The dot product (also called scalar product) of two vectors \(\vec{a}\) and \(\vec{b}\) is defined as
\(
\vec{a} \cdot \vec{b}=a b \cos \theta
\)

As we know \(b \cos \theta\) is the projection of \(b\) onto \(a\) and \(a \cos \theta\) is the projection of \(a\) on \(b\), the scalar product can be defined as the product of the magnitude of \(\mathrm{a}\) and the component of \(\mathrm{b}\) along with \(\mathrm{a}\) or the product of the magnitude of \(\mathrm{a}\) and the component of \(\mathrm{b}\) along with \(\mathrm{a}\).

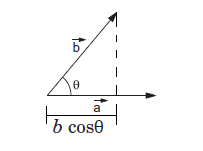
where \(a\) and \(b\) are the magnitudes of \(\vec{a}\) and \(\vec{b}\) respectively and \(\theta\) is the angle between them. The dot product between two mutually perpendicular vectors is zero as \(\cos 90^{\circ}=0\).

The dot product is commutative

\(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\)

The dot product is distributive

\(\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}\)

Example 1: The work done by a force \(\vec{F}\) during a displacement \(\vec{r}\) is given by \(\vec{F} \cdot \vec{r}\). Suppose a force of \(12 \mathrm{~N}\) acts on a particle in the vertically upward direction and the particle is displaced through \(2.0 \mathrm{~m}\) in the vertically downward direction. Find the work done by the force during this displacement.

Solution:

The angle between the force \(\vec{F}\) and the displacement \(\vec{r}\) is \(180^{\circ}\). Thus, the work done is
\(
\begin{aligned}
W &=\vec{F} \cdot \vec{r} \\
&=F r \cos \theta \\
&=(12 \mathrm{~N})(2 \cdot 0 \mathrm{~m})\left(\cos 180^{\circ}\right) \\
&=-24 \mathrm{~N}-\mathrm{m}=-24 \mathrm{~J}
\end{aligned}
\)

Example 2: Let there be two vectors \([6,2,-1]\) and \([5,-8,2]\). Find the dot product of the vectors.

Solution:
Given vectors: \([6,2,-1]\) and \([5,-8,2]\) be \(a\) and \(b\) respectively.
\(a \cdot b=(6)(5)+(2)(-8)+(-1)(2)\)
\(a \cdot b=30-16-2\)
a. \(b=12\)

Example 3: Let there be two vectors \(|\mathrm{a}|=6\) and \(|\mathrm{b}|=2\) and \(\theta=60^{\circ}\). Find their dot product.

Solution:
\(a \cdot b=|a||b| \cos \theta\)
a. \(b=6.2 \cos 60^{\circ}\)
\(a . b=6.2 \times(1 / 2)\)
\(a \cdot b=6\)

The dot product of two vectors in three-dimension

Consider two vectors \(\vec{a}\) and \(\vec{b}\) represented in terms of the unit vectors \(\overrightarrow{i,} \overrightarrow{j,} \vec{k}\) along the coordinate axes as
\(
\begin{array}{ll}
& \vec{a}=a_x \vec{i}+a_y \vec{j}+a_z \vec{k} \\
\text { and } & \vec{b}=b_x \vec{i}+b_y \vec{j}+b_z \vec{k}
\end{array}
\)
Then
\(
\begin{aligned}
\vec{a} \cdot \vec{b}=&\left(a_x \vec{i}+a_y \vec{j}+a_z \vec{k}\right) \cdot\left(b_x \vec{i}+b_y \vec{j}+b_z \vec{k}\right) \\
=& a_x b_x \vec{i} \cdot \vec{i}+a_x b_y \vec{i} \cdot \vec{j}+a_x b_z \vec{i} \cdot \vec{k} \\
&+a_y b_x \vec{j} \cdot \vec{i}+a_y b_y \vec{j} \cdot \vec{j}+a_y b_z \vec{j} \cdot \vec{k} \\
&+a_z b_x \vec{k} \cdot \vec{i}+a_z b_y \vec{k} \cdot \vec{j}+a_z b_z \vec{k} \cdot \vec{k} \dots(i)
\end{aligned}
\)
Since, \(\overrightarrow{i, ~} \vec{j}\) and \(\vec{k}\) are mutually orthogonal,
we have \(\vec{i} \cdot \vec{j}=\vec{i} \cdot \vec{k}=\vec{j} \cdot \vec{i}=\vec{j} \cdot \vec{k}=\vec{k} \cdot \vec{i}=\vec{k} \cdot \vec{j}=0\).
Also, \(\quad \vec{i} \cdot \vec{i}=1 \times 1 \cos 0=1\).
Similarly, \(\vec{j} \cdot \vec{j}=\vec{k} \cdot \vec{k}=1\).
Using these relations in equation (i) we get
\(
\vec{a} \cdot \vec{b}=a_x b_x+a_y b_y+a_z b_z \text {. }
\)

Dot Product Properties of Vector

• Dot product of two vectors is commutative i.e. \(a \cdot b=b. a=a b \cos \theta\).
• If \(a \cdot b=0\) then it can be clearly seen that either \(b\) or \(a\) is zero or \(\cos \theta=0\). \(\Rightarrow \theta=\frac{\pi}{2}\).
  It suggests that either of the vectors is zero or they are perpendicular to each other.
• Also, we know that using the scalar product of vectors \((p a) . (q b)=(p b) .(q a)=p q\) a.b
• The dot product of a vector to itself is the magnitude squared of the vector i.e. a.a \(=a \cdot a \cos 0\) \(=\mathrm{a}^2\)
• The dot product follows the distributive law also i.e. a.(b +c) = a.b + a.c
• In terms of orthogonal coordinates for mutually perpendicular vectors, it is seen that \(\hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1\)
• In terms of unit vectors, if \(a=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}\) and \(b=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}\)
  then
  \(a . b=\left(a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}\right) \cdot\left(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}\right)\)
  \(
  \Rightarrow a_1 b_1+a_2 b_2+a_3 b_3=a b \cos \theta
  \)

Example 4: Finding the Dot Product of Two Vectors given as \(\vec{A}=(-6,-3,5)\) and \(\vec{B}=(7,-4,-1)\), determine \(\vec{A} \cdot \vec{B}\).

Solution:
We calculate here the dot product using
\(
\vec{A} \cdot \vec{B}=A_x B_x+A_y B_y+A_z B_z,
\)
where the subscripts \(x, y\), and \(z\) denote the components along the \(x, y\), and \(z\)-axes. We thus have
\(
\begin{aligned}
\vec{A} \cdot \vec{B} &=(-6) \cdot 7+(-3) \cdot(-4)+5 \cdot(-1) \\
&=-42+12+(-5) \\
&=-35
\end{aligned}
\)

Example 5: Finding Missing Components of Orthogonal Vectors
For what value of \(k\) are vectors \(\vec{A}=(7,-7 k,-6)\) and \(\vec{B}=(7,-3, k)\) perpendicular?

Solution:
If two vectors are perpendicular, then the angle between them is \(90^{\circ}\) or \(-90^{\circ}\) (or \(270^{\circ}\) ). In both cases, the cosine of the angle between them is zero. Therefore, the dot product between the two vectors is zero. In this question, it means that \(\vec{A} \cdot \vec{B}=0\); that is,
\(
A_x B_x+A_y B_y+A_z B_z=0 .
\)
Hence, we have
\(
\begin{aligned}
7 \cdot 7+(-7 k) \cdot(-3)+(-6) \cdot k &=0 \\
49+21 k-6 k &=0 \\
k &=\frac{-49}{15} .
\end{aligned}
\)

Example 6: Which of the following is true of the vectors \(\vec{A}=(-3,7,-8)\) and \(\vec{B}=(-6,-1,-1)\) ?
A. They are parallel.
B. They are perpendicular.
C. They are neither parallel nor perpendicular.

Solution:
If \(\vec{A}\) and \(\vec{B}\) are parallel, then there is a number \(k\) such that \(\vec{A}=k \vec{B}\). We would have
\(
\begin{gathered}
-3=-6 k \\
7=-k \\
-8=-k .
\end{gathered}
\)
There is clearly no value of \(k\) that verifies the three equations since we get three different solutions for each of them \(\left(\frac{1}{2},-7\right.\), and 8\()\). Therefore, \(\vec{A}\) and \(\vec{B}\) are not parallel.
If \(\vec{A}\) and \(\vec{B}\) are perpendicular, then their dot product is zero. Let us work out their dot product:
\(
\begin{aligned}
\vec{A} \cdot \vec{B} &=A_x B_x+A_y B_y+A_z B_z \\
&=(-3) \cdot(-6)+7 \cdot(-1)+(-8) \cdot(-1) \\
&=18+(-7)+8=19 .
\end{aligned}
\)
Their dot product is not zero; therefore, \(\vec{A}\) and \(\vec{B}\) are not perpendicular.
The correct answer is that \(\vec{A}\) and \(\vec{B}\) are neither parallel nor perpendicular.