The operation to add two or more vectors together to form a vector sum is known as the addition of vectors. The addition of vectors is done in two ways, either through triangle law or parallelogram law.

Triangle law of vector addition

The triangle law of vector addition states that when two vectors are represented as two sides of a triangle with the same order of magnitude and direction, the magnitude and direction of the resultant vector is represented by the third side of the triangle.

The triangle rule of vector addition is already described above. If \(\vec{a}\) and \(\vec{b}\) are the two vectors to be added, a diagram is drawn in which the tail of \(\vec{b}\) coincides with the head of \(\vec{a}\). The vector joining the tail of \(\vec{a}\) with the head of \(\vec{b}\) is the vector sum of \(\vec{a}\) and \(\vec{b}\). Figure (1-a) shows the construction.

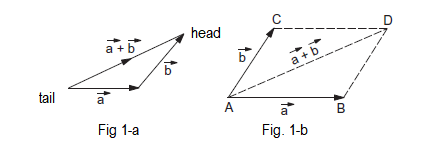
The same rule may be stated in a slightly different way. We draw the vectors \(\vec{a}\) and \(\vec{b}\) with both the tails coinciding (figure 1-b). Taking these two as the adjacent sides we complete the parallelogram. The diagonal through the common tails gives the sum of the two vectors.
Thus, in figure,(1-b) \(\overrightarrow{A B}+\overrightarrow{A C}=\overrightarrow{A D}\).

How to calculate the Magnitude and Direction of the resultant Vector?

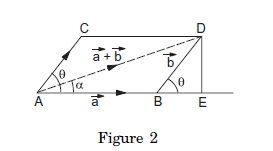
Suppose assume the magnitude of \(\vec{a}=a\) and that of \(\vec{b}=b\). What is the magnitude of the resultant vector \(\vec{a}+\vec{b}\) and what is its direction? Suppose assume the angle between \(\vec{a}\) and \(\vec{b}\) is \(\theta\). It is easy to see from figure (2) that (using the Pythagorean theorem),

\(
\begin{aligned}
A D^2 &=(A B+B E)^2+(D E)^2 \\
&=(a+b \cos \theta)^2+(b \sin \theta)^2 \\
&=a^2+2 a b \cos \theta+b^2
\end{aligned}
\)
Thus, the magnitude of the resultant vector \(\vec{a}+\vec{b}\) is
\(
\sqrt{a^2+b^2+2 a b \cos \theta} \dots(2.1)
\)
Its angle with \(\vec{a}\) is \(\alpha\) where
\(
\tan \alpha=\frac{D E}{A E}=\frac{b \sin \theta}{a+b \cos \theta} \dots(2.2)
\)

Example-1: Two vectors having equal magnitudes A make an angle \(\theta\) with each other. Find the magnitude and direction of the resultant.

Solution: The magnitude of the resultant will be
\(
\begin{aligned}
B &=\sqrt{A^2+A^2+2 A A \cos \theta} \\
&=\sqrt{2 A^2(1+\cos \theta)}=\sqrt{4 A^2 \cos ^2 \frac{\theta}{2}} \\
&=2 A \cos \frac{\theta}{2} .
\end{aligned}
\)
The resultant will make an angle \(\alpha\) with the first vector where
\(
\tan \alpha=\frac{A \sin \theta}{A+A \cos \theta}=\frac{2 A \sin \frac{\theta}{2} \cos \frac{\theta}{2}}{2 A \cos ^2 \frac{\theta}{2}}=\tan \frac{\theta}{2}
\)
or, \(\quad \alpha=\frac{\theta}{2}\)
Thus, the resultant of two equal vectors bisects the angle between them.

Parallelogram law of vector addition

Parallelogram law of vector addition states that If two vectors act along two adjacent sides of a parallelogram (with magnitude equal to the length of the sides) both pointing away from the common vertex, the resultant is represented by the diagonal of the parallelogram passing through the same common vertex.

If \(\vec{a}\) and \(\vec{b}\) represent the adjacent sides of the parallelogram \(A B C D\) as shown in the figure, then the result is the diagonal \(A C\) of the parallelogram \(A B C D\) which passes through the same common vertex.

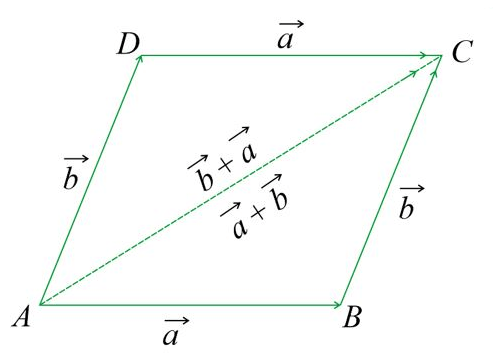
Hence, we can deduce that the triangle laws of vector addition and the parallelogram laws of vector addition are equivalent.

Example-2: Find the magnitude of the sum of a \(15 \mathrm{~km}\) displacement and a \(25 \mathrm{~km}\) displacement when the angle between them is \(60^{\circ}\)

Solution: Here, \(a=\) magnitude of \(\vec{a}=15\)
\(b=\) magnitude of \(\vec{b}=25\)
\(\theta=\) Angle between \(\vec{a}\) and \(\vec{b}=60^{\circ}\)
Hence, Then, the magnitude of \(\vec{a}+\vec{b}\) which is the resultant sum will be \(=\sqrt{a^2+b^2+2 a b \cos \theta}\)
\(
\begin{aligned}
&=\sqrt{15^2+25^2+2 \times 15 \times 25 \cos 60^{\circ}} \\
&=\sqrt{225+625+\frac{750}{2}} \\
&=\sqrt{850+375} \\
&=\sqrt{1225} \\
&=35
\end{aligned}
\)

Addition of Vectors: Properties

The addition of vectors differs from the addition of algebraic numbers. Here are some of the most significant properties to think about when adding vectors:

• Vector addition is commutative: It means the order of vectors does not affect the result of the addition. If two vectors \(\vec{a}\) and \(\vec{b}\) are added together, then \(\vec{a}+\vec{b}=\vec{b}+\vec{a}\)

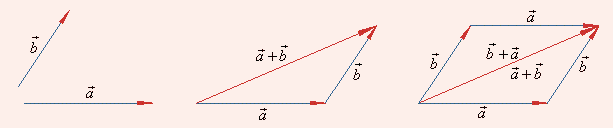
• Vector addition is associative: The mutual grouping of vectors has no effect on the result when adding three or more vectors together.
  \(
  (\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})
  \)

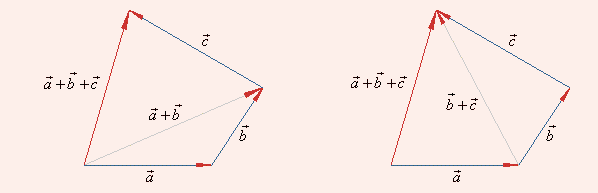
• Vector addition is distributive: It indicates that the sum of scalar times the sum of two vectors equals the sum of the scalar times of the two vectors separately.
  \(
  m(\vec{a}+\vec{b})=m \vec{a}+m \vec{b}
  \)
• Existence of Identity: For any vector \(\vec{a}, \vec{a}+\overrightarrow{0}=\vec{a}\)
  Here, \(\overrightarrow{0}\) is the additive identity.
• Existence of inverse: For any vector \(\vec{a}, \vec{a}+(-\vec{a})=\overrightarrow{0}\)
  So, an additive inverse exists for every vector.

Analytical Method of Vector Addition and Subtraction

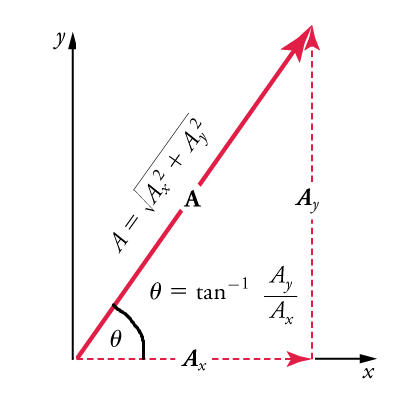
Calculating a resultant vector (or vector addition) is the reverse of breaking the resultant down into its components. If the perpendicular components \(\mathbf{A}_x\) and \(\mathbf{A}_y\) of a vector \(\mathbf{A}\) are known, then we can find A analytically. How do we do this? Since, by definition,
\(
\tan \theta=y / x\left(\text { or in this case } \tan \theta=A_y / A_x\right)
\)
we solve for \(\theta\) to find the direction of the resultant.
\(
\theta=\tan ^{-1}\left(A_y / A_x\right)
\)
Since this is a right triangle, the Pythagorean theorem \(\left(x^2+y^2=h^2\right)\) for finding the hypotenuse applies. In this case, it becomes
\(
A^2=A_x^2+A_y^2 .
\)
Solving for A gives
\(
A=\sqrt{A_x{ }^2+{A_y}^2} .
\)
In summary, to find the magnitude \(A\) and direction \(\theta\) of a vector from its perpendicular components \(\mathbf{A}_x\) and \(\mathbf{A}_y\), as illustrated in Figure above, we use the following relationships:
\(
\begin{aligned}
A=& \sqrt{A_x^2+A_y^2} \\
& \theta=\tan ^{-1}\left(A_y / A_x\right)
\end{aligned}
\)

How to add vectors that are not perfectly perpendicular to one another?

Sometimes, the vectors added are not perfectly perpendicular to one another. An example of this is the case below, where the vectors \(\mathbf{A}\) and \(\mathbf{B}\) are added to produce the resultant \(\mathbf{R}\), as illustrated in Figure below.

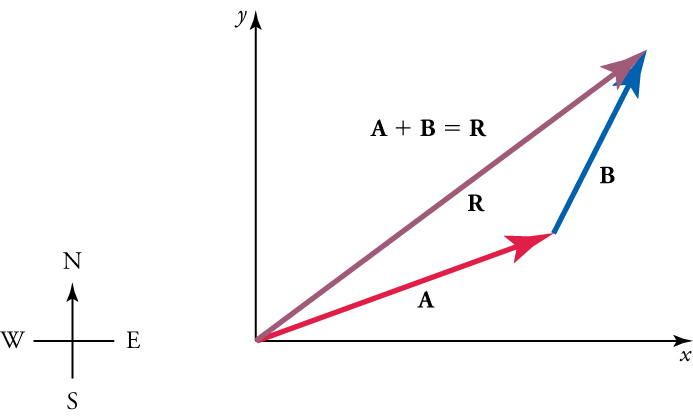
If \(\mathbf{A}\) and \(\mathbf{B}\) represent two legs of a walk (two displacements), then \(\mathbf{R}\) is the total displacement. The person taking the walk ends up at the tip of \(\mathbf{R}\). There are many ways to arrive at the same point. The person could have walked straight ahead first in the \(x\)-direction and then in the \(y\)-direction. Those paths are the \(x\)-and \(y\)-components of the resultant, \(\mathbf{R}_x\) and \(\mathbf{R}_y\). If we know \(\mathbf{R}_x\) and \(\mathbf{R}_y\), we can find \(R\) and \(\theta\) using the equations \(R=\sqrt{R_{\mathrm{x}}{ }^2+R_{\mathrm{y}}{ }^2}\) and \(\theta=\tan ^{-1}\left(R_y / R_x\right)\).

Step-1: Draw in the \(x\) and \(y\) components of each vector (including the resultant) with a dashed line. Use the equations \(A_x=A \cos \theta\) and \(A_y=A \sin \theta\) to find the components. In the Figure below, these components are \(A_x, A_y, B_x\), and \(B_y\). Vector \(\mathbf{A}\) makes an angle of \(\theta_A\) with the \(x\)-axis, and vector \(\mathbf{B}\) makes and angle of \(\theta_B\) with its own \(x\)-axis (which is slightly above the \(x\)-axis used by vector A).

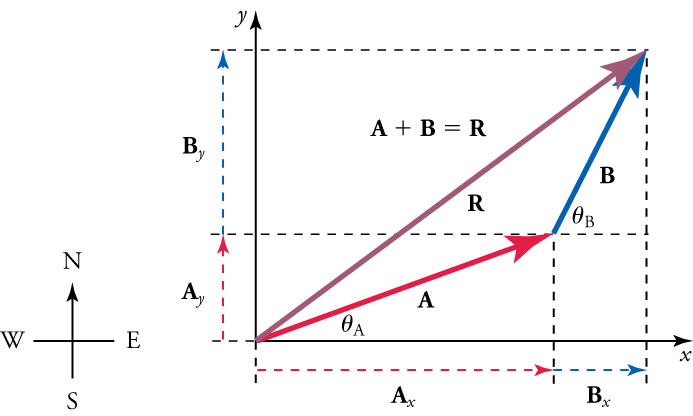
Step-2: Find the \(x\) component of the resultant by adding the \(x\) component of the vectors
\(R_x=A_x+B_x\)
and find the \(y\) component of the resultant (as illustrated in Figure below) by adding the \(y\) component of the vectors.
\(R_y=A_y+B_y .\)

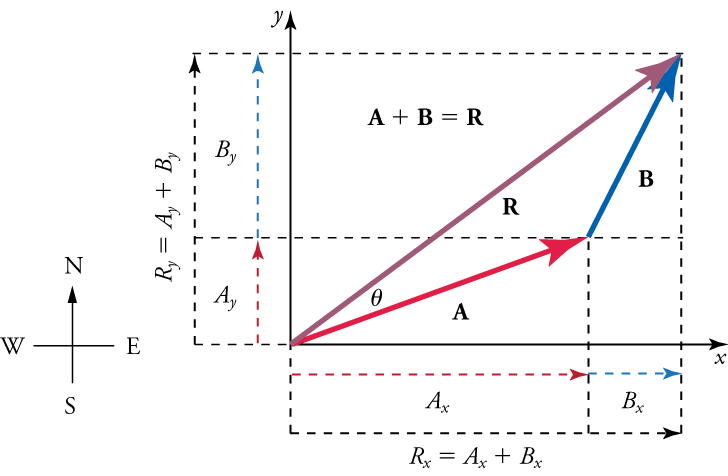
Now that we know the components of \(\mathbf{R}\), we can find its magnitude and direction.
Step-3: To get the magnitude of the resultant \(\mathrm{R}\), use the Pythagorean theorem.
\(
R=\sqrt{R_x^2+R_y^2}
\)
Step-4: To get the direction of the resultant
\(
\theta=\tan ^{-1}\left(R_y / R_x\right)
\)

Example 3: Add the vector \(\mathbf{A}\) to the vector \(\mathbf{B}\) shown in Figure below, using the steps above. The \(x\)-axis is along the east-west direction, and the \(y\)-axis is along the north-south directions. A person first walks \(53.0 \mathrm{~m}\) in a direction \(20.0^{\circ}\) north of east, represented by vector \(\mathbf{A}\). The person then walks \(34.0 \mathrm{~m}\) in a direction \(63.0^{\circ}\) north of east, represented by vector B.

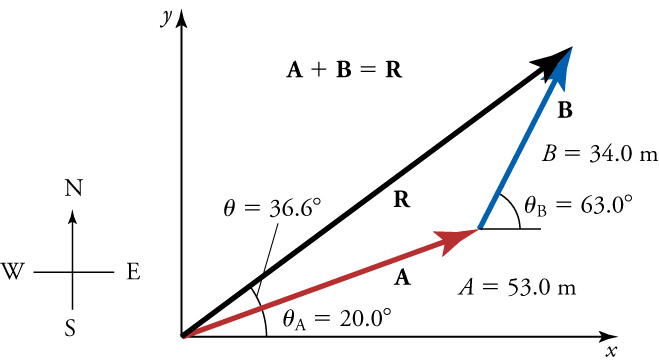
Solution: First, we find the components of \(\mathbf{A}\) and \(\mathbf{B}\) along the \(x\) – and \(y\)-axes. From the problem, we know that \(A=53.0 \mathrm{~m}, \theta_{\mathrm{A}}=20.0^{\circ}, B=34.0 \mathrm{~m}\), and \(\theta_{\mathrm{B}}=63.0^{\circ}\). We find the \(x\) components by using \(A_x=A \cos \theta\), which gives
\(
\begin{aligned}
A_x &=A \cos \theta_A=(53.0 \mathrm{~m})\left(\cos 20.0^{\circ}\right) \\
&=(53.0 \mathrm{~m})(0.940)=49.8 \mathrm{~m}
\end{aligned}
\)
and
\(
\begin{aligned}
B_x &=B \cos \theta_B=(34.0 \mathrm{~m})\left(\cos 63.0^{\circ}\right) \\
&=(34.0 \mathrm{~m})(0.454)=15.4 \mathrm{~m}
\end{aligned}
\)
Similarly, the \(y\)-components are found using \(A_y=A \sin \theta_A\)
\(
\begin{aligned}
A_y &=A \sin \theta_A=(53.0 \mathrm{~m})\left(\sin 20.0^{\circ}\right) \\
&=(53.0 \mathrm{~m})(0.342)=18.1 \mathrm{~m}
\end{aligned}
\)
and
\(
\begin{aligned}
B_y &=B \sin \theta_B=(34.0 \mathrm{~m})\left(\sin 63.0^{\circ}\right) \\
&=(34.0 \mathrm{~m})(0.891)=30.3 \mathrm{~m}
\end{aligned}
\)
The \(x\) – and \(y\)-components of the resultant are
\(
R_x=A_x+B_x=49.8 \mathrm{~m}+15.4 \mathrm{~m}=65.2 \mathrm{~m}
\)
and
\(
R_y=A_y+B_y=18.1 \mathrm{~m}+30.3 \mathrm{~m}=48.4 \mathrm{~m} .
\)
Now we can find the magnitude of the resultant by using the Pythagorean theorem
\(
R=\sqrt{R_x^2+R_y^2}=\sqrt{(65.2)^2+(48.4)^2} \mathrm{~m}
\)
so that
\(
R=\sqrt{6601 \mathrm{~m}}=81.2 \mathrm{~m} .
\)
Finally, we find the direction of the resultant
\(
\theta=\tan ^{-1}\left(R_y / R_x\right)=+\tan ^{-1}(48.4 / 65.2) \text {. }
\)
This is
\(
\theta=\tan ^{-1}(0.742)=36.6^{\circ} .
\)