Past JEE PYQs (Quadratic Equations)
Solution of a quadratic equation
The equations \(a x^2+b x+c=0\), where \(a, b\) and \(c\) are numbers (real or complex, \(a \neq 0\) ) is called the general quadratic equation in variable \(x\). The values of the variable satisfying the given equation are called roots of the equation.
The quadratic equation \(a x^2+b x+c=0\) with real coefficients has two roots given by \(\frac{-b+\sqrt{ D }}{2 a}\) and \(\frac{-b-\sqrt{ D }}{2 a}\), where \(D =b^2-4 a c\), called the discriminant of the equation.
- When \(D=0\), roots of the quadratic equation are real and equal. When \(D>0\), roots are real and unequal. Further, if \(a, b, c \in Q\) and \(D\) is a perfect square, then the roots of the equation are rational and unequal, and if \(a, b, c \in Q\) and \(D\) is not a perfect square, then the roots are irrational and occur in pair. When \(D <0\), roots of the quadratic equation are non real (or complex).
- Let \(\alpha, \beta\) be the roots of the quadratic equation \(a x^2+b x+c=0\), then sum of the roots
\((\alpha+\beta)=\frac{-b}{a}\) and the product of the roots \((\alpha \times \beta)=\frac{c}{a}\).
- Let \(S\) and \(P\) be the sum of roots and product of roots, respectively, of a quadratic equation. Then the quadratic equation is given by \(x^2-S x+P=0\).
Quiz Summary
0 of 161 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 161 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 161
1. Question
Let \(\mathrm{a}, \mathrm{b} \in R\) and \(\mathrm{a}^2+\mathrm{b}^2 \neq 0\).
Suppose \(S=\left\{z \in C: Z=\frac{1}{a+i b t},+\in \mathbb{R}, t \neq 0\right\}\), where \(i=\sqrt{-1}\). If \(\mathrm{z}=\mathrm{x}+\) iy and \(\mathrm{z} \in \mathrm{S}\), then ( \(\mathrm{x}, \mathrm{y})\) lies on [JEE Adv. 2016]CorrectIncorrectHint
\(
\begin{aligned}
&\quad(\mathbf{a}, \mathbf{c}, \mathbf{d}) \mathrm{z}=\frac{1}{a+i b t}=x+i y \\
&\Rightarrow x+i y=\frac{a-i b t}{a^2+b^2 t^2} \\
&\Rightarrow x=\frac{a}{a^2+b^2 t^2}, y=\frac{-b t}{a^2+b^2 t^2} \\
&\Rightarrow x^2+y^2=\frac{1}{a^2+b^2 t^2}=\frac{x}{a}
\end{aligned}
\)
\(
\Rightarrow x^2+y^2-\frac{x}{a}=0
\)
\(\therefore\) Locus of \(z\) is a circle with centre \(\left(\frac{1}{2 a}, 0\right)\) and radius \(\frac{1}{2|a|}\) irrespective of ‘ a’ +ve or -ve
Also for \(b=0, a \neq 0\), we get, \(y=0\)
\(\therefore\) locus is \(\mathrm{x}\)-axis
and for \(\mathrm{a}=0, \mathrm{~b} \neq 0\) we get \(\mathrm{x}=0\)
\(\therefore\) locus is y-axis.
Hence, a, c, and d are the correct options. -
Question 2 of 161
2. Question
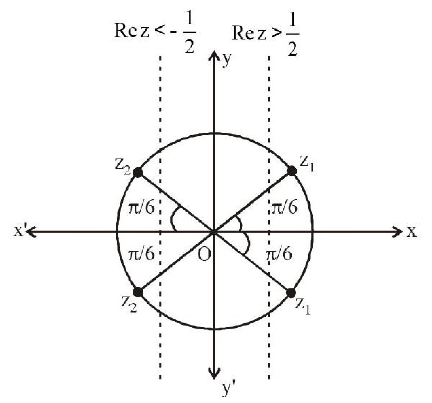
Let \(w=\frac{\sqrt{3}+i}{2}\) and \(\mathrm{P}=\left\{w^{\mathrm{n}}: n=1,2,3, \ldots\right\}\). Further \(\mathrm{H}_1=\) \(\left\{z \in \mathbb{C}: \operatorname{Re} z>\frac{1}{2}\right\}\) and \(H_2=\left\{z \in \mathbb{C}: \operatorname{Re} z<\frac{-1}{2}\right\}\), where \(\mathrm{c}\) is the set of all complex numbers. If \(z_1 \in P \cap H_1, z_2 \in P \cap H_2\) and \(O\) represents the origin, then \(\angle \mathrm{z}_1 O z_2=\) [JEE Adv. 2013]
CorrectIncorrectHint
(c, d) We have \(w=\frac{\sqrt{3}+i}{2}=\cos \frac{\pi}{6}+i \sin \frac{\pi}{6}\)
\(\Rightarrow w=\cos \frac{n \pi}{6}+i \sin \frac{n \pi}{6}\)
\(\therefore \mathrm{P}\) contains all those points which lie on unit circle and have arguments \(\frac{\pi}{6}, \frac{2 \pi}{6}, \frac{3 \pi}{6}\) and so on.
Since, \(\mathrm{z}_1 \in \mathrm{P} \cap \mathrm{H}_1\) and \(\mathrm{z}_2 \in \mathrm{P} \cap \mathrm{H}_2\), therefore \(\mathrm{z}_1\) and \(\mathrm{z}_2\) can have possible positions as shown in the figure.
\(
\therefore \angle \mathrm{z}_1 \mathrm{Oz}_2 \text { can be } \frac{2 \pi}{3} \text { or } \frac{5 \pi}{6} \text {. }
\)
-
Question 3 of 161
3. Question
If \(\omega\) is an imaginary cube root of unity, then \(\left(1+\omega-\omega^2\right)^7\) equals [1998 – 2 Marks]
CorrectIncorrectHint
(d) We have \(\left(1+\omega+\omega^2\right)^7=\left(-\omega^2-\omega^2\right)^7\)
\(
=(-2)^7\left(\omega^2\right)^7=-128 \omega^{14}=-128 \omega^2
\) -
Question 4 of 161
4. Question
Match the statements in column-I with those in column-II.
[Note: Here \(z\) takes the values in the complex plane and \(\operatorname{Im} z\) and \(\operatorname{Re} z\) denote, respectively, the imaginary part and the real part of \(z\) ] [2010]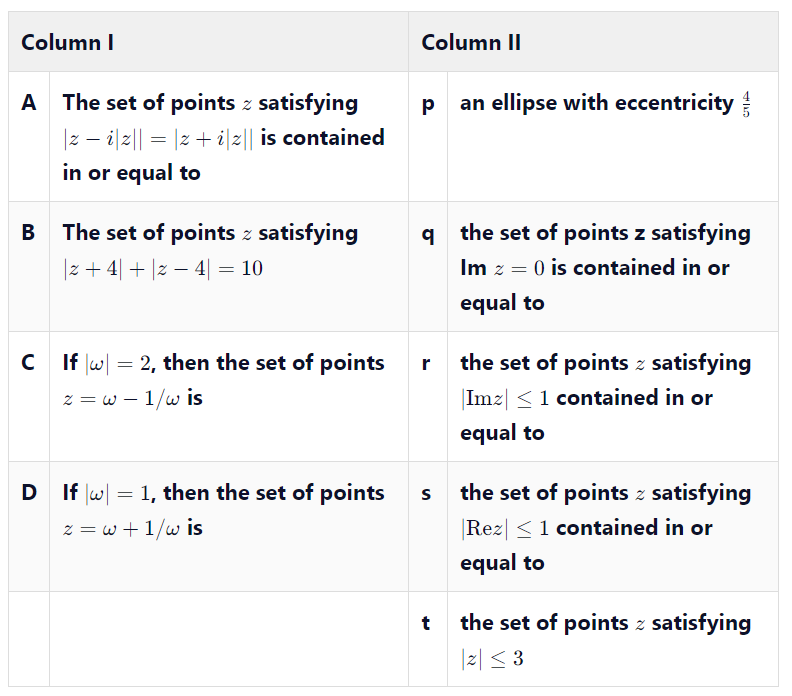 CorrectIncorrect
CorrectIncorrectHint
\((\mathrm{A}) \rightarrow(\mathrm{q}, \mathrm{r})\)
\(|z-i| z||=|z+i| z \mid\)
\(\Rightarrow z\) is equidistant from two points \((0,|z|)\) and
\((0,-|z|)\), which lie on imaginary axis.
\(\therefore z\) must lie on real axis \(\Rightarrow \operatorname{Im}(z)=0\). Also \(\left|I_m(z)\right| \leq 1\)
(B) \(\rightarrow\) p
\(z=\omega-\frac{1}{\omega}=2(\cos \theta+i \sin \theta)-\frac{1}{2}(\cos \theta-i \sin \theta)\)
\(\Rightarrow x+i y=\frac{3}{2} \cos \theta+i \frac{5}{2} \sin \theta\)
Here, \(|z|=\sqrt{\frac{9+25}{4}}=\sqrt{\frac{34}{4}} \leq 3\) and \(\left|R_e(z)\right| \leq 2\)
Also \(x=\frac{3}{2} \cos \theta, y=\frac{5}{2} \sin \theta \Rightarrow \frac{4 x^2}{9}+\frac{4 y^2}{25}=1\)
Which is an ellipse with \(e=\sqrt{1-\frac{9}{25}}=\frac{4}{5}\)
\((\mathrm{D}) \rightarrow(\mathrm{q}, \mathrm{r}, \mathrm{s}, \mathrm{t})\)
Let \(\omega=\cos \theta+i \sin \theta\) then \(z=2 \cos \theta \Rightarrow \operatorname{Im} z=0\) Also \(|z| \leq 3\) and \(|\operatorname{Im}(z)| \leq 1,\left|\mathrm{R}_e(z)\right| \leq 2\) -
Question 5 of 161
5. Question
\(z \neq 0\) is a complex number\( \text { [1992 – } 2 \text { Marks] }
\)\(
\begin{array}{|l|l|}
\hline \text { Column 1 } & \text { Column 2 } \\
\hline \operatorname{A. Re}(\mathrm{z})=0 & \operatorname{p. Re{(z^2)}}=0 \\
\hline \operatorname{B. Argz}=\pi / 4 & \operatorname{q. Im{(z^2)}}=0 \\
\hline & \operatorname{r. Re{(z^2)}}=\mathrm{Im{(z^2)}} \\
\hline
\end{array}
\)CorrectIncorrectHint
Given : \(z \neq 0 \quad\) Let \(z=a+i b\)
\(\operatorname{Re}(\mathrm{z})=0 \Rightarrow z=i b \Rightarrow z^2=-b^2\)
\(\therefore \operatorname{Im}(z^2)=0\)
\(\therefore(\mathrm{A})\) corresponds to (q)
\(\operatorname{Arg} z=\frac{\pi}{4} \Rightarrow a=\mathrm{b} \Rightarrow z=a+i a\) \(\Rightarrow z^2=a^2-a^2+2 i a^2 \Rightarrow z^2=2 i a^2 \Rightarrow \operatorname{Re}(z^2)=0\)
\(\therefore(B)\) corresponds to \((\mathrm{p})\). -
Question 6 of 161
6. Question
If one the vertices of the square circumscribing the circle \(|z-1|=\) \(\sqrt{2}\) is \(2+\sqrt{3} i\). Find the other vertices of the square. [2005-4 Marks]
CorrectIncorrectHint
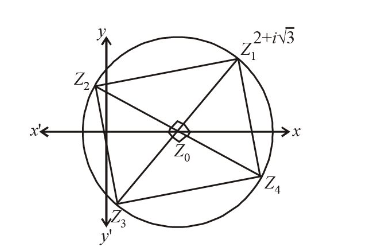
The given circle is \(|\mathrm{z}-1|=\sqrt{2}\), where \(\mathrm{z}_0=1\) is the centre and \(\sqrt{2}\) is radius of circle. \(z_1\) is one of the vertex of the square inscribed in the given circle.
Clearly \(z_2\) can be obtained by rotating \(z_1\) by an angle \(90^{\circ}\) in anticlockwise direction, about centre \(z_0\)
Thus, \(z_2-z_0=\left(z_1-z_0\right) e^{i \pi / 2}\)
or \(z_2-1=(2+i \sqrt{3}-1) i \Rightarrow z_2=i-\sqrt{3}+1\)
\(
z_2=(1-\sqrt{3})+i
\)
Again rotating \(z_2\) by \(90^{\circ}\) about \(z_0\), we get
\(
\begin{aligned}
&z_3-z_0=\left(z_2-z_0\right) i \\
&\Rightarrow z_3-1=[(1-\sqrt{3})+i-1] i=-\sqrt{3} i-1 \Rightarrow z_3=-i \sqrt{3}
\end{aligned}
\)
And similarly \(1=(-i \sqrt{3}-1) i=\sqrt{3}-i\)
\(
\Rightarrow \quad z_4=(\sqrt{3}+1)-i
\)
Hence, the remaining vertices are
\(
(1-\sqrt{3})+i,-i \sqrt{3},(\sqrt{3}+1)-i
\) -
Question 7 of 161
7. Question
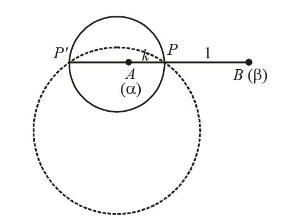
Find the centre and radius of circle given by
\(
\left|\frac{z-\alpha}{z-\beta}\right|=k, k \neq 1
\)
where, \(z=x+i y, \alpha=\alpha_1+i \alpha_2, \beta=\beta_1+i \beta_2\) [2004 – 2 Marks]CorrectIncorrectHint
\(
\text { Given : }\left|\frac{z-\alpha}{z-\beta}\right|=k \Rightarrow|z-\alpha|=k|z-\beta|
\)
Let pt. A represents complex number \(\alpha\) and \(B\) that of \(\beta\), and \(P\) represents \(z\). then \(|z-\alpha|=k|z-\beta|\)
\(\Rightarrow z\) is the complex number whose distance from \(A\) is \(k\) times its distance from \(B\).
i.e. \(P A=k P B\)
\(\Rightarrow P\) divides \(A B\) in the ratio \(k: 1\) internally or externally (at \(P^{\prime}\) ).
Then \(P=\left(\frac{k \beta+\alpha}{k+1}\right)\) and \(P^{\prime}=\left(\frac{k \beta-\alpha}{k-1}\right)\)
Now through \(P P^{\prime}\) a number of circles can pass, but with given data we can find radius and centre of that circle for which \(P P^{\prime}\) is diameter.
\(
\begin{aligned}
&\therefore \text { Centre }=\text { mid. point of } P P^{\prime}=\left(\frac{k \beta+\alpha}{k+1}+\frac{k \beta-\alpha}{k-1}\right) \\
&= \\
&=\frac{k^2 \beta+k \alpha-k \beta-\alpha+k^2 \beta-k \alpha+k \beta-\alpha}{2\left(k^2-1\right)} \\
&=\frac{k^2 \beta-\alpha}{k^2-1}=\frac{\alpha-k^2 \beta}{1-k^2}
\end{aligned}
\)
Also radius \(=\frac{1}{2}\left|P P^{\prime}\right|\)
\(
\begin{aligned}
&=\frac{1}{2}\left|\frac{k \beta+\alpha}{k+1}-\frac{k \beta-\alpha}{k-1}\right| \\
&=\frac{1}{2}\left|\frac{k^2 \beta+k \alpha-k \beta-\alpha-k^2 \beta+k \alpha-k \beta+\alpha}{k^2-1}\right|=\frac{k|\alpha-\beta|}{\left|1-k^2\right|}
\end{aligned}
\) -
Question 8 of 161
8. Question
Given that there exists no complex number \(z\) such that \(|z|<\frac{1}{3}\) and \(\sum_{r=1}^n a_r z^r=1\) where \(\left|a_r\right|<2\). Is this statement true? [2003 – 2 Marks]
CorrectIncorrectHint
Let us consider, \(\sum_{r=1}^n a_r z^r=1\) where \(\left|a_r\right|<2\)
\(
\begin{aligned}
&\Rightarrow a_1 z+a_2 z^2+a_3 z^3+\ldots+a_n z^n=1 \\
&\Rightarrow\left|a_1 z+a_2 z^2+a_3 z^3+\ldots+a_n z^n\right|=1
\end{aligned}
\)
But we know that \(\left|z_1+z_2\right| \leq\left|z_1\right|+\left|z_2\right|\)
\(\therefore \quad\) Using its generalised form, we get
\(
\begin{gathered}
\left|a_1 z+a_2 z^2+a_3 z^3+\ldots+a_n z^n\right| \\
\quad \leq\left|a_1 z\right|+\left|a_2 z^2\right|+\ldots+\left|a_n z^n\right| \\
\Rightarrow 1 \leq\left|a_1\right||z|+\left|a_2\right|\left|z^2\right|+\left|a_3\right||z|+\ldots+\left|a_n\right|\left|z^n\right| \\
\quad\left[\operatorname{using~eq}{ }^{\mathrm{n}}(\mathrm{i})\right]
\end{gathered}
\)
But given that \(\left|a_r\right|<2 \forall r=1, \ldots, n\)\(
\begin{aligned}
\therefore & 1<2\left[|z|+|z|^2+|z|^3+\ldots+|z|^n\right] \\
\Rightarrow & \quad 1<2\left[\frac{|z|\left(1-|z|^n\right)}{1-|z|}\right] \Rightarrow 2\left[\frac{|z|-|z|^{n+1}}{1-|z|}\right]>1 \\
\Rightarrow & 2\left[|z|-|z|^{n+1}\right]>1-|z| \quad(\because 1-|z|>0 \text { as }|z|<1 / 3) \\
\Rightarrow & {\left[|z|-|z|^{n+1}\right]>\frac{1}{2}-\frac{1}{2}|z| } \\
\Rightarrow & \frac{3}{2}|z|>\frac{1}{2}+|z|^{n+1} \\
\Rightarrow &|z|>\frac{1}{3}+\frac{2}{3}|z|^{n+1} \Rightarrow|z|>\frac{1}{3}
\end{aligned}
\)
which is a contradiction as given that \(|z|<\frac{1}{3}\)
\(
\therefore \quad \text { There exists no such complex number. }
\) -
Question 9 of 161
9. Question
Let a complex number \(\alpha, \alpha \neq 1\), be a root of the equation \(z^{p+q}-z^p-z^q+\) \(1=0\), where \(p, q\) are distinct primes. Given that either \(1+\alpha+\alpha^2+\ldots\). \(+\alpha^{p-1}=0\) or \(1+\alpha+\alpha^2+\ldots+\alpha^{q-1}=0\), but not both together. Is this true? [2002 – 5 Marks]
CorrectIncorrectHint
The given equation can be written as
\(
\left(z^p-1\right)\left(z^q-1\right)=0
\)
\(
\therefore \quad z=(1)^{1 / p} \quad \text { or } \quad(1)^{1 / q}
\)
where \(\mathrm{p}\) and \(\mathrm{q}\) are distinct prime numbers.
Hence both the equations will have distinct roots and as \(z \neq 1\), both will not be simultaneously zero for any value of \(z\) given by equations in (i)
Also \(1+\alpha+\alpha^2+\ldots+\alpha^{p-1}=\frac{1-\alpha^p}{1-\alpha}=0(\alpha \neq 1)\)
or \(1+\alpha+\alpha^2+\ldots+\alpha^p=\frac{1-\alpha^q}{1-\alpha}=0(\alpha \neq 1)\)
Because of (i) either \(\alpha^p=1\) and if \(\alpha^q=1\) but not both simultaneously as \(p\) and \(q\) are distinct primes. -
Question 10 of 161
10. Question
For complex numbers \(z\) and \(w\), find \(|z|^2 w-|w|^2 z=?\) if and only if \(z=w\) or \(z \bar{w}=1\). [1999 – 10 Marks]
CorrectIncorrectHint
Let, \(|z|^2 w-|w|^2 z=y\)
Now,
\(
\begin{aligned}
& |z|^2=z \bar{z} \\
& |w|^2=w \bar{w}
\end{aligned}
\)
and \(z=w \Rightarrow \bar{z}=\bar{w} \dots(i)\)
\(
z \bar{w}=1 \dots(ii)
\)
\(
\begin{aligned}
&\text { Since, multiplication is commutative, }\\
&\therefore \quad z \bar{w}=\bar{w} z=1 \dots(iii)
\end{aligned}
\)
Now, \(y=z \bar{z} w – w \bar{w} z\)
\(y=z \bar{w} z – w z \bar{w} \) (Using Eqn(i) & (ii))
\(
\Rightarrow \quad y=(z-w)(1)
\) (Using eqn (iii))
\(
\Rightarrow \quad y=(z-w)
\)
\(
\therefore \quad|z|^2 w-|w|^2 z=z-w \text { if and only if } z=w \text { ore } z \bar{w}=1
\) -
Question 11 of 161
11. Question
Let \(z_1\) and \(z_2\) be roots of the equation \(z^2+p z+q=0\), where the coefficients \(p\) and \(q\) may be complex numbers. Let \(A\) and \(B\) represent \(z_1\) and \(z_2\) in the complex plane. If \(\angle A O B=\alpha \neq 0\) and \(O A=O B\), where \(O\) is the origin, given that \(p^2=4 q \cos ^2\left(\frac{\alpha}{2}\right) \text {. }\). Is this true? [1997 – 5 Marks]
CorrectIncorrectHint
True
\(z^2+p z+q=0\)
\(z_1+z_2=-p, z_1 z_2=\mathrm{q}\)
By rotation through \(\alpha\) in anticlockwise direction,
\(
\begin{aligned}
&z_2=z_1 e^{i \alpha} \\
&\frac{z_2}{z_1}=\frac{e^{i \alpha}}{1}=\frac{\cos \alpha+i \sin \alpha}{1}
\end{aligned}
\)
Add 1 in both sides to get \(z_1+z_2=-\mathrm{p}\)
\(
\begin{aligned}
&\therefore \frac{z_1+z_2}{z_1}=\frac{1+\cos \alpha+i \sin \alpha}{1}=2 \cos \frac{\alpha}{2}\left[\cos \frac{\alpha}{2}+i \sin \frac{\alpha}{2}\right] \\
&\Rightarrow \frac{\left(z_2+z_1\right)}{z_1}=2 \cos \frac{\alpha}{2} e^{i \alpha / 2}
\end{aligned}
\)
On squaring, \(\left(z_2+z_1\right)^2=4 \cos ^2(\alpha / 2) z_1^2 \cdot e^{i \alpha}\)
\(
=4 \cos ^2 \frac{\alpha}{2} z_1^2 \cdot \frac{z_2}{z_1}=4 \cos ^2 \frac{\alpha}{2} z_1 z_2
\)
\(
\Rightarrow \quad p^2=4 q \cos ^2 \frac{\alpha}{2}
\) -
Question 12 of 161
12. Question
Find all non-zero complex numbers \(Z\) satisfying \(\bar{Z}=i Z^2\). [1996 – 2 Marks]
CorrectIncorrectHint
Let \(z=x+i y\) then \(\bar{z}=i z^2\)
\(
\begin{aligned}
&\Rightarrow x-i y=i\left(x^2-y^2+2 i x y\right) \\
&\Rightarrow x-i y=i\left(x^2-y^2\right)-2 x y \\
&\Rightarrow x(1+2 y)=0 ; x^2-y^2+y=0 \\
&\Rightarrow x=0 \text { or } y=-\frac{1}{2} \Rightarrow x=0, y=0,1
\end{aligned}
\)
or \(y=-\frac{1}{2} \quad x=\pm \frac{\sqrt{3}}{2}\)
For non zero complex number \(z\),
\(
\begin{aligned}
&x=0, y=1 ; x=\frac{\sqrt{3}}{2}, y=-\frac{1}{2} ; x=\frac{-\sqrt{3}}{2}, y=-\frac{1}{2} \\
&\therefore \quad z=i, \frac{\sqrt{3}}{2}-\frac{i}{2},-\frac{\sqrt{3}}{2}-\frac{i}{2}
\end{aligned}
\) -
Question 13 of 161
13. Question
If \(|Z| \leq 1,|W| \leq 1\), Find the right statement from the given choices [1995 – 5 Marks]
CorrectIncorrectHint
Let \(z=r_1\left(\cos \theta_1+i \sin \theta_1\right)\) and \(w=r_2\left(\cos \theta_2+i \sin \theta_2\right)\)
We have, \(|z|=r_1,|w|=r_2, \arg (z)=\theta_1\) and \(\arg (w)=\theta_2\)
Given, \(|z| \leq 1,|w|<1\)
\(\Rightarrow \quad r_1 \leq 1\) and \(r_2 \leq 1\)
Now, \(z-w=\left(r_1 \cos \theta_1-r_2 \cos \theta_2\right)+i\left(r_1 \sin \theta_1-r_2 \sin \theta_2\right)\)
\(\Rightarrow|z-w|^2=\left(r_1 \cos \theta_1-r_2 \cos \theta_2\right)^2+\left(r_1 \sin \theta_1-r_2 \sin \theta_2\right)^2\)
\(=3 \cos ^2 \theta_1+r_2^2 \cos ^2 \theta_2-2 r_1 r_2 \cos \theta_1 \cos \theta_2\)
\(+7 \sin ^2 \theta_1+r_2^2 \sin ^2 \theta_2-2 r_1 r_2 \sin \theta_1 \sin \theta_2\)
\(=r_1\left(\cos ^2 \theta_1+\sin ^2 \theta_1\right)+r_2^2\left(\cos ^2 \theta_2+\sin ^2 \theta_2\right)\)
\(-2 r_1 r_2\left(\cos \theta_1 \cos \theta_2+\sin \theta_1 \sin \theta_2\right)\)
\(=r_1+r_2^2-2 r_1 r_2 \cos \left(\theta_1-\theta_2\right)\)
\(=\left(r_1-r_2\right)^2+2 r_1 r_2\left[1-\cos \left(\theta_1-\theta_2\right)\right]\)
\(=\left(r_1-r_2\right)^2+4 r_1 r_2 \sin ^2\left(\frac{\theta_1-\theta_2}{2}\right)\)
\(
\leq\left|r_1-r_2\right|^2+4\left|\sin \left(\frac{\theta_1-\theta_2}{2}\right)\right|^2 \quad\left[ r_1, r_2 \leq 1\right]
\)
and \(|\sin \theta| \leq|\theta|, \forall \theta \in \mathrm{R}\)
Therefore, \(|z-w|^2 \leq\left|r_1-r_2\right|^2+4\left|\frac{\theta_1-\theta_2}{2}\right|^2\)
\(
\leq\left|r_1-r_2\right|^2+\left|\theta_1-\theta_2\right|^2
\)
\(
\Rightarrow \quad|z-w|^2 \leq(|z|-|w|)^2+(\arg z-\arg w)^2
\) -
Question 14 of 161
14. Question
If \(i z^3+z^2-z+i=0\), then find \(|z|\). [1995 – 5 Marks]
CorrectIncorrectHint
Dividing throughout by \(i\) and knowing that \(\frac{1}{i}=-i\), we get
\(
\begin{aligned}
&z^3-i z^2+i z+1=0 \\
&\Rightarrow \quad z^2(z-i)+i(z-i)=0 \quad \text { as } \quad 1=-i^2 \\
&\Rightarrow \quad(z-i)\left(z^2+i\right)=0 \quad \therefore z=i \quad \text { or } \quad z^2=-i \\
&\therefore \quad|z|=|i|=1 \text { or }\left|z^2\right|=|z|^2=|-i|=1 \Rightarrow|z|=1
\end{aligned}
\)
Hence, in either case \(|z|=1\) -
Question 15 of 161
15. Question
If \(1, a_1, a_2 \ldots \ldots, a_{n-1}\) are the \(\mathrm{n}\) roots of unity, Find \(\left(1-a_1\right)(1-\) \(\left.a_2\right)\left(1-a_3\right) \ldots\left(1-a_{n-1}\right)= ?\) [1984 – 2 Marks]
CorrectIncorrectHint
\(1, a_1, a_2, \ldots, a_{n-1}\) are the \(n\) roots of unity. Therefore they are roots of eq. \(x^n-1=0\)
Therefore by factor theorem,
\(x^n-1=(x-1)\left(x-a_1\right)\left(x-a_2\right) \ldots .\left(x-a_{n-1}\right) \dots(i)\)
\(\Rightarrow \frac{x^n-1}{x-1}=\left(x-a_1\right)\left(x-a_2\right) \ldots .\left(x-a_{n-1}\right) \dots(ii)\) On differentiating both sides of eq. (i), we get
\(
n x^{n-1}=\left(x-a_1\right)\left(x-a_2\right) \ldots\left(x-a_{n-1}\right)+(x-1)\left(x-a_2\right)
\)
\(\ldots .\left(x-a_{n-1}\right)+\ldots .+(x-1)\left(x-a_1\right) \ldots\left(x-a_{n-2}\right)\)
For \(x=1\), we get \(n=\left(1-a_1\right)\left(1-a_2\right) \ldots\left(1-a_{n-1}\right)\)
[Since the terms except first, contain \((x-1)\) and hence become zero for \(x\) \(=1]\) -
Question 16 of 161
16. Question
Show that the complex numbers \(z_1, z_2\) and the origin form an equilateral triangle only if \(z_1^2+z_2^2-z_1 z_2\). [1983 – 3 Marks]
CorrectIncorrectHint
We know that if \(z_1, z_2, z_3\) are vertices of an equilateral triangle, then
\(
\frac{z_1-z_2}{z_3-z_2}=\frac{z_3-z_1}{z_2-z_1}
\)
Here \(z_3=0\),
\(
\therefore \frac{z_1-z_2}{-z_2}=\frac{-z_1}{z_2-z_1}
\)
\(
\Rightarrow-z_1^2-z_2^2+2 z_1 z_2=z_1 z_2, \quad \therefore z_1^2+z_2^2-z_1 z_2=0 \text {. }
\)
-
Question 17 of 161
17. Question
Let the complex number \(z_1, z_2\) and \(z_3\) be the vertices of an equilateral triangle. Let \(z_0\) be the circumcentre of the triangle. Then find \(z_1^2\) \(+z_2^2+z_3^2= ?\). [1981 – 4 Marks]
CorrectIncorrectHint
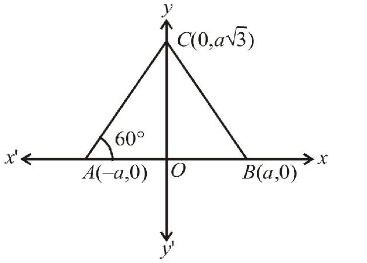
Let us consider the equilateral triangle with each side of length \(2 a\) and having two of its vertices \(A(-a, 0)\) and \(B(a, 0)\) on \(x\)-axis, then third vertex \(C\) will clearly lie on y-axissuch that \(O C=2 a \sin 60^{\circ}=a \sqrt{3}, \therefore\) \(C=(0, a \sqrt{3)}\).
Now if \(A, B\) and \(C\) are represented by complex number \(z_1, z_2, z_3\) then \(z_1=-a ; z_2=a ; z_3=a \sqrt{3} i\)
Since in an equilateral triangle, centriod and circumcentre coincide,
\(
\begin{aligned}
&\therefore \text { Circumcentre, } z_0=\frac{z_1+z_2+z_3}{3} \\
&\Rightarrow z_0=\frac{-a+a+a \sqrt{3} i}{3}=\frac{i a}{\sqrt{3}}
\end{aligned}
\)
Now, \(z_1^2+z_2^2+z_3^2=a^2+a^2-3 a^2=-a^2\)
and \(3 z_0^2=(i a)^2=-a^2\)
\(\therefore\) Clearly \(3 z_0^2=z_1^2+z_2^2+z_3^2\) -
Question 18 of 161
18. Question
If \(x=a+b, y=a \gamma+b \beta\) and \(z=a \beta+b \gamma\) where \(\gamma\) and \(\beta\) are the complex cube roots of unity, find \(x y z= ?\). [1978]
CorrectIncorrectHint
Since, \(\beta\) and \(\gamma\) are the complex cube roots of unity therefore, we can suppose \(\beta=\omega\) and \(\gamma=\omega^2\) so that \(\omega+\omega^2+1=0\) and \(\omega^3=1\).
Then \(x y z=(a+b)\left(a \omega^2+b \omega\right)\left(a \omega+b \omega^2\right)\)
\(=(a+b)\left(a^2 \omega^3+a b \omega^4+a b \omega^2+b^2 \omega^3\right)\)
\(=(a+b)\left(a^2+a b \omega+a b \omega^2+b^2\right)\left(\mathrm{using} \omega^3=1\right)\)
\(=(a+b)\left(a^2+a b\left(\omega+\omega^2\right)+b^2\right)\)
\(=(a+b)\left(a^2-a b+b^2\right)=a^3+b^3\) -
Question 19 of 161
19. Question
If \(\alpha\) and \(\beta\) be two roots of the equation \(x^2-64 x+256=0\). Then the value of \(\left(\frac{\alpha^3}{\beta^5}\right)^{\frac{1}{8}}+\left(\frac{\beta^3}{\alpha^5}\right)^{\frac{1}{8}}\) is: [Main Sep. \(\left.06,2020(\mathrm{I})\right]\)
CorrectIncorrectHint
(a) \(\alpha+\beta=64, \alpha \beta=256\)
\(
\frac{\alpha^{3 / 8}}{\beta^{5 / 8}}+\frac{\beta^{3 / 8}}{\alpha^{5 / 8}}=\frac{\alpha+\beta}{(\alpha \beta)^{5 / 8}}=\frac{64}{\left(2^8\right)^{5 / 8}}=\frac{64}{32}=2
\) -
Question 20 of 161
20. Question
If \(\alpha\) and \(\beta\) are the roots of the equation \(2 x(2 x+1)=1\), then \(\beta\) is equal to: [Main Sep. 06, 2020 (II)]
CorrectIncorrectHint
(b) Let \(\alpha\) and \(\beta\) be the roots of the given quadratic equation, \(2 x^2+2 x-1=0\)
Then, \(\alpha+\beta=-\frac{1}{2} \Rightarrow-1=2 \alpha+2 \beta\) and \(4 \alpha^2+2 \alpha-1=0 \quad[\because \alpha\) is root of eq. (i) \(]\)
\(
\Rightarrow 4 \alpha^2+2 \alpha+2 \alpha+2 \beta=0 \Rightarrow \beta=-2 \alpha(\alpha+1)
\) -
Question 21 of 161
21. Question
The product of the roots of the equation \(9 x^2-18|x|+5=0\), is: [Main Sep. 05, 2020 (I)]
CorrectIncorrectHint
(b) Let \(|x|=y\) then
\(
\begin{aligned}
&9 y^2-18 y+5=0 \\
&\Rightarrow 9 y^2-15 y-3 y+5=0 \\
&\Rightarrow(3 y-1)(3 y-5)=0 \\
&\Rightarrow y=\frac{1}{3} \text { or } \frac{5}{3} \Rightarrow|x|=\frac{1}{3} \text { or } \frac{5}{3}
\end{aligned}
\)
Roots are \(\pm \frac{1}{3}\) and \(\pm \frac{5}{3}\)
\(
\therefore \text { Product }=\frac{25}{81}
\) -
Question 22 of 161
22. Question
If \(\alpha\) and \(\beta\) are the roots of the equation, \(7 x^2-3 x-2=0\), the the value of \(\frac{\alpha}{1-\alpha^2}+\frac{\beta}{1-\beta^2}\) is equal to: [Main Sep. 05, 2020 (II)]
CorrectIncorrectHint
\(
\text { (d) Let } \alpha \text { and } \beta \text { be the roots of the quadratic equation }
\)
\(
\begin{aligned}
&7 x^2-3 x-2=0\\
&\therefore \alpha+\beta=\frac{3}{7}, \alpha \beta=\frac{-2}{7}\\
&\text { Now, } \frac{\alpha}{1-\alpha^2}+\frac{\beta}{1-\beta^2}\\
&=\frac{\alpha-\alpha \beta(\alpha+\beta)+\beta}{1-\left(\alpha^2+\beta^2\right)+(\alpha \beta)^2}\\
&=\frac{(\alpha+\beta)-\alpha \beta(\alpha+\beta)}{1-(\alpha+\beta)^2+2 \alpha \beta+(\alpha \beta)^2}\\
&=\frac{\frac{3}{7}+\frac{2}{7} \times \frac{3}{7}}{1-\frac{9}{49}+2 \times \frac{-2}{7}+\frac{4}{49}}=\frac{27}{16}
\end{aligned}
\) -
Question 23 of 161
23. Question
Let \(u=\frac{2 z+i}{z-k i}, z=x+i y\) and \(k>0\). If the curve represented by \(\operatorname{Re}(\mathrm{u})\) \(+\operatorname{Im}(\mathrm{u})=1\) intersects the \(y\)-axis at the points \(P\) and \(Q\) where \(P Q=5\), then the value of \(k\) is: [Main Sep. 04, 2020 (I)]
CorrectIncorrectHint
(d) \(u=\frac{2(x+i y)+i}{(x+i y)-k i}=\frac{2 x+i(2 y+1)}{x+i(y-k)}\)
Real part of \(u=\operatorname{Re}(u)=\frac{2 x^2+(y-K)(2 y+1)}{x^2+(y-K)^2}\)
Imaginary part of \(u\)
\(
\begin{aligned}
&=\operatorname{Im}(u)=\frac{-2 x(y-K)+x(2 y+1)}{x^2+(y-K)^2} \\
&\because \operatorname{Re}(u)+\operatorname{Im}(u)=1 \\
&\Rightarrow 2 x^2+2 y^2-2 K y+y-K-2 x y+2 K x+2 x y+x \\
&=x^2+y^2+K^2-2 K y
\end{aligned}
\)
Since, the curve intersect at \(y\)-axis
\(
\begin{aligned}
&\therefore x=0 \\
&\Rightarrow y^2+y-K(K+1)=0
\end{aligned}
\)
Let \(y_1\) and \(y_2\) are roots of equations if \(x=0\)
\(
\begin{aligned}
&\because y_1+y_2=-1 \\
&y_1 y_2=-\left(K^2+K\right)
\end{aligned}
\)
\(
\begin{aligned}
&\therefore\left(y_1-y_2\right)^2=\left(1+4 K^2+4 K\right) \\
&\text { Given } P Q=5 \Rightarrow\left|y_1-y_2\right|=5 \\
&\quad \Rightarrow 4 K^2+4 K-24=0 \Rightarrow K=2 \text { or }-3 \\
&\text { as } K>0, \therefore K=2
\end{aligned}
\) -
Question 24 of 161
24. Question
Let \(\lambda \neq 0\) be in \(\mathbf{R}\). If \(\alpha\) and \(\beta\) are roots of the equation, \(x^2-x+2 \lambda=0\) and \(\alpha\) and \(\gamma\) are the roots of the equation, \(3 x^2-10 x+27 \lambda=0\), then \(\frac{\beta \gamma}{\lambda}\) is equal to: [Main Sep. 04, 2020 (II)]
CorrectIncorrectHint
(b) Since \(\alpha\) is common root of \(x^2-x+2 \lambda=0\) and \(3 x^2-10 x+27 \lambda=0\) \(\therefore 3 \alpha^2-10 \alpha+27 \lambda=0\) \(3 \alpha^2-3 \alpha+6 \lambda=0\)
\(\therefore\) On subtract, we get \(\alpha=3 \lambda\)
Now, \(\alpha \beta=2 \lambda \Rightarrow 3 \lambda \cdot \beta=2 \lambda \Rightarrow \beta=\frac{2}{3}\)
\(
\begin{aligned}
&\Rightarrow \alpha+\beta=1 \Rightarrow 3 \lambda+\frac{2}{3}=1 \Rightarrow \lambda=\frac{1}{9} \text { and } \\
&\alpha \gamma=9 \lambda \Rightarrow 3 \lambda \cdot \gamma=9 \lambda \Rightarrow \gamma=3 \\
&\therefore \frac{\beta \gamma}{\lambda}=18
\end{aligned}
\) -
Question 25 of 161
25. Question
If \(\alpha\) and \(\beta\) are the roots of the equation \(x^2+p x+2=0\) and \(\frac{1}{\alpha}\) and \(\frac{1}{\beta}\) are the roots of the equation \(2 x^2+2 q x+1=0\), then \(\left(\alpha-\frac{1}{\alpha}\right)\left(\beta-\frac{1}{\beta}\right)\left(\alpha+\frac{1}{\beta}\right)\left(\beta+\frac{1}{\alpha}\right)\) is equal to: Main Sep. 03, 2020 (I)]
CorrectIncorrectHint
(d) \(\alpha \cdot \beta=2\) and \(\alpha+\beta=-p\) also \(\frac{1}{\alpha}+\frac{1}{\beta}=-q\)
\(
\Rightarrow p=2 q
\)
\(
\text { Now } \begin{aligned}
&\left(\alpha-\frac{1}{\alpha}\right)\left(\beta-\frac{1}{\beta}\right)\left(\alpha+\frac{1}{\beta}\right)\left(\beta+\frac{1}{\alpha}\right) \\
&=\left[\alpha \beta+\frac{1}{\alpha \beta}-\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right]\left[\alpha \beta+\frac{1}{\alpha \beta}+\right] \\
=& \frac{9}{2}\left[\frac{5}{2}-\frac{\alpha^2+\beta^2}{2}\right]=\frac{9}{4}\left[5-\left(p^2-4\right)\right]
\end{aligned}
\)
\(
=\frac{9}{4}\left(9-p^2\right) \quad\left[\because \alpha^2+\beta^2=(\alpha+\beta)^2-2 \alpha \beta\right]
\) -
Question 26 of 161
26. Question
The set of all real values of \(\lambda\) for which the quadratic equations, \(\left(\lambda^2+1\right) x^2-4 \lambda x+2=0\) always have exactly one root in the interval \(\)(0,1)\(\) is : [Main Sep. 03, 2020(II)]
CorrectIncorrectHint
(c) The given quadratic equation is
\(
\left(\lambda^2+1\right) x^2-4 \lambda x+2=0
\)
\(\because\) One root is in the interval \((0,1)\)
\(\therefore f(0) f(1) \leq 0\)
\(\Rightarrow 2\left(\lambda^2+1-4 \lambda+2\right) \leq 0\)
\(\Rightarrow 2\left(\lambda^2-4 \lambda+3\right) \leq 0\)
\((\lambda-1)(\lambda-3) \leq 0 \Rightarrow \lambda \in[1,3]\)
But at \(\lambda=1\), both roots are 1 so \(\lambda \neq 1\)
\(\therefore \lambda \in(1,3]\) -
Question 27 of 161
27. Question
Let \(\alpha\) and \(\beta\) be the roots of the equation, \(5 x^2+6 x-2=0\). If \(S_n=\alpha^n+\beta^n, n=1,2,3, \ldots\), then: [Main Sep. 02, 2020 (I)]
CorrectIncorrectHint
(c) Since, \(\alpha\) and \(\beta\) are the roots of the equaton \(5 x^2+6 x-2=0\)
Then, \(5 \alpha^2+6 \alpha-2=0,5 \beta^2+6 \beta-2=0\)
\(
\begin{aligned}
&5 \alpha^2+6 \alpha=2 \\
&\begin{aligned}
5 S_6 &+6 S_5=5\left(\alpha^6+\beta^6\right)+6\left(\alpha^5+\beta^5\right) \\
&=\left(5 \alpha^4+6 \alpha^5\right)+\left(5 \beta^6+6 \beta^5\right) \\
&=\alpha^4\left(5 \alpha^2+6 \alpha\right)+\beta^4\left(5 \beta^2+6 \beta\right) \\
&=2\left(\alpha^4+\beta^4\right)=2 S_4
\end{aligned}
\end{aligned}
\) -
Question 28 of 161
28. Question
The number of real roots of the equation, \(e^{4 x}+e^{3 x}-4 e^{2 x}+e^x+1=0\) is: [Main Jan. 9, 2020 (I)]
CorrectIncorrectHint
(a) Let \(e^x=t \in(0, \infty)\)
Given equation
\(
\begin{aligned}
&t^4+t^3-4 t^2+t+1=0 \\
&\Rightarrow t^2+t-4+\frac{1}{t}+\frac{1}{t^2}=0 \\
&\Rightarrow \quad\left(t^2+\frac{1}{t^2}\right)+\left(t+\frac{1}{t}\right)-4=0
\end{aligned}
\)
Let \(t+\frac{1}{t}=y\)
\(\begin{aligned}\left(y^2-2\right)+y-4 &=0 \quad \Rightarrow \quad \\ y^2+y-6=0 \end{aligned} \quad \Rightarrow \quad \begin{array}{r}y^2+y-6=0 \\ y=-3,2\end{array}\)
\(\Rightarrow y=2 \quad \Rightarrow t+\frac{1}{t}=2\)
\(\Rightarrow e^x+e^{-x}=2\)
\(x=0\), is the only solution of the equation
Hence, there is only one solution to the given equation. -
Question 29 of 161
29. Question
If the equation, \(x^2+b x+45=0(b \in R)\) has conjugate complex roots and they satisfy \(|z+1|=2 \sqrt{10}\), then: [Main Jan. 8, 2020 (I)]
CorrectIncorrectHint
(a) Let \(z=\alpha \pm i \beta\) be the complex roots of the equation
So, sum of roots \(=2 \alpha=-b\) and
Product of roots \(=\alpha^2+\beta^2=45\)
\(
(\alpha+1)^2+\beta^2=40
\)
Given, \(|z+1|=2 \sqrt{10}\)
\(
\begin{array}{lll}
\Rightarrow & (\alpha+1)^2-\alpha^2=-5 & {\left[Q \beta^2=45-\alpha^2\right]} \\
\Rightarrow & 2 \alpha+1=-5 \quad \Rightarrow & 2 \alpha=-6
\end{array}
\)
Hence, \(b=6\) and \(b^2-b=30\) -
Question 30 of 161
30. Question
Let \(\alpha\) and \(\beta\) be the roots of the equation \(x^2-x-1=0\). If \(p_k=(\alpha)^k+(\beta)^k, k \geq 1\), then which one of the following statements is not true? [Main Jan. 7, 2020(II)]
CorrectIncorrectHint
\(
\begin{aligned}
&(d) \alpha^5=5 \alpha+3 \\
&\beta^5=5 \beta+3 \\
&p_5=5(\alpha+\beta)+6=5(1)+6 \\
&\quad\left[\mathrm{Q} \text { from } x^2-x-1=0, \alpha+\beta=\frac{-b}{a}=1\right] \\
&p_5=11 \text { and } p_5=\alpha^2+\beta^2=\alpha+1+\beta+1 \\
&p_2=3 \text { and } p_3=\alpha^3+\beta^3=2 \alpha+1+2 \beta+1 \\
&=2(1)+2=4 \\
&p_2 \times p_3=12 \text { and } p_5=11 \Rightarrow p_5 \neq p_2 \times p_3
\end{aligned}
\) -
Question 31 of 161
31. Question
Let \(\alpha\) and \(\beta\) be two real roots of the equation \((k+1) \tan ^2 x-\sqrt{2} \lambda \tan x=(1-k)\), where \(k(\equiv-1)\) and \(\lambda\) are real numbers. If \(\tan ^2(\alpha+\beta)=50\), then a value of \(\lambda\) is: [Main Jan. 7, 2020(I)]
CorrectIncorrectHint
(b) \((k+1) \tan ^2 x-\sqrt{2} \lambda \tan x+(k-1)=0\)
\(
\begin{gathered}
\tan \alpha+\tan \beta=\frac{\sqrt{2} \lambda}{k+1} \\
\tan \alpha \cdot \tan \beta=\frac{k-1}{k+1} \\
\therefore \quad \tan (\alpha+\beta)=\frac{\frac{\sqrt{2} \lambda}{k+1}}{1-\frac{k-1}{k+1}}=\frac{\lambda}{\sqrt{2}} \\
\text { [Product of root } = \frac{k-1}{k+1}] \\
\tan ^2(\alpha+\beta)=\frac{\lambda^2}{2}=50 \\
\lambda=10 .
\end{gathered}
\) -
Question 32 of 161
32. Question
Suppose \(a, b\) denote the distinct real roots of the quadratic polynomial \(x^2+20 x-2020\) and suppose \(c, d\) denote the distinct complex roots of the quadratic polynomial \(x^2-20 x+2020\). Then the value of [Adv. 2020]
\(
a c(a-c)+a d(a-d)+b c(b-c)+b d(b-d)
\)
isCorrectIncorrectHint
(d) Consider the quadratic polynomials in the form of the equation
\(
\begin{aligned}
&x^2+20 x-2020=0 \dots(i)\\
&x^2-20 x+2020=0 \dots(ii)
\end{aligned}
\)
Since, \(a\) and \(b\) are roots of the equation(i), then
\(
a+b=-20, a b=-2020
\)
\(c\) and \(d\) are the roots of the equation (ii), then \(c+d=20, c d=2020\)
Now,
\(
\begin{aligned}
& \quad a c(a-c)+a d(a-d)+b c(b-c)+b d(b-d) \\
=& a^2 c-a c^2+a^2 d-a d^2+b^2 c-b c^2+b^2 d-b d^2 \\
=& a^2(c+d)+b^2(c+d)-c^2(a+b)-d^2(a+b) \\
=&(c+d)\left(a^2+b^2\right)-(a+b)\left(c^2+d^2\right) \\
=&(c+d)\left((a+b)^2-2 a b\right)-(a+b)\left((c+d)^2-2 c d\right) \\
=& 20\left[(20)^2+4040\right]+20\left[(20)^2-4040\right] \\
=& 20 \times 800=16000
\end{aligned}
\)
Note: We know that, for a quadratic polynomial of the form \(\mathrm{ax}^2+\mathrm{bx}+\mathrm{c}\), Sum of roots \(=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^2}=\frac{-b}{a}\),
And product of roots \(=\frac{\text { Constant term }}{\text { Coefficient of } \mathrm{x}^2}=\frac{\mathrm{c}}{\mathrm{a}}\) -
Question 33 of 161
33. Question
If \(\mathrm{a}\) and \(\mathrm{b}\) are the roots of the quadratic equation, \(\mathrm{x}^2+\mathrm{x} \sin \mathrm{\theta}-2 \operatorname{sin \theta}=\) \(00, \theta \in\left(0, \frac{\pi}{2}\right)\), then \(\frac{\alpha^{12}+\beta^{12}}{\left(\alpha^{-12}+\beta^{-12}\right)(\alpha-\beta)^{24}}\) is equal to: [Main April 10, 2019 (I)]
CorrectIncorrectHint
(b) Given equation is, \(x^2+x \sin \mathrm{\theta}-2 \sin \mathrm{\theta}=0\)
\(a+b=-\sin \theta\) and \(a b=-2 \sin \theta\)
\(
\begin{aligned}
&\frac{\left(\alpha^{12}+\beta^{12}\right) \alpha^{12} \beta^{12}}{\left(\alpha^{12}+\beta^{12}\right)(\alpha-\beta)^{24}}=\frac{(\alpha \beta)^{12}}{(\alpha-\beta)^{24}} \\
&|\alpha-\beta|=\sqrt{(\alpha+\beta)^2-4 \alpha \beta}=\sqrt{\sin ^2 \theta+8 \sin \theta} \\
& \frac{(\alpha \beta)^{12}}{(\alpha-\beta)^{24}}=\frac{(2 \sin \theta)^{12}}{\sin ^{12} \theta(\sin \theta+8)^{12}}=\frac{2^{12}}{(\sin \theta+8)^{12}}
\end{aligned}
\) -
Question 34 of 161
34. Question
The number of real roots of the equation \(5+\left|2^x-1\right|=2^x\left(2^x-2\right)\) is: [Main April 10, 2019 (II)]
CorrectIncorrectHint
According to question,
\(
5+\left|2^x-1\right|=2^x\left(2^x-2\right)
\)
Case I
\(
\begin{aligned}
&2^x \geq 1 \\
&\Rightarrow 5+2^x-1=2^x\left(2^x-2\right)
\end{aligned}
\)
Let \(2^x=\mathrm{t}\)
\(\Rightarrow 5+\mathrm{t}-1=\mathrm{t}(\mathrm{t}-2)\)
\(=t^2-3 t-4=0\)
\(\Rightarrow \mathrm{t}=4\) or \(-1\) (invalid) \(\left(\because 2^{\mathrm{x}} \neq-1\right)\)
\(\Rightarrow 2^x=4\)
\(\Rightarrow x=2\)
\(\therefore\) only one solution
Case II
\(2^x<1\)
\(\Rightarrow 5+1-2^x=2^x\left(2^x-2\right)\)
Let \(2^x=t\)
\(\Rightarrow 5+1-t=t(t-2)\)
\(\Rightarrow \mathrm{t}^2-\mathrm{t}-6=0\)
\(\Rightarrow(\mathrm{t}-3)(\mathrm{t}-2)=0\)
\(\Rightarrow \mathrm{t}=3,-2\)
\(2^x=3\) (invalid as \(2^x<1\) ), or \(2^x=-2\) (invalid)
Therefore, number of real roots is one. -
Question 35 of 161
35. Question
Let \(\mathrm{p}, \mathrm{q} \in \mathrm{R}\). If \(2-\sqrt{3}\) is a root of the quadratic equation, \(x^2+p x+q=0\), then: [Main April 9, 2019 (I)]
CorrectIncorrectHint
(d) Since \(2-\sqrt{3}\) is a root of the quadratic equation \(\mathrm{x}^2+\mathrm{px}+\mathrm{q}=0\)
\(\therefore 2+\sqrt{3}\) is the other root
\(\Rightarrow x^2+p x+q=[x-(2-\sqrt{3})[x-(2+\sqrt{3})]\)
\(
\begin{aligned}
&=x^2-(2+\sqrt{3}) x-(2-\sqrt{3}) x+\left(2^2-(\sqrt{3})^2\right) \\
&=x^2-4 x+1
\end{aligned}
\)
Now, by comparing \(p=-4, q=1\)
\(
p^2-4 q-12=16-4-12=0
\) -
Question 36 of 161
36. Question
The sum of the solutions of the equation \(|\sqrt{x}-2|+\sqrt{x}(\sqrt{x}-4)+2=\) \(0,(x>0)\) is equal to: [Main April 8, 2019 (I)]
CorrectIncorrectHint
(d) Let \(\sqrt{x}=a\)
given equation will become:
\(
\begin{aligned}
&|a-2|+a(a-4)+2=0 \\
&\quad \Rightarrow|a-2|+a^2-4 a+4-2=0 \\
&\quad \Rightarrow|a-2|+(a-2)^2-2=0
\end{aligned}
\)
Let \(|a-2|=y(\) Clearly \(y \geq 0)\)
\(
\begin{aligned}
&\Rightarrow \quad y+y^2-2=0 \\
&\Rightarrow \quad y=1 \text { or }-2 \text { (rejected) } \\
&\Rightarrow \quad|a-2|=1 \Rightarrow a=1,3
\end{aligned}
\)
When \(\sqrt{x}=1 \Rightarrow x=1\)
When \(\sqrt{x}=3 \Rightarrow x=9\)
Hence, the required sum of solutions of the equation \(=10\) -
Question 37 of 161
37. Question
If \(\alpha\) and \(\beta\) be the roots of the equation \(x^2-2 x+2=0\), then the least value of \(n\) for which \(\left(\frac{\alpha}{\beta}\right)^n=1\) is: [Main April 8, \(2019(\mathrm{I})\) ]
CorrectIncorrectHint
(c) The given quadratic equation is \(x^2-2 x+2=0\)
Then, the roots of the this equation are \(\frac{2 \pm \sqrt{-4}}{2}=1 \pm i\)
Now, \(\frac{\alpha}{\beta}=\frac{1-i}{1+i}=\frac{(1-i)^2}{1-i^2}=i\)
or \(\frac{\alpha}{\beta}=\frac{1-i}{1+i}=\frac{(1-i)^2}{1-i^2}=-i \quad\) So, \(\frac{\alpha}{\beta}=\pm i\)
Now, \(\left(\frac{\alpha}{\beta}\right)^n=1 \Rightarrow(\pm \mathrm{i})^n=1\)
\(\Rightarrow n\) must be a multiple of 4.
Hence, the required least value of \(n=4\). -
Question 38 of 161
38. Question
If \(\lambda\) be the ratio of the roots of the quadratic equation in \(\mathrm{x}, 3 \mathrm{~m}^2 \mathrm{x}^2+\mathrm{m}(\mathrm{m}-4) \mathrm{x}+2=\) 0 , then the least value of \(\mathrm{m}\) for which \(\lambda+\frac{1}{\lambda}=1\), is: [Main Jan. 12, 2019(I)]
CorrectIncorrectHint
\(
\text { (b) Let roots of the quadratic equation are } \alpha, \beta \text {. }
\)Given, \(\lambda=\frac{\alpha}{\beta}\) and \(\lambda+\frac{1}{\lambda}=1 \Rightarrow \frac{\alpha}{\beta}+\frac{\beta}{\alpha}=1\) \(\frac{(\alpha+\beta)^2-2 \alpha \beta}{\alpha \beta}=1 \ldots\) (i)
The quadratic equation is, \(3 m^2 x^2+m(m-4) x+2=0\) \( \mathrm{a}+\mathrm{b}=\frac{m(4-m)}{3 m^2}=\frac{4-m}{3 m}\) and \(\alpha \beta=\frac{2}{3 m^2}\)
Put these values in eq (1),
\(
\begin{aligned}
&\frac{\left(\frac{4-m}{3 m}\right)^2}{\frac{2}{3 m^2}}=3 \\
&\Rightarrow(m-4)^2=18 \Rightarrow m=4 \pm \sqrt{18}
\end{aligned}
\)
Therefore, least value is \(4-\sqrt{18}=4-3 \sqrt{2}\) -
Question 39 of 161
39. Question
Consider the quadratic equation \((\mathrm{c}-5) x^2-2 \mathrm{c} x+(\mathrm{c}-4)=0\),
\(c \neq 5\). Let \(\mathrm{S}\) be the set of all integral values of \(\mathrm{c}\) for which one root of the equation lies in the interval \((0,2)\) and its other root lies in the interval \((2,3)\). Then the number of elements in \(\mathrm{S}\) is: [Main Jan. 10, 2019 (I)]CorrectIncorrectHint
(d) Consider the quadratic equation
\(
(c-5) x^2-2 c x+(c-4)=0
\)
Now, \(f(0) . f(3)>0\) and \(f(0) . f(2)<0\)
\(
\begin{aligned}
&\Rightarrow \quad(c-4)(4 c-49)>0 \text { and }(c-4)(c-24)<0 \\
&\Rightarrow \quad c \in(-\infty, 4) \cup\left(\frac{49}{4}, \infty\right) \text { and } c \in(4,24) \\
&\Rightarrow \quad c \in\left(\frac{49}{4}, 24\right)
\end{aligned}
\)
Integral values in the interval \(\left(\frac{49}{4}, 24\right)\) are \(13,14, \ldots, 23\).
\(
\therefore \quad S=\{13,14, \ldots, 23\}
\) -
Question 40 of 161
40. Question
Let \(\mathrm{a}\) and \(\mathrm{b}\) be two roots of the equation \(x^2+2 x+2=0\), then \(\mathrm{a}^{15}+\mathrm{b}^{15}\) is equal to: [Main Jan. 9, 2019 (I)]
CorrectIncorrectHint
(a) Consider the equation
\(
\begin{aligned}
&x^2+2 x+2=0 \\
&x=\frac{-2 \pm \sqrt{4-8}}{2}=-1 \pm i
\end{aligned}
\)
Let \(\alpha=-1+i, \beta=-1-i\)
\(
\begin{aligned}
&\alpha^{15}+\beta^{15}=(-1+i)^{15}+(-1-i)^{15} \\
&=\left(\sqrt{2} e^{i \frac{3 \pi}{4}}\right)^{15}+\left(\sqrt{2} e^{-i \frac{3 \pi}{4}}\right)^{15} \\
&=(\sqrt{2})^{15}\left[e^{\frac{i 45 \pi}{4}}+e^{\frac{-i 45 \pi}{4}}\right] \\
&=(\sqrt{2})^{15} \cdot 2 \cos \frac{45 \pi}{4}=(\sqrt{2})^{15} \cdot 2 \cos \frac{3 \pi}{4} \\
&=\frac{-2}{\sqrt{2}}(\sqrt{2})^{15} \\
&=-2(\sqrt{2})^{14}=-256
\end{aligned}
\) -
Question 41 of 161
41. Question
The number of all possible positive integral values of \(\alpha\) for which the roots of the quadratic equation, \(6 x^2-11 x+\alpha=0\) are rational numbers is: [Main Jan. 09, 2019 (II)]
CorrectIncorrectHint
\(
6 x^2-11 x+ \alpha=0
\)
If roots are rational numbers, then discriminant should be a perfect square.
\(
D=121-24 \alpha
\)
So, If \(\alpha=1, D=97\), which is not a perfect square.
\(\alpha=2, D=73\), which is not a perfect square.
\(\alpha=3, D=49\), it is a perfect square.
\(\alpha=4, D=25\), it is a perfect square.
\(\alpha=5, D=1\), it is a perfect square.
So, number of possible values of \(\alpha\) is 3. -
Question 42 of 161
42. Question
If an angle \(A\) of a \(\triangle A B C\) satisfies \(5 \cos A+3=0\), then the roots of the quadratic equation, \(9 x^2+27 x+20=0\) are. [Main Online April 16, 2018]
CorrectIncorrectHint
(b) Here, \(9 x^2+27 x+20=0\)
\(
\begin{aligned}
&\therefore x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a} \\
&\Rightarrow x=\frac{-27 \pm \sqrt{27^2-4 \times 9 \times 20}}{2 \times 9} \\
&\Rightarrow x=-\frac{4}{3},-\frac{5}{3}
\end{aligned}
\)
Given, \(\cos A=-\frac{3}{5}\)
\(\therefore \sec A=\frac{1}{\cos A}=-\frac{5}{3}\)
Here, A is an obtuse angle.
\(
\therefore \tan A=-\sqrt{\sec ^2 A-1}=-\frac{4}{3} .
\) -
Question 43 of 161
43. Question
If \(\tan A\) and \(\tan B\) are the roots of the quadratic equation, \(3 x^2-10 x-\) \(25=0\) then the value of \(3 \sin ^2(A+B)-10 \sin (A+B) \cdot \cos (A+B)-25 \cos ^2(A+B)\) is [Main Online April 15, 2018]
CorrectIncorrectHint
(b) As \(\tan A\) and \(\tan B\) are the roots of \(3 x^2-10 x-25=0\), So, \(\tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B}=\frac{\frac{10}{3}}{1+\frac{25}{3}}=\frac{10 / 3}{28 / 3}=\frac{5}{14}\)
Now, \(\cos 2(A+B)=-1+2 \cos ^2(A+B)\)
\(
\begin{aligned}
=& \frac{1-\tan ^2(A+B)}{1+\tan ^2(A+B)} \Rightarrow \cos ^2(A+B)=\frac{196}{221} \\
& \therefore 3 \sin ^2(A+B)-10 \sin (A+B) \cos (A+B)-25 \cos ^2(A+B) \\
=& \cos ^2(A+B)\left[3 \tan ^2(A+B)-10 \tan (A+B)-25\right] \\
=& \frac{75-700-4900}{196} \times \frac{196}{221}=-\frac{5525}{196} \times \frac{196}{221}=-25
\end{aligned}
\) -
Question 44 of 161
44. Question
If \(\alpha, \beta \in \mathrm{C}\) are the distinct roots, of the equation \(\mathrm{x}^2-\mathrm{x}+1=0\), then \(\alpha^{101}+\beta^{107}\) is equal to: [Main 2018]
CorrectIncorrectHint
(b) \(\alpha, \beta\) are roots of \(x^2-x+1=0\)
\(\therefore \quad \alpha=-\omega\) and \(\beta=-\omega^2\)
where \(\omega\) is cube root of unity
\(
\begin{gathered}
\therefore \quad \alpha^{101}+\beta^{107}=(-\omega)^{101}+(-\omega)^{107} \\
=-\left[\omega^2+\omega\right]=-[-1]=1
\end{gathered}
\) -
Question 45 of 161
45. Question
If, for a positive integer \(\mathrm{n}\), the quadratic equation, \(\mathrm{x}(\mathrm{x}+1)+(\mathrm{x}+1)(\mathrm{x}+2)+\ldots . .+(\mathrm{x}+\overline{\mathrm{n}-1})(\mathrm{x}+\mathrm{n})=10 \mathrm{n}\) has two consecutive integral solutions, then \(n\) is equal to: [Main 2017]
CorrectIncorrectHint
\(
\begin{aligned}
&\text { (a) We have, } \sum_{r=1}^n(x+r-1)(x+r)=10 n\\
&\sum_{r=1}^n\left(x^2+x r+(r-1) x+r^2-r\right)=10 n\\
&\Rightarrow \quad \sum_{\mathrm{r}=1}^{\mathrm{n}}\left(\mathrm{x}^2+(2 \mathrm{r}-1) \mathrm{x}+\mathrm{r}(\mathrm{r}-1)\right)=10 \mathrm{n}\\
&\Rightarrow \mathrm{nx}^2+\{1+3+5+\ldots .+(2 \mathrm{n}-1)\} \mathrm{x}\\
&+\{1.2+2.3+\ldots .+(n-1) n\}=10 n
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow \quad \mathrm{nx}^2+\mathrm{n}^2 \mathrm{x}+\frac{(\mathrm{n}-1) \mathrm{n}(\mathrm{n}+1)}{3}=10 \mathrm{n} \\
&\Rightarrow \quad \mathrm{x}^2+\mathrm{nx}+\frac{\mathrm{n}^2-31}{3}=0
\end{aligned}
\)
Let \(\alpha\) and \(\alpha+1\) be its two solutions
\(\Rightarrow \quad \alpha+(\alpha+1)=-\mathrm{n} \quad\) ( \(\because\) it has two consequtive integral solutions) \(\Rightarrow \quad \alpha=\frac{-\mathrm{n}-1}{2} \dots(i)\) Also \(\alpha(\alpha+1)=\frac{\mathrm{n}^2-31}{3} \quad\)…(ii)
Putting value of (i) in (ii), we get
\(
\begin{aligned}
&-\left(\frac{\mathrm{n}+1}{2}\right)\left(\frac{1-\mathrm{n}}{2}\right)=\frac{\mathrm{n}^2-31}{3} \\
\Rightarrow \quad \mathrm{n}^2 &=121 \Rightarrow \mathrm{n}=11
\end{aligned}
\) -
Question 46 of 161
46. Question
The sum of all the real values of \(x\) satisfying the equation \(2^{(x-1)\left(x^2+5 x-50\right)}=1\) is: [Main Online April 9, 2017]
CorrectIncorrectHint
(c) \((x-1)\left(x^2+5 x-50\right)=0\)
\(\Rightarrow \quad(\mathrm{x}-1)(\mathrm{x}+10)(\mathrm{x}-5)=0\)
\(\Rightarrow \quad x=1,5,-10\)
Sum \(=-4\) -
Question 47 of 161
47. Question
The sum of all real values of \(\mathrm{x}\) satisfying the equation \(\left(x^2-5 x+5\right)^{x^2+4 x-60}=1\) is: [Main 2016]
CorrectIncorrectHint
(c) \(\left(x^2-5 x+5\right)^{x^2+4 x-60}=1\)
Case I
\(x^2-5 x+5=1\) and \(x^2+4 x-60\) can be any real number \(\Rightarrow \mathrm{x}=1,4\)
Case II
\(x^2-5 x+5=-1\) and \(x^2+4 x-60\) has to be an even number \(\Rightarrow \mathrm{x}=2,3\)
where 3 is rejected because for \(x=3\),
\(x^2+4 x-60\) is odd.
Case III
\(x^2-5 x+5\) can be any real number and
\(x^2+4 x-60=0\)
\(\Rightarrow \mathrm{x}=-10,6\)
\(\Rightarrow\) Sum of all values of \(x\)
\(
=-10+6+2+1+4=3
\) -
Question 48 of 161
48. Question
If \(x\) is a solution of the equation,
\(\sqrt{2 x+1}-\sqrt{2 x-1}=1,\left(x \geq \frac{1}{2}\right)\), then \(\sqrt{4 x^2-1}\) is equal to: [Main Online April 10, 2016]CorrectIncorrectHint
(a) \(\sqrt{2 x+1}-\sqrt{2 x-1}=1 \dots(i)\)
\(\Rightarrow \quad 2 x+1+2 x-1-2 \sqrt{4 x^2-1}=1\)
\(\Rightarrow \quad 4 x-1=2 \sqrt{4 x^2-1}\)
\(\Rightarrow \quad 16 x^2-8 x+1=16 x^2-4\)
\(\Rightarrow \quad 8 x=5\)
\(\Rightarrow \quad x=\frac{5}{8}\) which satisfies equation (i)
So, \(\sqrt{4 x^2-1}=\frac{3}{4}\) -
Question 49 of 161
49. Question
Let \(\alpha\) and \(\beta\) be the roots of equation \(x^2-6 x-2=0\). If \(a_n=\alpha^n-\beta^n\), for \(\mathrm{n} \geq 1\), then the value of \(\frac{\mathrm{a}_{10}-2 \mathrm{a}_8}{2 \mathrm{a}_9}\) is equal to: [Main 2015]
CorrectIncorrectHint
(a) \(\alpha, \beta=\frac{6 \pm \sqrt{36+8}}{2}=3 \pm \sqrt{11}\) \(\alpha=3+\sqrt{11}, \beta=3-\sqrt{11}\)
\(
\begin{aligned}
& \therefore \mathrm{a}_{\mathrm{n}}=(3+\sqrt{11})^{\mathrm{n}}-(3-\sqrt{11})^{\mathrm{n}} \frac{\mathrm{a}_{10}-2 \mathrm{a}_8}{2 \mathrm{a}_9} \\
=& \frac{(3+\sqrt{11})^{10}-(3-\sqrt{11})^{10}-2(3+\sqrt{11})^8+2(3-\sqrt{11})^8}{2\left[(3+\sqrt{11})^9-(3-\sqrt{11})^9\right]} \\
=& \frac{(3+\sqrt{11})^8\left[(3+\sqrt{11})^2-2\right]+(3-\sqrt{11})^8\left[2-(3-\sqrt{11})^2\right]}{2\left[(3+\sqrt{11})^9-(3-\sqrt{11})^9\right]} \\
=& \frac{(3+\sqrt{11})^8(9+11+6 \sqrt{11}-2)+(3-\sqrt{11})^8(2-9-11+6 \sqrt{11})}{2\left[(3+\sqrt{11})^9(3-\sqrt{11})^9\right]} \\
=& \frac{6(3+\sqrt{11})^9-6(3-\sqrt{11})^9}{2\left[(3+\sqrt{11})^9-(3-\sqrt{11})^9\right]}=\frac{6}{2}=3
\end{aligned}
\) -
Question 50 of 161
50. Question
Let \(-\frac{\pi}{6}<\theta<-\frac{\pi}{12}\). Suppose \(\alpha_1\) and \(\beta_1\) are the roots of the equation \(x^2\) \(-2 \mathrm{x} \sec \alpha+1=0\) and \(\alpha_2\) and \(\beta_2\) are the roots of the equation \(x^2+2 x\) \(\tan \theta-1=0\). If \(\alpha_1>\beta_1\) and \(\alpha_2>\beta_2\), then \(\alpha_1+\beta_2\) equals [Adv. 2016]
CorrectIncorrectHint
(c) \(x^2-2 x \sec \theta+1=0 \Rightarrow x=\sec \theta \pm \tan \theta\) and \(\mathrm{x}^2+2 \mathrm{x} \tan \theta-1=0 \Rightarrow \mathrm{x}=-\tan \theta \pm \sec \theta\)
\(
\begin{aligned}
&\because-\frac{\pi}{6}<\theta<-\frac{\pi}{12} \\
&\Rightarrow \sec \frac{\pi}{6}>\sec \theta>\sec \frac{\pi}{12}
\end{aligned}
\)
and \(-\tan \frac{\pi}{6}<\tan \theta<-\tan \frac{\pi}{12}\)
Also \(\tan \frac{\pi}{12}<-\tan \theta<\tan \frac{\pi}{6}\)
Since, \(\alpha_1, \beta_1\) are roots of \(\mathrm{x}^2-2 \mathrm{x} \sec \theta+1=0\) and \(\alpha_1>\beta_1\)
\(\therefore \alpha_1=\sec \theta-\tan \theta\) and \(\beta_1=\sec \theta+\tan \theta\)
Since, \(\alpha_2, \beta_2\) are roots of \(\mathrm{x}^2+2 \mathrm{x} \tan \theta-1=0\) and \(\alpha_2>\beta_2\)
\(
\begin{aligned}
&\therefore \alpha_2=-\tan \theta+\sec \theta, \beta_2=-\tan \theta-\sec \theta \\
&\therefore \alpha_1+\beta_2=\sec \theta-\tan \theta-\tan \theta-\sec \theta=-2 \tan \theta
\end{aligned}
\) -
Question 51 of 161
51. Question
If \(a \in \mathrm{R}\) and the equation
\(
-3(x-[x])^2+2(x-[x])+a^2=0
\)
(where \([x]\) denotes the greatest integer \(\leq x\) ) has no integral solution, then all possible values of a lie in the interval: [Main 2014]CorrectIncorrectHint
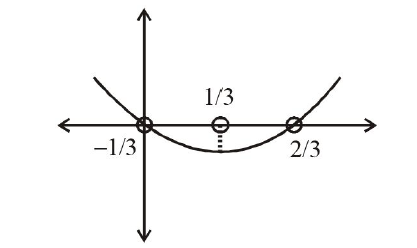
(c) Consider \(-3(x-[x])^2+2[x-[x])+a^2=0\)
\(\Rightarrow \quad 3\{x\}^2-2\{x\}-a^2=0 \quad(x-[x]=\{x\})\)
\(
\begin{aligned}
&\Rightarrow \quad 3\left(\{x\}^2-\frac{2}{3}\{x\}\right)=a^2, a \neq 0 \\
&\Rightarrow \quad a^2=3\{x\}\left(\{x\}-\frac{2}{3}\right)
\end{aligned}
\)
Now, \(\{x\} \in(0,1)\) and \(\frac{-2}{3} \leq a^2<1\)
(by graph)
Since, \(x\) is not an integer
\(
\therefore \quad a \in(-1,1)-\{0\}
\)
\(
\Rightarrow a \in(-1,0) \cup(0,1)
\) -
Question 52 of 161
52. Question
The sum of the roots of the equation, \(\mathrm{x}^2+|2 \mathrm{x}-3|-4=0\), is: [Main Online April 12, 2014]
CorrectIncorrectHint
(c) \(x^2+|2 x-3|-4=0\)
\(|2 x-3|=\left\{\begin{array}{ccc}(2 x-3) & \text { if } & \mathrm{x}>\frac{3}{2} \\ -(2 x-3) & \text { if } & \mathrm{x}<\frac{3}{2}\end{array}\right.\)
for \(x>\frac{3}{2}, x^2+2 x-3-4=0\)
\(
x^2+2 x-7=0
\)
\(
x=\frac{-2 \pm \sqrt{4+28}}{2}=\frac{-2 \pm 4 \sqrt{2}}{2}=-1 \pm 2 \sqrt{2}
\)
Here \(x=2 \sqrt{2}-1 \quad\left\{2 \sqrt{2}-1<\frac{3}{2}\right\}\)
for \(x<\frac{3}{2}\)
\(
\begin{aligned}
&x^2-2 x+3-4=0 \\
&\Rightarrow x^2-2 x-1=0 \\
&\Rightarrow x=\frac{2 \pm \sqrt{4+4}}{2}=\frac{2 \pm 2 \sqrt{2}}{2}=1 \pm \sqrt{2}
\end{aligned}
\)
Here \(x=1-\sqrt{2} \quad\left\{(1-\sqrt{2})<\frac{3}{2}\right\}\)
Sum of roots: \((2 \sqrt{2}-1)+(1-\sqrt{2})=\sqrt{2}\) -
Question 53 of 161
53. Question
The quadratic equation \(p(x)=0\) with real coefficients has purely imaginary roots. Then the equation \(p(p(x))=0\) has [Adv. 2014]
CorrectIncorrectHint
(d) Quadratic equation with real coefficients and purely imaginary roots can be considered as \(p(x)=x^2+a=0\) where \(a>0\) and \(a \in R\)
\(
\begin{aligned}
&\text { The } p[p(x)]=0 \Rightarrow\left(x^2+a\right)^2+a=0 \\
&\quad \Rightarrow x^4+2 a x^2+\left(a^2+a\right)=0 \\
&\Rightarrow x^2=\frac{-2 a \pm \sqrt{4 a^2-4 a^2-4 a}}{2} \\
&\Rightarrow x^2=-a \pm \sqrt{a} i
\end{aligned}
\)
\(\Rightarrow x=\sqrt{-a \pm \sqrt{a} i}=\alpha \pm i \beta\), where \(\alpha, \beta \neq 0\)
\(\therefore p[p(x)]=0\), has complex roots which are neither purely real nor purely imaginary. -
Question 54 of 161
54. Question
If \(p\) and \(q\) are non-zero real numbers and \(\alpha^3+\beta^3=-p, \alpha \beta=q\), then a quadratic equation whose roots are \(\frac{\alpha^2}{\beta}, \frac{\beta^2}{\alpha}\) is: [Main Online April 25, 2013]
CorrectIncorrectHint
(b) Given \(\alpha^3+\beta^3=-p\) and \(\alpha \beta=q\)
Let \(\frac{\alpha^2}{\beta}\) and \(\frac{\beta^2}{\alpha}\) be the root of required quadratic equation.
So, \(\frac{\alpha^2}{\beta}+\frac{\beta^2}{\alpha}=\frac{\alpha^3+\beta^3}{\alpha \beta}=\frac{-p}{q}\)
and \(\frac{\alpha^2}{\beta} \times \frac{\beta^2}{\alpha}=\alpha \beta=q\)
Hence, required quadratic equation is
\(
\begin{aligned}
&x^2-\left(\frac{-p}{q}\right) x+q=0 \\
&\Rightarrow x^2+\frac{p}{q} x+q=0 \Rightarrow q x^2+p x+q^2=0
\end{aligned}
\) -
Question 55 of 161
55. Question
Let \(\alpha\) and \(\beta\) be the roots of \(x^2-6 x-2=0\), with \(\alpha>\beta\). If \(a_n=\alpha^n-\beta^n\) for \(n \geq 1\), then the value of \(\frac{a_{10}-2 a_8}{2 a_9}\) is [2011]
CorrectIncorrectHint
(c) \(\because \alpha, \beta\) are the roots of \(x^2-6 x-2=0\)
\(
\begin{aligned}
&\therefore \alpha^2-6 \alpha-2=0 \\
&\quad \Rightarrow \alpha^{10}-6 \alpha^9-2 \alpha^8=0 \\
&\quad \Rightarrow \alpha^{10}-2 \alpha^8=6 \alpha^9 \quad \ldots \text { (i) } \\
&\text { Similarly } \beta^{10}-2 \beta^8=6 \beta^9 \quad \ldots \text { (ii) } \\
&\text { On subtracting (ii) from (i), } \\
&\alpha^{10}-\beta^{10}-2\left(\alpha^8-\beta^8\right)=6\left(\alpha^9-\beta^9\right) \\
&\quad \Rightarrow a_{10}-2 a_8=6 a_9 \Rightarrow \frac{a_{10}-2 a_8}{2 a_9}=3
\end{aligned}
\) -
Question 56 of 161
56. Question
Let \(\left(x_0, y_0\right)\) be the solution of the following equations
\(
\begin{aligned}
&(2 x)^{\ln 2}=(3 y)^{\ln 3} \\
&3^{\ell n x}=2^{\ell n y}
\end{aligned}
\)
Then \(x_0\) is [2011]CorrectIncorrectHint
\(
(2 x)^{\ln 2}=(3 y)^{\ln 3}
\)
Taking \(\ln\) both sides,
\(
\begin{aligned}
&\Rightarrow(\ln 2)(\ln 2 x)=(\ln 3)(\ln 3 y) \\
&\Rightarrow(\ln 2)(\ln 2+\ln x)=(\ln 3)(\ln 3+\ln y) \rightarrow(1)
\end{aligned}
\)
Now, we will take the second equation,
\(
3^{\ln x}=2^{\ln y}
\)
Taking \(\ln\) both sides,
\(
\begin{aligned}
&\Rightarrow(\ln x)(\ln 3)=(\ln y)(\ln 2) \\
&\Rightarrow(\ln y)=\frac{(\ln x)(\ln 3)}{\ln 2}
\end{aligned}
\)
Putting value of \(\ln y\) in (1),
\(
\begin{aligned}
&(\ln 2)(\ln 2+\ln x)=(\ln 3)\left(\ln 3+\frac{(\ln x)(\ln 3)}{\ln 2}\right) \\
&\Rightarrow(\ln x)\left(\ln 2-\left(\frac{(\ln 3)^2}{\ln 2}\right)\right)=(\ln 3)^2-(\ln 2)^2 \\
&\Rightarrow \frac{\ln x}{\ln 2}\left((\ln 2)^2-(\ln 3)^2\right)=(\ln 3)^2-(\ln 2)^2 \\
&\Rightarrow \frac{\ln x}{\ln 2}=-1 \\
&\Rightarrow(\ln x)=\ln (2)^{-1} \\
&\Rightarrow x=2^{-1} \Rightarrow x=\frac{1}{2}, \text { which is the required value of } x_0 \text {. }
\end{aligned}
\) -
Question 57 of 161
57. Question
Let \(p\) and \(q\) be real numbers such that \(p \neq 0, p^3 \neq q\) and \(p^3 \neq-q\). If \(\alpha\) and \(\beta\) are nonzero complex numbers satisfying \(\alpha+\beta=-p\) and \(\alpha^3+\) \(\beta^3=q\), then a quadratic equation having \(\frac{\alpha}{\beta}\) and \(\frac{\beta}{\alpha}\) as its roots is [2010]
CorrectIncorrectHint
(b)
\(
\begin{aligned}
& \alpha^3+\beta^3=q \\
& \Rightarrow(\alpha+\beta)^3-3 \alpha \beta(\alpha+\beta)=q \\
& \Rightarrow-p^3+3 p \alpha \beta=q \\
& \Rightarrow \alpha \beta=\frac{q+p^3}{3 p} \\
& x^2-\left(\frac{\alpha}{\beta}+\frac{\beta}{\alpha}\right) x+\frac{\alpha}{\beta} \cdot \frac{\beta}{\alpha}=0 \\
& \Rightarrow x^2-\frac{p^2-2\left(\frac{p^3+q}{3 p}\right)}{\frac{p^3+q}{3 p}} x+1=0 \\
& \Rightarrow x^2-\left(\frac{(\alpha+\beta)^2-2 \alpha \beta}{\alpha \beta}\right) x+1=0 \\
& \Rightarrow\left(p^3+q\right) x^2-\left(3 p^3-2 p^3-2 q\right) x+\left(p^3+q\right)=0 \\
& \Rightarrow\left(p^3+q\right) x^2-\left(p^3-2 q\right) x+\left(p^3+q\right)=0
\end{aligned}
\) -
Question 58 of 161
58. Question
Let \(\alpha, \beta\) be the roots of the equation \(x^2-p x+r=0\) and \(\frac{\alpha}{2}, 2 \beta\) be the roots of the equation \(x^2-q x+r=0\). Then the value of \(r\) is [2007 -3 marks]
CorrectIncorrectHint
(d) Since \(\alpha\) and \(\beta\) are the roots of \(x^2-p x+r=0\) \(\therefore \quad \alpha+\beta=p \dots(i)\)
and \(\alpha \beta=r \dots(ii)\)
Also \(\frac{\alpha}{2}\) and \(2 \beta\) are the roots of \(x^2-q x+r=0\)
\(
\therefore \quad \frac{\alpha}{2}+2 \beta=q \Rightarrow \alpha+4 \beta=2 q \dots(iii)
\)
Solving (i) and (iii) for \(\alpha\) and \(\beta\), we get
\(
\beta=\frac{1}{3}(2 q-p) \text { and } \alpha=\frac{2}{3}(2 q-q)
\)
On substituting the values of \(\alpha\) and \(\beta\), in equation (ii), we get \(\frac{2}{9}(2 p-q)(2 q-p)=r\). -
Question 59 of 161
59. Question
Let \(a, b, c\) be the sides of a triangle where \(a \neq b \neq c\) and \(\lambda \in R\). If the roots of the equation \(x^2+2(a+b+c) x+3 \lambda(a b+b c+c a)=0\) are real, then [2006 -3M, -1]
CorrectIncorrectHint
(a) \(\because a, b, c\) are sides of a triangle and \(a \neq b \neq c\) \(\therefore \quad|a-b|<|c| \Rightarrow a^2+b^2-2 a b<c^2 \dots(i)\)
Similarly,
\(
b^2+c^2-2 b c<a^2 \quad \ldots \text {. (ii) } ; c^2+a^2-2 c a<b^2 \dots(iii)
\)
On adding, (i), (ii) and (iii) we get
\(
\begin{aligned}
&a^2+b^2+c^2<2(a b+b c+c a) \\
&\Rightarrow \quad \frac{a^2+b^2+c^2}{a b+b c+c a}<2 \dots(iv) \\
&\because \quad \text { Roots of the given equation are real } \\
&\therefore \quad(a+b+c)^2-3 \lambda(a b+b c+c a) \geq 0 \\
&\Rightarrow \quad \frac{a^2+b^2+c^2}{a b+b c+c a} \geq 3 \lambda-2 \dots(v)
\end{aligned}
\)
From (iv) and (v), \(3 \lambda-2<2 \Rightarrow \lambda<\frac{4}{3}\) -
Question 60 of 161
60. Question
If one root is square of the other root of the equation \(x^2+p x+q=0\), then the relation between \(p\) and \(q\) is [2004S]
CorrectIncorrectHint
(a) \(x^2+p x+q=0\)
Let roots be \(\alpha\) and \(\alpha^2\), then
\(
\alpha+\alpha^2=-p, \alpha \alpha^2=q \Rightarrow \alpha=q^{1 / 3}
\)
\(
\therefore \quad(q)^{1 / 3}+\left(q^{1 / 3}\right)^2=-p
\)
On taking cube on both sides, we get
\(
\begin{aligned}
&q+q^2+3 q\left(q^{1 / 3}+q^{2 / 3}\right)=-p^3 \\
&\Rightarrow q+q^2-3 p q=-p^3 \Rightarrow p^3+q^2-q(3 p-1)=0
\end{aligned}
\) -
Question 61 of 161
61. Question
For the equation \(3 x^2+p x+3=0, p>0\), if one of the root is square of the other, then \(p\) is equal to [2000S]
CorrectIncorrectHint
(c) Let \(\alpha, \alpha^2\) be the roots of \(3 x^2+p x+3\).
\(\therefore \quad \alpha+\alpha^2=-p / 3\) and \(\alpha^3=1\)
\(\Rightarrow(\alpha-1)\left(\alpha^2+\alpha+1\right)=0 \Rightarrow \alpha=1\) or \(\alpha^2+\alpha=-1\)
If \(\alpha=1\), then \(p=-6\), which is not possible as \(p>0\)
If \(\alpha^2+\alpha=-1 \Rightarrow-p / 3=-1 \Rightarrow p=3\). -
Question 62 of 161
62. Question
If \(b>a\), then the equation \((x-a)(x-b)-1=0\) has [2000S]
CorrectIncorrectHint
(d) Given: \((x-a)(x-b)-1=0, b>a\).
or \(x^2-(a+b) x+(a b-1)=0\)
Let \(f(x)=x^2-(a+b) x+(a b-1)\)
\(
\begin{aligned}
D=(a+b)^2-4(a b-1) \\
=(a-b)^2+1>0
\end{aligned}
\)
Since coeff. of \(x^2\) i.e. \(1>0, \therefore f(x)\) represents upward parabola, intersecting \(x\)-axis at two points corresponding to two real roots, \(D\) being \(+\mathrm{ve}\).
\(\operatorname{Also} f(a)=f(b)=-1\)
\(\Rightarrow\) curve is below \(x\)-axis at \(a\) and \(b\)
\(\therefore \quad a\) and \(b\) both lie between the roots.
Therefore, the graph of the given equation is as shown.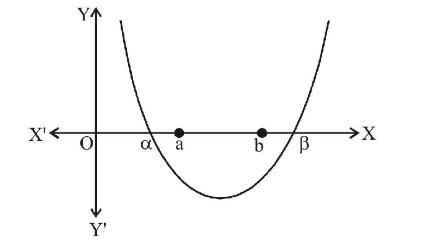
It is clear from graph, that one root of the equation lies in \((-\infty, a)\) and other in \((b, \infty)\).
-
Question 63 of 161
63. Question
If \(\alpha\) and \(\beta(\alpha<\beta)\) are the roots of the equation \(x^2+b x+c=0\), where \(c\) \(<0<b\), then [2000S]
CorrectIncorrectHint
(b) Given : \(\mathrm{c}<0<\mathrm{b}\) and \(\alpha+\beta=-\mathrm{b} \dots(i)\)
\(\alpha \beta=\mathrm{c} \quad\)….(ii)
From (ii), c \(<0 \Rightarrow \alpha \beta<0 \Rightarrow\) Either \(\alpha\) is -ve or \(\beta\) is – ve and second quantity is positive.
From (i), \(b>0 \Rightarrow-\mathrm{b}<0 \Rightarrow \alpha+\beta<0\)
\(\Rightarrow\) the sum is negative
\(\Rightarrow\) (Modules of negative quantity) \(>\) (Modulus of positive quantity)
But given \(\alpha<\beta\). Therefore, it is clear that \(\alpha\) is negative and \(\beta\) is positive and modulus of \(\alpha\) is greater than modulus of \(\beta\)
\(
\Rightarrow \alpha<0<\beta<|\alpha|
\) -
Question 64 of 161
64. Question
If the roots of the equation \(x^2-2 a x+a^2+a-3=0\) are real and less than 3 , then [1999 – 2 Marks]
CorrectIncorrectHint
(a) If both roots of a quadratic equation \(a x^2+b x+c=0\) are less than \(\mathrm{k}\), then \(f(k)>0, \mathrm{D} \geq 0, \alpha+\beta<2 \mathrm{k}\)
\(
\begin{aligned}
f(x) &=x^2-2 a x+a^2+a-3=0 \\
f(3)>0, & \alpha+\beta<6, D \geq 0 . \\
& \Rightarrow a^2-5 a+6>0, a<3,-4 a+12 \geq 0 \\
& \Rightarrow a<2 \text { or } a>3, a<3, a<3 \Rightarrow a<2
\end{aligned}
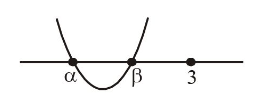
\)
-
Question 65 of 161
65. Question
Let \(p, q \in\{1,2,3,4\}\). The number of equations of the form \(p x^2+q x+\) \(1=0\) having real roots is [1994]
CorrectIncorrectHint
(c) For the equation \(p x^2+q x+1=0\) to have real roots \(D \geq 0 \Rightarrow q^2 \geq 4 p\)
If \(p=1\) then \(q^2 \geq 4 \quad \Rightarrow q=2,3,4\)
If \(p=2\) then \(q^2 \geq 8 \quad \Rightarrow q=3,4\)
If \(p=3\) then \(q^2 \geq 12 \Rightarrow q=4\)
If \(p=4\) then \(q^2 \geq 16 \Rightarrow q=4\)
\(\therefore \quad\) Number of required equations \(=7\) -
Question 66 of 161
66. Question
Let \(\alpha, \beta\) be the roots of the equation \((x-a)(x-b)=c, c \neq 0\). Then the roots of the equation \((x-\alpha)(x-\beta)+c=0\) are [1992 – 2 Marks]
CorrectIncorrectHint
(c) \(\alpha, \beta\) are roots of the equation \((x-a)(x-b)=c, c \neq 0\)
\(\therefore \quad(x-a)(x-b)-c=(x-\alpha)(x-\beta)\)
\(\Rightarrow(x-\alpha)(x-\beta)+c=(x-\mathbf{a})(x-b)\)
\(\Rightarrow\) Roots of \((x-\alpha)(x-\beta)+c=0\) are \(a\) and \(b\) -
Question 67 of 161
67. Question
Let \(a, b, c\) be real numbers, \(a \neq 0\). If \(\alpha\) is a root of \(a^2 x^2+b x+c=0\). \(\beta\) is the root of \(a^2 x^2-b x-c=0\) and \(0<\alpha<\beta\), then the equation \(a^2 x^2+\) \(2 b x+2 c=0\) has a root \(\gamma\) that always satisfies [1989 – 2 Marks]
CorrectIncorrectHint
(d) If \(f(\alpha)\) and \(f(\beta)\) are of opposite signs then there must lie a value \(\gamma\) between \(\alpha\) and \(\beta\) such that \(f(\gamma)=0\).
\(a, b, c\) are real numbers and \(a \neq 0\).
Since \(\alpha\) is a root of \(a^2 x^2+b x+c=0\)
\(
\therefore a^2 \alpha^2+b \alpha+c=0 \dots(i)
\)
Also \(\beta\) is a root of \(a^2 x^2-b x-c=0\) \(\therefore a^2 \beta^2-b \beta-c=0 \quad\)… (ii)
Now, let \(f(x)=a^2 x^2+2 b x+2 c\)
Then \(f(\alpha)=a^2 \alpha^2+2 b \alpha+2 c=a^2 \alpha^2+2(b \alpha+\mathrm{c})\) \(=a^2 \alpha^2+2\left(-a^2 \alpha^2\right)\)
[using eq. (i) \(]\) \(=-a^2 \alpha^2\).
\(
\begin{aligned}
&\text { and } f(\beta)=a^2 \beta^2+2 b \beta+2 c=a^2 \beta^2+2(b \beta+c) \\
&=a^2 \beta^2+2\left(a^2 \beta^2\right) \\
&=3 a^2 \beta^2>0 \text {. } \\
&\text { Since } f(\alpha) \text { and } f(\beta) \text { are of opposite signs and } \gamma \text { is a root of equation } f(x)= \\
&\quad 0 \\
&\quad \therefore \gamma \text { must lie between } \alpha \text { and } \beta \\
&\quad \Rightarrow \alpha<\gamma<\beta \text {. }
\end{aligned}
\) -
Question 68 of 161
68. Question
The equation \(x-\frac{2}{x-1}=1-\frac{2}{x-1}\) has [1984 – 2 Marks]
CorrectIncorrectHint
(a) Given : \(x-\frac{2}{x-1}=1-\frac{2}{x-1}\)
Clearly \(x \neq 1\) for the given equation to be defined. If \(x \neq 1\), we can cancel the common term \(\frac{-2}{x-1}\) on both sides to get \(x=1\), but it is not possible. So given equation has no roots. -
Question 69 of 161
69. Question
If \(\left(x^2+p x+1\right)\) is a factor of \(\left(a x^3+b x+c\right)\), then [1980]
CorrectIncorrectHint
(c) Since, \(\left(x^2+p x+1\right)\) is a factor of \(a x^3+b x+c\), hence we can assume that zeros of \(x^2+p x+1\) are \(\alpha, \beta\) and that of \(a x^3+b x+c\) be \(\alpha, \beta, \gamma\)
\(
\begin{gathered}
\therefore \quad \alpha+\beta=-p \dots(i)\\
\alpha \beta=1 \quad \ldots .(\text { ii) } \\
\text { and } \alpha+\beta+\gamma=0 \dots(iii) \\
\alpha \beta+\beta \gamma+\gamma \alpha=\frac{b}{a} \dots(iv) \\
\alpha \beta \gamma=\frac{-c}{a} \dots(v)
\end{gathered}
\)
On solving (ii) and (v), we get \(\gamma=-c / a\).
On solving (i) and (iii), we get \(\gamma=p\) \(\therefore \quad p=\gamma=-c / a\)
Using equations (i), (ii) and (iv), we get
\(
\begin{aligned}
&1+\gamma(-p)=\frac{b}{a} \\
&\Rightarrow 1+\left(-\frac{c}{a}\right)\left(\frac{c}{a}\right)=\frac{b}{a} \quad( \gamma=p=-c / a) \\
&\Rightarrow 1-\frac{c^2}{a^2}=\frac{b}{a} \Rightarrow a^2-c^2=a b
\end{aligned}
\) -
Question 70 of 161
70. Question
Both the roots of the equation \((x-b)(x-c)+(x-a)(x-c)+(x-a)(x-b)=0\) are always [1980]
CorrectIncorrectHint
(b) Given :
\(
\begin{aligned}
&(x-b)(x-c)+(x-a)(x-c)+(x-a)(x-b)=0 \\
& \Rightarrow 3 x^2-2(a+b+c) x+(a b+b c+c a)=0 \\
D=& 4(a+b+c)^2-12(a b+b c+c a) \\
&=4\left[a^2+b^2+c^2-a b-b c-c a\right] \\
&=2\left[(a-b)^2+(b-c)^2+(c-a)^2\right] \geq 0 \quad \forall a, b, c \\
& \therefore \quad \text { Roots of given equation are always real. }
\end{aligned}
\) -
Question 71 of 161
71. Question
If \(l, m\) are real, \(l \neq m\), then the roots by the equation:
\((l-m) x^2-5(l+m) x-2(l-m)=0 \text { are }\) [1979]CorrectIncorrectHint
\((l-m) x^2-5(l+m) x-2(l-m)=0\) is the given equation.
Comparing given equation with standard form of quadratic equation \(a x^2+b x+c=0\)
we get \(a=l-m, b=-5(l+m), c=-2(l-m)\)
The nature of the roots of a quadratic equation depends on the value of where \(D\) is given as
\(
D=b^2-4 a c
\)
Substituting the values of \(a, b, c\) for the given equation we get
\(
\begin{aligned}
&\Rightarrow D=5^2(l+m)^2-4(l-m)(-2)(l-m) \\
&\Rightarrow D=25(l+m)^2+8(l-m)^2
\end{aligned}
\)
For all real values of \(l, m(l+m)^2>0,(l-m)^2>0\) as \(l \neq m\) \(\Rightarrow D>0\)
When \(D>0\) for a quadratic equation, the equation has real and unequal roots.
Hence, the given quadratic equation \((l-m) x^2-5(l+m) x-2(l-m)=0\) has real and unequal roots, -
Question 72 of 161
72. Question
The least positive value of ‘ \(a\) ‘ for which the equation, \(2 x^2+(a-10) x\) \(+\frac{33}{2}=2 a\) has real roots is [Main Jan. 8, 2020 (I)]
CorrectIncorrectHint
(8) Since, \(2 x^2+(a-10) x+\frac{33}{2}=2 a\) has real roots, \(\therefore \quad D \geq 0\)
\(
\Rightarrow \quad(a-10)^2-4(2)\left(\frac{33}{2}-2 a\right) \geq 0
\)
\(
\begin{aligned}
&\Rightarrow \quad(a-10)^2-4(33-4 a) \geq 0 \\
&\Rightarrow \quad a^2-4 a-32 \geq 0 \\
&\Rightarrow \quad(a-8)(a+4) \geq 0
\end{aligned}
\)
\(\Rightarrow \quad a \leq-4 \cup a \geq 8\)
\(\Rightarrow \quad a \in(-\infty,-4] \cup[8, \infty)\) -
Question 73 of 161
73. Question
The smallest value of \(k\), for which both the roots of the equation \(x^2-\) \(8 k x+16\left(k^2-k+1\right)=0\) are real, distinct and have values at least 4 , is [2009]
CorrectIncorrectHint
(2) The given equation is
\(
x^2-8 k x+16\left(k^2-k+1\right)=0
\)
\(\because \quad\) Both the roots are real and distinct.
\(
\begin{aligned}
&\therefore \quad D>0 \Rightarrow(8 k)^2-4 \times 16\left(k^2-k+1\right)>0\\
&\Rightarrow \mathrm{k}>1 \dots(i) \\
&\because \quad \text { Both the roots are greater than or equal to } 4\\
&\therefore \quad \alpha+\beta>8 \text { and } f(4) \geq 0\\
&\Rightarrow k>1 \dots(ii) \\
&\text { and } 16-32 k+16\left(k^2-k+1\right) \geq 0\\
&\Rightarrow k^2-3 k+2 \geq 0 \Rightarrow(k-1)(k-2) \geq 0\\
&\Rightarrow k \in(-\infty, 1] \cup[2, \infty) \dots(iii) \\
&\text { Combining (i), (ii) and (iii), we get } k \geq 2\\
&\therefore \quad \text { Smallest value of } k=2 .
\end{aligned}
\) -
Question 74 of 161
74. Question
If the product of the roots of the equation \(\mathrm{x}^2-3 \mathrm{kx}+2 e^{2 \operatorname{lnk}}-1=0\) is 7 , then the roots are real for \(k= ……. \) [1984-2 Marks]
CorrectIncorrectHint
The given equation : \(x^2-3 k x+2 e^{2 \ln k}-1=0\)
\(
\Rightarrow x^2-3 k x+\left(2 k^2-1\right)=0
\)
Now, product of roots \(=2 k^2-1\)
\(
\therefore 2 \mathrm{k}^2-1=7 \Rightarrow \mathrm{k}^2=4 \quad \Rightarrow \mathrm{k}=2,-2
\)
For real roots, \(D \geq 0\)
\(
\Rightarrow 9 k^2-4\left(2 k^2-1\right) \geq 0 \quad \Rightarrow k^2+4 \geq 0
\)
which is true for all \(k\). Thus \(k=2,-2\)
But for \(k=-2, \ln k\) is not defined
We reject \(k=-2\), we get \(k=2\). -
Question 75 of 161
75. Question
If \(2+i \sqrt{3}\) is a root of the equation \(x^2+p x+q=0\), where \(p\) and \(q\) are real, then \((p, q)=(\ldots \ldots \ldots \ldots \ldots . . . \ldots \ldots \ldots \ldots \ldots .)\) [1982 – 2 Marks]
CorrectIncorrectHint
Since, \(p\) and \(q\) are real and one root is \(2+\mathrm{i} \sqrt{3}\), therefore other root should be \(2-i \sqrt{3}\)
\(\therefore \quad p=-(\) sum of roots \()=-4, q=\) product of roots \(=4+3=7\) -
Question 76 of 161
76. Question
If \(a<b<c<d\), then the roots of the equation \((x-a)(x-c)+2(x-b)(x-d)=0\) are real and distinct. [1984 – 1 Mark]
Is this statement true or false?
CorrectIncorrectHint
(True) \(f(x)=(x-a)(x-c)+2(x-b)(x-d)\).
\(f(\mathrm{a})=+v e ; f(b)=-v e ; f(c)=-v e ; f(d)=+v e\)
\(\therefore \quad\) There exists two real and distinct roots one in the interval \((a, b)\) and other in \((c, d)\). -
Question 77 of 161
77. Question
The equation \(2 x^2+3 x+1=0\) has an irrational root. [1983-1 Mark]
Is this statement true or false?
CorrectIncorrectHint
(False) \(2 x^2+3 x+1=0 \Rightarrow x=-1,-1 / 2\); both are rationals \(\therefore \quad\) Statement is false.
-
Question 78 of 161
78. Question
Let \(\mathrm{p}, \mathrm{q}\) be integers and let \(\alpha, \beta\) be the roots of the equation, \(\mathrm{x}^2-\mathrm{x}-1=0\), where \(\alpha \neq \beta\). For \(\mathrm{n}=0,1,2, \ldots\), let \(\mathrm{a}_{\mathrm{n}}=\mathrm{p} \alpha^{\mathrm{n}}+\mathrm{q} \beta^{\mathrm{n}}\).
FACT : If \(a\) and \(b\) are rational numbers and \(a+b \sqrt{5}=0\), then \(a=0=b\) [Adv. 2017]\(a_{12}= ….\)
CorrectIncorrectHint
(b) \(\alpha^2=\alpha+1\)
\(
\beta^2=\beta+1
\)
\(a_n=p \alpha^n+q \beta^n\)
\(
\begin{aligned}
=& p\left(\alpha^{n-1}+\alpha^{n-2}\right)+q\left(\beta^{n-1}+\beta^{n-2}\right) \\
=a_{n-1} &+a_{n-2} \\
\therefore \quad & a_{12}=a_{11}+a_{10}
\end{aligned}
\) -
Question 79 of 161
79. Question
Let \(\mathrm{p}, \mathrm{q}\) be integers and let \(\alpha, \beta\) be the roots of the equation, \(\mathrm{x}^2-\mathrm{x}-1=0\), where \(\alpha \neq \beta\). For \(\mathrm{n}=0,1,2, \ldots\), let \(\mathrm{a}_{\mathrm{n}}=\mathrm{p} \alpha^{\mathrm{n}}+\mathrm{q} \beta^{\mathrm{n}}\).
FACT : If \(a\) and \(b\) are rational numbers and \(a+b \sqrt{5}=0\), thena \(=0=b\) [Adv. 2017]\(
\text { If } \mathrm{a}_4=28, \text { then } p+2 \mathrm{q}=…..
\)CorrectIncorrectHint
\(
\begin{aligned}
{ (d) } \alpha=\frac{1+\sqrt{5}}{2}, \beta=\frac{1-\sqrt{5}}{2} \\
a_4=a_3+a_2 \\
= 2 a_2+a_1 \\
\quad=3 a_1+2 a_0 \\
28= p(3 \alpha+2)+q(3 \beta+2) \\
28=(p+q)\left(\frac{3}{2}+2\right)+(p-q)\left(\frac{3 \sqrt{5}}{2}\right) \\
\therefore \quad p-q=0 \text { and }(p+q) \times \frac{7}{2}=28 \\
\Rightarrow p+q=8 \Rightarrow p=q=4 \\
\therefore p+2 q=12
\end{aligned}
\) -
Question 80 of 161
80. Question
Let \(a, b, c, p, q\) be real numbers. Suppose \(\alpha, \beta\) are the roots of the equation \(x^2+2 p x+q=0\) and \(\alpha, \frac{1}{\beta}\) are the roots of the equation \(a x^2+\) \(2 b x+c=0\), where \(\beta^2 \notin\{-1,0,1\}\)
STATEMENT – 1: \(\left(p^2-q\right)\left(b^2-a c\right) \geq 0\)
and
STATEMENT – 2: \(b \neq p a\) or \(c \neq q a\) [2008]CorrectIncorrectHint
(b) As \(a, b, c, p, q, \in R\) and the two given equations have exactly one common root
\(\Rightarrow\) Either both equations have real roots
or both eqations have imaginary roots
or \(p^2-q \leq 0\) and \(b^2-a c \leq 0\)
\(
\Rightarrow\left(p^2-q\right)\left(b^2-a c\right) \geq 0
\)
\(\therefore\) Statement 1 is true.
Also we have \(\alpha \beta=q\) and \(\frac{\alpha}{\beta}=\frac{c}{a}\)
\(
\therefore \frac{\alpha \beta}{\alpha / \beta}=\frac{q}{c} \times a \Rightarrow \beta^2=\frac{q a}{c}
\)
As \(\hat{\mathrm{a}} \neq 1\) or \(-1 \Rightarrow \hat{\mathrm{a}}^2 \neq 1 \Rightarrow \frac{q a}{c} \neq 1\) or \(c \neq q a\)
Again, as exactly one root á is common, and \(\hat{a} \neq 1\)
\(
\therefore \text { á }+\hat{\mathrm{a}} \neq \mathrm{á}+\frac{1}{\hat{\mathrm{a}}} \Rightarrow \frac{-2 b}{a} \neq-2 p \quad \Rightarrow b \neq a p
\)
\(\therefore\) Statement 2 is correct.
But Statement 2 is not a correct explanation of Statement 1. -
Question 81 of 161
81. Question
Let \(a\) and \(b\) be the roots of the equation \(x^2-10 c x-11 d=0\) and those of \(x^2-10 a x-11 b=0\) are \(c, d\) then the value of \(a+b+c+d\), when \(a \neq b \neq c \neq d\), is. [2006-6 M]
CorrectIncorrectHint
Roots of \(x^2-10 c x-11 d=0\) are \(a\) and \(b\) \(\Rightarrow a+b=10 c\) and \(a b=-11 d\)
Similarly \(c\) and \(d\) are the roots of \(x^2-10 a x-11 b=0 \Rightarrow c+d=10 a\) and \(c d\)
\(
\begin{aligned}
&=-11 b \\
&\Rightarrow a+b+c+d=10(a+c) \text { and } a b c d=121 b d \\
&\Rightarrow b+d=9(a+c) \text { and } a c=121
\end{aligned}
\)
Also we have \(a^2-10 a c-11 d=0\) and \(c^2-10 a c-11 b=0\)
\(
\begin{aligned}
&\Rightarrow a^2+c^2-20 a c-11(b+d)=0 \\
&\Rightarrow(a+c)^2-22 \times 121-99(a+c)=0 \\
&\Rightarrow a+c=121 \text { or }-22
\end{aligned}
\)
For \(a+c=-22\), we get \(a=c\)
\(\therefore \quad\) Rejecting this value we have \(a+c=121\)
\(
\therefore \quad a+b+c+d=10(a+c)=1210
\) -
Question 82 of 161
82. Question
If \(x^2+(a-b) x+(1-a-\mathrm{b})=0\) where \(a, b \in \mathrm{R}\) then find the values of a for which equation has unequal real roots for all values of \(b\). [2003 – 4 Marks]
CorrectIncorrectHint
Given :
\(
x^2+(a-b) x+(1-a-b)=0, a, b \in R
\)
For this equation to have unequal real roots for all value of \(b\)
\(
\text { if } \quad \begin{aligned}
D &>0 \\
& \Rightarrow(a-b)^2-4(1-a-b)>0 \\
& \Rightarrow a^2+b^2-2 a b-4+4 a+4 b>0 \\
& \Rightarrow b^2+b(4-2 a)+a^2+4 a-4>0
\end{aligned}
\)
Which is a quadratic expression in \(b\), and it will be true for all \(b \in R\), if discriminant of above equation is less than zero.
\(
\text { i.e., } \begin{aligned}
&(4-2 a)^2-4\left(a^2+4 a-4\right)<0 \\
& \Rightarrow \quad(2-a)^2-\left(a^2+4 a-4\right)<0 \\
& \Rightarrow \quad 4-4 a+a^2-a^2-4 a+a<0 \\
& \Rightarrow \quad-8 a+8<0 \therefore a>1
\end{aligned}
\) -
Question 83 of 161
83. Question
If \(\alpha, \beta\) are the roots of \(a x^2+b x+c=0,(a \neq 0)\) and \(\alpha+\delta, \beta+\delta\) are the roots of \(A x^2+B x+C=0, \quad(A \neq 0)\) for some constant \(\delta\), then \(\frac{b^2-4 a c}{a^2}=\frac{B^2-4 A C}{A^2}\). Is this statement true? [2000 – 4 Marks]
CorrectIncorrectHint
We know \((\alpha-\beta)^2=[(\alpha+\delta)-(\beta+\delta)]^2\)
\(
\Rightarrow \quad(\alpha+\beta)^2-4 \alpha \beta=(\alpha+\delta+\beta+\delta)^2-4(\alpha+\delta)(\beta+\delta)
\)
\(
\Rightarrow \frac{b^2}{a^2}-\frac{4 c}{a}=\frac{B^2}{A^2}-\frac{4 C}{A} \Rightarrow \frac{4 a c-b^2}{a^2}=\frac{4 A C-B^2}{A^2}
\)
\(\left[\operatorname{Here} \alpha+\beta=-\frac{b}{a}, \alpha \beta=\frac{c}{a}\right.\),
\(
\left.(\alpha+\delta)(\beta+\delta)=-\frac{B}{A} \operatorname{and}(\alpha+\delta)(\beta+\delta)=\frac{C}{A}\right]
\) -
Question 84 of 161
84. Question
Let \(a, b, c\) be real. If \(a x^2+b x+c=0\) has two real roots \(\alpha\) and \(\beta\), where \(\alpha<-1\) and \(\beta>1\), then \(1+\frac{c}{a}+\left|\frac{b}{a}\right|<0\). Is this statement true? [1995 – 5 Marks]
CorrectIncorrectHint
Given : For \(a, b, c \in R, a x^2+b x+c=0\) has two real roots \(\alpha\) and \(\beta\), where \(\alpha<-1\) and \(\beta>1\). There may be two cases depending upon the value of a, as shown below.
In each of cases (i) and (ii) \(a f(-1)<0\) and \(a f(1)<0\)
\(\Rightarrow a(a-b+c)<0\) and \(a(a+b+c)<0\)
Dividing by \(a^2(>0)\), we get
\(
1-\frac{b}{a}+\frac{c}{a}<0 \dots(i)
\)
and \(1+\frac{b}{a}+\frac{c}{a}<0 \dots(ii)\)
On combining (i) and (ii) we get
\(
1+\left|\frac{b}{a}\right|+\frac{c}{a}<0 \quad \text { or } \quad 1+\frac{c}{a}+\left|\frac{b}{a}\right|<0
\) -
Question 85 of 161
85. Question
Find solutions to the equation \(\left|x^2+4 x+3\right|+2 x+5=0\) [1988 – 5 Marks]
CorrectIncorrectHint
Given \(
\left|x^2+4 x+3\right|+2 x+5=0
\)
Here two cases are possible.
Case I: \(x^2+4 x+3 \geq 0 \Rightarrow(x+1)(x+3) \geq 0\)
\(\Rightarrow x \in(-\infty,-3] \cup[-1, \infty) \dots(i)\)
Then the given equation becomes,
\(
\begin{aligned}
&\Rightarrow x^2+6 x+8=0 \\
&\Rightarrow(x+4)(x+2)=0, \quad \therefore x=-4,-2
\end{aligned}
\)
But \(x=-2\) does not satisfy (i) and hence rejected.
\(\therefore \quad\) Solution is \(x=-4\)
Case II : \(x^2+4 x+3<0\)
\(\Rightarrow \quad(x+1)(x+3)<0\)
\(\Rightarrow \quad x \in(-3,-1) \dots(ii)\)
Then the given equation becomes,
\(
-\left(x^2+4 x+3\right)+2 x+5=0
\)
\(
\begin{aligned}
&\Rightarrow-x^2-2 x+2=0 \Rightarrow x^2+2 x-2=0 \\
&\Rightarrow x=\frac{-2 \pm \sqrt{4+8}}{2} \quad \therefore x=-1+\sqrt{3},-1-\sqrt{3}
\end{aligned}
\)
But \(x=-1+\sqrt{3}\) does not satisfy (ii) and hence rejected.
\(\therefore \quad\) Solution is \(x=-1-\sqrt{3}\)
On combining solutions in the two cases, we get the solutions : \(x=-4,-1-\) \(\sqrt{3}\). -
Question 86 of 161
86. Question
For a \(\leq 0\), determine all real roots of the equation
\(x^2-2 a|x-a|-3 a^2=0\) [1986 – 5 Marks]CorrectIncorrectHint
Given:
\(x^2-2 a|x-a|-3 a^2=0 \dots(i)\)
Here two cases are possible.
Case I : \(x-a>0\), then \(|x-a|=x-a\)
Hence, Eq. (i) becomes
\(
\begin{aligned}
&x^2-2 a(x-a)-3 a^2=0 \\
&\Rightarrow \quad x^2-2 a x-a^2=0 \Rightarrow \quad x=\frac{2 a \pm \sqrt{4 a^2+4 a^2}}{2} \\
&\therefore \quad x=a \pm a \sqrt{2}
\end{aligned}
\)
Case II : \(x-a<0\), then \(|x-a|=-(x-a)\)
Hence, Eq. (i) becomes
\(
\begin{aligned}
&x^2+2 a(x-a)-3 a^2=0 \\
&\Rightarrow \quad x^2+2 a x-5 a^2=0 \Rightarrow \quad x=\frac{-2 a \pm \sqrt{4 a^2+20 a^2}}{2} \\
&\therefore \quad x=\frac{-2 a \pm 2 a \sqrt{6}}{2} \Rightarrow \quad x=-a \pm a \sqrt{6}
\end{aligned}
\)
Hence, the solution set is \(\{a \pm a \sqrt{2},-a \pm a \sqrt{6}\}\) -
Question 87 of 161
87. Question
Solve for \(x ; \quad(5+2 \sqrt{6})^{x^2-3}+(5-2 \sqrt{6})^{x^2-3}=0\) [1985 – 5 Marks]
CorrectIncorrectHint
Given, \((5+2 \sqrt{6})^{x^2-3}+(5-2 \sqrt{6})^{x^2-3}=10 \dots(i)\)
Put \(y=(5+2 \sqrt{6})^{x^2-3} \Rightarrow(5-2 \sqrt{6})^{x^2-3}=\frac{1}{y}\)
From Eq. (i), \(y+\frac{1}{y}=10\)
\(
\begin{array}{ll}
& \Rightarrow y^2-10 y+1=0 \Rightarrow y=5 \pm 2 \sqrt{6} \\
& \Rightarrow(5+2 \sqrt{6})^{x^2-3}=5+2 \sqrt{6} \\
\text { or } & (5+2 \sqrt{6})^{x^2-3}=5-2 \sqrt{6} \\
& \Rightarrow x^2-3=1 \quad \text { or } x^2-3=-1 \\
& \Rightarrow x=\pm 2 \text { or } x=\pm \sqrt{2} \\
& \Rightarrow x=\pm 2, \pm \sqrt{2}
\end{array}
\) -
Question 88 of 161
88. Question
\(
\text { Solve the following equation for } x \text { : }
\)
\(
2 \log _x a+\log _{a x} a+3 \log _{a^2 x} a=0, a>0
\) [1978]CorrectIncorrectHint
Given \(a>0\), so we have to consider two cases :
\(a \neq 1\) and \(a=1\).
Also it is clear that \(x>0\)
and \(x \neq 1, a x \neq 1, a^2 x \neq 1\).
Case I : If \(a>0, \neq 1\)
then given equation can be simplified as
\(
\frac{2}{\log _a x}+\frac{1}{1+\log _a x}+\frac{3}{2+\log _a x}=0
\)
Putting \(\log _a x=y\), we get
\(
2(1+y)(2+y)+y(2+y)+3 y(1+y)=0
\)
\(
\begin{aligned}
&\Rightarrow \quad 6 y^2+11 y+4=0 \Rightarrow y=-4 / 3 \text { and }-1 / 2 \\
&\Rightarrow \log _a x=-4 / 3 \text { and } \log _a x=-1 / 2 \\
&\Rightarrow x=a^{-4 / 3} \text { and } x=a^{-1 / 2}
\end{aligned}
\) -
Question 89 of 161
89. Question
Solve for \(x: \sqrt{x+1}-\sqrt{x-1}=1\). [1978]
CorrectIncorrectHint
\(\sqrt{x+1}=1+\sqrt{x-1}\)
Squaring both sides, we get
\(
\begin{aligned}
&x+1=1+x-1+2 \sqrt{x-1} \Rightarrow 1=2 \sqrt{x-1} \\
&\Rightarrow 1=4(x-1) \\
&\Rightarrow \quad x=5 / 4
\end{aligned}
\) -
Question 90 of 161
90. Question
Let \(a, b \in \mathrm{R}, a \neq 0\) be such that the equation, \(a x^2-2 b x+5=0\) has a repeated root \(\alpha\), which is also a root of the equation, \(x^2-2 b x-10=0\). If \(\beta\) is the other root of this equation, then \(\alpha^2+\beta^2\) is equal to: [Main Jan. 9, 2020 (II)]
CorrectIncorrectHint
(a) \(a x^2-2 b x+5=0\),
If \(\alpha\) and \(\alpha\) are roots of equations, then sum of roots
\(
2 \alpha=\frac{2 b}{a} \quad \Rightarrow \quad \alpha=\frac{b}{a}
\)
and product of roots \(=\alpha^2=\frac{5}{a} \Rightarrow \frac{b^2}{a^2}=\frac{5}{a}\)
\(\quad \Rightarrow \quad b^2=5 a \quad(a \neq 0)\)
For \(x^2-2 b x-10=0\)
\(\alpha+\beta=2 b\)
and \(\alpha \beta=-10\)
\(\alpha=\frac{b}{a}\) is also root of \(x^2-2 b x-10=0\)
\(\Rightarrow \quad b^2-2 a b^2-10 a^2=0\)
By eqn. (i) \(\Rightarrow 5 a-10 a^2-10 a^2=0\)
\(
\Rightarrow 20 a^2=5 a \Rightarrow a=\frac{1}{4} \text { and } b^2=\frac{5}{4}
\)
\(\alpha^2=20\) and \(\beta^2=5\)
Now, \(\alpha^2+\beta^2=5+20=25\) -
Question 91 of 161
91. Question
If \(5,5 \mathrm{r}, 5 \mathrm{r}^2\) are the lengths of the sides of a triangle, then \(\mathrm{r}\) cannot be equal to: [Main Jan. 10, 2019 (I)]
CorrectIncorrectHint
The triangle is possible if,
\(
\begin{aligned}
&5+5 r>5 r^2 \cdots(1) \\
&5 r+5 r^2>5 \cdots(2) \\
&5 r^2+5>5 r \cdots(3)
\end{aligned}
\)
From eqn (1)
\(
\begin{aligned}
&5 r^2-5 r-5<0 \\
&\Rightarrow r^2-r-1<0 \\
&\Rightarrow\left[r-\left(\frac{1-\sqrt{5}}{2}\right)\right]\left[r-\left(\frac{1+\sqrt{5}}{2}\right)\right]<0 \\
&\Rightarrow 0<r<\frac{1+\sqrt{5}}{2} \quad \cdots(4) \\
&\because r>0
\end{aligned}
\)
From eqn (2)
\(
5 r^2+5 r-5>0
\)
\(
\begin{aligned}
&r^2+r-1>0 \\
&\left(r-\left(\frac{-1-\sqrt{5}}{2}\right)\right)\left(r-\left(\frac{-1+\sqrt{5}}{2}\right)\right)>0 \\
&r>\frac{-1+\sqrt{5}}{2} \quad \cdots(5)
\end{aligned}
\)
\(
\because r>0
\)
From eqn (3)
\(
\begin{aligned}
&5 r^2-5 r+5>0 \\
&\Rightarrow r^2-r+1>0 \\
&\Rightarrow r \in R^{+} \cdots(6) \\
&(\because D=1-4=-3<0)
\end{aligned}
\)
Therefore, from (4), (5) and (6), we get \(\left(\frac{-1+\sqrt{5}}{2}\right)<r<\left(\frac{1+\sqrt{5}}{2}\right)\) \(r \in(0.618,1.618)\)
Hence, \(r \neq \frac{7}{4}\) -
Question 92 of 161
92. Question
If \(|z-3+2 i| \leq 4\) then the difference between the greatest value and the least value of \(|z|\) is [Main Online April 15, 2018]
CorrectIncorrectHint
(b) \(|z-(3-2 i)| \leq 4\) represents a circle whose centre is \((3,-2)\) and radius \(=4\).
\(|z|=|z-0|\) represents the distance of point ‘ \(z\) ‘ from origin \((0,0)\)
Suppose \(R S\) is the normal of the circle passing through origin ‘ \(O\) ‘ and \(G\) is its center \((3,-2)\).
Here, \(O R\) is the least distance and \(O S\) is the greatest distance
\(O R=R G-O G\) and \(O S=O G+G S \dots(i)\)
As, \(R G=G S=4\)
\(
O G=\sqrt{3^2+(-2)^2}=\sqrt{9+4}=\sqrt{13}
\)
From (i), \(O R=4-\sqrt{13}\) and \(O S=4+\sqrt{13}\)
So, required difference \(=(4+\sqrt{13})-(4-\sqrt{13})\)
\(
=\sqrt{13}+\sqrt{13}=2 \sqrt{13}
\) -
Question 93 of 161
93. Question
If the equations \(x^2+b x-1=0\) and \(x^2+x+b=0\) have a common root different from \(-1\), then \(|\mathrm{b}|\) is equal to: [Main Online April 9, 2016]
CorrectIncorrectHint
\(x^2+b x-1=0 \dots(i)\) common root
\(x^2+x+b=0 \dots(ii)\)
By solving eqn(i) & (ii) we get, \({x=\frac{b+1}{b-1}}\)
Put \(x=\frac{b+1}{b-1}\) in equation
\(
\begin{aligned}
&\left(\frac{b+1}{b-1}\right)^2+\left(\frac{b+1}{b-1}\right)+b=0 \\
&(b+1)^2+(b+1)(b-1)+b(b-1)^2=0 \\
&b^2+1+2 b+b^2-1+b\left(b^2-2 b+1\right)=0 \\
&2 b^2+2 b+b^3-2 b^2+b=0 \\
&b^3+3 b=0 \\
&b\left(b^2+3\right)=0 \\
&b^2=-3 \\
&b=\pm \sqrt{3} i \\
&|b|=\sqrt{3}
\end{aligned}
\) -
Question 94 of 161
94. Question
If non-zero real numbers b and c are such that \(\min f(x)>\max g(x)\), where \(f(x)=x^2+2 b x+2 c^2\) and \(g(x)=-x^2-2 c x+\) \(\mathrm{b}^2(\mathrm{x} \in \mathrm{R})\)
then \(\left|\frac{\mathrm{c}}{\mathrm{b}}\right|\) lies in the interval: [Main Online April 19, 2014]CorrectIncorrectHint
(d) We have
\(
f(x)=x^2+2 b x+2 c^2
\)
and \(g(x)=-x^2-2 c x+b^2,(x \in R)\)
\(
\Rightarrow f(x)=(x+b)^2+2 c^2-b^2
\)
and \(g(x)=-(x+c)^2+b^2+c^2\)
Now, \(f_{\min }=2 c^2-b^2\) and \(g_{\max }=b^2+c^2\)
\(
\text { Given : } \begin{aligned}
& \min f(x)>\max g(x) \\
& \Rightarrow 2 c^2-b^2>b^2+c^2 \\
& \Rightarrow c^2>2 b^2 \Rightarrow|c|>|b| \sqrt{2} \\
& \Rightarrow \frac{|c|}{|b|}>\sqrt{2} \Rightarrow\left|\frac{c}{b}\right|>\sqrt{2} \Rightarrow\left|\frac{c}{b}\right| \in(\sqrt{2}, \infty) .
\end{aligned}
\) -
Question 95 of 161
95. Question
If the equations \(x^2+2 x+3=0\) and \(a x^2+b x+c=0, a, b, c \in \mathrm{R}\), have a common root, then \(a: b: c\) is [Main 2013]
CorrectIncorrectHint
(a) Given equations are
\(
\begin{aligned}
&x^2+2 x+3=0 \quad \text {… (i) } \\
&a x^2+b x+c=0 \quad \text {… (ii) }
\end{aligned}
\)
Roots of equation (i) are imaginary roots in order pair.
According to the question (ii) will also have both roots same as (i). Thus
\(
\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\lambda \text { (say) }
\)
\(
\Rightarrow \quad a=\lambda, b=2 \lambda, c=3 \lambda
\)
Hence, the required ratio is \(1: 2: 3\) -
Question 96 of 161
96. Question
A value of \(b\) for which the equations
\(x^2+b x-1=0\)
\(x^2+x+b=0\)
have one root in common is [2011]CorrectIncorrectHint
(b) Let \(\alpha\) be the common root of given equations, then \(a^2+b \alpha-1=0 \quad\)…(i)
and \(\alpha^2+\alpha+b=0\)…(ii)
On subtracting (ii) from (i), we get
\(
\begin{gathered}
(b-1) \alpha-(b+1)=0 \\
\Rightarrow \alpha=\frac{b+1}{b-1}
\end{gathered}
\)
Substituting this value of \(\alpha\) in equation (i), we get
\(
\begin{aligned}
&\left(\frac{b+1}{b-1}\right)^2+b\left(\frac{b+1}{b-1}\right)-1=0 \Rightarrow b^3+3 b=0 \\
\Rightarrow \quad & b=0, i \sqrt{3},-i \sqrt{3}
\end{aligned}
\) -
Question 97 of 161
97. Question
For all ‘ \(x\) ‘, \(x^2+2 a x+10-3 a>0\), then the interval in which ‘ \(a\) ‘ lies is [2004S]
CorrectIncorrectHint
(b) \(f(x)=a x^2+b x+c\) has same sign as that of a if \(D<0\).
Since \(x^2+2 a x+10-3 a>0 \forall x\)
\(
\begin{aligned}
&\therefore \quad D<0 \Rightarrow 4 a^2-4(10-3 a)<0 \Rightarrow a^2+3 a-10<0 \\
&\Rightarrow \quad(a+5)(a-2)<0 \Rightarrow a \in(-5,2)
\end{aligned}
\) -
Question 98 of 161
98. Question
If the quadratic equations \(x^2+a x+b=0\) and \(x^2+b x+a=0(a \neq b)\) have a common root, then the numerical value of \(a+b\) is [1986 – 2 Marks]
CorrectIncorrectHint
\(
\begin{aligned}
&x^2+a x+b=0 \dots(1) \\
&x^2+b x+a=0 \dots(2)
\end{aligned}
\)
then a will satisfy for both the equations
\(
\begin{aligned}
&a^2+a a+b=a^2+b a+a=a(a-b)=a-b \\
&a=1 \\
&a=1 \text { is the common root from equation } 1 \\
&(1)^2+a(1)+b=0 \\
&1+a+b=0 \\
&a+b=-1
\end{aligned}
\) -
Question 99 of 161
99. Question
If \(P(x)=a x^2+b x+c\) and \(Q(x)=-a x^2+d x+c\), where \(a \neq 0\), then \(P(\mathrm{x}) Q(\mathrm{x})=0\) has at least two real roots. Is this statement true or false? [1985 – 1 Mark]
CorrectIncorrectHint
(True) \(P(x) \cdot Q(x)=\left(a x^2+b x+c\right)\left(-a x^2+b x+c\right)\)
\(\Rightarrow \quad D_1=b^2-4 a c\) and \(D_2=b^2+4 a c\)
clearly, \(\mathrm{D}_1+\mathrm{D}_2=2 \mathrm{~b}^2 \geq 0\)
\(\therefore\) At least one of \(\mathrm{D}_1\) and \(\mathrm{D}_2\) is positive. Hence, at least two real roots. -
Question 100 of 161
100. Question
Let \(S\) be the set of all non-zero real numbers \(\alpha\) such that the quadratic equation \(\alpha x^2-x+\alpha=0\) has two distinct real roots \(x_1\) and \(x_2\) satisfying the inequality \(\left|x_1-x_2\right|<1\). Which of the following intervals is(are) \(a\) subset(s) of \(S\)? [JEE Adv. 2015]
CorrectIncorrectHint
(a, d) Given, \(x_1\) and \(x_2\) are roots of \(\alpha x^2-x+\alpha=0\). \(\therefore \quad x_1+x_2=\frac{1}{\alpha}\) and \(x_1 x_2=1\)
Also, \(\left|x_1-x_2\right|<1\)
\(\Rightarrow\left|x_1-x_2\right|^2<1 \Rightarrow\left(x_1-x_2\right)^2<1\)
or \(\left(x_1+x_2\right)^2-4 x_1 x_2<1\)
\(\Rightarrow \quad \frac{1}{\alpha^2}-4<1\) or \(\frac{1}{\alpha^2}<5\)
or \(5 \alpha^2-1>0\) or \((\sqrt{5} \alpha-1)(\sqrt{5} \alpha+1)>0\)
\(\therefore \quad \alpha \in\left(-\infty,-\frac{1}{\sqrt{5}}\right) \cup\left(\frac{1}{\sqrt{5}}, \infty\right) \dots(i)\)
Also, \(D>0\)
\(\Rightarrow 1-4 \alpha^2>0\) or \(\alpha \in\left(-\frac{1}{2}, \frac{1}{2}\right) \dots(ii)\)
From Eqs. (i) and (ii), we get
\(
\alpha \in\left(-\frac{1}{2}, \frac{-1}{\sqrt{5}}\right) \cup\left(\frac{1}{\sqrt{5}}, \frac{1}{2}\right)
\) -
Question 101 of 161
101. Question
If \(a, b, c, d\) and \(p\) are distinct real numbers such that \(\left(a^2+b^2+c^2\right) p^2-2(a b+b c+c d) p+\left(b^2+c^2+d^2\right) \leq 0\) then \(a, b, c, d\) [1987 – 2 Marks]
CorrectIncorrectHint
(b) Given : \(a, b, c, d, p\) are real and distinct numbers such that
\(
\begin{aligned}
&\left(a^2+b^2+c^2\right) p^2-2(a b+b c+c d) p+\left(b^2+c^2+d^2\right) \leq 0 \\
&\Rightarrow \quad\left(a^2 p^2+b^2 p^2+c^2 p^2\right)-(2 a b p+2 b c p+2 c d p)+\left(b^2+c^2+d^2\right) \leq 0 \\
&\Rightarrow \quad\left(a^2 p^2-2 a b p+b^2\right)+\left(b^2 p^2-2 b c p+c^2\right)+\left(c^2 p^2-2 c d p+d^2\right) \leq 0
\end{aligned}
\)
\(
\Rightarrow(a p-b)^2+(b p-c)^2+(c p-d)^2 \leq 0
\)
Since, LHS is the sum of perfect squares, therefore LHS can never be -ve.
\(
\therefore(a p-b)^2+(b p-c)^2+(c p-d)^2=0
\)
Which is possible only when each term is zero individually
i.e. \(a p-b=0 ; b p-c=0 ; c p-d=0\)
\(
\begin{aligned}
&\Rightarrow \quad \frac{b}{a}=p ; \frac{c}{b}=p ; \frac{d}{c}=p \Rightarrow \frac{b}{a}=\frac{c}{b}=\frac{d}{c}=p \\
&\therefore \quad a, b, c, d \text { are in G.P. }
\end{aligned}
\) -
Question 102 of 161
102. Question
For real \(x\), the function \(\frac{(x-a)(x-b)}{x-c}\) will assume all real values provided [1984 – 3 Marks]
CorrectIncorrectHint
(c, d) Let \(y=\frac{(x-a)(x-b)}{(x-c)}\)
\(
\begin{aligned}
&\Rightarrow \quad(x-c) y=x^2-(a+b) x+a b \\
&\Rightarrow \quad x^2-(a+b+y) x+a b+c y=0
\end{aligned}
\)
Here, \(D=(a+b+y)^2-4(a b+c y)\)
\(
=y^2+2 y(a+b-2 c)+(a-b)^2
\)
Since \(x\) is real and y assumes all real values.
\(\therefore \quad D \geq 0\) for all real values of \(y\)
\(
\Rightarrow \quad y^2+2 y(a+b-2 c)+(a-b)^2 \geq 0
\)
As we know that the sign of a quadratic polynomial is same as that of coefficient of \(y^2\) if its descriminant \(<0\)
\(
\begin{aligned}
&\therefore \quad 4(a+b-2 c)^2-4(a-b)^2<0 \\
&\Rightarrow \quad 4(a+b-2 c+a-b)(a+b-2 c-a+b)<0 \\
&\Rightarrow \quad 16(a-c)(b-c)<0 \\
&\Rightarrow \quad 16(c-a)(c-b)<0 \dots(i)
\end{aligned}
\)
If \(a<b\) then from inequation (i), we get \(\mathrm{c} \in(\mathrm{a}, \mathrm{b})\)
\(
\Rightarrow a<c<b
\)
If \(a>b\) then from inequation (i), we get \(c \in(b, a)\)
\(
\Rightarrow a>c>b
\)
Thus, both (c) and (d) are the correct answer. -
Question 103 of 161
103. Question
Let \(a, b, c\) be real numbers with \(a \neq 0\) and let \(\alpha, \beta\) be the roots of the equation \(a x^2+b x+c=0\). Express the roots of \(a^3 x^2+a b c x+c^3=0\) in terms of \(\alpha, \beta\). [2001 – 4 Marks]
CorrectIncorrectHint
Given : \(a x^2+b x+c=0 \dots(i)\)
and \(\quad a^3 x^2+a b c x+c^2=0 \dots(ii)\)
\(
\therefore \quad \alpha+\beta=-\frac{b}{a}, \alpha \cdot \beta=\frac{c}{a}
\)
Divide the equation (ii) by \(a^3\), we get
\(
\begin{aligned}
& x^2+\frac{b}{a} \cdot \frac{c}{a} \cdot x+\left(\frac{c}{a}\right)^3=0 \\
\Rightarrow & x^2-(\alpha+\beta) \cdot(\alpha \beta) x+(\alpha \beta)^3=0 \\
\Rightarrow & x^2-\alpha^2 \beta x-\alpha \beta^2 x+(\alpha \beta)^3=0 \\
\Rightarrow & x\left(x-\alpha^2 \beta\right)-\alpha \beta^2\left(x-\alpha^2 \beta\right)=0 \\
\Rightarrow &\left(x-\alpha^2 \beta\right)\left(x-\alpha \beta^2\right)=0 \\
\Rightarrow & x=\alpha^2 \beta, \alpha \beta^2
\end{aligned}
\) -
Question 104 of 161
104. Question
Find all real values of \(x\) which satisfy \(x^2-3 x+2>0\) and \(x^2-2 x-4 \leq 0\) [1983 – 2 Marks]
CorrectIncorrectHint
\(
\begin{aligned}
&x^2-3 x+2>0 \text { and } x^2-3 x-4 \leq 0 \\
&x^2-3 x+2>0 \\
&\Rightarrow(x-1)(x-2)>0 \\
&\Rightarrow x \in(-\infty, 1) \cup(2, \infty) \cdots(1) \\
&x^2-3 x-4 \leq 0 \\
&\Rightarrow(x+1)(x-4) \leq 0 \\
&\Rightarrow x \in[-1,4] \cdots(2) \\
&\text { From }(1) \text { and }(2) \\
&x \in[-1,1) \cup(2,4]
\end{aligned}
\) -
Question 105 of 161
105. Question
If \(\alpha, \beta\) are the roots of \(x^2+p x+q=0\) and \(\gamma, \delta\) are the roots of \(x^2+r x+\) \(s=0\), then evaluate \((\alpha-\gamma)(\alpha-\delta)(\beta-\gamma)(\beta-\delta)\) in terms of \(p, q, r\) and \(s\).
Deduce the condition that the equations have a common root. [1979]CorrectIncorrectHint
\(\alpha, \beta\) are the roots of \(x^2+p x+q=0\) \(\alpha+\beta=-p, \quad \alpha \beta=q\)
\(\gamma, \delta\) are the roots of \(x^2+r x+s=0\) \(\gamma+\delta=-r, \gamma \delta=s\)
Now, \((\alpha-\gamma)(\alpha-\delta)(\beta-\gamma)(\beta-\delta)\)
\(
\begin{aligned}
=& {\left[\alpha^2-(\gamma+\delta) \alpha+\gamma \delta\right]\left[\beta^2-(\gamma+\delta) \beta+\gamma \delta\right] } \\
=\quad & {\left[\alpha^2+r \alpha+s\right]\left[\beta^2+r \beta+s\right] } \\
& \because \quad \alpha, \beta \text { are roots of } x^2+p x+q=0 \\
& \therefore \quad \alpha^2+p \alpha+q=0 \text { and } \beta^2+p \beta+q=0 \\
& \Rightarrow \quad \alpha^2=-p \alpha-q \text { and } \beta^2=-p \beta-q
\end{aligned}
\)
\(
\begin{aligned}
& \quad \therefore(\alpha-\gamma)(\alpha-\delta)(\beta-\gamma)(\beta-\delta)=\left[\alpha^2+r \alpha+s\right]\left[\beta^2+r \beta+s\right] \\
=& {[(r-p) \alpha+(s-q)][(r-p) \beta+(s-q)] } \\
=\quad &(r-p)^2 \alpha \beta+(r-p)(s-q)(\alpha+\beta)+(s-q)^2 \\
=& q(r-p)^2-p(r-p)(s-q)+(s-q)^2
\end{aligned}
\)
Now if the equations \(x^2+p x+q=0\) and \(x^2+r x+s=0\) have a common root say \(\alpha\), then \(\alpha^2+p \alpha+q=0\) and \(\alpha^2+r \alpha+s=0\)
\(
\begin{aligned}
&\Rightarrow \frac{\alpha^2}{p s-q r}=\frac{\alpha}{q-s}=\frac{1}{r-p} \\
&\Rightarrow \alpha^2=\frac{p s-q r}{r-p} \text { and } \alpha=\frac{q-s}{r-p}
\end{aligned}
\)
\(\Rightarrow(q-s)^2=(r-p)(p s-q r)\), which is the required condition. -
Question 106 of 161
106. Question
Let \(S=\left\{x \in R:(\sqrt{3}+\sqrt{2})^x+(\sqrt{3}-\sqrt{2})^x=10\right\}\). Then the number of elements in \(S\) is : [JEE Main 2024 1st Feb Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& (\sqrt{3}+\sqrt{2})^x+(\sqrt{3}-\sqrt{2})^x=10 \\
& \text { Let }(\sqrt{3}+\sqrt{2})^{ x }= t \\
& t +\frac{1}{ t }=10 \\
& t ^2-10 t +1=0 \\
& t=\frac{10 \pm \sqrt{100-4}}{2}=5 \pm 2 \sqrt{6} \\
& (\sqrt{3}+\sqrt{2})^x=(\sqrt{3} \pm \sqrt{2})^2 \\
& x =2 \text { or } x =-2 \\
& \text { Number of solutions }=2
\end{aligned}
\) -
Question 107 of 161
107. Question
Let \(\alpha\) and \(\beta\) be the roots of the equation \(px ^2+ qx -r=0\), where \(p \neq 0\). If \(p, q\) and \(r\) be the consecutive terms of a non-constant G.P and \(\frac{1}{\alpha}+\frac{1}{\beta}=\frac{3}{4}\), then the value of \((\alpha-\beta)^2\) is : [JEE Main 2024 1st Feb Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& px ^2+ qx – r =0<_\beta^\alpha \\
& p=A, q=A R, r=A R^2 \\
& A x^2+A R x-A R^2=0 \\
& x^2+R x-R^2=0<_\beta^\alpha
\end{aligned}
\)
\(
\begin{aligned}
& \because \frac{1}{\alpha}+\frac{1}{\beta}=\frac{3}{4} \\
& \therefore \frac{\alpha+\beta}{\alpha \beta}=\frac{3}{4} \Rightarrow \frac{- R }{- R ^2}=\frac{3}{4} \Rightarrow R =\frac{4}{3} \\
& (\alpha-\beta)^2=(\alpha+\beta)^2-4 \alpha \beta= R ^2-4\left(- R ^2\right)=5\left(\frac{16}{9}\right) \\
& =80 / 9
\end{aligned}
\) -
Question 108 of 161
108. Question
If \(\alpha, \beta\) are the roots of the equation, \(x^2-x-1=0\) and \(S_n=2023 \alpha^n+2024 \beta^n\), then [JEE Main 2024 27th Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& x ^2- x -1=0 \\
& S _{ n }=2023 \alpha^{ n }+2024 \beta^{ n } \\
& S _{ n -1}+ S _{ n -2}=2023 \alpha^{ n -1}+2024 \beta^{ n -1}+2023 \alpha^{ n -2}+2024 \beta^{ n -2} \\
& =2023 \alpha^{ n -2}[1+\alpha]+2024 \beta^{ n -2}[1+\beta] \\
& =2023 \alpha^{ n -2}\left[\alpha^2\right]+2024 \beta^{ n -2}\left[\beta^2\right] \\
& =2023 \alpha^{ n }+2024 \beta^{ n } \\
& S _{ n -1}+ S _{ n -2}= S _{ n } \\
& \text { Put } n =12 \\
& S _{11}+ S _{10}= S _{12}
\end{aligned}
\) -
Question 109 of 161
109. Question
\(\text { Let the set } C=\left\{(x, y) \mid x^2-2^y=2023, x, y \in N \right\} \text {. Then } \sum_{(x, y)=C}(x+y) \text { is equal to }\) [JEE Main 2024 29th Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2-2^y=2023 \\
& \Rightarrow x=45, y=1 \\
& \sum_{(x, y)=C}(x+y)=46 .
\end{aligned}
\)
Explanation:First, let’s consider the equation \(x^2-2^y=2023\) where \(x\) and \(y\) are natural numbers. Our goal is to find all the pairs \((x, y)\) that satisfy this equation and then sum the values of \(x+y\) for each pair in set \(C\).
Since 2023 is an odd number, and \(x^2\), the square of any natural number, is even when \(x\) is even and odd when \(x\) is odd, we can determine that for the left-hand side of the equation to be odd (thus equal to 2023), \(x\) must be odd since the right-hand side of the equation \(\left(2^y\right)\) is always even as it represents a power of two.
Also, 2023 can be factored into prime factors to further analyze the possible solutions:
\(
2023=7 \times 17 \times 17
\)
Thus, allowing us to rewrite the equation as:
\(
x^2-2^y=7 \times 17^2
\)
The next step is to check for potential values of \(x\) that would fit the equation, keeping in mind that \(x\) must be odd. We can try to express \(x^2\) as \(7 \times 17^2\) plus a power of 2 , recognizing that we are looking for the decomposition of the form:
\(
x^2=7 \times 17^2+2^y
\)
By examining the powers of 2 and keeping in mind that they grow very quickly, we can reason that \(y\) cannot be very large because \(x^2\) must not exceed 2023 by a large margin.
Let’s start by trying the lowest values for \(y\) since that would make \(2^y\) small and \(x\) has a better chance of being a natural number:
For \(y=1\) :
\(
x^2=2023+2^1=2023+2=2025
\)
Surprisingly, we find a perfect square since \(45^2=2025\). Therefore, \((x, y)=(45,1)\) is one solution.
For \(y=2\) or higher:
\(2^y\) becomes at least 4 and increases exponentially, so \(x^2\) must be at least 2027 or higher in such cases. There’s no natural number between 45 and 46 , and \(46^2\) far exceeds the target (2116), making it impossible for \(x^2\) to be less than 2116 for any larger \(y\).
Hence, it appears there is only one possible solution: \((x, y)=(45,1)\).
Therefore, the sum \(\sum_{(x, y) \in C}(x+y)\) for this set will consist of only this one pair:
\(
\sum_{(x, y) \in C}(x+y)=45+1=46
\) -
Question 110 of 161
110. Question
Let \(\alpha, \beta \in N\) be roots of equation \(x ^2-70 x +\lambda=0\), where \(\frac{\lambda}{2}, \frac{\lambda}{3} \notin N\). If \(\lambda\) assumes the minimum possible value, then \(\frac{(\sqrt{\alpha-1}+\sqrt{\beta-1})(\lambda+35)}{|\alpha-\beta|}\) is equal to: [JEE Main 2024 30th Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2-70 x+\lambda=0 \\
& \alpha+\beta=70 \\
& \alpha \beta=\lambda \\
& \therefore \alpha(70-\alpha)=\lambda
\end{aligned}
\)
Since, 2 and 3 does not divide \(\lambda\)
\(
\therefore \alpha=5, \beta=65, \lambda=325
\)
By putting value of \(\alpha, \beta, \lambda\) we get the required value 60 . -
Question 111 of 161
111. Question
The number of real solutions of the equation \(x\left(x^2+3|x|+5|x-1|+6|x-2|\right)=0\) is [JEE Main 2024 30th Jan Shift 2]
CorrectIncorrectHint
\(
x=0 \text { and } x^2+3|x|+5|x-1|+6|x-2|=0
\)
Here all terms are + ve except at \(x=0\)
So there is no value of \(x\)
Satisfies this equation
Only solution \(x =0\)
No of solution 1 . -
Question 112 of 161
112. Question
For \(0< c < b < a\), let \(( a + b -2 c ) x ^2+( b + c -2 a ) x +(c+a-2 b)=0\) and \(\alpha \neq 1\) be one of its root.
Then, among the two statements
(I) If \(\alpha \in(-1,0)\), then \(b\) cannot be the geometric mean of \(a\) and \(c\)
(II) If \(\alpha \in(0,1)\), then \(b\) may be the geometric mean of \(a\) and \(c\) [JEE Main 2024 31st Jan Shift 1]CorrectIncorrectHint
\(
\begin{aligned}
& f(x)=(a+b-2 c) x^2+(b+c-2 a) x+(c+a-2 b) \\
& f(x)=a+b-2 c+b+c-2 a+c+a-2 b=0 \\
& f(1)=0 \\
& \therefore \alpha \cdot 1=\frac{c+a-2 b}{a+b-2 c} \\
& \alpha=\frac{c+a-2 b}{a+b-2 c} \\
& \text { If }-1<\alpha<0 \\
& -1<\frac{c+a-2 b}{a+b-2 c}<0
\end{aligned}
\)
\(
b+c<2 a \text { and } b>\frac{a+c}{2}
\)
therefore, \(b\) cannot be G.M. between \(a\) and \(c\).
If, \(0<\alpha<1\)
\(
0<\frac{c+a-2 b}{a+b-2 c}<1
\)
\(b > c\) and \(b <\frac{ a + c }{2}\)
Therefore, \(b\) may be the G.M. between \(a\) and \(c\). -
Question 113 of 161
113. Question
Let \(S\) be the set of positive integral values of a for which \(\frac{a x^2+2(a+1) x+9 a+4}{x^2-8 x+32}<0, \forall x \in R\) Then, the number of elements in \(S\) is: [JEE Main 2024 31st Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{a x^2+2(a+1) x+9 a+4}{x^2-8 x+32}<0 \\
& D=64-4 \times 32<0 \\
& \& a=1>0 \\
& \therefore x^2-8 x+32>0 \forall x \in R \\
& a x^2+2(a+1) x+9 a+4<0 \forall x \in R
\end{aligned}
\)Only possible when
\(
a <0 \& D <0
\)
but we need positive integral value of \(a\).
So, No solution -
Question 114 of 161
114. Question
The number of solutions, of the equation \(e^{\sin x}-2 e^{-\sin x}=2\) is [JEE Main 2024 31st Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Take } e^{\sin x}=t(t>0) \\
& \Rightarrow t-\frac{2}{t}=2 \\
& \Rightarrow \frac{t^2-2}{t}=2 \\
& \Rightarrow t^2-2 t-2=0 \\
& \Rightarrow t^2-2 t+1=3 \\
& \Rightarrow(t-1)^2=3 \\
& \Rightarrow t=1 \pm \sqrt{3} \\
& \Rightarrow t=1 \pm 1.73 \\
& \Rightarrow t=2.73 \text { or }-0.73 \text { (rejected as } t>0 \text { ) } \\
& \Rightarrow e^{\sin x}=2.73 \\
& \Rightarrow \log _e e^{\sin x}=\log _e 2.73 \\
& \Rightarrow \sin x=\log _e 2.73>1
\end{aligned}
\)
So no solution. -
Question 115 of 161
115. Question
Let \(a, b, c\) be the length of three sides of a triangle satisfying the condition \(\left(a^2+b^2\right) x^2-2 b(a+c)\). \(x+\left(b^2+c^2\right)=0\). If the set of all possible values of \(x\) is the interval \((\alpha, \beta)\), then \(12\left(\alpha^2+\beta^2\right)\) is equal to [JEE Main 2024 31st Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(a^2+b^2\right) x^2-2 b(a+c) x+b^2+c^2=0 \\
& \Rightarrow a^2 x^2-2 a b x+b^2+b^2 x^2-2 b c x+c^2=0 \\
& \Rightarrow(a x-b)^2+(b x-c)^2=0 \\
& \Rightarrow a x-b=0, \quad b x-c=0 \\
& \Rightarrow a+b>c \quad b+c>a \quad c+a>b \\
& a+a x>b x \quad|a x+b x>a| a x^2+a>a x \\
& a+a x>a x^2 \left\lvert\, \begin{array}{l}
a x+a x^2>a \\
x^2-x+1>0
\end{array}\right. \\
&
\end{aligned}
\)
\(
x^2-x-1<0\left|x^2+x-1>0\right| \text { always true }
\)
\(
\begin{aligned}
& \frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2} \\
& x<\frac{-1-\sqrt{5}}{2}, \text { or } x>\frac{-1+\sqrt{5}}{2} \\
& \Rightarrow \frac{\sqrt{5}-1}{2}< x <\frac{\sqrt{5}+1}{2} \\
& \Rightarrow \alpha=\frac{\sqrt{5}-1}{2}, \beta=\frac{\sqrt{5}+1}{2} \\
& 2\left(\alpha^2+\beta^2\right)=12\left(\frac{(\sqrt{5}-1)^2+(\sqrt{5}+1)^2}{4}\right)=36
\end{aligned}
\) -
Question 116 of 161
116. Question
Let \(\alpha\) be a root of the equation \((a-c) x^2+(b-a) x+(c-b)=0\) where \(a, b, c\) are distinct real numbers such that the matrix
\(
\left[\begin{array}{ccc}
\alpha^2 & \alpha & 1 \\
1 & 1 & 1 \\
a & b & c
\end{array}\right]
\)
is singular. Then the value of \(\frac{(a-c)^2}{(b-a)(c-b)}+\frac{(b-a)^2}{(a-c)(c-b)}+\frac{(c-b)^2}{(a-c)(b-a)}\) is [JEE Main 2023 24th Jan Shift 1]CorrectIncorrectHint
\(
\Delta=0=
\)\(
\left[\begin{array}{ccc}
\alpha^2 & \alpha & 1 \\
1 & 1 & 1 \\
a & b & c
\end{array}\right]
\)\(\alpha^2( c – b )-\alpha( c – a )+( b – a )=0\)
It is singular when \(\alpha=1\)
\(
\begin{aligned}
& \frac{(a-c)^2}{(b-a)(c-b)}+\frac{(b-a)^2}{(a-c)(c-b)}+\frac{(c-b)^2}{(a-c)(b-a)} \\
& \frac{(a-b)^3+(b-c)^3+(c-a)^3}{(a-b)(b-c)(c-a)} \\
& =3 \frac{(a-b)(b-c)(c-a)}{(a-b)(b-c)(c-a)}=3
\end{aligned}
\) -
Question 117 of 161
117. Question
Let \(\lambda \in R\) and let the equation \(E\) be \(|x|^2-2|x|+|\lambda-3|=0\). Then the largest element in the set \(S=\) \(\{x+\lambda: x\) is an integer solution of \(E\}\) is [JEE Main 2023 24th Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& |x|^2-2|x|+|\lambda-3|=0 \\
& |x|^2-2|x|+|\lambda-3|-1=0 \\
& (|x|-1)^2+|\lambda-3|=1
\end{aligned}
\)
At \(\lambda=3, x=0\) and 2 ,
at \(\lambda=4\) or 2 , then
\(
x =1 \text { or }-1
\)
So maximum value of \(x+\lambda=5\) -
Question 118 of 161
118. Question
The number of real solutions of the equation \(3\left(x^2+\frac{1}{x^2}\right)-2\left(x+\frac{1}{x}\right)+5=0\), is [JEE Main 2023 24th Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& 3\left(x^2+\frac{1}{x^2}\right)-2\left(x+\frac{1}{x}\right)+5=0 \\
& 3\left[\left(x+\frac{1}{x}\right)^2-2\right]-2\left(x+\frac{1}{x}\right)+5=0 \\
& \text { Let } x+\frac{1}{x}=t \\
& 3 t^2-2 t-1=0 \\
& 3 t^2-3 t+t-1=0 \\
& 3 t(t-1)+1(t-1)=0 \\
& (t-1)(3 t+1)=0 \\
& t=1,-\frac{1}{3} \\
& x+\frac{1}{x}=1,-\frac{1}{3} \Rightarrow \text { No solution. }
\end{aligned}
\) -
Question 119 of 161
119. Question
Let
\(
S=\left\{\alpha: \log _2\left(9^{2 \alpha-4}+13\right)-\log _2\left(\frac{5}{2} \cdot 3^{2 \alpha-4}+1\right)=2\right\}
\)
Then the maximum value of \(\beta\) for which the equation \(x^2-2\left(\sum_{\alpha \in S} \alpha\right)^2 x+\sum_{\alpha \in S}(\alpha+1)^2 \beta=0 \text { has real roots, is }\) [JEE Main 2023 25th Jan Shift 1]CorrectIncorrectHint
\(
\begin{aligned}
& \log _2\left(9^{2 \alpha-4}+13\right)-\log _2\left(\frac{5}{2} \cdot 3^{2 \alpha-4}+1\right)=2 \\
& \Rightarrow \frac{9^{2 \alpha-4}+13}{\frac{5}{2} 3^{2 \alpha-4}+1}=4
\end{aligned}
\)
\(
\Rightarrow \alpha=2 \quad \text { or } \quad 3
\)
\(
\sum_{\alpha \in S} \alpha=5 \text { and } \sum_{\alpha \in S}(\alpha+1)^2=25
\)
\(
\begin{aligned}
& \Rightarrow x^2-50 x+25 \beta=0 \text { has real roots } \\
& \Rightarrow \beta \leq 25 \\
& \Rightarrow \beta_{\max }=25
\end{aligned}
\) -
Question 120 of 161
120. Question
Let \(a \in R\) and let \(\alpha, \beta\) be the roots of the equation \(x^2+60^{\frac{1}{4}} x+a=0\). If \(\alpha^4+\beta^4=-30\), then the product of all possible values of \(a\) is [JEE Main 2023 25th Jan Shift 2]
CorrectIncorrectHint
\(x^2+60^{\frac{1}{4}} x+a=0 \)
\(
\alpha+\beta=-60^{\frac{1}{4}} \quad \& \quad \alpha \beta= a
\)
Given \(\alpha^4+\beta^4=-30\)
\(
\begin{aligned}
& \Rightarrow\left(\alpha^2+\beta^2\right)^2-2 \alpha^2 \beta^2=-30 \\
& \Rightarrow\left\{(\alpha+\beta)^2-2 \alpha \beta\right\}^2-2 a^2=-30
\end{aligned}
\)
\(
\Rightarrow\left\{60^{\frac{1}{2}}-2 a \right\}^2-2 a ^2=-30
\)
\(
\begin{aligned}
& \Rightarrow 60+4 a ^2-4 a \times 60^{\frac{1}{2}}-2 a ^2=-30 \\
& \Rightarrow 2 a ^2-4.60^{\frac{1}{2}} a +90=0 \\
& \text { Product }=\frac{90}{2}=45
\end{aligned}
\) -
Question 121 of 161
121. Question
Let \(\lambda \neq 0\) be a real number. Let \(\alpha, \beta\) be the roots of the equation \(14 x^2-31 x+3 \lambda=0\) and \(\alpha, \gamma\) be the roots of the equation \(35 x^2-53 x+4 \lambda=0\). Then \(\frac{3 \alpha}{\beta}\) and \(\frac{4 \alpha}{\gamma}\) are the roots of the equation : [JEE Main 2023 29th Jan Shift 1]
CorrectIncorrectHint
\(
14 x^2-31 x+3 \lambda=0
\)
\(\alpha+\beta=\frac{31}{14} \dots(1)\)
and \(\alpha \beta=\frac{3 \lambda}{14} \dots(2)\)
\(
35 x^2-53 x+4 \lambda=0
\)
\(\alpha+\gamma=\frac{53}{35} \dots(3)\)
and \(\alpha \gamma=\frac{4 \lambda}{35} \dots(4)\)
\(
\begin{aligned}
& \frac{(2)}{(4)} \Rightarrow \frac{\beta}{\gamma}=\frac{3 \times 35}{4 \times 14}=\frac{15}{8} \Rightarrow \beta=\frac{15}{8} \gamma \\
& \text { (1) }-(3) \Rightarrow \beta-\gamma=\frac{31}{14}-\frac{53}{35}=\frac{155-106}{70}=\frac{7}{10} \\
& \frac{15}{8} \gamma-\gamma=\frac{7}{10} \Rightarrow \gamma=\frac{4}{5} \\
& \Rightarrow \beta=\frac{15}{8} \times \frac{4}{5}=\frac{3}{2}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \alpha=\frac{31}{14}-\beta=\frac{31}{14}-\frac{3}{2}=\frac{5}{7} \\
& \Rightarrow \lambda=\frac{14}{3} \alpha \beta=\frac{14}{3} \times \frac{5}{7} \times \frac{3}{2}=5 \\
& \text { so, sum of roots } \frac{3 \alpha}{\beta}+\frac{4 \alpha}{\gamma}=\left(\frac{3 \alpha \gamma+4 \alpha \beta}{\beta \gamma}\right) \\
& =\frac{\left(3 \times \frac{4 \lambda}{35}+4 \times \frac{3 \lambda}{14}\right)}{\beta \gamma}=\frac{12 \lambda(14+35)}{14 \times 35 \beta \gamma}
\end{aligned}
\)
\(
=\frac{49 \times 12 \times 5}{490 \times \frac{3}{2} \times \frac{4}{5}}=5
\)
Product of roots
\(
=\frac{3 \alpha}{\beta} \times \frac{4 \alpha}{\gamma}=\frac{12 \alpha^2}{\beta \gamma}=\frac{12 \times \frac{25}{49}}{\frac{3}{2} \times \frac{4}{5}}=\frac{250}{49}
\)
So, required equation is \(x^2-5 x+\frac{250}{49}=0\)
\(
\Rightarrow 49 x^2-245 x+250=0
\) -
Question 122 of 161
122. Question
If the value of real number \(a>0\) for which \(x^2-5 a x\) \(+1=0\) and \(x^2-a x-5=0\) have a common real roots is \(\frac{3}{\sqrt{2 \beta}}\) then \(\beta\) is equal to [JEE Main 2023 30th Jan Shift 2]
CorrectIncorrectHint
Two equations have common root
\(
\begin{aligned}
& \therefore(4 a)(26 a)=(-6)^2=36 \\
& \Rightarrow a^2=\frac{9}{26} \\
& \therefore a=\frac{3}{\sqrt{26}} \\
& \Rightarrow \beta=13
\end{aligned}
\) -
Question 123 of 161
123. Question
The number of real roots of the equation \(\sqrt{x^2-4 x+3}+\sqrt{x^2-9}=\sqrt{4 x^2-14 x+6}\), is: [JEE Main 2023 31st Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \sqrt{(x-1)(x-3)}+\sqrt{(x-3)(x+3)} \\
& =\sqrt{4\left(x-\frac{12}{4}\right)\left(x-\frac{2}{4}\right)} \\
& \Rightarrow \sqrt{ x -3}=0 \Rightarrow x =3 \text { which is in domain }
\end{aligned}
\)
or
\(
\begin{aligned}
& \sqrt{ x -1}+\sqrt{ x +3}=\sqrt{4 x -2} \\
& 2 \sqrt{(x-1)(x+3)}=2 x-4 \\
& x^2+2 x-3=x^2-4 x+4 \\
& 6 x =7 \\
& x =7 / 6 \text { (rejected) }
\end{aligned}
\) -
Question 124 of 161
124. Question
The equation \(e ^{4 x }+8 e ^{3 x }+13 e ^{2 x }-8 e ^{ x }+1=0, x \in R\) has: [JEE Main 2023 31st Jan Shift 2]
CorrectIncorrectHint
\(
e^{4 x}+8 e^{3 x}+13 e^{2 x}-8 e^x+1=0
\)
Let \(e ^{ x }= t\)
Now, \(t ^4+8 t ^3+13 t ^2-8 t +1=0\)
Dividing equation by \(t ^2\),
\(
\begin{aligned}
& t ^2+8 t +13-\frac{8}{ t }+\frac{1}{ t ^2}=0 \\
& t ^2+\frac{1}{ t ^2}+8\left( t -\frac{1}{ t }\right)+13=0 \\
& \left( t -\frac{1}{ t }\right)^2+2+8\left( t -\frac{1}{ t }\right)+13=0
\end{aligned}
\)
Let \(t -\frac{1}{ t }= z\)
\(
\begin{aligned}
& z^2+8 z+15=0 \\
& (z+3)(z+5)=0 \\
& z=-3 \text { or } z=-5
\end{aligned}
\)
So, \(t -\frac{1}{ t }=-3\) or \(t -\frac{1}{ t }=-5\)
\(
\begin{aligned}
& t ^2+3 t -1=0 \text { or } t ^2+5 t -1=0 \\
& t =\frac{-3 \pm \sqrt{13}}{2} \text { or } t =\frac{-5 \pm \sqrt{29}}{2}
\end{aligned}
\)
as \(t = e ^{ x }\) so \(t\) must be positive,
\(
t =\frac{\sqrt{13}-3}{2} \text { or } \frac{\sqrt{29}-5}{2}
\)
So, \(x=\ln \left(\frac{\sqrt{13}-3}{2}\right)\)
or \(x =\ln \left(\frac{\sqrt{29}-5}{2}\right)\)
Hence two solution and both are negative. -
Question 125 of 161
125. Question
Two dice are thrown independently. Let \(A\) be the event that the number appeared on the \(1^{\text {st }}\) die is less than the number appeared on the \(2^{\text {nd }}\) die, \(B\) be the event that the number appeared on the \(1^{\text {st }}\) die is even and that on the second die is odd, and \(C\) be the event that the number appeared on the \(1^{\text {st }}\) die is odd and that on the \(2^{\text {nd }}\) is even. Then [JEE Main 2023 1st Feb Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& A=\{(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5), \\
& n(A)=15 \\
& B=\{(2,1),(2,3),(2,5),(4,1),(4,3),(4,5),(6,1),(6,3),(6,5)\} \\
& n(B)=9 \\
& C=\{(1,2),(1,4),(1,6),(3,2),(3,4),(3,6),(5,2),(5,4),(5,6)\} \\
& n(C)=9 \\
& (4,5) \in A \text { and }(4,5) \in B \\
& \therefore A \text { and } B \text { are not exclusive events } \\
& \quad n((A \cup B) \cap C)=n(A \cap C)+n(B \cap C)-n(A \cap B \cap C) \\
& =3+3-0 \\
& =6
\end{aligned}
\)
\(
\begin{aligned}
& n(B)=\frac{9}{36}, n(C)=\frac{9}{36}, n(B \cap C)=0 \\
& \Rightarrow n(B) \cdot n(C) \neq n(B \cap C)
\end{aligned}
\)
\(\therefore B\) and \(C\) are not independent. -
Question 126 of 161
126. Question
If the sum of the squares of the reciprocals of the roots \(\alpha\) and \(\beta\) of the equation \(3 x^2+\lambda x-1=0\) is 15 , then \(6\left(\alpha^3+\beta^3\right)^2\) is equal to: [JEE Main 2022 24th June Shift 1]
CorrectIncorrectHint
Here \(\alpha, \beta\) roots of equation \(3 x^2+\lambda x-1=0\)
\(
\begin{aligned}
& \alpha+\beta=\frac{-\lambda}{3}, \alpha \beta=\frac{-1}{3} \\
& \frac{1}{\alpha^2}+\frac{1}{\beta^2}=\frac{(\alpha+\beta)^2-2 \alpha \beta}{\alpha^2 \beta^2}=15 \\
& \lambda^2=9
\end{aligned}
\)
Now \(6\left(\alpha^3+\beta^3\right)^2=6\left((\alpha+\beta)\left((\alpha+\beta)^2-3 \alpha \beta\right)\right)^2\)
\(
=6\left(\frac{\lambda^2}{9}\right)\left\{\frac{\lambda^2}{9}+1\right\}^2=24
\) -
Question 127 of 161
127. Question
The sum of all the real roots of the equation \(\left(e^{2 x}-4\right)\left(6 e^{2 x}-5 e^x+1\right)=0\) is [JEE Main 2022 24th June Shift 2]
CorrectIncorrectHint
Let \(e ^{ x }= t\)
then given equation converts into
\(
\begin{aligned}
& \left(t^2-4\right)\left(6 t^2-5 t+1\right)=0 \\
& \Rightarrow(t-2)(t+2)(2 t-1)(3 t-1)=0 \\
& \Rightarrow t=2,-2, \frac{1}{2}, \frac{1}{3} \\
& \because t=e^x>0 \\
& \therefore t \neq-2
\end{aligned}
\)
\(\because\) If \(t =2\) then \(e ^{ x }=2 \Rightarrow x =\log _e 2\)
If \(t =\frac{1}{2}\) then \(e ^{ x }=\frac{1}{2} \Rightarrow x =-\log _e 2\)
If \(t =\frac{1}{3}\) then \(e ^{ x }=\frac{1}{3} \Rightarrow x =-\log _e 3\)
\(\therefore\) Sum of real roots \(=\log _e 2-\log _e 2-\log _e 3\)
\(
\begin{aligned}
& =-\log _e 3 \\
& =\log _e\left(\frac{1}{3}\right)
\end{aligned}
\) -
Question 128 of 161
128. Question
For a natural number \(n\), let \(a_n=19^n-12^n\). Then, the value of \(\frac{31 \alpha_9-\alpha_{10}}{57 \alpha_8}\) is [JEE Main 2022 25th June Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{31 \alpha_9-\alpha_{10}}{57 \alpha_8}=\frac{31\left(19^9-12^9\right)-\left(19^{10}-12^{10}\right)}{57 \alpha_8} \\
& =\frac{19^9(31-19)-12^9(31-12)}{57 \alpha_8} \\
& =\frac{19^9 \cdot 12-12^{19} \cdot 19}{57 \alpha_8} \\
& =\frac{12 \cdot 19\left(19^8-12^8\right)}{57 \alpha_8}=4
\end{aligned}
\) -
Question 129 of 161
129. Question
Let \(a, b \in R\) be such that the equation \(ax ^2-2 bx +15=0\) has a repeated root \(\alpha\). If \(\alpha\) and \(\beta\) are the roots of the equation \(x^2-2 b x+21=0\), then \(\alpha^2+\beta^2\) is equal to: [JEE Main 2022 25th June Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& a x^2-2 b x+15=0 \\
& 2 \alpha=\frac{2 b}{a}, \alpha^2=\frac{15}{a} \\
& \frac{\alpha}{2}=\frac{15}{2 b} \\
& \alpha=\frac{15}{b} \\
& x^2-2 b x+21=0 \\
& \left(\frac{15}{b}\right)^2-2 b\left(\frac{15}{b}\right)+21=0 \\
& b^2=25 \\
& \alpha+\beta=2 b, \alpha \beta=21 \\
& \alpha^2+\beta^2=4 b^2-42 \\
& =58
\end{aligned}
\) -
Question 130 of 161
130. Question
The sum of the cubes of all the roots of the equation \(x^4-3 x^3-2 x^2+3 x+1=10\) is [JEE Main 2022 26th June Shift 1]
CorrectIncorrectHint
\(
x^4-3 x^3-2 x^2+3 x+1=10
\)
\(x=0\) is not the root of this equation so divide it by \(x^2\)
\(
\begin{aligned}
& x^2-3 x-2+\frac{3}{x}+\frac{1}{x^2}=0 \\
& x^2+\frac{1}{x^2}-2+2-3\left(x-\frac{1}{x}\right)-2=0 \\
& \left(x-\frac{1}{x}\right)^2-3\left(x-\frac{1}{x}\right)=0
\end{aligned}
\)
\(
\begin{array}{ll}
x-\frac{1}{x}=0, & x-\frac{1}{x}=3 \\
x^2-1=0 & x^2-3 x-1=0 \\
x= \pm 1 & \gamma+\delta=3 \\
\alpha=1, \beta=-1 & \gamma \delta=-1
\end{array}
\)
\(
\begin{aligned}
& \alpha^3+\beta^3+\gamma^3+\delta^3 \\
& 1-1+(\gamma+\delta)\left((\gamma+\delta)^2-3 \gamma \delta\right) \\
& 0+3(9-3(-1)) \\
& \quad+3(12)=36
\end{aligned}
\) -
Question 131 of 161
131. Question
If the sum of all the roots of the equation \(e^{2 x}-11 e^x-45 e^{-x}+\frac{81}{2}=0\) is \(\log _{ e } P\), then \(p\) is equal to [JEE Main 2022 27th June Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& e^{2 x}-11 e^x-45 e^{-x}+\frac{81}{2}=0 \\
& e^{x^3}-11 e^{x^2}-45+\frac{81 e^x}{2}=0
\end{aligned}
\)
\(
\begin{aligned}
& e^x=t \\
& 2 t^3-22 t^2+81 t-90=0 \\
& t_1 t_2 t_3=45 \\
& e^{x_1} \cdot e^{x_2} \cdot e^{x_3}=45 \\
& e^{x_1+x_2+x_3}=45 \\
& \log _e e^{x_1+x_2+x_3}=\log _e 45 \\
& x_1+x_2+x_3=\log _e 45 \\
& \log _e P=\log _e 45 \\
& P=45
\end{aligned}
\) -
Question 132 of 161
132. Question
Let \(\alpha, \beta\) be the roots of the equation \(x^2-4 \lambda x+5=0\) and \(\alpha, \gamma\) be the roots of the equation \(x^2-(3 \sqrt{2}+2 \sqrt{3}) x+7+3 \lambda \sqrt{3}=0\).
If \(\beta+\gamma=3 \sqrt{2}\), then \((\alpha+2 \beta+\gamma)^2\) is equal to : [JEE Main 2022 27th June Shift 2]CorrectIncorrectHint
\(
\begin{aligned}
& x^2-4 \lambda x+5=0\left\langle_\beta^\alpha\right. \\
& x^2-(3 \sqrt{2}+2 \sqrt{3}) x+(7+3 \lambda \sqrt{3})=0\left\langle\begin{array}{l}
\alpha \\
\gamma
\end{array}\right.
\end{aligned}
\)
\(
\begin{aligned}
& \alpha+\beta=4 \lambda \\
& \alpha+\gamma=3 \sqrt{2}+2 \sqrt{3} \\
& \beta+\lambda=3 \sqrt{2} \\
& \therefore \alpha=2 \lambda+\sqrt{3} \\
& \beta=2 \lambda-\sqrt{3} \\
& \alpha \gamma=7+3 \lambda \sqrt{3} \\
& \alpha \beta=5 \\
& 4 \lambda^2=8 \Rightarrow \lambda=\sqrt{2} \\
& \therefore(\alpha+2 \beta+\lambda)^2=(4 \alpha+3 \sqrt{2})^2=(7 \sqrt{2})^2=98
\end{aligned}
\) -
Question 133 of 161
133. Question
The number of real solutions of the equation \(e ^{4 x}+4 e ^{3 x }-58 e ^{2 x }+4 e ^x+1=0\) is [JEE Main 2022 28th June Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& e^{4 x}+4 e^{3 x}-58 e^{2 x}+4 e^x+1=0 \\
& \text { Let } f(x)=e^{2 x}\left(e^{2 x}+\frac{1}{e^{2 x}}+4\left(e^x+\frac{1}{e^x}\right)-58\right)
\end{aligned}
\)
\(
e ^{ x }+\frac{1}{ e ^{ x }}
\)
Let \(h ( t )= t ^2+4 t -58=0\)
\(
t=\frac{-4 \pm \sqrt{16+4.58}}{2}
\)
\(
\begin{aligned}
& =\frac{-4 \pm 2 \sqrt{62}}{2} \\
& t_1=-2+2 \sqrt{62} \\
& t_2=-2-2 \sqrt{62} \text { (not possible) } \\
& t \geq 2
\end{aligned}
\)
\(
\begin{aligned}
& e ^{ x }+\frac{1}{ e ^{ x }}=-2+2 \sqrt{62} \\
& e ^{2 x }-(-2+2 \sqrt{62}) e ^{ x }+1=0 \\
& (-2+2 \sqrt{62})-4 \\
& 4+4.62-8 \sqrt{62}-4 \\
& 248-8 \sqrt{62}>0 \\
& \frac{-b}{2 a }>0
\end{aligned}
\)
both roots are positive 2 real roots -
Question 134 of 161
134. Question
Let \(f(x)\) be a quadratic polynomial such that \(f(-2)\) \(+f(3)=0\). If one of the roots of \(f(x)=0\) is -1 , then the sum of the roots of \(f(x)=0\) is equal to : [JEE Main 2022 28th June Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& f(-2)+f(3)=0 \\
& f(x)=(x+1)(a x+b) \\
& f(-2)+f(3)=-1(-2 a+b)+4(3 a+b)=0 \\
& 2 a-b+12 a+4 b=0 \\
& 14 a+3 b=0 \\
& \frac{-b}{a}=\frac{14}{3}
\end{aligned}
\)
\(
\text { Sum of roots }=\left(-1+\frac{-b}{a}\right)=-1+\frac{14}{3}=\frac{11}{3}
\) -
Question 135 of 161
135. Question
Let \(\alpha\) be a root of the equation \(1+ x ^2+ x ^4=0\).
Then the value of \(\alpha^{1011}+\alpha^{2022}-\alpha^{3033}\) is equal to: [JEE Main 2022 29th June Shift 2]CorrectIncorrectHint
\(
\begin{aligned}
& x^4+x^2+1=0 \\
& \Rightarrow\left(x^2+x+1\right)\left(x^2-x+1\right)=0
\end{aligned}
\)
\(\Rightarrow x= \pm \omega, \pm \omega^2\) where \(\omega=1^{1 / 3}\) and imaginary.
So \(\alpha^{1011}+\alpha^{2022}-\alpha^{3033}=1+1-1=1\) -
Question 136 of 161
136. Question
If \(\alpha\) and \(\beta\) are the distinct roots of the equation \(x^2+(3)^{1 / 4} x+3^{1 / 2}=0\), then the value of \(\alpha^{96}\left(\alpha^{12}-1\right)+\beta^{96}\left(\beta^{12}-1\right)\) is equal to : [JEE Main 2021 20th July Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { As, }\left(\alpha^2+\sqrt{3}\right)=-(3)^{1 / 4} \cdot \alpha \\
& \Rightarrow\left(\alpha^4+2 \sqrt{3} \alpha^2+3\right)=\sqrt{3} \alpha^2 \text { (On squaring) } \\
& \therefore\left(\alpha^4+3\right)=(-) \sqrt{3} \alpha^2 \\
& \Rightarrow \alpha^8+6 \alpha^4+9=3 \alpha^4 \quad \text { (Again squaring) } \\
& \therefore \alpha^8+3 \alpha^4+9=0 \\
& \Rightarrow \alpha^8=-9-3 \alpha^4
\end{aligned}
\)
(Multiply by \(\alpha^4\) )
\(
\begin{aligned}
& \text { So, } \alpha^{12}=-9 \alpha^4-3 \alpha^8 \\
& \therefore \quad \alpha^{12}=-9 \alpha^4-3\left(-9-3 \alpha^4\right) \\
& \Rightarrow \alpha^{12}=-9 \alpha^4+27+9 \alpha^4
\end{aligned}
\)
Hence, \(\alpha^{12}=(27)^2\)
\(
\begin{aligned}
& \Rightarrow\left(\alpha^{12}\right)^8=(27)^8 \\
& \Rightarrow \alpha^{96}=(3)^{24} \\
& \text { Similarly } \beta^{96}=(3)^{24} \\
& \therefore \alpha^{96}\left(\alpha^{12}-1\right)+\beta^{96}\left(\beta^{12}-1\right)=(3)^{24} \times 52
\end{aligned}
\) -
Question 137 of 161
137. Question
If \(\alpha, \beta\) are roots of the equation \(x ^2+5(\sqrt{2}) x +10=0, \alpha>\beta\) and \(P _{ n }=\alpha^{ n }-\beta^{ n }\) for each positive integer \(n\), then the value of \(\left(\frac{P_{17} P_{20}+5 \sqrt{2} P_{17} P_{19}}{P_{18} P_{19}+5 \sqrt{2} P_{18}^2}\right)\) is equal to [JEE Main 2021 25th July Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
&\begin{aligned}
& x^2+5 \sqrt{2} x+10=0 \\
& \& p _{ a }=\alpha^{ n }-\beta^{ n } \text { (Given) } \\
& \text { Now } \frac{P_{17} P_{20}+5 \sqrt{2} P_{17} P_{19}}{P_{18} P_{19}+5 \sqrt{2} P_{18}^2}=\frac{P_{17}\left(P_{20}+5 \sqrt{2} P_{19}\right)}{P_{18}\left(P_{19}+5 \sqrt{2} P_{18}\right)} \\
& \frac{P_{17}\left(\alpha^{20}-\beta^{20}+5 \sqrt{2}\left(\alpha^{19}-\beta^{19}\right)\right)}{P_{18}\left(\alpha^{19}-\beta^{19}+5 \sqrt{2}\left(\alpha^{18}-\beta^{18}\right)\right)} \\
& \frac{P_{17}\left(\alpha^{19}(\alpha+5 \sqrt{2})-\beta^{19}(\beta+5 \sqrt{2})\right)}{P_{18}\left(\alpha^{18}(\alpha+5 \sqrt{2})-\beta^{18}(\beta+5 \sqrt{2})\right)}
\end{aligned}\\
&\text { Since } \alpha+5 \sqrt{2}=-10 / \alpha \text {. }
\end{aligned}
\)
\(1 \& \beta+5 \sqrt{2}=-10 / \beta\)
Now put there values in above expression \(=-\frac{10 P _{17} P _{18}}{-10 P _{18} P _{17}}=1\) -
Question 138 of 161
138. Question
If \(a + b + c =1, ab + bc + ca =2\) and \(abc =3\), then the value of \(a^4+b^4+c^4\) is equal to [JEE Main 2021 25th July Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& a^2+b^2+c^2=(a+b+c)^2-2 \Sigma a b=-3 \\
& (a b+b c+c a)^2=\Sigma(a b)^2+2 a b c \Sigma a
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \Sigma(a b)^2=-2 \\
& \begin{aligned}
a^4+b^4+c^4 & =\left(a^2+b^2+c^2\right)^2-2 \Sigma(a b)^2 \\
& =9-2(-2)=13
\end{aligned}
\end{aligned}
\) -
Question 139 of 161
139. Question
Let \(\alpha, \beta\) be two roots of the equation \(x ^2+(20)^{1 / 4} x +(5)^{1 / 2}=0\). Then \(\alpha^8+\beta^8\) is equal to [JEE Main 2021 27th July Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(x^2+\sqrt{5}\right)^2=\sqrt{20} x^2 \\
& x^4=-5 \Rightarrow x^8=25 \\
& \alpha^8+\beta^8=50
\end{aligned}
\) -
Question 140 of 161
140. Question
The number of real roots of the equation \(e ^{4 x }- e ^{3 x }-4 e ^{2 x }- e ^{ x }+1=0\) is equal to [JEE Main 2021 27th July Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& t ^4- t ^3-4 t ^2- t +1=0, e ^x= t >0 \\
& \Rightarrow t ^2- t -4-\frac{1}{ t }+\frac{1}{ t ^2}=0 \\
& \Rightarrow \alpha^2-\alpha-6=0, \alpha= t +\frac{1}{ t } \geq 2 \\
& \Rightarrow \alpha=3,-2 \text { (reject) } \\
& \Rightarrow t +\frac{1}{ t }=3 \\
& \Rightarrow \text { The number of real roots }=2
\end{aligned}
\) -
Question 141 of 161
141. Question
The numbers of pairs \((a, b)\) of real numbers, such that whenever \(\alpha\) is a root of the equation \(x^2+a x+b=0, \alpha^2-2\) is also a root of this equation, is : [JEE Main 2021 1st Sept Shift 2]
CorrectIncorrectHint
Consider the equation \(x^2+a x+b=0\)
If has two roots (not necessarily real \(\alpha \& \beta\) )
Either \(\alpha=\beta\) or \(\alpha \neq \beta\)
Case (1) If \(\alpha=\beta\), then it is repeated root. Given that \(\alpha^2-2\) is also a root
So, \(\alpha=\alpha^2-2 \Rightarrow(\alpha+1)(\alpha-2)=0\)
\(\Rightarrow \alpha=-1\) or \(\alpha=2\)
When \(\alpha=-1\) then \((a, b)=(2,1)\)
\(\alpha=2\) then \((a, b)=(-4,4)\)
Case (2) If \(\alpha \neq \beta\)
Then
(I) \(\alpha=\alpha^2-2\) and \(\beta=\beta^2-2\)
Hence, \(( a , b )=(-(\alpha+\beta), \alpha \beta)\)
\(
(-1,-2)
\)
(II) \(\alpha=\beta^2-2\) and \(\beta=\alpha^2-2\)
Then \(\alpha-\beta=\beta^2-\alpha^2=(\beta-\alpha)(\beta+\alpha)\)
Since \(\alpha \neq \beta\) we get \(\alpha+\beta=\beta^2+\alpha^2-4\)
\(
\alpha+\beta=(\alpha+\beta)^2-2 \alpha \beta-4
\)
Thus \(-1=1-2 \alpha \beta-4\) which implies
\(
\begin{aligned}
& \alpha \beta=-1 \text { Therefore }( a , b )=(-(\alpha+\beta), \alpha \beta) \\
& =(1,-1)
\end{aligned}
\)
(III) \(\alpha=\alpha^2-2=\beta^2-2\) and \(\alpha \neq \beta\)
\(
\Rightarrow \alpha=-\beta
\)
Thus \(\alpha=2, \beta=-2\)
\(
\alpha=-1, \beta=1
\)
Therefore \((a, b)=(0,-4) \&(0,1)\)
(IV) \(\beta=\alpha^2-2=\beta^2-2\) and \(\alpha \neq \beta\) is same as (III) Therefore we get 6 pairs of (a, b)
Which are \((2,1),(-4,4),(-1,-2),(1,-1),(0,-4)\) -
Question 142 of 161
142. Question
\(\operatorname{cosec} 18^{\circ}\) is a root of the equation : [JEE Main 2021 31st Aug Shift 1]
CorrectIncorrectHint
\(
\operatorname{cosec} 18^{\circ}=\frac{1}{\sin 18^{\circ}}=\frac{4}{\sqrt{5}-1}=\sqrt{5}+1
\)
Let \(\operatorname{cosec} 18^{\circ}=x=\sqrt{5}+1\)
\(
\Rightarrow x-1=\sqrt{5}
\)
Squaring both sides, we get
\(
\begin{aligned}
& x^2-2 x+1=5 \\
& \Rightarrow x^2-2 x-4=0
\end{aligned}
\) -
Question 143 of 161
143. Question
The number of real roots of the equation \(e ^{4 x }+2 e ^{3 x }- e ^{ x }-6=0\) is: [JEE Main 2021 31st Aug Shift 1]
CorrectIncorrectHint
Let \(e^x=t>0\)
\(
\begin{aligned}
& f(t)=t^4+2 t^3-t-6=0 \\
& f^{\prime}(t)=4 t^3+6 t^2-1
\end{aligned}
\)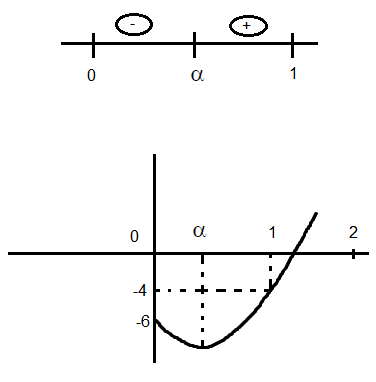
\(
f^{\prime \prime}(t)=12 t^2+12 t>0
\)\(
f(0)=-6, f(1)=-4, f(2)=24
\)
\(\Rightarrow\) Number of real roots \(=1\) -
Question 144 of 161
144. Question
The set of all values of \(k >-1\), for which the equation \(\left(3 x^2+4 x+3\right)^2-(k+1)\left(3 x^2+4 x+3\right)\) \(\left(3 x^2+4 x+2\right)+k\left(3 x^2+4 x+2\right)^2=0\) has real roots is : [JEE Main 2021 27th Aug Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(3 x^2+4 x+3\right)^2-(k+1)\left(3 x^2+4 x+3\right)\left(3 x^2+4 x+2\right) \\
& +k\left(3 x^2+4 x+2\right)^2=0 \\
& \text { Let } 3 x^2+4 x+3=a \\
& \text { and } 3 x^2+4 x+2=b \Rightarrow b=a-1 \\
& \text { Given equation becomes } \\
& \Rightarrow a^2-(k+1) a b+k b^2=0 \\
& \Rightarrow a(a-k b)-b(a-k b)=0 \\
& \Rightarrow(a-k b)(a-b)=0 \Rightarrow a=k b \text { or } a=b(\text { reject }) \\
& \because a=k b \\
& \Rightarrow 3 x^2+4 x+3=k\left(3 x^2+4 x+2\right) \\
& \Rightarrow 3(k-1) x^2+4(k-1) x+(2 k-3)=0
\end{aligned}
\)
\(
D \geq 0
\)
\(
\begin{aligned}
& \Rightarrow 16( k -1)^2-4(3( k -1))(2 k -3) \geq 0 \\
& \Rightarrow 4( k -1)\{4( k -1)-3(2 k -3)\} \geq 0 \\
& \Rightarrow 4( k -1)\{-2 k +5\} \geq 0 \\
& \Rightarrow-4( k -1)\{2 k -5\} \geq 0 \\
& \Rightarrow( k -1)(2 k -5) \leq 0
\end{aligned}
\)
\(
\begin{aligned}
& \therefore k \in\left[1, \frac{5}{2}\right] \\
& \because k \neq 1 \\
& \therefore k \in\left(1, \frac{5}{2}\right]
\end{aligned}
\) -
Question 145 of 161
145. Question
The number of distinct real roots of the equation \(3 x^4+4 x^3-12 x^2+4=0\) is [JEE Main 2021 27th Aug Shift 1]
CorrectIncorrectHint
Let \(f(x)=3 x^4+4 x^3-12 x^2+4\)
differentiation w.r.t. \(x\), we get
\(
\begin{aligned}
& \Rightarrow f^{\prime}(x)=12 x^3+12 x^2-24 x \\
& \Rightarrow f^{\prime}(x)=12 x(x+2)(x-1)
\end{aligned}
\)
For \(\max / \min , f^{\prime}(x)=0\)
\(
\begin{aligned}
& \Rightarrow x =0,-2,1 \\
& \Rightarrow f (0)=4, f (-2)=-28, f (1)=-1
\end{aligned}
\)
So, using intermediate value theorem on the given function, 4 real roots exist. -
Question 146 of 161
146. Question
Let \(\lambda \neq 0\) be in \(R\). If \(\alpha\) and \(\beta\) are the roots of the equation \(x^2-x+2 \lambda=0\), and \(\alpha\) and \(\gamma\) are the roots of equation \(3 x^2-10 x+27 \lambda=0\), then \(\frac{\beta \gamma}{\lambda}\) is equal to [JEE Main 2021 26th Aug Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& 3 \alpha^2-10 \alpha+27 \lambda=0 \dots(1) \\
& \alpha^2-\alpha+2 \lambda=0 \dots(2)
\end{aligned}
\)
\((1)-3(2)\) gives
\(
-7 \alpha+21 \lambda=0 \Rightarrow \alpha=3 \lambda
\)
Put \(\alpha=3 \lambda\) in equation (1) we get
\(
\begin{aligned}
& 9 \lambda^2-3 \lambda+2 \lambda-0 \\
& 9 \lambda^2=\lambda \Rightarrow \lambda=\frac{1}{9} \text { as } \lambda \neq 0
\end{aligned}
\)
Now \(\alpha=3 \lambda \Rightarrow \lambda=\frac{1}{3}\)
\(
\begin{aligned}
& \alpha+\beta=1 \Rightarrow \beta=2 / 3 \\
& \alpha+\gamma=\frac{10}{3} \Rightarrow \gamma=3 \\
& \frac{\beta \gamma}{\lambda}=\frac{\frac{2}{3} \times 3}{\frac{1}{9}}=18
\end{aligned}
\) -
Question 147 of 161
147. Question
The sum of all integral values of \(k ( k \neq 0)\) for which the equation \(\frac{2}{x-1}-\frac{1}{x-2}=\frac{2}{k}\) in \(x\) has no real roots, is [JEE Main 2021 26th Aug Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{2}{x-1}-\frac{1}{x-2}=\frac{2}{k} \\
& x \in R-\{1,2\} \\
& \Rightarrow k (2 x -4- x +1)=2\left( x ^2-3 x +2\right) \\
& \Rightarrow k ( x -3)=2\left( x ^2-3 x +2\right) \\
& \text { for } x \neq 3, \quad k=2\left(x-3+\frac{2}{x-3}+3\right) \\
& x -3+\frac{2}{ x -3} \geq 2 \sqrt{2}, \forall x >3 \\
& \& x-3+\frac{2}{x-3} \leq-2 \sqrt{2}, \forall x<-3 \\
& \Rightarrow 2\left(x-3+\frac{2}{x-3}+3\right) \in(-\infty, 6-4 \sqrt{2}] \cup[6+4 \sqrt{2}, \infty)
\end{aligned}
\)
for no real roots
\(
k \in(6-4 \sqrt{2}, 6+4 \sqrt{2})-\{0\}
\)
Integral \(k \in\{1,2 \ldots \ldots .11\}\)
Sum of \(k =66\) -
Question 148 of 161
148. Question
Let \(p\) and \(q\) be two positive number such that \(p+q=2\) and \(p^4+q^4=272\). Then \(p\) and \(q\) are roots of the equation : [JEE Main 2021 24th Feb Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(p^2+q^2\right)^2-2 p^2 q^2=272 \\
& \left((p+q)^2-2 p q\right)^2-2 p^2 q^2=272 \\
& 16+16 p q+2 p^2 q^2=272 \\
& (p q)^2-8 p q-128=0 \\
& pq =\frac{8 \pm 24}{2}=16,-8 \\
& pq =16 \\
& \text { Now } \\
& x^2-(p+q) x+p q=0 \\
& x^2-2 x+16=0
\end{aligned}
\) -
Question 149 of 161
149. Question
Let \(a, b, c\) be in arithmetic progression. Let the centroid of the triangle with vertices \((a, c),(2, b)\) and \((a, b)\) be \(\left(\frac{10}{3}, \frac{7}{3}\right)\). If \(\alpha, \beta\) are the roots of the equation \(a x^2+b x+1=0\), then the value of \(\alpha^2+\beta^2-\alpha \beta\) is: [JEE Main 2021 24th Feb Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& 2 b=a+c \\
& \frac{2 a+2}{3}=\frac{10}{3} \text { and } \frac{2 b+c}{3}=\frac{7}{3} \\
& \left.a=4, \begin{array}{l}
2 b+c=7 \\
2 b-c=4
\end{array}\right\} \text {, solving } \\
& b=\frac{11}{4} \\
& c=\frac{3}{2} \\
&
\end{aligned}
\)
\(\therefore\) Quadratic Equation is \(4 x^2+\frac{11}{4} x+1=0\)
\(\therefore\) The value of \((\alpha+\beta)^2-3 \alpha \beta=\frac{121}{256}-\frac{3}{4}=-\frac{71}{256}\) -
Question 150 of 161
150. Question
The number of the real roots of the equation \((x+1)^2+|x-5|=\frac{27}{4}\) is [JEE Main 2021 24th Feb Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& x \geq 5 \\
& (x+1)^2+(x-5)=\frac{27}{4} \\
& \Rightarrow x^2+3 x-4=\frac{27}{4} \\
& \Rightarrow x^2+3 x-\frac{43}{4}=0 \\
& \Rightarrow 4 x^2+12 x-43=0 \\
& x=\frac{-12 \pm \sqrt{144+688}}{8} \\
& x=\frac{-12 \pm \sqrt{832}}{8}=\frac{-12 \pm 28.8}{8}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{-3 \pm 7.2}{2} \\
& =\frac{-3+7.2}{2}, \frac{-3-7.2}{2} \text { (Therefore no solution) }
\end{aligned}
\)
For \(x \leq 5\)
\(
\begin{aligned}
& (x+1)^2-(x-5)=\frac{27}{4} \\
& x^2+x+6-\frac{27}{4}=0 \\
& 4 x^2+4 x-3=0 \\
& x=\frac{-4 \pm \sqrt{16+48}}{8} \\
& x=\frac{-4 \pm 8}{8} \Rightarrow x=-\frac{12}{8}, \frac{4}{8}
\end{aligned}
\)
\(\therefore 2\) Real Root’s -
Question 151 of 161
151. Question
The coefficients \(a, b\) and \(c\) of the quadratic equation, \(a x^2+b x+c=0\) are obtained by throwing a dice three times. The probability that this equation has equal roots is: [JEE Main 2021 25th Feb Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& a x^2+b x+c=0 \\
& a, b, c \in\{1,2,3,4,5,6\} \\
& n(s)=6 \times 6 \times 6=216 \\
& D=0 \Rightarrow b^2=4 a c \\
& a c=\frac{b^2}{4} \text { If } b=2, a c=1 \Rightarrow a=1, c=1 \\
& \text { If } b=4, a c=4 \Rightarrow a=1, c=4
\end{aligned}
\)
\(
\begin{gathered}
a =4, c =1 \\
\text { If } ~b =6, ac =9 \Rightarrow a=3, c=3 \\
\therefore \text { probability }=\frac{5}{216}
\end{gathered}
\) -
Question 152 of 161
152. Question
The integer ‘ \(k\) ‘, for which the inequality \(x^2-2(3 k-1) x+8 k^2-7>0\) is valid for every \(x\) in \(R\) is : [JEE Main 2021 25th Feb Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& D<0 \\
& (2(3 k-1))^2-4\left(8 k^2-7\right)<0 \\
& 4\left(9 k^2-6 k+1\right)-4\left(8 k^2-7\right)<0 \\
& k^2-6 k+8<0 \\
& (k-4)(k-2)<0
\end{aligned}
\)
\(
2<k<4
\)
then \(k=3\) -
Question 153 of 161
153. Question
If \(\alpha, \beta \in R\) are such that \(1-2 i\) (here \(i ^2=-1\) ) is a root of \(z ^2+\alpha z +\beta=0\), then \((\alpha-\beta)\) is equal to: [JEE Main 2021 25th Feb Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& (1-2 i)^2+\alpha(1-2 i)+\beta=0 \\
& 1-4-4 i+\alpha-2 i \alpha+\beta=0 \\
& (\alpha+\beta-3)-i(4+2 \alpha)=0 \\
& \alpha+\beta-3=0 \quad \& 4+2 \alpha=0 \\
& \alpha=-2 \quad \beta=5 \\
& \alpha-\beta=-7
\end{aligned}
\) -
Question 154 of 161
154. Question
Let \(\alpha\) and \(\beta\) be the roots of \(x^2-6 x-2=0\). If \(a_n=\alpha^n-\beta^n\) for \(n \geq 1\), then the value of \(\frac{a_{10}-2 a_8}{3 a_9}\) is: [JEE Main 2021 25th Feb Shift 2]
CorrectIncorrectHint
Step 1: Equating the quadratic equation by substituting \(\alpha\) and \(\beta\) in the equation
The given quadratic equation is
\(
x^2-6 x-2=0 \ldots(i)
\)
And \(\alpha\) and \(\beta\) be the roots of this equation
Substituting \(x=\alpha\) in \((i)\)
\(
\begin{aligned}
& \Rightarrow \alpha^2-6 \alpha-2=0 \\
& \Rightarrow \quad \alpha^2-2=6 \alpha \dots(ii)
\end{aligned}
\)
And substituting \(x=\beta\) in \((i)\)
\(
\begin{aligned}
& \Rightarrow \beta^2-6 \beta-2=0 \\
& \Rightarrow \quad \beta^2-2=6 \beta \ldots(i i i)
\end{aligned}
\)
Step 2: Equating for \(\frac{\left(a_{10}-2 a_8\right)}{\left(3 a_9\right)}\)
Since given that \(a_n=\alpha^n-\beta^n\)
Therefore,
\(
\Rightarrow \frac{\left(a_{10}-2 a_8\right)}{\left(3 a_9\right)}=\frac{\left(\alpha^{10}-\beta^{10}\right)-2\left(\alpha^8-\beta^8\right)}{3\left(\alpha^9-\beta^9\right)}
\)
\(
\begin{aligned}
& =\frac{\left(\alpha^{10}-2 \alpha^8\right)-\left(\beta^{10}-2 \beta^8\right)}{3\left(\alpha^9-\beta^9\right)} \\
& =\frac{\alpha^8\left(\alpha^2-2\right)-\beta^8\left(\beta^2-2\right)}{3\left(\alpha^9-\beta^9\right)} \\
& =\frac{\alpha^8(6 \alpha)-\beta^8(6 \beta)}{3\left(\alpha^9-\beta^9\right)} \quad[\text { from equation }(i i) and (i i i)]
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{6\left(\alpha^9-\beta^9\right)}{3\left(\alpha^9-\beta^9\right)} \\
& =\frac{6}{3} \\
& =2
\end{aligned}
\)
Thus, \(\frac{\left(a_{10}-2 a_8\right)}{\left(3 a_9\right)}=2\) -
Question 155 of 161
155. Question
The number of solutions of the equation \(\log _4(x-1)=\log _2(x-3)\) is [JEE Main 2021 26th Feb Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{1}{2} \log _2(x-1)=\log _2(x-3) \\
& x-1=(x-3)^2 \\
& x^2-6 x+9=x-1 \\
& x^2-7 x+10=0
\end{aligned}
\)
\(
x=2,5
\)
\(X=2 \quad\) Not possible as \(\log _2(x-3)\) is not defined \(\Rightarrow\) No. of solution \(=1\) -
Question 156 of 161
156. Question
Let \(\alpha\) and \(\beta\) be two real numbers such that \(\alpha+\beta=1\) and \(\alpha \beta=-1\). Let \(P_n=(\alpha)^n+(\beta)^n, P_{n-1}=11\) and \(P_{n+1}=29\) for some integer \(n \geq 1\). Then, the value of \(P_n^2\) is [JEE Main 2021 26th Feb Shift 2]
CorrectIncorrectHint
Given, \(\alpha+\beta=1, \alpha \beta=-1\)
\(\therefore\) Quadratic equation with roots \(\alpha, \beta\) is \(x^2-x-1=0 \Rightarrow \alpha^2=\alpha+1\)
Multiplying both sides by \(\alpha^{n-1} \alpha^{n+1}=\alpha^n+\alpha^{n-1} \dots(1)\)
Similarly, \(\beta^{n+1}=\beta^n+\beta^{n-1} \dots(2)\)
\(
\begin{aligned}
& \text { Adding (1)\&(2) } \alpha^{ n +1}+\beta^{ n +1}=\left(\alpha^{ n }+\beta^{ n }\right)+\left(\alpha^{ n -1}+\beta^{ n -1}\right) \\
& \Rightarrow P_{n+1}=P_n+P_{n-1} \\
& \Rightarrow 29= P _{ n }+11 \text { ( Given }, P _{ n +1}=29, P _{ n -1}=11 \text { ) } \\
& \Rightarrow P_n=18 \\
& \therefore P_n^2=18^2=324
\end{aligned}
\) -
Question 157 of 161
157. Question
The number of elements in the set \(\{ x \in R :(| x |-3)| x +4|=6\}\) is equal to [JEE Main 2021 16th March Shift 1]
CorrectIncorrectHint
Case 1:
\(
\begin{aligned}
& x \leq-4 \\
& (-x-3)(-x-4)=6 \\
& \Rightarrow(x+3)(x+4)=6 \\
& \Rightarrow x^2+7 x+6=0 \\
& \Rightarrow x=-1 \text { or }-6 \\
& \text { but } x \leq-4 \\
& x=-6
\end{aligned}
\)
Case 2 :
\(
\begin{aligned}
& x \in(-4,0) \\
& (-x-3)(x+4)=6 \\
& \Rightarrow-x^2-7 x-12-6=0 \\
& \Rightarrow x^2+7 x+18=0 \\
& D<0 \text { No solution }
\end{aligned}
\)
Case 3 :
\(
\begin{aligned}
& x \geq 0 \\
& (x-3)(x+4)=6 \\
& \Rightarrow x^2+x-12-6=0 \\
& \Rightarrow x^2+x-18=0 \\
& x=\frac{-1 \pm \sqrt{1+72}}{2} \\
& \therefore x=\frac{\sqrt{73}-1}{2} \text { only }
\end{aligned}
\)Number of solutions = 2
-
Question 158 of 161
158. Question
Let \(P ( x )= x ^2+ bx + c\) be a quadratic polynomial with real coefficients such that \(\int_0^1 P ( x ) dx =1\) and \(P ( x )\) leaves remainder 5 when it is divided by \((x-2)\). Then the value of \(9(b+c)\) is equal to: [JEE Main 2021 16th March Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \int_0^1\left(x^2+b x+c\right) d x=1 \\
& \frac{1}{3}+\frac{b}{2}+c=1 \\
& \Rightarrow \frac{b}{2}+c=\frac{2}{3} \\
& 3 b+6 c=4 \dots(1) \\
& P(2)=5 \\
& 4+2 b+c=5 \\
& 2 b+c=1 \dots(2)
\end{aligned}
\)
From (1) & (2)
\(
\begin{aligned}
& b =\frac{2}{9} \quad \& \quad c =\frac{5}{9} \\
& 9( b + c )=7
\end{aligned}
\) -
Question 159 of 161
159. Question
The value of \(4+\frac{1}{5+\frac{1}{4+\frac{1}{5+\frac{1}{4+\ldots \ldots \infty}}}}\) [JEE Main 2021 17th March Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& y=4+\frac{1}{\left(5+\frac{1}{y}\right)} \\
& y-4=\frac{y}{(5 y+1)} \\
& 5 y^2-20 y-4=0 \\
& y=\frac{20+\sqrt{480}}{10} \\
& y=\frac{20-\sqrt{480}}{10} \rightarrow \text { rejected } \\
& y=2+\sqrt{\frac{480}{100}}
\end{aligned}
\) -
Question 160 of 161
160. Question
The value of \(3+\frac{1}{4+\frac{1}{3+\frac{1}{4+\frac{1}{3+\ldots \infty}}}}\) is equal to [JEE Main 2021 18th March Shift 1]
CorrectIncorrectHint
Let \(x=3+\frac{1}{4+\frac{1}{3+\frac{1}{4+\frac{1}{3+\ldots \infty}}}}\)
\(
\begin{aligned}
& \text { So, } x=3+\frac{1}{4+\frac{1}{x}}=3+\frac{1}{\frac{4 x+1}{x}} \\
& \Rightarrow(x-3)=\frac{x}{(4 x+1)} \\
& \Rightarrow(4 x+1)(x-3)=x \\
& \Rightarrow 4 x^2-12 x+x-3=x \\
& \Rightarrow 4 x^2-12 x-3=0 \\
& x =\frac{12 \pm \sqrt{(12)^2+12 \times 4}}{2 \times 4}=\frac{12 \pm \sqrt{12(16)}}{8} \\
& =\frac{12 \pm 4 \times 2 \sqrt{3}}{8}=\frac{3 \pm 2 \sqrt{3}}{2} \\
& x=\frac{3}{2} \pm \sqrt{3}=1.5 \pm \sqrt{3}
\end{aligned}
\)
But only positive value is accepted
So, \(x=1.5+\sqrt{3}\) -
Question 161 of 161
161. Question
If \(f(x)\) and \(g(x)\) are two polynomials such that the polynomial \(P ( x )=f\left( x ^3\right)+ xg \left( x ^3\right)\) is divisible by \(x^2+x+1\), then \(P(1)\) is equal to [JEE Main 2021 18th March Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& P(x)=f\left(x^3\right)+x g\left(x^3\right) \\
& P(1)=f(1)+g(1) \ldots(1)
\end{aligned}
\)
Now \(P ( x )\) is divisible by \(x ^2+ x +1\)
\(
\Rightarrow P ( x )= Q ( x )\left( x ^2+ x +1\right)
\)
\(P ( w )=0= P \left( w ^2\right)\) where \(w , w ^2\) are non-real cube roots of units.
\(
\begin{aligned}
& P(x)=f\left(x^3\right)+x g\left(x^3\right) \\
& P(w)=f\left(w^3\right)+w g\left(w^3\right)=0 \\
& f(1)+w g(1)=2 \ldots(2) \\
& P\left(w^2\right)=f\left(w^6\right)+w^2 g\left(w^6\right)=0 \\
& f(1)+w^2 g(1)=0 \ldots(3)
\end{aligned}
\)
\(
\begin{aligned}
&\begin{aligned}
& (2)+(3) \\
& \Rightarrow 2 f(1)+\left(w+w^2\right) g(1)=0 \\
& 2 f(1)=g(1) \ldots(4)
\end{aligned}\\
&\begin{aligned}
& (2)-(3) \\
& \Rightarrow\left(w-w^2\right) g(1)=0 \\
& g(1)=0=f(1) \text { from (4) } \\
& \text { from (1) } P(1)=f(1)+g(1)=0
\end{aligned}
\end{aligned}
\)