Derivatives

A derivative in calculus is the rate of change of a quantity \(y\) with respect to another quantity \(x\). It is also termed the differential coefficient of \(y\) with respect to \(\mathrm{x}\). Differentiation is the process of finding the derivative of a function.

To find the derivative of a function we need to understand how to calculate the slope of a line because the definition of the derivative is derived from the formula for the slope of a line.

\(\text { Slope }=\frac{\text { Change in } y}{\text { Change in } x}\)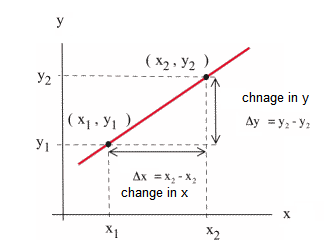

We can find the average slope between two points P and Q as shown in figure(a) and figure(b) shows the slope at a point that shows there is nothing to measure.

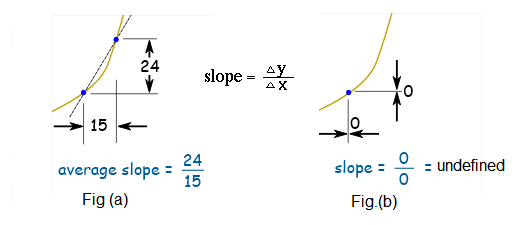
We can not find the derivative of a function at a particular point as there is nothing to measure as the result turns out to be \(\frac{0}{0}\). But using limits we can calculate the derivative of a function at a point by shrinking \(\Delta x\) towards 0.

Definition of Derivative

The derivative of a function is the rate of change of the function’s output relative to its input value. Given \(y=f(x)\), the derivative of \(f(x)\), denoted \(f^{\prime}(x)\) (or \(\left.d f(x) / d x\right)\), is defined by the following limit:
\(
f^{\prime}(x)=\frac{\Delta y}{\Delta x}=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}
\)

This formula is popularly known as the “limit definition of the derivative” (or) “derivative by using the first principle”.

We know the slope of a line is the rate of change of the line, which is computed as the ratio of the change in \(y\) to the change in \(x\). Geometrically, the derivative is the slope of the line tangent to the curve at a point of interest. Typically, we calculate the slope of a line using two points on the line. This is not possible for a curve, since the slope of a curve changes from point to point. Consider the figure below.

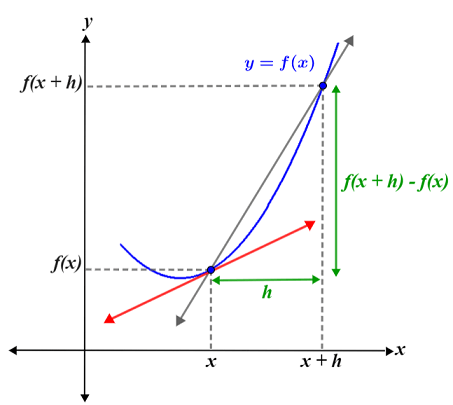
The figure shows a curve (blue) with two points: \((x, f(x))\) and \((x+h, f(x+h))\). The grey secant line represents the slope between these two points and is computed as:
\(
m=\frac{\Delta y}{\Delta x}=\frac{f(x+h)-f(x)}{h}
\)

Similarly, we can find the slope of a function \(f(x)\) at a point “a” defined as \(f^{\prime}(a)\) and is given by

\(f^{\prime}(a)=\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\)

Essentially, this limit finds the rate of change between two points as those points become increasingly close to each other and converge to a point with no distance between each other \(h=0)\)

Example 23: Find the derivative of the function \(f(x)=x^2\)

Solution:

\(
\begin{aligned}
&f^{\prime}(x)=\lim _{h \rightarrow 0}\left[(x+h)^2-x^2\right] / h \\
&=\lim _{h \rightarrow 0}\left[x^2+2 x h+h^2-x^2\right] / h \\
&=\lim _{h \rightarrow 0}\left[2 x h+h^2\right] / h \\
&=\lim _{h \rightarrow 0}[h(2 x+h)] / h \\
&=\lim _{h \rightarrow 0}(2 x+h) \\
&=2 x+0 \\
&=2 x
\end{aligned}
\)

If we want to find the derivative of the function at \(x=2\), \(f^{\prime}(2)=2(2)=4\).

Example 24: Find the derivative of the function \(f(x)=\sin (x)\)

Solution: To solve this problem, we will use the following trigonometric identities and limits.

\(
\begin{aligned}
&\begin{aligned}
&\sin (x+h)=\sin (x) \cos (h)+\sin (h) \cos (x) \dots(1)\\
&\lim _{h \rightarrow 0} \cos (h)=\cos (0)=1 \dots(2)
\end{aligned}\\
&\lim _{h \rightarrow 0} \frac{\sin (h)}{h}=1 \dots(3)
\end{aligned}
\)

The points at which the above identities and limits are applied will be denoted using their respective identifiers: (1), (2), and (3).

\(
\begin{aligned}
f^{\prime}(x) &=\lim _{h \rightarrow 0} \frac{\sin (x+h)-\sin (x)}{h} \\
&=\lim _{h \rightarrow 0} \frac{\sin (x) \cos (h)+\sin (h) \cos (x)-\sin (x)}{h} \\
&=\lim _{h \rightarrow 0} \frac{\sin (x)+\sin (h) \cos (x)-\sin (x)}{h} \\
&=\lim _{h \rightarrow 0} \frac{\sin (h) \cos (x)}{h} \\
&=1 \cdot \cos (x)=\cos (x)
\end{aligned}
\)

Thus, the derivative of \(\sin (x)\) is \(\cos (x)\), or:
\(f^{\prime}(x)=\frac{d}{d x}(\sin (x))=\cos (x)\)

Derivative Formulas in Calculus

Fortunately, the rules for computing the derivatives for different types of functions are well-defined, so simply knowing (or being able to reference) these rules enables us to differentiate most functions.

Derivatives of Log/Exponential functions

\(d / d x(\ln x)=1 / x \)
\(d / d x\left(\log _a x\right)=1 /(x \ln a)\)
\(d / d x\left(e^x\right)=e^x\)
\(d / d x\left(a^x\right)=a^x \ln a\)

Derivatives of Trigonometric Functions

\(
\begin{aligned}
&\frac{d}{d x}(\sin x)=\cos x \\
&\frac{d}{d x}(\cos x)=-\sin x \\
&\frac{d}{d x}(\tan x)=\sec ^2 x \\
&\frac{d}{d x}(\cot x)=-\operatorname{cosec}^2 x \\
&\frac{d}{d x}(\sec x)=\sec x \tan x \\
&\frac{d}{d x}(\operatorname{cosec} x)=-\operatorname{cosec} x \cot x
\end{aligned}
\)

Derivatives of Inverse Trigonometric Functions

\(
\begin{aligned}
&\frac{d}{d x}\left(\sin ^{-1} x\right)=\frac{1}{\sqrt{1-x^2}}\\
&\frac{d}{d x}\left(\cos ^{-1} x\right)=-\frac{1}{\sqrt{1-x^2}}\\
&\frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{1+x^2}\\
&\frac{d}{d x}\left(\csc ^{-1} x\right)=-\frac{1}{|x| \sqrt{x^2-1}}\\
&\frac{d}{d x}\left(\sec ^{-1} x\right)=\frac{1}{|x| \sqrt{x^2-1}}\\
&\frac{d}{d x}\left(\cot ^{-1} x\right)=-\frac{1}{1+x^2}
\end{aligned}
\)

Fundamental Rules of Derivatives

Power Rule of Derivatives

\(d / d x\left(x^n\right)=n x^{n-1}\)

Example 25: Evaluate derivative of the function \(y = (x^5)\)

Solution: \(dy / d x=5 x^4\)

Sum Rule of Differentiation

If the function is the sum or difference of two functions, then the derivative of the functions is the sum or difference of the individual functions, i.e.,

If \(f(x)=u(x) \pm v(x)\), then;
\(f^{\prime}(x)=u^{\prime}(x) \pm v^{\prime}(x)\)

Example 26: \(f(x)=2x+x^3\)

Solution:
By applying the sum rule of derivative here, we have:
\(f^{\prime}(x)=u^{\prime}(x)+v^{\prime}(x)\)
Now, differentiating the given function, we get;
\(
\begin{aligned}
&f^{\prime}(x)=d / d x\left(2x+x^3\right) \\
&f^{\prime}(x)=d / d x(2x)+d / d x\left(x^3\right) \\
&f^{\prime}(x)=2+3 x^2
\end{aligned}
\)

Example 27: \(f(x)=3 x^2-4 x\)

Solution:

Given function is: \(f(x)=3 x^2-4 x\)
This is of the form \(f(x)=u(x)-v(x)\)
So by applying the difference rule of derivatives, we get,
\(
\begin{aligned}
&f^{\prime}(x)=d / d x\left(3 x^2\right)-d / d x(4 x) \\
&=3(2 x)-4(1) \\
&=6 x-4
\end{aligned}
\)
Therefore, \(f^{\prime}(x)=6 x-4\)

Product Rule of Differentiation

According to the product rule of derivatives, if the function f(x) is the product of two functions u(x) and v(x), then the derivative of the function is given by:

If \(f(x)=u(x) \times v(x)\), then:
\(f^{\prime}(x)=u^{\prime}(x) \times v(x)+u(x) \times v^{\prime}(x)\)

Example 28: Find the derivative of \(x^2(x+5)\)

Solution:

As per the product rule of derivative, we know;
\(
f^{\prime}(x)=u^{\prime}(x) \times v(x)+u(x) \times v^{\prime}(x)
\)
Here,
\(u(x)=x^2\) and \(v(x)=x+5\)
Therefore, on differentiating the given function, we get;
\(
\begin{aligned}
&f^{\prime}(x)=d / d x\left[x^2(x+5)\right] \\
&f^{\prime}(x)=d / d x\left(x^2\right)(x+5)+x^2 d / d x(x+5) \\
&f^{\prime}(x)=2 x(x+5)+x^2(1) \\
&f^{\prime}(x)=2 x^2+10 x+x^2 \\
&f^{\prime}(x)=3 x^2+10 x
\end{aligned}
\)

Quotient Rule of Differentiation

If \(f(x)\) is a function, which is equal to ratio of two functions \(u(x)\) and \(v(x)\) such that; \(f(x)=u(x) / v(x)\)
Then, as per the quotient rule, the derivative of \(f(x)\) is given by;
\(
\mathbf{f}^{\prime}(\mathbf{x})=\frac{\mathbf{u}^{\prime}(\mathbf{x}) \times \mathbf{v}(\mathbf{x})-\mathbf{u}(\mathbf{x}) \times \mathbf{v}^{\prime}(\mathbf{x})}{(\mathbf{v}(\mathbf{x}))^2}
\)

Example 29: Find derivative of the function \(g(x)=x /(x+1)\)

Solution:

The derivative of the given function is \(g^{\prime}(x)=d / d t .[x /(x+1)]\) \([(x+1) d / d x(x)-x d / d x(x+1)] /(x+1)^2[\) Applying the quotient rule of derivatives]
\(=[(x+1)(1)-x(1+0)] /(x+1)^2\)
Thus \(g^{\prime}(x)=1 /(x+1)^2\)

Chain Rule of Differentiation (Derivatives of composite functions)

If a function \(y=f(x)=g(u)\) and if \(u=h(x)\), then the chain rule for differentiation is defined as;
\(d y / d x=(d y / d u) \times(d u / d x)\)
This rule is majorly used in the method of substitution where we can perform differentiation of composite functions.

Example 30: Find the derivative of \(f(x)=e^{\sin (2 x)}\)

Solution:

Given, \(f(x)=e^{\sin (2 x)}\)
Let \(t=g(x)=\sin 2 x\) and \(u(t)=e^t\)
According to the chain rule,
\(\mathrm{df} / \mathrm{dx}=(\mathrm{du} / \mathrm{dt}) \times(\mathrm{dt} / \mathrm{dx})\)
Here,
\(d u / d t=d / d t\left(e^t\right)=e^t\)
\(d t / d x=(d / d x) \times g(x)\)
\(=\mathrm{d} / \mathrm{dx}(\sin 2 \mathrm{x})\)
\(=2 \cos 2 \mathrm{x}\)
Thus, \(d f / d x=e^t \times 2 \cos 2 x\)
\(=e^{\sin (2 x)} \times 2 \cos 2 x\)
\(=2 \cos (2 x) e^{\sin (2 x)}\)

Constant multiple Rule

The constant multiple rule of derivatives states that \(d / d x[c(f(x)]=c \cdot d / d x f(x)\). i.e., the constant which when multiplied by a function, comes out of the differentiation process.

Example 31: \(d / d x\left(5 x^2\right)=5 \mathrm{~d} / d x\left(x^2\right)=5(2 x)=10 x\).

Derivatives of Implicit Functions

In equations where \(y\) as a function of \(x\) cannot be explicitly defined by the variables \(x\) and \(y\), we use implicit differentiation. In this case, we take derivatives of the question on both sides and solve for \(dy / dx\). Let’s look at the example below:

Example 32: Find the derivative of the equation \(2 x+y=12\)

Solution:

\(
\begin{aligned}
&d / d x(2 x+y)=d / d x(0) \\
&2+d y / d x=0 \\
&d y / d x=-2
\end{aligned}
\)

Parametric Derivatives

In a function, we may have the dependent variables \(x\) and \(y\) which are dependent on the third independent variable.

If \(x=f(t)\) and \(y=g(t)\), then derivative is calculated as \(d y / d x=g^{\prime}(x) / f^{\prime}(x)\).

Suppose, if \(x=4+t^2\) and \(y\) \(=4 t^2-5 t^4\), then we find \(d y / d x\) as follows.
\(\mathrm{dx} / \mathrm{dt}=2 \mathrm{t}\) and \(\mathrm{dy} / \mathrm{dt}=8 \mathrm{t}-20 \mathrm{t}^3\)
\(\mathrm{dy} / \mathrm{dx}=(\mathrm{dy} / \mathrm{dt}) /(\mathrm{dx} / \mathrm{dt})\)
\(\mathrm{d} y / \mathrm{dx}=\left(8 \mathrm{t}-20 \mathrm{t}^3\right) / 2 \mathrm{t}\)
\(=2 \mathrm{t}\left(4-10 \mathrm{t}^2\right) / 2 \mathrm{t}\)
\(\mathrm{d} y / \mathrm{dx}=4-10 \mathrm{t}^2\)

It says that the limit when we divide one function by another is the same after we take the derivative of each function (with some special conditions shown later).

\(
\begin{aligned}
&\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{f^{\prime}(a)}{g^{\prime}(a)} \\
&\text {, if } \\
&\lim _{x \rightarrow a} \frac{f(x)}{g(x)}
\end{aligned}
\)
gives the form \(0 / 0\), Which is indeterminate, so we are stuck?
Where, \(f(a)=0\) and \(g(a)=0\).

Example 34: Evaluate the limit \(\lim _{x \rightarrow 2} \frac{x^2+x-6}{x^2-4}\)

Solution: At \({x}={2}\) we would normally get:
\(
\frac{2^2+2-6}{2^2-4}=\frac{0}{0}
\)
Which is indeterminate, so we are stuck. Or are we?
Let’s try L’Hôpital!
Differentiate both top and bottom (see Derivative Rules ):
\(
\lim _{x \rightarrow 2} \frac{x^2+x-6}{x^2-4}=\lim _{x \rightarrow 2} \frac{2 x+1-0}{2 x-0}
\)
Now we just substitute \({x}={2}\) to get our answer:
\(
\lim _{x \rightarrow 2} \frac{2 x+1-0}{2 x-0}=\frac{5}{4}
\)

Example 35: Evaluate \(\lim _{x \rightarrow \infty} \frac{e^x}{x^2}\)

Solution:
Normally this is the result:
\(
\lim _{x \rightarrow \infty} \frac{e^x}{x^2}=\frac{\infty}{\infty}
\)
Both head to infinity. Which is indeterminate.
But let’s differentiate both top and bottom (note that the derivative of \(\mathrm{e}^{\mathrm{x}}\) is \(\mathrm{e}^{\mathrm{x}}\) ):
\(
\lim _{x \rightarrow \infty} \frac{e^x}{x^2}=\lim _{x \rightarrow \infty} \frac{e^x}{2 x}
\)
This is still not solved, both tending towards infinity. But we can use it again:
\(
\lim _{x \rightarrow \infty} \frac{e^x}{x^2}=\lim _{x \rightarrow \infty} \frac{e^x}{2 x}=\lim _{x \rightarrow \infty} \frac{e^x}{2}
\)
Now we have:
\(
\lim _{x \rightarrow \infty} \frac{e^x}{2}=\infty
\)

Conditions

Differentiable: For a limit approaching \(\mathrm{a}\), the original functions must be differentiable either side of “a”, but not necessarily at “a”.
Likewise \(g^{\prime}(x)\) is not equal to zero either side of \(a\).
The Limit must exist
\(
\lim _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}
\)

Example 36: Evaluate \(\lim _{x \rightarrow \infty} \frac{x+\cos (x)}{x}\)

Solution:
Which is a \(\frac{\infty}{\infty}\) case. Let’s differentiate top and bottom:
\(
\lim _{x \rightarrow \infty} \frac{1-\sin (x)}{1}
\)
And because it just wiggles up and down it never approaches any value.
So that new limit does not exist!
And so L’Hôpital’s Rule is not usable in this case.
But we can do this:
\(
\lim _{x \rightarrow \infty} \frac{x+\cos (x)}{x}=\lim _{x \rightarrow \infty}\left(1+\frac{\cos (x)}{x}\right)
\)
As \(x\) goes to infinity then \(\frac{\cos (x)}{x}\) tends to between \(\frac{-1}{\infty}\) and \(\frac{+1}{\infty}\), and both tend to zero.
And we are left with just the “1”, so:
\(
\lim _{x \rightarrow \infty} \frac{x+\cos (x)}{x}=\lim _{x \rightarrow \infty}\left(1+\frac{\cos (x)}{x}\right)=1
\)

Example 37: What is the equation of the tangent line to \(f(x)=x^2+\) \(5 x\) at \(x=4 ?\)

Solution: 

Given \(f(x)=x^2+5 x\)
\(
f(4)=4^2+5(4)=16+20=36
\)
The derivative of \(f(x)\) at the given point is the slope of the tangent line.
\(
\begin{aligned}
&f^{\prime}(x)=d / d x\left(x^2+5 x\right)=2 x+5 \\
&f^{\prime}(4)=2(4)+5=13 \\
&m=13
\end{aligned}
\)
Thus the equation of the tangent at \((4,36)\) is given by the slope formula: \(y-y_1=m\left(x-x_1\right)\)
\(
\begin{aligned}
&y-36=13(x-4) \\
&y-36=13 x-52 \\
&y=13 x-52+36 \\
&y=13 x-16
\end{aligned}
\)