Angles on the Coordinate Plane

We have heard sometimes people say they’ve done ‘a complete 180?’ What does that really mean? For example, if  you are facing North and you complete a 180-degree rotation, you’d now be facing South. It doesn’t matter which direction, clockwise or counterclockwise, you turn because 180 degrees is exactly halfway from completing a full revolution. You can think about the coordinate plane in terms of direction. We can see North, South, East and West.

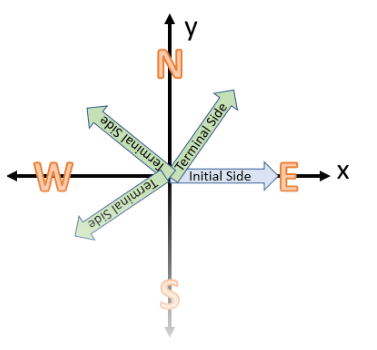
We can turn in two different directions, clockwise or counterclockwise.

• Angles that turn in a counterclockwise direction are positive angles.
• Angles that turn in a clockwise direction are negative.

All angles have an initial side and a terminal side. The initial side of the angle is where the angle starts. Angles on the coordinate plane have an initial side on the positive x-axis. If we think of it in terms of directions, all angles start on East.

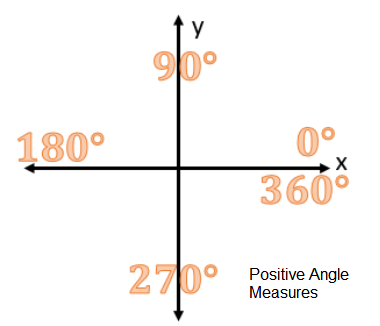
Angle Measurements

Angle measurements are done corresponding to the axes on the coordinate plane. One full revolution, or circle, measures 360 degrees. If we only turn halfway, we are making an angle of 180 degrees. If we go only one quarter, we make an angle of 90 degrees. The angle measured is positive when we measure in an anti-clockwise direction with respect to the positive x-axis as shown below.

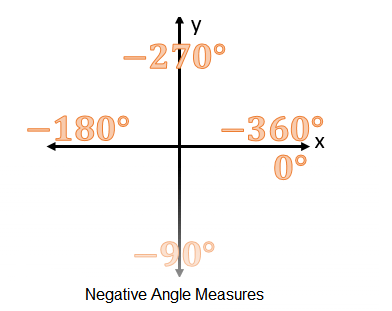
Similarly, if we complete these turns in a clockwise direction, the angles become negative.

Application of Angle Measurement in Trigonometry

In trigonometry, angles are placed on coordinate axes. The vertex is always placed at the origin and one ray is always placed on the positive x-axis. This ray is called the initial side of the angle. The other ray is called the terminal side of the angle. This positioning of an angle is called the standard position. The Greek letter theta \(\theta\) is often used to represent an angle measure. Two angles in standard position are shown below.

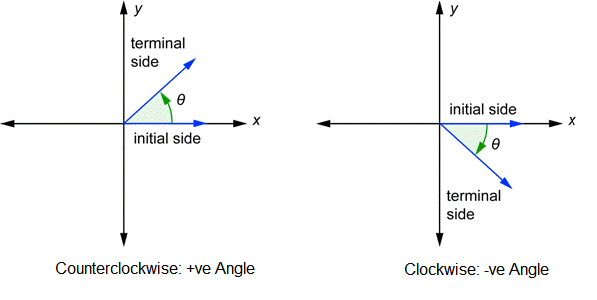
When an angle is drawn in a standard position, it has a direction. Notice that there are little curved arrows in the above drawing. The one on the left goes counterclockwise and is defined to be a positive angle. The one on the right goes clockwise and is defined to be a negative angle. Why is counterclockwise positive? This is just a convention that mathematicians have agreed on because one way has to be positive and the other way negative.

Since the \(x\) and \(y\) axes are perpendicular, each axis then represents an increment of ninety degrees of rotation. The diagrams below show a variety of angles formed by rotating a ray through the quadrants of the coordinate plane.

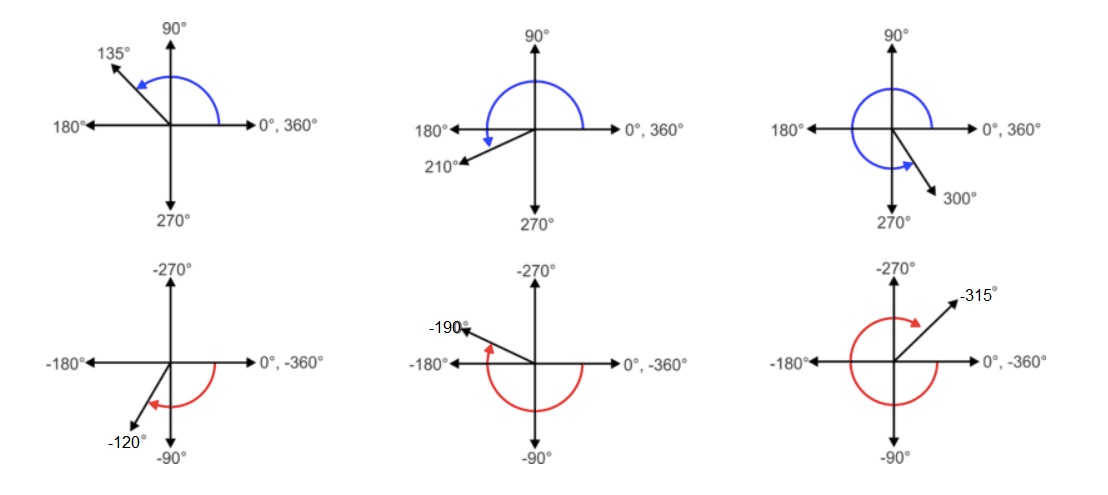
An angle of rotation can be described infinitely in many ways. It can be described by a positive or negative angle of rotation or by making multiple full-circle rotations through \(360^{\circ}\). The example below illustrates this concept.

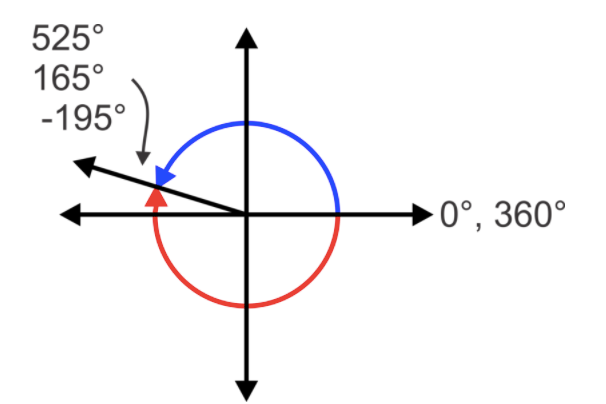
For the angle \(525^{\circ}\), an entire \(360^{\circ}\) rotation is made and then we keep going another \(165^{\circ}\) to \(525^{\circ}\). Therefore, the resulting angle is equivalent to \(525^{\circ}-360^{\circ}\), or \(165^{\circ}\). In other words, the terminal side is in the same location as the terminal side for a \(165^{\circ}\) angle. If we subtract \(360^{\circ}\) again, we get a negative angle, – \(195^{\circ}\). Since they all share the same terminal side, they are called coterminal angles.

Two angles in a standard position that share a common terminal side are said to be coterminal. The angles in the figure below are all coterminal with an angle that measures \(30^{\circ}\).

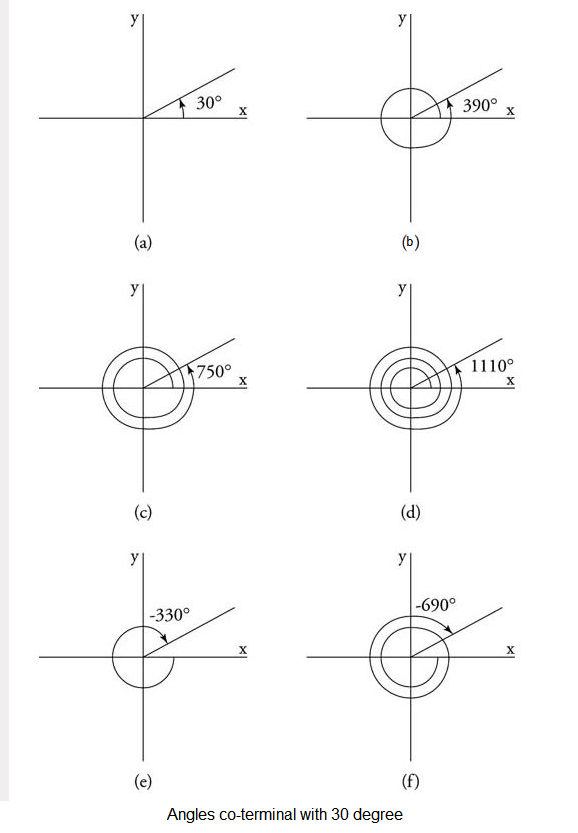
All angles that are coterminal with \(\theta^{\circ}\) can be written as
\(
\theta^{\circ}+n \cdot 360^{\circ}
\)
where \(n\) is an integer (positive, negative, or zero).

Example 1: \(\text { Is an angle measuring } 200^{\circ} \text { coterminal with an angle measuring } 940^{\circ} \text { ? }\)

Solution: If an angle measuring \(940^{\circ}\) and an angle measuring \(200^{\circ}\) were coterminal, then

\(
\begin{gathered}
940^{\circ}=200^{\circ}+n \cdot 360^{\circ} \\
740^{\circ}=n \cdot 360^{\circ}
\end{gathered}
\)
Because \(740^{\circ}\) is not a multiple of \(360^{\circ}\) , these angles are not coterminal.

Example 2: \(\text { Name } 5 \text { angles that are coterminal with }-70^{\circ} \text {. }\)

Solution:

\(
\begin{gathered}
-70^{\circ}+(1) 360^{\circ}=290^{\circ} \\
-70^{\circ}+(2) 360^{\circ}=650^{\circ} \\
-70^{\circ}+(3) 360^{\circ}=1010^{\circ} \\
-70^{\circ}+(-1) 360^{\circ}=-430^{\circ} \\
-70^{\circ}+(-2) 360^{\circ}=-790^{\circ}
\end{gathered}
\)

Reference Angles in different Quadrants

A reference angle is an acute angle between the terminal side of an angle and the \(x-\) axis. The diagram below shows the reference angles for the terminal sides of angles in each of the four quadrants.

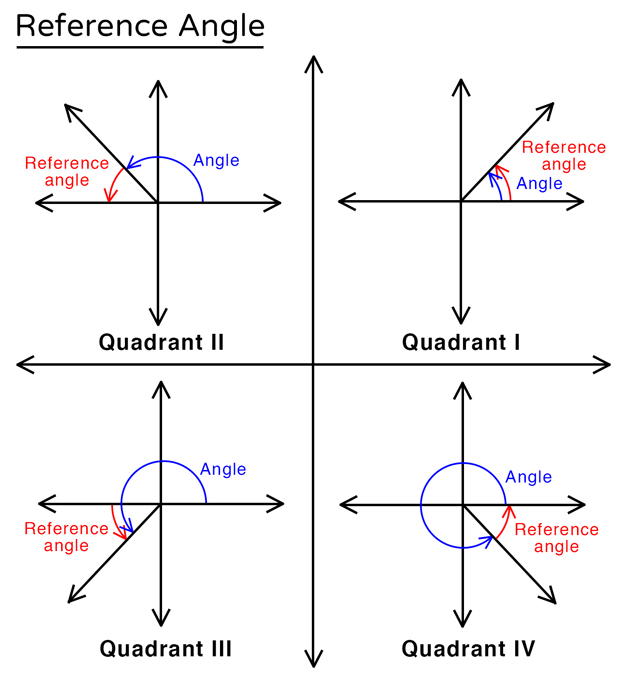
Note: A reference angle is never determined by the angle between the terminal side and the \(y\) – axis. This is a common error for students, especially when the terminal side appears to be closer to the \(y\) – axis than the \(x\) – axis.

For example, let’s determine the quadrant in which \(-745^{\circ}\) lies and hence determine the reference angle. 

Since our angle is more than one rotation, we need to add \(360^{\circ}\) until we get an angle whose absolute value is less than \(360^{\circ}:-745^{\circ}+360^{\circ}=-385^{\circ}\), again \(-385^{\circ}+360^{\circ}=-25^{\circ}\)
Now we can plot the angle and determine the reference angle:

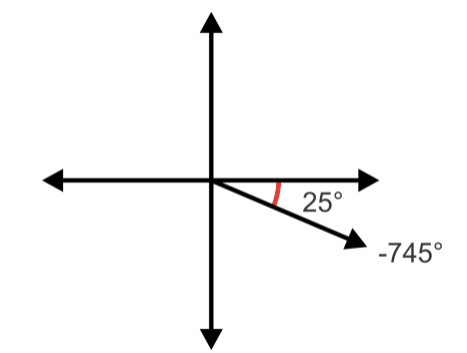
Note that the reference angle is positive \(25^{\circ}\). All reference angles will be positive as they are acute angles (between \(0^{\circ}\) and \(90^{\circ}\) ).

Finally, let’s give two coterminal angles to \(595^{\circ}\), one positive and one negative, and find the reference angle. To find the coterminal angles we can add/subtract \(360^{\circ}\). In this case, our angle is greater than \(360^{\circ}\) so it makes sense to subtract \(360^{\circ}\) to get a positive coterminal angle: \(595^{\circ}-360^{\circ}=235^{\circ}\). Now subtract again to get a negative angle: \(235^{\circ}-360^{\circ}=-125^{\circ}\).

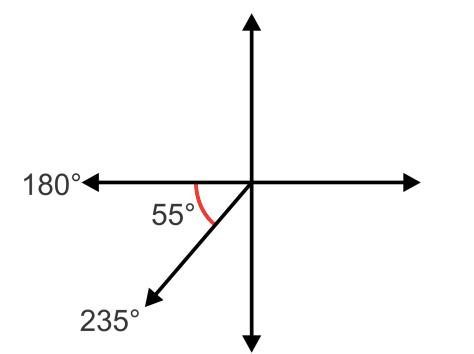
By plotting any of these angles we can see that the terminal side lies in the third quadrant as shown. Since the terminal side lies in the third quadrant, we need to find the angle between \(180^{\circ}\) and \(235^{\circ}\), so \(235^{\circ}-180^{\circ}=55^{\circ}\).

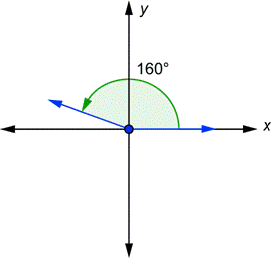
Example 3: Draw a \(160^{\circ}\) angle in standard position.

Solution: The angle is positive, so you start at the x-axis and go \(160^{\circ}\) counterclockwise.

Example 4: Draw a \(-200^{\circ}\) angle in standard position.

Solution: The angle is negative, so you start at the \(x\)-axis and go \(200^{\circ}\) clockwise. Remember that \(180^{\circ}\) is a straight line. That will bring you to the negative \(x\) axis, and then you have to go \(20^{\circ}\) farther.

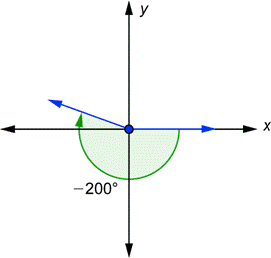
Notice that the terminal sides in the two examples above are the same, but they represent different angles. Such pairs of angles are said to be coterminal angles.

For each angle drawn in the standard position, there is a related angle known as a reference angle. This is the angle formed by the terminal side and the x-axis. The reference angle is always considered to be positive and has a value anywhere from \(0^{\circ}\) to \(90^{\circ}\). Two angles are shown below in the standard position.

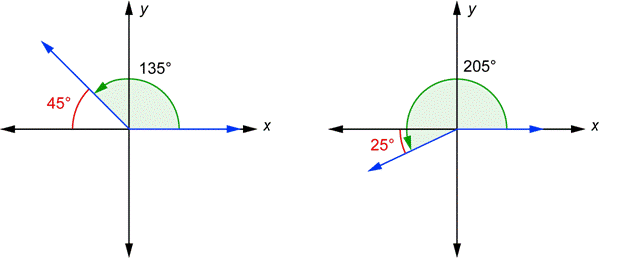
You can see that the terminal side of the 135° angle and the x-axis form a 45° angle (this is because the two angles must add up to 180°). This 45° angle, shown in red, is the reference angle for 135°. The terminal side of the 205° angle and the x-axis form a 25° angle. It is 25° because. This 25° angle, shown in red, is the reference angle for 205°.

Note: Think “reference” means to refer to the nearest part of the  x-axis

Finding Angles in other Quadrants using Reference Angle

To determine the other angles in other quadrants using reference angles follow the table below.

\(
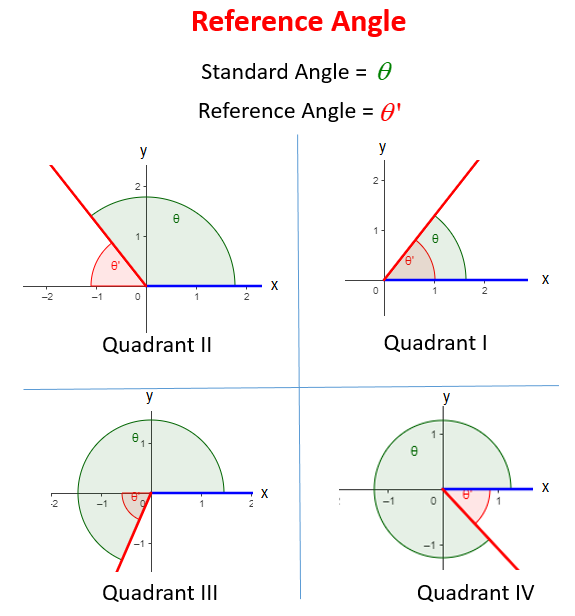
\begin{array}{|l|l|l|l|}
\hline \text { Quadrant } & \text { Angle, } \theta & \begin{array}{l}
\text { Reference Angle } \\
\text { Formula in } \\
\text { Degrees }
\end{array} & \begin{array}{l}
\text { Reference Formula in } \\
\text { Radians }
\end{array} \\
\hline \text { I } & \begin{array}{l}
\text { lies between } \\
0^{\circ} \text { and } 90^{\circ}
\end{array} & \theta & \theta \\
\hline \text { II } & \begin{array}{l}
\text { lies between } \\
90^{\circ} \text { and } 180^{\circ}
\end{array} & 180-\theta & \pi-\theta \\
\hline \text { III } & \begin{array}{l}
\text { lies between } \\
180^{\circ} \text { and } 270^{\circ}
\end{array} & \theta-180 & \theta-\pi \\
\hline \text { IV } & \begin{array}{l}
\text { lies between } \\
270^{\circ} \text { and } 360^{\circ}
\end{array} & 360-\theta & 2 \pi-\theta \\
\hline
\end{array}
\)

Example 5: Determine the reference angle that corresponds to each of the following angles.
a) \(165^{\circ}\)
b) \(249^{\circ}\)
c) \(328^{\circ}\)

Solution:

a) \(165^{\circ}\) is in quadrant II \(\left(90^{\circ}<165^{\circ}<180^{\circ}\right)\)
The reference angle is \(180^{\circ}-165^{\circ}=15^{\circ}\)

b) \(249^{\circ}\) is in quadrant III \(\left(180^{\circ}<249^{\circ}<270^{\circ}\right)\)
The reference angle is \(249^{\circ}-180^{\circ}=69^{\circ}\)

c) \(328^{\circ}\) is in quadrant III \(\left(270^{\circ}<328^{\circ}<360^{\circ}\right)\)
The reference angle is \(360^{\circ}-328^{\circ}=32^{\circ}\)

Example 6: \(\text { In which quadrant, do the following angles lie? (a) } 420^{\circ} \text { (b) }-570^{\circ} \text { (c) } 600^{\circ}\)

Solution:

(a) Look at the figure below, the angle \(420^{\circ}\) starts from OA and counterclockwise rotates a full circle to the OA position and continues to rotate to the \(\mathrm{OB}\) position. Since \(420^{\circ}=360^{\circ}+60^{\circ}\), so, the terminal side of \(420^{\circ}\) lies in quadrant \(\mathrm{I}\). That is, \(420^{\circ}\) is the angle of quadrant \(\mathrm{I}\).

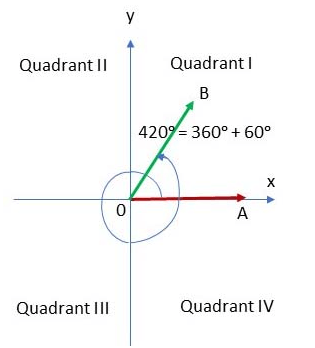
Note: Both angles \(420^{\circ}\) and \(60^{\circ}\) have the same terminal side that lies in quadrant I and they are the angles of the quadrant \(\mathrm{I}\).

(b) Look at the figure below, the angle \(-570^{\circ}\) starts from OA and clockwise rotates two full circles then change direction to counterclockwise rotate to the \(O B\) position. Since \(-570^{\circ}=-2 \times 360^{\circ}+150^{\circ}\), so, the terminal side of \(-570^{\circ}\) lies in quadrant II. That is, \(-570^{\circ}\) is the angle of quadrant II.

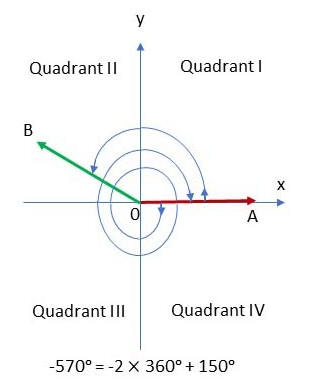
Note: Both angles \(-570^{\circ}\) and \(150^{\circ}\) have the same terminal side that lies in quadrant II and they are the angles of the quadrant II.

(c) Look at the figure below, the angle \(600^{\circ}\) starts from OA and counterclockwise rotates two full circles then change direction to clockwise rotate to the \(\mathrm{OB}\) position. Since \(600^{\circ}=2 \times 360^{\circ}-120^{\circ}\), so, the terminal side of \(600^{\circ}\) lies in quadrant III. That is, \(600^{\circ}\) is the angle of quadrant III.

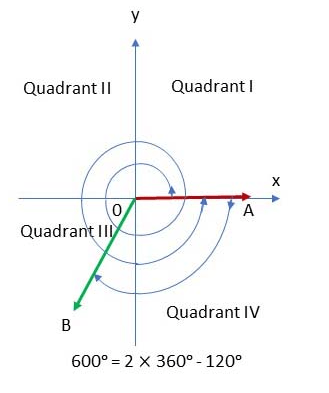
Note: Both angles \(600^{\circ}\) and \(-120^{\circ}\) have the same terminal side that lies in quadrant III and they are the angles of the quadrant III.

Example 7: \(\text { find the reference angle of }-500^{\circ} \text { and find the quadrant in which the terminal side lies. }\)

Solution:

Since our angle is more than one rotation, we need to add \(360^{\circ}\) until we get an angle whose absolute value is less than \(360^{\circ}:-500^{\circ}+360^{\circ}=-200^{\circ}\).
If we plot this angle we see that it is \(-200^{\circ}\) clockwise from the origin or \(160^{\circ}\) counterclockwise. \(160^{\circ}\) lies in the second quadrant.
Now determine the reference angle: \(180^{\circ}-160^{\circ}=20^{\circ}\).

Example 8: \(\text { Find two coterminal angles to } 138^{\circ} \text {, one positive and one negative. }\)

Solution:

\(
138^{\circ}+360^{\circ}=498^{\circ} \text { and } 138^{\circ}-360^{\circ}=-222^{\circ}
\)

Example 9: \(\text { Find the reference angle for } 895^{\circ} \text {. }\)

Solution:

\(895^{\circ}-360^{\circ}=535^{\circ}, 535^{\circ}-360^{\circ}=175^{\circ}\). The terminal side lies in the second quadrant, so we need to determine the angle between \(175^{\circ}\) and \(180^{\circ}\), which is \(5^{\circ}\).

Example 10: \(\text { Find the reference angle for } 343^{\circ} \text {. }\)

Solution:

\(
343^{\circ} \text { is in the fourth quadrant so we need to find the angle between } 343^{\circ} \text { and } 360^{\circ} \text { which is } 17^{\circ} \text {. }
\)