Cofunction identities in trigonometry give the relationship between the different trigonometric functions and their complementary angles. Let us recall the meaning of complementary angles. Two angles are said to be complementary angles if their sum is equal to \(\pi / 2\) radians or \(90^{\circ}\). The cofunction identities give a relationship between trigonometric functions sine and cosine, tangent and cotangent, and secant and cosecant. These functions are referred to as cofunctions of each other.

A function \(f\) is cofunction of a function \(g\) if \(f(A)=g(B)\) when A and B are complementary angles.

Cofunction Identities Proof

Consider a right-angled triangle \(A B C\) right angled at \(B\). Assume angle \(C=\theta\), then using the angle sum property of a triangle we have,

\(
\begin{aligned}
&\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}=180^{\circ} \\
&\Rightarrow \angle \mathrm{A}+90^{\circ}+\angle \mathrm{C}=180^{\circ} \text {[Because angle } \mathrm{B} \text { is a right angle] } \\
&\Rightarrow \angle \mathrm{A}+\angle \mathrm{C}=180^{\circ}-90^{\circ} \\
&\Rightarrow \angle \mathrm{A}+\theta=90^{\circ} \\
&\Rightarrow \angle \mathrm{A}=90^{\circ}-\theta
\end{aligned}
\)

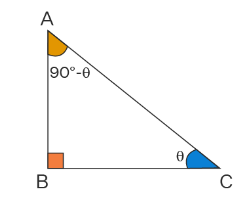
Therefore, we have the three angles of the triangle \(\mathrm{ABC}\) as \(\angle \mathrm{A}=90^{\circ}-\theta\), \(\angle B=90^{\circ}\) and \(\angle \mathrm{C}=\theta\).

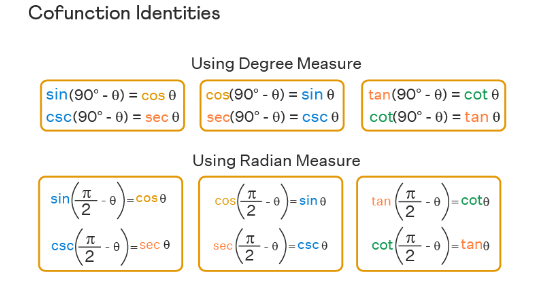
Cofunction Identities in Degrees

\(
\begin{aligned}
&\sin \left(90^{\circ}-\theta\right)=\cos \theta \\
&\cos \left(90^{\circ}-\theta\right)=\sin \theta \\
&\tan \left(90^{\circ}-\theta\right)=\cot \theta \\
&\cot \left(90^{\circ}-\theta\right)=\tan \theta \\
&\sec \left(90^{\circ}-\theta\right)=\operatorname{cosec} \theta \\
&\csc \left(90^{\circ}-\theta\right)=\sec \theta
\end{aligned}
\)

Cofunction Identities in Radians

\(\sin (\pi / 2-\theta)=\cos \theta\)
\(\cos (\pi / 2-\theta)=\sin \theta\)
\(\tan (\pi / 2-\theta)=\cot \theta\)
\(\cot (\pi / 2-\theta)=\tan \theta\)
\(\sec (\pi / 2-\theta)=\operatorname{cosec} \theta\)
\(\csc (\pi / 2-\theta)=\sec \theta\)

Example 1: Determine the value of \(\sin 150^{\circ}\) using cofunction identities.

Solution: To find the value of \(\sin 150^{\circ}\), we will use the formula sin \(\theta=\cos \left(90^{\circ}-\theta\right)\). So, we have
\(
\begin{aligned}
&\sin 150^{\circ}=\cos \left(90^{\circ}-150^{\circ}\right) \\
&=\cos \left(-60^{\circ}\right) \\
&=\cos \left(60^{\circ}\right) [\text { Because } \cos (-x)=\cos x \text { for all } x .] \\
&=1 / 2 \left[\text { Because } \cos 60^{\circ}=1 / 2\right]
\end{aligned}
\)

Example 2: Find the value of \(\theta\) if \(\tan \theta=\cot (\theta / 2+\pi / 12)\) using cofunction identities.

Solution: To find the value of \(\theta\), we will use the formula \(\tan \theta=\) \(\cot (\pi / 2-\theta)\). So, we have
\(
\begin{aligned}
&\tan \theta=\cot (\theta / 2+\pi / 12) \\
&\Rightarrow \cot (\pi / 2-\theta)=\cot (\theta / 2+\pi / 12) \\
&\Rightarrow \pi / 2-\theta=\theta / 2+\pi / 12 \\
&\Rightarrow \theta+\theta / 2=\pi / 2-\pi / 12 \\
&\Rightarrow 3 \theta / 2=6 \pi / 12-\pi / 2 \\
&\Rightarrow \theta=5 \pi / 12 \times 2 / 3 \\
&=5 \pi / 18
\end{aligned}
\)