Properties of Definite Integrals
Properties of Definite Integrals
1. The variable \(x\) that appears in definite integrals is called the dummy variable and we can replace this with another to get the same result:
\(
\int_a^b f(x) \mathrm{d} x=\int_a^b f(t) \mathrm{d} t .
\)
Proof:
\(\begin{aligned}
L H S &=\int_a^b f(x)+c \\
&=[g(x)+c]_a^b \\
&=[g(b)+c]-[g(a)+c] \\
&=g(b)-g(a)
\end{aligned}
\) \(
\begin{aligned}
\text { RHS } &=\int_a^b f(t) d t \\
&=[g(t)+c]_a^b \\
&=[g(b)+c]-[g(a)+c] \\
&=g(b)-g(a)
\end{aligned}
\)
Thus LHS = RHS
2. The definite integral of a constant \(c \in \mathbf{R}\) is proportional to the width of the interval:
\(\int_a^b c \mathrm{~d} x=c(b-a)\)
Proof:
\(\begin{aligned}
\int_a^b c d x \\
&=c [x]_a^b \\
&=c(b-a) \\
\end{aligned}
\)
3. The zero-width limit when \(b=a\) implies that
\(
\int_a^a f(x) \mathrm{d} x=0 .
\)
Example 1:
\(\begin{aligned}
\int_2^2 2 x d x &=\left[x^2\right]_2^2 \\
&=2^2-2^2 \\
&=0
\end{aligned}
\)
4. We can interchange the limits on any definite integral using
\(
\int_a^b f(x) \mathrm{d} x=-\int_b^a f(x) \mathrm{d} x .
\)
Proof:
\(\begin{aligned}
L H S &=\int_a^b f(x)+c \\
&=[g(x)+c]_a^b \\
&=[g(b)+c]-[g(a)+c] \\
&=g(b)-g(a)
\end{aligned}
\) \(
\begin{aligned}
L H S &=-\int_b^a f(x)+c \\
&=-[g(x)+c]_b^a \\
&=-([g(a)+c]-[g(b)+c]) \\
&=g(b)-g(a)
\end{aligned}
\)
LHS = RHS
5. We can split up definite integrals with a sum or difference:
\(
\int_a^b(f(x) \pm g(x)) \mathrm{d} x=\int_a^b f(x) \mathrm{d} x \pm \int_a^b g(x) \mathrm{d} x
\)
Example 2: Integral of Sum of functions: Evaluate the integral \(\int\left[x+e^x\right] d x\)
According to the above property
\(\int_a^b(f(x) + g(x)) \mathrm{d} x=\int_a^b f(x) \mathrm{d} x + \int_a^b g(x) \mathrm{d} x \\\) \(\int\left[x+e^x\right] d x=\int x d x+\int e^x d x \\
=x^2 / 2+e^x+c
\)
Proof: Integral of difference of functions
Evaluate the integral
\(
\int[2-1 / x] d x
\)
\(
\int[2-1 / x] d x=\int 2 d x-\int(1 / x) d x
\)
\(
=2 x-\ln |x|+c
\)
6. We can factor out a constant \(c \in \mathbf{R}\) from definite integrals:
\(\int_a^b c f(x) \mathrm{d} x=c \int_a^b f(x) \mathrm{d} x .\)
Example 3:
\(\int_1^2 5 f(x) \mathrm{d} x=5 \int_1^2 f(x) \mathrm{d} x . \)
7. We can also split up the integral with the limits \([a, b]\) for some value \(c \in \mathbf{R}\) over two adjacent intervals \([a, c]\) and \([c, b]\):
\(
\int_a^b f(x) \mathrm{d} x=\int_a^c f(x) \mathrm{d} x+\int_c^b f(x) \mathrm{d} x .
\)
Example 4:
\(\text { If } \int_0^8 f(x) d x=10 \text { and } \int_0^5 f(x) d x=5 \text {, find the value of } \int_5^8 f(x) d x
\)
We know that
\(\begin{aligned}
\int_a^b f(x) d x &=\int_a^c f(x) d x+\int_c^b f(x) d x . \\
\int_0^8 f(x) d x &=\int_0^5 f(x) d x+\int_5^8 f(x) d x \\
10 &=5+\int_5^8 f(x) d x \\
5 &=\int_5^8 f(x) d x
\end{aligned}
\)
8. If \(f(x) \geq 0\), then \(\int_a^b f(x) \mathrm{d} x \geq 0\)
Example 5:
In this example \(f(x)\) = 4 \(x\), As \(f(x) \geq 0 \) its integral is also \(\int_1^2 4 x d x \geq 0 \)
\(\begin{aligned}
\int_1^2 4 x d x &=2 \left[x^2\right]_1^2 \\
&= 2(2^2-1^2) \\
&=6
\end{aligned}
\)
9. If \(f(x) \geq g(x)\), then \(\int_a^b f(x) \mathrm{d} x \geq \int_a^b g(x) \mathrm{d} x .\)
Example 6:
\(
\text { Compare } f(x)=\sqrt{1+x^2} \text { and } g(x)=\sqrt{1+x} \text { over the interval }[0,1]
\)
Graphing these functions is necessary to understand how they compare over the interval \([0,1]\). Initially, when graphed on a graphing calculator, \(f(x)\) appears to be above \(g(x)\) everywhere. However, on the interval \([0,1]\), the graphs appear to be on top of each other. We need to zoom in to see that, on the interval \([0,1], g(x)\) is above \(f(x)\). The two functions intersect at \(x=0\) and \(x=1\) (as shown in figure a & b).
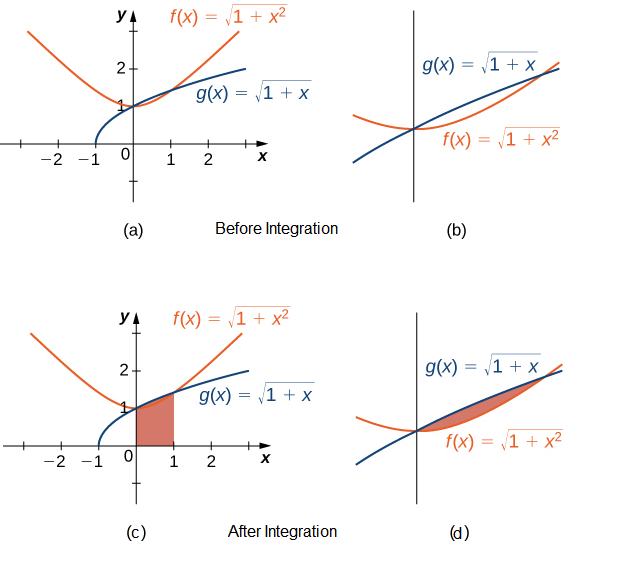
We can see from the graph that over the interval \([0,1], g(x) \geq f(x)\). Comparing the integrals over the specified interval \([0,1]\), we also see that \(\int_0^1 g(x) d x \geq \int_0^1 f(x) d x\) (Figure c & d). The thin, red-shaded area shows just how much difference there is between these two integrals over the interval \([0,1]\).
10. We also have the bounded property; if \(m \leq f(x) \leq M\), then
\(
m(b-a) \leq \int_a^b f(x) \mathrm{d} x \leq M(b-a)
\)
Example 7:
Suppose that on \([-2,5]\), the values of \(f\) lie in the interval \([m, M]\). Between which bounds does \(\int_{-2}^5 f(x) \mathrm{d} x\) lie?
In this example, we want to find the bounds of an integral using the property where the values of \(f\) lie in a particular interval.
In particular, the following property states that if \(m \leq f(x) \leq M\), then
\(
m(b-a) \leq \int_a^b f(x) \mathrm{d} x \leq M(b-a)
\)
On applying this property with \(a=-2\) and \(b=5\), we have \(b-a=7\). Thus,
\(
7 m \leq \int_{-2}^5 f(x) \mathrm{d} x \leq 7 M
\)
11. The modulus property is given by
\(
\left|\int_a^b f(x) \mathrm{d} x\right| \leq \int_a^b|f(x)| \mathrm{d} x .
\)
Proof:
From Negative of Absolute Value, we have for all \(a \in[a \ldots b]\) :
\(
-|f(t)| \leq f(t) \leq|f(t)|
\)
Thus from Relative Sizes of Definite Integrals:
\(
-\int_a^b|f(t)| \mathrm{d} t \leq \int_a^b f(t) \mathrm{d} t \leq \int_a^b|f(t)| \mathrm{d} t
\)
Hence the result.
12. Finally, we have a property for even and odd functions when integrating over the interval \([-a, a]\). For even functions \(f(-x)=f(x)\), we have
\(
\int_{-a}^a f(x) \mathrm{d} x=2 \int_0^a f(x) \mathrm{d} x .
\)
Example 8:
Evaluate \(\int_{-\pi / 2}^{\pi / 2} \cos ^3 x d x\)
Solution:
\(
\begin{aligned}
&\text { Let } f(x)=\cos ^3 x \\
&f(x)=(\cos x)^3 \\
&f(-x)=(\cos (-x))^3 \\
&f(-x)=(\cos x)^3 \\
&f(-x)=\cos ^3 x \\
&f(-x)=f(x)
\end{aligned}
\)
The function \(f(x)\) is even.
\(
\begin{aligned}
\int_{-\pi / 2}^{\pi / 2} \cos ^3 x d x &=2 \int_0^{\pi / 2} \cos ^3 x d x \\
&=2 \int_0^{\pi / 2} \frac{(\cos 3 x+3 \cos x)}{4} \\
&=(1 / 2)\left[\frac{\sin 3 x}{3}+3 \sin x\right]_0^{\pi / 2} \\
&=(1 / 2)[(-1 / 3)+3)] \\
&=(1 / 2)(8 / 3) \\
&=4 / 3
\end{aligned}
\)
For odd functions \(f(-x)=-f(x)\), we have
\(
\int_{-a}^a f(x) \mathrm{d} x=0
\)
Example 9:
Evaluate \(\int_{-\pi / 4}^{\pi / 4} x^3 \cos ^3 x d x\)
Solution:
\(
\begin{aligned}
&\int^{\pi / 4} x^3 \cos ^3 x d x \\
&-\pi / 4 \\
&f(x)=x^3 \cos ^3 x \\
&f(x)=(x \cos x)^3 \\
&f(-x)=(-x \cos (-x))^3 \\
&f(-x)=-x \cos ^3 x
\end{aligned}
\)
The given function is odd.
\(
\int_{-\pi / 4}^{\pi / 4} x^3 \cos ^3 x d x=0
\)
13. \(\int_a^b f(x) d x=\int_a^b f(a+b-x) d x\)
Proof: Let \(u=a+b-x\)
\(
\Rightarrow d u=-d x
\)
\(
\int_a^b f(x) d x=\int_a^b f(u) d u
\)
\(
\begin{aligned}
&\Rightarrow \int_b^a f(a+b-x)(-d x) \\
&\Rightarrow-\int_b^a f(a+b-x) d x \\
&\Rightarrow \int_a^b f(a+b-x) d x
\end{aligned}
\)
Hence Proved.
14. \(\int_0^a f(x) d x=\int_0^a f(a-x) d x\)
Proof:
\(I=\int_0^a f(x) d x\)
now, put \(a-t=x; -d t=d x\)
also when,
\(
\begin{aligned}
&x=0; t=a \\
&x=a; t=0
\end{aligned}
\)
\(
\begin{array}{rlr}
I=\int_a^0 f(a-t)(-d t)=\int_0^a f(a-t) d t \\
=\int_0^a f(a-x) d x
\end{array}
\)
Hence proved. The dummy variable does not affect the definite integral. So replacing \(t\) with \(x\) does not make any difference
15. \(\int_0^{2 a} f(x) d x=\int_0^a f(x) d x+\int_0^a f(2 a-x) d x\)
Proof:
\(I=\int_0^{2a} f(x) d x=\int_0^a f(x) d x + \int_a^{2 a} f(x) d x\)
now, put \(2a-x=t; -d t=d x\)
also when,
\(
\begin{aligned}
&x=a; t=a \\
&x=2a; t=0
\end{aligned}
\)
\begin{array}{rlr}
I=\int_0^{2a} f(x) d x=\int_0^a f(x) d x + \int_a^0 f(2a-t) (-d t) \\
=\int_0^a f(x) d x +\int_0^a f(2a-t) d t \\
=\int_0^a f(x) d x +\int_0^a f(2a-x) d x
\end{array}
\)
Hence proved.
16. \(
\int_0^{2 a} f(x) d x=\left\{\begin{array}{l}
2 \int_0^a f(x) d x, \text { if } f(2 a-x)=f(x) \\
0, \text { if } f(2 a-x)=-f(x)
\end{array}\right.
\)
Proof:
Let’s use the following substitution
put \(2a-x=t; -d t=d x\)
also when,
\(
\begin{aligned}
&x=a; t=a \\
&x=2a; t=0
\end{aligned}
\)
\begin{array}{rlr}
I=\int_0^{2a} f(x) d x =\int_0^{a} f(x) d x + \int_a^{2a} f(x) d x [x = (2a-t)] \\
=\int_0^a f(x) d x + \int_a^0 f(2a-t) (-d t) \\
=\int_0^a f(x) d x +\int_0^a f(2a-t) d t \\
=\int_0^a f(x) d x +\int_0^a f(2a-x) d x \\
=2\int_0^{2a} f(x) d x (f(2 a-x)=f(x))
\end{array}
\)
\(
\begin{array}{rlr}
I=\int_0^{2a} f(x) d x=\int_0^a f(x) d x + \int_a^0 f(2a-t) (-d t) \\
=\int_0^a f(x) d x +\int_0^a f(2a-t) d t \\
=\int_0^a f(x) d x +\int_0^a f(2a-x) d x \\
=\int_0^a f(x) d x -\int_0^a f(x) d x = 0 [f(2a-x) = -f(x)]
\end{array}
\)