integration is a method of adding or summing up the parts (slices) to find the whole. Integration is the process of finding the area of the region under the curve. Integration is a reverse process of differentiation.

Integration can be used to find areas, volumes, and many useful things. But it is easier to understand by taking an example that illustrates the area under the curve of a function as shown below:

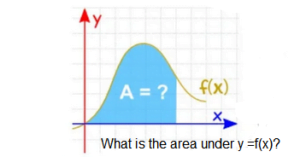
Slices (Parts)

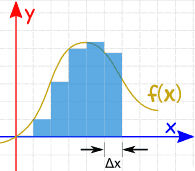
First, we can divide the function into different rectangular slices of width Δx. We could calculate the function at a few points and add up slices of width Δx as shown in the figure below to find the area(but the answer won’t be very accurate as some portion is left out).

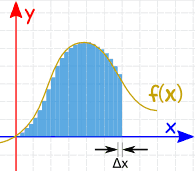
To improve the accuracy of the calculation of the area under the curve we can make Δx a lot smaller and add up many small slices as shown in the figure below (the answer is getting better).

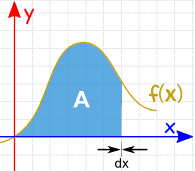
And as the slices approach zero in width, we get the true area under the curve. We now write dx to mean the Δx slices are approaching zero in width. You can see the waveform looks exactly the same as the one we started from.

But the above process of the calculating area under the curve is cumbersome and requires the addition of a lot of slices. 

Fortunately, there is an easy method or shortcut that exists. We know that finding integration is the reverse of finding differentiation. If we know the derivatives of a function we can easily calculate the integral of the function.

Example 1: \(\text { Find an integral of } 2 x\)

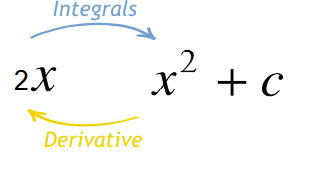
Solution: 

An integral of \(2 x\) is \(x^2 \ldots\) because the derivative of \(x^2\) is \(2 x\)

What is +C Here?

We wrote the answer as \(x^2\) but why \(+C\)?
It is the “Constant of Integration”. It is there because of all the functions whose derivative is \(\mathbf{2 x}\):

• the derivative of \(x^2\) is \(2 x\)
• and the derivative of \(x^2+8\) is also \(2 x\),
• and the derivative of \(\mathrm{x}^2+49\) is also \(2 \mathrm{x}\), and so on….

Because the derivative of a constant is zero. So when we reverse the operation (to find the integral) we only know \(\mathbf{2 x}\), but there could have been a constant of any value. So we wrap up the idea by just writing \(+C\) at the end.

Integration Notation:

The formula for the integration of \(2 x\) is given by, \(\sqrt{2 x} d x=x^2+C\), with \(C\) as the integration constant. The image given below shows the formula for the integration of \(2 \mathrm{x}\):

Example 2: \(\text { what is } \int \cos (x) d x \text { ? }\)

Solution: From the Rules of Derivatives table we see the derivative of \(\sin (x)\) is \(\cos (x)\) so:
\(\int \cos (x) d x=\sin (x)+C\)

Example 3: \(\text { What is } \int x^4 d x \text { ? }\)

Solution: On Rules of Integration there is a “Power Rule” that says:
\(
\int x^n d x=\frac{x^{n+1}}{n+1}+C
\)
We can use that rule with \(\mathrm{n}=4\) :
\(
\int x^4 d x=\frac{x^5}{5}+C
\)

Integration Rules

\(
\begin{aligned}
&\int x^n d x=\frac{x^{n+1}}{n+1}+C, n \neq-1 \\
&\int d x=x+C \\
&\int \cos x d x=\sin x+C \\
&\int \sin x d x=-\cos x+C \\
&\int \sec ^2 x d x=\tan x+C \\
&\int \operatorname{cosec} 2 x d x=-\cot x+C \\
&\int \sec x \tan x d x=\sec x+C \\
&\int \operatorname{cosec} x \cot x d x=-\operatorname{cosec} x+C
\end{aligned}
\)
\(
\begin{aligned}
&\int \frac{d x}{\sqrt{1-x^2}}=\sin ^{-1} x+C\\
&\int \frac{d x}{\sqrt{1-x^2}}=-\cos ^{-1} x+C\\
&\int \frac{d x}{1+x^2}=\tan ^{-1} x+C\\
&\int \frac{d x}{1+x^2}=-\cot ^{-1} x+C\\
&\int \frac{d x}{x \sqrt{x^2-1}}=\sec ^{-1} x+C\\
&\int \frac{d x}{x \sqrt{x^2-1}}=-\operatorname{cosec}^{-1} x+C\\
&\int e^x d x=e^x+C\\
&\int \frac{d x}{x}=\ln |x|+C\\
&\int a^x d x=\frac{a^x}{\ln a}+C
\end{aligned}
\)

What are the Key Differences Between Log and Ln?

\(
\begin{array}{|l|l|}
\hline {\text { Log }} & {\text { Ln }} \\
\hline \text { Log refers to a logarithm to the base } 10 & \text { Ln refers to a logarithm to the base e } \\
\hline \text { This is also called as a common logarithm } & \text { This is also called as a natural logarithm } \\
\hline \text { The common log is represented as } \log _{10}(\mathrm{x}) & \text { The natural log is represented as } \log _{\mathrm{e}}(\mathrm{x}) \\
\hline \begin{array}{l}
\text { The exponent form of the common logarithm } \\
\text { is } 10^{\mathrm{x}}=\mathrm{y}
\end{array} & \text { The exponent form of the natural logarithm is } \mathrm{e}^{\mathrm{x}}=\mathrm{y} \\
\hline
\end{array}
\)

Basic Integration Rules

Here are the basic integration rules where each of them can be cross-verified by differentiating the result. If you want to see how each of these rules are derived, click on the respective links.

Power rule of integration is, \(\int x^n d x=x^{n+1} /(n+1)+C\)

Integral of 1 is, \(\int 1 \mathrm{dx}=\mathrm{x}+\mathrm{C}\).

Integral of \(e^x\) is, \(\int e^x d x=e^x+C\)

Integral of \(a^x\) is, \(\int a^x d x=a^x / \ln a+C\)

Integral of \(1 / x\) is, \(\int 1 / x d x=\ln |x|+C\)

Apart from these, we use the following properties of integrals when sum/difference of terms is present in the place of the integrand.

\(\int[f(x)+g(x)] d x=\int f(x) d x+\int g(x) d x\)

\(\int[f(x)-g(x)] d x=\int f(x) d x-\int g(x) d x\)

\(\int a f(x) d x=\int f(x) d x+C\), where ‘a’ is a constant

Integration Rules of Trigonometric Functions

There are 6 trigonometric functions: \(\sin , \cos , \tan , \mathrm{csc}, \mathrm{sec}\), and cot. Here are the integration rules of all these trigonometric functions:

\(\begin{aligned}
&\int \sin x d x=-\cos x+C \\
&\int \cos x d x=\sin x+C \\
&\int \sec ^2 x d x=\tan x+C \\
&\int \operatorname{cosec}^2 x d x=-\cot x+C \\
&\int \sec x \tan x d x=\sec x+C \\
&\int \operatorname{cosec} x \cot x d x=-\operatorname{cosec} x+C \\
&\int \cot x d x=\ln |\sin x|+C \\
&\int \sec x d x=\ln |\sec x+\tan x|+C \\
&\int \operatorname{cosec} x d x=\ln |\operatorname{cosec} x-\cot x|+C
\end{aligned}\)

Integrate trigonometric functions with power?

\(
\begin{aligned}
&\int \sin ^n(x) d x=\frac{-1}{n} \sin ^{n-1}(x) \cos (x)+\frac{n-1}{n} \int \sin ^{n-2}(x) d x \\
&\int \cos ^n(x) d x=\frac{1}{n} \cos ^{n-1}(x) \sin (x)+\frac{n-1}{n} \int \cos ^{n-2}(x) d x \\
&\int \tan ^n(x) d x=\frac{1}{n-1} \tan ^{n-1}(x)-\int \tan ^{n-2}(x) d x \\
&\int \sec ^n(x) d x=\frac{1}{n-1} \sec ^{n-2}(x) \tan (x)+\frac{n-2}{n-1} \int \sec ^{n-2}(x) d x \\
&\int \csc ^n(x) d x=\frac{-1}{n-1} \csc ^{n-2}(x) \cot (x)+\frac{n-2}{n-1} \int \csc ^{n-2}(x) d x
\end{aligned}
\)

Integration Rules of Inverse Trigonometric Functions

There are 6 inverse trigonometric functions:
\(\arcsin \left(\sin ^{-1}\right), \arccos \left(\cos ^{-1}\right)\), \(\arctan \left(\tan ^{-1}\right), \operatorname{arccsc}\left(\csc ^{-1}\right), \operatorname{arcsec}\left(\sec ^{-1}\right)\), and \(\operatorname{arccot}\left(\cot ^{-1}\right)\).

Here are the integration rules of these inverse trigonometric functions.

\(\int \sin ^{-1} x d x=x \sin ^{-1} x+\sqrt{ }\left(1-x^2\right)+C \\\) \(\int \cos ^{-1} x d x=x \cos ^{-1} x-\sqrt{ }\left(1-x^2\right)+C \\\) \(\int \tan ^{-1} x d x=x \tan ^{-1} x-1 / 2 \ln \left|1+x^2\right|+C \\\) \(\int \csc ^{-1} x d x=x \csc ^{-1} x+\ln \left|x+\sqrt{ }\left(x^2-1\right)\right|+C \\\) \(\int \sec ^{-1} x d x=x \sec ^{-1} x-\ln \left|x+\sqrt{ }\left(x^2-1\right)\right|+C \\\) \(\int \cot ^{-1} x d x=x \cot ^{-1} x+1 / 2 \ln \left|1+x^2\right|+C\)

We actually do not need to remember these rules, instead, we can apply the integration by parts rule to derive each of these quickly.

Besides these, we have several other integration rules that involve the inverse trigonometric functions:

\(\int 1 / \sqrt{ }\left(1-x^2\right) \cdot d x=\sin ^{-1} x+C \\\) \(\int 1 /\left(1-x^2\right) \cdot d x=-\cos ^{-1} x+C \\\) \(\int 1 / x \sqrt{ }\left(x^2-1\right) \cdot d x=\sec ^{-1} x+C \\\) \(\int 1 / x \sqrt{ }\left(x^2-1\right) \cdot d x=-\operatorname{cosec}^{-1} x+C \\\) \(\int 1 /\left(1+x^2\right) \cdot d x=\tan ^{-1} x+C \\\) \(\int 1 /\left(1+x^2\right) \cdot d x=-\cot ^{-1} x+C \\\)

Integration Rules of Special Functions

Other than the rules that we have seen in the previous sections, we have some integration rules that are used to integrate some special type of rational functions where the denominator involves squares. They are as follows:

\(\int 1 /\left(x^2-a^2\right) d x=(1 / 2 a) \ln |(x-a) /(x+a)|+C \\\)
\(\int 1 /\left(a^2-x^2\right) d x=(1 / 2 a) \ln |(a+x) /(a-x)|+C \\\)
\(\int 1 / \sqrt{ }\left(x^2+a^2\right) d x=\ln \left|x+\sqrt{ }\left(x^2+a^2\right)\right|+C \\\)
\(\int 1 / \sqrt{ }\left(x^2-a^2\right) d x=\ln \left|x+\sqrt{ }\left(x^2-a^2\right)\right|+C \\\)
\(\int 1 /\left(a^2+x^2\right) d x=(1 / a) \tan ^{-1}(x / a)+C \\\)
\(\int 1 / \sqrt{ }\left(a^2-x^2\right) d x=\sin ^{-1}(x / a)+C \\\)

There are some other integration rules that involve square roots in integrands.

\(
\begin{aligned}
&\int \sqrt{ }\left(a^2-x^2\right) \cdot d x=x / 2 \cdot \sqrt{ }\left(a^2-x^2\right)+a^2 / 2 \cdot \sin ^{-1} x / a+C \\
&\int \sqrt{ }\left(x^2+a^2\right) \cdot d x=x / 2 \cdot \sqrt{ }\left(x^2+a^2\right)+a^2 / 2 \cdot \ln \left|x+\sqrt{ }\left(x^2+a^2\right)\right|+C \\
&\int \sqrt{ }\left(x^2-a^2\right) \cdot d x=x / 2 \cdot \sqrt{ }\left(x^2-a^2\right)-a^2 / 2 \cdot \ln \left|x+\sqrt{ }\left(x^2-a^2\right)\right|+C
\end{aligned}
\)