The derivative of a function is the rate of change of the function’s output relative to its input value. Given \(y=f(x)\), the derivative of \(f(x)\), denoted \(f^{\prime}(x)\) (or \(\left.d f(x) / d x\right)\), is defined by the following limit:

\(f^{\prime}(x)=\frac{\Delta y}{\Delta x}=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

The definition of the derivative is derived from the formula for the slope of a line. Recall that the slope of a line is the rate of change of the line, which is computed as the ratio of the change in \(y\) to the change in \(x\). Geometrically, the derivative is the slope of the line tangent to the curve at a point of interest. It is sometimes referred to as the instantaneous rate of change. Typically, we calculate the slope of a line using two points on the line. This is not possible for a curve, since the slope of a curve changes from point to point. Consider the figure below.

Alternatively, derivatives can be defined as the limit of the average rate of change in the function as the length of the interval on which the average is computed tends to 0.

What is a Tangent Line?

The tangent line (red line shown in the figure below) of a curve at a given point is a line that just touches the curve (function) at that point. The tangent line in calculus may touch the curve at any other point(s) and it also may cross the graph at some other point(s) as well. 

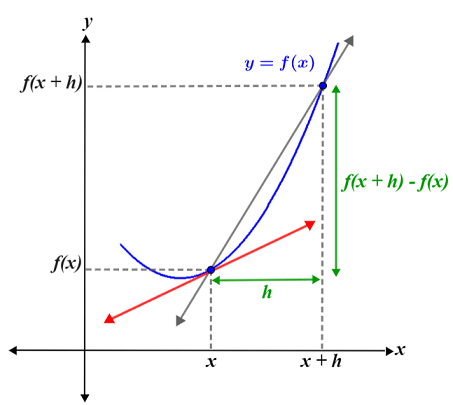
The figure shows a curve (blue) with two points: \((x, f(x))\) and \((x+h, f(x+h))\). The grey secant line represents the slope between these two points and is computed as:
\(m=\frac{\Delta y}{\Delta x}=\frac{f(x+h)-f(x)}{h}\)

However, this formula gives us the slope between the two points, which is an average of the slope of the curve. The derivative at \(x\) is represented by the red line in the figure. To calculate the slope of this line, we need to modify the slope formula so that it can be used for a single point. We do this by computing the limit of the slope formula as the change in \(x(\Delta x)\), denoted \(h\), approaches 0 . By doing this, we find the slope between two points separated by a difference so small that it provides an approximation for the slope at a single point, leading us to the definition of the derivative stated above.

Definition 1: Suppose \(f\) is a real-valued function and “a” is a point in its domain of definition. The derivative of \(f\) at “a” is defined by
\(f^{\prime}(a) = \lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\)
provided this limit exists. Derivative of \(f(x)\) at “a” is denoted by \(f^{\prime}(a)\). Observe that \(f^{\prime}(a)\) quantifies the change in \(f(x)\) at \(a\) with respect to \(x\).

Example 1: Find the derivative at \(x=2\) of the function \(f(x)=3 x\).

Solution:

We have
\(
\begin{aligned}
f^{\prime}(2) &=\lim _{h \rightarrow 0} \frac{f(2+h)-f(2)}{h}=\lim _{h \rightarrow 0} \frac{3(2+h)-3(2)}{h} \\
&=\lim _{h \rightarrow 0} \frac{6+3 h-6}{h}=\lim _{h \rightarrow 0} \frac{3 h}{h}=\lim _{h \rightarrow 0} 3=3 .
\end{aligned}
\)
The derivative of the function \(3 x\) at \(x=2\) is 3.

Example 2: Find the derivative of the function \(f(x)=2 x^2+3 x-5\) at \(x=-1\). Also prove that \(f^{\prime}(0)+3 f^{\prime}(-1)=0\).

Solution:

We first find the derivatives of \(f(x)\) at \(x=-1\) and at \(x=0\). We have
\(
f^{\prime}(-1)=\lim _{h \rightarrow 0} \frac{f(-1+h)-f(-1)}{h}
\)
\(
=\lim _{h \rightarrow 0} \frac{\left[2(-1+h)^2+3(-1+h)-5\right]-\left[2(-1)^2+3(-1)-5\right]}{h}
\)
\(=\lim _{h \rightarrow 0} \frac{2 h^2-h}{h}=\lim _{h \rightarrow 0}(2 h-1)=2(0)-1=-1\)
and
\(f^{\prime}(0)=\lim _{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}\)
\(
=\lim _{h \rightarrow 0} \frac{\left[2(0+h)^2+3(0+h)-5\right]-\left[2(0)^2+3(0)-5\right]}{h}
\)
\(
=\lim _{h \rightarrow 0} \frac{2 h^2+3 h}{h}=\lim _{h \rightarrow 0}(2 h+3)=2(0)+3=3
\)
Clearly \(\quad f^{\prime}(0)+3 f^{\prime}(-1)=0\)

Example 3: Find the derivative of \(\sin x\) at \(x=0\).

Solution:
Let \(f(x)=\sin x\). Then
\(
\begin{aligned}
f^{\prime}(0) &=\lim _{h \rightarrow 0} \frac{f(0+h)-f(0)}{h} \\
&=\lim _{h \rightarrow 0} \frac{\sin (0+h)-\sin (0)}{h}=\lim _{h \rightarrow 0} \frac{\sin h}{h}=1
\end{aligned}
\)

Definition 2: Suppose \(f\) is a real-valued function, the function defined by
\(
\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}
\)
wherever the limit exists is defined to be the derivative of \(f\) at \(x\) and is denoted by \(f^{\prime}(x)\). This definition of derivative is also called the first principle of derivative. Thus \(\quad f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

Clearly, the domain of definition of \(f^{\prime}(x)\) is wherever the above limit exists. There are different notations for the derivative of a function. Sometimes \(f^{\prime}(x)\) is denoted by \(\frac{d}{d x}(f(x))\) or if \(y=f(x)\), it is denoted by \(\frac{d y}{d x}\). This is referred to as derivative of \(f(x)\) or \(y\) with respect to \(x\). It is also denoted by \(\mathrm{D}(f(x))\). Further, derivative of \(f\) at \(x=a\) is also denoted by \(\left.\frac{d}{d x} f(x)\right|_a\) or \(\left.\frac{d f}{d x}\right|_a\) or even \(\left(\frac{d f}{d x}\right)_{x=a}\).

Example 4: Find the derivative of \(f(x)=x^2\).

Solution:
We have, \(f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
\(
=\lim _{h \rightarrow 0} \frac{(x+h)^2-(x)^2}{h}=\lim _{h \rightarrow 0}(h+2 x)=2 x
\)

Example 5: Find the derivative of \(f(x)=\frac{1}{x}\)

Solution: We have \(f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
\(
\begin{aligned}
&=\lim _{h \rightarrow 0} \frac{\frac{1}{(x+h)}-\frac{1}{x}}{h} \\
&=\lim _{h \rightarrow 0} \frac{1}{h}\left[\frac{x-(x+h)}{x(x+h)}\right] \\
&=\lim _{h \rightarrow 0} \frac{1}{h}\left[\frac{-h}{x(x+h)}\right]=\lim _{h \rightarrow 0} \frac{-1}{x(x+h)}=-\frac{1}{x^2}
\end{aligned}
\)

Algebra of derivative of functions

The following are the rules called the differentiation rules that represent the algebra of derivatives of functions. Suppose \(f(x)\) and \(g(x)\) are two functions such that their derivatives are defined in a common domain. Then we can define the following rules for the functions \(f\) and \(g\).

Derivative of the sum of two functions

Derivative of the sum of two functions is the sum of the derivatives of the functions.

\(\frac{d}{d x}[f(x)+g(x)]=\frac{d}{d x} f(x)+\frac{d}{d x} g(x)\)

 

Example 6:
Find the derivative of the function \(x+(1 / x)\).

Solution:

Given: \(x+(1 / x)\)
Let \(f(x)=x\) and \(g(x)=1 / x\)
Using the sum rule of differentiation,
\(\frac{d}{d x}[f(x)+g(x)]=\frac{d}{d x} f(x)+\frac{d}{d x} g(x)\)
\(\frac{d}{d x}[x+(1 / x)]=\frac{d}{d x}(x)+\frac{d}{d x}(1 / x)\)
\(=1+\left(-1 / x^2\right)\)
\(=1-\left(1 / x^2\right)\)

Derivative of difference of two functions

Derivative of difference of two functions is difference of the derivatives of the functions.

\(\frac{d}{d x}[f(x)-g(x)]=\frac{d}{d x} f(x)-\frac{d}{d x} g(x)\)

Example 7: Find the derivative of \(\sin x-\cos x\).

Solution:

Given function is: \(\sin x-\cos x\)
Let \(f(x)=\sin x\) and \(g(x)=\cos x\)
Using the difference rule of differentiation,
\(\frac{d}{d x}[f(x)-g(x)]=\frac{d}{d x} f(x)-\frac{d}{d x} g(x)\)
\(
\begin{aligned}
&\frac{d}{d x}(\sin x-\cos x)=\frac{d}{d x}(\sin x)-\frac{d}{d x}(\cos x) \\
&=\cos x-(-\sin x) \\
&=\cos x+\sin x
\end{aligned}
\)

Derivative of the product of two functions

Derivative of the product of two functions is given by the following product rule.

\(\frac{d}{d x}[f(x) \cdot g(x)]=\frac{d}{d x} f(x) \cdot g(x)+f(x) \cdot \frac{d}{d x} g(x)\)

Leibnitz rule for differentiating product of functions: 

Let \(u=f(x)\) and \(v=g(x)\). Then
\((u v)^{\prime}=u^{\prime} v+u v^{\prime}\)

Example 8: Compute the derivative of \(f(x)=\sin ^2 x\).

Solution:
We use the Leibnitz product rule to evaluate this.
\(
\begin{aligned}
\frac{d f(x)}{d x} &=\frac{d}{d x}(\sin x \sin x) \\
&=(\sin x)^{\prime} \sin x+\sin x(\sin x)^{\prime} \\
&=(\cos x) \sin x+\sin x(\cos x) \\
&=2 \sin x \cos x=\sin 2 x
\end{aligned}
\)

Derivative of the quotient of two functions

Derivative of the quotient of two functions is given by the following quotient rule (whenever the denominator is non–zero).

\(\frac{d}{d x}\left(\frac{f(x)}{g(x)}\right)=\frac{\frac{d}{d x} f(x) \cdot g(x)-f(x) \frac{d}{d x} g(x)}{(g(x))^2}\)

We can rewrite this Let \(u=f(x)\) and \(v=g(x)\). Then
\(\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v- v^{\prime}u} {v^2}\)

Example 9: Find the derivative of \(f(x)=\frac{x+1}{x}\)

Solution: Clearly this function is defined everywhere except at \(x=0\). We use the quotient rule with \(u=x+1\) and \(v=x\). Hence \(u^{\prime}=1\) and \(v^{\prime}=1\). Therefore
\(
\frac{d f(x)}{d x}=\frac{d}{d x}\left(\frac{x+1}{x}\right)=\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{u^{\prime} v-u v^{\prime}}{v^2}=\frac{1(x)-(x+1) 1}{x^2}=-\frac{1}{x^2}
\)

Example 10: prove that derivative of \(f(x)=x^n\) is \(n x^{n-1}\) for any positive integer \(n\).

Proof: By definition of the derivative function, we have

\(
\begin{aligned}
\frac{d}{d x}\left(x^n\right) &=\frac{d}{d x}\left(x \cdot x^{n-1}\right) \\
&=\frac{d}{d x}(x) \cdot\left(x^{n-1}\right)+x \cdot \frac{d}{d x}\left(x^{n-1}\right) \text { (by product rule) } \\
&=1 \cdot x^{n-1}+x \cdot\left((n-1) x^{n-2}\right) \text { (by induction hypothesis) } \\
&=x^{n-1}+(n-1) x^{n-1}=n x^{n-1}
\end{aligned}
\)

Derivative of Polynomial Functions

Let, \(f(x)=a_n x^n+a_{n-1} x^{n-1}+\ldots+a_1 x+a_0\)
be a polynomial function, then the derivative function is given by:
\(
\frac{d}{d x} f(x)=\frac{d}{d x}\left[a_n x^n+a_{n-1} x^{n-1}+\ldots+a_1 x+a_0\right]
\)
This can be expanded as:
\(
\frac{d f(x)}{d x}=n a_n x^{n-1}+(n-1) a_{n-1} x^{n-2}+\ldots+2 a_2 x+a_1
\)
Here, \(a_1, a_2, \ldots, a_n\) are all real numbers and \(a_n \neq 0\)

Derivatives of Polynomial Formulas

To find the derivative of a given polynomial function, it is required to get thoroughly familiar with the following basic derivative formulas and rules. These are used while calculating the derivative of a simple or complex polynomial function.

• \(\frac{d}{d x}(c)=0\)
• \(\frac{d}{d x}(x)=1\)
• \(\frac{d}{d x}\left(x^n\right)=n x^{n-1}\)
• \(\frac{d}{d x}(u \pm v)=\frac{d u}{d x} \pm \frac{d v}{d x}\)
• \(\frac{d}{d x}(c u)=c \frac{d u}{d x}\)
• \(\frac{d}{d x}(u v)=u \frac{d v}{d x}+v \frac{d u}{d x}\)
• \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^2}\)

Derivatives of Trigonometric Functions Formulas

• \(\frac{d}{d x}(\sin x)=\cos x\)
• \(\frac{d}{d x}(\cos x)=-\sin x\)
• \(\frac{d}{d x}(\tan x)=\sec ^2 x\)
• \(\frac{d}{d x}\left(\cot x=-\operatorname{cosec}^2 x\right.\)
• \(\frac{d}{d x}(\sec x)=\sec x \tan x\)
• \(\frac{d}{d x}(\operatorname{cosec} x)=-\operatorname{cosec} x \cot x\)
• \(\frac{d}{d x}(\sinh x)=\cosh x\)
• \(\frac{d}{d x}(\cosh x)=\sinh x\)
• \(\frac{d}{d x}(\tanh x)=\operatorname{sech}^2 x\)
• \(\frac{d}{d x}(\operatorname{coth} x)=-\operatorname{cosech}^2 x\)
• \(\frac{d}{d x}(\operatorname{sech} x)=-\operatorname{sech} x \tanh x\)
• \(\frac{d}{d x}(\operatorname{cosech} x)=-\operatorname{cosech} x \operatorname{coth} x\)

Differentiation Formulas for Inverse Trigonometric Functions

• \(\frac{d}{d x}\left(\sin ^{-1} x\right)=\frac{1}{\sqrt{1-x^2}}\)
• \(\frac{d}{d x}\left(\cos ^{-1} x\right)=-\frac{1}{\sqrt{1-x^2}}\)
• \(\frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{1+x^2}\)
• \(\frac{d}{d x}\left(\cot ^{-1} x\right)=-\frac{1}{1+x^2}\)
• \(\frac{d}{d x}\left(\sec ^{-1} x\right)=\frac{1}{|x| \sqrt{x^2-1}}\)
• \(\frac{d}{d x}\left(\operatorname{cosec}^{-1} x\right)=-\frac{1}{|x| \sqrt{x^2-1}}\)

Other Differentiation Formulas

• \(\frac{d}{d x}\left(a^x\right)=a^x \ln a\)
• \(\frac{d}{d x}\left(e^x\right)=e^x\)
• \(\frac{d}{d x}\left(\log _a x\right)=\frac{1}{(\ln a) x}\)
• \(\frac{d}{d x}(\ln x)=1 / x\)
• Chain Rule: \(\frac{d y}{d x}=\frac{d y}{d u} \times \frac{d u}{d x}=\frac{d y}{d v} \times \frac{d v}{d u} \times \frac{d u}{d x}
  \)

Example 11: Find the derivative of \(f(x)=1+x+x^2+x^3+\ldots+x^{50}\) at \(x=1\)

Solution: A direct application of the above Theorem 6 tells that the derivative of the above function is \(1+2 x+3 x^2+\ldots+50 x^{49}\). At \(x=1\) the value of this function equals
\(
1+2(1)+3(1)^2+\ldots+50(1)^{49}=1+2+3+\ldots+50=\frac{(50)(51)}{2}=1275
\)

Example 12: Compute the derivative of
(i) \(f(x)=\sin 2 x\)
(ii) \(g(x)=\cot x\)

Solution:

(i) Recall the trigonometric formula \(\sin 2 x=2 \sin x \cos x\). Thus
\(
\begin{aligned}
\frac{d f(x)}{d x} &=\frac{d}{d x}(2 \sin x \cos x)=2 \frac{d}{d x}(\sin x \cos x) \\
&=2\left[(\sin x)^{\prime} \cos x+\sin x(\cos x)^{\prime}\right] \\
&=2[(\cos x) \cos x+\sin x(-\sin x)] \\
&=2\left(\cos ^2 x-\sin ^2 x\right)
\end{aligned}
\)

(ii)

\(
\begin{aligned}
\frac{d g}{d x} &=\frac{d}{d x}(\cot x)=\frac{d}{d x}\left(\frac{1}{\tan x}\right) \\
&=\frac{(1)^{\prime}(\tan x)-(1)(\tan x)^{\prime}}{(\tan x)^2} \\
&=\frac{(0)(\tan x)-(\sec x)^2}{(\tan x)^2} \\
&=\frac{-\sec ^2 x}{\tan ^2 x}=-\operatorname{cosec}^2 x
\end{aligned}
\)

Example 13: Find the derivative of \(\frac{x^5-\cos x}{\sin x}\)

Solution: Let \(h(x)=\frac{x^5-\cos x}{\sin x}\). We use the quotient rule on this function wherever it is defined.
\(
h^{\prime}(x)=\frac{\left(x^5-\cos x\right)^{\prime} \sin x-\left(x^5-\cos x\right)(\sin x)^{\prime}}{(\sin x)^2}
\)
\(
\begin{aligned}
&=\frac{\left(5 x^4+\sin x\right) \sin x-\left(x^5-\cos x\right) \cos x}{\sin ^2 x} \\
&=\frac{-x^5 \cos x+5 x^4 \sin x+1}{(\sin x)^2}
\end{aligned}
\)

Example 14: Find the derivative of \(\frac{x+\cos x}{\tan x}\)

Solution: We use quotient rule on the function \(\frac{x+\cos x}{\tan x}\) wherever it is defined.
\(
\begin{aligned}
h^{\prime}(x) &=\frac{(x+\cos x)^{\prime} \tan x-(x+\cos x)(\tan x)^{\prime}}{(\tan x)^2} \\
&=\frac{(1-\sin x) \tan x-(x+\cos x) \sec ^2 x}{(\tan x)^2}
\end{aligned}
\)

Example 15: \(\text { The Derivative of } \mathrm{e}^{\mathrm{x}}\)

Solution: Let us consider the series expression for the exponential function
\(
e^x=1+x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\text { etc. }
\)
We can calculate the derivative of the left side by applying the rule for the derivative of a sum. That is, the derivative of a sum equals the sum of the derivatives of each term
\(
\left(e^x\right)^{\prime}=1^{\prime}+(x)^{\prime}+\left(\frac{x^2}{2 !}\right)^{\prime}+\left(\frac{x^3}{3 !}\right)^{\prime}+(\text { etc. })^{\prime}
\)
We calculate the derivative term by term, We know the derivatives of each of those terms
\(
\left(e^x\right)^{\prime}=0+1+2 \frac{x}{1.2}+3 \frac{x^2}{1.2 .3}+4 \frac{x^3}{1.2 .3 .4}+(\text { etc. })^{\prime}
\)
We apply the power rule to calculate the derivative of each term
\(
\left(e^x\right)^{\prime}=1+x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+e t c .
\)
We cancel out some of the numbers and we arrive to a surprising result. The expression for the derivative is the same as the one for the original function. That is
\(\left(e^x\right)^{\prime}=e^x\)
The derivative of \(e^x \text { is } e^x\)

Example 16: Find the derivative of the function \(y=\cos \left(2 x^2+1\right)\) using the chain rule.

Solution:

Assume that \(u=2 x^2+1\). Then \(y=\cos u\).
By the chain rule formula,
\(\mathrm{dy} / \mathrm{dx}=\mathrm{dy} / \mathrm{du} \cdot \mathrm{du} / \mathrm{dx}\)
\(\mathrm{dy} / \mathrm{dx}=\mathrm{d} / \mathrm{du}(\cos u) \cdot \mathrm{d} / \mathrm{dx}\left(2 x^2+1\right)\)
\(\mathrm{dy} / \mathrm{dx}=-\sin u \cdot 4 x\)
\(\mathrm{dy} / \mathrm{dx}=-4 x \sin \left(2 x^2+1\right)\left(\right.\) because \(\left.u=2 x^2+1\right)\)
Therefore, derivative of the given function is, \(\mathrm{dy} / \mathrm{dx}=-4 x \sin\) \(\left(2 x^2+1\right)\)

What is L Hospital Rule?

L’Hospital’s rule states that the limit of the ratio of two functions (where the denominator is not equal to 0) that results in an indeterminate form by the direct application of the limit is equal to the limit of the ratio of their derivatives. Let us see the mathematical definition of L’Hopital’s rule below.

L’Hopital’s Rule

If \(\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\) indeterminate form then:
\(
\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\lim _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}
\)

Important Notes on L’Hospital’s Rule:

• The limit of a fraction of two functions (that results in an indeterminate form) is equal to the limit of the fraction of their derivatives.
• Do not apply L’Hospital’s rule if the limit is not resulting in an indeterminate form.
• We can apply L’Hopital’s rule as many times as required but before the application of each time, we should check whether the limit in that particular step is giving an indeterminate form.
• When we are trying to apply L’Hopital’s rule for the product \(f(x) \cdot g(x)\), first, write it as fraction (i.e., either as \(f(x) /(1 / g(x))\) or as \(g(x) /(1 /\) \(f(x)))\)

 

Example 17: Evaluate the \(\operatorname{limit}^{\lim } \lim _{x \rightarrow \infty}\left(2 x^2+5 x+3\right) /\left(3 x^2-7 x\right.\) \(+2\) )

(i) without using and

(ii) using L’Hopital’s rule.

Solution:

(i) without using L’Hopitals rule:
\(
\begin{aligned}
&\lim _{x \rightarrow \infty}\left(2 x^2+5 x+3\right) /\left(3 x^2-7 x+2\right) \\
&=\lim _{x \rightarrow \infty}\left[x^2\left(2+5 / x+3 / x^2\right)\right] /\left[x^2\left(3-7 / x+2 / x^2\right)\right] \\
&=\lim _{x \rightarrow \infty}\left(2+5 / x+3 / x^2\right) /\left(3-7 / x+2 / x^2\right) \\
&=(2+0+0) /(3-0+0) \\
&=2 / 3
\end{aligned}
\)

(ii) Using L’Hospitals rule:
\(\lim _{x \rightarrow \infty}\left(2 x^2+5 x+3\right) /\left(3 x^2-7 x+2\right)\)
Apply \(x \rightarrow \infty\) gives indeterminate form \(\infty / \infty\). So we apply
L’Hospital’s rule. The derivatives of numerator and denominator are \(4 x+5\) and \(6 x-7\) respectively. So the above limit becomes: \(=\lim _{\mathrm{x} \rightarrow \infty}(4 \mathrm{x}+5) /(6 \mathrm{x}-7)\)

Direct application of \(x \rightarrow \infty\) again gives \(\infty / \infty\). So we again apply the rule. Then we get:
\(=\lim _{x \rightarrow \infty}(4) /(6)\)
\(=4 / 6\)
\(=2 / 3\)
In both the methods, we found that \(\lim _{x \rightarrow \infty}\left(2 x^2+5 x\right.\) \(+3) /\left(3 x^2-7 x+2\right)=2 / 3\)

Example 18: \(\text { Evaluate the limit } \lim _{x \rightarrow \infty}\left(e^x / x^2\right)\)

Solution:

If we apply the limit \(x \rightarrow \infty\), it gives \(\infty / \infty\). So we apply L’Hpoital’s rule. Then we get:
\(\lim _{x \rightarrow \infty}\left(e^x / x^2\right)=\lim _{x \rightarrow \infty}\left(e^x / 2 x\right)\)
(This is by using the derivative of \(e^x\) formula)
Again, the application of limit gives \(\infty / \infty\). So we apply the rule again. Then the above limit becomes:
\(\lim _{x \rightarrow \infty}\left(e^x / 2\right)=\infty / 2=\infty\)
Therefore, \(\lim _{x \rightarrow \infty}\left(e^x / x^2\right)=\infty\).

Example 19: Evaluate \(\lim _{x \rightarrow 0}(1-\cos 2 x) / x^2\)

Solution:

By the direct application of limit \(x \rightarrow 0\), we get \((1-\cos 0) / 0=(1-1) / 0=\) \(\mathrm{0} / \mathrm{0}\), which is an indeterminate form.
So we apply L’Hospital’s rule. We know that the derivatives of \(1-\cos 2 x\) and \(x^2\) are \(2 \sin 2 x\) and \(2 x\) respectively.
Then the above limit becomes: \(\lim _{x \rightarrow 0}(2 \sin 2 x / 2 x)=\lim _{x \rightarrow 0}(\sin 2 x / x)\)
Let us try to apply the limit now.
Then we get \((\sin 0) / 0=0 / 0\), which is again an indeterminate form.
So we apply the L’Hospital’s rule again.
We know that the derivatives of \(\sin 2 x\) and \(x\) are \(2 \cos 2 x\) and 1 respectively.
Then the above limit becomes:
\(\lim _{x \rightarrow 0}(2 \cos 2 x / 1)=2 \cos 0=2(1)=2 .^x\)
Therefore, \(\lim _{x \rightarrow 0}(1-\cos 2 x) / x^2=2\)

When Can’t We apply L’Hospital’s Rule?

Application of L’Hopital’s rule when the limit does not give an indeterminate form throws the wrong result.

Example 20: Evaluate \(\lim _{x \rightarrow 2}(3 x+1) /(2 x+2)\)

Solution: 

\(\lim _{x \rightarrow 2}(3 x+1) /(2 x+2)=(3(2)+1) /(2(2)+2)=7 / 6\) (correct answer)
The limit didn’t result in an indeterminate form and so we can’t apply the L’Hospital’s rule.

Let us see what we get if we apply. We know that the derivatives of \(3 x+1\) and \(2 x+2\) are 3 and 2 respectively. So the above limit after the application of the rule becomes:
\(\lim _{x \rightarrow 2}(3 / 2)=3 / 2\) (incorrect answer)

Note1: So do apply the limit first and make sure that an indeterminate form is resulted before applying the rule.

Simplify the Fraction Before Each Application

When we apply L’Hospital’s rule for multiple times, simplify the rational expression each time before applying the limit every time. Otherwise, we result in a wrong answer. Here is an example.
\(
\begin{aligned}
&\lim _{x \rightarrow 1}\left(x^3-1\right) /\left(x^2-1\right) \\
&=\lim _{x \rightarrow 1}\left(3 x^2 / 2 x\right) \\
&=\lim _{x \rightarrow 1}(3 x / 2) \\
&=3(1) / 2 \\
&=3 / 2 \text { (correct answer) }
\end{aligned}
\)
But what happens if we don’t simplify the fraction (in the third step) and try to apply L’Hopital’s rule again?
\(
\begin{aligned}
&\lim _{x \rightarrow 1}\left(x^3-1\right) /\left(x^2-1\right) \\
&=\lim _{x \rightarrow 1}\left(3 x^2 / 2 x\right) \\
&=\lim _{x \rightarrow 1}(6 x / 2) \\
&=\lim _{x \rightarrow 1} 3 x \\
&=3(1) \\
&=3 \text { (incorrect answer) }
\end{aligned}
\)

Note2: Thus, simplify everything into the lowest terms before the application of the rule.

Example 21: Evaluate \(\lim _{x \rightarrow 1} \frac{x^4-1}{x-1}\)

Solution: \(\lim _{x \rightarrow 1} \frac{x^4-1}{x-1}\)
If we put lim x=1, we have indeterminate form \(\frac{0}{0}\), Let’s first factorize.
\(=\lim _{x \rightarrow 1} \frac{\left(x^2-1\right)\left(x^2+1\right)}{x-1}\)
\(=\lim _{x \rightarrow 1} \frac{(x-1)(x+1)\left(x^2+1\right)}{x-1}\)
\(=\lim _{x \rightarrow 1}(x+1)\left(x^2+1\right)\)
\(=4\)

Example 22: Evaluate \(\lim _{x \rightarrow 1} \frac{\left(x^{\frac{1}{3}}-1\right)}{\left(x^{\frac{1}{2}}-1\right)}\)

Solution: \(\lim _{x \rightarrow 1} \frac{\left(x^{\frac{1}{3}}-1\right)}{\left(x^{\frac{1}{2}}-1\right)}\)
\(=\lim _{x \rightarrow 1} \frac{\frac{\mathrm{d}}{\mathrm{d} x}\left(x^{\frac{1}{3}}-1\right)}{\frac{\mathrm{d}}{\mathrm{d} x}\left(x^{\frac{1}{2}}-1\right)}\)
we have indeterminate form \(\frac{0}{0}\) L’Hopital’s rule applies
\(
=\lim _{x \rightarrow 1} \frac{\left(\frac{1}{3} x^{-\frac{2}{3}}\right)}{\left(\frac{1}{2} x^{-\frac{1}{2}}\right)}=\frac{2}{3}
\)

Example 23: \(\text { Evaluate } \lim _{\mathrm{x} \rightarrow 0}\left(\frac{e^{4 \mathrm{x}}-1}{\mathrm{x}}\right)\)

Solution: \(
\lim _{x \rightarrow 0} \frac{e^{4 x}-1}{x}=\frac{0}{0}
\)
This represents an indeterminate form. Thus applying L’Hospital’s rule, we get
\(
\lim _{x \rightarrow 0} \frac{e^{4 x}-1}{x}=\lim _{x \rightarrow 0} \frac{\frac{d}{d x}\left(e^{4 x}-1\right)}{\frac{d}{d x}(x)}
\)
\(
=\lim _{x \rightarrow 0} \frac{4 e^{4 x}}{1} = 4
\)

Example 24: Evaluate \(\lim _{x \rightarrow 1} \frac{x-1}{\ln (x)}\)

Solution: Substituting 1 into the limit results in the indeterminate form \(0 / 0\):
\(
\lim _{x \rightarrow 1} \frac{x-1}{\ln (x)}=\frac{1-1}{\ln (1)}=0 / 0
\)
Since the above expression fits the necessary criteria, we can use L’Hôpital’s rule to determine the limit:
\(
\begin{aligned}
\lim _{x \rightarrow 1} \frac{x-1}{\ln (x)} &=\lim _{x \rightarrow 1} \frac{(x-1)^{\prime}}{\ln (x)^{\prime}} \\
&=\lim _{x \rightarrow 1} \frac{1}{1 / x}=1
\end{aligned}
\)

Example 25: Evaluate \(\lim _{x \rightarrow \infty} \frac{x^2}{e^x}\)

Solution:
As \(x\) approaches \(\infty\), both the numerator and denominator approach infinity, resulting in the indeterminate form \(\infty / \infty\). Thus, we can use L’Hôpital’s rule, and differentiate the expression:
\(
\lim _{x \rightarrow \infty} \frac{\left(x^2\right)^{\prime}}{\left(e^x\right)^{\prime}}=\lim _{x \rightarrow \infty} \frac{2 x}{e^x}
\)
Notice that the resulting expression has the indeterminate form \(\infty / \infty\), so we still cannot determine the limit, and instead differentiate the expression once more:
\(
\lim _{x \rightarrow \infty} \frac{(2 x)^{\prime}}{\left(e^x\right)^{\prime}}=\lim _{x \rightarrow \infty} \frac{2}{e^x}
\)
After differentiating the expression a second time, we get an expression that is no longer an indeterminate form, so we can compute the limit and find that:
\(
\lim _{x \rightarrow \infty} \frac{2}{e^x}=0
\)

Other indeterminate forms

Although L’Hôpital’s rule can only be applied to limits of the indeterminate forms \(0 / 0\) and \(\infty / \infty\), it is sometimes possible to algebraically re-arrange expressions such that they meet the criteria necessary to use L’Hôpital’s rule. The examples below illustrate this for different cases.

Example 26: \(\text { Evaluate } \lim _{x \rightarrow \frac{\pi}{2}} \tan (x)\left(\frac{\pi}{2}-x\right)\)

Solution:

Plugging \(\pi / 2\) in results in an expression of the indeterminate form \(0 \cdot \infty\). In order to make use of L’Hôpital’s rule, re-write the limit as a quotient such that substitution results in an expression of the indeterminate form \(0 / 0\) :
\(
\begin{aligned}
\lim _{x \rightarrow \frac{\pi}{2}} \tan (x)\left(\frac{\pi}{2}-x\right) &=\lim _{x \rightarrow \frac{\pi}{2}} \frac{\frac{\pi}{2}-x}{\frac{1}{\tan (x)}} \\
&=\lim _{x \rightarrow \frac{\pi}{2}} \frac{\frac{\pi}{2}-x}{\cot (x)}
\end{aligned}
\)
Then, we use L’Hôpital’s rule and differentiate the expression to find the limit:
\(
\begin{aligned}
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\left(\frac{\pi}{2}-x\right)^{\prime}}{\cot (x)^{\prime}} &=\lim _{x \rightarrow \frac{\pi}{2}} \frac{-1}{-\csc ^2(x)} \\
&=\lim _{x \rightarrow \frac{\pi}{2}} \sin ^2(x)=1
\end{aligned}
\)

When not to use L’Hôpital’s rule

It is important to note that L’Hôpital’s rule cannot be used for just any limit. To reiterate, it can only be used for limits that result in (or can be converted to) the indeterminate forms 0/0 or ∞/∞ after having evaluated the limit through substitution. Using it in situations where this is not the case will result in an incorrect outcome.

Example 27: Find \(\lim _{x \rightarrow 0} \frac{1+\cos (x)}{e^x}\)

Solution: This limit can be evaluated through substitution. Plugging \(x=0\) into the limit,
\(\lim _{x \rightarrow 0} \frac{1+\cos (x)}{e^x}=\frac{1+1}{1}=2\)
we find that the limit is 2. However, if we had applied L’Hôpital’s rule instead of computing the limit as we did above, we would find an incorrect limit:
\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{(1+\cos (x))^{\prime}}{\left(e^x\right)^{\prime}} &=\lim _{x \rightarrow 0} \frac{-\sin (x)}{e^x} \\
&=\frac{0}{1}=0
\end{aligned}
\)

Thus, it is important to first confirm that we have a limit of the appropriate form by using substitution before applying L’Hôpital’s rule to a limit.
It is also important to note that even in cases where a limit is of the indeterminate form \(0 / 0\) or \(\infty / \infty\), this does not guarantee that the limit exists, or that it can be determined using L’Hôpital’s rule. It is entirely possible that repeated applications of L’Hôpital’s rule always results in an indeterminate form. In such cases, the limit may not exist. However, just because a limit cannot be determined using L’Hôpital’s rule does not necessarily mean that the limit does not exist; sometimes, it may be possible to use other methods to compute the limit.

Example 28: \(\text { Find } \lim _{x \rightarrow \infty} \frac{x+1}{\sqrt{x^2+2 x+3}}\)

Solution:

As \(x \rightarrow \infty\), both terms approach \(\infty\), so we have a limit of the indeterminate form \(\infty / \infty\), and can apply L’Hôpital’s rule:
\(
\lim _{x \rightarrow \infty} \frac{(x+1)^{\prime}}{\left(\sqrt{x^2+2 x+3}\right)^{\prime}}=\lim _{x \rightarrow \infty} \frac{1}{\frac{(x+1)}{\left(\sqrt{\left.x^2+2 x+3\right)}\right.}}
\)
\(
=\lim _{x \rightarrow \infty} \frac{\sqrt{x^2+2 x+3}}{x+1}
\)
The resulting limit is still of the form \(\infty / \infty\), and if we were to apply L’Hôpital’s rule once more, we would end up with the same limit we began with. Regardless how many times we apply L’Hôpital’s rule, we would continue to alternate between the same two results.

Thus, this limit cannot be computed using L’Hôpital’s rule. However, it can be computed by simplifying the
expression algebraically. To do so, we first rewrite \(x+1\) as \(\sqrt{(x+1)^2}\). We also complete the square of the denominator to find that \(x^2+2 x+3=(x+1)^2+2\), allowing us to simplify the expression:
\(
\begin{aligned}
\lim _{x \rightarrow \infty} \frac{x+1}{\sqrt{x^2+2 x+3}} &=\lim _{x \rightarrow \infty} \frac{\sqrt{(x+1)^2}}{\sqrt{(x+1)^2+2}} \\
&=\lim _{x \rightarrow \infty} \sqrt{\frac{1}{\frac{(x+1)^2+2}{(x+1)^2}}} \\
&=\lim _{x \rightarrow \infty} \sqrt{\frac{1}{1+\frac{2}{(x+1)^2}}} \\
&=\sqrt{\frac{1}{1+0}}=1
\end{aligned}
\)