What is a natural domain of a function? This leads to the following theorem.

Theorem 1:

If \(a\) is any number in the natural domain of the corresponding trigonometric function, then
1. \(\lim _{x \rightarrow a} \sin (x)=\sin (a)\).
2. \(\lim _{x \rightarrow a} \cos (x)=\cos (a)\).
3. \(\lim _{x \rightarrow a} \tan (x)=\tan (a)\).
4. \(\lim _{x \rightarrow a} \csc (x)=\csc (a)\).
5. \(\lim _{x \rightarrow a} \sec (x)=\sec (a)\).
6. \(\lim _{x \rightarrow a} \cot (x)=\cot (a)\).

Proof: Since the trigonometric functions are continuous on their natural domain, the statements are valid.

Note: While evaluating the limits of a function never get it in 0/0 form (or something/0 which is undefined). Use the factorization method to avoid an undefined state.

Methods used to avoid undefined state

Method-1: Direct substitution method

Consider an example where we use direct substitution to calculate the function limits.

Evaluate the following limit: \(\lim _{x \rightarrow 4} \frac{4 x+3}{x-2}\)

Solution:
Directly Subsubstituting value of \(x\)
\(
\frac{4 \times 4+3}{4-2}=\frac{19}{2}
\)

Method-2: Factorization Method

Use this method when the direct substitution method fails.

Evaluate the following limit: \(\lim _{x \rightarrow 2} \frac{3 x^2-x-10}{x^2-4}\)

Solution: 
\(
\begin{aligned}
&=\lim _{x \rightarrow 2} \frac{3 x^2-x-10}{x^2-4} \\
&=\lim _{x \rightarrow 2} \frac{3 x^2-6 x+5 x-10}{(x+2)(x-2)} \\
&=\lim _{x \rightarrow 2} \frac{3 x(x-2)+5(x-2)}{(x+2)(x-2)} \\
&=\lim _{x \rightarrow 2} \frac{(3 x+5)(x-2)}{(x+2)(x-2)}
\end{aligned}
\)

We can now directly Substitute the value of \(x\).
\(=\frac{3 \times 2+5}{2+2}=\frac{11}{4}\)

Method-3: Use the formula if both the direct and factorization method fails

For any positive integer \(n\)

\(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}=n a^{n-1}\)

Note: The expression in the above theorem for the limit is true even if \(n\) is any rational number and \(a\) is positive.

Evaluate the following limit:
\(\lim _{x \rightarrow 0} \frac{(x+1)^5-1}{x}\)

Solution: Let, 
\(
\begin{aligned}
x &+1=y \\
x & \rightarrow 0 \\
y & \rightarrow 0+1 \\
y & \rightarrow 1
\end{aligned}
\)
\(
=\lim _{y \rightarrow 1} \frac{y^5-1}{y-1}
\)
compare with the formula
\(
\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}=n a^{n-1}
\)
We have now
\(
\begin{aligned}
&n=5, &a=1
\end{aligned}
\)
Therefore answer will be
\(
\begin{aligned}
&=5 \times(1)^{5-1} \\
&=5
\end{aligned}
\)

Method-4: Use trigonometric functions such as

\(
\begin{aligned}
&\lim _{x \rightarrow 0} \frac{\sin x}{x}=1 \\
&\lim _{x \rightarrow 0} \frac{1-\cos x}{x}=0
\end{aligned}
\)

Let’s consider an example

Evaluate the following limit:
\(\lim _{x \rightarrow 0} \frac{\sin a x}{b x}\)
Solution: Let’s try to bring the given function in the following format: \(\lim _{x \rightarrow 0} \frac{\sin x}{x}=1\)

\(
\lim _{x \rightarrow 0} \frac{\sin a x}{b x}
\)
Divide & Multiply by \(a x\)
\(
\begin{aligned}
{\left[\lim _{x \rightarrow 0} \frac{\sin a x}{a x}\right] \times \frac{a x}{b x} } =\frac{a}{b} \\
\end{aligned}
\)

Example 1: \(\text { Evaluate } \lim _{\theta \rightarrow 0} \frac{1-\cos \theta}{\theta} \text {. }\)

Solution:

In the first step, we multiply by the conjugate so that we can use a trigonometric identity to convert the cosine in the numerator to a sine:
\(
\begin{aligned}
\lim _{\theta \rightarrow 0} \frac{1-\cos \theta}{\theta}=& \lim _{\theta \rightarrow 0} \frac{1-\cos \theta}{\theta} \cdot \frac{1+\cos \theta}{1+\cos \theta} \\
&=\lim _{\theta \rightarrow 0} \frac{1-\cos ^2 \theta}{\theta(1+\cos \theta)} \\
&=\lim _{\theta \rightarrow 0} \frac{\sin ^2 \theta}{\theta(1+\cos \theta)} \\
&=\lim _{\theta \rightarrow 0} \frac{\sin \theta}{\theta} \cdot \frac{\sin \theta}{1+\cos \theta} \\
&=1 \cdot \frac{0}{2}=0
\end{aligned}
\)
Therefore,
\(
\lim _{\theta \rightarrow 0} \frac{1-\cos \theta}{\theta}=0
\)

limits of all six trigonometric functions when \(x\) tends to \(\pm{\infty}\)

We know that the graphs of the functions \(y=\sin x\) and \(y=\cos x\) approach different values between \(-1\) and 1 as shown in the above figure. Thus, the function is oscillating between the values, so it will be impossible for us to find the limit of \(y=\sin x\) and \(y=\cos x\) as \(x\) tends to \(\pm{\infty}\). Therefore, the limits of all six trigonometric functions when \(x\) tends to \(\pm{\infty}\) are tabulated below: 

\(
\begin{array}{|l|l|}
\hline \text { Function } & \text { Limit of the function for } \pm \infty \\
\hline \sin x & \lim _{x \rightarrow \pm \infty} \sin x=\text { not de fined } \\
\hline \cos x & \lim _{x \rightarrow \pm \infty} \cos x=\text { not defined } \\
\hline \tan x & \lim _{x \rightarrow \pm \infty} \tan x=\text { not defined } \\
\hline \operatorname{cosec} x & \lim _{x \rightarrow \pm \infty} \operatorname{cosec} x=\text { not defined } \\
\hline \sec x & \lim _{x \rightarrow \pm \infty} \sec x=\text { not defined } \\
\hline \cot x & \lim _{x \rightarrow \pm \infty} \cot x=\text { not defined } \\
\hline
\end{array}
\)

Apart from the above formulas, we can define the following theorems that come in handy in calculating the limits of some trigonometric functions.

Area of a Sector

\(
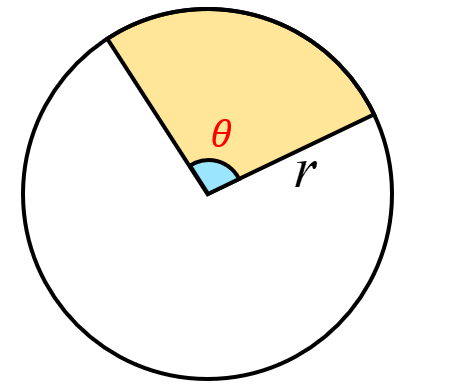
A=\left(\frac{\theta}{360}\right) \pi r^2
\)
For the other formula with radians as the input value, we will perform some work. Note that the ratio of the central angle with the circle’s complete revolution is \(\frac{\theta}{2 \pi}\). If we multiply this to the formula of the area of the circle, we get
\(
\frac{\theta}{2 \pi} \times \pi r^2=\frac{\theta}{2} \times r^2
\)

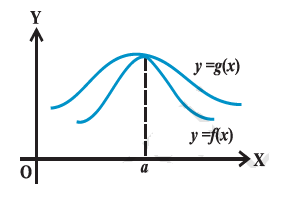
Theorem 2:

Let \(f\) and \(g\) be two real-valued functions with the same domain such that \(f(x) \leq g(x)\) for all \(x\) in the domain of definition, For some \(a\), if both
\(
\lim _{x \rightarrow a} f(x)
\)
and
\(\lim _{x \rightarrow a} g(x)\)
exist, then
\(
\lim _{x \rightarrow a} f(x) \leq \lim _{x \rightarrow a} g(x)
\)

This is shown in the Figure below.

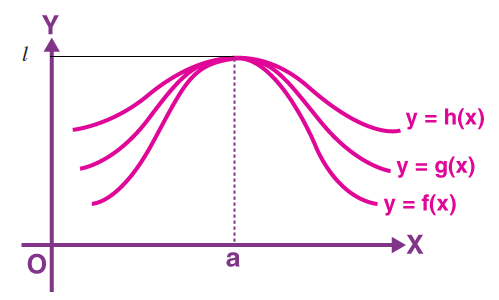
Theorem 3(Sandwich or Squeeze theorem):

Let \(f, g\) and \(h\) be real functions such that \(f(x) \leq g(x) \leq h(x)\) for all \(x\) in the common domain of definition. For some real number a, if
\(
\begin{aligned}
&\lim _{x \rightarrow a} f(x)=l=\lim _{x \rightarrow a} h(x) \\
&\text {, then } \lim _{x \rightarrow a} g(x)=l
\end{aligned}
\)

We use the Sandwich theorem to find the limit of a function when it becomes difficult or complicated or sometimes when we failed to find the limit by other methods. This is illustrated in the figure below.

Sandwich Theorem proof

Let’s have a look at the geometric proof of the above statement using an inequality involving trigonometric functions.
Consider the inequality as,
\(\cos x<\frac{\sin x}{x}<1\) for \(0<|x|<\pi / 2 \ldots .(1)\)
We know that,
\(\sin (-x)=-\sin x\)
\(\cos (-x)=\cos x\)
Hence, it is sufficient to prove the above inequality for \(0<x<\pi / 2\).
For this, we need to draw a unit circle.
Let O be the centre of the unit circle such that the \(\angle A O C\) is \(x\) radians and \(0<x<\pi / 2\).
Also, the line segments \(B A\) and \(C D\) are perpendiculars to \(O A\). Finally, join \(A C\) as shown in the figure below:

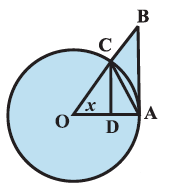
Area of \(\triangle \mathrm{OAC}<\) Area of sector OAC \(<\) Area of \(\triangle \mathrm{OAB}\)
i.e., \(\quad \frac{1}{2} \mathrm{OA} \cdot \mathrm{CD}<\frac{x}{2 \pi} \cdot \pi \cdot(\mathrm{OA})^2<\frac{1}{2} \mathrm{OA} \cdot \mathrm{AB}\).
i.e., \(\mathrm{CD}<x . \mathrm{OA}<\mathrm{AB}\).
From \(\triangle \mathrm{OCD}\),
\(\sin x=\frac{\mathrm{CD}}{\mathrm{OA}}\) (since \(\left.\mathrm{OC}=\mathrm{OA}\right)\) and hence \(\mathrm{CD}=\mathrm{OA} \sin x\). Also \(\tan x=\frac{\mathrm{AB}}{\mathrm{OA}}\) and
hence \(\quad \mathrm{AB}=\mathrm{OA} . \tan x\). Thus
OA \(\sin x<\) OA. \(x<\) OA. \(\tan x\).
Since length \(\mathrm{OA}\) is positive, we have
\(\sin x<x<\tan x\)
Since \(0<x<\frac{\pi}{2}, \sin x\) is positive and thus by dividing throughout by \(\sin x\), we have
\(1<\frac{x}{\sin x}<\frac{1}{\cos x}\). Taking reciprocals throughout, we have
\(
\cos x<\frac{\sin x}{x}<1
\)
which completes the proof.

Example 2: Find the limit \(\lim _{x \rightarrow 0} x^2 \cos \left(\frac{1}{x}\right) \text {. }\)

Solution:We know that \(-1 \leq \cos x \leq 1\)
Using the above relation we can write
\(
\begin{gathered}
-1 \leq \cos \left(\frac{1}{x}\right) \leq 1 \\
\text { i.e., }-x^2 \leq x^2 \cos \left(\frac{1}{x}\right) \leq x^2
\end{gathered}
\)
Comparing the above relation with the Squeeze theorem (i.e., Sandwich theorem) we get,
\(f(x)=-x^2, g(x)=x^2 \cos \left(\frac{1}{x}\right)\) and \(h(x)=-x^2\)
We have squeezed the given function \(x^2 \cos \left(\frac{1}{x}\right)\) between \(-x^2\) and \(x^2\)

Our next steps are to find the limits of \(x^2\) and \(-x^2\) as \(x\) approaches 0 .
\(
\begin{gathered}
\lim _{x \rightarrow 0} x^2=(0)^2=0 \\
\lim _{x \rightarrow 0}\left(-x^2\right)=-\lim _{x \rightarrow 0} x^2=-(0)^2=0
\end{gathered}
\)
So using Squeeze Theorem we can say \(\lim _{x \rightarrow 0} x^2 \cos \left(\frac{1}{x}\right)\) exists and
\(
\lim _{x \rightarrow 0} x^2 \cos \left(\frac{1}{x}\right)=0
\)

Squeeze theorem graph

We can represent the Squeeze theorem graphically.
For a clear concept, we take the previous example to explain the Squeeze theorem graphically.

If we put the functions \(f(x)=-x^2, g(x)=x^2 \cos \left(\frac{1}{x}\right)\) and \(h(x)=-x^2\) on the graph, the graph looks like this:

 

 

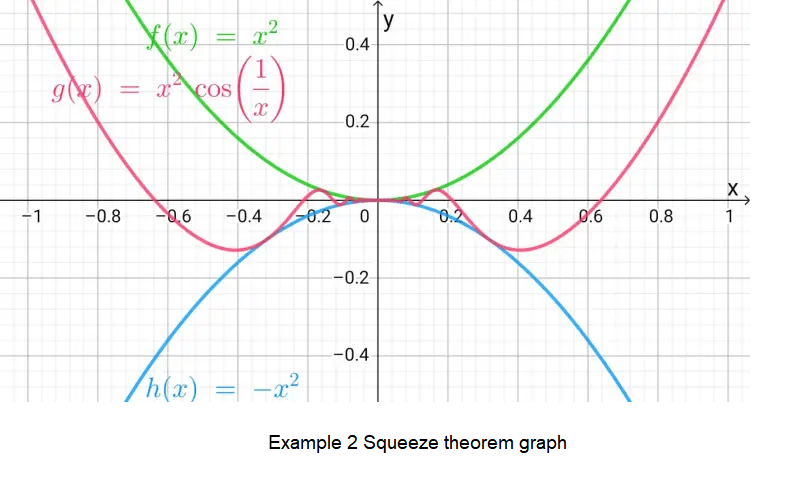
You can see that as \(-x^2 \leq x^2 \cos \left(\frac{1}{x}\right)\) the graph of \(x^2 \cos \left(\frac{1}{x}\right)\) is lied above \(-x^2\).

Also as \(x^2 \cos \left(\frac{1}{x}\right) \leq x^2\) the graph of \(x^2 \cos \left(\frac{1}{x}\right)\) is lied below \(x^2\).
The function \(g(x)=x^2 \cos \left(\frac{1}{x}\right)\) is squeezed in between \(f(x)=\) \(-x^2\) and \(f(x)=x^2\) at \((0,0)\).

We can say using limit that \(g(x)=x^2 \cos \left(\frac{1}{x}\right)\) approaches 0 as \(x\) approaches \(0 .\)
Therefore the limit
\(
\lim _{x \rightarrow 0} x^2 \cos \left(\frac{1}{x}\right)=0
\) 

Example 3:Evaluate:
\(\lim _{x \rightarrow 0} \frac{\sin a x}{b x}\)

Solution:
\(\lim _{x \rightarrow 0} \frac{\sin a x}{b x}\)
Multiplying and dividing the function by \({a x}\),
\(
\begin{aligned}
&=\lim _{x \rightarrow 0} \frac{\sin a x}{a x} \times \frac{a x}{b x} \\
&=\lim _{x \rightarrow 0} \frac{\sin a x}{a x} \times \frac{a}{b}
\end{aligned}
\)
Now, take the constant term out of the limit.
\(
=\frac{a}{b} \times \lim _{x \rightarrow 0} \frac{\sin a x}{a x}
\)
As we know,
\(
\lim _{x \rightarrow 0} \frac{\sin x}{x}=1
\)
So, replacing “\({x}\)” with “\({a x}\)“,
\(
\frac{a}{b} \times \lim _{a x \rightarrow 0} \frac{\sin a x}{a x}=\frac{a}{b} \times 1=\frac{a}{b}
\)
Therefore,
\(
\lim _{x \rightarrow 0} \frac{\sin a x}{b x}=\frac{a}{b}
\)

Example 4:
Find the value of
\(
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cos 2 x}{\sin x}
\)

Solution:

We know that,
\(\lim _{x \rightarrow a} \sin x=\sin a\)
and
\(\lim _{x \rightarrow a} \cos x=\cos a\)
Now,
\(
\begin{aligned}
&\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cos 2 x}{\sin x}=\frac{\lim _{x \rightarrow \frac{\pi}{2}} \cos 2 x}{\lim _{x \rightarrow \frac{\pi}{2}} \sin x}=\frac{\cos 2\left(\frac{\pi}{2}\right)}{\sin \frac{\pi}{2}} \\
&=\cos \pi /(\sin \pi / 2) \\
&=-1 / 1 \\
&=-1
\end{aligned}
\)
Therefore,
\(
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cos 2 x}{\sin x}=-1
\)

Example 5: Prove that \(\lim _{x \rightarrow 0} \frac{\sin x}{x} = 1\)

Solution: As the angle tends to zero, a special close relation between angle and sine of angle is revealed. In this special case, the value of sine function is approximately equal to the angle. Look at the table below.

\(
\begin{array}{|l|l|}
\hline \text { Angle }(x) \text { in Radian } & \sin x \\
\hline 0 & 0 \\
\hline 0.1 & 0.099833417 \approx 0.1 \\
\hline 0.02 & 0.019998667 \approx 0.02 \\
\hline 0.003 & 0.002999996 \approx 0.03 \\
\hline 0.0004 & 0.0004 \\
\hline 0.00005 & 0.00005 \\
\hline 0.000123 & 0.000123 \\
\hline 0.0006583 & 0.0006583 \\
\hline 0.00027595 & 0.00027595 \\
\hline 0.000039178 & 0.000039178 \\
\hline
\end{array}
\)

Therefore, \(\sin x \approx x\) as \(x\) approaches zero.
\(
\begin{aligned}
&\Longrightarrow \lim _{x \rightarrow 0} \frac{\sin x}{x}=\lim _{x \rightarrow 0} \frac{x}{x} \\
&\Longrightarrow \lim _{x \rightarrow 0} \frac{\sin x}{x}=\lim _{x \rightarrow 0} 1 \\
&\therefore \quad \lim _{x \rightarrow 0} \frac{\sin x}{x}=1
\end{aligned}
\)
Therefore, it is proved that the value of the ratio of the sine function to the angle is equal to one as the angle approaches zero.

Example 6: Evaluate \(\lim _{x \rightarrow 0} \frac{\sin (4 x)}{\sin (5 x)}\)

Solution:

\(
\begin{aligned}
&=\lim _{x \rightarrow 0} \frac{\sin (4 x)}{x} \cdot \frac{x}{\sin (5 x)} \\
&=\lim _{x \rightarrow 0} \frac{\sin (4 x)}{x}\left(\lim _{x \rightarrow 0} \frac{\sin (5 x)}{x}\right)^{-1} \\
&=4 \cdot 5^{-1}=\frac{4}{5}
\end{aligned}
\)

Example 7: Evaluate \(\lim _{x \rightarrow 0} \frac{\tan (3 x)}{\sin (x)}\)

Solution:

\(
=\lim _{x \rightarrow 0} \frac{\sin (3 x)}{\sin (x) \cos (3 x)}
\)
Multiply by \({x} / {x}\) :
\(
\begin{aligned}
&=\lim _{x \rightarrow 0} \frac{\sin (3 x)}{x} \cdot\left(\frac{\sin (x)}{x}\right)^{-1} \cdot \frac{1}{\cos (3 x)} \\
&=3 \cdot 1 \cdot 1=3
\end{aligned}
\)

Example 8: Evaluate \(\lim _{x \rightarrow 0} \frac{\cos (x)-1}{\sin (x)}\)

Solution:
\(
\begin{aligned}
&=\lim _{x \rightarrow 0}\left(\frac{\cos (x)-1}{\sin (x)}\right) \frac{x}{x} \\
&=\lim _{x \rightarrow 0} \frac{\cos (x)-1}{x} \cdot \lim _{x \rightarrow 0}\left(\frac{\sin (x)}{x}\right)^{-1} \\
&=0 \cdot 1=0
\end{aligned}
\)

Example 9: Evaluate \(\lim _{x \rightarrow 0} \frac{\sin ^2(5 x)}{x^2}\)

Solution:

\(
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{\sin ^2(5 x)}{x^2} \\
=& \lim _{x \rightarrow 0}\left(\frac{\sin (5 x)}{x}\right)^2 \\
=&\left(\lim _{x \rightarrow 0} \frac{\sin (5 x)}{x}\right)^2 \\
=& 5^2=25
\end{aligned}
\)

Example 10: \(\lim _{x \rightarrow 1} \frac{\sin (x-1)}{x^2+x-2}\)

Solution: 
\(
\begin{aligned}
& \frac{\sin (x-1)}{x^2+x-2}=\frac{\sin (x-1)}{(x+2)(x-1)}=\left(\frac{\sin (x-1)}{x-1}\right) \frac{1}{x+2} \\
& \lim _{x \rightarrow 1} \frac{\sin (x-1)}{x^2+x-2}=\lim _{x \rightarrow 1}\left(\frac{\sin (x-1)}{x-1}\right) \frac{1}{x+2}=1 \cdot \frac{1}{3}
\end{aligned}
\)

Example 11: Evaluate \(\lim _{x \rightarrow \frac{\pi}{4}} \frac{1-\tan (x)}{\sin (x)-\cos (x)}\)

Solution: 

\(
\begin{aligned}
&\lim _{x \rightarrow \frac{\pi}{4}} \frac{1-\frac{\sin (x)}{\cos (x)}}{\sin (x)-\cos (x)} \\
&=\lim _{x \rightarrow \frac{\pi}{4}} \frac{\frac{\cos (x)-\sin (x)}{\cos (x)}}{\sin (x)-\cos (x)} \\
&=\lim _{x \rightarrow \frac{\pi}{4}} \frac{\cos (x)-\sin (x)}{-\cos (x)[\cos (x)-\sin (x)]} \\
&=\lim _{x \rightarrow \frac{\pi}{4}} \frac{1}{-\cos (x)} \\
&=\frac{-2}{\sqrt{2}}=-\sqrt{2}
\end{aligned}
\)

Example 12: \(\lim _{x \rightarrow 0} \frac{\sin (x)}{x \tan (x)}\)

Solution:

\(
\begin{aligned}
&=\lim _{x \rightarrow 0} \frac{\sin (x)}{\frac{x \sin (x)}{\cos (x)}} \\
&=\lim _{x \rightarrow 0} \frac{\sin (x) \cos (x)}{x \sin (x)} \\
&=\lim _{x \rightarrow 0} \frac{\cos (x)}{x} \rightarrow \infty
\end{aligned}
\)

Example 13: \(\lim _{x \rightarrow 0} \frac{\sin \left(x^2\right)}{x}\)

Solution:

Let \(u=x^2\), then \(x=u^{1 / 2}\). Now convert to u’s and multiply by \(u^{1 / 2} / u^{1 / 2}\) :
\(
\begin{aligned}
&=\lim _{u \rightarrow 0} \frac{\sin (u)}{u^{1 / 2}} \frac{u^{1 / 2}}{u^{1 / 2}} \\
&=\lim _{u \rightarrow 0} \frac{u^{1 / 2} \sin (u)}{u} \\
&=\lim _{u \rightarrow 0} u^{1 / 2} \cdot \lim _{u \rightarrow 0} \frac{\sin (u)}{u} \\
&=0 \cdot 1=0
\end{aligned}
\)

Example 14: Evaluate \(\lim _{x \rightarrow 1} \frac{\sin (x-1)}{x^2-1}\)

Solution: 

Step 1: Eliminate the indeterminate form by factoring

\(
=\lim _{x \rightarrow 1} \frac{\sin (x-1)}{(x+1)(x-1)}
\)
Now, let’s try to factorize this rational function as a product of two fractions by the multiplication rule of fractions.
\(
\begin{aligned}
&=\lim _{x \rightarrow 1} \frac{\sin (x-1)}{(x+1) \times(x-1)} \\
&=\lim _{x \rightarrow 1} \frac{\sin (x-1)}{(x-1) \times(x+1)} \\
&=\lim _{x \rightarrow 1} \frac{\sin (x-1) \times 1}{(x-1) \times(x+1)} \\
&=\lim _{x \rightarrow 1}\left(\frac{\sin (x-1)}{(x-1)} \times \frac{1}{(x+1)}\right) \\
&=\lim _{x \rightarrow 1}\left(\frac{\sin (x-1)}{x-1} \times \frac{1}{x+1}\right)
\end{aligned}
\)
According to the product rule of limits, the limit of a product of \(\sin (x-1)\) by \(x-1\) and 1 by \(x+1\) can be calculated by the product of their limits.
\(
=\lim _{x \rightarrow 1} \frac{\sin (x-1)}{x-1} \times \lim _{x \rightarrow 1} \frac{1}{x+1}
\)
According to the commutative property of multiplication, the above product of two functions can be written as follows.
\(
=\lim _{x \rightarrow 1} \frac{1}{x+1} \times \lim _{x \rightarrow 1} \frac{\sin (x-1)}{x-1}
\)

Step 2: Find the Limit by Direct Substitution

Look at the first factor of the mathematical expression. The limit of 1 by \(x\) plus 1 can be evaluated by the direct substitution as the value of \(x\) approaches 1.
\(
\begin{aligned}
&=\frac{1}{1+1} \times \lim _{x \rightarrow 1} \frac{\sin (x-1)}{x-1} \\
&=\frac{1}{2} \times \lim _{x \rightarrow 1} \frac{\sin (x-1)}{x-1}
\end{aligned}
\)

Step 3: Find the Limit by the Trigonometric Limit rule

The second factor is similar to the trigonometric limit rule in the sine function. So, let’s try to convert the limit of sine of \(x\) minus 1 by \(x\) minus 1 as \(x\) approaches 1 into trigonometric limit rule in sine function.
If \(x \rightarrow 1\), then \(x-1 \rightarrow 1-1\). Therefore, \(x-1 \rightarrow 0\)
It clears that the value of \(x\) minus 1 tends to zero when the value of \(x\) is closer to 1 . \(=\frac{1}{2} \times \lim _{x-1 \rightarrow 0} \frac{\sin (x-1)}{x-1}\)
Assume \(y=x-1\) for our convenience. Now, transform the function in the second-factor position in terms of \(y\).
\(
\begin{aligned}
&=\frac{1}{2} \times \lim _{y \rightarrow 0} \frac{\sin (y)}{y} \\
&=\frac{1}{2} \times \lim _{y \rightarrow 0} \frac{\sin y}{y}
\end{aligned}
\)
According to the trigonometric limit rule in sine function, the limit of sine of angle \(y\) by \(y\) as the value of \(y\) tends to 0 is equal to one.
\(
\begin{aligned}
&=\frac{1}{2} \times 1 \\
&=\frac{1}{2}
\end{aligned}
\)

Example 15: Evaluate \(\lim _{x \rightarrow 0} \frac{\sin 4 x}{\sin 2 x}\)

Solution:

\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{\sin 4 x}{\sin 2 x} &=\lim _{x \rightarrow 0}\left[\frac{\sin 4 x}{4 x} \cdot \frac{2 x}{\sin 2 x} \cdot 2\right] \\
&=2 \cdot \lim _{x \rightarrow 0}\left[\frac{\sin 4 x}{4 x}\right] \div\left[\frac{\sin 2 x}{2 x}\right] \\
&=2 \cdot \lim _{4 x \rightarrow 0}\left[\frac{\sin 4 x}{4 x}\right] \div \lim _{2 x \rightarrow 0}\left[\frac{\sin 2 x}{2 x}\right] \\
&=2.1 .1=2(\text { as } x \rightarrow 0,4 x \rightarrow 0 \text { and } 2 x \rightarrow 0)
\end{aligned}
\)

Example 16: \(\lim _{x \rightarrow 0} \frac{\tan x}{x}\)

Solution: 

\(
\text { We have } \lim _{x \rightarrow 0} \frac{\tan x}{x}=\lim _{x \rightarrow 0} \frac{\sin x}{x \cos x}=\lim _{x \rightarrow 0} \frac{\sin x}{x} \cdot \lim _{x \rightarrow 0} \frac{1}{\cos x}=1.1=1
\)