NCERT Exemplar MCQs
Summary
- In three dimensions, the coordinate axes of a rectangular Cartesian coordinate system are three mutually perpendicular lines. The axes are called the \(x, y\) and \(z\)-axes.
- The three planes determined by the pair of axes are the coordinate planes, called XY, YZ and ZX-planes.
- The three coordinate planes divide the space into eight parts known as octants.
- The coordinates of a point \(P\) in three dimensional geometry is always written in the form of triplet like \((x, y, z)\). Here \(x, y\) and \(z\) are the distances from the YZ, ZX and XY-planes.
(i) Any point on \(x\)-axis is of the form \((x, 0,0)\)
(ii) Any point on \(y\)-axis is of the form \((0, y, 0)\)
(iii) Any point on \(z\)-axis is of the form \((0,0, z)\). - Distance between two points \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\) is given by
\(
PQ =\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}
\) - The coordinates of the point \(R\) which divides the line segment joining two points \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\) internally and externally in the ratio \(m: n\) are given by
\(
\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}, \frac{m z_2+n z_1}{m+n}\right) \text { and }\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}, \frac{m z_2-n z_1}{m-n}\right) \text {, }
\)
respectively. - The coordinates of the mid-point of the line segment joining two points \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\) are \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)\).
- The coordinates of the centroid of the triangle, whose vertices are \(\left(x_1, y_1, z_1\right)\) \(\left(x_2, y_2, z_2\right)\) and \(\left(x_3, y_3, z_3\right)\), are \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\).
Quiz Summary
0 of 81 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 81 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 81
1. Question
Which Octant the following points located:
(i) \((1,-1,3)\)
(ii) \((-1,2,4)\)
(iii) \((-2,-4,-7)\)
(iv) \((-4,2,-5)\)CorrectIncorrectHint
(i) Location of \(P (1,-1,3)=(x,-y, z)=\) IV octant
(ii) Location of \(Q (-1,2,4)=(-x, y, z)=\) II octant
(iii) Location of \(R (-2,-4,-7)=(-x,-y,-z)=\) VII octant
(iv) Location of \(S(-4,2,-5)=(-x, y,-z)= VI\) octant -
Question 2 of 81
2. Question
Name the octant in which each of the following points lie.
(i) \((1,2,3)\)
(ii) \((4,-2,3)\)
(iii) \((4,-2,-5)\)
(iv) \((4,2,-5)\)
(v) \((-4,2,5)\)
(vi) \((-3,-1,6)\)
(vii) \((2,-4,-7) \quad\)
(viii) \((-4,2,-5)\)CorrectIncorrectHint
(i) Point \((1,2,3)\) lies in I octant
(ii) Point \((4,-2,3)\) lies in IV octant
(iii) Point \((4,-2,-5)\) lies in VIII octant
(iv) Point \((4,2,-5)\) lies in \(V\) octant
(v) Point \((-4,2,5)\) lies in II octant
(vi) Point \((-3,-1,6)\) lies in III octant
(vii) Point \((2,-4,-7)\) lies in VIII octant
(viii) Point \((-4,2,-5)\) lies in VI octant -
Question 3 of 81
3. Question
Let A, B, C be the feet of perpendiculars from a point \(P\) on \(x, y\), \(z\)-axis respectively. Find the coordinates of \(A, B\) and \(C\) in each of the following where the \(P\) is
(i) \((3,4,2)\)
(ii) \((-5,3,7)\)
(iii) \((4,-3,-5)\)CorrectIncorrectHint
The coordinates of \(A , B\) and \(C\) are
(i) \(A (3,0,0), B (0,4,0)\) and \(C (0,0,2)\)
(ii) \(A (-5,0,0), B (0,3,0)\) and \(C (0,0,7)\)
(iii) \(A (4,0,0), B (0,-3,0)\) and \(C (0,0,-5)\) -
Question 4 of 81
4. Question
Let A, B, C be the feet of perpendiculars from a point \(P\) on the \(x y, y z\) and \(z x\) planes respectively. Find the coordinates of A, B, C in each of the following where the point \(P\) is
(i) \((3,4,5)\)
(ii) \((-5,3,7)\)
(iii) \((4,-3,-5)\).CorrectIncorrectHint
The coordinates of \(A , B\) and \(C\) are
(i) \(A (3,4,0), B (0,4,5)\) and \(C (3,0,5)\)
(ii) \(A (-5,3,0), B (0,3,7)\) and \(C (-5,0,7)\)
(iii) \(A (4,-3,0), B (0,-3,-5)\) and \(C (4,0,-5)\) -
Question 5 of 81
5. Question
How far apart are the points \((2,0,0)\) and \((-3,0,0)\) ?
CorrectIncorrectHint
Given points are \((2,0,0)\) and \((-3,0,0)\)
\(\therefore\) Distance between the given points
\(
=\sqrt{(2+3)^2+(0-0)^2+(0-0)^2}=\sqrt{25}=5
\)
Hence, the required distance \(=5\). -
Question 6 of 81
6. Question
Find the distance from the origin to \((6,6,7)\).
CorrectIncorrectHint
Coordinates of the origin are \((0,0,0)\)
\(\therefore\) Distance from \((0,0,0)\) to \((6,6,7)\)
\(
\begin{aligned}
& =\sqrt{(6-0)^2+(6-0)^2+(7-0)^2} \\
& =\sqrt{36+36+49}=\sqrt{121} \\
& =11 \text { units. }
\end{aligned}
\)
Hence, the required distance \(=11\) units. -
Question 7 of 81
7. Question
If \(x^2+y^2=1\), then the point \(\left(x, y, \sqrt{1-x^2-y^2}\right)\) is at a distance ____ unit from the origin.
CorrectIncorrectHint
Given point is \(\left(x, y, \sqrt{1-x^2-y^2}\right)\)
\(\therefore\) Distance between the origin and the point is
\(
\begin{aligned}
& =\sqrt{(x-0)^2+(y-0)^2+\left(\sqrt{1-x^2-y^2}-0\right)^2} \\
& =\sqrt{1}=1 .
\end{aligned}
\) -
Question 8 of 81
8. Question
Are the point \(A (1,-1,3), B (2,-4,5)\) and \((5,-13,11)\) are collinear?
CorrectIncorrectHint
Given points are \(A (1,-1,3), B (2,-4,5)\) and \(C (5,-13,11)\)
\(
\begin{aligned}
AB & =\sqrt{(2-1)^2+(-4+1)^2+(5-3)^2} \\
& =\sqrt{1+9+4}=\sqrt{14} \\
BC & =\sqrt{(5-2)^2+(-13+4)^2+(11-5)^2} \\
& =\sqrt{9+81+36}=\sqrt{126}=3 \sqrt{14} \\
AC & =\sqrt{(5-1)^2+(-13+1)^2+(11-3)^2} \\
& =\sqrt{16+144+64}=\sqrt{224}=4 \sqrt{14}
\end{aligned}
\)
Here we observe that \(\sqrt{14}+3 \sqrt{14}=4 \sqrt{14}\)
So \(AB + BC = AC\).
Hence, the given points are collinear. -
Question 9 of 81
9. Question
Three consecutive vertices of a parallelogram \(ABCD\) are \(A (6,-2,4), B (2,4,-8)\), \(C(-2,2,4)\). Find the coordinates of the fourth vertex.
[Hint: Diagonals of a parallelogram have the same mid-point.]CorrectIncorrectHint
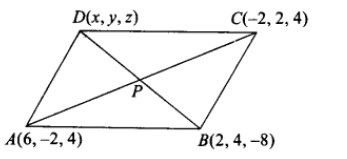
Let the coordinates of the fourth vertex \(D\) be \((x, y, z)\)
Mid-point of diagonal \(A C\) is \(P\left(\frac{6-2}{2}, \frac{-2+2}{2}, \frac{4+4}{2}\right) \equiv P(2,0,4)\)
Also, mid-point of \(B D\) is \(P\left(\frac{x+2}{2}, \frac{y+4}{2}, \frac{z-8}{2}\right)\).
Now, \(P\left(\frac{x+2}{2}, \frac{y+4}{2}, \frac{z-8}{2}\right) \equiv P(2,0,4)\)
One equating coordinates, we get
\(
\begin{aligned}
& \frac{x+2}{2}=2 \Rightarrow x=2 ; \\
& \frac{y+4}{2}=0 \Rightarrow y=-4 ; \\
& \frac{z-8}{2}=4 \Rightarrow z=16
\end{aligned}
\)
So, the coordinate of fourth vertex \(D\) are given as \((2,-4,16)\). -
Question 10 of 81
10. Question
The triangle \(ABC\) with vertices \(A (0,4,1), B (2,3,-1)\) and \(C (4,5,0)\) is ____ angled.
CorrectIncorrectHint
Given vertices are \(A(0,4,1), B(2,3,-1)\) and \(C(4,5,0)\)
\(
\begin{aligned}
AB & =\sqrt{(2-0)^2+(3-4)^2+(-1-1)^2} \\
& =\sqrt{4+1+4}=\sqrt{9}=3 \\
BC & =\sqrt{(4-2)^2+(5-3)^2+(0+1)^2} \\
& =\sqrt{4+4+1}=\sqrt{9}=3 \\
AC & =\sqrt{(4-0)^2+(5-4)^2+(0-1)^2} \\
& =\sqrt{16+1+1}=\sqrt{18}
\end{aligned}
\)
\(
\because \quad(3)^2+(3)^2=(\sqrt{18})^2 \text {. }
\)
So \(AB ^2+ BC ^2= AC ^2\)
Hence, \(\triangle ABC\) is a right angled triangle. -
Question 11 of 81
11. Question
Find the third vertex of triangle whose centroid is origin and two vertices are \((2,4,6)\) and \((0,-2,-5)\)
CorrectIncorrectHint
Using formula for co-ordinates of centroid of a triangle, the coordinates of the centroid of the triangle, whose vertices are \(\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)\) and \(\left(x_3, y_3, z_3\right)\) are
\(
\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)
\)
Given two vertices are \(A(2,4,6)\) and \(B(0,-2,-5)\)
Let the third vertex \(C(x, y, z)\)
\(\therefore\) Centroid of \(\triangle ABC\),
\(
\begin{aligned}
& G=\left(\frac{x+2+0}{3}, \frac{y+4-2}{3}, \frac{z+6-5}{3}\right) \\
& \Rightarrow G=\left(\frac{x+2}{3}, \frac{y+2}{3}, \frac{z+1}{3}\right)
\end{aligned}
\)
Simplifying using given coordinates of centroid
Given centroid is at origin
\(
\therefore G\left(\frac{x+2}{3}, \frac{y+2}{3}, \frac{z+1}{3}\right)=G(0,0,0)
\)
Comparing coordinates, we get
\(
\frac{x+2}{3}=0 \Rightarrow x=-2
\)
\(
\begin{aligned}
& \frac{y+2}{3}=0 \Rightarrow y=-2 \\
& \frac{z+1}{3}=0 \Rightarrow z=-1
\end{aligned}
\)
Therefore, third vertex of the triangle is \((-2,-2,-1)\) -
Question 12 of 81
12. Question
Find the centroid of a triangle, the mid-point of whose sides are \(D (1,2,-3)\), \(E(3,0,1)\) and \(F(-1,1,-4)\).
CorrectIncorrectHint
Let the coordinates of the vertices of \(\triangle A B C\) be \(A \left(x_1, y_1, z_1\right), B \left(x_2, y_2, z_2\right)\) and \(C \left(x_3, y_3, z_3\right)\).
\(
\begin{aligned}
& \text { Mid-point of } BC =(1,2,-3) \\
\therefore \quad & 1=\frac{x_2+x_3}{2} \Rightarrow x_2+x_3=2 \dots(i)
\end{aligned}
\)
\(
\begin{aligned}
2 & =\frac{y_2+y_3}{2} \Rightarrow y_2+y_3=4 \dots(ii) \\
-3 & =\frac{z_2+z_3}{2} \Rightarrow z_2+z_3=-6 \dots(iii)
\end{aligned}
\)
Mid-point of \(AB =(3,0,1)\)
\(
\therefore \quad 3=\frac{x_1+x_2}{2} \Rightarrow x_1+x_2=6 \dots(iv)
\)
\(
\begin{aligned}
& 0=\frac{y_1+y_2}{2} \Rightarrow y_1+y_2=0 \dots(v) \\
& 1=\frac{z_1+z_2}{2} \Rightarrow z_1+z_2=2 \dots(vi)
\end{aligned}
\)
Similarly, mid-point of \(AC =(-1,1,-4)\)
\(
\begin{aligned}
\therefore \quad-1 & =\frac{x_1+x_3}{2} \Rightarrow x_1+x_3=-2 \dots(vii)\\
1 & =\frac{y_1+y_3}{2} \Rightarrow y_1+y_3=2 \dots(viii)\\
-4 & =\frac{z_1+z_3}{2} \Rightarrow z_1+z_3=-8 \dots(ix)
\end{aligned}
\)
Adding eq. (i), (iv) and (vii) we get,
\(
\begin{aligned}
& 2 x_1+2 x_2+2 x_3=2+6-2=6 \\
& \Rightarrow \quad x_1+x_2+x_3=3 \\
& \Rightarrow \quad 6+x_3=3 \Rightarrow x_3=-3 \quad \text { [from eq. (iv)] } \\
& \Rightarrow \quad x_1+2=3 \Rightarrow x_1=1 \quad \text { [from eq. (i)] } \\
& \Rightarrow \quad x_2-2=3 \Rightarrow x_2=5 \quad \text { [from eq. (vii)] } \\
&
\end{aligned}
\)
\(
\text { So, } x_1=1, x_2=5 \text { and } x_3=-3 \text {. }
\)
Similarly, Adding (ii), (v) and (viii) we get
\(
\begin{aligned}
& 2\left(y_1+y_2+y_3\right)=4+0+2=6 \\
& \therefore \quad y_1+y_2+y_3=3 \\
& y_1+4=3 \Rightarrow y_1=-1 \\
& 0+y_3=3 \Rightarrow y_3=3 \\
& y_2+2=3 \Rightarrow y_2=1 \\
&
\end{aligned}
\)
So, \(y_1=-1, y_2=1, y_3=3\)
Adding (iii), (vi) and (ix) we have
\(
2\left(z_1+z_2+z_3\right)=-6+2-8=-12
\)
\(
\begin{aligned}
& \therefore \quad z_1+z_2+z_3=-6 \\
& z_1-6=-6 \quad \Rightarrow \quad z_1=0 \quad \text { [from eq. (iii)] } \\
& 2+z_3=-6 \Rightarrow z_3=-8 \quad \text { [from eq. (vi)] } \\
& \text { and } z_2-8=-6 \quad \Rightarrow \quad z_2=2 \\
&
\end{aligned}
\)
\(
\therefore z_1=1, z_2=1, z_3=-8
\)
So, the points are \(A (1,-1,0), B (5,1,2)\) and \(C (-3,3,-8)\).
\(\therefore\) Centroid of the triangle
\(
G=\left(\frac{1+5-3}{3}, \frac{-1+1+3}{3}, \frac{0+2-8}{3}\right)=(1,1,-2)
\)
Hence, the required coordinates \(=(1,1,-2)\). -
Question 13 of 81
13. Question
The mid-points of the sides of a triangle are \((5,7,11),(0,8,5)\) and \((2,3,-1)\). Find its vertices.
CorrectIncorrectHint
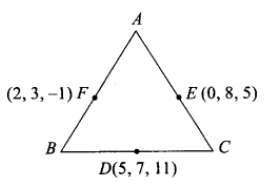
Given that The mid-points of the sides of a triangle \(A B C\) are \(D(5,7,11), E(0,8,5)\) and \(F(2,3,-1)\)
Let the vertices of triangle be \(A\left(x_1, y_1, z_1\right)\), \(B\left(x_2, y_2, z_2\right)\) and \(C\left(x_3, y_3, z_3\right)\).
Mid-point of \(A C\) is \(E\).
\(
\therefore \quad\left(\frac{x_1+x_3}{2}, \frac{y_1+y_3}{2}, \frac{z_1+z_3}{2}\right) \equiv(0,8,5)
\)
So, \(C\left(x_3, y_3, z_3\right) \equiv C\left(-x_1, 16-y_1, 10-z_1\right)\) (i)
Mid-point of \(A B\) is \(F\).
\(
\therefore \quad\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right) \equiv(2,3,-1)
\)
\(
\text { So, } B\left(x_2, y_2, z_2\right) \equiv B\left(4-x_1, 6-y_1,-2-z_1\right) \dots(ii)
\)
Mid-point of \(B C\) is \(D\)
\(
\begin{aligned}
\therefore \quad \frac{-x_1+4-x_1}{2} & =5, \frac{16-y_1+6-y_1}{2}=7, \\
\frac{10-z_1-2-z_1}{2} & =11
\end{aligned}
\)
\(
\begin{array}{llr}
\Rightarrow & x_1=-3, y_1=4 \text { and } z_1=-7 \\
\therefore & A \equiv(-3,4,-7) \\
\text { So, } & B \equiv(7,2,5) & \text { [Using (ii)] } \\
\text { and } & C \equiv(3,12,17) \quad \text { [Using (i)] }
\end{array}
\) -
Question 14 of 81
14. Question
Three vertices of a Parallelogram \(ABCD\) are \(A (1,2,3), B (-1,-2,-1)\) and \(C (2,3,2)\). Find the fourth vertex \(D\).
CorrectIncorrectHint
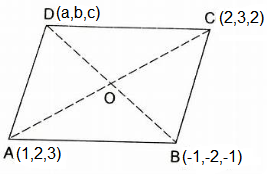
\(
\text { Let the coordinates of } D \text { be }(a, b, c) \text {. }
\)
We know that the diagonals of a parallelogram bisect each other.
\(\therefore\) Mid-point of \(AC\) i.e. \(O =\left(\frac{1+2}{2}, \frac{2+3}{2}, \frac{3+2}{2}\right)\)
\(
=\left(\frac{3}{2}, \frac{5}{2}, \frac{5}{2}\right)
\)
\(
\text { Mid-point of } BD \text { i.e. } O =\left(\frac{a-1}{2}, \frac{b-2}{2}, \frac{c-1}{2}\right)
\)
Equating the corresponding coordinate, we have
\(
\begin{aligned}
& \frac{a-1}{2}=\frac{3}{2} \quad \Rightarrow \quad a=4 \\
& \frac{b-2}{2}=\frac{5}{2} \quad \Rightarrow \quad b=7
\end{aligned}
\)
and \(\frac{c-1}{2}=\frac{5}{2} \Rightarrow c=6\)
Hence, the coordinates of \(D=(4,7,6)\). -
Question 15 of 81
15. Question
Find the coordinate of the points which trisect the line segment joining the points \(A (2,1,-3)\) and \(B (5,-8,3)\).
CorrectIncorrectHint
Let \(C\) and \(D\) be the points which divide the given line \(AB\) into three equal parts.
Here \(AC : CB =1: 2\)
Let \(\left(x_1, y_1, z_1\right)\) be the coordinates of \(C\)
\(
\begin{aligned}
\therefore \quad x_1 & =\frac{1 \times 5+2 \times 2}{1+2}=3 \\
y_1 & =\frac{1 \times-8+2 \times 1}{1+2}=-2
\end{aligned}
\)
\(
z_1=\frac{1 \times 3+2 \times-3}{1+2}=-1
\)
So \(C=(3,-2,-1)\).
Now \(D\) is the mid-point \(=C B\)
Let the coordinates of \(D\) be \(\left(x_2, y_2, z_2\right)\)
\(
\begin{aligned}
& x_2=\frac{3+5}{2}=4 \\
& y_2=\frac{-8-2}{2}=-5 \\
& z_2=\frac{3-1}{2}=1
\end{aligned}
\)
So, \(D=(4,-5,1)\).
Hence, the required coordinates are \(C(3,-2,-1)\) and \(D(4,-5,1)\). -
Question 16 of 81
16. Question
If the origin is the centriod of a triangle \(ABC\) having vertices \(A (a, 1,3)\), \(B (-2, b,-5)\) and \(C (4,7, c)\), find the values of \(a, b, c\).
CorrectIncorrectHint
Coordinates of the centroid \(G =(0,0,0)\)
\(
\begin{aligned}
\therefore & 0 =\frac{x_1+x_2+x_3}{3} \Rightarrow 0=\frac{a-2+4}{3} \Rightarrow a=-2 \\
& 0 =\frac{y_1+y_2+y_3}{3} \Rightarrow 0=\frac{1+b+7}{3} \Rightarrow b=-8 \\
\text { and } & 0 =\frac{z_1+z_2+z_3}{3} \Rightarrow 0=\frac{3-5+c}{3} \Rightarrow c=2
\end{aligned}
\)
Hence, the required values are \(a=-2, b=-8\) and \(c=2\). -
Question 17 of 81
17. Question
Let \(A (2,2,-3), B (5,6,9)\) and \(C (2,7,9)\) be the vertices of a triangle. The internal bisector of the angle \(A\) meets \(BC\) at the point \(D\). Find the coordinates of \(D\).
CorrectIncorrectHint
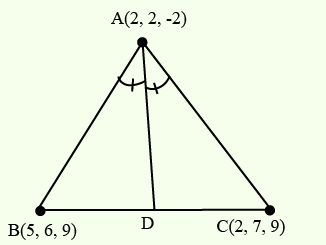
Given that \(AD\) is the internal bisector of \(\angle A\)
\(
\begin{aligned}
\therefore \quad \frac{ AB }{ AC } & =\frac{ BD }{ DC } \\
AB & =\sqrt{(5-2)^2+(6-2)^2+(9+3)^2} \\
& =\sqrt{9+16+144}=\sqrt{169}=13 \\
\therefore \quad AC & =\sqrt{(2-2)^2+(7-2)^2+(9+3)^2} \\
& =\sqrt{0+25+144}=13 \\
\therefore \quad \frac{ AB }{ AC } & =\frac{ BD }{ DC }=\frac{13}{13} \Rightarrow BD = DC
\end{aligned}
\)
\(\Rightarrow D\) is the mid-point of \(B C\)
\(
\begin{aligned}
\therefore \quad \text { Coordinates of } D & =\left(\frac{5+2}{2}, \frac{6+7}{2}, \frac{9+9}{2}\right) \\
& =\left(\frac{7}{2}, \frac{13}{2}, 9\right)
\end{aligned}
\)
Hence, the required coordinates are \(\left(\frac{7}{2}, \frac{13}{2}, 9\right)\). -
Question 18 of 81
18. Question
Given that the three points \(A (2,3,4), B (-1,2,-3)\) and \(C (-4,1,-10)\) are collinear and find the ratio in which \(C\) divides \(AB\).
CorrectIncorrectHint
Given points are \(A (2,3,4), B (-1,2,-3)\) and \(C (-4,1,-10)\)
\(
\begin{aligned}
AB & =\sqrt{(2+1)^2+(3-2)^2+(4+3)^2} \\
& =\sqrt{9+1+49}=\sqrt{59} \\
BC & =\sqrt{(-1+4)^2+(2-1)^2+(-3+10)^2} \\
& =\sqrt{9+1+49}=\sqrt{59} \\
AC & =\sqrt{(2+4)^2+(3-1)^2+(4+10)^2} \\
& =\sqrt{36+4+196}=\sqrt{236}=2 \sqrt{59} \\
\therefore \quad AB + BC & = AC \\
\sqrt{59}+\sqrt{59} & =2 \sqrt{59}
\end{aligned}
\)
Hence, \(A , B\) and \(C\) are collinear and \(AC : BC =2 \sqrt{59}: \sqrt{59}=2: 1\) Hence, \(C\) divides \(AB\) is \(2: 1\) externally. -
Question 19 of 81
19. Question
The mid-point of the sides of a triangle are \((1,5,-1),(0,4,-2)\) and \((2,3,4)\). Find its vertices. Also find the centroid of the triangle.
CorrectIncorrectHint
Let the vertices of the given triangle be \(A \left(x_1, y_1, z_1\right), B \left(x_2, y_2, z_2\right)\) and \(C \left(x_3, y_3, z_3\right)\).
\(D\) is the mid-point of \(B C\)
\(
\begin{aligned}
& \therefore \quad 1=\frac{x_2+x_3}{2} \Rightarrow x_2+x_3=2 \dots(i)\\
& 5=\frac{y_2+y_3}{2} \Rightarrow y_2+y_3=10 \dots(ii)\\
& -1=\frac{z_2+z_3}{2} \Rightarrow z_2+z_3=-2 \dots(iii)\\
&
\end{aligned}
\)
\(E\) is the mid-point of \(A B\)
\(
\begin{aligned}
\therefore \quad 0 & =\frac{x_1+x_2}{2} \quad \Rightarrow x_1+x_2=0 \dots(iv) \\
4 & =\frac{y_1+y_2}{2} \Rightarrow y_1+y_2=8 \dots(v) \\
-2 & =\frac{z_1+z_2}{2} \Rightarrow z_1+z_2=-4 \dots(vi)
\end{aligned}
\)
\(F\) is the mid-point of \(AC\)
\(
\begin{aligned}
\therefore \quad 2 & =\frac{x_1+x_3}{2} \Rightarrow x_1+x_3=4 \dots(vii)\\
3 & =\frac{y_1+y_3}{2} \Rightarrow y_1+y_3=6 \dots(viii)\\
4 & =\frac{z_1+z_3}{2} \Rightarrow z_1+z_3=8 \dots(ix)
\end{aligned}
\)
Adding eq. (i), (iv) and (vii) we get
\(
\begin{aligned}
2\left(x_1+x_2+x_3\right) & =2+0+4 \\
\therefore \quad x_1+x_2+x_3 & =3 \dots(x)
\end{aligned}
\)
Adding (ii), (v) and (viii) we get
\(
\Rightarrow \quad \begin{aligned}
2\left(y_1+y_2+y_3\right) & =10+8+6\\
y_1+y_2+y_3 & =12 \dots(xi)
\end{aligned}
\)
Adding (iii), (vi) and (ix) we get
\(
\begin{aligned}
2\left(z_1+z_2+z_3\right) & =-2-4+8 \\
z_1+z_2+z_3 & =1 \dots(xii)
\end{aligned}
\)
Solving the above equations
Here, the coordinates of \(B (-1,6,-7)\) Hence, the required coordinates are
\(
\begin{aligned}
& A (1,2,3), B (-1,6,-7) \text { and } C (3,4,5) \\
& \text { and Centroid } G=\left(\frac{1-1+3}{3}, \frac{2+6+4}{3}, \frac{3-7+5}{3}\right) \\
& =\left(1,4, \frac{1}{3}\right) \text {. } \\
&
\end{aligned}
\) -
Question 20 of 81
20. Question
The points \((0,-1,-7),(2,1,-9)\) and \((6,5,-13)\) are collinear. Find the ratio in which the first point divides the join of the other two.
CorrectIncorrectHint
Let the given points are \(A (0,-1,-7), B (2,1,-9)\) and \(C (6,5,-13)\)
\(
\begin{aligned}
AB & =\sqrt{(2-0)^2+(1+1)^2+(-9+7)^2} \\
& =\sqrt{4+4+4}=\sqrt{12}=2 \sqrt{3} \\
BC & =\sqrt{(6-2)^2+(5-1)^2+(-13+9)^2} \\
& =\sqrt{16+16+16}=\sqrt{48}=4 \sqrt{3}
\end{aligned}
\)
\(
\begin{aligned}
AC & =\sqrt{(6-0)^2+(5+1)^2+(-13+7)^2} \\
& =\sqrt{36+36+36}=\sqrt{108}=6 \sqrt{3} \\
2 \sqrt{3}+4 \sqrt{3} & =6 \sqrt{3}
\end{aligned}
\)
\(
\begin{array}{ll}
\text { i.e. } & A B+B C=A C \\
\therefore & A B: A C=2 \sqrt{3}: 6 \sqrt{3}=1: 3
\end{array}
\)
\(
\text { Hence, point } A \text { divides } B \text { and } C \text { in } 1: 3 \text { externally. }
\) -
Question 21 of 81
21. Question
What are the coordinates of the vertices of a cube whose edge is 2 units, one of whose vertices coincides with the origin and the three edges passing through the origin, coincides with the positive direction of the axes through the origin?
CorrectIncorrectHint
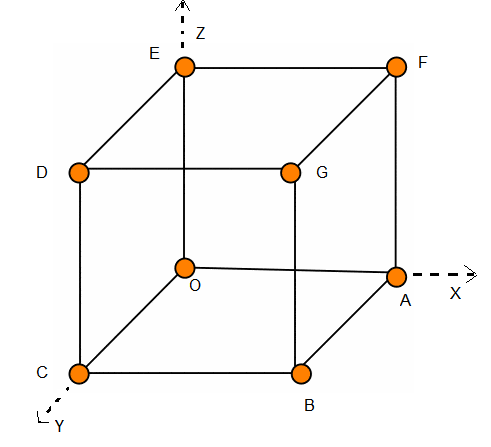
Given that each edge of the cuboid is 2 units.
\(\therefore\) Coordinates of the vertices are
\(
\begin{aligned}
& A (2,0,0), B (2,2,0), C (0,2,0) \\
& D (0,2,2), E (0,0,2), F (2,0,2), \\
& G (2,2,2) \text { and } O (0,0,0) \text {. }
\end{aligned}
\) -
Question 22 of 81
22. Question
The distance of point \(P (3,4,5)\) from the \(y z\)-plane is
CorrectIncorrectHint
Given point is \(P (3,4,5)\)
\(\therefore\) Distance of \(P\) from \(y z\)-plane
\(
\begin{aligned}
& =\sqrt{(0-3)^2+(4-4)^2+(5-5)^2} \\
& =\sqrt{9}=3 \text { units }
\end{aligned}
\) -
Question 23 of 81
23. Question
What is the length of foot of perpendicular drawn from the point \(P (3,4,5)\) on \(y\)-axis
CorrectIncorrectHint
On \(y\)-axis, \(x=0\) and \(z=0\) and given point \(P (3,4,5)\)
\(\therefore\) The point \(A\) is \((0,4,0)\)
\(
\begin{aligned}
\therefore \quad PA & =\sqrt{(0-3)^2+(4-4)^2+(0-5)^2} \\
& =\sqrt{9+0+25}=\sqrt{34}
\end{aligned}
\) -
Question 24 of 81
24. Question
Distance of the point \((3,4,5)\) from the origin \((0,0,0)\) is
CorrectIncorrectHint
Given points \(A (3,4,5)\) and the given \(O (0,0,0)\)
\(
\begin{aligned}
\therefore \quad OA & =\sqrt{(3-0)^2+(4-0)^2+(5-0)^2} \\
& =\sqrt{9+16+25}=\sqrt{50}
\end{aligned}
\) -
Question 25 of 81
25. Question
If the distance between the points \((a, 0,1)\) and \((0,1,2)\) is \(\sqrt{27}\), then the value of \(a\) is
CorrectIncorrectHint
Let the given points be \(A (a, 0,1)\) and \(B (0,1,2)\)
\(
\begin{aligned}
\therefore \quad AB & =\sqrt{(a-0)^2+(0-1)^2+(1-2)^2} \\
\sqrt{27} & =\sqrt{a^2+1+1}
\end{aligned}
\)
Squaring both sides, we get
\(
27=a^2+2 \quad \Rightarrow \quad a^2=25 \quad \therefore a= \pm 5
\) -
Question 26 of 81
26. Question
\(x\)-axis is the intersection of two planes
CorrectIncorrectHint
We know that on the \(x y\) and \(x z\)-planes, the line of intersection is \(x\)-axis.
-
Question 27 of 81
27. Question
Equation of \(y\)-axis is considered as
CorrectIncorrectHint
\(
\text { On } y \text {-axis, } x=0 \text { and } z=0
\) -
Question 28 of 81
28. Question
The point \((-2,-3,-4)\) lies in the
CorrectIncorrectHint
\(
\text { The point }(-2,-3,-4) \text { lies in seventh octant. }
\) -
Question 29 of 81
29. Question
A plane is parallel to \(y z\)-plane so it is perpendicular to :
CorrectIncorrectHint
\(
\text { Any plane parallel to } y z \text {-plane is perpendicular to } x \text {-axis. }
\) -
Question 30 of 81
30. Question
The locus of a point for which \(y=0, z=0\) is
CorrectIncorrectHint
We know that one equation of \(x\)-axis, \(y=0, z=0\) Hence, the locus of the point is equation of \(x\)-axis.
-
Question 31 of 81
31. Question
The locus of a point for which \(x=0\) is
CorrectIncorrectHint
On the \(y z\)-plane, \(x=0\)
Hence, the locus of the point is \(y z\)-plane. -
Question 32 of 81
32. Question
If a parallelopiped is formed by planes drawn through the points \((5,8,10)\) and \((3,6,8)\) parallel to the coordinate planes, then the length of diagonal of the parallelopiped is
CorrectIncorrectHint
Given points are \(A(5,8,10)\) and \(B(3,6,8)\)
\(
\begin{aligned}
\therefore \quad AB & =\sqrt{(5-3)^2+(8-6)^2+(10-8)^2} \\
& =\sqrt{4+4+4}=\sqrt{12}=2 \sqrt{3}
\end{aligned}
\) -
Question 33 of 81
33. Question
\(L\) is the foot of the perpendicular drawn from a point \(P (3,4,5)\) on the \(x y\)-plane. The coordinates of point \(L\) are
CorrectIncorrectHint
We know that on \(x y\)-plane, \(z=0\).
So, the coordinate of the point \(L\) are \((3,4,0)\). -
Question 34 of 81
34. Question
\(L\) is the foot of the perpendicular drawn from a point \((3,4,5)\) on \(x\)-axis. The coordinates of \(L\) are
CorrectIncorrectHint
We know that \(x\)-axis, \(y=0\) and \(z=0\).
So, the required coordinates are \((3,0,0)\). -
Question 35 of 81
35. Question
The three axes OX, OY, OZ determine ____.
CorrectIncorrectHint
The three axes OX, OY and OZ determine three coordinate planes.
Hence, the filler value is three coordinate planes. -
Question 36 of 81
36. Question
The three planes determine a rectangular parallelopiped which has _____ of rectangular faces.
CorrectIncorrectHint
Three pairs. Hence, the value of the filler is three pairs.
-
Question 37 of 81
37. Question
The coordinates of a point are the perpendicular distance from the _____ on respective axes.
CorrectIncorrectHint
Given points.
Hence, the value of the filler is given points. -
Question 38 of 81
38. Question
The three coordinates planes divide the space into _____ parts.
CorrectIncorrectHint
Eight. Hence, the values of the filler is eight.
-
Question 39 of 81
39. Question
If a point \(P\) lies in \(y z\)-plane, then the coordinates of a point on \(y z\)-plane is of the form _____.
CorrectIncorrectHint
We know that on \(y z\)-plane, \(x=0\)
So, the coordinates of the required point is \((0, y, z)\). Hence, the value of the filler is \((0, y, z)\). -
Question 40 of 81
40. Question
The equation of \(y z\)-plane is _____.
CorrectIncorrectHint
The equation of \(y z\)-plane is \(x=0\).
Hence, the value of the filler is \(x=0\). -
Question 41 of 81
41. Question
If the point \(P\) lies on \(z\)-axis, then coordinates of \(P\) are of the form _____.
CorrectIncorrectHint
On the \(z\)-axis, \(x=0\) and \(y=0\).
\(\therefore\) The required coordinate is in the form of \((0,0, z)\).
Hence, the value of the filler is \((0,0, z)\). -
Question 42 of 81
42. Question
The equation of \(z\)-axis are _____.
CorrectIncorrectHint
The equation of \(z\)-axis are, \(x=0\) and \(y=0\).
Hence, the value of the filler is \(x=0\) and \(y=0\). -
Question 43 of 81
43. Question
A line is parallel to \(x y\)-plane if all the points on the line have equal _____.
CorrectIncorrectHint
\(z\)-coordinates
Hence, the value of the filler is \(z\)-coordinates. -
Question 44 of 81
44. Question
A line is parallel to \(x\)-axis if all the points on the line have equal ________.
CorrectIncorrectHint
Hence, the value of the filler is \(y\) and \(z\) coordinates.
-
Question 45 of 81
45. Question
\(x=a\) represents a plane parallel to ____.
CorrectIncorrectHint
\(x=a\) represents a plane parallel to \(y z\)-plane.
-
Question 46 of 81
46. Question
The plane parallel to \(y z\)-plane is perpendicular to _____.
CorrectIncorrectHint
The plane parallel to \(y z\)-plane is perpendicular to \(x\)-axis. Hence, the value of the filler is \(x\)-axis.
-
Question 47 of 81
47. Question
The length of the longest piece of a string that can be stretched straight in a rectangular room whose dimensions are 10,13 and 8 units are _____.
CorrectIncorrectHint
The given dimensions are 10,13 and 8
Let \(a=10, b=13\) and \(c=8\)
\(
\begin{aligned}
\therefore \quad \text { Required length } & =\sqrt{a^2+b^2+c^2} \\
& =\sqrt{(10)^2+(13)^2+(8)^2} \\
& =\sqrt{100+169+64}=\sqrt{333}
\end{aligned}
\)
Hence, the value of the filler is \(\sqrt{333}\). -
Question 48 of 81
48. Question
If the distance between the points \((a, 2,1)\) and \((1,-1,1)\) is 5 , then \(a\) ____.
CorrectIncorrectHint
Given points are \((a, 2,1)\) and \((1,-1,1)\)
\(
\begin{aligned}
\therefore \quad \text { Distance } & =\sqrt{(a-1)^2+(2+1)^2+(1-1)^2} \\
5 & =\sqrt{a^2+1-2 a+9}
\end{aligned}
\)
Squaring both sides, we have
\(
\begin{aligned}
& 25=a^2-2 a+10 \\
& \Rightarrow \quad a^2-2 a-15=0 \\
& \Rightarrow \quad a^2-5 a+3 a-15=0 \\
& \Rightarrow \quad a(a-5)+3(a-5)=0 \\
& \Rightarrow \quad(a+3)(a-5)=0 \\
& \therefore \quad a=-3 \text { or } 5 \\
&
\end{aligned}
\)
Hence, the value of the filler is 5 or -3 . -
Question 49 of 81
49. Question
If the mid-points of the sides of a triangle \(AB ; BC\); \(CA\) are \(D (1,2,-3), E (3,0,1)\) and \(F(-1,1,-4)\), then the centroid of the triangle \(A B C\) is _____.
CorrectIncorrectHint
Given that mid-point of a triangle are \(D(1,2,-3), E(3,0,1)\) and \(F(-1,1,-4)\).
From Geometry of centroid, centroid of triangle is same as the centroid of the triangle formed by mid-points of the sides.
The coordinates of the centroid of the triangle, whose vertices are \(\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)\) and \(\left(x_3, y_3, z_3\right)\) are \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\)
\(\therefore\) Centroid of triangle
\(
\begin{aligned}
& =G\left(\frac{1+3-1}{3}, \frac{2+0+1}{3}, \frac{-3+1-4}{3}\right) \\
& =G(1,1,-2)
\end{aligned}
\)
Hence, \((1,1,-2)\) are the coordinates of the centroid. -
Question 50 of 81
50. Question
Match each item under the Column I to its correct answer given under Column II.
\(
\begin{array}{|l|l|r|l|}
\hline & \text { Column I } & & \text { Column II } \\
\hline \text { (a) } & \text { In } x y \text {-plane } & \text { (i) } & \text { Ist octant } \\
\hline \text { (b) } & \text { Point }(2,3,4) \text { lies in the } & \text { (ii) } & y z \text {-plane } \\
\hline \text { (c) } & \begin{array}{l}
\text { Locus of the points } \\
\text { having } x \text {-coordinate } 0 \text { is }
\end{array} & \text { (iii) } & z \text {-coordinate is zero } \\
\hline \text { (d) } & \begin{array}{l}
\text { A line is parallel to } \\
x \text {-axis if and only }
\end{array} & \text { (iv) } & z \text {-axis } \\
\hline \text { (e) } & \begin{array}{l}
\text { If } x=0, y=0 \text { taken } \\
\text { together will represent } \\
\text { the }
\end{array} & \text { (v) } & \text { Parallel to } x y \text {-plane } \\
\hline \text { (f) } & \begin{array}{l}
z=c \text { represent the plane. }
\end{array} & \text { (vi) } & \begin{array}{l}
\text { If all the points on the } \\
\text { line have equal } y \text { and } \\
z \text {-coordinates }
\end{array} \\
\hline \text { (g) } & \begin{array}{l}
\text { Planes } x=a, y=b \\
\text { represent the line }
\end{array} & \text { (vii) } & \begin{array}{l}
\text { From the point on the } \\
\text { respective axes }
\end{array} \\
\hline \text { (h) } & \begin{array}{l}
\text { Coordinates of a point } \\
\text { are the distances from } \\
\text { the origin to the feet of } \\
\text { perpendiculars }
\end{array} & \text { (viii) } & \text { Parallel to } z \text {-axis } \\
\hline \text { (i) } & \begin{array}{l}
\text { A ball is a solid region } \\
\text { in the space enclosed } \\
\text { by a }
\end{array} & (i x) & \text { disc } \\
\hline \text { (j) } & \begin{array}{l}
\text { Region in the plane } \\
\text { enclosed by a circle is } \\
\text { known as a }
\end{array} & (x) & \text { sphere } \\
\hline
\end{array}
\)CorrectIncorrectHint
(a) In \(x y\)-plane, \(z\)-coordinate is zero.
Hence, \((a) \leftrightarrow(i i i)\).
(b) The point \((2,3,4)\) lies in first octant.
Hence, \((b) \leftrightarrow(i)\).
(c) Locus of the points with \(x\)-coordinate is zero is \(y z\)-plane. Hence, \((c) \leftrightarrow(i i)\).
(d) A line is parallel to \(x\)-axis if and only if all the points on the line have equal \(y\) and \(z\)-coordinates.
Hence, \((d) \leftrightarrow(v i)\).
(e) \(x=0, y=0\) represent \(z\)-axis.
Hence, \((e) \leftrightarrow(i v)\).
(f) \(z=c\) represent a plane parallel to \(x y\)-plane.
Hence, \((f) \leftrightarrow(v)\).
(g) The planes \(x=a, y=b\) represent the line parallel to \(z\)-axis. Hence, \((g) \leftrightarrow\) (viii).
(h) Coordinates of a point are the distances from the origin to the feet of perpendicular from the point on the respective axes.
Hence, \((h) \leftrightarrow\) (vii).
(i) A ball is solid region in the space enclosed by a sphere. Hence, \((i) \leftrightarrow(x)\).
(j) The region in the plane enclosed by a circle is known as a disc. Hence, \((j) \leftrightarrow(i x)\). -
Question 51 of 81
51. Question
The length of the foot of perpendicular drawn from the point \(P (3,4,5)\) on \(y\)-axis is
CorrectIncorrectHint
Let \(l\) be the foot of perpendicular from point \(P\) on the \(y\)-axis. Therefore, its \(x\) and \(z\)-coordinates are zero, i.e., \((0,4,0)\). Therefore, distance between the points ( 0 , \(4,0)\) and \((3,4,5)\) is \(\sqrt{9+25}\) i.e., \(\sqrt{34}\).
-
Question 52 of 81
52. Question
What is the perpendicular distance of the point \(P (6,7,8)\) from \(x y\)-plane?
CorrectIncorrectHint
Let \(L\) be the foot of perpendicular drawn from the point \(P (6,7,8)\) to the \(x y\) plane and the distance of this foot \(L\) from \(P\) is \(z\)-coordinate of \(P\), i.e., 8 units.
-
Question 53 of 81
53. Question
\(L\) is the foot of the perpendicular drawn from a point \(P (6,7,8)\) on the \(x y\) plane. What are the coordinates of point \(L\) ?
CorrectIncorrectHint
Since \(L\) is the foot of perpendicular from \(P\) on the \(x y\)-plane, \(z\)-coordinate is zero in the \(x y\)-plane. Hence, coordinates of \(L\) are \((6,7,0)\).
-
Question 54 of 81
54. Question
\(L\) is the foot of the perpendicular drawn from a point \((6,7,8)\) on \(x\)-axis. The coordinates of \(L\) are
CorrectIncorrectHint
Since \(L\) is the foot of perpendicular from \(P\) on the \(x\)-axis, \(y\) and \(z\)-coordinates are zero. Hence, the coordinates of \(L\) are \((6,0,0)\).
-
Question 55 of 81
55. Question
What is the locus of a point for which \(y=0, z=0\) ?
CorrectIncorrectHint
Locus of the point \(y=0, z=0\) is \(x\)-axis, since on \(x\)-axis both \(y=0\) and \(z=0\).
-
Question 56 of 81
56. Question
\(L\), is the foot of the perpendicular drawn from a point \(P(3,4,5)\) on the \(x z\) plane. What are the coordinates of point \(L\) ?
CorrectIncorrectHint
Since \(L\) is the foot of perpendicular segment drawn from the point \(P(3,4,5)\) on the \(x z\)-plane. Since the \(y\)-coordinates of all points in the \(x z\)-plane are zero, coordinate of the foot of perpendicular are \((3,0,5)\).
-
Question 57 of 81
57. Question
A line is parallel to \(x y\)-plane if all the points on the line have equal _____.
CorrectIncorrectHint
A line parallel to xy-plane if all the points on the line have equal \(z\)-coordinates.
-
Question 58 of 81
58. Question
The equation \(x=b\) represents a plane parallel to ____ plane.
CorrectIncorrectHint
Since \(x=0\) represent \(y z\)-plane, therefore \(x=b\) represent a plane parallel to \(y z\)-plane at a unit distance \(b\) from the origin.
-
Question 59 of 81
59. Question
Perpendicular distance of the point \(P (3,5,6)\) from \(y\)-axis is ____.
CorrectIncorrectHint
Since \(M\) is the foot of perpendicular from \(P\) on the \(y\)-axis, therefore, its \(x\) and \(z\)-coordinates are zero. The coordinates of \(M\) is \((0,5,0)\). Therefore, the perpendicular distance of the point \(P\) from \(y\)-axis \(\sqrt{3^2+6^2}=\sqrt{45}\).
-
Question 60 of 81
60. Question
\(L\) is the foot of perpendicular drawn from the point \(P (3,4,5)\) on \(z x\) planes. The coordinates of \(L\) are ____.
CorrectIncorrectHint
Since \(L\) is the foot of perpendicular from \(P\) on the \(z x\)-plane, \(y\)-coordinate of every point is zero in the \(z x\)-plane. Hence, coordinate of \(L\) are \((3,0,5)\).
-
Question 61 of 81
61. Question
The length of the foot of perpendicular drawn from the point \(P (a, b, c)\) on \(z\)-axis is _____.
CorrectIncorrectHint
The coordinates of the foot of perpendicular from the point \(P (a, b, c)\) on \(z\) axis is \((0,0, c )\). The distance between the point \(P (a, b, c)\) and \((0,0, c)\) is \(\sqrt{a^2+b^2}\).
-
Question 62 of 81
62. Question
The \(y\)-axis and \(z\)-axis, together determine a plane known as \(y z\)-plane.
CorrectIncorrectHint
True
-
Question 63 of 81
63. Question
The point \((4,5,-6)\) lies in the VI th octant.
CorrectIncorrectHint
False, the point \((4,5,-6)\) lies in the \(V ^{ \text {th} }\) octant.
-
Question 64 of 81
64. Question
The \(x\)-axis is the intersection of two planes \(x y\)-plane and \(x z\) plane.
CorrectIncorrectHint
true
-
Question 65 of 81
65. Question
Three mutually perpendicular planes divide the space into 8 octants.
CorrectIncorrectHint
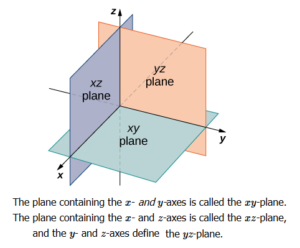
Three mutually perpendicular planes divide the space into 8 octants. True
-
Question 66 of 81
66. Question
The equation of the plane \(z=6\) represent a plane parallel to the \(x y\)-plane, having a \(z\)-intercept of 6 units.
CorrectIncorrectHint
True
-
Question 67 of 81
67. Question
The equation of the plane \(x=0\) represent the \(y z\)-plane.
CorrectIncorrectHint
true
-
Question 68 of 81
68. Question
The point on the \(x\)-axis with \(x\)-coordinate equal to \(x_0\) is written as \(\left(x_0, 0,0\right)\).
CorrectIncorrectHint
true
-
Question 69 of 81
69. Question
\(x=x_0\) represent a plane parallel to the \(y z\)-plane.
CorrectIncorrectHint
true
-
Question 70 of 81
70. Question
Match each item under the Column I to its correct answer given under Column II.
\(
\begin{array}{|l|l|r|l|}
\hline & \text { Column I } & & \text { Column II } \\
\hline \text { (a) } & \begin{array}{l}
\text { If the centroid of the triangle is } \\
\text { origin and two of its vertices } \\
\text { are (3, – 5, 7) and (–1, 7, – 6) } \\
\text { then the third vertex is }
\end{array} & \text { (i) } & \text { Parallelogram } \\
\hline \text { (b) } & \begin{array}{l}
\text { If the mid-points of the sides of } \\
\text { triangle are (1, 2, – 3), (3, 0, 1) } \\
\text { and (–1, 1, – 4) then the centroid is }
\end{array} & \text { (ii) } & \text { (–2, –2, –1) } \\
\hline \text { (c) } & \begin{array}{l}
\text { The points (3, – 1, – 1), (5, – 4, 0), } \\
\text { (2, 3, – 2) and (0, 6, – 3) are the } \\
\text { vertices of a }
\end{array} & \text { (iii) } & \text { as Isosceles right-angled triangle } \\
\hline \text { (d) } & \begin{array}{l}
\text { Point A(1, –1, 3), B (2, – 4, 5) and } \\
\text { C (5, – 13, 11) are }
\end{array} & \text { (iv) } & \text { (1, 1, – 2) } \\
\hline \text { (e) } & \begin{array}{l}
\text { Point A(2, 4, 3), B (4, 1, 9) and } \\
\text { C (10, – 1, 6) are the vertices of }
\end{array} & \text { (v) } & \text { Collinear } \\
\hline
\end{array}
\)CorrectIncorrectHint
(a) Let \(A (3,-5,7), B (-1,7,-6), C (x, y, z)\) be the vertices of a \(\Delta ABC\) with centroid \((0\), 0,0 )
Therefore, \((0,0,0)=\left(\frac{3-1+x}{3}, \frac{-5+7+y}{3}, \frac{7-6+z}{3}\right)\). This implies \(\frac{x+2}{3}=0, \frac{y+2}{3}=0\), \(\frac{z+1}{3}=0\)
Hence \(x=-2, y=-2\), and \(z=-1\). Therefore (a) \(\leftrightarrow\) (ii)
(b) Let \(ABC\) be the given \(\triangle\) and \(DEF\) be the mid-points of the sides \(BC , CA , AB\), respectively. We know that the centroid of the \(\triangle ABC =\) centriod of \(\triangle DEF\).
Therefore, centroid of \(\triangle DEF\) is \(\left(\frac{1+3-1}{3}, \frac{2+0+1}{3}, \frac{-3+1-4}{3}\right)=(1,1,-2)\)
Hence (b) \(\leftrightarrow\) (iv)
(c) Mid-point of diagonal AC is \(\left(\frac{3+2}{2}, \frac{-1+3}{2}, \frac{-1-2}{2}\right)=\left(\frac{5}{2}, 1, \frac{-3}{2}\right)\)
Mid-point of diagonal BD is \(\left(\frac{5+0}{2}, \frac{-4+6}{2}, \frac{0-3}{2}\right)=\left(\frac{5}{2}, 1, \frac{-3}{2}\right)\)
Diagonals of parallelogram bisect each other. Therefore (c) \(\leftrightarrow\) (i)
(d)
\(
\begin{aligned}
& |A B|=\sqrt{(2-1)^2+(-4+1)^2+(5-3)^2}=\sqrt{14} \\
& |B C|=\sqrt{(5-2)^2+(-13+4)^2+(11-5)^2}=3 \sqrt{14} \\
& |A C|=\sqrt{(5-1)^2+(-13+1)^2+(11-3)^2}=4 \sqrt{14}
\end{aligned}
\)
Now \(|A B|+|B C|=|A C|\). Hence Points A, B, C are collinear. Hence (d) \(\leftrightarrow\) (v)
(e) \(AB =\sqrt{4+9+36}=7\)
\(
\begin{aligned}
& BC =\sqrt{36+4+9}=7 \\
& CA =\sqrt{64+25+9}=7 \sqrt{2}
\end{aligned}
\)
Now \(AB ^2+ BC ^2= AC ^2\). Hence \(ABC\) is an isosceles right angled triangle and hence (e) \(\leftrightarrow\) (iii) -
Question 71 of 81
71. Question
The points \(P(2,4,6), Q(-2,-2,-2)\) and \(R (6,10,14)\) are collinear. Is this true?
CorrectIncorrectHint
Three points are collinear if the sum of any two distances is equal to the third distance.
\(
\begin{aligned}
& P Q=\sqrt{(-2-2)^2+(-2-4)^2+(-2-6)^2}=\sqrt{16+36+64}=\sqrt{116}=2 \sqrt{29} \\
& QR =\sqrt{(6+2)^2+(10+2)^2+(14+2)^2}=\sqrt{64+144+256}=\sqrt{464}=4 \sqrt{29} \\
& PR =\sqrt{(6-2)^2+(10-4)^2+(14-6)^2}=\sqrt{16+36+64}=\sqrt{116}=2 \sqrt{29}
\end{aligned}
\)
Since \(QR = PQ + PR\). Therefore, the given points are collinear. -
Question 72 of 81
72. Question
Find the coordinates of a point equidistant from the four points \(O (0,0,0)\), \(A (l, 0,0), B (0, m, 0)\) and \(C (0,0, n)\).
CorrectIncorrectHint
Let \(P (x, y, z)\) be the required point. Then \(OP = PA = PB = PC\).
Now \(OP = PA \Rightarrow OP ^2= PA ^2 \Rightarrow x^2+y^2+z^2=(x-l)^2+(y-0)^2+(z-0)^2 \Rightarrow x=\frac{l}{2}\)
Similarly, \(OP = PB \Rightarrow y=\frac{m}{2}\) and \(OP = PC \Rightarrow z=\frac{n}{2}\)
Hence, the coordinate of the required point are \(\left(\frac{l}{2}, \frac{m}{2}, \frac{n}{2}\right)\). -
Question 73 of 81
73. Question
Find the point on \(x\)-axis which is equidistant from the point \(A (3,2,2)\) and B \((5,5,4)\).
CorrectIncorrectHint
The point on the \(x\)-axis is of form \(P (x, 0,0)\). Since the points \(A\) and \(B\) are equidistant from \(P\). Therefore \(PA ^2= PB ^2\), i.e.,
\(
\begin{aligned}
& (x-3)^2+(0-2)^2+(0-2)^2=(x-5)^2+(0-5)^2+(0-4)^2 \\
& \Rightarrow 4 x=25+25+16-17 \text { i.e., } x=\frac{49}{4} .
\end{aligned}
\)
Thus, the point \(P\) on the \(x\)-axis is \(\left(\frac{49}{4}, 0,0\right)\) which is equidistant from \(A\) and \(B\). -
Question 74 of 81
74. Question
Find the point on \(y\)-axis which is at a distance \(\sqrt{10}\) from the point \((1,2,3)\)
CorrectIncorrectHint
Let the point \(P\) be on \(y\)-axis. Therefore, it is of the form \(P (0, y, 0)\).
The point \((1,2,3)\) is at a distance \(\sqrt{10}\) from \((0, y, 0)\). Therefore
\(
\begin{aligned}
& \sqrt{(1-0)^2+(2-y)^2+(3-0)^2}=\sqrt{10} \\
& \Rightarrow y^2-4 y+4=0 \Rightarrow(y-2)^2=0 \Rightarrow y=2
\end{aligned}
\)
Hence, the required point is \((0,2,0)\). -
Question 75 of 81
75. Question
If a parallelopiped is formed by planes drawn through the points \((2,3,5)\) and \((5,9,7)\) parallel to the coordinate planes, then find the length of edges of a parallelopiped and length of the diagonal.
CorrectIncorrectHint
Length of edges of the parallelopiped are \(5-2,9-3,7-5\) i.e., \(3,6,2\).
Length of diagonal is \(\sqrt{3^2+6^2+2^2}=7\) units. -
Question 76 of 81
76. Question
The points \((0,7,10),(-1,6,6)\) and \((-4,9,6)\) form a right angled isosceles triangle. Is this true?
CorrectIncorrectHint
Let \(P (0,7,10), Q (-1,6,6)\) and \(R (-4,9,6)\) be the given three points.
Here \(PQ =\sqrt{1+1+16}=3 \sqrt{2}\)
\(
\begin{aligned}
& QR =\sqrt{9+9+0}=3 \sqrt{2} \\
& PR =\sqrt{16+4+16}=6
\end{aligned}
\)
Now \(PQ ^2+ QR ^2=(3 \sqrt{2})^2+(3 \sqrt{2})^2=18+18=36=( PR )^2\)
Therefore, \(\triangle PQR\) is a right angled triangle at \(Q\). Also \(PQ = QR\). Hence \(\triangle PQR\) is an isosceles triangle. -
Question 77 of 81
77. Question
The points \((5,-1,1),(7,-4,7),(1-6,10)\) and \((-1,-3,4)\) are the vertices of a rhombus. Is this true?
CorrectIncorrectHint
Let \(A (5,-1,1), B (7,-4,7), C (1,-6,10)\) and \(D (-1,-3,4)\) be the four points of a quadrilateral. Here
\(
\begin{aligned}
& AB =\sqrt{4+9+36}=7, BC =\sqrt{36+4+9}=7, CD =\sqrt{4+9+36}=7, \\
& DA =\sqrt{23+4+9}=7
\end{aligned}
\)
Note that \(AB = BC = CD = DA\). Therefore, \(ABCD\) is a rhombus. -
Question 78 of 81
78. Question
Find the ratio in which the line segment joining the points \((2,4,5)\) and \((3,5,-4)\) is divided by the \(x z\)-plane.
CorrectIncorrectHint
Let the joint of \(P (2,4,5)\) and \(Q (3,5,-4)\) be divided by \(x z\)-plane in the ratio \(k: 1\) at the point \(R (x, y, z)\). Therefore
\(
x=\frac{3 k+2}{k+1}, y=\frac{5 k+4}{k+1}, z=\frac{-4 k+5}{k+1}
\)
Since the point \(R (x, y, z)\) lies on the \(x z\)-plane, the \(y\)-coordinate should be zero,i.e.,
\(
\frac{5 k+4}{k+1}=0 \Rightarrow k=-\frac{4}{5}
\)
Hence, the required ratio is \(-4: 5\), i.e.; externally in the ratio \(4: 5\). -
Question 79 of 81
79. Question
Find the coordinate of the point \(P\) which is five – sixth of the way from \(A\) \((-2,0,6)\) to \(B (10,-6,-12)\).
CorrectIncorrectHint
Let \(P (x, y, z)\) be the required point, i.e., \(P\) divides \(AB\) in the ratio \(5: 1\). Then
\(
P(x, y, z)=\left(\frac{5 \times 10+1 \times-2}{5+1}, \frac{5 \times-6+1 \times 0}{5+1}, \frac{5 \times-12+1 \times 6}{5+1}\right)=(8,-5,-9)
\) -
Question 80 of 81
80. Question
Let \(A (3,2,0), B (5,3,2), C (-9,6,-3)\) be three points forming a triangle. \(A D\), the bisector of \(\angle B A C\), meets \(B C\) in \(D\). Find the coordinates of the point \(D\).
CorrectIncorrectHint
Note that
\(
\begin{aligned}
& AB =\sqrt{(5-3)^2+(3-2)^2+(2-0)^2}=\sqrt{4+1+4}=3 \\
& AC =\sqrt{(-9-3)^2+(6-2)^2+(-3-0)^2}=\sqrt{144+16+9}=13
\end{aligned}
\)
Since \(AD\) is the bisector of \(\angle BAC\), We have \(\frac{ BD }{ DC }=\frac{ AB }{ AC }=\frac{3}{13}\)
i.e., \(D\) divides \(BC\) in the ratio \(3: 13\). Hence, the coordinates of \(D\) are
\(
\left(\frac{3(-9)+13(5)}{3+13}, \frac{3(6)+13(3)}{3+13}, \frac{3(-3)+13(2)}{3+13}\right)=\left(\frac{19}{8}, \frac{57}{16}, \frac{17}{16}\right)
\) -
Question 81 of 81
81. Question
Determine the point in \(y z\)-plane which is equidistant from three points \(A\) \((2,0,3)\) B \((0,3,2)\) and \(C(0,0,1)\).
CorrectIncorrectHint
Since \(x\)-coordinate of every point in \(y z\)-plane is zero. Let \(P (0, y, z)\) be a point on the \(y z\)-plane such that \(PA = PB = PC\). Now
\(
\begin{aligned}
& PA = PB \Rightarrow(0-2)^2+(y-0)^2+(z-3)^2=(0-0)^2+(y-3)^2+(z-2)^2, \text { i.e. } z-3 y=0 \\
& \text { and } PB = PC \\
& \Rightarrow y^2+9-6 y+z^2+4-4 z=y^2+z^2+1-2 z \text {, i.e. } 3 y+z=6
\end{aligned}
\)
Simplifying the two equating, we get \(y=1, z=3\)
Here, the coordinate of the point \(P\) are \((0,1,3)\).