12.5 Section Formula

Section Formula for Internal Division

In two dimensional geometry, we have learnt how to find the coordinates of a point dividing a line segment in a given ratio internally. Now, we extend this to three dimensional geometry as follows:

Let the two given points be \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\). Let the point \(R (x, y, z)\) divide \(PQ\) in the given ratio \(m: n\) internally. Draw PL, QM and RN perpendicular to the XY-plane. Obviously PL || RN || QM and feet of these perpendiculars lie in a XY-plane. The points \(L , M\) and \(N\) will lie on a line which is the intersection of the plane containing PL, RN and QM with the XY-plane. Through the point R draw a line ST parallel to the line LM. Line ST will intersect the line LP externally at the point \(S\) and the line MQ at T, as shown in Fig 12.5.

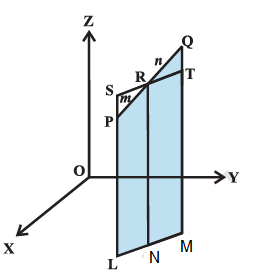
Also note that quadrilaterals LNRS and NMTR are parallelograms. The triangles PSR and QTR are similar. Therefore,
\(
\frac{m}{n}=\frac{ PR }{ QR }=\frac{ SP }{ QT }=\frac{ SL – PL }{ QM – TM }=\frac{ NR – PL }{ QM – NR }=\frac{z-z_1}{z_2-z}
\)
This implies
\(
z=\frac{m z_2+n z_1}{m+n}
\)
Similarly, by drawing perpendiculars to the \(XZ\) and \(YZ\)-planes, we get
\(
y=\frac{m y_2+n y_1}{m+n} \text { and } x=\frac{m x_2+n x_1}{m+n}
\)
Hence, the coordinates of the point \(R\) which divides the line segment joining two points \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\) internally in the ratio \(m: n\) are
\(
\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}, \frac{m z_2+n z_1}{m+n}\right)
\)

Section Formula for External Division

If the point \(R\) divides \(PQ\) externally in the ratio \(m: n\), then its coordinates are obtained by replacing \(n\) by \(-n\) so that coordinates of point \(R\) will be
\(
\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}, \frac{m z_2-n z_1}{m-n}\right)
\)

Case I: Coordinates of the mid-point

Coordinates of the mid-point: In case \(R\) is the mid-point of \(PQ\), then \(m: n=1: 1\) so that \(x=\frac{x_1+x_2}{2}, y=\frac{y_1+y_2}{2}\) and \(z=\frac{z_1+z_2}{2}\).
These are the coordinates of the mid point of the segment joining \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\).

Case-II: The coordinates of the point \(R\) which divides \(PQ\) in the ratio \(k: 1\)

The coordinates of the point \(R\) which divides \(PQ\) in the ratio \(k: 1\) are obtained by taking \(k=\frac{m}{n}\) which are as given below:
\(
\left(\frac{k x_2+x_1}{1+k}, \frac{k y_2+y_1}{1+k}, \frac{k z_2+z_1}{1+k}\right)
\)

Example 1: Find the coordinates of the point which divides the line segment joining the points \((1,-2,3)\) and \((3,4,-5)\) in the ratio \(2: 3\) (i) internally, and (ii) externally.

Solution:

(i) Let \(P (x, y, z)\) be the point which divides line segment joining \(A (1,-2,3)\) and \(B (3,4,-5)\) internally in the ratio \(2: 3\). Therefore
\(
x=\frac{2(3)+3(1)}{2+3}=\frac{9}{5}, y=\frac{2(4)+3(-2)}{2+3}=\frac{2}{5}, \quad z=\frac{2(-5)+3(3)}{2+3}=\frac{-1}{5}
\)
Thus, the required point is \(\left(\frac{9}{5}, \frac{2}{5}, \frac{-1}{5}\right)\)

(ii) Let \(P (x, y, z)\) be the point which divides segment joining \(A (1,-2,3)\) and \(B (3,4,-5)\) externally in the ratio \(2: 3\). Then
\(
x=\frac{2(3)+(-3)(1)}{2+(-3)}=-3, \quad y=\frac{2(4)+(-3)(-2)}{2+(-3)}=-14, z=\frac{2(-5)+(-3)(3)}{2+(-3)}=19
\)
Therefore, the required point is \((-3,-14,19)\).

Example 2: Using section formula, prove that the three points \((-4,6,10),(2,4,6)\) and \((14,0,-2)\) are collinear.

Solution: Let \(A (-4,6,10), B (2,4,6)\) and \(C (14,0,-2)\) be the given points. Let the point \(P\) divides \(AB\) in the ratio \(k: 1\). Then coordinates of the point \(P\) are
\(
\left(\frac{2 k-4}{k+1}, \frac{4 k+6}{k+1}, \frac{6 k+10}{k+1}\right)
\)
Let us examine whether for some value of \(k\), the point \(P\) coincides with point \(C\).
On putting \(\frac{2 k-4}{k+1}=14\), we get \(k=-\frac{3}{2}\)
When \(k=-\frac{3}{2}\), then \(\frac{4 k+6}{k+1}=\frac{4\left(-\frac{3}{2}\right)+6}{-\frac{3}{2}+1}=0\)
and
\(
\frac{6 k+10}{k+1}=\frac{6\left(-\frac{3}{2}\right)+10}{-\frac{3}{2}+1}=-2
\)
Therefore, \(C (14,0,-2)\) is a point which divides \(AB\) externally in the ratio \(3: 2\) and is same as P.Hence A, B, C are collinear.

Example 3: Find the coordinates of the centroid of the triangle whose vertices are \(\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)\) and \(\left(x_3, y_3, z_3\right)\).

Solution: Let \(ABC\) be the triangle. Let the coordinates of the vertices \(A , B , C\) be \(\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)\) and \(\left(x_3, y_3, z_3\right)\), respectively. Let \(D\) be the mid-point of \(BC\). Hence coordinates of \(D\) are
\(
\left(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2}, \frac{z_2+z_3}{2}\right)
\)
Let \(G\) be the centroid of the triangle. Therefore, it divides the median \(AD\) in the ratio \(2: 1\). Hence, the coordinates of \(G\) are
\(
\left(\frac{2\left(\frac{x_2+x_3}{2}\right)+x_1}{2+1}, \frac{2\left(\frac{y_2+y_3}{2}\right)+y_1}{2+1}, \frac{2\left(\frac{z_2+z_3}{2}\right)+z_1}{2+1}\right)
\)
\(
\text { or } \quad\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)
\)

Example 4: Find the ratio in which the line segment joining the points \((4,8,10)\) and \((6,10,-8)\) is divided by the YZ-plane.

Solution: Let YZ-plane divides the line segment joining A \((4,8,10)\) and B \((6,10,-8)\) at \(P (x, y, z)\) in the ratio \(k: 1\). Then the coordinates of \(P\) are
\(
\left(\frac{4+6 k}{k+1}, \frac{8+10 k}{k+1}, \frac{10-8 k}{k+1}\right)
\)
Since \(P\) lies on the YZ-plane, its \(x\)-coordinate is zero, i.e., \(\frac{4+6 k}{k+1}=0\)
\(
\text { or } \quad k=-\frac{2}{3}
\)
Therefore, YZ-plane divides AB externally in the ratio \(2: 3\).

Example 5: Find the ratio in which \(2 x+3 y+5 z=1\) divides the line joining the points \((1,0,-3)\) and \((1,-5,7)\).

Solution: Let \(2 x+3 y+5 z=1\) divides \((1,0,-3)\) and \((1,-5,7)\) in the ratio of \(k: 1\) at point \(P\).
Then, \(P=\left(\frac{k+1}{k+1}, \frac{-5 k}{k+1}, \frac{7 k-3}{k+1}\right)\) which must satisfy
\(
\begin{aligned}
& 2 x+3 y+5 z=1 \\
& \Rightarrow \quad 2\left(\frac{k+1}{k+1}\right)+3\left(\frac{-5 k}{k+1}\right)+5\left(\frac{7 k-3}{k+1}\right)=1 \\
& \Rightarrow \quad 2 k+2-15 k+35 k-15=k+1 \\
& \Rightarrow \quad 21 k=14 \Rightarrow k=\frac{2}{3}
\end{aligned}
\)
\(\therefore 2 x+3 y+5 z=1\), divides \((1,0,-3)\) and \((1,-5,7)\) in the ratio of \(2: 3\).

Example 6: If \(A(3,2,-4), B(5,4,-6)\) and \(C(9,8,-10)\) are three collinear points, then find the ratio in which point \(C\) divides \(A B\).

Solution: Let \(C\) divide \(A B\) in the ratio \(\lambda: 1\). Then,
\(
C \equiv\left(\frac{5 \lambda+3}{\lambda+1}, \frac{4 \lambda+2}{\lambda+1}, \frac{-6 \lambda-4}{\lambda+1}\right)=(9,8,10)
\)
Comparing, \(5 \lambda+3=9 \lambda+9\) or \(4 \lambda=-6\)
\(
\therefore \quad \lambda=-\frac{3}{2}
\)
Also, from \(4 \lambda+2=8 \lambda+8\) and \(-6 \lambda-4=-10 \lambda-10\), we get the same value of \(\lambda\).
\(\therefore C\) divides \(A B\) in the ratio \(3: 2\) externally.

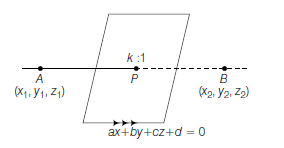
Example 7: Show that the plane \(a x+b y+c z+d=0\) divides the line joining \(\left(x_1, y_1, z_1\right)\) and \(\left(x_2, y_2, z_2\right)\) in the ratio of \(\left(-\frac{a x_1+a y_1+c z_1+d}{a x_2+b y_2+c z_2+d}\right)\).

Solution: Let the plane \(a x+b y+c z+d=0\) divides the line joining \(\left(x_1, y_1, z_1\right)\) and \(\left(x_2, y_2, z_2\right)\) in the ratio \(k: 1\) as shown in figure.

\(
\begin{aligned}
& \therefore \text { Coordinates of } P\left(\frac{k x_2+x_1}{k+1}, \frac{k y_2+y_1}{k+1}, \frac{k z_2+z_1}{k+1}\right) \\
& \text { must satisfy } a x+b y+c z+d=0 \\
& \text { i.e., } a\left(\frac{k x_2+x_1}{k+1}\right)+b\left(\frac{k y_2+y_1}{k+1}\right)+c\left(\frac{k z_2+z_1}{k+1}\right)+d=0 \\
& \Rightarrow a\left(k x_2+x_1\right)+b\left(k y_2+y_1\right)+c\left(k z_2+z_1\right)+d(k+1)=0 \\
& \Rightarrow \quad k\left(a x_2+b y_2+c z_2+d\right)+\left(a x_1+b y_1+c z_1+d\right)=0 \\
& \Rightarrow \quad k=-\frac{\left(a x_1+b y_1+c z_1+d\right)}{\left(a x_2+b y_2+c z_2+d\right)}
\end{aligned}
\)

Remark

• Students are advised to learn above result as a formula i.e. \(a x+b y+c z+d=0\) divides join of \(\left(x_1, y_1, z_1\right)\) and \(\left(x_2, y_2, z_2\right)\) in ratio of \(-\frac{\left(a x_1+b y_1+c z_1+d\right)}{\left(a x_2+b y_2+c z_2+d\right)}\).

Example 8: Find the ratio in which the join of \((2,1,5)\), \((3,4,3)\) is divided by the plane \(2 x+2 y-2 z-1=0\).

Solution: Let the given plane divides the join of \(A B\) in \(k: 1\) at point \(C\). Hence, the coordinates \(C\) using Section Formula will be:
\(
\left(\frac{3 k+2}{k+1}, \frac{4 k+1}{k+1}, \frac{3 k+5}{k+1}\right)
\)
Since, point \(C\) lies on given plane
\(
\Rightarrow 2\left(\frac{3 k+2}{k+1}\right)+2\left(\frac{4 k+1}{k+1}\right)-2\left(\frac{3 k+5}{k+1}\right)=1
\)
On solving, we get
\(
\begin{aligned}
& 8 k -4= k +1 \\
& \Rightarrow k =\frac{5}{7}
\end{aligned}
\)
Hence, the required ratio is \(5: 7\).

Alternate:

Using above result,
\(
\begin{aligned}
\text { Required ratio } & =- \frac{\{(2(2)+2(1)-2(5)-1\}}{\{2(3)+2(4)-2(3)-1\}} \\
& =- \frac{\{6-11\}}{\{14-7\}}=-\frac{-5}{7}
\end{aligned}
\)
\(\Rightarrow 2 x+2 y-2 z-1=0\) divides \((2,1,5)\) and \((3,4,5)\) externally in ratio of \(5: 7\).

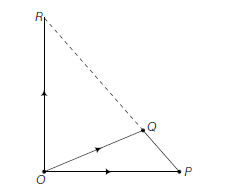
Example 9: Let \(P\) and \(Q\) be two points whose position vectors are \(r _1\) and \(r _2\) respectively. Let \(R\) be a point on \(P Q\) dividing it in the ratio \(m: n\). Then, show that the position vector of \(R\) is given by \(r =\frac{m r _2+n r _1}{m+n}\)

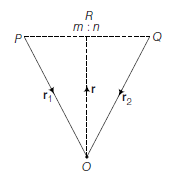
Solution: Let \(O\) be the origin. Then, \(OP = r _1, OQ = r _2\) and \(OR = r\)
Now, \(\frac{P R}{R Q}=\frac{m}{n}\)
\(
\begin{gathered}
n PR =m RQ \\
n( OR – OP )=m( OQ – OR ) \\
n\left( r – r _1\right)=m\left( r _2- r \right) \\
(m+n) r =m r _2+n r _1 \\
r =\frac{m r _2+n r _1}{m+n}
\end{gathered}
\)

Corollary

• Mid-point formula Let \(P\) and \(Q\) be two points whose position vectors are given by \(r _1\) and \(r _2\) respectively. Then, the position vector of the mid-point \(R\) of \(P Q\) is given by, \(r =\frac{ r _1+ r _2}{2}\)

Example 10: Let \(P\) and \(Q\) be the points whose position vectors are \(r _1\) and \(r _2\) respectively. Let \(R\) be a point on \(P Q\) dividing it externally in the ratio \(m: n\). Then, show that the position vector of \(R\) is given by,
\(
r =\frac{m r _2-n r _1}{m-n}
\)

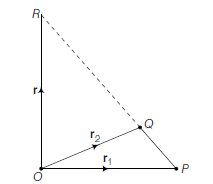
Solution: Let \(O\) be the origin. Then, \(OP = r _1, OQ = r _2\) and \(OR = r\)
Now,
\(
\frac{P R}{Q R}=\frac{m}{n}
\)
\(
\begin{aligned}
n PR & =m QR \\
n( OR – OP ) & =m( OR – OQ ) \\
n\left( r – r _1\right) & =m\left( r – r _2\right) \\
(m-n) r & =m r _2-n r _1 \\
r & =\left(\frac{m r _2-n r _1}{m-n}\right)
\end{aligned}
\)

Corollary 1: If \(R(x, y, z)\) is a point dividing the join of \(P\left(x_1, y_1, z_1\right)\) and \(Q\left(x_2, y_2, z_2\right)\) in the ratio \(m: n\).
Then, \(x=\frac{m x_2+n x_1}{m+n}, y=\frac{m y_2+n y_1}{m+n}, z=\frac{m z_2+n z_1}{m+n}\)

Corollary 2: The coordinates of the mid-point of the joint of \(P\left(x_1, y_1, z_1\right)\) and \(Q\left(x_2, y_2, z_2\right)\) are
\(
\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)
\)

Corollary 3: The coordinates of a point \(R\) which divides the join of \(P\left(x_1, y_1, z_1\right)\) and \(Q\left(x_2, y_2, z_2\right)\) externally in the ratio \(m: n\) are
\(
\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}, \frac{m z_2-n z_1}{m-n}\right)
\)

Corollary 4: The coordinate of centroid of triangle with vertices \(\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right),\left(x_3, y_3, z_3\right)\) is
\(
\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)
\)

Corollary 5: Centroid of tetrahedron with vertices \(\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right),\left(x_3, y_3, z_3\right),\left(x_4, y_4, z_4\right)\) is
\(
\begin{aligned}
\left(\frac{x_1+x_2+x_3+x_4}{4}, \frac{y_1+y_2+y_3+y_4}{4},\right. & \left.\frac{z_1+z_2+z_3+z_4}{4}\right)
\end{aligned}
\)