12.3 Coordinates of a Point in Space

Let’s see given a point in the space, how we associate with it three coordinates \((x, y, z)\) and conversely, given a triplet of three numbers \((x, y, z)\), how, we locate a point in the space.

Given a point \(P\) in space, we drop a perpendicular PM on the \(XY\)-plane with \(M\) as the foot of this perpendicular (Fig 11.2).

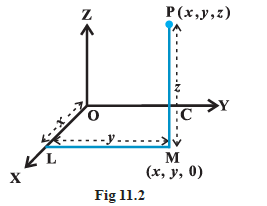
Then, from the point \(M\), we draw a perpendicular ML to the \(x\)-axis, meeting it at \(L\). Let OL be \(x, LM\) be \(y\) and MP be \(z\). Then \(x, y\) and \(z\) are called the \(x, y\) and \(z\) coordinates, respectively, of the point \(P\) in the space. In Fig 11.2, we may note that the point \(P (x, y, z)\) lies in the octant \(XOYZ\) and so all \(x, y\), \(z\) are positive. If \(P\) was in any other octant, the signs of \(x, y\) and \(z\) would change accordingly. Thus, to each point \(P\) in the space there corresponds an ordered triplet \((x, y, z)\) of real numbers.

Alternatively, through the point \(P\) in the space, we draw three planes parallel to the coordinate planes, meeting the \(x\)-axis, \(y\)-axis and \(z\)-axis in the points \(A , B\) and \(C\), respectively (Fig 11.3). Let \(OA =x, OB =y\) and \(OC =z\). Then, the point \(P\) will have the coordinates \(x, y\) and \(z\) and we write \(P (x, y, z)\).

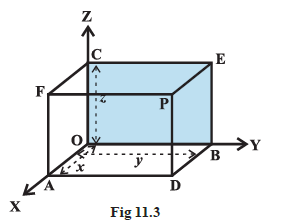
Conversely, given \(x, y\) and \(z\), we locate the three points A, B and \(C\) on the three coordinate axes. Through the points \(A , B\) and \(C\) we draw planes parallel to the YZ-plane, ZX-plane and XY-plane, respectively. The point of intersection of these three planes, namely, ADPF, BDPE and CEPF is obviously the point \(P\), corresponding to the ordered triplet \((x, y, z)\). We observe that if \(P (x, y, z)\) is any point in the space, then \(x, y\) and \(z\) are perpendicular distances from \(YZ , ZX\) and \(XY\) planes, respectively.

Remark

• The coordinates of the origin \(O\) are \((0,0,0)\). The coordinates of any point on the \(x\)-axis will be as \((x, 0,0)\) and the coordinates of any point in the YZ-plane will be as \((0, y, z)\).

Position Vector of a Point in Space

Let \(\hat{ i }, \hat{ j }\), \(\hat{ k }\) be unit vector (called base vector) along \(O X, O Y\) and \(O Z\), respectively.
Let \(P(x, y, z)\) be a point in space, let the position of \(P\) be \(r\).
Then, \(\quad r = OP = OM + MP\)
\(
=( OA + AM )+ MP = OA + OB + OC
\)
\(
r =x \hat{ i }+y \hat{ j }+z \hat{ k }
\)
Thus, the position vector of a point \(P\) is, \(x \hat{ i }+\hat{y j }+z \hat{ k }\).

Remark

• Any point on
  \(
  \begin{aligned}
  X \text {-axis } & =(x, 0,0) \\
  Y \text {-axis } & =(0, y, 0) \\
  Z \text {-axis } & =(0,0, z) \\
  X Y \text {-plane } & =(x, y, 0) \\
  Y Z \text {-plane } & =(0, y, z) \\
  Z \text {-plane } & =(x, 0, z)
  \end{aligned}
  \)
• \(O P=\sqrt{x^2+y^2+z^2}\)

Example 1: Planes are drawn parallel to the coordinate planes through the points \((1,2,3)\) and \((3,-4,-5)[latex]. Find the lengths of the edges of the parallelopiped so formed.

Solution: Let [latex]P=(1,2,3), Q=(3,-4,-5)\) through which planes are drawn parallel to the coordinate planes shown as,

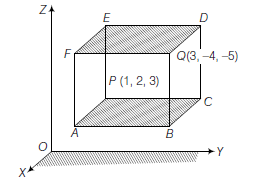
\(\therefore P E=\) Distance between parallel planes \(A B C P\) and \(F Q D E\), i.e. (along \(Z\)-axis)
\(
=|-5-3|=8
\)
\(P A=\) Distance between parallel planes \(A B Q F\) and \(P C D E\), i.e. (along \(X\)-axis)
\(
=|3-1|=2
\)
\(P C=\) Distance between parallel planes \(B C D Q\) and \(A P E F\), i.e. (along \(Y\)-axis)
\(
=|-4-2|=6
\)
\(\therefore\) Lengths of edges of the parallelopiped are \(2,6,8\).

Shifting of Origin

Shifting the origin to another point without changing the directions of the axes is called the translation of axes. Let the origin \(O(0,0,0)\) be shifted to another point \(O^{\prime}\left(x^{\prime}, y^{\prime}, z^{\prime}\right)\) without changing the direction of axes. Let the new coordinate frame be \(O^{\prime} X^{\prime} Y^{\prime} Z^{\prime}\). Let \(P(x, y, z)\) be a point with respect to the coordinate frame \(O X Y Z\). Then, coordinate of point \(P\) with respect to new coordinate frame \(O^{\prime} X^{\prime} Y^{\prime} Z^{\prime}\) is \(\left(x_1, y_1, z_1\right)\), where \(x_1=x-x^{\prime}\),
\(
y_1=y-y^{\prime}, z_1=z-z^{\prime}
\)

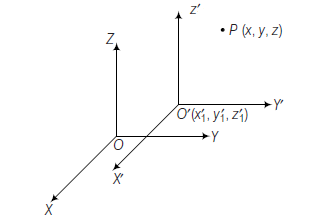
Example 2: If the origin is shifted \((1,2,-3)\) without changing the directions of the axis, then find the new coordinates of the point \((0,4,5)\) with respect to new frame.

Solution: In the new frame \(x^{\prime}=x-x_1, y^{\prime}=y-y_1, z^{\prime}=z-z_1\), where \(\left(x_1, y_1, z_1\right)\) is shifted origin.
\(
\Rightarrow \quad \begin{aligned}
& x^{\prime}=0-1=-1, \\
& y^{\prime}=4-2=2, z^{\prime}=5+3=8
\end{aligned}
\)
Hence, the coordinates of the point with respect to the new coordinates frame are \((-1,2,8)\).

Example 3: In Fig 11.3, if \(P\) is \((2,4,5)\), find the coordinates of \(F\).

Solution: For the point F, the distance measured along OY is zero (it is in x-z plane so y is 0). Therefore, the coordinates of \(F\) are \((2,0,5)\).

Example 4: Find the octant in which the points (–3,1,2) and (–3,1,– 2) lie.

Solution: 

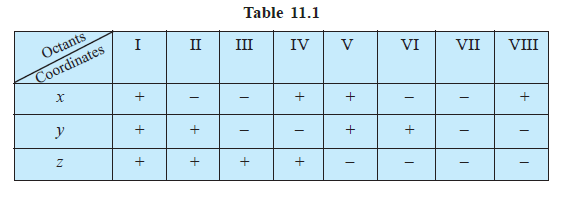
From the Table 11.1, the point (–3,1, 2) lies in second octant and the point (–3, 1, – 2) lies in octant VI.