12.2 Coordinate Axes and Coordinate Planes in Three Dimensional Space

Consider three planes intersecting at a point \(O\) such that these three planes are mutually perpendicular to each other (Fig 11.1).

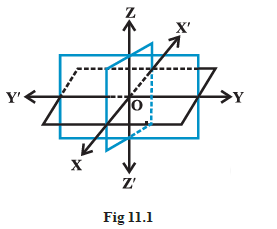
These three planes intersect along the lines \(X ^{\prime} OX , Y ^{\prime} OY\) and \(Z^{\prime} O Z\), called the \(x, y\) and \(z\)-axes, respectively We may note that these lines are mutually perpendicular to each other. These lines constitute the rectangular coordinate system.

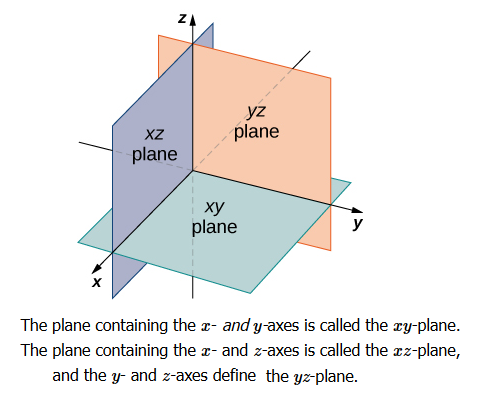
The planes \(XOY , YOZ\) and ZOX, called, respectively the XY-plane, YZ-plane and the ZX-plane, are known as the three coordinate planes. We take the XOY plane as the plane of the paper and the line \(Z ^{\prime} OZ\) as perpendicular to the plane \(XOY\). If the plane of the paper is considered as horizontal, then the line \(Z ^{\prime} OZ\) will be vertical. The distances measured from \(XY\)-plane upwards in the direction of \(OZ\) are taken as positive and those measured downwards in the direction of \(OZ ^{\prime}\) are taken as negative. Similarly, the distance measured to the right of ZX-plane along OY are taken as positive, to the left of \(ZX\)-plane and along \(OY ^{\prime}\) as negative, in front of the \(YZ\)-plane along \(OX\) as positive and to the back of it along \(OX ^{\prime}\) as negative. The point \(O\) is called the origin of the coordinate system. The three coordinate planes divide the space into eight parts known as octants (as described in introduction section).

How to Visualize in 3-D

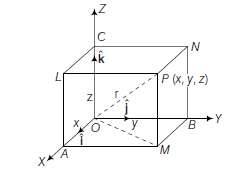
Let \(O Y\) and \(O Z\) be two perpendicular lines which intersect at \(O\) and let a third straight line \(O X\) be perpendicular to the plane in which they lie. The three mutually perpendicular lines form a set of coordinate axis. They determine three mutually perpendicular planes called coordinate planes.

    ⇒          

Remarks

• The axes to coordinate form a right handed set (in the figure) i.e. a right handed screw, driven from \(O\) to \(X\) would rotate in the sense from \(O Y\) to \(O Z\).
• The points \(A, B\) and \(C\) are the orthogonal projections of \(P\) on the \(X, Y\) and \(Z\)-axes.
• Points \(L, M\) and \(N\) are \((x, 0, z),(x, y, 0),(0, y, z)\) and \(A, B\) and \(C\) are \((x, 0,0),(0, y, 0),(0,0, z)\), respectively.