12.1 Introduction

You may recall that to locate the position of a point in a plane, we need two intersecting mutually perpendicular lines in the plane. These lines are called the coordinate axes and the two numbers are called the coordinates of the point with respect to the axes. In actual life, we do not have to deal with points lying in a plane only. For example, consider the position of a ball thrown in space at different points of time or the position of an aeroplane as it flies from one place to another at different times during its flight.

Similarly, if we were to locate the position of the lowest tip of an electric bulb hanging from the ceiling of a room or the position of the central tip of the ceiling fan in a room, we will not only require the perpendicular distances of the point to be located from two perpendicular walls of the room but also the height of the point from the floor of the room. Therefore, we need not only two but three numbers representing the perpendicular distances of the point from three mutually perpendicular planes, namely the floor of the room and two adjacent walls of the room. The three numbers representing the three distances are called the coordinates of the point with reference to the three coordinate planes. So, a point in space has three coordinates. 

Three-Dimensional Coordinate Systems

As we have learned, the two-dimensional rectangular coordinate system contains two perpendicular axes: the horizontal \(x\)-axis and the vertical \(y\)-axis. We can add a third dimension, the \(z\)-axis, which is perpendicular to both the \(x\)-axis and the \(y\)-axis. We call this system the three-dimensional rectangular coordinate system. It represents the three dimensions we encounter in real life.

The three-dimensional rectangular coordinate system consists of three perpendicular axes: the \(x\)-axis, the \(y\)-axis, and the \(z\)-axis.

In Figure a below, the positive \(z\)-axis is shown above the plane containing the \(x\)-and \(y\)-axes. The positive \(x\)-axis appears to the left and the positive \(y\)-axis is to the right. A natural question to ask is: How was this arrangement determined? The system displayed follows the right-hand rule. If we take our right hand and align the fingers with the positive \(x\)-axis, then curl the fingers so they point in the direction of the positive \(y\)-axis, our thumb points in the direction of the positive \(z\)-axis (Figure b). In this text, we always work with coordinate systems set up in accordance with the right-hand rule.

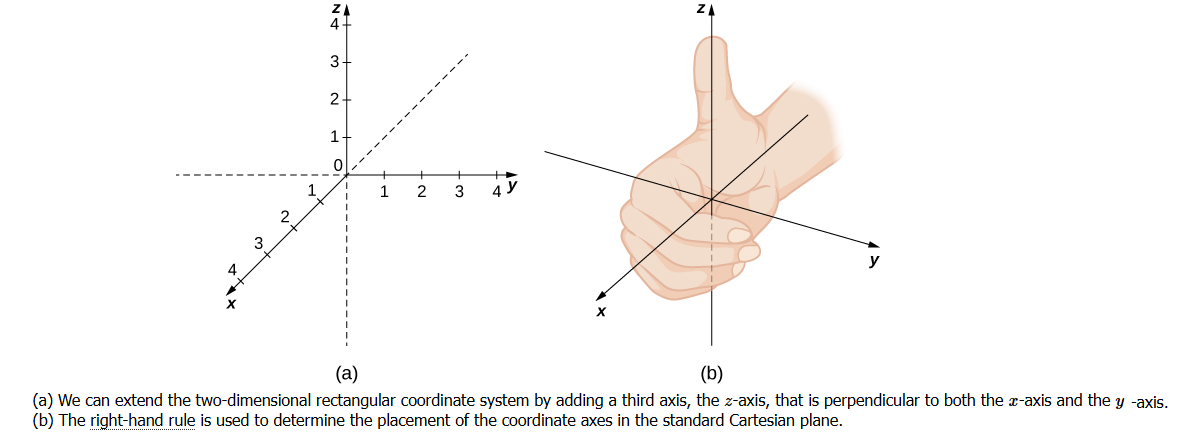
In two dimensions, we describe a point in the plane with the coordinates \((x, y)\). Each coordinate describes how the point aligns with the corresponding axis. In three dimensions, a new coordinate, \(z\), is appended to indicate alignment with the \(z\)-axis: \((x, y, z)\). A point in space is identified by all three coordinates (Figure below). To plot the point \((x, y, z)\), go \(x\) units along the \(x\)-axis, then \(y\) units in the direction of the \(y\)-axis, then \(z\) units in the direction of the \(z\)-axis.

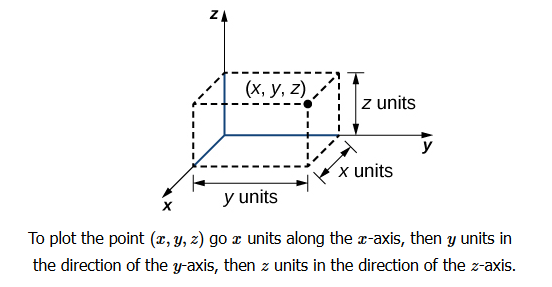
Example 1: Sketch the point \((1,-2,3)\) in three-dimensional space.

Solution: To sketch a point, start by sketching three sides of a rectangular prism along the coordinate axes: one unit in the positive \(x\) direction, 2 units in the negative \(y\) direction, and 3 units in the positive \(z\) direction. Complete the prism to plot the point (Figure below).

Octants Rule in 3-Dimension

In two-dimensional space, the coordinate plane is defined by a pair of perpendicular axes. These axes allow us to name any location within the plane. In three dimensions, we define coordinate planes by the coordinate axes, just as in two dimensions. There are three axes now, so there are three intersecting pairs of axes. Each pair of axes forms a coordinate plane: the \(x y\)-plane, the \(x z\)-plane, and the \(y z\)-plane (Figure below). We define the \(x y\)-plane formally as the following set: \(\{(x, y, 0): x, y \in R \}\). Similarly, the \(x z\)-plane and the \(y z\)-plane are defined as \(\{(x, 0, z): x, z \in R \}\) and \(\{(0, y, z): y, z \in R \}\), respectively.

To visualize this, imagine you’re building a house and are standing in a room with only two of the four walls finished. (Assume the two finished walls are adjacent to each other.) If you stand with your back to the corner where the two finished walls meet, facing out into the room, the floor is the \(x y\)-plane, the wall to your right is the \(x z\)-plane, and the wall to your left is the \(y z\)-plane.

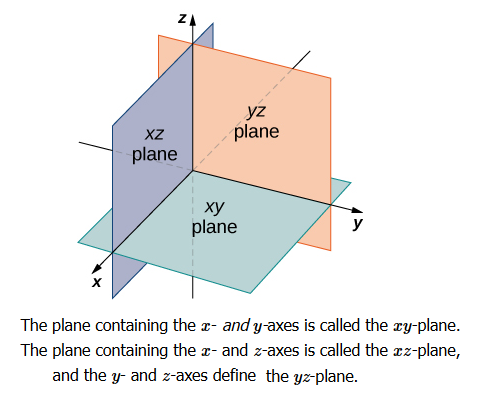
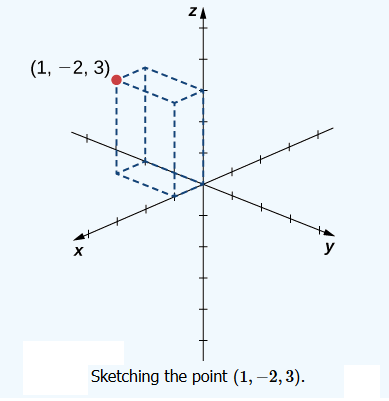
In two dimensions, the coordinate axes partition the plane into four quadrants. Similarly, the coordinate planes divide space between them into eight regions about the origin, called octants (as shown below).

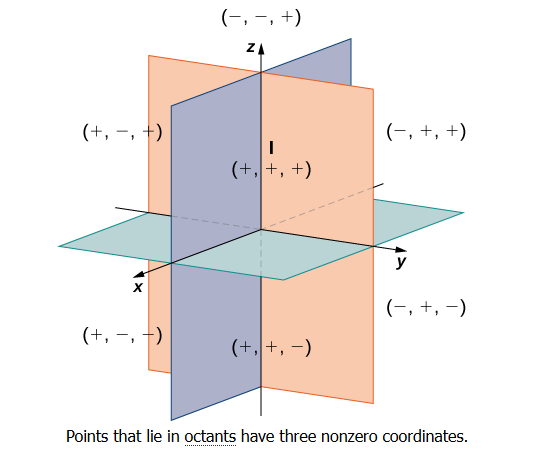
The sign of the coordinates of a point determine the octant in which the point lies. The following table shows the signs of the coordinates in eight octants.