11.6 Hyperbola

Definition

A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant.

                                                                                              or 

The locus of a point which moves in a plane such that its distance from a fixed point (i.e. focus) is \(e\) times its distance from a fixed line (i.e. directrix) is known as hyperbola. For hyperbola \(e>1\).

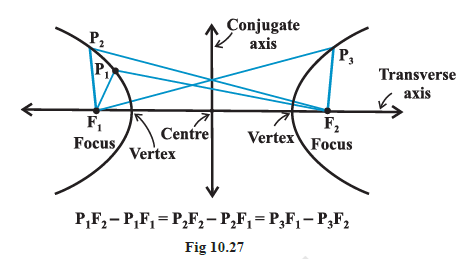
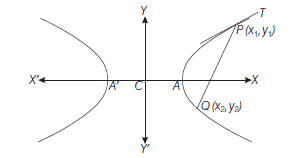
The term “difference” that is used in the definition means the distance to the farther point minus the distance to the closer point. The two fixed points are called the foci of the hyperbola. The mid-point of the line segment joining the foci is called the centre of the hyperbola. The line through the foci is called the transverse axis and the line through the centre and perpendicular to the transverse axis is called the conjugate axis. The points at which the hyperbola intersects the transverse axis are called the vertices of the hyperbola (Fig 10.27).

We denote the distance between the two foci by \(2 c\), the distance between two vertices (the length of the transverse axis) by \(2 a\) and we define the quantity \(b\) as
\(
b=\sqrt{c^2-a^2}
\)
Also \(2 b\) is the length of the conjugate axis (Fig 10.28).

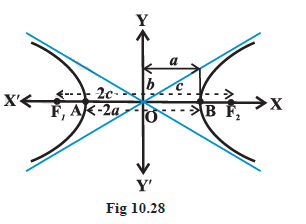
To find the constant \(P_1 F_2-P_1 F_1\) :
By taking the point \(P\) at \(A\) and \(B\) in the Fig 10.28 , we have \(BF _1- BF _2= AF _2- AF _1\) (by the definition of the hyperbola)
\(
\begin{aligned}
& BA + AF _1- BF _2= AB + BF _2- AF _1 \\
& \text { i.e., } AF _1= BF _2
\end{aligned}
\)
So that, \(BF _1- BF _2= BA + AF _1- BF _2= BA =2 a\)

Eccentricity

Definition 8 Just like an ellipse, the ratio \(e=\frac{c}{a}\) is called the eccentricity of the hyperbola. Since \(c \geq a\), the eccentricity is never less than one. In terms of the eccentricity, the foci are at a distance of \(a e\) from the centre.

Standard equation of Hyperbola

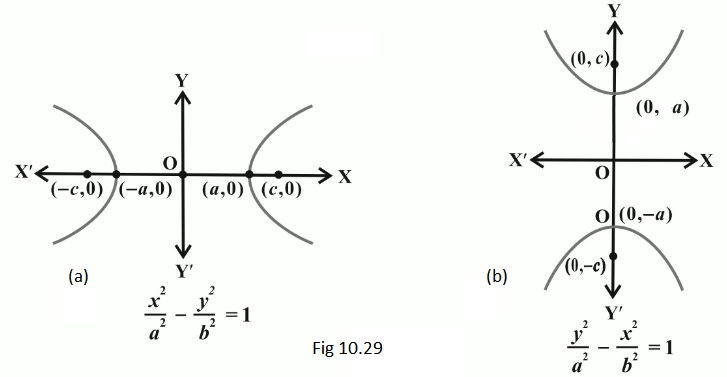
The equation of a hyperbola is simplest if the centre of the hyperbola is at the origin and the foci are on the \(x\)-axis or \(y\)-axis. The two such possible orientations are shown in Fig10.29.

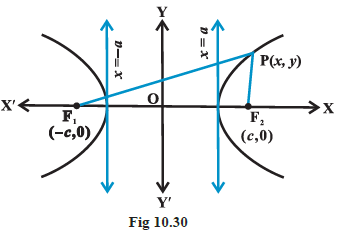
Let \(F_1\) and \(F_2\) be the foci and \(O\) be the mid-point of the line segment \(F_1 F_2\). Let \(O\) be the origin and the line through \(O\) through \(F _2\) be the positive \(x\)-axis and that through \(F _1\) as the negative \(x\)-axis. The line through \(O\) perpendicular to the \(x\)-axis be the \(y\)-axis. Let the coordinates of \(F_1\) be \((-c, 0)\) and \(F _2\) be \((c, 0)\) (Fig 10.30).

Let \(P (x, y)\) be any point on the hyperbola such that the difference of the distances from \(P\) to the farther point minus the closer point be \(2 a\). So given, \(PF _1- PF _2=2 a\)

Using the distance formula, we have
\(
\begin{aligned}
& \sqrt{(x+c)^2+y^2}-\sqrt{(x-c)^2+y^2}=2 a \\
& \sqrt{(x+c)^2+y^2}=2 a+\sqrt{(x-c)^2+y^2}
\end{aligned}
\)
Squaring both side, we get
\(
(x+c)^2+y^2=4 a^2+4 a \sqrt{(x-c)^2+y^2}+(x-c)^2+y^2
\)
and on simplifying, we get
\(
\frac{c x}{a}-a=\sqrt{(x-c)^2+y^2}
\)
On squaring again and further simplifying, we get
\(
\frac{x^2}{a^2}-\frac{y^2}{c^2-a^2}=1
\)
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text { (Since } c^2-a^2=b^2 \text { ) }
\)
Hence any point on the hyperbola satisfies \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Conversely, let \(P (x, y)\) satisfy the above equation with \(0<a<c\). Then
\(
y^2=b^2\left(\frac{x^2-a^2}{a^2}\right)
\)
\(
\begin{aligned}
\text { Therefore, } PF _1 & =+\sqrt{(x+c)^2+y^2} \\
& =+\sqrt{(x+c)^2+b^2\left(\frac{x^2-a^2}{a^2}\right)}=a+\frac{c}{a} x
\end{aligned}
\)
Similarly, \(\quad PF _2=a-\frac{a}{c} x\)
In hyperbola \(c>a\); and since \(P\) is to the right of the line \(x=a, x>a, \frac{c}{a} x>a\). Therefore, \(a-\frac{c}{a} x\) becomes negative. Thus, \(PF _2=\frac{c}{a} x-a\).
Therefore
\(
PF _1- PF _2=a+\frac{c}{a} x-\frac{c x}{a}+a=2 a
\)
Also, note that if \(P\) is to the left of the line \(x=-a\), then
\(
PF _1=-\left(a+\frac{c}{a} x\right), PF _2=a-\frac{c}{a} x .
\)
In that case \(PF _2- PF _1=2 a\). So, any point that satisfies \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), lies on the hyperbola.
Thus, we proved that the equation of hyperbola with origin \((0,0)\) and transverse axis along \(x\)-axis is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), \(\text { where, } b^2=a^2\left(e^2-1\right)\) and \(e=\frac{c}{a}\)

Generally : The equation of the hyperbola whose focus is the point \((h, k)\) and directrix is \(l x+m y+n=0\) and whose eccentricity is \(e\), is
\(
(x-h)^2+(y-k)^2=e^2 \frac{(l x+m y+n)^2}{\left(l^2+m^2\right)}
\)

Remarks

• A hyperbola in which \(a=b\) is called an equilateral hyperbola.
• From the equation of the hyperbola we have obtained, it follows that, we have for every point \((x, y)\) on the hyperbola, \(\frac{x^2}{a^2}=1+\frac{y^2}{b^2} \geq 1\).
  i.e, \(\left|\frac{x}{a}\right| \geq 1\), i.e., \(x \leq-a\) or \(x \geq a\). Therefore, no portion of the curve lies between the lines \(x=+a\) and \(x=-a\), (i.e. no real intercept on the conjugate axis).
• Hyperbola is symmetric with respect to both the axes, since if \((x, y)\) is a point on the hyperbola, then \((-x, y),(x,-y)\) and \((-x,-y)\) are also points on the hyperbola.
• The foci are always on the transverse axis. It is the positive term whose denominator gives the transverse axis. For example, \(\frac{x^2}{9}-\frac{y^2}{16}=1\) has transverse axis along \(x\)-axis of length 6 , while \(\frac{y^2}{25}-\frac{x^2}{16}=1\) has transverse axis along y-axis of length 10.

Latus rectum

Latus rectum of hyperbola is a line segment perpendicular to the transverse axis through any of the foci and whose end points lie on the hyperbola. As in ellipse, it is easy to show that the length of the latus rectum in hyperbola is \(\frac{2 b^2}{a}\).

Example 1: Find the coordinates of the foci and the vertices, the eccentricity, the length of the latus rectum of the hyperbolas:
(i) \(\frac{x^2}{9}-\frac{y^2}{16}=1\),
(ii) \(y^2-16 x^2=16\)

Answer: (i) Comparing the equation \(\frac{x^2}{9}-\frac{y^2}{16}=1\) with the standard equation
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\)
Here, \(a=3, b=4\) and \(c=\sqrt{a^2+b^2}=\sqrt{9+16}=5\)
Therefore, the coordinates of the foci are \(( \pm 5,0)\) and that of vertices are \(( \pm 3,0)\).Also, The eccentricity \(e=\frac{c}{a}=\frac{5}{3}\). The latus rectum \(=\frac{2 b^2}{a}=\frac{32}{3}\)
(ii) Dividing the equation by 16 on both sides, we have \(\frac{y^2}{16}-\frac{x^2}{1}=1\)
Comparing the equation with the standard equation \(\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\), we find that \(a=4, b=1\) and \(c=\sqrt{a^2+b^2}=\sqrt{16+1}=\sqrt{17}\).
Therefore, the coordinates of the foci are \((0, \pm \sqrt{17})\) and that of the vertices are \((0, \pm 4)\). Also,
The eccentricity \(e=\frac{c}{a}=\frac{\sqrt{17}}{4}\). The latus rectum \(=\frac{2 b^2}{a}=\frac{1}{2}\).

Example 2: Find the equation of the hyperbola with foci \((0, \pm 3)\) and vertices
\(
\left(0, \pm \frac{\sqrt{11}}{2}\right) \text {. }
\)

Answer:  Since the foci is on y-axis, the equation of the hyperbola is of the form
\(
\frac{y^2}{a^2}-\frac{x^2}{b^2}=1
\)
Since vertices are \(\left(0, \pm \frac{\sqrt{11}}{2}\right), a=\frac{\sqrt{11}}{2}\)
Also, since foci are \((0, \pm 3) ; c=3\) and \(b^2=c^2-a^2=\frac{25}{4}\).
Therefore, the equation of the hyperbola is
\(
\frac{y^2}{\left(\frac{11}{4}\right)}-\frac{x^2}{\left(\frac{25}{4}\right)}=1 \text {, i.e., } 100 y^2-44 x^2=275 \text {. }
\)

Example 3: Find the equation of the hyperbola where foci are \((0, \pm 12)\) and the length of the latus rectum is 36.

Answer: Since foci are \((0, \pm 12)\), it follows that \(c=12\).
Length of the latus rectum \(=\frac{2 b^2}{a}=36\) or \(b^2=18 a\)
\(
\begin{aligned}
\text { Therefore } & c^2=a^2+b^2 ; \text { gives } \\
& 144=a^2+18 a \\
& a^2+18 a-144=0, \\
& a=-24,6 .
\end{aligned}
\)
Since \(a\) cannot be negative, we take \(a=6\) and so \(b^2=108\).
Therefore, the equation of the required hyperbola is \(\frac{y^2}{36}-\frac{x^2}{108}=1\), i.e., \(3 y^2-x^2=108\)

Example 4: The focus of a parabolic mirror as shown in Fig 10.31 is at a distance of \(5 cm\) from its vertex. If the mirror is \(45 cm\) deep, find the distance \(AB\) (Fig 10.31).

Answer: 

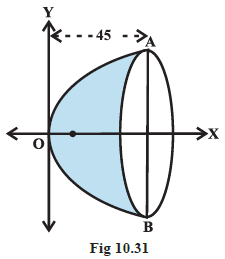
Since the distance from the focus to the vertex is \(5 cm\). We have, \(a=5\). If the origin is taken at the vertex and the axis of the mirror lies along the positive \(x\)-axis, the equation of the parabolic section is
\(
y^2=4(5) x=20 x
\)
Note that \(\quad x=45\). Thus
\(
y^2=900
\)
\(
\begin{aligned}
\text { Therefore } & y= \pm 30 \\
\text { Hence } & AB = 2 y=2 \times 30=160 cm
\end{aligned}
\)

Example 5: A beam is supported at its ends by supports which are 12 metres apart. Since the load is concentrated at its centre, there is a deflection of \(3 cm\) at the centre and the deflected beam is in the shape of a parabola. How far from the centre is the deflection \(1 cm\) ?

Answer: Let the vertex be at the lowest point and the axis vertical. Let the coordinate axis be chosen as shown in Fig 10.32.

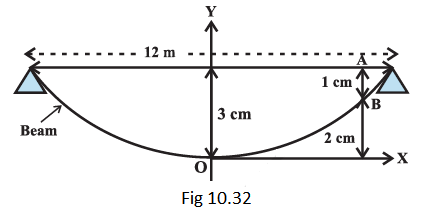
The equation of the parabola takes the form \(x^2=4 a y\). Since it passes through \(\left(6, \frac{3}{100}\right)\), we have \((6)^2=4 a\left(\frac{3}{100}\right)\), i.e., \(a=\frac{36 \times 100}{12}=300 pm\)
Let \(AB\) be the deflection of the beam which is \(\frac{1}{100} m\). Coordinates of \(B\) are \(\left(x, \frac{2}{100}\right)\).
Therefore
\(
\begin{aligned}
& x^2=4 \times 300 \times \frac{2}{100}=24 \\
& x=\sqrt{24}=2 \sqrt{6} \text { metres }
\end{aligned}
\)

The Foci and Two Directrices of a Hyperbola

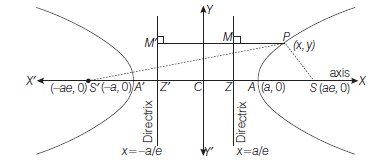
On the negative side of origin take a point \(S^{\prime}\) which is such that
\(
C S=C S^{\prime}=a e
\)
and another point \(Z^{\prime}\), then \(C Z=C Z^{\prime}=\frac{a}{e}\)
\(\therefore\) Coordinates of \(S^{\prime}\) are \((-a e, 0)\) and equation of second directrix (i.e. \(Z^{\prime} M^{\prime}\) ) is
\(
x=-\frac{a}{e}
\)
Let \(P(x, y)\) be any point on the hyperbola, then
\(
S^{\prime} P=e P M^{\prime} \text { or }\left(S^{\prime} P\right)^2=e^2\left(P M^{\prime}\right)^2
\)
\(
\begin{aligned}
(x+a e)^2+(y-0)^2 & =e^2\left(x+\frac{a}{e}\right)^2 \\
(x+a e)^2+y^2 & =(e x+a)^2 \\
x^2+2 a e x+a^2 e^2+y^2 & =e^2 x^2+2 a e x+a^2 \\
x^2\left(e^2-1\right)-y^2 & =a^2\left(e^2-1\right) \\
\frac{x^2}{a^2}-\frac{y^2}{a^2\left(e^2-1\right)} & =1
\end{aligned}
\)
\(
\text { or } \quad \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text {, where, } b^2=a^2\left(e^2-1\right)
\)
The equation being the same as that of hyperbola when \(S(a e, 0)\) is focus and \(M Z\) i.e. \(x=\frac{a}{e}\) is directrix.
Hence, coordinates of foci are \(( \pm a e, 0)\) and equations of directrices are
\(
x= \pm a / e
\)

Remarks

• Distance between foci \(S S^{\prime}=2 a\) and distance between directrices
  \(
  Z ^{\prime}=2 a / e
  \)
• Two hyperbolas are said to be similar if they have the same value of eccentricity.
• Since,
  \(
  \frac{x^2}{a^2}-\frac{y^2}{b^2}=1
  \)
  \(
  \begin{aligned}
  & \Rightarrow \quad \frac{y^2}{b^2}=\frac{x^2}{a^2}-1 \\
  & \frac{y^2}{b^2}=\frac{(x-a)(x+a)}{a^2} \dots(i) \\
  &
  \end{aligned}
  \)
  \(
  \begin{aligned}
  & \because \quad A N=C N-C A=(x-a) \\
  & \text { and } \quad A^{\prime} N=C N+C A^{\prime}=(x+a) \\
  & \text { and } \quad P N=y \\
  & \therefore \text { From Eq. (i), } \frac{(P N)^2}{A N \cdot A^{\prime} N}=\frac{b^2}{a^2} \\
  &
  \end{aligned}
  \)

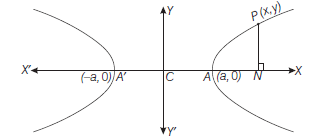
Tracing of the Hyperbola

Equation of the hyperbola is
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)

• Since only even powers of \(x\) and \(y\) occur in this equation so it (hyperbola) is symmetrical about the both axes.
• The hyperbola (i) does not cut \(Y\)-axis in real points where as it cuts \(X\)-axis at \((a, 0)\) and \((-a, 0)\).
• The Eq. (i) may be written as
  \(
  y= \pm \frac{b}{a} \sqrt{\left(x^2-a^2\right)}
  \)
  If follows that \(x^2-a^2 \geq 0\)
  \(
  \begin{array}{ll}
  \therefore & x^2 \geq a^2 \\
  \Rightarrow & x \leq-a \text { or } x \geq a \\
  \text { Hence, } & x \notin(-a, a)
  \end{array}
  \)
  The curve does not exist in the region
  \(
  x=-a \text { to } x=a .
  \)
• As \(x\) increases, \(y\) also increases i.e. the curve extends to infinity.

Some Terms Related to Hyperbola

Let the equation of hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)

• Centre : All chords passing through \(C\) and bisected at C.
  Here \(C \equiv(0,0)\)
• Eccentricity: For the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) we have
  \(
  \begin{aligned}
  b^2 & =a^2\left(e^2-1\right) \\
  \Rightarrow \quad e^2 & =\frac{a^2+b^2}{a^2}
  \end{aligned}
  \)
  \(
  \Rightarrow \quad e=\sqrt{1+\left(\frac{b^2}{a^2}\right)} \Rightarrow e=\sqrt{\left\{1+\frac{(2 b)^2}{(2 a)^2}\right\}}
  \)
  \(
  \Rightarrow \quad e=\sqrt{\left\{1+\frac{(\text { conjugate axis })^2}{\text { (transverse axis) }^2}\right\}}
  \)
• Foci and directrices: \(S\) and \(S^{\prime}\) are the foci of the ellipse and their coordinates are \((a e, 0)\) and \((-a e, 0)\) respectively and \(Z M\) and \(Z^{\prime} M^{\prime}\) are two directrices of the hyperbola and their equations are
  \(
  x=\frac{a}{e} \text { and } x=-\frac{a}{e} \text { respectively. }
  \)

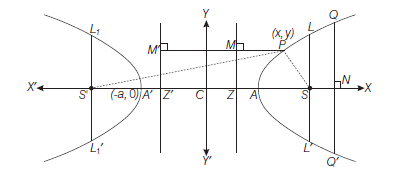
• Axes: The points \(A(a, 0)\) and \(A^{\prime}(-a, 0)\) are called the vertices of the hyperbola and line \(A A^{\prime}\) is called transverse axis and the line perpendicular to its through the centre \((0,0)\) of the hyperbola is called conjugate axis.
  The length of transverse and conjugate axes are taken as \(2 a\) and \(2 b\) respectively.
• Double ordinates: If \(Q\) be a point on the hyperbola draw \(Q N\) perpendicular to the axis of the hyperbola and produced to meet the curve again at \(Q^{\prime}\). Then \(Q Q^{\prime}\) is called a double ordinate of \(Q\).
  If abscissa of \(Q\) is \(h\), then ordinates of \(Q\) are
  \(
  \begin{aligned}
  \frac{y^2}{b^2} & =\frac{h^2}{a^2}-1 \\
  y & = \pm \frac{b}{a} \sqrt{\left(h^2-a^2\right)} \\
  y & =\frac{b}{a} \sqrt{\left(h^2-a^2\right)} \text { (for I quadrant) }
  \end{aligned}
  \)
  and ordinate of \(Q^{\prime}\) is
  \(
  y=-\frac{b}{a} \sqrt{\left(h^2-a^2\right)} \text { (for IV quadrant) }
  \)
  Hence, coordinates of \(Q\) and \(Q^{\prime}\) are
  \(
  \begin{aligned}
  & \left(h, \frac{b}{a} \sqrt{\left(h^2-a^2\right)}\right) \text { and }\left(h,-\frac{b}{a} \sqrt{\left(h^2-a^2\right)}\right) \\
  & \text { respectively. }
  \end{aligned}
  \)

• Latusrectum : The double ordinates \(L L^{\prime}\) and \(L_1 L_1{ }^{\prime}\) are the latusrectums of the hyperbola. These lines are perpendicular to transverse axis \(A A^{\prime}\) and through the foci \(S\) and \(S^{\prime}\) respectively.

  Length of latusrectum

  Now, let \(L L^{\prime}=2 k\), then \(L S=L^{\prime} S=k\)
  Coordinates of \(L\) and \(L^{\prime}\) are \((a e, k)\) and \((a e,-k)\)
  lie on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
  \(
  \therefore \quad \frac{a^2 e^2}{a^2}-\frac{k^2}{b^2}=1
  \)
  \(
  \text { or } \quad k^2=b^2\left(e^2-1\right)=b^2\left(\frac{b^2}{a^2}\right) \quad\left[\because b^2=a^2\left(e^2-1\right)\right]
  \)
  \(
  \therefore \quad k=\frac{b^2}{a} \quad(\because k>0)
  \)
  \(
  \therefore \quad 2 k=\frac{2 b^2}{a}=L L^{\prime}
  \)
  \(\therefore\) Length of latusrectum \(L L^{\prime}=L_1 L_1^{\prime}=\frac{2 b^2}{a}\) and end points of latusrectums are
  \(
  \begin{aligned}
  L & \equiv\left(a e, \frac{b^2}{a}\right) ; L^{\prime} \equiv\left(a e,-\frac{b^2}{a}\right) \\
  L_1 & \equiv\left(-a e, \frac{b^2}{a}\right) ; L_1{ }^{\prime} \equiv\left(-a e,-\frac{b^2}{a}\right) \text { respectively. }
  \end{aligned}
  \)

• Focal chord : A chord of hyperbola passing through its focus is called a focal chord.
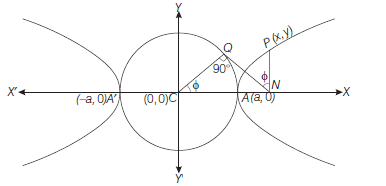
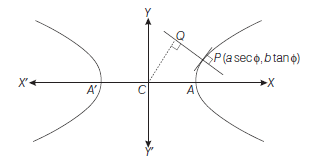
• Parametric equations of the hyperbola : Let \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) be the hyperbola with centre \(C\) and transverse axis \(A^{\prime} A\). Therefore, circle drawn with centre \(C\) and segment \(A^{\prime} A\) as a diameter is called auxiliary circle of the hyperbola.
  \(
  \frac{x^2}{a^2}-\frac{y^2}{b^2}=1
  \)
  \(\therefore\) Equation of the auxiliary circle is \(x^2+y^2=a^2\)
  Let \(P(x, y)\) be any point on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) Draw \(P N\) perpendicular to \(X\)-axis.
  Let \(N Q\) be a tangent to the auxiliary circle \(x^2+y^2=a^2\). Join \(C Q\)
  Let \(\angle Q C N=\phi\)
  Here, \(P\) and \(Q\) are the corresponding points of the hyperbola and the auxiliary circle. \(\phi\) is the eccentric angle of \(P \cdot(0 \leq \phi<2 \pi)\)
  Since, \(Q \equiv(a \cos \phi, a \sin \phi)\)
  Now,
  \(
  x=C N=\frac{C N}{C Q} \cdot C Q=\sec \phi \cdot a
  \)
  \(\therefore \quad x=C N=a \sec \phi\)
  \(\therefore \quad P(x, y) \equiv(a \sec \phi, y)\)
  \(\because P\) lies on \(\quad \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
  \(\therefore \quad \frac{a^2 \sec ^2 \phi}{a^2}-\frac{y^2}{b^2}=1\)
  \(
  \text { or } \quad \frac{y^2}{b^2}=\sec ^2 \phi-1=\tan ^2 \phi
  \)
  \(
  \begin{array}{ll}
  \therefore & y= \pm b \tan \phi \\
  \therefore & y=b \tan \phi \text { ( } P \text { lies in I quadrant) }
  \end{array}
  \)
  The equations of \(x=a \sec \phi\) and \(y=b \tan \phi\) are known as the parametric equations of the hyperbola
  \(
  \frac{x^2}{a^2}-\frac{y^2}{b^2}=1
  \)
  Position of points \(Q\) an auxiliary circle and the corresponding point \(P\) which describes the hyperbola and \(0 \leq \phi<2 \pi\).

\(
\begin{array}{ccc}
\hline \phi \text { varies from } & Q( a \cos \phi, a \sin \phi) & P ( a \sec \phi, b \tan \phi) \\
\hline 0 \text { to } \frac{\pi}{2} & \text { I } & \text { I } \\
\hline \frac{\pi}{2} \text { to } \pi & \text { II } & \text { III } \\
\hline \pi \text { to } \frac{3 \pi}{2} & \text { III } & \text { II } \\
\hline \frac{3 \pi}{2} \text { to } 2 \pi & \text { IV } & \text { IV } \\
\hline
\end{array}
\)

Remarks

• Equation of the chord joining the points \(P \equiv\left(a \sec \phi_1, b \tan \phi_1\right)\) and \(Q \equiv\left(a \sec \phi_2, b \tan \phi_2\right)\) is
  \(
  \frac{x}{a} \cos \left(\frac{\phi_1-\phi_2}{2}\right)-\frac{y}{b} \sin \left(\frac{\phi_1+\phi_2}{2}\right)=\cos \left(\frac{\phi_1+\phi_2}{2}\right)
  \)
  If it is focal chord, then pass through \((a e, 0)\) or \((-a e, 0)\). Suppose it pass through \((a e, 0)\), then
  \(
  \begin{aligned}
  & e \cos \left(\frac{\phi_1-\phi_2}{2}\right)-0=\cos \left(\frac{\phi_1+\phi_2}{2}\right) \\
  & \frac{\cos \left(\frac{\phi_1-\phi_2}{2}\right)}{\cos \left(\frac{\phi_1+\phi_2}{2}\right)}=\frac{1}{e} \\
  & \Rightarrow \frac{\cos \left(\frac{\phi_1-\phi_2}{2}\right)-\cos \left(\frac{\phi_1+\phi_2}{2}\right)}{\cos \left(\frac{\phi_1-\phi_2}{2}\right)+\cos \left(\frac{\phi_1+\phi_2}{2}\right)}=\frac{1-e}{1+e} \\
  & \tan \left(\frac{\phi_1}{2}\right) \tan \left(\frac{\phi_2}{2}\right)=\frac{1-e}{1+e} \\
  &
  \end{aligned}
  \)
  Hence, if \(\phi_1\) and \(\phi_2\) are the eccentric angles of extremities of a focal chord of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), then
  \(
  \tan \left(\frac{\phi_1}{2}\right) \tan \left(\frac{\phi_2}{2}\right)=\frac{1-e}{1+e} \text { or } \frac{1+e}{1-e}
  \)
  according as focus \((a e, 0)\) or \((-a e, 0)\).

Focal Distances of a Point

The difference of the focal distances of any point on the hyperbola is constant and equal to length of the transverse axis of the hyperbola.
The hyperbola is
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
The foci \(S\) and \(S^{\prime}\) are \((a e, 0)\) and \((-a e, 0)\).
The equation of its directrices \(M Z\) and \(M^{\prime} Z^{\prime}\) are
\(
x=\frac{a}{e} \text { and } x=-\frac{a}{e}
\)
respectively.

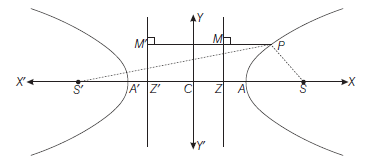
Let \(P\left(x_1, y_1\right)\) be any point on Eq. (i). Now \(\quad S P=e P M=e\left(x_1-\frac{a}{e}\right)=e x_1-a\)
\(
\text { and } \quad S^{\prime} P^{\prime}=e P M^{\prime}=e\left(x_1+\frac{a}{e}\right)=e x_1+a
\)
\(
\begin{aligned}
\therefore \quad S^{\prime} P-S P & =\left(e x_1+a\right)-\left(e x_1-a\right)=2 a=A A^{\prime} \\
& =\text { Transverse axis }
\end{aligned}
\)

A hyperbola is the locus of a point which moves in a plane such that the difference of its distances from two fixed point (foci) is always constant.

Example 6: Find the equation of the hyperbola from the definition that hyperbola is the locus of a point which moves such that the difference of its distances from two fixed points is constant with the fixed point as foci.

Answer: Let two fixed point be \(S(a e, 0)\) and \(S^{\prime}(-a e, 0)\). Let \(P(x, y)\) be a moving point such that
\(
S^{\prime} P-S P=\text { constant }=2 a(\text { say })
\)
\(
\begin{aligned}
& \text { i.e. } \sqrt{(x+a e)^2+(y-0)^2}-\sqrt{(x-a e)^2+(y-0)^2}=2 a \\
& \text { or } \quad \sqrt{\left(x^2+y^2+2 a e x+a^2 e^2\right)}
\end{aligned}
\)
\(
\begin{aligned}
& -\sqrt{\left(x^2+y^2-2 a e x+a^2 e^2\right)}=2 a \dots(i) \\
& \text { Let } \quad l=x^2+y^2+2 a e x+a^2 e^2 \dots(ii) \\
& \text { and } \quad m=x^2+y^2-2 a e x+a^2 e^2 \dots(iii) \\
&
\end{aligned}
\)
Eq. (i) can be re-written as
\(
\sqrt{l}-\sqrt{m}=2 a \dots(iv)
\)
From Eqs. (ii) and (iii),
\(
\begin{aligned}
& l-m=4 a e x \\
& \Rightarrow \quad(\sqrt{l}+\sqrt{m})(\sqrt{l}-\sqrt{m})=4 \text { aex } \\
& \Rightarrow \quad 2 a(\sqrt{l}+\sqrt{m})=4 a e x \text { [from Eq. (iv)] } \\
& \text { or } \quad \sqrt{l}+\sqrt{m}=2 e x \dots(v) \\
&
\end{aligned}
\)
Adding Eqs. (iv) and (v), then
\(
\begin{aligned}
& 2 \sqrt{l}=2 a+2 e x \\
& \Rightarrow \quad \sqrt{l}=a+e x \Rightarrow l=(a+e x)^2 \\
& x^2+y^2+2 a e x+a^2 e^2=a^2+2 a e x+e^2 x^2 \\
& \text { or } \quad x^2\left(e^2-1\right)-y^2=a^2\left(e^2-1\right) \\
& \text { or } \quad \frac{x^2}{a^2}-\frac{y^2}{a^2\left(e^2-1\right)}=1 \\
& \text { or } \quad \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text {, where } b^2=a^2\left(e^2-1\right) \text {. } \\
&
\end{aligned}
\)

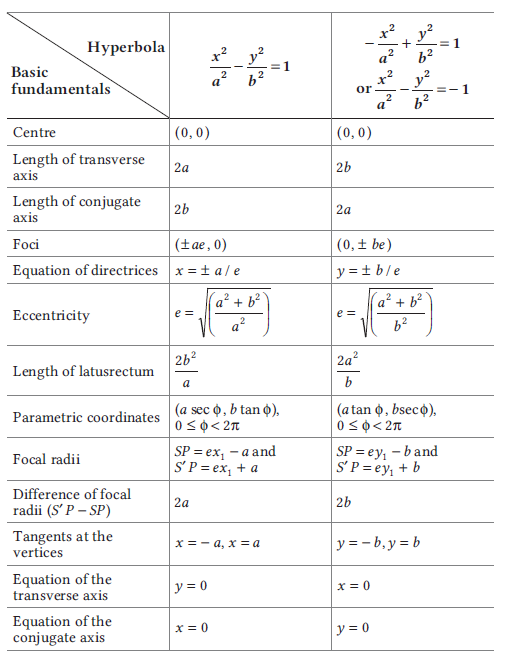
Conjugate Hyperbola

The hyperbola whose transverse and conjugate axes are respectively the conjugate and transverse axes of a given hyperbola is called the conjugate hyperbola of the given hyperbola.
The conjugate hyperbola of the hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text { is }-\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\)
its shape is shown alongside.

Various results related to hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) and its conjugate
\(
-\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \text { or } \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1
\)
are given in the following table

Remarks

• If the centre of hyperbola is \((h, k)\) and axes are parallel to the coordinates axes, then its equation is
  \(
  \frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1 .
  \)
  By shifting the origin at \((h, k)\) without rotating the coord inate axes, the above equation reduces to
  \(
  \frac{x^2}{a^2}-\frac{y^2}{b^2}=1
  \)
  where, \(X=X+h, y=Y+k\)
• If \(e_1\) and \(e_2\) are the eccentricities of a hyperbola and its conjugate, respectively, then \(e_1^2+e_2^2=1\).
  Proof For hyperbola \(b^2=a^2\left(e^2-1\right)\)
  \(
  \epsilon^2=1+\frac{b^2}{a^2}=\frac{a^2+b^2}{a^2} \dots(i)
  \)
  and for conjugate hyperbola \(a^2=b^2\left(e_2^2-1\right)\)
  \(
  \theta_2^2=1+\frac{a^2}{b^2}=\frac{a^2+b^2}{b^2} \dots(ii)
  \)
  From Eqs. (i) and (ii), we get
  \(
  \frac{1}{e_1^2}+\frac{1}{e_2^2}=1 \text { or } e^{-2}+e_2^{-2}=1
  \)
• The foci of a hyperbola and its conjugate are concyclic and form the vertices of a square.
• A simple method to find the coordinates of the centre of the hyperbola expressed as a general equation of degree two should be remembered as :
  Let \(\phi(x, y)=0\) represents a hyperbola.
  Find \(\frac{\partial \phi}{\partial x}\) (differentiate w.r.t \(x\) keeping \(y\) as constant) and \(\frac{\partial \phi}{\partial y}\)
  (differentiate w.r.t. \(y\) keeping \(x\) as constant).
  Then the point of intersection of \(\frac{\partial \phi}{\partial x}=0\) and \(\frac{\partial \phi}{\partial y}=0\) gives the centre of the hyperbola.

Example 7: Find the equation of the hyperbola whose directrix is \(2 x+y=1\), focus \((1,2)\) and eccentricity \(\sqrt{3}\).

Answer: Let \(P(x, y)\) be any point on the hyperbola. Draw \(P M\) perpendicular from \(P\) on the directrix.
Then, by definition \(\quad S P=e P M\)
\(
\Rightarrow \quad(S P)^2=e^2(P M)^2
\)

\(
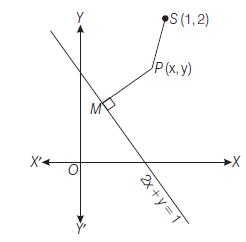
\begin{aligned}
& \Rightarrow(x-1)^2+(y-2)^2=3\left\{\frac{2 x+y-1}{\sqrt{4+1}}\right\}^2 \\
& \Rightarrow 5\left\{x^2+y^2-2 x-4 y+5\right\}
\end{aligned}
\)
\(
=3\left(4 x^2+y^2+1+4 x y-2 y-4 x\right)
\)
\(
\Rightarrow 7 x^2-2 y^2+12 x y-2 x+14 y-22=0
\)
which is the required hyperbola.

Example 8: Find the lengths of transverse axis and conjugate axis, eccentricity, the coordinates of foci, vertices, lengths of the latusrectum and equations of the directrices of the following hyperbolas
(i) \(9 x^2-y^2=1\)
(ii) \(16 x^2-9 y^2=-144\)

Answer: (i) The equation \(9 x^2-y^2=1\) can be written as
\(
\frac{x^2}{(1 / 9)}-\frac{y^2}{1}=1 \text {. }
\)
This is of the form \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
\(
\begin{array}{ll}
\therefore & a^2=\frac{1}{9}, b^2=1 \\
\Rightarrow & a=\frac{1}{3}, b=1
\end{array}
\)
Length of transverse axis: The length of transverse, axis
\(=2 a=\frac{2}{3}\)
Length of conjugate axis: The length of conjugate axis \(=2 b=2\)
Eccentricity : \(e=\sqrt{\left(1+\frac{b^2}{a^2}\right)}=\sqrt{1+\frac{1}{(1 / 9)}}=\sqrt{10}\)
Foci : The coordinates of the foci are \(( \pm a e, 0)\) i.e. \(\left( \pm \frac{\sqrt{10}}{3}, 0\right)\).
Vertices: The coordinates of the vertices are \(( \pm a, 0)\) i.e. \(\left( \pm \frac{1}{3}, 0\right)\)
Length of latusrectum : The length of latusrectum
\(
=\frac{2 b^2}{a}=\frac{2(1)^2}{1 / 3}=6
\)
Equation of the directrices: The equations of the directrices are
\(
\begin{aligned}
x & = \pm \frac{a}{e} \\
\text { i.e. } \quad x & = \pm \frac{1 / 3}{\sqrt{10}} \\
\text { or } \quad x & = \pm \frac{1}{3 \sqrt{10}}
\end{aligned}
\)
(ii) The equation \(16 x^2-9 y^2=-144\) can be written as
\(
\frac{x^2}{9}-\frac{y^2}{16}=-1
\)
This is of the form \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1\)
\(
\begin{aligned}
& \therefore \quad a^2=9, b^2=16 \\
& \Rightarrow \quad a=3, b=4
\end{aligned}
\)
Length of transverse axis : The length of transverse axis \(=2 b=8\).
Length of conjugate axis: The length of conjugate axis \(=2 a=6\).
Eccentricity : \(\quad e=\sqrt{\left(1+\frac{a^2}{b^2}\right)}=\sqrt{\left(1+\frac{9}{16}\right)}=\frac{5}{4}\)
Foci : The coordinates of the foci are \((0, \pm b e)\) i.e. \((0, \pm 5)\) Vertices: The coordinates of the vertices are \((0, \pm b)\) i.e. \((0, \pm 4)\).
\(
\begin{aligned}
& \text { Length of latusrectum : The length of latusrectum }=\frac{2 a^2}{b} \\
& \qquad=\frac{2(3)^2}{4}=\frac{9}{2}
\end{aligned}
\)
Equation of directrices: The equation of directrices are
\(
\begin{aligned}
y & = \pm \frac{b}{e} \\
y & = \pm \frac{4}{(5 / 4)} \\
\Rightarrow \quad y & = \pm \frac{16}{5}
\end{aligned}
\)

Example 9: Find the eccentricity of the hyperbola whose latusrectum is half of its transverse axis.

Answer: Let the equation of hyperbola be
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\)
Then, transverse axis \(=2 a\) and latusrectum \(=\frac{2 b^2}{a}\)
According to question \(\frac{2 b^2}{a}=\frac{1}{2}(2 a)\)
\(
\Rightarrow \quad 2 b^2=a^2 \quad\left(\because b^2=a^2\left(e^2-1\right)\right)
\)
\(
\begin{aligned}
\Rightarrow & 2 a^2\left(e^2-1\right) & =a^2 \\
\Rightarrow & 2 e^2-2 & =1 \\
\Rightarrow & e^2 & =\frac{3}{2}
\end{aligned}
\)
\(
\therefore \quad e=\sqrt{\frac{3}{2}}
\)
Hence, the required eccentricity is \(\sqrt{\frac{3}{2}}\).

Example 10: Prove that the point \(\left\{\frac{a}{2}\left(t+\frac{1}{t}\right), \frac{b}{2}\left(t-\frac{1}{t}\right)\right\}\) lies on the hyperbola for all values of \(t(t \neq 0)\).

Answer: Let \(x=\frac{a}{2}\left(t+\frac{1}{t}\right)\)
or \(\frac{2 x}{a}=t+\frac{1}{t}\)
or \(\left(\frac{2 x}{a}\right)^2=t^2+\frac{1}{t^2}+2 \dots(i)\)
\(
\begin{aligned}
& \text { and let } & y & =\frac{b}{2}\left(t-\frac{1}{t}\right) \\
& \text { or } & \frac{2 y}{b} & =t-\frac{1}{t} \\
& \text { or } & \left(\frac{2 y}{b}\right)^2 & =t^2+\frac{1}{t^2}-2 \dots(ii)
\end{aligned}
\)
Subtracting Eqs. (ii) from (i),
\(
\begin{aligned}
& \frac{4 x^2}{a^2}-\frac{4 y^2}{b^2}=4 \\
& \frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\end{aligned}
\)
which is hyperbola.

Example 11: Show that the equation \(7 y^2-9 x^2+54 x-28 y-116=0\) represent a hyperbola. Find the coordinates of the centre, lengths of transverse and conjugate axes, eccentricity, latusrectum, coordinate of foci, vertices and equations of the directrices of the hyperbola.

Answer:

\(
\text { We have, } 7 y^2-9 x^2+54 x-28 y-116=0
\)
\(
\begin{aligned}
7\left(y^2-4 y\right)-9\left(x^2-6 x\right)-116 & =0 \\
7\left(y^2-4 y+4\right)-9\left(x^2-6 x+9\right) & =116+28-81 \\
7(y-2)^2-9(x-3)^2 & =63 \\
\frac{(y-2)^2}{9}-\frac{(x-3)^2}{7} & =1 \\
\frac{Y^2}{9}-\frac{X^2}{7} & =1
\end{aligned}
\)
where \(X=x-3\) and \(Y=y-2\)
This equation represents conjugate hyperbola. Comparing it with
\(
\frac{Y^2}{b^2}-\frac{X^2}{a^2}=1
\)
we get,
\(b^2=9\) and \(a^2=7\)
\(\therefore \quad b=3\) and \(a=\sqrt{7}\)
Centre : \(\quad X=0, Y=0\)
i.e. \(\quad x-3=0, y-2=0\)
\(\therefore\) Centre is \((3,2)\).
Length of transverse axis : Length of transverse axis
\(=2 b=6 \text {. }\)

Length of conjugate axis: Length of conjugate axis
\(=2 a=2 \sqrt{7} \text {. }\)

Eccentricity: The eccentricity \(e\) is given by
\(
e=\sqrt{1+\frac{a^2}{b^2}}=\sqrt{1+\frac{7}{9}}=\frac{4}{3}
\)

Length of latusrectum : The length of latusrectum
\(
=\frac{2 a^2}{b}=\frac{2(7)}{3}=\frac{14}{3}
\)

Foci : The coordinates of foci are \((0, \pm b e)\)
\(
\begin{array}{lc}
\therefore & X=0, Y= \pm b e \\
\Rightarrow & x-3=0, y-2= \pm 3 \times \frac{4}{3} \\
\text { or } & (3,2 \pm 4) \\
\text { i.e. } & (3,-2) \text { and }(3,6)
\end{array}
\)

Vertices: The coordinates of vertices are \((0, \pm b)\)
or \(X=0, Y= \pm b\)
or \(x-3=0, y-2= \pm 3 \text { or }(3,2 \pm 3)\)
or vertices are \((3,-1)\) and \((3,5)\)

Equation of directrices: The equation of directrices are
\(
\begin{aligned}
\qquad & Y = \pm \frac{b}{e} \\
\Rightarrow & y-2 = \pm \frac{3}{4 / 3} \\
\Rightarrow & y =\left(2 \pm \frac{9}{4}\right) \\
\text { i.e. } & y =\frac{17}{4} \text { and } y=-\frac{1}{4}
\end{aligned}
\)

Example 12: Find the equation of the hyperbola whose foci are \((6,4)\) and \((-4,4)\) and eccentricity is 2.

Answer: The centre of the hyperbola is the mid-point of the line joining the two foci. So, the coordinates of the centre are
\(
\left(\frac{6-4}{2}, \frac{4+4}{2}\right) \text { i.e. }(1,4)
\)
Let \(2 a\) and \(2 b\) be the lengths of transverse and conjugate axes and let \(e\) be the eccentricity. Then, equation of hyperbola is
\(
\frac{(x-1)^2}{a^2}-\frac{(y-4)^2}{b^2}=1
\)
\(\because \quad\) Distance between the foci \(=2 a e\)
\(
\sqrt{(6+4)^2+(4-4)^2}=2 a \times 2
\)
\(
\begin{array}{ll}
\Rightarrow & 10=4 a \\
\therefore & a=5 / 2 \\
\therefore & b^2=a^2\left(e^2-1\right)=\frac{25}{4}(4-1)=\frac{75}{4}
\end{array}
\)
Thus, the equation of the hyperbola is
\(
\begin{aligned}
& \frac{(x-1)^2}{\left(\frac{25}{4}\right)}-\frac{(y-4)^2}{\left(\frac{75}{4}\right)}=1 \\
& 12(x-1)^2-4(y-4)^2=75 \\
& 12\left(x^2-2 x+1\right)-4\left(y^2-8 y+16\right)=75 \\
& 12 x^2-4 y^2-24 x+32 y-127=0
\end{aligned}
\)

Example 13: Obtain the equation of a hyperbola with coordinate axes as principal axes given that the distances of one of its vertices from the foci are 9 and 1 units.

Answer: Let equation of hyperbola is
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
If vertices are \(A(a, 0)\) and \(A^{\prime}(-a, 0)\) and foci are \(S(a e, 0)\) and \(S^{\prime}(-a e, 0)\).
\(
\begin{aligned}
& \text { Given } \quad l\left(S^{\prime} A\right)=9 \text { and } l(S A)=1 \\
& \Rightarrow \quad a+a e=9 \text { and } a e-a=1 \\
& \text { or } \quad a(1+e)=9 \text { and } a(e-1)=1 \\
& \therefore \quad \frac{a(1+e)}{a(e-1)}=\frac{9}{1} \\
& \Rightarrow \quad 1+e=9 e-9 \quad \Rightarrow \quad e=\frac{5}{4} \\
& \because \quad a(1+e)=9 \\
& \therefore \quad a\left(1+\frac{5}{4}\right)=9 \quad \Rightarrow a=4 \\
& b^2=a^2\left(e^2-1\right)=16\left(\frac{25}{16}-1\right) \\
& \therefore \quad b^2=9 \\
&
\end{aligned}
\)
From Eq. (i) equation of hyperbola is
\(
\frac{x^2}{16}-\frac{y^2}{9}=1
\)

Example 14: The foci of a hyperbola coincide with the foci of the ellipse \(\frac{x^2}{25}+\frac{y^2}{9}=1\). Find the equation of the hyperbola if its eccentricity is 2.

Answer: The given ellipse is \(\frac{x^2}{25}+\frac{y^2}{9}=1\)
Comparing with \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\therefore \quad a^2=25\) and \(b^2=9\)
then eccentricity \(e=\sqrt{1-\frac{b^2}{a^2}}=\sqrt{1-\frac{9}{25}}=\frac{4}{5}\)
\(\therefore\) Foci of ellipse are \(( \pm a e, 0)\) i.e. \(( \pm 4,0)\)
So, the coordinates of foci of the hyperbola are \(( \pm 4,0)\).
Let \(e^{\prime}\) be the eccentricity of the required hyperbola and its equation be
\(
\frac{x^2}{A^2}-\frac{y^2}{B^2}=1 \dots(i)
\)
the coordinates of foci are \(\left( \pm A e^{\prime}, 0\right)\)
\(
\therefore \quad A e^{\prime}=4 \Rightarrow A \times 2=4 \Rightarrow A=2
\)
\(
\text { Also } \quad B^2=A^2\left(e^{\prime 2}-1\right) \quad\left(\because \text { given } e^{\prime}=2\right)
\)
\(
=4(4-1)=12
\)
Substituting the values of \(A\) and \(B\) in Eq. (i), we get
\(
\frac{x^2}{4}-\frac{y^2}{12}=1 \text { or } 3 x^2-y^2-12=0
\)
which is required hyperbola.

Example 15: If two points \(P\) and \(Q\) on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) whose centre is \(C\), are such that \(C P\) is perpendicular to \(C Q, a<b\), then prove that
\(
\frac{1}{(C P)^2}+\frac{1}{(C Q)^2}=\frac{1}{a^2}-\frac{1}{b^2} .
\)

Answer: Let \(P(x, y)\) be any point on the given hyperbola. Let slope of \(C P\) is \(m\), then equation of \(C P\) is \(y=m x\).
Solving, \(y=m x\) and \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)

\(
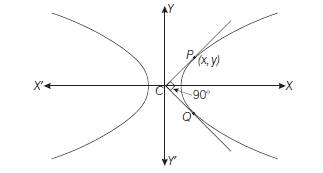
\begin{aligned}
& \frac{x^2}{a^2}-\frac{m^2 x^2}{b^2}=1 \\
& \therefore \quad x^2=\frac{a^2 b^2}{\left(b^2-a^2 m^2\right)} \\
& \text { and } \quad y^2=m^2 x^2=\frac{a^2 m^2 b^2}{b^2-a^2 m^2} \\
& \therefore \quad x^2+y^2=\frac{a^2 b^2}{\left(b^2-a^2 m^2\right)}\left(1+m^2\right) \\
& \therefore \quad(C P)^2=x^2+y^2=\frac{a^2 b^2\left(1+m^2\right)}{\left(b^2-a^2 m^2\right)} \\
& \Rightarrow \quad \frac{1}{(C P)^2}=\frac{b^2-a^2 m^2}{a^2 b^2\left(1+m^2\right)} \dots(i) \\
& \text { and equation of } C Q \text { is } \quad y=-\frac{1}{m} x \\
&
\end{aligned}
\)
replacing \(m\) by \(-\frac{1}{m}\) in Eq. (i)
then \(\frac{1}{(C Q)^2}=\frac{b^2-a^2\left(-\frac{1}{m}\right)^2}{a^2 b^2\left(1+\left(-\frac{1}{m}\right)^2\right)}=\frac{b^2 m^2-a^2}{a^2 b^2\left(1+m^2\right)} \dots(ii)\)
Adding Eqs. (i) and (ii), then
\(
\begin{aligned}
\frac{1}{(C P)^2} & +\frac{1}{(C Q)^2}=\frac{b^2\left(1+m^2\right)-a^2\left(1+m^2\right)}{a^2 b^2\left(1+m^2\right)} \\
& =\frac{b^2-a^2}{a^2 b^2}=\frac{1}{a^2}-\frac{1}{b^2}
\end{aligned}
\)

Position of a Point with Respect to a Hyperbola

Theorem : The point \(\left(x_1, y_1\right)\) lies outside, on or inside the hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\)
\(
\text { according as } \frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}-1<==\text { or }>0
\)

Proof : Let \(P \equiv\left(x_1, y_1\right)\) then \(Q \equiv\left(x_1, y_2\right)\) Draw PL perpendicular to \(X\)-axis

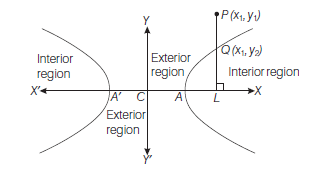
Clearly, \(P L>Q L\)
\(
\begin{array}{ll}
\Rightarrow & y_1>y_2 \\
\Rightarrow & \frac{y_1^2}{b^2}>\frac{y_2^2}{b^2} \\
\Rightarrow & -\frac{y_1^2}{b^2}<-\frac{y_2^2}{b^2} \\
\Rightarrow & \frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}<\frac{x_1^2}{a^2}-\frac{y_2^2}{b^2} \\
\Rightarrow & \frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}<1\left(\because Q\left(x_1, y_2\right) \text { lies on } \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\right) \\
\Rightarrow & \frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}-1<0
\end{array}
\)
Thus, the point \(P\left(x_1, y_1\right)\) lies outside the hyperbola. Hence the point \(\left(x_1, y_1\right)\) lies outside, on or inside the hyperbola
\(
\begin{gathered}
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \\
\text { according as } \frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}-1<,=\text { or }>0 .
\end{gathered}
\)

Example 16: Find the position of the point \((5,-4)\) relative to the hyperbola \(9 x^2-y^2=1\).

Answer: Since, \(9(5)^2-(-4)^2-1=225-16-1=208>0\), So, the point \((5,-4)\) inside the hyperbola \(9 x^2-y^2=1\).

Intersection of a Line and a Hyperbola

Let the hyperbola be \(\quad \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)\)
and the given line be \(\quad y=m x+c \dots(ii)\)
Eliminating \(y\) from Eqs. (i) and (ii),
\(
\begin{aligned}
& \frac{x^2}{a^2}-\frac{(m x+c)^2}{b^2}=1 \Rightarrow b^2 x^2-a^2(m x+c)^2=a^2 b^2 \\
\Rightarrow \quad & \left(a^2 m^2-b^2\right) x^2+2 m c a^2 x+a^2\left(b^2+c^2\right)=0 \dots(iii)
\end{aligned}
\)
Above equation being a quadratic in \(x\) gives two values of \(x\). It shows that every straight line will cut the hyperbola in two points, may be real, coincident or imaginary, according as discriminant of Eq. (iii) \(>,=,<0\)
\(
\begin{gathered}
4 m^2 c^2 a^4-4\left(a^2 m^2-b^2\right) a^2\left(b^2+c^2\right)>,=,<0 \\
-a^2 m^2+b^2+c^2>,=,<0 \\
c^2>,=,<a^2 m^2-b^2 \dots(iv)
\end{gathered}
\)

Condition of Tangency: If the line (ii) touches the hyperbola (i), then Eq. (iii) has equal roots.
\(
\begin{aligned}
& \therefore \text { Discriminant of Eq. (iii) }=0 \\
& \Rightarrow \quad c^2=a^2 m^2-b^2 \\
& \text { or } \quad c= \pm \sqrt{\left(a^2 m^2-b^2\right)} \dots(v)\\
&
\end{aligned}
\)
So, the line \(y=m x+c\) touches the hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text { if } c^2=a^2 m^2-b^2 \text { (which is condition of tangency) }
\)
Substituting the value of \(c\) from Eq. (v) in Eq. (ii)
\(
y=m x \pm \sqrt{\left(a^2 m^2-b^2\right)}
\)
Hence, the line \(y=m x \pm \sqrt{\left(a^2 m^2-b^2\right)}\) will always be tangent to the hyperbola.

Point of contact : Substituting \(c= \pm \sqrt{\left(a^2 m^2-b^2\right)}\) in Eq. (iii)
\(
\left(a^2 m^2-b^2\right) x^2 \pm 2 m a^2 \sqrt{\left(a^2 m^2-b^2\right)} x+a^4 m^2=0
\)
or \(\quad\left(x \sqrt{\left(a^2 m^2-b^2\right)} \pm a^2 m\right)^2=0\)
\(
\therefore \quad x= \pm \frac{a^2 m}{\sqrt{\left(a^2 m^2-b^2\right)}}= \pm \frac{a^2 m}{c}
\)
\(
\begin{aligned}
& \text { From Eq. (i), } \quad \frac{a^4 m^2}{c^2} \cdot \frac{1}{a^2}-\frac{y^2}{b^2}=1 \\
& \Rightarrow \quad \frac{y^2}{b^2}=\frac{a^2 m^2}{c^2}-1=-\frac{\left(c^2-a^2 m^2\right)}{c^2}=\frac{b^2}{c^2} \\
& \therefore \quad y= \pm \frac{b^2}{c} \\
&
\end{aligned}
\)
Hence, the point of contact is \(\left( \pm \frac{a^2 m}{c}, \pm \frac{b^2}{c}\right)\). This is known as \(m\)-point on the hyperbola.

Remark

• If \(m=0\), then Eq. (iii) gives \(-b^2 x^2+a^2\left(b^2+c^2\right)=0\)
  \(
  \begin{aligned}
  x^2 & =\frac{a^2\left(b^2+c^2\right)}{b^2} \\
  \therefore \quad x & = \pm \frac{a}{b} \sqrt{\left(b^2+c^2\right)}
  \end{aligned}
  \)
  which gives two values of \(x\).

Example 17: Prove that the straight linel \(x+m y+n=0\) touches the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) if
\(
a^2 l^2-b^2 m^2=n^2 \text {. }
\)

Answer: The given line is \(l x+m y+n=0\) or \(y=-\frac{l}{m} x-\frac{n}{m}\)
Comparing this line with
\(
\begin{aligned}
y & =M x+c \dots(i) \\
\therefore \quad M & =-\frac{l}{m} \quad \text { and } \quad c=-\frac{n}{m}
\end{aligned}
\)
This line (i) will touch the hyperbola
\(
\begin{aligned}
& \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text { if } c^2=a^2 M^2-b^2 \\
\Rightarrow \quad & \frac{n^2}{m^2}=\frac{a^2 l^2}{m^2}-b^2 \text { or } a^2 l^2-b^2 m^2=n^2
\end{aligned}
\)

Example 18: Show that the line \(x \cos \alpha+y \sin \alpha=p\) touches the hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text { if } a^2 \cos ^2 \alpha-b^2 \sin ^2 \alpha=p^2 \text {. }
\)

Answer: The given line is
\(
x \cos \alpha+y \sin \alpha=p
\)
\(
\begin{aligned}
\Rightarrow & & y \sin \alpha & =-x \cos \alpha+p \\
\Rightarrow & & y & =-x \cot x+p \operatorname{cosec} \alpha
\end{aligned}
\)
Comparing this line with \(y=m x+c\)
\(
\Rightarrow \quad m=-\cot \alpha, c=p \operatorname{cosec} \alpha
\)
Since, the given line touches the hyperbola
\(
\begin{aligned}
& \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text {, then } c^2=a^2 m^2-b^2 \\
& \Rightarrow \quad p^2 \operatorname{cosec}^2 \alpha=a^2 \cot ^2 \alpha-b^2 \\
& \text { or } \quad p^2=a^2 \cos ^2 \alpha-b^2 \sin ^2 \alpha \\
&
\end{aligned}
\)

Example 19: For what value of \(\lambda\) does the line \(y=2 x+\lambda\) touches the hyperbola \(16 x^2-9 y^2=144\) ?

Answer: Equation of hyperbola is
\(
\begin{aligned}
16 x^2-9 y^2 & =144 \\
\text { or } \quad \frac{x^2}{9}-\frac{y^2}{16} & =1
\end{aligned}
\)
Comparing this with \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), we get \(a^2=9, b^2=16\) and comparing this line \(y=2 x+\lambda\) with \(y=m x+c\) \(\therefore \quad m=2\) and \(c=\lambda\)
If the line \(y=2 x+\lambda\) touches the hyperbola
\(
16 x^2-9 y^2=144
\)
\(
\text { then } \quad c^2=a^2 m^2-b^2
\)
\(
\begin{aligned}
& \Rightarrow \quad \lambda^2=9(2)^2-16=36-16=20 \\
& \therefore \quad \lambda= \pm 2 \sqrt{5} \\
&
\end{aligned}
\)

Example 20: If it possible to draw the tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) having slope 2 , then find its range of eccentricity.

Answer: Tangent having slope \(m\) is \(y=m x \pm \sqrt{\left(a^2 m^2-b^2\right)}\)
The tangent having slope 2 is \(y=2 x \pm \sqrt{\left(4 a^2-b^2\right)}\), which is real if
\(
\begin{aligned}
& 4 a^2-b^2 \geq 0 \\
& \frac{b^2}{a^2} \leq 4 \text { or } e^2-1 \leq 4 \text { or } e^2 \leq 5
\end{aligned}
\)
\(
1<e \leq \sqrt{5} \text { (for hyperbola } e>1 \text { ) }
\)

Equations of Tangents in Different Forms

Case-I: Point form (first principal method) :

Theorem : The equation of the tangent to the hyperbola
\(
\begin{aligned}
\frac{x^2}{a^2}-\frac{y^2}{b^2} & =1 \text { at }\left(x_1, y_1\right) \text { is } \\
\frac{x x_1}{a^2}-\frac{y y_1}{b^2} & =1 .
\end{aligned}
\)

Proof : Equation of hyperbola is
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
Let \(P \equiv\left(x_1, y_1\right)\) and \(Q \equiv\left(x_2, y_2\right)\) be any two points in Eq. (i), then
\(
\begin{aligned}
\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}=1 \dots(ii) \\
\text { and } \quad \frac{x_2^2}{a^2}-\frac{y_2^2}{b^2}=1 \dots(iii)
\end{aligned}
\)

Subtracting Eq. (ii) from Eq. (iii), then
\(
\begin{gathered}
\frac{1}{a^2}\left(x_2^2-x_1^2\right)-\frac{1}{b^2}\left(y_2^2-y_1^2\right)=0 \\
\Rightarrow \quad \frac{\left(x_2-x_1\right)\left(x_2+x_1\right)}{a^2}-\frac{\left(y_2-y_1\right)\left(y_2+y_1\right)}{b^2}=0
\end{gathered}
\)
\(
\Rightarrow \quad \frac{y_2-y_1}{x_2-x_1}=\frac{b^2}{a^2} \frac{\left(x_1+x_2\right)}{\left(y_1+y_2\right)} \dots(iv)
\)
Equation of \(P Q\) is
\(
y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right) \dots(v)
\)
From Eqs. (iv) and (v),
\(
y-y_1=\frac{b^2}{a^2} \cdot \frac{\left(x_1+x_2\right)}{\left(y_1+y_2\right)}\left(x-x_1\right) \dots(vi)
\)
Now, tangent at \(P, Q \rightarrow P\)
i.e. \(x_2 \rightarrow x_1\) and \(y_2 \rightarrow y_1\), then Eq. (vi) becomes
\(
y-y_1=\frac{b^2}{a^2} \cdot \frac{\left(2 x_1\right)}{\left(2 y_1\right)}\left(x-x_1\right)
\)
\(
\text { or } \quad \frac{y y_1-y_1^2}{b^2}=\frac{x x_1-x_1^2}{a^2} \text { or } \frac{x x_1}{a^2}-\frac{y y_1}{b^2}=\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}
\)
or \(\quad \frac{x x_1}{a^2}-\frac{y y_1}{b^2}=1 \text { [from Eq. (ii)] }\)
which is the required equation of tangent at \(\left(x_1, y_1\right)\).

Remark

The equation of tangent at \(\left(x_1, y_1\right)\) can be obtained by replacing \(x^2\) by \(x x_1, y^2\) by \(y y_1, x\) by \(\frac{x+x_1}{2}\), by \(\frac{y+y_1}{2}\) and \(x y\) by \(\frac{x y_1+x_1 y}{2}\). This method is applied only when the equation of conic is a polynomial of second degree in \(x\) and \(y\).

Case-II: Parametric form :

Theorem : The equation of tangent to the hyperbola
\(
\begin{aligned}
& \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text { at }(a \sec \phi, b \tan \phi) \text { is } \\
& \frac{x}{a} \sec \phi-\frac{y}{b} \tan \phi=1
\end{aligned}
\)

Proof : Since, equation of tangent at \(\left(x_1, y_1\right)\) is
\(
\frac{x x_1}{a^2}-\frac{y y_1}{b^2}=1
\)
Now, replacing \(x_1\) by \(a \sec \phi\) and \(y_1\) by \(b \tan \phi\), we get
\(
\frac{x}{a} \sec \phi-\frac{y}{b} \tan \phi=1
\)

Remark

• The point of intersection of tangents at ‘ \(\theta\) ‘ and ‘ \(\phi\) ‘ on the hyperbola
  \(
  \begin{aligned}
  & \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text { is } \\
  & \left(\frac{a \cos \left(\frac{\theta-\phi}{2}\right)}{\cos \left(\frac{\theta+\phi}{2}\right)}, \frac{b \sin \left(\frac{\theta+\phi}{2}\right)}{\cos \left(\frac{\theta+\phi}{2}\right)}\right) \\
  &
  \end{aligned}
  \)

Case III:  Slope form:

Theorem : The equations of tangents of slope \(m\) to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is given by
\(
y=m x \pm \sqrt{\left(a^2 m^2-b^2\right)}
\)
The coordinates of the points of contact are
\(
\left( \pm \frac{a^2 m}{\sqrt{\left(a^2 m^2-b^2\right.}}, \pm \frac{b^2}{\sqrt{\left(a^2 m^2-b^2\right)}}\right)
\)

Proof : Let \(y=m x+c\) be a tangent to the hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
Substituting the value of \(y=m x+c\) in Eq. (i), then
\(
\frac{x^2}{a^2}-\frac{(m x+c)^2}{b^2}=1
\)
or \(\left(a^2 m^2-b^2\right) x^2+2 m c a^2 x+a^2\left(c^2+b^2\right)=0\)
must have equal roots
\(
\therefore \quad 4 a^4 m^2 c^2-4\left(a^2 m^2-b^2\right) a^2\left(c^2+b^2\right)=0 \left[\because B^2-4 A C=0\right]
\)
\(
\begin{array}{lc}
\Rightarrow & a^2 m^2 c^2-\left(a^2 m^2-b^2\right)\left(b^2+c^2\right)=0 \\
\Rightarrow & a^2 m^2 c^2-a^2 b^2 m^2-a^2 m^2 c^2+b^4+b^2 c^2=0 \\
\Rightarrow & -a^2 b^2 m^2+b^4+b^2 c^2=0 \Rightarrow c^2=a^2 m^2-b^2
\end{array}
\)
\(
\therefore \quad c= \pm \sqrt{\left(a^2 m^2-b^2\right)}
\)
Substituting this value of \(c\) in \(y=m x+c\), we get
\(
y=m x \pm \sqrt{\left(a^2 m^2-b^2\right)} \dots(ii)
\)
as the required equation of tangents of hyperbola in terms of slope.
\(\because\) Tangent at \(\left(x_1, y_1\right)\) to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is
\(
\frac{x x_1}{a^2}-\frac{y y_1}{b^2}=1 \dots(iii)
\)
On comparing Eqs. (ii) and (iii) we get
\(
\frac{x_1 / a^2}{m}=\frac{y_1 / b^2}{1}= \pm \frac{1}{\sqrt{a^2 m^2-b^2}}
\)
Thus, the coordinates of the points of contact are
\(
\left(\frac{ \pm a^2 m}{\sqrt{\left(a^2 m-b^2\right)}}, \pm \frac{b^2}{\sqrt{\left(a^2 m-b^2\right)}}\right)
\)

Remark

• The equations of tangents of slope \(m\) to the hyperbola \(-\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) are given by \(y=m x \pm \sqrt{\left(b^2-a^2 m^2\right)}\) and the coordinates of the points of contact are
  \(
  \left(\mp \frac{a^2 m}{\sqrt{\left(b^2-a^2 m^2\right)}} \mp \frac{b^2}{\sqrt{\left(b^2-a^2 m^2\right)}}\right)
  \)

Example 21: Find the equation of the tangent to the hyperbola \(x^2-4 y^2=36\) which is perpendicular to the line \(x-y+4=0\).

Answer: Let \(m\) be the slope of the tangent. Since, the tangent is perpendicular to the line \(x-y+4=0\)
\(
\begin{aligned}
\therefore & & m \times 1 & =-1 \\
\Rightarrow & & m & =-1
\end{aligned}
\)
Since \(\quad x^2-4 y^2=36\) or \(\frac{x^2}{36}-\frac{y^2}{9}=1\)
Comparing this with \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
\(\therefore \quad a^2=36\) and \(b^2=9\)
So the equation of tangents are
\(
\begin{aligned}
& y=(-1) x \pm \sqrt{36 \times(-1)^2-9} \\
& \Rightarrow \quad y=-x \pm \sqrt{27} \\
& \text { or } & x+y \pm 3 \sqrt{3}=0 \\
&
\end{aligned}
\)

Example 22: Find the equation and the length of the common tangents to hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text { and } \frac{y^2}{a^2}-\frac{x^2}{b^2}=1 \text {. }
\)

Answer: Tangent at ( \(a \sec \phi, b \tan \phi\) ) on the 1st hyperbola is
\(
\frac{x}{a} \sec \phi-\frac{y}{b} \tan \phi=1 \dots(i)
\)
Similarly tangent at any point \((b \tan \theta, a \sec \theta)\) on 2 nd hyperbola is
\(
\frac{y}{a} \sec \theta-\frac{x}{b} \tan \theta=1 \dots(ii)
\)
If Eqs. (i) and (ii) are common tangents then they should be identical. Comparing the coefficients of \(x\) and \(y\)
\(
\Rightarrow \quad \frac{\sec \theta}{a}=-\frac{\tan \phi}{b}
\)
or \(\quad \sec \theta=-\frac{a}{b} \tan \phi \dots(iii)\)
\(
\begin{array}{ll}
\text { or } & \tan \theta=-\frac{b}{a} \sec \phi \dots(iv) \\
\because & \sec ^2 \theta-\tan ^2 \theta=1
\end{array}
\)
\(\Rightarrow \quad \frac{a^2}{b^2} \tan ^2 \phi-\frac{b^2}{a^2} \sec ^2 \phi=1 \quad\) [from Eqs. (iii) and (iv)]
or \(\quad \frac{a^2}{b^2} \tan ^2 \phi-\frac{b^2}{a^2}\left(1+\tan ^2 \phi\right)=1\)
or \(\quad\left(\frac{a^2}{b^2}-\frac{b^2}{a^2}\right) \tan ^2 \phi=1+\frac{b^2}{a^2}\)
\(\therefore \quad \tan ^2 \phi=\frac{b^2}{a^2-b^2}\)
and \(\quad \sec ^2 \phi=1+\tan ^2 \phi=\frac{a^2}{a^2-b^2}\)
Hence, the points of contact are
\(
\left\{ \pm \frac{a^2}{\sqrt{\left(a^2-b^2\right)}}, \pm \frac{b^2}{\sqrt{\left(a^2-b^2\right)}}\right\}
\)
and \(\left\{\mp \frac{b^2}{\sqrt{\left(a^2-b^2\right)}}, \mp \frac{a^2}{\sqrt{\left(a^2-b^2\right)}}\right\}\) [from Eqs. (iii) and (iv)]
Length of common tangent i.e. the distance between the above points is \(\sqrt{2} \frac{\left(a^2+b^2\right)}{\sqrt{\left(a^2-b^2\right)}}\) and equation of common tangent on putting the values of \(\sec \phi\) and \(\tan \phi\) in Eqs. (i) is
\(
\begin{aligned}
& \pm \frac{x}{\sqrt{\left(a^2-b^2\right)}} \mp \frac{y}{\sqrt{\left(a^2-b^2\right)}}=1 \\
\text { or } & x \mp y= \pm \sqrt{\left(a^2-b^2\right)}
\end{aligned}
\)

Example 23: \(18 PQ\) is the chord joining the points \(\phi_1\) and \(\phi_2\) on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\). If \(\phi_1-\phi_2=2 \alpha\), where \(\alpha\) is constant, prove that \(P Q\) touches the hyperbola
\(
\frac{x^2}{a^2} \cos ^2 \alpha-\frac{y^2}{b^2}=1 .
\)

Answer:

\(
\text { Given hyperbola is } \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
Equation of the chord \(P Q\) to the hyperbola (i) is
\(
\begin{aligned}
& \frac{x}{a} \cos \left(\frac{\phi_1-\phi_2}{2}\right)-\frac{y}{b} \sin \left(\frac{\phi_1+\phi_2}{2}\right)=\cos \left(\frac{\phi_1+\phi_2}{2}\right) \\
& \Rightarrow \quad \frac{x}{a} \cos \alpha-\frac{y}{b} \sin \left(\frac{\phi_1+\phi_2}{2}\right)=\cos \left(\frac{\phi_1+\phi_2}{2}\right) \left(\text { Given } \phi_1-\phi_2=2 \alpha\right)
\end{aligned}
\)
\(
\text { i.e. } \quad y=\frac{b}{a} \frac{\cos \alpha}{\sin \left(\frac{\phi_1+\phi_2}{2}\right)} x+\frac{b \cos \left(\frac{\phi_1+\phi_2}{2}\right)}{\sin \left(\frac{\phi_1+\phi_2}{2}\right)} \dots(ii)
\)
Comparing this line with \(y=m x+c\)
\(
\therefore \quad m=\frac{b}{a} \cdot \frac{\cos \alpha}{\sin \left(\frac{\phi_1+\phi_2}{2}\right)} \text { and } c=\frac{b \cos \left(\frac{\phi_1+\phi_2}{2}\right)}{\sin \left(\frac{\phi_1+\phi_2}{2}\right)}
\)
For line \(y=m x+c\) to be a tangent on \(\frac{x^2}{a^2} \cos ^2 \alpha-\frac{y^2}{b^2}=1\), we have
\(
\begin{gathered}
c^2=\frac{a^2}{\cos ^2 \alpha} m^2-b^2 \\
\therefore \quad \text { LHS }=c^2=\frac{b^2 \cos ^2\left(\frac{\phi_1+\phi_2}{2}\right)}{\sin ^2\left(\frac{\phi_1+\phi_2}{2}\right)}
\end{gathered}
\)
\(
\begin{aligned}
\text { and } \text { RHS } & =\frac{a^2}{\cos ^2 \alpha} m^2-b^2 \\
& =\frac{a^2}{\cos ^2 \alpha} \times \frac{b^2 \cos ^2 \alpha}{a^2 \sin ^2\left(\frac{\phi_1+\phi_2}{2}\right)}-b^2 \\
& =\frac{b^2}{\sin ^2\left(\frac{\phi_1+\phi_2}{2}\right)}-b^2
\end{aligned}
\)
\(
\quad \quad  =\frac{b^2 \cos ^2\left(\frac{\phi_1+\phi_2}{2}\right)}{\sin \left(\frac{\phi_1+\phi_2}{2}\right)}
\)
Hence proved.

Example 24: If the line \(y=m x+\sqrt{\left(a^2 m^2-b^2\right)}\) touches the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) at the point \((a \sec \theta, b \tan \theta)\), show that \(\theta=\sin ^{-1}\left(\frac{b}{a m}\right)\).

Answer: Since \((a \sec \theta, b \tan \theta)\) lies on
\(
\begin{aligned}
y & =m x+\sqrt{\left(a^2 m^2-b^2\right)} \\
\therefore \quad b \tan \theta & =a m \sec \theta+\sqrt{\left(a^2 m^2-b^2\right)}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad(b \tan \theta-a m \sec \theta)^2=a^2 m^2-b^2 \\
& \Rightarrow \quad b^2 \tan ^2 \theta+a^2 m^2 \sec ^2 \theta-2 a b m \tan \theta \sec \theta=a^2 m^2-b^2 \\
& \Rightarrow \quad a^2 m^2 \tan ^2 \theta-2 a b m \tan \theta \theta+b^2 \sec ^2 \theta=0
\end{aligned}
\)
\(
\text { or } \quad a^2 m^2 \sin ^2 \theta-2 a b m \sin \theta+b^2=0 \quad(\because \cos \theta \neq 0)
\)
\(
\therefore \quad \sin \theta=\frac{2 a b m \pm \sqrt{4 a^2 b^2 m^2-4 a^2 b^2 m^2}}{2 a^2 m^2}=\left(\frac{b}{a m}\right)
\)
\(
\therefore \quad \theta=\sin ^{-1}\left(\frac{b}{a m}\right)
\)

Example 25: If \(S Y\) and \(S^{\prime} Y^{\prime}\) be drawn perpendiculars from foci to any tangent to a hyperbola. Prove that \(Y\) and \(Y^{\prime}\) lie on the auxiliary circle and that product of these perpendiculars is constant.

Answer: Let hyperbola be
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
Tangent at \(P(a \sec \phi, b \tan \phi)\) on Eq. (i) is
\(
\frac{x}{a} \sec \phi-\frac{y}{b} \tan \phi=1 \dots(ii)
\)
Its slope is \(\quad \frac{(b \sec \phi)}{(a \tan \phi)}\)
Equation of \(S Y\) which is perpendicular to Eq. (i) and passes through focus \(S\) i.e. \((a e, 0)\) is
\(
\begin{gathered}
y-0=-\frac{a \tan \phi}{b \sec \phi}(x-a e) \\
\text { or } \quad \frac{x}{b} \tan \phi+\frac{y}{a} \sec \phi=\frac{a e}{b} \tan \phi \dots(iii)
\end{gathered}
\)
\(\because\) Lines (ii) and (iii) intersect at \(Y\) and in order to find its locus we have to eliminate \(\phi\) between Eqs. (ii) and (iii), for which squaring and adding Eqs. (ii) and (iii) then, we get
\(
\left(x^2+y^2\right)\left(\frac{\sec ^2 \phi}{a^2}+\frac{\tan ^2 \phi}{b^2}\right)=1+\frac{a^2 e^2}{b^2} \tan ^2 \phi
\)
\(
=1+\frac{a^2+b^2}{b^2} \tan ^2 \phi=\left(1+\tan ^2 \phi\right)+\frac{a^2}{b^2} \tan ^2 \phi
\)
\(
=\left(\sec ^2 \phi+\frac{a^2}{b^2} \tan ^2 \phi\right)=a^2\left(\frac{\sec ^2 \phi}{a^2}+\frac{\tan ^2 \phi}{b^2}\right)
\)
\(\therefore x^2+y^2=a^2\) is the required locus.
Similarly the point \(Y^{\prime}\) also lies on it. Again, if \(p_1\) and \(p_2\) be the length of perpendiculars from \(S(a e, 0)\) and \(S^{\prime}(-a e, 0)\) on the tangent (ii), then
\(
\begin{aligned}
p_1 p_2 & =\frac{(e \sec \phi-1) \cdot(e \sec \phi+1)}{\sqrt{\left(\frac{\sec ^2 \phi}{a^2}+\frac{\tan ^2 \phi}{b^2}\right)} \sqrt{\left(\frac{\sec ^2 \phi}{a^2}+\frac{\tan ^2 \phi}{b^2}\right)}} \\
& =\frac{a^2 b^2\left(e^2 \sec ^2 \phi-1\right)}{b^2 \sec ^2 \phi+a^2 \tan ^2 \phi} \\
& =\frac{a^2 b^2\left(e^2 \sec ^2 \phi-1\right)}{a^2\left(e^2-1\right) \sec ^2 \phi+a^2 \tan ^2 \phi}
\end{aligned}
\)
\(
=\frac{b^2\left(e^2 \sec ^2 \phi-1\right)}{\left(e^2 \sec ^2 \phi-1\right)}=b^2 \quad\left[\left(\because b^2=a^2\left(e^2-1\right)\right]\right.
\)

Equations of Normals in Different Forms

Case I: Point form :

Theorem : The equation of the normal to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) at \(\left(x_1, y_1\right)\) is \(\frac{a^2 x}{x_1}+\frac{b^2 y}{y_1}=a^2+b^2\)
Proof: Since the equation of tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) at \(\left(x_1, y_1\right)\) is \(\frac{x x_1}{a^2}-\frac{y y_1}{b^2}=1\)
The slope of tangent at \(\left(x_1, y_1\right)=\frac{b^2 x_1}{a^2 y_1}\)
\(\therefore \quad\) Slope of normal at \(\left(x_1, y_1\right)=-\frac{a^2 y_1}{b^2 x_1}\)

Hence, the equation of normal at \(\left(x_1, y_1\right)\)
\(
\begin{aligned}
y-y_1 & =-\frac{a^2 y_1}{b^2 x_1}\left(x-x_1\right) \\
\text { or } \quad \frac{a^2 x}{x_1}+\frac{b^2 y}{y_1} & =a^2+b^2
\end{aligned}
\)

Case II: Parametric form :

Theorem : The equation of normal at ( \(a \sec \phi, b \tan \phi\) ) to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is \(a x \cos \phi+b y \cot \phi=a^2+b^2\)

Proof: Since the equation of normals of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) at \(\left(x_1, y_1\right)\) is
\(
\frac{a^2 x}{x_1}+\frac{b^2 y}{y_1}=a^2+b^2 \dots(i)
\)
Replacing \(x_1\) by \(a \sec \phi\) and \(y_1\) by \(b \tan \phi\), then Eq. (i) becomes
\(
\frac{a^2 x}{a \sec \phi}+\frac{b^2 y}{b \tan \phi}=a^2+b^2
\)
\(
\text { or } \quad a x \cos \phi+b y \cot \phi=a^2+b^2
\)
is equation of normal at ( \(a \sec \phi, b \tan \phi\) ).

Case III: Slope form:

Theorem : The equations of normals of slope \(m\) to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) are given by
\(
\begin{gathered}
y=m x \mp \frac{m\left(a^2+b^2\right)}{\sqrt{\left(a^2-m^2 b^2\right)}} \\
\text { at the points }\left( \pm \frac{a^2}{\sqrt{\left(a^2-m^2 b^2\right)}}, \mp \frac{m b^2}{\sqrt{\left(a^2-m^2 b^2\right)}}\right)
\end{gathered}
\)

Proof: The equation of normal to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) at \(\left(x_1, y_1\right)\) is
\(
\frac{a^2 x}{x_1}+\frac{b^2 y}{y_1}=a^2+b^2 \dots(i)
\)
Since ‘ \(m\) ‘ is the slope of the normal, then
\(
\begin{gathered}
m=-\frac{a^2 y_1}{b^2 x_1} \\
y_1=-\frac{b^2 x_1 m}{a^2} \dots(ii)
\end{gathered}
\)
\(
\begin{array}{lr}
\text { Since }\left(x_1, y_1\right) \text { lies on } \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \\
\therefore \frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}=1 \\
\text { or } \frac{x_1^2}{a^2}-\frac{b^4 x_1^2 m^2}{a^4 b^2}=1 \\
\text { or } x_1^2=\frac{a^4}{a^2-b^2 m^2}
\end{array}
\)
\(
\therefore \quad x_1= \pm \frac{a^2}{\sqrt{\left(a^2-b^2 m^2\right)}}
\)
From Eq. (ii), \(\quad y_1=\mp \frac{m b^2}{\sqrt{\left(a^2-b^2 m^2\right)}}\)
\(\therefore\) Equation of normal in terms of slope is
\(
y-\left(\mp \frac{m b^2}{\sqrt{\left(a^2-m^2 b^2\right)}}\right)=m\left(x-\left( \pm \frac{a^2}{\sqrt{\left(a^2-m^2 b^2\right)}}\right)\right)
\)
\(
\Rightarrow \quad y=m x \mp \frac{m\left(a^2+b^2\right)}{\sqrt{\left(a^2-m^2 b^2\right)}} \dots(iii)
\)
Thus Eq. (iii) is a normal to the hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\)
where \(m\) is the slope of the normal.
The coordinates of the point of contact are
\(
\left( \pm \frac{a^2}{\sqrt{\left(a^2-b^2 m^2\right)}}, \mp \frac{m b^2}{\sqrt{\left(a^2-b^2 m^2\right)}}\right)
\)
Comparing Eq. (iii) with \(y=m x+c\)
\(\therefore \quad c=\mp \frac{m\left(a^2+b^2\right)}{\sqrt{\left(a^2-m^2 b^2\right)}}\)
\(
c^2=\frac{m^2\left(a^2+b^2\right)^2}{\left(a^2-m^2 b^2\right)}
\)
which is condition of normality, where \(y=m x+c\) is the normal of
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\)

Remark

• Normal other than transverse axis, never passes through the focus.

Example 26: A normal to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) meets the axes in \(M\) and \(N\) and lines MP and NP are drawn perpendiculars to the axes meeting at \(P\). Prove that the locus of \(P\) is the hyperbola
\(
a^2 x^2-b^2 y^2=\left(a^2+b^2\right)^2 .
\)

Answer: The equation of normal at the point \((a \sec \phi, b \tan \phi\) ) to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is
\(
a x \cos \phi+b y \cot \phi=a^2+b^2 \dots(i)
\)
The normal (i) meets the \(X\)-axis in \(M\left(\frac{a^2+b^2}{a} \sec \phi, 0\right)\) and \(Y[latex]-axis in [latex]N\left(0, \frac{a^2+b^2}{b} \tan \phi\right)\)

\(\therefore\) Equation of \(M P\), the line through \(M\) and perpendicular to \(X\) axis, is
\(
x=\left(\frac{a^2+b^2}{a}\right) \sec \phi
\)
\(
\text { or } \quad \sec \phi=\frac{a x}{\left(a^2+b^2\right)} \dots(ii)
\)
and the equation of \(N P\), the line through \(N\) and perpendicular to the \(Y\)-axis, is
\(
\begin{aligned}
y & =\left(\frac{a^2+b^2}{b}\right) \tan \phi \\
\text { or } \quad \tan \phi & =\frac{b y}{\left(a^2+b^2\right)} \dots(iii)
\end{aligned}
\)
The locus of the point of intersection of \(M P\) and \(N P\) will be obtained by elminating \(\phi\) from Eqs. (ii) and (iii), we have
\(
\begin{aligned}
& \sec ^2 \phi-\tan ^2 \phi=1 \\
& \Rightarrow \quad \frac{a^2 x^2}{\left(a^2+b^2\right)^2}-\frac{b^2 y^2}{\left(a^2+b^2\right)^2}=1 \\
& \text { or }  a^2 x^2-b^2 y^2=\left(a^2+b^2\right)^2 \\
&
\end{aligned}
\)
is the required locus of \(P\).

Example 27: Prove that the line \(l x+m y-n=0\) will be a normal to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) if
\(
\frac{a^2}{l^2}-\frac{b^2}{m^2}=\frac{\left(a^2+b^2\right)^2}{n^2} .
\)

Answer: The equation of any normal to \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is
\(
\begin{gathered}
a x \cos \phi+b y \cot \phi=a^2+b^2 \\
\text { or } \quad a x \cos \phi+b y \cot \phi-\left(a^2+b^2\right)=0 \dots(i)
\end{gathered}
\)
The straight line \(l x+m y-n=0\) will be a normal to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), then Eq. (i) and \(I x+m y-n=0\) represent the same line
\(
\begin{aligned}
& \frac{a \cos \phi}{l}=\frac{b \cot \phi}{m}=\frac{\left(a^2+b^2\right)}{n} \\
& \text { or } \sec \phi=\frac{n a}{l\left(a^2+b^2\right)} \text { and } \tan \phi=\frac{n b}{m\left(a^2+b^2\right)} \\
& \because \quad \sec ^2 \phi-\tan ^2 \phi=1 \\
& \therefore \quad \frac{n^2 a^2}{l^2\left(a^2+b^2\right)^2}-\frac{n^2 b^2}{m^2\left(a^2+b^2\right)^2}=1 \\
& \Rightarrow \quad \frac{a^2}{l^2}-\frac{b^2}{m^2}=\frac{\left(a^2+b^2\right)^2}{n^2} \\
&
\end{aligned}
\)

Example 28: If the normal at ‘ \(\phi\) ‘ on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) meet transverse axis at \(G\), prove that
\(
A G \cdot A^{\prime} G=a^2\left(e^4 \sec ^2 \phi-1\right) \text {. }
\)
where \(A\) and \(A^{\prime}\) are the vertices of the hyperbola.

Answer: The equation of normal at ( \(a \sec \phi, b \tan \phi\) ) to the given hyperbola is \(a x \cos \phi+b y \cot \phi=\left(a^2+b^2\right)\)
This meets the transverse axis i.e. \(X\)-axis at \(G\). So, the coordinates of \(G\) are \(\left(\left(\frac{a^2+b^2}{a}\right) \sec \phi, 0\right)\) and the
coordinates of the vertices \(A\) and \(A^{\prime}\) are \(A(a, 0)\) and \(A^{\prime}(-a, 0)\) respectively.
\(
\begin{aligned}
\therefore A G \cdot A^{\prime} G & =\left(-a+\left(\frac{a^2+b^2}{a}\right) \sec \phi\right)\left(a+\left(\frac{a^2+b^2}{a}\right) \sec \phi\right) \\
& =\left(\frac{a^2+b^2}{a}\right)^2 \sec ^2 \phi-a^2 \\
& =\left(a e^2\right)^2 \sec ^2 \phi-a^2=a^2\left(e^4 \sec ^2 \phi-1\right)
\end{aligned}
\)

Example 29: Find the locus of the foot of perpendicular from the centre upon any normal to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).

Answer: Normal at \(P(a \sec \phi, b \tan \phi)\) is
\(
a x \cos \phi+b y \cot \phi=a^2+b^2 \dots(i)
\)
and equation of line perpendicular to Eq. (i) and passing through origin is
\(
b x-a y \sin \phi=0 \dots(ii)
\)

Eliminating \(\phi\) from Eqs. (i) and (ii), we will get the equation of locus of \(Q\), as from Eq. (ii),

\(
\begin{aligned}
\sin \phi & =\frac{b x}{a y} \\
\therefore \quad \cos \phi & =\frac{\sqrt{\left(a^2 y^2-b^2 x^2\right)}}{a y} \\
\text { and } \quad \cot \phi & =\frac{\sqrt{\left(a^2 y^2-b^2 x^2\right)}}{b x}
\end{aligned}
\)
From Eq. (i),
\(
\begin{aligned}
& a x \times \frac{\sqrt{a^2 y^2-b^2 x^2}}{a y}+b y \times \frac{\sqrt{\left(a^2 y^2-b^2 x^2\right)}}{b x}=a^2+b^2 \\
& \Rightarrow \quad\left(x^2+y^2\right) \sqrt{\left(a^2 y^2-b^2 x^2\right)}=\left(a^2+b^2\right) x y \\
& \text { or } \quad\left(x^2+y^2\right)^2\left(a^2 y^2-b^2 x^2\right)=\left(a^2+b^2\right)^2 x^2 y^2
\end{aligned}
\)
which is required locus.

Pair of Tangents

Theorem : The combined equation of the pair of tangents drawn from a point \(P\left(x_1, y_1\right)\), lying outside the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is
\(
\left(\frac{x^2}{a^2}-\frac{y^2}{b^2}-1\right)\left(\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}-1\right)=\left(\frac{x x_1}{a^2}-\frac{y y_1}{b^2}-1\right)^2
\)
\(
S S_1=T^2
\)
where
\(
\begin{aligned}
S & =\frac{x^2}{a^2}-\frac{y^2}{b^2}-1 ; \\
S_1 & =\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}-1 \text { and } T=\frac{x x_1}{a^2}-\frac{y y_1}{b^2}-1
\end{aligned}
\)

Proof : Let \(T(h, k)\) be any point on the pair of tangents \(P Q\) or \(P R\) drawn from any external point \(P\left(x_1, y_1\right)\) to the hyperbola

\(
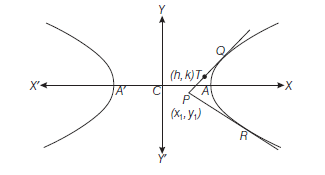
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\)
\(\therefore\) Equation of PT is \(y-y_1=\frac{k-y_1}{h-x_1}\left(x-x_1\right)\)
\(
\text { or } y=\left(\frac{k-y_1}{h-x_1}\right) x+\left(\frac{h y_1-k x_1}{h-x_1}\right)
\)
which is the tangent to the hyperbola
\(
\begin{aligned}
\frac{x^2}{a^2}-\frac{y^2}{b^2} & =1 \\
\therefore \quad c^2 & =a^2 m^2-b^2
\end{aligned}
\)
\(
\begin{aligned}
& \text { or } \quad\left(\frac{h y_1-k x_1}{h-x_1}\right)^2=a^2\left(\frac{k-y_1}{h-x_1}\right)^2-b^2 \\
& \Rightarrow \quad\left(h y_1-k x_1\right)^2=a^2\left(k-y_1\right)^2-b^2\left(h-x_1\right)^2
\end{aligned}
\)
Hence, locus of \((h, k)\) is
\(
\left(x y_1-x_1 y\right)^2=a^2\left(y-y_1\right)^2-b^2\left(x-x_1\right)^2
\)
\(
\left(x y_1-x_1 y\right)^2=-\left(b^2 x^2-a^2 y^2\right)-\left(b^2 x_1^2-a^2 y_1^2\right)-2\left(a^2 y y_1-b^2 x x_1\right)
\)
\(
\text { or } \quad\left(\frac{x y_1-x_1 y}{a b}\right)^2=-\left(\frac{x^2}{a^2}-\frac{y^2}{b^2}\right)-\left(\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}\right)+2\left(\frac{x x_1}{a^2}-\frac{y y_1}{b^2}\right)
\)
\(
\text { or } \quad-\left(\frac{x y_1-x_1 y}{a b}\right)^2-\left(\frac{x^2}{a^2}-\frac{y^2}{b^2}\right)-\left(\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}\right)+1+\left(\frac{x x_1}{a^2}-\frac{y y_1}{b^2}\right)^2
\)
\(
\begin{aligned}
& =\left(\frac{x x_1}{a^2}-\frac{y y_1}{b^2}\right)^2-2\left(\frac{x x_1}{a^2}-\frac{y y_1}{b^2}\right)+1 \\
& \left(\frac{x^2}{a^2}-\frac{y^2}{b^2}-1\right)\left(\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}-1\right)=\left(\frac{x x_1}{a^2}-\frac{y y_1}{b^2}-1\right)^2
\end{aligned}
\)
or \(\quad S S_1=T^2\)

Remark

• \(S=0\) is the equation of the curve, \(S_1\) is obtained from \(S\) by replacing \(x\) by \(x_1\) and \(y\) by \(y_1\) and \(T=0\) is the equation of the tangent at \(\left(x_1, y_1\right)\) to \(S=0\).

Chord of Contact

Theorem : If the tangents from a point \(P\left(x_1, y_1\right)\) to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) touch the hyperbola at \(Q\) and \(R\), then the equation of the chord of contact \(Q R\) is
\(
\frac{x x_1}{a^2}-\frac{y y_1}{b^2}=1
\)

Proof : Let \(Q \equiv\left(x^{\prime}, y^{\prime}\right)\) and \(R \equiv\left(x^{\prime \prime}, y^{\prime \prime}\right)\)

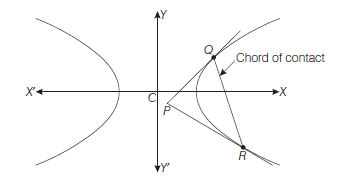
Now, equation of tangents \(P Q\) and \(P R\) are
\(
\frac{x x^{\prime}}{a^2}-\frac{y y^{\prime}}{b^2}=1 \dots(i)
\)
\(
\text { and } \frac{x x^{\prime \prime}}{a^2}-\frac{y y^{\prime \prime}}{b^2}=1 \dots(ii)
\)
Since, Eqs. (i) and (ii) pass through \(P\left(x_1, y_1\right)\), then
\(
\frac{x^{\prime} x_1}{a^2}-\frac{y^{\prime} y_1}{b^2}=1 \dots(iii)
\)
\(
\text { and } \quad \frac{x^{\prime \prime} x_1}{a^2}-\frac{y^{\prime \prime} y_1}{b^2}=1 \dots(iv)
\)
Hence, it is clear that \(Q\left(x^{\prime}, y^{\prime}\right)\) and \(R\left(x^{\prime \prime}, y^{\prime \prime}\right)\) lie on
\(
\frac{x x_1}{a^2}-\frac{y y_1}{b^2}=1 \text { or } T=0
\)
which is chord of contact \(Q R\).

Equation of the Chord Bisected at a Given Point

Theorem : The equation of the chord of the hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1,
\)
bisected at the point \(\left(x_1, y_1\right)\) is
\(
\frac{x x_1}{a^2}-\frac{y y_1}{b^2}-1=\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}-1
\)
or \(\quad T=S_1\), where \(T=\frac{x x_1}{a^2}-\frac{y y_1}{b^2}-1\)
and \(\quad S_1=\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}-1\).

Proof : Since equation of the hyperbola is
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
Let \(Q R\) be the chord of the hyperbola whose mid-point is \(P\left(x_1, y_1\right)\). Since \(Q\) and \(R\) lie on the hyperbola (i).

\(
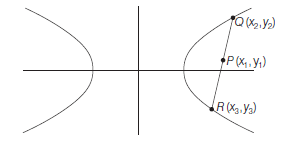
\therefore \quad \frac{x_2^2}{a^2}-\frac{y_2^2}{b^2}=1 \dots(ii)
\)
\(
\text { and } \frac{x_3^2}{a^2}-\frac{y_3^2}{b^2}=1 \dots(iii)
\)
Subtracting Eq. (iii) from Eq. (ii),
\(
\begin{gathered}
\frac{1}{a^2}\left(x_2^2-x_3^2\right)-\frac{1}{b^2}\left(y_2^2-y_3^2\right)=0 \\
\Rightarrow \quad \frac{\left(x_2+x_3\right)\left(x_2-x_3\right)}{a^2}-\frac{\left(y_2+y_3\right)\left(y_2-y_3\right)}{b^2}=0 \\
\Rightarrow \quad \frac{y_2-y_3}{x_2-x_3}=\frac{b^2\left(x_2+x_3\right)}{a^2\left(y_2+y_3\right)}
\end{gathered}
\)
\(
=\frac{b^2}{a^2} \frac{\left(2 x_1\right)}{\left(2 y_1\right)} \quad[P \text { is the mid-point of } Q R]
\)
\(
=\frac{b^2 x_1}{a^2 y_1} \dots(iv)
\)
\(\therefore\) Equation of \(Q R\) is
\(
y-y_1=\frac{y_2-y_3}{x_2-x_3}\left(x-x_1\right)
\)
\(
\Rightarrow \quad y-y_1=\frac{b^2 x_1}{a^2 y_1}\left(x-x_1\right) \quad \text { [from Eq. (iv)] }
\)
\(
\begin{aligned}
\frac{y y_1}{b^2}-\frac{y_1^2}{b^2} & =\frac{x x_1}{a^2}-\frac{x_1^2}{a^2} \\
\frac{x x_1}{a^2}-\frac{y y_1}{b^2} & =\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2} \\
\frac{x x_1}{a^2}-\frac{y y_1}{b^2}-1 & =\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}-1 \\
T & =S_1
\end{aligned}
\)

Example 30: Find the locus of the mid-points of the chords of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) which subtend a right angle at the origin.

Answer: Let \((h, k)\) be the mid-point of the chord of the hyperbola. Then its equation is
\(
\begin{gathered}
\frac{h x}{a^2}-\frac{k y}{b^2}-1=\frac{h^2}{a^2}-\frac{k^2}{b^2}-1 \\
\frac{h x}{a^2}-\frac{k y}{b^2}=\frac{h^2}{a^2}-\frac{k^2}{b^2} \dots(i)
\end{gathered}
\)
The equation of the lines joining the origin to the points of intersection of the hyperbola and the chord (i) is obtained by making homogeneous hyperbola with the help of Eq. (i)
\(
\begin{gathered}
\therefore \quad \frac{x^2}{a^2}-\frac{y^2}{b^2}=\frac{\left(\frac{h x}{a^2}-\frac{k y}{b^2}\right)^2}{\left(\frac{h^2}{a^2}-\frac{k^2}{b^2}\right)^2} \\
\Rightarrow \quad \frac{1}{a^2}\left(\frac{h^2}{a^2}-\frac{k^2}{b^2}\right)^2 x^2-\frac{1}{b^2}\left(\frac{h^2}{a^2}-\frac{k^2}{b^2}\right)^2 y^2 \\
=\frac{h^2}{a^4} x^2+\frac{k^2}{b^4} y^2-\frac{2 h k}{a^2 b^2} x y \dots(ii)
\end{gathered}
\)
The lines represented by Eq. (ii) will be at right angle if Coefficient of \(x^2+\) Coefficient of \(y^2=0\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{1}{a^2}\left(\frac{h^2}{a^2}-\frac{k^2}{b^2}\right)^2-\frac{h^2}{a^4}-\frac{1}{b^2}\left(\frac{h^2}{a^2}-\frac{k^2}{b^2}\right)^2-\frac{k^2}{b^4}=0 \\
& \Rightarrow \quad\left(\frac{h^2}{a^2}-\frac{k^2}{b^2}\right)^2\left(\frac{1}{a^2}-\frac{1}{b^2}\right)=\frac{h^2}{a^4}+\frac{k^2}{b^4}
\end{aligned}
\)
Hence, the locus of \((h, k)\) is
\(
\left(\frac{x^2}{a^2}-\frac{y^2}{b^2}\right)^2\left(\frac{1}{a^2}-\frac{1}{b^2}\right)=\frac{x^2}{a^4}+\frac{y^2}{b^4}
\)

Example 31: From the points on the circle \(x^2+y^2=a^2\), tangents are drawn to the hyperbola \(x^2-y^2=a^2\); prove that the locus of the middle-points of the chords of contact is the curve \(\left(x^2-y^2\right)^2=a^2\left(x^2+y^2\right)\).

Answer: Since any point on the circle \(x^2+y^2=a^2\) is \((a \cos \theta, a \sin \theta)\) chord of contact of this point w.r.t. hyperbola \(x^2-y^2=a^2\) is
\(
\begin{gathered}
x(a \cos \theta)-y(a \sin \theta)=a^2 \\
x \cos \theta-y \sin \theta=a \dots(i)
\end{gathered}
\)
If its mid-point be \((h, k)\), then it is same as
\(
\begin{array}{rlrl}
T & =S_1 \\
& \text { i.e. } \quad h x-k y-a^2 & =h^2-k^2-a^2 \\
& \text { or } \quad h x-k y =h^2-k^2 \dots(ii)
\end{array}
\)
On comparing Eqs. (i) and (ii), we get
\(
\frac{\cos \theta}{h}=\frac{\sin \theta}{k}=\frac{a}{\left(h^2-k^2\right)}
\)
\(
\begin{array}{ll}
\text { or } & \left(h^2-k^2\right) \cos \theta=a h \dots(iii) \\
\text { and } & \left(h^2-k^2\right) \sin \theta=a k \dots(iv)
\end{array}
\)
Squaring and adding Eqs. (iii) and (iv), we get
\(
\begin{aligned}
\quad\left(h^2-k^2\right)^2 & =a^2 h^2+a^2 k^2 \\
\Rightarrow \quad\left(h^2-k^2\right)^2 & =a^2\left(h^2+k^2\right)
\end{aligned}
\)
Hence, the required locus is
\(
\left(x^2-y^2\right)^2=a^2\left(x^2+y^2\right) \text {. }
\)

Example 32: Prove that the locus of the middle-points of the chords of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) which pass through a fixed point \((\alpha, \beta)\) is a hyperbola whose centre is \(\left(\frac{\alpha}{2}, \frac{\beta}{2}\right)\).

Answer: Let the mid-point of the chord be \((h, k)\). The equation of the chord whose mid-point is \((h, k)\) is
\(
\frac{h x}{a^2}-\frac{k y}{b^2}-1=\frac{h^2}{a^2}-\frac{k^2}{b^2}-1 \text { or } \frac{h x}{a^2}-\frac{k y}{b^2}=\frac{h^2}{a^2}-\frac{k^2}{b^2}
\)
It passes through \((\alpha, \beta)\), then
\(
\frac{\alpha h}{a^2}-\frac{\beta k}{b^2}=\frac{h^2}{a^2}-\frac{k^2}{b^2}
\)
\(\therefore\) locus of \((h, k)\) is
\(
\begin{array}{r}
\frac{x \alpha}{a^2}-\frac{y \beta}{b^2}=\frac{x^2}{a^2}-\frac{y^2}{b^2} \\
\Rightarrow \quad \frac{1}{a^2}\left(x^2-\alpha x\right)-\frac{1}{b^2}\left(y^2-\beta y\right)=0
\end{array}
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{1}{a^2}\left\{\left(x-\frac{\alpha}{2}\right)^2-\frac{\alpha^2}{4}\right\}-\frac{1}{b^2}\left\{\left(y-\frac{\beta}{2}\right)^2-\frac{\beta^2}{4}\right\}=0 \\
& \text { or } \quad \frac{\left(x-\frac{\alpha}{2}\right)^2}{a^2}-\frac{\left(y-\frac{\beta}{2}\right)^2}{b^2}=\frac{1}{4}\left\{\frac{\alpha^2}{a^2}-\frac{\beta^2}{b^2}\right\}=\lambda \text { (say) } \\
& \therefore \quad \frac{\left(x-\frac{\alpha}{2}\right)^2}{a^2 \lambda}-\frac{\left(y-\frac{\beta}{2}\right)^2}{b^2 \lambda}=1
\end{aligned}
\)
The centre of this hyperbola is \(\left(\frac{\alpha}{2}, \frac{\beta}{2}\right)\)

Diameter

The locus of the middle points of a system of parallel chords of a hyperbola is called a diameter and the point where the diameter intersects the hyperbola is called the vertex of the diameter.

Theorem : The equation of a diameter bisecting a system of parallel chords of slope \(m\) of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is
\(
y=\frac{b^2}{a^2 m} x
\)

Proof : Let \(y=m x+c\) be a system of a parallel chords to \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) for different chords. As \(c\) varies, \(m\) remain constant.

Let the extremities of any chord \(P Q\) of the set be \(P\left(x_1, y_1\right)\) and \(Q\left(x_2, y_2\right)\) and let its middle point be \(R(h, k)\). Then solving equations
\(
\begin{aligned}
& \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text { and } y=m x+c \\
& \text { we get } \quad \frac{x^2}{a^2}-\frac{(m x+c)^2}{b^2}=1
\end{aligned}
\)
\(
\Rightarrow \quad\left(a^2 m^2-b^2\right) x^2+2 m c a^2 x+a^2\left(c^2+b^2\right)=0
\)
Since, \(x_1\) and \(x_2\) be the roots of this equation, then
\(
x_1+x_2=\frac{-2 m c a^2}{a^2 m^2-b^2} \dots(i)
\)
Since, \((h, k)\) be the middle point of \(Q R\), then
\(
\begin{aligned}
& \qquad h=\frac{x_1+x_2}{2} \\
& \text { then from Eq. (i), } h=-\frac{m c a^2}{a^2 m^2-b^2} \\
& \text { but }(h, k) \text { lies on } y=m x+c \\
& \quad \therefore \quad k \quad=m h+c \\
& \text { or } \quad c \quad=k-m h \dots(ii)
\end{aligned}
\)
From Eqs. (i) and (ii),
\(
\begin{aligned}
h & =-\frac{m a^2(k-m h)}{a^2 m^2-b^2} \\
\Rightarrow \quad a^2 m^2 h-b^2 h & =-m a^2 k+m^2 a^2 h \\
\Rightarrow \quad-b^2 h & =-m a^2 k \quad \text { or } k=\frac{b^2 h}{a^2 m}
\end{aligned}
\)
Hence, locus of \(R(h, k)\) is \(y=\frac{b^2 x}{a^2 m}\)
which is the diameter of the hyperbola passing through \((0,0)\).

Alternate: Let \((h, k)\) be the middle-point of the chord \(y=m x+c\) of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) then
\(
\begin{array}{rlrl}
& T & =S_1 \\
\Rightarrow & & \frac{x h}{a^2}-\frac{y k}{b^2}=\frac{h^2}{a^2}-\frac{k^2}{b^2} \\
\therefore & & \text { Slope }=\frac{h b^2}{a^2 k} & =m \\
\Rightarrow & k =\frac{b^2 h}{a^2 m}
\end{array}
\)
Hence, the locus of mid-point is \(y=\frac{b^2 x}{a^2 m}\).

Conjugate Diameters

Two diameters are said to be conjugate when each bisects all chords parallel to the others.
If \(y=m x, y=m_1 x\) be conjugate diameters, then \(m m_1=\frac{b^2}{a^2}\).
Let \(y=m_1 x+c\) be a set of chords parallel to \(y=m_1 x\), then the diameter \(y=\frac{b^2}{a^2 m} x\) bisects them all. But being the conjugate diameter \(y=m x\) also bisects them. Hence, these two lines must be identical
\(
\therefore \quad m=\frac{b^2}{a^2 m_1} \Rightarrow m m_1=\frac{b^2}{a^2}
\)

Properties of Hyperbola

Property 1: If a pair of diameters be conjugate with respect to a hyperbola, they are conjugate with respect to its conjugate hyperbola also.

Let \(y=m x\) and \(y=m_1 x\) be two conjugate diameters of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), then
\(
m m_1=\frac{b^2}{a^2} \dots(i)
\)
Now conjugate hyperbola of \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is
\(
\begin{aligned}
& -\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\
& \frac{x^2}{-a^2}-\frac{y^2}{-b^2}=1 \dots(ii)
\end{aligned}
\)
If \(y=m_2 x\) and \(y=m_3 x\) are the conjugate diameters of Eq. (ii), then
\(
\begin{aligned}
m_2 m_3 & =\frac{\left(-b^2\right)}{\left(-a^2\right)} \\
& =\frac{b^2}{a^2}=m m_1 \text { [from Eq. (i)] }
\end{aligned}
\)
This proves the proposition.

Property 2: The parallelogram formed by the tangents at the extremities of conjugate diameters of a hyperbola has its vertices lying on the asymptotes and is of constant area.

Since, \(P\) and \(D\) lie on hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) and its conjugate diameter \(-\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
then coordinates of \(P\) and \(D\) are \((a \sec \phi, b \tan \phi)\) and ( \(a \tan \phi, b \sec \phi\) ) respectively.

Then \(\quad D^{\prime} \equiv(-a \tan \phi,-b \sec \phi)\)
and \(P^{\prime} \equiv(-a \sec \phi,-b \tan \phi)\)
Since, equations of asymptotes \(C Q\) and \(C R\) are \(y=\frac{b}{a} x\) and
\(y=-\frac{b}{a} x\) respectively and the equations of tangents at
\(P, P^{\prime}, D\) and \(D^{\prime}\) are
\(
\begin{aligned}
& \frac{x}{a} \sec \phi-\frac{y}{b} \tan \phi=1 \dots(i) \\
– & \frac{x}{a} \sec \phi+\frac{y}{b} \tan \phi=1 \dots(ii) \\
– & \frac{x}{a} \tan \phi+\frac{y}{b} \sec \phi=1 \dots(iii) \\
& \frac{x}{a} \tan \phi-\frac{y}{b} \sec \phi & =1 \dots(iv)
\end{aligned}
\)
Now, the lines (i) and (ii) are parallel and so are Eqs. (iii) and (iv).
Hence these tangents form a parallelogram. Solving Eqs. (i) and (iii), we get the coordinate of \(Q\) as \([a(\sec \phi+\tan \phi), b(\sec \phi+\tan \phi)]\) which clearly lies on the asymptote \(y=\frac{b}{a} x\) similarly the other points of intersection lies on the asymptotes.
The equations of \(P C P^{\prime}\) and \(D C D^{\prime}\) are
\(
\begin{aligned}
y & =\frac{b}{a} \frac{\tan \phi}{\sec \phi} x \text { or } b x \tan \phi-a y \sec \phi=0 \dots(v) \\
\text { and } \quad y & =\frac{b}{a} \frac{\sec \phi}{\tan \phi} x \text { or } b x \sec \phi-a y \tan \phi=0 \dots(vi)
\end{aligned}
\)
Hence by symmetry.
Area of parallelogram \(Q R Q^{\prime} R^{\prime}=4\) (Area of parallelogram
\(
\begin{aligned}
&Q D C P) \\
&=4 \cdot C P \times(\text { Perpendicular length from } C \text { on } Q D)
\end{aligned}
\)
\(
\begin{aligned}
& =4 \cdot \sqrt{\left(a^2 \sec ^2 \phi+b^2 \tan ^2 \phi\right)} \times \frac{1}{\sqrt{\frac{\tan ^2 \phi}{a^2}+\frac{\sec ^2 \phi}{b^2}}} \\
& =4 a b=\text { Constant. }
\end{aligned}
\)

Property 3: If the normal at \(P\) meets the transverse axis in \(G\), then \(S G=e \cdot S P\). Prove also that the tangent and normal bisect the angle between the focal distances of \(P\).

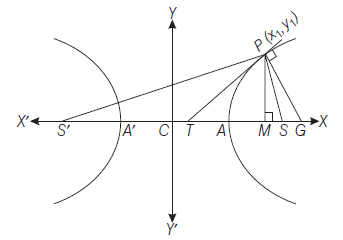
Let the coordinates of \(P[latex] be [latex]\left(x_1, y_1\right)\). The equation of normal at \(P\) on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is
\(
\frac{a^2 x}{x_1}+\frac{b^2 y}{y_1}=a^2+b^2 \dots(i)
\)
The normal (i) meets the \(X\)-axis i.e. \(y=0\) in Eq. (i), then coordinates of \(G\) are
\(
\begin{array}{ll}
& \left(\frac{\left(a^2+b^2\right)}{a^2} x_1, 0\right) \text { or }\left(e^2 x_1, 0\right) \\
\therefore & C G=e^2 x_1 \\
\text { Now } & S G=C G-C S
\end{array}
\)
\(
\begin{aligned}
& =e^2 x_1-a e=e\left(e x_1-a\right)=e \cdot S P \\
& \text { Similarly, } \quad S^{\prime} G=e \cdot S^{\prime} P \\
& \therefore \quad \frac{S G}{S^{\prime} G}=\frac{S P}{S^{\prime} P} \\
&
\end{aligned}
\)
This relation shows that the normal \(P G\) is the external bisector of the angle SPS’. The tangent \(P T\) being perpendicular to \(P G\) is therefore the internal bisector of the angle \(S P S^{\prime}\).

Property 4: If a pair of conjugate diameters meet the hyperbola in \(P, P^{\prime}\) and its conjugate in \(D, D^{\prime}\), then the asymptotes bisect \(P D, P D^{\prime}, P^{\prime} D\) and \(P^{\prime} D^{\prime}\).

The coordinates of four points \(P, D, P^{\prime}, D^{\prime}\) are \((a \sec \phi, b \tan \phi) ;(a \tan \phi, b \sec \phi)\); \((-a \sec \phi,-b \tan \phi) ;(-a \tan \phi,-b \sec \phi)\) respectively. If \((h, k)\) be the middle point of \(P D\), then
\(
h=\frac{a}{2}(\sec \phi+\tan \phi)
\)
\(
\begin{aligned}
& \text { and } & k & =\frac{b}{2}(\tan \phi+\sec \phi) \\
& \therefore & \frac{h}{k} & =\frac{a}{b}
\end{aligned}
\)
\(\therefore\) Locus of mid-point \((h, k)\) is \(y=\frac{b}{a} x\) which is equation of asymptote of hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).
Similarly other mid-points lie on the other asymptotes.

Intersection of Conjugate Diameters and Hyperbola

To prove that of a pair of conjugate diameters of a hyperbola, only one meets the curve in real points
\(
\begin{aligned}
\text { Let } & y=m x \dots(i) \\
\text { and } & y=m_1 x \dots(ii)
\end{aligned}
\)
be a pair of conjugate diameters of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), then
\(
m m_1=\frac{b^2}{a^2} \dots(iii)
\)
On solving Eq. (i) and the equation of hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), we get
\(
\frac{x^2}{a^2}-\frac{m^2 x^2}{b^2}=1
\)
or \(x^2=\frac{a^2 b^2}{b^2-a^2 m^2} \dots(iv)\)
Similarly Eq. (ii) meets the hyperbola at points whose abscissa are given by
\(
x^2=\frac{a^2 b^2}{b^2-a^2 m_1^2} \dots(v)
\)
The two values of \(x\) given by Eq. (iv) will be real if \(b^2-a^2 m^2>0\) i.e. \(m<\left(\frac{b}{a}\right)\)
\(
\text { i.e. } \quad \frac{b^2}{a^2 m_1}<\left(\frac{b}{a}\right) \quad\left\{\because m m_1=\frac{b^2}{a^2}\right\}
\)
\(\Rightarrow \quad \frac{b}{a}<m_1\) i.e. if \(b^2<a^2 m_1^2\)
i.e. if \(b^2-a^2 m_1^2<0\)
Then from Eq. (v) the values of \(x\) are imaginary.
Hence, if Eq. (i) meets the hyperbola in real points then Eq. (ii) meets it in imaginary points and vice-versa.

Remark

• If \(C D\) is the conjugate diameter of a diameter \(C P\) of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), where \(P\) is ( \(a \sec \phi, b \tan \phi\) ), then equation of \(C P\), where \(C\) is \((0,0)\) is
  \(
  y-0=\frac{b \tan \phi-0}{a \sec \phi-0}(x-0) \Rightarrow y=\frac{b}{a} \sin \phi \cdot x
  \)
  Comparing this with \(y=m x\)
  \(
  m=\frac{b}{a} \sin \phi
  \)
  \(
  \because \quad m m^{\prime}=\frac{b^2}{a^2} \Rightarrow \frac{b}{a} \sin \phi \times m^{\prime}=\frac{b^2}{a^2}
  \)
  \(
  \therefore \quad m^{\prime}=\left(\frac{b}{a}\right) \operatorname{cosec} \phi
  \)
  \(\therefore\) Equation of conjugate diameter is \(y=m^{\prime} x=(b / a) \operatorname{cosec} \phi x\) on solving
  \(
  y=(b / a) \operatorname{cosec} \phi \cdot x \text { and }-\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 .
  \)
  Then we get coordinates of \(D\)
  i.e. \(D \equiv(a \tan \phi, b \sec \phi)\)

Example 33: If a pair of conjugate diameters meets the hyperbola and its conjugate in \(P\) and \(D\) respectively, then prove that \(C P^2-C D^2=a^2-b^2\).

Answer: \(\because\) Coordinates of \(P\) and \(D\) are \((a \sec \phi, b \tan \phi)\) and \((a \tan \phi, b \sec \phi\) ) respectively.
\(
\begin{aligned}
& \text { Then }(C P)^2-(C D)^2=a^2 \sec ^2 \phi \\
& +b^2 \tan ^2 \phi-a^2 \tan ^2 \phi-b^2 \sec ^2 \phi \\
& =a^2\left(\sec ^2 \phi-\tan ^2 \phi\right)-b^2\left(\sec ^2 \phi-\tan ^2 \phi\right) \\
& =a^2(1)-b^2(1)=a^2-b^2 \\
&
\end{aligned}
\)

Example 34: For the hyperbola \(x^2-y^2=a^2\), prove that the triangle CPD is isosceles and has constant area, where \(C P\) and \(C D\) are a pair of its conjugate diameters.

Answer: Since, \(C P\) and \(C D\) are the conjugate diameters of \(x^2-y^2=a^2\), hence coordinates of \(P\) and \(D\) are \(P \equiv(a \sec \phi, a \tan \phi), D \equiv(a \tan \phi, a \sec \phi)\) respectively.

\(
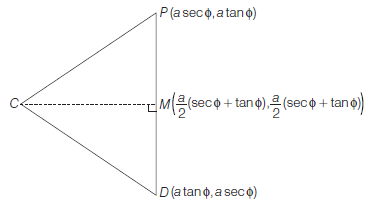
\therefore \quad C P=\sqrt{a^2\left(\sec ^2 \phi+\tan ^2 \phi\right)}=C D \quad[\because C=0(0,0)]
\)
Hence, \(\triangle C P D\) is isosceles triangle.
Draw \(\perp\) from \(C\) on \(P D\), where \(M\) is the mid-point of \(P D\)
\(
\begin{aligned}
& \therefore \quad M \equiv\left(\frac{a}{2}(\sec \phi+\tan \phi), \frac{a}{2}(\sec \phi+\tan \phi)\right) \\
& \therefore \quad C M=\frac{|(\sec \phi+\tan \phi)|}{2} \sqrt{\left(a^2+a^2\right)} \\
& \text { and } \quad P D=\sqrt{[a(\sec \phi-\tan \phi)]^2+[a(\sec \phi-\tan \phi)]^2} \\
& =\mid \sec \phi-\tan \phi) \mid \sqrt{\left(a^2+a^2\right)} \\
& \therefore \quad \text { Area of } \triangle P C D=\frac{1}{2} \cdot P D \cdot C M \\
& =\frac{1}{4}\left(a^2+a^2\right)=\frac{a^2}{2}=\text { constant } \\
&
\end{aligned}
\)

Example 35: Find the condition for the lines \(A x^2+2 H x y+B y^2=0\) to be conjugate diameters of \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).

Answer: Let the lines represented by
\(
A x^2+2 H x y+B y^2=0
\)
are \(y=m x\) and \(y=m_1 x\)
\(
\therefore \quad m m_1=\frac{A}{B} \dots(i)
\)
But \(y=m x\) and \(y=m_1 x\) are the conjugate diameters of
\(
\begin{aligned}
\frac{x^2}{a^2}-\frac{y^2}{b^2} & =1 \\
\text { then } m m_1 & =\frac{b^2}{a^2} \dots(ii)
\end{aligned}
\)
\(\therefore\) From Eqs. (i) and (ii), \(\frac{A}{B}=\frac{b^2}{a^2}\)
or \(a^2 A=b^2 B\)
which is the required condition.

Example 36: If the lines \(l x+m y+n=0\) passes through the extremities of a pair of conjugate diameters of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), show that \(a^2 l^2-b^2 m^2=0\).

Answer: The extremities of a pair of conjugate diameters of \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) are \((a \sec \phi, b \tan \phi)\) and \((a \tan \phi, b \sec \phi)\) respectively.
According to the question, since extremities of a pair of conjugate diameters lie on \(l x+m y+n=0\)
\(
\begin{array}{ll}
\therefore & l(a \sec \phi)+m(b \tan \phi)+n=0 \dots(i) \\
\Rightarrow & l(a \tan \phi)+m(b \sec \phi)+n=0 \dots(ii)
\end{array}
\)
then from Eq. (i), \(a l \sec \phi+b m \tan \phi=-n\)
or \(a^2 l^2 \sec ^2 \phi+b^2 m^2 \tan ^2 \phi+2 a b l m \sec \phi \tan \phi=n^2 \dots(iii)\)
and from Eq. (ii), al \(\tan \phi+b m \sec \phi=-n\)
or \(a^2 l^2 \tan ^2 \phi+b^2 m^2 \sec ^2 \phi+2 a b l m \sec \phi \tan \phi=n^2 \dots(iv)\)
then subtracting Eq. (iv) from Eq. (iii),
\(
a^2 l^2\left(\sec ^2 \phi-\tan ^2 \phi\right)+b^2 m^2\left(\tan ^2 \phi-\sec ^2 \phi\right)=0
\)
\(
\text { or } \quad a^2 l^2-b^2 m^2=0
\)

Director Circle

The locus of the point of intersection of the tangents to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), which are perpendicular to each other is called director circle.
Let any tangent in terms of slope of hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is

\(
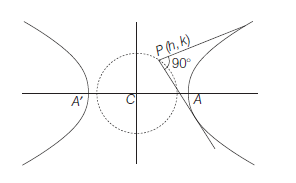
y=m x+\sqrt{\left(a^2 m^2-b^2\right)}
\)
It passes through \((h, k)\)
\(
\begin{array}{ll}
\therefore & k=m h+\sqrt{\left(a^2 m^2-b^2\right)} \\
\text { or } & (k-m h)^2=a^2 m^2-b^2 \\
\Rightarrow & k^2+m^2 h^2-2 m h k=a^2 m^2-b^2 \\
\Rightarrow & m^2\left(h^2-a^2\right)-2 h k m+k^2+b^2=0
\end{array}
\)
It is quadratic equation in \(m\). Let slopes of two tangents are \(m_1\) and \(m_2\)
\(
\begin{aligned}
\therefore \quad m_1 m_2 & =\frac{k^2+b^2}{h^2-a^2} \\
-1 & =\frac{k^2+b^2}{h^2-a^2} \quad(\because \text { tangents are perpendicular })
\end{aligned}
\)
\(
\begin{aligned}
\Rightarrow & -h^2+a^2 =k^2+b^2 \\
\text { or } & h^2+k^2 =a^2-b^2
\end{aligned}
[latex]
Hence, locus of [latex]P(h, k)\) is
\(
x^2+y^2=a^2-b^2 (a>b)
\)
Hence, \(x^2+y^2=a^2-b^2\) is the director circle of the hyperbola.

Remarks

• For director circle of \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), a must be greater than \(b\). If \(a<b\), then director circle \(x^2+y^2=a^2-b^2\) does not exist.
• The equation of director circle of \(-\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is \(x^2+y^2=b^2-a^2(b>a)\),
  If \(b<a\), then director circle does not exist.

Example 37: If any tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) with centre \(C\), meets its director circle in \(P\) and \(Q\), show that \(C P\) and \(C Q\) are conjugate semi-diameters of the hyperbola.

Answer: Since, equation of hyperbola is
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
Equation of tangent at ( \(a \sec \phi, b \tan \phi\) ) on Eq. (i) is
\(
\frac{x}{a} \sec \phi-\frac{y}{b} \tan \phi=1 \dots(ii)
\)
Equation of director circle of Eq. (i) is
\(
x^2+y^2=a^2-b^2 \dots(iii)
\)
Equation of lines joining the point of intersection of Eqs. (i) and (ii) to the origin is obtained by making Eq. (iii) homogeneous with the help of Eq. (ii).
\(
\therefore \quad x^2+y^2=\left(a^2-b^2\right)\left(\frac{x}{a} \sec \phi-\frac{y}{b} \tan \phi\right)^2
\)
\(
\text { or } \quad x^2\left(1-\frac{\left(a^2-b^2\right) \sec ^2 \phi}{a^2}\right)+y^2\left(1-\frac{\left(a^2-b^2\right) \tan ^2 \phi}{b^2}\right)+\frac{2\left(a^2-b^2\right) \sec \phi \tan \phi}{a b} x y=0 \dots(iv)
\)
Let \(m\) and \(m^{\prime}\) represent the slopes of the lines given by Eq. (iv), then

\(
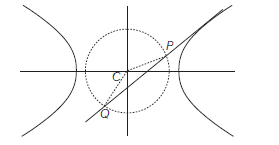
\begin{aligned}
m m^{\prime} & =\frac{1-\frac{\left(a^2-b^2\right) \sec ^2 \phi}{a^2}}{1-\frac{\left(a^2-b^2\right) \tan ^2 \phi}{b^2}}=\frac{b^2}{a^2} \cdot \frac{a^2-\left(a^2-b^2\right) \sec ^2 \phi}{b^2-\left(a^2-b^2\right) \tan ^2 \phi} \\
& =\frac{b^2}{a^2} \cdot \frac{b^2 \sec ^2 \phi-a^2 \tan ^2 \phi}{b^2 \sec ^2 \phi-a^2 \tan ^2 \phi}=\frac{b^2}{a^2}
\end{aligned}
\)
Hence, the lines \(C P\) and \(C Q\) are conjugate semi-diameters of the hyperbola.

Asymptotes

An asymptotes of any hyperbola or a curve is a straight line which touches in it two points at infinity.
Asymptotes of hyperbola: The equations of two asymptotes of the hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \text { are } y = \pm \frac{ b }{ a } x \text { or } \frac{x}{a} \pm \frac{y}{b}=0 \text {. }
\)

Proof : Let \(y=m x+c\) be an asymptote of the hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
Substituting the value of \(y\) in Eq. (i),
\(
\begin{gathered}
\frac{x^2}{a^2}-\frac{(m x+c)^2}{b^2}=1 \\
\text { or } \quad\left(a^2 m^2-b^2\right) x^2+2 a^2 m c x+a^2\left(b^2+c^2\right)=0 \dots(ii)
\end{gathered}
\)
If the line \(y=m x+c\) is an asymptote to the given hyperbola, then it touches the hyperbola at infinity. So both roots of Eq. (ii) must be infinite.
\(
\begin{aligned}
& \therefore \quad a^2 m^2-b^2=0 \\
& \text { and } & -2 a^2 m c=0 \\
& \text { then } & m= \pm \frac{b}{a} \text { and } c=0 \\
&
\end{aligned}
\)
Substituting the value of \(m\) and \(c\) in \(y=m x+c\), we get
\(
y= \pm \frac{b}{a} x \Rightarrow \frac{x}{a} \pm \frac{y}{b}=0
\)

Remarks

• If \(b=a\), then \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) reduces to \(x^2-y^2=a^2\). The asymptotes of rectangular hyperbola \(x^2-y^2=a^2\) are \(y= \pm x\) which are at right angles.
• A hyperbola and its conjugate hyperbola have the same asymptotes.
• The angle between the asymptotes of \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is \(2 \tan ^{-1}\left(\frac{b}{a}\right)\)

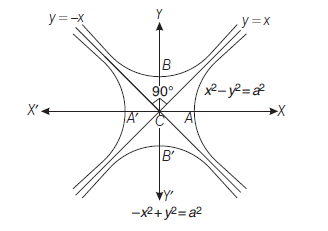
• If the angle between the asymptotes of a hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is \(2 \theta\), then \(e=\sec \theta\).
• The asymptotes pass through the centre of the hyperbola.
• The bisectors of the angles between the asymptotes are the coordinate axes.
• Let \(H \equiv \frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0\)
  \(
  A \equiv \frac{x^2}{a^2}-\frac{y^2}{b^2}=0 \text { and } C \equiv \frac{x^2}{a^2}-\frac{y^2}{b^2}+1=0
  \)
  be the equation of the hyperbola, asymptotes and the conjugate hyperbola respectively, then clearly \(C + H =2 A\).

Example 38: Find the asymptotes of the hyperbola \(x y-3 y-2 x=0\).

Answer: Since equation of a hyperbola and its asymptotes differ in constant terms only,
\(\therefore\) Pair of asymptotes is given by
\(
x y-3 y-2 x+\lambda=0 \dots(i)
\)
where, \(\lambda\) is any constant such that it represents two straight lines.
\(
\therefore \quad a b c+2 f g h-a f^2-b g^2-c h^2=0
\)
\(
\Rightarrow \quad 0+2 \times-\frac{3}{2} \times-1 \times \frac{1}{2}-0-0-\lambda\left(\frac{1}{2}\right)^2=0
\)
\(
\therefore \quad \lambda=6
\)
From Eq. (i), the asymptotes of given hyperbola are given by
\(
x y-3 y-2 x+6=0
\)
or \(\quad(y-2)(x-3)=0\).
\(\therefore\) Asymptotes are \(x-3=0\) and \(y-2=0\).

Example 39: The asymptotes of a hyperbola having centre at the point \((1,2)\) are parallel to the lines \(2 x+3 y=0\) and \(3 x+2 y=0\). If the hyperbola passes through the point \((5,3)\), show that its equation is
\(
(2 x+3 y-8)(3 x+2 y+7)=154
\)

Answer: Let the asymptotes be \(2 x+3 y+\lambda=0\) and \(3 x+2 y+\mu=0\). Since asymptotes passes through \((1,2)\), then
\(
\lambda=-8 \text { and } \mu=-7
\)
Thus, the equation of asymptotes are
\(
2 x+3 y-8=0 \text { and } 3 x+2 y-7=0
\)
Let the equation of hyperbola be
\(
(2 x+3 y-8)(3 x+2 y-7)+v=0 \dots(i)
\)
It passes through \((5,3)\), then
\(
\begin{aligned}
& (10+9-8)(15+6-7)+v=0 \\
& \Rightarrow \quad 11 \times 14+v=0 \\
& \therefore \quad \gamma=-154 \\
&
\end{aligned}
\)
Putting the value of \(v\) in Eq. (i), we obtain
\(
(2 x+3 y-8)(3 x+2 y-7)-154=0
\)
which is the equation of required hyperbola.

Example 40: Show that the tangent at any point of a hyperbola cuts off a triangle of constant area from the asymptotes and that the portion of it intercepted between the asymptotes is bisected at the point of contact.

Answer: Let \(P(a \sec \phi, b \tan \phi)\) be any point on the hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
Asymptotes of Eq. (i) are
\(
y= \pm \frac{b}{a} x
\)
Equation of tangent of Eq. (i) at \(P(a \sec \phi, b \tan \phi)\) is
\(
\frac{x}{a} \sec \phi-\frac{y}{b} \tan \phi=1 \dots(ii)
\)
Solving Eq. (ii) and \(y=\frac{b}{a} x\)
We get \(\frac{x}{a}(\sec \phi-\tan \phi)=\left(\sec ^2 \phi-\tan ^2 \phi\right)\)
\(
\begin{array}{ll}
\therefore & x=a(\sec \phi+\tan \phi) \\
\text { and } & y=b(\sec \phi+\tan \phi)
\end{array}
\)

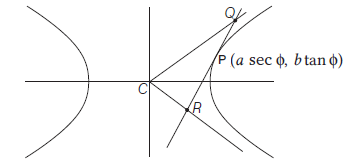
Let \(Q \equiv[a(\sec \phi+\tan \phi), b(\sec \phi+\tan \phi)]\)
Now solving Eq. (ii) and \(y=-\frac{b}{a} x\)
We get, \(\quad \frac{x}{a}(\sec \phi+\tan \phi)=\left(\sec ^2 \phi-\tan ^2 \phi\right)\)
or \(\quad x=a(\sec \phi-\tan \phi)\)
and \(\quad y=-b(\sec \phi-\tan \phi)\)
Let \(R \equiv[a(\sec \phi-\tan \phi),-b(\sec \phi-\tan \phi)]\)
Mid-point of \(Q R\) is ( \(a \sec \phi, b \tan \phi\) ) which is coordinate of \(P\).
Area of \(\triangle C Q R=\frac{1}{2}\left|\left(x_1 y_2-x_2 y_1\right)\right|\)
\(
=\frac{1}{2}|-a b-a b|=a b=\text { constant. }
\)

Rectangular Hyperbola

A hyperbola whose asymptotes include a right angle is said to be rectangular hyperbola.
                            OR
If the lengths of transverse and conjugate axes of any hyperbola be equal, it is called rectangular or equilateral hyperbola.
According to the first definition
\(
\begin{aligned}
2 \tan ^{-1}\left(\frac{b}{a}\right) & =\frac{\pi}{2} \\
\tan ^{-1}\left(\frac{b}{a}\right) & =\frac{\pi}{4} \Rightarrow \frac{b}{a}=1 \\
a & =b
\end{aligned}
\)
then, \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) becomes \(x^2-y^2=a^2\)
According to the second definition
When \(a=b, \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) becomes
\(
x^2-y^2=a^2
\)
Eccentricity, \(e=\sqrt{\left(1+\frac{b^2}{a^2}\right)}=\sqrt{2}\)
Hence, \(x^2-y^2=a^2\) is the general form of the equation of the rectangular hyperbola.

Remark

• All the results of \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) are applicable to the hyperbola \(x^2-y^2=a^2\) after changing \(b\) by \(a\).

The Rectangular Hyperbola \(x y=c^2\)

When the centre of any rectangular hyperbola be at the origin and its asymptotes coincide with the coordinate axes its, equation is \(x y=c^2\).
Since, asymptotes coincides the coordinate axes.
Hence, asymptotes are \(y=0\) and \(x=0\).
\(\therefore\) Combined equation of asymptotes is \(x y=0\). Now equation of any hyperbola and its asymptotes differ in respect of constant terms only.
\(\therefore\) Equation of rectangular hyperbola is \(x y=c^2\) where \(c\) is any constant.

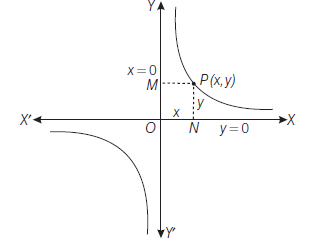
Second method (By rotation of axes) :

The equation of rectangular hyperbola is \(x^2-y^2=a^2\) and its asymptotes are \(x-y=0\) and \(x+y=0\). Since, asymptotes are inclined at \(45^{\circ}\) and \(135^{\circ}\) to the \(X\)-axis respectively.

If we rotate the axes through \(\theta=-45^{\circ}\) without changing the origin. Thus, when we replace \((x, y)\) by
\(
\begin{array}{r}
{\left[x \cos \left(-45^{\circ}\right)-y \sin \left(-45^{\circ}\right), x \sin (-45)^{\circ}\right.} \left.+y \cos \left(-45^{\circ}\right)\right]
\end{array}
\)
\(
\text { i.e. } \quad\left(\frac{x+y}{\sqrt{2}}, \frac{-x+y}{\sqrt{2}}\right)
\)
then equation \(x^2-y^2=a^2\) reduces to
\(
\left(\frac{x+y}{\sqrt{2}}\right)^2-\left(\frac{-x+y}{\sqrt{2}}\right)^2=a^2
\)
\(
\begin{aligned}
\frac{1}{2}\left\{(x+y)^2-(-x+y)^2\right\} & =a^2 \\
\frac{1}{2}(2 y)(2 x) & =a^2 \\
x y=\frac{a^2}{2}=\left(\frac{a}{\sqrt{2}}\right)^2 & =c^2 \text { (say) } \\
x y & =c^2
\end{aligned}
\)

Study of Hyperbola \(x y=c^2\)

• Vertices : \(A(c, c)\) and \(A^{\prime}(-c,-c)\).
• Transverse axis : \(y=x\).
• Conjugate axis : \(y=-x\).
• Foci : \(S(c \sqrt{2}, c \sqrt{2})\) and \(S^{\prime}(-c \sqrt{2},-c \sqrt{2})\).
• Length of latusrectum \(=\) Length of \(A A^{\prime}=2 \sqrt{2} c\).
• Equation of auxiliary circle : \(x^2+y^2=2 c^2\).
• Equation of director circle \(x^2+y^2=0\).
• Asymptotes : \(x=0, y=0\).

Remarks

• The equations of the asymptotes and the conjugate hyperbola of the rectangular hyperbola \(x y=c^2\), where the axes are the asymptotes, are \(x y=0\) and \(x y=-c^2\) respectively.
• The equation of a rectangular hyperbola having coord inate axes as its asymptotes is \(x y=c^2\). If the asymptotes of a rectangular hyperbola are \(x=\alpha, y=\beta\) then its equation is \((x-\alpha)(y-\beta)=c^2\) or \(x y-\alpha y-\beta x+\lambda=0\).
• Since \(x=c t, y=\frac{c}{t}\) satisfies \(x y=c^2\)
  \(\therefore(x, y)=\left(c t, \frac{c}{t}\right)(t \neq 0)\) is called a ‘ \(t\) ‘ point on the rectangular hyperbola. The set \(\left\{x=c t, y=\frac{c}{t}\right\}\) represents its parametric equations with parameter ‘ \(t\) ‘.

Properties of Rectangular Hyperbola \(x y=c^2\)

• Equation of the chord joining ‘ \(t_1\) ‘ and ‘ \(t_2\) ‘ is \(x+y t_1 t_2-c\left(t_1+t_2\right)=0\).
• Equation of tangent at \(\left(x_1, y_1\right)\) is \(x y_1+x_1 y=2 c^2\).
• Equation of tangent at ‘ \(t\) ‘ is \(\frac{x}{t}+y t=2 c\).
• Point of intersection of tangents at ‘ \(t_1\) ‘ and ‘ \(t_2\) ‘ is
  \(
  \left(\frac{2 c t_1 t_2}{t_1+t_2}, \frac{2 c}{t_1+t_2}\right) \text {. }
  \)
• Equation of normal at \(\left(x_1, y_1\right)\) is \(x x_1-y y_1=x_1^2-y_1^2\).
• Equation of normal at ‘ \(t\) ‘ is \(x t^3-y t-c t^4+c=0\).
• Point of intersection of normals at ‘ \(t_1\) ‘ and ‘ \(t_2\) ‘ is.
  \(
  \left(\frac{c\left\{t_1 t_2\left(t_1^2+t_1 t_2+t_2^2\right)-1\right\}}{t_1 t_2\left(t_1+t_2\right)}, \frac{c\left\{t_1^3 t_2^3+\left(t_1^2+t_1 t_2+t_2^2\right)\right\}}{t_1 t_2\left(t_1+t_2\right)}\right) .
  \)

Example 41: If the normal at the point ‘ \(t\) ‘ to the rectangular hyperbola \(x y=c^2\) meets it again at the point ‘ \(t_2\) ‘, prove that \(t_1^3 t_2=-1\).

Answer: Since, the equation of normal at \(\left(c t_1, \frac{c}{t_1}\right)\) to the hyperbola \(x y=c^2\) is
\(
x t_1^3-y t_1-c t_1^4+c=0
\)
but this passes through \(\left(c t_2, \frac{c}{t_2}\right)\), then
\(
c t_2 t_1^3-\frac{c}{t_2} t_1-c t_1^4+c=0
\)
\(
\begin{array}{lr}
\Rightarrow & t_2^2 t_1^3-t_1-t_1^4 t_2+t_2=0 \\
\Rightarrow & t_2 t_1^3\left(t_2-t_1\right)+\left(t_2-t_1\right)=0 \\
\Rightarrow & \left(t_1^3 t_2+1\right)\left(t_2-t_1\right)=0
\end{array}
\)
\(
\Rightarrow \quad t_1^3 t_2+1=0 \quad\left[\because t_2 \neq t_1\right]
\)
\(
\therefore \quad t_1^3 t_2=-1
\)

Example 42: A triangle has its vertices on a rectangular hyperbola. Prove that the orthocentre of the triangle also lies on the same hyperbola.

Answer: Let ” \(t_1\) “, ” \(t_2\) ” and ” \(t_3\) ” are the vertices of the triangle \(A B C\), described on the rectangular hyperbola \(x y=c^2\).

\(\therefore\) Coordinates of \(A, B\) and \(C\) are \(\left(c t_1, \frac{c}{t_1}\right),\left(c t_2, \frac{c}{t_2}\right)\) and \(\left(c t_3, \frac{c}{t_3}\right)\) respectively.
Now, slope of \(B C\) is \(\frac{\frac{c}{t_3}-\frac{c}{t_2}}{c t_3-c t_2}=-\frac{1}{t_2 t_3}\)
\(\therefore\) Slope of \(A D\) is \(t_2 t_3\)
Equation of altitude \(A D\) is
\(
y-\frac{c}{t_1}=t_2 t_3\left(x-c t_1\right)
\)
\(
\text { or } \quad t_1 y-c=x t_1 t_2 t_3-c t_1^2 t_2 t_3 \dots(i)
\)
Similarly equation of altitude \(B E\) is
\(
t_2 y-c=x t_1 t_2 t_3-c t_1 t_2^2 t_3 \dots(ii)
\)
Solving Eqs. (i) and (ii), we get the orthocentre \(\left(-\frac{c}{t_1 t_2 t_3},-c t_1 t_2 t_3\right)\) which lies on \(x y=c^2\).

Reflection Property of a Hyperbola

If an incoming light ray passing through one focus \(S\) strike convex side of the hyperbola then it will get reflected towards other focus \(S^{\prime}\).

Example 43: A ray emanating from the point \((5,0)\) is incident on the hyperbola \(9 x^2-16 y^2=144\) at the point \(P\) with abscissa 8 . Find the equation of the reflected ray after first reflection and point \(P\) lies in first quadrant.

Answer: Given, hyperbola is \(9 x^2-16 y^2=144\). This equation can be rewritten as
\(
\frac{x^2}{16}-\frac{y^2}{9}=1 \dots(i)
\)
Coordinates of foci are \((0, \pm \sqrt{16+9})\) i.e., \((0, \pm 5)\)

Since \(x\)-coordinate of \(P\) is 8 . Let \(y\)-coordinate of \(P\) is \(\alpha\).
\(
\begin{aligned}
& \therefore(8, \alpha) \text { lies on Eq. (i) } \\
& \therefore \quad \frac{64}{16}-\frac{\alpha^2}{9}=1 \\
& \Rightarrow \quad \alpha^2=27 \\
& \Rightarrow \quad \alpha=3 \sqrt{3} (\because P \text { lies in first quadrant) } \\
&
\end{aligned}
\)
Hence coordinate of point \(P\) is \((8,3 \sqrt{3})\).
\(\because\) Equation of reflected ray passing through \(P(8,3 \sqrt{3})\) and \(S^{\prime}(-5,0)\).
\(\therefore\) Its equation is \(y-3 \sqrt{3}=\frac{0-3 \sqrt{3}}{-5-8}(x-8)\)
\(
\begin{aligned}
& \text { or } \quad 13 y-39 \sqrt{3}=3 \sqrt{3} x-24 \sqrt{3} \\
& \text { or } \quad 3 \sqrt{3} x-13 y+15 \sqrt{3}=0 .
\end{aligned}
\)

Equation of a Hyperbola Referred to Two Perpendicular Lines

Let \(P(x, y)\) be any point on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\),
\(
\text { then } P M=y \text { and } P N=x
\)
\(
\begin{array}{ll}
\therefore & \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \\
\Rightarrow & \frac{(P N)^2}{a^2}-\frac{(P M)^2}{b^2}=1
\end{array}
\)

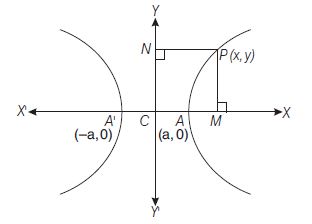
If perpendicular lines represented by
\(
\begin{aligned}
& L_1 \equiv a_1 x+b_1 y+c_1=0 \\
& \text { and } \quad L_2 \equiv b_1 x-a_1 y+c_2=0 \\
& \text { then } \\
& P N=p_1=\left(\frac{a_1 x+b_1 y+c_1}{\sqrt{\left(a_1^2+b_1^2\right)}}\right) \\
&
\end{aligned}
\)

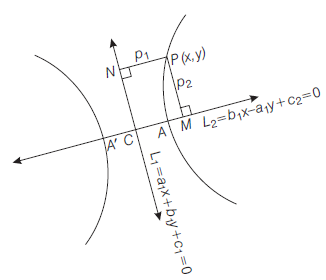
and \(P M=p_2=\left(\frac{b_1 x-a_1 y+c_2}{\sqrt{\left(b_1^2+a_1^2\right)}}\right)\)
Now equation of hyperbola becomes
\(
\frac{\left(\frac{a_1 x+b_1 y+c_1}{\sqrt{\left(a_1^2+b_1^2\right)}}\right)^2}{a^2}-\frac{\left(\frac{b_1 x-a_1 y+c_2}{\sqrt{\left(b_1^2+a_1^2\right)}}\right)^2}{b^2}=1
\)
Then the point \(P\) describes a hyperbola in the plane of the given lines such that :

• Centre : The centre of the hyperbola is the point of intersection of the lines \(L_1=0\) and \(L_2=0\).
• Transverse axis : The transverse axis lies along \(L_2=0\).
• Conjugate axis : The conjugate axis lies along \(L_1=0\).
• Length of transverse and conjugate axes: The length of transverse and conjugate axes are \(2 a\) and \(2 b\) respectively.
• Foci : The foci of the hyperbola is the point of intersection of the lines
  \(
  \frac{a_1 x+b_1 y+c_1}{\sqrt{\left(a_1^2+b_1^2\right)}}= \pm a e \text { and } L_2=0 .
  \)
  (v) Directrix : The directrices of the hyperbola are
  \(
  \frac{a_1 x+b_1 y+c_1}{\sqrt{\left(a_1^2+b_1^2\right)}}= \pm \frac{a}{e}
  \)
• Latusrectum : The latusrectum of the hyperbola is
  \(
  \frac{2 b^2}{a} \text {. }
  \)

Example 44: The equations of the transverse and conjugate axes of a hyperbola are respectively \(3 x+4 y-7=0,4 x-3 y+8=0\) and their respective lengths are 4 and 6 . Find the equation of the hyperbola.

Answer: The equation of the required hyperbola is
\(
\frac{\left(\frac{3 x+4 y-7}{\sqrt{\left(3^2+4^2\right)}}\right)^2}{\left(\frac{4}{2}\right)^2}-\frac{\left(\frac{4 x-3 y+8}{\sqrt{4^2+(-3)^2}}\right)^2}{\left(\frac{6}{2}\right)^2}=1
\)
\(
\Rightarrow \quad \frac{1}{100}(3 x+4 y-7)^2-\frac{1}{225}(4 x-3 y+8)^2=1
\)
\(
\Rightarrow \quad 9(3 x+4 y-7)^2-4(4 x-3 y+8)^2=900
\)
\(
\begin{aligned}
& \Rightarrow \quad 9\left(9 x^2+16 y^2+49+24 x y-42 x-56 y\right) \\
& \quad-4\left(16 x^2+9 y^2+64-24 x y+64 x-48 y\right)=900
\end{aligned}
\)
\(
\Rightarrow \quad 17 x^2+312 x y+108 y^2-634 x-312 y-715=0 \text {. }
\)