11.4 Parabola

3D View

The locus of a point which moves in a plane such that the ratio of its distance from a fixed point to its perpendicular distance from a fixed straight line is always constant, is known as a conic section or a conic.

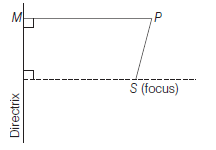
The fixed point is called the focus of the conic and this fixed line is called the directrix of the conic. Also, this constant ratio is called the eccentricity of the conic and is denoted by \(e\).
In the figure, \(\frac{S P}{P M}=\) constant \(=e\)
\(
\Rightarrow \quad S P=e P M
\)

Equation of Conic Section

If the focus is \((\alpha, \beta)\) and the directrix is \(a x+b y+c=0\), then the equation of the conic section whose eccentricity \(=e\) is \(S P=e P M\)

\(
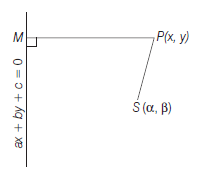
\begin{aligned}
& \Rightarrow \sqrt{(x-\alpha)^2+(y-\beta)^2}=e \cdot \frac{|a x+b y+c|}{\sqrt{\left(a^2+b^2\right)}} \\
& \Rightarrow \quad(x-\alpha)^2+(y-\beta)^2=e^2 \cdot \frac{(a x+b y+c)^2}{\left(a^2+b^2\right)} .
\end{aligned}
\)

Important Terms

• Axis: The straight line passing through the focus and perpendicular to the directrix is called the axis of the conic section.
• Vertex: The points of intersection of the conic section and the axis is (are) called vertex (vertices) of the conic section.
• Focal Chord: Any chord passing through the focus is called focal chord of the conic section.
• Double Ordinate: A straight line drawn perpendicular to the axis and terminated at both end of the curve is a double ordinate of the conic section.
• Latusrectum: The double ordinate passing through the focus is called the latusrectum of the conic section.
• Centre: The point which bisects every chord of the conic passing through it, is called the centre of the conic section.
• Directrix: The fixed straight line is called the directrix of the conic section. In general, every conic has four foci, two of them are real and the other two are imaginary. Due to two real foci, every conic has two directrices corresponding to each real focus.
• Eccentricity: The constant ratio is called the eccentricity of the conic section and is denoted by \(e\).

Remark

• Parabola has no centre but circle, ellipse and hyperbola have centre.

Example 1: Find the locus of a point, which moves such that its distance from the point \((0,-1)\) is twice its distance from the line \(3 x+4 y+1=0\).

Answer: Let \(P\left(x_1, y_1\right)\) be the point, whose locus is required.
Its distance from \((0,-1)=2 \times\) its distance from the line
\(
\begin{aligned}
& 3 x+4 y+1=0 \\
& \Rightarrow \quad \sqrt{\left(x_1-0\right)^2+\left(y_1+1\right)^2}=2 \times \frac{\left|3 x_1+4 y_1+1\right|}{\sqrt{\left(3^2+4^2\right)}} \\
& \Rightarrow \quad 5 \sqrt{x_1^2+\left(y_1+1\right)^2}=2\left|3 x_1+4 y_1+1\right|
\end{aligned}
\)
Squaring and simplifying, we have
\(
\begin{aligned}
25\left(x_1^2+y_1^2+2 y_1\right. & +1) \\
& =4\left(9 x_1^2+16 y_1^2+24 x_1 y_1+6 x_1+8 y_1+1\right)
\end{aligned}
\)
or \(11 x_1^2+39 y_1^2+96 x_1 y_1+24 x_1-18 y_1-21=0\)
Hence, the locus of \(\left(x_1, y_1\right)\) is
\(
11 x^2+39 y^2+96 x y+24 x-18 y-21=0
\)

Example 2: What conic does the equation
\(
25\left(x^2+y^2-2 x+1\right)=(4 x-3 y+1)^2 \text { represent? }
\)

Answer: Given equation is
\(
25\left(x^2+y^2-2 x+1\right)=(4 x-3 y+1)^2 \dots(i)
\)
Write the right hand side of this equation, so that it appears in perpendicular distance form, then
\(
(4 x-3 y+1)^2=25\left(\frac{4 x-3 y+1}{\sqrt{\left(4^2+3^2\right)}}\right)^2
\)
then, Eq. (i) can be re-written as
\(
25\left[(x-1)^2+(y-0)^2\right]=25\left[\frac{4 x-3 y+1}{\sqrt{\left(4^2+3^2\right)}}\right]^2
\)
or \(\sqrt{(x-1)^2+(y-0)^2}=\frac{|4 x-3 y+1|}{\sqrt{\left(4^2+3^2\right)}}\)
Here, \(e=1\)
Thus, the given equation represents a parabola. It may noted that \((1,0)\) is the focus and \(4 x-3 y+1=0\) is the directrix of the parabola.

How to Recognize types of Conics

The equation of conics represented by the general equation of second degree
\(
a x^2+2 h x y+b y^2+2 g x+2 f y+c=0 \dots(i)
\)
can be recognised easily by the condition given in the tabular form. For this, first we have to find discriminant of the equation. We know that the discriminant of above equation is represented by \(\Delta\), where
\(
\Delta=a b c+2 f g h-a f^2-b g^2-c h^2
\)
The nature of the conic section depends upon the position of the focus \(S\) with respect to the directrix and also upon the value of the eccentricity \(e\). Two different cases arise.

Case I: (When the focus lies on the directrix)
In this case Eq. (i) represents the Degenerate conic whose nature is given in the following table :
\(
\begin{array}{cc}
\hline \text { Condition } \quad \quad \quad \quad   & & & \text { Nature of Conic } \\
\hline
\end{array}
\)
\(
e>1 ; \Delta=0, h^2>a b \quad \text { The lines will be real and distinct intersecting at S.} 
\)
\(
e=1 ; \Delta=0, h^2=a b \quad \text { The lines will coincident }
\)
\(
e<1 ; \Delta=0, h^2<a b \quad \text { The lines will be imaginary. }
\)

Case II: (When the focus does not lie on the directrix)
In this case Eq. (i) represents the Non-degenerate conic whose nature is given in the following table:
\(
\begin{array}{cc}
\hline \text { Condition } \quad \quad \quad \quad \quad \quad & & & \text { Nature of Conic } \\
\hline
\end{array}
\)
\(
e=1 ; \Delta \neq 0, h^2=a b \quad \quad \quad \quad \quad \quad \text { a parabola }
\)
\(
0<e<1 ; \Delta \neq 0, h^2<a b \quad \quad \quad \quad \text { an ellipse }
\)
\(
e>1 ; \Delta \neq 0, h^2>a b \quad \quad \quad \quad \quad \quad \text { a hyperbola }
\)
\(
e>1 ; \Delta \neq 0, h^2>a b ; a+b=0 \quad \quad \text { rectangular hyperbola }
\)

Remark

• If conic represents an empty set, then \(\Delta \neq 0, h^2<a b\)
• If conic represents a single point, the \(\Delta=0, h^2<a b\).

Example 3: What conic does \(13 x^2-18 x y+37 y^2+2 x+14 y-2=0\) represent?

Answer: Compare the given equation with
\(
\begin{aligned}
& a x^2+2 h x y+b y^2+2 g x+2 f y+c=0 \\
& \therefore \quad a=13, h=-9, b=37, g=1, f=7, c=-2 \text {, } \\
& \text { then, } \Delta=a b c+2 f g h-a f^2-b g^2-c h^2 \\
& =(13)(37)(-2)+2(7)(1)(-9) \\
& -13(7)^2-37(1)^2+2(-9)^2 \\
& =-962-126-637-37+162=-1600 \neq 0 \\
&
\end{aligned}
\)
and also \(h^2=(-9)^2=81\) and \(a b=13 \times 37=481\)
Here, \(h^2<a b\)
So, we have \(h^2<a b\) and \(\Delta \neq 0\).
Hence, the given equation represents an ellipse.

Example 4: what conic is represented by the equation \(\sqrt{a x}+\sqrt{b y}=1\)?

Answer: Given conic is \(\sqrt{a x}+\sqrt{b y}=1\)
On squaring both sides, we get
\(
\begin{array}{rlrl}
& & a x+b y+2 \sqrt{a b x y} & =1 \\
\Rightarrow & a x+b y-1 =-2 \sqrt{a b x y}
\end{array}
\)
Again, on squaring both sides, then
\(
\begin{aligned}
& (a x+b y-1)^2=4 a b x y \\
\Rightarrow & a^2 x^2+b^2 y^2+1+2 a b x y-2 b y-2 a x=4 a b x y \\
\Rightarrow & a^2 x^2+b^2 y^2-2 a b x y-2 a x-2 b y+1=0 \\
\Rightarrow & a^2 x^2-2 a b x y+b^2 y^2-2 a x-2 b y+1=0 \quad \dots(i)
\end{aligned}
\)
Comparing the Eq. (i) with the equation
\(
\begin{gathered}
A x^2+2 H x y+B y^2+2 G x+2 F y+C=0 \\
\therefore \quad A=a^2, H=-a b, B=b^2, G=-a, F=-b, C=1 \\
\text { then, } \Delta=A B C+2 F G H-A F^2-B G^2-C H^2 \\
=a^2 b^2-2 a^2 b^2-a^2 b^2-a^2 b^2-a^2 b^2 \\
=-4 a^2 b^2 \neq 0 \text { and } H^2=a^2 b^2=A B
\end{gathered}
\)
So, we have \(\Delta \neq 0\) and \(H^2=A B\).
Hence, the given equation represents a parabola.

Example 5: If the equation \(x^2-y^2-2 x+2 y+\lambda=0\) represents a degenerate conic, find the value of \(\lambda\).

Answer: For degenerate conic \(\Delta=0\)
Comparing the given equation of conic with
\(
\begin{aligned}
& a x^2+2 h x y+b y^2+2 g x+2 f y+c=0 \\
& \therefore \quad a=1, b=-1, h=0, g=-1, f=1, c=\lambda \\
& \therefore \quad \Delta=a b c+2 f g h-a f^2-b g^2-c h^2=0 \\
& \Rightarrow(1)(-1)(\lambda)+0-1 \times(1)^2+1 \times(-1)^2-\lambda(0)^2=0 \\
& \Rightarrow \quad-\lambda-1+1=0 \Rightarrow \lambda=0 \\
&
\end{aligned}
\)

Example 6: If the equation \(x^2+y^2-2 x-2 y+c=0\) represents an empty set, then find the value of \(c\).

Answer: For empty set \(\Delta \neq 0\) and \(h^2<a b\).
Now, comparing the given equation of conic with
\(
a x^2+2 h x y+b y^2+2 g x+2 f y+c^{\prime}=0
\)
then \(a=1, h=0, b=1, g=-1, f=-1, c^{\prime}=c\)
\(
\begin{array}{ll}
\because & h^2<a b \\
\therefore & 0<1 \text { which is true } \\
\text { and } & \Delta=a b c^{\prime}+2 f g h-a f^2-b g^2-c^{\prime} h^2 \neq 0 \\
\Rightarrow & (1)(1)(c)+0-1 \times(-1)^2-1 \times(-1)^2-0 \neq 0 \\
\Rightarrow & c-2 \neq 0 \\
\therefore & c \neq 2 \\
\text { Hence, } & c \in R \sim(2)
\end{array}
\)

Example 7: If the equation of conic
\(
2 x^2+x y+3 y^2-3 x+5 y+\lambda=0
\)
represent a single point, then find the value of \(\lambda\).

Answer: For single point,
\(
h^2<a b \text { and } \Delta=0
\)
Comparing the given equation with
\(
a x^2+2 h x y+b y^2+2 g x+2 f y+c=0
\)
\(
\text { then, } a=2, h=\frac{1}{2}, b=3, g=-\frac{3}{2}, f=\frac{5}{2}, c=\lambda \text {. }
\)
\(
\begin{array}{ll}
\because & h^2=\frac{1}{4}, a b=6 \\
\therefore & h^2<a b
\end{array}
\)
\(
\text { and } \quad \Delta=a b c+2 f g h-a f^2-b g^2-c h^2
\)
\(
\begin{aligned}
= & (2)(3)(\lambda)+2 \times \frac{5}{2} \times-\frac{3}{2} \times \frac{1}{2} \\
& -2 \times \frac{25}{4}-3 \times \frac{9}{4}-\lambda \times \frac{1}{4} \\
= & 6 \lambda-\frac{15}{4}-\frac{25}{2}-\frac{27}{4}-\frac{\lambda}{4} \\
= & \frac{23 \lambda}{4}-23=0 \\
\lambda & =4
\end{aligned}
\)

Example 8: For what value of \(\lambda\) the equation of conic \(2 x y+4 x-6 y+\lambda=0\) represents two intersecting straight lines, if \(\lambda=17\), then this equation represents?

Answer: Comparing the given equation of conic with
\(
\begin{aligned}
& a x^2+2 h x y+b y^2+2 g x+2 f y+c=0 \\
\therefore \quad & a=0, b=0, h=1, g=2, f=-3, c=\lambda
\end{aligned}
\)
For two intersecting lines,
\(
\begin{aligned}
& & h^2 & >a b, \Delta=0 \\
\because & & a b & =0, h=1 \\
\therefore & & h^2 & >a b
\end{aligned}
\)
\(
\text { and } \quad \Delta=a b c+2 f g h-a f^2-b g^2-c h^2
\)
\(
\begin{aligned}
& =0+2 \times-3 \times 2 \times 1-0-0-\lambda(1)^2 \\
& =-12-\lambda=0 \\
\therefore \quad \lambda & =-12
\end{aligned}
\)
For \(\lambda=17\), then the given equation of conic \(2 x y+4 x-6 y+17=0\) according to the first system but here \(c=17\).
\(
\begin{array}{ll}
\therefore & a=0, b=0, h=1, g=2, f=-3, c=17, \\
\therefore & \Delta=a b c+2 f g h-a f^2-b g^2-c h^2
\end{array}
\)
\(
\begin{aligned}
& =0+2 \times-3 \times 2 \times 1-0-0-17 \times(1)^2 \\
& =-12-17=-29 \neq 0 \\
\therefore \quad \Delta & \neq 0 \text { and } h^2>a b
\end{aligned}
\)
So, we have \(\Delta \neq 0\) and \(h^2>a b\).
Hence, the given equation represents a hyperbola.

How to Find the Centre of Conics

If \(S \equiv a x^2+2 h x y+b y^2+2 g x+2 f y+c=0\).
Partially differentiating w.r.t. \(x\) and \(y\), we get
\(
\frac{\partial S}{\partial x}=2 a x+2 h y+2 g ; \text { (Treating } y \text { as constant) }
\)
\(
\frac{\partial S}{\partial y}=2 h x+2 b y+2 f \text { (Treating } x \text { as constant) }
\)
\(
\text { For centre, } \frac{\partial S}{\partial x}=0 \text { and } \frac{\partial S}{\partial y}=0
\)
\(
\therefore \quad 2 a x+2 h y+2 g=0 \text { and } \quad 2 h x+2 b y+2 f=0
\)
\(
\Rightarrow \quad a x+h y+g=0 \text { and } \quad h x+b y+f=0
\)

Remembering Method

Since,
\(
\Delta=\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|
\)
Write first two rows,

\(
\begin{aligned}
& \therefore \quad a b-h^2, h f-b g, g h-a f \\
& \text { or points }\left(\frac{h f-b g}{a b-h^2}, \frac{g h-a f}{a b-h^2}\right) \text { or }\left(\frac{C_{13}}{C_{33}}, \frac{C_{23}}{C_{33}}\right) .
\end{aligned}
\)

\(\quad \quad \quad \quad \text { OR }\)
According to first two rows,
\(
a x+h y+g=0 \text { and } h x+b y+f=0 .
\)
After solving we get find the centre of conic.

Example 9: Find the centre of the conic
\(
14 x^2-4 x y+11 y^2-44 x-58 y+71=0
\)

Answer: Let \(f(x, y) \equiv 14 x^2-4 x y+11 y^2-44 x-58 y+71=0\)
Differentiating partially w.r.t. \(x\) and \(y\), then
\(\frac{\partial f}{\partial x}=28 x-4 y-44\) and \(\frac{\partial f}{\partial y}=-4 x+22 y-58\)
\(
\text { For centre, } \frac{\partial f}{\partial x}=0 \text { and } \frac{\partial f}{\partial y}=0 \text {, }
\)
\(
\begin{array}{r}
28 x-4 y-44=0 \\
7 x-y-11=0 \dots(i)
\end{array}
\)
and \(-4 x+22 y-58=0\)
\(
-2 x+11 y=29 \dots(ii)
\)
On solving Eqs. (i) and (ii) we get,
\(
x=2 \text { and } y=3
\)
\(\therefore\) Centre is \((2,3)\).

Alternate: Comparing the given conic with
\(
\begin{gathered}
a x^2+2 h x y+b y^2+2 g x+2 f y+c=0 \\
\therefore \quad a=14, h=-2, b=11, g=-22, f=-29, c=71
\end{gathered}
\)
\(
\therefore \quad \text { Centre }\left(\frac{h f-b g}{a b-h^2}, \frac{g h-a f}{a b-h^2}\right)
\)
\(
\begin{aligned}
& =\left(\frac{(-2)(-29)-(11)(-22)}{(14)(11)-(-2)^2}, \frac{(-22)(-2)-(14)(-29)}{(14)(11)-(-2)^2}\right) \\
& =(2,3)
\end{aligned}
\)

Parabola Definition

A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point (not on the line) in the plane. The fixed line is called the directrix of the parabola and the fixed point \(F\) is called the focus (Fig 10.13). (‘Para’ means ‘for’ and ‘bola’ means ‘throwing’, i.e., the shape described when you throw a ball in the air).

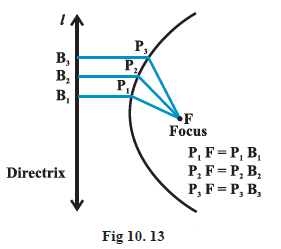
A line through the focus and perpendicular to the directrix is called the axis of the parabola. The point of intersection of parabola with the axis is called the vertex of the parabola (Fig10.14).

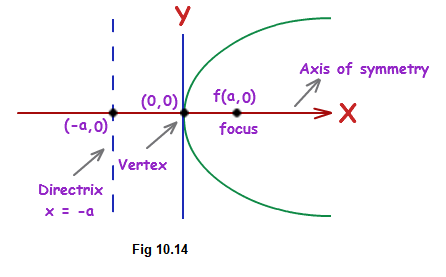
Standard Equation of Parabola

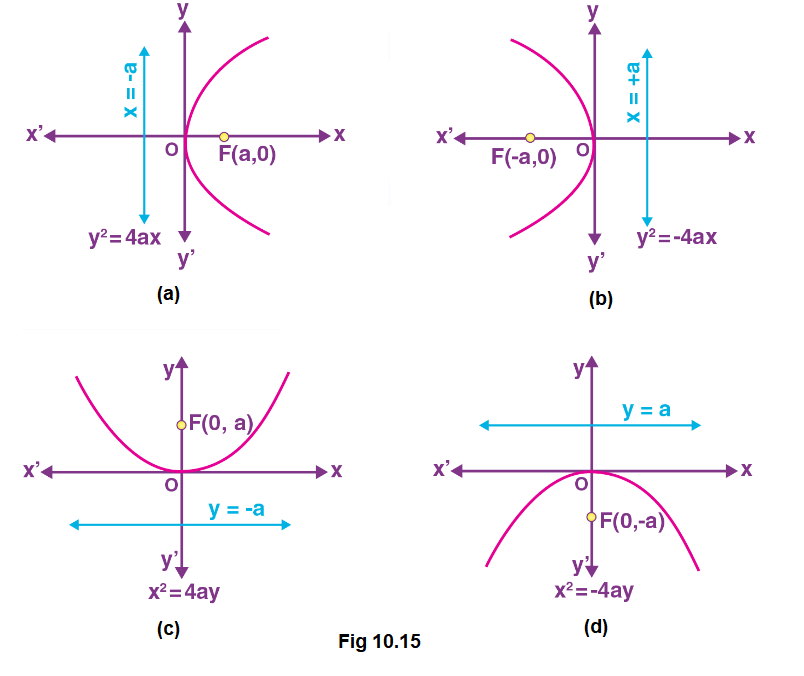
The equation of a parabola is simplest if the vertex is at the origin and the axis of symmetry is along the \(x\)-axis or \(y\)-axis. The four possible such orientations of parabola are shown below in Fig10.15 (a) to (d).

Derive Equation of Parabola

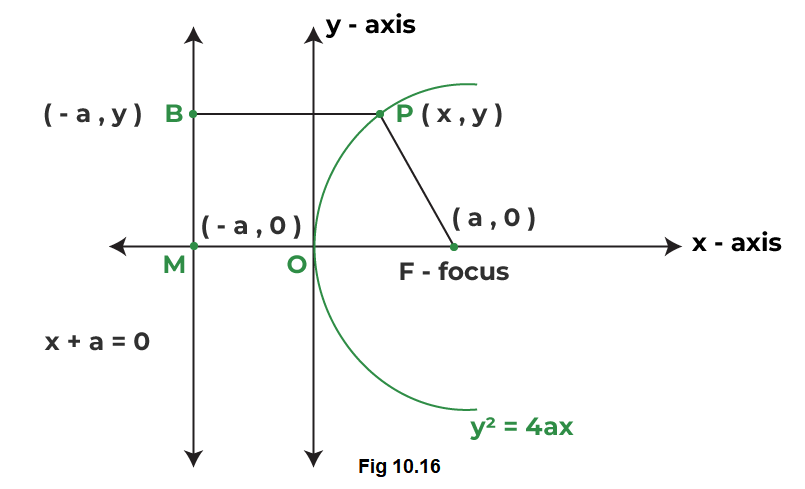
We will derive the equation for the parabola shown above in Fig 10.15 (a) with focus at \((a, 0) a>0\); and directricx \(x=-a\) as below:

Let \(F\) be the focus and \(l\) the directrix. Let \(FM\) be perpendicular to the directrix and bisect \(FM\) at the point \(O\). Produce \(MO\) to \(X\). By the definition of parabola, the mid-point \(O\) is on the parabola and is called the vertex of the parabola. Take \(O\) as origin, \(O X\) the \(x\)-axis and \(O Y\) perpendicular to it as the \(y\)-axis. Let the distance from the directrix to the focus be \(2 a\). Then, the coordinates of the focus are \((a, 0)\), and the equation of the directrix is \(x+a=0\) as in Fig10.16. Let \(P (x, y)\) be any point on the parabola such that

\(
PF = PB \dots(1)
\)
where PB is perpendicular to \(l\). The coordinates of \(B\) are \((-a, y)\). By the distance formula, we have
\(
PF =\sqrt{(x-a)^2+y^2} \text { and } PB =\sqrt{(x+a)^2}
\)
Since \(P F=P B\), we have
\(
\sqrt{(x-a)^2+y^2}=\sqrt{(x+a)^2}
\)
i.e. \((x-a)^2+y^2=(x+a)^2\)
or \(x^2-2 a x+a^2+y^2=x^2+2 a x+a^2\)
or \(y^2=4 a x(a>0)\).
Hence, any point on the parabola satisfies
\(
y^2=4 a x \dots(2)
\)
Conversely, let \(P (x, y)\) satisfy the equation (2)
\(
\begin{aligned}
PF & =\sqrt{(x-a)^2+y^2} \quad=\sqrt{(x-a)^2+4 a x} \\
& =\sqrt{(x+a)^2}= PB \dots(3)
\end{aligned}
\)
and so \(P (x, y)\) lies on the parabola.
Thus, from (2) and (3) we have proved that the equation to the parabola with vertex at the origin, focus at \((a, 0)\) and directrix \(x=-a\) is \(y^2=4 a x\).

Note: Discussion In equation (2), since \(a>0, x\) can assume any positive value or zero but no negative value and the curve extends indefinitely far into the first and the fourth quadrants. The axis of the parabola is the positive \(x\)-axis.
Similarly, we can derive the equations of the parabolas in:
Fig 11.15 (b) as \(y^2=-4 a x\),
Fig 11.15 (c) as \(x^2=4 a y\),
Fig 11.15 (d) as \(x^2=-4 a y\),
These four equations are known as standard equations of parabolas.

From the standard equations of the parabolas, Fig10.15, we have the following observations:

• Parabola is symmetric with respect to the axis of the parabola. If the equation has a \(y^2\) term, then the axis of symmetry is along the \(x\)-axis and if the equation has an \(x^2\) term, then the axis of symmetry is along the \(y\)-axis.
• When the axis of symmetry is along the \(x\)-axis the parabola opens to the
  (a) right if the coefficient of \(x\) is positive,
  (b) left if the coefficient of \(x\) is negative.
• When the axis of symmetry is along the \(y\)-axis the parabola opens
  (c) upwards if the coefficient of \(y\) is positive.
  (d) downwards if the coefficient of \(y\) is negative.

Some Terms Related to Parabola

Axis

The axis of the parabola is the straight line which is passes through focus and perpendicular to the directrix of the parabola.
For the parabola \(y^2=4 a x, X\)-axis is the axis.
Here, all powers of \(y\) are even in \(y^2=4 a x\) then, parabola \(y^2=4 a x\) is symmetrical about its axis (i.e. \(X\)-axis).
\(
\quad \quad \quad \quad \text { or }
\)
If the point \((x, y)\) lie on the parabola \(y^2=4 a x\), then the point \((x,-y)\) also lies on it. Hence, the parabola is symmetrical about \(X\)-axis (i.e. axis of parabola).

Vertex

The point of intersection of the parabola and its axis is called the vertex of the parabola. For the parabola \(y^2=4 a x\). \(A(0,0)\) i.e. the origin is the vertex.

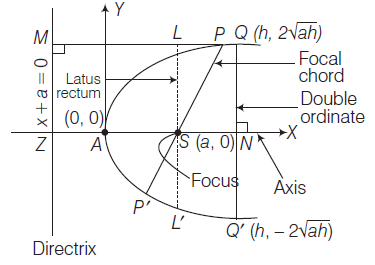
Double ordinate

If \(Q\) be the point on the parabola, draw \(Q N\) perpendicular to the axis of parabola and produced to meet the curve again at \(Q^{\prime}\), then \(Q Q^{\prime}\) is called a double ordinate.
If abscissa of \(Q\) is \(h\), then ordinate of \(Q\),
\(
y^2=4 a h \text { or } y=2 \sqrt{a h} \quad \text { (for first quadrant) }
\)
and ordinate of \(Q^{\prime}\) is \(y=-2 \sqrt{a h}\) (for fourth quadrant)
Hence, coordinates of \(Q\) and \(Q^{\prime}\) are \((h, 2 \sqrt{a h})\) and \((h,-2 \sqrt{a h})\), respectively.

Latusrectum

The double ordinate \(L L^{\prime}\) passes through the focus is called the latusrectum of the parabola.
Since focus \(S(a, 0)\) the equation of the latusrectum of the parabola is \(x=a\), then solving
\(
x=a \text { and } y^2=4 a x
\)
then, we get \(\quad y= \pm 2 a\)
Hence, the coordinates of the extremities of the latusrectum are \(L(a, 2 a)\) and \(L^{\prime}(a,-2 a)\), respectively.
Since, \(L S=L^{\prime} S=2 a\)
\(\therefore\) Length of latusrectum \(L L^{\prime}=2(L S)=2\left(L^{\prime} S\right)=4 a\).

Focal chord

A chord of a parabola which is passing through the focus is called a focal chord of the parabola. In the given figure, \(P P^{\prime}\) and \(L L^{\prime}\) are the focal chords.

Focal distance

The focal distance of any point \(P\) on the parabola is its distance from the focus \(S\) i.e. \(S P\)
Also, \(S P=P M=\) Distance of \(P\) from the directrix.
If \(\quad P \equiv(x, y)\)
then, \(\quad S P=P M=x+a\)

Parametric equations

From the equation of the parabola \(y^2=4 a x\), we can write \(\frac{y}{2 a}=\frac{2 x}{y}=t\)
where ‘ \(t\) ‘ is a parameter.
Then, \(y=2 a t\) and \(x=a t^2\)
The equations \(x=a t^2\) and \(y=2 a t\) are called parametric equations. The point \(\left(a t^2, 2 a t\right)\) is also referred to as the point ‘ \(t\) ‘.

Remarks

• Coordinates of any point on the parabola \(y^2=4 a x\), may be taken as ( \(\left.a t^2, 2 a t\right)\).
• Equation of chord joining \(t_1\) and \(t_2\) is \(2 x-\left(t_1+t_2\right) y+2 a t_1 t_2=0\).
• If the chord joining \(t_1, t_2\) and \(t_3, t_4\) pass through a point \((c, 0)\) on the axis, then \(t_1 t_2=t_3 t_4=-\frac{c}{a}\)

Other forms of Parabola with Latusrectum \(4 a\)

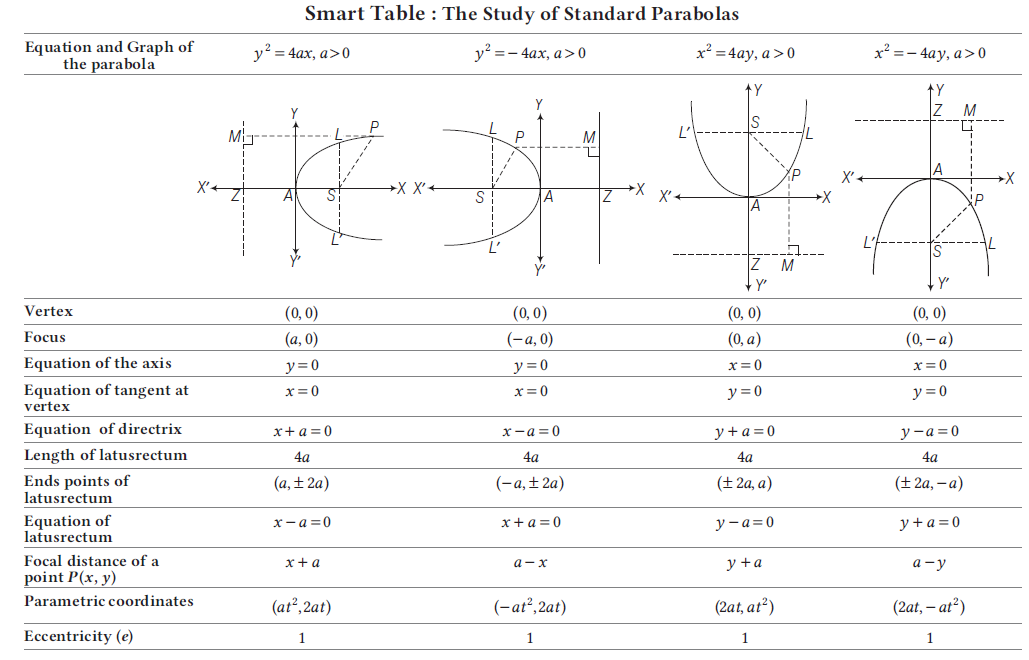
General Equation of a Parabola

Let \(S(a, b)\) be the focus, and \(l x+m y+n=0\) is the equation of the directrix. Let \(P(x, y)\) be any point on the parabola. Then by definition \(S P=P M\)

\(
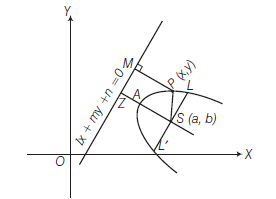
\begin{aligned}
& \Rightarrow \quad \sqrt{(x-a)^2+(y-b)^2}=\frac{|l x+m y+n|}{\sqrt{\left(l^2+m^2\right)}} \\
& \Rightarrow \quad(x-a)^2+(y-b)^2=\frac{(l x+m y+n)^2}{\left(l^2+m^2\right)}
\end{aligned}
\)
\(
\Rightarrow m^2 x^2+l^2 y^2-2 l m x y+x \text { term }+y \text { term }+ \text { constant }=0
\)

This is of the form \((m x-l y)^2+2 g x+2 f y+c=0\).
This equation is the general equation of parabola.

Remark

• Second degree terms in the general equation of a parabola forms a perfect square.

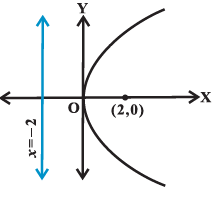
Example 10: Find the coordinates of the focus, axis, the equation of the directrix and latus rectum of the parabola \(y^2=8 x\).

Answer: The given equation involves \(y^2\), so the axis of symmetry is along the \(x\)-axis.
The coefficient of \(x\) is positive so the parabola opens to the right. Comparing with the given equation \(y^2=4 a x\), we find that \(a=2\).
Thus, the focus of the parabola is \((2,0)\) and the equation of the directrix of the parabola is \(x=-2\) (Fig below).
Length of the latus rectum is \(4 a=4 \times 2=8\).

Example 11: Find the equation of the parabola with focus \((2,0)\) and directrix \(x=-2\).

Answer: Since the focus \((2,0)\) lies on the \(x\)-axis, the \(x\)-axis itself is the axis of the parabola. Hence the equation of the parabola is of the form either \(y^2=4 a x\) or \(y^2=-4 a x\). Since the directrix is \(x=-2\) and the focus is \((2,0)\), the parabola is to be of the form \(y^2=4 a x\) with \(a=2\). Hence the required equation is \(y^2=4(2) x=8 x\)

Example 12: Find the equation of the parabola with vertex at \((0,0)\) and focus at \((0,2)\). 

Answer: Since the vertex is at \((0,0)\) and the focus is at \((0,2)\) which lies on \(y\)-axis, the \(y\)-axis is the axis of the parabola. Therefore, equation of the parabola is of the form \(x^2=4 a y\). thus, we have
\(
x^2=4(2) y \text {, i.e., } x^2=8 y \text {. }
\)

Example 13: Find the equation of the parabola which is symmetric about the \(y\)-axis, and passes through the point \((2,-3)\).

Answer: Since the parabola is symmetric about \(y\)-axis and has its vertex at the origin, the equation is of the form \(x^2=4 a y\) or \(x^2=-4 a y\), where the sign depends on whether the parabola opens upwards or downwards. But the parabola passes through \((2,-3)\) which lies in the fourth quadrant, it must open downwards. Thus the equation is of the form \(x^2=-4 a y\).
Since the parabola passes through \((2,-3)\), we have
\(
2^2=-4 a(-3) \text {, i.e., } a=\frac{1}{3}
\)
Therefore, the equation of the parabola is
\(
x^2=-4\left(\frac{1}{3}\right) y \text {, i.e., } 3 x^2=-4 y \text {. }
\)

Example 14: Find the equation of the parabola whose focus is at \((-1,-2)\) and the directrix is the straight line \(x-2 y+3=0\).

Answer: Let \(P(x, y)\) be any point on the parabola whose focus is \(S(-1,-2)\) and the directrix \(x-2 y+3=0\). Draw \(P M\) perpendicular from \(P(x, y)\) on the directrix \(x-2 y+3=0\).

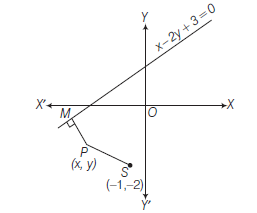
Then, by definition
\(
\begin{aligned}
& S P=P M \\
& \Rightarrow \quad(S P)^2=(P M)^2 \\
&
\end{aligned}
\)
\(
\Rightarrow(x+1)^2+(y+2)^2=\left(\frac{|x-2 y+3|}{\sqrt{(1)^2+(-2)^2}}\right)^2
\)
\(
5\left(x^2+y^2+2 x+4 y+5\right)=\left(x^2+4 y^2-4 x y+6 x-12 y+9\right)
\)
\(
\therefore \quad 4 x^2+y^2+4 x y+4 x+32 y+16=0
\)

Example 15: Find the equation of the parabola whose focus is \((-3,2)\) and the directrix is \(x+y=4\).

Answer:

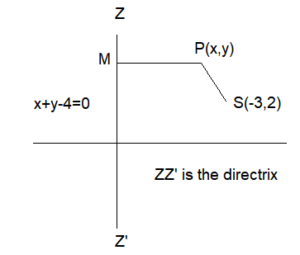
Let \(P(x, y)\) be any point on the parabola whose focus is \(S(-3,2)\) and the directrix \(x+y-4=0\). Draw \(P M\) perpendicular to \(x+y-4=0\). Then,
\(
\begin{aligned}
& S P=P M \\
& S P^2=P M^2 \\
& (x+3)^2+(y-2)^2=\left|\frac{x+y-4}{\sqrt{1+1}}\right|^2
\end{aligned}
\)
\(
\begin{aligned}
& 2\left(x^2+y^2+6 x-4 y+13\right)=\left(x^2+y^2+16+2 x y-8 x-8 y\right) \\
& x^2+y^2-2 x y+20 x+10=0
\end{aligned}
\)
Thus, the required equation of the parabola is \(x^2+y^2-2 x y+20 x+10=0\).

Example 16: Find the equation of the parabola whose focus is \((4,-3)\) and vertex is \((4,-1)\).

Answer: Let \(A(4,-1)\) be the vertex and \(S(4,-3)\) be the focus.
\(\therefore \quad\) Slope of \(A S=\frac{-3+1}{4-4}=\infty\)
which is parallel to \(Y\)-axis.
\(\therefore\) Directrix parallel to \(X\)-axis.

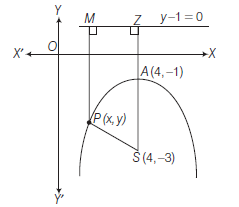
Let \(Z\left(x_1, y_1\right)\) be any point on the directrix, then \(A\) is the mid-point of \(S Z\).
\(
\begin{aligned}
& \therefore \quad 4=\frac{x_1+4}{2} \Rightarrow x_1=4 \\
& \text { and } \quad-1=\frac{y_1-3}{2} \Rightarrow y_1=1 \\
& \therefore \quad Z=(4,1) \\
&
\end{aligned}
\)
Also, directrix is parallel to \(X\)-axis and passes through \(Z(4,1)\), so equation of directrix is
\(
y=1 \text { or } y-1=0
\)
Now, let \(P(x, y)\) be any point on the parabola. Join \(S P\) and draw \(P M\) perpendicular to the directrix. Then, by definition
\(
\begin{aligned}
& S P=P M \\
& \Rightarrow \quad(S P)^2=(P M)^2 \\
& \Rightarrow \quad(x-4)^2+(y+3)^2=\left(\frac{|y-1|}{\sqrt{1^2}}\right)^2 \\
& \Rightarrow \quad(x-4)^2+(y+3)^2=(y-1)^2 \\
& \therefore \quad x^2-8 x+8 y+24=0 \\
&
\end{aligned}
\)

Alternate: Here \(a=A S=2\)
\(\therefore\) Length of latusrectum \(=4 a=8\)
Equation of parabola with vertex \((0,0)\) and open downward is \(x^2=-8 y\).
Shifting \((4,-1)\) on \((0,0)\), we get required parabola
\(
\begin{array}{rlrl}
(x-4)^2 & =-8(y+1) \\
\therefore \quad x^2-8 x+8 y+24 & =0
\end{array}
\)

Example 17: The focal distance of a point on a parabola \(y^2=8 x\) is 8 . Find it.

Answer: Comparing \(y^2=8 x\) with \(y^2=4 a x\)

\(\therefore \quad 4 a=8 \Rightarrow a=2\)
\(\therefore\) Equation of directrix is \(x+2=0\).
Let \(P\left(x_1, y_1\right)\) on the parabola
\(
y^2=8 x
\)
\(
\begin{array}{ll}
\therefore & y_1^2=8 x_1 \dots(i) \\
\because & S P=8 \\
\Rightarrow & P M=8 \quad [\because S P=P M]
\end{array}
\)
\(
\begin{array}{lll}
\Rightarrow & x_1+2 & =8 \\
\text { or } & x_1 & =6 \\
\text { From Eq. (i), } & y_1^2 & =8 \times 6 \\
\therefore & y_1 & = \pm 4 \sqrt{3}
\end{array}
\)
\(\therefore\) The required points are \((6,4 \sqrt{3})\) and \((6,-4 \sqrt{3})\).

Example 18: \(13 Q Q^{\prime}\) is a double ordinate of a parabola \(y^2=4 a x\). Find the locus of its point of trisection.

Answer: 

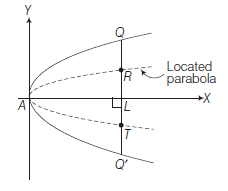
Let \(R\) and \(T\) be the points of trisection of double ordinates \(Q Q^{\prime}\). Let \((h, k)\) be the coordinates of \(R\), then,
\(
\begin{aligned}
& A L=h \quad \text { and } \quad R L=k \\
& R T=R L+L T=k+k=2 k .
\end{aligned}
\)
Since,
\(
\begin{array}{ll}
\text { Since, } & R Q=T R=Q^{\prime} T=2 k \\
\therefore & L Q=L R+R Q=k+2 k=3 k
\end{array}
\)
Thus, the coordinates of \(Q\) are \((h, 3 k)\).
Since, \((h, 3 k)\) lies on \(y^2=4 a x\)
\(
\Rightarrow \quad 9 k^2=4 a h
\)
Hence, the locus of \((h, k)\) is \(9 y^2=4 a x\).

Example 19: Find the length of the side of an equilateral triangle inscribed in the parabola \(y^2=4 a x\), so that one angular point is at the vertex.

Answer: Let \(A B C\) be the inscribed equilateral triangle, with one angular point at the vertex \(A\) of the parabola
\(
y^2=4 a x \dots(i)
\)
Let the length of the side of equilateral triangle \(=l\)
\(
\therefore \quad A B=B C=C A=l
\)

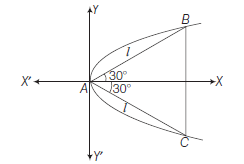
\(\therefore\) The coordinates of \(B\) is \(\left(l \cos 30^{\circ}, l \sin 30^{\circ}\right)\)
i.e., \(\quad\left(\frac{l \sqrt{3}}{2}, \frac{l}{2}\right)\).
Since, \(B\) lies on Eq. (i), then \(\left(\frac{l}{2}\right)^2=4 a\left(\frac{l \sqrt{3}}{2}\right)\) or \(l=8 a \sqrt{3}\)

Example 20: Prove that the equation of the parabola whose focus is \((0,0)\) and tangent at the vertex is \(x-y+1=0\) is \(x^2+y^2+2 x y-4 x+4 y-4=0\).

Answer: Let focus is \(S(0,0)\) and \(A\) is the vertex of the parabola take any point \(Z\) such that \(A S=A Z\) given tangent at vertex is \(x-y+1=0\), since directrix is parallel to the tangent at the vertex.

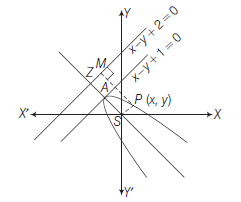
\(\therefore\) Equation of directrix is \(x-y+\lambda=0\) where, \(\lambda\) is constant.
\(\because A\) is the mid-point of \(S Z\).
\(
\begin{aligned}
& \therefore \quad S Z=2 S A \\
& \Rightarrow \quad \frac{|0-0+\lambda|}{\sqrt{\left(1^2+(-1)^2\right)}}=2 \times \frac{|0-0+1|}{\sqrt{\left(1^2+(-1)^2\right)}} \\
& \Rightarrow \quad \frac{|\lambda|}{\sqrt{2}}=\frac{2}{\sqrt{2}} \\
& \therefore \quad \lambda= \pm 2 \\
& \Rightarrow \quad \lambda=2 \\
&
\end{aligned}
\)
\([\because \lambda\) is positive since directrix in this case always lies in II quadrant]
\(\therefore\) Equation of directrix is \(x-y+2=0\).
Now, take \(P(x, y)\) be any point on the parabola, draw \(P M \perp Z M\), then from definition,
\(
\begin{aligned}
& S P=P M \\
& \Rightarrow \quad(S P)^2=(P M)^2 \\
&
\end{aligned}
\)
\(
\begin{aligned}
(x-0)^2+(y-0)^2 & =\left(\frac{|x-y+2|}{\sqrt{2}}\right)^2 \\
2\left(x^2+y^2\right) & =(x-y+2)^2 \\
2 x^2+2 y^2 & =x^2+y^2-2 x y+4 x-4 y+4
\end{aligned}
\)
\(
x^2+y^2+2 x y-4 x+4 y-4=0
\)

Equation of Parabola if Equation of axis, Tangent at Vertex and Latusrectum are given

Let equation of axis is \(a x+b y+c=0\) and equation of tangent at vertex is \(b x-a y+d=0\).

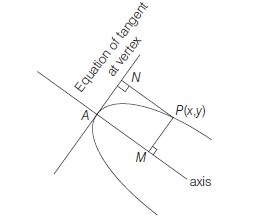
Equation of parabola is
\(
(P M)^2=(\text { Latusrectum) }(P N)
\)
\(
\Rightarrow\left(\frac{a x+b y+c}{\sqrt{\left(a^2+b^2\right)}}\right)^2=(\text { Latusrectum })\left(\frac{b x-a y+d}{\sqrt{\left(b^2+a^2\right)}}\right)
\)

Example 21: Find the equation of the parabola whose latusrectum is 4 units, axis is the line \(3 x+4 y-4=0\) and the tangent at the vertex is the line \(4 x-3 y+7=0\).

Answer: Let \(P(x, y)\) be any point on the parabola and let \(P M\) and \(P N\) are perpendiculars from \(P\) on the axis and tangent at the vertex respectively, then

\(
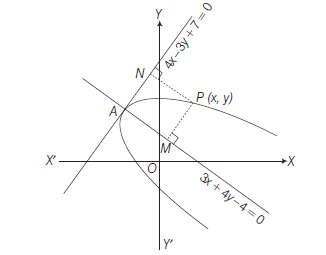
\begin{aligned}
&(P M)^2= \text { (latusrectum) }(P N) \\
& \Rightarrow \quad\left(\frac{3 x+4 y-4}{\sqrt{3^2+4^2}}\right)^2=4\left(\frac{4 x-3 y+7}{\sqrt{4^2+(-3)^2}}\right) \\
& \therefore \quad(3 x+4 y-4)^2=20(4 x-3 y+7)
\end{aligned}
\)
which is required parabola.

The Generalised form \((y-k)^2=4 a(x-h)\)
The parabola
\(
y^2=4 a x \dots(i)
\)
can be written as \((y-0)^2=4 a(x-0)\).
The vertex of this parabola is \(A(0,0)\)

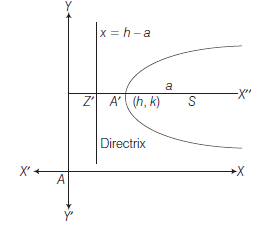
Now, when origin is shifted at \(A^{\prime}(h, k)\) without changing the direction of axes, its equation becomes
\(
(y-k)^2=4 a(x-h) \dots(ii)
\)
This is called generalised form of the parabola Eq. (i) and axis \(A^{\prime} X^{\prime \prime} \| A X\) with its vertex at \(A^{\prime}(h, k)\). Its focus is at \((a+h, k)\) and length of latusrectum \(=4 a\), the equation of the directrix is
\(
x=h-a \Rightarrow x+a-h=0
\)

Another form is \((x-h)^2=4 a(y-k)\) axis parallel to

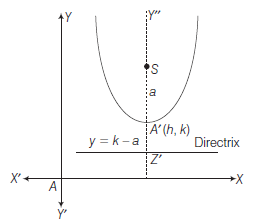
\(Y\)-axis with its vertex \((h, k)\) its focus is at \((h, a+k)\) and length of latusrectum \(=4 a\), the equation of the directrix is
\(
y=k-a \Rightarrow y+a-k=0 .
\)

Remark

• The parametric equation of \((y-k)^2=4 a(x-h)\) are \(x=h+a t^2\) and \(y=k+2 a t\).

Parabolic Curve

The equations \(y=A x^2+B x+C\) and \(x=A y^2+B y+C\) are always represents parabolas generally called parabolic curve.
Now,
\(
\begin{aligned}
y & =A x^2+B x+C \\
& =A\left\{x^2+\frac{B}{A} x+\frac{C}{A}\right\} \\
& =A\left\{\left(x+\frac{B}{2 A}\right)^2-\frac{B^2}{4 A^2}+\frac{C}{A}\right\} \\
& =A\left\{\left(x+\frac{B}{2 A}\right)^2-\frac{\left(B^2-4 A C\right)}{4 A^2}\right\}
\end{aligned}
\)
or \(\left(x+\frac{B}{2 A}\right)^2=\frac{1}{A}\left(y+\frac{B^2-4 A C}{4 A}\right)\)
Comparing it with \((x-h)^2=4 a(y-k)\) it represent a parabola with vertex at \((h, k)=\left(-\frac{B}{2 A},-\frac{B^2-4 A C}{4 A}\right)\)
and axis parallel to \(Y\)-axis and latusrectum \(=\frac{1}{|A|}\) and the curve opening upwards and downwards depending upon the sign of \(A\) and \(B\).

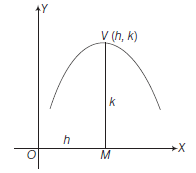
The optimum distance of its vertex \(V\) from \(O X\) is
\(
\left|-\frac{B^2-4 A C}{4 A}\right|
\)
\(
\begin{aligned}
\text { and } x & =A y^2+B y+C \\
& =A\left\{y^2+\frac{B}{A} y+\frac{C}{A}\right\} \\
& =A\left\{\left(y+\frac{B}{2 A}\right)^2-\frac{B^2}{4 A^2}+\frac{C}{A}\right\} \\
& =A\left\{\left(y+\frac{B}{2 A}\right)^2-\frac{B^2-4 A C}{4 A^2}\right\}
\end{aligned}
\)
\(
\Rightarrow\left(y+\frac{B}{2 A}\right)^2=\frac{1}{A}\left(x+\frac{B^2-4 A C}{4 A}\right)
\)
Comparing it with \((y-k)^2=4 a(x-h)\), it represent a parabola with vertex at
\(
(h, k)=\left(-\frac{B^2-4 A C}{4 A},-\frac{B}{2 A}\right)
\)
and axis parallel to \(X\)-axis and latusrectum \(=\frac{1}{|A|}\)
and the curve opening left and right depending upon the sign of \(A\) and \(B\).

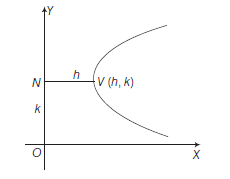
The optimum distance of its vertex \(V\) from \(O Y\) is
\(
\left|-\frac{B^2-4 A C}{4 A}\right| \text {. }
\)

Remarks

• The optimum distance of vertex from \(O X\) or \(O Y\) can be easily obtained using calculus Method.
• Equation of the parabola with axis parallel to the \(X\)-axis is of the form \(x=A y^2+B y+C\).
• Equation of the parabola with axis parallel to the \(Y\)-axis is of the form \(y=A x^2+B x+C\).

Method to Make Perfect Square

If \(\quad x=\alpha y^2 \pm \beta y+\gamma\)
first make the coefficient of \(y^2\) is unity
i.e., \(x=\alpha\left\{y^2 \pm \frac{\beta}{\alpha} y+\frac{\gamma}{\alpha}\right\}\)
Now, in braces write \(y\) and put the sign after \(y\) which between \(y^2\) and \(y\) i.e. \(\pm\) and after this sign write the half the coefficient of \(y\) i.e. \(\frac{\beta}{2 \alpha}\).
Now, write in braces \(\left(y \pm \frac{\beta}{2 \alpha}\right)^2\)
and always subtract \(\left(\frac{\beta}{2 \alpha}\right)^2=\frac{\beta^2}{4 \alpha^2}\)
\(
\begin{aligned}
\therefore \quad x & =\alpha\left\{\left(y \pm \frac{\beta}{2 \alpha}\right)^2-\frac{\beta^2}{4 \alpha^2}+\frac{\gamma}{\alpha}\right\} \\
& =\alpha\left\{\left(y \pm \frac{\beta}{2 \alpha}\right)^2-\frac{\left(\beta^2-4 \gamma \alpha\right)}{4 \alpha^2}\right\}
\end{aligned}
\)

Example 22: Find the vertex, focus, latusrectum, axis and the directrix of the parabola \(x^2+8 x+12 y+4=0\).

Answer: The equation of parabola is
\(
\begin{aligned}
& x^2+8 x+12 y+4=0 \dots(i) \\
& \Rightarrow \quad(x+4)^2-16+12 y+4=0 \\
& \Rightarrow \quad(x+4)^2-12+12 y=0 \\
& \Rightarrow \quad(x+4)^2=-12 y+12 \\
& \Rightarrow \quad(x+4)^2=-12(y-1) \\
\text { Let } & x+4=X, y-1=Y \dots(ii) \\
& \therefore \quad X^2=-12 Y \dots(iii) \\
& \therefore \quad a=3 \\
&
\end{aligned}
\)
Comparing it with \(X^2=-4 a Y\)
\(\therefore\) Vertex of Eq. (iii) is \((0,0)\)
i.e. \(X=0, Y=0\)
From Eq. (ii),
\(
\begin{aligned}
& & x+4 & =0, y-1=0 \\
& & x & =-4, y=1
\end{aligned}
\)
\(\therefore\) Vertex of Eq. (i) is \((-4,1)\).
Foucs of Eq. (iii) is \((0,-3)\)
\(
\text { i.e. } \quad X=0, Y=-3
\)
From Eq. (ii),
\(
\begin{aligned}
& & x+4 & =0, y-1=-3 \\
& \therefore & x & =-4, y=-2
\end{aligned}
\)
\(\therefore\) Focus of Eq. (i) is \((-4,-2)\).
and latusrectum \(=4 a=12\).
Equation of axis of Eq. (iii) is \(X=0\)
\(\therefore\) Equation of axis of Eq. (i) is \(x+4=0\)
Equation of directrix of Eq. (iii) is
\(
\begin{array}{rlrl}
Y & =3 \text { or } y-1=3 \\
\therefore & y-4 & =0
\end{array}
\)
\(\therefore\) Equation of directrix of Eq. (i) is
\(
y-4=0 .
\)

Example 23: Prove that the equation \(y^2+2 a x+2 b y+c=0\) represents a parabola whose axis is parallel to the axis of \(x\). Find its vertex.

Answer: The equation of parabola is
\(
\begin{aligned}
& y^2+2 a x+2 b y+c=0 \\
& (y+b)^2-b^2+2 a x+c=0 \\
& \Rightarrow \quad(y+b)^2=-2 a x+b^2-c \\
& \Rightarrow \quad(y+b)^2=-2 a\left(x-\frac{b^2-c}{2 a}\right) \dots(i)\\
& \text { Let } \quad y+b=Y, x-\frac{b^2-c}{2 a}=X \\
\text { From Eq. (i), } & Y^2=-2 a X \dots(ii) \\
&
\end{aligned}
\)
axis of its parabola is \(Y=0\)
or \(y+b=0,\)
which is parallel to \(X\)-axis
and vertex of Eq. (ii) is \(X=0, Y=0\)
\(
\begin{aligned}
& \Rightarrow \quad x-\frac{b^2-c}{2 a}=0, \quad y+b=0 \\
& \Rightarrow \quad x=\frac{b^2-c}{2 a}, \quad y=-b
\end{aligned}
\)
\(\therefore\) Vertex of given parabola is \(\left(\frac{b^2-c}{2 a},-b\right)\).

Example 24: Find the equation of the parabola with its vertex at \((3,2)\) and its focus at \((5,2)\).

Answer: Let Vertex \(A(3,2)\) and focus is \(S(5,2)\)
Slope of \(A S=\frac{2-2}{5-3}=0\), which is parallel to \(X\)-axis.
Hence, axis of parabola parallel to \(X\)-axis.

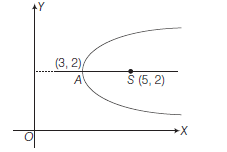
The equation is of the form
\(
\begin{aligned}
& (y-k)^2=4 a(x-h) \\
& (y-2)^2=4 a(x-3)
\end{aligned}
\)
as \((h, k)\) is the vertex \((3,2)\)
\(
\begin{aligned}
a & =\text { distance between the focus and the vertex } \\
& =\sqrt{(5-3)^2+(2-2)^2}=2
\end{aligned}
\)
Hence, the required equation is
\(
\begin{aligned}
(y-2)^2 & =8(x-3) \\
y^2-8 x-4 y-28 & =0 .
\end{aligned}
\)

Example 25: Find the equation of the parabola with latusrectum joining the points \((3,6)\) and \((3,-2)\).

Answer: Slope of \((3,6)\) and \((3,-2)\) is \(\frac{-2-6}{3-3}=\infty\), since latusrectum is perpendicular to axis. Hence, axis parallel to \(X\)-axis. The equation of the two possible parabolas will be of the form
\(
(y-k)^2= \pm 4 a(x-h) \dots(i)
\)
\(
\begin{aligned}
& \text { Since, latusrectum }=\sqrt{(3-3)^2+(6+2)^2}=8 \\
& \therefore \quad 4 a=8 \\
& \Rightarrow \quad a=2 \\
& \therefore \text { From Eq. (i), } \\
& (y-k)^2= \pm 8(x-h) \\
&
\end{aligned}
\)
Since, \((3,6)\) and \((3,-2)\) lie on the parabola, then
\(
\begin{aligned}
(6-k)^2 & = \pm 8(3-h) \\
\text { and } \quad(-2-k)^2 & = \pm 8(3-h)
\end{aligned}
\)

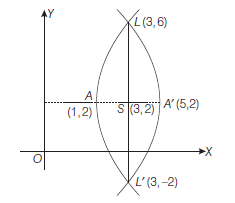
On solving Eqs. (ii) and (iii), we get
\(
k=2
\)
From Eq. (ii),
\(
\begin{aligned}
& & 16 & = \pm 8(3-h), \\
& \therefore & h & =3 \pm 2 \\
& & h & =5,1
\end{aligned}
\)
Hence, values of \((h, k)\) are \((5,2)\) and \((1,2)\).
The required parabolas are
\(
\begin{aligned}
(y-2)^2 & =8(x-5) \\
\text { and } \quad(y-2)^2 & =-8(x-1) .
\end{aligned}
\)

Example 26: Find the equation to the parabola whose axis parallel to the \(Y\)-axis and which passes through the points \((0,4)(1,9)\) and \((4,5)\) and determine its latusrectum .

Answer: The equation of parabola parallel to \(Y\)-axis is
\(
y=A x^2+B x+C \dots(i)
\)
The points \((0,4),(1,9)\) and \((4,5)\) lie on Eq. (i), then
\(
\begin{aligned}
4 & =0+0+C \Rightarrow C=4 \dots(ii) \\
\Rightarrow \quad & 9=A+B+C
\end{aligned}
\)
\(
\Rightarrow \quad 9=A+B+4 \quad[\because C=4]
\)
\(
\therefore \quad A+B=5 \dots(iii)
\)
and \(5=16 A+4 B+C \quad[\because C=4]\)
\(
\begin{array}{ll}
\Rightarrow & 5=16 A+4 B+4 \\
\therefore & 16 A+4 B=1 \\
\Rightarrow & 4 A+B=\frac{1}{4} \dots(iv)
\end{array}
\)
On solving Eqns. (iii) and (iv), we get
\(
A=-\frac{19}{12}, B=\frac{79}{12} \dots(v)
\)
On substituting the values of \(A, B\) and \(C\) from Eqs. (ii) and Eq. (v) in Eq. (i), then equation of parabola is
\(
y=-\frac{19}{12} x^2+\frac{79}{12} x+4
\)
Hence, length of latusrectum \(=\frac{1}{\left|-\frac{19}{12}\right|}=\frac{12}{19}\)

Position of a Point \(\left(x_1, y_1\right)\) with Respect to a Parabola \(y ^2=4 ax\)

Theorem: The point \(\left(x_1, y_1\right)\) lies outside, on or inside the parabola \(y^2=4 a x\) according as
\(
y_1^2-4 a x_1>,=\text {, or }<0 .
\)

Proof: Let \(P\left(x_1, y_1\right)\) be a point. From \(P\) draw \(P M \perp A X\) (on the axis of parabola) meeting the parabola \(y^2=4 a x\) at \(Q\) let the coordinate of \(Q\) be \(\left(x_1, y_2\right)\).

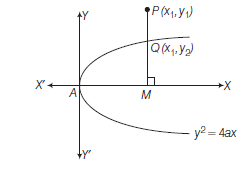
Since, \(Q\left(x_1, y_2\right)\) lies on the parabola
\(
\begin{aligned}
& y_1^2=4 a x \\
\text { then, } & y_2^2=4 a x_1 \dots(i)
\end{aligned}
\)
Now, \(P\) will be outside, on or inside the parabola \(y^2=4 a x\) according as
\(
\begin{array}{rlrl}
& P M & >,=\text { or }<Q M \\
\Rightarrow & & (P M)^2>,=\text { or }<(Q M)^2 \\
\Rightarrow & & y_1^2>,=\text {, or }<y_2^2
\end{array}
\)
\(\Rightarrow \quad y_1^2>,=\), or \(<4 a x_1 \text { [from Eq. (i)] }\)
Hence, \(\quad y_1^2-4 a x_1>,=\), or \(<0\)

Remarks

• The point \(\left(x_1, y_1\right)\) lies inside, on or outside \(y^2=-4 a x\) according as \(y_1^2+4 a x_1<=\), or \(>0\)
• The point \(\left(x_1, y_1\right)\) lies inside, on or outside \(x^2=4 a y\) according as \(x_1^2-4 a y_1<_1=\), or \(>0\)
• The point \(\left(x_1, y_1\right)\) lies inside, on or outside \(x^2=-4 a y\) according as \(x_1^2+4 a y_1<=\), or \(>0\)

Example 27: Show that the point \((2,3)\) lies outside the parabola \(y^2=3 x\).

Answer: Let the point \((h, k)=(2,3)\)
We have, \(k^2-3 h=3^2-3.2=9-6=3>0\)
\(
\therefore \quad k^2-3 h>0
\)
This shows that \((2,3)\) lies outside the parabola \(y^2=3 x\).

Example 28: Find the position of the point \((-2,2)\) with respect to the parabola \(y^2-4 y+9 x+13=0\).

Answer: Let the point \((h, k)=(-2,2)\)
We have, \(k^2-4 k+9 h+13=(2)^2\)
\(
\begin{gathered}
-4(2)+9(-2)+13=4-8-18+13=-9<0 \\
\quad k^2-4 k+9 h+13<0
\end{gathered}
\)
Hence, \(\quad k^2-4 k+9 h+13<0\)
Therefore, the point \((-2,2)\) lies inside the parabola
\(
y^2-4 y+9 x+13=0 .
\)

Parameteric Relation between the Coordinates of the Ends of a Focal Chord of a Parabola

Let \(y^2=4 a x\) be a parabola, if \(P Q\) be a focal chord.
Then, \(P \equiv\left(a t_1^2, 2 a t_1\right)\) and \(Q \equiv\left(a t_2^2, 2 a t_2\right)\)
Since, \(P Q\) passes through the focus \(S(a, 0)\).
\(
\therefore \quad Q, S, P \text { are collinear. }
\)

\(
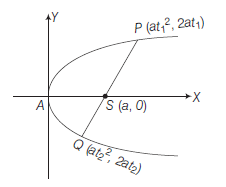
\begin{array}{ll}
\therefore & \text { Slope of } P S=\text { Slope of } Q S \\
\Rightarrow & \frac{2 a t_1-0}{a t_1^2-a}=\frac{0-2 a t_2}{a-a t_2^2} \Rightarrow \frac{2 t_1}{t_1^2-1}=\frac{2 t_2}{t_2^2-1} \\
\Rightarrow & t_1\left(t_2^2-1\right)=t_2\left(t_1^2-1\right) \\
\Rightarrow & t_1 t_2\left(t_2-t_1\right)+\left(t_2-t_1\right)=0 \\
\Rightarrow & t_2-t_1 \neq 0 \text { or } t_1 t_2+1=0 \\
\Rightarrow & t_1 t_2=-1 \text { or } t_2=-\frac{1}{t_1}, \dots(i)
\end{array}
\)
which is required relation.

Remark

• If one extremity of a focal chord is \(\left(a t_1^2, 2 a t_1\right)\) then the other extremity \(\left(a t_2^2, 2 a t_2\right)\) becomes \(\left(\frac{a}{t_1^2},-\frac{2 a}{t_1}\right)\) by virtue of relation Eq. (i).

Example 29: If the point \(\left(a t^2, 2 a t\right)\) be the extremity of a focal chord of parabola \(y^2=4 a x\) then show that the length of the focal chord is \(a\left(t+\frac{1}{t}\right)^2\).

Answer: Since, one extremity of focal chord is \(P\left(a t^2, 2 a t\right)\), then the other extremity is \(Q\left(\frac{a}{t^2},-\frac{2 a}{t}\right)\) [Replacing \(t\) by \(-1 / t\) ]

\(
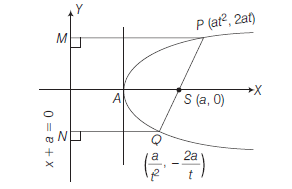
\begin{aligned}
& \therefore \text { Length of focal chord }=P Q \\
& =S P+S Q \quad[\because S P=P M \text { and } S Q=Q N] \\
& =P M+Q N \\
& =a t^2+a+\frac{a}{t^2}+a \\
&
\end{aligned}
\)
\(
=a\left(t^2+\frac{1}{t^2}+2\right)=a\left(t+\frac{1}{t}\right)^2
\)

Remark

\(\because \quad\left|t+\frac{1}{t}\right| \geq 2\) for all \(t \neq 0\) \([\because AM \geq GM ]\)
\(
\therefore \quad a\left(t+\frac{1}{t}\right)^2 \geq 4 a
\)
\(\Rightarrow\) Length of focal chord \(\geq\) latusrectum i.e. The length of smallest focal chord of the parabola is \(4 a\). Hence, the latusrectum of a parabola is the smallest focal chord.

Example 30: Prove that the semi-latusrectum of the parabola \(y^2=4 a x\) is the harmonic mean between the segments of any focal chord of the parabola.

Answer: Let parabola be \(y^2=4 a x\)
If \(P Q\) be the focal chord, if
\(
P \equiv\left(a t^2, 2 a t\right) \text { then } Q \equiv\left(\frac{a}{t^2}, \frac{-2 a}{t}\right)
\)
\(\therefore\) Length of latusrectum \(L L^{\prime}=4 a\).
\(\therefore\) Semi-latusrectum \(=\frac{1}{2}(4 a)=2 a\).
If sections of focal chord are \(k_1\) and \(k_2\),
then, \(\quad k_1=S P=P M=a+a t^2=a\left(1+t^2\right)\)
and \(\quad k_2=S Q=Q N=a+\frac{a}{t^2}=\frac{a\left(1+t^2\right)}{t^2}\)

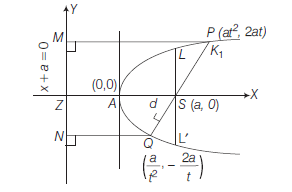
\(\therefore\) Harmonic mean of \(k_1\)
\(
\begin{aligned}
\text { and } \quad k_2 & =\frac{2 k_1 k_2}{k_1+k_2} \\
& =\frac{2}{\frac{1}{k_2}+\frac{1}{k_1}}=\frac{2}{\frac{t^2}{a\left(1+t^2\right)}+\frac{1}{a\left(1+t^2\right)}} \\
& =\frac{2}{\frac{1}{a}}=2 a=\text { Semi-latusrectum. }
\end{aligned}
\)

Remarks

• The length of focal chord having parameters \(t_1\) and \(t_2\) for its end points is \(a\left(t_2-t_1\right)^2\)
• If \(l_1\) and \(l_2\) are the length of segments of a focal chord of a parabola, then its latusrectum is \(\frac{4 l_1 l_2}{l_1+l_2}\).

Example 31: Show that the focal chord of parabola \(y^2=4 a x\) makes an angle \(\alpha\) with the \(X\)-axis is of length \(4 a \operatorname{cosec}^2 \alpha\).

Answer: Let \(P\left(a t_1^2, 2 a t_1\right)\) and \(Q\left(a t_2^2, 2 a t_2\right)\) be the end points of a focal chord \(P Q\) which makes an angle \(\alpha\) with the axis of the parabola. Then,
\(
P Q=a\left(t_2-t_1\right)^2
\)
\(
\begin{aligned}
&\begin{aligned}
& =a\left[\left(t_2+t_1\right)^2-4 t_1 t_2\right] \dots(i)\\
& =a\left[\left(t_2+t_1\right)^2+4\right] &\left[\because t_1 t_2=-1\right]
\end{aligned}\\
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \quad \tan \alpha=\text { slope of } P Q \\
& =\frac{2 a t_2-2 a t_1}{a t_2^2-a t_1^2} \\
& \Rightarrow \quad \tan \alpha=\frac{2}{t_2+t_1} \\
& \Rightarrow \quad t_2+t_1=2 \cot \alpha \dots(ii) \\
&
\end{aligned}
\)
On substituting the value of \(t_2+t_1\) from Eq. (ii) in Eq. (i), then
\(
\begin{aligned}
P Q & =a\left(4 \cot ^2 \alpha+4\right) \\
& =4 a \operatorname{cosec}^2 \alpha .
\end{aligned}
\)

Example 32: Prove that the length of a focal chord of a parabola varies inversely as the square of its distance from the vertex.

Answer: Let \(P\left(a t^2, 2 a t\right)\) be one end of a focal chord of the parabola \(y^2=4 a x\). The focus of its parabola is \(S(a, 0)\).

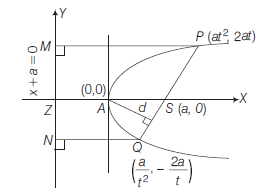
\(\therefore\) Equation of focal chord is (i.e. equation of \(P S\) )
\(
y-0=\frac{2 a t-0}{a t^2-a}(x-a)
\)
\(
\begin{array}{ll}
\Rightarrow & y=\frac{2 t}{\left(t^2-1\right)}(x-a) \\
\Rightarrow & \left(t^2-1\right) y=2 t x-2 a t \\
\Rightarrow & 2 t x-\left(t^2-1\right) y-2 a t=0
\end{array}
\)
If \(d\) be the distance of this focal chord from the vertex \((0,0)\) of the parabola \(y^2=4 a x\), then
\(
d=\frac{|0-0-2 a t|}{\sqrt{(2 t)^2+\left(t^2-1\right)^2}}
\)
\(
\begin{aligned}
& =\frac{|2 a t|}{\left(t^2+1\right)}=\frac{2 a}{\left|t+\frac{1}{t}\right|} \\
\Rightarrow \quad d^2 & =\frac{4 a^2}{\left(t+\frac{1}{t}\right)^2} \dots(i)
\end{aligned}
\)
The other end of the focal chord is \(Q\left(\frac{a}{t^2},-\frac{2 a}{t}\right)\)
If length of focal chord \(=P Q=(l\) say \()\)
\(
\begin{aligned}
& \therefore \quad l=P Q=P S+S Q=P M+Q N \\
& \therefore \quad l=a t^2+a+\frac{a}{t^2}+a \\
& \Rightarrow \quad l=a\left(t^2+\frac{1}{t^2}+2\right) \Rightarrow l=a\left(t+\frac{1}{t}\right)^2 \\
&
\end{aligned}
\)
\(
\Rightarrow \quad \frac{l}{a}=\left(t+\frac{1}{t}\right)^2 \dots(ii)
\)
From Eqns. (i) and (ii), \(d^2=\frac{4 a^2}{(l / a)}=\frac{4 a^3}{l}\)
\(
\therefore \quad l=\frac{4 a^3}{d^2} \Rightarrow l \propto \frac{1}{d^2}
\)
i.e. the length of the focal chord varies inversely as the square of its distance from vertex.

Intersection of a Line and a Parabola

Let the parabola be
\(
y^2=4 a x \dots(i)
\)
and the given line be \(\quad y=m x+c \dots(ii)\)
On eliminating \(x\) from Eqs. (i) and (ii), then
\(
\begin{aligned}
y^2 & =4 a\left(\frac{y-c}{m}\right) \\
\Rightarrow \quad m y^2-4 a y+4 a c & =0 \dots(iii)
\end{aligned}
\)
This equation being quadratic in \(y\), gives two values of \(y\), shows that every straight line will cut the parabola in two points may be real, coincident or imaginary according as discriminant of Eq. (iii) \(>,=<0\)
i.e. \((-4 a)^2-4 \cdot m \cdot 4 a c>,=,<0 \quad\) or \(a-m c>,=,<0\)
\(
a>,=,<m c \dots(iv)
\)

Condition of tangency

If the line Eq. (ii) touches the parabola Eq. (i), then Eq. (iii) has equal roots
\(\therefore\) Discriminant of Eq. (iii) \(=0\)
\(
\Rightarrow \quad(-4 a)^2-4 m \cdot 4 a c=0
\)
\(
\Rightarrow \quad c=\frac{a}{m}, m \neq 0 \dots(v)
\)
So, the line \(y=m x+c\) touches the parabola \(y^2=4 a x\) if \(c=\frac{a}{m}\) (which is condition of tangency).
Substituting the value of \(c\) from Eq. (v) in Eq. (ii), then
\(
y=m x+\frac{a}{m}, m \neq 0
\)
Hence, the line \(y=m x+\frac{a}{m}\) will always be a tangent to the parabola \(y^2=4 a x\).
The point of contact Substituting \(c=\frac{a}{m}\) in Eq. (iii), then
\(
\begin{aligned}
& m y^2-4 a y+4 a\left(\frac{a}{m}\right)=0 \\
& m^2 y^2-4 a m y+4 a^2=0 \\
&(m y-2 a)^2=0 \\
& m y-2 a=0 \\
& y=\frac{2 a}{m}
\end{aligned}
\)
Substituting this value of \(y\) in \(y=m x+\frac{a}{m}\)
\(\therefore \quad \frac{2 a}{m}=m x+\frac{a}{m}\)
\(
\Rightarrow \quad m x=\frac{a}{m} \text { or } x=\frac{a}{m^2}
\)
Hence, the point of contact is \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right),(m \neq 0)\) this known as \(m\)-point on the parabola.

Remark

• If \(m=0\), then Eq. (iii) gives
  \(
  \begin{aligned}
  & 0-4 a y+4 a c =0 \\
  \Rightarrow & y =c
  \end{aligned}
  \)
  which gives only one value of \(y\) and so every line parallel to \(x\)-axis cuts the parabola only in one real point.

Example 33: Prove that the straight line \(1 x+m y+n=0\) touches the parabola \(y^2=4 a x\), if \(\ln =a m^2\).

Answer: The given line is \(l x+m y+n=0\)
or \(\quad y=-\frac{l}{m} x-\frac{n}{m} \dots(i)\)
Comparing this line with \(y=M x+c\)
\(\therefore \quad M=-\frac{l}{m} \quad\) and \(\quad c=-\frac{n}{m}\)
The line Eq. (i) will touch the parabola \(y^2=4 a x\), if
\(
c=\frac{a}{M} \Rightarrow c M=a
\)
\(
\begin{aligned}
\left(-\frac{n}{m}\right)\left(-\frac{l}{m}\right) & =a \\
\ln & =a m^2
\end{aligned}
\)

Example 34: Show that the line \(x \cos \alpha+y \sin \alpha=p\)
touches the parabola \(y^2=4 a x\), if \(p \cos \alpha+a \sin ^2 \alpha=0\) and that the point of contact is \(\left(a \tan ^2 \alpha,-2 a \tan \alpha\right)\).

Answer: The given line is
\(
\begin{aligned}
& x \cos \alpha+y \sin \alpha=p \\
& \Rightarrow \quad y=-x \cot \alpha+p \operatorname{cosec} \alpha \\
&
\end{aligned}
\)
Comparing this line with \(y=m x+c\).
\(\therefore \quad m=-\cot \alpha\) and \(c=p \operatorname{cosec} \alpha\)
since, the given line touches the parabola
\(
\begin{aligned}
& \therefore \quad c=\frac{a}{m} \text { or } c m=a \\
& \Rightarrow \quad(p \operatorname{cosec} \alpha)(-\cot \alpha)=a \\
& \Rightarrow \quad a \sin ^2 \alpha+p \cos \alpha=0 \\
& \text { and point of contact is }\left(\frac{a}{m^2}, \frac{2 a}{m}\right) \\
&
\end{aligned}
\)
i.e. \(\left(\frac{a}{\cot ^2 \alpha},-\frac{2 a}{\cot \alpha}\right)\)
or \(\left(a \tan ^2 \alpha,-2 a \tan \alpha\right)\)

Example 35: Prove that the line \(\frac{x}{1}+\frac{y}{m}=1\) touches the parabola \(y^2=4 a(x+b)\), if \(m^2(l+b)+a l^2=0\).

Answer: The given parabola is
\(
y^2=4 a(x+b) \dots(i)
\)
Vertex of this parabola is \((-b, 0)\).
Now, shifting \((0,0)\) at \((-b, 0)\),
then, \(x=X+(-b)\) and \(y=Y+0\)
or \(\quad x+b=X\) and \(y=Y \dots(ii)\)
From Eq. (i), \(Y^2=4 a X \dots(iii)\)
and the line \(\frac{x}{l}+\frac{y}{m}=1\)
\(
\begin{array}{ll}
\text { reduces to } & \frac{X-b}{l}+\frac{Y}{m}=1 \\
& Y=m\left(1-\frac{X-b}{l}\right) \\
\Rightarrow \quad & Y=\left(-\frac{m}{l}\right) X+m\left(1+\frac{b}{l}\right) \dots(iv)
\end{array}
\)
The line Eq. (iv) will touch the parabola Eq. (iii), if
\(
m\left(1+\frac{b}{l}\right)=\frac{a}{\left(-\frac{m}{l}\right)}
\)
\(
\begin{aligned}
\frac{m^2}{l}\left(1+\frac{b}{l}\right) & =-a \\
m^2(l+b)+a l^2 & =0
\end{aligned}
\)

Example 36: Find the equations of the straight lines touching both \(x^2+y^2=2 a^2\) and \(y^2=8 a x\).

Answer: The given curves are

\(
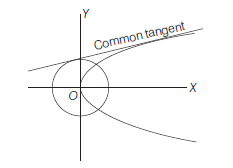
x^2+y^2=2 a^2 \dots(i)
\)
and \(y^2=8 a x \dots(ii)\)
The parabola Eq. (ii) is \(y^2=8 a x\)
or \(y^2=4(2 a) x\)
\(\therefore\) Equation of tangent of Eq. (ii) is
\(
y=m x+\frac{2 a}{m}
\)
\(
\text { or } \quad m^2 x-m y+2 a=0 \dots(iii)
\)
It is also tangent of Eq. (i), then the length of perpendicular from centre of Eq. (i) i.e. \((0,0)\) to Eq. (iii) must be equal to the radius of Eq. (i) i.e. \(a \sqrt{2}\).
\(
\begin{aligned}
& \therefore \quad \frac{|0-0+2 a|}{\sqrt{\left(m^2\right)^2+(-m)^2}}=a \sqrt{2} \Rightarrow \frac{4 a^2}{m^4+m^2}=2 a^2 \\
& \Rightarrow \quad m^4+m^2-2=0 \\
& \Rightarrow \quad\left(m^2+2\right)\left(m^2-1\right)=0 \\
& \because \quad m^2+2 \neq 0 \quad \text { [gives the imaginary values] } \\
& \therefore \quad m^2-1=0 \\
& \Rightarrow \quad m= \pm 1 \\
&
\end{aligned}
\)
Hence, from Eq. (iii) the required tangents are
\(
x \pm y+2 a=0
\)

Equation of Tangent in Different Forms

Point Form :

To find the equation of the tangent to the parabola \(y^2=4 a x\) at the point \(\left(x_1, y_1\right)\).
(First Principal Method) Equation of parabola is
\(
y^2=4 a x \dots(i)
\)
Let \(P \equiv\left(x_1, y_1\right)\) and \(Q \equiv\left(x_2, y_2\right)\) be any two points on parabola (i), then

\(
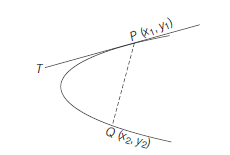
\begin{aligned}
& y_1^2=4 a x_1 \dots(ii) \\
\text { and } & y_2^2=4 a x_2 \dots(iii) \\
&
\end{aligned}
\)
Subtracting Eq. (ii) from Eq. (iii), then
\(
\begin{aligned}
y_2^2-y_1^2 & =4 a\left(x_2-x_1\right) \\
\Rightarrow \quad \frac{y_2-y_1}{x_2-x_1} & =\frac{4 a}{y_2+y_1} \dots(iv)
\end{aligned}
\)
Equation of \(P Q\) is
\(
y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right) \dots(v)
\)
From Eqs. (iv) and (v), then
\(
y-y_1=\frac{4 a}{y_2+y_1}\left(x-x_1\right) \dots(vi)
\)
Now, for tangent at \(P, Q \rightarrow P\), i.e. \(x_2 \rightarrow x_1\) and \(y_2 \rightarrow y_1\), then Eq. (vi) becomes
\(
y-y_1=\frac{4 a}{2 y_1}\left(x-x_1\right) \Rightarrow y y_1-y_1^2=2 a x-2 a x_1
\)
\(
\begin{aligned}
& y y_1=2 a x+y_1^2-2 a x_1 \\
& y y_1=2 a x+4 a x_1-2 a x_1 \quad \text { [from Eq. (ii)] } \\
& y y_1=2 a x+2 a x_1 \\
& y y_1=2 a\left(x+x_1\right),
\end{aligned}
\)
which is the required equation of tangent at \(\left(x_1, y_1\right)\).

Remarks

• The equation of tangent at \(\left(x_1, y_1\right)\) can also be obtained by replacing \(x^2\) by \(x x_1, y^2\) by \(y y_1, x\) by \(\frac{x+x_1}{2}, y\) by \(\frac{y+y_1}{2}\) and \(x y\) by \(\frac{x y_1+x_1 y}{2}\) and without changing the constant (if any) in the equation of curve. This method is apply only when the equations of parabola is polynomial of second degree in \(x\) and \(y\).
• Equation of tangents of all standard parabolas at \(\left(x_1, y_1\right)\).
  \(
  \begin{array}{ll}
  \hline \text { Equations of Parabolas } & \text { Tangent at }\left( x _{ 1 }, y _{ 1 }\right) \\
  \hline y^2=4 a x & y y_1=2 a\left(x+x_1\right) \\
  \hline y^2=-4 a x & y y_1=-2 a\left(x+x_1\right) \\
  \hline x^2=4 a y & x x_1=2 a\left(y+y_1\right) \\
  \hline x^2=-4 a y & x x_1=-2 a\left(y+y_1\right) \\
  \hline
  \end{array}
  \)

Parametric Form :

To find the equation of tangent to the parabola \(y^2=4 a x\) at the point \(\left(a t^2, 2 a t\right)\) or ‘ \(t\) ‘.
Since, the equation of tangent of the parabola \(y^2=4 a x\) at \(\left(x_1, y_1\right)\) is \(y y_1=2 a\left(x+x_1\right)\) replacing \(x_1\) by \(a t^2\) and \(y_1\) by 2at, then Eq. (i) becomes
\(
y(2 a t)=2 a\left(x+a t^2\right) \Rightarrow t y=x+a t^2
\)

Remark

The equations of tangent of all standard parabolas at ‘ \(t\) ‘.
\(
\begin{array}{lll}
\hline \text { Equations of Parabolas } & \text { Parametric Coordinates t} & \text { Tangent at t} \\
\hline y^2=4 a x & \left(a t^2, 2 a t\right) & t y=x+a t^2 \\
\hline y^2=-4 a x & \left(-a t^2, 2 a t\right) & t y=-x+a t^2 \\
\hline x^2=4 a y & \left(2 a t, a t^2\right) & t x=y+a t^2 \\
\hline x^2=-4 a y & \left(2 a t,-a t^2\right) & t x=-y+a t^2 \\
\hline
\end{array}
\)

Slope Form :

To find the equation of tangent and point of contact in terms of \(m\) (slope) to the parabola \(y^2=4 a x\).
The equation of tangent to the parabola \(y^2=4 a x\) at \(\left(x_1, y_1\right)\) is \(y y_1=2 a\left(x+x_1\right) \dots(i)\).
Since, \(m\) is the slope of the tangent, then
\(
m=\frac{2 a}{y_1} \Rightarrow y_1=\frac{2 a}{m}
\)
Since, \(\left(x_1, y_1\right)\) lies on \(y^2=4 a x\), therefore
\(
\begin{aligned}
& y_1^2=4 a x_1 \Rightarrow \frac{4 a^2}{m^2}=4 a x_1 \\
\therefore & x_1=\frac{a}{m^2}
\end{aligned}
\)
Substituting the values of \(x_1\) and \(y_1\) in Eq. (i), we get
\(
y=m x+\frac{a}{m} \dots(ii)
\)
Thus, \(y=m x+\frac{a}{m}\) is a tangent to the parabola \(y^2=4 a x\), where, \(m\) is the slope of the tangent. The coordinates of the point of contact are \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\). Comparing Eq. (ii) with \(y=m x+c\),
\(
c=\frac{a}{m}
\)
which is condition of tangency.
when, \(y=m x+c\) is the tangent of \(y^2=4 a x\).

Remark

The equation of tangent, condition of tangency and point of contact in terms of slope \((m)\) of all standard parabolas.

\(
\begin{array}{llll}
\hline \text { Equations of Parabolas } & \text { Point of contact in terms of slope (m)} & \text { Equation of tangent in terms of slope (m)} & \text { Condition of tangency } \\
\hline y^2=4 a x & \left(\frac{a}{m^2}, \frac{2 a}{m}\right) & y=m x+\frac{a}{m} & c=\frac{a}{m} \\
\hline y^2=-4 a x & \left(-\frac{a}{m^2}, \frac{2 a}{m}\right) & y=m x-\frac{a}{m} & c=-\frac{a}{m} \\
\hline x^2=4 a y & \left(2 a m, a m^2\right) & y=m x-a m^2 & c=-a m^2 \\
\hline x^2=-4 a y & \left(2 a m,-a m^2\right) & y=m x+a m^2 & c=a m^2 \\
\hline(y-k)^2=4 a(x-h) & \left(h+\frac{a}{m^2}, k+\frac{2 a}{m}\right) & y=m x-m h+k+\frac{a}{m} & c+m h=k+\frac{a}{m} \\
\hline(y-k)^2=-4 a(x-h) & \left(h-\frac{a}{m^2}, k+\frac{2 a}{m}\right) & y=m x-m h+k-a m^2 & c+m h=k-\frac{a}{m} \\
\hline(x-h)^2=4 a(y-k) & \left(h+2 a m, k+a m^2\right) & y=m x-m h+k+a m^2 & c+m h=k+a m^2 \\
\hline
\end{array}
\)

Point of Intersection of Tangents at any two Points on the Parabola

Let the parabola be \(y^2=4 a x\)
let two points on the parabola are
\(
P \equiv\left(a t_1^2, 2 a t_1\right) \text { and } Q \equiv\left(a t_2^2, 2 a t_2\right) \text {. }
\)
Equation of tangents at \(P\left(a t_1^2, 2 a t_1\right)\)
and \(Q\left(a t_2^2, 2 a t_2\right)\)
are \(t_1 y=x+a t_1^2 \dot(i)\)
and \(t_2 y=x+a t_2^2 \dots(ii)\)

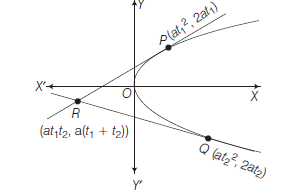
On solving these equations, we get \(x=a t_1 t_2, y=a\left(t_1+t_2\right)\) Thus, the coordinates of the point of intersection of tangents at
\(
\left(a t_1^2, 2 a t_1\right) \text { and }\left(a t_2^2, 2 a t_2\right) \text { are }\left(a t_1 t_2, a\left(t_1+t_2\right)\right) \text {. }
\)

Remarks

• The geometric mean of the \(x\)-coordinates of \(P\) and \(Q\) (i.e. \(\sqrt{a t_1^2 \times a t_2^2}=a t_1 t_2\) ) is the \(x\)-coordinate of the point of intersection of tangents at \(P\) and \(Q\) on the parabola. If \(P\) and \(Q\) are the ends points of focal chord, then \(x\)-coordinate of point of intersection of tangents at \(P\) and \(Q\) is \(\left(-a t_1 t_2\right)\).
• The arithmetic mean of the \(y\)-coordinates of \(P\) and \(Q\) \(\left(\right.\) i.e. \(\left.\frac{2 a t_1+2 a t_2}{2}=a\left(t_1+t_2\right)\right)\) is the \(y\)-coordinate of the point of intersection of tangents at \(P\) and \(Q\) on the parabola.

Example 37: Find the equation of the common tangents to the parabola \(y^2=4 a x\) and \(x^2=4 b y\).

Answer: The equation of any tangent in terms of slope \((m)\) to the parabola \(y^2=4 a x\) is
\(
y=m x+\frac{a}{m} \dots(i)
\)
If this line is also tangent to the parabola \(x^2=4 a y\), then Eq. (i) meets \(x^2=4 b y\) in two coincident points.
Substituting the value of \(y\) from Eq. (i) in \(x^2=4 b y\), we get
\(
\begin{aligned}
& x^2=4 b\left(m x+\frac{a}{m}\right) \\
& \Rightarrow \quad x^2-4 b m x-\frac{4 a b}{m}=0
\end{aligned}
\)
The roots of this quadratic are equal provided
\(
\begin{aligned}
& B^2=4 A C \\
& \text { i.e., } \quad(-4 b m)^2=4 \cdot 1\left(\frac{-4 a b}{m}\right) \\
& \Rightarrow \quad 16 b^2 m^3+16 a b=0, m \neq 0 \\
& \text { or } \\
& m^3=-a / b \\
& \therefore \quad m=-a^{1 / 3} / b^{1 / 3} \\
&
\end{aligned}
\)
Substituting the value of \(m\) in Eq. (i) the required equation is
\(
y=-\frac{a^{1 / 3}}{b^{1 / 3}} x-\frac{a b^{1 / 3}}{a^{1 / 3}}
\)
\(
\begin{array}{r}
y=-\frac{a^{1 / 3}}{b^{1 / 3}} x-a^{2 / 3} b^{1 / 3} \\
a^{1 / 3} x+b^{1 / 3} y+a^{2 / 3} b^{2 / 3}=0
\end{array}
\)

Example 38: The tangents to the parabola \(y^2=4 a x\) make angle \(\theta_1\) and \(\theta_2\) with \(X\)-axis. Find the locus of their point of intersection, if \(\cot \theta_1+\cot \theta_2=c\).

Answer: Let the equation of any tangent to the parabola \(y^2=4 a x\) is
\(
y=m x+(a / m) \dots(i)
\)
Let \(\left(x_1, y_1\right)\) be the point of intersection of the tangents to \(y^2=4 a x\), then Eq. (i) passes through \(\left(x_1, y_1\right)\).
\(
\begin{array}{ll}
\therefore & y_1=m x_1+(a / m) \\
\text { or } & m^2 x_1-m y_1+a=0
\end{array}
\)
Let \(m_1\) and \(m_2\) be the roots of this quadratic equation, then
\(
m_1+m_2=y_1 / x_1 \quad \text { and } \quad m_1 m_2=a / x_1
\)
\(
\begin{aligned}
& \text { or } \quad \tan \theta_1+\tan \theta_2=y_1 / x_1 \\
& \text { and } \quad \tan \theta_1 \tan \theta_2=a / x_1 \dots(ii) \\
&
\end{aligned}
\)
Now, \(\quad \cot \theta_1+\cot \theta_2=c \quad\) (given)
\(
\begin{aligned}
\frac{1}{\tan \theta_1}+\frac{1}{\tan \theta_2} & =c \\
\frac{\tan \theta_1+\tan \theta_2}{\tan \theta_1 \tan \theta_2} & =c \quad \text { [from Eq. (ii)] } \\
\frac{y_1 / x_1}{a / x_1} & =c \\
y_1 & =a c
\end{aligned}
\)
The required locus is \(y=a c\), which is a line parallel to \(X\)-axis.

Example 39: Show that the locus of the points of intersection of the mutually perpendicular tangents to a parabola is the directrix of the parabola.

Answer: Let the points \(P\left(a t_1^2, 2 a t_1\right)\) and \(Q\left(a t_2^2, 2 a t_2\right)\) on the parabola \(y^2=4 a x\) tangents at \(P\) and \(Q\) are
\(
t_1 y=x+a t_1^2 \dots(i)
\)
\(
\text { and } t_2 y=x+a t_2^2 \dots(ii)
\)

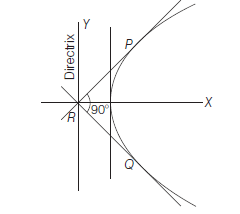
\(\because\) Point of intersection of these tangents is \(\left(a t_1 t_2, a\left(t_1+t_2\right)\right)\)
Let this point is \((h, k)\),
then,
\(
\begin{aligned}
& h=a t_1 t_2 \dots(iii) \\
\text { and } & k=a\left(t_1+t_2\right) \dots(iv)
\end{aligned}
\)
Slope of tangents Eqs. (i) and (ii) are \(\frac{1}{t_1}\) and \(\frac{1}{t_2}\), respectively.
Since, tangents are perpendicular, then
\(
\frac{1}{t_1} \times \frac{1}{t_2}=-1
\)
or \(t_1 t_2=-1 \dots(v)\)
From Eqs. (iii) and (v), we get
\(
h=-a \text { or } h+a=0
\)
\(\therefore\) Locus of the point of intersection of tangents is
\(
x+a=0
\)
which is directrix of \(y^2=4 a x\).

Remark

• Locus of the point of intersection of the perpendicular tangents to the parabola \(y^2=4 a x\) is called the director circle. Its equation is \(x+a=0\), which is parabola’s own directrix.

Example 40: The tangents to the parabola \(y^2=4 a x\) at \(P\left(a t_1^2, 2 a t_1\right)\) and \(Q\left(a t_2^2, 2 a t_2\right)\) intersect at \(R\). Prove that the area of the \(\triangle P Q R\) is \(\frac{1}{2} a^2\left|\left(t_1-t_2\right)\right|^3\).

Answer: Equations of tangents at \(P\left(a t_1^2, 2 a t_1\right)\) and \(Q\left(a t_2^2, 2 a t_2\right)\) are
\(
\begin{aligned}
t_1 y & =x+a t_1^2 \dots(i) \\
\text { and } \quad t_2 y & =x+a t_2^2 \dots(ii)
\end{aligned}
\)

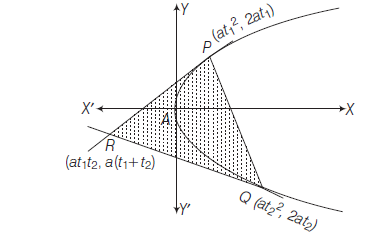
Since, point of intersect of Eqs. (i) and (ii) is \(R\left(a t_1 t_2, a\left(t_1+t_2\right)\right)\).
\(
\therefore \text { Area of } \triangle P Q R=\frac{1}{2}\left|\begin{array}{ccc}
a t_1^2 & 2 a t_1 & 1 \\
a t_2^2 & 2 a t_2 & 1 \\
a t_1 t_2 & a\left(t_1+t_2\right) & 1
\end{array}\right|
\)
Applying \(R_2 \rightarrow R_2-R_1\) and \(R_3 \rightarrow R_3-R_1\)
\(
=\frac{1}{2}\left|\begin{array}{ccc}
a t_1^2 & 2 a t_1 & 1 \\
a\left(t_2^2-t_1^2\right) & 2 a\left(t_2-t_1\right) & 0 \\
a t_1\left(t_2-t_1\right) & a\left(t_2-t_1\right) & 0
\end{array}\right|
\)
Expanding with respect to first row
\(
\begin{aligned}
& =\frac{1}{2}\left|\begin{array}{cc}
a\left(t_2^2-t_1^2\right) & 2 a\left(t_2-t_1\right) \\
a t_1\left(t_2-t_1\right) & a\left(t_2-t_1\right)
\end{array}\right| \\
& =\frac{1}{2} a^2\left(t_2-t_1\right)^2\left|\begin{array}{cc}
t_2+t_1 & 2 \\
t_1 & 1
\end{array}\right| \\
& =\frac{1}{2} a^2\left(t_1-t_2\right)^2\left|\left(t_2-t_1\right)\right| \\
& =\frac{1}{2} a^2\left(t_1-t_2\right)^2\left|\left(t_1-t_2\right)\right| \\
& =\frac{1}{2} a^2\left|\left(t_1-t_2\right)^3\right| .
\end{aligned}
\)

Equations of Normals in Different Forms

Point Form:

To find the equation of the normal to the parabola \(y^2=4 a x\) at the point \(\left(x_1, y_1\right)\).
Since, the equation of the tangent to the parabola \(y^2=4 a x\) at \(\left(x_1, y_1\right)\) is
\(
y y_1=2 a\left(x+x_1\right)
\)

The slope of the tangent at \(\left(x_1, y_1\right)=2 a / y_1\) Since, the normal at \(\left(x_1, y_1\right)\) is perpendicular to the tangent at \(\left(x_1, y_1\right)\).
\(\therefore \quad\) Slope of normal at \(\left(x_1, y_1\right)=-y_1 / 2 a\)
Hence, the equation of normal at \(\left(x_1, y_1\right)\) is
\(
y-y_1=-\frac{y_1}{2 a}\left(x-x_1\right)
\)

Remarks

• Equations of normals of all standard parabolas at \(\left(x_1, y_1\right)\).
  \(
  \begin{array}{ll}
  \hline \text { Equations of Parabolas } & \text { Normal at }\left(x_1, y_1\right) \\
  \hline y^2=4 a x & y-y_1=-\frac{y_1}{2 a}\left(x-x_1\right) \\
  \hline y^2=-4 a x & y-y_1=\frac{y_1}{2 a}\left(x-x_1\right) \\
  \hline x^2=4 a y & y-y_1=-\frac{2 a}{x_1}\left(x-x_1\right) \\
  \hline x^2=-4 a y & y-y_1=\frac{2 a}{x_1}\left(x-x_1\right) \\
  \hline
  \end{array}
  \)

Parametric form :

To find the equation of normal to the parabola \(y^2=4 a x\) at the point \(\left(a t^2, 2 a t\right)\) or ‘ \(t\) ‘.
Since, the equation of normal of the parabola \(y^2=4 a x\) at \(\left(x_1, y_1\right)\) is
\(
y-y_1=-\frac{y_1}{2 a}\left(x-x_1\right) \dots(i)
\)
Replacing \(x_1\) by \(a t^2\) and \(y_1\) by 2at, then Eq. (i) becomes
\(
\begin{aligned}
y-2 a t & =-t\left(x-a t^2\right) \\
\text { or } \quad y+t x & =2 a t+a t^3
\end{aligned}
\)

Remarks

• The equations of normals of all standard parabolas at ‘ \(t\) ‘
  Equations of normals of all standard parabolas at \(\left(x_1, y_1\right)\).
  \(
  \begin{array}{ll}
  \hline \text { Equations of Parabolas } & \text { Parametric coordinates ‘ t ‘} & \text { Normals at ‘ t ‘} \\
  \hline y^2=4 a x & \left(a t^2, 2 a t\right) & y+t x=2 a t+a t^3 \\
  \hline y^2=-4 a x & \left(-a t^2, 2 a t\right) & y-t x=2 a t+a t^3 \\
  \hline x^2=4 a y & \left(2 a t, a t^2\right) & x+t y=2 a t+a t^3 \\
  \hline x^2=-4 a y & \left(2 a t,-a t^2\right) & x-t y=2 a t+a t^3 \\
  \hline
  \end{array}
  \)

Slope form:

To find the Equation of normal, condition for normality and point of contact in terms of \(m\) (slope) to the parabola \(y^2=4 a x\)
The equation of normal to the parabola \(y^2=4 a x\) at \(\left(x_1, y_1\right)\) is
\(
y-y_1=-\frac{y_1}{2 a}\left(x-x_1\right) \dots(i)
\)
Since, \(m\) is the slope of the normal, then,
\(
m=-\frac{y_1}{2 a} \Rightarrow y_1=-2 a m
\)
Since, \(\left(x_1, y_1\right)\) lies on \(y^2=4 a x\), therefore
\(
\begin{array}{rlrl}
y_1^2 & =4 a x_1 \\
\Rightarrow & 4 a^2 m^2 & =4 a x_1 \\
& \therefore x_1 & =a m^2
\end{array}
\)
On substituting the values of \(x_1\) and \(y_1\) in Eq. (i) we get
\(
\begin{array}{rlrl}
& y+2 a m & =m\left(x-a m^2\right) \\
\therefore & y & =m x-2 a m-a m^3 \dots(ii)
\end{array}
\)
Thus, \(y=m x-2 a m-a m^3\) is a normal to the parabola \(y^2=4 a x\), where \(m\) is the slope of the normal. The coordinates of the point of contact are \(\left( am ^2,-2 am \right)\) On comparing Eq. (ii) with
\(
\begin{aligned}
& y & =m x+c \\
\therefore & c & =-2 a m-a m^3
\end{aligned}
\)
which is condition of normality when \(y=m x+c\) is the normal of \(y^2=4 a x\).

Remark

The equations of normals, point of contact and condition of normality in terms of slope \((m)\) of all standard parabolas.

\(
\begin{array}{|c|c|c|c|}
\hline \text { Equation of parabolas } & \begin{array}{l}
\text { Point of contact in terms of } \\
\text { slope }(m)
\end{array} & \begin{array}{l}
\text { Equation of normals in } \\
\text { terms of slope }(m)
\end{array} & \begin{array}{l}
\text { Condition of } \\
\text { normality }
\end{array} \\
\hline y^2=4 a x & \left(a m^2,-2 a m\right) & y=m x-2 a m-a m^3 & c=-2 a m-a m^3 \\
\hline y^2=-4 a x & \left(-a m^2, 2 a m\right) & y=m x+2 a m+a m^3 & c=2 a m+a m^3 \\
\hline x^2=4 a y & \left(-\frac{2 a}{m}, \frac{a}{m^2}\right) & y=m x+2 a+\frac{a}{m^2} & c=2 a+\frac{a}{m^2} \\
\hline x^2=-4 a y & \left(\frac{2 a}{m},-\frac{a}{m^2}\right) & y=m x-2 a-\frac{a}{m^2} & c=-2 a-\frac{a}{m^2} \\
(y-k)^2=4 a(x-h) & \left(h+a m^2, k-2 a m\right) & \begin{array}{l}
y-k=m(x-h) \\
-2 a m-a m^3
\end{array} & c=k-m h-2 a m-a m^3 \\
\hline(y-k)^2=-4 a(x-h) & \left(h-a m^2, k+2 a m\right) & \begin{array}{l}
y-k=m(x-h) \\
+2 a m+a m^3
\end{array} & c=k-m h+2 a m+a m^3 \\
\hline(x-h)^2=4 a(y-k) & \left(h-\frac{2 a}{m}, k+\frac{a}{m^2}\right) & \begin{array}{r}
y-k=m(x-h) \\
+2 a+\frac{a}{m^2}
\end{array} & c=k-m h+2 a+\frac{a}{m^2} \\
\hline
\end{array}
\)

Point of Intersection of Normals at any Two Points on the Parabola

Let the parabola be \(y^2=4 a x\).
Let the points on the parabola are
\(P \equiv\left(a t_1^2, 2 a t_1\right) \quad\) and \(\quad Q=\left(a t_2^2, 2 a t_2\right)\).

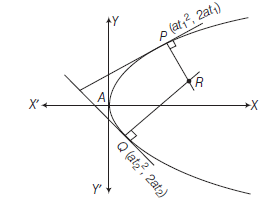
Equations of normals at \(P\left(a t_1^2, 2 a t_1\right)\) and \(Q\left(a t_2^2, 2 a t_2\right)\) are
\(
\text { and } \quad \begin{aligned}
y & =-t_1 x+2 a t_1+a t_1^3 \\
y & =-t_2 x+2 a t_2+a t_2^3
\end{aligned}
\)
On solving Eqs. (i) and (ii), we get
\(
x=2 a+a\left(t_1^2+t_2^2+t_1 t_2\right) \text { and } y=-a t_1 t_2\left(t_1+t_2\right)
\)

If \(R\) is the point of intersection, then
\(
R \equiv\left[2 a+a\left(t_1^2+t_2^2+t_1 t_2\right),-a t_1 t_2\left(t_1+t_2\right)\right] \text { (Remember) }
\)

Point of intersection of normals at \(t_1\) and \(t_2\)

\(
\begin{array}{ccc}
\hline \text { Parabola } & \begin{array}{c}
\text { Equation of normal } \\
\text { at any point } t
\end{array} & \begin{array}{c}
\text { Point of intersection of } \\
\text { normals at } t _1 \text { and } t _2
\end{array} \\
\hline y^2=4 a x & y+t x=2 a t+a t^3 & \left(2 a+a\left(t_1^2+t_1 t_2+t_2^2\right),\right. \\
& & \left.-a t_1 t_2\left(t_1+t_2\right)\right) \\
\hline y^2=-4 a x & y-t x=2 a t+a t^3 & \left(-2 a-a\left(t_1^2+t_1 t_2+t_2^2\right),\right. \\
& & \left.a t_1 t_2\left(t_1+t_2\right)\right) \\
\hline x^2=4 a y & x+t y=2 a t+a t^3 & \left(-a t_1 t_2\left(t_1+t_2\right), 2 a\right. \\
& & \left.+a\left(t_1^2+t_1 t_2+t_2^2\right)\right) \\
\hline x^2=-4 a y & x-t y=2 a t+a t^3 & \left(a t_1 t_2\left(t_1+t_2\right),-2 a\right. \\
& & \left.-a\left(t_1^2+t_1 t_2+t_2^2\right)\right) \\
\hline
\end{array}
\)

Relation between ‘ \(t_1\) ‘ and ‘ \(t_2\) ‘ if Normal at ‘ \(t_1\) ‘ meets the Parabola Again at ‘ \(t_2\) ‘

Let the parabola be \(y^2=4 a x\), equation of normal at \(P\left(a t_1^2, 2 a t_1\right)\) is
\(
y=-t_1 x+2 a t_1+a t_1^3 \dots(i)
\)

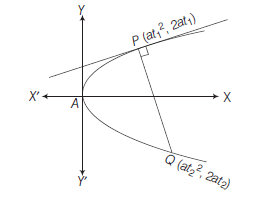
Since, it meet the parabola again at \(Q\left(a t_2^2, 2 a t_2\right)\), then Eq. (i) passes through \(Q\left(a t_2^2, 2 a t_2\right)\).
\(
\begin{array}{rr}
\therefore & 2 a t_2=-a t_1 t_2^2+2 a t_1+a t_1^3 \\
\Rightarrow & 2 a\left(t_2-t_1\right)+a t_1\left(t_2^2+t_1^2\right)=0 \\
\Rightarrow & a\left(t_2-t_1\right)\left[2+t_1\left(t_2+t_1\right)\right]=0 \\
\because & a\left(t_2-t_1\right) \neq 0 \quad \left[\because t_1 \text { and } t_2 \text { are different }\right]
\end{array}
\)
\(
\begin{aligned}
& \therefore \quad 2+t_1\left(t_2+t_1\right)=0 \\
& \therefore \quad t_2=-t_1-\frac{2}{t_1} \\
&
\end{aligned}
\)

Remarks

• If normals at ‘ \(t_1\) ‘ and ‘ \(t_2\) ‘ meets the parabola \(y^2=4 a x\) at same point, then \(t_1 t_2=2\).
  Proof Suppose normals meet at ‘ \(T\) ‘, then
  \(
  \begin{aligned}
  T & =-t_1-\frac{2}{t_1}=-t_2-\frac{2}{t_2} \\
  \Rightarrow \quad\left(t_1-t_2\right) & =2\left(\frac{1}{t_2}-\frac{1}{t_1}\right)
  \end{aligned}
  \)
  or \(\quad t_1 t_2=2 \left[\because t_1 \neq t_2\right]\)
• If the normals to the parabola \(y^2=4 a x\) at the points \(t_1\) and \(t_2\) intersect again on the parabola at the point \(t_3\), then \(t_3=-\left(t_1+t_2\right)\) and the line joining \(t_1\) and \(t_2\) passes through a fixed point \((-2 a, 0)\).

Example 41: Show that normal to the parabola \(y^2=8 x\) at the point \((2,4)\) meets it again at \((18,-12)\). Find also the length of the normal chord.

Answer: Comparing the given parabola (i.e. \(y^2=8 x\) ) with \(y^2=4 a x\).
\(
\therefore \quad 4 a=8 \quad \Rightarrow \quad a=2
\)
Since, normal at \(\left(x_1, y_1\right)\) to the parabola \(y^2=4 a x\) is
\(
y-y_1=-\frac{y_1}{2 a}\left(x-x_1\right)
\)
Here, \(x_1=2\) and \(y_1=4\).
\(\therefore\) Equation of normal is
\(
y-4=-\frac{4}{4}(x-2)
\)

\(
\begin{array}{rlrl}
\Rightarrow & y-4 & =-x+2 \\
\Rightarrow & x+y-6 & =0 \dots(i)
\end{array}
\)
On solving Eq. (i) and \(y^2=8 x\), then,
\(
y^2=8(6-y)
\)
\(
\begin{aligned}
& \Rightarrow \quad y^2+8 y-48=0 \\
& \Rightarrow \quad(y+12)(y-4)=0
\end{aligned}
\)
\(\therefore \quad y=-12\) and \(y=4\)
then, \(x=18\) and \(x=2\).
Hence, the point of intersection of normal and parabola are \((18,-12)\) and \((2,4)\), therefore normal meets the parabola at \((18,-12)\) and length of normal chord is distance between their points
\(
=P Q=\sqrt{(18-2)^2+(-12-4)^2}=16 \sqrt{2}
\)

Example 42: Prove that the chord \(y-x \sqrt{2}+4 a \sqrt{2}=0\) is a normal chord of the parabola \(y^2=4 a x\). Also, find the point on the parabola when the given chord is normal to the parabola.

Answer: We have, \(\quad y-x \sqrt{2}+4 a \sqrt{2}=0\)
i.e., \(\quad y=x \sqrt{2}-4 a \sqrt{2} \dots(i)\)
Comparing the Eq. (i) with the equation \(y=m x+c\), then
\(
m=\sqrt{2}, c=-4 a \sqrt{2}
\)
Since,
\(
\begin{aligned}
-2 a m-a m^3 & =-2 a \sqrt{2}-a(\sqrt{2})^3 \\
& =-2 a \sqrt{2}-2 a \sqrt{2}=-4 a \sqrt{2}=c
\end{aligned}
\)
Hence, the given chord is normal to the parabola \(y^2=4 a x\).
The coordinates of the points are \(\left(a m^2,-2 a m\right)\) i.e. \((2 a,-2 \sqrt{2} a) \text {. }\)

Example 43: If the normal to a parabola \(y^2=4 a x\), makes an angle \(\phi\) with the axis. Show that it will cut the curve again at an angle \(\tan ^{-1}\left(\frac{1}{2} \tan \phi\right)\).

Answer: Let the normal at \(P\left(a t_1^2, 2 a t_1\right)\) be
\(
y=-t_1 x+2 a t_1+a t_1^3 .
\)
\(\therefore \tan \phi=-t_1=\text { slope of the normal, } \dots(i)\)
it meet the curve again \(Q\) say \(\left(a t_2^2, 2 a t_2\right)\).
\(
\therefore \quad t_2=-t_1-\frac{2}{t_1} \dots(ii)
\)

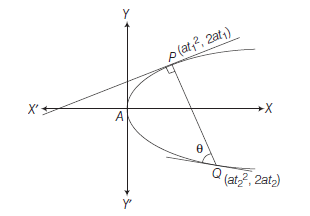
Now, angle between the normal and parabola
\(=\) Angle between the normal and tangent at \(Q\)
\(
\text { (i.e. } t_2 y=x+a t_2^2 \text { ) }
\)
If \(\theta\) be the angle, then
\(
\tan \theta=\frac{m_1-m_2}{1+m_1 m_2}=\frac{-t_1-\frac{1}{t_2}}{1+\left(-t_1\right)\left(\frac{1}{t_2}\right)}=-\frac{t_1 t_2+1}{t_2-t_1}
\)
\(
=-\frac{t_1\left(-t_1-\frac{2}{t_1}\right)+1}{-t_1-\frac{2}{t_1}-t_1} \quad \text { [from Eq. (ii)] }
\)
\(
=-\frac{-t_1^2-1}{-2\left(\frac{1+t_1^2}{t_1}\right)}=-\frac{t_1}{2}
\)
\(
=\frac{\tan \phi}{2} \text { [from Eq. (i)] }
\)
\(
\therefore \quad \theta=\tan ^{-1}\left(\frac{1}{2} \tan \phi\right)
\)

Example 44: Prove that the normal chord to a parabola \(y^2=4 a x\) at the point whose ordinate is equal to abscissa subtends a right angle at the focus.

Answer: Let the normal at \(P\left(a t_1^2, 2 a t_1\right)\) meet the curve at \(Q\left(a t_2^2, 2 a t_2\right)\).
\(\therefore P Q\) is a normal chord
and \(t_2=-t_1-\frac{2}{t_1} \dots(i)\)
By given condition, \(2 a t_1=a t_1^2\)
\(\therefore t_1=2\) from Eq. (i), \(t_2=-3\)
then, \(P(4 a, 4 a)\) and \(Q(9 a,-6 a)\)
but focus \(S(a, 0)\).
\(
\therefore \quad \text { Slope of } S P=\frac{4 a-0}{4 a-a}=\frac{4 a}{3 a}=\frac{4}{3}
\)

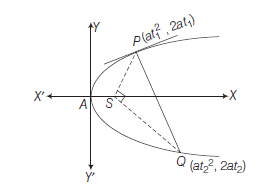
and slope of \(S Q=\frac{-6 a-0}{9 a-a}=-\frac{6 a}{8 a}=-\frac{3}{4}\)
\(\because\) Slope of \(S P \times\) Slope of \(S Q=\frac{4}{3} \times-\frac{3}{4}=-1\)
\(\therefore \quad \angle P S Q=\pi / 2\)
i.e. \(P Q\) subtends a right angle at the focus \(S\).

Example 45: If the normal to the parabola \(y^2=4 a x\) at point \(t_1\) cuts the parabola again at point \(t_2\), prove that \(t_2^2=8\).

Answer: A normal at point \(t_1\) cuts the parabola again at \(t_2\). Then,
\(
t_2=-t_1-\frac{2}{t_1} \Rightarrow t_1^2+t_1 t_2+2=0
\)
Since, \(t_1\) is real, so \(\left(t_2\right)^2-4 \cdot 1 \cdot 2 \geq 0\)
\(
\Rightarrow \quad t_2^2 \geq 8
\)

Co-normal Points

In general three normals can be drawn from a point to a parabola and their feet, points where they meet the parabola are called conormal points.
Let \(P(h, k)\) be any given point and \(y^2=4 a x\) be a parabola.
The equation of any normal to \(y^2=4 a x\) is
\(
y=m x-2 a m-a m^3
\)

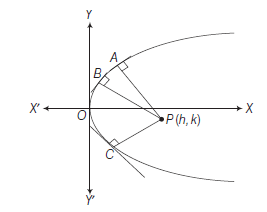
If it passes through \((h, k)\), then
\(
\begin{aligned}
k & =m h-2 a m-a m^3 \\
\Rightarrow a m^3+m(2 a-h)+k & =0 \dots(i)
\end{aligned}
\)
This is a cubic equation in \(m\), so it has three roots, say \(m_1, m_2\) and \(m_3\).
\(
\begin{aligned}
\therefore \quad m_1+m_2+m_3 & =0, \\
m_1 m_2+m_2 m_3+m_3 m_1 & =\frac{(2 a-h)}{a}, \\
m_1 m_2 m_3 & =-\frac{k}{a} \dots(ii)
\end{aligned}
\)
Hence, for any given point \(P(h, k)\), Eq. (i) has three real or imaginary roots. Corresponding to each of these three roots, we have one normal passing through \(P(h, k)\). Hence, in total, we have three normals \(P A, P B\) and \(P C\) drawn through \(P\) to the parabola.
Points \(A, B, C\) in which the three normals from \(P(h, k)\) meet the parabola are called co-normal points.

Corollary 1: The algebraic sum of the slopes of three concurrent normals is zero. This follows from Eq. (ii).

Corollary 2: The algebraic sum of ordinates of the feets of three normals drawn to a parabola from a given point is zero. Let the ordinates of \(A, B, C\) be \(y_1, y_2, y_3\) respectively, then
\(
y_1=-2 a m_1, y_2=-2 a m_2 \text { and } y_3=-2 a m_3
\)
\(\therefore\) Algebraic sum of these ordinates is
\(
\begin{aligned}
y_1+y_2+y_3 & =-2 a m_1-2 a m_2-2 a m_3 \\
& =-2 a\left(m_1+m_2+m_3\right) \\
& =-2 a \times 0 \quad \quad \text { [from Eq. (ii)] } \\
& =0
\end{aligned}
\)

Corollary 3: If three normals drawn to any parabola \(y^2=4 a x\) from a given point \((h, k)\) be real then \(h>2 a\).
When normals are real, then all the three roots of Eq. (i) are real and in that case
\(
\begin{aligned}
& m_1^2+m_2^2+m_3^2>0 \quad \text { (for any values of } m_1, m_2, m_3 \text { ) } \\
\Rightarrow & \left(m_1+m_2+m_3\right)^2-2 \quad\left(m_1 m_2+m_2 m_3+m_3 m_1\right)>0 \\
\Rightarrow & (0)^2-\frac{2(2 a-h)}{a}>0 \Rightarrow h-2 a>0 \\
\therefore & h>2 a \\
&
\end{aligned}
\)

Remark

• For \(a=1\) normals drawn to the parabola \(y^2=4 x\) from any point ( \(h, k\) ) are real, if \(h>2\).

Corollary 4: If three normals drawn to any parabola \(y^2=4 a x\) from a given point \((h, k)\) be real and distinct, then \(27 a k^2<4(h-2 a)^3\)
Let \(\quad f(m)=a m^3+m(2 a-h)+k\)
\(
\therefore \quad f^{\prime}(m)=3 a m^2+(2 a-h)
\)
Two distinct roots of \(f^{\prime}(m)=0\) are
\(
\begin{array}{ll}
& \alpha=\sqrt{\left(\frac{h-2 a}{3 a}\right)} \text { and } \beta=-\sqrt{\left(\frac{h-2 a}{3 a}\right)}, \\
\text { Now, } \quad & f(\alpha) f(\beta)<0 \Rightarrow f(\alpha) f(-\alpha)<0
\end{array}
\)
\(
\begin{array}{ll}
\Rightarrow & \left(a \alpha^3+\alpha(2 a-h)+k\right)\left(-a \alpha^3-\alpha(2 a-h)+k\right)<0 \\
\Rightarrow & k^2-\left(a \alpha^2+(2 a-h)\right)^2 \alpha^2<0
\end{array}
\)
\(
\begin{array}{ll}
\Rightarrow & k^2-\left(\frac{h-2 a}{3}+(2 a-h)\right)^2 \frac{(h-2 a)}{3 a}<0 \\
\Rightarrow & k^2-\left(\frac{4 a-2 h}{3}\right)^2\left(\frac{h-2 a}{3 a}\right)<0 \\
\Rightarrow & k^2-\frac{4(h-2 a)^3}{27 a}<0 \Rightarrow 27 a k^2-4(h-2 a)^3<0 \\
\therefore & \quad 27 a k^2<4(h-2 a)^3
\end{array}
\)

Corollary 5: The centroid of the triangle formed by the feet of the three normals lies on the axis of the parabola.
If \(A\left(x_1, y_1\right), B\left(x_2, y_2\right)\) and \(C\left(x_3, y_3\right)\) be vertices of \(\triangle A B C\), then its centroid is
\(
\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)=\left(\frac{x_1+x_2+x_3}{3}, 0\right) \text {. }
\)
Since, \(y_1+y_2+y_3=0\) (from corollary 2). Hence, the centroid lies on the \(X\)-axis \(O X\), which is the axis of the parabola also.
Now, \(\frac{x_1+x_2+x_3}{3}=\frac{1}{3}\left(a m_1^2+a m_2^2+a m_3^2\right)\)
\(
\begin{aligned}
= & \frac{a}{3}\left(m_1^2+m_2^2+m_3^2\right) \\
= & \frac{a}{3}\left\{\left(m_1+m_2+m_3\right)^2\right. \\
& \left.-2\left(m_1 m_2+m_2 m_3+m_3 m_1\right)\right\} \\
= & \frac{a}{3}\left[(0)^2-2\left\{\frac{2 a-h}{a}\right\}\right]=\frac{2 h-4 a}{3}
\end{aligned}
\)
\(\therefore\) Centroid of \(\triangle A B C\) is \(\left(\frac{2 h-4 a}{3}, 0\right)\).

Example 46: Find the locus of the point through which pass three normals to the parabola \(y^2=4 a x\) such that two of them make angles \(\alpha\) and \(\beta\) respectively with the axis such that \(\tan \alpha \tan \beta=2\).

Answer: Let \((h, k)\) be the point of intersection of three normals to the parabola \(y^2=4 a x\).
The equation of any normal to \(y^2=4 a x\) is
\(
y=m x-2 a m-a m^3
\)
If it passes through \(\left(h_1, k\right)\), then
\(
\begin{array}{r}
k=m h-2 a m-a m^3 \\
\Rightarrow \quad a m^3+m(2 a-h)+k=0 \dots(i)
\end{array}
\)
Let roots of Eq. (i) be \(m_1, m_2, m_3\) then from Eq. (i)
\(
m_1 m_2 m_3=-\frac{k}{a} \dots(ii)
\)
Also \(m_1=\tan \alpha, m_2=\tan \beta\) and \(\tan \alpha \tan \beta=2\)
\(\therefore \quad m_1 m_2=2 \dots(iii)\)
From Eqs. (ii) and (iii), \(2 m_3=-\frac{k}{a}\)
or \(m_3=-\frac{k}{2 a}\)
Which being a root of Eq. (i) must satisfy it
\(
\begin{aligned}
& \text { i.e. } \quad a m_3^3+m_3(2 a-h)+k=0 \\
& \Rightarrow \quad a\left(-\frac{k}{2 a}\right)^3-\frac{k}{2 a}(2 a-h)+k=0 \\
& \Rightarrow \quad-\frac{k^3}{8 a^2}-k+\frac{k h}{2 a}+k=0 \\
& \Rightarrow \quad k^2-4 a h=0 \\
& \therefore \text { Required locus of }(h, k) \text { is } y^2-4 a x=0 \text {. } \\
&
\end{aligned}
\)

Example 47: Find the point on the axis of the parabola \(3 y^2+4 y-6 x+8=0\) from when three distinct normals can be drawn.

Answer: Given, parabola is \(3 y^2+4 y-6 x+8=0\)
\(
\begin{aligned}
& \Rightarrow \quad 3\left(y^2+\frac{4}{3} y\right)=6 x-8 \\
& \Rightarrow \quad 3\left\{\left(y+\frac{2}{3}\right)^2-\frac{4}{9}\right\}=6 x-8 \\
& \Rightarrow \quad 3\left(y+\frac{2}{3}\right)^2=\left(6 x-8+\frac{4}{3}\right) \\
& \therefore \quad\left(y+\frac{2}{3}\right)^2=2\left(x-\frac{10}{9}\right) \\
&
\end{aligned}
\)
Let \(\quad y+\frac{2}{3}=Y, x-\frac{10}{9}=X\)
Then, \(\quad Y^2=2 X\)
Comparing with \(\quad Y^2=4 a X\)
\(\therefore \quad a=\frac{1}{2}\)
any point on the axis of parabola is \(\left(x,-\frac{2}{3}\right)\)
and \(X>2 a \Rightarrow x-\frac{10}{9}>1\)
\(\Rightarrow \quad x>\frac{19}{9}\)

Pair of Tangents \(S S_1=T^2\)

If \(y_1^2-4 a x_1>0\), then any point \(P\left(x_1, y_1\right)\) lies outside the parabola and a pair of tangents \(P Q, P R\) can be drawn to it from \(P\). We find their equation as follows.
Let \(T(h, k)\) be any point on the pair of tangents \(P Q\) or \(P R\) drawn from any external point \(P\left(x_1, y_1\right)\) to the parabola \(y^2=4 a x\).

Equation of \(P T\) is
\(
\begin{aligned}
y-y_1 & =\frac{k-y_1}{h-x_1}\left(x-x_1\right) \\
\Rightarrow \quad y & =\left(\frac{k-y_1}{h-x_1}\right) x+\left(\frac{h y_1-k x_1}{h-x_1}\right)
\end{aligned}
\)
which is tangent to the parabola
\(
\begin{aligned}
y^2 & =4 a x \\
\therefore \quad \quad \quad c & =\frac{a}{m}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad c m=a \Rightarrow\left(\frac{h y_1-k x_1}{h-x_1}\right)\left(\frac{k-y_1}{h-x_1}\right)=a \\
& \Rightarrow \quad\left(k-y_1\right)\left(h y_1-k x_1\right)=a\left(h-x_1\right)^2
\end{aligned}
\)
\(\therefore \quad\) Locus of \((h, k)\), equation of pair of tangents is
\(
\begin{aligned}
\left(y-y_1\right)\left(x y_1-x_1 y\right) & =a\left(x-x_1\right)^2 \\
\Rightarrow\left(y^2-4 a x\right)\left(y_1^2-4 a x_1\right) & =\left\{y y_1-2 a\left(x+x_1\right)\right\}^2
\end{aligned}
\)
\(
\begin{array}{lc}
\therefore & S S_1=T^2 \\
\text { where } & S=y^2-4 a x, S_1=y_1^2-4 a x_1 \\
\text { and } & T=y y_1-2 a\left(x+x_1\right) .
\end{array}
\)

Remark

• \(S=0\) is the equation of the curve, \(S_1\) is obtained from \(S\) by replacing \(x\) by \(x_1\) and \(y\) by \(y_1\) and \(T=0\) is the equation tangent at \(\left(x_1, y_1\right)\) to \(S=0\).

Chord of Contact

The chord joining the points of contact of two tangents drawn from an external point to a parabola is known as the chord of contact of tangents drawn from external point.
Theorem: The chord of contact of tangents drawn from a point \(\left(x_1, y_1\right)\) to the parabola \(y^2=4 a x\) is
\(
y y_1=2 a\left(x+x_1\right) .
\)

Proof: Let \(P Q\) and \(P R\) be tangents to the parabola \(y^2=4 a x\) drawn from any external point \(P\left(x_1, y_1\right)\), then \(Q R\) is called chord of contact of the parabola \(y^2=4 a x\).

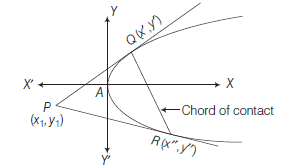
Let \(\quad Q \equiv\left(x^{\prime}, y^{\prime}\right)\) and \(R \equiv\left(x^{\prime \prime}, y^{\prime \prime}\right)\)
Equation of tangent \(P Q\) is
\(
y y^{\prime}=2 a\left(x+x^{\prime}\right) \dots(i)
\)
and equation of tangent \(P R\) is
\(
y y^{\prime \prime}=2 a\left(x+x^{\prime \prime}\right) \dots(ii)
\)
Since, lines Eqs. (i) and (ii) pass through \(\left(x_1, y_1\right)\), then
\(
y_1 y^{\prime}=2 a\left(x_1+x^{\prime}\right) \text { and } y_1 y^{\prime \prime}=2 a\left(x_1+x^{\prime \prime}\right)
\)
Hence, it is clear \(Q\left(x^{\prime}, y^{\prime}\right)\) and \(R\left(x^{\prime \prime}, y^{\prime \prime}\right)\) lie on
\(
y y_1=2 a\left(x+x_1\right)
\)
which is chord of contact \(Q R\).

Example 48: Tangents are drawn from the point \(\left(x_1, y_1\right)\) to the parabola \(y^2=4 a x\), show that the length of their chord of contact is \(\frac{1}{|a|} \sqrt{\left(y_1^2-4 a x_1\right)\left(y_1^2+4 a^2\right)}\).

Answer: Given parabola is
\(
y^2=4 a x \dots(i)
\)

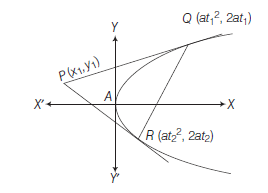
Let
\(
P \equiv\left(x_1, y_1\right)
\)
and the tangents from \(P\) touch the parabola at \(Q\left(a t_1^2, 2 a t_1\right)\) and \(R\left(a t_2^2, 2 a t_2\right)\) then \(P\) is the point of intersection of tangents.
\(
\begin{array}{ll}
\therefore & x_1=a t_1 t_2 \text { and } y_1=a\left(t_1+t_2\right) \\
\Rightarrow & t_1 t_2=\frac{x_1}{a} \text { and } t_1+t_2=\frac{y_1}{a} \ldots \text { (ii) }
\end{array}
\)
Now, \(\quad Q R=\sqrt{\left(a t_1^2-a t_2^2\right)^2+\left(2 a t_1-2 a t_2\right)^2}\)
\(
\begin{aligned}
& =\sqrt{a^2\left(t_1-t_2\right)^2\left[\left(t_1+t_2\right)^2+4\right]} \\
& =|a|\left|t_1-t_2\right| \sqrt{\left\{\left(t_1+t_2\right)^2+4\right\}} \\
& =|a| \sqrt{\left\{\left(t_1+t_2\right)^2-4 t_1 t_2\right\}} \sqrt{\left\{\left(t_1+t_2\right)^2+4\right\}} \\
& =|a| \sqrt{\left(\frac{y_1^2}{a^2}-\frac{4 x_1}{a}\right)} \cdot \sqrt{\left(\frac{y_1^2}{a^2}+4\right)} \text { [from Eq. (ii)] }
\end{aligned}
\)
\(
\begin{aligned}
& =|a| \frac{\sqrt{\left(y_1^2-4 a x_1\right)}}{|a|} \cdot \frac{\sqrt{\left(y_1^2+4 a^2\right)}}{|a|} \\
& =\frac{1}{|a|} \sqrt{\left(y_1^2-4 a x_1\right)\left(y_1^2+4 a^2\right)}
\end{aligned}
\)

Example 49: Prove that the area of the triangle formed by the tangents drawn from \(\left(x_1, y_1\right)\) to \(y^2=4 a x\) and their chord of contact is \(\left(y_1^2-4 a x_1\right)^{3 / 2} / 2 a\).

Answer: Equation of \(Q R\) (chord of contact) is
\(
\begin{aligned}
& y y_1=2 a\left(x+x_1\right) \\
& \Rightarrow \quad y y_1-2 a\left(x+x_1\right)=0 \\
& \because P M=\text { Length of perpendicular from } P\left(x_1, y_1\right) \text { on } Q R \\
& =\frac{\left|y_1 y_1-2 a\left(x_1+x_1\right)\right|}{\sqrt{\left(y_1^2+4 a^2\right)}}=\frac{\left|\left(y_1^2-4 a x_1\right)\right|}{\sqrt{\left(y_1^2+4 a^2\right)}} \\
&
\end{aligned}
\)
[Since, \(P\left(x_1, y_1\right)\) lies outside the parabola. So, \(y_1^2-4 a x_1>0\) ]

\(
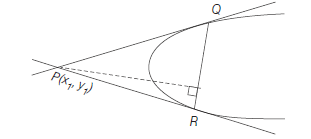
\begin{aligned}
& \text { Now, area of } \triangle P Q R=\frac{1}{2} Q R \cdot P M \\
& =\frac{1}{2} \frac{1}{|a|} \sqrt{\left(y_1^2-4 a x_1\right)\left(y_1^2+4 a^2\right)} \frac{\left(y_1^2-4 a x_1\right)}{\sqrt{\left(y_1^2+4 a^2\right)}} \\
& =\left(y_1^2-4 a x_1\right)^{3 / 2} / 2 a, \text { if } a>0
\end{aligned}
\)

Equation of the Chord Bisected at a Given Point

Theorem: The equation of the chord of the parabola \(y^2=4 a x\) which is bisected at \(\left(x_1, y_1\right)\) is
\(
y y_1-2 a\left(x+x_1\right)=y_1^2-4 a x_1
\)
or \(T=S_1 \text {, }\)
where, \(T=y y_1-2 a\left(x+x_1\right)\) and \(S_1=y_1^2-4 a x_1\).

Proof: Since, equation of the parabola is
\(
y^2=4 a x \dots(i)
\)
Let \(Q R\) be the chord of the parabola whose mid-point is \(P\left(x_1, y_1\right)\)

Since, \(Q\) and \(R\) lie on parabola (i),
\(
\begin{array}{rlrl}
y_2^2 & =4 a x_2 \text { and } y_3^2=4 a x_3 \\
\therefore & \quad y_3^2-y_2^2 =4 a\left(x_3-x_2\right) \\
\Rightarrow \quad & \frac{y_3-y_2}{x_3-x_2} =\frac{4 a}{y_3+y_2}
\end{array}
\)
\(
=\frac{4 a}{2 y_1}\left[\because P\left(x_1, y_1\right) \text { is mid-point of } Q R\right]
\)
\(
\begin{aligned}
& \therefore \quad \frac{y_3-y_2}{x_3-x_2}=\frac{2 a}{y_1}=\text { Slope of } Q R \\
& \text { Equation of } Q R \text { is } y-y_1=\frac{2 a}{y_1}\left(x-x_1\right) \\
& \Rightarrow \quad y y_1-y_1^2=2 a x-2 a x_1 \\
& \Rightarrow \quad y y_1-2 a\left(x+x_1\right)=y_1^2-4 a x_1 \\
& \text { [subtracting } 2 a x_1 \text { from both sides] } \\
& \therefore \quad T=S_1 \text {, } \\
& \text { where } \quad T=y y_1-2 a\left(x+x_1\right) \text { and } S_1=y_1^2-4 a x_1 \text {. } \\
&
\end{aligned}
\)

Example 50: Find the locus of the mid-points of the chords of the parabola \(y^2=4 a x\) which subtend a right angle at the vertex of the parabola.

Answer: Let \(P(h, k)\) be the mid-point of a chord \(Q R\) of the parabola \(y^2=4 a x\) then equation of chord \(Q R\) is
\(
T=S_1
\)
\(
\text { or } \quad y k-2 a(x+h)=k^2-4 a h
\)
\(
\Rightarrow \quad y k-2 a x=k^2-2 a h \dots(i)
\)
If \(A\) is the vertex of the parabola. For combined equation of \(A Q\) and \(A R\) making homogeneous of \(y^2=4 a x\) with the help of Eq. (i).
\(
\begin{array}{ll}
\therefore & y^2=4 a x \\
\Rightarrow & y^2=4 a x\left(\frac{y k-2 a x}{k^2-2 a h}\right)
\end{array}
\)
\(
\Rightarrow \quad y^2\left(k^2-2 a h\right)-4 a k x y+8 a^2 x^2=0
\)

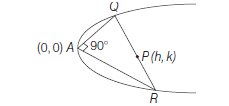
Since, \(\angle Q A R=90^{\circ}\)
\(\therefore\) Coefficient of \(x^2+\) Coefficient of \(y^2=0\)
\(
k^2-2 a h+8 a^2=0
\)
Hence, the locus of \(P(h, k)\) is \(y^2-2 a x+8 a^2=0\).

Diameter

The locus of the middle points of a system of parallel chords is called a diameter and in case of a parabola this diameter is shown to be a straight line which is parallel to the axis of the parabola.
Theorem: The equation of the diameter bisecting chords of slope \(m\) of the parabola \(y^2=4 a x\) is \(y=\frac{2 a}{m}\).

Proof: Let \(y=m x+c\) be system of parallel chords to \(y^2=4 a x\) for different chords \(c\) varies, \(m\) remains constant. Let the extremities of any chord \(P Q\) of the set be \(P\left(x_1, y_1\right)\) and \(Q\left(x_2, y_2\right)\) and let its middle point be \(M(h, k)\).

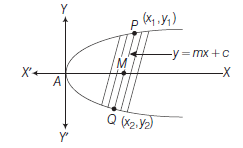
On solving equations
\(
\begin{aligned}
y^2 & =4 a x \text { and } y=m x+c . \\
\therefore \quad y^2 & =4 a\left(\frac{y-c}{m}\right)
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \quad m y^2-4 a y+4 a c=0 \\
& \therefore \quad y_1+y_2=\frac{4 a}{m} \quad \text { or } \frac{y_1+y_2}{2}=\frac{2 a}{m} [\because(h, k) \text { is the mid-point of } P Q]
\end{aligned}
\)
Hence, locus of \(M(h, k)\) is \(y=\frac{2 a}{m}\).

Remarks

• The point in which any diameter meets the curve is called the extremity of the diameter.
• Any line which is parallel to the axis of the parabola drawn through any point on the parabola is called diameter and its equation is \(y\)-coordinate of that point.
  If point on diameter \(\left(x_1, y_1\right)\), then diameter is \(y=y_1\).

Corollary 1: The tangent at the extremity of a diameter of a parabola is parallel to the system of chords it bisects.

Let \(y=m x+c\) (c variable) represents the system of parallel chords, then the equation of diameter of \(y^2=4 a x\) is \(y=\frac{2 a}{m}\). The diameter meets the parabola \(y^2=4 a x\) at \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\) and tangent is \(y=m x+\frac{a}{m}\) which is parallel to \(y=m x+c\).

Corollary 2: Tangents at the end of any chord meet on the diameter which bisects the chords.
If extremities of the chord be \(P\left(a t_1^2, 2 a t_1\right)\) and \(Q\left(a t_2^2, 2 a t_2\right)\) then its slope
\(
m=\frac{2 a t_2-2 a t_1}{a t_2^2-a t_1^2} \Rightarrow m=\frac{2}{\left(t_2+t_1\right)} .
\)

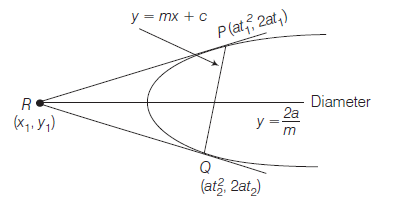
\(\therefore \quad\) Equation of diameter is
\(
y=2 a / m \Rightarrow y=a\left(t_1+t_2\right) \dots(i)
\)
Now, tangents at \(P\left(a t_1^2, 2 a t_1\right)\) and \(Q\left(a t_2^2, 2 a t_2\right)\) meet at a point \(\left[a t_1 t_2, a\left(t_1+t_2\right)\right]\) which lies on Eq. (i).

Lengths of Tangent, Subtangent, Normal and Subnormal

Let the parabola \(y^2=4 a x\). Let the tangent and normal at \(P(x, y)\) meet the axis of parabola at \(T\) and \(G\) respectively and let tangent at \(P(x, y)\) makes angle \(\psi\) with the positive direction of \(X\)-axis.

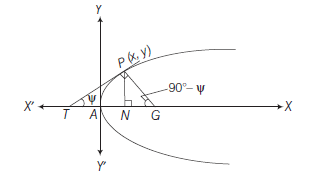
Then, \(\quad P T=\) Length of Tangent
\(P G=\) Length of Normal
\(
\begin{array}{ll}
& T N=\text { Length } \text { of Subtangent } \\
\text { and } & N G=\text { Length } \text { of Subnormal }
\end{array}
\)
If \(A(0,0)\) is the vertex of the parabola.
\(
\begin{array}{ll}
\because & P N=y \\
\therefore & P T=P N \operatorname{cosec} \psi=y \operatorname{cosec} \psi
\end{array}
\)
\(
\begin{aligned}
P G & =P N \operatorname{cosec}\left(90^{\circ}-\psi\right)=y \sec \psi \\
T N & =P N \cot \psi=y \cot \psi \\
N G & =P N \cot \left(90^{\circ}-\psi\right)=y \tan \psi
\end{aligned}
\)
where, \(\tan \psi=\frac{2 a}{y}=m \text { [slope of tangent at } P(x, y) \text { ] }\)

Example 51: Find the length of tangent, subtangent, normal and subnormal to \(y^2=4 a x\) at \(\left(a t^2, 2 a t\right)\).

Answer: \(\because\) Equation of tangent of \(\left(a t^2, 2 a t\right)\) of parabola \(y^2=4 a x\) is
\(
t y=x+a t^2
\)
Slope of this tangent \(m=\frac{1}{t}\)
Let tangent makes angle \(\psi\) with positive direction of \(X\)-axis
\(
\tan \psi=\frac{1}{t}
\)
then \(t=\cot \psi\)
\(\therefore\) Length of tangent at
\(
\begin{aligned}
\left(a t^2, 2 a t\right) & =2 a t \operatorname{cosec} \psi \\
& =2 a t \sqrt{\left(1+\cot ^2 \psi\right)}=2 a t \sqrt{\left(1+t^2\right)}
\end{aligned}
\)
Length of normals at
\(
\begin{aligned}
\left(a t^2, 2 a t\right) & =2 a t \sec \psi=2 a t \sqrt{\left(1+\tan ^2 \psi\right)} \\
& =2 a \sqrt{\left(t^2+t^2 \tan ^2 \psi\right)}=2 a \sqrt{\left(t^2+1\right)}
\end{aligned}
\)
Length of subtangent at \(\left(a t^2, 2 a t\right)=2 a t \cot \psi\)
\(
=2 a t^2
\)
Length of subnormal at \(\left(a t^2, 2 a t\right)=2 a t \tan \psi\)
\(
=2 a
\)

Some Standard Properties of the Parabola

Property-1: The tangents at the extremities of a focal chord intersect at right angles on the directrix.
The extremities of a focal chord \(P Q\) are
\(
P \equiv\left(a t^2, 2 a t\right) \text { and } Q \equiv\left(\frac{a}{t^2},-\frac{2 a}{t}\right)
\)

Let parabola is \(y^2=4 a x\)
\(\therefore\) Tangent at \(P\left(a t^2, 2 a t\right)\) is
\(
t y=x+a t^2 \dots(i)
\)
Its slope \(\frac{1}{t}=m_1 \text { (say) }\)
and tangent at \(Q\left(\frac{a}{t^2},-\frac{2 a}{t}\right)\) is
\(
-\frac{y}{t}=x+\frac{a}{t^2} \dots(ii)
\)
\(
\begin{array}{lrl}
\Rightarrow & -t y & =x t^2+a \\
\text { Its slope } & -t & =m_2 \text { (say) }
\end{array}
\)
\(
\begin{array}{ll}
\because & m_1 m_2=-1 \\
\therefore & \angle P T Q=90^{\circ}
\end{array}
\)
and adding Eqs. (i) and (ii), we get
\(
(x+a)\left(1+t^2\right)=0 \Rightarrow 1+t^2 \neq 0
\)
\(\therefore \quad x+a=0\), which is directrix.

Property-2: The portion of a tangent to a parabola intercepted between the directrix and the curve subtends a right angle at the focus.
The equation of the tangent to the parabola \(y^2=4 a x\) at \(P\left(a t^2, 2 a t\right)\) is
\(
t y=x+a t^2 \dots(i)
\)
Let Eq. (i) meet the directrix \(x+a=0\) at \(Q\), then coordinates of \(Q\) are \(\left(-a, \frac{a t^2-a}{t}\right)\), also focus \(S\) is \((a, 0)\).

\(
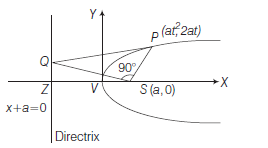
\begin{aligned}
\therefore \quad \text { Slope of } S P & =\frac{2 a t-0}{a t^2-a} \\
& =\frac{2 t}{t^2-1}=m_1 \text { (say) }
\end{aligned}
\)
\(
\begin{aligned}
& \text { and slope of } S Q=\frac{\frac{a t^2-a}{t}-0}{-a-a}=\frac{t^2-1}{-2 t}=m_2 \quad \text { (say) } \\
& \therefore \quad m_1 m_2=-1 \\
&
\end{aligned}
\)
i.e. \(S P\) is perpendicular to \(S Q\) i.e. \(\angle P S Q=90^{\circ}\)

Property-3: The tangent at any point \(P\) of a parabola bisects the angle between the focal chord through \(P\) and the perpendicular from \(P\) to the directrix.
Let the tangent at \(P\left(a t^2, 2 a t\right)\) to the parabola \(y^2=4 a x\) meets the axis of the parabola i.e. \(X\)-axis or \(y=0\) at \(T\). The equation of tangent to the parabola \(y^2=4 a x\) at \(P\left(a t^2, 2 a t\right)\) is
\(
t y=x+a t^2
\)

For coordinates of \(T\) solve it with \(y=0\).
\(
\begin{array}{cc}
\therefore & T\left(-a t^2, 0\right) \\
\therefore & S T=S V+V T=a+a t^2=a\left(1+t^2\right)
\end{array}
\)
\(
\begin{array}{lc}
\text { Also, } & S P=P M=a+a t^2=a\left(1+t^2\right) \\
\therefore & S P=S T, \quad \text { i.e. } \quad \angle S T P=\angle S P T \\
\text { But } & \angle S T P=\angle M P T \quad \text { [alternate angles] } \\
& \angle S P T=\angle M P T
\end{array}
\)

Property-4: The foot of the perpendicular from the focus on any tangent to a parabola lies on the tangent at the vertex.
Equation of tangent at \(P\left(a t^2, 2 a t\right)\)
On the parabola \(y^2=4 a x\) is \(\quad t y=x+a t^2\)
\(\Rightarrow \quad x-t y+a t^2=0 \dots(i)\)
Now, the equation of line through \(S(a, 0)\) and perpendicular to Eq. (i) is
\(
t x+y=\lambda
\)
Since, it passes through \((a, 0)\).
\(
\therefore \quad t a+0=\lambda
\)
\(\therefore \quad\) Equation \(t x+y=t a\) or \(t^2 x+t y-a t^2=0 \dots(ii)\)
By adding Eqs. (i) and (ii), we get
\(
x\left(1+t^2\right)=0
\)
\(
\Rightarrow \quad x=0 \quad\left[\because 1+t^2 \neq 0\right]
\)
Hence, the point of intersection of Eq. (i) and (ii) lies on \(x=0\) i.e. on \(Y\)-axis (which is tangent at the vertex of a parabola).

Property-5:  If \(S\) be the focus of the parabola and tangent and normal at any point \(P\) meet its axis in \(T\) and \(G\) respectively then \(S T=S G=S P\).
Let \(P\left(a t^2, 2 a t\right)\) be any point on the parabola \(y^2=4 a x\), then equation of tangent and normal at \(P\left(a t^2, 2 a t\right)\) are
\(
t y=x+a t^2 \text { and } y=-t x+2 a t+a t^2 \text {, respectively. }
\)
Since, tangent and normal meet its axis in \(T\) and \(G\).
\(\therefore\) Coordinates of \(T^{\prime}\) and \(G\) are \(\left(-a t^2, 0\right)\) and \(\left(2 a+a t^2, 0\right)\) respectively.

\(
\begin{aligned}
\therefore \quad S P & =P M=a+a t^2 \\
S G & =V G-V S=2 a+a t^2-a \\
& =a+a t^2
\end{aligned}
\)
and \(\quad S T=V S+V T=a+a t^2\)
Hence, \(S P=S G=S T\)

Property-6:  If \(S\) be the focus and \(S H\) be perpendicular to the tangent at \(P\), then \(H\) lies on the tangent at the vertex and \(S H^2=O S \cdot S P\), where \(O\) is the vertex of the parabola.
Let \(P\left(a t^2, 2 a t\right)\) be any point on the parabola
\(
y^2=4 a x \dots(i)
\)
then, tangent at \(P\left(a t^2, 2 a t\right)\) to the parabola Eq. (i) is
\(
t y=x+a t^2
\)
It meets the tangent at the vertex i.e. \(x=0\).

\(\therefore \quad\) Coordinates of \(H\) is \((0, a t)\)
and \(S P=P M=a+a t^2 \Rightarrow \quad O S=a\)
and \(S H=\sqrt{(a-0)^2+(0-a t)^2}=\sqrt{a^2+a^2 t^2}\)
or \((S H)^2=a\left\{a\left(1+t^2\right)\right\}=O S \cdot S P\).

Reflection Property of Parabola

The tangent \((P T)\) and normal \((P N)\) of the parabola
\(
y^2=4 a x
\)
at \(P\) are the internal and external bisectors of \(\angle S P M\) and \(B P\) is parallel to the axis of the parabola and
\(\angle B P N=\angle S P N\).

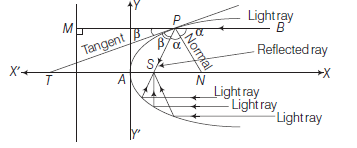
All rays of light coming from the positive direction of \(X\)-axis and parallel to the axis of the parabola after reflection pass through the focus of the parabola.

Example 52: A ray of light is coming along the line \(y=b\) from the positive direction of \(X\)-axis and strikes a concave mirror whose intersection with the \(x y\)-plane is a parabola \(y^2=4 a x\). Find the equation of the reflected ray and show that it passes through the focus of the parabola. Both \(a\) and \(b\) are positive.

Answer: Given parabola is \(y^2=4 a x\)

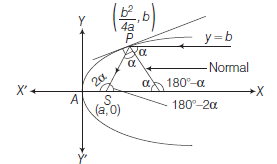
Equation of tangent at \(P\left(\frac{b^2}{4 a}, b\right)\) is \(y b=2 a\left(x+\frac{b^2}{4 a}\right)\), Slope of tangent is \(\frac{2 a}{b}\).
\(
\begin{aligned}
& \text { Hence, slope of normal }=-\frac{b}{2 a}=\tan \left(180^{\circ}-\alpha\right) . \\
& \therefore \quad \tan \alpha=\frac{b}{2 a} \\
& \therefore \quad \text { Slope of reflected ray }=\tan \left(180^{\circ}-2 \alpha\right) \\
& \qquad=-\tan 2 \alpha \\
& \qquad=-\left\{\frac{2 \tan \alpha}{1-\tan ^2 \alpha}\right\}=-\left\{\frac{2 \cdot \frac{b}{2 a}}{1-\frac{b^2}{4 a^2}}\right\}=-\frac{4 a b}{\left(4 a^2-b^2\right)}
\end{aligned}
\)
Hence, equation of reflected ray is
\(
\begin{aligned}
y-b & =-\frac{4 a b}{\left(4 a^2-b^2\right)}\left(x-\frac{b^2}{4 a}\right) \\
\Rightarrow \quad(y-b)\left(4 a^2-b^2\right) & =-\left(4 a x-b^2\right)
\end{aligned}
\)
which obviously passes through the focus \(S(a, 0)\).

Study of Parabola of the Form \((\alpha x+\beta y)^2+2 g x+2 f y+c=0\)

Given equation can be written as
\(
(\alpha x+\beta y)^2=-2 g x-2 f y-c
\)
Now, add an arbitrary constant \(\lambda\) in the square root of the second degree terms. Then the equation will be of the form
\(
\text { i.e. } \quad(\alpha x+\beta y+\lambda)^2=x f_1(\lambda)+y f_2(\lambda)+f_3(\lambda) \dots(i)
\)
Now, choose \(\lambda\) such that the lines
\(
\alpha x+\beta y+\lambda=0 \text { and } x f_1(\lambda)+y f_2(\lambda)+f_3(\lambda)=0
\)
are perpendicular
\(
\begin{aligned}
& \text { i.e. } \quad \text { slope of } \alpha x+\beta y+\lambda=0) \times(\text { slope of } \\
& \left.\qquad x f_1(\lambda)+y f_2(\lambda)+f_3(\lambda)=0\right)=-1 \\
& \Rightarrow \quad-\frac{\alpha}{\beta} \times-\frac{f_1(\lambda)}{f_2(\lambda)}=-1
\end{aligned}
\)
\(
\Rightarrow \quad \alpha f_1(\lambda)+\beta f_2(\lambda)=0 \dots(ii)
\)
Now, substitute the value of \(\lambda\) in Eq. (i) from Eq. (ii).
Multiply and divide \(\left(\alpha^2+\beta^2\right)\) in LHS of Eq. (i)
i.e. \((\alpha x+\beta y+\lambda)^2=\left(\alpha^2+\beta^2\right)\left(\frac{\alpha x+\beta y+\lambda}{\sqrt{\alpha^2+\beta^2}}\right)^2\)
and RHS of Eq. (i) by \(\sqrt{\left(\alpha^2+\beta^2\right)}\)
i.e. \(\begin{aligned}
& x f_1(\lambda)+y f_2(\lambda)+f_3(\lambda) \\
= & \sqrt{\left(\alpha^2+\beta^2\right)}\left(\frac{x f_1(\lambda)+y f_2(\lambda)+f_3(\lambda)}{\sqrt{\left(\alpha^2+\beta^2\right)}}\right)
\end{aligned}
\)
Then, Eq. (i) reduce in the form
\(
\left(\frac{\alpha x+\beta y+\lambda}{\sqrt{\alpha^2+\beta^2}}\right)^2=4 \rho\left(\frac{\beta x-\alpha y+\mu}{\sqrt{\left(\alpha^2+\beta^2\right)}}\right)
\)
which is of the form \(Y^2=4 \rho X\)
\(
Y=\frac{\alpha x+\beta y+\lambda}{\sqrt{\left(\alpha^2+\beta^2\right)}}, X=\frac{\beta x-\alpha y+\mu}{\sqrt{\left(\alpha^2+\beta^2\right)}} \text { and } \quad 4 \rho=\frac{1}{\sqrt{\left(\alpha^2+\beta^2\right)}} \text {. }
\)
Axis is \(Y=0 \quad\) or \(\quad \alpha x+\beta y+\lambda=0\). Equation of tangent at vertex is
\(
X=0 \text { or } \beta x-\alpha y+\mu=0 .
\)
Vertex is the point of intersection of
\(
X=0 \quad \text { and } \quad Y=0
\)
i.e. \(\beta x-\alpha y+\mu=0\) and \(\alpha x+\beta y+\lambda=0\).
Equation of directrix is \(X+\rho=0\).
Equation of latusrectum is \(X-\rho=0\).
FFocus Since, axis and latusrectum intersect at the focus \(S\) its coordinates are detained by solving
\(
X-\rho=0 \quad \text { and } \quad Y=0 .
\)

Example 53: Find the length of latusrectum of the parabola \(\left(a^2+b^2\right)\left(x^2+y^2\right)=(b x+a y-a b)^2\).

Answer: Given equation may be written as
\(
\begin{aligned}
a^2 x^2+a^2 y^2+b^2 x^2+b^2 y^2=b^2 x^2 & +a^2 y^2+a^2 b^2 \\
& +2 a b x y-2 a^2 b y-2 a b^2 x
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad a^2 x^2-2 a b x y+b^2 y^2=-2 a b^2 x-2 a^2 b y+a^2 b^2 \\
& \Rightarrow \quad(a x-b y)^2=-2 a b\left(b x+a y-\frac{a b}{2}\right)
\end{aligned}
\)
Since, \(a x-b y=0\) and \(b x+a y-\frac{a b}{2}=0\) are perpendicular.
\(
\begin{aligned}
& \therefore\left(a^2+b^2\right)\left(\frac{a x-b y}{\sqrt{a^2+b^2}}\right)^2=-2 a b \sqrt{\left(a^2+b^2\right)}\left(\frac{b x+a y-\frac{a b}{2}}{\sqrt{\left(a^2+b^2\right)}}\right) \\
& \Rightarrow\left(\frac{a x-b y}{\sqrt{a^2+b^2}}\right)^2=\frac{-2 a b}{\sqrt{\left(a^2+b^2\right)}}\left(\frac{b x+a y-\frac{a b}{2}}{\sqrt{\left(a^2+b^2\right)}}\right)
\end{aligned}
\)
which is of the form \(Y^2=-4 \rho X\).
Therefore, the latusrectum \(=4 \rho=\frac{2 a b}{\sqrt{\left(a^2+b^2\right)}}\).

Alternate:

Given equation may be written as
\(
x^2+y^2=\frac{(b x+a y-a b)^2}{\left(a^2+b^2\right)}
\)
\(
\begin{gathered}
\Rightarrow \sqrt{\left(x^2+y^2\right)}=\frac{|b x+a y-a b|}{\sqrt{\left(a^2+b^2\right)}} \\
\Rightarrow \sqrt{(x-0)^2+(y-0)^2} \\
=\frac{|b x+a y-a b|}{\sqrt{\left(a^2+b^2\right)}}
\end{gathered}
\)
which is of the form \(S P=P M\).

Since, distance from focus \(S\) to \((b x+a y-a b=0)=\frac{1}{2}(4 \rho)\)
\(
\begin{array}{ll}
\Rightarrow & \frac{1}{2}(4 \rho)=\frac{a b}{\sqrt{a^2+b^2}} \\
\therefore & 4 \rho=\frac{2 a b}{\sqrt{\left(a^2+b^2\right)}}
\end{array}
\)

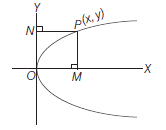
Remark

• Consider the equation of parabola is \(y^2=4 a x\). i.e. \((M P)^2=(\) Latusrectum) \(N P\).
  i.e. if \(P\) is any point on the given parabola, then (the distance of \(P\) from its axis) \({ }^2=\) (Latusrectum) (The distance of \(P\) from the tangent at its vertex).