11.2 Sections of a Cone

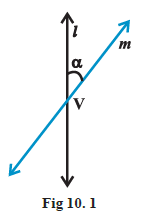
Let \(l\) be a fixed vertical line and \(m\) be another line intersecting it at a fixed point \(V\) and inclined to it an angle \(\alpha\) (Fig10.1).

Suppose we rotate the line \(m\) around the line \(l\) in such a way that the angle \(\alpha\) remains constant. Then the surface generated is a double-napped right circular hollow cone herein after referred as cone and extending indefinitely far in both directions (Fig10.2).

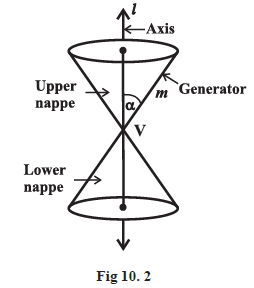
The point \(V\) is called the vertex; the line \(l\) is the axis of the cone. The rotating line \(m\) is called a generator of the cone. The vertex separates the cone into two parts called nappes.

If we take the intersection of a plane with a cone, the section so obtained is called a conic section. Thus, conic sections are the curves obtained by intersecting a right circular cone by a plane.

We obtain different kinds of conic sections depending on the position of the intersecting plane with respect to the cone and by the angle made by it with the vertical axis of the cone. Let \(\beta\) be the angle made by the intersecting plane with the vertical axis of the cone (Fig10.3).

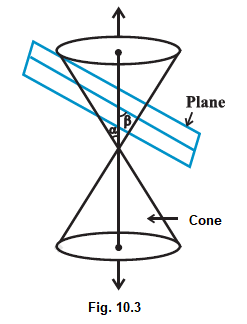
The intersection of the plane with the cone can take place either at the vertex of the cone or at any other part of the nappe either below or above the vertex.

Circle, ellipse, parabola and hyperbola When the plane cuts the nappe (other than the vertex) of the cone, we have the following situations:

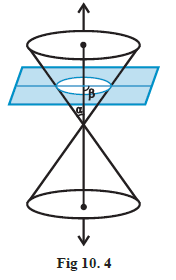
Case-I: When \(\beta=90^{\circ}\), the section is a circle (Fig10.4).

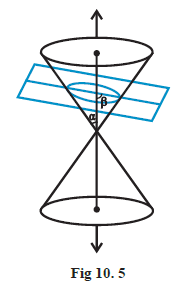
Case II: When \(\alpha<\beta<90^{\circ}\), the section is an ellipse (Fig10.5).

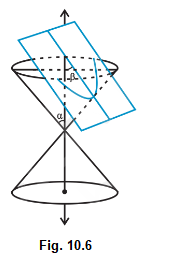
Case III: When \(\beta=\alpha\); the section is a parabola (Fig10.6).

(In each of the above three situations, the plane cuts entirely across one nappe of the cone).

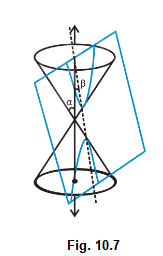
Case iv:  When \(0 \leq \beta<\alpha\); the plane cuts through both the nappes and the curves of intersection is a hyperbola (Fig10.7).

Degenerated conic sections

When the plane cuts at the vertex of the cone, we have the following different cases:
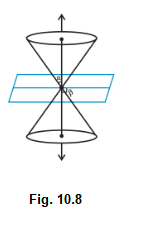
Case I: When \(\alpha<\beta \leq 90^{\circ}\), then the section is a point (Fig10.8).

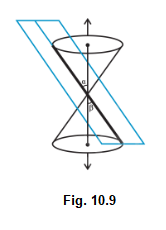
Case II: When \(\beta=\alpha\), the plane contains a generator of the cone and the section is a straight line (Fig10.9). It is the degenerated case of a parabola.

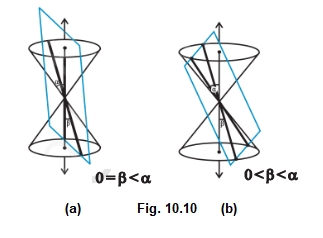
Case III: When \(0 \leq \beta<\alpha\), the section is a pair of intersecting straight lines (Fig10.10). It is the degenerated case of a hyperbola.

In the following sections, we shall obtain the equations of each of these conic sections in standard form by defining them based on geometric properties.