10.5 Distance of a Point From a Line

Distance of a Point From a Line

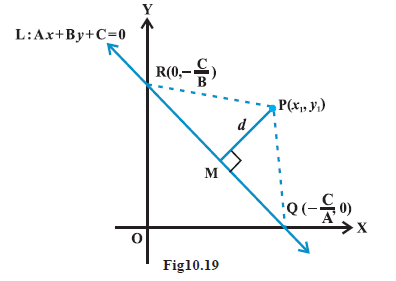
The distance of a point from a line is the length of the perpendicular drawn from the point to the line. Let \(\mathrm{L}: \mathrm{A} x+\mathrm{By}+\mathrm{C}=0\) be a line, whose distance from the point \(\mathrm{P}\left(x_1, y_1\right)\) is \(d\). Draw a perpendicular \(\mathrm{PM}\) from the point \(\mathrm{P}\) to the line \(\mathrm{L}\) (Fig10.19). If the line meets the \(x\)-and \(y\)-axes at the points \(\mathrm{Q}\) and \(\mathrm{R}\), respectively. Then, coordinates of the points are \(Q\left(-\frac{C}{A}, 0\right)\) and \(R\left(0,-\frac{C}{B}\right)\). Thus, the area of the triangle \(P Q R\) is given by
\(
\text { area }(\triangle \mathrm{PQR})=\frac{1}{2} \mathrm{PM} \cdot \mathrm{QR} \text {, which gives } \mathrm{PM}=\frac{2 \text { area }(\triangle \mathrm{PQR})}{\mathrm{QR}} \dots(1)
\)
\(
\text { Also, area }(\Delta \mathrm{PQR})=\frac{1}{2}\left|x_1\left(0+\frac{\mathrm{C}}{\mathrm{B}}\right)+\left(-\frac{\mathrm{C}}{\mathrm{A}}\right)\left(-\frac{\mathrm{C}}{\mathrm{B}}-y_1\right)+0\left(y_1-0\right)\right|
\)
\(
=\frac{1}{2}\left|x_1 \frac{\mathrm{C}}{\mathrm{B}}+y_1 \frac{\mathrm{C}}{\mathrm{A}}+\frac{\mathrm{C}^2}{\mathrm{AB}}\right|
\)
\(
\text { or } 2 \text { area }(\triangle \mathrm{PQR})=\left|\frac{\mathrm{C}}{\mathrm{AB}}\right| \cdot\left|\mathrm{A} x_1+\mathrm{B} y_1+\mathrm{C}\right| \text {, and }
\)
\(
\mathrm{QR}=\sqrt{\left(0+\frac{\mathrm{C}}{\mathrm{A}}\right)^2+\left(\frac{\mathrm{C}}{\mathrm{B}}-0\right)^2}=\left|\frac{\mathrm{C}}{\mathrm{AB}}\right| \sqrt{\mathrm{A}^2+\mathrm{B}^2}
\)
Substituting the values of area ( \(\triangle \mathrm{PQR})\) and \(\mathrm{QR}\) in (1), we get
\(
\begin{array}{l}
\mathrm{PM}=\frac{\left|\mathrm{A} x_1+\mathrm{B} y_1+\mathrm{C}\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}} \\
\text { or } \quad d=\frac{\left|\mathrm{A} x_1+\mathrm{B} y_1+\mathrm{C}\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}} .
\end{array}
\)
Thus, the perpendicular distance \((d)\) of a line \(\mathrm{Ax}+\mathrm{By}+\mathrm{C}=0\) from a point \(\left(x_1, y_1\right)\) is given by
\(
d=\frac{\left|\mathrm{A} x_1+\mathrm{B} y_1+\mathrm{C}\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}} .
\)

Corollary 1: The length of perpendicular from the origin to the line \(a x+b y+c=0\) is
\(
\frac{|a \cdot 0+b \cdot 0+c|}{\sqrt{\left(a^2+b^2\right)}} \text { i.e. } \frac{|c|}{\sqrt{\left(a^2+b^2\right)}}
\)

Corollary 2 : The length of perpendicular from \(\left(x_1, y_1\right)\) to the line \(x \cos \alpha+y \sin \alpha=p\) is
\(
\frac{\left|x_1 \cos \alpha+y_1 \sin \alpha-p\right|}{\sqrt{\left(\cos ^2 \alpha+\sin ^2 \alpha\right)}}=\left|x_1 \cos \alpha+y_1 \sin \alpha-p\right|
\)

Working Rule

• Put the point \(\left(x_1, y_1\right)\) for \((x, y)\) on the LHS while the RHS is zero.
• Divide LHS after Eq. (i) by \(\sqrt{\left(a^2+b^2\right)}\), where \(a\) and \(b\) are the coefficients of \(x\) and \(y\) respectively.

Example 1: Find the sum of the abscissas of all the points on the line \(x+y=4\) that lie at a unit distance from the line \(4 x+3 y-10=0\).

Answer: Any point on the line \(x+y=4\) can be taken as \(\left(x_1, 4-x_1\right)\). As it is at a unit distance from the line \(4 x+3 y-10=0\), we get
\(
\frac{\left|4 x_1+3\left(4-x_1\right)-10\right|}{\sqrt{\left(4^2+3^2\right)}}=1
\)
\(
\begin{array}{l}
\qquad \begin{aligned}
\left|x_1+2\right| & =5 \Rightarrow x_1+2= \pm 5 \\
x_1=3 & \text { or }-7
\end{aligned} \\
\text { Required sum }=3-7=-4 .
\end{array}
\)

Example 2: If \(p\) and \(p^{\prime}\) are the length of the perpendiculars from the origin to the straight lines whose equations are \(x \sec \theta+y \operatorname{cosec} \theta=a\) and \(x \cos \theta-y \sin \theta=a \cos 2 \theta\), then find the value of \(4 p^2+p^{\prime 2}\).

Answer: We have, \(p=\frac{|-a|}{\sqrt{\left(\sec ^2 \theta+\operatorname{cosec}^2 \theta\right)}}\)
\(
\therefore \quad p^2=\frac{a^2}{\sec ^2 \theta+\operatorname{cosec}^2 \theta}=\frac{a^2 \sin ^2 \theta \cos ^2 \theta}{1}
\)
\(
4 p^2=a^2 \sin ^2 2 \theta \dots(1)
\)
and
\(
p^{\prime}=\frac{|-a \cos 2 \theta|}{\sqrt{\left(\cos ^2 \theta+\sin ^2 \theta\right)}}=|-a \cos 2 \theta|
\)
\(
\left(p^{\prime}\right)^2=a^2 \cos ^2 2 \theta \dots(2)
\)
\(\therefore\) Adding Eqs. (i) and (ii), we get
\(
4 p^2+p^2=a^2
\)

Example 3: If \(p\) is the length of the perpendicular from the origin to the line \(\frac{x}{a}+\frac{y}{b}=1\), then prove that
\(
\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{p^2} \text {. }
\)

Answer: \(p=\) length of perpendicular from origin to
\(
\begin{aligned}
\frac{x}{a}+\frac{y}{b} & =1 \\
& =\frac{|0+0-1|}{\sqrt{\left(\frac{1}{a}\right)^2+\left(\frac{1}{b}\right)^2}}=\frac{1}{\sqrt{\left(\frac{1}{a^2}+\frac{1}{b^2}\right)}} \\
\frac{1}{p^2} & =\frac{1}{a^2}+\frac{1}{b^2} \text { or } \frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{p^2}
\end{aligned}
\)

Example 4: Prove that no line can be drawn through the point \((4,-5)\) so that its distance from \((-2,3)\) will be equal to 12.

Answer: Suppose, if possible.
Equation of line through \((4,-5)\) with slope of \(m\) is
\(
\begin{array}{l}
\quad y+5=m(x-4) \\
\Rightarrow \quad m x-y-4 m-5=0 \\
\text { Then, } \frac{|m(-2)-3-4 m-5|}{\sqrt{m^2+1}}=12
\end{array}
\)
\(
\begin{array}{ll}
\Rightarrow & |-6 m-8|=12 \sqrt{\left(m^2+1\right)} \\
\text { On squaring, } & (6 m+8)^2=144\left(m^2+1\right) \\
\Rightarrow & 4(3 m+4)^2=144\left(m^2+1\right) \\
\Rightarrow & (3 m+4)^2=36\left(m^2+1\right) \\
\Rightarrow & 27 m^2-24 m+20=0 \dots(i)
\end{array}
\)
Since, the discriminant of Eq. (i) is \((-24)^2-4 \cdot 27 \cdot 20=-1584\) which is negative, there is no real value of \(m\). Hence no such line is possible.

Distance between two parallel lines

We know that slopes of two parallel lines are equal. Therefore, two parallel lines can be taken in the form
\(
y=m x+c_1 \dots(1)
\)
and \(y=m x+c_2 \dots(2)\)
Line (1) will intersect \(x\)-axis at the point A \(\left(-\frac{c_1}{m}, 0\right)\) as shown in Fig10.20.

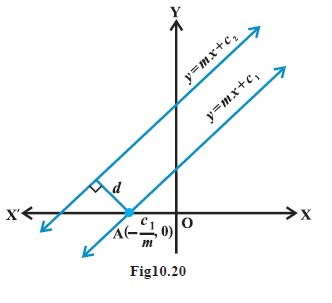
Distance between two lines is equal to the length of the perpendicular from point A to line (2). Therefore, distance between the lines (1) and (2) is
\(
\frac{\left|(-m)\left(-\frac{c_1}{m}\right)+\left(-c_2\right)\right|}{\sqrt{1+m^2}} \text { or } d=\frac{\left|c_1-c_2\right|}{\sqrt{1+m^2}} \text {. }
\)
Thus, the distance \(d\) between two parallel lines \(y=m x+c_1\) and \(y=m x+c_2\) is given by
\(
d=\frac{\left|c_1-c_2\right|}{\sqrt{1+m^2}}
\)
If lines are given in general form, i.e., \(\mathrm{A} x+\mathrm{B} y+\mathrm{C}_1=0\) and \(\mathrm{A} x+\mathrm{B} y+\mathrm{C}_2=0\),
then above formula will take the form \(d=\frac{\left|\mathrm{C}_1-\mathrm{C}_2\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}\)

Example 5: Find the distance of the point \((3,-5)\) from the line \(3 x-4 y-26=0\).

Answer: Given line is \(\quad 3 x-4 y-26=0 \dots(1)\)
Comparing (1) with general equation of line \(\mathrm{Ax}+\mathrm{By}+\mathrm{C}=0\), we get
\(
\mathrm{A}=3, \mathrm{~B}=-4 \text { and } \mathrm{C}=-26 \text {. }
\)
Given point is \(\left(x_1, y_1\right)=(3,-5)\). The distance of the given point from given line is
\(
d=\frac{\left|\mathrm{A} x_1+\mathrm{B} y_1+\mathrm{C}\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}=\frac{|3.3+(-4)(-5)-26|}{\sqrt{3^2+(-4)^2}}=\frac{3}{5} .
\)

Example 6: Find the distance between the parallel lines \(3 x-4 y+7=0\) and
\(
3 x-4 y+5=0
\)

Answer: Here \(\mathrm{A}=3, \mathrm{~B}=-4, \mathrm{C}_1=7\) and \(\mathrm{C}_2=5\). Therefore, the required distance is
\(
d=\frac{|7-5|}{\sqrt{3^2+(-4)^2}}=\frac{2}{5} .
\)

Example 7: Find the equations of the line parallel to \(5 x-12 y+26=0\) and at a distance of 4 units from it.

Answer: Equation of any line parallel to \(5 x-12 y+26=0\) is
\(
5 x-12 y+\lambda=0 \dots(1)
\)
Since, the distance between the parallel lines is 4 units, then
\(
\frac{|\lambda-26|}{\sqrt{(5)^2+(-12)^2}}=4
\)
or \(\quad|\lambda-26|=52\) or \(\lambda-26= \pm 52\)
or \(\quad \lambda=26 \pm 52 \quad \therefore \lambda=-26\) or 78
Substituting the values of \(\lambda\) in Eq. (i), we get
\(
5 x-12 y-26=0
\)
and
\(
5 x-12 y+78=0
\)

Example 8: If the lines \(2 x+y-3=0,5 x+k y-3=0\) and \(3 x-y-2=0\) are concurrent, find the value of \(k\).

Answer: Three lines are said to be concurrent, if they pass through a common point, i.e., point of intersection of any two lines lies on the third line. Here given lines are
\(
\begin{array}{l}
2 x+y-3=0 \dots(1) \\
5 x+k y-3=0 \dots(2)
\end{array}
\)
\(
3 x-y-2=0 \dots(3)
\)
Solving (1) and (3) by cross-multiplication method, we get
\(
\frac{x}{-2-3}=\frac{y}{-9+4}=\frac{1}{-2-3} \text { or } x=1, y=1 \text {. }
\)
Therefore, the point of intersection of two lines is \((1,1)\). Since above three lines are concurrent, the point \((1,1)\) will satisfy equation \((2)\) so that
\(
5.1+k .1-3=0 \text { or } k=-2 \text {. }
\)

Example 9: Find the distance of the line \(4 x-y=0\) from the point \(\mathrm{P}(4,1)\) measured along the line making an angle of \(135^{\circ}\) with the positive \(x\)-axis.

Answer: Given line is \(4 x-y=0 \dots(1)\)

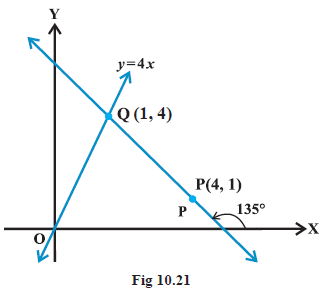
In order to find the distance of the line (1) from the point \(P(4,1)\) along another line, we have to find the point of intersection of both the lines. For this purpose, we will first find the equation of the second line (Fig 10.21). Slope of second line is \(\tan 135^{\circ}=-1\). Equation of the line with slope -1 through the point \(P(4,1)\) is
\(
y-1=-1(x-4) \text { or } x+y-5=0 \dots(2)
\)
Solving (1) and (2), we get \(x=1\) and \(y=4\) so that point of intersection of the two lines is \(Q(1,4)\). Now, distance of line (1) from the point \(P(4,1)\) along the line (2)
\(=\) the distance between the points \(P(4,1)\) and \(Q(1,4)\).
\(=\sqrt{(1-4)^2+(4-1)^2}=3 \sqrt{2}\) units.

Example 10: Assuming that straight lines work as the plane mirror for a point, find the image of the point \((1,2)\) in the line \(x-3 y+4=0\).

Answer: Let \(\mathbf{Q}(h, k)\) is the image of the point \(\mathrm{P}(1,2)\) in the line
\(
x-3 y+4=0 \dots(1)
\)

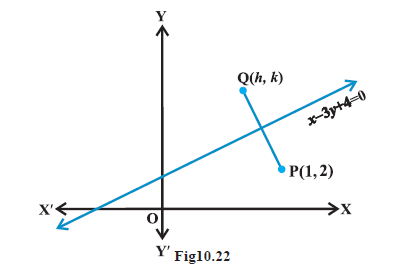
Therefore, the line (1) is the perpendicular bisector of line segment PQ (Fig 10.22).
Hence Slope of line \(\mathrm{PQ}=\frac{-1}{\text { Slope of line } x-3 y+4=0}\),
so that \(\frac{k-2}{h-1}=\frac{-1}{\frac{1}{3}} \quad\) or \(\quad 3 h+k=5 \dots(2)\)
and the mid-point of \(\mathrm{PQ}\), i.e., point \(\left(\frac{h+1}{2}, \frac{k+2}{2}\right)\) will satisfy the equation (1) so that
\(
\frac{h+1}{2}-3\left(\frac{k+2}{2}\right)+4=0 \text { or } h-3 k=-3
\)
Solving (2) and (3), we get \(h=\frac{6}{5}\) and \(k=\frac{7}{5}\).
Hence, the image of the point \((1,2)\) in the line (1) is \(\left(\frac{6}{5}, \frac{7}{5}\right)\).

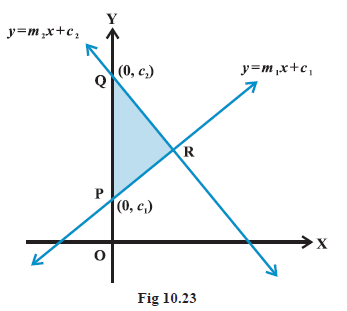
Example 11: Show that the area of the triangle formed by the lines \(y=m_1 x+c_1, y=m_2 x+c_2\) and \(x=0\) is \(\frac{\left(c_1-c_2\right)^2}{2\left|m_1-m_2\right|}\).

Answer: Given lines are

\(
\begin{array}{l}
y=m_1 x+c_1 \dots(1) \\
y=m_2 x+c_2 \dots(2) \\
x=0 \dots(3)
\end{array}
\)
We know that line \(y=m x+c\) meets the line \(x=0\) (y-axis) at the point \((0, c)\). Therefore, two vertices of the triangle formed by lines (1) to (3) are \(\mathrm{P}\left(0, c_1\right)\) and \(\mathrm{Q}\left(0, c_2\right)\) (Fig 10.23).
Third vertex can be obtained by solving equations (1) and (2). Solving (1) and (2), we get
\(
x=\frac{\left(c_2-c_1\right)}{\left(m_1-m_2\right)} \text { and } y=\frac{\left(m_1 c_2-m_2 c_1\right)}{\left(m_1-m_2\right)}
\)
Therefore, third vertex of the triangle is \(\mathrm{R}\left(\frac{\left(c_2-c_1\right)}{\left(m_1-m_2\right)}, \frac{\left(m_1 c_2-m_2 c_1\right)}{\left(m_1-m_2\right)}\right)\). Now, the area of the triangle is
\(
=\frac{1}{2}\left|0\left(\frac{m_1 c_2-m_2 c_1}{m_1-m_2}-c_2\right)+\frac{c_2-c_1}{m_1-m_2}\left(c_2-c_1\right)+0\left(c_1-\frac{m_1 c_2-m_2 c_1}{m_1-m_2}\right)\right|=\frac{\left(c_2-c_1\right)^2}{2\left|m_1-m_2\right|}
\)

Example 12: A line is such that its segment between the lines
\(5 x-y+4=0\) and \(3 x+4 y-4=0\) is bisected at the point \((1,5)\). Obtain its equation.

Answer: Given lines are
\(
\begin{array}{l}
5 x-y+4=0 \\
3 x+4 y-4=0
\end{array}
\)
Let the required line intersects the lines (1) and (2) at the points, \(\left(\alpha_1, \beta_1\right)\) and \(\left(\alpha_2, \beta_2\right)\), respectively (Fig10.24). Therefore
\(
\begin{array}{l}
5 \alpha_1-\beta_1+4=0 \text { and } \\
3 \alpha_2+4 \beta_2-4=0
\end{array}
\)

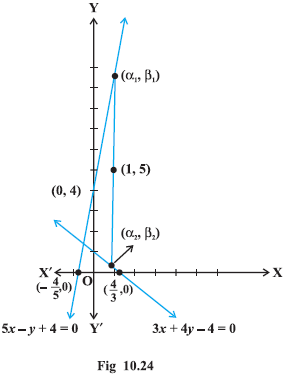
or \(\beta_1=5 \alpha_1+4\) and \(\beta_2=\frac{4-3 \alpha_2}{4}\).
We are given that the mid point of the segment of the required line between \(\left(\alpha_1, \beta_1\right)\) and \(\left(\alpha_2, \beta_2\right)\) is \((1,5)\). Therefore
\(
\begin{array}{l}
\frac{\alpha_1+\alpha_2}{2}=1 \text { and } \frac{\beta_1+\beta_2}{2}=5, \\
\alpha_1+\alpha_2=2 \text { and } \frac{5 \alpha_1+4+\frac{4-3 \alpha_2}{4}}{2}=5,
\end{array}
\)
or \(\alpha_1+\alpha_2=2\) and \(20 \alpha_1-3 \alpha_2=20\)
Solving equations in (3) for \(\alpha_1\) and \(\alpha_2\), we get
\(
\alpha_1=\frac{26}{23} \text { and } \alpha_2=\frac{20}{23} \text { and hence, } \beta_1=5 \cdot \frac{26}{23}+4=\frac{222}{23} .
\)
Equation of the required line passing through \((1,5)\) and \(\left(\alpha_1, \beta_1\right)\) is
\(
y-5=\frac{\beta_1-5}{\alpha_1-1}(x-1) \text { or } y-5=\frac{\frac{222}{23}-5}{\frac{26}{23}-1}(x-1)
\)
or \(\quad 107 x-3 y-92=0\),
which is the equation of required line.

Example 13: Show that the path of a moving point such that its distances from two lines \(3 x-2 y=5\) and \(3 x+2 y=5\) are equal is a straight line.

Answer: Given lines are
\(
\text { and } \quad \begin{aligned}
3 x-2 y & =5 \\
3 x+2 y & =5
\end{aligned}
\)
Let \((h, k)\) is any point, whose distances from the lines (1) and (2) are equal. Therefore
\(
\frac{|3 h-2 k-5|}{\sqrt{9+4}}=\frac{|3 h+2 k-5|}{\sqrt{9+4}} \text { or }|3 h-2 k-5|=|3 h+2 k-5| \text {, }
\)
which gives \(3 h-2 k-5=3 h+2 k-5\) or \(-(3 h-2 k-5)=3 h+2 k-5\).
Solving these two relations we get \(k=0\) or \(h=\frac{5}{3}\). Thus, the point \((h, k)\) satisfies the equations \(y=0\) or \(x=\frac{5}{3}\), which represent straight lines. Hence, path of the point equidistant from the lines (1) and (2) is a straight line.

The Distance form or Symmetric form or Parametric form of a line

Theorem : The equation of the straight line passing through \(\left(x_1, y_1\right)\) and making an angle \(\theta\) with the positive direction of \(X\)-axis is
\(
\frac{x-x_1}{\cos \theta}=\frac{y-y_1}{\sin \theta}=r
\)
where, \(r\) is the directed distance between the points \((x, y)\) and \(\left(x_1, y_1\right)\).

Proof: Let \(A B\) be a line which passes through the point \(Q\left(x_1, y_1\right)\) and meet \(X\)-axis at \(R\) and makes an angle \(\theta\) with the positive direction of \(X\)-axis.

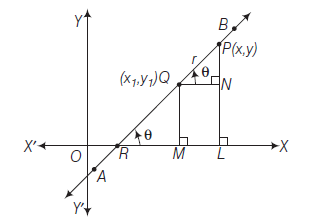
Let \(P(x, y)\) be any point on the line at a distance \(r\) from \(Q\). Draws \(P L\) and \(Q M\) are perpendiculars from \(P\) and \(Q\) on \(X\)-axis respectively and draw \(Q N\) perpendicular on \(P L\). Then,
\(
\begin{aligned}
& Q N=M L=O L-O M=x-x_1 \\
& P N=P L-N L=P L-Q M=y-y_1
\end{aligned}
\)
from \(\triangle P Q N\),
\(
\begin{aligned}
& \cos \theta=\frac{Q N}{P Q}=\frac{x-x_1}{r} \text { or } \quad \frac{x-x_1}{\cos \theta}=r \dots(i) \\
& \sin \theta=\frac{P N}{P Q}=\frac{y-y_1}{r} \text { or } \frac{y-y_1}{\sin \theta}=r \dots(ii)
\end{aligned}
\)
From Eqs. (i) and (ii), we get
\(
\frac{x-x_1}{\cos \theta}=\frac{y-y_1}{\sin \theta}=r
\)

Corollary \(1: \because \frac{x-x_1}{\cos \theta}=\frac{y-y_1}{\sin \theta}=r\), then
\(
\left.\begin{array}{l}
x=x_1+r \cos \theta \\
y=y_1+r \sin \theta
\end{array}\right\}
\)
parametric equations of straight line \(A B\).
Corollary 2: If \(P\) point above \(Q\) then \(r\) is positive then coordinates of \(P\) are \(\left(x_1+r \cos \theta, y_1+r \sin \theta\right)\) and if \(P\) below \(Q\) then \(r\) is negative then coordinates of \(P\) are \(\left(x_1-r \cos \theta, y_1-r \sin \theta\right)\).

Example 14: Find the direction in which a straight line must be drawn through the point \((1,2)\) so that its point of intersection with the line \(x+y=4\) may be at a distance \(\frac{1}{3} \sqrt{6}\) from this point.

Answer: Let the straight line makes an angle \(\theta\) with the positive direction of \(X\)-axis.
\(\therefore\) Equation of the line through \((1,2)\) in parametric form is
\(
\frac{x-1}{\cos \theta}=\frac{y-2}{\sin \theta}=\frac{1}{3} \sqrt{6}
\)

\(
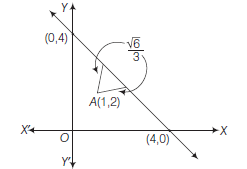
\text { or } \quad x=1+\frac{\sqrt{6}}{3} \cos \theta \text { and } y=2+\frac{\sqrt{6}}{3} \sin \theta
\)
\(
\text { Since, the point }\left(1+\frac{\sqrt{6}}{3} \cos \theta, 2+\frac{\sqrt{6}}{3} \sin \theta\right) \text { lies on the line }
\)
\(
\begin{aligned}
& x+y=4 \\
& 1+\frac{\sqrt{6}}{3} \cos \theta+2+\frac{\sqrt{6}}{3} \sin \theta=4
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{\sqrt{6}}{3}(\cos \theta+\sin \theta)=1 \\
& \Rightarrow \quad \cos \theta+\sin \theta=\frac{3}{\sqrt{6}}=\frac{\sqrt{3}}{\sqrt{2}} \\
& \Rightarrow \quad \frac{1}{\sqrt{2}} \cos \theta+\frac{1}{\sqrt{2}} \sin \theta=\frac{\sqrt{3}}{2} \\
& \Rightarrow \quad \cos \left(\theta-\frac{\pi}{4}\right)=\cos \left(\frac{\pi}{6}\right) \\
&
\end{aligned}
\)
\(
\theta-\frac{\pi}{4}=2 n \pi \pm \frac{\pi}{6} ; n \in I
\)
\(
\text { for } n=0, \quad \theta= \pm \frac{\pi}{6}+\frac{\pi}{4} \quad(\because 0 \leq \theta<\pi)
\)
\(
=15^{\circ}, 75^{\circ}
\)

Special Corollaries

Case-I: Angle made by \(A B\) with positive \(X\)-axis (where \(A\) and \(B\) are given points) :be two points and let \(A B\) makes an angle \(\theta\) with the positive direction of \(X\)-axis and let \(d\) be the distance between \(A\) and \(B\). Then Let \(A\left(x_1, y_1\right)\) and \(B\left(x_2, y_2\right)\)
\(
\cos \theta=\frac{x_2-x_1}{d}, \sin \theta=\frac{y_2-y_1}{d}
\)

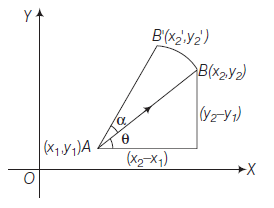
where, \(d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}=A B\) and \(x_2=x_1+d \cos \theta, y_2=y_1+d \sin \theta\)
If \(A B\) rotates an angle \(\alpha\) about \(A\), then new coordinates of \(B\) are
\(
\begin{aligned}
& x_2^{\prime}=x_1+d \cos (\theta+\alpha), \\
& y_2^{\prime}=y_1+d \sin (\theta+\alpha)
\end{aligned}
\)
and here, \(A B=A B^{\prime}=d\).

Example 15: The line joining the points \(A(2,0)\) and \(B(3,1)\) is rotated about \(A\) in the anticlockwise direction through an angle of \(15^{\circ}\). Find the equation of the line in the new position. If \(B\) goes to \(C\) in the new position, what will be the coordinates of \(C\) ?

Answer: Here \(\quad A B=\sqrt{(2-3)^2+(0-1)^2}=\sqrt{2}\) and slope of \(A B=\frac{1-0}{3-2}=1=\tan 45^{\circ}\)

\(
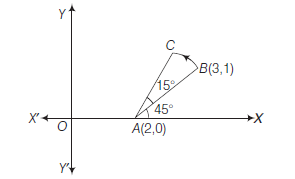
\therefore \quad \angle B A X=45^{\circ}
\)
Now line \(A B\) is rotated through an angle of \(15^{\circ}\)
\(
\begin{array}{rlrl}
\Rightarrow & & \angle C A X & =45^{\circ}+15^{\circ}=60^{\circ} \\
\text { and } & A B & =A C=\sqrt{2}
\end{array}
\)
Equation of line \(A C\) in parametric form is
\(
\left.\begin{array}{l}
x=2+r \cos 60^{\circ} \\
y=0+r \sin 60^{\circ}
\end{array}\right\} \dots(i)
\)
Since, \(A C=r=\sqrt{2}\)
Put \(r=\sqrt{2}\) in Eq. (i), then
\(
\begin{aligned}
& x=2+\sqrt{2} \cdot \frac{1}{2}=\frac{4+\sqrt{2}}{2} \\
& y=\sqrt{2} \cdot \frac{\sqrt{3}}{2}=\frac{\sqrt{6}}{2}
\end{aligned}
\)
Equation of the line \(A C\) is or
\(
\begin{aligned}
& \frac{x-2}{y}=\cot 60^{\circ}=\frac{1}{\sqrt{3}} \\
& x \sqrt{3}-y-2 \sqrt{3}=0
\end{aligned}
\)
and coordinates of \(C\) are \(\left(\frac{4+\sqrt{2}}{2}, \frac{\sqrt{6}}{2}\right)\).

Case-II:  Complex number as a rotating arrow in Argand plane :

Let \(z=r(\cos \theta+i \sin \theta)=r e^{i \theta}\), where \(i=\sqrt{-1} \dots(i)\)
be a complex number representing a point \(P\) in the Argand plane.

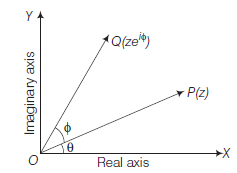
Then, \(\quad O P=|z|=r\) and \(\angle P O X=\theta\)
Now, consider complex number \(z_1=z e^{i \phi}\)
or
\(
z_1=r e^{i \theta} \cdot e^{i \phi}=r \cdot e^{i(\theta+\phi)} \quad \text { [from Eq. (i)] }
\)
Clearly the complex number \(z_1\) represents a point \(Q\) in the Argand plane, when
\(
O Q=r \text { and } \angle Q O X=\theta+\phi
\)
Clearly multiplication of \(z\) with \(e^{i \phi}\) rotates the vector \(\overrightarrow{O P}\) through angle \(\phi\) in anti-clockwise sense. Similarly multiplication of \(z\) with \(e^{-i \phi}\) will rotate the vector \(\overrightarrow{O P}\) in clockwise sense.

Example 16: The centre of a square is at the origin and one vertex is \(A(2,1)\). Find the coordinates of other vertices of the square.

Answer: [By special corollary (case-II)]
\(
\begin{array}{ll}
\because & A \equiv(2,1) \\
\therefore & z_A=2+i, \text { where } i=\sqrt{-1}
\end{array}
\)

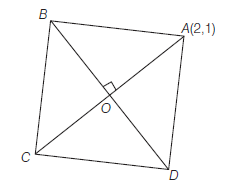
Now, in triangle \(A O B\),
\(
\begin{aligned}
& O A=O B, \angle A O B=90^{\circ}=\frac{\pi}{2} \\
& \therefore \quad z_B=z_A e^{i \frac{\pi}{2}}=i z_A=2 i-1 \\
& \therefore \quad B \equiv(-1,2) \\
& \because O \text { is the mid-point of } A C \text { and } B D \\
& \therefore \quad C \equiv(-2,-1) \text { and } D \equiv(1,-2) \text {. } \\
&
\end{aligned}
\)

Position of Two Points Relative to a Given Line

Theorem : The points \(P\left(x_1, y_1\right)\) and \(Q\left(x_2, y_2\right)\) lie on the same or opposite sides of the line \(a x+b y+c=0\) according as
\(
\frac{a x_1+b y_1+c}{a x_2+b y_2+c}>0 \text { or }<0 .
\)
Proof : Let the line \(P Q\) be divided by the line \(a x+b y+c=0\) in the ratio \(\lambda: 1\) (internally) at the point \(R\).
\(\therefore\) The coordinates of \(R\) are \(\left(\frac{x_1+\lambda x_2}{1+\lambda}, \frac{y_1+\lambda y_2}{1+\lambda}\right)\)
The point of \(R\) lies on the line \(a x+b y+c=0\)
\(
\begin{array}{ll}
\text { then } \quad a\left(\frac{x_1+\lambda x_2}{1+\lambda}\right)+b\left(\frac{y_1+\lambda y_2}{1+\lambda}\right)+c=0 \\
\Rightarrow \quad \lambda\left(a x_2+b y_2+c\right)+\left(a x_1+b y_1+c\right)=0 \\
\Rightarrow \quad \lambda=-\left(\frac{a x_1+b y_1+c}{a x_2+b y_2+c}\right) \quad\left(\because a x_2+b y_2+c \neq 0\right)
\end{array}
\)

Case I : Let \(P\) and \(Q\) are on same side of the line \(a x+b y+c=0\).
\(\therefore R\) divides \(P Q\) externally.

\(\therefore \lambda\) is negative
\(
\begin{array}{ll}
\Rightarrow & -\left(\frac{a x_1+b y_1+c}{a x_2+b y_2+c}\right)<0 \\
\Rightarrow & \left(\frac{a x_1+b y_1+c}{a x_2+b y_2+c}\right)>0
\end{array}
\)
or \(\quad \frac{f\left(x_1, y_1\right)}{f\left(x_2, y_2\right)}>0\)
where, \(f(x, y) \equiv a x+b y+c\).

Case II : Let \(P\) and \(Q\) are on opposite sides of the line \(a x+b y+c=0\)
\(\therefore R\) divides \(P Q\) internally.
\(\therefore \lambda\) is positive.

\(
\begin{aligned}
\Rightarrow & -\left(\frac{a x_1+b y_1+c}{a x_2+b y_2+c}\right) & >0 \\
\Rightarrow & \left(\frac{a x_1+b y_1+c}{a x_2+b y_2+c}\right) & <0 \\
\text { or } & \frac{f\left(x_1, y_1\right)}{f\left(x_2, y_2\right)} & <0
\end{aligned}
\)
where, \(f(x, y)=a x+b y+c\)

Important Points

• The side of the line where orig in lies is known as origin side.
• A point \((\alpha, \beta)\) will lie on origin side of the line \(a x+b y+c=0\), if \(a \alpha+b \beta+c\) and \(c\) have same sign.
• A point \((\alpha, \beta)\) will lie on non-origin side of the line \(a x+b y+c=0\), if \(a \alpha+b \beta+c\) and \(c\) have opposite sign.

Example 17: Are the points \((2,1)\) and \((-3,5)\) on the same or opposite side of the line \(3 x-2 y+1=0\) ?

Answer: Let \(f(x, y) \equiv 3 x-2 y+1\)
\(
\therefore \quad \frac{f(2,1)}{f(-3,5)}=\frac{3(2)-2(1)+1}{3(-3)-2(5)+1}=-\frac{5}{18}<0
\)
Therefore, the two points are on the opposite sides of the given line.

Example 18: Is the point \((2,-7)\) lies on origin side of the line \(2 x+y+2=0\) ?

Answer:

\(
\begin{aligned}
& \text { Let } f(x, y) \equiv 2 x+y+2 \\
& \therefore \quad f(2,-7)=2(2)-7+2=-1 \\
& \quad f(2,-7)<0 \text { and constant } 2>0
\end{aligned}
\)
Hence, the point \((2,-7)\) lies on non-origin side.

Example 19: A straight canal is at a distance of \(4 \frac{1}{2} km\) from a city and the nearest path from the city to the canal is in the north-east direction. Find whether a village which is at \(3 km\) north and \(4 km\) east from the city lies on the canal or not. If not, then on which side of the canal is the village situated?

Answer: Let \(O(0,0)\) be the given city and \(A B\) be the straight canal. Given, \(O L=\frac{9}{2} km\)

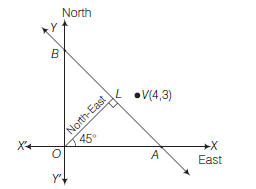
\(\therefore\) Equation of \(A B\)
i.e. Equation of canal is
\(
x \cos 45^{\circ}+y \sin 45^{\circ}=\frac{9}{2}
\)
\(
x+y=\frac{9}{\sqrt{2}} \dots(i)
\)
Let \(V\) be the given village, then \(V \equiv(4,3)\) Putting \(x=4\) and \(y=3\) in Eq. (i), then \(4+3=\frac{9}{\sqrt{2}}\), i.e. \(7=\frac{9}{\sqrt{2}}\) which is impossible.
Hence, the given village \(V\) does not lie on the canal.
Also if \(f(x, y) \equiv x+y-\frac{9}{\sqrt{2}}\)
\(
\therefore \quad \frac{f(4,3)}{f(0,0)}=\left(\frac{4+3-\frac{9}{\sqrt{2}}}{0+0-\frac{9}{\sqrt{2}}}\right)=-\left(\frac{7 \sqrt{2}-9}{9}\right)<0
\)
Hence, the village is on that side of the canal on which origin or the city lies.

Position of a Point Which Lies Inside a Triangle

Let \(P\left(x_1, y_1\right)\) be the point and equations of the sides of a triangle are
\(
\begin{array}{r}
B C: a_1 x+b_1 y+c_1=0 \\
C A: a_2 x+b_2 y+c_2=0 \\
\text { and } \quad A B: a_3 x+b_3 y+c_3=0
\end{array}
\)

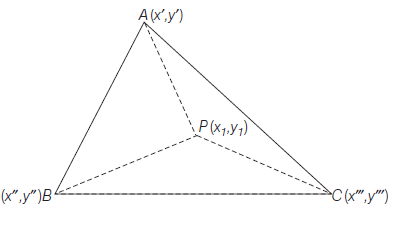
First find the coordinates of \(A, B\) and \(C\) say,
\(
A \equiv\left(x^{\prime}, y^{\prime}\right) ; B \equiv\left(x^{\prime \prime}, y^{\prime \prime}\right) \text { and } C \equiv\left(x^{\prime \prime \prime}, y^{\prime \prime \prime}\right)
\)
and if coordinates of \(A, B, C\) are given, then find equations of \(B C, C A\) and \(A B\).
If \(P\left(x_1, y_1\right)\) lies inside the triangle, then \(P\) and \(A\) must be on the same side of \(B C, P\) and \(B\) must be on the same side of \(A C, P\) and \(C\) must be on the same side of \(A B\), then
\(
\begin{aligned}
& \frac{a_1 x_1+b_1 y_1+c_1}{a_1 x^{\prime}+b_1 y^{\prime}+c_1}>0 \dots(i)\\
& \frac{a_2 x_1+b_2 y_1+c_2}{a_2 x^{\prime \prime}+b_2 y^{\prime \prime}+c_2}>0 \dots(ii)\\
& \text { and } \quad \frac{a_3 x_1+b_3 y_1+c_3}{a_3 x^{\prime \prime \prime}+b_3 y^{\prime \prime \prime}+c_3}>0 \dots(iii) \\
&
\end{aligned}
\)
The required values of \(P\left(x_1, y_1\right)\) must be intersection of these inequalities Eqs. (i), (ii) and (iii).

Alternate Method (Best Method):

First draw the exact diagram of the problem. If the point \(P\left(x_1, y_1\right)\)
move on the line \(y=a x+b\) for all \(x_1\), then
\(
P \equiv\left(x_1, a x_1+b\right)
\)
and the portion \(D E\) of the line \(y=a x+b\) (Excluding \(D\) and \(E)\) lies within the triangle. Now line \(y=a x+b\) cuts any two sides out of three sides, then find coordinates of \(D\) and E.
\(
\begin{array}{ll}
& D \equiv(\alpha, \beta) \\
\text { and } & E \equiv(\gamma, \delta) \text { (say) } \\
\text { then } & \alpha<x_1<\gamma \\
\text { and } & \beta<a x_1+b<\delta
\end{array}
\)

Example 20: For what values of the parameter \(t\) does the point \(P(t, t+1)\) lies inside the triangle \(A B C\) where \(A \equiv(0,3), B \equiv(-2,0)\) and \(C \equiv(6,1)\).

Answer: Equations of sides
\(
\begin{aligned}
& B C: x-8 y+2=0 \\
& C A: x+3 y-9=0 \\
& A B: 3 x-2 y+6=0
\end{aligned}
\)
Since, \(P(t, t+1)\) lies inside the triangle \(A B C\), then \(P\) and \(A\) must be on the same side of \(B C\)
\(\therefore \quad \frac{\text { value of }(x-8 y+2) \text { at } P(t, t+1)}{\text { value of }(x-8 y+2) \text { at } A(0,3)}>0\)
i.e. \(\quad \frac{t-8(t+1)+2}{0-24+2}>0\)
or
\(
\frac{-7 t-6}{-22}>0
\)
\(
7 t+6>0
\)
\(\therefore \quad t>-\frac{6}{7} \dots(i)\)

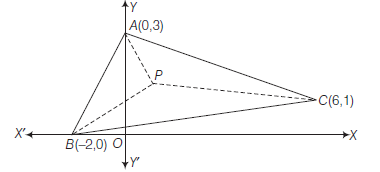
and \(P, B\) must be on the same side of \(C A\)
\(
\begin{aligned}
& \therefore \quad \frac{\text { value of }(x+3 y-9) \text { at } P(t, t+1)}{\text { value of }(x+3 y-9) \text { at } B(-2,0)}>0 \\
& \text { i.e. } \quad \frac{t+3(t+1)-9}{-2+0-9}>0 \\
& \text { or } \frac{4 t-6}{-11}>0 \\
&
\end{aligned}
\)
\(
\begin{array}{lr}
\text { or } & 4 t-6<0 \\
\therefore & t<\frac{3}{2} \dots(ii)
\end{array}
\)
and \(P, C\) must be on the same side of \(A B\)
\(
\begin{aligned}
& \therefore \quad \frac{\text { value of }(3 x-2 y+6) \text { at } P(t, t+1)}{\text { value of }(3 x-2 y+6) \text { at } C(6,1)}>0 \\
& \text { i.e. } \quad \frac{3 t-2(t+1)+6}{18-2+6}>0 \\
& \text { or } \quad \frac{t+4}{22}>0 \\
& \text { or } \quad t+4>0 \\
& \therefore \quad t>-4 \dots(iii)\\
&
\end{aligned}
\)
From Eqs. (i), (ii) and (iii), we get
\(
\begin{array}{ll}
& -\frac{6}{7}<t<\frac{3}{2} \\
\text { i.e. } & t \in\left(-\frac{6}{7}, \frac{3}{2}\right)
\end{array}
\)

Alternate Method: 

First draw the exact diagram of \(\triangle A B C\), the point \(P(t, t+1)\) move on the line
\(
y=x+1
\)
for all \(t\).

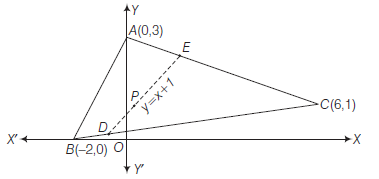
Now, \(D\) and \(E\) are the intersection of
\(
\begin{aligned}
& y=x+1, x-8 y+2=0 \\
& y=x+1, \quad x+3 y-9=0
\end{aligned}
\)
respectively.
\(
y=x+1, \quad x+3 y-9=0
\)
\(\therefore \quad D \equiv\left(-\frac{6}{7}, \frac{1}{7}\right)\)
\(
E \equiv\left(\frac{3}{2}, \frac{5}{2}\right)
\)
Thus, the points on the line \(y=x+1\) whose \(x\)-coordinates lies between \(-\frac{6}{7}\) and \(\frac{3}{2}\) lie within the triangle \(A B C\).
Hence, \(\quad-\frac{6}{7}<t<\frac{3}{2}\)
i.e. \(\quad t \in\left(-\frac{6}{7}, \frac{3}{2}\right)\)

Example 21: Find \(\lambda\) if \((\lambda, 2)\) is an interior point of \(\triangle A B C\) formed by \(x+y=4,3 x-7 y=8\) and \(4 x-y=31\).

Answer: Let \(P \equiv(\lambda, 2)\)
First draw the exact diagram of \(\triangle A B C\), the point \(P(\lambda, 2)\) move on the line \(y=2\) for all \(\lambda\).

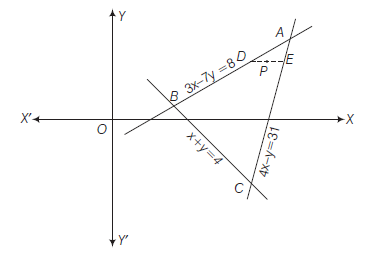
Now, \(D\) and \(E\) are the intersection of
\(
3 x-7 y=8, y=2
\)
and \(4 x-y=31, y=2\) respectively.
\(
\therefore \quad D \equiv\left(\frac{22}{3}, 2\right) \text { and } E \equiv\left(\frac{33}{4}, 2\right)
\)
Thus, the points on the line \(y=2\) whose \(x\)-coordinates lies between \(\frac{22}{3}\) and \(\frac{33}{4}\) lie within the \(\triangle A B C\).
Hence, \(\quad \frac{22}{3}<\lambda<\frac{33}{4}\)
i.e. \(\quad \lambda \in\left(\frac{22}{3}, \frac{33}{4}\right)\)

Example 22: Determine all values of \(\alpha\) for which the point \(\left(\alpha, \alpha^2\right)\) lies inside the triangle formed by the lines \(2 x+3 y-1=0, x+2 y-3=0\) and \(5 x-6 y-1=0\).

Answer: The coordinates of the vertices are

\(
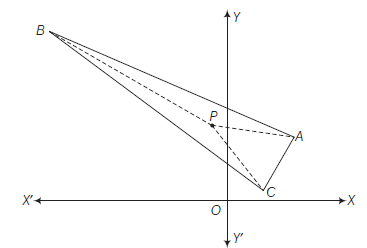
A\left(\frac{5}{4}, \frac{7}{8}\right), B(-7,5) \text { and } C\left(\frac{1}{3}, \frac{1}{9}\right)
\)
\(\because P\left(\alpha, \alpha^2\right)\) lies inside the \(\triangle A B C\), then
(i) \(A\) and \(P\) must lie on the same side of \(B C\)
(ii) \(B\) and \(P\) must lie on the same side of \(C A\)
(iii) \(C\) and \(P\) must lie on the same side of \(A B\), then
\(
\begin{aligned}
& \frac{\frac{5}{2}+\frac{21}{8}-1}{2 \alpha+3 \alpha^2-1}>0 \\
& \frac{33}{2 \alpha+3 \alpha^2-1}>0 \\
& 3 \alpha^2+2 \alpha-1>0 \\
&(\alpha+1)\left(\alpha-\frac{1}{3}\right)>0 \\
& \alpha \in(-\infty,-1) \cup\left(\frac{1}{3}, \infty\right) \dots(i)
\end{aligned}
\)
\(
\begin{array}{lc}
\text { and } & \frac{-35-30-1}{5 \alpha-6 \alpha^2-1}>0 \\
\Rightarrow & 5 \alpha-6 \alpha^2-1<0 \\
\Rightarrow & \left(\alpha-\frac{1}{3}\right)\left(\alpha-\frac{1}{2}\right)>0 \\
\therefore & \alpha \in(-\infty, 1 / 3) \cup(1 / 2, \infty) \dots(ii)
\end{array}
\)
\(
\begin{array}{ll}
\text { and } & \frac{\frac{1}{3}+\frac{2}{9}-3}{\alpha+2 \alpha^2-3}>0 \\
\Rightarrow & \alpha+2 \alpha^2-3<0 \\
\Rightarrow & (2 \alpha+3)(\alpha-1)<0 \\
\therefore & \alpha \in(-3 / 2,1) \dots(iii)
\end{array}
\)
From Eq. (i), Eq. (ii) and Eq. (iii), we get
\(
\alpha \in(-3 / 2,-1) \cup(1 / 2,1) \text {. }
\)

Equations of Lines Parallel and Perpendicular to a Given Line

Theorem 1: The equation of line parallel to \(a x+b y+c=0\) is \(a x+b y+\lambda=0\), where \(\lambda\) is some constant.

Proof:
\(
\begin{aligned}
&\text { Let the equation of any line parallel to }\\
&\begin{array}{lrl}
& a x+b y+c & =0 \dots(i) \\
\text { be } & a_1 x+b_1 y+c_1 & =0 \dots(ii) \\
\text { then } & \frac{a_1}{a}=\frac{b_1}{b} & =k \text { (say) } \\
\therefore & a_1=a k, b_1 & =b k
\end{array}
\end{aligned}
\)
Then from Eq. (ii),
\(
a k x+b k y+c=0
\)
Dividing it by \(k\), then
\(
\begin{aligned}
& a x+b y+\frac{c}{k}=0 \\
& a x+b y+\lambda=0 \left(\text { writing } \lambda \text { for } \frac{c}{k}\right)
\end{aligned}
\)
Hence, any line parallel to \(a x+b y+c=0\) is
\(
a x+b y+\lambda=0
\)
where \(\lambda\) is some constant.

Alternate Method:

The given line is
\(
a x+b y+c=0 \dots(i)
\)
Its slope \(=-\frac{a}{b}\)
Thus, any line parallel to Eq. (i) is given by
\(
\begin{array}{ll}
& y=\left(-\frac{a}{b}\right) x+\lambda_1 \\
\Rightarrow & a x+b y-b \lambda_1=0 \\
\Rightarrow \quad & \left.a x+b y+\lambda=0 \quad \text { (writing } \lambda \text { for }-b \lambda_1\right)
\end{array}
\)
where, \(\lambda\) is some constant.

Corollary: The equation of the line parallel to \(a x+b y+c=0\) and passing through \(\left(x_1, y_1\right)\) is
\(
a\left(x-x_1\right)+b\left(y-y_1\right)=0
\)

Working Rule :

• Keep the terms containing \(x\) and \(y\) unaltered.
• Change the constant.
• The constant \(\lambda\) is determined from an additional condition given in the problem.

Example 23: Find the general equation of the line which is parallel to \(3 x-4 y+5=0\). Also find such line through the point \((-1,2)\).

Answer: Equation of any parallel to \(3 x-4 y+5=0\) is
\(
3 x-4 y+\lambda=0 \dots(i)
\)
which is general equation of the line.
Also Eq. (i) passes through \((-1,2)\), then
\(
\begin{aligned}
3(-1)-4(2)+\lambda & =0 \\
\lambda & =11
\end{aligned}
\)
Then from Eq. (i) required line is
\(3 x-4 y+11=0\)

Theorem 2 : The equation of the line perpendicular to the line \(a x+b y+c=0\) is \(b x-a y+\lambda=0\), where \(\lambda\) is some constant.

Proof : Let the equation of any line perpendicular to be
\(
\begin{array}{r}
a x+b y+c=0 \dots(i) \\
a_1 x+b_1 y+c_1=0 \dots(ii) \\
a a_1+b b_1=0
\end{array}
\)
\(
\begin{aligned}
a a_1 & =-b b_1 \\
\frac{a_1}{b}=\frac{b_1}{-a} & =k \text { (say) } \\
a_1=b k, b_1 & =-a k
\end{aligned}
\)
Then, from Eq. (ii), \(b k x-a k y+c_1=0\) dividing it by \(k\), then
\(
b x-a y+\frac{c_1}{k}=0
\)
\(
\text { or } \quad b x-a y+\lambda=0 \quad\left(\text { writing } \lambda \text { for } \frac{c_1}{k}\right)
\)
Hence, any line perpendicular to \(a x+b y+c=0\) is
\(
b x-a y+\lambda=0
\)
where, \(\lambda\) is some constant.

Alternate Method:

The given line is
\(
\begin{aligned}
& a x+b y+c=0 \dots(i) \\
& \text { Its slope }=-\frac{a}{b}
\end{aligned}
\)
Slope of perpendicular line of Eq. (i) is \(\frac{b}{a}\). Thus any line perpendicular to Eq. (i) is given by
\(
y=\left(\frac{b}{a}\right) x+\lambda_1
\)
\(
\begin{aligned}
& b x-a y+a \lambda_1=0 \\
& b x-a y+\lambda=0 \quad \quad\left(\text { writing } \lambda \text { for } a \lambda_1\right)
\end{aligned}
\)
where, \(\lambda\) is some constant.

Corollary 1: The equation of the line through \(\left(x_1, y_1\right)\) and perpendicular to \(a x+b y+c=0\) is
\(
b\left(x-x_1\right)-a\left(y-y_1\right)=0
\)

Corollary 2 : Also equation of the line perpendicular to \(a x+b y+c=0\) is written as
\(\frac{x}{a}-\frac{y}{b}+k=0\), where \(k\) is some constant.

Working Rule :

• Interchange the coefficients of \(x\) and \(y\) and changing sign of one of these coefficients.
• Changing the constant term.
• The value of \(\lambda\) can be determined from an additional condition given in the problem.

Example 24: Find the general equation of the line which is perpendicular to \(x+y+4=0\). Also find such line through the point \((1,2)\).

Answer: Equation of any line perpendicular to \(x+y+4=0\) is
\(
x-y+\lambda=0 \dots(i)
\)
which is general equation of the line.
Also Eq. (i) passes through \((1,2)\), then
\(
\begin{aligned}
1-2+\lambda & =0 \\
\lambda & =1
\end{aligned}
\)
\(
\therefore \quad \lambda=1
\)
Then from Eq. (i), required line is
\(
x-y+1=0
\)

Example 25: Show that the equation of the line passing through the point \(\left(a \cos ^3 \theta, a \sin ^3 \theta\right)\) and perpendicular to the line
\(
\begin{aligned}
& x \sec \theta+y \operatorname{cosec} \theta=a \text { is } \\
& x \cos \theta-y \sin \theta=a \cos 2 \theta
\end{aligned}
\)

Answer:The given equation \(x \sec \theta+y \operatorname{cosec} \theta=a\) can be written as
\(
x \sin \theta+y \cos \theta=a \sin \theta \cos \theta \dots(i)
\)
\(\therefore\) equation of perpendicular line of Eq. (i) is
\(
x \cos \theta-y \sin \theta=\lambda \dots(ii)
\)
Also it is pass through \(\left(a \cos ^3 \theta, a \sin ^3 \theta\right)\)
\(
\begin{aligned}
& \therefore \quad a \cos ^3 \theta \cdot \cos \theta-a \sin ^3 \theta \cdot \sin \theta=\lambda \\
& \Rightarrow \quad \lambda=a\left(\cos ^4 \theta-\sin ^4 \theta\right) \\
& =a\left(\cos ^2 \theta+\sin ^2 \theta\right)\left(\cos ^2 \theta-\sin ^2 \theta\right) \\
& =a \cdot 1 \cdot \cos 2 \theta=a \cos 2 \theta \\
&
\end{aligned}
\)
From Eq. (ii), the required equation of the line is
\(
x \cos \theta-y \sin \theta=a \cos 2 \theta
\)

Alternate Method:

(From corollary (2) of Theorem (2)
Equation of any line perpendicular to the line
\(
x \sec \theta+y \operatorname{cosec} \theta=a \text {, is }
\)
\(
\frac{x}{\sec \theta}-\frac{y}{\operatorname{cosec} \theta}=k
\)
\(
x \cos \theta-y \sin \theta=k \dots(iii)
\)
Also, it pass through \(\left(a \cos ^3 \theta, a \sin ^3 \theta\right)\)
\(
\begin{aligned}
& \therefore \quad a \cos ^3 \theta \cdot \cos \theta-a \sin ^3 \theta \cdot \sin \theta=k \\
& \text { or } \\
& k=a\left(\cos ^4 \theta-\sin ^4 \theta\right) \\
& =a\left(\cos ^2 \theta+\sin ^2 \theta\right)\left(\cos ^2 \theta-\sin ^2 \theta\right) \\
& =a \cdot 1 \cdot \cos 2 \theta \\
& =a \cos 2 \theta \\
&
\end{aligned}
\)
From Eq. (iii), the required equation of the line is
\(
x \cos \theta-y \sin \theta=a \cos 2 \theta
\)

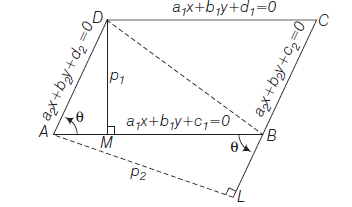
Area of Parallelogram

Theorem : Area of parallelogram \(A B C D\) whose sides \(A B, B C, C D\) and \(D A\) are represented by \(a_1 x+b_1 y+c_1=0\), \(a_2 x+b_2 y+c_2=0, a_1 x+b_1 y+d_1=0\)
and \(\quad a_2 x+b_2 y+d_2=0\) is
\(
\frac{p_1 p_2}{\sin \theta} \text { or } \frac{\left|c_1-d_1\right|\left|c_2-d_2\right|}{|| \begin{array}{ll}
a_1 & b_1 \\
a_2 & b_2
\end{array}||}
\)
where, \(p_1\) and \(p_2\) are the distances between parallel sides and \(\theta\) is the angle between two adjacent sides.

Proof: Since, \(p_1\) and \(p_1\) are the distances between the pairs of parallel sides of the parallelogram and \(\theta\) is the angle between two adjacent sides, then

\(
\begin{aligned}
& \text { Area of parallelogram } A B C D \\
&=2 \times \text { Area of } \triangle A B D \\
&=2 \times \frac{1}{2} \times A B \times p_1 \\
&=A B \times p_1 \\
&=\frac{p_2}{\sin \theta} \times p_1 \quad\left(\because \text { in } \triangle A B L, \sin \theta=\frac{p_2}{A B}\right) \\
&=\frac{p_1 p_2}{\sin \theta} \dots(i)
\end{aligned}
\)
Now, \(p_1=\) Distance between parallel sides \(A B\) and \(D C\)
\(
=\frac{\left|c_1-d_1\right|}{\sqrt{\left(a_1^2+b_1^2\right)}}
\)
and \(p_2=\) Distance between parallel sides \(A D\) and \(B C\)
\(
=\frac{\left|c_2-d_2\right|}{\sqrt{\left(a_2^2+b_2^2\right)}}
\)
\(
\text { Also, } \tan \theta=\left|\frac{m_1-m_2}{1+m_1 m_2}\right|=\left|\frac{-\frac{a_1}{b_1}-\left(-\frac{a_2}{b_2}\right)}{1+\left(-\frac{a_1}{b_1}\right)\left(-\frac{a_2}{b_2}\right)}\right|
\)
\(
\left(\begin{array}{c}
\because m_1=\text { slope of } A B=-\frac{a_1}{b_1} \\
\text { and } m_2=\text { slope of } A D=-\frac{a_2}{b_2}
\end{array}\right)
\)
\(
\begin{aligned}
& =\left|\frac{a_1 b_2-a_2 b_1 \mid}{a_1 a_2+b_1 b_2}\right| \\
\therefore \quad \sin \theta & =\frac{\left|a_1 b_2-a_2 b_1\right|}{\sqrt{\left(a_1^2+b_1^2\right)\left(a_2^2+b_2^2\right)}}
\end{aligned}
\)

Now, substitute the values of \(p_1, p_2\) and \(\sin \theta\) in Eq. (i)
\(\therefore\) Area of parallelogram \(A B C D=\frac{\left|c_1-d_1\right|\left|c_2-d_2\right|}{\left|a_1 b_2-a_2 b_1\right|}\)
\(
=\frac{\left|c_1-d_1\right|\left|c_2-d_2\right|}{|| \begin{array}{ll}
a_1 & b_1 \\
a_2 & b_2
\end{array}||}
\)

Corollaries :

• If \(p_1=p_2\), then \(A B C D\) becomes a rhombus
  \(\therefore\) Area of rhombus \(A B C D=\frac{p_1^2}{\sin \theta}\)
  \(
  =\frac{\left(c_1-d_1\right)^2}{\left|a_1 b_2-a_2 b_1\right| \sqrt{\left(\frac{a_1^2+b_1^2}{a_2^2+b_2^2}\right)}}
  \)
• If \(d_1\) and \(d_2\) are the lengths of two perpendicular diagonals of a rhombus, then
  Area of rhombus \(=\frac{1}{2} d_1 d_2\)
• Area of the parallelogram whose sides are \(y=m x+a\), \(y=m x+b, y=n x+c\) and \(y=n x+d\) is \(\frac{|a-b||c-d|}{|m-n|}\).

Example 26: Show that the area of the parallelogram formed by the lines \(x+3 y-a=0,3 x-2 y+3 a=0\), \(x+3 y+4 a=0\) and \(3 x-2 y+7 a=0\) is \(\frac{20}{11} a^2\) sq units.

Answer: Required area of the parallelogram
\(
=\frac{|-a-4 a||3 a-7 a|}{\left.|| \begin{array}{cc}
1 & 3 \\
3 & -2
\end{array} \right\rvert\,}=\frac{20}{11} a^2 \text { sq units }
\)

Example 27: Show that the area of the parallelogram formed by the lines
\(
\begin{aligned}
& x \cos \alpha+y \sin \alpha=p, x \cos \alpha+y \sin \alpha=q, \\
& x \cos \beta+y \sin \beta=r, x \cos \beta+y \sin \beta=s \text { is } \\
& |(p-q)(r-s) \operatorname{cosec}(\alpha-\beta)|
\end{aligned}
\)

Answer: The equation of sides of the parallelogram are
\(
\begin{aligned}
x \cos \alpha+y \sin \alpha-p & =0, \\
x \cos \alpha+y \sin \alpha-q & =0, \\
x \cos \beta+y \sin \beta-r & =0, \\
x \cos \beta+y \sin \beta-s & =0
\end{aligned}
\)
\(\therefore\) Required area of the parallelogram
\(
\begin{aligned}
& =\frac{|-p-(-q)||-r-(-s)|}{\left.|| \begin{array}{cc}
\cos \alpha & \sin \alpha \\
\cos \beta & \sin \beta
\end{array} \right\rvert\,}=\frac{|p-q||r-s|}{|\sin (\beta-\alpha)|} \\
& =|(p-q)(r-s) \operatorname{cosec}(\alpha-\beta)|
\end{aligned}
\)

Example 28: Prove that the diagonals of the parallelogram formed by the lines
\(
\frac{x}{a}+\frac{y}{b}=1, \frac{x}{b}+\frac{y}{a}=1, \frac{x}{a}+\frac{y}{b}=2 \text { and } \frac{x}{b}+\frac{y}{a}=2
\)
are at right angles. Also find its area \((a \neq b)\).

Answer: The distance between the parallel sides
\(
\frac{x}{a}+\frac{y}{b}=1 \text { and } \frac{x}{a}+\frac{y}{b}=2
\)
\(
\text { is } \quad \frac{|2-1|}{\sqrt{\left(\frac{1}{a^2}+\frac{1}{b^2}\right)}}=\frac{1}{\sqrt{\left(\frac{1}{a^2}+\frac{1}{b^2}\right)}}=p_1 \text { (say) }
\)
and the distance between the parallel sides
\(
\frac{x}{b}+\frac{y}{a}=1 \text { and } \frac{x}{b}+\frac{y}{a}=2
\)
\(
\text { is } \quad \frac{|2-1|}{\sqrt{\left(\frac{1}{b^2}+\frac{1}{a^2}\right)}}=\frac{1}{\sqrt{\left(\frac{1}{a^2}+\frac{1}{b^2}\right)}}=p_2 \text { (say) }
\)
Here, \(\quad p_1=p_2\).
\(\therefore\) Parallelogram is a rhombus.
But we know that diagonals of rhombus are perpendicular to each other.
\(
\begin{aligned}
\therefore \quad \text { Area of the rhombus } & =\frac{|(-1+2)(-1+2)|}{\left|\begin{array}{cc}
\frac{1}{a} & \frac{1}{b} \\
\frac{1}{b} & \frac{1}{a}
\end{array}\right|} \\
& =\frac{a^2 b^2}{\left|b^2-a^2\right|}(a \neq b)
\end{aligned}
\)

Example 29: Show that the four lines \(a x \pm b y \pm c=0\) enclose a rhombus whose area is \(\frac{2 c^2}{|a b|}\).

Answer: The given lines are
\(
\begin{aligned}
& a x+b y+c=0 \dots(i) \\
& a x+b y-c=0 \dots(ii) \\
& a x-b y+c=0 \dots(iii) \\
& a x-b y-c=0 \dots(iv)
\end{aligned}
\)
Distance between the parallel lines Eqs. (i) and (ii) is \(\frac{2 c}{\sqrt{\left(a^2+b^2\right)}}=p_1\) (say) and distance between the parallel lines Eqs. (iii) and (iv) is
\(
\frac{2 c}{\sqrt{\left(a^2+b^2\right)}}=p_2 \text { (say) }
\)
Here, \(p_1=p_2\)
\(\therefore\) it is a rhombus.
\(\therefore\) Area of rhombus \(=\frac{|(c+c)(c+c)|}{\left|\begin{array}{cc}a & b \\ a & -b\end{array}\right|}=\frac{4 c^2}{|-2 a b|}=\frac{2 c^2}{|a b|}\)

Points of Intersection of Two Lines

Let \(a_1 x+b_1 y+c_1=0\) and \(a_2 x+b_2 y+c_2=0\) be two non-parallel lines. If \(\left(x_1, y_1\right)\) be the coordinates of their point of intersection, then \(a_1 x_1+b_1 y_1+c_1=0\) and \(a_2 x_1+b_2 y_1+c_2=0\) Solving these two by cross multiplication, then
\(
\frac{x_1}{b_1 c_2-b_2 c_1}=\frac{y_1}{c_1 a_2-c_2 a_1}=\frac{1}{a_1 b_2-a_2 b_1}
\)
we get $\quad\left(x_1, y_1\right) \equiv\left(\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1}, \frac{c_1 a_2-c_2 a_1}{a_1 b_2-a_2 b_1}\right)$
\(
\equiv\left(\frac{\left|\begin{array}{ll}
b_1 & b_2 \\
c_1 & c_2
\end{array}\right|}{\left|\begin{array}{ll}
a_1 & a_2 \\
b_1 & b_2
\end{array}\right|}, \frac{\left|\begin{array}{ll}
c_1 & c_2 \\
a_1 & a_2
\end{array}\right|}{\left|\begin{array}{ll}
a_1 & a_2 \\
b_1 & b_2
\end{array}\right|}\right)
\)

Important Points

• Here lines are not parallel, they have unequal slopes, then, \(a_2 b_2-a_2 b_1 \neq 0\)
• In solving numerical questions, we should not be remember the coordinates \(\left(x_1, y_1\right)\) given above, but we solve the equations directly.

Concurrent Lines

The three given lines are concurrent, if they meet in a point. Hence to prove that three given lines are concurrent, we proceed as follows :

Method I: Find the point of intersection of any two lines by solving them simultaneously. If this point satisfies the third equation also, then the given lines are concurrent.

Method II: The three lines \(a_i x+b_i y+c_i=0, i=1,2,3\) are concurrent if
\(
\left|\begin{array}{lll}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2 \\
a_3 & b_3 & c_3
\end{array}\right|=0
\)

Method III: The condition for the lines \(P=0, Q=0\) and \(R=0\) to be concurrent is that three constants \(l, m, n\) (not all zeros at the same time) can be obtained such that
\(
l P+m Q+n R=0
\)

Important Points

• The reader is advised to follow method \(I\) in numerical problems.
• For finding unknown quantity applying method II.

Example 30: Show that the lines \(2 x+3 y-8=0, x-5 y+9=0\) and \(3 x+4 y-11=0\) are concurrent.

Answer: Method II: We have \(\left|\begin{array}{lll}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{array}\right|=\left|\begin{array}{ccc}2 & 3 & 8 \\ 1 & -5 & 9 \\ 3 & 4 & -11\end{array}\right|\) Applying \(C_3 \rightarrow C_3+C_1+2 C_2\)
\(
=\left|\begin{array}{rrr}
2 & 3 & 0 \\
1 & -5 & 0 \\
3 & 4 & 0
\end{array}\right|=0
\)
Hence the given lines are concurrent.

Method III: Suppose
\(
\begin{gathered}
l(2 x+3 y-8)+m(x-5 y+9)+n(3 x+4 y-11)=0 \\
\Rightarrow \quad x(2 l+m+3 n)+y(3 l-5 m+4 n)+(-8 l+9 m-11 n)=0 \\
=0 \cdot x+0 \cdot y+0
\end{gathered}
\)
On comparing,
\(
2 l+m+3 n=0,3 l-5 m+4 n=0,-8 l+9 m-11 n=0
\)
After solving, we get \(l=19, m=1, n=-13\)
Hence, \(19(2 x+3 y-8)+(x-5 y+9)-13(3 x+4 y-11)=0\)
Hence the given lines are concurrent.

Example 31: If the lines \(a x+y+1=0, x+b y+1=0\) and \(x+y+c=0(a, b\) and \(c\) being distinct and different from 1) are concurrent, then find the value of \(\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c}\).

Answer: The given lines are concurrent, then
\(
\left|\begin{array}{lll}
a & 1 & 1 \\
1 & b & 1 \\
1 & 1 & c
\end{array}\right|=0 \Rightarrow\left|\begin{array}{ccc}
a & 1-a & 1-a \\
1 & b-1 & 0 \\
1 & 0 & c-1
\end{array}\right|=0
\)
(applying \(C_2 \rightarrow C_2-C_1\) and \(C_3 \rightarrow C_3-C_1\) )
Expanding along first row
\(
\begin{array}{ll}
\Rightarrow & a(b-1)(c-1)-(1-a)(c-1)-(1-a)(b-1)=0 \\
\Rightarrow & a(1-b)(1-c)+(1-a)(1-c)+(1-a)(1-b)=0
\end{array}
\)
Dividing by \((1-a)(1-b)(1-c)\), then
\(
\begin{aligned}
\frac{a}{1-a}+\frac{1}{1-b}+\frac{1}{1-c} & =0 \\
\Rightarrow \quad-1+\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c} & =0 \\
\text { Hence, } \quad \frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c} & =1
\end{aligned}
\)

Example 32: Show that the three straight lines \(2 x-3 y+5=0,3 x+4 y-7=0\) and \(9 x-5 y+8=0\) meet in a point.

Answer: If we multiply these three equations by 3,1 and -1 , we have
\(
3(2 x-3 y+5)+(3 x+4 y-7)-(9 x-5 y+8)=0
\)
which is an identity.
Hence, three lines meet in a point.

Family of Lines

Theorem : Any line through the point of intersection of the lines \(a_1 x+b_1 y+c_1=0\) and \(a_2 x+b_2 y+c_2=0\) can be represented by the equation
\(
\left(a_1 x+b_1 y+c_1\right)+\lambda\left(a_2 x+b_2 y+c_2\right)=0
\)
where \(\lambda\) is a parameter which depends on the other property of line.

Proof: The equations of the lines are
\(
a_1 x+b_1 y+c_1=0 \dots(i)
\)
and
\(
a_2 x+b_2 y+c_2=0 \dots(ii)
\)
Multiplying \(\mu\) and \(v\) in Eqs. (i) and (ii) and adding, we get
\(
\mu\left(a_1 x+b_1 y+c_1\right)+v\left(a_2 x+b_2 y+c_2\right)=0
\)
where \(\mu, v\) are any constants not both zero.
Dividing both sides by \(\mu\), then
\(
\left(a_1 x+b_1 y+c_1\right)+\frac{\nu}{\mu}\left(a_2 x+b_2 y+c_2\right)=0
\)
\(
\Rightarrow\left(a_1 x+b_1 y+c_1\right)+\lambda\left(a_2 x+b_2 y+c_2\right)=0\left(\text { where, } \lambda=\frac{v}{\mu}\right)
\)
It is a first degree equation in \(x\) and \(y\). So it represents family of lines through the point of intersection of Eqs. (i) and (ii).
Thus, the family of straight lines through the intersection of lines
\(
L_1 \equiv a_1 x+b_1 y+c_1=0
\)
and
\(
\begin{aligned}
& L_2 \equiv a_2 x+b_2 y+c_2=0 \text { is } \\
& \left(a_1 x+b_1 y+c_1\right)+\lambda\left(a_2 x+b_2 y+c_2\right)=0
\end{aligned}
\)
i.e. \(\quad L_1+\lambda L_2=0\)

Corollaries :

• The equation \(L_1+\lambda L_2=0\) or \(\mu L_1+v L_2=0\) represent a line passing through the intersection of the lines \(L_1=0\) and \(L_2=0\) which is a fixed point, where \(\lambda, \mu, v\) are constants.
• For finding fixed point, the number of constants in family of lines are one or two. If number of constants more than two, then convert in two or one constant form.

Example 33: Find the equation of the straight line passing through the point \((2,1)\) and through the point of intersection of the lines \(x+2 y=3\) and \(2 x-3 y=4\).

Answer: Equation of any straight line passing through the intersection of the lines \(x+2 y=3\) and \(2 x-3 y=4\) is
\(
\lambda(x+2 y-3)+(2 x-3 y-4)=0 \dots(i)
\)
Since, it passes through the point \((2,1)\)
\(
\begin{array}{ll}
\therefore & \lambda(2+2-3)+(4-3-4)=0 \\
\Rightarrow & \lambda-3=0 \\
\therefore & \lambda=3
\end{array}
\)
Now, substituting this value of \(\lambda\) in (i), we get
i.e.
\(
\begin{array}{r}
3(x+2 y-3)+(2 x-3 y-4)=0 \\
5 x+3 y-13=0
\end{array}
\)
which is the equation of required line.

Example 34: The family of lines \(x(a+2 b)+y(a+3 b)=a+b\) passes through the point for all values of \(a\) and \(b\). Find the point.

Answer: The given equation can be written as
\(
a(x+y-1)+b(2 x+3 y-1)=0
\)
which is equation of a line passing through the point of intersection of the lines \(x+y-1=0\) and \(2 x+3 y-1=0\). The point of intersection of these lines is \((2,-1)\). Hence the given family of lines passes through the point \((2,-1)\) for all values of \(a\) and \(b\).

Example 35: If \(3 a+2 b+6 c=0\) the family of straight lines \(a x+b y+c=0\) passes through a fixed point. Find the coordinates of fixed point.

Answer:

\(
\begin{aligned}
& \text { Given, } 3 a+2 b+6 c=0 \\
& \text { or } \quad \frac{a}{2}+\frac{b}{3}+c=0 \dots(i)
\end{aligned}
\)
and family of straight lines is
\(
a x+b y+c=0 \dots(ii)
\)
Subtracting Eqs. (i) from (ii), then
\(
a\left(x-\frac{1}{2}\right)+b\left(y-\frac{1}{3}\right)=0
\)
which is equation of a line passing through the point of intersection of the lines
\(
x-\frac{1}{2}=0 \text { and } y-\frac{1}{3}=0
\)
\(\therefore\) The coordinates of fixed point are \(\left(\frac{1}{2}, \frac{1}{3}\right)\).

Example 36: If \(4 a^2+9 b^2-c^2+12 a b=0\), then the family of straight lines \(a x+b y+c=0\) is either concurrent at … or at ….

Answer: Given, \(\quad 4 a^2+9 b^2-c^2+12 a b=0\)
or \((2 a+3 b)^2-c^2=0\)
or \(c= \pm(2 a+3 b) \dots(i)\)
and family of straight lines is
\(
a x+b y+c=0 \dots(ii)
\)
Substituting the value of \(c\) from Eqs. (i) in (ii), then
\(
\begin{aligned}
& a x+b y \pm(2 a+3 b)=0 \\
& \Rightarrow \quad a(x \pm 2)+b(y \pm 3)=0 \\
&
\end{aligned}
\)
Taking ‘+’ sign : \(a(x+2)+b(y+3)=0\)
which is equation of a line passing through the point of intersection of the lines \(x+2=0\) and \(y+3=0\)
\(\therefore\) coordinates of fixed point are \((-2,-3)\).
Taking ‘-‘ sign : \(\quad a(x-2)+b(y-3)=0\) which is equation of a line passing through the point of intersection of the lines
\(
x-2=0 \text { and } y-3=0
\)
\(\therefore\) coordinates of fixed point are \((2,3)\)
Hence, the family of straight lines \(a x+b y+c=0\) is either concurrent at \((-2,-3)\) or at \((2,3)\).

Example 37: Find the equation of the line passing through the point of intersection of the lines
\(
x+5 y+7=0,3 x+2 y-5=0
\)
and
(a) parallel to the line \(7 x+2 y-5=0\)
(b) perpendicular to the line \(7 x+2 y-5=0\)

Answer: The point of intersection of the given lines \(x+5 y-7=0\) and \(3 x+2 y-5=0\) is \((3,-2)\).
\(\therefore\) Equation of line through \((3,-2)\) is
\(
y+2=m(x-3) \dots(i)
\)
(a) Line (i) is parallel to \(7 x+2 y-5=0\)
\(
\therefore \quad m=-\frac{7}{2}
\)
Hence, the equation of the required line is
\(
\begin{aligned}
& y+2=-\frac{7}{2}(x-3) \\
& \text { or } \quad 7 x+2 y-17=0
\end{aligned}
\)
(b) Line (i) is perpendicular to \(7 x+2 y-5=0\) then \(m \times\left(-\frac{7}{2}\right)=-1\) or
\(
m=\frac{2}{7}
\)
Hence, the equation of the required line is
\(
y+2=\frac{2}{7}(x-3)
\)
or \(2 x-7 y-20=0\)

Example 38: Find the equation of straight line which passes through the intersection of the straight lines
\(
3 x-4 y+1=0 \text { and } 5 x+y-1=0
\)
and cuts off equal intercepts from the axes.

Answer: Equation of any line passing through the intersection of the given lines is
\(
\begin{array}{cc}
& (3 x-4 y+1)+\lambda(5 x+y-1)=0 \\
\Rightarrow & x(3+5 \lambda)+y(-4+\lambda)+(1-\lambda)=0 \\
\Rightarrow & \frac{x}{\left(\frac{\lambda-1}{3+5 \lambda}\right)}+\frac{y}{\left(\frac{\lambda-1}{\lambda-4}\right)}=1 \dots(i)
\end{array}
\)
but given \(x\)-intercept \(=y\)-intercept i.e.
\(
\left(\frac{\lambda-1}{3+5 \lambda}\right)=\left(\frac{\lambda-1}{\lambda-4}\right)
\)
\(
\Rightarrow \quad \frac{1}{3+5 \lambda}=\frac{1}{\lambda-4}
\)
\((\lambda \neq 1 \because\) if \(\lambda=1\) then line (i) pass through origin)
\(
\begin{aligned}
& \therefore & \lambda-4 & =3+5 \lambda \\
& \text { or } & 4 \lambda & =-7 \\
& \therefore & \lambda & =-\frac{7}{4}
\end{aligned}
\)
Substituting the value of \(\lambda\) in Eq. (i), we get required equation is \(23 x+23 y=11\).

Example 39: If \(t_1\) and \(t_2\) are roots of the equation \(t^2+\lambda t+1=0\), where \(\lambda\) is an arbitrary constant. Then prove that the line joining the points \(\left(a t_1^2, 2 a t_1\right)\) and \(\left(a t_2^2, 2 a t_2\right)\) always passes through a fixed point. Also find that point.

Answer: \(\because t_1\) and \(t_2\) are the roots of the equation \(t^2+\lambda t+1=0\)
\(
\therefore \quad t_1+t_2=-\lambda \text { and } t_1 t_2=1 \dots(i)
\)
Equation of the line joining the points \(\left(a t_1^2, 2 a t_1\right)\) and \(\left(a t_2^2, 2 a t_2\right)\) is
\(
\begin{gathered}
y-2 a t_1=\frac{2 a t_2-2 a t_1}{a t_2^2-a t_1^2}\left(x-a t_1^2\right) \\
y-2 a t_1=\frac{2}{\left(t_2+t_1\right)}\left(x-a t_1^2\right) \\
y\left(t_1+t_2\right)-2 a t_1 t_2-2 a t_1^2=2 x-2 a t_1^2 \\
y\left(t_1+t_2\right)-2 a t_1 t_2=2 x \\
y(-\lambda)-2 a=2 x \text { [from Eq. (i)] }\\
(x+a)+\lambda\left(\frac{y}{2}\right)=0
\end{gathered}
\)
which is equation of a line passing through the point of intersection of the lines \(x+a=0\) and \(\frac{y}{2}=0\).
\(\therefore\) coordinates of fixed point are \((-a, 0)\).

Example 40: A variable straight line through the point of intersection of the lines \(\frac{x}{a}+\frac{y}{b}=1\) and \(\frac{x}{b}+\frac{y}{a}=1\) meets the coordinate axes in \(A\) and \(B\). Show that the locus of the mid-point of \(A B\) is the curve \(2 x y(a+b)=a b(x+y)\).

Answer: Any line through the point of intersection of given lines is
\(
\begin{aligned}
& \left(\frac{x}{a}+\frac{y}{b}-1\right)+\lambda\left(\frac{x}{b}+\frac{y}{a}-1\right)=0 \\
& x\left(\frac{1}{a}+\frac{\lambda}{b}\right)+y\left(\frac{1}{b}+\frac{\lambda}{a}\right)=(1+\lambda) \\
& \Rightarrow \quad x\left(\frac{b+a \lambda}{a b}\right)+y\left(\frac{a+b \lambda}{a b}\right)=(1+\lambda) \\
& \Rightarrow \quad \frac{x}{\left\{\frac{a b(1+\lambda)}{b+a \lambda}\right\}}+\frac{y}{\left\{\frac{a b(1+\lambda)}{a+b \lambda}\right\}}=1 \\
&
\end{aligned}
\)

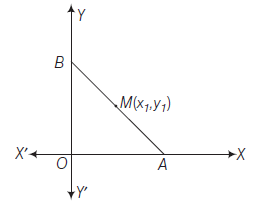
This meets the \(X\)-axis at
\(
A \equiv\left(\frac{a b(1+\lambda)}{b+a \lambda}, 0\right)
\)
and meets the \(Y\)-axis at
\(
B \equiv\left(0, \frac{a b(1+\lambda)}{a+b \lambda}\right)
\)
Let the mid-point of \(A B\) is \(M\left(x_1, y_1\right)\), then
\(
\begin{aligned}
x_1 & =\frac{a b(1+\lambda)}{2(b+a \lambda)} \text { and } y_1=\frac{a b(1+\lambda)}{2(a+b \lambda)} \\
\therefore \quad \frac{1}{x_1}+\frac{1}{y_1} & =\frac{2(b+a \lambda)}{a b(1+\lambda)}+\frac{2(a+b \lambda)}{a b(1+\lambda)} \\
& =\frac{2}{a b(1+\lambda)}(b+a \lambda+a+b \lambda) \\
& =\frac{2}{a b(1+\lambda)}(a+b)(1+\lambda)
\end{aligned}
\)
\(
\begin{array}{ll}
\Rightarrow & \frac{\left(x_1+y_1\right)}{x_1 y_1}=\frac{2(a+b)}{a b} \\
\Rightarrow & 2 x_1 y_1(a+b)=a b\left(x_1+y_1\right)
\end{array}
\)
Hence, the locus of mid point of \(A B\) is
\(
2 x y(a+b)=a b(x+y) \text {. }
\)

How to Find Circumcentre and Orthocentre by Slopes

Circumcentre

The circumcentre of a triangle is the point of intersection of the perpendicular bisectors of the sides of a triangle. It is the centre of the circle which passes through the vertices of the triangle and so its distance from the vertices of the triangle is the same and this distance is known as the circumradius of the triangle.

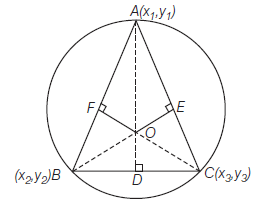
Let \(O(x, y)\) be the circumcentre.
If \(D, E\) and \(F\) are the mid points of \(B C, C A\) and \(A B\) respectively and \(O D \perp B C, O E \perp C A\) and \(O F \perp A B\)
\(\therefore \quad\) slope of \(O D \times\) slope of \(B C=-1\)
and slope of \(O E \times\) slope of \(C A=-1\)
and slope of \(O F \times\) slope of \(A B=-1\)
Solving any two, we get \((x, y)\).

Example 41: Find the coordinates of the circumcentre of the triangle whose vertices are \(A(5,-1), B(-1,5)\) and \(C(6,6)\). Find its radius also.

Answer: Let circumcentre be \(O^{\prime}(\alpha, \beta)\) and mid points of sides \(B C, C A\) and \(A B\) are \(D\left(\frac{5}{2}, \frac{11}{2}\right), E\left(\frac{11}{2}, \frac{5}{2}\right)\) and \(F(2,2)\) respectively. Since \(O^{\prime} D \perp B C\).
\(\therefore\) Slope of \(O^{\prime} D \times\) slope of \(B C=-1\)
\(
\Rightarrow \quad \frac{\beta-\frac{11}{2}}{\alpha-\frac{5}{2}} \times \frac{6-5}{6+1}=-1
\)

\(
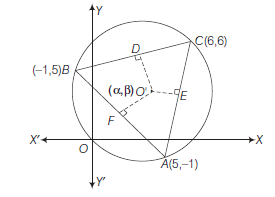
\begin{array}{lc}
\Rightarrow & \frac{2 \beta-11}{7(2 \alpha-5)}=-1 \\
\Rightarrow & 2 \beta-11=-14 \alpha+35 \\
\Rightarrow & 14 \alpha+2 \beta=46 \\
\therefore & 7 \alpha+\beta=23 \dots(i)
\end{array}
\)
and \(\quad O^{\prime} E \perp C A\)
\(\therefore\) Slope of \(O^{\prime} E \times\) Slope of \(C A=-1\)
\(
\begin{array}{ll}
\Rightarrow & \frac{\beta-\frac{5}{2}}{\alpha-\frac{11}{2}} \times \frac{-1-6}{5-6}=-1 \\
\Rightarrow & \frac{2 \beta-5}{2 \alpha-11} \times \frac{7}{1}=-1 \\
\Rightarrow & 14 \beta-35=-2 \alpha+11 \\
\therefore & 2 \alpha+14 \beta=46 \\
\therefore & \alpha+7 \beta=23 \dots(ii)
\end{array}
\)
Solving Eqs. (i) and (ii), we get
\(
\begin{aligned}
\alpha & =\beta=\frac{23}{8} \\
\therefore \text { Circumcentre } & =\left(\frac{23}{8}, \frac{23}{8}\right) \\
\therefore \text { Circumradius } & =O^{\prime} A=O^{\prime} B=O^{\prime} C \\
& =O^{\prime} C=\sqrt{(\alpha-6)^2+(\beta-6)^2} \\
& =\sqrt{\left(\frac{23}{8}-6\right)^2+\left(\frac{23}{8}-6\right)^2} \\
& =\sqrt{\left(\frac{25}{8}\right)^2+\left(\frac{25}{8}\right)^2}=\frac{25 \sqrt{2}}{8} \text { units. }
\end{aligned}
\)

Orthocentre

The orthocentre of a triangle is the point of intersection of altitudes.

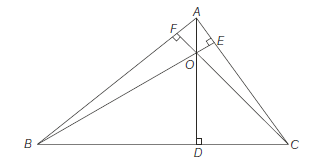
Here \(O\) is the orthocentre since \(A D \perp B C, B E \perp C A\) and \(C F \perp A B\), then \(O A \perp B C, O B \perp C A\), and \(O C \perp A B\)
Solving any two we can get coordinates of \(O\).

Important Points

• If any two lines out of three lines i.e. \(A B, B C\) and \(C A\) are perpendicular, then orthocentre is the point of intersection of two perpendicular lines.
• Firstly find the slope of lines \(B C, C A\) and \(A B\).

Example 42: Find the orthocentre of the triangle formed by the lines \(x y=0\) and \(x+y=1\).

Answer: Three sides of the triangle are \(x=0, y=0\) and \(x+y=1\). The coordinates of the vertices are \(O(0,0), A(1,0)\) and \(B(0,1)\). The triangle \(O A B\) is a right angled triangle having right angle at \(O\). Therefore \(O(0,0)\) is the orthocentre. Since we know that the point of intersection of two perpendicular lines is the orthocentre of the triangle \(O A B\).

Example 43: Find the orthocentre of the triangle \(A B C\) whose angular points are \(A(1,2), B(2,3)\) and \(C(4,3)\).

Answer: Now, Slope of \(B C=\frac{3-3}{4-2}=0\)

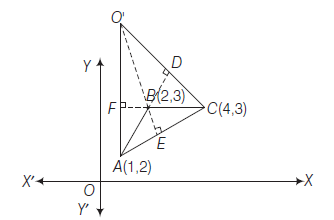
Slope of \(C A=\frac{2-3}{1-4}=\frac{1}{3}\) and Slope of \(A B=\frac{3-2}{2-1}=1\)
Let orthocentre be \(O^{\prime}(\alpha, \beta)\) then Slope of \(O^{\prime} A \times\) slope of \(B C=-1\)
\(
\begin{aligned}
\frac{2-\beta}{1-\alpha} \times 0 & =-1 \\
\frac{0}{1-\alpha} & =-1 \\
1-\alpha & =0 \\
\alpha & =1
\end{aligned}
\)
and Slope of \(O B \times\) slope of \(C A=-1\)
\(
\begin{aligned}
&\begin{aligned}
\frac{3-\beta}{2-\alpha} \times \frac{1}{3} & =-1 \\
3-\beta & =3 \alpha-6 \\
3 \alpha+\beta & =9 \\
\beta & =6 (\because \alpha=1)
\end{aligned}\\
\end{aligned}
\)
Hence, orthocentre of the given triangle is \((1,6)\).

Example 44: The equations of two sides of a triangle are \(3 x-2 y+6=0\) and \(4 x+5 y=20\) and the orthocentre is \((1,1)\). Find the equation of the third side.

Answer: Let \(3 x-2 y+6=0\) and \(4 x+5 y=20\) are the equations of the sides \(A B\) and \(A C\). The point of intersection of \(A B\) and \(A C\) is \(\left(\frac{10}{23}, \frac{84}{23}\right)\). Let slope of \(B C\) is \(m\). Since \(O^{\prime} A \perp B C\)

\(
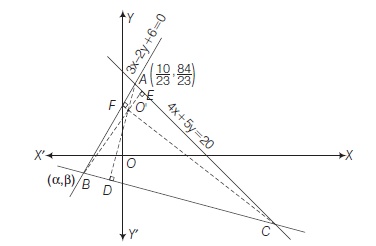
\therefore \text { Slope of } O^{\prime} A \times \text { Slope of } B C=-1
\)
\(
\begin{aligned}
\frac{\frac{84}{23}-1}{\frac{10}{23}-1} \times m & =-1 \\
\frac{61}{-13} m & =-1 \\
m & =\frac{13}{61}
\end{aligned}
\)
Let the vertex \(B\) is \((\alpha, \beta)\).
\(
\begin{array}{rr}
(\alpha, \beta) \text { lies on } 3 x-2 y+6=0 \\
\therefore 3 \alpha-2 \beta+6=0 \dots(i)
\end{array}
\)
and \(\quad O^{\prime} B \perp A C\)
\(\therefore\) Slope of \(O^{\prime} B \times\) slope of \(A C=-1\)
\(
\begin{array}{ll}
& \frac{\beta-1}{\alpha-1} \times\left(-\frac{4}{5}\right)=-1 \\
\Rightarrow & 4 \beta-4=5 \alpha-5 \\
\Rightarrow & 5 \alpha-4 \beta-1=0 \dots(ii)
\end{array}
\)
Solving Eqs. (i) and (ii), we get
\(
\alpha=-13 \text { and } \beta=-\frac{33}{2}
\)
Since, third side passes through \(\left(-13,-\frac{33}{2}\right)\) with slope \(\frac{13}{61}\), therefore its equation is
\(
\begin{aligned}
& y+\frac{33}{2}=\frac{13}{61}(x+13) \\
& \Rightarrow \quad 122 y+33 \times 61=26 x+2 \times 169 \\
& \Rightarrow \quad 26 x-122 y-1675=0 \\
&
\end{aligned}
\)

Example 45: If the orthocentre of the triangle formed by the lines \(2 x+3 y-1=0, x+2 y-1=0\), \(a x+b y-1=0\) is at origin, then find \((a, b)\).

Answer: The equation of a line through \(A\) i.e. the point of intersection of \(A B\) and \(A C\), is
\(
(2 x+3 y-1)+\lambda(a x+b y-1)=0 \dots(i)
\)
It passes through \(O(0,0)\), then
\(
\begin{array}{ll}
& -1-\lambda=0 \\
\therefore & \lambda=-1
\end{array}
\)

\(
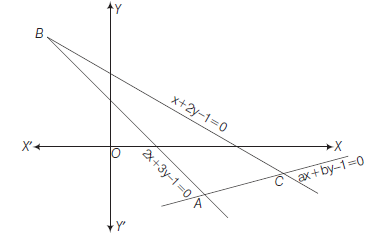
\begin{aligned}
& \text { From Eq. (i), } \\
& \qquad \begin{array}{r}
2 x+3 y-1-a x-b y+1=0 \\
\Rightarrow \quad(2-a) x+(3-b) y=0
\end{array}
\end{aligned}
\)
Since, \(A D \perp B C\)
\(
\begin{aligned}
& \therefore & -\frac{(2-a)}{(3-b)} \times\left(-\frac{1}{2}\right) & =-1 \\
\Rightarrow & & 2-a & =-6+2 b \\
\Rightarrow & & a+2 b & =8 \dots(ii)
\end{aligned}
\)
Similarly, \(B E \perp A C\), we get
\(
a+b=0 \dots(iii)
\)
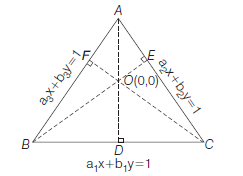
Solving Eqs. (ii) and (iii), we get
\(
\begin{array}{ll}
& b=8 \text { and } a=-8 \\
\therefore & (a, b) \text { is }(-8,8)
\end{array}
\)

Example 46: If the equations of the sides of a triangle are \(a_r x+b_r y=1 ; r=1,2,3\) and the orthocentre is the origin, then prove that
\(
a_1 a_2+b_1 b_2=a_2 a_3+b_2 b_3=a_3 a_1+b_3 b_1 \text {. }
\)

Answer: The equation of the line through \(A\), i.e. the point of intersection of \(A B\) and \(A C\) is
\(
\left(a_2 x+b_2 y-1\right)+\lambda\left(a_3 x+b_3 y-1\right)=0 \dots(i)
\)
It passes through \((0,0)\), then

\(
\begin{aligned}
& -1-\lambda & =0 \\
\therefore & \lambda & =-1
\end{aligned}
\)
From Eq. (i), \(a_2 x+b_2 y-1-a_3 x-b_3 y+1=0\)
\(
\therefore \quad\left(a_2-a_3\right) x+\left(b_2-b_3\right) y=0
\)
Since, \(A D \perp B C\)
\(\therefore\) Slope of \(A D \times\) slope of \(B C=-1\)
\(
\begin{aligned}
&-\frac{\left(a_2-a_3\right)}{\left(b_2-b_3\right)} \times\left(-\frac{a_1}{b_1}\right)=-1 \\
& \Rightarrow \quad a_1 a_2-a_3 a_1=-b_1 b_2+b_1 b_3
\end{aligned}
\)
\(
a_1 a_2+b_1 b_2=a_3 a_1+b_3 b_1 \dots(ii)
\)
Similarly, \(B E \perp C A\), then we get
\(
a_1 a_2+b_1 b_2=a_2 a_3+b_2 b_3 \dots(iii)
\)
From Eqs. (ii) and (iii), we get
\(
a_1 a_2+b_1 b_2=a_2 a_3+b_2 b_3=a_3 a_1+b_3 b_1
\)

Equations of Straight Lines Passing Through a Given Point and Making a Given Angle with a Given Line

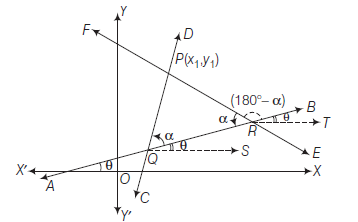
Theorem : Prove that the equations of the straight lines which pass through a given point \(\left(x_1, y_1\right)\) and make a given angle \(\alpha\) with the given straight line \(y=m x+c\) are where,
\(
\begin{aligned}
y-y_1 & =\tan (\theta \pm \alpha)\left(x-x_1\right) \\
m & =\tan \theta .
\end{aligned}
\)

Proof : Let \(A B\) be the given line which makes an angle \(\theta\) with \(X\)-axis.
\(
\therefore \quad m=\tan \theta
\)
Let \(C D\) and \(E F\) are two required lines which make angle \(\alpha\) with the given line. Let these lines meet the given line \(A B\) at \(Q\) and \(R\) respectively

\(
\therefore \quad \angle D Q S=\angle P Q R+\angle R Q S=(\alpha+\theta)
\)
\(\therefore\) Equation of line \(C D\) is
\(
\begin{aligned}
y-y_1 & =\tan (\theta+\alpha)\left(x-x_1\right) \dots(i)\\
\angle F R T & =\angle F R B+\angle B R T \\
& =180^{\circ}-\alpha+\theta \\
& =180^{\circ}+(\theta-\alpha)
\end{aligned}
\)
\(
\begin{aligned}
& =180^{\circ}-\alpha+\theta \\
& =180^{\circ}+(\theta-\alpha)
\end{aligned}
\)
\(\therefore\) Equation of line \(E F\) is
\(
\begin{aligned}
& y-y_1=\tan \left(180^{\circ}+\theta-\alpha\right)\left(x-x_1\right) \\
& y-y_1=\tan (\theta-\alpha)\left(x-x_1\right) \dots(ii)
\end{aligned}
\)
\(
y-y_1=\tan (\theta-\alpha)\left(x-x_1\right)
\)
From Eqs. (i) and (ii), we get
\(
y-y_1=\tan (\theta \pm \alpha)\left(x-x_1\right)
\)
These are the equations of the two required lines.

Example 47: Find the equations of the straight lines passing through the point \((2,3)\) and inclined at \(\pi / 4\) radians to the line \(2 x+3 y=5\).

Answer: Let the line \(2 x+3 y=5\) make an angle \(\theta\) with positive \(X\)-axis.
Then
\(
\tan \theta=-\frac{2}{3}
\)
Now \(\tan \theta \cdot \tan \frac{\pi}{4}=-\frac{2}{3} \times 1\)
\(
=-\frac{2}{3} \neq \pm 1
\)
Slopes of required lines are
\(
\tan \left(\theta+\frac{\pi}{4}\right) \text { and } \tan \left(\theta-\frac{\pi}{4}\right)
\)
\(
\begin{aligned}
& \therefore \tan \left(\theta+\frac{\pi}{4}\right)=\frac{\tan \theta+\tan \left(\frac{\pi}{4}\right)}{1-\tan \theta \tan \left(\frac{\pi}{4}\right)}=\frac{\left(-\frac{2}{3}\right)+1}{1-\left(-\frac{2}{3}\right)(1)}=\frac{1}{5} \\
& \text { and } \tan \left(\theta-\frac{\pi}{4}\right)=\frac{\tan \theta-\tan \left(\frac{\pi}{4}\right)}{1+\tan \theta \tan \left(\frac{\pi}{4}\right)} \\
& =\frac{\left(-\frac{2}{3}\right)-1}{1+\left(-\frac{2}{3}\right)(1)}=-5 \\
&
\end{aligned}
\)
\(\therefore\) Equations of required lines are
\(
y-3=\frac{1}{5}(x-2) \text { and } y-3=-5(x-2)
\)
i.e. \(\quad x-5 y+13=0\) and \(5 x+y-13=0\)

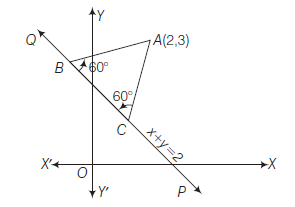
Example 48: A vertex of an equilateral triangle is \((2,3)\) and the opposite side is \(x+y=2\). Find the equations of the other sides.

Answer: Let \(A(2,3)\) be one vertex and \(x+y=2\) be the opposite side of an equilateral triangle. Clearly remaining two sides pass through the point \(A(2,3)\) and make an angle \(60^{\circ}\) with \(x+y=2\)
\(\because \quad\) Slope of \(x+y=2\) is -1

\(
\begin{aligned}
& \text { Let } & \tan \theta & =-1 \\
& \therefore & \theta & =135^{\circ}
\end{aligned}
\)
\(\therefore\) Equations of the other two sides are
\(
y-3=\tan \left(135^{\circ} \pm 60^{\circ}\right)(x-2)
\)
i.e. sides are
\(
y-3=\tan \left(195^{\circ}\right)(x-2) \quad \text { (taking ‘ }+ \text { ‘ sign) }
\)
\(
\begin{array}{ll}
\Rightarrow & y-3=\tan \left(180^{\circ}+15^{\circ}\right)(x-2) \\
\Rightarrow & y-3=\tan 15^{\circ}(x-2) \\
\Rightarrow & y-3=(2-\sqrt{3})(x-2) \\
\Rightarrow & (2-\sqrt{3}) x-y=1-2 \sqrt{3} \\
\text { and } & y-3=\tan \left(75^{\circ}\right)(x-2) \text { (taking ‘-‘ sign) }
\end{array}
\)
\(
\begin{array}{ll}
\Rightarrow & y-3=\cot 15^{\circ}(x-2) \\
\Rightarrow & y-3=(2+\sqrt{3})(x-2)
\end{array}
\)
\(
\Rightarrow \quad(2+\sqrt{3}) x-y=1+2 \sqrt{3}
\)
Hence, equations of other sides are
\(
\begin{aligned}
(2-\sqrt{3}) x-y & =1-2 \sqrt{3} \\
\text { and } \quad(2+\sqrt{3}) x-y & =1+2 \sqrt{3}
\end{aligned}
\)

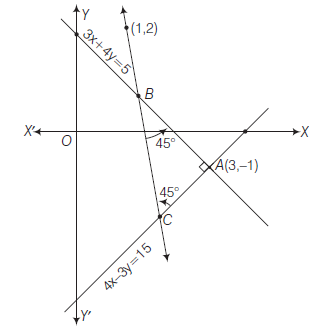
Example 49: The straight lines \(3 x+4 y=5\) and \(4 x-3 y=15\) intersect at a point \(A\). On these lines, the points \(B\) and \(C\) are chosen so that \(A B=A C\). Find the possible equations of the line \(B C\) passing through the point \((1,2)\).

Answer: Clearly \(\angle B A C=90^{\circ}\)
\(
\because \quad A B=A C
\)
\(
\begin{aligned}
\therefore \quad \angle A B C & =\angle B C A=45^{\circ} \\
\alpha & =45^{\circ}
\end{aligned}
\)
\(\because\) Slope of \(3 x+4 y=5\) is \(-\frac{3}{4}\)
Let \(\tan \theta=-\frac{3}{4}\)
So, possible equations of \(B C\) are given by
\(
y-2=\tan (\theta \pm \alpha)(x-1)
\)

\(
\begin{aligned}
& \Rightarrow \quad y-2=\left(\frac{\tan \theta \pm \tan \alpha}{1 \mp \tan \theta \tan \alpha}\right)(x-1) \\
& \Rightarrow \quad y-2=\left(\frac{-\frac{3}{4} \pm 1}{1 \mp\left(-\frac{3}{4}\right)(1)}\right)(x-1) \\
& \Rightarrow \quad y-2=\left(\frac{-3 \pm 4}{4 \mp(-3)}\right)(x-1)
\end{aligned}
\)
\(
\Rightarrow \quad y-2=\frac{1}{4-(-3)}(x-1) \quad \text { (taking upper sign) }
\)
\(
\text { or } \quad x-7 y+13=0
\)
\(
\text { and } \quad y-2=\frac{(-3-4)}{(4+(-3))}(x-1) \quad \text { (taking below sign) }
\)
or \(\quad 7 x+y-9=0\)
Hence, possible equation of the line \(B C\) are \(x-7 y+13=0\) and \(7 x+y-9=0\)

A Line Equally Inclined with Two Lines

Theorem: If two lines with slopes \(m_1\) and \(m_2\) be equally inclined to a line with slope \(m\), then
\(
\left(\frac{m_1-m}{1+m m_1}\right)=-\left(\frac{m_2-m}{1+m m_2}\right)
\)

Proof: Let be two lines of slopes \(m_1\) and \(m_2\) intersecting at a point \(P\).
Let \(\angle C P A=\angle B P C=\theta\)

\(
\tan (\angle C P A)=\left(\frac{m-m_1}{1+m m_1}\right)
\)
\(
\tan \theta=\left(\frac{m-m_1}{1+m m_1}\right) \quad\left(\because m>m_1\right) \dots(i)
\)
\(
\text { and } \quad \tan (\angle B P C)=\left(\frac{m_2-m}{1+m_2 m}\right)
\)
\(
\text { or } \quad \tan \theta=\left(\frac{m_2-m}{1+m_2 m}\right) \quad\left(\because m_2>m\right) \dots(ii)
\)
From Eqs. (i) and (ii), we get
\(
\left(\frac{m-m_1}{1+m m_1}\right)=\left(\frac{m_2-m}{1+m_2 m}\right) \text { or }\left(\frac{m_1-m}{1+m m_1}\right)=-\left(\frac{m_2-m}{1+m m_2}\right)
\)

Important Points

• The above equation gives two values of \(m\) which are the slopes of the lines parallel to the bisectors of the angles between the two given lines.
• Sign of \(m\) in both brackets is same.

Example 50: Find the equations to the straight lines passing through the point \((2,3)\) and equally inclined to the lines \(3 x-4 y-7=0\) and \(12 x-5 y+6=0\).

Answer: Let \(m\) be the slope of the required line. Then its equation is
\(
y-3=m(x-2) \dots(i)
\)
It is given that line (i) is equally inclined to the lines
\(
3 x-4 y-7=0 \text { and } 12 x-5 y+6=0 \text { then }
\)
\(
\Rightarrow \quad\left(\frac{\frac{3}{4}-m}{1+\frac{3}{4} m}\right)=-\left(\frac{\frac{12}{5}-m}{1+\frac{12}{5} m}\right) \left(\begin{array}{c}
\text { slope of } 3 x-4 y-7=0 \text { is } \frac{3}{4} \\
\text { and slope of } 12 x-5 y+6=0 \text { is } \frac{12}{5}
\end{array}\right)
\)
\(
\begin{aligned}
& \Rightarrow \quad\left(\frac{3-4 m}{4+3 m}\right)=-\left(\frac{12-5 m}{5+12 m}\right) \\
& \Rightarrow \quad(3-4 m)(5+12 m)+(4+3 m)(12-5 m)=0 \\
& \Rightarrow \quad 63 m^2-32 m-63=0 \\
& \Rightarrow \quad(7 m-9)(9 m+7)=0 \\
& \therefore \quad m=\frac{9}{7},-\frac{7}{9}
\end{aligned}
\)
Putting these values of \(m\) in Eq. (i) we obtain the equations of required lines as \(9 x-7 y+3=0\) and \(x+9 y-41=0\).

Example 51: Two equal sides of an isosceles triangle are given by the equations \(7 x-y+3=0\) and \(x+y-3=0\) and its third side passes through the point \((1,-10)\). Determine the equation of the third side.

Answer: Let \(m\) be the slope of \(B C\). Since \(A B=A C\).
Therefore \(B C\) makes equal angles with \(A B\) and \(A C\).

\(
\begin{aligned}
& \text { Then }\left(\frac{7-m}{1+7 m}\right)=-\left(\frac{-1-m}{1+(-1) m}\right) \\
& \Rightarrow \quad(7-m)(1-m)-(1+7 m)(1+m)=0 \\
& \Rightarrow \quad 6 m^2+16 m-6=0 \\
& \Rightarrow \quad 3 m^2+8 m-3=0
\end{aligned}
\)
\(
\begin{aligned}
\Rightarrow & (3 m-1)(m+3) =0 \\
\Rightarrow & m =\frac{1}{3},-3
\end{aligned}
\)
Equation of third side \(B C\) is \(y+10=m(x-1)\) i.e. \(y+10=\frac{1}{3}(x-1)\) and \(y+10=-3(x-1)\) or \(\quad x-3 y-31=0 \quad\) and \(\quad 3 x+y+7=0\)

Equation of the Bisectors

Theorem : Prove that the equation of the bisectors of the angles between the lines
\(
a_1 x+b_1 y+c_1=0 \text { and } a_2 x+b_2 y+c_2=0
\)
are given by \(\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}}= \pm \frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}}\)

Proof : Let the given lines be \(A A^{\prime}\) and \(B B^{\prime}\) whose equations are
\(
\begin{aligned}
& a_1 x+b_1 y+c_1=0  \dots(i) \\
& a_2 x+b_2 y+c_2=0 \dots(ii) 
\end{aligned}
\)
Since bisectors of the angles between the two lines are the locus of a point which moves in a plane such that whose distance from two lines are equal.

Let \(C C^{\prime}\) and \(D D^{\prime}\) be the two bisectors of the angle between the lines \(A A^{\prime}\) and \(B B^{\prime}\). Let \(P(x, y)\) be any point on \(C C^{\prime}\), then Length of the perpendicular from \(P\) on \(A A^{\prime}\)
\(=\) length of the perpendicular from \(P\) on \(B B^{\prime}\)
\(
\begin{aligned}
& \therefore \quad \frac{\left|a_1 x+b_1 y+c_1\right|}{\sqrt{\left(a_1^2+b_1^2\right)}}=\frac{\left|a_2 x+b_2 y+c_2\right|}{\sqrt{\left(a_2^2+b_2^2\right)}} \\
& \text { or } \quad \frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}}= \pm \frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}}
\end{aligned}
\)
These are the required equations of the bisectors.

Note: The two bisectors are perpendicular to each other.

Example 52: Find the equations of the bisectors of the angles between the straight lines \(3 x-4 y+7=0\) and \(12 x+5 y-2=0\).

Answer: The equations of the bisectors of the angles between \(3 x-4 y+7=0\) and \(12 x+5 y-2=0\) are
\(
\begin{array}{ll}
& \frac{(3 x-4 y+7)}{\sqrt{(3)^2+(-4)^2}}= \pm \frac{(12 x+5 y-2)}{\sqrt{(12)^2+(5)^2}} \\
\text { or } \quad & \frac{(3 x-4 y+7)}{5}= \pm \frac{(12 x+5 y-2)}{13} \\
\text { or } \quad(39 x-52 y+91) & = \pm(60 x+25 y-10)
\end{array}
\)
Taking the positive sign, we get
\(
21 x+77 y-101=0
\)
as one bisector.
Taking the negative sign, we get \(99 x-77 y+81=0\) as the second bisector.

Bisector of the Angle Containing the Origin

Let equations of lines be
\(
\begin{aligned}
& a_1 x+b_1 y+c_1=0 \dots(i) \\
& a_2 x+b_2 y+c_2=0 \dots(ii)
\end{aligned}
\)
where \(c_1\) and \(c_2\) are positive.
Let \(P(x, y)\) be taken on the bisector of the angle which contains the origin.

Let \(P(x, y)\) lies on \(D D^{\prime}\), then either \(O(0,0)\) and \(P(x, y)\) will lie on the same side of the two lines Eqs. (i) and (ii), then
\(
\frac{a_1 x+b_1 y+c_1}{0+0+c_1}>0
\)
\(
\text { and } \quad \frac{a_2 x+b_2 y+c_2}{0+0+c_2}>0
\)
\(
\text { or } \quad a_1 x+b_1 y+c_1>0
\)
and \(a_2 x+b_2 y+c_2>0 \quad\left(\because c_1, c_2>0\right)\)
If the origin \(O(0,0)\) and \(P(x, y)\) lie on the opposite side of the two lines Eqs. (i) and (ii), then
\(
\frac{a_1 x+b_1 y+c_1}{0+0+c_1}<0 \text { and } \frac{a_2 x+b_2 y+c_2}{0+0+c_2}<0
\)
or \(\quad a_1 x+b_1 y+c_1<0\) and \(a_2 x+b_2 y+c_2<0 \left(\because c_1, c_2>0\right)\)
Then equation of bisectors will be
\(
\frac{\left|a_1 x+b_1 y+c_1\right|}{\sqrt{\left(a_1^2+b_1^2\right)}}=\frac{\left|a_2 x+b_2 y+c_2\right|}{\sqrt{\left(a_2^2+b_2^2\right)}}
\)

Case I: If \(a_1 x+b_1 y+c_1>0\) and \(a_2 x+b_2 y+c_2>0\)
then \(\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}}=\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}}\)

Case II : If \(a_1 x+b_1 y+c_1<0\) and \(a_2 x+b_2 y+c_2<0\)
then \(-\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}}=-\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}}\)
i.e. \(\quad \frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}}=\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}}\)
Thus is both cases equation of the bisector containing the origin, when \(c_1\) and \(c_2\) are positive is
\(
\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}}=\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}}
\)
and equation of the bisector of the angle between the lines
\(
a_1 x+b_1 y+c_1=0 \text { and } a_2 x+b_2 y+c_2=0
\)
which does not contain the origin when \(c_1\) and \(c_2\) are positive is
\(
\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}}=-\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}}
\)

Working Rule :

• First re-write the equations of the two lines so that their constant terms are positive.
• The bisector of the angle containing the origin and does not containing the origin, then taking +ve and – ve sign in
  \(
  \frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}}= \pm \frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}} \text { respectively. }
  \)

Example 53: Find the equations of angular bisector bisecting the angle containing the origin and not containing the origin of the lines \(4 x+3 y-6=0\) and \(5 x+12 y+9=0\).

Answer: Firstly make the constant terms \(\left(c_1, c_2\right)\) positive, then
\(
-4 x-3 y+6=0 \text { and } 5 x+12 y+9=0
\)
\(\therefore\) The equation of the bisector bisecting the angle containing origin is
\(
\frac{(-4 x-3 y+6)}{\sqrt{\left(-4^2\right)+(-3)^2}}=\frac{(5 x+12 y+9)}{\sqrt{(5)^2+(12)^2}}
\)
\(
\begin{aligned}
& \Rightarrow \quad\left(\frac{-4 x-3 y+6}{5}\right)=\left(\frac{5 x+12 y+9}{13}\right) \\
& \Rightarrow \quad-52 x-39 y+78=25 x+60 y+45 \\
& \Rightarrow \quad 77 x+99 y-33=0 \text { or } 7 x+9 y-3=0 \\
&
\end{aligned}
\)
and the equation of the bisector bisecting the angle not containing origin is
\(
\frac{(-4 x-3 y+6)}{\sqrt{\left.(-4)^2+(-3)^2\right)}}=-\frac{(5 x+12 y+9)}{\sqrt{\left(5^2\right)+(12)^2}}
\)
\(
\begin{array}{ll}
\Rightarrow & \left(\frac{-4 x-3 y+6}{5}\right)=-\left(\frac{5 x+12 y+9}{13}\right) \\
\Rightarrow & -52 x-39 y+78=-25 x-60 y-45 \\
\Rightarrow & 27 x-21 y-123=0 \text { or } 9 x-7 y-41=0
\end{array}
\)

Equation of that Bisector of the Angle between Two Lines which Contains a Given Point

Let the equations of the two lines be
\(
\begin{aligned}
& a_1 x+b_1 y+c_1=0 \dots(i) \\
& a_2 x+b_2 y+c_2=0 \dots(ii)
\end{aligned}
\)
\(
a_2 x+b_2 y+c_2=0
\)
The equation of the bisector of the angle between the two lines containing the points \((h, k)\) will be
\(
\begin{aligned}
\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}} & =\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}} \\
\text { or } \quad \frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}} & =-\frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}}
\end{aligned}
\)
according as \(a_1 h+b_1 k+c_1\) and \(a_2 h+b_2 k+c_2\) are of the same sign or opposite sign.

Example 54: Find the bisector of the angle between the lines \(2 x+y-6=0\) and \(2 x-4 y+7=0\) which contains the point \((1,2)\).

Answer: Value of \(2 x+y-6\) at \((1,2)\) is -2 (negative)
and value of \(2 x-4 y+7\) at \((1,2)\) is 1 (positive) i.e. opposite sign.
\(\therefore\) Equation of bisector containing the point \((1,2)\) is
\(
\begin{aligned}
& \frac{(2 x+y-6)}{\sqrt{\left(2^2+1^2\right)}}=-\frac{(2 x-4 y+7)}{\sqrt{(2)^2+(-4)^2}} \\
\Rightarrow \quad & 2(2 x+y-6)+(2 x-4 y+7)=0
\end{aligned}
\)
or \(6 x-2 y-5=0\)

How to Distinguish the Acute (Internal) and Obtuse (External) Angle Bisectors?

Let the equations of the two lines be
\(
\begin{aligned}
& a_1 x+b_1 y+c_1=0 \dots(i) \\
& \text { and } \quad a_2 x+b_2 y+c_2=0 \dots(ii)
\end{aligned}
\)
\(
\text { where, } c_1>0, c_2>0 \text {. }
\)
\(\because\) Equations of bisectors are
\(
\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}}= \pm \frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}} \dots(iii)
\)
when Eq. (iii) be simplified, let the bisectors be and
\(
\begin{aligned}
& p_1 x+q_1 y+r_1=0 \dots(iv) \\
& p_2 x+q_2 y+r_2=0 \dots(v)
\end{aligned}
\)
Since the two bisectors are at right angles, the angle \(\alpha\) between the acute (internal ) bisector and any one of the given lines must lie between 0 and \(45^{\circ}\) i.e. \(0<\alpha<45^{\circ}\).
\(
\therefore \quad 0<\tan \alpha<1
\)
If \(m_1\) and \(m_2\) are the slopes of Eqs. (i) and (iii) respectively.
Then, \(\quad m_1=-\frac{a_1}{b_1} \quad\) and \(\quad m_2=-\frac{p_1}{q_1}\)
\(
\begin{aligned}
\therefore \quad \tan \alpha & =\left|\frac{m_1-m_2}{1+m_1 m_2}\right| \\
& =\left|\frac{\left(-\frac{a_1}{b_1}\right)-\left(-\frac{p_1}{q_1}\right)}{1+\left(-\frac{a_1}{b_1}\right)\left(-\frac{p_1}{q_1}\right)}\right|=\left|\frac{a_1 q_1-b_1 p_1}{b_1 q_1+a_1 p_1}\right|
\end{aligned}
\)
Hence, if \(0<\tan \alpha<1, p_1 x+q_1 y+r_1=0\) is the acute (internal) bisector and if \(\tan \alpha>1, p_2 x+q_2 y+r_2=0\) is the obtuse (external ) bisector.

Shortcut Method for finding Acute (Internal) and Obtuse (External) Angle Bisectors

Let the equations of the two lines be
\(
\begin{aligned}
& a_1 x+b_1 y+c_1=0 \\
& a_2 x+b_2 y+c_2=0
\end{aligned}
\)
Taking \(\quad c_1>0, c_2>0\) and \(a_1 b_2 \neq a_2 b_1\)
Then equations of the bisectors are
\(
\frac{\left(a_1 x+b_1 y+c_1\right)}{\sqrt{\left(a_1^2+b_1^2\right)}}= \pm \frac{\left(a_2 x+b_2 y+c_2\right)}{\sqrt{\left(a_2^2+b_2^2\right)}}
\)
\(
\begin{array}{c|l|l}
\hline \text { Conditions } & \text { Acute angle bisector } & \text { Obtuse angle bisector } \\
\hline a_1 a_2+b_1 b_2>0 & – & + \\
\hline a_1 a_2+b_1 b_2<0 & + & – \\
\hline
\end{array}
\)

Important Points

• Bisectors are perpendiculars to each other.
•  ‘ + ‘ sign gives the bisector of the angle containing origin.
• If \(a_1 a_2+b_1 b_2>0\) then the origin lies in obtuse angle and if \(a_1 a_2+b_1 b_2<0\), then the origin lies in acute angle.

Explanation: Equations of given lines in normal form will be respectively
\(
-\frac{a_1 x}{\sqrt{\left(a_1^2+b_1^2\right)}}-\frac{b_1 y}{\sqrt{\left(a_1^2+b_1^2\right)}}=\frac{c_1}{\sqrt{\left(a_1^2+b_1^2\right)}}\left(\because c_1>0\right)
\)
\(
\text { and } \quad-\frac{a_2 x}{\sqrt{\left(a_2^2+b_2^2\right)}}-\frac{b_2 y}{\sqrt{\left(a_2^2+b_2^2\right)}}=\frac{c_2}{\sqrt{\left(a_2^2+b_2^2\right)}}\left(\because c_2>0\right)
\)
If \(\quad \cos \alpha=-\frac{a_1}{\sqrt{\left(a_1^2+b_1^2\right)}}\) then \(\sin \alpha=-\frac{b_1}{\sqrt{\left(a_1^2+b_1^2\right)}}\) and \(\cos \beta=-\frac{a_2}{\sqrt{\left(a_2^2+b_2^2\right)}}\) then \(\sin \beta=-\frac{b_2}{\sqrt{\left(a_2^2+b_2^2\right)}}\)
Now, \(\cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\)
\(
=\frac{\left(a_1 a_2+b_1 b_2\right)}{\sqrt{\left(a_1^2+b_1^2\right)} \sqrt{\left(a_2^2+b_2^2\right)}}
\)
\(
\cos (\alpha-\beta)>0 \quad \text { or }<0
\)
according as \((\alpha-\beta)\) is acute or obtuse.
i.e. \(\quad a_1 a_2+b_1 b_2>0\) or \(<0\)
Hence, bisector of the angle between the lines will be the bisector of the acute or obtuse angle according as origin lies in the acute or obtuse angle according as \(a_1 a_2+b_1 b_2<0\) or \(>0\).

Example 55: Find the equation of the bisector of the obtuse angle between the lines \(3 x-4 y+7=0\) and \(12 x+5 y-2=0\).

Answer: Firstly make the constant terms \(\left(c_1, c_2\right)\) positive
\(
\begin{aligned}
& 3 x-4 y+7=0 \text { and }-12 x-5 y+2=0 \\
& \because a_1 a_2+b_1 b_2=(3)(-12)+(-4)(-5)=-36+20=-16 \\
& \therefore \quad a_1 a_2+b_1 b_2<0 \\
&
\end{aligned}
\)
Hence “-” sign gives the obtuse bisector.
\(\therefore\) Obtuse bisector is
\(
\begin{aligned}
\frac{(3 x-4 y+7)}{\sqrt{(3)^2+(-4)^2}} & =-\frac{(-12 x-5 y+2)}{\sqrt{(-12)^2+(-5)^2}} \\
\Rightarrow \quad 13(3 x-4 y+7) & =-5(-12 x-5 y+2) \\
\Rightarrow \quad 21 x+77 y-101 & =0 \text { is the obtuse angle bisector. }
\end{aligned}
\)

Example 56: Find the bisector of acute angle between the lines \(x+y-3=0\) and \(7 x-y+5=0\).

Answer: Firstly, make the constant terms \(\left(c_1, c_2\right)\) positive then
\(
\begin{aligned}
& -x-y+3=0 \text { and } 7 x-y+5=0 \\
& \because \quad a_1 a_2+b_1 b_2=(-1)(7)+(-1)(-1)=-7+1=-6 \\
& \text { i.e. } \quad a_1 a_2+b_1 b_2<0
\end{aligned}
\)
Hence “+” sign gives the acute bisector.
\(
\begin{aligned}
& \therefore \quad \text { Acute bisector is } \frac{-x-y+3}{\sqrt{(-1)^2+(-1)^2}}=+\frac{7 x-y+5}{\sqrt{(7)^2+(-1)^2}} \\
& \Rightarrow \quad \frac{-x-y+3}{\sqrt{2}}=\frac{7 x-y+5}{5 \sqrt{2}} \\
& \Rightarrow \quad-5 x-5 y+15=7 x-y+5 \\
& \therefore \quad 12 x+4 y-10=0 \text { or } 6 x+2 y-5=0
\end{aligned}
\)
is the acute angle bisector.

Example 57: Find the coordinates of incentre of the triangle. The equation of whose sides are
\(
\begin{aligned}
& A B: x+y-1=0, B C: 7 x-y-15=0 \\
& \text { and } C A: x-y-1=0
\end{aligned}
\)

Answer: Firstly, make the constant terms \(\left(c_1, c_2\right.\), and \(\left.c_3\right)\) positive i.e.
\(
\begin{array}{r}
A B:-x-y+1=0 \dots(i) \\
B C:-7 x+y+15=0 \dots(ii) \\
C A:-x+y+1=0 \dots(iii)
\end{array}
\)
\(\because\) The incentre of triangle is the point of intersection of internal or acute angle bisectors.
Internal bisector of \(A B\) and \(B C\) :
\(
\begin{array}{r}
-x-y+1=0 \\
-7 x+y+15=0
\end{array}
\)
\(
\because \quad a_1 a_2+b_1 b_2=(-1)(-7)+(-1)(1)=6>0
\)
\(\therefore\) Acute or internal bisector is
\(
\frac{(-x-y+1)}{\sqrt{(-1)^2+(-1)^2}}=-\frac{(-7 x+y+15)}{\sqrt{(-7)^2+(1)^2}}
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{(-x-y+1)}{\sqrt{2}}=-\frac{(-7 x+y+15)}{5 \sqrt{2}} \\
& \Rightarrow \quad-5 x-5 y+5=7 x-y-15 \\
& \text { or } \quad 12 x+4 y-20=0 \\
& \text { or } \quad 3 x+y-5=0 \dots(iv) \\
&
\end{aligned}
\)
Internal bisector of \(BC\) and \(CA\) :
\(
\begin{gathered}
-7 x+y+15=0 \\
-x+y+1=0 \\
\because a_1 a_2+b_1 b_2=(-7)(-1)+(1)(1)=8>0
\end{gathered}
\)
\(\because\) Acute or internal bisector is
\(
\begin{aligned}
& \frac{(-7 x+y+15)}{\sqrt{(-7)^2+(1)^2}}=-\frac{(-x+y+1)}{\sqrt{(-1)^2+(1)^2}} \\
& \Rightarrow \quad \frac{-7 x+y+15}{5 \sqrt{2}}=\frac{(x-y-1)}{\sqrt{2}} \\
& \Rightarrow \quad-7 x+y+15=5 x-5 y-5 \\
& \text { or } \quad 12 x-6 y-20=0 \\
& \text { or } \\
& 6 x-3 y-10=0 \dots(v) \\
&
\end{aligned}
\)
Finally, solve Eqs. (iv) and (v), we get
\(
x=\frac{5}{3} \text { and } y=0
\)
Hence coordinates of incentre are \(\left(\frac{5}{3}, 0\right)\).

The Foot of Perpendicular Drawn from the Point \(\left(x_1, y_1\right)\) to the Line \(a x+b y+c=0\)

Let \(P \equiv\left(x_1, y_1\right)\) and let \(M\) be the foot of perpendicular drawn from \(P\) on \(a x+b y+c=0\). In order to find the coordinates of \(M\), find the equation of the line \(P M\) which is perpendicular to \(R S\) and passes through \(P\left(x_1, y_1\right)\), i.e. \(b x-a y=b x_1-a y_1\) or \(b\left(x-x_1\right)-a\left(y-y_1\right)=0\) and solving it with \(a x+b y+c=0\), then we get coordinates of \(M\).

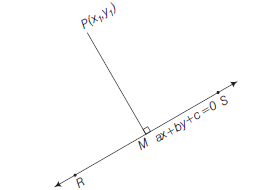
Method 1:  Let the coordinates of \(M\) are \(\left(x_2, y_2\right)\) then \(M\left(x_2, y_2\right)\) lies on \(a x+b y+c=0\)
\(
\Rightarrow \quad a x_2+b y_2+c=0 \dots(i)
\)
and \(\quad \because P M \perp R S\)
then \(\quad(\) Slope of \(P M)(\) Slope of \(R S)=-1\)
\(
\begin{array}{ll}
\Rightarrow & \left(\frac{y_2-y_1}{x_2-x_1}\right) \times\left(-\frac{a}{b}\right)=-1 \\
\text { or } & b x_2-a y_2=b x_1-a y_1 \dots(ii)
\end{array}
\)
Solving Eqns. (i) and (ii), we get \(\left(x_2, y_2\right)\).

Method II: Let the coordinates of \(M\) are \(\left(x_2, y_2\right)\)
\(
\begin{aligned}
\because & P M & \perp R S \\
\text { and } M \text { lies on } & a x+b y+c & =0 \\
\text { i.e. } & a x_2+b y_2+c & =0 \dots(iii)
\end{aligned}
\)
\(
\begin{aligned}
& \frac{x_2-x_1}{a}=\frac{y_2-y_1}{b} \\
& \frac{x_2-x_1}{a}=\frac{y_2-y_1}{b}=\frac{a\left(x_2-x_1\right)+b\left(y_2-y_1\right)}{\left(a^2+b^2\right)}
\end{aligned}
\)
(By ratio proportion method)
\(
\begin{aligned}
& =\frac{\left(a x_2+b y_2\right)-\left(a x_1+b y_1\right)}{a^2+b^2} \\
& =\frac{-c-\left(a x_1+b y_1\right)}{a^2+b^2} \text { [from Eq. (iii)] }\\
\frac{x_2-x_1}{a} & =\frac{y_2-y_1}{b}=-\frac{\left(a x_1+b y_1+c\right)}{\left(a^2+b^2\right)}
\end{aligned}
\)

Example 58: Find the coordinates of the foot of the perpendicular drawn from the point \((2,3)\) to the line \(y=3 x+4\)

Answer: Given line is
\(
3 x-y+4=0 \dots(i)
\)
Let Eq.
\(
P \equiv(2,3) \text {. }
\)
Let, \(M\) be the foot of perpendicular drawn from \(P\) on \(R S\).
Then equation of \(P M\) passes through \(P(2,3)\) and perpendicular to \(R S\) is i.e.
\(
\begin{array}{r}
x+3 y-(2+3 \times 3)=0 \\
x+3 y-11=0 \dots(ii)
\end{array}
\)
Solving Eqs. (i) and (ii), we get
\(
\begin{aligned}
x & =-\frac{1}{10}, y=\frac{37}{10} \\
\therefore \quad M & \equiv\left(-\frac{1}{10}, \frac{37}{10}\right)
\end{aligned}
\)

Method I: Let the coordinates of \(M\) be \(\left(x_2, y_2\right)\) then \(M\left(x_2, y_2\right)\) lies on \(3 x-y+4=0\)
\(
\Rightarrow \quad 3 x_2-y_2+4=0 \dots(iii)
\)
\(
\text { and } \quad \because P M \perp R S
\)
\(\therefore(\) Slope of \(P M) \times(\) Slope of \(R S)=-1\)
\(\Rightarrow \quad\left(\frac{y_2-3}{x_2-2}\right) \times(3)=-1\)
or \(\quad x_2+3 y_2-11=0 \dots(iv)\)
Solving Eqs. (iii) and (iv), we get
\(
\begin{aligned}
& x_2=-\frac{1}{10}, y_2=\frac{37}{10} \\
& \therefore \quad M \equiv\left(-\frac{1}{10}, \frac{37}{10}\right) \\
&
\end{aligned}
\)

Method II: By Ratio Proportion Method:
\(
\frac{x_2-2}{3}=\frac{y_2-3}{-1}=\frac{-(3 \times 2-3+4)}{3^2+(-1)^2}
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{x_2-2}{3}=\frac{y_2-3}{-1}=-\frac{7}{10} \\
& x_2=-\frac{1}{10} \text { and } y_2=\frac{37}{10} \\
& \therefore \quad M \equiv\left(-\frac{1}{10}, \frac{37}{10}\right) \\
&
\end{aligned}
\)

Image or Reflection of a Point \(\left(x_1, y_1\right)\) About a Line Mirror

Let \(Q \equiv\left(x_2, y_2\right)\) be the image of \(P \equiv\left(x_1, y_1\right)\) then find coordinates of the foot of perpendicular \(M\) drawn from the point \(P\left(x_1, y_1\right)\) on \(R S\) and use fact that \(M\) is the mid- point \(P\) and \(Q\).

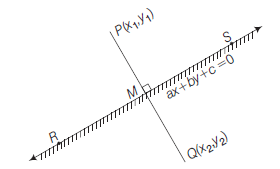
i.e. \(M \equiv\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)

Method I: Method Ratio Proportion Method :
\(
P Q \perp R S
\)
\(
\begin{aligned}
& \therefore \quad(\text { Slope of } P Q) \times(\text { Slope of } R S)=-1 \\
& \text { or }\left(\frac{y_2-y_1}{x_2-x_1}\right) \times\left(-\frac{a}{b}\right)=-1 \\
& \text { or } \quad \frac{\left(x_2-x_1\right)}{a}=\frac{\left(y_2-y_1\right)}{b} \\
& \text { or } \quad \frac{x_2-x_1}{a}=\frac{y_2-y_1}{b}=\frac{a\left(x_2-x_1\right)+b\left(y_2-y_1\right)}{a^2+b^2} \\
& =\frac{a\left(2 x-x_1-x_1\right)+b\left(2 y-y_1-y_1\right)}{a^2+b^2} \\
&
\end{aligned}
\)
\(
\left(\begin{array}{l}
\because M(x, y) \text { is mid-point of } P \text { and } Q \\
\therefore x_2=2 x-x_1 \text { and } y_2=2 y-y_1
\end{array}\right)
\)
\(
\begin{aligned}
& =\frac{-2 a x_1-2 b y_1+2(a x+b y)}{a^2+b^2} \\
& =\frac{-2 a x_1-2 b y_1+2(-c)}{a^2+b^2}(\because a x+b y=-c) \\
& =\frac{-2\left(a x_1+b y_1+c\right)}{\left(a^2+b^2\right)}
\end{aligned}
\)
i.e. \(\quad \frac{x_2-x_1}{a}=\frac{y_2-y_1}{b}=-\frac{2\left(a x_1+b y_1+c\right)}{\left(a^2+b^2\right)}\)

Method II: By Distance form or Symmetric form or parametric form:
\(
\begin{array}{ll}
\because & \text { Slope of } R S=-\frac{a}{b} \\
\therefore & \text { Slope of } P Q=\frac{b}{a}
\end{array}
\)

\(
\begin{aligned}
\text { Let } & \tan \theta & =\frac{b}{a} \\
\therefore & \sin \theta & =\frac{b}{\sqrt{\left(a^2+b^2\right)}}
\end{aligned}
\)
\(
\text { and } \quad \cos \theta=\frac{a}{\sqrt{\left(a^2+b^2\right)}}
\)
Put the equation of the mirror line such that the coefficient of \(y\) becomes negative.
Suppose if
\(
b>0
\)
then
\(
a x+b y+c=0
\)
becomes
\(
-a x-b y-c=0
\)
\(
\text { and } \quad p=P M=\text { Directed distance from } P\left(x_1, y_1\right) \text { on }
\)
\(
=\left(\frac{-a x_1-b y_1-c}{\sqrt{\left(a^2+b^2\right)}}\right)
\)
\(
\therefore \quad P Q=2 P M=2 p=2\left(\frac{-a x_1-b y_1-c}{\sqrt{\left(a^2+b^2\right)}}\right)=r
\)
\(\Rightarrow \quad\) Required image has the coordinates
\(
\left(x_1+r \cos \theta, y_1+r \sin \theta\right) \text {. }
\)

Example 59: Find the image of the point \((4,-13)\) with respect to the line mirror \(5 x+y+6=0\).

Answer: Let, \(P \equiv(4,-13)\) and Let, \(Q \equiv\left(x_2, y_2\right)\) be mirror image \(P\) with respect to line mirror \(5 x+y+6=0\).
Let, \(M(\alpha, \beta)\) be the foot of perpendicular from \(P(4,-13)\) on the line mirror \(5 x+y+6=0\), then
\(
\begin{aligned}
\frac{\alpha-4}{5} & =\frac{\beta+13}{1}=\frac{-(5 \times 4-13+6)}{5^2+1^2} \\
\frac{\alpha-4}{5} & =\frac{\beta+13}{1}=-\frac{1}{2} \\
M & \equiv\left(\frac{3}{2},-\frac{27}{2}\right)
\end{aligned}
\)
\(\because M\) is the mid-point of \(P\) and \(Q\), then
\(
Q \equiv\left(x_2, y_2\right) \equiv\left(2 \times \frac{3}{2}-4,2 \times\left(-\frac{27}{2}\right)+13\right)
\)
i.e. \(Q \equiv(-1,-14)\)

Method I: By Ratio Proportion Method
Let, \(Q\left(x_2, y_2\right)\) the image of \(P(4,-13)\) with respect to line mirror \(5 x+y+6=0\), then
\(
\begin{aligned}
\frac{x_2-4}{5} & =\frac{y_2+13}{1}=-\frac{2(5 \times 4-13+6)}{5^2+1^2}=-1 \\
x_2-4 & =-5 \text { and } y_2+13=-1 \\
x_2 & =-1 \text { and } y_2=-14
\end{aligned}
\)
\(
\text { Hence } Q \equiv(-1,-14) \text {. }
\)

Method II: By distance form or Symmetric form or Parametric form
Let, \(P \equiv(4,-13)\) and \(Q[latex] be the image of [latex]P\) with respect to line mirror \((R S) 5 x+y+6=0\)
\(
\because \quad \text { Slope of } R S=-5
\)

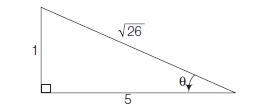
\(\therefore \quad\) Slope of \(P Q=\frac{1}{5}=\tan \theta\)
\(\therefore \quad \sin \theta=\frac{1}{\sqrt{26}}\) and \(\cos \theta=\frac{5}{\sqrt{26}}\)
Now, put the equation of the mirror line such that the coefficient of \(y\) becomes negative.
Then, \(5 x+y+6=0\) becomes \(-5 x-y-6=0\) and \(p=\perp\) Directed distance from \(P(4,-13)\) on \((-5 x-y-6=0)\)
\(
\begin{array}{r}
=\frac{-5 \times 4+13-6}{\sqrt{(-5)^2+(-1)^2}}=-\frac{13}{\sqrt{26}} \\
\therefore \quad P Q=r=2 p=-\frac{26}{\sqrt{26}}=-\sqrt{26}
\end{array}
\)
Hence, required image has the coordinates
\(
Q \equiv(4-\sqrt{26} \cos \theta,-13-\sqrt{26} \sin \theta)
\)
i.e. \(\quad\left(4-\sqrt{26} \times \frac{5}{\sqrt{26}},-13-\sqrt{26} \times \frac{1}{\sqrt{26}}\right)\)
i.e. \((4-5,-13-1)\)
Hence, \(Q \equiv(-1,-14)\)

Image or Reflection of a Point in Different Cases

Case I: The image or reflection of a point with respect to \(X\)-axis
Let \(P(\alpha, \beta)\) be any point and \(Q(x, y)\) be its image about \(X\)-axis, then \((M\) is the mid-point of \(P\) and \(Q)\)

\(
\begin{array}{rlrl}
& x & =\alpha \text { and } y=-\beta \\
\therefore & Q \equiv(\alpha,-\beta)
\end{array}
\)
i.e. sign change of ordinate.

Important Point:

• The image of the line \(a x+b y+c=0\) about \(X\)-axis is \(a x-b y+c=0\)

Case II: The image or reflection of a point with respect to \(Y\)-axis

Let \(P(\alpha, \beta)\) be any point and \(Q(x, y)\) be its image about \(Y\)-axis, then \((M\) is the mid-point of \(P Q)\)

\(
\begin{aligned}
& x=-\alpha \text { and } y=\beta \\
& \therefore \quad Q \equiv(-\alpha, \beta) \\
&
\end{aligned}
\)
i.e. sign change of abscissae.

Important Point

• The image of the line \(a x+b y+c=0\) about \(Y\)-axis is \(-a x+b y+c=0\)

Case III: The image or reflection of a point with respect to origin
Let \(P(\alpha, \beta)\) be any point and \(Q(x, y)\) be its image about the origin \((O\) is the mid point of \(P Q)\), then

\(
\begin{aligned}
& x=-\alpha \text { and } y=-\beta \\
& \therefore \quad Q \equiv(-\alpha,-\beta) \\
&
\end{aligned}
\)
i.e. sign change of abscissae and ordinate.

Important Point

• The image of the line \(a x+b y+c=0\) about origin is \(-a x-b y+c=0\).

Case iv: The image or reflection of a point with respect to the line \(x=a\)

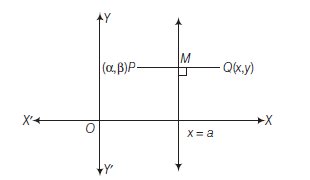
Let \(P(\alpha, \beta)\) be any point and \(Q(x, y)\) be its image about the line \(x=a\), then \(y=\beta\)
\(
\begin{aligned}
& \therefore \text { Coordinates of } M \text { are }(a, \beta) \\
& \because M \text { is the mid-point of PQ } \\
& \therefore Q \equiv(2 a-\alpha, \beta)
\end{aligned}
\)

Important Point

• The image of the line \(a x+b y+c=0\) about the line \(x=\lambda\) is
  \(
  a(2 \lambda-x)+b y+c=0
  \)

Case v: The image or reflection of a point with respect to the line \(y=b\)

Let \(P(\alpha, \beta)\) be any point and \(Q(x, y)\) be its image about the line \(y = b\), then \(x=\alpha\)

\(\therefore\) Co-ordinates of \(M\) are \((\alpha, b)\)
\(\because M\) is the mid-point of PQ \(\therefore Q \equiv(\alpha, 2 b-\beta)\)

Important Point

• The image of the line \(a x+b y+c=0\) about the line \(y=\mu\) is \(a x+b(2 \mu-y)+c=0\).

Case vi: The image or reflection of a point with respect to the line \(y = x\)

Let \(P(\alpha, \beta)\) be any point and \(Q\left(x_1, y_1\right)\) be its image about the line \(y=x(R S)\), then \(P Q \perp R S\)

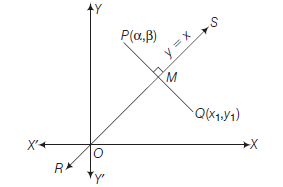
\(\therefore(\) Slope of \(P Q) \times(\) Slope of \(R S)=-1\)
or \(\quad \frac{y_1-\beta}{x_1-\alpha} \times 1=-1\)
or \(\quad x_1-\alpha=\beta-y_1 \dots(i)\)
and mid-point of \(P Q\) lie on \(y=x\)
i.e. \(\quad\left(\frac{y_1+\beta}{2}\right)=\left(\frac{x_1+\alpha}{2}\right)\)
or \(x_1+\alpha=\beta+y_1 \dots(ii)\)
Solving Eqs. (i) and (ii), we get \(x_1=\beta\) and \(y_1=\alpha\)
\(\therefore Q \equiv(\beta, \alpha)\) i.e. interchange of \(x\) and \(y\).

Important Point

• The image of the line \(a x+b y+c=0\) about the line \(y=x\) is \(a y+b x+c=0\).

Case vii: The image or reflection of a point with respect to the line \(y=x \tan \theta\)

Let \(P(\alpha, \beta)\) be any point and \(Q\left(x_1, y_1\right)\) be its image about the line \(y=x \tan \theta(R S)\), then \(P Q \perp R S\)
\(\therefore(\) Slope of \(P Q) \times(\) Slope of \(R S)=-1\)
\(\begin{array}{ll}\text { or } & \frac{y_1-\beta}{x_1-\alpha} \times \tan \theta=-1 \\ \Rightarrow & y_1-\beta=\left(\alpha-x_1\right) \cot \theta \dots(i) \end{array}\)
and mid-point of PQ lie on \(y=x \tan \theta\)
i.e. \(\quad\left(\frac{y_1+\beta}{2}\right)=\left(\frac{x_1+\alpha}{2}\right) \tan \theta\)

\(
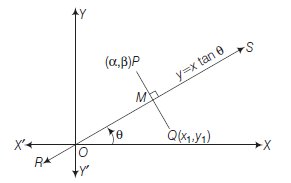
\text { or } \quad y_1+\beta=\left(x_1+\alpha\right) \tan \theta \dots(ii)
\)
Solving Eqs. (i) and (ii), we get
\(
x_1=\alpha \cos 2 \theta+\beta \sin 2 \theta
\)
\(
\begin{aligned}
& \text { and } \quad y_1=\alpha \sin 2 \theta-\beta \cos 2 \theta \\
& \therefore \quad Q \equiv(\alpha \cos 2 \theta+\beta \sin 2 \theta, \alpha \sin 2 \theta-\beta \cos 2 \theta) \\
&
\end{aligned}
\)

Example 60: The point \(P(\alpha, \beta)\) undergoes a reflection in the \(X\)-axis followed by a reflection in the \(Y\)-axis. Show that their combined effect is the same as the single reflection of \(P(\alpha, \beta)\) in the origin when \(\alpha, \beta>0\).

Answer: Let \(P_1\left(x_1, y_1\right)\) be the image of \((\alpha, \beta)\) after reflection in the \(X\)-axis. Then
\(
x_1=\alpha \text { and } y_1=-\beta \dots(i)
\)
Now, let \(P_2\left(x_2, y_2\right)\) be the image of \(P_1\left(x_1, y_1\right)\) in the \(Y\)-axis. Then

\(
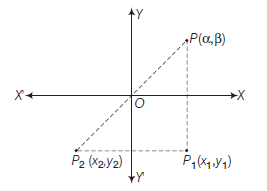
\begin{aligned}
& x_2=-x_1, y_2=y_1 \dots(ii)\\
\Rightarrow \quad & x_2=-\alpha, y_2=-\beta \quad \text { [from Eq. (i)] …(ii) }
\end{aligned}
\)
further let \(P_3\left(x_3, y_3\right)\) be the image of \(P(\alpha, \beta)\) in the origin \(O\). Then
\(
x_3=-\alpha, y_3=-\beta \dots(iii)
\)
From Eqs. (ii) and (iii), we get
\(
x_3=x_2 \text { and } y_3=y_2 \text {. }
\)
Hence the image of \(P_2\) of \(P\) after successive reflection in their \(X\)-axis and \(Y\)-axis is the same as the single reflection of \(P\) in the origin.

Example 61: Find the image of the point \((-2,-7)\) under the transformations \((x, y) \rightarrow(x-2 y,-3 x+y)\).

Answer: Let \(\left(x_1, y_1\right)\) be the image of the point \((x, y)\) under the given transformation. Then
\(
\begin{aligned}
& x_1=x-2 y=(-2)-2(-7)=12 \\
& x_1=12 \text { and } y_1=-3 x+y=-3(-2)-7=-1 \\
& y_1=-1
\end{aligned}
\)
Hence, the image is \((12,-1)\).

Example 62: The image of the point \(A(1,2)\) by the line mirror \(y=x\) is the point \(B\) and the image of \(B\) by the line mirror \(y=0\) is the point \((\alpha, \beta)\). Find \(\alpha\) and \(\beta\).

Answer: Let \(\left(x_1, y_1\right)\) be the image of the point \((1,2)\) about the line \(y=x\).
Then
\(
x_1=2, y_1=1 \dots(i)
\)

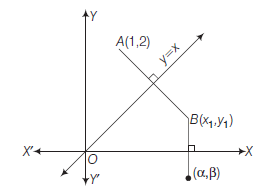
Also given image of \(B\left(x_1, y_1\right)\) by the line mirror \(y=0\) is \((\alpha, \beta)\). Then \(\alpha=x_1=2\)
and \(\beta=-y_1=-1 \text { [from Eq. (i)] }\)
\(
\text { Hence, } \quad \alpha=2 \text { and } \beta=-1
\)

Example 63: The point \((4,1)\) undergoes the following three transformations successively :
(i) Reflection about the line \(y=x\).
(ii) Translation through a distance 2 units along the positive direction of \(X\)-axis.
(iii) Rotation through an angle \(\pi / 4\) about the origin in the anticlockwise direction.
Then, find the coordinates of the final position.

Answer: Let \(Q\left(x_1, y_1\right)\) be the reflection of \(P\) about the line \(y=x\). Then
\(
\left.\begin{array}{l}
x_1=1 \\
y_1=4
\end{array}\right\}
\)
\(\therefore\) Coordinates of \(Q\) is \((1,4)\).
Given that \(Q\) move 2 units along the positive direction of \(X\)-axis.

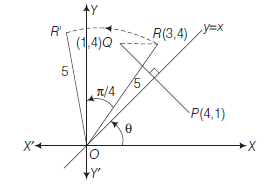
\(\therefore\) Coordinates of \(R\) is \(\left(x_1+2, y_1\right)\)
or \(\quad R(3,4)\)
If \(O R\) makes an angle \(\theta\), then
\(
\begin{aligned}
\tan \theta & =\frac{4}{3} \\
\therefore \quad \sin \theta & =\frac{4}{5} \text { and } \cos \theta=\frac{3}{5}
\end{aligned}
\)
After rotation of \(\frac{\pi}{4}\) let new position of \(R\) is \(R^{\prime}\) and
\(
O R=O R^{\prime}=\sqrt{3^2+4^2}=5
\)
\(\therefore \quad O R^{\prime}\) makes an angle \((\pi / 4+\theta)\) with \(X\)-axis.
Coordinates of \(R^{\prime}\left(O R^{\prime} \cos \left(\frac{\pi}{4}+\theta\right), O R^{\prime} \sin \left(\frac{\pi}{4}+\theta\right)\right)\)
\(
\begin{array}{r}
\text { i.e. } R^{\prime}\left(O R^{\prime}\left(\frac{1}{\sqrt{2}} \cos \theta-\frac{1}{\sqrt{2}} \sin \theta\right)\right. \text {, } \\
\left.O R^{\prime} \sin \left(\frac{1}{\sqrt{2}} \cos \theta+\frac{1}{\sqrt{2}} \sin \theta\right)\right)
\end{array}
\)
\(
\begin{aligned}
& \Rightarrow \quad R^{\prime}\left(5\left(\frac{3}{5 \sqrt{2}}-\frac{4}{5 \sqrt{2}}\right), 5\left(\frac{3}{5 \sqrt{2}}+\frac{4}{5 \sqrt{2}}\right)\right) \\
& \Rightarrow \quad R^{\prime}\left(-\frac{1}{\sqrt{2}}, \frac{7}{\sqrt{2}}\right)
\end{aligned}
\)

Alternate Method: (Use of complex number)
Let \(Q\) be the reflection of \(P(4,1)\) about the line \(y=x\), then \(Q \equiv(1,4)\)
\(\because Q\) move 2 units along the +ve direction of \(X\)-axis, if new point is,\(R\) then \(R \equiv(3,4)\).
If
\(
\begin{aligned}
R(3,4) & =R\left(z_1\right) \\
\text { when } z_1 & =(3+4 i)
\end{aligned}
\)
\(
\begin{aligned}
& \text { then } & R^{\prime}(x, y) & =R^{\prime}\left(z_2\right) \\
& \therefore & z_2 & =z_1 e^{i \pi / 4} \left(\because \angle R O R^{\prime}=\frac{\pi}{4}\right)
\end{aligned}
\)
\(
\begin{aligned}
& =(3+4 i)\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right) \\
& =(3+4 i)\left(\frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}}\right)=\left(-\frac{1}{\sqrt{2}}+\frac{7 i}{\sqrt{2}}\right)
\end{aligned}
\)
Hence, new coordinates are \(\left(-\frac{1}{\sqrt{2}}, \frac{7}{\sqrt{2}}\right)\).

Use of Image or Reflection

To make problems simpler and easier use Image or reflection.
Types of problems :

Case I: If vertex of a \(\triangle A B C\) and equations of perpendicular bisectors of \(A B\) and \(A C\) are given, then \(B\) and \(C\) are the images or reflections of \(A\) about the perpendicular bisectors of \(A B\) and \(A C\) (where \(M\) and \(N\) are the mid-points of \(A B\) and \(A C\) ).

Example 64: The base of a triangle passes through a fixed point \((f, g)\) and its sides are respectively bisected at right angles by the lines \(y+x=0\) and \(y-9 x=0\). Determine the locus of its vertex.

Answer: Let \(A \equiv(\alpha, \beta)\) the image of \(A(\alpha, \beta)\) about \(y+x=0\) is \(B\), then \(B \equiv(-\beta,-\alpha)\) and if image of \(A(\alpha, \beta)\) about \(y-9 x=0\) is \(C\left(x_2, y_2\right)\), then
\(
\begin{aligned}
& \frac{x_2-\alpha}{-9}=\frac{y_2-\beta}{1}=\frac{-2(\beta-9 \alpha)}{1+81} \\
\therefore \quad & x_2=\frac{9 \beta-40 \alpha}{41} \text { and } y_2=\frac{40 \beta+9 \alpha}{41}
\end{aligned}
\)
\(
\therefore \quad C \equiv\left(\frac{9 \beta-40 \alpha}{41}, \frac{40 \beta+9 \alpha}{41}\right)
\)

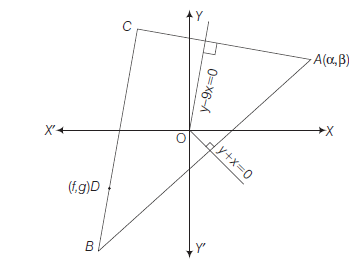
Hence, \(B, D, C\) are collinear, then
\(
\begin{aligned}
& \frac{1}{2}\left|\begin{array}{ccc}
-\beta & -\alpha & 1 \\
f & g & 1 \\
\frac{9 \beta-40 \alpha}{41} & \frac{40 \beta+9 \alpha}{41} & 1
\end{array}\right|=0 \\
\Rightarrow & 4\left(\alpha^2+\beta^2\right)+(4 g+5 f) \alpha+(4 f-5 g) \beta=0
\end{aligned}
\)
Hence, locus of vertex is
\(
4\left(x^2+y^2\right)+(4 g+5 f) x+(4 f-5 g) y=0
\)

Case II: The images or reflections of vertex \(A\) of a \(\triangle A B C\) about the angular bisectors of angles \(B\) and \(C\) lie on the side \(B C\). (By congruence) \(A_1\) and \(A_2\) are the images of \(A\) about the angle bisectors \(B E\) and \(C F\) respectively, where \(M\) and \(N\) are the mid-points of \(A A_1\) and \(A A_2\).

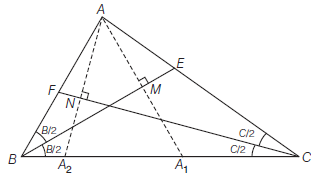
Example 65: Find the equations of the sides of the triangle having \((3,-1)\) as a vertex, \(x-4 y+10=0\) and \(6 x+10 y-59=0\) being the equations of an angle bisector and a median respectively drawn from different vertices.

Answer: Let \(B E\) be the angle bisector and \(C F\) be the median. Given equations of \(B E\) and \(C F\) are \(x-4 y+10=0\) and \(6 x+10 y-59=0\) respectively.
Since, image of \(A\) with respect to \(B E\) lie on \(B C\). If image of \(A\) is \(L(h, k)\).
then \(\quad \frac{h-3}{1}=\frac{k+1}{-4}=\frac{-2(3+4+10)}{1^2+(-4)^2}=-2\)
i.e. \(\quad h=1, k=7\)
\(\therefore \quad L \equiv(1,7)\)
\(\because F\) be the mid-point of \(A B\).

Let \(\quad F \equiv(\alpha, \beta)\)
then \(\quad B \equiv(2 \alpha-3,2 \beta+1)\)
\(\because B\) lie on \(B E\), then
\(
(2 \alpha-3)-4(2 \beta+1)+10=0
\)
i.e. \(2 \alpha-8 \beta+3=0 \dots(i)\)
and \(F\) lie on \(C F\), then
\(
6 \alpha+10 \beta-59=0 \dots(ii)
\)
Solving Eqs. (i) and (ii), we get
then
\(
\alpha=\frac{13}{2}, \beta=2
\)
\(F \equiv\left(\frac{13}{2}, 2\right)\)
and \(B=(10,5)\)
Equation of \(A B\) is
\(
\begin{array}{ll}
& y+1=\frac{2+1}{\frac{13}{2}-3}(x-3) \\
\Rightarrow & y+1=\frac{6}{7}(x-3) \\
\text { or } & 6 x-7 y-25=0
\end{array}
\)
Equation of \(B C\) is
\(
\begin{array}{ll}
& y-5=\frac{7-5}{1-10}(x-10) \\
\Rightarrow & y-5=-\frac{2}{9}(x-10) \\
\text { or } & 2 x+9 y-65=0
\end{array}
\)
\(\because C A\) is the family of lines of \(C B\) and \(C F\)
\(
\begin{aligned}
& \text { then }(2 x+9 y-65)+\lambda(6 x+10 y-59)=0 \dots(iii)\\
& \text { it pass through } A(3,-1) \\
& \text { then } \quad(6-9-65)+\lambda(18-10-59)=0 \\
& \therefore \quad \lambda=-\frac{4}{3}
\end{aligned}
\)
From Eq. (iii), we get equation of \(A C\) is
\(
18 x+13 y-41=0
\)

Case III: Optimization (Minimization or Maximization)

Minimization : Let \(A\) and \(B\) are two given points on the same side of \(a x+b y+c=0\). Suppose we want to determine a point \(P\) on \(a x+b y+c=0\) such that \(P A+P B\) is minimum. Then find the image of \(A\) or \(B\) about the line \(a x+b y+c=0\) (say \(A^{\prime}\) or \(B^{\prime}\) ) then join \(B^{\prime}\) with \(A\) or \(A^{\prime}\) with \(B\) wherever it intersects \(a x+b y+c=0\) is the required point.

\(
\therefore \quad P A+P B=P A+P B^{\prime}
\)
\(
\text { or } \quad P A+P B=P A^{\prime}+P B
\)

Important Point

• By triangle in equality Sum of two sides of a triangle \(>\) Third side i.e. \(|P A+P B|=\left|P A+P B^{\prime}\right|=\left|A B^{\prime}\right|\) (minimum value).

Example 66: Find a point \(R\) on the \(X\)-axis such that \(P R+R Q\) is the minimum, when \(P \equiv(1,1)\) and \(Q \equiv(3,2)\).

Answer: Since \(P\) and \(Q\) lie on the same side of \(X\)-axis.
The image of \(Q(3,2)\) about \(X\)-axis is \(Q^{\prime}(3,-2)\) then the equation of line \(P Q^{\prime}\) is
\(
\begin{aligned}
& y-1=\frac{-2-1}{3-1}(x-1) \\
\Rightarrow \quad & 3 x+2 y-5=0
\end{aligned}
\)

This line meets \(X\)-axis at \(R\left(\frac{5}{3}, 0\right)\) which is the required point.

Maximization : Let \(A\) and \(B\) are two given points on the same side of \(a x+b y+c=0\). Suppose we want to determine a point \(P\) on \(a x+b y+c=0\) such that \(|P A-P B|\) is maximum, then find the equation of line \(A B\) wherever it intersects \(a x+b y+c=0\) is the required point.

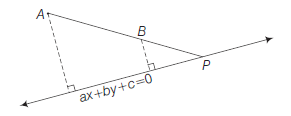
Important Point

• By triangle inequality Difference of two sides of a triangle \(<\) Third side i.e. \(\quad|P A-P B|=|A B|\) (maximum value)

Example 67: Find a point \(P\) on the line \(3 x+2 y+10=0\) such that \(|P A-P B|\) is maximum where \(A\) is \((4,2)\) and \(B\) is \((2,4)\).

Answer:

\(
\begin{array}{ll}
\text { Let, } & L(x, y)=3 x+2 y+10 \\
\therefore & L(4,2)=12+4+10=26 \\
\text { and } & L(2,4)=6+8+10=24
\end{array}
\)
\(\therefore A\) and \(B\) lie on the same side of the line
\(
3 x+2 y+10=0 \dots(i)
\)
Equation of line \(A B\) is
\(
\begin{aligned}
& y-2=\frac{4-2}{2-4}(x-4) \\
& \text { or } \quad x+y-6=0 \dots(ii)
\end{aligned}
\)
This line Eq. (ii) meets Eq. (i) at \(P \equiv(-22,28)\) which is the required point.

Alternate: Let \(\quad P\) be \(\left(x_1, y_1\right)\) and \(\angle A P B=\theta\)
then \(\quad \cos \theta=\frac{(P A)^2+(P B)^2-(A B)^2}{2 P A \cdot P B}\)

\(
\begin{array}{lr}
\text { since } & \cos \theta \leq 1 \\
\Rightarrow & \frac{(P A)^2+(P B)^2-(A B)^2}{2 P A \cdot P B} \leq 1
\end{array}
\)
\(
\begin{array}{ll}
\Rightarrow & (P A-P B)^2 \leq(A B)^2 \\
\Rightarrow & |P A-P B| \leq|A B| \\
\Rightarrow & |P A-P B| \leq 2 \sqrt{2}
\end{array}
\)
Maximum value of \(|P A-P B|\) is \(2 \sqrt{2}\) when, \(\theta=0\).
i.e. \(P\) lies on the line \(A B\) as well as on the given line.
\(\therefore\) Equation of \(A B\) is
\(
\begin{array}{rlrl}
& & y-2 =\frac{4-2}{2-4}(x-4) \\
\Rightarrow & y-2 =-x+4 \\
\Rightarrow & x+y =6 \dots(i)
\end{array}
\)
and given line
\(
3 x+2 y+10=0 \dots(ii)
\)
Solving Eqs. (i) and (ii), we get \(P(-22,28)\).

Reflection of Light

When a ray of light falls on a smooth polished surface (Mirror) separating two media, a part of it is reflected back into the first medium.

\(I P\) is the incident ray and \(P R\) is the reflected ray. A perpendicular drawn to the surface, at the point of incidence \(P\) is called the normal. Hence \(P N\) is the normal. The angle between the incident ray and the normal \((\angle I P N)\) is called the angle of incidence which is represented by \(\angle i\)
i.e. \(\angle I P N=\angle i=\) Angle of incidence and the angle between the reflected ray and the normal \((\angle I P R)\) is called the angle of reflection which is represented by \(\angle r\). i.e. \(\angle I P R=\angle r=\) Angle of reflection.

Laws of Reflection :

• The incident ray, normal and the reflected ray to a surface at the point of incidence all lie in the same plane.
• The angle of incidence \(=\) angle of reflection i.e.
  \(
  \angle i=\angle r
  \)

Example 68: A ray of light is sent along the line \(x-2 y-3=0\). Upon reaching the line \(3 x-2 y-5=0\), the ray is reflected from it. Find the equation of the line containing the reflected ray.

Answer: To get coordinates of point \(P\), we solve the given equation of lines together as
\(
x-2 y-3=0
\)
\(
\begin{aligned}
& 3 x-2 y-5=0 \\
& \therefore \quad x=1, y=-1 \\
&
\end{aligned}
\)
\(
\therefore \text { Coordinates of } P \text { are }(1,-1) \text {. }
\)

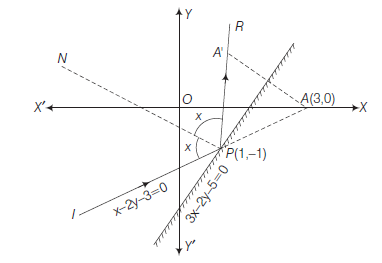
Let slope of reflected ray be \(m\).
Since, slope of line mirror is \(3 / 2\).
\(\therefore \quad\) Slope of \(P N=-2 / 3\) and
slope of \(P =1 / 2\), line \(P N\) is equally inclined to \(P\) and \(P R\), then
\(
\left(\frac{m-\left(-\frac{2}{3}\right)}{1+m\left(-\frac{2}{3}\right)}\right)=-\left(\frac{\frac{1}{2}-\left(-\frac{2}{3}\right)}{1+\frac{1}{2}\left(-\frac{2}{3}\right)}\right)
\)
\(
\begin{aligned}
\frac{3 m+2}{3-2 m} & =-\frac{7}{4} \\
12 m+8 & =-21+14 m \\
2 m & =29 \\
m & =\frac{29}{2}
\end{aligned}
\)
\(\therefore\) Equation of reflected ray \(y+1=\frac{29}{2}(x-1)\)
\(
\begin{array}{ll}
\Rightarrow & 2 y+2=29 x-29 \\
\Rightarrow & 29 x-2 y-31=0 .
\end{array}
\)

Alternate: (Image method)

Take A \((3,0)\) be any point on IP and if \(A^{\prime}(\alpha, \beta)\) be the image of \(A\) about the mirror line \(3 x-2 y-5=0\), then
\(
\frac{\alpha-3}{3}=\frac{\beta-0}{-2}=\frac{-2(9-0-5)}{9+4}
\)
\(
\begin{array}{lll}
\therefore & \alpha=\frac{15}{13} \text { and } \beta=\frac{16}{13} \\
\therefore & A^{\prime} \equiv\left(\frac{15}{13}, \frac{16}{13}\right) &
\end{array}
\)
\(\therefore\) Equation of \(A^{\prime} P\) is the equation of the reflected ray then its equation is,
\(
y+1=\frac{\left(\frac{16}{13}+1\right)}{\left(\frac{15}{13}-1\right)}(x-1)
\)
\(
y+1=\frac{29}{2}(x-1) \text { or } 29 x-2 y-31=0
\)

Example 69: A light beam, emanating from the point \((3,10)\) reflects from the straight line \(2 x+y-6=0\) and, then passes through the point \((7,2)\). Find the equations of the incident and reflected beams.

Answer: Let images of \(A\) and \(B\) about the line \(2 x+y-6=0\) are \(A^{\prime}(\alpha, \beta)\) and \(B^{\prime}(\gamma, \delta)\) respectively.
Then,
\(
\frac{\alpha-3}{2}=\frac{\beta-10}{1}=\frac{-2(6+10-6)}{2^2+1^2}
\)
\(
\begin{aligned}
& & =-4 \\
\therefore & \alpha & =-5, \beta=6 \\
\text { i.e. } & A^{\prime} \equiv(-5,6)
\end{aligned}
\)

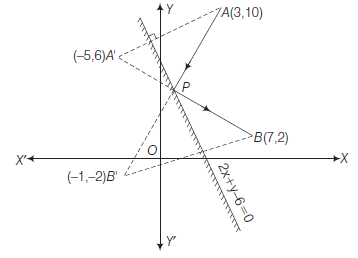
and \(\quad \frac{\gamma-7}{2}=\frac{\delta-2}{1}=\frac{-2(14+2-6)}{2^2+1^2}=-4\)
\(\therefore \quad \gamma=-1, \delta=-2\)
i.e. \(\quad B^{\prime} \equiv(-1,-2)\).
\(\therefore\) Equation of incident ray \(A B^{\prime}\) is
\(
y+2=\frac{10+2}{3+1}(x+1) \text { or } 3 x-y+1=0
\)
and equation of reflected ray \(A^{\prime} B\) is
\(
\begin{array}{ll}
& y-6=\frac{2-6}{7+5}(x+5) \\
\Rightarrow & y-6=-\frac{1}{3}(x+5) \\
\text { or } & x+3 y-13=0
\end{array}
\)

Refraction of Light

When a ray of light falls on the boundary separating the two transparent media, there is a change in direction of ray. This phenomenon is called refraction.

Laws of Refraction

• The incident ray, normal and the refracted ray to the surface separating the two transparent media all lie in the same plane.
• The ratio of sine of angle of incidence to the sine of the angle of refraction is constant for the two given media. The constant is called the refractive index of medium 2 with respect to medium 1.
  i.e. \({ }_1 \mu_2=\frac{\sin i}{\sin r}\)

Example 70: A ray of light is sent along the line \(x-6 y=8\). After refracting across the line \(x+y=1\) it enters the opposite side after turning by \(15^{\circ}\) away from the line \(x+y=1\). Find the equation of the line along which the refracted ray travels.

Answer: The point of intersection of \(x-6 y=8\) and \(x+y=1\) is \(A \equiv(2,-1)\).
Let the required ray have the slope \(=m\), then

\(
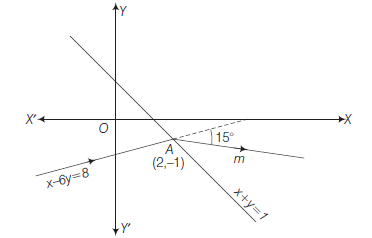
\tan 15^{\circ}=\left|\frac{m-\frac{1}{6}}{1+\frac{m}{6}}\right|
\)
\(
\begin{aligned}
& \Rightarrow \quad 2-\sqrt{3}= \pm\left(\frac{6 m-1}{m+6}\right) \\
& \text { then, } \quad \frac{6 m-1}{m+6}=2-\sqrt{3} \text { or } \sqrt{3}-2 \\
& \Rightarrow \quad m=\frac{70-37 \sqrt{3}}{13} \\
& \text { or } m=\frac{37 \sqrt{3}-70}{61} \\
&
\end{aligned}
\)
Let the angle between \(x+y=1\) and the line through \(A(2,-1)\) with the slope \(\frac{70-37 \sqrt{3}}{13}\) be \(\alpha\), then
\(
\tan \alpha=\left|\frac{\frac{70-37 \sqrt{3}}{13}-(-1)}{1-\left(\frac{70-37 \sqrt{3}}{13}\right)}\right|=\left|\frac{83-37 \sqrt{3}}{37 \sqrt{3}-57}\right|
\)
\(
=\frac{83-37 \sqrt{3}}{37 \sqrt{3}-57}
\)
and if angle between \(x+y=1\) and the line through \(A(2,-1)\) with the slope \(\frac{37 \sqrt{3}-70}{61}\) be \(\beta\), then
\(
\begin{aligned}
\tan \beta & =\left|\frac{\frac{37 \sqrt{3}-70}{61}-(-1)}{1-\left(\frac{37 \sqrt{3}-70}{61}\right)}\right|=\left|\frac{37 \sqrt{3}-9}{131-37 \sqrt{3}}\right| \\
& =\frac{37 \sqrt{3}-9}{131-37 \sqrt{3}}
\end{aligned}
\)
Here \(\tan \alpha>\tan \beta, \therefore \alpha>\beta\)
therefore the slope of the refracted ray \(=\frac{70-37 \sqrt{3}}{13}\)
\(\therefore\) The equation of the refracted ray is
\(
y+1=\frac{(70-37 \sqrt{3})}{13}(x-2)
\)
\(
\begin{array}{ll}
\Rightarrow & 13 y+13=(70-37 \sqrt{3}) x-140+74 \sqrt{3} \\
\text { or } & (70-37 \sqrt{3}) x-13 y-153+74 \sqrt{3}=0
\end{array}
\)

Conditions of Collinearity if Three given points are in Cyclic Order

Let the three given points
\(
A \equiv(f(a), g(a)), B \equiv(f(b), g(b))
\)
and \(C \equiv(f(c), g(c))\) lie on the line \(l x+m y+n=0\), where \(l, m\) and \(n\) are constants.
Then, \(l f(t)+m g(t)+n=0 \dots(i)\)
where, \(\quad t=a, b, c\)
i.e. \(a, b, c\) are the roots of the Eq. (i).
In this case Eq. (i) must be cubic in \(t\).
\(
A t^3+B t^2+C t+D=0 \text { (say) }
\)
then
\(
\begin{aligned}
a+b+c & =-\frac{B}{A}, a b+b c+c a=\frac{C}{A} \\
a b c & =-\frac{D}{A}
\end{aligned}
\)
which are the required conditions.

Example 71: If the points \(\left(\frac{a^3}{a-1}, \frac{a^2-3}{a-1}\right),\left(\frac{b^3}{b-1}, \frac{b^2-3}{b-1}\right)\) and \(\left(\frac{c^3}{c-1}, \frac{c^2-3}{c-1}\right)\) are collinear for three distinct values \(a, b, c\) and different from 1 , then show that \(a b c-(b c+c a+a b)+3(a+b+c)=0\).

Answer: Let the three given points lie on the line \(l x+m y+n=0, \quad\) where \(l, m\) and \(n\) are constants.
Then, \(l\left(\frac{t^3}{t-1}\right)+m\left(\frac{t^2-3}{t-1}\right)+n=0\)
\(
\Rightarrow \quad l t^3+m t^2+n t-(3 m+n)=0
\)
for \(t=a, b, c\)
i.e. \(a, b, c\) are the roots of
\(
l t^3+m t^2+n t-3 m-n=0
\)
then \(a+b+c=-\frac{m}{l}, a b+b c+c a=\frac{n}{l}\)
and \(a b c=\left(\frac{3 m+n}{l}\right)\)
Now, \(a b c-(b c+c a+a b)+3(a+b+c)\)
\(
=\left(\frac{3 m+n}{l}\right)-\frac{n}{l}-\frac{3 m}{l}=0
\)
Hence, \(a b c-(b c+c a+a b)+3(a+b+c)=0\)

Example 72: If \(t_1, t_2\) and \(t_3\) are distinct, the points \(\left(t_1, 2 a t_1+a t_1^3\right),\left(t_2, 2 a t_2+a t_2^3\right)\) and \(\left(t_3, 2 a t_3+a t_3^3\right)\) are collinear, then prove that \(t_1+t_2+t_3=0\).

Answer: Let the three given points lie on the line \(l x+m y+n=0\), where \(l, m\) and \(n\) are constants. Then,
\(
\begin{aligned}
l(t)+m\left(2 a t+a t^3\right)+n & =0 \\
\Rightarrow \quad(a m) t^3+(2 a m+l) t+n & =0 \dots(i)
\end{aligned}
\)
for \(t=t_1, t_2, t_3\)
i.e., \(t_1, t_2, t_3\) are the roots of Eq. (i), then
\(
t_1+t_2+t_3=0
\)

Homogeneous Equation in Two Variables

An equation of the form
\(
a_0 y^n+a_1 y^{n-1} x+a_2 y^{n-2} x^2+\ldots .+a_n x^n=0 \dots(i)
\)
in which the sum of the powers of \(x\) and \(y\) in every term is the same (here \(n\) ), is called a homogeneous equation (of degree \(n\) ).
We will prove that Eq. (i) represents \(n\) straight lines passing through the origin.
\(
a_0 y^n+a_1 y^{n-1} x+a_2 y^{n-2} x^2+\ldots .+a_n x^n=0
\)
Dividing each term by \(x^n\), we get
\(
a_0\left(\frac{y}{x}\right)^n+a_1\left(\frac{y}{x}\right)^{n-1}+a_2\left(\frac{y}{x}\right)^{n-2}+\ldots+a_n=0
\)
Above is an equation of \(n\)th degree in \(\frac{y}{x}\). Let the roots of this equation be \(m_1, m_2, m_3, \ldots, m_n\).
Then, the above equation will be identical with
\(
\begin{aligned}
a_0\left(\frac{y}{x}-m_1\right)\left(\frac{y}{x}-m_2\right)\left(\frac{y}{x}-m_3\right) \ldots\left(\frac{y}{x}-m_n\right) & =0 \\
\Rightarrow a_0\left(y-m_1 x\right)\left(y-m_2 x\right)\left(y-m_3 x\right) \ldots\left(y-m_n x\right) & =0
\end{aligned}
\)
Hence, Eq. (i) represents \(n\) straight lines
\(
\begin{aligned}
& y-m_1 x=0, y-m_2 x=0, \\
& y-m_3 x=0, \ldots, y-m_n x=0
\end{aligned}
\)
all of which clearly pass through the origin.

Example 73: Find the condition that the slope of one of the lines represented by \(a x^2+2 h x y+b y^2=0\) should be \(n\) times the slope of the other.

Answer: Let the lines represented by \(a x^2+2 h x y+b y^2=0\) are \(y=m_1 x\) and \(y=m_2 x\).
Therefore, \(\quad m_1+m_2=-\frac{2 h}{b} \dots(i)\)
and
\(
m_1 m_2=\frac{a}{b} \dots(ii)
\)
Given,
\(
m_2=n m_1
\)
\(
m_1=-\frac{2 h}{b(1+n)}
\)
From Eq. (i), \(\quad m_1+n m_1=-\frac{2 h}{b}\)
\(
m_1=-\frac{2 h}{b(1+n)} \dots(iii)
\)
\(
\begin{aligned}
& \text { and from Eq. (ii), } m_1\left(n m_1\right)=\frac{a}{b} \\
& \therefore \quad n m_1^2=\frac{a}{b} \\
& \Rightarrow \quad n\left\{\frac{-2 h}{b(1+n)}\right\}^2=\frac{a}{b} \text { [from Eq. (iii)] }
\end{aligned}
\)
\(
\begin{aligned}
\Rightarrow & \frac{4 n h^2}{b^2(1+n)^2} =\frac{a}{b} \\
\Rightarrow & 4 n h^2 =a b(1+n)^2 \dots(iv)
\end{aligned}
\)
This is the required condition.

Corollary: If slope of one line is double of the other, then put \(n=2\) in Eq. (iv), we have
\(
8 h^2=9 a b .
\)

Angle between the Pair of Lines \(a x^2+2 h x y+b y^2\)

Theorem: The angle \(\theta\) between the pair of lines represented by \(a x^2+2 h x y+b y^2=0\) is given by \(\theta=\tan ^{-1}\left\{\frac{2 \sqrt{\left(h^2-a b\right)}}{|a+b|}\right\}\).

Proof: Let \(y=m_1 x\) and \(y=m_2 x\) be the lines represented by
\(
a x^2+2 h x y+b y^2=0 .
\)

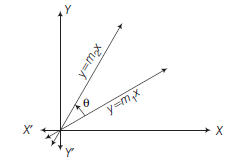
Then, \(\quad m_1+m_2=-\frac{2 h}{b}, m_1 m_2=\frac{a}{b}\)
Since, \(\theta\) be the angle between the lines
\(
y=m_1 x \text { and } y=m_2 x .
\)
Then, \(\tan \theta=\left|\frac{m_1-m_2}{1+m_1 m_2}\right|=\frac{\sqrt{\left(m_1+m_2\right)^2-4 m_1 m_2}}{\left|1+m_1 m_2\right|}\)
\(
\begin{aligned}
& =\frac{\sqrt{\left(\frac{-2 h}{b}\right)^2-4\left(\frac{a}{b}\right)}}{\left|1+\frac{a}{b}\right|}=\frac{2 \sqrt{\left(h^2-a b\right)}}{|a+b|} \\
\therefore \quad \theta & =\tan ^{-1}\left\{\frac{2 \sqrt{\left(h^2-a b\right)}}{|a+b|}\right\}
\end{aligned}
\)

Example 74: Find the angle between the lines
\(
\left(x^2+y^2\right) \sin ^2 \alpha=(x \cos \beta-y \sin \beta)^2 \text {. }
\)

Answer: Given equation is
\(
\begin{array}{r}
\left(x^2+y^2\right) \sin ^2 \alpha=(x \cos \beta-y \sin \beta)^2 \\
\Rightarrow \quad x^2\left(\sin ^2 \alpha-\cos ^2 \beta\right)+2 x y \sin \beta \cos \beta \\
+y^2\left(\sin ^2 \alpha-\sin ^2 \beta\right)=0 \dots(i)
\end{array}
\)
The homogeneous equation of second degree is
\(
a x^2+2 h x y+b y^2=0 \dots(ii)
\)
On comparing Eqs. (i) and (ii), we get
\(
\begin{aligned}
& a=\sin ^2 \alpha-\cos ^2 \beta, h=\sin \beta \cos \beta, \\
& b=\sin ^2 \alpha-\sin ^2 \beta
\end{aligned}
\)
Let the angle between the lines representing by Eq. (i) is \(\theta\).
\(
\therefore \tan \theta=2 \frac{\sqrt{h^2-a b}}{|a+b|}
\)
\(
=2 \frac{\sqrt{\sin ^2 \beta \cos ^2 \beta-\left(\sin ^2 \alpha-\cos ^2 \beta\right)\left(\sin ^2 \alpha-\sin ^2 \beta\right)}}{\left|\sin ^2 \alpha-\cos ^2 \beta+\sin ^2 \alpha-\sin ^2 \beta\right|}
\)
\(
\begin{aligned}
& =2 \frac{\sqrt{\sin ^2 \alpha\left(1-\sin ^2 \alpha\right)}}{|-\cos 2 \alpha|} \\
& =\frac{2 \sin \alpha \cos \alpha}{|-\cos 2 \alpha|}=\tan 2 \alpha \\
\therefore \quad \theta & =2 \alpha
\end{aligned}
\)

Bisectors of the Angle between the Lines Given by a Homogeneous Equation

Theorem: The joint equation of the bisectors of the angles between the lines represented by the equation
\(
a x^2+2 h x y+b y^2=0 \quad \text { is } \quad \frac{x^2-y^2}{a-b}=\frac{x y}{h} .
\)

Proof: Let the lines represented by \(a x^2+2 h x y+b y^2=0\) be \(y-m_1 x=0\) and \(y-m_2 x=0\), then
\(
m_1+m_2=-\frac{2 h}{b} \text { and } m_1 m_2=\frac{a}{b}
\)
Since, the bisectors of the angles between the lines are the locus of a point which is equidistant from the two given lines.

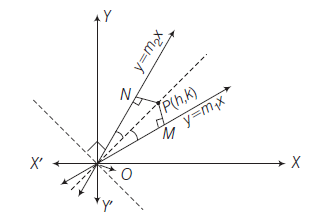
Let \(P(h, k)\) be a point on a bisector of the angle between the given lines. Then, \(P M=P N\)
\(
\begin{array}{ll}
\Rightarrow & \frac{\left|k-m_1 h\right|}{\sqrt{\left(1+m_1^2\right)}}=\frac{\left|k-m_2 h\right|}{\sqrt{\left(1+m_2^2\right)}} \\
\Rightarrow & \frac{\left(k-m_1 h\right)}{\sqrt{\left(1+m_1^2\right)}}= \pm \frac{\left(k-m_2 h\right)}{\sqrt{\left(1+m_2^2\right)}}
\end{array}
\)
Hence, the locus of a \(P(h, k)\) is
\(
\frac{\left(y-m_1 x\right)}{\sqrt{\left(1+m_1^2\right)}}= \pm \frac{\left(y-m_2 x\right)}{\sqrt{\left(1+m_2^2\right)}}
\)
\(\therefore\) The pair of bisectors is
\(
\left(\frac{\left(y-m_1 x\right)}{\sqrt{\left(1+m_1^2\right)}}+\frac{\left(y-m_2 x\right)}{\sqrt{\left(1+m_2^2\right)}}\right)\left(\frac{\left(y-m_1 x\right)}{\sqrt{\left(1+m_1^2\right)}}-\frac{\left(y-m_2 x\right)}{\sqrt{\left(1+m_2^2\right)}}\right)=0
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{\left(y-m_1 x\right)^2}{\left(1+m_1^2\right)}-\frac{\left(y-m_2 x\right)^2}{\left(1+m_2^2\right)}=0 \\
& \Rightarrow \quad\left(1+m_2^2\right)\left(y^2+m_1^2 x^2-2 m_1 x y\right) \\
& \quad-\left(1+m_1^2\right)\left(y^2+m_2^2 x^2-2 m_2 x y\right)=0
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow\left(m_2^2-m_1^2\right) y^2-\left(m_2^2-m_1^2\right) x^2 \\
& +2 x y\left(m_2-m_1\right)-2 m_1 m_2\left(m_2-m_1\right) x y=0 \\
& \Rightarrow \quad\left(m_2+m_1\right)\left(y^2-x^2\right)+2 x y-2 m_1 m_2 x y=0 \left[\because m_1-m_2 \neq 0\right]\\
&
\end{aligned}
\)
\(
\Rightarrow \quad\left(x^2-y^2\right)\left(-\frac{2 h}{b}\right)=2 x y\left(1-\frac{a}{b}\right) \left[\begin{array}{c}
\because m_1+m_2=-\frac{2 h}{b} \\
m_1 m_2=\frac{a}{b}
\end{array}\right]
\)
\(
\therefore \quad \frac{x^2-y^2}{a-b}=\frac{x y}{h} \quad[b \neq 0]
\)

Example 75: Find the equation of the bisectors of the angle between the lines represented by
\(
3 x^2-5 x y+4 y^2=0 .
\)

Answer: Given equation is
\(
3 x^2-5 x y+4 y^2=0 \dots(i)
\)
Comparing it with the equation
\(
\begin{array}{r}
a x^2+2 h x y+b y^2=0 \dots(ii) \\
\text { then } a=3, h=-\frac{5}{2}, b=4
\end{array}
\)
Hence, the equation of bisectors of the angle between the pair of the lines (i) is
\(
\begin{array}{rlrl}
& \frac{x^2-y^2}{3-4} & =\frac{x y}{-5 / 2} \\
\Rightarrow & \frac{x^2-y^2}{-1} & =\frac{2 x y}{-5} \\
& \therefore & 5 x^2-2 x y-5 y^2 & =0
\end{array}
\)

Example 76: Show that the line \(y=m x\) bisects the angle between the lines
\(
\begin{aligned}
a x^2-2 h x y+b y^2 & =0, \\
\text { if } \quad h\left(1-m^2\right)+m(a-b) & =0 .
\end{aligned}
\)

Answer: Equation of pair of bisectors of angles between lines
\(
\begin{aligned}
a x^2-2 h x y+b y^2 & =0 \text { is } \\
\frac{x^2-y^2}{a-b} & =\frac{x y}{-h} \\
\Rightarrow \quad-h\left(x^2-y^2\right) & =(a-b) x y \dots(i)
\end{aligned}
\)
But \(y=m x\) is one of these lines, then it will satisfy it. Substituting \(y=m x\) in Eq. (i),
\(
-h\left(x^2-m^2 x^2\right)=(a-b) x \cdot m x
\)
Dividing by \(x^2, h\left(1-m^2\right)+m(a-b)=0\)

Example 77: If pairs of straight lines \(x^2-2 p x y-y^2=0\) and \(x^2-2 q x y-y^2=0\) be such that each pair bisects the angle between the other pair, then prove that \(p q=-1\).

Answer: According to the question, the equation of the bisectors of the angle between the lines
\(
\begin{aligned}
& x^2-2 p x y-y^2=0 \dots(i)\\
& x^2-2 q x y-y^2=0 \dots(ii)
\end{aligned}
\)
\(\therefore\) The equation of bisectors of the angle between the lines (i) is
\(
\begin{aligned}
\frac{x^2-y^2}{1-(-1)} & =\frac{x y}{-p} \\
\Rightarrow \quad-p x^2-2 x y+p y^2 & =0 \dots(iii)
\end{aligned}
\)
Since, Eqs. (ii) and (iii) are identical, comparing Eqs. (ii) and (iii), we get
\(
\frac{1}{-p}=\frac{-2 q}{-2}=\frac{-1}{p} \Rightarrow p q=-1
\)

General Equation of Second Degree

The equation \(a x^2+2 h x y+b y^2+2 g x+2 f y+c=0\) is the general equation of second degree and represents a conics (pair of straight lines, circle, parabola, ellipse, hyperbola). It contains six constants \(a, b, c, f, g, h\).
\(
\begin{aligned}
& \text { i.e. } a=\text { coefficient of } x^2, b=\text { coefficient of } y^2, \\
& c=\text { constant term }, \quad g=\text { half the coefficient of } x, \\
& f=\text { half the coefficient of } y, \\
& h=\text { half the coefficient of } x y .
\end{aligned}
\)

Theorem: The necessary and sufficient condition for
\(
a x^2+2 h x y+b y^2+2 g x+2 f y+c=0
\)
to represent a pair of straight lines is that
\(
a b c+2 f g h-a f^2-b g^2-c h^2=0 \text { or }\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=0 .
\)

Proof: Necessary condition: Let the equation be
\(
a x^2+2 h x y+b y^2+2 g x+2 f y+c=0 \dots(i)
\)
represent a pair of lines. Assuming that these lines are not parallel, we suppose further that their point of intersection is \(\left(x_1, y_1\right)\). Shifting the origin at \(\left(x_1, y_1\right)\) without rotating the coordinate axes, we have the Eq. (i) transforms to
\(
\begin{aligned}
& a\left(X+x_1\right)^2+2 h\left(X+x_1\right)\left(Y+y_1\right)+b\left(Y+y_1\right)^2 \\
& +2 g\left(X+x_1\right)+2 f\left(Y+y_1\right)+c=0 \dots(ii)
\end{aligned}
\)
Now this Eq. (ii) represents a pair of lines through the new origin and consequently, it is homogeneous in \(X\) and \(Y\). Hence, the coefficients of \(X\) and \(Y\) and the constant term in Eq. (ii) must vanish separately.
i.e. coefficient of \(X=\) coefficient of \(Y=\) constant term \(=0\)
\(
\begin{aligned}
& \Rightarrow \quad a x_1+h y_1+g=0 \dots(iii)\\
& h x_1+b y_1+f=0 \dots(iv)\\
& \text { and } a x_1^2+2 h x_1 y_1+b y_1^2+2 g x_1+2 f y_1+c=0 \dots(v)\\
&
\end{aligned}
\)
Now, \(a x_1^2+2 h x_1 y_1+b y_1^2+2 g x_1+2 f y_1+c=0\)
\(
\begin{aligned}
& \Rightarrow \quad x_1\left(a x_1+h y_1+g\right)+y_1\left(h x_1+b y_1+f\right) \\
& \quad+\left(g x_1+f y_1+c\right)=0 \\
& \Rightarrow x_1 \cdot 0+y_1 \cdot 0+g x_1+f y_1+c=0 \text { [from Eqs. (iii) and (iv)] }
\end{aligned}
\)
\(
g x_1+f y_1+c=0 \dots(vi)
\)
On eliminating \(x_1, y_1\) from Eqs. (iii), (iv) and (vi), we get the determinant
\(
\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=0
\)
\(
\therefore a b c+2 f g h-a f^2-b g^2-c h^2=0,
\)
as the required condition.

Example 78: For what value of \(\lambda\) does the equation \(12 x^2-10 x y+2 y^2+11 x-5 y+\lambda=0\) represent a pair of straight lines? Find the angle between them.

Answer: Comparing the given equation with the equation
\(
a x^2+2 h x y+b y^2+2 g x+2 f y+c=0,
\)
we get \(a=12, h=-5, b=2, g=\frac{11}{2}, f=-\frac{5}{2}\) and \(c=\lambda\)
If the given equation represents a pair of straight lines, then
\(
a b c+2 f g h-a f^2-b g^2-c h^2=0
\)
\(
\begin{aligned}
\Rightarrow 12 \times 2 \times \lambda+2 \times\left(-\frac{5}{2}\right) \times \frac{11}{2} \times(-5) & -12 \times \frac{25}{4} \\
& -2 \times \frac{121}{4}-\lambda \times 25=0
\end{aligned}
\)
\(
\therefore \quad \lambda=2 \text {, also } h^2-a b=25-24=1>0
\)
\(\therefore\) The given equation will represent a pair of straight lines, if \(\lambda=2\).
To find the angle between the lines If \(\theta\) be the angle between the lines, then
\(
\begin{aligned}
\tan \theta & =\frac{2 \sqrt{h^2-a b}}{|a+b|} \\
& =\frac{2 \sqrt{25-24}}{|12+2|}=\frac{1}{7} \\
\therefore \quad \theta & =\tan ^{-1}\left(\frac{1}{7}\right)
\end{aligned}
\)

To Find the Point of Intersection of Lines Represented by
\(
\begin{aligned}
& a x^2+2 h x y+b y^2+2 g x \\
& +2 f y+c=0
\end{aligned}
\)

Let \(\phi(x, y) \equiv a x^2+2 h x y+b y^2+2 g x+2 f y+c=0\)
\(\therefore \quad \frac{\partial \phi}{\partial x}=2 a x+2 h y+2 g \quad\) [treating \(y\) as constant]
and \(\frac{\partial \phi}{\partial y}=2 h x+2 b y+2 f \quad\) [treating \(x\) as constant]
For point of intersection \(\frac{\partial \phi}{\partial x}=0\) and \(\frac{\partial \phi}{\partial y}=0\),
we obtain \(\quad a x+h y+g=0\) and \(h x+b y+f=0\)
Solving them \(\frac{x}{f h-b g}=\frac{y}{g h-a f}=\frac{1}{a b-h^2}\)
\(
(x, y)=\left(\frac{b g-f h}{h^2-a b}, \frac{a f-g h}{h^2-a b}\right)
\)

Working rule

In practice, therefore, the general equation of second degree \(\phi=0\), represents a pair of straight lines, we solve its partial derivatives \(\frac{\partial \phi}{\partial x}=0, \frac{\partial \phi}{\partial y}=0\) for their intersecting point \((x, y)=(\alpha, \beta)\).

Remembering Method (without use of partial derivatives)
Since,
\(
\Delta=\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|
\)
From the first two rows
\(
\begin{aligned}
& a \quad h \quad g \Rightarrow a x+h y+g=0 \\
& h \quad b \quad f \Rightarrow h x+b y+f=0 \text { and then solve. } \\
&
\end{aligned}
\)

Example 79: Find the point of intersection of lines represented by \(2 x^2-7 x y-4 y^2-x+22 y-10=0\).

Answer: Let \(\quad \phi \equiv 2 x^2-7 x y-4 y^2-x+22 y-10=0\)
\(
\begin{array}{llrl}
\therefore & \frac{\partial \phi}{\partial x} & \equiv 4 x-7 y-1=0 \\
\text { and } & \frac{\partial \phi}{\partial y} & \equiv-7 x-8 y+22=0
\end{array}
\)
then, the point of intersection is \((x, y)=(2,1)\).

Equation of the Lines Joining the Origin to the Points of Intersection of a Given Line and a Given Curve

Theorem: The combined equation of the straight lines joining the origin to the points of intersection of a second degree curve
\(
a x^2+2 h x y+b y^2+2 g x+2 f y+c=0
\)
and a straight line \(l x+m y+n=0\) is :
\(
\begin{aligned}
a x^2+2 h x y+b y^2+2 g x\left(\frac{l x+m y}{-n}\right)+2 f y\left(\frac{l x+m y}{-n}\right) & \\
+c\left(\frac{l x+m y}{-n}\right)^2 & =0
\end{aligned}
\)

Proof: The equation of the curve \((P A Q)\) is
\(
a x^2+2 h x y+b y^2+2 g x+2 f y+c=0 \dots(i)
\)
and the equation of the line \(P Q\) be
\(
l x+m y+n=0 \dots(ii)
\)

From the equation of the line Eq. (ii), find the value of ‘ 1 ‘ in terms of \(x\) and \(y\), i.e.
\(
\frac{l x+m y}{-n}=1 \dots(iii)
\)
Now, the Eq. (i) can be written as
\(
\begin{aligned}
& \text { or } a x^2+2 h x y+b y^2+(2 g x+2 f y)(1)+c(1)^2=0 \\
& \text { or } a x^2+2 h x y+b y^2+(2 g x+2 f y)\left(\frac{l x+m y}{-n}\right) +c\left(\frac{l x+m y}{-n}\right)^2=0 \dots(iv)
\end{aligned}
\)
\(
\text { [replacing } 1 \text { by } \frac{l x+m y}{-n} \text { from Eq. (iii)] }
\)
Hence, the Eq. (iv) is homogeneous equation of second degree. Above Eq. (iv) on simplification will be of the form \(A x^2+2 H x y+B y^2=0\) and will represent the required straight lines. If \(\theta\) be the angle between them, then
\(
\theta=\tan ^{-1}\left(\frac{2 \sqrt{\left(H^2-A B\right)}}{|A+B|}\right)
\)
Hence, the equation of pairs of straight lines passing through the origin and the points of intersection of a curve and a line is obtained by making the curve homogeneous with the help of the line.

Example 80: Prove that the angle between the lines joining the origin to the points of intersection of the straight line \(y=3 x+2\) with the curve
\(
x^2+2 x y+3 y^2+4 x+8 y-11=0 \text { is } \tan ^{-1}\left(\frac{2 \sqrt{2}}{3}\right)
\)

Answer: Equation of curve is \(x^2+2 x y+3 y^2+4 x+8 y-11=0 \dots(i)\)
and line \(\quad y=3 x+2 \Rightarrow \frac{y-3 x}{2}=1 \dots(ii)\)
Making Eq. (i) homogeneous with the help of Eq. (ii), then
\(
x^2+2 x y+3 y^2+4 x\left(\frac{y-3 x}{2}\right)+8 y\left(\frac{y-3 x}{2}\right)-11\left(\frac{y-3 x}{2}\right)^2=0
\)
\(
\begin{array}{lc}
\Rightarrow & x^2+2 x y+3 y^2+2 x y-6 x^2+4 y^2-12 x y \\
& -\frac{11}{4}(y-3 x)^2=0 \\
\Rightarrow & -5 x^2-8 x y+7 y^2-\frac{11}{4}\left(y^2-6 x y+9 x^2\right)=0 \\
\Rightarrow & -20 x^2-32 x y+28 y^2-11 y^2+66 x y-99 x^2=0 \\
\Rightarrow & 119 x^2-34 x y-17 y^2=0 \\
\Rightarrow & 7 x^2-2 x y-y^2=0 \dots(iii)
\end{array}
\)
This is the equation of lines joining the origin to the points of intersection of Eqs. (i) and (ii).
Comparing Eq. (iii) with \(a x^2+2 h x y+b y^2=0\)
\(
a=7, h=-1, b=-1
\)
If \(\theta\) is the acute angle between pair of lines of Eq. (iii), then
\(
\begin{aligned}
\tan \theta & =\frac{2 \sqrt{h^2-a b}}{|a+b|}=\frac{2 \sqrt{(1+7)}}{|7-1|}=\frac{2 \sqrt{8}}{6}=\frac{4 \sqrt{2}}{6}=\frac{2 \sqrt{2}}{3} \\
\therefore \quad \theta & =\tan ^{-1}\left(\frac{2 \sqrt{2}}{3}\right)
\end{aligned}
\)