10.4 General Equation of a Line

In earlier classes, we have studied general equation of first degree in two variables, \(\mathrm{Ax}+\mathrm{B} y+\mathrm{C}=0\), where \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\) are real constants such that \(\mathrm{A}\) and \(\mathrm{B}\) are not zero simultaneously. Graph of the equation \(\mathrm{A} x+\mathrm{B} y+\mathrm{C}=0\) is always a straight line. Therefore, any equation of the form \(\mathrm{Ax}+\mathrm{B} y+\mathrm{C}=0\), where \(\mathrm{A}\) and \(\mathrm{B}\) are not zero simultaneously is called general linear equation or general equation of a line.

Different forms of \(\mathrm{Ax}+\mathrm{B} y+C=0\) The general equation of a line can be reduced into various forms of the equation of a line, by the following procedures:

Case-I: Slope-intercept form 

If \(\mathrm{B} \neq 0\), then \(\mathrm{Ax}+\mathrm{B} y+\mathrm{C}=0\) can be written as
\(
y=-\frac{\mathrm{A}}{\mathrm{B}} x-\frac{\mathrm{C}}{\mathrm{B}} \text { (Assuming } B \neq 0 \text { ) } \dots(1)
\)
Comparing it with \(y=m x+c\)
we get slope \((m)=-\frac{A}{B}=-\frac{\text { coefficient of } x}{\text { coefficient of } y}\)
and \(\quad y\) intercept \((c)=-\frac{C}{B}=-\frac{\text { constant term }}{\text { coefficient of } y}\)
We know that Equation (1) is the slope-intercept form of the equation of a line whose slope is \(-\frac{\mathrm{A}}{\mathrm{B}}\), and \(y\)-intercept is \(-\frac{\mathrm{C}}{\mathrm{B}}\).
If \(\mathrm{B}=0\), then \(x=-\frac{\mathrm{C}}{\mathrm{A}}\), which is a vertical line whose slope is undefined and \(x\)-intercept is \(-\frac{\mathrm{C}}{\mathrm{A}}\).

Corollary 1 : Find angle between the lines \(A_1 x+B_1 y+C_1=0\) and \(A_2 x+B_2 y+C_2=0\).
Slope of the line
\(
A_1 x+B_1 y+C_1=0 \text { is }-\frac{A_1}{B_1}=m_1 \text { (say) }
\)
and slope of the line
\(
A_2 x+B_2 y+C_2=0 \text { is }-\frac{A_2}{B_2}=m_2 \text { (say) }
\)
If \(\theta\) is the angle between the two lines, then
\(
\begin{aligned}
\tan \theta & =\left|\frac{m_1-m_2}{1+m_1 m_2}\right|=\left\lvert\, \frac{\left.\left(-\frac{A_1}{B_1}\right)-\left(-\frac{A_2}{B_2}\right) \right\rvert\,}{\left.1+\left(-\frac{A_1}{B_1}\right)\left(-\frac{A_2}{B_2}\right) \right\rvert\,}\right. \\
& =\left|\frac{A_1 B_2-A_2 B_1}{A_1 A_2+B_1 B_2}\right| \\
\therefore \quad \theta & =\tan ^{-1}\left|\frac{A_1 B_2-A_2 B_1}{A_1 A_2+B_1 B_2}\right|
\end{aligned}
\)

Corollary 2 : Find the condition of (i) parallelism (ii) perpendicularity of the lines
\(
\quad \begin{array}{l}
A_1 x+B_1 y+C_1=0 \\
A_2 x+B_2 y+C_2=0
\end{array}
\)
(i) If the two lines are parallel, \(\theta=0^{\circ}\)
\(
\begin{array}{ll}
\therefore & \tan \theta=\tan 0^{\circ}=0 \\
\Rightarrow & \left|\frac{A_1 B_2-A_2 B_1 \mid}{A_1 A_2+B_1 B_2}\right|=0 \\
\Rightarrow & A_1 B_2-A_2 B_1=0
\end{array}
\)
\(
\frac{A_1}{A_2}=\frac{B_1}{B_2} \quad \text { (Remember) }
\)
which is required condition of parallelism.
(ii) If the two lines are perpendicular, \(\theta=90^{\circ}\)
\(
\begin{array}{ll}
\therefore & \tan \theta=\tan 90^{\circ}=\infty \\
\Rightarrow & \left|\frac{A_1 B_2-A_2 B_1}{A_1 A_2+B_1 B_2}\right|=\infty
\end{array}
\)
\(
\Rightarrow \quad A_1 A_2+B_1 B_2=0 \text { (Remember) }
\)
which is required condition of perpendicularity.

Note: If two lines are coincident, then
\(
\frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2} \text { (Remember) }
\)

Example 1: Reduce \(x+\sqrt{3} y+4=0\) to the slope-intercept form and find its slope and \(y\)-intercept.

Answer: Given equation is \(x+\sqrt{3} y+4=0\)
\(
\begin{aligned}
\Rightarrow & & \sqrt{3} y & =-x-4 \\
\Rightarrow & & y & =\left(-\frac{1}{\sqrt{3}}\right) x+\left(-\frac{4}{\sqrt{3}}\right)
\end{aligned}
\)
which is in the slope-intercept form \(y=m x+c\)
Where slope \((m)=-\frac{1}{\sqrt{3}}\) and \(y\)-intercept \((c)=-\frac{4}{\sqrt{3}}\)

Case-II: Intercept form 

Given equation is \(A x+B y+C=0\)
\(
\begin{aligned}
A x+B y & =-C \\
\frac{A}{-C} x+\frac{B}{-C} y & =1 \quad(\text { Assuming } C \neq 0)
\end{aligned}
\)
\(
\left.\frac{x}{(-C / A)}+\frac{y}{(-C / B)}=1 \text { (Assuming } A \neq 0, B \neq 0\right) \dots(2)
\)
Comparing with \(\frac{x}{a}+\frac{y}{b}=1\)
we get, \(x\)-intercept \((a)=-\frac{C}{A}=-\frac{\text { constant term }}{\text { coefficient of } x}\)
and \(\quad y\)-intercept \((b)=-\frac{C}{B}=-\frac{\text { constant term }}{\text { coefficient of } y}\)

Example 2: Reduce \(x+\sqrt{3} y+4=0\) to the Intercept form and find its intercepts on the axes.

Answer: Given equation is
\(
\begin{aligned}
x+\sqrt{3} y+4 & =0 \\
x+\sqrt{3} y & =-4 \\
\frac{x}{-4}+\frac{\sqrt{3} y}{-4} & =1 \\
\frac{x}{-4}+\frac{y}{-4 / \sqrt{3}} & =1
\end{aligned}
\)
which is in the intercept form \(\frac{x}{a}+\frac{y}{b}=1\) where \(x\)-intercept \((a)=-4\) and \(y\)-intercept \((b)=-\frac{4}{\sqrt{3}}\)

Case-III: Normal Form

Let \(x \cos \omega+y \sin \omega=p\) be the normal form of the line represented by the equation \(\mathrm{A} x+\mathrm{B} y+\mathrm{C}=0\) or \(\mathrm{A} x+\mathrm{B} y=-\mathrm{C}\). Thus, both the equations are same and therefore,
\(
\frac{A}{\cos \omega}=\frac{B}{\sin \omega}=-\frac{C}{p}
\)
which gives \(\cos \omega=-\frac{\mathrm{A} p}{\mathrm{C}} \text { and } \sin \omega=-\frac{\mathrm{B} p}{\mathrm{C}}\)
Now
\(
\sin ^2 \omega+\cos ^2 \omega=\left(-\frac{\mathrm{A} p}{\mathrm{C}}\right)^2+\left(-\frac{\mathrm{B} p}{\mathrm{C}}\right)^2=1
\)
or
\(
p^2=\frac{\mathrm{C}^2}{\mathrm{~A}^2+\mathrm{B}^2} \quad \text { or } \quad p= \pm \frac{\mathrm{C}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}
\)
Therefore
\(
\cos \omega= \pm \frac{A}{\sqrt{A^2+B^2}} \text { and } \sin \omega= \pm \frac{B}{\sqrt{A^2+B^2}}
\)
Thus, the normal form of the equation \(\mathrm{Ax}+\mathrm{B} y+\mathrm{C}=0\) is
\(
x \cos \omega+y \sin \omega=p,
\)
where \(\cos \omega= \pm \frac{\mathrm{A}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}, \sin \omega= \pm \frac{\mathrm{B}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}\) and \(p= \pm \frac{\mathrm{C}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}\).
Proper choice of signs is made so that \(p\) should be positive.

Example 3: Reduce \(x+\sqrt{3} y+4=0\) to the Normal form and find the values of \(p\) and \(\alpha\).

Answer: Given equation is \(x+\sqrt{3} y+4=0\)
\(
\begin{aligned}
\Rightarrow & & x+\sqrt{3} y & =-4 \\
\Rightarrow & & -x-\sqrt{3} y & =4 \quad \text { (RHS made positive) }
\end{aligned}
\)
Dividing both sides by \(\sqrt{(-1)^2+(-\sqrt{3})^2}=2\), we get
\(
\left(-\frac{1}{2}\right) x+\left(-\frac{\sqrt{3}}{2}\right) y=2
\)
Which is the normal form \(x \cos \alpha+y \sin \alpha=p\).
where, \(\quad \cos \alpha=-\frac{1}{2}=-\cos 60^{\circ}=\cos \left(180^{\circ}-60^{\circ}\right)\)
\(
\begin{array}{l}
\text { or } \cos \left(180^{\circ}+60^{\circ}\right) \\
\therefore \alpha=120^{\circ} \text { or } 240^{\circ} \\
\text { and } \sin \alpha=-\frac{\sqrt{3}}{2}=-\sin 60^{\circ}=\sin \left(180^{\circ}+60^{\circ}\right) \\
\text { or } \sin \left(360^{\circ}-60^{\circ}\right) \\
\therefore \alpha=240^{\circ} \text { or } 300^{\circ} \\
\text { Hence, } \alpha=240^{\circ}, p=2
\end{array}
\)
\(\therefore\) Required normal form is
\(
x \cos 240^{\circ}+y \sin 240^{\circ}=2
\)

Example 4: Equation of a line is \(3 x-4 y+10=0\). Find its (i) slope, (ii) \(x\) – and \(y\)-intercepts.

Answer: (i) Given equation \(3 x-4 y+10=0\) can be written as
\(
y=\frac{3}{4} x+\frac{5}{2} \dots(1)
\)
Comparing (1) with \(y=m x+c\), we have slope of the given line as \(m=\frac{3}{4}\).
(ii) Equation \(3 x-4 y+10=0\) can be written as
\(3 x-4 y=-10\) or \(\frac{x}{-\frac{10}{3}}+\frac{y}{\frac{5}{2}}=1 \dots(2)\)
Comparing (2) with \(\frac{x}{a}+\frac{y}{b}=1\), we have \(x\)-intercept as \(a=-\frac{10}{3}\) and \(y\)-intercept as \(b=\frac{5}{2}\).

Example 5: Reduce the equation \(\sqrt{3} x+y-8=0\) into normal form. Find the values of \(p\) and \(\omega\).

Answer: Given equation is
\(
\sqrt{3} x+y-8=0 \dots(1)
\)
Dividing (1) by \(\sqrt{(\sqrt{3})^2+(1)^2}=2\), we get
\(
\frac{\sqrt{3}}{2} x+\frac{1}{2} y=4 \text { or } \cos 30^{\circ} x+\sin 30^{\circ} y=4 \dots(2)
\)
Comparing (2) with \(x \cos \omega+y \sin \omega=p\), we get \(p=4\) and \(\omega=30^{\circ}\).

Example 6: Find the angle between the lines \(y-\sqrt{3} x-5=0\) and \(\sqrt{3} y-x+6=0\).

Answer: Given lines are
\(
y-\sqrt{3} x-5=0 \text { or } y=\sqrt{3} x+5 \dots(1)
\)
and \(\sqrt{3} y-x+6=0\) or \(y=\frac{1}{\sqrt{3}} x-2 \sqrt{3} \dots(2)\)
Slope of line (1) is \(m_1=\sqrt{3}\) and slope of line (2) is \(m_2=\frac{1}{\sqrt{3}}\).
The acute angle (say) \(\theta\) between two lines is given by
\(
\tan \theta=\left|\frac{m_2-m_1}{1+m_1 m_2}\right| \dots(3)
\)
Putting the values of \(m_1\) and \(m_2\) in (3), we get
\(
\tan \theta=\left|\frac{\frac{1}{\sqrt{3}}-\sqrt{3}}{1+\sqrt{3} \times \frac{1}{\sqrt{3}}}\right|=\left|\frac{1-3}{2 \sqrt{3}}\right|=\frac{1}{\sqrt{3}}
\)
which gives \(\theta=30^{\circ}\). Hence, angle between two lines is either \(30^{\circ}\) or \(180^{\circ}-30^{\circ}=150^{\circ}\).

Example 7: Show that two lines \(a_1 x+b_1 y+c_1=0\) and \(a_2 x+b_2 y+c_2=0\), where \(b_1, b_2 \neq 0\) are: (i) Parallel if \(\frac{a_1}{b_1}=\frac{a_2}{b_2}\), and (ii) Perpendicular if \(a_1 a_2+b_1 b_2=0\).

Answer: Given lines can be written as
\(
\begin{array}{l}
y=-\frac{a_1}{b_1} x-\frac{c_1}{b_1} \dots(1) \\
\text { and } y=-\frac{a_2}{b_2} x-\frac{c_2}{b_2} \dots(2)
\end{array}
\)
Slopes of the lines (1) and (2) are \(m_1=-\frac{a_1}{b_1}\) and \(m_2=-\frac{a_2}{b_2}\), respectively. Now
(i) Lines are parallel, if \(m_1=m_2\), which gives
\(
-\frac{a_1}{b_1}=-\frac{a_2}{b_2} \text { or } \frac{a_1}{b_1}=\frac{a_2}{b_2} .
\)
(ii) Lines are perpendicular, if \(m_1 \cdot m_2=-1\), which gives
\(
\frac{a_1}{b_1} \cdot \frac{a_2}{b_2}=-1 \text { or } a_1 a_2+b_1 b_2=0
\)

Example 8: Find the equation of a line perpendicular to the line \(x-2 y+3=0\) and passing through the point \((1,-2)\).

Answer: Given line \(x-2 y+3=0\) can be written as
\(
y=\frac{1}{2} x+\frac{3}{2} \dots(1)
\)
Slope of the line (1) is \(m_1=\frac{1}{2}\). Therefore, slope of the line perpendicular to line (1) is
\(
m_2=-\frac{1}{m_1}=-2
\)
Equation of the line with slope -2 and passing through the point \((1,-2)\) is
\(
y-(-2)=-2(x-1) \text { or } y=-2 x \text {, }
\)
which is the required equation.

Example 9: Find the measure of the angle of intersection of the lines whose equations are \(3 x+4 y+7=0\) and \(4 x-3 y+5=0\).

Answer: Given lines are \(3 x+4 y+7=0,4 x-3 y+5=0\). Comparing
the given lines with \(A_1 x+B_1 y+C_1=0, A_2 x+B_2 y+C_2=0\)
respectively, we get
\(
\begin{array}{c}
A_1=3, B_1=4 \text { and } A_2=4, B_2=-3 \\
\because \quad A_1 A_2+B_1 B_2=3 \times 4+4(-3)=0
\end{array}
\)
Hence, the given lines are perpendicular.

Example 10: Find the angle between the lines
\(
\begin{array}{l}
\left(a^2-a b\right) y=\left(a b+b^2\right) x+b^3 \\
\text { and }\left(a b+a^2\right) y=\left(a b-b^2\right) x+a^3 \\
\text { where } a>b>0 \text {. } \\
\end{array}
\)

Answer: The given equations of lines can be written as
\(
\begin{aligned}
\left(a b+b^2\right) x-\left(a^2-a b\right) y+b^3 & =0 \dots(i) \\
\text { and } \quad\left(a b-b^2\right) x-\left(a b+a^2\right) y+a^3 & =0 \dots(ii)
\end{aligned}
\)
Comparing the given lines (i) and (ii) with the lines
\(
A_1 x+B_1 y+C_1=0 \text { and } A_2 x+B_2 y+C_2=0
\)
respectively, we get
\(
\begin{aligned}
A_1 & =a b+b^2, B_1=-\left(a^2-a b\right) \\
\text { and } \quad A_2 & =a b-b^2, B_2=-\left(a b+a^2\right)
\end{aligned}
\)
Let \(\theta\) be the acute angle between the lines, then
\(
\tan \theta=\left|\frac{A_1 B_2-A_2 B_1}{A_1 A_2+B_1 B_2}\right|
\)
\(
\begin{aligned}
\tan \theta & =\left|\frac{\left(a b+b^2\right) \times\left(-\left(a b+a^2\right)\right)-\left(a b-b^2\right) \times\left(-\left(a^2-a b\right)\right)}{\left(a b+b^2\right)\left(a b-b^2\right)+\left(a^2-a b\right)\left(a b+a^2\right)}\right| \\
& =\left|\frac{-\left\{a^2 b^2+a^3 b+a b^3+a^2 b^2-a^3 b+a^2 b^2+a^2 b^2-b^3 a\right\}}{\left(a^2 b^2-b^4+a^4-a^2 b^2\right)}\right| \\
& =\left|\frac{-4 a^2 b^2}{a^4-b^4}\right|=\frac{4 a^2 b^2}{a^4-b^4} \\
\therefore \theta & =\tan ^{-1}\left(\frac{4 a^2 b^2}{a^4-b^4}\right)
\end{aligned}
\)

Example 11: Two equal sides of an isosceles triangle are given by the equations \(7 x-y+3=0\) and \(x+y-3=0\) and its third side passes through the point \((1,-10)\). Determine the equation of the third side.

Answer: Given equations
\(
\begin{array}{r}
7 x-y+3=0 \dots(i)\\
x+y-3=0 \dots(ii)
\end{array}
\)
represents two equal sides \(A B\) and \(A C\) of an isosceles
triangle \(A B C\). Since its third side passes through \(D(1,-10)\) then its equation is
\(
y+10=m(x-1) \dots(iii)
\)
\(
\because \quad A B=A C
\)
Let \(\angle A B C=\angle A C B=\theta\)
then \(\quad \angle A C E=\pi-\theta\)

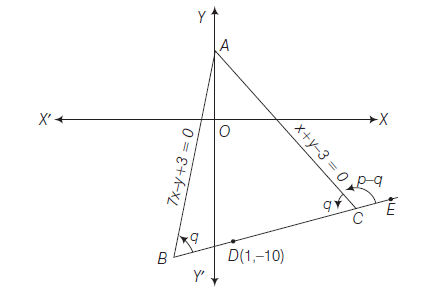
From Eqs. (i) and (ii), slopes of \(A B\) and \(A C\) are
\(
m_1=7 \text { and } m_2=-1
\)
respectively.
\(
\therefore \quad \tan \theta=\frac{7-m}{1+7 m}
\)
and \(\tan (\pi-\theta)=\frac{-1-m}{1+(-1) m}=-\left(\frac{1+m}{1-m}\right)\)
\(\Rightarrow \quad-\tan \theta=-\left(\frac{1+m}{1-m}\right) \Rightarrow \tan \theta=\left(\frac{1+m}{1-m}\right)\)
\(\therefore \quad \frac{7-m}{1+7 m}=\frac{1+m}{1-m}\)
\(\Rightarrow \quad(7-m)(1-m)=(1+7 m)(1+m)\)
\(\Rightarrow \quad 6 m^2+16 m-6=0\)
or \(\quad 3 m^2+8 m-3=0\) or \((3 m-1)(m+3)=0\)
\(\Rightarrow \quad m=\frac{1}{3},-3\)
Hence from Eq. (iii), the third side \(B C\) has two equations
\(
y+10=\frac{1}{3}(x-1) \text { and } y+10=-3(x-1)
\)
or \(\quad x-3 y-31=0\) and \(3 x+y+7=0\)