10.1 Introduction

The great philospher and mathematician of France Rane Descartes (1596-1650) published a book ‘La Geometric’ in 1637. Descartes gave a new idea i.e. each point in a plane is expressed by an ordered pair of algebraic real numbers like \((x, y),(r, \theta)\) etc., called coordinates of the point.
The point \((x, y)\) is called cartesian coordinates and \((r, \theta)\) is called polar coordinates of the point. Then represents different forms of equations which are developed for all types of straight lines and curves.

Thus the Coordinate Geometry (or Analytical Geometry) is that branch of mathematics in which geometrical problems are solved with the help of Algebra.

Coordinate Axes
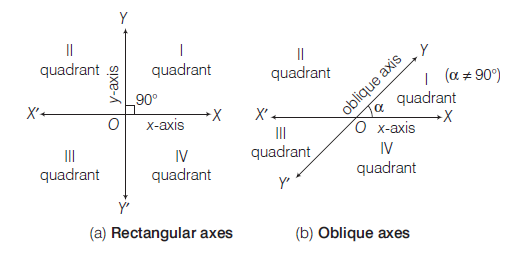
The position of a point in a plane is determined with reference to two intersecting straight lines called the coordinate axes and their point of intersection is called the origin of coordinates. If these two axes of reference (generally we call them \(x\) and \(y\) axes) cut each other at right angle, they are called rectangular axes otherwise they are called oblique axes. The axes divide the coordinate plane in four quadrants.

Rectangular Cartesian Coordinates of a Point

Let \(X^{\prime} O X\) and \(Y^{\prime} O Y\) be two perpendicular axes in the plane of paper intersecting at \(O\). Let \(P\) be any point in the plane of the paper. Draw PM perpendicular to \(O X\). Then the lengths \(O M\) and \(P M\) are called the rectangular cartesian coordinates or briefly the coordinates of \(P\).

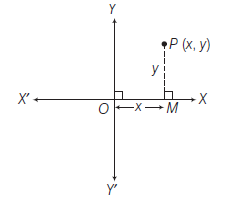
Let \(\quad O M=x\) and \(M P=y\)
Then, the position of the point \(P\) in the plane with respect to the coordinate axes is represented by the ordered pair \((x, y)\). The ordered pair \((x, y)\) is called the coordinates of point \(P\).
i.e. \(\quad O M=x\)-coordinate or abscissa of the point \(P\)
and \(\quad M P=y\)-coordinate or ordinate of the point \(P\).

Points to remember

• The ordinate of every point on \(X\)-axis is 0 .
• The abscissa of every point on \(Y\)-axis is 0 .
• The abscissa and ordinate of the origin \(O(0,0)\) are both zero.
• The abscissa and ordinate of a point are at perpendicular distance from \(Y\)-axis and \(X\)-axis respectively.

Polar Coordinates of a Point

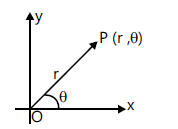
Let \(O X\) be any fixed line, known as initial line, and \(O\) be the origin. If the distance of any point \(P\) from the origin \(O\) is ‘ \(r\) ‘ and \(\angle X O P=\theta\), then \((r, \theta)\) are known as polar co-ordinates of point \(P\). If \((x, y)\) are the Cartesian co-ordinates of a point \(P\), then
\(x=r \cos \theta ; y=r \sin \theta\) and
\(|r|=\sqrt{x^2+y^2}, \theta=\tan ^{-1}\left(\frac{y}{x}\right), \theta \in(-\pi, \pi)\)

As an example: If the Cartesian co-ordinates of any point are \((\sqrt{3}, 1)\), find the polar co-ordinates. (JEE Main)

Answer: Polar co-ordinates of any point are \((r, \theta)\), where \(r=\sqrt{x^2+y^2}\) and \(\theta=\tan ^{-1}\left(\frac{y}{x}\right)\). \(x=\sqrt{3} ; y=1\)
Let their polar co-ordinates be \((r, \theta) \Rightarrow x=r \cos \theta ; y=r \sin \theta\)
\(
\begin{array}{ll}
\text { So } r \Rightarrow \sqrt{x^2+y^2} & r=\sqrt{3+1} \\
\theta \Rightarrow \tan ^{-1}\left(\frac{y}{x}\right)=2 & \theta \Rightarrow \tan ^{-1}\left(\frac{1}{\sqrt{3}}\right)=\frac{\pi}{6} \\
\therefore(r, \theta)=\left(2, \frac{\pi}{6}\right) . &
\end{array}
\)

Points to remember

• \(r\) may be positive or negative according as \(\theta\) is measured in anticlockwise or clockwise direction. \(\theta\) lies between \(-\pi\) to \(\pi\) i.e. \(-\pi<\theta \leq \pi\). If it is greater than \(\pi\), then we subtract \(2 \pi\) from it and if it is less than \(-\pi\), then we add \(2 \pi\), to it. It is also known as principal value of \(P\).
• Always taken \(\theta\) in radian.

Example 1: Draw the polar coordinates \(\left(2, \frac{\pi}{3}\right),\left(-2, \frac{\pi}{3}\right),\left(-2,-\frac{\pi}{3}\right)\) and \(\left(2,-\frac{\pi}{3}\right)\) on the plane.

Answer: 

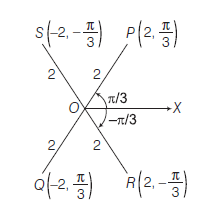
Example 2: Draw the polar coordinate \(\left(3, \frac{5 \pi}{4}\right)\) on the plane.

Answer: Here, \(\quad \theta=\frac{5 \pi}{4}>\pi\)

\(
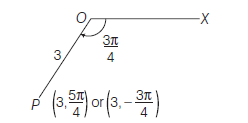
\begin{array}{l}
\text { then, } \quad \theta-2 \pi=\frac{5 \pi}{4}-2 \pi=-\frac{3 \pi}{4} \\
\therefore\left(3, \frac{5 \pi}{4}\right) \text { is same }\left(3,-\frac{3 \pi}{4}\right)
\end{array}
\)

Relation between the Polar and Cartesian Coordinates

Let \(P(x, y)\) be the cartesian coordinates with respect to axes \(O X\) and \(O Y\) and \((r, \theta)\) be its polar coordinates with respect to pole \(O\) and initial line \(O X\).

It is clear from figure
\(
\begin{array}{l}
O M=x=r \cos \theta \dots(i)\\
M P=y=r \sin \theta \dots(ii)\\
\end{array}
\)

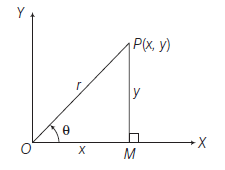
Squaring and adding Eqs. (i) and (ii), we get
\(
x^2+y^2=r^2 \quad \text { or } r=\sqrt{\left(x^2+y^2\right)}
\)
Dividing Eqs. (ii) by (i), then
i.e.
\(
\tan \theta=\left(\frac{y}{x}\right) \text { or } \theta=\tan ^{-1}\left(\frac{y}{x}\right)
\)
\((r \cos \theta, r \sin \theta) \Rightarrow(x, y) \dots(iii)\)
and \(\left(\sqrt{\left(x^2+y^2\right)}, \tan ^{-1}\left(\frac{y}{x}\right)\right) \Rightarrow(r, \theta) \dots(iv)\)
If \(r\) and \(\theta\) are known then we can find \((x, y)\) from Eq. (iii) and if \(x\) and \(y\) are known then we can find \((r, \theta)\) from Eq. (iv).
\(
\begin{array}{ll}
\because & \theta=\tan ^{-1}\left(\frac{y}{x}\right) \\
\text { If } & \alpha=\tan ^{-1}\left|\frac{y}{x}\right|
\end{array}
\)
Then, values of \(\theta\) in four quadrants.

\(
\begin{array}{ccccc}
\hline \text { Quadrant } & \text { I } & \text { II } & \text { III } & \text { IV } \\
\hline \theta & \alpha & \pi-\alpha & -\pi+\alpha & -\alpha \\
\hline
\end{array}
\)

Example 3: Find the cartesian coordinates of the points whose polar coordinates are
(i) \(\left(5, \pi-\tan ^{-1}\left(\frac{4}{3}\right)\right)\)
(ii) \(\left(5 \sqrt{2}, \frac{\pi}{4}\right)\)

Answer: (i) Given, \(r=5, \theta=\pi-\tan ^{-1}\left(\frac{4}{3}\right)\)
Now,
\(
\begin{aligned}
x & =r \cos \theta=5 \cos \left(\pi-\tan ^{-1}\left(\frac{4}{3}\right)\right) \\
& =-5 \cos \left(\tan ^{-1}\left(\frac{4}{3}\right)\right) \\
& =-5 \cos \left(\cos ^{-1}\left(\frac{3}{5}\right)\right)=-5 \times \frac{3}{5}=-3
\end{aligned}
\)
and
\(
\begin{aligned}
y & =r \sin \theta=5 \sin \left(\pi-\tan ^{-1}\left(\frac{4}{3}\right)\right) \\
& =5 \sin \left(\tan ^{-1}\left(\frac{4}{3}\right)\right) \\
& =5 \sin \left(\sin ^{-1}\left(\frac{4}{5}\right)\right)=5 \times \frac{4}{5}=4
\end{aligned}
\)
Hence, cartesian coordinates of the given point will be \((-3,4)\).
(ii) Given, \(\quad r=5 \sqrt{2}, \theta=\frac{\pi}{4}\)
Now,
\(
x=r \cos \theta=5 \sqrt{2} \cos \left(\frac{\pi}{4}\right)=5 \sqrt{2} \times \frac{1}{\sqrt{2}}=5
\)
and
\(
y=r \sin \theta=5 \sqrt{2} \sin \left(\frac{\pi}{4}\right)=5 \sqrt{2} \times \frac{1}{\sqrt{2}}=5
\)
Hence, cartesian coordinates of the given point, will be \((5,5)\).

Example 4: Find the polar coordinates of the points whose cartesian coordinates are
(i) \((-2,-2)\)
(ii) \((-3,4)\)

Answer: (i) Given, \(x=-2, y=-2\)
\(\therefore \quad r=\sqrt{\left(x^2+y^2\right)}=\sqrt{(4+4)}=2 \sqrt{2}\)
and \(\quad \alpha=\tan ^{-1}\left|\frac{y}{x}\right|=\tan ^{-1}\left|\frac{-2}{-2}\right|=\tan ^{-1} 1=\frac{\pi}{4}\)
Since, point \((-2,-2)\) lies in III quadrant.
\(
\therefore \quad \theta=-\pi+\alpha=-\pi+\frac{\pi}{4}=-\frac{3 \pi}{4}
\)
Hence, polar coordinates of the given points will be
\(
\left(2 \sqrt{2},-\frac{3 \pi}{4}\right)
\)
Remark: If we find \(\theta\), from the equation,
\(
\tan \theta=\frac{y}{x}=\frac{-2}{-2}=1
\)
then, \(\quad \theta=\frac{\pi}{4}\) and then
\(
\begin{aligned}
(x, y) & =(r \cos \theta, r \sin \theta)=\left(2 \sqrt{2} \times \frac{1}{\sqrt{2}}, 2 \sqrt{2} \times \frac{1}{\sqrt{2}}\right) \\
& =(2,2) \neq(-2,-2)
\end{aligned}
\)

\(
\begin{array}{l}
\text { (ii) Given, } x=-3, y=4 \\
\therefore \quad r=\sqrt{\left(x^2+y^2\right)}=\sqrt{(9+16)}=5 \\
\text { and } \\
\alpha=\tan ^{-1}\left|\frac{y}{x}\right|=\tan ^{-1}\left|\frac{4}{-3}\right|=\tan ^{-1}\left(\frac{4}{3}\right) \\
\end{array}
\)
Since, point \((-3,4)\) lies in II quadrant
\(
\therefore \quad \theta=\pi-\alpha=\pi-\tan ^{-1}\left(\frac{4}{3}\right)
\)
Hence, polar coordinates of the given points, will be
\(
\left(5, \pi-\tan ^{-1}\left(\frac{4}{3}\right)\right) \text {. }
\)

Example 5: Transform the equation \(r^2=a^2 \cos 2 \theta\) into cartesian form.

Answer: \(\because \quad r=\sqrt{\left(x^2+y^2\right)} \quad\) and \(\quad \theta=\tan ^{-1}\left(\frac{y}{x}\right)\)
or \(\quad r^2=\left(x^2+y^2\right) \quad\) and \(\quad \tan \theta=\frac{y}{x}\)
Given, \(r^2=a^2 \cos 2 \theta=a^2\left(\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\right)\)
\(
\begin{array}{l}
\left(x^2+y^2\right)=a^2\left(\frac{1-\frac{y^2}{x^2}}{1+\frac{y^2}{x^2}}\right) \\
\left(x^2+y^2\right)^2=a^2\left(x^2-y^2\right)
\end{array}
\)
This is the required equation in cartesian form.

Alternate:
\(r^2=a^2 \cos 2 \theta\)
or \(\quad r^2=a^2\left(\cos ^2 \theta-\sin ^2 \theta\right)\)
\(\because \quad x=r \cos \theta\) and \(y=r \sin \theta\)
and \(\quad r^2=x^2+y^2\)
then \(\quad r^2=a^2\left(\frac{x^2}{r^2}-\frac{y^2}{r^2}\right)\)
or \(\quad r^4=a^2\left(x^2-y^2\right)\)
or \(\left(x^2+y^2\right)^2=a^2\left(x^2-y^2\right)\).

Example 6: Transform the equation \(x^2+y^2=a x\) into polar form.

Answer:

\(
\begin{aligned}
\because \quad x=r \cos \theta, y & =r \sin \theta \\
\text { Given, } \quad x^2+y^2 & =a x
\end{aligned}
\)
\(
\begin{aligned}
r^2 & =a(r \cos \theta) \\
r & =a \cos \theta
\end{aligned}
\)
This is the required equation in polar form.

Distance Between Two Points

The distance between two points \(P\left(x_1, y_1\right)\) and \(Q\left(x_2, y_2\right)\) is given by
\(
|P Q|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}
\)

Proof: Let \(P\left(x_1, y_1\right)\) and \(Q\left(x_2, y_2\right)\) be any two points in the plane. Let us assume that the points \(P\) and \(Q\) are both in 1st quadrant (for the sake of exactness).

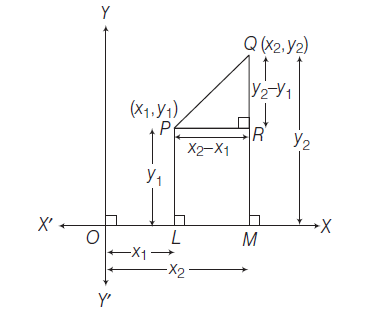
From \(P\) and \(Q\) draw \(P L\) and \(Q M\) perpendiculars to \(X\)-axis. From \(P\) draw \(P R\) perpendicular to \(Q M\) and join \(P Q\). Then
\(
\begin{array}{l}
O L=x_1, O M=x_2, P L=y_1, Q M=y_2 \\
P R=L M=O M-O L=x_2-x_1
\end{array}
\)
\(
\text { and } \quad Q R=Q M-R M=Q M-P L=y_2-y_1
\)
Since, \(P R Q\) is a right angled triangle, therefore by pythagoras theorem.
\(
\begin{aligned}
(P Q)^2 & =(P R)^2+(Q R)^2 \\
\therefore \quad|P Q| & =\sqrt{(P R)^2+(Q R)^2}(\because P Q \text { is always positive }) \\
& =\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}
\end{aligned}
\)
\(\therefore\) The distance \(P Q\) between the points \(P\left(x_1, y_1\right)\) and \(Q\left(x_2, y_2\right)\) is given by \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

Note: We shall denote the distance between two points \(P\) and \(Q\) of the coordinate plane, either by \(|P Q|\) or by \(P Q\) or by \(\overline{P Q}\)

As an example: Find the distance between \(\mathrm{P}\left(2,-\frac{\pi}{6}\right)\) and \(\mathrm{Q}\left(3, \frac{\pi}{6}\right)\). [JEE Main]

Answer: The distance between two points \(=\sqrt{r_1^2+r_2^2-2 r_1 r_2 \cos \left(\theta_1-\theta_2\right)}\). Therefore,
\(
P Q=\sqrt{r_1^2+r_2^2-2 r_1 r_2 \cos \left(\theta_1-\theta_2\right)}=\sqrt{4+9-2.2 \cdot 3 \cos \left(-\frac{\pi}{6}-\frac{\pi}{6}\right)}=\sqrt{4+9-12 \cos \left(\frac{\pi}{3}\right)}=\sqrt{13-12 \cdot \frac{1}{2}}=\sqrt{7}
\)

As an example: The point whose abscissa is equal to its ordinate and which is equidistant from the points \(A(1,0)\), \(B(0,3)\) is (JEE Main)

Answer: Given, abscissa = ordinate. Therefore distance can be found by considering the co-ordinates of required point be \(\mathrm{P}(\mathrm{k}, \mathrm{k})\).
Now given \(\mathrm{PA}=\mathrm{PB} \Rightarrow \sqrt{(\mathrm{k}-1)^2+\mathrm{k}^2}=\sqrt{\mathrm{k}^2+(\mathrm{k}-3)^2}\)
\(
2 k^2-2 k+1=2 k^2-6 k+9 \Rightarrow 4 k=8 \Rightarrow k=2
\)

Important Remarks for Objective Questions

• If \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) are the ends of the hypotenuse of a right angled isosceles triangle, then the third vertex is given by
  \(
  \left(\frac{\left(x_1+x_2\right) \pm\left(y_1-y_2\right)}{2}, \frac{\left(y_1+y_2\right) \mp\left(x_1-x_2\right)}{2}\right)
  \)
• If two vertices of an equilateral triangle are \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\), then coordinates of the third vertex are
  \(
  \left(\frac{x_1+x_2 \mp \sqrt{3}\left(y_2-y_1\right)}{2}, \frac{y_1+y_2 \pm \sqrt{3}\left(x_2-x_1\right)}{2}\right)
  \)

Example 7: Prove that the distance of the point \((a \cos \alpha, a \sin \alpha)\) from the origin is independent of \(\alpha\).

Answer: Let \(P \equiv(a \cos \alpha, a \sin \alpha)\) and \(O \equiv(0,0)\) then
\(
\begin{aligned}
|O P| & =\sqrt{(a \cos \alpha-0)^2+(a \sin \alpha-0)^2} \\
& =\sqrt{\left(a^2 \cos ^2 \alpha+a^2 \sin ^2 \alpha\right)} \\
& =\sqrt{a^2\left(\cos ^2 \alpha+\sin ^2 \alpha\right)}=\sqrt{a^2} \\
& =|a|, \text { which is independent of } \alpha .
\end{aligned}
\)

Example 8: Find the distance between the points \((a \cos \alpha, a \sin \alpha)\) and \((a \cos \beta, a \sin \beta)\), where \(a>0\).

Answer: Let \(P \equiv(a \cos \alpha, a \sin \alpha)\) and \(Q \equiv(a \cos \beta, a \sin \beta)\)
then
\(
\begin{array}{l}
|P Q|=\sqrt{(a \cos \alpha-a \cos \beta)^2+(a \sin \alpha-a \sin \beta)^2} \\
=\sqrt{a^2\left\{(\cos \alpha-\cos \beta)^2+(\sin \alpha-\sin \beta)^2\right\}} \\
=\sqrt{\begin{array}{c}
a^2\left\{\cos ^2 \alpha+\cos ^2 \beta-2 \cos \alpha \cos \beta+\sin ^2 \alpha\right. \\
\left.+\sin ^2 \beta-2 \sin \alpha \sin \beta\right\}
\end{array}} \\
=\sqrt{a^2\{1+1-2(\cos \alpha \cos \beta+\sin \alpha \sin \beta)\}} \\
=\sqrt{a^2(2-2 \cos (\alpha-\beta))} \\
=\sqrt{2 a^2(1-\cos (\alpha-\beta))} \\
=\sqrt{\left(2 a^2 \cdot 2 \sin ^2\left(\frac{\alpha-\beta}{2}\right)\right)} \\
=\sqrt{4 a^2 \sin ^2\left(\frac{\alpha-\beta}{2}\right)} \\
=\left|2 a \sin \left(\frac{\alpha-\beta}{2}\right)\right| \\
=2 a\left|\sin \left(\frac{\alpha-\beta}{2}\right)\right| \quad(\because a>0) \\
\end{array}
\)

Example 9: If the point \((x, y)\) be equidistant from the points \((6,-1)\) and \((2,3)\), prove that \(x-y=3\).

Answer: Let \(P \equiv(x, y), A \equiv(6,-1)\) and \(B \equiv(2,3)\)
By the given condition, \(P A=P B\)
\(
\begin{array}{l}
\sqrt{(x-6)^2+(y+1)^2}=\sqrt{(x-2)^2+(y-3)^2} \\
(x-6)^2+(y+1)^2=(x-2)^2+(y-3)^2 \\
x^2-12 x+36+y^2+2 y+1 \\
=x^2-4 x+4+y^2-6 y+9 \\
8 x-8 y=24 \\
x-y=3
\end{array}
\)

Example 10: Using distance formula, show that the points \((1,5),(2,4)\) and \((3,3)\) are collinear (points lying in the same straight line).

Answer: Let \(A \equiv(1,5), B \equiv(2,4)\) and \(C \equiv(3,3)\) be the given points, then
\(
|A B|=\sqrt{(1-2)^2+(5-4)^2}=\sqrt{2}
\)

\(
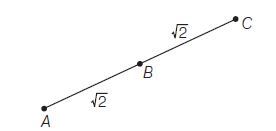
\begin{array}{ll}
& |B C|=\sqrt{(2-3)^2+(4-3)^2}=\sqrt{2} \\
\text { and } & |A C|=\sqrt{(1-3)^2+(5-3)^2}=2 \sqrt{2} \\
\text { Clearly, } & |A B|+|B C|=\sqrt{2}+\sqrt{2}=2 \sqrt{2}=|A C| .
\end{array}
\)
Hence, \(A, B, C\) are collinear.

Example 11: An equilateral triangle has one vertex at the point \((0,0)\) and another at \((3, \sqrt{3})\). Find the coordinates of the third vertex.

Answer: Let \(O \equiv(0,0)\) and \(A \equiv(3, \sqrt{3})\) be the given points and let \(B \equiv(x, y)\) be the required point. Then
\(
O A=O B=A B
\)

\(
\begin{aligned}
(O A)^2 & =(O B)^2=(A B)^2 \\
(3-0)^2+(\sqrt{3}-0)^2 & =(x-0)^2+(y-0)^2 \\
& =(x-3)^2+(y-\sqrt{3})^2 \\
12=x^2+y^2 & =x^2+y^2-6 x-2 \sqrt{3} y+12
\end{aligned}
\)
Taking first two members then
\(
x^2+y^2=12 \dots(i)
\)
and taking last two members, then
\(
6 x+2 \sqrt{3} y=12 \text { or } y=\sqrt{3}(2-x) \dots(ii)
\)
From Eqns. (i) and (ii), we get
\(
\begin{aligned}
x^2+3(2-x)^2 & =12 \\
4 x^2-12 x & =0 \\
x & =0,3
\end{aligned}
\)
Putting \(x=0,3\) in Eq. (ii), we get \(y=2 \sqrt{3},-\sqrt{3}\)
Hence, the coordinates of the third vertex \(B\) are \((0,2 \sqrt{3})\) or \((3,-\sqrt{3})\).

Short Cut Method : According to important note :

\(
\begin{array}{l}
\left(\frac{x_1+x_2 \mp \sqrt{3}\left(y_2-y_1\right)}{2}, \frac{y_1+y_2 \pm \sqrt{3}\left(x_2-x_1\right)}{2}\right) \\
\left(\frac{0+3 \mp \sqrt{3}(\sqrt{3}-0)}{2}, \frac{0+\sqrt{3} \pm \sqrt{3}(3-0)}{2}\right) \\
=\left(\frac{3 \mp 3}{2}, \frac{\sqrt{3} \pm 3 \sqrt{3}}{2}\right) \\
=(0,2 \sqrt{3}) \text { or }(3,-\sqrt{3})
\end{array}
\)

Example 12: Show that four points \((1,-2),(3,6)\), \((5,10)\) and \((3,2)\) are the vertices of a parallelogram.

Answer: Let \(A \equiv(1,-2), B \equiv(3,6), C \equiv(5,10)\) and \(D \equiv(3,2)\) be the given points. Then
\(
|A B|=\sqrt{(1-3)^2+(-2-6)^2}=\sqrt{4+64}=2 \sqrt{17}
\)
\(
\begin{array}{l}
|B C|=\sqrt{(3-5)^2+(6-10)^2}=\sqrt{4+16}=2 \sqrt{5} \\
|C D|=\sqrt{(5-3)^2+(10-2)^2}=\sqrt{4+64}=2 \sqrt{17} \\
|A D|=\sqrt{(1-3)^2+(-2-2)^2}=\sqrt{4+16}=2 \sqrt{5} \\
|A C|=\sqrt{(1-5)^2+(-2-10)^2}=\sqrt{16+144}=4 \sqrt{10} \\
|B D|=\sqrt{(3-3)^2+(6-2)^2}=4
\end{array}
\)

Clearly, \(|A B|=|C D|,|B C|=|A D|\) and \(|A C| \neq|B D|\) Hence, \(A B C D\) is a parallelogram.

Example 13: Let the opposite angular points of a square be \((3,4)\) and \((1,-1)\). Find the coordinates of the remaining angular points.

Answer: Let \(A(3,4)\) and \(C(1,-1)\) be the given angular points of a square \(A B C D\) and let \(B(x, y)\) be the unknown vertex. Then
\(
\begin{array}{l}
A B=B C \\
\Rightarrow \quad(A B)^2=(B C)^2 \\
\Rightarrow \quad(x-3)^2+(y-4)^2=(x-1)^2+(y+1)^2 \\
\Rightarrow \quad 4 x+10 y-23=0 \\
\Rightarrow \quad x=\left(\frac{23-10 y}{4}\right) \dots(i) \\
\end{array}
\)

Also, in \(\triangle A B C\), \((A B)^2+(B C)^2=(A C)^2\)
\(
\begin{array}{c}
(x-3)^2+(y-4)^2+(x-1)^2+(y+1)^2 \\
=(3-1)^2+(4+1)^2 \\
x^2+y^2-4 x-3 y-1=0 \dots(ii)
\end{array}
\)
Substituting the value of \(x\) from Eqs. (i) into (ii), we get
\(
\left(\frac{23-10 y}{4}\right)^2+y^2-4\left(\frac{23-10 y}{4}\right)-3 y-1=0
\)
\(
\begin{array}{c}
4 y^2-12 y+5=0 \\
(2 y-1)(2 y-5)=0 \\
y=\frac{1}{2} \text { or } \frac{5}{2}
\end{array}
\)
Putting \(y=\frac{1}{2}\) in Eq. (i), we get \(x=\frac{9}{2}\), and putting \(y=\frac{5}{2}\) in Eq. (i), we get \(x=-\frac{1}{2}\)
Hence, the required vertices of the square are \(\left(\frac{9}{2}, \frac{1}{2}\right)\) and \(\left(-\frac{1}{2}, \frac{5}{2}\right)\)

Example 14: Find the circumcentre of the triangle whose vertices are \((-2,-3),(-1,0)\) and \((7,-6)\). Also find the radius of the circumcircle.

Answer: Let \(A \equiv(-2,-3), B \equiv(-1,0)\) and \(C \equiv(7,-6)\). Let \(P \equiv(x, y)\) be the circumcentre of \(\triangle A B C\).

Since, \(P\) is the circumcentre
\(
\therefore \quad|P A|=|P B|=|P C| \Rightarrow(P A)^2=(P B)^2=(P C)^2
\)
\(
\begin{array}{c}
(x+2)^2+(y+3)^2=(x+1)^2+(y-0)^2 \\
=(x-7)^2+(y+6)^2
\end{array}
\)
\(
\begin{array}{c}
x^2+y^2+4 x+6 y+13=x^2+y^2+2 x+1 \\
=x^2+y^2-14 x+12 y+85
\end{array}
\)
Taking first two members, we get
\(
x+3 y+6=0 \dots(i)
\)
and taking 1st and last member then, we get
\(
3 x-y-12=0 \dots(ii)
\)
Solving Eqs. (i) and (ii), we get
\(
x=3, y=-3
\)
Hence, circumcentre is \((3,-3)\).
Radius of the circumcircle
\(
\begin{array}{l}
=P B=\sqrt{(3+1)^2+(-3-0)^2} \\
=\sqrt{16+9}=5 \text { units }
\end{array}
\)

Example 15: If the line segment joining the points \(A(a, b)\) and \(B(c, d)\) subtends an angle \(\theta\) at the origin \(O\), prove that
\(
\cos \theta=\frac{a c+b d}{\sqrt{\left(a^2+b^2\right)\left(c^2+d^2\right)}}
\)
or
\(
O A \cdot O B \cos \theta=a c+b d
\)

Answer: Let \(O A=r_1\) and \(O B=r_2\)
Now, and
\(
\begin{array}{l}
r_1=|O A|=\sqrt{\left(a^2+b^2\right)} \dots(i)\\
r_2=|O B|=\sqrt{\left(c^2+d^2\right)} \dots(ii)
\end{array}
\)
Also,
\(
\begin{aligned}
|A B| & =\sqrt{(a-c)^2+(b-d)^2} \\
& =\sqrt{a^2+b^2+c^2+d^2-2 a c-2 b d} \\
& =\sqrt{r_1^2+r_2^2-2(a c+b d)} \text { [from Eqs. (i) and (ii)] }
\end{aligned}
\)

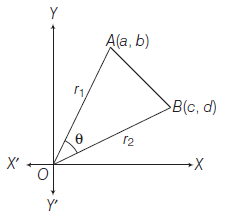
By using Cosine formula in \(\triangle A O B\)
\(
\begin{aligned}
\cos \theta & =\frac{(O A)^2+(O B)^2-(A B)^2}{2 \cdot O A \cdot O B} \\
& =\frac{r_1^2+r_2^2-\left(r_1^2+r_2^2-2(a c+b d)\right)}{2 r_1 r_2} \\
& =\frac{2(a c+b d)}{2 r_1 r_2}=\frac{(a c+b d)}{r_1 r_2} \dots(iii) \\
& =\frac{(a c+b d)}{\sqrt{\left(a^2+b^2\right)} \sqrt{\left(c^2+d^2\right)}} \text { [from Eqs. (i) and (ii)] } \\
& =\frac{(a c+b d)}{\sqrt{\left(a^2+b^2\right)\left(c^2+d^2\right)}}
\end{aligned}
\)
Also from Eq. (iii),
\(
r_1 r_2 \cos \theta=a c+b d \quad \text { or } \quad O A . O B \cos \theta=a c+b d
\)

Choice of Axes

For simplification we carefully choose the axes or the origin. Some situations are given below :

• If two lines are perpendicular then point of intersection is taken as origin and these lines must be taken as the coordinate axes.
• If two fixed points \(A\) and \(B\) are given then we take \(|A B|=2 a\) and the mid-point of \(A B\) as origin ‘ \(O\) ‘, line \(A O B\) as \(X\)-axis and the line perpendicular to \(A B\) through \(O\) is taken as \(Y\)-axis then the coordinates of the fixed points are \(( \pm a, 0)\). Similarly if \(A O B\) as \(Y\)-axis and the line perpendicular to \(A B\) through \(O\) is taken as \(X\)-axis then the coordinates of the fixed points are \((0, \pm a)\).
• If there is a symmetry of any kind then take the coordinates of the points in a general way i.e. \(\left(x_i, y_i\right)\), \(i=1,2,3, \ldots\) etc.

Example 16: Show that the triangle, the coordinates of whose vertices are given by integers, can never be an equilateral triangle.

Answer: Let \(A \equiv(0,0), B \equiv(a, 0)\) and \(C \equiv(b, c)\) be the vertices of equilateral triangle \(A B C\) where \(a, b, c\) are integers then,
\(
\begin{array}{rlrl}
|A B| & =|B C|=|C A| \\
\Rightarrow & (A B)^2 =(B C)^2=(C A)^2 \\
\Rightarrow & a^2 =(a-b)^2+c^2=b^2+c^2
\end{array}
\)
From first two members, we get
\(
b^2+c^2=2 a b \dots(i)
\)
and taking first and third members, then
\(
b^2+c^2=a^2 \dots(ii)
\)
From Eqs. (i) and (ii) we get
\(
a=2 b (\because a \neq 0)
\)
From Eq. (ii), \(b^2+c^2=(2 b)^2\)
or
\(
c^2=3 b^2
\)
or
\(
c= \pm b \sqrt{3}
\)
which is impossible, since \(b\) and \(c\) are integers.

Example 17: In any triangle \(A B C\), show that
\(
A B^2+A C^2=2\left(A D^2+B D^2\right)
\)
where, \(D\) is the middle point of \(B C\).

Answer: Let \(D\) as the origin and \(D C\) and \(D Y\) as the \(X\) and \(Y\)-axes respectively. Let \(B C=2 a\), then
\(
B \equiv(-a, 0), C \equiv(a, 0) \text { and let } A \equiv(b, c)
\)

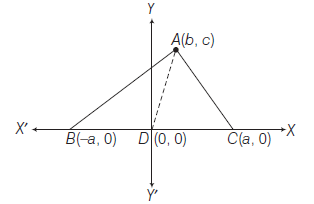
Now,
\(
\begin{aligned}
\text { LHS } & =A B^2+A C^2 \\
& =(b+a)^2+(c-0)^2+(b-a)^2+(c-0)^2 \\
& =2\left(a^2+b^2+c^2\right) \dots(i)
\end{aligned}
\)
and
\(
\begin{aligned}
\text { RHS } & =2\left(A D^2+B D^2\right) \\
& =2\left\{(b-0)^2+(c-0)^2+a^2\right\} \\
& =2\left(a^2+b^2+c^2\right) \dots(ii)
\end{aligned}
\)
From Eqs. (i) and (ii), we get
\(
A B^2+A C^2=2\left(A D^2+B D^2\right)
\)

Example 18: Let \(A B C D\) be a rectangle and \(P\) be any point in its plane. Show that \(P A^2+P C^2=P B^2+P D^2\)

Answer: Let \(A\) as the origin and \(A B\) and \(A D\) as the \(X\) and \(Y\)-axes respectively. Let \(A B=a\) and \(A D=b\), then
\(
B \equiv(a, 0), D \equiv(0, b) \text { and } C \equiv(a, b)
\)
Let \(P \equiv(\alpha, \beta)\)

Now,
\(
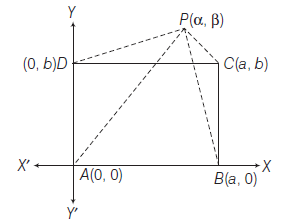
\begin{aligned}
\text { Now, LHS } & =P A^2+P C^2 \\
& =(\alpha-0)^2+(\beta-0)^2+(\alpha-a)^2+(\beta-b)^2 \\
& =2 \alpha^2+2 \beta^2-2 a \alpha-2 b \beta+a^2+b^2 \dots(i) \\
\text { and RHS } & =P B^2+P D^2 \\
& =(\alpha-a)^2+(\beta-0)^2+(\alpha-0)^2+(\beta-b)^2 \\
& =2 \alpha^2+2 \beta^2-2 a \alpha-2 b \beta+a^2+b^2 \dots(ii)
\end{aligned}
\)
From Eqs. (i) and (ii), we get
\(
P A^2+P C^2=P B^2+P D^2
\)

Distance between Two Points in Polar Coordinates

Let \(O\) be the pole and \(O X\) be the initial line. Let \(P\) and \(Q\) be two given points whose polar coordinates are \(\left(r_1, \theta_1\right)\) and \(\left(r_2, \theta_2\right)\) respectively.

\(
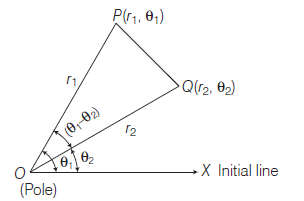
\begin{aligned}
& \text { Then, } & O P & =r_1, O Q=r_2 \\
& \text { and } & \angle P O X & =\theta_1, \angle Q O X=\theta_2 \\
& \therefore & \angle P O Q & =\theta_1-\theta_2
\end{aligned}
\)
By using Cosine formula in \(\triangle P O Q\),
\(
\begin{array}{rlrl}
& \cos (\angle P O Q) =\frac{(O P)^2+(O Q)^2-(P Q)^2}{2(O P)(O Q)} \\
& \text { or } \cos \left(\theta_1-\theta_2\right) =\frac{r_1^2+r_2^2-(P Q)^2}{2 r_1 r_2} \\
& \therefore |P Q| =\sqrt{\left(r_1^2+r_2^2-2 r_1 r_2 \cos \left(\theta_1-\theta_2\right)\right)}
\end{array}
\)

Example 19: Prove that the points \((0,0),\left(3, \frac{\pi}{2}\right)\) and \(\left(3, \frac{\pi}{6}\right)\) are the vertices of an equilateral triangle.

Answer: Let \(A \equiv(0,0), B \equiv\left(3, \frac{\pi}{2}\right)\) and \(C \equiv\left(3, \frac{\pi}{6}\right)\)
Here, given coordinates are in polar form
\(
\begin{array}{l}
\therefore \quad|A B|=\sqrt{\left(0^2+3^2-2 \cdot 0 \cdot 3 \cos \left(\frac{\pi}{2}-0\right)\right.}=3 \text { units } \\
|B C|=\sqrt{\left(3^2+3^2-2 \cdot 3 \cdot 3 \cos \left(\frac{\pi}{2}-\frac{\pi}{6}\right)\right)} \\
=\sqrt{\left(18-18 \sin \frac{\pi}{6}\right)}=\sqrt{(18-9)}=3 \text { units } \\
\text { and }|C A|=\sqrt{\left(3^2+0^2-2 \cdot 3 \cdot 0 \cos \left(\frac{\pi}{6}-0\right)\right)}=3 \text { units } \\
\end{array}
\)
\(
\therefore \quad|A B|=|B C|=|C A|
\)
Hence, points \(A, B, C\) are the vertices of an equilateral triangle.

Alternate:

\(
\begin{array}{l}
\angle B A X=\frac{\pi}{2} \\
\angle C A X=\frac{\pi}{6}
\end{array}
\)

\(
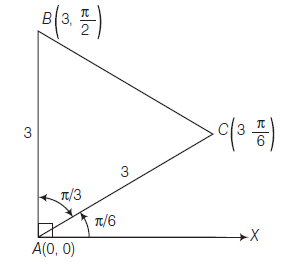
\begin{array}{l}
\begin{array}{l}
\therefore \quad \angle B A C=\frac{\pi}{2}-\frac{\pi}{6}=\frac{\pi}{3} \\
\because \text { In } \triangle A B C \\
A B=A C \\
\therefore \quad \angle A C B=\angle A B C=\alpha \text { (say) } \\
\therefore \quad \alpha+\alpha+\frac{\pi}{3}=\pi \\
\text { or } \\
\alpha=\frac{\pi}{3} \\
\end{array}\\
\text { Hence, } \quad|A B|=|B C|=|C A| \text {. }
\end{array}
\)

Section Formula

Definition: If \(P\) be any point on the line \(A B\) between \(A\) and \(B\) then we say that \(P\) divides segment \(A B\) internally in the ratio \(A P: P B\).

Also, if \(P\) be any point on the line \(A B\) but not between \(A\) and \(B\) ( \(P\) may be to the right or the left of the points \(A, B)\) then \(P\) divides \(A B\) externally in the ratio \(A P: P B\)

Case-I: Formula for Internal Division

Theorem: If the point \(P(x, y)\) divides the line segment joining the points \(A\left(x_1, y_1\right)\) and \(B\left(x_2, y_2\right)\) internally in the ratio \(m: n\), then prove that
\(
\begin{array}{l}
x=\frac{m x_2+n x_1}{m+n} \\
y=\frac{m y_2+n y_1}{m+n}
\end{array}
\)

Proof: The given points are \(A\left(x_1, y_1\right)\) and \(B\left(x_2, y_2\right)\). Let us assume that the points \(A\) and \(B\) are both in 1st quadrant (for the sake of exactness). Since \(P(x, y)\) divides \(A B\) internally in the ratio \(m: n\) i.e. \(A P: P B=m: n\). From \(A, B\) and \(P\) draw \(A L, B M\) and \(P N\) perpendiculars to \(X\)-axis. From \(A\) and \(P\) draw \(A H\) and \(P J\) perpendiculars to \(P N\) and \(B M\) respectively, then
\(
\begin{array}{l}
O L=x_1, O N=x, O M=x_2, A L=y_1, P N=y \text { and } B M=y_2 \\
\therefore \quad A H=L N=O N-O L=x-x_1 \\
P J=N M=O M-O N=x_2-x \\
P H=P N-H N=P N-A L=y-y_1 \\
\text { and } \quad B J=B M-J M=B M-P N=y_2-y \\
\end{array}
\)

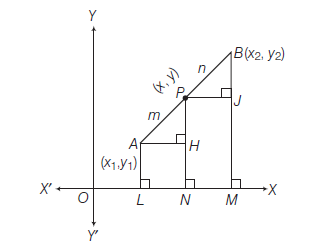
Clearly, the \(\triangle \mathrm{s} A H P\) and \(P J B\) are similar and therefore, their sides are proportional
\(
\begin{array}{l}
\therefore \quad \frac{A H}{P J}=\frac{P H}{B J}=\frac{A P}{P B} \\
\text { or } \quad \frac{x-x_1}{x_2-x} \dots(i)=\frac{y-y_1}{y_2-y}\dots(ii)=\frac{m}{n} \dots(iii)\\
\end{array}
\)
From Eqs. (i) and (iii), we have
\(
\begin{aligned}
\frac{x-x_1}{x_2-x} & =\frac{m}{n} \\
n x-n x_1 & =m x_2-m x \\
(m+n) x & =m x_2+n x_1 \\
x & =\frac{m x_2+n x_1}{m+n}
\end{aligned}
\)
and from Eqs. (ii) and (iii), we have
\(
\begin{aligned}
\frac{y-y_1}{y_2-y} & =\frac{m}{n} \\
n y-n y_1 & =m y_2-m y \\
(m+n) y & =m y_2+n y_1 \\
y & =\frac{m y_2+n y_1}{m+n}
\end{aligned}
\)
Thus, the coordinates of \(P\) are
\(
\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)
\)

Important Points to remember

• If \(P(\alpha, \beta)\) be the mid-point of \(A B\) and if coordinates of \(A\) are \((\lambda, \mu)\) then the coordinates of \(B\) are \((2 \alpha-\lambda, 2 \beta-\mu)\), i.e. (Double the \(x\)-co-ordinate of mid point – \(x\)-coordinate of given point, Double the \(y\)-co-ordinate of mid point \(-y\)-coordinate of given point).
• If \(P\) is the mid-point of \(A B\) then \(m=n\), the coordinates of the middle-point of \(A B\) are
  \(
  \left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)
  \)
• From the above the co-ordinates of a point dividing AB in the ratio \(\lambda: 1\) are \(\left(\frac{x_1+\lambda x_2}{1+\lambda}, \frac{y_1+\lambda y_2}{1+\lambda}\right)\). Considering \(\lambda\) as a variable parameter, i.e. of all values positive or negative, the co-ordinates of any point on the line joining the points \(\left(\mathrm{x}_1, \mathrm{y}_1\right)\) and \(\left(\mathrm{x}_2, \mathrm{y}_2\right)\) can be expressed in the above forms. If \(\lambda\) is positive then divides intemally and if \(\lambda\) is negative, then divides externally.
• The straight line \(a x+b y+c=0\) divides the joint of points \(A\left(x_1, y_1\right)\) and \(B\left(x_2, y_2\right)\) in the ratio
  \(
  \frac{A P}{P B}=\frac{\lambda}{1}=-\frac{\left(a x_1+b y_1+c\right)}{\left(a x_2+b y_2+c\right)}
  \)

       

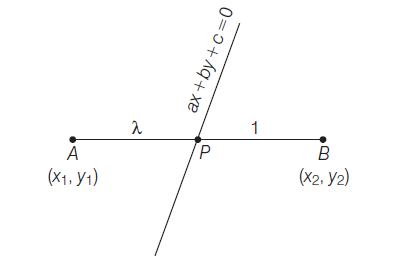
If ratio is positive, then divides internally and if ratio is negative then divides externally.

• The line joining the points \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) is divided by the \(X\)-axis in the ratio \(-\frac{y_1}{y_2}\) and by \(Y\)-axis in the ratio \(-\frac{x_1}{x_2}\).

Proof: Coordinates of \(P\) are \(\left(\frac{x_1+\lambda x_2}{1+\lambda}, \frac{y_1+\lambda y_2}{1+\lambda}\right)\)
\(\because P\) lies on the line \(a x+b y+c=0\), then
\(
a\left(\frac{x_1+\lambda x_2}{1+\lambda}\right)+b\left(\frac{y_1+\lambda y_2}{1+\lambda}\right)+c=0
\)
\(
\begin{array}{l}
\left(a x_1+b y_1+c\right)+\lambda\left(a x_2+b y_2+c\right)=0 \\
\frac{\lambda}{1}=-\frac{\left(a x_1+b y_1+c\right)}{\left(a x_2+b y_2+c\right)}
\end{array}
\)

Example 20: Find the coordinates of the point which divides the line segment joining the points \((5,-2)\) and \((9,6)\) in the ratio \(3: 1\).

Answer: Let the required point be \((x, y)\), then
\(
\begin{array}{l}
x=\left(\frac{3 \times 9+1 \times 5}{3+1}\right)=8 \\
y=\left(\frac{3 \times 6+1 \times(-2)}{3+1}\right)=4
\end{array}
\)
Thus, the coordinates of the required point are \((8,4)\).

Example 21: Find the length of median through \(A\) of a triangle whose vertices are \(A(-1,3), B(1,-1)\) and \(C(5,1)\).

Answer: Let \(D\) be the mid-point of \(B C\), then coordinates of \(D\) are \(\left(\frac{1+5}{2}, \frac{-1+1}{2}\right)\) i.e. \((3,0)\)

\(
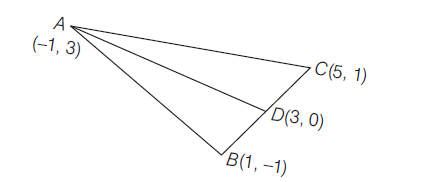
\begin{aligned}
\text { Median } A D & =\sqrt{(3+1)^2+(0-3)^2} \\
& =\sqrt{16+9}=\sqrt{25} \\
& =5 \text { units }
\end{aligned}
\)

Example 22: Determine the ratio in which \(y-x+2=0\) divides the line joining \((3,-1)\) and \((8,9)\).

Answer: Suppose the line \(y-x+2=0\) divides the line segment joining \(A(3,-1)\) and \(B(8,9)\) in the ratio \(\lambda: 1\) at point \(P\), then the coordinates of the point \(P\) are \(\left(\frac{8 \lambda+3}{\lambda+1}, \frac{9 \lambda-1}{\lambda+1}\right)\).
But \(P\) lies on \(y-x+2=0\) therefore
\(
\begin{array}{c}
\left(\frac{9 \lambda-1}{\lambda+1}\right)-\left(\frac{8 \lambda+3}{\lambda+1}\right)+2=0 \\
\Rightarrow \quad 9 \lambda-1-8 \lambda-3+2 \lambda+2=0 \\
\Rightarrow \quad 3 \lambda-2=0 \text { or } \lambda=\frac{2}{3}
\end{array}
\)
So, the required ratio is \(\frac{2}{3}: 1\), i.e. \(2: 3\) (internally) since here \(\lambda\) is positive.

Shortcut Method:

\(
\begin{aligned}
\lambda & =-\left(\frac{-1-3+2}{9-8+2}\right)=\frac{2}{3} \\
\text { or } \quad \lambda: 1 & =2: 3
\end{aligned}
\)

Example 23: The coordinates of three consecutive vertices of a parallelogram are \((1,3),(-1,2)\) and \((2,5)\). Then find the coordinates of the fourth vertex.

Answer: Let the fourth vertex be \(D(\alpha, \beta)\). Since \(A B C D\) is a parallelogram, the diagonals bisect to each other. i.e. mid-point of \(B D=\) mid-point of \(A C\)
\(
\therefore \quad\left(\frac{\alpha-1}{2}, \frac{\beta+2}{2}\right)=\left(\frac{2+1}{2}, \frac{5+3}{2}\right)
\)
\(
\left(\frac{\alpha-1}{2}, \frac{\beta+2}{2}\right)=\left(\frac{3}{2}, 4\right)
\)

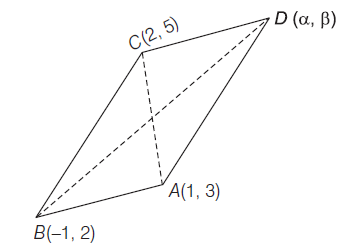
On equating abscissaes and ordinates, we get
\(
\frac{\alpha-1}{2}=\frac{3}{2} \quad \text { or } \quad \alpha-1=3 \quad \text { or } \quad \alpha=4
\)
and \(\frac{\beta+2}{2}=4\) or \(\beta+2=8\) or \(\beta=6\)
Hence, the coordinates of the fourth vertex \(D(\alpha, \beta)\) is \((4,6)\).

Example 24: In what ratio does \(X\)-axis divide the line segment joining \((2,-3)\) and \((5,6)\)?

Answer: Let the given points be \(A(2,-3)\) and \(B(5,6)\). Let \(A B\) be divided by the \(X\)-axis at \(P(x, 0)\) in the ratio \(\lambda: 1\) internally. Considering the ordinate of \(P\), then
\(
\begin{array}{l}
0=\frac{\lambda \times 6+1 \times(-3)}{\lambda+1} \\
\lambda=\frac{1}{2}
\end{array}
\)
\(\therefore\) The ratio is \(\frac{1}{2}: 1\) i.e. \(1: 2\) (Internally)

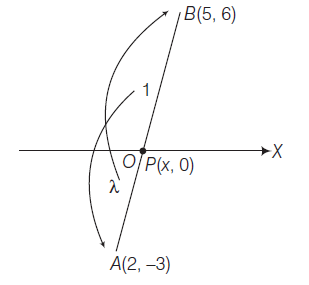
Shortcut Method

According to Important points :
\(
\frac{\lambda}{1}=-\frac{y_1}{y_2}=\frac{-(-3)}{6}=\frac{1}{2}
\)
\(\therefore\) The ratio is \(\frac{1}{2}: 1\) i.e. \(1: 2\) (internally)

Example 25: The mid-points of the sides of a triangle are \((1,2),(0,-1)\) and \((2,-1)\). Find the coordinates of the vertices of a triangle with the help of two unknowns.

Answer: Let \(D(1,2), E(0,-1)\) and \(F(2,-1)\) be the mid-points of \(B C, C A\) and \(A B\) respectively.
Let the coordinates of \(A\) be \((\alpha, \beta)\) then coordinates of \(B\) and \(C\) are \((4-\alpha,-2-\beta)\) and \((-\alpha,-2-\beta)\) respectively (see important point)
\(\because D\) is the mid-point of \(B\) and \(C\)

\(
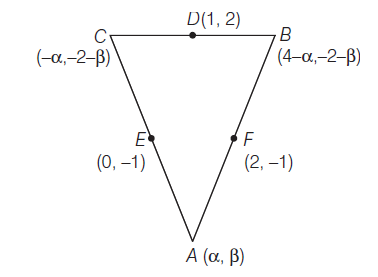
\text { then } \quad 1=\frac{4-\alpha-\alpha}{2}
\)
\(
\begin{array}{l}
1=2-\alpha \text { or } \alpha=1 \\
2=\frac{-2-\beta-2-\beta}{2} \\
2=-2-\beta \text { or } \beta=-4
\end{array}
\)
Hence, coordinates of \(A, B\) and \(C\) are \((1,-4),(3,2)\) and \((-1,2)\) respectively.

Example 26: Prove that in a right angled triangle the mid-point of the hypotenuse is equidistant from its vertices.

Answer: Let the given right angled triangle be \(A B C\), with right angled at \(B\). We take \(B\) as the origin and \(B A\) and \(B C\) as the \(X\) and \(Y\)-axes respectively.
Let \(B A=a\) and \(B C=b\)
then \(A \equiv(a, 0)\) and \(C \equiv(0, b)\)
Let \(M\) to be the mid-point of the hypotenuse \(A C\), then coordinates of \(M\) are \(\left(\frac{a}{2}, \frac{b}{2}\right)\)

\(
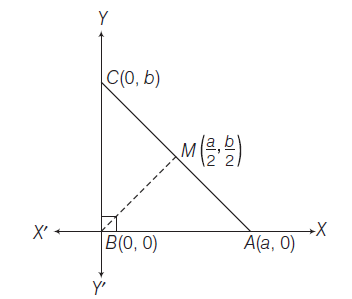
|A M|=\sqrt{\left(a-\frac{a}{2}\right)^2+\left(0-\frac{b}{2}\right)^2}=\frac{\sqrt{\left(a^2+b^2\right)}}{2} \dots(i)
\)
\(
|B M|=\sqrt{\left(0-\frac{a}{2}\right)^2+\left(0-\frac{b}{2}\right)^2}=\frac{\sqrt{\left(a^2+b^2\right)}}{2} \dots(ii)
\)
\(
\text { and } \quad|C M|=\sqrt{\left(0-\frac{a}{2}\right)^2+\left(b-\frac{b}{2}\right)^2}=\frac{\sqrt{\left(a^2+b^2\right)}}{2} \dots(iii)
\)
From Eqs. (i), (ii) and (iii), we get
\(
|A M|=|B M|=|C M|
\)

Example 27: Show that the line joining the mid-points of any two sides of a triangle is half the third side.

Answer: We take \(O\) as the origin and \(O C\) and \(O Y\) as the \(X\) and \(Y\)-axes respectively.

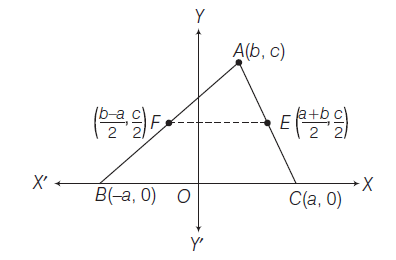
Let \(B C=2 a\), then \(B \equiv(-a, 0), C \equiv(a, 0)\)
Let \(A \equiv(b, c)\), if \(E\) and \(F\) are the mid-points of sides \(A C\) and \(A B\) respectively.
Then,
\(
E \equiv\left(\frac{a+b}{2}, \frac{c}{2}\right) \text { and } F \equiv\left(\frac{b-a}{2}, \frac{c}{2}\right)
\)
Now,
\(
\begin{aligned}
F E & =\sqrt{\left(\frac{a+b}{2}-\frac{b-a}{2}\right)^2+\left(\frac{c}{2}-\frac{c}{2}\right)^2}=a \\
& =\frac{1}{2}(2 a)=\frac{1}{2}(B G)
\end{aligned}
\)
Hence, the line joining the mid-points of any two sides of a triangle is half the third side.

Case-II: Formula for External Division

Theorem : If the point \(P(x, y)\) divides the line joining the points \(A\left(x_1, y_1\right)\) and \(B\left(x_2, y_2\right)\) externally in the ratio \(m: n\) then prove that
\(
x=\frac{m x_2-n x_1}{m-n}, y=\frac{m y_2-n y_1}{m-n}
\)
Proof : The given points are \(A\left(x_1, y_1\right)\) and \(B\left(x_2, y_2\right)\). Let us assume that the points \(A\) and \(B\) are both in the 1st quadrant (for the sake of exactness). Let \(P(x, y)\) be the point which divides \(A B\) externally in the ratio \(m: n\), so that \(\frac{A P}{B P}=\frac{m}{n}\)

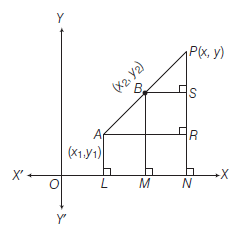
From \(A, B\) and \(P\) draw \(A L, B M\) and \(P N\) perpendiculars on \(X\)-axis. Also, from \(A\) and \(B\) draw \(A R\) and \(B S\) perpendiculars on \(P N\),
then
\(
\begin{array}{l}
A R=L N=O N-O L=x-x_1 \\
B S=M N=O N-O M=x-x_2 \\
P R=P N-R N=P N-A L=y-y_1 \\
P S=P N-S N=P N-B M=y-y_2
\end{array}
\)
Clearly, the \(\triangle ‘s A P R\) and \(B P S\) are similar and therefore their sides are proportional.
\(
\begin{array}{ll}
\therefore & \frac{A P}{P B}=\frac{A R}{B S}=\frac{P R}{P S} \\
\text { or } & \frac{m}{n} \dots(i)=\frac{x-x_1}{x-x_2} \dots(ii)=\frac{y-y_1}{y-y_2} \dots(iii)
\end{array}
\)
From Eqs. (i) and (ii), we have
\(
\frac{m}{n}=\frac{x-x_1}{x-x_2}
\)
\(
\begin{aligned}
m x-m x_2 & =n x-n x_1 \\
(m-n) x & =m x_2-n x_1 \\
x & =\frac{m x_2-n x_1}{m-n}
\end{aligned}
\)
Also, from Eqs. (i) and (iii), we have
\(
\begin{array}{c}
\frac{m}{n}=\frac{y-y_1}{y-y_2} \\
m y-m y_2=n y-n y_1 \\
(m-n) y=m y_2-n y_1 \\
y=\frac{m y_2-n y_1}{m-n}
\end{array}
\)
\(
\text { Thus, the coordinates of } P \text { are }\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}\right) \text {. } \text { (Here, } m \neq n \text { ) }
\)

Points to Remember

• Corollary 1 : The above formula is true for all positions of the points, keeping in mind, the proper signs of their coordinates.
• Corollary 2 : The above coordinates can also be expressed as
  \(
  \left(\frac{m x_2+(-n) x_1}{m+(-n)}, \frac{m y_2+(-n) y_1}{m+(-n)}\right)
  \)
  and this can be thought of as the coordinates of the point dividing \(A B\) internally in the ratio \(m:-n\)
• Corollary \(3: \because \quad \frac{A P}{P B}=\frac{m}{n}\)

       

\(
\begin{aligned}
\frac{A P}{P B}-1 & =\frac{m}{n}-1 \\
\frac{A P-P B}{P B} & =\frac{m-n}{n} \\
\frac{A B}{P B} & =\frac{m-n}{n}
\end{aligned}
\)
Now, we can say that \(B\) divides \(A P\) in the ratio \(m-n: n\) internally.
i.e. \(\quad x_2=\frac{(m-n) x+n x_1}{(m-n)+n} \Rightarrow x=\frac{m x_2-n x_1}{m-n}\)
and \(\quad y_2=\frac{(m-n) y+n y_1}{(m-n)+n} \Rightarrow y=\frac{m y_2-n y_1}{m-n}\)

• Corollary 4 : (for proving \(A, B\) and \(C\) are collinear)
  If \(A, B, C\) three points are collinear then let \(C\) divides \(A B\) in the ratio \(\lambda: 1\) internally.
  If \(\lambda=+\) ve rational, then divide internally and if \(\lambda=-\) ve rational, then divide externally.
• Let \(\frac{m}{n}=\lambda\), then \(\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}\right)\) or \(\left(\frac{\frac{m}{n} x_2-x_1}{\frac{m}{n}-1}, \frac{\frac{m}{n} y_2-y_1}{\frac{m}{n}-1}\right)\) or \(\left(\frac{\lambda x_2-x_1}{\lambda-1}, \frac{\lambda y_2-y_1}{\lambda-1}\right)\)

Example 28: Find the coordinates of a point which divides externally the line joining \((1,-3)\) and \((-3,9)\) in the ratio \(1: 3\).

Answer: Let the coordinates of the required point be \(P(x, y)\), Then,
\(
\begin{array}{l}
x=\left(\frac{1 \times(-3)-3 \times 1}{1-3}\right) \\
y=\left(\frac{1 \times 9-3 \times(-3)}{1-3}\right)
\end{array}
\)
i.e. \(\quad x=3\) and \(y=-9\)
Hence, the required point is \((3,-9)\).

Example 29: The line segment joining \(A(6,3)\) to \(B(-1,-4)\) is doubled in length by having its length added to each end. Find the coordinates of the new ends.

Answer:

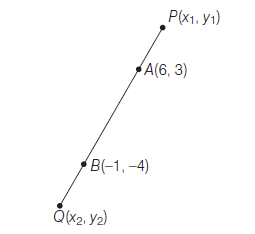
Let \(P\) and \(Q\) be the required new ends
Let the coordinates of \(P\) be \(\left(x_1, y_1\right)\)
\(
\begin{aligned}
\text { Given, } & & A B=2 A P \\
\Rightarrow & & \frac{A B}{A P}=\frac{2}{1}
\end{aligned}
\)
i.e. \(A\) divides \(B P\) internally in the ratio \(2: 1\). Then, \(\quad 6=\frac{2 \times x_1+1 \times(-1)}{2+1}\)
\(
\begin{aligned}
19 & =2 x_1 \text { or } x_1=\frac{19}{2} \\
3 & =\frac{2 \times y_1+1 \times(-4)}{2+1} \\
13 & =2 y_1 \text { or } y_1=\frac{13}{2}
\end{aligned}
\)
\(\therefore\) Coordinates of \(P\) are \(\left(\frac{19}{2}, \frac{13}{2}\right)\)
Also, let coordinates of \(Q\) be \(\left(x_2, y_2\right)\)
Given,
\(
A B=2 B Q \Rightarrow \frac{A B}{B Q}=\frac{2}{1}
\)
i.e. \(B\) divides \(A Q\) internally in the ratio \(2: 1\)
\(
\begin{array}{ll}
\text { Then } & -1=\frac{2 \times x_2+1 \times 6}{2+1} \\
\Rightarrow & -9=2 x_2 \text { or } x_2=-\frac{9}{2} \\
\text { and } & -4=\frac{2 \times y_2+1 \times 3}{2+1} \\
\Rightarrow & -15=2 y_2 \text { or } y_2=-\frac{15}{2}
\end{array}
\)
\(
\therefore \text { Coordinates of } Q \text { are }\left(-\frac{9}{2},-\frac{15}{2}\right)
\)

Example 30: Using section formula show that the points \((1,-1),(2,1)\) and \((4,5)\) are collinear.

Answer: 

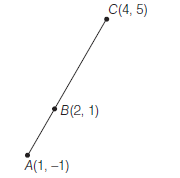
Let \(A \equiv(1,-1), B \equiv(2,1)\) and \(C \equiv(4,5)\)
Suppose \(C\) divides \(A B\) in the ratio \(\lambda: 1\) internally, then
\(
4=\frac{\lambda \times 2+1 \times 1}{\lambda+1}
\)
\(
\begin{array}{c}
4 \lambda+4=2 \lambda+1 \\
\lambda=-\frac{3}{2}
\end{array}
\)
i.e. \(C\) divides \(A B\) in the ratio \(3: 2\) (externally).
Hence, \(A, B, C\) are collinear.

Example 31: Find the ratio in which the point \((2, y)\) divides the line segment joining \((4,3)\) and \((6,3)\) and hence find the value of \(y\).

Answer: 

Let \(A \equiv(4,3), B \equiv(6,3)\) and \(P \equiv(2, y)\)
Let \(P\) divides \(A B\) internally in the ratio \(\lambda: 1\) then,
\(
2=\frac{6 \lambda+4}{\lambda+1} \Rightarrow 2 \lambda+2=6 \lambda+4
\)
\(
\Rightarrow \quad-4 \lambda=2 \text { or } \lambda=-\frac{1}{2}
\)
\(\therefore \quad P\) divides \(A B\) externally in the ratio \(1: 2(\because \lambda\) is negative \()\) Now, \(y=\frac{1 \times 3-2 \times 3}{1-2}=3\)

Case-III: Harmonic Conjugates

If four points in a line, then the system is said to form a range. Let four points say \(P, Q, R, S\).
If the range \((P Q, R S)\) has a cross ratio equal to -1 , then it is called harmonic.
i.e. \(\quad \frac{P R}{R Q} \cdot \frac{S Q}{S P}=-1 \Rightarrow \frac{P R}{R Q}=-\frac{S P}{S Q}=\lambda\)
\(\therefore \quad \frac{P R}{R Q}=\frac{\lambda}{1} \Rightarrow P R: R Q=\lambda: 1 \quad\) (internally)
and \(\quad \frac{S P}{S Q}=-\frac{\lambda}{1} \Rightarrow P S: S Q=\lambda: 1 \quad\) (externally)

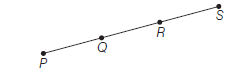
Hence, \(R\) and \(S\) are called the harmonic conjugates to each other with respect to the points \(P\) and \(Q\).

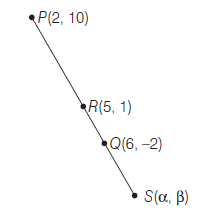
Example 32: Find the harmonic conjugates of the point \(R(5,1)\) with respect to the points \(P(2,10)\) and \(Q(6,-2)\).

Answer: Let \(S(\alpha, \beta)\) (be the harmonic conjugates of the point \(R(5,1)\) ). Suppose \(R\) divides \(P Q\) in the ratio \(\lambda: 1\) internally, then \(S\) divides \(P Q\) in the ratio \(\lambda: 1\) externally, then

\(
\begin{array}{l}
5=\frac{6 \lambda+2}{\lambda+1} \Rightarrow 5 \lambda+5=6 \lambda+2 \\
\therefore \quad \lambda=3 \\
\text { Also, } \quad 1=\frac{-2 \lambda+10}{\lambda+1} \\
\lambda+1=-2 \lambda+10 \Rightarrow 3 \lambda=9 \\
\therefore \quad \lambda=3 \\
\text { Now, } \quad \alpha=\frac{3 \times 6-1 \times 2}{3-1}=8 \\
\beta=\frac{3 \times(-2)-1 \times 10}{3-1} \\
=-8 \\
\end{array}
\)
Hence, harmonic conjugates of \(R(5,1)\) is \(S(8,-8)\).

Centroid of a Triangle

Definition : The point of intersection of the medians of a triangle is called the centroid of the triangle and it divides the median internally in the ratio \(2: 1\).
Theorem : Prove that the coordinates of the centroid of the triangle whose vertices are \(\left(x_1, y_1\right),\left(x_2, y_2\right)\) and \(\left(x_3, y_3\right)\) are
\(
\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)
\)
Also, deduce that the medians of a triangle are concurrent.
Proof : Let \(A \equiv\left(x_1, y_1\right), B \equiv\left(x_2, y_2\right)\) and \(C \equiv\left(x_3, y_3\right)\) be the vertices of the triangle \(A B C\). Let us assume that the points \(A, B\) and \(C\) are in the 1st quadrant (for the sake of exactness) whose medians are \(A D, B E\) and \(C F\) respectively so \(D, E\) and \(F\) are respectively the mid-points of \(B C, C A\) and \(A B\) then the coordinates of \(D, E, F\) are
\(
\begin{array}{l}
D \equiv\left(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2}\right) \\
E \equiv\left(\frac{x_3+x_1}{2}, \frac{y_3+y_1}{2}\right) \\
F \equiv\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)
\end{array}
\)

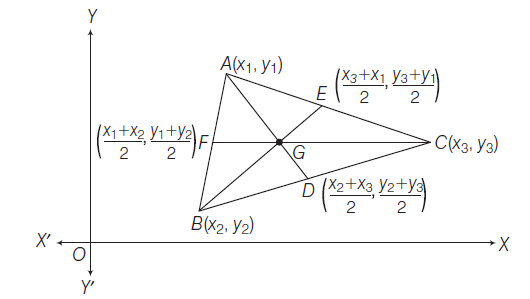
The coordinates of a point dividing \(A D\) in the ratio \(2: 1\) are
\(
\left(\frac{2 \cdot\left(\frac{x_2+x_3}{2}\right)+1 \cdot x_1}{2+1}, \frac{2 \cdot\left(\frac{y_2+y_3}{2}\right)+1 \cdot y_1}{2+1}\right)
\)
\(
\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)
\)
and the coordinates of a point dividing \(B E\) in the ratio \(2: 1\) are
\(
\left(\frac{2 \cdot\left(\frac{x_3+x_1}{2}\right)+1 \cdot x_2}{2+1}, \frac{2 \cdot\left(\frac{y_3+y_1}{2}\right)+1 \cdot y_2}{2+1}\right)
\)
\(
\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)
\)
Similarly the coordinates of a point dividing \(C F\) in the ratio \(2: 1\) are
\(
\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)
\)
\(\therefore\) The common point which divides \(A D, B E\) and \(C F\) in the ratio \(2: 1\) is
\(
\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)
\)
Hence, medians of a triangle are concurrent and the coordinates of the centroid are
\(
\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)
\)

Important Theorem

Centroid of the triangle obtained by joining the middle points of the sides of a triangle is the same as the centroid of the original triangle.

Or If \(\left(a_1, b_1\right),\left(a_2, b_2\right)\) and \(\left(a_3, b_3\right)\) are the mid-points of the sides of a triangle, then its centroid is given by
\(
\left(\frac{a_1+a_2+a_3}{3}, \frac{b_1+b_2+b_3}{3}\right)
\)

Proof : Let \(D, E, F\) are the mid-points of \(B C, C A\) and \(A B\) respectively now let coordinates of \(A\) are \((\alpha, \beta)\) then coordinates of \(B\) and \(C\) are \(\left(2 a_3-\alpha, 2 b_3-\beta\right)\) and \(\left(2 a_2-\alpha, 2 b_2-\beta\right)\) are respectively.

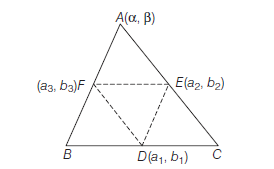
\(\because D\left(a_1, b_1\right)\) is the mid-point of \(B\) and \(C\), then
\(
\quad \begin{array}{l}
2 a_1=2 a_3-\alpha+2 a_2-\alpha \Rightarrow \alpha=a_2+a_3-a_1 \\
2 b_1=2 b_3-\beta+2 b_2-\beta \Rightarrow \beta=b_2+b_3-b_1
\end{array}
\)
Now, coordinates of \(B\) are \(\left(2 a_3-\alpha, 2 b_3-\beta\right)\)
\(
\left(a_3+a_1-a_2, b_3+b_1-b_2\right)
\)
and coordinates of \(C\) are \(\left(2 a_2-\alpha, 2 b_2-\beta\right)\)
\(
\left(a_2+a_1-a_3, b_2+b_1-b_3\right)
\)
Hence, coordinates of \(A, B\) and \(C\) are
\(
\begin{array}{l}
A \equiv\left(a_2+a_3-a_1, b_2+b_3-b_1\right), \\
B \equiv\left(a_3+a_1-a_2, b_3+b_1-b_2\right) \\
C \equiv\left(a_2+a_1-a_3, b_2+b_1-b_3\right)
\end{array}
\)
\(\therefore\) Coordinates of centroid of triangle \(A B C\) are
\(
\begin{array}{l}
\left(\frac{a_1+a_2+a_3}{3}, \frac{b_1+b_2+b_3}{3}\right)
\end{array}
\)
which is same as the centroid of triangle \(D E F\).

Corollary 1 (Finger Rule) : If mid-points of the sides of a triangle are \(\left(x_1, y_1\right),\left(x_2, y_2\right)\) and \(\left(x_3, y_3\right)\), then coordinates of the original triangle are
\(
\begin{array}{ll}
& \left(x_2+x_3-x_1, y_2+y_3-y_1\right), \\
& \left(x_3+x_1-x_2, y_3+y_1-y_2\right) \\
\text { and } \quad & \left(x_1+x_2-x_3, y_1+y_2-y_3\right) \text {. }
\end{array}
\)

Corollary 2 : If two vertices of a triangle are \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) and the coordinates of centroid are \((\alpha, \beta)\), then coordinates of the third vertex are
\(
\left(3 \alpha-x_1-x_2, 3 \beta-y_1-y_2\right)
\)

Corollary 3 : According to important theorem \(\triangle s A B C\) and \(D E F\) are similar
\(
\begin{aligned}
\therefore \quad \frac{\text { Area of } \triangle A B C}{\text { Area of } \triangle D E F} & =\frac{(B C)^2}{(E F)^2} \\
& =\frac{4\left\{\left(a_2-a_3\right)^2+\left(b_2-b_3\right)^2\right\}}{\left\{\left(a_2-a_3\right)^2+\left(b_2-b_3\right)^2\right\}}=4
\end{aligned}
\)
\(\therefore \quad\) Area of \(\triangle A B C=4 \times\) Area of \(\triangle D E F\)
i.e. Area of a triangle is four times the area of the triangle formed by joining the mid-points of its sides.

Example 33: Two vertices of a triangle are \((-1,4)\) and \((5,2)\). If its centroid is \((0,-3)\), find the third vertex.

Answer: Let the third vertex be \((x, y)\) then the coordinates of the centroid of triangle are
\(
\left(\frac{-1+5+x}{3}, \frac{4+2+y}{3}\right) \text { i.e. }\left(\frac{4+x}{3}, \frac{6+y}{3}\right)
\)
Now, \(\left(\frac{4+x}{3}, \frac{6+y}{3}\right)=(0,-3)\)
\(\Rightarrow \quad \frac{4+x}{3}=0\) and \(\frac{6+y}{3}=-3\)
\(\Rightarrow \quad 4+x=0\) and \(y+6=-9\)
or \(\quad x=-4\) and \(y=-15\)
Hence, the third vertex is \((-4,-15)\).

Shortcut Method

According to corollary 2
\(
\begin{aligned}
(x, y) & =(3 \times 0-(-1)-5,3 \times(-3)-4-2) \\
& =(-4,-15)
\end{aligned}
\)

Example 34: The vertices of a triangle are \((1,2),(h,-3)\) and \((-4, k)\). Find the value of \(\sqrt{\left\{(h+k)^2+(h+3 k)^2\right\}}\). If the centroid of the triangle be at the point \((5,-1)\).

Answer: Here, \(\quad \frac{1+h-4}{3}=5\) and \(\frac{2-3+k}{3}=-1\) then, we get \(h=18, k=-2\)
\(
\begin{aligned}
\therefore \quad & \sqrt{(h+k)^2+(h+3 k)^2} \\
& =\sqrt{(18-2)^2+(18-6)^2} \\
& =\sqrt{\left(16^2+12^2\right)}=20
\end{aligned}
\)

Example 35: If \(D(-2,3), E(4,-3)\) and \(F(4,5)\) are the mid-points of the sides \(B C, C A\) and \(A B\) of triangle \(A B C\), then find \(\sqrt{\left(|A G|^2+|B G|^2-|C G|^2\right)}\) where, \(G\) is the centroid of \(\triangle A B C\).

Answer: Let the coordinates of \(A\) be \((\alpha, \beta)\) then coordinates of \(B\) are \((8-\alpha, 10-\beta)\) and coordinates of \(C\) are \((8-\alpha,-6-\beta)\)

\(\because D\) is the mid-point of \(B C\), then

\(\begin{array}{ll} & \frac{8-\alpha+8-\alpha}{2}=-2 \\ \text { and } & \frac{10-\beta-6-\beta}{2}=3 \\ \text { i.e. } \quad \alpha=10 \text { and } \beta=-1\end{array}\)

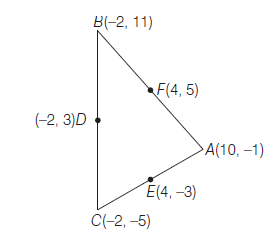
\(\therefore\) Coordinates of \(A, B, C\) are \((10,-1),(-2,11)\) and \((-2,-5)\) respectively.
Now, coordinates of centroid
\(
G \equiv\left(\frac{10-2-2}{3}, \frac{-1+11-5}{3}\right)
\)
i.e.
\(
G \equiv\left(2, \frac{5}{3}\right)
\)
\(
\begin{aligned}
\therefore \quad A G & =\sqrt{(10-2)^2+\left(-1-\frac{5}{3}\right)^2} \\
& =\sqrt{\left(64+\frac{64}{9}\right)}=\frac{8}{3} \sqrt{(10)}
\end{aligned}
\)
\(
\begin{aligned}
B G & =\sqrt{(-2-2)^2+\left(11-\frac{5}{3}\right)^2} \\
& =\sqrt{16+\frac{(28)^2}{9}}=\frac{4}{3} \sqrt{(58)}
\end{aligned}
\)
and
\(
\begin{aligned}
C G & =\sqrt{(-2-2)^2+\left(-5-\frac{5}{3}\right)^2} \\
& =\sqrt{\left(16+\frac{400}{9}\right)}=\frac{4}{3} \sqrt{(34)}
\end{aligned}
\)
Hence,
\(
\begin{array}{l}
\sqrt{\left(|A G|^2+|B G|^2-|C G|^2\right)} \\
=\sqrt{\left(\frac{64}{9} \times 10+\frac{16}{9} \times 58-\frac{16}{9} \times 34\right)} \\
=\sqrt{\frac{32}{9}(20+29-17)} \\
=\sqrt{\left(\frac{32}{9} \times 32\right)}=\frac{32}{3} \\
\end{array}
\)

Example 36: If \(G\) be the centroid of the \(\triangle A B C\) and \(O\) be any other point in the plane of the triangle \(A B C\), then show that \(O A^2+O B^2+O C^2=G A^2+G B^2+G C^2+3 G O^2\).

Answer: Let \(G\) be the origin and \(G O\) be \(X\)-axis.
\(
\begin{array}{l}
\quad O \equiv(a, 0), A \equiv\left(x_1, y_1\right), B \equiv\left(x_2, y_2\right) \\
\text { and } C \equiv\left(x_3, y_3\right) \\
\text { Now, LHS }=O A^2+O B^2+O C^2 \\
=\left(x_1-a\right)^2+y_1^2+\left(x_2-a\right)^2+y_2^2+\left(x_3-a\right)^2+y_3^2 \\
=\left(x_1^2+x_2^2+x_3^2\right)+\left(y_1^2+y_2^2+y_3^2\right) -2 a\left(x_1+x_2+x_3\right)+3 a^2
\end{array}
\)
\(
=\sum x_1^2+\sum y_1^2-0+3 a^2 \quad\left(\begin{array}{ll}
\because \frac{x_1+x_2+x_3}{3}=0 \\
\text { i.e., } x_1+x_2+x_3=0
\end{array}\right)
\)
\(
=\sum x_1^2+\sum y_1^2+3 a^2 \dots(i)
\)
\(
\begin{aligned}
\mathrm{RHS} & =G A^2+G B^2+G C^2+3 G O^2 \\
& =x_1^2+y_1^2+x_2^2+y_2^2+x_3^2+y_3^2+3\left\{(a-0)^2\right\} \\
& =\sum x_1^2+\sum y_1^2+3 a^2 \dots(ii)
\end{aligned}
\)
Hence, from Eqs. (i) and (ii), we get
\(
O A^2+O B^2+O C^2=G A^2+G B^2+G C^2+3 G O^2
\)

Example 37: If \(G\) be the centroid of \(\triangle A B C\), show that
\(
A B^2+B C^2+C A^2=3\left(G A^2+G B^2+G C^2\right) .
\)

Answer: We take \(B\) as the origin and \(B C\) and \(B Y\) as the \(X\) and \(Y\)-axes respectively.

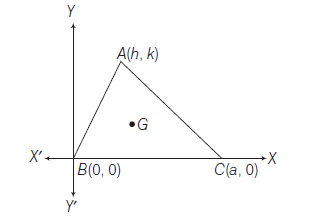
Let \(\quad B C=a\), then \(B \equiv(0,0)\) and \(C \equiv(a, 0)\) and let \(A \equiv(h, k)\) then, coordinates of \(G\) will be
\(
\left(\frac{h+0+a}{3}, \frac{k+0+0}{3}\right) \text {, i.e. }\left(\frac{h+a}{3}, \frac{k}{3}\right)
\)
Take \(\triangle A B C\) as in 1st quadrant (for the sake of exactness).
Now,
\(
\begin{aligned}
\text { LHS } & =(A B)^2+(B C)^2+(C A)^2 \\
& =(h-0)^2+(k-0)^2+a^2+(h-a)^2+(k-0)^2 \\
& =2 h^2+2 k^2-2 a h+2 a^2 \dots(i)
\end{aligned}
\)
\(
\mathrm{RHS}=3\left((G A)^2+(G B)^2+(G C)^2\right)
\)
\(
=3\left\{\left(\frac{a+h}{3}-h\right)^2+\left(\frac{k}{3}-k\right)^2+\left(\frac{a+h}{3}-0\right)^2\right.
\)
\(
\left.+\left(\frac{k}{3}-0\right)^2+\left(\frac{a+h}{3}-a\right)^2+\left(\frac{k}{3}-0\right)^2\right\}
\)
\(
\begin{aligned}
=\frac{3}{9}\left\{(a-2 h)^2+(-2 k)^2+(a+h)^2+\right. & k^2 \\
& \left.+(h-2 a)^2+k^2\right\}
\end{aligned}
\)
\(
\begin{array}{l}
=\frac{1}{3}\left\{6 a^2+6 h^2+6 k^2-6 a h\right\} \\
=2 h^2+2 k^2-2 a h+2 a^2 \dots(ii)
\end{array}
\)
Hence, from Eqs. (i) and (ii), we get
\(
A B^2+B C^2+C A^2=3\left(G A^2+G B^2+G C^2\right)
\)

Example 38: The vertices of a triangle are \((1, a),(2, b)\) and \(\left(c^2,-3\right)\)
(i) Prove that its centroid can not lie on the \(Y\)-axis.
(ii) Find the condition that the centroid may lie on the \(x\)-axis.

Answer: Centroid of the triangle is
\(
G \equiv\left(\frac{1+2+c^2}{3}, \frac{a+b-3}{3}\right) \text { i.e. }\left(\frac{3+c^2}{3}, \frac{a+b-3}{3}\right)
\)
(i) \(\because G\) will lie on \(Y\)-axis, then
\(
\begin{array}{rlrl}
& \frac{3+c^2}{3} & =0 \\
\Rightarrow & c^2 & =-3 \\
& \text { or } & c & = \pm i \sqrt{3}
\end{array}
\)
\(\because\) Both values of \(c\) are imaginary.
Hence, \(G\) can not lie on \(Y\)-axis.
(ii) \(\because G\) will lie on \(X\)-axis, then \(\frac{a+b-3}{3}=0\)
\(
\begin{array}{l}
\Rightarrow \quad a+b-3=0 \\
\text { or } \\
a+b=3 \\
\end{array}
\)

Incentre

Definition : The point of intersection of internal angle bisectors of triangle is called the incentre of the triangle.
Theorem : Prove that the coordinates of the incentre of a triangle whose vertices are \(A\left(x_1, y_1\right), B\left(x_2, y_2\right), C\left(x_3, y_3\right)\) are
\(
\left(\frac{a x_1+b x_2+c x_3}{a+b+c}, \frac{a y_1+b y_2+c y_3}{a+b+c}\right)
\)
where, \(a, b, c[latex] are the lengths of sides [latex]B C, C A\) and \(A B\) respectively.
Also, prove that the internal bisectors of the angles of a triangle are concurrent.

Proof : Given \(A \equiv\left(x_1, y_1\right), B\left(x_2, y_2\right), C \equiv\left(x_3, y_3\right)\) be the vertices of \(\triangle A B C\) and \(B C=a, C A=b\) and \(A B=c\). Let \(A D\) be the bisector of \(A\). We know that the bisector of an angle of a triangle divides the opposite side in the ratio of the sides containing the triangle.
\(
\therefore \quad \frac{B D}{D C}=\frac{A B}{A C}=\frac{c}{b} \dots(i)
\)

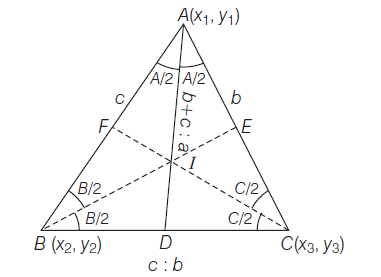
Hence, \(D\) divides \(B C\) in the ratio \(c: b\)
\(\therefore\) Coordinates of \(D\) are \(\left(\frac{c x_3+b x_2}{c+b}, \frac{c y_3+b y_2}{c+b}\right)\)
From Eq. (i), \(\quad \frac{D C}{B D}=\frac{b}{c}\) or \(\frac{D C}{B D}+1=\frac{b}{c}+1\)
\(
\frac{D C+B D}{B D}=\left(\frac{b+c}{c}\right) \text { or } \frac{a}{B D}=\left(\frac{b+c}{c}\right)
\)
\(\therefore \quad B D=\frac{a c}{(b+c)}\)
Also, in \(\triangle A B D, B I\) is the bisector of \(B\).
Then,
\(
\frac{A I}{I D}=\frac{A B}{B D}=\frac{c}{\left(\frac{a c}{b+c}\right)}=\frac{b+c}{a}
\)
\(\therefore\) I divides \(A D\) in the ratio \(b+c: a\)
\(\therefore\) Coordinates of \(I\) are
\(
\begin{array}{l}
\left(\frac{(b+c) \cdot \frac{c x_3+b x_2}{c+b}+a \cdot x_1}{b+c+a}, \frac{(b+c) \cdot \frac{c y_3+b y_2}{c+b}+b \cdot y_1}{b+c+a}\right) \\
\text { i.e. } \quad\left(\frac{a x_1+b x_2+c x_3}{a+b+c}, \frac{a y_1+b y_2+c y_3}{a+b+c}\right)
\end{array}
\)
Similarly we can show that the coordinates of the point which divides \(B E\) internally in the ratio \(c+a: b\) and the coordinates of the point which divides \(C F\) internally in the ratio \(a+b: c\) will be each
\(
\left(\frac{a x_1+b x_2+c x_3}{a+b+c}, \frac{a y_1+b y_2+c y_3}{a+b+c}\right)
\)
and
\(
\begin{array}{l}
C E=\frac{a b}{(c+a)}, A E=\frac{b c}{(c+a)}, \\
A F=\frac{b c}{a+b}, B F=\frac{a c}{a+b}
\end{array}
\)
Thus, the three internal bisectors of the angles of a triangle meet in a point \(I\).
\(
I \equiv\left(\frac{a x_1+b x_2+c x_3}{a+b+c}, \frac{a y_1+b y_2+c y_3}{a+b+c}\right)
\)

Corollary 1 : If \(\triangle A B C\) is equilateral, then \(a=b=c\) incentre \(=\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)=\) centroid i.e. incentre and centroid coincide in equilateral, triangle.

Corollary 2 :

\(
\begin{aligned}
A E & =A F=s-a \\
B D & =B F=s-b \\
C D & =C E=s-c
\end{aligned}
\)

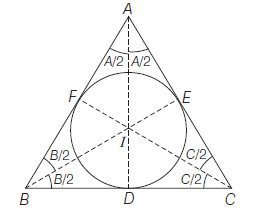
where, \(\quad s=\frac{a+b+c}{2}\)
and \(\quad|B C|=a,|C A|=b,|A B|=c\)
Proof : Let \(A E=A F=\alpha\) ( \(\because\) Lengths of tangents are equal from a point to a circle)
\(
\begin{aligned}
B D & =B F=\beta \\
C D & =C E=\gamma \\
a & =B C=B D+D C=\beta+\gamma \dots(i) \\
b & =C A=C E+A E=\gamma+\alpha \dots(ii) \\
c & =A B=A F+B F=\alpha+\beta \dots(iii)
\end{aligned}
\)
Adding all, we get
\(
\begin{aligned}
a+b+c & =2(\alpha+\beta+\gamma) \\
2 s & =2(\alpha+\beta+\gamma) \\
s & =\alpha+\beta+\gamma
\end{aligned}
\)
From Eqs. (i), (ii) and (iii), we get
\(
\alpha=s-a, \beta=s-b, \gamma=s-c
\)

Example 39: Find the coordinates of incentre of the triangle whose vertices are \((4,-2),(-2,4)\) and \((5,5)\).

Answer: Let \(A(4,-2), B(-2,4)\) and \(C(5,5)\) be the vertices of the given triangle. Then
\(
\begin{array}{l}
a=B C=\sqrt{(-2-5)^2+(4-5)^2}=\sqrt{50}=5 \sqrt{2} \\
b=C A=\sqrt{(5-4)^2+(5+2)^2}=\sqrt{50}=5 \sqrt{2} \\
c=A B=\sqrt{(4+2)^2+(-2-4)^2}=\sqrt{72}=6 \sqrt{2}
\end{array}
\)

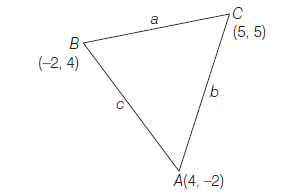
Let \((x, y)\) be the coordinates of incentre of \(\triangle A B C\). Then
\(
\begin{aligned}
x & =\frac{a x_1+b x_2+c x_3}{a+b+c} \\
& =\frac{5 \sqrt{2} \times 4+5 \sqrt{2} \times(-2)+6 \sqrt{2} \times 5}{5 \sqrt{2}+5 \sqrt{2}+6 \sqrt{2}} \\
& =\frac{20 \sqrt{2}-10 \sqrt{2}+30 \sqrt{2}}{16 \sqrt{2}} \\
& =\frac{40}{16}=\frac{5}{2} \\
y & =\frac{a y_1+b y_2+c y_3}{a+b+c} \\
& =\frac{5 \sqrt{2} \times(-2)+5 \sqrt{2} \times 4+6 \sqrt{2} \times 5}{5 \sqrt{2}+5 \sqrt{2}+6 \sqrt{2}} \\
& =\frac{40}{16}=\frac{5}{2}
\end{aligned}
\)
\(\therefore\) The coordinates of the incentre are \(\left(\frac{5}{2}, \frac{5}{2}\right)\)

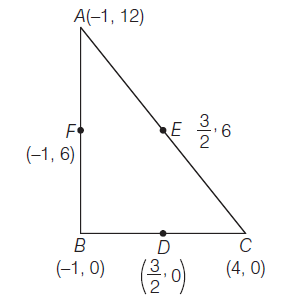
Example 40: If \(\left(\frac{3}{2}, 0\right),\left(\frac{3}{2}, 6\right)\) and \((-1,6)\) are mid-points of the sides of a triangle, then find
(i) Centroid of the triangle
(ii) Incentre of the triangle

Answer: Let \(A \equiv(\alpha, \beta)\), then coordinates of \(B \equiv(-2-\alpha, 12-\beta)\) and coordinates of \(C \equiv(3-\alpha, 12-\beta)\). But mid-point of \(B C\) is \(\left(\frac{3}{2}, 0\right)\)

\(
\begin{array}{ll}
\text { then } & 3=-2-\alpha+3-\alpha \\
\Rightarrow & \alpha=-1 \\
\text { and } & 0=12-\beta+12-\beta \\
\Rightarrow & \beta=12
\end{array}
\)
\(\therefore\) Coordinates of vertices are
\(
A \equiv(-1,12), B \equiv(-1,0) \text { and } C \equiv(4,0)
\)
(i) Centroid : The centroid of \(\triangle A B C\) is
\(
\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)
\)
\(
\left(\frac{-1-1+4}{3}, \frac{12+0+0}{3}\right) \text { i.e. }\left(\frac{2}{3}, 4\right)
\)
(ii) Incentre : We have
\(
\begin{array}{l}
a=B C=\sqrt{(-1-4)^2+(0-0)^2}=5 \\
b=C A=\sqrt{(4+1)^2+(0-12)^2}=13
\end{array}
\)
and \(\quad c=A B=\sqrt{(-1+1)^2+(12-0)^2}=12\)
\(\therefore\) The incentre of \(\triangle A B C\) is
\(
\begin{array}{c}
\left(\frac{a x_1+b x_2+c x_3}{a+b+c}, \frac{a y_1+b y_2+c y_3}{a+b+c}\right) \\
\text { or }\left(\frac{5 \times(-1)+13 \times(-1)+12 \times 4}{5+13+12}, \frac{5 \times 12+13 \times 0+12 \times 0}{5+13+12}\right)
\end{array}
\)
i.e. \((1,2)\)

Example 41: If a vertex of a triangle be \((1,1)\) and the middle points of two sides through it be \((-2,3)\) and \((5,2)\), then find the centroid and the incentre of the triangle.

Answer: Let coordinate of \(A\) be \((1,1)\) and mid-points of \(A B\) and \(A C\) are \(F\) and \(E\).
\(
\therefore \quad F \equiv(-2,3) \text { and } E \equiv(5,2)
\)

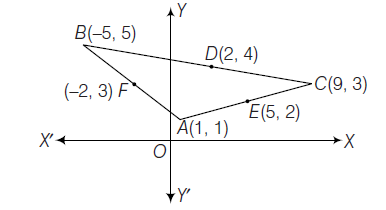
Hence, coordinates of \(B\) and \(C\) are \((2 \times(-2)-1,(2 \times 3-1)\) and \((2 \times 2-(-5), 2 \times 4-5)\) respectively.
i.e. \(B \equiv(-5,5)\) and \(C \equiv(9,3)\)
Then, centroid is \(\left(\frac{1-5+9}{3}, \frac{1+5+3}{3}\right)\) i.e., \(\left(\frac{5}{3}, 3\right)\)
\(
\begin{array}{ll}
\text { Also, } & a=|B C|=\sqrt{(-5-9)^2+(5-3)^2}=\sqrt{200}=10 \sqrt{2} \\
& b=|C A|=\sqrt{(9-1)^2+(3-1)^2}=\sqrt{68}=2 \sqrt{17} \\
\text { and } & c=|A B|=\sqrt{(1+5)^2+(1-5)^2}=\sqrt{52}=2 \sqrt{13}
\end{array}
\)
Then, incentre is
\(
\left(\frac{10 \sqrt{2} \times 1+2 \sqrt{17} \times(-5)+2 \sqrt{13} \times 9}{10 \sqrt{2}+2 \sqrt{17}+2 \sqrt{13}},\right. \left.\frac{10 \sqrt{2} \times 1+2 \sqrt{17} \times 5+2 \sqrt{13} \times 3}{10 \sqrt{2}+2 \sqrt{17}+2 \sqrt{13}}\right)
\)
\(
\text { i.e. } \quad\left(\frac{5 \sqrt{2}-5 \sqrt{17}+9 \sqrt{13}}{5 \sqrt{2}+\sqrt{17}+\sqrt{13}}, \frac{5 \sqrt{2}+5 \sqrt{17}+3 \sqrt{13}}{5 \sqrt{2}+\sqrt{17}+\sqrt{13}}\right)
\)

Example 42: If \(G\) be the centroid and \(I\) be the incentre of the triangle with vertices \(A(-36,7), B(20,7)\) and \(C(0,-8)\) and \(G I=\frac{25}{3} \sqrt{(205)} \lambda\), then find the value of \(\lambda\).

Answer: Coordinates of centroid are
\(
\begin{aligned}
G & \equiv\left(-\frac{16}{3}, 2\right) \\
a & =|B C|=\sqrt{(20-0)^2+(7+8)^2} \\
& =\sqrt{625}=25 \\
b & =|C A|=\sqrt{(0+36)^2+(-8-7)^2} \\
& =\sqrt{1521}=39 \\
c & =|A B|=\sqrt{(-36-20)^2+(7-7)^2} \\
& =\sqrt{(56)^2}=56
\end{aligned}
\)
Therefore, the coordinates of incentre are
\(
I \equiv\left(\frac{25 \times(-36)+39 \times 20+56 \times 0}{25+39+56}, \frac{25 \times 7+39 \times 7+56 \times(-8)}{25+39+56}\right)
\)
i.e., \(\quad I \equiv(-1,0)\)
\(\therefore \quad G I=\sqrt{\left(-\frac{16}{3}+1\right)^2+(2-0)^2}=\frac{\sqrt{(205)}}{3}\)
but given \(\quad G I=\frac{25}{3} \sqrt{(205)} \lambda\)
\(\therefore \quad \frac{1}{3} \sqrt{(205)}=\frac{25}{3} \sqrt{(205)} \lambda\)
\(\Rightarrow \quad \lambda=\frac{1}{25}\)

Excentres of a Triangle

This is the point of intersection of the external bisectors of the angles of a triangle.

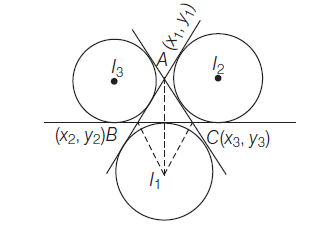
The circle opposite to the vertex \(A\) is called the escribed circle opposite \(A\) or the circle escribed to the side \(B C\). If \(I_1\) is the point of intersection of internal bisector of \(\angle B A C\) and external bisector of \(\angle A B C\) and \(\angle A C B\), then 
\(
\begin{array}{l}
I_1 \equiv\left(\frac{a x_1-b x_2-c x_3}{a-b-c}, \frac{a y_1-b y_2-c y_3}{a-b-c}\right) \\
I_1 \equiv\left(\frac{-a x_1+b x_2+c x_3}{-a+b+c}, \frac{-a y_1+b y_2+c y_3}{-a+b+c}\right)
\end{array}
\)
Similarly, \(\quad I_2 \equiv\left(\frac{a x_1-b x_2+c x_3}{a-b+c}, \frac{a y_1-b y_2+c y_3}{a-b+c}\right)\) and
\(
I_3 \equiv\left(\frac{a x_1+b x_2-c x_3}{a+b-c}, \frac{a y_1+b y_2-c y_3}{a+b-c}\right)
\)
where, \(|B C|=a,|C A|=b\) and \(|A B|=c\)

Example 43: If the coordinates of the mid-points of sides \(B C, C A\) and \(A B\) of triangle \(A B C\) are \((1,1),(2,-3)\) and \((3,4)\), then find the excentre opposite to the vertex \(A\).

Answer: Let \(D(1,1), E(2,-3)\) and \(F(3,4)\) are the mid-points of the sides of the triangle \(B C, C A\) and \(A B\) respectively. Let \(A \equiv(\alpha, \beta)\)

then \(B \equiv(6-\alpha, 8-\beta)\)
and \(C \equiv(4-\alpha,-6-\beta)\)
Also, \(D\) is the mid-point of \(B\) and \(C\), then
\(
\begin{array}{l}
1=\frac{6-\alpha+4-\alpha}{2} \Rightarrow \alpha=4 \\
\text { and } \quad 1=\frac{8-\beta-6-\beta}{2} \Rightarrow \beta=0 \\
\therefore \quad A \equiv(4,0), B \equiv(2,8) \text { and } C \equiv(0,-6) \text {, then } \\
a=|B C|=\sqrt{(2-0)^2+(8+6)^2}=\sqrt{200}=10 \sqrt{2} \\
b=|C A|=\sqrt{(0-4)^2+(-6-0)^2}=\sqrt{52}=2 \sqrt{13} \\
\text { and } \quad c=|A B|=\sqrt{(4-2)^2+(0-8)^2}=\sqrt{68}=2 \sqrt{17} \\
\end{array}
\)
Hence, the coordinates of the excentre opposite to \(A\) are
\(
\left(\frac{-a x_1+b x_2+c x_3}{-a+b+c}, \frac{a y_1+b y_2+c y_3}{-a+b+c}\right)
\)
\(
\text { i.e., } \quad\left(\frac{-10 \sqrt{2} \times 4+2 \sqrt{13} \times 2+2 \sqrt{17} \times 0}{-10 \sqrt{2}+2 \sqrt{13}+2 \sqrt{17}}\right. \text {, }\left.\frac{-10 \sqrt{2} \times 0+2 \sqrt{13} \times 8+2 \sqrt{17} \times(-6)}{-10 \sqrt{2}+2 \sqrt{13}+2 \sqrt{17}}\right)
\)
\(
\left(\frac{-20 \sqrt{2}+2 \sqrt{13}}{-5 \sqrt{2}+\sqrt{13}+\sqrt{17}}, \frac{8 \sqrt{13}-6 \sqrt{17}}{-5 \sqrt{2}+\sqrt{13}+\sqrt{17}}\right)
\)

Circumcentre of a Triangle

The circumcentre of a triangle is the point of intersection of the perpendicular bisectors of the sides of a triangle (i.e., the lines through the mid-point of a side and perpendicular to it). Let \(A\left(x_1, y_1\right), B\left(x_2, y_2\right)\) and \(C\left(x_3, y_3\right)\) be the vertices of \(\triangle A B C\) and if angles of \(\triangle A B C\) are given, then coordinates of circumcentre are

\(
\left(\frac{x_1 \sin 2 A+x_2 \sin 2 B+x_3 \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C},\right.\left.\frac{y_1 \sin 2 A+y_2 \sin 2 B+y_3 \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C}\right)
\)
\(
\left(\frac{a x_1 \cos A+b x_2 \cos B+c x_3 \cos C}{a \cos A+b \cos B+c \cos C},\right.\left.\frac{a y_1 \cos A+b y_2 \cos B+c y_3 \cos C}{a \cos A+b \cos B+c \cos C}\right)
\)
\(
\text { where, }|B C|=a,|C A|=b \text { and }|A B|=c
\)

Example 44: In a \(\triangle A B C\) with vertices \(A(1,2), B(2,3)\) and \(C(3,1)\) and \(\angle A=\angle B=\cos ^{-1}\left(\frac{1}{\sqrt{10}}\right)\), \(\angle C=\cos ^{-1}\left(\frac{4}{5}\right)\), then find the circumcentre of \(\triangle A B C\).

Answer: Since, \(\angle A=\angle B=\cos ^{-1}\left(\frac{1}{\sqrt{10}}\right)\)
\(
\Rightarrow \quad \cos A=\cos B=\frac{1}{\sqrt{10}}
\)
then, \(\quad \sin A=\sin B=\frac{3}{\sqrt{10}}\)
\(\therefore \quad \sin 2 A=\sin 2 B=2 \times \frac{3}{\sqrt{10}} \times \frac{1}{\sqrt{10}}=\frac{3}{5}\)
and \(\quad \angle C=\cos ^{-1}\left(\frac{4}{5}\right)\)
\(\Rightarrow \quad \cos C=\frac{4}{5}\) then, \(\sin C=\frac{3}{5}\)
\(\therefore \quad \sin 2 C=2 \times \frac{3}{5} \times \frac{4}{5}=\frac{24}{25}\)
Let the circumcenter be \((x, y)\), then
\(
\begin{aligned}
x & =\frac{x_1 \sin 2 A+x_2 \sin 2 B+x_3 \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C} \\
& =\frac{1 \times \frac{3}{5}+2 \times \frac{3}{5}+3 \times \frac{24}{25}}{\frac{3}{5}+\frac{3}{5}+\frac{24}{25}}=\frac{13}{6}
\end{aligned}
\)
\(
\begin{aligned}
y & =\frac{y_1 \sin 2 A+y_2 \sin 2 B+y_3 \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C} \\
& =\frac{2 \times \frac{3}{5}+3 \times \frac{3}{5}+1 \times \frac{24}{25}}{\frac{3}{5}+\frac{3}{5}+\frac{24}{25}}=\frac{11}{6}
\end{aligned}
\)
Hence, coordinates of circumcenter are \(\left(\frac{13}{6}, \frac{11}{6}\right)\).

Two Important Tricks for Circumcentre

• If angles of triangle \(A B C[latex] are not given and the vertices [latex]A\left(x_1, y_1\right), B\left(x_2, y_2\right)\) and \(C\left(x_3, y_3\right)\) are given, then the circumcentre of the \(\triangle A B C\) is given by
  \(
  \left(\frac{\left(x_1+x_2\right)+\lambda\left(y_1-y_2\right)}{2}, \frac{\left(y_1+y_2\right)-\lambda\left(x_1-x_2\right)}{2}\right)
  \)
  Here, we observe that
  \(
  \begin{array}{ll}
  & P=\left[\begin{array}{ll}
  x_1-x_3 & y_1-y_3 \\
  x_2-x_3 & y_2-y_3
  \end{array}\right] \\
  \therefore \quad & \lambda=\frac{\overrightarrow{\mathbf{R}}_1 \cdot \overrightarrow{\mathbf{R}}_2}{|P|}
  \end{array}
  \)
• If the angle \(C\) is given instead of coordinates of the vertex \(C\) and the vertices \(A\left(x_1, y_1\right), B\left(x_2, y_2\right)\) of \(\triangle A B C\) are given, then the circumcentre of \(\triangle A B C\) is given by
  \(
  \left(\frac{\left(x_1+x_2\right) \pm \cot C\left(y_1-y_2\right)}{2}, \frac{\left(y_1+y_2\right) \pm \cot C\left(x_1-x_2\right)}{2}\right)
  \)

Important Points to remember

Circumcentre of the right angled triangle \(A B C\), right angled at \(A\) is \(\frac{B+C}{2}\).

Example 45: Find the circumcentre of the triangle whose vertices are \((2,2),(4,2)\) and \((0,4)\).

Answer: Let the given points are \(\left(x_1, y_1\right),\left(x_2, y_2\right)\) and \(\left(x_3, y_3\right)\) respectively.
for the matrix
\(
\begin{aligned}
P & =\left[\begin{array}{ll}
x_1-x_3 & y_1-y_3 \\
x_2-x_3 & y_2-y_2
\end{array}\right]=\left[\begin{array}{ll}
2 & -2 \\
4 & -2
\end{array}\right] \\
\therefore \quad \lambda & =\frac{\overrightarrow{\mathbf{R}}_1 \cdot \overrightarrow{\mathbf{R}}_2}{|P|} \\
& =\frac{2 \times 4+(-2) \times(-2)}{2 \times(-2)-4 \times(-2)}=\frac{12}{4}=3
\end{aligned}
\)
\(\therefore\) Circumcentre of the triangle
\(
\begin{array}{l}
\equiv\left(\frac{\left(x_1+x_2\right)+\lambda\left(y_1-y_2\right)}{2}, \frac{\left(y_1+y_2\right)-\lambda\left(x_1-x_2\right)}{2}\right) \\
\equiv\left(\frac{2+4+3(2-2)}{2}, \frac{2+2-3(2-4)}{2}\right) \\
\equiv(3,5)
\end{array}
\)

Example 46: Find the circumcentre of triangle \(A B C\) if \(A \equiv(7,4), B \equiv(3,-2)\) and \(\angle C=\frac{\pi}{3}\).

Answer: Here, \(x_1=7, y_1=4, x_2=3, y_2=-2\) and \(\angle C=\frac{\pi}{3}\)
\(\therefore\) The circumcentre of \(\triangle A B C\)
\(
\begin{array}{l}
\equiv\left(\frac{\left(x_1+x_2\right) \pm \cot C\left(y_1-y_2\right)}{2}, \frac{\left(y_1+y_2\right) \mp \cot C\left(x_1-x_2\right)}{2}\right) \\
\equiv\left(\frac{(7+3) \pm \frac{1}{\sqrt{3}}(4+2)}{2}, \frac{(4-2) \mp \frac{1}{\sqrt{3}}(7-3)}{2}\right) \\
\equiv\left(5+\sqrt{3}, 1-\frac{2}{\sqrt{3}}\right) \text { or }\left(5-\sqrt{3}, 1+\frac{2}{\sqrt{3}}\right)
\end{array}
\)

Orthocentre of a Triangle

The orthocentre of a triangle is the point of intersection of altitudes (i.e., the lines through the vertices and perpendicular to opposite sides).
Let \(A\left(x_1, y_1\right), B\left(x_2, y_2\right)\) and \(C\left(x_3, y_3\right)\) be the vertices of \(\triangle A B C\) and if angles of \(\triangle A B C\) are given, then coordinates of orthocentre are

\(
\left(\frac{x_1 \tan A+x_2 \tan B+x_3 \tan C}{\tan A+\tan B+\tan C},\right.\left.\frac{y_1 \tan A+y_2 \tan B+y_3 \tan C}{\tan A+\tan B+\tan C}\right)
\)
\(
\left(\frac{a x_1 \sec A+b x_2 \sec B+c x_3 \sec C}{a \sec A+b \sec B+c \sec C},\right.\left.\frac{a y_1 \sec A+b y_2 \sec B+c y_3 \sec C}{a \sec A+b \sec B+c \sec C}\right)
\)
where, \(|B C|=a,|C A|=b\) and \(|A B|=c\)

Important trick for orthocentre :

Orthocentre of the triangle whose vertices are \((0,0),\left(x_1, y_1\right)\) is given by
\(
\begin{array}{l}
\left(\lambda\left(y_2-y_1\right),-\lambda\left(x_2-x_1\right)\right) \\
\text { where, } \lambda=\frac{x_1 x_2+y_1 y_2}{x_1 y_2-x_2 y_1}
\end{array}
\)
Important points to remember

• The orthocentre of a triangle having vertices \((\alpha, \beta),(\beta, \alpha)\) and \((\alpha, \alpha)\) is \((\alpha, \alpha)\).
• The orthocentre of a triangle having vertices is \(\left(-\frac{1}{\alpha \beta \gamma},-\alpha \beta \gamma\right)\)
• The orthocentre of right angled triangle \(A B C\), right angled at \(A\) is \(A\).

Example 47: Find the orthocentre of \(\triangle A B C\) if \(A \equiv(0,0), B \equiv(3,5)\) and \(C \equiv(4,7)\).

Answer: Here, \(x_1=3, y_1=5, x_2=4, y_2=7\)
\(
\begin{array}{c}
\therefore \quad \lambda=\frac{3 \times 4+5 \times 7}{3 \times 7-4 \times 5}=47 \\
\Rightarrow \text { Orthocentre of } \triangle A B C \equiv(47(7-5),-47(4-3)) \\
\equiv(94,-47)
\end{array}
\)

Nine Point Centre of a Triangle

If a circle passing through the feet of perpendiculars (i.e., \(D, E, F)\) mid-points of sides \(B C, C A, A B\) respectively (i.e., \(H, I, J)\) and the \(n x\) mid-points of the line joining the orthocentre \(O\) to the angular points \(A, B, C\) (i.e., \(K, L, M\) ) thus the nine points \(D, E, F, H, I, J, K, L, M\) all lie on a circle.

This circle is known as nine point circle and its centre is called the nine point centre. The nine-point centre of a triangle is collinear with the circumcentre and the orthocentre and bisects the segments joining them and radius of nine point circle of a triangle is half the radius of the circumcircle.

• Corollary 1 : The orthocentre, the nine point centre, the centroid and the circumcentre therefore all lie on a straight line.
• Corollary 2 : If \(O\) is orthocentre, \(N\) is nine point centre, \(G\) is centroid and \(C\) is circumcentre, then to remember it see ONGC (i.e. Oil Natural Gas Corporation) in left of \(G\) are 2 and in right is 1 , therefore \(G\) divides \(O\) and \(C\) in the ratio 2 : 1 (internally).
• Corollary 3 : \(N\) is the mid-point of \(O\) and \(C\)
• Corollary 4 : Radius of nine point circle \(=\frac{1}{2} \times\) Radius of circumcircle

Points to remember

• The distance between the orthocentre and circumcentre in an equilateral triangle is zero.
• If the circumcentre and centroid of a triangle are respectively \((\alpha, \beta)(\gamma, \delta)\) then orthocentre will be \((3 \gamma-2 \alpha, 3 \delta-2 \beta)\).

Example 48: If a triangle has its orthocentre at \((1,1)\) and circumcentre at \(\left(\frac{3}{2}, \frac{3}{4}\right)\), then find the centroid and nine point centre.

Answer: Since, centroid divides the orthocentre and circumcentre in the ratio \(2: 1\) (internally) and if centroid \(G(x, y)\), then

\(
\begin{array}{l}
x=\frac{2 \times \frac{3}{2}+1 \times 1}{2+1}=\frac{4}{3} \\
\text { and } \quad y=\frac{2 \times \frac{3}{4}+1 \times 1}{2+1}=\frac{5}{6}
\end{array}
\)
\(\therefore\) Centroid is \(\left(\frac{4}{3}, \frac{5}{6}\right)\) and nine point centre is the mid-point of orthocentre and circumcentre.
\(\therefore\) Nine point centre is \(\left(\frac{1+\frac{3}{2}}{2}, \frac{1+\frac{3}{4}}{2}\right)\), i.e. \(\left(\frac{5}{4}, \frac{7}{8}\right)\).

Area of a Triangle

Theorem : The area of a triangle, the coordinates of whose vertices \(\operatorname{are}\left(x_1, y_1\right),\left(x_2, y_2\right)\) and \(\left(x_3, y_3\right)\) is

Let \(A, B, C\) be the vertices of the triangle having \(\left(x_1, y_1\right),\left(x_2, y_2\right)\) and \(\left(x_3, y_3\right)\) as their respective co-ordinates. Draw \(A L, B M, C N\) perpendicular to the \(x\)-axis.
Then \(\triangle \mathrm{ABC}=\) trapezium ALNC + trapezium CNMB – trapezium ALMB
\(
\begin{array}{l}
=\frac{1}{2}(L A+N C) L N+\frac{1}{2}(N C+M B) N M-\frac{1}{2}(L A+M B) L M \\
=\frac{1}{2}\left(y_1+y_3\right)\left(x_3-x_1\right)+\frac{1}{2}\left(y_3+y_2\right)\left(x_2-x_3\right)-\frac{1}{2}\left(y_1+y_2\right)\left(x_2-x_1\right) \\
=\frac{1}{2}|\left\{x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right\}|
\end{array}
\)
\(
=\frac{1}{2}|\left|\begin{array}{lll}
\mathrm{x}_1 & \mathrm{y}_1 & 1 \\
\mathrm{x}_2 & \mathrm{y}_2 & 1 \\
\mathrm{x}_3 & \mathrm{y}_3 & 1
\end{array}\right||
\)
If the area of the triangle formed by the points \(\left(x_1, y_1\right),\left(x_2, y_2\right)\) and \(\left(x_3, y_3\right)\) is zero, the points lie on a straight line. Using this, we can determine whether three point are in a straight line. i.e. the condition for \(\left(x_1, y_1\right),\left(x_2, y_2\right)\) and \(\left(x_3,y_3\right)\) to be collinear is that \(\left|\begin{array}{lll}x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1\end{array}\right|=0\).

Corollary 1 : Area of triangle can also be found by easy method

\(
\Delta=\frac{1}{2}|\left|\begin{array}{ll}
x_1 & y_1 \\
x_2 & y_2
\end{array}\right|+\frac{1}{2}\left|\begin{array}{cc}
x_2 & y_2 \\
x_3 & y_3
\end{array}\right|+\frac{1}{2}\left|\begin{array}{cc}
x_3 & y_3 \\
x_1 & y_1
\end{array}\right||
\)

Note: The area of triangle \(A B C\) will come out to be a positive quantity only when the vertices \(A, B, C\) are taken in anticlockwise direction and if points \(A, B, C\) are taken in clockwise direction then the area will be negative and if the points \(A, B, C\) are taken arbitrary then the area will be positive or negative, the numerical value being the same in all cases.

Area of quadrilateral \(A B C D\) : The area of a quadrilateral can be found out by dividing the quadrilateral into two triangles.
\(\therefore\) Area of quadrilateral \(A B C D\)

\(
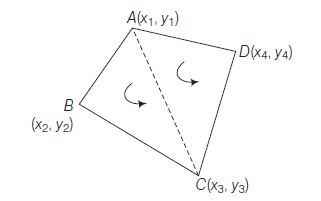
\begin{array}{l}
=\text { Area of } \triangle A B C+\text { Area of } \triangle D A C \\
=\frac{1}{2}\left|\begin{array}{ll}
x_1 & y_1 \\
x_2 & y_2
\end{array}\right|+\frac{1}{2}\left|\begin{array}{ll}
x_2 & y_2 \\
x_3 & y_3
\end{array}\right|+\frac{1}{2}\left|\begin{array}{ll}
x_3 & y_3 \\
x_1 & y_1
\end{array}\right|
\end{array}
\)
\(
+\frac{1}{2}\left|\begin{array}{ll}
x_4 & y_4 \\
x_1 & y_1
\end{array}\right|+\frac{1}{2}\left|\begin{array}{ll}
x_1 & y_1 \\
x_3 & y_3
\end{array}\right|+\frac{1}{2}\left|\begin{array}{ll}
x_3 & y_3 \\
x_4 & y_4
\end{array}\right|
\)
\(
=|\frac{1}{2}\left|\begin{array}{ll}
x_1 & y_1 \\
x_2 & y_2
\end{array}\right|+\frac{1}{2}\left|\begin{array}{ll}
x_2 & y_2 \\
x_3 & y_3
\end{array}\right|+\frac{1}{2}\left|\begin{array}{ll}
x_3 & y_3 \\
x_4 & y_4
\end{array}\right||+\frac{1}{2}\left|\begin{array}{ll}
x_4 & y_4 \\
x_1 & y_1
\end{array}\right|
\)
\(
\left(\because\left|\begin{array}{ll}
x_3 & y_3 \\
x_1 & y_1
\end{array}\right|=-\left|\begin{array}{ll}
x_1 & y_1 \\
x_3 & y_3
\end{array}\right|\right)
\)

Area of polygon whose vertices are \(\left(x_1, y_1\right),\left(x_2, y_2\right),\left(x_3, y_3\right), \ldots,\left(x_n, y_n\right)\) is

\(
\frac{1}{2}|\left|\begin{array}{ll}
x_1 & y_1 \\
x_2 & y_2
\end{array}\right|
+\left|\begin{array}{ll}
x_2 & y_2 \\
x_3 & y_3
\end{array}\right|+\left|\begin{array}{ll}
x_3 & y_3 \\
x_4 & y_4
\end{array}\right|+\ldots .+\left|\begin{array}{cc}
x_n & y_n \\
x_1 & y_1
\end{array}\right||
\)

Stair Method Repeat first coordinates one time in last for down arrow use positive sign and for up arrow use negative sign.

\(
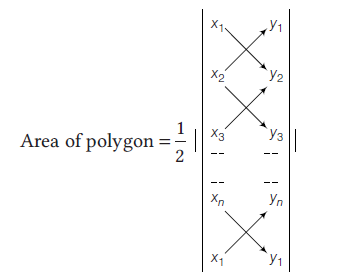
\begin{array}{l}
\left.=\frac{1}{2} \right\rvert\,\left\{\left(x_1 y_2+x_2 y_3+\ldots+x_n y_1\right)\right. \\
\left.\quad-\left(y_1 x_2+y_2 x_3+\ldots+y_n x_1\right)\right\} \mid
\end{array}
\)

Corollary 2 : If the coordinates of the vertices of the triangle are given in polar form i.e.,
\(
A\left(r_1, \theta_1\right), B\left(r_2, \theta_2\right), C\left(r_3, \theta_3\right) \text {. }
\)

Then, area of triangle
\(
\begin{array}{l}
=\frac{1}{2}\left|r_1 r_2 \sin \left(\theta_1-\theta_2\right)+r_2 r_3 \sin \left(\theta_2-\theta_3\right)+r_3 r_1 \sin \left(\theta_3-\theta_1\right)\right| \\
=\frac{1}{2}\left|\sum r_1 r_2 \sin \left(\theta_1-\theta_2\right)\right|
\end{array}
\)

Corollary 3: If \(a_1 x+b_1 y+c_1=0, a_2 x+b_2 y+c_2=0\) and \(a_3 x+b_3 y+c_3=0\) are the sides of a triangle, then the area of the triangle is given by (without solving the vertices)
\(
\Delta=\frac{1}{2\left|C_1 C_2 C_3\right|}\left|\begin{array}{lll}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2 \\
a_3 & b_3 & c_3
\end{array}\right|^2
\)
where, \(C_1, C_2, C_3\) are the cofactors of \(c_1, c_2, c_3\) in the determinant

or, Area of triangle \(=\frac{\Delta^2}{2\left|\Delta_1 \Delta_2 \Delta_3\right|}\)
where, \(\quad \Delta=\left|\begin{array}{lll}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{array}\right|, \Delta_1=\left|\begin{array}{ll}a_1 & b_1 \\ a_2 & b_2\end{array}\right|, \Delta_2=\left|\begin{array}{ll}a_2 & b_2 \\ a_3 & b_3\end{array}\right|\)
and \(\quad \Delta_3=\left|\begin{array}{ll}a_3 & b_3 \\ a_1 & b_1\end{array}\right|\)

Corollary 4 : Area of the triangle formed by the lines of the form \(y=m_1 x+c_1, y=m_2 x+c_2\) and \(y=m_3 x+c_3\) is
\(
\Delta=\frac{1}{2}\left|\frac{\left(c_2-c_3\right)^2}{\left(m_2-m_3\right)}+\frac{\left(c_3-c_1\right)^2}{\left(m_3-m_1\right)}+\frac{\left(c_1-c_2\right)^2}{\left(m_1-m_2\right)}\right|
\)

Important points to remember

• If area of a triangle is given then, use \(\pm\) sign.
• The points \(A\left(x_1, y_1\right), B\left(x_2, y_2\right)\) and \(C\left(x_3, y_3\right)\) are collinear, then area of \((\triangle A B C)=0\).
• Four given points will be collinear, then area of the quadrilateral is zero.
• Area of the triangle formed by the points \(\left(x_1, y_1\right),\left(x_2, y_2\right)\) and
  \(
  \left(x_3, y_3\right) \text { is } \Delta=\frac{1}{2}|\left|\begin{array}{ll}
  x_1-x_3 & x_2-x_3 \\
  y_1-y_3 & y_2-y_3
  \end{array}\right||
  \)
• If one vertex \(\left(x_3, y_3\right)\) is at \((0,0)\) then, \(\Delta=\frac{1}{2}\left|x_1 y_2-x_2 y_1\right|\)

Example 49: The coordinates of \(A, B, C\) are \((6,3),(-3,5)\) and \((4,-2)\) respectively and \(P\) is any points \((x, y)\). Show that the ratio of the areas of the triangles \(P B C\) and \(A B C\) is \(\frac{|x+y-2|}{7}\).

Answer: We have

\(
\frac{\text { Area of } \triangle P B C}{\text { Area of } \triangle A B C}=\frac{\frac{1}{2}|\{x(5+2)-3(-2-y)+4(y-5)\}|}{\frac{1}{2}|\{6(5+2)-3(-2-3)+4(3-5)\}|}
\)
\(
=\frac{|7 x+7 y-14|}{|49|}=\frac{7|x+y-2|}{49}=\frac{|x+y-2|}{7}
\)

Example 50: Find the area of the pentagon whose vertices are \(A(1,1), B(7,21), C(7-3), D(12,2)\) and \(E(0,-3)\).

Answer: The required area
\(
=\frac{1}{2}|\left|\begin{array}{rr}
1 & 1 \\
7 & 21
\end{array}\right|+\left|\begin{array}{rr}
7 & 21 \\
7 & -3
\end{array}\right|+\left|\begin{array}{rr}
7 & -3 \\
12 & 2
\end{array}\right|+\left|\begin{array}{rr}
12 & 2 \\
0 & -3
\end{array}\right|+\left|\begin{array}{rr}
0 & -3 \\
1 & 1
\end{array}\right||
\)
\(
\begin{array}{l}
=\frac{1}{2}|(21-7)+(-21-147)+(14+36)+(-36-0)+(0+3)| \\
=\frac{1}{2}|-137|=\frac{137}{2} \text { sq units }
\end{array}
\)

Example 51: Show that the points \((a, 0),(0, b)\) and \((1,1)\) are collinear, if \(\frac{1}{a}+\frac{1}{b}=1\)

Answer: Let \(A \equiv(a, 0), B \equiv(0, b)\) and \(C \equiv(1,1)\)
Now, points \(A, B, C\) will be collinear, if area of \(\triangle A B C=0\) or
\(
\frac{1}{2}
|\left|\begin{array}{ll}
a & 0 \\
0 & b
\end{array}\right|+\left|\begin{array}{ll}
0 & b \\
1 & 1
\end{array}\right|+\left|\begin{array}{ll}
1 & 1 \\
a & 0
\end{array}\right||
=0
\)

\(
\begin{array}{r}
|(a b-0)+(0-b)+(0-a)|=0 \\
a b-a-b=0 \\
a+b=a b \text { or } \frac{1}{a}+\frac{1}{b}=1
\end{array}
\)

Example 52: Prove that the coordinates of the vertices of an equilateral triangle can not all be rational.

Answer: Let \(A\left(x_1, y_1\right), B\left(x_2, y_2\right)\) and \(C\left(x_3, y_3\right)\) be the vertices of a triangle \(A B C\). If possible let \(x_1, y_1, x_2, y_2, x_3, y_3\) be all rational.

Now, area of \(\triangle A B C=\frac{1}{2}\mid x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\mid\)
\(
=\text { Rational } \dots(i)
\)

Since, \(\triangle A B C\) is equilateral
\(
\begin{aligned}
\therefore \text { Area of } \triangle A B C & =\frac{\sqrt{3}}{4}(\text { side })^2 \\
& =\frac{\sqrt{3}}{4}(A B)^2 \\
& =\frac{\sqrt{3}}{4}\left\{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2\right\} \\
& =\text { Irrational } \dots(ii)
\end{aligned}
\)
From Eqs. (i) and (ii),
Rational \(=\) Irrational
which is contradiction.
Hence, \(x_1, y_1, x_2, y_2, x_3, y_3\) cannot all be rational.

Example 53: The coordinates of two points \(A\) and \(B\) are \((3,4)\) and \((5,-2)\) respectively. Find the coordinates of any point \(P\) if \(P A=P B\) and area of \(\triangle A P B\) is 10.

Answer: Let coordinates of \(P\) be \((h, k)\).
\(
\begin{array}{ll}
\because & P A=P B \Rightarrow(P A)^2=(P B)^2 \\
\Rightarrow & (h-3)^2+(k-4)^2=(h-5)^2+(k+2)^2 \\
\Rightarrow & (h-3)^2-(h-5)^2+(k-4)^2-(k+2)^2=0 \\
\Rightarrow & (2 h-8)(2)+(2 k-2)(-6)=0 \\
\Rightarrow & (h-4)-3(k-1)=0 \\
\Rightarrow & h-3 k-1=0 \dots(i)
\end{array}
\)
\(
\text { Now, Area of } \triangle P A B=\frac{1}{2} \left|\begin{array}{rrr}
h & k & 1 \\
3 & 4 & 1 \\
5 & -2 & 1
\end{array}\right|=10
\)
\(
\begin{array}{l}
6 h+2 k-26= \pm 20 \\
6 h+2 k-46=0 \text { or } 6 h+2 k-6=0 \\
3 h+k-23=0 \text { or } 3 h+k-3=0 \\
\end{array}
\)
Solving \(\quad h-3 k-1=0\) and \(3 h+k-23=0\),
we get \(\quad h=7, k=2\)
Solving \(\quad h-3 k-1=0\) and \(3 h+k-3=0\),
we get \(\quad h=1, k=0\)
Hence, the coordinates of \(P\) are \((7,2)\) or \((1,0)\).

Example 54: Find the area of the triangle formed by the straight lines \(7 x-2 y+10=0,7 x+2 y-10=0\) and \(9 x+y+2=0\) (without solving the vertices of the triangle).

Answer: The given lines are :
\(
\begin{array}{r}
7 x-2 y+10=0 \\
7 x+2 y-10=0 \\
9 x+y+2=0
\end{array}
\)
\(
\therefore \text { Area of triangle } \Delta=\frac{1}{2\left|C_1 C_2 C_3\right|}\left|\begin{array}{rrr}
7 & -2 & 10 \\
7 & 2 & -10 \\
9 & 1 & 2
\end{array}\right|^2 \dots(i)
\)
where,
\(
\begin{array}{l}
C_1=\left|\begin{array}{ll}
7 & 2 \\
9 & 1
\end{array}\right|=7-18=-11, \\
C_2=\left|\begin{array}{rr}
9 & 1 \\
7 & -2
\end{array}\right|=-118-7=-25 \\
C_3=\left|\begin{array}{rr}
7 & -2 \\
7 & 2
\end{array}\right|=14+14=28,
\end{array}
\)
\(
\begin{aligned}
& \left|\begin{array}{rrr}
7 & -2 & 10 \\
7 & 2 & -10 \\
9 & 1 & 2
\end{array}\right|=10 C_1-10 C_2+2 C_3 \\
= & 10 \times(-11)-10 \times(-25)+2 \times 28=196
\end{aligned}
\)
\(
\therefore \text { From Eq. (i), } \begin{aligned}
\Delta & =\frac{1}{2|-11 \times(-25) \times 28|} \times(196)^2 \\
& =\frac{196 \times 196}{2 \times 11 \times 25 \times 28}=\frac{686}{275} \text { sq units }
\end{aligned}
\)

Example 55: If \(\Delta_1\) is the area of the triangle with vertices \((0,0),(a \tan \alpha, b \cot \alpha),(a \sin \alpha, b \cos \alpha) ; \Delta_2\) is the area of the triangle with vertices \((a, b),\left(a \sec ^2 \alpha, b \operatorname{cosec}^2 \alpha\right),\left(a+a \sin ^2 \alpha, b+b \cos ^2 \alpha\right)\) and \(\Delta_3\) is the area of the triangle with vertices \((0,0)\), \((a \tan \alpha,-b \cot \alpha),(a \sin \alpha, b \cos \alpha)\). Show that there is no value of \(\alpha\) for which \(\Delta_1, \Delta_2\) and \(\Delta_3\) are in GP.

Answer: We have, \(\Delta_1=\frac{1}{2}|(a \tan \alpha)(b \cos \alpha)-(a \sin \alpha)(b \cot \alpha)|\)
\((\because\) one vertex is \((0,0))\)
\(
=\frac{1}{2}|a b \| \sin \alpha-\cos \alpha| \dots(i)
\)
\(
\text { and } \Delta_2=\frac{1}{2}|
\left|\begin{array}{lc}
a-\left(a+a \sin ^2 \alpha\right) & a \sec ^2 \alpha-\left(a+a \sin ^2 \alpha\right) \\
b-\left(b+b \cos ^2 \alpha\right) & b \operatorname{cosec}^2 \alpha-\left(b+b \cos ^2 \alpha\right)
\end{array}\right||
\)
\(
=\frac{1}{2}|\left|\begin{array}{ll}
-a \sin ^2 \alpha & a\left(\tan ^2 \alpha-\sin ^2 \alpha\right) \\
-b \cos ^2 \alpha & b\left(\cot ^2 \alpha-\cos ^2 \alpha\right)
\end{array}\right||
\)
\(
=\frac{1}{2}|a b| \times|
\left|\begin{array}{cc}
-\sin ^2 \alpha & \sin ^2 \alpha\left(\sec ^2 \alpha-1\right) \\
-\cos ^2 \alpha & \cos ^2 \alpha\left(\operatorname{cosec}^2 \alpha-1\right)
\end{array}\right||
\)
\(
=\frac{1}{2}|a b| \times|\left|\begin{array}{cc}
-\sin ^2 \alpha & \sin ^2 \alpha \tan ^2 \alpha \\
-\cos ^2 \alpha & \cos ^2 \alpha \cot ^2 \alpha
\end{array}\right||
\)
\(
=\frac{1}{2}|a b| \times\left|-\sin ^2 \alpha \cos ^2 \alpha \cot ^2 \alpha+\sin ^2 \alpha \cos ^2 \alpha \tan ^2 \alpha\right|
\)
\(
\begin{array}{l}
=\frac{1}{2}|a b| \times\left|-\cos ^4 \alpha+\sin ^4 \alpha\right| \\
=\frac{1}{2}|a b| \times\left|\sin ^2 \alpha+\cos ^2 \alpha\right| \times\left|\sin ^2 \alpha-\cos ^2 \alpha\right| \\
=\frac{1}{2}|a b| \times|1| \times|-\cos 2 \alpha| \\
=\frac{1}{2}|a b| \times|\cos 2 \alpha| \dots(ii)
\end{array}
\)
\(
\text { and } \quad \Delta_3=\frac{1}{2}|(a \tan \alpha)(b \cos \alpha)-(-b \cot \alpha)(a \sin \alpha)|
\)
\(
=\frac{1}{2}|a b||\sin \alpha+\cos \alpha| \dots(iii)
\)
\(
\text { Since, } \Delta_1, \Delta_2, \Delta_3 \text { are in GP, then } \Delta_1 \Delta_3=\Delta_2^2
\)
\(
\frac{1}{2}|a b||\sin \alpha-\cos \alpha| \times \frac{1}{2}|a b||\sin \alpha+\cos \alpha|
\)
\(
=\frac{1}{4}|a b|^2|\cos 2 \alpha|^2 \quad \text { [from Eqs. (i), (ii) and (iii)] }
\)
\(
\begin{array}{c}
\left|\sin ^2 \alpha-\cos ^2 \alpha\right|=|\cos 2 \alpha|^2 \\
|-\cos 2 \alpha|=|\cos 2 \alpha|^2 \\
|\cos 2 \alpha|=|\cos 2 \alpha|^2 \\
|\cos 2 \alpha|(1-|\cos 2 \alpha|)=0
\end{array}
\)
\(
1-|\cos 2 \alpha|=0 \quad(\because|\cos 2 \alpha| \neq 0)
\)
\(
\begin{array}{c}
|\cos 2 \alpha|=1 \\
\cos 2 \alpha= \pm 1 \quad \text { or } \cos 2 \alpha=1 \\
\cos 2 \alpha=-1 \\
2 \alpha=2 n \pi, 2 \alpha=(2 p+1) \pi \\
\alpha=n \pi, \alpha=p \pi+\frac{\pi}{2} ; n, p \in I
\end{array}
\)
For these values of \(\alpha\) the vertices of the given triangles are not defined. Hence \(\Delta_1, \Delta_2\) and \(\Delta_3\) cannot be in GP for any value of \(\alpha\).

Example 56: The vertices of a triangle are \(A(a, a \tan \alpha), B(b, b \tan \beta)\) and \(C(c, c \tan \gamma)\). If the circumcentre of \(\triangle A B C\) coincides with the origin and \(H(\bar{x}, \bar{y})\) is the orthocentre, then show that
\(
\frac{\bar{y}}{\bar{x}}=\left(\frac{\sin \alpha+\sin \beta+\sin \gamma}{\cos \alpha+\cos \beta+\cos \gamma}\right) .
\)

Answer: If \(R\) be the circumradius and \(O\) be the circumcentre
\(
\begin{array}{ll}
\therefore \quad O A =O B=O C=R \\
\text { or } \sqrt{\left(a^2+a^2 \tan ^2 \alpha\right)} & =\sqrt{\left(b^2+b^2 \tan ^2 \beta\right)} \\
& =\sqrt{\left(c^2+c^2 \tan ^2 \gamma\right)}=R
\end{array}
\)
or \(\quad a \sec \alpha=b \sec \beta=c \sec \gamma=R\)
or \(\quad a=R \cos \alpha, b=R \cos \beta, c=R \cos \gamma\)
then, \(\quad a \tan \alpha=R \cos \alpha \cdot \frac{\sin \alpha}{\cos \alpha}=R \sin \alpha\)

Similarly,
\(
b \tan \beta=R \sin \beta \text { and } c \tan \gamma=R \sin \gamma
\)
\(\therefore\) Coordinates of the vertices of a triangle are :
\(A(R \cos \alpha, R \sin \alpha), B(R \cos \beta, R \sin \beta)\)
and \(C(R \cos \gamma, R \sin \gamma)\)
\(\therefore\) Centroid
\(
(G) \equiv\left(\frac{R(\cos \alpha+\cos \beta+\cos \gamma)}{3}, \frac{R(\sin \alpha+\sin \beta+\sin \gamma)}{3}\right)
\)
Since, \(G\) divides \(H[latex] and [latex]O\) in the ratio \(2: 1\) (internally), then
\(
\frac{R}{3}(\cos \alpha+\cos \beta+\cos \gamma)=\frac{2 \cdot 0+1 \cdot \bar{x}}{2+1}
\)
or \(\quad \frac{R}{3}(\cos \alpha+\cos \beta+\cos \gamma)=\frac{\bar{x}}{3} \dots(i)\)
and \(\frac{R}{3}(\sin \alpha+\sin \beta+\sin \gamma)=\frac{2 \cdot 0+1 \cdot \bar{y}}{2+1}\)
or \(\quad \frac{R}{3}(\sin \alpha+\sin \beta+\sin \gamma)=\frac{\bar{y}}{3} \dots(ii)\)
Dividing Eqs. (ii) by (i), then we get
\(
\frac{\bar{y}}{\bar{x}}=\left(\frac{\sin \alpha+\sin \beta+\sin \gamma}{\cos \alpha+\cos \beta+\cos \gamma}\right)
\)

Locus and its Equation

Locus: The locus of a moving point is the path traced out by that point under one or more given conditions.

Locus is a set of points which satisfies a given geometrical data. Thus, for example, locus of a point moving at a constant distance from a given point is a circle. Locus of a point which is equidistance from two fixed points is a perpendicular bisector of the line joining the two points. All the points in a locus can be represented by an equation. For example 1,

(a) If the distance of the point \((x, y)\) from \((2,3)\) is 4 , then
\(
(x-2)^2+(y-3)^2=4^2 \text {. }
\)
i.e. \(\quad x^2+y^2-4 x-6 y-3=0\).
This equation will represent a circle with its centre at \((2,3)\) and radius 4.

(b) If \((x, y)\) be the point equidistant from the points \((3,4)\) and \((2,1)\), then
\(
(x-3)^2+(y-4)^2=(x-2)^2+(y-1)^2
\)
i.e. \(x+3 y=10\).
From the geometrical constraint, which governs the motion, we can find a relation (locus) between the coordinates of the moving point in any of its positions. Equation of locus is therefore merely on equation relating the \(x\) and \(y\) co-ordinates of every point on the locus.
Steps to find locus

• Assume the co-ordinates of point for which locus is to be determined as (h, k).
• Apply the given geometrical conditions.
• Transform the geometrical conditions into algebraic equation and simplify.
• Eliminate variables (if any).
• Replace \(\mathrm{h} \rightarrow \mathrm{x}\) and \(\mathrm{k} \rightarrow \mathrm{y}\) to get the equation of locus.
• Note: Simplify the equation by squaring both sides if square roots are there and taking LCM to remove the denominators.

Note: (a) Locus should not contain any other variables except \(x\) and \(y\).
(b) The algebraic relation between \(x\) and \(y\) satisfied by the co-ordinates at every point on the curve and not off the curve is called the equation of curve.

For example 2. If a point \(P\) moves in a plane such that whose distance from a fixed point \(O\) (say) in the plane is always constant distance \(a\). Thus the locus of the moving point \(P\) is clearly a circle with centre \(O\) and radius \(a\).

Equation of a Locus

A relation \(f(x, y)=0\) between \(x\) and \(y\) which is satisfied by each point on the locus and such that each point satisfying the equation is on the locus is called the equation of the locus.

Example 57: Find the locus of a point which moves such that its distance from the point \((0,0)\) is twice its distance from the \(Y\)-axis.

Answer: Let \(P\left(x_1, y_1\right)\) be the moving point whose locus is required.
By hypothesis \(|O P|=2|P M| \quad(\because P\) lies in any quadrant \()\)
\(
\Rightarrow \sqrt{\left(x_1^2+y_1^2\right)}=2\left|x_1\right|
\)

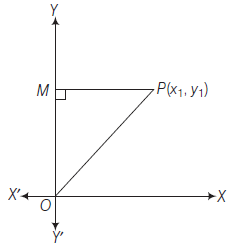
Squaring both sides, then
\(
\begin{array}{l}
x_1^2+y_1^2=4 x_1^2 \\
\Rightarrow \quad 3 x_1^2-y_1^2=0 \\
\end{array}
\)
Changing \(\left(x_1, y_1\right)\) to \((x, y)\), then
\(
3 x^2-y^2=0
\)
which is the required locus of \(P\).

Example 58: Find the locus of the moving point \(P\) such that \(2 P A=3 P B\), where \(A\) is \((0,0)\) and \(B\) is \((4,-3)\).

Answer: Let \(P\left(x_1, y_1\right)\) be the moving point whose locus is required.

By hypothesis,
\(
\begin{aligned}
& 2 P A=3 P B \text { or } 4(P A)^2=9(P B)^2 \\
\Rightarrow \quad & 4\left\{x_1^2+y_1^2\right\}=9\left\{\left(x_1-4\right)^2+\left(y_1+3\right)^2\right\} \\
\Rightarrow \quad & 4\left(x_1^2+y_1^2\right)=9\left(x_1^2+y_1^2-8 x_1+6 y_1+25\right)
\end{aligned}
\)
\(
\text { or } 5 x_1^2+5 y_1^2-72 x_1+54 y_1+225=0
\)
Changing \(\left(x_1, y_1\right)\) to \((x, y)\), then
\(
5 x^2+5 y^2-72 x+54 y+225=0
\)
which is the required locus of \(P\).

Example 59: A point moves so that the sum of the squares of its distances from two fixed points \(A(a, 0)\) and \(B(-a, 0)\) is constant and equal to \(2 c^2\), find the locus of the point.

Answer: Let \(P\left(x_1, y_1\right)\) be the moving point whose locus is required.

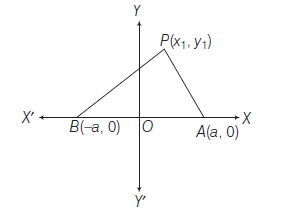
By hypothesis, \(\quad(P A)^2+(P B)^2=2 c^2\)
\(
\begin{array}{lc}
\Rightarrow & \left(x_1-a\right)^2+\left(y_1-0\right)^2+\left(x_1+a\right)^2+\left(y_1-0\right)^2=2 c^2 \\
\Rightarrow & 2 x_1^2+2 y_1^2+2 a^2=2 c^2 \\
\text { or } & x_1^2+y_1^2=c^2-a^2
\end{array}
\)
Changing \(\left(x_1, y_1\right)\) to \((x, y)\), then
\(
x^2+y^2=c^2-a^2
\)
which is the required locus of \(P\).

Example 60: A point moves such that the sum of its distances from two fixed points \((a e, 0)\) and \((-a e, 0)\) is always \(2 a\). Prove that the equation of the locus is
\(
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \text {, where } b^2=a^2\left(1-e^2\right)
\)

Answer: Let \(P\left(x_1, y_1\right)\) be the moving point whose locus is required and \(A(a e, 0)\) and \(B(-a e, 0)\) be the given fixed points.

\(
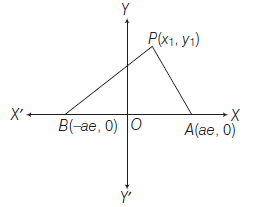
\begin{array}{l}
\text { By hypothesis, } \quad|P A|+|P B|=2 a \\
\text { or } \sqrt{\left(x_1-a e\right)^2+\left(y_1-0\right)^2}+\sqrt{\left(x_1+a e\right)^2+\left(y_1-0\right)^2}=2 a \\
\text { or } \sqrt{\left(x_1^2+y_1^2-2 a e x_1+a^2 e^2\right)}+\sqrt{\left(x_1^2+y_1^2+2 a e x_1+a^2 e^2\right)} \\
\quad=2 a \dots(i)
\end{array}
\)
Let \(\quad l=x_1^2+y_1^2-2 a e x_1+a^2 e^2\)
and \(\quad m=x_1^2+y_1^2+2 a e x_1+a^2 e^2 \quad(l-m\) method \()\)
then, Eq. (i) can be written as
\(
\sqrt{l}+\sqrt{m}=2 a \dots(ii)
\)
and \(\quad l-m=-4 a e x_1\)
or \(\quad(\sqrt{l}+\sqrt{m})(\sqrt{l}-\sqrt{m})=-4 a e x_1\)
or \(\quad 2 a(\sqrt{l}-\sqrt{m})=-4 a e x_1 \quad\) [from Eq. (ii)]
\(
\sqrt{l}-\sqrt{m}=-2 e x_1 \dots(iii)
\)
Adding Eqs. (ii) and (iii), then
\(
2 \sqrt{l}=2 a-2 e x_1 \text { or } \sqrt{l}=a-e x_1
\)
Squaring both sides,
\(
\begin{array}{ll}
& l=a^2-2 a e x_1+e^2 x_1^2 \\
\Rightarrow & x_1^2+y_1^2-2 a e x_1+a^2 e^2=a^2-2 a e x_1+e^2 x_1^2 \\
\Rightarrow & \left(1-e^2\right) x_1^2+y_1^2=a^2\left(1-e^2\right)
\end{array}
\)
\(
\begin{array}{rlr}
\frac{x_1^2}{a^2}+\frac{y_1^2}{a^2\left(1-e^2\right)} & =1 & \\
\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2} & =1 & {\left[\because b^2=a^2\left(1-e^2\right)\right]}
\end{array}
\)
Changing \(\left(x_1, y_1\right)\) to \((x, y)\), then
\(
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\)
which is the required locus of \(P\).

Example 61: Find the equation of the locus of a point which moves so that the difference of its distances from the points \((3,0)\) and \((-3,0)\) is 4 units.

Answer: Let \(P\left(x_1, y_1\right)\) be the moving point whose locus is required and \(A(3,0)\) and \(B(-3,0)\) be the given fixed points.

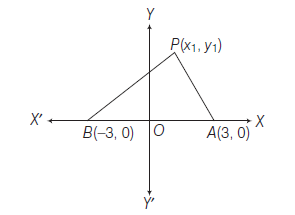
By hypothesis
\(
|P B|-|P A|=4 \text { (assume }|P B|>|P A|)
\)
\(
\begin{array}{l}
\sqrt{\left(x_1+3\right)^2+\left(y_1-0\right)^2}-\sqrt{\left(x_1-3\right)^2+\left(y_1-0\right)^2}=4 \\
\sqrt{\left(x_1^2+y_1^2+6 x_1+9\right)}=4+\sqrt{\left(x_1^2+y_1^2-6 x_1+9\right)}
\end{array}
\)
Squaring both sides then,
\(
x_1^2+y_1^2+6 x_1+9=16+x_1^2+y_1^2-6 x_1+9+8\sqrt{\left(x_1^2+y_1^2-6 x_1+9\right)}
\)
\(
\begin{aligned}
\left(12 x_1-16\right) & =8 \sqrt{\left(x_1^2+y_1^2-6 x_1+9\right)} \\
\left(3 x_1-4\right) & =2 \sqrt{\left(x_1^2+y_1^2-6 x_1+9\right)}
\end{aligned}
\)
Again, squaring both sides, then
\(
9 x_1^2-24 x_1+16=4 x_1^2+4 y_1^2-24 x_1+36
\)
or
\(
5 x_1^2-4 y_1^2=20
\)
\(
\Rightarrow \quad \frac{x_1^2}{4}-\frac{y_1^2}{5}=1
\)
Changing \(\left(x_1, y_1\right)\) by \((x, y)\), then
\(
\frac{x^2}{4}-\frac{y^2}{5}=1
\)
which is the required locus of \(P\).

Example 62: The ends of the hypotenuse of a right angled triangle are \((6,0)\) and \((0,6)\). Find the locus of the third vertex.

Answer: Let \(C\left(x_1, y_1\right)\) be the moving point (third vertex) whose locus is required and \(A(6,0)\) and \(B(0,6)\) be the given vertices.

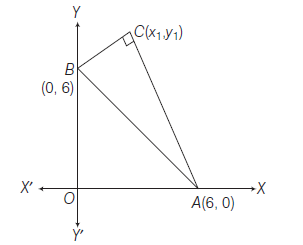
By hypothesis
\(
(A C)^2+(B C)^2=(A B)^2 \quad\left(\because \angle A C B=90^{\circ}\right)
\)
\(
\begin{array}{l}
\left(x_1-6\right)^2+\left(y_1-0\right)^2+\left(x_1-0\right)^2+\left(y_1-6\right)^2=6^2+6^2 \\
2 x_1^2+2 y_1^2-12 x_1-12 y_1=0 \\
x_1^2+y_1^2-6 x_1-6 y_1=0
\end{array}
\)
Changing \(\left(x_1, y_1\right)\) by \((x, y)\), then
\(
x^2+y^2-6 x-6 y=0
\)
which is the required locus of third vertex \(C\).

Example 63: Find the equation of the locus of a point which moves so that the sum of their distances from \((3,0)\) and \((-3,0)\) is less than 9 .

Answer: Let \(P\left(x_1, y_1\right)\) be the moving point whose locus is required and \(A(3,0)\) and \(B(-3,0)\) are the given points.

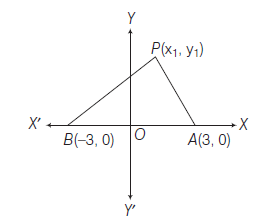
By hypothesis,
\(
|P A|+|P B|<9
\)
\(
\begin{array}{l}
\sqrt{\left\{\left(x_1-3\right)^2+\left(y_1-0\right)^2\right\}}+\sqrt{\left\{\left(x_1+3\right)^2+\left(y_1-0\right)^2\right\}}<9 \\
\sqrt{\left(x_1^2+y_1^2-6 x_1+9\right)}<9-\sqrt{\left(x_1^2+y_1^2+6 x_1+9\right)}
\end{array}
\)
On squaring, we get
\(
\left(x_1^2+y_1^2-6 x_1+9\right)<\left(81+x_1^2+y_1^2+6 x_1+9\right)-18 \sqrt{\left(x_1^2+y_1^2+6 x_1+9\right)}
\)
\(
\left(\because a<b \Rightarrow a^2<b^2 \text { provided } a>0\right)
\)
\(
\begin{array}{l}
-12 x_1-81<-18 \sqrt{\left(x_1^2+y_1^2+6 x_1+9\right)} \\
\left(4 x_1+27\right)>6 \sqrt{\left(x_1^2+y_1^2+6 x_1+9\right)} (\because \text { If } a>b \text {, then }-a<-b)
\end{array}
\)
On squaring, we get
\(
16 x_1^2+729+216 x>36 x_1^2+36 y_1^2+216 x_1+324
\)
\(
20 x_1^2+36 y_1^2<405
\)
Changing \(\left(x_1, y_1\right)\) by \((x, y)\), then
\(
20 x^2+36 y^2<405
\)
which is the required locus of \(P\).

Example 64: Find the locus of a point whose coordinate are given by \(x=t+t^2, y=2 t+1\), where \(t\) is variable.

Answer: Given,
\(
\begin{array}{l}
x=t+t^2 \dots(i) \\
y=2 t+1 \dots(ii)
\end{array}
\)
From Eq. (ii),
\(
t=\left(\frac{y-1}{2}\right) \dots(iii)
\)
On eliminating \(t\) from Eqs. (i) and (iii), we get required locus as
\(
x=\left(\frac{y-1}{2}\right)+\left(\frac{y-1}{2}\right)^2
\)
\(
\begin{aligned}
x & =\left(\frac{y-1}{2}\right)\left(1+\frac{y-1}{2}\right) \\
x & =\left(\frac{y-1}{2}\right)\left(\frac{y+1}{2}\right) \\
4 x & =y^2-1 \\
y^2 & =4 x+1
\end{aligned}
\)

Example 65: A stick of length \(l\) rests against the floor and a wall of a room. If the stick begins to slide on the floor, find the locus of its middle point.

Answer: Let the cross section of the floor and wall be taken as the coordinate axes and \(A B\) be one of the position of the stick. Let the mid-point of \(A B\) be \(P\left(x_1, y_1\right)\), then coordinates of \(A\) and \(B\) are \(\left(2 x_1, 0\right)\) and \(\left(0,2 y_1\right)\) respectively.

\(
\text { But given, }|A B|=l
\)
\(
\begin{aligned}
(A B)^2 & =l^2 \\
\left(2 x_1-0\right)^2+\left(0-2 y_1\right)^2 & =l^2 \\
4 x_1^2+4 y_1^2 & =l^2
\end{aligned}
\)
Changing \(\left(x_1, y_1\right)\) by \((x, y)\), then
\(
4\left(x^2+y^2\right)=l^2
\)
which is the required locus of \(P\).

Example 66: Find the locus of the point of intersection of the lines \(x \cos \alpha+y \sin \alpha=a\) and \(x \sin \alpha-y \cos \alpha=b\), where \(\alpha\) is variable.

Answer: Given equations are
\(
\begin{array}{l}
x \cos \alpha+y \sin \alpha=a \dots(i)\\
x \sin \alpha-y \cos \alpha=b \dots(ii)
\end{array}
\)
Here, \(\alpha\) is a variable, on eliminating \(\alpha\). Squaring and adding Eqs. (i) and (ii), we get required locus as
\(
(x \cos \alpha+y \sin \alpha)^2+(x \sin \alpha-y \cos \alpha)^2=a^2+b^2
\)
\(
\begin{array}{l}
\left(x^2 \cos ^2 \alpha+y^2 \sin ^2 \alpha+2 x y \cos \alpha \sin \alpha\right) \\
\quad+\left(x^2 \sin ^2 \alpha+y^2 \cos ^2 \alpha-2 x y \sin \alpha \cos \alpha\right)=a^2+b^2 \\
x^2\left(\cos ^2 \alpha+\sin ^2 \alpha\right)+y^2\left(\sin ^2 \alpha+\cos ^2 \alpha\right)=a^2+b^2 \\
x^2+y^2=a^2+b^2
\end{array}
\)

Example 67: A variable line cuts \(X\)-axis at \(A, Y\)-axis at \(B\), where \(O A=a, O B=b\) ( \(O\) as origin) such that \(a^2+b^2=1\).
Find the locus of
(i) centroid of \(\triangle O A B\)
(ii) circumcentre of \(\triangle O A B\)

Answer: (i) Coordinates of \(A\) and \(B\) are \((a, 0)\) and \((0, b)\) respectively.
If centroid of \(\triangle O A B\) be \(G(x, y)\) then
and
\(
\begin{array}{l}
x=\frac{0+a+0}{3} \Rightarrow a=3 x \\
y=\frac{0+0+b}{3} \Rightarrow b=3 y
\end{array}
\)

On substituting in \(a^2+b^2=1\), we get
\(
\begin{aligned}
(3 x)^2+(3 y)^2 & =1 \\
x^2+y^2 & =\frac{1}{9}
\end{aligned}
\)
which is the required locus of \(G\).
(ii) If the circumcentre be \(C(x, y)\). Since in semicircle angle \(90^{\circ}\), then \(A B\) is the diameter of the circumcircle \(O A B\).
\(\therefore\) Circumcentre is the mid-point of \(A B\).
Then
\(
\begin{array}{l}
x=\frac{a+0}{2} \Rightarrow a=2 x \\
y=\frac{0+b}{2} \Rightarrow b=2 y
\end{array}
\)
On substituting in \(a^2+b^2=1\), we get
\(
(2 x)^2+(2 y)^2=1
\)
or
\(
x^2+y^2=\frac{1}{4}
\)
which is the required locus of \(C\).

Example 68: Two points \(P\) and \(Q\) are given, \(R\) is a variable point on one side of the line \(P Q\) such that \(\angle R P Q-\angle R Q P\) is a positive constant \(2 \alpha\). Find the locus of the point \(R\).

Answer: Let the \(X\)-axis along \(Q P\) and the middle point of \(P Q\) is origin and let coordinates of moving point \(R\) be \(\left(x_1, y_1\right)\).

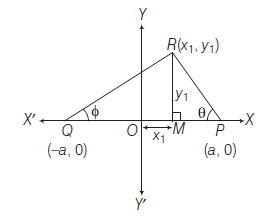
Let
\(O P=O Q=a\)
then coordinates of \(P\) and \(Q\) are \((a, 0)\) and \((-a, 0)\) respectively.
Draw \(R M\) perpendicular on \(Q P\)
\(\therefore \quad O M=x_1\) and \(\quad M R=y_1\)
and let \(\quad \angle R P M=\theta \quad\) and \(\quad \angle R Q M=\phi\)
Now, in \(\triangle R M P\),
\(
\tan \theta=\frac{R M}{M P}=\frac{R M}{O P-O M}=\frac{y_1}{a-x_1} \dots(i)
\)
and in \(\triangle R M Q\),
\(
\tan \phi=\frac{R M}{Q M}=\frac{R M}{O Q+O M}=\frac{y_1}{a+x_1} \dots(ii)
\)
But given
\(
\begin{array}{cc}
& \angle R P Q-\angle R Q P=2 \alpha \text { (constant) }\\
\Rightarrow & \theta-\phi=2 \alpha \\
\therefore & \tan (\theta-\phi)=\tan 2 \alpha \\
\Rightarrow & \frac{\tan \theta-\tan \phi}{1+\tan \theta \tan \phi}=\tan 2 \alpha
\end{array}
\)
\(
\frac{\frac{y_1}{a-x_1}-\frac{y_1}{a+x_1}}{1+\left(\frac{y_1}{a-x_1}\right) \cdot\left(\frac{y_1}{a+x_1}\right)}=\tan 2 \alpha \text { [from Eqs. (i) and (ii)] }
\)
\(
\begin{array}{l}
\frac{2 x_1 y_1}{a^2-x_1^2+y_1^2}=\tan 2 \alpha \\
a^2-x_1^2+y_1^2=2 x_1 y_1 \cot 2 \alpha \\
x_1^2-y_1^2+2 x_1 y_1 \cot 2 \alpha=a^2
\end{array}
\)
Hence, locus of the point \(R\left(x_1, y_1\right)\) is
\(
x^2-y^2+2 x y \cot 2 \alpha=a^2
\)

Change of Axes OR the Transformations of Axes

In coordinate geometry we have discussed the coordinates of a point or the equation of a curve are always considered on taking a fixed point \(O\) as the origin and two perpendicular straight lines through \(O\) as the coordinates axes. For convenient the coordinates of the point or the equation of the curve changes when either the origin is changed or the direction of axes or both are suitably. These processes in coordinate geometry are known as the transformations or change of axes. This process of transformation of coordinates will be of great advantage to solve most of the problems very easily.

Case-I: Change of origin OR Shifting of origin (Translation of Axes)

To change the origin of coordinates to another point \((h, k)\) whereas the directions of axes remain unaltered.

Let \(O\) be the origin of coordinates and \(O X, O Y\) be the original coordinate axes. Let \(O^{\prime}\) be the new origin and \((h, k)\) its coordinates referred to the original axes. Draw two lines \(O^{\prime} X^{\prime}\) and \(O^{\prime} Y^{\prime}\) through \(O^{\prime}\) and parallel to \(O X\) and \(O Y\) respectively. Let \(P(x, y)\) be any point referred to the original axes \(O X, O Y\). Again suppose that the coordinates of the same point \(P\) referred to the new axes \(O^{\prime} X^{\prime}, O^{\prime} Y^{\prime}\) are \((X, Y)\). From \(O^{\prime}\) draw \(O^{\prime} L\) perpendicular to \(O X\). from \(P\) draw \(P M\) perpendicular to \(O X\) to meet \(O^{\prime} X^{\prime}\) in \(N\). Then

\(
\begin{array}{ll}
& O L=h, O^{\prime} L=k, O M=x, P M=y, O^{\prime} N=X text { and } & P N=Y
\end{array}
\)
we have \(\quad x=O M=O L+L M=O L+O^{\prime} N=h+X\)
i.e. \(\quad x=X+h \dots(i)\)
and \(\quad y=P M=P N+N M=P N+O^{\prime} L=Y+k\)
i.e. \(y=Y+k \dots(ii)\)

Important Points to remember

• In this case axes are shifted parallel to themselves, then it is also called Transformation by parallel axes.
• Inverse translation or shifting the origin back: Some times it is required to shift the new origin back. Then putting \(x-h\) in place of \(x\) and \(y-k\) in place of \(y\) in any equation of curve referred to the new origin to get the corresponding equation referred to the old origin.
• The above transformation is true whether the axes be rectangular or oblique.

Example 69: Find the equation of the curve \(2 x^2+y^2-3 x+5 y-8=0\) when the origin is transferred to the point \((-1,2)\) without changing the direction of axes.

Answer: Here, we want to shift the origin to the point \((-1,2)\) without changing the direction of axes. Then we replace \(x\) by \(x-1\) and \(y\) by \(y+2\) in the equation of given curve, then the transformed equation is
\(
\begin{array}{l}
2(x-1)^2+(y+2)^2-3(x-1)+5(y+2)-8=0 \\
\Rightarrow \quad 2 x^2+y^2-7 x+9 y+11=0 \\
\end{array}
\)

Example 70: The equation of a curve referred to the new axes, axes retaining their direction and origin is \((4,5)\) is \(x^2+y^2=36\). Find the equation referred to the original axes.

Answer: Here we want to shift the \((4,5)\) to the origin without changing the direction of axes. Then we replace \(x\) by \(x-4\) and \(y\) by \(y-5\) in the equation of given curve then the required equation is
\(
\begin{aligned}
(x-4)^2+(y-5)^2 & =36 \\
\Rightarrow \quad x^2+y^2-8 x-10 y+5 & =0
\end{aligned}
\)

Example 71: Shift the origin to a suitable point so that the equation \(y^2+4 y+8 x-2=0\) will not contain term in \(y\) and the constant.

Answer: Since, this equation is required to be free from the term containing \(y\) and the constant, we have
\(
\begin{array}{l}
2 k+4=0 \quad \text { and } \quad k^2+4 k+8 h-2=0 \\
\therefore \quad k=-2 \quad \text { and } \quad h=\frac{3}{4} \\
\end{array}
\)
Hence, the point to which the origin be shifted is \(\left(\frac{3}{4},-2\right)\).

Example 72: At what point the origin be shifted, if the coordinates of a point \((-1,8)\) become \((-7,3)\)?

Answer: Let the origin be shifted to the point \((h, k)\) without changing the direction of axes. Then we replace \(x\) by \(x+h\) and \(y\) by \(y+k\) and we get new co-ordinates. Here, given old coordinates and new coordinates are \((-1,8)\) and \((-7,3)\) respectively.
We have \(\quad-1+h=-7\) and \(8+k=3\)
\(
\Rightarrow \quad h=-6 \text { and } k=-5
\)
Hence, the origin must be shifted to \((-6,-5)\).

Case-II: Rotation of Axes (Change of Directions of Axes)

To find the change in the coordinates of a point when the directions of axes are rotated through an angle \(\theta\) the origin being fixed.

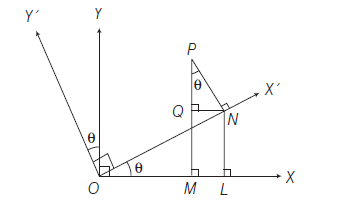
Let \(O X\) and \(O Y\) be the original system of coordinate axes. Let \(O X^{\prime}\) and \(O Y^{\prime}\) be the new axes obtained by rotating the original axes through an angle \(\theta\). Let \(P\) be a point in the plane whose coordinates are \((x, y)\) and \((X, Y)\) referred to old and new axes respectively. Draw \(P M\) and \(P N\) perpendiculars to \(O X\) and \(O X^{\prime}\) and also \(N L\) and \(N Q\) perpendiculars to \(O X\) and \(P M\). We have

\(
\begin{aligned}
O M & =x, P M=y, O N=X, P N=Y \\
x & =O M=O L-M L
\end{aligned}
\)
\(
\left(\begin{array}{c}
\because \text { Angle between any two lines }=\text { Angle between } \\
\text { their perpendiculars i.e. } \angle X O X^{\prime}=\angle N P M=\theta
\end{array}\right)
\)
\(
\begin{aligned}
& =O L-Q N=O N \cos \theta-P N \sin \theta \\
& =X \cos \theta-Y \sin \theta \\
x & =X \cos \theta-Y \sin \theta \dots(i)
\end{aligned}
\)
\(
\begin{aligned}
y & =P M=P Q+Q M=P Q+N L \\
& =P N \cos \theta+O N \sin \theta \\
& =Y \cos \theta+X \sin \theta \\
y & =X \sin \theta+Y \cos \theta \dots(ii)
\end{aligned}
\)
Now, multiplying Eqs. (i) by \(\cos \theta\) and Eq. (ii) by \(\sin \theta\) and adding we get
\(
X=x \cos \theta+y \sin \theta \dots(iii)
\)
Also, subtracting the product of Eq. (i) by \(\sin \theta\) from the product of Eq. (ii) by \(\cos \theta\), we get
\(
Y=-x \sin \theta+y \cos \theta \dots(iv)
\)
also \(x^2+y^2=X^2+Y^2=O P^2\) are unchanged i.e. the distance of the point \(P\) from the origin \(O\) remains unaffected by the rotation of axes.

Important Points to Remember

• Rule : When the axes are rotated through \(\theta\), replace \((x, y)\) by \((x \cos \theta-y \sin \theta, x \sin \theta+y \cos \theta)\).
• Shifting the coordinate axes back : Some times it is required to shift the new coordinates axes back. Then replace \((x, y)\) by
  \(
  (x \cos \theta+y \sin \theta,-x \sin \theta+y \cos \theta) \text {. }
  \)

Example 73: If the axes are turned through \(45^{\circ}\), find the transformed form of the equation
\(
3 x^2+3 y^2+2 x y=2
\)

Answer: Here, \(\theta=45^{\circ}\) so \(\sin \theta=\cos \theta=\frac{1}{\sqrt{2}}\)
Replacing \((x, y)\) by \((x \cos \theta-y \sin \theta, x \sin \theta+y \cos \theta)\)
i.e. \(\quad\left(\frac{x-y}{\sqrt{2}}, \frac{x+y}{\sqrt{2}}\right)\)
Then, \(3 x^2+3 y^2+2 x y=2\) becomes
\(
3\left(\frac{x-y}{\sqrt{2}}\right)^2+3\left(\frac{x+y}{\sqrt{2}}\right)^2+2\left(\frac{x-y}{\sqrt{2}}\right)\left(\frac{x+y}{\sqrt{2}}\right)=2
\)
\(
\begin{array}{lr}
\Rightarrow & 3\left(2 x^2+2 y^2\right)+2\left(x^2-y^2\right)=4 \\
\Rightarrow & 8 x^2+4 y^2=4 \\
\text { or } & 2 x^2+y^2=1
\end{array}
\)
which is free from the term containing \(x y\).

Example 74: Prove that if the axes be turned through \(\frac{\pi}{4}\) the equation \(x^2-y^2=a^2\) is transformed to the form \(x y=\lambda\). Find the value of \(\lambda\).

Answer: Here, \(\theta=\frac{\pi}{4} \quad\) so \(\quad \sin \theta=\cos \theta=\frac{1}{\sqrt{2}}\)
Replacing \((x, y)\) by \((x \cos \theta-y \sin \theta, x \sin \theta+y \cos \theta)\)
i.e. \(\quad\left(\frac{x-y}{\sqrt{2}}, \frac{x+y}{\sqrt{2}}\right)\)
then, \(x^2-y^2=a^2\) becomes
\(
\begin{array}{ll}
& \left(\frac{x-y}{\sqrt{2}}\right)^2-\left(\frac{x+y}{\sqrt{2}}\right)^2=a^2 \\
\Rightarrow \quad & \left(\frac{x-y}{\sqrt{2}}+\frac{x+y}{\sqrt{2}}\right)\left(\frac{x-y}{\sqrt{2}}-\frac{x+y}{\sqrt{2}}\right)=a^2 \\
\Rightarrow \quad & \left(\frac{2 x}{\sqrt{2}}\right)\left(\frac{-2 y}{\sqrt{2}}\right)=a^2 \\
\text { or } \quad & x y=-\frac{a^2}{2}
\end{array}
\)
Comparing it with \(x y=\lambda\), then we get \(\lambda=-\frac{a^2}{2}\).

Example 75: Through what angle should the axes be rotated so that the equation \(9 x^2-2 \sqrt{3} x y+7 y^2=10\) may be changed to \(3 x^2+5 y^2=5\) ?

Answer: Let angle be \(\theta\) then replacing \((x, y)\) by \((x \cos \theta-y \sin \theta, x \sin \theta+y \cos \theta)\)
\(
\begin{array}{l}
\text { then, } \quad 9 x^2-2 \sqrt{3} x y+7 y^2=10 \text { becomes } \\
9(x \cos \theta-y \sin \theta)^2-2 \sqrt{3} \\
(x \cos \theta-y \sin \theta)(x \sin \theta+y \cos \theta) \\
+7(x \sin \theta+y \cos \theta)^2=10 \\
\end{array}
\)
\(
\begin{aligned}
\Rightarrow \quad x^2(9 & \left.\cos ^2 \theta-2 \sqrt{3} \sin \theta \cos \theta+7 \sin ^2 \theta\right) \\
+ & 2 x y(-9 \sin \theta \cos \theta-\sqrt{3} \cos 2 \theta+7 \sin \theta \cos \theta) \\
+ & y^2\left(9 \cos ^2 \theta+2 \sqrt{3} \sin \theta \cos \theta+7 \cos ^2 \theta\right)=10
\end{aligned}
\)
On comparing with \(3 x^2+5 y^2=5\) (coefficient of \(x y\) ) we get \(-9 \sin \theta \cos \theta-\sqrt{3} \cos 2 \theta+7 \sin \theta \cos \theta=0\)
\(
\begin{aligned}
\sin 2 \theta & =-\sqrt{3} \cos 2 \theta \\
\tan 2 \theta & =-\sqrt{3}=\tan \left(180^{\circ}-60^{\circ}\right) \\
2 \theta & =120^{\circ} \\
\theta & =60^{\circ}
\end{aligned}
\)

Example 76: If \((x, y)\) and \((X, Y)\) be the coordinates of the same point referred to two sets of rectangular axes with the same origin and if \(u x+v y\), when \(u\) and \(v\) are independent of \(X\) and \(Y\) become \(V X+U Y\), show that \(u^2+v^2=U^2+V^2\)

Answer: Let the axes rotate an angle \(\theta\) and if \((x, y)\) be the point with respect to old axes and \((X, Y)\) be the co-ordinates with respect to new axes, then
\(
x+i y=(X+i Y) e^{i \theta}=(X+i Y)(\cos \theta+i \sin \theta)
\)
On comparing real and imaginary parts, we get
\(
\left\{\begin{array}{l}
x=X \cos \theta-Y \sin \theta \\
y=X \sin \theta+Y \cos \theta
\end{array}\right.
\)
Then, \(u x+v y=u(X \cos \theta-Y \sin \theta)+v(X \sin \theta+Y \cos \theta)\)
\(
=(u \cos \theta+v \sin \theta) X+(-u \sin \theta+v \cos \theta) Y
\)
but given new curve \(V X+U Y\)
then, \(V X+U Y=(u \cos \theta+v \sin \theta)\)
\(
X+(-u \sin \theta+v \cos \theta) Y
\)
On comparing the coefficients of \(X\) and \(Y\), we get
\(
\begin{array}{c}
V=u \cos \theta+v \sin \theta \dots(i) \\
U=-u \sin \theta+v \cos \theta \dots(ii)
\end{array}
\)
Squaring and adding Eqs. (i) and (ii), we get
\(
\begin{array}{c}
V^2+U^2=(u \cos \theta+v \sin \theta)^2+(-u \sin \theta+v \cos \theta)^2 \\
=u^2+v^2
\end{array}
\)
Hence, \(\quad u^2+v^2=U^2+V^2\)

Case-III: Double Transformation (Origin Shifted and Axes Rotated)

If origin is shifted to the point. \(O^{\prime}(h, k)\) and at the same time the directions of axes are rotated through an angle \(\theta\) in the anticlockwise sense such that new coordinates of \(P(x, y)\) become \((X, Y)\).

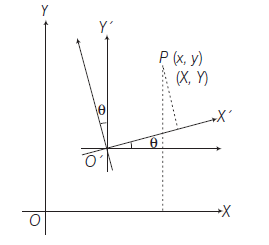
Then, we get \(\quad x=h+X \cos \theta-Y \sin \theta \dots(i)\)
\(
y=k+X \sin \theta+Y \cos \theta \dots(ii)
\)
In practice we have to replace \(x\) by \(h+x \cos \theta-y \sin \theta\) and \(y\) by \(k+x \sin \theta+y \cos \theta\).
Again, if we want to shift the coordinate axes back to their original positions, then we obtained \(X\) and \(Y\) by solving Eqs. (i) and (ii), then
\(
\begin{array}{l}
X=(x-h) \cos \theta+(y-k) \sin \theta \\
Y=-(x-h) \sin \theta+(y-k) \cos \theta
\end{array}
\)

Example 77: What does the equation \(2 x^2+4 x y-5 y^2+20 x-22 y-14=0\) becomes when referred to rectangular axes through the point \((-2,-3)\), the new axes being inclined at an angle of \(45^{\circ}\) with the old?

Answer: Let \(O^{\prime}(-2,-3)\) be the new origin and axes are rotated about \(O^{\prime}\) through an angle \(45^{\circ}\) in anticlockwise direction then replacing \(x\) and \(y\) by
\(
\begin{array}{l}
-2+x \cos 45^{\circ}-y \sin 45^{\circ} \\
-3+x \sin 45^{\circ}+y \cos 45^{\circ}
\end{array}
\)
i.e. \(-2+\left(\frac{x-y}{\sqrt{2}}\right)\) and \(-3+\left(\frac{x+y}{\sqrt{2}}\right)\) respectively in the given curve, then the new equation of curve will be
\(
2\left\{-2+\left(\frac{x-y}{\sqrt{2}}\right\}\right\}^2+4\left\{-2+\left(\frac{x-y}{\sqrt{2}}\right)\right\}\left\{-3+\left(\frac{x+y}{\sqrt{2}}\right)\right\}
\)
\(
\begin{array}{l}
\begin{aligned}
-5\left\{-3+\left(\frac{x+y}{\sqrt{2}}\right)\right\}^2 & +20\left\{-2+\left(\frac{x-y}{\sqrt{2}}\right)\right\} \\
& -22\left\{-3+\left(\frac{x+y}{\sqrt{2}}\right)\right\}-14=0
\end{aligned}\\
x^2-14 x y-7 y^2-2=0
\end{array}
\)

Removal of the Term \(x y\) from \(f(x, y)=a x^2+2 h x y+b y^2\) without Changing the Origin

Clearly, \(h \neq 0\)
Rotating the axes through an angle \(\theta\), we have
\(
\begin{array}{l}
x=X \cos \theta-Y \sin \theta \\
y=X \sin \theta+Y \cos \theta \\
\because \quad f(x, y)=a x^2+2 h x y+b y^2 \\
\end{array}
\)
After rotation, new equation is
\(
\begin{array}{l}
F(X, Y)=\left(a \cos ^2 \theta+2 h \cos \theta \sin \theta+b \sin ^2 \theta\right) X^2 \\
+2\left\{(b-a) \cos \theta \sin \theta+h\left(\cos ^2 \theta-\sin ^2 \theta\right)\right\} X Y \\
+\left(a \sin ^2 \theta-2 h \cos \theta \sin \theta+b \cos ^2 \theta\right) Y^2
\end{array}
\)
Now, coefficient of \(X Y=0\)
Then, we get \(\cot 2 \theta=\frac{a-b}{2 h}\)

Important points to Remember

• Usually, we use the formula, \(\tan 2 \theta=\frac{2 h}{a-b}\) for finding the angle of rotation, \(\theta\).
• However, if \(a=b\), we use \(\cot 2 \theta=\frac{a-b}{2 h}\) as in this case \(\tan 2 \theta\) is not defined.

Example 78: Given the equation \(4 x^2+2 \sqrt{3} x y+2 y^2=1\), through what angle should the axes be rotated so that the term in \(x y\) be wanting from the transformed equation.

Answer: Comparing the given equation with \(a x^2+2 h x y+b y^2\), we get \(a=4, h=\sqrt{3} b=2\). If axes are to be rotated at \(\theta\), then
\(
\begin{aligned}
\tan 2 \theta & =\frac{2 h}{a-b}=\frac{2 \sqrt{3}}{2}=\sqrt{3}=\tan \frac{\pi}{3} \\
2 \theta & =\frac{\pi}{3}, \pi+\frac{\pi}{3} \Rightarrow 2 \theta=\frac{\pi}{3}, \frac{4 \pi}{3} \\
\therefore \quad \theta & =\frac{\pi}{6}, \frac{2 \pi}{3}
\end{aligned}
\)

Position of a Point which Lies Inside a Triangle

If any point say \((P)\) lies within the triangle \(A B C\), then
\(
\Delta_1+\Delta_2+\Delta_3=\Delta
\)

where, \(\Delta=\) Area of triangle \(A B C\),
\(\Delta_1=\) Area of \(\triangle P B C\),
\(\Delta_2=\) Area of \(\triangle P C A\),
\(\Delta_3=\) Area of \(\triangle P A B\)
Also,
\(
\Delta_1 \neq 0, \Delta_2 \neq 0, \Delta_3 \neq 0, \Delta \neq 0
\)
(Each individual area must be non-zero)

Example 79: Find \(\lambda\) if \((\lambda, \lambda+1)\) is an interior point of \(\triangle A B C\) where, \(A \equiv(0,3) ; B \equiv(-2,0)\) and \(C \equiv(6,1)\).

Answer: The point \(P(\lambda, \lambda+1)\) will be inside the triangle \(A B C\), then Area of \(\triangle P B C+\) Area of \(\triangle P C A+\) Area of \(\triangle P A B=\) Area of \(\triangle A B C\)
\(
=\frac{1}{2}|\left|\begin{array}{rrr}
\lambda & \lambda+1 & 1 \\
-2 & 0 & 1 \\
6 & 1 & 1
\end{array}\right||+\frac{1}{2}|\left|\begin{array}{rrr}
\lambda & \lambda+1 & 1 \\
6 & 1 & 1 \\
0 & 3 & 1
\end{array}\right||+\frac{1}{2}|\left|\begin{array}{rrr}
\lambda & \lambda+1 & 1 \\
0 & 3 & 1 \\
-2 & 0 & 1
\end{array}\right||
\)
\(
=\frac{1}{2}|\left|\begin{array}{rrr}
0 & 3 & 1 \\
-2 & 0 & 1 \\
6 & 1 & 1
\end{array}\right||
\)
\(
\Rightarrow \quad|7 \lambda+6|+|8 \lambda-12|+|\lambda+4|=22
\)
\(
\text { For } \lambda<-4 \text { : }
\)

\(
\begin{array}{l}
\text { Then, }-(7 \lambda+6)-(8 \lambda-12)-(\lambda+4)=22 \\
\Rightarrow \quad-16 \lambda=20 \quad \therefore \quad \lambda=-\frac{5}{4}
\end{array}
\)
which is impossible.
For \(-4 \leq \lambda<-\frac{6}{7}\) :
Then, \(-(7 \lambda+6)-(8 \lambda-12)+(\lambda+4)=22\)
\(\Rightarrow \quad-14 \lambda=12 \quad \therefore=-\frac{6}{7}\)
which is impossible.
For \(-\frac{6}{7} \leq \lambda<\frac{3}{2}\) :
Then, \((7 \lambda+6)-(8 \lambda-12)+\lambda+4=22 \Rightarrow 22=22\)
\(\because\) at \(\lambda=-\frac{6}{7}\), area of \(\triangle P B C=0\)
\(\therefore \quad \lambda \neq \frac{-6}{7}\)
\(\therefore \quad \lambda \in\left(-\frac{6}{7}, \frac{3}{2}\right)\)
For \(\lambda \geq \frac{3}{2}\) :
Then, \(7 \lambda+6+8 \lambda-12+\lambda+4=22 \Rightarrow 16 \lambda=24\)
\(
\therefore \quad \lambda=\frac{3}{2}
\)
\(\because \quad\) at \(\lambda=\frac{3}{2}\), area of \(\triangle P C A=0\)
\(
\therefore \quad \lambda \neq \frac{3}{2}
\)
Hence, value of \(\lambda \in\left(-\frac{6}{7}, \frac{3}{2}\right)\).