NCERT Exemplar MCQs
Overview
- An expression consisting of two terms, connected by + or – sign is called a binomial expression. For example, \(x+a, 2 x-3 y, \frac{1}{x}-\frac{1}{x^3}, 7 x-\frac{4}{5 y}\), etc., are all binomial expressions.
Binomial theorem
If \(a\) and \(b\) are real numbers and \(n\) is a positive integer, then \((a+b)^n={ }^n C _0 a^n+{ }^n C _1 a^{n-1} b^1+{ }^n C _2 a^{n-2} b^2+\ldots\)
\(
\ldots+{ }^n C _r a^{n-r} b^r+\ldots+{ }^n C _n b^n \text {, where }{ }^n C _r=\frac{{n!}}{{r!} {(n-r)}!} \text { for } 0 \leq r \leq n
\)
The general term or \((r+1)^{ th }\) term in the expansion is given by
\(
T _{r+1}={ }^n C _r a^{n-r} b^r
\)
Some important observations
- The total number of terms in the binomial expansion of \((a+b)^n\) is \(n+1\), i.e. one more than the exponent \(n\).
- In the expansion, the first term is raised to the power of the binomial and in each subsequent terms the power of \(a\) reduces by one with simultaneous increase in the power of \(b\) by one, till power of \(b\) becomes equal to the power of binomial, i.e., the power of \(a\) is \(n\) in the first term, ( \(n-1)\) in the second term and so on ending with zero in the last term. At the same time power of \(b\) is 0 in the first term, 1 in the second term and 2 in the third term and so on, ending with \(n\) in the last term.
- In any term the sum of the indices (exponents) of ‘ \(a\) ‘ and ‘ \(b\) ‘ is equal to \(n\) (i.e., the power of the binomial).
- The coefficients in the expansion follow a certain pattern known as pascal’s triangle.
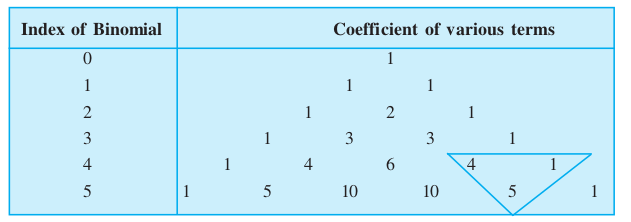
Each coefficient of any row is obtained by adding two coefficients in the preceding row, one on the immediate left and the other on the immediate right and each row is bounded by 1 on both sides.
The \((r+1)^{ \text {th} }\) term or general term is given by
\(
T _{r+1}={ }^n C _r a^{n-r} b^r
\)
Some particular cases
If \(n\) is a positive integer, then
\(
\begin{aligned}
& (a+b)^n={ }^n C _0 a^n b^0+{ }^n C _1 a^n b^1+{ }^n C _2 a^{n-2} b^2+\ldots+{ }^n C _r a^{n-r} b^r+\ldots+ { }^n C _n a^0 b^n \dots(1)
\end{aligned}
\)
In particular
- Replacing \(b\) by \(-b\) in (1), we get
\(
\begin{aligned}
& (a-b)^n={ }^n C _0 a^n b^0-{ }^n C _1 a^{n-1} b^1+{ }^n C _2 a^{n-2} b^2+\ldots+(-1)^r{ }^n C _r a^{n-r} b^r+\ldots+ \\
& (-1)^n{ }^n C _n a^0 b^n \dots(2)
\end{aligned}
\) - Adding (1) and (2), we get
\(
\begin{aligned}
(a+b)^n+(a-b)^n & =2\left[{ }^n C _0 a^n b^0+{ }^n C _2 a^{n-2} b^2+{ }^n C _4 a^{n-4} b^4+\ldots\right] \\
& =2[\text { terms at odd places }]
\end{aligned}
\) - Subtracting (2) from (1), we get
\(
\begin{aligned}
(a+b)^n-(a-b)^n & =2\left[{ }^n C _1 a^{n-1} b^1+{ }^n C _3 a^{n-3} b^3+\ldots\right] \\
& =2[\text { sum of terms at even places }]
\end{aligned}
\) - Replacing \(a\) by 1 and \(b\) by \(x\) in (1), we get
\(
(1+x)^n={ }^n C _0 x^0+{ }^n C _1 x+{ }^n C _2 x^2+\ldots+{ }^n C _r x^r+\ldots+{ }^n C _{n-1} x^{n-1}+{ }^n C _n x^n
\)
i.e. \(\quad(1+x)^n=\sum_{r=0}^n{ }^n C _r x^r\) - Replacing \(a\) by 1 and \(b\) by \(-x\) in … (1), we get
\(
(1-x)^n={ }^n C _0 x^0-{ }^n C _1 x+{ }^n C _2 x^2 \ldots+{ }^n C _{n-1}(-1)^{n-1} x^{n-1}+{ }^n C _n(-1)^n x^n
\)
i.e., \(\quad(1-x)^n=\sum_{r=0}^n(-1)^r{ }^n C _r x^r\)
The \(p~{\text {th }}\) term from the end
The \(p~{\text {th }}\) term from the end in the expansion of \((a+b)^n\) is \((n-p+2)^{\text {th }}\) term from the beginning.
Middle terms
The middle term depends upon the value of \(n\).
- If \(n\) is even: then the total number of terms in the expansion of \((a+b)^n\) is \(n+1\) (odd). Hence, there is only one middle term, i.e., \(\left(\frac{n}{2}+1\right)^{\text {th }}\) term is the middle term.
- If \(n\) is odd: then the total number of terms in the expansion of \((a+b)^n\) is \(n+1\) (even). So there are two middle terms i.e., \(\left(\frac{n+1}{2}\right)^{ th }\) and \(\left(\frac{n+3}{2}\right)^{\text {th }}\) are two middle terms.
Binomial coefficient
In the Binomial expression, we have
\(
(a+b)^n={ }^n C _0 a^n+{ }^n C _1 a^{n-1} b+{ }^n C _2 a^{n-2} b^2+\ldots+{ }^n C _n b^n \dots(1)
\)
The coefficients \({ }^n C _0,{ }^n C _1,{ }^n C _2, \ldots,{ }^n C _n\) are known as binomial or combinatorial coefficients.
Putting \(a=b=1\) in (1), we get
\(
{ }^n C _0+{ }^n C _1+{ }^n C _2+\ldots+{ }^n C _n=2^n
\)
Thus the sum of all the binomial coefficients is equal to \(2^n\).
Again, putting \(a=1\) and \(b=-1\) in (1), we get
\(
{ }^n C _0+{ }^n C _2+{ }^n C _4+\ldots={ }^n C _1+{ }^n C _3+{ }^n C _5+\ldots
\)
Thus, the sum of all the odd binomial coefficients is equal to the sum of all the even binomial coefficients and each is equal to \(\frac{2^n}{2}=2^{n-1}\).
\(
{ }^n C _0+{ }^n C _2+{ }^n C _4+\ldots={ }^n C _1+{ }^n C _3+{ }^n C _5+\ldots=2^{n-1}
\)
Quiz Summary
0 of 63 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 63 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 63
1. Question
\(
\text { Find the } r^{\text {th }} \text { term in the expansion of }\left(x+\frac{1}{x}\right)^{2 r}
\)CorrectIncorrectHint
We have \(\mathrm{T}_{\mathrm{r}}={ }^{2 r} \mathrm{C}_{r-1}(x)^{2 r-r+1}\left(\frac{1}{x}\right)^{r-1}\).
\(
\begin{aligned}
& =\frac{2 r!}{(r-1)!(r+1)!} x^{r+1-r+1} \\
& =\frac{2 r!}{(r-1)!(r+1)!} x^2
\end{aligned}
\) -
Question 2 of 63
2. Question
\(
\text { Expand the following }\left(1-x+x^2\right)^4
\)CorrectIncorrectHint
Put \(1-x=y\). Then
\(
\begin{aligned}
\left(1-x+x^2\right)^4= & \left(y+x^2\right)^4 \\
= & { }^4 \mathrm{C}_0 \quad y^4\left(x^2\right)^0+{ }^4 \mathrm{C}_1 y^3\left(x^2\right)^1 \\
& +{ }^4 \mathrm{C}_2 \quad y^2\left(x^2\right)^2+{ }^4 \mathrm{C}_3 \quad y\left(x^2\right)^3+{ }^4 \mathrm{C}_4\left(x^2\right)^4 \\
= & y^4+4 y^3 x^2+6 y^2 x^4+4 y x^6+x^8 \\
= & (1-x)^4+4 x^2(1-x)^3+6 x^4(1-x)^2+4 x^6(1-x)+x^8 \\
= & 1-4 x+10 x^2-16 x^3+19 x^4-16 x^5+10 x^6-4 x^7+x^8
\end{aligned}
\) -
Question 3 of 63
3. Question
\(
\text { Find the } 4^{\text {th }} \text { term from the end in the expansion of }\left(\frac{x^3}{2}-\frac{2}{x^2}\right)^9
\)CorrectIncorrectHint
Since \(r^{\text {th }}\) term from the end in the expansion of \((a+b)^n\) is \((n-r+2)^{\text {th }}\) term from the beginning. Therefore \(4^{\text {th }}\) term from the end is \(9-4+2\), i.e., \(7^{\text {th }}\) term from the beginning, which is given by
\(
\mathrm{T}_7={ }^9 \mathrm{C}_6\left(\frac{x^3}{2}\right)^3\left(\frac{-2}{x^2}\right)^6={ }^9 \mathrm{C}_3 \frac{x^9}{8} \cdot \frac{64}{x^{12}}=\frac{9 \times 8 \times 7}{3 \times 2 \times 1} \times \frac{64}{x^3}=\frac{672}{x^3}
\) -
Question 4 of 63
4. Question
\(
\text { Evaluate: }\left(x^2-\sqrt{1-x^2}\right)^4+\left(x^2+\sqrt{1-x^2}\right)^4
\)CorrectIncorrectHint
Putting \(\sqrt{1-x^2}=y\), we get
The given expression \(=\left(x^2-y\right)^4+\left(x^2+y\right)^4=2\left[x^8+{ }^4 \mathrm{C}_2 x^4 y^2+{ }^4 \mathrm{C}_4 y^4\right]\)
\(
\begin{aligned}
& =2 x^8+\frac{4 \times 3}{2 \times 1} x^4 \cdot\left(1-x^2\right)+\left(1-x^2\right)^2 \\
& =2\left[x^8+6 x^4\left(1-x^2\right)+\left(1-2 x^2+x^4)\right]\right. \\
& =2 x^8-12 x^6+14 x^4-4 x^2+2
\end{aligned}
\) -
Question 5 of 63
5. Question
\(
\text { Find the coefficient of } x^{11} \text { in the expansion of } (x^3-\frac{2}{x^2})^{12}
\)CorrectIncorrectHint
Let the general term, i.e., \((r+1)^{\text {th }}\) contain \(x^{11}\).
We have
\(
\begin{aligned}
\mathrm{T}_{r+1} & ={ }^{12} \mathrm{C}_r\left(x^3\right)^{12-r}\left(-\frac{2}{x^2}\right)^r \\
& ={ }^{12} \mathrm{C}_r x^{36-3 r-2 r}(-1)^r 2^r \\
& ={ }^{12} \mathrm{C}_r(-1)^r 2^r x^{36-5 r}
\end{aligned}
\)
Now for this to contain \(x^{11}\), we observe that
\(
36-5 r=11 \text {, i.e., } r=5
\)
Thus, the coefficient of \(x^{11}\) is
\(
{ }^{12} C_5(-1)^5 2^5=-\frac{12 \times 11 \times 10 \times 9 \times 8}{5 \times 4 \times 3 \times 2} \times 32=-25344
\) -
Question 6 of 63
6. Question
Determine whether the expansion of \((x^2-\frac{2}{x})^{18}\) will contain a term containing \(x^{10}\) ?
CorrectIncorrectHint
Let \(\mathrm{T}_{r+1}\) contain \(x^{10}\). Then
\(
\begin{aligned}
\mathrm{T}_{r+1} & ={ }^{18} \mathrm{C}_r\left(x^2\right)^{18-r} \frac{-2}{x} \\
& ={ }^{18} \mathrm{C}_r x^{36-2 r}(-1)^r \cdot 2^r x^r \\
& =(-1)^r 2^r{ }^{18} \mathrm{C}_r x^{36-3 r}
\end{aligned}
\)
Thus,
\(
36-3 r=10 \text {, i.e., } r=\frac{26}{3}
\)\(
\text { Since } r \text { is a fraction, the given expansion cannot have a term containing } x^{10} \text {. }
\) -
Question 7 of 63
7. Question
\(
\text { Find the term independent of } x \text { in the expansion of }\left(\frac{\sqrt{x}}{\sqrt{3}}+\frac{\sqrt{3}}{2 x^2}\right)^{10} \text {. }
\)CorrectIncorrectHint
Let \((r+1)^{\text {th }}\) term be independent of \(x\) which is given by
\(
\mathrm{T}_{r+1}={ }^{10} \mathrm{C}_r \sqrt{\frac{x}{3}}^{10-r}{\frac{\sqrt{3}}{2 x^2}}^r
\)
\(
\begin{aligned}
& ={ }^{10} \mathrm{C}_r \frac{x}{3}{ }^{\frac{10-r}{2}} 3^{\frac{r}{2}} \frac{1}{2^r x^{2 r}} \\
& ={ }^{10} \mathrm{C}_r 3^{\frac{r}{2}-\frac{10-r}{2}} 2^{-r} x^{\frac{10-r}{2}-2 r} \\
&
\end{aligned}
\)
Since the term is independent of \(x\), we have
\(
\frac{10-r}{2}-2 r=0 \quad \Rightarrow \quad r=2
\)
Hence \(3^{\text {rd }}\) term is independent of \(x\) and its value is given by
\(
\mathrm{T}_3={ }^{10} \mathrm{C}_2 \frac{3^{-3}}{4}=\frac{10 \times 9}{2 \times 1} \times \frac{1}{9 \times 12}=\frac{5}{12}
\) -
Question 8 of 63
8. Question
Find the middle term in the expansion of \((2 a x-{\frac{b}{x^2}})^{12}\).
CorrectIncorrectHint
Since the power of binomial is even, it has one middle term which is the \(\frac{12+2}{2}\) th term and it is given by
\(
\begin{aligned}
\mathrm{T}_7 & ={ }^{12} \mathrm{C}_6(2 a x)^6\left(\frac{-b}{x^2}\right)^6 \\
& ={ }^{12} \mathrm{C}_6 \frac{2^6 a^6 x^6 \cdot(-b)^6}{x^{12}} \\
& ={ }^{12} \mathrm{C}_6 \frac{2^6 a^6 b^6}{x^6}=\frac{59136 a^6 b^6}{x^6}
\end{aligned}
\) -
Question 9 of 63
9. Question
\(
\text { Find the middle term (terms) in the expansion of }\left(\frac{p}{x}+\frac{x}{p}\right)^9 \text {. }
\)CorrectIncorrectHint
Since the power of binomial is odd. Therefore, we have two middle terms which are \(5^{\text {th }}\) and \(6^{\text {th }}\) terms. These are given by
\(
\mathrm{T}_5={ }^9 \mathrm{C}_4\left(\frac{p}{x}\right)^5\left(\frac{x}{p}\right)^4={ }^9 \mathrm{C}_4 \frac{p}{x}=\frac{126 p}{x}
\)
and
\(
\mathrm{T}_6={ }^9 \mathrm{C}_5\left(\frac{p}{x}\right)^4\left(\frac{x}{p}\right)^5={ }^9 \mathrm{C}_5 \frac{x}{p}=\frac{126 x}{p}
\) -
Question 10 of 63
10. Question
\(
\text { Is the equation } 2^{4 n+4}-15 n-16 \text {, where } n \in \mathbf{N} \text { is divisible by } 225 \text {. }
\)CorrectIncorrectHint
We have
\(
\begin{aligned}
2^{4 n+4}-15 n-16= & 2^{4(n+1)}-15 n-16 \\
= & 16^{n+1}-15 n-16 \\
= & (1+15)^{n+1}-15 n-16 \\
= & { }^{n+1} \mathrm{C}_0 15^0+{ }^{n+1} \mathrm{C}_1 15^1+{ }^{n+1} \mathrm{C}_2 15^2+{ }^{n+1} \mathrm{C}_3 15^3 \\
& +\ldots+{ }^{n+1} \mathrm{C}_{n+1}(15)^{n+1}-15 n-16 \\
= & 1+(n+1) 15+{ }^{n+1} \mathrm{C}_2 15^2+{ }^{n+1} \mathrm{C}_3 15^3 \\
& +\ldots+{ }^{n+1} \mathrm{C}_{n+1}(15)^{n+1}-15 n-16 \\
= & 1+15 n+15+{ }^{n+1} \mathrm{C}_2 15^2+{ }^{n+1} \mathrm{C}_3 15^3 \\
& +\ldots+{ }^{n+1} \mathrm{C}_{n+1}(15)^{n+1}-15 n-16 \\
= & 15^2\left[{ }^{n+1} \mathrm{C}_2+{ }^{n+1} \mathrm{C}_3 15+\ldots \text { so on }\right]
\end{aligned}
\)
Thus, \(2^{4 n+4}-15 n-16\) is divisible by 225 . -
Question 11 of 63
11. Question
Find numerically the greatest term in the expansion of \((2+3 x)^9\), where
\(x=\frac{3}{2}\)CorrectIncorrectHint
\(
\text { We have }(2+3 x)^9=2^9\left(1+\frac{3 x}{2}\right)^9
\)
\(
\frac{\mathrm{T}_{r+1}}{\mathrm{~T}_r}=\frac{2^9\left[{ }^9 \mathrm{C}_r\left(\frac{3 x}{2}\right)^r\right]}{2^9\left[{ }^9 \mathrm{C}_{r-1}\left(\frac{3 x}{2}\right)^{r-1}\right]}
\)
\(
=\frac{{ }^9 \mathrm{C}_r}{{ }^9 \mathrm{C}_{r-1}}\left|\frac{3 x}{2}\right|
\)
\(
=\frac{10-r}{r}\left|\frac{3 x}{2}\right|=\frac{10-r}{r}\left(\frac{9}{4}\right) \quad \text { Since } \quad x=\frac{3}{2}
\)
Therefore,
\(
\begin{aligned}
\frac{\mathrm{T}_{r+1}}{\mathrm{~T}_r} \geq 1 & \Rightarrow \frac{90-9 r}{4 r} \geq 1 \\
& \Rightarrow 90-9 r \geq 4 r \\
& \Rightarrow r \leq \frac{90}{13} \\
& \Rightarrow r \leq 6 \frac{12}{13}
\end{aligned}
\)
Thus the maximum value of \(r\) is 6 . Therefore, the greatest term is \(\mathrm{T}_{r+1}=\mathrm{T}_7\).
Hence,
\(
\begin{aligned}
\mathrm{T}_7 & =2^9\left[{ }^9 \mathrm{C}_6\left(\frac{3 x}{2}\right)^6\right], \quad \text { where } x=\frac{3}{2} \\
& =2^9 \cdot{ }^9 \mathrm{C}_6\left(\frac{9}{4}\right)^6=2^9 \cdot \frac{9 \times 8 \times 7}{3 \times 2 \times 1}\left(\frac{3^{12}}{2^{12}}\right)=\frac{7 \times 3^{13}}{2}
\end{aligned}
\) -
Question 12 of 63
12. Question
If \(n\) is a positive integer, find the coefficient of \(x^{-1}\) in the expansion of
\(
(1+x)^n\left(1+\frac{1}{x}\right)^n
\)CorrectIncorrectHint
We have
\(
(1+x)^n (1+\frac{1}{x})^n=(1+x)^n \quad (\frac{x+1}{x})^n \quad=\frac{(1+x)^{2 n}}{x^n}
\)
Now to find the coefficient of \(x^{-1}\) in \((1+x)^n \quad (1+\frac{1}{x})^n\), it is equivalent to finding coefficient of \(x^{-1}\) in \(\frac{(1+x)^{2 n}}{x^n}\) which in turn is equal to the coefficient of \(x^{n-1}\) in the expansion of \((1+x)^{2 n}\).
Since \((1+x)^{2 n}={ }^{2 n} \mathrm{C}_0 x^0+{ }^{2 n} \mathrm{C}_1 x^1+{ }^{2 n} \mathrm{C}_2 x^2+\ldots+{ }^{2 n} \mathrm{C}_{n-1} x^{n-1}+\ldots+{ }^{2 n} \mathrm{C}_{2 n} x^{2 n}\)
Thus the coefficient of \(x^{n-1}\) is \({ }^{2 n} \mathrm{C}_{n-1}\) -
Question 13 of 63
13. Question
Which of the following is larger?
\(
99^{50}+100^{50} \text { or } 101^{50}
\)CorrectIncorrectHint
We have \((101)^{50}=(100+1)^{50}\)
\(
=100^{50}+50(100)^{49}+\frac{50.49}{2.1}(100)^{48}+\frac{50.49 .48}{3.2 .1}(100)^{47}+\ldots \dots(1)
\)
Similarly \(\quad 99^{50}=(100-1)^{50}\)
\(
=100^{50}-50.100^{49}+\frac{50.49}{2.1}(100)^{48}-\frac{50.49 .48}{3.2 .1}(100)^{47}+\ldots \dots(2)
\)
Subtracting (2) from (1), we get
\(
\begin{aligned}
& 101^{50}-99^{50}=2 \\
& 50 \cdot(100)^{49}+\frac{50 \cdot 49 \cdot 48}{3 \cdot 2 \cdot 1} 100^{47}+\ldots \\
& \Rightarrow \quad 101^{50}-99^{50}=100^{50}+2 \frac{50 \cdot 49 \cdot 48}{3 \cdot 2 \cdot 1} 100^{47}+\ldots \\
& \Rightarrow \quad 101^{50}-99^{50}>100^{50} \\
& \text { Hence } 101^{50}>99^{50}+100^{50}
\end{aligned}
\) -
Question 14 of 63
14. Question
Find the coefficient of \(x^{50}\) after simplifying and collecting the like terms in the expansion of \((1+x)^{1000}+x(1+x)^{999}+x^2(1+x)^{998}+\ldots+x^{1000}\).
CorrectIncorrectHint
Since the above series is a geometric series with the common ratio \(\mathrm{x} /(1+\mathrm{x})\), its sum is
\(
\frac{(1+x)^{1000}\left[1-\left(\frac{x}{1+x}\right)^{1001}\right]}{\left[1-\left(\frac{x}{1+x}\right)\right]}
\)
\(
\begin{aligned}
& =\frac{(1+x)^{1000}-\frac{x^{1001}}{1+x}}{\frac{1+x-x}{1+x}} \\
& =(1+x)^{1001}-x^{1001}
\end{aligned}
\)
\(
\text { Hence, coefficient of } x^{50} \text { is given by }
\)
\(
{ }^{1001} \mathrm{C}_{50} = \frac{(1001) !}{(951) !(50) !}
\) -
Question 15 of 63
15. Question
If \(a_1, a_2, a_3\) and \(a_4\) are the coefficient of any four consecutive terms in the expansion of \((1+x)^n\), then
\(
\frac{a_1}{a_1+a_2}+\frac{a_3}{a_3+a_4}=\frac{2 a_2}{a_2+a_3}
\). Is this true?CorrectIncorrectHint
Let \(a_1, a_2, a_3\) and \(a_4\) be the coefficient of four consecutive terms \(\mathrm{T}_{r+1}, \mathrm{~T}_{r+}\) \({ }_2, \mathrm{~T}_{r+3}\), and \(\mathrm{T}_{r+4}\) respectively. Then
\(
\begin{aligned}
& a_1=\text { coefficient of } \mathrm{T}_{r+1}={ }^n \mathrm{C}_r \\
& a_2=\text { coefficient of } \mathrm{T}_{r+2}={ }^n \mathrm{C}_{r+1} \\
& a_3=\text { coefficient of } \mathrm{T}_{r+3}={ }^n \mathrm{C}_{r+2} \\
& a_4=\text { coefficient of } \mathrm{T}_{r+4}={ }^n \mathrm{C}_{r+3}
\end{aligned}
\)
and, Thus
\(
\begin{aligned}
\frac{a_1}{a_1+a_2} & =\frac{{ }^n \mathrm{C}_r}{{ }^n \mathrm{C}_r+{ }^n \mathrm{C}_{r+1}} \\
& =\frac{{ }^n \mathrm{C}_r}{{ }^{n+1} \mathrm{C}_{r+1}} \quad\left(\because{ }^n \mathrm{C}_r+{ }^n \mathrm{C}_{r+1}={ }^{n+1} \mathrm{C}_{r+1}\right) \\
& =\frac{r+1}{n+1}
\end{aligned}
\)
Similarly,
\(
\begin{aligned}
\frac{a_3}{a_3+a_4} & =\frac{{ }^n \mathrm{C}_{r+2}}{{ }^n \mathrm{C}_{r+2}+{ }^n \mathrm{C}_{r+3}} \\
& =\frac{{ }^n \mathrm{C}_{r+2}}{{ }^{n+1} \mathrm{C}_{r+3}}=\frac{r+3}{n+1}
\end{aligned}
\)
Hence,
\(
\text { L.H.S. }=\frac{a_1}{a_1+a_2}+\frac{a_3}{a_3+a_4}=\frac{r+1}{n+1}+\frac{r+3}{n+1}=\frac{2 r+4}{n+1}
\)
and
\(
\text { R.H.S. }=\frac{2 a_2}{a_2+a_3}=\frac{2\left({ }^n \mathrm{C}_{r+1}\right)}{{ }^n \mathrm{C}_{r+1}+{ }^n \mathrm{C}_{r+2}}=\frac{2\left({ }^n \mathrm{C}_{r+1}\right)}{{ }^{n+1} \mathrm{C}_{r+2}}
\)
\(
=\frac{2(r+2)}{n+1}
\) -
Question 16 of 63
16. Question
The total number of terms in the expansion of \((x+a)^{51}-(x-a)^{51}\) after simplification is
CorrectIncorrectHint
(c)
\(
\begin{array}{l}
\text { for }(x+a)^{51}-(x-a)^{51} \\
\text { Since }(x+a)^{51}={ }^{51} C_0 x^{51}+{ }^{51} C_1 x^{50} a+{ }^{51} C_2 x^{49} a^2+\ldots+{ }^{51} C_{51} a^{51} \\
\text { and }(x-a)^{51}={ }^{51} C_0 x^{51}-{ }^{51} C_1 x^{50} a+{ }^{51} C_2 x^{49} a^2 \ldots{ }^{51} C_{51} a^{51}
\end{array}
\)
Subtracting above values,
\(
(x+a)^{51}-(x-a)^{51}=2\left({ }^{51} C_1 x^{50} a+{ }^{51} C_3 x^{48} a^3+\ldots+{ }^{51} C_{51} a^{51}\right)
\)
i.e. \(1^{\text {st, }} 3^{\text {rd }}, 5^{\text {th, }} 7^{\text {th }} \ldots\) \(49^{\text {th }}, 51^{\text {th }}\) term are there.
\(\therefore\) applying A.P.
\(
a+(n-1) d=51
\)
i.e. \(1+(n-1) 2=51\)
i.e. \(2(n-1)=50\)
i.e. \(n=26\) -
Question 17 of 63
17. Question
\(
\text { If the coefficients of } x^7 \text { and } x^8 \text { in } (2+\frac{x}{3})^{n} \text { are equal, then } n \text { is }
\)CorrectIncorrectHint
b is the correct choice. Since \(\mathrm{T}_{r+1}={ }^n \mathrm{C}_r a^{n-r} x^r\) in expansion of \((a+x)^n\),
Therefore,
\(
\mathrm{T}_8={ }^n \mathrm{C}_7(2)^{n-7}\left(\frac{x}{3}\right)^7={ }^n \mathrm{C}_7 \frac{2^{n-7}}{3^7} x^7
\)
and
\(
\mathrm{T}_9={ }^n \mathrm{C}_8(2)^{n-8}\left(\frac{x}{3}\right)^8={ }^n \mathrm{C}_8 \frac{2^{n-8}}{3^8} x^8
\)
Therefore, \({ }^n \mathrm{C}_7 \frac{2^{n-7}}{3^7}={ }^n \mathrm{C}_8 \frac{2^{n-8}}{3^8}\) (since it is given that coefficient of \(x^7=\operatorname{coefficient} x^8\) )
\(
=\frac{2^{n-8}}{3^8} \cdot \frac{3^7}{2^{n-7}}
\)
\(
\Rightarrow \quad \frac{8}{n-7}=\frac{1}{6} \Rightarrow n=55
\) -
Question 18 of 63
18. Question
If \(\left(1-x+x^2\right)^n=a_0+a_1 x+a_2 x^2+\ldots+a_{2 n} x^{2 n}\), then \(a_0+a_2+a_4+\ldots\) \(+a_{2 n}\) equals.
CorrectIncorrectHint
a is the correct choice. Putting \(x=1\) and \(-1\) in
we get
\(
\begin{aligned}
\left(1-x+x^2\right)^n & =a_0+a_1 x+a_2 x^2+\ldots+a_{2 n} x^{2 n} \\
1 & =a_0+a_1+a_2+a_3+\ldots+a_{2 n} \dots(1)\\
3^n & =a_0-a_1+a_2-a_3+\ldots+a_{2 n} \dots(2)
\end{aligned}
\)
and
Adding (1) and (2), we get
\(
3^n+1=2\left(a_0+a_2+a_4+\ldots+a_{2 n}\right)
\)
Therefore \(a_0+a_2+a_4+\ldots+a_{2 n}=\frac{3^n+1}{2}\) -
Question 19 of 63
19. Question
The coefficient of \(x^p\) and \(x^q\) ( \(p\) and \(q\) are positive integers) in the expansion of \((1+x)^{p+q}\) are
CorrectIncorrectHint
Coefficient of \(x^p\) and \(x^q\) in the expansion of \((1+x)^p\) \({ }^{+q}\) are \({ }^{p+q} \mathrm{C}_p\) and \({ }^{p+q} \mathrm{C}_q\)
and
\(
{ }^{p+q} \mathrm{C}_p={ }^{p+q} \mathrm{C}_q
\)
Hence (a) is the correct answer. -
Question 20 of 63
20. Question
The number of terms in the expansion of \((a+b+c)^n\), where \(n \in \mathbf{N}\) is
CorrectIncorrectHint
a is the correct choice. We have
\(
\begin{aligned}
(a+b+c)^n= & {[a+(b+c)]^n } \\
= & a^n+{ }^n \mathrm{C}_1 a^{n-1}(b+c)^1+{ }^n \mathrm{C}_2 a^{n-2}(b+c)^2 \\
& +\ldots+{ }^n \mathrm{C}_n(b+c)^n
\end{aligned}
\)
Further, expanding each term of R.H.S., we note that
First term consist of 1 term.
Second term on simplification gives 2 terms.
Third term on expansion gives 3 terms.
Similarly, fourth term on expansion gives 4 terms and so on.
The total number of terms \(=1+2+3+\ldots+(n+1)\)
\(
=\frac{(n+1)(n+2)}{2}
\) -
Question 21 of 63
21. Question
The ratio of the coefficient of \(x^{15}\) to the term independent of \(x\) in \((x^2+\frac{2}{x})^{15}\) is
CorrectIncorrectHint
(b) is the correct choice. Let \(\mathrm{T}_{r+1}\) be the general term of \(x^2+\frac{2}{x}\), so,
\(
\begin{aligned}
\mathrm{T}_{r+1} & ={ }^{15} \mathrm{C}_r\left(x^2\right)^{15-r} \frac{2}{x} \\
& ={ }^{15} \mathrm{C}_r(2)^r x^{30-3 r} \dots(1)
\end{aligned}
\)
Now, for the coefficient of term containing \(x^{15}\),
\(
30-3 r=15, \quad \text { i.e., } \quad r=5
\)
Therefore, \({ }^{15} \mathrm{C}_5(2)^5\) is the coefficient of \(x^{15}\) (from (1))
To find the term independent of \(x\), put \(30-3 r=0\)
Thus \({ }^{15} \mathrm{C}_{10} 2^{10}\) is the term independent of \(x\) (from (1))
Now the ratio is \(\frac{{ }^{15} \mathrm{C}_5 2^5}{{ }^{15} \mathrm{C}_{10} 2^{10}}=\frac{1}{2^5}=\frac{1}{32}\) -
Question 22 of 63
22. Question
If \(z=(\frac{\sqrt{3}}{2}+\frac{i}{2})^{5}+(\frac{\sqrt{3}}{2}-\frac{i}{2})^{5}\), then
CorrectIncorrectHint
b is the correct choice. On simplification, we get
\(
z=2{ }^5 \mathrm{C}_0 \frac{\sqrt{3}^2}{2}+{ }^5 \mathrm{C}_2 \frac{\sqrt{3}^3}{2} \frac{i}{2}^2+{ }^5 \mathrm{C}_4 \frac{\sqrt{3}}{2} \frac{i}{2}^4
\)
Since \(i^2=-1\) and \(i^4=1, z\) will not contain any \(i\) and hence \(\mathrm{I}_m(z)=0\). -
Question 23 of 63
23. Question
\(
\text { Find the term independent of } x, x \neq 0 \text {, in the expansion of }\left(\frac{3 x^2}{2}-\frac{1}{3 x}\right)^{15} \text {. }
\)CorrectIncorrectHint
\(
\begin{aligned}
& \left(\frac{3 x^2}{2}-\frac{1}{3 x}\right)^{15} \text { (Given) }\\
& T_{r+1}={ }^{15} \mathrm{C}_r\left(\frac{3 x^2}{2}\right)^{15-r}\left(-\frac{1}{3 x}\right)^r \text { (standard formula of Tr+1) } \\
& T_{r+1}={ }^{15} \mathrm{C}_r(-1)^r 3^{15-2 r} 2^{r-15} X^{30-3 r} \ldots \dots(i)
\end{aligned}
\)
Now, for \(x\),
\(
\begin{aligned}
& 30-3 r=0 \\
& \rightarrow r=10
\end{aligned}
\)
Substituting the value of \(r\) in eq (i),
\(
\begin{aligned}
T_{r+1} & ={ }^{15} \mathrm{C}_{10} 3^{-5} 2^{-5} \\
& ={ }^{15} \mathrm{C}_{10}\left(\frac{1}{6}\right)^5
\end{aligned}
\) -
Question 24 of 63
24. Question
If the term free from \(x\) in the expansion of \((\sqrt{x}-{\frac{k}{x^2}})^{10}\) is 405 , find the value of \(k\).
CorrectIncorrectHint
\(
\begin{aligned}
\therefore \quad & T_{r+1}={ }^{10} C_r(\sqrt{x})^{10-r}\left(\frac{-k}{x^2}\right)^r \\
& ={ }^{10} C_r(x)^{\frac{1}{2}(10-r)}(-k)^r x^{-2 r} \\
& ={ }^{10} C_r(x)^{5-\frac{r}{2}-2 r}(-k)^r \\
& ={ }^{10} C_r x^{\frac{10-5 r}{2}}(-k)^r
\end{aligned}
\)
For the term free from \(x\),
\(
\frac{10-5 r}{2}=0 \Rightarrow r=2
\)
So, the term free from \(x\) is
\(
\begin{aligned}
& T_{2+1}={ }^{10} C_2(-k)^2 . \\
& \Rightarrow{ }^{10} C_2(-k)^2=405 \\
& \Rightarrow \frac{10 \times 9 \times 8 !}{2 ! \times 8 !}(-k)^2=405 \\
& \Rightarrow 45 k^2=405 \\
& \Rightarrow k^2=9 \quad \therefore k=\pm 3
\end{aligned}
\) -
Question 25 of 63
25. Question
\(
\text { Find the coefficient of } x \text { in the expansion of }\left(1-3 x+7 x^2\right)(1-x)^{16} \text {. }
\)CorrectIncorrectHint
The given expression is \(\left(1-3 x+7 x^2\right)(1-x)^{16}\).
\(
\begin{aligned}
& =\left(1-3 x+7 x^2\right)\left[{ }^{16} C_0(1)^{16}(-x)^0+{ }^{16} C_1(1)^{15}(-x)+{ }^{16} C_2(1)^{14}(-x)^2+\ldots\right] \\
& =\left(1-3 x+7 x^2\right)\left(1-16 x+120 x^2 \ldots\right)
\end{aligned}
\)
Collecting the term containing \(\mathrm{x}\)
We get \(-16 x-3 x=-19 x\)
Hence, the coefficient of \(x=-19\) -
Question 26 of 63
26. Question
\(
\text { Find the term independent of } x \text { in the expansion of, } (3 x-{\frac{2}{x^2}})^{15} \text {. }
\)CorrectIncorrectHint
\(
\begin{aligned}
& \therefore \mathrm{T}_{r+1}={ }^{15} C_r(3 x)^{15-r}\left(\frac{-2}{x^2}\right)^r \\
& ={ }^{15} C_r 3^{15-r} x^{15-3 r}(-2)^r
\end{aligned}
\)
For the term independent of \(x\),
\(
15-3 r=0 \Rightarrow r=5
\)
\(\therefore\) The term independent of \(x\) is
\(
\begin{aligned}
& T_{5+1}={ }^{15} C_5 3^{15-5}(-2)^5 \\
& =\frac{15 \times 14 \times 13 \times 12 \times 11 \times 10 !}{5 \times 4 \times 3 \times 2 \times 1 \times 10 !} \cdot 3^{10} \cdot 2^5 \\
& =-3003 \times 3^{10} \times 2^5
\end{aligned}
\) -
Question 27 of 63
27. Question
Find the middle term (terms) in the expansion of \((\frac{x}{a}-\frac{a}{x})^{10}\)
CorrectIncorrectHint
Given Expression (i) \((x / a-a / x)^{10}\)
Here index, \(n=10\) (even). So, there is one middle term which is \((10 / 2+1)\) th term, i.e,6th term.
\(
\begin{aligned}
& \therefore T_6=T_{5+1}={ }^{10} C_5\left(\frac{x}{a}\right)^{10-5}\left(\frac{-a}{x}\right)^5 \\
& =-{ }^{10} C_5\left(\frac{x}{a}\right)^5\left(\frac{a}{x}\right)^5 \\
& =-\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 !}{5 ! \times 5 \times 4 \times 3 \times 2 \times 1}\left(\frac{x}{a}\right)^5\left(\frac{x}{a}\right)^{-5} \\
& =-252
\end{aligned}
\) -
Question 28 of 63
28. Question
Find the middle term (terms) in the expansion of \((3 x-\frac{x^3}{6})^{9}\)
CorrectIncorrectHint
Given Expression (ii) \(\left(3 x-x^3 / 6\right)^9\)
Here index, \(n=9\) (odd)
So, there are two middle terms, which are \(((9+1) / 2)\) th i.e, 5 th term and \(((9+1) / 2\) +1)th i.e, 6th term.
\(
\begin{aligned}
& \therefore T_5=T_{4+1}={ }^9 C_4(3 x)^{9-4}\left(-\frac{x^3}{6}\right)^4 \\
& =\frac{9 \times 8 \times 7 \times 6 \times 5 !}{4 \times 3 \times 2 \times 1 \times 5 !} 3^5 x^5 x^{12} 6^{-4} \\
& =\frac{9 \times 8 \times 7 \times 6}{4 \times 3 \times 2 \times 1} \times \frac{3^5}{3^4 \times 2^4} x^{17} \\
& =\frac{189}{8} x^{17}
\end{aligned}
\)
And \(T_6=T_{5+1}={ }^9 C_5(3 x)^{9-5}\left(-\frac{x^3}{6}\right)^5\)
\(
\begin{aligned}
& =-\frac{9 \times 8 \times 7 \times 6 \times 5 !}{5 ! \times 4 \times 3 \times 2 \times 1} \cdot 3^4 \cdot x^4 \cdot x^{15} \cdot 6^{-5} \\
& =-\frac{21}{16} x^{19}
\end{aligned}
\) -
Question 29 of 63
29. Question
\(
\text { Find the coefficient of } x^{15} \text { in the expansion of }\left(x-x^2\right)^{10} \text {. }
\)CorrectIncorrectHint
The given expression is \(\left(x-x^2\right)^{10}\)
General Term \(\mathrm{T}_{r+1}={ }^n \mathrm{C}_r x^{n-r} y^r\)
\(
\begin{aligned}
& ={ }^{10} C_r(x)^{10-r}\left(-x^2\right) r \\
& ={ }^{10} C_r(x)^{10-r}(-1)^r \cdot\left(x^2\right)^r \\
& =(-1)^r \cdot{ }^{10} C_r(x)^{10-r+2 r} \\
& =(-1)^r \cdot{ }^{10} C_r(x)^{10+r}
\end{aligned}
\)
To find the coefficient of \(x^{15}\)
Put \(10+r=15\)
\(
\begin{aligned}
& \Rightarrow r=5 \\
& \therefore \text { Coefficient of } x^{15}=(-1)^5{ }^{10} C_5 \\
& =-{ }^{10} C_5 \\
& =-252
\end{aligned}
\)
Hence, the required coefficient \(=-252\) -
Question 30 of 63
30. Question
Find the coefficient of \(\frac{1}{x^{17}}\) in the expansion of \((x^4-{\frac{1}{x^3}})^{15}\)
CorrectIncorrectHint
The given expression is \(\left(x^4-\frac{1}{x^3}\right)^{15}\)
General Term \(T_{r+1}={ }^n C_r x^{n-r} y^r\)
\(
\begin{aligned}
& ={ }^{15} C_r\left(x^4\right)^{15-r}\left(-\frac{1}{x^3}\right)^r \\
& ={ }^{15} C_r(x)^{60-4 r}(-1)^r \cdot \frac{1}{x^{3 r}} \\
& ={ }^{15} C_r(-1)^r \cdot \frac{1}{x^{3 r-60+4 r}} \\
& ={ }^{15} C_r(-1)^r \cdot \frac{1}{x^{7 r-60}}
\end{aligned}
\)
To find the coefficient of \(\frac{1}{x^{17}}\)
Put \(7 r-60=17\)
\(
\begin{aligned}
& \Rightarrow 7 r=60+17 \\
& \Rightarrow 7 r=77 \\
& \therefore r=11
\end{aligned}
\)
Putting the value of \(r\) in the above expression, we get
\(
\begin{aligned}
& ={ }^{15} C_{11}(-1)^{11} \cdot \frac{1}{x^{17}} \\
& =-{ }^{15} C_4 \cdot \frac{1}{x^{17}} \\
& =-\frac{15 \times 14 \times 13 \times 12}{4 \times 3 \times 2 \times 1} \cdot \frac{1}{x^{17}} \\
& =-1365 \cdot \frac{1}{x^{17}}
\end{aligned}
\)
Hence, the coefficient of \(\frac{1}{x^{17}}=-1365\) -
Question 31 of 63
31. Question
Find the sixth term of the expansion \(\left(y^{\frac{1}{2}}+x^{\frac{1}{3}}\right)^n\), if the binomial coefficient of the third term from the end is 45.
[Hint: Binomial coefficient of third term from the end \(=\) Binomial coefficient of third term from beginning \(={ }^n \mathrm{C}_2\).]CorrectIncorrectHint
Given expression is \(\left(y^{1 / 2}+x^{1 / 3}\right)^n\)
Binomial coefficient of third term from the end \(=45\)
\(
\begin{aligned}
& \Rightarrow \quad{ }^n C_{n-2}=45 \\
& \Rightarrow \quad{ }^n C_2=45 \\
& \Rightarrow \frac{n(n-1)(n-2) !}{2 !(n-2) !}=45 \\
& \Rightarrow \quad n(n-1)=90 \\
& \Rightarrow \quad n^2-n-90=0 \\
& \Rightarrow(n-10)(n+9)=0 \\
& \Rightarrow \quad n=10[\because n \neq-9]
\end{aligned}
\)
Now, sixth term
\(
\begin{aligned}
& ={ }^{10} C_5\left(y^{1 / 2}\right)^{10-5}\left(x^{1 / 3}\right)^5 \\
& =252 y^{5 / 2} \cdot x^{5 / 3}
\end{aligned}
\) -
Question 32 of 63
32. Question
Find the value of \(r\), if the coefficients of \((2 r+4)^{\text {th }}\) and \((r-2)^{\text {th }}\) terms in the expansion of \((1+x)^{18}\) are equal.
CorrectIncorrectHint
General Term \({T}_{r+1}={ }^n C_r x^{n-r} y^r\)
For coefficient of \((2 r+4)^{\text {th }}\) term, we have
\(
\begin{aligned}
& \mathrm{T}_{2 r+4}=\mathrm{T}_{2 r+3+1} \\
& ={ }^{18} \mathrm{C}_{2 r+3}(1)^{18-2 r-3} \cdot x^{2 r+3} \\
& \therefore \text { Coefficient of }(2 r+4)^{\text {th }} \text { term }={ }^{18} \mathrm{C}_{2 r+3}
\end{aligned}
\)
Similarly, \(\mathrm{T}_{r-2}=\mathrm{T}_{r-3+1}\)
\(
\begin{aligned}
& ={ }^{18} C_{r-3}(1)^{18-r+3} \cdot x^{r-3} \\
& \therefore \text { Coefficient of }(r-2)^{\text {th }} \text { term }={ }^{18} C_{r-3}
\end{aligned}
\)
As per the condition of the questions,
We have \({ }^{18} C_{2 r+3}={ }^{18} C_{r-3}\)
\(
\begin{aligned}
& \Rightarrow 2 r+3+r-3=18 \\
& \Rightarrow 3 r=18 \\
& \Rightarrow r=6
\end{aligned}
\) -
Question 33 of 63
33. Question
If the coefficient of second, third and fourth terms in the expansion of \((1+x)^{2 n}\) are in A.P. Then \(2 n^2-9 n+7=0\). Is this statement true?
CorrectIncorrectHint
\(
\begin{aligned}
& (1+x)^{2 n}={ }^{2 n} C_0+{ }^{2 n} C_1 x+{ }^{2 n} C_2 x^2+\ldots . .+{ }^{2 n} C_n x^n+\ldots . .+{ }^{2 n} C_{2 n} x^{2 n} \\
& T_2={ }^{2 n} C_1 x, T_3={ }^{2 n} C_2 x^2, T_4={ }^{2 n} C_3 x{ }^3
\end{aligned}
\)
Given, coefficients of \(T_2, T_3\) and \(T_4\) are in A.P.
\(
\begin{aligned}
& \Rightarrow 2 \cdot{ }^{2 n} C_2={ }^{2 n} C_1+{ }^{2 n} C_3 \\
& \Rightarrow \quad 2 \cdot \frac{(2 n) !}{(2 n-2) ! 2 !}=\frac{(2 n) !}{(2 n-1) !}+\frac{(2 n) !}{(2 n-3) ! 3 !} \\
& \Rightarrow(2 n)(2 n-1)=2 n+\frac{2 n(2 n-1)(2 n-2)}{6} \\
& \Rightarrow 6(2 n-1)=6+(2 n-1)(2 n-2) \\
& \Rightarrow 12 n-6=6+4 n^2-6 n+2 \\
& \Rightarrow 4 n^2-18 n+14=0 \\
& \Rightarrow \mathbf2 n^2-9 n+7=0
\end{aligned}
\) -
Question 34 of 63
34. Question
\(
\text { Find the coefficient of } x^4 \text { in the expansion of }\left(1+x+x^2+x^3\right)^{11} \text {. }
\)CorrectIncorrectHint
Given expression is \(\left(1+x+x^2+x^3\right)^{11}\)
\(
\begin{aligned}
& =\left[(1+x)+x^2(1+x)\right]^{11} \\
& =\left[(1+x)\left(1+x^2\right)\right]^{11} \\
& =(1+x)^{11} \cdot\left(1+x^2\right)^{11}
\end{aligned}
\)
Expanding the above expression, we get
\(
\begin{aligned}
& \left({ }^{11} C_0+{ }^{11} C_1 x+{ }^{11} C_2 x^2+{ }^{11} C_3 x^3+{ }^{11} C_4 x^4+\ldots\right) \cdot\left({ }^{11} C_0+{ }^{11} C_1 x^2+{ }^{11} C_2 x^4+\right) \\
& =\left(1+11 x+55 x^2+165 x^3+330 x^4 \ldots\right) \cdot\left(1+11 x^2+55 x^4+\ldots\right)
\end{aligned}
\)
Collecting the terms containing \(x^4\), we get
\(
(55+605+330) x^4=990 x^4
\)
Hence, the coefficient of \(x^4=990\) -
Question 35 of 63
35. Question
If \(p\) is a real number and if the middle term in the expansion of \((\frac{p}{2}+2)^8\) is 1120 , find \(p\).
CorrectIncorrectHint
Given expression is \((p / 2+2)^8\)
Since index is \(n=8\) there is only one middle term, i.e., \((8 / 2+1)^{\text {th }}=5^{\text {th }}\) term
\(
\begin{aligned}
& T_5=T_{4+1}={ }^8 C_4\left(\frac{p}{2}\right)^{8-4} \cdot 2^4 \\
& \Rightarrow 1120={ }^8 C_4 p^4 \\
& \Rightarrow 1120=\frac{8 \times 7 \times 6 \times 5 \times 4 !}{4 ! \times 4 \times 3 \times 2 \times 1} p^4 \\
& \Rightarrow \quad 1120=7 \times 2 \times 5 \times p^4 \\
& \Rightarrow \quad p^4=\frac{1120}{70} \\
& \Rightarrow p^4=16 \\
& \Rightarrow p^2=4 \\
& \Rightarrow p=\pm 2
\end{aligned}
\) -
Question 36 of 63
36. Question
Is the middle term in the expansion of \(\left(x-\frac{1}{x}\right)^{2 n}\) is
\(
\frac{1 \times 3 \times 5 \times \ldots(2 n-1)}{n!} \times(-2)^n
\)?CorrectIncorrectHint
Given, expansion is \(\left(x-\frac{1}{x}\right)^{2 n}\). This Binomial expansion has even power. So, this has one middle term.
i.e., \(\left(\frac{2 n}{2}+1\right)\) th term \(=(n+1) t h\) term
\(
\begin{aligned}
& T_{n+1}={ }^{2 n} C_n(x)^{2 n-n}\left(-\frac{1}{x}\right)^n={ }^{2 n} C_n x^n(-1)^n x^{-n} \\
& ={ }^{2 n} C_n(-1)^n=(-1)^n \frac{(2 n) !}{n ! n !}=\frac{1.2 \cdot 3 \cdot 4 \cdot 5 \ldots .(2 n-1)(2 n)}{n ! n !}(-1)^n \\
& =\frac{1.3 \cdot 5 \ldots(2 n-1) \cdot 2 \cdot 4 \cdot 6 \ldots(2 n)}{12.3 \ldots n(n !)}(-1)^n \\
& =\frac{1.3 .5 \ldots(2 n-1) \cdot 2^n(1.2 \cdot 3 \ldots n)(-1)^n}{(1.2 .3 \ldots n)(n !)} \\
& =\frac{[1.3 .5 \ldots(2 n-1)]}{n !}(-2)^n
\end{aligned}
\) -
Question 37 of 63
37. Question
Find \(n\) in the binomial \((\sqrt[3]{2}+\frac{1}{\sqrt[3]{3}})^{n} \quad\) if the ratio of \(7^{\text {th }}\) term from the beginning to the \(7^{\text {th }}\) term from the end is \(\frac{1}{6}\).
CorrectIncorrectHint
In the binomial expansion of \(\left(\sqrt[3]{2}+\frac{1}{\sqrt[3]{3}}\right)^n[(n+1)-7+1]^{\text {th }}\) i.e., \((n-5)^{\text {th }}\) term from the beginning is the \(7^{\text {th }}\) term from the end.
Now,
\(
T_7={ }^n C_6(\sqrt[3]{2})^{n-6}\left(\frac{1}{\sqrt[3]{3}}\right)^6={ }^n C_6 \times 2^{\frac{n}{3}}-2 \times \frac{1}{3^2}
\)
And,
\(
T_{n-5}={ }^n C_{n-6}(\sqrt[3]{2})^6\left(\frac{1}{\sqrt[3]{3}}\right)^{n-6}={ }^n C_6 \times 2^2 \times \frac{1}{3^{\frac{n}{3}}-2}
\)
It is given that,
\(
\begin{aligned}
& \frac{T_7}{T_{n-5}}=\frac{1}{6} \\
& \Rightarrow \frac{{ }^n C_6 \times 2^{\frac{n}{3}}-2 \times \frac{1}{3^2}}{{ }^n C_6 \times 2^2 \times \frac{1}{3^{\frac{n}{3}}-2}}=\frac{1}{6} \\
& \Rightarrow 2^{\frac{n}{3}}-2-2 \times 3^{\frac{n}{3}}-2-2=\frac{1}{6} \\
& \Rightarrow\left(\frac{1}{6}\right)^{4-\frac{n}{3}}=\frac{1}{6} \\
& \Rightarrow 4-\frac{n}{3}=1 \\
& \Rightarrow n=9
\end{aligned}
\)
Hence, the value of \(n\) is 9 . -
Question 38 of 63
38. Question
\(\text { In the expansion of }(x+a)^n \text { if the sum of odd terms is denoted by } \mathrm{O} \text { and the sum of }\) even term by \(E\). Then
(i) \(\mathrm{O}^2-\mathrm{E}^2=\left(x^2-a^2\right)^n\)
(ii) \(4 \mathrm{OE}=(x+a)^{2 n}-(x-a)^{2 n}\)
Is this statement true?CorrectIncorrectHint
We have \((x+a)^n\)
\(
\begin{aligned}
={ }^n C_0 x^n+{ }^n C_1 x^{n-1} a^1+{ }^n C_2 x^{n-2} a^2 \\
+{ }^n C_3 x^{n-3} a^3+\ldots+{ }^n C_n a^n
\end{aligned}
\)
Sum of odd terms,
\(
O={ }^n C_0 x^n+{ }^n C_2 x^{n-2} a^2+\ldots
\)
And sum of even terms,
\(
\begin{gathered}
E={ }^n C_1 x^{n-1} a+{ }^n C_3 x^{n-3} a^3+\ldots \\
\quad \text { Since }(x+a)^n=O+E \cdots \text { (i) } \\
(x-a)^n=O-E \ldots \text { (ii) } \\
\therefore(O+E)(O-E)=(x+a)^n(x-a)^n \\
\Rightarrow O^2-E^2=\left(x^2-a^2\right)^n
\end{gathered}
\)
(ii)
\(
\begin{aligned}
4 O E & =(O+E)^2-(O-E)^2 \\
& =\left[(x+a)^n\right]^2-\left[(x-a)^n\right]^2 \\
& =(x+a)^{2 n}-(x-a)^{2 n}
\end{aligned}
\) -
Question 39 of 63
39. Question
If \(x^p\) occurs in the expansion of \(\left(x^2+1 / x\right)^{2 n}\), then its coefficient is
\(
\frac{(2 n) !}{\left[\frac{1}{3}(4 n-p)\right] !\left[\frac{1}{3}(2 n+p)\right] !}
\). Is this true?CorrectIncorrectHint
The general term in the expansion of \(\left(x^2+\frac{1}{x}\right)^{2 n}\) is given by
\(
\begin{aligned}
& T_{r+1}=\cdot{ }^{2 n} C_r \times\left(x^2\right)^{(2 n-r)} \times\left(\frac{1}{x}\right)^r \\
& \Rightarrow T_{r+1}=.{ }^{2 n} C_r \times x^{(4 n-3 r)} . \quad \ldots \text { (i) }
\end{aligned}
\)
This term contains \(x^p\) only when \(4 n-3 r=p\).
And, \(4 n-3 r=p \Rightarrow \frac{(4 n-p)}{3}\).
Putting \(4 n-3 r=p\) in (i), we get
coefficent of \(x^p={ }^{2 n} C_r\), where \(r=\frac{(4 n-p)}{3}\)
\(\frac{(2 n) !}{(r !) \times(2 n-r) !}=\frac{(2 n)}{\left\{\left(\frac{4 n-p}{3}\right) !\right\} \times\left\{\left[2 n-\frac{(4 n-p)}{3}\right] !\right\}}\)
\(\frac{(2 n) !}{\left\{\left(\frac{4 n-p}{3}\right) !\right\} \times\left\{\left(\frac{2 n+p}{3}\right) !\right\}}\)
Hence, the coefficent of \(x^p\) in the expansion of \(\left(x^2+\frac{1}{x}\right)^{2 n}\) is
\(
\frac{(2 n) !}{\left\{\frac{(4 n-p)}{3} !\right\} \times\left\{\left(\frac{2 n+p}{3}\right) !\right\}}
\) -
Question 40 of 63
40. Question
\(
\text { Find the term independent of } x \text { in the expansion of }\left(1+x+2 x^3\right)\left(\frac{3}{2} x^2-\frac{1}{3 x}\right)^9
\)CorrectIncorrectHint
In the expansion of \(E=\left(\frac{3}{2} x^2-\frac{1}{3 x}\right)^9\), we have
\(
\begin{aligned}
& T_{r+1}=(-1)^r \cdot{ }^9 C_r \cdot\left(\frac{3}{2} x^2\right)(9-r)\left(\frac{1}{3 x}\right)^r \\
& \Rightarrow T_{r+1}=(-1)^r \cdot{ }^9 C_r \cdot \frac{3(9-2 r)}{2^{(9-r)}} \cdot x^{(18-3 r)} . \\
& \left(1+x+2 x^3\right)\left[\left(a_0 \times \frac{1}{x^3}+a_1 \times \frac{1}{x}+a^2\right) \text { from E }\right] \\
& =\left(1+x+2 x^3\right)\left[\left\{(-1)^7 \cdot{ }^9 C_7 \cdot \frac{3^{-5}}{2^2} \times \frac{1}{x^3}\right\}+\left\{(-1)^6 \cdot{ }^9 C_6 \cdot \frac{3^{-3}}{2^3} \times x^0\right\}\right] \\
& {[\quad x=-1 \Rightarrow 18-3 r=-1 \Rightarrow \quad \mathrm{r} \text { is faction }} \\
& 18-3 r=0 \Rightarrow r=6 \text { and } 18-3 r=-3 \Rightarrow r=7] \\
& =\left(1+x+2 x^3\right)\left[\frac{-1}{27 x^3}+\frac{7}{18}\right] \\
& \therefore \quad \text { required term }\left(\frac{-2}{27}+\frac{7}{18}\right)=\frac{17}{54} .
\end{aligned}
\) -
Question 41 of 63
41. Question
The total number of terms in the expansion of \((x+a)^{100}+(x-a)^{100}\) after simplification is
CorrectIncorrectHint
Given expression is
\(
(x+a)^{100}+(x-a)^{100}
\)
Here, \(n=100\) which is even.
\(\therefore\) Total number of terms \(=\frac{n}{2}+1\) \(=\frac{100}{2}+1=51\) -
Question 42 of 63
42. Question
Given the integers \(r>1, n>2\), and coefficients of \((3 r)^{\text {th }}\) and \((r+2)^{\text {nd }}\) terms in the binomial expansion of \((1+x)^{2 n}\) are equal, then
CorrectIncorrectHint
Given that \(r>1\) and \(n>2\)
Then \(\mathrm{T}_{3 r}=\mathrm{T}_{3 r-1+1}\)
\(
={ }^{2 n} C_{3 r-1} \cdot x^{3 r-1}
\)
And \(T_{r+2}=T_{r+1+1}\)
\(
={ }^{2 n} C_{r+1} x^{r+1}
\)
We have \({ }^{2 n} C_{3 r-1}={ }^{2 n} C_{r+1}\)
\(
\begin{aligned}
& \Rightarrow 3 \mathrm{r}-1+\mathrm{r}+1=2 \mathrm{n} \quad \ldots \cdot\left[\because{ }^n C_p={ }^n C_q \Rightarrow n=p+q\right] \\
& \Rightarrow 4 \mathrm{r}=2 \mathrm{n} \\
& \mathrm{n}=2 \mathrm{r}
\end{aligned}
\) -
Question 43 of 63
43. Question
The two successive terms in the expansion of \((1+x)^{24}\) whose coefficients are in the ratio \(1: 4\) are
\(\left[\right.\) Hint: \(\left.\frac{{ }^{24} \mathrm{C}_r}{{ }^{24} \mathrm{C}_{r+1}}=\frac{1}{4} \quad \frac{r+1}{24-r} \quad \frac{1}{4} \Rightarrow 4 r+4=24-4 \Rightarrow r=4\right]\)
CorrectIncorrectHint
Let the two successive terms in the expansion of \((1+x)^{24}\) be \((r+1)\) th and \((r+2)\) th terms.
Now, \(T_{r+1}={ }^{24} C_r x^r\) and
\(
T_{r+2}={ }^{24} C_{r+1} x^{r+1}
\)
Given that, \(\frac{{ }^{24} C_r}{{ }^{24} C_{r+1}}=\frac{1}{4}\)
\(
\begin{aligned}
& \frac{(24) !}{r !(24-r) !} \\
\Rightarrow & \frac{(24) !}{(r+1) !(24-r-1) !}=\frac{1}{4} \\
\Rightarrow & \frac{(r+1) r !(23-r) !}{r !(24-r)(23-r) !}=\frac{1}{4} \\
\Rightarrow & \frac{r+1}{24-r}=\frac{1}{4} \\
\Rightarrow & 4 r+4=24-r \\
\Rightarrow & r=4 \\
\therefore & T_{4+1}=T_5 \text { and } \\
& T_{4+2}=T_6
\end{aligned}
\)
Hence, \(5^{\text {th }}\) and \(6^{\text {th }}\) terms. -
Question 44 of 63
44. Question
The coefficient of \(x^n\) in the expansion of \((1+x)^{2 n}\) and \((1+x)^{2 n-1}\) are in the ratio.
\(\left[\right.\) Hint : \({ }^{2 n} \mathrm{C}_n:{ }^{2 n-1} \mathrm{C}_n]\)
CorrectIncorrectHint
General Term \(\mathrm{T}_{r+1}={ }^{\mathrm{n}} \mathrm{C}_r x^{n-r} y^r\)
In the expansion of \((1+x)^{2 n}\)
We get \(\mathrm{T}_{r+1}={ }^{2 n} \mathrm{C}_r x^r\)
To get the coefficient of \(x^n\)
Put \(r=n\)
\(\therefore\) Coefficient of \(x^n={ }^{2 n} C_n\)
In the expansion of \((1+x)^{2 n-1}\)
We get \(\mathrm{T}_{r+1}={ }^{2 n-1} C_r x^r\)
\(\therefore\) Coefficient of \(x^n={ }^{2 n-1} C_{n-1}\)
The required ratio is \(\frac{{ }^{2 n} C_n}{{ }^{2 n-1} C_{n-1}}\)
\(
\begin{aligned}
& =\frac{\frac{2 n !}{n !(n !)}}{\frac{(2 n-1) !}{(n-1) !(2 n-1-n+1) !}} \\
& =\frac{\frac{2 n !}{n ! n !}}{\frac{(2 n-1) !}{(n-1)(n !)}} \\
& =\frac{2 n !}{n ! n !} \times \frac{(n-1) ! \cdot n !}{(2 n-1) !} \\
& =\frac{2 n(2 n-1) !}{n ! n(n-1) !} \times \frac{(n-1) ! \cdot n !}{(2 n-1) !} \\
& =\frac{2}{1} \\
& =2: 1
\end{aligned}
\) -
Question 45 of 63
45. Question
If the coefficients of \(2^{\text {nd }}, 3^{\text {rd }}\) and the \(4^{\text {th }}\) terms in the expansion of \((1+x)^n\) are in A.P., then value of \(n\) is
\(
\text { [Hint: } 2{ }^n \mathrm{C}_2={ }^n \mathrm{C}_1+{ }^n \mathrm{C}_3 \Rightarrow n^2-9 n+14=0 \Rightarrow n=2 \text { or } 7
\)CorrectIncorrectHint
\(
\begin{aligned}
(1+x)^n= & { }^n C_0+{ }^n C_1 x+{ }^n C_2 x^2 \\
& +{ }^n C_3 x^3+\ldots+{ }^n C_n x^n
\end{aligned}
\)
So coefficients of \(2 n d\), 3rd and 4th terms are \({ }^n C_1,{ }^n C_2\), and \({ }^n C_3\) respectively.
Given that, \({ }^n C_1,{ }^n C_2\), and \({ }^n C_3\) are in A.P.
\(
\begin{aligned}
& \therefore 2{ }^n C_2={ }^n C_1+{ }^n C_3 \\
& \Rightarrow 2\left[\frac{n !}{(n-2) ! 2 !}\right]=n+\frac{n !}{3 !(n-3) !} \\
& \Rightarrow 2\left[\frac{n(n-1)}{2 !}\right]=n+\frac{n(n-1)(n-2)}{3 !} \\
& \Rightarrow(n-1)=1+\frac{(n-1)(n-2)}{6} \\
& \Rightarrow \quad 6 n-6=6+n^2-3 n+2 \\
& \Rightarrow n^2-9 n+14=0 \\
& \Rightarrow \quad(n-7)(n-2)=0 \\
& \therefore n=2 \text { or } n=7
\end{aligned}
\)
Since \(n=2\) is not possible, so \(n=7\) -
Question 46 of 63
46. Question
If \(\mathrm{A}\) and \(\mathrm{B}\) are coefficient of \(x^n\) in the expansions of \((1+x)^{2 n}\) and \((1+x)^{2 n-1}\) respectively, then \(\frac{\mathrm{A}}{\mathrm{B}}\) equals
CorrectIncorrectHint
The coefficient of \(x^n\) in the expansion of \((1+x)^{2 n}\) is \({ }^{2 n} C_n\)
\(
A={ }^{2 n} C_n
\)
The coefficient of \(x^n\) in the expansion of \((1+x)^{2 n-1}\) is \({ }^{2 n-1} C_n\)
\(
\begin{aligned}
& \mathrm{B}={ }^{2 n-1} \mathrm{C}_n \\
& \therefore \frac{A}{B}=\frac{{ }^{2 n} C_n}{{ }^{2 n-1} C_n}=\frac{2}{1}=2
\end{aligned}
\) -
Question 47 of 63
47. Question
If the middle term of \((\frac{1}{x}+x \sin x)^{10} \quad\) is equal to \(7 \frac{7}{8}\), then value of \(x\) is
CorrectIncorrectHint
Given expression is \(\left(\frac{1}{x}+x \sin x\right)^{10}\)
Number of terms \(=10+1=11\) odd
\(\therefore\) Middle term \(=\frac{11+1}{2}\) th term \(=6^{\text {th }}\) term
\(\mathrm{T}_6=\mathrm{T}_{5+1}\)
\(={ }^{10} C_5\left(\frac{1}{x}\right)^{10-5}(x \sin x)^5\)
\(\therefore{ }^{10} C_5\left(\frac{1}{x}\right)^5 \cdot x^5 \cdot \sin ^5 x=7 \frac{7}{8}\)
\(\Rightarrow{ }^{10} C_5 \cdot \sin ^5 x=\frac{63}{8}\)
\(\Rightarrow \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \cdot \sin ^5 x=\frac{63}{8}\)
\(\Rightarrow 252 \cdot \sin ^5 x=\frac{63}{8}\)
\(\Rightarrow \sin ^5 x=\frac{63}{8 \times 252}\)
\(\Rightarrow \sin ^5 x=\frac{1}{32}\)
\(\Rightarrow \sin ^5 x=\left(\frac{1}{2}\right)^5\)
\(\Rightarrow \sin x=\frac{1}{2}\)
\(
\begin{aligned}
& \Rightarrow \sin \mathrm{x}=\sin \frac{\pi}{6} \\
& \therefore \mathrm{x}=\mathrm{n} \pi+(-1)^{\mathrm{n}} \cdot \frac{\pi}{6}
\end{aligned}
\)Alternate:
[Hint: \(\mathrm{T}_6={ }^{10} \mathrm{C}_5 \frac{1}{x^5} \cdot x^5 \sin ^5 x=\frac{63}{8} \Rightarrow \sin ^5 x=\frac{1}{2^5} \quad \sin \quad \frac{1}{2}\)
\(
\left.\Rightarrow x=n \pi+(-1)^n \frac{\pi}{6}\right]
\) -
Question 48 of 63
48. Question
\(
\text { The largest coefficient in the expansion of }(1+x)^{30} \text { is }………
\)CorrectIncorrectHint
Here \(n=30\) which is even
\(\therefore\) The largest coefficient in \((1+\mathrm{x})^n={ }^n C_{\frac{n}{2}}\)
So, the largest coefficient in \((1+x)^{30}={ }^{30} C_{15}\)
Hence, the value of the filler is \({ }^{30} C_{15}\). -
Question 49 of 63
49. Question
\(
\text { The number of terms in the expansion of }(x+y+z)^n …….
\)CorrectIncorrectHint
The expression \((x+y+z)^n\) can be written \(a[x+(y+z)]^n\)
\(
\begin{aligned}
& \therefore[x+y+z]^n={ }^n C_0 x^n(y+z)^0+{ }^n C_1(x)^{n-1} (y+z)+{ }^n C_2(x){ }^{n-2}(y+z)^2+\ldots+{ }^n C n(y+z)^n \\
& \therefore \text { Number of terms } 1+2+3+4+\ldots(n+1) \\
& =\frac{(n+1)(n+2)}{2}
\end{aligned}
\) -
Question 50 of 63
50. Question
\(
\text { In the expansion of } (x^2-{\frac{1}{x^2}})^{16} \text {, the value of constant term is } …….
\)CorrectIncorrectHint
Given \(\left(x^2-1 / x^2\right)^{16}\)
\(
\begin{aligned}
T_{r+1} & ={ }^{16} C_r\left(x^2\right)^{16-r}\left(-\frac{1}{x^2}\right)^r \\
& ={ }^{16} C_r x^{32-4 r}(-1)^r
\end{aligned}
\)
For constant term,
\(
\begin{aligned}
& 32-4 r=0 \Rightarrow r=8 \\
& \therefore T_{8+1}={ }^{16} C_8
\end{aligned}
\) -
Question 51 of 63
51. Question
If the seventh terms from the beginning and the end in the expansion of \((\sqrt[3]{2}+\frac{1}{\sqrt[3]{3}})^{n}\) are equal, then \(n\) equals ……..
CorrectIncorrectHint
The given expansion is \(\left(\sqrt[3]{2}+\frac{1}{\sqrt[3]{3}}\right)^n\)
\(
\begin{aligned}
& \therefore \mathrm{T}_7=\mathrm{T}_{6+1} \\
& ={ }^n \mathrm{C}_6\left(2^{\frac{1}{3}}\right)^{n-6} \cdot \frac{1}{\left(3^{\frac{1}{3}}\right)^6} \\
& ={ }^n \mathrm{C}_6(2)^{\frac{n-6}{3}} \cdot \frac{1}{(3)^2}
\end{aligned}
\)
Now the \(T_7\) from the end \(=T_7\) from the beginning in \(\left(\frac{1}{\sqrt[3]{2}}+\sqrt[3]{2}\right)^n\).
\(
\begin{aligned}
& \therefore \mathrm{T}_7=\mathrm{T}_{6+1} \\
& ={ }^n \mathrm{C}_6\left(\frac{1}{3^{\frac{1}{3}}}\right)^{n-6} \cdot\left(2^{\frac{1}{3}}\right)^6
\end{aligned}
\)
We get \({ }^n C_6(2)^{\frac{n-6}{3}} \cdot\left(\frac{1}{3^2}\right)={ }^n C_6 \frac{1}{\frac{n-6}{3}} \cdot(2)^2\)
\(
\begin{aligned}
& \Rightarrow(2)^{\frac{n-6}{3}} \cdot(3)^{-2}=(3)^{-\left(\frac{n-5}{3}\right)} \cdot(2)^2 \\
& \Rightarrow(2)^{\frac{n-6}{3}} 2 \cdot(3)^{-2+\frac{n-6}{3}}=1 \\
& \Rightarrow 2^{\frac{n-12}{3}} \cdot(3)^{\frac{n-12}{3}}=1 \\
& \Rightarrow(6)^{\frac{n-12}{3}}=(6)^0
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \frac{n-12}{3}=0 \\
& \Rightarrow \mathrm{n}=12
\end{aligned}
\) -
Question 52 of 63
52. Question
The coefficient of \(a^{-6} b^4\) in the expansion of \((\frac{1}{a}-\frac{2 b}{3})^{10}\) is
CorrectIncorrectHint
The given expansion is \(\left(\frac{1}{a}-\frac{2 b}{3}\right)^{10}\)
From \(a^{-6} b^4\)
We can take \(r=4\)
\(
\begin{aligned}
& \therefore T_5=T_{4+1} \\
& ={ }^{10} C_4\left(\frac{1}{a}\right)^{10-4}\left(-\frac{2 b}{3}\right)^4 \\
& ={ }^{10} C_4\left(\frac{1}{a}\right)^6\left(\frac{-2}{3}\right)^4 \cdot b^4 \\
& =\frac{10 \cdot 9 \cdot 8 \cdot 7}{4 \cdot 3 \cdot 2 \cdot 1} \times \frac{16}{81} \cdot a^{-6} b^4 \\
& =210 \times \frac{16}{81} a^{-6} b^4 \\
& =\frac{1120}{27} a^{-6} b^4
\end{aligned}
\) -
Question 53 of 63
53. Question
\(
\text { Middle term in the expansion of }\left(a^3+b a\right)^{28} \text { is }………
\)CorrectIncorrectHint
Number of term in the expansion \(\left(a^3+b a\right)^{28}\)
\(
\begin{aligned}
& =28+1 \\
& =29 \text { (odd) } \\
& \therefore \text { Middle term }=\frac{29+1}{2}=15^{\text {th }} \text { term } \\
& \therefore T_{15}=T_{14+1} \\
& ={ }^{28} C_{14}\left(a^3\right)^{28-14} \cdot(b a)^{14} \\
& ={ }^{28} C_{14}(a)^{42} \cdot b^{14} \cdot a^{14} \\
& ={ }^{28} C_{14} a^{56} b^{14}
\end{aligned}
\) -
Question 54 of 63
54. Question
\(
\text { The ratio of the coefficients of } x^p \text { and } x^q \text { in the expansion of }(1+x)^{p+q} \text { is }…….
\)CorrectIncorrectHint
Coefficient of \(x^p\) in the expansion of \((1+x)^{p+q}\) is \({ }^{p+q} C_p\).
Coefficient of \(x^q\) in the expansion of \((1+x)^{p+q}\) is \({ }^{p+q} C_q\)
Now,
\(
\frac{{ }^{p+q} C_p}{p+q C_q}=\frac{\frac{(p+q) !}{p ! q !}}{\frac{(p+q) !}{q ! p !}}=1
\)
Hence, the ratio of the coefficients of \(x^p\) and \(x^q\) in the expansion of \((1+x)^{p+q}\) is \(1: 1\). -
Question 55 of 63
55. Question
The position of the term independent of \(x\) in the expansion of \((\sqrt{\frac{x}{3}}+\frac{3}{2 x^2})^{10}\) is ……
CorrectIncorrectHint
Given: \(\left(\sqrt{\frac{x}{3}}+\frac{3}{2 x^2}\right)^{10}\)
Thus, \(T_{r+1}={ }^{10} C_r\left(\sqrt{\frac{x}{3}}\right)^{10-r}\left(\frac{3}{2 x^2}\right)^r\)
Now, for constant term,
\(10-5 r=0\)
Thus, \(r=2\)
Therefore, the third term is independent of \(x\). -
Question 56 of 63
56. Question
\(
\text { If } 25^{15} \text { is divided by } 13 \text {, the reminder is }……..
\)CorrectIncorrectHint
Given \(25^{15}=(26-1)^{15}\)
\(
\begin{aligned}
& ={ }^{15} C_0 26^{15}-{ }^{15} C_1 26^{14}+\ldots+{ }^{15} C_{14} 26-{ }^{15} C_{15} \\
& =\left({ }^{15} C_0 26^{15}-{ }^{15} C_1 26^{14}+\ldots+{ }^{15} C_{14} 26-13\right)+12
\end{aligned}
\)
Clearly when \(25^{15}\) is divided by 13 , then remainder will be 12 . -
Question 57 of 63
57. Question
State if this statement is True or False
\(
\text { The sum of the series }\sum_{r=0}^{10}{ }^{20} C_r \text { is } 2^{19}+\frac{{ }^{20} \mathrm{C}_{10}}{2}
\)CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{r=0}^{10}{ }^{20} C_r \\
& \left({ }^{20} C_0+{ }^{20} C_1+\ldots+{ }^{20} C_{10}\right) \\
& =\frac{1}{2}\left\{2\left({ }^{20} C_0+{ }^{20} C_1+\ldots+{ }^{20} C_{10}\right)\right\} \\
& =\frac{2}{2}\left\{\left({ }^{20} C_0+{ }^{20} C_1+\ldots+{ }^{20} C_{10}\right)+\left({ }^{20} C_{20}+{ }^{20} C_{19}+\ldots+{ }^{20} C_{10}\right)\right\} \\
& =\frac{1}{2}\left\{\left({ }^{20} C_0+{ }^{20} C_1+\ldots+{ }^{20} C_{10}+{ }^{20} C_{11}+\ldots+{ }^{20} C_{20}\right)+{ }^{20} C_{10}\right\} \\
& =\frac{1}{2}\left\{22^{20}+{ }^{20} C_{10}\right\}=22^{19}+\frac{1}{2}{ }^{20} C_{10}
\end{aligned}
\) -
Question 58 of 63
58. Question
State if the statement is True or False.
\(
\text { The expression } 7^9+9^7 \text { is divisible by } 64
\)CorrectIncorrectHint
\(
\begin{aligned}
& 7^9+9^7=(1+8)^7-(1-8)^9 \\
& =\left[{ }^7 C_0+{ }^7 C_1 \cdot 8+{ }^7 C_2(8)^2+{ }^7 C_3(8)^3+\ldots+{ }^7 C_7(8)^7\right]-\left[{ }^9 C_0-{ }^9 C_1 8+{ }^9 C_2(8)^2-{ }^9 C_3(8)^3+\ldots{ }^9 C_9(8)^9\right] \\
& =(7 \times 8+9 \times 8)+\left(21 \times 8^2-36 \times 8^2\right)+\ldots \\
& =(56+72)+(21-36) 8^2+\ldots \\
& =128+64(21-36)+\ldots \\
& =64[2+(21-36)+\ldots]
\end{aligned}
\)
Which is divisible by 64 -
Question 59 of 63
59. Question
State if the statement is True or False.
\(
\text { The number of terms in the expansion of }\left[\left(2 x+y^3\right)^4\right]^7 \text { is } 8
\)CorrectIncorrectHint
Given expression is \(\left[\left(2 x+y^3\right)^4\right]^7=(2 x+3 y)^{28}\)
So, the number of terms \(=28+1=29\) -
Question 60 of 63
60. Question
State if the statement is True or False.
The sum of coefficients of the two middle terms in the expansion of \((1+x)^{2 n-1}\) is equal to \({ }^{2 n-1} C_n\).
CorrectIncorrectHint
\(
(1+x)^{2 n-1}
\)
Here, \(\mathrm{n}\) is an odd number.
Therefore, the middle terms are \(\left(\frac{2 n-1+1}{2}\right)\) th and \(\left(\frac{2 n-1+1}{2}+1\right)\) th, i.e., \(n\)th and \((n+1)\) th terms.
Now, we have
\(
T_n=T_{n-1+1}={ }^{2 n-1} C_{n-1}(x)^{n-1}
\)
And,
\(
T_{n+1}=T_{n+1}={ }^{2 n-1} C_n(x)^n
\)
\(\therefore\) the coefficients of two middle terms are \({ }^{2 n-1} C_{n-1}\) and \({ }^{2 n-1} C_n\).
Now,
\(
{ }^{2 n-1} C_{n-1}+{ }^{2 n-1} C_n={ }^{2 n} C_n
\)
Hence, the sum of the coefficients of two middle terms in the binomial expansion of \((1+x)^{2 n-1}\) is \(^{2 n} C_n\). -
Question 61 of 63
61. Question
State if the statement is True or False.
\(
\text { The last two digits of the numbers } 3^{400} \text { are } 01 \text {. }
\)CorrectIncorrectHint
Given that \(3^{400}=(9)^{200}=(10-1)^{200}\)
\(
\begin{aligned}
& \therefore(10-1)^{200}={ }^{200} C_0(10)^{200}-{ }^{200} C_1(10)^{199}+\ldots-{ }^{200} C_{199}(10)^1+{ }^{200} C_{200}(1)^{200} \\
& =10^{200}-200 \times 10^{199}+\ldots-10 \times 200+1
\end{aligned}
\)
So, it is clear that last two digits are 01 . -
Question 62 of 63
62. Question
State if the statement is True or False.
If the expansion of \((x-\frac{1}{x^2})^{2n}\) contains a term independent of \(x\), then \(\)n\(\) is a multiple of 2.
CorrectIncorrectHint
Given Binomial expansion is \(\left(x-\frac{1}{x^2}\right)^{2 n}\)
Let \(T_{r+1}\) term is independent of \(x\)
Then, \(T_{r+1}={ }^{2 n} C_r(x)^{2 n-r}\left(-\frac{1}{x^2}\right)^r\) \(={ }^{2 n} C_r x^{2 n-r}(-1)^r x^{-2 r}={ }^{2 n} C_r x^{2 n-3 r}(-1)^r\)
For independent of \(x\)
\(
\begin{aligned}
& 2 n-3 r=0 \\
& \therefore r=\frac{2 n}{3}
\end{aligned}
\)
Which is not a integer
So, the given expansion is not possible -
Question 63 of 63
63. Question
State if the statement is True or False.
Number of terms in the expansion of \((a+b)^n\) where \(n \in \mathbf{N}\) is one less than the power \(n\).
CorrectIncorrectHint
The given statement is False.
In the given expression \((a+b)^n\), the no. of terms is just 1 more than \(n\), i.e., \(n+1\).