Past JEE Main Entrance Paper
Overview
- An expression consisting of two terms, connected by + or – sign is called a binomial expression. For example, \(x+a, 2 x-3 y, \frac{1}{x}-\frac{1}{x^3}, 7 x-\frac{4}{5 y}\), etc., are all binomial expressions.
Binomial theorem
If \(a\) and \(b\) are real numbers and \(n\) is a positive integer, then \((a+b)^n={ }^n C _0 a^n+{ }^n C _1 a^{n-1} b^1+{ }^n C _2 a^{n-2} b^2+\ldots\)
\(
\ldots+{ }^n C _r a^{n-r} b^r+\ldots+{ }^n C _n b^n \text {, where }{ }^n C _r=\frac{{n!}}{{r!} {(n-r)}!} \text { for } 0 \leq r \leq n
\)
The general term or \((r+1)^{ th }\) term in the expansion is given by
\(
T _{r+1}={ }^n C _r a^{n-r} b^r
\)
Some important observations
- The total number of terms in the binomial expansion of \((a+b)^n\) is \(n+1\), i.e. one more than the exponent \(n\).
- In the expansion, the first term is raised to the power of the binomial and in each subsequent terms the power of \(a\) reduces by one with simultaneous increase in the power of \(b\) by one, till power of \(b\) becomes equal to the power of binomial, i.e., the power of \(a\) is \(n\) in the first term, ( \(n-1)\) in the second term and so on ending with zero in the last term. At the same time power of \(b\) is 0 in the first term, 1 in the second term and 2 in the third term and so on, ending with \(n\) in the last term.
- In any term the sum of the indices (exponents) of ‘ \(a\) ‘ and ‘ \(b\) ‘ is equal to \(n\) (i.e., the power of the binomial).
- The coefficients in the expansion follow a certain pattern known as pascal’s triangle.
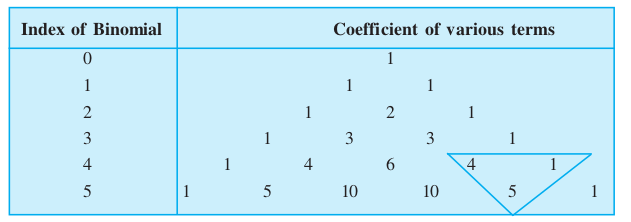
Each coefficient of any row is obtained by adding two coefficients in the preceding row, one on the immediate left and the other on the immediate right and each row is bounded by 1 on both sides.
The \((r+1)^{ \text {th} }\) term or general term is given by
\(
T _{r+1}={ }^n C _r a^{n-r} b^r
\)
Some particular cases
If \(n\) is a positive integer, then
\(
\begin{aligned}
& (a+b)^n={ }^n C _0 a^n b^0+{ }^n C _1 a^n b^1+{ }^n C _2 a^{n-2} b^2+\ldots+{ }^n C _r a^{n-r} b^r+\ldots+ { }^n C _n a^0 b^n \dots(1)
\end{aligned}
\)
In particular
- Replacing \(b\) by \(-b\) in (1), we get
\(
\begin{aligned}
& (a-b)^n={ }^n C _0 a^n b^0-{ }^n C _1 a^{n-1} b^1+{ }^n C _2 a^{n-2} b^2+\ldots+(-1)^r{ }^n C _r a^{n-r} b^r+\ldots+ \\
& (-1)^n{ }^n C _n a^0 b^n \dots(2)
\end{aligned}
\) - Adding (1) and (2), we get
\(
\begin{aligned}
(a+b)^n+(a-b)^n & =2\left[{ }^n C _0 a^n b^0+{ }^n C _2 a^{n-2} b^2+{ }^n C _4 a^{n-4} b^4+\ldots\right] \\
& =2[\text { terms at odd places }]
\end{aligned}
\) - Subtracting (2) from (1), we get
\(
\begin{aligned}
(a+b)^n-(a-b)^n & =2\left[{ }^n C _1 a^{n-1} b^1+{ }^n C _3 a^{n-3} b^3+\ldots\right] \\
& =2[\text { sum of terms at even places }]
\end{aligned}
\) - Replacing \(a\) by 1 and \(b\) by \(x\) in (1), we get
\(
(1+x)^n={ }^n C _0 x^0+{ }^n C _1 x+{ }^n C _2 x^2+\ldots+{ }^n C _r x^r+\ldots+{ }^n C _{n-1} x^{n-1}+{ }^n C _n x^n
\)
i.e. \(\quad(1+x)^n=\sum_{r=0}^n{ }^n C _r x^r\) - Replacing \(a\) by 1 and \(b\) by \(-x\) in … (1), we get
\(
(1-x)^n={ }^n C _0 x^0-{ }^n C _1 x+{ }^n C _2 x^2 \ldots+{ }^n C _{n-1}(-1)^{n-1} x^{n-1}+{ }^n C _n(-1)^n x^n
\)
i.e., \(\quad(1-x)^n=\sum_{r=0}^n(-1)^r{ }^n C _r x^r\)
The \(p~{\text {th }}\) term from the end
The \(p~{\text {th }}\) term from the end in the expansion of \((a+b)^n\) is \((n-p+2)^{\text {th }}\) term from the beginning.
Middle terms
The middle term depends upon the value of \(n\).
- If \(n\) is even: then the total number of terms in the expansion of \((a+b)^n\) is \(n+1\) (odd). Hence, there is only one middle term, i.e., \(\left(\frac{n}{2}+1\right)^{\text {th }}\) term is the middle term.
- If \(n\) is odd: then the total number of terms in the expansion of \((a+b)^n\) is \(n+1\) (even). So there are two middle terms i.e., \(\left(\frac{n+1}{2}\right)^{ th }\) and \(\left(\frac{n+3}{2}\right)^{\text {th }}\) are two middle terms.
Binomial coefficient
In the Binomial expression, we have
\(
(a+b)^n={ }^n C _0 a^n+{ }^n C _1 a^{n-1} b+{ }^n C _2 a^{n-2} b^2+\ldots+{ }^n C _n b^n \dots(1)
\)
The coefficients \({ }^n C _0,{ }^n C _1,{ }^n C _2, \ldots,{ }^n C _n\) are known as binomial or combinatorial coefficients.
Putting \(a=b=1\) in (1), we get
\(
{ }^n C _0+{ }^n C _1+{ }^n C _2+\ldots+{ }^n C _n=2^n
\)
Thus the sum of all the binomial coefficients is equal to \(2^n\).
Again, putting \(a=1\) and \(b=-1\) in (1), we get
\(
{ }^n C _0+{ }^n C _2+{ }^n C _4+\ldots={ }^n C _1+{ }^n C _3+{ }^n C _5+\ldots
\)
Thus, the sum of all the odd binomial coefficients is equal to the sum of all the even binomial coefficients and each is equal to \(\frac{2^n}{2}=2^{n-1}\).
\(
{ }^n C _0+{ }^n C _2+{ }^n C _4+\ldots={ }^n C _1+{ }^n C _3+{ }^n C _5+\ldots=2^{n-1}
\)
Quiz Summary
0 of 226 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 226 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 226
1. Question
If \(\{p\}\) denotes the fractional part of the number \(p\), then \(\left\{\frac{3^{200}}{8}\right\}\), is equal to : [Main Sep. 06, 2020 (I)]
CorrectIncorrectHint
(d)
\(
\begin{aligned}
& \frac{3^{200}}{8}=\frac{1}{8}\left(9^{100}\right) \\
& =\frac{1}{8}(1+8)^{100}=\frac{1}{8}\left[1+n \cdot 8+\frac{n(n+1)}{2} \cdot 8^2+\ldots\right] \\
& =\frac{1}{8}+\text { Integer } \\
& \therefore\left\{\frac{3^{200}}{8}\right\}=\left\{\frac{1}{8}+\text { integer }\right\}=\frac{1}{8}
\end{aligned}
\) -
Question 2 of 226
2. Question
If \(\alpha\) and \(\beta\) be the coefficients of \(x^4\) and \(x^2\) respectively in the expansion of \(\left(x+\sqrt{x^2-1}\right)^6+\left(x-\sqrt{x^2-1}\right)^6\), then: [Main Jan. 8, 2020 (II)]
CorrectIncorrectHint
\(
(x+a)^n+(x-a)^n=2\left(T_1+T_3+T_5+\ldots . .\right)
\)
\(
\begin{aligned}
& \left(\mathrm{x}+\sqrt{\mathrm{x}^2-1}\right)^6+\left(\mathrm{x}-\sqrt{\mathrm{x}^2-1}\right)^6 \\
& =2\left[T_1+T_3+T_5+T_7\right] \\
& =2\left[{ }^6 \mathrm{C}_0 \mathrm{x}^6+{ }^6 \mathrm{C}_2 \mathrm{x}^4\left(\mathrm{x}^2-1\right)+{ }^6 \mathrm{C}_4 \mathrm{x}^2\left(\mathrm{x}^2-1\right)^2+{ }^6 \mathrm{C}_6\left(\mathrm{x}^2-1\right)^3\right] \\
& =2\left[\mathrm{x}^6+15\left(\mathrm{x}^6-\mathrm{x}^4\right)+15 \mathrm{x}^2\left(\mathrm{x}^4-2 \mathrm{x}^2+1\right)+\left(-1+3 \mathrm{x}^2-3 \mathrm{x}^2+\mathrm{x}^6\right)\right] \\
& =2\left[32 \mathrm{x}^6-48 \mathrm{x}^4+18 \mathrm{x}^2-1\right] \\
& =64 \mathrm{x}^6-96 \mathrm{x}^4+36 \mathrm{x}^2-2 \\
& \alpha=-96 \\
& \beta=36 \\
& \therefore \alpha-\beta=-96-36 \\
& \quad=-132
\end{aligned}
\) -
Question 3 of 226
3. Question
The smallest natural number \(n\), such that the coefficient of \(x\) in the expansion of \(\left(x^2+\frac{1}{x^3}\right)^n\) is \({ }^n \mathrm{C}_{23}\), is : [Main April 10, 2019 (II)]
CorrectIncorrectHint
Given,
\(\left(x^2+\frac{1}{x^3}\right)^n\), its \((r+1)^{\text {th }}\) term, is
\(
\begin{aligned}
T_{r+1} & ={ }^n C_r x^{2 n-2 r} \cdot x^{-3 r} \\
& ={ }^n C_r x^{2 n-5 r}
\end{aligned}
\)
\(
\begin{aligned}
& \therefore 2 n-5 r=1 \\
& \Rightarrow r=\frac{2 n-1}{5}
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \text { Coeff. of } x={ }^n C_{\left(\frac{2 n-1}{5}\right)}={ }^n C_{23} \\
& \therefore \frac{2 n-1}{5}=23 \text { or } n-\left(\frac{2 n-1}{5}\right)=23 \\
& \Rightarrow n=58 \text { or } n=38
\end{aligned}
\)
Minimum value is \(n=38\) -
Question 4 of 226
4. Question
If the fourth term in the Binomial expansion of \(\left(\frac{2}{x}+x^{\log _8 x}\right)^6(\mathrm{x}>0)\) is \(20 \times 8^7\), then a value of \(\mathrm{x}\) is: [Main April 9, 2019 (I)]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(\frac{2}{x}+x^{\log _8 x}\right)^6(x>0) \\
& \Rightarrow T_4=20 \times 8^7 \\
& \Rightarrow{ }^6 C_3\left(\frac{2}{x}\right)^3\left(x^{\log _8 x}\right)^3=20 \times 8^7 \\
& \Rightarrow \frac{160}{x^3} x^{3 \log _8 x}=20 \times 8^7 \\
& \Rightarrow x^{3 \log _8 x-3}=8^6 \\
& \Rightarrow x^{\log _2 x-3}=8^6=2^{18} \\
& \Rightarrow \log _2\left(x^{\log _2 x-3}\right)=\log _2 2^{18} \\
& \Rightarrow\left(\log _2 x-3\right)\left(\log _2 x\right)=18 \\
& \text { Let } \log _2 x =t \\
& \Rightarrow t^2-3 t-18=0 \\
& \Rightarrow t=6,-3 \\
& \Rightarrow \log _2 x=6 \quad \Rightarrow x=2^6=8^2 \\
& \Rightarrow \log _2 x=-3 \quad \Rightarrow x=2^{-3}=1 / 8 \\
\end{aligned}
\) -
Question 5 of 226
5. Question
The sum of the coefficients of all even degree terms in \(x\) in the expansion of \(\left(x+\sqrt{x^3-1}\right)^6+\left(x-\sqrt{x^3-1}\right)^6,(x>1)\) is equal to: [Main April 8, 2019 (I)]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(\mathrm{x}+\sqrt{\mathrm{x}^3-1}\right)^6+\left(\mathrm{x}-\sqrt{\mathrm{x}^3-1}\right)^6 \\
& =2\left[{ }^6 \mathrm{C}_0 \mathrm{x}^6+{ }^6 \mathrm{C}_2 \mathrm{x}^4\left(\mathrm{x}^3-1\right)+{ }^6 \mathrm{C}_4 \mathrm{x}^2\left(\mathrm{x}^3-1\right)^2+{ }^6 \mathrm{C}_6\left(\mathrm{x}^3-1\right)^3\right] \\
& =2\left[{ }^6 \mathrm{C}_0 \mathrm{x}^6+{ }^6 \mathrm{C}_2 \mathrm{x}^7 – { }^6 \mathrm{C}_2 \mathrm{x}^4+{ }^6 \mathrm{C}_4 \mathrm{x}^8+{ }^6 \mathrm{C}_4 \mathrm{x}^2-2^6 \mathrm{C}_4 \mathrm{x}^5+\left(\mathrm{x}^9-1-3 \mathrm{x}^6+3 \mathrm{x}^3\right)\right] \\
& \Rightarrow \text { sum of coefficient of even powers of } \mathrm{x}=2[1-15+15+15-1-3]=24
\end{aligned}
\) -
Question 6 of 226
6. Question
Let \((x+10)^{50}+(x-10)^{50}=\mathrm{a}_0+\mathrm{a}_1 x+\mathrm{a}_2 x^2+\ldots .+\mathrm{a}_{50} x^{50}\), for all \(x \in \mathbf{R}\); then \(\frac{a_2}{a_0}\) is equal to : [Main Jan. 11, 2019 (II)]
CorrectIncorrectHint
\(
\begin{aligned}
& (x+10)^{50}={ }^{50} C_0(10)^{50}+{ }^{50} C_1 x \cdot 10^{49}+{ }^{50} C_2 x^2 \cdot 10^{48}+\cdots(1) \\
& (x-10)^{50}={ }^{50} C_0(10)^{50}-{ }^{50} C_1 x \cdot 10^{49}+{ }^{50} C_2 x^2 \cdot 10^{48}-\cdots(2)
\end{aligned}
\)
Add equation (1) and (2)
\(
\begin{aligned}
& (x+10)^{50}+(x-10)^{50} \\
& =2 \cdot{ }^{50} C_0 \cdot(10)^{50}+2 \cdot{ }^{50} C_2(10)^{48} \cdot x^2+\cdots \\
& \therefore a_0=2 \cdot{ }^{50} C_0(10)^{50}, a_2=2 \cdot{ }^{50} C_2(10)^{48} \\
& \Rightarrow \frac{a_2}{a_0}=\frac{2 \cdot{ }^{50} C_2(10)^{48}}{2 \cdot{ }^{50} C_0(10)^{50}} \\
& \therefore \frac{a_2}{a_0}=\frac{50 \times 49}{2 \times 100}=12.25
\end{aligned}
\) -
Question 7 of 226
7. Question
If the third term in the binomial expansion of \(\left(1+x^{\log _2 x}\right)^5\) equals 2560 , then a possible value of \(x\) is: [Main Jan. 10, 2019 (I)]
CorrectIncorrectHint
(a) Third term of \(\left(1+x^{\log _2 x}\right)^5={ }^5 C_2\left(x^{\log _2 x}\right)^{5-3}\)
\(
={ }^5 C_2\left(x^{\log _2 x}\right)^2
\)
Given, \({ }^5 \mathrm{C}_2\left(x^{\log _2 x}\right)^2=2560\)
\(
\begin{aligned}
& \Rightarrow \quad\left(x^{\log _2 x}\right)^2=256=(\pm 16)^2 \\
& \Rightarrow \quad x^{\log _2 x}=16 \text { or } x^{\log _2 x=-16 \text { (rejected) }} \\
& \Rightarrow \quad x^{\log _2 x}=16 \Rightarrow \log _2 x \log _2 x=\log _2 16=4 \\
& \Rightarrow \quad \log _2 x=\pm 2 \Rightarrow x=2^2 \text { or } 2^{-2} \\
& \Rightarrow x=4 \text { or } \frac{1}{4}
\end{aligned}
\) -
Question 8 of 226
8. Question
If the fractional part of the number \(\frac{2^{403}}{15}\) is \(\frac{k}{15}\), then \(\mathrm{k}\) is equal to: [Main Jan. 9, 2019 (I)]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{2^{403}}{15}=2^3 \times\left(\frac{2^{400}}{15}\right)=8 \times\left(\frac{16^{100}}{15}\right) \\
& =\frac{8}{15}(1+15)^{100}
\end{aligned}
\)
Using binomial theorem we can write above expression as
\(
\begin{aligned}
& \frac{8}{15}(1+15 . n), n \in N \\
& =\frac{8}{15}+8 . n
\end{aligned}
\)
So the fractional part is \(\frac{8}{15}=\frac{k}{15}\)
Hence, the value of \(k=8\) -
Question 9 of 226
9. Question
The coefficient of \(x^2\) in the expansion of the product \(\left(2-x^2\right) .((1+2 x+\) \(\left.\left.3 x^2\right)^6+\left(1-4 x^2\right)^6\right)\) is [Main Online April 16, 2018]
CorrectIncorrectHint
(a) Let \(a=\left(\left(1+2 x+3 x^2\right)^6+\left(1-4 x^2\right)^6\right)\)
\(\therefore\) Coefficient of \(x^2\) in the expansion of the product \(\left(2-x^2\right)\left(\left(1+2 x+3 x^2\right)^6+\left(1-4 x^2\right)^6\right)\) \(=2\) (Coefficient of \(x^2\) in a) \(-1\) (Constant of expansion) In the expansion of \(\left(\left(1+2 x+3 x^2\right)^6+\left(1-4 x^2\right)^6\right)\).
Constant \(=1+1=2\)
Coefficient of \(x^2=\left[\right.\) Coefficient of \(x^2\) in \(\left.\left({ }^6 C_0(1+2 x)^6\left(3 x^2\right)^0\right)\right]+[\) Coefficient of \(x^2\) in \(\left.\left({ }^6 C_1(1+2 x)^5\left(3 x^2\right)^1\right)\right]\)
– Coefficient of \(x^2\) in \(\left[{ }^6 \mathrm{C}_1\left(4 x^2\right)\right]\)
\(=60+6 \times 3-24=54\)
\(\therefore\) The coefficient of \(x^2\) in
\(
\begin{aligned}
& \left(2-x^2\right)\left(\left(1+2 x+3 x^2\right)^6+\right. \\
& \left.\left(1-4 x^2\right)^6\right) \\
& =2 \times 54-1(2)=108-2=106
\end{aligned}
\) -
Question 10 of 226
10. Question
The sum of the co-efficients of all odd degree terms in the expansion of \(\left(x+\sqrt{x^3-1}\right)^5+\left(x-\sqrt{x^3-1}\right)^5,(x>1)\) is : [Main 2018]
CorrectIncorrectHint
(c) Since we know that,
\(
\begin{aligned}
& (\mathrm{x}+\mathrm{a})^5+(\mathrm{x}-\mathrm{a})^5 \\
& =2\left[{ }^5 \mathrm{C}_0 \mathrm{x}^5+{ }^5 \mathrm{C}_2 \mathrm{x}^3 \cdot \mathrm{a}^2+{ }^5 \mathrm{C}_4 \mathrm{x} \cdot \mathrm{a}^4\right] \\
& \quad \therefore \quad\left(\mathrm{x}+\sqrt{\mathrm{x}^3-1}\right)^5+\left(\mathrm{x}-\sqrt{\mathrm{x}^3-1}\right)^5 \\
& =2\left[{ }^5 \mathrm{C}_0 \mathrm{x}^5+{ }^5 \mathrm{C}_2 \mathrm{x}^3\left(\mathrm{x}^3-1\right)+{ }^5 \mathrm{C}_4 \mathrm{x}\left(\mathrm{x}^3-1\right)^2\right] \\
& \quad \Rightarrow \quad 2\left[\mathrm{x}^5+10 \mathrm{x}^6-10 \mathrm{x}^3+5 \mathrm{x}^7-10 \mathrm{x}^4+5 \mathrm{x}\right]
\end{aligned}
\)
\(\therefore\) Sum of coefficients of odd degree terms \(=2\). -
Question 11 of 226
11. Question
The coefficient of \(x^{-5}\) in the binomial expansion of \(\left(\frac{x+1}{x^{\frac{2}{3}}-x^{\frac{1}{3}}+1}-\frac{x-1}{x-x^{\frac{1}{2}}}\right)^{10}\) where \(x \neq 0,1\), is : [Main Online April 9, 2017]
CorrectIncorrectHint
(a) \(\left[\frac{\left(x^{1 / 3}+1\right)\left(x^{2 / 3}-x^{1 / 3}+1\right)}{\left(x^{2 / 3}-x^{1 / 3}+1\right)}-\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}-1)}\right]^{10}\)
\(
\begin{aligned}
& =\left(\mathrm{x}^{1 / 3}+1-1-1 / \mathrm{x}^{1 / 2}\right)^{10}=\left(x^{1 / 3}-1 / x^{1 / 2}\right)^{10} \\
& \mathrm{~T}_{r+1}={ }^{10} C_{\mathrm{r}} \frac{20-5 \mathrm{r}}{6} \\
& \text { for } \mathrm{r}=10 \\
& \quad \mathrm{~T}_{11}={ }^{10} \mathrm{C}_{10} \mathrm{x}^{-5}
\end{aligned}
\)
Coefficient of \(\mathrm{x}^{-5}={ }^{10} C_{10}(1)(-1)^{10}=1\) -
Question 12 of 226
12. Question
If the coefficients of \(x^{-2}\) and \(x^{-4}\) in the expansion of \(\left(x^{\frac{1}{3}}+\frac{1}{2 x^{\frac{1}{3}}}\right)^{18},(x\) \(>0\) ), are \(m\) and \(n\) respectively, then \(\frac{\mathrm{m}}{\mathrm{n}}\) is equal to : [Main Online April 10, 2016]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (b) } T_{r+1}={ }^{18} C_r\left(x^{\frac{1}{3}}\right)^{18-r}\left(\frac{1}{2 x^{\frac{1}{3}}}\right)^r={ }^{18} C_r x^{6-\frac{2 r}{3}} \frac{1}{2^r} \\
& \left\{\begin{array}{l}
6-\frac{2 r}{3}=-2 \Rightarrow r=12 \\
\& 6-\frac{2 r}{3}=-4 \Rightarrow r=15
\end{array}\right\}
\end{aligned}
\)\(
\Rightarrow \frac{\text { coefficient of } x^{-2}}{\text { coefficient of } x^{-4}}=\frac{{ }^{18} C_{12} \frac{1}{2^{12}}}{{ }^{18} C_{15} \frac{1}{2^{15}}}=182
\) -
Question 13 of 226
13. Question
If the coefficents of \(x^3\) and \(x^4\) in the expansion of \(\left(1+a x+b x^2\right)(1-2 x)^{18}\) in powers of \(x\) are both zero, then \((a, b)\) is equal to: [Main 2014]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(1+a x+b x^2\right)(1-2 x)^{18}=1(1-2 x)^{18}+a x(1-2 x)^{18}+b x^2(1-2 x)^{18} \\
& \text { Coefficient of } x^3:(-2)^3{ }^{18} C_3+a(-2)^2{ }^{18} C_2+b(-2)^{18} C_1=0 \\
& \frac{4 \times(17 \times 16)}{(3 \times 2)}-2 a \times \frac{17}{2}+b=0-(1) \\
& \text { Coefficient of } x^4:(-2)^4{ }^{18} C_4+a(-2)^3{ }^{18} C_3+b(-2)^2{ }^{18} C_2=0 \\
& (4 \times 20)-2 a \times \frac{16}{3}+b=0-(2) \\
& \text { From equations }(1) \text { and }(2), \text { we get } \\
& 4\left(\frac{17 \times 8}{3}-20\right)+2 a\left(\frac{16}{3}-\frac{17}{2}\right)=0 \\
& \Rightarrow a=16 \\
& \Rightarrow b=\frac{2 \times 16 \times 16}{3}-80=\frac{272}{3}
\end{aligned}
\) -
Question 14 of 226
14. Question
If \(X=\left\{4^n-3 n-1: n \in N\right\}\) and \(Y=\{9(n-1): n \in N\}\), where \(N\) is the set of natural numbers, then \(X \cup Y\) is equal to: [Main 2014]
CorrectIncorrectHint
\(
\begin{aligned}
\because X & =\left\{4^n-3 n-1: n \in N\right\} \\
X & =\{0,9,54,243, \ldots\} \text { [put } n=1,2,3, \ldots] \\
Y & =\{9(n-1): n \in N\} \\
Y & =\{0,1,18,27, \ldots\}
\end{aligned}
\)
It is clear that \(X \subset Y\).
\(
\therefore \quad X \cup Y=Y
\) -
Question 15 of 226
15. Question
The number of terms in the expansion of \((1+x)^{101}\left(1+x^2-x\right)^{100}\) in powers of \(x\) is: [Main Online April 9, 2014]
CorrectIncorrectHint
(c) Given expansion is
\(
\begin{aligned}
&(1+x)^{101}\left(1-x+x^2\right)^{100} \\
&=(1+x)(1+x)^{100}\left(1-x+x^2\right)^{100} \\
&=(1+x)\left[(1+x)\left(1-x+x^2\right)\right]^{100} \\
&=(1+x)\left[\left(1-x^3\right)^{100}\right]
\end{aligned}
\)
Expansion \(\left(1-x^3\right)^{100}\) will have \(100+1=101\) terms.
So, \((1+x)\left(1-x^3\right)^{100}\) will have \(2 \times 101=202\) terms -
Question 16 of 226
16. Question
The sum of the rational terms in the binomial expansion of \(\left(2^{\frac{1}{2}}+3^{\frac{1}{5}}\right)^{10}\) is : [Main Online April 23, 2013]
CorrectIncorrectHint
\(
\text { (d) }\left(2^{1 / 2}+3^{1 / 5}\right)^{10}={ }^{10} \mathrm{C}_0\left(2^{1 / 2}\right)^{10} +{ }^{10} \mathrm{C}_1\left(2^{1 / 2}\right)^9\left(3^{1 / 5}\right)+\ldots \ldots+{ }^{10} \mathrm{C}_{10}\left(3^{1 / 5}\right)^{10}\)
There are only two rational terms – first term and last term. Now sum of two rational terms
\(
=(2)^5+(3)^2=32+9=41
\) -
Question 17 of 226
17. Question
For \(\mathrm{r}=0,1, \ldots, 10\), let \(A_r, B_r\) and \(C_r\) denote, respectively, the coefficient of \(\mathrm{x}^{\mathrm{r}}\) in the expansions of \((1+x)^{10}\), [2010]
\((1+x)^{20}\) and \((1+x)^{30}\). Then \(\sum_{\mathrm{r}=1}^{10} A_r\left(B_{10} B_{\mathrm{r}}-C_{10} A_r\right)\) is equal toCorrectIncorrectHint
Let \(y=\sum_{r=1}^{10} A_r\left(B_{10} B_r-C_{10} A_r\right)\).
Now, \(\sum_{r=1}^{10} A_r B_r=\) coefficient of \(x^{10}\) in \(\left[(1+x)^{10}(1+x)^{20}\right]-1\)
\(
\Rightarrow \sum_{\mathrm{r}=1}^{10} \mathrm{~A}_{\mathrm{r}} \mathrm{B}_{\mathrm{r}}=\mathrm{C}_{20}-1=\mathrm{C}_{10}-1
\)
And \(\sum_{r=1}^{10} A_r^2=\) coefficient of \(x^{10}\) in \(\left[(1+x)^{10}(1+x)^{10}\right]-1\) \(\Rightarrow \sum_{\mathrm{r}=1}^{10} \mathrm{~A}_{\mathrm{r}}^2=\mathrm{B}_{10}-1\)Therefore, \(\mathrm{y}=\mathrm{B}_{10}\left(\mathrm{C}_{10}-1\right)-\mathrm{C}_{10}\left(\mathrm{~B}_{10}-1\right)=\mathrm{C}_{10}-\mathrm{B}_{10}\).
-
Question 18 of 226
18. Question
Coefficient of \(t^{24}\) in \(\left(1+t^2\right)^{12}\left(1+t^{12}\right)\left(1+t^{24}\right)\) is [2003S]
CorrectIncorrectHint
(d) \(\left(1+t^2\right)^{12}\left(1+t^{12}\right)\left(1+t^{24}\right)\)
\(
\begin{aligned}
& =\left(1+t^{12}+t^{24}+t^{36}\right)\left(1+t^2\right)^{12} \\
& \therefore \text { Coeff. of } t^{24}=1 \times \text { Coeff. of } t^{24} \text { in }\left(1+t^2\right)^{12}+1 \times \\
& \text { Coeff. of } t^{12} \text { in }\left(1+t^2\right)^{12}+1 \times \text { constant term in }\left(1+t^2\right)^{12} \\
& ={ }^{12} C_{12}+{ }^{12} C_6+{ }^{12} C_0=1+{ }^{12} C_6+1={ }^{12} C_6+2 \\
&
\end{aligned}
\) -
Question 19 of 226
19. Question
In the binomial expansion of \((a-b)^n, n \geq 5\), the sum of the \(5^{\text {th }}\) and \(6^{\text {th }}\) terms is zero. Then \(a / b\) equals [2001S]
CorrectIncorrectHint
(b) In binomial expansion \((a-b)^n, \mathrm{n} \geq 5\);
\(
\begin{aligned}
& T_5+T_6=0 \\
& \Rightarrow{ }^n C_4 a^{n-4} b^4-{ }^n C_5 a^{n-5} b^5=0 \\
& \Rightarrow \frac{{ }^n C_4}{{ }^n C_5} \cdot \frac{a}{b}=1 \Rightarrow \frac{5}{n-4} \cdot \frac{a}{b}=1 \Rightarrow \quad \frac{a}{b}=\frac{n-4}{5}
\end{aligned}
\) -
Question 20 of 226
20. Question
The coefficient of \(x^4\) in \(\left(\frac{x}{2}-\frac{3}{x^2}\right)^{10}\) is [1983- 1 Mark]
CorrectIncorrectHint
(a) General term in the expansion \(\left(\frac{x}{2}-\frac{3}{x^2}\right)^{10}\) is
\(
T_{r+1}={ }^{10} C_r\left(\frac{x}{2}\right)^{10-r}\left(\frac{-3}{x^2}\right)^r={ }^{10} C_r x^{10-3 r} \frac{(-1)^r 3^r}{2^{10-r}}
\)
To find coeff of \(x^4\), put \(10-3 \mathrm{r}=4 \Rightarrow \mathrm{r}=2\)
\(\therefore\) Coeff of \(\mathrm{x}^4={ }^{10} \mathrm{C}_2 \frac{(-1)^2 3^2}{2^8}=\frac{405}{256}\) -
Question 21 of 226
21. Question
Given positive integers \(r>1, n>2\) and that the coefficient of \((3 r)\) th and \((r+2)\) th terms in the binomial expansion of \((1+x)^{2 n}\) are equal . Then [1983 – 1 Mark]
CorrectIncorrectHint
(a) Given : \(\mathrm{r}\) and \(\mathrm{n}\) are positive integers such that \(\mathrm{r}>1, \mathrm{n}>2\)
Also, in the expansion of \((1+x)^{2 n}\)
Coeff. of \((3 \mathrm{r})^{\text {th }}\) term \(=\) Coeff. of \((\mathrm{r}+2)^{\mathrm{th}}\) term
\(
\begin{aligned}
& \Rightarrow{ }^{2 \mathrm{n}} \mathrm{C}_{3 \mathrm{r}-1}={ }^{2 \mathrm{n}} \mathrm{C}_{\mathrm{r}+1} \\
& \Rightarrow 3 \mathrm{r}-1=\mathrm{r}+1 \text { or } 3 \mathrm{r}-1+\mathrm{r}+1=2 \mathrm{n} \\
& {\left[\because \text { If }{ }^n C_p={ }^n C_q \text {, then } p=q \text { or } p+q=n\right]} \\
& \Rightarrow \mathrm{r}=1 \text { or } 2 \mathrm{r}=\mathrm{n} \\
&
\end{aligned}
\)
But \(\mathrm{r}>1 \quad \therefore \quad \mathrm{n}=2 \mathrm{r}\) -
Question 22 of 226
22. Question
Let \(X=\left({ }^{10} C_1\right)^2+2\left({ }^{10} C_2\right)^2+3\left({ }^{10} C_3\right)^2+\cdots+10\left({ }^{10} C_{10}\right)^2,\)
where \({ }^{10} C_r, r \in\{1,2, \cdots, 10\}\) denote binomial coefficients. Then, the value of \(\frac{1}{1430} X\) is [Adv. 2018]CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{\mathrm{r}=0}^{\mathrm{n}} \mathrm{r}\left({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}\right)^2=\mathrm{n} \sum_{\mathrm{r}=0}^{\mathrm{n}}{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}{ }^{\mathrm{n}-1} \mathrm{C}_{\mathrm{r}-1} \\
& =\mathrm{n} \sum_{\mathrm{r}=1}^{\mathrm{n}}{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{n}-\mathrm{r}}{ }^{\mathrm{n}-1} \mathrm{C}_{\mathrm{r}-1}={ }^{2 \mathrm{n}-1} \mathrm{C}_{\mathrm{n}-1}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\mathrm{X} & =\left({ }^{10} \mathrm{C}_1\right)^2+2\left({ }^{10} \mathrm{C}_2\right)^2+3\left({ }^{10} \mathrm{C}_3\right)^2+\ldots+10\left({ }^{10} \mathrm{C}_{10}\right)^2 \\
& =\sum_{\mathrm{n}=0}^{10} \mathrm{r}\left({ }^{10} \mathrm{C}_{\mathrm{r}}\right)^2=10^{19} \mathrm{C}_9 \\
\therefore & \frac{\mathrm{X}}{1430}=\frac{1}{143}{ }^{19} \mathrm{C}_9=646
\end{aligned}
\) -
Question 23 of 226
23. Question
Let \(m\) be the smallest positive integer such that the coefficient of \(x^2\) in the expansion of \((1+x)^2+(1+x)^3+\ldots+(1+x)^{49}+(1+m x)^{50}\) is \((3 n+\) 1) \({ }^{51} C_3\) for some positive integer \(n\). Then the value of \(n\) is [Adv. 2016]
CorrectIncorrectHint
(5) \((1+x)^2+(1+x)^3+\ldots .+(1+x)^{49}+(1+m x)^{50}\)
\(
\begin{aligned}
& =(1+x)^2\left[\frac{(1+x)^{48}-1}{(1+x)-1}\right]+(1+m x)^{50} \\
& =\frac{1}{x}\left[(1+x)^{50}-(1+x)^2\right]+(1+m x)^{50}
\end{aligned}
\)
Coeff. of \(x^2\) in the above expansion
\(
\begin{aligned}
& =\text { Coeff. of } x^3 \text { in }(1+x)^{50}+\text { Coeff. of } x^2 \text { in }(1+m x)^{50} \\
& ={ }^{50} \mathrm{C}_3+{ }^{50} \mathrm{C}_2 \mathrm{~m}^2 \\
& \therefore(3 \mathrm{n}+1){ }^{51} \mathrm{C}_3={ }^{50} \mathrm{C}_3+{ }^{50} \mathrm{C}_2 \mathrm{~m}^2 \\
& \Rightarrow(3 \mathrm{n}+1)=\frac{{ }^{50} \mathrm{C}_3}{{ }^{51} \mathrm{C}_3}+\frac{{ }^{50} \mathrm{C}_2}{{ }^{51} \mathrm{C}_3} \mathrm{~m}^2 \\
& \Rightarrow 3 \mathrm{n}+1=\frac{16}{17}+\frac{1}{17} \mathrm{~m}^2 \Rightarrow \mathrm{n}=\frac{\mathrm{m}^2-1}{51} \\
&
\end{aligned}
\)
\(\therefore\) Least positive integer \(\mathrm{m}\) for which \(\mathrm{n}\) is an integer is m \(=16\) and then \(n=5\) -
Question 24 of 226
24. Question
The coefficients of three consecutive terms of \((1+x)^{n+5}\) are in the ratio \(5: 10: 14\). Then \(\mathrm{n}=\) [Adv. 2013]
CorrectIncorrectHint
(6) Let the coefficients of three consecutive terms of \((1+x)^{n+5}\) be \({ }^{n+}\) \({ }^5 C_{r-1},{ }^{n+5} C_r,{ }^{n+5} C_{r+1}\), then we have
\(
\begin{aligned}
& { }^{n+5} C_{r-1}:{ }^{n+5} C_r:{ }^{n+5} C_{r+1}=5: 10: 14 \\
& \frac{{ }^{n+5} C_{r-1}}{{ }^{n+5} C_r}=\frac{5}{10} \Rightarrow \frac{r}{n+6-r}=\frac{1}{2}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow n-3 r+6=0 \\
\text { Also } & \frac{{ }^{n+5} C_r}{{ }^{n+5} C_{r+1}}=\frac{10}{14} \Rightarrow \frac{r+1}{n-r+5}=\frac{5}{7} \\
& \Rightarrow 5 n-12 r+18=0
\end{aligned}
\)
Solving (i) and (ii), we get \(n=6\). -
Question 25 of 226
25. Question
The natural number \(m\), for which the coefficient of \(x\) in the binomial expansion of \(\left(x^m+\frac{1}{x^2}\right)^{22}\) is 1540 , is [Main Sep. 05, 2020 (I)]
CorrectIncorrectHint
(13)
\(
\begin{aligned}
& T_{r+1}={ }^{22} C_r \cdot\left(x^m\right)^{22-r} \cdot\left(\frac{1}{x^2}\right)^r \\
& T_{r+1}={ }^{22} C_r \cdot x^{22 m-m r-2 r} \\
& \because 22 m-m r-2 r=1 \\
& \Rightarrow r=\frac{22 m-1}{m+2} \Rightarrow r=22-\frac{3 \cdot 3 \cdot 5}{m+2}
\end{aligned}
\)
So, possible value of \(m=1,3,7,13,43\)
But \({ }^{22} C_r=1540\)
\(\therefore\) Only possible value of \(m=13\). -
Question 26 of 226
26. Question
The coefficient of \(x^4\) in the expansion of \(\left(1+x+x^2+x^3\right)^6\) in powers of \(x\), is [Main Sep. 05, 2020 (II)]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Coefficient of } x^4 \text { in }\left(\frac{1-x^4}{1-x}\right)^6=\text { coefficient of } x^4 \text { in }\left(1-6 x^4\right)(1-x)^{-6} \\
& =\text { coefficient of } x^4 \text { in }\left(1-6 x^4\right)\left[1+{ }^6 C_1 x+{ }^7 C_2 x^2+\ldots\right] \\
& \quad={ }^9 C_4-6 \cdot 1=126-6=120
\end{aligned}
\) -
Question 27 of 226
27. Question
Let \(\left(2 x^2+3 x+4\right)^{10}=\sum_{r=0}^{20} a_r x^r\). Then \(\frac{a_7}{a_{13}}\) is equal to [Main Sep. 04, 2020 (I)]
CorrectIncorrectHint
Finding the value of \(\frac{a_7}{a_{13}}\) :
Given, \(\left(2 x^2+3 x+4\right)^{10}=\sum_{r=0}^{20} a_r x^r \quad \ldots \ldots(1)\)
To obtain the symmetry, replace \(x\) by \(\frac{2}{x}\) in above equation we get,
\(
\begin{aligned}
& {\left[2\left(\frac{2}{x}\right)^2+3\left(\frac{2}{x}\right)+4\right]^{10}=\sum_{r=0}^{20} a_r \frac{2^r}{x^r}} \\
& \Rightarrow \quad\left[\frac{8}{x^2}+\frac{6}{x}+4\right]^{10}=\sum_{r=0}^{20} a_r \times 2^r\left(\frac{1}{x^r}\right) \\
& \Rightarrow \quad \frac{2^{10}}{x^{20}}\left[2 x^2+3 x+4\right]^{10}=\sum_{r=0}^{20} a_r 2^r\left(\frac{1}{x^r}\right) \\
& \Rightarrow \quad\left[2 x^2+3 x+4\right]^{10}=\sum_{r=0}^{20} a_r 2^{(r-10)} x^{(20-r)} \\
&
\end{aligned}
\)
Substituting equation (1) in equation (2), we get
\(
\sum_{r=0}^{20} a_r x^r=\sum_{r=0}^{20} a_r 2^{(r-10)} x^{(20-r)}
\)
Put \(r=7\) in LHS and \(r=13\) on RHS to find the coefficients of \(x^7\) on both sides and compare them we get,
\(
\begin{aligned}
& a_7= a_{13}(2)^3 \\
& \Rightarrow \frac{a_7}{a_{13}}=8
\end{aligned}
\)
Hence, the value of the ratio \(\frac{a_7}{a_{13}}=8\). -
Question 28 of 226
28. Question
The sum of the rational terms in the expansion of \(\left(\sqrt{2}+3^{1 / 5}\right)^{10}\) is [1997 – 2 Marks]
CorrectIncorrectHint
Given expression : \(\left(\sqrt{2}+3^{1 / 5}\right)^{10}\)
\(
\begin{aligned}
\therefore & T_{r+1}={ }^{10} C_r(\sqrt{2})^{10-r} \cdot\left(3^{1 / 5}\right)^r \cdot(0 \leq r \leq 10) \\
& =\frac{10 !}{r !(10-r) !} \cdot 2^{5-r / 2} \cdot 3^{r / 5}
\end{aligned}
\)
\(\mathrm{T}_{\mathrm{r}+1}\) will be rational if \(2^{5-r / 2}\) and \(3^{\mathrm{r} / 5}\) are rational numbers.
\(\Rightarrow 5-\frac{r}{2}\) and \(\frac{r}{5}\) are integers
\(\Rightarrow \mathrm{r}=0\) and \(\mathrm{r}=10 \Rightarrow \mathrm{T}_1\) and \(\mathrm{T}_{11}\) are rational terms.
Now, \(\mathrm{T}_1+\mathrm{T}_{11}={ }^{10} \mathrm{C}_0 2^{5-0} \cdot 3^0+{ }^{10} \mathrm{C}_{10} 2^{5-5} \cdot 3^2\)
\(
=1.32 .1+1.1 .9=32+9=41
\) -
Question 29 of 226
29. Question
Let \(n\) be positive integer. If the coefficients of \(2 \mathrm{nd}\), 3rd, and 4 th terms in the expansion of \((1+x)^n\) are in A.P., then the value of \(n\) is [1994- 2 Marks]
CorrectIncorrectHint
We know that for \(a\) positive integer \(n\)
\(
(1+x)^n={ }^n C_0+{ }^n C_1 x+{ }^n C_2 x^2+\ldots . .+{ }^n C_n x^n
\)
Since coefficients of \(2^{\text {nd }}, 3^{\text {rd }}\) and \(4^{\text {th }}\) terms are in A.P.
\(
\begin{aligned}
& \therefore{ }^n C_1,{ }^n C_2,{ }^n C_3 \text { are in A.P. } \\
& \Rightarrow 2 \cdot{ }^n C_2={ }^n C_1+{ }^n C_3 \\
& \Rightarrow 2 \times \frac{n(n-1)}{2}=n+\frac{n(n-1)(n-2)}{3 !} \\
& \Rightarrow n-1=1+\frac{n^2-3 n+2}{6} \Rightarrow n^2-9 n+14=0 \\
& \Rightarrow(n-7)(n-2)=0 \Rightarrow \mathrm{n}=7 \text { or } 2
\end{aligned}
\)
But for the existence of \(4^{\text {th }}\) term, \(n=7\). -
Question 30 of 226
30. Question
\(
\text { The larger of } 99^{50}+100^{50} \text { and } 101^{50} \text { is }……
\) [1982- 2 Marks]CorrectIncorrectHint
\(
\begin{aligned}
& (101)^{50}-\left\{(99)^{50}+(100)^{50}\right\} \\
& =(100+1)^{50}-(100-1)^{50}-(100)^{50} \\
& =(100)^{50}\left[(1+0.01)^{50}-(1-0.01)^{50}-1\right] \\
& =(100)^{50}\left[2\left(\left(^{50} C_1(0.01)+{ }^{50} C_3(0.01)^3+\ldots .\right)-1\right]\right. \\
& \quad=(100)^{50}\left[2 \times 50 \times \frac{1}{100}+2\left({ }^{50} C_3(0.01)^3+\ldots .\right)-1\right] \\
& =(100)^{50}\left[2\left(\left(^{50} C_3(0.01)^3+\ldots .\right)\right]>0\right. \\
& \quad \therefore(101)^{50}>(99)^{50}+(100)^{50} \quad \therefore(101)^{50} \text { is greater. }
\end{aligned}
\) -
Question 31 of 226
31. Question
If \(a_n=\sum_{r=0}^n \frac{1}{{ }^n C_r}\), then \(\sum_{r=0}^n \frac{r}{{ }^n C_r}\) equals [1998 – 2 Marks]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (c) Let } b=\sum_{r=0}^n \frac{r}{{ }^n C_r}=\sum_{r=0}^n \frac{n-(n-r)}{{ }^n C_r} \\
& =n a_n-\sum_{r=0}^n \frac{n-r}{{ }^n C_{n-r}} \quad\left[\because{ }^n C_r={ }^n C_{n-r}\right] \\
& =n a_n-b \\
& \Rightarrow 2 b=n a_n \Rightarrow b=\frac{n}{2} a_n \\
&
\end{aligned}
\) -
Question 32 of 226
32. Question
If the constant term in the binomial expansion of \(\left(\sqrt{x}-\frac{k}{x^2}\right)^{10}\) is 405 , then \(|k|\) equals: [Main Sep. 06, 2020 (II)]
CorrectIncorrectHint
\(
\text { (c) } \begin{aligned}
\text { General term }=T_{r+1}= & { }^{10} C_r(\sqrt{x})^{10-r} \cdot\left(-\frac{k}{x^2}\right)^r \\
& ={ }^{10} C_r(-k)^r \cdot x^{\frac{10-r}{2}-2 r} \\
& ={ }^{10} C_r(-k)^r \cdot x^{\frac{10-5 r}{2}}
\end{aligned}
\)
Since, it is constant term, then
\(
\begin{aligned}
& \frac{10-5 r}{2}=0 \Rightarrow r=2 \\
& \therefore{ }^{10} C_2(-k)^2=405 \\
& \Rightarrow k^2=\frac{405 \times 2}{10 \times 9}=\frac{81}{9}=9 \\
& \therefore|k|=3
\end{aligned}
\) -
Question 33 of 226
33. Question
If for some positive integer \(n\), the coefficients of three consecutive terms in the binomial expansion of \((1+x)^{n+5}\) are in the ratio \(5: 10: 14\), then the largest coefficient in this expansion is : [Main Sep. 04, 2020 (II)]
CorrectIncorrectHint
Let the three consecutive terms in the binomial expansion of \((1+\mathrm{x})^{\mathrm{n}+5}\) are \({ }^{\mathrm{n}+5} \mathrm{C}_{\mathrm{r}-1},{ }^{\mathrm{n}+5} \mathrm{C}_{\mathrm{r}}\) and \({ }^{\mathrm{n}+5} \mathrm{C}_{\mathrm{r}+1}\)
Now, according to the given information \({ }^{\mathrm{n}+5} \mathrm{C}_{\mathrm{r}-1}:{ }^{\mathrm{n}+5} \mathrm{C}_{\mathrm{r}}:{ }^{\mathrm{n}+5} \mathrm{C}_{\mathrm{r}+1}=5: 10: 14\)
\(
\Rightarrow \quad \frac{(\mathrm{n}+5) !}{(\mathrm{r}-1) !(\mathrm{n}-\mathrm{r}+6) !}: \frac{(\mathrm{n}+5) !}{\mathrm{r} !(\mathrm{n}-\mathrm{r}+5) !}: \frac{(\mathrm{n}+5) !}{(\mathrm{r}+1) !(\mathrm{n}-\mathrm{r}+4) !}=5: 10: 14
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{1}{(n-\mathrm{r}+6)(\mathrm{n}-\mathrm{r}+5)}: \frac{1}{\mathrm{r}(\mathrm{n}-\mathrm{r}+5)}: \frac{1}{(\mathrm{r}+1) \mathrm{r}} \\
& \text { So, } \quad \frac{\mathrm{r}}{\mathrm{n}-\mathrm{r}+6}=\frac{5}{10} \\
& \Rightarrow \quad 2 \mathrm{r}=\mathrm{n}-\mathrm{r}+6 \Rightarrow \mathrm{n}+6=3 \mathrm{r} \dots(i)\\
& \text { and } \quad \frac{\mathrm{r}+1}{\mathrm{n}-\mathrm{r}+5}=\frac{5}{7} \\
& \Rightarrow \quad 7 \mathrm{r}+7 \quad=5 \mathrm{n}-5 \mathrm{r}+25 \\
& \Rightarrow \quad 5 \mathrm{n}+18=12 \mathrm{r} \dots(ii)
\end{aligned}
\)
From Eqs. (i) and (ii), we have \(n=6\).
So, the largest coefficient in the expansion is same as the greatest binomial coefficient
\(
\begin{aligned}
& ={ }^{11} \mathrm{C}_5 \text { or }{ }^{11} \mathrm{C}_6 \\
& =\frac{11 !}{5 ! 6 !}=\frac{11 \times 10 \times 9 \times 8 \times 7}{5 \times 4 \times 3 \times 2}=462
\end{aligned}
\) -
Question 34 of 226
34. Question
If the number of integral terms in the expansion of \(\left(3^{1 / 2}+5^{1 / 8}\right)^n\) is exactly 33 , then the least value of \(n\) is : [Main Sep. 03, 2020 (I)]
CorrectIncorrectHint
(c) Here, \(\left(3^{\frac{1}{2}}+5^{\frac{1}{8}}\right)^n\)
\(
T_{r+1}={ }^n C_r(3)^{\frac{n-r}{2}}(5)^{\frac{r}{8}}
\)
\(\because \frac{n-r}{2}\) and \(\frac{r}{8}\) are integer
So, \(r\) must be \(0,8,16,24 \ldots \ldots\)
Now \(n=t_{33}=a+(n-1) d=0+32 \times 8=256\)
\(
\Rightarrow n=256
\) -
Question 35 of 226
35. Question
If the term independent of \(x\) in the expansion of \(\left(\frac{3}{2} x^2-\frac{1}{3 x}\right)^9\) is \(k\), then \(18 k\) is equal to : [Main Sep. 03, 2020 (II)]
CorrectIncorrectHint
(c) General term \(=T_{r+1}={ }^9 C_r\left(\frac{3 x^2}{2}\right)^{9-r}\left(-\frac{1}{3 x}\right)^r\)
\(
={ }^9 C_r\left(\frac{3}{2}\right)^{9-r}\left(-\frac{1}{3}\right)^r x^{18-3 r}
\)
The term is independent of \(x\), then
\(
\begin{aligned}
& 18-3 r=0 \Rightarrow r=6 \\
& \therefore T_7={ }^9 C_6\left(\frac{3}{2}\right)^3\left(-\frac{1}{3}\right)^6={ }^9 C_3\left(\frac{1}{6}\right)^3 \\
& =\frac{9 \times 8 \times 7}{3 \times 2 \times 1}\left(\frac{1}{6}\right)^3=\left(\frac{7}{18}\right) . \\
& \therefore 18 k=18 \times \frac{7}{18}=7 .
\end{aligned}
\) -
Question 36 of 226
36. Question
Let \(\alpha>0, \beta>0\) be such that \(\alpha^3+\beta^2=4\). If the maximum value of the term independent of \(x\) in the binomial expansion of \(\left(\alpha x^{\frac{1}{9}}+\beta x^{-\frac{1}{6}}\right)^{10}\) is \(10 k\), then \(k\) is equal to : [Main Sep. 02, 2020 (I)]
CorrectIncorrectHint
(a) General term of
\(
\begin{gathered}
\left(\alpha x^{\frac{1}{9}}+\beta x^{\frac{-1}{6}}\right)^{10}={ }^{10} C_r\left(\alpha x^{\frac{1}{9}}\right)^{10-r}\left(\beta x^{\frac{-1}{6}}\right)^r \\
={ }^{10} C_r \alpha^{10-r} \beta^r(x)^{\frac{10-r}{9}-\frac{r}{6}}
\end{gathered}
\)
Term independent of \(x\) if \(\frac{10-r}{9}-\frac{r}{6}=0 \Rightarrow r=4\).
\(\therefore\) Term independent of \(x={ }^{10} C_4 \alpha^6 \beta^4\)
Since \(\alpha^3+\beta^2=4\)
Then, by AM-GM inequality
\(
\begin{aligned}
& \frac{\alpha^3+\beta^2}{2} \geq\left(\alpha^3 b^2\right)^{\frac{1}{2}} \\
& \Rightarrow(2)^2 \geq \alpha^3 \beta^2 \Rightarrow \alpha^6 \beta^4 \leq 16
\end{aligned}
\)
\(\because\) The maximum value of the term independent of \(x=10 \mathrm{k}\)
\(
\therefore 10 k={ }^{10} C_4 \cdot 16 \Rightarrow k=336 .
\) -
Question 37 of 226
37. Question
In the expansion of \(\left(\frac{x}{\cos \theta}+\frac{1}{x \sin \theta}\right)^{16}\), if \(l_1\) is the least value of the term independent of \(x\) when \(\frac{\pi}{8} \leq \theta \leq \frac{\pi}{4}\) and \(l_2\) is the least value of the term independent of \(x\) when \(\frac{\pi}{16} \leq \theta \leq \frac{\pi}{8}\), then the ratio \(l_2: l_1\) is equal to : [Main Jan. 9, 2020 (II)]
CorrectIncorrectHint
(b) General term of the given expansion
\(
T_{r+1}={ }^{16} C_r\left(\frac{x}{\sin \theta}\right)^{16-r}\left(\frac{1}{x \cos \theta}\right)^r
\)
For \(r=8\) term is free from ‘ \(x\) ‘
\(
\begin{aligned}
& T_9={ }^{16} C_8 \frac{1}{\sin ^8 \theta \cos ^8 \theta} \\
& T_9={ }^{16} C_8 \frac{2^8}{(\sin 2 \theta)^8}
\end{aligned}
\)
When \(\theta \in\left[\frac{\pi}{8}, \frac{\pi}{4}\right]\), then least value of the term independent of \(x\),
\(
l_1={ }^{16} C_8 2^8
\)
[Q min. value of \(l_1\) at \(\theta=\pi / 4\) ]
When \(\theta \in\left[\frac{\pi}{16}, \frac{\pi}{8}\right]\), then least value of the term independent of \(x\),
\(
l_2={ }^{16} C_8=\frac{2^8}{\left(\frac{1}{\sqrt{2}}\right)^8}={ }^{16} \mathrm{C}_8 \cdot 2^8 \cdot 2^4
\)
[Q min. value of \(l_2\) at \(\theta=\pi / 8\) ]
Now, \(\frac{l_2}{l_1}=\frac{{ }^{16} C_8 \cdot 2^8 \cdot 2^4}{{ }^{16} C_8 \cdot 2^8}=16: 1\) -
Question 38 of 226
38. Question
The total number is irrational terms in the binomial expansion of \(\left(7^{\frac{1}{5}}-3^{\frac{1}{10}}\right)^{60}\) is: [Main Jan. 12, 2019 (II)]
CorrectIncorrectHint
\(
\text { (d) Let the general term of the expansion }
\)\(
\begin{gathered}
T_{r+1}={ }^{60} C_r\left(7^{\frac{1}{5}}\right)^{60-r}\left(-3^{\frac{1}{10}}\right)^r \\
={ }^{60} C_r \cdot(7)^{12-\frac{r}{5}}(-1)^r \cdot(3)^{\frac{r}{10}}
\end{gathered}
\)
Then, for getting rational terms, \(r\) should be multiple of L.C.M. of \((5,10)\) Then, \(r\) can be \(0,10,20,30,40,50,60\).
Since, total number of terms \(=61\)
Hence, total irrational terms \(=61-7=54\) -
Question 39 of 226
39. Question
A ratio of the \(5^{\text {th }}\) term from the beginning to the 5 th term from the end in the binomial expansion of \(\left(2^{\frac{1}{3}}+\frac{1}{2(3)^{\frac{1}{3}}}\right)^{10}\) is: [Main Jan. 12, 2019 (I)]
CorrectIncorrectHint
(c) \(\left(2^{\frac{1}{3}}+\frac{1}{2(3)^{\frac{1}{3}}}\right)^{10}={ }^{10} C_0\left(2^{\frac{1}{3}}\right)^0\left(\frac{1}{2(3)^{1 / 3}}\right)^{10}+\)
\(
\cdots+{ }^{10} C_{10}\left(2^{\frac{1}{3}}\right)^{10}\left(\frac{1}{2(3)^{1 / 3}}\right)^0
\)
\(
\begin{aligned}
& 5^{\text {th }} \text { term from beginning } T_5={ }^{10} C_4\left(2^{\frac{1}{3}}\right)^6 \frac{1}{\left(2.3^{\frac{1}{3}}\right)^4}+{ }^{10} C_{10}\left(2^{\frac{1}{3}}\right)^{10}\left(\frac{1}{2(3)^{1 / 3}}\right)^0 \\
& \text { and } 5^{\text {th }} \text { term from end } T_{11-5+1}={ }^{10} C_6\left(2^{\frac{1}{3}}\right)^4\left(\frac{1}{2.3^{\frac{1}{3}}}\right)^6 \\
& \therefore T_5: T_7={ }^{10} C_4\left(2^{\frac{1}{3}}\right)^6\left(\frac{1}{2.3^{\frac{1}{3}}}\right)^4:{ }^{10} C_6\left(2^{\frac{1}{3}}\right)^4\left(\frac{1}{2.3^{\frac{1}{3}}}\right)^6 \\
& =\left(2^{\frac{1}{3}}\right)^2:\left(\frac{1}{2.3^{\frac{1}{3}}}\right)^2
\end{aligned}
\)
\(
=\frac{2^{\frac{2}{3}} \cdot 2^2 \cdot 3^{\frac{2}{3}}}{1}=4(6)^{\frac{2}{3}}: 1=4 \cdot(36)^{\frac{1}{3}}: 1
\) -
Question 40 of 226
40. Question
The term independent of \(\mathrm{x}\) in expansion of \(\left(\frac{x+1}{x^{2 / 3}-x^{1 / 3}+1}-\frac{x-1}{x-x^{1 / 2}}\right)^{10}\) is [Main 2013]
CorrectIncorrectHint
(c) Given expression can be written as
\(
\begin{aligned}
& \quad\left[\frac{\left(x^{1 / 3}\right)^3+1^3}{x^{2 / 3}-x^{1 / 3}+1}-\frac{(\sqrt{x})^2-1^2}{\sqrt{x}(\sqrt{x}-1)}\right]^{10} \\
& =\left(\left(x^{1 / 3}+1\right)-\left(\frac{\sqrt{x}+1}{\sqrt{x}}\right)\right)^{10}=\left(x^{1 / 3}+1-1-\frac{1}{\sqrt{x}}\right)^{10} \\
& =\left(x^{1 / 3}-x^{-1 / 2}\right)^{10} \\
& \text { General term }=\mathrm{T}_{r+1} \\
& ={ }^{10} \mathrm{C}_{\mathrm{r}}\left(x^{1 / 3}\right)^{10-r}\left(-x^{-1 / 2}\right)^r={ }^{10} C_r x^{\frac{10-r}{3}} \cdot(-1)^r \cdot x^{-\frac{r}{2}} \\
& ={ }^{10} C_r(-1)^r \cdot x^{\frac{10-r}{3}-\frac{r}{2}}
\end{aligned}
\)
Term will be independent of \(x\) when \(\frac{10-r}{3}-\frac{r}{2}=0\)
\(
\Rightarrow r=4
\)
So, required term \(=\mathrm{T}_5={ }^{10} \mathrm{C}_4=210\) -
Question 41 of 226
41. Question
For a positive integer \(n,\left(1+\frac{1}{x}\right)^n\) is expanded in increasing powers of \(x\). If three consecutive coefficients in this expansion are in the ratio, 2 \(: 5: 12\), then \(n\) is equal to [Main Sep. 02, 2020 (II)]
CorrectIncorrectHint
According to the question,
\(
\begin{aligned}
& { }^n C_{r-1}:{ }^n C_r:{ }^n C_{r+1}=2: 5: 12 \\
& \Rightarrow \frac{{ }^n C_r}{{ }^n C_{r-1}}=\frac{5}{2} \Rightarrow \frac{n-r+1}{r}=\frac{5}{2} \\
& \Rightarrow 2 n-7 r+2=0 \dots(i)\\
& \frac{{ }^n C_{r+1}}{{ }^n C_r}=\frac{12}{5} \Rightarrow \frac{n-r}{r+1}=\frac{12}{5} \\
& \Rightarrow 5 n-17 r-12=0 \dots(ii)
\end{aligned}
\)
Solving eqns. (i) and (ii),
\(
n=118, r=34
\) -
Question 42 of 226
42. Question
\(\sum_{r=1}^k(-3)^{r-1} 3 n C_{2 r-1}=0\), where \(k=(3 n) / 2\) and \(n\) is an even positive integer. Is this statement true? [1993 – 5 Marks]
CorrectIncorrectHint
Given, \(\mathrm{n}\) is an even positive integer.
Let \(n=2 m, \therefore k=3 m, n \in N\)
\(
\begin{aligned}
& \text { LHS } \sum_{r=1}^k(-3)^{r-1} \cdot{ }^{3 n} C_{2 r-1}=\sum_{r=1}^{3 m}(-3)^{r-1} \quad{ }^{6 m} C_{2 r-1} \\
& ={ }^{6 m} C_1-3 \cdot{ }^{6 m} C_3+3^2 \cdot{ }^{6 m} C_5 \\
& -\ldots+(-3)^{3 m-16 m} C_{6 m-1} \ldots \text { (i) }
\end{aligned}
\)
Consider \((1+i \sqrt{3})^{6 m}={ }^{6 m} C_0+{ }^{6 m} C_1(i \sqrt{3})+{ }^{6 m} C_2(i \sqrt{3})^2\)
\(+{ }^{6 m} C_3(i \sqrt{3})^3+{ }^{6 m} C_4(i \sqrt{3})^4+{ }^{6 m} C_5(i \sqrt{3})^5\)
\(+\ldots+{ }^{6 m} C_{6 m-1}(i \sqrt{3})^{6 m-1}+{ }^{6 m} C_{6 m}(i \sqrt{3})^{6 m} \ldots(i i)\)
Now, \((1+i \sqrt{3})^{6 m}=\left\{(-2)\left(\frac{-1-i \sqrt{3}}{(2)}\right)\right\}^{6 m}=\left(-2 \omega^2\right)^{6 m}\) \(=2^{6 m}\), where \(\omega\) is cube root of unity.
Then, Eq . (ii) can be written as
\(
\begin{aligned}
& 2^{6 m}=\left\{{ }^{6 m} C_0-{ }^{6 m} C_2 \cdot 3+{ }^{6 m} C_4 \cdot 3^2\right. \\
& \left.-\ldots+(-3)^{3 m} \cdot{ }^{6 m} C_{6 m}\right\}+i \sqrt{3}\left\{{ }^{6 m} C_1-{ }^{6 m} C_3 \cdot 3+\right. \\
& \left.+{ }^{6 m} C_5 \cdot 3^2-\ldots+(-3)^{3 m-1} \cdot{ }^{6 m} C_{6 m-1}\right\}
\end{aligned}
\)
On comparing the imaginary part on both sides, we get
\(\sqrt{3}\left({ }^{6 m} C_1-3+{ }^{6 m} C_3+3^2 \cdot{ }^{6 m} C_5-\ldots+(-3)^{3 m-1} \cdot{ }^{6 m} C_{6 m-1}\right)=0\)
or \({ }^{6 m} C_1-3+{ }^{6 m} C_3+3^2 \cdot{ }^{6 m} C_5-\ldots+(-3)^{3 m-1} \cdot{ }^{6 m} C_{6 m-1}=0\)
\(\Rightarrow \sum_{r=1}^{3 m}(-3)^{3 m-1} \cdot{ }^{3 n} C_{2 r-1}=0\)
or \(\sum_{r=1}^k(-3)^{r-1} \cdot{ }^{3 n} C_{2 r-1}=0\), where \(\mathrm{n}=2 \mathrm{~m}\) and \(\mathrm{k}=3 \mathrm{~m}\). -
Question 43 of 226
43. Question
Let \(R=(5 \sqrt{5}+11)^{2 n+1}\) and \(f=R-[R]\), where [] denotes the greatest integer function. Then \(R f=4^{2 n+1}\). Is this statement true? [1988 – 5 Marks]
CorrectIncorrectHint
Given, \(G=(5 \sqrt{5}+11)^{2 n+1}, 0<G<1\)
and \(R=(5 \sqrt{5}+11)^{2 n+1}\)
\(
\begin{aligned}
& \therefore \quad R-G=2\left\{^{2 n+1} C_1(5 \sqrt{5})^{2 n} \cdot 11+{ }^{2 n+1} C_3\right. \\
&\left.(5 \sqrt{5})^{2 n-2} \cdot(11)^3+\ldots\right\}
\end{aligned}
\)
\(\Rightarrow R-G=\) even integer.
or \(I+f-G=\) even integer
\(
f-G=\text { integer } . . \text { (i) }
\)
where \(0 \leq f<1\) and \(0<G<1\)
\(
\therefore \quad-\mathrm{i}<f-G<1 \dots(ii)
\)
From Eqs. (i) and (ii), we get
\(
\begin{aligned}
& f-G=0 \\
& \therefore \quad f=G \\
& \text { Thus, } R \cdot f=R \cdot G \\
&=(5 \sqrt{5}+11)^{2 n+1} \cdot(5 \sqrt{5}-11)^{2 n+1} \\
&= 4^{2 n+1}
\end{aligned}
\) -
Question 44 of 226
44. Question
The value of \(\sum_{r=0}^{20}{ }^{50-r} C_6\) is equal to: [Main Sep. 04, 2020 (I)]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{r=0}^{20}{ }^{50-r} C_6={ }^{50} C_6+{ }^{49} C_6+{ }^{48} C_6+\ldots . .+{ }^{30} C_6 \\
& ={ }^{50} C_6+{ }^{49} C_6+\ldots . .+{ }^{31} C_6+\left({ }^{30} C_6+{ }^{30} C_7\right)-{ }^{30} C_7 \\
& ={ }^{50} C_6+{ }^{49} C_6+\ldots . .+\left({ }^{31} C_6+{ }^{31} C_7\right)-{ }^{30} C_7 \\
& ={ }^{50} C_6+{ }^{50} C_7-{ }^{30} C_7 \\
& ={ }^{51} C_7-{ }^{30} C_7 \\
& { }^n C_r+{ }^n C_{r-1}={ }^{n+1} C_r
\end{aligned}
\) -
Question 45 of 226
45. Question
If \({ }^{20} \mathrm{C}_1+\left(2^2\right){ }^{20} \mathrm{C}_2+\left(3^2\right){ }^{20} \mathrm{C}_3+\ldots \ldots .+\left(20^2\right){ }^{20} \mathrm{C}_{20}=\mathrm{A}\left(2^{\mathrm{b}}\right)\), then the ordered pair \((\mathrm{A}, \mathrm{b})\) is equal to: [Main April 12, 2019 (II)]
CorrectIncorrectHint
(b) Given, \({ }^{20} C_1+2^2 \cdot{ }^{20} C_2+3^2{ }^{20} C_3+\ldots+20^2 \cdot{ }^{20} C_{20}\) \(=A\left(2^b\right)\)
Taking L.H.S.,
\(
\begin{aligned}
& =\sum_{r=1}^{20} r^2 \cdot{ }^{20} C_r=20 \sum_{r=1}^{20} r \cdot{ }^{19} C_{r-1} \\
& =20\left[\sum_{r=1}^{20}(r-1){ }^{19} C_{r-1}+\sum_{r=1}^{20}{ }^{19} C_{r-1}\right] \\
& =20\left[19 \sum_{r=2}^{20}{ }^{18} C_{r-2}+2^{19}\right]=20\left[19 \cdot 2^{18}+2^{19}\right]
\end{aligned}
\)
\(
=420 \times 2^{18}
\)
Now, compare it with R.H.S., \(\mathrm{A}=420\) and \(\mathrm{b}=18\) -
Question 46 of 226
46. Question
If the coefficients of \(x^2\) and \(x^3\) are both zero, in the expansion of the expression \(\left(1+a x+b x^2\right)(1-3 x)^{15}\) in powers of \(x\), then the ordered pair \((a, b)\) is equal to: [Main April 10, 2019 (I)]
CorrectIncorrectHint
(c) Given expression is \(\left(1+a x+b x^2\right)(1-3 x)^{15}\)
Co-efficient of \(x^2=0\)
\(
\begin{aligned}
& \left.\Rightarrow{ }^{15} \mathrm{C}_2(-3)\right)^2+a \cdot{ }^{15} \mathrm{C}_1(-3)+b \cdot{ }^{15} \mathrm{C}_0=0 \\
& \Rightarrow \frac{15 \times 14}{2} \times 9-15 \times 3 a+b=0 \\
& \Rightarrow 945-45 a+b=0 \dots(i)
\end{aligned}
\)
Now, co-efficient of \(x^3=0\)
\(
\begin{aligned}
& \Rightarrow{ }^{15} \mathrm{C}_3(-3)^3+a \cdot{ }^{15} \mathrm{C}_2(-3)^2+b \cdot{ }^{15} \mathrm{C}_1(-3)=0 \\
& \Rightarrow \frac{15 \times 14 \times 13}{3 \times 2} \times(-3 \times 3 \times 3)+a \times \frac{15 \times 14 \times 9}{2}-b \times 3 \times 15=0 \\
& \Rightarrow 15 \times 3[-3 \times 7 \times 13+a \times 7 \times 3-b]=0 \\
& \Rightarrow 21 a-b=273 \dots(ii)
\end{aligned}
\)
From (i) and (ii), we get,
\(
a=28, b=315 \Rightarrow(a, b) \equiv(28,315)
\) -
Question 47 of 226
47. Question
The sum of the series \(2 \cdot{ }^{20} \mathrm{C}_0+5 \cdot{ }^{20} \mathrm{C}_1+8 \cdot{ }^{20} \mathrm{C}_2+11 \cdot{ }^{20} \mathrm{C}_3+\ldots+62 \cdot{ }^{20} \mathrm{C}_{20}
\) is equal to: [Main April 8, 2019 (I)]CorrectIncorrectHint
(b) \(2 .{ }^{20} \mathrm{C}_0+5 .{ }^{20} \mathrm{C}_1+8 .{ }^{20} \mathrm{C}_2+\ldots \ldots . .+62 .{ }^{20} \mathrm{C}_{20}\)
\(
\begin{aligned}
& =\sum_{r=0}^{20}(3 r+2){ }^{20} C_r=3 \sum_{r=0}^{20} r \cdot{ }^{20} C_r+2 \sum_{r=0}^{20}{ }^{20} C_r \\
& =60 \sum_{r=1}^{20}{ }^{19} C_{n-1}+2 \sum_{r=0}^{20}{ }^{20} C_r \\
& =60 \times 2^{19}+2 \times 2^{20}=2^{21}[15+1]=2^{25}
\end{aligned}
\) -
Question 48 of 226
48. Question
The value of \(\mathrm{r}\) for which \({ }^{20} C_r{ }^{20} C_0+{ }^{20} C_{r-1}{ }^{20} C_1+{ }^{20} C_{r-2}{ }^{20} C_2+\ldots\) \(+{ }^{20} C_0{ }^{20} C_r\) is maximum, is : [Main Jan. 11, 2019 (I)]
CorrectIncorrectHint
Let \(S={ }^{20} \mathrm{C}_r{ }^{20} \mathrm{C}_0+{ }^{20} \mathrm{C}_{r-1}{ }^{20} \mathrm{C}_1+{ }^{20} \mathrm{C}_{r-2}{ }^{20} \mathrm{C}_2+\ldots+{ }^{20} \mathrm{C}_0{ }^{20} \mathrm{C}_r\) The sum \(S\) is the coefficient of \(x^r\) in the expansion of \((1+x)^{20}(x+1)^{20}=(1+x)^{40}\) \(\therefore \mathrm{S}={ }^{40} \mathrm{C}_{\mathrm{r}}\)
\(\mathrm{S}\) is maximum when \(r=20\) -
Question 49 of 226
49. Question
If \(\sum_{\mathrm{r}=0}^{25}\left\{{ }^{50} \mathrm{C}_{\mathrm{r}} \cdot{ }^{50-\mathrm{r}} \mathrm{C}_{25-\mathrm{r}}\right\}=\mathrm{K}\left({ }^{50} \mathrm{C}_{25}\right)\), then K is equal to: [Main Jan. 10, 2019 (II)]
CorrectIncorrectHint
From question, the summation given is:
\(
\begin{aligned}
& \sum_{\mathrm{r}=0}^{25}\left\{{ }^{50} \mathrm{C}_{\mathrm{r}} \cdot 50-\mathrm{r}_{\mathrm{C}_{25}-\mathrm{r}}\right\}=\mathrm{K}\left({ }^{50} \mathrm{C}_{25}\right) \\
& \because\left[{ }^n C_r=\frac{n !}{r !(n-r) !}\right] \\
& \Rightarrow \sum_{r=0}^{25}\left(\frac{50 !}{r !(50-r) !} \times \frac{(50-r) !}{(25-r) ! 25 !}\right)=K^{50} C_{25} \\
& \Rightarrow \sum_{r=0}^{25}\left(\frac{50 !}{25 ! 25 !} \times \frac{25 !}{r !(25-r) !}\right)=K^{50} C_{25}
\end{aligned}
\)
[On multiplying 25! numerator and denominator]
\(
\begin{aligned}
& \because\left[{ }^{50} C_{25}=\frac{50}{25 ! 25 !}\right] \\
& \Rightarrow{ }^{50} \mathrm{C}_{25} \sum_{r=0}^{25}{ }^{25} \mathrm{C}_r=K^{50} C_{25} \\
& \because\left[{ }^{\mathrm{n}} \mathrm{C}_0+{ }^{\mathrm{n}} \mathrm{C}_1+{ }^{\mathrm{n}} \mathrm{C}_2+\ldots+{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{n}}=2^{\mathrm{n}}\right] \\
& \Rightarrow \mathrm{K}=\sum_{\mathrm{r}=0}^{25}{ }^{25} \mathrm{C}_r \\
& \therefore \mathrm{K}=2^{25}
\end{aligned}
\) -
Question 50 of 226
50. Question
The coefficient of \(t^4\) in the expansion of \(\left(\frac{1-t^6}{1-t}\right)^3\) [Main Jan. 09, 2019 (II)]
CorrectIncorrectHint
(b) Consider the expression
\(
\begin{gathered}
\left(\frac{1-t^6}{1-t}\right)^3=\left(1-t^6\right)^3(1-t)^{-3} \\
=\left(1-3 t^6+3 t^{12}-t^{18}\right)\left(1+3 t+\frac{3 \cdot 4}{2 !} t^2\right. \\
\left.+\frac{3 \cdot 4 \cdot 5}{3 !} t^3+\frac{3 \cdot 4 \cdot 5 \cdot 6}{4 !} t^4+\ldots \infty\right)
\end{gathered}
\)
Hence, the coefficient of \(t^4=1 \cdot \frac{3 \cdot 4 \cdot 5 \cdot 6}{4 !}\)
\(
=\frac{3 \times 4 \times 5 \times 6}{4 \times 3 \times 2 \times 1}=15
\) -
Question 51 of 226
51. Question
The value of
\(\begin{aligned}
& \left({ }^{21} \mathrm{C}_1-{ }^{10} \mathrm{C}_1\right)+\left({ }^{21} \mathrm{C}_2-{ }^{10} \mathrm{C}_2\right)+\left({ }^{21} \mathrm{C}_3-{ }^{10} \mathrm{C}_3\right)+\left({ }^{21} \mathrm{C}_4-{ }^{10} \mathrm{C}_4\right) \\
& +\ldots . .+\left({ }^2 \mathrm{C}_{10}-{ }^{10} \mathrm{C}_{10}\right) \text { is : }
\end{aligned}\) [Main 2017]CorrectIncorrectHint
(a) We have \(\left({ }^{21} \mathrm{C}_1+{ }^{21} \mathrm{C}_2 \ldots \ldots . .+{ }^{21} \mathrm{C}_{10}\right)\)
\(
\begin{aligned}
& -\left({ }^{10} \mathrm{C}_1+{ }^{10} \mathrm{C}_2 \ldots .{ }^{10} \mathrm{C}_{10}\right) \\
& =\frac{1}{2}\left[\left({ }^{21} \mathrm{C}_1+\ldots .+{ }^{21} \mathrm{C}_{10}\right)+\left({ }^{21} \mathrm{C}_{11}+\ldots .{ }^{21} \mathrm{C}_{20}\right)\right]-\left(2^{10}-1\right) \\
& \left(\because{ }^{10} \mathrm{C}_1+{ }^{10} \mathrm{C}_2+\ldots .+{ }^{10} \mathrm{C}_{10}=2^{10}-1\right) \\
& =\frac{1}{2}\left[2^{21}-2\right]-\left(2^{10}-1\right) \\
& =\left(2^{20}-1\right)-\left(2^{10}-1\right)=2^{20}-2^{10} \\
&
\end{aligned}
\) -
Question 52 of 226
52. Question
If the number of terms in the expansion of \(\left(1-\frac{2}{x}+\frac{4}{x^2}\right)^n\), \(x \neq 0\), is 28 , then the sum of the coefficients of all the terms in this expansion, is : [Main 2016]
CorrectIncorrectHint
(b) Total number of terms \(={ }^{\mathrm{n}+2} \mathrm{C}_2=28\) \((n+2)(n+1)=56 ; n=6\)
\(\therefore\) Put \(x=1\) in expansion \(\left(1-\frac{2}{x}+\frac{4}{x^2}\right)^6\),
we get sum of coefficient \(=(1-2+4)^6\) \(=3^6=729\). -
Question 53 of 226
53. Question
The sum of coefficients of integral power of \(x\) in the binomial expansion \((1-2 \sqrt{\mathrm{x}})^{50}\) is : [Main 2015]
CorrectIncorrectHint
(c) We know that \((a+b)^n+(a-b)^n\)
\(
\begin{aligned}
& =2\left[{ }^n C_0 a^n b^0+{ }^n C_2 a^{n-2} b^2+{ }^n C_4 a^{n-4} b^4 \ldots\right] \\
& (1-2 \sqrt{\mathrm{x}})^{50}+(1+2 \sqrt{\mathrm{x}})^{50} \\
& 2\left[{ }^{50} C_0+{ }^{50} C_2(2 \sqrt{x})^2+{ }^{50} C_4(2 \sqrt{x})^4 \ldots\right] \\
& =2\left[{ }^{50} \mathrm{C}_0+{ }^{50} \mathrm{C}_2 2^2 \mathrm{x}+{ }^{50} \mathrm{C}_4 2^4 \mathrm{x}^2+\ldots\right]
\end{aligned}
\)
Putting \(\mathrm{x}=1\), we get,
\(
{ }^{50} C_0+{ }^{50} C_2 2^2+{ }^{50} C_4 2^4 \ldots=\frac{3^{50}+1}{2}
\) -
Question 54 of 226
54. Question
Coefficient of \(x^{11}\) in the expansion of \(\left(1+x^2\right)^4\left(1+x^3\right)^7\left(1+x^4\right)^{12}\) is [Adv. 2014]
CorrectIncorrectHint
(c) Coeff. of \(x^{11}\) in exp. of \(\left(1+x^2\right)^4\left(1+x^3\right)^7\left(1+x^4\right)^{12}\) \(=\left[\right.\) Coeff. of \(x^a\) in \(\left.\left(1+x^2\right)^4\right] \times\left[\right.\) Coeff. of \(x^b\) in \(\left.\left(1+x^3\right)^7\right]\)
Such that \(a+b+c=11\)
Here \(a=2 m, b=3 n, c=4 p\)
\(\therefore 2 m+3 n+4 p=11\)
Case I : \(m=0, n=1, p=2\)
Case II : \(m=1, n=3, p=0\)
Case III : \(m=2, n=1, p=1\)
Case IV : \(m=4, n=1, p=0\)
\(\therefore\) Required coefficient.
\(={ }^4 C_0 \times{ }^7 C_1 \times{ }^{12} C_2+{ }^4 C_1 \times{ }^7 C_3 \times{ }^{12} C_0+{ }^4 C_2 \times{ }^7 C_1 \times{ }^{12} C_1+{ }^4 C_4 \times{ }^7 C_1 \times{ }^{12} C_0\)
[Coeff. of \(x^c\) in \(\left.(1+x)^4\right]\)
\(
=462+140+504+7=1113
\) -
Question 55 of 226
55. Question
The value of \(\left(\begin{array}{c}30 \\ 0\end{array}\right)\left(\begin{array}{c}30 \\ 10\end{array}\right)-\left(\begin{array}{c}30 \\ 1\end{array}\right)\left(\begin{array}{c}30 \\ 11\end{array}\right)+\left(\begin{array}{c}30 \\ 2\end{array}\right)\left(\begin{array}{c}30 \\ 12\end{array}\right) \ldots . .+\left(\begin{array}{l}30 \\ 20\end{array}\right)\left(\begin{array}{l}30 \\ 30\end{array}\right)\) is where \(\left(\begin{array}{l}n \\ r\end{array}\right)={ }^n C_r [2005 \mathrm{~S}]\)
CorrectIncorrectHint
\(
\begin{aligned}
& (1-x)^{30}={ }^{30} C_0 x^0-{ }^{30} C_1 x^1+{ }^{30} C_2 x^2 \\
& +\ldots \ldots \ldots \ldots+(-1)^{30}{ }^{30} C_{30} x^{30} \ldots \ldots \ldots \ldots(i) \\
& (x+1)^{30}={ }^{30} C_0 x^3 \mathrm{O}-{ }^{30} C_1 x^{29}+{ }^{30} C_2 x^{28} \\
& +\ldots \ldots \ldots \ldots+{ }^{30} C_{10} x^{20}+\ldots \ldots \ldots . .+{ }^{30} C_{30} x^0 \ldots \ldots(ii)
\end{aligned}
\)
Multiplying (i) and (ii) and equating the coefficient of \(x^{20}\) on both sides, we get the required sum \(=\) coefficient of \(x^{20}\) in \(\left(1-x^2\right)^{30}={ }^{30} C_{10}\). -
Question 56 of 226
56. Question
The \(\operatorname{sum} \sum_{i=0}^m\left(\begin{array}{l}10 \\ i\end{array}\right)\left(\begin{array}{c}20 \\ m-i\end{array}\right)\), (where \(\left(\begin{array}{l}p \\ q\end{array}\right)=0\) if \(\mathrm{p}>\mathrm{q}\) ) is maximum when \(m\) is [2002S]
CorrectIncorrectHint
(c) \(\begin{aligned} \sum_{i=0}^m{ }^{10} C_i^{20} C_{m-i}={ }^{10} C_0{ }^{20} C_m & +{ }^{10} C_1{ }^{20} C_{m-1} \\ & +{ }^{10} C_2{ }^{20} C_{m-2}+\ldots . .+{ }^{10} C_m{ }^{20} C_0\end{aligned}\) \(=\) Coeff. of \(x^m\) in the expansion of product \((1+x)^{10}\)
\(=\) Coeff. of \(x^m\) in the expansion of \((1+x)^{30}\) \(={ }^{30} C_m\)
\(\sum_{i=0}^n{ }^{10} C_i{ }^{20} C_{m-1}\) will be maximum, if \({ }^{30} C_m\) will be maximum.
Clearly, \({ }^{30} C_m\) will be maximum when \(m=\frac{30}{2}=15\)
\(
\left[\because \operatorname{Max} \cdot\left({ }^n C_r\right)=\left\{\begin{array}{l}
{ }^n C_{n / 2} \text { if } n \text { is even } \\
{ }^n C_{\frac{n+1}{2}} \text { if } n \text { is odd }
\end{array}\right]\right.
\) -
Question 57 of 226
57. Question
For \(2 \leq r \leq n,\left(\begin{array}{l}n \\ r\end{array}\right)+2\left(\begin{array}{c}n \\ r-1\end{array}\right)+\left(\begin{array}{c}n \\ r-2\end{array}\right)=\)
CorrectIncorrectHint
(d) \(\left(\begin{array}{l}n \\ r\end{array}\right)+2\left(\begin{array}{c}n \\ r-1\end{array}\right)+\left(\begin{array}{c}n \\ r-2\end{array}\right)\)
\(
\begin{gathered}
\left.=\left[\left(\begin{array}{l}
n \\
r
\end{array}\right)+\left(\begin{array}{c}
n \\
r-1
\end{array}\right)\right]+\left[\left(\begin{array}{c}
n \\
r-1
\end{array}\right)+\left(\begin{array}{c}
n \\
r-2
\end{array}\right)\right\}\right] \\
=\left[\begin{array}{l}
\text { Here }\left[\begin{array}{l}
n \\
r
\end{array}\right],\left[\begin{array}{c}
n \\
r-1
\end{array}\right] \text { and }\left[\begin{array}{c}
n \\
r-2
\end{array}\right] \\
\text { represent }{ }^n C_r,{ }^n \mathrm{C}_{\mathrm{r}-1} \text { and }{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}-2}
\end{array}\right]
\end{gathered}
\)
\(
=\left(\begin{array}{c}
n+1 \\
r
\end{array}\right)+\left(\begin{array}{c}
n+1 \\
r
\end{array}\right)=\left(\begin{array}{c}
n+2 \\
r
\end{array}\right) \quad\left[\because{ }^n C_r+{ }^n C_{r-1}={ }^{n+1} C_r\right]
\) -
Question 58 of 226
58. Question
If in the expansion of \((1+x)^m(1-x)^n\), the coefficients of \(x\) and \(x^2\) are 3 and \(-6\) respectively, then \(m\) is [1999 – 2 Marks]
CorrectIncorrectHint
(c) \((1+x)^m(1-x)^n\)
\(
\begin{gathered}
=\left[1+m x+\frac{m(m-1)}{2 !} x^2+\ldots\right]\left[1-n x+\frac{n(n-1)}{2 !} x^2-\ldots\right] \\
=1+(m-n) x+\left[\frac{m(m-1)}{2}+\frac{n(n-1)}{2}-m n\right] x^2+\ldots
\end{gathered}
\)
Given, \(m-n=3 \dots(i)\)
\(
\text { and } \begin{aligned}
& \frac{1}{2} m(m-1)+\frac{1}{2} n(n-1)-m n=-6 \\
& \Rightarrow m^2+n^2-2 m n-(m+n)=-12 \\
& \Rightarrow(m-n)^2-(m+n)=-12 \\
& \Rightarrow m+n=9+12=21 \dots(ii)
\end{aligned}
\)
From (i) and (ii), we get \(m=12\) -
Question 59 of 226
59. Question
The expression \(\left(x+\left(x^3-1\right)^{\frac{1}{2}}\right)^5+\left(x-\left(x^3-1\right)^{\frac{1}{2}}\right)^5\) is a polynomial of degree [1992 – 2 Marks]
CorrectIncorrectHint
(c) Given expression:
\(
\left(x+\sqrt{x^3-1}\right)^5+\left(x-\sqrt{x^3-1}\right)^5
\)
We know that using binomial theorem,
\(
(x+a)^n+(x-a)^n=2\left[{ }^n C_0 x^n+{ }^n C_2 x^{n-2} a^2\right.
\)
\(\therefore\) The given expression
\(
=2\left[{ }^5 C_0 x^5+{ }^5 C_2 x^3\left(x^3-1\right)+{ }^5 C_4 x\left(x^3-1\right)^2\right]
\)
since maximum power of \(x\) involved in the expansionis 7 . Also, only +ve integral powers of \(x\) are involved in the expansion, therefore given expression is a polynomial of degree 7. -
Question 60 of 226
60. Question
The coefficient of \(x^4\) in the expansion of \(\left(1+x+x^2\right)^{10}\) is ….. [Main Jan. 9, 2020 (I)]
CorrectIncorrectHint
(615) General term of the expansion \(=\frac{10 !}{\alpha ! \beta ! \gamma !} x^{\beta+2 \gamma}\)
For coefficient of \(x^4 ; \beta+2 \gamma=4\)
Here, three cases arise
Case-1: When \(\gamma=0, \beta=4, \alpha=6\)
\(
\Rightarrow \frac{10 !}{\alpha ! \beta ! \gamma !} x^{\beta+2 \gamma}
\)
Case-2: When \(\gamma=1, \beta=2, \alpha=7\)
\(
\Rightarrow \frac{10 !}{7 ! 2 ! 1 !}=360
\)
Case-3: When \(\gamma=2, \beta=0, \alpha=8\)
\(
\Rightarrow \frac{10 !}{8 ! 0 ! 2 !}=45
\)
Hence, total \(=615\) -
Question 61 of 226
61. Question
If the sum of the coefficients of all even powers of \(x\) in the product \(\left(1+x+x^2+\ldots+x^{2 n}\right)\left(1-x+x^2-x^3+\ldots+x^{2 n}\right)\) is 61, then \(n\) is equal to …. [Main Jan. 7, 2020 (I)]
CorrectIncorrectHint
(30)Let \(\left(1-x+x^2 \ldots \ldots x^{2 n}\right)\left(1+x+x^2 \ldots \ldots x^{2 n}\right)\) \(=a_0+a_1 x+a_2 x^2+\ldots \ldots\)
put \(x=1\)
\(
1(2 n+1)=a_0+a_1+a_2+\ldots . a_{2 n} \dots(i)
\)
put \(x=-1\)
\(
1(2 n+1)=a_0+a_1+a_2+\ldots \ldots a_{2 n} \dots(ii)
\)
Adding (i) and (ii), we get,
\(
\begin{aligned}
4 n+2 & =2\left(a_0+a_2+\ldots .\right)=2 \times 61 \\
\Rightarrow & 2 n+1=61 \Rightarrow n=30 .
\end{aligned}
\) -
Question 62 of 226
62. Question
Suppose
\(
\operatorname{det}\left[\begin{array}{cc}
\sum_{k=0}^n k & \sum_{k=0}^n{ }^n C_k k^2 \\
\sum_{k=0}^n{ }^n C_k k & \sum_{k=0}^n{ }^n C_k 3^k
\end{array}\right]=0
\)
holds for some positive integer \(\mathrm{n}\). The \(\sum_{k=0}^n \frac{{ }^n C_k}{k+1}\) equals …… [Adv. 2019]CorrectIncorrectHint
Finding the value of \(\sum_{k=0}^n \frac{{ }^n C_k}{k+1}\)
Step 1: Consider the given determinant as,
\(
\left|\begin{array}{cc}
\sum_{k=0}^n k & \sum_{k=0}^n{ }^n C_k k^2 \\
\sum_{k=0}^n{ }^n C_k k & \sum_{k=0}^n{ }^n C_k 3^k
\end{array}\right|=0
\)
From the standard formula, we can write the above determinant as,
\(
\left|\begin{array}{cc}
\frac{n(n+1)}{2} & n(n+1) 2^{n-2} \\
n .2^{n-1} & 4^n
\end{array}\right|=0
\)
Step 2: Simplify the above determinant as,
\(
\begin{aligned}
& \Rightarrow \frac{n(n+1)}{2} \cdot 4^n-n^2(n+1) 2^{2 n-3}=0 \\
& \Rightarrow \frac{4^n}{2}-n \frac{4^{n-1}}{2}=0 \\
& \Rightarrow \frac{4^n}{2}=n \frac{4^{n-1}}{2} \\
& \Rightarrow n=\frac{2}{4^{n-1}} \times \frac{4^n}{2} \\
& \Rightarrow n=4^{n-n+1} \\
& \Rightarrow n=4
\end{aligned}
\)
Step 3: Find the value of \(\sum_{k=0}^n \frac{{ }^n C_k}{k+1}\)
\(
\begin{aligned}
& \begin{aligned}
\sum_{k=0}^n \frac{{ }^n C_k}{k+1} & =\sum_{k=0}^4 \frac{{ }^4 C_k}{k+1} \\
& =\frac{1}{5} \sum_{k=0}^4{ }^5 C_{k+1} \\
& =\frac{1}{5}\left(2^5-1\right) \\
& =\frac{1}{5}(32-1) \\
& =\frac{31}{5} \\
& =6.20
\end{aligned} \\
& \text { Therefore, the value of } \sum_{k=0}^n \frac{{ }^n C_k}{k+1}=6.20
\end{aligned}
\) -
Question 63 of 226
63. Question
The sum of the coefficients of the polynomial \(\left(1+x-3 x^2\right)^{2163}\) is \(\text { [1982 – } 2 \text { Marks] }\)
CorrectIncorrectHint
Sum of coefficients is obtained by putting \(x=1\)
ie, \((1+1-3)^{2163}=-1\)
Thus, sum of the coefficients of the polynomial
\(\left(1+x-3 x^2\right)^{2163}\) is \(-1\) -
Question 64 of 226
64. Question
If \(C_r\) stands for \({ }^n C_r\), then the sum of the series
\(
\frac{2\left(\frac{n}{2}\right) !\left(\frac{n}{2}\right) !}{n !}\left[C_0^2-2 C_1^2+3 C_2^2-\ldots \ldots \ldots+(-1)^n(n+1) C_n^2 {]}\right.
\)
where \(n\) is an even positive integer, is equal to [1986 – 2 Marks]CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{C}_0^2-2 \mathrm{C}_1^2+3 \mathrm{C}_2^2-4 \mathrm{C}_3^2+\ldots+(-1)^{\mathrm{n}}(\mathrm{n}+1) \mathrm{C}_{\mathrm{n}}^2 \\
& =\left[\mathrm{C}_0^2-\mathrm{C}_1^2+\mathrm{C}_2^2-\mathrm{C}_3^2+\ldots+(-1)^{\mathrm{n}} \mathrm{C}_{\mathrm{n}}^2\right]-\left[\mathrm{C}_1^2-2 \mathrm{C}_2^2+3 \mathrm{C}_3^2-\ldots+(-1)^{\mathrm{n}} \mathrm{nC}_{\mathrm{n}}^2\right] \\
& =(-1)^{\frac{n}{2}} \frac{\mathrm{n} !}{\left(\frac{n}{2}\right) !\left(\frac{n}{2}\right) !}-(-1)^{\frac{n}{2}-1} \frac{n}{2} \cdot{ }^{\mathrm{n}} \mathrm{C}_{\frac{n}{2}} \\
& =(-1)^{\frac{n}{2}} \frac{\mathrm{n} !}{\left(\frac{n}{2}\right) !\left(\frac{n}{2}\right) !}\left(1+\frac{n}{2}\right) \\
& \therefore 2\left(\frac{\mathrm{n}}{2}\right) !\left(\frac{\mathrm{n}}{2}\right) !\left[\mathrm{C}_0^2-2 \mathrm{C}_1^2+3 \mathrm{C}_2^2-\ldots+(-1)^{\mathrm{n}}(\mathrm{n}+2) \mathrm{C}_{\mathrm{n}}^2\right] \\
& =(-1)^{\frac{n}{2}}(\mathrm{n}+2)
\end{aligned}
\) -
Question 65 of 226
65. Question
If the following statement true?
\(
\begin{aligned}
& 2^k\left(\begin{array}{l}
n \\
0
\end{array}\right)\left(\begin{array}{l}
n \\
k
\end{array}\right)-2^{k-1}\left(\begin{array}{l}
n \\
1
\end{array}\right)\left(\begin{array}{l}
n-1 \\
k-1
\end{array}\right) \\
& +2^{k-2\left(\begin{array}{l}
n \\
2
\end{array}\right)}\left(\begin{array}{l}
n-2 \\
k-2
\end{array}\right)-\ldots . .(-1)^k\left(\begin{array}{l}
n \\
k
\end{array}\right)\left(\begin{array}{c}
n-k \\
0
\end{array}\right)=\left(\begin{array}{l}
n \\
k
\end{array}\right) \\
&
\end{aligned}
\)CorrectIncorrectHint
To show that
\(
\begin{aligned}
& 2^{k, n} C_0 \cdot{ }^n C_k-2^{k-1} \cdot{ }^n C_1 \cdot{ }^{n-1} C_{k-1}+2^{k-2} \cdot{ }^n C_2 \cdot{ }^{n-2} C_{k-2} \\
&-\ldots . .+(-1)^{k n} C_k{ }^{n-k} C_0={ }^n C_k
\end{aligned}
\)
Taking LHS
\(
\begin{aligned}
& 2^k \cdot{ }^n C_0 \cdot{ }^n C_k-2^{k-1} \cdot{ }^n C_1 \cdot{ }^{n-1} C_{k-1}+\ldots+ (-1)^k \cdot{ }^n C_k \cdot{ }^{n-k} C_0\\
&=\sum_{r=0}^k(-1)^r \cdot 2^{k-r} \cdot{ }^n C_r \cdot{ }^{k-r} C_k \cdot{ }^{n-k} C_{k-r} \\
&=\sum_{r=0}^k(-1)^r 2^{k-r} \cdot \frac{n !}{r !(n-r) !} \cdot \frac{(n-r) !}{(k-r) !(n-k) !}
\end{aligned}
\)
\(
\begin{aligned}
& =\sum_{r=0}^k(-1)^r \cdot 2^{k-r} \cdot \frac{n !}{(n-k) ! \cdot k !} \cdot \frac{k !}{r !(k-r) !} \\
& \quad=\sum_{r=0}^k(-1)^r \cdot 2^{k-r}{ }^n C_k \cdot{ }^k C_r=2^k \cdot{ }^n C_k\left\{\sum_{r=0}^k(-1)^r \cdot \frac{1}{2^r} \cdot{ }^k C_r\right\} \\
& \quad=2^k \cdot{ }^n C_k\left(1-\frac{1}{2}\right)^k={ }^n C_k=\text { R.H.S. }
\end{aligned}
\) -
Question 66 of 226
66. Question
For any positive integer \(m, n\left(\right.\) with \(\mathrm{n} \geq \mathrm{m}\) ), let \(\left(\begin{array}{l}n \\ m\end{array}\right)={ }^n C_m\). Given that \(\left(\begin{array}{c}n \\ m\end{array}\right)+\left(\begin{array}{c}n-1 \\ m\end{array}\right)+\left(\begin{array}{c}n-2 \\ m\end{array}\right)+\ldots . .+\left(\begin{array}{c}m \\ m\end{array}\right)=\left(\begin{array}{c}n+1 \\ m+2\end{array}\right)\). Given that
\(
\left(\begin{array}{l}
n \\
m
\end{array}\right)+2\left(\begin{array}{c}
n-1 \\
m
\end{array}\right)+3\left(\begin{array}{c}
n-2 \\
m
\end{array}\right)+\ldots . .+(n-m+1)\left(\begin{array}{c}
m \\
m
\end{array}\right)=\left(\begin{array}{c}
n+2 \\
m+2
\end{array}\right) \text {. }
\) Are these statements true? [2000 – 6 Marks]CorrectIncorrectHint
Given that for positive integers \(m\) and \(n\) such that \(n \geq m\), then to prove that
\(
\begin{aligned}
& \begin{array}{c}
{ }^n C_m+{ }^{n-1} C_m+{ }^{n-2} C_m+\ldots .+{ }^m C_m={ }^{n+1} C_{m+1} \\
\text { L.H.S. }{ }^m C_m+{ }^{m+1} C_m+{ }^{m+2} C_m+\ldots .+{ }^{n-1} C_m+{ }^n C_m \\
\text { [writing L.H.S. in reverse order] }
\end{array} \\
& \begin{array}{l}
\left({ }^{m+1} C_{m+1}+{ }^{m+1} C_m\right)+{ }^{m+2} C_m+\ldots .+{ }^{n-1} C_m+{ }^n C_m \quad\left[\because \quad{ }^m C_m={ }^{m+1} C_{m+1}\right]
\end{array} \\
& =\left({ }^{m+2} C_{m+1}+{ }^{m+2} C_m\right)+{ }^{m+3} C_m+\ldots .+{ }^n C_m \quad\left[\because \quad{ }^n C_{r+1}+{ }^n C_r={ }^{n+1} C_{r+1}\right]
\end{aligned}
\)
Combining in the same way we get
\(
={ }^n C_{m+1}+{ }^n C_m={ }^{n+1} C_{m+1}=\text { R.H.S. }
\)
Again we have to prove
\(
\begin{aligned}
& \quad{ }^n C_m+2^{n-1} C_m+3{ }^{n-2} C_m+\ldots+(n-m+1){ }^m C_m \\
& ={ }^{n+2} C_{m+2} \\
& =\left[{ }^n C_m+{ }^{n-1} C_m+{ }^{n-2} C_m+\ldots+{ }^m C_m\right]+\left[{ }^{n-1} C_m\right. \\
& \left.+{ }^{n-2} C_m+\ldots .+{ }^m C_m\right]+\left[{ }^{n-2} C_m+\ldots .+{ }^m C_m\right]+\ldots .+\left[{ }^m C_m\right] \\
& {[n-m+1 \text { bracketed terms }]} \\
& ={ }^{n+1} C_{m+1}+{ }^n C_{m+1}{ }^{n-1} C_{m+1} \ldots+{ }^{m+1} C_{m+1} \\
& ={ }^{n+2} C_{m+2} \\
& {[\text { Replacing } n \text { by } n+1 \text { and } m \text { by } m+1 \text { in the previous result.] }} \\
& =\text { R.H.S. }
\end{aligned}
\) -
Question 67 of 226
67. Question
Let \(n\) be a positive integer and
\(
\left(1+x+x^2\right)^n=a_0+a_1 x+\ldots \ldots \ldots . .+a_{2 n} x^{2 n}
\)
It is given that \(a_0^2-a_1^2+a_2^2 \ldots \ldots \ldots \ldots . .+a_{2 n}^2=a_n\). Is this statement true or false? [1994 – 5 Marks]CorrectIncorrectHint
\(
\text { Given : }\left(1+x+x^2\right)^n=a_0+a_1 x+\ldots .+\mathrm{a}_{2 n} x^{2 n} \dots(i)
\)
where \(n\) is a +ve integer.
On replacing \(\mathrm{x}\) by \(-\frac{1}{x}\) in equation(i), we get
\(
\left(1-\frac{1}{x}+\frac{1}{x^2}\right)^n=a_0-\frac{a_1}{x}+\frac{a_2}{x^2}-\frac{a_3}{x^3}+\ldots .+\frac{a_{2 n}}{x^{2 n}} \dots(ii)
\)
Multiplying equation (i) and (ii) :
\(
\begin{gathered}
\frac{\left(1+x+x^2\right)^n\left(x^2-x+1\right)^n}{x^{2 n}} \\
=\left(a_0+a_1 x+\ldots .+a_{2 n} x^{2 n}\right)\left(a_0-\frac{a_1}{x}+\frac{a_2}{x^2}+\ldots+\frac{a_{2 n}}{x^{2 n}}\right)
\end{gathered}
\)
Equating the constant terms on both sides we get
\(a_0^2-a_1^2+a_2^2-a_3^2+\ldots .+a_{2 n}^2=\) constant term in the expansion of
\(
\frac{\left[\left(1+x+x^2\right)\left(1-x+x^2\right)\right]^n}{x^{2 n}}
\)
\(=\) Coeff. of \(x^{2 n}\) in the expansion of \(\left(1+x^2+x^4\right)^n\)
But replacing \(x\) by \(x^2\) in equation (i), we have
\(
\begin{aligned}
& \left(1+x^2+x^4\right)^n=a_0+a_1 x^2+\ldots+a_{2 n}\left(x^2\right)^{2 n} \\
& \quad \therefore \quad \text { Coeff. of } x^{2 n}=a_n \\
& \therefore \quad a_0^2-a_1^2+a_2^2-a_3^2+\ldots .+a_{2 n}^2=a_n
\end{aligned}
\) -
Question 68 of 226
68. Question
If \(\sum_{r=0}^{2 n} a_r(x-2)^r=\sum_{r=0}^{2 n} b_r(x-3)^r\) and \(a_k=1\) for all \(k \geq n\), then \(b_n={ }^{2 n+1} C_{n+1}\). Is this statement true or false? [1992 – 6 Marks]
CorrectIncorrectHint
Given : \(\sum_{r=0}^{2 n} a_r(x-2)^r=\sum_{r=0}^{2 n} b_r(x-3)^r \dots(i)\)
and \(a_k=1, \forall k \geq n\)
To prove \(: b_n={ }^{2 n+1} C_{n+1}\)
In the given equation (i) let us put \(x-3=y\)
\(
\begin{aligned}
& \Rightarrow x-2=y+1 \\
& \therefore \sum_{r=0}^{2 n} a_r(1+y)^r=\sum_{r=0}^{2 n} b_r(y)^r[\text { From (i) }] \\
& \Rightarrow a_0+a_1(1+y)+\ldots .+a_{n-1}(1+y)^{n-1}+(1+y)^n \\
& +(1+y)^{n+1}+\ldots .+(1+y)^{2 n}
\end{aligned}
\)
\(
=\sum_{r=0}^{2 n} b_r y^r
\)
[Using \(a_k=1, \forall k \geq n\) ]
Equating the coefficients of \(y^n\) on both sides we get
\(
\begin{aligned}
& \Rightarrow{ }^n C_n+{ }^{n+1} C_n+{ }^{n+2} C_n+\ldots .+{ }^{2 n} C_n=b_n \\
& \Rightarrow\left({ }^{n+1} C_{n+1}+{ }^{n+1} C_n\right)+{ }^{n+2} C_n+\ldots .+{ }^{2 n} C_n=b_n
\end{aligned}
\)
\(\left[{ }^n C_n={ }^{n+1} C_{n+1}=1\right]\)
\(
\Rightarrow b_n={ }^{n+2} C_{n+1}+{ }^{n+2} C_n+\ldots .+{ }^{2 n} C_n
\)
\(
\left[{ }^m C_r+{ }^m C_{r-1}={ }^{m+1} C_r\right]
\)
Combining the terms in similar way, we get
\(
\Rightarrow b_n={ }^{2 n} C_{n+1}+{ }^{2 n} C_n \Rightarrow \quad b_n={ }^{2 n+1} C_{n+1}
\) -
Question 69 of 226
69. Question
Given that
\(
C_0-2^2 C_1+3^2 C_2-\ldots \ldots \ldots . .+(-1)^n(n+1)^2 C_n=0,
\)
\(n>2\), where \(C_r={ }^n C_r\).
\(
\text { [1989 – } 5 \text { Marks] }
\). Is this statement true or false?CorrectIncorrectHint
We know
\(
(1-x)^n=C_0-C_1 x+C_2 x^2-C_3 x^3+\ldots .+(-1)^n C_n x^n
\)
On multiplying both sides by \(x\),
\(
x(1-x)^n=C_0 x-C_1 x^2+C_2 x^3-C_3 x^4+\ldots .+(-1)^n C_n x^{n+1}
\)
On differentiating both sides w.r. to \(x\),
\(
\begin{aligned}
& (1-x)^n-n x(1-x)^{n-1} \\
& =C_0-2 C_1 x+3 C_2 x^2-4 C_3 x^3+\ldots .+(-1)^n(n+1) C_n x^n
\end{aligned}
\)
Again on multiplying both sides by \(x\),
\(
\begin{gathered}
x(1-x)^n-n x^2(1-x)^{n-1} \\
=C_0 x-2 C_1 x^2+3 C_2 x^3-4 C_3 x^4+\ldots .+(-1)^n(n+1) C_n x^{n+1}
\end{gathered}
\)
On differentiating both sides with respect to \(x\),
\(
\begin{aligned}
& (1-x)^n-n x(1-x)^{n-1}-2 n x(1-x)^{n-1}+n x^2(n-1)(1-x)^{n-2} \\
& =C_0-2^2 C_1 x+3^2 C_2 x^2-4^2 C_3 x^3+\ldots .+(-1)^n(n+1)^2 C_n x^n
\end{aligned}
\)
Putting \(x=1\), in above, we get
\(
0=C_0-2^2 C_1+3^2 C_2-4^2 C_3+\ldots .+(-1)^n(n+1)^2 C_n
\) -
Question 70 of 226
70. Question
\(
\text { Given } s_n=1+q+q^2+\ldots \ldots+q^n
\)
\(
\begin{aligned}
& S_n=1+\frac{q+1}{2}+\left(\frac{q+1}{2}\right)^2+\ldots . .+\left(\frac{q+1}{2}\right)^n, q \neq 1 \text { Given that } \\
& { }^{n+1} C_1+{ }^{n+1} C_2 s_1+{ }^{n+1} C_3 s_2+\ldots . .+{ }^{n+1} C_{n+1} s_n=2^n S_n
\end{aligned}
\)[1984 – 4 Marks]. Is this statement true or false?
CorrectIncorrectHint
\(
\begin{aligned}
& { }^{n+1} C_1+{ }^{n+1} C_2 s_1+{ }^{n+1} C_3 s_2+\ldots .+{ }^{n+1} C_{n+1} s_n \\
& =\sum_{r=1}^{n+1}{ }^{n+1} C_r s_{r-1},
\end{aligned}
\)
where
\(
\begin{aligned}
& s_n=1+q+q^2+\ldots+q^n=\frac{1-q^{n+1}}{1-q} \\
& \therefore \sum_{r=1}^{n+1}{ }^{n+1} C_r\left(\frac{1-q^r}{1-q}\right)=\frac{1}{1-q}\left(\sum_{r=1}^{n+1}{ }^{n+1} C_r-\sum_{r=1}^{n+1}{ }^{n+1} C_r q^r\right) \\
& =\frac{1}{1-q}\left[(1+1)^{n+1}-(1+q)^{n+1}\right] \\
& =\frac{1}{1-q}\left[2^{n+1}-(1+q)^{n+1}\right] \quad \ldots \text { (i) }
\end{aligned}
\)
Also, \(S_n=1+\left(\frac{q+1}{2}\right)+\left(\frac{q+1}{2}\right)^2+\ldots+\left(\frac{q+1}{2}\right)^n\)
\(
=\frac{1-\left(\frac{q+1}{2}\right)^{n+1}}{1-\left(\frac{q+1}{2}\right)}=\frac{2^{n+1}-(q+1)^{n+1}}{2^n(1-q)} \dots(ii)
\)
From equations (i) and (ii),
\(
{ }^{n+1} C_1+{ }^{n+1} C_2 s_1+{ }^{n+1} C_3 s_2+\ldots+{ }^{n+1} C_{n+1} s_n=2^n S_n
\) -
Question 71 of 226
71. Question
If \((1+x)^n=C_0+C_1 x+C_2 x^2+\ldots \ldots+C_n x^n\) then Given that the sum of the products of the \(\mathrm{C}_{\mathrm{i}}\) ‘s taken two at a time, represented by \(\sum_{0 \leq i<j \leq n} \sum C_i C_j\) is equal to \(2^{2 n-1}-\frac{(2 n) !}{2(n !)^2}\). Is this true? [1983 – 3 Marks]
CorrectIncorrectHint
\(
\begin{aligned}
& S=\sum \sum C_i C_j \\
& 0 \leq i<j \leq n \\
& \Rightarrow S=C_0\left(C_1+C_2+C_3+\ldots .+C_n\right)+C_1\left(C_2+C_3+\ldots .+C_n\right) \\
& +C_2\left(C_3+C_4+C_5+\ldots C_n\right)+\ldots C_{n-1}\left(C_n\right) \\
& \Rightarrow S=C_0\left(2^n-C_0\right)+C_1\left(2^n-C_0-C_1\right)+ \\
& C_2\left(2^n-C_0-C_1-C_2\right) \\
& +\ldots .+C_{n-1}\left(2^n-C_0-C_1 \ldots . C_{n-1}\right) \\
& +C_n\left(2^n-C_0-C_1 \ldots C_n\right) \\
& \Rightarrow S=2^n\left(C_0+C_1+C_2+\ldots .+C_{n-1}+C_n\right) \\
& -\left(C_0^2+C_1^2+C_2^2+\ldots .+C_n^2\right)-S \\
& \Rightarrow 2 S=2^n \cdot 2^n-\frac{2 n !}{(n !)^2}=2^{2 n}-\frac{2 n !}{(n !)^2} \\
&
\end{aligned}
\) -
Question 72 of 226
72. Question
Given that
\(
C_1+2 C_2 x+3 C_3 x^2+\ldots \ldots \ldots . .+2 n C_{2 n} x^{2 n-1}=2 n(1+x)^{2 n-1}
\)
where \(C_r=\frac{(2 n) !}{r !(2 n-r) !} \quad r=0,1,2, \ldots \ldots \ldots \ldots \ldots, 2 n\)
then
\(
C_1^2-2 C_2^2+3 C_3^2-\ldots \ldots \ldots \ldots \ldots \ldots .2 n C_{2 n}^2=(-1)^n n C_n \text {. }
\).
Is this statement true? [1979]CorrectIncorrectHint
Given : \(C_1+2 C_2 x+3 C_3 x^2+\ldots . .+2 n C_{2 n} \pi^{2 n-1}=2 n(1+x)^{2 n-1} \ldots .(\mathrm{i})\)
where \(C_r=\frac{2 n !}{r !(2 n-r) !}\)
Integrating both sides with respect to \(x\), under the limits 0 to \(x\), we get
\(
\begin{aligned}
& {\left[C_1 x+C_2 x^2+C_3 x^3+\ldots .+C_{2 \pi} x^{2 n}\right]{ }_0^x=\left[(1+x)^{2 n}\right]_0^x} \\
& \quad \Rightarrow C_1 x+C_2 x^2+C_3 x^3+\ldots .+C_{2 n} x^{2 n}=(1+x)^{2 n}-1 \\
& \quad \Rightarrow C_0+C_1 x+C_2 x^2+C_3 x^3+\ldots .+C_{2 \pi} x^{2 n}=(1+x)^{2 n} \dots(ii)
\end{aligned}
\)
Changing \(x\) by \(-\frac{1}{x}\), we get
\(
\begin{aligned}
& \Rightarrow C_0-\frac{C_1}{x}+\frac{C_2}{x^2}-\frac{C_3}{x^3}+\ldots .+(-1)^{2 n} \frac{C_{2 n}}{x^{2 n}}=\left(1-\frac{1}{x}\right)^{2 n} \\
& \Rightarrow C_0 x^{2 n}-C_1 x^{2 n-1}+C_2 x^{2 n-2}-C_3 x^{2 n-3} \\
& +\ldots . .+C_{2 n}=(x-1)^{2 n} \dots(iii)
\end{aligned}
\)
Multiplying eqn. (i) and (iii) and equating the coefficients of \(\mathrm{x}^{2 \mathrm{n}-1}\) on both sides, we get
\(
\begin{aligned}
& \quad C_1^2+2 C_2^2-3 C_3^2+\ldots+2 n C_{2 n}^2 \\
&=\text { coeff.of } x^{2 n-1} \text { in } 2 n(x-1)\left(x^2-1\right)^{2 n-1} \\
&=2 n \text { [coeff. of } x^{2 n-2} \text { in }\left(x^2-1\right)^{2 n-1} \left.-\text { coeff. of } x^{2 n-1} \text { in }\left(x^2-1\right)^{2 n-1}\right]\\
&=2 n\left[\left[^{2 n-1} C_{n-1}(-1)^{n-1}-0\right]\right. \\
&=(-1)^{n-1} \cdot 2 n^{2 n-1} C_{n-1} \\
& \quad \Rightarrow\left.-\text { coeff. of } x^{2 n-1} \text { in }\left(x^2-1\right)^{2 n-1}\right] \\
&=(-1)^n \cdot 2 n^{2 n-1} C_{n-1}=(-1)^n n \cdot\left(\frac{2 n}{n} \cdot{ }^{2 n-1} C_{n-1}\right) \\
&=(-1)^n n \cdot{ }^{2 n} C_n=(-1)^n n \cdot C_n . \quad\left(\because 3 C_3^2+\ldots .+2 n C_n C_n\right)
\end{aligned}
\) -
Question 73 of 226
73. Question
The remainder when \(428^{2024}\) is divided by 21 is ____. [JEE Main 2024 (Online) 9th April Morning Shift]
CorrectIncorrectHint
(a)
\(
\begin{aligned}
& 428=21 \times 20+8 \\
\Rightarrow \quad & (428)^{2024} =(20 \times 21+8)^{2024} = 8^{2024}(\bmod 21) \\
& 8^2=21 \times 3+1 \\
& 8^{2024}=(21 \times 3+1)^{1012} \\
\Rightarrow \quad & 8^{2024} =(21 \times 3+1)^{1012}(\bmod 21) \\
& = 1^{2012}(\bmod 21) \\
& 428^{2024} = 1(\bmod 21)
\end{aligned}
\) -
Question 74 of 226
74. Question
If the second, third and fourth terms in the expansion of \((x+y)^n\) are 135,30 and \(\frac{10}{3}\), respectively, then \(6\left(n^3+x^2+y\right)\) is equal to ______. [JEE Main 2024 (Online) 6th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T_2={ }^n C_1 y^1 \cdot x^{n-1}=135 \dots(i)\\
& T_3={ }^n C_2 y^2 \cdot x^{n-2}=30 \dots(ii) \\
& T_4={ }^n C_3 y^3 x^{n-3}=\frac{10}{3} \dots(iii)
\end{aligned}
\)
By \(\frac{\text { (i) }}{\text { (ii) }}\)
\(
\frac{{ }^n C_1}{{ }^n C_2} \frac{x}{y}=\frac{9}{2} \dots(iv)
\)
\(
\begin{aligned}
& \text { By } \frac{\text { (ii) }}{\text { (iii) }} \\
& \frac{{ }^n C_2}{{ }^n C_3} \frac{x}{y}=9 \dots(v) \\
&
\end{aligned}
\)
\(
\begin{aligned}
& \text { By } \frac{( iv )}{( v )} \\
& \frac{{ }^n C_1{ }^n C_3}{{ }^n C_2{ }^n C_2}=\frac{1}{2} \\
& \frac{2 n ^2( n -1)( n -2)}{6}=\frac{ n ( n -1)}{2} \frac{ n ( n -1)}{2} \\
& 4 n-8=3 n-3 \\
& \Rightarrow n =5 \\
& \text { put in (v) } \\
& \frac{x}{y}=9 \\
& x=9 y \\
& \text { put in (i) } \\
& { }^5 C_1 x^4\left(\frac{x}{9}\right)=135 \\
& x^5=27 \times 9 \\
& \Rightarrow x=3, \quad y=\frac{1}{3} \\
& 6\left(n^3+x^2+y\right) \\
& =6\left(125+9+\frac{1}{3}\right) \\
& =806
\end{aligned}
\) -
Question 75 of 226
75. Question
If the constant term in the expansion of \(\left(1+2 x-3 x^3\right)\left(\frac{3}{2} x^2-\frac{1}{3 x}\right)^9\) is \(p\), then \(108 p\) is equal to ____. [JEE Main 2024 (Online) 5th April Morning Shift]
CorrectIncorrectHint
General term of \(\left(\frac{3}{2} x^2-\frac{1}{3 x}\right)^9\)
\(
T_{r+1}={ }^9 C_r\left(\frac{3}{2} x^2\right)^{9-r}\left(-\frac{1}{3 x}\right)^r={ }^9 C_r(-1)^r 3^{9-2 r} 2^{r-9} x^{18-35}
\)
Constant term in expansion of \(\left(1+2 x-3 x^3\right)\)
\(
\begin{aligned}
& \left(\frac{3}{2} x^2-\frac{1}{3 x}\right)^9 \\
& =T_7-3 T_8={ }^9 C_6 3^{-3} \cdot 2^{-3}+3^9 C_7 \cdot 3^{-5} \cdot 2^{-2} \\
& =\frac{3 \times 4 \times 7}{3^3 \cdot 2^3}+\frac{3 \times 9 \times 4}{3^5 \times 2^2}= \\
& p=\frac{42+12}{108}=\frac{54}{108} \\
& 108 p=54
\end{aligned}
\) -
Question 76 of 226
76. Question
Let \(a=1+\frac{{ }^2 C _2}{3!}+\frac{{ }^3 C _2}{4!}+\frac{{ }^4 C _2}{5!}+\ldots, b =1+\frac{{ }^1 C _0+{ }^1 C _1}{1!}+\frac{{ }^2 C _0+{ }^2 C _1+{ }^2 C _2}{2!}+\frac{{ }^3 C _0+{ }^3 C _1+{ }^3 C _2+{ }^3 C _3}{3!}+\ldots\)
Then \(\frac{2 b}{a^2}\) is equal to ____. [JEE Main 2024 (Online) 4th April Morning Shift]CorrectIncorrectHint
\(
\begin{aligned}
& a=1+\frac{{ }^2 C_2}{3!}+\frac{{ }^3 C_2}{4!}+\frac{{ }^4 C_2}{5!}+\ldots \\
& b=1+\frac{{ }^1 C_0+{ }^1 C_1}{1!}+\frac{{ }^2 C_0+{ }^2 C_1+{ }^2 C_2}{2!}+\ldots \\
& b=1+\frac{2}{1!}+\frac{2^2}{2!}+\frac{2}{3!}+\ldots=e^2 \\
& \text { Using } e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x}{3!}+\ldots \\
& a=1+\sum_{r=2}^{\infty} \frac{{ }^r C_2}{(r+1)!}=1+\sum_{r=2} \frac{r(r-1)}{2(r+1)!} \\
& =1+\frac{1}{2} \sum_{r=2}^{\infty} \frac{(r+1) r-2 r}{(r+1)!} \\
& =1+\frac{1}{2} \sum_{r=2}^{\infty} \frac{1}{(r-1)!}-\frac{1}{2} \sum_{r=2} \frac{2 r}{(r+1)!} \\
& =1+\frac{1}{2}\left(\frac{1}{1!}+\frac{1}{2!}+\ldots\right)-\sum_{r=2}^{\infty} \frac{(r+1)-1}{(r+1)!} \\
& =1+\frac{1}{2}(e-1)-\sum_{r=2}^{\infty} \frac{1}{r!}+\sum_{r=2} \frac{1}{(r+1)!} \\
& =1+\frac{1}{2}(e-1)-\left(e-\frac{1}{1!}-\frac{1}{0!}\right)+\left(e-\frac{1}{1!}-\frac{1}{0!}-\frac{1}{2!}\right) \\
& =1+\frac{e}{2}-\frac{1}{2}-e+2+e-2-\frac{1}{2}=\frac{e}{2} \\
& \Rightarrow \frac{2 b}{a^2}=\frac{2 {e^2}}{\frac{e^2}{4}}= 8 \\
&
\end{aligned}
\) -
Question 77 of 226
77. Question
If the Coefficient of \(x^{30}\) in the expansion of \(\left(1+\frac{1}{x}\right)^6\left(1+x^2\right)^7\left(1-x^3\right)^8 ; x \neq 0\) is \(\alpha\), then \(|\alpha|\) equals _____. [JEE Main 2024 (Online) 1st February Morning Shift]
CorrectIncorrectHint
(b) We are given the product of three binomial expansions:
\(
\left(1+\frac{1}{x}\right)^6\left(1+x^2\right)^7\left(1-x^3\right)^8
\)
We need to find the coefficient of \(x^{30}\) in the expansion of this product.
Step 1: Expanding each binomial term
1. Expand \(\left(1+\frac{1}{x}\right)^6\) : The general term for \(\left(1+\frac{1}{x}\right)^6\) is:
2. Expand \(\left(1+x^2\right)^7\) : The general term for \(\left(1+x^2\right)^7\) is:
3. Expand \(\left(1-x^3\right)^8\) : The general term for \(\left(1-x^3\right)^8\) is:
Step 2: Finding the coefficient of \(x^{30}\)
Now, we need to find the values of \(r, s\), and \(t\) such that the exponents of \(x\) from all three expansions sum to 30 :
\(
-r+2 s+3 t=30
\)
We need to solve for \(r, s\), and \(t\) such that this equation holds.
Case 1: \(r=6\)
For \(r=6\), we have:
\(
2 s+3 t=36
\)
Solving this equation for integer values of \(s\) and \(t\), we get: \(s=12, t=8\). The corresponding terms are:
\(
\binom{6}{6} \times\binom{ 7}{12} \times\binom{ 8}{8}=678
\)
Thus, the coefficient \(\alpha\) is 678 . -
Question 78 of 226
78. Question
Let the coefficient of \(x^r\) in the expansion of \((x+3)^{n-1}+(x+3)^{n-2}(x+2)+(x+3)^{n-3}(x+2)^2+\ldots \ldots \ldots \ldots+(x+2)^{n-1}\) be \(\alpha_r\). If \(\sum_{r=0}^n \alpha_r=\beta^n-\gamma^n, \beta, \gamma \in N\), then the value of \(\beta^2+\gamma^2\) equals _____. [JEE Main 2024 (Online) 31st January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& (x+3)^{n-1}+(x+3)^{n-2}(x+2)+(x+3)^{n-3} \\
& (x+2)^2+\ldots \ldots+(x+2)^{n-1} \\
& \sum \alpha_r=4^{n-1}+4^{n-2} \times 3+4^{n-3} \times 3^2 \ldots \ldots+3^{n-1} \\
& =4^{n-1}\left[1+\frac{3}{4}+\left(\frac{3}{4}\right)^2 \ldots+\left(\frac{3}{4}\right)^{n-1}\right] \\
& =4^{n-1} \times \frac{1-\left(\frac{3}{4}\right)^n}{1-\frac{3}{4}} \\
& =4^n-3^n=\beta^n-\gamma^n \\
& \beta=4, \gamma=3 \\
& \beta^2+\gamma^2=16+9=25
\end{aligned}
\) -
Question 79 of 226
79. Question
In the expansion of \((1+x)\left(1-x^2\right)\left(1+\frac{3}{x}+\frac{3}{x^2}+\frac{1}{x^3}\right)^5, x \neq 0\), the sum of the coefficients of \(x^3\) and \(x^{-13}\) is equal to ____. [JEE Main 2024 (Online) 31st January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& (1+x)\left(1-x^2\right)\left(1+\frac{3}{x}+\frac{3}{x^2}+\frac{1}{x^3}\right)^5 \\
& =(1+x)\left(1-x^2\right)\left(\left(1+\frac{1}{x}\right)^3\right)^5 \\
& =\frac{(1+x)^2(1-x)(1+x)^{15}}{x^{15}} \\
& =\frac{(1+x)^{17}-x(1+x)^{17}}{x^{15}}
\end{aligned}
\)
\(=\operatorname{coeff}\left( x ^3\right)\) in the expansion \(\approx \operatorname{coeff}\left( x ^{18}\right)\) in
\(
\begin{aligned}
& (1+x)^{17}-x(1+x)^{17} \\
& =0-1 \\
& =-1
\end{aligned}
\)
coeff \(\left( x ^{-13}\right)\) in the expansion \(\approx \operatorname{coeff}\left( x ^2\right)\) in
\(
\begin{aligned}
& (1+x)^{17}-x(1+x)^{17} \\
& =\binom{17}{2}-\binom{17}{1} \\
& =17 \times 8-17 \\
& =17 \times 7 \\
& =119
\end{aligned}
\)
Hence Answer \(=119-1=118\) -
Question 80 of 226
80. Question
Let \(\alpha=\sum_{k=0}^n\left(\frac{\left({ }^n C_k\right)^2}{k+1}\right)\) and \(\beta=\sum_{k=0}^{n-1}\left(\frac{{ }^n C_k{ }^n C_{k+1}}{k+2}\right)\) If \(5 \alpha=6 \beta\), then \(n\) equals ____. [JEE Main 2024 (Online) 30th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
\alpha= & \sum_{k=0}^n \frac{{ }^n C_k \cdot{ }^n C_k}{k+1} \cdot \frac{n+1}{n+1} \\
& =\frac{1}{n+1} \sum_{k=0}^n{ }^{n+1} C_{k+1} \cdot{ }^n C_{n-k} \\
\alpha & =\frac{1}{n+1} \cdot{ }^{2 n+1} C_{n+1} \\
\beta & =\sum_{k=0}^{n-1} C_k \cdot \frac{{ }^n C_{k+1}}{k+2} \frac{n+1}{n+1} \\
& \frac{1}{n+1} \sum_{k=0}^{n-1}{ }^n C_{n-k} \cdot{ }^{n+1} C_{k+2} \\
& =\frac{1}{n+1} \cdot{ }^{2 n+1} C_{n+2} \\
\frac{\beta}{\alpha} & =\frac{2 n+1}{2 n+1} C_{n+2} \\
\frac{\beta}{\alpha} & =\frac{2 n+1-(n+2)+1}{n+2}=\frac{5}{6} \\
n & =10
\end{aligned}
\) -
Question 81 of 226
81. Question
Number of integral terms in the expansion of \(\left\{7^{\left(\frac{1}{2}\right)}+11^{\left(\frac{1}{6}\right)}\right\}^{824}\) is equal to ____. [JEE Main 2024 (Online) 30th January Morning Shift]
CorrectIncorrectHint
General term in expansion of \(\left((7)^{1 / 2}+(11)^{1 / 6}\right)^{824}\) is
\(t _{ r +1}={ }^{824} C _{ r }(7)^{\frac{824- r }{2}}(11)^{ r / 6}\)
For integral term, \(r\) must be multiple of 6 .
Hence \(r=0,6,12, \ldots \ldots .822\)
Total = 138. -
Question 82 of 226
82. Question
Remainder when \(64^{32^{32}}\) is divided by 9 is equal to ____. [JEE Main 2024 (Online) 29th January Evening Shift]
CorrectIncorrectHint
Let \(32^{32}= t\)
\(
\begin{aligned}
& 64^{32^{32}}=64^t=8^{2 t}=(9-1)^{2 t} \\
& =9 k +1
\end{aligned}
\)
Hence remainder \(=1\) -
Question 83 of 226
83. Question
If \(\frac{{ }^{11} C_1}{2}+\frac{{ }^{11} C_2}{3}+\ldots+\frac{{ }^{11} C_9}{10}=\frac{n}{m}\) with \(\operatorname{gcd}(n, m)=1\), then \(n+m\) is equal to ____. [JEE Main 2024 (Online) 29th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{ r =1}^9 \frac{{ }^{11} C _{ r }}{ r +1} \\
& =\frac{1}{12} \sum_{ r =1}^9{ }^{12} C _{ r +1} \\
& =\frac{1}{12}\left[2^{12}-26\right]=\frac{2035}{6} \\
& \therefore m + n =2041
\end{aligned}
\) -
Question 84 of 226
84. Question
The coefficient of \(x^{2012}\) in the expansion of \((1-x)^{2008}\left(1+x+x^2\right)^{2007}\) is equal to ____. [JEE Main 2024 (Online) 27th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& (1-x)(1-x)^{2007}\left(1+x+x^2\right)^{2007} \\
& (1-x)\left(1-x^3\right)^{2007} \\
& (1-x)\left({ }^{2007} C_0-{ }^{2007} C_1\left(x^3\right)+\ldots \ldots\right)
\end{aligned}
\)
General term
\(
\begin{aligned}
& (1-x)\left((-1)^{r 2007} C_r x^{3 r}\right) \\
& (-1)^{r 2007} C_r x^{3 r}-(-1)^{r 2007} C_r x^{3 r+1} \\
& 3 r=2012 \\
& r \neq \frac{2012}{3} \\
& 3 r+1=2012 \\
& 3 r=2011 \\
& r \neq \frac{2011}{3}
\end{aligned}
\)
Hence there is no term containing \(x ^{2012}\).
So coefficient of \(x^{2012}=0\) -
Question 85 of 226
85. Question
The remainder, when \(7^{103}\) is divided by 17 , is ____. [JEE Main 2023 (Online) 13th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 7^{103}=7 \times 7^{102} \\
& =7 \times(49)^{51} \\
& =7 \times(51-2)^{51} \\
& \text { Remainder }=7 \times(-2)^{51} \\
& =-7\left(2^3 \cdot(16)^{12}\right) \\
& =-56(17-1)^{12} \\
& \text { Remainder }=-56 \times(-1)^{12}=-56+68=12
\end{aligned}
\) -
Question 86 of 226
86. Question
Let \(\alpha\) be the constant term in the binomial expansion of \(\left(\sqrt{x}-\frac{6}{x^{\frac{3}{2}}}\right)^n, n \leq 15\). If the sum of the coefficients of the remaining terms in the expansion is 649 and the coefficient of \(x^{-n}\) is \(\lambda \alpha\), then \(\lambda\) is equal to ____. [JEE Main 2023 (Online) 13th April Morning Shift]
CorrectIncorrectHint
Given expression \(\left(\sqrt{x}-\frac{6}{x^{3 / 2}}\right)^n\). Here, \(a=\sqrt{x}\) and \(b=-\frac{6}{x^{3 / 2}}\).
The \(r\)-th term of the binomial expansion of \((a+b)^n\) is given by
\(
T_r={ }^n C_r a^{n-r} b^r \text {. }
\)
Substitute \(a\) and \(b\) in this formula, we get:
\(
T_r={ }^n C_r(\sqrt{x})^{n-r}\left(-\frac{6}{x^{3 / 2}}\right)^r={ }^n C_r(-6)^r x^{\frac{n-4 r}{2}} .
\)
The constant term in the binomial expansion is obtained when the power of \(x\) in the terms equals zero.
This happens when \(\frac{n-4 r}{2}=0\), which gives \(n=4 r\).
\(
\begin{aligned}
& { }^n C_{\frac{n}{4}}(-6)^{\frac{n}{4}}=\alpha \\
& (-5)^n-{ }^n C_{\frac{n}{4}}(-6)^{n / 4}=649
\end{aligned}
\)
By observation \((625+24=649)\), we get \(n=4\)
\(
\therefore \alpha=-24
\)
Now, for coefficient of \(x^{-4}\)
\(
\begin{aligned}
& \frac{n-4 r}{2}=-4 \\
& n=4 r-8 \Rightarrow r=3 \\
& \lambda(-24)=(-6)^3 \cdot{ }^4 C_3 \\
& \Rightarrow \lambda=36
\end{aligned}
\) -
Question 87 of 226
87. Question
The mean of the coefficients of \(x, x^2, \ldots, x^7\) in the binomial expansion of \((2+x)^9\) is ____. [JEE Main 2023 (Online) 11th April Morning Shift]
CorrectIncorrectHint
We have, binomial coefficient, \((2+x)^9\)
\(
T_{r+1}={ }^n C_r 2^{n-r} \times x^r
\)
Coefficient of \(x\left(T_1\right)={ }^9 C_1 \times 2^8\)
Coefficient of \(x^2\left(T_2\right)={ }^9 C_2 \times 2^7\)
Coefficient of \(x^3\left(T_3\right)={ }^9 C_3 \times 2^6\)
. .
. .
. .
Coefficient of \(x^7\left(T_7\right)={ }^9 C_7 \times 2^2\)
Mean \(=\frac{{ }^9 C_1 \times 2^8+{ }^9 C_2 \times 2^7+{ }^9 C_3 \times 2^6+\ldots+{ }^9 C_7 \times 2^2}{7}\)
\(
\begin{aligned}
& { }^9 C_0 \times 2^9+{ }^9 C_1 \times 2^8+{ }^9 C_2 \times 2^7+{ }^9 C_3 \times 2^6+\ldots+{ }^9 C_7 \times 2^2 \\
& =\frac{+{ }^9 C_8 \times 2^1+{ }^9 C_9 \times 2^0-{ }^9 C_0 \times 2^9-{ }^9 C_8 \times 2^1-{ }^9 C_9 \times 2^0}{7} \\
& =\frac{(1+2)^9-2^9-18-1}{7}=\frac{19152}{7}=2736
\end{aligned}
\) -
Question 88 of 226
88. Question
The number of integral terms in the expansion of \(\left(3^{\frac{1}{2}}+5^{\frac{1}{4}}\right)^{680}\) is equal to ____. [JEE Main 2023 (Online) 11th April Morning Shift]
CorrectIncorrectHint
General term of the expansion \(\left(3^{\frac{1}{2}}+5^{\frac{1}{4}}\right)^{680}\)
\(
={ }^{680} C_r\left(3^{1 / 2}\right)^{680-r}\left(5^{1 / 4}\right)^r={ }^{680} C_r \times 3^{\frac{680-r}{2}} \times 5^{\frac{r}{4}}
\)
The term will be integral if \(r\) is a multiple of 4 .
\(\therefore r=0,4,8,12, \ldots, 680\) (which is an AP)
\(
\begin{aligned}
& 680=0+(n-1) 4 \\
& n=\frac{680}{4}+1=171
\end{aligned}
\) -
Question 89 of 226
89. Question
The coefficient of \(x^7\) in \(\left(1-x+2 x^3\right)^{10}\) is ______. [JEE Main 2023 (Online) 10th April Morning Shift]
CorrectIncorrectHint
Given expression is \(\left(1-x+2 x^3\right)^{10}\)
So, general term is \(\frac{10!}{r_{1}!r_{2}!r_{3}!}(1)^{r_1}(-1)^{r_2} \cdot(2)^{r_3} \cdot(x)^{r_2+r_3}\)
Where, \(r_1+r_2+r_3=10\) and \(r_2+3 r_3=7\)
\(
\begin{aligned}
&\text { Now, for possibility, }\\
&\begin{array}{ccc}
r_1 & r_2 & r_3 \\
3 & 7 & 0 \\
7 & 1 & 2 \\
5 & 4 & 1
\end{array}
\end{aligned}
\)
Thus, required co-efficient
\(
\begin{aligned}
& =\frac{10!}{3!7!}(-1)^7+\frac{10!}{5!4!}(-1)^4(2)+\frac{10!}{7!2!}(-1)^1(2)^2 \\
& =-120+2520-1440 \\
& =2520-1560=960
\end{aligned}
\) -
Question 90 of 226
90. Question
Let \([t]\) denote the greatest integer \(\leq t\). If the constant term in the expansion of \(\left(3 x^2-\frac{1}{2 x^5}\right)^7\) is \(\alpha\), then \([\alpha]\) is equal to ____. [JEE Main 2023 (Online) 8th April Morning Shift]
CorrectIncorrectHint
Let \(T _{r+1}\) be the constant term.
\(
T _{r+1}={ }^7 C _r\left(3 x^2\right)^{7-r}\left(\frac{-1}{2 x^5}\right)^r
\)
For constant term, power of \(x\) should be zero.
i.e., \(14-2 r-5 r=0\)
\(
\Rightarrow 14=7 r \Rightarrow r=2
\)
Now, constant term \(=\alpha\)
\(
\begin{aligned}
& \Rightarrow{ }^7 C_2(3)^5\left(\frac{-1}{2}\right)^2=\alpha \\
& \Rightarrow 21 \times 243 \times \frac{1}{4}=\alpha \\
& \Rightarrow[\alpha]=[1275.75]=1275
\end{aligned}
\) -
Question 91 of 226
91. Question
The largest natural number \(n\) such that \(3^n\) divides 66 ! is ____. [JEE Main 2023 (Online) 8th April Morning Shift]
CorrectIncorrectHint
We have,
\(
\begin{aligned}
& {\left[\frac{66}{3}\right]=22} \\
& {\left[\frac{66}{3^2}\right]=7} \\
& {\left[\frac{66}{3^3}\right]=2}
\end{aligned}
\)
Highest powers of 3 is greater than 66 . So, their g.i.f. is always 0 .
\(\therefore\) Required natural number \(=22+7+2=31\) -
Question 92 of 226
92. Question
The coefficient of \(x^{18}\) in the expansion of \(\left(x^4-\frac{1}{x^3}\right)^{15}\) is ___. [JEE Main 2023 (Online) 6th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
T_{r+1} & ={ }^{15} C_r\left(x^4\right)^{15-r}\left(-\frac{1}{x^3}\right)^r={ }^{15} C_r(-1)^r x^{60-4 r-3 r} \\
& ={ }^{15} C_r(-1)^r x^{60-7 r}
\end{aligned}
\)
\(
\begin{array}{r}
\therefore 60-7 r=18 \\
\Rightarrow 7 r=42 \\
\Rightarrow r=6
\end{array}
\)
\(\therefore\) The coefficient of \(x^{18}\)
\(
={ }^{15} C_6(-1)^6=\frac{15 \times 14 \times 13 \times 12 \times 11 \times 10}{6 \times 5 \times 4 \times 3 \times 2 \times 1}=5005
\) -
Question 93 of 226
93. Question
Let the sixth term in the binomial expansion of \(\left(\sqrt{2^{\log _2\left(10-3^x\right)}}+\sqrt[5]{2^{(x-2) \log _2 3}}\right)^m\) in the increasing powers of \(2^{(x-2) \log _2 3}\), be 21 . If the binomial coefficients of the second, third and fourth terms in the expansion are respectively the first, third and fifth terms of an A.P., then the sum of the squares of all possible values of \(x\) is ____. [JEE Main 2023 (Online) 1st February Evening Shift]
CorrectIncorrectHint
\({ }^m C_1,{ }^m C_2,{ }^m C_3\) are first, third and fifth term of \(A P\)
\(
\begin{aligned}
\therefore \quad & a={ }^m C_1 \\
& a+2 d={ }^m C_2 \\
& a+4 d={ }^m C_3
\end{aligned}
\)
\(
\begin{gathered}
\therefore \quad 2{ }^m C_2-{ }^m C_3=m \\
\Rightarrow m=7 \text { or } m=2
\end{gathered}
\)
\(\because m=2\) is not possible
\(
\therefore m=7
\)
\(
T _6={ }^{ m } C _5\left(10-3^{ x }\right)^{\frac{ m -5}{2}} \cdot\left(3^{ x -2}\right)=21
\)
Putting value of \(m=7\), we get
\(
\begin{aligned}
& T_{5+1}={ }^7 C_5\left(10-3^x\right)^{\frac{7-5}{2}} 3^{x-2}=21 \\
& \Rightarrow \frac{10.3^x-\left(3^x\right)^2}{3^2}=1 \\
& \Rightarrow\left(3^x\right)^2-10 \cdot 3^x+9=0 \\
& \Rightarrow 3^x=9,1 \\
& \Rightarrow x=0,2
\end{aligned}
\)
Sum of squares of values of \(x=0^2+2^2=4\) -
Question 94 of 226
94. Question
If the term without \(x\) in the expansion of \(\left(x^{\frac{2}{3}}+\frac{\alpha}{x^3}\right)^{22}\) is 7315 , then \(|\alpha|\) is equal to ____. [JEE Main 2023 (Online) 1st February Evening Shift]
CorrectIncorrectHint
Given expansion \(\left(x^{\frac{2}{3}}+\frac{\alpha}{x^3}\right)^{22}\)
\(
T_{r+1}={ }^{22} C_r\left(x^{\frac{2}{3}}\right)^{22-r}\left(\frac{\alpha}{x^3}\right)^r
\)
For constant term
\(
\begin{aligned}
& \frac{44-2 r}{3}-3 r=0 \\
& \Rightarrow r=4
\end{aligned}
\)
Now \({ }^{22} C _4 \alpha^4=7315\)
\(
\frac{22 \times 21 \times 20 \times 19}{4 \times 3 \times 2 \times 1} \alpha^4=7315
\)
\(
\begin{aligned}
& \therefore \alpha^4=1 \\
& \therefore|\alpha|=1
\end{aligned}
\) -
Question 95 of 226
95. Question
The remainder, when \(19^{200}+23^{200}\) is divided by 49 , is ____. [JEE Main 2023 (Online) 1st February Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 19^{200}+23^{200} \\
& =(21-2)^{200}+(21+2)^{200}=49 \lambda+2^{201}
\end{aligned}
\)
Now, \(2^{201}=8^{67}=(7+1)^{67}=49 \lambda+7 \times 67+1\)
\(
\begin{aligned}
& =49 \lambda+470 \\
& =49(\lambda+9)+29 \\
& \therefore \text { Remainder }=29
\end{aligned}
\) -
Question 96 of 226
96. Question
The coefficient of \(x^{-6}\), in the expansion of \(\left(\frac{4 x}{5}+\frac{5}{2 x^2}\right)^9\), is ____. [JEE Main 2023 (Online) 31st January Evening Shift]
CorrectIncorrectHint
Coeff of \(x^{-6}\) in \(\left(\frac{4 x}{5}+\frac{5}{2 x^2}\right)^9\)
\(
\begin{aligned}
T_{r+1} & ={ }^9 C_r\left(\frac{4 x}{5}\right)^{9-r}\left(\frac{5}{2 x^2}\right)^r \\
9-3 r & =-6 \\
r & =5
\end{aligned}
\)
Coeff of \(x^{-6}={ }^9 C_5\left(\frac{4}{5}\right)^4\left(\frac{5}{2}\right)^5=5040\) -
Question 97 of 226
97. Question
If the constant term in the binomial expansion of \(\left(\frac{x^{\frac{5}{2}}}{2}-\frac{4}{x^l}\right)^9\) is -84 and the coefficient of \(x^{-3 l}\) is \(2^\alpha \beta\), where \(\beta<0\) is an odd number, then \(|\alpha l-\beta|\) is equal to ____. [JEE Main 2023 (Online) 31st January Evening Shift]
CorrectIncorrectHint
Given binomial expansion of \(\left(\frac{x^{\frac{5}{2}}}{2}-\frac{4}{x^l}\right)^9\)
\(
\begin{aligned}
T_{r+1} & ={ }^9 C_r\left(\frac{x^{\frac{5}{2}}}{2}\right)^{9-r}\left(\frac{-4}{x^l}\right)^r \\
& ={ }^9 C_r x^{\frac{45-5 r}{2}-l r} \cdot 2^{r-9} \cdot 4^r \cdot(-1)^r
\end{aligned}
\)
For constant term, power of \(x\) is zero.
So, \(\frac{45-5 r}{2}=l r \Rightarrow 2 l r+5 r=45\)
Now constant term \(=-84\)
and \({ }^9 C_r \cdot 2^{3 r-9}(-1)^r=-84\)
So, \(r=3\) and \(l=5\)
Now for \(x^{-15}, \frac{45-5 r}{2}-5 r=-15\)
\(
\begin{aligned}
& \Rightarrow 45-15 r=-30 \\
& \Rightarrow r=5
\end{aligned}
\)
\(\therefore\) Coefficient \(=-{ }^9 C_5 2^6=-63.2^7\)
\(
\therefore \alpha=7, \beta=-63
\)
and \(|\alpha l-\beta|=|7 \times 5+63|=98\) -
Question 98 of 226
98. Question
The remainder on dividing \(5^{99}\) by 11 is ____. [JEE Main 2023 (Online) 31st January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 5^{99}=5^4 \cdot 5^{95} \\
& =625\left[5^5\right]^{19} \\
& =625[3125]^{19} \\
& =625[3124+1]^{19} \\
& =625[11 k \times 19+1] \\
& =625 \times 11 k \times 19+625 \\
& =11 k _1+616+9 \\
& =11\left( k _2\right)+9 \\
& \text { Remainder }=9
\end{aligned}
\) -
Question 99 of 226
99. Question
Let \(\alpha>0\), be the smallest number such that the expansion of \(\left(x^{\frac{2}{3}}+\frac{2}{x^3}\right)^{30}\) has a term \(\beta x^{-\alpha}, \beta \in N\). Then \(\alpha\) is equal to ____. [JEE Main 2023 (Online) 31st January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T _{ r +1}={ }^{30} C _{ r }\left( x ^{2 / 3}\right)^{30- r }\left(\frac{2}{ x ^3}\right)^{ r } \\
& ={ }^{30} C _{ r } \cdot 2^{ r } \cdot x ^{\frac{60-11 r }{3}} \\
& \frac{60-11 r }{3}<0 \\
& \Rightarrow 11 r >60 \\
& \Rightarrow r >\frac{60}{11} \\
& \Rightarrow r =6 \\
& T _7={ }^{30} C _6 \cdot 2^6 x ^{-2}
\end{aligned}
\)
We have also observed \(\beta={ }^{30} C _6(2)^6\) is a natural number.
\(
\therefore \alpha=2
\) -
Question 100 of 226
100. Question
\(50^{\text {th }}\) root of a number \(x\) is 12 and \(50^{\text {th }}\) root of another number \(y\) is 18 . Then the remainder obtained on dividing \((x+y)\) by 25 is ____. [JEE Main 2023 (Online) 30th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Given } x^{\frac{1}{50}}=12 \Rightarrow x=12^{50} \\
& y^{\frac{1}{50}}=18 \Rightarrow y=18^{50} \\
& 12 \equiv 13(\operatorname{Mod} 25) \\
& 12^2 \equiv 19(\operatorname{Mod} 25) \\
& 12^3 \equiv-3(\operatorname{Mod} 25) \\
& 12^9 \equiv-2(\operatorname{Mod} 25) \\
& 12^{10} \equiv-1(\operatorname{Mod} 25) \\
& 12^{50} \equiv-1(\operatorname{Mod} 25) \dots(i)
\end{aligned}
\)
Now
\(18 \equiv 7(\operatorname{Mod} 25)\)
\(18^2 \equiv-1(\operatorname{Mod} 25)\)
\(18^{-50} \equiv-1(\operatorname{Mod} 25) \dots(ii)\)
\(\therefore 12^{50}+18^{50} \equiv-2(\operatorname{Mod} 25)\)
\(\equiv 23(\operatorname{Mod} 25)\)
\(\therefore\) Answer \(=23\) -
Question 101 of 226
101. Question
Let the coefficients of three consecutive terms in the binomial expansion of \((1+2 x)^n\) be in the ratio \(2: 5: 8\). Then the coefficient of the term, which is in the middle of those three terms, is ____. [JEE Main 2023 (Online) 29th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& t _{ r +1}={ }^{ n } C _{ r }(2 x )^{ r } \\
& \Rightarrow \frac{{ }^{ n } C _{ r -1}(2)^{ r -1}}{{ }^{ n } C _{ r }(2)^{ r }}=\frac{2}{5} \\
& \Rightarrow \frac{\frac{n!}{(r-1)!(n-r+1)!}}{\frac{n!(2)}{r!(n-r)!}}=\frac{2}{5} \\
& \Rightarrow \frac{ r }{ n – r +1}=\frac{4}{5} \Rightarrow 5 r =4 n -4 r +4 \\
& \Rightarrow 9 r =4( n +1) \quad \ldots(1)
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \frac{{ }^n C_r(2)^{ r }}{{ }^{ n } C _{ r +1}(2)^{ r +1}}=\frac{5}{8} \\
& \Rightarrow \frac{\frac{n!}{r!(n-r)!}}{\frac{n!}{(r+1)!(n-r-1)!}}=\frac{5}{4} \Rightarrow \frac{r+1}{n-r}=\frac{5}{4}
\end{aligned}
\)
\(
\Rightarrow 4 r+4=5 n-5 r \Rightarrow 5 n-4=9 r \dots(2)
\)
From (1) and (2)
\(
\Rightarrow 4 n +4=5 n -4 \Rightarrow n =8
\)
(1) \(\Rightarrow r=4\)
so, coefficient of middle term is
\(
{ }^8 C _4 2^4=16 \times \frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1}=16 \times 70=1120
\) -
Question 102 of 226
102. Question
If the co-efficient of \(x^9\) in \(\left(\alpha x^3+\frac{1}{\beta x}\right)^{11}\) and the co-efficient of \(x^{-9}\) in \(\left(\alpha x-\frac{1}{\beta x^3}\right)^{11}\) are equal, then \((\alpha \beta)^2\) is equal to ____. [JEE Main 2023 (Online) 29th January Morning Shift]
CorrectIncorrectHint
Coefficient of \(x ^9\) in \(\left(\alpha x^3+\frac{1}{\beta x}\right)={ }^{11} C_6 \cdot \frac{\alpha^5}{\beta^6}\)
\(\because\) Both are equal
\(
\begin{aligned}
& \therefore { }^{11} C_6 \cdot \frac{\alpha^5}{\beta^6}=-{ }^{11} C_6 \cdot \frac{\alpha^6}{\beta^5} \\
& \Rightarrow \frac{1}{\beta}=-\alpha \\
& \Rightarrow \alpha \beta=-1 \\
& \Rightarrow(\alpha \beta)^2=1
\end{aligned}
\) -
Question 103 of 226
103. Question
The remainder when \((2023)^{2023}\) is divided by 35 is ____. [JEE Main 2023 (Online) 25th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& (2023)^{2023} \\
& =(2030-7)^{2023} \\
& =(35 K -7)^{2023}
\end{aligned}
\)
\(
={ }^{2023} C _0(35 K )^{2023}(-7)^0+{ }^{2023} C _1(35 K )^{2022}(-7)+\ldots \ldots+\ldots \ldots .+{ }^{2023} C _{2023}(-7)^{2023}
\)
\(
=35 N -7^{2023}
\)
Now,\(-7^{2023}=-7 \times 7^{2022}=-7\left(7^2\right)^{1011}\)
\(
=-7(50-1)^{1011}
\)
\(
=-7\left({ }^{1011} C _0 50^{1011}-{ }^{1011} C _1(50)^{1010}+\ldots . .{ }^{1011} C _{1011}\right)
\)
\(
\begin{aligned}
& =-7(5 \lambda-1) \\
& =-35 \lambda+7
\end{aligned}
\)
\(\therefore\) when \((2023)^{2023}\) is divided by 35 remainder is 7. -
Question 104 of 226
104. Question
The constant term in the expansion of \(\left(2 x+\frac{1}{x^7}+3 x^2\right)^5\) is ____. [JEE Main 2023 (Online) 25th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(2 x+\frac{1}{x^7}+3 x^2\right)^5 \\
& \frac{1}{x^{35}}\left(2 x^8+1+3 x^9\right)^5 \\
& \frac{1}{x^{35}}\left(1+x^8(3 x+2)\right)^5
\end{aligned}
\)
Term independent of \(x=\) coefficient of \(x^{35}\) in
\(
\begin{aligned}
& { }^5 C_4\left(x^8(3 x+2)\right)^4 \\
= & { }^5 C_4 \text { coefficient of } x^3 \text { in }(2+3 x)^4 \\
= & { }^5 C_4 \times{ }^4 C_3(2)^1(3)^3 \\
= & 5 \times 4 \times 2 \times 27 \\
= & 1080
\end{aligned}
\) -
Question 105 of 226
105. Question
Let the sum of the coefficients of the first three terms in the expansion of \(\left(x-\frac{3}{x^2}\right)^n, x \neq 0 . n \in N\), be 376. Then the coefficient of \(x^4\) is ______. [JEE Main 2023 (Online) 24th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S=1-3 n+\frac{9 n(n-1)}{2}=376 \\
& 3 n^2-5 n-250=0 \\
& n=10, \frac{-25}{3} \text { (Rejected) } \\
& T_{r+1}={ }^n C_r \cdot x^{n-r}\left(\frac{-3}{x^2}\right)^r \\
& ={ }^n C_r x^{n-3 r}(-3)^r \\
& ={ }^{10} C_r x^{10-3 r}(-3)^r
\end{aligned}
\)
Here \(r=2\)
\(
\begin{aligned}
\text { Required coefficient } & ={ }^{10} C _2(-3)^2 \\
& =45 \times 9 \\
& =405
\end{aligned}
\) -
Question 106 of 226
106. Question
Suppose \(\sum_{r=0}^{2023} r^2{ }^{2023} C_r=2023 \times \alpha \times 2^{2022}\). Then the value of \(\alpha\) is ____. [JEE Main 2023 (Online) 24th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (1) }{ }^n C_r=\frac{n}{r} \cdot{ }^{n-1} C_{r-1} \\
& \text { Given, } \\
& \sum_{r=0}^{2023} r^2 \cdot{ }^{2023} C_r \\
& =\sum_{r=0}^{2023} r^2 \cdot \frac{2023}{r} \cdot{ }^{2022} C_{r-1} \\
& =2023 \sum_{r=0}^{2023} r \cdot{ }^{2022} C_{r-1} \\
& =2023 \sum_{r=0}^{2023}[(r-1)+1] \cdot{ }^{2022} C_{r-1} \\
& =2023\left[\sum_{r=0}^{2023}(r-1) \cdot{ }^{2022} C_{r-1}+\sum_{r=0}^{2023}{ }^{2022} C_{r-1}\right] \\
& =2023\left[\sum_{r=0}^{2023}(r-1) \cdot \frac{2022}{(r-1)} \cdot{ }^{2021} C_{r-2}+2^{2022}\right] \\
& =2023\left[2022 \sum_{r=0}^{2023}{ }^{2021} C_{r-2}+2^{2022}\right] \\
& =2023\left[2022 \cdot 2^{2021}+2^{2022}\right] \\
& =2023 \cdot 2^{2021}[2022+2] \\
& =2023 \cdot 2^{2021} \cdot 2024
\end{aligned}
\)
\(
\begin{aligned}
& =2023 \cdot \frac{2^{2022}}{2} \cdot 2024 \\
& =2023 \cdot 2^{2022} \cdot 1012 \\
& \therefore \alpha=1012
\end{aligned}
\) -
Question 107 of 226
107. Question
If \(\sum_{k=1}^{10} K^2\left({ }^{10}{C_K}\right)^2=22000 L\), then \(L\) is equal to ____. [JEE Main 2022 (Online) 29th July Evening Shift]
CorrectIncorrectHint
Given,
\(
\begin{aligned}
& \sum_{k=1}^{10} k^2\left({ }^{10} C_k\right)^2=2200 L \\
& \Rightarrow \sum_{k=1}^{10}\left(k \cdot{ }^{10} C_k\right)^2=22000 L \\
& \Rightarrow \sum_{k=1}^{10}\left(k \cdot \frac{10}{k} \cdot{ }^9 C_{k-1}\right)^2=22000 L \\
& \Rightarrow \sum_{k=1}^{10}\left(10 \cdot{ }^9 C_{k-1}\right)^2=22000 L
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow 100 \cdot \sum_{k=1}^{10}\left({ }^9 C_{k-1}\right)^2=22000 L \\
& \Rightarrow 100\left(\left({ }^9 C_0\right)^2+\left({ }^9 C_1\right)^2+\ldots .+\left({ }^9 C_9\right)^2\right)=22000 L \\
& \Rightarrow 100\left({ }^{18} C_9\right)=22000 L
\end{aligned}
\)
[Note : \(\left({ }^n C_1\right)^2+\left({ }^n C_2\right)^2+\ldots+\left({ }^n C_n\right)^2={ }^{2 n} C_n\) ]
\(
\begin{aligned}
& \Rightarrow 100 \times \frac{18!}{9!9!}=22000 L \\
& \Rightarrow L=221
\end{aligned}
\) -
Question 108 of 226
108. Question
Let the ratio of the fifth term from the beginning to the fifth term from the end in the binomial expansion of \(\left(\sqrt[4]{2}+\frac{1}{\sqrt[4]{3}}\right)^n\), in the increasing powers of \(\frac{1}{\sqrt[4]{3}}\) be \(\sqrt[4]{6}: 1\). If the sixth term from the beginning is \(\frac{\alpha}{\sqrt[4]{3}}\), then \(\alpha\) is equal to _____. [JEE Main 2022 (Online) 29th July Morning Shift]
CorrectIncorrectHint
Fifth term from beginning \(={ }^n C_4\left(2^{\frac{1}{4}}\right)^{n-4}\left(3^{\frac{-1}{4}}\right)^4\)
Fifth term from end \(=(n-5+1)^{\text {th }}\) term from begin \(={ }^n C_{n-4}\left(2^{\frac{1}{4}}\right)^3\left(3^{\frac{-1}{4}}\right)^{n-4}\)
\(
\begin{aligned}
& \text { Given } \frac{{ }^n C_4 2^{\frac{n-4}{4}} \cdot 3^{-1}}{{ }^n C_{n-3} 2^{\frac{4}{4}} \cdot 3^{-\left(\frac{n-4}{4}\right)}}=6^{\frac{1}{4}} \\
& \Rightarrow 6^{\frac{n-8}{4}}=6^{\frac{1}{4}} \\
& \Rightarrow \frac{n-8}{4}=\frac{1}{4} \Rightarrow n=9 \\
& T_6=T_{5+1}={ }^9 C_5\left(2^{\frac{1}{4}}\right)^4\left(3^{\frac{-1}{4}}\right)^5 \\
& =\frac{{ }^9 C_5 \cdot 2}{3^{\frac{1}{4}} \cdot 3}=\frac{84}{3^{\frac{1}{4}}}=\frac{\alpha}{3^{\frac{1}{4}}} \\
& \Rightarrow \alpha=84
\end{aligned}
\) -
Question 109 of 226
109. Question
Let the coefficients of the middle terms in the expansion of \(\left(\frac{1}{\sqrt{6}}+\beta x\right)^4,(1-3 \beta x)^2\) and \(\left(1-\frac{\beta}{2} x\right)^6, \beta>0\), respectively form the first three terms of an A.P. If \(d\) is the common difference of this A.P. , then \(50-\frac{2 d}{\beta^2}\) is equal to _______. [JEE Main 2022 (Online) 28th July Evening Shift]
CorrectIncorrectHint
Coefficients of middle terms of given expansions are \({ }^4 C_2 \frac{1}{6} \beta^2,{ }^2 C_1(-3 \beta),{ }^6 C_3\left(\frac{-\beta}{2}\right)^3\) form an A.P.
\(
\begin{aligned}
& \therefore 2.2(-3 \beta)=\beta^2-\frac{5 \beta^3}{2} \\
& \Rightarrow-24=2 \beta-5 \beta^2 \\
& \Rightarrow 5 \beta^2-2 \beta-24=0 \\
& \Rightarrow 5 \beta^2-12 \beta+10 \beta-24=0 \\
& \Rightarrow \beta(5 \beta-12)+2(5 \beta-12)=0 \\
& \beta=\frac{12}{5} \\
& d=-6 \beta-\beta^2 \\
& \therefore 50-\frac{2 d}{\beta^2}=50-2 \frac{\left(-6 \beta-\beta^2\right)}{\beta^2}=50+\frac{12}{\beta}+2=57
\end{aligned}
\) -
Question 110 of 226
110. Question
If \(1+\left(2+{ }^{49} C_1+{ }^{49} C_2+\ldots+{ }^{49} C_{49}\right)\left({ }^{50} C_2+{ }^{50} C_4+\ldots+{ }^{50} C_{50}\right)\) is equal to \(2^{ n } \cdot m\), where \(m\) is odd, then \(n + m\) is equal to _____. [JEE Main 2022 (Online) 28th July Evening Shift]
CorrectIncorrectHint
\(
l=1+\left(1+{ }^{49} C_0+{ }^{49} C_1+\ldots+{ }^{49} C_{49}\right)\left({ }^{50} C_2+{ }^{50} C_4+\ldots+{ }^{50} C_{50}\right)
\)
As \({ }^{49} C_0+{ }^{49} C_1+\ldots \ldots+{ }^{49} C_{49}=2^{49}\)
and \({ }^{50} C_0+{ }^{50} C_2+\ldots+{ }^{50} C_{50}=2^{49}\)
\(
\begin{aligned}
& \Rightarrow{ }^{50} C_2+{ }^{50} C_4+\ldots+{ }^{50} C_{50}=2^{49}-1 \\
& \therefore l=1+\left(2^{49}+1\right)\left(2^{49}-1\right) \\
& =2^{98} \\
& \therefore m=1 \text { and } n=98 \\
& m+n=99
\end{aligned}
\) -
Question 111 of 226
111. Question
Let for the \(9^{\text {th }}\) term in the binomial expansion of \((3+6 x)^{ n }\), in the increasing powers of \(6 x\), to be the greatest for \(x=\frac{3}{2}\), the least value of \(n\) is \(n _0\). If \(k\) is the ratio of the coefficient of \(x^6\) to the coefficient of \(x^3\), then \(k + n _0\) is equal to : [JEE Main 2022 (Online) 27th July Evening Shift]
CorrectIncorrectHint
\(
(3+6 x)^n=3^n(1+2 x)^n
\)
If \(T _9\) is numerically greatest term
\(
\begin{aligned}
& \therefore T_8 \leq T_9 \leq T_{10} \\
& { }^n C_7 3^{n-7}(6 x)^7 \leq{ }^n C_8 3^{n-8}(6 x)^8 \geq{ }^n C_9 3^{n-9}(6 x)^9 \\
& \Rightarrow \frac{n!}{(n-7)!7!} 9 \leq \frac{n!}{(n-8)!8!} 3 \cdot(6 x) \geq \frac{n!}{(n-9)!9!}(6 x)^2 \\
& \Rightarrow \underbrace{\frac{9}{(n-7)(n-8)}} \leq \underbrace{\frac{18\left(\frac{3}{2}\right)}{(n-8) 8} \geq \frac{36}{9.8} \frac{9}{4}}
\end{aligned}
\)
\(
\begin{aligned}
& 72 \leq 27(n-7) \text { and } 27 \geq 9(n-8) \\
& \frac{29}{3} \leq n \text { and } n \leq 11 \\
& \therefore n_0=10 \\
& \text { For }(3+6 x)^{10} \\
& T_{r+1}={ }^{10} C_r \\
& 3^{10-r}(6 x)^r
\end{aligned}
\)
For coeff. of \(x^6\)
\(
r=6 \Rightarrow{ }^{10} C_6 3^4 \cdot 6^6
\)
For coeff. of \(x^3\)
\(
\begin{aligned}
& r=3 \Rightarrow{ }^{10} C_3 3^7 \cdot 6^3 \\
& \therefore k=\frac{{ }^{10} C_6}{{ }^{10} C_3} \cdot \frac{3^4 \cdot 6^6}{3^7 \cdot 6^3}=\frac{10!7!3!}{6!4!10!} \cdot 8 \\
& \Rightarrow k=14 \\
& \therefore k+n_0=24
\end{aligned}
\) -
Question 112 of 226
112. Question
If the coefficients of \(x\) and \(x^2\) in the expansion of \((1+x)^{ p }(1-x)^{ q }, p , q \leq 15\), are -3 and -5 respectively, then the coefficient of \(x^3\) is equal to _____. [JEE Main 2022 (Online) 26th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Coefficient of } x \text { in }(1+x)^p(1-x)^q \\
& -{ }^p C_0{ }^q C_1+{ }^p C_1{ }^q C_0=-3 \Rightarrow p-q=-3 \\
& \text { Coefficient of } x ^2 \text { in }(1+x)^p(1-x)^q \\
& { }^p C_0{ }^q C_2-{ }^p C_1{ }^q C_1+{ }^p C_2{ }^q C_0=-5 \\
& \frac{q(q-1)}{2}-p q+\frac{p(q-1)}{2}=-5 \\
& \frac{q^2-q}{2}-(q-3) q+\frac{(q-3)(q-4)}{2}=-5 \\
& \Rightarrow q=11, p=8 \\
& \text { Coefficient of } x ^3 \text { in }(1+x)^8(1-x)^{11} \\
& =-{ }^{11} C_3+{ }^8 C_1{ }^{11} C_2-{ }^8 C_2{ }^{11} C_1+{ }^8 C_3=23
\end{aligned}
\) -
Question 113 of 226
113. Question
If the maximum value of the term independent of \(t\) in the expansion of \(\left( t ^2 x^{\frac{1}{5}}+\frac{(1-x)^{\frac{1}{10}}}{ t }\right)^{15}, x \geqslant 0\), is \(K\), then \(8 K\) is equal to _____. [JEE Main 2022 (Online) 25th July Morning Shift]
CorrectIncorrectHint
General term of \(\left(t^2 x^{\frac{1}{5}}+\frac{(1-x)^{\frac{1}{10}}}{t}\right)^{15}\) is
\(
\begin{aligned}
& T_{r+1}={ }^{15} C_r \cdot\left(t^2 x^{\frac{1}{5}}\right)^{15-r} \cdot\left(\frac{(1-x)^{\frac{1}{10}}}{t}\right)^r \\
& ={ }^{15} C_r \cdot t^{30-2 r} \cdot x^{\frac{15-r}{5}} \cdot(1-x)^{\frac{r}{10}} \cdot t^{-r} \\
& ={ }^{15} C_r \cdot t^{30-3 r} \cdot x^{\frac{15-r}{5}} \cdot(1-x)^{\frac{r}{10}}
\end{aligned}
\)
Term will be independent of \(t\) when \(30-3 r=0 \Rightarrow r=10\)
\(\therefore T_{10+1}=T_{11}\) will be independent of \(t\)
\(
\begin{aligned}
& \therefore T_{11}={ }^{15} C_{10} \cdot x^{\frac{15-10}{5}} \cdot(1-x)^{\frac{10}{10}} \\
& ={ }^{15} C_{10} \cdot x^1 \cdot(1-x)^1
\end{aligned}
\)
\(T _{11}\) will be maximum when \(x(1-x)\) is maximum.
Let \(f(x)=x(1-x)=x-x^2\)
\(f(x)\) is maximum or minimum when \(f^{\prime}(x)=0\)
\(
\therefore f^{\prime}(x)=1-2 x
\)
For maximum \(/\) minimum \(f^{\prime}(x)=0\)
\(
\begin{aligned}
& \therefore 1-2 x=0 \\
& \Rightarrow x=\frac{1}{2}
\end{aligned}
\)
Now, \(f^{\prime \prime}(x)=-2<0\)
\(\therefore\) At \(x=\frac{1}{2}, f(x)\) maximum
\(\therefore\) Maximum value of \(T _{11}\) is
\(
\begin{aligned}
& ={ }^{15} C_{10} \cdot \frac{1}{2}\left(1-\frac{1}{2}\right) \\
& ={ }^{15} C_{10} \cdot \frac{1}{4}
\end{aligned}
\)
Given \(K={ }^{15} C_{10} \cdot \frac{1}{4}\)
Now, \(8 K=2\left({ }^{15} C_{10}\right)\)
\(
=6006
\) -
Question 114 of 226
114. Question
Let the coefficients of \(x ^{-1}\) and \(x ^{-3}\) in the expansion of \(\left(2 x^{\frac{1}{5}}-\frac{1}{x^{\frac{1}{5}}}\right)^{15}, x>0\), be \(m\) and \(n\) respectively. If \(r\) is a positive integer such that \(m n^2={ }^{15} C_r \cdot 2^r\), then the value of \(r\) is equal to _____. [JEE Main 2022 (Online) 29th June Evening Shift]
CorrectIncorrectHint
Given, Binomial expansion
\(
\left(2 x^{\frac{1}{5}}-\frac{1}{x^{\frac{1}{5}}}\right)^{15}
\)
\(\therefore\) General Term
\(
\begin{aligned}
& T_{r+1}={ }^{15} C_r \cdot\left(2 x^{\frac{1}{5}}\right)^{15-r} \cdot\left(-\frac{1}{x^{\frac{1}{5}}}\right)^r \\
& ={ }^{15} C_r \cdot 2^{15-r} \cdot x^{\frac{1}{5}(15-r-r)} \cdot(-1)^r
\end{aligned}
\)
For \(x^{-1}\) term;
\(
\begin{aligned}
& \frac{1}{5}(15-2 r)=-1 \\
& \Rightarrow 15-2 r=-5 \\
& \Rightarrow 2 r=20 \\
& \Rightarrow r=10
\end{aligned}
\)
\(m\) is the coefficient of \(x^{-1}\) term,
\(
\begin{aligned}
& \therefore m={ }^{15} C_{10} \cdot 2^{15-10} \cdot(-1)^{10} \\
& ={ }^{15} C_{10} \cdot 2^5
\end{aligned}
\)
For \(x^{-3}\) term;
\(
\begin{aligned}
& \frac{1}{5}(15-2 r)=-3 \\
& \Rightarrow 15-2 r=-15 \\
& \Rightarrow 2 r=30 \\
& \Rightarrow r=15
\end{aligned}
\)
\(n\) is the coefficient of \(x^{-3}\) term,
\(
\begin{aligned}
& \therefore n={ }^{15} C_{15} \cdot 2^{15-15} \cdot(-1)^{15} \\
& =1 \cdot 1 \cdot-1 \\
& =-1
\end{aligned}
\)
Given,
\(
\begin{aligned}
& m n^2={ }^{15} C_r \cdot 2^r \\
& \left.\Rightarrow{ }^{15} C_{10} \cdot 2^5 \cdot(1)^2={ }^{15} C_r \cdot 2^r \text { [putting value of } m \text { and } n \right] \\
& \Rightarrow{ }^{15} C_{15-10} \cdot 2^5={ }^{15} C_r \cdot 2^r \\
& \Rightarrow{ }^{15} C_5 \cdot 2^5={ }^{15} C_r \cdot 2^r
\end{aligned}
\)
Comparing both side, we get
\(
r=5
\) -
Question 115 of 226
115. Question
The number of positive integers \(k\) such that the constant term in the binomial expansion of \(\left(2 x^3+\frac{3}{x^k}\right)^{12}, x \neq 0 \text { is } 2^8 . I,\) \(
\text { where I is an odd integer, is }\) _____. [JEE Main 2022 (Online) 28th June Morning Shift]CorrectIncorrectHint
(b) Given Binomial expression is
\(
\left(2 x^3+\frac{3}{x^k}\right)^{12}
\)
General term,
\(
\begin{aligned}
& T_{r+1}={ }^{12} C_r\left(2 x^3\right)^r \cdot\left(\frac{3}{x^k}\right)^{12-r} \\
& =\left({ }^{12} C_r \cdot 2^r \cdot 3^{12-r}\right) \cdot x^{3 r-12 k+k r}
\end{aligned}
\)
For constant term,
\(
\begin{aligned}
& 3 r-12 k+k r=0 \\
& \Rightarrow k(12-r)=3 r \\
& \Rightarrow k=\frac{3 r}{12-r}
\end{aligned}
\)
For \(r =1, k=\frac{3}{11}\) (not integer)
For \(r =2, k=\frac{6}{10}\) (not integer)
For \(r =3, k=\frac{9}{9}=1\) (integer)
For \(r =6, k=\frac{18}{6}=3\) (integer)
For \(r =8, k=\frac{24}{4}=6\) (integer)
For \(r =9, k=\frac{27}{3}=9\) (integer)
For \(r =10, k=\frac{30}{2}=15\) (integer)
For \(r =11, k=\frac{33}{1}=33\) (integer)
So, for \(r=3,6,8,9,10\) and 11, \(k\) is positive integer.
When \(k =1\) then \(r =3\) and constant term is
\(
\begin{aligned}
& ={ }^{12} C_3 \cdot 2^3 \cdot 3^9 \\
& =\frac{12 \cdot 11 \cdot 10}{3 \cdot 2 \cdot 1} \cdot 2^3 \cdot 3^9 \\
& =2 \cdot 11 \cdot 2 \cdot 5 \cdot 2^3 \cdot 3^9 \\
& =11 \cdot 5 \cdot 2^5 \cdot 3^9 \\
& =2^5 \cdot\left(55 \cdot 3^9\right) \\
& =2^5(I) \\
& \neq 2^8 \cdot I
\end{aligned}
\)
When \(x =3\) then \(r =6\) and constant term
\(
\begin{aligned}
& ={ }^{12} C_6 \cdot 2^6 \cdot 3^6 \\
& =\frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \cdot 2^6 \cdot 3^6 \\
& =2^8 \cdot 231 \cdot 3^6 \\
& =2^8(I)
\end{aligned}
\)
When \(k =6\) then \(r =8\) and constant term
\(
\begin{aligned}
& ={ }^{12} C_8 \cdot 2^8 \cdot 3^4 \\
& =\frac{12 \cdot 11 \cdot 10 \cdot 9}{4 \cdot 3 \cdot 2 \cdot 1} \cdot 2^8 \cdot 3^4 \\
& =2^8 \cdot 55 \cdot 3^6 \\
& =2^8(I)
\end{aligned}
\)
When \(x=9\) then \(r=9\) and constant term
\(
\begin{aligned}
& ={ }^{12} C_9 \cdot 2^9 \cdot 3^3 \\
& =\frac{12 \cdot 11 \cdot 10}{3 \cdot 2 \cdot 1} \cdot 2^9 \cdot 3^3 \\
& =2^{11} \cdot 55 \cdot 3^3
\end{aligned}
\)
Here power of 2 is 11 which is greater than 8 . So, \(k=9\) is not possible.
Similarly for \(k =15\) and \(k =33,2^8 . I\) form is not possible.
\(\therefore k =3\) and \(k =6\) is accepted.
\(\therefore\) For 2 positive integer value of \(k , 2^8\). \(I\) form of constant term possible. -
Question 116 of 226
116. Question
If the sum of the coefficients of all the positive powers of \(x\), in the Binomial expansion of \(\left(x^n+\frac{2}{x^5}\right)^7\) is 939 , then the sum of all the possible integral values of \(n\) is _____. [JEE Main 2022 (Online) 27th June Evening Shift]
CorrectIncorrectHint
Given, Binomial expression is
\(
\begin{aligned}
& =\left(x^n+\frac{2}{x^5}\right)^7 \\
& \therefore \text { General term } \\
& T_{r+1}={ }^7 C_r \cdot\left(x^n\right)^{7-r} \cdot\left(\frac{2}{x^5}\right)^r \\
& ={ }^7 C_r \cdot x^{7 n-n r-5 r} \cdot 2^r
\end{aligned}
\)
For positive power of \(x\),
\(
\begin{aligned}
& 7 n-n r-5 r>0 \\
& \Rightarrow 7 n>r(n+5) \\
& \Rightarrow r<\frac{7 n}{n+5}
\end{aligned}
\)
As \(r\) represent term of binomial expression so \(r\) is always integer.
Given that sum of coefficient is 939 .
When \(r=0\),
sum of coefficient \(={ }^7 C_0 \cdot 2^0=1\)
when \(r=1\),
sum of coefficient \(={ }^7 C_0 \cdot 2^0+{ }^7 C_1 \cdot 2^1=1+14=15\)
when \(r=2\),
sum of coefficient
\(={ }^7 C_0 \cdot 2^0+{ }^7 C_1 \cdot 2^1+{ }^7 C_2 \cdot 2^2\)
\(=1+14+84\)
\(=99\)
when \(r=3\),
sum of coefficient
\(={ }^7 C_0 \cdot 2^0+{ }^7 C_1 \cdot 2^1+{ }^7 C_2 \cdot 2^2+{ }^7 C_3 \cdot 2^3\)
\(=1+14+84+280\)
\(=379\)
when \(r=4\),
sum of coefficient
\(
\begin{aligned}
& ={ }^7 C_0 \cdot 2^0+{ }^7 C_1 \cdot 2^1+{ }^7 C_2 \cdot 2^2+{ }^7 C_3 \cdot 2^3+{ }^7 C_4 \cdot 2^4 \\
& =1+14+84+280+560 \\
& =939
\end{aligned}
\)
\(\therefore\) For \(r=4\) sum of coefficient \(=939\)
To get value of \(r=4\), value of \(\frac{7 n}{n+5}\) should be between 4 and 5 .
\(
\begin{aligned}
& \therefore 4<\frac{7 n}{n+5}<5 \\
& \Rightarrow 4 n+20<7 n<5 n+25 \\
& \therefore 4 n+20<7 n \\
& \Rightarrow 3 n>20 \\
& \Rightarrow n>\frac{20}{3} \\
& \Rightarrow n>6.66
\end{aligned}
\)
and
\(
\begin{aligned}
& 7 n<5 n+25 \\
& \Rightarrow 2 n<25 \\
& \Rightarrow n<12.5 \\
& \therefore 6.66<n<12.5
\end{aligned}
\)
\(\therefore\) Possible integer values of \(n=7,8,9,10,11,12\)
\(\therefore\) Sum of values of \(n=7+8+9+10+11+12=57\) -
Question 117 of 226
117. Question
If the coefficient of \(x^{10}\) in the binomial expansion of \(\left(\frac{\sqrt{x}}{5^{\frac{1}{4}}}+\frac{\sqrt{5}}{x^{\frac{1}{3}}}\right)^{60}\) is \(5^k . l\), where \(l , k \in N\) and \(l\) is co-prime to 5 , then \(k\) is equal to _____ [JEE Main 2022 (Online) 27th June Morning Shift]
CorrectIncorrectHint
Given Binomial Expansion
\(
=\left(\frac{\sqrt{x}}{5^{\frac{1}{4}}}+\frac{\sqrt{x}}{5^{\frac{1}{3}}}\right)^{60}
\)
\(\therefore\) General term
\(
\begin{aligned}
& T_{r+1}={ }^{60} C_r \cdot\left(\frac{x^{1 / 2}}{5^{1 / 4}}\right)^{60-r} \cdot\left(\frac{5^{1 / 2}}{x^{1 / 3}}\right)^r \\
& ={ }^{60} C_r \cdot 5^{\left(\frac{r}{4}-15+\frac{r}{2}\right)} \cdot x^{\left(30-\frac{r}{2}-\frac{r}{3}\right)} \\
& ={ }^{60} C_r \cdot 5^{\left(\frac{3 r-60}{4}\right)} \cdot x^{\left(\frac{180-5 r}{6}\right)}
\end{aligned}
\)
For \(x ^{10}\) term,
\(
\begin{aligned}
& \frac{180-5 r}{6}=10 \\
& \Rightarrow 5 r=120 \\
& \Rightarrow r=24
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \text { Coefficient of } x^{10}={ }^{60} C_{24} \cdot 5\left(\frac{3 \times 24-60}{4}\right) \\
& ={ }^{60} C_{24} \cdot 5^3 \\
& =\frac{60!}{24!36!} \cdot 5^3
\end{aligned}
\)
It is given that,
\(
\frac{60!}{24!36!} \cdot 5^3=5^k \cdot l \dots(1)
\)
Also given that, I is coprime to 5 means I can’t be multiple of 5 . So we have to find all the factors of 5 in 60 !, 24 ! and 36 !
[Note : Formula for exponent or degree of prime number in n!.
Exponent of \(p\) in \(n!=\left\lceil\frac{n}{p}\right\rceil+\left\lceil\frac{n}{p^2}\right\rceil+\left\lceil\frac{n}{p^3}\right\rceil+\ldots .\). until 0 comes here \(p\) is a prime number. ]
\(\therefore\) Exponent of 5 in 60 !
\(
\begin{aligned}
& =\left\lceil\frac{60}{5}\right\rceil+\left\lceil\frac{60}{5^2}\right\rceil+\left\lceil\frac{60}{5^3}\right\rceil+\ldots . . \\
& =12+2+0+\ldots . . \\
& =14
\end{aligned}
\)
Exponent of 5 in 24 !
\(
\begin{aligned}
& =\left\lceil\frac{24}{5}\right\rceil+\left\lceil\frac{24}{5^2}\right\rceil+\left\lceil\frac{24}{5^3}\right\rceil+\ldots \ldots \\
& =4+0+0 \ldots \ldots \\
& =4
\end{aligned}
\)
Exponent of 5 in 36 !
\(
\begin{aligned}
& =\left\lceil\frac{36}{5}\right\rceil+\left\lceil\frac{36}{5^2}\right\rceil+\left\lceil\frac{36}{5^3}\right\rceil+\ldots \ldots . . \\
& =7+1+0 \ldots \ldots \\
& =8
\end{aligned}
\)
\(\therefore\) From equation (1), exponent of 5 overall
\(
\begin{aligned}
& \frac{5^{14}}{5^4 \cdot 5^8} \cdot 5^3=5^k \\
& \Rightarrow 5^5=5^k \\
& \Rightarrow k=5
\end{aligned}
\) -
Question 118 of 226
118. Question
If \(\left({ }^{40} C_0\right)+\left({ }^{41} C_1\right)+\left({ }^{42} C_2\right)+\ldots \ldots+\left({ }^{60} C_{20}\right)=\frac{m}{n}{ }^{60} C_{20} m\) and \(n\) are coprime, then \(m+n\) is equal to _____. [JEE Main 2022 (Online) 26th June Evening Shift]
CorrectIncorrectHint
Here property used is
\(
{ }^n C_r+{ }^n C_{r+1}={ }^{n+1} C_{r+1}
\)
Given, \({ }^{40} C_0+{ }^{41} C_1+{ }^{42} C_2+\ldots+{ }^{60} C_{20}=\frac{m}{n}{ }^{60} C_{20}\)
As \({ }^{40} C_0={ }^{41} C_0=1\)
So, we replace \({ }^{40} C_0\) with \({ }^{41} C_0\).
\(
\begin{aligned}
& \Rightarrow{ }^{41} C_0+{ }^{41} C_1+{ }^{42} C_2+\ldots \ldots+{ }^{60} C_{20}=\frac{m}{n} \cdot{ }^{60} C_{20} \\
& \Rightarrow{ }^{42} C_1+{ }^{42} C_2+\ldots \ldots+{ }^{60} C_{20}=\frac{m}{n} \cdot{ }^{60} C_{20} \\
& \Rightarrow{ }^{43} C_2+{ }^{43} C_3+\ldots \ldots+{ }^{60} C_{20}=\frac{m}{n} \cdot{ }^{60} C_{20} \\
& \Rightarrow{ }^{44} C_3+{ }^{44} C_4+\ldots \ldots+{ }^{60} C_{20}=\frac{m}{n} \cdot{ }^{60} C_{20} \\
& \Rightarrow{ }^{45} C_4+{ }^{45} C_5+\ldots \ldots+{ }^{60} C_{20}=\frac{m}{n} \cdot{ }^{60} C_{20}
\end{aligned}
\)
\(\vdots\)
\(
\begin{aligned}
& \Rightarrow{ }^{60} C_{19}+{ }^{60} C_{20}=\frac{m}{n} \cdot{ }^{60} C_{20} \\
& \Rightarrow{ }^{61} C_{20}=\frac{m}{n} \cdot{ }^{60} C_{20} \\
& \Rightarrow \frac{61!}{20!41!}=\frac{m}{n} \cdot \frac{60!}{20!40!} \\
& \Rightarrow \frac{61}{41}=\frac{m}{n} \\
& \therefore m=61 \text { and } n=41 \\
& \therefore m+n=61+41=102
\end{aligned}
\) -
Question 119 of 226
119. Question
If the sum of the co-efficient of all the positive even powers of \(x\) in the binomial expansion of \(\left(2 x^3+\frac{3}{x}\right)^{10}\) is \(5^{10}-\beta \cdot 3^9\), then \(\beta\) is equal to _____. [JEE Main 2022 (Online) 25th June Evening Shift]
CorrectIncorrectHint
Given, Binomial Expansion
\(
\left(2 x^3+\frac{3}{x}\right)^{10}
\)
General term
\(
\begin{aligned}
& T_{r+1}={ }^{10} C_r \cdot\left(2 x^3\right)^{10-r} \cdot\left(\frac{3}{x}\right)^r \\
& ={ }^{10} C_r \cdot 2^{10-r} \cdot 3^r \cdot x^{30-3 r} \cdot x^{-r} \\
& ={ }^{10} C_r \cdot 2^{10-r} \cdot 3^r \cdot x^{30-4 r}
\end{aligned}
\)
For positive even power of \(x, 30-4 r\) should be even and positive.
For \(r =0,30-4 \times 0=30\) (even and positive)
For \(r =1,30-4 \times 1=26\) (even and positive)
For \(r=2,30-4 \times 2=22\) (even and positive)
For \(r=3,30-4 \times 3=18\) (even and positive)
For \(r=4,30-4 \times 4=14\) (even and positive)
For \(r=5,30-4 \times 5=10\) (even and positive)
For \(r=6,30-4 \times 6=6\) (even and positive)
For \(r =7,30-4 \times 7=2\) (even and positive)
For \(r =8,30-4 \times 8=-2\) (even but not positive)
So, for \(r=1,2,3,4,5,6\) and 7 we can get positive even power of \(x\).
\(\therefore\) Sum of coefficient for positive even power of \(x\)
\(
\begin{aligned}
& ={ }^{10} C_0 \cdot 2^{10} \cdot 3^0+{ }^{10} C_1 \cdot 2^9 \cdot 3^1+{ }^{10} C_2 \cdot 2^8 \cdot 3^2+{ }^{10} C_3 \cdot 2^7 \cdot 3^3+{ }^{10} C_4 \cdot 2^6 \\
& ={ }^{10} C_{10} \cdot 2^{10} \cdot 3^0+{ }^{10} C_1 \cdot 2^9 \cdot 3^1+\ldots \ldots+{ }^{10} C_{10} \cdot 2^0 \cdot 3^{10}-\left[{ }^{10} C_8 \cdot 2^2 \cdot 3\right. \\
& =(2+3)^{10}-\left[45 \cdot 4 \cdot 3^8+10 \cdot 2 \cdot 3^9+1 \cdot 1 \cdot 3^{10}\right]
\end{aligned}
\)
\(
\begin{aligned}
& =5^{10}-\left[60 \times 3^9+20 \cdot 3^9+3 \cdot 3^9\right] \\
& =5^{10}-(60+20+3) 3^9 \\
& =5^{10}-83 \cdot 3^9 \\
& \therefore \beta=83
\end{aligned}
\) -
Question 120 of 226
120. Question
Let \(C _{ r }\) denote the binomial coefficient of \(x ^{ r }\) in the expansion of \((1+x)^{10}\). If for \(\alpha, \beta\) \(\in R , C_1+3.2 C_2+5.3 C_3+\ldots . . .\). upto 10 terms \(=\frac{\alpha \times 2^{11}}{2^\beta-1}\left(C_0+\frac{C_1}{2}+\frac{C_2}{3}+\ldots \ldots \text { upto } 10 \text { terms }\right)\) then the value of \(\alpha+\beta\) is equal to ____. [JEE Main 2022 (Online) 25th June Morning Shift]
CorrectIncorrectHint
Given,
\(C_1+3.2 C_2+5.3 C_3+\ldots . .\). upto 10 terms
\(
=\frac{\alpha \cdot 2^{11}}{2^\beta-1}\left(C_0+\frac{C_1}{2}+\frac{C_2}{3}+\ldots . . \text { upto } 10 \text { terms }\right)
\)
Now, L.H.S. :
\(
\begin{aligned}
& C_1+3 \cdot 2 C_2+5 \cdot 3 C_3+\ldots . . \text { upto } 10 \text { terms } \\
& =1 \cdot 1 C_1+3 \cdot 2 C_2+5 \cdot 3 C_3+\ldots . . \text { upto } 10 \text { terms } \\
& =\sum_{r=1}^{10} r \cdot(2 r-1)^{10} C_r \\
& =\sum_{r=1}^{10}\left(2 r^2-r\right) \cdot{ }^{10} C_r \\
& =2 \cdot \sum_{r=1}^{10} r^2 \cdot{ }^{10} C_r-\sum_{r=1}^{10} r \cdot{ }^n C_r
\end{aligned}
\)
[We know, \(\sum_{r=1}^n r \cdot{ }^n C_r=n \cdot 2^{n-1}\)
\(
\begin{aligned}
& \text { and } \sum_{r=1}^n r^2 \cdot{ }^n C_r=\sum_{r=1}^n\left(r \cdot{ }^n C_r\right) \cdot r \\
& =\sum_{r=1}^n\left(r \cdot \frac{n}{r} \cdot{ }^{n-1} C_{r-1}\right) \cdot r \\
& =\sum_{r=1}^n\left(n \cdot{ }^{n-1} C_{r-1}\right) \cdot r \\
& =n \sum_{r=1}^n(r-1+1)^{n-1} C_{r-1} \\
& =n \cdot \sum_{r=1}^n(r-1) \cdot{ }^{n-1} C_{r-1}+n \cdot \sum_{r=1}^n{ }^{n-1} C_{r-1} \\
& \left.=n \cdot(n-1) \cdot 2^{n-2}+n \cdot 2^{n-1}\right] \\
& =2\left(n(n-1) 2^{n-2}+n \cdot 2^{n-1}\right)-n \cdot 2^{n-1}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Put } n=10 \\
& =2\left(10 \cdot 9 \cdot 2^8+10 \cdot 2^9\right)-10 \cdot 2^9 \\
& =45 \cdot 2^{10}+10 \cdot 2^{10}-5 \cdot 2^{10} \\
& =2^{10}(45+10-5) \\
& =2^{10} \cdot(50) \\
& =25 \cdot 2^{11}
\end{aligned}
\)
R.H.S. :-
\(\frac{\alpha \cdot 2^{11}}{2^\beta-1}\left(C_0+\frac{C_1}{2}+\frac{C_2}{3}+\ldots .\right.\). upto 10 terms \()\)
\(\frac{\alpha \cdot 2^{11}}{2^\beta-1}\left(\frac{C_0}{1}+\frac{C_1}{2}+\frac{C_2}{3}+\ldots .\right.\). upto 10 terms \()\)
\(
\begin{aligned}
& \frac{\alpha \cdot 2^{11}}{2^\beta-1}\left(\sum_{r=0}^n \frac{{ }^n C_r}{r+1}\right) \\
& =\frac{\alpha \cdot 2^{11}}{2^\beta-1}\left(\sum_{r=0}^n \frac{{ }^{n+1} C_{r+1}}{n+1}\right) \\
& =\frac{\alpha \cdot 2^{11}}{2^\beta-1}\left(\frac{{ }^{n+1} C_1+{ }^{n+1} C_2+\ldots .+{ }^{n+1} C_{n+1}}{n+1}\right) \\
& =\frac{\alpha \cdot 2^{11}}{2^\beta-1}\left(\frac{{ }^{n+1} C_0+{ }^{n+1} C_2+\ldots .+{ }^{n+1} C_{n+1}-{ }^{n+1} C_0}{n+1}\right) \\
& =\frac{\alpha \cdot 2^{11}}{2^\beta-1}\left(\frac{2^{n+1}-1}{n+1}\right)
\end{aligned}
\)
Putting value of \(n=10\), we get
\(
=\frac{\alpha \cdot 2^{11}}{2^\beta-1}\left(\frac{2^{11}-1}{11}\right)
\)
Using L.H.S. = R.H.S.
\(
\begin{aligned}
& \Rightarrow 25 \cdot 2^{11}=\frac{\alpha \cdot 2^{11}}{2^\beta-1}\left(\frac{2^{11}-1}{11}\right) \\
& \Rightarrow 25 \cdot 2^{11}=2^{11}\left(\frac{\alpha}{11}\right)\left(\frac{2^{11}-1}{2^\beta-1}\right)
\end{aligned}
\)
By comparing both sides,
\(
\begin{aligned}
& \frac{\alpha}{11}=25 \Rightarrow \alpha=275 \\
& \text { and } \frac{2^{11}-1}{2^\beta-1}=1 \\
& \Rightarrow 2^{11}=2^\beta \\
& \Rightarrow \beta=11 \\
& \therefore \alpha+\beta=275+11=286
\end{aligned}
\) -
Question 121 of 226
121. Question
The remainder on dividing \(1+3+3^2+3^3+\ldots . .+3^{2021}\) by 50 is ____. [JEE Main 2022 (Online) 24th June Evening Shift]
CorrectIncorrectHint
Given,
\(
\begin{aligned}
& 1+3+3^2+3^3+\ldots \ldots+3^{2021} \\
& =3^0+3^1+3^2+3^3+\ldots+3^{2021}
\end{aligned}
\)
This is a G.P with common ratio \(=3\)
\(
\begin{aligned}
& \therefore \text { Sum }=\frac{1\left(3^{2022}-1\right)}{3-1} \\
& =\frac{3^{2022}-1}{2} \\
& =\frac{\left(3^2\right)^{2011}-1}{2} \\
& =\frac{(10-1)^{1011}-1}{2}
\end{aligned}
\)
\(
=\frac{\left[{ }^{1011} C_0 \cdot 10^{1011} \_{ }^{1011} C_1 \cdot 10^{1010}+\ldots . . \cdot-{ }^{1011} C_{1009} \cdot(10)^2+{ }^{1011} C_{1010} \cdot 10-{ }^{1011} C_{1011}\right]-1}{2}
\)
\(
\begin{aligned}
& =\frac{10^2\left[{ }^{1011} C_0 \cdot(10)^{1009} \_{ }^{1011} C_1 \cdot(1008)+\ldots . .{ }^{1011} C_{1000}\right]+10110-1-1}{2} \\
& =\frac{100 k+10110-2}{2} \\
& =\frac{100 k+10108}{2} \\
& =50 k+5054 \\
& =50 k+50 \times 101+4 \\
& =50[k+101]+4 \\
& =50 k^{\prime}+4
\end{aligned}
\)
\(\therefore\) By dividing 50 we get remainder as 4 . -
Question 122 of 226
122. Question
If the sum of the coefficients in the expansion of \((x+y)^n\) is 4096 , then the greatest coefficient in the expansion is _____. [JEE Main 2021 (Online) 1st September Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& (x+y)^n \Rightarrow 2^n=4096 \\
& 2^{10}=1024 \times 2 \\
& \Rightarrow 2^n=2^{12} \\
& 2^{11}=2048 \\
& n=12 \\
& 2^{12}=4096 \\
& { }^{12} C_6=\frac{12 \times 11 \times 10 \times 9 \times 8 \times 7}{6 \times 5 \times 4 \times 3 \times 2 \times 1} \\
& =11 \times 3 \times 4 \times 7 \\
& =924
\end{aligned}
\) -
Question 123 of 226
123. Question
If the coefficient of \(a^7 b^8\) in the expansion of \((a+2 b+4 a b)^{10}\) is \(K .2^{16}\), then \(K\) is equal to _____. [JEE Main 2021 (Online) 31st August Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{10!}{\alpha!\beta!\gamma!} a^\alpha(2 b)^\beta \cdot(4 a b)^\gamma \\
& \frac{10!}{\alpha!\beta!\gamma!} a^{\alpha+\gamma} \cdot b^{\beta+\gamma} \cdot 2^\beta \cdot 4^\gamma
\end{aligned}
\)
\(
\begin{aligned}
&\alpha+\beta+\gamma=10 \ldots (1)\\
&\alpha+\gamma=7 \ldots (2) \\
&\beta+\gamma=8 \ldots (3)
\end{aligned}
\)
\(
(2)+(3)-(1) \Rightarrow \gamma=5
\)
\(
\begin{aligned}
& \alpha=2 \\
& \beta=3 \\
& \text { so coefficients }=\frac{10!}{2!3!5!} 2^3 .2^{10} \\
& =\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5}{2 \times 3 \times 2 \times 5!} \times 2^{13} \\
& =315 \times 2^{16} \Rightarrow k=315
\end{aligned}
\) -
Question 124 of 226
124. Question
If \(\left(\frac{3^6}{4^4}\right) k\) is the term, independent of \(x\), in the binomial expansion of \(\left(\frac{x}{4}-\frac{12}{x^2}\right)^{12}\), then \(k\) is equal to _____. [JEE Main 2021 (Online) 31st August Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(\frac{x}{4}-\frac{12}{x^2}\right)^{12} \\
& T_{r+1}=(-1)^r \cdot{ }^{12} C_r\left(\frac{x}{4}\right)^{12-r}\left(\frac{12}{x^2}\right)^r \\
& T_{r+1}=(-1)^r \cdot{ }^{12} C_r\left(\frac{1}{4}\right)^{12-r}(12)^r \cdot(x)^{12-3 r}
\end{aligned}
\)
Term independent of \(x \Rightarrow 12-3 r=0 \Rightarrow r=4\)
\(
\begin{aligned}
& T_5=(-1)^r \cdot{ }^{12} C_r\left(\frac{1}{4}\right)^8(12)^4=\frac{3^6}{4^4} \cdot k \\
& \Rightarrow k =55
\end{aligned}
\) -
Question 125 of 226
125. Question
\(3 \times 7^{22}+2 \times 10^{22}-44\) when divided by 18 leaves the remainder ____. [JEE Main 2021 (Online) 27th August Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 3(1+6)^{22}+2 \cdot(1+9)^{22}-44=(3+2-44)+18 \cdot 1 \\
& =-39+18 \cdot 1 \\
& =(54-39)+18(1-3) \\
& =15+18 c_1 \\
& \Rightarrow \text { Remainder }=15
\end{aligned}
\) -
Question 126 of 226
126. Question
Let \(\binom{n}{k}\) denotes \({ }^n C_k\) and \(\left[\begin{array}{l}n \\ k\end{array}\right]=\) \(
\left\{\begin{array}{c}
\binom{n}{k}, \quad \text { if } 0 \leq k \leq n \\
0, \quad \text { otherwise }
\end{array}\right.
\)
If \(A_k=\sum_{i=0}^9\binom{9}{i}\left[\begin{array}{c}12 \\ 12-k+i\end{array}\right]+\sum_{i=0}^8\binom{8}{i}\left[\begin{array}{c}13 \\ 13-k+i\end{array}\right]\) and \(A _4- A _3=190 p\), then \(p\) is equal to :CorrectIncorrectHint
\(
\begin{aligned}
& A_k=\sum_{i=0}^9{ }^9 C_i{ }^{12} C_{k-i}+\sum_{i=0}^8{ }^8 C_i{ }^{13} C_{k-i} \\
& A_k={ }^{21} C_k+{ }^{21} C_k=2 \cdot{ }^{21} C_k \\
& A_4-A_3=2\left({ }^{21} C_4-{ }^{21} C_3\right)=2(5985-1330) \\
& 190 p=2(5985-1330) \Rightarrow p=49
\end{aligned}
\) -
Question 127 of 226
127. Question
Let \(n \in N\) and \([x]\) denote the greatest integer less than or equal to \(x\). If the sum of \((n+\) 1) terms \({ }^n C_0, 3 \cdot{ }^n C_1, 5 \cdot{ }^n C_2, 7 \cdot{ }^n C_3, \ldots\). is equal to \(2^{100} \cdot 101\), then \(2\left[\frac{n-1}{2}\right]\) is equal to ____. [JEE Main 2021 (Online) 25th July Evening Shift]
CorrectIncorrectHint
\(
\text { 1. }{ }^n C_0+3 \cdot{ }^n C_1+5 \cdot{ }^n C_2+\ldots+(2 n+1) \cdot{ }^n C_n
\)
\(
\begin{aligned}
& T_r=(2 r+1)^n C_r \\
& S=\sum T_r \\
& S=\sum(2 r+1)^n C_r=\sum 2 r^n C_r+\sum{ }^n C_r \\
& S=2\left(n .2^{n-1}\right)+2^n=2^n(n+1) \\
& 2^n(n+1)=2^{100} .101 \Rightarrow n=100 \\
& 2\left[\frac{n-1}{2}\right]=2\left[\frac{99}{2}\right]=98
\end{aligned}
\) -
Question 128 of 226
128. Question
If the co-efficient of \(x^7\) and \(x^8\) in the expansion of \(\left(2+\frac{x}{3}\right)^n\) are equal, then the value of \(n\) is equal to _____. [JEE Main 2021 (Online) 25th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& { }^n C_7 2^{n-7} \frac{1}{3^7}={ }^n C_8 2^{n-8} \frac{1}{3^8} \\
& \Rightarrow n -7=48 \Rightarrow n =55
\end{aligned}
\) -
Question 129 of 226
129. Question
The ratio of the coefficient of the middle term in the expansion of \((1+x)^{20}\) and the sum of the coefficients of two middle terms in expansion of \((1+x)^{19}\) is _____. [JEE Main 2021 (Online) 25th July Morning Shift]
CorrectIncorrectHint
Coeff. of middle term in \((1+ x )^{20}={ }^{20} C_{10}\) & Sum of coeff. of two middle terms in \((1+\) \(x )^{19}={ }^{19} C_9+{ }^{19} C_{10}\)
\(
\text { So required ratio }=\frac{{ }^{20} C_{10}}{{ }^{19} C_9+{ }^{19} C_{10}}=\frac{{ }^{20} C_{10}}{{ }^{20} C_{10}}=1
\) -
Question 130 of 226
130. Question
The term independent of ‘ \(x\) ‘ in the expansion of \(\left(\frac{x+1}{x^{2 / 3}-x^{1 / 3}+1}-\frac{x-1}{x-x^{1 / 2}}\right)^{10}\), where \(x \neq 0,1\) is equal to ____. [JEE Main 2021 (Online) 25th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(\frac{x+1}{x^{2 / 3}-x^{1 / 3}+1}-\frac{x-1}{x-x^{1 / 2}}\right)^{10} \\
& =\left(\frac{\left(x^{1 / 3}\right)^3+\left(1^{1 / 3}\right)^3}{x^{2 / 3}-x^{1 / 3}+1}-\frac{(\sqrt{x})^2-(1)^2}{x-x^{1 / 2}}\right)^{10} \\
& =\left(\frac{\left(x^{1 / 3}+1\right)\left(x^{2 / 3}-x^{1 / 3}+1\right)}{x^{2 / 3}-x^{1 / 3}+1}-\frac{(\sqrt{x}+1)(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-1)}\right)^{10} \\
& =\left(\left(x^{1 / 3}+1\right)-\frac{(\sqrt{x}+1)}{\sqrt{x}}\right)^{10} \\
& =\left(\left(x^{1 / 3}+1\right)-\left(1+\frac{1}{\sqrt{x}}\right)\right)^{10} \\
& =\left(x^{1 / 3}-\frac{1}{x^{1 / 2}}\right)^{10}
\end{aligned}
\)
[Note:For \(\left(x^\alpha \pm \frac{1}{x^\beta}\right)^n\) the \((r+1)^{\text {th }}\) term with power \(m\) of \(x\) is
\(
\left.r=\frac{n \alpha-m}{\alpha+\beta}\right]
\)
Here \(\alpha=\frac{1}{3}, \beta=\frac{1}{2}\) and \(m =0\) then \(r=\frac{10 \times \frac{1}{3}-0}{\frac{1}{3}+\frac{1}{2}}=\frac{10}{3} \times \frac{6}{5}=4\)
\(\therefore T_5\) is the term independent of \(x\).
\(
\therefore T _5={ }^{10} C_4=210
\) -
Question 131 of 226
131. Question
If the constant term, in binomial expansion of \(\left(2 x^r+\frac{1}{x^2}\right)^{10}\) is 180 , then \(r\) is equal to ____. [JEE Main 2021 (Online) 22th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(2 x^r+\frac{1}{x^2}\right)^{10} \\
& \text { General term }={ }^{10} C_R\left(2 x^2\right)^{10-R} x^{-2 R} \\
& \Rightarrow 2^{10-R 10} C_R=180 \ldots \ldots .(1)
\end{aligned}
\)
\(
\begin{aligned}
& \&(10- R ) r -2 R =0 \\
& r=\frac{2 R}{10-R} \\
& r=\frac{2(R-10)}{10-R}+\frac{20}{10-R} \\
& \Rightarrow r=-2+\frac{20}{10-R} \dots(2)
\end{aligned}
\)
\(R=8\) or 5 reject equation (1) not satisfied
At \(R=8\)
\(
\Rightarrow 2^{10-R} \times{ }^{10} C_R=180 \Rightarrow r=8
\) -
Question 132 of 226
132. Question
The number of elements in the set \(\left\{n \in\{1,2,3, \ldots \ldots ., 100\} \mid(11)^n>(10)^n+(9)^n\right\}\) is ____. [JEE Main 2021 (Online) 22th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 11^n>10^n+9^n \\
& \Rightarrow 11^n-9^n>10^n \\
& \Rightarrow(10+1)^n-(10-1)^n>10^n
\end{aligned}
\)
\(
\Rightarrow 2\left\{{ }^n C_1 \cdot 10^{n-1}+{ }^n C_3 10^{n-10}+{ }^n C_5 10^{n-5}+\ldots \ldots\right\}>10^n
\)
\(
\Rightarrow \frac{1}{5}\left[{ }^n C_1 10^n+{ }^n C_3 10^{n-2}+{ }^n C_5 10^{n-4}+\ldots . .\right]>10^n
\)
\(
\Rightarrow \frac{1}{5}\left[{ }^n C_1+{ }^n C_3 10^{-2}+{ }^n C_5 10^{-4}+\ldots . .\right]>1
\)
Clearly the above inequality is true for \(n \geq 5\)
For \(n=4\), we have \(\frac{1}{5}\left[4+\frac{4}{10^2}\right]=\frac{4}{5}\left(\frac{101}{100}\right)<1\)
\(\Rightarrow\) Inequality does not hold good for \(n=1,2,3,4\)
So, required number of elements \(=\{5,6,7\), \(\ldots\) \(100\}=96\) -
Question 133 of 226
133. Question
The number of rational terms in the binomial expansion of \(\left(4^{\frac{1}{4}}+5^{\frac{1}{6}}\right)^{120}\) is ____. [JEE Main 2021 (Online) 20th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(4^{\frac{1}{4}}+5^{\frac{1}{6}}\right)^{120} \\
& T_{r+1}={ }^{120} C_r\left(2^{1 / 2}\right)^{120-r}(5)^{r / 6}
\end{aligned}
\)
for rational terms \(r=6 \lambda\)
\(
0 \leq r \leq 120
\)
So total no of terms are 21. -
Question 134 of 226
134. Question
The term independent of \(x\) in the expansion of \(\left[\frac{x+1}{x^{2 / 3}-x^{1 / 3}+1}-\frac{x-1}{x-x^{1 / 2}}\right]^{10}, x \neq 1\), is equal to ____. [JEE Main 2021 (Online) 18th March Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(\frac{x+1}{x^{2 / 3}-x^{1 / 3}+1}-\frac{x-1}{x-x^{1 / 2}}\right)^{10} \\
& =\left(\frac{\left(x^{1 / 3}\right)^3+\left(1^{1 / 3}\right)^3}{x^{2 / 3}-x^{1 / 3}+1}-\frac{(\sqrt{x})^2-(1)^2}{x-x^{1 / 2}}\right)^{10} \\
& =\left(\frac{\left(x^{1 / 3}+1\right)\left(x^{2 / 3}-x^{1 / 3}+1\right)}{x^{2 / 3}-x^{1 / 3}+1}-\frac{(\sqrt{x}+1)(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-1)}\right)^{10} \\
& =\left(\left(x^{1 / 3}+1\right)-\frac{(\sqrt{x}+1)}{\sqrt{x}}\right)^{10} \\
& =\left(\left(x^{1 / 3}+1\right)-\left(1+\frac{1}{\sqrt{x}}\right)\right)^{10} \\
& =\left(x^{1 / 3}-\frac{1}{x^{1 / 2}}\right)^{10}\left(x^{-\frac{1}{2}}\right)^r
\end{aligned}
\)
For being independent of \(x: \frac{10-r}{3}-\frac{r}{2}=0 \Rightarrow r=4\)
Term independent of \(x={ }^{10} C_4=210\) -
Question 135 of 226
135. Question
Let \({ }^n C_r\) denote the binomial coefficient of \(x ^{\Gamma}\) in the expansion of \((1+ x )^n\). If \(\sum_{k=0}^{10}\left(2^2+3 k\right)^{10} C_k=\alpha \cdot 3^{10}+\beta \cdot 2^{10}, \alpha, \beta \in R\), then \(\alpha+\beta\) is equal to ____. [JEE Main 2021 (Online) 18th March Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{k=0}^{10}\left(2^2+3 k\right)^{10} C_k \\
& =4 \sum_{k=0}^{10}{ }^{10} C_k+3 \sum_{k=0}^{10} k \cdot{ }^{10} C_k \\
& =4\left(2^{10}\right)+3 \sum_{k=0}^{10} k \cdot \frac{10}{k} \cdot{ }^9 C_{k-1} \\
& =4\left(2^{10}\right)+3 \cdot 10\left(2^9\right) \\
& =4\left(2^{10}\right)+3.5 \cdot 2^{10} \\
& =2^{10}(19)
\end{aligned}
\)
According to question,
\(
\begin{aligned}
& 19\left(2^{10}\right)=\alpha .3^{10}+\beta \cdot 2^{10} \\
& \therefore \alpha=0, \beta=19 \\
& \Rightarrow \alpha+\beta=19
\end{aligned}
\) -
Question 136 of 226
136. Question
Let the coefficients of third, fourth and fifth terms in the expansion of \(\left(x+\frac{a}{x^2}\right)^n, x \neq 0\), be in the ratio \(12: 8: 3\). Then the term independent of \(x\) in the expansion, is equal to _____. [JEE Main 2021 (Online) 17th March Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T_{r+1}=n_{C_r} x^{n-r} \cdot\left(\frac{a}{x^2}\right)^r \\
& ={ }^n C_r a^r x^{n-3 r} \\
& T_3={ }^n C_2 a^2 x^{n-6}, T_4={ }^n C_3 a^3 x^{n-9}, T_5={ }^n C_4 a^4 x^{n-12}
\end{aligned}
\)
\(
\Rightarrow a(n-2)=2 \dots(i)
\)
and \(\frac{\text { coefficient of } T_4}{\text { coefficient of } T_5}=\frac{{ }^n C_3 \cdot a^3}{{ }^n C_4 \cdot a^4}=\frac{4}{a(n-3)}=\frac{8}{3}\)
\(
\Rightarrow a(n-3)=\frac{3}{2} \dots(ii)
\)
by (i) and (ii) \(n=6, a=\frac{1}{2}\)
for term independent of ‘ \(x\) ‘
\(
\begin{aligned}
& n-3 r=0 \Rightarrow r=\frac{n}{3} \Rightarrow r=\frac{6}{3}=2 \\
& T_3={ }^6 C_2\left(\frac{1}{2}\right)^2 x^0=\frac{15}{4}=3.75 \approx 4
\end{aligned}
\) -
Question 137 of 226
137. Question
If \((2021)^{3762}\) is divided by 17 , then the remainder is ______. [JEE Main 2021 (Online) 17th March Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 2021=17 m-2 \\
& (2021)^{3762}=(17 m-2)^{3762}=\text { multiple of } 17+2^{3762} \\
& =17 \lambda+2^2\left(2^4\right)^{940} \\
& =17 \lambda+4(17-1)^{940} \\
& =17 \lambda+4(17 \mu+1) \\
& =17 k+4 ;(k \in I) \\
& \therefore \text { Remainder }=4
\end{aligned}
\) -
Question 138 of 226
138. Question
Let \(n\) be a positive integer. Let
\(
A=\sum_{k=0}^n(-1)^{k n} C_k\left[\left(\frac{1}{2}\right)^k+\left(\frac{3}{4}\right)^k+\left(\frac{7}{8}\right)^k+\left(\frac{15}{16}\right)^k+\left(\frac{31}{32}\right)^k\right] \text {. If }
\)
\(63 A=1-\frac{1}{2^{30}}\), then \(n\) is equal to [JEE Main 2021 (Online) 16th March Evening Shift]CorrectIncorrectHint
\(
A=\sum(-1)^{k_n} C_k\left(\frac{1}{2}\right)^k+\sum(-1)^{k_n} C_k\left(\frac{3}{4}\right)^k+\ldots \ldots
\)
\(
\begin{aligned}
& =\left(1-\frac{1}{2}\right)^n+\left(1-\frac{3}{4}\right)^n+\ldots \ldots+\left(1-\frac{31}{32}\right)^n \\
& =\left(\frac{1}{2}\right)^n+\left(\frac{1}{2}\right)^{2 n}+\left(\frac{1}{2}\right)^{3 n}+\ldots \ldots+\left(\frac{1}{2}\right)^{5 n}
\end{aligned}
\)
\(
=\left(\frac{1}{2}\right)^n\left(\frac{1-\left(\frac{1}{2}\right)^{5 n}}{1-\left(\frac{1}{2}\right)^n}\right)=\frac{2^{5 n}-1}{2^{5 n}\left(2^n-1\right)}
\)
\(
\therefore 63 A=\frac{63\left(2^{5 n}-1\right)}{2^{5 n}\left(2^n-1\right)}=\frac{63}{\left(2^n-1\right)}\left(1-\frac{1}{2^{5 n}}\right)
\)
Given, \(63 A=1-\frac{1}{2^{30}}\)
\(
\therefore \frac{63}{\left(2^n-1\right)}\left(1-\frac{1}{2^{5 n}}\right)=1-\frac{1}{2^{30}}
\)
For \(n=6\), L.H.S \(=\) R.H.S
\(
\therefore n =6
\) -
Question 139 of 226
139. Question
Let \(m , n \in N\) and \(\operatorname{gcd}(2, n )=1\). If \(30\binom{30}{0}+29\binom{30}{1}+\ldots \ldots+2\binom{30}{28}+1\binom{30}{29}=n .2^m\), then \(n+m\) is equal to _____. [JEE Main 2021 (Online) 26th February Morning Shift]
\(
\text { (Here }\binom{n}{k}={ }^n C_k \text { ) }
\)CorrectIncorrectHint
\(
30\left({ }^{30} C_0\right)+29\left({ }^{30} C_1\right)+\ldots .+2\left({ }^{30} C_{28}\right)+1\left({ }^{30} C_{29}\right)
\)
\(
=30\left({ }^{30} C_{30}\right)+29\left({ }^{30} C_{29}\right)+\ldots \ldots+2\left({ }^{30} C_2\right)+1\left({ }^{30} C_1\right)
\)
\(
\begin{aligned}
& =\sum_{r=1}^{30} r\left({ }^{30} C_r\right) \\
& =\sum_{r=1}^{30} r\left(\frac{30}{r}\right)\left({ }^{29} C_{r-1}\right) \\
& =30 \sum_{r=1}^{30}{ }^{29} C_{r-1}
\end{aligned}
\)
\(
\begin{aligned}
& =30\left({ }^{29} C_0+{ }^{29} C_1+{ }^{29} C_2+\ldots .+{ }^{29} C_{29}\right) \\
& =30\left(2^{29}\right)=15(2)^{30}=n(2)^m
\end{aligned}
\)
\(
\begin{aligned}
& \therefore n =15, m =30 \\
& \Rightarrow n + m =45
\end{aligned}
\) -
Question 140 of 226
140. Question
If the remainder when \(x\) is divided by 4 is 3 , then the remainder when \((2020+x)^{2022}\) is divided by 8 is ____. [JEE Main 2021 (Online) 25th February Evening Shift]
CorrectIncorrectHint
(d)
\(
\begin{aligned}
& \text { Let } x=4 k+3 \\
& (2020+x)^{2022} \\
& =(2020+4 k+3)^{2022} \\
& =(4(505)+4 k+3)^{2022} \\
& =(4 P+3)^{2022} \\
& =(4 P+4-1)^{2022} \\
& =(4 A-1)^{2022} \\
& 2022 C_0(4 A)^0(-1)^{2022}+{ }^{2022} C_1(4 A)^1(-1)^{2021}+\ldots . . \\
& =1+2022(4 A)(-1)+\ldots . . \\
& =1+8 \lambda
\end{aligned}
\)
\(\therefore\) Remainder is 1 . -
Question 141 of 226
141. Question
The total number of two digit numbers ‘ \(n\) ‘, such that \(3^n+7^n\) is a multiple of 10 , is ____. [JEE Main 2021 (Online) 25th February Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \because 7^n=(10-3)^n=10 k+(-3)^n \\
& 7^n+3^n=10 k+(-3)^n+3^n
\end{aligned}
\)
\(
10 K+(-3)^n+3^n
\)
\(10 K\) if \(n=\) odd \(10 K+2.3^n\) if \(n=\) even
\(
\text { Let } n =2 t ; t \in N
\)
\(
\begin{aligned}
& \therefore 3^n=3^{2 t}=(10-1)^t \\
& =10 p+(-1)^t \\
& =10 p \pm 1
\end{aligned}
\)
\(\therefore\) if \(n=\) even then \(7^n+3^n\) will not be multiply of 10So if \(n\) is odd then only \(7^n+3^n\) will be multiply of 10
\(\therefore n=11,13,15 \ldots 99\)
Hence, there are 45 two digit number. -
Question 142 of 226
142. Question
For integers \(n\) and \(r\), let \(\binom{n}{r}=\left\{\begin{array}{cc}{ }^n C_r, & \text { if } n \geq r \geq 0 \\ 0, & \text { otherwise }\end{array}\right.\) The maximum value of \(k\)
for which the sum \(\sum_{i=0}^k\binom{10}{i}\binom{15}{k-i}+\sum_{i=0}^{k+1}\binom{12}{i}\binom{13}{k+1-i}\) exists, is equal to ____. [JEE Main 2021 (Online) 24th February Evening Shift]CorrectIncorrectHint
Finding the maximum value for which the sum
\(
\sum_{i=0}^k\binom{10}{i}\binom{15}{k-i}+\sum_{i=0}^{k+1}\binom{12}{i}\binom{13}{k+1-i}:
\)
Given that \(\binom{n}{r}= \begin{cases}n C_r, & \text { if } n \geq r \geq 0 \\ 0, & \text { Otherwise }\end{cases}\)
\(
\begin{aligned}
& (1+x)^{10}=10 C_0+10 C_1 x+10 C_2 x^2+\ldots \ldots+10 C_{10} x^{10} \\
& (1+x)^{15}=15 C_0+15 C_1 x+15 C_2 x^2+\ldots \ldots+15 C_{k-1} x^{k-1}+15 C_{k+1} \\
& x^{k+1}+\ldots 15 C_{15} x^{15} \\
& \sum_{i=0}^k\left(10 C_i\right)\left(15 C_{k-i}\right)=10 C_0 15 C_k+10 C_1 15 C_{k-1}+\ldots+10 C_k 15 C_0
\end{aligned}
\)
Coefficient of \(x_k\) in \((1+x)^{25}=25 C_k\)
\(
\sum_{i=0}^{k+1}\left(12 C_i\right)\left(13 C_{k+1-i}\right)=12 C_0 13 C_{k+1}+12 C_1 13 C_k+\ldots+12 C_{k+1} 13 C_0
\)
Coefficient of \(x^{k+1}\) in \((1+x)^{25}=25 C_{k+1}\)
\(
25 C_k+25 C_{k+1}=26 C_{k+1}
\)
For maximum value
As per given, \(k\) can be as large as possible.
Hence, \(k\) can be as large as possible . -
Question 143 of 226
143. Question
The sum of the coefficient of \(x^{2 / 3}\) and \(x^{-2 / 5}\) in the binomial expansion of \(\left(x^{2 / 3}+\frac{1}{2} x^{-2 / 5}\right)^9\) is [JEE Main 2024 (Online) 9th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T_{r+1}={ }^9 C_r\left(\frac{x^{-2 / 5}}{2}\right)^r\left(x^{2 / 3}\right)^{9-r} \\
& ={ }^9 C_r \frac{1}{2^r} x^{\frac{2}{3}(9-r)+\left(\frac{-2 r}{5}\right)} \\
& ={ }^9 C_r \cdot \frac{1}{2^r} \cdot x^{6-\frac{16 r}{15}}
\end{aligned}
\)
For coefficient of \(x^{2 / 3}\)
\(
\begin{aligned}
& \Rightarrow 6-\frac{16 r}{15}=\frac{2}{3} \\
& \Rightarrow 90-16 r=10 \\
& \Rightarrow r=5
\end{aligned}
\)
For coefficient of \(x^{-2 / 5}\)
\(
\begin{aligned}
& \Rightarrow 6-\frac{16 r}{15}=\frac{-2}{5} \\
& \Rightarrow 90-16 r=-6 \\
& \Rightarrow r=6
\end{aligned}
\)
Sum of coefficient of \(x^{2 / 3} \& x^{-2 / 5}\)
\(
\begin{aligned}
& ={ }^9 C_5 \cdot \frac{1}{2^5}+{ }^9 C_6 \cdot \frac{1}{2^6} \\
& =\frac{9!}{5!4!}\left(\frac{1}{2^5}\right)+\frac{9!}{6!3!}\left(\frac{1}{2^6}\right)=\frac{21}{4}
\end{aligned}
\) -
Question 144 of 226
144. Question
The coefficient of \(x^{70}\) in \(x^2(1+x)^{98}+x^3(1+x)^{97}+x^4(1+x)^{96}+\ldots+x^{54}(1+x)^{46}\) is \({ }^{99} C _{ p }-{ }^{46} C_{q}\). Then a possible value of \(p + q\) is : [JEE Main 2024 (Online) 9th April Morning Shift]
CorrectIncorrectHint
\(
x^2(1+x)^{98}+x^3(1+x)^{97}+\ldots+x^{54}(1+x)^{46}
\)
It is a G.P. with first term \(=x^2(1+x)^{98}\) and common ratio \(=\frac{x}{1+x}\)
sum of these term \(=x^2(1+x)^{98}\left(\frac{\left(\frac{x}{1+x}\right)^{53}-1}{\frac{x}{1+x}-1}\right)\)
\(
=x^2(1+x)^{98}\left((1+x)-x^{53}(1+x)^{-52}\right)
\)
\(
=x^2(\underbrace{1+x)^{99}}_{\begin{array}{l}
\text { Coeff } \\
\text { of } x^{68}
\end{array}}-x^{55} \underbrace{(1+x)^{46}}_{\text {Coeff of } x^{15}}
\)
\(
\begin{aligned}
& ={ }^{99} C _{68}-{ }^{46} C _{15} \\
& \Rightarrow p=68, q=15 \\
& \Rightarrow p+q=83
\end{aligned}
\) -
Question 145 of 226
145. Question
If the term independent of \(x\) in the expansion of \(\left(\sqrt{ a } x^2+\frac{1}{2 x^3}\right)^{10}\) is 105 , then \(a ^2\) is equal to : [JEE Main 2024 (Online) 8th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(\sqrt{a} x^2+\frac{1}{2 x^3}\right)^{10} \\
& T_{r+1}={ }^{10} C_r\left(\sqrt{a} x^2\right)^{10-r}\left(\frac{1}{2 x^3}\right)^r
\end{aligned}
\)
Independent of \(x \Rightarrow 20-2 r-3 r=0\)
\(
r=4
\)
Independent of \(x\) is \({ }^{10} C_4(\sqrt{a})^6\left(\frac{1}{2}\right)^4=105\)
\(
\begin{gathered}
\frac{210}{2 \times 8} a^3=105 \\
\Rightarrow \quad a=2 \\
a^2=4
\end{gathered}
\) -
Question 146 of 226
146. Question
If the constant term in the expansion of \(\left(\frac{\sqrt[5]{3}}{x}+\frac{2 x}{\sqrt[3]{5}}\right)^{12}, x \neq 0\), is \(\alpha \times 2^8 \times \sqrt[5]{3}\), then \(25 \alpha\) is equal to : [JEE Main 2024 (Online) 5th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(\frac{\sqrt[5]{3}}{x}+\frac{2 x}{\sqrt[5]{3}}\right)^{12} \\
& T_{r+1}={ }^{12} C r\left(\frac{\sqrt[5]{3}}{x}\right)^{12-r}\left(\frac{2 x}{\sqrt[3]{5}}\right)^r
\end{aligned}
\)
For constant term \(-12+r+r=0\)
\(
\begin{aligned}
& \Rightarrow \quad r=6 \\
& \therefore \quad \text { Constant term }={ }^{12} C_6 \frac{(3)^{\frac{6}{5}}}{(5)^{\frac{6}{3}}}(2)^6 \\
& ={ }^{12} C_6 \times \frac{2^6}{25} \times 3.3^{\frac{1}{5}} \\
& =\frac{231}{25} \times 2^8 \cdot 3^{\frac{1}{5}} \cdot 3 \\
& =\frac{693}{25} \cdot 2^8 \sqrt[5]{3} \\
& \therefore \quad \alpha=\frac{693}{25} \\
& 25 \alpha=693
\end{aligned}
\) -
Question 147 of 226
147. Question
If the coefficients of \(x^4, x^5\) and \(x^6\) in the expansion of \((1+x)^n\) are in the arithmetic progression, then the maximum value of \(n\) is: [JEE Main 2024 (Online) 4th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& (1+x)^n={ }^n C_0+{ }^n C_1 x^1+{ }^n C_2 x^2+\ldots{ }^n C_n x^n \\
& { }^n C_4,{ }^n C_5 \text { and } { }^n C_6 \text { are in A. P. } \Rightarrow { }^n C_5-{ }^n C_4={ }^n C_6-{ }^n C_5 \\
& \Rightarrow \frac{n!}{5!(n-5)!}-\frac{n!}{4!(n-4)!}=\frac{n!}{6!(n-6)!}-\frac{n!}{5!(n-5)!} \\
& \Rightarrow 30(n-9)(n-6)=5(n-4)(n-11) \\
& \Rightarrow 30 n^2-450 n+1620=5 n^2 \\
& \Rightarrow \frac{1}{n-5}\left[\frac{n-4-5}{5(n-4)}\right]=\frac{1}{5}\left[\frac{n-5-6}{6(n-5)}\right] \\
& \Rightarrow \frac{n-9}{5(n-4)}=\frac{1}{5}\left[\frac{n-11}{6}\right] \\
& \Rightarrow n^2-21 n+98=0 \\
& n_{\max }=14
\end{aligned}
\) -
Question 148 of 226
148. Question
The sum of all rational terms in the expansion of \(\left(2^{\frac{1}{5}}+5^{\frac{1}{3}}\right)^{15}\) is equal to: [JEE Main 2024 (Online) 4th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T_{r+1}={ }^{15} C _r\left(2^{1 / 5}\right)^{15-r}\left(5^{1 / 3}\right)^r \\
& ={ }^{15} C_r 5^{r / 3} 2^{\left(3-\frac{r}{5}\right)}
\end{aligned}
\)
For rational terms,
\(\frac{r}{3}\) and \(\frac{r}{5}\) must be integer
3 and 5 divide \(r \Rightarrow 15\) divides \(r \Rightarrow r=0\) and \(r=15\)
\(
\begin{aligned}
& { }^{15} C_0 5^0 2^3+{ }^{15} C_{15} 5^5 2^{(0)} \\
& =8+3125 \\
& =3133
\end{aligned}
\) -
Question 149 of 226
149. Question
Let \(m\) and \(n\) be the coefficients of seventh and thirteenth terms respectively in the expansion of \(\left(\frac{1}{3} x^{\frac{1}{3}}+\frac{1}{2 x^{\frac{2}{3}}}\right)^{18}\). Then \(\left(\frac{ n }{ m }\right)^{\frac{1}{3}}\) is :[JEE Main 2024 (Online) 1st February Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& t _7={ }^{18} C _6\left(\frac{ x ^{\frac{1}{3}}}{3}\right)^{12}\left(\frac{ x ^{\frac{-2}{3}}}{2}\right)^6={ }^{18} C _6 \frac{1}{(3)^{12}} \cdot \frac{1}{2^6} \\
& t _{13}={ }^{18} C _{12}\left(\frac{ x ^{\frac{1}{3}}}{3}\right)^6\left(\frac{ x ^{\frac{-2}{3}}}{2}\right)^{12}={ }^{18} C _{12} \frac{1}{(3)^6} \cdot \frac{1}{2^{12}} \cdot x ^{-6} \\
& \therefore m={ }^{18} C_6\left(\frac{1}{3}\right)^{12}\left(\frac{1}{2}\right)^6 \\
& n={ }^{18} C_{12}\left(\frac{1}{3}\right)^6\left(\frac{1}{2}\right)^{12}
\end{aligned}
\)
\(
\begin{aligned}
\left(\frac{m}{n}\right)^{\frac{1}{3}} & =\left(\frac{{ }^{18} C_6\left(\frac{1}{3}\right)^{12}\left(\frac{1}{2}\right)^6}{{ }^{18} C_{12}\left(\frac{1}{3}\right)^6\left(\frac{1}{2}\right)^{12}}\right)^{\frac{1}{3}} \\
& =\left(\frac{\left(\frac{1}{3}\right)^6}{\left(\frac{1}{2}\right)^6}\right)^{\frac{1}{3}}=\left(\left(\frac{2}{3}\right)^6\right)^{\frac{1}{3}}=\frac{4}{9} \\
\therefore\left(\frac{n}{m}\right)^{\frac{1}{3}} & =\frac{9}{4}
\end{aligned}
\) -
Question 150 of 226
150. Question
Let \(a\) be the sum of all coefficients in the expansion of \(\left(1-2 x+2 x^2\right)^{2023}\left(3-4 x^2+2 x^3\right)^{2024}\) and \(b=\lim _{x \rightarrow 0}\left(\frac{\int_0^x \frac{\log (1+t)}{t^{2024}+1} d t}{x^2}\right)\). If the equation \(c x^2+d x+e=0\) and \(2 b x^2+a x+4=0\) have a common root, where \(c, d, e \in R\), then \(d : c : e\) equals [JEE Main 2024 (Online) 31st January Morning Shift]
CorrectIncorrectHint
Put \(x=1\)
\(
\begin{aligned}
& \therefore a=1 \\
& b=\lim _{x \rightarrow 0} \frac{\int_0^x \frac{\ln (1+t)}{1+t^{2024}} dt }{x^2}
\end{aligned}
\)
Using L’ HOPITAL Rule
\(
b =\lim _{ x \rightarrow 0} \frac{\ln (1+ x )}{\left(1+ x ^{2024}\right)} \times \frac{1}{2 x }=\frac{1}{2}
\)
Now, \(cx ^2+ dx + e =0, x ^2+ x +4=0\)
\(
\begin{aligned}
& ( D <0) \\
& \therefore \frac{ c }{1}=\frac{ d }{1}=\frac{ e }{4}
\end{aligned}
\) -
Question 151 of 226
151. Question
Suppose \(2-p, p, 2-\alpha, \alpha\) are the coefficients of four consecutive terms in the expansion of \((1+x)^n\). Then the value of \(p^2-\alpha^2+6 \alpha+2 p\) equals [JEE Main 2024 (Online) 30th January Evening Shift]
CorrectIncorrectHint
\(
2-p, p, 2-\alpha, \alpha
\)
Binomial coefficients are
\(
\begin{aligned}
& { }^n C_r,{ }^n C_{r+1},{ }^n C_{r+2},{ }^n C_{r+3} \text { respectively } \\
\Rightarrow \quad & { }^n C_r+{ }^n C_{r+1}=2 \\
\Rightarrow \quad & { }^{n+1} C_{r+1}=2 \quad \ldots \ldots(1)
\end{aligned}
\)
Also, \({ }^{ n } C _{ r +2}+{ }^{ n } C _{ r +3}=2\)
\(
\Rightarrow \quad{ }^{n+1} C_{r+3}=2 \dots(2)
\)
From (1) and (2)
\(
\begin{aligned}
& { }^{n+1} C_{r+1}={ }^{n+1} C_{r+3} \\
& \Rightarrow \quad 2 r +4= n +1 \\
& n =2 r +3 \\
& { }^{2 r +4} C _{ r +1}=2
\end{aligned}
\) -
Question 152 of 226
152. Question
\({ }^{n-1} C_r=\left(k^2-8\right)^n C_{r+1} \text { if and only if : }\) [JEE Main 2024 (Online) 27th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& { }^{ n -1} C _{ r }=\left( k ^2-8\right)^{ n } C _{ r +1} \\
& \underbrace{ r +1 \geq 0, \quad r \geq 0}_{ r \geq 0} \\
& \frac{{ }^{n-1} C_r}{{ }^n C_{r+1}}=k^2-8 \\
& \frac{r+1}{n}=k^2-8 \\
& \Rightarrow k^2-8>0 \\
& (k-2 \sqrt{2})(k+2 \sqrt{2})>0
\end{aligned}
\)
\(
\begin{aligned}
& k \in(-\infty,-2 \sqrt{2}) \cup(2 \sqrt{2}, \infty) \dots(i)\\
& \therefore n \geq r +1, \frac{ r +1}{ n } \leq 1 \\
& \Rightarrow k ^2-8 \leq 1 \\
& \quad k ^2-9 \leq 0 \\
& \quad-3 \leq k \leq 3 \quad \text {…. (ii) }
\end{aligned}
\)
From equation (i) and (ii) we get
\(
k \in[-3,-2 \sqrt{2}) \cup(2 \sqrt{2}, 3]
\) -
Question 153 of 226
153. Question
If A denotes the sum of all the coefficients in the expansion of \(\left(1-3 x+10 x^2\right)^{ n }\) and \(B\) denotes the sum of all the coefficients in the expansion of \(\left(1+x^2\right)^n\), then : [JEE Main 2024 (Online) 27th January Morning Shift]
CorrectIncorrectHint
Sum of coefficients in the expansion of \(\left(1-3 x+10 x^2\right)^n=A\) then \(A=(1-3+10)^n=8^n\) (put \(x=1\) ) and sum of coefficients in the expansion of
\(
\begin{aligned}
& \left(1+x^2\right)^n=B \\
& \text { then } B=(1+1)^n=2^n \\
& A=B^3
\end{aligned}
\) -
Question 154 of 226
154. Question
Let \(\left(a+b x+c x^2\right)^{10}=\sum_{i=0}^{20} p_i x^i, a, b, c \in N\). If \(p_1=20\) and \(p_2=210\), then \(2(a+b+c)\) is equal to : [JEE Main 2023 (Online) 15th April Morning Shift]
CorrectIncorrectHint
We are given that \(\left(a+b x+c x^2\right)^{10}=\sum_{i=0}^{20} p_i x^i\), and we are given that \(p_1=20\) and \(p_2=210\).
We need to find the value of \(2(a+b+c)\).
Using the multinomial theorem, we can express the expansion of \(\left(a+b x+c x^2\right)^{10}\) as follows:
\(
\sum_{k_1+k_2+k_3=10} \frac{10!}{k_{1}!k_{2}!k_{3}!} a^{k_1}(b x)^{k_2}\left(c x^2\right)^{k_3}
\)
Now we need to find the coefficients of \(x^1\) and \(x^2\) in the expansion:
For \(x^1\) term, we have:
\(
k_2=1, k_1=9, k_3=0
\)
So, \(p_1=\frac{10!}{9!1!0!} a^9 b^1=10 a^9 b\)
For \(x^2\) term, there are two possibilities:
\(
k_2=2, k_1=8, k_3=0 \quad \text { and } \quad k_2=0, k_1=9, k_3=1
\)
So, \(p_2=\frac{10!}{8!2!!} a^8 b^2+\frac{10!}{9!0!1!} a^9 c=45 a^8 b^2+10 a^9 c\)
Now we are given \(p_1=20\) and \(p_2=210\). So, \(10 a^9 b=20 \Longrightarrow a^9 b=2\) and \(45 a^8 b^2+10 a^9 c=210\)
Now, divide the second equation by \(a^8: 45 b^2+10 a c=210\)
We know that \(a^9 b=2\). Taking the \(9^{\text {th }}\) root of both sides: \(a b=\sqrt[9]{2}\)
Now, let \(k=a b=\sqrt[9]{2}\). We can rewrite the equation for \(x^2\) term as:
\(
45 k^2+10 k^9=210
\)
From the equation \(a b=k=\sqrt[9]{2}\), we know that \(a\) and \(b\) are positive integers. Thus, \(k=2\) (as both \(a\) and \(b\) must be factors of 2 ). Now we have:
\(
a+b=2
\)
and from the equation \(a^9 b=2\), we get \(a=1, b=2\) or vice versa.
Now we need to find the value of \(c\). We can use the equation for the \(x^2\) term again:
\(
45 a^8 b^2+10 a^9 c=210
\)
Using \(a=1\) and \(b=2\), we get:
\(
45(1)^8(2)^2+10(1)^9 c=210 \Longrightarrow 180+10 c=210 \Longrightarrow c=3
\)
So, \(a=1, b=2\), and \(c=3\). Now, we need to find the value of \(2(a+b+c)\) :
\(
2(a+b+c)=2(1+2+3)=2(6)=12
\) -
Question 155 of 226
155. Question
The coefficient of \(x^5\) in the expansion of \(\left(2 x^3-\frac{1}{3 x^2}\right)^5\) is: [JEE Main 2023 (Online) 13th April Evening Shift]
CorrectIncorrectHint
Given, \(\left(2 x^3-\frac{1}{3 x^2}\right)^5\)
General term,
\(
\begin{aligned}
& T_{r+1}={ }^5 C_r\left(2 x^3\right)^{5-r}\left(\frac{-1}{3 x^2}\right)^r={ }^5 C_r \frac{(2)^{5-r}}{(-3)^r}(x)^{15-5 r} \\
& \therefore 15-5 r =5 \\
& \therefore r =2 \\
& T_3=10\left(\frac{8}{9}\right) x^5
\end{aligned}
\)
So, coefficient is \(\frac{80}{9}\). -
Question 156 of 226
156. Question
Fractional part of the number \(\frac{4^{2022}}{15}\) is equal to [JEE Main 2023 (Online) 13th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \left\{\frac{4^{2022}}{15}\right\}=\left\{\frac{2^{4044}}{15}\right\} \\
& =\left\{\frac{(1+15)^{1011}}{15}\right\} \\
& =\frac{1}{15}
\end{aligned}
\) -
Question 157 of 226
157. Question
If \(\frac{1}{n+1}{ }^n C _n+\frac{1}{n}{ }^n C _{n-1}+\ldots+\frac{1}{2}{ }^n C _1+{ }^n C _0=\frac{1023}{10}\) then \(n\) is equal to : [JEE Main 2023 (Online) 12th April Morning Shift]
CorrectIncorrectHint
\(
\frac{1}{n+1}{ }^n C _n+\frac{1}{n}{ }^n C _{n-1}+\ldots+\frac{1}{2}{ }^n C _1+{ }^n C _0=\frac{1023}{10}
\)
\(
\begin{aligned}
& \Rightarrow \sum_{r=0}^n \frac{1}{r+1}{ }^n C_r=\frac{1023}{10} \\
& \left(\because{ }^{n+1} C_{r+1}=\frac{n+1}{r+1}{ }^n C_r\right) \\
& \Rightarrow \sum_{r=0}^n \frac{1}{n+1}^{n+1} C_{r+1}=\frac{1023}{10}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \frac{1}{n+1}\left[{ }^{n+1} C_1+{ }^{n+1} C_2+\ldots+{ }^{n+1} C_{n+1}\right]=\frac{1023}{10} \\
& \Rightarrow \frac{2^{n+1}-1}{n+1}=\frac{1023}{10}=\frac{2^{10}-1}{10} \\
& \Rightarrow n+1=10 \\
& \Rightarrow n=9
\end{aligned}
\) -
Question 158 of 226
158. Question
The sum, of the coefficients of the first 50 terms in the binomial expansion of \((1-x)^{100}\), is equal to [JEE Main 2023 (Online) 12th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \left({ }^{100} C_0-{ }^{100} C_1+{ }^{100} C_2-\ldots . .{ }^{100} C_{49}\right)+{ }^{100} C_{50} \\
& +\left(-{ }^{100} C_{51}+{ }^{100} C_{52}-\ldots .+{ }^{100} C_{100}\right)=0 \\
& \lambda_1+{ }^{100} C_{50}+\lambda_2=0 \\
& \lambda_1=-\frac{1}{2}{ }^{100} C_{50} \quad\left(\because \lambda_1=\lambda_2\right) \\
& =-{ }^{99} C_{49}
\end{aligned}
\) -
Question 159 of 226
159. Question
The sum of the coefficients of three consecutive terms in the binomial expansion of \((1+ x )^{ n +2}\), which are in the ratio \(1: 3: 5\), is equal to : [JEE Main 2023 (Online) 11th April Evening Shift]
CorrectIncorrectHint
The problem asks for the sum of the coefficients of three consecutive terms in the binomial expansion of \((1+x)^{n+2}\), which are in the ratio \(1: 3: 5\).
Given that the ratios of the coefficients are 1:3:5, we let the terms be \(T_r, T_{r+1}\), and \(T_{r+2}\). The coefficients of these terms are \({ }^{n+2} C_{r-1},{ }^{n+2} C_r\), and \({ }^{n+2} C_{r+1}\), respectively.
\(
\begin{aligned}
& \frac{T_{r+1}}{T_r}=\frac{{ }^{n+2} C_r}{{ }^{n+2} C_{r-1}}=\frac{n+2-r+1}{r}=\frac{n+3-r}{r}=3 \\
& n-4 r+3=0 \ldots \ldots(1) \\
& \frac{T_{r+2}}{T_{r+1}}=\frac{{ }^{n+2} C_{r+1}}{{ }^{n+2} C_r}=\frac{(n+2)-(r+1)+1}{r+1}=\frac{n-r+2}{r+1}=\frac{5}{3} \\
& 3 n-8 r+1=0 \ldots \ldots(2)
\end{aligned}
\)
By solving (1) and (2), we get
\(
\begin{aligned}
& \Rightarrow n=5, r=2 \\
& \begin{aligned}
T_r+T_{r+1}+T_{r+2} & ={ }^7 C_1+{ }^7 C_2+{ }^7 C_3 \\
& =7+21+35=63
\end{aligned}
\end{aligned}
\) -
Question 160 of 226
160. Question
If the \(1011^{\text {th }}\) term from the end in the binominal expansion of \(\left(\frac{4 x}{5}-\frac{5}{2 x}\right)^{2022}\) is 1024 times \(1011^{\text {th }}\) term from the beginning, then \(|x|\) is equal to [JEE Main 2023 (Online) 11th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T _{1011} \text { from beginning }= T _{1010+1} \\
& ={ }^{2022} C _{1010}\left(\frac{4 x }{5}\right)^{1012}\left(\frac{-5}{2 x }\right)^{1010} \\
& T _{1011} \text { from end } \\
& ={ }^{2022} C _{1010}\left(\frac{-5}{2 x }\right)^{1012}\left(\frac{4 x }{5}\right)^{1010} \\
& \text { Given: }{ }^{2022} C _{1010}\left(\frac{-5}{2 x }\right)^{1012}\left(\frac{4 x }{5}\right)^{1010} \\
& =2^{10} \cdot{ }^{2022} C _{1010}\left(\frac{-5}{2 x }\right)^{1010}\left(\frac{4 x }{5}\right)^{1012} \\
& \Rightarrow\left(\frac{-5}{2 x}\right)^2=2^{10}\left(\frac{4 x}{5}\right)^2 \\
& \Rightarrow x^4=\frac{5^4}{2^{16}} \\
& \Rightarrow|x|=\frac{5}{16}
\end{aligned}
\) -
Question 161 of 226
161. Question
Let the number \((22)^{2022}+(2022)^{22}\) leave the remainder \(\alpha\) when divided by 3 and \(\beta\) when divided by 7 . Then \(\left(\alpha^2+\beta^2\right)\) is equal to: [JEE Main 2023 (Online) 10th April Evening Shift]
CorrectIncorrectHint
We have, \((22)^{2022}+(2022)^{22}\)
As 2022 is completely divisible by 3
So, \((2022)^{22}\) is also divisible by 3
\(
(22)^{2022}=(21+1)^{2022}=(3 \times 7+1)^{2022}=7 m+1
\)
\(\Rightarrow(22)^{2022}\) leave a remainder 1 , when divisible by 3 .
\(\therefore(22)^{2022}+(2022)^{22}\) leave a remainder when divisible by 3
\(
\therefore \alpha=1
\)
\(
\begin{aligned}
(22)^{2022}+(2022)^{22} & =(21+1)^{2022}+(2023-1)^{22} \\
& =7 K+1+7 \mu+1=7(K+\mu)+2
\end{aligned}
\)
\(\Rightarrow(22)^{2022}+(2022)^{22}\) leave a remainder 2 when divisible by 7
\(
\therefore \beta=2
\)
Hence, \(\alpha^2+\beta^2=1^2+2^2=5\) -
Question 162 of 226
162. Question
If the coefficients of \(x\) and \(x^2\) in \((1+x)^{ p }(1-x)^{ q }\) are 4 and -5 respectively, then \(2 p+3 q\) is equal to : [JEE Main 2023 (Online) 10th April Evening Shift]
CorrectIncorrectHint
We have, coefficient of \(x\) in \((1+x)^p(1-x)^q=4\) and coefficient of \(x^2\) in \((1+x)^p(1-x)^q=-5\)
\(
\begin{aligned}
& (1+x)^p(1-x)^q \\
& =\left(1+p x+\frac{p(p-1)}{2} x^2+\ldots\right)\left(1-q x+\frac{q(q-1)}{2} x^2+\ldots\right) \\
& =1+(p-q) x+\left(\frac{p(p-1)}{2}+\frac{q(q-1)}{2}-p q\right) x^2+\ldots \ldots
\end{aligned}
\)
Coefficient of \(x\) in \((1+x)^p(1-x)^q=-q+p\)
\(
\Rightarrow p-q=4 \dots(i)
\)
Coefficient of \(x^2\) in \((1+x)^p(1-x)^q=\frac{q(q-1)}{2}-p q+\frac{p(p-1)}{2}\)
\(
\begin{aligned}
& \Rightarrow \frac{q^2-q-2 p q+p^2-p}{2}=-5 \\
& \Rightarrow \frac{p^2+q^2-2 p q-(p+q)}{2}=-5 \\
& \Rightarrow(p-q)^2-(p+q)=-10
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow(4)^2-(p+q)=-10 \quad[\because \text { From Eq. (i) }] \\
& \Rightarrow p+q=26 \ldots \ldots \ldots \ldots(i i)
\end{aligned}
\)
Form Eqs. (i) and (ii), we get \(p=15, q=11\)
\(
\therefore 2 p+3 q=2 \times 15+3 \times 11=30+33=63
\) -
Question 163 of 226
163. Question
If the coefficient of \(x^7\) in \(\left(a x-\frac{1}{b x^2}\right)^{13}\) and the coefficient of \(x^{-5}\) in \(\left(a x+\frac{1}{b x^2}\right)^{13}\) are equal, then \(a^4 b^4\) is equal to : [JEE Main 2023 (Online) 10th April Morning Shift]
CorrectIncorrectHint
The given expression is \(\left(a x-\frac{1}{b x^2}\right)^{13}\)
So,
\(
\begin{aligned}
T_{r+1} & ={ }^{13} C_r(a x)^{13-r}\left(-\frac{1}{b x^2}\right)^r \\
& ={ }^{13} C_r(a)^{13-r} x^{13-r-2 r}(-1 / b)^r \\
& ={ }^{13} C_r(a)^{13-r}\left(-\frac{1}{b}\right)^r x^{13-3 r}
\end{aligned}
\)
For coefficient of \(x^7\) in \(\left(a x-\frac{1}{b x^2}\right)^{13}\)
\(
\begin{gathered}
13-3 r=7 \\
\Rightarrow 3 r=6 \Rightarrow r=2
\end{gathered}
\)
\(\therefore\) Coefficient of \(x^7={ }^{13} C_2 \cdot(a)^{11} \cdot \frac{1}{b^2}\)
Again, the another expression is \(\left(a x+\frac{1}{b x^2}\right)^{13}\)
So, \(T_{n+1}={ }^{13} C_r(a x)^{13-r}\left(\frac{1}{b x^2}\right)^r={ }^{13} C_r(a)^{13-r}\left(\frac{1}{b}\right)^r x^{13-3 r}\)
For coefficient \(x^{-5}\) in \(\left(a x+\frac{1}{b x^2}\right)^{13}\)
\(13-3 r=-5\)
\(
\Rightarrow r=6
\)
So, coefficient of \(x^{-5}={ }^{13} C_6(a)^7 \frac{1}{b^6}\)
Now, according to the question,
\(
\begin{aligned}
& { }^{13} C_2(a)^{11} \frac{1}{b^2}={ }^{13} C_6(a)^7 \frac{1}{b^6} \\
& \Rightarrow a^4 b^4=\frac{{ }^{13} C_6}{{ }^{13} C_2} \\
& \therefore a^4 b^4=22
\end{aligned}
\) -
Question 164 of 226
164. Question
\(25^{190}-19^{190}-8^{190}+2^{190}\) is divisible by : [JEE Main 2023 (Online) 8th April Evening Shift]
CorrectIncorrectHint
The given expression is divisible by 6 and 17 .
Also, \(25^{190}-8^{190}\) is not divisible by 7
but \(19^{190}-2^{190}\) is divisible by 7 ,
So, \(25^{190}-19^{190}-8^{190}+2^{190}\) is divisible by 34 but not by 14 . -
Question 165 of 226
165. Question
The absolute difference of the coefficients of \(x^{10}\) and \(x^7\) in the expansion of \(\left(2 x^2+\frac{1}{2 x}\right)^{11}\) is equal to : [JEE Main 2023 (Online) 8th April Evening Shift]
CorrectIncorrectHint
\(
\text { General term of }\left(2 x^2+\frac{1}{2 x}\right)^{11} \text { is : }
\)
\(
\begin{aligned}
& T _{ r +1}={ }^{11} C _r\left(2 x^2\right)^{11-r}\left(\frac{1}{2 x}\right)^r \\
& ={ }^{11} C _r 2^{11-r} x^{22-2 r} 2^{-r} x^{-r} \\
& ={ }^{11} C _r 2^{11-2r} x^{22-3 r}
\end{aligned}
\)
Now, \(22-3 r=10\) and \(22-3 r=7\)
\(
\begin{array}{ll}
\Rightarrow 3 r=12 & \Rightarrow 3 r=15 \\
\Rightarrow r=4 & \Rightarrow r=5
\end{array}
\)
\(
\therefore \text { Coeff. of } x^{10}={ }^{11} C _4 \cdot 2^{11-8}={ }^{11} C _4 \times 8
\)
Coeff. of \(x^7={ }^{11} C_5 \cdot 2^{11-10}={ }^{11} C_4 \times 2\)
Now, required difference
\(
\begin{aligned}
& ={ }^{11} C _4 \times 8-{ }^{11} C _5 \times 2 \\
& =\frac{11 \times 10 \times 9 \times 8 \times 7!}{4!\times 7!} \times 8-\frac{11 \times 10 \times 9 \times 8 \times 7 \times 6!\times 2}{5!6!} \\
& =\frac{11 \times 10 \times 9 \times 8 \times 8}{24}-\frac{11 \times 10 \times 9 \times 8 \times 7 \times 2}{120} \\
& =11 \times 10 \times 8 \times 3-11 \times 3 \times 4 \times 7 \\
& =11 \times 3 \times 4[20-7] \\
& =11 \times 12 \times 13=(12-1) \times 12 \times(12+1) \\
& =12\left(12^2-1\right)=12^3-12
\end{aligned}
\) -
Question 166 of 226
166. Question
If the coefficients of three consecutive terms in the expansion of \((1+x)^n\) are in the ratio \(1: 5: 20\), then the coefficient of the fourth term is [JEE Main 2023 (Online) 8th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Given: }{ }^n C _{r-1}:{ }^n C _r:{ }^n C _{r+1} \\
& =1: 5: 20 \\
& \Rightarrow \frac{n!}{(r-1)!(n-r+1)!} \times \frac{r!(n-r)!}{n!}=\frac{1}{5} \\
& \Rightarrow \frac{r}{(n-r+1)}=\frac{1}{5} \\
& \Rightarrow 5 r=n-r+1 \\
& \Rightarrow n=6 r-1 \ldots \ldots . .(i)
\end{aligned}
\)
Also, \(\frac{n!}{r!(n-r)!} \times \frac{(r+1)!(n-r-1)!}{n!}=\frac{5}{20}=\frac{1}{20}\)
\(
\begin{aligned}
& \Rightarrow \frac{(r+1)}{(n-r)}=\frac{1}{4} \\
& \Rightarrow 4 r+4=n-r \\
& \Rightarrow n=5 r+4 \ldots \ldots . .(ii)
\end{aligned}
\)
From (i) and (ii), we get
\(
\begin{aligned}
& 6 r-1=5 r+4 \\
& \Rightarrow r=5
\end{aligned}
\)
So, \(n=5(5)+4=29\)
So, coefficient of \(4^{\text {th }}\) terms \(={ }^n C _3={ }^{29} C _3\)
\(
=\frac{29!}{3!26!}=\frac{29 \times 28 \times 27}{3 \times 2}=3654
\) -
Question 167 of 226
167. Question
If the coefficient of \(x^7\) in \(\left(a x^2+\frac{1}{2 b x}\right)^{11}\) and \(x^{-7}\) in \(\left(a x-\frac{1}{3 b x^2}\right)^{11}\) are equal, then : [JEE Main 2023 (Online) 6th April Evening Shift]
CorrectIncorrectHint
General term of \(\left(a x^2+\frac{1}{2 b x}\right)^{11}\) is
\(
T_{r+1}={ }^{11} C_r\left(a x^2\right)^{11-r}\left(\frac{1}{2 b x}\right)^r={ }^{11} C_r(a)^{11-r}\left(\frac{1}{2 b}\right)^r x^{22-3 r}
\)
Now, \(22-3 r=7\)
\(
\begin{aligned}
& \Rightarrow 15=3 r \\
& \Rightarrow r=5
\end{aligned}
\)
and general term of \(\left(a x-\frac{1}{3 b x^2}\right)^{11}\) is
\(
\begin{aligned}
T_{r+1} & ={ }^{11} C_r(a x)^{11-r}\left(-\frac{1}{3 b x^2}\right)^r \\
& ={ }^{11} C_r a^{11-r}\left(-\frac{1}{3 b}\right)^r x^{11-3 r}
\end{aligned}
\)
Now, \(11-3 r=-7\)
\(
\Rightarrow 18=3 r \Rightarrow r=6
\)
Since, coefficient of \(x^7\) in \(\left(a x^2+\frac{1}{2 b x}\right)^{11}\)
\(=\) Coefficient of \(x^{-7}\) in \(\left(a x-\frac{1}{3 b x^2}\right)^{11}\)
\(
\begin{aligned}
& \Rightarrow{ }^{11} C_5(a)^6\left(\frac{1}{2 b}\right)^5={ }^{11} C_6(a)^5\left(-\frac{1}{3 b}\right)^6 \\
& \Rightarrow \frac{a}{32 b^5}=\frac{1}{729 b^6} \Rightarrow 729 a b=32
\end{aligned}
\) -
Question 168 of 226
168. Question
Among the statements :
(S1) : \(2023^{2022}-1999^{2022}\) is divisible by 8
(S2) : \(13(13)^n-12 n-13\) is divisible by 144 for infinitely many \(n \in N\)CorrectIncorrectHint
\(
\begin{aligned}
& \text { We have, } S_1:(2023)^{2022}-(1999)^{2022} \\
& =(1999+24)^{2022}-(1999)^{2022}={ }^{2022} C_0(1999)^{2022}(24)^0 \\
& +{ }^{2022} C_1(1999)^{2021}(24)^1+{ }^{2022} C_2(1999)^{2020}(24)^2 \\
& +\ldots-(1999)^{2022}
\end{aligned}
\)
\(
\begin{aligned}
& ={ }^{2022} C_1(1999)^{2021}(24)+{ }^{2022} C_2(1999)^{2022}(24)^2 \\
& =24\left({ }^{(2022} C_1(1999)^{2021}+{ }^{2022} C_2(1999)^{2022}(24)+\ldots+\ldots\right)
\end{aligned}
\)
\(\Rightarrow S_1\) is divisible by 24
Now, \(S_2: 13(13)^n-12 n-13\)
Here, \(13^n=(1+12)^n\)
\(
\begin{aligned}
& =1+{ }^n C_1 12+{ }^n C_2(12)^2+{ }^n C_3(12)^3 \\
\therefore S_2 & : 13\left(1+{ }^n C_1(12)+{ }^n C_2(12)^2+{ }^n C_3(12)^3+\ldots\right)-12 n-13 \\
& =13+156 n+13\left({ }^n C_2(12)^2+{ }^n C_3(12)^3+\ldots\right)-12 n-13 \\
& =144 n+144 \times 13\left({ }^n C_2+{ }^n C_3(12)+\ldots\right)
\end{aligned}
\)
\(\Rightarrow S_2\) is divisible by 144 for infinitely many \(n \in N\) -
Question 169 of 226
169. Question
If \({ }^{2 n} C_3:{ }^n C_3=10: 1\), then the ratio \(\left(n^2+3 n\right):\left(n^2-3 n+4\right)\) is: [JEE Main 2023 (Online) 6th April Morning Shift]
CorrectIncorrectHint
We have, \({ }^{2 n} C_3:{ }^n C_3=10: 1\)
\(
\begin{aligned}
& \Rightarrow \frac{{ }^{2 n} C_3}{{ }^n C_3}=\frac{10}{1} \\
& \Rightarrow \frac{(2 n)!}{3!(2 n-3)!} \times \frac{3!(n-3)!}{n!}=\frac{10}{1} \\
& \Rightarrow \frac{(2 n)(2 n-1)(2 n-2)}{(n)(n-1)(n-2)}=\frac{10}{1} \\
& \Rightarrow 4 n^2-6 n+2=5\left(n^2-3 n+2\right) \\
& \Rightarrow n^2-9 n+8=0 \\
& \Rightarrow n^2-8 n-n+8=0 \\
& \Rightarrow n(n-8)-1(n-8)=0 \\
& \Rightarrow(n-8)(n-1)=0 \\
& \Rightarrow n=8(n=1 \text { not valid }) \\
& \therefore \frac{n^2+3 n}{n^2-3 n+4}=\frac{88}{44}=\frac{2}{1}=2: 1
\end{aligned}
\) -
Question 170 of 226
170. Question
If the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of \(\left(\sqrt[4]{2}+\frac{1}{\sqrt[4]{3}}\right)^{ n }\) is \(\sqrt{6}: 1\), then the third term from the beginning is : [JEE Main 2023 (Online) 6th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T _{r+1}={ }^n C _r x^{n-r} a^r \\
& \frac{T_5}{T_5^{\prime}}=\frac{{ }^n C_4 \times\left((2)^{\frac{1}{4}}\right)^{n-4}\left(\frac{1}{3^{1 / 4}}\right)^4}{{ }^n C_4\left(\frac{1}{3^{1 / 4}}\right)^{n-4}\left(2^{1 / 4}\right)^4}=\sqrt{6}
\end{aligned}
\)
\(\left[\because r\right.\) th term from end in the expansion of \((x+y)^n=r\) th term from beginning in the expansion of \((y+x)^n\) ]
\(
\begin{aligned}
& \Rightarrow \frac{{ }^n C_4(2)^{\frac{n-4}{4}}\left(\frac{1}{3}\right)^{4 / 4}}{{ }^n C_4\left(\frac{1}{3}\right)^{\frac{n-4}{4}}(2)^{4 / 4}}=\frac{\sqrt{6}}{1} \\
& \Rightarrow(2)^{\frac{n-8}{4}}(3)^{\frac{n-8}{4}}=6^{1 / 2} \\
& \Rightarrow 6^{\frac{n-8}{4}}=6^{1 / 2}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \frac{n-8}{4}=\frac{1}{2} \\
& \Rightarrow n-8=2 \Rightarrow n=10 \\
& \therefore T_3={ }^{10} C_2(\sqrt[4]{2})^8\left(\frac{1}{\sqrt[4]{3}}\right)^2=45(2)^{\frac{8}{4}} \frac{1}{3^{1 / 2}} \\
& =45(4) \times \frac{\sqrt{3}}{3}=60 \sqrt{3}
\end{aligned}
\) -
Question 171 of 226
171. Question
Let \(x=(8 \sqrt{3}+13)^{13}\) and \(y=(7 \sqrt{2}+9)^9\). If \([t]\) denotes the greatest integer \(\leq t\), then : [JEE Main 2023 (Online) 30th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { If } I_1+f=(8 \sqrt{3}+13)^{13}, f^{\prime}=(8 \sqrt{3}-13)^{13} \\
& I_1+f-f^{\prime}=\text { Even } \\
& I_1=\text { Even } \\
& I_2+f-f^{\prime}=(7 \sqrt{2}+9)^9+(7 \sqrt{2}-9)^9 \\
& =\text { Even } \\
& I_2=\text { Even }
\end{aligned}
\) -
Question 172 of 226
172. Question
If the coefficient of \(x^{15}\) in the expansion of \(\left( a x^3+\frac{1}{ b x^{1 / 3}}\right)^{15}\) is equal to the coefficient of \(x^{-15}\) in the expansion of \(\left(a x^{1 / 3}-\frac{1}{b x^3}\right)^{15}\), where \(a\) and \(b\) are positive real numbers, then for each such ordered pair \(( a , b )\) : [JEE Main 2023 (Online) 30th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { For }\left(a x^3+\frac{1}{b x^{\frac{1}{3}}}\right) \\
& T_{r+1}={ }^{15} C_r\left(a x^3\right)^{15-r}\left(\frac{1}{b x^{\frac{1}{3}}}\right)^1 \\
& \therefore x^{15} \rightarrow 3(15-r)-\frac{r}{3}=15 \\
& \Rightarrow 30=\frac{10 r}{3} \Rightarrow r=9
\end{aligned}
\)
Similarly, for \(\left(a x^{\frac{1}{3}}-\frac{1}{b x^3}\right)^{15}\)
\(
T_{r+1}={ }^{15} C_r\left(a x^{\frac{1}{3}}\right)^{15-r}\left(-\frac{1}{b x^3}\right)^r
\)
\(\therefore\) For \(x^{-15} \rightarrow \frac{15-r}{3}-3 r=-15 \Rightarrow r=6\)
\(
\therefore{ }^{15} C_9 \frac{a^6}{b^9}={ }^{15} C_6 \frac{a^9}{b^6} \Rightarrow a b=1
\) -
Question 173 of 226
173. Question
The coefficient of \(x^{301}\) in \((1+x)^{500}+x(1+x)^{499}+x^2(1+x)^{498}+\ldots+x^{500}\) is : [JEE Main 2023 (Online) 30th January Morning Shift]
CorrectIncorrectHint
The coefficient of \(x^{301}\) in
\(
\begin{aligned}
& (1+x)^{500}+x(1+x)^{499}+x^2(1+x)^{498}+\ldots+x^{500} \\
& { }^{500} C_{301}+{ }^{499} C_{300}+{ }^{498} C_{299}+\ldots+{ }^{199} C_0 \\
& ={ }^{500} C_{199}+{ }^{499} C_{199}+{ }^{498} C_{199}+\ldots+{ }^{199} C_{199} \\
& ={ }^{501} C_{200}
\end{aligned}
\) -
Question 174 of 226
174. Question
Let \(K\) be the sum of the coefficients of the odd powers of \(x\) in the expansion of \((1+x)^{99}\). Let \(a\) be the middle term in the expansion of \(\left(2+\frac{1}{\sqrt{2}}\right)^{200}\). If \(\frac{{ }^{200} C_{99} K}{a}=\frac{2^l m}{n}\), where \(m\) and \(n\) are odd numbers, then the ordered pair \((l, n )\) is equal to [JEE Main 2023 (Online) 29th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& K=2^{98} \\
& a={ }^{200} C_{100} 2^{50} \\
& \therefore{ }^{200} C_{99} \cdot 2^{98} C_{100} \cdot 2^{50}=\frac{2^l m}{n} \\
& \Rightarrow \frac{100}{101} \cdot 2^{48}=\frac{2^l m}{n} \\
& \Rightarrow \frac{25}{101} \cdot 2^{50}=\frac{2^l m}{n} \\
& \therefore l=50, m=25, n=101
\end{aligned}
\) -
Question 175 of 226
175. Question
If \(a_r\) is the coefficient of \(x^{10-r}\) in the Binomial expansion of \((1+x)^{10}\), then \(\sum_{r=1}^{10} r^3\left(\frac{a_r}{a_{r-1}}\right)^2\) is equal to [JEE Main 2023 (Online) 25th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& a _{ r }={ }^{10} C _{10- r }={ }^{10} C _{ r } \\
& \Rightarrow \sum_{ r =1}^{10} r ^3\left(\frac{{ }^{10} C _{ r }}{{ }^{10} C _{ r -1}}\right)^2=\sum_{ r =1}^{10} r ^3\left(\frac{11- r }{ r }\right)^2=\sum_{ r =1}^{10} r (11- r )^2 \\
& =\sum_{ r =1}^{10}\left(121 r + r ^3-22 r ^2\right)=1210
\end{aligned}
\) -
Question 176 of 226
176. Question
If \(\left({ }^{30} C_1\right)^2+2\left({ }^{30} C_2\right)^2+3\left({ }^{(30} C_3\right)^2+\ldots+30\left({ }^{30} C_{30}\right)^2=\frac{\alpha 60!}{(30!)^2}\) then \(\alpha\) is equal to : [JEE Main 2023 (Online) 24th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S =0 \cdot\left({ }^{30} C _0\right)^2+1 \cdot\left({ }^{30} C _1\right)^2+2 \cdot\left({ }^{30} C _2\right)^2+\ldots \ldots+30 \cdot\left({ }^{30} C _{30}\right)^2 \\
& S =30 \cdot\left({ }^{30} C _0\right)^2+29 \cdot\left({ }^{30} C _1\right)^2+28 \cdot\left({ }^{30} C _2\right)^2+\ldots .+0 \cdot\left({ }^{30} C _0\right)^2 \\
& 2 S =30 \cdot\left({ }^{30} C _0{ }^2+{ }^{30} C _1{ }^2+\ldots \ldots .+{ }^{30} C _{30}{ }^2\right) \\
& S =15 \cdot{ }^{60} C _{30}=15 \cdot \frac{60!}{(30!)^2} \\
& \frac{15 \cdot 10!}{(30!)^2}=\frac{\alpha \cdot 60!}{(30!)^2} \\
& \Rightarrow \alpha=15
\end{aligned}
\)Alternate:
\(
\begin{aligned}
& 1 \cdot\left({ }^{30} C_1\right)^2+2 \cdot\left({ }^{30} C_2\right)^2+3 \cdot\left({ }^{30} C_3\right)^2+\ldots \ldots+30 \cdot\left({ }^{30} C_{30}\right)^2 \\
& =\sum_{r=1}^{30} r \cdot\left({ }^{30} C_r\right)^2 \\
& =\sum_{r=1}^{30} r \cdot{ }^{30} C_r \cdot{ }^{30} C_r \\
& =\sum_{r=1}^{30} r \cdot \frac{30}{r} \cdot{ }^{29} C_{r-1} \cdot{ }^{30} C_r \\
& =30 \sum_{r=1}^{30}{ }^{29} C_{r-1} \cdot{ }^{30} C_r
\end{aligned}
\)
\(
\begin{aligned}
& =30 \times\left(\text { Coefficient of } x^{29} \text { in }(1+x)^{59}\right) \\
& =30 \times\left({ }^{59} C_{29}\right) \\
& =30 \times \frac{60}{30} \times{ }^{59} C_{29} \times \frac{30}{60} \\
& =30 \times{ }^{60} C_{30} \times \frac{30}{60} \\
& =15 \times \frac{60!}{30!30!} \\
& \therefore \alpha=15
\end{aligned}
\) -
Question 177 of 226
177. Question
The value of \(\sum_{r=0}^{22}{ }^{22} C_r{ }^{23} C_r\) is [JEE Main 2023 (Online) 24th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{r=0}^{22}{ }^{22} C_r \cdot{ }^{23} C_r \\
& =\sum_{r=0}^{22}{ }^{22} C_r{ }^{23} C_{23-r}\left[\text { using }{ }^n C_r={ }^n C_{n-r}\right] \\
& ={ }^{22} C_0{ }^{23} C_{23}+{ }^{22} C_1{ }^{23} C_{22}+\ldots+{ }^{22} C_{21}{ }^{23} C_2+{ }^{22} C_{22}{ }^{23} C_1
\end{aligned}
\)
We know,
\(
(1+x)^{22}={ }^{22} C_0+{ }^{22} C_1 x+{ }^{22} C_2 x^2+{ }^{22} C_3 x^3+\ldots+{ }^{22} C_{22} x^{22}
\)
and \((1+x)^{23}={ }^{23} C_0+{ }^{23} C_1 x+{ }^{23} C_2 x^2+\ldots+{ }^{23} C_{22} x^{22}+{ }^{23} C_{23} x^{23}\)
Now coefficient of \(x^{23}\) in \((1+x)^{22}(1+x)^{23}\) or \((1+x)^{45}\)
\(
\begin{aligned}
& ={ }^{22} C_0{ }^{23} C_{23}+{ }^{22} C_1{ }^{23} C_{22}+\ldots+{ }^{22} C_{21} \cdot{ }^{23} C_2+{ }^{22} C_{22} \cdot{ }^{23} C_1 \\
& =\sum_{r=0}^{22}{ }^{22} C_r \cdot{ }^{23} C_{23-r}
\end{aligned}
\)
\(\therefore\) Coefficient of \(x^{23}\) in \((1+x)^{45}={ }^{45} C_{23}\) -
Question 178 of 226
178. Question
\(\sum_{r=1}^{20}\left(r^2+1\right)(r!) \text { is equal to }\) [JEE Main 2022 (Online) 29th July Evening Shift]
CorrectIncorrectHint
Given,
\(
\begin{aligned}
& \sum_{r=1}^{20}\left(r^2+1\right)(r!) \\
& \text { Let, } f(r)=\left(r^2+1\right)(r!) \\
& =\left(r^2\right)(r!)+r! \\
& =r(r r!)+r! \\
& =r[(r+1-1) r!]+r! \\
& =r[(r+1) r!-r!]+r! \\
& =r[(r+1)!-(r!)]+r! \\
& =r(r+1)!-r(r!)+r! \\
& =(r+2-2)(r+1)!-r(r!)+r! \\
& =(r+2)(r+1)!-2(r+1)!-[(r+1-1)(r!)]+r! \\
& =(r+2)!-2(r+1)!-(r+1)!+r!+r! \\
& =(r+2)!-3(r+1)!+2 r! \\
& =[(r+2)!-(r+1)!]-2[(r+1)!-r!]
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \sum_{r=1}^{20} f(r) \\
& =\sum_{r=1}^{20}[(r+2)!-(r+1)!]-2 \sum_{r=1}^{20}[(r+1)!-r!]
\end{aligned}
\)
\(
=[(22!+21!+20!+\ldots \ldots+4!+3!)-(21!+20!+19!+\ldots .+3!+2!]-2[(21!+20!+\ldots \ldots+3!+2!)-(20!+19!+\ldots \ldots 1!)]
\)
\(
\begin{aligned}
& =[(22!)-(2!)]-2[(21)!-(1!)] \\
& =22!-2!-2 \cdot(21)!+2 \cdot 1! \\
& =22!-2 \cdot(21)!
\end{aligned}
\) -
Question 179 of 226
179. Question
The remainder when \(7^{2022}+3^{2022}\) is divided by 5 is : [JEE Main 2022 (Online) 28th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 7^{2022}+3^{2022} \\
& =\left(7^2\right)^{1011}+\left(3^2\right)^{1011} \\
& =(50-1)^{1011}+(10-1)^{1011} \\
& =\left(50^{1011}-1011.50^{1010}+\ldots-1\right) \\
& +\left(10^{1011}-1011.10^{1010}+\ldots \ldots-1\right) \\
& =5 m-1+5 n-1=5(m+n)-2 \\
& =5(m+n)-5+3=5(m+n-1)+3 \\
& =5 k+3 \\
& \therefore \text { Remainder }=3
\end{aligned}
\) -
Question 180 of 226
180. Question
The remainder when \((2021)^{2022}+(2022)^{2021}\) is divided by 7 is [JEE Main 2022 (Online) 27th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& (2021)^{2022}+(2022)^{2021} \\
& =(7 k-2)^{2022}+\left(7 k_1-1\right)^{2021} \\
& =\left[(7 k-2)^3\right]^{674}+\left(7 k_1\right)^{2021}-2021\left(7 k_1\right)^{2020}+\ldots .-1 \\
& =\left(7 k_2-1\right)^{674}+(7 m-1) \\
& =(7 n+1)+(7 m-1)=7(m+n) \text { (multiple of } 7 \text { ) } \\
& \therefore \text { Remainder }=0
\end{aligned}
\) -
Question 181 of 226
181. Question
\(\sum_{i, j=0}^n { }^n C_i{ }^n C_j \text { is equal to }, i \neq j\) [JEE Main 2022 (Online) 26th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{i, j=0}^n{ }_{i \neq j}^n C_i{ }^n C_j=\sum_{i, j=0}^n{ }^n C_i{ }^n C_j-\sum_{i=j}^n{ }^n C_i{ }^n C_j \\
& =\sum_{j=0}^n{ }^n C_i \sum_{j=0}^n{ }^n C_j-\sum_{i=0}^n{ }^n C_i C_i \\
& =2^n \cdot 2^n-{ }^{2 n} C_n \\
& =2^{2 n}-{ }^{2 n} C_n \\
&
\end{aligned}
\) -
Question 182 of 226
182. Question
The remainder when \((11)^{1011}+(1011)^{11}\) is divided by 9 is [JEE Main 2022 (Online) 25th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \operatorname{Re}\left(\frac{(11)^{1011}+(1011)^{11}}{9}\right)=\operatorname{Re}\left(\frac{2^{1011}+3^{11}}{9}\right) \\
& \text { For } \operatorname{Re}\left(\frac{2^{1011}}{9}\right)
\end{aligned}
\)
\(
2^{1011}=(9-1)^{337}={ }^{337} C_0 9^{337}(-1)^0+{ }^{337} C_1 9^{336}(-1)^1+{ }^{337} C_2 9^{335}(-1)^2+\ldots \ldots+{ }^{337} C_{337} 9^0(-1)^{337}
\)
So, remainder is 8 and \(\operatorname{Re}\left(\frac{3^{11}}{9}\right)=0\)
So, remainder is 8. -
Question 183 of 226
183. Question
For two positive real numbers \(a\) and \(b\) such that \(\frac{1}{a^2}+\frac{1}{b^3}=4\), then minimum value of the constant term in the expansion of \(\left(a x^{\frac{1}{8}}+b x^{-\frac{1}{12}}\right)^{10}\) is : [JEE Main 2022 (Online) 30th June Morning Shift]
CorrectIncorrectHint
Given, Binomial expansion,
\(
\left(a x^{\frac{1}{8}}+b x^{-\frac{1}{12}}\right)^{10}
\)
General term,
\(
\begin{aligned}
& T_{r+1}={ }^{10} C_r \cdot\left(a x^{\frac{1}{8}}\right)^{10-r} \cdot\left(b x^{-\frac{1}{12}}\right)^r \\
& ={ }^{10} C_r \cdot a^{10-r} \cdot b^r \cdot x^{\frac{10-r}{8}} \cdot x^{-\frac{r}{12}} \\
& ={ }^{10} C_r \cdot a^{10-r} \cdot b^r \cdot x^{\left(\frac{10-r}{8}-\frac{r}{12}\right)} \\
& ={ }^{10} C_r \cdot a^{10-r} \cdot b^r \cdot x^{\frac{30-3 r-2 r}{24}} \\
& ={ }^{10} C_r \cdot a^{10-r} \cdot b^r \cdot x^{\frac{30-5 r}{24}}
\end{aligned}
\)
For constant term,
\(
\begin{aligned}
& \frac{30-5 r}{24}=0 \\
& \Rightarrow r=6
\end{aligned}
\)
\(\therefore\) Constant term,
\(
\begin{aligned}
& T_{r+1}=T_{6+1}={ }^{10} C_6 \cdot a^4 \cdot b^6 \\
& =\frac{10!}{6!4!} a^4 \cdot b^6 \\
& =\frac{10 \times 9 \times 8 \times 7}{4 \times 3 \times 2 \times 1} \cdot a^4 \cdot b^6 \\
& =210 a^4 b^6
\end{aligned}
\)
We know, \(G M \geq H M\)
For terms \(a ^2\) and \(b ^3\),
\(
\begin{aligned}
& \sqrt{a^2 b^3} \geq \frac{2}{\frac{1}{a^2}+\frac{1}{b^3}} \\
& \Rightarrow \sqrt{a^2 b^3} \geq \frac{2}{4} \\
& \Rightarrow a^2 b^3 \geq \frac{1}{4} \\
& \Rightarrow\left(a^2 b^3\right)^2 \geq \frac{1}{16} \\
& \therefore a^4 b^6 \geq \frac{1}{16}
\end{aligned}
\)
\(\therefore\) Minimum value of \(a^4 b^6=\frac{1}{16}\)
\(\therefore\) Minimum value of constant term
\(
\begin{aligned}
& T_7=210 \times a^4 b^6 \\
& =210 \times \frac{1}{16} \\
& =\frac{105}{8}
\end{aligned}
\) -
Question 184 of 226
184. Question
Let \(n \geq 5\) be an integer. If \(9^n-8 n-1=64 \alpha\) and \(6^n-5 n-1=25 \beta\), then \(\alpha-\) \(\beta\) is equal to [JEE Main 2022 (Online) 29th June Evening Shift]
CorrectIncorrectHint
Given,
\(
\begin{aligned}
& 9^n-8 n-1=64 \alpha \\
& \Rightarrow \alpha=\frac{(1+8)^n-8 n-1}{64}
\end{aligned}
\)
\(
=\frac{\left({ }^n C_0 \cdot 1+{ }^n C_1 \cdot 8^1+{ }^n C_2 \cdot 8^2+\ldots . .+{ }^n C_n \cdot 8^n\right)-8 n-1}{8^2}
\)
\(
=\frac{1+8 n+{ }^n C_2 \cdot 8^2+\ldots .+{ }^n C_n \cdot 8^n-8 n-1}{8^2}
\)
\(
=\frac{{ }^n C_2 \cdot 8^2+{ }^n C_3 \cdot 8^3+\ldots . .+{ }^n C_n \cdot 8^n}{8^2}
\)
\(
={ }^n C_2+{ }^n C_3 \cdot 8+{ }^n C_4 \cdot 8^2+\ldots .{ }^n C_n \cdot 8^{n-2}
\)
Also given,
\(
\begin{aligned}
& 6^n-5 n-1=25 \beta \\
& \Rightarrow \beta=\frac{(1+5)^n-5 n-1}{25}
\end{aligned}
\)
\(
=\frac{{ }^n C_0 \cdot 1+{ }^n C_1 \cdot 5+{ }^n C_2 \cdot 5^2+\ldots . .+{ }^n C_n \cdot 5^n-5 n-1}{5^2}
\)
\(
=\frac{1+5 n+{ }^n C_2 \cdot 5^2+{ }^n C_3 \cdot 5^3+\ldots .+{ }^n C_n \cdot 5^2-5 n-1}{5^2}
\)
\(
=\frac{{ }^n C_2 \cdot 5^2+{ }^n C_3 \cdot 5^3+{ }^n C_4 \cdot 5^4+\ldots .+{ }^n C_n \cdot 5^n}{5^2}
\)
\(
\begin{aligned}
& ={ }^n C_2+{ }^n C_3 \cdot 5+{ }^n C_4 \cdot 5^2+\ldots \ldots+{ }^n C_n \cdot 5^{n-2} \\
& \therefore \alpha-\beta
\end{aligned}
\)
\(
=\left({ }^n C_2+{ }^n C_3 \cdot 8+{ }^n C_4 \cdot 8^2+\ldots .+{ }^n C_n \cdot 8^{n-2}\right)-\left({ }^n C_2+{ }^n C_3 \cdot 5\right.\left.+{ }^n C_4 \cdot 5^2+\ldots+{ }^n C_n \cdot 5^{n-2}\right)
\)
\(
={ }^n C_3 \cdot(8-5)+{ }^n C_4 \cdot\left(8^2-5^2\right)+\ldots+{ }^n C_n\left(8^{n-2}-5^{n-2}\right)
\) -
Question 185 of 226
185. Question
If the constant term in the expansion of \(\left(3 x^3-2 x^2+\frac{5}{x^5}\right)^{10}\) is \(2^{ k } . l\), where \(l\) is an odd integer, then the value of \(k\) is equal to: [JEE Main 2022 (Online) 29th June Morning Shift]
CorrectIncorrectHint
The general term of \(\left(x_1+x_2+\ldots+x_n\right)^n\) the expansion is
\(
\begin{aligned}
& \frac{n!}{n_{1}!n_{2}!\ldots n_{n}!} x_1^{n_1} x_2^{n_2} \ldots x_n^{n_n} \\
& \text { where } n _1+ n _2+\ldots .+ n _{ n }= n
\end{aligned}
\)
Given,
\(
\begin{aligned}
& \left(3 x^2-2 x^2+\frac{5}{x^5}\right)^{10} \\
& =\frac{\left(3 x^8-2 x^7+5\right)^{10}}{x^{50}}
\end{aligned}
\)
Now constant term in \(\left(3 x^3-2 x^2+\frac{5}{x^5}\right)^{10}=x^{50}\) term in \(\left(3 x^8-2 x^7+5\right)^{10}\)
General term in \(\left(3 x^8-2 x^7+5\right)^{10}\) is
\(
\begin{aligned}
& =\frac{10!}{n_{1}!n_{2}!n_{3}!}\left(3 x^8\right)^{n_1}\left(-2 x^7\right)^{n_2}(5)^{n_3} \\
& =\frac{10!}{n_{1}!n_{2}!n_{3}!}(3)^{n^1}(-2)^{n_2}(5)^{n^3} \cdot x^{8 n_1+7 n_2}
\end{aligned}
\)
\(\therefore\) Coefficient of \(x^{8 n_1+7 n_2}\) is
\(
=\frac{10!}{n_{1}!n_{2}!n_{3}!}(3)^{n_1}(-2)^{n_2}(5)^{n_3}
\)
where \(n_1+n_2+n_3=0\)
For coefficient of \(x ^{50}\) :
\(
8 n_1+7 n_2=50
\)
\(\therefore\) Possible values of \(n_1, n_2\) and \(n_3\) are
\(
\begin{array}{|c|c|c|}
\hline n_1 & n_2 & n_3 \\
\hline 1 & 6 & 3 \\
\hline
\end{array}
\)
\(
\begin{aligned}
& \therefore \text { Coefficient of } x ^{50} \\
& =\frac{10!}{1!6!3!}(3)^1(-2)^6(5)^3 \\
& =\frac{10 \times 9 \times 8 \times 7}{6} \times 3 \times 5^3 \times 2^6 \\
& =5 \times 3 \times 8 \times 7 \times 3 \times 5^3 \times 2^6 \\
& =7 \times 5^4 \times 3^2 \times 2^9 \\
& =2^k . l \\
& \therefore l=7 \times 5^4 \times 3^2=\text { An odd integer } \\
& \text { and } 2^k=2^9 \\
& \Rightarrow k=9
\end{aligned}
\) -
Question 186 of 226
186. Question
The term independent of \(x\) in the expansion of \(\left(1-x^2+3 x^3\right)\left(\frac{5}{2} x^3-\frac{1}{5 x^2}\right)^{11}, x \neq 0\) is : [JEE Main 2022 (Online) 28th June Evening Shift]
CorrectIncorrectHint
General term of Binomial expansion \(\left(\frac{5}{2} x^3-\frac{1}{5 x^2}\right)^{11}\) is
\(
\begin{aligned}
& T_{r+1}={ }^{11} C_r \cdot\left(\frac{5}{2} x^3\right)^{11-r} \cdot\left(-\frac{1}{5 x^2}\right)^r \\
& ={ }^{11} C_r \cdot\left(\frac{5}{2}\right)^{11-r} \cdot\left(-\frac{1}{5}\right)^r \cdot x^{33-5 r}
\end{aligned}
\)
In the term,
\(
\left(1-x^2+3 x^3\right)\left(\frac{5}{2} x^3-\frac{1}{5 x^2}\right)^{11}
\)
Term independent of \(x\) is when
(1) \(33-5 r=0\)
\(\Rightarrow r=\frac{33}{5} \notin\) integer
(2) \(33-5 r=-2\)
\(\Rightarrow 5 r=35\)
\(\Rightarrow r=7 \in\) integer
(3) \(33-5 r=-3\)
\(\Rightarrow 5 r=36\)
\(\Rightarrow r=\frac{36}{5} \notin\) integer
\(\therefore\) Only for \(r=7\) independent of \(x\) term possible.
\(\therefore\) Independent of \(x\) term
\(
\begin{aligned}
& =-\left({ }^{11} C_7\left(\frac{5}{2}\right)^4 \cdot\left(-\frac{1}{5}\right)^7\right) \\
& =-\left(\frac{11 \cdot 10 \cdot 9 \cdot 8}{4 \cdot 3 \cdot 2 \cdot 1} \cdot \frac{5^4}{2^4} \cdot-\frac{1}{5^7}\right) \\
& =\frac{11 \cdot 10 \cdot 3}{2^4 \cdot 5^3} \\
& =\frac{11 \cdot 3}{2^3 \cdot 5^2} \\
& =\frac{33}{200}
\end{aligned}
\) -
Question 187 of 226
187. Question
If \(\sum_{k=1}^{31}\left({ }^{31} C_k\right)\left({ }^{31} C_{k-1}\right)-\sum_{k=1}^{30}\left({ }^{30} C_k\right)\left({ }^{30} C_{k-1}\right)=\frac{\alpha(60!)}{(30!)(31!)}\) where \(\alpha \in R\), then the value of \(16 \alpha\) is equal to [JEE Main 2022 (Online) 28th June Morning Shift]
CorrectIncorrectHint
Given,
\(
\sum_{k=1}^{31}\left({ }^{31} C_k\right)\left({ }^{31} C_{k-1}\right)-\sum_{k=1}^{30}\left({ }^{30} C_k\right)\left({ }^{30} C_{k-1}\right)=\frac{\alpha(60!)}{(30!)(31!)}
\)
Now,
\(
\begin{aligned}
& \sum_{k=1}^{31}\left({ }^{31} C_k\right)\left({ }^{31} C_{k-1}\right) \\
& =\left({ }^{31} C_1 \cdot{ }^{31} C_0+{ }^{31} C_2 \cdot{ }^{31} C_1+{ }^{31} C_3 \cdot{ }^{31} C_2+\ldots \ldots+{ }^{31} C_{31} \cdot{ }^{31} C_{30}\right) \\
& =\left({ }^{31} C_0 \cdot{ }^{31} C_{31-1}+{ }^{31} C_1 \cdot{ }^{31} C_{31-2}+\ldots \ldots+{ }^{31} C_{30} \cdot{ }^{31} C_{31-31}\right) \\
& \text { [using }{ }^n C_r={ }^n C_{n-r} \text { ] } \\
& =\left({ }^{31} C_0 \cdot{ }^{31} C_{30}+{ }^{31} C_1 \cdot{ }^{31} C_{29}+\ldots \ldots+{ }^{31} C_{30} \cdot{ }^{31} C_0\right) \\
& ={ }^{62} C_{30}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Now, } \sum_{k=1}^{30}{ }^{30} C_k \cdot{ }^{30} C_{k-1} \\
& =\left({ }^{30} C_1 \cdot{ }^{30} C_0+{ }^{30} C_2 \cdot{ }^{30} C_1+\ldots \ldots+{ }^{30} C_{30} \cdot{ }^{30} C_{29}\right) \\
& =\left({ }^{30} C_0 \cdot{ }^{30} C_{29}+{ }^{30} C_1 \cdot{ }^{30} C_{28}+\ldots \ldots+{ }^{30} C_{29} \cdot{ }^{30} C_0\right) \\
& ={ }^{60} C_{29}
\end{aligned}
\)
\(
\begin{aligned}
& \therefore{ }^{60} C_{30}-{ }^{60} C_{29}=\frac{\alpha(60!)}{30!31!} \\
& \Rightarrow \frac{62.61 \cdot 60!}{30!32!}-\frac{60!}{29!31!}=\frac{\alpha(60!)}{30!31!} \\
& \Rightarrow \frac{62.61 \cdot 60!}{30!32!}-\frac{60!}{\frac{30!}{30} \cdot 31!}=\frac{\alpha(60!)}{30!31!}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \frac{60!}{30!31!}\left(\frac{62.61}{32}-30\right)=\frac{\alpha(60!)}{30!31!} \\
& \Rightarrow \alpha=\frac{62.61}{32}-30 \\
& \Rightarrow 16 \alpha=\frac{62.61-30 \times 32}{2} \\
& \Rightarrow 16 \alpha=\frac{2822}{2}=1411
\end{aligned}
\) -
Question 188 of 226
188. Question
The remainder when \((2021)^{2023}\) is divided by 7 is : [JEE Main 2022 (Online) 26th June Morning Shift]
CorrectIncorrectHint
\(
(2021)^{2023}
\)
\(=(2016+5)^{2023}\) [here 2016 is divisible by 7]
\(
\begin{aligned}
& ={ }^{2023} C_0(2016)^{2023}+\ldots \ldots \ldots .+{ }^{2023} C_{2022}(2016)(5)^{2022}+{ }^{2023} C_{2023}(5)^{2023} \\
& =2016\left[{ }^{2023} C_0 \cdot(2016)^{2022}+\ldots \ldots . .+{ }^{2023} C_{2022} \cdot(5)^{2022}\right]+(5)^{2023}
\end{aligned}
\)
\(
\begin{aligned}
& =2016 \lambda+(5)^{2023} \\
& =7 \times 288 \lambda+(5)^{2023}
\end{aligned}
\)
\(
=7 K+(5)^{2023} \dots(1)
\)
Now, \((5)^{2023}\)
\(
\begin{aligned}
& =(5)^{2022} \cdot 5 \\
& =\left(5^3\right)^{674} \cdot 5 \\
& =(125)^{674} \cdot 5 \\
& =(126-1)^{674} \cdot 5
\end{aligned}
\)
\(
=5\left[{ }^{674} C_0(126)^{674}+\ldots \ldots \ldots . .-{ }^{674} C_{673}(126)+{ }^{674} C_{674}\right]
\)
\(
\begin{aligned}
& =5 \times 126\left[{ }^{674} C_0(126)^{673}+\ldots \ldots .-{ }^{674} C_{673}\right]+5 \\
& =5.7 .18\left[{ }^{674} C_0(126)^{673}+\ldots \ldots .-{ }^{674} C_{673}\right]+5 \\
& =7 \lambda+5
\end{aligned}
\)
Replacing (5) \({ }^{2023}\) in equation (1) with \(7 \lambda+5\), we get,
\(
\begin{aligned}
& (2021)^{2023}=7 K+7 \lambda+5 \\
& =7(K+\lambda)+5
\end{aligned}
\)
\(\therefore\) Remainder \(=5\) -
Question 189 of 226
189. Question
The coefficient of \(x ^{101}\) in the expression \((5+x)^{500}+x(5+x)^{499}+x^2(5+x)^{498}+\ldots . .+x^{500}, x >0\), is [JEE Main 2022 (Online) 25th June Evening Shift]
CorrectIncorrectHint
Given,
\(
(5+x)^{500}+x(5+x)^{499}+x^2(5+x)^{498}+\ldots \ldots . . x^{500}
\)
This is a G.P. with first term \((5+x)^{500}\)
Common ratio \(=\frac{x(5+x)^{499}}{(5+x)^{500}}=\frac{x}{5+x}\) and 501 terms present.
\(
\begin{aligned}
& \therefore \text { Sum }=\frac{(5+x)^{500}\left(\left(\frac{x}{5+x}\right)^{501}-1\right)}{\frac{x}{5+x}-1} \\
& =\frac{(5+x)^{500}\left(\frac{x^{501}-(5+x)^{501}}{(5+x)^{501}}\right)}{\frac{x-5-x}{5+x}} \\
& =\frac{\frac{x^{501}-(5+x)^{501}}{5+x}}{\frac{-5}{5+x}}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{5}\left((5+x)^{501}-x^{501}\right) \\
& \text { Coefficient of } x ^{101} \text { in }(5+x)^{501} \text { is }={ }^{501} C_{101} \cdot 5^{400} \\
& \therefore \ln \frac{1}{5}\left((5+x)^{500}-x^{501}\right) \text { coefficient of } x { }^{101} \text { is }=\frac{1}{5} \cdot{ }^{501} C_{101} \cdot 5^{400} \\
& ={ }^{501} C_{101} \cdot 5^{399}
\end{aligned}
\) -
Question 190 of 226
190. Question
If \(\frac{1}{2.3^{10}}+\frac{1}{2^2 .3^9}+\ldots \ldots+\frac{1}{2^{10} .3}=\frac{K}{2^{10} .3^{10}}\), then the remainder when \(K\) is divided by 6 is : [JEE Main 2022 (Online) 25th June Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{1}{2 \cdot 3^{10}}+\frac{1}{2^2 \cdot 3^9}+\ldots+\frac{1}{2^{10} \cdot 3}=\frac{K}{2^{10} \cdot 3^{10}} \\
& \Rightarrow \frac{1}{2 \cdot 3^{10}}\left[\frac{\left(\frac{3}{2}\right)^{10}-1}{\frac{3}{2}-1}\right]=\frac{K}{2^{10} \cdot 3^{10}} \\
& =\frac{3^{10}-2^{10}}{2^{10} \cdot 3^{10}}=\frac{K}{2^{10} \cdot 3^{10}} \Rightarrow K=3^{10}-2^{10}
\end{aligned}
\)
Now \(K=(1+2)^{10}-2^{10}\)
\(
\begin{aligned}
& ={ }^{10} C_0+{ }^{10} C_1 2+{ }^{10} C_2 2^3+\ldots .+{ }^{10} C_{10} 2^{10}-2^{10} \\
& ={ }^{10} C_0+{ }^{10} C_1 2+6 \lambda+{ }^{10} C_9 \cdot 2^9 \\
& =1+20+5120+6 \lambda \\
& =5136+6 \lambda+5 \\
& =6 \mu+5 \\
& \lambda, \mu \in N \\
& \therefore \text { remainder }=5
\end{aligned}
\) -
Question 191 of 226
191. Question
The remainder when \(3^{2022}\) is divided by 5 is : [JEE Main 2022 (Online) 24th June Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 3^{2022} \\
& =\left(3^2\right)^{1011} \\
& =(9)^{1011} \\
& =(10-1)^{1011}
\end{aligned}
\)
\(
={ }^{1011} C_0(10)^{1011}+\ldots \ldots+{ }^{1011} C_{1010} \cdot(10)^1-{ }^{1011} C_{1011}
\)
\(
=10\left[{ }^{1011} C_0(10)^{1010}+\ldots \ldots+{ }^{1011} C_{1010}\right]-1
\)
\(
=10 K-1
\)
[As \(10\left[{ }^{1011} C_0 \cdot(10)^{1010}+\ldots \ldots+{ }^{1011} C_{1010}\right]\) is multiple of 10 ]
\(
\begin{aligned}
& =10 K+5-5-1 \\
& =10 K-5+5-1 \\
& =5(2 K-1)+4
\end{aligned}
\)
\(\therefore\) Unit digit \(=4\) when divided by 5 . -
Question 192 of 226
192. Question
\(\sum_{k=0}^{20}\left({ }^{20} C_k\right)^2 \text { is equal to : }\) [JEE Main 2021 (Online) 27th August Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{k=0}^{20}\left({ }^{20} C_k\right)^2 \\
& =\left({ }^{20} C_0\right)^2+\left({ }^{20} C_1\right)^2+\left({ }^{20} C_2\right)^2+\ldots+\left({ }^{20} C_{20}\right)^2 \\
& ={ }^{40} C_{20}
\end{aligned}
\)Using the formula :
\(
\left({ }^n C_0\right)^2+\left({ }^n C_1\right)^2+\left({ }^n C_2\right)^2+\ldots+\left({ }^n C_n\right)^2={ }^{2 n} C_n
\) -
Question 193 of 226
193. Question
If \({ }^{20} C_r\) is the co-efficient of \(x ^{r}\) in the expansion of \((1+ x )^{20}\), then the value of \(\sum_{r=0}^{20} r^2 \cdot{ }^{20} C_r\) is equal to : [JEE Main 2021 (Online) 26th August Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{r=0}^{20} r^2 \cdot{ }^{20} C_r \\
& \sum(4(r-1)+r) \cdot{ }^{20} C_r \\
& \sum r(r-1) \cdot \frac{20 \times 19}{r(r-1)} \cdot{ }^{18} C_r+r \cdot \frac{20}{r} \cdot \sum{ }^{19} C_{r-1} \\
& \Rightarrow 20 \times 19.2^{18}+20.2^{19} \\
& \Rightarrow 420 \times 2^{18}
\end{aligned}
\) -
Question 194 of 226
194. Question
A possible value of ‘ \(x\) ‘, for which the ninth term in the expansion of \(\left\{3^{\log _3 \sqrt{25^{x-1}+7}}+3^{\left(-\frac{1}{8}\right) \log _3\left(5^{x-1}+1\right)}\right\}^{10}\) in the increasing powers of \(3^{\left(-\frac{1}{8}\right) \log _3\left(5^{x-1}+1\right)}\) is equal to 180 , is : [JEE Main 2021 (Online) 27th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& { }^{10} C_8\left(25^{(x-1)}+7\right) \times\left(5^{(x-1)}+1\right)^{-1}=180 \\
& \Rightarrow \frac{25^{x-1}+7}{5^{(x-1)}+1}=4
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \frac{t^2+7}{t+1}=4 ; \\
& \Rightarrow t =1,3=5^{x-1}
\end{aligned}
\)
\(\Rightarrow x-1=0\) (one of the possible value).
\(
\Rightarrow x =1
\) -
Question 195 of 226
195. Question
If the coefficients of \(x ^7\) in \(\left(x^2+\frac{1}{b x}\right)^{11}\) and \(x ^{-7}\) in \(\left(x-\frac{1}{b x^2}\right)^{11}, b \neq 0\), are equal, then the value of \(b\) is equal to : [JEE Main 2021 (Online) 27th July Morning Shift]
CorrectIncorrectHint
Coefficient of \(x ^7\) in \(\left(x^2+\frac{1}{b x}\right)^{11}\) :
General Term \(={ }^{11} C_r\left(x^2\right)^{11-r} \cdot\left(\frac{1}{b x}\right)^r\)
\(={ }^{11} C_r x^{22-3 r} \cdot \frac{1}{b^r}\)
\(22-3 r=7\)
\(r=5\)
\(\therefore\) Required Term \(={ }^{11} C_5 \cdot \frac{1}{b^5} \cdot x^7\)
Coefficient of \(x ^{-7}\) in \(\left(x-\frac{1}{b x^2}\right)^{11}\) :
General Term \(={ }^{11} C_r(x)^{11-r} \cdot\left(-\frac{1}{b x^2}\right)^r\)
\(={ }^{11} C_r x^{11-3 r} \cdot \frac{(-1)^r}{b^r}\)
\(11-3 r=-7 \therefore r=6\)
\(\therefore\) Required Term \(={ }^{11} C_6 \cdot \frac{1}{b^6} x^{-7}\)According to the question,
\({ }^{11} C_5 \cdot \frac{1}{b^5}={ }^{11} C_6 \cdot \frac{1}{b^6}\)
Since, \(b \neq 0 \therefore b=1\) -
Question 196 of 226
196. Question
The sum of all those terms which are rational numbers in the expansion of \(\left(2^{1 / 3}+3^{1 / 4}\right)^{12}\) is : [JEE Main 2021 (Online) 25th July Evening Shift]
CorrectIncorrectHint
\(
T_{r+1}={ }^{12} C_r\left(2^{1 / 3}\right)^r \cdot\left(3^{1 / 4}\right)^{12-4}
\)
\(T_{r+1}\) will be rational number when \(r=0,3,6,9,12 \text { and } r=0,4,8,12\)
\(
\begin{aligned}
& \Rightarrow r =0,12 \\
& T _1+ T _{13}=1 \times 3^3+1 \times 2^4 \times 1 \\
& =27+16=43
\end{aligned}
\) -
Question 197 of 226
197. Question
If the greatest value of the term independent of ‘ \(x\) ‘ in the expansion of \(\left(x \sin \alpha+a \frac{\cos \alpha}{x}\right)^{10}\) is \(\frac{10!}{(5!)^2}\), then the value of ‘a’ is equal to : [JEE Main 2021 (Online) 25th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T_{r+1}={ }^{10} C_r(x \sin \alpha)^{10-r}\left(\frac{a \cos \alpha}{x}\right)^r \\
& r =0,1,2, \ldots \ldots ., 10
\end{aligned}
\)
\(T_{r+1}\) will be independent of \(x\) when \(10-2 r=0 \Rightarrow r=5\)
\(
\begin{aligned}
& T_6={ }^{10} C_5(x \sin \alpha)^5 \times\left(\frac{a \cos \alpha}{x}\right)^5 \\
& ={ }^{10} C_5 \times a^5 \times \frac{1}{2^5}(\sin 2 \alpha)^5
\end{aligned}
\)
will be greatest when \(\sin 2 \alpha=1\)
\(
\Rightarrow{ }^{10} C_5 \frac{a^5}{2^5}={ }^{10} C_5 \Rightarrow a=2
\) -
Question 198 of 226
198. Question
The lowest integer which is greater than \(\left(1+\frac{1}{10^{100}}\right)^{10^{100}}\) is ____. [JEE Main 2021 (Online) 25th July Evening Shift]
CorrectIncorrectHint
Let \(10^{100}=n\)
Then, \(\left(1+\frac{1}{n}\right)^n\)
\(
\begin{aligned}
& ={ }^n C_0+{ }^n C_1 \cdot \frac{1}{n}+{ }^n C_2 \cdot \frac{1}{n^2}+{ }^n C_3 \cdot \frac{1}{n^3}+\cdots \\
& =1+1+\frac{n(n-1)}{2 n^2}+\frac{n(n-1)(n-2)}{6 n^3}+\cdots \\
& \Rightarrow\left(1+\frac{1}{n}\right)^{n^n}>2
\end{aligned}
\)We know that
\(
\lim _{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^n=e \approx 2.72
\)Hence, lowest integer is 3 which is greater than \(\left(1+\frac{1}{10^{100}}\right)^{10^{100}}\)
-
Question 199 of 226
199. Question
If \(b\) is very small as compared to the value of \(a\), so that the cube and other higher powers of \(\frac{b}{a}\) can be neglected in the identity \(\frac{1}{a-b}+\frac{1}{a-2 b}+\frac{1}{a-3 b}+\ldots \ldots+\frac{1}{a-n b}=\alpha n+\beta n^2+\gamma n^3\), then the value of \(\gamma\) is : [JEE Main 2021 (Online) 25th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& (a-b)^{-1}+(a-2 b)^{-1}+\ldots+(a-n b)^{-1} \\
& =\frac{1}{a} \sum_{r=1}^n\left(1-\frac{r b}{a}\right)^{-1} \\
& =\frac{1}{a} \sum_{r=1}^n\left\{\left(1+\frac{r b}{a}+\frac{r^2 b^2}{a^2}\right)+(\text { terms to be neglected })\right\} \\
& =\frac{1}{a}\left[n+\frac{n(n+1)}{2} \cdot \frac{b}{a}+\frac{n(n+1)(2 n+1)}{6} \cdot \frac{b^2}{a^2}\right] \\
& =\frac{1}{a}\left[n^3\left(\frac{b^2}{3 a^2}\right)+\ldots .\right]
\end{aligned}
\)So, \(\gamma=\frac{b^2}{3 a^3}\)
-
Question 200 of 226
200. Question
For the natural numbers \(m, n\), if \((1-y)^m(1+y)^n=1+a_1 y+a_2 y^2+\ldots+a_{m+n} y^{m+n}\) and \( a_1=a_2=10 \text {, then the value of }( m + n ) \text { is equal to : }\) [JEE Main 2021 (Online) 20th July Evening Shift]
CorrectIncorrectHint
\(
(1-y)^m(1+y)^n=1+a_1 y+a_2 y^2+\ldots+a_{m+n} y^{m+n}
\)
Given, \(\left(a_1=a_2=10\right)\)
\(
\left(1-m y+{ }^m C_2 y^2+\ldots \ldots\right)\left(1+n y+{ }^n C_2 y^2+\ldots \ldots\right)=1+a_1 y+a_2 y^2+\ldots
\)
\(
\begin{aligned}
& \Rightarrow n-m=10 \ldots . . \text { (i) } \\
& \Rightarrow{ }^m C_2+{ }^n C_2-m n=10 \ldots \ldots \text { (ii) } \\
& \frac{m(m-1)}{2}+\frac{n(n-1)}{2}-m n=10 \\
& \Rightarrow \frac{m^2-m}{2}+\frac{(10+m)(9+m)}{2}-m(10+m)=10 \\
& \Rightarrow m^2-m+m^2+19 m+90-2\left(m^2+10 m\right)=20 \\
& \Rightarrow 18 m+90-20 m=20 \\
& \Rightarrow 2 m=70 \\
& \Rightarrow m=35 \& n=45 \\
& m+n=80
\end{aligned}
\) -
Question 201 of 226
201. Question
The coefficient of \(x^{256}\) in the expansion of \((1-x)^{101}\left(x^2+x+1\right)^{100}\) is : [JEE Main 2021 (Online) 20th July Morning Shift]
CorrectIncorrectHint
\(
(1-x)^{101}\left(x^2+x+1\right)^{100}
\)
Coefficient of
\(
\begin{aligned}
& x^{256}=\left[(1-x)\left(1+x+x^2\right)\right]^{100}(1-x)=\left(1-x^3\right)^{100}(1-x) \\
& \Rightarrow\left({ }^{100} C_0-{ }^{100} C_1 x^3+{ }^{100} C_2 x^6-{ }^{100} C_3 x^9 \ldots\right)(1-x)
\end{aligned}
\)
\(
\begin{aligned}
& \sum(-1)^r 100 C_r x^{3 r}(1-x) \\
& \Rightarrow 3 r=256 \text { or } 255 \Rightarrow r=\frac{256}{3} \text { (Reject) } \\
& r =85 \\
& \text { Coefficient }={ }^{100} C_{85}={ }^{100} C_{15}
\end{aligned}
\) -
Question 202 of 226
202. Question
Let \(\left(1+x+2 x^2\right)^{20}=a_0+a_1 x+a_2 x^2+\ldots .+a_{40} x^{40}\). Then \(a_1+a_3+a_5+\ldots . .+a_{37}\) is equal to [JEE Main 2021 (Online) 18th March Morning Shift]
CorrectIncorrectHint
\(
\left(1+x+2 x^2\right)^{20}=a_0+a_1 x+a_2 x^2+\ldots+a_{40} x^{40}
\)
Put \(x=1\)
\(
\Rightarrow 4^{20}=a_0+a_1+\ldots \ldots .+a_{40 \ldots} \text { (i) }
\)
Put \(x=-1\)
\(
\Rightarrow 2^{20}=a_0-a_1+\ldots \ldots+-a_{39}+a_{40} \ldots \ldots. (ii)
\)
by (i) – (ii) we get,
\(
\begin{aligned}
& 4^{20}-2^{20}=2\left(a_1+a_3+\ldots \ldots+a_{37}+a_{39}\right) \\
& \Rightarrow a_1+a_3+\ldots \ldots+a_{37}=2^{39}-2^{19}-a_{39} \ldots .(iii)
\end{aligned}
\)
\(
\begin{aligned}
& a_{39}=\text { coeff. } x^{39} \text { in }\left(1+x+2 x^2\right)^{20} \\
& =\frac{20!}{0!1!!}(1)^0(1)^1(2)^{19} \\
& =20.2^{19} \\
& \therefore a_1+a_3+\ldots \ldots+a_{37}=2^{39}-2^{19} .21 \\
& \Rightarrow 2^{19}\left(2^{20}-21\right)
\end{aligned}
\) -
Question 203 of 226
203. Question
The value of \(\sum_{r=0}^6 \left({ }^6 C_r \cdot{ }^6 C_{6-r}\right) \text { is equal to: }\) [JEE Main 2021 (Online) 17th March Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{r=0}^6{ }^6 C_r{ }^6 C_{6-r} \\
& ={ }^6 C_0 \cdot{ }^6 C_6+{ }^6 C_1 \cdot{ }^6 C_5+\ldots+{ }^6 C_6 \cdot{ }^6 C_0
\end{aligned}
\)
Now,
\(
\begin{aligned}
& =\left({ }^6 C_0+{ }^6 C_1 x+{ }^6 C_2 x^2+\ldots+{ }^6 C_6 x^6\right) \\
& \left({ }^6 C_0+{ }^6 C_1 x+{ }^6 C_2 x^2+\ldots+{ }^6 C_6 x^6\right)
\end{aligned}
\)
Comparing coefficient of \(x^6\) both sides
\(
\begin{aligned}
& { }^6 C_0 \cdot{ }^6 C_6+{ }^6 C_1 \cdot{ }^6 C_5+\ldots+{ }^6 C_6 \cdot{ }^6 C_0 \\
& ={ }^{12} C_6=924
\end{aligned}
\) -
Question 204 of 226
204. Question
If the fourth term in the expansion of \(\left(x+x^{\log _2 x}\right)^7\) is 4480 , then the value of \(x\) where \(x \in N\) is equal to : [JEE Main 2021 (Online) 17th March Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T _4={ }^7 C_3 x^4\left(x^{\log _2 x}\right)^3=4480 \\
& \Rightarrow 35 x^4\left(x^{\log _2 x}\right)^3=4480 \\
& \Rightarrow x^4\left(x^{\log _2 x}\right)^3=128
\end{aligned}
\)
take \(\log\) w.r.t. base 2 we get,
\(
\begin{aligned}
& 4 \log _2 x+3 \log _2\left(x^{\log _2 x}\right)=\log _2 128 \\
& \text { Let } \log _2 x=y \\
& 4 y+3 y^2=7 \\
& \Rightarrow y=1, \frac{-7}{3} \\
& \Rightarrow \log _2 x=1, \frac{-7}{3} \\
& \Rightarrow x=2, x=2^{-7 / 3}
\end{aligned}
\) -
Question 205 of 226
205. Question
If \(n\) is the number of irrational terms in the expansion of \(\left(3^{1 / 4}+5^{1 / 8}\right)^{60}\), then \((n-1)\) is divisible by: [JEE Main 2021 (Online) 16th March Morning Shift]
CorrectIncorrectHint
\(
T_{r+1}={ }^{60} C_r\left(3^{1 / 4}\right)^{60-r}\left(5^{1 / 8}\right)^r
\)
rational if \(\frac{60-r}{4}, \frac{r}{8}\), both are whole numbers, \(r \in\{0,1,2, \ldots \ldots 60\}\)
\(
\frac{60-r}{4} \in W \Rightarrow r \in\{0,4,8, \ldots .60\}
\)
and \(\frac{r}{8} \in W \Rightarrow r \in\{0,8,16, \ldots .56\}\)
\(\therefore\) Common terms \(r \in\{0,8,16, \ldots . .56\}\)
So, 8 terms are rational
Then Irrational terms \(=61-8=53=n\)
\(
\therefore n-1=52=13 \times 2^2
\)
Factors 1, 2, 4, 13, 26, 52 -
Question 206 of 226
206. Question
Let \([x]\) denote greatest integer less than or equal to \(x\). If for \(n \in N\),
\(
\left(1-x+x^3\right)^n=\sum_{j=0}^{3 n} a_j x^j
\)
then \(\sum_{j=0}^{\left[\frac{3 n}{2}\right]} a_{2 j}+4 \sum_{j=0}^{\left[\frac{3 n-1}{2}\right]} a_{2 j}+1\) is equal to : [JEE Main 2021 (Online) 16th March Morning Shift]CorrectIncorrectHint
\(
\begin{aligned}
& \left(1-x+x^3\right)^n=\sum_{j=0}^{3 n} a_j x^j \\
& \left(1-x+x^3\right)=a_0+a_1 x+a_2 x^2+\ldots \ldots+a_{3 n} x^{3 n}
\end{aligned}
\)
Put \(x=1\)
\(
1=a_0+a_1+a_2+a_3+a_4+\ldots \ldots \ldots+a_{3 n} \dots(1)
\)
Put \(x=-1\)
\(
1=a_0-a_1+a_2-a_3+a_4+\ldots \ldots \ldots(-1)^{3 n} a_{3 n} \ldots \ldots (2)
\)
Add (1) + (2)
\(
\Rightarrow a_0+a_2+a_4+a_6+\ldots \ldots=1
\)
Sub (1) – (2)
\(
\Rightarrow a_1+a_3+a_5+a_7+\ldots \ldots=0
\)
Now, \(\sum_{j=0}^{\left[\frac{3 n}{2}\right]} a_{2 j}+4 \sum_{j=0}^{\left[\frac{3 n-1}{2}\right]} a_{2 j}+1\)
\(
\begin{aligned}
& =\left(a_0+a_2+a_4+\ldots \ldots\right)+4\left(a_1+a_3+\ldots \ldots\right) \\
& =1+4 \times 0+1 \\
& =1+1=2
\end{aligned}
\) -
Question 207 of 226
207. Question
The maximum value of the term independent of ‘ \(t\) ‘ in the expansion of \(\left(t x^{\frac{1}{5}}+\frac{(1-x)^{\frac{1}{10}}}{t}\right)^{10}\) where \(x \in(0,1)\) is : [JEE Main 2021 (Online) 26th February Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T_{r+1}={ }^{10} C_r\left(t x^{1 / 5}\right)^{10-r}\left[\frac{(1-x)^{1 / 10}}{t}\right]^r \\
& ={ }^{10} C_r t^{(10-2 r)} \times x^{\frac{10-r}{5}} \times(1-x)^{\frac{r}{10}} \\
& \Rightarrow 10-2 r=0 \Rightarrow r=5 \\
& \therefore T_6={ }^{10} C_5 \times x \sqrt{1-x}
\end{aligned}
\)
At maximum, \(\frac{d T_6}{d x}={ }^{10} C_5\left[\sqrt{1-x}-\frac{x}{2 \sqrt{1-x}}\right]=0\)
\(
\begin{aligned}
& \Rightarrow 1-x=x / 2 \Rightarrow 3 x=2 \Rightarrow x=2 / 3 \\
& \left.T_6\right|_{\max }=\frac{10!}{5!5!} \times \frac{2}{3 \sqrt{3}}=\frac{2.10!}{3 \sqrt{3}(5!)^2}
\end{aligned}
\) -
Question 208 of 226
208. Question
If \(n \geq 2\) is a positive integer, then the sum of the series \({ }^{n+1} C_2+2\left({ }^2 C_2+{ }^3 C_2+{ }^4 C_2+\ldots+{ }^n C_2\right)\) is: [JEE Main 2021 (Online) 24th February Evening Shift]
CorrectIncorrectHint
Given that \(n \geq 2\) is a positive integer
\(
\begin{array}{ll}
\therefore{ }^{n+1} C_2+2\left({ }^2 C_2+{ }^3 C_2+{ }^4 C_2+. .+{ }^n C_2\right) & \\
={ }^{n+1} C_2+2\left({ }^3 C_3+{ }^3 C_2+{ }^4 C_2+. .+{ }^n C_2\right) & {\left[\because{ }^n C_n={ }^m C_m\right]} \\
={ }^{n+1} C_2+2\left({ }^4 C_3+{ }^4 C_2+. .+{ }^n C_2\right) & {\left[\because{ }^n C_m+{ }^n C_{m-1}={ }^{n+1} C_m\right]} \\
={ }^{n+1} C_2+2\left({ }^5 C_3+. .+{ }^n C_2\right) & {\left[\because{ }^n C_m+{ }^n C_{m-1}={ }^{n+1} C_m\right]}
\end{array}
\)
Proceeding in this way we get
\(
\begin{gathered}
={ }^{n+1} C_2+2\left({ }^n C_3+{ }^n C_2\right) \\
={ }^{n+1} C_2+2 .{ }^{n+1} C_3
\end{gathered}
\)
\(
=\frac{(n+1)!}{2!(n+1-2)!}+\frac{2 \cdot(n+1)!}{3!(n+1-3)!} \quad\left[\because{ }^n C_m=\frac{n!}{m!(n-m)!}\right]
\)
\(
\begin{aligned}
& =\frac{(n+1)!}{2!(n-1)!}+\frac{2 \cdot(n+1)!}{3!(n-2)!} \\
& =\frac{n(n+1)}{2}+\frac{(n-1)(n)(n+1)}{3} \\
& =n(n+1)\left[\frac{1}{2}+\frac{n-1}{3}\right] \\
& =n(n+1)\left[\frac{3+2 n-2}{6}\right] \\
& =n(n+1)\left[\frac{2 n+1}{6}\right] \\
& =\frac{n(n+1)(2 n+1)}{6}
\end{aligned}
\) -
Question 209 of 226
209. Question
The value of \(-{ }^{15} C_1+2 \cdot{ }^{15} C_2-3 \cdot{ }^{15} C_3+\ldots-15 \cdot{ }^{15} C_{15}+{ }^{14} C_1+{ }^{14} C_3+{ }^{14} C_5+\) \(\ldots+{ }^{14} C_{11}\) is [JEE Main 2021 (Online) 24th February Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& -{ }^{15} C_1+2 \cdot{ }^{15} C_2-3 \cdot{ }^{15} C_3+\ldots .-15 \cdot{ }^{15} C_{15} \\
& =\sum_{r=1}^{15}(-1)^r \cdot r \cdot{ }^{15} C_r \\
& =\sum_{r=1}^{15}(-1)^2 \cdot r \cdot \frac{15}{r} \cdot{ }^{14} C_{r-1} \\
& =15 \sum_{r=1}^{15}(-1)^2 \cdot{ }^{14} C_{r-1} \\
& =15\left(-{ }^{14} C_0+{ }^{14} C_1-{ }^{14} C_2+\ldots .-{ }^{14} C_{14}\right) \\
& =15(0)=0
\end{aligned}
\)
We know
\(
\begin{aligned}
& \Rightarrow 2^{14-1}={ }^{14} C_1+{ }^{14} C_3+{ }^{14} C_5 \ldots+{ }^{14} C_{13} \\
& \Rightarrow 2^{13}={ }^{14} C_1+{ }^{14} C_3+{ }^{14} C_5 \ldots+{ }^{14} C_{13} \\
& \text { Also let, } S={ }^{14} C_1+{ }^{14} C_3+{ }^{14} C_5+\ldots+{ }^{14} C_{11} \\
& \Rightarrow S+{ }^{14} C_{13}={ }^{14} C_1+{ }^{14} C_3+{ }^{14} C_5+\ldots+{ }^{14} C_{11}+{ }^{14} C_{13} \\
& \Rightarrow S+{ }^{14} C_{13}=2^{13} \\
& \Rightarrow S+14=2^{13} \\
& \Rightarrow S=2^{13}-14
\end{aligned}
\) -
Question 210 of 226
210. Question
The number of integral terms in the expansion of \(\left(5^{\frac{1}{2}}+7^{\frac{1}{8}}\right)^{1016}\) is: [JEE Main 2025 (Online) 8th April Evening Shift]
CorrectIncorrectHint
(b)
\(
\begin{aligned}
&\begin{aligned}
& \mathrm{T}_{\mathrm{r}}={ }^{1016} \mathrm{C}_{\mathrm{r}}(5)^{\frac{1016-\mathrm{r}}{2}} 7^{\frac{\mathrm{r}}{8}} \\
& \Rightarrow \mathrm{r}=0,8,16,24, \ldots, 1016 \\
& 1016=0+(\mathrm{n}-1) 8 \\
& \Rightarrow \mathrm{n}-1=\frac{1016}{8}=127
\end{aligned}\\
&\text { So, } \mathrm{n}=128 \text {. }
\end{aligned}
\)Explanation: Step 1: Formulate the general term
The general term \(T_{r+1}\) in the binomial expansion of \((a+b)^n\) is given by \(T_{r+1}=\binom{n}{r} a^{n-r} b^r\). For the given expression \(\left(5^{\frac{1}{2}}+7^{\frac{1}{8}}\right)^{1016}\), the general term is:
\(
\begin{gathered}
T_{r+1}=\binom{1016}{r}\left(5^{\frac{1}{2}}\right)^{1016-r}\left(7^{\frac{1}{8}}\right)^r \\
T_{r+1}=\binom{1016}{r} 5^{\frac{1016-r}{2}} 7^{\frac{r}{8}}
\end{gathered}
\)
Step 2: Determine conditions for integer terms
For the term \(\boldsymbol{T}_{\boldsymbol{r}+1}\) to be an integer, the exponents of 5 and 7 must be integers. The value of \(r\) must be an integer such that \(0 \leq r \leq 1016\).
The conditions are:
(i) \(\frac{1016-r}{2}\) must be an integer.
(ii) \(\frac{r}{8}\) must be an integer.
Step 3: Solve for possible values of r
The second condition requires \(\boldsymbol{r}\) to be a multiple of 8, so we can write \(\boldsymbol{r}=8 k\), where \(k\) is an integer.
Substitute \(r=8 k\) into the first condition:
\(
\frac{1016-8 k}{2}=508-4 k, \text { which is always an integer for any integer } k.
\)
We must also satisfy the range \(0 \leq r \leq 1016\) :
\(
\begin{gathered}
0 \leq 8 k \leq 1016 \\
0 \leq k \leq \frac{1016}{8} \\
0 \leq k \leq 127
\end{gathered}
\)
Step 4: Count the number of terms
The possible values of \(k\) are integers from 0 to 127 , inclusive. The number of such values is \(127-0+1=128\). Each value of \(k\) corresponds to a unique integer value of \(\boldsymbol{r}\) (and thus a unique integral term).
The number of integral terms in the expansion is 128. -
Question 211 of 226
211. Question
The remainder when \(\left((64)^{(64)}\right)^{(64)}\) is divided by 7 is equal to [JEE Main 2025 (Online) 7th April Morning Shift]
CorrectIncorrectHint
(a)
\(
\begin{aligned}
&\begin{aligned}
& 64^{64} \Rightarrow(63+1)^{64}=63 \lambda+1 \\
& 64^{664^{64}} \Rightarrow(63+1)^{64^{64}} \\
& 63 \lambda_1+1
\end{aligned}\\
&\text { Required remainder when divided } 7 \text { is } 1 \text {. }
\end{aligned}
\)Explanation: We find the remainder of
\(
\left((64)^{64}\right)^{64}
\)
when divided by 7.
Step 1: Simplify the expression
\(
\left((64)^{64}\right)^{64}=64^{64 \times 64}=64^{4096}
\)
Step 2: Reduce the base modulo 7
\(
64 \equiv 1(\bmod 7)
\)
Step 3: Raise to the power
\(
64^{4096} \equiv 1^{4096} \equiv 1 \quad(\bmod 7)
\) -
Question 212 of 226
212. Question
If \(1^2 \cdot\left({ }^{15} C_1\right)+2^2 \cdot\left({ }^{15} C_2\right)+3^2 \cdot\left({ }^{15} C_3\right)+\ldots+15^2 \cdot\left({ }^{15} C_{15}\right)=2^m \cdot 3^n \cdot 5^k\), where \(m, n, k \in \mathbf{N}\), then \(\mathrm{m}+\mathrm{n}+\mathrm{k}\) is equal to: [JEE Main 2025 (Online) 4th April Evening Shift]
CorrectIncorrectHint
(b) The given sum is \(S=\sum_{r=1}^{15} r^2 \cdot\left({ }^{15} C_r\right)\).
A known identity for this type of summation is:
\(
\sum_{r=1}^n r^2 \cdot\left({ }^n C_r\right)=n(n+1) 2^{n-2}
\)
In this problem, \(n=15\). Substituting this value into the formula:
\(
\begin{gathered}
S=15(15+1) 2^{15-2} \\
S=15 \cdot 16 \cdot 2^{13}
\end{gathered}
\)
Next, express the terms in their prime factor form:
\(
\begin{gathered}
15=3 \cdot 5 \\
16=2^4 \\
S=(3 \cdot 5) \cdot 2^4 \cdot 2^{13} \\
S=3^1 \cdot 5^1 \cdot 2^{4+13} \\
S=2^{17} \cdot 3^1 \cdot 5^1
\end{gathered}
\)
We are given that \(S=2^m \cdot 3^n \cdot 5^k\). Comparing the exponents:
\(m=17\)
\(n=1\)
\(k=1\)
The question asks for the value of \(m+n+k\) :
\(
m+n+k=17+1+1=19
\) -
Question 213 of 226
213. Question
For an integer \(n \geq 2\), if the arithmetic mean of all coefficients in the binomial expansion of \((x+y)^{2 n-3}\) is 16, then the distance of the point \(\mathrm{P}\left(2 n-1, n^2-4 n\right)\) from the line \(x+y=8\) is [JEE Main 2025 (Online) 4th April Morning Shift]
CorrectIncorrectHint
(d)
\(
\begin{aligned}
& \text { Mean }=\frac{{ }^{2 n-3} C_0+{ }^{2 n-3} C_1+{ }^{2 n-3} C_2+\cdots{ }^{2 n-3} C_{2 n-3}}{2 n-2}=16 \\
& =2^{2 n-3}=16(2 n-2) \\
& =2^{2 n-3}=2^5(n-1) \\
& \Rightarrow n=5 \\
& \therefore P(9,5) \\
& d=\left|\frac{9+5-8}{\sqrt{2}}\right|=\frac{6}{\sqrt{2}}=3 \sqrt{2}
\end{aligned}
\)Explanation: Step 1: Use the given condition (arithmetic mean of coefficients)
For the binomial expansion
\(
(x+y)^k
\)
Number of coefficients \(=k+1\)
Sum of coefficients \(=2^k\)
So the arithmetic mean of coefficients is
\(
\frac{2^k}{k+1}
\)
Here,
\(
k=2 n-3
\)
Given mean \(=16\) :
\(
\frac{2^{2 n-3}}{(2 n-3)+1}=\frac{2^{2 n-3}}{2 n-2}=16
\)
Step 2: Simplify
\(
2^{2 n-3}=16(2 n-2)=2^4 \cdot 2(n-1)=2^5(n-1)
\)
So,
\(
2^{2 n-3}=2^5(n-1)
\)
Comparing powers of 2:
\(
2 n-3=5+\log _2(n-1)
\)
Try integer values \(n \geq 2\).
Check \(n=5\) :
\(
2 n-3=7, \quad n-1=4 \Rightarrow 5+\log _2 4=5+2=7
\)
So,
\(
n=5
\)
Step 3: Coordinates of point \(P\)
\(
P\left(2 n-1, n^2-4 n\right)
\)
Substitute \(n=5\) :
\(
P(9,25-20)=(9,5)
\)
Step 4: Distance from line \(x+y=8\)
Write line in standard form:
\(
x+y-8=0
\)
Distance formula:
\(
d=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}}
\)
Here \(A=1, B=1, C=-8\).
\(
d=\frac{|9+5-8|}{\sqrt{2}}=\frac{6}{\sqrt{2}}=3 \sqrt{2}
\) -
Question 214 of 226
214. Question
In the expansion of \(\left(\sqrt[3]{2}+\frac{1}{\sqrt[3]{3}}\right)^n, n \in \mathrm{~N}\), if the ratio of \(15^{\text {th }}\) term from the beginning to the \(15^{\text {th }}\) term from the end is \(\frac{1}{6}\), then the value of \({ }^n \mathrm{C}_3\) is [JEE Main 2025 (Online) 4th April Morning Shift]
CorrectIncorrectHint
(b) Given
\(
\left(\sqrt[3]{2}+\frac{1}{\sqrt[3]{3}}\right)^n
\)
Here,
\(
a=2^{1 / 3}, \quad b=3^{-1 / 3}
\)
Step 1: Write the required terms
15th term from the beginning
\(
T_{15}=\binom{n}{14} a^{n-14} b^{14}
\)
15th term from the end
(The 15th from end \(=(n-14)^{\text {th }}\) from beginning)
\(
T_{15}^{\prime}=\binom{n}{14} b^{n-14} a^{14}
\)
Step 2: Take the ratio
\(
\frac{T_{15}}{T_{15}^{\prime}}=\left(\frac{a}{b}\right)^{n-28}
\)
Given:
\(
\frac{T_{15}}{T_{15}^{\prime}}=\frac{1}{6}
\)
Step 3: Evaluate \(\frac{a}{b}\)
\(
\frac{a}{b}=\frac{2^{1 / 3}}{3^{-1 / 3}}=(2 \cdot 3)^{1 / 3}=6^{1 / 3}
\)
So,
\(
\left(6^{1 / 3}\right)^{n-28}=6^{-1}
\)
Step 4: Solve for \(n\)
\(
\frac{n-28}{3}=-1 \Rightarrow n-28=-3 \Rightarrow n=25
\)
Step 5: Find \(\binom{n}{3}\)
\(
\binom{25}{3}=\frac{25 \cdot 24 \cdot 23}{6}=2300
\)Explanation: Calculation Steps
Step 1: General Term: The general term in the expansion of \((a+b)^n\) is given by \(T_{r+1}={ }^n \mathrm{C}_r a^{n-r} b^r\). In this problem, \(a=\sqrt[3]{2}=2^{1 / 3}[latex] and [latex]b=\frac{1}{\sqrt[3]{3}}=3^{-1 / 3}\).
Step 2: \(15^{\text {th }}\) Term from the Beginning: The 15 th term from the beginning is \(T_{15}\), which corresponds to \(r=14\) :
\(
T_{15}={ }^n \mathrm{C}_{14}\left(2^{1 / 3}\right)^{n-14}\left(3^{-1 / 3}\right)^{14}
\)
Step 3: \(15^{\text {th }}\) Term from the End: The 15th term from the end is equivalent to the \((n+1-15+1)=(n-13)^{\text {th }}\) term from the beginning, which corresponds to \(r=n-14\).
\(
T_{15}^{\prime}=T_{n-13}={ }^n \mathrm{C}_{n-14}\left(2^{1 / 3}\right)^{n-(n-14)}\left(3^{-1 / 3}\right)^{n-14}
\)
Since \({ }^n \mathrm{C}_{14}={ }^n \mathrm{C}_{n-14}\), the expression simplifies to:
\(
T_{15}^{\prime}={ }^n \mathrm{C}_{14}\left(2^{1 / 3}\right)^{14}\left(3^{-1 / 3}\right)^{n-14}
\)
Step 4: Ratio and Solving for \(n\) : The ratio of the 15 th term from the beginning to the 15 th term from the end is given as \(\frac{1}{6}\) :
\(
\frac{T_{15}}{T_{15}^{\prime}}=\frac{{ }^n \mathrm{C}_{14}\left(2^{1 / 3}\right)^{n-14}\left(3^{-1 / 3}\right)^{14}}{{ }^n \mathrm{C}_{14}\left(2^{1 / 3}\right)^{14}\left(3^{-1 / 3}\right)^{n-14}}=\frac{1}{6}
\)
The binomial coefficients cancel out:
\(
\frac{\left(2^{1 / 3}\right)^{n-14}\left(3^{-1 / 3}\right)^{14}}{\left(2^{1 / 3}\right)^{14}\left(3^{-1 / 3}\right)^{n-14}}=\frac{2^{(n-14) / 3} \cdot 3^{-14 / 3}}{2^{14 / 3} \cdot 3^{-(n-14) / 3}}=\frac{1}{6}
\)
Combining terms with the same base:
\(
\begin{aligned}
& 2^{(n-14) / 3-14 / 3} \cdot 3^{-14 / 3-(-(n-14) / 3)}=2^{(n-28) / 3} \cdot 3^{(n-28) / 3}=\frac{1}{6} \\
& (2 \cdot 3)^{(n-28) / 3}=6^{(n-28) / 3}=6^{-1}
\end{aligned}
\)
Equating the exponents:
\(
\frac{n-28}{3}=-1 \Longrightarrow n-28=-3 \Longrightarrow n=25
\)
Step 5: Calculate \({ }^n \mathrm{C}_3\) : With \(n=25\), we calculate \({ }^{25} \mathrm{C}_3\) :
\(
{ }^{25} \mathrm{C}_3=\frac{25!}{3!(25-3)!}=\frac{25 \times 24 \times 23}{3 \times 2 \times 1}=25 \times 4 \times 23=2300
\) -
Question 215 of 226
215. Question
The sum of all rational terms in the expansion of \((2+\sqrt{3})^8\) is : [JEE Main 2025 (Online) 3rd April Morning Shift]
CorrectIncorrectHint
(b) Step 1: Determine the general term formula
The general term in the expansion of the binomial \((a+b)^n\) is given by \(T_{r+1}=\binom{n}{r} a^{n-r} b^r\). For the given expression \((2+\sqrt{3})^8\), we have \(a=2, b=\sqrt{3}\), and \(n=8\). The general term is:
\(
T_{r+1}=\binom{8}{r} 2^{8-r}(\sqrt{3})^r=\binom{8}{r} 2^{8-r} 3^{r / 2}
\)
Step 2: Identify rational terms
For a term to be rational, the exponent of 3 , which is \(\boldsymbol{r} / 2\), must be an integer. This requires \(\boldsymbol{r}\) to be an even integer. The possible values for \(\boldsymbol{r}\) in the range \(0 \leq \boldsymbol{r} \leq 8\) are \(0,2,4,6\), and 8.
Step 3: Calculate the rational terms
We calculate the value of the term for each even value of \(r\) :
For \(r=0: T_1=\binom{8}{0} 2^8 \cdot 3^0=1 \cdot 256 \cdot 1=256\)
For \(r=2: T_3=\binom{8}{2} 2^6 \cdot 3^1=28 \cdot 64 \cdot 3=5376\)
For \(r=4: T_5=\binom{8}{4} 2^4 \cdot 3^2=70 \cdot 16 \cdot 9=10080\)
For \(r=6: T_7=\binom{8}{6} 2^2 \cdot 3^3=28 \cdot 4 \cdot 27=3024\)
For \(r=8: T_9=\binom{8}{8} 2^0 \cdot 3^4=1 \cdot 1 \cdot 81=81\)
Step 4: Sum the rational terms
The sum of all rational terms is the sum of these values:
\(
\text { Sum }=256+5376+10080+3024+81=18817
\)Alternate: Step 1: Use a shortcut identity
For any expression \((a+\sqrt{b})^n\), sum of rational terms is given by:
\(
\frac{(a+\sqrt{b})^n+(a-\sqrt{b})^n}{2}
\)
Here,
\(
a=2, \quad b=3, \quad n=8
\)
So,
\(
S=\frac{(2+\sqrt{3})^8+(2-\sqrt{3})^8}{2}
\)
Step 2: Evaluate
Note:
\(
(2+\sqrt{3})(2-\sqrt{3})=1
\)
Hence,
\(
(2-\sqrt{3})^8=\frac{1}{(2+\sqrt{3})^8}
\)
Also,
\(
\begin{gathered}
(2+\sqrt{3})^2=7+4 \sqrt{3} \\
(2+\sqrt{3})^4=(7+4 \sqrt{3})^2=97+56 \sqrt{3} \\
(2+\sqrt{3})^8=(97+56 \sqrt{3})^2=18817+10864 \sqrt{3}
\end{gathered}
\)
Thus,
\(
(2-\sqrt{3})^8=18817-10864 \sqrt{3}
\)
\(
\begin{aligned}
&\text { Step 3: Add and divide by } 2\\
&S=\frac{(18817+10864 \sqrt{3})+(18817-10864 \sqrt{3})}{2}=\frac{37634}{2}=18817
\end{aligned}
\) -
Question 216 of 226
216. Question
If \(\sum_{r=1}^9\left(\frac{r+3}{2^r}\right) \cdot{ }^9 C_r=\alpha\left(\frac{3}{2}\right)^9-\beta, \alpha, \beta \in \mathbb{N}\), then \((\alpha+\beta)^2\) is equal to [JEE Main 2025 (Online) 3rd April Morning Shift]
CorrectIncorrectHint
(b) Step 1: Split the sum
\(
S=\sum_{r=1}^9 \frac{r}{2^r}\binom{9}{r}+3 \sum_{r=1}^9 \frac{1}{2^r}\binom{9}{r}
\)
Step 2: Evaluate standard binomial sums
(i)
\(
\begin{aligned}
& \sum_{r=0}^9\binom{9}{r}\left(\frac{1}{2}\right)^r \\
& =\left(1+\frac{1}{2}\right)^9=\left(\frac{3}{2}\right)^9
\end{aligned}
\)
So,
\(
\sum_{r=1}^9\binom{9}{r}\left(\frac{1}{2}\right)^r=\left(\frac{3}{2}\right)^9-1
\)
(ii) \(\sum_{r=0}^9 r\binom{9}{r}\left(\frac{1}{2}\right)^r\)
Using
\(
\sum r\binom{n}{r} x^r=n x(1+x)^{n-1}
\)
For \(n=9, x=\frac{1}{2}\) :
\(
\sum_{r=0}^9 r\binom{9}{r}\left(\frac{1}{2}\right)^r=9 \cdot \frac{1}{2}\left(\frac{3}{2}\right)^8
\)
(Note: the \(r=0\) term is zero, so this already equals the sum from \(r=1\) to 9.)
Step 3: Combine
\(
S=\frac{9}{2}\left(\frac{3}{2}\right)^8+3\left[\left(\frac{3}{2}\right)^9-1\right]
\)
Write the first term with \(\left(\frac{3}{2}\right)^9\) :
\(
\frac{9}{2}\left(\frac{3}{2}\right)^8=3\left(\frac{3}{2}\right)^9
\)
So,
\(
\begin{gathered}
S=3\left(\frac{3}{2}\right)^9+3\left(\frac{3}{2}\right)^9-3 \\
S=6\left(\frac{3}{2}\right)^9-3
\end{gathered}
\)
Step 4: Identify \(\alpha, \beta\)
\(
\alpha=6, \quad \beta=3
\)
Step 5: Final value
\(
(\alpha+\beta)^2=(6+3)^2=9^2=81
\) -
Question 217 of 226
217. Question
If \(\sum_{r=0}^{10}\left(\frac{10^{r+1}-1}{10^r}\right) \cdot{ }^{11} C_{r+1}=\frac{{ }_\alpha 11-11^{11}}{10^{10}}\), then \(\alpha\) is equal to : [JEE Main 2025 (Online) 2nd April Evening Shift]
CorrectIncorrectHint
(b) Step 1: Simplify the general term
\(
\frac{10^{r+1}-1}{10^r}=10-\frac{1}{10^r}
\)
So the sum becomes
\(
S=\sum_{r=0}^{10}\left(10-\frac{1}{10^r}\right)\binom{11}{r+1}
\)
Split it:
\(
S=10 \sum_{r=0}^{10}\binom{11}{r+1}-\sum_{r=0}^{10} \frac{\binom{11}{r+1}}{10^r}
\)
Step 2: Evaluate the first sum
\(
\sum_{r=0}^{10}\binom{11}{r+1}=\sum_{k=1}^{11}\binom{11}{k}=2^{11}-1=2047
\)
So,
\(
10 \sum_{r=0}^{10}\binom{11}{r+1}=20470
\)
Step 3: Evaluate the second sum
Let \(k=r+1\) :
\(
\begin{aligned}
& \sum_{r=0}^{10} \frac{\binom{11}{r+1}}{10^r}=\sum_{k=1}^{11} \frac{\binom{11}{k}}{10^{k-1}}=10 \sum_{k=1}^{11}\binom{11}{k}\left(\frac{1}{10}\right)^k \\
& =10\left[\left(1+\frac{1}{10}\right)^{11}-1\right]=10\left(\frac{11^{11}}{10^{11}}-1\right)
\end{aligned}
\)
Step 4: Combine
\(
S=20470-10\left(\frac{11^{11}}{10^{11}}-1\right)=20480-\frac{11^{11}}{10^{10}}
\)
Write over a common denominator:
\(
S=\frac{20480 \cdot 10^{10}-11^{11}}{10^{10}}
\)
Step 5: Compare with the given form
\(
\frac{\alpha^{11}-11^{11}}{10^{10}}
\)
This means
\(
{ }_\alpha 11=20480 \cdot 10^{10}
\)
Note:
\(
20480=2^{11} \cdot 10=2^{12} \cdot 5
\)
So,
\(
20480 \cdot 10^{10}=2^{12} \cdot 5 \cdot(2 \cdot 5)^{10}=2^{22} \cdot 5^{11}=\left(2^2 \cdot 5\right)^{11}=20^{11}
\)
Hence,
\(
{ }_\alpha 11=20^{11} \Rightarrow \alpha=20
\) -
Question 218 of 226
218. Question
The largest \(\mathrm{n} \in \mathbf{N}\) such that \(3^{\mathrm{n}}\) divides 50! is : [JEE Main 2025 (Online) 2nd April Morning Shift]
CorrectIncorrectHint
(a) Step 1: Use Legendre’s formula
For a prime \(p\), the exponent of \(p\) in \(n!\) is:
\(
v_p(n!)=\left\lfloor\frac{n}{p}\right\rfloor+\left\lfloor\frac{n}{p^2}\right\rfloor+\left\lfloor\frac{n}{p^3}\right\rfloor+\cdots
\)
Here \(p=3, n=50\).
Step 2: Compute the terms
\(
\begin{aligned}
& \left\lfloor\frac{50}{3}\right\rfloor=16 \\
& \left\lfloor\frac{50}{9}\right\rfloor=5 \\
& \left\lfloor\frac{50}{27}\right\rfloor=1 \\
& \left\lfloor\frac{50}{81}\right\rfloor=0
\end{aligned}
\)
Step 3: Add them
\(
v_3(50!)=16+5+1=22
\) -
Question 219 of 226
219. Question
The term independent of \(x\) in the expansion of \(\left(\frac{(x+1)}{\left(x^{2 / 3}+1-x^{1 / 3}\right)}-\frac{(x-1)}{\left(x-x^{1 / 2}\right)}\right)^{10}, x>1\), is : [JEE Main 2025 (Online) 2nd April Morning Shift]
CorrectIncorrectHint
(d) Simplify the first term: The numerator \(x+1\) can be factored as a sum of cubes, \(\left(x^{1 / 3}\right)^3+1^3\). Using the identity \(a^3+b^3=(a+b)\left(a^2-a b+b^2\right)\), we get:
\(
\frac{x+1}{x^{2 / 3}-x^{1 / 3}+1}=\frac{\left(x^{1 / 3}+1\right)\left(x^{2 / 3}-x^{1 / 3}+1\right)}{\left(x^{2 / 3}-x^{1 / 3}+1\right)}=x^{1 / 3}+1
\)
Simplify the second term: The denominator \(x-x^{1 / 2}\) can be factored by taking out \(x^{1 / 2}\) as a common factor. The numerator \(x-1\) can be factored as a difference of squares, \(\left(x^{1 / 2}-1\right)\left(x^{1 / 2}+1\right)\).
\(
\frac{x-1}{x-x^{1 / 2}}=\frac{\left(x^{1 / 2}-1\right)\left(x^{1 / 2}+1\right)}{x^{1 / 2}\left(x^{1 / 2}-1\right)}=\frac{x^{1 / 2}+1}{x^{1 / 2}}=1+x^{-1 / 2}
\)
Combine the simplified terms: Substitute the simplified terms back into the original expression inside the parentheses:
\(
\left(x^{1 / 3}+1\right)-\left(1+x^{-1 / 2}\right)=x^{1 / 3}+1-1-x^{-1 / 2}=x^{1 / 3}-x^{-1 / 2}
\)
The expression to be expanded is thus \(\left(x^{1 / 3}-x^{-1 / 2}\right)^{10}\).
Finding the term independent of \(\boldsymbol{x}\)
The general term, \(T_{r+1}\), in the expansion of \((a+b)^n\) is given by \(T_{r+1}=\binom{n}{r} a^{n-r} b^r\).
In this case, \(n=10, a=x^{1 / 3}\), and \(b=-x^{-1 / 2}\).
\(
\begin{aligned}
& T_{r+1}=\binom{10}{r}\left(x^{1 / 3}\right)^{10-r}\left(-x^{-1 / 2}\right)^r \\
& T_{r+1}=\binom{10}{r} x^{(10-r) / 3}(-1)^r x^{-r / 2} \\
& T_{r+1}=\binom{10}{r}(-1)^r x^{(10-r) / 3-r / 2}
\end{aligned}
\)
For the term to be independent of \(x\), the exponent of \(x\) must be zero:
\(
\begin{gathered}
\frac{10-r}{3}-\frac{r}{2}=0 \\
\frac{2(10-r)-3 r}{6}=0 \\
20-2 r-3 r=0 \\
20-5 r=0 \\
5 r=20 \\
r=4
\end{gathered}
\)
Substitute \(r=4\) back into the general term formula to find the value of the term:
\(
\begin{aligned}
T_{4+1} & =T_5=\binom{10}{4}(-1)^4 x^0 \\
T_5 & =\frac{10!}{4!(10-4)!} \times 1 \times 1 \\
T_5 & =\frac{10 \times 9 \times 8 \times 7}{4 \times 3 \times 2 \times 1} \\
T_5 & =10 \times 3 \times 7=210
\end{aligned}
\)
The term independent of \(x\) in the expansion is 210. -
Question 220 of 226
220. Question
The remainder, when \(7^{103}\) is divided by 23 , is equal to: [JEE Main 2025 (Online) 29th January Evening Shift]
CorrectIncorrectHint
(c) Step 1: Use Fermat’s Little Theorem
Since 23 is prime and \(\operatorname{gcd}(7,23)=1\),
\(
7^{22} \equiv 1(\bmod 23)
\)
Step 2: Reduce the exponent
\(
103=22 \times 4+15
\)
So,
\(
7^{103}=\left(7^{22}\right)^4 \cdot 7^{15} \equiv 1^4 \cdot 7^{15} \equiv 7^{15} \quad(\bmod 23)
\)
Step 3: Compute \(7^{15}(\bmod 23)\)
First,
\(
\begin{gathered}
7^2=49 \equiv 3 \quad(\bmod 23) \\
7^4 \equiv 3^2=9 \\
7^8 \equiv 9^2=81 \equiv 12 \quad(\bmod 23)
\end{gathered}
\)
\(
\begin{aligned}
&\text { Now, }\\
&\begin{gathered}
7^{15}=7^8 \cdot 7^4 \cdot 7^2 \cdot 7 \\
\equiv 12 \cdot 9 \cdot 3 \cdot 7 \equiv 12 \cdot 9 \cdot 21 \\
12 \cdot 9=108 \equiv 16 \quad(\bmod 23) \\
16 \cdot 21=336 \equiv 14 \quad(\bmod 23)
\end{gathered}
\end{aligned}
\)Alternate: Since 23 is prime and \(\operatorname{gcd}(7,23)=1\),
\(
7^{22} \equiv 1 \quad(\bmod 23)
\)
Write the exponent:
\(
\begin{gathered}
103=22 \times 4+15 \\
7^{103} \equiv 7^{15} \quad(\bmod 23)
\end{gathered}
\)
Now compute small powers modulo 23:
\(
\begin{gathered}
7^2=49 \equiv 3 \quad(\bmod 23) \\
7^4 \equiv 3^2=9 \\
7^8 \equiv 9^2=81 \equiv 12 \\
7^{15}=7^8 \cdot 7^4 \cdot 7^2 \cdot 7 \\
\equiv 12 \cdot 9 \cdot 3 \cdot 7 \equiv 14 \quad(\bmod 23)
\end{gathered}
\)Note: 49 modulo 23 is 3.
Perform division: Divide 49 by 23 to find the largest integer quotient. The calculation is \(49 \div 23=2\) (since \(2 \times 23=46\) ). -
Question 221 of 226
221. Question
The least value of \(\mathbf{n}\) for which the number of integral terms in the Binomial expansion of \((\sqrt[3]{7}+\sqrt[12]{11})^n\) is 183 , is : [JEE Main 2025 (Online) 29th January Morning Shift]
CorrectIncorrectHint
(a) Step 1: General Term Formula
The general term, \(T_{r+1}\), in the binomial expansion of \((\sqrt[3]{7}+\sqrt[12]{11})^n\) is given by the formula:
\(
T_{r+1}=\binom{n}{r}(\sqrt[3]{7})^{n-r}(\sqrt[12]{11})^r=\binom{n}{r} 7^{(n-r) / 3} 11^{r / 12}
\)
Step 2: Conditions for Integral Terms
For \(T_{r+1}\) to be an integral term, both exponents must be non-negative integers. This requires:
(i) \((n-r) / 3\) must be an integer, which implies \(n-r\) is a multiple of 3.
(ii) \(r / 12\) must be an integer, which implies \(r\) is a multiple of 12.
The constraints on \(\boldsymbol{r}\) are \(0 \leq \boldsymbol{r} \leq \boldsymbol{n}\). Since \(\boldsymbol{r}\) must be a multiple of 12, we can write \(r=12 k\), where \(k\) is an integer.
Substituting \(r\) into the first condition, we get \(n-12 k\) must be a multiple of 3. Since \(12 k\) is always divisible by \(3, n\) must also be a multiple of 3 for any integral term to exist.
Step 3: Determine the Number of Terms
The number of integral terms is the number of possible values for \(\boldsymbol{r}\) in the range \(0 \leq \boldsymbol{r} \leq \boldsymbol{n}\) that are multiples of 12.
These values are \(0,12,24, \ldots, 12 k_{\text {max }}\), where \(12 k_{\text {max }} \leq n<12\left(k_{\text {max }}+1\right)\). The number of multiples of 12 in the range \([0, n]\) is given by \(\lfloor n / 12\rfloor+1\). The problem states that there are 183 integral terms.
\(
\left\lfloor\frac{n}{12}\right\rfloor+1=183
\)
Step 4: Solve for \(\mathbf{n}\)
From the equation in Step 3:
\(
\left\lfloor\frac{n}{12}\right\rfloor=182
\)
This inequality is equivalent to:
\(
182 \leq \frac{n}{12}<183
\)
Multiplying by 12 gives the range for \(n\) :
\(
\begin{aligned}
182 \times 12 & \leq n<183 \times 12 \\
2184 & \leq n<2196
\end{aligned}
\)
We previously established that \(n\) must be a multiple of 3. The least value of \(n\) in this range that is divisible by 3 is 2184. -
Question 222 of 226
222. Question
Let the coefficients of three consecutive terms \(T_r, T_{r+1}\) and \(T_{r+2}\) in the binomial expansion of \((a+b)^{12}\) be in a G.P. and let \(p\) be the number of all possible values of \(r\). Let \(q\) be the sum of all rational terms in the binomial expansion of \((\sqrt[4]{3}+\sqrt[3]{4})^{12}\). Then \(p+q\) is equal to: [JEE Main 2025 (Online) 28th January Evening Shift]
CorrectIncorrectHint
(b) Step 1: Determine the value of \(p\)
The coefficients of three consecutive terms \(\boldsymbol{T}_{\boldsymbol{r}}, \boldsymbol{T}_{\boldsymbol{r}+1}\), and \(\boldsymbol{T}_{\boldsymbol{r}+2}\) in the binomial expansion of \((a+b)^{12}\) are \(\binom{12}{r},\binom{12}{r+1}\), and \(\binom{12}{r+2}\) respectively, where \(0 \leq r \leq 10\).
For these coefficients to be in a Geometric Progression (G.P.), the middle coefficient squared must equal the product of the other two:
\(
\left(\binom{12}{r+1}\right)^2=\binom{12}{r} \times\binom{ 12}{r+2}
\)
This condition simplifies to the equation \(r^2-12 r+13=0\).
The solutions to this quadratic equation are
\(
r=\frac{12 \pm \sqrt{144-52}}{2}=\frac{12 \pm \sqrt{92}}{2}=6 \pm \sqrt{23} .
\)
Since \(\boldsymbol{r}\) must be a non-negative integer (term index in the expansion), there are no possible integer values for \(r\).
Therefore, the number of all possible values of \(\boldsymbol{r}, \boldsymbol{p}\), is \(\mathbf{0}\).
Step 2: Determine the value of \(q\)
The general term in the binomial expansion of \((\sqrt[4]{3}+\sqrt[3]{4})^{12}\), which is \(\left(3^{1 / 4}+4^{1 / 3}\right)^{12}\), is given by:
\(
T_{k+1}=\binom{12}{k}\left(3^{1 / 4}\right)^{12-k}\left(4^{1 / 3}\right)^k=\binom{12}{k} 3^{\frac{12-k}{4}} 4^{\frac{k}{3}}
\)
For a term to be rational, the exponents of 3 and 4 must be integers.
\(\frac{12-k}{4}\) must be an integer, which means \(12-k\) must be a multiple of 4. So, \(k\) must be a multiple of 4 (since \(0 \leq k \leq 12\) ). The possible values for \(k\) are \(0,4,8,12\).
\(\frac{k}{3}\) must be an integer, which means \(k\) must be a multiple of 3. The possible values for \(k\) are \(0,3,6,9,12\).
The values of \(k\) that satisfy both conditions are the common values in both sets: \(k=0\) and \(k=12\).
The rational terms are \(T_1\) (for \(k=0\) ) and \(T_{13}\) (for \(k=12\) ).
For \(k=0: T_1=\binom{12}{0} 3^{\frac{12-0}{4}} 4^{\frac{0}{3}}=1 \times 3^3 \times 4^0=27\).
For \(k=12: T_{13}=\binom{12}{12} 3^{\frac{12-12}{4}} 4^{\frac{12}{3}}=1 \times 3^0 \times 4^4=256\).
The sum of all rational terms, \(q\), is \(27+256=283\).
The value of \(p+q\) is \(0+283=283\).Alternate: Part A: Coefficients in G.P.
\(\ln (a+b)^{12}\), the coefficients of
\(
T_r, T_{r+1}, T_{r+2}
\)
are
\(
\binom{12}{r-1},\binom{12}{r},\binom{12}{r+1} .
\)
G.P. condition
\(
\left(\binom{12}{r}\right)^2=\binom{12}{r-1}\binom{12}{r+1}
\)
Using the standard identity:
\(
\frac{\binom{n}{r}^2}{\binom{n}{r-1}\binom{n}{r+1}}=\frac{(r+1)(n-r+1)}{r(n-r)}
\)
For \(n=12\) :
\(
\begin{gathered}
\frac{(r+1)(13-r)}{r(12-r)}=1 \\
(r+1)(13-r)=r(12-r)
\end{gathered}
\)
Expand both sides:
\(
\begin{gathered}
13 r+13-r^2-r=12 r-r^2 \\
12 r+13-r^2=12 r-r^2 \\
13=0 \quad \text { (impossible) }
\end{gathered}
\)
Conclusion
There is no value of \(r\) for which three consecutive coefficients are in G.P.
\(
p=0
\)
Part B: Rational terms in
\(
(\sqrt[4]{3}+\sqrt[3]{4})^{12}
\)
General term
\(
T_{k+1}=\binom{12}{k} 3^{\frac{12-k}{4}} 4^{\frac{k}{3}}
\)
For rationality:
\(
\begin{gathered}
\frac{12-k}{4} \in \mathbb{Z} \Rightarrow k \equiv 0(\bmod 4) \\
\frac{k}{3} \in \mathbb{Z} \Rightarrow k \equiv 0(\bmod 3) \\
\Rightarrow k \equiv 0(\bmod 12)
\end{gathered}
\)
Valid k: 0,12
Rational terms
\(k=0: 3^3=27\)
\(k=12: 4^4=256\)
\(
q=27+256=283
\)
\(
p+q=0+283=283
\) -
Question 223 of 226
223. Question
Suppose \(A\) and \(B\) are the coefficients of \(30^{\text {th }}\) and \(12^{\text {th }}\) terms respectively in the binomial expansion of \((1+x)^{2 \mathrm{n}-1}\). If \(2 \mathrm{~A}=5 \mathrm{~B}\), then \(n\) is equal to: [JEE Main 2025 (Online) 24th January Evening Shift]
CorrectIncorrectHint
(d) The general term in the binomial expansion of \((1+x)^m\) is \(T_{r+1}=\binom{m}{r} x^r\), where the coefficient is \(\binom{m}{r}\). In our case, \(m=2 n-1\).
The coefficient of the 30 th term \(\left(T_{30}\right.\), so \(\left.r=29\right)\) is \(A=\binom{2 n-1}{29}\).
The coefficient of the 12 th term ( \(T_{12}\), so \(r=11\) ) is \(B=\binom{2 n-1}{11}\).
Given, \(2 A=5 B\)
Step 1: Write in factorial form
\(
\begin{aligned}
2\binom{2 n-1}{29} & =5\binom{2 n-1}{11} \\
2 \cdot \frac{(2 n-1)!}{29!(2 n-30)!} & =5 \cdot \frac{(2 n-1)!}{11!(2 n-12)!}
\end{aligned}
\)
Cancel \((2 n-1)\) !:
\(
\frac{2}{29!(2 n-30)!}=\frac{5}{11!(2 n-12)!}
\)
Step 2: Rearrange
\(
\frac{2 \cdot 11!}{5 \cdot 29!}=\frac{(2 n-30)!}{(2 n-12)!}
\)
Write factorial ratios:
\(
\frac{2}{5} \cdot \frac{1}{29 \cdot 28 \cdots 12}=\frac{1}{(2 n-12)(2 n-13) \cdots(2 n-29)}
\)
Invert both sides (this is important):
\(
\frac{5}{2}(29 \cdot 28 \cdots 12)=(2 n-12)(2 n-13) \cdots(2 n-29)
\)
Now everything is positive and we are comparing products.
Both sides are products of 18 consecutive integers:
LHS: 12, 13, . . . , 29
RHS: \((2 n-29), \ldots,(2 n-12)\)
\(
2 n-12=30 \Rightarrow 2 n=42 \Rightarrow n=21
\)Explanation:
\(
\frac{(2 n-12)(2 n-13) \cdots(2 n-29)}{29 \cdot 28 \cdots 12}=\frac{5}{2}
\)
Take logarithms / monotonicity argument (rigorous)
Define:
\(
F(x)=\frac{x(x-1) \cdots(x-17)}{29 \cdot 28 \cdots 12} \quad \text { for } x \geq 29
\)
\(F(x)\) is strictly increasing
Therefore equation has at most one solution
Now test the natural candidate:
\(
x=30 \Rightarrow \frac{30 \cdot 29 \cdots 13}{29 \cdot 28 \cdots 12}=\frac{30}{12}=\frac{5}{2}
\)
So:
\(
F(30)=\frac{5}{2}
\)
By strict monotonicity, this is the only solution.
Thus:
\(
2 n-12=30
\) -
Question 224 of 226
224. Question
For some \(\mathrm{n} \neq 10\), let the coefficients of the 5 th, 6 th and 7 th terms in the binomial expansion of \((1+\mathrm{x})^{\mathrm{n}+4}\) be in A.P. Then the largest coefficient in the expansion of \((1+\mathrm{x})^{\mathrm{n}+4}\) is: [JEE Main 2025 (Online) 24th January Morning Shift]
CorrectIncorrectHint
(b) Let
\(
(1+x)^{n+4}=(1+x)^N \quad \text { where } N=n+4
\)
Identify the required coefficients
In a binomial expansion:
5th term coefficient \(=\binom{N}{4}\)
6 th term coefficient \(=\binom{N}{5}\)
7th term coefficient \(=\binom{N}{6}\)
Apply the A.P. condition: Since the coefficients are in an arithmetic progression (A.P.), the middle term’s coefficient is the average of the other two:
\(
2\binom{N}{5}=\binom{N}{4}+\binom{N}{6}
\)
Use binomial identities
\(
\binom{N}{4}=\binom{N}{5} \cdot \frac{5}{N-4}, \quad\binom{N}{6}=\binom{N}{5} \cdot \frac{N-5}{6}
\)
Substitute:
\(
2=\frac{5}{N-4}+\frac{N-5}{6}
\)
Multiply by \(6(N-4)\) :
\(
\begin{gathered}
12(N-4)=30+(N-5)(N-4) \\
12 N-48=N^2-9 N+50 \\
N^2-21 N+98=0 \\
N=\frac{21 \pm 7}{2} \Rightarrow N=14 \text { or } 7
\end{gathered}
\)
Find \(n\)
\(
n+4=N \Rightarrow n=10 \text { or } 3
\)
Given \(n \neq 10\), hence:
\(
n=3
\)
So the expansion is:
\(
(1+x)^7
\)
Largest coefficient
For \((1+x)^7\), the coefficients are:
\(
1,7,21,35,35,21,7,1
\)
The largest coefficient is: 35 -
Question 225 of 226
225. Question
If in the expansion of \((1+x)^{\mathrm{p}}(1-x)^{\mathrm{q}}\), the coefficients of \(x\) and \(x^2\) are 1 and -2 , respectively, then \(\mathrm{p}^2+\mathrm{q}^2\) is equal to: [JEE Main 2025 (Online) 23rd January Evening Shift]
CorrectIncorrectHint
(c) Given
\(
(1+x)^p(1-x)^q
\)
Use binomial expansions up to \(x^2\) :
\(
\begin{aligned}
& (1+x)^p=1+p x+\frac{p(p-1)}{2} x^2+\cdots \\
& (1-x)^q=1-q x+\frac{q(q-1)}{2} x^2+\cdots
\end{aligned}
\)
Multiply and collect terms
Coefficient of \(x\) :
\(
p-q
\)
Given coefficient of \(x=1\) :
\(
p-q=1 \dots(1)
\)
Coefficient of \(x^2\) :
From multiplication:
\(
\frac{p(p-1)}{2}+\frac{q(q-1)}{2}-p q
\)
Given coefficient of \(x^2=-2\) :
\(
\frac{p(p-1)+q(q-1)}{2}-p q=-2
\)
Multiply by 2:
\(
\begin{gathered}
p^2-p+q^2-q-2 p q=-4 \\
(p-q)^2-(p+q)=-4
\end{gathered}
\)
Using \(p-q=1\) :
\(
\begin{gathered}
1-(p+q)=-4 \\
p+q=5 \dots(2)
\end{gathered}
\)
Solve for \(p\) and \(q\)
From (1) and (2):
\(
p=3, \quad q=2
\)
Required value
\(
p^2+q^2=3^2+2^2=9+4=13
\) -
Question 226 of 226
226. Question
Let \(\alpha, \beta, \gamma\) and \(\delta\) be the coefficients of \(x^7, x^5, x^3\) and \(x\) respectively in the expansion of \(\left(x+\sqrt{x^3-1}\right)^5+\left(x-\sqrt{x^3-1}\right)^5, x>1\). If \(u\) and \(v\) satisfy the equations \(\alpha u+\beta v=18\),
\(
\gamma u+\delta v=20,
\)
then \({u}+{v}\) equals : [JEE Main 2025 (Online) 22nd January Evening Shift]CorrectIncorrectHint
(c) Let
\(
E=\left(x+\sqrt{x^3-1}\right)^5+\left(x-\sqrt{x^3-1}\right)^5
\)
Step 1: Use binomial symmetry
For
\(
(a+b)^5+(a-b)^5
\)
only odd powers of b cancel, and even powers remain:
\(
(a+b)^5+(a-b)^5=2\left[a^5+10 a^3 b^2+5 a b^4\right]
\)
Here,
\(
a=x, \quad b=\sqrt{x^3-1}
\)
So,
\(
E=2\left[x^5+10 x^3\left(x^3-1\right)+5 x\left(x^3-1\right)^2\right]
\)
Step 2: Simplify
\(
\begin{aligned}
& E=2\left[x^5+10 x^6-10 x^3+5 x\left(x^6-2 x^3+1\right)\right] \\
& E=2\left[x^5+10 x^6-10 x^3+5 x^7-10 x^4+5 x\right] \\
& E=2\left(5 x^7+10 x^6+x^5-10 x^4-10 x^3+5 x\right) \\
& E=10 x^7+20 x^6+2 x^5-20 x^4-20 x^3+10 x
\end{aligned}
\)
Step 3: Identify coefficients
Comparing with powers:
Coefficient of \(x^7\) :
\(
\alpha=10
\)
Coefficient of \(x^5\) :
\(
\beta=2
\)
Coefficient of \(x^3\) :
\(
\gamma=-20
\)
Coefficient of \(x\) :
\(
\delta=10
\)
The equations for \(u\) and \(v\) are \(\alpha u+\beta v=18\) and \(\gamma u+\delta v=20\). Substituting the coefficients:
\(10 u+2 v=18\) (which simplifies to \(5 u+v=9\) )
\(-20 u+10 v=20\) (which simplifies to \(-2 u+v=2\) )
Step 4: Solve for \(\boldsymbol{u}\) and \(\boldsymbol{v}\)
Subtracting the second simplified equation from the first gives \(7 u=7\), so \(u=1\).
Substituting \(u=1\) into the second simplified equation yields \(-2(1)+v=2\), so \(v=4\)
The value of \(u+v\) is 5.