NCERT Exemplar MCQs
Summary
- Two real numbers or two algebraic expressions related by the symbols \(<,>, \leq\) or \(\geq\) form an inequality.
- Equal numbers may be added to (or subtracted from ) both sides of an inequality.
- Both sides of an inequality can be multiplied (or divided) by the same positive number. But when both sides are multiplied (or divided) by a negative number, then the inequality is reversed.
- The values of \(x\), which make an inequality a true statement, are called solutions of the inequality.
- To represent \(x<a\) (or \(x>a\) ) on a number line, put a circle on the number \(a\) and dark line to the left (or right) of the number \(a\).
- To represent \(x \leq a\) (or \(x \geq a\) ) on a number line, put a dark circle on the number \(a\) and dark the line to the left (or right) of the number \(x\).
- \(a \leq b\) either \(a<b\) or \(a=b\)
- \(a<b\) and \(b<c \Rightarrow a<c\) (transition property)
- \(a<b \Rightarrow-a>-b\), i.e., inequality sign reverses if both sides are multiplied by a negative number
- \(a<b\) and \(c<d \Rightarrow a+c<b+d\) and \(a-d<b-c\).
- If both sides of inequality are multiplied (or divided) by a positive number, inequality does not change. When both of its sides are multiplied (or divided) by a negative number, inequality gets reversed.
i.e., \(a<b \Rightarrow k a<k b\) if \(k>0\) and \(k a>k b\) if \(k<0\) - \(0<a<b \Rightarrow a^r<b^r\) if \(r>0\) and \(a^r>b^r\) if \(r<0\)
- \(a+\frac{1}{a} \geq 2\) for \(a>0\) and equality holds for \(a=1\)
- \(a+\frac{1}{a} \leq-2\) for \(a<0\) and equality holds for \(a=-1\)
- Squaring an inequality:
If \(a<b\), then \(a^2<b^2\) does not follows always:
Consider the following illustrations:
\(2<3 \Rightarrow 4<9\), but \(-4<3 \Rightarrow 16>9\)
Also if \(x>2 \Rightarrow x^2>4\), but for \(x<2 \Rightarrow x^2 \geq 0\)
If \(2<x<4 \Rightarrow 4<x^2<16\)
If \(-2<x<4 \Rightarrow 0 \leq x^2<16\)
If \(-5<x<4 \Rightarrow 0 \leq x^2<25\)
In fact \(a<b \Rightarrow a^2<b^2\) follows only when absolute value of \(a\) is less than the absolute value of \(b\) or distance of \(a\) from zero is less than the distance of \(b\) from zero on real number line. - Law of reciprocal:
If both sides of inequality have same sign, while taking its reciprocal the sign of inequality gets reversed. i.e., \(a\). \(>b>0 \Rightarrow \frac{1}{a}<\frac{1}{b}\) and \(a<b<0 \Rightarrow \frac{1}{a}>\frac{1}{b}\)
But if both sides of inequality have opposite sign, then while taking reciprocal sign of inequality does not change, i.e.
\(
a<0<b \Rightarrow \frac{1}{a}<\frac{1}{b}
\)
If \(x \in[a, b] \Rightarrow\left\{\begin{array}{l}\frac{1}{x} \in\left[\frac{1}{b}, \frac{1}{a}\right], \text { if } a \text { and } b \text { have same sign } \\ \frac{1}{x} \in\left(-\infty, \frac{1}{a}\right] \cup\left[\frac{1}{b}, \infty\right), \text { if } a \text { and } b \text { have opposite signs }\end{array}\right.\) - \(|x|<a \Leftrightarrow-a<x<a\) i.e. \(x \in(-a, a)\)
- \(|x| \leq a \Leftrightarrow-a \leq x \leq a\) i.e. \(x \in[-a, a]\)
- \(|x|>a \Leftrightarrow x<-a\) or \(x>a\) i.e. \(x \in(-\infty,-a) \cup(a, \infty)\)
- \(|x| \geq a \Leftrightarrow x \leq-a\) or \(x \geq a\) i.e. \(x \in(-\infty,-a] \cup[a, \infty)\)
If \(r\) is a positive real number and \(a\) is any real number, then
- \(|x-a|<r \Leftrightarrow a-r<x<a+r\) i.e. \(x \in(a-r, a+r)\)
- \(|x-a| \leq r \Leftrightarrow a-r \leq x \leq a+r\) i.e. \(x \in[a-r, a+r]\)
- \(|x-a|>r \Leftrightarrow x<a-r\) or, \(x>a+r\)
\(
\text { i.e. } x \in(-\infty, a-r) \cup(a+r, \infty)
\) - \(|x-a| \geq r \Leftrightarrow x \leq a-r\) or, \(x \geq a+r\)
\(
\text { i.e. } x \in(-\infty, a-r] \cup[a+r, \infty)
\)
If \(a, b>0\) and \(c\) are real numbers, then
- \(a<|x|<b \Leftrightarrow x \in(-b,-a) \cup(a, b)\)
- \(a \leq|x| \leq b \Leftrightarrow x \in[-b,-a] \cup[a, b]\)
- \(a \leq|x-c| \leq b \Leftrightarrow x \in[-b+c,-a+c] \cup[a+c, b+c]\)
- \(a<|x-c|<b \Leftrightarrow x \in(-b+c,-a+c) \cup(a+c, b+c)\)
- If \(a, b, c \in R\) such that \(b^2-4 a c<0\), then
\(
\begin{aligned}
& a>0 \Rightarrow a x^2+b x+c>0 \text { for all } x \in R \\
& a<0 \Rightarrow a x^2+b x+c<0 \text { for all } x \in R
\end{aligned}
\)
i.e. \(a x^2+b x+c\) and \(a\) are of the same sign for all \(x \in R\).
Quadratic Equation
An equation of the form
\(
a x^2+b x+c=0 \dots(i)
\)
where \(a \neq 0, a, b, c \in R\) is called a quadratic equation with real coefficients.
The quantity \(D=b^2-4 a c\) is known as the discriminant of the quadratic equation in (i) whose roots are given by
\(
\alpha=\frac{-b+\sqrt{b^2-4 a c}}{2 a} \text { and } \beta=\frac{-b-\sqrt{b^2-4 a c}}{2 a}
\)
Where \(\alpha, \beta\) are roots of the quadratic equation \(a x^2+b x+c=0\), then
\(
\alpha+\beta=-\frac{b}{a} \text { and } \alpha \beta=\frac{c}{a}
\)
The nature of the roots is as given below :
- The roots are real and distinct iff \(D>0\).
- The roots are real and equal iff \(D=0\).
- The roots are complex with non-zero imaginary part iff \(D<0\).
- The roots are rational iff \(a, b, c\) are rational and \(D\) is a perfect square.
- The roots are of the form \(p+\sqrt{q}(p, q \in Q)\) iff \(a, b, c\) are rational and \(D\) is not a perfect square.
- If \(a=1, b, c \in I\) and the roots are rational numbers, then these roots must be integers.
- If a quadratic equation in \(x\) has more than two roots, then it is an identity in \(x\) that is \(a=b=c=0\).
Quiz Summary
0 of 64 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 64 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 64
1. Question
\(
\text { Solve the inequality, } 3 x-5<x+7 \text {, when } x
\) is a natural numberCorrectIncorrectHint
(a)
We have \(3 x-5<x+7\)
\(
\Rightarrow 3 \mathrm{x}<\mathrm{x}+12
\) ….(Adding 5 to both sides)
\(\Rightarrow 2 \mathrm{x}<12\) (Subtracting \(\mathrm{x}\) from both sides)
\(\Rightarrow x<6\)
(Dividing by 2 on both sides)
Solution set is \(\{1,2,3,4,5\}\) -
Question 2 of 64
2. Question
\(
\text { Solve the inequality, } 3 x-5<x+7 \text {, when } x
\) is a whole numberCorrectIncorrectHint
We have \(3 x-5<x+7\)
\(
\Rightarrow 3 \mathrm{x}<\mathrm{x}+12
\) ….(Adding 5 to both sides)
\(\Rightarrow 2 \mathrm{x}<12\)
(Subtracting \(\mathrm{x}\) from both sides)
\(\Rightarrow x<6\)
(Dividing by 2 on both sides)
Solution set is \(\{0,1,2,3,4,5\}\) -
Question 3 of 64
3. Question
Solve the inequality, \(3 x-5<x+7\), when \(x\) is an integer
CorrectIncorrectHint
We have \(3 x-5<x+7\)
\(\Rightarrow 3 x<x+12 \quad \ldots\). (Adding 5 to both sides)
\(\Rightarrow 2 \mathrm{x}<12 \ldots .\). (Subtracting \(\mathrm{x}\) from both sides)
\(\Rightarrow x<6\) (Dividing by 2 on both sides)
Solution set is \(\{\ldots .-3,-2,-1,0,1,2,3,4,5\}\) -
Question 4 of 64
4. Question
Solve the inequality, \(3 x-5<x+7\), when \(x\) is a real number
CorrectIncorrectHint
(a) We have \(3 x-5<x+7\)
\(\Rightarrow 3 \mathrm{x}<\mathrm{x}+12\) (Adding 5 to both sides)
\(\Rightarrow 2 x<12\) (Subtracting \(x\) from both sides)
\(\Rightarrow x<6\) (Dividing by 2 on both sides)
\(
\text { Solution set is }\{x: x \in R \text { and } x<6\} \text {, i.e., any real number less than } 6 \text {. }
\) -
Question 5 of 64
5. Question
\(
\text { Solve } \frac{x-2}{x+5}>2
\)CorrectIncorrectHint
We have \(\frac{x-2}{x+5}>2\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{x-2}{x+5}-2>0 \\
& \Rightarrow \quad \frac{-(x+12)}{x+5}>0 \\
& \Rightarrow \quad \frac{x+12}{x+5}<0 \\
& \Rightarrow \quad x+12>0 \text { and } x+5<0 \quad \text { [Since } \frac{a}{b}<0 \Rightarrow a \text { and } b \text { are of opposite signs] } \\
& \text { or } \\
& x+12<0 \text { and } x+5>0 \\
& \Rightarrow \quad x>-12 \text { and } x<-5 \\
& x<-12 \text { and } x>-5 \quad \text { (Not possible) } \\
& \text { Therefore, } \quad-12<x<-5, \quad \text { i.e. } x \in(-12,-5) \\
&
\end{aligned}
\) -
Question 6 of 64
6. Question
Solutions of the inequality \(|3-4 x| \geq 9\) is
CorrectIncorrectHint
We have \(|3-4 x| \geq 9\).
\(
\begin{array}{lll}
\Rightarrow & 3-4 x \leq-9 \text { or } 3-4 x \geq 9 & \text { (Since }|x| \geq a \Rightarrow x \leq-a \text { or } x \geq a) \\
\Rightarrow & -4 x \leq-12 \text { or }-4 x \geq 6 \\
\Rightarrow & \left.x \geq 3 \quad \text { or } \quad x \leq \frac{-3}{2} \quad \text { (Dividing both sides by }-4\right) \\
\Rightarrow \quad & x \in\left(-\infty, \frac{-3}{2}\right] \cup[3, \infty) &
\end{array}
\) -
Question 7 of 64
7. Question
Find \(\text { Solution to the inequality } 1 \leq|x-2| \leq 3\)
CorrectIncorrectHint
We have \(1 \leq|x-2| \leq 3\)
\(
\begin{array}{ll}
\Rightarrow & |x-2| \geq 1 \text { and }|x-2| \leq 3 \\
\Rightarrow & (x-2 \leq-1 \text { or } x-2 \geq 1) \text { and }(-3 \leq x-2 \leq 3) \\
\Rightarrow & (x \leq 1 \text { or } x \geq 3) \text { and }(-1 \leq x \leq 5) \\
\Rightarrow & x \in(-\infty, 1] \cup[3, \infty) \text { and } x \in[-1,5]
\end{array}
\)
Combining the solutions of two inequalities, we have
\(
x \in[-1,1] \cup[3,5]
\) -
Question 8 of 64
8. Question
The cost and revenue functions of a product are given by \(\mathrm{C}(x)=20 x+4000\) and \(\mathrm{R}(x)=60 x+2000\), respectively, where \(x\) is the number of items produced and sold. How many items must be sold to realise some profit?
CorrectIncorrectHint
We have, profit \(=\) Revenue \(–\) Cost
\(
\begin{aligned}
& =(60 x+2000)-(20 x+4000) \\
& =40 x-2000
\end{aligned}
\)
To earn some profit, \(40 x-2000>0\)
\(
\Rightarrow \quad x>50
\)
Hence, the manufacturer must sell more than 50 items to realise some profit. -
Question 9 of 64
9. Question
\(\text { Solve for } x,|x+1|+|x|>3\)
CorrectIncorrectHint
(d) On LHS of the given inequality, we have two terms both containing modulus. By equating the expression within the modulus to zero, we get \(x=-1,0\) as critical points. These critical points divide the real line in three parts as \((-\infty,-1),[-1,0),[0, \infty)\).
Case I: When \(-\infty<x<-1\)
\(
|x+1|+|x|>3 \Rightarrow-x-1-x>3 \Rightarrow x<-2
\)
Case II: When \(-1 \leq x<0\),
\(
|x+1|+|x|>3 \Rightarrow x+1-x>3 \Rightarrow 1>3 \quad \text { (not possible) }
\)
Case III When \(0 \leq x<\infty\),
\(
|x+1|+|x|>3 \Rightarrow x+1+x>3 \Rightarrow x>1 .
\)
Combining the results of cases (I), (II) and (III), we get
\(
x \in(-\infty,-2) \cup(1, \infty)
\) -
Question 10 of 64
10. Question
\(
\text { Solve for } x, \frac{|x+3|+x}{x+2}>1
\)CorrectIncorrectHint
We have \(\frac{|x+3|+x}{x+2}>1\)
\(
\begin{array}{ll}
\Rightarrow & \frac{|x+3|+x}{x+2}-1>0 \\
\Rightarrow & \frac{|x+3|-2}{x+2}>0
\end{array}
\)
Now two cases arise:
Case I: When \(x+3 \geq 0\), i.e., \(x \geq-3\). Then
\(
\begin{array}{ll}
& \frac{|x+3|-2}{x+2}>0 \Rightarrow \frac{x+3-2}{x+2}>0 \\
\Rightarrow & \frac{x+1}{x+2}>0 \\
\Rightarrow & \{(x+1)>0 \text { and } x+2>0\} \text { or }\{x+1<0 \text { and } x+2<0\} \\
\Rightarrow & \{x>-1 \text { and } x>-2\} \text { or }\{x<-1 \text { and } x<-2\} \\
\Rightarrow & x>-1 \text { or } x<-2 \\
\Rightarrow & x \in(-1, \infty) \text { or } x \in(-\infty,-2) \\
\Rightarrow & x \in(-3,-2) \cup(-1, \infty) \quad[\text { Since } x \geq-3] \dots(1)
\end{array}
\)
Case II: When \(x+3<0\), i.e., \(x<-3\)
\(
\begin{array}{ll}
& \frac{|x+3|-2}{x+2}>0 \quad \Rightarrow \quad \frac{-x-3-2}{x+2}>0 \\
\Rightarrow \quad & \frac{-(x+5)}{x+2}>0 \quad \Rightarrow \quad \frac{x+5}{x+2}<0 \\
\Rightarrow \quad & (x+5<0 \text { and } x+2>0) \quad \text { or }(x+5>0 \text { and } x+2<0) \\
\Rightarrow \quad & (x<-5 \text { and } x>-2) \quad \text { or } \quad(x>-5 \text { and } x<-2) \\
\Rightarrow \quad & \text { it is not possible. } \\
\Rightarrow & x \in(-5,-2) \dots(2)
\end{array}
\)
Combining (I) and (II), the required solution is
\(
x \in(-5,-2) \cup(-1, \infty)
\) -
Question 11 of 64
11. Question
Solve the following system of inequalities :
\(
\frac{x}{2 x+1} \geq \frac{1}{4}, \frac{6 x}{4 x-1}<\frac{1}{2}
\)CorrectIncorrectHint
From the first inequality, we have \(\frac{x}{2 x+1}-\frac{1}{4} \geq 0\)
\(
\begin{array}{ll}
\Rightarrow & \frac{2 x-1}{2 x+1} \geq 0 \\
\Rightarrow & (2 x-1 \geq 0 \text { and } 2 x+1>0) \text { or }(2 x-1 \leq 0 \text { and } 2 x+1<0)[\text { Since } 2 x+1 \neq 0) \\
\Rightarrow & \left(x \geq \frac{1}{2} \text { and } x>-\frac{1}{2}\right) \text { or }\left(x \leq \frac{1}{2} \text { and } x<-\frac{1}{2}\right) \\
\Rightarrow & x \geq \frac{1}{2} \text { or } x<-\frac{1}{2} \\
\Rightarrow & x \in\left(-\infty,-\frac{1}{2}\right) \cup\left[\frac{1}{2}, \infty\right) \dots(1)
\end{array}
\)
From the second inequality, we have \(\frac{6 x}{4 x-1}-\frac{1}{2}<0\)
\(
\begin{array}{llll}
\Rightarrow & \frac{8 x+1}{4 x-1}<0 & \\
\Rightarrow & (8 x+1<0 \text { and } 4 x-1>0) \quad & \text { or } & (8 x+1>0 \text { and } 4 x-1<0) \\
\Rightarrow & \left(x<-\frac{1}{8} \text { and } x>\frac{1}{4}\right) \quad \text { or } \quad\left(x>-\frac{1}{8} \text { and } x<\frac{1}{4}\right) \\
\Rightarrow & x \in\left(-\frac{1}{8}, \frac{1}{4}\right) \quad \text { (Since the first is not possible) } \dots(2)
\end{array}
\)Note that the common solution of (1) and (2) is null set. Hence, the given system of
inequalities has no solution. -
Question 12 of 64
12. Question
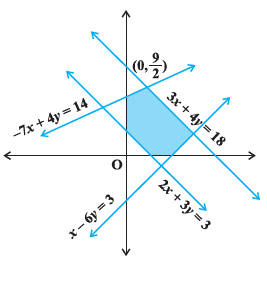
Find the linear inequalities for which the shaded region in the given figure is the solution set.
 CorrectIncorrect
CorrectIncorrectHint
We have \(2 x+3 y \geq 3\) as linear inequality corresponding to the line \(2 x+3 y=3\).
(ii) Consider \(3 x+4 y=18\). We observe that the shaded region and the origin lie on the same side of this line and \((0,0)\) satisfies \(3 x+4 y \leq 18\). Therefore, \(3 x+4 y \leq 18\) is the linear inequality corresponding to the line \(3 x+4 y=18\).
(iii) Consider \(-7 x+4 y=14\). It is clear from the figure that the shaded region and the origin lie on the same side of this line and \((0,0)\) satisfies the inequality \(-7 x+4 y \leq 14\). Therefore, \(-7 x+4 y \leq 14\) is the inequality corresponding to the line \(-7 x+4 y=14\)
(iv) Consider \(x-6 y=3\). It may be noted that the shaded portion and origin lie on the same side of this line and \((0,0)\) satisfies \(x-6 y \leq 3\). Therefore, \(x-6 y \leq 3\) is the inequality corresponding to the line \(x-6 y=3\).
(v) Also the shaded region lies in the first quadrant only. Therefore, \(x \geq 0, y \geq 0\). Hence, in view of (i), (ii), (iii), (iv) and (v) above, the linear inequalities corresponding to the given solution set are :
\(
2 x+3 y \geq 3,3 x+4 y \leq 18-7 x+4 y \leq 14, x-6 y \leq 3, x \geq 0, y \geq 0 \text {. }
\) -
Question 13 of 64
13. Question
\(
\text { If } \frac{|x-2|}{x-2} \geq 0, \text { then }
\)CorrectIncorrectHint
\(
\text { (b) is the correct choice. Since } \frac{|x-2|}{x-2} \geq 0 \text {, for }|x-2| \geq 0 \text {, and } x-2 \neq 0 \text {. }
\)Therefore, \(x \in(2, \infty)\)
-
Question 14 of 64
14. Question
The length of a rectangle is three times the breadth. If the minimum perimeter of the rectangle is 160 cm, then
CorrectIncorrectHint
(c) is the correct choice. If \(x \mathrm{~cm}\) is the breadth, then
\(
2(3 x+x) \geq 160 \Rightarrow x \geq 20
\) -
Question 15 of 64
15. Question
Solutions of the inequalities comprising a system in variable x are represented on number lines as given below, then
 CorrectIncorrect
CorrectIncorrectHint
(a) is the correct choice. Common solution of the inequalities is from \(-\infty\) to \(-4\) and 3 to \(\infty\).
-
Question 16 of 64
16. Question
\(
\text { If }|x+3| \geq 10 \text {, then }
\)CorrectIncorrectHint
(d) is the correct choice, since \(|x+3| \geq 10, \Rightarrow x+3 \leq-10\) or \(x+3 \geq 10\)
\(
\begin{array}{ll}
\Rightarrow & x \leq-13 \text { or } \quad x \geq 7 \\
\Rightarrow & x \in(-\infty,-13] \cup[7, \infty)
\end{array}
\) -
Question 17 of 64
17. Question
State whether the following statements are True or False.
\(
\text { If } x>y \text { and } b<0 \text {, then } b x<b y
\)CorrectIncorrectHint
(a) True, because the sign of inequality is reversed when we multiply both sides of an inequality by a negative quantity.
-
Question 18 of 64
18. Question
State whether the following statements are True or False.
\(
\text { If } x y>0 \text {, then } x>0 \text {, and } y<0
\)CorrectIncorrectHint
False, product of two numbers is positive if they have the same sign.
-
Question 19 of 64
19. Question
State whether the following statements are True or False.
\(
\text { If } x y<0 \text {, then } x>0 \text {, and } y>0
\)CorrectIncorrectHint
False, product of two numbers is negative if they have opposite signs.
-
Question 20 of 64
20. Question
State whether the following statements are True or False.
\(
\text { If } x>5 \text { and } x>2 \text {, then } x \in(5, \infty)
\)CorrectIncorrectHint
(a)
\(
\text { If } x>5 \text {, then } x \in(5, \infty)
\)\(
\text { If } x>2 \text {, then } x \in(2, \infty)
\)Therefore, \(x \in(5, \infty)\)
-
Question 21 of 64
21. Question
State whether the following statements are True or False.
\(
\text { If }|x|<5 \text {, then } x \in(-5,5)
\)CorrectIncorrectHint
\(
\text { True if }|x|<5 \Rightarrow-5<x<5 \Rightarrow x \in(-5,5) \text {. }
\) -
Question 22 of 64
22. Question
Fill in the blanks in the following:
If \(x \geq-3\), then \(x+5\) ……..2
CorrectIncorrectHint
\((\geq)\), because same number can be added to both sides of inequality without changing the sign of inequality.
-
Question 23 of 64
23. Question
Fill in the blanks in the following:
If \(-x \leq-4\), then \(2 x\)……….8
CorrectIncorrectHint
\(
(\geq) \text {, after multiplying both sides by }-2, \text { the sign of inequality is reversed. }
\) -
Question 24 of 64
24. Question
If \(\frac{1}{x-2}<0\), then \(x\) ………..2
CorrectIncorrectHint
\(
(<) \text {, because if } \frac{a}{b}<0 \text { and } a>0 \text {, then } b<0 \text {. }
\) -
Question 25 of 64
25. Question
Fill in the blanks in the following:
\(
\text { If } a<b \text { and } c<0 \text {, then } \frac{a}{c} \ldots \ldots \ldots . \frac{b}{c}
\)CorrectIncorrectHint
(>), if both sides are divided by the same negative quantity, then the sign of inequality is reversed.
-
Question 26 of 64
26. Question
Fill in the blanks in the following:
\(
\text { If }|x-1| \leq 2 \text {, then }-1 \ldots \ldots \quad x \ldots 3
\)CorrectIncorrectHint
\(
(\leq, \leq),|x-1| \leq 2 \Rightarrow-2 \leq x-1 \leq 2 \Rightarrow-1 \leq x \leq 3
\) -
Question 27 of 64
27. Question
Fill in the blanks in the following:
\(
\text { If }|3 x-7|>2 \text {, then } x \ldots \frac{5}{3} \text { or } x \ldots 3
\)CorrectIncorrectHint
\(
\begin{aligned}
& (<,>),|3 x-7|>2 \Rightarrow 3 x-7<-2 \text { or } 3 x-7>2 \\
& \Rightarrow x<\frac{5}{3} \quad \text { or } x>3
\end{aligned}
\) -
Question 28 of 64
28. Question
Fill in the blanks in the following:
\(
\text { If } p>0 \text { and } q<0 \text {, then } p+q \ldots p
\)CorrectIncorrectHint
\(
(<) \text {, as } p \text { is positive and } q \text { is negative, therefore, } p+q \text { is always smaller than } p \text {. }
\) -
Question 29 of 64
29. Question
\(
\text { Solve for } x \text {, the inequalities }
\)\(
\frac{4}{x+1} \leq 3 \leq \frac{6}{x+1},(x>0)
\)CorrectIncorrectHint
Given that
\(
\begin{aligned}
& \frac{4}{x+1} \leq 3 \leq \frac{6}{x+1}, x>0 \\
& \Rightarrow \quad 4 \leq 3(x+1) \leq 6 \Rightarrow 4 \leq 3 x+3 \leq 6 \\
& \Rightarrow \quad 4-3 \leq 3 x \leq 6-3 \Rightarrow 1 \leq 3 x \leq 3 \\
& \Rightarrow \quad \frac{1}{3} \leq x \leq 1
\end{aligned}
\)
Hence, the solution is \((1 / 3) \leq x \leq 1\). -
Question 30 of 64
30. Question
Solve for x, the inequalities below
\(
\frac{|x-2|-1}{|x-2|-2} \leq 0
\)CorrectIncorrectHint
\(
\begin{aligned}
& \text { Let }|\mathrm{x}-2|=\mathrm{y} \\
& \therefore \frac{y-1}{y-2} \leq 0 \\
& \Rightarrow y-1 \leq 0 \text { and } y-2>0 \quad \text { or } y-1 \geq 0 \text { and } y-2<0 \\
& \Rightarrow y \leq 1 \text { and } y>2 \text { or } y \geq 1 \text { and } y<2 \\
& \Rightarrow 1 \leq y<2 \\
& \Rightarrow 1 \leq|x-2|<2 \\
& \Rightarrow-2<x-2 \leq-1 \text { or } 1 \leq x-2<2 \\
& \Rightarrow 0<x \leq 1 \text { or } 3 \leq x<4 \\
& \Rightarrow x \in(0,1] \cup[3,4)
\end{aligned}
\) -
Question 31 of 64
31. Question
Solve for x, the inequalities below
\(
\frac{1}{|x|-3} \leq \frac{1}{2}
\)CorrectIncorrectHint
Given that
\(
\begin{aligned}
& \frac{1}{|x|-3} \leq \frac{1}{2} \\
& \Rightarrow \quad|x|-3 \geq 2 \\
& {\left[\because \frac{1}{x}<\frac{1}{y} \Rightarrow x>y\right]} \\
& \Rightarrow \quad|x| \geq 5 \\
& \text { So, } x \in(-\infty,-5)] \cup[5, \infty) \dots(i)\\
& \text { Here } \quad|x|-3 \neq 0 \\
& \Rightarrow \quad|x|-3<0 \text { (or) }|x|-3>0 \\
& \Rightarrow \quad|x|<3 \quad \text { (or) } \quad|x|>3 \\
& \Rightarrow-3<x<3 \text { (or) } x<-3 \text { or } x>3 \ldots \text { (ii) } \\
& \text { From (i) and (ii) we get } \\
& x \in(-\infty,-5] \cup(-3,3) \cup[5, \infty)
\end{aligned}
\) -
Question 32 of 64
32. Question
Solve for x, the inequalities is
\(
|x-1| \leq 5, \quad|x| \geq 2
\)CorrectIncorrectHint
\(
\mid x-1 \mid \leq 5
\)
There are two cases,
\(
x-1 \leq 5
\)
Adding 1 to L.H.S. and R.H.S
\(
\begin{aligned}
& \Rightarrow x \leq 6 \\
& \Rightarrow-(x-1) \leq 5 \\
& \Rightarrow-x+1 \leq 5
\end{aligned}
\)
Subtracting 1 from L.H.S. and R.H.S.,
\(
\begin{aligned}
& \Rightarrow-x \leq 4 \\
& \Rightarrow x \geq-4
\end{aligned}
\)
From cases 1 and 2, we have
\(
\Rightarrow-4 \leq x \leq 6 \ldots \ldots .[i]
\)
Also,
\(
\begin{aligned}
& |x| \geq 2 \\
& \Rightarrow x \geq 2 \text { and } \\
& \Rightarrow-x \geq 2 \\
& \Rightarrow x \leq-2 \\
& \Rightarrow x \in(\infty,-2] \cup[2, \infty) \dots(ii)
\end{aligned}
\)
Combining equation [i] and [ii], we get
\(
x \in[-4,-2] \cup[2,6]
\) -
Question 33 of 64
33. Question
Solve for x, the inequalities below
\(
-5 \leq \frac{2-3 x}{4} \leq 9
\)CorrectIncorrectHint
(b)
\(
-5 \leq \frac{2-3 x}{4} \leq 9
\)
Multiplying each term by 4 , we get
\(
\Rightarrow-20 \leq 2-3 x \leq 36
\)
Adding \(-2\) each term, we get
\(
\Rightarrow-22 \leq-3 x \leq 34
\)
Dividing each term by 3 , we get
\(
\Rightarrow-\frac{22}{3} \leq-x \leq \frac{34}{3}
\)
We know that,
Multiplication by \(-1\) inverts the inequality.
So, multiplying each term by \(-1\), we get
\(
\Rightarrow-\frac{34}{3} \leq \mathrm{x} \leq \frac{22}{3}
\) -
Question 34 of 64
34. Question
Solve for x, the inequalities below
\(
4 x+3 \geq 2 x+17,3 x-5<-2
\)CorrectIncorrectHint
\(
\begin{aligned}
& 4 x+3 \geq 2 x+17 \\
& \Rightarrow 4 x-2 x \geq 17-3 \\
& \Rightarrow 2 x \geq 14 \\
& \Rightarrow x \geq 7 \dots(i)
\end{aligned}
\)
Also,
\(
\begin{aligned}
& 3 x-5<-2 \\
& \Rightarrow 3 x<3 \\
& \Rightarrow x<1 \dots(ii)
\end{aligned}
\)
Since, equations [i] and [ii] cannot be possible
Simultaneously
We conclude that \(x\) has no solution. -
Question 35 of 64
35. Question
A company manufactures cassettes. Its cost and revenue functions are \(\mathrm{C}(x)=26,000+30 x\) and \(\mathrm{R}(x)=43 x\), respectively, where \(x\) is the number of cassettes produced and sold in a week. How many cassettes must be sold by the company to realise some profit?
CorrectIncorrectHint
We know that
Profit \(=\) Revenue \(–\) cost
The requirement is, profit \(>0\)
According to the question,
Revenue, \(R(x)=43 x\)
Cost, \(C(x)=26,000+30 x\)
Where \(\mathrm{x}\) is number of cassettes
\(
\begin{aligned}
& \Rightarrow \text { Profit }=43 x-(26,000+30 x)>0 \\
& \Rightarrow 13 x-26,000>0 \\
& \Rightarrow 13 x>26000 \\
& \Rightarrow x>2000
\end{aligned}
\)
Therefore, the company should sell more than 2000 cassettes to realise profit. -
Question 36 of 64
36. Question
The water acidity in a pool is considered normal when the average \(\mathrm{pH}\) reading of three daily measurements is between \(8.2\) and 8.5. If the first two \(\mathrm{pH}\) readings are \(8.48\) and \(8.35\), find the range of \(\mathrm{pH}\) value for the third reading that will result in the acidity level being normal.
CorrectIncorrectHint
(c) Let the third \(\mathrm{pH}\) value be \(\mathrm{x}\).
Given that first \(\mathrm{pH}\) value \(=8.48\)
And second \(\mathrm{pH}\) value \(=8.35\)
\(\therefore\) Average value of \(\mathrm{pH}=\frac{8.48+8.35+x}{3}\)
But average value of \(\mathrm{pH}\) lies between \(8.2\) and \(8.5\)
\(
\begin{aligned}
& \therefore 8 \cdot 2<\frac{8.48+8 \cdot 35+x}{3}<8 \cdot 5 \\
& \Rightarrow 24.6<16.83+\mathrm{x}<25.5 \\
& \Rightarrow 24.6-16.83<\mathrm{x}<25.5-16.83 \\
& \Rightarrow 7.77<\mathrm{x}<8.67
\end{aligned}
\)
Hence, the third pH value lies between \(7.77\) and \(8.67\). -
Question 37 of 64
37. Question
A solution of \(9 \%\) acid is to be diluted by adding \(3 \%\) acid solution to it. The resulting mixture is to be more than \(5 \%\) but less than \(7 \%\) acid. If there is 460 litres of the \(9 \%\) solution, how many litres of \(3 \%\) solution will have to be added?
CorrectIncorrectHint
Let \(\mathrm{x}\) litres of \(3 \%\) solution be added to 460 litres of \(9 \%\).
\(\therefore\) Total amount of mixture \(=(460+\mathrm{x})\) litres
Given that the acid contents in the resulting mixture is more than \(5 \%\) but less than \(7 \%\) acid.
\(
\begin{aligned}
& \therefore 5 \% \text { of }(460+\mathrm{x})<\frac{9}{100}+\frac{3}{100} \times x<7 \% \text { of }(460+\mathrm{x}) \\
& \Rightarrow \frac{5}{100}(460+x)<\frac{4140+3 x}{100}<\frac{7}{100}(460+x) \\
& \Rightarrow 5(460+\mathrm{x})<4140+3 \mathrm{x}<3220+7 \mathrm{x} \\
& \Rightarrow 2300+5 \mathrm{x}<4140+3 \mathrm{x}<3220+7 \mathrm{x} \\
& \Rightarrow 2300+5 \mathrm{x}<4140+3 \mathrm{x} \text { and } 4140+3 \mathrm{x}<3220+7 \mathrm{x} \\
& \Rightarrow 5 \mathrm{x}-3 \mathrm{x}<4140-2300 \text { and } 3 \mathrm{x}-7 \mathrm{x}<3220-4140 \\
& \Rightarrow 2 \mathrm{x}<1840 \text { and }-4 \mathrm{x}<-920 \\
& \Rightarrow x<\frac{1840}{2} \text { and } 4 \mathrm{x}>920 \\
& \Rightarrow \mathrm{x}<920 \\
& \therefore x>\frac{920}{4} \text { and } \mathrm{x}>230
\end{aligned}
\)
Hence the required amount of acid solution is more than 230 litres and less than 920 litres. -
Question 38 of 64
38. Question
A solution is to be kept between \(40^{\circ} \mathrm{C}\) and \(45^{\circ} \mathrm{C}\). What is the range of temperature in degree fahrenheit, if the conversion formula is \(\mathrm{F}=\frac{9}{5} \mathrm{C}+32\)?
CorrectIncorrectHint
Let temperature in Celsius be \(C\)
Let temperature in Fahrenheit be \(\mathrm{F}\)
Solution should be kept between \(40^{\circ} \mathrm{C}\) and \(45^{\circ} \mathrm{C}\)
\(
\Rightarrow 40<C<45
\)
Multiplying each term by \(\frac{9}{5}\), we get
\(
\Rightarrow 72<\frac{9}{5} C<81
\)
Adding 32 to each term, we get
\(
\begin{aligned}
& \Rightarrow 104<\frac{9}{5} C+32<113 \\
& \Rightarrow 104<F<113
\end{aligned}
\)
Hence, the range of temperature in Fahrenheit should be between \(104^{\circ} \mathrm{F}\) and \(113^{\circ} \mathrm{F}\). -
Question 39 of 64
39. Question
The longest side of a triangle is twice the shortest side and the third side is 2cm longer than the shortest side. If the perimeter of the triangle is more than 166 cm then find the minimum length of the shortest side.
CorrectIncorrectHint
Let the length of shortest side \(={ }^{\prime} x\) ‘ \(\mathrm{cm}\)
The longest side of a triangle is twice the shortest side
\(\Rightarrow\) Length of largest side \(=2 x\)
Also, the third side is \(2 \mathrm{~cm}\) longer than the shortest side
\(\Rightarrow\) Length of third side \(=(x+2) \mathrm{cm}\)
Perimeter of triangle \(=\) sum of three sides
\(
\begin{aligned}
& =x+2 x+x+2 \\
& =4 x+2 \mathrm{~cm}
\end{aligned}
\)
Now, we know that,
Perimeter is more than \(166 \mathrm{~cm}\)
\(
\begin{aligned}
& \Rightarrow 4 x+2 \geq 166 \\
& \Rightarrow 4 x \geq 164 \\
& \Rightarrow x \geq 41
\end{aligned}
\)
Hence, the minimum length of the shortest side should be \(=41 \mathrm{~cm}\). -
Question 40 of 64
40. Question
In drilling world’s deepest hole it was found that the temperature \(\mathrm{T}\) in degree celcius, \(x \mathrm{~km}\) below the earth’s surface was given by \(\mathrm{T}=30+25(x-3)\), \(3 \leq x \leq 15\). At what depth will the temperature be between \(155^{\circ} \mathrm{C}\) and \(205^{\circ} \mathrm{C}\)?
CorrectIncorrectHint
\(
T=30+25(x-3), 3 \leq x \leq 15
\)
Where, \(\mathrm{T}=\) temperature and \(\mathrm{x}=\) depth inside the earth
The Temperature should be between \(155^{\circ} \mathrm{C}\) and \(205^{\circ} \mathrm{C}\)
So, we get,
\(
\begin{aligned}
& \Rightarrow 155<\mathrm{T}<205 \\
& \Rightarrow 155<30+25(\mathrm{x}-3)<205 \\
& \Rightarrow 155<30+25 \mathrm{x}-75<205 \\
& \Rightarrow 155<25 \mathrm{x}-45<205
\end{aligned}
\)
Adding 45 to each term, we get
\(
\Rightarrow 200<25 \mathrm{x}<250
\)
Dividing each term by 25 , we get
\(
\Rightarrow 8<\mathrm{x}<10
\)
Hence, temperature varies from \(155^{\circ} \mathrm{C}\) to \(205^{\circ} \mathrm{C}\) at a depth of \(8 \mathrm{~km}\) to \(10 \mathrm{~km}\). -
Question 41 of 64
41. Question
\(
\text { Solve the following system of inequalities } \frac{2 x+1}{7 x-1}>5, \frac{x+7}{x-8}>2
\)CorrectIncorrectHint
(a) We have,
\(
(2 x+1) /(7 x-1)>5,(x+7) /(x-8)>2
\)
Now, \(\frac{2 x+1}{7 x-1}-5>0\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{(2 x+1)-5(7 x-1)}{7 x-1}>0 \Rightarrow \frac{2 x+1-35 x+5}{7 x-1}>0 \\
& \Rightarrow \quad \frac{-33 x+6}{7 x-1}>0 \Rightarrow \frac{11 x-2}{7 x-1}<0 \\
& \Rightarrow \quad 11 x-2<0 \text { and } 7 x-1>0 \text { or } 11 x-2>0 \text { and } 7 x-1<0 \\
& \Rightarrow \quad x<2 / 11 \text { and } x>1 / 7 \quad \text { or } x>2 / 11 \text { and } x<1 / 7 \\
& \Rightarrow \quad x \in(1 / 7,2 / 11) \quad \text { (i) }
\end{aligned}
\)
Also \(\frac{x+7}{x-8}>2\)
\(
\begin{aligned}
& \Rightarrow \frac{x+7}{x-8}-2>0 \Rightarrow \frac{x+7-2(x-8)}{x-8}>0 \\
& \Rightarrow \frac{x+7-2 x+16}{x-8}>0 \Rightarrow \frac{-x+23}{x-8}>0 \Rightarrow \frac{x-23}{x-8}<0 \\
& \Rightarrow \quad x-23<0 \text { and } x-8>0 \text { or } x-23>0 \text { and } x-8<0 \\
& \Rightarrow \quad x<23 \text { and } x>8 \text { or } x>23 \text { and } x<8 \\
& \Rightarrow \quad x \in(8,23) \quad \text { (ii) } \\
&
\end{aligned}
\)
From (i) and (ii), we can find that there is no common set of values of \(x\). So, the given system of equation has no solution. -
Question 42 of 64
42. Question
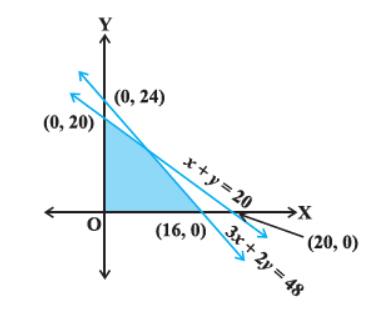
Find the linear inequalities for which the shaded region in the given figure is the solution set.
 CorrectIncorrect
CorrectIncorrectHint
Consider the line \(3 x+2 y=48\), we observe that the shaded and the origin are on the same side of the line \(3 x+2 y=48\) and \((0,0)\) satisfy the linear constraint \(3 x+2 y \leq 48\). So, we must have one inequation as \(3 x+2 y \leq 48\).
Now, consider the line \(x+y=20\). We find that the shaded region and the origin are on the same side of the line \(x+y=20\) and \((0,0)\) satisfy the constraints \(x+y \leq 20\). So, the second inequation is \(x+y \leq 20\).
We also notice that the shaded region is above \(\mathrm{X}\) – axis and is on the right side of \(y\)-axis, so we must have \(x \geq 0, y \geq 0\).
Thus, the linear inequations corresponding to the given solution set are \(3 x+2 y \leq 48, x+y \leq 20\) and \(x \geq 0, y \geq 0\). -
Question 43 of 64
43. Question
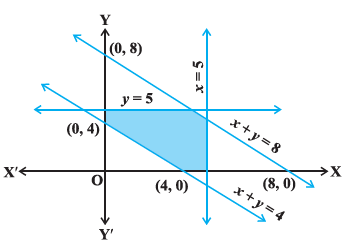
Find the linear inequalities for which the shaded region in the given figure is the solution set.
 CorrectIncorrect
CorrectIncorrectHint
(i) Consider the line \(x+y=8\). We observe that the shaded region and origin lie on the same side of this line and \((0,0)\) satisfies \(x+y \leq 8\)
Therefore, \(x+y \leq 8\) is the linear inequality corresponding to the line \(x+y=8\).(ii) Consider \(x+y=4\). We observe that shaded region and origin are on the opposite side of this line and \((0,0)\) satisfies \(x+y \leq 4\)
Therefore, we must have \(x+y \geq 4\) as linear inequalities corresponding to the line \(x+y=4\)(iii) Shaded portion lie below the line \(y=5\). So, \(y \leq 5\) is the linear inequality corresponding to \(y=5\).
(iv) Shaded portion lie on the left side of the line \(x=5\), So, \(x \leq 5\) is the linear inequality corresponding to \(x=5\)
(v) Also, the shaded region lies in the first quadrant only. Therefore, \(x \geq 0, y \geq 0\).
In view of (i), (ii), (iii), (iv) and (v) above the linear inequalities corresponding to the given solutions are: \(x+y \leq 8, x+y \geq 4, y \leq 5, x \leq 5, x \geq 0\) and \(y \geq 0\) -
Question 44 of 64
44. Question
Is the following system of linear inequalities has no solution?
\(
x+2 y \leq 3,3 x+4 y \geq 12, x \geq 0, y \geq 1
\)CorrectIncorrectHint
Given: \(x+2 y \leq 3 \quad\) Line: \(x+2 y=3\)
\(
\begin{array}{|l|l|l|}
\hline x & 3 & 1 \\
\hline y & 0 & 1 \\
\hline
\end{array}
\)
Now, \((0,0)\) doesn’t satisfies \(3 x+4 y \geq 12\),
Thus, the region is not towards the origin
region is to the right of the \(y\) axis, thus,
\(x \geq 0\)
& Region is above the line \(x=1\), thus,
\(y \geq 1\)
Thus, the graph can be plotted as,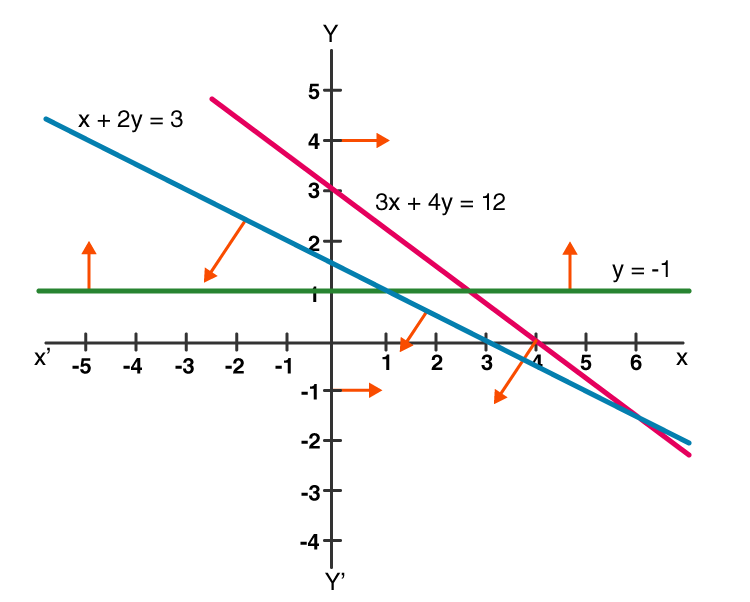
Therefore, the system has no common region as solution.
-
Question 45 of 64
45. Question
Solve the following system of linear inequalities:
\(3 x+2 y \geq 24,3 x+y \leq 15, x \geq 4\)CorrectIncorrectHint
\(
3 x+2 y \geq 24
\)
Line: \(3 x+2 y=24\)\(
\begin{array}{|l|l|l|}
\hline x & 0 & 8 \\
\hline y & 12 & 0 \\
\hline
\end{array}
\)Also, \((0,0)\) doesn’t satisfy the \(3 x+2 y \geq 24\), hence region is away from the origin
\(
3 x+y \leq 15
\)
Line: \(3 x+y=15\)\(
\begin{array}{|l|l|l|}
\hline \mathrm{x} & 0 & 5 \\
\hline \mathrm{y} & 15 & 0 \\
\hline
\end{array}
\)Also, \((0,0)\) satisfies the \(3 x+y \leq 15\), hence region is towards the origin \(x \geq 4\) implies that region is right to the line \(x=4\), therefore graph is
It is clear from the graph the above system has no common region as solution.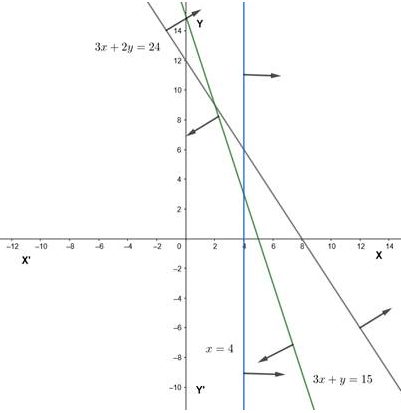
-
Question 46 of 64
46. Question
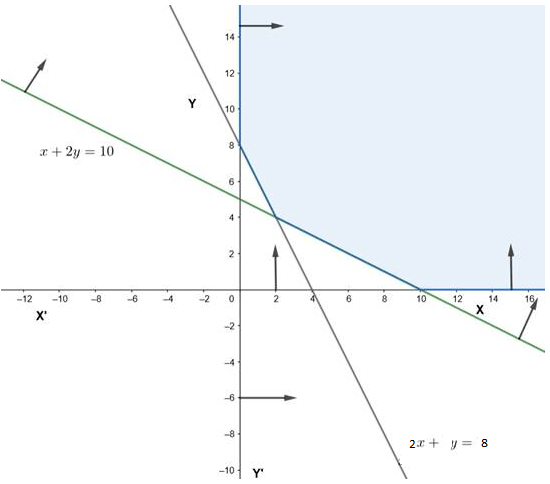
Is the solution set of the following system of linear inequalities in an unbounded region?
\(
2 x+y \geq 8, x+2 y \geq 10, x \geq 0, y \geq 0
\)CorrectIncorrectHint
(a) Let’s plot the region of each inequality and then find the common region of all
\(
2 x+y \geq 8
\)
Line: \(2 x+y=8\)
\(
\begin{array}{|c|c|c|}
\hline x & 0 & 4 \\
\hline y & 8 & 0 \\
\hline
\end{array}
\)
Also, \((0,0)\) doesn’t satisfy the \(2 x+y \geq 8\), hence region is away from the origin
\(
x+2 y \geq 10
\)
Line: \(x+2 y=10\)
\(
\begin{array}{|c|c|c|}
\hline \mathrm{X} & 0 & 10 \\
\hline \mathrm{Y} & 5 & 0 \\
\hline
\end{array}
\)
\(
\text { Also, }(0,0) \text { doesn’t satisy the } x+2 y \geq 10 \text {, hence region is away from the origin }
\)
-
Question 47 of 64
47. Question
If \(x<5\), then
CorrectIncorrectHint
\(
x<5
\)
Multiplication or dividing by negative number inverts the inequality sign.
\(
\Rightarrow-x>-5
\) -
Question 48 of 64
48. Question
Given that \(x, y\) and \(b\) are real numbers and \(x<y, b<0\), then
CorrectIncorrectHint
Given that \(\mathrm{x}, \mathrm{y}\) and \(\mathrm{b}\) are real numbers and \(\mathrm{x}<\mathrm{y}, \mathrm{b}<0\), then \(\frac{x}{b}>\frac{y}{b}\).
Explanation:
Given that \(x<y, b<0\)
\(
\Rightarrow \frac{x}{b}>\frac{y}{b}, b<0
\) -
Question 49 of 64
49. Question
If \(-3 x+17<-13\), then
CorrectIncorrectHint
\(
\begin{aligned}
& -3 x+17<-13 \\
& \Rightarrow-3 x<-30 \text { [Subtracting } 17 \text { both side] } \\
& \Rightarrow x>10 \text { [Division by negative number inverts the inequality sign] } \\
& \Rightarrow x \in(10, \infty)
\end{aligned}
\) -
Question 50 of 64
50. Question
If \(x\) is a real number and \(|x|<3\), then
CorrectIncorrectHint
\(|x|<3\)
Hence, there are two cases,
\(x<3 \dots(1)\)
and
\(
\begin{aligned}
& -x<3 \\
& \Rightarrow x>-3 \dots(2)
\end{aligned}
\)
From [1] and [2], we get
\(
\Rightarrow-3<x<3
\) -
Question 51 of 64
51. Question
\(x\) and \(b\) are real numbers. If \(b>0\) and \(|x|>b\), then
CorrectIncorrectHint
\(
|x|>b
\)
Hence, there are two cases,
\(
\begin{aligned}
& x>b \\
& \Rightarrow x \in(b, \infty)……[1]
\end{aligned}
\)
and
\(
\begin{aligned}
& -x>b \\
& \Rightarrow x<-b \\
& \Rightarrow x \in(-\infty,-b)…..[2]
\end{aligned}
\)
From [1] and [2], we get
\(
\Rightarrow x \in(-\infty,-b) \cup(b, \infty)
\) -
Question 52 of 64
52. Question
If \(|x-1|>5\), then
CorrectIncorrectHint
(c)
\(
\begin{aligned}
& |x-1|>5 \\
& x-1<-5 \text { and } x-1>5 \\
& x<-4 \text { and } x>6 \\
& x \in(-\infty,-4) \cup (6, \infty)
\end{aligned}
\) -
Question 53 of 64
53. Question
If \(|x+2| \leq 9\), then
CorrectIncorrectHint
Given that \(|x+2| \leq 9\)
\(
\begin{aligned}
& \Rightarrow-9 \leq x+2 \leq 9 \\
& \Rightarrow-9-2 \leq x \leq 9-2 \quad \ldots \ldots[|x|<a \Rightarrow-a \leq x \leq a] \\
& \Rightarrow-11 \leq x \leq 7 \\
& \Rightarrow x \in[-11,7]
\end{aligned}
\) -
Question 54 of 64
54. Question
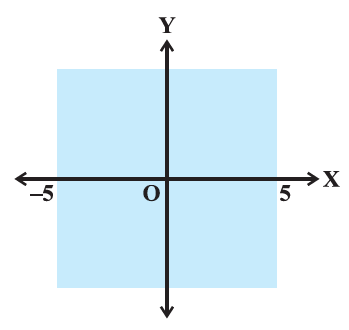
The inequality representing the following graph is:
 CorrectIncorrect
CorrectIncorrectHint
(a) The inequality representing the following graph is \(|\underline{\mathbf{x}}| \mathbf{\leq 5}\).
Explanation:
The given graph represents \(x>-5\) and \(x<5\)
Combining the two inequalities \(|x|<5\) -
Question 55 of 64
55. Question
The solution of a linear inequality in variable x is represented on number line in the following Exercises
 CorrectIncorrect
CorrectIncorrectHint
The gives graph represents all values of \(x\) greater than 5 including 5 on the real number line
\(
\text { So } x \in(5, \infty)
\) -
Question 56 of 64
56. Question
The solution of a linear inequality in variable x is represented on number line in the Exercises shown below.
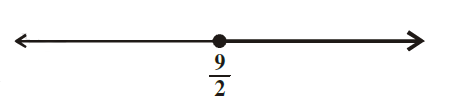 CorrectIncorrect
CorrectIncorrectHint
The given graph has all real values of \(x\) greater than and equal to \(\frac{9}{2}\).
So, \(x \geq \frac{9}{2}\)
\(
\Rightarrow x \in\left[\frac{9}{2}, \infty\right)
\) -
Question 57 of 64
57. Question
Solution of a linear inequality in variable x is represented on number line in the Exercises below.
 CorrectIncorrect
CorrectIncorrectHint
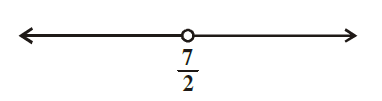
The given graph represents all the values of \(\mathrm{x}\) less than \(\frac{7}{2}\) on real number line. So, \(x \in\left(-\infty, \frac{7}{2}\right)\)
-
Question 58 of 64
58. Question
Solution of a linear inequality in variable x is represented on number line in the Exercises below.
 CorrectIncorrect
CorrectIncorrectHint
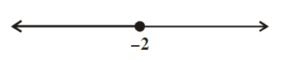
The given graph represents all real values of \(\mathrm{x}\) less than and equal to \(-2\)
So, \(x \in(-\infty,-2]\) -
Question 59 of 64
59. Question
State which of the following statement is True or False
\(
\text { If } x<y \text { and } b<0 \text {, then } \frac{x}{b}<\frac{y}{b} \text {. }
\)CorrectIncorrectHint
Given that \(x<y, b<0\)
\(
\Rightarrow \frac{x}{b}>\frac{y}{b}, b<0
\) -
Question 60 of 64
60. Question
State which of the following statement is True or False.
\(
\text { If } x y>0 \text {, then } x>0 \text { and } y<0
\)CorrectIncorrectHint
\(
\text { If } x, y>0 \text { then } x>0, y>0 \text { or } x<0, y<0
\) -
Question 61 of 64
61. Question
State which of the following statement is True or False.
\(
\text { If } x<-5 \text { and } x<-2 \text {, then } x \in(-\infty,-5)
\)CorrectIncorrectHint
\(x<-5\) and \(x<-2\)
\(
\Rightarrow x \in(-\infty,-5)
\) -
Question 62 of 64
62. Question
State which of the following statement is True or False.
\(
\text { If } x<-5 \text { and } x>2, \text { then } x \in(-5,2)
\)CorrectIncorrectHint
\(
\text { If } x<-5 \text { and } x>2 \text {, then } x \text { have no value. }
\) -
Question 63 of 64
63. Question
State which of the following statement is True or False.
\(
\text { If }|x|>5 \text {, then } x \in(-\infty,-5) \cup[5, \infty)
\)CorrectIncorrectHint
\(
\begin{aligned}
& \text { If }|x|>5 \text { then } x<-5 \text { or } x>5 \\
& \Rightarrow x \in(-\infty,-5) \cup(5, \infty)
\end{aligned}
\) -
Question 64 of 64
64. Question
State which of the following statement is True or False.
\(
\text { If }|x| \leq 4, \text { then } x \in[-4,4]
\)CorrectIncorrectHint
If \(|x| \leq 4\), then \(-4 \leq x \leq 4\)
\(
\Rightarrow x \in[-4,4]
\)