Past JEE Main Entrance Paper
Overview
A statement involving the symbols \({ }^{\prime}>{ }^{\prime},{ }^{\prime}<,{ }^{\prime} \geq{ }^{\prime},{ }^{\prime} \leq\) ‘ is called an inequality. For example \(5>3, x \leq 4, x+y \geq 9\).
- Inequalities which do not involve variables are called numerical inequalities. For example \(3<8,5 \geq 2\).
- Inequalities which involve variables are called literal inequalities. For example, \(x>3, y \leq 5, x-y \geq 0\).
- An inequality may contain more than one variabe and it can be linear, quadratic or cubic etc. For eaxmple, \(3 x-2<0\) is a linear inequality in one variable, \(2 x+3 y \geq 4\) is a linear inequality in two variables and \(x^2+3 x+2<0\) is a quadratic inequality in one variable.
- Inequalities involving the symbol ‘ \(>\) ‘ or ‘ \(<\) ‘ are called strict inequalities. For example, \(3 x-y>5, x<3\).
- Inequalities involving the symbol \(\geq^{\prime}\) or \(\leq\) ‘ are called slack inequalities. For example, \(3 x-y \geq 5, x \leq 5\).
Solution of an inequality
The value(s) of the variable(s) which makes the inequality a true statement is called its solutions. The set of all solutions of an inequality is called the solution set of the inequality. For example, \(x-1 \geq 0\), has infinite number of solutions as all real values greater than or equal to one make it a true statement. The inequality \(x^2+1<0\) has no solution in \(R\) as no real value of \(x\) makes it a true statement.
To solve an inequality we can
- Add (or subtract) the same quantity to (from) both sides without changing the sign of inequality.
- Multiply (or divide) both sides by the same positive quantity without changing the sign of inequality. However, if both sides of inequality are multiplied (or divided) by the same negative quantity the sign of inequality is reversed, i.e., ‘ \(>\) ‘ changes into ‘ \(<\) ‘ and vice versa.
Representation of solution of linear inequality in one variable on a number line
To represent the solution of a linear inequality in one variable on a number line, we use the following conventions:
- If the inequality involves ‘ \(\geq\) ‘ or ‘ \(\leq\) ‘, we draw filled circle ( \(\bullet\) ) on the number line to indicate that the number corresponding to the filled circle is included in the solution set.
- If the inequality involves ‘ \(>\) ‘ or ‘ \(<\) ‘, we draw an open circle (O) on the number line to indicate that the number corresponding to the open circle is excluded from the solution set.
Graphical representation of the solution of a linear inequality
- To represent the solution of a linear inequality in one or two variables graphically in a plane, we proceed as follows:
- If the inequality involves ‘ \(\geq\) ‘ or ‘ \(\leq\) ‘, we draw the graph of the line as a thick line to indicate that the points on this line are included in the solution set.
- If the inequality involves ‘ \(>\) ‘ or ‘ \(<\) ‘, we draw the graph of the line as dotted line to indicate that the points on the line are excluded from the solution set.
- Solution of a linear inequality in one variable can be represented on number line as well as in the plane but the solution of a linear inequality in two variables of the type \(a x+b y>c, a x+b y \geq c, a x+b y<c\) or \(a x+b y \leq c(a \neq 0, b \neq 0)\) can be represented in the plane only.
- Two or more inequalities taken together comprise a system of inequalities and the solutions of the system of inequalities are the solutions common to all the inequalities comprising the system.
Two important results
- If \(a, b \in R\) and \(b \neq 0\), then
- \(a b>0\) or \(\frac{a}{b}>0 \Rightarrow a\) and \(b\) are of the same sign.
- \(a b<0\) or \(\frac{a}{b}<0 \Rightarrow a\) and \(b\) are of opposite sign.
-
If \(a\) is any positive real number, i.e., \(a>0\), then
-
\(
\begin{aligned}
& |x|<a \Leftrightarrow-a<x<a \\
& |x| \leq a \Leftrightarrow-a \leq x \leq a
\end{aligned}
\) -
\(
\begin{aligned}
& |x|>a \Leftrightarrow x<-a \text { or } x>a \\
& |x| \geq a \Leftrightarrow x \leq-a \text { or } x \geq a
\end{aligned}
\)
-
\(
Quiz Summary
0 of 103 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 103 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 103
1. Question
The region represented by \(\{z=x+i y \in \mathrm{C}:|z|-\operatorname{Re}(z) \leq 1\}\) is also given by the inequality: [ Main Sep. 06, 2020 (I)]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (b) } \because|z|-\operatorname{Re}(z) \leq 1 \quad(\because z=x+i y) \\
& \Rightarrow \sqrt{x^2+y^2}-x \leq 1 \Rightarrow \sqrt{x^2+y^2} \leq 1+x \\
& \Rightarrow x^2+y^2 \leq 1+x^2+2 x \\
& \Rightarrow y^2 \leq 1+2 x \Rightarrow y^2 \leq 2\left(x+\frac{1}{2}\right)
\end{aligned}
\) -
Question 2 of 103
2. Question
Consider the two sets :
\(A=\left\{m \in \mathbf{R}\right.\) : both the roots of \(x^2-(m+1) x+m+4=0\) are real \(\}\) and \(B=[-3,5)\).
Which of the following is not true? [Main Sep. 03, 2020 (I)]CorrectIncorrectHint
(a) Given sets \(A=\left\{m \in R\right.\) : both the roots of \(x^2-(m+1) x+m+4=0\) are real \(\}\) and \(B=[-3,5)\) \(\because\) Roots of \(x^2-(m+1) x+m+4=0\) are real, \(m \in R\)
\(\therefore \quad D \geq 0 \Rightarrow(m+1)^2-4(m+4) \geq 0\)
\(\Rightarrow \quad m^2-2 m-15 \geq 0\)
\(\Rightarrow \quad m^2-5 m+3 m-15 \geq 0\)
\(\Rightarrow \quad m(m-5)+3(m-5) \geq 0\)
\(\Rightarrow \quad(m+3)(m-5) \geq 0\)
\(\Rightarrow \quad m \in(-\infty,-3] \cup[5, \infty) \quad[\because A=(-\infty,-3] \cup[5, \infty)]\)
\(\therefore \quad A-B=(-\infty,-3) \cup[5, \infty)\)
\(A \cap B=\{-3\}, B-A=(-3,5)\) and \(A \cup B=R\)
Hence, option (a) is correct. -
Question 3 of 103
3. Question
If \(\mathrm{A}=\{x \in \mathrm{R}:|x|<2\}\) and \(\mathrm{B}=\{x \in \mathrm{R}:|x-2| \geq 3\}\); then: [Main Jan. 9, 2020 (II)]
CorrectIncorrectHint
(b) \(A=\{x: x \in(-2,2)\}\)
\(
\begin{aligned}
& B=\{x: x \in(-\infty,-1] \cup[5, \infty)\} \\
& A \cap B=\{x: x \in(-2,-1]\} \\
& A \cup B=\{x: x \in(-\infty, 2) \cup[5, \infty)\} \\
& A-B=\{x: x \in(-1,2)\} \\
& B-A=\{x: x \in(-\infty,-2] \cup[5, \infty)\}
\end{aligned}
\) -
Question 4 of 103
4. Question
Let \(S\) be the set of all real roots of the equation, \(3^x\left(3^x-1\right)+2=\left|3^x-1\right|+\left|3^x-2\right|\). Then \(S\): [Main Jan. 8, 2020 (II)]
CorrectIncorrectHint
(b)
Let \(3^x=y\)
\(
\therefore \quad y(y-1)+2=|y-1|+|y-2|
\)
Case 1: when \(y>2\)
\(
\begin{aligned}
& y^2-y+2=y-1+y-2 \\
& y^2-3 y+5=0
\end{aligned}
\)
\(D<0[\therefore\) Equation not satisfy. \(]\)
Case 2: when \(1 \leq y \leq 2\)
\(
\begin{aligned}
& y^2-y^2+2=y-1-y+2 \\
& y^2-y+1=0 \\
& \quad D<0[\therefore \text { Equation not satisfy. }]
\end{aligned}
\)
Case 3: when \(y \leq 1\)
\(
\begin{aligned}
& y^2-y+2=-y+1-y+2 \\
& y^2+y-1=0 \\
& \therefore y=\frac{-1+\sqrt{5}}{2} \\
& =\frac{-1-\sqrt{5}}{2}[\therefore \text { Equation not Satisfy }]
\end{aligned}
\)
\(\therefore\) Only one \(-1+\frac{\sqrt{5}}{2}\) satisfy equation -
Question 5 of 103
5. Question
All the pairs \((\mathrm{x}, \mathrm{y})\) that satisfy the inequality \(2 \sqrt{\sin ^2 x-2 \sin x+5} \cdot \frac{1}{4 \sin ^2 y} \leq 1\) also satisfy the equation: [Main April 10, 2019 (I)]
CorrectIncorrectHint
(d) Given inequality is,
\(
\begin{aligned}
& 2 \sqrt{\sin ^2 x-2 \sin x+5} \leq 2^{2 \sin ^2 y} \\
& \Rightarrow \sqrt{\sin ^2 x-2 \sin x+5} \leq 2 \sin ^2 y \\
& \Rightarrow \sqrt{(\sin x-1)^2+4} \leq 2 \sin ^2 y
\end{aligned}
\)
We know that for \(\sin ^2 y \leqslant 1\)
max value is \(\left|\sin ^2 y\right|=1\)
Now max value for \(\sqrt{(\sin x-1)^2+4}=2\) is
\(
\begin{aligned}
& (\sin x-1)^2+4=4 \\
& \sin x-1=0 \\
& \sin x=1 \\
\therefore & \sin x=|\sin y|
\end{aligned}
\)
\(\Rightarrow\) all the pairs that satisfy the inequality along with the equation \(
\sin x=|\sin y|\) -
Question 6 of 103
6. Question
The number of integral values of \(\mathrm{m}\) for which the quadratic expression, \((1+2 \mathrm{~m}) x^2-2(1+3 \mathrm{~m}) x+4(1+\mathrm{m}), x \in \mathrm{R}\), is always positive, is: [Main Jan. 12, 2019 (II)]
CorrectIncorrectHint
\(
\begin{aligned}
& (1+2 m) x^2-2(1+3 m) x+4(1+m)>0 \\
& \therefore D<0 \\
& 4(1+3 m)^2-16(1+2 m)(1+m)<0 \\
& \Rightarrow 1+9 m^2+6 m-4-12 m-8 m^2<0 \\
& \Rightarrow m^2-6 m-3<0 \\
& \Rightarrow(m-3)^2<12 \\
& \Rightarrow-2 \sqrt{3}<m-3<2 \sqrt{3} \\
& \Rightarrow 3-2 \sqrt{3}<m<3+2 \sqrt{3}
\end{aligned}
\)
Also
\(
\begin{aligned}
& 2 m+1>0 \\
& \Rightarrow m>-\frac{1}{2}
\end{aligned}
\)
Possible integral values of \(m\) are \(0,1,2,3,4,5,6\)
Hence, number of integral values of \(m\) is 7. -
Question 7 of 103
7. Question
If \(\mathrm{f}(\mathrm{x})=\left(\frac{3}{5}\right)^{\mathrm{x}}+\left(\frac{4}{5}\right)^{\mathrm{x}}-1, \mathrm{x} \in \mathrm{R}\), then the equation \(f(x)=0\) has: [Main Online April 9, 2014]
CorrectIncorrectHint
(b) \(f(x)=\left(\frac{3}{5}\right)^x+\left(\frac{4}{5}\right)^x-1\)
Put \(f(x)=0\)
\(
\begin{gathered}
\Rightarrow \quad 0=\left(\frac{3}{5}\right)^x+\left(\frac{4}{5}\right)^x-1 \\
\Rightarrow \quad\left(\frac{3}{5}\right)^x+\left(\frac{4}{5}\right)^x=1 \\
\Rightarrow 3^x+4^x=5^x \dots(i)
\end{gathered}
\)
For \(x=1\)
\(
3^1+4^1>5^1
\)
For \(x=3\)
\(
3^3+4^3=91<5^3
\)
Only for \(x=2\), equation (i) Satisfy
So, only one solution \((x=2)\) -
Question 8 of 103
8. Question
If \(\alpha \in\left(0, \frac{\pi}{2}\right)\) then \(\sqrt{x^2+x}+\frac{\tan ^2 \alpha}{\sqrt{x^2+x}}\) is always greater than or equal to [2003S]
CorrectIncorrectHint
(a) Let \(a=\sqrt{x^2+x}\) and \(b=\frac{\tan ^2 \alpha}{\sqrt{x^2+x}}\)
\(
\begin{array}{ll}
\quad & \mathrm{AM} \geq \mathrm{GM}, \quad \therefore \quad \frac{a+b}{2} \geq \sqrt{a b} \\
\Rightarrow & a+b \geq 2 \sqrt{a b} \\
\Rightarrow & \sqrt{x^2+x}+\frac{\tan ^2 \alpha}{\sqrt{x^2+x}} \geq 2 \sqrt{\tan ^2 \alpha}=2 \tan \alpha
\end{array}
\)
\(
[\because \alpha \in(0, \pi / 2)]
\) -
Question 9 of 103
9. Question
The set of all real numbers \(x\) for which \(x^2-|x+2|+x>0\), is [2002S]
CorrectIncorrectHint
(b) For \(x<-2,|x+2|=-(x+2)\)
\(
\begin{array}{ll}
\therefore & x^2-|x+2|+x>0 \\
\Rightarrow & x^2+x+2+x>0 \quad \Rightarrow(x+1)^2+1>0,
\end{array}
\)
which is valid \(\forall x \in R\)
But \(x<-2, \quad \therefore x \in(-\infty,-2) \dots(1)\)
For \(x \geq 2,|x+2|=x+2\)
\(
\begin{aligned}
& \therefore x^2-|x+2|+x>0 \Rightarrow x^2-x-2+x>0 \\
& \Rightarrow x^2>2 \Rightarrow x>\sqrt{2} \text { or } x<-\sqrt{2}
\end{aligned}
\)
i.e., \(x \in(-\infty,-\sqrt{2)} \cup(\sqrt{2, \infty})\)
But \(x \geq-2 \Rightarrow x \in[-2,-\sqrt{2}) \cup(\sqrt{2, \infty}) \dots(ii)\)
From (i) and (ii),
\(
\begin{aligned}
& x \in(-\infty,-2) \cup[-2,-\sqrt{2}) \cup(\sqrt{2}, \infty) \\
\Rightarrow \quad & x \in(-\infty,-\sqrt{2}) \cup(\sqrt{2}, \infty)
\end{aligned}
\) -
Question 10 of 103
10. Question
If \(a_1, a_2 \ldots ., a_n\) are positive real numbers whose product is a fixed number \(\mathrm{c}\), then the minimum value of \(a_1+a_2+\ldots \ldots+a_{n-1}+2 a_n\) is [2002S]
CorrectIncorrectHint
(a) Since for positive real numbers,
\(
\begin{aligned}
& \text { A.M. } \geq \text { G.M. } \\
& \therefore \quad \frac{\left(a_1+a_2+\ldots+a_{n-1}+2 a_n\right)}{n} \geq\left(a_1 a_2 \ldots a_{n-1} 2 a_n\right)^{1 / n} \\
& \Rightarrow \quad a_1+a_2+a_3+\ldots .+a_{n-1}+2 a_n \geq n(2 c)^{1 / n}
\end{aligned}
\)
Hence, required minimum value \(=n(2 c)^{1 / n}\) -
Question 11 of 103
11. Question
If \(a, b, c, d\) are positive real numbers such that \(a+b+c+d=2\), then \(M=(a+b)(c+d)\) satisfies the relation [2000S]
CorrectIncorrectHint
(a) Since, for positive real numbers,
A.M. \(\geq\) G.M.
\(
\begin{aligned}
& \quad \frac{(a+b)+(c+d)}{2} \geq \sqrt{(a+b)(c+d)} \Rightarrow M \leq 1 \\
& \text { Also }(\mathrm{a}+\mathrm{b})(\mathrm{c}+\mathrm{d})>0 \\
& \therefore \quad 0 \leq M \leq 1
\end{aligned}
\) -
Question 12 of 103
12. Question
If \(p, q, r\) are \(+\) ve and are in A.P., the roots of quadratic equation \(p x^2+\) \(q x+r=0\) are all real for [1994]
CorrectIncorrectHint
(b) For real roots \(q^2-4 p r \geq 0\)
\(
\begin{aligned}
& \Rightarrow\left(\frac{p+r}{2}\right)^2-4 p r \geq 0 \quad(\because p, q, r \text { are in A.P. }) \\
& \Rightarrow \quad p^2+r^2-14 p r \geq 0 \Rightarrow \frac{p^2}{r^2}-14 \frac{p}{r}+1 \geq 0 \\
& \Rightarrow \quad\left(\frac{p}{r}-7\right)^2-48 \geq 0 \Rightarrow\left|\frac{p}{r}-7\right| \geq 4 \sqrt{3}
\end{aligned}
\) -
Question 13 of 103
13. Question
The number of points of intersection of two curves \(y=2 \sin x\) and \(y=5 x^2+2 x+3\) is [1994]
CorrectIncorrectHint
(a) Given: \(y=5 x^2+2 x+3=5\left(x+\frac{1}{5}\right)^2+\frac{14}{5}>2, \forall x \in R\) While \(y=2 \sin x \leq 2, \forall x \in R\)
\(\therefore\) The two curves do not meet at all.Alternate:
We have
\(
\begin{aligned}
& y=5 x^2+2 x+3=5\left[x^2+\frac{2}{5} x+\frac{3}{5}\right] \\
& =5\left[\left(x+\frac{1}{5}\right)^2+\frac{3}{5}-\frac{1}{25}\right] \\
& =5\left[\left(x+\frac{1}{5}\right)^2+\frac{14}{25}\right]=5\left(x+\frac{1}{5}\right)^2+\frac{14}{25}>2
\end{aligned}
\)
Since \(y=2 \sin x \leq 2[latex]
[latex]\therefore\) we cannot have any point of intersection.
Hence number of points of intersection is \({ }^{\prime} 0^{\prime}\) -
Question 14 of 103
14. Question
The number of solutions of the equation \(\sin (e)^x=5^x+5^{-x}\) is
\(
\text { [1990 – } 2 \text { Marks] }
\)CorrectIncorrectHint
(a) Given : \(\sin \left(e^x\right)=5^x+5^{-x}\)
We know \(5^x\) and \(5^{-x}\) both are +ve real numbers.
By using \(\mathrm{AM} \geq \mathrm{GM}, 5^x+\frac{1}{5^x} \geq 2 \Rightarrow 5^x+5^{-x} \geq 2\)
\(\therefore \quad\) R.H.S. of given equation \(\geq 2\)
While \(\sin e^x \in[-1,1]\) i.e. LHS \(\in[-1,1]\)
\(\therefore\) The equation is not possible for any real value of \(x\). -
Question 15 of 103
15. Question
If \(\log _{0.3}(\mathrm{x}-1)<\log _{0.09}(x-1)\), then \(x\) lies in the interval – [1985 – 2 Marks]
CorrectIncorrectHint
(a) First of all for \(\log (x-1)\) to be defined, \(x-1>0\)
\(
\Rightarrow x>1
\)
Now, \(\log _{0.3}(x-1)<\log _{0.09}(x-1)\)
\(
\begin{aligned}
& \Rightarrow \log _{0.3}(x-1)<\log _{(0.3)}(x-1) \\
& \Rightarrow \log _{0.3}(x-1)<\frac{1}{2} \log _{0.3}(x-1) \\
& \Rightarrow 2 \log _{0.3}(x-1)<\log _{0.3}(x-1) \\
& \Rightarrow \log _{0.3}(x-1)^2<\log _{0.3}(x-1) \\
& \Rightarrow(x-1)^2>(x-1)
\end{aligned}
\)
[Here inequality is reversed because base lies between 0 and 1]
\(
\Rightarrow(x-1)^2-(x-1)>0 \Rightarrow(x-1)(x-2)>0
\)
On combining (i) and (ii), we get \(x>2\)
\(
\therefore \quad x \in(2, \infty)
\) -
Question 16 of 103
16. Question
If \(a^2+b^2+c^2=1\), then \(a b+b c+c a\) lies in the interval [1984 – 2 Marks]
CorrectIncorrectHint
(c) Given : \(a^2+b^2+c^2=1 \ldots .(\mathrm{i})\)
We know \((a+b+c)^2 \geq 0\)
\(
\begin{aligned}
& \Rightarrow \quad a^2+b^2+c^2+2 a b+2 b c+2 c a \geq 0 \\
& \Rightarrow \quad 2(a b+b c+c a) \geq-1 \quad \text { [using (i)] } \\
& \Rightarrow \quad a b+b c+c a \geq-1 / 2 \dots(ii)
\end{aligned}
\)
Also we know that
\(
\begin{aligned}
& \frac{1}{2}\left[(a-b)^2+(b-c)^2+(c-a)^2\right] \geq 0 \\
\Rightarrow & a^2+b^2+c^2-a b-b c-c a \geq 0 \\
\Rightarrow & a b+b c+c a \leq 1 \quad \text { [using (i) }]
\end{aligned}
\)
On combining (ii) and (iii), we get
\(
-1 / 2 \leq a b+b c+c a \leq 1, \therefore a b+b c+c a \in[-1 / 2,1]
\) -
Question 17 of 103
17. Question
The largest interval for which \(x^{12}-x^9+x^4-x+1>0\) is [1982 – 2 Marks]
CorrectIncorrectHint
\(
\text { (d) Given expression } x^{12}-x^9+x^4-x+1=f(x) \text { (let) }
\)
For \(\mathrm{x}<0\), put \(x=-y\) where \(y>0\) then we get
\(
f(x)=y^{12}+y^9+y^4+y+1>0 \text { for } y>0
\)
For \(0<x<1, \quad x^9<x^4 \Rightarrow-x^9+x^4>0\)
Also \(1-x>0\) and \(x^{12}>0\)
\(
\Rightarrow x^{12}-x^9+x^4+1-x>0 \quad \Rightarrow f(x)>0
\)
For \(x>1 ; f(x)=x\left(x^3-1\right)\left(x^8+1\right)+1>0\)
So, \(f(x)>0\) for \(-\infty<x<\infty\). -
Question 18 of 103
18. Question
If \(p, q, r\) are any real numbers, then [1982 – 2 Marks]
CorrectIncorrectHint
(b) If \(p=5, q=3, r=2 ; \max (p, q)=5 ; \max (p, q, r)=5\) \(\Rightarrow \max (p, q)=\max (p, q, r)\)
\(\therefore \quad\) (a) is not true. Similarly we can show that (c) is not true.
Also \(\min (p, q)=\frac{1}{2}(p+q-|p-q|)\)
Let \(p<q\), then \(\mathrm{LHS}=p\)
and R.H.S. \(=\frac{1}{2}(p+q-q+p)=p\)
Similarly, we can prove that \((b)\) is true for \(q<p\) too. -
Question 19 of 103
19. Question
Two towns A and B are 60 km apart. A school is to be built to serve 150 students in town A and 50 students in town B. If the total distance to be travelled by all 200 students is to be as small as possible, then the school should be built at [1982- 2 Marks]
CorrectIncorrectHint
(c) Let the distance of school from \(A=x\)
\(\therefore \quad\) The distance of the school form \(B=60-x\) Total distance covered by 200 students
\(
=2[150 x+50(60-x)]=2[100 x+3000] \text {, }
\)
Which is minimum, when \(x=0\)
\(\therefore \quad\) School should be built at town \(A\). -
Question 20 of 103
20. Question
The number of real solutions of the equation \(|x|^2-3|x|+2=0\) is [1982 – 2 Marks]
CorrectIncorrectHint
(a) \(|x|^2-3|x|+2=0\)
Case I : \(x<0\), then \(|x|=-x\)
\(\Rightarrow x^2+3 x+2=0 \Rightarrow(x+1)(x+2)=0\)
\(x=-1,-2(\) both acceptable as \(x<0)\)
Case II : \(x>0\), then \(|x|=x\)
\(\Rightarrow x^2-3 x+2=0 \Rightarrow(x-1)(x-2)=0\)
\(x=1,2\) ( both acceptable as \(x>0\) )
Hence, there are 4 real solutions. -
Question 21 of 103
21. Question
The least value of the expression \(2 \log _{10} x-\log _x(0.01)\), for \(x>1\), is [1980]
CorrectIncorrectHint
\(
\text { (b) Let } y=2 \log _{10} x-\log _x 0.01
\)
\(
\begin{aligned}
& =2 \log _{10} x-\frac{\log _{10} 0.01}{\log _{10} x}=2 \log _{10} x+\frac{2}{\log _{10} x} \\
& =2\left[\log _{10} x+\frac{2}{\log _{10} x}\right]
\end{aligned}
\)
Here \(x>1 \Rightarrow \log _{10} x>0\)
Also the sum of a real positive number and its reciprocal is always greater than or equal to 2.
\(\therefore \quad y \geq 2 \times 2 \Rightarrow y \geq 4, \therefore\) Least value of \(y\) is 4. -
Question 22 of 103
22. Question
Let \(a>0, b>0\) and \(c>0\). Then the roots of the equation \(a x^2+b x+c=0\) [1979]
CorrectIncorrectHint
(c) Since, \(a, b, c>0\); therefore \(a, b, c\) should be real because order relation is not defined in the set of complex numbers.
\(\therefore \quad\) Roots of equation are either real or complex conjugate.
Let \(\alpha, \beta\) be the roots of \(a x^2+b x+c=0\), then
\(
\alpha+\beta=-\frac{b}{a}=-v e, \quad \alpha \beta=\frac{c}{a}=+v e
\)
\(\Rightarrow\) Either both \(\alpha, \beta\) are – ve, if roots are real or both \(\alpha, \beta\) have \(–\) ve real parts, if roots are complex conjugate. -
Question 23 of 103
23. Question
If \(x, y\) and \(z\) are real and different and \(u=x^2+4 y^2+9 z^2-6 y z-3 z x-2 x y\), then \(u\) is always. [1979]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (a) } u=x^2+4 y^2+9 z^2-6 y x-3 z x-2 x y \\
& \quad=\frac{1}{2}\left[2 x^2+8 y^2+18 z^2-12 y z-6 z x-4 x y\right] \\
& =\frac{1}{2}\left[\left(x^2-4 x y+4 y^2\right)+\left(4 y^2+9 z^2-12 y z\right)\right. \\
& \left.+\left(x^2+9 z^2-6 z x\right)\right] \\
& =\frac{1}{2}\left[(x-2 y)^2+(2 y-3 z)^2+(3 z-x)^2\right] \geq 0
\end{aligned}
\)
Hence, \(\)u\(\) is always non-negative. -
Question 24 of 103
24. Question
\(
\text { The equation } x+2 y+2 z=1 \text { and } 2 x+4 y+4 z=9 \text { have }
\) [1979]CorrectIncorrectHint
(d) The given equations are
\(
x+2 y+2 z=1 \dots(i)
\)
and \(2 x+4 y+4 z=9 \dots(ii)\)
On multiplying (i), by 2 and then subtracting from (ii), we get \(0=7\), which is not possible
\(\therefore \quad\) No solution. -
Question 25 of 103
25. Question
The number of distinct real roots of \(x^4-4 x^3+12 x^2+x-1=0\) is [2011]
CorrectIncorrectHint
(2) Given : \(x^4-4 x^3+12 x^2+x-1=0\)
\(
\Rightarrow x^4-4 x^3+6 x^2-4 x+1+6 x^2+5 x-2=0
\)
\(
\begin{aligned}
& \Rightarrow(x-1)^4+6 x^2+5 x-2=0 \\
& \Rightarrow(x-1)^4=-6 x^2-5 x+2
\end{aligned}
\)
The solution of the above polynomial is the intersection points of the curves \(y=(x-1)^4\) and
\(
y=-6 x^2-5 x+2 \text { or } y=(x-1)^4 \text { and }\left(x+\frac{5}{12}\right)^2=-\frac{1}{6}\left(y-\frac{73}{24}\right)
\)
Clearly, the two curves have two points of intersection. Hence the given polynomial has two real roots.
-
Question 26 of 103
26. Question
The minimum value of the sum of real numbers \(a^{-5}, a^{-4}, 3 a^{-3}, 1, a^8\) and \(a^{10}\) where \(a>0\) is [2011]
CorrectIncorrectHint
(8) \(\because a>0, \therefore a^{-5}, a^{-4}, 3 a^{-3}, 1, a^8, a^{10}>0\)
Using AM \(\geq\) GM for positive real numbers, we get
\(
\begin{aligned}
& \frac{\frac{1}{a^5}+\frac{1}{a^4}+\frac{1}{a^3}+\frac{1}{a^3}+\frac{1}{a^3}+1+a^8+a^{10}}{8} \geq \\
& \left(\frac{1}{a^5} \cdot \frac{1}{a^4} \cdot \frac{1}{a^3} \cdot \frac{1}{a^3} \cdot \frac{1}{a^3} \cdot 1 \cdot a^8 \cdot a^{10}\right)^{\frac{1}{8}} \\
& \Rightarrow \frac{1}{a^5}+\frac{1}{a^4}+\frac{3}{a^3}+1+a^8+a^{10} \geq 8(1)^{\frac{1}{8}}
\end{aligned}
\) -
Question 27 of 103
27. Question
Let \((x, y, z)\) be points with integer coordinates satisfying the system of homogeneous equations :
\(
\begin{array}{r}
3 x-y-z=0 \\
-3 x+z=0 \\
-3 x+2 y+z=0
\end{array}
\)
Then the number of such points for which \(x^2+y^2+z^2 \leq 100\) is [2009]CorrectIncorrectHint
(7) Given system of equations:
\(
\begin{aligned}
& 3 x-y-z=0 \\
& -3 x+z=0
\end{aligned}
\)
and \(-3 x+2 y+z=0\)
Let \(x=p\), where \(p\) is an integer, then \(y=0\) and \(z=3 p\)
But \(x^2+y^2+z^2 \leq 100 \Rightarrow p^2+9 p^2 \leq 100\)
\(
\Rightarrow p^2 \leq 10 \Rightarrow p=0, \pm 1, \pm 2 \pm 3
\)
i.e. \(p\) can take 7 different values.
\(\therefore \quad\) Number of points \((x, y, z)\) are 7. -
Question 28 of 103
28. Question
The sum of all the real roots of the equation \(|x-2|^2+|x-2|-2=0 \text { is }\) [1997 – 2 Marks]
CorrectIncorrectHint
\(|x-2|^2+|x-2|-2=0\)
Case 1: \(x \geq 2\)
\(
\begin{aligned}
& \Rightarrow \quad(x-2)^2+(x-2)-2=0 \\
& \Rightarrow \quad x^2-3 x=0 \Rightarrow x(x-3)=0 \\
& \Rightarrow \quad x=0,3
\end{aligned}
\)
But 0 is rejected as \(x \geq 2\)
\(
\therefore \quad x=3
\)
Case 2: \(x<2\)
\(
\begin{aligned}
& \{-(x-2)\}^2-(x-2)-2=0 \\
& \Rightarrow x^2+4-4 x-x=0 \Rightarrow(x-1)(x-4)=0 \\
& \Rightarrow x=1,4
\end{aligned}
\)
But 4 is rejected as \(x<2\)
\(
\therefore \quad x=1
\)
\(\therefore\) the sum of the roots is \(3+1=4\). -
Question 29 of 103
29. Question
Let \(n\) and \(k\) be positive such that \(n \geq \frac{k(k+1)}{2}\). The number of solutions \(\left(x_1, x_2, \ldots . x_k\right), x_1 \geq 1, x_2 \geq 2, \ldots, x_k \geq k\), all integers, satisfying \(x_1+x_2+\ldots .+x_k=n\), is [1996 – 2 Marks]
CorrectIncorrectHint
The number of solution of \(x_1+x_2+\ldots+x_k=n\) \(=\) Coefficient of \(t^n\) in \(\left(t+t^2+t^3+\ldots\right)\left(t^2+t^3+\ldots\right)\left(t^k+t^{k+1}+\ldots\right)\) \(=\) Coefficient of \(t^n\) in \(t^{1+2+\ldots+k}\left(1+t+t^2+\ldots\right)^k\)
Now, \(1+2+\ldots+k=\frac{k(k+1)}{2}=p\) [say]
and \(1+t+t^2+\ldots=\frac{1}{1-t}\)
Thus, the number of required solutions
\(=\) Coefficient of \(t^{n-p}\) in \((1-t)^{-k}\)
\(=\) Coefficient of \(t^{n-p}\) in \(\left[1+{ }^k C_1 t+{ }^{k+1} C_2 t^2+{ }^{k+2} C_3 t^3+\ldots\right]\)
\(={ }^{k+n-p-1} C_{n-p}={ }^r C_{n-p}\)
where, \(r=k+n-p-1=k+n-1-\frac{1}{2} k(k+1)\)
\(
=\frac{1}{2}\left(2 k+2 n-2+k^2-k\right)=\frac{1}{2}\left(2 n-k^2+k-2\right)
\) -
Question 30 of 103
30. Question
If \(x<0, y<0, x+y+\frac{x}{y}=\frac{1}{2}\) and \((x+y) \frac{x}{y}=-\frac{1}{2}\), then \(x=\) and \(y=\ldots \ldots\) [1990 – 2 Marks]
CorrectIncorrectHint
Given \(x<0, \quad y<0\),
\(
x+y+\frac{x}{y}=\frac{1}{2} \quad \text { and } \quad(x+y) \cdot \frac{x}{y}=-\frac{1}{2}
\)
Let \(x+y=a\) and \(\frac{x}{y}=b\)
\(
\therefore \quad a+b=\frac{1}{2} \text { and } a b=-\frac{1}{2}
\)
On solving the above two equations, we get \(a+\left(-\frac{1}{2 a}\right)=\frac{1}{2}\)
\(
\Rightarrow 2 a^2-a-1=0 \Rightarrow a=1,-1 / 2 \Rightarrow b=-1 / 2,1
\)
Hence, from equation (i), \(x+y=1\) and \(\frac{x}{y}=-\frac{1}{2}\)
or \(x+y=\frac{-1}{2}\) and \(\frac{x}{y}=1\)
But \(x, y<0\)
\(
\therefore x+y<0 \Rightarrow x+y=\frac{-1}{2} \text { and } \frac{x}{y}=1
\)
On solving the above equations, we get \(x=-1 / 4\) and \(y=-1 / 4\). -
Question 31 of 103
31. Question
The solution of equation \(\log _7 \log _5(\sqrt{x+5}+\sqrt{x})=0\) is [1986 – 2 Marks]
CorrectIncorrectHint
\(
\begin{aligned}
& \log _7 \log _5(\sqrt{x+5}+\sqrt{x})=0 \\
& \Rightarrow \quad \log _5(\sqrt{x+5}+\sqrt{x})=1 \\
& \Rightarrow \quad \sqrt{x+5}+\sqrt{x}=5 \Rightarrow x+5=25+x-10 \sqrt{x} \\
& \Rightarrow \quad 2=\sqrt{x} \Rightarrow x=4, \text { which satisfies the given equation. }
\end{aligned}
\) -
Question 32 of 103
32. Question
Is the given statement below true?
If \(x\) and \(y\) are positive real numbers and \(m, n\) are any positive integers, then \(\frac{x^n y^m}{\left(1+x^{2 n}\right)\left(1+y^{2 m}\right)}>\frac{1}{4}\) [1989 – 1 Mark]CorrectIncorrectHint
\(\mathrm{x} \& \mathrm{y}\) are positive real numbers and \(\mathrm{m} \& \mathrm{n}\) are positive integers Since for two +ve numbers A.M. \(\geq\) G.M.
\(
\begin{aligned}
& \therefore \quad \frac{1+x^{2 n}}{2} \geq\left(1 \times x^{2 n}\right)^{1 / 2} \text { and } \frac{1+y^{2 m}}{2} \geq\left(1 \times y^{2 m}\right)^{1 / 2} \\
& \Rightarrow\left(\frac{1+x^{2 n}}{2}\right) \geq x^n \dots(i)
\end{aligned}
\)
and \(\left(\frac{1+y^{2 m}}{2}\right) \geq y^m\) \dots(ii)
Multiplying (i) and (ii), we get
\(
\frac{\left(1+x^{2 n}\right)\left(1+y^{2 m}\right)}{4} \geq x^n y^m \Rightarrow \frac{1}{4} \geq \frac{x^n y^m}{\left(1+x^{2 n}\right)\left(1+y^{2 m}\right)}
\)
Hence, the statement is false. -
Question 33 of 103
33. Question
Is this statement true or False?
If \(n_1, n_2, \ldots . . n_p\) are \(p\) positive integers, whose sum is an even number, then the number of odd integers among them is odd. [1985 – 1 Mark]CorrectIncorrectHint
Consider \(N=n_1+n_2+n_3+\ldots+n_p\), where \(N\) is an even number.
Let \(k\) numbers among these \(p\) numbers be odd, then \((p-k)\) numbers are even numbers. Now sum of \((p-k)\) even numbers is even and for \(N\) to be an even number, sum of \(k\) odd numbers must be even which is possible only when \(k\) is even.
\(\therefore \quad\) The given statement is false. -
Question 34 of 103
34. Question
Is this statement true or false? For every integer \(n>1\), the inequality \((n !)^{1 / n}<\frac{n+1}{2}\) holds. [1981-2 Marks]
CorrectIncorrectHint
Consider \(n\) numbers, namely \(1,2,3,4, \ldots, n\). Since, A.M. > G.M.
\(
\begin{aligned}
& \therefore \quad \frac{1+2+3+4 \ldots+n}{n}>(1.2 .3 .4 \ldots n)^{1 / n} \\
& \Rightarrow \frac{n(n+1)}{2 n}>(n !)^{1 / n} \Rightarrow(n !)^{1 / n}<\frac{n+1}{2}, \text { True }
\end{aligned}
\) -
Question 35 of 103
35. Question
If \(3^x=4^{x-1}\), then \(x=\) [Adv. 2013]
CorrectIncorrectHint
\(
\begin{aligned}
& (\mathbf{a}, \mathbf{b}, \mathbf{c}) \\
& 3^{\mathrm{x}}=4^{\mathrm{x}-1} \Rightarrow \mathrm{x} \log 3=2(\mathrm{x}-1) \log 2 \\
& \quad \Rightarrow \mathrm{x}=\frac{2 \log 2}{2 \log 2-\log 3} \Rightarrow \mathrm{x}=\frac{2 \log _3 2}{2 \log _3 2-1}=\frac{2}{2-\log _2 3}
\end{aligned}
\)\(
\text { Also } x=\frac{1}{1-\frac{1}{2} \log _2 3}=\frac{1}{1-\log _4 3}
\) -
Question 36 of 103
36. Question
Number of divisor of the form \(4 n+2(n \geq 0)\) of the integer 240 is [1998-2 Marks]
CorrectIncorrectHint
We can write 240 as \(2^4 .3^1 .5^1\)
But we want divisors of the form \(4 \mathrm{n}+2\)
That is, we want even divisors of the form \(2(2 n+1)\) and \(n \geqslant 0\)
The divisor is 2 ( when \(\mathrm{n}=0\) ) or divisors are odd multiples of 2
So the divisors are \(2,6,10\) and 30
Hence the answer is 4 -
Question 37 of 103
37. Question
The product of \(n\) positive numbers is unity Then their sum is [1991-2 Marks]
CorrectIncorrectHint
(d) Let \(x_1, x_2, \ldots, x_n\) be the \(n\) +ve numbers
According to the question,
\(
x_1 x_2 x_3 \ldots x_n=1 \dots(i)
\)
We know that for positive numbers A.M. \(\geq\) G.M.
\(
\begin{array}{ll}
\therefore & \frac{x_1+x_2+\ldots+x_n}{n} \geq \sqrt[n]{x_1 x_2 \ldots x_n} \\
\Rightarrow & \frac{x_1+x_2+\ldots+x_n}{n} \geq 1 \\
& \text { [using eq. (i)] } \\
\Rightarrow x_1+x_2+\ldots+x_n \geq n
\end{array}
\) -
Question 38 of 103
38. Question
\(
\text { The equation } x^{3 / 4\left(\log _2 x\right)^2+\log _2 x-5 / 4}=\sqrt{2} \text { has }
\) [1989- 2 Marks]CorrectIncorrectHint
(a, b, c) Given equation: \(\frac{3}{x^4}\left(\log _2 x\right)^2+\log _2 x-\frac{5}{4}=\sqrt{2}\) For \(x>0\), taking log on both sides to the base \(x\), we get
\(
\frac{3}{4}\left(\log _2 x\right)^2+\left(\log _2 x\right)-\frac{5}{4}=\log _x \sqrt{2}=\frac{1}{2} \log _x 2
\)
Let \(\log _2 x=y\), then we get, \(\frac{3}{4} y^2+y-\frac{5}{4}=\frac{1}{2 y}\)
\(
\begin{aligned}
& \Rightarrow \quad 3 y^3+4 y^2-5 y-2=0 \\
& \Rightarrow \quad(y-1)(y+2)(3 y+1)=0 \Rightarrow y=1,-2,-1 / 3 \\
& \Rightarrow \quad \log _2 x=1,-2,-1 / 3 \Rightarrow x=2,2^{-2}, 2^{-1 / 3} \\
& \Rightarrow \quad x=2, \frac{1}{4}, \frac{1}{2^{1 / 3}}, \text { all are possible because they are positive }
\end{aligned}
\) -
Question 39 of 103
39. Question
If \(a, b\) and \(c\) are distinct positive numbers, then the expression \((b+c-\) \(a)(c+a-b)(a+b-c)-a b c\) is [1986- 2 Marks]
CorrectIncorrectHint
Since, as AM \(>\) GM
\(
\begin{aligned}
& \Rightarrow \frac{(b+c-a)+(c+a-b)}{2}>((b+c-a)(c+a-b))^{1 / 2} \\
& \Rightarrow \quad \quad c>((b+c-a)(c+a-b))^{1 / 2} \dots(i)
\end{aligned}
\)
Similarly, \(b>((a+b-c)(b+c-a))^{1 / 2} \dots(ii)\)
and \(\quad a>((a+b-c)(c+a-b))^{1 / 2} \dots(iii)\)
On multiplying Eqs. (i), (ii) and (iii), we get \(a b c>(a+b-c)(b+c-a)(c+a-b)\)
Hence, \(\quad(a+b-c)(b+c-a)(c+a-b)-a b c<0\) -
Question 40 of 103
40. Question
If \(S\) is the set of all real \(x\) such that \(\frac{2 x-1}{2 x^3+3 x^2+x}\) is positive, then \(S\) contains [1986- 2 Marks]
CorrectIncorrectHint
(a, d) Wavy curve method:
Let \(f(x)=\left(x-\alpha_1\right)\left(x-\alpha_2\right) \ldots\left(x-\alpha_n\right)\)
To find sign of \(f(x)\), plot \(\alpha_1, \alpha_2, \ldots \alpha_n\) on number line in ascending order of magnitude. Starting from right extreme interval i.e., interval \(\left(\frac{1}{2}, \infty\right)\) , put \(+\) ve, \(–\) ve signs alternately in the intervals on the number line. \(f\) \((x)\) is positive in the intervals having + ve sign and negative in the intervals having -ve sign.
Using the wavy curve method for the function,
\(
f(x)=\frac{2 x-1}{2 x^3+3 x^2+x}=\frac{2 x-1}{x(2 x+1)(x+1)}
\)
We get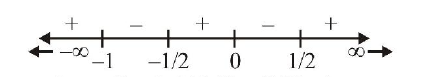
Clearly \(f(x)>0\), when \(x \in(-\infty,-1) \cup(-1 / 2,0) \cup(1 / 2, \infty)\)
Hence, \(S\) contains \((-\infty,-3 / 2)\) and \((1 / 2,3)\) -
Question 41 of 103
41. Question
Find the set of all \(\mathrm{x}\) for which \(\frac{2 x}{\left(2 x^2+5 x+2\right)}>\frac{1}{(x+1)}\) [1987 – 3 Marks]
CorrectIncorrectHint
Given : \(\frac{2 x}{2 x^2+5 x+2}>\frac{1}{x+1}\)
\(
\begin{aligned}
& \Rightarrow \frac{2 x}{2 x^2+5 x+2}-\frac{1}{x+1}>0 \\
& \Rightarrow \frac{2 x^2+2 x-2 x^2-5 x-2}{\left(2 x^2+5 x+2\right)(x+1)}>0 \\
& \Rightarrow \frac{-3 x-2}{(2 x+1)(x+1)(x+2)}>0 \Rightarrow \frac{(3 x+2)}{(x+1)(x+2)(2 x+1)}<0 \\
& \Rightarrow \frac{(3 x+2)(x+1)(x+2)(2 x+1)}{(x+1)^2(x+2)^2(2 x+1)^2}<0 \\
& \Rightarrow(3 x+2)(x+1)(x+2)(2 x+1)<0
\end{aligned}
\)
Using wavey curve method, we get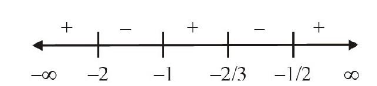
\(
\text { Clearly Inequality (i) holds for, } x \in(-2,-1) \cup(-2 / 3,-1 / 2)
\) -
Question 42 of 103
42. Question
If one root of the quadratic equation \(a x^2+b x+c=0\) is equal to the \(n\) th power of the other, then \(
\begin{aligned}
& \left(a c^n\right)^{\frac{1}{n+1}}+\left(a^n c\right)^{\frac{1}{n+1}}+b=0 \\
& {[1983 \text { – 2 Marks] }}\end{aligned}\).Is this true?
CorrectIncorrectHint
Let \(\alpha, \beta\) be the roots of eq. \(a x^2+b x+c=0\)
According to the question, \(\beta=\alpha^n\)
\(
\begin{gathered}
\text { Also, } \alpha+\beta=-b / a ; \alpha \beta=c / a \\
\alpha \beta=\frac{c}{a} \Rightarrow \alpha \cdot \alpha^n=\frac{c}{a} \\
\Rightarrow \quad a^{n+1}=\frac{c}{a} \Rightarrow \alpha=\left(\frac{c}{a}\right)^{\frac{1}{n+1}}
\end{gathered}
\)
then
\(
\begin{aligned}
& \alpha+\beta=-b / a \Rightarrow \alpha+\alpha^n=\frac{-b}{a} \\
& \Rightarrow\left(\frac{c}{a}\right)^{\frac{1}{n+1}}+\left(\frac{c}{a}\right)^{\frac{n}{n+1}}=\frac{-b}{a} \\
& \Rightarrow \quad a \cdot\left(\frac{c}{a}\right)^{\frac{1}{n+1}}+a \cdot\left(\frac{c}{a}\right)^{\frac{n}{n+1}}+b=0 \\
& \Rightarrow \quad \frac{n}{n+1} c^{\frac{1}{n+1}}+a^{\frac{1}{n+1}} c^{\frac{n}{n+1}}+b=0 \\
& \Rightarrow \quad\left(a^n c\right)^{\frac{1}{n+1}}+\left(a c^n\right)^{\frac{1}{n+1}}+b=0
\end{aligned}
\) -
Question 43 of 103
43. Question
\(\mathrm{mn}\) squares of euqal size are arranged to from a rectangle of dimension \(m\) by \(n\), where \(m\) and \(n\) are natural numbers. Two squares will be called ‘neighbours’ if they have exactly one common side. A natural number is written in each square such that the number written in any square is the arithmetic mean of the numbers written in its neighbouring squares. This is possible only if all the numbers used are equal. Is this statement true or false? [1982 – 5 Marks]
CorrectIncorrectHint
\(
\text { For any square there can be at most } 4 \text {, neighbouring squares. }
\)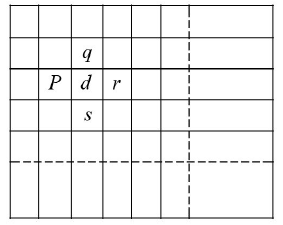
Let us consider a square \(d\) as shown in the figure. It has four neighbouring square \(p, q, r, s\) as shown.
According to the question,
\(
\begin{array}{ll}
& p+q+r+s=4 d \\
\Rightarrow \quad & (d-p)+(d-q)+(d-r)+(d-s)=0
\end{array}
\)
Sum of four tve numbers can be zero only if these are zero individually
\(
\begin{aligned}
& \therefore \quad d-p=0=d-q=d-r=d-s \\
& \Rightarrow \quad p=q=r=s=d
\end{aligned}
\)
Hence, all the numbers written are same. -
Question 44 of 103
44. Question
Is that the equation \(\)e^{\sin x}-e^{-\sin x}-4=0\(\) has no real solution. [1982- 2 Marks]
CorrectIncorrectHint
\(e^{\sin x}-e^{-\sin x}-4=0\)
Let \(e^{\sin x}=y\) then \(e^{-\sin x}=1 / y\)
\(\therefore \quad\) Given equation becomes, \(y-\frac{1}{y}-4=0\)
\(
\Rightarrow y^2-4 y-1=0 \Rightarrow y=2+\sqrt{5}, 2-\sqrt{5}
\)
But \(\mathrm{y}\) is real \(+\mathrm{ve}\) number,
\(
\begin{aligned}
& \therefore \quad y \neq 2-\sqrt{5} \Rightarrow y=2+\sqrt{5} \\
& \Rightarrow \quad e^{\sin x}=2+\sqrt{5} \Rightarrow \sin x=\log _e(2+\sqrt{5})
\end{aligned}
\)
But \(2+\sqrt{5}>e \Rightarrow \log _e\left(2+\sqrt{5)}>\log _e e\right.\)
\(
\Rightarrow \log _e(2+\sqrt{5})>1
\)
Hence, \(\sin x>1\), which is not possible.
\(\therefore \quad\) Given equation has no real solution. -
Question 45 of 103
45. Question
Find the solution set of the system [1980]
\(
\begin{gathered}
x+2 y+z=1 \\
2 x-3 y-w=2 \\
x \geq 0 ; y \geq 0 ; z \geq 0 ; w \geq 0
\end{gathered}
\)CorrectIncorrectHint
The given system is
\(
\begin{aligned}
& x+2 y+z=1 \dots(i)\\
& 2 x-3 y-\omega=2 \dots(ii)
\end{aligned}
\)
where \(x, y, z\), then \(\omega \geq 0\)
Multiplying eqn. (i) by 2 and subtracting from (ii), we get \(7 y+2 z+\omega=0 \Rightarrow \omega=-(7 y+2 z)\)
Now if \(y, z>0\), then \(\omega<0\) (not possible)
If \(y=0, z=0\), then \(x=1\) and \(\omega=0\).
\(\therefore \quad\) The only solution is \(x=1, y=0, z=0, \omega=0\). -
Question 46 of 103
46. Question
For what values of \(m\), does the system of equations
\(
\begin{aligned}
& 3 x+m y=m \\
& 2 x-5 y=20
\end{aligned}
\)
has solution satisfying the conditions \(x>0, y>0\). [1980]CorrectIncorrectHint
The given equations are \(3 x+m y-m=0\) and \(2 x-5 y-20=0\)
By cross-multiplication method, we get
\(
\begin{aligned}
& \frac{x}{-20 m-5 m}=\frac{y}{-2 m+60}=\frac{1}{-15-2 m} \\
& \Rightarrow \quad x=\frac{25 m}{2 m+15}, y=\frac{2 m-60}{2 m+15}
\end{aligned}
\)
If \(x>0\), then \(\frac{25 m}{2 m+15}>0\)
\(
\Rightarrow m<-\frac{15}{2} \text { or } m>0 \dots(i)
\)
If \(y>0\), then \(\frac{2(m-30)}{2 m+15}>0\)
\(
\Rightarrow \mathrm{m}<-\frac{15}{2} \text { or } \mathrm{m}>30 \dots(ii)
\)
On combining (i) and (ii), we get the common values of \(\mathrm{m}\) as follows :
\(
\mathrm{m}<-\frac{15}{2} \text { or } \mathrm{m}>30 \quad \therefore \quad \mathrm{m} \in\left(-\infty, \frac{-15}{2}\right) \cup(30, \infty)
\) -
Question 47 of 103
47. Question
Let \(y=\sqrt{\frac{(x+1)(x-3)}{(x-2)}}\)
Find all the real values of \(x\) for which \(y\) takes real values. [1980]CorrectIncorrectHint
\(y=\sqrt{\frac{(x+1)(x-3)}{(x-2)}}\)
\(\mathrm{y}\) will take all real values if \(\frac{(x+1)(x-3)}{(x-2)} \geq 0\)
By wavy curve method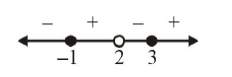
\(
x \in[-1,2) \cup[3, \infty)
\)
[2 is not included as it makes the denominator zero, and hence \(\)y\(\) an undefined number.] -
Question 48 of 103
48. Question
Given \(n^4<10^n\) for a fixed positive integer \(n \geq 2\),then \((n+1)^4<10^{n+1} .\)Is this statement true? [1980]
CorrectIncorrectHint
Given : \(n^4<10^n\) for a fixed \(+\) ve integer \(n \geq 2\).
To prove : \((n+1)^4<10^{n+1}\)
Proof : Since \(n^4<10^n \Rightarrow 10 n^4<10^{n+1} \dots(i)\)
So it is sufficient to prove that \((n+1)^4<10 n^4\)
Now \(\left(\frac{n+1}{n}\right)^4=\left(1+\frac{1}{n}\right)^4 \leq\left(1+\frac{1}{2}\right)^4[\because n \geq 2]\)
\(
\begin{aligned}
& =\frac{81}{16}<10 \\
\Rightarrow \quad(n+1)^4 & <10 n^4 \dots(ii)
\end{aligned}
\)
From (i) and (ii), \((n+1)^4<10^{n+1}\) -
Question 49 of 103
49. Question
Find all integers \(x\) for which \((5 x-1)<(x+1)^2<(7 x-3)\) [1978]
CorrectIncorrectHint
There are two parts of this question
\((5 x-1)<(x+1)^2\) and \((x+1)^2<(7 x-3)\)
Taking first part
\(
\begin{aligned}
& (5 x-1)<(x+1)^2 \Rightarrow 5 x-1<x^2+2 x+1 \\
& \Rightarrow x^2-3 x+2>0 \Rightarrow(x-1)(x-2)>0
\end{aligned}
\)
Using wavy curve method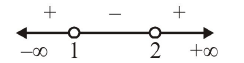
\(
\Rightarrow x<1 \text { or } x>2 \dots(i)
\)Taking second part
\(
\begin{aligned}
& (x+1)^2<(7 x-3) \Rightarrow x^2-5 x+4<0 \\
& \Rightarrow \quad(x-1)(x-4)<0
\end{aligned}
\)
Using wavy curve method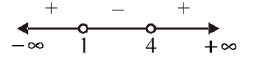
\(
\Rightarrow \quad 1<x<4 \dots(ii)
\)
On combining (i) and (ii) [taking common solution], we get \(2<\mathrm{x}<4\), but \(x\) is an integer therefore \(x=3\). -
Question 50 of 103
50. Question
Sketch the solution set of the following system of inequalities: \(x^2+y^2-2 x \geq 0 ; 3 x-y-12 \leq 0 ; y-x \leq 0 ; y \geq 0 .\) [1978]
CorrectIncorrectHint
\(x^2+y^2-2 x \geq 0 \Rightarrow x^2-2 x+1+y^2 \geq 1\)
\(\Rightarrow(x-1)^2+y^2 \geq 1\), which represents the boundary and exterior region of the circle with centre at \((1,0)\) and radius as 1 .
For \(3 x-y \leq 12\), the corresponding equation is \(3 x-y=12\). Two points on it can be taken as \((4,0),(2,-6)\). Also putting \((0,0)\) in given inequation, we get \(0 \leq 12\) which is true.
\(\therefore\) given inequation represents that half plane region on one side of the line \(3 x-y=12\), which contains origin.
For \(y \leq x\), the corresponding equation is \(y=x\). Two points on it can be taken as \((0,0)\) and \((1,1)\). Also putting \((2,1)\) in the given inequation, we get \(1 \leq 2\), which is true. So \(y \leq x\) represents that half plane on one side of the line \(y=x\), which contains the points \((2,1) \cdot y \geq 0\) represents upper half cartesian plane.
Combining all we find the solution set as the shaded region in the graph.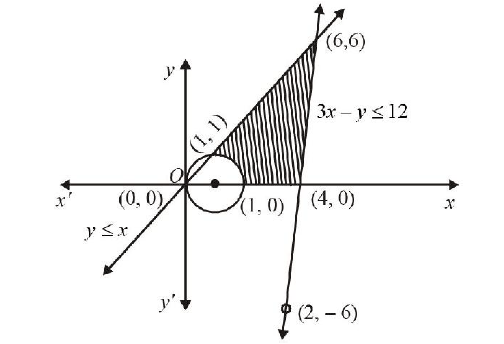
-
Question 51 of 103
51. Question
\(
\text { Show that the square of } \frac{\sqrt{26-15 \sqrt{3}}}{5 \sqrt{2}-\sqrt{38+5 \sqrt{3}}} \text { is a rational number. }
\) [1978]CorrectIncorrectHint
\(
\begin{aligned}
& \text { Let } x=\frac{\sqrt{26-15 \sqrt{3}}}{5 \sqrt{2}-\sqrt{38+5 \sqrt{3}}} \\
& \Rightarrow \quad x^2=\frac{26-15 \sqrt{3}}{50+38+5 \sqrt{3}-10 \sqrt{76+10 \sqrt{3}}} \\
& \Rightarrow x^2=\frac{26-15 \sqrt{3}}{88+5 \sqrt{3}-10 \sqrt{75+1+10 \sqrt{3}}} \\
& \Rightarrow x^2=\frac{26-15 \sqrt{3}}{88+5 \sqrt{3}-10 \sqrt{\left(5 \sqrt{3)^2}+(1)^2+2 \times 5 \sqrt{3} \times 1\right.}} \\
& \Rightarrow \quad x^2=\frac{26-15 \sqrt{3}}{88+5 \sqrt{3}-10 \sqrt{(5 \sqrt{3}+1)^2}} \\
& =\frac{26-15 \sqrt{3}}{3(26-15 \sqrt{3})}=\frac{1}{3} \text {, which is a rational number. } \\
&
\end{aligned}
\) -
Question 52 of 103
52. Question
If \((m, n)=\frac{\left(1-x^m\right)\left(1-x^{m-1}\right) \ldots \ldots \ldots\left(1-x^{m-n+1}\right)}{(1-x)\left(1-x^2\right) \ldots \ldots \ldots \ldots\left(1-x^n\right)}\)
where \(m\) and \(n\) are positive integers \((n \leq m)\), then \((m, n+1)=(m-1, n+1)+x^{m-n-1}(m-1, n)\). Is this true?[1978]CorrectIncorrectHint
\(
\mathrm{RHS}=(\mathrm{m}-1, \mathrm{n}+1)+\mathrm{x}^{\mathrm{m}-\mathrm{n}-1}(m-1, n)
\)
\(
\begin{aligned}
& =\frac{\left(1-x^{m-1}\right)\left(1-x^{m-2}\right) \ldots\left(1-x^{m-n-1}\right)}{(1-x)\left(1-x^2\right) \ldots\left(1-x^{n+1}\right)} \\
& +x^{m-n-1}\left[\frac{\left(1-x^{m-1}\right)\left(1-x^{m-2}\right) \ldots\left(1-x^{m-n}\right)}{(1-x)\left(1-x^2\right) \ldots\left(1-x^n\right)}\right] \\
& =\frac{\left(1-x^{m-1}\right)\left(1-x^{m-2}\right) \ldots\left(1-x^{m-n}\right)}{(1-x)\left(1-x^2\right) \ldots\left(1-x^n\right)} \\
& {\left[\frac{1-x^{m-n-1}}{1-x^{n+1}}+x^{m-n-1}\right]} \\
& {\left[\frac{1-x^{m-n-1}+x^{m-n-1}-x^m}{1-x^{n+1}}\right]} \\
& =\frac{\left(1-x^m\right)\left(1-x^{m-1}\right) \ldots\left(1-x^{m-n}\right)}{(1-x)\left(1-x^2\right) \ldots\left(1-x^n\right)\left(1-x^{n+1}\right)} \\
& =(m, n+1)=\text { L.H.S. } \\
&
\end{aligned}
\) -
Question 53 of 103
53. Question
\(\text { Solve for } x: 4^x-3^{x-\frac{1}{2}}=3^{x+\frac{1}{2}}-2^{2 x-1}\) [1978]
CorrectIncorrectHint
\(
\begin{aligned}
& 4^x-3^{x-1 / 2}=3^{x+1 / 2}-\frac{\left(2^2\right)^x}{2} \\
& \Rightarrow 4^x-\frac{3^x}{\sqrt{3}}=3^x \sqrt{3}-\frac{4^x}{2} \\
& \Rightarrow \frac{3}{2} \cdot 4^x=3^x\left(\sqrt{3}+\frac{1}{\sqrt{3}}\right) \Rightarrow \frac{3}{2} \cdot 4^x=3^x \frac{4}{\sqrt{3}} \\
& \Rightarrow \frac{4^{x-1}}{4^{1 / 2}}=\frac{3^{x-1}}{\sqrt{3}} \Rightarrow 4^{x-3 / 2}=3^{x-3 / 2} \\
& \Rightarrow\left(\frac{4}{3}\right)^{x-3 / 2}=1 \Rightarrow x-\frac{3}{2}=0 \Rightarrow x=3 / 2
\end{aligned}
\) -
Question 54 of 103
54. Question
Let \([\alpha]\) denote the greatest integer \(\leq \alpha\). Then \([\sqrt{1}]+[\sqrt{2}]+[\sqrt{3}]+\ldots+[\sqrt{120}]\) is equal to [JEE Main 2023]
CorrectIncorrectHint
\(
\begin{aligned}
& {[\sqrt{1}]+[\sqrt{2}]+[\sqrt{3}]+\ldots+[120]} \\
& E=1+1+1+2+2+2+2+2+3+3+3+3+3 \\
& +3+3+4+4+\ldots \\
& E=3 \times 1+5 \times 2+7 \times 3+\ldots+19 \times 9+10 \times 21 \\
& =\sum_{r=1}^{10}(2 r+1) r=2\left[\frac{10 \times 11 \times 21}{6}\right]+\frac{10 \times 11}{2} \\
& =770+55 \\
& =825
\end{aligned}
\) -
Question 55 of 103
55. Question
The number of points, where the curve \(f(x)=e^{8 x}-e^{6 x}-3 e^{4 x}-e^{2 x}+1, x \in R\) cuts \(x\)-axis, is equal to [JEE Main 2023]
CorrectIncorrectHint
Firstly, we know that the given function
\(f(x)=e^{8 x}-e^{6 x}-3 e^{4 x}-e^{2 x}+1\) intersects the \(x\)-axis where \(f(x)=0\). Setting \(f(x)\) equal to zero gives us:
\(
e^{8 x}-e^{6 x}-3 e^{4 x}-e^{2 x}+1=0 \text {. }
\)
Let \(t=e^{2 x}\). The equation now becomes:
\(
t^4-t^3-3 t^2-t+1=0 \text {. }
\)
Dividing by \(t^2\) and rearranging the equation gives :
\(
t^2-t-3-\frac{1}{t}+\frac{1}{t^2}=0
\)
If we let \(y=t+\frac{1}{t}\), we get :
\(
y^2-y-5=0
\)
This quadratic equation in y can be solved using the quadratic formula to give two roots :
\(
y=\frac{1 \pm \sqrt{21}}{2} .
\)
Since \(y=t+\frac{1}{t}\), and \(t>0\) (as \(t=e^{2 x}\) ), we must choose the root where \(y>2\). Thus, we take \(y=\frac{1+\sqrt{21}}{2}\).
So, we have :
\(
t+\frac{1}{t}=\frac{1+\sqrt{21}}{2}
\)
Solving for \(t\) gives us :
\(
t^2-y t+1=0
\)
or \(t=\frac{y \pm \sqrt{y^2-4}}{2} .\)
Substituting \(y=\frac{1+\sqrt{21}}{2}\) into the formula gives :
\(
t=\frac{\frac{1+\sqrt{21}}{2} \pm \sqrt{\left(\frac{1+\sqrt{21}}{2}\right)^2-4}}{2} .
\)
This quadratic formula for \(t\) yields two possible values \((t=2.37\) and \(t=0.42)\). Both of them are positive, thus both are acceptable values for \(t=e^{2 x}\).
Finally, to get \(x\), take the natural \(\log\) of both sides and divide by 2 :
\(
x=\frac{1}{2} \ln (t)
\)
This gives us two solutions for \(x\), corresponding to the two positive solutions for \(t\). So, the number of points where the curve \(f(x)=e^{8 x}-e^{6 x}-3 e^{4 x}-e^{2 x}+1\) intersects the \(x\)-axis is 2 . -
Question 56 of 103
56. Question
If \(a\) and \(b\) are the roots of the equation \(x^2-7 x-1=0\), then the value of \(\frac{a^{21}+b^{21}+a^{17}+b^{17}}{a^{19}+b^{19}}\) is equal to [JEE Main 2023]
CorrectIncorrectHint
\(
x^2-7 x-1=0<_b^a
\)
By newton’s theorem
\(
\begin{aligned}
& S _{ n +2}-7 S _{ n +1}- S _{ n }=0 \\
& S _{21}-7 S _{20}- S _{19}=0 \\
& S _{20}-7 S _{19}- S _{18}=0 \\
& S _{19}-7 S _{18}- S _{17}=0 \\
& \frac{ S _{21}+ S _{17}}{ S _{19}}=\frac{ S _{21}+\left( S _{19}-7 S _{18}\right)}{ S _{19}} \\
& =\frac{ S _{21}+ S _{19}-7\left( S _{20}-7 S _{19}\right)}{ S _{19}} \\
& =\frac{50 S _{19}+\left( S _{21}-7 S _{20}\right)}{ S _{19}} \\
& =51 \cdot \frac{ S _{19}}{ S _{19}}=51
\end{aligned}
\) -
Question 57 of 103
57. Question
If the value of real number \(a>0\) for which \(x^2-5 a x+1=0\) and \(x^2-a x-5=0\) have a common real root is \(\frac{3}{\sqrt{2 \beta}}\) then \(\beta\) is equal to [JEE Main 2023]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2-5 \alpha x+1=0 \dots(1)\\
& x^2-\alpha x-5=0 \dots(2)
\end{aligned}
\)
have a common root.
Subtracting (1) with (2) we’ll get \(x=\frac{6}{4 \alpha}\)
Substituting in (1)
\(
\begin{aligned}
& \frac{36}{16 \alpha^2}-\frac{30}{4}+1=0 \\
& \Rightarrow \alpha^2=\frac{9}{26} \\
& \alpha=\frac{3}{\sqrt{2 \times 13}} \\
& \therefore \beta=13
\end{aligned}
\) -
Question 58 of 103
58. Question
Let \(\alpha_1, \alpha_2, \ldots, \alpha_7\) be the roots of the equation \(x^7+3 x^5-13 x^3-15 x=0\) and \(\left|\alpha_1\right| \geq\left|\alpha_2\right| \geq \ldots \geq\left|\alpha_7\right|\). Then \(\alpha_1 \alpha_2-\alpha_3 \alpha_4+\alpha_5 \alpha_6\) is equal to [JEE Main 2023]
CorrectIncorrectHint
\(
\begin{aligned}
& x^7+3 x^5-13 x^3-15 x=0 \\
& x\left(x^6+3 x^4-13 x^2-15\right)=0 \\
& x=0=\alpha_7 \\
& \text { Let } x^2=t \\
& t^3+3 t^2-13 t-15=0 \\
& (t+1)(t+5)(t-3)=0 \\
& t=x^2=-1,-5,3 \\
& x= \pm i, \pm \sqrt{5} i, \pm \sqrt{3} \\
& \alpha_1, \alpha_2= \pm \sqrt{5} i, \alpha_3, \alpha_4= \pm \sqrt{3}, \alpha_5, \alpha_6= \pm i \\
& \alpha_1 \alpha_2-\alpha_3 \alpha_4+\alpha_5 \alpha_6=5+3+1=9
\end{aligned}
\) -
Question 59 of 103
59. Question
Let \(\alpha \in R\) and let \(\alpha, \beta\) be the roots of the equation \(x^2+60^{\frac{1}{4}} x+a=0\). If \(\alpha^4+\beta^4=-30\), then the product of all possible values of \(a\) is [JEE Main 2023]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2+60^{\frac{1}{4}} x+a=0 \\
& \therefore \alpha+\beta=-60^{\frac{1}{4}}, \alpha \beta=a \\
& \text { Now } \alpha^4+\beta^4=-30 \\
& \Rightarrow\left(\alpha^2+\beta^2\right)^2-2 a^2=-30 \\
& \Rightarrow\left[(\alpha+\beta)^2-2 a\right]^2-2 a^2=-30 \\
& \Rightarrow\left(60^{\frac{1}{2}}-2 a\right)^2-2 a^2=-30 \\
& \Rightarrow 60+4 a^2-4 \cdot 60^{\frac{1}{2}} a-2 a^2+30=0 \\
& \Rightarrow 2 a^2-8 \sqrt{15} a+90=0
\end{aligned}
\)
Product of value of \(a=45\) -
Question 60 of 103
60. Question
Let \(\lambda \in R\) and let the equation \(E\) be \(|x|^2-2|x|+|\lambda-3|=0\). Then the largest element in the set \(S =\{x+\lambda: x\) is an integer solution of \(E \}\) is [JEE Main 2023]
CorrectIncorrectHint
\(
\begin{aligned}
& D \geq 0 \Rightarrow 4-4|\lambda-3| \geq 0 \\
& |\lambda-3| \leq 1 \\
& -1 \leq \lambda-3 \leq 1 \\
& 2 \leq \lambda \leq 4 \\
& |x|=\frac{2 \pm \sqrt{4-4|\lambda-3|}}{2} \\
& =1 \pm \sqrt{1-|\lambda-3|} \\
& x_{\text {largest }} \quad=1+1=2 \text {, when } \lambda=3
\end{aligned}
\)
Largest element of \(S=2+3=5\) -
Question 61 of 103
61. Question
The number of real roots of the equation \(x|x|-5|x+2|+6=0\), is : [JEE Main 2023]
CorrectIncorrectHint
Case-I:
When \(x<-2\) then
\(
\begin{aligned}
& -x^2+5(x+2)+6=0 \\
& \Rightarrow x^2-5 x-16=0
\end{aligned}
\)
\(
\Rightarrow x=\frac{5 \pm \sqrt{25+64}}{2}
\)
\(\therefore x=\frac{5-\sqrt{89}}{2}\) is acceptedCase-II :
When \(-2 \leq x<0\) then
\(
\begin{aligned}
& -x^2-5(x+2)+6=0 \\
\Rightarrow & x^2+5 x+4=0 \\
\Rightarrow & (x+1)(x+4)=0
\end{aligned}
\)
\(x=-1\) is acceptedCase-III :
When \(x \geq 0\) then
\(
\begin{gathered}
x^2-5(x+2)+6=0 \\
\Rightarrow x^2-5 x-4=0 \\
x=\frac{5 \pm \sqrt{25+16}}{2} \\
=\frac{5 \pm \sqrt{41}}{2} \\
x=\frac{5-\sqrt{41}}{2} \text { is accepted }
\end{gathered}
\)
\(\therefore 3\) real roots are possible. -
Question 62 of 103
62. Question
Let \(\alpha, \beta\) be the roots of the equation \(x^2-\sqrt{2} x+2=0\). Then \(\alpha^{14}+\beta^{14}\) is equal to [JEE Main 2023]
CorrectIncorrectHint
Find the roots of the quadratic equation:
The quadratic formula is \(x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\). For the quadratic equation \(x^2-\sqrt{2} x+2=0\), we have \(a=1, b=-\sqrt{2}, c=2\). Plugging these into the quadratic formula gives:
\(
x=\frac{\sqrt{2} \pm \sqrt{(-\sqrt{2})^2-4(1)(2)}}{2(1)}=\frac{\sqrt{2} \pm \sqrt{2-8}}{2}=\frac{\sqrt{2} \pm \sqrt{6} i}{2} .
\)
So, we have two roots, \(\alpha\) and \(\beta\), which are:
So, we have two roots, \(\alpha\) and \(\beta\), which are:
\(
\begin{aligned}
& \alpha=\frac{\sqrt{2}+\sqrt{6} i}{2}, \\
& \beta=\frac{\sqrt{2}-\sqrt{6} i}{2} .
\end{aligned}
\)
Express the roots in exponential form:
We can express complex numbers in the form \(r e^{i \theta}\). For \(\alpha\) and \(\beta\), we find the magnitude \(r=\sqrt{2}\) and the arguments \(\theta=\frac{\pi}{3},-\frac{\pi}{3}\) respectively. So, we have:
\(
\begin{aligned}
& \alpha=\sqrt{2} e^{i \frac{\pi}{3}} \\
& \beta=\sqrt{2} e^{-i \frac{\pi}{3}}
\end{aligned}
\)
Calculate the 14 th power of the roots:
To find \(\alpha^{14}\) and \(\beta^{14}\), we use the property of exponents which says that \(\left(a^m\right)^n=a^{m n}\). So, we have:
\(
\begin{aligned}
& \alpha^{14}=\left(\sqrt{2} e^{i \frac{\pi}{3}}\right)^{14}=2^7 e^{i \frac{14 \pi}{3}}=128 e^{i \frac{2 \pi}{3}}, \\
& \beta^{14}=\left(\sqrt{2} e^{-i \frac{\pi}{3}}\right)^{14}=2^7 e^{-i \frac{14 \pi}{3}}=128 e^{-i \frac{2 \pi}{3}} .
\end{aligned}
\)
Add the 14th powers of the roots:
We want to find the real part of \(\alpha^{14}+\beta^{14}\). To do this, we use the property that \(e^{i x}=\cos (x)+i \sin (x)\). We have:
\(
\alpha^{14}+\beta^{14}=128 e^{i \frac{2 \pi}{3}}+128 e^{-i \frac{2 \pi}{3}}=128(2) \cos \left(\frac{2 \pi}{3}\right)=-128
\) -
Question 63 of 103
63. Question
The set of all \(a \in R\) for which the equation \(x|x-1|+|x+2|+a=0\) has exactly one real root, is : [JEE Main 2023]
CorrectIncorrectHint
\(
x|x-1|+|x+2|+a=0
\)Case I: If \(x<-2\) then
\(
\begin{aligned}
& -x^2+x-x-2+a=0 \\
& a=x^2+2
\end{aligned}
\)
\(y=x^2+2\) is decreasing \(\forall x \in(-\infty,-2)\)
Case II: If \(-2 \leq x<1\) then
\(
\begin{aligned}
& -x^2+x+x+2+a=0 \\
& a=x^2-2 x-2
\end{aligned}
\)
\(y=x^2-2 x-2\) is decreasing \(\forall x \in[-2,1)\).
Case III: If \(x \geq 1\) then
\(
\begin{aligned}
& x^2-x+x+2+a=0 \\
& a=-\left(x^2+2\right)
\end{aligned}
\)
\(y=-\left(x^2+2\right)\) is decreasing \(\forall x \in[1, \infty)\)
\(\therefore\) Exactly one real root \(\forall x \in R\) -
Question 64 of 103
64. Question
Let \(\alpha, \beta\) be the roots of the quadratic equation \(x^2+\sqrt{6} x+3=0\). Then \(\frac{\alpha^{23}+\beta^{23}+\alpha^{14}+\beta^{14}}{\alpha^{15}+\beta^{15}+\alpha^{10}+\beta^{10}}\) is equal to : [JEE Main 2023]
CorrectIncorrectHint
Given quadratic equation: \(x^2+\sqrt{6} x+3=0\)
We can find the roots using the quadratic formula: \(x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
Here, \(a=1, b=\sqrt{6}[latex], and [latex]c=3\).
Substituting these values into the quadratic formula, we have:
\(
x=\frac{-\sqrt{6} \pm \sqrt{(\sqrt{6})^2-4(1)(3)}}{2(1)}
\)
Simplifying further :
\(
\begin{aligned}
& x=\frac{-\sqrt{6} \pm \sqrt{6-12}}{2} \\
& x=\frac{-\sqrt{6} \pm \sqrt{-6}}{2}
\end{aligned}
\)
Since the discriminant is negative, the roots are complex numbers. We can express them using the imaginary unit \(i\) :
\(
\begin{aligned}
& x=\frac{-\sqrt{6} \pm \sqrt{6} i}{2} \\
& \Rightarrow x=\frac{-1}{2} \sqrt{6} \pm \frac{1}{2} \sqrt{6} i \\
& \therefore \alpha, \beta=\sqrt{3} e ^{ \pm \frac{3 \pi i}{4}} .
\end{aligned}
\)
The required expression can be rewritten in terms of the argument of the exponential form of the roots, which simplifies the calculation:
\(
=\frac{(\sqrt{3})^{23}\left(2 \cos \frac{69 \pi}{4}\right)+(\sqrt{3})^{14}\left(2 \cos \frac{42 \pi}{4}\right)}{(\sqrt{3})^{15}\left(2 \cos \frac{45 \pi}{4}\right)+(\sqrt{3})^{10}\left(2 \cos \frac{30 \pi}{4}\right)}
\)
Here, the exponential power of \(\sqrt{3}\) in the numerator is larger by 8 compared to the denominator, so we can divide the numerator and denominator by \((\sqrt{3})^8=81\) to simplify:
\(
=\frac{(\sqrt{3})^{15}\left(2 \cos \frac{69 \pi}{4}\right)+(\sqrt{3})^6\left(2 \cos \frac{42 \pi}{4}\right)}{(\sqrt{3})^7\left(2 \cos \frac{45 \pi}{4}\right)+(\sqrt{3})^2\left(2 \cos \frac{30 \pi}{4}\right)}
\)
Since the cosine function has a period of \(2 \pi\), we can reduce the arguments of the cosine function in the numerator and denominator.
We have \(69 \pi / 4=\pi / 4+17 \pi=\pi / 4\),
\(
\begin{aligned}
& 42 \pi / 4=2 \pi / 4+10 \pi=\pi / 2, \\
& 45 \pi / 4=\pi / 4+11 \pi=\pi / 4, \text { and } \\
& 30 \pi / 4=2 \pi / 4+7 \pi=\pi / 2 .
\end{aligned}
\)
Therefore, the required expression simplifies to :
\(
\begin{aligned}
& =\frac{(\sqrt{3})^{15}\left(2 \cos \frac{\pi}{4}\right)+(\sqrt{3})^6\left(2 \cos \frac{\pi}{2}\right)}{(\sqrt{3})^7\left(2 \cos \frac{\pi}{4}\right)+(\sqrt{3})^2\left(2 \cos \frac{\pi}{2}\right)} \\
& =\frac{(\sqrt{3})^{15} \sqrt{2}+(\sqrt{3})^6 \cdot 0}{(\sqrt{3})^7 \sqrt{2}+(\sqrt{3})^2 \cdot 0} \\
& =\frac{(\sqrt{3})^{15} \sqrt{2}}{(\sqrt{3})^7 \sqrt{2}} \\
& =(\sqrt{3})^{15-7} \\
& =(\sqrt{3})^8 \\
& =81
\end{aligned}
\) -
Question 65 of 103
65. Question
Let \(\alpha, \beta, \gamma\) be the three roots of the equation \(x^3+b x+c=0\). If \(\beta \gamma=1=-\alpha\), then \(b^3+2 c^3-3 \alpha^3-6 \beta^3-8 \gamma^3\) is equal to : [JEE Main 2023]
CorrectIncorrectHint
Concept:
For a cubic equation, \(a x^3+b x^2+c x+d=0\)
Sum of roots \(=\frac{-b}{a}\)
Product of roots taken two at a time \(=\frac{c}{a}\)
Product of roots \(=\frac{-d}{a}\)
Given cubic equation is :
\(
x^3+b x+c=0
\)
\(\because \alpha, \beta, \gamma\) are the roots of above equation.
And \(\beta \gamma=1=-\alpha\)
So, product of roots \(=-c\)
\(
\begin{aligned}
& \Rightarrow \alpha \beta \gamma=-c \\
& \Rightarrow(-1)(1)=-c \\
& \Rightarrow c=1
\end{aligned}
\)
Since, \(\alpha=-1\) is the root. So,
\(
\begin{aligned}
& \Rightarrow-1-b+c=0 \\
& \Rightarrow c-b=1 \\
& \Rightarrow 1-b=1 \Rightarrow b=0
\end{aligned}
\)
The given equation becomes \(x^3+1=0\)
So, roots are \(-1,-\omega,-\omega^2\)
\(
\begin{aligned}
& \therefore b^3+2 c^3-3 \alpha^3-6 \beta^3-8 \gamma^3 \\
& =0+2-3(-1)^3-6(-\omega)^3-8\left(-\omega^2\right)^3 \\
& =2+3+6 \omega^3+8 \omega^6 \\
& =5+6+8=19
\end{aligned}
\) -
Question 66 of 103
66. Question
Let \(A=\{x \in R:[x+3]+[x+4] \leq 3\}\), \(B=\left\{x \in R: 3^x\left(\sum_{r=1}^{\infty} \frac{3}{10^x}\right)^{x-3}<3^{-3 x}\right\}\), Then, [JEE Main 2023]
CorrectIncorrectHint
We have,
\(
\begin{aligned}
& A=\{x \in R:[x+3]+[x+4] \leq 3\} \\
& \text { Here, }[x+3]+[x+4] \leq 3 \\
& \Rightarrow[x]+3+[x]+4 \leq 3 \\
& (\because[x+n]=[x]+n, n \in I) \\
& \Rightarrow 2[x]+4 \leq 0 \Rightarrow[x] \leq-2 \\
& \Rightarrow x \in(-\infty,-1)
\end{aligned}
\)
\(
A \equiv(-\infty,-1) \dots(i)
\)
Also,
\(
B=\left\{x \in R: 3^x\left(\sum_{r=1}^{\infty} \frac{3}{10^x}\right)^{x-3}<3^{-3 x}\right\}
\)
Here,
\(
\begin{aligned}
& 3^x\left(\frac{3}{10}+\frac{3}{10^2}+\frac{3}{10^3}+\ldots\right)^{x-3}<3^{-3 x} \\
\Rightarrow & 3^x\left(\frac{\frac{3}{10}}{1-\frac{1}{10}}\right)^{x-3}<3^{-3 x} \\
\Rightarrow & 3^x\left(\frac{1}{3}\right)^{x-3}<3^{-3 x} \\
\Rightarrow & 3^{x-x+3}<3^{-3 x} \Rightarrow 3^3<3^{-3 x}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad-3 x>3 \Rightarrow x<-1 \\
& \Rightarrow \quad x \in(-\infty,-1) \\
& \Rightarrow \quad B \equiv(-\infty,-1) \ldots \ldots . . .(i i)
\end{aligned}
\)
From equations (i) and (ii), we get
\(
A=B
\) -
Question 67 of 103
67. Question
The sum of all the roots of the equation \(\left|x^2-8 x+15\right|-2 x+7=0\) is : [JEE Main 2023]
CorrectIncorrectHint
We have, \(\left|x^2-8 x+15\right|-2 x+7=0\)
\(
\Rightarrow|(x-3)(x-5)|-2 x+7=0
\)
Now, when \(x \leq 3\) or \(x \geq 5\), then
\(
\begin{gathered}
x^2-8 x+15-2 x+7=0 \\
\Rightarrow x^2-10 x+22=0 \\
\Rightarrow x^2-10 x+25-3=0 \\
\Rightarrow(x-5)^2-3=0 \\
\Rightarrow(x-5)= \pm \sqrt{3} \\
\Rightarrow x=5+\sqrt{3}, 5-\sqrt{3}
\end{gathered}
\)
Since, \(x \leq 3\) or \(x \geq 5\)
\(
\therefore x=5+\sqrt{3}
\)
When, \(3<x<5\), then
\(
\begin{aligned}
& -\left(x^2-8 x+15\right)-2 x+7=0 \\
& \Rightarrow-x^2+8 x-15-2 x+7=0 \\
& \Rightarrow-x^2+6 x-8=0 \\
& \Rightarrow x^2-6 x+8=0 \\
& \Rightarrow(x-4)(x-2)=0 \Rightarrow x=2,4
\end{aligned}
\)
Since, \(3<x<5\)
\(
\therefore x=4
\)
\(\therefore\) Sum of roots \(=(5+\sqrt{3})+4=9+\sqrt{3}\) -
Question 68 of 103
68. Question
The number of integral values of \(k\), for which one root of the equation \(2 x^2-8 x+k=0\) lies in the interval \((1,2)\) and its other root lies in the interval \((2,3)\), is : [JEE Main 2023]
CorrectIncorrectHint
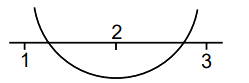
\(
2 x^2-8 x+k=0
\)
\(
\begin{aligned}
& f(1)>0 \Rightarrow k>6 \\
& f(2)<0 \Rightarrow k<8 \\
& f(3)>0 \Rightarrow k>6 \\
& k \in(6,8)
\end{aligned}
\)
Only 1 integral value of \(k\) is 7 . -
Question 69 of 103
69. Question
Let \(S=\left\{x: x \in R\right.\) and \(\left.(\sqrt{3}+\sqrt{2})^{x^2-4}+(\sqrt{3}-\sqrt{2})^{x^2-4}=10\right\}\). Then \(n(S)\) is equal to [JEE Main 2023]
CorrectIncorrectHint
Let \((\sqrt{3}+\sqrt{2})^{x^2-4}=t\)
\(
\begin{aligned}
& t+\frac{1}{t}=10 \\
\Rightarrow & t^2-10 t+1=0 \\
\Rightarrow & t=\frac{10 \pm \sqrt{100-4}}{2}=5 \pm 2 \sqrt{6}
\end{aligned}
\)Case-I:
\(
\begin{gathered}
t=5+2 \sqrt{6}=(\sqrt{3}+\sqrt{2})^2 \\
\Rightarrow(\sqrt{3}+\sqrt{2})^{x^2-4}=(\sqrt{3}+\sqrt{2})^2 \\
\Rightarrow x^2-4=2 \Rightarrow x^2=6 \Rightarrow x= \pm \sqrt{6}
\end{gathered}
\)Case-II :
\(
\begin{aligned}
& t=5-2 \sqrt{6}=(\sqrt{3}-\sqrt{2})^2 \\
& (\sqrt{3}+\sqrt{2})^{x^2-4}=(\sqrt{3}-\sqrt{2})^2 \\
& \Rightarrow\left((\sqrt{3}-\sqrt{2})^{-1}\right)^{x^2-4}=(\sqrt{3}-\sqrt{2})^2 \\
& \Rightarrow 4-x^2=2 \\
& \Rightarrow x^2=2 \\
& \Rightarrow x= \pm \sqrt{2}
\end{aligned}
\) -
Question 70 of 103
70. Question
The equation \(e ^{4 x}+8 e ^{3 x}+13 e ^{2 x}-8 e ^x+1=0, x \in R\) has : [JEE Main 2023]
CorrectIncorrectHint
\(
e^{4 x}+8 e^{3 x}+13 e^{2 x}-8 e^x+1=0
\)
Let \(e ^{ x }= t\)
Now, \(t ^4+8 t ^3+13 t ^2-8 t +1=0\)
Dividing equation by \(t ^2\)
\(
\begin{aligned}
& t^2+8 t+13-\frac{8}{t}+\frac{1}{t^2}=0 \\
& t^2+\frac{1}{t^2}+8\left(t-\frac{1}{t}\right)+13=0 \\
& \left(t-\frac{1}{t}\right)^2+2+8\left(t-\frac{1}{t}\right)+13=0
\end{aligned}
\)
Let \(t -\frac{1}{ t }= z\)
\(
\begin{aligned}
& z^2+8 z+15=0 \\
& (z+3)(z+5)=0 \\
& z=-3 \text { or } z=-5
\end{aligned}
\)
So, \(t-\frac{1}{t}=-3\) or \(t-\frac{1}{t}=-5\)
\(t^2+3 t-1=0\) or \(t^2+5 t-1=0\)
\(t =\frac{-3 \pm \sqrt{13}}{2}\) or \(t =\frac{-5 \pm \sqrt{29}}{2}\)
as \(t=e^x\) so \(t\) must be positive,
\(t=\frac{\sqrt{13}-3}{2}\) or \(\frac{\sqrt{29}-5}{2}\)
So, \(x=\ln \left(\frac{\sqrt{13}-3}{2}\right)\) or \(x=\ln \left(\frac{\sqrt{29}-5}{2}\right)\)
Hence two solutions and both are negative. -
Question 71 of 103
71. Question
The equation \(x^2-4 x+[x]+3=x[x]\), where \([x]\) denotes the greatest integer function, has : [JEE Main 2022]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2-4 x+[x]+3=x[x] \\
& \Rightarrow x^2-4 x+[x]+3-x[x]=0 \\
& \Rightarrow(x-1)(x-3)-[x](x-1)=0 \\
& \Rightarrow(x-1)(x-[x]-3)=0 \\
& \therefore x=1
\end{aligned}
\)
Or
\(
\begin{aligned}
& x-[x]-3=0 \\
& \Rightarrow\{x\}-3=0[\text { As }\{x\}=x-[x]] \\
& \Rightarrow\{x\}=3
\end{aligned}
\)
But we know, \(0<\{x\}<1\)
\(
\therefore\{x\} \neq 3
\)
\(\therefore x\) has only one solution in \((-\infty, \infty)\) which is \(x=1\). -
Question 72 of 103
72. Question
If \(\frac{1}{(20-a)(40-a)}+\frac{1}{(40-a)(60-a)}+\ldots+\frac{1}{(180-a)(200-a)}=\frac{1}{256}\), then the maximum value of \(a\) is : [JEE Main 2022]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{1}{20}\left(\frac{1}{20-a}-\frac{1}{40-a}+\frac{1}{40-a}-\frac{1}{60-a}+\ldots .+\frac{1}{180-a}-\frac{1}{200-a}\right)=\frac{1}{256} \\
& \Rightarrow \frac{1}{20}\left(\frac{1}{20-a}-\frac{1}{200-a}\right)=\frac{1}{256} \\
& \Rightarrow \frac{1}{20}\left(\frac{180}{(20-a)(200-a)}\right)=\frac{1}{256} \\
& \Rightarrow(20-a)(200-a)=9.256
\end{aligned}
\)OR \(a^2-220 a+1696=0\)
\(
\Rightarrow a=212,8
\) -
Question 73 of 103
73. Question
Let \(S=\left\{x \in[-6,3]-\{-2,2\}: \frac{|x+3|-1}{|x|-2} \geq 0\right\}\) and \(T=\left\{x \in Z : x^2-7|x|+9 \leq 0\right\}\). Then the number of elements in \(S \cap T\) is : [JEE Main 2022]
CorrectIncorrectHint
\(
\begin{aligned}
& \left|x^2\right|-7|x|+9 \leq 0 \\
& \Rightarrow|x| \in\left[\frac{7-\sqrt{13}}{2}, \frac{7+\sqrt{13}}{2}\right]
\end{aligned}
\)
As \(x \in Z\)
So, \(x\) can be \(\pm 2, \pm 3, \pm 4, \pm 5\)
Out of these values of \(x\),
\(
x=3,-4,-5
\)
satisfy \(S\) as well
\(
n(S \cap T)=3
\) -
Question 74 of 103
74. Question
Let \(\alpha, \beta\) be the roots of the equation \(x^2-\sqrt{2} x+\sqrt{6}=0\) and \(\frac{1}{\alpha^2}+1, \frac{1}{\beta^2}+1\) be the roots of the equation \(x^2+a x+b=0\). Then the roots of the equation \(x^2-(a+b-2) x+(a+b+2)=0\) are : [JEE Main 2022]
CorrectIncorrectHint
\(
\begin{aligned}
& \alpha+\beta=\sqrt{2}, \alpha \beta=\sqrt{6} \\
& \frac{1}{\alpha^2}+1+\frac{1}{\beta^2}+1=2+\frac{\alpha^2+\beta^2}{6} \\
& =2+\frac{2-2 \sqrt{6}}{6}=-a \\
& \left(\frac{1}{\alpha^2}+1\right)\left(\frac{1}{\beta^2}+1\right)=1+\frac{1}{\alpha^2}+\frac{1}{\beta^2}+\frac{1}{\alpha^2 \beta^2} \\
& =\frac{7}{6}+\frac{2-2 \sqrt{6}}{6}=b \\
& \Rightarrow a+b=\frac{-5}{6}
\end{aligned}
\)
So, equation is \(x^2+\frac{17 x}{6}+\frac{7}{6}=0\)
Or \(6 x^2+17 x+7=0\)
Both roots of equation are – ve and distinct -
Question 75 of 103
75. Question
If \(\alpha, \beta\) are the roots of the equation
\(
x^2-\left(5+3^{\sqrt{\log _3 5}}-5^{\sqrt{\log _5 3}}\right) x+3\left(3^{\left(\log _3 5\right)^{\frac{1}{3}}}-5^{\left(\log _5 3\right)^{\frac{2}{3}}}-1\right)=0
\)
then the equation, whose roots are \(\alpha+\frac{1}{\beta}\) and \(\beta+\frac{1}{\alpha}\), is : [JEE Main 2022]CorrectIncorrectHint
\(
\begin{aligned}
& 3^{\sqrt{\log _3 5}}-5^{\sqrt{\log _5 3}}=3^{\sqrt{\log _3 5}}-\left(3^{\log _3 5}\right)^{\sqrt{\log _5 3}} \\
& 3^{\left(\log _3 5\right)^{\frac{1}{3}}}-5^{\left(\log _5 3\right)^{\frac{2}{3}}}=5^{\left(\log _5 3\right)^{\frac{2}{3}}}-5^{\left(\log _5 3\right)^{\frac{2}{3}}}=0
\end{aligned}
\)
Note: In the given equation ‘ \(x\) ‘ is missing.So \(x^2-5 x+3(-1)=0 <_\beta^\alpha\)
\(
\begin{aligned}
& \alpha+\beta+\frac{1}{\alpha}+\frac{1}{\beta}=(\alpha+\beta)+\frac{\alpha+\beta}{\alpha \beta} \\
& =5-\frac{5}{3}=\frac{10}{3} \\
& \left(\alpha+\frac{1}{\beta}\right)\left(\beta+\frac{1}{\alpha}\right)=2+\alpha \beta+\frac{1}{\alpha \beta}=2-3-\frac{1}{3}=\frac{-4}{3}
\end{aligned}
\) -
Question 76 of 103
76. Question
The minimum value of the sum of the squares of the roots of \(x^2+(3-a) x+1=2 a\) is: [JEE Main 2022]
CorrectIncorrectHint
\(
x^2+(3-a) x+1=2 a <_\beta^\alpha
\)
\(
\begin{aligned}
& \alpha+\beta=a-3, \alpha \beta=1-2 a \\
& \Rightarrow \alpha^2+\beta^2=(a-3)^2-2(1-2 a) \\
& =a^2-6 a+9-2+4 a \\
& =a^2-2 a+7 \\
& =(a-1)^2+6
\end{aligned}
\)
So, \(\alpha^2+\beta^2 \geq 6\) -
Question 77 of 103
77. Question
If \(\alpha, \beta, \gamma, \delta\) are the roots of the equation \(x^4+x^3+x^2+x+1=0\), then \(\alpha^{2021}+\beta^{2021}+\gamma^{2021}+\delta^{2021}\) is equal to : [JEE Main 2022]
CorrectIncorrectHint
When, \(x^5=1\)
then \(x^5-1=0\)
\(
\Rightarrow(x-1)\left(x^4+x^3+x^2+x+1\right)=0
\)
Given, \(x^4+x^3+x^2+x+1=0\) has roots \(\alpha, \beta, \gamma\) and 8 .
\(\therefore\) Roots of \(x^5-1=0\) are \(1, \alpha, \beta, \gamma\) and 8 .
We know, Sum of \(p^{\text {th }}\) power of \(n^{\text {th }}\) roots of unity \(=0\). (If \(p\) is not multiple of \(n\) ) or \(n\) (If \(p\) is multiple of \(n\) )
\(\therefore\) Here, Sum of \(p ^{\text {th }}\) power of \(n ^{\text {th }}\) roots of unity
Here, \(p=2021\), which is not multiple of 5 .
\(
\begin{aligned}
& \therefore 1^{2021}+\alpha^{2021}+\beta^{2021}+\gamma^{2021}+8^{2021}=0 \\
& \Rightarrow \alpha^{2021}+\beta^{2021}+\gamma^{2021}+8^{2021}=-1
\end{aligned}
\) -
Question 78 of 103
78. Question
Let \(S_1=\left\{x \in R-\{1,2\}: \frac{(x+2)\left(x^2+3 x+5\right)}{-2+3 x-x^2} \geq 0\right\}\) and \(S_2=\left\{x \in R: 3^{2 x}-3^{x+1}-3^{x+2}+27 \leq 0\right\}\). Then, \(S_1 \cup S_2\) is equal to : [JEE Main 2022]
CorrectIncorrectHint
Given,
\(
\frac{(x+2)\left(x^2+3 x+5\right)}{-2+3 x-x^2} \geq 0
\)
\(x^2+3 x+5\) is a quadratic equation
\(
\begin{aligned}
& a=1>0 \text { and } D=(-3)^2-4 \cdot 1 \cdot 5=-11<0 \\
& \therefore x^2+3 x+5>0 \text { (always) }
\end{aligned}
\)
So, we can ignore this quadratic term
\(
\begin{aligned}
& \frac{(x+2)}{-2+3 x-x^2} \geq 0 \\
\Rightarrow & \frac{x+2}{-\left(x^2-3 x+2\right)} \geq 0 \\
\Rightarrow & \frac{x+2}{x^2-3 x+2} \leq 0 \\
\Rightarrow & \frac{x+2}{x^2-2 x-x+2} \leq 0 \\
\Rightarrow & \frac{x+2}{(x-1)(x-2)} \leq 0
\end{aligned}
\)
\(
\begin{aligned}
& \therefore x \in(-\alpha,-2] \cup(1,2) \\
& \therefore S_1=(-\alpha,-2] \cup(1,2)
\end{aligned}
\)
Now,
\(
\begin{aligned}
& 3^{2 x}-3^{x+1}-3^{x+2}+27 \leq 0 \\
& \Rightarrow\left(3^x\right)^2-3 \cdot 3^x-3^2 \cdot 3^x+27 \leq 0
\end{aligned}
\)
Let \(3^x=t\)
\(
\begin{aligned}
& \Rightarrow t^2-3 \cdot t-3^2 \cdot t+27 \leq 0 \\
& \Rightarrow t(t-3)-9(t-3) \leq 0 \\
& \Rightarrow(t-3)(t-9) \leq 0
\end{aligned}
\)
\(
\begin{aligned}
& \therefore 3 \leq t \leq 9 \\
& \Rightarrow 3^1 \leq 3^x \leq 3^2 \\
& \Rightarrow 1 \leq x \leq 2 \\
& \therefore x \in[1,2] \\
& \therefore S_2=[1,2] \\
& \therefore S_1 \cup S_2=(-\alpha, 2] \cup(1,2) \cup[1,2] \\
& =(-\alpha, 2] \cup[1,2]
\end{aligned}
\) -
Question 79 of 103
79. Question
Let \(S\) be the set of all integral values of \(\alpha\) for which the sum of squares of two real roots of the quadratic equation \(3 x^2+(\alpha-6) x+(\alpha+3)=0\) is minimum. Then \(S\) : [JEE Main 2022]
CorrectIncorrectHint
Given quadratic equation,
\(
3 x^2+(\alpha-6) x+(\alpha+3)=0
\)
Let, \(a\) and \(b\) are the roots of the equation,
\(
\therefore a+b=-\frac{\alpha-6}{3}
\)
and \(a b=\frac{\alpha+3}{3}\)
For real roots,
\(
\begin{aligned}
& D \geq 0 \\
& \Rightarrow(\alpha-6)^2-4 \cdot 3 \cdot(\alpha+9) \geq 0 \\
& \Rightarrow \alpha^2-12 \alpha+36-12 \alpha-36 \geq 0 \\
& \Rightarrow \alpha^2-24 \alpha \geq 0 \\
& \Rightarrow \alpha(\alpha-24) \geq 0
\end{aligned}
\)
\(
\therefore \alpha>24 \text { or } \alpha<0
\)
\(\therefore\) Real roots of the equation possible for \(\alpha>24\) or \(\alpha<0\).
Now, sum of square of roots
\(
\begin{aligned}
& =a^2+b^2 \\
& =(a+b)^2-2 a b \\
& =\frac{(\alpha-6)^2}{9}-2 \cdot \frac{(\alpha+3)}{3} \\
& =\frac{\alpha^2-12 \alpha+36-6 \alpha-18}{9} \\
& =\frac{\alpha^2-18 \alpha+18}{9}=f(x)
\end{aligned}
\)
\(\therefore\) Sum of square of roots are minimum when \(a^2+b^2=\) minimum.
\(
\therefore f(\alpha)_{\min }=\frac{\alpha^2-18 \alpha+18}{9}
\)
Value of quadratic equation \(\alpha^2-18 \alpha+18\) is minimum at \(\alpha=-\frac{b}{2 a}=-\frac{(-18)}{2.1}=9\)
But for real roots \(\alpha\) should be less than 0 or greater than 24 .
So, there is no value of \(\alpha\) in the range \(\alpha>24 \cup \alpha<0\) where sum of squares of two real roots is minimum.
\(\therefore S\) is an empty set. -
Question 80 of 103
80. Question
The number of distinct real roots of \(x^4-4 x+1=0\) is : {JEE Main 2022]
CorrectIncorrectHint
\(
\begin{aligned}
& f(x)=x^4-4 x+1=0 \\
& f^{\prime}(x)=4 x^3-4 \\
& =4(x-1)\left(x^2+1+x\right)
\end{aligned}
\)
\(
f^{\prime}(x)=0 \Rightarrow x=1
\)
\(x=1\) is point of minima.
\(
\begin{aligned}
& f(1)=-2 \\
& f(0)=1
\end{aligned}
\)
-
Question 81 of 103
81. Question
Let \(A=\{x \in R:|x+1|<2\}\) and \(B=\{x \in R:|x-1| \geq 2\}\). Then which one of the following statements is NOT true? [JEE Main 2022]
CorrectIncorrectHint
\(
A=(-3,1) \text { and } B=(-\infty,-1] \cup[3, \infty)
\)
So, \(A-B=(-1,1)\)
\(
B-A=(-\infty,-3] \cup[3, \infty)=R-(-3,3)
\)
\(A \cap B=(-3,-1]\)
and \(A \cup B=(-\infty, 1) \cup[3, \infty)=R-[1,3)\) -
Question 82 of 103
82. Question
The number of distinct real roots of the equation \(x^7-7 x-2=0\) is [JEE Main 2022]
CorrectIncorrectHint
Given equation \(x^7-7 x-2=0\)
Let \(f(x)=x^7-7 x-2\)
\(
f^{\prime}(x)=7 x^6-7=7\left(x^6-1\right)
\)
and \(f^{\prime}(x)=0 \Rightarrow x=+1\)
and \(f(-1)=-1+7-2=5>0\)
\(
f(1)=1-7-2=-8<0
\)
So, roughly sketch of \(f(x)\) will be
So, number of real roots of \(f(x)=0\) and 3\(
f(x)=2 \text { has } 3 \text { real distinct solution. }
\)
-
Question 83 of 103
83. Question
The sum of the roots of the equation \(x+1-2 \log _2\left(3+2^x\right)+2 \log _4\left(10-2^{-x}\right)=0\), is : [JEE Main 2021]
CorrectIncorrectHint
\(
\begin{aligned}
& x+1-2 \log _2\left(3+2^x\right)+2 \log _4\left(10-2^{-x}\right)=0 \\
& \log _2\left(2^{x+1}\right)-\log _2\left(3+2^x\right)^2+\log _2\left(10-2^{-x}\right)=0 \\
& \log _2\left(\frac{2^{x+1} \cdot\left(10-2^{-x}\right)}{\left(3+2^x\right)^2}\right)=0 \\
& \frac{2\left(10.2^{-x}-1\right)}{\left(3+2^x\right)^2}=1 \\
& \Rightarrow 20.2^x-2=9+2^{2 x}+6.2^x \\
& \therefore\left(2^x\right)^2-14\left(2^x\right)+11=0
\end{aligned}
\)
Roots are \(2^{x_1} \& 2^{x_2}\)
\(
\begin{aligned}
& \therefore 2^{x_1} \cdot 2^{x_2}=11 \\
& x_1+x_2=\log _2(11)
\end{aligned}
\) -
Question 84 of 103
84. Question
Let \(\alpha=\max _{x \in R}\left\{8^{2 \sin 3 x} \cdot 4^{4 \cos 3 x}\right\}\) and \(\beta=\min _{x \in R}\left\{8^{2 \sin 3 x} \cdot 4^{4 \cos 3 x}\right\}\). If \(8 x^2+b x+c=0\) is a quadratic equation whose roots are \(\alpha^{1 / 5}\) and \(\beta^{1 / 5}\), then the value of \(c – b\) is equal to [JEE Main 2021]
CorrectIncorrectHint
\(
\begin{aligned}
& \alpha=\max _{x \in R}\left\{8^{2 \sin 3 x} \cdot 4^{4 \cos 3 x}\right\} \\
& =\max \left\{2^{6 \sin 3 x} \cdot 2^{8 \cos 3 x}\right\} \\
& =\max \left\{2^{6 \sin 3 x+8 \cos 3 x}\right\}
\end{aligned}
\)
and \(\beta=\min \left\{8^{2 \sin 3 x} \cdot 4^{4 \cos 3 x}\right\}=\min \left\{2^{6 \sin 3 x+8 \cos 3 x}\right\}\)
Now range of \(6 \sin 3 x+8 \cos 3 x\)
\(
\begin{aligned}
& =\left[-\sqrt{6^2+8^2},+\sqrt{6^2+8^2}\right]=[-10,10] \\
& \alpha=2^{10} \& \beta=2^{-10}
\end{aligned}
\)
So, \(\alpha^{1 / 5}=2^2=4\)
\(
\Rightarrow \beta^{1 / 5}=2^{-2}=1 / 4
\)
quadratic \(8 x^2+b x+c=0\)
\(
\begin{aligned}
& -\frac{b}{8}=\frac{17}{4} \Rightarrow b=-34 \\
& \frac{c}{8}=1 \Rightarrow c=8 \\
& \therefore c-b=8+34=42
\end{aligned}
\) -
Question 85 of 103
85. Question
Let \(\alpha, \beta\) be two roots of the equation \(x^2+(20)^{1 / 4} x +(5)^{1 / 2}=0\). Then \(\alpha^8+\beta^8\) is equal to [JEE Main 2021]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2+(20)^{1 / 4} x+(5)^{1 / 2}=0 \\
& \Rightarrow x^2+\sqrt{5}=-(20)^{1 / 4} x
\end{aligned}
\)
Squaring both sides, we get
\(
\begin{aligned}
& \left(x^2+\sqrt{5}\right)^2=\sqrt{20} x^2 \\
& \Rightarrow x^4=-5 \Rightarrow x^8=25 \\
& \Rightarrow \alpha^8+\beta^8=50
\end{aligned}
\) -
Question 86 of 103
86. Question
If \([x]\) be the greatest integer less than or equal to \(x\), then \(\sum_{n=8}^{100}\left[\frac{(-1)^n n}{2}\right]\) is equal to: [JEE Main 2021]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{n=8}^{100}\left[\frac{(-1)^n n}{2}\right] \\
& =[4]+[-4.5]+[5]+[-5.5]+[6]+\ldots . .+[-49.5]+[50] \\
& =4-5+5-6+6 \ldots . .-50+50 \\
& =4
\end{aligned}
\) -
Question 87 of 103
87. Question
The number of real solutions of the equation, \(x^2-|x|-12=0\) is : [JEE Main 2021]
CorrectIncorrectHint
\(
\begin{aligned}
& |x|^2-|x|-12=0 \\
& \Rightarrow(|x|+3)(|x|-4)=0 \\
& \Rightarrow|x|=4 \\
& \Rightarrow x= \pm 4
\end{aligned}
\) -
Question 88 of 103
88. Question
The number of real roots of the equation \(e^{6 x}-e^{4 x}-2 e^{3 x}-12 e^{2 x}+e^x+1=0\) is : [JEE Main 2021]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Let } e^{6 x}-e^{4 x}-2 e^{3 x}-12 e^{2 x}+e^x+1=0 \\
& \Rightarrow e^{6 x}-2 e^{3 x}+1-e^x\left[e^{3 x}+12 e^x-1\right]=0 \\
& \Rightarrow\left(e^{3 x}-1\right)^2-e^x\left(e^{3 x}-1\right)-12 e^{2 x}=0 \\
& \Rightarrow\left(e^{3 x}-1\right)^2-4 e^x\left(e^{3 x}-1\right)+3 e^x\left(e^{3 x}-1\right)-12 e^{2 x}=0 \\
& \Rightarrow\left(e^{3 x}-1\right)\left[e^{3 x}-1-4 e^x\right]+3 e^x\left[e^{3 x}-1-4 e^x\right]=0 \\
& \Rightarrow\left(e^{3 x}-1+3 e^x\right)\left(e^{3 x}-1-4 e^x\right)=0 \\
& \text { Either } e^{3 x}=1+4 e^x
\end{aligned}
\)
From the above graphs, only two roots are possible.
-
Question 89 of 103
89. Question
Let \([x]\) denote the greatest integer less than or equal to \(x\). Then, the values of \(x \in R[latex] satisfying the equation [latex]\left[e^x\right]^2+\left[e^x+1\right]-3=0\) lie in the interval : [JEE Main 2021]
CorrectIncorrectHint
\(
\begin{aligned}
& {\left[e^x\right]^2+\left[e^x+1\right]-3=0} \\
& \Rightarrow\left[e^x\right]^2+\left[e^x\right]+1-3=0 \\
& \text { Let }\left[e^x\right]=t \\
& \Rightarrow t^2+t-2=0 \\
& \Rightarrow t=-2,1 \\
& {\left[e^x\right]=-2 \text { (Not possible) }} \\
& \text { or }\left[e^x\right]=1 \therefore 1 \leq e^x<2 \\
& \Rightarrow \ln (1) \leq x<\ln (2) \\
& \Rightarrow 0 \leq x<\ln (2) \\
& \Rightarrow x \in[0, \ln 2)
\end{aligned}
\) -
Question 90 of 103
90. Question
If \(\alpha\) and \(\beta\) are the distinct roots of the equation \(x^2+(3)^{1 / 4} x+3^{1 / 2}=0\), then the value of \(\alpha^{96}\left(\alpha^{12}-1\right)+\beta^{96}\left(\beta^{12}-1\right)\) is equal to : [JEE Main 2021]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { As, }\left(\alpha^2+\sqrt{3}\right)=-(3)^{1 / 4} . \alpha \\
& \Rightarrow\left(\alpha^4+2 \sqrt{3} \alpha^2+3\right)=\sqrt{3} \alpha^2 \text { (On squaring) } \\
& \therefore\left(\alpha^4+3\right)=(-) \sqrt{3} \alpha^2 \\
& \Rightarrow \alpha^8+6 \alpha^4+9=3 \alpha^4 \text { (Again squaring) } \\
& \therefore \alpha^8+3 \alpha^4+9=0 \\
& \Rightarrow \alpha^8=-9-3 \alpha^4
\end{aligned}
\)
(Multiply by \(\alpha^4\) )
So, \(\alpha^{12}=-9 \alpha^4-3 \alpha^8\)
\(
\begin{aligned}
& \therefore \alpha^{12}=-9 \alpha^4-3\left(-9-3 \alpha^4\right) \\
& \Rightarrow \alpha^{12}=-9 \alpha^4+27+9 \alpha^4
\end{aligned}
\)
Hence, \(\alpha^{12}=(27)^2\)
\(
\begin{aligned}
& \Rightarrow\left(\alpha^{12}\right)^8=(27)^8 \\
& \Rightarrow \alpha^{96}=(3)^{24}
\end{aligned}
\)
\(
\therefore \alpha^{96}\left(\alpha^{12}-1\right)+\beta^{96}\left(\beta^{12}-1\right)=(3)^{24} \times 52
\) -
Question 91 of 103
91. Question
Let \(\alpha, \beta ; \alpha>\beta\), be the roots of the equation \(x^2-\sqrt{2} x-\sqrt{3}=0\). Let \(P _n=\alpha^n-\beta^n, n \in N\). Then \((11 \sqrt{3}-10 \sqrt{2}) P _{10}+(11 \sqrt{2}+10) P _{11}-11 P _{12}\) is equal to [JEE Main 2024]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2-\sqrt{2} x-\sqrt{3}=0 \\
& P_n=\alpha^n-\beta^n
\end{aligned}
\)
\(\alpha\) and \(\beta\) are the roots of the equation
Using Newton’s theorem
\(
\begin{aligned}
& P_{n+2}-\sqrt{2} P_{n+1}-\sqrt{3} P_n=0 \\
& \text { Put } n=10 \\
& P_{12}-\sqrt{2} P_{11}-\sqrt{3} P_{10}=0 \\
& P_{12}=\sqrt{2} P_{11}+\sqrt{3} P_{10}
\end{aligned}
\)
Put \(n=9\)
\(
\begin{aligned}
& P_{11}-\sqrt{2} P_{10}-\sqrt{3} P_9=0 \\
& P_{11}=\sqrt{2} P_{10}+\sqrt{3} P_9 \\
& (11 \sqrt{3}-10 \sqrt{2}) P_{10}+(11 \sqrt{2}+10) P_{11}-11 P_{12}
\end{aligned}
\)
Put the value of \(P_{12} \& P_{12}\) in above equation.
\(
\begin{aligned}
& =(11 \sqrt{3}-10 \sqrt{2}) P_{10}+(11 \sqrt{2}+10)\left(\sqrt{2} P_{10}+\sqrt{3} P_9\right)-11\left(\sqrt{2} P_{11}+\sqrt{3} P_{10}\right. \\
& =11 \sqrt{3} P_{10}-10 \sqrt{2} P_{10}+22 P_{10}+10 \sqrt{2} P_{10}+11 \sqrt{6} P_9+10 \sqrt{3} P_9-11 \sqrt{2} P_{11} \\
& =22 P_{10}+11 \sqrt{6} P_9+10 \sqrt{3} P_9-11 \sqrt{2}\left(\sqrt{2} P_{10}+\sqrt{3} P_9\right) \\
& =22 P_{10}+11 \sqrt{6} P_9+10 \sqrt{3} P_9-22 P_{10}-11 \sqrt{6} P_9 \\
& =10 \sqrt{3} P_9
\end{aligned}
\) -
Question 92 of 103
92. Question
Let \(\alpha, \beta\) be the roots of the equation \(x^2+2 \sqrt{2} x-1=0\). The quadratic equation, whose roots are \(\alpha^4+\beta^4\) and \(\frac{1}{10}\left(\alpha^6+\beta^6\right)\), is: [JEE Main 2024]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2+2 \sqrt{2 x}-1=0 \\
& \alpha+\beta=-2 \sqrt{2} \text { and } \alpha \beta=-1 \\
& \alpha^2+\beta^2=(\alpha+\beta)^2-2 \alpha \beta \\
& =8+2=10 \\
& \alpha^4+\beta^4=\left(\alpha^2+\beta^2\right)^2-2(\alpha \beta)^2 \\
& =100-2=98 \\
& \alpha^6+\beta^6=\left(\alpha^2+\beta^2\right)^3-3 \alpha^2 \beta^2\left(\alpha^2+\beta^2\right) \\
& =1000-3(10) \\
& =970 \\
& \therefore \quad \frac{1}{10}\left(\alpha^6+\beta^6\right)=97
\end{aligned}
\)
Equation whose roots are \(\alpha^4+\beta^4\) and \(\frac{1}{10}\left(\alpha^6+\beta^6\right)\) is
\(
\begin{aligned}
& x^2-(98+97) x+98 \times 97=0 \\
& x^2-195 x+9506=0
\end{aligned}
\) -
Question 93 of 103
93. Question
The sum of all the solutions of the equation \((8)^{2 x}-16 \cdot(8)^x+48=0\) is : [JEE Main 2024]
CorrectIncorrectHint
First, let’s start by substituting \(y=(8)^x\) in the given equation. By substituting, the equation \(8^{2 x}-16 \cdot 8^x+48=0\) will be transformed into
\(
y^2-16 y+48=0
\)
Now, we have a quadratic equation in \(y\). To find the roots of this quadratic equation, we can use the quadratic formula:
\(
y=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}
\)
In this case, \(a=1, b=-16\), and \(c=48\). Substituting these values into the formula, we get:
\(
\begin{aligned}
& y=\frac{16 \pm \sqrt{256-192}}{2} \\
& y=\frac{16 \pm \sqrt{64}}{2} \\
& y=\frac{16 \pm 8}{2}
\end{aligned}
\)
Solving for the two possible values of \(y\), we have:
\(
\begin{aligned}
& y=\frac{16+8}{2}=12 \\
& y=\frac{16-8}{2}=4
\end{aligned}
\)
Now, recall that we substituted \(y=(8)^x\). So, we need to solve for \(x\) when \(y=12\) and \(y=4\).
\(
8^x=12
\)
\(
\begin{aligned}
& x=\log _8(12) \\
& 8^x=4 \\
& x=\log _8(4)
\end{aligned}
\)
Therefore, the solutions for \(x\) are \(\log _8(12)\) and \(\log _8(4)\). The sum of these solutions is:
\(
\log _8(12)+\log _8(4)
\)
Using the logarithmic property that \(\log _b(m)+\log _b(n)=\log _b(m \cdot n)\), we get:
\(
\begin{aligned}
& \log _8(12)+\log _8(4)=\log _8(12 \cdot 4) \\
& =\log _8(48)
\end{aligned}
\)
Now, we note that:
\(
48=8 \cdot 6
\)
Thus,
\(
\log _8(48)=\log _8(8 \cdot 6)=\log _8(8)+\log _8(6)=1+\log _8(6)
\)
Therefore, the sum of all the solutions of the equation is: \(1+\log _8(6)\) -
Question 94 of 103
94. Question
Let \(\alpha, \beta\) be the distinct roots of the equation \(x^2-\left(t^2-5 t+6\right) x+1=0, t \in R\) and \(a_n=\alpha^n+\beta^n\). Then the minimum value of \(\frac{a_{2023}+a_{2025}}{a_{2024}}\) is [JEE Main 2024]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2-\left(t^2-5 t+6\right) x+1=0 \\
& \therefore a_{2025}-\left(t^2-5 t+6\right) a_{2024}+a_{2023}=0 \\
& \Rightarrow \frac{a_{2025}+a_{2023}}{a_{2024}}=t^2-5 t+6 \\
& =\left(t+\frac{5}{2}\right)^2+\left(\frac{-1}{4}\right) \\
& \text { Minimum value }=\frac{-1}{4}
\end{aligned}
\) -
Question 95 of 103
95. Question
The coefficients \(a , b , c\) in the quadratic equation \(a x^2+ bx + c =0\) are from the set \(\{1,2,3,4,5,6\}\). If the probability of this equation having one real root bigger than the other is \(p\), then 216 p equals : [JEE Main 2024]
CorrectIncorrectHint
Equation is \(a x^2+b x+c=0\)
\(D >0\) [for roots to be real & distinct]
\(
\Rightarrow b^2-4 a c>0
\)
For \(b<2\) no value of \(a \& c\) are possible
For \(b=3 \Rightarrow a c<\frac{9}{4}\)
\(
(a, c) \in\{(1,1),(1,2),(2,1)\} \Rightarrow 3 \text { cases }
\)
For \(b=4 \Rightarrow a c<4\)
\(
(a, c) \in\{(1,1),(1,2),(2,1),(3,1),(1,3)\} \Rightarrow 5 \text { cases }
\)
For \(b=5 \Rightarrow a c<\frac{25}{4}\)
\(
\begin{aligned}
& (a, c) \in\{(1,1),(1,2),(2,1),(3,1),(1,3),(2,2), \\
& (4,1),(1,4),(3,2),(2,3),(5,1),(1,5),(1,6), \\
& (6,1)\}=14 \text { cases }
\end{aligned}
\)
For \(b=6 \Rightarrow a c<9\)
\(
\begin{aligned}
& (a, c) \in\{(1,1),(1,2),(2,1),(3,1),(1,3),(2,2) \\
& (4,1),(1,4),(3,2),(2,3),(5,1),(1,5),(1,6), \\
& (6,1),(2,4),(4,2)\}=16 \text { cases }
\end{aligned}
\)
Total cases \(=3+5+14+16=38\) cases
\(\Rightarrow\) Probability, \(p=\frac{38}{216}\)
\(
\Rightarrow 216 p=38
\) -
Question 96 of 103
96. Question
If 2 and 6 are the roots of the equation \(a x^2+b x+1=0\), then the quadratic equatio whose roots are \(\frac{1}{2 a+b}\) and \(\frac{1}{6 a+b}\), is : [JEE Main 2024]
CorrectIncorrectHint
\(
\begin{aligned}
& (x-2)(x-6)=0 \\
& \Rightarrow x^2-8 x+12=0 \\
& \Rightarrow \frac{x^2}{12}-\frac{8 x}{12}+1=0 \\
& \therefore a=\frac{1}{12}, b=\frac{-2}{3} \\
& \frac{1}{2 a+b}=\frac{1}{\frac{1}{6}-\frac{2}{3}} \Rightarrow \frac{6}{-3}=-2 \\
& \frac{1}{6 a+b}=\frac{1}{\frac{1}{2}-\frac{2}{3}} \Rightarrow \frac{6}{-1}=-6 \\
& \therefore(x+2)(x+6)=0 \\
& \Rightarrow x^2+8 x+12=0
\end{aligned}
\) -
Question 97 of 103
97. Question
If \(\alpha, \beta\) are the roots of the equation, \(x^2-x-1=0\) and \(S_n=2023 \alpha^n+2024 \beta^n\), then: [JEE Main 2024]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2-x-1=0 \\
& S_n=2023 \alpha^n+2024 \beta^n \\
& S_{n-1}+S_{n-2}=2023 \alpha^{n-1}+2024 \beta^{n-1}+2023 \alpha^{n-2}+2024 \beta^{n-2} \\
& =2023 \alpha^{n-2}[1+\alpha]+2024 \beta^{n-2}[1+\beta] \\
& =2023 \alpha^{n-2}\left[\alpha^2\right]+2024 \beta^{n-2}\left[\beta^2\right] \\
& =2023 \alpha^n+2024 \beta^n \\
& S_{n-1}+S_{n-2}=S_n \\
& P_{u t} n=12 \\
& S_{11}+S_{10}=S_{12}
\end{aligned}
\) -
Question 98 of 103
98. Question
The number of distinct real roots of the equation \(|x+1||x+3|-4|x+2|+5=0\), is [JEE Main 2024]
CorrectIncorrectHint
\(
|x+1||x+3|-4|x+2|+5=0
\)
(I) If \(x<-3\)
\(
\begin{aligned}
& x^2+4 x+3+4 x+8+5=0 \\
& x^2+8 x+16=0 \Rightarrow x=-4 \Rightarrow \text { one solution }
\end{aligned}
\)
\(
\begin{aligned}
& \text { (II) If }-3 \leq x<-2 \\
& -x^2-4 x-3+4 x+8+5=0 \\
& x^2-10=0 \Rightarrow x= \pm \sqrt{10} \Rightarrow \text { do not satisfy }-3 \leq \\
& x<-2
\end{aligned}
\)
\(
\begin{aligned}
& \text { (III) If }-2 \leq x<-1 \\
& -x^2-4 x-3-4 x-8+5=0 \\
& x^2-8 x+6=0 \\
& (x+4)^2=10 \Rightarrow x=-4 \pm \sqrt{10} \Rightarrow \text { do not satisfy } \\
& -2 \leq x<-1
\end{aligned}
\)
(IV) If \(x \geq-1\)
\(
\begin{aligned}
& x^2+4 x+3-4 x-8+5=0 \\
& x^2=0 \\
& x=0 \text { (One solution) }
\end{aligned}
\)
\(x=0\) (One solution)
\(\Rightarrow\) The number of distinct real roots are two -
Question 99 of 103
99. Question
Let \(x_1, x_2, x_3, x_4\) be the solution of the equation \(4 x^4+8 x^3-17 x^2-12 x+9=0\) and \(\left(4+x_1^2\right)\left(4+x_2^2\right)\left(4+x_3^2\right)\left(4+x_4^2\right)=\frac{125}{16} m\). Then the value of \(m\) is [JEE Main 2024]
CorrectIncorrectHint
\(
\begin{aligned}
& 4 x^4+8 x^3-17 x^2-12 x+9=0 \\
& (x+1)\left(4 x^3+4 x^2-21 x+9\right)=0 \\
& (x+1)(x+3)\left(4 x^2-8 x+3\right)=0 \\
& (x+1)(x+3)\left(4 x^2-6 x-2 x+3\right)=0 \\
& (x+1)(x+3)(2 x(2 x-3)-1(2 x-3))=0
\end{aligned}
\)
\(
\frac{(x+1)}{x=-1}
\)
\(
\begin{gathered}
\underset{\downarrow}{(x+1)} \\
x=-3
\end{gathered}
\)
\(
\frac{(2 x-1)}{x=\frac{1}{2}}
\)
\(
\begin{aligned}
& (2 x-3) \\
& x=\frac{3}{2}=0
\end{aligned}
\)
\(
\begin{aligned}
& (4+1)(4+9)\left(4+\frac{1}{4}\right)\left(4+\frac{9}{4}\right)=\frac{125}{16} m \\
& 5 \times 13 \times\left(\frac{17}{4}\right) \times\left(\frac{25}{4}\right)=\frac{125}{16} m \\
& \frac{125}{16} \times[13 \times 17]=\frac{125}{16} m \\
& m=13 \times 17 \\
& m=221
\end{aligned}
\) -
Question 100 of 103
100. Question
The number of real solutions of the equation \(x|x+5|+2|x+7|-2=0\) is [JEE Main 2024]
CorrectIncorrectHint
\(
x|x+5|+2|x+7|-2=0
\)
\(
\begin{aligned}
& \text { (i) } d x \geq-5 \Rightarrow x(x+5)+2(x+7)-2=0 \\
& x^2+7 x+12=0 \Rightarrow x=-3,-4
\end{aligned}
\)
(ii)
\(
\begin{aligned}
& x \in(-7,-5) \\
& x(-x-5)+2(x+7)-2=0 \\
& -x^2-3 x+12=0 \\
& \Rightarrow x^2+3 x-12=0 \\
& \Rightarrow x=\frac{-3-\sqrt{57}}{2} \text { satisfy }
\end{aligned}
\)
(iii)
\(
\begin{aligned}
& x \leq-7 \\
& \Rightarrow x(-x-5)+2(-x-7)-2=0 \\
& -x^2-7 x-16=0 \Rightarrow x^2+7 x+16=0
\end{aligned}
\)
No solution -
Question 101 of 103
101. Question
The number of distinct real roots of the equation \(|x||x+2|-5|x+1|-1=0\) is [JEE Main 2024]
CorrectIncorrectHint
\(
|x| \quad|x+2|-5|x+1|-1=0
\)
\(
\begin{aligned}
& \text { (I) if } x<-2 \\
& x^2+2 x+5 x+5-1=0 \\
& x^2+7 x+4=0 \Rightarrow \text { one root satisfying } x<-2
\end{aligned}
\)
(I) if \(x<-2\)
\(
\begin{aligned}
& \text { (II) if }-2 \leq x<-1 \\
& -x^2-2 x+5 x+5-1=0 \\
& x^2-3 x-4=0 \Rightarrow \text { not root satisfying }-2 \leq x<-1
\end{aligned}
\)
\(
\begin{aligned}
& \text { (III) if }-1 \leq x<0 \\
& -x^2-2 x-5 x-5-1=0 \\
& x^2+7 x+6=0 \\
& x=-1 \text { is only root satisfying }-1 \leq x<0
\end{aligned}
\)
(IV) if \(x \geq 0\)
\(
\begin{aligned}
& x^2+2 x-5 x-5-1=0 \\
& x^2-3 x-6=0
\end{aligned}
\)
one root satisfying \(x \geq 0\)
\(\Rightarrow\) The number of distinct real roots are three. -
Question 102 of 103
102. Question
The number of real solutions of the equation \(x\left(x^2+3|x|+5|x-1|+6|x-2|\right)=0\) is [JEE Main 2024]
CorrectIncorrectHint
The given equation is \(x\left(x^2+3|x|+5|x-1|+6|x-2|\right)=0\), which can be solved by analyzing it in parts. It can be broken down into: \(x=0\) and
\(
x^2+3|x|+5|x-1|+6|x-2|=0 \text {. }
\)
For \(x=0\), it’s clear that it is a solution to the equation since it makes the entire expression equal to zero.
Case (I)
\(
\begin{aligned}
& x<0 \\
& x^2-3 x-5(x-1)-6(x-2)=0 \\
& x^2-14 x+17=0
\end{aligned}
\)
\(\because\) All roots are positive \(\Rightarrow\) no solution
Case (II)
\(
\begin{aligned}
& 0<x<1 \\
& x^2+3 x-5(x-1)-6(x-2)=0 \\
& x^2-8 x+17=0 \\
& \because D<0 \Rightarrow \text { no solution }
\end{aligned}
\)
\(
\begin{aligned}
& \text { Case (III) } \\
& 1<x<2 \\
& x^2+3 x+5(x-1)-6(x-2)=0 \\
& x^2+2 x+7=0 \\
& \Rightarrow \text { no solution } \\
& \text { Case (IV) } \\
& x>2 \\
& x^2+3 x+5(x-1)+6(x-2)=0 \\
& x^2+14 x-19=0 \\
& \text { All roots less than } 2 \\
& \Rightarrow \text { no solution }
\end{aligned}
\)
Here \(x=0\) is only solution. -
Question 103 of 103
103. Question
If \(a, b, c\) are distinct + ve real numbers and \(a^2+b^2+c^2=1\) then \(a b+b c+c a\) is [JEE Main 2002]
CorrectIncorrectHint
\(
\begin{aligned}
& \because(a-b)^2+(b-c)^2+(c-a)^2>0 \\
& \Rightarrow 2\left(a^2+b^2+c^2-a b-b c-c a\right)>0 \\
& \Rightarrow 2>2(a b+b c+c a) \Rightarrow a b+b c+c a<1
\end{aligned}
\)