5.4 The Modulus and the Conjugate of a Complex Number

The absolute value of a complex number, \(z=a+b i\), is defined as the distance between the origin \((0,0)\) and the point \((a, b)\) in the complex plane. In other words, it is the length of the hypotenuse of the right triangle formed (by the Pythagorean Theorem).
\(|z|=|a+b i|=\sqrt{a^2+b^2}\)
This is also called the modulus of a complex number.

 

 

Example 1:  Find the absolute value of \(3+2 i\).

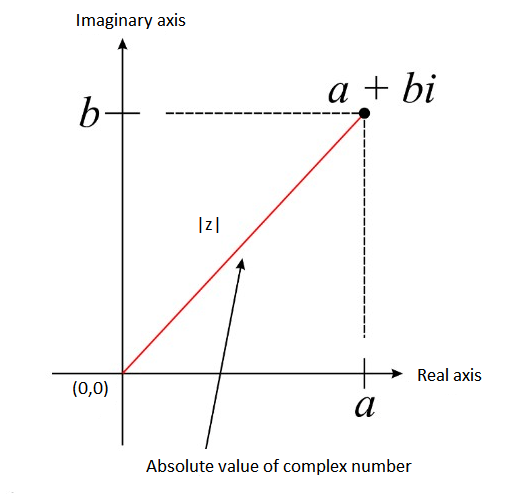
Solution: \(|3+2 i|=\sqrt{3^2+2^2}\)
\(=\sqrt{9+4}\)
\(=\sqrt{13}\)
The absolute value of \(3+2 i=\sqrt{13}\).

Example 2: Find \(|1-3 i|\).

Solution: \(|1-3 i|=\sqrt{1^2+3^2}\)
\(=\sqrt{1+9}\)
\(=\sqrt{10}\)
Therefore, \(|1-3 i|=\sqrt{10}\).

 

Example 3: If \(z\) is a complex number of magnitude \(\sqrt{45}\) and its real part is 3 . Find the imaginary part and \(z\).

Solution: Let \(z=a+ib\), \(\sqrt{a^2+b^2}=\sqrt{45}\)
\(
\begin{aligned}
&\sqrt{3^2+b^2}=\sqrt{45} \\
&\sqrt{9+b^2}=\sqrt{45} \\
&9+b^2=45 \\
&b^2=45-9 \\
&b^2=36 \\
&b=\sqrt{36} \\
&b=\pm 6
\end{aligned}
\)
The complex number \(z=3\pm 6 i\)

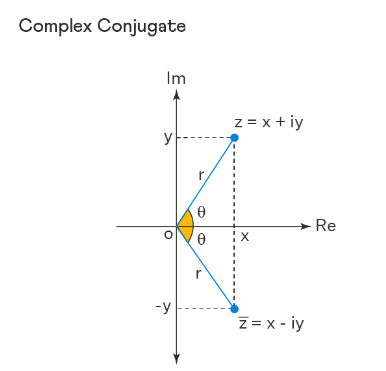
Complex Conjugate Number

The complex conjugate of a complex number, z, is its mirror image with respect to the horizontal axis (or \(x\)-axis). The complex conjugate of complex number \(z\) is denoted by \(\bar{z}\). An easy way to determine the conjugate of a complex number is to replace ‘ \(i\) ‘ with ‘- \(i\) ‘ in the original complex number. The complex conjugate of \(x+iy\) is \(x- iy\) and the complex conjugate of \(x- iy\) is \(x+iy\). As in the image given below, if the complex number z lies in the first quadrant, its image about the horizontal axis, that is, the complex conjugate \(\bar{z}\) lies in the fourth quadrant.

Properties of conjugate: If \(\mathrm{z}, \mathrm{z}_1, \mathrm{z}_2\) are complex numbers, then
(i) \(\overline{\overline{(z)}}=z\)
(ii) \(z+\bar{z}=2 \operatorname{Re}(z)\)
(iii) \(z-\bar{z}=2 i \operatorname{Im}(z)\)
(iv) \(z=\bar{z} \Leftrightarrow z\) is purely real
(v) \(z+\bar{z}=0 \Rightarrow z\) is purely imaginary
(vi) \(z \bar{z}=\{\operatorname{Re}(z)\}^2+\{\operatorname{Im}(z)\}^2\)
(vii) \(\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}\)
(viii) \(\overline{z_1-z_2}=\overline{z_1}-\overline{z_2}\)
(ix) \(\overline{z_1 z_2}=\overline{z_1}\) \(\overline{z_2}\)
(x) \(\frac{z_1}{z_2}=\frac{\overline{z_1}}{\overline{z_2}}, z_2 \neq 0\).

Example 4: Find the complex conjugate of \(5-3 \mathbf{i}\)

Solution: \(5+3 \mathbf{i}\) (Replace \(\mathbf{i}\) with \(\mathbf{-i}\))

Example 5: Prove that \(z \bar{z}=|z|^2\), where \(z=a+i b\) is a complex number and \(\bar{z}\) its conjugate.

Proof: Let \(z=a+i b\) be a complex number. Then, the modulus of \(z\), denoted by \(|z|\), is defined to be the non-negative real number \(\sqrt{a^2+b^2}\), i.e., \(|z|=\sqrt{a^2+b^2}\) and the conjugate of \(z\), denoted as \(\bar{z}\), is the complex number \(a-i b\), i.e., \(\bar{z}=a-i b\).
Observe that the multiplicative inverse of the non-zero complex number \(z\) is given by
\(
z^{-1}=\frac{1}{a+i b}=\frac{a}{a^2+b^2}+i \frac{-b}{a^2+b^2}=\frac{a-i b}{a^2+b^2}=\frac{\bar{z}}{|z|^2}
\)
or \(\quad z \bar{z}=|z|^2\)

Important Note:

For any two complex numbers \(z_1\) and \(z_2\), we have
(i) \(\left|z_1 z_2\right|=\left|z_1\right|\left|z_2\right|\)
(ii) \(\left|\frac{z_1}{z_2}\right|=\frac{\left|z_1\right|}{\left|z_2\right|}\) provided \(\left|z_2\right| \neq 0\)

Example 6: Find the multiplicative inverse of \(2-3 i\).

Solution:  Let \(z=2-3 i\)
Then \(\quad \bar{z}=2+3 i\) and \(\quad|z|^2=2^2+(-3)^2=13\)
Therefore, the multiplicative inverse of \(2-3 i\) is given by
\(z^{-1}=\frac{\bar{z}}{|z|^2}=\frac{2+3 i}{13}=\frac{2}{13}+\frac{3}{13} i\)
The above working can be reproduced in the following manner also,
\(
\begin{aligned}
z^{-1} &=\frac{1}{2-3 i}=\frac{2+3 i}{(2-3 i)(2+3 i)} \\
&=\frac{2+3 i}{2^2-(3 i)^2}=\frac{2+3 i}{13}=\frac{2}{13}+\frac{3}{13} i
\end{aligned}
\)

Example 7: Express the following in the form \(a+i b\)
(i) \(\frac{5+\sqrt{2} i}{1-\sqrt{2} i}\)

(ii) \(i^{-35}\)

Solution: (i) We have, \(\frac{5+\sqrt{2} i}{1-\sqrt{2} i}=\frac{5+\sqrt{2} i}{1-\sqrt{2} i} \times \frac{1+\sqrt{2} i}{1+\sqrt{2} i}=\frac{5+5 \sqrt{2} i+\sqrt{2} i-2}{1-(\sqrt{2} i)^2}\)

\(
=\frac{3+6 \sqrt{2} i}{1+2}=\frac{3(1+2 \sqrt{2} i)}{3}=1+2 \sqrt{2} i .
\)

(ii) \(i^{-35}=\frac{1}{i^{35}}=\frac{1}{\left(i^2\right)^{17} i}=\frac{1}{-i} \times \frac{i}{i}=\frac{i}{-i^2}=i\)

Example 8: The conjugate of a complex number is \(\frac{1}{i-1}\). Then, that complex number is [AIEEE 2008]
(a) \(\frac{-1}{i+1}\)
(b) \(\frac{1}{i-1}\)
(c) \(\frac{-1}{i-1}\)
(d) \(\frac{1}{i+1}\)

Solution: (a) Let the required complex number be \(z\). Then,
\(
\bar{z}=\frac{1}{i-1} \Rightarrow z=\left(\overline{\frac{1}{i-1}}\right)=\frac{1}{-i-1}=-\frac{1}{i+1}
\)

Example 9: If \(\operatorname{Im}\left(\frac{z-1}{2 z+1}\right)=-4\), then the locus of \(z\) is [CEE (Delhi) 2006]
(a) an ellipse
(b) a parabola
(c) a straight line
(d) a circle

Solution: (d) Let \(z=x+i y\). Then,
\(
\frac{z-1}{2 z+1}=\frac{(x-1)+i y}{(2 x+1)+2 i y}=\frac{\mid(x-1)+i y)|(2 x+1)-2 i y|}{|(2 x+1)+2 i y||(2 x+1)-2 i y|}
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{z-1}{2 z+1}=\frac{\left|(x-1)(2 x+1)+2 y^2\right|+i|y(2 x+1)-2 y(x-1)|}{(2 x+1)^2+4 y^2} \\
& \therefore \quad \operatorname{Im}\left(\frac{z-1}{2 z+1}\right)=\frac{3 y}{(2 x+1)^2+4 y^2}
\end{aligned}
\)
Now, \(\operatorname{Im}\left(\frac{z-1}{2 z+1}\right)=-4\)
\(
\Rightarrow \quad \frac{3 y}{(2 x+1)^2+4 y^2}=-4 \Rightarrow x^2+y^2+x+\frac{3}{16} y+\frac{1}{4}=0
\)
Clearly, it represents a circle.
\(
x^2+x+y^2+\frac{3}{16} y=-\frac{1}{4}
\)
Add the square of half the coefficient of \(x\) (which is \(\left(\frac{1}{2}\right)^2=\frac{1}{4}\) ) to both sides:
\(
\begin{gathered}
x^2+x+\frac{1}{4}+y^2+\frac{3}{16} y=-\frac{1}{4}+\frac{1}{4} \\
\left(x+\frac{1}{2}\right)^2+y^2+\frac{3}{16} y=0
\end{gathered}
\)
Add the square of half the coefficient of \(y\) (which is \(\left(\frac{1}{2} \cdot \frac{3}{16}\right)^2=\left(\frac{3}{32}\right)^2=\frac{9}{1024}\) ) to both sides:
\(
\begin{gathered}
\left(x+\frac{1}{2}\right)^2+y^2+\frac{3}{16} y+\frac{9}{1024}=0+\frac{9}{1024} \\
\left(x+\frac{1}{2}\right)^2+\left(y+\frac{3}{32}\right)^2=\frac{9}{1024}
\end{gathered}
\)
The equation is now in the standard form \((x-h)^2+(y-k)^2=r^2\).
The center of the circle \((h, k)\) is \(\left(-\frac{1}{2},-\frac{3}{32}\right)\), and the radius \(r\) is \(\sqrt{\frac{9}{1024}}=\frac{3}{32}\).
Since the radius squared \(\left(r^2=\frac{9}{1024}\right)\) is positive, the equation describes a real circle.

Modulus of a Complex Number

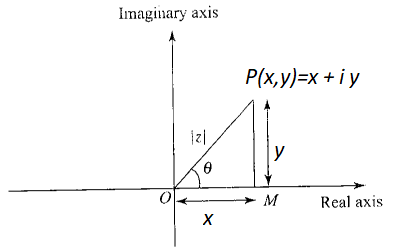
The length of the line segment \(O P\) is called the modulus of \(z\) and is denoted by \(|z|\). From Figure above, we have
\(
\begin{aligned}
O P^2 & =O M^2+M P^2 \\
\Rightarrow \quad O P^2 & =x^2+y^2 \Rightarrow O P=\sqrt{x^2+y^2}
\end{aligned}
\)
Thus,
\(
|z|=\sqrt{x^2+y^2}=\sqrt{\{\operatorname{Re}(z)\}^2+\{\operatorname{Im}(z)\}^2}
\)
Clearly, \(|z| \geq 0\) for all \(z \in C\).

If \(z_1=3-4 i, z_2=-5+2 i\) and \(z_3 =1+\sqrt{-3}\), then \(\left|z_1\right|=\sqrt{3^2+(-4)^2}=5,\left|z_2\right|=\sqrt{(-5)^2+2^2}=\sqrt{29}\) and \(\left|z_3\right|=|1+i \sqrt{3}|=\sqrt{1^2+(\sqrt{3})^2}=2\).

Remark: In the set \(C\) of all complex numbers, the order relation is not defined. As such \(z_1>z_2\) or \(z_1<z_2\) has no meaning but \(\left|z_1\right|>\left|z_2\right|\) or \(\left|z_1\right|<\left|z_2\right|\) has got its meaning since \(\left|z_1\right|\) and \(\left|z_1\right|\) are real numbers.

Argument of Complex Number

The angle \(\theta\) which \(O P\) makes with \(x\)-axis is called the argument or amplitude of \(z\) and is denoted by \(\arg (z)\) or \(\operatorname{amp}(z)\). From Figure above, we have
\(
\tan \theta=\frac{P M}{O M}=\frac{y}{x}=\frac{\operatorname{Im}(z)}{\operatorname{Re}(z)} \Rightarrow \theta=\tan ^{-1}\left(\frac{\operatorname{Im}(z)}{\operatorname{Re}(z)}\right)
\)
This angle \(\theta\) has infinitely many values differing by multiples of \(2 \pi\).

Example 10: If \(z=1+i \tan \alpha\), where \(\pi<\alpha<3 \pi / 2\), then \(|z|\) is equal to
(a) \(\sec \alpha\)
(b) \(-\sec \alpha\)
(c) \(\operatorname{cosec} \alpha\)
(d) none of these

Solution: (b) We have,
\(
\begin{aligned}
& z=1+i \tan \alpha \\
\Rightarrow \quad & |z|=\sqrt{1+\tan ^2 \alpha}=|\sec \alpha|=-\sec \alpha
\end{aligned}
\)

Properties of Modulus:

Theorem: If \(z, z_1, z_2 \in C\), then
(i) \(|z|=0 \Leftrightarrow z=0\) i.e. \(\operatorname{Re}(z)=\operatorname{Im}(z)=0\)
(ii) \(|z|=|\bar{z}|=|-z|\)
(iii) \(-|z| \leq \operatorname{Re}(z) \leq|z| ;-|z| \leq \operatorname{Im}(z) \leq|z|\)
(iv) \(z \bar{z}=|z|^2\)
(v) \(\left|z_1 z_2\right|=\left|z_1\right|\left|z_2\right|\)
(vi) \(\left|\frac{z_1}{z_2}\right|=\frac{\left|z_1\right|}{\left|z_2\right|}, z_2 \neq 0\)
(vii) \(\left|z_1+z_2\right|^2=\left|z_1\right|^2+\left|z_2\right|^2+2 \operatorname{Re}\left(z_1 \overline{z_2}\right)\)
(viii) \(\left|z_1-z_2\right|^2=\left|z_1\right|^2+\left|z_2\right|^2-2 \operatorname{Re}\left(z_1 \overline{z_2}\right)\)
(ix) \(\left|z_1+z_2\right|^2+\left|z_1-z_2\right|^2=2\left(\left|z_1\right|^2+\left|z_2\right|^2\right)\)
(x) \(\left|a z_1-b z_2\right|^2+\left|b z_1+a z_2\right|^2=\left(a^2+b^2\right)\left(\left|z_1\right|^2+\left|z_2\right|^2\right)\), where \(a, b \in R\).

Reciprocal of a Complex Number

Let \(z\) be a complex number. Then,
\(
\frac{1}{z}=\frac{\bar{z}}{z \bar{z}}=\frac{\bar{z}}{|z|^2}
\)

Example 11: If \(\left|\frac{z+i}{z-i}\right|=\sqrt{3}\), then the radius of the circle is [CEE (Delhi) 2007]
(a) \(\frac{2}{\sqrt{21}}\)
(b) \(\frac{1}{\sqrt{21}}\)
(c) \(\sqrt{3}\)
(d) \(\sqrt{21}\)

Solution: (c) We have,
\(
\left|\frac{z+i}{z-i}\right|=\sqrt{3}
\)
\(
\begin{aligned}
& \Rightarrow \quad|z+i|=\sqrt{3}|z-i| \\
& \Rightarrow \quad|x+i(y+1)|=\sqrt{3}|x+i(y-1)| \\
& \Rightarrow \quad x^2+(y+1)^2=3\left\{x^2+(y-1)^2\right\} \\
& \Rightarrow \quad x^2+y^2-4 y+1=0 \\
& \Rightarrow \quad(x-0)^2+(y-2)^2=(\sqrt{3})^2
\end{aligned}
\)
Clearly, it represents a circle of radius \(\sqrt{3}\).

Example 12: The smallest positive integral value of \(n\) for which \(\left(\frac{1-i}{1+i}\right)^n\) is purely imaginary with positive imaginary part, is
(a) 1
(b) 3
(c) 5
(d) none of these

Solution: (b) We have,
\(
\left(\frac{1-i}{1+i}\right)^n=\left(\frac{1-i}{1+i} \times \frac{1-i}{1-i}\right)^n=\left(\frac{1-2 i+i^2}{1-i^2}\right)^n=(-i)^n
\)
\(\therefore \quad\left(\frac{1-i}{1+i}\right)^n\) will be purely imaginary if \(n\) is an odd integer.
For \(n=1\), we have \(\left(\frac{1+i}{1-i}\right)^1=(-i)^1=-i\), which has negative imaginary part.
For \(n=3\), we have
\(\left(\frac{1+i}{1-i}\right)^3=(-i)^3=i\), which has positive imaginary part.
Hence, \(n=3\).

Example 13: The least positive integer \(n\) for which \(\left(\frac{1+i}{1-i}\right)^n\) is real, is
(a) 2
(b) 4
(c) 8
(d) none of these

Solution: (a) We have,
\(
\left(\frac{1+i}{1-i}\right)^n=\left(\frac{(1+i)^2}{1-i^2}\right)^n=(i)^n
\)
Clearly, it is real for \(n=2\).

Example 14: The smallest positive integer \(n\) for which \(\frac{(1+i)^n}{(1-i)^{n-2}}\) is a real number, is [CEE (Delhi) 2001]
(a) 2
(b) 1
(c) 3
(d) 4

Solution: (b) We have,
\(
\begin{aligned}
& \frac{(1+i)^n}{(1-i)^{n-2}}=\left(\frac{1+i}{1-i}\right)^n(1-i)^2 \\
\Rightarrow \quad & \frac{(1+i)^n}{(1-i)^{n-2}}=\left\{\frac{(1+i)^2}{1-i^2}\right\}\left(1-2 i+i^2\right)=(i)^n(-2 i)=-2 i^{n+1}
\end{aligned}
\)
This will be a real number if \(n+1\) is an even integer i.e. \(n\) is an odd integer.
Since the smallest odd positive integer is 1. Therefore, \(n=1\).

Example 15: If \(z=x-iy\) and \(z^{1 / 3}=p+i q\), then \(\left(\frac{x}{p}+\frac{y}{q}\right) / p^2+q^2\) is equal to [AIEEE 2004]
(a) -2
(b) -1
(c) 2
(d) 1

Solution: (a) We have,
\(
\begin{aligned}
& z=x-i y \text { and } z^{1 / 3}=p+i q \\
\Rightarrow & z=x-i y \text { and } z=(p+i q)^3 \\
\Rightarrow & x-i y=(p+i q)^3 \\
\Rightarrow & x-i y=\left(p^3-3 p q^2\right)+i\left(-3 p^2 q+q^3\right) \\
\Rightarrow & x=p^3-3 p q^2 \text { and } y=q^3-3 p^2 q \\
\Rightarrow & \frac{x}{p}+\frac{y}{q}=\left(p^2+q^2\right)-3\left(p^2+q^2\right) \Rightarrow \frac{\frac{x}{p}+\frac{y}{q}}{p^2+q^2}=-2 .
\end{aligned}
\)

Example 16: If \(z=x+i y, z^{1 / 3}=a-i b\) and \(\frac{x}{a}-\frac{y}{b}=k\left(a^2-b^2\right)\), then the value of \(k\) equals [CEE (Delhi) 2005)]
(a) 2
(b) 4
(c) 6
(d) 1

Solution: (b) We have,
\(
\begin{aligned}
& z=x+i y \text { and } z^{1 / 3}=a-i b \\
\Rightarrow & x+i y=(a-i b)^3 \\
\Rightarrow & x+i y=\left(a^3-3 a b^2\right)+i\left(-3 a^2 b+b^3\right) \\
\Rightarrow & x=a^3-3 a b^2 \text { and } y=-3 a^2 b+b^3 \\
\Rightarrow & \frac{x}{a}-\frac{y}{b}=a^2-3 b^2+3 a^2-b^2 \\
\Rightarrow & \frac{x}{a}-\frac{y}{b}=4\left(a^2-b^2\right) \\
\Rightarrow & k\left(a^2-b^2\right)=4\left(a^2-b^2\right) \quad \quad\left[\because \frac{x}{a}-\frac{y}{b}=k\left(a^2-b^2\right)\right] \\
\Rightarrow & k=4
\end{aligned}
\)

Square Root of a Complex Number

Let \(a+i b\) be a complex number such that \(\sqrt{a+i b}=x+i y\), where \(x\) and \(y\) are real numbers. Then,
\(
\begin{array}{ll}
\sqrt{a+i b} & =x+i y \\
\Rightarrow \quad(a+i b) & =(x+i y)^2 \\
\Rightarrow \quad a+i b & =\left(x^2-y^2\right)+2 i x y
\end{array}
\)
On equating real and imaginary parts, we get
\(
\begin{aligned}
&\begin{aligned}
& x^2-y^2=a \dots(i)\\
& 2 x y=b
\end{aligned}\\
&\text { Now, }\\
&\begin{aligned}
& \left(x^2+y^2\right)^2=\left(x^2-y^2\right)^2+4 x^2 y^2 \\
\Rightarrow & \left(x^2+y^2\right)^2=a^2+b^2 \\
\Rightarrow & \left(x^2+y^2\right)=\sqrt{a^2+b^2} \quad\left[\because x^2+y^2 \geq 0\right] \dots(ii)
\end{aligned}
\end{aligned}
\)
Solving equations (i) and (ii), we get
\(
\begin{aligned}
x^2 & =\left(\frac{1}{2}\right)\left[\sqrt{a^2+b^2}+a\right] \text { and } y^2=\left(\frac{1}{2}\right)\left[\sqrt{a^2+b^2}-a\right] \\
\Rightarrow x & = \pm \sqrt{\left(\frac{1}{2}\right)\left[\sqrt{a^2+b^2}+a\right]} \text { and } y= \pm \sqrt{\left(\frac{1}{2}\right)\left[\sqrt{a^2+b^2}-a\right]}
\end{aligned}
\)
If \(b\) is positive, then by the relation \(2 x y=b, x\) and \(y\) are of the same sign. Hence,
\(
\sqrt{a+i b}= \pm\left\{\sqrt{\frac{1}{2}\left[\sqrt{a^2+b^2}+a\right]}+i \sqrt{\frac{1}{2}\left[\sqrt{a^2+b^2}-a\right]}\right\}
\)
If \(b\) is negative, then by the relation \(2 x y=b, x\) and \(y\) are of different signs. Hence,
\(
\sqrt{a+i b}= \pm\left\{\sqrt{\frac{1}{2}\left[\sqrt{a^2+b^2}+a\right]}-i \sqrt{\frac{1}{2}\left[\sqrt{a^2+b^2}-a\right]}\right\}
\)

Remark: The square root of a complex number \(z\) is given by
\(\sqrt{z}= \pm\left[\sqrt{\frac{1}{2}\{|z|+\operatorname{Re}(z)\}}+i \sqrt{\frac{1}{2}\{|z|-\operatorname{Re}(z)\}}\right], \text { if } \operatorname{Im}|z|>0\)
and, \(\sqrt{z}= \pm\left[\sqrt{\frac{1}{2}\{|z|+\operatorname{Re}(z)\}}-i \sqrt{\frac{1}{2}\{|z|-\operatorname{Re}(z)\}}\right]\), if \(\operatorname{Im}|z|<0\)

Example 17: Taking the value of the square root with positive real part only, the value of \(\sqrt{7+24 i}+\sqrt{-7-24 i}\) is
(a) \(1+7 i\)
(b) \(-1-7 i\)
(c) \(7-i\)
(d) \(-7+i\)

Solution: (c) If \(z=a+i b\), then
\(
\begin{array}{rlrl}
& \sqrt{a \pm i b}  = \pm\left\{\sqrt{\frac{|z|+\operatorname{Re}(z)}{2}} \pm i \sqrt{\frac{|z|-\operatorname{Re}(z)}{2}}\right\} \\
& \therefore \sqrt{7+24 i}  = \pm(4+3 i) \text { and, } \sqrt{-7-24 i}= \pm(3-4 i) \\
\therefore \sqrt{7+24 i} & \pm \sqrt{-7-24 i} \\
& =4+3 i +3-4 i=7-i \quad \text { [Taking +ive real part only]] }
\end{array}
\)

Example 18: Given that the real parts of \(\sqrt{5+12 i}\) and \(\sqrt{5-12 i}\) are positive. The value of \(z=\frac{\sqrt{5+12 i}+\sqrt{5-12 i}}{\sqrt{5+12 i}-\sqrt{5-12 i}}\), is
(a) \(\frac{3}{2} i\)
(b) \(\frac{-3}{2} i\)
(c) \(-3+\frac{2}{5} i\)
(d) none of these

Solution: (b) Taking positive real parts, we have
\(
\sqrt{5+12 i}=\sqrt{\frac{13+5}{2}}+i \sqrt{\frac{13-5}{2}}=3+2 i
\)
and, \(\sqrt{5-12 i}=\sqrt{\frac{13+5}{2}}-i \sqrt{\frac{13-5}{2}}=3-2 i\)
\(
\therefore \quad z=\frac{(3+2 i)+(3-2 i)}{(3+2 i)-(3-2 i)}=\frac{6}{4 i}=\frac{-3}{2} i
\)

Example 19: Find the value of \(\frac{i^{592}+i^{590}+i^{588}+i^{586}+i^{584}}{i^{582}+i^{580}+i^{578}+i^{576}+i^{574}}-1\)

Solution: The given expression is \(\frac{i^{592}+i^{590}+i^{588}+i^{586}+i^{584}}{i^{582}+i^{580}+i^{578}+i^{576}+i^{574}}-1\). We observe a common factor in the numerator related to the denominator. The difference in powers is \(592-582=10\).
We can factor out \(i^{10}\) from the numerator terms:
\(
i^{592}+i^{590}+i^{588}+i^{586}+i^{584}=i^{10}\left(i^{582}+i^{580}+i^{578}+i^{576}+i^{574}\right)
\)
The fraction simplifies to:
\(
\frac{i^{10}\left(i^{582}+i^{580}+i^{578}+i^{576}+i^{574}\right)}{i^{582}+i^{580}+i^{578}+i^{576}+i^{574}}=i^{10}
\)
The expression becomes \(i^{10}-1\).
Evaluate the power of the imaginary unit
The imaginary unit \(i\) has the property that its powers cycle every four integers: \(i^1=i\), \(i^2=-1, i^3=-i, i^4=1\). We can determine \(i^{10}\) by finding the remainder when 10 is divided by 4 , which is 2.
\(
i^{10}=i^{4 \cdot 2+2}=\left(i^4\right)^2 \cdot i^2=1^2 \cdot(-1)=-1
\)
Substituting this value back into the simplified expression \(i^{10}-1\) :
\(
-1-1=-2
\)

Example 20: The value of \(i^{1+3+5+\cdots+(2 n+1)}\) is ____.

Solution: Step 1: Sum the exponent series
The exponent is an arithmetic series of odd numbers: \(S=1+3+5+\ldots+(2 n+1)\). There are \(n+1\) terms in this series. The sum of the first \(k\) odd integers is \(k^2\).
Therefore, the sum \(S\) is given by:
\(
S=(n+1)^2
\)
Step 2: Evaluate the power of \(i\)
The expression becomes \(i^S=i^{(n+1)^2}\). The value of \(i^m\) cycles every four powers depending on \(m(\bmod 4)\). We analyze \((n+1)^2(\bmod 4)\) (Modulo 4 means finding the remainder after dividing by 4):
\(
(n+1)^2=n^2+2 n+1
\)
If \(n\) is even, \(n=2 k\), then \(S=(2 k+1)^2=4 k^2+4 k+1 \equiv 1(\bmod 4)\).
If \(n\) is odd, \(n=2 k+1\), then \(S=(2 k+2)^2=4(k+1)^2 \equiv 0(\bmod 4)\).
Step 3: Determine the final value
The value of the expression is \(i^S\).
If \(n\) is even, \(i^S=i^1=i\).
If \(n\) is odd, \(i^S=i^0=1\).
The value of the expression is \(\boldsymbol{i}\) for even \(\boldsymbol{n}\) and \(\mathbf{1}\) for odd \(\boldsymbol{n}\).