7.3 Oxidation Number

The oxidation number of an atom is defined as the charge that an atom appears to have on forming ionic bonds with other heteroatoms. An atom having higher electronegativity (even if it forms a covalent bond) is assigned a negative oxidation state. Oxidation number is also called oxidation state. The definition assigns an oxidation state to an atom on conditions that the atom:

• Bonds with heteroatoms.
• Always form ionic bonding by either gaining or losing electrons, irrespective of the actual nature of bonding.

A less obvious example of electron transfer is realised when hydrogen combines with oxygen to form water by the reaction:
\(
2 \mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \dots(8.18)
\)
Though not simple in its approach, yet we can visualise the \(\mathrm{H}\) atom as going from a neutral (zero) state in \(\mathrm{H}_2\) to a positive state in \(\mathrm{H}_2 \mathrm{O}\), the \(\mathrm{O}\) atom goes from a zero state in \(\mathrm{O}_2\) to a dinegative state in \(\mathrm{H}_2 \mathrm{O}\). It is assumed that there is an electron transfer from \(\mathrm{H}\) to \(\mathrm{O}\) and consequently \(\mathrm{H}_2\) is oxidised and \(\mathrm{O}_2\) is reduced.

However, as we shall see later, the charge transfer is only partial and is perhaps better described as an electron shift rather than a complete loss of electron by \(\mathrm{H}\) and gain by \(\mathrm{O}\). What has been said here with respect to equation (8.18) may be true for a good number of other reactions involving covalent compounds. Two such examples of this class of the reactions are:
\(
\mathrm{H}_2(\mathrm{~s})+\mathrm{Cl}_2(\mathrm{~g}) \rightarrow 2 \mathrm{HCl}(\mathrm{g}) \dots(8.19)
\)
and,
\(
\mathrm{CH}_4(\mathrm{~g})+4 \mathrm{Cl}_2(\mathrm{~g}) \rightarrow \mathrm{CCl}_4(\mathrm{l})+4 \mathrm{HCl}(\mathrm{g}) \dots(8.20)
\)
In order to keep track of electron shifts in chemical reactions involving formation of covalent compounds, a more practical method of using oxidation number has been developed. In this method, it is always assumed that there is a complete transfer of electron from a less electronegative atom to a more electronegative atom. For example, we rewrite equations (8.18 to 8.20 ) to show charge on each of the atoms forming part of the reaction:

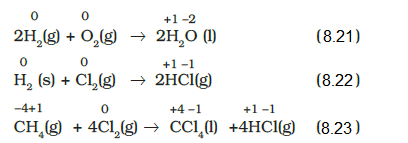
It may be emphasized that the assumption of electron transfer is made for book-keeping purpose only and it will become obvious at a later stage in this unit that it leads to the simple description of redox reactions.

Oxidation number denotes the oxidation state of an element in a compound ascertained according to a set of rules formulated on the basis that electron pair in a covalent bond belongs entirely to more electronegative element.

Rules for Assigning Oxidation Number

A set of rules has been formulated to determine the oxidation number of an element in a compound/ion. If two or more than two atoms of an element are present in the molecule/ion such as \(\mathrm{Na}_2 \mathrm{~S}_2 \mathrm{O}_3 / \mathrm{Cr}_2 \mathrm{O}_7^{2-}\), the oxidation number of the atom of that element will then be the average of the oxidation number of all the atoms of that element. We may at this stage, state the rules for the calculation of oxidation number. These rules are:

• In elements, in the free or the uncombined state, each atom bears an oxidation number of zero. Evidently each atom in \(\mathrm{H}_2\), \(\mathrm{O}_2, \mathrm{Cl}_2, \mathrm{O}_3, \mathrm{P}_4, \mathrm{~S}_8, \mathrm{Na}, \mathrm{Mg}, \mathrm{Al}\) has the oxidation number zero.
• For ions composed of only one atom, the oxidation number is equal to the charge on the ion. Thus \(\mathrm{Na}^{+}\)ion has an oxidation number of \(+1, \mathrm{Mg}^{2+}\) ion, \(+2, \mathrm{Fe}^{3+}\) ion, +3, \(\mathrm{Cl}^{-}\)ion, \(-1, \mathrm{O}^{2-}\) ion, -2 ; and so on. In their compounds all alkali metals have oxidation number of +1 , and all alkaline earth metals have an oxidation number of +2 . Aluminium is regarded to have an oxidation number of +3 in all its compounds.
• The oxidation number of oxygen in most compounds is -2 . However, we come across two kinds of exceptions here. One arises in the case of peroxides and superoxides, the compounds of oxygen in which oxygen atoms are directly linked to each other. While in peroxides (e.g., \(\mathrm{H}_2 \mathrm{O}_2, \mathrm{Na}_2 \mathrm{O}_2\) ), each oxygen atom is assigned an oxidation number of -1 , in superoxides (e.g., \(\mathrm{KO}_2\), \(\mathrm{RbO}_2\) ) each oxygen atom is assigned an oxidation number of \(-(1 / 2)\). The second exception appears rarely, i.e. when oxygen is bonded to fluorine. In such compounds e.g., oxygen difluoride \(\left(\mathrm{OF}_2\right)\) and dioxygen difluoride \(\left(\mathrm{O}_2 \mathrm{~F}_2\right)\), the oxygen is assigned an oxidation number of +2 and +1 , respectively. The number assigned to oxygen will depend upon the bonding state of oxygen but this number would now be a positive figure only.
• The oxidation number of hydrogen is +1 , except when it is bonded to metals in binary compounds (that is compounds containing two elements). For example, in \(\mathrm{LiH}, \mathrm{NaH}\), and \(\mathrm{CaH}_2\), its oxidation number is -1 .
• In all its compounds, fluorine has an oxidation number of -1 . Other halogens \((\mathrm{Cl}\), \(\mathrm{Br}\), and I) also have an oxidation number of -1 , when they occur as halide ions in their compounds. Chlorine, bromine and iodine when combined with oxygen, for example in oxoacids and oxoanions, have positive oxidation numbers.
• The algebraic sum of the oxidation number of all the atoms in a compound must be zero. In polyatomic ion, the algebraic sum of all the oxidation numbers of atoms of the ion must equal the charge on the ion. Thus, the sum of oxidation number of three oxygen atoms and one carbon atom in the carbonate ion, \(\left(\mathrm{CO}_3\right)^{2-}\) must equal -2.

By the application of above rules, we can find out the oxidation number of the desired element in a molecule or in an ion. It is clear that the metallic elements have positive oxidation number and nonmetallic elements have positive or negative oxidation number. The atoms of transition elements usually display several positive oxidation states. The highest oxidation number of a representative element is the group number for the first two groups and the group number minus 10 (following the long form of periodic table) for the other groups. Thus, it implies that the highest value of oxidation number exhibited by an atom of an element generally increases across the period in the periodic table. In the third period, the highest value of oxidation number changes from 1 to 7 as indicated below in the compounds of the elements.

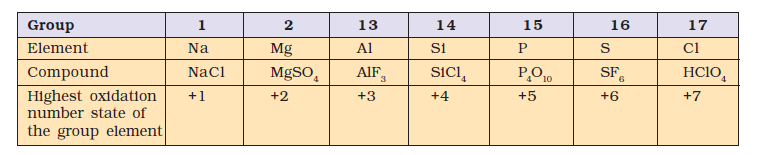
A term that is often used interchangeably with the oxidation number is the oxidation state. Thus in \(\mathrm{CO}_2\), the oxidation state of carbon is +4 , that is also its oxidation number and similarly the oxidation state as well as oxidation number of oxygen is -2 . This implies that the oxidation number denotes the oxidation state of an element in a compound. The oxidation number/state of a metal in a compound is sometimes presented according to the notation given by German chemist, Alfred Stock. It is popularly known as Stock notation. According to this, the oxidation number is expressed by putting a Roman numeral representing the oxidation number in parenthesis after the symbol of the metal in the molecular formula. Thus aurous chloride and auric chloride are written as \(\mathrm{Au}(\mathrm{I}) \mathrm{Cl}\) and \(\mathrm{Au}(\mathrm{III}) \mathrm{Cl}_3\). Similarly, stannous chloride and stannic chloride are written as \(\mathrm{Sn}(\mathrm{II})\) \(\mathrm{Cl}_2\) and \(\mathrm{Sn}(\mathrm{IV}) \mathrm{Cl}_4\). This change in oxidation number implies change in oxidation state, which in turn helps to identify whether the species is present in oxidised form or reduced form. Thus, \(\mathrm{Hg}_2(\mathrm{I}) \mathrm{Cl}_2\) is the reduced form of \(\mathrm{Hg}(\mathrm{II}) \mathrm{Cl}_2\).

The idea of oxidation number has been invariably applied to define oxidation, reduction, oxidising agent (oxidant), reducing agent (reductant) and the redox reaction. To summarise, we may say that:

Oxidation: An increase in the oxidation number of the element in the given substance.

Reduction: A decrease in the oxidation number of the element in the given substance.

Oxidising agent: A reagent which can increase the oxidation number of an element in a given substance. These reagents are called as oxidants also.

Reducing agent: A reagent which lowers the oxidation number of an element in a given substance. These reagents are also called as reductants.

Redox reactions: Reactions which involve change in oxidation number of the interacting species.

Example 8.3: Using Stock notation, represent the following compounds : \(\mathrm{HAuCl}_4, \mathrm{Tl}_2 \mathrm{O}, \mathrm{FeO}\), \(\mathrm{Fe}_2 \mathrm{O}_3, \mathrm{CuI}, \mathrm{CuO}, \mathrm{MnO}\) and \(\mathrm{MnO}_2\).

Answer: By applying various rules of calculating the oxidation number of the desired element in a compound, the oxidation number of each metallic element in its compound is as follows:
\(
\begin{array}{lll}
\mathrm{HAuCl}_4 & \rightarrow & \mathrm{Au} \text { has 3 } \\
\mathrm{Tl}_2 \mathrm{O} & \rightarrow & \mathrm{Tl} \text { has 1 } \\
\mathrm{FeO} & \rightarrow & \mathrm{Fe} \text { has 2 } \\
\mathrm{Fe}_2 \mathrm{O}_3 & \rightarrow & \mathrm{Fe} \text { has 3 } \\
\mathrm{CuI} & \rightarrow & \text { Cu has 1 } \\
\mathrm{CuO} & \rightarrow & \mathrm{Cu} \text { has 2 } \\
\mathrm{MnO} & \rightarrow & \text { Mn has 2 } \\
\mathrm{MnO}_2 & \rightarrow & \text { Mn has 4 }
\end{array}
\)
Therefore, these compounds may be represented as:
\(\mathrm{HAu}(\mathrm{III}) \mathrm{Cl}_4, \mathrm{Tl}_2(\mathrm{I})\)O, \(\mathrm{Fe}(\mathrm{II})\)O, \(\mathrm{Fe}_2(\mathrm{III})\)O \({ }_3\), \(\mathrm{Cu}(\mathrm{I}) \mathrm{I}, \mathrm{Cu}(\mathrm{II}) \mathrm{O}, \mathrm{Mn}(\mathrm{II}) \mathrm{O}, \mathrm{Mn}(\mathrm{IV}) \mathrm{O}_2\).

Example 8.4: Justify that the reaction:
\(
2 \mathrm{Cu}_2 \mathrm{O}(\mathrm{s})+\mathrm{Cu}_2 \mathrm{~S}(\mathrm{~s}) \rightarrow 6 \mathrm{Cu}(\mathrm{s})+\mathrm{SO}_2(\mathrm{~g})
\)
is a redox reaction. Identify the species oxidised/reduced, which acts as an oxidant and which acts as a reductant.

Answer: Let us assign oxidation number to each of the species in the reaction under examination. This results into:
\(
\begin{aligned}
& \begin{array}{llllll}
+1 & -2 & +1 & -2 & & \quad 0 & \quad +4-2
\end{array} \\
& 2 \mathrm{Cu}_2 \mathrm{O}(\mathrm{s})+\mathrm{Cu}_2 \mathrm{~S}(\mathrm{~s}) \rightarrow 6 \mathrm{Cu}(\mathrm{s})+\mathrm{SO}_2 \\
&
\end{aligned}
\)
We therefore, conclude that in this reaction copper is reduced from +1 state to zero oxidation state and sulphur is oxidised from -2 state to +4 state. The above reaction is thus a redox reaction. Further, \(\mathrm{Cu}_2 \mathrm{O}\) helps sulphur in \(\mathrm{Cu}_2 \mathrm{~S}\) to increase its oxidation number, therefore, \(\mathrm{Cu}(\mathrm{I})\) is an oxidant; and sulphur of \(\mathrm{Cu}_2 \mathrm{~S}\) helps copper both in \(\mathrm{Cu}_2 \mathrm{~S}\) itself and \(\mathrm{Cu}_2 \mathrm{O}\) to decrease its oxidation number; therefore, sulphur of \(\mathrm{Cu}_2 \mathrm{~S}\) is reductant.

Applications of Oxidation Number

• To compare the strength of acid and base : Strength of acid \(\propto\) Oxidation Number
  Strength of base \(\propto \frac{1}{\text { Oxidation number }}\)
• To determine the oxidising and reducing nature : Oxidising strength \(\propto\) Oxidation number
  Reducing strength \(\propto \frac{1}{\text { Oxidation number }}\)
• To determine the molecular formula of compound

Types of Redox Reactions

1. Combination reactions

A combination reaction may be denoted in the manner:
\(
\mathrm{A}+\mathrm{B} \rightarrow \mathrm{C}
\)
Either A and B or both A and B must be in the elemental form for such a reaction to be a redox reaction. All combustion reactions, which make use of elemental dioxygen, as well as other reactions involving elements other than dioxygen, are redox reactions. Some important examples of this category are: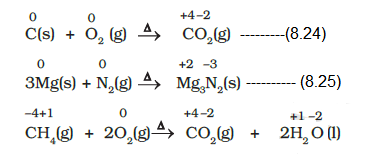

2. Decomposition reactions

Decomposition reactions are the opposite of combination reactions. Precisely, a decomposition reaction leads to the breakdown of a compound into two or more components at least one of which must be in the elemental state. Examples of this class of reactions are:

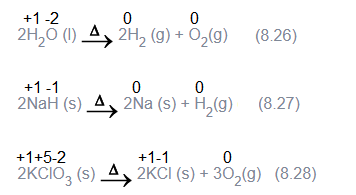
It may carefully be noted that there is no change in the oxidation number of hydrogen in methane under combination reactions and that of potassium in potassium chlorate in reaction (8.28). This may also be noted here that all decomposition reactions are not redox reactions. For example, decomposition of calcium carbonate is not a redox reaction.

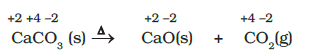
3. Displacement reactions

In a displacement reaction, an ion (or an atom) in a compound is replaced by an ion (or an atom) of another element. It may be denoted as:
\(
\mathrm{X}+\mathrm{YZ} \rightarrow \mathrm{XZ}+\mathrm{Y}
\)
Displacement reactions fit into two categories: metal displacement and non-metal displacement.

(a) Metal displacement: A metal in a compound can be displaced by another metal in the uncombined state. Metal displacement reactions find many applications in metallurgical processes in which pure metals are obtained from their compounds in ores. A few such examples are:

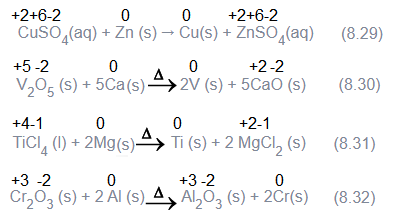
In each case, the reducing metal is a better reducing agent than the one that is being reduced which evidently shows more capability to lose electrons as compared to the one that is reduced.

(b) Non-metal displacement: The non-metal displacement redox reactions include hydrogen displacement and a rarely occurring reaction involving oxygen displacement. All alkali metals and some alkaline earth metals \((\mathrm{Ca}, \mathrm{Sr}\), and \(\mathrm{Ba})\) which are very good reductants, will displace hydrogen from cold water.

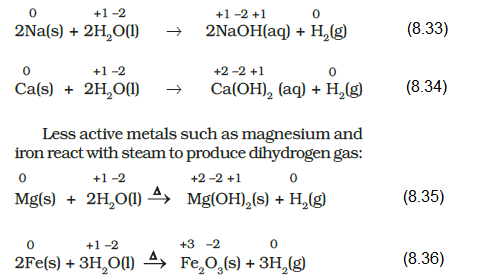
Many metals, including those which do not react with cold water, are capable of displacing hydrogen from acids. Dihydrogen from acids may even be produced by such metals which do not react with steam. Cadmium and tin are the examples of such metals. A few examples for the displacement of hydrogen from acids are: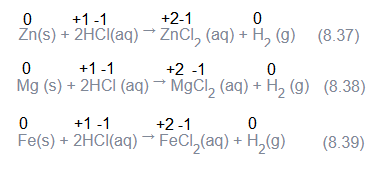

Reactions ( 8.37 to 8.39 ) are used to prepare dihydrogen gas in the laboratory. Here, the reactivity of metals is reflected in the rate of hydrogen gas evolution, which is the slowest for the least active metal \(\mathrm{Fe}\), and the fastest for the most reactive metal, Mg. Very less active metals, which may occur in the native state such as silver (Ag), and gold (Au) do not react even with hydrochloric acid.

We have already discussed that the metals – zinc ( \(\mathrm{Zn})\), copper \((\mathrm{Cu})\) and silver \((\mathrm{Ag})\) through tendency to lose electrons show their reducing activity in the order \(\mathrm{Zn}>\mathrm{Cu}>\mathrm{Ag}\). Like metals, activity series also exists for the halogens. The power of these elements as oxidising agents decreases as we move down from fluorine to iodine in group 17 of the periodic table. This implies that fluorine is so reactive that it can replace chloride, bromide and iodide ions in solution. In fact, fluorine is so reactive that it attacks water and displaces the oxygen of water:

It is for this reason that the displacement reactions of chlorine, bromine and iodine using fluorine are not generally carried out in aqueous solution. On the other hand, chlorine can displace bromide and iodide ions in an aqueous solution as shown below:
\(
\begin{aligned}
& \begin{array}{lll}
0  & & & +1-1  & & & +1-1 & & & 0
\end{array} \\
& \mathrm{Cl}_2(\mathrm{~g})+2 \mathrm{KBr}(\mathrm{aq}) \rightarrow 2 \mathrm{KCl}(\mathrm{aq})+\mathrm{Br}_2(\mathrm{l}) \dots(8.41) \\
&
\end{aligned}
\)
\(
\begin{aligned}
& \begin{array}{lll}
0  & & & +1-1  & & +1-1 & & & 0
\end{array} \\
& \mathrm{Cl}_2(\mathrm{~g})+2 \mathrm{KI}(\mathrm{aq}) \rightarrow 2 \mathrm{KCl}(\mathrm{aq})+\mathrm{I}_2(\mathrm{~s}) \dots(8.42) \\
&
\end{aligned}
\)
As \(\mathrm{Br}_2\) and \(\mathrm{I}_2\) are coloured and dissolve in \(\mathrm{CCl}_4\), can easily be identified from the colour of the solution. The above reactions can be written in ionic form as: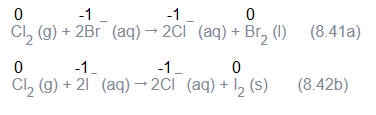

Reactions (8.41) and (8.42) form the basis of identifying \(\mathrm{Br}^{-}\)and \(\mathrm{I}^{-}\)in the laboratory through the test popularly known as ‘Layer Test’. It may not be out of place to mention here that bromine likewise can displace iodide ion in solution:
\(
\begin{aligned}
& \begin{array}{lll}
0  & & & -1  & & & & -1 & & & & 0
\end{array} \\
& \mathrm{Br}_2(\mathrm{l})+2 \mathrm{I}^{-}(\mathrm{aq}) \rightarrow 2 \mathrm{Br}^{-}(\mathrm{aq})+\mathrm{I}_2(\mathrm{~s}) \dots(8.43) \\
&
\end{aligned}
\)
The halogen displacement reactions have a direct industrial application. The recovery of halogens from their halides requires an oxidation process, which is represented by:
\(
2 \mathrm{X}^{-} \rightarrow \mathrm{X}_2+2 \mathrm{e}^{-} \dots(8.44)
\)
here \(\mathrm{X}\) denotes a halogen element. Whereas chemical means are available to oxidise \(\mathrm{Cl}^{-}\), \(\mathrm{Br}^{-}\)and \(\mathrm{I}^{-}\), as fluorine is the strongest oxidising agent; there is no way to convert \(\mathrm{F}^{-}\)ions to \(\mathrm{F}_2\) by chemical means. The only way to achieve \(\mathrm{F}_2\) from \(\mathrm{F}^{-}\)is to oxidise electrolytically, the details of which you will study at a later stage.

4. Disproportionation reactions

Disproportionation reactions are a special type of redox reactions. In a disproportionation reaction an element in one oxidation state is simultaneously oxidised and reduced. One of the reacting substances in a disproportionation reaction always contains an element that can exist in at least three oxidation states. The element in the form of reacting substance is in the intermediate oxidation state; and both higher and lower oxidation states of that element are formed in the reaction. The decomposition of hydrogen peroxide is a familiar example of the reaction, where oxygen experiences disproportionation.

\(
\begin{aligned}
& \begin{array}{lll}
+1-1   & & & +1-2 & & 0
\end{array} \\
& 2 \mathrm{H}_2 \mathrm{O}_2(\mathrm{aq}) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{O}_2(\mathrm{~g}) \dots(8.45) \\
&
\end{aligned}
\)
Here the oxygen of peroxide, which is present in -1 state, is converted to zero oxidation state in \(\mathrm{O}_2\) and decreases to -2 oxidation state in \(\mathrm{H}_2 \mathrm{O}\).

Phosphorous, sulphur and chlorine undergo disproportionation in the alkaline medium as shown below:
\(
\begin{aligned}
& \begin{array}{lll}
0  & & & & & & & & & & & & & & -3  & & & & +1
\end{array} \\
& \mathrm{P}_4(\mathrm{~s})+3 \mathrm{OH}^{-}(\mathrm{aq})+3 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{PH}_3(\mathrm{~g})+3 \mathrm{H}_2 \mathrm{PO}_2^{-}(\mathrm{aq}) \dots(8.46) \\
&
\end{aligned}
\)
\(
\begin{aligned}
& \begin{array}{lll}
0  & & & & & & & & & & -2  & & & & +2
\end{array} \\
& \mathrm{S}_8(\mathrm{~s})+12 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow 4 \mathrm{~S}^{2-}(\mathrm{aq})+2 \mathrm{~S}_2 \mathrm{O}_3^{2-}(\mathrm{aq})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \dots(8.47) \\
&
\end{aligned}
\)
\(
\begin{aligned}
& \begin{array}{lll}
0  & & & & & & & & & +1  & & & & -1
\end{array} \\
& \mathrm{Cl}_2(\mathrm{~g})+2 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow \mathrm{ClO}^{-}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \dots(8.48) \\
&
\end{aligned}
\)

The reaction ( 8.48 ) describes the formation of household bleaching agents. The hypochlorite ion \(\left(\mathrm{ClO}^{-}\right)\)formed in the reaction oxidises the colour-bearing stains of the substances to colourless compounds.
It is of interest to mention here that whereas bromine and iodine follow the same trend as exhibited by chlorine in reaction (8.48), fluorine shows deviation from this behaviour when it reacts with alkali. The reaction that takes place in the case of fluorine is as follows:
\(
2 \mathrm{~F}_2(\mathrm{~g})+2 \mathrm{OH}(\mathrm{aq}) \rightarrow 2 \mathrm{~F}^{-}(\mathrm{aq})+\mathrm{OF}_2(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \dots(8.49)
\)
(It is to be noted with care that fluorine in reaction (8.49) will undoubtedly attack water to produce some oxygen also). This departure shown by fluorine is not surprising for us as we know the limitation of fluorine that, being the most electronegative element, it cannot exhibit any positive oxidation state. This means that among halogens, fluorine does not show a disproportionation tendency.

Example 8.5: Which of the following species, do not show disproportionation reaction and why?
\(
\mathrm{ClO}^{-}, \mathrm{ClO}_2^{-}, \mathrm{ClO}_3^{-} \text {and } \mathrm{ClO}_4^{-}
\)
Also write reaction for each of the species that disproportionates.

Answer: Among the oxoanions of chlorine listed above, \(\mathrm{ClO}_4^{-}\)does not disproportionate because in this oxoanion chlorine is present in its highest oxidation state that is, +7 . The disproportionation reactions for the other three oxoanions of chlorine are as follows:

\(
\stackrel{+1}{\quad 3 \mathrm{ClO}^{-}} \rightarrow \stackrel{-1}{2\mathrm{Cl}^{-}}+\stackrel{+5}{\quad \mathrm{ClO}_3^{-}}
\)
\(
\stackrel{+3}{\quad 6 \mathrm{ClO}_2^{-}} \stackrel{h v}{\longrightarrow} \stackrel{+5}{\quad 4 \mathrm{ClO}_3^{-}}+\stackrel{-1}{2 \mathrm{Cl}^{-}}
\)
\(
\stackrel{+5}{\quad 4 \mathrm{ClO}_3^{-}} \rightarrow \stackrel{-1}{\mathrm{Cl}^{-}}+\stackrel{+7}{\quad \mathrm{ClO}_4^{-}}
\)

Example 8.6: Suggest a scheme of classification of the following redox reactions
\(
\text { (a) } \mathrm{N}_2 \text { (g) }+\mathrm{O}_2 \text { (g) } \rightarrow 2 \mathrm{NO} \text { (g) }
\)
\(
\text { (b) } 2 \mathrm{~Pb}\left(\mathrm{NO}_3\right)_2 \text { (s) } \rightarrow 2 \mathrm{PbO}(\mathrm{s})+4 \mathrm{NO}_2 \text { (g) }+\mathrm{O}_2(\mathrm{~g})
\)
\(
\text { (c) } \mathrm{NaH} \text { (s) }+\mathrm{H}_2 \mathrm{O} \text { (l) } \rightarrow \mathrm{NaOH} \text { (aq) }+\mathrm{H}_2 \text { (g) }
\)
\(
\text { (d) } 2 \mathrm{NO}_2(\mathrm{~g})+2 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow \mathrm{NO}_2^{-}(\mathrm{aq})+\mathrm{NO}_3^{-}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})
\)

Answer: In reaction
(a) the compound nitric oxide is formed by the combination of the elemental substances, nitrogen and oxygen; therefore, this is an example of combination redox reactions. The reaction
(b) involves the breaking down of lead nitrate into three components; therefore, this is categorised under decomposition redox reaction. In reaction
(c) hydrogen of water has been displaced by hydride ion into dihydrogen gas. Therefore, this may be called as displacement redox reaction. The reaction
(d) involves disproportionation of \(\mathrm{NO}_2\) (+4 state) into \(\mathrm{NO}_2^{-}\)(+3 state) and \(\mathrm{NO}_3^{-}\) ( +5 state). Therefore reaction (d) is an example of disproportionation redox reaction.

Example 8.7: Why do the following reactions proceed differently ?
\(
\mathrm{Pb}_3 \mathrm{O}_4+8 \mathrm{HCl} \rightarrow 3 \mathrm{PbCl}_2+\mathrm{Cl}_2+4 \mathrm{H}_2 \mathrm{O}
\)
and
\(
\begin{array}{r}
\mathrm{Pb}_3 \mathrm{O}_4+4 \mathrm{HNO}_3 \rightarrow 2 \mathrm{~Pb}\left(\mathrm{NO}_3\right)_2+\mathrm{PbO}_2+2 \mathrm{H}_2 \mathrm{O}
\end{array}
\)

Answer: \(\mathrm{Pb}_3 \mathrm{O}_4\) is actually a stoichiometric mixture of \(2 \mathrm{~mol}\) of \(\mathrm{PbO}\) and \(1 \mathrm{~mol}\) of \(\mathrm{PbO}_2\). In \(\mathrm{PbO}_2\), lead is present in +4 oxidation state, whereas the stable oxidation state of lead in \(\mathrm{PbO}\) is \(+2 . \mathrm{PbO}_2\) thus can act as an oxidant (oxidising agent) and, therefore, can oxidise \(\mathrm{Cl}^{-}\)ion of \(\mathrm{HCl}\) into chlorine. We may also keep in mind that \(\mathrm{PbO}\) is a basic oxide. Therefore, the reaction
\(
\mathrm{Pb}_3 \mathrm{O}_4+8 \mathrm{HCl} \rightarrow 3 \mathrm{PbCl}_2+\mathrm{Cl}_2+4 \mathrm{H}_2 \mathrm{O}
\)
can be splitted into two reactions namely:
\(
2 \mathrm{PbO}+4 \mathrm{HCl} \rightarrow 2 \mathrm{PbCl}_2+2 \mathrm{H}_2 \mathrm{O} \quad \text { (acid-base reaction) }
\)
\(
\begin{array}{llll}
+4 & & -1 & & \quad +2 & & & 0
\end{array}
\)
\(
\mathrm{PbO}_2+4 \mathrm{HCl} \rightarrow \mathrm{PbCl}_2+\mathrm{Cl}_2+2 \mathrm{H}_2 \mathrm{O} \quad \text { (redox reaction) }
\)
Since \(\mathrm{HNO}_3\) itself is an oxidising agent therefore, it is unlikely that the reaction may occur between \(\mathrm{PbO}_2\) and \(\mathrm{HNO}_3\). However, the acid-base reaction occurs between \(\mathrm{PbO}\) and \(\mathrm{HNO}_3\) as:
\(
2 \mathrm{PbO}+4 \mathrm{HNO}_3 \rightarrow 2 \mathrm{~Pb}\left(\mathrm{NO}_3\right)_2+2 \mathrm{H}_2 \mathrm{O}
\)
It is the passive nature of \(\mathrm{PbO}_2\) against \(\mathrm{HNO}_3\) that makes the reaction different from the one that follows with \(\mathrm{HCl}\).

Balancing of Redox Reactions

Two methods are used to balance chemical equations for redox processes.

• Oxidation Number Method: This method is based on the change in the oxidation number of reducing agent and the oxidising agent.
• Half Reaction Method: This method is based on splitting the redox reaction into two half reactions – one involving oxidation and the other involving reduction.

Oxidation Number Method:

In writing equations for oxidation-reduction reactions, just as for other reactions, the compositions and formulas must be known for the substances that react and for the products that are formed. The oxidation number method is now best illustrated in the following steps:

Step 1: Write the correct formula for each reactant and product.

Step 2: Identify atoms which undergo change in oxidation number in the reaction by assigning the oxidation number to all elements in the reaction.

Step 3: Calculate the increase or decrease in the oxidation number per atom and for the entire molecule/ion in which it occurs. If these are not equal then multiply by suitable number so that these become equal. (If you realise that two substances are reduced and nothing is oxidised or vice-versa, something is wrong. Either the formulas of reactants or products are wrong or the oxidation numbers have not been assigned properly).

Step 4: Ascertain the involvement of ions if the reaction is taking place in water, add \(\mathrm{H}^{+}\)or \(\mathrm{OH}\) ions to the expression on the appropriate side so that the total ionic charges of reactants and products are equal. If the reaction is carried out in acidic solution, use \(\mathrm{H}^{+}\)ions in the equation; if in basic solution, use \(\mathrm{OH}^{-}\)ions.

Step 5: Make the numbers of hydrogen atoms in the expression on the two sides equal by adding water \(\left(\mathrm{H}_2 \mathrm{O}\right)\) molecules to the reactants or products. Now, also check the number of oxygen atoms. If there are the same number of oxygen atoms in the reactants and products, the equation then represents the balanced redox reaction.

Let us now explain the steps involved in the method with the help of a few problems given below:

Example 8.8: Write the net ionic equation for the reaction of potassium dichromate(VI), \(\mathrm{K}_2 \mathrm{Cr}_2 \mathrm{O}_7\) with sodium sulphite, \(\mathrm{Na}_2 \mathrm{SO}_3\), in an acid solution to give chromium(III) ion and the sulphate ion.

Answer:

Step 1: The skeletal ionic equation is:
\(
\mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq})+\mathrm{SO}_3^{2-}(\mathrm{aq}) \rightarrow \mathrm{Cr}^{3+}(\mathrm{aq})+\mathrm{SO}_4^{2-}(\mathrm{aq})
\)

Step 2: Assign oxidation numbers for \(\mathrm{Cr}\) and \(\mathrm{S}\)
\(
\begin{aligned}
& \begin{array}{llll}
+6-2 & & & +4-2 & & & +3 & & +6-2
\end{array} \\
& \mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq})+\mathrm{SO}_3^{2-}(\mathrm{aq}) \rightarrow \mathrm{Cr}(\mathrm{aq})+\mathrm{SO}_4^{2-}(\mathrm{aq}) \\
&
\end{aligned}
\)
This indicates that the dichromate ion is the oxidant and the sulphite ion is the reductant.

Step 3: Calculate the increase and decrease of oxidation number, and make them equal: from step- 2 we can notice that there is change in oxidation state of chromium and sulphur. Oxidation state of chromium changes form +6 to +3 . There is decrease of +3 in oxidation state of chromium on right hand side of the equation. Oxidation state of sulphur changes from +4 to +6 . There is an increase of +2 in the oxidation state of sulphur on right hand side. To make the increase and decrease of oxidation state equal, place numeral 2 before cromium ion on right hand side and numeral 3 before sulphate ion on right hand side and balance the chromium and sulphur atoms on both the sides of the equation. Thus we get
\(
\begin{aligned}
& \begin{array}{lll}
+6-2 & & & +4-2 & & & & +3 & & & & +6-2
\end{array} \\
& \mathrm{Cr}_2 \mathrm{O}_7{ }^{2-}(\mathrm{aq})+3 \mathrm{SO}_3^{2-}(\mathrm{aq}) \rightarrow 2 \mathrm{Cr}^{3+}(\mathrm{aq})+3 \mathrm{SO}_4^{2-}(\mathrm{aq}) \\
&
\end{aligned}
\)

Step 4: As the reaction occurs in the acidic medium, and further the ionic charges are not equal on both the sides, add \(8 \mathrm{H}^{+}\)on the left to make ionic charges equal
\(
\mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq})+3 \mathrm{SO}_3^{2-}(\mathrm{aq})+8 \mathrm{H}^{+} \rightarrow 2 \mathrm{Cr}^{3+}(\mathrm{aq})+3 \mathrm{SO}_4^{2-}(\mathrm{aq})
\)

Step 5: Finally, count the hydrogen atoms, and add appropriate number of water molecules (i.e., \(4 \mathrm{H}_2 \mathrm{O}\) ) on the right to achieve balanced redox change.
\(
\mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq})+3 \mathrm{SO}_3^{2-}(\mathrm{aq})+8 \mathrm{H}^{+}(\mathrm{aq}) \rightarrow2 \mathrm{Cr}^{3+}(\mathrm{aq})+3 \mathrm{SO}_4^{2-}(\mathrm{aq})+4 \mathrm{H}_2 \mathrm{O}(\mathrm{l})
\)

Example 8.9: Permanganate ion reacts with bromide ion in basic medium to give manganese dioxide and bromate ion. Write the balanced ionic equation for the reaction.

Answer:

Step 1: The skeletal ionic equation is:
\(
\mathrm{MnO}_4^{-}(\mathrm{aq})+\mathrm{Br}^{-}(\mathrm{aq}) \rightarrow \mathrm{MnO}_2(\mathrm{~s})+\mathrm{BrO}_3^{-}(\mathrm{aq})
\)

Step 2: Assign oxidation numbers for \(\mathrm{Mn}\) and \(\mathrm{Br}\)
\(
\begin{array}{llll}
+7 & & & & -1 & & & & +4 & & & & +5
\end{array}
\)
\(
\mathrm{MnO}_4^{-}(\mathrm{aq})+\mathrm{Br}^{-}(\mathrm{aq}) \rightarrow \mathrm{MnO}_2(\mathrm{~s})+\mathrm{BrO}_3^{-}(\mathrm{aq})
\)
this indicates that permanganate ion is the oxidant and bromide ion is the reductant.

Step 3: Calculate the increase and decrease of oxidation number, and make the increase equal to the decrease.
\(
\begin{array}{llll}
+7 & & & & -1 & & & & +4 & & & & +5
\end{array}
\)
\(
2 \mathrm{MnO}_4(\mathrm{aq})+\mathrm{Br}(\mathrm{aq}) \rightarrow 2 \mathrm{MnO}_2(\mathrm{~s})+\mathrm{BrO}_3(\mathrm{aq})
\)

Step 4: As the reaction occurs in the basic medium, and the ionic charges are not equal on both sides, add \(2 \mathrm{OH}^{-}\) ions on the right to make ionic charges equal.
\(
\begin{aligned}
& 2 \mathrm{MnO}_4^{-}(\mathrm{aq})+\mathrm{Br}^{-}(\mathrm{aq}) \rightarrow 2 \mathrm{MnO}_2(\mathrm{~s})+\mathrm{BrO}_3^{-}(\mathrm{aq})+2 \mathrm{OH}^{-}(\mathrm{aq})
\end{aligned}
\)

Step 5: Finally, count the hydrogen atoms and add appropriate number of water molecules (i.e. one \(\mathrm{H}_2 \mathrm{O}\) molecule) on the left side to achieve balanced redox change.
\(
\begin{array}{r}
2 \mathrm{MnO}_4^{-}(\mathrm{aq})+\mathrm{Br}^{-}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow 2 \mathrm{MnO}_2(\mathrm{~s})+\mathrm{BrO}_3^{-}(\mathrm{aq})+2 \mathrm{OH}^{-}(\mathrm{aq})
\end{array}
\)

Half Reaction Method: In this method, the two half equations are balanced separately and then added together to give balanced equation.

Suppose we are to balance the equation showing the oxidation of \(\mathrm{Fe}^{2+}\) ions to \(\mathrm{Fe}^{3+}\) ions by dichromate ions \(\left(\mathrm{Cr}_2 \mathrm{O}_7\right)^{2-}\) in acidic medium, wherein, \(\mathrm{Cr}_2 \mathrm{O}_7^{2-}\) ions are reduced to \(\mathrm{Cr}^{3+}\) ions. The following steps are involved in this task.

Step 1: Produce unbalanced equation for the reaction in ionic form:
\(
\mathrm{Fe}^{2+}(\mathrm{aq})+\mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq}) \rightarrow \mathrm{Fe}^{3+}(\mathrm{aq})+\mathrm{Cr}^{3+}(\mathrm{aq}) \dots(8.50)
\)

Step 2: Separate the equation into halfreactions:
\(\quad \quad \quad \quad \quad \quad \quad +2 \quad \quad \quad \quad +3\)
\(
\text { Oxidation half: } \mathrm{Fe}^{2+}(\mathrm{aq}) \rightarrow \mathrm{Fe}^{3+}(\mathrm{aq}) \dots(8.51)
\)
\(
\quad \quad \quad \quad \quad \quad \quad +6-2 \quad \quad \quad \quad +3
\)
\(
\text { Reduction half : } \mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq}) \rightarrow \mathrm{Cr}^{3+}(\mathrm{aq}) \dots(8.52)
\)

Step 3: Balance the atoms other than \(\mathrm{O}\) and \(\mathrm{H}\) in each half reaction individually. Here the oxidation half reaction is already balanced with respect to \(\mathrm{Fe}\) atoms. For the reduction half reaction, we multiply the \(\mathrm{Cr}^{3+}\) by 2 to balance Cr atoms.
\(
\mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq}) \rightarrow 2 \mathrm{Cr}^{3+}(\mathrm{aq}) \dots(8.53)
\)

Step 4: For reactions occurring in acidic medium, add \(\mathrm{H}_2 \mathrm{O}\) to balance \(\mathrm{O}\) atoms and \(\mathrm{H}^{+}\) to balance \(\mathrm{H}\) atoms.
Thus, we get:
\(
\mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq})+14 \mathrm{H}^{+}(\mathrm{aq}) \rightarrow 2 \mathrm{Cr}^{3+}(\mathrm{aq})+7 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \dots(8.54)
\)

Step 5: Add electrons to one side of the half reaction to balance the charges. If need be, make the number of electrons equal in the two half reactions by multiplying one or both half reactions by appropriate number.
The oxidation half reaction is thus rewritten to balance the charge:
\(
\mathrm{Fe}^{2+}(\mathrm{aq}) \rightarrow \mathrm{Fe}^{3+}(\mathrm{aq})+\mathrm{e}^{-} \dots(8.55)
\)
Now in the reduction half reaction there are net twelve positive charges on the left hand side and only six positive charges on the right hand side. Therefore, we add six electrons on the left side.
\(
\mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq})+14 \mathrm{H}^{+}(\mathrm{aq})+6 \mathrm{e}^{-} \rightarrow 2 \mathrm{Cr}^{3+}(\mathrm{aq})+7 \mathrm{H}_2 \mathrm{O}(1) \dots(8.56)
\)
To equalise the number of electrons in both the half reactions, we multiply the oxidation half reaction by 6 and write as :
\(
6 \mathrm{Fe}^{2+}(\mathrm{aq}) \rightarrow 6 \mathrm{Fe}^{3+}(\mathrm{aq})+6 \mathrm{e}^{-} \dots(8.57)
\)

Step 6: We add the two half reactions to achieve the overall reaction and cancel the electrons on each side. This gives the net ionic equation as :
\(
6 \mathrm{Fe}^{2+}(\mathrm{aq})+\mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq})+14 \mathrm{H}^{+}(\mathrm{aq}) \rightarrow 6 \mathrm{Fe}^{3+}(\mathrm{aq})+2 \mathrm{Cr}^{3+}(\mathrm{aq})+7 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \dots(8.58)
\)

Step 7: Verify that the equation contains the same type and number of atoms and the same charges on both sides of the equation. This last check reveals that the equation is fully balanced with respect to number of atoms and the charges.

For the reaction in a basic medium, first balance the atoms as is done in acidic medium. Then for each \(\mathrm{H}^{+}\)ion, add an equal number of \(\mathrm{OH}^{-}\)ions to both sides of the equation. Where \(\mathrm{H}^{+}\)and \(\mathrm{OH}^{-}\)appear on the same side of the equation, combine these to give \(\mathrm{H}_2 \mathrm{O}\).

Example 8.10: Permanganate(VII) ion, \(\mathrm{MnO}_4^{-}\)in basic solution oxidises iodide ion, \(\mathrm{I}^{-}\)to produce molecular iodine \(\left(\mathrm{I}_2\right)\) and manganese (IV) oxide \(\left(\mathrm{MnO}_2\right)\). Write a balanced ionic equation to represent this redox reaction.

Answer: 

Step 1: First we write the skeletal ionic equation, which is
\(
\mathrm{MnO}_4^{-}(\mathrm{aq})+\mathrm{I}^{-}(\mathrm{aq}) \rightarrow \mathrm{MnO}_2(\mathrm{~s})+\mathrm{I}_2(\mathrm{~s})
\)

Step 2: The two half-reactions are:
\(
\begin{array}{ll}
& & & & & &  -1 & & & & 0
\end{array}
\)
\(
\text { Oxidation half: } \mathrm{I}^{-}(\mathrm{aq}) \rightarrow \mathrm{I}_2 \text { (s) }
\)
\(
\begin{array}{ll}
& & & & & & & +7 & & & & & +4
\end{array}
\)
\(
\text { Reduction half: } \mathrm{MnO}_4^{-}(\mathrm{aq}) \rightarrow \mathrm{MnO}_2(\mathrm{~s})
\)

Step 3: To balance the I atoms in the oxidation half reaction, we rewrite it as:
\(
2 \mathrm{I}^{-}(\mathrm{aq}) \rightarrow \mathrm{I}_2(\mathrm{~s})
\)

Step 4: To balance the \(\mathrm{O}\) atoms in the reduction half reaction, we add two water molecules on the right:
\(
\mathrm{MnO}_4^{-}(\mathrm{aq}) \rightarrow \mathrm{MnO}_2(\mathrm{~s})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})
\)
To balance the \(\mathrm{H}\) atoms, we add four \(\mathrm{H}^{+}\) ions on the left:
\(
\mathrm{MnO}_4^{-}(\mathrm{aq})+4 \mathrm{H}^{+}(\mathrm{aq}) \rightarrow \mathrm{MnO}_2(\mathrm{~s})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})
\)
As the reaction takes place in a basic solution, therefore, for four \(\mathrm{H}^{+}\)ions, we add four \(\mathrm{OH}^{-}\)ions to both sides of the equation:
\(
\mathrm{MnO}_4^{-}(\mathrm{aq})+4 \mathrm{H}^{+}(\mathrm{aq})+4 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow\mathrm{MnO}_2(\mathrm{~s})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})+4 \mathrm{OH}^{-}(\mathrm{aq})
\)
Replacing the \(\mathrm{H}^{+}\)and \(\mathrm{OH}\) ions with water, the resultant equation is:
\(
\mathrm{MnO}_4^{-}(\mathrm{aq})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{MnO}_2(\mathrm{~s})+4 \mathrm{OH}^{-}(\mathrm{aq})
\)

Step 5: In this step we balance the charges of the two half-reactions in the manner depicted as:
\(
2 \mathrm{I}^{-}(\mathrm{aq}) \rightarrow \mathrm{I}_2(\mathrm{~s})+2 \mathrm{e}^{-}
\)
\(
\mathrm{MnO}_4^{-}(\mathrm{aq})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})+3 \mathrm{e}^{-} \rightarrow \mathrm{MnO}_2(\mathrm{~s}) +4 \mathrm{OH}^{-}(\mathrm{aq})
\)
Now to equalise the number of electrons, we multiply the oxidation half-reaction by 3 and the reduction half-reaction by 2 .
\(
6 \mathrm{I}^{-}(\mathrm{aq}) \rightarrow 3 \mathrm{I}_2(\mathrm{~s})+6 \mathrm{e}^{-}
\)
\(
2 \mathrm{MnO}_4^{-}(\mathrm{aq})+4 \mathrm{H}_2 \mathrm{O}(\mathrm{l})+6 \mathrm{e}^{-} \rightarrow 2 \mathrm{MnO}_2(\mathrm{~s})+8 \mathrm{OH}^{-}(\mathrm{aq})
\)

Step 6: Add two half-reactions to obtain the net reactions after cancelling electrons on both sides.
\(
6 \mathrm{I}^{-}(\mathrm{aq})+2 \mathrm{MnO}_4^{-}(\mathrm{aq})+4 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow 3 \mathrm{I}_2(\mathrm{~s})+2 \mathrm{MnO}_2(\mathrm{~s})+8 \mathrm{OH}^{-}(\mathrm{aq})
\)

Step 7: A final verification shows that the equation is balanced in respect of the number of atoms and charges on both sides.

Redox Reactions as the Basis for Titrations

In acid-base systems we come across with a titration method for finding out the strength of one solution against the other using a \(\mathrm{pH}\) sensitive indicator. Similarly, in redox systems, the titration method can be adopted to determine the strength of a reductant/oxidant using a redox sensitive indicator. The usage of indicators in redox titration is illustrated below:

(i) In one situation, the reagent itself is intensely coloured, e.g., permanganate ion, \(\mathrm{MnO}_4^{-}\). Here \(\mathrm{MnO}_4^{-}\)acts as the self indicator. The visible end point in this case is achieved after the last of the reductant \(\left(\mathrm{Fe}^{2+}\right.\) or \(\left.\mathrm{C}_2 \mathrm{O}_4{ }^{2-}\right)\) is oxidised and the first lasting tinge of pink colour appears at \(\mathrm{MnO}_4^{-}\) concentration as low as \(10^{-6} \mathrm{~mol} \mathrm{~dm}^{-3}\) \(\left(10^{-6} \mathrm{~mol} \mathrm{~L}^{-1}\right)\). This ensures a minimal ‘overshoot’ in colour beyond the equivalence point, the point where the reductant and the oxidant are equal in terms of their mole stoichiometry.

(ii) If there is no dramatic auto-colour change (as with \(\mathrm{MnO}_4^{-}\)titration), there are indicators which are oxidised immediately after the last bit of the reactant is consumed, producing a dramatic colour change. The best example is afforded by \(\mathrm{Cr}_2 \mathrm{O}_7^{2-}\), which is not a self-indicator, but oxidises the indicator substance diphenylamine just after the equivalence point to produce an intense blue colour, thus signalling the end point.

(iii) There is yet another method which is interesting and quite common. Its use is restricted to those reagents which are able to oxidise \(\mathrm{I}^{-}\) ions, say, for example, Cu(II):
\(
2 \mathrm{Cu}^{2+}(\mathrm{aq})+4 \mathrm{I}^{-}(\mathrm{aq}) \rightarrow \mathrm{Cu}_2 \mathrm{I}_2(\mathrm{~s})+\mathrm{I}_2(\mathrm{aq}) \dots(8.59)
\)
This method relies on the facts that iodine itself gives an intense blue colour with starch and has a very specific reaction with thiosulphate ions \(\left(\mathrm{S}_2 \mathrm{O}_3{ }^{2-}\right)\), which too is a redox reaction:
\(
\mathrm{I}_2(\mathrm{aq})+2 \mathrm{~S}_2 \mathrm{O}_3^{2-}(\mathrm{aq}) \rightarrow 2 \mathrm{I}^{-}(\mathrm{aq})+\mathrm{S}_4 \mathrm{O}_6{ }^{2-}(\mathrm{aq}) \dots(8.60)
\)
\(\mathrm{I}_2\), though insoluble in water, remains in solution containing \(\mathrm{KI}\) as \(\mathrm{KI}_3\).

On addition of starch after the liberation of iodine from the reaction of \(\mathrm{Cu}^{2+}\) ions on iodide ions, an intense blue colour appears. This colour disappears as soon as the iodine is consumed by the thiosulphate ions. Thus, the end-point can easily be tracked and the rest is the stoichiometric calculation only.

Limitations of Concept of Oxidation Number

As you have observed in the above discussion, the concept of redox processes has been evolving with time. This process of evolution is continuing. In fact, in recent past the oxidation process is visualised as a decrease in electron density and reduction process as an increase in electron density around the atom(s) involved in the reaction.