Past JEE Main Entrance Paper
Overview
Relation between degree and radian
The circumference of a circle always bears a constant ratio to its diameter. This constant ratio is a number denoted by \(\pi\) which is taken approximately as \(\frac{22}{7}\) for all practical purposes. The relationship between degree and radian measurements is as follows:
\(
\begin{aligned}
& 2 \text { right angle }=180^{\circ}=\pi \text { radians } \\
& 1 \text { radian }=\frac{180^{\circ}}{\pi}=57^{\circ} 16^{\prime} \text { (approx) } \\
& 1^{\circ}=\frac{\pi}{180} \text { radian }=0.01746 \text { radians (approx) } \\
&
\end{aligned}
\)
Trigonometric functions
Trigonometric ratios are defined for acute angles as the ratio of the sides of a right angled triangle. The extension of trigonometric ratios to any angle in terms of radian measure (real numbers) are called trigonometric functions. The signs of trigonometric functions in different quadrants have been given in the following table:
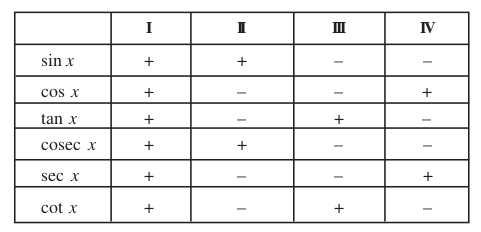
Domain and range of trigonometric functions
\(\begin{array}{|l|l|l|}
\hline \text { Functions } & \text { Domain } & \text { Range } \\
\hline \text { sine } & R & {[-1,1]} \\
\hline \text { cosine } & R & {[-1,1]} \\
\hline \text { tan } & R -\left\{(2 n+1) \frac{\pi}{2}: n \in Z \right\} & R \\
\hline \text { cot } & R -\{n \pi: n \in Z \} & R \\
\hline \text { sec } & R -\left\{(2 n+1) \frac{\pi}{2}: n \in Z \right\} & R -(-1,1) \\
\hline \text { cosec } & R -\{n \pi: n \in Z \} & R -(-1,1) \\
\hline
\end{array}
\)
Sine, cosine and tangent of some angles less than \(90^{\circ}\)
\(
\begin{array}{|l|c|c|c|c|c|c|c|c|}
\hline & 0^{\circ} & 15^{\circ} & 18^{\circ} & 30^{\circ} & 36^{\circ} & 45^{\circ} & 6 0 & 90^{\circ} \\
\hline \text { sine } & 0 & \frac{\sqrt{6}-\sqrt{2}}{4} & \frac{\sqrt{5}-1}{4} & \frac{1}{2} & \frac{\sqrt{10-2 \sqrt{5}}}{4} & \frac{1}{\sqrt{2}} & \frac{\sqrt{3}}{2} & 1 \\
\text { cosine } & 1 & \frac{\sqrt{6}+\sqrt{2}}{4} & \frac{\sqrt{10+2 \sqrt{5}}}{4} & \frac{\sqrt{3}}{2} & \frac{\sqrt{5}+1}{4} & \frac{1}{\sqrt{2}} & \frac{1}{2} & 0 \\
\hline \text { tan } & 0 & 2-\sqrt{3} & \frac{\sqrt{25-10 \sqrt{5}}}{5} & \frac{1}{\sqrt{3}} & \sqrt{5-2 \sqrt{5}} & 1 & \sqrt{3} & \text { defined } \\
\hline
\end{array}
\)
Allied or related angles
The angles \(\frac{n \pi}{2} \pm \theta\) are called allied or related angles and \(\theta \pm n \times 360^{\circ}\) are called coterminal angles. For general reduction, we have the following rules. The value of any trigonometric function for \(\left(\frac{n \pi}{2} \pm \theta\right)\) is numerically equal to
- The value of the same function if \(n\) is an even integer with algebaric sign of the function as per the quadrant in which angles lie.
- Corresponding cofunction of \(\theta\) if \(n\) is an odd integer with algebraic sign of the function for the quadrant in which it lies. Here sine and cosine; tan and cot; sec and cosec are cofunctions of each other.
Functions of negative angles
Let \(\theta\) be any angle. Then
\(
\begin{aligned}
\sin (-\theta) & =-\sin \theta, \cos (-\theta)=\cos \theta \\
\tan (-\theta) & =-\tan \theta, \cot (-\theta)=-\cot \theta \\
\sec (-\theta) & =\sec \theta, \operatorname{cosec}(-\theta)=-\operatorname{cosec} \theta
\end{aligned}
\)
Some formulae regarding compound angles
An angle made up of the sum or differences of two or more angles is called a compound angle. The basic results in this direction are called trigonometric identities as given below:
- \(\sin ( A + B )=\sin A \cos B +\cos A \sin B\)
- \(\sin (A-B)=\sin A \cos B-\cos A \sin B\)
- \(\cos ( A + B )=\cos A \cos B -\sin A \sin B\)
- \(\cos ( A – B )=\cos A \cos B +\sin A \sin B\)
- \(\tan ( A + B )=\frac{\tan A +\tan B }{1-\tan A \tan B }\)
- \(\tan ( A – B )=\frac{\tan A -\tan B }{1+\tan A \tan B }\)
- \(\cot ( A + B )=\frac{\cot A \cot B -1}{\cot A +\cot B }\)
- \(\cot ( A – B )=\frac{\cot A \cot B +1}{\cot B -\cot A }\)
- \(\sin 2 A =2 \sin A \cos A =\frac{2 \tan A }{1+\tan ^2 A }\)
- \(\cos 2 A =\cos ^2 A -\sin ^2 A =1-2 \sin ^2 A =2 \cos ^2 A -1=\frac{1-\tan ^2 A }{1+\tan ^2 A }\)
- \(\tan 2 A =\frac{2 \tan A }{1-\tan ^2 A }\)
- \(\sin 3 A =3 \sin A -4 \sin ^3 A\)
- \(\cos 3 A =4 \cos ^3 A -3 \cos A\)
- \(\tan 3 A =\frac{3 \tan A -\tan ^3 A }{1-3 \tan ^2 A }\)
- \(\cos A +\cos B =2 \cos \frac{ A + B }{2} \cos \frac{ A – B }{2}\)
- \(\cos A -\cos B =2 \sin \frac{ A + B }{2} \sin \frac{ B – A }{2}\)
- \(\sin A +\sin B =2 \sin \frac{ A + B }{2} \cos \frac{ A – B }{2}\)
- \(\sin A -\sin B =2 \cos \frac{ A + B }{2} \sin \frac{ A – B }{2}\)
- \(2 \sin A \cos B =\sin ( A + B )+\sin ( A – B )\)
- \(2 \cos A \sin B =\sin ( A + B )-\sin ( A – B )\)
- \(2 \cos A \cos B =\cos ( A + B )+\cos ( A – B )\)
- \(2 \sin A \sin B =\cos ( A – B )-\cos ( A + B )\)
- \(
\sin \frac{ A }{2}= \pm \sqrt{\frac{1-\cos A }{2}}\left[\begin{array}{l}
+ \text { if } \frac{ A }{2} \text { lies in quadrants I or II } \\
– \text { if } \frac{ A }{2} \text { lies in III or IV quadrants }
\end{array}\right.
\) - \(
\cos \frac{ A }{2}= \pm \sqrt{\frac{1+\cos A }{2}}\left[\begin{array}{l}
+ \text { if } \frac{ A }{2} \text { lies in } I \text { or IV quadrants } \\
– \text { if } \frac{ A }{2} \text { lies in II or } I I \text { quadrants }
\end{array}\right.
\) - \(
\tan \frac{ A }{2}= \pm \sqrt{\frac{1-\cos A }{1+\cos A }} \quad\left[\begin{array}{l}
+ \text { if } \frac{ A }{2} \text { lies in I or III quadrants } \\
– \text { if } \frac{ A }{2} \text { lies in II or IV quadrants }
\end{array}\right.
\)
Trigonometric functions of an angle of \(18^{\circ}\)
Let \(\theta=18^{\circ}\). Then \(2 \theta=90^{\circ}-3 \theta\)
Therefore, \(\quad \sin 2 \theta=\sin \left(90^{\circ}-3 \theta\right)=\cos 3 \theta\)
or \(\sin 2 \theta=4 \cos ^3 \theta-3 \cos \theta\)
Since, \(\quad \cos \theta \neq 0\), we get
\(
2 \sin \theta=4 \cos ^2 \theta-3=1-4 \sin ^2 \theta \text { or } \quad 4 \sin ^2 \theta+2 \sin \theta-1=0 \text {. }
\)
Hence, \(\quad \sin \theta=\frac{-2 \pm \sqrt{4+16}}{8}=\frac{-1 \pm \sqrt{5}}{4}\)
Since, \(\quad \theta=18^{\circ}, \sin \theta>0\), therefore, \(\sin 18^{\circ}=\frac{\sqrt{5}-1}{4}\)
Also, \(\cos 18^{\circ}=\sqrt{1-\sin ^2 18^{\circ}}=\sqrt{1-\frac{6-2 \sqrt{5}}{16}}=\sqrt{\frac{10+2 \sqrt{5}}{4}}\)
Now, we can easily find \(\cos 36^{\circ}\) and \(\sin 36^{\circ}\) as follows:
\(
\begin{aligned}
& \cos 36^{\circ}=1-2 \sin ^2 18^{\circ}=1-\frac{6-2 \sqrt{5}}{8}=\frac{2+2 \sqrt{5}}{8}=\frac{\sqrt{5}+1}{4} \\
& \cos 36^{\circ}=\frac{\sqrt{5}+1}{4}
\end{aligned}
\)
Also, \(\sin 36^{\circ}=\sqrt{1-\cos ^2 36^{\circ}}=\sqrt{1-\frac{6+2 \sqrt{5}}{16}}=\frac{\sqrt{10-2 \sqrt{5}}}{4}\)
Trigonometric equations
Equations involving trigonometric functions of a variables are called trigonometric equations. Equations are called identities, if they are satisfied by all values of the unknown angles for which the functions are defined. The solutions of a trigonometric equations for which \(0 \leq \theta<2 \pi\) are called principal solutions. The expression involving integer \(n\) which gives all solutions of a trigonometric equation is called the general solution.
General Solution of Trigonometric Equations
- If \(\sin \theta=\sin \alpha\) for some angle \(\alpha\), then \(\theta=n \pi+(-1)^n \alpha\) for \(n \in Z\), gives general solution of the given equation
- If \(\cos \theta=\cos \alpha\) for some angle \(\alpha\), then \(\theta=2 n \pi \pm \alpha, n \in Z\), gives general solution of the given equation
- If \(\tan \theta=\tan \alpha\) or \(\cot \theta=\cot \alpha\), then \(\theta=n \pi+\alpha, n \in Z\), gives general solution for both equations
- The general value of \(\theta\) satisfying any of the equations \(\sin ^2 \theta=\sin ^2 \alpha, \cos ^2 \theta=\) \(\cos ^2 \alpha\) and \(\tan ^2 \theta=\tan ^2 \alpha\) is given by \(\theta=n \pi \pm \alpha\)
- The general value of \(\theta\) satisfying equations \(\sin \theta=\sin \alpha\) and \(\cos \theta=\cos \alpha\) simultaneously is given by \(\theta=2 n \pi+\alpha, n \in Z\).
- To find the solution of an equation of the form \(a \cos \theta+b \sin \theta=c\), we put \(a=r \cos \alpha\) and \(b=r \sin \alpha\), so that \(r^2=a^2+b^2\) and \(\tan \alpha=\frac{b}{a}\).
Thus we find \(a \cos \theta+b \sin \theta=c\) changed into the form \(r(\cos \theta \cos \alpha+\sin \theta \sin \alpha)=c\)
or \(r \cos (\theta-\alpha)=c\) and hence \(\cos (\theta-\alpha)=\frac{c}{r}\). This gives the solution of the given equation.
Maximum and Minimum values of the expression \(A \cos \theta+ B \sin \theta\) are \(\sqrt{ A ^2+ B ^2}\) and \(-\sqrt{ A ^2+ B ^2}\) respectively, where \(A\) and \(B\) are constants.
Quiz Summary
0 of 158 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 158 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 158
1. Question
For any \(\theta \in(\pi / 4, \pi / 2)\), the expression \(3(\sin \theta-\cos \theta)^{4}+6(\sin \theta+\) \(\cos \theta)^{2}+4 \sin ^{6} \theta\) equals [Main Jan. 9, 2019 (I)]
Hint
(a) \(3(\sin \theta-\cos \theta)^{4}+6(\sin \theta+\cos \theta)^{2}+4 \sin ^{6} \theta\)
\(
\begin{aligned}
&=3(1-2 \sin \theta \cos \theta)^{2}+6(1+2 \sin \theta \cos \theta)+4 \sin ^{6} \theta \\
&=3\left(1+4 \sin ^{2} \theta \cos ^{2} \theta-4 \sin \theta \cos \theta\right)+6 -12 \sin \theta \cos \theta+4 \sin ^{6} \theta\\
&=9+12 \sin ^{2} \theta \cos ^{2} \theta+4 \sin ^{6} \theta \\
&=9+12 \cos ^{2} \theta\left(1-\cos ^{2} \theta\right)+4\left(1-\cos ^{2} \theta\right)^{3} \\
&=9+12 \cos ^{2} \theta-12 \cos ^{4} \theta+4\left(1-\cos ^{6} \theta-3 \cos ^{2} \theta+3 \cos ^{4} \theta\right) \\
&=9+4-4 \cos ^{6} \theta \\
&=13-4 \cos ^{6} \theta
\end{aligned}
\) -
Question 2 of 158
2. Question
Let \(f_{k}(x)=\frac{1}{k}\left(\sin ^{k} x+\cos ^{k} x\right)\) where \(x \in R \quad\) and \(k \geq 1\). Then \(f_{4}(x)-f_{6}(x)\) equals
[Main 2014]Hint
(b) Let \(f_{k}(x)=\frac{1}{k}\left(\sin ^{k} x+\cos ^{k} x\right)\)
Consider \(f_{4}(x)-f_{6}(x)=\frac{1}{4}\left(\sin ^{4} x+\cos ^{4} x\right)\)
\(
\begin{aligned}
&-\frac{1}{6}\left(\sin ^{6} x+\cos ^{6} x\right) \\
&=\frac{1}{4}\left[1-2 \sin ^{2} x \cos ^{2} x\right]-\frac{1}{6}\left[1-3 \sin ^{2} x \cos ^{2} x\right] \\
&=\frac{1}{4}-\frac{1}{6}=\frac{1}{12}
\end{aligned}
\) -
Question 3 of 158
3. Question
If \(2 \cos \theta+\sin \theta=1\left(\theta \neq \frac{\pi}{2}\right)\), then \(7 \cos \mathrm{\theta}+6 \sin \mathrm{\theta}\) is equal to: [Main Online April 11, 2014]
Hint
(d) Given \(2 \cos \theta+\sin \theta=1\)
Squaring both sides, we get
\(
\begin{aligned}
&(2 \cos \theta+\sin \theta)^{2}=1^{2} \\
&\Rightarrow 4 \cos ^{2} \theta+\sin ^{2} \theta+4 \sin \theta \cos \theta=1 \\
&\Rightarrow 3 \cos ^{2} \theta+\left(\cos ^{2} \theta+\sin ^{2} \theta\right)+4 \sin \theta \cos \theta=1
\end{aligned}
\)
\(\begin{aligned}
&\Rightarrow 3 \cos ^{2} \theta+4 \sin \theta \cos \theta=0\\
&\Rightarrow 3 \cos ^{2} \theta+4 \sin \theta \cos \theta=0\\
&\Rightarrow \cos \theta(3 \cos \theta+4 \sin \theta)=0\\
&\Rightarrow 3 \cos \theta+4 \sin \theta=0 \Rightarrow 3 \cos \theta=-4 \sin \theta\\
&\Rightarrow \frac{-3}{4}=\tan \theta=\sqrt{\sec ^{2} \theta-1}=\frac{-3}{4}\left(\because \tan \theta=\sqrt{\sec ^{2} \theta-1}\right)\\
&\Rightarrow \sec ^{2} \theta-1=\left(\frac{-3}{4}\right)^{2}=\frac{9}{16}\\
&\Rightarrow \sec ^{2} \theta=\frac{9}{16}+1=\frac{25}{16} \Rightarrow \sec \theta=\frac{5}{4}\\
&\text { or } \cos \theta=\frac{4}{5}\\
&\sin ^{2} \theta+\frac{16}{25}=1 \Rightarrow \sin ^{2} \theta=1-\frac{16}{25}=\frac{9}{25}\\
&\sin \theta=\pm \frac{3}{5}\\
&=7 \times \frac{4}{5}+6 \times \frac{3}{5}=\frac{28}{5}+\frac{18}{5}=\frac{46}{5}
\end{aligned}\) -
Question 4 of 158
4. Question
The expression \(\frac{\tan \mathrm{A}}{1-\cot \mathrm{A}}+\frac{\cot \mathrm{A}}{1-\tan \mathrm{A}}\) can be written as: [Main 2013]
Hint
(b) Given expression can be written as
\(
\begin{aligned}
\frac{\sin A}{\cos A} \times \frac{\sin A}{\sin A-\cos A}+\frac{\cos A}{\sin A} \times \frac{\cos A}{\cos A-\sin A} \\
&\left(\because \tan A=\frac{\sin A}{\cos A} \text { and } \cot A=\frac{\cos A}{\sin A}\right)
\end{aligned}
\)
\(\begin{aligned}
&=\frac{1}{\sin A-\cos A}\left\{\frac{\sin ^{3} A-\cos ^{3} A}{\cos A \sin A}\right\} \\
&\because a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right) \\
&=\frac{\sin ^{2} A+\sin A \cos A+\cos ^{2} A}{\sin A \cos A} \\
&=1+\sec \mathrm{A} \operatorname{cosec} \mathrm{A}
\end{aligned}\) -
Question 5 of 158
5. Question
Given both \(\theta\) and \(\varphi\) are acute angles and \(\sin \theta=\frac{1}{2}, \cos \varphi=\frac{1}{3}\), then the value of \(\theta+\varphi\) belongs to \([2004 \mathrm{~S}]\)
Hint
(b) Given : \(\sin \theta=1 / 2\) and \(\theta\) is acute angle
\(
\therefore \theta=\pi / 6
\)
Also given, \(\cos \phi=\frac{1}{2}\) and \(\varphi\) is acute angle.
\(
\begin{aligned}
&\therefore 0<\frac{1}{3}<\frac{1}{2} \\
&\Rightarrow \cos \pi / 2<\cos \phi<\cos \pi / 3 \text { or } \pi / 3<\phi<\pi / 2 \\
&\therefore \frac{\pi}{3}+\frac{\pi}{6}<\theta+\phi<\frac{\pi}{2}+\frac{\pi}{6} \text { or } \frac{\pi}{2}<\theta+\phi<\frac{2 \pi}{3} \\
&\Rightarrow \theta+\phi \in\left(\frac{\pi}{2}, \frac{2 \pi}{3}\right)
\end{aligned}
\) -
Question 6 of 158
6. Question
If \(\omega\) is an imaginary cube root of unity then the value of \(\sin \left\{\left(\omega^{10}+\omega^{23}\right) \pi-\frac{\pi}{4}\right\}\) is [1994]
Hint
\(\begin{aligned}
&\text { (c) } \sin \left\{\left(\omega^{10}+\omega^{23}\right) \pi-\frac{\pi}{4}\right\}=\sin \left\{\left(\omega+\omega^{2}\right) \pi-\frac{\pi}{4}\right\} \\
&=\sin \left(-\pi-\frac{\pi}{4}\right)=-\sin \left(\pi+\frac{\pi}{4}\right)=\sin \pi / 4=1 / \sqrt{2}
\end{aligned}\) -
Question 7 of 158
7. Question
If \(\tan \theta=-\frac{4}{3}\), then \(\sin \theta\) is [1979]
Hint
(b) \(\tan \theta=\frac{-4}{3} \Rightarrow \theta \in\) II quad or IV quad.
\(
\begin{aligned}
&\Rightarrow 0<\sin \theta<1 \text { or }-1<\sin \theta<0 \\
&\Rightarrow \sin \theta=\frac{4}{5} \text { or }-\frac{4}{5}
\end{aligned}
\) -
Question 8 of 158
8. Question
Which of the following number(s) is/are rational? [1998 – 2 Marks]
Hint
(c) We know, \(\sin 15^{\circ}=\frac{\sqrt{3}-1}{2 \sqrt{2}}\) (irrational) \(\cos 15^{\circ}=\frac{\sqrt{3}+1}{2 \sqrt{2}}(\) irrational \()\)
\(\begin{aligned}
&\sin 15^{\circ} \cdot \cos 15^{\circ}=\frac{1}{2}\left(2 \sin 15^{\circ} \cos 15^{\circ}\right) \\
&=\frac{1}{2} \sin 30^{\circ}=\frac{1}{4}(\text { rational }) \\
&\sin 15^{\circ} \cos 75^{\circ}=\sin 15^{\circ} \cos \left(90-15^{\circ}\right) \\
&=\sin 15^{\circ} \sin 15^{\circ}=\sin ^{2} 15^{\circ}=\frac{1}{2}\left(1+\cos 30^{\circ}\right) \\
&=\frac{1}{2}\left(1-\frac{\sqrt{3}}{2}\right) \text { (irrational) }
\end{aligned}\) -
Question 9 of 158
9. Question
In this questions there are entries in columns 1 and 2. Each entry in column 1 is related to exactly one entry in column 2. Write the correct letter from column 2 against the entry number in column 1 in your answer book. \(\frac{\sin 3 \alpha}{\cos 2 \alpha}\) is [1992 – 2 Marks]
Column I Column II
(A) positive (p) \(\left(\frac{13 \pi}{48}, \frac{14 \pi}{48}\right)\)
(B) negative (q) \(\left(\frac{14 \pi}{48}, \frac{18 \pi}{48}\right)\)
(r) \(\left(\frac{18 \pi}{48}, \frac{23 \pi}{48}\right)\)
(s) \(\left(0, \frac{\pi}{2}\right)\)Hint
(a) \((\mathrm{A} \rightarrow \mathrm{r} ; \mathrm{B} \rightarrow \mathbf{p})\)
(p) If \(\frac{13 \pi}{48}<\alpha<\frac{14 \pi}{48}\) then \(\frac{13 \pi}{16}<3 \alpha<\frac{14 \pi}{16}\)
and \(\frac{13 \pi}{24}<2 \alpha<\frac{14 \pi}{24}\)
\(\Rightarrow 3 \alpha \in\) II quad and \(2 \alpha \in\) II quad \(\Rightarrow \sin 3 \alpha=+\) ve
\(\cos 2 \alpha=-\mathrm{ve} \therefore \frac{\sin 3 \alpha}{\cos 2 \alpha}=-v e\)
\(\therefore\) (B) corresponds to \((\mathrm{p})\).
(q) If \(\alpha \in\left(\frac{14 \pi}{48}, \frac{18 \pi}{48}\right)\) then \(\frac{14 \pi}{16}<3 \alpha<\frac{18 \pi}{16}\)
and \(\frac{14 \pi}{24}<2 \alpha<\frac{18 \pi}{24}\)
\(\Rightarrow 3 \alpha \in\) II or III quad and \(2 \alpha \in\) II quad
\(\Rightarrow\) Nothing can be said about the sign of \(\frac{\sin 3 \alpha}{\cos 2 \alpha}\) over this interval.
(r) If \(\alpha \in\left(\frac{18 \pi}{48}, \frac{23 \pi}{48}\right)\) then \(\frac{18 \pi}{16}<3 \alpha<\frac{23 \pi}{16}\)
and \(\frac{18 \pi}{24}<2 \alpha<\frac{23 \pi}{24}\)
\(\Rightarrow 3 \alpha \in\) III quad and \(2 \alpha \in\) II quad
\(\Rightarrow \quad \sin 3 \alpha=-\mathrm{ve}, \cos 2 \mathrm{a}=-\mathrm{ve}, \quad \therefore \frac{\sin 3 \alpha}{\cos 2 \alpha}=+v e\)
\(\therefore\) (A) corresponds to (r)
(s) If \(\alpha \in(0, \pi / 2)\), then \(0<3 \alpha<3 \pi / 2\) and \(0<2 \alpha<\pi\)
\(\Rightarrow\) Nothing can be said about the sign of \(\frac{\sin 3 \alpha}{\cos 2 \alpha}\) over the given interval. -
Question 10 of 158
10. Question
Let \(\mathrm{O}\) be the origin, and \(\overrightarrow{\mathrm{OX}}, \overrightarrow{\mathrm{OY}}, \overrightarrow{\mathrm{OZ}}\) be three unit vectors in the directions of the sides \(\overrightarrow{\mathrm{QR}}, \overrightarrow{\mathrm{RP}}, \overrightarrow{\mathrm{PQ}}\) respectively, of a triangle \(\mathrm{PQR}\). [Adv. 2017]
\(|\overrightarrow{\mathrm{OX}} \times \overrightarrow{\mathrm{OY}}|=\)
Hint
(a) \(\overrightarrow{\mathrm{OX}}, \overrightarrow{\mathrm{OY}}, \overrightarrow{\mathrm{OZ}}\) are unit vectors in the directions of sides \(\overrightarrow{\mathrm{OR}}, \overrightarrow{\mathrm{RP}}\) and \(\overrightarrow{\mathrm{PQ}}\) respectively,
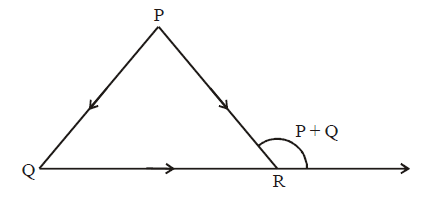
\(\begin{aligned}
&\therefore \quad \overrightarrow{\mathrm{OX}}=\frac{\overrightarrow{\mathrm{QR}}}{|\overrightarrow{\mathrm{QR}}|}, \overrightarrow{\mathrm{OY}}=\frac{\overrightarrow{\mathrm{RP}}}{|\overrightarrow{\mathrm{RP}}|}, \overrightarrow{\mathrm{OZ}}=\frac{\overrightarrow{\mathrm{PQ}}}{|\overrightarrow{\mathrm{PQ}}|} \\
&\therefore \quad|\overrightarrow{\mathrm{OX}} \times \overrightarrow{\mathrm{OY}}|=\frac{|\overrightarrow{\mathrm{OR}} \times \overrightarrow{\mathrm{RP}}|}{|\overrightarrow{\mathrm{QR}}||\overrightarrow{\mathrm{RP}}|}=\frac{|\overrightarrow{\mathrm{QR}}||\overrightarrow{\mathrm{RP}}| \sin (\mathrm{P}+\mathrm{Q})}{|\overrightarrow{\mathrm{QR}}||\overrightarrow{\mathrm{RP}}|} \\
&=\sin (\mathrm{P}+\mathrm{Q})
\end{aligned}\) -
Question 11 of 158
11. Question
Let \(\mathrm{O}\) be the origin, and \(\overrightarrow{\mathrm{OX}}, \overrightarrow{\mathrm{OY}}, \overrightarrow{\mathrm{OZ}}\) be three unit vectors in the directions of the sides \(\overrightarrow{\mathrm{QR}}, \overrightarrow{\mathrm{RP}}, \overrightarrow{\mathrm{PQ}}\) respectively, of a triangle \(\mathrm{PQR}\). [Adv. 2017]
If the triangle \(\mathrm{PQR}\) varies, then the minimum value of \(\cos (\mathrm{P}+\mathrm{Q})+\) \(\cos (\mathrm{Q}+\mathrm{R})+\cos (\mathrm{R}+\mathrm{P})\) is
Hint
(b) \(\cos (\mathrm{P}+\mathrm{Q})+\cos (\mathrm{Q}+\mathrm{R})+\cos (\mathrm{R}+\mathrm{P})\)
\(=\cos (180-\mathrm{R})+\cos (180-\mathrm{P})+\cos (180-\mathrm{Q})\)
\(=-[\cos P+\cos Q+\cos R]\)
In any \(\mathrm{PQR}, \cos P+\cos Q+\cos R \leq \frac{3}{2}\)
\(\Rightarrow \quad-(\cos P+\cos Q+\cos R) \geq-\frac{3}{2}\)
\(\therefore \quad\) Required minimum value \(=-\frac{3}{2}\) -
Question 12 of 158
12. Question
Find the range of values of \(t\) for which \(2 \sin t=\frac{1-2 x+5 x^{2}}{3 x^{2}-2 x-1}, t \in\) \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\). [2005 – 2 Marks]
Hint
(a) \(\text { Given : } 2 \sin t=\frac{1-2 x+5 x^{2}}{3 x^{2}-2 x-1}, \quad t \in[-\pi / 2, \pi / 2]\)
\(\Rightarrow(6 \sin t-5) x^{2}+2(1-2 \sin t) x-(1+2 \sin t)=0\)
The given equation will hold, if \(x\) be some real number, and hence, \(D \geq 0\)
\(
\begin{aligned}
&\Rightarrow 4(1-2 \sin t)^{2}+4(6 \sin t-5)(1+2 \sin t) \geq 0 \\
&\Rightarrow 16 \sin ^{2} t-8 \sin t-4 \geq 0 \Rightarrow\left(4 \sin ^{2} t-2 \sin t-1\right) \geq 0 \\
&\Rightarrow 4\left(\sin t-\frac{\sqrt{5}+1}{4}\right)\left(\sin t+\frac{\sqrt{5}-1}{4}\right) \geq 0 \\
&\Rightarrow \sin t \leq-\left(\frac{\sqrt{5}-1}{4}\right) \text { or } \sin t \geq \frac{\sqrt{5}+1}{4} \\
&\Rightarrow \sin t \leq \sin (-\pi / 10) \text { or } \quad \sin t \geq \sin (3 \pi / 10) \\
&\Rightarrow t \leq-\pi / 10 \quad \text { or } \quad t \geq 3 \pi / 10 \\
&\text { [Note that } \sin x \text { is an increasing function from }-\pi / 2 \text { to } \pi / 2] \\
&\therefore \quad \text { range of } t \text { is }[-\pi / 2,-\pi / 10] \cup[3 \pi / 10, \pi / 2]
\end{aligned}
\) -
Question 13 of 158
13. Question
If \(L=\sin ^{2}\left(\frac{\pi}{16}\right)-\sin ^{2}\left(\frac{\pi}{8}\right)\) and \(M=\cos ^{2}\left(\frac{\pi}{16}\right)-\sin ^{2}\left(\frac{\pi}{8}\right)\), then \(:\) [Main Sep. 05, 2020 (II)]
Hint
(d) \(\mathrm{L}+\mathrm{M}=1-2 \sin ^{2} \frac{\pi}{8}=\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}}\dots….(i)\)
and \(\mathrm{L}-\mathrm{M}=-\cos \frac{\pi}{8} \dots….(ii)\)
From equations (i) and (ii),
\(
\begin{aligned}
&L=\frac{1}{2}\left(\frac{1}{\sqrt{2}}-\cos \frac{\pi}{8}\right)=\frac{1}{2 \sqrt{2}}-\frac{1}{2} \cos \frac{\pi}{8} \text { and } \\
&M=\frac{1}{2}\left(\frac{1}{\sqrt{2}}+\cos \frac{\pi}{8}\right)=\frac{1}{2 \sqrt{2}}+\frac{1}{2} \cos \frac{\pi}{8}
\end{aligned}
\) -
Question 14 of 158
14. Question
The set of all possible values of \(\theta\) in the interval \((0, \pi)\) for which the points \((1,2)\) and \((\sin \theta, \cos \theta)\) lie on the same side of the line \(x+y=\) 1 is: [Main Sep. 02, 2020 (II)]
Hint
(a) Let \(f(x, y)=x+y-1\)
Given \((1,2)\) and \((\sin \theta, \cos \theta)\) are lies on same side.
\(
\begin{aligned}
&\therefore f(1,2) \cdot f(\sin \theta, \cos \theta)>0 \\
&\Rightarrow 2[\sin \theta+\cos \theta-1]>0 \\
&\Rightarrow \sin \theta+\cos \theta>1 \Rightarrow \sin \left(\theta+\frac{\pi}{4}\right)>\frac{1}{\sqrt{2}} \\
&\Rightarrow \theta+\frac{\pi}{4} \in\left(\frac{\pi}{4}, \frac{3 \pi}{4}\right) \Rightarrow \theta \in\left(0, \frac{\pi}{2}\right)
\end{aligned}
\) -
Question 15 of 158
15. Question
The value of \(\cos ^{3}\left(\frac{\pi}{8}\right) \cdot \cos \left(\frac{3 \pi}{8}\right)+\sin ^{3}\left(\frac{\pi}{8}\right) \cdot \sin \left(\frac{3 \pi}{8}\right)\) is [Main Jan. 9, 2020 (I)]
Hint
\(
\begin{aligned}
&\text { (b) } \cos ^{3} \frac{\pi}{8}\left[4 \cos ^{3} \frac{\pi}{8}-3 \cos \frac{\pi}{8}\right]\\
&+\sin ^{3} \frac{\pi}{8}\left[3 \sin \frac{\pi}{8}-4 \sin ^{3} \frac{\pi}{8}\right]\\
&=4 \cos ^{6} \frac{\pi}{8}-4 \sin ^{6} \frac{\pi}{8}-3 \cos ^{4} \frac{\pi}{8}+3 \sin ^{4} \frac{\pi}{8}\\
&=4\left[\left(\cos ^{2} \frac{\pi}{8}-\sin ^{2} \frac{\pi}{8}\right)\right]\\
&\left[\left(\sin ^{4} \frac{\pi}{8}+\cos ^{4} \frac{\pi}{8}+\sin ^{2} \frac{\pi}{8} \cos ^{2} \frac{\pi}{8}\right)\right]\\
&-3\left[\left(\cos ^{2} \frac{\pi}{8}-\sin ^{2} \frac{\pi}{8}\right)\left(\cos ^{2} \frac{\pi}{8}+\sin ^{2} \frac{\pi}{8}\right)\right]\\
&=\cos \frac{\pi}{4}\left[4\left(1-\sin ^{2} \frac{\pi}{8} \cos ^{2} \frac{\pi}{8}\right)-3\right]\\
&=\frac{1}{\sqrt{2}}\left[1-\frac{1}{2}\right]=\frac{1}{2 \sqrt{2}}
\end{aligned}
\) -
Question 16 of 158
16. Question
The angle of elevation of the top of a vertical tower standing on a horizontal plane is observed to be \(45^{\circ}\) from a point \(\mathrm{A}\) on the plane. Let \(B\) be the point \(30 \mathrm{~m}\) vertically above the point \(A\). If the angle of elevation of the top of the tower from \(\mathrm{B}\) be \(30^{\circ}\), then the distance (in \(\mathrm{m})\) of the foot of the tower from the point \(A\) is: [Main April 12, 2019(II)]
Hint
(a) Let the height of the tower be \(h\) and the distance of the foot of the tower from the point \(A\) is \(d\).
By the diagram,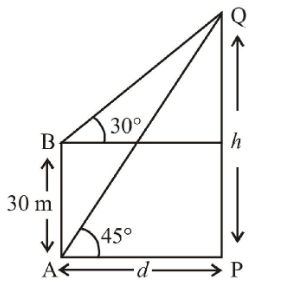
\(
\begin{gathered}
\tan 45^{\circ}=\frac{h}{d}=1 \\
h=d \dots ….(i)
\end{gathered}
\)
\(\tan 30^{\circ}=\frac{h-30}{d}\)
\(
\sqrt{3}(h-30)=d \dots ….(ii)
\)
Put the value of \(h\) from (i) to (ii),
\(
\begin{aligned}
&\sqrt{3} d=d+30 \sqrt{3} \\
&d=\frac{30 \sqrt{3}}{\sqrt{3-1}}=15 \sqrt{3}(\sqrt{3}+1)=15(3+\sqrt{3})
\end{aligned}
\) -
Question 17 of 158
17. Question
The value of \(\cos ^{2} 10^{\circ}-\cos 10^{\circ} \cos 50^{\circ}+\cos ^{2} 50^{\circ}\) is: [Main April 9, 2019 (II)]
Hint
(b) \(\cos ^{2} 10^{\circ}-\cos 10^{\circ} \cos 50^{\circ}+\cos ^{2} 50^{\circ}\)
\(
\begin{aligned}
&=\left(\frac{1+\cos 20^{\circ}}{2}\right)+\left(\frac{1+\cos 100^{\circ}}{2}\right)-\frac{1}{2}\left(2 \cos 10^{\circ} \cos 50^{\circ}\right) \\
&=1+\frac{1}{2}\left(\cos 20^{\circ}+\cos 100^{\circ}\right)-\frac{1}{2}\left[\cos 60^{\circ}+\cos 40^{\circ}\right] \\
&=\left(1-\frac{1}{4}\right)+\frac{1}{2}\left[\cos 20^{\circ}+\cos 100^{\circ}-\cos 40^{\circ}\right] \\
&=\frac{3}{4}+\frac{1}{2}\left[2 \cos 60^{\circ} \times \cos 40^{\circ}-\cos 40^{\circ}\right] \\
&=\frac{3}{4}
\end{aligned}
\) -
Question 18 of 158
18. Question
If \(\cos (\alpha+\beta)=\frac{3}{5}, \sin (\alpha-\beta)=\frac{5}{13}\) and \(0<\alpha, \beta<\frac{\pi}{4}\), then \(\tan (2 \alpha)\) is equal to : [Main April 8, 2019(I)]
Hint
(b) \(\alpha+\beta\) and \(\alpha-\beta\) both are acute angles.
\(\cos (\alpha+\beta)=\frac{3}{5}\), then \(\sin (\alpha+\beta)=\sqrt{1-\left(\frac{3}{5}\right)^{2}}=\frac{4}{5}\)
\(\tan (\alpha+\beta)=\frac{4}{3}\)
And \(\sin (\alpha-\beta)=\frac{5}{13}\), then
\(\cos (\alpha-\beta)=\sqrt{1-\left(\frac{5}{13}\right)^{2}}=\frac{12}{13}\)
\(\Rightarrow \tan (\alpha-\beta)=\frac{5}{12}\)
Now, \(\tan 2 \alpha=\tan ((\alpha+\beta)+(\alpha-\beta))\)
\(=\frac{\tan (\alpha+\beta)+\tan (\alpha-\beta)}{1-\tan (\alpha+\beta) \cdot \tan (\alpha-\beta)}=\frac{\frac{4}{3}+\frac{5}{12}}{1-\frac{4}{3} \cdot \frac{5}{12}}=\frac{63}{16}\) -
Question 19 of 158
19. Question
If \(\sin ^{4} \alpha+4 \cos ^{4} \beta+2=4 \sqrt{2} \sin \alpha \cos \beta ; \alpha, \beta \in[0, \pi]\), then \(\cos (\alpha+\beta)\) \(-\cos (\alpha-\beta)\) is equal to: [Main Jan. 12, 2019 (II)]
Hint
(d)
\(
\text { A.M. } \geq \text { G.M. }
\)
\(\frac{\sin ^{4} \alpha+4 \cos ^{4} \beta+1+1}{4} \geq\left(\sin ^{4} \alpha \cdot 4 \cdot \cos ^{4} \beta .1 .1\right) \frac{1}{4}\)
\(
\begin{aligned}
&\Rightarrow \text { A.M. }=\text { G.M. } \Rightarrow \sin ^{4} \alpha=1=4 \cos ^{4} \beta \\
&\sin \alpha=1, \cos \beta=\pm \frac{1}{\sqrt{2}} \\
&\sin \beta=\frac{1}{\sqrt{2}} \operatorname{as} \beta \in[0, \pi] \\
&\cos (\alpha+\beta)-\cos (\alpha-\beta)=-2 \sin \alpha \sin \beta \\
&=-\sqrt{2}
\end{aligned}
\) -
Question 20 of 158
20. Question
Let \(f_{k}(x)=\frac{1}{k}\left(\sin ^{k} x+\cos ^{k} x\right)\) for \(\mathrm{k}=1,2,3, \ldots\) Then for all \(\mathrm{x} \in \mathrm{R}\), the value of \(f_{4}(x)-f_{6}(x)\) is equal to: [Main Jan. 11, 2019(I)]
Hint
\(
\begin{aligned}
&\text { (a) } f_{k}(x)=\frac{1}{k}\left(\sin ^{k} x+\cos ^{k} x\right)\\
&f_{4}(x)=\frac{1}{4}\left[\sin ^{4} x+\cos ^{4} x\right]\\
&=\frac{1}{4}\left[\left(\sin ^{2} x+\cos ^{2} x\right)^{2}-\frac{(\sin 2 x)^{2}}{2}\right]\\
&=\frac{1}{4}\left[1-\frac{(\sin 2 x)^{2}}{2}\right]
\end{aligned}
\)
\(
\begin{aligned}
& f_{6}(x)=\frac{1}{6}\left[\sin ^{6} x+\cos ^{6} x\right] \\
=& \frac{1}{6}\left[\left(\sin ^{2} x+\left(\cos ^{2} x\right)-\frac{3}{4}\left(\sin ^{2} x\right)^{2}\right]\right.\\
=& \frac{1}{6}\left[1-\frac{3}{4}(\sin 2 x)^{2}\right] \\
& \text { Now } f_{4}(x)-f_{(6)}(x)=\frac{1}{4}-\frac{1}{6}-\frac{(\sin 2 x)^{2}}{8}+\frac{1}{8}(\sin 2 x)^{2} \\
=& \frac{1}{12}
\end{aligned}
\) -
Question 21 of 158
21. Question
If \(5\left(\tan ^{2} x-\cos ^{2} x\right)=2 \cos 2 x+9\), then the value of \(\cos 4 x\) is: [Main 2017]
Hint
(a) We have
\(
\begin{aligned}
&5 \tan ^{2} \mathrm{x}-5 \cos ^{2} \mathrm{x}=2\left(2 \cos ^{2} \mathrm{x}-1\right)+9 \\
&\quad \Rightarrow 5 \tan ^{2} \mathrm{x}-5 \cos ^{2} \mathrm{x}=4 \cos ^{2} \mathrm{x}-2+9 \\
&\quad \Rightarrow 5 \tan ^{2} \mathrm{x}=9 \cos ^{2} \mathrm{x}+7 \\
&\quad \Rightarrow 5\left(\sec ^{2} \mathrm{x}-1\right)=9 \cos ^{2} \mathrm{x}+7 \\
&\text { Let } \cos ^{2} \mathrm{x}=\mathrm{t} \\
&\quad \Rightarrow \frac{5}{\mathrm{t}}-9 \mathrm{t}-12=0 \\
&\Rightarrow 9 \mathrm{t}^{2}+12 \mathrm{t}-5=0 \\
&\quad \Rightarrow 9 \mathrm{t}^{2}+15 \mathrm{t}-3 \mathrm{t}-5=0 \\
&\Rightarrow(3 \mathrm{t}-1)(3 \mathrm{t}+5)=0 \\
&\Rightarrow \mathrm{t}=\frac{1}{3} \text { as } \mathrm{t} \neq-\frac{5}{3} \\
&\cos 2 \mathrm{x}=2 \cos ^{2} \mathrm{x}-1=2\left(\frac{1}{3}\right)-1=-\frac{1}{3} \\
&\cos 4 \mathrm{x}=2 \cos ^{2} 2 \mathrm{x}-1=2\left(-\frac{1}{3}\right)^{2}-1=-\frac{7}{9}
\end{aligned}
\) -
Question 22 of 158
22. Question
If \(\mathrm{m}\) and \(\mathrm{M}\) are the minimum and the maximum values of \(4+\frac{1}{2} \sin ^{2} 2 x-2 \cos ^{4} x, x \in R\), then \(M-m\) is equal to : [Main Online April 9, 2016]
Hint
(b) \(4+\frac{1}{2} \sin ^{2} 2 x-2 \cos ^{4} x\)
\(
=4+2\left(1-\cos ^{2} x\right) \cos ^{2} x-2 \cos ^{4} x
\)
\(
\begin{aligned}
=-4 &\left\{\cos ^{4} x-\frac{\cos ^{2} x}{2}-1+\frac{1}{16}-\frac{1}{16}\right\} \\
=-4 &\left\{\left(\cos ^{2} x-\frac{1}{4}\right)^{2}-\frac{17}{16}\right\} \\
0 \leq \cos ^{2} x & \leq 1 \\
-\frac{1}{4} & \leq \cos ^{2} x-\frac{1}{4} \leq \frac{3}{4} \\
0 & \leq\left(\cos ^{2} x-\frac{1}{4}\right)^{2} \leq \frac{9}{16} \\
-\frac{17}{16} & \leq\left(\cos ^{2} x-\frac{1}{4}\right)^{2}-\frac{17}{16} \leq \frac{9}{16}-\frac{17}{16} \\
\frac{17}{4} & \geq-4\left\{\left(\cos ^{2} x-\frac{1}{4}\right)^{2}-\frac{17}{16}\right\} \geq \frac{1}{2} \\
M &=\frac{17}{4} \\
m &=\frac{1}{2} \\
M-m &=\frac{17}{4}-\frac{2}{4}=\frac{15}{4}
\end{aligned}
\) -
Question 23 of 158
23. Question
The value of \(\sum_{k=1}^{13} \frac{1}{\sin \left(\frac{\pi}{4}+\frac{(k-1) \pi}{6}\right) \sin \left(\frac{\pi}{4}+\frac{k \pi}{6}\right)}\) is equal to [Adv. 2016]
Hint
(c)
\(
\begin{aligned}
& 2 \sum_{k=1}^{13} \frac{\sin \left(\frac{\pi}{6}\right)}{\sin \left(\frac{\pi}{4}+\frac{(k-1) \pi}{6}\right) \sin \left(\frac{\pi}{4}+\frac{k \pi}{6}\right)} \\
& =2 \sum \frac{\sin \left\{\left(\frac{\pi}{4}+\frac{k \pi}{6}\right)-\left(\frac{\pi}{4}+\frac{(k-1) \pi}{6}\right)\right\}}{\sin \left(\frac{\pi}{4}+\frac{(k-1) \pi}{6}\right) \cdots \in\left(\frac{\pi}{4}+\frac{k \pi}{6}\right)} \\
& =2 \sum_{k=1}^{13}\left\{\cot \left(\frac{\pi}{4}+\frac{(k-1) \pi}{6}\right)-\cot \left(\frac{\pi}{4}+\frac{k \pi}{6}\right)\right\} \\
& =2\left[\cot \left(\frac{\pi}{4}\right)-\cot \left(\frac{\pi}{4}+\frac{13 \pi}{6}\right)\right] \\
& =2[1-(2-\sqrt{3})] \\
& =2(\sqrt{3}-1)
\end{aligned}
\) -
Question 24 of 158
24. Question
If \(\cos \alpha+\cos \beta=\frac{3}{2}\) and \(\sin \alpha+\sin \beta =\frac{1}{2}\) and \(\theta\) is the the arithmetic mean of \(\alpha\) and \(\beta\), then \(\sin 2 \theta+\cos 2 \theta\) is equal to: [Main Online April 11, 2015]
Hint
(b) Let \(\cos \alpha+\cos \beta=\frac{3}{2}\)
\(\Rightarrow 2 \cos \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2}=\frac{3}{2}\)
and \(\sin \alpha+\sin \beta=\frac{1}{2}\)
\(
\Rightarrow 2 \sin \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2}=\frac{1}{2}
\)
On dividing (ii) by (i), we get
\(
\tan \left(\frac{\alpha+\beta}{2}\right)=\frac{1}{3}
\)
Given : \(\theta=\frac{\alpha+\beta}{2} \Rightarrow 2 \theta=\alpha+\beta\)
Consider \(\sin 2 \theta+\cos 2 \theta=\sin (\alpha+\beta)+\cos (\alpha+\beta)\)
\(
=\frac{\frac{2}{3}}{1+\frac{1}{9}}+\frac{1-\frac{1}{9}}{1+\frac{1}{9}}=\frac{6}{10}+\frac{8}{10}=\frac{7}{5}
\) -
Question 25 of 158
25. Question
Let \(\theta \in\left(0, \frac{\pi}{4}\right)\) and \(t_{1}=(\tan \theta)^{\tan \theta}, t_{2}=(\tan \theta)^{\cot \theta}, t_{3}=(\cot \theta)^{\tan \theta}\) and \(t_{4}=\) \((\cot \theta)^{\cot \theta}\), then [2006-3 M,-1]
Hint
(b) Given: \(\theta \in\left(0, \frac{\pi}{4}\right) \Rightarrow \tan \theta<1\) and \(\cot \theta>1\)
Let \(\tan \theta=1-x\) and \(\cot \theta=1+y\),
where \(x, y>0\) and are very small, then
\(
\begin{aligned}
&\therefore t_{1}=(1-x)^{1-x}, t_{2}=(1-x)^{1+y} \\
&\mathrm{t}_{3}=(1+y)^{1-x}, t_{4}=(1+y)^{1+y} \\
&\text { Clearly, } t_{4}>t_{3} \text { and } t_{1}>t_{2} \text { also, } t_{3}>t_{1} \\
&\therefore t_{4}>t_{3}>t_{1}>t_{2}
\end{aligned}
\) -
Question 26 of 158
26. Question
The values of \(\theta \in(0,2 \pi)\) for which \(2 \sin ^{2} \theta-5 \sin \theta+2>0\), are [2006-3M, -1]
Hint
(a) \(2 \sin ^{2} \theta-5 \sin \theta+2>0\)
\(
\begin{aligned}
&\Rightarrow(\sin \theta-2)(2 \sin \theta-1)>0 \\
&\because-1 \leq \sin \theta \leq 1, \quad \therefore \sin \theta<\frac{1}{2}
\end{aligned}
\)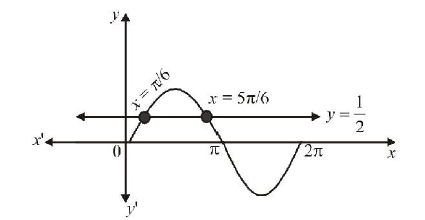
\(
\text { From graph, we get } x \in\left(0, \frac{\pi}{6}\right) \cup\left(\frac{5 \pi}{6}, 2 \pi\right)
\) -
Question 27 of 158
27. Question
If \(\alpha+\beta=\pi / 2\) and \(\beta+\gamma=\alpha\), then \(\tan \alpha\) equals [2001S]
Hint
(c) Given : \(\alpha+\beta=\pi / 2 \Rightarrow \alpha=\pi / 2-\beta\)
\(
\begin{aligned}
&\Rightarrow \tan \alpha=\tan (\pi / 2-\beta)=\cot \beta=\frac{1}{\tan \beta} \\
&\Rightarrow \tan \alpha \tan \beta=1 \Rightarrow 1+\tan \alpha \tan \beta=2 .
\end{aligned}
\)
Now, \(\tan (\alpha-\beta)=\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}\)
\(
\begin{aligned}
&\Rightarrow \tan \gamma=\frac{\tan \alpha-\tan \beta}{2} \\
&\Rightarrow 2 \tan \gamma=\tan \alpha-\tan \beta \Rightarrow \tan \alpha=2 \tan \gamma+\tan \beta
\end{aligned}
\) -
Question 28 of 158
28. Question
The maximum value of \(\left(\cos \alpha_{1}\right) \cdot\left(\cos \alpha_{2}\right) \ldots\left(\cos \alpha_{n}\right)\), under the restrictions
\(0 \leq \alpha_{1}, \alpha_{2}, \ldots, \alpha_{n} \leq \frac{\pi}{2}\) and \(\left(\cot \alpha_{1}\right) \cdot\left(\cot \alpha_{2}\right) \ldots\left(\cot \alpha_{n}\right)=1\) is [2001S]Hint
(a) Given : \(\left(\cot \alpha_{1}\right) \cdot\left(\cot \alpha_{2}\right) \ldots\left(\cot \alpha_{n}\right)=1\)
\(
\begin{aligned}
\Rightarrow\left(\cos \alpha_{1}\right)\left(\cos \alpha_{2}\right) \ldots\left(\cos \alpha_{n}\right) \\
=&\left(\sin \alpha_{1}\right)\left(\sin \alpha_{2}\right) \ldots\left(\sin \alpha_{n}\right) \dots ….(i)
\end{aligned}
\)
Let \(\mathrm{y}=\left(\cos \alpha_{1}\right)\left(\cos \alpha_{2}\right) \ldots\left(\cos \alpha_{n}\right)\) (to be max.)
\(
\Rightarrow \mathrm{y}^{2}=\left(\cos ^{2} \alpha_{1}\right)\left(\cos ^{2} \alpha_{2}\right) \ldots\left(\cos ^{2} \alpha_{n}\right)
\)
\(
\begin{aligned}
&=\cos \alpha_{1} \sin \alpha_{1} \cos \alpha_{2} \sin \alpha_{2} \ldots \cos \alpha_{n} \sin \alpha_{n} \quad(\text { From(i)) } \\
&=\frac{1}{2^{n}}\left[\sin 2 \alpha_{1} \sin 2 \alpha_{2} \ldots . \sin 2 \alpha_{n}\right] \\
&\text { Now, } 0 \leq \alpha_{1}, \alpha_{2}, \ldots \ldots \alpha_{n} \leq \pi / 2 \\
&\therefore 0 \leq 2 \alpha_{1}, 2 \alpha_{2}, \ldots \ldots, 2 \alpha_{n} \leq \pi \\
&\Rightarrow 0 \leq \sin 2 \alpha_{1}, \sin 2 \alpha_{2}, \ldots ., \sin 2 \alpha_{n} \leq 1 \\
&\therefore y^{2} \leq \frac{1}{2^{n}} \cdot 1 \Rightarrow y \leq \frac{1}{2^{n / 2}} \\
&\therefore \text { Max. value of } y \text { i.e. }\left(\cos \alpha_{1}\right) \cdot\left(\cos \alpha_{2}\right) \ldots .\left(\cos \alpha_{n}\right)=\frac{1}{2^{n / 2}} .
\end{aligned}
\) -
Question 29 of 158
29. Question
Let \(f(\theta)=\sin \theta(\sin \theta+\sin 3 \theta)\). Then \(f(\theta)\) is [2000S]
Hint
(c) \(f(\theta)=\sin \theta(\sin \theta+\sin 3 \theta)\)
\(
\begin{aligned}
&=\sin \theta\left(\sin \theta+3 \sin \theta-4 \sin ^{3} \theta\right) \\
&=\sin \theta\left(4 \sin \theta-4 \sin ^{3} \theta\right)=\sin ^{2} \theta\left(4-4 \sin ^{2} \theta\right) \\
&=4 \sin ^{2} \theta\left(1-\sin ^{2} \theta\right) \\
&=4 \sin ^{2} \theta \cos ^{2} \theta=(2 \sin \theta \cos \theta)^{2}=(\sin 2 \theta)^{2} \geq 0,
\end{aligned}
\)
which is true for all \(\theta\). -
Question 30 of 158
30. Question
\(3(\sin x-\cos x)^{4}+6(\sin x+\cos x)^{2}+4\left(\sin ^{6} x+\cos ^{6} x\right)=\) [1995S]
Hint
\(
\begin{aligned}
&\text { (c) } 3(\sin x-\cos x)^{4}+6(\sin x+\cos x)^{2}+4\left(\sin ^{6} x+\cos ^{6} x\right) \\
&=3(1-\sin 2 x)^{2}+6(1+\sin 2 x) \\
&\qquad+4\left[\left(\sin ^{2} x+\cos ^{2} x\right)^{3}-3 \sin ^{2} x \cos ^{2} x\left(\sin ^{2} x+\cos ^{2} x\right)\right]
\end{aligned}
\) -
Question 31 of 158
31. Question
Let \(0<x<\frac{\pi}{4}\) then \((\sec 2 x-\tan 2 x)\) equals [1994]
Hint
(b) \(\sec 2 \mathrm{x}-\tan 2 \mathrm{x}=\frac{1-\sin 2 x}{\cos 2 x}=\frac{1-\cos 2\left(\frac{\pi}{4}-x\right)}{\sin 2\left(\frac{\pi}{4}-x\right)}\)
\(
=\frac{2 \sin ^{2}\left(\frac{\pi}{4}-x\right)}{2 \sin \left(\frac{\pi}{4}-x\right) \cos \left(\frac{\pi}{4}-x\right)}=\tan \left(\frac{\pi}{4}-x\right)
\) -
Question 32 of 158
32. Question
Given \(A=\sin ^{2} \theta+\cos ^{4} \theta\) then for all real values of \(\theta\) [1980]
Hint
\(
\text { (b) } A=\sin ^{2} \theta+\cos ^{4} \theta=\sin ^{2} \theta+\left(1-\sin ^{2} \theta\right)^{2}
\)
\(
=\sin ^{4} \theta-\sin ^{2} \theta+1 \Rightarrow A=\left(\sin ^{2} \theta-\frac{1}{2}\right)^{2}+\frac{3}{4}
\)
Now,
\(
\begin{aligned}
&0 \leq\left(\sin ^{2} \theta-\frac{1}{2}\right)^{2} \leq \frac{1}{4} \\
&\Rightarrow \frac{3}{4} \leq\left(\sin ^{2} \theta-\frac{1}{2}\right)^{2}+\frac{3}{4} \leq 1 \Rightarrow \frac{3}{4} \leq A \leq 1
\end{aligned}
\) -
Question 33 of 158
33. Question
If \(\alpha+\beta+\gamma=2 \pi\), then [1979]
Hint
(a) \(\alpha+\beta+\gamma=2 \pi \Rightarrow \frac{\alpha}{2}+\frac{\beta}{2}+\frac{\gamma}{2}=\pi\)
\(
\begin{gathered}
\therefore \tan \left(\frac{\alpha}{2}+\frac{\beta}{2}\right)=\tan \left(\pi-\frac{\gamma}{2}\right)=-\tan \frac{\gamma}{2} \\
\Rightarrow \frac{\tan \alpha / 2+\tan \beta / 2}{1-\tan \alpha / 2 \tan \beta / 2}=-\tan \gamma / 2 \\
\Rightarrow \tan \alpha / 2+\tan \beta / 2+\tan \gamma / 2 \\
=\tan \alpha / 2 \tan \beta / 2 \tan \gamma / 2
\end{gathered}
\) -
Question 34 of 158
34. Question
The maximum value of the expression \(\frac{1}{\sin ^{2} \theta+3 \sin \theta \cos \theta+5 \cos ^{2} \theta}\) is [2010]
Hint
(b) Let \(f(\theta)=\frac{1}{g(\theta)}\),
where \(g(\theta)=\sin ^{2} \theta+3 \sin \theta \cos \theta+5 \cos ^{2} \theta\)
Clearly \(f\) is maximum when \(g\) is minimum
Now \(g(\theta)=\frac{1-\cos 2 \theta}{2}+\frac{3}{2} \sin 2 \theta+\frac{5}{2}(1+\cos 2 \theta)\)
\(
\begin{aligned}
&=3+2 \cos 2 \theta+\frac{3}{2} \sin 2 \theta \geq 3+\left(-\sqrt{4+\frac{9}{4}}\right) \\
&\therefore g_{\min }=3-\frac{5}{2}=\frac{1}{2} \Rightarrow f_{\max }=2 .
\end{aligned}
\) -
Question 35 of 158
35. Question
\(\text { If } \frac{\sqrt{2} \sin \alpha}{\sqrt{1+\cos 2 \alpha}}=\frac{1}{7} \text { and } \sqrt{\frac{1-\cos 2 \beta}{2}}=\frac{1}{\sqrt{10}} . \alpha, \beta \in\left(0, \frac{\pi}{2}\right) \text {, then } \tan (\alpha+2 \beta) \text { is equal to }\) [Main Jan. 8, 2020 (II)]
Hint
\(
\begin{aligned}
&\text { (c) } \frac{\sqrt{2} \sin \alpha}{\sqrt{2} \cos \alpha} = \frac{1}{\sqrt{7}} \text { and } \sqrt{\frac{1-\cos {2} \beta}{2}}=\frac{1}{10} \\
&\Rightarrow \frac{\sqrt{2} \sin \beta}{\sqrt{2}}=\frac{1}{\sqrt{10}}
\end{aligned}
\)
\(
\begin{gathered}
\therefore \quad \tan \alpha=\frac{1}{7} \text { and } \sin \beta=\frac{1}{\sqrt{10}} \\
\tan \beta=\frac{1}{3} \\
\therefore \quad \tan 2 \beta=\frac{2 \tan \beta}{1-\tan ^{2} \beta}=\frac{2 \cdot \frac{1}{3}}{1-\frac{1}{9}}=\frac{\frac{2}{3}}{\frac{8}{9}}=\frac{3}{4} \\
\tan (\alpha+2 \beta)=\frac{\tan \alpha+\tan 2 \beta}{1-\tan \alpha \tan 2 \beta} \\
=\frac{\frac{1}{7}+\frac{3}{4}}{1-\frac{1}{7} \cdot \frac{3+2}{4}}=\frac{\frac{42}{28}}{\frac{25}{2}}=1
\end{gathered}
\) -
Question 36 of 158
36. Question
Let \(f:[0,2] \rightarrow \mathbf{R}\) be the function defined by
\(f(x)=(3-\sin (2 \pi x)) \sin \left(\pi x-\frac{\pi}{4}\right)-\sin \left(3 \pi x+\frac{\pi}{4}\right) \text {. }\)
If \(\alpha, \beta \in[0,2]\) are such that \(\{x \in[0,2]: f(x) \geq 0\}=[\alpha, \beta]\), then the value of \(\beta-\alpha\) is ___ [Adv. 2020]Hint
(d)
\(
\begin{aligned}
&\text { Let } \pi x-\frac{\pi}{4}=\theta \in\left[\frac{-\pi}{4}, \frac{7 \pi}{4}\right] \\
&\text { So, }\left(3-\sin \left(\frac{\pi}{2}+2 \theta\right)\right) \sin \theta \geq \sin (\pi+3 \theta) \\
&\Rightarrow(3-\cos 2 \theta) \sin \theta \geq-\sin 3 \theta \\
&\Rightarrow \sin \theta\left[3-4 \sin ^{2} \theta+3-\cos 2 \theta\right] \geq 0 \\
&\Rightarrow \sin \theta(6-2(1-\cos 2 \theta)-\cos 2 \theta) \geq 0 \\
&\Rightarrow \sin \theta(4+\cos 2 \theta) \geq 0 \\
&\Rightarrow \sin \theta \geq 0 \\
&\Rightarrow \theta \in[0, \pi] \Rightarrow 0 \leq \pi x-\frac{\pi}{4} \leq \pi \\
&\Rightarrow x \in\left[\frac{1}{4}, \quad \frac{5}{4}\right] \\
&\Rightarrow[\alpha, \beta]=\left[\frac{1}{4}, \frac{5}{4}\right] \\
&\therefore \beta-\alpha=\frac{5}{4}-\frac{1}{4}=1
\end{aligned}
\) -
Question 37 of 158
37. Question
If \(A>0, B>0\) and \(A+B=\pi / 3\), then the maximum value of \(\tan\) \(A \tan B\) is ____ [1993 – 2 Marks]
Hint
(a) \(\text { Given : } A+B=\pi / 3 \Rightarrow \tan (A+B)=\sqrt{3}\)
\(
\begin{aligned}
&\Rightarrow \frac{\tan A+\tan B}{1-\tan A \tan B}=\sqrt{3} \Rightarrow \frac{\tan A+\frac{y}{\tan A}}{1-y}=\sqrt{3} \\
&\Rightarrow \tan ^{2} A+\sqrt{3}(y-1) \tan A+y=0 \quad \text { [Let } y=\tan A \tan B \text { ] }
\end{aligned}
\)
For real value of \(\tan A, 3(y-1)^{2}-4 y \geq 0\)
\(
\begin{aligned}
&\Rightarrow 3 y^{2}-10 y+3 \geq 0 \Rightarrow(y-3)\left(y-\frac{1}{3}\right) \geq 0 \\
&\Rightarrow y \leq \frac{1}{3} \text { or } \geq 3
\end{aligned}
\)
But \(A, B>0\) and \(A+B=\pi / 3 \Rightarrow A, B<\pi / 3\)
\(
\begin{aligned}
&\Rightarrow \tan A \tan B<3 \\
&\Rightarrow y \leq \frac{1}{3} \Rightarrow \text { Max. value of } y \text { is } 1 / 3 .
\end{aligned}
\) -
Question 38 of 158
38. Question
If \(K=\sin (\pi / 18) \sin (5 \pi / 18) \sin (7 \pi / 18)\), then the numerical value of \(\mathrm{K}\) is [1993 – 2 Marks]
Hint
(c) \(K=\sin \frac{\pi}{18} \sin \frac{5 \pi}{18} \sin \frac{7 \pi}{18}\) \(=\cos \left(\frac{\pi}{2}-\frac{\pi}{18}\right) \cos \left(\frac{\pi}{2}-\frac{5 \pi}{18}\right) \cos \left(\frac{\pi}{2}-\frac{7 \pi}{18}\right)\) \(=\cos \frac{\pi}{9} \cos \frac{2 \pi}{9} \cos \frac{4 \pi}{9}=\frac{1}{2^{3} \sin \frac{\pi}{9}} \cdot \sin \frac{8 \pi}{9}\) \(\left[\cos \alpha \cos 2 \alpha \quad \cos 2^{2} \alpha \ldots \ldots \ldots \cos 2^{n-1} \alpha=\frac{1}{2^{n} \sin \alpha} \cdot \sin \left(2^{n} \alpha\right)\right]\) \(=\frac{1}{8 \sin \pi / 9} \cdot \sin \pi / 9=\frac{1}{8}\)
-
Question 39 of 158
39. Question
The value of \(\sin \frac{\pi}{14} \sin \frac{3 \pi}{14} \sin \frac{5 \pi}{14} \sin \frac{7 \pi}{14} \sin \frac{9 \pi}{14} \sin \frac{11 \pi}{14} \sin \frac{13 \pi}{14}\) is equal to [1991 – 2 Marks]
Hint
(b)
\(\sin \frac{\pi}{14} \sin \frac{3 \pi}{14} \sin \frac{5 \pi}{14} \sin \frac{7 \pi}{14} \sin \frac{9 \pi}{14} \sin \frac{11 \pi}{14} \sin \frac{13 \pi}{14}\)
\(
\begin{aligned}
=\left(\sin \frac{\pi}{14} \sin \frac{3 \pi}{14} \sin \frac{5 \pi}{14}\right)^{2} \times 1 \\
& {\left[\because \sin \frac{13 \pi}{14}=\sin \frac{\pi}{14}, \sin \frac{11 \pi}{14}=\sin \frac{3 \pi}{14} \text { and } \sin \frac{3 \pi}{14}=\sin \frac{5 \pi}{14}\right] }
\end{aligned}
\)
\(\begin{aligned}
&=\left[\cos \left(\frac{\pi}{2}-\frac{\pi}{14}\right) \cos \left(\frac{\pi}{2}-\frac{3 \pi}{14}\right) \cos \left(\frac{\pi}{2}-\frac{5 \pi}{14}\right)\right]^{2} \\
&=\left[\cos \frac{3 \pi}{7} \cos \frac{2 \pi}{7} \cos \frac{\pi}{7}\right]^{2}=\left[\cos \frac{\pi}{7} \cos \frac{2 \pi}{7} \cos \frac{4 \pi}{7}\right]^{2}
\end{aligned}\)\(\left[\cos \alpha \cos 2 \alpha \quad \cos 2^{2} \alpha \ldots \ldots \ldots \cos 2^{n-1} \alpha\right.\)\(\left.=\frac{1}{2^{n} \sin \alpha} \cdot \sin \left(2^{n} \alpha\right)\right]\)
\(
\begin{aligned}
&=\left(\frac{1}{8 \sin \pi / 7} \sin \frac{8 \pi}{7}\right)^{2}=\left(\frac{\sin (\pi+\pi / 7)}{8 \sin \pi / 7}\right)^{2} \\
&=\left(\frac{-\sin \pi / 7}{8 \sin \pi / 7}\right)^{2}=\left(\frac{1}{8}\right)^{2}=\frac{1}{64}
\end{aligned}
\) -
Question 40 of 158
40. Question
Suppose \(\sin ^{3} x \sin 3 x=\sum_{m=0}^{n} C_{m} \cos m x\) is an identity in \(x\), where \(C_{0}, C_{1}\), \(C_{\mathrm{n}}\) are constants, and \(C_{n} \neq 0\). then the value of \(n\) is [1981 – 2 Marks]
Hint
(c) Given \(\sin ^{3} x \cdot \sin 3 x=\sum_{m=0}^{n} C_{m} \cos m x\)
\(
\begin{aligned}
&\sin ^{3} x \sin 3 x=\frac{1}{4}[3 \sin x-\sin 3 x] \sin 3 x \\
&=\quad \frac{1}{4}\left[\frac{3}{2} \cdot 2 \sin x \cdot \sin 3 x-\sin ^{2} 3 x\right] \\
&=\frac{1}{4}\left[\frac{3}{2}(\cos 2 x-\cos x)-\frac{1}{2}(1-\cos 6 x)\right] \\
&=\frac{1}{8}[\cos 6 x+3 \cos 2 x-3 \cos x-1] \\
&\quad \therefore \quad \text { Max value of } m=6 \quad \therefore \quad n=6
\end{aligned}
\) -
Question 41 of 158
41. Question
If \(\tan A=(1-\cos B) / \sin B\), then \(\tan 2 A=\tan B\). True or False? [1983 – 1 Mark]
Hint
(b) (True) \(\tan A=\frac{1-\cos B}{\sin B}=\frac{2 \sin ^{2} B / 2}{2 \sin B / 2 \cos / 2}=\tan B / 2\)
Now, \(\tan 2 A=\frac{2 \tan A}{1-\tan ^{2} A}=\frac{2 \tan B / 2}{1-\tan ^{2} B / 2}=\tan B\) Hence, statement is true. -
Question 42 of 158
42. Question
Let \(f(x)=x \sin \pi x, x>0\). Then for all natural numbers \(n, f^{\prime}(x)\) vanishes at [Adv. 2013]
Hint
(b, c) Given: \(f(x)=x \sin \pi x, x>0\) \(\Rightarrow f^{\prime}(x)=\sin \pi x+x \pi \cos \pi x\)
Now, \(f^{\prime}(x)=0 \Rightarrow \tan \pi x=-\pi x\)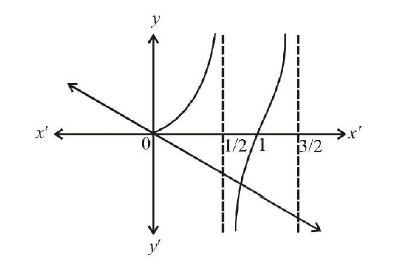
From graph of \(y=\tan \pi x\) and \(y=-\pi x\), it is clear that they intersect each other at unique point in the intervals
\((n, n+1) \text { and }\left(n+\frac{1}{2}, n+1\right)\) -
Question 43 of 158
43. Question
\(
\begin{gathered}
\text { Let } \theta, \phi \in[0,2 \pi] \text { be such that } 2 \cos \theta(1-\sin \phi) \\
=\sin ^{2} \theta\left(\tan \frac{\theta}{2}+\cot \frac{\theta}{2}\right) \cos \varphi-1, \tan (2 \pi-\theta)>0 \text { and } \\
-1<\sin \theta<-\frac{\sqrt{3}}{2}, \text { then } \phi \text { cannot satisfy }
\end{gathered}\) [2012]Hint
\((a, c, d)\)
As \(\tan (2 \pi-\theta)>0\) and \(-1<\sin \theta<-\frac{\sqrt{3}}{2}, \theta \in[0,2 \pi]\)
Hence \(\frac{3 \pi}{2}<\theta<\frac{5 \pi}{3}\)
Now \(2 \cos \theta(1-\sin \phi)=\sin ^{2} \theta\left(\tan \frac{\theta}{2}+\cot \frac{\theta}{2}\right) \cos \phi-1\)
\(
\Rightarrow 2 \cos \theta(1-\sin \phi)=2 \sin \theta \cos \phi-1
\)
\(
\Rightarrow 2 \cos \theta+1=2 \sin (\theta+\phi)
\)
As \(\theta \in\left(\frac{3 \pi}{2}, \frac{5 \pi}{3}\right), 1<2 \sin (\theta+\phi)<2\)
As \(\theta+\varphi \in\left(\frac{\pi}{6}, \frac{5 \pi}{6}\right)\) or \((\theta+\phi) \in\left(\frac{13 \pi}{6}, \frac{17 \pi}{6}\right)\)
We have \(\varphi \in\left(-\frac{3 \pi}{2},-\frac{2 \pi}{3}\right) \cup\left(\frac{2 \pi}{3}, \frac{7 \pi}{6}\right)\) -
Question 44 of 158
44. Question
If \(\frac{\sin ^{4} x}{2}+\frac{\cos ^{4} x}{3}=\frac{1}{5}\), then [2009]
Hint
(a, b) Given:
\(
\frac{\sin ^{4} x}{2}+\frac{\cos ^{4} x}{3}=\frac{1}{5} \Rightarrow 3 \sin ^{4} x+2 \cos ^{4} x=\frac{6}{5}
\)
\(
\begin{aligned}
&\Rightarrow \sin ^{4} x+2\left[\sin ^{4} x+\cos ^{4} x\right]=\frac{6}{5} \\
&\Rightarrow \sin ^{4} x+2\left[1-2 \sin ^{2} x \cos ^{2} x\right]=\frac{6}{5} \\
&\Rightarrow \sin ^{4} x+2-4 \sin ^{2} x\left(1-\sin ^{2} x\right)=\frac{6}{5} \\
&\Rightarrow 5 \sin ^{4} x-4 \sin ^{2} x+2-\frac{6}{5}=0 \\
&\Rightarrow 25 \sin ^{4} x-20 \sin ^{2} x+4=0 \\
&\Rightarrow\left(5 \sin ^{2} x-2\right)^{2}=0 \Rightarrow \sin ^{2} x=\frac{2}{5} \\
&\Rightarrow \cos ^{2} x=\frac{3}{5} \text { and } \tan ^{2} x=\frac{2}{3} \\
&\text { Also } \frac{\sin ^{8} x}{8}+\frac{\cos ^{8} x}{27}=\frac{2}{625}+\frac{3}{625}=\frac{5}{625}=\frac{1}{125}
\end{aligned}
\) -
Question 45 of 158
45. Question
For a positive integer \(n\), let \(f_{n}(\theta)\)
\(=\left(\tan \frac{\theta}{2}\right)(1+\sec \theta)(1+\sec 2 \theta)(1+\sec 4 \theta) \ldots .\left(1+\sec 2^{n} \theta\right) \text {. Then } \) [1999 – 3 Marks]Hint
(a, b, c, d) Note that the multiplicative loop is very important approach in IIT Mathematics
\(
\begin{aligned}
&\left(\tan \frac{\theta}{2}\right)(1+\sec \theta)=\frac{\sin \theta / 2}{\cos \theta / 2} \cdot\left[1+\frac{1}{\cos \theta}\right] \\
&=\frac{(\sin \theta / 2) 2 \cos ^{2} \theta / 2}{(\cos \theta / 2) \cos \theta} \\
&=\frac{(2 \sin \theta / 2) \cos \theta / 2}{\cos \theta}=\frac{\sin \theta}{\cos \theta}=\tan \theta \\
&\therefore \quad f_{n}(\theta)=(\tan \theta / 2)(1+\sec \theta) \\
&(1+\sec 2 \theta)\left(1+\sec 2^{2} \theta\right) \ldots\left(1+\sec 2^{n} \theta\right) \\
&=(\tan \theta)(1+\sec 2 \theta)\left(1+\sec 2^{2} \theta\right) \ldots\left(1+\sec 2^{n} \theta\right) \\
&=\tan 2 \theta \cdot\left(1+\sec 2^{2} \theta\right) \ldots\left(1+\sec 2^{n} \theta\right)=\tan \left(2^{n} \theta\right) \\
&\text { Now, } f_{2}\left(\frac{\pi}{16}\right)=\tan \left(2^{2} \cdot \frac{\pi}{16}\right)=\tan \left(\frac{\pi}{4}\right)=1
\end{aligned}
\)
Therefore, (a) is the correct option.
\(
f_{3}\left(\frac{\pi}{32}\right)=\tan \left(2^{3} \cdot \frac{\pi}{32}\right)=\tan \left(\frac{\pi}{4}\right)=1
\)
Therefore, (b) is the correct option.
\(
f_{4}\left(\frac{\pi}{64}\right)=\tan \left(2^{4} \cdot \frac{\pi}{64}\right)=\tan \left(\frac{\pi}{4}\right)=1
\)
Therefore, (c) is the correct option.
\(
f_{5}\left(\frac{\pi}{128}\right)=\tan \left(2^{5} \cdot \frac{\pi}{128}\right)=\tan \left(\frac{\pi}{4}\right)=1
\)
Therefore, (d) is the correct option. -
Question 46 of 158
46. Question
The minimum value of the expression \(\sin \alpha+\sin \beta+\sin \gamma\), where \(\alpha, \beta, \gamma\) are real numbers satisfying \(\alpha+\beta+\gamma=\pi\) is [1995]
Hint
(c) \(\sin \alpha+\sin \beta+\sin \gamma\)
\(
=2 \sin \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2}+2 \sin \frac{\gamma}{2} \cos \frac{\gamma}{2}
\)
\(
\begin{aligned}
&=2 \sin \left(\frac{\pi}{2}-\frac{\gamma}{2}\right) \cos \frac{\alpha-\beta}{2}+2 \sin \left(\frac{\pi}{2}-\frac{\alpha+\beta}{2}\right) \cos \frac{\gamma}{2} \\
&=2 \cos \frac{\gamma}{2}\left[\cos \frac{\alpha-\beta}{2}+\cos \frac{\alpha+\beta}{2}\right] \\
&=2 \cos (\alpha / 2) \cos (\beta / 2) \cos (\gamma / 2)
\end{aligned}
\)
\(\therefore\) Each \(\cos ((\alpha / 2), \cos (\beta / 2), \cos (\gamma / 2)\) lies between \(-1\) and 1 .
\(
\begin{aligned}
&\Rightarrow-1 \leq \cos \alpha / 2, \cos \beta / 2, \cos \gamma / 2 \leq 1 \\
&\Rightarrow-2 \leq 2 \cos \alpha / 2, \cos \beta / 2, \cos \gamma / 2 \leq 2 \\
&\Rightarrow-2 \leq \cos \alpha+\cos \beta+\cos \gamma \leq 2 \\
&\therefore \quad \text { Min value of } \sin \alpha+\sin \beta+\sin \gamma=-2
\end{aligned}
\) -
Question 47 of 158
47. Question
Let \(2 \sin ^{2} x+3 \sin x-2>0\) and \(x^{2}-x-2<0(x\) is measured in radians). Then \(x\) lies in the interval [1994]
Hint
(d) \(2 \sin ^{2} x+3 \sin x-2>0\)
\(
\begin{aligned}
&(2 \sin x-1)(\sin x+2)>0 \\
&\quad \Rightarrow 2 \sin x-1>0 \quad(\because-1 \leq \sin x \leq 1) \\
&\quad \Rightarrow \sin x>1 / 2 \Rightarrow x \in(\pi / 6,5 \pi / 6) \\
&\text { Also } x^{2}-x-2<0 \\
&\Rightarrow(x-2)(x+1)<0 \Rightarrow-1<x<2
\end{aligned}
\)
On combining (i) and (ii), we get \(x \in(\pi / 6,2)\). -
Question 48 of 158
48. Question
The expression \(3\left[\sin ^{4}\left(\frac{3 \pi}{2}-\alpha\right)+\sin ^{4}(3 \pi+\alpha)\right]-\) \(2\left[\sin ^{6}\left(\frac{\pi}{2}+\alpha\right)+\sin ^{6}(5 \pi-\alpha)\right]\) is equal to [1986 – 2 Marks]
Hint
(b) \(3\left[\sin ^{4}\left(\frac{3 \pi}{2}-\alpha\right)+\sin ^{4}(3 \pi+\alpha)\right]\)
\(
-2\left[\sin ^{6}(\pi / 2+\alpha)+\sin ^{6}(5 \pi-\alpha)\right]
\)
\(
\begin{aligned}
&=3\left[\cos ^{4} \alpha+\sin ^{4} \alpha\right]-2\left[\cos ^{6} \alpha+\sin ^{6} \alpha\right] \\
&=3\left[\left(\cos ^{2} \alpha+\sin ^{2} \alpha\right)^{2}-2 \sin ^{2} \alpha \cos ^{2} \alpha\right] \\
&-2\left[\left(\cos ^{2} \alpha+\sin ^{2} \alpha\right)^{3}-3 \cos ^{2} \alpha \sin ^{2} \alpha\left(\cos ^{2} \alpha+\sin ^{2} \alpha\right)\right]= \\
&\quad 3\left[1-2 \sin ^{2} \alpha \cos ^{2} \alpha\right]-2\left[1-3 \cos ^{2} \alpha \sin ^{2} \alpha\right] \\
&=3-6 \sin ^{2} \alpha \cos ^{2} \alpha-2+6 \sin ^{2} \alpha \cos ^{2} \alpha=1
\end{aligned}
\) -
Question 49 of 158
49. Question
\(\left(1+\cos \frac{\pi}{8}\right)\left(1+\cos \frac{3 \pi}{8}\right)\left(1+\cos \frac{5 \pi}{8}\right)\left(1+\cos \frac{7 \pi}{8}\right)\) is equal to [1984 – 3 Marks]
Hint
(c) Given,
\(
\begin{aligned}
&(1+\cos \pi / 8)(1+\cos 3 \pi / 8)(1+\cos 5 \pi / 8)(1+\cos 7 \pi / 8) \\
=&(1+\cos \pi / 8)(1+\cos 3 \pi / 8)(1+\cos (\pi-3 \pi / 8)) (1+\cos (\pi-\pi / 8)) \\
=&(1+\cos \pi / 8)(1+\cos 3 \pi / 8)(1-\cos 3 \pi / 8)(1-\cos \pi / 8)=\\
&\left(1-\cos ^{2} \pi / 8\right)\left(1-\cos ^{2} 3 \pi / 8\right)=\sin ^{2} \pi / 8 \sin ^{2} 3 \pi / 8 \\
=& \frac{1}{4} \cdot[2 \sin \pi / 8 \sin (\pi / 2-\pi / 8)]^{2} \\
=& \frac{1}{4} \cdot[2 \sin \pi / 8 \cos (\pi / 8)]^2=\frac{1}{4} \cdot \sin ^{2} \pi / 4=\frac{1}{4} \times \frac{1}{2}=\frac{1}{8}
\end{aligned}
\)\(\) -
Question 50 of 158
50. Question
In any triangle \(A B C\), prove that
\(\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}=\cot \frac{A}{2} \cot \frac{B}{2} \cot \frac{C}{2} \text {. }\) [2000 – 3 Marks]Hint
\(
\begin{aligned}
&\because A+B+C=\pi \\
&\Rightarrow \quad \frac{A}{2}+\frac{B}{2}+\frac{C}{2}=\frac{\pi}{2} \Rightarrow \frac{A}{2}+\frac{B}{2}=\frac{\pi}{2}-\frac{C}{2} \\
&\Rightarrow \cot \left(\frac{A}{2}+\frac{B}{2}\right)=\cot \left(\frac{\pi}{2}-\frac{C}{2}\right) \\
&\Rightarrow \quad \frac{\cot \frac{A}{2} \cdot \cot \frac{B}{2}-1}{\cot \frac{A}{2}+\cot \frac{B}{2}}=\tan \frac{C}{2} \\
&\Rightarrow \cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}=\cot \frac{A}{2} \cdot \cot \frac{B}{2} \cdot \cot \frac{C}{2}
\end{aligned}
\) -
Question 51 of 158
51. Question
Prove that \(\sum_{k=1}^{n-1}(n-k) \cos \frac{2 k \pi}{n}=-\frac{n}{2}\), where \(n \geq 3\) is an integer. [1997 – 5 Marks]
Hint
\(\text { Let } S=\sum_{k=1}^{n-1}(n-k) \cos \frac{2 k \pi}{n}\)
\(
\begin{aligned}
\Rightarrow S=&(n-1) \cos \frac{2 \pi}{n}+(n-2) \cos 2 . \frac{2 \pi}{n}+\ldots \ldots \\
&+1 \cdot \cos (n-1) \cos \frac{2(\mathrm{n}-1) \pi}{n} \quad \ldots \text { (i) }
\end{aligned}
\)
We know that \(\cos \theta=\cos (2 \pi-\theta)\)
Replacing each angle \(\theta\) by \(2 \pi-\theta\) in (i), we get
\(
\begin{array}{r}
S=(n-1) \cos (n-1) \frac{2 \pi}{n}+(n-2) \cos (n-2) \frac{2 \pi}{n}+\ldots \ldots \\
+1 . \cos \frac{2 \pi}{n} \ldots \text { (ii) }
\end{array}
\)
On adding terms in (i) and (ii) having the same angle and taking \(n\) common, we get
\(
\therefore 2 S=n\left[\cos \frac{2 \pi}{n}+\cos \frac{4 \pi}{n}+\cos \frac{6 \pi}{n}+\ldots .+\cos (n-1) \frac{2 \pi}{n}\right]
\)
Angles are in A.P. with common difference \((d)=\frac{2 \pi}{n}\)
\(
\begin{aligned}
2 S &=n\left[\frac{\sin (n-1) \frac{\pi}{n}}{\sin \frac{\pi}{n}} \cos \frac{\frac{2 \pi}{n}+(n-1) \frac{2 \pi}{n}}{2}\right] \\
&=n .1 \cos \pi=-n, \quad \because \sin (\pi-\theta)=\sin \theta, \quad \therefore S=-n / 2
\end{aligned}
\) -
Question 52 of 158
52. Question
Prove that the values of the function \(\frac{\sin x \cos 3 x}{\sin 3 x \cos x}\) do not lie between \(\frac{1}{3}\) and 3 for any real \(x\). [1997 – 5 Marks]
Hint
Let \(y=\frac{\sin x \cos 3 x}{\sin 3 x \cos x}=\frac{\tan x}{\tan 3 x}\)
\(
\begin{aligned}
&=\frac{\tan x\left(1-3 \tan ^{2} x\right)}{3 \tan x-\tan ^{3} x}=\frac{1-3 \tan ^{2} x}{3-\tan ^{2} x} \\
\Rightarrow & 3 y-\left(\tan ^{2} x\right) y=1-3 \tan ^{2} x \Rightarrow 3 y-1=(y-3) \tan ^{2} x \\
\Rightarrow & \tan ^{2} x=\frac{3 y-1}{y-3}=\frac{(3 y-1)(y-3)}{(y-3)^{2}} \\
\text { Since, } \tan ^{2} x>0, \quad \therefore(3 y-1)(y-3)>0 \\
\Rightarrow &\left(y-\frac{1}{3}\right)(y-3)>0 \Rightarrow y<\frac{1}{3} \quad \text { or } \quad y>3
\end{aligned}
\)
\(
\therefore y \text { cannot lie between } \frac{1}{3} \text { and } 3 \text {. }
\) -
Question 53 of 158
53. Question
Find the smallest positive number \(p\) for which the equation \(\cos (p \sin\) \(x)=\sin (p \cos x)\) has a solution \(x \in[0,2 \pi]\). [1995 – 5 Marks]
Hint
Given: \(\cos \theta=\sin \varphi\), where \(\theta=p \sin x, \varphi=p \cos x\)
Above is possible when both \(\theta=\varphi=\frac{\pi}{4}\) or \(\theta=\varphi=\frac{5 \pi}{4}\)
\(
\therefore \quad p \sin x=\frac{\pi}{4} \quad \text { or } \quad p \sin x=\frac{5 \pi}{4}
\)
and \(p \cos x=\frac{\pi}{4}\) or \(p \cos x=\frac{5 \pi}{4}\)
On squaring and adding, \(p^{2}=\frac{\pi^{2}}{16} .2\) or \(\frac{25 \pi^{2}}{16} .2\)
\(\therefore \quad p=\frac{\pi}{4} \sqrt{2}\) only for least positive value or \(p=\frac{\pi}{4} \sqrt{2}\) -
Question 54 of 158
54. Question
Determine the smallest positive value of \(x\) (in degrees) for which \(\tan \left(x+100^{\circ}\right)=\tan \left(x+50^{\circ}\right) \tan (x) \tan \left(x-50^{\circ}\right)\). [1993 – 5 Marks]
Hint
Given: \(\tan \left(x+100^{\circ}\right)=\tan \left(x+50^{\circ}\right) \tan x \tan \left(x-50^{\circ}\right)\)
\(
\begin{aligned}
&\Rightarrow \frac{\tan \left(x+100^{\circ}\right)}{\tan x}=\tan \left(x+50^{\circ}\right) \tan \left(x-50^{\circ}\right) \\
&\Rightarrow \frac{\sin \left(x+100^{\circ}\right) \cos x}{\cos \left(x+100^{\circ}\right) \sin x}=\frac{\sin \left(x+50^{\circ}\right) \sin \left(x-50^{\circ}\right)}{\cos \left(x+50^{\circ}\right) \cos \left(x-50^{\circ}\right)} \\
&\Rightarrow \frac{\sin \left(2 x+100^{\circ}\right)+\sin 100^{\circ}}{\sin \left(2 x+100^{\circ}\right)-\sin 100^{\circ}}=\frac{\cos 100^{\circ}-\cos 2 x}{\cos 100^{\circ}+\cos 2 x}
\end{aligned}
\)
By componendo and dividendo,
\(/
\begin{aligned}
&\Rightarrow \frac{2 \sin \left(2 x+100^{\circ}\right)}{2 \sin 100^{\circ}}=\frac{2 \cos 100^{\circ}}{-2 \cos 2 x} \\
&\Rightarrow 2 \sin \left(2 x+100^{\circ}\right) \cos 2 x=-2 \sin 100^{\circ} \cos 100^{\circ} \\
&\Rightarrow \sin \left(4 x+100^{\circ}\right)+\sin 100^{\circ}=-\sin 200^{\circ} \\
&\Rightarrow \sin \left(4 x+10^{\circ}+90^{\circ}\right)+\sin \left(90^{\circ}+10^{\circ}\right)=-\sin \left(180+20^{\circ}\right) \\
&\Rightarrow \cos \left(4 x+10^{\circ}\right)+\cos 10^{\circ}=\sin 20^{\circ} \\
&\Rightarrow \cos \left(4 x+10^{\circ}\right)=\sin 20^{\circ}-\cos 10^{\circ} \\
&\Rightarrow \cos \left(4 x+10^{\circ}\right)=\sin 20^{\circ}-\sin 80^{\circ} \\
&=-2 \cos 50^{\circ} \sin 30^{\circ}=-2 \cos 50^{\circ} \cdot \frac{1}{2} \\
&=-\cos 50^{\circ}=\cos 130^{\circ}
\end{aligned}
\)
\(\Rightarrow 4 x+10^{\circ}=130^{\circ} \Rightarrow x=30^{\circ}\) -
Question 55 of 158
55. Question
Show that the value of \(\frac{\tan x}{\tan 3 x}\), wherever defined never lies between \(\frac{1}{3}\) and \(3 .\) [1992 – 4 Marks]
Hint
Let \(y=\frac{\tan x}{\tan 3 x} \Rightarrow y=\frac{\tan x\left(1-3 \tan ^{2} x\right)}{3 \tan x-\tan ^{3} x}\) \(\Rightarrow 3 y-3 \tan ^{2} x=1-3 \tan ^{2} x\)
\(\Rightarrow(y-3) \tan ^{2} x=3 y-1 \Rightarrow \tan ^{2} x=\frac{3 y-1}{y-3}\)
\(\Rightarrow \frac{3 y-1}{y-3}>0 \quad(\because\) L.H.S. is a prefect square \()\)
\(\Rightarrow \frac{(3 y-1)(y-3)}{(y-3)^{2}}>0 \Rightarrow(3 y-1)(y-3)>0\)
\(\Rightarrow y<\frac{1}{3}\) or \(y>3\)
Thus \(y\) never lies between \(\frac{1}{3}\) and 3 . -
Question 56 of 158
56. Question
If \(\exp \left\{\left(\sin ^{2} x+\sin ^{4} x+\sin ^{6} x+\ldots \ldots \ldots \ldots\right)\right.\) ln 2\(\}\) satisfies the equation \(x^{2}-9 x+8=0\), find the value of \(\frac{\cos x}{\cos x+\sin x}, 0<x<\frac{\pi}{2}\). [1991 – 4 Marks]
Hint
Let \(y=\exp \left[\sin ^{2} x+\sin ^{4} x+\sin ^{6} x+\ldots \infty\right] \ln 2\)
\(
\begin{aligned}
&=e^{I n \cdot 2^{\sin ^{2} x+\sin ^{4} x+\sin ^{6} x+\ldots \infty}} \\
&=2^{\sin ^{2} x+\sin ^{4} x+\sin ^{6} x+\ldots . \infty}=\frac{\sin ^{2} x}{2^{1-\sin ^{2} x}}=2^{\tan ^{2} x}
\end{aligned}
\)
As \(y\) satisfies the eq. \(x^{2}-9 x+8=0\)
\(\therefore y^{2}-9 y+8=0\)
\(
\begin{aligned}
&\Rightarrow(y-1)(y-8)=0 \Rightarrow y=1,8 \\
&\Rightarrow 2^{\tan ^{2} x}=1 \text { or } 2^{\tan ^{2} x}=8 \\
&\Rightarrow \tan ^{2} x=0 \text { or } \tan ^{2} x=3 \\
&\Rightarrow \tan x=0 \text { or } \tan x=\sqrt{3},-\sqrt{3} \\
&\Rightarrow x=0 \text { or } x=\pi / 3,2 \pi / 3
\end{aligned}
\)
But given \(0<x<\pi / 2 \Rightarrow x=\pi / 3\)
\(\therefore \frac{\cos x}{\cos x+\sin x}=\frac{1}{1+\tan x}=\frac{1}{1+\sqrt{3}}=\frac{\sqrt{3}-1}{2}\) -
Question 57 of 158
57. Question
\(A B C\) is a triangle such that
\(
\sin (2 A+B)=\sin (C-A)=-\sin (B+2 C)=\frac{1}{2} \text {. }
\)
If \(A, B\) and \(C\) are in arithmetic progression, determine the values of \(A, B\) and \(C\). [1990 – 5 Marks]Hint
Given : In \(\triangle A B C, A, B\) and \(C\) are in A.P.
\(\therefore A+C=2 B\)
\(\mathrm{Also} A+B+C=180^{\circ} \Rightarrow B+2 B=180^{\circ} \Rightarrow B=60^{\circ}\)
Also given that, \(\sin (2 A+B)=\sin (C-A)=-\sin (B+2 C)=\frac{1}{2}\)
\(
\Rightarrow \quad \sin \left(2 A+60^{\circ}\right)=\sin (C-A)=-\sin (60+2 C)=\frac{1}{2} \ldots \text { (i) }
\)
From eq. (i), \(\sin \left(2 A+60^{\circ}\right)=\frac{1}{2} \Rightarrow 2 A+60^{\circ}=30^{\circ}, 150^{\circ}\)
But \(A\) can not be -ve
\(
\therefore 2 A+60^{\circ}=150^{\circ} \Rightarrow 2 A=90^{\circ} \Rightarrow A=45^{\circ}
\)
Again from (i), \(\sin \left(60^{\circ}+2 C\right)=-\frac{1}{2}\)
\(
\begin{aligned}
&\Rightarrow \quad 60^{\circ}+2 C=210^{\circ} \text { or } 330^{\circ} \\
&\Rightarrow C=75^{\circ} \text { or } 135^{\circ}
\end{aligned}
\)
Also from (i), \(\sin (C-A)=\frac{1}{2} \Rightarrow C-A=30^{\circ}, 150^{\circ}\)
For \(A=45^{\circ} ; C=75^{\circ}, 195^{\circ}\)
But \(\mathrm{C}=195^{\circ}\) is not possible.
\(\begin{aligned}
&\therefore C=75^{\circ} \\
&\therefore A=45^{\circ}, B=60^{\circ}, C=75^{\circ} .
\end{aligned}\) -
Question 58 of 158
58. Question
Prove that \(\tan \alpha+2 \tan 2 \alpha+4 \tan 4 \alpha+8 \cot 8 \alpha=\cot \alpha\) [1988 – 2 Marks]
Hint
We know \(\tan 2 \alpha=\frac{2 \tan \alpha}{1-\tan ^{2} \alpha}\) \(\Rightarrow \frac{1-\tan ^{2} \alpha}{\tan \alpha}=2 \cot 2 \alpha \Rightarrow \cot \alpha-\tan \alpha=2 \cot 2 \alpha \dots …(i)\)
Now, we have to prove \(\tan \alpha+2 \tan 2 \alpha+4 \tan 4 \alpha+8 \cot 8 \alpha=\cot \alpha\)
LHS \(=\tan \alpha+2 \tan 2 \alpha+4 \tan 4 \alpha+4(2 \cot 2.4 \alpha)\) \(=\tan \alpha+2 \tan 2 \alpha+4 \tan 4 \alpha+4(\cot 4 \alpha-\tan 4 \alpha)\) [From (i)]
\(=\tan \alpha+2 \tan 2 \alpha+4 \tan 4 \alpha+4 \cot 4 \alpha-4 \tan 4 \alpha\)
\(=\tan \alpha+2 \tan 2 \alpha+2(2 \cot 2.2 \alpha)\)
\(=\tan \alpha+2 \tan 2 \alpha+2(\cot \alpha-\tan 2 \alpha)\)
\(=\tan \alpha+2 \tan 2 \alpha+2(2 \cot 2 \alpha-\tan 2 \alpha) \quad\) [From (i)]
\(=\tan \alpha+2 \cot 2 \alpha\)
\(=\tan \alpha+(\cot \alpha-\tan \alpha) \quad\) [From (i)]
\(=\cot \alpha=\) RHS. -
Question 59 of 158
59. Question
Show that \(16 \cos \left(\frac{2 \pi}{15}\right) \cos \left(\frac{4 \pi}{15}\right) \cos \left(\frac{8 \pi}{15}\right) \cos \left(\frac{16 \pi}{15}\right)=1\) [1983 – 2 Marks]
Hint
We know,
\(
\begin{aligned}
&\cos A \cos 2 A \cos 4 A \ldots \cos 2^{n} A=\frac{1}{2^{n+1} \sin A} \sin \cdot\left(2^{n+1} A\right) \\
&\therefore 16 \cos \frac{2 \pi}{15} \cos 2\left(\frac{2 \pi}{15}\right) \cos 2^{2}\left(\frac{2 \pi}{15}\right) \cos 2^{3}\left(\frac{2 \pi}{15}\right) \\
&=16 \cdot \frac{\sin \left(2^{4} A\right)}{2^{4} \sin A}, \text { where } A=2 \pi / 15 \\
&=16 . \frac{\sin (32 \pi / 15)}{16 \sin 2 \pi / 15}=\frac{\sin (32 \pi / 15)}{\sin (2 \pi+2 \pi / 15)}=\frac{\sin (32 \pi / 15)}{\sin (32 \pi / 15)}=1
\end{aligned}
\) -
Question 60 of 158
60. Question
Without using tables, Calculate \(\left(\sin 12^{\circ}\right)\left(\sin 48^{\circ}\right)\left(\sin 54^{\circ}\right)=?\) [1982 – 2 Marks]
Hint
(b)
\(
\begin{aligned}
& =\frac{1}{2}\left(2 \sin 12^{\circ} \sin 48^{\circ}\right) \sin 54^{\circ} \\
& =\frac{1}{2}\left[\cos \left(36^{\circ}\right)-\cos \left(60^{\circ}\right)\right] \sin 54^{\circ} \\
& =\frac{1}{2}\left(\cos 36^{\circ}-\frac{1}{2}\right) \sin 54^{\circ} \\
& =\frac{1}{4}\left(2 \cos 36^{\circ} \sin 54^{\circ}-\sin 54^{\circ}\right) \\
& =\frac{1}{4}\left(\sin 90^{\circ}+\sin 18^{\circ}-\sin 54^{\circ}\right) \\
& =\frac{1}{4}\left(1+\frac{\sqrt{5}-1}{4}-\frac{\sqrt{5}+1}{4}\right) \\
& =\frac{1}{4}\left(1+\frac{\sqrt{5}-1-\sqrt{5}-1}{4}\right) \\
& =\frac{1}{4}\left(1-\frac{1}{2}\right)=\frac{1}{8}
\end{aligned}
\) -
Question 61 of 158
61. Question
For all \(\theta\) in \([0, \pi / 2]\) show that, \(\cos (\sin \theta) \geq \sin (\cos \theta)\). [1981 – 4 Marks]
Hint
\(\begin{aligned}
&\text {We know, }\\
&\cos \theta+\sin \theta=\sqrt{2}\left[\frac{1}{\sqrt{2}} \cos \theta+\frac{1}{\sqrt{2}} \sin \theta\right]\\
&=\sqrt{2} \sin (\pi / 4+\theta)\\
&\therefore \cos \theta+\sin \theta \leq \sqrt{2}<\pi / 2\left[\begin{array}{c}
\because \sqrt{2}=1.414 \\
\pi / 2=1.57
\end{array}\right]\\
&\therefore \quad \cos \theta+\sin \theta<\pi / 2 \quad \Rightarrow \quad \cos \theta<\pi / 2-\sin \theta \quad \ldots \text { (i) } \quad \text { As }\\
&\theta \in[0, \pi / 2] \text { in which } \sin \theta \text { increases. }\\
&\therefore \text { Taking sin on both sides of eq. (i), we get }\\
&\sin (\cos \theta)<\sin (\pi / 2-\sin \theta)\\
&\sin (\cos \theta)<\cos (\sin \theta)\\
&\Rightarrow \cos (\sin \theta)>\sin (\cos \theta)
\end{aligned}\) -
Question 62 of 158
62. Question
Given \(A=\left\{x: \frac{\pi}{6} \leq x \leq \frac{\pi}{3}\right\}\) and \(f(x)=\cos x-x(1+x)[latex]; find [latex]f(A)\). [1980]
Hint
\(
\begin{aligned}
&A=\left\{x: \frac{\pi}{6} \leq x \leq \frac{\pi}{3}\right\} \\
&f(x)=\cos x-x(1+x) \\
&f^{\prime}(x)=-\sin x-1-2 x<0, \forall x \in A
\end{aligned}
\)
\(\therefore f\) is a decreasing function.
As
\(
\begin{aligned}
\frac{\pi}{6} & \leq x \leq \frac{\pi}{3} \Rightarrow f\left(\frac{\pi}{3}\right) \leq f(x) \leq\left(\frac{\pi}{6}\right) \\
& \Rightarrow \cos \frac{\pi}{3}-\frac{\pi}{3}\left(1+\frac{\pi}{3}\right) \leq f(x) \leq \cos \frac{\pi}{6}-\frac{\pi}{6}\left(1+\frac{\pi}{6}\right) \\
\therefore & f(A)=\left[\frac{1}{2}-\frac{\pi}{3}\left(1+\frac{\pi}{3}\right), \frac{\sqrt{3}}{2}-\frac{\pi}{6}\left(1+\frac{\pi}{6}\right)\right]
\end{aligned}
\) -
Question 63 of 158
63. Question
Given \(\alpha+\beta-\gamma=\pi\), prove that \(\sin ^{2} \alpha+\sin ^{2} \beta-\sin ^{2} \gamma=2 \sin \alpha \sin \beta \cos \gamma\) [1980]
Hint
Given \(\alpha+\beta-\gamma=\pi\) and we have to prove that
\(\sin ^{2} \alpha+\sin ^{2} \beta-\sin ^{2} \gamma=2 \sin \alpha \sin \beta \cos \gamma\)
L.H.S. \(=\sin ^{2} \alpha+\sin ^{2} \beta-\sin ^{2} \gamma\)
\(=\sin ^{2} \alpha+\sin (\beta+\gamma) \sin (\beta-\gamma)\)
\(=\sin ^{2} \alpha+\sin (\beta+\gamma) \sin (\pi-\alpha) \quad\left[\text { Since }, \sin ^{2} A-\sin ^{2} B=\sin (A+B) \sin (A-B)\right]\)
\(=\sin ^{2} \alpha+\sin (\beta+\gamma) \sin (\pi-\gamma)\) \(=\sin ^{2} \alpha+\sin (\beta+\gamma) \sin \alpha\)
\(=\sin \alpha(\sin \alpha+\sin (\beta+\gamma))\)
\(=\sin \alpha[\sin [\pi-(\beta-\gamma)]+\sin (\beta+\gamma)]\)
\(=\sin \alpha[\sin (\beta-\gamma)+\sin (\beta+\gamma)]\)
\(=\sin \alpha[2 \sin \beta \cos \gamma]=2 \sin \alpha \sin \beta \cos \gamma=\) R.H.S. -
Question 64 of 158
64. Question
\(\tan \alpha=\frac{m}{m+1}\) and \(\tan \beta=\frac{1}{2 m+1}\), find the possible values of \((\alpha+\beta)\). [1978]
Hint
\(
\begin{aligned}
&\text { 52. We know } \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta} \\
&\Rightarrow \tan (\alpha+\beta)=\frac{\frac{m}{m+1}+\frac{1}{2 m+1}}{1-\frac{m}{m+1} \cdot \frac{1}{2 m+1}}=\frac{2 m^{2}+2 m+1}{2 m^{2}+2 m+1}=1 \\
&\Rightarrow \alpha+\beta=n \pi+\pi / 4, \text { where } n \in Z
\end{aligned}
\) -
Question 65 of 158
65. Question
If the equation \(\cos ^{4} \theta+\sin ^{4} \theta+\lambda=0\) has real solutions for \(\theta\), then \(\lambda\) lies in the interval: [Main Sep. 02, 2020 (II)]
Hint
\(
\begin{aligned}
&\text { (b) } \sin ^{4} \theta+\cos ^{4} \theta=-\lambda\\
&\Rightarrow\left(\sin ^{2} \theta+\cos ^{2} \theta\right)^{2}-2 \sin ^{2} \theta \cdot \cos ^{2} \theta=-\lambda\\
&\Rightarrow 1-2 \sin ^{2} \theta \cos ^{2} \theta=-\lambda\\
&\Rightarrow \lambda=\frac{(\sin 2 \theta)^{2}}{2}-1\\
&\Rightarrow \text { as } \sin ^{2} 2 \theta \in[0,1]
\end{aligned}
\)\(
\Rightarrow \lambda \in\left[-1, \frac{-1}{2}\right]
\) -
Question 66 of 158
66. Question
If \([x]\) denotes the greatest integer \(\leq x\), then the system of linear equations
\([\sin \mathrm{q}] x+[-\cos \mathrm{q}] y=0\)
\([\cot \mathrm{q}] x+y=0\) [Main April 12, 2019 (II)]Hint
(a) According to the question, there are two cases.
Case \(1: \theta \in\left(\frac{\pi}{2}, \frac{2 \pi}{3}\right)\)
In this interval, \([\sin \theta]=0,[-\cos \theta]=0\) and \([\cot \theta]=-1\)
Then the system of equations will be ;
\(0 \cdot x+0 \cdot y=0\) and \(-x+y=0\)
Which have infinitely many solutions.
Case 2: \(\theta \in\left(\pi, \frac{7 \pi}{6}\right)\)
In this interval, \([\sin \theta]=-1\) and \([-\cos \theta]=0\),
Then the system of equations will be;
\(-x+0 \cdot y=0\) and \([\cot \theta] x+y=0\)
Clearly, \(x=0\) and \(y=0\) which has unique solution. -
Question 67 of 158
67. Question
Let \(\mathrm{S}=\left\{\theta \in[-2 \pi, 2 \pi]: 2 \cos ^{2} \theta+3 \sin \theta=0\right\}\). Then the sum of the elements of \(\mathrm{S}\) is: [Main April 9, 2019(I)]
Hint
(c) \(2 \cos ^{2} \theta+3 \sin \theta=0\)
\((2 \sin \theta+1)(\sin \theta-2)=0\)
\(\Rightarrow \sin \theta=-\frac{1}{2}\) or \(\sin \theta=2 \rightarrow\) Not possible
The required sum of all solutions in \([-2 \pi, 2 \pi]\) is
\(
=\left(\pi+\frac{\pi}{6}\right)+\left(2 \pi-\frac{\pi}{6}\right)+\left(-\frac{\pi}{6}\right)+\left(-\pi+\frac{\pi}{6}\right)=2 \pi
\) -
Question 68 of 158
68. Question
If \(0 \leq x<\frac{\pi}{2}\), then the number of values of \(\mathrm{x}\) for which \(\sin x-\sin 2 x+\) \(\sin 3 x=0\), is: [Main Jan. 09, \(\)2019(II)]
Hint
(d)
\(
\begin{aligned}
&\sin x+\sin 3 x=\sin 2 x \Rightarrow 2 \sin 2 x \cos x=\sin 2 x \\
&\Rightarrow \sin 2 x=0 \text { or } \cos x=1 / 2 \\
&\Rightarrow 2 x \in\{0\}, \quad x \in\{\pi / 3\} \\
&\Rightarrow x={0, \frac{\pi}{3}}, \quad x \in\left[0, \frac{\pi}{2}\right]
\end{aligned}
\) -
Question 69 of 158
69. Question
If sum of all the solutions of the equation \(8 \cos x \cdot\left(\cos \left(\frac{\pi}{6}+x\right) \cdot \cos \left(\frac{\pi}{6}-x\right)-\frac{1}{2}\right)-1\) in \([0, \pi]\) is \(k \pi\), then \(k\) is equal to: [Main 2018]
Hint
(a) \(8 \cos x\left(\cos ^{2} \frac{\pi}{6}-\sin ^{2} x-\frac{1}{2}\right)=1\)
\(\Rightarrow \quad 8 \cos x\left(\frac{3}{4}-\frac{1}{2}-\sin ^{2} x\right)=1\)
\(\Rightarrow \quad 8 \cos x\left(\frac{1}{4}-\left(1-\cos ^{2} x\right)\right)=1\)
\(\Rightarrow \quad 8 \cos x\left(\frac{1}{4}-1+\cos ^{2} x\right)=1\)
\(\Rightarrow 8 \cos x\left(\cos ^{2} x-\frac{3}{4}\right)=1\)
\(\Rightarrow 8\left(\frac{4 \cos ^{3} x-3 \cos x}{4}\right)=1\)
\(\Rightarrow 2\left(4 \cos ^{3} x-3 \cos x\right)=1\)
\(\Rightarrow 2 \cos 3 x=1 \Rightarrow \cos 3 x=\frac{1}{2}\)
\(\therefore 3 \mathrm{x}=2 \mathrm{n} \pi \pm \frac{\pi}{3}, \mathrm{n} \in 1\)
\(\Rightarrow \mathrm{x}=\frac{2 \mathrm{n} \pi}{3} \pm \frac{\pi}{9}\)
In \(x \in[0, \pi]: x=\frac{\pi}{9}, \frac{2 \pi}{3}+\frac{\pi}{9}, \frac{2 \pi}{3}-\frac{\pi}{9}\), only Sum of all the solutions of the equation \(=\left(\frac{1}{9}+\frac{2}{3}+\frac{1}{9}+\frac{2}{3}-\frac{1}{9}\right) \pi=\frac{13}{9} \pi\) -
Question 70 of 158
70. Question
If \(0 \leq x<2 \pi\), then the number of real values of \(x\), which satisfy the equation \(\cos x+\cos 2 x+\cos 3 x+\cos 4 x=0\) is: [Main 2016]
Hint
\(
\begin{aligned}
&\text { (a) } \cos x+\cos 2 x+\cos 3 x+\cos 4 x=0\\
&\Rightarrow 2 \cos 2 \mathrm{x} \cos \mathrm{x}+2 \cos 3 \mathrm{x} \cos \mathrm{x}=0\\
&\Rightarrow 2 \cos x\left(2 \cos \frac{5 x}{2} \cos \frac{x}{2}\right)=0\\
&\cos x=0, \cos \frac{5 x}{2}=0, \cos \frac{x}{2}=0\\
&\mathrm{x}=\pi, \frac{\pi}{2}, \frac{3 \pi}{2}, \frac{\pi}{5}, \frac{3 \pi}{5}, \frac{7 \pi}{5}, \frac{9 \pi}{5}
\end{aligned}
\) -
Question 71 of 158
71. Question
The number of \(x \in[0,2 \pi]\) for which \(\left|\sqrt{2 \sin ^{4} x+18 \cos ^{2} x}-\sqrt{2 \cos ^{4} x+18 \sin ^{2} x}\right|=1\) is [Main Online April 9, 2016]
Hint
(d) \(\left|\sqrt{2 \sin ^{4} x+18 \cos ^{2} x}-\sqrt{2 \cos ^{4} x+18 \sin ^{2} x}\right|=1\)
\(\sqrt{2 \sin ^{4} x+18 \cos ^{2} x}-\sqrt{2 \cos ^{4} x+18 \sin ^{2} x}=\pm 1\)
\(\sqrt{2 \sin ^{4} x+18 \cos ^{2} x}=\pm 1+\sqrt{2 \cos ^{4} x+18 \sin ^{2} x}\)
by squaring both the sides we will get 8 solutions -
Question 72 of 158
72. Question
Let \(S=\left\{x \in(-\pi, \pi): x \neq 0, \pm \frac{\pi}{2}\right\}\). The sum of all distinct solutions of the equation
\(\sqrt{3} \sec x+\operatorname{cosec} x+2(\tan x-\cot x)=0\) in the set \(S\) is equal to [Adv. 2016]Hint
(c) \(\sqrt{3} \sec x+\operatorname{cosec} x+2(\tan x-\cot x)=0\)
\(
\begin{aligned}
&\Rightarrow \frac{\sqrt{3}}{2} \sin \mathrm{x}+\frac{1}{2} \cos \mathrm{x}=\cos ^{2} \mathrm{x}-\sin ^{2} \mathrm{x} \\
&\Rightarrow \cos \left(\mathrm{x}-\frac{\pi}{3}\right)=\cos 2 \mathrm{x} \Rightarrow \mathrm{x}-\frac{\pi}{3}=2 \mathrm{n} \pi \pm 2 \mathrm{x} \\
&\Rightarrow \mathrm{x}=\frac{2 \mathrm{n} \pi}{3}+\frac{\pi}{9} \text { or } \mathrm{x}=-2 \mathrm{n} \pi-\frac{\pi}{3}
\end{aligned}
\)
For \(\mathrm{x} \in \mathrm{S}, \mathrm{n}=0 \Rightarrow \mathrm{x}=\frac{\pi}{9},-\frac{\pi}{3}\)
Now, \(\mathrm{n}=1 \Rightarrow \mathrm{x}=\frac{7 \pi}{9} ; \quad\) and \(\mathrm{n}=-1 \Rightarrow \mathrm{x}=\frac{-5 \pi}{9}\)
Hence, sum of all values of \(x=\frac{\pi}{9}-\frac{\pi}{3}+\frac{7 \pi}{9}-\frac{5 \pi}{9}=0\) -
Question 73 of 158
73. Question
The number of values of \(\alpha\) in \([0,2 \pi]\) for which \(2 \sin ^{3} \alpha-7 \sin ^{2} \alpha+7 \sin \alpha=2\), is: [Main Online April 9, 2014]
Hint
\(
\begin{aligned}
&\text { (c) } 2 \sin ^{3} \alpha-7 \sin ^{2} \alpha+7 \sin \alpha-2=0 \\
&\Rightarrow 2 \sin ^{2} \alpha(\sin \alpha-1)-5 \sin \alpha(\sin \alpha-1) +2(\sin \alpha-1)=0 \\
&\Rightarrow(\sin \alpha-1)\left(2 \sin ^{2} \alpha-5 \sin \alpha+2\right)=0 \\
&\Rightarrow \sin \alpha-1=0 \text { or } 2 \sin ^{2} \alpha-5 \sin \alpha+2=0
\end{aligned}
\)\(\sin \alpha=1\) or \(\sin \alpha=\frac{5 \pm \sqrt{25-16}}{4}=\frac{5 \pm 3}{4}\) \(\alpha=\frac{\pi}{2}\) or \(\sin \alpha=\frac{1}{2}, 2\)
Now, \(\sin \alpha \neq 2\)
for, \(\sin \alpha=\frac{1}{2}\)
\(
\alpha=\frac{\pi}{3}, \frac{2 \pi}{3}
\)
There are three values of \(\alpha\) between \([0,2 \pi]\) -
Question 74 of 158
74. Question
For \(x \in(0, \pi)\), the equation \(\sin x+2 \sin 2 x-\sin 3 x=3\) has [Adv. 2014]
Hint
(d) \(\sin x+2 \sin 2 x-\sin 3 x=3\)
\(\Rightarrow \quad \sin x+4 \sin x \cos x-3 \sin x+4 \sin ^{3} x=3\)
\(\Rightarrow \quad \sin x\left(-2+2 \cos x+4 \sin ^{2} x\right)=3\)
\(\Rightarrow \quad \sin x\left(-2+2 \cos x+4-4 \cos ^{2} x\right)=3\)
\(\Rightarrow \quad 2+2 \cos x-4 \cos ^{2} x=\frac{3}{\sin x}\)
\(\Rightarrow \quad 2-\left(4 \cos ^{2} x-2.2 \cos x \cdot \frac{1}{2}+\frac{1}{4}\right)+\frac{1}{4}=\frac{3}{\sin x}\)
\(\Rightarrow \frac{9}{4}-\left(2 \cos x-\frac{1}{2}\right)^{2}=\frac{3}{\sin x}\)
\(\therefore\) LHS \(\leq \frac{9}{4}\) and RHS \(\geq 3 \quad[\because 0 \leq \sin x \leq 1]\) -
Question 75 of 158
75. Question
The number of solutions of the pair of equations
\(
\begin{aligned}
&2 \sin ^{2} \theta-\cos 2 \theta=0 \\
&2 \cos ^{2} \theta-3 \sin \theta=0
\end{aligned}
\)
in the interval \([0,2 \pi]\) is [2007 – 3 Marks]Hint
(c) \(2 \sin ^{2} \theta-\cos 2 \theta=0 \Rightarrow 1-2 \cos 2 \theta=0\) \(\Rightarrow \cos 2 \theta=\frac{1}{2} \Rightarrow 2 \theta=\frac{\pi}{3}, \frac{5 \pi}{3}, \frac{7 \pi}{3}, \frac{11 \pi}{3}\) \(\Rightarrow \theta=\frac{\pi}{6}, \frac{5 \pi}{6}, \frac{7 \pi}{6}, \frac{11 \pi}{6} \dots…(i)\)
where \(\theta \in[0,2 \pi]\)
Also,
\(
\begin{aligned}
& 2 \cos ^{2} \theta-3 \sin \theta=0 \\
\Rightarrow & 2 \sin ^{2} \theta+3 \sin \theta-2=0
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow(2 \sin \theta-1)(\sin \theta+2)=0 \Rightarrow \sin \theta=\frac{1}{2} \quad[\because \sin \theta \neq-2] \\
&\Rightarrow \theta=\frac{\pi}{6}, \frac{5 \pi}{6} \quad \ldots . \text { (ii), }
\end{aligned}
\)
where \(\theta \in[0,2 \pi]\)
Combining (i) and (ii), we get \(\theta=\frac{\pi}{6}, \frac{5 \pi}{6}\)
Hence, there are two solutions. -
Question 76 of 158
76. Question
\(\cos (\alpha-\beta)=1\) and \(\cos (\alpha+\beta)=1 / e\) where \(\alpha, \beta \in[-\pi, \pi]\). Pairs of \(\alpha, \beta\) which satisfy both the equations is/are \([2005 \mathrm{~S}]\)
Hint
(d) Given : \(\cos (\alpha-\beta)=1\) and \(\cos (\alpha+\beta)=1 / \mathrm{e}\),
where \(\alpha, \beta \in[-\pi, \pi]\)
Now, \(\cos (\alpha-\beta)=1 \Rightarrow \alpha-\beta=0 \Rightarrow \alpha=\beta\)
and \(\cos (\alpha+\beta)=1 / \mathrm{e} \Rightarrow \cos 2 \alpha=1 / \mathrm{e}\)
\(\because 0<1 / e<1\)
Now \(2 \alpha \in[-2 \pi, 2 \pi]\)
\(\Rightarrow\) There will be two values of \(2 \alpha\) satisfying \(\cos 2 \alpha=1 / \mathrm{e}\) and two values in \([0,2 \pi]\) in \([-2 \pi, 0]\).
\(\Rightarrow\) There will be four values of \(\alpha\) in \([-\pi, \pi]\) and correspondingly four values of \(\beta\). Hence there are four sets of \((\alpha, \beta)\). -
Question 77 of 158
77. Question
The number of integral values of \(k\) for which the equation \(7 \cos x+5\) \(\sin x=2 k+1\) has a solution is [2002S]
Hint
(b) We know, \(-\sqrt{a^{2}+b^{2}} \leq a \cos \theta+b \sin \theta \leq \sqrt{a^{2}+b^{2}}\)
\(\Rightarrow-\sqrt{74} \leq 7 \cos x+5 \sin x \leq \sqrt{74}\)
\(\Rightarrow-\sqrt{74} \leq 2 k+1 \leq \sqrt{74} \Rightarrow-8.6 \leq 2 k+1 \leq 8.6\)
\(\Rightarrow-4.8 \leq k \leq 3.8\)
Hence, \(k\) can take only 8 integral values. -
Question 78 of 158
78. Question
The number of distinct real roots of \(\left|\begin{array}{ccc}\sin x & \cos x & \cos x \\ \cos x & \sin x & \cos x \\ \cos x & \cos x & \sin x\end{array}\right|=0\) in the interval \(-\frac{\pi}{4} \leq x \leq \frac{\pi}{4}\) is [2001S]
Hint
(c) To simplify the det. let \(\sin x=a ; \cos x=b\), then equation becomes
\(
\left|\begin{array}{lll}
a & b & b \\
b & a & b \\
b & b & a
\end{array}\right|=0
\)
\(
\begin{aligned}
&\left|\begin{array}{ccc}
a & b-a & 0 \\
b & a-b & b-a \\
b & 0 & a-b
\end{array}\right|=0\left[C_{2}-C_{1} ; C_{3}-C_{2}\right] \\
&\Rightarrow a(a-b)^{2}-(b-a)[b(a-b)-b(b-a)]=0 \\
&\Rightarrow a(a-b)^{2}-2 b(b-a)(a-b)=0 \\
&\Rightarrow(a-b)^{2}(a-2 b)=0 \Rightarrow(a=b) \text { or } a=2 b \\
&\therefore \frac{a}{b}=1 \text { or } \frac{a}{b}=2 \\
&\Rightarrow \tan x=1 \text { or } \tan x=2
\end{aligned}
\)
But we have \(-\pi / 4 \leq x \leq \pi / 4\)
\(
\begin{aligned}
&\Rightarrow \tan (-\pi / 4) \leq \tan x \leq \tan (\pi / 4) \Rightarrow-1 \leq \tan x \leq 1 \\
&\therefore \tan x=1 \Rightarrow x=\pi / 4
\end{aligned}
\)
Hence, there is only one real not. -
Question 79 of 158
79. Question
In a triangle \(P Q R, \angle R=\pi / 2\). If \(\tan (P / 2)\) and \(\tan (Q / 2)\) are the roots of the equation \(a x^{2}+b x+c=0(a \neq 0)\) then. [1999 – 2 Marks]
Hint
(a) Given : In \(\triangle P Q R, \angle R=\pi / 2\)
\(
\Rightarrow \angle P+\angle Q=\pi / 2 \Rightarrow \frac{\angle P}{2}+\frac{\angle Q}{2}=\frac{\pi}{4}
\)
Also \(\tan P / 2\) and \(\tan Q / 2\) are roots of the equation \(a x^{2}+b x+c=0(a \neq 0)\)
\(
\therefore \tan P / 2+\tan Q / 2=-\frac{b}{a} ; \tan P / 2 \tan Q / 2=c / a
\)
Now \(\tan \left(\frac{P+Q}{2}\right)=\frac{\tan P / 2+\tan Q / 2}{1-\tan P / 2 \tan Q / 2}\)
\(
\begin{aligned}
&\Rightarrow \tan \frac{\pi}{4}=\frac{-b / a}{1-c / a} \Rightarrow 1-\frac{c}{a}=-\frac{b}{a} \\
&\Rightarrow a-c=-b \Rightarrow a+b=c
\end{aligned}
\) -
Question 80 of 158
80. Question
\(\sec ^{2} \theta=\frac{4 x y}{(x+y)^{2}}\) is true if and only if [1996 – 1 Mark]
Hint
(b) Given: \(\sec ^{2} \theta=\frac{4 x y}{(x+y)^{2}}\)
But \(\sec ^{2} \theta \geq 1 \Rightarrow \frac{4 x y}{(x+y)^{2}} \geq 1\)
\(
\Rightarrow 4 x y \geq x^{2}+y^{2}+2 x y
\)
\(
\Rightarrow x^{2}+y^{2}-2 x y \leq 0 \Rightarrow(x-y)^{2} \leq 0
\)
\(\Rightarrow x=y\), because perfect square of real number can not be negative.
Also \(x \neq 0\), otherwise \(\sec ^{2} \theta\) will become indeterminate. -
Question 81 of 158
81. Question
The general values of \(\theta\) satisfying the equation \(2 \sin ^{2} \theta-3 \sin \theta-2=0\) is [1995S]
Hint
\(
\begin{aligned}
&\text { (d) } 2 \sin ^{2} \theta-3 \sin \theta-2=0 \\
&\Rightarrow(2 \sin \theta+1)(\sin \theta-2)=0 \\
&\Rightarrow \sin \theta=-\frac{1}{2} \quad[\because \sin \theta-2=0, \text { is not possible }] \\
&\Rightarrow \quad \sin \theta=\sin (-\pi / 6) \text { and } \sin (7 \pi / 6) \\
&\Rightarrow \quad \theta=n \pi+(-1)^{n}(-\pi / 6) \text { and } n \pi+(-1)^{n} 7 \pi / 6 \\
&\Rightarrow \text { Thus, } \theta=n \pi+(-1)^{n} 7 \pi / 6
\end{aligned}
\) -
Question 82 of 158
82. Question
Let \(n\) be a positive integer such that \(\sin \frac{\pi}{2 n}+\cos \frac{\pi}{2 n}=\frac{\sqrt{n}}{2}\). Then [1994]
Hint
(d) \(\sin \frac{\pi}{2 n}+\cos \frac{\pi}{2 n}=\frac{\sqrt{n}}{2}\)
\(\Rightarrow \sin ^{2} \frac{\pi}{2 n}+\cos ^{2} \frac{\pi}{2 n}+2 \sin \frac{\pi}{2 n} \cos \frac{n}{2 n}=\frac{n}{4}\)
\(\Rightarrow 1+\sin \frac{\pi}{n}=\frac{n}{4} \Rightarrow \sin \frac{\pi}{n}=\frac{n-4}{4}\)
For \(n=2\) the given equation is not satisfied.
Considering \(n>1\) and \(n \neq 2,0<\sin \frac{\pi}{n}<1\)
\(
\Rightarrow 0<\frac{n-4}{4}<1 \Rightarrow 4<n<8 .
\) -
Question 83 of 158
83. Question
Number of solutions of the equation [1993 – 1 Mark]
\(\tan x+\sec x=2 \cos x \text { lying in the interval }[0,2 \pi] \text { is : }\)
Hint
\(
\begin{aligned}
&\text { (c) } \tan x+\sec x=2 \cos x\\
&\Rightarrow \frac{\sin x}{\cos x}+\frac{1}{\cos x}=2 \cos x\\
&\Rightarrow \sin x+1=2 \cos ^{2} x \Rightarrow 2 \sin ^{2} x+\sin x-1=0\\
&\Rightarrow(2 \sin x-1)(\sin x+1)=0 \Rightarrow \sin x=\frac{1}{2},-1\\
&\Rightarrow x=\frac{\pi}{6}, \frac{5 \pi}{6}, \frac{3 \pi}{2} \in[0,2 \pi]
\end{aligned}
\)But for \(x=\frac{3 \pi}{2}\), given eq. is not defined, Hence, there are only 2 solutions.
-
Question 84 of 158
84. Question
The equation \((\cos p-1) x^{2}+(\cos p) x+\sin p=0\)
In the variable \(x\), has real roots. Then \(p\) can take any value in the interval [1990 – 2 Marks]Hint
(d) \((\cos p-1) x^{2}+(\cos p) x+\sin p=0\)
For real roots \(D \geq 0\)
\(
\begin{aligned}
& \Rightarrow \cos ^{2} p-4 \sin p(\cos p-1) \geq 0 \\
& \Rightarrow \cos ^{2} p-4 \sin p \cos p+4 \sin ^{2} p+4 \sin p-4 \sin ^{2} p \geq 0 \\
& \Rightarrow(\cos p-2 \sin p)^{2}+4 \sin p(1-\sin p) \geq 0 \\
\text { Since, } p &(\cos p-2 \sin p)^{2} \geq 0 \text { and } 1-\sin p \geq 0 \\
\therefore D \geq 0, & \forall p \in(0, \pi)
\end{aligned}
\) -
Question 85 of 158
85. Question
The general solution of \(\sin x-3 \sin 2 x+\sin 3 x=\cos x-3 \cos 2 x+\cos 3 x\) is [1989 – 2 Marks]
Hint
(b) \(\sin x-3 \sin 2 x+\sin 3 x=\cos x-3 \cos 2 x+\cos 3 x\)
\(\Rightarrow 2 \sin 2 x \cos x-3 \sin 2 x=2 \cos 2 x \cos x-3 \cos 2 x\)
\(\Rightarrow \sin 2 x(2 \cos x-3)=\cos 2 x(2 \cos x-3)\)
\(\Rightarrow \sin 2 x=\cos 2 x \quad[\because \cos x \neq 3 / 2]\)
\(\Rightarrow \tan 2 x=1 \Rightarrow 2 x=n \pi+\pi / 4\)
\(\Rightarrow x=\frac{n \pi}{2}+\frac{\pi}{8}\) -
Question 86 of 158
86. Question
The value of the expression \(\sqrt{3} \operatorname{cosec} 20^{\circ}-\sec 20^{\circ}\) is equal to [1988 – 2 Marks]
Hint
(c) \(\sqrt{3} \operatorname{cosec} 20^{\circ}-\sec 20^{\circ}\)
\(
\begin{aligned}
&=\frac{\sqrt{3}}{\sin 20^{\circ}}-\frac{1}{\cos 20^{\circ}}=\frac{\sqrt{3} \cos 20^{\circ}-\sin 20^{\circ}}{\sin 20^{\circ} \cos 20^{\circ}} \\
&=4\left[\frac{\left.\frac{\sqrt{3}}{2} \cos 20^{\circ}-\frac{1}{2} \sin 20^{\circ}\right]}{2 \sin 20^{\circ} \cos 20^{\circ}}\right] \\
&=4\left[\frac{\sin 60^{\circ} \cos 20^{\circ}-\cos 60^{\circ} \sin 20^{\circ}}{\sin \left(2 \times 20^{\circ}\right)}\right] \\
&=\frac{4 \sin 40^{\circ}}{\sin 40^{\circ}}=4
\end{aligned}
\) -
Question 87 of 158
87. Question
The general solution of the trigonometric equation \(\sin x+\cos x=1\) is given by: [1981 – 2 Marks]
Hint
(c) Given: \(\sin x+\cos x=1\)
\(
\Rightarrow \frac{1}{\sqrt{2}} \sin x+\frac{1}{\sqrt{2}} \cos =\frac{1}{\sqrt{2}}
\)
\(
\begin{aligned}
&\Rightarrow \sin x \cos \frac{\pi}{4}+\cos x \sin \frac{\pi}{4}=\sin \frac{\pi}{4} \\
&\Rightarrow \sin (x+\pi / 4)=\sin \pi / 4 \\
&\Rightarrow x+\pi / 4=n \pi+(-1)^{n} \pi / 4, n \in Z \text { (the set of integers) } \\
&\Rightarrow x=n+(-1)^{n} \pi / 4-\pi / 4
\end{aligned}
\)
where \(n=0, \pm 1, \pm 2, \ldots\) -
Question 88 of 158
88. Question
The equation \(2 \cos ^{2} \frac{x}{2} \sin ^{2} x=x^{2}+x^{-2} ; 0<x \leq \frac{\pi}{2}\) has
Hint
(a) Given :
\(2 \cos ^{2}\left(\frac{x}{2}\right) \sin ^{2} x=x^{2}+\frac{1}{x^{2}}\) where \(0<x \leq \frac{\pi}{2}\)
\(
\begin{aligned}
\text { LHS }=& 2 \cos ^{2} \frac{x}{2} \sin ^{2} x=(1+\cos x) \sin ^{2} x \\
& \because 1+\cos x<2 \text { and } \sin ^{2} x \leq 1 \text { for } 0<x \leq \frac{\pi}{2} \\
\therefore(1+\cos x) \sin ^{2} x<2
\end{aligned}
\)
And R.H.S. \(=x^{2}+\frac{1}{x^{2}} \geq 2\)
Thus for \(0<x \leq \frac{\pi}{2}\), given equation is not possible -
Question 89 of 158
89. Question
The number of distinct solutions of the equation \(\frac{5}{4} \cos ^{2} 2 x+\cos ^{4} x+\sin ^{4} x+\cos ^{6} x+\sin ^{6} x=2\) in the interval \([0,2 \pi]\) is [Adv. 2015]
Hint
\(
\begin{aligned}
&\text { (b) } \frac{5}{4} \cos ^{2} 2 x+\cos ^{4} x+\sin ^{4} x+\cos ^{6} x+\sin ^{6} x=2 \\
&\Rightarrow \quad \frac{5}{4} \cos ^{2} 2 x+1-\frac{1}{2} \sin ^{2} 2 x+1-\frac{3}{4} \sin ^{2} 2 x=2 \\
&\Rightarrow \quad \frac{5}{4}\left(\cos ^{2} 2 x-\sin ^{2} 2 x\right)=0 \Rightarrow \cos 4 x=0 \\
&\Rightarrow \quad 4 x=(2 n+1) \frac{\pi}{2} \text { or } \quad x=(2 n+1) \frac{\pi}{8}
\end{aligned}
\)
For \(x \in[0,2 \pi]\), \(\mathrm{n}\) can take values 0 to 7 Hence, there are 8 solutions. -
Question 90 of 158
90. Question
The positive integer value of \(n>3\) satisfying the equation \(\frac{1}{\sin \left(\frac{\pi}{n}\right)}=\frac{1}{\sin \left(\frac{2 \pi}{n}\right)}+\frac{1}{\sin \left(\frac{3 \pi}{n}\right)}\) is [2011]
Hint
\(
\text { (c) } \frac{1}{\sin \frac{\pi}{n}}-\frac{1}{\sin \frac{3 \pi}{n}}=\frac{1}{\sin \frac{2 \pi}{n}}
\)
\(
\begin{aligned}
&\Rightarrow \frac{\sin \frac{3 \pi}{n}-\sin \frac{\pi}{n}}{\sin \frac{\pi}{n} \sin \frac{3 \pi}{n}}=\frac{1}{\sin \frac{2 \pi}{n}} \Rightarrow \frac{2 \cos \frac{2 \pi}{n} \sin \frac{\pi}{n}}{\sin \frac{\pi}{n} \sin \frac{3 \pi}{n}}=\frac{1}{\sin \frac{2 \pi}{n}} \\
&\Rightarrow \quad 2 \sin \frac{2 \pi}{n} \cos \frac{2 \pi}{n}=\sin \frac{3 \pi}{n} \Rightarrow \sin \frac{4 \pi}{n}-\sin \frac{3 \pi}{n}=0 \\
&\Rightarrow \quad 2 \cos \frac{7 \pi}{2 n} \sin \frac{\pi}{2 n}=0 \Rightarrow \cos \frac{7 \pi}{2 n}=0 \text { or } \sin \frac{\pi}{2 n}=0 \\
&\Rightarrow \quad \frac{7 \pi}{2 n}=(2 k+1) \frac{\pi}{2} \text { or } \frac{\pi}{2 n}=2 \mathrm{k} \pi, \text { where } k \in Z \\
&\Rightarrow \quad n=\frac{7}{2 k+1} \text { or } \mathrm{n}=\frac{1}{4 k}
\end{aligned}
\)
( \(n=\frac{1}{4 k}\) not possible for any integral value of \(k\) )
As \(n>3\); for \(k=0\), we get \(n=7\). -
Question 91 of 158
91. Question
Two parallel chords of a circle of radius 2 are at a distance \(\sqrt{3}+1\) apart. If the chords subtend at the center, angles of \(\frac{\pi}{k}\) and \(\frac{2 \pi}{k}\), where \(k>0\), then the value of \([k]\) is [2010]
[Note : \([k]\) denotes the largest integer less than or equal to \(k\) ]Hint
(d) From the figure,
\(
2 \cos \frac{\pi}{k}+2 \cos \frac{\pi}{2 k}=\sqrt{3}+1
\)
\(
\begin{gathered}
\Rightarrow 2 \times 2 \cos ^{2} \frac{\pi}{2 k}+2 \cos \frac{\pi}{2 k}-2 \\
=\sqrt{3}+1
\end{gathered}
\)
\(
\Rightarrow 4 \cos ^{2} \frac{\pi}{2 k}+2 \cos \frac{\pi}{2 k}-(3+\sqrt{3})=0
\)
\(
\begin{aligned}
&\Rightarrow \cos \frac{\pi}{2 k}=\frac{-2 \pm \sqrt{4+16(3+\sqrt{3})}}{8}=\frac{-1 \pm \sqrt{13+4 \sqrt{3}}}{4} \\
&=\frac{-1 \pm(2 \sqrt{3}+1)}{4}=\frac{\sqrt{3}}{2} \text { or }-\left(\frac{\sqrt{3}+1}{2}\right)
\end{aligned}
\)
As \(\frac{\pi}{2 k}\) is an acute angle, \(\cos \frac{\pi}{2 k}=\frac{\sqrt{3}}{2}=\cos \frac{\pi}{6} \Rightarrow k=3\)
-
Question 92 of 158
92. Question
The number of values of \(\theta\) in the interval, \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) such that \(\theta \neq \frac{\mathrm{n} \pi}{5}\) for \(\mathrm{n}=0, \pm 1, \pm 2\) and \(\tan \theta=\cot 5 \theta\) as well as \(\sin 2 \theta=\cos 4 \theta\) is [2010]
Hint
(b) \(\tan \theta=\cot 5 \theta, \theta \neq \frac{n \pi}{5}\)
\(
\begin{aligned}
&\Rightarrow \cos \theta \cos 5 \theta-\sin 5 \theta \sin \theta=0 \Rightarrow \cos 6 \theta=0 \\
&\Rightarrow 6 \theta=\frac{-5 \pi}{2}, \frac{-3 \pi}{2}, \frac{-\pi}{2}, \frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2} \\
&\Rightarrow \theta=\frac{-5 \pi}{12}, \frac{-\pi}{4}, \frac{-\pi}{12}, \frac{\pi}{12}, \frac{\pi}{4}, \frac{5 \pi}{12}
\end{aligned}
\)
Again \(_{\sin 2 \theta} 2=\cos 4 \theta=1-2 \sin ^{2} 2 \theta\)
\(
\begin{aligned}
&\Rightarrow 2 \sin ^{2} 2 \theta+\sin 2 \theta-1=0 \Rightarrow \sin 2 \theta=-1, \frac{1}{2} \\
&\Rightarrow 2 \theta=\frac{-\pi}{2}, \frac{\pi}{6}, \frac{5 \pi}{6} \Rightarrow \theta=\frac{-\pi}{4}, \frac{\pi}{12}, \frac{5 \pi}{12}
\end{aligned}
\)
So, common solutions are \(\theta=\frac{-\pi}{4}, \frac{\pi}{12}\) and \(\frac{5 \pi}{12}\)
\(\therefore\) Number of solutions \(=3\). -
Question 93 of 158
93. Question
The number of all possible values of \(\theta\) where \(0<\theta<\pi\), for which the system of equations
\(
\begin{gathered}
(y+z) \cos 3 \theta=(x y z) \sin 3 \theta \\
x \sin 3 \theta=\frac{2 \cos 3 \theta}{y}+\frac{2 \sin 3 \theta}{z} \\
(x y z) \sin 3 \theta=(y+2 z) \cos 3 \theta+y \sin 3 \theta
\end{gathered}
\)
have a solution \(\left(x_{0}, y_{0}, z_{0}\right)\) with \(y_{0} z_{0} \neq 0\), is [2010]Hint
(d) Given equations are
\(x y z \sin 3 \theta=(y+z) \cos 3 \theta\)…(i)
\(x y z \sin 3 \theta=2 z \cos 3 \theta+2 y \sin 3 \theta \quad\)…(ii)
\(x y z \sin 3 \theta=(y+2 z) \cos 3 \theta+y \sin 3 \theta\)…(iii)
On subtracting eq. (ii) from (i), we get
\((\cos 3 \theta-2 \sin \theta) y-(\cos 3 \theta) z=0\)…(iv)
On subtracting eq. (i) from (iii), we get \((\sin 3 \theta) y+(\cos 3 \theta) z=0\)…(v)
Eq. (iv) and (v) from homogeneous system of linear equation.
But \(y \neq 0, z \neq 0\)
\(
\begin{aligned}
&\therefore \frac{\cos 3 \theta-2 \sin 3 \theta}{\sin 3 \theta}=-\frac{\cos 3 \theta}{\cos 3 \theta} \Rightarrow \cos 3 \theta=\sin 3 \theta \\
&\Rightarrow \tan 3 \theta=1 \Rightarrow 3 \theta=n \pi+\frac{\pi}{4} \Rightarrow \theta=(4 n+1) \frac{\pi}{12}, n \in Z \\
&\text { For } \theta \in(0, \pi) \Rightarrow \theta=\frac{\pi}{12}, \frac{5 \pi}{12}, \frac{3 \pi}{4}
\end{aligned}
\)
Three such solutions are possible. -
Question 94 of 158
94. Question
The number of distinct solutions of the equation, \(\log _{1 / 2}|\sin x|=2-\log _{1 / 2}|\cos x|\) in the interval \([0,2 \pi]\), is ____ [Main Jan. 9,2020(I)]
Hint
\(
\begin{aligned}
&\text { (c) } \log _{1 / 2}|\sin x|=2-\log _{1 / 2}|\cos x| \\
&\Rightarrow \quad \log _{1 / 2}|\sin x \cos x|=2 \\
&\Rightarrow \quad|\sin x \cos x|=\frac{1}{4} \\
&\Rightarrow \quad \sin 2 x=\pm \frac{1}{2}
\end{aligned}
\)\(\text { Hence, total number of solutions }=8 \text {. }\)
-
Question 95 of 158
95. Question
Let \(a, b, c\) be three non-zero real numbers such that the equation: \(\sqrt{3} a \cos x+2 b \sin x=c, x \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\), has two distinct real roots \(\alpha\) and \(\beta\) with \(\alpha+\beta=\frac{\pi}{3}\). Then, the value of \(\frac{b}{a}\) is ____ [Adv. 2018]
Hint
(c) Given : \(\sqrt{3} a \cos x+2 b \sin x=c\)
which has two roots \(\alpha\) and \(\beta\), such that \(\alpha+\beta=\frac{\pi}{3}\)
\(\therefore \sqrt{3} \mathrm{a} \cos \alpha+2 \mathrm{~b} \sin \alpha=\mathrm{c}\)…(i)
and \(\sqrt{3}\) a \(\cos \beta+2 b \sin \beta=c\)…(ii)
On subtracting equation (ii) from (i),
\(
\begin{aligned}
& \sqrt{3} \text { a }(\cos \alpha-\cos \beta)+2 b(\sin \alpha-\sin \beta)=0 \Rightarrow \\
&-\sqrt{3} \mathrm{a} 2 \sin \frac{\alpha+\beta}{2} \sin \frac{\alpha-\beta}{2}+2 b \cdot 2 \cos \frac{\alpha+\beta}{2} \sin \frac{\alpha-\beta}{2}=0 \\
\Rightarrow &-2 \sqrt{3} \mathrm{a} \sin \frac{\pi}{6}+4 \mathrm{~b} \cos \frac{\pi}{6}=0 \\
\Rightarrow &-2 \sqrt{3} \mathrm{a} \times \frac{1}{2}+4 \mathrm{~b} \frac{\sqrt{3}}{2}=0 \Rightarrow \frac{\mathrm{b}}{\mathrm{a}}=\frac{1}{2}=0.5
\end{aligned}
\) -
Question 96 of 158
96. Question
The real roots of the equation \(\cos ^{7} x+\sin ^{4} x=1\) in the interval \((-\pi\), \(\pi)\) are \(\ldots, \ldots\), and ____ [ 1997 – 2 Marks]
Hint
(a) \(\cos ^{7} x=1-\sin ^{4} x=\left(1-\sin ^{2} x\right)\left(1+\sin ^{2} x\right)=\cos ^{2} x\left(1+\sin ^{2} x\right)\)
\(\therefore \cos x=0 \Rightarrow x=\pi / 2,-\pi / 2\)
or \(\cos ^{5} x=1+\sin ^{2} x \Rightarrow \cos ^{5} x-\sin ^{2} x=1\)
Now maximum value of each \(\cos x\) or \(\sin x\) is 1.
Hence the above equation will hold when
\(\cos x=1\) and \(\sin x=0\)
Both these imply \(x=0\)
\(
\therefore x=-\frac{\pi}{2}, \frac{\pi}{2}, 0
\) -
Question 97 of 158
97. Question
General value of \(\theta\) satisfying the equation \(\tan ^{2} \theta+\sec 2 \theta=1\) is _____ [1996 – 1 Mark]
Hint
(b)
\(
\begin{aligned}
&\tan ^{2} \theta+\sec 2 \theta=1 \\
&\left.t^{2}+\frac{1+t^{2}}{1-t^{2}}=1, \text { [but } t=\tan \theta\right] \\
&\Rightarrow \quad t^{2}\left(t^{2}-3\right)=0 \Rightarrow \tan \theta=0, \pm \sqrt{3} \\
&\Rightarrow \quad \theta=n \pi \text { and } \theta=n \pi \pm \pi / 3
\end{aligned}
\) -
Question 98 of 158
98. Question
The sides of a triangle inscribed in a given circle subtend angles \(\alpha, \beta\) and \(\gamma\) at the centre. The minimum value of the arithmetic mean of \(\cos \left(\alpha+\frac{\pi}{2}\right), \cos \left(\beta+\frac{\pi}{2}\right)\) and \(\left.\cos (\left(\alpha+\frac{\pi}{2}\right) \cos \beta+\frac{\pi}{2}\right)\) is equal to ____ [1987 – 2 Marks]
Hint
(a) We know that A.M. \(\geq\) G.M.
\(\Rightarrow\) Minimum value of \(\mathrm{AM}\). is obtained when \(\mathrm{AM}=\mathrm{GM}\)
\(\Rightarrow\) The quantities whose \(\mathrm{AM}\) is being taken are equal
i.e., \(\cos \left(\alpha+\frac{\pi}{2}\right)=\cos \left(\beta+\frac{\pi}{2}\right)\)
\(
=\cos \left(\gamma+\frac{\pi}{2}\right)
\)
\(\Rightarrow \sin \alpha=\sin \beta=\sin \gamma\)
Also \(\alpha+\beta+\gamma=360^{\circ} \Rightarrow \alpha=\beta=\gamma=120^{\circ}=2 \pi / 3\)
\(\therefore\) Min value of A.M.
\(
\begin{aligned}
&=\frac{\cos \left(\frac{2 \pi}{3}+\frac{\pi}{2}\right)+\cos \left(\frac{2 \pi}{3}+\frac{\pi}{2}\right)+\cos \left(\cos \left(\frac{2 \pi}{3}+\frac{\pi}{2}\right)\right)}{3} \\
&=\frac{-3 \sin \frac{2 \pi}{3}}{3}=-\frac{\sqrt{3}}{2}
\end{aligned}
\)
-
Question 99 of 158
99. Question
The set of all \(x\) in the interval \([0, \pi]\) for which \(2 \sin ^{2} x-3 \sin x+1 \geq\) 0 , is ____ [1987 – 2 Marks]
Hint
(c) Given: \(2 \sin ^{2} x-3 \sin x+1 \geq 0\)
\(\Rightarrow(2 \sin x-1)(\sin x-1) \geq 0\)
\(\Rightarrow\left(\sin x-\frac{1}{2}\right)(\sin x-1) \geq 0 \Rightarrow \sin x \leq \frac{1}{2}\) or \(\sin x \geq 1\)
But we know that \(0 \leq \sin x \leq 1\) for \(x \in[0, \pi]\)
\(
\begin{aligned}
&\Rightarrow \quad 0 \leq \sin x \leq \frac{1}{2} \text { or } \sin x=1 \\
&\Rightarrow \quad x \in[0, \pi / 6] \cup[5 \pi / 6, \pi] \text { or } x=\pi / 2
\end{aligned}
\)
On combining, we get \(x \in[0, \pi / 6] \cup\{\pi / 2\} \cup[5 \pi / 6, \pi]\)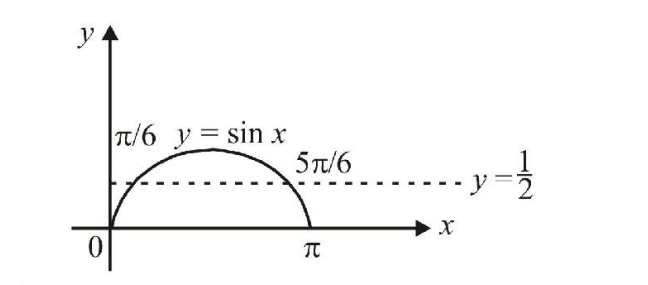
-
Question 100 of 158
100. Question
The solution set of the system of equations \(\mathrm{x}+\mathrm{y}=\frac{2 \pi}{3}\), \(\cos x+\cos y=\frac{3}{2}\), where \(x\) and \(y\) are real, is ___ [1987 – 2 Marks]
Hint
(a) Given equations: \(x+y=2 \pi / 3\)
and \(\cos x+\cos y=3 / 2\)
From eq. (ii), \(2 \cos \frac{x+y}{2} \cos \frac{x-y}{2}=\frac{3}{2}\)
\(
\begin{aligned}
&\Rightarrow \quad 2 \cos \frac{\pi}{3} \cos \frac{x-y}{2}=\frac{3}{2} \quad \text { [From eq. (i)] } \\
&\Rightarrow \quad 2 . \frac{1}{2} \cos \frac{x-y}{2}=\frac{3}{2} \Rightarrow \cos \frac{x-y}{2}=\frac{3}{2}
\end{aligned}
\)
which is not possible because \(-1 \leq \cos \theta \leq 1\).
Hence, solution of given equations is \(\phi\). -
Question 101 of 158
101. Question
There exists a value of \(\theta\) between 0 and \(2 \pi\) that satisfies the equation \(\sin ^{4} \theta-2 \sin ^{2} \theta-1=0\). The statement is True or False? [1984 – 1 Mark]
Hint
(b) (False) Given : \(\sin ^{4} \theta-2 \sin ^{2} \theta-1=0\)
\(
\therefore \quad D=4+4=8
\)
\(
\because \sin ^{2} \theta=\frac{2 \pm \sqrt{8}}{2}=1 \pm \sqrt{2} \text {. }
\)
\(\because\) value of \(\sin ^{2} \theta\) is +ve, \(\quad \therefore \sin ^{2} \theta=\sqrt{2}+1\)
\(\because-1 \leq \sin \theta \leq 1, \quad \therefore \sin ^{2} \theta \neq \sqrt{2}+1\)
Hence, there is no value of \(\theta\), which satisfy the given equation. Hence, the statement is false. -
Question 102 of 158
102. Question
Let \(\alpha\) and \(\beta\) be non-zero real numbers such that \(2(\cos \beta-\cos \alpha)+\cos \alpha\) \(\cos \beta=1\). Then which of the following is/are true? [Adv. 2017]
Hint
(a, c) If we consider \(\tan \alpha / 2=x\) and \(\tan \beta / 2=y\), then \(2(\cos \beta-\cos \alpha)+\cos \alpha \cos \beta=1\)
\(
\begin{aligned}
&\Rightarrow \quad 2\left[\frac{1-y^{2}}{1+y^{2}}-\frac{1-x^{2}}{1+x^{2}}\right]=1-\frac{\left(1-x^{2}\right)\left(1-y^{2}\right)}{\left(1+x^{2}\right)\left(1+y^{2}\right)} \\
&\Rightarrow \quad 2\left[\left(1+x^{2}\right)\left(1-y^{2}\right)-\left(1-x^{2}\right)\left(1+y^{2}\right)\right] \\
&\Rightarrow \quad 4\left(x^{2}-y^{2}\right)=2\left(x^{2}+y^{2}\right) \\
&\Rightarrow \quad x^{2}=3 y^{2} \Rightarrow x=\pm \sqrt{3} y \\
&\Rightarrow \quad \tan \frac{\alpha}{2} \pm \sqrt{3} \tan \frac{\beta}{2}=0
\end{aligned}
\) -
Question 103 of 158
103. Question
The number of points in \((-\infty , \infty)\) for which \(x^{2}-x \sin x-\cos x=0\), is [Adv. 2013]
Hint
(c) Let \(f(x)=x^{2}-x \sin x-\cos x\)
\(\therefore f(x)=2 x-x \cos x=x(2-\cos x)\)
\(\therefore f\) is increasing on \((0, \infty)\) and decreasing on \((-\infty, 0)\)
Also \(\lim _{x \rightarrow \infty} f(x)=\infty, \lim _{x \rightarrow-\infty} f(x)=\infty\) and \(f(0)=-1\)
\(\therefore \quad y=f(x)\) meets \(x\)-axis twice.
i.e., \(f(x)=0\) has two points in \((-\infty, \infty)\). -
Question 104 of 158
104. Question
\(\text { For } 0<\theta<\frac{\pi}{2} \text {, the solution (s) of }\)
\(\sum_{m = 1}^{6} \operatorname{cosec}\left(\theta+\frac{(m-1) \pi}{4}\right) \operatorname{cosec}\left(\theta+\frac{m \pi}{4}\right)=4 \sqrt{2}\) is (are) [2009]Hint
(c,d) Given:
\(
\begin{aligned}
&\frac{1}{\sin (\pi / 4)}\left[\frac{\sin (\theta+\pi / 4-\theta)}{\sin \theta \sin (\theta+\pi / 4)}+\frac{\sin (\theta+\pi / 2-(\theta+\pi / 4))}{\sin (\theta+\pi / 4) \cdot \sin (\theta+\pi / 2)}+\ldots+\right. \\
&\left.\frac{\sin ((\theta+3 \pi / 2)-(\theta+5 \pi / 4))}{\sin (\theta+3 \pi / 2) \cdot \sin (\theta+5 \pi / 4)}\right]=4 \sqrt{2}
\end{aligned}
\)
Using Formula for splitting numerator of first term:
\(
\sin (\theta+\pi / 4-\theta)=\sin (\theta+\pi / 4) \cos (\theta)-\cos (\theta+\pi / 4) \sin (\theta)
\)
\(
\begin{aligned}
&\Rightarrow \sqrt{2}[\cot \theta-\cot (\theta+\pi / 4)+\cot (\theta+\pi / 4)-\cot (\theta+\pi / 2)+\ldots+\cot (\theta+5 \pi / 4)-\cot (\theta+ \\
&3 \pi / 2)]=4 \sqrt{2}
\end{aligned}
\)
\(
\Rightarrow \tan \theta+\cot \theta=4 \Rightarrow \tan \theta=2 \pm \sqrt{3}
\)
\(
\Rightarrow \theta=\frac{\pi}{12} \text { or } \frac{5 \pi}{12}
\) -
Question 105 of 158
105. Question
The number of values of \(x\) in the interval \([0,5 \pi]\) satisfying the equation \(3 \sin ^{2} x-7 \sin x+2=0\) is [1998 – 2 Marks]
Hint
(c) \(3 \sin ^{2} x-7 \sin x+2=0\), put \(\sin x=s\)
\(\Rightarrow(s-2)(3 s-1)=0\)
\(\because \quad s=2\) is not possible, \(\quad \therefore s=1 / 3 \Rightarrow \sin x=\frac{1}{3}\)
Number of solutions of \(\sin x=\frac{1}{3}\) from the following graph is 6 between \([0,5 \pi]\)
-
Question 106 of 158
106. Question
The values of \(\theta\) lying between \(\theta=0\) and \(\theta=\pi / 2\) and satisfying the equation
[1988 – 2 Marks]\(\left|\begin{array}{ccc}1+\sin ^{2} \theta & \cos ^{2} \theta & 4 \sin 4 \theta \\ \sin ^{2} \theta & 1+\cos ^{2} \theta & 4 \sin 4 \theta \\ \sin ^{2} \theta & \cos ^{2} \theta & 1+4 \sin 4 \theta\end{array}\right|=0\) are
Hint
\(
\text { (a, c) }\left|\begin{array}{rrr}
1+\sin ^{2} \theta & \cos ^{2} \theta & 4 \sin 4 \theta \\
\sin ^{2} \theta & 1+\cos ^{2} \theta & 4 \sin 4 \theta \\
\sin ^{2} \theta & \cos ^{2} \theta & 1+4 \sin 4 \theta
\end{array}\right|=0
\)
Applying \(C_{1} \rightarrow C_{1}+C_{2}\)
\(
\left|\begin{array}{rrr}
2 & \cos ^{2} \theta & 4 \sin 4 \theta \\
2 & 1+\cos ^{2} \theta & 4 \sin 4 \theta \\
1 & \cos ^{2} \theta & 1+4 \sin 4 \theta
\end{array}\right|=0
\)
Applying \(R_{1} \rightarrow R_{1}-R_{2} ; R_{2} \rightarrow R_{2}-R_{3}\)
\(
\left|\begin{array}{rrr}
0 & -1 & 0 \\
1 & 1 & -1 \\
1 & \cos ^{2} \theta & 1+4 \sin 4 \theta
\end{array}\right|=0
\)
\(
\begin{aligned}
&\Rightarrow \quad[1+4 \sin 4 \theta+1]=0 \\
&\Rightarrow \quad 2(1+2 \sin 4 \theta)=0 \Rightarrow \sin 4 \theta=-\frac{1}{2} \\
&\Rightarrow 4 \theta=\pi+\pi / 6 \text { or } 2 \pi-\pi / 6 \\
&\Rightarrow 4 \theta=7 \pi / 6 \text { or } 11 \pi / 6 \\
&\Rightarrow \quad \theta=7 \pi / 24 \text { or } 11 \pi / 24
\end{aligned}
\) -
Question 107 of 158
107. Question
The number of all possible triplets \(\left(a_{1}, a_{2}, \mathrm{a}_{3}\right)\) such that \(a_{1}+a_{2} \cos (2 x)\) \(+a_{3} \sin ^{2}(x)=0\) for all \(x\) is [1987-2 Marks]
Hint
(d) \(a_{1}+a_{2} \cos 2 x+a_{3} \sin ^{2} x=0, \forall x\)
For \(x=0\) and \(x=\pi / 2\), we get \(a_{1}+a_{2}=0\)….(i)
and \(a_{1}-a_{2}+a_{3}=0\)
\(\Rightarrow a_{2}=-a_{1}\) and \(a_{3}=-2 a_{1}\)
\(\therefore\) The given equation becomes
\(
\begin{aligned}
&a_{1}-a_{1} \cos 2 x-2 a_{1} \sin ^{2} x=0, \quad \forall x \\
&\Rightarrow a_{1}\left(1-\cos 2 x-2 \sin ^{2} x\right)=0, \forall x \\
&\Rightarrow a_{1}\left(2 \sin ^{2} x-2 \sin ^{2} x\right)=0, \forall x
\end{aligned}
\)
The above is satisfied for all values of \(a_{1}\).
Hence, infinite number of triplets \(\left(a_{1},-a_{1},-2 a_{1}\right)\) are possible. -
Question 108 of 158
108. Question
Let \(f(x)=\sin (\pi \cos x)\) and \(g(x)=\cos (2 \pi \sin x)\) be two functions defined for \(x>\) 0 . Define the following sets whose elements are written in the increasing order: [Adv. 2019]
\(
X=\left\{x: f^{\prime}(x)=0\right\}, \quad Y=\{x: f(x)=0\} \text {, }
\)
\(Z=[x: g(x)=0\}, W=\left[x: g^{\prime}(x)=0\right\}\).List – 1 contains the sets \(X, Y, Z\) and \(W\). List – II contains some information regarding these sets.
Column I Column II
(I) \(\quad X \quad(P) \supseteq\left\{\frac{\pi}{2}, \frac{3 \pi}{2}, 4 \pi, 7 \pi\right\}\)
(II) \(\quad Y \quad(Q)\) an arithmetic progression
(III) \(\quad Z \quad(R)\) not an arithmetic progression
(IV) \(\quad W \quad(S) \supseteq\left\{\frac{\pi}{6}, \frac{7 \pi}{6}, \frac{13 \pi}{6}\right\}\)
(T) \(\supseteq\left\{\frac{\pi}{3}, \frac{2 \pi}{3}, \pi\right\}\)
\((U) \supseteq\left\{\frac{\pi}{6}, \frac{3 \pi}{4}\right\}\)\(
\text { Which of the following is the only correct combination? }
\)Hint
\(
\begin{aligned}
&f(x)=\sin (\pi \cos x) \\
& X=\left\{x: f^{\prime}(x)=0\right\} \\
&f(x)=0 \Rightarrow \sin (\pi \cos x)=0 \Rightarrow \cos x=n \Rightarrow \cos x=1,-1,0 \Rightarrow x=\frac{n \pi}{2} \\
&X=\left\{\frac{n \pi}{2}: n \in N\right\}=\left\{\frac{\pi}{2}, \pi, \frac{3 \pi}{2}, 2 \pi \ldots .\right\} \\
&g(x)=\cos (2 \pi \sin x) \\
&Z=\{x: g(x)=0\} \\
&\cos (2 \pi \sin x)=0 \Rightarrow 2 \pi \sin x=(2 n+1) \frac{\pi}{2} \Rightarrow \sin x=\frac{(2 n+1)}{4} \\
&\sin x=-\frac{1}{4}, \frac{1}{4}, \frac{-3}{4}, \frac{3}{4} \\
&Z=\left\{n \pi \pm \sin -1\left(\frac{1}{4}\right), n \pi \pm \sin ^{-1}\left(\frac{3}{4}\right), n \in I\right\} \\
&Y=\{x: f(x)=0\} \\
&f(x)=\sin (\pi \cos x) \Rightarrow f^{\prime}(x)=\cos (\pi \cos x) \cdot(-\pi \sin x)=0 \\
&\sin x=0 \Rightarrow x=n \pi . \\
&\cos (\pi \cos x)=0 \pi \cos x=(2 n+1) \frac{\pi}{2} \Rightarrow \cos =\frac{(2 n+1)}{2} \Rightarrow \cos x=-\frac{1}{2}, \frac{1}{2} \\
&Y=\left\{n \pi, n \pi \pm \frac{\pi}{3}\right\}=\left\{\frac{\pi}{3}, \frac{2 \pi}{3}, \pi, \frac{4 \pi}{3}, \frac{5 \pi}{3}, 2 \pi, \ldots \ldots\right\} \\
&W=\left\{x: g^{\prime}(x)=0\right\}
\end{aligned}
\)\(
\begin{aligned}
&g(x)=\cos (2 \pi \sin x) \Rightarrow g^{\prime}(x)=-\sin (2 \pi \sin x) \cdot(2 \pi \cos x)=0 \\
&\cos x=0 \Rightarrow x=(2 n+1) \frac{\pi}{2} \\
&\sin (2 \pi \sin x)=0 \Rightarrow 2 \pi \sin x=n \pi \Rightarrow \sin x=\frac{n}{2}=-1,-\frac{1}{2}, 0, \frac{1}{2}, 1 \\
&W=\left\{\frac{n \pi}{2}, n \pi \pm \frac{\pi}{6}, n \in 1\right\}=\left\{\frac{\pi}{6}, \frac{\pi}{2}, \frac{5 \pi}{6}, \pi, \frac{7 \pi}{6}, \frac{3 \pi}{2}, \ldots . .\right\}
\end{aligned}
\) -
Question 109 of 158
109. Question
Let \(f(x)=\sin (\pi \cos x)\) and \(g(x)=\cos (2 \pi \sin x)\) be two functions defined for \(x>\) 0 . Define the following sets whose elements are written in the increasing order: [Adv. 2019]
\(
X=\left\{x: f^{\prime}(x)=0\right\}, \quad Y=\{x: f(x)=0\} \text {, }
\)
\(Z=[x: g(x)=0\}, W=\left[x: g^{\prime}(x)=0\right\}\).List – 1 contains the sets \(X, Y, Z\) and \(W\). List – II contains some information regarding these sets.
Column I Column II
(I) \(\quad X \quad(P) \supseteq\left\{\frac{\pi}{2}, \frac{3 \pi}{2}, 4 \pi, 7 \pi\right\}\)
(II) \(\quad Y \quad(Q)\) an arithmetic progression
(III) \(\quad Z \quad(R)\) not an arithmetic progression
(IV) \(\quad W \quad(S) \supseteq\left\{\frac{\pi}{6}, \frac{7 \pi}{6}, \frac{13 \pi}{6}\right\}\)
(T) \(\supseteq\left\{\frac{\pi}{3}, \frac{2 \pi}{3}, \pi\right\}\)
\((U) \supseteq\left\{\frac{\pi}{6}, \frac{3 \pi}{4}\right\}\)\(
\text { Which of the following is the only correct combination? }
\)Hint
(d)
\(
\begin{aligned}
&f^{\prime}(\mathrm{x})=0 \quad \Rightarrow \quad \cos (\pi \cos x)(-\pi \sin x)=0 \\
&\quad \Rightarrow \quad \cos (\pi \cos x)=0, \sin x=0 \\
&\Rightarrow \quad \pi \cos x=(2 n-1) \frac{\pi}{2}, x=n \pi \\
&\Rightarrow \quad \cos x=(2 n-1) \frac{1}{2}, x=\pi, 2 \pi, 3 \pi, \ldots \ldots \\
&\Rightarrow \quad \cos x=\frac{-1}{2}, \frac{1}{2} . \\
&\Rightarrow \quad x=\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3}, \frac{7 \pi}{3}, \frac{8 \pi}{3}, \frac{10 \pi}{3}, \frac{11 \pi}{3}, \frac{13 \pi}{3}, \ldots . . \\
&\therefore Y=\left\{\frac{\pi}{3}, \frac{2 \pi}{3}, \pi, \frac{4 \pi}{3}, \frac{5 \pi}{3}, 2 \pi, \ldots \ldots \ldots\right\} . \\
&\therefore \quad(\mathrm{II})-\mathrm{Q}, \mathrm{T} .
\end{aligned}
\) -
Question 110 of 158
110. Question
Find all values of \(\theta\) in the interval \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) satisfying the equation \((1-\tan \theta)(1+\tan \theta) \sec ^{2} \theta+2^{\tan ^{2} \theta}=0\) [1996 – 2 Marks]
Hint
Given : \((1-\tan \theta)(1+\tan \theta) \sec ^{2} \theta+2^{\tan ^{2} \theta}=0\) \(\Rightarrow \quad\left(1-\tan ^{2} \theta\right)\left(1+\tan ^{2} \theta\right)+2^{\tan ^{2} \theta}=0\)
Put \(\tan ^{2} \theta=t\)
\(\therefore \quad(1-t)(1+t)+2^{t}=0\) or \(1-t^{2}+2^{t}=0\)
It is clearly satisfied by \(t=3\).
As \(-8+8=0 \quad \therefore \quad \tan ^{2} \theta=3\)
\(\therefore \quad \theta=\pm \pi / 3\) in the given interval. -
Question 111 of 158
111. Question
Find the values of \(x \in(-\pi,+\pi)\) which satisfy the equation \(8^{\left(1+|\cos x|+\left|\cos ^{2} x\right|+\left|\cos ^{3} x\right|+\ldots \ldots\right)}=4^{3}\) [1984 – 2 Marks]
Hint
\(
\begin{aligned}
&8^{\left(1+|\cos x|+\left|\cos ^{2} x\right|+\left|\cos ^{3} x\right|+\ldots .\right)}=4^{3} \\
&\Rightarrow 2^{3\left(1+|\cos x|+\left|\cos ^{2} x\right|+\left|\cos ^{3} x\right|+\ldots\right)}=2^{6} \\
&\Rightarrow 3\left(1+|\cos x|+\left|\cos ^{2} x\right|+\left|\cos ^{3} x\right|+\ldots\right)=6 \\
&\Rightarrow 1+|\cos x|+\left|\cos ^{2} x\right|+\left|\cos ^{3} x\right|+\ldots .=2 \\
&\Rightarrow \frac{1}{1-|\cos x|}=2 \\
&\Rightarrow 1-\cos x=1 / 2 \Rightarrow|\cos x|=\frac{1}{2} \\
&\Rightarrow x=\pi / 3,-\pi / 3,2 \pi / 3,-2 \pi / 3, \ldots .
\end{aligned}
\)
The values of \(x \in(-\pi, \pi)\) are \(\pm \pi / 3, \pm 2 \pi / 3\). -
Question 112 of 158
112. Question
Find all the solution of \(4 \cos ^{2} x \sin x-2 \sin ^{2} x=3 \sin x\) [1983 – 2 Marks]
Hint
Given : \(4 \cos ^{2} x \sin x-2 \sin ^{2} x=3 \sin x\)
\(\Rightarrow 4 \cos ^{2} x \sin x-2 \sin ^{2} x-3 \sin x=0\)
\(\Rightarrow 4\left(1-\sin ^{2} x\right) \sin x-2 \sin ^{2} x-3 \sin x=0\)
\(\Rightarrow \sin x\left[4 \sin ^{2} x+2 \sin x-1\right]=0\)
\(\therefore \quad\) Either \(\sin x=0\) or \(4 \sin ^{2} x+2 \sin x-1=0\)
If \(\sin x=0\), then \(x=n \pi\)
\(\Rightarrow\) If \(4 \sin ^{2} x+2 \sin x-1=0\), then \(\sin x=\frac{-1 \pm \sqrt{5}}{4}\)
If \(\sin x=\frac{-1 \pm \sqrt{5}}{4}=\sin 18^{\circ}=\sin \frac{\pi}{10}\), then
\(x=n x+(-1)^{4} \frac{\pi}{10}\)
If \(\sin x=-\left(\frac{\sqrt{5}+1}{4}\right)=\sin \left(-54^{\circ}\right)=\sin \left(\frac{-3 \pi}{10}\right)\),
then \(x=n \pi+(-1)^{n}\left(\frac{-3 \pi}{10}\right)\)
Hence, \(x=n \pi, n \pi+(-1)^{n} \frac{\pi}{10}\) or \(n \pi+(-1)^{n}\left(\frac{-3 \pi}{10}\right)\),
where \(n\) is some integer -
Question 113 of 158
113. Question
(a) Draw the graph of \(y=\frac{1}{\sqrt{2}}(\sin x+\cos x)\) from \(x=-\frac{\pi}{2}\) to \(x=\frac{\pi}{2}\).
(b) If \(\cos (\alpha+\beta)=\frac{4}{5}, \sin (\alpha-\beta)=\frac{5}{13}\), and \(\alpha, \beta\) lies between 0 and \(\frac{\pi}{4}\), find \(\tan 2 \alpha\). [1979]Hint
(a) Given: \(y=\frac{1}{\sqrt{2}}(\sin x+\cos x)=\sin \left(x+\frac{\pi}{4}\right)\)
To draw the graph of \(y=\sin \left(x+\frac{\pi}{4}\right)\), we first draw the graph of \(y=\sin x\) and then on shifting it by \(-\frac{\pi}{4}\).\(
\begin{aligned}
&\text { (b) } \cos (\alpha+\beta)=\frac{4}{5} \\
&\Rightarrow \tan (\alpha+\beta)=\frac{3}{4}, 0<\alpha, \beta<\frac{\pi}{4} \\
&\sin (\alpha-\beta)=\frac{5}{13} \Rightarrow \tan (\alpha-\beta)=\frac{5}{12} \\
&=\frac{\tan (\alpha+\beta)+\tan (\alpha-\beta)}{1-\tan (\alpha+\beta) \tan (\alpha-\beta)} =\tan 2 \alpha=\tan [(\alpha+\beta)+(\alpha-\beta)] \\
&=\frac{\frac{3}{4}+\frac{5}{12}}{1-\frac{3}{4} \times \frac{5}{12}}=\frac{9+5}{12} \times \frac{16}{11}=\frac{56}{33}
\end{aligned}
\)
-
Question 114 of 158
114. Question
The number of solutions of the equation \(4 \sin ^2 x-4 \cos ^3 x+9-4 \cos x=0 ; x \in[-2 \pi, 2 \pi]\) is : [JEE Main 2024 1st Feb Shift 2]
Hint
(d) We start by recognizing that \(\sin ^2 x+\cos ^2 x=1\). Substituting \(\sin ^2 x=1-\cos ^2 x\) into the original equation gives:
\(
4\left(1-\cos ^2 x\right)-4 \cos ^3 x+9-4 \cos x=0
\)
Rearranging and simplifying this equation, we have:
\(
\begin{aligned}
& 4-4 \cos ^2 x-4 \cos ^3 x+9-4 \cos x=0 \\
& 4 \cos ^3 x+4 \cos ^2 x+4 \cos x-13=0 \\
& 4 \cos ^3 x+4 \cos ^2 x+4 \cos x=13
\end{aligned}
\)
Observing the bounds given, \(x \in[-2 \pi, 2 \pi]\), we want to find how many solutions satisfy this cubic equation in terms of \(\cos x\). However, we note that the left-hand side (LHS) of the equation, representing a combination of cosines, could at most approach a maximum sum when \(\cos x=1\), that being \(4(1)+4(1)+4(1)=12\). Yet, we have the equation set to equal 13 , which is impossible given the maximum sum of the LHS can only be 12.
The above reasoning indicates that, within the domain specified, there is no value of \(x\) for which the equation holds true. Therefore, the number of solutions to the equation is zero. -
Question 115 of 158
115. Question
Let the set of all \(a \in R\) such that the equation \(\cos 2 x+a \sin x=2 a-7\) has a solution be \([p, q]\) and \(r=\tan 9^{\circ}-\tan 27^{\circ}-\frac{1}{\cot 63^{\circ}}+\tan 81^{\circ}\), then \(pqr\) is equal to [JEE Main 2024 27th Jan Shift 1]
Hint
(c)
\(
\begin{aligned}
& \cos 2 x+a \cdot \sin x=2 a-7 \\
& a(\sin x-2)=2(\sin x-2)(\sin x+2) \\
& \sin x=2, a=2(\sin x+2) \\
& \Rightarrow a \in[2,6] \\
& p=2 \quad q=6 \\
& r=\tan 9^{\circ}+\cot 9^{\circ}-\tan 27^{\circ}-\cot 27^{\circ} \\
& r=\frac{1}{\sin 9 \cdot \cos 9}-\frac{1}{\sin 27 \cdot \cos 27} \\
& =2\left[\frac{4}{\sqrt{5}-1}-\frac{4}{\sqrt{5}+1}\right] \\
& r=4 \\
& p \cdot q \cdot r=2 \times 6 \times 4=48
\end{aligned}
\) -
Question 116 of 158
116. Question
If \(2 \tan ^2 \theta-5 \sec \theta=1\) has exactly 7 solutions in the interval \(\left[0, \frac{n \pi}{2}\right]\), for the least value of \(n \in N\) then \(\sum_{k=1}^n \frac{k}{2^k}\) is equal to : [JEE Main 2024 27th Jan Shift 1]
Hint
(d)
\(
\begin{aligned}
& 2 \tan ^2 \theta-5 \sec \theta-1=0 \\
& \Rightarrow 2 \sec ^2 \theta-5 \sec \theta-3=0 \\
& \Rightarrow(2 \sec \theta+1)(\sec \theta-3)=0 \\
& \Rightarrow \sec \theta=-\frac{1}{2}, 3 \\
& \Rightarrow \cos \theta=-2, \frac{1}{3} \\
& \Rightarrow \cos \theta=\frac{1}{3}
\end{aligned}
\)
For 7 solutions \(n=13\)
\(
\begin{aligned}
& \text { So, } \sum_{ k =1}^{13} \frac{ k }{2^{ k }}= S \text { (say) } \\
& S =\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+\ldots+\frac{13}{2^{13}} \\
& \frac{1}{2} S =\frac{1}{2^2}+\frac{1}{2^3}+\ldots+\frac{12}{2^{13}}+\frac{13}{2^{14}} \\
& \Rightarrow \frac{ S }{2}=\frac{1}{2} \cdot \frac{1-\frac{1}{2^{13}}}{1-\frac{1}{2}}-\frac{13}{2^{14}} \Rightarrow S =2 \cdot\left(\frac{2^{13}-1}{2^{13}}\right)-\frac{13}{2^{13}}=\frac{1}{2^{13}}\left(2^{14}-15\right)
\end{aligned}
\) -
Question 117 of 158
117. Question
If \(\alpha,-\frac{\pi}{2}<\alpha<\frac{\pi}{2}\) is the solution of \(4 \cos \theta+5 \sin \theta=1\), then the value of \(\tan \alpha\) is [JEE Main 2024 29th Jan Shift 1]
Hint
(c)
\(
4+5 \tan \theta=\sec \theta
\)
Squaring: \(24 \tan ^2 \theta+40 \tan \theta+15=0\)
\(
\tan \theta=\frac{-10 \pm \sqrt{10}}{12}
\)
and \(\tan \theta=-\left(\frac{10+\sqrt{10}}{12}\right)\) is Rejected. -
Question 118 of 158
118. Question
The sum of the solutions
 of the equation \(\frac{3 \cos 2 x+\cos ^3 2 x}{\cos ^6 x-\sin ^6 x}=x^3-x^2+6\) is [JEE Main 2024 29th Jan Shift 2]
of the equation \(\frac{3 \cos 2 x+\cos ^3 2 x}{\cos ^6 x-\sin ^6 x}=x^3-x^2+6\) is [JEE Main 2024 29th Jan Shift 2]Hint
(c)
\(
\begin{aligned}
& \frac{3 \cos 2 x+\cos ^3 2 x}{\cos ^6 x-\sin ^6 x}=x^3-x^2+6 \\
& \Rightarrow \frac{\cos 2 x\left(3+\cos ^2 2 x\right)}{\cos 2 x\left(1-\sin ^2 x \cos ^2 x\right)}=x^3-x^2+6 \\
& \Rightarrow \frac{4\left(3+\cos ^2 2 x\right)}{\left(4-\sin ^2 2 x\right)}=x^3-x^2+6 \\
& \Rightarrow \frac{4\left(3+\cos ^2 2 x\right)}{\left(3+\cos ^2 2 x\right)}=x^3-x^2+6 \\
& x^3-x^2+2=0 \Rightarrow(x+1)\left(x^2-2 x+2\right)=0
\end{aligned}
\)
so, sum of real solutions \(=-1\) -
Question 119 of 158
119. Question
If \(2 \sin ^3 x+\sin 2 x \cos x+4 \sin x-4=0\) has exactly 3 solutions in the interval \(\left[0, \frac{ n \pi}{2}\right], n \in N\), then the roots of the equation \(x^2+n x+(n-3)=0\) belong to : [JEE Main 2024 30th Jan Shift 1]
Hint
(b)
\(
\begin{aligned}
& 2 \sin ^3 x+2 \sin x \cdot \cos ^2 x+4 \sin x-4=0 \\
& 2 \sin ^3 x+2 \sin x \cdot\left(1-\sin ^2 x\right)+4 \sin x-4=0 \\
& 6 \sin x-4=0 \\
& \sin x=\frac{2}{3}
\end{aligned}
\)
\(n = 5\) (in the given interval)
\(
\begin{aligned}
& x^2+5 x+2=0 \\
& x=\frac{-5 \pm \sqrt{17}}{2}
\end{aligned}
\)
Required interval \((-\infty, 0)\) -
Question 120 of 158
120. Question
If \(\tan A =\frac{1}{\sqrt{x\left(x^2+x+1\right)}}, \tan B=\frac{\sqrt{x}}{\sqrt{x^2+x+1}}\) and \(\tan C=\left(x^{-3}+x^{-2}+x^{-1}\right)^{\frac{1}{2}}, 0<A, B, C<\frac{\pi}{2}\), then \(A + B\) is equal to : [JEE Main 2024 1st Feb Shift 1]
Hint
(a)
\(
\begin{aligned}
& \text { Finding } \tan (A+B) \text { we get } \\
& \Rightarrow \tan ( A + B )= \\
& \frac{\tan A+\tan B}{1-\tan A \tan B}=\frac{\frac{1}{\sqrt{x\left(x^2+x+1\right)}}+\frac{\sqrt{x}}{\sqrt{x^2+x+1}}}{1-\frac{1}{x^2+x+1}} \\
& \Rightarrow \tan ( A + B )=\frac{(1+x)\left(\sqrt{x^2+x+1}\right)}{\left(x^2+x\right)(\sqrt{x})} \\
& \frac{(1+x)\left(\sqrt{x^2+x+1}\right)}{\left(x^2+x\right)(\sqrt{x})} \\
& \tan (A+B)=\frac{\sqrt{x^2+x+1}}{x \sqrt{x}}=\tan C \\
& A+B=C
\end{aligned}
\) -
Question 121 of 158
121. Question
For \(\alpha, \beta \in\left(0, \frac{\pi}{2}\right)\), let \(3 \sin (\alpha+\beta)=2 \sin (\alpha-\beta)\) and a real number \(k\) be such that \(\tan \alpha= k \tan \beta\). Then the value of \(k\) is equal to : [JEE Main 2024 30th Jan Shift 2]
Hint
(b)
\(
\begin{aligned}
& 3 \sin \alpha \cos \beta+3 \sin \beta \cos \alpha \\
& =2 \sin \alpha \cos \beta-2 \sin \beta \cos \alpha \\
& 5 \sin \beta \cos \alpha=-\sin \alpha \cos \beta \\
& \tan \beta=-\frac{1}{5} \tan \alpha \\
& \tan \alpha=-5 \tan \beta
\end{aligned}
\) -
Question 122 of 158
122. Question
If \(m\) and \(n\) respectively are the numbers of positive and negative value of \(\theta\) in the interval \([-\pi, \pi]\) that satisfy the equation \(\cos 2 \theta \cos \frac{\theta}{2}=\cos 3 \theta \cos \frac{9 \theta}{2}\), then \(mn\) is equal to [JEE Main 2023 25th Jan Shift 2]
Hint
(d)
\(
\begin{aligned}
& \cos 2 \theta \cdot \cos \frac{\theta}{2}=\cos 3 \theta \cdot \cos \frac{9 \theta}{2} \\
& \Rightarrow 2 \cos 2 \theta \cdot \cos \frac{\theta}{2}=2 \cos \frac{9 \theta}{2} \cdot \cos 3 \theta \\
& \Rightarrow \cos \frac{5 \theta}{2}+\cos \frac{3 \theta}{2}=\cos \frac{15 \theta}{2}+\cos \frac{3 \theta}{2} \\
& \Rightarrow \cos \frac{15 \theta}{2}=\cos \frac{5 \theta}{2} \\
& \Rightarrow \frac{15 \theta}{2}=2 k \pi \pm \frac{5 \theta}{2} \\
& 5 \theta=2 k \pi \text { or } 10 \theta=2 k \pi \\
& \theta=\frac{2 k \pi}{5} \theta=\frac{k \pi}{5} \\
& \therefore \theta=\left\{-\pi, \frac{-4 \pi}{5}, \frac{-3 \pi}{5}, \frac{-2 \pi}{5}, \frac{-\pi}{5}, 0, \frac{\pi}{5}, \frac{2 \pi}{5}, \frac{3 \pi}{5}, \frac{4 \pi}{5}, \pi\right\} \\
& m=5, n=5 \\
& \therefore m \cdot n=25
\end{aligned}
\) -
Question 123 of 158
123. Question
Let \(f(\theta)=3\left(\sin ^4\left(\frac{3 \pi}{2}-\theta\right)+\sin ^4(3 \pi+\theta)\right)-2\left(1-\sin ^2 2 \theta\right)\) and \(S=\left\{\theta \in[0, \pi]: f^{\prime}(\theta)=-\frac{\sqrt{3}}{2}\right\}\). If \(4 \beta=\sum_{\theta \in S} \theta\), then \(f(\beta)\) is equal to [JEE Main 2023 29th Jan Shift 1]
Hint
(b)
\(
f(\theta)=3\left(\sin ^4\left(\frac{3 \pi}{2}-\theta\right)+\sin ^4(3 x+\theta)\right)-2\left(1-\sin ^2 2 \theta\right)
\)
\(
\begin{aligned}
& S=\left\{\theta \in[0, \pi]: f^{\prime}(\theta)=-\frac{\sqrt{3}}{2}\right\} \\
& \Rightarrow f(\theta)=3\left(\cos ^4 \theta+\sin ^4 \theta\right)-2 \cos ^2 2 \theta
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow f(\theta)=3\left(1-\frac{1}{2} \sin ^2 2 \theta\right)-2 \cos ^2 2 \theta\\
&\begin{aligned}
\Rightarrow f(\theta) & =3-\frac{3}{2} \sin ^2 2 \theta-2 \cos ^2 \theta \\
& =\frac{3}{2}-\frac{1}{2} \cos ^2 2 \theta=\frac{3}{2}-\frac{1}{2}\left(\frac{1+\cos 4 \theta}{2}\right)
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
& f(\theta)=\frac{5}{4}-\frac{\cos 4 \theta}{4} \\
& f^{\prime}(\theta)=\sin 4 \theta \\
& \Rightarrow f^{\prime}(\theta)=\sin 4 \theta=-\frac{\sqrt{3}}{2} \\
& \Rightarrow 4 \theta= n \pi+(-1)^{ n } \frac{\pi}{3} \\
& \Rightarrow \theta=\frac{ n \pi}{4}+(-1)^{ n } \frac{\pi}{12} \\
& \Rightarrow \theta=\frac{\pi}{12},\left(\frac{\pi}{4}-\frac{\pi}{12}\right),\left(\frac{\pi}{2}+\frac{\pi}{12}\right),\left(\frac{3 \pi}{4}-\frac{\pi}{12}\right) \\
& \Rightarrow 4 \beta=\frac{\pi}{4}+\frac{\pi}{2}+\frac{3 \pi}{4}=\frac{3 \pi}{2} \\
& \Rightarrow \beta=\frac{3 \pi}{8} \Rightarrow f(\beta)=\frac{5}{4}-\frac{\cos \frac{3 \pi}{2}}{4}=\frac{5}{4} \\
&
\end{aligned}
\) -
Question 124 of 158
124. Question
Let \(S=\{\theta \in[0,2 \pi): \tan (\pi \cos \theta)+\tan (\pi \sin \theta)=0\}\)
Then \(\sum_{\theta \in S} \sin ^2\left(\theta+\frac{\pi}{4}\right)\) is equal to [JEE Main 2023 24th Jan Shift 2]Hint
(b)
\(
\begin{aligned}
& \tan (\pi \cos \theta)+\tan (\pi \sin \theta)=0 \\
& \tan (\pi \cos \theta)=-\tan (\pi \sin \theta) \\
& \tan (\pi \cos \theta)=\tan (-\pi \sin \theta) \\
& \pi \cos \theta=n \pi-\pi \sin \theta \\
& \sin \theta+\cos \theta=n \text { where } n \in I
\end{aligned}
\)
possible values are \(n =0,1\) and -1 because
\(
-\sqrt{2} \leq \sin \theta+\cos \theta \leq \sqrt{2}
\)
Now it gives \(\theta \in\left\{0, \frac{\pi}{2}, \frac{3 \pi}{4}, \frac{7 \pi}{4}, \frac{3 \pi}{2}, \pi\right\}\)
\(
\text { So } \sum_{\theta=S} \sin ^2\left(\theta+\frac{\pi}{4}\right)=2(0)+4\left(\frac{1}{2}\right)=2
\) -
Question 125 of 158
125. Question
The set of all values of \(\lambda\) for which the equation \(\cos ^2 2 x-2 \sin ^4 x-2 \cos ^2 x=\lambda\) [JEE Main 2023 29th Jan Shift 2]
Hint
(d)
\(
\lambda=\cos ^2 2 x-2 \sin ^4 x-2 \cos ^2 x
\)
convert all in to \(\cos x\).
\(
\begin{aligned}
\lambda & =\left(2 \cos ^2 x-1\right)^2-2\left(1-\cos ^2 x\right)^2-2 \cos ^2 x \\
& =4 \cos ^4 x-4 \cos ^2 x+1-2\left(1-2 \cos ^2 x+\cos ^4 x\right)- \\
& 2 \cos ^2 x \\
& =2 \cos ^4 x-2 \cos ^2 x+1-2 \\
& =2 \cos ^4 x-2 \cos ^2 x-1 \\
& =2\left[\cos ^4 x-\cos ^2 x-\frac{1}{2}\right] \\
& =2\left[\left(\cos ^2 x-\frac{1}{2}\right)^2-\frac{3}{4}\right] \\
\lambda_{\max } & =2\left[\frac{1}{4}-\frac{3}{4}\right]=2 \times\left(-\frac{2}{4}\right)=-1 \text { (max Value) } \\
\lambda_{\min } & =2\left[0-\frac{3}{4}\right]=-\frac{3}{2}(\text { MinimumValue) }
\end{aligned}
\)
So, Range \(=\left[-\frac{3}{2},-1\right]\) -
Question 126 of 158
126. Question
If \(\tan 15^{\circ}+\frac{1}{\tan 75^{\circ}}+\frac{1}{\tan 105^{\circ}}+\tan 195^{\circ}=2 a\), then the value of \(\left(a+\frac{1}{a}\right)\) is : [JEE Main 2023 30th Jan Shift 1]
Hint
(a)
\(
\begin{aligned}
& \tan 15^{\circ}=2-\sqrt{3} \\
& \frac{1}{\tan 75^{\circ}}=\cot 75^{\circ}=2-\sqrt{3} \\
& \frac{1}{\tan 105^{\circ}}=\cot \left(105^{\circ}\right)=-\cot 75^{\circ}=\sqrt{3}-2 \\
& \tan 195^{\circ}=\tan 15^{\circ}=2-\sqrt{3} \\
\therefore \quad & 2(2-\sqrt{3})=2 a \Rightarrow a =2-\sqrt{3} \\
\Rightarrow & a +\frac{1}{ a }=4
\end{aligned}
\) -
Question 127 of 158
127. Question
If the solution of the equation \(\log _{\cos x} \cot x+4 \log _{\sin x} \tan x=1, x \in\left(0, \frac{\pi}{2}\right)\), is \(\sin ^{-1}\left(\frac{\alpha+\sqrt{\beta}}{2}\right)\), where \(\alpha, \beta\) are integers, then \(\alpha+\beta\) is equal to: [JEE Main 2023 30th Jan Shift 1]
Hint
(d)
\(
\begin{aligned}
& \log _{\cos x} \cot x+4 \log _{\sin x} \tan x=1 \\
& \Rightarrow \frac{\ln \cos x-\ln \sin x}{\ln \cos x}+4 \frac{\ln \sin x-\ln \cos x}{\ln \sin x}=1 \\
& \Rightarrow(\ln \sin x)^2-4(\ln \sin x)(\ln \cos x)+4(\ln \cos x)^2= \\
& \Rightarrow \ln \sin x=2 \ln \cos x \\
& \Rightarrow \sin ^2 x+\sin x-1=0 \Rightarrow \sin x=\frac{-1+\sqrt{5}}{2} \\
& \therefore \alpha+\beta=4
\end{aligned}
\) -
Question 128 of 158
128. Question
Let
\(
S=\left\{\theta \in[-\pi, \pi]-\left\{ \pm \frac{\pi}{2}\right\}: \sin \theta \tan \theta+\tan \theta=\sin 2 \theta\right\} \text {. }
\)
\(
\text { If } T =\sum_{\theta \in S} \cos 2 \theta, \text { then } T + n ( S ) \text { is equal }
\) [JEE Main 2022 24th June Shift 1]Hint
(b)
\(
\begin{aligned}
& \sin \theta \tan \theta+\tan \theta=\sin 2 \theta \\
& \tan \theta(\sin \theta+1)=\frac{2 \tan \theta}{1+\tan ^2 \theta} \\
& \tan \theta=0 \Rightarrow \theta=-\pi, 0, \pi \\
& (\sin \theta+1)=2 \cdot \cos ^2 \theta=2(1+\sin \theta)(1-\sin \theta) \\
& \sin \theta=-1 \text { which is not possible } \\
& \sin \theta=\frac{1}{2} \quad \theta=\frac{\pi}{6}, \frac{5 \pi}{6} \\
& n ( s )=5 \\
& T =\cos 0+\cos 2 \pi+\cos 2 \pi+\cos \frac{\pi}{3}+\cos \frac{5 \pi}{3} \\
& T =4 \\
& T + n ( s )=9
\end{aligned}
\) -
Question 129 of 158
129. Question
The number of values of \(x\) in the interval \(\left(\frac{\pi}{4}, \frac{7 \pi}{4}\right)\) for which \(14 \operatorname{cosec}^2 x-2 \sin ^2 x=21\) \(-4 \cos ^2 x\) holds, is [JEE Main 2022 25th June Shift 1]
Hint
(c)
\(
\begin{aligned}
& x \in\left(\frac{\pi}{4}, \frac{7 \pi}{4}\right) \\
& 14 \operatorname{cosec}^2 x-2 \sin ^2 x=21-4 \cos ^2 x \\
& =21-4\left(1-\sin ^2 x\right) \\
& =17+4 \sin ^2 x \\
& 14 \operatorname{cosec}^2 x-6 \sin ^2 x=17 \\
& \text { let } \sin ^2 x=p \\
& \frac{14}{p}-6 p=17 \Rightarrow 14-6 p^2=17 p \\
& 6 p^2+17 p-14=0 \\
& p=-3.5, \frac{2}{3} \Rightarrow \sin ^2 x=\frac{2}{3} \\
& \Rightarrow \sin x= \pm \sqrt{\frac{2}{3}}
\end{aligned}
\)So total four solutions
-
Question 130 of 158
130. Question
The number of elements in the set \(S=\) \(\left\{\theta \epsilon[-4 \pi, 4 \pi]: 3 \cos ^2 2 \theta+6 \cos 2 \theta-\right.\) \(\left.10 \cos ^2 \theta+5=0\right\}\) is [JEE Main 2022 29th June Shift 1]
Hint
(a)
\(
\begin{aligned}
& 3 \cos ^2 2 \theta+6 \cos 2 \theta-10 \cos ^2 \theta+5=0 \\
& 3 \cos ^2 2 \theta+6 \cos 2 \theta-5(1+\cos 2 \theta)+5=0 \\
& 3 \cos ^2 2 \theta+\cos 2 \theta=0 \\
& \operatorname{Cos} 2 \theta=0 \text { OR } \cos 2 \theta=-1 / 3 \\
& \theta \in[-4 \pi, 4 \pi] \\
& 2 \theta=(2 n+1) \cdot \frac{\pi}{2} \\
& \therefore \theta= \pm \pi / 4 . \pm 3 \pi / 4 \ldots \ldots . . \pm 15 \pi / 4
\end{aligned}
\)
Similarly \(\cos 2 \theta=-1 / 3\) gives 16 solution. Total 32 solutions. -
Question 131 of 158
131. Question
The number of solutions of the equation \(2 \theta-\cos ^2 \theta+\sqrt{2}=0\) is \(R\) is equal to [JEE Main 2022 29th June Shift 1]
Hint
(d) Given,
\(
\begin{aligned}
& 2 \theta-\cos ^2 \theta+\sqrt{2}=0 \\
& \Rightarrow 2 \theta+\sqrt{2}=\cos ^2 \theta \\
& \Rightarrow 2 \theta+\sqrt{2}=\frac{1+\cos 2 \theta}{2} \\
& \Rightarrow 4 \theta+2 \sqrt{2}=1+\cos 2 \theta=y \text { (Assume) } \\
& \therefore y=4 \theta+2 \sqrt{2} \text { and } \\
& y=1+\cos 2 \theta
\end{aligned}
\)
For \(y=1+\cos 2 \theta\)
when \(\theta=0, y=1+1=2\)
when \(\theta=\frac{\pi}{4}, y=1+\cos \frac{\pi}{2}=1\)
\(
\theta=\frac{\pi}{2}, y=1+\cos \pi=1-1=0
\)
For \(y=4 \theta+2 \sqrt{2}\)
when \(\theta=0, y=2 \sqrt{2}\)
when \(\theta=\frac{\pi}{2}, y=2 \pi+2 \sqrt{2}\)
\(
\begin{aligned}
& =2(\pi+\sqrt{2}) \\
& =2(3.14+1.41) \\
& =2(4.55) \\
& =9.1
\end{aligned}
\)
when \(\theta=-\frac{\pi}{2}, y=-2 \pi+2 \sqrt{2}\)
\(
\begin{aligned}
& =2(-\pi+\sqrt{2}) \\
& =2(-3.14+1.41) \\
& =-3.46
\end{aligned}
\)
\(\therefore\) Two graph cut’s at only one point so one solution possible. -
Question 132 of 158
132. Question
The number of solutions of the equation \(\sin x =\) \(\cos ^2 x\) in the interval \((0,10)\) is [JEE Main 2022 29th June Shift 2]
Hint
(a) Given equation \(\sin x=\cos ^2 x\)
\(
\begin{aligned}
& \Rightarrow \sin ^2 x+\sin x-1=0 \\
& \Rightarrow \sin x=\frac{-1 \pm \sqrt{5}}{2} \\
& \Rightarrow \sin x=\frac{\sqrt{5}-1}{2}
\end{aligned}
\)
\(\therefore\) Number of solution \(= 4\)
-
Question 133 of 158
133. Question
The number of solutions of the equation \(\cos \left(x+\frac{\pi}{3}\right) \cos \left(\frac{\pi}{3}-x\right)=\frac{1}{4} \cos ^2 2 x, x \in[-3 \pi \text {, } 3 \pi] \) is [JEE Main 2022 24th June Shift 2]
Hint
(d)
\(
\begin{aligned}
& \cos \left(\frac{\pi}{3}+x\right) \cos \left(\frac{\pi}{3}-x\right)=\frac{1}{4} \cos ^2 2 x \\
& x \in[-3 \pi, 3 \pi] \\
& 4\left(\cos ^2\left(\frac{\pi}{3}\right)-\sin ^2 x\right)=\cos ^2 2 x \\
& 4\left(\frac{1}{4}-\sin ^2 x\right)=\cos ^2 2 x \\
& 1-4 \sin ^2 x=\cos ^2 2 x \\
& 1-2(1-\cos 2 x)=\cos ^2 2 x \\
& l e t \cos 2 x=t \\
& -1+2 \cos 2 x=\cos ^2 2 x \\
& t^2-2 t+1=0 \\
& (t-1)^2=0
\end{aligned}
\)
\(
\begin{aligned}
& t=1 \quad \cos 2 x=1 \\
& 2 x=2 n \pi \\
& x=n \pi \\
& n=-3,-2,-1,0,1,2,3
\end{aligned}
\) -
Question 134 of 158
134. Question
The value of \(2 \sin \left(12^{\circ}\right)-\sin \left(72^{\circ}\right)\) is : [JEE Main 2022 25th June Shift 2]
Hint
(d)
\(
\begin{aligned}
& \sin 12^{\circ}+\sin 12^{\circ}-\sin 72^{\circ} \\
& =\sin 12^{\circ}-2 \cos 42^{\circ} \sin 30^{\circ} \\
& =\sin 12^{\circ}-\sin 48^{\circ} \\
& =-2 \cos 30^{\circ} \sin 18^{\circ} \\
& =-2 \times \frac{\sqrt{3}}{2} \times \frac{\sqrt{5}-1}{4} \\
& =\frac{\sqrt{3}}{4}(1-\sqrt{5})
\end{aligned}
\) -
Question 135 of 158
135. Question
If \(\sin ^2\left(10^{\circ}\right) \sin \left(20^{\circ}\right) \sin \left(40^{\circ}\right) \sin \left(50^{\circ}\right) \sin \left(70^{\circ}\right)=\alpha-\) \(\frac{1}{16} \sin \left(10^{\circ}\right)\), then \(16+\alpha^{-1}\) is equal to [JEE Main 2022 26th June Shift 1]
Hint
(b)
\(
\begin{aligned}
& \sin 10^{\circ}\left(\frac{1}{2} \cdot 2 \sin 20^{\circ} \sin 40^{\circ}\right) \cdot \sin 10^{\circ} \sin \left(60^{\circ}-10^{\circ}\right) \sin \left(60^{\circ}+10^{\circ}\right) \\
& \sin 10^{\circ} \frac{1}{2}\left(\cos 20^{\circ}-\cos 60^{\circ}\right) \cdot \frac{1}{4} \sin 30^{\circ} \\
& \frac{1}{2} \cdot \frac{1}{4} \cdot \frac{1}{2} \cdot \sin 10^{\circ}\left(\cos 20^{\circ}-\frac{1}{2}\right) \\
& =\frac{1}{32}\left(2 \sin 10^{\circ} \cos 20^{\circ}-\sin 10^{\circ}\right)
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{32}\left(\sin 30^{\circ}-\sin 10^{\circ}-\sin 10^{\circ}\right) \\
& =\frac{1}{32}\left(\frac{1}{2}-2 \sin 10^{\circ}\right) \\
& =\frac{1}{64}\left(1-4 \sin 10^{\circ}\right) \\
& =\frac{1}{64}-\frac{1}{16} \sin 10^{\circ}
\end{aligned}
\)
Hence \(\alpha=\frac{1}{64}\)
\(
16+\alpha^{-1}=80
\) -
Question 136 of 158
136. Question
\(16 \sin \left(20^{\circ}\right) \sin \left(40^{\circ}\right) \sin \left(80^{\circ}\right)\) is equal to : [JEE Main 2022 26th June Shift 2]
Hint
(b)
\(
\begin{aligned}
& 16 \sin 20^{\circ} \sin 40^{\circ} \sin 80^{\circ} \\
& =16 \sin 40^{\circ} \sin 20^{\circ} \sin 80^{\circ} \\
& =4(4 \sin (60-20) \sin (20) \sin (60+20)) \\
& =4 \times \sin \left(3 \times 20^{\circ}\right) \\
& {[\because \sin 3 \theta=4 \sin (60-\theta) \times \sin \theta \times \sin (60+\theta)]} \\
& =4 \times \sin 60^{\circ} \\
& =4 \times \frac{\sqrt{3}}{2}=2 \sqrt{3}
\end{aligned}
\) -
Question 137 of 158
137. Question
The value of \(\cos \left(\frac{2 \pi}{7}\right)+\cos \left(\frac{4 \pi}{7}\right)+\cos \left(\frac{6 \pi}{7}\right)\) is equal to : [JEE Main 2022 27 June Shift 1]
Hint
(b)
\(
\begin{aligned}
& \cos \frac{2 \pi}{7}+\cos \frac{4 \pi}{7}+\cos \frac{6 \pi}{7} \\
& =\frac{\sin \left(3 \times \frac{\pi}{7}\right)}{\sin \frac{\pi}{7}} \times \cos \left(\frac{\frac{2 \pi}{7}+\frac{6 \pi}{7}}{2}\right) \\
& =\frac{2 \sin \left(\frac{3 \pi}{7}\right)}{2 \sin \frac{\pi}{7}} \times \cos \left(\frac{4 \pi}{7}\right) \\
& =\frac{\sin \left(\frac{7 \pi}{7}\right)+\sin \left(\frac{-\pi}{7}\right)}{2 \sin \frac{\pi}{7}} \\
& =\frac{-\sin \frac{\pi}{7}}{2 \sin \frac{\pi}{7}} \\
& =-\frac{1}{2} \\
&
\end{aligned}
\) -
Question 138 of 158
138. Question
\(\alpha=\sin 36^{\circ}\) is a root of which of the following equation [JEE Main 2022 27th June Shift 2]
Hint
(c)
\(
\begin{aligned}
& \cos 72^{\circ}=\frac{\sqrt{5}-1}{4} \\
& \Rightarrow 1-2 \sin ^2 36^{\circ}=\frac{\sqrt{5}-1}{4} \\
& \Rightarrow 4-8 x^2=\sqrt{5}-1 \\
& \Rightarrow 5-8 x^2=\sqrt{5} \\
& \Rightarrow\left(5-8 x^2\right)^2=5 \\
& \Rightarrow 25+64 x^4-80 x^2=5 \\
& \Rightarrow 64 x^4-80 x^2+20=0 \\
& \Rightarrow 16 x^4-20 x^2+5=0
\end{aligned}
\) -
Question 139 of 158
139. Question
If \(\cot \alpha=1\) and \(\sec \beta=-\frac{5}{3}\), where \(\pi<\alpha<\frac{3 \pi}{2}\) and \(\frac{\pi}{2}<\beta<\pi\), then the value of \(\tan (\alpha+\beta)\) and the quadrant in which \(\alpha+\beta\) lies, respectively are [JEE Main 2022 28th June Shift 2]
Hint
(a)
\(
\begin{aligned}
& \cot \alpha=1, \sec \beta=\frac{-5}{3}, \cos \beta=\frac{-3}{5}, \tan \beta=\frac{-4}{3} \\
& \tan (\alpha+\beta)=\frac{1-\frac{4}{3}}{1+\frac{4}{3} \times 1}=\frac{-1}{7}
\end{aligned}
\) -
Question 140 of 158
140. Question
If \(e ^{\left(\cos ^2 x+\cos ^4 x+\cos ^5 x+\ldots \infty\right) \log _e 2}\) satisfies the equation \(t^2-9 t+8=0\), then the value of \(\frac{2 \sin x}{\sin x+\sqrt{3} \cos x}\left(0<x<\frac{\pi}{2}\right)\) is [JEE Main 2021 24th Feb Shift 1]
Hint
(c) Step 1: Simplifying the given equation:
Given that,
\(
e^{\left(\cos ^2 x+\cos ^4 x+\cos ^6 x+\ldots \infty\right) \log _e 2}
\)
Here, \(\cos ^2 x+\cos ^4 x+\ldots+\infty\) is in GP. Then
\(
\begin{aligned}
\cos ^2 x+\cos ^4 x+\ldots \infty & =\frac{\cos ^2 x}{1-\cos ^2 x} \quad\left[\because S _{ n }=\frac{ a }{1- r }\right] \\
& =\frac{\cos ^2 x}{\sin ^2 x} \\
& =\cot ^2 x
\end{aligned}
\)
Substitute this in the given function, we get
\(
\begin{aligned}
e^{\left(\cos ^2 x+\cos ^4 x+\cos ^6 x+\ldots \infty\right) \log _e 2} & =e^{\cot ^2 x \log _e 2} \\
& =e^{\log _e 2^{\cot x}} \quad\left[\because \text { mloga }=\log ^{ m }\right] \\
& =2^{\cot ^2 x}
\end{aligned}
\)
Step 2: Find the value of \(t\) :
\(t^2-9 t+8=0 \quad\) [given]
\(
\begin{array}{lrl}
\Rightarrow & t^2-8 t-t+8=0 \\
\Rightarrow & t(t-8)-1(t-8)=0 \\
\Rightarrow & (t-8)(t-1)=0 \\
\Rightarrow & t=8 \text { or } 1
\end{array}
\)
\(\text { Since, the given equation satisfies the equation } t^2-9 t+8=0 \text {,then }\)
\(
\begin{aligned}
2^{\cot ^2 x} & =8 \\
& \Rightarrow 2^{\cot ^2 x}=2^3 \\
& \Rightarrow \cot ^2 x=3 \quad \quad \quad \text { by comparing] } \\
& \Rightarrow \cot x=\sqrt{3} \\
& \Rightarrow \quad x=\frac{\pi}{6}
\end{aligned}
\)
\(
\begin{aligned}
2^{\cot ^2 x} & =1 \\
& \Rightarrow 2^{\cot ^2 x}=2^0 \\
& \Rightarrow \cot ^2 x=0 \quad \text { by comparing] } \\
& \Rightarrow \cot x=\cot \left(\frac{\pi}{2}\right) \\
& \Rightarrow \quad x=\frac{\pi}{2}
\end{aligned}
\)
But it is given \(0<x<\frac{\pi}{2}\) so, take only \(x=\frac{\pi}{6}\).
Step 4: Find the value of the expression:
By substituting \(x=\frac{\pi}{6}\) in the expression.
\(
\begin{aligned}
\frac{2 \sin x}{\sin x+\sqrt{3} \cos x} & =\frac{2 \sin \left(\frac{\pi}{6}\right)}{\sin \left(\frac{x}{6}\right)+\sqrt{3} \cos \left(\frac{\pi}{6}\right)} \\
& =\frac{2 \times \frac{1}{2}}{\frac{1}{2}+\sqrt{3} \times \frac{\sqrt{3}}{2}} \\
& =\frac{2}{4} \\
& =\frac{1}{2}
\end{aligned}
\) -
Question 141 of 158
141. Question
All possible values of \(\theta \in[0,2 \pi]\) for which \(\sin 2 \theta+\tan 2 \theta>0\) lie in: [JEE Main 2021 25th Feb Shift 1]
Hint
(b)
\(
\begin{aligned}
& \tan 2 \theta(1+\cos 2 \theta)>0 \\
& 2 \theta \in\left(0, \frac{\pi}{2}\right) \cup\left(\pi, \frac{3 \pi}{2}\right) \cup\left(2 \pi, \frac{5 \pi}{2}\right) \cup\left(3 \pi, \frac{7 \pi}{2}\right) \\
& \Rightarrow \theta \in\left(0, \frac{\pi}{4}\right) \cup\left(\frac{\pi}{2}, \frac{3 \pi}{4}\right) \cup\left(\pi, \frac{5 \pi}{4}\right) \cup\left(\frac{3 \pi}{2}, \frac{7 \pi}{4}\right)
\end{aligned}
\) -
Question 142 of 158
142. Question
If \(0<x, y<\pi\) and \(\cos x+\cos y-\cos (x+y)=\frac{3}{2}\), then \(\sin x+\cos y\) is equal to : [JEE Main 2021 25th Feb Shift1]
Hint
(a)
\(
\begin{aligned}
& 2 \cos \left(\frac{x+y}{2}\right) \cos \left(\frac{x-y}{2}\right)-\left[2 \cos ^2\left(\frac{x+y}{2}\right)-1\right]=\frac{3}{2} \\
& 2 \cos \left(\frac{x+y}{2}\right)\left[\cos \left(\frac{x-y}{2}\right)-\cos \left(\frac{x+y}{2}\right)\right]=\frac{1}{2} \\
& 2 \cos \left(\frac{x+y}{2}\right)\left[2 \sin \left(\frac{x}{2}\right) \cdot \sin \left(\frac{y}{2}\right)\right]=\frac{1}{2} \\
& \cos \left(\frac{x+y}{2}\right) \cdot \sin \left(\frac{x}{2}\right) \cdot \sin \left(\frac{y}{2}\right)=\frac{1}{8} \\
& \text { Possible when } \frac{x}{2}=30^{\circ} \& \frac{y}{2}=30^{\circ} \\
& x=y=60^{\circ} \\
& \sin x+\cos y=\frac{\sqrt{3}}{2}+\frac{1}{2}=\frac{\sqrt{3}+1}{2}
\end{aligned}
\) -
Question 143 of 158
143. Question
The number of integral values of ‘ \(k\) ‘ for which the equation \(3 \sin x +4 \cos x = k +1\) has a solution, \(k \in R\) is [JEE Main 2021 26th Feb Shift 1]
Hint
(d)
\(
3 \sin x+4 \cos x=k+1
\)
The equation has a solution if
\(
\begin{aligned}
& -\sqrt{3^2+4^2} \leq k+1 \leq \sqrt{3^2+4^2} \\
& \Rightarrow-5 \leq k+1 \leq 5 \\
& \Rightarrow-6 \leq k \leq 4 \\
& \Rightarrow k=-6,-5,-4,-3,-2,-1,0,1,2,3,4
\end{aligned}
\)
\(\therefore\) There are 11 possible integral values. -
Question 144 of 158
144. Question
If \(\sqrt{3}\left(\cos ^2 x\right)=(\sqrt{3}-1) \cos x+1\), the number of solutions of the given equation when \(x \in\left[0, \frac{\pi}{2}\right]\) is [JEE Main 2021 26th Feb Shift 1]
Hint
(c)
\(
\left.\sqrt{3} t^2-(\sqrt{3}-1) t-1=0 \text { (where } t=\cos x\right)
\)
Now, \(t=\frac{(\sqrt{3}-1) \pm \sqrt{4+2 \sqrt{3}}}{2 \sqrt{3}}\)
\(t=\cos x=1\) or \(-\frac{1}{\sqrt{3}} \rightarrow\) rejected as \(x \in\left[0, \frac{\pi}{2}\right]\)
\(
\Rightarrow \cos x=1
\)
\(\Rightarrow\) No. of solution \(=1\) -
Question 145 of 158
145. Question
The value of \(\tan 9^{\circ}-\tan 27^{\circ}-\tan 63^{\circ}+\tan 81^{\circ}\) is [JEE Main 2023 (Online) 6th April Evening Shift]
Hint
(a)
\(
\begin{aligned}
& \tan 9^{\circ}-\tan 27^{\circ}-\tan 63^{\circ}+\tan 81^{\circ} \\
& =\tan 9^{\circ}+\tan \left(90^{\circ}-9^{\circ}\right)-\tan 27^{\circ}-\tan \left(90^{\circ}-27^{\circ}\right) \\
& =\tan 9^{\circ}+\cot 9^{\circ}-\tan 27^{\circ}-\cot 27^{\circ} \\
& =\frac{\sin 9^{\circ}}{\cos 9^{\circ}}+\frac{\cos 9^{\circ}}{\sin 9^{\circ}}-\left(\frac{\sin 27^{\circ}}{\cos 27^{\circ}}+\frac{\cos 27^{\circ}}{\sin 27^{\circ}}\right) \\
& =\frac{\sin ^2 9^{\circ}+\cos ^2 9^{\circ}}{\sin 9^{\circ} \cos 9^{\circ}}-\left(\frac{\sin ^2 27^{\circ}+\cos ^2 27^{\circ}}{\cos 27^{\circ} \sin 27^{\circ}}\right) \\
& =\frac{2}{\sin 18^{\circ}}-\frac{2}{\sin 54^{\circ}} \\
& =\frac{2 \times 4}{\sqrt{5}-1}-\frac{2 \times 4}{\sqrt{5}+1} \\
& =8\left(\frac{\sqrt{5}+1-\sqrt{5}+1}{5-1}\right)=2(2)=4
\end{aligned}
\) -
Question 146 of 158
146. Question
Let \(\alpha\) and \(\beta\) be two real roots of the \((k+1) \tan ^2 x-\sqrt{2} \cdot \lambda \tan x=(1-k)\), where \(k(\neq-1)\) and \(\lambda\) are real numbers. If \(\tan ^2(\alpha+\beta)=50\), then a value of \(\lambda\) is: [JEE Main 2020 7th Jan Morning]
Hint
(a)
\(
\begin{aligned}
& (k+1) \tan ^2 x-\sqrt{2} \lambda \tan x+(k-1)=0 \\
& \tan \alpha+\tan \beta=\frac{\sqrt{2} \lambda}{k+1} \\
& \tan \alpha \tan \beta=\frac{k-1}{k+1} \\
& \tan (\alpha+\beta)=(k-1)=0 \frac{\frac{\sqrt{2} \lambda}{k+1}}{1-\frac{k-1}{k+1}}=\frac{\sqrt{2} \lambda}{2}=\frac{\lambda}{\sqrt{2}} \\
& \tan ^2(\alpha+\beta)=\frac{\lambda^2}{2}=50 \\
& \lambda=10
\end{aligned}
\) -
Question 147 of 158
147. Question
Let \(\frac{\sqrt{2} \sin \alpha}{\sqrt{1+\cos 2 \alpha}}=\frac{1}{7}\) and \(\sqrt{\frac{1-\cos 2 \beta}{2}}=\frac{1}{\sqrt{10}}\) where \(\alpha, \beta \in\left(0, \frac{\pi}{2}\right)\). Then \(\tan (\alpha+2 \beta)\) is equal to [JEE Main 2020 8th Jan Evening]
Hint
(a)
\(
\begin{aligned}
& \frac{\sqrt{2} \sin \alpha}{\sqrt{2} \cos \alpha}=\frac{1}{7} \text { and } \frac{\sqrt{2} \sin \beta}{\sqrt{2}}=\frac{1}{\sqrt{10}} \\
& \tan \alpha=\frac{1}{7} \\
& \sin \beta=\frac{1}{\sqrt{10}} \\
& \tan \beta=\frac{1}{3} \\
& \tan 2 \beta=\frac{2 \cdot \frac{1}{3}}{1-\frac{1}{9}}=\frac{\frac{2}{3}}{\frac{8}{9}}=\frac{3}{4} \\
& \tan (\alpha+2 \beta)=\frac{\tan \alpha+\tan 2 \beta}{1-\tan \alpha \tan 2 \beta}=\frac{\frac{1}{7}+\frac{3}{4}}{1-\frac{1}{7} \cdot \frac{3}{4}}=\frac{\frac{4+21}{28}}{\frac{25}{28}}=1
\end{aligned}
\) -
Question 148 of 158
148. Question
If the equation \(\cos ^4 \theta+\sin ^4 \theta+\lambda=0\) has real solutions for \(\theta\), then \(\lambda\) lies in the interval [JEE Main 2020 2nd Sept Evening]
Hint
(a)
\(
\begin{aligned}
& \sin ^4 \theta+\cos ^4 \theta=-\lambda \\
& \Rightarrow \quad 1-2 \sin ^2 \theta \cos ^2 \theta=-\lambda \\
& \Rightarrow \quad \lambda=\frac{(\sin 2 \theta)^2}{2}-1 \\
& \Rightarrow \quad \text { as } \sin ^2 2 \theta \in[0,1] \\
& \Rightarrow \quad \lambda \in\left[-1, \frac{-1}{2}\right]
\end{aligned}
\) -
Question 149 of 158
149. Question
Two vertical poles \(A B=15 m\) and \(CD =10 m\) are standing apart on a horizontal ground with points \(A\) and \(C\) on the ground. If \(P\) is the point of intersection of \(BC\) and \(AD\), then the height of \(P(\) in \(m)\) above the line \(A C\) is : [JEE Main 2020 4th Sept Morning]
Hint
(a)
\(
\begin{aligned}
& \tan \theta=\frac{10}{ x }=\frac{ h }{ x _2} \Rightarrow x _2=\frac{ hx }{10} \\
& \tan \phi=\frac{15}{ x }=\frac{ h }{ x _1} \Rightarrow x _1=\frac{ hx }{15} \\
& \text { Now, } x _1+ x _2= x =\frac{ hx }{15}+\frac{ hx }{10} \\
& \Rightarrow 1=\frac{ h }{10}+\frac{ h }{15} \Rightarrow h =6
\end{aligned}
\) -
Question 150 of 158
150. Question
The angle of elevation of a cloud \(C\) from a point \(P , 200 m\) above a still lake is \(30^{\circ}\). If the angle of depression of the image of \(C\) in the lake from the point \(P\) is \(60^{\circ}\), then \(P C(\) in \(m)\) is equal to : [JEE Main 2020 4th Sept Evening]
Hint
(a)
\(
\begin{aligned}
& \Rightarrow \ell=\frac{\ell}{2}+200 \\
& \Rightarrow \ell=400
\end{aligned}
\)
So \(\quad PC =\ell=400 m\) -
Question 151 of 158
151. Question
If \(L=\sin ^2\left(\frac{\pi}{16}\right)-\sin ^2\left(\frac{\pi}{8}\right)\) and \(M=\cos ^2\left(\frac{\pi}{16}\right)-\sin ^2\left(\frac{\pi}{8}\right)\), then [JEE Main 2020 5th Sept evening]
Hint
(b)
\(L + M =1-2 \sin ^2 \frac{\pi}{8}=\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}} \dots(i)\) and \(L – M =-\cos \frac{\pi}{8} \dots(ii)\)
By (i) and (ii)
\(
\begin{aligned}
& L=\frac{1}{2}\left(\frac{1}{\sqrt{2}}-\cos \frac{\pi}{8}\right)=\frac{1}{2 \sqrt{2}}-\frac{1}{2} \cos \frac{\pi}{8} \\
& \& M=\frac{1}{2}\left(\frac{1}{\sqrt{2}}+\cos \frac{\pi}{8}\right)=\frac{1}{2 \sqrt{2}}+\frac{1}{2} \cos \frac{\pi}{8}
\end{aligned}
\) -
Question 152 of 158
152. Question
The angle of elevation of the top of a hill from a point on the horizontal plane passing through the foot of the hill is found to be \(45^{\circ}\). After walking a distance of 80 meters towards the top, up a slope inclined at an angle of \(30^{\circ}\) to the horizontal plane, the angle of elevation of the top of the hill becomes \(75^{\circ}\). Then the height of the hill (in meters) is [JEE Main 2020 6th Sept Morning]
Hint
(b)
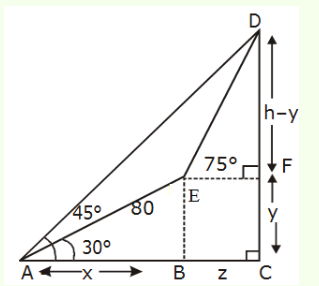
\(
\begin{aligned}
& x=80 \cos 30^{\circ}=40 \sqrt{3} \\
& y=80 \sin 30^{\circ}=40 \\
& \text { In } \triangle A D C \\
& \tan 45^{\circ}=\frac{h}{x+z} \Rightarrow h=x+z \\
& \Rightarrow h=40 \sqrt{3}+z \cdots \text { (1) }
\end{aligned}
\)
In \(\triangle E D F\)
\(
\begin{aligned}
& \tan 75^{\circ}=\frac{h-y}{z} \\
& 2+\sqrt{3}=\frac{h-40}{z} \Rightarrow z=\frac{h-40}{2+\sqrt{3}} \dots(2)
\end{aligned}
\)
Put the value of \(z\) from (1)
\(
\begin{aligned}
& h-40 \sqrt{3}=\frac{h-40}{2+\sqrt{3}} \\
& h(1+\sqrt{3})=40(2 \sqrt{3}+3-1) \\
& h(1+\sqrt{3})=80(1+\sqrt{3}) \\
& h=80
\end{aligned}
\) -
Question 153 of 158
153. Question
The angle of elevation of the summit of a mountain from a point on the ground is \(45^{\circ}\). After climbing up one \(km\) towards the summit at an inclination of \(30^{\circ}\) from the ground, the angle of elevation of the summit is found to be \(60^{\circ}\). Then the height (in \(km\) ) of the summit from the ground is : [JEE Main 2020 6th Sept Evening]
Hint
(b)
\(
\begin{aligned}
& \because \angle S R P=\angle S P R=15^{\circ} \\
& \therefore P P=S R=1 km
\end{aligned}
\)
\(
\begin{aligned}
&\begin{aligned}
& \text { In } \Delta SPT \\
& \frac{P T}{S P}=\sin 60^{\circ} \\
& P T=\frac{\sqrt{3}}{2} k m
\end{aligned}\\
&\ln \Delta R S U, \sin 30^{\circ}=\frac{S U}{R S} \Rightarrow S U=\frac{1}{2} km
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \text { Height of mountain }=\left(\frac{\sqrt{3}}{2}+\frac{1}{2}\right)=\left(\frac{\sqrt{3}+1}{2}\right) km \\
& =\frac{1}{\sqrt{3}-1} km
\end{aligned}
\) -
Question 154 of 158
154. Question
If \(\sin x+\sin ^2 x=1, x \in\left(0, \frac{\pi}{2}\right)\), then \(\left(\cos ^{12} x+\tan ^{12} x\right)+3\left(\cos ^{10} x+\tan ^{10} x+\cos ^8 x+\tan ^8 x\right)+\left(\cos ^6 x+\tan ^6 x\right)\) is equal to: [JEE Main 2025]
Hint
(c) Given \(\sin x+\sin ^2 x=1\)
Rearrange the equation: \(\sin x=1-\sin ^2 x\).
Using the identity \(\sin ^2 x+\cos ^2 x=1\), we have \(\sin x=\cos ^2 x\).
Substitute \(\sin x=\cos ^2 x\) into \(\tan x=\frac{\sin x}{\cos x}\) to get \(\tan x=\frac{\cos ^2 x}{\cos x}=\cos x\) into the given expression
\(
\left(\cos ^{12} x+\tan ^{12} x\right)+3\left(\cos ^{10} x+\tan ^{10} x+\cos ^8 x+\tan ^8 x\right)+\left(\cos ^6 x+\tan ^6 x\right) .
\)
\(\left(\cos ^{12} x+\cos ^{12} x\right)+3\left(\cos ^{10} x+\cos ^{10} x+\cos ^8 x+\cos ^8 x\right)+\left(\cos ^6 x+\cos ^6 x\right)\)
\(
2 \cos ^{12} x+6 \cos ^{10} x+6 \cos ^8 x+2 \cos ^6 x
\)
Replace \(\cos ^2 x=\sin x\)
\(
\begin{aligned}
& =2\left[\sin ^6 x+3 \sin ^5 x+3 \sin ^4 x+\sin ^3 x\right] \\
& =2 \sin ^3 x\left[(\sin x+1)^3\right] \\
& =2\left[\sin ^2 x+\sin x\right]^3 \\
& =2
\end{aligned}
\) -
Question 155 of 158
155. Question
If \(\sum_{r=1}^{13}\left\{\frac{1}{\sin \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right) \sin \left(\frac{\pi}{4}+\frac{r \pi}{6}\right)}\right\}=a \sqrt{3}+b, a, b \in Z\), then \(a^2+b^2\) is equal to : [JEE Main 2025]
Hint
(c)
\(
\sum_{r=1}^{13}\left\{\frac{1}{\sin \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right) \sin \left(\frac{\pi}{4}+\frac{r \pi}{6}\right)}\right\}=a \sqrt{3}+b, a, b \in Z
\)
\(
\begin{aligned}
& \sin (A-B)=\sin A \cos B-\cos A \sin B \\
& \sin \left(\frac{\pi}{6}\right)=\frac{1}{2} \\
& \cos \left(\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}
\end{aligned}
\)
Simplify the general term of the summation.
Multiply and divide by \(\sin \left(\frac{\pi}{6}\right)\) :
\(\frac{1}{\sin \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right) \sin \left(\frac{\pi}{4}+\frac{r \pi}{6}\right)}=\frac{\sin \left(\frac{\pi}{6}\right)}{\sin \left(\frac{\pi}{6}\right) \sin \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right) \sin \left(\frac{\pi}{4}+\frac{r \pi}{6}\right)}\)
Rewrite \(\sin \left(\frac{\pi}{6}\right)\) using the difference of angles formula:
\(\sin \left(\frac{\pi}{6}\right)=\sin \left(\left(\frac{\pi}{4}+\frac{r \pi}{6}\right)-\left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right)\right)\)
\(\sin \left(\frac{\pi}{6}\right)=\sin \left(\frac{\pi}{4}+\frac{r \pi}{6}\right) \cos \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right)-\cos \left(\frac{\pi}{4}+\frac{r \pi}{6}\right) \sin \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right)\)
Substitute back into the expression:
\(
\frac{\sin \left(\frac{\pi}{6}\right)}{\sin \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right) \sin \left(\frac{\pi}{4}+\frac{r \pi}{6}\right)}
\)
\(
=\frac{\sin \left(\frac{\pi}{4}+\frac{r \pi}{6}\right) \cos \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right)-\cos \left(\frac{\pi}{4}+\frac{r \pi}{6}\right) \sin \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right)}{\sin \left(\frac{\pi}{6}\right) \sin \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right) \sin \left(\frac{\pi}{4}+\frac{r \pi}{6}\right)}
\)
Simplify:
\(\frac{1}{\sin \left(\frac{\pi}{6}\right)}\left[\cot \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right)-\cot \left(\frac{\pi}{4}+\frac{r \pi}{6}\right)\right]\)
\(2\left[\cot \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right)-\cot \left(\frac{\pi}{4}+\frac{r \pi}{6}\right)\right]\)
\(
\begin{aligned}
& \sum_{r=1}^{13} 2\left[\cot \left(\frac{\pi}{4}+(r-1) \frac{\pi}{6}\right)-\cot \left(\frac{\pi}{4}+\frac{r \pi}{6}\right)\right] \\
& 2\left[\cot \left(\frac{\pi}{4}\right)-\cot \left(\frac{\pi}{4}+\frac{13 \pi}{6}\right)\right] \\
& 2\left[1-\cot \left(\frac{\pi}{4}+\frac{\pi}{6}\right)\right] \\
& 2\left[1-\frac{\cot \left(\frac{\pi}{4}\right) \cot \left(\frac{\pi}{6}\right)-1}{\cot \left(\frac{\pi}{4}\right)+\cot \left(\frac{\pi}{6}\right)}\right] \\
& 2\left[1-\frac{\sqrt{3}-1}{\sqrt{3}+1}\right] \\
& 2\left[1-\frac{(\sqrt{3}-1)^2}{2}\right] \\
& 2\left[1-\frac{4-2 \sqrt{3}}{2}\right] \\
& 2[1-(2-\sqrt{3})] \\
& 2(\sqrt{3}-1) \\
& 2 \sqrt{3}-2
\end{aligned}
\)
\(
\begin{aligned}
& a=2 \text { and } b=-2 \\
& a^2+b^2=2^2+(-2)^2=4+4=8
\end{aligned}
\) -
Question 156 of 158
156. Question
Let the range of the function \(f(x)=6+16 \cos x \cdot \cos \left(\frac{\pi}{3}-x\right) \cdot \cos \left(\frac{\pi}{3}+x\right) \cdot \sin 3 x \cdot \cos 6 x, x \in \mathbf{R}\) be \([\alpha, \beta]\). Then the distance of the point \((\alpha, \beta)\) from the line \(3 x+4 y+12=0\) is : [JEE Main 2025]
Hint
(a) The distance of the point \((\alpha, \beta)\) from the line \(3 x+4 y+12=0\), where \([\alpha, \beta]\) is the range of the function
\(
f(x)=6+16 \cos x \cdot \cos \left(\frac{\pi}{3}-x\right) \cdot \cos \left(\frac{\pi}{3}+x\right) \cdot \sin 3 x \cdot \cos 6 x
\)
What’s given in the problem
\(f(x)=6+16 \cos x \cdot \cos \left(\frac{\pi}{3}-x\right) \cdot \cos \left(\frac{\pi}{3}+x\right) \cdot \sin 3 x \cdot \cos 6 x\)
\(x \in \mathbf{R}\)
Range of \(f(x)\) is \([\alpha, \beta]\)
Line equation: \(3 x+4 y+12=0\)Helpful Formulas:
\(
\begin{aligned}
&\begin{aligned}
& \cos a \cos b=\frac{1}{2}[\cos (a+b)+\cos (a-b)] \\
& \cos (a+b) \cos (a-b)=\cos ^2 a-\sin ^2 b \\
& \cos 3 x=4 \cos ^3 x-3 \cos x \\
& \sin 2 x=2 \sin x \cos x \\
& \sin 3 x=3 \sin x-4 \sin ^3 x \\
& \sin 3 x=\sin x\left(3-4 \sin ^2 x\right)=\sin x\left(4 \cos ^2 x-1\right) \\
& \sin 3 x=\sin x(2 \cos 2 x+1) \\
& \cos 6 x=1-2 \sin ^2 3 x
\end{aligned}\\
&\text { Distance from point }\left(x_0, y_0\right) \text { to line } A x+B y+C=0 \text { is } \frac{\left|A x_0+B y_0+C\right|}{\sqrt{A^2+B^2}}
\end{aligned}
\)How to solve
Simplify \(f(x)\) using trigonometric identities.
Find the range \([\alpha, \beta]\) of \(f(x)\).
Calculate the distance from \((\alpha, \beta)\) to the line \(3 x+4 y+12=0\).Step 1: Simplify \(f(x)\)
\(
\begin{aligned}
& f(x)=6+16 \cos x \cdot \cos \left(\frac{\pi}{3}-x\right) \cdot \cos \left(\frac{\pi}{3}+x\right) \cdot \sin 3 x \cdot \cos 6 x \\
& f(x)=6+16 \cos x\left(\cos ^2 \frac{\pi}{3}-\sin ^2 x\right) \sin 3 x \cos 6 x \\
& f(x)=6+16 \cos x\left(\frac{1}{4}-\sin ^2 x\right) \sin 3 x \cos 6 x \\
& f(x)=6+4 \cos x\left(1-4 \sin ^2 x\right) \sin 3 x \cos 6 x \\
& f(x)=6+4 \cos x\left(1-4\left(1-\cos ^2 x\right)\right) \sin 3 x \cos 6 x \\
& f(x)=6+4 \cos x\left(4 \cos ^2 x-3\right) \sin 3 x \cos 6 x \\
& f(x)=6+4 \cos 3 x \sin 3 x \cos 6 x \\
& f(x)=6+2 \sin 6 x \cos 6 x \\
& f(x)=6+\sin 12 x
\end{aligned}
\)Step 2: Find the range of \(f(x)\)
\(
\begin{aligned}
& \text { Since }-1 \leq \sin 12 x \leq 1, \\
& 6-1 \leq 6+\sin 12 x \leq 6+1 \\
& 5 \leq f(x) \leq 7
\end{aligned}
\)
Thus, \(\alpha=5\) and \(\beta=7\).Step 3: Calculate the distance
\(
\begin{aligned}
& \text { Distance }=\frac{|3 \alpha+4 \beta+12|}{\sqrt{3^2+4^2}} \\
& \text { Distance }=\frac{|3(5)+4(7)+12|}{\sqrt{9+16}} \\
& \text { Distance }=\frac{|15+28+12|}{5} \\
& \text { Distance }=\frac{55}{5} \\
& \text { Distance }=11
\end{aligned}
\)
The distance of the point \((\alpha, \beta)\) from the line \(3 x+4 y+12=0\) is 11. -
Question 157 of 158
157. Question
The value of \(\left(\sin 70^{\circ}\right)\left(\cot 10^{\circ} \cot 70^{\circ}-1\right)\) is [JEE Main 2025]
Hint
(b) The expression is given as \(\left(\sin 70^{\circ}\right)\left(\cot 10^{\circ} \cot 70^{\circ}-1\right)\).
We can write,
\(
\sin 70^{\circ}\left(\frac{\cos 10^{\circ} \times \cos 70^{\circ}}{\sin 10^{\circ} \times \sin 70^{\circ}}-1\right)
\)
\(
={Sin} 70^{\circ}\left[\frac{\cos 10^{\circ} \times \cos 70^{\circ}-\sin 10^{\circ} \times \sin 70^{\circ}}{\sin 10^{\circ} \times \sin 70^{\circ}}\right]
\)
\(
=\frac{\sin 70^{\circ} \times \cos \left(10^{\circ}+70^{\circ}\right)}{\sin 10^{\circ} \times \sin 70^{\circ}}
\)
\(
=\frac{\cos 80^{\circ}}{\sin 10^{\circ}}=\frac{\cos \left(90^{\circ}-10^{\circ}\right)}{\sin 10^{\circ}}
\)
\(
=\frac{\sin 10^{\circ}}{\sin 10^{\circ}}=1
\) -
Question 158 of 158
158. Question
The sum of all values of \(\theta \in[0,2 \pi]\) satisfying \(2 \sin ^2 \theta=\cos 2 \theta\) and \(2 \cos ^2 \theta=3 \sin \theta\) is [JEE Main 2025]
Hint
(a) Given, \(2 \sin ^2 \theta=\cos 2 \theta\)
\(
\begin{aligned}
& 2 \sin ^2 \theta=1-2 \sin ^2 \theta \\
& 4 \sin ^2 \theta=1 \Rightarrow \sin \theta= \pm \frac{1}{2}
\end{aligned}
\)
Given \(2 \cos ^2 \theta=3 \sin \theta\)
\(
\begin{aligned}
& 2\left(1-\sin ^2 \theta\right)=3 \sin \theta \\
& 2 \sin ^2 \theta+3 \sin \theta-2=0 \\
& (2 \sin \theta-1)(\sin \theta+2)=0 \\
& \sin \theta=\frac{1}{2},-2 ( -2 \text { is not possible} )
\end{aligned}
\)
Since \(\sin \theta=\frac{1}{2}\), the values of \(\theta\) in \([0,2 \pi]\) are:
\(\theta_1=\frac{\pi}{6}\)
\(\theta_2=\pi-\frac{\pi}{6}=\frac{5 \pi}{6}\)
\(
\begin{aligned}
& \text { Sum }=\theta_1+\theta_2 \\
& \text { Sum }=\frac{\pi}{6}+\frac{5 \pi}{6} \\
& \text { Sum }=\frac{6 \pi}{6} \\
& \text { Sum }=\pi
\end{aligned}
\)