3.4 Trigonometric Functions of Sum and Difference of Two Angles

In this Section, we shall derive expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions. We shall prove the following cases:

\(\text { 1. } \quad \sin (-x)=-\sin x\)

Proof:

\(\begin{aligned}
&\sin (-x) \\
&=\sin (0-x) \\
&=\sin 0 \cos x-\cos 0 \sin x \\
&=0(\cos x)-1(\sin x) \\
&=-\sin x
\end{aligned}\)

Note: The sine function is an odd function that is anti-mirrored perfectly around the y-axis. So, for every absolute value on the x-axis, the value of y will be the same but opposite sign – whether the point x is chosen on the positive x-axis or the negative x-axis.

\(\text { 2. } \quad \cos (-x)=\cos x\)

Proof:

Cosine and Sine values are complementary.
Thus, \(\cos x=\sin \left(90^{\circ}-x\right)\)
\(
\Rightarrow \cos (-x)=\sin \left(90^{\circ}+x\right)
\)
We know that, \(\sin (A+B)=\sin A \cos B+\cos A \sin B\)
Thus, using this formula we can expand \(\sin \left(90^{\circ}+x\right)\)
\(
\begin{aligned}
&=\sin 90^{\circ} \times \cos x+\cos 90^{\circ} \times \sin x \\
&=1 \times \cos x+0 \times \sin x \quad \quad\left(\text { Since, } \sin 90^{\circ}=1, \cos 90^{\circ}=0\right) \\
&=\cos x
\end{aligned}
\)

Note: The cosine function is an even function that is mirrored perfectly around the y-axis. So, for every absolute value on the x-axis, the value of y will be the same – whether the point x is chosen on the positive x-axis or the negative x-axis.

\(\text { 3. } \quad \cos (x+y)=\cos x \cos y-\sin x \sin y\)

Proof:

Consider the unit circle with centre at the origin. Let \(x\) be the angle \(\mathrm{P}_{4} \mathrm{OP}_{1}\) and \(y\) be the angle \(\mathrm{P}_{1} \mathrm{OP}_{2^{*}}\). Then \((x+y)\) is the angle \(\mathrm{P}_{4} \mathrm{OP}_{2}\). Also let \((-y)\) be the angle \(\mathrm{P}_{4} \mathrm{OP}_{3}\). Therefore, \(P_{1}, P_{2}, P_{3}\) and \(P_{4}\) will have the coordinates \(P_{1}(\cos x\), \(\sin x)\), \(\mathrm{P}_{2}[\cos (x+y), \sin (x+y)], \mathrm{P}_{3}[\cos (-y), \sin (-y)]\) and \(\mathrm{P}_{4}(1,0)\) (Fig 3.13).

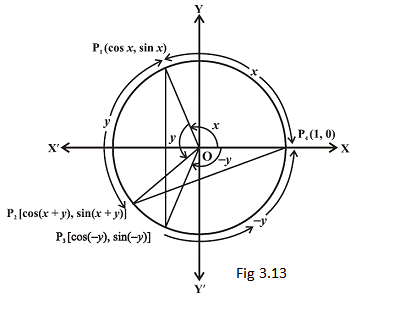
Consider the triangles \(\mathrm{P}_{1} \mathrm{OP}_{3}\) and \(\mathrm{P}_{2} \mathrm{OP}_{4}\). They are congruent (Why?). Therefore, \(\mathrm{P}_{1} \mathrm{P}_{3}\) and \(\mathrm{P}_{2} \mathrm{P}_{4}\) are equal. By using distance formula, we get
\(
\begin{aligned}
\mathrm{P}_{1} \mathrm{P}_{3}^{2} &=[\cos x-\cos (-y)]^{2}+\left[\sin x-\sin (-y]^{2}\right.\\
&=(\cos x-\cos y)^{2}+(\sin x+\sin y)^{2} \\
&=\cos ^{2} x+\cos ^{2} y-2 \cos x \cos y+\sin ^{2} x+\sin ^{2} y+2 \sin x \sin y \\
&=2-2(\cos x \cos y-\sin x \sin y) \quad(\text { Why?) }
\end{aligned}
\)
Also,
\(
\begin{aligned}
\mathrm{P}_{2} \mathrm{P}_{4}^{2} &=[1-\cos (x+y)]^{2}+[0-\sin (x+y)]^{2} \\
&=1-2 \cos (x+y)+\cos ^{2}(x+y)+\sin ^{2}(x+y) \\
&=2-2 \cos (x+y)
\end{aligned}
\)
Since \(\mathrm{P}_{1} \mathrm{P}_{3}=\mathrm{P}_{2} \mathrm{P}_{4}\), we have \(\mathrm{P}_{1} \mathrm{P}_{3}^{2}=\mathrm{P}_{2} \mathrm{P}_{4}^{2}\).
Therefore, \(2-2(\cos x \cos y-\sin x \sin y)=2-2 \cos (x+y)\).
Hence \(\cos (x+y)=\cos x \cos y-\sin x \sin y\)

\(\text { 4. } \quad\cos (x-y)=\cos x \cos y+\sin x \sin y\)

Proof:

Replacing \(y\) by \(-y\) in identity 3 , we get
\(\cos (x+(-y))=\cos x \cos (-y)-\sin x \sin (-y)\)
or \(\cos (x-y)=\cos x \cos y+\sin x \sin y\)

\(\text { 5. } \quad\cos \left(\frac{\pi}{2}-x\right)=\sin x\)

Proof:

If we replace \(x\) by \(\frac{\pi}{2}\) and \(y\) by \(x\) in Identity (4), we get
\(
\cos \left(\frac{\pi}{2}-x\right)=\cos \frac{\pi}{2} \cos x+\sin \frac{\pi}{2} \sin x=\sin x
\)

\(\text { 6. } \quad\sin \left(\frac{\pi}{2}-x\right)=\cos x\)

Proof:

Using the Identity 5 , we have
\(
\sin \left(\frac{\pi}{2}-x\right)=\cos \left[\frac{\pi}{2}-\left(\frac{\pi}{2}-x\right)\right]=\cos x .
\)

\(\text { 7. } \quad\sin (x+y)=\sin x \cos y+\cos x \sin y\)

Proof:

We know that
\(
\begin{aligned}
\sin (x+y) &=\cos \left(\frac{\pi}{2}-(x+y)\right)=\cos \left(\left(\frac{\pi}{2}-x\right)-y\right) \\
&=\cos \left(\frac{\pi}{2}-x\right) \cos y+\sin \left(\frac{\pi}{2}-x\right) \sin y \\
&=\sin x \cos y+\cos x \sin y
\end{aligned}
\)

\(\text { 8. } \quad\sin (x-y)=\sin x \cos y-\cos x \sin y\)

Proof:

If we replace \(y\) by \(-y\), in the Identity 7 , we get the result.

9. By taking suitable values of \(x\) and \(y\) in the identities \(3,4,7\) and 8 , we get the following results:

Proof:

\(\begin{array}{ll}
\cos \left(\frac{\pi}{2}+x\right)=-\sin x & \sin \left(\frac{\pi}{2}+x\right)=\cos x \\
\cos (\pi-x)=-\cos x & \sin (\pi-x)=\sin x
\end{array}
\)

\(
\begin{array}{ll}
\cos (\pi+x)=-\cos x & \sin (\pi+x)=-\sin x \\
\cos (2 \pi-x)=\cos x & \sin (2 \pi-x)=-\sin x
\end{array}
\)
Similar results for \(\tan x, \cot x, \sec x\) and \(\operatorname{cosec} x\) can be obtained from the results of \(\sin\) \(x\) and \(\cos x\).

10. If none of the angles \(x, y\) and \((x+y)\) is an odd multiple of \(\frac{\pi}{2}\), then
\(
\tan (x+y)=\frac{\tan x+\tan y}{1-\tan x \tan y}
\)

Proof:

Since none of the \(x, y\) and \((x+y)\) is an odd multiple of \(\frac{\pi}{2}\), it follows that \(\cos x\), \(\cos y\) and \(\cos (x+y)\) are non-zero. Now
\(
\tan (x+y)=\frac{\sin (x+y)}{\cos (x+y)}=\frac{\sin x \cos y+\cos x \sin y}{\cos x \cos y-\sin x \sin y} .
\)
Dividing numerator and denominator by \(\cos x \cos y\), we have
\(
\begin{aligned}
\tan (x+y) &=\frac{\frac{\sin x \cos y}{\cos x \cos y}+\frac{\cos x \sin y}{\cos x \cos y}}{\frac{\cos x \cos y}{\cos x \cos y}-\frac{\sin x \sin y}{\cos x \cos y}} \\
&=\frac{\tan x+\tan y}{1-\tan x \tan y}
\end{aligned}
\)

11. \(\tan (x-y)=\frac{\tan x-\tan y}{1+\tan x \tan y}\)

Proof:

If we replace \(y\) by \(-y\) in Identity 10 , we get
\(
\begin{aligned}
\tan (x-y) &=\tan [x+(-y)] \\
&=\frac{\tan x+\tan (-y)}{1-\tan x \tan (-y)}=\frac{\tan x-\tan y}{1+\tan x \tan y}
\end{aligned}
\)

12. If none of the angles \(x, y\) and \((x+y)\) is a multiple of \(\pi\), then
\(
\cot (x+y)=\frac{\cot x \cot y-1}{\cot y+\cot x}
\)

Proof:

Since, none of the \(x, y\) and \((x+y)\) is multiple of \(\pi\), we find that \(\sin x, \sin y\) and \(\sin (x+y)\) are non-zero. Now,
\(
\cot (x+y)=\frac{\cos (x+y)}{\sin (x+y)}=\frac{\cos x \cos y-\sin x \sin y}{\sin x \cos y+\cos x \sin y}
\)
Dividing numerator and denominator by \(\sin x \sin y\), we have
\(
\cot (x+y)=\frac{\cot x \cot y-1}{\cot y+\cot x}
\)

13. \(\cot (x-y)=\frac{\cot x \cot y+1}{\cot y-\cot x}\) if none of angles \(x, y\) and \(x-y\) is a multiple of \(\pi\)

Proof:

If we replace \(y\) by \(-y\) in identity 12 , we get the result

14. \(\cos 2 x=\cos ^{2} x-\sin ^{2} x=2 \cos ^{2} x-1=1-2 \sin ^{2} x=\frac{1-\tan ^{2} x}{1+\tan ^{2} x}\)

Proof:

We know that \(\cos (x+y)=\cos x \cos y-\sin x \sin y\)
Replacing \(y\) by \(x\), we get
\( \begin{aligned} \cos 2 x &=\cos ^{2} x-\sin ^{2} x \\ &=\cos ^{2} x-\left(1-\cos ^{2} x\right)=2 \cos ^{2} x-1 \end{aligned} \)
\(\cos 2 x=\frac{1-\tan ^{2} x}{1+\tan ^{2} x}, \quad x \neq n \pi+\frac{\pi}{2}\), where \(\mathrm{n}\) is an integer

Note:

\(
\begin{aligned}
\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta} & =\frac{1-\frac{\sin ^2 \theta}{\cos ^2 \theta}}{1+\frac{\sin ^2 \theta}{\cos ^2 \theta}} \\
& =\frac{\left(\cos ^2 \theta-\sin ^2 \theta\right) / \cos ^2 \theta}{\left(\cos ^2 \theta+\sin ^2 \theta\right) / \cos ^2 \theta} \\
& =\frac{\cos ^2 \theta-\sin ^2 \theta}{\cos ^2 \theta+\sin ^2 \theta} \\
& =\cos ^2 \theta-\sin ^2 \theta \\
& =\cos ^2 \theta-\left(1-\cos ^2 \theta\right) \\
& =2 \cos ^2 \theta-1
\end{aligned}
\)

15. \(\sin 2 x=2 \sin x \cos x=\frac{2 \tan x}{1+\tan ^{2} x} x \neq n \pi+\frac{\pi}{2}\), where \(\mathrm{n}\) is an integer

Proof:

We have
\(
\sin (x+y)=\sin x \cos y+\cos x \sin y
\)
Replacing \(y\) by \(x\), we get \(\sin 2 x=2 \sin x \cos x\).
\(
\text { Again } \quad \sin 2 x=\frac{2 \sin x \cos x}{\cos ^{2} x+\sin ^{2} x}
\)
Dividing each term by \(\cos ^{2} x\), we get
\(
\sin 2 x=\frac{2 \tan x}{1+\tan ^{2} x}
\)

16. \(\tan 2 x=\frac{2 \tan x}{1-\tan ^{2} x}\) if \(2 x \neq n \pi+\frac{\pi}{2}\), where \(\mathrm{n}\) is an integer

Proof:

We know that
\(
\tan (x+y)=\frac{\tan x+\tan y}{1-\tan x \tan y}
\)
Replacing \(y\) by \(x\), we get \(\tan 2 x=\frac{2 \tan x}{1-\tan ^{2} x}\)

17. \(\sin 3 x=3 \sin x-4 \sin ^{3} x\)

Proof:

We have,
\(
\begin{aligned}
\sin 3 x &=\sin (2 x+x) \\
&=\sin 2 x \cos x+\cos 2 x \sin x \\
&=2 \sin x \cos x \cos x+\left(1-2 \sin ^{2} x\right) \sin x \\
&=2 \sin x\left(1-\sin ^{2} x\right)+\sin x-2 \sin ^{3} x \\
&=2 \sin x-2 \sin ^{3} x+\sin x-2 \sin ^{3} x \\
&=3 \sin x-4 \sin ^{3} x
\end{aligned}
\)

18. \(\cos 3 x=4 \cos ^{3} x-3 \cos x\)

Proof:

We have,
\(
\begin{aligned}
\cos 3 x &=\cos (2 x+x) \\
&=\cos 2 x \cos x-\sin 2 x \sin x \\
&=\left(2 \cos ^{2} x-1\right) \cos x-2 \sin x \cos x \sin x \\
&=\left(2 \cos ^{2} x-1\right) \cos x-2 \cos x\left(1-\cos ^{2} x\right) \\
&=2 \cos ^{3} x-\cos x-2 \cos x+2 \cos ^{3} x \\
&=4 \cos ^{3} x-3 \cos x
\end{aligned}
\)

19. \(\tan 3 x=\frac{3 \tan x-\tan ^{3} x}{1-3 \tan ^{2} x}\) if \(3 x \neq n \pi+\frac{\pi}{2}\), where \(\mathrm{n}\) is an integer

Proof:

We have \(\tan 3 x=\tan (2 x+x)\)
\(
=\frac{\tan 2 x+\tan x}{1-\tan 2 x \tan x}=\frac{\frac{2 \tan x}{1-\tan ^{2} x}+\tan x}{1-\frac{2 \tan x \cdot \tan x}{1-\tan ^{2} x}}
\)
\(=\frac{2 \tan x+\tan x-\tan ^{3} x}{1-\tan ^{2} x-2 \tan ^{2} x}=\frac{3 \tan x-\tan ^{3} x}{1-3 \tan ^{2} x}\)

20. (i) \(\cos x+\cos y=2 \cos \frac{x+y}{2} \cos \frac{x-y}{2}\)
(ii) \(\cos x-\cos y=-2 \sin \frac{x+y}{2} \sin \frac{x-y}{2}\)
(iii) \(\sin x+\sin y=2 \sin \frac{x+y}{2} \cos \frac{x-y}{2}\)
(iv) \(\sin x-\sin y=2 \cos \frac{x+y}{2} \sin \frac{x-y}{2}\)

Proof:

We know that
\(\cos (x+y)=\cos x \cos y-\sin x \sin y \quad \ldots\) (1)
and \(\quad \cos (x-y)=\cos x \cos y+\sin x \sin y \quad \ldots\) (2)
Adding and subtracting (1) and (2), we get
\(\cos (x+y)+\cos (x-y)=2 \cos x \cos y \quad \ldots\) (3)
and \(\quad \cos (x+y)-\cos (x-y)=-2 \sin x \sin y \quad \ldots\) (4)
Further \(\quad \sin (x+y)=\sin x \cos y+\cos x \sin y \quad \ldots\) (5)
and \(\quad \sin (x-y)=\sin x \cos y-\cos x \sin y \quad \ldots\) (6)
Adding and subtracting (5) and (6), we get
\(\begin{array}{ll}\sin (x+y)+\sin (x-y)=2 \sin x \cos y & \ldots(7) \\ \sin (x+y)-\sin (x-y)=2 \cos x \sin y & \ldots(8)\end{array}\)
Let \(x+y=\theta\) and \(x-y=\phi\). Therefore
\(
x=\left(\frac{\theta+\phi}{2}\right) \text { and } y=\left(\frac{\theta-\phi}{2}\right)
\)
Substituting the values of \(x\) and \(y\) in (3), (4), (7) and (8), we get
\(
\begin{aligned}
&\cos \theta+\cos \phi=2 \cos \left(\frac{\theta+\phi}{2}\right) \cos \left(\frac{\theta-\phi}{2}\right) \\
&\cos \theta-\cos \phi=-2 \sin \left(\frac{\theta+\phi}{2}\right) \sin \left(\frac{\theta-\phi}{2}\right) \\
&\sin \theta+\sin \phi=2 \sin \left(\frac{\theta+\phi}{2}\right) \cos \left(\frac{\theta-\phi}{2}\right)
\end{aligned}
\)
\(
\sin \theta-\sin \phi=2 \cos \left(\frac{\theta+\phi}{2}\right) \sin \left(\frac{\theta-\phi}{2}\right)
\)
Since \(\theta\) and \(\phi\) can take any real values, we can replace \(\theta\) by \(x\) and \(\phi\) by \(y\).
Thus, we get
\(
\begin{aligned}
&\cos x+\cos y=2 \cos \frac{x+y}{2} \cos \frac{x-y}{2} ; \cos x-\cos y=-2 \sin \frac{x+y}{2} \sin \frac{x-y}{2}, \\
&\sin x+\sin y=2 \sin \frac{x+y}{2} \cos \frac{x-y}{2} ; \sin x-\sin y=2 \cos \frac{x+y}{2} \sin \frac{x-y}{2} .
\end{aligned}
\)

Example 10: Prove that
\(
3 \sin \frac{\pi}{6} \sec \frac{\pi}{3}-4 \sin \frac{5 \pi}{6} \cot \frac{\pi}{4}=1
\)

Solution: We have
\(
\begin{aligned}
\text { L.H.S. } &=3 \sin \frac{\pi}{6} \sec \frac{\pi}{3}-4 \sin \frac{5 \pi}{6} \cot \frac{\pi}{4} \\
&=3 \times \frac{1}{2} \times 2-4 \sin \left(\pi-\frac{\pi}{6}\right) \times 1=3-4 \sin \frac{\pi}{6} \\
&=3-4 \times \frac{1}{2}=1=\text { R.H.S. }
\end{aligned}
\)

Example 11: Find the value of \(\sin 15^{\circ}\).

Solution: We have
\(
\begin{aligned}
\sin 15^{\circ} &=\sin \left(45^{\circ}-30^{\circ}\right) \\
&=\sin 45^{\circ} \cos 30^{\circ}-\cos 45^{\circ} \sin 30^{\circ} \\
&=\frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}} \times \frac{1}{2}=\frac{\sqrt{3}-1}{2 \sqrt{2}} .
\end{aligned}
\)

Example 12: \(\text { Find the value of } \tan \frac{13 \pi}{12} \text {. }\)

Solution: We have
\(
\begin{aligned}
\tan \frac{13 \pi}{12} &=\tan \left(\pi+\frac{\pi}{12}\right)=\tan \frac{\pi}{12}=\tan \left(\frac{\pi}{4}-\frac{\pi}{6}\right) \\
&=\frac{\tan \frac{\pi}{4}-\tan \frac{\pi}{6}}{1+\tan \frac{\pi}{4} \tan \frac{\pi}{6}}=\frac{1-\frac{1}{\sqrt{3}}}{1+\frac{1}{\sqrt{3}}}=\frac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3}
\end{aligned}
\)

Example 13: Prove that
\(
\frac{\sin (x+y)}{\sin (x-y)}=\frac{\tan x+\tan y}{\tan x-\tan y} .
\)

Solution: We have
\(
\text { L.H.S. }=\frac{\sin (x+y)}{\sin (x-y)}=\frac{\sin x \cos y+\cos x \sin y}{\sin x \cos y-\cos x \sin y}
\)
Dividing the numerator and denominator by \(\cos x \cos y\), we get
\(
\frac{\sin (x+y)}{\sin (x-y)}=\frac{\tan x+\tan y}{\tan x-\tan y} .
\)

Example 14: Show that
\(
\tan 3 x \tan 2 x \tan x=\tan 3 x-\tan 2 x-\tan x
\)

Solution: We know that \(3 x=2 x+x\)
Therefore, \(\tan 3 x=\tan (2 x+x)\)
or \(\quad \tan 3 x=\frac{\tan 2 x+\tan x}{1-\tan 2 x \tan x}\)
or \(\quad \tan 3 x-\tan 3 x \tan 2 x \tan x=\tan 2 x+\tan x\)
or \(\quad \tan 3 x-\tan 2 x-\tan x=\tan 3 x \tan 2 x \tan x\)

Example 15: Prove that
\(
\cos \left(\frac{\pi}{4}+x\right)+\cos \left(\frac{\pi}{4}-x\right)=\sqrt{2} \cos x
\)

Solution:
\(\begin{aligned}
\text { L.H.S. } \quad &=\cos \left(\frac{\pi}{4}+x\right)+\cos \left(\frac{\pi}{4}-x\right) \\
&=2 \cos \left(\frac{\frac{\pi}{4}+x+\frac{\pi}{4}-x}{2}\right) \cos \left(\frac{\frac{\pi}{4}+x-\left(\frac{\pi}{4}-x\right)}{2}\right) \\
&=2 \cos \frac{\pi}{4} \cos x=2 \times \frac{1}{\sqrt{2}} \cos x=\sqrt{2} \cos x=\text { R.H.S. }
\end{aligned}\)

Example 16: Prove that \(\frac{\cos 7 x+\cos 5 x}{\sin 7 x-\sin 5 x}=\cot x\)

Solution: Using the Identities 20 (i) and 20 (iv), we get
\(
\text { L.H.S. }=\frac{2 \cos \frac{7 x+5 x}{2} \cos \frac{7 x-5 x}{2}}{2 \cos \frac{7 x+5 x}{2} \sin \frac{7 x-5 x}{2}}=\frac{\cos x}{\sin x}=\cot x=\text { R.H.S. }
\)

Example 17: Prove that \(=\frac{\sin 5 x-2 \sin 3 x+\sin x}{\cos 5 x-\cos x}=\tan x\)

Solution: We have
\(
\begin{aligned}
\text { L.H.S. } &=\frac{\sin 5 x-2 \sin 3 x+\sin x}{\cos 5 x-\cos x}=\frac{\sin 5 x+\sin x-2 \sin 3 x}{\cos 5 x-\cos x} \\
&=\frac{2 \sin 3 x \cos 2 x-2 \sin 3 x}{-2 \sin 3 x \sin 2 x}=-\frac{\sin 3 x(\cos 2 x-1)}{\sin 3 x \sin 2 x} \\
&=\frac{1-\cos 2 x}{\sin 2 x}=\frac{2 \sin ^{2} x}{2 \sin x \cos x}=\tan x=\text { R.H.S. }
\end{aligned}
\)