2.1 Introduction
“Relations and Functions” are the most important topics in algebra. Relations and functions – these are the two different words having different meanings mathematically. You might get confused about their difference. Before we go deeper, let’s understand the difference between both with a simple example.
An ordered pair is represented as (INPUT, OUTPUT):
The relation shows the relationship between INPUT and OUTPUT. Whereas, a function is a relation that derives one OUTPUT for each given INPUT.
Note: All functions are relations, but not all relations are functions.
What is a Function?
A function is a relation that describes that there should be only one output for each input (or) we can say that a special kind of relation (a set of ordered pairs), which follows a rule i.e., every \(X\)-value should be associated with only one \(y\)-value is called a function.
\(\begin{aligned}
&\text { For example: }\\
&\begin{array}{|l|l|}
\hline \text { Domain } & \text { Range } \\
\hline-1 & -4 \\
\hline 1 & 4 \\
\hline 3 & 8 \\
\hline
\end{array}
\end{aligned}
\)
\(
\begin{aligned}
&\text { Let us also look at the definition of Domain and Range of a function. }\\
&\begin{array}{|l|l|}
\hline \text { Domain } & \text { It is a collection of the first values in the ordered pair (Set of all input }(\mathrm{x}) \text { values). } \\
\hline \text { Range } & \text { It is a collection of the second values in the ordered pair (Set of all output (y) values). } \\
\hline
\end{array}
\end{aligned}
\)
Example:
In the relation, \(\{(-2,3),\{4,5),(6,-5),(-2,3)\}\),
The domain is \(\{-2,4,6\}\) and range is \(\{-5,3,5\}\).
Note: Don’t consider duplicates while writing the domain and range and also write it in increasing order.
What is the Relation?
It is a subset of the Cartesian product. Or simply, a bunch of points (ordered pairs). In other words, the relation between the two sets is defined as the collection of the ordered pair, in which the ordered pair is formed by the object from each set.
Example: \({(-2,1),(4,3),(7,-3)}\), usually written in set notation form with curly brackets.
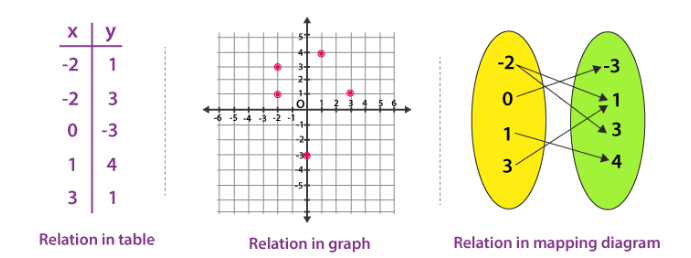
Relation Representation
There are other ways too to write the relation, apart from set notation such as through tables, plotting it on \(\mathrm{XY}\) – axis or through mapping diagram.