NCERT Exampler Questions
Quiz Summary
0 of 34 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 34 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 34
1. Question
We know that the relationship between \(K_c\) and \(K_p\) is
\(
K_p=K_c(\mathrm{RT})^{\Delta n}
\)
What would be the value of \(\Delta n\) for the reaction
\(
\mathrm{NH}_4 \mathrm{Cl}(\mathrm{s}) \rightleftharpoons \mathrm{NH}_3(\mathrm{~g})+\mathrm{HCl}(\mathrm{g})
\)CorrectIncorrectHint
(d) The relationship between \(K_p\) and \(K_c\) is
\(
K_p=K_c(R T)^{\Delta n}
\)
Where \(\Delta n=\) (number of moles of gaseous products) – (number of moles of gaseous reactants)
For the reaction,
\(
\mathrm{NH}_4 \mathrm{Cl}(\mathrm{s}) \rightleftharpoons \mathrm{NH}_3(\mathrm{~g})+\mathrm{HCl}(\mathrm{g})
\)
\(
\Delta n=2-0=2
\) -
Question 2 of 34
2. Question
For the reaction \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\), the standard free energy is \(\Delta G^{\ominus}>0\). The equilibrium constant \((K)\) would be
CorrectIncorrectHint
(d) \(\Delta G^{\ominus}=-R T \ln K; \Delta G^{\ominus}>0\) means \(\Delta G^{\ominus}\) is +ve. This can be so only if In \(K\) is -ve, i.e., \(K<1\).
-
Question 3 of 34
3. Question
Which of the following is not a general characteristic of equilibria involving physical processes?
CorrectIncorrectHint
(c) All the physical processes like melting of ice and freezing of water, etc., do not stop at equilibrium.
-
Question 4 of 34
4. Question
\(\mathrm{PCl}_5, \mathrm{PCl}_3\) and \(\mathrm{Cl}_2\) are at equilibrium at \(500 \mathrm{~K}\) in a closed container and their concentrations are \(0.8 \times 10^{-3} \mathrm{~mol} \mathrm{~L}^{-1}, 1.2 \times 10^{-3} \mathrm{~mol} \mathrm{~L}^{-1}\) and \(1.2 \times 10^{-3} \mathrm{~mol} \mathrm{~L}^{-1}\) respectively. The value of \(K_c\) for the reaction \(\mathrm{PCl}_5(\mathrm{~g}) \rightleftharpoons \mathrm{PCl}_3(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g})\) will be
CorrectIncorrectHint
(b)
\(
\begin{aligned}
K_{\mathrm{C}} & =\frac{\left[\mathrm{PCl}_3\right]\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}=\frac{1 .2 \times 10^{-3} \times 1.2 \times 10^{-3}}{0.8 \times 10^{-3}} \\
& =1.8 \times 10^{-3} \mathrm{~mol} \mathrm{~L}^{-1}
\end{aligned}
\) -
Question 5 of 34
5. Question
Which of the following statements is incorrect?
CorrectIncorrectHint
(b) \(\mathrm{Fe}^{3+}+\mathrm{SCN}^{-} \rightleftharpoons \mathrm{FeSCN}^{2+}(\mathrm{Red})\)
When oxalic acid is added to a solution containing iron nitrate and potassium thiocyanate, oxalic acid reacts with \(\mathrm{Fe}^{3+}\) ions to form a stable complex ion \(\left[\mathrm{Fe}\left(\mathrm{C}_2 \mathrm{O}_4\right)_3\right]^{3-}\), thus, decreasing the concentration of free \(\mathrm{Fe}^{3+}\) ions which in \(\mathrm{mm}\) decreases the intensity of red colour.
\(
\mathrm{Fe}^{3+}+\mathrm{SCN}^{-} \rightleftharpoons[\mathrm{Fe}(\mathrm{SCN})]^{2+}(\mathrm{Blood Red})
\) -
Question 6 of 34
6. Question
When hydrochloric acid is added to cobalt nitrate solution at room temperature, the following reaction takes place and the reaction mixture becomes blue. On cooling the mixture it becomes pink. On the basis of this information mark the correct answer.
\(
\left[\mathrm{Co}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{3+}(a q)+4 \mathrm{Cl}^{-}(a q) \rightleftharpoons\left[\mathrm{CoCl}_4\right]^{2-}(a q)+6 \mathrm{H}_2 \mathrm{O}(l)
\)
\(
\text { (pink) } \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \text { (blue) }
\)CorrectIncorrectHint
(a) Since the reaction shifts to backward direction on cooling, this means that the backward reaction is exothermic reaction. Therefore, the forward reaction is endothermic reaction and \(\Delta \mathrm{H}>0\).
-
Question 7 of 34
7. Question
The \(\mathrm{pH}\) of neutral water at \(25^{\circ} \mathrm{C}\) is 7.0 . As the temperature increases, ionisation of water increases, however, the concentration of \(\mathrm{H}^{+}\)ions and \(\mathrm{OH}\) ions are equal. What will be the \(\mathrm{pH}\) of pure water at \(60^{\circ} \mathrm{C}\) ?
CorrectIncorrectHint
(c) At \(25^{\circ} \mathrm{C},\left[\mathrm{H}^{+}\right]=\left[\mathrm{OH}^{-}\right]=10^7\) and \(\mathrm{K}_W=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]=10^{-14}\).
On heating, \(\mathrm{K}_w\) increases, i.e., \(\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]>10^{-}\) \({ }^{14}\) As \(\left[\mathrm{H}^{+}\right]=\left[\mathrm{OH}^{-}\right],\left[\mathrm{H}^{+}\right]^2>10^{-14}\) or \(\left[\mathrm{H}^{+}\right]>10^{-7} \mathrm{~M}\) or \(\mathrm{pH}<7\). -
Question 8 of 34
8. Question
The ionisation constant of an acid, \(K_{\mathrm{a}}\), is the measure of strength of an acid. The \(K_{\mathrm{a}}\) values of acetic acid, hypochlorous acid and formic acid are \(1.74 \times 10^{-5}, 3.0 \times 10^{-8}\) and \(1.8 \times 10^{-4}\) respectively. Which of the following orders of \(\mathrm{pH}\) of \(0.1 \mathrm{~mol} \mathrm{~dm}^{-3}\) solutions of these acids is correct?
CorrectIncorrectHint
(d) \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\sqrt{K_{\mathrm{a}} \cdot \mathrm{C}}\) for the same concentration, \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \propto \sqrt{K_{\mathrm{a}}}\). But \(\mathrm{pH}=-\log \left[\mathrm{H}_3 \mathrm{O}^{+}\right]\)
Larger the value of \(K_{\mathrm{a}}\), larger will be \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\)and lower will be \(\mathrm{pH}\). -
Question 9 of 34
9. Question
\(K_{a_1}, K_{a_2}\) and \(K_{a_3}\) are the respective ionisation constants for the following reactions.
\(
\begin{aligned}
& \mathrm{H}_2 \mathrm{~S} \rightleftharpoons \mathrm{H}^{+}+\mathrm{HS}^{-} \\
& \mathrm{HS}^{-} \rightleftharpoons \mathrm{H}^{+}+\mathrm{S}^{2-} \\
& \mathrm{H}_2 \mathrm{~S} \rightleftharpoons 2 \mathrm{H}^{+}+\mathrm{S}^{2-}
\end{aligned}
\)
The correct relationship between \(K_{a_1}, K_{a_2}\) and \(K_{a_3}\) isCorrectIncorrectHint
(a) For the reaction, \(\mathrm{H}_2 \mathrm{S} \rightleftharpoons \mathrm{H}^{+}+\mathrm{HS}^{-}\)
\(
K_{\mathrm{a}_1}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{HS}^{-}\right]}{\left[\mathrm{H}_2 \mathrm{~S}\right]}
\)
For the reaction, \(\quad \mathrm{HS}^{-} \rightleftharpoons \mathrm{H}^{+}+\mathrm{S}^{2-}\)
\(
K_{\mathrm{a}_2}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{S}^{2-}\right]}{\left[\mathrm{HS}^{-}\right]}
\)
When the above two reactions are added, their equilibrium constants are multiplied. Thus
\(
K_{\mathrm{a}_3}=\frac{\left[\mathrm{H}^{+}\right]^2\left[\mathrm{~S}^{2-}\right]}{\left[\mathrm{H}_2 \mathrm{~S}\right]}=K_{\mathrm{a}_1} \times K_{\mathrm{a}_2}
\)
Hence, \(K_{\mathrm{a}_3}=K_{\mathrm{a}_1} \times K_{\mathrm{a}_2}\) -
Question 10 of 34
10. Question
Acidity of \(\mathrm{BF}_3\) can be explained on the basis of which of the following concepts?
CorrectIncorrectHint
(c) According to Lewis concept, a positively charged or an electron deficient species acts as Lewis acid. \(\mathrm{BF}_3\) is an electron deficient compound with \(\mathrm{B}\) having 6 electrons only.
-
Question 11 of 34
11. Question
Which of the following will produce a buffer solution when mixed in equal volumes?
CorrectIncorrectHint
(c) In (c), all \(\mathrm{HCl}\) will be neutralized and \(\mathrm{NH}_4 \mathrm{C} l\) will be formed. Also some \(\mathrm{NH}_4 \mathrm{OH}\) will be left unneutralized. Thus, the final solution will contain \(\mathrm{NH}_4 \mathrm{OH}\) and \(\mathrm{NH}_4 \mathrm{Cl}\) and hence will form a buffer.
-
Question 12 of 34
12. Question
In which of the following solvents is silver chloride most soluble?
CorrectIncorrectHint
(d) Silver chloride forms a soluble complex with aqueous ammonia. \(\mathrm{AgCl}+2 \mathrm{NH}_3 \rightarrow\left[\mathrm{Ag}\left(\mathrm{NH}_3\right)_2\right] \mathrm{Cl}\)
-
Question 13 of 34
13. Question
What will be the value of \(\mathrm{pH}\) of \(0.01 \mathrm{~mol} \mathrm{dm}^{-3} \mathrm{CH}_3 \mathrm{COOH}\left(K_{\mathrm{a}}=1.74 \times 10^{-5}\right)\)?
CorrectIncorrectHint
(a)
\(\mathrm{pH}\) for weak acid is given by:
\(
\mathrm{pH}=\frac{1}{2}\left[\mathrm{pK}_{\mathrm{a}}-\log \mathrm{C}\right]
\)
\(
=\frac{1}{2}\left[-\log \left(1.74 \times 10^{-5}\right)-\log 10^{-2}\right]
\)
\(
=\frac{1}{2}[(5-0.2405)+2]=\frac{1}{2}(6.76)=3.38 \cong 3.4
\)Alternate:
Hint: \(\left[\mathrm{H}^{+}\right]=\sqrt{\mathrm{K}_{\mathrm{a} \cdot} \cdot \mathrm{C}}\)
Step 1:
Calculate the concentration of \(\mathrm{H}^{+}\)ion as follows:
Given that, \(\left(\mathrm{K}_{\mathrm{a}}=1.74 \times 10^{-5}\right)\)
Concentration of \(\mathrm{CH}_3 \mathrm{COOH}=0.01 \mathrm{~mol} \mathrm{~dm}{ }^{-3}\)
\(
\begin{aligned}
& {\left[\mathrm{H}^{+}\right]=\sqrt{\mathrm{K}_{\mathrm{a}} \cdot \mathrm{C}}} \\
& =\sqrt{1.74 \times 10^{-5} \times 0.01}=4.17 \times 10^{-4}
\end{aligned}
\)Step 2 :
\(
\begin{aligned}
& \mathrm{pH}=-\log \left[\mathrm{H}^{+}\right] \\
& =-\log \left(4.17 \times 10^{-4}\right) \\
& =3.4
\end{aligned}
\) -
Question 14 of 34
14. Question
\(K_{\mathrm{a}}\) for \(\mathrm{CH}_3 \mathrm{COOH}\) is \(1.8 \times 10^{-5}\) and \(K_{\mathrm{b}}\) for \(\mathrm{NH}_4 \mathrm{OH}\) is \(1.8 \times 10^{-5}\). The \(\mathrm{pH}\) of ammonium acetate will be
CorrectIncorrectHint
(c)
\(
\begin{aligned}
\mathrm{pH} & =\frac{1}{2}\left[\mathrm{p} K_{\mathrm{w}}+\mathrm{p} K_{\mathrm{a}}-\mathrm{p} K_{\mathrm{b}}\right] \\
& =\frac{1}{2}\left[14-\log \left(1.8 \times 10^{-5}\right)+\log \left(1.8 \times 10^{-5}\right)\right]=7.0
\end{aligned}
\) -
Question 15 of 34
15. Question
Which of the following options will be correct for the stage of half completion of the reaction \(A \rightleftharpoons B\).
CorrectIncorrectHint
(a)
\(
\Delta G^{\ominus}=-R T \ln K
\)
At the stage of half completion of reaction \([A]=[B]\),
Therefore, \(K=1\). Thus, \(\Delta G^{\ominus}=0\). -
Question 16 of 34
16. Question
On increasing the pressure, in which direction will the gas phase reaction proceed to re-establish equilibrium, is predicted by applying the Le Chatelier’s principle. Consider the reaction.
\(
\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH}_3(\mathrm{~g})
\)
Which of the following is correct, if the total pressure at which the equilibrium is established, is increased without changing the temperature?CorrectIncorrectHint
(a) According to Le Chatelier’s principle, at constant temperature, the equilibrium composition will change but \(\mathrm{K}\) will remain same. If the total pressure at which the equilibrium is established, is increased without changing the temperature, \(\mathrm{K}\) will remain same. \(\mathrm{K}\) changes only with change in temperature.
-
Question 17 of 34
17. Question
What will be the correct order of vapour pressure of water, acetone and ether at \(30^{\circ} \mathrm{C}\). Given that among these compounds, water has maximum boiling point and ether has minimum boiling point?
CorrectIncorrectHint
(b) Greater the boiling point, less is the vapour pressure. Hence, the correct order of vapour pressures will be:
water < acetone < ether.Hint: Magnitude of vapour pressure and boiling point are inversely proportional to each other
Greater the boiling point, lower is the vapour pressure of the solvent.
The boiling point of water is \(100^{\circ} \mathrm{C}\), acetone boiling point is \(56^{\circ} \mathrm{C}\), and ether boiling point is \(34.6^{\circ} \mathrm{C}\).
-
Question 18 of 34
18. Question
At \(500 \mathrm{~K}\), equilibrium constant, \(K_c\), for the following reaction is 5 .
\(
\frac{1}{2} \mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{I}_2(\mathrm{~g}) \rightleftharpoons \mathrm{HI}(\mathrm{g})
\)
What would be the equilibrium constant \(K_{\mathrm{c}}\) for the reaction
\(
2 \mathrm{HI}(\mathrm{g}) \rightleftharpoons \mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g})
\)CorrectIncorrectHint
If the given equation is multiplied by 2 , the equilibrium constant for the new equation will be squared, and on reversing the reaction the value of the equilibrium constant is reciprocated.
Thus
\(
K=5^2=25
\)
For the required reaction equation \(K=\frac{1}{25}=0.04\)Alternate:
The equilibrium constant for the reverse reaction is the inverse of the equilibrium constant for the reaction in the forward direction
\(
\text { For the reaction, } \frac{1}{2} \mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{I}_2(\mathrm{~g}) \rightleftharpoons \mathrm{HI}(\mathrm{g})
\)
\(
\mathrm{K}_{\mathrm{c}}=\frac{[\mathrm{HI}]}{\left[\mathrm{H}_2\right]^{1 / 2}\left[\mathrm{I}_2\right]^{1 / 2}}=5
\)
\(
\text { Thus, for the reaction, } 2 \mathrm{HI}(\mathrm{g}) \rightleftharpoons \mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g})
\)
\(
\mathrm{K}_{\mathrm{c}_1}=\frac{\left[\mathrm{H}_2\right]\left[\mathrm{I}_2\right]}{[\mathrm{HI}]^2}=\left(\frac{1}{\mathrm{~K}_{\mathrm{c}}}\right)^2=\left(\frac{1}{5}\right)^2=\frac{1}{25}=0.04
\) -
Question 19 of 34
19. Question
In which of the following reactions, the equilibrium remains unaffected on addition of small amount of argon at constant volume?
CorrectIncorrectHint
(d) The equilibrium will remain unaffected in all three cases on addition of small amount of inert gas at constant volume.
Alternate:
Hint: Inert gas doesn’t affect equilibrium at constant volume according to Le – Chatelier’s principle.
Explanation:
Step 1:
Le- Chatelier’s principle, states that changes in the temperature, pressure, volume, or concentration of a system will result in predictable and opposing changes in the system in order to achieve a new equilibrium state.The reaction is as follows:
\(
\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})
\)
\(\mathrm{PCl}_5(\mathrm{~g}) \rightleftharpoons \mathrm{PCl}_3(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g})\)
\(
\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH}_3(\mathrm{~g})
\)Step 2:
According to Le chatelier’s principle, the equilibrium constant (K) remains unaffected by the addition of inert gas in constant volume. Hence, in all three cases equilibrium remain unaffected. -
Question 20 of 34
20. Question
For the reaction \(\mathrm{N}_2 \mathrm{O}_4(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}_2(\mathrm{~g})\), the value of \(K\) is 50 at \(400 \mathrm{~K}\) and 1700 at \(500 \mathrm{~K}\). Which of the following options is correct?
CorrectIncorrectHint
(a) As the value of \(\mathrm{K}\) increases with increase of temperature and \(\mathrm{K}=\mathrm{K}_{\mathrm{f}} / \mathrm{K}_{\mathrm{b}}\), this means that \(\mathrm{K}_{\mathrm{f}}\) increases, i.e., forward reaction is favoured.
Hence, reaction is endothermic.
(c). At \(400 \mathrm{~K}, Q=\frac{p_{\mathrm{NO}_2}^2}{P_{\mathrm{N}_2 \mathrm{O}_4}}=\frac{(20)^2}{2}=200\). Thus, \(Q>K\). Equilibrium will shift backward to form more \(\mathrm{N}_2 \mathrm{O}_4\).
(d) As reaction is accompanied by increase in the number of moles, entropy increases. -
Question 21 of 34
21. Question
At a particular temperature and atmospheric pressure, the solid and liquid phases of a pure substance can exist in equilibrium. Which of the following term defines this temperature?
CorrectIncorrectHint
(a, d) These are normal melting point and freezing point since they are measured at atmospheric pressure.
-
Question 22 of 34
22. Question
Match the following equilibria with the corresponding condition
\(
\begin{array}{|l|l|}
\hline \text { (i) Liquid } \rightleftarrows \text { Vapour } & \text { (a) Saturated solution } \\
\hline \text { (ii) Solid } \rightleftarrows \text { Liquid } & \text { (b) Boiling point } \\
\hline \text { (iii) Solid } \rightleftarrows \text { Vapour } & \text { (c) Sublimation point } \\
\hline \text { (iv) Solute (s) } \rightleftarrows \text { Solute (solution) } & \text { (d) Melting point } \\
\hline & \text { (e) Unsaturated solution } \\
\hline
\end{array}
\)CorrectIncorrectHint
(a)
(i) \(\rightarrow\) (b), (ii) \(\rightarrow\) (d), (iii) \(\rightarrow\) (c), (iv) \(\rightarrow\) (a)
(i) Liquid \(\rightleftharpoons\) Vapour equilibrium exists at the boiling point.
(ii) Solid \(\rightleftharpoons\) Liquid equilibrium exists at the melting point.
(iii) Solid \(\rightleftharpoons\) Vapour equilibrium exists at the sublimation point.
(iv) Solute(s) \(\rightleftharpoons\) Solute (solution) equilibrium exists in saturated solution. -
Question 23 of 34
23. Question
For the reaction: \(\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH}_3(\mathrm{~g})\)
Equilibrium constant \(K_c=\frac{\left[\mathrm{NH}_3\right]^2}{\left[\mathrm{~N}_2\right]\left[\mathrm{H}_2\right]^3}\)
Some reactions are written below in Column I and their equilibrium constants in terms of \(K_c\) are written in Column II. Match the following reactions with the corresponding equilibrium constant CorrectIncorrect
CorrectIncorrectHint
(c)
\(
\text { (i) } \rightarrow \text { (d), (ii) } \rightarrow \text { (c), (iii) } \rightarrow \text { (b) }
\)
For \(\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH}_3(\mathrm{~g})\)
\(
K_{\mathrm{C}}=\frac{\left[\mathrm{NH}_3\right]^2}{\left[\mathrm{~N}_2\right]\left[\mathrm{H}_2\right]^3}
\)
\(
\text { (i) } 2 \mathrm{~N}_2(\mathrm{~g})+6 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons 4 \mathrm{NH}_3(\mathrm{~g}) ; K_{\mathrm{C}}^{\prime}=K_{\mathrm{C}}^2
\)
\(
\text { (ii) } 2 \mathrm{NH}_3(\mathrm{~g}) \rightleftharpoons \mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) ; K_{\mathrm{C}}^{\prime}=\frac{1}{K_{\mathrm{C}}}
\)
\(
\text { (iii) } \frac{1}{2} \mathrm{~N}_2(\mathrm{~g})+\frac{3}{2} \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons \mathrm{NH}_3(\mathrm{~g}) ; K_{\mathrm{C}}^{\prime}=K_{\mathrm{C}}^{1 / 2}
\) -
Question 24 of 34
24. Question
Match standard free energy of the reaction with the corresponding equilibrium constant
 CorrectIncorrect
CorrectIncorrectHint
(b)
(i) \(\rightarrow\) (d), (ii) \(\rightarrow\) (a), (iii) \(\rightarrow\) (b)
As we know that, \(\Delta G^{\ominus}=-\mathrm{R} T \ln K\)
(i) If \(\Delta G^{\ominus}>0\), i.e., \(\Delta G^{\ominus}\) is positive, then \(\ln K\) is negative i.e., \(K<1\)
(ii) If \(\Delta G^{\ominus}<0\), i.e., \(\Delta G^{\ominus}\) is negative then \(\ln K\) is positive i.e., \(K>1\).
(iii) If \(\Delta G^{\ominus}=0, \ln K=0\), i.e., \(K=1\) -
Question 25 of 34
25. Question
Match the following species with the corresponding conjugate acid
\(
\begin{array}{|c|c|}
\hline \text { Species } & \text { Conjugate Acid } \\
\hline \text { (i) } \mathrm{NH}_3 & \text { (a) } \mathrm{CO}_3{ }^{2-} \\
\hline \text { (ii) } \mathrm{HCO}_3{ }^{-} & \text {(b) } \mathrm{NH}_4{ }^{+} \\
\hline \text { (iii) } \mathrm{H}_2 \mathrm{O} & \text { (c) } \mathrm{H}_3 \mathrm{O}^{+} \\
\hline \text { (iv) } \mathrm{HSO}_4^{-} & \text {(d) } \mathrm{H}_2 \mathrm{SO}_4 \\
\hline & \text { (e) } \mathrm{H}_2 \mathrm{CO}_3 \\
\hline
\end{array}
\)CorrectIncorrectHint
(d) Hint: Conjugate acids are a type of acid that is formed when a base accepts a proton in solution. Explanation:
As conjugate base \(\rightarrow\) Base \(+\mathrm{H}^{+}\)
A. \(\mathrm{NH}_3+\mathrm{H}^{+} \rightarrow \mathrm{NH}_4^{+}\)
B. \(\mathrm{HCO}_3^{-}+\mathrm{H}^{+} \rightarrow \mathrm{H}_2 \mathrm{CO}_3\)
C. \(\mathrm{H}_2 \mathrm{O}+\mathrm{H}^{+} \rightarrow \mathrm{H}_3 \mathrm{O}^{+}\)
D. \(\mathrm{HSO}_4^{-}+\mathrm{H}^{+} \rightarrow \mathrm{H}_2 \mathrm{SO}_4\) -
Question 26 of 34
26. Question
Match the following graphical variation with their description
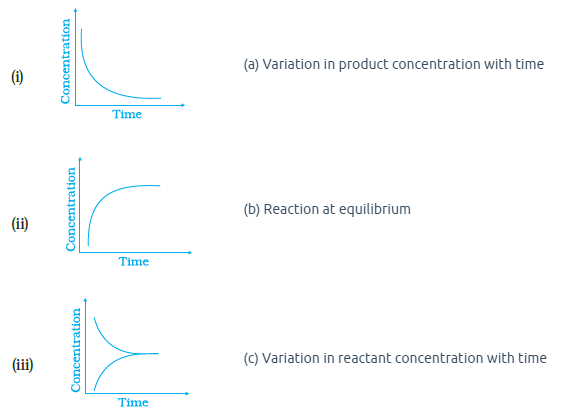 CorrectIncorrect
CorrectIncorrectHint
(a)
c) Variation in Reactant conc. \(\mathrm{v} / \mathrm{s}\) time.
\(\therefore\) Reactant concentration decreases with time as it gets converted to product. So, it matches curve \((i)\).
a) Variation of product concentration with time.Since, Concentration of Product increases with time as products will get produced from reactants. So, it matches curve (ii)
b) Reaction at equilibriumThe time from where concentration of [reactant \(]\) and [ product \(]\) becomes constant, the equilibrium is established. As at this time both rates of forward and backward reaction are equal. So, it matches curve \((\) iii \()\)
-
Question 27 of 34
27. Question
Match Column (I) with Column (II).
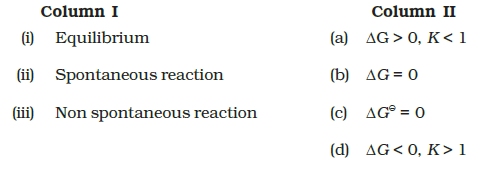 CorrectIncorrect
CorrectIncorrectHint
(b)
(i) \(\rightarrow\) (b) and (c) (ii) \(\rightarrow\) (d) (iii) \(\rightarrow\) (a)
Hint: The relation between \(\Delta_{\mathrm{r}} \Delta G^{\ominus}\) and \(\mathrm{K}\) is \(\Delta_{\mathrm{r}} \Delta G^{\ominus}=-\mathrm{RT} \ln \mathrm{K}\)
A. \(\Delta \mathrm{G}\) is 0 , the reaction has achieved equilibrium: at this point, there is no longer any free energy left to drive the reaction.
B. If \(\Delta G<0\), then \(\mathrm{K}>1\) which implies a spontaneous reaction or the reaction which proceeds in the forward direction to such an extent that the products are present predominantly.
C. If \(\Delta \mathrm{G}>\mathbf{0}\), then \(\mathrm{K}<1\), which implies a non-spontaneous reaction or a reaction that proceeds in the forward direction to such a small degree that only a very minute quantity of product is formed. -
Question 28 of 34
28. Question
In the following questions a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A) : Increasing order of acidity of hydrogen halides is \(\mathrm{HF}<\mathrm{HCl}<\mathrm{HBr}<\mathrm{HI}\)
Reason (R) : While comparing acids formed by the elements belonging to the same group of periodic table, \(\mathrm{H}-\mathrm{A}\) bond strength is a more important factor in determining acidity of an acid than the polar nature of the bond.CorrectIncorrectHint
(a) Hint: Down the group acidity of hydrogen halide increases.
Explanation:In the hydrogen halides, the \(\mathrm{HI}\) is the strongest acid while \(\mathrm{HF}\) is the weak acid. It is because while comparing acids formed by the elements belonging to the same group of the periodic table, \(\mathrm{H}-\mathrm{A}\) bond strength is a more important factor in determining the acidity of acid than the polar nature of the bond.
Down the group strength of \(\mathrm{HI}\) bond decreases because bond dissociation energy decreases. Hence, acidity increases.
-
Question 29 of 34
29. Question
In the following questions a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A) : A solution containing a mixture of acetic acid and sodium acetate maintains a constant value of \(\mathrm{pH}\) on addition of small amounts of acid or alkali.
Reason (R) : A solution containing a mixture of acetic acid and sodium acetate acts as a buffer solution around \(\mathrm{pH} 4.75\).CorrectIncorrectHint
(a) Hint: Buffer solution resist the \(\mathrm{pH}\) change.
Explanation:
A buffer solution is an acid or a base aqueous solution consisting of a mixture of a weak acid and its conjugate base, or vice versa. Its pH changes very little when a small amount of strong acid or base is added to it.
A solution containing a mixture of acetic acid and sodium acetate acts as a buffer solution as it maintains a constant pH which is not affected by the addition of small amounts of acid or alkali.
So, option a is the correct answer.
-
Question 30 of 34
30. Question
In the following questions a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): The ionisation of hydrogen sulphide in water is low in the presence of hydrochloric acid.
Reason (R) : Hydrogen sulphide is a weak acid.CorrectIncorrectHint
(b) Hint: Common ion effect
\(\mathrm{H}_2 \mathrm{~S}\) is a weak acid and forms an equilibrium in the solution. The reaction is as follows:
\(
\mathrm{H}_2 \mathrm{~S} \rightleftharpoons 2 \mathrm{H}^{+}+2 \mathrm{~S}^{2-}
\)When a strong acid like \(\mathrm{HCl}\) is added to the solution, due to the common ion effect the ionization of \(\mathrm{H}_2 \mathrm{~S}\) is suppressed. Hence, Both assertion and reason are true and the reason is not the correct explanation of assertion.
-
Question 31 of 34
31. Question
In the following questions a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): For any chemical reaction at a particular temperature, the equilibrium constant is fixed and is a characteristic property.
Reason (R) : Equilibrium constant is independent of temperature.CorrectIncorrectHint
(c)
Hint: The equilibrium constant of a reaction depends upon temperature.
Equilibrium constants are changed if we change the temperature of the system. For any chemical reaction at a particular temperature, the equilibrium constant is fixed and is a characteristic property. Hence, Assertion is true but the reason is false. -
Question 32 of 34
32. Question
In the following questions a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A) : Aqueous solution of ammonium carbonate is basic.
Reason (R) : Acidic/basic nature of a salt solution of a salt of weak acid and weak base depends on \(K_{\mathrm{a}}\) and \(K_{\mathrm{b}}\) value of the acid and the base forming it.CorrectIncorrectHint
(a) Analyzing the assertion
It is correct because aqueous solution of ammonium carbonate is basic in nature.Analyzing the reason
It is also correct because for a solution of salt of weak acid and weak base, the acidic/basic nature depends upon value of \(K_a\) for weak acid and \(K_b\) for weak base.Solution is basic if
\(\mathrm{K}_{\mathrm{b}}\) (weak base) \(>\mathrm{K}_{\mathrm{a}}\) (weak acid).
\(
\begin{aligned}
& \mathrm{Ka}\left(\mathrm{H}_2 \mathrm{CO}_3\right)=4.3 \times 10^{-7} \\
& \mathrm{~Kb}\left(\mathrm{NH}_4 \mathrm{OH}\right)=1.8 \times 10^{-5}
\end{aligned}
\)
\(\mathrm{K}_{\mathrm{b}}\) (Ammonium hydroxide) \(>\mathrm{K}_{\mathrm{a}}\) (Hydrogen carbonate)
\(\therefore\) Hence, solution of Ammonium carbonate is basic in nature.
Both \(\mathrm{A}\) and \(\mathrm{R}\) are true and \(\mathrm{R}\) is the correct explanation of \(\mathrm{A}\).
\(\therefore\) Correct answer is option (a). -
Question 33 of 34
33. Question
In the following questions a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): An aqueous solution of ammonium acetate can act as a buffer.
Reason (R) : Acetic acid is a weak acid and \(\mathrm{NH}_4 \mathrm{OH}\) is a weak base.CorrectIncorrectHint
(c)
Hint: An aqueous solution of ammonium acetate can act as a buffer.
Explanation:
A buffer solution is an aqueous solution consisting of a mixture of a weak acid and its conjugate base, or vice versa. Its \(\mathrm{pH}\) changes very little when a small amount of strong acid or base is added to it.
Ammonium acetate is a salt of a weak acid \(\left(\mathrm{CH}_3 \mathrm{COOH}\right)\) and weak base \(\left(\mathrm{NH}_4 \mathrm{OH}\right)\).
Hence, both assertion and reason are true and the reason is the correct explanation of assertion. -
Question 34 of 34
34. Question
In the following questions a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
Assertion (A): In the dissociation of \(\mathrm{PCl}_5\) at constant pressure and temperature addition of helium at equilibrium increases the dissociation of \(\mathrm{PCl}_5\).
Reason (R) : Helium removes \(\mathrm{Cl}_2\) from the field of action.CorrectIncorrectHint
(d)
Explanation: If the volume remains constant and an inert gas such as argon(helium) is added, the equilibrium remains undisturbed because it does not take part in the reaction.