6.11 Ionization of Acids and Bases

Ionization of a compound refers to a process in which a neutral molecule splits into charged ions when exposed to a solution. The compound which is dissolved in a solvent produces positive and negative ions called electrolytes and the degree of ionisation is defined as the ratio of a number of molecules undergoing dissociation to a total number of molecules.
\(\alpha=\) number of molecules undergoing dissociation/ total number of molecules
Where \(\alpha\) is called as the degree of ionization

Arrhenius concept of Acid and base ionization

According to Arrhenius theory, acids are the compounds that dissociate in an aqueous medium to generate hydrogen ions, \(\mathrm{H}^{+}(\mathrm{aq})\). On the other hand, bases are the compounds which furnish hydroxyl ions, \(\mathrm{OH}^{-}(\mathrm{aq})\) in an aqueous medium.

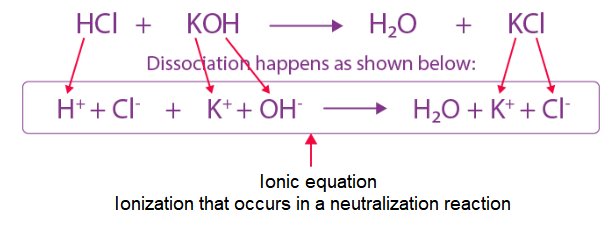
Arrhenius concept of acids and bases becomes useful in case of ionization of acids and bases as mostly ionizations in chemical and biological systems occur in aqueous medium. Strong acids like perchloric acid \(\left(\mathrm{HClO}_4\right)\), hydrochloric acid \((\mathrm{HCl})\), hydrobromic acid (HBr), hyrdoiodic acid (HI), nitric acid \(\left(\mathrm{HNO}_3\right)\) and sulphuric acid \(\left(\mathrm{H}_2 \mathrm{SO}_4\right)\) are termed strong because they are almost completely dissociated into their constituent ions in an aqueous medium, thereby acting as proton \(\left(\mathrm{H}^{+}\right)\)donors. Similarly, strong bases like lithium hydroxide \((\mathrm{LiOH})\), sodium hydroxide \((\mathrm{NaOH})\), potassium hydroxide \((\mathrm{KOH})\), caesium hydroxide \((\mathrm{CsOH})\) and barium hydroxide \(\mathrm{Ba}(\mathrm{OH})_2\) are almost completely dissociated into ions in an aqueous medium giving hydroxyl ions, \(\mathrm{OH}^{-}\). According to Arrhenius concept they are strong acids and bases as they are able to completely dissociate and produce \(\mathrm{H}_3 \mathrm{O}^{+}\) and \(\mathrm{OH}^{-}\)ions respectively in the medium. Alternatively, the strength of an acid or base may also be gauged in terms of Brönsted-Lowry concept of acids and bases, wherein a strong acid means a good proton donor and a strong base implies a good proton acceptor. Consider, the acid-base dissociation equilibrium of a weak acid HA,

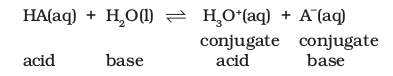
Explanation of Arrhenius acid and base ionization

We saw that acid (or base) dissociation equilibrium is dynamic involving a transfer of proton in forward and reverse directions. Consider the two acids \(\mathrm{HA}\) and \(\mathrm{H}_3 \mathrm{O}^{+}\)present in the above mentioned acid-dissociation equilibrium. We have to see which amongst them is a stronger proton donor. Whichever exceeds in its tendency of donating a proton over the other shall be termed as the stronger acid and the equilibrium will shift in the direction of weaker acid. Say, if HA is a stronger acid than \(\mathrm{H}_3 \mathrm{O}^{+}\), then HA will donate protons and not \(\mathrm{H}_3 \mathrm{O}^{+}\), and the solution will mainly contain \(\mathrm{A}^{-}\)and \(\mathrm{H}_3 \mathrm{O}^{+}\)ions. The equilibrium moves in the direction of formation of weaker acid and weaker base because the stronger acid donates a proton to the stronger base.

It follows that as a strong acid dissociates completely in water, the resulting base formed would be very weak i.e., strong acids have very weak conjugate bases. Strong acids like perchloric acid \(\left(\mathrm{HClO}_4\right)\), hydrochloric acid \((\mathrm{HCl})\), hydrobromic acid (HBr), hydroiodic acid (HI), nitric acid \(\left(\mathrm{HNO}_3\right)\) and sulphuric acid \(\left(\mathrm{H}_2 \mathrm{SO}_4\right)\) will give conjugate base ions \(\mathrm{ClO}_4^{-}, \mathrm{Cl}\), \(\mathrm{Br}^{-}, \mathrm{I}^{-}, \mathrm{NO}_3^{-}\)and \(\mathrm{HSO}_4^{-}\), which are much weaker bases than \(\mathrm{H}_2 \mathrm{O}\). Similarly, a very strong base would give a very weak conjugate acid. On the other hand, a weak acid say HA is only partially dissociated in aqueous medium and thus, the solution mainly contains undissociated HA molecules. Typical weak acids are nitrous acid \(\left(\mathrm{HNO}_2\right)\), hydrofluoric acid (HF) and acetic acid \(\left(\mathrm{CH}_3 \mathrm{COOH}\right)\). It should be noted that the weak acids have very strong conjugate bases. For example, \(\mathrm{NH}_2^{-}, \mathrm{O}^{2-}\) and \(\mathrm{H}^{-}\)are very good proton acceptors and thus, much stronger bases than \(\mathrm{H}_2 \mathrm{O}\).

Certain water soluble organic compounds like phenolphthalein and bromothymol blue behave as weak acids and exhibit different colours in their acid (HIn) and conjugate base \(\left(\mathrm{In}^{-}\right)\)forms.

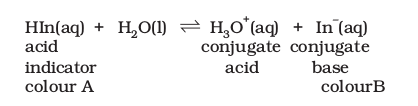
Such compounds are useful as indicators in acid-base titrations, and finding out \(\mathrm{H}^{+}\)ion concentration.

The Ionization Constant of Water and its Ionic Product

Some substances like water are unique in their ability of acting both as an acid and a base. In the presence of an acid, HA it accepts a proton and acts as the base while in the presence of a base, \(\mathrm{B}^{-}\)it acts as an acid by donating a proton. In pure water, one \(\mathrm{H}_2 \mathrm{O}\) molecule donates proton and acts as an acid and another water molecules accepts a proton and acts as a base at the same time. The following equilibrium exists:

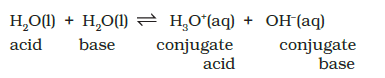
The dissociation constant is represented by,
\(
K=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right] /\left[\mathrm{H}_2 \mathrm{O}\right] \dots(7.26)
\)
The concentration of water is omitted from the denominator as water is a pure liquid and its concentration remains constant. \(\left[\mathrm{H}_2 \mathrm{O}\right]\) is incorporated within the equilibrium constant to give a new constant, \(K_w\), which is called the ionic product of water.
\(
K_{\mathrm{W}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right] \dots(7.27)
\)
The concentration of \(\mathrm{H}^{+}\)has been found out experimentally as \(1.0 \times 10^{-7} \mathrm{M}\) at \(298 \mathrm{~K}\). And, as dissociation of water produces an equal number of \(\mathrm{H}^{+}\)and \(\mathrm{OH}^{-}\)ions, the concentration of hydroxyl ions, \(\left[\mathrm{OH}^{-}\right]=\left[\mathrm{H}^{+}\right]=1.0 \times 10^{-7} \mathrm{M}\). Thus, the value of \(K_w\) at \(298 \mathrm{~K}\),
\(
K_{\mathrm{w}}=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=\left(1 \times 10^{-7}\right)^2=1 \times 10^{-14} \mathrm{M}^2 \dots(7.28)
\)
The value of \(K_w\) is temperature-dependent as it is an equilibrium constant.
The density of pure water is \(1000 \mathrm{~g} / \mathrm{L}\) and its molar mass is \(18.0 \mathrm{~g} / \mathrm{mol}\). From this, the molarity of pure water can be given as,
\(
\left[\mathrm{H}_2 \mathrm{O}\right]=(1000 \mathrm{~g} / \mathrm{L})(1 \mathrm{~mol} / 18.0 \mathrm{~g})=55.55 \mathrm{M} \text {. }
\)
Therefore, the ratio of dissociated water to that of undissociated water can be given as: \(10^{-7} /(55.55)=1.8 \times 10^{-9}\) or \(\sim 2\) in \(10^{-9}\) (thus, the equilibrium lies mainly towards undissociated water)
We can distinguish acidic, neutral, and basic aqueous solutions by the relative values of the \(\mathrm{H}_3 \mathrm{O}^{+}\)and \(\mathrm{OH}^{-}\)concentrations:
Acidic: \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]>\left[\mathrm{OH}^{-}\right]\)
Neutral: \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]\)
Basic : \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]<\left[\mathrm{OH}^{-}\right]\)

The pH Scale

Hydronium ion concentration in molarity is more conveniently expressed on a logarithmic scale known as the \(\mathbf{p H}\) scale. The \(\mathrm{pH}\) of a solution is defined as the negative logarithm to base 10 of the activity \(\left(\mathrm{a}_{\mathrm{H}^{+}}\right)\)of hydrogen ion. In dilute solutions \((<0.01 \mathrm{M})\), activity of hydrogen ion \(\left(\mathrm{H}^{+}\right)\)is equal in magnitude to molarity represented by \(\left[\mathrm{H}^{+}\right]\). It should be noted that activity has no units and is defined as:
\(
=\left[\mathrm{H}^{+}\right] / \mathrm{mol} \mathrm{L}^{-1}
\)
From the definition of \(\mathrm{pH}\), the following can be written,
\(
\mathrm{pH}=-\log \mathrm{a}_{\mathrm{H}^{+}}=-\log \left\{\left[\mathrm{H}^{+}\right] / \mathrm{mol} \mathrm{L}^{-1}\right\}
\)
Thus, an acidic solution of \(\mathrm{HCl}\left(10^{-2} \mathrm{M}\right)\) will have a \(\mathrm{pH}=2\). Similarly, a basic solution of \(\mathrm{NaOH}\) having \(\left[\mathrm{OH}^{-}\right]=10^{-4} \mathrm{M}\) and \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\) \(10^{-10} \mathrm{M}\) will have a \(\mathrm{pH}=10\). At \(25^{\circ} \mathrm{C}\), pure water has a concentration of hydrogen ions, \(\left[\mathrm{H}^{+}\right]=10^{-7} \mathrm{M}\). Hence, the \(\mathrm{pH}\) of pure water is given as:
\(
\mathrm{pH}=-\log \left(10^{-7}\right)=7
\)
Acidic solutions possess a concentration of hydrogen ions, \(\left[\mathrm{H}^{+}\right]>10^{-7} \mathrm{M}\), while basic solutions possess a concentration of hydrogen ions, \(\left[\mathrm{H}^{+}\right]<10^{-7} \mathrm{M}\). thus, we can summarise that

Acidic solution has \(\mathrm{pH}<7\)
Basic solution has \(\mathrm{pH}>7\)
Neutral solution has \(\mathrm{pH}=7\)
Now again, consider the equation (7.28) at \(298 \mathrm{~K}\)
\(
K_w=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=10^{-14}
\)

Taking negative logarithm on both sides of the equation, we obtain
\(
\begin{aligned}
-\log K_{\mathrm{w}} & =-\log \left\{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]\right\} \\
& =-\log \left[\mathrm{H}_3 \mathrm{O}^{+}\right]-\log \left[\mathrm{OH}^{-}\right] \\
& =-\log 10^{-14} \\
\mathrm{p} K_{\mathrm{w}} & =\mathrm{pH}+\mathrm{pOH}=14 \dots(7.29)
\end{aligned}
\)

Note that although \(K_w\) may change with temperature the variations in \(\mathrm{pH}\) with temperature are so small that we often ignore it.
\(\mathrm{p} K_{\mathrm{w}}\) is a very important quantity for aqueous solutions and controls the relative concentrations of hydrogen and hydroxyl ions as their product is a constant. It should be noted that as the \(\mathrm{pH}\) scale is logarithmic, a change in \(\mathrm{pH}\) by just one unit also means change in \(\left[\mathrm{H}^{+}\right]\)by a factor of 10. Similarly, when the hydrogen ion concentration, \(\left[\mathrm{H}^{+}\right]\)changes by a factor of 100, the value of \(\mathrm{pH}\) changes by 2 units. Now you can realise why the change in \(\mathrm{pH}\) with temperature is often ignored.

Measurement of \(\mathrm{pH}\) of a solution is very essential as its value should be known when dealing with biological and cosmetic applications. The \(\mathrm{pH}\) of a solution can be found roughly with the help of \(\mathrm{pH}\) paper that has different colour in solutions of different \(\mathrm{pH}\). Now-a-days \(\mathrm{pH}\) paper is available with four strips on it. The different strips have different colours (Fig. 7.11) at the same \(\mathrm{pH}\). The \(\mathrm{pH}\) in the range of 1-14 can be determined with an accuracy of \(\sim 0.5\) using \(\mathrm{pH}\) paper.

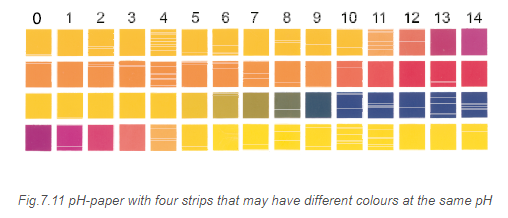
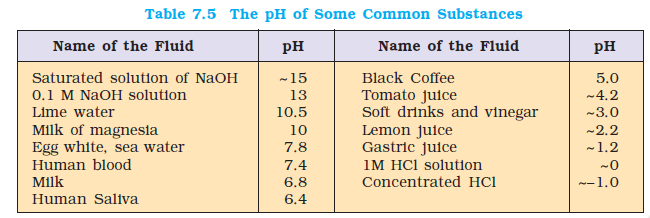
For greater accuracy \(\mathrm{pH}\) meters are used. \(\mathrm{pH}\) meter is a device that measures the \(\mathrm{pH}\)-dependent electrical potential of the test solution within 0.001 precision. \(\mathrm{pH}\) meters of the size of a writing pen are now available in the market. The \(\mathrm{pH}\) of some very common substances are given in Table 7.5.

Example 7.16: The concentration of hydrogen ion in a sample of soft drink is \(3.8 \times 10^{-3} \mathrm{M}\). what is its \(\mathrm{pH}\)?

Answer:

\(
\begin{aligned}
\mathrm{pH} & =-\log \left[3.8 \times 10^{-3}\right] \\
& =-\left\{\log [3.8]+\log \left[10^{-3}\right]\right\} \\
& =-\{(0.58)+(-3.0)\}=-\{-2.42\}=2.42
\end{aligned}
\)
Therefore, the \(\mathrm{pH}\) of the soft drink is 2.42 and it can be inferred that it is acidic.

Example 7.17: Calculate \(\mathrm{pH}\) of a \(1.0 \times 10^{-8} \mathrm{M}\) solution of \(\mathrm{HCl}\).

Answer: 

\(
\begin{aligned}
& 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) \\
& K_{\mathrm{w}}=\left[\mathrm{OH}^{-}\right]\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \\
& \quad=10^{-14}
\end{aligned}
\)
Let, \(\mathrm{x}=\left[\mathrm{OH}^{-}\right]=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\)from \(\mathrm{H}_2 \mathrm{O}\). The \(\mathrm{H}_3 \mathrm{O}^{+}\) concentration is generated
(i) from the ionization of \(\mathrm{HCl}\) dissolved i.e., \(\mathrm{HCl}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\), and
(ii) from ionization of \(\mathrm{H}_2 \mathrm{O}\). In these very dilute solutions, both sources of \(\mathrm{H}_3 \mathrm{O}^{+}\)must be considered:
\(
\begin{aligned}
& {\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=10^{-8}+\mathrm{x}} \\
& K_{\mathrm{w}}=\left(10^{-8}+\mathrm{x}\right)(\mathrm{x})=10^{-14} \\
& \text { or } \mathrm{x}^2+10^{-8} \mathrm{x}-10^{-14}=0 \\
& {\left[\mathrm{OH}^{-}\right]=\mathrm{x}=9.5 \times 10^{-8}}
\end{aligned}
\)
So, \(\mathrm{pOH}=7.02\) and \(\mathrm{pH}=6.98\)

Ionization Constants of Weak Acids

Consider a weak acid \(\mathrm{HX}\) that is partially ionized in the aqueous solution. The equilibrium can be expressed by:

Here, \(c=\) initial concentration of the undissociated acid, \(\mathrm{HX}\) at time, \(\mathrm{t}=0 . \alpha=\) extent up to which \(\mathrm{HX}\) is ionized into ions. Using these notations, we can derive the equilibrium constant for the above-discussed acid dissociation equilibrium:
\(
K_{\mathrm{a}}=\mathrm{c}^2 \alpha^2 / \mathrm{c}(1-\alpha)=\mathrm{c} \alpha^2 / 1-\alpha
\)
\(K_{\mathrm{a}}\) is called the dissociation or ionization constant of acid HX. It can be represented alternatively in terms of molar concentration as follows,
\(
K_{\mathrm{a}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{-}\right] /[\mathrm{HX}] \dots(7.30)
\)
At a given temperature \(T, K_{\mathrm{a}}\) is a measure of the strength of the acid \(\mathrm{HX}\) i.e., larger the value of \(K_a\), the stronger is the acid. \(K_{\mathrm{a}}\) is a dimensionless quantity with the understanding that the standard state concentration of all species is \(1 \mathrm{M}\).
The values of the ionization constants of some selected weak acids are given in Table 7.6.

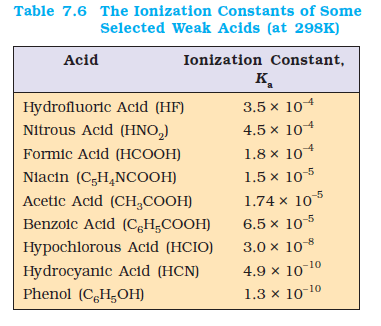
The \(\mathrm{pH}\) scale for the hydrogen ion concentration has been so useful that besides \(\mathrm{p} K_{\mathrm{w}}\), it has been extended to other species and quantities. Thus, we have:
\(
\mathrm{p} K_{\mathrm{a}}=-\log \left(K_{\mathrm{a}}\right) \dots(7.31)
\)
Knowing the ionization constant, \(K_{\mathrm{a}}\) of an acid and its initial concentration, c, it is possible to calculate the equilibrium concentration of all species and also the degree of ionization of the acid and the \(\mathrm{pH}\) of the solution.

A general step-wise approach can be adopted to evaluate the \(\mathrm{pH}\) of the weak electrolyte as follows:

Step 1. The species present before dissociation are identified as Brönsted-Lowry acids / bases.
Step 2. Balanced equations for all possible reactions i.e., with a species acting both as acid as well as base are written.
step 3. The reaction with the higher \(K_a\) is identified as the primary reaction whilst the other is a subsidiary reaction.
Step 4. Enlist in a tabular form the following values for each of the species in the primary reaction
(a) Initial concentration, c.
(b) Change in concentration on proceeding to equilibrium in terms of \(\alpha\), degree of ionization.
(c) Equilibrium concentration.
Step 5. Substitute equilibrium concentrations into the equilibrium constant equation for the principal reaction and solve for \(\alpha\).
Step 6. Calculate the concentration of species in the principal reaction.
Step 7. Calculate \(\mathrm{pH}=-\log \left[\mathrm{H}_3 \mathrm{O}^{+}\right]\)

The above-mentioned methodology has been elucidated in the following examples.

Example 7.18: The ionization constant of HF is \(3.2 \times 10^{-4}\). Calculate the degree of dissociation of \(\mathrm{HF}\) in its \(0.02 \mathrm{M}\) solution. Calculate the concentration of all species present \(\left(\mathrm{H}_3 \mathrm{O}^{+}, \mathrm{F}^{-}\right.\)and \(\left.\mathrm{HF}\right)\) in the solution and its \(\mathrm{pH}\).

Answer:

The following proton transfer reactions are possible:
1) \(\mathrm{HF}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{F}^{-}\)
\(
K_{\mathrm{a}}=3.2 \times 10^{-4}
\)
2) \(\mathrm{H}_2 \mathrm{O}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{OH}^{-}\)
\(
K_w=1.0 \times 10^{-14}
\)

As \(K_a \gg K_w\), [1] is the principle reaction.
\(
\mathrm{HF}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{F}^{-}
\)
Initial concentration (M)
\(
\begin{array}{lcc}
0.02 & 0 & 0 \\
\text { Change (M) } & & \\
\quad-0.02 \alpha & +0.02 \alpha & +0.02 \alpha \\
\text { Equilibrium } \\
\text { concentration (M) } \\
0.02-0.02 \alpha & 0.02 \alpha & 0.02 \alpha
\end{array}
\)
Substituting equilibrium concentrations in the equilibrium reaction for the principal reaction gives:
\(
\begin{aligned}
& K_{\mathrm{a}}=(0.02 \alpha)^2 /(0.02-0.02 \alpha) \\
& =0.02 \alpha^2 /(1-\alpha)=3.2 \times 10^{-4}
\end{aligned}
\)

We obtain the following quadratic equation:
\(
\alpha^2+1.6 \times 10^{-2} \alpha-1.6 \times 10^{-2}=0
\)

The quadratic equation in \(\alpha\) can be solved and the two values of the roots are:
\(
\alpha=+0.12 \text { and }-0.12
\)

The negative root is not acceptable and hence,
\(
\alpha=0.12
\)
This means that the degree of ionization, \(\alpha=0.12\), then equilibrium concentrations of other species viz., \(\mathrm{HF}, \mathrm{F}^{-}\)and \(\mathrm{H}_3 \mathrm{O}^{+}\)are given by:
\(
\begin{aligned}
& {\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\left[\mathrm{F}^{-}\right]=\mathrm{c} \alpha=0.02 \times 0.12} \\
& =2.4 \times 10^{-3} \mathrm{M} \\
& {[\mathrm{HF}]=\mathrm{c}(1-\alpha)=0.02(1-0.12)} \\
& =17.6 \times 10^{-3} \mathrm{M} \\
& \mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]=-\log \left(2.4 \times 10^{-3}\right)=2.62 \\
&
\end{aligned}
\)

Example 7.19: The \(\mathrm{pH}\) of \(0.1 \mathrm{M}\) monobasic acid is 4.50 . Calculate the concentration of species \(\mathrm{H}^{+}\), \(\mathrm{A}^{-}\)and \(\mathrm{HA}\) at equilibrium. Also, determine the value of \(K_a\) and \(\mathrm{p} K_a\) of the monobasic acid.

Answer:

\(
\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]
\)
Therefore,
\(
\begin{aligned}
{\left[\mathrm{H}^{+}\right]=10^{-\mathrm{pH}} } & =10^{-4.50} \\
& =3.16 \times 10^{-5}
\end{aligned}
\)
\(
\left[\mathrm{H}^{+}\right]=\left[\mathrm{A}^{-}\right]=3.16 \times 10^{-5}
\)
\(
\text { Thus, } \quad K_{\mathrm{a}}=\left[\mathrm{H}^{+}\right][\mathrm{A}] /[\mathrm{HA}]
\)
\(
\begin{aligned}
& {[\mathrm{HA}]_{\text {eqlbm }}=0.1-\left(3.16 \times 10^{-5}\right)=0.1} \\
& K_{\mathrm{a}}=\left(3.16 \times 10^{-5}\right)^2 / 0.1=1.0 \times 10^{-8} \\
& \mathrm{p} K_{\mathrm{a}}=-\log \left(10^{-8}\right)=8
\end{aligned}
\)
Alternatively, “Percent dissociation” is another useful method for measure of strength of a weak acid and is given as:
Percent dissociation
\(
=[\mathrm{HA}]_{\text {dissoctated }} /[\mathrm{HA}]_{\text {initial }} \times 100 \% \dots(7.32)
\)

Example 7.20: Calculate the \(\mathrm{pH}\) of \(0.08 \mathrm{M}\) solution of hypochlorous acid, \(\mathrm{HOCl}\). The ionization constant of the acid is \(2.5 \times 10^{-5}\). Determine the percent dissociation of \(\mathrm{HOCl}\).

Answer:

\(
\hspace {9em} \mathrm{HOCl}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{ClO}^{-}(\mathrm{aq})
\)
Initial concentration \((\mathrm{M}): 0.08 \hspace {9em} 0 \hspace {5em} 0\)
Change to reach equilibrium concentration (M): \(-\mathrm{x} \quad +\mathrm{x} \quad +\mathrm{x}\)
equilibrium concentration (M): \(0.08-\mathrm{x} \hspace {6em} \mathrm{x} \hspace {5em} \mathrm{x}\)
\(
\begin{aligned}
K_{\mathrm{a}} & =\left\{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{ClO}^{-}\right] /[\mathrm{HOCl}]\right\} \\
& =\mathrm{x}^2 /(0.08-\mathrm{x})
\end{aligned}
\)

As \(\mathrm{x}<<0.08\), therefore \(0.08-\mathrm{x}=0.08\)
\(
\mathrm{x}^2 / 0.08=2.5 \times 10^{-5}
\)
\(\mathrm{x}^2=2.0 \times 10^{-6}\), thus, \(\mathrm{x}=1.41 \times 10^{-3}\) \(\left[\mathrm{H}^{+}\right]=1.41 \times 10^{-3} \mathrm{M}\).
Therefore,
Percent dissociation
\(
=\left\{[\mathrm{HOCl}]_{\text {dissoccated }} /[\mathrm{HOCl}]_{\text {initial }}\right] \times 100
\)
\(
\begin{aligned}
& =1.41 \times 10^{-3} \times 10^2 / 0.08=1.76 \% \\
& \mathrm{pH}=-\log \left(1.41 \times 10^{-3}\right)=2.85 .
\end{aligned}
\)

Ionization of Weak Bases

The ionization of base \(\mathrm{MOH}\) can be represented by equation:
\(
\mathrm{MOH}(\mathrm{aq}) \rightleftharpoons \mathrm{M}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})
\)
In a weak base there is partial ionization of \(\mathrm{MOH}\) into \(\mathrm{M}^{+}\)and \(\mathrm{OH}^{-}\), the case is similar to that of acid-dissociation equilibrium. The equilibrium constant for base ionization is called base ionization constant and is represented by \(K_b\). It can be expressed in terms of concentration in molarity of various species in equilibrium by the following equation:
\(
K_{\mathrm{b}}=\left[\mathrm{M}^{+}\right]\left[\mathrm{OH}^{-}\right] /[\mathrm{MOH}] \dots(7.33)
\)
Alternatively, if \(c=\) initial concentration of base and \(\alpha=\) degree of ionization of base i.e. the extent to which the base ionizes. When equilibrium is reached, the equilibrium constant can be written as:
\(
K_b=(\mathrm{c} \alpha)^2 / \mathrm{c}(1-\alpha)=\mathrm{c} \alpha^2 /(1-\alpha)
\)
The values of the ionization constants of some selected weak bases, \(K_b\) are given in Table 7.7.

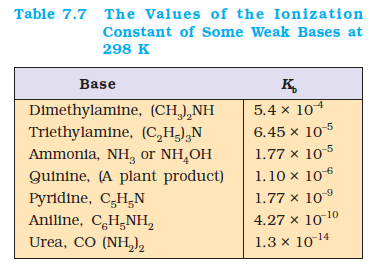
Many organic compounds like amines are weak bases. Amines are derivatives of ammonia in which one or more hydrogen atoms are replaced by another group. For example, methylamine, codeine, quinine and nicotine all behave as very weak bases due to their very small \(K_{\mathrm{b}}\). Ammonia produces \(\mathrm{OH}^{-}\) in aqueous solution:
\(
\mathrm{NH}_3(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})
\)
The \(\mathrm{pH}\) scale for the hydrogen ion concentration has been extended to get:
\(
\mathrm{p} K_b=-\log \left(K_b\right) \dots(7.34)
\)

Example 7.21: The \(\mathrm{pH}\) of \(0.004 \mathrm{M}\) hydrazine solution is 9.7. Calculate its ionization constant \(K_{\mathrm{b}}\) and \(\mathrm{p} K_{\mathrm{b}}\).

Answer: 

\(
\mathrm{NH}_2 \mathrm{NH}_2+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{NH}_2 \mathrm{NH}_3^{+}+\mathrm{OH}^{-}
\)
From the \(\mathrm{pH}\) we can calculate the hydrogen ion concentration. Knowing hydrogen ion concentration and the ionic product of water we can calculate the concentration of hydroxyl ions. Thus we have:
\(
\left[\mathrm{H}^{+}\right]=\operatorname{antilog}(-\mathrm{pH})
\)
\(
=\operatorname{antilog}(-9.7)=1.67 \times 10^{-10}
\)
\(
\begin{aligned}
{\left[\mathrm{OH}^{-}\right]=K_{\mathrm{w}} /\left[\mathrm{H}^{+}\right] } & =1 \times 10^{-14} / 1.67 \times 10^{-10} \\
& =5.98 \times 10^{-5}
\end{aligned}
\)
The concentration of the corresponding hydrazinium ion is also the same as that of hydroxyl ion. The concentration of both these ions is very small so the concentration of the undissociated base can be taken equal to \(0.004 \mathrm{M}\).
Thus,
\(
\begin{aligned}
& K_{\mathrm{b}}=\left[\mathrm{NH}_2 \mathrm{NH}_3^{+}\right][\mathrm{OH}] /\left[\mathrm{NH}_2 \mathrm{NH}_2\right] \\
& =\left(5.98 \times 10^{-5}\right)^2 / 0.004=8.96 \times 10^{-7} \\
& \mathrm{p} K_{\mathrm{b}}=-\log K_{\mathrm{b}}=-\log \left(8.96 \times 10^{-7}\right)=6.04 .
\end{aligned}
\)

Example 7.22: Calculate the \(\mathrm{pH}\) of the solution in which \(0.2 \mathrm{M} \mathrm{NH}_4 \mathrm{Cl}\) and \(0.1 \mathrm{M} \mathrm{NH}_3\) are present. The \(\mathrm{pK}_{\mathrm{b}}\) of ammonia solution is 4.75.

Answer:

\(
\mathrm{NH}_3+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{NH}_4^{+}+\mathrm{OH}^{-}
\)
The ionization constant of \(\mathrm{NH}_3\) \(K_{\mathrm{b}}=\operatorname{antilog}\left(-\mathrm{p} K_{\mathrm{b}}\right)\) i.e.
\(
\begin{aligned}
K_{\mathrm{b}}= & 10^{-4.75}=1.77 \times 10^{-5} \mathrm{M} \\
& \hspace { 6em} \mathrm{NH}_3+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{NH}_4^{+}+\mathrm{OH}
\end{aligned}
\)
Initial concentration (M): \(0.10 \hspace { 5em} 0.20 \hspace {2em} 0\)
Change to reach equilibrium (M): \(-\mathrm{x} \quad +\mathrm{x} \quad +\mathrm{x}\)
At equilibrium (M): \(\hspace { 2em} 0.10-\mathrm{x} \hspace { 3em} 0.20+\mathrm{x} \quad  \mathrm{x}\)
\(
\begin{aligned}
& K_{\mathrm{b}}=\left[\mathrm{NH}_4^{+}\right]\left[\mathrm{OH}^{-}\right] /\left[\mathrm{NH}_3\right] \\
& =(0.20+\mathrm{x})(\mathrm{x}) /(0.1-\mathrm{x})=1.77 \times 10^{-5}
\end{aligned}
\)
As \(K_{\mathrm{b}}\) is small, we can neglect \(\mathrm{x}\) in comparison to \(0.1 \mathrm{M}\) and \(0.2 \mathrm{M}\). Thus,
\(
\left[\mathrm{OH}^{-}\right]=\mathrm{x}=0.88 \times 10^{-5}
\)
Therefore, \(\left[\mathrm{H}^{+}\right]=1.12 \times 10^{-9}\)
\(
\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]=8.95 \text {. }
\)

Relation between \(K_{\mathrm{a}}\) and \(K_{\mathrm{b}}\)

As seen earlier in this chapter, \(K_{\mathrm{a}}\) and \(K_{\mathrm{b}}\) represent the strength of an acid and a base, respectively. In the case of a conjugate acid-base pair, they are related in a simple manner so that if one is known, the other can be deduced. Considering the example of \(\mathrm{NH}_4^{+}\)and \(\mathrm{NH}_3\) we see,
\(
\begin{aligned}
& \mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{NH}_3(\mathrm{aq}) \\
& \quad K_{\mathrm{a}}=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{NH}_3\right] /\left[\mathrm{NH}_4^{+}\right]=5.6 \times 10^{-10} \\
& \mathrm{NH}_3(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) \\
& K_{\mathrm{b}}=\left[\mathrm{NH}_4^{+}\right]\left[\mathrm{OH}^{-}\right] / \mathrm{NH}_3=1.8 \times 10^{-5} \\
& \mathrm{Net}: 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) \\
& K_{\mathrm{w}}=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.0 \times 10^{-14} \mathrm{M}
\end{aligned}
\)
Where, \(K_{\mathrm{a}}\) represents the strength of \(\mathrm{NH}_4^{+}\)as an acid and \(K_b\) represents the strength of \(\mathrm{NH}_3\) as a base.
It can be seen from the net reaction that the equilibrium constant is equal to the product of equilibrium constants \(K_{\mathrm{a}}\) and \(K_{\mathrm{b}}\) for the reactions added. Thus,
\(
\begin{array}{r}
K_{\mathrm{a}} \times K_{\mathrm{b}}=\left\{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{NH}_3\right] /\left[\mathrm{NH}_4^{+}\right]\right\} \times\left\{\left[\mathrm{NH}_4^{+}\right]\right. \\
\left.\left[\mathrm{OH}^{-}\right] /\left[\mathrm{NH}_3\right]\right\}
\end{array}
\)
\(
\begin{aligned}
& =\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=K_{\mathrm{w}} \\
& =\left(5.6 \times 10^{-10}\right) \times\left(1.8 \times 10^{-5}\right)=1.0 \times 10^{-14} \mathrm{M}
\end{aligned}
\)
This can be extended to make a generalization. The equilibrium constant for a net reaction obtained after adding two (or more) reactions equals the product of the equilibrium constants for individual reactions:
\(
K_{\mathrm{NET}}=K_1 \times K_2 \times \ldots \ldots(7.35)
\)
Similarly, in case of a conjugate acid-base pair,
\(
K_{\mathrm{a}} \times K_{\mathrm{b}}=K_{\mathrm{w}} \dots(7.36)
\)
Knowing one, the other can be obtained. It should be noted that a strong acid will have a weak conjugate base and vice-versa.
Alternatively, the above expression \(K_{\mathrm{w}}=K_{\mathrm{a}} \times K_{\mathrm{b}}\), can also be obtained by considering the base-dissociation equilibrium reaction:
\(
\begin{aligned}
& \mathrm{B}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{BH}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) \\
& K_{\mathrm{b}}=\left[\mathrm{BH}^{+}\right]\left[\mathrm{OH}^{-}\right] /[\mathrm{B}]
\end{aligned}
\)
As the concentration of water remains constant it has been omitted from the denominator and incorporated within the dissociation constant. Then multiplying and dividing the above expression by \(\left[\mathrm{H}^{+}\right]\), we get:
\(
\begin{aligned}
& \begin{aligned}
K_{\mathrm{b}} & =\left[\mathrm{BH}^{+}\right]\left[\mathrm{OH}^{-}\right]\left[\mathrm{H}^{+}\right] /[\mathrm{B}]\left[\mathrm{H}^{+}\right] \\
& \left.=\left\{\left[\mathrm{OH}^{-}\right]\left[\mathrm{H}^{+}\right]\right\}\left[\mathrm{BH}^{+}\right] /[\mathrm{B}]\left[\mathrm{H}^{+}\right]\right\} \\
& =K_{\mathrm{w}} / K_{\mathrm{a}}
\end{aligned} \\
& \text { or } K_{\mathrm{a}} \times K_{\mathrm{b}}=K_{\mathrm{w}}
\end{aligned}
\)
It may be noted that if we take the negative logarithm of both sides of the equation, then \(\mathrm{pK}\) values of the conjugate acid and base are related to each other by the equation:
\(
\mathrm{p} K_{\mathrm{a}}+\mathrm{p} K_{\mathrm{b}}=\mathrm{p} K_{\mathrm{w}}=14(\text { at } 298 \mathrm{~K})
\)

Example 7.23: Determine the degree of ionization and \(\mathrm{pH}\) of a \(0.05 \mathrm{M}\) of ammonia solution. The ionization constant of ammonia can be taken from Table 7.7. Also, calculate the ionization constant of the conjugate acid of ammonia.

Answer: The ionization of \(\mathrm{NH}_3\) in water is represented by equation:
\(
\mathrm{NH}_3+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{NH}_4^{+}+\mathrm{OH}
\)
We use equation (7.33) to calculate hydroxyl ion concentration,
\(
\begin{aligned}
& {\left[\mathrm{OH}^{-}\right]=\mathrm{c} \alpha=0.05 \alpha} \\
& K_{\mathrm{b}}=0.05 \alpha^2 /(1-\alpha)
\end{aligned}
\)
The value of \(\alpha\) is small, therefore the quadratic equation can be simplified by neglecting \(\alpha\) in comparison to 1 in the denominator on right-hand side of the equation,
Thus,
\(
\begin{aligned}
K_{\mathrm{b}}=\mathrm{c} \alpha^2 \text { or } \alpha & =\sqrt{\left(1.77 \times 10^{-5} / 0.05\right)} \\
& =0.018.
\end{aligned}
\)
\(
\begin{aligned}
& {\left[\mathrm{OH}^{-}\right]=\mathrm{c} \alpha=0.05 \times 0.018=9.4 \times 10^{-4} \mathrm{M}} \\
& \begin{aligned}
{\left[\mathrm{H}^{+}\right]=K_{\mathrm{w}} /[\mathrm{OH}] } & =10^{-14} /\left(9.4 \times 10^{-4}\right) \\
& =1.06 \times 10^{-11}
\end{aligned}
\end{aligned}
\)
\(
\mathrm{pH}=-\log \left(1.06 \times 10^{-11}\right)=10.97
\)
Now, using the relation for conjugate acid-base pair,
\(
K_{\mathrm{a}} \times K_{\mathrm{b}}=K_{\mathrm{w}}
\)
using the value of \(K_{\mathrm{b}}\) of \(\mathrm{NH}_3\) from Table 7.7.
We can determine the concentration of conjugate acid \(\mathrm{NH}_4^{+}\)
\(
\begin{aligned}
K_{\mathrm{a}}=K_{\mathrm{w}} / K_{\mathrm{b}} & =10^{-14} / 1.77 \times 10^{-5} \\
& =5.64 \times 10^{-10}
\end{aligned}
\)

Di- and Polybasic Acids and Di- and Polyacidic Bases

Some of the acids like oxalic acid, sulphuric acid and phosphoric acids have more than one ionizable proton per molecule of the acid. Such acids are known as polybasic or polyprotic acids.
The ionization reactions for example for a dibasic acid \(\mathrm{H}_2 \mathrm{X}\) are represented by the equations:
\(
\begin{aligned}
\mathrm{H}_2 \mathrm{X}(\mathrm{aq}) & \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{HX}^{-}(\mathrm{aq}) \\
\mathrm{HX}^{-}(\mathrm{aq}) & \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{X}^{2-}(\mathrm{aq})
\end{aligned}
\)
And the corresponding equilibrium constants are given below:
\(
K_{a_1}=\left\{\left[\mathrm{H}^{+}\right]\left[\mathrm{HX}^{-}\right]\right\} /\left[\mathrm{H}_2 \mathrm{X}\right] \text { and }
\)
\(
K_{\mathrm{a}_2}=\left\{\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{2-}\right]\right\} /\left[\mathrm{HX}^{-}\right]
\)
Here, \(K_{\mathrm{a}_1}\) and \(K_{\mathrm{a}_2}\) are called the first and second ionization constants respectively of the acid \(\mathrm{H}_2\) X. Similarly, for tribasic acids like \(\mathrm{H}_3 \mathrm{PO}_4\) we have three ionization constants. The values of the ionization constants for some common polyprotic acids are given in Table 7.8.

It can be seen that higher-order ionization constants \(\left(K_{\mathrm{a}_2}, K_{\mathrm{a}_3}\right)\) are smaller than the lower order ionization constant \(\left(K_{\mathrm{a}_1}\right)\) of a polyprotic acid. The reason for this is that it is more difficult to remove a positively charged proton from a negative ion due to electrostatic forces. This can be seen in the case of removing a proton from the uncharged \(\mathrm{H}_2 \mathrm{CO}_3\) as compared from a negatively charged \(\mathrm{HCO}_3^{-}\). Similarly, it is more difficult to remove a proton from a doubly charged \(\mathrm{HPO}_4^{2-}\) anion as compared to \(\mathrm{H}_2 \mathrm{PO}_4^{-}\).

Polyprotic acid solutions contain a mixture of acids like \(\mathrm{H}_2 \mathrm{~A}, \mathrm{HA}^{-}\)and \(\mathrm{A}^{2-}\) in case of a diprotic acid. \(\mathrm{H}_2 \mathrm{~A}\) being a strong acid, the primary reaction involves the dissociation of \(\mathrm{H}_2 \mathrm{~A}\), and \(\mathrm{H}_3 \mathrm{O}^{+}\)in the solution comes mainly from the first dissociation step.

Factors Affecting Acid Strength

Having discussed quantitatively the strengths of acids and bases, we come to a stage where we can calculate the \(\mathrm{pH}\) of a given acid solution. But, broadly speaking we can say that the extent of dissociation of an acid depends on the strength and polarity of the H-A bond.
In general, when the strength of H-A bond decreases, that is, the energy required to break the bond decreases, HA becomes a stronger acid. Also, when the H-A bond becomes more polar i.e., the electronegativity difference between the atoms \(\mathrm{H}\) and \(\mathrm{A}\) increases and there is marked charge separation, cleavage of the bond becomes easier thereby increasing the acidity.

But it should be noted that while comparing elements in the same group of the periodic table, H-A bond strength is a more important factor in determining acidity than its polar nature. As the size of A increases down the group, H-A bond strength decreases and so the acid strength increases. For example,

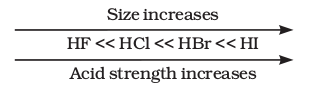
Similarly, \(\mathrm{H}_2 \mathrm{~S}\) is stronger acid than \(\mathrm{H}_2 \mathrm{O}\).
But, when we discuss elements in the same row of the periodic table, \(\mathrm{H}-\mathrm{A}\) bond polarity becomes the deciding factor for determining the acid strength. As the electronegativity of A increases, the strength of the acid also increases. For example,

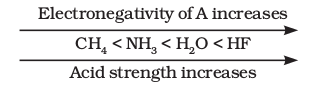
Common Ion Effect in the Ionization of Acids and Bases

Consider an example of acetic acid dissociation equilibrium represented as:
\(
\begin{aligned}
& \mathrm{CH}_3 \mathrm{COOH}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq}) \\
& \text { or } \mathrm{HAc}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{Ac}^{-}(\mathrm{aq}) \\
& K_{\mathrm{a}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{Ac}^{-}\right] /[\mathrm{HAc}]
\end{aligned}
\)
Addition of acetate ions to an acetic acid solution results in decreasing the concentration of hydrogen ions, \(\left[\mathrm{H}^{+}\right]\). Also, if \(\mathrm{H}^{+}\)ions are added from an external source then the equilibrium moves in the direction of undissociated acetic acid i.e., in a direction of reducing the concentration of hydrogen ions, \(\left[\mathrm{H}^{+}\right]\). This phenomenon is an example of common ion effect. It can be defined as a shift in equilibrium on adding a substance that provides more of an ionic species already present in the dissociation equilibrium. Thus, we can say that common ion effect is a phenomenon based on the Le Chatelier’s principle.

In order to evaluate the \(\mathrm{pH}\) of the solution resulting in addition of \(0.05 \mathrm{M}\) acetate ion to \(0.05 \mathrm{M}\) acetic acid solution, we shall consider the acetic acid dissociation equilibrium once again,
\(
\mathrm{HAc}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{Ac}^{-}(\mathrm{aq})
\)
\(
\begin{array}{ccc}
\text { Initial concentration }(\mathrm{M}) \\
0.05 & 0 & 0.05
\end{array}
\)
Let \(\mathrm{x}\) be the extent of ionization of acetic acid.
Change in concentration (M)
\(
\begin{array}{ccc}
-\mathrm{x} & +\mathrm{x} & +\mathrm{x}
\end{array}
\)
Equilibrium concentration (M)
\(
0.05-x \quad x \quad 0.05+x
\)
Therefore,
\(
K_{\mathrm{a}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{Ac}^{-}\right] /[\mathrm{H} \mathrm{Ac}]=\{(0.05+\mathrm{x})(\mathrm{x})\} /(0.05-\mathrm{x})
\)
As \(K_{\mathrm{a}}\) is small for a very weak acid, \(\mathrm{x}<<0.05\).
Hence, \((0.05+x) \approx(0.05-x) \approx 0.05\)
Thus,
\(
\begin{aligned}
& 1.8 \times 10^{-5}=(\mathrm{x})(0.05+\mathrm{x}) /(0.05-\mathrm{x}) \\
& =\mathrm{x}(0.05) /(0.05)=\mathrm{x}=\left[\mathrm{H}^{+}\right]=1.8 \times 10^{-5} \mathrm{M} \\
& \mathrm{pH}=-\log \left(1.8 \times 10^{-5}\right)=4.74
\end{aligned}
\)

Example 7.24: Calculate the \(\mathrm{pH}\) of a \(0.10 \mathrm{M}\) ammonia solution. Calculate the \(\mathrm{pH}\) after \(50.0 \mathrm{~mL}\) of this solution is treated with \(25.0 \mathrm{~mL}\) of \(0.10 \mathrm{M} \mathrm{HCl}\). The dissociation constant of ammonia, \(K_{\mathrm{b}}=1.77 \times 10^{-5}\)

Answer: 

\(
\begin{aligned}
& \mathrm{NH}_3+\mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{NH}_4^{+}+\mathrm{OH}^{-} \\
& K_{\mathrm{b}}=\left[\mathrm{NH}_4^{+}\right]\left[\mathrm{OH}^{-}\right] /\left[\mathrm{NH}_3\right]=1.77 \times 10^{-5}
\end{aligned}
\)
Before neutralization,
\(
\begin{aligned}
& {\left[\mathrm{NH}_4^{+}\right]=\left[\mathrm{OH}^{-}\right]=x} \\
& {\left[\mathrm{NH}_3\right]=0.10-\mathrm{x}=0.10} \\
& \mathrm{x}^2 / 0.10=1.77 \times 10^{-5}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Thus, } \mathrm{x}=1.33 \times 10^{-3}=\left[\mathrm{OH}^{-}\right] \\
& \text {Therefore, }\left[\mathrm{H}^{+}\right]=K_w /\left[\mathrm{OH}^{-}\right]=10^{-14} / \\
& \qquad\left(1.33 \times 10^{-3}\right)=7.51 \times 10^{-12} \\
& \mathrm{pH}=-\log \left(7.5 \times 10^{-12}\right)=11.12
\end{aligned}
\)
On addition of \(25 \mathrm{~mL}\) of \(0.1 \mathrm{M} \mathrm{HCl}\) solution (i.e., \(2.5 \mathrm{mmol}\) of \(\mathrm{HCl}\) ) to \(50 \mathrm{~mL}\) of \(0.1 \mathrm{M}\) ammonia solution (i.e., \(5 \mathrm{mmol}\) of \(\mathrm{NH}_3\) ), \(2.5 \mathrm{mmol}\) of ammonia molecules are neutralized. The resulting \(75 \mathrm{~mL}\) solution contains the remaining unneutralized \(2.5 \mathrm{mmol}\) of \(\mathrm{NH}_3\) molecules and \(2.5 \mathrm{mmol}\) of \(\mathrm{NH}_4^{+}\).
\(
\mathrm{NH}_3+\mathrm{HCl} \rightarrow \mathrm{NH}_4^{+}+\mathrm{Cl}^{-}
\)
\(
\begin{array}{llll}
2.5 & & 2.5 & & & 0 & & 0
\end{array}
\)
At equilibrium
\(
\begin{array}{llll}
0 & & & 0 & & &  2.5 & & 2.5
\end{array}
\)
The resulting \(75 \mathrm{~mL}\) of solution contains \(2.5 \mathrm{mmol}\) of \(\mathrm{NH}_4^{+}\)ions (i.e., \(0.033 \mathrm{M}\) ) and \(2.5 \mathrm{mmol}\) (i.e., \(0.033 \mathrm{M}\) ) of uneutralised \(\mathrm{NH}_3\) molecules. This \(\mathrm{NH}_3\) exists in the following equilibrium:
\(
\mathrm{NH}_4 \mathrm{OH} \rightleftharpoons \mathrm{NH}_4^{+}+\mathrm{OH}^{-}
\)
\(
0.033 \mathrm{M}-\mathrm{y} \quad \mathrm{y} \quad \quad \quad \mathrm{y}
\)
\(
\text { where, } \mathrm{y}=\left[\mathrm{OH}^{-}\right]=\left[\mathrm{NH}_4^{+}\right]
\)
The final \(75 \mathrm{~mL}\) solution after neutralisation already contains \(2.5 \mathrm{~m} \mathrm{~mol} \mathrm{~NH}_4^{+}\)ions (i.e. \(0.033 \mathrm{M}\) ), thus total concentration of \(\mathrm{NH}_4^{+}\)ions is given as:
\(
\left[\mathrm{NH}_4^{+}\right]=0.033+\mathrm{y}
\)
As \(\mathrm{y}\) is small, \(\left[\mathrm{NH}_4 \mathrm{OH}\right] \simeq 0.033 \mathrm{M}\) and \(\left[\mathrm{NH}_4^{+}\right]=0.033 \mathrm{M}\).
We know,
\(
\begin{aligned}
K_{\mathrm{b}} & =\left[\mathrm{NH}_4^{+}[\mathrm{OH}] /\left[\mathrm{NH}_4 \mathrm{OH}\right]\right. \\
& =\mathrm{y}(0.033) /(0.033)=1.77 \times 10^{-5} \mathrm{M}
\end{aligned}
\)
Thus, \(\mathrm{y}=1.77 \times 10^{-5}=\left[\mathrm{OH}^{-}\right]\)
\(
\left[\mathrm{H}^{+}\right]=10^{-14} / 1.77 \times 10^{-5}=0.56 \times 10^{-9}
\)
Hence, \(\mathrm{pH}=9.24\)

Hydrolysis of Salts and the pH of their Solutions

Salts formed by the reactions between acids and bases in definite proportions, undergo ionization in water. The cations/anions formed on ionization of salts either exist as hydrated ions in aqueous solutions or interact with water to reform corresponding acids/bases depending upon the nature of salts. The later process of interaction between water and cations/anions or both of salts is called hydrolysis. The \(\mathrm{pH}\) of the solution gets affected by this interaction. The cations (e.g., \(\mathrm{Na}^{+}, \mathrm{K}^{+}\), \(\mathrm{Ca}^{2+}, \mathrm{Ba}^{2+}\), etc.) of strong bases and anions (e.g., \(\mathrm{Cl}^{-}, \mathrm{Br}^{-}, \mathrm{NO}_3^{-}, \mathrm{ClO}_4^{-}\), etc.) of strong acids simply get hydrated but do not hydrolyse, and therefore the solutions of salts formed from strong acids and bases are neutral i.e., their \(\mathrm{pH}\) is 7. However, the other category of salts do undergo hydrolysis.

We now consider the hydrolysis of the salts of the following types:
(i) salts of weak acid and strong base e.g., \(\mathrm{CH}_3 \mathrm{COONa}\).
(ii) salts of strong acid and weak base e.g., \(\mathrm{NH}_4 \mathrm{Cl}\), and
(iii) salts of weak acid and weak base, e.g., \(\mathrm{CH}_3 \mathrm{COONH}_4\).

In the first case, \(\mathrm{CH}_3 \mathrm{COONa}\) being a salt of weak acid, \(\mathrm{CH}_3 \mathrm{COOH}\) and strong base, \(\mathrm{NaOH}\) gets completely ionised in aqueous solution. \(\mathrm{CH}_3 \mathrm{COONa}(\mathrm{aq}) \rightarrow \mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq})+\mathrm{Na}^{+}(\mathrm{aq})\)

Acetate ion thus formed undergoes hydrolysis in water to give acetic acid and \(\mathrm{OH}^{-}\) ions
\(
\mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{CH}_3 \mathrm{COOH}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})
\)
Acetic acid being a weak acid \(\left(K_{\mathrm{a}}=1.8 \times 10^{-5}\right)\) remains mainly unionised in solution. This results in increase of \(\mathrm{OH}^{-}\)ion concentration in solution making it alkaline. The \(\mathrm{pH}\) of such a solution is more than 7.

Similarly, \(\mathrm{NH}_4 \mathrm{Cl}\) formed from weak base, \(\mathrm{NH}_4 \mathrm{OH}\) and strong acid, \(\mathrm{HCl}\), in water dissociates completely.
\(
\mathrm{NH}_4 \mathrm{Cl}(\mathrm{aq}) \rightarrow \mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})
\)

Ammonium ions undergo hydrolysis with water to form \(\mathrm{NH}_4 \mathrm{OH}\) and \(\mathrm{H}^{+}\)ions
\(
\mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(1) \rightleftharpoons \mathrm{NH}_4 \mathrm{OH}(\mathrm{aq})+\mathrm{H}^{+}(\mathrm{aq})
\)

Ammonium hydroxide is a weak base \(\left(K_{\mathrm{b}}=1.77 \times 10^{-5}\right)\) and therefore remains almost unionised in solution. This results in increased of \(\mathrm{H}^{+}\)ion concentration in solution making the solution acidic. Thus, the \(\mathrm{pH}\) of \(\mathrm{NH}_4 \mathrm{Cl}\) solution in water is less than 7.

Consider the hydrolysis of \(\mathrm{CH}_3 \mathrm{COONH}_4\) salt formed from weak acid and weak base. The ions formed undergo hydrolysis as follows:
\(
\mathrm{CH}_3 \mathrm{COO}^{-}+\mathrm{NH}_4^{+}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{CH}_3 \mathrm{COOH}+\mathrm{NH}_4 \mathrm{OH}
\)
\(\mathrm{CH}_3 \mathrm{COOH}\) and \(\mathrm{NH}_4 \mathrm{OH}\), also remain into partially dissociated form:
\(
\begin{aligned}
& \mathrm{CH}_3 \mathrm{COOH} \rightleftharpoons \mathrm{CH}_3 \mathrm{COO}^{-}+\mathrm{H}^{+} \\
& \mathrm{NH}_4 \mathrm{OH} \rightleftharpoons \mathrm{NH}_4^{+}+\mathrm{OH}^{-} \\
& \mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}^{+}+\mathrm{OH}^{-}
\end{aligned}
\)
Without going into detailed calculation, it can be said that degree of hydrolysis is independent of concentration of solution, and \(\mathrm{pH}\) of such solutions is determined by their \(\mathrm{pK}\) values:
\(
\mathrm{pH}=7+1 / 2\left(\mathrm{p} K_{\mathrm{a}}-\mathrm{p} K_{\mathrm{b}}\right) \dots(7.38)
\)
The \(\mathrm{pH}\) of solution can be greater than 7, if the difference is positive and it will be less than 7, if the difference is negative.

Example 7.25: The \(\mathrm{p} K_{\mathrm{a}}\) of acetic acid and \(\mathrm{p} K_b\) of ammonium hydroxide are 4.76 and 4.75 respectively. Calculate the \(\mathrm{pH}\) of ammonium acetate solution.

Answer: 

\(
\begin{aligned}
\mathrm{pH} & =7+1 / 2\left[\mathrm{p} K_{\mathrm{a}}-\mathrm{p} K_{\mathrm{b}}\right] \\
& =7+1 / 2[4.76-4.75] \\
& =7+1 / 2[0.01]=7+0.005=7.005
\end{aligned}
\)