NCERT Exemplar MCQs
Summary
This chapter deals with some basic definitions and operations involving sets. These are summarised below:
- A set is a well-defined collection of objects.
- A set which does not contain any element is called empty set.
- A set which consists of a definite number of elements is called finite set, otherwise, the set is called infinite set.
- Two sets \(A\) and \(B\) are said to be equal if they have exactly the same elements.
- A set \(A\) is said to be subset of a set \(B\), if every element of \(A\) is also an element of B. Intervals are subsets of \(R\).
- The union of two sets \(A\) and \(B\) is the set of all those elements which are either in \(A\) or in \(B\).
- The intersection of two sets \(A\) and \(B\) is the set of all elements which are common. The difference of two sets \(A\) and \(B\) in this order is the set of elements which belong to \(A\) but not to \(B\).
- The complement of a subset \(A\) of universal set \(U\) is the set of all elements of \(U\) which are not the elements of \(A\).
- For any two sets \(A\) and \(B ,( A \cup B )^{\prime}= A ^{\prime} \cap B ^{\prime}\) and \(( A \cap B )^{\prime}= A ^{\prime} \cup B ^{\prime}\)
Quiz Summary
0 of 47 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 47 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 47
1. Question
Suppose \(A_{1}, A_{2}, \ldots, A_{30}\) are thirty sets each having 5 elements and \(B_{1}, B_{2}, \ldots, B_{n}\) are \(n\) sets each with 3 elements, let \(\bigcup_{i=1}^{30} \mathrm{~A}_{i}=\bigcup_{j=1}^{n} \mathrm{~B}_{j}=\mathrm{S}\) and each element of \(\mathrm{S}\) belongs to exactly 10 of the \(\mathrm{A}_{i}\)’s and exactly 9 of the \(\mathrm{B}_{j}\)’s. then \(n\) is equal to
CorrectIncorrectHint
(c) If elements are not repeated, then number of elements in \(A_{1} \cup A_{2} \cup A_{3} \cdots\) \(\cup A_{30}\) is \(30 \times 5\).
But each element is used 10 times.
So, \(\quad S=\frac{30 \times 5}{10}=15\)
If elements in \(B_{1}, B_{2}, \ldots, B_{n}\), are not repeated, then total number of elements in \(B_{1} \cup B_{2} \cup B_{3} \ldots \cup B_{n}\) is \(3 n\)
But each element is repeated 9 times.
So, \(\quad S=\frac{3 n}{9} \Rightarrow 15=\frac{3 n}{9} \Rightarrow n=45\) -
Question 2 of 47
2. Question
Two finite sets have \(m\) and \(n\) elements. The number of subsets of the first set is 112 more than that of the second set. The values of \(m\) and \(n\) are, respectively,
CorrectIncorrectHint
(b) According to the question,
\(
\begin{array}{ll}
& 2^{m}-2^{n}=112 \\
\Rightarrow & 2^{n}\left(2^{m-n}-1\right)=2^{4} \cdot 7 \\
\Rightarrow & 2^{n}=2^{4} \text { and } 2^{m-n}-1=7 \\
\Rightarrow & n=4 \text { and } 2^{m-n}=8 \\
\Rightarrow & 2^{m-n}=2^{3} \Rightarrow m-n=3 \Rightarrow m-4=3 \Rightarrow m=7
\end{array}
\) -
Question 3 of 47
3. Question
The set \(\left(\mathrm{A} \cap \mathrm{B}^{\prime}\right)^{\prime} \cup(\mathrm{B} \cap \mathrm{C})\) is equal to
CorrectIncorrectHint
(b)
\(
\begin{aligned}
\left(A \cap B^{\prime}\right)^{\prime} \cup(B \cap C) =\left(\left(A^{\prime} \cup\left(B^{\prime}\right)^{\prime}\right) \cup(B \cap C)\right.\\
=\left(A^{\prime} \cup B\right) \cup(C \cap B)=A^{\prime} \cup(B \cup(C \cap B))=A^{\prime} \cup B
\end{aligned}
\) -
Question 4 of 47
4. Question
Let \(\mathrm{F}_{1}\) be the set of parallelograms, \(\mathrm{F}_{2}\) the set of rectangles, \(\mathrm{F}_{3}\) the set of rhombuses, \(\mathrm{F}_{4}\) the set of squares and \(\mathrm{F}_{5}\) the set of trapeziums in a plane. Then \(\mathrm{F}_{1}\) may be equal to
CorrectIncorrectHint
(d) We know that every rectangle, rhombus, and square in a plane is a parallelogram but every trapezium is not a parallelogram.
So, \(F_{1}\) is either of \(F_{1}\) or \(F_{2}\) or \(F_{3}\) or \(F_{4}\).
\(
\therefore F_{1}=F_{1} \cup F_{2} \cup F_{3} \cup F_{4}
\) -
Question 5 of 47
5. Question
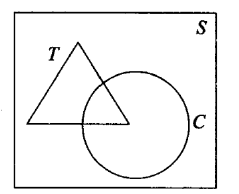
Let \(\mathrm{S}=\) set of points inside the square, \(\mathrm{T}=\) the set of points inside the triangle and \(\mathrm{C}=\) the set of points inside the circle. If the triangle and circle intersect each other and are contained in a square. Then
CorrectIncorrectHint
(c) The given sets are represented in Venn diagram as shown below:
\(
\text { It is clear from the diagram that, } S \cup T \cup C=S \text {. }
\) -
Question 6 of 47
6. Question
Let \(\mathrm{R}\) be set of points inside a rectangle of sides \(a\) and \(b(a, b>1)\) with two sides along the positive direction of \(x\)-axis and \(y\)-axis. Then
CorrectIncorrectHint
(d) Since, \(R\) be the set of points inside the rectangle.
\(
\therefore \quad R=\{(x, y): 0<x<a \text { and } 0<y<b\}
\) -
Question 7 of 47
7. Question
In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Then, the number of students who play neither is
CorrectIncorrectHint
(b)
Let ‘ \(\mathrm{A}\) ‘ be the set of students who play cricket, ‘ \(\mathrm{B}\) ‘ be the set of students who play tennis.It is given that, \(n(A)=25, n(B)=20\) and \(n(A \cap B)=10=\) students who play both the games
Thus \(n(\mathrm{~A} \cup \mathrm{B})=\mathrm{n}(\mathrm{A})+\mathrm{n}(\mathrm{B})-\mathrm{n}(\mathrm{A} \cap \mathrm{B})=20+25-10=35\)
Therefore the students who play neither of the cricket and tennis \(=60-35=25\) -
Question 8 of 47
8. Question
In a town of 840 persons, 450 persons read Hindi, 300 read English and 200 read both. Then the number of persons who read neither is
CorrectIncorrectHint
(b) Let \(H\) and \(E\) denote the number of persons who read Hindi and English newspaper respectively.
Given, total number of persons, \(n(U)=840\)
Total number of persons who read Hindi newspaper,
\(
n(H)=450
\)
Total number of persons who read English newspaper,
\(
n(E)=300
\)
and \(n(H \cap E)=200\)
\(
\because n(H \cup E)=n(H)+n(E)-n(H \cap E)=550
\)
\(\therefore\) The number of persons who read neither of the newspaper
\(
=n\left(H^{\prime} \cap E^{\prime}\right)=n(U)-n(H \cup E)=290
\) -
Question 9 of 47
9. Question
If \(\mathrm{X}=\left\{8^{n}-7 n-1 \mid n \in \mathbf{N}\right\}\) and \(\mathrm{Y}=\{49 n-49 \mid n \in \mathbf{N}\}\). Then
CorrectIncorrectHint
(a) \(\begin{aligned}
X &=\left\{8^{n}-7 n-1 \mid n \in N\right\}=\{0,49,490, \ldots\} \\
Y &=\{49 n-49 \mid n \in N\}=\{0,49,98,147, \ldots, 490, \ldots\}
\end{aligned}\)Clearly, every element of \(X\) is in \(Y\) but every element of \(Y\) is not in \(X\).
\(
\therefore \quad X \subset Y
\) -
Question 10 of 47
10. Question
A survey shows that \(63 \%\) of the people watch a News Channel whereas \(76 \%\) watch another channel. If \(x \%\) of the people watch both channel, then
CorrectIncorrectHint
(c) Let \(\mathrm{p} \%\) of the people watch a channel and \(\mathrm{q} \%\) of the people watch another channel
\(\therefore \mathrm{n}(\mathrm{p} \cap \mathrm{q})=\mathrm{x} \%\) and \(\mathrm{n}(\mathrm{p} \cup \mathrm{q}) \leq 100\)
So \(n(p \cup q) \geq n(p)+n(q)-n(p \cap q)\)
\(100 \geq 63+76-x\)
\(100 \geq 139-x\)
\(\Rightarrow x \geq 139-100\)
\(\Rightarrow x \geq 39\)
Now \(n(p)=63\)
\(
\begin{aligned}
&\therefore \mathrm{n}(\mathrm{p} \cap \mathrm{q}) \leq \mathrm{n}(\mathrm{p}) \\
&\Rightarrow \mathrm{x} \leq 63
\end{aligned}
\)
So \(39 \leq x \leq 63\). -
Question 11 of 47
11. Question
If sets \(\mathrm{A}\) and \(\mathrm{B}\) are defined as
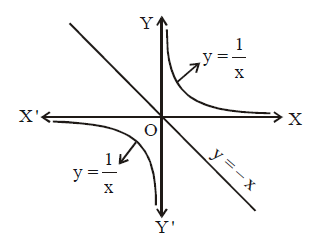
\(\mathrm{A}=\left\{(x, y) \mid y=\frac{1}{x}, 0 \neq x \in \mathbf{R}\right\} \quad \mathrm{B}=\{(x, y) \mid y=-x, x \in \mathbf{R}\}\), thenCorrectIncorrectHint
(c) Graph of set A represents the rectangular hyperbola and graph of set B represents a straight line passing through the origin.
Clearly, from the graph nothing is common between them.
\(
\therefore A \cap B=\phi
\)
-
Question 12 of 47
12. Question
If \(\mathrm{A}\) and \(\mathrm{B}\) are two sets, then \(\mathrm{A} \cap(\mathrm{A} \cup \mathrm{B})\) equals
CorrectIncorrectHint
(a) \(
\begin{aligned}
&A \cap(A \cup B) \\
&=(A \cap A) \cup(A \cap B) \\
&=A
\end{aligned}
\) -
Question 13 of 47
13. Question
If \(\mathrm{A}=\{1,3,5,7,9,11,13,15,17\} \mathrm{B}=\{2,4, \ldots, 18\}\) and \(\mathbf{N}\) the set of natural numbers is the universal set, then \(\left.\mathrm{A}^{\prime} \cup((\mathrm{A} \cup \mathrm{B}) \cap \mathrm{B}^{\prime}\right)\) is
CorrectIncorrectHint
(b)
\(
\begin{aligned}
&\mathrm{A} \cup \mathrm{B} \\
&=(1,2,3,4,5 \ldots 17,18) \\
&\mathrm{B}^{\prime}=(1,3,5,7,9 \ldots 17,19,20,21 \ldots) \\
&(\mathrm{A} \cup \mathrm{B}) \cap \mathrm{B}^{\prime}=(1,3,5,7,9 . .17)=\mathrm{A} \\
&\mathrm{A}^{\prime} \cup \mathrm{A} \\
&=\text { Universal Set } \\
&=\mathrm{N}
\end{aligned}
\) -
Question 14 of 47
14. Question
Let \(S=\{x \mid x\) is a positive multiple of 3 less than 100\(\}\) \(\mathrm{P}=\{x \mid x\) is a prime number less than 20\(\}\). Then \(n(\mathrm{~S})+n(\mathrm{P})\) is
CorrectIncorrectHint
(a) Given: \(S=\{x \mid x\) is a positive multiple of 3 less than 100\(\}\) and \(P=\{x \mid x\) is a prime number less than 20}
To find: \(n(S)+n(P)\)
\(S=\{x \mid x\) is a positive multiple of 3 less than 100\(\}\)
\(\Rightarrow \mathrm{S}=\{3,6,9,12,15, \ldots \ldots, 99\}\)
\(n(S)=99 / 3=33\)
\(P=\{x \mid x\) is a prime number less than 20\(\}\)
\(\Rightarrow P=\{2,3,5,7,11,13,17,19\}\)
\(\Rightarrow n(P)=8\)
\(n(S)+n(P)=33+8=41\)
Hence, the answer is 41 -
Question 15 of 47
15. Question
If \(\mathrm{X}\) and \(\mathrm{Y}\) are two sets and \(\mathrm{X}^{\prime}\) denotes the complement of \(\mathrm{X}\), then \(\mathrm{X} \cap(\mathrm{X} \cup \mathrm{Y})^{\prime}\) is equal to
CorrectIncorrectHint
(c)
\(
\begin{aligned}
&X \cap(X \cup Y)^{\prime}\\
&=X \cap\left(X^{\prime} \cap Y^{\prime}\right) \quad\left[\because(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}\right]\\
&=\left(X \cap X^{\prime}\right) \cap Y^{\prime}\\
&=\phi \cap Y^{\prime}\\
&=\phi \quad[\because \phi \cap A=\phi]
\end{aligned}
\) -
Question 16 of 47
16. Question
Each set \(\mathrm{X}_{r}\) contains 5 elements and each set \(\mathrm{Y}_{r}\) contains 2 elements and \(\bigcup_{r=1}^{20} \mathrm{X}_{r}=\mathrm{S}=\bigcup_{r=1}^{n} \mathrm{Y}_{r}\). If each element of \(\mathrm{S}\) belong to exactly 10 of the \(\mathrm{X}_{r} s\) and to exactly 4 of the \(\mathrm{Y}_{r}^{\prime} s\), then \(n\) is
CorrectIncorrectHint
(b) Since, \(n\left(\mathrm{X}_{r}\right)=5, \bigcup_{r=1}^{20} \mathrm{X}_{r}=\mathrm{S}\), we get \(n(\mathrm{~S})=100\)
But each element of \(\mathrm{S}\) belong to exactly 10 of the \(\mathrm{X}_{r}\) ‘ \(s\)
So, \(\frac{100}{10}=10\) are the number of distinct elements in \(\mathrm{S}\).
Also each element of \(\mathrm{S}\) belong to exactly 4 of the \(\mathrm{Y}_{r}{ }^{\prime} s\) and each \(\mathrm{Y}_{r}\) contain 2 elements. If \(\mathrm{S}\) has \(n\) number of \(\mathrm{Y}_{r}\) in it. Then
\(
\frac{2 n}{4}=10
\)
which gives
\(
n=20
\) -
Question 17 of 47
17. Question
Two finite sets have \(m\) and \(n\) elements respectively. The total number of subsets of first set is 56 more than the total number of subsets of the second set. The values of \(m\) and \(n\) respectively are.
CorrectIncorrectHint
(c) Since, let \(\mathrm{A}\) and \(\mathrm{B}\) be such sets, i.e., \(n(\mathrm{~A})=m, \quad n(\mathrm{~B})=n\)
So \(n(\mathrm{P}(\mathrm{A}))=2^{m}, n(\mathrm{P}(\mathrm{B}))=2^{n}\)
\(\Rightarrow\)
Thus, \(n(\mathrm{P}(\mathrm{A}))-n(\mathrm{P}(\mathrm{B}))=56\), i.e., \(2^{m}-2^{n}=56\)
\(2^{n}\left(2^{m-n}-1\right)=2^{3} 7\)
\(\Rightarrow\)
\(n=3,2^{m-n}-1=7\)
\(\Rightarrow\)
\(m=6\) -
Question 18 of 47
18. Question
The set \((\mathrm{A} \cup \mathrm{B} \cup \mathrm{C}) \cap\left(\mathrm{A} \cap \mathrm{B}^{\prime} \cap \mathrm{C}^{\prime}\right)^{\prime} \cap \mathrm{C}^{\prime}\) is equal to
CorrectIncorrectHint
(a) \(\text { Since }(A \cup B \cup C) \cap\left(A \cap B^{\prime} \cap C^{\prime}\right)^{\prime} \cap C^{\prime}\)
\(\begin{aligned}
&=(\mathrm{A} \cup(\mathrm{B} \cup \mathrm{C})) \cap\left(\mathrm{A}^{\prime} \cup(\mathrm{B} \cup \mathrm{C})\right) \cap \mathrm{C}^{\prime} \\
&=\left(\mathrm{A} \cap \mathrm{A}^{\prime}\right) \cup(\mathrm{B} \cup \mathrm{C}) \cap \mathrm{C}^{\prime} \\
&=\phi \cup(\mathrm{B} \cup \mathrm{C}) \cap \mathrm{C}^{\prime} \\
&=\mathrm{B} \cap \mathrm{C}^{\prime} \cup \phi=\mathrm{B} \cap \mathrm{C}^{\prime}
\end{aligned}\) -
Question 19 of 47
19. Question
If \(\mathrm{A}\) and \(\mathrm{B}\) are two finite sets, then \(n(\mathrm{~A})+n(\mathrm{~B})\) is equal to _____
CorrectIncorrectHint
(a) Since \(n(\mathrm{~A} \cup \mathrm{B})=n(\mathrm{~A})+n(\mathrm{~B})-n(\mathrm{~A} \cap \mathrm{B})\)
So, \(n(\mathrm{~A})+n(\mathrm{~B})=n(\mathrm{~A} \cup \mathrm{B})+n(\mathrm{~A} \cap \mathrm{B})\) -
Question 20 of 47
20. Question
\(\text { If } \mathrm{A} \text { is a finite set containing } n \text { element, then number of subsets of } \mathrm{A} \text { is }\) ____
CorrectIncorrectHint
(c) \(2^{n}\)
-
Question 21 of 47
21. Question
Let R and \(\mathrm{S}\) be the sets defined as follows:
\(\mathrm{R}=\{x \in \mathbf{Z} \mid x\) is divisible by 2\(\}\)
\(\mathrm{S}=\{y \in \mathbf{Z} \mid y\) is divisible by 3\(\}\)
then \(\mathrm{R} \cap \mathrm{S}=\phi\). Is this statement true or false?CorrectIncorrectHint
(b) False
Since 6 is divisible by both 3 and 2.
Thus \(\quad R \cap S \neq \phi\) -
Question 22 of 47
22. Question
\(\mathbf{Q} \cap \mathbf{R}=\mathbf{Q}\), where \(\mathbf{Q}\) is the set of rational numbers and \(\mathbf{R}\) is the set of real numbers. Is this statement true?
CorrectIncorrectHint
(a) True, Since\(\mathbf{Q} \subset \mathbf{R}\)
So, \(\mathbf{Q} \cap \mathbf{R}=\mathbf{Q}\) -
Question 23 of 47
23. Question
\(\text { The set }\{x \in \mathbf{R}: 1 \leq x<2\} \text { can be written as }\) _____
CorrectIncorrectHint
(a) Glven: \(\{x \in R: 1 \leq x<2\}\)
To find: roster form of given set
Let \(A=\{x \in R: 1 \leq x<2\}\)
\(
\Rightarrow A=[1,2)
\) -
Question 24 of 47
24. Question
\(\text { When } \mathrm{A}=\phi \text {, then number of elements in } \mathrm{P}(\mathrm{A}) \text { is }\) ____
CorrectIncorrectHint
(d) \(P(A)\) is the power set of set \(A\)
\(
\mathrm{P}(\mathrm{A})=2^{\mathrm{n}}(\mathrm{n}=0)
\)
\(P(A)=2^{0} =1 \) -
Question 25 of 47
25. Question
\(\text { If } \mathrm{A} \text { and } \mathrm{B} \text { are finite sets such that } \mathrm{A} \subset \mathrm{B} \text {, then } n(\mathrm{~A} \cup \mathrm{B}) \)= ____
CorrectIncorrectHint
(a) \(A\) and \(B\) are finite set and \(A \subset B\)
\(A \subset B\) means \(A\) is a subset of \(B\)
If \(A\) is subset of \(B\), then all elements of \(A\) are present in \(B\)
\(
\therefore \mathrm{n}(\mathrm{A} \cup \mathrm{B})=\mathrm{n}(\mathrm{B})
\) -
Question 26 of 47
26. Question
\(\text { If } \mathrm{A} \text { and } \mathrm{B} \text { are any two sets, then } \mathrm{A}-\mathrm{B} \text { is equal to }\) ____
CorrectIncorrectHint
(c) From Venn diagram you can clearly see,
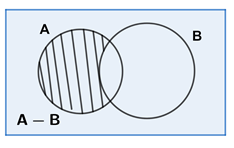
\(A-B=A \cap B^{\prime}\) -
Question 27 of 47
27. Question
\(\text { Power set of the set } \mathrm{A}=\{1,2\} \text { is }\) ____
CorrectIncorrectHint
(d) Given: set \(A=\{1,2\}\)
To find: power set of \(A\)
A power set is a set of all the subsets of set \(A\)
Subsets of \(A\) are \(\{1\},\{2\},\{1,2\}, \Phi\) -
Question 28 of 47
28. Question
Given the sets \(\mathrm{A}=\{1,3,5\} . \mathrm{B}=\{2,4,6\}\) and \(\mathrm{C}=\{0,2,4,6,8\}\). Then the universal set of all the three sets \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\) can be ____
CorrectIncorrectHint
(a) Given: \(A=\{1,3,5\} . B=\{2,4,6\}\) and \(C=\{0,2,4,6,8\}\)
To find: Universal set of all the three sets
Universal set is a set which contains elements of all sets
\(
\Rightarrow U=\{0,1,2,3,4,5,6,8\}
\) -
Question 29 of 47
29. Question
If \(\mathrm{U}=\{1,2,3,4,5,6,7,8,9,10\}, \mathrm{A}=\{1,2,3,5\}, \mathrm{B}=\{2,4,6,7\}\) and \(\mathrm{C}=\{2,3,4,8\}\). Then (i) \((\mathrm{B} \cup \mathrm{C})^{\prime}\) is ____ (ii) \((\mathrm{C}-\mathrm{A})^{\prime}\) is ____
CorrectIncorrectHint
(a) Given: \(U=\{1,2,3,4,5,6,7,8,9,10\}\)
\(
A=\{1,2,3,5\}, B=\{2,4,6,7\}
\)
And \(C=\{2,3,4,8\}\)
Given that: \(U=\{1,2,3,4,5,6,7,8,9,10\}, A=\{1,2,3,5\}, B=\{2,4,6,7\}\) and \(C=\{2,3,4,8\}\)
(i) \((B \cup C)^{\prime}=\{2,3,4,6,7,8\}^{\prime}=\{1,5,9,10\}\)
(ii) \((C-A)^{\prime}=\{1,2,3,5,6,7,9,10\}\) -
Question 30 of 47
30. Question
\(\text { For all sets } \mathrm{A} \text { and } \mathrm{B}, \mathrm{A}-(\mathrm{A} \cap \mathrm{B}) \text { is equal to }\)
CorrectIncorrectHint
(d) Since \(A-B=A \cap B^{\prime}\)
\(A-(A \cap B)=A \cap B^{\prime}\) -
Question 31 of 47
31. Question
Match the following sets for all sets A, B and C
(i) \(\left(\left(A^{\prime} \cup B^{\prime}\right)-A\right)^{\prime}\) (a) \(A-B\)
(ii) \(\left[B^{\prime} \cup\left(B^{\prime}-A\right)\right]^{\prime}\) (b) \(\mathrm{A}\)
(iii) \((A-B)-(B-C)\) (c) \(\mathrm{B}\)
(iv) \((A-B) \cap(C-B)\) (d) \((A \times B) \cap(A \times C)\)
(v) \(A \times(B \cap C)\) (e) \((A \times B) \cup(A \times C)\)
(vi) \(A \times(B \cup C)\) (f) \((A \cap C)-B\)CorrectIncorrectHint
(c) (I)
\(\begin{aligned}
\left(\left(A^{\prime} \cup B^{\prime}\right)-A\right)^{\prime} &=\left[A^{\prime} \cup B^{\prime} \cap A\right]^{\prime} & &\left.\quad \text { As } A-B=A \cap B^{\prime}\right] \\
&\left.=[A \cap B)^{\prime} \cap A^{\prime}\right]^{\prime} & & \\
&=\left[(A \cap B)^{\prime}\right]^{\prime} \cup\left(A^{\prime}\right)^{\prime} & & {\left[\text { As }\left(A^{\prime}\right)^{\prime}=A\right] } \\
&=(A \cup B) \cup A & \\
&=A
\end{aligned}\)
(II)
\(\begin{aligned}
{\left[B^{\prime} \cup\left(B^{\prime}-A^{\prime}\right)\right]^{\prime} } &=\left[B^{\prime} \cup\left(B^{\prime} \cap A^{\prime}\right)\right]^{\prime} \\
&=\left(B^{\prime}\right)^{\prime} \cap\left(B^{\prime} \cap A^{\prime}\right)^{\prime} \\
&=B \cap(B \cup A) \\
&=B
\end{aligned}\)
(iii)
\(
\begin{aligned}
(A-B)-(B-C) &=\left(A \cap B^{\prime}\right)-\left(B \cap C^{\prime}\right) \\
&=\left(A \cap B^{\prime}\right) \cap\left(B \cap C^{\prime}\right)^{\prime} \\
&=\left(A \cap B^{\prime}\right) \cap\left(B^{\prime} \cap C\right) \\
&=\left[A \cap\left(B^{\prime} \cap C\right)\right] \cap\left[B^{\prime} \cap\left(B^{\prime} \cap C\right)\right] \\
&=\left[A \cap\left(B^{\prime} \cap C\right)\right] \cap B^{\prime} \\
&=\left(A \cap B^{\prime}\right) \cap B^{\prime} \\
&=\left(A \cap B^{\prime}\right) \\
&=A-B
\end{aligned}\)
(iv)
\(
\begin{aligned}
(A-B) \cap(C-B) &=\left(A \cap B^{\prime}\right) \cap\left(C \cap B^{\prime}\right) \\
&=(A \cap C) \cap B^{\prime} \\
&=(A \cap C)-B
\end{aligned}
\)
(v) \(A \times(B \cap C)=(A \times B) \cap(A \times C)\)
(vi) \(A \times(B \cup C)=(A \times B) \cup(A \times C)\) -
Question 32 of 47
32. Question
\(\text { If } \mathrm{A} \text { is any set, then } \mathrm{A} \subset \mathrm{A}\). Is this statement true or false?
CorrectIncorrectHint
(b) Every set is a subset of itself. Hence, A \(\subset\) A Is true
-
Question 33 of 47
33. Question
\(\text { Given that } \mathrm{M}=\{1,2,3,4,5,6,7,8,9\} \text { and if } \mathrm{B}=\{1,2,3,4,5,6,7,8,9\} \text {, then } \mathrm{B} \not \subset \mathrm{M}\). Is this statement true or false?
CorrectIncorrectHint
(a)
\(
\begin{aligned}
&M=\{1,2,3,4,5,6,7,8,9\} \\
&B=\{1,2,3,4,5,6,7,8,9\}
\end{aligned}
\)
Every element of \(M\) and \(B\) is same
Hence, \(M=B\) and \(B \subset M\)
So, the given statement Is false. -
Question 34 of 47
34. Question
The sets A={1, 2, 3, 4} and B={3, 4, 5, 6} are equal?
CorrectIncorrectHint
(d) Sets A and B have the same number of elements but all the elements are not equal. Therefore, A and B are equivalent sets, not equal sets.
-
Question 35 of 47
35. Question
\(\mathbf{Q} \cup \mathbf{Z}=\mathbf{Q} \text {, where } \mathbf{Q} \text { is the set of rational numbers and } \mathbf{Z} \text { is the set of integers. }\) Is this statement true?
CorrectIncorrectHint
(b) Since every integer is a rational number
\(\therefore Z \subset Q \Rightarrow Q \cup Z=Q\)
Hence the statement is true. -
Question 36 of 47
36. Question
Let sets \(\mathrm{R}\) and \(\mathrm{T}\) be defined as
\(\mathrm{R}=\{x \in \mathbf{Z} \mid x\) is divisible by 2\(\}\)
\(\mathrm{T}=\{x \in \mathbf{Z} \mid x\) is divisible by 6\(\} .\) Then \(\mathrm{T} \subset \mathrm{R}\), Is this statement true?CorrectIncorrectHint
(a) This statement is True.
Explanation:
\(R\) and \(T\) can be represented in roster form as follows:
\(
\begin{aligned}
&R=\{\ldots,-8,-6,-4,-2,0,2,4,6,8, \ldots\} \\
&T=\{\ldots,-18,-12,-6,0,6,12,18, \ldots\}
\end{aligned}
\)
Since, every element of \(\mathrm{T}\) is present in \(\mathrm{R}\).
So, \(T \subset R\) -
Question 37 of 47
37. Question
\(\text { Given } \mathrm{A}=\{0,1,2\}, \mathrm{B}=\{x \in \mathbf{R} \mid 0 \leq x \leq 2\} . \text { Then } \mathrm{A}=\mathrm{B} \text {. }\). Is this statement true or false?
CorrectIncorrectHint
(c) \(
A=\{0,1,2\}, B=\{x \in \mathbf{R} \mid 0 \leq x \leq 2\}
\)
Roster form of \(B\) :
\(
B=\{0,1,2\}
\)
Every element of both the sets \(A\) and \(B\) are same
\(
\Rightarrow A=B
\)
So, the given statement Is true. -
Question 38 of 47
38. Question
What is the roaster form of the following sets?
(i) \(\mathrm{A}=\left\{x \mid x\right.\) is a positive integer less than 10 and \(2^{x}-1\) is an odd number \(\}\)
(ii) \(\mathrm{C}=\left\{x: x^{2}+7 x-8=0, x \in \mathbf{R}\right\}\)CorrectIncorrectHint
(a)
(i) \(2^{x}-1\) is always an odd number for all positive integral values of \(x\). In particular, \(2^{x}-1\) is an odd number for \(x=1,2, \ldots, 9\). Thus, \(\mathrm{A}=\{1,2,3,4,5,6,7,8,9\}\).
(ii) \(x^{2}+7 x-8=0 \quad\) or \((x+8)(x-1)=0\) giving \(x=-8\) or \(x=1\)
Thus, \(\mathrm{C}=\{-8,1\}\) -
Question 39 of 47
39. Question
State which of the following statements are true and which are false.
(i) \(37 \notin\{x \mid x\) has exactly two positive factors \(\}\)
(ii) \(28 \in\{y \mid\) the sum of the all positive factors of \(y\) is \(2 y\}\)
(iii) \(7,747 \in\{t \mid t\) is a multiple of 37 \(\}\)CorrectIncorrectHint
(b)
(i) False
Since, 37 has exactly two positive factors, 1 and 37,37 belongs to the set.
(ii) True
Since, the sum of positive factors of 28
\(
\begin{aligned}
&=1+2+4+7+14+28 \\
&=56=2(28)
\end{aligned}
\)
(iii) False
7,747 is not a multiple of \(37 .\) -
Question 40 of 47
40. Question
If \(\mathrm{X}\) and \(\mathrm{Y}\) are subsets of the universal set \(\mathrm{U}\), then identify which of the following statements are true and which are false.
(i) \(\mathrm{Y} \subset \mathrm{X} \cup \mathrm{Y}\)
(ii) \(\mathrm{X} \cap \mathrm{Y} \subset \mathrm{X}\)
(iii) \(\mathrm{X} \subset \mathrm{Y} \Rightarrow \mathrm{X} \cap \mathrm{Y}=\mathrm{X}\)CorrectIncorrectHint
(c)
(i) \(\mathrm{X} \cup \mathrm{Y}=\{x \mid x \in \mathrm{X}\) or \(x \in \mathrm{Y}\}\)
Thus \(x \in \mathrm{Y} \Rightarrow x \in \mathrm{X} \cup \mathrm{Y}\)
Hence, \(\mathrm{Y} \subset \mathrm{X} \cup \mathrm{Y}\)
(ii) \(\mathrm{X} \cap \mathrm{Y}=\{x \mid x \in \mathrm{X}\) and \(x \in \mathrm{Y}\}\)
Thus \(\quad x \in \mathrm{X} \cap \mathrm{Y} \Rightarrow x \in \mathrm{X}\)
Hence \(\mathrm{X} \cap \mathrm{Y} \subset \mathrm{X}\)
(iii) Note that
\(x \in \mathrm{X} \cap \mathrm{Y} \Rightarrow x \in \mathrm{X}\)
Thus \(\mathrm{X} \cap \mathrm{Y} \subset \mathrm{X}\)
Also, since \(\quad \mathrm{X} \subset \mathrm{Y}\),
\(x \in \mathrm{X} \Rightarrow x \in \mathrm{Y} \Rightarrow x \in \mathrm{X} \cap \mathrm{Y}\)
so that \(\mathrm{X} \subset \mathrm{X} \cap \mathrm{Y}\)
Hence the result \(\mathrm{X}=\mathrm{X} \cap \mathrm{Y}\) follows. -
Question 41 of 47
41. Question
Given that \(\mathrm{N}=\{1,2,3, \ldots, 100\}\), then
(i) What is the subset A of \(\mathrm{N}\), whose element are odd numbers.
(ii) What is the subset \(\mathrm{B}\) of \(\mathrm{N}\), whose element are represented by \(x+2\), where \(x \in \mathrm{N}\).CorrectIncorrectHint
(d)
(i) \(\mathrm{A}=\{x \mid x \in \mathrm{N}\) and \(x\) is odd \(\}=\{1,3,5,7, \ldots, 99\}\)
(ii) \(\mathrm{B}=\{y \mid y=x+2, x \in \mathrm{N}\}\)
So, for
\(
\begin{gathered}
1 \in \mathrm{N}, y=1+2=3 \\
2 \in \mathrm{N}, y=2+2=4,
\end{gathered}
\)
and so on. Therefore, \(\mathrm{B}=\{3,4,5,6, \ldots, 100\}\) -
Question 42 of 47
42. Question
Given that \(\mathrm{E}=\{2,4,6,8,10\}\). If \(n\) represents any member of \(\mathrm{E}\), then, Find the following sets containing all numbers represented by
(i) \(n+1\)
(ii) \(n^{2}\)CorrectIncorrectHint
(a)
Given \(\mathrm{E}=\{2,4,6,8,10\}\)
(i) Let \(\mathrm{A}=\{x \mid x=n+1, n \in \mathrm{E}\}\)
Thus, for
\(
\begin{aligned}
&2 \in \mathrm{E}, x=3 \\
&4 \in \mathrm{E}, x=5,
\end{aligned}
\)
and so on. Therefore, \(\mathrm{A}=\{3,5,7,9,11\}\).
(ii) Let \(\mathrm{B}=\left\{x \mid x=n^{2}, n \in \mathrm{E}\right\}\)
So, for \(\quad 2 \in \mathrm{E}, x=(2)^{2}=4,4 \in \mathrm{E}, x=(4)^{2}=16,6 \in \mathrm{E}, x=(6)^{2}=36\), and so on. Hence, \(B=\{4,16,36,64,100\}\) -
Question 43 of 47
43. Question
For all sets A, B and C Is \((\mathrm{A} \cap \mathrm{B}) \cup \mathrm{C}=\mathrm{A} \cap(\mathrm{B} \cup \mathrm{C})\)? Is this statement true?
CorrectIncorrectHint
(b) False
Consider the following sets \(A, B\) and \(C\):
\(
\begin{aligned}
&A=\{1,2,3\} \\
&B=\{2,3,5\} \\
&C=\{4,5,6\}
\end{aligned}
\)
Now
\((\mathrm{A} \cap \mathrm{B}) \cup \mathrm{C}=(\{1,2,3\} \cap\{2,3,5\}) \cup\{4,5,6\}\)
\(=\{2,3\} \cup\{4,5,6\}\)
\(=\{2,3,4,5,6\}\)
And
\(
\begin{aligned}
\mathrm{A} \cap(\mathrm{B} \cup \mathrm{C}) &=\{1,2,3\} \cap[\{2,3,5\} \cup\{4,5,6\}\\
&=\{1,2,3\} \cap\{2,3,4,5,6\} \\
&=\{2,3\} \\
(\mathrm{A} \cap \mathrm{B}) \cup \mathrm{C} & \neq \mathrm{A} \cap(\mathrm{B} \cup \mathrm{C})
\end{aligned}
\) -
Question 44 of 47
44. Question
Is it possible to prove that for all the sets \(A\) and \(B\)
\(\mathrm{A}-(\mathrm{A} \cap \mathrm{B})=\mathrm{A}-\mathrm{B}\)?CorrectIncorrectHint
(a)
We have
\(
\begin{aligned}
\mathrm{A}-(\mathrm{A} \cap \mathrm{B}) &=\mathrm{A} \cap(\mathrm{A} \cap \mathrm{B})^{\prime} \quad\left(\text { since } \mathrm{A}-\mathrm{B}=\mathrm{A} \cap \mathrm{B}^{\prime}\right) \\
&\left.=\mathrm{A} \cap\left(\mathrm{A}^{\prime} \cup \mathrm{B}^{\prime}\right) \quad \text { [by De Morgan’s law }\right) \\
&=\left(\mathrm{A} \cap \mathrm{A}^{\prime}\right) \cup\left(\mathrm{A} \cap \mathrm{B}^{\prime}\right) \quad \text { [by distributive law] } \\
&=\phi \cup\left(\mathrm{A} \cap \mathrm{B}^{\prime}\right) \\
&=\mathrm{A} \cap \mathrm{B}^{\prime}=\mathrm{A}-\mathrm{B}
\end{aligned}
\) -
Question 45 of 47
45. Question
For all sets A, B and C Is \((\mathrm{A}-\mathrm{B}) \cap(\mathrm{C}-\mathrm{B})=(\mathrm{A} \cap \mathrm{C})-\mathrm{B}\)?
CorrectIncorrectHint
(b) Yes
Let \(x \in(\mathrm{A}-\mathrm{B}) \cap(\mathrm{C}-\mathrm{B})\)
\(\Rightarrow \quad x \in \mathrm{A}-\mathrm{B}\) and \(x \in \mathrm{C}-\mathrm{B}\)
\(\Rightarrow \quad(x \in \mathrm{A}\) and \(x \notin \mathrm{B})\) and \((x \in \mathrm{C}\) and \(x \notin \mathrm{B})\)
\(\Rightarrow \quad(x \in \mathrm{A}\) and \(x \in \mathrm{C})\) and \(x \notin \mathrm{B}\)
\(\Rightarrow \quad(x \in \mathrm{A} \cap \mathrm{C})\) and \(x \notin \mathrm{B}\)
\(\Rightarrow \quad x \in(\mathrm{A} \cap \mathrm{C})-\mathrm{B}\)
So \(\quad(\mathrm{A}-\mathrm{B}) \cap(\mathrm{C}-\mathrm{B}) \subset(\mathrm{A} \cap \mathrm{C})-\mathrm{B} \dots ….(1)\)
Now, conversely\(
\begin{array}{ll}
\text { Let } y \in(\mathrm{A} \cap \mathrm{C})-\mathrm{B} \\
\Rightarrow y \in(\mathrm{A} \cap \mathrm{C}) \text { and } y \notin \mathrm{B} \\
\Rightarrow (y \in \mathrm{A} \text { and } y \in \mathrm{C}) \text { and }(y \notin \mathrm{B}) \\
\Rightarrow (y \in \mathrm{A} \text { and } y \notin \mathrm{B}) \text { and }(y \in \mathrm{C} \text { and } y \notin \mathrm{B}) \\
\Rightarrow y \in(\mathrm{A}-\mathrm{B}) \text { and } y \in(\mathrm{C}-\mathrm{B}) \\
\Rightarrow y \in(\mathrm{A}-\mathrm{B}) \cap(\mathrm{C}-\mathrm{B}) \\
\text { So } (\mathrm{A} \cap \mathrm{C})-\mathrm{B} \subset(\mathrm{A}-\mathrm{B}) \cap(\mathrm{C}-\mathrm{B}) \dots ….(2) \\
\text { From }(1) \text { and }(2),(\mathrm{A}-\mathrm{B}) \cap(\mathrm{C}-\mathrm{B})=(\mathrm{A} \cap \mathrm{C})-\mathrm{B}
\end{array}
\) -
Question 46 of 47
46. Question
Let \(\mathrm{P}\) be the set of prime numbers and let \(\mathrm{S}=\left\{t \mid 2^{t}-1\right.\) is a prime \(\}\).
Statement \(\mathrm{S} \subset \mathrm{P}\) is true or false.CorrectIncorrectHint
(b)
Now the equivalent contrapositive statement of \(x \in \mathrm{S} \Rightarrow x \in \mathrm{P}\) is \(x \notin \mathrm{P} \Rightarrow\) \(x \notin \mathrm{S} .\)
Now, we will prove the above contrapositive statement by contradiction method
\(\begin{array}{ll}\text { Let } & x \notin \mathrm{P} \\ \Rightarrow & x \text { is a composite number }\end{array}\)
Let us now assume that \(x \in \mathrm{S}\)
\(\Rightarrow \quad 2^{x}-1=m \quad\) (where \(m\) is a prime number)
\(\Rightarrow \quad 2^{x}=m+1\)
Which is not true for all composite number, say for \(x=4\) because
\(2^{4}=16\) which can not be equal to the sum of any prime number \(m\) and \(1 .\)
Thus, we arrive at a contradiction
\(\Rightarrow \quad x \notin \mathrm{S}\).
Thus, when \(x \notin \mathrm{P}\), we arrive at \(x \notin \mathrm{S}\)
So \(\quad \mathrm{S} \subset \mathrm{P}\). -
Question 47 of 47
47. Question
From 50 students taking examinations in Mathematics, Physics and Chemistry, each of the student has passed in at least one of the subject, 37 passed Mathematics, 24 Physics and 43 Chemistry. At most 19 passed Mathematics and Physics, at most 29 Mathematics and Chemistry and at most 20 Physics and Chemistry. What is the largest possible number that could have passed all three examination?
CorrectIncorrectHint
(d) Let \(\mathrm{M}\) be the set of students passing in Mathematics
\(\mathrm{P}\) be the set of students passing in Physics
\(C\) be the set of students passing in Chemistry
\(
\begin{array}{ll}
\text { Now, } \quad & n(\mathrm{M} \cup \mathrm{P} \cup \mathrm{C})=50, n(\mathrm{M})=37, n(\mathrm{P})=24, n(\mathrm{C})=43 \\
& n(\mathrm{M} \cap \mathrm{P}) \leq 19, n(\mathrm{M} \cap \mathrm{C}) \leq 29, n(\mathrm{P} \cap \mathrm{C}) \leq 20 \text { (Given }) \\
& n(\mathrm{M} \cup \mathrm{P} \cup \mathrm{C})=n(\mathrm{M})+n(\mathrm{P})+n(\mathrm{C})-n(\mathrm{M} \cap \mathrm{P})-n(\mathrm{M} \cap \mathrm{C}) \\
& -n(\mathrm{P} \cap \mathrm{C})+n(\mathrm{M} \cap \mathrm{P} \cap \mathrm{C}) \leq 50 \\
\Rightarrow & 37+24+43-19-29-20+n(\mathrm{M} \cap \mathrm{P} \cap \mathrm{C}) \leq 50 \\
\Rightarrow & n(\mathrm{M} \cap \mathrm{P} \cap \mathrm{C}) \leq 50-36 \\
\Rightarrow & n(\mathrm{M} \cap \mathrm{P} \cap \mathrm{C}) \leq 14
\end{array}
\)
Thus, the largest possible number that could have passed all the three examinations is \(\)14.\(\)