1.12 Practical Problems on Union and Intersection of Two Sets
In earlier Section, we have learnt the union, intersection, and difference of two sets. In this Section, we will go through some practical problems related to our daily life. The formulae derived in this Section will also be used in subsequent Chapter on Probability.
Formulae to solve practical problems on union and intersection of two sets
Let \(\mathrm{A}\) and \(\mathrm{B}\) be finite sets. If \(\mathrm{A} \cap \mathrm{B}=\phi\), then
(a) \(n(\mathrm{~A} \cup \mathrm{B})=n(\mathrm{~A})+n(\mathrm{~B}) \ldots \text { (i) }\)
The elements in \(\mathrm{A} \cup \mathrm{B}\) are either in \(\mathrm{A}\) or in \(\mathrm{B}\) but not in both as \(\mathrm{A} \cap \mathrm{B}=\phi\). So, (i) follows immediately.
In general, if \(\mathrm{A}\) and \(\mathrm{B}\) are finite sets, then
(b) \(n(\mathrm{~A} \cup \mathrm{B})=n(\mathrm{~A})+n(\mathrm{~B})-n(\mathrm{~A} \cap \mathrm{B})\ldots \text { (ii) }\)
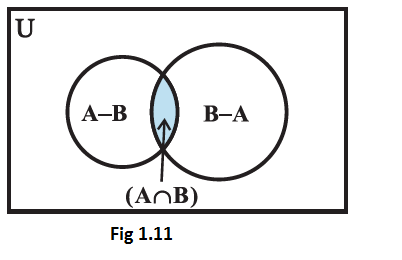
Note that the sets \(\mathrm{A}-\mathrm{B}, \mathrm{A} \cap \mathrm{B}\) and \(\mathrm{B}-\mathrm{A}\) are disjoint and their union is \(\mathrm{A} \cup \mathrm{B}\) (Fig 1.9). Therefore
\(
\begin{aligned}
n(\mathrm{~A} \cup \mathrm{B}) &=n(\mathrm{~A}-\mathrm{B})+n(\mathrm{~A} \cap \mathrm{B})+n(\mathrm{~B}-\mathrm{A}) \\
&=n(\mathrm{~A}-\mathrm{B})+n(\mathrm{~A} \cap \mathrm{B})+n(\mathrm{~B}-\mathrm{A})+n(\mathrm{~A} \cap \mathrm{B})-n(\mathrm{~A} \cap \mathrm{B}) \\
&=n(\mathrm{~A})+n(\mathrm{~B})-n(\mathrm{~A} \cap \mathrm{B}), \text { which verifies } \ldots \text { (ii) }
\end{aligned}
\)
(c) If \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\) are finite sets, then \(n(\mathrm{~A} \cup \mathrm{B} \cup \mathrm{C})=n(\mathrm{~A})+n(\mathrm{~B})+n(\mathrm{C})-n(\mathrm{~A} \cap \mathrm{B})-n(\mathrm{~B} \cap \mathrm{C})\) \(-n(\mathrm{~A} \cap \mathrm{C})+n(\mathrm{~A} \cap \mathrm{B} \cap \mathrm{C})\ldots \text { (iii) }\)
In fact, we have
\(
\begin{array}{ll}
n(\mathrm{~A} \cup \mathrm{B} \cup \mathrm{C})=n(\mathrm{~A})+n(\mathrm{~B} \cup \mathrm{C})-n[\mathrm{~A} \cap(\mathrm{B} \cup \mathrm{C})] & {[\text { by { (ii) } }]} \\
=n(\mathrm{~A})+n(\mathrm{~B})+n(\mathrm{C})-n(\mathrm{~B} \cap \mathrm{C})-n[\mathrm{~A} \cap(\mathrm{B} \cup \mathrm{C})] & {[\text { by { (ii) } ] }}
\end{array}
\)
Since \(A \cap(B \cup C)=(A \cap B) \cup(A \cap C)\), we get
\(
n[\mathrm{~A} \cap(\mathrm{B} \cup \mathrm{C})]=n(\mathrm{~A} \cap \mathrm{B})+n(\mathrm{~A} \cap \mathrm{C})-n[(\mathrm{~A} \cap \mathrm{B}) \cap(\mathrm{A} \cap \mathrm{C})]
\)
\(
=n(\mathrm{~A} \cap \mathrm{B})+n(\mathrm{~A} \cap \mathrm{C})-n(\mathrm{~A} \cap \mathrm{B} \cap \mathrm{C})
\)
Therefore
\(
\begin{aligned}
n(\mathrm{~A} \cup \mathrm{B} \cup \mathrm{C}) &=n(\mathrm{~A})+n(\mathrm{~B})+n(\mathrm{C})-n(\mathrm{~A} \cap \mathrm{B})-n(\mathrm{~B} \cap \mathrm{C}) \\
&-n(\mathrm{~A} \cap \mathrm{C})+n(\mathrm{~A} \cap \mathrm{B} \cap \mathrm{C})
\end{aligned}
\)
This proves (iii).
Example 1: If \(\mathrm{X}\) and \(\mathrm{Y}\) are two sets such that \(\mathrm{X} \cup \mathrm{Y}\) has 50 elements, \(\mathrm{X}\) has 28 elements and \(\mathrm{Y}\) has 32 elements, how many elements does \(\mathrm{X} \cap \mathrm{Y}\) have?
Solution: Given that
\(
n(\mathrm{X} \cup \mathrm{Y})=50, n(\mathrm{X})=28, n(\mathrm{Y})=32 \text {, }
\)
\(n(\mathrm{X} \cap \mathrm{Y})=\)?
By using the formula
\(n(\mathrm{X} \cup \mathrm{Y})=n(\mathrm{X})+n(\mathrm{Y})-n(\mathrm{X} \cap \mathrm{Y})\),
we find that
\(
\begin{aligned}
n(\mathrm{X} \cap \mathrm{Y}) &=n(\mathrm{X})+n(\mathrm{Y})-n(\mathrm{X} \cup \mathrm{Y}) \\
&=28+32-50=10
\end{aligned}
\)
Example 2: In a school there are 20 teachers who teach mathematics or physics. Of these, 12 teach mathematics and 4 teach both physics and mathematics. How many teach physics?
Solution: Let M denote the set of teachers who teach mathematics and \(\mathrm{P}\) denote the set of teachers who teach physics. In the statement of the problem, the word ‘or’ gives us a clue of union and the word ‘and’ gives us a clue of intersection. We, therefore, have
We wish to determine \(n(\mathrm{M} \cup \mathrm{P})=20, n(\mathrm{M})=12\) and \(n(\mathrm{M} \cap \mathrm{P})=4\)
wish to determine \(n(\mathrm{P})\)
Using the result
\(
n(\mathrm{M} \cup \mathrm{P})=n(\mathrm{M})+n(\mathrm{P})-n(\mathrm{M} \cap \mathrm{P}),
\)
we obtain
Thus
\(
\begin{aligned}
&20=12+n(\mathrm{P})-4 \\
&n(\mathrm{P})=12
\end{aligned}
\)
Hence 12 teachers teach physics.
Example 3: In a class of 35 students, 24 like to play cricket and 16 like to play football. Also, each student likes to play at least one of the two games. How many students like to play both cricket and football?
Solution: Let \(\mathrm{X}\) be the set of students who like to play cricket and \(\mathrm{Y}\) be the set of students who like to play football. Then \(\mathrm{X} \cup \mathrm{Y}\) is the set of students who like to play at least one game, and \(\mathrm{X} \cap \mathrm{Y}\) is the set of students who like to play both games. Given \(n(\mathrm{X})=24, n(\mathrm{Y})=16, n(\mathrm{X} \cup \mathrm{Y})=35, n(\mathrm{X} \cap \mathrm{Y})=\)?
Using the formula \(n(\mathrm{X} \cup \mathrm{Y})=n(\mathrm{X})+n(\mathrm{Y})-n(\mathrm{X} \cap \mathrm{Y})\), we get
\(
35=24+16-n(\mathrm{X} \cap \mathrm{Y})
\)
Thus,
\(
n(\mathrm{X} \cap \mathrm{Y})=5
\)
i.e., 5 students like to play both games.
Example 4: In a survey of 400 students in a school, 100 were listed as taking apple juice, 150 as taking orange juice and 75 were listed as taking both apple as well as orange juice. Find how many students were taking neither apple juice nor orange juice.
Solution: Let \(\mathrm{U}\) denote the set of surveyed students and A denote the set of students taking apple juice and \(\mathrm{B}\) denote the set of students taking orange juice. Then
\(n(\mathrm{U})=400, n(\mathrm{~A})=100, n(\mathrm{~B})=150\) and \(n(\mathrm{~A} \cap \mathrm{B})=75 .\)
Now
\(
\begin{aligned}
n\left(\mathrm{~A}^{\prime} \cap \mathrm{B}^{\prime}\right) &=n(\mathrm{~A} \cup \mathrm{B})^{\prime} \\
&=n(\mathrm{U})-n(\mathrm{~A} \cup \mathrm{B}) \\
&=n(\mathrm{U})-n(\mathrm{~A})-n(\mathrm{~B})+n(\mathrm{~A} \cap \mathrm{B}) \\
&=400-100-150+75=225
\end{aligned}
\)
Hence 225 students were taking neither apple juice nor orange juice.
Example 5: There are 200 individuals with a skin disorder, 120 had been exposed to the chemical \(\mathrm{C}_{1}, 50\) to chemical \(\mathrm{C}_{2}\), and 30 to both the chemicals \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\). Find the number of individuals exposed to
(i) Chemical \(\mathrm{C}_{1}\) but not chemical \(\mathrm{C}_{2}\)
(ii) Chemical \(\mathrm{C}_{2}\) but not chemical \(\mathrm{C}_{1}\)
(iii) Chemical \(\mathrm{C}_{1}\) or chemical \(\mathrm{C}_{2}\)
Solution: Let \(\mathrm{U}\) denote the universal set consisting of individuals suffering from the skin disorder, A denote the set of individuals exposed to the chemical \(\mathrm{C}_{1}\) and \(\mathrm{B}\) denote the set of individuals exposed to the chemical \(\mathrm{C}_{2}\).
Here \(n(\mathrm{U})=200, n(\mathrm{~A})=120, n(\mathrm{~B})=50\) and \(n(\mathrm{~A} \cap \mathrm{B})=30\)
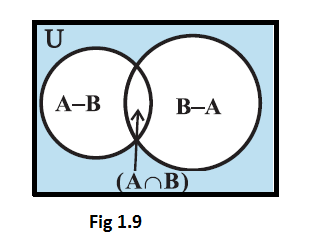
(i) From the Venn diagram given in Fig 1.11, we have
\(
\mathrm{A}=(\mathrm{A}-\mathrm{B}) \cup(\mathrm{A} \cap \mathrm{B}) \text {. }
\)
\(n(\mathrm{~A})=n(\mathrm{~A}-\mathrm{B})+n(\mathrm{~A} \cap \mathrm{B}) \quad(\) Since \(\mathrm{A}-\mathrm{B})\) and \(\mathrm{A} \cap \mathrm{B}\) are disjoint. \()\)
or \(n(\mathrm{~A}-\mathrm{B})=n(\mathrm{~A})-n(\mathrm{~A} \cap \mathrm{B})=120-30=90\)
Hence, the number of individuals exposed to chemical \(\mathrm{C}_{1}\) but not to chemical \(\mathrm{C}_{2}\) is 90 .
(ii) From Fig 1.11, we have
\(\mathrm{B}=(\mathrm{B}-\mathrm{A}) \cup(\mathrm{A} \cap \mathrm{B}) \text {. }\)
and so, \(n(\mathrm{~B})=n(\mathrm{~B}-\mathrm{A})+n(\mathrm{~A} \cap \mathrm{B})\)
(Since \(\mathrm{B}-\mathrm{A}\) and \(\mathrm{A} \cap \mathrm{B}\) are disjoint. \()\)
\(
\text { or } \quad \begin{aligned}
n(\mathrm{~B}-\mathrm{A}) &=n(\mathrm{~B})-n(\mathrm{~A} \cap \mathrm{B}) \\
&=50-30=20
\end{aligned}
\)
Thus, the number of individuals exposed to chemical \(\mathrm{C}_{2}\) and not to chemical \(\mathrm{C}_{1}\) is 20.
(iii) The number of individuals exposed either to chemical \(\mathrm{C}_{1}\) or to chemical \(\mathrm{C}_{2}\), i.e.,
\(
\begin{aligned}
n(\mathrm{~A} \cup \mathrm{B}) &=n(\mathrm{~A})+n(\mathrm{~B})-n(\mathrm{~A} \cap \mathrm{B}) \\
&=120+50-30=140 .
\end{aligned}
\)