1.9 Venn Diagrams
Most of the relationships between sets can be represented by means of diagrams which are known as Venn diagrams. Venn diagrams are named after the English logician, John Venn (1834-1883). A Venn diagram typically uses intersecting and non-intersecting circles (although other closed figures like squares may be used) to denote the relationship between sets. The universal set is represented usually by a rectangle and its subsets by circles.
Universal Set
The universal set contains all of the elements in all of the sets that are being considered and is represented following way using the Venn diagram:
- A large rectangle is used to represent the universal set and it is usually denoted by the symbol U.
- All the other sets are represented by circles or closed figures within this larger rectangle.
- Every set is the subset of the universal set U.
Example 1:
Consider the Venn Diagram image shown in Fig 1.1.
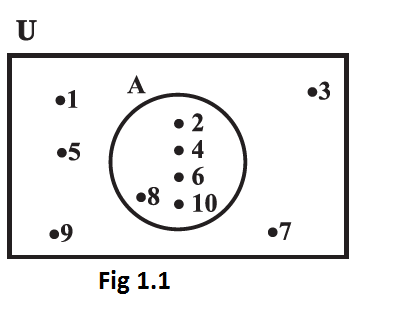
- U is the universal set with all the numbers 1-10, enclosed within the rectangle.
- A is the set of even numbers 1-10, which is the subset of the universal set U and it is placed inside the rectangle.
Fig 1.1, \(\mathrm{U}=\{1,2,3, \ldots, 10\}\) is the universal set of which \(\mathrm{A}=\{2,4,6,8,10\} \text { is a subset. }\)