1.7 Power Set
Power set
The set or family of all the subsets of a given set \(A\) is said to be the power set of \(A\) and is denoted by \(P(A)\).
Symbolically, \(P(A)=\{X \mid X \subseteq A\}\)
Thus, \(X \in P(A) \Leftrightarrow X \subseteq A\)
Also, \(\phi \in P(A)\) and \(A \in P(A)\) for all sets \(A\).
The elements of the power set \(P(A)\) are the subsets of \(A\).
For example,
(i) If \(A=\{1\}\), then \(P(A)=\{\phi,\{1\}\}\)
(ii) If \(B=\{1,2\}\), then \(P(B)=\{\phi,\{1\},\{2\},\{1,2\}\}\)
(iii) If \(C=\{1,2,3\}\), then \(P(C)=\{\phi,\{1\},\{2\},\{3\},\{1,2\}\), \(\{2,3\},\{1,3\},\{1,2,3\}\}\)
We observe that number of elements in power set of a given set is \(2^n\), where \(n\) is the number of elements in the given set.
Note: If \(A \subseteq B \Rightarrow P(A) \subseteq P(B)\). We know that \(\phi\) is a subset of every set.
Example 1: Write down the power set of the set \(A=\{a, e, i, o, u\}\).
Solution:
\(
\begin{aligned}
&\text { Consider a set } A=\{a, e, i, o, u\} \text {, therefore power set of } A \text { is given by } P(A) \text {, i.e. }\\
&\begin{aligned}
& P(A)=\{\phi \\
& \{a\},\{e\},\{i\},\{o\},\{u\}, \\
& \{a, e\},\{a, i\},\{a, o\},\{a, u\},\{e, i\},\{e, o\},\{e, u\},\{i, o\},\{i, u\},\{o, u\}, \\
& \{a, e, i\},\{a, e, o\},\{a, e, u\},\{a, i, o\},\{a, i, u\},\{a, o, u\},\{e, i, o\},\{e, i, u\},\{e, ~ \\
& o, u\},\{i, o, u\}, \\
& \{a, e, i, o\},\{a, e, i, u\},\{a, e, o, u\},\{a, i, o, u\},\{e, i, o, u\}, \\
& \{a, e, i, o, u\}\}
\end{aligned}
\end{aligned}
\)
Power Set of the Empty Set
A power set is all possible subsets of the original set, including the null or empty set. So a power set of the Empty Set is basically the empty set itself. We can prove this with simple steps.
Let’s find out the total number of elements of the power set.
No. of elements of empty set = 0 [From Definition of Empty Set]
No. of elements of power set \(=2^0=1\)
Therefore, the power set of the empty set, i.e., \(P(\phi)=\{\phi\}\).
Cardinal Number of Set
The number of distinct elements or members in a finite set is called the cardinal number of a set. Through cardinality, we define the size of a set. The cardinal number of a set \(A\) is denoted as \(n(A)\), where \(n(A)\) represents the number of elements in set \(A\).
Equivalent sets
Two or more sets having the same number of elements are called equivalent sets.
Thus, if sets \(A\) and \(B\) are equivalent sets then \(n(A)=n(B)\).
Also, we understand that equal sets have same number of elements so are equivalent.
But equivalent sets may not be equal sets as they may have different elements.
The principle of inclusion and exclusion (PIE)
The principle of inclusion and exclusion (PIE) is a counting technique that computes the number of elements that satisfy at least one of several properties while guaranteeing that elements satisfying more than one property are not counted twice.
An underlying idea behind PIE is that summing the number of elements that satisfy at least one of two categories and subtracting the overlap prevents double-counting. For instance, the number of people that have at least one cat or at least one dog can be found by taking the number of people who own a cat, adding the number of people that have a dog, then subtracting the number of people who have both.
PIE is particularly useful in combinatorics and probability problem solving when it is necessary to devise a counting method that ensures an object is not counted twice.
Formula for Two Sets
\(
\begin{aligned}
&\text { For two sets } \mathrm{A} \text { and } \mathrm{B}\\
&|A \cup B|=|A|+|B|-|A \cap B|
\end{aligned}
\)
Where,
\(|{A}|=n(A)\) is the number of elements in set \(A\).
\(|B|=n(B)\) is the number of element \(\sin \operatorname{set} B\).
\(|A \cap B|=n(A \cap B)\) is the number of elements in both set \(A\) and \(B\).
Derivation of Inclusion and Exclusion Principle Using Venn Diagrams
We can visualize this using Venn diagram, for finite number of sets. Here we will discuss formula for Principle of Inclusion and Exclusion for two and three sets and derive it using Venn diagram,
Venn Diagram for Two Sets
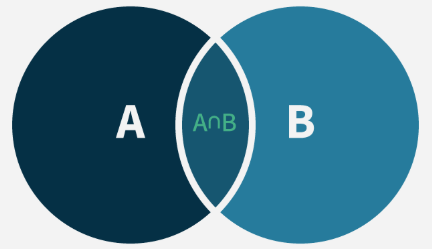
First Step (Inclusion): Add the sizes of the two sets \(|\mathrm{A}|\) and \(|B|\). This counts all the elements in \(A\) and \(B\), but elements in the intersection \(A \cap B\) are counted twice (once in \(A\) and once in \(B\) ).
Second Step (Exclusion): Subtract the size of the intersection \(|A \cap B|\), because these elements were counted twice in the first step.
Thus, the number of elements in the union of these two sets, \(|A \cup B|\), is given by:
\(
|A \cup B|=|A|+|B|-|A \cap B|
\)
Example 2: In a class of 100 students:
60 study Math.
45 study Science.
20 study both Math and Science.
How many students study either Math or Science?
Solution:
As we know, \(n(A \cup B)=n(A)+n(B)-n(A \cap B)\)
Given:
\(n(A)=60\)
\(n(B)=45\)
\(n(A \cap B)=20\)
\(n(A \cup B)=n(A)+n(B)-n(A \cap B)=60+45-20=85\)
Thus, 85 students study either Math or Science.
Formula for Three Sets
For three sets \(\mathrm{A}, \mathrm{B}, \mathrm{C}\) the Principle of Inclusion and Exclusion (PIE) formula to find the size of the union is:
\(
|A \cup B \cup C|=|A|+|B|+|C|-|A \cap B|-|A \cap C|-|B \cap C|+|A \cap B \cap C|
\)
Where,
\(|\mathrm{A}|,|\mathrm{B}|,|\mathrm{C}|\) are number of elements in the sets \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\) respectively.
\(|\mathrm{A} \cap \mathrm{B}|,|\mathrm{A} \cap \mathrm{C}|,|\mathrm{B} \cap \mathrm{C}|\) are the numbers of elements in the pairwise intersections of the sets.
\(|A \cap B \cap C|\) is the number of elements that are in all three sets.
Venn Diagram for Three Sets
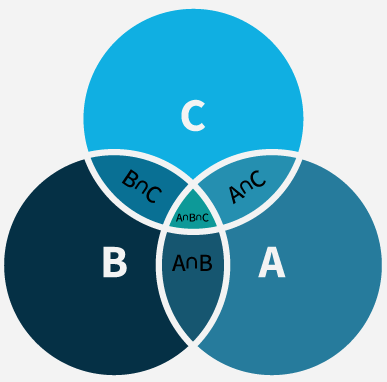
First Step (Inclusion): Add the sizes of the individual sets \(|A|\), \(|\mathrm{B}|\), and \(|\mathrm{C}|\). This counts all the elements in \(\mathrm{A}, \mathrm{B}\), and \(\mathrm{C}\) , but it also counts the elements in the intersections more than once.
Second Step (Exclusion): Subtract the pairwise intersections \(|A \cap B|,|B \cap C|\), and \(|C \cap A|\) because these elements were counted twice in the first step.
Third Step (Inclusion of Intersection of All Three Sets): Add back the intersection of all three sets \(|A \cap B \cap C|\), as it was subtracted three times (once for each pairwise intersection) in the previous step.
Thus, the number of elements in the union of these three sets, \(|A \cup B \cup C|\), is given by:
\(
\begin{gathered}
|A \cup B \cup C|=|A|+|B|+|C|-|A \cap B|-|B \cap C|-|C \cap A|+ \\
|A \cap B \cap C|
\end{gathered}
\)
Example 3: In a survey of 200 people:
120 like pizza.
100 like burgers.
80 like tacos.
60 like both pizza and burgers.
40 like both burgers and tacos.
30 like both pizza and tacos.
20 like all three: pizza, burgers, and tacos.
How many people like at least one of these three foods?
Solution: As we know, \(|A \cup B \cup C|=|A|+|B|+|C|-|A \cap B|-|A \cap C|-\) \(|B \cap C|+|A \cap B \cap C|\)
Given:
\(|A|=120\) Pizza lovers
\(|B|=100\) Burger lovers
\(|C|=80\) Taco lovers
\(|A \cap B|=60\)
\(|A \cap C|=30\)
\(|B \cap C|==40\)
\(|A \cap B \cap C|=20\)
Substituting in the formula, we get,
\(
|A \cup B \cup C|=120+100+80-60-30-40+20=190
\)
Thus, 190 people like at least one of the three foods.
Cardinal Number of Union of Two Sets
Consider sets \(A=\{1,3,5,7\}\) and \(B=\{2,4,6,8,10\}\)
Here, sets \(A\) and \(B\) are disjoint.
\(
n(A)=4 \text { and } n(B)=5
\)
Also, \(A \cup B=\{1,2,3,4,5,6,7,8,10\}\)
\(
\therefore \quad n(A \cup B)=9=n(A)+n(B)
\)
Thus, when sets \(A\) and \(B\) are disjoint, \(n(A \cup B)=n(A)+n(B)\).
Also, if sets \(A, B\) and \(C\) are pairwise disjoint, then
\(
n(A \cup B \cup C)=n(A)+n(B)+n(C)
\)
When sets are not disjoint:
Now, consider sets \(A=\{1,2,3,4,5,6\}\) and \(B=\{4,5,6,7,8\}\).
Here, \(A \cap B=\{4,5,6\}\).
Now: \(A \cup B=\{1,2,3,4,5,6,7,8\}\)
\(
\therefore \quad n(A \cup B)=8
\)
Also. \(n(A)+n(B)=6+5=11\)
Thus. \(n(A \cup B) \neq n(A)+n(B)\)
This is because common elements 4.5 and 6 are counted twice in \(n(A)+n(B)\), with \(n(A)\) and with \(n(B)\).
So, actually, we should have
\(
n(A \cup B)=n(A)+n(B)-n(A \cap B)
\)
The above relation is for any type of set. When sets \(A\) and \(B\) are disjoint, \(n(A \cap B)=0\).
\(
\therefore \quad n(A \cup B)=n(A)+n(B)
\)
Cardinal Number of Union of more than Two Sets
For three sets \(A, B\) and \(C\). which are not disjoint pairwise, let us calculate \(n(A \cup B \cup C)\).
Clearly, first we need to take the sum \(n(A)+n(B)+n(C)\).
Here, in sum \(n(A)+n(B), n(A \cap B)\) is taken twice, once with \(n(A)\) and once with \(n(B)\), so \(n(A \cap B)\) needs to be subtracted once. Similarly, \(n(B \cap C)\) and \(n(C \cap A)\) are also taken twice and hence, each needs to be subtracted once.
Also, \(n(A \cap B \cap C)\) is taken once in each of \(n(A), n(B), n(C)\), \(n(A \cap B), n(B \cap C), n(C \cap A)\). So, in the sum \(n(A)+n(B)+n(C)\) \(-n(A \cap B)-n(B \cap C)-n(C \cap A)\), term \(n(A \cap B \cap C)\) vanishes. Hence, \(n(A \cap B \cap C)\) needs to be added once.
So, finally we have
\(
\begin{aligned}
n(A \cup B \cup C)= & n(A)+n(B)+n(C)-n(A \cap B) \\
& -n(B \cap C)-n(C \cap A)+n(A \cap B \cap C)
\end{aligned}
\)
The concept used in the above formula is called the Principle of Inclusion and Exclusion. Here, the sum \(n(A)+n(B)+n(C)\) gives greater value, so we exclude \(n(A \cap B)+n(B \cap C)+n(C \cap A)\). But, doing this, we lose \(n(A \cap B \cap C)\), so we include it.
With the help of the above Jogic,
\(
n(A \cup B \cup C \cup D)
\)
\(=[\) Sum of number of elements in sets \(A, B, C\) and \(D]\)
– [Sum of the number of elements of the intersection of sets taken two at a time]
+[Sum of number of elements of intersection of sets taken three at a time]
– Elements of the intersection of all sets
\(
=n(A)+n(B)+n(C)+n(D)-n(A C, B)-n(A \cap C)-n(A \cap D)-n(B \cap C)
\)
\(
\begin{aligned}
& -n(B \cap D)-n(C \cap D)+n(A \cap B C, C) \\
& +n(B \cap C \cap D)+n(C \cap D \cap A) \\
& +n(D \cap A \cap B)-n(A \cap B \cap C \cap D)
\end{aligned}
\)
Thus, \(n\left(A_1 \cup A_2 \cup A_3 \cup \ldots \cup A_n\right)\)
\(
=\sum_{i=1}^n n\left(A_i\right)-\sum_{1 \leq i<j \leq n} n\left(A_i \cap A_j\right)
\)
\(
+\sum_{1 \leq i<j<k \leq n} n\left(A_i \cap A_j \cap A_k\right)+\ldots
\)
\(
+(-1)^n \sum n\left(A_1 \cap A_2 \cap \ldots \cap A_n\right)
\)
From the above discussion, it is easy to establish the following:
(i) \(n(A-B)=n(A)-n(A \cap B)=n\left(A \cap B^{\prime}\right)\)
(ii) \(n\left(A^{\prime}\right)=n(U)-n(A)\)
(iii) \(n\left(A^{\prime} \cup B^{\prime}\right)=n(U)-n(A \cap B)\)
(iv) \(n\left(A^{\prime} \cap B^{\prime}\right)=n(U)-n(A \cup B)\)
Cardinality of Power Set
Cardinality (cardinality of a set means the number of elements of a set) of a power set denotes the number of elements present in the power set. It is denoted by \(|P(A)|\). Thus, the number of elements in the power set is given by:
\(
|P(A)|=2^n
\)
Where ” \(n\) ” is the number of elements of Set \(A\).
Let’s consider an example for better understanding.
Example 4: Find the cardinality of the Power Set of \(A\), where \(A=\{1,2,9\}\).
Solution: As \(n=|A|=3\), the number of elements in the Power Set of \(A=2^{n}\)
Thus, \(|P(A)|=2^3=8\)
Therefore, there are 8 elements in the power set of \(A\).