5.5 Enthalpies for Different Types of Reactions

It is convenient to give name to enthalpies specifying the types of reactions.

(a) Standard Enthalpy of Combustion (symbol : \(\Delta_c H^{\ominus}\) )

Combustion reactions are exothermic in nature. These are important in industry, rocketry, and other walks of life.

Standard enthalpy of combustion is defined as the enthalpy change per mole (or per unit amount) of a substance when it undergoes combustion and all the reactants and products being in their standard states at the specified temperature (It is the heat evolved when 1 mole of substance is completely burnt or oxidised in oxygen. It is represented as \(\Delta_c H\).)

\(
\text { ex: } \mathrm{CH}_4(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{g})
\)
\(\Delta_C H^{\ominus}\) is the standard enthalpy of combustion i.e. combustion taking place under standard conditions, i.e., \(298 \mathrm{~K}\) and \(1 \mathrm{bar}\) pressure.

Another example is cooking gas in cylinders contains mostly butane \(\left(\mathrm{C}_4 \mathrm{H}_{10}\right)\). During the complete combustion of one mole of butane, \(2658 \mathrm{~kJ}\) of heat is released. We can write the thermochemical reactions for this as:
\(
\mathrm{C}_4 \mathrm{H}_{10}(\mathrm{~g})+\frac{13}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow 4 \mathrm{CO}_2(\mathrm{~g})+5 \mathrm{H}_2 \mathrm{O}(\mathrm{l}); \Delta_C H^{\ominus}=-2658.0 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
Similarly, combustion of glucose gives out \(2802.0 \mathrm{~kJ} / \mathrm{mol}\) of heat, for which the overall equation is :
\(
\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6(\mathrm{~g})+6 \mathrm{O}_2(\mathrm{~g}) \rightarrow 6 \mathrm{CO}_2(\mathrm{~g})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{l}); \Delta_C H^{\ominus}=-2802.0 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
Our body also generates energy from food by the same overall process as combustion, although the final products are produced after a series of complex biochemical reactions involving enzymes.

Example 6.9: The combustion of one mole of benzene takes place at \(298 \mathrm{~K}\) and \(1 \mathrm{~atm}\). After combustion, \(\mathrm{CO}_2(\mathrm{~g})\) and \(\mathrm{H}_2 \mathrm{O}(1)\) are produced and \(3267.0 \mathrm{~kJ}\) of heat is liberated. Calpulate the standard enthalpy of formation, \(\Delta_f H^{\ominus}\) of benzene. Standard enthalpies of formation of \(\mathrm{CO}_2(\mathrm{~g})\) and \(\mathrm{H}_2 \mathrm{O}(\mathrm{l})\) are \(-393.5 \mathrm{~kJ} \mathrm{~mol}^{-1}\) and \(-285.83 \mathrm{~kJ} \mathrm{~mol}^{-1}\) respectively.

Answer: The formation reaction of benzene is given by :
\(
6 \mathrm{C}(\text { graphite })+3 \mathrm{H}_2(\mathrm{~g}) \rightarrow \mathrm{C}_6 \mathrm{H}_6(\mathrm{l}) ;\Delta_f H^{\ominus}=? \ldots \text { (i) }
\)
The enthalpy of combustion of \(1 \mathrm{~mol}\) of benzene is:
\(
\mathrm{C}_6 \mathrm{H}_6(\mathrm{l})+\frac{15}{2} \mathrm{O}_2 \rightarrow 6 \mathrm{CO}_2(\mathrm{~g})+3 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \text {; }\Delta_C H^{\ominus}=-3267 \mathrm{~kJ} \mathrm{~mol}^{-1} \ldots \text { (ii) }
\)
The enthalpy of formation of \(1 \mathrm{~mol}\) of \(\mathrm{CO}_2(\mathrm{~g}):\)
\(
\mathrm{C}(\text { graphite })+\mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g}) \text {; }\Delta_f H^{\ominus}=-393.5 \mathrm{~kJ} \mathrm{~mol}^{-1} \ldots \text { (iii) }
\)
The enthalpy of formation of \(1 \mathrm{~mol}\) of \(\mathrm{H}_2 \mathrm{O}(\mathrm{l})\) is :
\(
\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l}) ;\Delta_C H^{\ominus}=-285.83 \mathrm{~kJ} \mathrm{~mol}^{-1} \ldots \text { (iv) }
\)
multiplying eqn. (iii) by 6 and eqn. (iv) by 3 we get:
\(
6 \mathrm{C}(\text { graphite })+6 \mathrm{O}_2(\mathrm{~g}) \rightarrow 6 \mathrm{CO}_2(\mathrm{~g}) ;\Delta_f H^{\ominus}=-2361 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
\(
3 \mathrm{H}_2(\mathrm{~g})+\frac{3}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow 3 \mathrm{H}_2 \mathrm{O}(1); \Delta_f H^{\ominus}=-857.49 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
Summing up the above two equations :
\(
6 \mathrm{C}(\text { graphite })+3 \mathrm{H}_2(\mathrm{~g})+\frac{15}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow 6 \mathrm{CO}_2(\mathrm{~g})+3 \mathrm{H}_2 \mathrm{O}(1);\Delta_f H^{\ominus}=-3218.49 \mathrm{~kJ} \mathrm{~mol}^{-1} \ldots(\mathrm{v})
\)
Reversing equation (ii);
\(
6 \mathrm{CO}_2(\mathrm{~g})+3 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{C}_6 \mathrm{H}_6(\mathrm{l})+\frac{15}{2} \mathrm{O}_2; \Delta_f H^{\ominus}=-3267.0 \mathrm{~kJ} \mathrm{~mol}^{-1} \ldots \text { (vi) }
\)
Adding equations (v) and (vi), we get
\(
6 \mathrm{C}(\text { graphite })+3 \mathrm{H}_2(\mathrm{~g}) \rightarrow \mathrm{C}_6 \mathrm{H}_6(\mathrm{l}) ;\Delta_f H^{\ominus}=-48.51 \mathrm{~kJ} \mathrm{~mol}^{-1} \ldots \text { (vii) }
\)

(b) Enthalpy of Atomization (symbol: \(\Delta_a H^{\boldsymbol{\theta}}\) )

It is the enthalpy change on breaking one mole of bonds completely to obtain atoms in the gas phase (When one mole of a given substance dissociates into gaseous atoms, the enthalpy change accompanying the process is called enthalpy of atomization. It is represented by \(\Delta_a H^{\ominus}\)).

Consider the following example of atomization of dihydrogen
\(
\mathrm{H}_2(\mathrm{~g}) \rightarrow 2 \mathrm{H}(\mathrm{g}) ; \Delta_a H^{\ominus}=435.0 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
You can see that \(\mathrm{H}\) atoms are formed by breaking \(\mathrm{H}-\mathrm{H}\) bonds in dihydrogen. The enthalpy change in this process is known as enthalpy of atomization, \(\Delta_a H^{\ominus}\).
In the case of diatomic molecules, like dihydrogen (given above), the enthalpy of atomization is also the bond dissociation enthalpy. The other examples of enthalpy of atomization can be
\(
\mathrm{CH}_4(\mathrm{~g}) \rightarrow \mathrm{C}(\mathrm{g})+4 \mathrm{H}(\mathrm{g}) ; \Delta_a H^{\ominus}=1665 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
Note that the products are only atoms of \(\mathrm{C}\) and \(\mathrm{H}\) in the gaseous phase. Now see the following reaction:
\(
\mathrm{Na}(\mathrm{s}) \rightarrow \mathrm{Na}(\mathrm{g}) ; \Delta_a H^{\ominus}=108.4 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
In this case, the enthalpy of atomization is the same as the enthalpy of sublimation.

(c) Bond Enthalpy (symbol: \(\Delta_{\text {bond }} H^{\ominus}\) )

It is the amount of energy released when one mole of bonds are formed from the isolated atom in gaseous state or the amount of energy required to dissociate one mole of bonds present between the atoms in gaseous molecules. 

Chemical reactions involve the breaking and making of chemical bonds. Energy is required to break a bond and energy is released when a bond is formed. It is possible to relate the heat of reaction to changes in energy associated with the breaking and making of chemical bonds. With reference to the enthalpy changes associated with chemical bonds, two different terms are used in thermodynamics.
(i) Bond dissociation enthalpy
(ii) Mean bond enthalpy

Let us discuss these terms with reference to diatomic and polyatomic molecules.

Diatomic Molecules: Consider the following process in which the bonds in one mole of dihydrogen gas \(\left(\mathrm{H}_2\right)\) are broken:
\(
\mathrm{H}_2(\mathrm{~g}) \rightarrow 2 \mathrm{H}(\mathrm{g}) ; \Delta_{\mathrm{H}-\mathrm{H}} H^{\ominus}=435.0 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)

The enthalpy change involved in this process is the bond dissociation enthalpy of \(\mathrm{H}-\mathrm{H}\) bond. The bond dissociation enthalpy is the change in enthalpy when one mole of covalent bonds of a gaseous covalent compound is broken to form products in the gas phase.

Note that it is the same as the enthalpy of atomization of dihydrogen. This is true for all diatomic molecules. For example:
\(
\begin{aligned}
& \mathrm{Cl}_2(\mathrm{~g}) \rightarrow 2 \mathrm{Cl}(\mathrm{g}) ; \Delta_{\mathrm{Cl}-\mathrm{Cl}} H^{\ominus}=242 \mathrm{~kJ} \mathrm{~mol}^{-1} \\
& \mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{O}(\mathrm{g}) ; \Delta_{\mathrm{O}=0} H^{\ominus}=428 \mathrm{~kJ} \mathrm{~mol}^{-1}
\end{aligned}
\)

In the case of polyatomic molecules, bond dissociation enthalpy is different for different bonds within the same molecule.

Polyatomic Molecules: Let us now consider a polyatomic molecule like methane, \(\mathrm{CH}_4\). The overall thermochemical equation for its atomization reaction is given below:
\(
\begin{aligned}
& \mathrm{CH}_4(\mathrm{~g}) \rightarrow \mathrm{C}(\mathrm{g})+4 \mathrm{H}(\mathrm{g}) ; \\
& \qquad \Delta_a H^{\ominus}=1665 \mathrm{~kJ} \mathrm{~mol}^{-1}
\end{aligned}
\)
In methane, all four \(\mathrm{C}-\mathrm{H}\) bonds are identical in bond length and energy. However, the energies required to break the individual \(\mathrm{C}-\mathrm{H}\) bonds in each successive step differ :
\(
\begin{aligned}
& \mathrm{CH}_4(\mathrm{~g}) \rightarrow \mathrm{CH}_3(\mathrm{~g})+\mathrm{H}(\mathrm{g}) ; \Delta_{\text {bond }} H^{\ominus}=+427 \mathrm{~kJ} \mathrm{~mol}^{-1} \\
& \mathrm{CH}_3(\mathrm{~g}) \rightarrow \mathrm{CH}_2(\mathrm{~g})+\mathrm{H}(\mathrm{g}) ; \Delta_{\text {bond }} H^{\ominus}=+439 \mathrm{~kJ} \mathrm{~mol}^{-1} \\
& \mathrm{CH}_2(\mathrm{~g}) \rightarrow \mathrm{CH}(\mathrm{g})+\mathrm{H}(\mathrm{g}) ; \Delta_{\text {bond }} H^{\ominus}=+452 \mathrm{~kJ} \mathrm{~mol}^{-1} \\
& \mathrm{CH}(\mathrm{g}) \rightarrow \mathrm{C}(\mathrm{g})+\mathrm{H}(\mathrm{g}) ; \Delta_{\text {band }} H^{\ominus}=+347 \mathrm{~kJ} \mathrm{~mol}^{-1}
\end{aligned}
\)
Therefore,
\(
\mathrm{CH}_4(\mathrm{~g}) \rightarrow \mathrm{C}(\mathrm{g})+4 \mathrm{H}(\mathrm{g}) ; \Delta_a H^{\ominus}=1665 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
In such cases we use mean bond enthalpy of \(\mathbf{C}-\mathbf{H}\) bond.
For example in \(\mathrm{CH}_4, \Delta_{\mathrm{C}-\mathrm{H}} \mathrm{H}^{\ominus}\) is calculated as:
\(
\begin{aligned}
\Delta_{\mathrm{C}-\mathrm{H}} H^{\ominus}=1 / 4\left(\Delta_a H^{\ominus}\right) & =1 / 4\left(1665 \mathrm{~kJ} \mathrm{~mol}^{-1}\right) \\
& =416 \mathrm{~kJ} \mathrm{~mol}^{-1}
\end{aligned}
\)
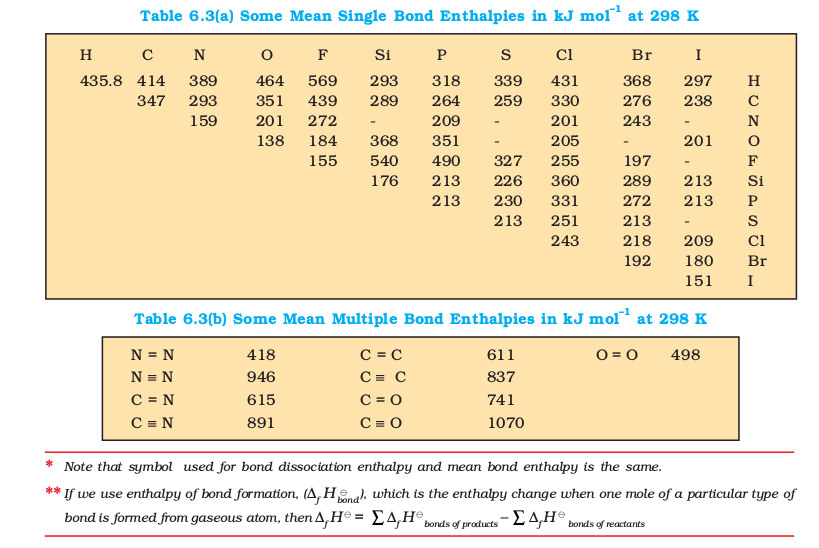
We find that mean \(\mathrm{C}-\mathrm{H}\) bond enthalpy in methane is \(416 \mathrm{~kJ} / \mathrm{mol}\). It has been found that mean \(\mathrm{C}-\mathrm{H}\) bond enthalpies differ slightly from compound to compound, as in \(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{Cl}, \mathrm{CH}_3 \mathrm{NO}_2\), etc, but it does not differ in a great deal*. Using Hess’s law, bond enthalpies can be calculated. Bond enthalpy values of some single and multiple bonds are given in Table 6.3. The reaction enthalpies are very important quantities as these arise from the changes that accompany the breaking of old bonds and formation of the new bonds. We can predict enthalpy of a reaction in gas phase, if we know different bond enthalpies. The standard enthalpy of reaction, \(\Delta_r H^{\ominus}\) is related to bond enthalpies of the reactants and products in gas phase reactions as:
\(
\Delta_r H^{\ominus}=\sum \text { bond enthalpies }_{\text {reactants }}-\sum \text { bond enthalpies }_{\text {products }} \dots(6.17)^{* *}
\)
This relationship is particularly more useful when the required values of \(\Delta_f H^{\ominus}\) are not available. The net enthalpy change of a reaction is the amount of energy required to break all the bonds in the reactant molecules minus the amount of energy required to break all the bonds in the product molecules. Remember that this relationship is approximate and is valid when all substances (reactants and products) in the reaction are in the gaseous state.

(d) Lattice Enthalpy

The lattice enthalpy of an ionic compound is the enthalpy change which occurs when one mole of an ionic compound dissociates into its ions in gaseous state.
\(
\mathrm{Na}^{+} \mathrm{Cl}^{-}(\mathrm{s}) \rightarrow \mathrm{Na}^{+}(\mathrm{g})+\mathrm{Cl}^{-}(\mathrm{g}); \Delta_{\text {lattlce }} H^{\ominus}=+788 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
Since it is impossible to determine lattice enthalpies directly by experiment, we use an indirect method where we construct an enthalpy diagram called a Born-Haber Cycle (Fig. 6.9).

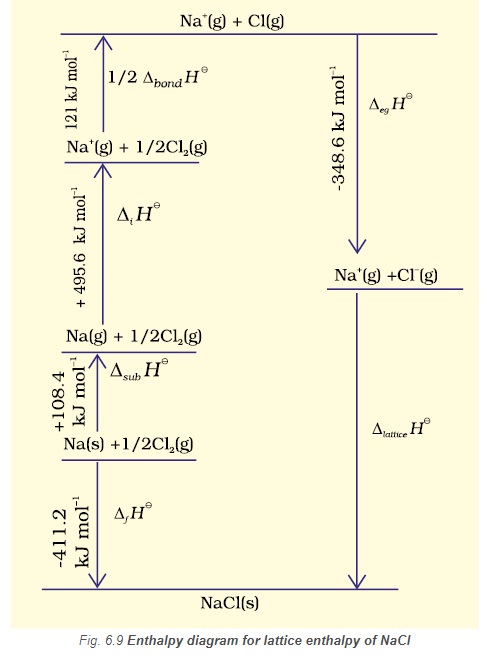
Let us now calculate the lattice enthalpy of \(\mathrm{Na}^{+} \mathrm{Cl}^{-}(\mathrm{s})\) by following the steps given below :

1. \(\mathrm{Na}(\mathrm{s}) \rightarrow \mathrm{Na}(\mathrm{g})\), sublimation of sodium metal, \(\Delta_{\text {sub }} H^{\ominus}=108.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\)
2. \(\mathrm{Na}(\mathrm{g}) \rightarrow \mathrm{Na}^{+}(\mathrm{g})+\mathrm{e}^{-1}(\mathrm{~g})\), the ionization of sodium atoms, ionization enthalpy \(\Delta_t H^{\ominus}=496 \mathrm{~kJ} \mathrm{~mol}^{-1}\)
3. \(\frac{1}{2} \mathrm{Cl}_2(\mathrm{~g}) \rightarrow \mathrm{Cl}(\mathrm{g})\), the dissociation of chlorine, the reaction enthalpy is half the bond dissociation enthalpy.
   \(
   \frac{1}{2} \Delta_{\text {bond }} H^{\ominus}=121 \mathrm{~kJ} \mathrm{~mol}^{-1}
   \)
4. \(\mathrm{Cl}(\mathrm{g})+\mathrm{e}^{-1}(\mathrm{~g}) \rightarrow \mathrm{Cl}(\mathrm{g})\) electron gained by chlorine atoms. The electron gain enthalpy, \(\Delta_{e g} H^{\ominus}=-348.6 \mathrm{~kJ} \mathrm{~mol}^{-1}\).
5. \(\mathrm{Na}^{+}(\mathrm{g})+\mathrm{Cl}^{-}(\mathrm{g}) \rightarrow \mathrm{Na}^{+} \mathrm{Cl}^{-}\)(s) The sequence of steps is shown in Fig. 6.9, and is known as a Born-Haber cycle. The importance of the cycle is that the sum of the enthalpy changes round a cycle is zero. Applying Hess’s law, we get,
   \(
   \begin{aligned}
   & \Delta_{\text {lattice }} H^{\ominus}=411.2+108.4+121+496-348.6 \\
   & \Delta_{\text {lattice }} H^{\ominus}=+788 \mathrm{~kJ}
   \end{aligned}
   \)
   \(
   \text { for } \mathrm{NaCl}(\mathrm{s}) \rightarrow \mathrm{Na}^{+}(\mathrm{g})+\mathrm{Cl}^{-}(\mathrm{g})
   \)
   Internal energy is smaller by \(2 \mathrm{RT}\) ( because \(\left.\Delta n_g=2\right)\) and is equal to \(+783 \mathrm{~kJ} \mathrm{~mol}^{-1}\).
   Now we use the value of lattice enthalpy to calculate the enthalpy of the solution from the expression:
   \(
   \Delta_{\text {sol }} H^{\ominus}=\Delta_{\text {lattice }} H^{\ominus}+\Delta_{\text {hyd }} H^{\ominus}
   \)
   For one mole of \(\mathrm{NaCl}(\mathrm{s})\), lattice enthalpy \(=+788 \mathrm{~kJ} \mathrm{~mol}^{-1}\)
   and \(\Delta_{\text {hyd }} H^{\ominus}=-784 \mathrm{~kJ} \mathrm{~mol}^{-1}\) (from the literature)
   \(
   \begin{aligned}
   \Delta_{\text {sol }} H^{\ominus} & =+788 \mathrm{~kJ} \mathrm{~mol}^{-1}-784 \mathrm{~kJ} \mathrm{~mol}^{-1} \\
   & =+4 \mathrm{~kJ} \mathrm{~mol}^{-1}
   \end{aligned}
   \)
   The dissolution of \(\mathrm{NaCl}(\mathrm{s})\) is accompanied by very little heat change.

Ionization Energy and Electron Affinity

Ionization energy and electron affinity are defined at absolute zero. At any other temperature, heat capacities for the reactants and the products have to be taken into account. Enthalpies of reactions for 

\(
\mathrm{M}(\mathrm{g}) \rightarrow \mathrm{M}^{+}(\mathrm{g})+\mathrm{e}^{-} \quad \text { (for ionization) }
\)
\(
\mathrm{M}(\mathrm{g})+\mathrm{e}^{-} \rightarrow \mathrm{M}^{-}(\mathrm{g}) \text { (for electron gain) }
\)
at temperature, \(T\) is
\(
\Delta_r H^{\ominus}(T)=\Delta_r H^{\ominus}(0)+\int_0^T \Delta_r C_p^{\ominus} d T
\)
The value of \(C_p\) for each species in the above reaction is \(5 / 2 \mathrm{R} \quad\left(C_V=3 / 2 \mathrm{R}\right)\)
\(
\text { So, } \Delta_r C_p{ }^{\ominus}=+5 / 2 \mathrm{R} \text { (for ionization) }
\)
\(
\Delta_{\mathrm{r}} C_p{ }^{\ominus}=-5 / 2 \mathrm{R} \text { (for electron gain) }
\)
Therefore,
\(
\begin{aligned}
& \Delta_r H^{\ominus} \text { (ionization enthalpy) } \\
& \quad=E_0 \text { (ionization energy) }+5 / 2 \mathrm{RT}
\end{aligned}
\)
\(
\begin{aligned}
& \Delta_r H^{\ominus} \text { (electron gain enthalpy) } \\
& \quad=-\mathrm{A} \text { (electron affinity) }-5 / 2 \mathrm{R} T
\end{aligned}
\)

(e) Enthalpy of Solution (symbol : \(\Delta_{\text {sol }} H^{\ominus}\) )

Enthalpy of solution of a substance is the enthalpy change when one mole of it dissolves in a specified amount of solvent. The enthalpy of solution at infinite dilution is the enthalpy change observed on dissolving the substance in an infinite amount of solvent when the interactions between the ions (or solute molecules) are negligible.

When an ionic compound dissolves in a solvent, the ions leave their ordered positions on the crystal lattice. These are now more free in solution. But solvation of these ions (hydration in case the solvent is water) also occurs at the same time. This is shown diagrammatically, for an ionic compound, \(\mathrm{AB}(\mathrm{s})\)

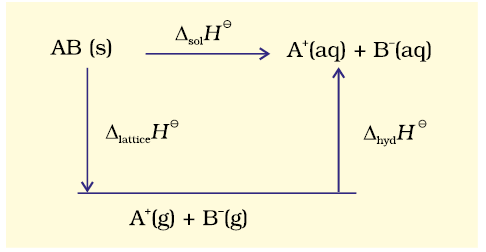
The enthalpy of solution of \(\mathrm{AB}(\mathrm{s}), \Delta_{\text {sol }} H^{\ominus}\), in water is, therefore, determined by the selective values of the lattice enthalpy, \(\Delta_{\text {lattice }} H^{\ominus}\) and enthalpy of hydration of ions, \(\Delta_{\text {hyd }} H^{\ominus}\) as
\(
\Delta_{\text {sol }} H^{\ominus}=\Delta_{\text {lattice }} H^{\ominus}+\Delta_{\text {hyd }} H^{\ominus}
\)
For most of the ionic compounds, \(\Delta_{\text {sol }} H^{\ominus}\) is positive and the dissociation process is endothermic. Therefore the solubility of most salts in water increases with the rise of temperature. If the lattice enthalpy is very high, the dissolution of the compound may not take place at all. Why do many fluorides tend to be less soluble than the corresponding chlorides? Estimates of the magnitudes of enthalpy changes may be made by using tables of bond energies (enthalpies) and lattice energies (enthalpies).

(f) Enthalpy of Dilution

It is known that enthalpy of solution is the enthalpy change associated with the addition of a specified amount of solute to the specified amount of solvent at a constant temperature and pressure. This argument can be applied to any solvent with slight modification. Enthalpy change for dissolving one mole of gaseous hydrogen chloride in \(10 \mathrm{~mol}\) of water can be represented by the following equation. For convenience, we will use the symbol aq. for water
\(
\begin{aligned}
&\mathrm{HCl}(\mathrm{g})+10 \text { aq. } \rightarrow \mathrm{HCl} .10 \text { aq. } \\
& \Delta \mathrm{H}=-69.01 \mathrm{~kJ} / \mathrm{mol}
\end{aligned}
\)
Let us consider the following set of enthalpy changes:
\(
\begin{aligned}
(\mathrm{S}-1) \mathrm{HCl}(\mathrm{g})+25 \text { aq. } \rightarrow & \mathrm{HCl} .25 \text { aq. } \\
& \Delta \mathrm{H}=-72.03 \mathrm{~kJ} / \mathrm{mol}
\end{aligned}
\)
\(
\begin{aligned}
(\mathrm{S}-2) \mathrm{HCl}(\mathrm{g})+40 \text { aq. } \rightarrow & \mathrm{HCl} .40 \text { aq. } \\
& \Delta \mathrm{H}=-72.79 \mathrm{~kJ} / \mathrm{mol}
\end{aligned}
\)
\(
\begin{aligned}
\text { (S-3) } \mathrm{HCl}(\mathrm{g})+\infty \text { aq. } \rightarrow & \mathrm{HCl}, \infty \text { aq. } \\
& \Delta \mathrm{H}=-74.85 \mathrm{~kJ} / \mathrm{mol}
\end{aligned}
\)

The values of \(\Delta \mathrm{H}\) show a general dependence of the enthalpy of solution on the amount of solvent. As more and more solvent is used, the enthalpy of the solution approaches a limiting value, i.e., the value in infinitely dilute solution. For hydrochloric acid this value of \(\Delta \mathrm{H}\) is given above in equation (S-3).
If we subtract the first equation (equation S-1) from the second equation (equation S-2) in the above set of equations, we obtain-
\(\mathrm{HCl} .25\) aq. +15 aq. \(\rightarrow \mathrm{HCl} .40\) aq.
\(
\begin{aligned}
\Delta \mathrm{H} & =[-72.79-(-72.03)] \mathrm{kJ} / \mathrm{mol} \\
& =-0.76 \mathrm{~kJ} / \mathrm{mol}
\end{aligned}
\)
This value \((-0.76 \mathrm{~kJ} / \mathrm{mol})\) of \(\Delta \mathrm{H}\) is enthalpy of dilution. It is the heat withdrawn from the surroundings when additional solvent is added to the solution. The enthalpy of dilution of a solution is dependent on the original concentration of the solution and the amount of solvent added.