11.11 Entrance Corner (Hyperbola)

The hyperbola is the set of all points in a plane, the difference of whose distance from two fixed points in the plane is a constant. The term “difference” that means the distance to the farther point minus the distance to the closer point. The two fixed points are called the foci of the hyperbola. The midpoint of the line segment joining the foci is called the centre of the hyperbola. The line through the foci is called the transverse axis and the line through the centre and perpendicular to the transverse axis is called the conjugate axis. The points at which the hyperbola intersects the transverse axis are called the vertices of the hyperbola.

\(
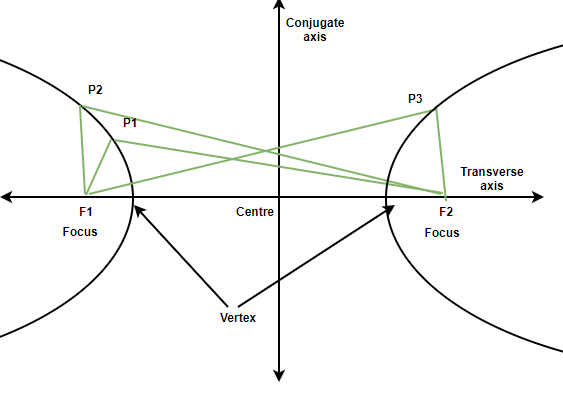
P_1 F_2-P_1 F_1=P_2 F_2-P_2 F_1=P_3 F_1-P_3 F_2
\)

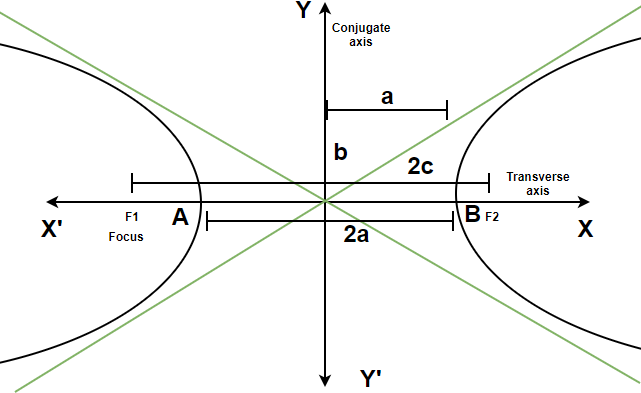
We denote the distance between the two foci by \(2 c\), the distance between the two vertices (the length of the transverse axis) by \(2 a\) and we define the quantity \(b\) as \(b=\sqrt{c^2-a^2}\).

Standard Equation of Hyperbola

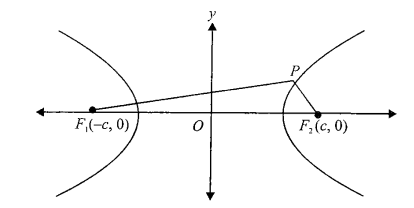
Let the foci of a hyperbola be \(( \pm c, 0)\). Then its centre is \((0,0)\).
According to the definition of hyperbola,
\(
P F_1-P F_2=2 a(2 a<2 c, \text { i.e. } c>a)
\)

\(
\sqrt{(x+c)^2+y^2}-\sqrt{(x-c)^2+y^2}=2 a
\)
\(
\sqrt{(x+c)^2+y^2}=2 a+\sqrt{(x-c)^2+y^2}
\)
Squaring both sides, we get
\(
\begin{aligned}
& (x+c)^2+y^2=4 a^2+4 a \sqrt{(x-c)^2+y^2} \\
& +(x-c)^2+y^2
\end{aligned}
\)
On simplifying, we get
\(
\frac{c x}{a}-a=\sqrt{(x-c)^2+y^2}
\)
On squaring again and further simplifying, we get
\(
\frac{x^2}{a^2}-\frac{y^2}{c^2-a^2}=1
\)
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \quad\left(\text { since } c^2-a^2=b^2\right)
\)
\(
\begin{aligned}
&\text { Hence, any point on the hyperbola satisfies the equation }\\
&\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\end{aligned}
\)
This is same as the standard equation of ellipse except \(b^2\) has been replaced by \(-b^2\).

This is a second degree equation in which the powers of \(x\) and \(y\) are even, hence the curve is symmetric about both the axes. For each \(x>a\) or \(x<-a\) there are two values of \(y\) symmetrically situated on either side of \(x\)-axis and for each value of \(x\) lying in \((-a, a)\) the curve fails to exist. Hence, the curve denoted by Eqn (i) consists of two symmetrical branches, each extending to infinity in two directions.

Equation of Hyperbola 

Eccentricity of Hyperbola

The eccentricity of a hyperbola is always greater than 1. i.e. \(\mathrm{e}>1\). The eccentricity of a hyperbola can be taken as the ratio of the distance of the point on the hyperbole, from the focus, and its distance from the directrix.
Eccentricity = Distance from Focus/Distance from Directrix
\(
\mathrm{e}=\frac{\mathrm{PF}}{\mathrm{PM}}=c / a
\)

Substituting the value of \(c\) we have the following value of eccentricity.
\(
e=\sqrt{1+\frac{b^2}{a^2}}
\)
Here a is the length of the semi-major axis and b is a constant value.

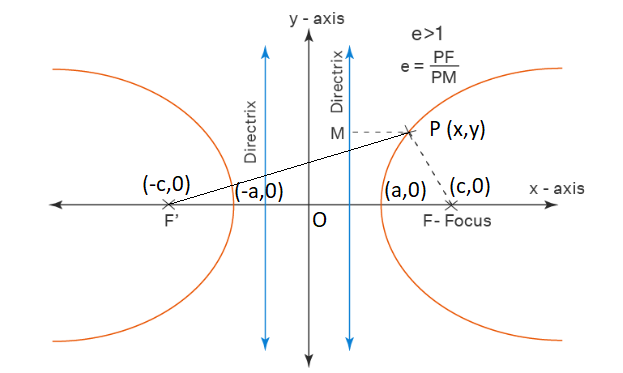
Derivation: The eccentricity of the hyperbola can be derived from the equation of the hyperbola. Let us consider the basic definition of Hyperbola. A hyperbola represents a locus of a point such that the difference of its distances from the two fixed points is a constant value. Let \(P(x, y)\) be a point on the hyperbola and the coordinates of the two foci are \(\mathrm{F}(\mathrm{c}, 0)\), and \(\mathrm{F}^{\prime}(-\mathrm{c}, 0)\). From the definition of hyperbola, we have the following expression.
\(\mathrm{PF}^{\prime}-\mathrm{PF}=2 \mathrm{a}\)
\(
\begin{aligned}
& \sqrt{(x+c)^2+y^2}-\sqrt{(x-c)^2+y^2}=2 a \\
& \sqrt{(x+c)^2+y^2}=2 a+\sqrt{(x-c)^2+y^2}
\end{aligned}
\)
Squaring this above expression on both sides, we have the below expression.
\(
(x+c)^2+y^2=4 a^2+(x-c)^2+y^2+4 a \sqrt{(x-c)^2+y^2}
\)
This on further simplification we have the following equation of hyperbola.
\(
\frac{x^2}{a^2}-\frac{y^2}{c^2-a^2}=1
\)
Here we replace \(c^2-a^2=b^2\) to obtain the equation of hyperbola as \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\). Further we simplify it to \(c^2=a^2+b^2\), and to \(c=\sqrt{a^2+b^2}\). This is now substituted in the expression \(\mathrm{e}=\mathrm{c} / \mathrm{a}\), to obtain the below formula of eccentricity of hyperbola.
\(
\begin{aligned}
& e=\frac{\sqrt{a^2+b^2}}{a} \\
& e=\sqrt{1+\frac{b^2}{a^2}}
\end{aligned}
\)

Hyperbola Equation in terms of Eccentricity

\(
\begin{aligned}
e & =\frac{\text { Distance from centre to focus }}{\text { Distance from centre to vertex }} \\
& =\frac{c}{a} \\
\Rightarrow \quad e^2 & =\frac{c^2}{a^2}=\frac{a^2+b^2}{a^2}=1+\frac{b^2}{a^2} \\
\Rightarrow \quad a^2 e^2 & =a^2+b^2
\end{aligned}
\)
Therefore, equation of hyperbola in terms of eccentricity can be written as
\(
\frac{x^2}{a^2}-\frac{y^2}{a^2\left(e^2-1\right)}=1
\)
Coordinates of the foci are \(( \pm a e, 0)\).
Two hyperbolas are said to be similar if they have the same value of eccentricity.
\(
e=\sqrt{1+\frac{(2 b)^2}{(2 a)^2}}=\sqrt{1+\frac{(\text { Conjugate axis })^2}{(\text { Transverse axis })^2}}
\)

Rectangular or Equilateral Hyperbola

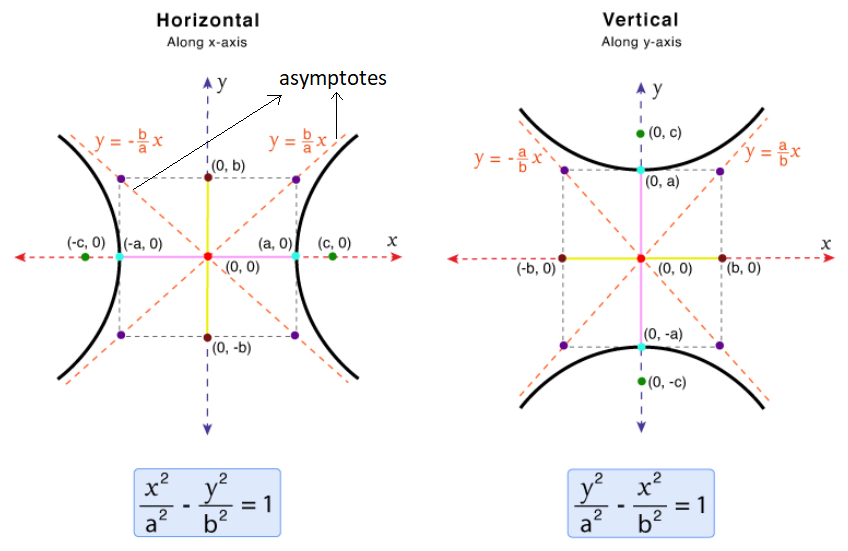
Step 1: For a standard hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), the hyperbola is rectangular if:
\(
a=b
\)
Substituting this into the standard equation gives:
\(
x^2-y^2=a^2
\)
Step 2: Key Properties
Because \(a=b\), the geometry of the hyperbola shifts in specific ways:
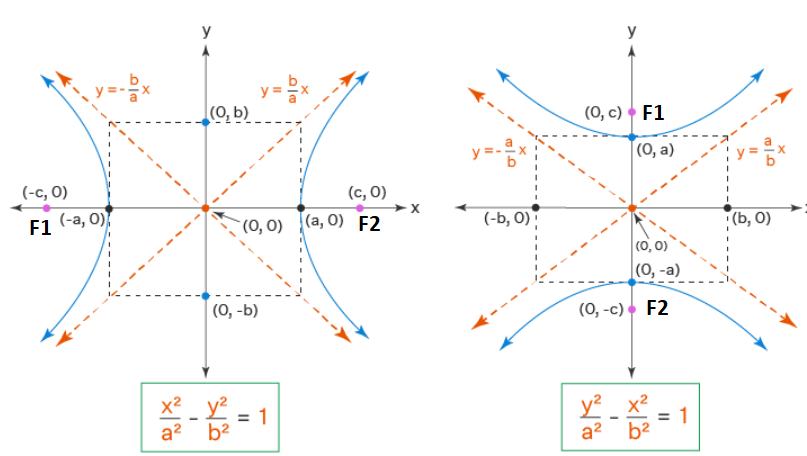
Asymptotes: The lines are \(y= \pm \frac{b}{a} x\). Since \(a=b\), these become \(y= \pm x\). These lines intersect at \(90^{\circ}\).
Eccentricity \((e)\) : Using the formula \(b^2=a^2\left(e^2-1\right)\) :
\(
a^2=a^2\left(e^2-1\right) \Longrightarrow 1=e^2-1 \Longrightarrow e^2=2
\)
Thus, for every rectangular hyperbola, \(e=\sqrt{2}\).
Foci: The distance \(c=a e=a \sqrt{2}\). The foci are at \(( \pm a \sqrt{2}, 0)\).
Step 3: Rotated Form: \(x y=c^2\)
The most famous form of a rectangular hyperbola occurs when the axes are rotated by \(\mathbf{4 5}^{\circ}\) so that the asymptotes become the \(x\) and \(y\) axes themselves.
The equation then becomes:
\(
x y=\frac{a^2}{2} \text { or } x y=c^2
\)
Vertices: Located at \((c, c)\) and \((-c,-c)\).
Foci: Located at \((c \sqrt{2}, c \sqrt{2})\) and \((-c \sqrt{2},-c \sqrt{2})\).
Parametric Coordinates: Any point on this curve can be represented as (\(ct,\frac{c}{t}\)).

Comparision Table:
\(
\begin{array}{lll}
\text { Feature } & \text { Standard Rectangular } & \text { Rotated Rectangular } \\
\text { Equation } & x^2-y^2=a^2 & x y=c^2 \\
\text { Asymptotes } & y=x \text { and } y=-x & x=0 \text { and } y=0 \text { (Axes) } \\
\text { Eccentricity } & \sqrt{2} & \sqrt{2} \\
\text { Vertices } & ( \pm a, 0) & (c, c) \text { and }(-c,-c)
\end{array}
\)

Directrix

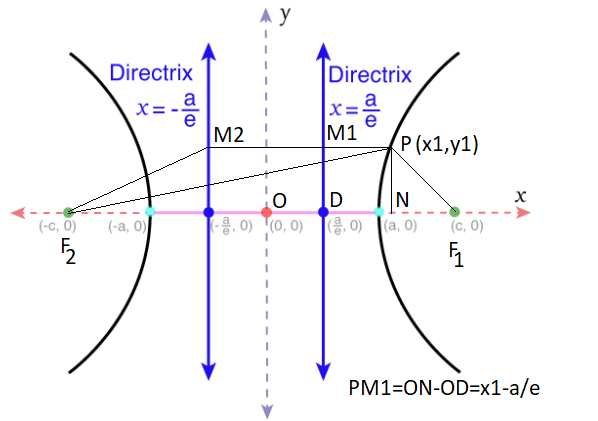
It is possible to define two lines, \(x= \pm \frac{a}{e}\), corresponding to each focus, which satisfy the focal directrix property of the hyperbola, i.e. \(P F_1=e P M_1\) and \(P F_2=e P M_2\).
Hence, for any point \(P\) on the hyperbola,
\(
\frac{P F_1}{P M_1}=e \text { (constant) }
\)

Focal Distance (Focal Radius)

The difference of the focal radii of any point on the hyperbola is equal to the length of the major axis. We have
\(
\begin{aligned}
P F_1 & =e P M_1=e\left(x_1-\frac{a}{e}\right) \\
& =e x_1-a \dots(i) \\
P F_2 & =e\left(x_1+\frac{a}{e}\right) \\
& =e x_1+a \dots(ii)
\end{aligned}
\)
Subtracting Eq. (i) from Eq. (ii), we get
\(
P F_2-P F_1=2 a
\)

Equation of Hyperbola Whose Axes are Parallel to Coordinate Axes and Centre is \(\boldsymbol{(} \boldsymbol{h} \boldsymbol{,} \boldsymbol{k}\) )

Equation of such hyperbola is
\(
\frac{(x-h)^2}{a^2}-\frac{(x-k)^2}{b^2}=1 \quad(a>b)
\)
Center: \((h, k)\)
Foci: \((h \pm a e, k)\)
Vertices: \((h \pm a, k)\)
Directrices: \(x=h \pm \frac{a}{e}\)
Asymptotes: \((y-k)= \pm \frac{b}{a}(x-h)\)

Definition and Basic Terminology

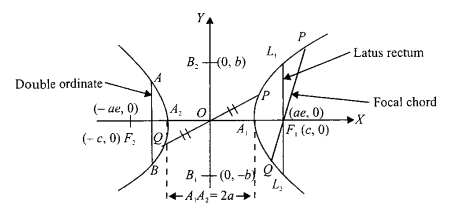
• Line containing the fixed points \(F_1\) and \(F_2\) (called foci) is called transverse axis (TA) or focal axis and the distance between \(F_1\) and \(F_2\) is called focal length.
• The points of intersection \(A_1\) and \(A_2\) of the curve with the transverse axis are called vertices of the hyperbola. The length ‘ \(2 a\) ‘ between the vertices is called the length of transverse axis (TA).
• The points \(B_1(0, b)\) and \(B_2(0,-b)\) which have special significance, are known as the extremities of conjugate axis and the length ‘ \(2 b\) ‘ is called the length of conjugate axis. The point of intersection of these two axes is called the centre ‘ \(O\) ‘ of the hyperbola. (Transverse axis and conjugate axis together are called the principal axes).
• Any chord passing through centre is called diameter (\(P Q\)) and is bisected by it.
• Any chord passing through focus is called a focal chord and any chord perpendicular to the transverse axis is called a double ordinate \((A B)\).
• A particular double ordinates which passes through focus and perpendicular to focal axis is called the latus rectum \(\left(L_1 L_2\right)\)

Latus-Rectum (LR) Length

The two foci are \(( \pm a e, 0)\)
We have the equation of the hyperbola,
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\)
Putting \(x=a e\), we get
\(
\begin{aligned}
\frac{y^2}{b^2} & =e^2-1=\left(\frac{b^2}{a^2}+1\right)-1 \\
& =\frac{b^2}{a^2} \\
y & = \pm \frac{b^2}{a}
\end{aligned}
\)
Hence, coordinate of the extremities of \(L R\)
\(
=\left( \pm a e, \pm b^2 / a\right)
\)
Length of \(L R\)
\(
\begin{aligned}
& =\frac{2 b^2}{a} \\
& =\frac{4 b^2}{2 a}=\frac{(\text { minor axis })^2}{\text { major axis }}
\end{aligned}
\)
Also
\(
\begin{aligned}
L_1 L_2= & 2 a\left(e^2-1\right) \\
= & 2 e\left(a e-\frac{a}{e}\right) \\
= & 2 e\left(O F_1-O A_1\right)(\text { as shown in Figure above) } \\
= & 2 e \times(\text { distance between focus } \\
& \text { and corresponding foot of the } \\
& \text { directrix) }
\end{aligned}
\)

Conjugate Hyperpola

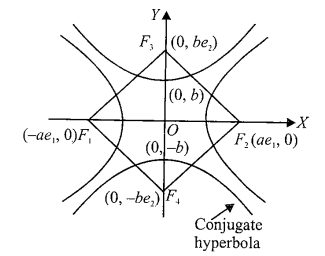
Corresponding to every hyperbola there exists a hyperbola such that the conjugate axis and transverse axis of one is equal to the transverse axis and conjugate axis of the other. Such hyperbolas are known as conjugate to each other.
Hence, for the hyperbola
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
The conjugate hyperbola is
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1 \dots(ii)
\)

Notes:

• If \(e_1\) and \(e_2\) are the eccentricities of a hyperbola and its conjugate, respectively, then \(e_1^{-2}+e_2^{-2}=1\).
  Proof:
  For hyperbola,
  \(
  e_1^2=1+\frac{b^2}{a^2}=\frac{a^2+b^2}{a^2}
  \)
  And for conjugate hyperbola,
  \(
  \begin{aligned}
  \therefore & e_2^2=1+\frac{a^2}{b^2}=\frac{a^2+b^2}{b^2} \\
  \therefore & \frac{1}{e_1^2}+\frac{1}{e_2^2}=1
  \end{aligned}
  \)
• The foci of a hyperbola and its conjugate are concyclic and form the vertices of a square.
  Proof:
  All the four sides of the quadrilateral \(F_1 F_3 F_2 F_4\) are obviously equal to their diagonals at right angles.
  Hence it is a rhombus.
  Now to prove that \(F_1 F_3 F_2 F_4\) is a square it is sufficient to prove that
  \(
  a e_1=b e_2
  \)
  \(
  a^2 e_1^2=b^2 e_2^2=a^2\left(e_1^2-1\right) e_2^2
  \)
  \(
  e_1^2=e_1^2 e_2^2-e_2^2
  \)
  \(
  e_1^2+e_2^2=e_1^2 e_2^2
  \)
  \(
  \frac{1}{e_1^2}+\frac{1}{e_2^2}=1 \text { which is true }
  \)
  Hence
  \(
  a e_1=b e_2
  \)
  \(
  \Rightarrow F_1 F_3 F_2 F_4 \text { is a square. }
  \)

Example 1: The equation \(16 x^2-3 y^2-32 x+12 y-44=0\) represents a hyperbola
(a) the length of whose transverse axis is \(4 \sqrt{3}\)
(b) the length of whose conjugate axis is 4
(c) whose centre is \((-1,2)\)
(d) whose eccentricity is \(\sqrt{\frac{19}{3}}\)

Solution: (d) We have,
\(
\begin{array}{ll}
& 16\left(x^2-2 x\right)-3\left(y^2-4 y\right)=44 \\
\Rightarrow & 16(x-1)^2-3(y-2)^2=48 \\
\Rightarrow & \frac{(x-1)^2}{3}-\frac{(y-2)^2}{16}=1
\end{array}
\)
This equation represents a hyperbola with eccentricity given by
\(
e=\sqrt{1+\frac{(\text { Conjugate axis })^2}{(\text { Transverse axis })^2}}=\sqrt{1+\left(\frac{4}{\sqrt{3}}\right)^2}=\sqrt{\frac{19}{3}}
\)
If the centre of the hyperbola is at the point \((h, k)\) and the directions of the axes are parallel to the coordinate axes, then its equation is
\(
\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1
\)
By shifting the origin at \((h, k)\) without rotating the coordinate axes, the above equation reduces to
\(
\frac{X^2}{a^2}-\frac{Y^2}{b^2}=1, \text { where } x=X+h \text { and } y=Y+k
\)

Example 2: The eccentricity of the hyperbola
\(
9 x^2-16 y^2+72 x-32 y-16=0 \text {, is }
\)
(a) \(\frac{5}{4}\)
(b) \(\frac{4}{5}\)
(c) \(\frac{9}{16}\)
(d) \(\frac{16}{9}\)

Solution: (a) We have,
\(
\begin{array}{ll}
& 9\left(x^2+8 x\right)-16\left(y^2-2 y\right)=16 \\
\Rightarrow & 9(x+4)^2-16(y+1)^2=144 \\
\Rightarrow & \frac{(x+4)^2}{16}-\frac{(y+1)^2}{9}=1
\end{array}
\)
\(
\begin{aligned}
&\text { Here, } a^2=16 \text { and } b^2=9\\
&\therefore \quad e^2=1+\frac{b^2}{a^2}=1+\frac{9}{16}=\frac{25}{16} \Rightarrow e=\frac{5}{4}
\end{aligned}
\)

Example 3: The equation of the hyperbola whose foci are \((8,3)(0,3)\) and eccentricity \(=\frac{4}{3}\), is
(a) \(49 x^2-3 y^2=147\)
(b) \(7 x^2-9 y^2=63\)
(c) \(7(x-4)^2-9(y-3)^2=63\)
(d) \(7(x+4)^2-9(y+3)^2=63\)

Solution: (c) Step 1: Find the Center (\(h, k\))
The center of a hyperbola is the midpoint of the line segment joining the two foci.
Foci: \(F_1(8,3)\) and \(F_2(0,3)\)
\(h=\frac{8+0}{2}=4\)
\(k=\frac{3+3}{2}=3\)
Center \((h, k)=(4,3)\)
Step 2: Determine the Distance between Foci (\(2ae\))
The distance between the foci \((8,3)\) and \((0,3)\) is:
\(
\begin{gathered}
2 a e=\sqrt{(8-0)^2+(3-3)^2}=8 \\
a e=4
\end{gathered}
\)
Step 3: Find \(a^2\) and \(b^2\)
We are given the eccentricity \(e=\frac{4}{3}\).
From \(a e=4\), we have: \(a\left(\frac{4}{3}\right)=4 \Longrightarrow a=3 \Longrightarrow a^2=9\)
Using the relation \(b^2=a^2\left(e^2-1\right)\) :
\(
\begin{gathered}
b^2=9\left(\left(\frac{4}{3}\right)^2-1\right) \\
b^2=9\left(\frac{16}{9}-1\right)=9\left(\frac{7}{9}\right)=7
\end{gathered}
\)
Step 4: Write the Equation
Since the \(y\)-coordinates of the foci are the same (\(y=3\)), the transverse axis is horizontal. The equation for a shifted horizontal hyperbola is:
\(
\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1
\)
Substitute our values:
\(
\frac{(x-4)^2}{9}-\frac{(y-3)^2}{7}=1
\)
To match the format of the options, multiply the entire equation by 63 (the LCM of 9 and 7):
\(
7(x-4)^2-9(y-3)^2=63
\)

Example 4: The equation of the hyperbola, the length of whose latus rectum is 8 and eccentricity is \(3 / \sqrt{5}\), is
(a) \(5 x^2-4 y^2=100\)
(b) \(4 x^2-5 y^2=100\)
(c) \(-4 x^2+5 y^2=100\)
(d) \(-5 x^2+4 y^2=100\)

Solution: (b) Let the equation of the hyperbola be
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
We have,
Length of the latusrectum \(=8\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{2 b^2}{a}=8 \\
& \Rightarrow \quad b^2=4 a \\
& \Rightarrow \quad a^2\left(e^2-1\right)=4 a \\
& \Rightarrow \quad a\left(e^2-1\right)=4 \Rightarrow a\left(\frac{9}{5}-1\right)=4 \Rightarrow a=5
\end{aligned}
\)
Putting \(a=5\) in \(b^2=4 a\), we get \(b^2=20\).
Hence, the equation of the required hyperbola is \(\frac{x^2}{25}-\frac{y^2}{20}=1\)

Example 5: The equations of the transverse and conjugate axes of a hyperbola are respectively \(x+2 y-3=0,2 x-y+4=0\), and their respective lengths are \(\sqrt{2}\) and \(2 / \sqrt{3}\). The equation of the hyperbola is
(a) \(\frac{2}{5}(x+2 y-3)^2-\frac{3}{5}(2 x-y+4)^2=1\)
(b) \(\frac{2}{5}(2 x-y+4)^2-\frac{3}{5}(x+2 y-3)^2=1\)
(c) \(2(2 x-y+4)^2-3(x+2 y-3)^2=1\)
(d) \(2(x+2 y-3)^2-3(2 x-y+4)^2=1\)

Solution: (b) Step 1: Identify the Axes and Lengths
Transverse Axis (\(T\)): \(x+2 y-3=0\)
Length of transverse axis \((2 a)=\sqrt{2} \Longrightarrow a=\frac{\sqrt{2}}{2} \Longrightarrow a^2=\frac{1}{2}\)
Conjugate Axis (C): \(2 x-y+4=0\)
Length of conjugate axis \((2 b)=\frac{2}{\sqrt{3}} \Longrightarrow b=\frac{1}{\sqrt{3}} \Longrightarrow \mathbf{b}^2=\frac{1}{3}\)
Note that these two lines are perpendicular (\(m_1=-1 / 2\) and \(m_2=2\)), which confirms they are valid axes for a hyperbola.
Step 2: Use the Distance Definition
For any point \(P(x, y)\) on the hyperbola:
\(d_1=\) Perpendicular distance from \(P\) to the Conjugate Axis
\(d_2=\) Perpendicular distance from \(P\) to the Transverse Axis
The standard equation relative to these axes is:
\(
\frac{d_1^2}{a^2}-\frac{d_2^2}{b^2}=1
\)
Step 3: Calculate Distances
\(d_1\) (distance to \(2 x-y+4=0\)):
\(
d_1=\frac{2 x-y+4}{\sqrt{2^2+(-1)^2}}=\frac{2 x-y+4}{\sqrt{5}}
\)
\(d_2\) (distance to \(x+2 y-3=0\)):
\(
d_2=\frac{x+2 y-3}{\sqrt{1^2+2^2}}=\frac{x+2 y-3}{\sqrt{5}}
\)
Step 4: Substitute into the Equation
\(
\frac{\left(\frac{2 x-y+4}{\sqrt{5}}\right)^2}{1 / 2}-\frac{\left(\frac{x+2 y-3}{\sqrt{5}}\right)^2}{1 / 3}=1
\)
Simplify the fractions:
\(
2\left(\frac{(2 x-y+4)^2}{5}\right)-3\left(\frac{(x+2 y-3)^2}{5}\right)=1
\)
Factoring out the \(1 / 5\) :
\(
\frac{2}{5}(2 x-y+4)^2-\frac{3}{5}(x+2 y-3)^2=1
\)

Example 6: The equation of the hyperbola whose conjugate axis is 5 and the distance between the foci is 13 , is
(a) \(25 x^2-144 y^2=900\)
(b) \(-25 x^2+144 y^2=900\)
(c) \(144 x^2-25 y^2=900\)
(d) \(-144 x^2+25 y^2=900\)

Solution: (a) Let \(2 a\) and \(2 b\) be the transverse and conjugate axes and \(e\) be the eccentricity. Let the centre be the origin and the transverse and the conjugate axes the coordinate axes.
Then, the equation of the hyperbola is
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
We have, \(2 b=5\) and \(2 a e=13\).
Now,
\(
\begin{aligned}
b^2 & =a^2\left(e^2-1\right) \\
\Rightarrow \quad b^2 & =a^2 e^2-a^2 \Rightarrow \frac{25}{4}=\frac{169}{4}-a^2 \Rightarrow a^2=\frac{144}{4} \Rightarrow a=6 .
\end{aligned}
\)
Substituting the values of \(a\) and \(b\) in (i), the equation of the hyperbola is
\(
\frac{x^2}{36}-\frac{y^2}{25 / 4}=1 \text { or, } 25 x^2-144 y^2=900
\)

Example 7: Find the vertices of the hyperbola \(9 x^2\)
\(
-16 y^2-36 x+96 y-252=0 .
\)

Solution: To find the vertices of the hyperbola, we need to transform the general equation into the standard shifted form \(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\) by completing the square.
Group and Factor the Terms:
First, group the \(x\) terms and the \(y\) terms together:
\(
\left(9 x^2-36 x\right)-\left(16 y^2-96 y\right)=252
\)
Factor out the leading coefficients:
\(
9\left(x^2-4 x\right)-16\left(y^2-6 y\right)=252
\)
Complete the Square:
To complete the square inside the parentheses:
For \(x:\left(\frac{-4}{2}\right)^2=4\). Add and subtract 4 inside.
For \(y:\left(\frac{-6}{2}\right)^2=9\). Add and subtract 9 inside.
\(
\begin{gathered}
9\left(x^2-4 x+4\right)-16\left(y^2-6 y+9\right)=252+9(4)-16(9) \\
9(x-2)^2-16(y-3)^2=252+36-144 \\
9(x-2)^2-16(y-3)^2=144
\end{gathered}
\)
Divide to get the Standard Form:
Divide the entire equation by 144 to set the right side to 1 :
\(
\begin{gathered}
\frac{9(x-2)^2}{144}-\frac{16(y-3)^2}{144}=1 \\
\frac{(x-2)^2}{16}-\frac{(y-3)^2}{9}=1
\end{gathered}
\)
Identify the Parameters:
Comparing this to \(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\) :
Center \((h, k):(2,3)\)
\(a^2=16 \Longrightarrow a=4\)
\(b^2=9 \Longrightarrow b=3\)
Since the \(x\) term is positive, the transverse axis is horizontal.
Calculate the Vertices:
The vertices for a horizontal hyperbola are given by (\(h \pm a, k\)).
Vertex 1: \((2+4,3)=(6,3)\)
Vertex 2: \((2-4,3)=(-2,3)\)

Example 8: Find the coordinates of foci, the eccentricity and latus – rectum, equations of directrices for the hyperbola \(9 x^2-16 y^2-72 x+96 y-144=0\).

Solution: Equation can be rewritten as So
\(
\begin{aligned}
\frac{(x-4)^2}{4^2}-\frac{(y-3)^2}{3^2 a} & =1 \\
a & =4, b=3
\end{aligned}
\)
\(
b^2=a^2\left(e^2-1\right) \text { gives } e=\frac{5}{4} .
\)
Foci:
\(
\begin{aligned}
& x-4= \pm a e \\
& y-3=0
\end{aligned}
\)
give the foci as \((9,3),(-1,3)\)
Centre:\(x-4=0, y-3=0\)
i.e. centre is \((4,3)\)
Directrices: \(x-4= \pm \frac{a}{e},\)
i.e.\(x-4= \pm \frac{16}{5}\)
Hence, directrices are \(5 x-36=0 ; 5 x-4=0\).
Latus rectum: \(\frac{2 b^2}{a}=2 \times \frac{9}{4}=\frac{9}{2}\)

Example 9: If the foci of the ellipse \(\frac{x^2}{16}+\frac{y^2}{b^2}=1\) and the hyperbola \(\frac{x^2}{144}-\frac{y^2}{81}=\frac{1}{25}\) coincide, then find the value of \(b^2\).

Solution: For hyperbola,
\(
\begin{aligned}
e^2 & =1+\frac{b^2}{a^2} \\
& =1+\frac{81}{144}=\frac{225}{144}
\end{aligned}
\)
\(
e=\frac{15}{12}=\frac{5}{4}
\)
Also,
\(
a^2=\frac{144}{25}
\)
Hence, the foci are \(( \pm a e, 0) \equiv\left( \pm \frac{12}{5} \times \frac{5}{4}, 0\right) \equiv( \pm 3,0)\)
Now for ellipse
\(
a e=3 \text { or } a^2 e^2=9
\)
Now
\(
b^2=a^2\left(1-e^2\right)
\)
\(
\begin{aligned}
b^2 & =a^2-a^2 e^2 \\
& =16-9=7
\end{aligned}
\)