11.9 Entrance Corner (Ellipse)

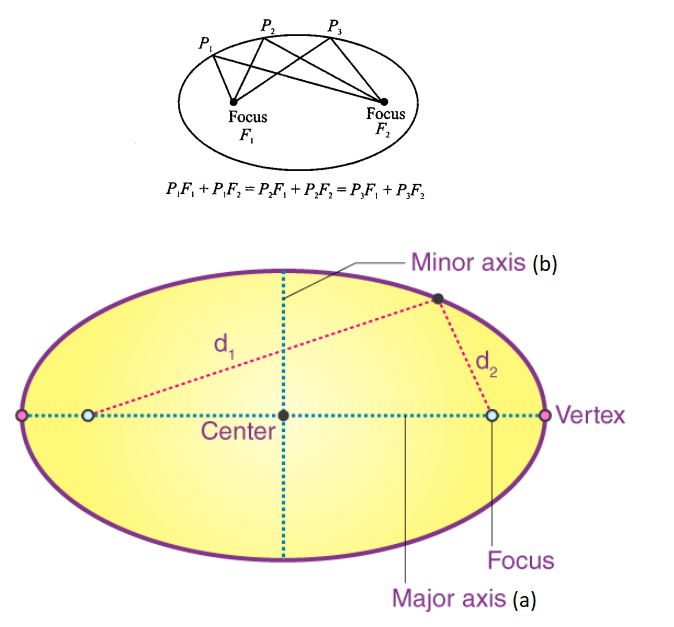
An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant. The two fixed points are called the foci (plural of ‘focus’) of the ellipse. The constant which is the sum of the distances of a point on the ellipse from the two fixed points is always greater than the distance between the two fixed points. The midpoint of the line segment joining the foci is called the centre of the ellipse. The line segment through the foci of the ellipse is called the major axis and the line segment through the centre and perpendicular to the major axis is called the minor axis. The end points of the major axis are called the vertices of the ellipse.

Ellipse Equation

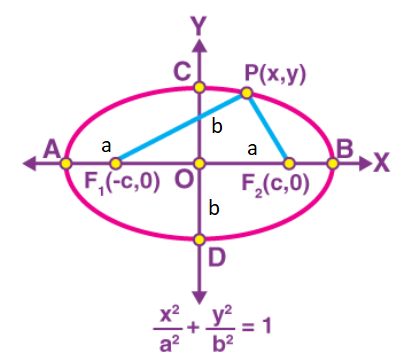
For an ellipse centered at the origin \((0,0)\) with a horizontal major axis, the standard equation is:
\(
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \quad (a > b)
\)
\(a=\) semi-major axis (half the length of the long side)
\(b=\) semi-minor axis (half the length of the short side)

Derivation of Ellipse Equation

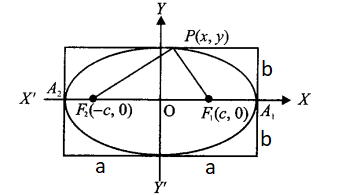
The line segment passing through the foci of the ellipse is the major axis and the line segment perpendicular to the major axis and passing through the center of the ellipse is the minor axis. The end points A and B as shown are known as the vertices which represent the intersection of major axes with the ellipse. ‘\(2a\)‘ denotes the length of the major axis and ‘ \(a\) ‘ is the length of the semi-major axis. ‘ \(2 b\) ‘ is the length of the minor axis and ‘ \(b\) ‘ is the length of the semi-minor axis. ‘ \(2 c\) ‘ represents the distance between two foci.

Let us consider the end points \(A\) and \(B\) on the major axis and points \(C\) and \(D\) at the end of the minor axis.

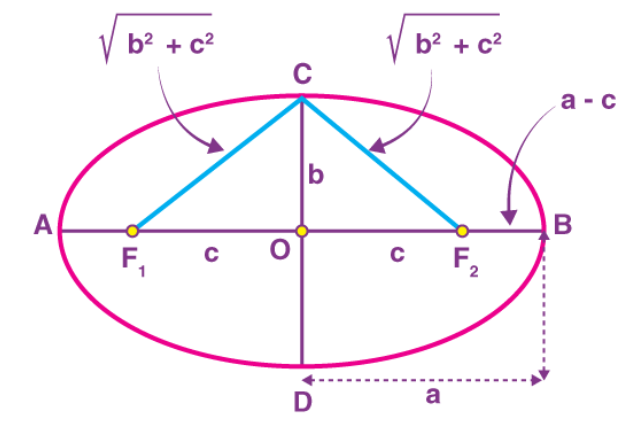
The sum of distances of \(B\) from \(F_1\) is \(F_1 B+F_2 B=F_1 O+O B+F_2 B\) (From the above figure)
\(
\Rightarrow c+a+a-c=2 a
\)
The sum of distances from point \(C\) to \(F_1\) is \(F_1 C+F_2 C\)
\(
\Rightarrow F_1 C+F_2 C=\sqrt{ }\left(b^2+c^2\right)+\sqrt{ }\left(b^2+c^2\right)=2 \sqrt{ }\left(b^2+c^2\right)
\)
By definition of ellipse;
\(
\begin{aligned}
& 2 \sqrt{ }\left(b^2+c^2\right)=2 a \\
& \Rightarrow a=\sqrt{ }\left(b^2+c^2\right) \\
& \Rightarrow a^2=b^2+c^2 \\
& \Rightarrow c^2=a^2-b^2 \dots(i)
\end{aligned}
\)

Special Cases:

• If \(c=0\) then \(F_1\) and \(F_2\), i.e. both foci merge together with center of ellipse. Also \(a^2\) becomes equal to \(b^2\), i.e. \(a=b\) so now we get \(a\) circle in this case.
• If \(c=a\) then \(b\) becomes 0 and we get \(a\) line segment \(F_1 F_2\).

Standard Equation of an Ellipse

The simplest method to determine the equation of an ellipse is to assume that centre of the ellipse is at the origin \((0,0)\) and the foci lie either on \(x\)-axis or \(y\)-axis of the Cartesian plane as shown below:

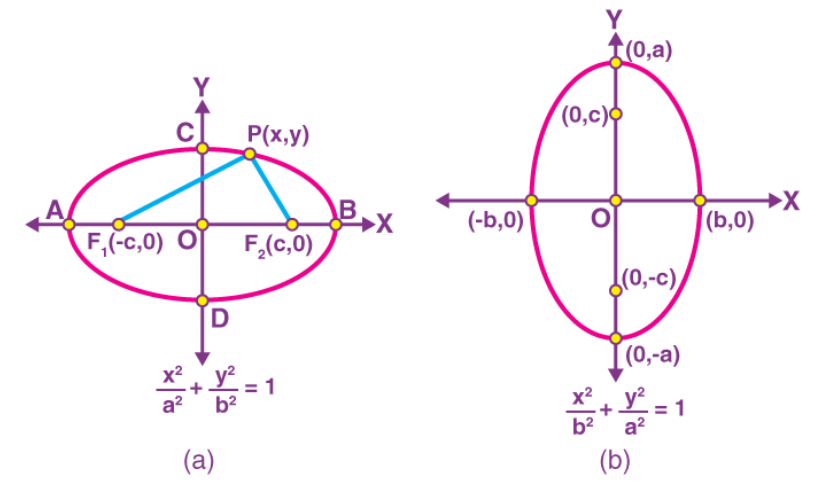
In Figure(a) both the foci lie on the x -axis and center O lies at the origin.
Let us consider the figure (a) to derive the equation of an ellipse. Let the coordinates of \(F_1\) and \(F_2\) be (\(-c, 0\)) and (\(c, 0\)) respectively as shown. Let us consider a point \(P(x, y)\) lying on the ellipse such that \(P\) satisfies the definition i.e. the sum of distances of \(P\) from \(F_1\) and \(F_2\) in the plane is a constant \(2 a\).
\(
\Rightarrow P F_1+P F_2=2 a \dots(ii)
\)
Using distance formula the distance can be written as:
\(
\begin{aligned}
& \sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}=2 a \\
\Rightarrow & \sqrt{(x+c)^2+y^2}=2 a-\sqrt{(x-c)^2+y^2}
\end{aligned}
\)
Squaring and simplifying both sides we get;
\(
\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1
\)
From eqn (i) we know \(a^2-c^2=b^2\)
\(
\Rightarrow \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \dots(iii)
\)
Now since \(P\) lies on the ellipse it should satisfy equation 2 such that \(0<c<a\).
\(
\Rightarrow y^2=b^2\left(1-\frac{x^2}{a^2}\right)
\)
Thus,
\(
\begin{aligned}
& P F_1=\sqrt{(x+c)^2+y^2} \\
= & \sqrt{(x+c)^2+b^2\left(1-\frac{x^2}{a^2}\right)}
\end{aligned}
\)
Substituting \(b^2=a^2-c^2\) into your equation:
\(
P F_1=\sqrt{(x+c)^2+\left(a^2-c^2\right)\left(1-\frac{x^2}{a^2}\right)}
\)
Now, expand the terms:
Expand the first part: \((x+c)^2=x^2+2 c x+c^2\)
Expand the second part: \(\left(a^2-c^2\right)-\frac{x^2\left(a^2-c^2\right)}{a^2}=a^2-c^2-x^2+\frac{c^2 x^2}{a^2}\)
Combining them:
\(
P F_1=\sqrt{x^2+2 c x+c^2+a^2-c^2-x^2+\frac{c^2 x^2}{a^2}}
\)
Notice how the \(x^2\) and \(c^2\) terms cancel out! This leaves us with:
\(
P F_1=\sqrt{a^2+2 c x+\frac{c^2 x^2}{a^2}}
\)
The expression inside the square root is actually a perfect square:
\(
P F_1=\sqrt{\left(a+\frac{c x}{a}\right)^2}
\)
Because \(x \leq a\) and \(c<a\), the term inside is positive, so:
\(
P F_1=a+\frac{c x}{a}
\)
If you repeat this exact process for the second focus \(\left(P F_2\right)\), you will find:
\(
P F_2=a-\frac{c x}{a}
\)
When you add them together:
\(
P F_1+P F_2=\left(a+\frac{c x}{a}\right)+\left(a-\frac{c x}{a}\right)=2 a
\)
Therefore the equation of the ellipse with centre at origin and major axis along the x-axis is:
\(
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\)
where \(-a \leq x \leq a\).
Similarly, the equation of the ellipse with center at origin and major axis along the \(y\) axis is (fig-b):
\(
\frac{x^2}{b^2}+\frac{y^2}{a^2}=1
\)
where \(-b \leq y \leq b\).

Latus Rectum

The line segments perpendicular to the major axis through any of the foci such that their endpoints lie on the ellipse are defined as the latus rectum. Show that \(L=\frac{2 b^2}{a}\)

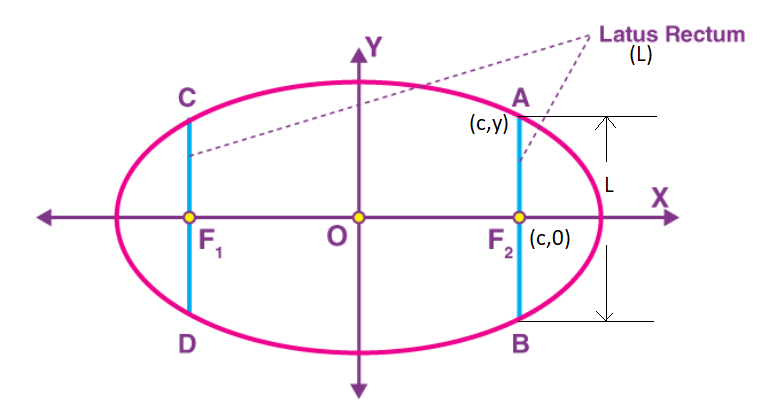
Proof: Identify the Point: A latus rectum passes through a focus, which has the coordinates \((c, 0)\). Let the point on the ellipse directly above the focus be \((c, y)\).
Substitute into the Equation:
\(
\frac{c^2}{a^2}+\frac{y^2}{b^2}=1
\)
Solve for \(y\) :
\(
\frac{y^2}{b^2}=1-\frac{c^2}{a^2}
\)
Using your earlier identity \(c^2=a^2-b^2\), we substitute:
\(
\frac{y^2}{b^2}=1-\frac{a^2-b^2}{a^2}=1-\left(1-\frac{b^2}{a^2}\right)=\frac{b^2}{a^2}
\)
Find the Semi-Latus Rectum:
\(
y^2=\frac{b^4}{a^2} \Rightarrow y=\frac{b^2}{a}
\)
Total Length: Since the latus rectum extends both above and below the axis, we double it:
\(
L=2 y=\frac{2 b^2}{a}
\)

Eccentricity of Ellipse

Eccentricity is defined as the ratio of the distance between the center and a focus (\(c\)) to the distance between the center and a vertex (\(a\)):
\(
e=\frac{c}{a}=\frac{O F_1}{O A_1}=\frac{\text { Distance from centre to focus }}{\text { Distance from centre to vertex }}
\)
Since we know from your previous derivation that \(c=\sqrt{a^2-b^2}\), we can also write the formula in terms of the axes:
\(
e=\frac{\sqrt{a^2-b^2}}{a}=\sqrt{1-\frac{b^2}{a^2}} \quad (<1)
\)

\(
e^2=1-\frac{4 b^2}{4 a^2}
\)
\(
e^2=1-\left(\frac{2 b}{2 a}\right)^2 \Rightarrow e=\sqrt{1-\left(\frac{\text { Minor axis }}{\text { Major axis }}\right)^2}
\)

The Range of Eccentricity: For any true ellipse, the value of \(e\) sits in the range \(0 \leq e<1\). The value tells a specific story about the shape:

• \(e=0\) (The Circle): If \(e=0\), then \(c=0\). The two foci are in the exact same spot (the center), making the distance to the edge uniform.
• \(e \rightarrow 0\) (Low Eccentricity): The ellipse looks very “fat” or nearly circular (like the orbits of most planets in our solar system).
• \(e \rightarrow 1\) (High Eccentricity): The ellipse looks very “flat” or elongated (like the orbits of many comets).
• \(e=1\) (The Parabola): Once \(e\) reaching 1, the curve “breaks open” and is no longer an ellipse.

Equation of an ellipse in terms of eccentricity 

\(
\frac{x^2}{a^2}+\frac{y^2}{a^2\left(1-e^2\right)}=1
\)
where \(b^2=a^2\left(1-e^2\right)\) or \(a^2 e^2=a^2-b^2(a>b)\).

Directrix of Ellipse

The ellipse’s directrix is drawn outside the ellipse and runs parallel to its latus rectum. The ellipse’s two directrix are located equidistant from its centre. The directrix of an ellipse is a line that is perpendicular to the major axis of the ellipse at a distance of \(x= \pm \frac{a}{e}\) from the center, where e is the eccentricity of the ellipse and a is the length of the major axis.

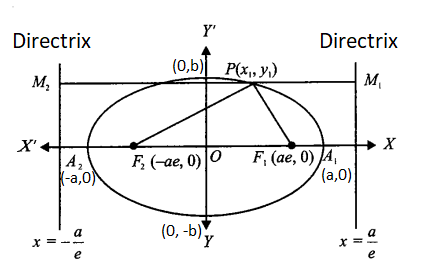
It is possible to define two lines \(x= \pm \frac{a}{e}\) corresponding to each focus, which satisfy the focal directrix property of the ellipse, i.e., \(P F_1=e P M_1\) and \(P F_2=e P M_2\).
Hence, for any point \(P\) on the ellipse \(\frac{P F_1}{P M_1}=e\) (constant)

The sum of the focal radii of any point on the ellipse is equal to the length of the major axis.
We have
\(
\begin{aligned}
& P F_1=e P M_1=e\left(\frac{a}{e}-x_1\right)=a-e x_1 \dots(1) \\
& P F_2=e P M_2=e\left(\frac{a}{e}+x_1\right)=a+e x_1 \dots(2)
\end{aligned}
\)
(1) + (2) gives \(P F_1+P F_2=2 a\)

Latus-rectum Length in terms of Eccentricity, major and minor axis

The two foci are \(( \pm a e, 0)\).
\(
\begin{array}{ll}
\text { Putting } & x=a e \text { in } \frac{x^2}{a^2}+\frac{y^2}{b^2}=1, \text { we get } \\
\Rightarrow & \frac{y^2}{b^2}=1-e^2=1-\left(1-\frac{b^2}{a^2}\right)=\frac{b^2}{a^2} ; \\
\therefore & y= \pm \frac{b^2}{a}
\end{array}
\)
∴ Coordinate of the extremities of the latus rectum
\(
=\left( \pm a e, \pm \frac{b^2}{a}\right)
\)
\(
\begin{aligned}
\text { Length of latus rectum } & =\frac{2 b^2}{a}=2 a\left(1-e^2\right) \quad b^2=a^2\left(1-e^2\right)\\
& =\frac{4 b^2}{2 a}=\frac{(\text { Minor axis })^2}{\text { Major axis }}
\end{aligned}
\)

Equation of an Ellipse Whose Axes are Parallel to Coordinate Axis and Centre is \(\boldsymbol{(} \boldsymbol{h} \boldsymbol{,} \boldsymbol{k}\) )

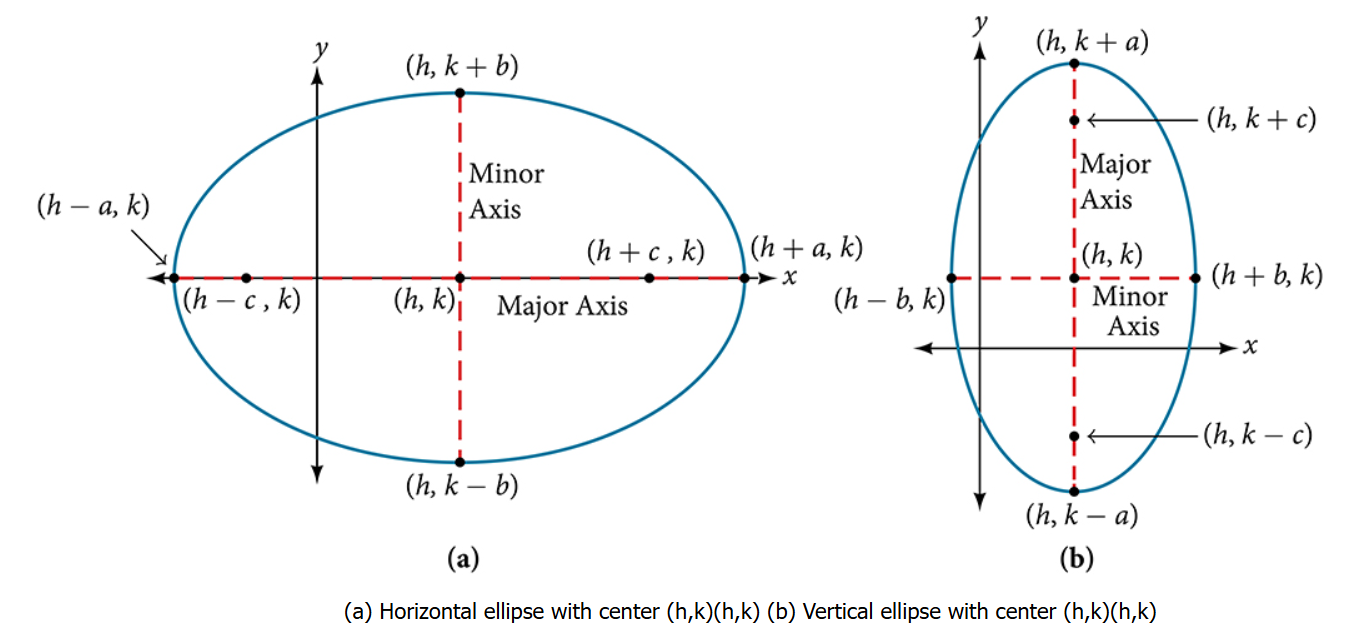
Equation of such an ellipse is \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1,(a>b)\)
Foci: \((h \pm a e, k)=(h \pm c, k)\)
Directrix:
\(
x=h \pm \frac{a}{e}
\)

Comparison of Standard Equation of an Ellipse when \(a>b\) and \(a<b\)

Various results related to \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b)\) and \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a<b)\) are given in the following table for ready reference.
\(
\begin{array}{|l|l|l|}
\hline & \frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a>b, & \frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a<b \\
\hline \text { Coordinates of the centre } & (0,0) & (0,0) \\
\hline \text { Coordinates of the vertices } & (a, 0) \text { and }(-a, 0) & (0,-b) \text { and }(0,-b) \\
\hline \text { Coordinates of foci } & (\mathrm{ae}, \mathrm{o}) \text { and }(-a e, 0) & (\mathrm{o}, \mathrm{be}) \text { and }(\mathrm{o},-\mathrm{be}) \\
\hline \text { Length of the major axis } & 2 a & 2 b \\
\hline \text { Length of the minor axis } & 2 b & 2 a \\
\hline \text { Equation of the major axis } & y=0 & x=0 \\
\hline \text { Equation of the minor axis } & x=0 & y=0 \\
\hline \text { Equations of the directrices } & x=\frac{a}{e} \text { and } x=-\frac{a}{e} & y=\frac{b}{e} \text { and } y=-\frac{b}{e} \\
\hline \text { Eccentricity } & e=\sqrt{1-\frac{b^2}{a^2}} & e=\sqrt{1-\frac{a^2}{b^2}} \\
\hline \text { Length of the latusrectum } & \frac{2 b^2}{a} & \frac{2 a^2}{b} \\
\hline \text { Focal distances of a point }(x, y) & a \pm e x & b \pm e y \\
\hline
\end{array}
\)

Position of a Point \((h, k)\) with Respect to an Ellipse

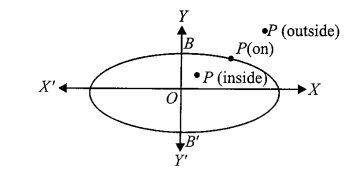
Let an ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Let \(P \equiv(h, k)\)
Now \(P\) will lie outside, on or inside the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) according to as \(S=\frac{h^2}{a^2}+\frac{k^2}{b^2}-1>,=,<0\)

For example, Take the ellipse \(\frac{x^2}{25}+\frac{y^2}{9}=1\). Let’s check the position of the point \((2,1)\) :
\(
\begin{gathered}
S=\frac{2^2}{25}+\frac{1^2}{9}-1 \\
S=\frac{4}{25}+\frac{1}{9}-1 \approx 0.16+0.11-1=-0.73
\end{gathered}
\)
Since \(-0.73<0\), the point \((2,1)\) lies inside the ellipse.

Example 1: The equation of the ellipse whose focus is \((1,0)\) and the directrix is \(x+y+1=0\) and eccentricity is equal to \(1 / \sqrt{2}\), is
(a) \((x-1)^2+y^2=(x+y+1)^2\)
(b) \(2\left\{(x-1)^2+y^2\right\}=(x+y+1)^2\)
(c) \(4\left\{(x-1)^2+y^2\right\}=(x+y+1)^2\)
(d) none of these

Solution: (c) Let \(S(1,0)\) be the focus and \(Z Z^{\prime}\) be the directrix. Let \(P(x, y)\) be any point on the ellipse and \(P M\) be perpendicular from \(P\) on the directrix. Then, by definition, we have

\(
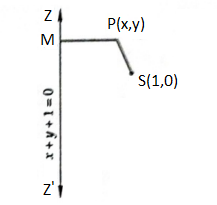
\begin{aligned}
& & S P=e P M, \text { where } e=1 / \sqrt{2} \\
\Rightarrow & & S P^2=e^2 P M^2 \\
\Rightarrow & & (x-1)^2+(y-0)^2=\left(\frac{1}{\sqrt{2}}\right)^2\left\{\frac{x+y+1}{\sqrt{1+1}}\right\}^2
\end{aligned}
\)
\(
\Rightarrow \quad 4\left\{(x-1)^2+y^2\right\}=(x+y+1)^2
\)

Example 2: The equation \(\frac{x^2}{10-a}+\frac{y^2}{4-a}=1\) represents an ellipse, if
(a) \(a<4\)
(b) \(a>4\)
(c) \(4<a<10\)
(d) \(a>10\)

Solution: (a) The standard form of an ellipse is:
\(
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\)
For this to represent a real ellipse, both denominators (\(a\) and \(b\)) must be positive. If one were negative, you would have a hyperbola; if both were negative, the equation would have no real solutions (since a sum of squares cannot be negative).
Given the equation:
\(
\frac{x^2}{10-a}+\frac{y^2}{4-a}=1
\)
We need to satisfy two conditions simultaneously:
First Denominator must be positive:
\(
10-a>0 \Longrightarrow 10>a \Longrightarrow a<10
\)
Second Denominator must be positive:
\(
4-a>0 \Longrightarrow 4>a \Longrightarrow a<4
\)
Finding the Intersection:
To satisfy both conditions, we must pick the more restrictive one.
If \(a\) is less than 10 but greater than 4 (e.g., \(a=7\)), the second denominator (\(4-7=-3\)) becomes negative, which fails the ellipse requirement.
Therefore, a must be less than 4 to keep both denominators positive.

Example 3: The curve with parametric equations \(x=1+4 \cos \theta, y=2+3 \sin \theta\), is
(a) an ellipse
(b) a parabola
(c) a hyperbola
(d) a circle

Solution: (a) We have,
\(
\begin{aligned}
x=1+4 \cos \theta, y & =2+3 \sin \theta \\
\therefore \quad\left(\frac{x-1}{4}\right)^2+\left(\frac{y-2}{3}\right)^2 & =1 \Rightarrow \frac{(x-1)^2}{16}+\frac{(y-2)^2}{9}=1
\end{aligned}
\)
Clearly, it is which is an ellipse.

Example 4: Length of the major axis of the ellipse \(9 x^2+7 y^2=63\), is
(a) 3
(b) 9
(c) 6
(d) \(2 \sqrt{7}\)

Solution: (c) Step 1: Normalize the Equation
The given equation is \(9 x^2+7 y^2=63\). To get a 1 on the right side, divide the entire equation by 63 :
\(
\begin{gathered}
\frac{9 x^2}{63}+\frac{7 y^2}{63}=\frac{63}{63} \\
\frac{x^2}{7}+\frac{y^2}{9}=1
\end{gathered}
\)
Step 2: Identify the Semi-Axes
In the standard form, \(a^2\) and \(b^2\) are the denominators.
Here, the denominator under \(y^2\) is larger (\(9>7\)).
This means the major axis is vertical (along the y-axis).
Let \(a\) represent the semi-major axis (the larger value) and \(b\) represent the semi-minor axis:
\(a^2=9 \Longrightarrow a=3\)
\(b^2=7 \Longrightarrow b=\sqrt{7}\)
Step 3: Calculate the Length of the Major Axis
The total length of the major axis is \(2 a\).
\(
\text { Length }=2 \times 3=6
\)

Example 5: The length of the axes of the conic \(9 x^2+4 y^2-6 x+4 y+1=0\) are: [JEE (Orissa) 2002]
(a) \(\frac{1}{2}, 9\)
(b) \(3, \frac{2}{5}\)
(c) \(1, \frac{2}{3}\)
(d) 3,2

Solution: (c) This problem is a bit more complex because the ellipse is not centered at the origin. To find the lengths of the axes, we need to complete the square to get it into the standard form: \(\frac{(x-h)^2}{a^2}+ \frac{(y-k)^2}{b^2}=1\).
Step 1: Group the terms
Group the \(x\) terms and \(y\) terms together:
\(
\left(9 x^2-6 x\right)+\left(4 y^2+4 y\right)=-1
\)
Step 2: Complete the square
Factor out the coefficients of the squared terms:
\(
9\left(x^2-\frac{2}{3} x\right)+4\left(y^2+y\right)=-1
\)
Now, add the necessary constants inside the parentheses (and balance the equation on the right):
For \(x\) : half of \(-\frac{2}{3}\) is \(-\frac{1}{3}\), and \(\left(-\frac{1}{3}\right)^2=\frac{1}{9}\).
For \(y\) : half of 1 is \(\frac{1}{2}\), and \(\left(\frac{1}{2}\right)^2=\frac{1}{4}\).
\(
\begin{gathered}
9\left(x^2-\frac{2}{3} x+\frac{1}{9}\right)+4\left(y^2+y+\frac{1}{4}\right)=-1+9\left(\frac{1}{9}\right)+4\left(\frac{1}{4}\right) \\
9\left(x-\frac{1}{3}\right)^2+4\left(y+\frac{1}{2}\right)^2=-1+1+1 \\
9\left(x-\frac{1}{3}\right)^2+4\left(y+\frac{1}{2}\right)^2=1
\end{gathered}
\)
Step 3: Standard Form
To match \(\frac{X^2}{a^2}+\frac{Y^2}{b^2}=1\), we rewrite the multipliers as denominators:
\(
\frac{\left(x-\frac{1}{3}\right)^2}{1 / 9}+\frac{\left(y+\frac{1}{2}\right)^2}{1 / 4}=1
\)
Step 4: Identify the lengths
The denominators are \(a^2\) and \(b^2\) :
\(a^2=\frac{1}{9} \Longrightarrow a=\frac{1}{3}\)
\(b^2=\frac{1}{4} \Longrightarrow b=\frac{1}{2}\)
The lengths of the axes are \(2 a\) and \(2 b\) :
Length 1: \(2 \times \frac{1}{3}=\frac{2}{3}\)
Length 2: \(2 \times \frac{1}{2}=1\)
Correct Option: (c) (The lengths are 1 and \(\frac{2}{3}\)).

Example 6: The eccentricity of the ellipse \(x^2+4 y^2+8 y-2 x+1=0\), is [CEE (Delhi) 2009]
(a) \(\frac{\sqrt{3}}{2}\)
(b) \(\frac{\sqrt{5}}{2}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{4}\)

Solution: (a) The equation of the ellipse is
\(
\begin{aligned}
& x^2+4 y^2+8 y-2 x+1=0 \\
\Rightarrow \quad & \left(x^2-2 x+1\right)+4\left(y^2+2 y+1\right)=4 \\
\Rightarrow & \frac{(x-1)^2}{2^2}+\frac{(y+1)^2}{1^2}=1
\end{aligned}
\)
This is of the form \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\).
On comparing, we get \(a=2\) and \(b=1\).
Let \(e\) be the eccentricity of the ellipse. Then,
\(
e=\sqrt{1-\frac{b^2}{a^2}} \Rightarrow e=\sqrt{1-\frac{1}{4}}=\frac{\sqrt{3}}{2}
\)

Example 7: The equation of the ellipse whose axes are along the coordinate axes, vertices are \(( \pm 5,0)\) are foci at \(( \pm 4,0)\), is
(a) \(9 x^2+25 y^2=1\)
(b) \(9 x^2+25 y^2=225\).
(c) \(25 x^2+9 y^2=225\)
(d) \(25 x^2+9 y^2=1\)

Solution: (b) Let the equation of the required ellipse be
\(
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \dots(i)
\)
The coordinates of its vertices and foci are (\(\pm a, 0\)) and (\(\pm a e, 0\)) respectively.
\(
\therefore \quad a=5 \text { and } a e=4 \Rightarrow e=\frac{4}{5}
\)
Now,
\(
b^2=a^2\left(1-e^2\right) \Rightarrow b^2=25\left(1-\frac{16}{25}\right)=9
\)
Substituting the values of \(a^2\) and \(b^2\) in (i), we get \(\frac{x^2}{25}+\frac{y^2}{9}=1\), which is the equation of the required ellipse.