Latest PYQs MCQs

Hint

(d) Step 1: Define the Total Series
Let \(S\) be the sum of the given infinite series:
\(
S=\sum_{n=1}^{\infty} \frac{1}{n^4}=\frac{1}{1^4}+\frac{1}{2^4}+\frac{1}{3^4}+\frac{1}{4^4}+\cdots=\frac{\pi^4}{90}
\)
This series can be split into its odd terms ( \(\alpha\) ) and its even terms ( \(\beta\) ):
\(
S=\alpha+\beta
\)
Step 2: Express \(\beta\) in terms of \(S\)
The series \(\beta\) consists of the even terms:
\(
\beta=\frac{1}{2^4}+\frac{1}{4^4}+\frac{1}{6^4}+\ldots
\)
We can factor out \(\frac{1}{2^4}\) from every term:
\(
\begin{gathered}
\beta=\frac{1}{2^4}\left(\frac{1}{1^4}+\frac{1}{2^4}+\frac{1}{3^4}+\ldots\right) \\
\beta=\frac{1}{16} \cdot S
\end{gathered}
\)
Step 3: Express \(\alpha\) in terms of \(S\)
Since \(S=\alpha+\beta\), we can substitute the value of \(\beta\) :
\(
\begin{gathered}
\alpha=S-\beta \\
\alpha=S-\frac{1}{16} S=\frac{15}{16} S
\end{gathered}
\)
Step 4: Find the Ratio \(\frac{\alpha}{\beta}\)
Now, we divide \(\alpha\) by \(\beta\) :
\(
\begin{gathered}
\frac{\alpha}{\beta}=\frac{\frac{15}{16} S}{\frac{1}{16} S} \\
\frac{\alpha}{\beta}=15
\end{gathered}
\)

Hint

(b) To solve for the \(n^{\text {th }}\) term \(a_n\), we first need to determine the first term ( \(a_1\) ) and the common difference ( \(d\) ) of the Arithmetic Progression using the given conditions.
Step 1: Set up the Equations
We are given:
\(a_6=7 \Longrightarrow a_1+5 d=7\)
\(S_7=7\)
Using the sum formula \(S_k=\frac{k}{2}\left[2 a_1+(k-1) d\right][latex] for [latex]S_7\) :
\(
S_7=\frac{7}{2}\left[2 a_1+6 d\right]=7
\)
Divide both sides by 7 :
\(
\frac{1}{2}\left[2 a_1+6 d\right]=1 \Longrightarrow a_1+3 d=1
\)
Step 2: Solve for \(a_1\) and \(d\)
Subtract (Eq. 2) from (Eq. 1):
\(
\begin{gathered}
\left(a_1+5 d\right)-\left(a_1+3 d\right)=7-1 \\
2 d=6 \Longrightarrow d=3
\end{gathered}
\)
Now, substitute \(d=3\) back into (Eq. 2):
\(
\begin{gathered}
a_1+3(3)=1 \\
a_1+9=1 \Longrightarrow a_1=-8
\end{gathered}
\)
Step 3: Use \(S_n=700\) to find \(n\)
Now we use the given total sum to find the value of \(n\) :
\(
S_n=\frac{n}{2}\left[2 a_1+(n-1) d\right]=700
\)
Substitute \(a_1=-8\) and \(d=3\) :
\(
\begin{gathered}
\frac{n}{2}[2(-8)+(n-1) 3]=700 \\
n[-16+3 n-3]=1400 \\
n(3 n-19)=1400 \\
3 n^2-19 n-1400=0
\end{gathered}
\)
Step 4: Solve the Quadratic Equation
Using the quadratic formula \(n=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\) :
\(
\begin{gathered}
n=\frac{19 \pm \sqrt{(-19)^2-4(3)(-1400)}}{6} \\
n=\frac{19 \pm \sqrt{361+16800}}{6} \\
n=\frac{19 \pm \sqrt{17161}}{6}
\end{gathered}
\)
Since \(\sqrt{17161}=131\) :
\(
n=\frac{19+131}{6}=\frac{150}{6}=25
\)
(We ignore the negative root as \(n \in \mathbb{N}\) ).
Step 5: Find \(a_n\) (which is \(a_{25}\) )
\(
\begin{gathered}
a_{25}=a_1+(25-1) d \\
a_{25}=-8+24(3) \\
a_{25}=-8+72=64
\end{gathered}
\)
The value of \(a_n\) is 64.

Hint

(a) To solve this, we will represent the terms of the Geometric Progression (G.P.) using the first term \(a\) and the common ratio \(r\). Since the G.P. consists of positive terms, both \(a>0\) and \(r>\) 0.
Step 1: Set up the Equations
The \(n^{\text {th }}\) term of a G.P. is given by \(T_n=a r^{n-1}\).
Condition 1: Sum of 2nd, 4th, and 6th terms is 21.
\(
\begin{array}{r}
a r+a r^3+a r^5=21 \\
a r\left(1+r^2+r^4\right)=21
\end{array}
\)
Condition 2: Sum of 8th, 10th, and 12th terms is 15309.
\(
\begin{array}{r}
a r^7+a r^9+a r^{11}=15309 \\
a r^7\left(1+r^2+r^4\right)=15309
\end{array}
\)
Step 2: Solve for \(r\) and \(a\)
Divide (Eq. 2) by (Eq. 1) to eliminate the common terms:
\(
\begin{gathered}
\frac{a r^7\left(1+r^2+r^4\right)}{a r\left(1+r^2+r^4\right)}=\frac{15309}{21} \\
r^6=729
\end{gathered}
\)
Since \(729=3^6\) and \(r\) must be positive: \(r=3\)
Now, substitute \(r=3\) back into (Eq. 1) to find \(a\) :
\(
\begin{gathered}
a(3)\left(1+3^2+3^4\right)=21 \\
3 a(1+9+81)=21 \\
3 a(91)=21 \\
a=\frac{21}{3 \times 91}=\frac{7}{91}=\frac{1}{13}
\end{gathered}
\)
Step 3: Calculate the Sum of the First Nine Terms ( \(S_9\) )
The formula for the sum of the first \(n\) terms is \(S_n=\frac{a\left(r^n-1\right)}{r-1}\). For \(n=9, a=1 / 13, r=3\) :
\(
\begin{gathered}
S_9=\frac{\frac{1}{13}\left(3^9-1\right)}{3-1} \\
S_9=\frac{3^9-1}{13 \times 2}=\frac{3^9-1}{26}
\end{gathered}
\)
Calculating \(3^9\) :
\(3^4=81\)
\(3^8=81 \times 81=6561\)
\(3^9=6561 \times 3=19683\)
\(
\begin{gathered}
S_9=\frac{19683-1}{26}=\frac{19682}{26} \\
S_9=757
\end{gathered}
\)
The sum of the first nine terms is 757.

Hint

(b) Step 1: Define the terms and equations
Let the geometric progression terms be \(x_1=a, x_2=a r, x_3=a r^2\), and \(x_4=a r^3\).
The terms after subtraction, \(a-2, a r-7, a r^2-9\), and \(a r^3-5\), are in an arithmetic progression, meaning the common difference between consecutive terms is equal. This gives us two equations:
\(
\begin{gathered}
(a r-7)-(a-2)=\left(a r^2-9\right)-(a r-7) \\
\left(a r^2-9\right)-(a r-7)=\left(a r^3-5\right)-\left(a r^2-9\right)
\end{gathered}
\)
Step 2: Simplify the equations
Simplifying the first equation yields \(a(r-1)^2=-3\). Simplifying the second equation yields \(\operatorname{ar}(r-1)^2=-6\).
Step 3: Solve for the common ratio and first term
Dividing the second simplified equation by the first simplified equation gives \(\frac{a r(r-1)^2}{a(r-1)^2}=\frac{-6}{-3}\), which results in \(r=2\). Substituting \(r=2\) back into the first equation, \(a(2-1)^2=-3\), gives \(a=-3\).
Step 4: Calculate the product of the terms
The product of the terms \(x_1 x_2 x_3 x_4\) is \(a^4 r^6\). Using the values \(a=-3\) and \(r=2\) :
\(
x_1 x_2 x_3 x_4=(-3)^4 \times 2^6=81 \times 64=5184
\)
Step 5: Calculate the final required value
The required value is \(\frac{1}{24}\left(x_1 x_2 x_3 x_4\right)\).
\(
\frac{1}{24} \times 5184=216
\)

Hint

(b) Step 1: Factoring the Denominator, factored the biquadratic expression \(r^4+3 r^2+4\)
\(
r^4+3 r^2+4=\left(r^4+4 r^2+4\right)-r^2=\left(r^2+2\right)^2-r^2
\)
Using the identity \(a^2-b^2=(a-b)(a+b)\) :
\(
\left(r^2+2-r\right)\left(r^2+2+r\right)
\)
Step 2: Partial Fractions The numerator \(4 r\) was split as \(2 \times 2 r\). You expressed \(2 r\) as the difference between the two factors:
\(
\left(r^2+r+2\right)-\left(r^2-r+2\right)=2 r
\)
This leads to the telescoping form:
\(
T_r=2\left[\frac{1}{r^2-r+2}-\frac{1}{r^2+r+2}\right]
\)
Step 3: Telescoping the Sum Let \(f(r)=\frac{1}{r^2-r+2}\). Then \(f(r+1)=\frac{1}{(r+1)^2-(r+1)+2}=\frac{1}{r^2+r+2}\). The sum becomes:
\(
S_n=2 \sum_{r=1}^n[f(r)-f(r+1)]=2[f(1)-f(n+1)]
\)
Step 4: Final Calculation for \(S_{20}\)
\(f(1)=\frac{1}{1^2-1+2}=\frac{1}{2}\)
\(f(21)=\frac{1}{20^2+20+2}=\frac{1}{422}\)
\(
S_{20}=2\left(\frac{1}{2}-\frac{1}{422}\right)=1-\frac{1}{211}=\frac{210}{211}
\)
Since \(\frac{m}{n}=\frac{210}{211}\) (which is irreducible as 211 is prime), we have:
\(
m+n=210+211=421
\)

Hint

(a) Step 1: Initial Setup
You correctly identified the middle terms for both progressions:
Set A: \(\{12-d, 12,12+d\} \Longrightarrow p=12\left(144-d^2\right)\)
Set B: \(\{12-D, 12,12+D\} \Longrightarrow q=12\left(144-D^2\right)\)
Step 2: The Ratio Calculation
Using the Componendo and Dividendo rule on \(\frac{p+q}{p-q}=\frac{19}{5}\) :
\(
\frac{(p+q)+(p-q)}{(p+q)-(p-q)}=\frac{19+5}{19-5} \Longrightarrow \frac{2 p}{2 q}=\frac{24}{14} \Longrightarrow \frac{p}{q}=\frac{12}{7}
\)
Which leads to your equation: \(7 p=12 q\).
Step 3: Solving for \(d[latex] and [latex]D\)
Substitute the expressions for \(p\) and \(q\) :
\(
\begin{gathered}
7\left[12\left(144-d^2\right)\right]=12\left[12\left(144-D^2\right)\right] \\
7\left(144-d^2\right)=12\left(144-D^2\right)
\end{gathered}
\)
In your notes, you substituted \((12-D)\) with \((15-d)\) and \((12+D)\) with \((9-d)\). This implies you are working with a specific problem where the terms of set \(B\) are related to set \(A\) (perhaps shifted).
If we take your solved values \(d=6\) and \(D=9\) :
Check Ratio:
\(p=12(144-36)=12(108)=1296\)
\(q=12(144-81)=12(63)=756\)
\(
\frac{p}{q}=\frac{1296}{756}=\frac{108}{63}=\frac{12}{7}(\text { Matches }!)
\)
Difference \(p-q = 540\)

Hint

(d) Step 1: Identify the Properties of Sets A and B
Set A: 1, 6, 11, 16, . . .
First term \(a_1=1\), Common difference \(d_1=5\)
Number of terms \(N=2025\)
Last term \(L_A=1+(2025-1) 5=1+10120=10121\)
Set B: 9, 16, 23,30,…
First term \(b_1=9\), Common difference \(d_2=7\)
Number of terms \(N=2025\)
Last term \(L_B=9+(2025-1) 7=9+14168=14177\)
Step 2: Identify the Intersection Set ( \(A \cap B\) )
Common terms of two APs form a new AP.
First common term ( \(a\) ): By inspection, the first common term is 16.
Common difference \((D): D=\operatorname{LCM}\left(d_1, d_2\right)=\operatorname{LCM}(5,7)=35\).
Step 3: Find the Number of Common Terms \(n(A \cap B)\)
The common terms must not exceed the smaller of the two last terms ( \(L_A=10121\) and \(L_B=14177\) ).
\(
16+(k-1) 35 \leq 10121
\)
\(
\begin{gathered}
(k-1) 35 \leq 10105 \\
k-1 \leq \frac{10105}{35}
\end{gathered}
\)
Dividing 10105 by \(35: 10105 \div 35=288.71 \ldots\)
\(
k-1 \leq 288 \Longrightarrow k \leq 289
\)
So, \(n(A \cap B)=289\).
Step 4: Final Calculation
Now, apply the inclusion-exclusion formula:
\(
\begin{gathered}
n(A \cup B)=n(A)+n(B)-n(A \cap B) \\
n(A \cup B)=2025+2025-289 \\
n(A \cup B)=4050-289 \\
n(A \cup B)=3761
\end{gathered}
\)

Hint

(b) Step 1: Analyze the Series Pattern and Define General Terms
The series alternates between the value of an odd number and the square of an odd number. The terms are as follows: \(1,3,5^2, 7,9^2, 11,13^2, 15, \ldots\)
The sequence of numbers is \(1,3,5,7,9,11, \ldots\), which are consecutive odd integers, with the general \(n\)-th odd integer being \(2 n-1\). The pattern applies a square to terms in the odd-numbered positions (1st, 3rd, 5th, etc.) and no square (implicitly power of 1) to terms in the even-numbered positions (2nd, 4th, 6th, etc.).
Step 2: Group Terms and Formulate a Summation
To sum up to 40 terms, we can group the terms into 20 pairs, as each pair contains two consecutive terms of the sequence:
\(
(1+3)+\left(5^2+7\right)+\left(9^2+11\right)+\left(13^2+15\right)+\ldots+\left(T_{39}^2+T_{40}\right)
\)
The \(k\)-th pair of terms (where \(k\) ranges from 1 to 20 ) involves the ( \(2 k-1\) )-th and ( \(2 k\) )th odd numbers.
The odd numbers involved are \(2(2 k-1)-1=4 k-3\) and \(2(2 k)-1=4 k-1\).
The \(k\)-th pair sum ( \(S_k\) ) is:
\(
S_k=(4 k-3)^2+(4 k-1)
\)
Expanding this expression:
\(
S_k=\left(16 k^2-24 k+9\right)+(4 k-1)=16 k^2-20 k+8
\)
Step 3: Calculate the Total Sum Using Summations
The total sum ( \(S\) ) for 40 terms (20 pairs) is the sum of \(S_k\) from \(k=1\) to 20 :
\(
S=\sum_{k=1}^{20}\left(16 k^2-20 k+8\right)=16 \sum_{k=1}^{20} k^2-20 \sum_{k=1}^{20} k+\sum_{k=1}^{20} 8
\)
Using the standard summation formulas for \(\sum k=\frac{n(n+1)}{2}\) and \(\sum k^2=\frac{n(n+1)(2 n+1)}{6}\) with \(n=20\) :
\(
\begin{gathered}
S=16\left(\frac{20(21)(41)}{6}\right)-20\left(\frac{20(21)}{2}\right)+8(20) \\
S=16(2870)-20(210)+160 \\
S=45920-4200+160 \\
S=41880
\end{gathered}
\)

Hint

(b) Step 1: Simplify the Numerator
The numerator of the \(n^{\text {th }}\) term is the sum of the first \(n\) odd natural numbers. Using the property that the sum of the first \(n\) odd numbers is \(n^2\) :
\(
1+3+5+\cdots+(2 n-1)=n^2
\)
Step 2: Identify the General Term \(T_n\)
The general term of the series is:
\(
T_n=\frac{n^2}{n!}
\)
We can simplify this by canceling out \(n\) from the factorial:
\(
T_n=\frac{n \cdot n}{n \cdot(n-1)!}=\frac{n}{(n-1)!}
\)
To further break this down for summation, we express the numerator \(n\) as \((n-1)+1\) :
\(
T_n=\frac{(n-1)+1}{(n-1)!}=\frac{n-1}{(n-1)!}+\frac{1}{(n-1)!}
\)
\(
T_n=\frac{1}{(n-2)!}+\frac{1}{(n-1)!}
\)
Step 3: Evaluate the Infinite Sum
The sum of the series \(S\) is:
\(
S=\sum_{n=1}^{\infty} T_n=\sum_{n=1}^{\infty}\left(\frac{1}{(n-2)!}+\frac{1}{(n-1)!}\right)
\)
Recall the power series expansion for \(e^x\) at \(x=1\) :
\(
e^1=\sum_{k=0}^{\infty} \frac{1}{k!}=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\ldots
\)
Let’s expand our sum carefully, noting that \(1 / k!=0\) if \(k<0\) :
First part: \(\sum_{n=1}^{\infty} \frac{1}{(n-2)!}=\frac{1}{(-1)!}+\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots=0+e=e\)
Second part: \(\sum_{n=1}^{\infty} \frac{1}{(n-1)!}=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots=e\)
Step 4: Final Calculation
\(
S=e+e=2 e
\)

Hint

(b) To solve for the required sum, we will express the terms of the Geometric Progression (G.P.) in terms of the first term \(a_1\) and the common ratio \(r\). Since it is an increasing G.P. of positive numbers, we know \(r>1\) and \(a_1>0\).
Step 1: Use the Product Property
The terms are \(a_1, a_1 r, a_1 r^2, \ldots\) We are given:
\(
\begin{gathered}
a_3 \cdot a_5=729 \\
\left(a_1 r^2\right) \cdot\left(a_1 r^4\right)=729 \\
a_1^2 r^6=729
\end{gathered}
\)
Taking the square root (since terms are positive):
\(
a_1 r^3=\sqrt{729}=27
\)
Note that \(a_1 r^3\) is actually the term \(a_4\). So, \(a_4=27\).
Step 2: Solve for the Common Ratio \(r\)
We are given the sum:
\(
a_2+a_4=\frac{111}{4}
\)
Substitute \(a_4=27\) :
\(
\begin{gathered}
a_2+27=\frac{111}{4} \\
a_2=\frac{111}{4}-27=\frac{111-108}{4}=\frac{3}{4}
\end{gathered}
\)
Now, relate \(a_2\) and \(a_4\) :
\(
\begin{gathered}
\frac{a_4}{a_2}=\frac{a_1 r^3}{a_1 r}=r^2 \\
r^2=\frac{27}{3 / 4}=27 \cdot \frac{4}{3}=9 \cdot 4=36
\end{gathered}
\)
Since the G.P. is increasing ( \(r>1\) ), we have: \(r=6\)
Step 3: Find the First Three Terms
Now we calculate \(a_1, a_2\), and \(a_3\) :
\(a_2=\frac{3}{4}\) (already found)
\(a_1=\frac{a_2}{r}=\frac{3 / 4}{6}=\frac{3}{24}=\frac{1}{8}\)
\(a_3=a_2 \cdot r=\frac{3}{4} \cdot 6=\frac{18}{4}=\frac{9}{2}\)
Step 4: Calculate the Final Expression
We need the value of \(24\left(a_1+a_2+a_3\right)\) :
\(
24\left(\frac{1}{8}+\frac{3}{4}+\frac{9}{2}\right)
\)
Multiply 24 into each term:
\(
\begin{gathered}
=\left(24 \cdot \frac{1}{8}\right)+\left(24 \cdot \frac{3}{4}\right)+\left(24 \cdot \frac{9}{2}\right) \\
=3+(6 \cdot 3)+(12 \cdot 9) \\
=3+18+108 \\
=129
\end{gathered}
\)

Hint

(a) Step 1: Find the General Term \(a_n\)
Let the series be \(S=1+3+11+25+45+71+\ldots\) The terms are: \(a_1=1, a_2= 3, a_3=11, a_4=25, a_5=45, a_6=71\).
Let’s look at the first differences:
\(3-1=2\)
\(11-3=8\)
\(25-11=14\)
\(45-25=20\)
\(71-45=26\)
The first differences are \(2,8,14,20,26, \ldots\). Now, let’s look at the second differences:
\(8-2=6\)
\(14-8=6\)
\(20-14=6\)
Since the second differences are constant (6), the general term \(a_n\) is a quadratic expression of the form:
\(
a_n=A n^2+B n+C
\)
Step 2: Solve for \(A, B\), and \(C\)
Using the first three terms:
1. For \(n=1: A+B+C=1\)
2. For \(n=2: 4 A+2 B+C=3\)
3. For \(n=3: 9 A+3 B+C=11\)
Subtracting (1) from (2): \(3 A+B=2\) Subtracting (2) from (3): \(5 A+B=8\) Subtracting these results: \(2 A=6 \Longrightarrow \mathrm{~A}=3\)
Substitute \(A=3\) into \(3 A+B=2: 3(3)+B=2 \Longrightarrow 9+B=2 \Longrightarrow \mathrm{~B}=-7\)
Substitute \(A=3, B=-7\) into \(A+B+C=1: 3-7+C=1 \Longrightarrow-4+C= 1 \Longrightarrow \mathbf{C}=\mathbf{5}\)
The general term is: \(a_n=3 n^2-7 n+5\).
Step 3: Calculate the Sum of 20 Terms ( \(S_{20}\) )
\(
\begin{gathered}
S_{20}=\sum_{n=1}^{20}\left(3 n^2-7 n+5\right) \\
S_{20}=3 \sum_{n=1}^{20} n^2-7 \sum_{n=1}^{20} n+\sum_{n=1}^{20} 5
\end{gathered}
\)
Using the standard summation formulas for \(n=20\) :
\(\sum n^2=\frac{n(n+1)(2 n+1)}{6}=\frac{20 \cdot 21 \cdot 41}{6}=2870\)
\(\sum n=\frac{n(n+1)}{2}=\frac{20 \cdot 21}{2}=210\)
\(\sum 5=5 \cdot 20=100\)
Step 4: Final Computation
\(
\begin{gathered}
S_{20}=3(2870)-7(210)+100 \\
S_{20}=8610-1470+100 \\
S_{20}=7140+100=7240
\end{gathered}
\)

Hint

(b) To solve this, let the number of terms be \(2 n\), the first term be \(a\), and the common difference be d.
Step 1: Set up the Equations for Sums
The Arithmetic Progression is: \(a, a+d, a+2 d, \ldots, a+(2 n-1) d\).
Odd terms \(\left(T_1, T_3, \ldots, T_{2 n-1}\right): a, a+2 d, a+4 d, \ldots, a+(2 n-2) d\) There are \(n\) such terms. Their sum is:
\(
S_{o d d}=\frac{n}{2}[2 a+(n-1) 2 d]=n[a+(n-1) d]=24 \dots(1)
\)
Even terms \(\left(T_2, T_4, \ldots, T_{2 n}\right): a+d, a+3 d, a+5 d, \ldots, a+(2 n-1) d\) There are \(n\) such terms. Their sum is:
\(
S_{\text {even }}=\frac{n}{2}[2(a+d)+(n-1) 2 d]=n[a+d+(n-1) d]=30 \dots(2)
\)
Step 2: Solve for \(n\) and \(d\)
Subtract (Eq. 1) from (Eq. 2):
\(
\begin{gathered}
n[a+n d]-n[a+(n-1) d]=30-24 \\
n[n d-(n-1) d]=6 \Longrightarrow n[d]=6
\end{gathered}
\)
So, \(n d=6\).
Step 3: Use the “Last Term” condition
The last term is \(a_{2 n}=a+(2 n-1) d\). We are given that the last term exceeds the first by 21/2:
\(
\begin{gathered}
(a+(2 n-1) d)-a=\frac{21}{2} \\
(2 n-1) d=\frac{21}{2} \\
2 n d-d=\frac{21}{2}
\end{gathered}
\)
Substitute \(n d=6\) :
\(
2(6)-d=\frac{21}{2} \Longrightarrow 12-d=10.5 \Longrightarrow d=1.5=\frac{3}{2}
\)
Now, find \(n\) :
\(
n(1.5)=6 \Longrightarrow n=4
\)
The total number of terms is \(2 n=8\).
Step 4: Solve for the first term \(a\)
Substitute \(n=4\) and \(d=1.5\) into (Eq. 1):
\(
\begin{gathered}
4[a+(3)(1.5)]=24 \\
a+4.5=6 \Longrightarrow a=1.5=\frac{3}{2}
\end{gathered}
\)
Step 5: Identify Integer Terms
The terms of the A.P. are \(a+(k-1) d\) for \(k=1\) to 8:
\(
T_k=\frac{3}{2}+(k-1) \frac{3}{2}=\frac{3}{2}[1+k-1]=\frac{3 k}{2}
\)
For \(T_k\) to be an integer, \(3 k[latex] must be divisible by 2. Since 3 is odd, [latex]k\) must be even. The even values of \(k\) within the 8 terms are \(k=2,4,6,8\).
The integer terms are:
\(T_2=\frac{3(2)}{2}=3\)
\(T_4=\frac{3(4)}{2}=6\)
\(T_6=\frac{3(6)}{2}=9\)
\(T_8=\frac{3(8)}{2}=12\)
There are 4 such terms.
The number of integer terms is 4.

Hint

(c) Step 1: Simplify the Summation of Odd Terms
The odd terms are \(a_1, a_3, a_5, \ldots, a_{23}\). These form an A.P. with:
First term: \(a_1\)
Common difference: \(2 d\)
Number of terms: 12
The sum is given by:
\(
\begin{gathered}
\sum_{k=1}^{12} a_{2 k-1}=\frac{12}{2}\left[2 a_1+(12-1)(2 d)\right]=-\frac{72}{5} a_1 \\
6\left[2 a_1+22 d\right]=-\frac{72}{5} a_1
\end{gathered}
\)
Divide both sides by 6:
\(
\begin{aligned}
& 2 a_1+22 d=-\frac{12}{5} a_1 \\
& 22 d=-\frac{12}{5} a_1-2 a_1
\end{aligned}
\)
\(
22 d=-\frac{22}{5} a_1 \Longrightarrow d=-\frac{a_1}{5}
\)
Step 2: Set the Sum of \(n\) Terms to Zero
We are given \(\sum_{k=1}^n a_k=0\). Using the sum formula for an A.P.:
\(
S_n=\frac{n}{2}\left[2 a_1+(n-1) d\right]=0
\)
Since \(n\) cannot be 0 , we solve for the term inside the bracket:
\(
2 a_1+(n-1) d=0
\)
Step 3: Substitute \(d=-\frac{a_1}{5}\)
\(
2 a_1+(n-1)\left(-\frac{a_1}{5}\right)=0
\)
Divide by \(a_1\) (given \(a_1 \neq 0\) ):
\(
2-\frac{n-1}{5}=0
\)
\(
\begin{aligned}
&2=\frac{n-1}{5}\\
&10=n-1\\
&n=11
\end{aligned}
\)

Hint

(b) Step 1: Formulate equations from given conditions
The sum of the first three terms of an A.P. with first term \(a[latex] and common difference [latex]d\) is \(S_3=\frac{3}{2}[2 a+(3-1) d]=3 a+3 d\).
Given \(S_3=54\), we have the equation:
\(
3 a+3 d=54 \Longrightarrow a+d=18
\)
The sum of the first twenty terms is \(S_{20}=\frac{20}{2}[2 a+(20-1) d]=10(2 a+19 d)\).
Given \(1600<S_{20}<1800\), we have the inequality:
\(
1600<10(2 a+19 d)<1800
\)
Step 2: Solve the inequality for \(\boldsymbol{a}\) and \(\boldsymbol{d}\)
Divide the inequality by 10 to get:
\(
160<2 a+19 d<180
\)
Substitute \(d=18-a\) (from the first equation) into the inequality:
\(
\begin{aligned}
160<2 a+19(18-a)<180 \\
160<2 a+342-19 a<180 \\
160<342-17 a<180
\end{aligned}
\)
Solving the two parts of the inequality for \(a\) :
From \(160<342-17 a\), we get \(17 a<182\), so \(a<\frac{182}{17} \approx 10.70\).
From \(342-17 a<180\), we get \(162<17 a\), so \(a>\frac{162}{17} \approx 9.52\).
Step 3: Determine the integer values of \(\boldsymbol{a}\) and \(\boldsymbol{d}\)
The term \(a\) must be a positive integer such that \(9.52<a<10.70\).
The only possible integer value is \(\boldsymbol{a} \boldsymbol{=} \mathbf{1 0}\).
Using \(a+d=18\), we find \(d=18-10=8\).
Both \(a\) and \(d\) are positive integers, satisfying the condition that the A.P. consists of positive integers.
Step 4: Calculate the 11 th term
The \(n^{\text {th }}\) term of an A.P. is given by \(a_n=a+(n-1) d\).
The 11th term ( \(a_{11}\) ) is:
\(
a_{11}=a+10 d=10+10(8)=10+80=90
\)

Hint

(b) Step 1: Simplify \(a_n\)
We are given:
\(
4 a_n=n^2+5 n+6
\)
Factorizing the quadratic expression \(n^2+5 n+6\) :
\(
\begin{aligned}
& 4 a_n=(n+2)(n+3) \\
& a_n=\frac{(n+2)(n+3)}{4}
\end{aligned}
\)
Step 2: Express \(\frac{1}{a_k}\) and \(S_n\)
The term we need to sum is the reciprocal of \(a_k\) :
\(
\frac{1}{a_k}=\frac{4}{(k+2)(k+3)}
\)
The sum \(S_n\) is:
\(
S_n=\sum_{k=1}^n \frac{4}{(k+2)(k+3)}=4 \sum_{k=1}^n \frac{1}{(k+2)(k+3)}
\)
Step 3: Apply the Telescoping Method
We can use partial fractions to split the term:
\(
\frac{1}{(k+2)(k+3)}=\frac{(k+3)-(k+2)}{(k+2)(k+3)}=\frac{1}{k+2}-\frac{1}{k+3}
\)
Now, expand the sum \(S_n\) :
\(
S_n=4\left[\left(\frac{1}{3}-\frac{1}{4}\right)+\left(\frac{1}{4}-\frac{1}{5}\right)+\cdots+\left(\frac{1}{n+2}-\frac{1}{n+3}\right)\right]
\)
Most terms cancel out, leaving only the first and last terms:
\(
S_n=4\left[\frac{1}{3}-\frac{1}{n+3}\right]
\)
Step 4: Calculate \(S_{2025}\)
Substitute \(n=2025\) :
\(
S_{2025}=4\left[\frac{1}{3}-\frac{1}{2025+3}\right]
\)
\(
S_{2025}=4\left[\frac{1}{3}-\frac{1}{2028}\right]
\)
To simplify inside the bracket:
\(
\frac{1}{3}-\frac{1}{2028}=\frac{676-1}{2028}=\frac{675}{2028}
\)
So, \(S_{2025}=4 \times \frac{675}{2028}=\frac{675}{507}\).
Step 5: Find the Final Value
We need the value of \(507 \times S_{2025}\) :
\(
507 \times \frac{675}{507}=675
\)

Hint

(b) Step 1: Identify the General Term
From the characteristic equation \(2 x^2-5 x+3=0\), we found the roots to be 1 and \(\frac{3}{2}\). Using the initial conditions \(a_0=0\) and \(a_1=\frac{1}{2}\), the general term is:
\(
a_n=\left(\frac{3}{2}\right)^n-1
\)
Step 2: Express \(a_{100}\)
Using the formula above:
\(
a_{100}=\left(\frac{3}{2}\right)^{100}-1
\)
This implies that \(\left(\frac{3}{2}\right)^{100}=a_{100}+1\).
Step 3: Simplify the Sum \(\sum_{k=1}^{100} a_k\)
We already calculated the sum as:
\(
\begin{aligned}
&S=3\left(\frac{3}{2}\right)^{100}-103\\
&\text { Now, substitute the expression for }\left(\frac{3}{2}\right)^{100} \text { in terms of } a_{100} \text { : }\\
&\begin{gathered}
S=3\left(a_{100}+1\right)-103 \\
S=3 a_{100}+3-103 \\
S=3 a_{100}-100
\end{gathered}
\end{aligned}
\)

Hint

(b) To solve this problem, we need to find the common difference \(d\), the first term \(a\), and the value of \(m\) for the given Arithmetic Progression (A.P.).
Step 1: Find the Common Difference ( \(d\) ) and First Term ( \(a\) )
We are given:
\(T_{25}=a+24 d=\frac{1}{20}\)
The sum of the first 25 terms: \(20 \sum_{r=1}^{25} T_r=13\)
Using the sum formula \(S_n=\frac{n}{2}[2 a+(n-1) d]\) :
\(
\begin{gathered}
20\left[\frac{25}{2}(2 a+24 d)\right]=13 \\
20[25(a+12 d)]=13 \\
500(a+12 d)=13 \Longrightarrow a+12 d=\frac{13}{500} \dots(1)
\end{gathered}
\)
From the given \(T_{25}\) :
\(
a+24 d=\frac{1}{20}=\frac{25}{500} \dots(2)
\)
Subtracting (Eq. 1) from (Eq. 2):
\(
\begin{gathered}
(a+24 d)-(a+12 d)=\frac{25}{500}-\frac{13}{500} \\
12 d=\frac{12}{500} \Longrightarrow d=\frac{1}{500}
\end{gathered}
\)
Now, substitute \(d\) back into (Eq. 1):
\(
\begin{aligned}
&a+12\left(\frac{1}{500}\right)=\frac{13}{500} \Longrightarrow a=\frac{13}{500}-\frac{12}{500}=\frac{1}{500}\\
&\text { So, } a=\frac{1}{500} \text { and } d=\frac{1}{500} \text {. This means } T_r=\frac{r}{500} \text {. }
\end{aligned}
\)
Step 2: Find the value of \(m\)
We are given \(T_m=\frac{1}{25}\) :
\(
\begin{gathered}
a+(m-1) d=\frac{1}{25} \\
\frac{1}{500}+(m-1) \frac{1}{500}=\frac{20}{500} \\
1+m-1=20 \Longrightarrow m=20
\end{gathered}
\)
Step 3: Calculate the required Sum
We need to find \(5 m \sum_{r=m}^{2 m} T_r\). With \(m=20\), we need to find \(100 \sum_{r=20}^{40} T_r\).
The number of terms in the sum \(\sum_{r=20}^{40} T_r\) is \(40-20+1=21\). Using the sum formula \(S= \frac{n}{2}\) (first term + last term):
\(
\sum_{r=20}^{40} T_r=\frac{21}{2}\left(T_{20}+T_{40}\right)
\)
Since \(T_r=\frac{r}{500}:\)
\(
\sum_{r=20}^{40} T_r=\frac{21}{2}\left(\frac{20}{500}+\frac{40}{500}\right)=\frac{21}{2}\left(\frac{60}{500}\right)=\frac{21 \times 30}{500}=\frac{630}{500}
\)
Now, multiply by \(5 m=100\) :
\(
100 \times \frac{630}{500}=\frac{630}{5}=126
\)

Hint

(d) Step 1: Formulate equations for \(S_{40}\) and \(S_{12}\)
Using the arithmetic progression sum formula \(S_n=\frac{n}{2}[2 a+(n-1) d]\), we derive two linear equations from the given information:
\(
\begin{aligned}
& S_{40}=1030 \Longrightarrow \frac{40}{2}[2 a+39 d]=1030 \Longrightarrow 2 a+39 d=51.5 \dots(1) \\
& S_{12}=57 \Longrightarrow \frac{12}{2}[2 a+11 d]=57 \Longrightarrow 2 a+11 d=9.5 \dots(2)
\end{aligned}
\)
Step 2: Solve the system of equations for \(\boldsymbol{a}\) and \(\boldsymbol{d}\)
Subtracting Equation 2 from Equation 1 allows us to solve for the common difference \(\boldsymbol{d}\) :
\(
(2 a+39 d)-(2 a+11 d)=51.5-9.5 \Longrightarrow 28 d=42 \Longrightarrow d=1.5
\)
Substituting \(\boldsymbol{d}\) back into Equation 2 gives the first term \(\boldsymbol{a}\) :
\(
2 a+11(1.5)=9.5 \Longrightarrow 2 a+16.5=9.5 \Longrightarrow 2 a=-7 \Longrightarrow a=-3.5
\)
Step 3: Express and calculate \(S_{30}-S_{10}\)
The required difference can be algebraically simplified:
\(
S_{30}-S_{10}=15(2 a+29 d)-5(2 a+9 d)=20 a+390 d=10(2 a+39 d)
\)
We recognize \(2 a+39 d\) as the expression from Equation 1.
\(
S_{30}-S_{10}=10 \times 51.5=515
\)

Hint

(d) Step 1: Identify the Series
Let the given sum be \(S\) :
\(
S=5+\frac{5+\alpha}{7}+\frac{5+2 \alpha}{7^2}+\frac{5+3 \alpha}{7^3}+\cdots=7
\)
This can be split into two separate infinite geometric series:
\(
S=\left(5+\frac{5}{7}+\frac{5}{7^2}+\ldots\right)+\left(\frac{\alpha}{7}+\frac{2 \alpha}{7^2}+\frac{3 \alpha}{7^3}+\ldots\right)
\)
Step 2: Solve the First Part
The first part is a simple infinite G.P. with first term \(a=5\) and common ratio \(r=\frac{1}{7}\) :
\(
S_1=\frac{a}{1-r}=\frac{5}{1-\frac{1}{7}}=\frac{5}{\frac{6}{7}}=\frac{35}{6}
\)
Step 3: Solve the Second Part (A.G.P. Method)
Let \(S_2=\frac{\alpha}{7}+\frac{2 \alpha}{7^2}+\frac{3 \alpha}{7^3}+\ldots\) Multiply \(S_2[latex] by the common ratio [latex]\frac{1}{7}\) :
\(
\frac{1}{7} S_2=\frac{\alpha}{7^2}+\frac{2 \alpha}{7^3}+\ldots
\)
Subtract the second equation from the first:
\(
\begin{gathered}
S_2-\frac{1}{7} S_2=\frac{\alpha}{7}+\left(\frac{2 \alpha}{7^2}-\frac{\alpha}{7^2}\right)+\left(\frac{3 \alpha}{7^3}-\frac{2 \alpha}{7^3}\right)+\ldots \\
\frac{6}{7} S_2=\frac{\alpha}{7}+\frac{\alpha}{7^2}+\frac{\alpha}{7^3}+\ldots
\end{gathered}
\)
The right side is an infinite G.P. with \(a=\frac{\alpha}{7}\) and \(r=\frac{1}{7}\) :
\(
\begin{gathered}
\frac{6}{7} S_2=\frac{\frac{\alpha}{7}}{1-\frac{1}{7}}=\frac{\frac{\alpha}{7}}{\frac{6}{7}}=\frac{\alpha}{6} \\
S_2=\frac{7 \alpha}{36}
\end{gathered}
\)
Step 4: Combine and Find \(\alpha\)
Now, substitute \(S_1\) and \(S_2\) back into the original equation \(S=7\) :
\(
\frac{35}{6}+\frac{7 \alpha}{36}=7
\)
Multiply the entire equation by 36 to clear the denominators:
\(
\begin{gathered}
6(35)+7 \alpha=7(36) \\
210+7 \alpha=252 \\
7 \alpha=252-210 \\
7 \alpha=42 \\
\alpha=6
\end{gathered}
\)

Hint

(d) To solve this problem, we first need to find the sum \(S_n\) and then use it to find the properties of the given Arithmetic Progression.
Step 1: Find the sum \(S_n\)
The series is given by:
\(
S_n=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\ldots
\)
Notice the denominators: \(2,6,12,20 \ldots\) can be written as \(1 \times 2,2 \times 3,3 \times 4,4 \times 5 \ldots\) The general term \(T_r\) is:
\(
T_r=\frac{1}{r(r+1)}=\frac{1}{r}-\frac{1}{r+1}
\)
This is a telescoping series:
\(
\begin{gathered}
S_n=\sum_{r=1}^n\left(\frac{1}{r}-\frac{1}{r+1}\right)=\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\cdots+\left(\frac{1}{n}-\frac{1}{n+1}\right) \\
S_n=1-\frac{1}{n+1}=\frac{n}{n+1}
\end{gathered}
\)
Step 2: Find the value of \(\sqrt{2026 S_{2025}}\)
Substituting \(n=2025\) into our formula for \(S_n\) :
\(
S_{2025}=\frac{2025}{2025+1}=\frac{2025}{2026}
\)
Therefore:
\(
\sqrt{2026 \times \frac{2025}{2026}}=\sqrt{2025}=45
\)
Step 3: Analyze the A.P.
We are given an A.P. where:
First term \(a=-p\)
Common difference \(d=p\)
Sum of first 6 terms \(\left(S_6^{\prime}\right)=45\)
Using the sum formula \(S_n=\frac{n}{2}[2 a+(n-1) d]\) :
\(
\frac{6}{2}[2(-p)+(6-1) p]=45
\)
\(
\begin{gathered}
3[-2 p+5 p]=45 \\
3[3 p]=45 \Longrightarrow 9 p=45 \Longrightarrow p=5
\end{gathered}
\)
Step 4: Find the absolute difference \(\left|T_{20}-T_{15}\right|\)
In any A.P., the difference between the \(n^{\text {th }}\) and \(m^{\text {th }}\) terms is \((n-m) d\) :
\(
\begin{aligned}
\left|T_{20}-T_{15}\right| & =|(20-15) d| \\
& =|5 d|
\end{aligned}
\)
Since \(d=p=5\) :
\(
5 \times 5=25
\)
The absolute difference is 25.

Hint

(c) To solve this, we will use the formula for the sum of the first \(n\) terms of an Arithmetic Progression: \(S_n=\frac{n}{2}[2 a+(n-1) d]\).
Step 1: Identify the given values
First term \((a)=3\)
Sum of first four terms \(\left(S_4\right): T_1+T_2+T_3+T_4\)
Sum of the next four terms: \(T_5+T_6+T_7+T_8\)
We are told that:
\(
S_4=\frac{1}{5}\left(T_5+T_6+T_7+T_8\right)
\)
Step 2: Set up the equation for the common difference (d)
The “sum of the next four terms” can be written as the sum of the first eight terms minus the sum of the first four terms ( \(S_8-S_4\) ). So the equation becomes:
\(
S_4=\frac{1}{5}\left(S_8-S_4\right)
\)
Multiply both sides by 5:
\(
5 S_4=S_8-S_4 \Longrightarrow 6 S_4=S_8
\)
Now, substitute the sum formula into the equation:
\(
\begin{aligned}
6\left[\frac{4}{2}(2(3)+3 d)\right] & =\frac{8}{2}(2(3)+7 d) \\
6[2(6+3 d)] & =4(6+7 d) \\
12(6+3 d) & =4(6+7 d)
\end{aligned}
\)
Divide both sides by 4 :
\(
\begin{gathered}
3(6+3 d)=6+7 d \\
18+9 d=6+7 d \\
2 d=-12 \Longrightarrow d=-6
\end{gathered}
\)
Step 3: Calculate the sum of the first 20 terms ( \(S_{20}\) )
Now that we have \(a=3\) and \(d=-6\) :
\(
\begin{gathered}
S_{20}=\frac{20}{2}[2(3)+(20-1)(-6)] \\
S_{20}=10[6+19(-6)] \\
S_{20}=10[6-114] \\
S_{20}=10[-108]=-1080
\end{gathered}
\)

Hint

(d) Step 1: Define the terms and sums
The A.P. has \(2 k\) terms, with the first term \(a_1\) and common difference \(d\). The sum of the odd terms ( \(\boldsymbol{S}_{\text {odd }}\) ) and even terms ( \(\boldsymbol{S}_{\text {even }}\) ) can be expressed as:
\(
\begin{gathered}
S_{\text {odd }}=k\left[a_1+(k-1) d\right]=40 \\
S_{\text {even }}=k\left(a_1+k d\right)=55
\end{gathered}
\)
Step 2: Use the last term condition
The last term exceeds the first term by 27 :
\(
\begin{gathered}
\left(a_1+(2 k-1) d\right)-a_1=27 \\
(2 k-1) d=27
\end{gathered}
\)
Step 3: Solve the system of equations
Subtract the equation for \(S_{\text {odd }}\) from the equation for \(S_{\text {even }}\) :
\(
\begin{gathered}
k\left(a_1+k d\right)-k\left[a_1+(k-1) d\right]=55-40 \\
k a_1+k^2 d-k a_1-k(k-1) d=15 \\
k^2 d-\left(k^2-k\right) d=15 \\
k^2 d-k^2 d+k d=15 \\
k d=15
\end{gathered}
\)
Substitute \(d=\frac{15}{k}\) into the equation from Step 2:
\(
\begin{gathered}
(2 k-1) \frac{15}{k}=27 \\
15(2 k-1)=27 k \\
30 k-15=27 k \\
3 k=15 \\
k=5
\end{gathered}
\)

Hint

(b) To solve this, we define the terms of the Geometric Progression (G.P.) as \(a_1=a_1 a_2=a r\), \(a_3=a r^2\), and so on. Since the terms are increasing and positive, we know that \(a>0\) and \(r>1\).
Step 1: We are given two pieces of information:
Product of terms: \(a_1 a_5=28\)
\(
a \cdot\left(a r^4\right)=28 \Longrightarrow a^2 r^4=28 \Longrightarrow\left(a r^2\right)^2=28
\)
Taking the square root (since terms are positive):
\(
a r^2=\sqrt{28}=2 \sqrt{7} \dots(1)
\)
(Note: \(a r^2\) is the third term, \(a_3\).)
Sum of terms: \(a_2+a_4=29\)
\(a r+a r^3=29 \Longrightarrow a r\left(1+r^2\right)=29 \dots(2)\)
Step 2: Solve for \(r^2\)
From (Eq. 1), we can express \(a\) in terms of \(r\) :
\(
a=\frac{2 \sqrt{7}}{r^2}
\)
Substitute this into (Eq. 2):
\(
\begin{gathered}
\left(\frac{2 \sqrt{7}}{r^2}\right) r\left(1+r^2\right)=29 \\
\frac{2 \sqrt{7}\left(1+r^2\right)}{r}=29 \Longrightarrow 2 \sqrt{7}\left(1+r^2\right)=29 r
\end{gathered}
\)
This is a quadratic-like equation in \(r\) :
\(
2 \sqrt{7} r^2-29 r+2 \sqrt{7}=0
\)
Using the quadratic formula \(r=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\) :
\(
\begin{gathered}
r=\frac{29 \pm \sqrt{29^2-4(2 \sqrt{7})(2 \sqrt{7})}}{2(2 \sqrt{7})} \\
r=\frac{29 \pm \sqrt{841-112}}{4 \sqrt{7}}=\frac{29 \pm \sqrt{729}}{4 \sqrt{7}}=\frac{29 \pm 27}{4 \sqrt{7}}
\end{gathered}
\)
We get two possible values for \(r\) :
\(r=\frac{29+27}{4 \sqrt{7}}=\frac{56}{4 \sqrt{7}}=\frac{14}{\sqrt{7}}=2 \sqrt{7}\)
\(r=\frac{29-27}{4 \sqrt{7}}=\frac{2}{4 \sqrt{7}}=\frac{1}{2 \sqrt{7}}\)
Since the G.P. consists of increasing terms, \(r\) must be greater than 1. Thus, \(r=2 \sqrt{7}\).
Step 3: Calculate \(a_6\)
We need to find \(a_6=a r^5\). We can rewrite this using \(a_3\) (which is \(a r^2\) ):
\(
a_6=\left(a r^2\right) \cdot r^3
\)
Substitute \(a r^2=2 \sqrt{7}\) (from Eq. 1) and \(r=2 \sqrt{7}\) :
\(
\begin{gathered}
a_6=(2 \sqrt{7}) \cdot(2 \sqrt{7})^3 \\
a_6=(2 \sqrt{7})^4 \\
a_6=2^4 \cdot(\sqrt{7})^4=16 \cdot 49 \\
a_6=784
\end{gathered}
\)

Hint

(c) To solve this, we use the formula for the sum of an infinite Geometric Progression (G.P.): \(S_{\infty}= \frac{a}{1-r}\), where \(|r|<1\).
Step 1: Set up the equations for the two series
First series: \(\sum_{n=0}^{\infty} a r^n=57\)
\(
\frac{a}{1-r}=57 \Longrightarrow a=57(1-r) \dots(1)
\)
Second series: \(\sum_{n=0}^{\infty} a^3 r^{3 n}=9747\) This is an infinite G.P. with first term \(a^3\) and common ratio \(r^3\).
\(
\frac{a^3}{1-r^3}=9747 \dots(2)
\)
Step 2: Solve for \(r\)
Substitute \(a\) from (Eq. 1) into (Eq. 2):
\(
\frac{[57(1-r)]^3}{1-r^3}=9747
\)
\(
\frac{57^3(1-r)^3}{(1-r)\left(1+r+r^2\right)}=9747
\)
Using the identity \(1-r^3=(1-r)\left(1+r+r^2\right)\), we can cancel one factor of \((1-r)\) :
\(
\frac{57^3(1-r)^2}{1+r+r^2}=9747
\)
Note that \(57^3=57 \times 57 \times 57=185193\). Let’s simplify the constant:
\(
\frac{185193}{9747}=19
\)
So, the equation becomes:
\(
19 \frac{(1-r)^2}{1+r+r^2}=1
\)
\(
\begin{aligned}
&19\left(1-2 r+r^2\right)=1+r+r^2\\
&19-38 r+19 r^2=1+r+r^2\\
&18 r^2-39 r+18=0
\end{aligned}
\)
\(
6 r^2-13 r+6=0
\)
Step 3: Find the value of \(r\) and \(a\)
Factor the quadratic:
\(
(2 r-3)(3 r-2)=0
\)
This gives \(r=\frac{3}{2}\) or \(r=\frac{2}{3}\). Since the sum of an infinite G.P. converges only if \(|r|<1\), we must have: \(r=\frac{2}{3}\)
Now, find \(a\) using (Eq. 1):
\(
a=57\left(1-\frac{2}{3}\right)=57\left(\frac{1}{3}\right)=19
\)
Step 4: Calculate \(a+18 r\)
Substitute \(a=19\) and \(r=\frac{2}{3}\) :
\(
\begin{gathered}
a+18 r=19+18\left(\frac{2}{3}\right) \\
=19+6(2) \\
=19+12=31
\end{gathered}
\)

Hint

(a) To solve this problem, we recognize the series as a telescoping sum. Each term is in the form \(\frac{1}{T_n T_{n+1}}\) where the terms in the denominator belong to an Arithmetic Progression (A.P.) with a common difference \(d\).
Step 1: General Term Decomposition
The general term of the series can be written as:
\(
T_r=\frac{1}{(1+(r-1) d)(1+r d)}
\)
We can split this using the method of differences. Notice that the difference between the two factors in the denominator is \((1+r d)-(1+(r-1) d)=d\). Therefore:
\(
\begin{gathered}
\frac{1}{(1+(r-1) d)(1+r d)}=\frac{1}{d}\left[\frac{(1+r d)-(1+(r-1) d)}{(1+(r-1) d)(1+r d)}\right] \\
\frac{1}{(1+(r-1) d)(1+r d)}=\frac{1}{d}\left[\frac{1}{1+(r-1) d}-\frac{1}{1+r d}\right]
\end{gathered}
\)
Step 2: Expand the Telescoping Series
Let the sum be \(S\). Applying the decomposition to all 10 terms:
\(
S=\frac{1}{d}\left[\left(\frac{1}{1}-\frac{1}{1+d}\right)+\left(\frac{1}{1+d}-\frac{1}{1+2 d}\right)+\cdots+\left(\frac{1}{1+9 d}-\frac{1}{1+10 d}\right)\right]
\)
In this telescoping sum, all intermediate terms cancel out, leaving only the first and the last terms:
\(
S=\frac{1}{d}\left[1-\frac{1}{1+10 d}\right]
\)
Step 3: Solve for d
We are given that \(S=5\).
\(
\begin{gathered}
5=\frac{1}{d}\left[\frac{(1+10 d)-1}{1+10 d}\right] \\
5=\frac{1}{d}\left[\frac{10 d}{1+10 d}\right] \\
5=\frac{10}{1+10 d}
\end{gathered}
\)
\(
\begin{aligned}
&5(1+10 d)=10\\
&1+10 d=2\\
&10 d=1 \Longrightarrow d=\frac{1}{10}
\end{aligned}
\)
Step 4: Calculate \(50 d\)
Substitute the value of \(d\) :
\(
50 d=50 \times \frac{1}{10}=5
\)

Hint

(c) Step 1: Define the geometric progression and conditions
Let the first term of the increasing geometric progression (GP) be \(a\) and the common ratio be \(r\). The terms are given by \(a_n=a r^{n-1}\). The problem states all terms are positive and the GP is increasing, so we have \(a>0\) and \(r>1\). The given conditions are:
Sum of the second and sixth terms: \(a_2+a_6=a r+a r^5=\frac{70}{3}\)
Product of the third and fifth terms: \(a_3 \cdot a_5=\left(a r^2\right)\left(a r^4\right)=49\)
Step 2: Use the product condition to find ar \(^3\)
The product condition simplifies to \(a^2 r^6=49\), which can be written as \(\left(a r^3\right)^2=49\). Taking the square root and noting all terms are positive:
\(
a r^3=7
\)
This value \(a r^3\) is the fourth term of the GP, \(a_4\).
Step 3: Use the sum condition to find the common ratio \(r\)
We can substitute \(a=\frac{7}{r^3}\) into the sum condition:
\(
\begin{gathered}
a r+a r^5=a r\left(1+r^4\right)=\frac{70}{3} \\
\frac{7}{r^3} \cdot r \cdot\left(1+r^4\right)=\frac{70}{3} \\
\frac{7\left(1+r^4\right)}{r^2}=\frac{70}{3} \\
21\left(1+r^4\right)=70 r^2
\end{gathered}
\)
Dividing by 7 gives \(3\left(1+r^4\right)=10 r^2\), which rearranges to a quadratic in \(r^2\) :
\(
3 r^4-10 r^2+3=0
\)
Factoring the equation as \(\left(3 r^2-1\right)\left(r^2-3\right)=0\) yields two possible values for \(r^2\) : \(r^2=\frac{1}{3}\) or \(r^2=3\). Since \(r>1\), we choose \(r^2=3\), so \(r=\sqrt{3}\).
Step 4: Calculate the required sum
We need to find the sum of the \(4^{\text {th }}, 6^{\text {th }}\), and \(8^{\text {th }}\) terms: \(S=a_4+a_6+a_8\). Using \(a_4=a r^3=7\) and \(r^2=3\) :
\(
\begin{gathered}
a_6=a r^5=a r^3 \cdot r^2=7 \cdot 3=21 \\
a_8=a r^7=a r^3 \cdot r^4=7 \cdot\left(r^2\right)^2=7 \cdot 3^2=7 \cdot 9=63
\end{gathered}
\)
The sum is \(S=7+21+63=91\).

Hint

(b)

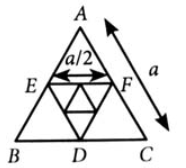
To solve this, let the side length of the initial equilateral triangle \(A B C\) be \(a\).
Step 1: Find the Sum of Perimeters ( \(P\) )
When you join the midpoints of an equilateral triangle, the side length of the new triangle is exactly half of the previous one.
Perimeter of 1st triangle ( \(P_1[latex] ): [latex]3 a\)
Perimeter of 2 nd triangle \(\left(P_2\right): 3\left(\frac{a}{2}\right)\)
Perimeter of 3rd triangle ( \(P_3[latex] ): [latex]3\left(\frac{a}{4}\right)\)
This is an infinite G.P. with first term \(3 a\) and common ratio \(r=1 / 2\) :
\(
P=\frac{3 a}{1-1 / 2}=6 a
\)
Step 2: Find the Sum of Areas (Q)
The area of an equilateral triangle with side \(a\) is \(\frac{\sqrt{3}}{4} a^2\). When the side is halved, the area becomes \((1 / 2)^2=1 / 4\) of the original area.
Area of 1st triangle \(\left(Q_1\right): \frac{\sqrt{3}}{4} a^2\)
Area of 2 nd triangle \(\left(Q_2\right): \frac{\sqrt{3}}{4}\left(\frac{a}{2}\right)^2=\frac{1}{4} Q_1\)
This is an infinite G.P. with first term \(\frac{\sqrt{3}}{4} a^2[latex] and common ratio [latex]r=1 / 4\) :
\(
Q=\frac{\frac{\sqrt{3}}{4} a^2}{1-1 / 4}=\frac{\frac{\sqrt{3}}{4} a^2}{3 / 4}=\frac{\sqrt{3} a^2}{3}=\frac{a^2}{\sqrt{3}}
\)
Step 3: Establish the Relationship between \(P\) and \(Q\)
We have:
\(P=6 a \Longrightarrow a=\frac{P}{6}\)
\(Q=\frac{a^2}{\sqrt{3}}\)
Substitute the value of \(a\) from the first equation into the second:
\(
\begin{aligned}
&\begin{aligned}
Q & =\frac{(P / 6)^2}{\sqrt{3}} \\
Q & =\frac{P^2}{36 \sqrt{3}}
\end{aligned}\\
&\text { Rearranging for } P^2 \text { : }\\
&P^2=36 \sqrt{3} Q
\end{aligned}
\)

Hint

(c) To solve this problem, we need to equate the total amount of “work” required to finish the assignment. We can define work in terms of “system-days”.
Step 1: Calculate Total Work Required
If \(m\) computer systems can finish the assignment in 17 days, the total work \(W\) is:
\(
\mathrm{W}=17 \mathrm{~m}
\)
Step 2: Calculate Work Done with Crashes
According to the problem, systems start crashing from the second day onwards. The assignment eventually took 8 more days, meaning it took \(17+8=25\) days in total.
The number of systems working each day forms an Arithmetic Progression (A.P.):
Day 1: \(m\) systems
Day 2: \((m-4)\) systems
Day 3: \((m-8)\) systems
… and so on for 25 days.
The total work done is the sum of this A.P. for \(n=25\) terms, where the first term \(a=m\) and the common difference \(d=-4\).
Using the sum formula \(S_n=\frac{n}{2}[2 a+(n-1) d]\) :
\(
\begin{gathered}
W=\frac{25}{2}[2 m+(25-1)(-4)] \\
W=\frac{25}{2}[2 m+24(-4)] \\
W=\frac{25}{2}[2 m-96] \\
W=25(m-48)
\end{gathered}
\)
Step 3: Equate the Work
Since the total work remains the same, we set the two expressions for \(W\) equal to each other:
\(
\begin{aligned}
& 17 m=25(m-48) \\
& 17 m=25 m-1200
\end{aligned}
\)
Rearrange the equation to solve for \(m\) :
\(
\begin{gathered}
1200=25 m-17 m \\
1200=8 m \\
m=\frac{1200}{8} \\
m=150
\end{gathered}
\)

Hint

(a) To find the value of \(K\), we use the property of an Arithmetic Progression (A.P.): if \(A, B, C\) are in A.P., then \(2 B=A+C\).
Step 1: Set up the Equation
Given terms:
\(A=4^{1+x}+4^{1-x}\)
\(B=\frac{K}{2}\)
\(C=16^x+16^{-x}\)
Applying the A.P. condition \(2\left(\frac{K}{2}\right)=A+C\) :
\(
\begin{aligned}
& K=\left(4^{1+x}+4^{1-x}\right)+\left(16^x+16^{-x}\right) \\
& K=4 \cdot 4^x+\frac{4}{4^x}+\left(4^x\right)^2+\left(4^x\right)^{-2}
\end{aligned}
\)
Step 2: Apply AM-GM Inequality
Let \(t=4^x\). Since \(x \geq 0\), then \(t=4^x \geq 4^0\), so \(t \geq 1\). The expression for \(K\) becomes:
\(
\begin{gathered}
K=4 t+\frac{4}{t}+t^2+\frac{1}{t^2} \\
K=4\left(t+\frac{1}{t}\right)+\left(t^2+\frac{1}{t^2}\right)
\end{gathered}
\)
To find the least value of \(K\), we look at the behavior of the function \(f(t)=4\left(t+\frac{1}{t}\right)+\left(t^2+\right. \left.\frac{1}{t^2}\right)\) for \(t \geq 1\). Both \(\left(t+\frac{1}{t}\right)\) and \(\left(t^2+\frac{1}{t^2}\right)\) are increasing functions for \(t \geq 1\).
Step 3: Find the Minimum Value
Since the function is monotonically increasing for \(t \geq 1\), the minimum value occurs at the smallest possible value of \(t\), which is \(t=1\) (at \(x=0\)).
Substitute \(t=1\) into the expression for \(K\) :
\(
\begin{gathered}
K_{\min }=4\left(1+\frac{1}{1}\right)+\left(1^2+\frac{1}{1^2}\right) \\
K_{\min }=4(2)+(2) \\
K_{\min }=8+2=10
\end{gathered}
\)

Hint

(b) To solve this, we will find the values of \(m\) and \(n\) individually. Both expressions are telescoping series, where terms cancel out to leave only the first and last values.
Step 1: Find the value of \(m\)
The general term of the first series is \(\frac{1}{\sqrt{r}+\sqrt{r+1}}\). We can rationalize the denominator:
\(
\frac{1}{\sqrt{r}+\sqrt{r+1}} \cdot \frac{\sqrt{r+1}-\sqrt{r}}{\sqrt{r+1}-\sqrt{r}}=\frac{\sqrt{r+1}-\sqrt{r}}{(r+1)-r}=\sqrt{r+1}-\sqrt{r}
\)
Now, expand the sum for \(m\) :
\(
m=(\sqrt{2}-\sqrt{1})+(\sqrt{3}-\sqrt{2})+(\sqrt{4}-\sqrt{3})+\cdots+(\sqrt{100}-\sqrt{99})
\)
All intermediate terms cancel out:
\(
m=\sqrt{100}-\sqrt{1}=10-1=9
\)
Step 2: Find the value of \(n\)
The general term of the second series is \(\frac{1}{r(r+1)}\). We can use partial fractions:
\(
\frac{1}{r(r+1)}=\frac{1}{r}-\frac{1}{r+1}
\)
Now, expand the sum for \(n\) :
\(
n=\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\cdots+\left(\frac{1}{99}-\frac{1}{100}\right)
\)
Again, all intermediate terms cancel out:
\(
n=1-\frac{1}{100}=\frac{99}{100}
\)
Step 3: Identify the Line
We have the point \((m, n)=\left(9, \frac{99}{100}\right)\). Let’s test this point in the given options:
Option (A): \(11(x-1)-100 y=0\) Substitute \(x=9, y=99 / 100\) :
\(
11(9-1)-100\left(\frac{99}{100}\right)=11(8)-99=88-99=-11 \neq 0
\)
Option (B): \(11 x-100 y=0\)
\(
11(9)-100\left(\frac{99}{100}\right)=99-99=0
\)
Since the point \(\left(9, \frac{99}{100}\right)\) satisfies the equation \(11 x-100 y=0\), the correct option is (B).
Final Answer: The point \((m, n)\) lies on the line \(11 x-100 y=0\).

Hint

(a) Step 1: Express the sums using summation notation
The problem can be written using summation notation to represent the numerator and denominator:
\(
\frac{1 \times 2^2+2 \times 3^2+\ldots+100 \times(101)^2}{1^2 \times 2+2^2 \times 3+\ldots+100^2 \times 101}=\frac{\sum_{n=1}^{100} n(n+1)^2}{\sum_{n=1}^{100} n^2(n+1)}
\)
Step 2: Expand the terms inside the summations
Expand the terms in the numerator and denominator to make use of standard summation formulas:
\(
\frac{\sum_{n=1}^{100} n\left(n^2+2 n+1\right)}{\sum_{n=1}^{100}\left(n^3+n^2\right)}=\frac{\sum_{n=1}^{100}\left(n^3+2 n^2+n\right)}{\sum_{n=1}^{100}\left(n^3+n^2\right)}
\)
Step 3: Apply standard summation formulas
Use the formulas for the sum of the first \(N\) integers, squares, and cubes, where \(N=100 ;\)
\(\sum n=\frac{N(N+1)}{2}\)
\(\sum n^2=\frac{N(N+1)(2 N+1)}{6}\)
\(\sum n^3=\left(\frac{N(N+1)}{2}\right)^2\)
Substitute \(N=100\) into the expression:
\(
\frac{\left(\frac{100(101)}{2}\right)^2+\frac{2 \cdot 100(101)(201)}{6}+\frac{100(101)}{2}}{\left(\frac{100(101)}{2}\right)^2+\frac{100(101)(201)}{6}}
\)
Step 4: Simplify the expression algebraically and calculate the final value
To simplify, factor out common terms like \(\frac{100(101)}{2}\) from both the numerator and the denominator. After algebraic manipulation and calculation, the expression simplifies to the final fraction:
\(
=\frac{300(101)+4(201)+6}{300(101)+2(201)}=\frac{305}{301}
\)

Hint

(a) Step 1: Formulate equations and find b
The given conditions are translated into the following equations:
AP condition: \(2 b=a+c\)
GP condition: \(b^2=(a+1)(c+3)\)
Arithmetic mean: \(\frac{a+b+c}{3}=8 \Longrightarrow a+b+c=24\)
Substituting the AP condition into the arithmetic mean equation: \(2 b+b=24\), which simplifies to \(3 b=24\).
Solving for \(b\), we find \(b=8\).
Step 2: Solve for a and c
From \(a+c=24-b\), we get \(a+c=16\), so \(c=16-a\).
Substitute \(b=8\) and \(c=16-a\) into the GP condition:
\(
\begin{gathered}
8^2=(a+1)((16-a)+3) \\
64=(a+1)(19-a) \\
64=19 a-a^2+19-a \\
a^2-18 a+45=0
\end{gathered}
\)
Factoring the quadratic equation yields \((a-3)(a-15)=0\). The possible values for \(a\) are 3 and 15. Given the condition \(a>10\), we select \(a=15\).
Then \(c=16-15=1\).
The numbers are \(a=15, b=8\), and \(c=1\).
Step 3: Calculate the cube of the geometric mean
The geometric mean (GM) of \(a, b, c\) is \(\sqrt[3]{a b c}\). The cube of the geometric mean is \(a b c\).
\(
a b c=15 \times 8 \times 1=120
\)

Hint

(c) Step 1: Define the terms of the G.P. and A.P.
Let the first term of the G.P. be \(a_g=2\) and the common ratio be \(r\). The terms are \(2,2 r\), and \(2 r^2\).
Let the first term of the A.P. be \(\boldsymbol{A}\) and the common difference be \(\boldsymbol{d}\). The terms are \(A+(k-1) d\).
Step 2: Formulate equations based on the given relationships
The terms \(2, p\), and \(q\) are the \(7^{\text {th }}, 8^{\text {th }}\), and \(13^{\text {th }}\) terms of the A.P., respectively:
\(2=A+6 d\)
\(p=2 r=A+7 d\)
\(q=2 r^2=A+12 d\)
Step 3: Solve for the common ratio of the G.P. (r)
Subtract the first equation from the second to find \(d\) :
\(
d=(A+7 d)-(A+6 d)=2 r-2
\)
Subtract the second equation from the third:
\(
(A+12 d)-(A+7 d)=2 r^2-2 r \Longrightarrow 5 d=2 r^2-2 r
\)
Substitute the expression for \(d\) into the second difference equation:
\(
5(2 r-2)=2 r^2-2 r
\)
\(
\begin{gathered}
10 r-10=2 r^2-2 r \Longrightarrow 2 r^2-12 r+10=0 \\
r^2-6 r+5=0 \Longrightarrow(r-1)(r-5)=0
\end{gathered}
\)
The possible values for \(r\) are 1 and 5. Since \(q \neq 2\), we have \(2 r^2 \neq 2 \Longrightarrow r^2 \neq 1 \Longrightarrow r \neq 1\). Therefore, we use \(r=5\).
Step 4: Find the common difference ( \(\boldsymbol{d}\) ) and the first term ( \(\boldsymbol{A}\) ) of the A.P.
Using \(r=5\), the common difference is:
\(
d=2 r-2=2(5)-2=8
\)
Using \(d=8\), the first term of the A.P. is:
\(
A=2-6 d=2-6(8)=2-48=-46
\)
Step 5: Find the \(5^{\text {th }}\) term of the G.P.
The \(5^{\text {th }}\) term of the G.P. is \(g_5=a_g r^{5-1}=2 r^4\).
\(
g_5=2(5)^4=2(625)=1250
\)
Step 6: Find \(n\) such that the \(5^{\text {th }}\) term of the G.P. is the \(n^{\text {th }}\) term of the A.P.
We set the \(n^{\text {th }}\) term of the A.P., \(A_n=A+(n-1) d\), equal to the \(5^{\text {th }}\) term of the G.P., \(g_5\) :
\(
\begin{gathered}
A+(n-1) d=1250 \\
-46+(n-1) 8=1250
\end{gathered}
\)
\(
\begin{gathered}
8(n-1)=1250+46=1296 \\
n-1=\frac{1296}{8}=162 \\
n=162+1=163
\end{gathered}
\)

Hint

(c) To solve this, we will find the first term \(a\) and the common difference \(d\) of the Arithmetic Progression (A.P.) using the given conditions.
STep 1: Set up the equations
We are given the sum of the first 10 terms ( \(S_{10}\) ) and the ratio of terms \(T_{10}\) and \(T_5\).
From \(S_{10}=390\) : Using the formula \(S_n=\frac{n}{2}[2 a+(n-1) d]\) :
\(
\begin{gathered}
\frac{10}{2}[2 a+9 d]=390 \\
5(2 a+9 d)=390 \\
2 a+9 d=78 \dots(1)
\end{gathered}
\)
From the ratio \(\frac{T_{10}}{T_5}=\frac{15}{7}\) : Using the formula \(T_n=a+(n-1) d\).
\(
\frac{a+9 d}{a+4 d}=\frac{15}{7}
\)
Cross-multiply to solve:
\(
\begin{aligned}
& 7(a+9 d)=15(a+4 d) \\
& 7 a+63 d=15 a+60 d
\end{aligned}
\)
\(
3 d=8 a \Longrightarrow d=\frac{8 a}{3} \dots(2)
\)
Step 2: Solve for \(a\) and \(d\)
Substitute (Eq. 2) into (Eq. 1):
\(
\begin{gathered}
2 a+9\left(\frac{8 a}{3}\right)=78 \\
2 a+3(8 a)=78 \\
2 a+24 a=78 \\
26 a=78 \Longrightarrow a=3
\end{gathered}
\)
Now, find \(d\) using (Eq. 2):
\(
d=\frac{8(3)}{3}=8
\)
Step 3: Calculate \(S_{15}-S_5\)
The expression \(S_{15}-S_5\) represents the sum of terms from \(T_6\) to \(T_{15}\). This is a series of 10 terms where the first term is \(T_6\).
\(
\sum_{r=6}^{15} T_r=\frac{10}{2}\left[T_6+T_{15}\right]
\)
First, find \(T_6\) and \(T_{15}\) :
\(T_6=a+5 d=3+5(8)=43\)
\(T_{15}=a+14 d=3+14(8)=3+112=115\)
Now, calculate the sum:
\(
\begin{aligned}
& S_{15}-S_5=5[43+115] \\
& S_{15}-S_5=5[158]=790
\end{aligned}
\)
Final Answer: The value of \(S_{15}-S_5\) is 790.

Hint

(d) To solve this, we will find the common difference of the Arithmetic Progression (A.P.) and use it to satisfy the conditions of the Geometric Progression (G.P.).
Step 1: Define the terms in A.P.
Let \(d\) be the common difference of the A.P. starting with 3.
\(a=3+d\)
\(b=3+2 d\)
\(c=3+3 d\)
Step 2: Set up the G.P. terms
Substituting the values of \(a, b\), and \(c\) into the given G.P. sequence:
\(G_1=3\)
\(G_2=(3+d)-1=2+d\)
\(G_3=(3+2 d)+1=4+2 d=2(2+d)\)
\(G_4=(3+3 d)+9=12+3 d=3(4+d)\)
Step 3: Solve for \(d\)
In a G.P., the common ratio \(r\) must be constant between consecutive terms:
\(
\begin{gathered}
r=\frac{G_2}{G_1}=\frac{2+d}{3} \\
r=\frac{G_3}{G_2}=\frac{2(2+d)}{2+d}=2
\end{gathered}
\)
Equating the two expressions for \(r\) :
\(
\frac{2+d}{3}=2 \Longrightarrow 2+d=6 \Longrightarrow d=4
\)
Now, let’s verify if this \(d\) satisfies the fourth term: If \(d=4\), then \(r=2\). The fourth term should be \(G_3 \times r=(4+2(4)) \times 2=12 \times 2=24\). Checking \(G_4\) from our formula: \(3(4+4)= 3(8)=24\). Since it matches, \(d=4\) is the correct common difference.
Step 4: Find the Arithmetic Mean of \(a, b\), and \(c\)
Calculate the values:
\(a=3+4=7\)
\(b=3+8=11\)
\(c=3+12=15\)
The Arithmetic Mean (A.M.) is:
\(
\mathrm{A} . \mathrm{M} .=\frac{a+b+c}{3}=\frac{7+11+15}{3}=\frac{33}{3}=11
\)
Note: In any A.P., the arithmetic mean of three consecutive terms is always the middle term (b). Since we found \(b=11\), the mean is 11.
Final Answer: The arithmetic mean of \(a, b\), and \(c\) is 11.

Hint

(d) Step 1: Establish the Geometric Progression (GP) Condition
The terms \(1+d, 1+7 d\), and \(1+43 d\) are in a geometric progression (GP), meaning the ratio of consecutive terms is constant, which leads to the condition:
\(
(1+7 d)^2=(1+d)(1+43 d)
\)
Step 2: Solve for the Common Difference \(\boldsymbol{d}\)
Expanding the equation from Step 1 gives:
\(
1+14 d+49 d^2=1+44 d+43 d^2
\)
Rearranging the terms to solve for \(d\) :
\(
6 d^2-30 d=0
\)
Factoring the expression yields \(6 d(d-5)=0\), providing two possible values for the common difference: \(d=0\) or \(d=5\). The non-trivial solution used is \(d=5\).
Step 3: Calculate the Sum of the First 20 Terms
Assuming the arithmetic progression has a first term \(a=1\) and common difference \(d=5\), the sum of the first 20 terms ( \(S_{20}\) ) is calculated using the arithmetic series formula \(S_n=\frac{n}{2}[2 a+(n-1) d]\) :
\(
\begin{gathered}
S_{20}=\frac{20}{2}[2 \times 1+(20-1) \times 5] \\
S_{20}=10[2+95]=970
\end{gathered}
\)

Hint

(b) To solve this, we first examine the given quadratic equation:
\(
(a+b-2 c) x^2+(b+c-2 a) x+(c+a-2 b)=0
\)
Step 1: Find the roots of the equation
Notice that the sum of the coefficients is:
\(
(a+b-2 c)+(b+c-2 a)+(c+a-2 b)=(a+b+c+a+b+c)-(2 c+2 a+2 b
\)
Since the sum of coefficients is zero, \(x=1\) must be one root.
We are given that \(\alpha \neq 1\) is the other root. Using the product of roots formula (Product \(= \frac{\text { constant term }}{\text { coefficient of } x^2}\)):
\(
1 \cdot \alpha=\frac{c+a-2 b}{a+b-2 c} \Longrightarrow \alpha=\frac{a+c-2 b}{a+b-2 c}
\)
Step 2: Relate \(\alpha\) to Arithmetic Progression
Let’s check the condition if \(a, b, c\) were in A.P. If they were in A.P., then \(2 b=a+c\). In that case:
\(
\alpha=\frac{(a+c)-(a+c)}{a+b-2 c}=0
\)
Since we are given \(0<c<b<a\), we know the denominator \(a+b-2 c\) is positive.
Step 3: Analyze the condition for Geometric Mean
If \(b\) is the Geometric Mean (G.M.) of \(a\) and \(c\), then \(b^2=a c\). Since \(a, b, c\) are distinct and positive, we know from the AM-GM Inequality that the Arithmetic Mean is greater than the Geometric Mean:
\(
\frac{a+c}{2}>\sqrt{a c} \Longrightarrow \frac{a+c}{2}>b \Longrightarrow a+c-2 b>0
\)
Now let’s look at the numerator and denominator of \(\alpha\) :
Numerator \((a+c-2 b)\) : As shown above, if \(b=\sqrt{a c}[latex], the numerator is positive.
Denominator [latex](a+b-2 c)\) : Since \(a>c\) and \(b>c\), then \(a+b>2 c\), so the denominator is positive.
Therefore, if \(b\) is the G.M. of \(a\) and \(c\), then \(\alpha>0\).
Step 4: Evaluate the Statements
Statement (I): “If \(\alpha \in(-1,0)\), then \(b\) cannot be the G.M.” Since we proved that \(b=\) G.M. \(\Longrightarrow \alpha>0\), it is impossible for \(\alpha\) to be negative if \(b\) is the G.M. Thus, the statement is True.
Statement (II): “If \(\alpha \in(0,1)\), then \(b\) may be the G.M.” As established, \(b=\mathrm{G} . \mathrm{M}\). results in \(\alpha>0\). We need to check if \(\alpha<1\) :
\(
\alpha=\frac{a+c-2 b}{a+b-2 c}<1 \Longleftrightarrow a+c-2 b<a+b-2 c \Longleftrightarrow 3 c<3 b \Longleftrightarrow c<b
\)
Since \(c<b[latex] is given, [latex]\alpha<1\) is always true when \(b\) is the G.M. Thus, it is possible for \(b\) to be the G.M. in this interval. The statement is True.
Final Answer: Both (I) and (II) are true. The correct option is (b).

Hint

(b) Step 1: General Term Expression
The general term \(T_r\) of the series is:
\(
T_r=\frac{r}{1-3 r^2+r^4}
\)
Step 2: Factorizing the Denominator
The denominator \(r^4-3 r^2+1\) can be rewritten to facilitate factorization:
\(
\begin{gathered}
r^4-3 r^2+1=\left(r^4-2 r^2+1\right)-r^2 \\
=\left(r^2-1\right)^2-r^2
\end{gathered}
\)
Using the difference of squares identity \(x^2-y^2=(x-y)(x+y)\) :
\(
\begin{aligned}
& =\left(r^2-1-r\right)\left(r^2-1+r\right) \\
& =\left(r^2-r-1\right)\left(r^2+r-1\right)
\end{aligned}
\)
Step 3: Partial Fraction Decomposition
Now, express \(T_r\) as a difference of two terms:
\(
T_r=\frac{r}{\left(r^2-r-1\right)\left(r^2+r-1\right)}
\)
Notice that the difference between the two factors is \(\left(r^2+r-1\right)-\left(r^2-r-1\right)=2 r\).
Therefore:
\(
\begin{aligned}
& T_r=\frac{1}{2}\left[\frac{2 r}{\left(r^2-r-1\right)\left(r^2+r-1\right)}\right] \\
& T_r=\frac{1}{2}\left[\frac{1}{r^2-r-1}-\frac{1}{r^2+r-1}\right]
\end{aligned}
\)
Step 4: Telescoping the Sum
Let \(f(r)=\frac{1}{r^2-r-1}\). Then \(f(r+1)=\frac{1}{(r+1)^2-(r+1)-1}=\frac{1}{r^2+2 r+1-r-1-1}=\frac{1}{r^2+r-1}\). So, \(T_r= \frac{1}{2}[f(r)-f(r+1)]\).
Summing from \(r=1\) to \(r=10\) :
\(
S_{10}=\frac{1}{2} \sum_{r=1}^{10}[f(r)-f(r+1)]
\)
\(
S_{10}=\frac{1}{2}[f(1)-f(11)]
\)
STep 5: Calculate final value
\(f(1)=\frac{1}{1^2-1-1}=\frac{1}{-1}=-1\)
\(f(11)=\frac{1}{11^2+11-1}=\frac{1}{121+10}=\frac{1}{131}\) (Note: we use the \(f(r+1)\) form for the last term, where \(r=10\), so \(r^2+r-1\) becomes \(10^2+10-1=109\))
Wait, let’s re-calculate \(f(11)\) carefully using \(r=10\) in the second part of the bracket: The last term in the sum is \(T_{10}=\frac{1}{2}\left[\frac{1}{10^2-10-1}-\frac{1}{10^2+10-1}\right]=\frac{1}{2}\left[\frac{1}{89}-\frac{1}{109}\right]\).
So the telescoping sum is:
\(
\begin{gathered}
S_{10}=\frac{1}{2}\left[\frac{1}{1^2-1-1}-\frac{1}{10^2+10-1}\right] \\
S_{10}=\frac{1}{2}\left[-1-\frac{1}{109}\right] \\
S_{10}=\frac{1}{2}\left[\frac{-109-1}{109}\right] \\
S_{10}=\frac{1}{2}\left[\frac{-110}{109}\right] \\
S_{10}=-\frac{55}{109}
\end{gathered}
\)

Hint

(c) To solve this, we will find the common ratios for both Geometric Progressions (G.P.s) and then equate the specific terms provided.
Step 1: Analyze the First G.P.
Let the first G.P. have common ratio \(r_1\).
First term \(\left(G_1\right)=a\)
Third term \(\left(G_3\right)=a r_1^2=b \Longrightarrow r_1^2=\frac{b}{a}\)
We need the \(11^{\text {th }}\) term of this G.P.:
\(
T_{11}=a r_1^{10}=a\left(r_1^2\right)^5
\)
Substitute \(r_1^2=\frac{b}{a}\) :
\(
T_{11}=a\left(\frac{b}{a}\right)^5\dots(1)
\)
Step 2: Analyze the Second G.P.
Let the second G.P. have common ratio \(r_2\).
First term \(\left(g_1\right)=a\)
Fifth term \(\left(g_5\right)=a r_2^4=b \Longrightarrow r_2^4=\frac{b}{a}\)
We need the \(p^{\text {th }}\) term of this G.P.:
\(
t_p=a r_2^{p-1}
\)
Since \(r_2^4=\frac{b}{a}\), we can write \(r_2=\left(\frac{b}{a}\right)^{1 / 4}\). So:
\(
t_p=a\left(\frac{b}{a}\right)^{\frac{p-1}{4}} \dots(2)
\)
Step 3: Equate the Terms
The problem states that \(T_{11}\) of the first G.P. is equal to \(t_p\) of the second G.P.:
\(
a\left(\frac{b}{a}\right)^5=a\left(\frac{b}{a}\right)^{\frac{p-1}{4}}
\)
Since \(a\) and \(b\) are distinct positive real numbers, the base \(\frac{b}{a}\) is not equal to 1. We can equate the exponents:
\(
5=\frac{p-1}{4}
\)
Step 4: Solve for \(p\)
\(
\begin{gathered}
5 \times 4=p-1 \\
20=p-1 \\
p=21
\end{gathered}
\)

Hint

(d) Step 1: Formulate equations for \(\boldsymbol{a}\) and \(\boldsymbol{d}\)
Given the sum of the first 20 terms is 790 and the sum of the first 10 terms is 145 , we use the formula for the sum of an arithmetic series, \(S_n=\frac{n}{2}[2 a+(n-1) d]\).
We derive two equations:
\(
\begin{aligned}
& 2 a+19 d=79 \\
& 2 a+9 d=29
\end{aligned}
\)
Step 2: Solve for \(\boldsymbol{a}\) and \(\boldsymbol{d}\)
Subtracting the second equation from the first allows us to solve for \(d\) :
\((2 a+19 d)-(2 a+9 d)=79-29\), which gives \(10 d=50\), so \(d=5\). Substituting \(d=5\) into the second equation yields \(2 a+9(5)=29\), leading to \(2 a+45=29\), so \(2 a=-16\) , and \(a=-8\).
Thus, we have \(a=-8\) and \(d=5\).
Step 3: Calculate \(S_{15}-S_5\)
Using the values of \(a\) and \(d\), we calculate \(S_{15}-S_5\) :
\(
S_{15}-S_5=\frac{15}{2}[2 a+14 d]-\frac{5}{2}[2 a+4 d]
\)
Substituting the values:
\(
S_{15}-S_5=\frac{15}{2}[2(-8)+14(5)]-\frac{5}{2}[2(-8)+4(5)]=395
\)

Hint

(b) Step 1: First A.P.: From \(\ln a, \ln b, \ln c\), we get \(b^2=a c\).
Step 2: Second A.P.: From the second set, we get:
\(
\begin{gathered}
\left(\frac{2 b}{3 c}\right)^2=\left(\frac{a}{2 b}\right)\left(\frac{3 c}{a}\right) \\
\frac{4 b^2}{9 c^2}=\frac{3 c}{2 b} \Longrightarrow 8 b^3=27 c^3
\end{gathered}
\)
Taking the cube root of both sides:
\(
2 b=3 c \Longrightarrow \frac{b}{c}=\frac{3}{2}
\)
Step 3: Final Ratio: Using \(a=\frac{b^2}{c}\) :
\(
a=b\left(\frac{b}{c}\right)=b\left(\frac{3}{2}\right) \Longrightarrow \frac{a}{b}=\frac{3}{2}
\)
Combining these: \(a: b=3: 2\) and \(b: c=3: 2\). To align them:
\(
a: b: c=9: 6: 4
\)

Hint

(a) To solve this, we first need to determine the common ratio \((r)\) of the geometric progression (G.P.) based on the relationship provided between the terms.
Step 1: Determine the Common Ratio ( \(r\) )
Let the G.P. be \(a, a r, a r^2, \ldots\) where \(a=a_1=\frac{1}{8}\). We are told that each term is the arithmetic mean of the next two terms. For any term \(a_n\) :
\(
a_n=\frac{a_{n+1}+a_{n+2}}{2}
\)
Substitute the G.P. terms into this relation:
\(
a r^{n-1}=\frac{a r^n+a r^{n+1}}{2}
\)
Since \(a_1 \neq 0\), we can divide by \(a r^{n-1}\) :
\(
\begin{gathered}
1=\frac{r+r^2}{2} \\
r^2+r-2=0
\end{gathered}
\)
Now, solve the quadratic equation:
\(
(r+2)(r-1)=0
\)
This gives \(r=1\) or \(r=-2\). The problem states that \(a_2 \neq a_1\), which means \(r \neq 1\). Therefore, \(r=-2\).
Step 2: Identify \(S_{20}-S_{18}\)
The expression \(S_{20}-S_{18}\) represents the sum of the first 20 terms minus the sum of the first 18 terms. This leaves only the \(19^{\text {th }}\) and \(20^{\text {th }}\) terms:
\(
S_{20}-S_{18}=a_{19}+a_{20}
\)
Step 3: Calculate the terms
Using the formula \(a_n=a_1 \cdot r^{n-1}\) :
\(a_{19}=a_1 \cdot r^{18}=\frac{1}{8} \cdot(-2)^{18}\)
\(a_{20}=a_1 \cdot r^{19}=\frac{1}{8} \cdot(-2)^{19}\)
Now, sum them:
\(
S_{20}-S_{18}=\frac{1}{8}\left[(-2)^{18}+(-2)^{19}\right]
\)
Factor out \((-2)^{18}\) :
\(
\begin{gathered}
S_{20}-S_{18}=\frac{1}{8} \cdot(-2)^{18}[1+(-2)] \\
S_{20}-S_{18}=\frac{1}{8} \cdot 2^{18} \cdot(-1)
\end{gathered}
\)
Since \(8=2^3\) :
\(
S_{20}-S_{18}=-\frac{2^{18}}{2^3}=-2^{15}
\)
Step 4: Final Calculation \(2^{10}=1024\) and \(2^5=32\).
\(
2^{15}=1024 \times 32=32768
\)
So, \(S_{20}-S_{18}=-32768\).
Final Answer: The value of \(S_{20}-S_{18}\) is \(-2^{15}\) (or -32768 ).

Hint

(b) To solve this, let’s represent the Geometric Progression (G.P.) and the specific sums mentioned in the problem.
Step 1: Define the G.P. and Sums
Let the G.P. have \(n=64\) terms with first term \(a\) and common ratio \(r\). The terms are: \(a, a r, a r^2, a r^3, \ldots, a r^{63}\)
Sum of all terms (\(S_{\text {total }}\)):
\(
S_{\text {total }}=\frac{a\left(r^{64}-1\right)}{r-1}
\)
Sum of odd terms \(\left(S_{\text {odd }}\right)\) : The odd terms are the \(1^{\text {st }}, 3^{\text {rd }}, 5^{\text {th }}, \ldots, 63^{\text {rd }}\) terms: \(a, a r^2, a r^4, \ldots, a r^{62}\). This is a new G.P. where:
First term = a
Common ratio \(=r^2\)
Number of terms = 32 (half of 64 )
\(
S_{o d d}=\frac{a\left(\left(r^2\right)^{32}-1\right)}{r^2-1}=\frac{a\left(r^{64}-1\right)}{r^2-1}
\)
Step 2: Set up the Equation
The problem states that \(S_{\text {total }}=7 \times S_{\text {odd }}\) :
\(
\frac{a\left(r^{64}-1\right)}{r-1}=7 \times \frac{a\left(r^{64}-1\right)}{r^2-1}
\)
Step 3: Solve for \(r\)
Assuming \(r \neq 1\) and \(r^{64} \neq 1\), we can cancel \(a\left(r^{64}-1\right)\) from both sides:
\(
\frac{1}{r-1}=\frac{7}{r^2-1}
\)
We know that \(r^2-1=(r-1)(r+1)\). Substituting this:
\(
\frac{1}{r-1}=\frac{7}{(r-1)(r+1)}
\)
Multiply both sides by \((r-1)\) :
\(
\begin{gathered}
1=\frac{7}{r+1} \\
r+1=7 \\
r=6
\end{gathered}
\)
The common ratio of the G.P. is 6.

Hint

(d) Step 1: Express terms using the common difference
We are given the sixth term \(a_6=2\). The general term of an A.P. is \(a_n=a_1+(n-1) d\). We can express the required terms \(\left(a_1, a_4, a_5\right)\) in terms of \(a_6\) and the common difference, \(d\).
\(a_5=a_6-d=2-d\)
\(a_4=a_6-2 d=2-2 d\)
\(a_1=a_6-5 d=2-5 d\)
Step 2: Formulate the product function
The product to be maximized is \(\boldsymbol{P}=a_1 a_4 a_5\). Substituting the expressions from Step 1:
\(
P(d)=(2-5 d)(2-2 d)(2-d)
\)
Expanding this expression gives a cubic polynomial in \(d\) :
\(
P(d)=8-32 d+34 d^2-10 d^3
\)
Step 3: Use calculus to find critical points
To find the value of \(d\) that maximizes \(P(d)\), we take the first derivative with respect to \(d\) and set it to zero:
\(
\frac{d P}{d d}=-32+68 d-30 d^2
\)
Setting \(\frac{d P}{d d}=0\), we solve the quadratic equation \(30 d^2-68 d+32=0\), which simplifies to \(15 d^2-34 d+16=0\).
Using the quadratic formula \(d=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\) :
\(
d=\frac{34 \pm \sqrt{(-34)^2-4 \cdot 15 \cdot 16}}{2 \cdot 15}=\frac{34 \pm \sqrt{196}}{30}=\frac{34 \pm 14}{30}
\)
The two critical points are \(d_1=\frac{48}{30}=\frac{8}{5}\) and \(d_2=\frac{20}{30}=\frac{2}{3}\).
Step 4: Determine which critical point is a maximum
We use the second derivative test to determine the nature of the critical points. The second derivative of \(P(d)\) is:
\(
\frac{d^2 P}{d d^2}=68-60 d
\)
For \(d=\frac{8}{5}: \frac{d^2 P}{d d^2}=68-60\left(\frac{8}{5}\right)=68-96=-28<0\), which indicates a local maximum.
For \(d=\frac{2}{3}: \frac{d^2 P}{d d^2}=68-60\left(\frac{2}{3}\right)=68-40=28>0\), which indicates a local minimum.
The common difference that yields the greatest product is \(d=\frac{8}{5}\).

Hint

(a) Step 1: Identify the properties of the arithmetic progression (AP)
The given progression is an arithmetic progression (AP) with:
First term, \(a=20\)
Common difference, \(d=19 \frac{1}{4}-20=\frac{77}{4}-\frac{80}{4}=-\frac{3}{4}=-0.75\)
Last term, \(L=-129 \frac{1}{4}=-\frac{517}{4}=-129.25\)
Step 2: Form an AP from the end of the progression
To find the \(20^{\text {th }}\) term from the end, we can consider the AP in reverse order. The reversed AP has:
First term (of reversed AP), \(d^{\prime}=L=-\frac{517}{4}=-129.25\)
Common difference (of reversed AP), \(d^{\prime}=-d=-\left(-\frac{3}{4}\right)=\frac{3}{4}=0.75\)
Step 3: Calculate the 20th term of the reversed AP
The \(n^{\text {th }}\) term of an AP is given by the formula \(T_n=d^{\prime}+(n-1) d^{\prime}\). We want to find the \(20^{\text {th }}\) term from the beginning of the reversed AP (which is the \(20^{\text {th }}\) term from the end of the original AP).
Using \(d^{\prime}=-\frac{517}{4}, d^{\prime}=\frac{3}{4}\), and \(n=20\) :
\(
\begin{gathered}
T_{20}=d^{\prime}+(20-1) d^{\prime} \\
T_{20}=-\frac{517}{4}+(19)\left(\frac{3}{4}\right) \\
T_{20}=-\frac{517}{4}+\frac{57}{4} \\
T_{20}=\frac{-517+57}{4} \\
T_{20}=\frac{-460}{4} \\
T_{20}=-115
\end{gathered}
\)

Hint

(d) To find the number of common terms between two Arithmetic Progressions (A.P.s), we need to identify the first common term, the common difference of the common terms, and the upper limit of both sequences.
Step 1: Identify the sequences and their limits
Progression 1 (A): 4, 9, 14, 19, . .
First term \(\left(a_1\right)=4\)
Common difference \(\left(d_1\right)=5\)
\(25^{\text {th }}\) term \(\left(T_{25}\right)=4+(25-1) 5=4+120=124\)
Progression 2 (B): 3, 6, 9, 12, . .
First term \(\left(b_1\right)=3\)
Common difference \(\left(d_2\right)=3\)
\(37^{\text {th }}\) term \(\left(T_{37}^{\prime}\right)=3+(37-1) 3=3+108=111\)
The common terms must be less than or equal to the smaller of the two last terms.
\(
\text { Upper Limit }=\min (124,111)=111
\)
Step 2: Find the first common term
Looking at the sequences:
Sequence A: 4, 9, 14, 19, …
Sequence B: \(3,6,9,12, \ldots\) The first common term (a) is 9.
Step 3: Find the common difference of the common terms
The common terms themselves form an A.P. The common difference ( \(D\) ) of this new sequence is the Least Common Multiple (LCM) of the common differences of the original two sequences.
\(
D=\operatorname{LCM}\left(d_1, d_2\right)=\operatorname{LCM}(5,3)=15
\)
Step 4: Calculate the number of common terms
The common terms follow the sequence: \(9,24,39, \ldots\) up to a maximum of 111. Using the general term formula \(T_n=a+(n-1) D\) :
\(
\begin{gathered}
9+(n-1) 15 \leq 111 \\
(n-1) 15 \leq 102 \\
n-1 \leq \frac{102}{15} \\
n-1 \leq 6.8
\end{gathered}
\)
\(
n \leq 7.8
\)
Since \(n\) must be an integer, the maximum value for \(n\) is 7.
Final Answer: The number of common terms is 7.

Hint

(a) Step 1: Define the Arithmetic Means
When \(A_1\) and \(A_2\) are inserted between \(a\) and \(b\), the sequence \(a, A_1, A_2, b\) is in Arithmetic Progression (A.P.). The sum of \(n\) arithmetic means between \(a\) and \(b\) is given by \(n \times\left(\frac{a+b}{2}\right)\). For two means:
\(
A_1+A_2=2 \times \frac{a+b}{2}=a+b \dots(1)
\)
Step 2: Define the Geometric Means
When \(G_1, G_2, G_3\) are inserted between \(a[latex] and [latex]b\), the sequence \(a, G_1, G_2, G_3, b\) is in Geometric Progression (G.P.). Let \(r\) be the common ratio. Then \(b=a \cdot r^4 \Longrightarrow r=\left(\frac{b}{a}\right)^{1 / 4}\). The means are:
\(G_1=a \cdot r=a\left(\frac{b}{a}\right)^{1 / 4}=a^{3 / 4} b^{1 / 4}\)
\(G_2=a \cdot r^2=a\left(\frac{b}{a}\right)^{2 / 4}=\sqrt{a b}\)
\(G_3=a \cdot r^3=a\left(\frac{b}{a}\right)^{3 / 4}=a^{1 / 4} b^{3 / 4}\)
Step 3: Simplify the Terms of the Expression
We need to calculate each part of \(G_1^4+G_2^4+G_3^4+G_1^2 G_3^2\) :
\(G_1^4=\left(a^{3 / 4} b^{1 / 4}\right)^4=a^3 b\)
\(G_2^4=(\sqrt{a b})^4=a^2 b^2\)
\(G_3^4=\left(a^{1 / 4} b^{3 / 4}\right)^4=a b^3\)
\(G_1^2 G_3^2=\left(G_1 G_3\right)^2=\left(a^{3 / 4} b^{1 / 4} \cdot a^{1 / 4} b^{3 / 4}\right)^2=(a b)^2=a^2 b^2\)
Step 4: Evaluate the Expression
Substitute these back into the given expression:
\(
\begin{gathered}
E=a^3 b+a^2 b^2+a b^3+a^2 b^2 \\
E=a^3 b+2 a^2 b^2+a b^3
\end{gathered}
\)
Factor out \(a b\) :
\(
\begin{gathered}
E=a b\left(a^2+2 a b+b^2\right) \\
E=a b(a+b)^2
\end{gathered}
\)
Step 5: Final Substitution
From Step 1, we know \(a+b=A_1+A_2\). From Step 2, we know \(a b=G_2^2\) (or \(G_1 G_3\) ). Substituting these into our result:
\(
E=G_2^2\left(A_1+A_2\right)^2
\)
Since \(G_2^2=G_1 G_3\), this is also equivalent to:
\(
E=G_1 G_3\left(A_1+A_2\right)^2
\)
In the context of JEE Main 2023, the options provided for this question usually simplify to:
\(
G_1 G_3\left(A_1+A_2\right)^2
\)
Final Answer: The expression is equal to \(G_1 G_3\left(A_1+A_2\right)^2\).

Hint

(d) To solve this, we will find the first term \(a\) and the common ratio \(r\) of the Geometric Progression (G.P.) using the given conditions.
Step 1: Set up the equations
Let the G.P. be \(a, a r, a r^2, \ldots\) where \(a>0\) and \(r>1\) (since it is an increasing progression of positive numbers).
From the product of \(3^{\text {rd }}\) and \(5^{\text {th }}\) terms:
\(
\begin{gathered}
a_3 \cdot a_5=\frac{1}{9} \\
\left(a r^2\right) \cdot\left(a r^4\right)=\frac{1}{9} \\
a^2 r^6=\frac{1}{9}
\end{gathered}
\)
Taking the square root (since \(a, r>0\)):
\(
a r^3=\frac{1}{3} \Longrightarrow a=\frac{1}{3 r^3} \dots(1)
\)
From the sum of \(6^{\text {th }}\) and \(8^{\text {th }}\) terms:
\(
\begin{gathered}
a_6+a_8=2 \\
a r^5+a r^7=2
\end{gathered}
\)
Factor out \(a r^5\) :
\(
a r^5\left(1+r^2\right)=2 \dots(2)
\)
Step 2: Solve for \(r\) and \(a\)
Substitute \(a\) from (Eq. 1) into (Eq. 2):
\(
\begin{gathered}
\left(\frac{1}{3 r^3}\right) r^5\left(1+r^2\right)=2 \\
\frac{r^2}{3}\left(1+r^2\right)=2 \\
r^2\left(1+r^2\right)=6 \\
r^4+r^2-6=0
\end{gathered}
\)
Factor the quadratic in terms of \(r^2\) :
\(
\left(r^2+3\right)\left(r^2-2\right)=0
\)
Since \(r\) is a real number, \(r^2 \neq-3\). Thus:
\(
r^2=2 \Longrightarrow r=\sqrt{2}
\)
Now find \(a\) using (Eq. 1):
\(
a=\frac{1}{3(\sqrt{2})^3}=\frac{1}{3(2 \sqrt{2})}=\frac{1}{6 \sqrt{2}}
\)
Step 3: Evaluate the required expression
We need to find \(6\left(a_2+a_4\right)\left(a_4+a_6\right)\). Let’s simplify the factors first:
\(\left(a_2+a_4\right)=a r+a r^3=a r\left(1+r^2\right)\)
\(\left(a_4+a_6\right)=a r^3+a r^5=a r^3\left(1+r^2\right)\)
Multiplying them:
\(
\left(a_2+a_4\right)\left(a_4+a_6\right)=\left[a r\left(1+r^2\right)\right] \cdot\left[a r^3\left(1+r^2\right)\right]=a^2 r^4\left(1+r^2\right)^2
\)
Now substitute \(a=\frac{1}{6 \sqrt{2}}, r^2=2\), and \(r^4=4\) :
\(
\begin{gathered}
=\left(\frac{1}{6 \sqrt{2}}\right)^2 \cdot(4) \cdot(1+2)^2 \\
=\frac{1}{36 \cdot 2} \cdot 4 \cdot 9 \\
=\frac{1}{72} \cdot 36=\frac{1}{2}
\end{gathered}
\)
Finally, multiply by the constant 6:
\(
6 \times \frac{1}{2}=3
\)

Hint

(c) Step 1: Define the formula for \(s_i\)
The sum to \(n\) terms of an AP is given by \(S_n=\frac{n}{2}[2 a+(n-1) d]\). For the \(i\)-th AP, \(n=12\), the first term is \(a_i=i\), and the common difference is \(d_i=2 i-1\). The sum \(s_i\) is given by the formula:
\(
\begin{gathered}
s_i=\frac{12}{2}\left[2 a_i+(12-1) d_i\right] \\
s_i=6[2 i+11(2 i-1)]
\end{gathered}
\)
Step 2: Simplify the expression for \(\boldsymbol{s}_{\boldsymbol{i}}\)
Simplify the expression for \(s_i\) algebraically:
\(
\begin{gathered}
s_i=6[2 i+22 i-11] \\
s_i=6[24 i-11]
\end{gathered}
\)
Step 3: Calculate the total sum
The total sum required is \(\sum_{i=1}^{10} s_i\) :
\(
\begin{gathered}
\sum_{i=1}^{10} s_i=\sum_{i=1}^{10} 6[24 i-11] \\
\sum_{i=1}^{10} s_i=6\left(24 \sum_{i=1}^{10} i-\sum_{i=1}^{10} 11\right)
\end{gathered}
\)
Using the summation formula \(\sum_{i=1}^n i=\frac{n(n+1)}{2}\) with \(n=10\) :
\(
\begin{aligned}
&\sum_{i=1}^{10} i=\frac{10(11)}{2}=55\\
&\text { Substitute this value back into the equation: }\\
&\begin{gathered}
\sum_{i=1}^{10} s_i=6(24 \times 55-11 \times 10) \\
\sum_{i=1}^{10} s_i=6(1320-110) \\
\sum_{i=1}^{10} s_i=6(1210) \\
\sum_{i=1}^{10} s_i=7260
\end{gathered}
\end{aligned}
\)

Hint

(c) To solve this, we first find the expression for the \(n^{\text {th }}\) term \(a_n\) from the given sum \(S_n\), and then evaluate the required sum of reciprocals.
Step 1: Find the general term \(a_n\)
Let \(S_n=\frac{n^2+3 n}{(n+1)(n+2)}=\frac{n(n+3)}{(n+1)(n+2)}\). The \(n^{\text {th }}\) term is given by \(a_n=S_n-S_{n-1}\) for \(n>1\).
For \(n=1\) :
\(
a_1=S_1=\frac{1(4)}{2(3)}=\frac{4}{6}=\frac{2}{3}
\)
For \(n>1\) :
\(
a_n=\frac{n(n+3)}{(n+1)(n+2)}-\frac{(n-1)(n+2)}{n(n+1)}
\)
Taking common denominator \(n(n+1)(n+2)\) :
\(
a_n=\frac{n^2(n+3)-(n-1)(n+2)^2}{n(n+1)(n+2)}
\)
Expand the numerators:
\(
n^2(n+3)=n^3+3 n^2
\)
\(
(n-1)\left(n^2+4 n+4\right)=n^3+4 n^2+4 n-n^2-4 n-4=n^3+3 n^2-4
\)
Subtracting them:
\(
a_n=\frac{\left(n^3+3 n^2\right)-\left(n^3+3 n^2-4\right)}{n(n+1)(n+2)}=\frac{4}{n(n+1)(n+2)}
\)
Notably, for \(n=1, \frac{4}{1(2)(3)}=\frac{4}{6}=\frac{2}{3}\), which matches \(a_1\). So, the general formula is:
\(
a_n=\frac{4}{n(n+1)(n+2)}
\)
Step 2: Evaluate the sum of reciprocals
We need to find \(\sum_{k=1}^{10} \frac{1}{a_k}\) :
\(
\begin{gathered}
\frac{1}{a_k}=\frac{k(k+1)(k+2)}{4} \\
\sum_{k=1}^{10} \frac{1}{a_k}=\frac{1}{4} \sum_{k=1}^{10}\left(k^3+3 k^2+2 k\right)
\end{gathered}
\)
Using the standard summation formulas:
\(\sum k=\frac{n(n+1)}{2}=\frac{10 \cdot 11}{2}=55\)
\(\sum k^2=\frac{n(n+1)(2 n+1)}{6}=\frac{10 \cdot 11 \cdot 21}{6}=385\)
\(\sum k^3=\left(\frac{n(n+1)}{2}\right)^2=55^2=3025\)
Substitute these into the sum:
\(
\begin{gathered}
\operatorname{Sum}=\frac{1}{4}[3025+3(385)+2(55)] \\
\operatorname{Sum}=\frac{1}{4}[3025+1155+110]=\frac{4290}{4}=\frac{2145}{2}
\end{gathered}
\)
Step 3: Solve for \(m\)
Now, use the given equation:
\(
28 \times\left(\frac{2145}{2}\right)=p_1 p_2 \ldots p_m
\)
\(
14 \times 2145=p_1 p_2 \ldots p_m
\)
Find the prime factorization of \(14 \times 2145\) :
\(14=2 \times 7\)
\(2145=5 \times 429=5 \times 3 \times 143=5 \times 3 \times 11 \times 13\)
Combining all factors:
\(
\text { Product }=2 \times 3 \times 5 \times 7 \times 11 \times 13
\)
The product consists of the first 6 prime numbers \((2,3,5,7,11,13)\). Therefore, \(m=6\).
Final Answer: The value of \(m\) is 6.

Hint

(c) To find the maximum value of the expression \(a^5 b^3 c^2 d\) given the constraint \(a+b+c+d=\) 11, we use the Weighted AM-GM Inequality.
Step 1: Apply the Weighted AM-GM Inequality
The general principle is that for a product \(a^p b^q c^r d^s\) to be maximum while the sum \(a+b+ c+d\) is constant, the variables must be divided into \(p, q, r\), and \(s\) equal parts respectively.
Specifically, the maximum occurs when:
\(
\frac{a}{5}=\frac{b}{3}=\frac{c}{2}=\frac{d}{1}=k
\)
Step 2: Solve for the constant \(k\)
From the ratios above, we can express all variables in terms of \(k\) :
\(a=5 k\)
\(b=3 k\)
\(c=2 k\)
\(d=k\)
Substitute these into the sum constraint \(a+b+c+d=11\) :
\(
\begin{gathered}
5 k+3 k+2 k+k=11 \\
11 k=11 \Longrightarrow k=1=\frac{11}{5+3+2+1}
\end{gathered}
\)
So, the values that maximize the product are \(a=5, b=3, c=2\), and \(d=1\).
Step 3: Calculate the Maximum Value
Substitute these values into the expression \(a^5 b^3 c^2 d\) :
\(
\begin{gathered}
\text { Max Value }=(5)^5 \cdot(3)^3 \cdot(2)^2 \cdot(1)^1 \\
\text { Max Value }=3125 \cdot 27 \cdot 4 \cdot 1
\end{gathered}
\)
To make calculation easier, group the terms:
\(
\begin{gathered}
\text { Max Value }=3125 \cdot(27 \cdot 4) \\
\text { Max Value }=3125 \cdot 108 \\
3125 \times 100=312,500 \\
3125 \times 8=25,000 \\
\text { Max Value }=312,500+25,000=337,500
\end{gathered}
\)
Step 4: Solve for \(\beta\)
The problem states the maximum value is \(3750 \beta\) :
\(
\begin{gathered}
3750 \beta=337,500 \\
\beta=\frac{337,500}{3750}
\end{gathered}
\)
Divide both sides by 10 and then by 25 :
\(
\begin{gathered}
\beta=\frac{33,750}{375} \\
\beta=\frac{1,350}{15} \\
\beta=90
\end{gathered}
\)

Hint

(b) Step 1: Find the common difference of the arithmetic progression
The sum of an arithmetic progression with \(n\) terms is \(S_n=\frac{n}{2}\left(2 x_1+(n-1) d\right)\), where \(x_1\) is the first term and \(d\) is the common difference. The mean is \(\frac{S_n}{n}\).
We are given \(n=100, x_1=2\), and the mean is 200 .
\(
\frac{S_{100}}{100}=200 \Longrightarrow S_{100}=200 \times 100=20000
\)
Substitute the values into the sum formula:
\(
\begin{gathered}
20000=\frac{100}{2}(2(2)+(100-1) d) \\
20000=50(4+99 d) \\
400=4+99 d \\
396=99 d \\
d=\frac{396}{99}=4
\end{gathered}
\)
Step 2: Express \(x_i\) and \(y_i\) in terms of \(i\)
The \(i\)-th term of the arithmetic progression is given by \(x_i=x_1+(i-1) d\).
\(
x_i=2+(i-1) 4=2+4 i-4=4 i-2
\)
The expression for \(y_i\) is given as \(y_i=i\left(x_i-i\right)\).
\(
y_i=i((4 i-2)-i)=i(3 i-2)=3 i^2-2 i
\)
Step 3: Calculate the mean of \(y_1, y_2, \ldots, y_{100}\)
The mean of \(y_i\) is \(\frac{1}{100} \sum_{i=1}^{100} y_i=\frac{1}{100} \sum_{i=1}^{100}\left(3 i^2-2 i\right)\).
\(
\text { Mean }=\frac{1}{100}\left(3 \sum_{i=1}^{100} i^2-2 \sum_{i=1}^{100} i\right)
\)
Using the formulas \(\sum_{i=1}^n i=\frac{n(n+1)}{2}\) and \(\sum_{i=1}^n i^2=\frac{n(n+1)(2 n+1)}{6}\) for \(n=100\) :
\(
\begin{gathered}
\sum_{i=1}^{100} i=\frac{100 \times 101}{2}=5050 \\
\sum_{i=1}^{100} i^2=\frac{100 \times 101 \times 201}{6}=338350
\end{gathered}
\)
Substitute these sums back into the mean equation:
\(
\begin{gathered}
\text { Mean }=\frac{1}{100}(3 \times 338350-2 \times 5050) \\
\text { Mean }=\frac{1}{100}(1015050-10100) \\
\text { Mean }=\frac{1004950}{100} \\
\text { Mean }=10049.5
\end{gathered}
\)