Latest PYQs MCQs (Integer)
Overview
By a sequence, we mean an arrangement of numbers in a definite order according to some rule. We denote the terms of a sequence by \(a_1, a_2, a_3, \ldots\), etc., the subscript denotes the position of the term.
In view of the above a sequence in the set \(X\) can be regarded as a mapping or a function \(f: N \rightarrow X\) defined by
\(
f(n)=t_n \forall n \in N .
\)
Domain of \(f\) is a set of natural numbers or some subset of it denoting the position of term. If its range denoting the value of terms is a subset of \(R\) real numbers then it is called a real sequence. A sequence is either finite or infinite depending upon the number of terms in a sequence. We should not expect that its terms will be necessarily given by a specific formula. However, we expect a theoretical scheme or rule for generating the terms.
Let \(a_1, a_2, a_3, \ldots\), be the sequence, then, the expression \(a_1+a_2+a_3+\ldots\) is called the series associated with given sequence. The series is finite or infinite according as the given sequence is finite or infinite.
Remark
- When the series is used, it refers to the indicated sum not to the sum itself. Sequence following certain patterns are more often called progressions. In progressions, we note that each term except the first progresses in a definite manner.
Arithmetic progression (A.P.)
A. P. is a sequence in which each term except the first is obtained by adding a fixed number (positive or negative) to the preceding term. Thus any sequence \(a_1, a_2, a_3 \ldots a_n, \ldots\) is called an arithmetic progression if \(a_{n+1}=a_n+d, n \in N\), where \(d\) is called the common difference of the A.P., usually we denote the first term of an A.P by \(a\) and the last term by \(l\)
The general term or the \(n ^{\text {th }}\) term of the A.P. is given by
\(
\begin{aligned}
& a_n=a+(n-1) d \\
& a_n=l-(n-1) d
\end{aligned}
\)
The \(\operatorname{sum} S _n\) of the first \(n\) terms of an A.P. is given by \(S _n=\frac{n}{2}[2 a+(n-1) d]=\frac{n}{2}(a+l)\), where \(l=a+(n-1) d\) is the last terms of the A.P., and the general term is given by \(a_n= S _n- S _{n-1}\) The arithmetic mean for any \(n\) positive numbers \(a_1, a_2, a_3, \ldots a_n\) is given by
\(
\text { A.M. }=\frac{a_1+a_2+\ldots+a_n}{n}
\)
If \(a, A\) and \(b\) are in A.P., then A is called the arithmetic mean of numbers \(a\) and \(b\) and
\(
A =\frac{a+b}{2}
\)
If the terms of an A.P. are increased, decreased, multiplied or divided by the same constant, they still remain in A.P.
If \(a_1, a_2, a_3 \ldots\) are in A.P. with common difference \(d\), then
- \(a_1 \pm k, a_2 \pm k, a_3 \pm k, \ldots\) are also in A.P with common difference \(d\).
- \(a_1 k, a_2 k, a_3 k, \ldots\) are also in A.P with common difference \(d k(k \neq 0)\).
and \(\frac{a_1}{k}, \frac{a_2}{k}, \frac{a_3}{k} \ldots\) are also in A.P. with common difference \(\frac{d}{k}(k \neq 0)\).
If \(a_1, a_2, a_3 \ldots\) and \(b_1, b_2, b_3 \ldots\) are two A.P., then
- \(a_1 \pm b_1, a_2 \pm b_2, a_3 \pm b_3, \ldots\) are also in A.P.
- \(a_1 b_1, a_2 b_2, a_3 b_3, \ldots\) and \(\frac{a_1}{b_1}, \frac{a_2}{b_2}, \frac{a_3}{b_3}, \ldots\) are not in A.P.
If \(a_1, a_2, a_3 \ldots\) and \(a_n\) are in A.Ps, then
- \(a_1+a_n=a_2+a_{n-1}=a_3+a_{n-2}=\ldots\)
- \(a_r=\frac{a_{r-k}+a_{r+k}}{2} \forall k, 0 \leq k \leq n-r\)
- If \(n^{\text {th }}\) term of any sequence is linear expression in \(n\), then the sequence is an A.P.
- If sum of \(n\) terms of any sequence is a quadratic expression in \(n\), then sequence is an A.P.
A Geometric progression (G.P.)
G. P. is a sequence in which each term except the first is obtained by multiplying the previous term by a non-zero constant called the common ratio. Let us consider a G.P. with first non-zero term \(a\) and common ratio \(r\), i.e.,
\(
a, a r, a r^2, \ldots, a r^{n-1}, \ldots
\)
Here, common ratio \(r=\frac{a r^{n-1}}{a r^{n-2}}\)
The general term or \(n^{\text {th }}\) term of G.P. is given by \(a_n=a r^{n-1}\).
Last term \(l\) of a G.P. is same as the \(n^{\text {mim }}\) term and is given by \(l=a r^{n-1}\).
and the \(n^{\text {th }}\) term from the last is given by \(a_n=\frac{l}{r^{n-1}}\)
The sum \(S _n\) of the first \(n\) terms is given by
\(
\begin{array}{ll}
S _n=\frac{a\left(r^n-1\right)}{r-1}, & \text { if } r \neq 1 \\
S _n=n a & \text { if } r=1
\end{array}
\)
If \(a, G\), and \(b\) are in G.P., then \(G\) is called the geometric mean of the numbers \(a\) and \(b\) and is given by
\(
G =\sqrt{a b}
\)
- If the terms of a G.P. are multiplied or divided by the same non-zero constant \((k \neq 0)\), they still remain in G.P.
If \(a_1, a_2, a_3, \ldots\), are in GP., then \(a_1 k, a_2 k, a_3 k, \ldots\) and \(\frac{a_1}{k}, \frac{a_2}{k}, \frac{a_3}{k}, \ldots\) are also in GP. with same common ratio, in particularly if \(a_1, a_2, a_3, \ldots\) are in GP., then
\(\frac{1}{a_1}, \frac{1}{a_2}, \frac{1}{a_3}, \ldots\) are also in G.P. - If \(a_1, a_2, a_3, \ldots\) and \(b_1, b_2, b_3, \ldots\) are two G.P.s, then \(a_1 b_1, a_2 b_2, a_3 b_3, \ldots\) and \(\frac{a_1}{b_1}, \frac{a_2}{b_2}, \frac{a_3}{b_3}, \ldots\) are also in G.P.
- If \(a_1, a_2, a_3, \ldots\) are in A.P. \(\left(a_i>0 \forall i\right)\), then \(x^{a_1}, x^{a_2}, x^{a_3}, \ldots\), are in G.P. \((\forall x>0)\)
- If \(a_1, a_2, a_3, \ldots, a_n\) are in G.P., then \(a_1 a_n=a_2 a_{n-1}=a_3 a_{n-2}=\ldots\)
Important results on the sum of special sequences
- Sum of the first \(n\) natural numbers:
\(
\sum n=1+2+3+\ldots+n=\frac{n(n+1)}{2}
\) - Sum of the squares of first \(n\) natural numbers.
\(
\sum n^2=1^2+2^2+3^2+\ldots+n^2=\frac{n(n+1)(2 n+1)}{6}
\) - Sum of cubes of first \(n\) natural numbers:
\(
\sum n^3=1^3+2^3+3^3+\ldots+n^3=\left[\frac{n(n+1)}{2}\right]^2
\)
Quiz Summary
0 of 17 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 17 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 17
1. Question
If the sum of the first 10 terms of the series \(\frac{4 \cdot 1}{1+4 \cdot 1^4}+\frac{4 \cdot 2}{1+4 \cdot 2^4}+\frac{4 \cdot 3}{1+4 \cdot 3^4}+\ldots\) is \(\frac{\mathrm{m}}{\mathrm{n}}\), where \(\operatorname{gcd}(\mathrm{m}, \mathrm{n})=1\), then \(\mathrm{m}+\mathrm{n}\) is equal to ___. [JEE Main 2025 (Online) 2nd April Evening Shift]
CorrectIncorrectHint
(b) Step 1: Simplify the General Term ( \(T_r\) )
The \(r^{\text {th }}\) term of the series is:
\(
T_r=\frac{4 r}{1+4 r^4}
\)
The denominator \(1+4 r^4\) can be factored as follows:
\(
1+4 r^4=\left(1+4 r^4+4 r^2\right)-4 r^2=\left(2 r^2+1\right)^2-(2 r)^2
\)
Using the difference of squares identity \(a^2-b^2=(a-b)(a+b)\) :
\(
1+4 r^4=\left(2 r^2-2 r+1\right)\left(2 r^2+2 r+1\right)
\)
Step 2: Express as Partial Fractions
Now we rewrite the numerator \(4 r\) as the difference between these two factors:
\(
\left(2 r^2+2 r+1\right)-\left(2 r^2-2 r+1\right)=4 r
\)
Thus, the general term becomes:
\(
\begin{gathered}
T_r=\frac{\left(2 r^2+2 r+1\right)-\left(2 r^2-2 r+1\right)}{\left(2 r^2-2 r+1\right)\left(2 r^2+2 r+1\right)} \\
T_r=\frac{1}{2 r^2-2 r+1}-\frac{1}{2 r^2+2 r+1}
\end{gathered}
\)
Step 3: Expand the Telescoping Series
Let’s calculate the sum of the first 10 terms \(\left(S_{10}\right)\) :
For \(r=1: T_1=\left(\frac{1}{1}-\frac{1}{5}\right)\)
For \(r=2: T_2=\left(\frac{1}{5}-\frac{1}{13}\right)\)
For \(r=3: T_3=\left(\frac{1}{13}-\frac{1}{25}\right)\)
…
For \(r=10: T_{10}=\left(\frac{1}{2(10)^2-2(10)+1}-\frac{1}{2(10)^2+2(10)+1}\right)\)
Summing these up, all intermediate terms cancel:
\(
\begin{gathered}
S_{10}=1-\frac{1}{200+20+1}=1-\frac{1}{221} \\
S_{10}=\frac{220}{221}
\end{gathered}
\)
Step 4: Final Calculation
We are given the sum is \(\frac{m}{n}\) where \(\operatorname{gcd}(m, n)=1\) :
\(m=220\)
\(n=221\)
Since 221 is \(13 \times 17\) and 220 is \(2^2 \times 5 \times 11\), their greatest common divisor is indeed 1.
\(
m+n=220+221=441
\)Alternate:
\(
\begin{aligned}
& \frac{4.1}{1+4.1^4}+\frac{4.2}{1+4.2^4}+\frac{4.3}{1+4.3^4}+\ldots \\
& T_r=\frac{4 r}{1+4 r^4}=\frac{4 r}{4 r^4+4 r^2+1-4 r^2} \\
& =\frac{4 r}{\left(2 r^2+1\right)^2-(2 r)^2} \\
& T_r=\frac{4 r}{\left(2 r^2-2 r+1\right)\left(2 r^2+2 r+1\right)} \\
& T_r=\frac{\left(2 r^2+2 r+1\right)-\left(2 r^2-2 r+1\right)}{\left(2 r^2-2 r+1\right)\left(2 r^2+2 r+1\right)} \\
& T_r=\left(\frac{1}{r^2+(r-1)^2}-\frac{1}{r^2+(r+1)^2}\right) \\
& \sum_{r=1}^{10} T_r=\left(\frac{1}{0^2+1^2}-\frac{1}{1^2+2^2}+\frac{1}{1^2+2^2}-\frac{1}{2^2+3^2}+\ldots\right. \\
& \frac{1}{9^2+10^2}-\frac{1}{10^2+11^2} \\
& =1-\frac{1}{221} \\
& =\frac{220}{221} \\
& \therefore \quad m+n=220+221 \\
& =441
\end{aligned}
\) -
Question 2 of 17
2. Question
Let \(a_1, a_2, \ldots, a_{2024}\) be an Arithmetic Progression such that \(a_1+\left(a_5+a_{10}+a_{15}+\ldots+a_{2020}\right)+a_{2024}=2233\). Then \(a_1+a_2+a_3+\ldots+a_{2024}\) is equal to ___. [JEE Main 2025 (Online) 29th January Evening Shift]
CorrectIncorrectHint
(a) Concepts: Your identification of the number of pairs is the most critical part of this problem. Since the indices in the bracket \((5,10,15, \ldots, 2020)\) form an arithmetic progression of their own, we can verify the count:
Number of terms in the bracket \(=\frac{2020-5}{5}+1=\frac{2015}{5}+1=403+1=404\) terms.
These 404 terms form 202 pairs where each pair \(a_k+a_{2024-k+1}=a_1+a_{2024}\).
Adding the external \(a_1\) and \(a_{2024}\) gives you exactly 203 pairs.
Summary of the Steps
Constant Sum Property: \(a_r+a_{n-r+1}=\) constant.
Pairing: \(203 \times\left(a_1+a_{2024}\right)=2233\) leads to \(\left(a_1+a_{2024}\right)=11\).
Total Sum Formula: \(S_n=\frac{n}{2}\) (sum of first and last terms) was applied correctly.Step 1: Determine the value of the sum of the first and last terms
In an arithmetic progression, the sum of terms equidistant from the ends is equal, e.g., \(a_1+a_{2024}=a_5+a_{2020}=a_{10}+a_{2015}\), which is a constant value. Given the sum of specific terms is 2233, and there are 203 terms in the sum:
\(
\begin{aligned}
& 203\left(a_1+a_{2024}\right)=2233 \\
& a_1+a_{2024}=\frac{2233}{203}=11
\end{aligned}
\)
Step 2: Calculate the sum of the first 2024 terms of the A.P.
The sum of the first \(n\) terms of an A.P. is given by the formula \(S_n=\frac{n}{2}\left(a_1+a_n\right)\). For \(n=2024\), using the value of \(a_1+a_{2024}\) from Step 1:
\(
\begin{gathered}
S_{2024}=\frac{2024}{2}\left(a_1+a_{2024}\right) \\
S_{2024}=1012 \times 11 \\
S_{2024}=11132
\end{gathered}
\) -
Question 3 of 17
3. Question
The interior angles of a polygon with \(n\) sides, are in an A.P. with common difference \(6^{\circ}\). If the largest interior angle of the polygon is \(219^{\circ}\), then \(n\) is equal to ___. [JEE Main 2025 (Online) 28th January Evening Shift]
CorrectIncorrectHint
(c) To solve this, we use two different ways to calculate the sum of the interior angles of a polygon and set them equal to each other.
Step 1: Geometric Sum Formula
For any polygon with \(n\) sides, the sum of the interior angles \(\left(S_n\right)\) is given by:
\(
S_n=(n-2) \times 180^{\circ}
\)
Step 2: Arithmetic Progression (AP) Sum Formula
We are told the angles are in an AP. Let:
\(n =\) number of sides (and number of angles)
\(d=6^{\circ}\) (common difference)
\(a_n=219^{\circ}\) (largest angle)
Since the angles are increasing, the largest angle is the \(n^{\text {th }}\) term. We can find the first term ( \(a_1 )\) in terms of \(n\) :
\(
\begin{gathered}
a_n=a_1+(n-1) d \\
219=a_1+(n-1) 6 \Longrightarrow a_1=219-6 n+6=225-6 n
\end{gathered}
\)
The sum of an AP is \(S_n=\frac{n}{2}\left(a_1+a_n\right)\) :
\(
\begin{gathered}
S_n=\frac{n}{2}(225-6 n+219) \\
S_n=\frac{n}{2}(444-6 n)=n(222-3 n)
\end{gathered}
\)
Step 3: Equating and Solving for \(n\)
\(
\begin{gathered}
(n-2) \times 180=n(222-3 n) \\
180 n-360=222 n-3 n^2 \\
3 n^2-42 n-360=0
\end{gathered}
\)
Divide the entire equation by 3 to simplify:
\(
n^2-14 n-120=0
\)
Now, factor the quadratic:
\(
(n-20)(n+6)=0
\)
Since the number of sides \(n\) must be positive, we have:
\(
n=20
\)Note:
\(
\begin{array}{|l|l|l|l|}
\hline \text { Polygon } & \text { Sides }(n) & \text { Number of Triangles }(n-2) & \text { Sum of Angles } \\
\hline \text { Triangle } & 3 & 3-2=1 & 1 \times 180=180^{\circ} \\
\hline \text { Quadrilateral } & 4 & 4-2=2 & 2 \times 180=360^{\circ} \\
\hline \text { Pentagon } & 5 & 5-2=3 & 3 \times 180=540^{\circ} \\
\hline \text { Hexagon } & 6 & 6-2=4 & 4 \times 180=720^{\circ} \\
\hline
\end{array}
\) -
Question 4 of 17
4. Question
The roots of the quadratic equation \(3 x^2-p x+q=0\) are \(10^{\text {th }}\) and \(11^{\text {th }}\) terms of an arithmetic progression with common difference \(\frac{3}{2}\). If the sum of the first 11 terms of this arithmetic progression is 88, then \(q-2 p\) is equal to ____. [JEE Main 2025 (Online) 23rd January Evening Shift]
CorrectIncorrectHint
(d) Step 1: Determine the first term of the arithmetic progression
Using the formula for the sum of the first \(\boldsymbol{n}\) terms of an arithmetic progression, \(S_n=\frac{n}{2}[2 a+(n-1) d]\), with \(S_{11}=88\) and common difference \(d=\frac{3}{2}\), we can solve for the first term \(\boldsymbol{a}\) :
\(
\frac{11}{2}\left[2 a+(11-1) \frac{3}{2}\right]=88
\)
Solving this equation gives \(a=\frac{1}{2}\).
Step 2: Calculate the tenth and eleventh terms
The roots of the quadratic equation are the 10th \((\alpha)\) and 11th \((\beta)\) terms of the progression. The formula for the \(n^{\text {th }}\) term is \(T_n=a+(n-1) d\).
\(
\begin{aligned}
& \alpha=T_{10}=\frac{1}{2}+9\left(\frac{3}{2}\right)=14 \\
& \beta=T_{11}=\frac{1}{2}+10\left(\frac{3}{2}\right)=\frac{31}{2}
\end{aligned}
\)
Step 3: Find the values of \(p\) and \(q\)
For the quadratic equation \(3 x^2-p x+q=0\), the sum and product of the roots are related to the coefficients: \(\alpha+\beta=\frac{p}{3}\) and \(\alpha \beta=\frac{q}{3}\).
\(
\begin{gathered}
\alpha+\beta=14+\frac{31}{2}=\frac{59}{2} \Longrightarrow \frac{p}{3}=\frac{59}{2} \Longrightarrow p=\frac{177}{2} \\
\alpha \beta=14 \cdot \frac{31}{2}=217 \Longrightarrow \frac{q}{3}=217 \Longrightarrow q=651
\end{gathered}
\)
Step 4: Compute the value of q – \(2 p\)
Substitute the calculated values of \(p\) and \(q\) into the expression \(q-2 p\).
\(
q-2 p=651-2\left(\frac{177}{2}\right)=651-177=474
\) -
Question 5 of 17
5. Question
If \(\left(\frac{1}{\alpha+1}+\frac{1}{\alpha+2}+\ldots \ldots+\frac{1}{\alpha+1012}\right)-\left(\frac{1}{2 \cdot 1}+\frac{1}{4 \cdot 3}+\frac{1}{6 \cdot 5}+\ldots \ldots+\frac{1}{2024 \cdot 2023}\right)=\frac{1}{2024}\), then \(\alpha\) is equal to ___. [JEE Main 2024 (Online) 9th April Evening Shift]
CorrectIncorrectHint
(a) To solve this problem, we need to simplify the second series using partial fractions and then relate it to the first series.
Step 1: Simplify the second series
Let the second expression be \(S\). Each term in \(S\) is of the form \(\frac{1}{2 r(2 r-1)}\). Using partial fractions:
\(
\frac{1}{2 r(2 r-1)}=\frac{1}{2 r-1}-\frac{1}{2 r}
\)
Expanding the series \(S\) for \(r=1\) to 1012 (since the last term is \(2024 \cdot 2023\) ):
\(
S=\left(1-\frac{1}{2}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\left(\frac{1}{5}-\frac{1}{6}\right)+\ldots+\left(\frac{1}{2023}-\frac{1}{2024}\right)
\)
This is the alternating harmonic series:
\(
S=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\ldots+\frac{1}{2023}-\frac{1}{2024}
\)
Step 2: Rearrange the series \(S\)
We can express this sum as:
\(
\begin{gathered}
S=\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{2024}\right)-2\left(\frac{1}{2}+\frac{1}{4}+\ldots+\frac{1}{2024}\right) \\
S=\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{2024}\right)-\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{1012}\right) \\
S=\frac{1}{1013}+\frac{1}{1014}+\ldots+\frac{1}{2023}+\frac{1}{2024}
\end{gathered}
\)
Step 3: Substitute back into the main equation
The given equation is:
\(
\left(\frac{1}{\alpha+1}+\frac{1}{\alpha+2}+\ldots+\frac{1}{\alpha+1012}\right)-\left(\frac{1}{1013}+\ldots+\frac{1}{2023}+\frac{1}{2024}\right)=\frac{1}{2024}
\)
Notice that the last term of the second bracket is \(\frac{1}{2024}\), which matches the right side of the equation. Let’s move it out:
\(
\begin{aligned}
& \left(\sum_{r=1}^{1012} \frac{1}{\alpha+r}\right)-\left(\sum_{r=1013}^{2023} \frac{1}{r}+\frac{1}{2024}\right)=\frac{1}{2024} \\
& \left(\sum_{r=1}^{1012} \frac{1}{\alpha+r}\right)-\left(\sum_{r=1013}^{2023} \frac{1}{r}\right)=\frac{2}{2024}=\frac{1}{1012}
\end{aligned}
\)
Step 4: Find the value of \(\alpha\)
By comparing the terms in the first sum to the second sum, we notice that if \(\alpha=1012\), the terms align beautifully. If \(\alpha=1012\) : The first sum is \(\frac{1}{1013}+\frac{1}{1014}+\ldots+\frac{1}{2024}\). Substitute this back into the very first simplified version of the equation:
\(
\left(\frac{1}{1013}+\ldots+\frac{1}{2023}+\frac{1}{2024}\right)-\left(\frac{1}{1013}+\ldots+\frac{1}{2023}+\frac{1}{2024}\right)=0
\)
Wait, let’s re-examine the original prompt’s structure:
\(
\operatorname{Sum} 1-\operatorname{Sum} 2=\frac{1}{2024}
\)
From Step 2, Sum \(2=\left(\frac{1}{1013}+\frac{1}{1014}+\ldots+\frac{1}{2023}+\frac{1}{2024}\right)\). So:
\(
\begin{gathered}
\left(\frac{1}{\alpha+1}+\cdots+\frac{1}{\alpha+1012}\right)-\left(\frac{1}{1013}+\cdots+\frac{1}{2023}+\frac{1}{2024}\right)=\frac{1}{2024} \\
\left(\frac{1}{\alpha+1}+\cdots+\frac{1}{\alpha+1012}\right)=\frac{1}{1013}+\frac{1}{1014}+\cdots+\frac{1}{2023}+\frac{2}{2024} \\
\left(\frac{1}{\alpha+1}+\cdots+\frac{1}{\alpha+1012}\right)=\frac{1}{1013}+\frac{1}{1014}+\cdots+\frac{1}{2023}+\frac{1}{1012}
\end{gathered}
\)
Rearranging the right side to be in order:
\(
\frac{1}{1012}+\frac{1}{1013}+\ldots+\frac{1}{2023}
\)
Comparing this to \(\frac{1}{\alpha+1}+\frac{1}{\alpha+2}+\ldots+\frac{1}{\alpha+1012}\), we see: \(\alpha+1=1012 \Longrightarrow \alpha=1011\). -
Question 6 of 17
6. Question
An arithmetic progression is written in the following way
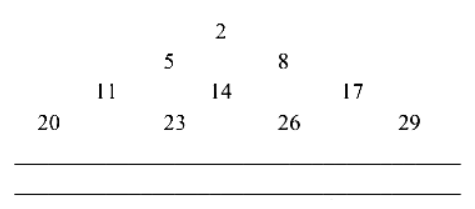
The sum of all the terms of the \(10^{\text {th }}\) row is ____. [JEE Main 2024 (Online) 8th April Evening Shift]
CorrectIncorrectHint
(b) Step 1: Finding the general term
The general term is given by:
\(
T_n=\frac{3 n^2-3 n+4}{2}
\)
Step 2: Finding the 10th term
\(
T_{10}=\frac{3(100)-3(10)+4}{2}
\)
Simplifying:
\(
T_{10}=\frac{300-30+4}{2}=\frac{274}{2}=137
\)
Hence, \(T_{10}=137\).
Step 3: Sum of 10 terms with common difference (c.d.) = 3
\(
S_{10}=\frac{10}{2}[2(137)+9(3)]
\)
Simplifying:
\(
S_{10}=5(274+27)=5 \times 301=1505
\)Note: First term is each row form pattern
Step 1: Verification of \(a\) and \(b\)
Starting from your simplified equations:
\(3 a+b=3 \dots(1)\)
\(5 a+b=6 \dots(2)\)
Subtracting (1) from (2):
\(
\begin{gathered}
(5 a-3 a)+(b-b)=6-3 \\
2 a=3 \Longrightarrow a=\frac{3}{2}
\end{gathered}
\)
Substituting \(a\) back into (1):
\(
\begin{gathered}
3\left(\frac{3}{2}\right)+b=3 \\
\frac{9}{2}+b=3 \Longrightarrow b=3-4.5 \Longrightarrow \mathrm{~b}=-\frac{3}{2}
\end{gathered}
\)
Step 2: Solving for \(c\)
Now, let’s substitute \(a\) and \(b\) into the first original equation ( \(T_1\) ):
\(
\begin{gathered}
a+b+c=2 \\
\frac{3}{2}+\left(-\frac{3}{2}\right)+c=2 \\
0+c=2 \Longrightarrow c=2
\end{gathered}
\)
You correctly identified \(c=2\).
Step 3: The Final Formula
Let’s plug \(a, b\), and \(c\) into the general form \(T_n=a n^2+ b n+c\) :
\(
T_n=\frac{3}{2} n^2-\frac{3}{2} n+2
\)
To write this as a single fraction:
\(
T_n=\frac{3 n^2-3 n+4}{2}
\) -
Question 7 of 17
7. Question
Let the positive integers be written in the form :

If the \(k^{\text {th }}\) row contains exactly \(k\) numbers for every natural number \(k\), then the row in which the number 5310 will be, is ___. [JEE Main 2024 (Online) 8th April Morning Shift]
CorrectIncorrectHint
(c) Step 1: Identify the Formula for the Last Number
The last number in row \(n\) is given by the sum of the first \(n\) natural numbers ( \(S_n\) ):
\(
S_n=\frac{n(n+1)}{2}
\)
We need to find the row \(n\) such that 5310 falls within it. This means we are looking for the smallest integer \(n\) where:
\(
\frac{n(n+1)}{2} \geq 5310
\)
Step 2: Solve for \(n\)
Let’s solve the inequality \(n(n+1) \geq 10620\) :
\(
n^2+n-10620 \geq 0
\)
To get an estimate, we can take the square root of 10620:
\(
\sqrt{10620} \approx 103.05
\)
Let’s test \(n=102\) and \(n=103\) :
For \(n=102\) :
\(
S_{102}=\frac{102 \times 103}{2}=51 \times 103=5253
\)
(This is the last number of row 102. Since \(5253<5310\), the number 5310 is not in this row.)
For \(n=103\) :
\(
S_{103}=\frac{103 \times 104}{2}=103 \times 52=5356
\)
(This is the last number of row 103. Since \(5356 \geq 5310\), the number 5310 must be in this row.)
Step 3: Conclusion
The number 5310 lies between the end of row 102 (5253) and the end of row 103 (5356).
The row in which the number 5310 will be is 103. -
Question 8 of 17
8. Question
Let \(\alpha=\sum_{r=0}^n\left(4 r^2+2 r+1\right)^n C_r\) and \(\beta=\left(\sum_{r=0}^n \frac{{ }^n C_r}{r+1}\right)+\frac{1}{n+1}\). If \(140<\frac{2 \alpha}{\beta}<281\), then the value of \(n\) is ____. [JEE Main 2024 (Online) 8th April Morning Shift]
CorrectIncorrectHint
(d) To solve this, we need to simplify \(\alpha\) and \(\beta\) using binomial expansion properties and then find the ratio \(\frac{2 \alpha}{\beta}\).
Step 1: Simplify \(\alpha\)
The general term of \(\alpha\) is \(\sum_{r=0}^n\left(4 r^2+2 r+1\right)\binom{n}{r}\). We use the following properties:
\(\sum\binom{n}{r}=2^n\)
\(\sum r\binom{n}{r}=n 2^{n-1}\)
\(\sum r^2\binom{n}{r}=n(n-1) 2^{n-2}+n 2^{n-1}=n(n+1) 2^{n-2}\)
Substituting these into the expression for \(\alpha\) :
\(
\begin{gathered}
\alpha=4\left[n(n-1) 2^{n-2}+n 2^{n-1}\right]+2\left[n 2^{n-1}\right]+2^n \\
\alpha=n(n-1) 2^n+2 n 2^n+n 2^n+2^n \\
\alpha=2^n\left[n^2-n+2 n+n+1\right]=2^n\left(n^2+2 n+1\right)=2^n(n+1)^2
\end{gathered}
\)
Step 2: Simplify \(\beta\)
We use the integration property of binomial coefficients: \(\frac{\binom{n}{r}}{r+1}=\frac{\binom{n+1}{r+1}}{n+1}\).
\(
\sum_{r=0}^n \frac{\binom{n}{r}}{r+1}=\frac{1}{n+1} \sum_{r=0}^n\binom{n+1}{r+1}
\)
The sum \(\sum_{r=0}^n\binom{n+1}{r+1}\) is the total sum of binomial coefficients for \((n+1)\) minus the first term \(\binom{n+1}{0}:\)
\(
\sum_{r=0}^n\binom{n+1}{r+1}=2^{n+1}-1
\)
Substituting this into \(\beta\) :
\(
\beta=\frac{2^{n+1}-1}{n+1}+\frac{1}{n+1}=\frac{2^{n+1}}{n+1}
\)
Step 3: Calculate the Ratio and Solve for \(n\)
Now find \(\frac{2 \alpha}{\beta}\) :
\(
\frac{2 \alpha}{\beta}=\frac{2 \cdot 2^n(n+1)^2}{\frac{2^{n+1}}{n+1}}=\frac{2^{n+1}(n+1)^2 \cdot(n+1)}{2^{n+1}}=(n+1)^3
\)
We are given the inequality:
\(
140<(n+1)^3<281
\)
Let’s check perfect cubes near this range:
\(5^3=125\) (Too small)
\(6^3=216\) (Within range)
\(7^3=343\) (Too large)
Therefore:
\(
\begin{gathered}
(n+1)^3=216 \\
n+1=6 \Longrightarrow n=5
\end{gathered}
\) -
Question 9 of 17
9. Question
If \(\mathrm{S}(x)=(1+x)+2(1+x)^2+3(1+x)^3+\cdots+60(1+x)^{60}, x \neq 0\), and \((60)^2 \mathrm{~S}(60)=\mathrm{a}(\mathrm{b})^{\mathrm{b}}+\mathrm{b}\), where \(a, b \in N\), then \((a+b)\) equal to ___. [JEE Main 2024 (Online) 6th April Evening Shift]
CorrectIncorrectHint
(d) Step 1: Identify the Series
The given series is:
\(
S(x)=(1+x)+2(1+x)^2+3(1+x)^3+\cdots+60(1+x)^{60}
\)
This is an Arithmetico-Geometric Progression (AGP). Let \(R=(1+x)\). Then:
\(
S=R+2 R^2+3 R^3+\cdots+60 R^{60}
\)
Step 2: Find the Sum of the AGP
To solve this, we multiply the series by \(R\) and subtract it from the original series:
\(
\begin{gathered}
S=R+2 R^2+3 R^3+\cdots+60 R^{60} \\
R S=\quad R^2+2 R^3+\cdots+59 R^{60}+60 R^{61}
\end{gathered}
\)
Subtracting the two equations:
\(
S(1-R)=\left(R+R^2+R^3+\cdots+R^{60}\right)-60 R^{61}
\)
The term in the parentheses is a Geometric Progression (GP) with \(a=R, r=R\), and \(n=60\) :
\(
S(1-R)=\frac{R\left(R^{60}-1\right)}{R-1}-60 R^{61}
\)
Since \(R=1+x\), we have \(1-R=-x\) and \(R-1=x\) :
\(
-x S(x)=\frac{(1+x)\left((1+x)^{60}-1\right)}{x}-60(1+x)^{61}
\)
Step 3: Evaluate at \(x=60\)
Substitute \(x=60\) into the equation:
\(
-60 S(60)=\frac{61\left(61^{60}-1\right)}{60}-60(61)^{61}
\)
Multiply the entire equation by -60 to isolate \((60)^2 S(60)\) :
\(
\begin{gathered}
(60)^2 S(60)=-61\left(61^{60}-1\right)+3600(61)^{61} \\
(60)^2 S(60)=-61^{61}+61+3600(61)^{61} \\
(60)^2 S(60)=(3600-1) 61^{61}+61 \\
(60)^2 S(60)=3599(61)^{61}+61
\end{gathered}
\)
Step 4: Compare with the Given Form
The problem states:
\(
(60)^2 S(60)=a(b)^b+b
\)
Comparing the two expressions:
\(b=61\)
\(a=3599\)
Step 5: Final Calculation
We need to find \((a+b)\) :
\(
a+b=3599+61=3660
\) -
Question 10 of 17
10. Question
Let the first term of a series be \(T_1=6\) and its \(r^{\text {th }}\) term \(T_r=3 T_{r-1}+6^r, r=2,3, \ldots \ldots \ldots . . n\). If the sum of the first \(n\) terms of this series is \(\frac{1}{5}\left(n^2-12 n+39\right)\left(4 \cdot 6^n-5 \cdot 3^n+1\right)\), then \(n\) is equal to ____. [JEE Main 2024 (Online) 6th April Morning Shift]
CorrectIncorrectHint
(d) Step 1: Find the general term \(T_r\)
The recurrence relation is given as:
\(
T_r=3 T_{r-1}+6^r
\)
This is a linear recurrence of the form \(T_r-3 T_{r-1}=6^r\). To solve this, we can divide both sides by \(3^r\) :
\(
\frac{T_r}{3^r}-\frac{T_{r-1}}{3^{r-1}}=\frac{6^r}{3^r}=2^r
\)
Let \(a_r=\frac{T_r}{3^r}\). Then the equation becomes:
\(
a_r-a_{r-1}=2^r
\)
We can find \(a_n\) by summing this difference from \(r=2\) to \(n\) :
\(
\begin{gathered}
\sum_{r=2}^n\left(a_r-a_{r-1}\right)=\sum_{r=2}^n 2^r \\
a_n-a_1=\frac{2^2\left(2^{n-1}-1\right)}{2-1}=4\left(2^{n-1}-1\right)=2^{n+1}-4
\end{gathered}
\)
Since \(T_1=6\), then \(a_1=\frac{T_1}{3^1}=\frac{6}{3}=2\).
\(
a_n=2+2^{n+1}-4=2^{n+1}-2
\)
Substituting back \(a_n=\frac{T_n}{3^n}\) :
\(
T_n=3^n\left(2^{n+1}-2\right)=2 \cdot 6^n-2 \cdot 3^n
\)
Step 2: Find the Sum \(S_n\)
The sum of the first \(n\) terms is:
\(
\begin{gathered}
S_n=\sum_{r=1}^n T_r=\sum_{r=1}^n\left(2 \cdot 6^r-2 \cdot 3^r\right) \\
S_n=2 \sum_{r=1}^n 6^r-2 \sum_{r=1}^n 3^r
\end{gathered}
\)
Using the GP sum formula \(\frac{a\left(r^n-1\right)}{r-1}\) :
\(
\begin{gathered}
S_n=2\left[\frac{6\left(6^n-1\right)}{6-1}\right]-2\left[\frac{3\left(3^n-1\right)}{3-1}\right] \\
S_n=\frac{12}{5}\left(6^n-1\right)-3\left(3^n-1\right)
\end{gathered}
\)
To compare this with the given format, let’s get a common denominator of 5 :
\(
\begin{gathered}
S_n=\frac{12 \cdot 6^n-12-15 \cdot 3^n+15}{5} \\
S_n=\frac{12 \cdot 6^n-15 \cdot 3^n+3}{5} \\
S_n=\frac{3}{5}\left(4 \cdot 6^n-5 \cdot 3^n+1\right)
\end{gathered}
\)
Step 3: Solve for \(n\)
We are given that:
\(
S_n=\frac{1}{5}\left(n^2-12 n+39\right)\left(4 \cdot 6^n-5 \cdot 3^n+1\right)
\)
By comparing our derived \(S_n\) with the given \(S_n\), we can see that:
\(
\begin{gathered}
n^2-12 n+39=3 \\
n^2-12 n+36=0 \\
(n-6)^2=0 \\
n=6
\end{gathered}
\) -
Question 11 of 17
11. Question
If \(1+\frac{\sqrt{3}-\sqrt{2}}{2 \sqrt{3}}+\frac{5-2 \sqrt{6}}{18}+\frac{9 \sqrt{3}-11 \sqrt{2}}{36 \sqrt{3}}+\frac{49-20 \sqrt{6}}{180}+\ldots\) upto \(\infty=2+\left(\sqrt{\frac{b}{a}}+1\right) \log _e\left(\frac{a}{b}\right)\), where a and b are integers with \(\operatorname{gcd}(a, b)=1\), then \(11 a+18 b\) is equal to ____. [JEE Main 2024 (Online) 5th April Evening Shift]
CorrectIncorrectHint
(c)
\(
\begin{aligned}
& S=1+\frac{\sqrt{3}-\sqrt{2}}{2 \sqrt{3}}+\frac{5-2 \sqrt{6}}{18}+\frac{9 \sqrt{3}-11 \sqrt{2}}{36 \sqrt{3}}+\ldots \infty \\
& =1+\frac{(1-\sqrt{2} / \sqrt{3})}{2}+\frac{(1-\sqrt{2} / \sqrt{3})^2}{6}+\frac{(1-\sqrt{2} / \sqrt{3})^3}{12}+\ldots \infty \\
& \text { let } 1-\frac{\sqrt{2}}{\sqrt{3}}=a \\
& S=1+\frac{a}{2}+\frac{a^2}{6}+\frac{a^3}{12}+\ldots \\
& =1+\left(1-\frac{1}{2}\right) a+\left(\frac{1}{2}-\frac{1}{3}\right) a^2+\left(\frac{1}{3}-\frac{1}{4}\right) a^3+\ldots \\
& =1+\left(a+\frac{a^2}{2}+\frac{a^3}{3} \ldots \infty\right)+\frac{1}{a}\left(\frac{-a^2}{2}-\frac{a^3}{3}-\frac{a^4}{4} \ldots \infty\right) \\
& =-\ln (1-a)+\frac{1}{a}\left(-a-\frac{a^2}{2}-\frac{a^3}{3} \ldots \infty\right)+2 \\
& =-\ln (1-a)+\frac{1}{a} \ln (1-a)+2 \\
& =2+\left(\frac{1}{a}-1\right) \ln (1-a)
\end{aligned}
\)
\(
\begin{aligned}
& =2+\left(\frac{\sqrt{3}}{\sqrt{3}-\sqrt{2}}-1\right) \ln \left(1-1+\sqrt{\frac{2}{3}}\right) \\
& =2+\frac{\sqrt{2}}{\sqrt{3}}-\sqrt{2} \ln \sqrt{\frac{2}{3}} \\
& =2+\left(\frac{\sqrt{6}+2}{1} \cdot \frac{1}{2} \ln \frac{2}{3}\right) \\
& \therefore 2+\left(\sqrt{\frac{3}{2}}+1\right) \ln \frac{2}{3} \\
& \therefore 11 a+18 b=76
\end{aligned}
\) -
Question 12 of 17
12. Question
Let \(a_1, a_2, a_3, \ldots\) be in an arithmetic progression of positive terms. Let \(A_k=a_1^2-a_2^2+a_3^2-a_4^2+\ldots+a_{2 k-1}^2-a_{2 k}^2\). If \(\mathrm{A}_3=-153, \mathrm{~A}_5=-435\) and \(\mathrm{a}_1^2+\mathrm{a}_2^2+\mathrm{a}_3^2=66\), then \(\mathrm{a}_{17}-\mathrm{A}_7\) is equal to ____. [JEE Main 2024 (Online) 5th April Morning Shift]
CorrectIncorrectHint
(b)
\(
\begin{aligned}
&\text { Let } a_n=a+(n-1) d \forall n \in N\\
&\begin{aligned}
A_k & =\left(a_1^2-a_2^2\right)+\left(a_3^2-a_4^2\right)+\ldots a_{2 k-1}^2-a_{2 k}^2 \\
& =(-d)\left(a_1+a_2+\ldots+a_{2 k}\right) \\
& A_k=(-d k)(2 a+(2 k-1) d) \\
\Rightarrow & A_3=(-3 d)(2 a+5 d)=-153 \\
\Rightarrow & d(2 a+5 d)=51 \quad \ldots \text { (i) } \\
& A_5=(-5 d)(2 a+9 d)=-435 \\
\Rightarrow & d(2 a+9 d)=87 \\
\Rightarrow & 4 d^2=36 \Rightarrow d= \pm 3(d=3 \text { positive terms }) \\
\Rightarrow & 3(2 a+27)=87 \\
\Rightarrow & 2 a=29-27 \\
\Rightarrow & a=1 \\
& a_{17}-A_7=(a+16 d)-(-7 d)(2+13 d) \\
& =49+7 \times 3(2+39) \\
& =49+21 \times 41=910
\end{aligned}
\end{aligned}
\)Explanation: Step 1: Simplify \(A_k\) using the Telescoping Method
Each pair in \(A_k\) is of the form \(a_{2 i-1}^2-a_{2 i}^2\). Using \(\left(x^2-y^2\right)=(x-y)(x+y)\) :
\(
a_{2 i-1}^2-a_{2 i}^2=\left(a_{2 i-1}-a_{2 i}\right)\left(a_{2 i-1}+a_{2 i}\right)
\)
In an Arithmetic Progression (AP), \(a_{2 i}-a_{2 i-1}=d\), so \(\left(a_{2 i-1}-a_{2 i}\right)=-d\). Therefore:
\(
\begin{gathered}
A_k=-d\left(a_1+a_2\right)-d\left(a_3+a_4\right)-\cdots-d\left(a_{2 k-1}+a_{2 k}\right) \\
A_k=-d\left[a_1+a_2+a_3+\cdots+a_{2 k}\right]
\end{gathered}
\)
Using the AP sum formula for \(2 k\) terms:
\(
A_k=-d\left[\frac{2 k}{2}\left(a_1+a_{2 k}\right)\right]=-k d\left(a_1+a_{2 k}\right)
\)
Step 2: Set up the Equations
Given \(A_3=-153\) and \(A_5=-435\) :
For \(A_3(k=3)\) :
\(
-3 d\left(a_1+a_6\right)=-153 \Longrightarrow d\left(a_1+a_1+5 d\right)=51 \Longrightarrow d\left(2 a_1+5 d\right)=51
\)
For \(A_5(k=5)\) :
\(
-5 d\left(a_1+a_{10}\right)=-435 \Longrightarrow d\left(a_1+a_1+9 d\right)=87 \Longrightarrow d\left(2 a_1+9 d\right)=87
\)
Subtracting the first equation from the second:
\(
\begin{gathered}
\left(2 a_1 d+9 d^2\right)-\left(2 a_1 d+5 d^2\right)=87-51 \\
4 d^2=36 \Longrightarrow d^2=9 \Longrightarrow d=3 \text { (since terms are positive) }
\end{gathered}
\)
Substitute \(d=3\) into \(d\left(2 a_1+5 d\right)=51\) :
\(
3\left(2 a_1+15\right)=51 \Longrightarrow 2 a_1+15=17 \Longrightarrow 2 a_1=2 \Longrightarrow a_1=1
\)
Step 3: Verify with the third condition
The problem states \(a_1^2+a_2^2+a_3^2=66\). With \(a_1=1\) and \(d=3\) :
\(a_1=1\)
\(a_2=1+3=4\)
\(a_3=1+2(3)=7\) Check: \(1^2+4^2+7^2=1+16+49=66\). (Matches!)
Step 4: Calculate \(a_{17}\) and \(A_7\)
Find \(a_{17}\) :
\(
a_{17}=a_1+16 d=1+16(3)=1+48=49
\)
Find \(A_7\) : Using our formula \(A_k=-k d\left(2 a_1+(2 k-1) d\right)\) for \(k=7\) :
\(
\begin{gathered}
A_7=-7(3)[2(1)+(13)(3)] \\
A_7=-21[2+39]=-21 \times 41=-861
\end{gathered}
\)
Step 5: Final Answer
The value of \(a_{17}-A_7\) is:
\(
49-(-861)=49+861=910
\) -
Question 13 of 17
13. Question
If three successive terms of a G.P. with common ratio \(r(r>1)\) are the lengths of the sides of a triangle and \([r]\) denotes the greatest integer less than or equal to \(r\), then \(3[r]+[-r]\) is equal to _____. [JEE Main 2024 (Online) 1st February Evening Shift]
CorrectIncorrectHint
(a) Step 1: Define the Sides
Let the three successive terms of the G.P. be:
\(
a, \quad a r, \quad a r^2
\)
Since \(a\) is a length, \(a>0\). Given \(r>1\), the sides are in increasing order: \(a<a r<a r^2\).
Step 2: Apply the Triangle Inequality
For these sides to form a triangle, the sum of the two smaller sides must be greater than the largest side:
\(
a+a r>a r^2
\)
Since \(a>0\), we can divide the entire inequality by \(a\) :
\(
1+r>r^2 \Longrightarrow r^2-r-1<0
\)
Step 3: Solve the Quadratic Inequality
First, find the roots of \(r^2-r-1=0\) using the quadratic formula:
\(
r=\frac{-(-1) \pm \sqrt{(-1)^2-4(1)(-1)}}{2(1)}=\frac{1 \pm \sqrt{5}}{2}
\)
The roots are approximately:
\(r_1=\frac{1-\sqrt{5}}{2} \approx-0.618\)
\(r_2=\frac{1+\sqrt{5}}{2} \approx 1.618\)
For the quadratic \(r^2-r-1<0\), the value of \(r\) must lie between these roots:
\(
\frac{1-\sqrt{5}}{2}<r<\frac{1+\sqrt{5}}{2}
\)
Step 4: Incorporate the Given Condition
The problem states that \(r>1\). Therefore, the valid range for \(r\) is:
\(
1<r<\frac{1+\sqrt{5}}{2}
\)
Approximating the upper bound: \(r<1.618\).
Step 5: Evaluate the Greatest Integer Functions
Now we find \([r]\) and \([-r]\) for \(r \in(1,1.618)\) :
For \([r]\) : Since \(1<r<1.618\), the greatest integer less than or equal to \(r\) is 1.
For \([-r]\) : If \(1<r<1.618\), then \(-1.618<-r<-1\). The greatest integer less than or equal to \(-r\) is -2.
Step 6: Final Calculation
Substitute these values into the required expression:
\(
\begin{gathered}
3[r]+[-r]=3(1)+(-2) \\
3-2=1
\end{gathered}
\) -
Question 14 of 17
14. Question
Let \(3,7,11,15, \ldots, 403\) and \(2,5,8,11, \ldots, 404\) be two arithmetic progressions. Then the sum, of the common terms in them, is equal to ___. [JEE Main 2024 (Online) 1st February Morning Shift]
CorrectIncorrectHint
(b) Step 1: Identify the Properties of the two APs
Series 1 ( \(S_1\) ): 3, 7, 11, 15, . . . , 403
First term \(\left(a_1\right)=3\)
Common difference \(\left(d_1\right)=7-3=4\)
Series \(2\left(S_2\right)\) : 2, 5, 8, 11, 14, . . . 404
First term \(\left(a_2\right)=2\)
Common difference \(\left(d_2\right)=5-2=3\)
Step 2: Find the First Common Term
By inspection:
\(S_1: 3,7,11,15, \ldots\)
\(S_2: 2,5,8,11,14, \ldots\) The first common term \((A)\) is 11.
Step 3: Find the Common Difference of Common Terms
The common terms of two APs themselves form an AP. The common difference ( \(D\) ) of this new AP is the Least Common Multiple (LCM) of the common differences of the original series.
\(
D=\operatorname{LCM}\left(d_1, d_2\right)=\operatorname{LCM}(4,3)=12
\)
Step 4: Find the Number of Common Terms ( \(n\) )
The common terms must be less than or equal to the last term of the shorter range. The maximum value possible is 403 . The \(n^{\text {th }}\) common term is given by:
\(
\begin{gathered}
T_n=A+(n-1) D \leq 403 \\
11+(n-1) 12 \leq 403 \\
(n-1) 12 \leq 392 \\
n-1 \leq \frac{392}{12} \approx 32.66 \\
n \leq 33.66
\end{gathered}
\)
So, the number of terms \(n=33\).
Step 5: Calculate the Sum of Common Terms
We use the sum formula for an AP: \(S_n=\frac{n}{2}[2 A+(n-1) D]\)
\(
\begin{gathered}
S_{33}=\frac{33}{2}[2(11)+(33-1) 12] \\
S_{33}=\frac{33}{2}[22+32 \times 12] \\
S_{33}=\frac{33}{2}[22+384] \\
S_{33}=\frac{33}{2}[406] \\
S_{33}=33 \times 203 \\
S_{33}=6699
\end{gathered}
\) -
Question 15 of 17
15. Question
Let \(S_n\) be the sum to \(n\)-terms of an arithmetic progression \(3,7,11\), If \(40<\left(\frac{6}{n(n+1)} \sum_{k=1}^n S_k\right)<42\), then \(n\) equals ____. [JEE Main 2024 (Online) 30th January Evening Shift]
CorrectIncorrectHint
(c) Step 1: Finding the General Term and \(S_n\)
The series \(3,7,11, .\). is an arithmetic progression (AP) with:
First term \(a=3\)
Common difference \(d=4\)
The sum of the first \(n\) terms is:
\(
S_n=\frac{n}{2}[2(3)+(n-1) 4]=\frac{n}{2}(4 n+2)=2 n^2+n
\)
Step 2: Finding the Sum of \(S_k\)
You used the standard summation formulas:
\(\sum k^2=\frac{n(n+1)(2 n+1)}{6}\)
\(\sum k=\frac{n(n+1)}{2}\)
Your simplification was spot on:
\(
\sum_{k=1}^n S_k=\frac{n(n+1)(4 n+5)}{6}
\)
Step 3: Solving for \(n\)
The inequality given is:
\(
40<\frac{6}{n(n+1)}\left[\frac{n(n+1)(4 n+5)}{6}\right]<42
\)
This simplifies beautifully because the \(\frac{6}{n(n+1)}\) terms cancel out perfectly, leaving:
\(
40<4 n+5<42
\)
Subtracting 5 from all sides:
\(
35<4 n<37
\)
Dividing by 4:
\(
8.75<n<9.25
\)
Since \(n\) must be an integer (as it represents the number of terms), the only possible value is \(n=9\). -
Question 16 of 17
16. Question
Let \(\alpha=1^2+4^2+8^2+13^2+19^2+26^2+\ldots\) upto 10 terms and \(\beta=\sum_{n=1}^{10} n^4\). If \(4 \alpha-\beta=55 k+40\), then \(k\) is equal to ___. [JEE Main 2024 (Online) 30th January Morning Shift]
CorrectIncorrectHint
(d)
\(
\begin{aligned}
&\begin{gathered}
\alpha=1^2+4^2+8^2 \cdots \\
t_n=a^2+b n+c \\
1=a+b+c \\
4=4 a+2 b+c \\
8=9 a+3 b+c
\end{gathered}\\
&\text { On solving we get, } \mathrm{a}=\frac{1}{2}, \mathrm{~b}=\frac{3}{2}, \mathrm{c}=-1\\
&\begin{aligned}
& \alpha=\sum_{n=1}^{10}\left(\frac{n^2}{2}+\frac{3 n}{2}-1\right)^2 \\
& 4 \alpha=\sum_{n=1}^{10}\left(n^2+3 n-2\right)^2, \beta=\sum_{n=1}^{10} n^4 \\
& 4 \alpha-\beta=\sum_{n=1}^{10}\left(6 n^3+5 n^2-12 n+4\right)=55(353)+40
\end{aligned}
\end{aligned}
\)Explanation: Step 1: Verification of the General Term ( \(t_n\) )
You defined the base sequence as \(1,4,8, \ldots\) and assumed a quadratic form \(t_n=a n^2+ b n+c\).
For \(n=1: a+b+c=1\)
For \(n=2: 4 a+2 b+c=4\)
For \(n=3: 9 a+3 b+c=8\)
Solving this system:
\((4 a+2 b+c)-(a+b+c)=3 a+b=3\)
\((9 a+3 b+c)-(4 a+2 b+c)=5 a+b=4\)
Subtracting these: \((5 a+b)-(3 a+b) \Rightarrow 2 a=1 \Rightarrow \mathbf{a}=\frac{1}{2}\)
Substituting \(a[latex] : [latex]3\left(\frac{1}{2}\right)+b=3 \Rightarrow \mathbf{b}=\frac{3}{2}\)
Substituting into first eq: \(\frac{1}{2}+\frac{3}{2}+c=1 \Rightarrow c=-1\)
Your general term \(t_n=\frac{n^2+3 n-2}{2}\) is correct.
Step 2: Expansion of \(4 \alpha-\beta\)
You are looking at the difference between \(4 \alpha\) and \(\beta\) over 10 terms:
\(
\begin{gathered}
4 \alpha=\sum_{n=1}^{10}\left(n^2+3 n-2\right)^2 \\
\beta=\sum_{n=1}^{10} n^4
\end{gathered}
\)
Expanding the term inside \(\mathbf{4} \boldsymbol{\alpha}\) :
\(
\left(n^2+3 n-2\right)^2=n^4+9 n^2+4+6 n^3-4 n^2-12 n=n^4+6 n^3+5 n^2-12 n+4
\)
Subtracting \(\beta=n^4\) :
\(
4 \alpha-\beta=\sum_{n=1}^{10}\left(6 n^3+5 n^2-12 n+4\right)
\)
Step 3: Final Summation Calculation
Using the standard power sum formulas for \(n=10\) :
\(\sum n^3=\left(\frac{10 \cdot 11}{2}\right)^2=55^2=3025\)
\(\sum n^2=\frac{10 \cdot 11 \cdot 21}{6}=385\)
\(\sum n=55\)
\(\sum 4=40\)
Plugging these in:
\(
\begin{gathered}
6(3025)+5(385)-12(55)+40 \\
18150+1925-660+40=19455
\end{gathered}
\)
Your expression \(55(353)+40\) also yields \(19415+40=19455\). -
Question 17 of 17
17. Question
If \(8=3+\frac{1}{4}(3+p)+\frac{1}{4^2}(3+2 p)+\frac{1}{4^3}(3+3 p)+\cdots \cdots \infty\), then the value of \(p\) is ___. [JEE Main 2024 (Online) 27th January Morning Shift]
CorrectIncorrectHint
(a) You have correctly applied the formula for the sum of an infinite A.G.P., where the sum \(S_{\infty}\) is given by:
\(
S_{\infty}=\frac{a}{1-r}+\frac{d r}{(1-r)^2}
\)
Verification of the Steps:
Given your equation:
\(
8=\frac{3}{1-\frac{1}{4}}+\frac{p \cdot \frac{1}{4}}{\left(1-\frac{1}{4}\right)^2}
\)
Step 1: Simplify the first term:
\(
\frac{3}{3 / 4}=3 \cdot \frac{4}{3}=4
\)
Step 2: Simplify the second term: The denominator is \(\left(\frac{3}{4}\right)^2=\frac{9}{16}\). So, the term becomes:
\(
\frac{\frac{p}{4}}{\frac{9}{16}}=\frac{p}{4} \cdot \frac{16}{9}=\frac{4 p}{9}
\)
Step 3: Solve for \(p\) :
\(
\begin{gathered}
8=4+\frac{4 p}{9} \\
4=\frac{4 p}{9} \\
1=\frac{p}{9} \Rightarrow \mathbf{p}=\mathbf{9}
\end{gathered}
\)