Past JEE Main Entrance Papers Set-II
Overview
DISTANCE FORMULA :
The distance between two points \(A \left( x _1, y _1, z _1\right)\) and \(B \left( x _2, y_2, z _2\right)\) is given by \(A B=\sqrt{\left[\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2\right]}\)
SECTION FORMULAE :
Let \(P \left( x _1, y _1, z _1\right)\) and \(Q \left( x _2, y _2, z _2\right)\) be two points and let \(R ( x , y , z )\) divide \(P Q\) in the ratio \(m_1: m_2\). Then \(R\) is
\(
(x, y, z)=\left(\frac{m_1 x_2+m_2 x_1}{m_1+m_2}, \frac{m_1 y_2+m_2 y_1}{m_1+m_2}, \frac{m_1 z_2+m_2 z_1}{m_1+m_2}\right)
\)
If \(\left(m_1 / m_2\right)\) is positive, \(R\) divides PQ internally and if \(\left(m_1 / m_2\right)\) is negative, then externally.
Mid point of \(P Q\) is given by \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)\)
CENTROID OF A TRIANGLE :
Let \(A \left( x _1, y_1, z _1\right), B\left(x_2, y_2, z_2\right), C\left(x_3, y_3, z_3\right)\) be the vertices of a triangle \(A B C\). Then its centroid \(G\) is given by
\(
G=\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)
\)
DIRECTION COSINES OF LINE :
If \(\alpha, \beta, \gamma\) be the angles made by a line with \(x\)-axis, \(y\)-axis & \(z\)-axis respectively then \(\cos \alpha, \cos \beta~ \& \cos \gamma\) are called direction cosines of a line, denoted by \(l, m~ \& ~n\) respectively and the relation between \(\ell\), \(m , n\) is given by \(\ell^2+ m ^2+ n ^2=1\)
Direction cosine of \(x\)-axis, \(y\)-axis & \(z\)-axis are respectively
\(
(1,0,0) ; (0,1,0) ; (0,0,1)
\)
DIRECTION RATIOS :
Any three numbers \(a , b , c\) proportional to direction cosines \(\ell, m , n\) are called direction ratios of the line.
i.e. \(\frac{\ell}{a}=\frac{m}{b}=\frac{n}{c}\)
It is easy to see that there can be infinitely many sets of direction ratios for a given line.
RELATION BETWEEN D.Cosine’S & D.Ratio’S :
\(
\begin{aligned}
& \frac{\ell}{ a }=\frac{ m }{ b }=\frac{ n }{ c } \\
\therefore & \frac{\ell^2}{ a ^2}=\frac{ m ^2}{ b ^2}=\frac{ n ^2}{ c ^2}=\frac{\ell^2+ m ^2+ n ^2}{ a ^2+ b ^2+ c ^2} \\
\therefore \quad & \ell=\frac{ \pm a }{\sqrt{ a ^2+ b ^2+ c ^2}} ; m =\frac{ \pm b }{\sqrt{ a ^2+ b ^2+ c ^2}} ; n =\frac{ \pm c }{\sqrt{ a ^2+ b ^2+ c ^2}}
\end{aligned}
\)
DIRECTION COSINE OF AXES :
Direction ratios and Direction cosines of the line joining two points :
Let \(A \left( x _1, y _1, z _1\right)\) and \(B \left( x _2, y _2, z _2\right)\) be two points, then d.r.’s of \(AB\) are \(x_2-x_1, y_2-y_1, z_2-z_1\) and the d.c.’ s of \(A B\) are \(\frac{1}{r}\left(x_2-x_1\right), \frac{1}{r}\left(y_2-y_1\right)\), \(\frac{1}{ r }\left( z _2- z _1\right)\) where \(r =\sqrt{\left[\Sigma\left( x _2- x _1\right)^2\right]}=|\vec{ AB }|\)
PROJECTION OF A LINE ON ANOTHER LINE :
Let \(P Q\) be a line segment with \(P\left(x_1, y_1, z_1\right)\) and \(Q\left(x_2, y_2, z_2\right)\) and let \(L\) be a straight line whose d.c.’s are \(\ell, m , n\). Then the length of projection of PQ on the line \(L\) is \(\left|\ell\left(x_2-x_1\right)+m\left(y_2-y_1\right)+n\left(z_2-z_1\right)\right|\)
ANGLE BETWEEN TWO LINES :
Let \(\theta\) be the angle between the lines with d.c.’ \(l _1, m _1, n _1\) and \(l _2, m _2\), \(n _2\) then \(\cos \theta= l _1 l _2+m_1 m _2+ n _1 n _2\). If \(a _1, b _1, c _1\) and \(a _2, b_2, c_2\) be D.R.’s of two lines then angle \(\theta\) between them is given by
\(
\cos \theta=\frac{\left(a_1 a_2+b_1 b_2+c_1 c_2\right)}{\sqrt{\left(a_1^2+b_1^2+c_1^2\right)} \sqrt{\left(a_2^2+b_2^2+c_2^2\right)}}
\)
PERPENDICULARITY AND PARALLELISM :
Let the two lines have their d.c.’s given by \(l _1, m _1, n _1\) and \(l _2, m _2, n _2\) respectively then they are perpendicular if \(\theta=90^{\circ}\) i.e. \(\cos \theta=0\), i.e. \(l_1 l_2+ m_1 m_2+ n _1 n _2=0\).
Also the two lines are parallel if \(\theta=0\) i.e. \(\sin \theta=0\), i.e. \(\frac{\ell_1}{\ell_2}=\frac{m_1}{m_2}=\frac{n_1}{n_2}\)
Note:
If instead of d.c.’s, d.r.’s \(a _1, b _1, c _1\) and \(a _2, b _2, c _2\) are given, then the lines are perpendicular if \(a_1 a_2+b_1 b_2+c_1 c_2=0\) and parallel if \(a _1 / a _2= b _1 / b _2= c _1 / c _2\).
EQUATION OF A STRAIGHT LINE IN SYMMETRICAL FORM :
(a) One point form : Let \(A \left( x _1, y_1, z_1\right)\) be a given point on the straight line and \(l , m , n\) the \(d\).c’s of the line, then its equation is
\(
\frac{x-x_1}{\ell}=\frac{y-y_1}{m}=\frac{z-z_1}{n}=r \quad \text { (say) }
\)
It should be noted that \(P \left( x _1+lr, y _1+ mr , z _1+ nr \right)\) is a general point on this line at a distance \(r\) from the point \(A\left(x_1, y_1, z_1\right)\) i.e. \(A P=r\). One should note that for \(AP = r ; l, m , n\) must be d.c.’s not d.r.’s. If \(a , b , c\) are direction ratios of the line, then equation of the line is \(\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}=r\) but here \(A P \neq r\)
(b) Equation of the line through two points \(A \left( x _1, y _1, z _1\right)\) and \(B \left( x _2, y _2, z _2\right)\) is \(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\)
FOOT, LENGTH AND EQUATION OF PERPENDICULAR FROM A POINT TO A LINE :
Let equation of the line be
\(
\frac{x-x_1}{\ell}=\frac{y-y_1}{m}=\frac{z-z_1}{n}=r \text { (say) } \dots(i)
\)
and \(A (\alpha, \beta, \gamma)\) be the point. Any point on the line \(( i )\) is
\(
P \left(\ell r + x _1, mr + y _1, nr + z _1\right) \dots(ii)
\)
If it is the foot of the perpendicular, from \(A\) on the line, then \(AP\) is \(\perp\) to the line, so \(\ell\left(\ell r+x_1-\alpha\right)+m\left(m r+y_1-\beta\right)+n\left(n r+z_1-\gamma\right)=0\) i.e. \(\quad r=\left(\alpha-x_1\right) \ell+\left(\beta-y_1\right) m+\left(\gamma-z_1\right) n\)
since \(\ell^2+ m ^2+ n ^2=1\)
Putting this value of \(r\) in (ii), we get the foot of perpendicular from point A to the line.
Length : Since foot of perpendicular \(P\) is known, length of perpendicular,
\(
AP =\sqrt{\left[\left(\ell r + x _1-\alpha\right)^2+\left( mr + y _1-\beta\right)^2+\left( nr + z _1-\gamma\right)^2\right]}
\)
Equation of perpendicular is given by
\(
\frac{x-\alpha}{\ell r+x_1-\alpha}=\frac{y-\beta}{m r+y_1-\beta}=\frac{z-\gamma}{n r+z_1-\gamma}
\)
EQUATIONS OF A PLANE :
The equation of every plane is of the first degree i.e. of the form \(a x+b y+c z+d=0\), in which \(a, b, c\) are constants, where \(a^2+b^2+c^2 \neq\) 0 (i.e. \(a , b , c \neq 0\) simultaneously).
(a) Vector form of equation of plane :
If \(\vec{a}\) be the position vector of a point on the plane and \(\vec{n}\) be a vector normal to the plane then it’s vectorial equation is given by \((\overrightarrow{ r }-\overrightarrow{ a }) \cdot \overrightarrow{ n }=0 \Rightarrow \overrightarrow{ r } \cdot \overrightarrow{ n }= d\) where \(d =\overrightarrow{ a } \cdot \overrightarrow{ n }=\) constant.
(b) Plane Parallel to the Coordinate Planes :
(i) Equation of \(y-z\) plane is \(x=0\).
(ii) Equation of \(z-x\) plane is \(y=0\).
(iii) Equation of \(x-y\) plane is \(z=0\).
(iv) Equation of the plane parallel to \(x-y\) plane at a distance \(c\) is \(z = c\). Similarly, planes parallel to \(y – z\) plane and \(z\)-x plane are respectively \(x = c\) and \(y = c\).
(c) Equations of Planes Parallel to the Axes :
If \(a =0\), the plane is parallel to \(x\)-axis i.e. equation of the plane parallel to \(x\)-axis is \(b y+c z+d=0\).
Similarly, equations of planes parallel to \(y\)-axis and parallel to \(z\)-axis are \(ax + cz + d =0\) and \(a x+b y+d=0\) respectively.
(d) Equation of a Plane in Intercept Form :
Equation of the plane which cuts off intercepts a, b, c from the axes is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\).
(e) Equation of a Plane in Normal Form :
If the length of the perpendicular distance of the plane from the origin is \(p\) and direction cosines of this perpendicular are ( \(l\), \(m , n )\), then the equation of the plane is \(lx + my + nz = p\).
(f) Vectoral form of Normal equation of plane :
If \(\hat{n}\) is a unit vector normal to the plane from the origin to the plane and \(d\) be the perpendicular distance of plane from origin then its vector equation is \(\overrightarrow{ r } \cdot \hat{ n }= d\).
(g) Equation of a Plane through three points :
The equation of the plane through three non-collinear points
\(
\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)\left(x_3, y_3, z_3\right) \text { is }
\)
\(
\left|\begin{array}{cccc}
x & y & z & 1 \\
x_1 & y_1 & z_1 & 1 \\
x_2 & y_2 & z_2 & 1 \\
x_3 & y_3 & z_3 & 1
\end{array}\right|=0
\)
ANGLE BETWEEN TWO PLANES :
Consider two planes \(ax + by + cz + d =0\) and \(a ^{\prime} x + b ^{\prime} y + c ^{\prime} z + d ^{\prime}=0\).
Angle between these planes is the angle between their normals.
\(
\cos \theta=\frac{a a^{\prime}+b b^{\prime}+c c^{\prime}}{\sqrt{a^2+b^2+c^2} \sqrt{a^{\prime 2}+b^{\prime 2}+c^{\prime 2}}}
\)
\(\therefore\) Planes are perpendicular if \(aa ^{\prime}+ bb ^{\prime}+ cc ^{\prime}=0\) and they are parallel if \(a / a ^{\prime}= b / b ^{\prime}= c / c ^{\prime}\).
Planes parallel to a given Plane :
Equation of a plane parallel to the plane \(ax + by + cz + d =0\) is \(a x+b y+c z+d^{\prime}=0\). \(d^{\prime}\) is to be found by other given condition.
ANGLE BETWEEN A LINE AND A PLANE :
Let equations of the line and plane be \(\frac{x-x_1}{\ell}=\frac{y-y_1}{m}=\frac{z-z_1}{n}\) and \(a x+b y+c z+d=0\) respectively and \(\theta\) be the angle which line makes with the plane. Then \((\pi / 2-\theta)\) is the angle between the line and the normal to the plane.
\(
\text { So } \sin \theta=\frac{ a \ell+ bm + cn }{\sqrt{\left( a ^2+ b ^2+ c ^2\right)} \sqrt{\left(\ell^2+ m ^2+ n ^2\right)}}
\)
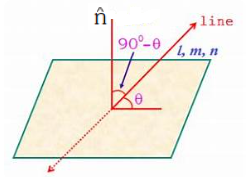
Line is parallel to plane if \(\theta=0\)
i.e. if \(al + bm + cn =0\).
Line is \(\perp\) to the plane if line is parallel to the normal of the plane
i.e. if \(\frac{ a }{\ell}=\frac{ b }{ m }=\frac{ c }{ n }\).
CONDITION IN ORDER THAT THE LINE MAY LIE ON THE GIVEN PLANE :
The line \(\frac{x-x_1}{\ell}=\frac{y-y_1}{m}=\frac{z-z_1}{n}\) will lie on the plane \(A x+B y+C z+D=0\)
if (a) \(A \ell+ Bm + Cn =0\) and (b) \(Ax _1+ By _1+ Cz _1+ D =0\)
POSITION OF TWO POINTS W.R.T. A PLANE :
Two points \(P \left( x _1, y _1, z _1\right) \& ~Q \left( x _2, y _2, z _2\right)\) are on the same or opposite sides of a plane \(ax + by + cz + d =0\) according to \(ax _1+ b y _1+ cz _1+ d~ \&\) \(~ax _2+ by _2+ cz _2+ d\) are of same or opposite signs.
IMAGE OF A POINT IN THE PLANE :
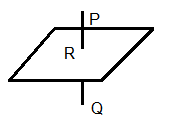
Let the image of a point \(P \left( x _1, y _1, z _1\right)\) in a plane \(a x+b y+c z+d=0\) is \(Q \left( x _2, y _2, z _2\right)\) and foot of perpendicular of point \(P\) on plane is \(R \left( x _3, y_3, z_3\right)\), then
(a) \(\frac{x_3-x_1}{a}=\frac{y_3-y_1}{b}=\frac{z_3-z_1}{c}=-\left(\frac{a x_1+b y_1+c z_1+d}{a^2+b^2+c^2}\right)\)
(b) \(\frac{x_2-x_1}{a}=\frac{y_2-y_1}{b}=\frac{z_2-z_1}{c}=-2\left(\frac{a x_1+b y_1+c z_1+d}{a^2+b^2+c^2}\right)\)
CONDITION FOR COPLANARITY OF TWO LINES :
Let the two lines be
\(
\begin{aligned}
& \frac{x-\alpha_1}{\ell_1}=\frac{y-\beta_1}{m_1}=\frac{z-\gamma_1}{n_1} \dots(i)\\
& \text { and } \quad \frac{x-\alpha_2}{\ell_2}=\frac{y-\beta_2}{m_2}=\frac{z-\gamma_2}{ n _2} \dots(ii)\\
&
\end{aligned}
\)
These lines will coplanar if \(\left|\begin{array}{ccc}\alpha_2-\alpha_1 & \beta_2-\beta_1 & \gamma_2-\gamma_1 \\ \ell_1 & m _1 & n _1 \\ \ell_2 & m _2 & n _2\end{array}\right|=0\)
the plane containing the two lines is \(\left|\begin{array}{ccc}x-\alpha_1 & y-\beta_1 & z-\gamma_1 \\ \ell_1 & m_1 & n_1 \\ \ell_2 & m_2 & n_2\end{array}\right|=0\)
PERPENDICULAR DISTANCE OF A POINT FROM THE PLANE :
Perpendicular distance \(p\), of the point \(A \left( x _1, y _1, z _1\right)\) from the plane \(a x+b y+c z+d=0\) is given by
\(
p =\frac{\left|a x_1+b y_1+c z_1+d\right|}{\sqrt{\left( a ^2+ b ^2+ c ^2\right)}}
\)
Distance between two parallel planes \(ax + by + cz + d _1=0\) \(\& ~a x+b y+c z+d_2=0\) is \(\left|\frac{d_1-d_2}{\sqrt{a^2+b^2+c^2}}\right|\)
A PLANE THROUGH THE LINE OF INTERSECTION OF TWO GIVEN PLANES :
Consider two planes
\(
u \equiv a x+b y+c z+d=0 \text { and } v \equiv a^{\prime} x+b^{\prime} y+c^{\prime} z+d^{\prime}=0 \text {. }
\)
The equation \(u+\lambda v=0, \lambda\) a real parameter, represents the plane passing through the line of intersection of given planes and if planes are parallel, this represents a plane parallel to them.
BISECTORS OF ANGLES BETWEEN TWO PLANES :
Let the equations of the two planes be \(ax + by + cz + d =0\) and \(a_1 x+b_1 y+c_1 z+d_1=0\).
Then equations of bisectors of angles between them are given by
\(
\frac{a x+b y+c z+d}{\sqrt{\left(a^2+b^2+c^2\right)}}= \pm \frac{a_1 x+b_1 y+c_1 z+d_1}{\sqrt{\left(a_1^2+b_1^2+c_1^2\right)}}
\)
(a) Equation of bisector of the angle containing origin : First make both constant terms positive. Then +ve sign give the bisector of the angle which contains the origin.
(b) Bisector of acute/obtuse angle : First making both constant terms positive,
\(aa _1+ bb _1+ cc _1>0 \quad \Rightarrow\) origin lies in obtuse angle
\(aa _1+ bb _1+ cc _1<0 \quad \Rightarrow\) origin lies in acute angle
Quiz Summary
0 of 202 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 202 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 202
1. Question
If \((a, b, c)\) is the image of the point \((1,2,-3)\) in the line \(\frac{x+1}{2}=\frac{y-3}{-2}=\frac{z}{-1}\), then \(a + b + c\) is : [JEE Main 2020 (Online) 5th September Morning Slot]
CorrectIncorrectHint
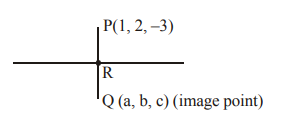
Line is \(\frac{x+1}{2}=\frac{y-3}{-2}=\frac{z}{-1}=\lambda\) : Let point \(R\) is
\(
(2 \lambda-1,-2 \lambda+3,-\lambda)
\)
Direction ratio of \(P Q \equiv(2 \lambda-2,-2 \lambda+1,3-\lambda)\)
\(P O\) is \(\perp^r\) to line
\(
\begin{aligned}
& \Rightarrow 2(2 \lambda-2)-2(-2 \lambda+1)-1(3-\lambda)=0 \\
& 4 \lambda-4+4 \lambda-2-3+\lambda=0 \\
& 9 \lambda=9 \Rightarrow \lambda=1 \\
& \Rightarrow \text { Point } R \text { is }(1,1,-1) \\
& \begin{array}{c|c|c}
\frac{a+1}{2}=1 & \frac{b+2}{2}=1 & \frac{c-3}{2}=-1 \\
a=1 & b=0 & c=1
\end{array} \\
& \Rightarrow a+b+c=2 \\
&
\end{aligned}
\) -
Question 2 of 202
2. Question
The distance of the point \((1,-2,3)\) from the plane \(x-y+z=5\) measured parallel to the line \(\frac{x}{2}=\frac{y}{3}=\frac{z}{-6}\) is : [JEE Main 2020 (Online) 4th September Evening Slot]
CorrectIncorrectHint
Equation of line parallel to \(\frac{x}{2}=\frac{y}{3}=\frac{z}{-6}\) passes through \((1,-2,3)\) is
\(
\begin{aligned}
& \frac{x-1}{2}=\frac{y+2}{3}=\frac{z-3}{-6}=r \\
& x=2 r+1 \\
& y=3 r-2 \\
& z=-6 r+3
\end{aligned}
\)
A point on whole line \(=(2 r+1,3 r-2,-6 r+3)\).
This point lies on plane \(x-y+2=5\)
\(
\begin{aligned}
& \text { so, } 2 r+1-3 r+2-6 r+3=5 \\
& \Rightarrow r=\frac{1}{7} \\
& \therefore x=\frac{9}{7}, y=\frac{-11}{7}, z=\frac{15}{7}
\end{aligned}
\)
Distance is \(=\sqrt{\left(\frac{9}{7}-1\right)^2+\left(2-\frac{11}{7}\right)^2+\left(3-\frac{15}{7}\right)^2}\)
\(
\begin{aligned}
& =\sqrt{\left(\frac{2}{7}\right)^2+\left(\frac{3}{7}\right)^2+\left(\frac{6}{7}\right)^2} \\
& =\frac{1}{7} \sqrt{4+9+36}=1
\end{aligned}
\) -
Question 3 of 202
3. Question
The plane which bisects the line joining, the points \((4,-2,3)\) and \((2,4,-1)\) at right angles also passes through the point : [JEE Main 2020 (Online) 3rd September Evening Slot]
CorrectIncorrectHint
Direction ratios of normal to plane are <2,-6,4>
Also plane passes through \((3,1,1)\)
\(\therefore\) Equation of plane
\(
\begin{aligned}
& 2( x -3)-6( y -1)+4( z -1)=0 \\
& \Rightarrow x -3 y +2 z =2
\end{aligned}
\)
By checking all options we can see this equation passes through \((4,0,-1)\) -
Question 4 of 202
4. Question
The foot of the perpendicular drawn from the point \((4,2,3)\) to the line joining the points \((1,-2,3)\) and \((1,1,0)\) lies on the plane: [JEE Main 2020 (Online) 3rd September Morning Slot]
CorrectIncorrectHint

Equation of \(A B\),
\(
\begin{aligned}
& \frac{x-1}{0}=\frac{y+2}{3}=\frac{z-3}{-3}=\lambda \\
& \therefore \text { Coordinates of any point on the line }( M )=(\lambda+1 ,3 \lambda-2,-3 \lambda+3) \\
& \overrightarrow{P M}=-3 \hat{i}+(3 \lambda-4) \hat{j}-3 \lambda \widehat{k} \\
& \overrightarrow{A B}=3 \hat{j}-3 \widehat{k}
\end{aligned}
\)
As \(\overrightarrow{P M} \perp \overrightarrow{A B}\)
\(
\begin{aligned}
& \therefore \overrightarrow{P M} \cdot \overrightarrow{A B}=0 \\
& \Rightarrow(-3) \cdot 0+(3 \lambda-4)(3)+(-3 \lambda)(-3)=0 \\
& \Rightarrow \lambda=\frac{2}{3} \\
& \therefore M=(1,0,1)
\end{aligned}
\)
By checking each options we can see \(M\) lies on \(2 x+y-z=1\). -
Question 5 of 202
5. Question
A plane passing through the point \((3,1,1)\) contains two lines whose direction ratios are \(1,-2,2\) and \(2,3,-1\) respectively. If this plane also passes through the point ( \(\alpha,-\) \(3,5)\), then \(\alpha\) is equal to: [JEE Main 2020 (Online) 2nd September Evening Slot]
CorrectIncorrectHint
As normal is perpendicular to both the lines so normal vector to the plane is
\(
\begin{aligned}
& \vec{n}=(\hat{i}-2 \hat{j}+2 \widehat{k}) \times(2 \hat{i}+3 \hat{j}-\widehat{k}) \\
& \vec{n}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
1 & -2 & 2 \\
2 & 3 & -1
\end{array}\right| \\
& \vec{n}=(2-6) \hat{i}-(-1-4) \hat{j}+(3+4) \widehat{k} \\
& \vec{n}=-4 \hat{i}+5 \hat{j}+7 \widehat{k}
\end{aligned}
\)
Now equation of plane passing through \((3,1,1)\) is
\(
\begin{aligned}
& \Rightarrow-4(x-3)+5(y-1)+7(z-1)=0 \\
& \Rightarrow-4 x+12+5 y-5+7 z-7=0 \\
& \Rightarrow-4 x+5 y+7 z=0 \dots(1)
\end{aligned}
\)
Plane is also passing through \((\alpha,-3,5)\) so this point satisfies the equation of plane so put in equation (1)
\(
\begin{aligned}
& -4 \alpha+5 \times(-3)+7 \times(5)=0 \\
& \Rightarrow-4 \alpha-15+35=0 \\
& \Rightarrow \alpha=5
\end{aligned}
\) -
Question 6 of 202
6. Question
The plane passing through the points \((1,2,1)\), \((2,1,2)\) and parallel to the line, \(2 x=3 y, z=1\) also passes through the point : [JEE Main 2020 (Online) 2nd September Morning Slot]
CorrectIncorrectHint
Equation of plane passing through \((2,1,2)\)
\(
a(x-2)+b(y-1)+c(z-2)=0
\)
As point \((1,2,1)\) also passes through the plane, so it satisfy the equation,
\(
\begin{aligned}
& a(1-2)+b(2-1)+c(1-2)=0 \\
& \Rightarrow-a+b-c=0 \ldots .(2)
\end{aligned}
\)
Given line \(2 x=3 y\) and \(z=1\),
So, symmetric form of the line
\(
\frac{x}{3}=\frac{y}{2}=\frac{z-1}{0}
\)
\(\therefore\) Direction ratio of this line is \((3,2,0)\) and Direction ratio of plane \(=(a, b, c)\)
As plane is parallel to the line so the normal of the plane is perpendicular to the line.
\(\therefore\) Dot product of direction ratio \(=0\)
\(
3 a+2 b+0(c)=0
\)
Equation of plane,
\(
\begin{aligned}
& \left|\begin{array}{ccc}
x-2 & y-1 & z-2 \\
-1 & 1 & -1 \\
3 & 2 & 0
\end{array}\right|=0 \\
& \Rightarrow 3(1-y+2-z)-2(-x+2+z-2)=0 \\
& \Rightarrow 9-3 y-3 z+2 x-2 z=0 \\
& \Rightarrow 2 x-3 y-5 z+9=0
\end{aligned}
\)
By checking all options you can see \((-2,0,1)\) satisfy the equation. -
Question 7 of 202
7. Question
The mirror image of the point \((1,2,3)\) in a plane is \(\left(-\frac{7}{3},-\frac{4}{3},-\frac{1}{3}\right)\). Which of the following points lies on this plane? [JEE Main 2020 (Online) 8th January Evening Slot]
CorrectIncorrectHint
Let \(A (1,2,3), B \left(-\frac{7}{3},-\frac{4}{3},-\frac{1}{3}\right)\)
\(\therefore\) Midpoint of \(A B=M=\left(\frac{\frac{-7}{3}+1}{2}, \frac{\frac{4}{3}+2}{2}, \frac{\frac{-1}{3}+3}{2}\right)\)
\(
=\left(\frac{-2}{3}, \frac{1}{3}, \frac{4}{3}\right)
\)
DR of AM \(=\left(1+\frac{2}{3}, 2-\frac{1}{3}, 3-\frac{4}{3}\right)\)
\(
\begin{aligned}
& =\left(\frac{5}{3}, \frac{5}{3}, \frac{5}{3}\right) \\
& =(1,1,1)
\end{aligned}
\)
Equation of plane
\(
\begin{aligned}
& a\left(x+\frac{2}{3}\right)+b\left(y-\frac{1}{3}\right)+c\left(z-\frac{4}{3}\right)=0 \\
& \Rightarrow 1\left(x+\frac{2}{3}\right)+1\left(y-\frac{1}{3}\right)+1\left(z-\frac{4}{3}\right)=0 \\
& \Rightarrow x+y+z=1
\end{aligned}
\)
\(\therefore(1,-1,1)\) lies on the plane. -
Question 8 of 202
8. Question
The shortest distance between the lines \(\frac{x-3}{3}=\frac{y-8}{-1}=\frac{z-3}{1}\) and \(\frac{x+3}{-3}=\frac{y+7}{2}=\frac{z-6}{4}\) is : [JEE Main 2020 (Online) 8th January Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& \vec{a}=\langle 3,8,3\rangle \\
& \vec{b}=\langle-3,-7,6\rangle \\
& \vec{p}=\langle 3,-1,1\rangle \\
& \vec{q}=\langle-3,2,4\rangle \\
& \vec{p} \times \vec{q}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
3 & -1 & 1 \\
-3 & 2 & 4
\end{array}\right|=\langle-6,-15,3\rangle \\
& \text { Shortest distance }=\left|\frac{(\vec{b}-\vec{a}) \cdot(\vec{p} \times \vec{q})}{|\vec{p} \times \vec{q}|}\right| \\
& =\left|\frac{(-6,-15,3) \cdot(-6,-15,3)}{\sqrt{36+225+9}}\right| \\
& =\left|\frac{36+225+9}{\sqrt{36+225+9}}\right| \\
& =\sqrt{270}=3 \sqrt{30} \\
&
\end{aligned}
\) -
Question 9 of 202
9. Question
Let \(P\) be a plane passing through the points \((2,1,0),(4,1,1)\) and \((5,0,1)\) and \(R\) be any point \((2,1,6)\). Then the image of \(R\) in the plane \(P\) is : [JEE Main 2020 (Online) 7th January Morning Slot]
CorrectIncorrectHint
Plane passing through \((2,1,0),(4,1,1)\) and \((5,0,1)\) is
\(
\left|\begin{array}{lll}
x-2 & y-1 & z-0 \\
4-2 & 1-1 & 1-0 \\
5-2 & 0-1 & 1-0
\end{array}\right|=0
\)
\(\therefore\) Image of \(R(2,1,6)\) in this plane is
\(
\begin{aligned}
& \frac{x-2}{1}=\frac{y-1}{1}=\frac{z-6}{-2}=-2 \frac{(2+1-12-3)}{1+1+4} \\
& \therefore( x , y , z )=(6,5,-2)
\end{aligned}
\) -
Question 10 of 202
10. Question
A plane which bisects the angle between the two given planes \(2 x-y+2 z-4=0\) and \(x+2 y+2 z-2=0\), passes through the point : [JEE Main 2019 (Online) 12th April Evening Slot]
CorrectIncorrectHint
Planes bisecting the given planes are
\(
\begin{aligned}
& \frac{2 x-y+2 z-4}{3}= \pm \frac{x+2 y+2 z-2}{3} \\
& \Rightarrow x -3 y =2 \text { or } 3 x + y +4 z =6
\end{aligned}
\)
Out of the four given points in question’s options only \((2,-4,1)\) lies on the plane \(3 x+y\) \(+4 z=6\) -
Question 11 of 202
11. Question
The length of the perpendicular drawn from the point \((2,1,4)\) to the plane containing the lines \(\vec{r}=(\hat{i}+\hat{j})+\lambda(\hat{i}+2 \hat{j}-\widehat{k})\) and \(\vec{r}=(\hat{i}+\hat{j})+\mu(-\hat{i}+\hat{j}-2 \widehat{k})\) is : [JEE Main 2019 (Online) 12th April Evening Slot]
CorrectIncorrectHint
Vector of the plane is
\(
\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & 2 & -1 \\
-1 & 1 & -2
\end{array}\right|=-3 \hat{i}+3 \hat{j}+3 \hat{k}
\)
Now equation of plane is
\(
-3 x+3 y+3 z=c
\)
\((1,1,0)\) will satisfy the plane
\(
\begin{aligned}
& \Rightarrow-3+3+0=c \\
& \Rightarrow c =0 \\
& -3 x+3 y+3 z=0
\end{aligned}
\)
distance from \((2,1,4)\) is
\(
\Rightarrow\left|\frac{-6+3+12}{\sqrt{27}}\right|=\left|\frac{9}{3 \sqrt{3}}\right|=\sqrt{3} \text { units }
\) -
Question 12 of 202
12. Question
If the line \(\frac{x-2}{3}=\frac{y+1}{2}=\frac{z-1}{-1}\) intersects the plane \(2 x+3 y-z+13=0\) at a point \(P\) and the plane \(3 x+y+4 z=16\) at a point \(Q\), then \(P Q\) is equal to : [JEE Main 2019 (Online) 12th April Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x-2}{3}=\frac{y+1}{2}=\frac{z-1}{-1}=\lambda \\
& A(3 \lambda+2,2 \lambda-1,-\lambda+1) \text { line on } 2 x+3 y-z+13=0 \\
& \Rightarrow 2(3 \lambda+2)+3(2 \lambda-1)-(-\lambda+1)+13=0 \\
& \Rightarrow 13 \lambda+13=0 \Rightarrow \lambda=-1
\end{aligned}
\)
Now point \(P(-1,-3,2)\) lie on \(3 x+y+4 z=16\)
\(
\begin{aligned}
& \Rightarrow 3(3 \lambda+2)+(3 \lambda+2)+4(3 \lambda+2)=16 \\
& \Rightarrow 9 \lambda+6+2 \lambda-4 \lambda-1+4=16 \\
& \Rightarrow 7 \lambda=7 \Rightarrow \lambda=1 \\
& \Rightarrow Q(5,1,0) \\
& \therefore P Q=\sqrt{36+16+4}=\sqrt{56}=2 \sqrt{14}
\end{aligned}
\) -
Question 13 of 202
13. Question
If the plane \(2 x-y+2 z+3=0\) has the distances \(\frac{1}{3}\) and \(\frac{2}{3}\) units from the planes \(4 x-\) \(2 y+4 z+\lambda=0\) and \(2 x-y+2 z+\mu=0\), respectively, then the maximum value of \(\lambda+\mu\) is equal to : [JEE Main 2019 (Online) 10th April Evening Slot]
CorrectIncorrectHint
\(
\text { (i) } \begin{aligned}
& \frac{|\lambda-6|}{\sqrt{16+4+16}}=\left|\frac{\lambda-6}{6}\right|=\frac{1}{3} \\
& \Rightarrow|\lambda-6|=2 \\
& \Rightarrow \lambda=8,4
\end{aligned}
\)
\(
\begin{aligned}
& \text { (ii) } \frac{|\mu-3|}{\sqrt{4+4+1}}=\frac{2}{3} \\
& \Rightarrow|\mu-3|=2 \\
& \Rightarrow \mu=5,1 \\
& \therefore(\mu+\lambda)_{\max }=13
\end{aligned}
\) -
Question 14 of 202
14. Question
A perpendicular is drawn from a point on the line \(\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z}{1}\) to the plane \(x + y\) \(+z=3\) such that the foot of the perpendicular \(Q\) also lies on the plane \(x-y+z=3\). Then the co-ordinates of \(Q\) are : [JEE Main 2019 (Online) 10th April Evening Slot]
CorrectIncorrectHint
\(
\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z}{1}=\lambda
\)
Let a point \(P\) on the line is
\(
(2 \lambda+1,-\lambda-1,+\lambda)
\)
Foot of \(\perp^r Q\) is given by
\(
\frac{x-2 \lambda-1}{1}=\frac{y+\lambda+1}{1}=\frac{z-\lambda}{1}=-\frac{(2 \lambda-3)}{3}
\)
\(\therefore Q\) lies on \(x+y+z=3 \& x-y+z=3\)
\(
\begin{aligned}
& \Rightarrow x+z=3 \& y=0 \\
& \therefore y=0 \Rightarrow \lambda+1=\frac{-2 \lambda+3}{3} \Rightarrow \lambda=0
\end{aligned}
\)
\(\therefore Q\) is \((2,0,1)\) -
Question 15 of 202
15. Question
If the length of the perpendicular from the point \((\beta, 0, \beta)(\beta \neq 0)\) to the line, \(\frac{x}{1}=\frac{y-1}{0}=\frac{z+1}{-1}\) is \(\sqrt{\frac{3}{2}}\), then \(\beta\) is equal to : [JEE Main 2019 (Online) 10th April Morning Slot]
CorrectIncorrectHint
\(
\frac{x}{1}=\frac{y-1}{0}=\frac{z+1}{-1}=p P(\beta, 0, \beta)
\)
any point on line \(A=(p, 1,-p-1)\)
Now, DR of \(AP \equiv< p -\beta, 1-0,- p -1-\beta>\)
Which is perpendicular to line so
\(
\begin{aligned}
& ( p -\beta) \cdot 1+0.1-1(- p -1-\beta)=0 \\
& \Rightarrow p -\beta+ p +1+\beta=0 \\
& p=\frac{-1}{2}
\end{aligned}
\)
Point \(A\left(\frac{-1}{2}, 1-\frac{1}{2}\right)\)
Now, distance AP \(=\sqrt{\frac{3}{2}}\)
\(
\Rightarrow A P^2=\frac{3}{2}
\)
\(
\begin{aligned}
& \Rightarrow\left(\beta+\frac{1}{2}\right)^2+1+\left(\beta+\frac{1}{2}\right)^2=\frac{3}{2} \\
& \Rightarrow 2\left(\beta+\frac{1}{2}\right)^2=\frac{1}{2} \\
& \Rightarrow\left(\beta+\frac{1}{2}\right)^2=\frac{1}{4} \\
& \Rightarrow \beta=0,-1,(\beta \neq 0) \\
& \therefore \beta=-1
\end{aligned}
\) -
Question 16 of 202
16. Question
If \(Q(0,-1,-3)\) is the image of the point \(P\) in the plane \(3 x-y+4 z=2\) and \(R\) is the point \((3,-1,-2)\), then the area (in sq. units) of \(\triangle P Q R\) is : [JEE Main 2019 (Online) 10th April Morning Slot]
CorrectIncorrectHint
Image of \(Q\) in plane
\(
\begin{aligned}
& \frac{(x-0)}{3}=\frac{(y+1)}{-1}=\frac{z+3}{+4}=\frac{-2(1-12-2)}{9+1+16}=1 \\
& x=3, y=-2, z=1 \\
& P(3,-2,1), Q(0,-1,-3), R(3,-1,-2)
\end{aligned}
\)
Now area of \(\triangle P Q R\) is
\(
\frac{1}{2}|\overline{P Q} \times \overline{Q R}|
\)
\(
=\frac{1}{2}\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
3 & -1 & 4 \\
3 & 0 & 1
\end{array}\right|
\)
\(
\begin{aligned}
& \Rightarrow \frac{1}{2}|\{\hat{i}(-1)-\hat{j}(3-12)+\widehat{k}(3)\}| \\
& \Rightarrow \frac{1}{2} \sqrt{(1+81+9)} \\
& \Rightarrow \frac{\sqrt{91}}{2}
\end{aligned}
\) -
Question 17 of 202
17. Question
The vertices \(B\) and \(C\) of a \(\triangle A B C\) lie on the line, \(\frac{x+2}{3}=\frac{y-1}{0}=\frac{z}{4}\) such that \(BC =5\) units.
Then the area (in sq. units) of this triangle, given that the point \(A(1,-1,2)\), is : [JEE Main 2019 (Online) 9th April Evening Slot]CorrectIncorrectHint
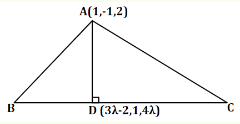
Let \(A D\) be a perpendicular drawn from point \(A\) on
The vertices \(B\) and \(C\) of a \(\triangle A B C\) lie on the line, \(\frac{x+2}{3}=\frac{y-1}{0}=\frac{z}{4}\) Coordinates of D can be expressed as \((3 \lambda-2,1,4 \lambda)\).
DR’s of AD are \((3 \lambda-3,2,4 \lambda-2)\)
\(A D\) is perpendicular to \(B C\)
\(
\begin{aligned}
& \therefore 3(3 \lambda-3)+0(2)+4(4 \lambda-2)=0 \\
& \Rightarrow 9 \lambda-9+0+16 \lambda-8=0 \\
& \Rightarrow \lambda=\frac{17}{25}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Coordinates of D are }\left(\frac{1}{25}, 1, \frac{68}{25}\right) \\
& \text { Length of } A D=\sqrt{\left(\frac{1}{25}-1\right)^2+(1-(-1))^2+\left(\frac{68}{25}-2\right)^2} \\
& =\sqrt{\frac{576}{625}+4+\frac{324}{625}} \\
& =\sqrt{\frac{3400}{625}}=\frac{2}{5} \sqrt{34} \\
&
\end{aligned}
\)
\(
\text { Area of triangle }=\frac{1}{2} \times 5 \times \frac{2}{5} \sqrt{34}=\sqrt{34} \text { sq. units }
\) -
Question 18 of 202
18. Question
Let \(P\) be the plane, which contains the line of intersection of the planes, \(x+y+z-6=\) 0 and \(2 x+3 y+z+5=0\) and it is perpendicular to the \(x y\)-plane. Then the distance of the point \((0,0,256)\) from \(P\) is equal to : [JEE Main 2019 (Online) 9th April Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& P_1: x+y+z-6=0 \\
& P_2: 2 x+3 y+z+5=0
\end{aligned}
\)
Equation of plane which passes through the line of intersection of \(P_1\) and \(P_2\) is
\(
\begin{aligned}
& P_1+\lambda P_2=0 \\
& \Rightarrow(x+y+z-6)+\lambda(2 x+3 y+z+5)=0 \\
& \Rightarrow(1+2 \lambda) x+(1+3 \lambda) y+(1+\lambda) z+(5 \lambda-6)=0
\end{aligned}
\)
As the above plane is perpendicular to xy plane
\(
\begin{aligned}
& \therefore \vec{n} \cdot \hat{k}=0 \\
& \Rightarrow[(2+\lambda) \hat{i}+(3+\lambda) \hat{j}+(1+\lambda) \widehat{k}] \cdot \widehat{k}=0 \\
& \Rightarrow 1+\lambda=0 \\
& \Rightarrow \lambda=-1
\end{aligned}
\)
So, equation of plane
\(
\begin{aligned}
& -x-2 y-11=0 \\
& \Rightarrow x+2 y+11=0
\end{aligned}
\)
Distance of the point \((0,0,256)\) from this plane
\(
=\left|\frac{0+0+11}{\sqrt{5}}\right|=\frac{11}{\sqrt{5}}
\) -
Question 19 of 202
19. Question
A plane passing through the points \((0,-1,0)\) and \((0,0,1)\) and making an angle \(\frac{\pi}{4}\) with the plane \(y-z+5=0\), also passes through the point [JEE Main 2019 (Online) 9th April Morning Slot]
CorrectIncorrectHint
Let \(a x+b y+c z=1\) be the equation of the plane
it passed through point \((0,-1,0)\).
\(
\begin{aligned}
& \therefore-b=1 \\
& \Rightarrow b=-1
\end{aligned}
\)
Also it passes through point \((0,0,1)\)
\(
\therefore c=1
\)
So the plane is \(a x-y+z=1\).
This plane an angle \(\frac{\pi}{4}\) with the plane \(y-z+5=0\).
Normal to the plane \(a x-y+z=1\) is
\(
\vec{a}=a \hat{i}-\hat{j}+\widehat{k}
\)
Normal to the plane \(y-z+5=0\) is
\(
\vec{b}=\hat{j}-\widehat{k}
\)
\(
\begin{aligned}
& \cos \theta=\left|\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\right| \\
& \Rightarrow \frac{1}{\sqrt{2}}=\left|\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\right| \\
& \Rightarrow \frac{|0-1-1|}{\sqrt{a^2+1+1} \sqrt{1^2+1^2}}=\frac{1}{\sqrt{2}} \\
& \Rightarrow a^2+2=4 \\
& \Rightarrow a= \pm \sqrt{2}
\end{aligned}
\)
\(\therefore\) Equation of plane
\(
\pm \sqrt{2} x-y+z=1
\)
Now by checking each options you can see equation \(-\sqrt{2} x-y+z=1\) satisfy by the point \((\sqrt{2}, 1,4)\) -
Question 20 of 202
20. Question
If the line, \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-2}{4}\) meets the plane, \(x +2 y +3 z =15\) at a point \(P\), then the distance of \(P\) from the origin is : [JEE Main 2019 (Online) 9th April Morning Slot]
CorrectIncorrectHint
Let \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-2}{4}=\lambda\)
Any arbitary point on the line is \(P (2 \lambda+1,3 \lambda-1,4 \lambda+2)\).
This point also lies on the plane \(x+2 y+3 z=15\).
\(
\begin{aligned}
& \therefore(2 \lambda+1)+2(3 \lambda-1)+3(4 \lambda+2)=15 \\
& \Rightarrow 20 \lambda=10 \\
& \Rightarrow \lambda=\frac{1}{2}
\end{aligned}
\)
So point \(P\) is \(\left(2, \frac{1}{2}, 4\right)\).
Distance from the origin \((0)\) of point \(P\left(2, \frac{1}{2}, 4\right)\) is
\(
\begin{aligned}
& OP =\sqrt{(2)^2+\left(\frac{1}{2}\right)^2+(4)^2} \\
& =\sqrt{4+\frac{1}{4}+16} \\
& =\sqrt{\frac{81}{4}} \\
& =\frac{9}{2}
\end{aligned}
\) -
Question 21 of 202
21. Question
The vector equation of the plane through the line of intersection of the planes \(x+y+z\) \(=1\) and \(2 x+3 y+4 z=5\) which is perpendicular to the plane \(x-y+z=0\) is : [JEE Main 2019 (Online) 8th April Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& P_1: x+y+z=1 \\
& P_1: 2 x+3 y+4 z=5
\end{aligned}
\)
Equation of the plane passing through the line of intersection of the plane \(P_1\) and \(P_2\) is
\(
\begin{aligned}
& P _1+\lambda P _2=0 \\
& \Rightarrow(x+y+z-1)+\lambda(2 x+3 y+4 z-5)=0 \\
& \Rightarrow x(1+2 \lambda)+y(1+3 \lambda)+z(1+4 \lambda)-5 \lambda-1=0 \dots(1)
\end{aligned}
\)
Direction Ratio (D.R) of this plane \(=(1+2 \lambda, 1+3 \lambda, 1+4 \lambda)\)
Plane (1) is perpendicular to \(x-y+z=0\), whose D.R \(=(1,-1,1)\)
As they are perpendicular so dot product of D.R \(=0\)
\(
\begin{aligned}
& \therefore(1)(1+2 \lambda)+(-1)(1+3 \lambda)+(1)(1+4 \lambda)=0 \\
& \Rightarrow 1+2 \lambda-1-3 \lambda+1+4 \lambda=0 \\
& \Rightarrow \lambda=-\frac{1}{3}
\end{aligned}
\)
Putting the value of \(\lambda\) in equation (1), we get
\(
\begin{aligned}
& \Rightarrow \frac{x}{3}-\frac{z}{3}+\frac{2}{3}=0 \\
& \Rightarrow x – z +2=0
\end{aligned}
\)
Vector form of this plane,
\(
\vec{r} \cdot(\hat{i}-\hat{k})+2=0
\) -
Question 22 of 202
22. Question
If a point \(R(4, y, z)\) lies on the line segment joining the points \(P(2,-3,4)\) and \(Q(8,0\), \(10)\), then the distance of \(R\) from the origin is : [JEE Main 2019 (Online) 8th April Evening Slot]
CorrectIncorrectHint
Equation of \(P Q\) is
\(
\begin{aligned}
& \frac{x-2}{8-2}=\frac{y+3}{0-(-3)}=\frac{z-4}{10-4} \\
& \Rightarrow \frac{x-2}{6}=\frac{y+3}{3}=\frac{z-4}{6}
\end{aligned}
\)
Point \(R(4, y, z)\) lies on this
\(
\begin{aligned}
& \therefore \frac{4-2}{6}=\frac{y+3}{3}=\frac{z-4}{6} \\
& \Rightarrow \frac{1}{3}=\frac{y+3}{3}=\frac{z-4}{6}
\end{aligned}
\)
\(y=-2\) and \(y=6\)
\(
\therefore R=(4,-2,6)
\)
Distance of \(R(4,-2,6)\) from the origin \(O(0,0,0)\) is
\(
\begin{aligned}
& RO =\sqrt{4^2+(-2)^2+6^2} \\
& =\sqrt{56}=2 \sqrt{14}
\end{aligned}
\) -
Question 23 of 202
23. Question
The length of the perpendicular from the point \((2,-1,4)\) on the straight line, \(\frac{x+3}{10}=\frac{y-2}{-7}=\frac{z}{1}\) is : [JEE Main 2019 (Online) 8th April Morning Slot]
CorrectIncorrectHint
Given,
\(P=(2,-1,4)\) and equation of line \(\frac{x+3}{10}=\frac{y-2}{-7}=\frac{z}{1}\)
Any point \(B\) on the line is \((10 \lambda-3,-7 \lambda+2, \lambda)\)
Now,
Direction ratios of \(PB =(10 \lambda-5,-7 \lambda+3, \lambda-4)\)
Direction ratios of the line \(=(10,-7,1)\)
As the lines are perpendicular, therefore dot product of given lines are 0 .
\(
\begin{aligned}
& \Rightarrow 10(10 \lambda-5)-7(-7 \lambda+3)+(\lambda-4)=0 \\
& \Rightarrow 100 \lambda-50+49 \lambda-21+\lambda-4=0 \\
& \Rightarrow 150 \lambda=75 \\
& \Rightarrow \lambda=\frac{1}{2}
\end{aligned}
\)
Point \(B=\left(2,-\frac{3}{2}, \frac{1}{2}\right)\)
\(
|P B|=\frac{5}{\sqrt{2}}=3.53
\) -
Question 24 of 202
24. Question
The magnitude of the projection of the vector \(2\hat{i}+3\hat{j}+\hat{k}\) on the vector perpendicular to the plane containing the vectors \(\hat{i}+\hat{j}+\hat{k}\) and \(\hat{i}+2\hat{j}+3\hat{k}\), is : [JEE Main 2019 (Online) 8th April Morning Slot]
CorrectIncorrectHint
Let vector \(\vec{p}\) is perpendicular to the both vectors \(\hat{i}+\hat{j}+\hat{k}\) and \(\hat{i}+\hat{2 j}+3\hat{k}\).
\(
\begin{aligned}
& \therefore \vec{p}=(\hat{i}+\hat{j}+\hat{k}) \times(\hat{i}+2\hat{j}+3 \hat{k}) \\
& =\left|\begin{array}{rrr}
\hat{i} & \hat{j} & \hat{k} \\
1 & 1 & 1 \\
1 & 2 & 3
\end{array}\right| \\
& =\hat{i}-2 \hat{j}+\widehat{k}
\end{aligned}
\)
Now a vector \(\vec{a}=\hat{2 i}+\hat{3 j}+\hat{k}\) is given and we have to findout projection of vector \(\vec{a}\) on \(\vec{p}\).
\(\therefore\) Projection of vector \(\vec{a}\) on \(\vec{p}\)
\(
\begin{aligned}
& =|\vec{a}| \cos \theta \\
& =|\vec{a}| \times \frac{\overrightarrow{a \cdot p}}{|\vec{a}||\vec{p}|} \\
& =\frac{\vec{a} \cdot \vec{p}}{|\vec{p}|} \\
& =\frac{(2 \hat{i}+3 \hat{j}+\hat{k}) \cdot(\hat{i}-2 \hat{j}+\hat{k})}{\sqrt{1+4+1}} \\
& =\frac{2-6+1}{\sqrt{6}} \\
& =\frac{-3}{\sqrt{6}}
\end{aligned}
\)
Magnitude of projection of vector \(\vec{a}\) on \(\vec{p}\)
\(
=\left|\frac{-3}{\sqrt{6}}\right|=\frac{3}{\sqrt{6}}=\frac{\sqrt{3}}{\sqrt{2}}
\) -
Question 25 of 202
25. Question
The equation of a plane containing the line of intersection of the planes \(2 x-y-4=0\) and \(y+2 z-4=0\) and passing through the point \((1,1,0)\) is : [JEE Main 2019 (Online) 8th April Morning Slot]
CorrectIncorrectHint
The equation of any plane passing through the intersection of the planes \(2 x-y-4=\) 0 and \(y+2 z-4=0\) is :
\(
(2 x-y-4)+\lambda(y+2 z-4)=0 \dots(1)
\)
As this plane passes through \((1,1,0)\) then this point satisfy the equation (1).
\(
\begin{aligned}
& \therefore(2-1-4)+\lambda(1+0-4)=0 \\
& \Rightarrow \lambda=-1
\end{aligned}
\)
Equation of required plane will be
\(
\begin{aligned}
& (2 x-y-4)-(y+2 z-4)=0 \\
& \Rightarrow 2 x-2 y-2 z=0 \\
& \Rightarrow x-y-z=0
\end{aligned}
\) -
Question 26 of 202
26. Question
Let \(S\) be the set of all real values of \(\lambda\) such that a plane passing through the points (\(\left.\lambda^2, 1,1\right),\left(1,-\lambda^2, 1\right)\) and \(\left(1,1,-\lambda^2\right)\) also passes through the point \((-1,-1,1)\). Then \(S\) is equal to: [JEE Main 2019 (Online) 12th January Evening Slot]
CorrectIncorrectHint
All four points are coplanar so
\(
\begin{aligned}
& \left|\begin{array}{ccc}
1-\lambda^2 & 2 & 0 \\
2 & -\lambda^2+1 & 0 \\
2 & 2 & -\lambda^2-1
\end{array}\right|=0 \\
& \left(\lambda^2+1\right)^2\left(3-\lambda^2\right)=0 \\
& \lambda= \pm \sqrt{3}
\end{aligned}
\) -
Question 27 of 202
27. Question
If an angle between the line, \(\frac{x+1}{2}=\frac{y-2}{1}=\frac{z-3}{-2}\) and the plane, \(x-2 y-k z=3\) is \(\cos ^{-1}\left(\frac{2 \sqrt{2}}{3}\right)\), then a value of \(k\) is : [JEE Main 2019 (Online) 12th January Evening Slot]
CorrectIncorrectHint
DR’s of line are \(2,1,-2\)
normal vector of plane is \(\hat{i}-2 \hat{j}- k \widehat{k}\)
\(
\sin \alpha=\frac{(2 \hat{i}+\hat{j}-2 \hat{k}) \cdot(\hat{i}-2 \hat{j}-k \hat{k})}{3 \sqrt{1+4+k^2}}
\)
\(
\begin{aligned}
&\begin{aligned}
& \sin \alpha=\frac{2 k}{3 \sqrt{k^2+5}} \quad \ldots \ldots . (1)\\
& \cos \alpha=\frac{2 \sqrt{2}}{3} \quad \ldots \ldots .(2)
\end{aligned}\\
&(1)^2+(2)^2=1 \Rightarrow k^2=\frac{5}{3}
\end{aligned}
\) -
Question 28 of 202
28. Question
The perpendicular distance from the origin to the plane containing the two lines, \(\frac{x+2}{3}=\frac{y-2}{5}=\frac{z+5}{7}\) and \(\frac{x-1}{1}=\frac{y-4}{4}=\frac{z+4}{7}\), is : [JEE Main 2019 (Online) 12th January Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& \left|\begin{array}{lll}
i & j & k \\
3 & 5 & 7 \\
1 & 4 & 7
\end{array}\right| \\
& =\hat{i}(35-28)-\hat{j}(21-7)+\widehat{k}(12-5)
\end{aligned}
\)
\(
\begin{aligned}
& =7 \hat{i}-14 \hat{j}+7 \widehat{k} \\
& =\hat{i}-2 \hat{j}+\widehat{k} \\
& 1( x +2)-2( y -2)+1( z +15)=0 \\
& x -2 y + z +11=0 \\
& \frac{11}{\sqrt{4+1+1}}=\frac{11}{\sqrt{6}}
\end{aligned}
\) -
Question 29 of 202
29. Question
A tetrahedron has vertices \(P(1,2,1), Q(2,1,3), R(-1,1,2)\) and \(O(0,0,0)\). The angle between the faces \(O P Q\) and \(P Q R\) is : [JEE Main 2019 (Online) 12th January Morning Slot]
CorrectIncorrectHint
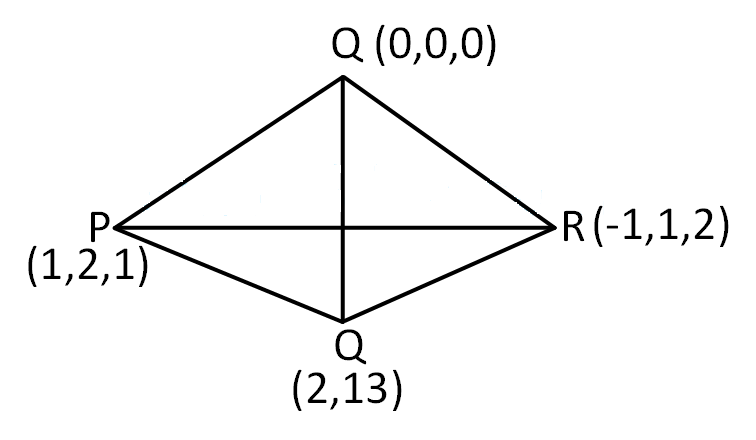
\(
\begin{aligned}
& \overrightarrow{O P} \times \overrightarrow{O Q}=(\hat{i}+2 \hat{j}+\widehat{k}) \times(2 \hat{i}+\hat{j}+3 \widehat{k}) \\
& =5 \hat{i}-\hat{j}-3 \widehat{k} \\
& \overrightarrow{P Q} \times \overrightarrow{P R}=(\hat{i}-\hat{j}+2 \widehat{k}) \times(-2 \hat{i}-\hat{j}+\widehat{k}) \\
& =\hat{i}-5 \hat{j}-3 \widehat{k} \\
& \cos \theta=\frac{5+5+9}{(\sqrt{25+9+1})^2}=\frac{19}{35}
\end{aligned}
\) -
Question 30 of 202
30. Question
Two lines \(\frac{x-3}{1}=\frac{y+1}{3}=\frac{z-6}{-1}\) and \(\frac{x+5}{7}=\frac{y-2}{-6}=\frac{z-3}{4}\) intersect at the point \(R\). The reflection of \(R\) in the \(x y\)-plane has coordinates : [JEE Main 2019 (Online) 11th January Evening Slot]
CorrectIncorrectHint
Point on \(L _1(\lambda+3,3 \lambda-1,-\lambda+6)\)
Point on \(L _2(7 \mu-5,-6 \mu+2,4 \mu+3)\)
\(
\Rightarrow \lambda+3=7 \mu-5
\)
\(3 \lambda-1=-6 \mu+2 \dots(i)\)
\(\Rightarrow \lambda=-1, \mu=1 \dots(ii)\)
point \(R(2,-4,7)\)
Reflection is \((2,-4,-7)\) -
Question 31 of 202
31. Question
If the point \((2, \alpha, \beta)\) lies on the plane which passes through the points \((3,4,2)\) and \((7\), \(0,6)\) and is perpendicular to the plane \(2 x-5 y=15\), then \(2 \alpha-3 \beta\) is equal to [JEE Main 2019 (Online) 11th January Evening Slot]
CorrectIncorrectHint
Normal vector of plane
\(
\begin{aligned}
& =\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
2 & -5 & 0 \\
4 & -4 & 5
\end{array}\right| \\
& =-4(5 \hat{i}+2 \hat{j}-3 \widehat{k})
\end{aligned}
\)
equation of plane is
\(
\begin{aligned}
& 5(x-7)+2 y-3(z-6)=0 \\
& 5 x+2 y-3 z=17 \\
& 5 \times 2+2 \alpha-3 \beta=17 \\
& \therefore 2 \alpha-3 \beta=17-10=7
\end{aligned}
\) -
Question 32 of 202
32. Question
The plane containing the line \(\frac{x-3}{2}=\frac{y+2}{-1}=\frac{z-1}{3}\) and also containing its projection on the plane \(2 x+3 y-z=5\), contains which one of the following points? [JEE Main 2019 (Online) 11th January Morning Slot]
CorrectIncorrectHint
The normal vector of required plane
\(
\begin{aligned}
& =(2 \hat{i}-\hat{j}+3 \widehat{k}) \times(2 \hat{i}+3 \hat{j}-\widehat{k}) \\
& =-8 \hat{i}+8 \hat{j}+8 \widehat{k}
\end{aligned}
\)
So, direction ratio of normal is \((-1,1,1)\)
So required plane is
\(
\begin{aligned}
& -(x-3)+(y+2)+(z-1)=0 \\
& \Rightarrow-x+y+z+4=0
\end{aligned}
\)
Which is satisfied by \((2,0,-2)\) -
Question 33 of 202
33. Question
The direction ratios of normal to the plane through the points \((0,-1,0)\) and \((0,0,1)\) and making an angle \(\frac{\pi}{4}\) with the plane \(y-z+5=0\) are : [JEE Main 2019 (Online) 11th January Morning Slot]
CorrectIncorrectHint
Let the equation of plane be
\(
a(x-0)+b(y+1)+c(z-0)=0
\)
It passes through \((0,0,1)\) then
\(
b+c=0 \quad \ldots .(1)
\)
Now \(\cos \frac{\pi}{4}=\frac{a(0)+b(1)+c(-1)}{\sqrt{2} \sqrt{a^2+b^2+c^2}}\)
\(\Rightarrow a ^2=-2 bc\) and \(b =- c\)
we get \(a^2=2 c^2\)
\(
\Rightarrow a = \pm \sqrt{2} c
\)
\(\Rightarrow\) direction ratio \(( a , b , c )=(\sqrt{2},-1,1)\) or \((\sqrt{2}, 1,-1)\) -
Question 34 of 202
34. Question
On which of the following lines lies the point of intersection of the line, \(\frac{x-4}{2}=\frac{y-5}{2}=\frac{z-3}{1}\) and the plane, \(x + y + z =2\) ? [JEE Main 2019 (Online) 10th January Evening Slot]
CorrectIncorrectHint
General point on the given line is
\(
\begin{aligned}
& x=2 \lambda+4 \\
& y=2 \lambda+5 \\
& z=\lambda+3
\end{aligned}
\)
Solving with plane,
\(
\begin{aligned}
& 2 \lambda+4+2 \lambda+5+\lambda+3=2 \\
& 5 \lambda+12=2 \\
& 5 \lambda=-10 \\
& \lambda=-2
\end{aligned}
\) -
Question 35 of 202
35. Question
The plane which bisects the line segment joining the points \((-3,-3,4)\) and \((3,7,6)\) at right angles, passes through which one of the following points ? [JEE Main 2019 (Online) 10th January Evening Slot]
CorrectIncorrectHint
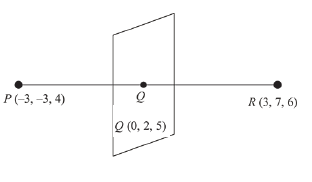
Since, direction ratios of normal to the plane is
\(
\vec{n}=6 \hat{i}+10 \hat{j}+2 \hat{k}
\)
Then, equation of the plane is
\(
\begin{aligned}
& (x-0) 6+(y-2) 10+(z-5) 2=0 \\
& 3 x+5 y-10+z-5=0 \\
& 3 x+5 y+z=15 \dots(1)
\end{aligned}
\)
Since, plane (1) satisfies the point \((4,1,-2)\)
Hence, required point is \((4,1,-2)\) -
Question 36 of 202
36. Question
The plane passing through the point \((4,-1,2)\) and parallel to the lines \(\frac{x+2}{3}=\frac{y-2}{-1}=\frac{z+1}{2}\) and \(\frac{x-2}{1}=\frac{y-3}{2}=\frac{z-4}{3}\) also passes through the point [JEE Main 2019 (Online) 10th January Morning Slot]
CorrectIncorrectHint
Equation of required plane is
\(
\left|\begin{array}{ccc}
x-4 & y+1 & z-2 \\
3 & -1 & 2 \\
1 & 2 & 3
\end{array}\right|=0
\)
\(
(x-4)(-3-4)-\left(y+1\right)(9-2)+(z-2)(6+1)=0
\)
\(
\begin{aligned}
& \Rightarrow-7(x-4)-7(y+1)+7(z-2)=0 \\
& \Rightarrow x-4+y+1-z+2=0 \\
& \Rightarrow x+y-z-1=0
\end{aligned}
\)
\(\because\) point \((1,1,1)\) satisfies this equation
\(\therefore\) point \((1,1,1)\) lies on the plane -
Question 37 of 202
37. Question
Let \(A\) be a point on the line \(\vec{r}=(1-3 \mu) \hat{i}+(\mu-1) \hat{j}+(2+5 \mu) \widehat{k}\) and \(B (3,2\), 6) be a point in the space. Then the value of \(\mu\) for which the vector \(\overrightarrow{A B}\) is parallel to the plane \(x-4 y+3 z=1\) is [JEE Main 2019 (Online) 10th January Morning Slot]
CorrectIncorrectHint
\(\because A\) be a point on given line.
\(\therefore\) Position vector of \(A\)
\(
\overrightarrow{O A}=(1-3 \mu) \hat{i}+(\mu-1) \hat{j}+(2+5 \mu) \hat{k}
\)
Position vector of \(B=\overrightarrow{O B}=3 \hat{i}+2 \hat{j}+6 \hat{k}\)
\(
\begin{aligned}
& \therefore \quad \overrightarrow{A B}=\overrightarrow{O B}-\overrightarrow{O A} \\
&=(3 \mu+2) \hat{i}+(3-\mu) \hat{j}+(4-5 \mu) \hat{k}
\end{aligned}
\)
Equation of plane is: \(x-4 y+3 z=1\)
\(\because \overrightarrow{A B}\) is parallel to this plane.
\(
\begin{aligned}
& \therefore 1(3 \mu+2)-4(3-\mu)+3(4-5 \mu)=0 \\
& \Rightarrow 3 \mu+2-12+4 \mu+12-15 \mu=0 \\
& \Rightarrow 2-8 \mu=0 \\
& \Rightarrow \mu=\frac{1}{4}
\end{aligned}
\) -
Question 38 of 202
38. Question
The equation of the plane containing the straight line \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\) and perpendicular to the plane containing the straight lines \(\frac{x}{3}=\frac{y}{4}=\frac{z}{2}\) and \(\frac{x}{4}=\frac{y}{2}=\frac{z}{3}\) is : [JEE Main 2019 (Online) 9th January Evening Slot]
CorrectIncorrectHint
\(
\text { Vector } \perp \text { to given plane }=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
3 & 4 & 2 \\
4 & 2 & 3
\end{array}\right|
\)
\(
\begin{aligned}
& =\hat{i}(12-4)-\hat{j}(9-8)+\widehat{k}(6-16) \\
& =8 \hat{i}-\hat{j}-10 \widehat{k} \quad \ldots(1)
\end{aligned}
\)
Vector parallel to given line
\(
=2 \hat{i}+3 \hat{j}+4 \widehat{k} \dots(2)
\)
Vector \(\perp\) to both (1) & (2) vector
\(
\begin{aligned}
& =\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
8 & -1 & -10 \\
2 & 3 & 4
\end{array}\right| \\
& =\hat{i}(-4+30)-\hat{j}(32+20)+\widehat{k}(24+2) \\
& =26 \hat{i}-52 \hat{j}+26 \widehat{k}
\end{aligned}
\)
Dr’s of normal of required plane is
\(
(26,-52,26) \Rightarrow(1,-2,1)
\)
Equation of plane whose Dr’s of Normal is \((1,-2,1)\) and passes through origin
\(
\begin{aligned}
& \text { 1. }(x-0)-2(y-0)+1 \cdot(z-0)=0 \\
& x-2 y+z=0
\end{aligned}
\) -
Question 39 of 202
39. Question
If the lines \(x=a y+b, z=c y+d\) and \(x=a^{\prime} z+b^{\prime}, y=c^{\prime} z+d^{\prime}\) are perpendicular, then : [JEE Main 2019 (Online) 9th January Evening Slot]
CorrectIncorrectHint
Equation of \(1^{\text {st }}\) line is
\(
\frac{x-b}{a}=\frac{y}{1}=\frac{z-d}{c}
\)
Dr’s of \(1^{\text {st }}\) line \(=(a, 1, c)\)
Equation of \(2^{\text {nd }}\) line is
\(
\frac{x-b^{\prime}}{a^{\prime}}=\frac{y-b^{\prime}}{c^{\prime}}=\frac{z}{1}
\)
Dr’s of \(2^{\text {nd }}\) line \(=\left(a^{\prime}, c^{\prime}, 1\right)\)
Lines are perpendicular, so the dot product of the Dr’s of two lines are zero.
\(
\therefore a a^{\prime}+c+c^{\prime}=0
\) -
Question 40 of 202
40. Question
The equation of the line passing through \((-4,3,1)\), parallel to the plane \(x+2 y-z-5=0\) and intersecting the line \(\frac{x+1}{-3}=\frac{y-3}{2}=\frac{z-2}{-1}\) is : [JEE Main 2019 (Online) 9th January Morning Slot]
CorrectIncorrectHint
Let any point on the intersecting line
\(
\frac{x+1}{-3}=\frac{y-3}{2}=\frac{z-2}{-1}=\lambda \text { (say) }
\)
is \(\quad(-3 \lambda-1,2 \lambda+3,-\lambda+2)\)
Since, the above point lies on a line which passes through the point \((-4,3,1)\)
Then, direction ratio of the required line
\(
\begin{aligned}
& =<-3 \lambda-1+4,2 \lambda+3-3,-\lambda+2-1\rangle> \\
& \text { or }\langle-3 \lambda+3,2 \lambda,-\lambda+1\rangle
\end{aligned}
\)
Since, line is parallel to the plane
\(
x+2 y-z-5=0
\)
Then, perpendicular vector to the line is \(\hat{i}+2 \hat{j}-\hat{k}\)
Now \((-3 \lambda+3)(1)+(2 \lambda)(2)+(-\lambda+1)(-1)=0\)
\(
\Rightarrow \lambda=-1
\)
Now direction ratio of the required line \(=\langle 6,-2,2\rangle\) or \(<3,-1,1>\)
Hence required equation of the line is
\(
\frac{(x+4)}{3}=\frac{y-3}{-1}=\frac{z-1}{1}
\) -
Question 41 of 202
41. Question
The plane through the intersection of the planes \(x+y+z=1\) and \(2 x+3 y-z+4=\) 0 and parallel to \(y\)-axis also passes through the point : [JEE Main 2019 (Online) 9th January Morning Slot]
CorrectIncorrectHint
The equation of plane
\(
\begin{aligned}
& (x+y+z-1)+\lambda(2 x+3 y-z+4)=0 \\
& \Rightarrow(1+2 \lambda) x+(1+3 \lambda) y+(1-\lambda) z+4 \lambda-1=0
\end{aligned}
\)
As plane is parallel to \(y\) axis so the normal vector of plane and dot product of \(\hat{j}\) is zero.
\(
\begin{aligned}
& \therefore 1+3 \lambda=0 \\
& \Rightarrow \lambda=-\frac{1}{3}
\end{aligned}
\)
\(\therefore\) So the equation of the plane is
\(
\begin{aligned}
& x\left(1-\frac{2}{3}\right)+\left(1-\frac{3}{3}\right) y+\left(1+\frac{1}{3}\right)-\frac{4}{3}-1=0 \\
& \Rightarrow x\left(\frac{1}{3}\right)+z\left(\frac{4}{3}\right)-\frac{7}{3}=0 \\
& \Rightarrow x+4 z-7=0
\end{aligned}
\)
By checking each options you can see only point \((3,2,1)\) lies on the plane. -
Question 42 of 202
42. Question
If the angle between the lines, \(\frac{x}{2}=\frac{y}{2}=\frac{z}{1}\) and \(\frac{5-x}{-2}=\frac{7 y-14}{p}=\frac{z-3}{4}\) is \(\cos ^{-1}\left(\frac{2}{3}\right)\), then \(p\) is equal to : [JEE Main 2018 (Online) 16th April Morning Slot]
CorrectIncorrectHint
Let \(\theta\) be the angle between the two lines
Here direction cosines of \(\frac{x}{2}=\frac{y}{2}=\frac{z}{1}\) are \(2,2,1\)
Also second line can be written as :
\(
\frac{x-5}{2}=\frac{y-2}{\frac{p}{7}}=\frac{z-3}{4}
\)
\(\therefore\) its direction cosines are \(2, \frac{P}{7}, 4\)
Also, \(\cos \theta=\frac{2}{3}\) (Given)
\(
\begin{aligned}
& \because \cos \theta=\left|\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^2+b_1^2+c_1^2 \sqrt{a_2^2+b_2^2+c_2^2}}}\right| \\
& \Rightarrow \quad \frac{2}{3}=\left|\frac{(2 \times 2)+\left(2 \times \frac{P}{7}\right)+(1 \times 4)}{\sqrt{2^2+2^2+1^2} \sqrt{2^2+\frac{P^2}{49}+4^2}}\right| \\
& =\frac{4+\frac{2 P}{7}+4}{3 \times \sqrt{2^2+\frac{P^2}{49}+4^2}} \\
& \Rightarrow\left(4+\frac{P}{7}\right)^2=20+\frac{P^2}{49} \\
& \Rightarrow 16+\frac{8 P}{7}+\frac{P^2}{49}=20+\frac{P^2}{49} \\
& \Rightarrow \frac{8 P}{7}=4 \Rightarrow P=\frac{7}{2} \\
&
\end{aligned}
\) -
Question 43 of 202
43. Question
The sum of the intercepts on the coordinate axes of the plane passing through the point \((-2,-2,2)\) and containing the line joining the points \((1,-1,2)\) and \((1,1,1)\) is : [JEE Main 2018 (Online) 16th April Morning Slot]
CorrectIncorrectHint
Equation of plane passing through three given points is :
\(
\begin{aligned}
& \left|\begin{array}{ccc}
x-x_1 & y-y_1 & z-z_1 \\
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
x_3-x_1 & y_3-y_1 & z_3-z_1
\end{array}\right|=0 \\
& \Rightarrow\left|\begin{array}{ccc}
x+2 & y+2 & z-2 \\
1+2 & -1+2 & 2-2 \\
1+2 & 1+2 & 1-2
\end{array}\right|=0 \\
& \Rightarrow\left|\begin{array}{ccc}
x+2 & y+2 & z-2 \\
3 & 1 & 0 \\
3 & 30 & -1
\end{array}\right|=0 \\
& \Rightarrow-x+3 y+6 z-8=0 \\
& \Rightarrow \frac{x}{8}-\frac{3 y}{8}-\frac{6 z}{8}+\frac{8}{8}=0 \\
& \Rightarrow \frac{x}{8}-\frac{y}{\frac{8}{3}}-\frac{z}{\frac{8}{6}}=-1 \\
& \Rightarrow \frac{x}{-8}+\frac{y}{\frac{8}{3}}+\frac{z}{\frac{8}{6}}=1
\end{aligned}
\)
\(
\therefore \text { Sum of intercepts }=-8+\frac{8}{3}+\frac{8}{6}=-4
\) -
Question 44 of 202
44. Question
If \(L_1\) is the line of intersection of the planes \(2 x-2 y+3 z-2=0, x-y+z+1=0\) and \(L_2\) is the line of intersection of the planes \(x+2 y-z-3=0,3 x-y+2 z-1=0\), then the distance of the origin from the plane, containing the lines \(L_1\) and \(L_2\), is : [JEE Main 2018 (Offline)]
CorrectIncorrectHint
Plane passing through line of intersection of first two planes is
\(
(2 x-2 y+3 z-2)+\lambda(x-y+z+1)=0
\)
\(x(\lambda+2)-y(2+\lambda)+z(\lambda+3)+(\lambda-2)=0 \dots(i)\)
is having infinite number of solutions with \(x+2 y-z-3=0\) and \(3 x-y+2 z-1=0\) then
\(
\left|\begin{array}{ccc}
\lambda+2 & -(\lambda+2) & \lambda+3 \\
1 & 2 & -1 \\
3 & -1 & 2
\end{array}\right|=0
\)
On solving, we have \(\lambda=5\)
Hence required equation of plane is \(7 x-7 y+8 z+3=0\)
Now, perpendicular distance from \((0,0,0)\) is \(\frac{3}{\sqrt{49+49+64}}\)
\(=\frac{3}{\sqrt{162}}=\frac{1}{3 \sqrt{2}}\) -
Question 45 of 202
45. Question
The length of the projection of the line segment joining the points \((5,-1,4)\) and \((4\), \(-1,3\) ) on the plane, \(x+y+z=7\) is : [JEE Main 2018 (Offline)]
CorrectIncorrectHint
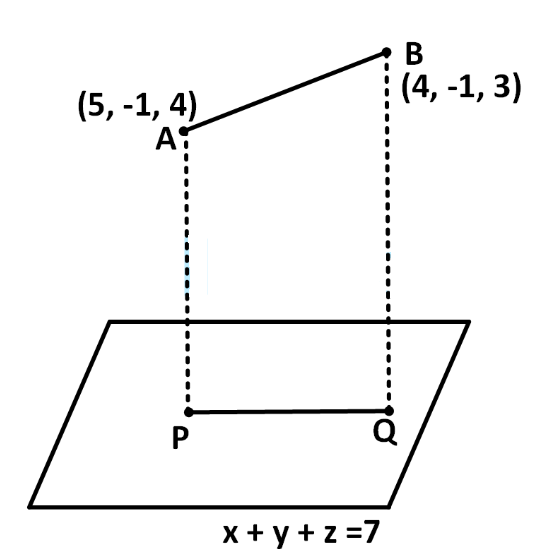
\(P Q\) is the projection of line segment \(A B\) on the plane \(x+y+z=7\)
\(P\) and \(Q\) are called foot of perpendicular on the plane \(x+y+z=7\)
Let \(P=(x, y, z)\) then
\(
\begin{aligned}
& \frac{x-5}{1}=\frac{y+1}{1}=\frac{z-4}{1}=\frac{-(5-1+4)}{1^2+1^2+1^2} \\
& \Rightarrow x-5=y+1=z-4=-\frac{8}{3} \\
& \therefore x =\frac{7}{3}, y =-\frac{11}{3}, z =\frac{4}{3} \\
& \therefore \text { Point } P =\left(\frac{7}{3},-\frac{11}{3}, \frac{4}{3}\right)
\end{aligned}
\)
Let \(Q =\left( x _1, y _1, z _1\right)\) then
\(
\begin{aligned}
& \frac{a_1-4}{1}=\frac{y_1+1}{1}=\frac{z_1-3}{1}=\frac{-(4-1+3)}{1^2+1^2+1^2} \\
& \Rightarrow x _1-4= y _1+1= z _1-3=-2 \\
& \therefore x =2, y =-3, z =1 \\
& \therefore \text { Point } Q =(2,-3,1)
\end{aligned}
\)
Now length of \(PQ\) is
\(
\sqrt{\left(\frac{7}{3}-2\right)^2+\left(-\frac{11}{3}+3\right)^2+\left(\frac{4}{3}-1\right)^2}=\sqrt{\frac{2}{3}}
\) -
Question 46 of 202
46. Question
An angle between the lines whose direction cosines are given by the equations, \(l+3 m+5 n=0\) and \(5 l m-2 m n+6 n l=0\), is : [JEE Main 2018 (Online) 15th April Evening Slot]
CorrectIncorrectHint
Given \(l+3 m+5 n=0 \dots(1)\)
and \(5 l m-2 m n+6 n l=0 \dots(2)\)
From eq. (1) we have
\(
l=-3 m-5 n
\)
Put the value of \(l\) in eq. (2), we get ;
\(
\begin{aligned}
& 5(-3 m-5 n) m-2 m n+6 n(-3 m-5 n)=0 \\
& \Rightarrow 15 m^2+45 m n+30 n^2=0 \\
& \Rightarrow m^2+3 m n+2 n^2=0 \\
& \Rightarrow m^2+2 m n+m n+2 n^2=0 \\
& \Rightarrow(m+n)(m+2 n)=0 \\
& \therefore m=-n \text { or } m=-2 n
\end{aligned}
\)
For \(m =-n, l=-2 n\)
And for \(m =-2 n , l= n\)
\(
\begin{aligned}
& \therefore(l, m , n )=(-2 n ,- n , n ) \operatorname{Or}(l, m , n )=( n ,-2 n , n ) \\
& \Rightarrow(l, m , n )=(-2,-1,1) \operatorname{Or}(l, m , n )=(1,-2,1)
\end{aligned}
\)
Therefore, angle between the lines is given as :
\(
\begin{aligned}
& \cos (\theta)=\frac{(-2)(1)+(-1) \cdot(-2)+(1)(1)}{\sqrt{6} \cdot \sqrt{6}} \\
& \Rightarrow \cos (\theta)=\frac{1}{6} \Rightarrow \theta=\cos ^{-1}\left(\frac{1}{6}\right)
\end{aligned}
\) -
Question 47 of 202
47. Question
A plane bisects the line segment joining the points \((1,2,3)\) and \((-3,4,5)\) at right angles. Then this plane also passes through the point : [JEE Main 2018 (Online) 15th April Evening Slot]
CorrectIncorrectHint
Since the plane bisects the line joining the points \((1,2,3)\) and \((-3,4,5)\) then the plane passes through the midpoint of the line which is:
\(
\left(\frac{1-3}{2}, \frac{2+4}{2}, \frac{5+3}{2}\right) \equiv\left(\frac{-2}{2}, \frac{6}{2}, \frac{8}{2}\right) \equiv(-1,3,4) \text {. }
\)
As plane cuts the line segment at right angle, so the direction cosines of the normal of the plane are \((-3-1,4-2,5-3)=(-4,2,2)\)
So the equation of the plane is : \(-4 x+2 y+2 z=\lambda\)
As plane passes through \((-1,3,4)\)
So, \(-4(-1)+2(3)+2(4)=\lambda \Rightarrow \lambda=18\)
Therefore, equation of plane is : \(-4 x+2 y+2 z=18\)
Now, only \((-3,2,1)\) satiesfies the given plane as
\(
-4(-3)+2(2)+2(1)=18
\) -
Question 48 of 202
48. Question
A variable plane passes through a fixed point \((3,2,1)\) and meets \(x, y\) and \(z\) axes at \(A\), \(B\) and \(C\) respectively. A plane is drawn parallel to \(yz\)-plane through \(A\), a second plane is drawn parallel \(zx\)-plane through \(B\) and a third plane is drawn parallel to \(xy\) plane through \(C\). Then the locus of the point of intersection of these three planes, is [JEE Main 2018 (Online) 15th April Morning Slot]
CorrectIncorrectHint
If \(a, b, c\) are the intercepts of the variable plane on the \(x, y, z\) axes respectively, then the equation of the plane is
\(
\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1
\)
And the point of intersection of the planes parallel to the \(x y, y z\) and \(z x\) planes is \((a, b, c)\)
As the point \((3,2,1)\) lies on the variables plane,
\(
\text { so } \frac{3}{a}+\frac{2}{b}+\frac{1}{c}=1
\)
Therefore, the required locus is
\(
\frac{3}{x}+\frac{2}{y}+\frac{1}{z}=1
\) -
Question 49 of 202
49. Question
An angle between the plane, \(x+y+z=5\) and the line of intersection of the planes, \(3 x+4 y+z-1=0\) and \(5 x+8 y+2 z+14=0\), is : [JEE Main 2018 (Online) 15th April Morning Slot]
CorrectIncorrectHint
Normal to \(3 x+4 y+z=1\) is \(3 \hat{i}+4 \hat{j}+\widehat{k}\)
Normal to \(5 x+8 y+2 z=-14\) is \(5 \hat{i}+8 \hat{j}+2 \widehat{k}\)
The line of intersection of the planes is perpendicular to both normals, so, direction ratios of the intersection line are directly proportional to the cross product of the normal vectors.
Therefore the direction ratios of the line is \(-\hat{j}+4 \widehat{k}\)
Hence the angle between the plane \(x+y+z+5=0\)
and the intersection line is \(\sin ^{-1}\left(\frac{-1+4}{\sqrt{17} \sqrt{3}}\right)=\sin ^{-1}\left(\sqrt{\frac{3}{17}}\right)\) -
Question 50 of 202
50. Question
The square of the distance of the image of the point \((6,1,5)\) in the line \(\frac{x-1}{3}=\frac{y}{2}=\frac{z-2}{4}\), from the origin is _____. [JEE Main 2024 (Online) 9th April Evening Shift]
CorrectIncorrectHint
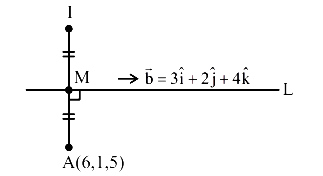
Let \(M(3 \lambda+1,2 \lambda, 4 \lambda+2)\)
\(
\begin{aligned}
& \overrightarrow{ AM } \cdot \overrightarrow{ b }=0 \\
& \Rightarrow \quad 9 \lambda-15+4 \lambda-2+16 \lambda-12=0 \\
& \Rightarrow \quad 29 \lambda=29 \\
& \Rightarrow \quad \lambda=1 \\
& M (4,2,6), I =(2,3,7)
\end{aligned}
\)
\(
\text { Required Distance }=\sqrt{4+9+49}=\sqrt{62}
\) -
Question 51 of 202
51. Question
Let \(P (\alpha, \beta, \gamma)\) be the image of the point \(Q (1,6,4)\) in the line \(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\). Then \(2 \alpha+\beta+\gamma\) is equal to ____. [JEE Main 2024 (Online) 8th April Evening Shift]
CorrectIncorrectHint
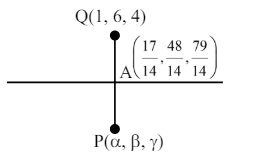
\(
\begin{aligned}
& \frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3} \\
& \vec{b}=\hat{i}+2 \hat{j}+3 \hat{k} \\
& A(t, 2 t+1,3 t+2) \\
& \overrightarrow{Q A}=(t-1) i+(2 t-5) j+(3 t-2) \hat{k} \\
& \overrightarrow{Q A} \cdot \vec{b}=0 \\
& (t-1)+2(2 t-5)+3(3 t-2)=0 \\
& 14 t=17 \\
& \alpha=\frac{20}{14} \\
& \beta=\frac{12}{14} \\
& \gamma=\frac{102}{14} \\
& 2 \alpha+\beta+\gamma=\frac{154}{14}=11 \text { Ans. }
\end{aligned}
\) -
Question 52 of 202
52. Question
If the shortest distance between the lines \(\frac{x-\lambda}{3}=\frac{y-2}{-1}=\frac{z-1}{1}\) and \(\frac{x+2}{-3}=\frac{y+5}{2}=\frac{z-4}{4}\) is \(\frac{44}{\sqrt{30}}\), then the largest possible value of \(|\lambda|\) is equal to ____. [JEE Main 2024 (Online) 6th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L_1: \frac{x-\lambda}{3}=\frac{y-2}{-1}=\frac{z-1}{1} \\
& L_2: \frac{x+2}{-3}=\frac{y+5}{2}=\frac{z-4}{4} \\
& n_1 \times n_2=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
3 & -1 & 1 \\
-3 & 2 & 4
\end{array}\right| \\
& =-6 \hat{i}-15 \hat{j}+3 \hat{k}
\end{aligned}
\)
\(
\begin{aligned}
& d=\left|\frac{[(\lambda+2) \hat{i}+7 \hat{j}-3 \hat{k}][-6 \hat{i}-15 \hat{j}+3 \hat{k}]}{|-6 \hat{i}-15 \hat{j}+3 \hat{k}|}\right| \\
& \left|\frac{-6 \lambda-12-105-9}{\sqrt{270}}\right|=\frac{44}{\sqrt{30}} \\
& |6 \lambda+126|=132 \\
& |\lambda+21|=22 \\
& \lambda+21= \pm 22 \\
& |\lambda|_{\max }=43
\end{aligned}
\) -
Question 53 of 202
53. Question
Let \(P\) be the point \((10,-2,-1)\) and \(Q\) be the foot of the perpendicular drawn from the point \(R(1,7,6)\) on the line passing through the points \((2,-5,11)\) and \((-6,7,-5)\). Then the length of the line segment \(P Q\) is equal to ____. [JEE Main 2024 (Online) 6th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& P(10,-2,-1) \\
& M N: \frac{x-2}{8}=\frac{y+5}{-12}=\frac{z-11}{16} \\
& \text { General point } \\
& (8 k+2,-12 k-5,16 k+11) \\
& \overrightarrow{R Q}=(8 k+2-1) \hat{i}+(-12 k-5-7) \hat{j}+(16 k+11-6) \widehat{k} \\
& \overrightarrow{R Q}=(8 k+1) \hat{i}-(12 k+12) \hat{j}+(16 k+5) \widehat{k} \\
& \overrightarrow{R Q} \cdot \overrightarrow{M N}=0(\text { as both are perpendicular }) \\
& 8(8 k+1)+12(12 k+12)+16(16 k+5)=0 \\
& 64 k+8+144 k+144+256 k+80=0 \\
& 464 k=-232 \\
& k=\frac{-232}{464}=\frac{-1}{2} \\
& Q(-4+2,6-5,-8+11) \\
& Q(-2,1,3) \\
& P Q=\sqrt{(10+2)^2+(-3)^2+(4)^2} \\
& P Q=\sqrt{12^2+3^2+4^2} \\
& P Q=\sqrt{169}=13
\end{aligned}
\) -
Question 54 of 202
54. Question
Let the point \((-1, \alpha, \beta)\) lie on the line of the shortest distance between the lines \(\frac{x+2}{-3}=\frac{y-2}{4}=\frac{z-5}{2}\) and \(\frac{x+2}{-1}=\frac{y+6}{2}=\frac{z-1}{0}\). Then \((\alpha-\beta)^2\) is equal to ___. [JEE Main 2024 (Online) 5th April Evening Shift]
CorrectIncorrectHint
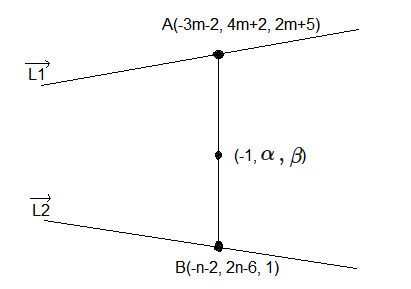
\(
\begin{aligned}
& \overrightarrow{A B} \perp \vec{L}_1 \text { and } \overrightarrow{A B} \perp \vec{L}_2 \\
& \overrightarrow{A B}=(-3 m-2+n+2,4 m+2-2 n+6,2 m+5-1) \\
& =(-3 m+n, 4 m-2 n+8,2 m+4) \\
& \overrightarrow{A B} \perp \vec{L}_1 \\
& \Rightarrow-3(-3 m+n)+4(4 m-2 n+8)+2(2 m+4)=0 \\
& (9 m+16 m+4 m)+(-3 n-8 n)+32+8=0 \\
& \Rightarrow 29 m-11 n+40=0 \quad \ldots(1) \\
& \overrightarrow{A B} \perp \vec{L}_2 \\
& \Rightarrow-1(-3 m+n)+2(4 m-2 n+8)+0(2 m+4)=0 \\
& \Rightarrow 3 m-n+8 m-4 n+16=0 \\
& \Rightarrow 11 m-5 n+16=0 \Rightarrow m=-1, n=1 \\
& \Rightarrow A \equiv(1,-2,3), \quad B \equiv(-3,-4,1) \\
& A B \text { line } \Rightarrow \frac{x-1}{2}=\frac{y+2}{1}=\frac{z-3}{1} \\
& \Rightarrow \alpha=-2, \quad \beta=3 \\
& \Rightarrow(\alpha-\beta)^2=25
\end{aligned}
\) -
Question 55 of 202
55. Question
Consider a line \(L\) passing through the points \(P (1,2,1)\) and \(Q (2,1,-1)\). If the mirror image of the point \(A (2,2,2)\) in the line \(L\) is \((\alpha, \beta, \gamma)\), then \(\alpha+\beta+6 \gamma\) is equal to ____. [JEE Main 2024 (Online) 4th April Evening Shift]
CorrectIncorrectHint
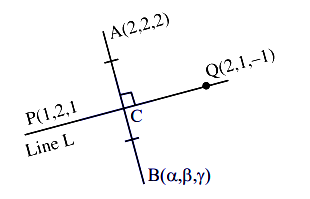
DR’s of Line \(L \equiv-1: 1: 2\)
DR’s of \(A B \equiv \alpha-2: \beta-2: \gamma-2\)
\(
\begin{aligned}
& AB \perp L \Rightarrow 2-\alpha+\beta-2+2 \gamma-4=0 \\
& 2 \gamma+\beta-\alpha=4 \quad \ldots \text { (1) }
\end{aligned}
\)
Let \(C\) is mid-point of \(AB\)
\(
C \left(\frac{\alpha+2}{2}, \frac{\beta+2}{2}, \frac{\gamma+2}{2}\right)
\)
DR’s of PC \(=\frac{\alpha}{2}: \frac{\beta-2}{2}: \frac{\gamma}{2}\)
line \(L \| PC \Rightarrow \frac{-\alpha}{2}=\frac{\beta-2}{2}=\frac{\gamma}{4}= K\) (let)
\(
\begin{aligned}
& \alpha=-2 K \\
& \beta=2 K +2 \\
& \gamma=4 K
\end{aligned}
\)
Use in (1) \(\Rightarrow K=\frac{1}{6}\)
Value of \(\alpha+\beta+6 \gamma=24 K+2=6\) -
Question 56 of 202
56. Question
Let the line of the shortest distance between the lines
\(L _1: \overrightarrow{ r }=(\hat{i}+2 \hat{j}+3 \hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})\) and
\(
L _2: \overrightarrow{ r }=(4 \hat{i}+5 \hat{j}+6 \hat{k})+\mu(\hat{i}+\hat{j}-\hat{k})
\)
intersect \(L _1\) and \(L _2\) at \(P\) and \(Q\) respectively. If \((\alpha, \beta, \gamma)\) is the mid point of the line segment \(PQ\), then \(2(\alpha+\beta+\gamma)\) is equal to ____. [JEE Main 2024 (Online) 1st February Morning Shift]CorrectIncorrectHint
\(
\begin{array}{ll}
L_1 \equiv \vec{r}=(1,2,3)+\lambda(1,-1,1) & \left(\vec{r}=\vec{a}_1+\lambda \vec{b}_1\right) \\
L_2 \equiv \vec{r}=(4,5,6)+\mu(1,1,-1) & \left(\vec{r}=\vec{a}_2+\lambda \vec{b}_2\right) \\
P \equiv(\lambda+1,-\lambda+2, \lambda+3) & \\
Q \equiv(\mu+4, \mu+5,-\mu+6)
\end{array}
\)
\(
\overrightarrow{P Q}=(\mu-\lambda+3, \mu+\lambda+3,-\mu-\lambda+3)
\)
\(
\overrightarrow{P Q} \cdot \vec{b}_1=0 \Rightarrow 3 \lambda+\mu=3 \dots(i)
\)
\(
\overrightarrow{P Q} \cdot \vec{b}_2=0 \Rightarrow 3 \mu+\lambda=3 \dots(ii)
\)
From (i) and (ii),
\(
\begin{aligned}
& P \equiv\left(\frac{5}{2}, \frac{1}{2}, \frac{9}{2}\right) \& Q \equiv\left(\frac{5}{2}, \frac{7}{2}, \frac{15}{2}\right) \\
& \alpha=\frac{5}{2}, \beta=\frac{4}{2}, \gamma=\frac{12}{2} \\
& 2(\alpha+\beta+\gamma)=21
\end{aligned}
\) -
Question 57 of 202
57. Question
A line passes through \(A(4,-6,-2)\) and \(B(16,-2,4)\). The point \(P(a, b, c)\), where \(a, b, c\) are non-negative integers, on the line \(A B\) lies at a distance of 21 units, from the point \(A\). The distance between the points \(P(a, b, c)\) and \(Q(4,-12,3)\) is equal to ____. [JEE Main 2024 (Online) 31st January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x-4}{12}=\frac{x+6}{4}=\frac{z+2}{6} \\
& \frac{x-4}{\frac{6}{7}}=\frac{y+6}{\frac{2}{7}}=\frac{z+2}{\frac{3}{7}}=21 \\
& \left(21 \times \frac{6}{7}+4, \frac{2}{7} \times 21-6, \frac{3}{7} \times 21-2\right) \\
& =(22,0,7)=(a, b, c) \\
& \therefore \sqrt{324+144+16}=22
\end{aligned}
\) -
Question 58 of 202
58. Question
Let \(Q\) and \(R\) be the feet of perpendiculars from the point \(P (a, a, a)\) on the lines \(x=y, z=1\) and \(x=-y, z=-1\) respectively. If \(\angle QPR\) is a right angle, then \(12 a^2\) is equal to ____. [JEE Main 2024 (Online) 31st January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x}{1}=\frac{y}{1}=\frac{z-1}{0}=r \rightarrow Q(r, r, 1) \\
& \frac{x}{1}=\frac{y}{-1}=\frac{z+1}{0}=k \rightarrow R(k,-k,-1)
\end{aligned}
\)
\(
\begin{aligned}
& \overline{P Q}=(a-r) \hat{i}+(a-r) \hat{j}+(a-1) \hat{k} \\
& a=r+a-r=0 \\
& 2 a=2 r \rightarrow a=r \\
& \overline{P R}=(a-k) i+(a+k) \hat{j}+(a+1) \hat{k} \\
& a-k-a-k=0 \Rightarrow k=0
\end{aligned}
\)
\(
\begin{aligned}
& A s, P Q \perp P R \\
& (a-r)(a-k)+(a-r)(a+k)+(a-1)(a+1)=0 \\
& a=1 \text { or }-1 \\
& 12 a^2=12
\end{aligned}
\) -
Question 59 of 202
59. Question
Let a line passing through the point \((-1,2,3)\) intersect the lines \(L_1: \frac{x-1}{3}=\frac{y-2}{2}=\frac{z+1}{-2}\) at \(M(\alpha, \beta, \gamma)\) and \(L_2: \frac{x+2}{-3}=\frac{y-2}{-2}=\frac{z-1}{4}\) at \(N(a, b, c)\). Then, the value of \(\frac{(\alpha+\beta+\gamma)^2}{(a+b+c)^2}\) equals ____. [JEE Main 2024 (Online) 30th January Evening Shift]
CorrectIncorrectHint
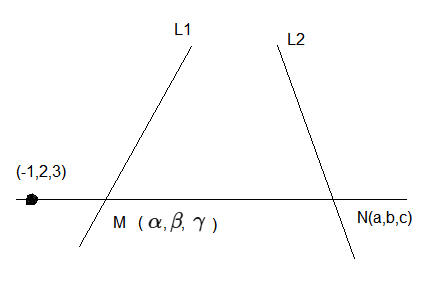
\(
\begin{aligned}
& M (3 \lambda+1,2 \lambda+2,-2 \lambda-1) \quad \therefore \alpha+\beta+\gamma=3 \lambda+2 \\
& N (-3 \mu-2,-2 \mu+2,4 \mu+1) \quad \therefore a + b + c =-\mu+1
\end{aligned}
\)
\(
\begin{aligned}
& \frac{3 \lambda+2}{-3 \mu-1}=\frac{2 \lambda}{-2 \mu}=\frac{-2 \lambda-4}{4 \mu-2} \\
& 3 \lambda \mu+2 \mu=3 \lambda \mu+\lambda \\
& 2 \mu=\lambda \\
& 2 \lambda \mu-\lambda=\lambda \mu+2 \mu \\
& \lambda \mu=\lambda+2 \mu \\
& \Rightarrow \lambda \mu=2 \lambda \\
& \Rightarrow \quad \mu=2 \quad(\lambda \neq 0) \\
& \therefore \quad \lambda=4 \\
& \quad \alpha+\beta+\gamma=14 \\
& \quad a+b+c=-1 \\
& \frac{(\alpha+\beta+\gamma)^2}{(a+b+c)^2}=196
\end{aligned}
\) -
Question 60 of 202
60. Question
If \(d _1\) is the shortest distance between the lines \(x+1=2 y=-12 z, x=y+2=6 z-6\) and \(d _2\) is the shortest distance between the lines \(\frac{x-1}{2}=\frac{y+8}{-7}=\frac{z-4}{5}, \frac{x-1}{2}=\frac{y-2}{1}=\frac{z-6}{-3}\), then the value of \(\frac{32 \sqrt{3} d_1}{d_2}\) is : [JEE Main 2024 (Online) 30th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L _1: \frac{ x +1}{1}=\frac{ y }{1 / 2}=\frac{ z }{-1 / 12}, L _2: \frac{ x }{1}=\frac{ y +2}{1}=\frac{ z -1}{\frac{1}{6}} \\
& d _1=\text { shortest distance between } L _1 \& L _2 \\
& =\left|\frac{\left(\vec{a}_2-\vec{a}_1\right) \cdot\left(\vec{b}_1 \times \vec{b}_2\right)}{\left|\left(\vec{b}_1 \times \vec{b}_2\right)\right|}\right| \\
& d_1=2 \\
& L _3: \frac{ x -1}{2}=\frac{ y +8}{-7}=\frac{ z -4}{5}, L _4: \frac{ x -1}{2}=\frac{ y -2}{1}=\frac{ z -6}{-3} \\
& d _2=\text { shortest distance between } L _3 \& L _4 \\
& d _2=\frac{12}{\sqrt{3}} \text { Hence } \\
& =\frac{32 \sqrt{3} d _1}{ d _2}=\frac{32 \sqrt{3} \times 2}{\frac{12}{\sqrt{3}}}=16
\end{aligned}
\) -
Question 61 of 202
61. Question
Let \(O\) be the origin, and \(M\) and \(N\) be the points on the lines \(\frac{x-5}{4}=\frac{y-4}{1}=\frac{z-5}{3}\) and \(\frac{x+8}{12}=\frac{y+2}{5}=\frac{z+11}{9}\) respectively such that \(MN\) is the shortest distance between the given lines. Then \(\overrightarrow{O M} \cdot \overrightarrow{O N}\) is equal to ____. [JEE Main 2024 (Online) 29th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L _1: \frac{ x -5}{4}=\frac{ y -4}{1}=\frac{ z -5}{3}=\lambda \quad \operatorname{drs}(4,1,3)= b _1 \\
& M (4 \lambda+5, \lambda+4,3 \lambda+5) \\
& L _2: \frac{ x +8}{12}=\frac{ y +2}{5}=\frac{ z +11}{9}=\mu \\
& N (12 \mu-8,5 \mu-2,9 \mu-11) \\
& \overrightarrow{ MN }=(4 \lambda-12 \mu+13, \lambda-5 \mu+6,3 \lambda-9 \mu+16) \dots(1)
\end{aligned}
\)
\(
\overrightarrow{ b }_1 \times \overrightarrow{ b }_2=\left|\begin{array}{ccc}
\hat{ i } & \hat{ j } & \hat{ k } \\
4 & 1 & 3 \\
12 & 5 & 9
\end{array}\right|=-6 \hat{ i }+8 \hat{ k } \dots(2)
\)
Equation (1) and (2)
\(
\therefore \frac{4 \lambda-12 \mu+13}{-6}=\frac{\lambda-5 \mu+6}{0}=\frac{3 \lambda-9 \mu+16}{8}
\)
Eqn 1 and 2 gives
\(
\lambda-5 \mu+6=0 \dots(3)
\)
Eqn 1 and 3 gives
\(
\lambda-3 \mu+4=0 \dots(4)
\)
Solve (3) and (4) we get
\(
\begin{aligned}
\lambda & =-1, \mu=1 \\
\therefore & M (1,3,2) \\
& N (4,3,-2) \\
\therefore & \overrightarrow{ OM } \cdot \overrightarrow{ ON }=4+9-4=9
\end{aligned}
\) -
Question 62 of 202
62. Question
A line with direction ratios \(2,1,2\) meets the lines \(x=y+2=z\) and \(x+2=2 y=2 z\) respectively at the points \(P\) and \(Q\). If the length of the perpendicular from the point \((1,2,12)\) to the line \(PQ\) is \(l\), then \(l^2\) is ____. [JEE Main 2024 (Online) 29th January Morning Shift]
CorrectIncorrectHint
Let \(P ( t , t -2, t )\) and \(Q (2 s -2, s , s )\)
D.R’s of \(P Q\) are \(2,1,2\)
\(
\begin{aligned}
& \frac{2 s -2- t }{2}=\frac{ s – t +2}{1}=\frac{ s – t }{2} \\
& \Rightarrow t =6 \text { and } s =2 \\
& \Rightarrow P (6,4,6) \text { and } Q (2,2,2) \\
& PQ : \frac{ x -2}{2}=\frac{ y -2}{1}=\frac{ z -2}{2}=\lambda
\end{aligned}
\)
Let \(F (2 \lambda+2, \lambda+2,2 \lambda+2)\)
\(
A (1,2,12)
\)
\(
\overrightarrow{ AF } \cdot \overrightarrow{ PQ }=0
\)
\(
\therefore \lambda=2
\)
So \(F(6,4,6)\) and \(A F=\sqrt{65}\) -
Question 63 of 202
63. Question
The lines \(\frac{x-2}{2}=\frac{y}{-2}=\frac{z-7}{16}\) and \(\frac{x+3}{4}=\frac{y+2}{3}=\frac{z+2}{1}\) intersect at the point \(P\). If the distance of \(P\) from the line \(\frac{x+1}{2}=\frac{y-1}{3}=\frac{z-1}{1}\) is \(l\), then \(14 l^2\) is equal to ____. [JEE Main 2024 (Online) 27th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{ x -2}{1}=\frac{ y }{-1}=\frac{ z -7}{8}=\lambda \\
& \frac{ x +3}{4}=\frac{ y +2}{3}=\frac{ z +2}{1}= k \\
& \Rightarrow \lambda+2=4 k -3 \\
& -\lambda=3 k -2 \\
& \Rightarrow k =1, \lambda=-1 \\
& 8 \lambda+7= k -2 \\
& \therefore P =(1,1,-1)
\end{aligned}
\)
Projection of \(2 \hat{i}-2 \hat{k}\) on \(2 \hat{i}+3 \hat{j}+\hat{k}\) is
\(
\begin{aligned}
& =\frac{4-2}{\sqrt{4+9+1}}=\frac{2}{\sqrt{14}} \\
& \therefore l^2=8-\frac{4}{14}=\frac{108}{14} \\
& \Rightarrow 14 l^2=108
\end{aligned}
\) -
Question 64 of 202
64. Question
Let the plane \(P\) contain the line \(2 x+y-z-3=0=5 x-3 y+4 z+9\) and be parallel to the line \(\frac{x+2}{2}=\frac{3-y}{-4}=\frac{z-7}{5}\). Then the distance of the point \(A (8,-1,-19)\) from the plane \(P\) measured parallel to the line \(\frac{x}{-3}=\frac{y-5}{4}=\frac{2-z}{-12}\) is equal to ____. [JEE Main 2023 (Online) 15th April Morning Shift]
CorrectIncorrectHint
Plane \(P \equiv P _1+\lambda P _2=0\)
\(
\begin{aligned}
& (2 x+y-z-3)+\lambda(5 x-3 y)+4 z+9)=0 \\
& (5 \lambda+2) x+(1-3 \lambda) y+(4 \lambda-1) z+9 \lambda-3=0
\end{aligned}
\)
\(\overrightarrow{ n } \cdot \overrightarrow{ b }=0\) where \(\overrightarrow{ b }(2,4,5)\)
\(
\begin{aligned}
& 2(5 \lambda+2)+4(1-3 \lambda)+5(4 \lambda-1)=0 \\
& \lambda=-\frac{1}{6}
\end{aligned}
\)
Plane \(7 x+9 y-10 z-27=0\)
Equation of line \(AB\) is
\(
\frac{ x -8}{-3}=\frac{ y +1}{4}=\frac{z+19}{12}=\lambda
\)
Let \(B=(8-3 \lambda,-1+4 \lambda,-19+12 \lambda)\) lies on plane \(P\)
\(
\begin{aligned}
& \therefore 7(8-3 \lambda)+9(4 \lambda-1)-10(12 \lambda-19)=27 \\
& \lambda=2
\end{aligned}
\)
\(\therefore\) Point \(B=(2,7,5)\)
\(
A B=\sqrt{6^2+8^2+24^2}=26
\) -
Question 65 of 202
65. Question
Let the image of the point \(\left(\frac{5}{3}, \frac{5}{3}, \frac{8}{3}\right)\) in the plane \(x-2 y+z-2=0\) be \(P\). If the distance of the point \(Q(6,-2, \alpha), \alpha>0\), from \(P\) is 13 , then \(\alpha\) is equal to ____. [JEE Main 2023 (Online) 13th April Morning Shift]
CorrectIncorrectHint
Image of point \(\left(\frac{5}{3}, \frac{5}{3}, \frac{8}{3}\right)\)
\(
\begin{aligned}
& \frac{x-\frac{5}{3}}{1}=\frac{y-\frac{5}{3}}{-2}=\frac{ z -\frac{8}{3}}{1}=\frac{-2\left(1 \times \frac{5}{3}+(-2) \times \frac{8}{3}+1 \times \frac{8}{3}-2\right)}{1^2+2^2+1^2}=\frac{1}{3} \\
& \therefore x=2, y=1, z =3 \\
& P Q^2=13^2=(6-2)^2+(-2-1)^2+(\alpha-3)^2 \\
& \Rightarrow(\alpha-3)^2=144 \Rightarrow \alpha=15(\because \alpha>0)
\end{aligned}
\) -
Question 66 of 202
66. Question
Let the plane \(x+3 y-2 z+6=0\) meet the co-ordinate axes at the points \(A , B , C\). If the orthocenter of the triangle \(ABC\) is \(\left(\alpha, \beta, \frac{6}{7}\right)\), then \(98(\alpha+\beta)^2\) is equal to ____. [JEE Main 2023 (Online) 12th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& A (-6,0,0) \quad B (0,-2,0) C =(0,0,3) \\
& \overrightarrow{ AB }=6 \hat{ i }-2 \hat{ j }, \quad \overrightarrow{ BC }=2 \hat{ j }+3 \hat{ k } \\
& \overrightarrow{ AC }=6 \hat{ i }+3 \hat{ k }
\end{aligned}
\)
\(
\begin{aligned}
& \overrightarrow{ AH } \cdot \overrightarrow{ BC }=0 \\
& \left(\alpha+6, \beta, \frac{6}{7}\right) \cdot(0,2,3)=0 \\
& \beta=\frac{-9}{7} \\
& \overrightarrow{ CH } \cdot \overrightarrow{ AB }=0 \\
& \left(\alpha, \beta, \frac{-15}{7}\right) \cdot(6,-2,0)=0 \\
& 6 \alpha-2 \beta=0 \\
& \alpha=\frac{-3}{7} \\
& 98(\alpha+\beta)^2=(98) \frac{(144)}{49}=288
\end{aligned}
\) -
Question 67 of 202
67. Question
Let the line \(l: x=\frac{1-y}{-2}=\frac{z-3}{\lambda}, \lambda \in R\) meet the plane \(P: x+2 y+3 z=4\) at the point \((\alpha, \beta, \gamma)\). If the angle between the line \(l\) and the plane \(P\) is \(\cos ^{-1}\left(\sqrt{\frac{5}{14}}\right)\), then \(\alpha+2 \beta+6 \gamma\) is equal to _____. [JEE Main 2023 (Online) 11th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L: \frac{x-0}{1}=\frac{y-1}{2}=\frac{z-3}{\lambda} \\
& P: x+2 y+3 z=4
\end{aligned}
\)
Vector parallel to line : \(\langle 1,2, \lambda\rangle=\vec{b}\)
Normal vector to plane \(P:<1,2,3\rangle=\vec{n}\)
Angle between plane and line is \(\theta\)
Then, \(\sin \theta=\frac{<1,2, \lambda>\cdot<1,2,3>}{\sqrt{1^2+2^2+\lambda^2} \cdot \sqrt{1^2+2^2+3^2}}\)
\(
\begin{aligned}
& \Rightarrow \frac{3}{\sqrt{14}}=\frac{1+4+3 \lambda}{\sqrt{\lambda^2+5} \sqrt{14}} \Rightarrow \lambda=\frac{2}{3} \\
& L_1 \equiv \frac{x-0}{3}=\frac{y-1}{6}=\frac{z-3}{2}=\mu
\end{aligned}
\)
Any point on line : \((3 \mu, 6 \mu+1,2 \mu+3)\)
It lies on \(P\)
\(
\begin{aligned}
& \therefore 3 \mu+12 \mu+2+6 \mu+9=4 \\
& \Rightarrow \mu=\frac{-1}{3}
\end{aligned}
\)
Hence, \(\alpha=3 \mu=-1, \beta=6 \mu+1=-1, \gamma=2 \mu+3=\frac{7}{3}\)
Now, \(\alpha+2 \beta+6 \gamma=11\) -
Question 68 of 202
68. Question
Let a line \(l\) pass through the origin and be perpendicular to the lines
\(
\begin{aligned}
& l_1: \vec{r}=(\hat{\imath}-11 \hat{\jmath}-7 \hat{k})+\lambda(\hat{i}+2 \hat{\jmath}+3 \hat{k}), \lambda \in R \text { and } \\
& l_2: \vec{r}=(-\hat{\imath}+\hat{ k })+\mu(2 \hat{\imath}+2 \hat{\jmath}+\hat{ k }), \mu \in R \text {. }
\end{aligned}
\)
If \(P\) is the point of intersection of \(l\) and \(l_1\), and \(Q (\alpha, \beta, \gamma)\) is the foot of perpendicular from \(P\) on \(l_2\), then \(9(\alpha+\beta+\gamma)\) is equal to ____. [JEE Main 2023 (Online) 11th April Morning Shift]CorrectIncorrectHint
We have,
\(l_1: \vec{r}=(\hat{\imath}-11 \hat{\jmath}-7 \hat{k})+\lambda(\hat{i}+2 \hat{\jmath}+3 \hat{k}), \lambda \in R\) and \(l_2: \vec{r}=(-\hat{\imath}+\hat{ k })+\mu(2 \hat{\imath}+2 \hat{\jmath}+\hat{ k }), \mu \in R\)
Let direction ratio of line \(l\) be \(a, b\) and \(c\) Equation of line \(l\)
\(
\begin{aligned}
\vec{r} & =(0 \hat{ i }+0 \hat{ j }+0 \hat{ k })+\delta(a \hat{ i }+b \hat{ j }+c \hat{ k }) \\
& =\delta(a \hat{ i }+b \hat{ j }+c \hat{ k })
\end{aligned}
\)
As, line \(l\) is perpendicular to \(l_1\) and \(l_2\),
\(
a \hat{ i }+b \hat{ j }+c \hat{ k }=\left|\begin{array}{ccc}
\hat{ i } & \hat{ j } & \hat{ k } \\
1 & 2 & 3 \\
2 & 2 & 1
\end{array}\right|=-4 \hat{ i }+5 \hat{ j }-2 \hat{ k }
\)
\(\therefore\) Equation of line \(l: \vec{r}=\delta(-4 \hat{ i }+5 \hat{ j }-2 \hat{ k })\)
As, \(P\) is the intersecting point of \(l\) and \(l_1\)
\(
-4 \delta=1+\lambda, 5 \delta=-11+2 \lambda,-2 \delta=-7+3 \lambda
\)
After solving the above three equation, we get
\(
\delta=-1 \text { and } \lambda=3
\)
\(\therefore\) Co-ordinate of point \(P\) is \((4,-5,2)\).
\(Q\) is a point on line \(l_2\)
Let co-ordinate of \(Q\) be \((-1+2 \mu, 2 \mu, 1+\mu)\)
\(
\begin{gathered}
\overrightarrow{P Q}=(-5+2 \mu) \hat{ i }+(2 \mu+5) \hat{ j }+(\mu-1) \hat{ k } \\
\overrightarrow{P Q} \cdot(2 \hat{ i }+2 \hat{ j }+\hat{ k })=0\left[\because \overrightarrow{P Q} \perp l_2\right] \\
2(-5+2 \mu)+2(2 \mu+5)+\mu-1=0 \\
9 \mu-1=0 \Rightarrow \mu=\frac{1}{9}
\end{gathered}
\)
\(
\therefore \alpha=-1+\frac{2}{9}=\frac{-7}{9}, \beta=2 \times \frac{1}{9}=\frac{2}{9}, r=1+\frac{1}{9}=\frac{10}{9}
\)
Hence, \(9(\alpha+\beta+\gamma)=9\left(-\frac{7}{9}+\frac{2}{9}+\frac{10}{9}\right)=5\) -
Question 69 of 202
69. Question
Let the foot of perpendicular from the point \(A (4,3,1)\) on the plane \(P : x-y+2 z+3=0\) be \(N\). If \(B (5, \alpha, \beta), \alpha, \beta \in Z\) is a point on plane \(P\) such that the area of the triangle \(ABN\) is \(3 \sqrt{2}\), then \(\alpha^2+\beta^2+\alpha \beta\) is equal to ____. [JEE Main 2023 (Online) 10th April Evening Shift]
CorrectIncorrectHint
We have, equation of plane \(P\) is \(x-y+2 z+3=0\)
Perpendicular distance from \(A\) to a plane \(P\) i.e. N
\(
=\frac{|4-3+2(1)+3|}{\sqrt{1^2+(-1)^2+2^2}}
\)
\(B(5, \alpha, \beta)\) lies on the plane \(P\), so
\(
5-\alpha+2 \beta+3=0 \Rightarrow \alpha=2 \beta+8 \dots(i)
\)
Direction ratio of \(A N\) is \(<1,-1,2>\)
Equation of \(A N\) is \(\frac{x-4}{1}=\frac{y-3}{-1}=\frac{z-1}{2}\)
Co-ordinate of \(N: \frac{x-4}{1}=\frac{y-3}{-1}=\frac{z-1}{2}=\frac{-(4-3+2+3)}{1+1+4}=-1\)
\(
\Rightarrow x=3, y=4, z=-1
\)
\(\therefore\) Co-ordinate of \(N\) is \((3,4,-1)\)
Also, Area of \((\triangle ABN )=3 \sqrt{2}\)
\(
\begin{aligned}
& \Rightarrow \frac{1}{2} \times AN \times BN =3 \sqrt{2} \\
& \Rightarrow \frac{1}{2} \times \sqrt{6} \times BN =3 \sqrt{2} \Rightarrow BN =2 \sqrt{3}
\end{aligned}
\)
\(
\begin{aligned}
& \text { or } BN ^2=12 \\
& \Rightarrow(5-3)^2+(\alpha-4)^2+(\beta+1)^2=12 \\
& 4+(2 \beta+4)^2+(\beta+1)^2=12(\text { using eqn (i)) } \\
& \Rightarrow 4 \beta^2+16+16 \beta+\beta^2+1+2 \beta=8 \\
& \Rightarrow 5 \beta^2+18 \beta+9=0 \\
& \Rightarrow(5 \beta+3)(\beta+3)=0 \\
& \Rightarrow \beta=-3\left[\because \beta \in z \text {, so rejecting } \beta=\frac{-3}{5}\right] \\
& \text { and } \alpha=2 \beta+8=2(-3)+8=2 \\
& \text { also } \alpha^2+\beta^2+\alpha \beta=9+4-6=7
\end{aligned}
\) -
Question 70 of 202
70. Question
Let \(P _1\) be the plane \(3 x-y-7 z=11\) and \(P _2\) be the plane passing through the points \((2,-1,0),(2,0,-1)\), and \((5,1,1)\). If the foot of the perpendicular drawn from the point \((7,4,-1)\) on the line of intersection of the planes \(P_1\) and \(P_2\) is \((\alpha, \beta, \gamma)\), then \(\alpha+\beta+\gamma\) is equal to ______. [JEE Main 2023 (Online) 8th April Evening Shift]
CorrectIncorrectHint
Equation of plane \(P _2\) passing through \((2,-1,0),(2,0,-1)\) and \((5,1,1)\) is
\(
\begin{aligned}
& \left|\begin{array}{ccc}
x-5 & y-1 & z-1 \\
3 & 2 & 1 \\
3 & 1 & 2
\end{array}\right|=0 \\
& \Rightarrow(x-5)(4-1)-(y-1)(6-3)+(z-1)(3-6)=0 \\
& \Rightarrow 3 x-15-3 y+3-3 z+3=0 \\
& \Rightarrow 3 x-3 y-3 z-9=0 \\
& \Rightarrow x-y-z=3 \ldots \ldots(i)
\end{aligned}
\)
Now, direction ratios of line of intersection of \(P_1\) and \(P _2\) is
\(
\begin{aligned}
& \left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & -1 & -1 \\
3 & -1 & -7
\end{array}\right| \\
& =\hat{i}(7-1)-\hat{j}(-7+3)+\hat{k}(-1+3) \\
& =6 \hat{i}+4 \hat{j}+2 \hat{k}
\end{aligned}
\)
At \(z=0, x-y=3\) [from (i)]
\(
3 x-y=11
\)
On solving, we get
\(
x=4 \text { and } y=1
\)
So, equation of line is
\(
\begin{aligned}
& \frac{x-4}{6}=\frac{y-1}{4}=\frac{z-2}{6}=k \\
& \therefore(\alpha, \beta, \gamma)=(6 k+4,4 k+1,2 k) \\
& \Rightarrow(6)(\alpha-7)+4(\beta-4)+2(\gamma+1)=0 \\
& \Rightarrow 6(6 k+4-7)+4(4 k+1-4)+2(2 k+1)=0 \\
& \Rightarrow 36 k-18+16 k-12+4 k+4=0 \\
& \Rightarrow 56 k=26 \Rightarrow k=\frac{1}{2}
\end{aligned}
\)
So, \(\alpha=7, \beta=3\) and \(\gamma=1\)
\(
\therefore \alpha+\beta+\gamma=7+3+1=11
\) -
Question 71 of 202
71. Question
Let \(\lambda_1, \lambda_2\) be the values of \(\lambda\) for which the points \(\left(\frac{5}{2}, 1, \lambda\right)\) and \((-2,0,1)\) are at equal distance from the plane \(2 x+3 y-6 z+7=0\). If \(\lambda_1>\lambda_2\), then the distance of the point \(\left(\lambda_1-\lambda_2, \lambda_2, \lambda_1\right)\) from the line \(\frac{x-5}{1}=\frac{y-1}{2}=\frac{z+7}{2}\) is ______. [JEE Main 2023 (Online) 8th April Morning Shift]
CorrectIncorrectHint
Since \(\left(\frac{5}{2}, 1, \lambda\right)\) and \((-2,0,1)\) are equidistant
\(
\begin{aligned}
& \text { from plane } 2 x+3 y-6 z+7=0 \\
& \therefore\left|\frac{2\left(\frac{5}{2}\right)+3(1)-6(\lambda)+7}{\sqrt{2^2+3^2+6^2}}\right|=\left|\frac{2(-2)+3(0)-6(1)+7}{\sqrt{2^2+3^2+6^2}}\right| \\
& \Rightarrow|5+3-6 \lambda+7|=|-4-6+7| \\
& \Rightarrow|15-6 \lambda|=|-3| \\
& \Rightarrow 15-6 \lambda= \pm 3 \\
& \Rightarrow 15-6 \lambda=3 \text { or } 15-6 \lambda=-3 \\
& \Rightarrow 6 \lambda=12 \text { or } 6 \lambda=18 \\
& \Rightarrow \lambda=2 \text { or } \lambda=3 \\
& \because \lambda_1>\lambda_2 \\
& \therefore \lambda_1=3 \text { and } \lambda_2=2
\end{aligned}
\)
So, point will be \((1,2,3)\)
Let \(M _0=(1,2,3)\)
\(M_1\) is the point through which line passes i.e, \((5,1,-7)\)
and \(\vec{s}=\hat{i}+2 \hat{j}+2 \hat{k}\)
\(
\therefore \overrightarrow{ M _0 M _1}=4 \hat{i}-\hat{j}-10 \hat{k}
\)
\(
\begin{aligned}
& =\frac{|(4 \hat{i}-\hat{j}-10 \hat{k}) \times(\hat{i}+2 \hat{j}+2 \hat{k})|}{\sqrt{1+4+4}} \\
& =\frac{|18 \hat{i}-18 \hat{j}+9 \hat{k}|}{3}=9
\end{aligned}
\) -
Question 72 of 202
72. Question
If the lines \(\frac{x-1}{2}=\frac{2-y}{-3}=\frac{z-3}{\alpha}\) and \(\frac{x-4}{5}=\frac{y-1}{2}=\frac{z}{\beta}\) intersect, then the magnitude of the minimum value of \(8 \alpha \beta\) is _____. [JEE Main 2023 (Online) 6th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x-1}{2}=\frac{2-y}{-3}=\frac{z-3}{\alpha} \\
& \Rightarrow \frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{\alpha}=\lambda \dots(i)
\end{aligned}
\)
Any point on the line (i)
\(
x=2 \lambda+1, y=3 \lambda+2, z=\alpha \lambda+3
\)
and line \(\frac{x-4}{5}=\frac{y-1}{2}=\frac{z}{\beta}=\mu \dots(ii)\)
Any point on line (ii)
\(
\Rightarrow x=5 \mu+4, y=2 \mu+1, z=\beta \mu
\)
Since, given lines intersects
\(
\therefore 2 \lambda+1=5 \mu+4 \dots(iii)
\)
\(3 \lambda+2=2 \mu+1 \dots(iv)\)
and \(\alpha \lambda+3=\beta \mu \dots(v)\)
On solving (iii) and (iv), we get
\(
\lambda=-1, \mu=-1
\)
On putting value of \(\lambda\) and \(\mu\) in (v), we get
\(
\begin{gathered}
\alpha(-1)+3=-\beta \\
\Rightarrow \alpha=\beta+3
\end{gathered}
\)
Now,
\(
\begin{aligned}
& 8 \alpha \beta=8(\beta+3)(\beta) \\
& =8\left(\beta^2+3 \beta\right) \\
& =8\left(\beta^2+3 \beta+\frac{9}{4}-\frac{9}{4}\right) \\
& =8\left\{\left(\beta+\frac{3}{2}\right)^2-\frac{9}{4}\right\} \\
& =8\left(\beta+\frac{3}{2}\right)^2-18
\end{aligned}
\)
Here, minimum value \(=-18\)
\(\therefore\) Magnitude of the minimum value of \(8 \alpha \beta\) is 18. -
Question 73 of 202
73. Question
Let the image of the point \(P (1,2,3)\) in the plane \(2 x-y+z=9\) be \(Q\). If the coordinates of the point \(R\) are \((6,10,7)\), then the square of the area of the triangle \(PQR\) is ____. [JEE Main 2023 (Online) 6th April Morning Shift]
CorrectIncorrectHint
Let \(Q(x, y, z)\) be the image of \(P(1,2,3)\) in the plane
\(
\begin{aligned}
& 2 x-y+z=9 \\
& \therefore \frac{x-1}{2}=\frac{y-2}{-1}=\frac{z-3}{1}=\frac{-2(2 \times 1+(-1)(2)+(1)(3)(-9)}{(2)^2+(-1)^2+(1)^2} \\
& \Rightarrow \frac{x-1}{2}=\frac{y-2}{-1}=\frac{z-3}{1}=\frac{-2(-6)}{6}=2 \\
& \Rightarrow x=5, y=0, z=5
\end{aligned}
\)
Now, \(\overrightarrow{P Q}=4 \hat{ i }-2 \hat{ j }+2 \hat{ k }\) and
\(
\overrightarrow{P R}=5 \hat{ i }+8 \hat{ j }+4 \hat{ k }
\)
\(\therefore\) Area of the \(\triangle P Q R=\frac{1}{2}|\overrightarrow{P Q} \times \overrightarrow{P R}|\)
Now, \(\overrightarrow{P Q} \times \overrightarrow{P R}\)
\(
\begin{aligned}
& =\left|\begin{array}{ccr}
\hat{ i } & \hat{ j } & \hat{ k } \\
4 & -2 & 2 \\
5 & 8 & 4
\end{array}\right| \\
& =\hat{ i }(-8-16)-\hat{ j }(16-10)+\hat{ k }(32+10) \\
& =-24 \hat{ i }-6 \hat{ j }+42 \hat{ k }
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \frac{1}{2}|(-24 \hat{ i }-6 \hat{ j }+42 \hat{ k })|=|-12 \hat{ i }-3 \hat{ j }+21 \hat{ k }| \\
& =\sqrt{(-12)^2+(-3)^2+(21)^2} \\
& =\sqrt{144+9+441}=\sqrt{594} \\
&
\end{aligned}
\)
\(\therefore\) The square of the area of the \(\triangle P Q R=594\) -
Question 74 of 202
74. Question
The point of intersection \(C\) of the plane \(8 x+y+2 z=0\) and the line joining the points \(A (-3,-6,1)\) and \(B (2,4,-3)\) divides the line segment \(AB\) internally in the ratio \(k : 1\). If \(a , b , c (| a |,| b |,| c |\) are coprime) are the direction ratios of the perpendicular from the point \(C\) on the line \(\frac{1-x}{1}=\frac{y+4}{2}=\frac{z+2}{3}\), then \(| a + b + c |\) is equal to _____. [JEE Main 2023 (Online) 1st February Evening Shift]
CorrectIncorrectHint
Plane: \(8 x+y+2 z=0\)
Given line \(AB : \frac{ x -2}{5}=\frac{ y -4}{10}=\frac{ z +3}{-4}=\lambda\)
Any point on line \((5 \lambda+2,10 \lambda+4,-4 \lambda-3)\)
Point of intersection of line and plane
\(
\begin{aligned}
& 8(5 \lambda+2)+10 \lambda+4-8 \lambda-6=0 \\
& \lambda=-\frac{1}{3} \\
& C \left(\frac{1}{3}, \frac{2}{3},-\frac{5}{3}\right)
\end{aligned}
\)
\(L : \frac{ x -1}{-1}=\frac{ y +4}{2}=\frac{ z +2}{3}=\mu\)
\(
\begin{aligned}
& \overrightarrow{ CD }=\left(-\mu+\frac{2}{3}\right) \hat{ i }+\left(2 \mu-\frac{14}{3}\right) \hat{ j }+\left(3 \mu-\frac{1}{3}\right) \hat{ k } \\
& \left(-\mu+\frac{2}{3}\right)(-1)+\left(2 \mu-\frac{14}{3}\right) 2+\left(3 \mu-\frac{1}{3}\right) 3=0 \\
& \Rightarrow \mu=\frac{11}{14} \\
& \overrightarrow{ CD }=\frac{-5}{42}, \frac{-130}{42}, \frac{85}{42}
\end{aligned}
\)
Direction ratios \(\rightarrow(-1,-26,17)\)
\(
|a+b+c|=10
\) -
Question 75 of 202
75. Question
Let \(\alpha x+\beta y+\gamma z=1\) be the equation of a plane passing through the point \((3,-2,5)\) and perpendicular to the line joining the points \((1,2,3)\) and \((-2,3,5)\). Then the value of \(\alpha \beta \gamma\) is equal to _____. [JEE Main 2023 (Online) 1st February Evening Shift]
CorrectIncorrectHint
Plane :
\(
a(x-3)+b(y+2)+c(z-5)=0
\)
Dr’s of plane : \(3 \hat{i}-\hat{j}-2 \hat{k}\)
\(
\begin{aligned}
& <3,-1,-2> \\
& P: 3(x-3)-1(y+2)-2(z-5)=0 \\
& 3 x-9-y-2-2 z+10=0 \\
& 3 x-y-2 z=1
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \alpha=3, \beta=-1, \gamma=-2 \\
& \Rightarrow \alpha \beta \gamma=6
\end{aligned}
\) -
Question 76 of 202
76. Question
Let the line \(L: \frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-3}{1}\) intersect the plane \(2 x+y+3 z=16\) at the point \(P\). Let the point \(Q\) be the foot of perpendicular from the point \(R(1,-1,-3)\) on the line \(L\). If \(\alpha\) is the area of triangle \(P Q R\), then \(\alpha^2\) is equal to ____. [JEE Main 2023 (Online) 31st January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L: \frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-3}{1}=r \text { (say) } \\
& \text { Let } P \equiv\left(2 r_1+1,-r_1, r_1+3\right) \\
& P \text { lies on } 2 x+y+3 z=16 \\
& \therefore 2\left(2 r_1+1\right)+\left(-r_1-1\right)+3\left(r_1+3\right)=16 \\
& r_1=1 \\
& P \equiv(3,-2,4) \\
& R \equiv(1,-1,-3) \\
& \text { Let } Q \equiv\left(2 r_2+1,-r_2-1, r_2+3\right) \\
& D R \text { of } Q R \equiv\left(2 r_2, -r_2, r_2+6\right) \\
& \text { DRs of } L \equiv(2,-1,1) \\
& Q R \perp L \Rightarrow 4 r_2+r_2+r_2+6=0 \\
& r_2=-1 \\
& Q \equiv(-1,0,2)
\end{aligned}
\)
\(
\begin{aligned}
& \overrightarrow{Q P} \times \overrightarrow{R P}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
4 & -2 & 2 \\
2 & -1 & 7
\end{array}\right|=-12 \hat{i}-24 \hat{j}+0 \hat{k} \\
& \alpha=[P Q R]=\frac{1}{2}|\overrightarrow{Q P} \times \overrightarrow{R P}|=\frac{1}{2} \times 12 \sqrt{5} \\
& =6 \sqrt{5} \\
& \alpha^2=180
\end{aligned}
\) -
Question 77 of 202
77. Question
Let \(\theta\) be the angle between the planes \(P_1: \vec{r} \cdot(\hat{i}+\hat{j}+2 \hat{k})=9\) and \(P_2: \vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})=15\). Let \(L\) be the line that meets \(P_2\) at the point \((4,-2,5)\) and makes an angle \(\theta\) with the normal of \(P_2\). If \(\alpha\) is the angle between \(L\) and \(P_2\), then \(\left(\tan ^2 \theta\right)\left(\cot ^2 \alpha\right)\) is equal to ____. [JEE Main 2023 (Online) 31st January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& P_1: \vec{r} \cdot(\hat{i}+\hat{j}+2 \hat{k})=9 \\
& P_2: \vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})=15 \\
& \text { then } \cos \theta=\frac{3}{\sqrt{6} \cdot \sqrt{6}}=\frac{1}{2} \\
& \therefore \theta=\frac{\pi}{3}, \text { Now } \alpha=\frac{\pi}{2}-\theta \\
& \therefore \tan ^2 \theta \cdot \cot ^2 \alpha=\tan ^4 \theta \\
& =(\sqrt{3})^4=9
\end{aligned}
\) -
Question 78 of 202
78. Question
Let a line \(L\) pass through the point \(P(2,3,1)\) and be parallel to the line \(x+3 y-2 z-2=0=x-y+2 z\). If the distance of \(L\) from the point \((5,3,8)\) is \(\alpha\), then \(3 \alpha^2\) is equal to : [JEE Main 2023 (Online) 30th January Evening Shift]
CorrectIncorrectHint
\(
L: \frac{x-2}{1}=\frac{y-3}{-1}=\frac{z-1}{-1}=\lambda
\)
Any point on \(L\) can be taken as
\(
B(\lambda+2,-\lambda+3,-\lambda+1)
\)
Let \(A(5,3,8)\)
\(
\begin{aligned}
& \text { So, } A B \cdot(\hat{i}-\hat{j}-\widehat{k})=0 \\
& {[(\lambda-3) \hat{i}-\lambda \hat{j}-(\lambda+7) \hat{k}] \cdot[\hat{i}-\hat{j}-\widehat{k}]=0} \\
& \lambda-3+\lambda+\lambda+7=0 \\
& \therefore \lambda=\frac{-4}{3} \\
& \overrightarrow{A B}=\frac{13}{3} \hat{i}+\frac{4}{3} \hat{i}-\frac{17}{3} \widehat{k} \\
& |\overrightarrow{A B}|=\sqrt{\frac{169}{9}+\frac{16}{9}+\frac{289}{9}} \\
& =\frac{\sqrt{474}}{3}=\alpha \\
& 3 \alpha^2=\frac{474}{9} \times 3=158
\end{aligned}
\) -
Question 79 of 202
79. Question
If the equation of the plane passing through the point \((1,1,2)\) and perpendicular to the line \(x-3 y+2 z-1=0=4 x-y+z\) is \(A x+ B y+ C z=1\), then \(140( C – B + A )\) is equal to _____. [JEE Main 2023 (Online) 30th January Morning Shift]
CorrectIncorrectHint
Line of intersection of the planes \(x-3 y+2 z-1=0\) and \(4 x-y+z=0\) is normal \((\vec{n})\) to the required plane.
\(
\vec{n}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
1 & -3 & 2 \\
4 & -1 & 1
\end{array}\right|=-\hat{i}+7 \hat{j}+11 \widehat{k}
\)
Equation of plane is
\(
-x+7 y+11 z=\lambda
\)
It passes through \((1,1,2)\)
\(
\therefore \lambda=28
\)
So, the plane is
\(
\begin{aligned}
& -x+7 y+11 z=28 \\
& \Rightarrow \frac{-1}{28} x+\frac{7}{28} y+\frac{11}{28} z=1 \\
& A=\frac{-1}{28}, B=\frac{7}{28}, C=\frac{11}{28} \\
& 140(C-B+A)=15
\end{aligned}
\) -
Question 80 of 202
80. Question
If \(\lambda_1<\lambda_2\) are two values of \(\lambda\) such that the angle between the planes \(P_1: \vec{r}(3 \hat{i}-5 \hat{j}+\hat{k})=7\) and \(P_2: \vec{r} \cdot(\lambda \hat{i}+\hat{j}-3 \hat{k})=9\) is \(\sin ^{-1}\left(\frac{2 \sqrt{6}}{5}\right)\), then the square of the length of perpendicular from the point \(\left(38 \lambda_1, 10 \lambda_2, 2\right)\) to the plane \(P_1\) is ____. [JEE Main 2023 (Online) 30th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& P_1: \vec{r} \cdot(3 \hat{i}-5 \hat{j}+\widehat{k})=7 \\
& P_2: \vec{r} \cdot(\lambda \hat{i}+\hat{j}-3 \widehat{k})=9
\end{aligned}
\)
Let angle between \(P_1\) and \(P_2\) is \(\theta\)
Then \(\cos \theta=\frac{3 \lambda-5-3}{\sqrt{35} \sqrt{\lambda^2+10}}\)
\(
\begin{aligned}
& \text { But } \sin \theta=\frac{2 \sqrt{6}}{5} \\
& \therefore \frac{(3 \lambda-8)^2}{35\left(\lambda^2+10\right)}=1-\frac{24}{25} \\
& \Rightarrow 5\left(9 \lambda^2+64-48 \lambda\right)=7 \lambda^2+70 \\
& \Rightarrow 38 \lambda^2-240 \lambda+250=0 \\
& \Rightarrow 19 \lambda^2-120 \lambda+125=0 \\
& \Rightarrow(19 \lambda-25)(\lambda-5)=0 \\
& \therefore \lambda_1=\frac{25}{19}, \lambda_2=5
\end{aligned}
\)
So, point \((50,50,2)\)
\(
\therefore d=\frac{|150-250+2-7|}{\sqrt{35}}=315
\) -
Question 81 of 202
81. Question
Let the equation of the plane \(P\) containing the line \(x+10=\frac{8-y}{2}=z\) be \(a x+b y+3 z=2(a+b)\) and the distance of the plane \(P\) from the point \((1,27,7)\) be \(c\). Then \(a^2+b^2+c^2\) is equal to ____. [JEE Main 2023 (Online) 29th January Morning Shift]
CorrectIncorrectHint
The line \(\frac{x+10}{1}=\frac{y-8}{-2}=\frac{z}{1}\) have a point \((-10,8,0)\) with d. r. \((1,-2,1)\)
\(\because\) the plane \(a x+b y+3 z=2(a+b)\)
\(
\Rightarrow b =2 a
\)
\(\&\) dot product of d.r.’s is zero
\(
\therefore a-2 b+3=0 \therefore a=1 \& b=2
\)
Distance from \((1,27,7)\) is
\(
\begin{aligned}
& c=\frac{1+54+21-6}{\sqrt{14}}=\frac{70}{\sqrt{14}}=5 \sqrt{14} \\
& \therefore a ^2+ b ^2+ c ^2=1+4+350 \\
& =355
\end{aligned}
\) -
Question 82 of 202
82. Question
Let the co-ordinates of one vertex of \(\triangle A B C\) be \(A(0,2, \alpha)\) and the other two vertices lie on the line \(\frac{x+\alpha}{5}=\frac{y-1}{2}=\frac{z+4}{3}\). For \(\alpha \in Z\), if the area of \(\triangle A B C\) is 21 sq. units and the line segment \(B C\) has length \(2 \sqrt{21}\) units, then \(\alpha^2\) is equal to _____. [JEE Main 2023 (Online) 29th January Morning Shift]
CorrectIncorrectHint
\(
\left|\frac{1}{2} \cdot 2 \sqrt{21}\right| \begin{array}{ccc}
i & j & k \\
\alpha & 1 & \alpha+4 \\
5 & 2 & 3
\end{array}\left|\frac{1}{\sqrt{25+4+9}}\right|=21 \sqrt{21}
\)
\(
\begin{aligned}
& \sqrt{(2 \alpha+5)^2+(2 \alpha+20)^2+(2 \alpha-5)^2}=\sqrt{21} \sqrt{38} \\
& \Rightarrow 12 \alpha^2+80 \alpha+450=798 \\
& \Rightarrow 12 \alpha^2+80 \alpha-348=0 \\
& \Rightarrow \alpha=3 \Rightarrow \alpha^2=9 \\
&
\end{aligned}
\) -
Question 83 of 202
83. Question
If the shortest distance between the line joining the points \((1,2,3)\) and \((2,3,4)\), and the line \(\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-2}{0}\) is \(\alpha\), then \(28 \alpha^2\) is equal to _____. [JEE Main 2023 (Online) 25th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Points }(1,2,3) \text { and }(2,3,4) \\
& L_1: \frac{(x-1)}{1}=\frac{(y-2)}{1}=\frac{(2-3)}{1} \\
& L_2: \frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-2}{0} \\
& \vec{b}_1=\hat{i}+\hat{j}+\hat{k} \\
& \vec{b}_2=2 \hat{i}-\hat{j}+0 \hat{k} \\
& \overrightarrow{a_1}-\overrightarrow{a_2}=0 \hat{i}-3 \hat{j}-\hat{k} \\
& d=\left|\frac{\left(\bar{a}_1-\bar{a}_2\right) \cdot\left(n_1 \times n_2\right)}{\left|n_1 \times n_2\right|}\right| \\
& =\left|\frac{6-3}{\sqrt{9+1+4}}\right|=\frac{3}{\sqrt{14}}=\alpha \\
& 28 \alpha^2=\frac{28 \times 9}{14}=18
\end{aligned}
\) -
Question 84 of 202
84. Question
Let the equation of the plane passing through the line \(x-2 y-z-5=0=x+y+3 z-5\) and parallel to the line \(x+y+2 z-7=0=2 x+3 y+z-2\) be \(a x+b y+c z=65\). Then the distance of the point \(( a , b , c )\) from the plane \(2 x+2 y-z+16=0\) is _____. [JEE Main 2023 (Online) 25th January Morning Shift]
CorrectIncorrectHint
Let the equation of the plane is
\(
(x-2 y-z-5)+\lambda(x+y+3 z-5)=0 \dots(i)
\)
\(\because \quad\) it’s parallel to the line
\(
x+y+2 z-7=0=2 x+3 y+z-2
\)
So, vector along the line \(\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & 2 \\ 2 & 3 & 1\end{array}\right|\)
\(
=-5 \hat{i}+3 \hat{j}+\hat{k}
\)
\(\because\) Plane is parallel to line
\(
\begin{aligned}
& \therefore-5(1+\lambda)+3(-2+\lambda)+1(-1+3 \lambda)=0 \\
& \lambda=12
\end{aligned}
\)
So, by (i)
\(
\begin{aligned}
& 13 x+10 y+35 z=65 \\
& \therefore a=13, b=10, c=35 \text { and } d=\frac{26+20-35+16}{\sqrt{9}}=9
\end{aligned}
\) -
Question 85 of 202
85. Question
If the shortest between the lines \(\frac{x+\sqrt{6}}{2}=\frac{y-\sqrt{6}}{3}=\frac{z-\sqrt{6}}{4}\) and \(\frac{x-\lambda}{3}=\frac{y-2 \sqrt{6}}{4}=\frac{z+2 \sqrt{6}}{5}\) is 6 , then the square of sum of all possible values of \(\lambda\) is : [JEE Main 2023 (Online) 24th January Evening Shift]
CorrectIncorrectHint
Shortest distance between the lines
\(
\begin{aligned}
& \frac{x+\sqrt{6}}{2}=\frac{y-\sqrt{6}}{3}=\frac{z-\sqrt{6}}{4} \\
& \frac{x-\lambda}{3}=\frac{y-2 \sqrt{6}}{4}=\frac{2+2 \sqrt{6}}{5} \text { is } 6
\end{aligned}
\)
Vector along line of shortest distance
\(=\left|\begin{array}{lll} i & j & k \\ 2 & 3 & 4 \\ 3 & 4 & 5\end{array}\right|, \Rightarrow-\hat{ i }+2 \hat{ j }- k\) (its magnitude is \(\sqrt{6}\) )
Now \(\frac{1}{\sqrt{6}}\left|\begin{array}{ccc}\sqrt{6}+\lambda & \sqrt{6} & -3 \sqrt{6} \\ 2 & 3 & 4 \\ 3 & 4 & 5\end{array}\right|= \pm 6\)
\(
\Rightarrow \lambda=-2 \sqrt{6}, 10 \sqrt{6}
\)
So, square of sum of these values
\(
=(10 \sqrt{6}-2 \sqrt{6})^2=(8 \sqrt{6})^2=384
\) -
Question 86 of 202
86. Question
The shortest distance between the lines \(\frac{x-2}{3}=\frac{y+1}{2}=\frac{z-6}{2}\) and \(\frac{x-6}{3}=\frac{1-y}{2}=\frac{z+8}{0}\) is equal to _____. [JEE Main 2023 (Online) 24th January Morning Shift]
CorrectIncorrectHint
Shortest distance between the lines
\(
\begin{aligned}
& =\frac{\left|\begin{array}{ccc}
4 & 2 & -14 \\
3 & 2 & 2 \\
3 & -2 & 0
\end{array}\right|}{\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
3 & 2 & 2 \\
3 & -2 & 0
\end{array}\right|} \\
& =\frac{16+12+168}{|4 \hat{i}+6 \hat{j}-12 \hat{k}|}=\frac{196}{14}=14
\end{aligned}
\) -
Question 87 of 202
87. Question
Let a line with direction ratios \(a,-4 a,-7\) be perpendicular to the lines with direction ratios \(3,-1,2 b\) and \(b, a,-2\). If the point of intersection of the line \(\frac{x+1}{a^2+b^2}=\frac{y-2}{a^2-b^2}=\frac{z}{1}\) and the plane \(x-y+z=0\) is \((\alpha, \beta, \gamma)\), then \(\alpha+\beta+\gamma\) is equal to _____. [JEE Main 2022 (Online) 29th July Morning Shift]
CorrectIncorrectHint
Given \(a \cdot 3+(-4 a)(-1)+(-7) 2 b=0 \dots(i)\)
and \(a b-4 a^2+14=0 \dots(ii)\)
\(\Rightarrow a^2=4\) and \(b^2=1\)
\(\therefore L \equiv \frac{x+1}{5}=\frac{y-2}{3}=\frac{z}{1}=\lambda\) (say)
\(\Rightarrow\) General point on line is \((5 \lambda-1,3 \lambda+2, \lambda)\) for finding point of intersection with \(x-y+z=0\) we get \((5 \lambda-1)-(3 \lambda+2)+(\lambda)=0\)
\(\Rightarrow 3 \lambda-3=0 \Rightarrow \lambda=1\)
\(\therefore\) Point at intersection \((4,5,1)\)
\(
\therefore \alpha+\beta+\gamma=4+5+1=10
\) -
Question 88 of 202
88. Question
Let \(P (-2,-1,1)\) and \(Q \left(\frac{56}{17}, \frac{43}{17}, \frac{111}{17}\right)\) be the vertices of the rhombus PRQS. If the direction ratios of the diagonal RS are \(\alpha,-1, \beta\), where both \(\alpha\) and \(\beta\) are integers of minimum absolute values, then \(\alpha^2+\beta^2\) is equal to _____. [JEE Main 2022 (Online) 28th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { d.r’s of } R S=<\alpha,-1, \beta> \\
& \text { d.r’s of } P Q=<\frac{90}{17}, \frac{60}{17}, \frac{94}{17}>=<45,30,47>
\end{aligned}
\)
as \(P Q\) and \(R S\) are diagonals of rhombus
\(
\begin{aligned}
& \alpha(45)+30(-1)+47(\beta)=0 \\
& \Rightarrow 45 \alpha+47 \beta=30 \\
& \text { i.e., } \alpha=\frac{30-47 \beta}{45}
\end{aligned}
\)
for minimum integral value \(\alpha=-15\) and \(\beta=15\)
\(
\Rightarrow \alpha^2+\beta^2=450
\) -
Question 89 of 202
89. Question
Let the line \(\frac{x-3}{7}=\frac{y-2}{-1}=\frac{z-3}{-4}\) intersect the plane containing the lines \(\frac{x-4}{1}=\frac{y+1}{-2}=\frac{z}{1}\) and \(4 a x-y+5 z-7 a=0=2 x-5 y-z-3, a \in R\) at the point \(P(\alpha, \beta, \gamma)\). Then the value of \(\alpha+\beta+\gamma\) equals _____. [JEE Main 2022 (Online) 27th July Morning Shift]
CorrectIncorrectHint
Equation of plane containing the line \(4 a x-y+5 z-7 a=0=2 x-5 y-z-3\) can be written as
\(
\begin{aligned}
& 4 a x-y+5 z-7 a+\lambda(2 x-5 y-z-3)=0 \\
& (4 a+2 \lambda) x-(1+5 \lambda) y+(5-\lambda) z-(7 z+3 \lambda)=0
\end{aligned}
\)
Which is coplanar with the line
\(
\begin{aligned}
& \frac{x-4}{1}=\frac{y+1}{-2}=\frac{z}{1} \\
& 4(4 a+2 \lambda)+(1+5 \lambda)-(7 a+3 \lambda)=0 \\
& 9 a+10 \lambda+1=0 \ldots . .(1) \\
& (4 a+2 \lambda) 1+(1+5 \lambda) 2+5-\lambda=0 \\
& 4 a+11 \lambda+7=0 \ldots \ldots .(2) \\
& a=1, \lambda=-1
\end{aligned}
\)
Equation of plane is \(x+2 y+3 z-2=0\)
Intersection with the line
\(
\begin{aligned}
& \frac{x-3}{7}=\frac{y-2}{-1}=\frac{z-3}{-4} \\
& (7 t+3)+2(-t+2)+3(-4 t+3)-2=0 \\
& -7 t+14=0 \\
& t=2
\end{aligned}
\)
So, the required point is \((17,0,-5)\)
\(
\alpha+\beta+\gamma=12
\) -
Question 90 of 202
90. Question
The largest value of \(a\), for which the perpendicular distance of the plane containing the lines \(\vec{r}=(\hat{i}+\hat{j})+\lambda(\hat{i}+a \hat{j}-\hat{k})\) and \(\vec{r}=(\hat{i}+\hat{j})+\mu(-\hat{i}+\hat{j}-a \hat{k})\) from the point \((2,1,4)\) is \(\sqrt{3}\), is ____. [JEE Main 2022 (Online) 26th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Normal to plane }=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
1 & a & -1 \\
-1 & 1 & -a
\end{array}\right| \\
& =\hat{i}\left(1-a^2\right)-\hat{j}(-a-1)+\widehat{k}(1+a) \\
& =(1-a) \hat{i}+\hat{j}+\widehat{k} \\
& \therefore \text { Plane }(1-a)(x-1)+(y-1)+z=0
\end{aligned}
\)
Distance from \((2,1,4)\) is \(\sqrt{3}\) i.e.
\(
\begin{aligned}
& \Rightarrow\left|\frac{(1-a)+0+4}{\sqrt{(1-a)^2+1+1}}\right|=\sqrt{3} \\
& \Rightarrow 25+a^2-10 a=3 a^2-6 a+9 \\
& \Rightarrow 2 a^2+4 a-16=0 \\
& \Rightarrow a^2+2 a-8=0 \\
& a=2 \text { or }-4 \\
& \therefore a_{\max }=2
\end{aligned}
\) -
Question 91 of 202
91. Question
The plane passing through the line \(L: l x-y+3(1-l) z=1, x+2 y-z=2\) and perpendicular to the plane \(3 x+2 y+z=6\) is \(3 x-8 y+7 z=4\). If \(\theta\) is the acute angle between the line \(L\) and the \(y\)-axis, then \(415 \cos ^2 \theta\) is equal to ____. [JEE Main 2022 (Online) 26th July Evening Shift]
CorrectIncorrectHint
\(L: l x-y+3(1-l) z=1, x+2 y-z=2\) and plane containing the line
\(
p: 3 x-8 y+7 z=4
\)
Let \(\vec{n}\) be the vector parallel to \(L\).
\(
\begin{aligned}
& \text { then } \vec{n}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
l & -1 & 3(1-l) \\
1 & 2 & -1
\end{array}\right| \\
& =(6 l-5) \hat{i}+(3-2 l) \hat{j}+(2 l+1) \hat{k}
\end{aligned}
\)
\(\because R\) containing \(L\)
\(
\begin{aligned}
& 3(6 l-5)-8(3-2 l)+7(2 l+1)=0 \\
& 18 l+16 l+14 l-15-24+7=0 \\
& \therefore l=\frac{32}{48}=\frac{2}{3}
\end{aligned}
\)
Let \(\theta\) be the acute angle between \(L\) and \(y\)-axis
\(
\begin{aligned}
& \therefore \cos \theta=\frac{\frac{5}{3}}{\sqrt{1+\frac{25}{9}+\frac{49}{9}}}=\frac{5}{\sqrt{83}} \\
& \therefore 415 \cos ^2 \theta=125
\end{aligned}
\) -
Question 92 of 202
92. Question
Let \(Q\) and \(R\) be two points on the line \(\frac{x+1}{2}=\frac{y+2}{3}=\frac{z-1}{2}\) at a distance \(\sqrt{26}\) from the point \(P(4,2,7)\). Then the square of the area of the triangle \(P Q R\) is ____. [JEE Main 2022 (Online) 26th July Morning Shift]
CorrectIncorrectHint
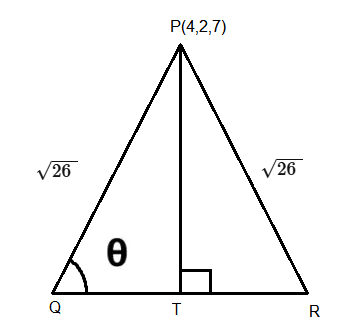
\(
L: \frac{x+1}{2}=\frac{y+2}{3}=\frac{2-1}{2}
\)
\(
\begin{aligned}
& \text { Let } T(2 t-1,3 t-2,2 t+1) \\
& \because P T \perp^r Q R \\
& \therefore 2(2 t-5)+3(3 t-4)+2(2 t-6)=0 \\
& 17 t=34 \\
& \therefore t=2
\end{aligned}
\)
So \(T(3,4,5)\)
\(
\begin{aligned}
& \therefore P T=\sqrt{1+4+4}=3 \\
& \therefore Q T=\sqrt{26-9}=\sqrt{17}
\end{aligned}
\)
\(\therefore\) Area of \(\triangle P Q R=\frac{1}{2} \times 2 \sqrt{17} \times 3=3 \sqrt{17}\)
\(\therefore\) Square of \(\operatorname{ar}(\triangle P Q R)=153\). -
Question 93 of 202
93. Question
The line of shortest distance between the lines \(\frac{x-2}{0}=\frac{y-1}{1}=\frac{z}{1}\) and \(\frac{x-3}{2}=\frac{y-5}{2}=\frac{z-1}{1}\) makes an angle of \(\cos ^{-1}\left(\sqrt{\frac{2}{27}}\right)\) with the plane \(P : a x-y-z=0,(a>0)\). If the image of the point \((1,1,-5)\) in the plane \(P\) is \((\alpha, \beta, \gamma)\), then \(\alpha+\beta-\gamma\) is equal to ______. [JEE Main 2022 (Online) 25th July Morning Shift]
CorrectIncorrectHint
DR’s of line of shortest distance
\(
\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
0 & 1 & 1 \\
2 & 2 & 1
\end{array}\right|=-\hat{i}+2 \hat{j}-2 \hat{k}
\)
angle between line and plane is \(\cos ^{-1} \sqrt{\frac{2}{27}}=\alpha\)
\(
\cos \alpha=\sqrt{\frac{2}{27}}, \sin \alpha=\frac{5}{3 \sqrt{3}}
\)
DR’s normal to plane \((1,-1,-1)\)
\(
\begin{aligned}
& \sin \alpha=\left|\frac{-a-2+2}{\sqrt{4+4+1} \sqrt{a^2+1+1}}\right|=\frac{5}{3 \sqrt{3}} \\
& \sqrt{3}|a|=5 \sqrt{a^2+2} \\
& 3 a^2=25 a^2+50
\end{aligned}
\)
No value of (a) -
Question 94 of 202
94. Question
Consider a triangle \(ABC\) whose vertices are \(A (0, \alpha, \alpha), B (\alpha, 0, \alpha)\) and \(C (\alpha, \alpha, 0), \alpha>0\). Let \(D\) be a point moving on the line \(x+z-3=0=y\) and \(G\) be the centroid of \(\triangle A B C\). If the minimum length of GD is \(\sqrt{\frac{57}{2}}\), then \(\alpha\) is equal to ____. [JEE Main 2022 (Online) 30th June Morning Shift]
CorrectIncorrectHint
Centroid of \(\triangle ABC =G\left(\frac{2 \alpha}{3}, \frac{2 \alpha}{3}, \frac{2 \alpha}{3}\right)\)
Given equation of line is \(\frac{x}{1}=\frac{z-3}{-1}=\frac{y}{0}=\lambda\)
\(
x=\lambda, y=0, z=-\lambda+3
\)
\(\therefore D(\lambda, 0-\lambda+3)\) be any point on given line
\(
\begin{aligned}
& \therefore G D=\sqrt{\left(\lambda-\frac{2 \alpha}{3}\right)^2+\left(\frac{2 \alpha}{3}\right)^2+\left(-\lambda+3-\frac{2 \alpha}{3}\right)^2} \\
& GD _1=\left(\lambda-\frac{2 \alpha}{3}\right)^2+\left(\frac{2 \alpha}{3}\right)^2+\left(-\lambda+3-\frac{2 \alpha}{3}\right)^2 \\
& \frac{d G D_1}{d \lambda}=2\left(\lambda-\frac{2 \alpha}{3}\right)-2\left(-\lambda+3-\frac{2 \alpha}{3}\right) \\
& =4 \lambda-6=0 \\
& \Rightarrow \lambda=\frac{3}{2}
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \text { Minimum GD }=\sqrt{\left(\frac{3}{2}-\frac{2 \alpha}{3}\right)^2+\left(\frac{2 \alpha}{3}\right)^2+\left(-\frac{3}{2}+3-\frac{2 \alpha}{3}\right)^2} \\
& \sqrt{\frac{57}{2}}=\sqrt{\left(\frac{9-4 \alpha}{6}\right)^2+\frac{4 \alpha^2}{9}+\left(\frac{9-4 \alpha}{6}\right)^2} \\
& \Rightarrow \frac{57}{2}=\frac{24 \alpha^2-72 \alpha+81}{18} \\
& \Rightarrow \alpha^2-3 \alpha-18=0 \ldots(\because \alpha>0) \\
& \Rightarrow \alpha=-3,6 \\
& \therefore \alpha=6
\end{aligned}
\) -
Question 95 of 202
95. Question
Let \(d\) be the distance between the foot of perpendiculars of the points \(P(1,2,-1)\) and \(Q(2,-1,3)\) on the plane \(-x+y+z=1\). Then \(d^2\) is equal to _____. [JEE Main 2022 (Online) 29th June Morning Shift]
CorrectIncorrectHint
Foot of perpendicular from \(P\)
\(
\begin{aligned}
& \frac{x-1}{-1}=\frac{y-2}{1}=\frac{z+1}{1}=\frac{-(-1+2-1-1)}{3} \\
& \Rightarrow p^{\prime} \equiv\left(\frac{2}{3}, \frac{7}{3}, \frac{-2}{3}\right)
\end{aligned}
\)
and foot of perpendicular from \(Q\)
\(
\begin{aligned}
& \frac{x-2}{-1}=\frac{y+1}{1}=\frac{z-3}{1}=\frac{-(-2-1+3-1)}{3} \\
& \Rightarrow Q^{\prime} \equiv\left(\frac{5}{3}, \frac{-2}{3}, \frac{10}{3}\right) \\
& P^{\prime} Q^{\prime}=\sqrt{(1)^2+(3)^2+(4)^2}=d=\sqrt{26} \\
& \Rightarrow d^2=26
\end{aligned}
\) -
Question 96 of 202
96. Question
Let \(P_1: \vec{r}\). \((2 \hat{i}+\hat{j}-3 \hat{k})=4\) be a plane. Let \(P_2\) be another plane which passes through the points \((2,-3,2),(2,-2,-3)\) and \((1,-4,2)\). If the direction ratios of the line of intersection of \(P _1\) and \(P _2\) be \(16, \alpha, \beta\), then the value of \(\alpha+\beta\) is equal to ____. [JEE Main 2022 (Online) 29th June Morning Shift]
CorrectIncorrectHint
Direction ratio of normal to \(\left.P_1 \equiv<2,1,-3\right\rangle\) and that of \(P_2 \equiv\left|\begin{array}{ccc}\hat{i} & \hat{j} & \widehat{k} \\ 0 & 1 & -5 \\ -1 & -2 & 5\end{array}\right|=-5 \hat{i}-\hat{j}(-5)+\widehat{k}(1)\)
i.e. \(\langle-5,5,1\rangle\)
d.r’s of line of intersection are along vector
\(
\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
2 & 1 & -3 \\
-5 & 5 & 1
\end{array}\right|=\hat{i}(16)-\hat{j}(-13)+\widehat{k}(15)
\)
i.e. \(\langle 16,13,15\rangle\)
\(
\therefore \alpha+\beta=13+15=28
\) -
Question 97 of 202
97. Question
Let the image of the point \(P (1,2,3)\) in the line \(L: \frac{x-6}{3}=\frac{y-1}{2}=\frac{z-2}{3}\) be \(Q\). Let \(R (\alpha\), \(\beta, \gamma)\) be a point that divides internally the line segment \(PQ\) in the ratio \(1: 3\). Then the value of \(22(\alpha+\beta+\gamma)\) is equal to ____. [JEE Main 2022 (Online) 28th June Evening Shift]
CorrectIncorrectHint
The point dividing \(P Q\) in the ratio \(1: 3\) will be mid-point of \(P \&\) foot of perpendicular from \(P\) on the line.
\(\therefore\) Let a point on line be \(\lambda\)
\(
\begin{aligned}
& \Rightarrow \frac{x-6}{3}=\frac{y-1}{2}=\frac{z-2}{3}=\lambda \\
& \Rightarrow P^{\prime}(3 \lambda+6,2 \lambda+1,3 \lambda+2)
\end{aligned}
\)
as \(P ^{\prime}\) is foot of perpendicular
\(
\begin{aligned}
& (3 \lambda+5) 3+(2 \lambda-1) 2+(3 \lambda-1) 3=0 \\
& \Rightarrow 22 \lambda+15-2-3=0 \\
& \Rightarrow \lambda=\frac{-5}{11} \\
& \therefore P^{\prime}\left(\frac{51}{11}, \frac{1}{11}, \frac{7}{11}\right)
\end{aligned}
\)
Mid-point of \(P P^{\prime} \equiv\left(\frac{\frac{51}{11}+1}{2}, \frac{\frac{1}{11}+2}{2}, \frac{\frac{7}{11}+3}{2}\right)\)
\(
\begin{aligned}
& \equiv\left(\frac{62}{22}, \frac{23}{22}, \frac{40}{22}\right) \equiv(\alpha, \beta, \gamma) \\
& \Rightarrow 22(\alpha, \beta, \gamma)=62+23+40=125
\end{aligned}
\) -
Question 98 of 202
98. Question
Let the mirror image of the point \((a, b, c)\) with respect to the plane \(3 x-4 y+12 z+19=0\) be \(( a -6, \beta, \gamma)\). If \(a + b + c =5\), then \(7 \beta-9 \gamma\) is equal to ____. [JEE Main 2022 (Online) 27th June Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x-a}{3}=\frac{y-b}{-4}=\frac{z-c}{12}=\frac{-2(3 a-4 b+12 c+19)}{3^2+(-4)^2+12^2} \\
& \frac{x-a}{3}=\frac{y-b}{-4}=\frac{z-c}{12}=\frac{-6 a+8 b-24 c-38}{169} \\
& (x, y, z) \equiv(a-6, \beta, \gamma) \\
& \frac{(a-6)-a}{3}=\frac{\beta-b}{-4}=\frac{\gamma-c}{12}=\frac{-6 a+8 b-24 c-38}{169} \\
& \frac{\beta-b}{-4}=-2 \Rightarrow \beta=8+b \\
& \frac{\gamma-c}{12}=-2 \Rightarrow \gamma=-24+c \\
& \frac{-6 a+8 b-24 c-38}{169}=-2
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow 3 a-4 b+12 c=150 \ldots . .(1)\\
&\begin{aligned}
& a+b+c=5 \\
& 3 a+3 b+3 c=15 \ldots \ldots .(2)
\end{aligned}
\end{aligned}
\)
Applying (1) – (2)
\(
\begin{aligned}
& -7 b+9 c=135 \\
& 7 b-9 c=-135 \\
& 7 \beta-9 \gamma=7(8+b)-9(-24+c) \\
& =56+216+7 b-9 c \\
& =56+216-135=137
\end{aligned}
\) -
Question 99 of 202
99. Question
Let \(l_1\) be the line in xy-plane with \(x\) and \(y\) intercepts \(\frac{1}{8}\) and \(\frac{1}{4 \sqrt{2}}\) respectively, and \(l_2\) be the line in \(zx\)-plane with \(x\) and \(z\) intercepts \(-\frac{1}{8}\) and \(-\frac{1}{6 \sqrt{3}}\) respectively. If \(d\) is the shortest distance between the line \(l_1\) and \(l_2\), then \(d ^{-2}\) is equal to _____. [JEE Main 2022 (Online) 25th June Evening Shift]
CorrectIncorrectHint
Equation of \(l_1\)
\(
\frac{x-\frac{1}{8}}{\frac{1}{8}}=\frac{y}{-\frac{1}{4 \sqrt{2}}}=\frac{z}{0}
\)
\(
\text { or } \frac{x-\frac{1}{8}}{1}=\frac{y}{-\sqrt{2}}=\frac{z}{0} \ldots . . \text { (i) }
\)
Equation of \(L _2\)
\(
\begin{aligned}
& \frac{x+\frac{1}{8}}{-6 \sqrt{3}}=\frac{y}{0}=\frac{z}{8} \dots(ii) \\
& d=\left|\frac{(\vec{c}-\vec{a}) \cdot \vec{b} \times \vec{d})}{|\vec{b} \times \vec{d}|}\right| \\
& =\frac{\left(\frac{1}{4} \hat{i}\right) \cdot(4 \sqrt{2} \hat{i}+4 \hat{j}+3 \sqrt{6 \hat{k}})}{\sqrt{(4 \sqrt{2})^2+4^2+(3 \sqrt{6})^2}} \\
& =\frac{\sqrt{2}}{\sqrt{32+16+54}}=\frac{1}{\sqrt{51}} \\
& d^{-2}=51 \\
&
\end{aligned}
\) -
Question 100 of 202
100. Question
Let the lines
\(
L_1: \vec{r}=\lambda(\hat{i}+2 \hat{j}+3 \widehat{k}), \lambda \in R
\)
\(
L_2: \vec{r}=(\hat{i}+3 \hat{j}+\hat{k})+\mu(\hat{i}+\hat{j}+5 \hat{k}) ; \mu \in R
\)
intersect at the point \(S\). If a plane \(a x+\) by \(-z+d=0\) passes through \(S\) and is parallel to both the lines \(L_1\) and \(L_2\), then the value of \(a+b+d\) is equal to _____. [JEE Main 2022 (Online) 25th June Morning Shift]CorrectIncorrectHint
Both the lines lie in the same plane
\(\therefore\) equation of the plane
\(
\begin{aligned}
& \left|\begin{array}{lll}
x & y & z \\
1 & 2 & 3 \\
1 & 1 & 5
\end{array}\right|=0 \\
& \Rightarrow 7 x -2 y – z =0 \\
& \therefore a + b + d =5
\end{aligned}
\) -
Question 101 of 202
101. Question
Let a line having direction ratios, \(1,-4,2\) intersect the lines \(\frac{x-7}{3}=\frac{y-1}{-1}=\frac{z+2}{1}\) and \(\frac{x}{2}=\frac{y-7}{3}=\frac{z}{1}\) at the points \(A\) and \(B\). Then \(( AB )^2\) is equal to ____. [JEE Main 2022 (Online) 24th June Morning Shift]
CorrectIncorrectHint
Let \(A(3 \lambda+7,-\lambda+1, \lambda-2)\) and \(B(2 \mu, 3 \mu+7, \mu)\)
So, DR’s of \(A B \propto 3 \lambda-2 \mu+7,-(\lambda+3 \mu+6), \lambda-\mu-2\)
Clearly \(\frac{3 \lambda-2 \mu+7}{1}=\frac{\lambda+3 \mu+6}{4}=\frac{\lambda-\mu-2}{2}\)
\(
\Rightarrow 5 \lambda-3 \mu=-16 \dots(i)
\)
And \(\lambda-5 \mu=10 \dots(ii)\)
From (i) and (ii) we get \(\lambda=-5, \mu=-3\)
So, \(A\) is \((-8,6,-7)\) and \(B\) is \((-6,-2,-3)\)
\(
A B=\sqrt{4+64+16} \Rightarrow(A B)^2=84
\) -
Question 102 of 202
102. Question
If the shortest distance between the lines
\(
\vec{r}=(-\hat{i}+3 \hat{k})+\lambda(\hat{i}-a \hat{j})
\)
and \(\vec{r}=(-\hat{j}+2 \widehat{k})+\mu(\hat{i}-\hat{j}+\widehat{k})\) is \(\sqrt{\frac{2}{3}}\), then the integral value of a is equal to ____. [JEE Main 2022 (Online) 24th June Morning Shift]CorrectIncorrectHint
\(
\begin{aligned}
& \vec{b}_1 \times \vec{b}_2=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & -a & 0 \\
1 & -1 & 1
\end{array}\right|=-a \hat{i}-\hat{j}+(a-1) \hat{k} \\
& \vec{a}_1-\vec{a}_2=-\hat{i}+\hat{j}+\hat{k} \\
& \text { Shortest distance }=\left|\frac{\left(\vec{a}_1-\vec{a}_2\right) \cdot\left(\vec{b}_1 \times \vec{b}_2\right)}{\left|\vec{b}_1 \times \vec{b}_2\right|}\right| \\
& \Rightarrow \quad \sqrt{\frac{2}{3}}=\frac{2(a-1)}{\sqrt{a^2+1+(a-1)^2}} \\
& \Rightarrow 6\left(a^2-2 a+1\right)=2 a^2-2 a+2 \\
& \Rightarrow \quad(a-2)(2 a-1)=0 \Rightarrow a=2 \text { because } a \in z .
\end{aligned}
\) -
Question 103 of 202
103. Question
Suppose, the line \(\frac{x-2}{\alpha}=\frac{y-2}{-5}=\frac{z+2}{2}\) lies on the plane \(x+3 y-2 z+\beta=0\). Then \((\alpha+\beta)\) is equal to _____. [JEE Main 2021 (Online) 31st August Evening Shift]
CorrectIncorrectHint
Given equation of line
\(
\frac{x-2}{\alpha}=\frac{y-2}{-5}=\frac{z+2}{2} \ldots \ldots \text { (i) }
\)
and plane \(x+3 y-2 z+\beta=0 \dots(ii)\)
Line (i) passes through \((2,2,-2)\)
which lies on plane (ii).
\(
\therefore 2+6+4+\beta=0 \Rightarrow \beta=-12
\)
Also, given line is perpendicular to normal of the plane
\(
\begin{aligned}
& \alpha(1)-5(3)+2(-2)=0 \Rightarrow \alpha=19 \\
& \therefore \alpha+\beta=19+(-12)=19-12=7
\end{aligned}
\) -
Question 104 of 202
104. Question
The square of the distance of the point of intersection of the line \(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z+1}{6}\) and the plane \(2 x-y+z=6\) from the point \((-1,-\) \(1,2)\) is _____. [JEE Main 2021 (Online) 31st August Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x-1}{2}=\frac{y-2}{3}=\frac{z+1}{6}=\lambda \\
& x=2 \lambda+1, y=3 \lambda+2, z=6 \lambda-1
\end{aligned}
\)
for point of intersection of line & plane
\(
\begin{aligned}
& 2(2 \lambda+1)-(3 \lambda+2)+(6 \lambda-1)=6 \\
& 7 \lambda=7 \Rightarrow \lambda=1
\end{aligned}
\)
point : \((3,5,5)\)
\(
\begin{aligned}
& (\text { distance })^2=(3+1)^2+(5+1)^2+(5-2)^2 \\
& =16+36+9=61
\end{aligned}
\) -
Question 105 of 202
105. Question
Let \(S\) be the mirror image of the point \(Q(1,3,4)\) with respect to the plane \(2 x-y+z+3\) \(=0\) and let \(R (3,5, \gamma)\) be a point of this plane. Then the square of the length of the line segment SR is _____. [JEE Main 2021 (Online) 27th August Evening Shift]
CorrectIncorrectHint
Since \(R(3,5, \gamma)\) lies on the plane \(2 x-y+z+3=0\).
Therefore, \(6-5+\gamma+3=0\)
\(
\Rightarrow \gamma=-4
\)
Now,
dr’s of line QS are \(2,-1,1\)
equation of line QS is
\(
\begin{aligned}
& \frac{x-1}{2}=\frac{y-3}{-1}=\frac{z-4}{1}=\lambda \text { (say) } \\
& \Rightarrow F(2 \lambda+1,-\lambda+3, \lambda+4)
\end{aligned}
\)
F lies in the plane
\(
\begin{aligned}
& \Rightarrow 2(2 \lambda+1)-(-\lambda+3)+(\lambda+4)+3=0 \\
& \Rightarrow 4 \lambda+2+\lambda-3+\lambda+7=0 \\
& \Rightarrow 6 \lambda+6=0 \Rightarrow \lambda=-1 \\
& \Rightarrow F(-1,4,3)
\end{aligned}
\)
Since, \(F\) is mid-point of QS.
Therefore, coordinated of \(S\) are \((-3,5,2)\).
So, \(S R=\sqrt{36+0+36}=\sqrt{72}\)
\(
SR ^2=72 \text {. }
\) -
Question 106 of 202
106. Question
Let \(Q\) be the foot of the perpendicular from the point \(P (7,-2,13)\) on the plane containing the lines \(\frac{x+1}{6}=\frac{y-1}{7}=\frac{z-3}{8}\) and \(\frac{x-1}{3}=\frac{y-2}{5}=\frac{z-3}{7}\). Then \((P Q)^2\), is equal to _____. [JEE Main 2021 (Online) 26th August Evening Shift]
CorrectIncorrectHint
Containing the line \(\left|\begin{array}{ccc}x+1 & y-1 & z-3 \\ 6 & 7 & 8 \\ 3 & 5 & 7\end{array}\right|=0\)
\(
\begin{aligned}
& 9(x+1)-18(y-1)+9(z-3)=0 \\
& x-2 y+z=0 \\
& P Q=\left|\frac{7+4+13}{\sqrt{6}}\right|=4 \sqrt{6} \\
& P Q^2=96
\end{aligned}
\) -
Question 107 of 202
107. Question
Let the line \(L\) be the projection of the line \(\frac{x-1}{2}=\frac{y-3}{1}=\frac{z-4}{2}\) in the plane \(x-2 y-z\) \(=3\). If \(d\) is the distance of the point \((0,0,6)\) from \(L\), then \(d^2\) is equal to _____. [JEE Main 2021 (Online) 26th August Morning Shift]
CorrectIncorrectHint
To find the projection let’s find the foot of perpendicular from \((1,3,4)\) to plane \(x-2 y-z=3\)
\(
\begin{aligned}
& \frac{x-1}{1}=\frac{y-3}{-2}=\frac{z-4}{-1}=\lambda_1 \\
& \left(\lambda_1+1\right)-2\left(-2 \lambda_1+3\right)-\left(-\lambda_1+4\right)=3 \\
& \Rightarrow 6 \lambda_1=12 \Rightarrow \lambda_1=2
\end{aligned}
\)
So, foot of perpendicular from \((1,3,4)\) to plane \(x-2 y-z=3\) is \(A(3,-1,2)\).
Let us also find the intersection point of the plane and line
\(
\frac{x-1}{2}=\frac{y-3}{1}=\frac{z-4}{2}=\lambda_2
\)
\(
\left(2 \lambda_2+1\right)-2\left(\lambda_2+3\right)-\left(2 \lambda_2+4\right)=3-2 \lambda_2=12 \Rightarrow \lambda_2=-6
\)
The intersection point of the plane and line is \(B(-11,-3,-8)\) Line passing through \(A\) and \(B\) is
\(
\begin{aligned}
& \frac{x-3}{-14}=\frac{y+1}{-2}=\frac{z-2}{-10}=\mu \\
& \frac{x-3}{7}=\frac{y+1}{1}=\frac{z-2}{5}=\mu
\end{aligned}
\)
Now, let’s find the distance from \(O(0,0,6)\) to this line \(L\).
Let’s say \(C(7 \mu+3, \mu-1,5 \mu+2)\) is any point on \(L\). Then,
\(
\begin{aligned}
& \{(7 \mu+3)-0\} \cdot 7+\{(\mu-1)-0\} \cdot 1+\{(5 \mu+2)-6\} \cdot 5=0 \\
& \Rightarrow 49 \mu+21+\mu-1+25 \mu-20=0 \Rightarrow \mu=0 \\
& \therefore C(3,-1,2)
\end{aligned}
\)
Distance \(=\sqrt{(3-0)^2+(-1-0)^2+(2-6)^2}=\sqrt{26}\)
\(
d^2=26
\) -
Question 108 of 202
108. Question
The distance of the point \(P(3,4,4)\) from the point of intersection of the line joining the points. \(Q(3,-4,-5)\) and \(R(2,-3,1)\) and the plane \(2 x+y+z=7\), is equal to ____. [JEE Main 2021 (Online) 27th July Evening Shift]
CorrectIncorrectHint
The equation of the line passing through the points \(A(3,-4,-5)\) and \(B(2,-3,1)\) is given by
\(
\begin{aligned}
& \frac{x-3}{2-3}=\frac{y-(-4)}{-3-(-4)}=\frac{z-(-5)}{1-(-5)} \\
& \text { Or } \frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}
\end{aligned}
\)
The coordinates of any point on the line
\(
\frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}=\lambda \text { (say) } \dots(1)
\)
If it lies on the plane \(2 x+y+z=7\), then
\(
\begin{aligned}
& 2(-\lambda+3)+(\lambda-4)+(6 \lambda-5)=7 \\
& \Rightarrow 5 \lambda-3=7 \\
& \Rightarrow 5 \lambda=10 \\
& \Rightarrow \lambda=2
\end{aligned}
\)
Putting
\(\lambda=2\) in (1), we get \((1,-2,7)\) as the coordinates of the point of intersection of the given line and plane.
\(
\begin{aligned}
& \therefore \text { Required distance }=\text { Distance between points }(3,4,4) \text { and }(1,-2,7) \\
& =\sqrt{(3-1)^2+(4+2)^2+(4-7)^2} \\
& =\sqrt{4+36+9} \\
& =\sqrt{49} \\
& =7 \text { units }
\end{aligned}
\) -
Question 109 of 202
109. Question
Let a plane \(P\) pass through the point \((3,7,-7)\) and contain the line, \(\frac{x-2}{-3}=\frac{y-3}{2}=\frac{z+2}{1}\). If distance of the plane \(P\) from the origin is \(d\), then \(d ^2\) is equal to ____. [JEE Main 2021 (Online) 27th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \overrightarrow{B A}=(\hat{i}+4 \hat{j}-5 \widehat{k}) \\
& \overrightarrow{B A} \times \vec{l}=\vec{n}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
-3 & 2 & 1 \\
1 & 4 & -5
\end{array}\right|
\end{aligned}
\)
\(
\begin{aligned}
& a \hat{i}+b \hat{j}+c \widehat{k}=-14 \hat{i}-\hat{j}(14)+\widehat{k}(-14) \\
& a=1, b=1, c=1
\end{aligned}
\)
Plane is \((x-2)+(y-3)+(z+2)=0\)
\(
\begin{aligned}
& \Rightarrow x + y + z -3=0 \\
& \therefore d =\sqrt{3} \Rightarrow d ^2=3
\end{aligned}
\) -
Question 110 of 202
110. Question
If the lines \(\frac{x-k}{1}=\frac{y-2}{2}=\frac{z-3}{3}\) and \(\frac{x+1}{3}=\frac{y+2}{2}=\frac{z+3}{1}\) are co-planar, then the value of \(k\) is ___. [JEE Main 2021 (Online) 25th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \left|\begin{array}{ccc}
k+1 & 4 & 6 \\
1 & 2 & 3 \\
3 & 2 & 1
\end{array}\right|=0 \\
& \Rightarrow(k+1)[2-6]-4[1-9]+6[2-6]=0 \\
& \Rightarrow k=1
\end{aligned}
\) -
Question 111 of 202
111. Question
Let \(P\) be a plane passing through the points \((1,0,1),(1,-2,1)\) and \((0,1,-2)\). Let a vector \(\vec{a}=\alpha \hat{i}+\beta \hat{j}+\gamma \widehat{k}\) be such that \(\vec{a}\) is parallel to the plane \(P\), perpendicular to \((\hat{i}+2 \hat{j}+3 \widehat{k})\) and \(\vec{a} \cdot(\hat{i}+\hat{j}+2 \widehat{k})=2\), then \((\alpha-\beta+\gamma)^2\) equals ____. [JEE Main 2021 (Online) 20th July Morning Shift]
CorrectIncorrectHint
Equation of plane :
\(
\begin{aligned}
& \left|\begin{array}{ccc}
x-1 & y-0 & z-1 \\
1-1 & 2 & 1-1 \\
1-0 & 0-1 & 1+2
\end{array}\right|=0 \\
& \Rightarrow 3 x-z-2=0 \\
& \vec{a}=\alpha \hat{i}+\beta \hat{j}+\gamma \hat{k} \| \text { to } 3 x-z-2=0
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow 3 \alpha-8=0 \ldots . .(1)\\
&\vec{a} \perp \hat{i}+\hat{j}+3 \widehat{k}
\end{aligned}
\)
\(
\Rightarrow \alpha+2 \beta+3 \gamma=0 \ldots \ldots . . \text { (2) }
\)
\(
\begin{aligned}
& \vec{a} \cdot(\hat{i}+\hat{j}+2 \widehat{k})=0 \\
& \Rightarrow \alpha+\beta+2 \gamma=2 \ldots . .(3)
\end{aligned}
\)
On solving \(1,2 \& 3\)
\(
\alpha=1, \beta=-5, \gamma=3
\)
So, \((\alpha-\beta+\gamma)^2=81\) -
Question 112 of 202
112. Question
Let the mirror image of the point \((1,3, a)\) with respect to the plane \(\vec{r} .(2 \hat{i}-\hat{j}+\widehat{k})-b=0\) be \((-3,5,2)\). Then, the value of \(| a + b |\) is equal to _____. [JEE Main 2021 (Online) 18th March Evening Shift]
CorrectIncorrectHint
Given equation of plane in vector form is \(\vec{r}\). \((2 \hat{i}-\hat{j}+\widehat{k})-b=0\)
Its Cartesian form will be
\(
2 x-y+z=b \dots(i)
\)
\(\because R\) is the mid-point of \(P Q\).
\(
\therefore R \equiv \frac{P+Q}{2} \Rightarrow R \equiv\left(-1,4, \frac{a+2}{2}\right)
\)
\(\because R\) lies on the plane (i).
\(
\begin{aligned}
& \therefore-2-4+\frac{a+2}{2}=b \Rightarrow a+2=2 b+12 \\
& \Rightarrow a=2 b+10 \ldots \ldots . . \text { (ii) }
\end{aligned}
\)
\(\because\) Direction ratio’s of QP is \((1-(-3), 3-5, a-2)\)
i.e. \((4,-2, a-2)\)
and direction ratios of normal to the given plane are \((2,-1,1)\)
\(\because n\) and \(Q P\) are parallel.
\(
\begin{aligned}
& \therefore \frac{2}{4}=\frac{-1}{-2}=\frac{1}{a-2} \\
& \therefore a-2=2 \Rightarrow a=4
\end{aligned}
\)
From Eq. (ii), b \(=-3\)
\(
\therefore|a+b|=|4-3|=|1|=1
\) -
Question 113 of 202
113. Question
Let \(P\) be a plane containing the line \(\frac{x-1}{3}=\frac{y+6}{4}=\frac{z+5}{2}\) and parallel to the line \(\frac{x-1}{4}=\frac{y-2}{-3}=\frac{z+5}{7}\). If the point \((1,-1, \alpha)\) lies on the plane \(P\), then the value of \(|5 \alpha|\) is equal to _____. [JEE Main 2021 (Online) 18th March Evening Shift]
CorrectIncorrectHint
Equation of required plane is \(\left|\begin{array}{ccc}x-1 & y+6 & z+5 \\ 3 & 4 & 2 \\ 4 & -3 & 7\end{array}\right|=0\)
Since, \((1,-1, \alpha)\) lies on it,
So, replace \(x\) by \(1, y\) by ( -1 ) and \(z\) and \(\alpha\).
\(\left|\begin{array}{ccc}0 & 5 & \alpha+5 \\ 3 & 4 & 2 \\ 4 & -3 & 7\end{array}\right|=0\)
\(
\begin{aligned}
& \Rightarrow 5 \alpha+38=0 \Rightarrow 5 \alpha=-38 \\
& \therefore|5 \alpha|=|-38|=38
\end{aligned}
\) -
Question 114 of 202
114. Question
Let the plane \(a x+b y+c z+d=0\) bisect the line joining the points \((4,-3,1)\) and \((2,3\), -5 ) at the right angles. If \(a, b, c, d\) are integers, then the minimum value of \(\left(a^2+b^2+c^2+d^2\right)\) is _____. [JEE Main 2021 (Online) 18th March Morning Shift]
CorrectIncorrectHint
\(
\begin{gathered}
a x+b y+c z+d=0 \\
\text { Dr’s: }(-2,6,-6)=(1,-3,3) \\
\text { mid } p t(3,0,-2)
\end{gathered}
\)
Equation of plane is \(1(x-3)-3(y-0)+3(z+2)=0\)
\(
\begin{gathered}
x-3-3 y+3 z+6=0 \\
x-3 y+3 z+3=0 \\
a=1, b=-3, c=3, d=3
\end{gathered}
\)
\(
a^2+b^2+c^2+d^2=1+9+9+9=28
\) -
Question 115 of 202
115. Question
The equation of the planes parallel to the plane \(x-2 y+2 z-3=0\) which are at unit distance from the point \((1,2,3)\) is \(a x+b y+c z+d=0\). If \((b-d)=k(c-a)\), then the positive value of \(k\) is : [JEE Main 2021 (Online) 18th March Morning Shift]
CorrectIncorrectHint
The equation of the planes parallel to the plane \(x-2 y+2 z-3=0\)
\(
x-2 y+2 z+\lambda=0
\)
Now given
\(
\begin{aligned}
& d=\frac{|1-4+6+\lambda|}{\sqrt{9}}=1 \\
& |\lambda+3|=3 \\
& \lambda+3= \pm 3 \Rightarrow \lambda=0,-6
\end{aligned}
\)
So planes are : \(x-2 y+2 z-6=0\)
and \(x-2 y+2 z=0\)
\(
\begin{aligned}
& b-d=-2+6=4 \\
& c-a=2-1=1 \\
& \therefore \frac{b-d}{c-a}=k \\
& \Rightarrow k=4
\end{aligned}
\) -
Question 116 of 202
116. Question
Let \(P\) be an arbitrary point having sum of the squares of the distances from the planes \(x+y+z=0,lx-n z=0\) and \(x-2 y+z=0\), equal to 9 . If the locus of the point \(P\) is \(x^2+\) \(y^2+z^2=9\), then the value of \(l-n\) is equal to _____. [JEE Main 2021 (Online) 17th March Evening Shift]
CorrectIncorrectHint
Let point \(P\) is \((\alpha, \beta, \gamma)\)
\(
\left(\frac{\alpha+\beta+\gamma}{\sqrt{3}}\right)^2+\left(\frac{l \alpha-n \gamma}{\sqrt{l^2+n^2}}\right)^2+\left(\frac{\alpha-2 \beta+\gamma}{\sqrt{6}}\right)^2=9
\)
Locus is \(\frac{(x+y+z)^2}{3}+\frac{(\ln -n z)^2}{l^2+n^2}+\frac{(x-2 y+z)^2}{6}=9\)
\(
x^2\left(\frac{1}{2}+\frac{l^2}{l^2+n^2}\right)+y^2+z^2\left(\frac{1}{2}+\frac{n^2}{l^2+n^2}\right)+2 z x\left(\frac{1}{2}-\frac{\ln }{l^2+n^2}\right)-9=0
\)
Since its given that \(x^2+y^2+z^2=9\)
After solving \(l = n\),
then, \(l – n =0\) -
Question 117 of 202
117. Question
If the equation of the plane passing through the line of intersection of the planes \(2 x-\) \(7 y+4 z-3=0,3 x-5 y+4 z+11=0\) and the point \((-2,1,3)\) is \(a x+b y+c z-7=0\), then the value of \(2 a+b+c-7\) is _____. [JEE Main 2021 (Online) 17th March Morning Shift]
CorrectIncorrectHint
Equation of plane can be written using family of planes: \(P_1+\lambda P_2=0\)
\(
(2 x-7 y+4 z-3)+\lambda(3 x-5 y+4 z+11)=0
\)
It passes through \((-2,1,3)\)
\(
\begin{aligned}
& \therefore(-4+7+12-3)+\lambda(-6-5+12+11)=0 \\
& -2+\lambda(12)=0 \\
& \lambda=\frac{1}{6} . \\
& \therefore 12 x-42 y+24 z-18+3 x-5 y+4 z+11=0 \\
& 15 x-47 y+28 z-7=0 \\
& \therefore a=15, b=-47, c=28 \\
& \therefore 2 a+b+c-7=30-47+28-7=4
\end{aligned}
\) -
Question 118 of 202
118. Question
If the distance of the point \((1,-2,3)\) from the plane \(x+2 y-3 z+10=0\) measured parallel to the line, \(\frac{x-1}{3}=\frac{2-y}{m}=\frac{z+3}{1}\) is \(\sqrt{\frac{7}{2}}\), then the value of \(| m |\) is equal to ____. [JEE Main 2021 (Online) 16th March Evening Shift]
CorrectIncorrectHint
\(
\text { DC of line } \equiv\left(\frac{3}{\sqrt{ m ^2+10}}, \frac{- m }{\sqrt{ m ^2+10}}, \frac{1}{\sqrt{ m ^2+10}}\right)
\)
\(
\begin{gathered}
Q \equiv\left(1+\frac{3 r }{\sqrt{ m ^2+10}},-2+\frac{- mr }{\sqrt{ m ^2+10}}, 3+\frac{ r }{\sqrt{ m ^2+10}}\right) \\
Q \text { lies on } x +2 y -3 z +10=0
\end{gathered}
\)
\(
1+\frac{3 r }{\sqrt{ m ^2+10}}-4-\frac{2 mr }{\sqrt{ m ^2+10}}-9-\frac{3 r }{\sqrt{ m ^2+10}}+10=0
\)
\(
\begin{aligned}
& \Rightarrow \frac{r}{\sqrt{m^2+10}}(3-2 m-3)=2 \\
& \Rightarrow \frac{r}{\sqrt{m^2+10}}(-2 m)=2 \\
& r^2 m^2=m^2+10
\end{aligned}
\)
\(
\begin{aligned}
& \frac{7}{2} m ^2= m ^2+10 \\
& \Rightarrow \frac{5}{2} m ^2=10 \\
& \Rightarrow m ^2=4 \\
& | m |=2
\end{aligned}
\) -
Question 119 of 202
119. Question
Let \((\lambda, 2,1)\) be a point on the plane which passes through the point \((4,-2,2)\). If the plane is perpendicular to the line joining the points \((-2,-21,29)\) and \((-1,-16,23)\), then \(\left(\frac{\lambda}{11}\right)^2-\frac{4 \lambda}{11}-4\) is equal to _____. [JEE Main 2021 (Online) 26th February Morning Shift]
CorrectIncorrectHint
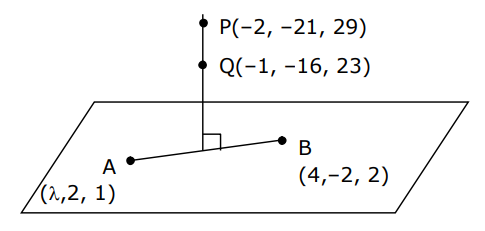
\(
\begin{aligned}
& \overrightarrow{A B} \perp \overrightarrow{P Q} \\
& {[(4-\lambda) \hat{i}-4 \hat{j}+\hat{k}] \cdot[+\hat{i}+5 \hat{j}-6 \hat{k}]=0} \\
& 4-\lambda-20-6=0 \\
& \Rightarrow \lambda=-22
\end{aligned}
\)
Now, \(\frac{\lambda}{11}=-2\)
\(
\begin{aligned}
& \Rightarrow\left(\frac{\lambda}{11}\right)^2-\frac{4 \lambda}{11}-4 \\
& \Rightarrow 4+8-4=8
\end{aligned}
\) -
Question 120 of 202
120. Question
A line ‘\(l\)’ passing through origin is perpendicular to the lines
\(
\begin{aligned}
& l_1: \vec{r}=(3+t) \hat{i}+(-1+2 t) \hat{j}+(4+2 t) \hat{k} \\
& l_2: \vec{r}=(3+2 s) \hat{i}+(3+2 s) \hat{j}+(2+s) \hat{k}
\end{aligned}
\)
If the co-ordinates of the point in the first octant on ‘ \(l_2\) ‘ at a distance of \(\sqrt{17}\) from the point of intersection of ‘ \(l\) ‘ and ‘ \(l_1\) ‘ are \((a, b, c)\) then \(18(a+b+c)\) is equal to _____. [JEE Main 2021 (Online) 25th February Evening Shift]CorrectIncorrectHint
\(
\begin{aligned}
& l_1: \vec{r}=(3+t) \hat{i}+(-1+2 t) \hat{j}+(4+2 t) \widehat{k} \\
& l_1: \frac{x-3}{1}=\frac{y+1}{2}=\frac{z-4}{2} \Rightarrow \text { D.R. of } l_1=1,2,2 \\
& l_2: \vec{r}=(3+2 s) \hat{i}+(3+2 s) \hat{j}+(2+s) \widehat{k} \\
& l_2: \frac{x-3}{2}=\frac{y-3}{2}=\frac{z-2}{1} \Rightarrow \text { D.R. of } l_2=2,2,1
\end{aligned}
\)
D.R. of \(l\) is \(\perp\) to \(l_1~ \& ~l _2\)
\(\therefore\) D.R. of \(l \|\left(l_1 \times l_2\right) \Rightarrow(-2,3-2)\)
\(\therefore\) Equation of \(l: \frac{x}{2}=\frac{y}{-3}=\frac{z}{2}\)
Solving \(l \& l_1\)
\(
\begin{aligned}
& (2 \lambda,-3 \lambda, 2 \lambda)=(\mu+3,2 \mu-1,2 \mu+\mu) \\
& \Rightarrow 2 \lambda=\mu+3 \\
& -3 \lambda=2 \mu-1 \\
& 2 \lambda=2 \mu+4 \\
& \Rightarrow \mu+3=2 \mu+4 \\
& \mu=-1 \\
& \lambda=1
\end{aligned}
\)
\(P(2,-3,2)\) {intersection point}
Let, \(Q(2 v+3,2 v+3, v+2)\) be point on \(l_2\)
Now, \(P Q=\sqrt{(2 v+3-2)^2+(2 v+3+3)^2+(v+2-2)^2}=\sqrt{17}\)
\(
\begin{aligned}
& \Rightarrow(2 v+1)^2+(2 v+6)^2+(v)^2=17 \\
& \Rightarrow 9 v^2+28 v+36+1-17=0 \\
& \Rightarrow 9 v^2+28 v+20=0 \\
& \Rightarrow 9 v^2+18 v+10 v+20=0 \\
& \Rightarrow(9 v+10)(v+2)=0 \\
& \Rightarrow v=-2 \text { (rejected), }-\frac{10}{9} \text { (accepted) } \\
& Q\left(3-\frac{20}{9}, 3-\frac{20}{9}, 2-\frac{10}{9}\right) \\
& \left(\frac{7}{9}, \frac{7}{9}, \frac{8}{9}\right) \\
& \therefore 18(a+b+c) \\
& =18\left(\frac{7}{9}, \frac{7}{9}, \frac{8}{9}\right) \\
& =44
\end{aligned}
\) -
Question 121 of 202
121. Question
Let \(\lambda\) be an integer. If the shortest distance between the lines \(x-\lambda=2 y-1=-2 z\) and \(x=y+2 \lambda=z-\lambda\) is \(\frac{\sqrt{7}}{2 \sqrt{2}}\), then the value of \(|\lambda|\) is ____. [JEE Main 2021 (Online) 24th February Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x-\lambda}{1}=\frac{y-\frac{1}{2}}{\frac{1}{2}}=\frac{z}{-\frac{1}{2}} \\
& \frac{x-\lambda}{2}=\frac{y-\frac{1}{2}}{1}=\frac{2}{-1} \dots(1) \\
& \text { Point on line }=\left(\lambda, \frac{1}{2}, 0\right) \\
& \frac{x}{1}=\frac{y+2 \lambda}{1}=\frac{z-\lambda}{1} \dots(2) \\
& \text { Point on line }=(0,-2 \lambda, \lambda) \\
& \text { Distance between skew lines }=\frac{\left[\overrightarrow{a_2}-\overrightarrow{a_1} \overrightarrow{b_1 b_2}\right]}{\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|} \\
\end{aligned}
\)\(
=\frac{\left|-5 \lambda-\frac{3}{2}\right|}{\sqrt{14}}=\frac{\sqrt{7}}{2 \sqrt{2}} \Rightarrow \lambda=-1
\)\(
\text { Since } \lambda \text { is an integer, the only solution is }|\lambda|=1 \text {. }
\) -
Question 122 of 202
122. Question
If the equation of a plane \(P\), passing through the intersection of the planes, \(x+4 y-z+7=0\) and \(3 x+y+5 z=8\) is \(a x+b y+6 z=15\) for some \(a, b \in R\), then the distance of the point \((3,2,-1)\) from the plane \(P\) is ______. [JEE Main 2020 (Online) 4th September Morning Slot]
CorrectIncorrectHint
Equation of plane \(P\) is
\(
\begin{aligned}
& (x+4 y-z+7)+\lambda(3 x+y+5 z-8)=0 \\
& \Rightarrow x(1+3 \lambda)+y(4+\lambda)+z(-1+5 \lambda)+(7-8 \lambda)=0 \\
& \frac{1+3 \lambda}{a}=\frac{4+\lambda}{b}=\frac{5 \lambda-1}{6}=\frac{7-8 \lambda}{-15} \\
& \therefore 15-75 \lambda=42-48 \lambda \\
& \Rightarrow-27=27 \lambda \\
& \Rightarrow \lambda=-1
\end{aligned}
\)
\(\therefore\) Plane is \((x+4 y-z+7)-1(3 x+y+5 z-8)=0\)
\(
\Rightarrow 2 x-3 y+6 z-15=0
\)
Distance of \((3,2,-1)\) from the plane \(P\)
\(
=\frac{|6-6-6-15|}{7}=\frac{21}{7}=3
\) -
Question 123 of 202
123. Question
Let a plane \(P\) contain two lines \(\vec{r}=\hat{i}+\lambda(\hat{i}+\hat{j}), \lambda \in R\) and \(\vec{r}=-\hat{j}+\mu(\hat{j}-\widehat{k}), \mu \in R\)
If \(Q (\alpha, \beta, \gamma)\) is the foot of the perpendicular drawn from the point \(M (1,0,1)\) to \(P\), then 3 ( \(\alpha+\beta+\gamma\) ) equals ____. [JEE Main 2020 (Online) 3rd September Evening Slot]CorrectIncorrectHint
Given lines,
\(\vec{r}=\hat{i}+\lambda(\hat{i}+\hat{j})\) parallel to \((\hat{i}+\hat{j})\)
Let, \(\overrightarrow{n_1}=(\hat{i}+\hat{j})\)
and \(\vec{r}=-\hat{j}+\mu(\hat{j}-\widehat{k})\) parallel to \((\hat{j}-\widehat{k})\)
Let, \(\overrightarrow{n_2}=(\hat{j}-\widehat{k})\)
\(\therefore\) Normal of plane, \(\vec{n}=\overrightarrow{n_1} \times \overrightarrow{n_2}\)
\(
\begin{aligned}
& \vec{n}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
2 & 1 & 0 \\
0 & 1 & -1
\end{array}\right| \\
& =-\hat{i}+\hat{j}+\widehat{k}
\end{aligned}
\)
Line \(\vec{r}=\hat{i}+\lambda(\hat{i}+\hat{j})\) is on the plane so, point on the line \((1,0,0)\) will be also on the plane.
\(\therefore\) Equation of the plane,
\(
\begin{aligned}
& -1(x-1)+1(y-0)+1(z-0)=0 \\
& \Rightarrow x-y-z-1=0
\end{aligned}
\)
Foot of perpendicular from \(\left(x_1, y_1, z_1\right)\) on the plane,
\(
\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}=-\frac{\left(a x_1+b y_1+c z_1+d\right)}{a^2+b^2+c^2}
\)
Here foot of perpendicular is drawn from \(M(1,0,1)\),
\(
\begin{aligned}
& \therefore \frac{x-1}{1}=\frac{y-0}{-1}=\frac{z-1}{-1}=-\frac{(1-0-1-1)}{3} \\
& \therefore x-1=\frac{1}{3} \Rightarrow x=\frac{4}{3} \\
& \frac{y}{-1}=\frac{1}{3} \Rightarrow y=-\frac{1}{3} \\
& \frac{z-1}{-1}=\frac{1}{3} \Rightarrow z=\frac{2}{3}
\end{aligned}
\)
According to the question,
\(
\begin{aligned}
& x=\alpha, y=\beta, z=\gamma \\
& \therefore \alpha=\frac{4}{3}, \beta=-\frac{1}{3}, \gamma=\frac{2}{3} \\
& \therefore 3(\alpha+\beta+\gamma)=3\left(\frac{4}{3}-\frac{1}{3}+\frac{2}{3}\right)=5
\end{aligned}
\) -
Question 124 of 202
124. Question
If the distance between the plane, \(23 x-10 y-2 z+48=0\) and the plane containing the lines \(\frac{x+1}{2}=\frac{y-3}{4}=\frac{z+1}{3}\) and \(\frac{x+3}{2}=\frac{y+2}{6}=\frac{z-1}{\lambda}(\lambda \in R)\) is equal to \(\frac{k}{\sqrt{633}}\), then \(k\) is equal to _____. [JEE Main 2020 (Online) 9th January Evening Slot]
CorrectIncorrectHint
Required distance \(=\) perpendicular distance of plane \(23 x-10 y-2 z+48=0\) either from \((-1,3,-1)\) or \((-3,-2,1)\)
\(
\begin{aligned}
& \Rightarrow\left|\frac{-23-30+2+48}{\sqrt{(23)^2+(10)^2+(2)^2}}\right|=\frac{k}{\sqrt{633}} \\
& \Rightarrow\left|\frac{3}{\sqrt{633}}\right|=\frac{k}{\sqrt{633}} \\
& \Rightarrow k =3
\end{aligned}
\) -
Question 125 of 202
125. Question
The projection of the line segment joining the points \((1,-1,3)\) and \((2,-4,11)\) on the line joining the points \((-1,2,3)\) and \((3,-2,10)\) is _____. [JEE Main 2020 (Online) 9th January Morning Slot]
CorrectIncorrectHint
\(
\text { Let } A(1,-1,3), B(2,-4,11), C(-1,2,3) \& D(3,-2,10)
\)
\(
\begin{aligned}
& \therefore \overrightarrow{A B}=\hat{i}-3 \hat{j}+8 \widehat{k} \\
& \Rightarrow \overrightarrow{C D}=4 \hat{i}-4 \hat{j}+7 \widehat{k}
\end{aligned}
\)
Projection of \(\overrightarrow{A B}\) on \(\overrightarrow{C D}=\frac{\overrightarrow{A B} \cdot \overrightarrow{C D}}{|\overrightarrow{C D}|}\)
\(
\begin{aligned}
& =\frac{4+12+56}{\sqrt{16+16+49}} \\
& =\frac{72}{9} \\
& =8
\end{aligned}
\) -
Question 126 of 202
126. Question
If the foot of the perpendicular drawn from the point \((1,0,3)\) on a line passing through \((\alpha, 7,1)\) is \(\left(\frac{5}{3}, \frac{7}{3}, \frac{17}{3}\right)\), then \(\alpha\) is equal to _____. [JEE Main 2020 (Online) 7th January Evening Slot]
CorrectIncorrectHint
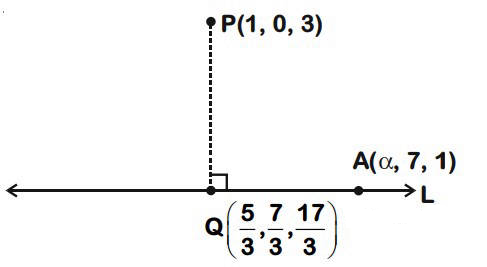
Step 1: Solve for the direction ratios of the lines
Let the points be \(P(1,0,3), Q\left(\frac{5}{3}, \frac{7}{3}, \frac{17}{3}\right)\) and \(A(\alpha, 7,1)\)
We know that the direction ratios of a vector line joining two points \(\left(x_1, y_1, z_1\right)\) and \(\left(x_2, y_2, z_2\right)\) are \(\left(x_2-x_1, y_2-y_1, z_2-z_1\right)\)
\(\therefore\) Direction ratios of line \(P Q=\left(\frac{5}{3}-1, \frac{7}{3}-0, \frac{17}{3}-3\right)=\left(\frac{2}{3}, \frac{7}{3}, \frac{8}{3}\right)\)
Direction ratios of line \(A Q=\left(\frac{5}{3}-\alpha, \frac{7}{3}-7, \frac{17}{3}-1\right)=\left(\frac{5-3 \alpha}{3}, \frac{-14}{3}, \frac{14}{3}\right)\)Step 2: Solve for the value of \(\alpha\)
Given that \(P Q \perp A Q \Rightarrow P Q . A Q=0\)
\(
\Rightarrow\left(\frac{2}{3}\right)\left(\frac{5-3 \alpha}{3}\right)+\left(\frac{7}{3}\right)\left(\frac{-14}{3}\right)+\left(\frac{8}{3}\right)\left(\frac{14}{3}\right)=0
\)
\(
\begin{aligned}
\frac{10-6 \alpha-98+112}{9} & =0 \\
6 \alpha & =112-98+10 \\
6 \alpha & =24 \\
\alpha & =\frac{24}{6} \\
\alpha & =4
\end{aligned}
\) -
Question 127 of 202
127. Question
\(ABC\) is triangle in a plane with vertices \(A (2,3,5), B (-1,3,2)\) and \(C(\lambda, 5, \mu)\). If the median through \(A\) is equally inclined to the coordinate axes, then the value of \(\left(\lambda^3+\mu^3+5\right)\) is : [Online April 10, 2016]
CorrectIncorrectHint
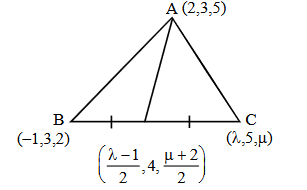
DR’s of AD are \(\frac{\lambda-1}{2}-2,4-3, \frac{\mu+2}{2}-5\)
i.e. \(\frac{\lambda-5}{2}, 1, \frac{\mu-8}{2}\)
\(\because\) This median is making equal angles with coordinate axes, therefore,
\(
\begin{aligned}
& \frac{\lambda-5}{2}=1=\frac{\mu-8}{2} \\
\Rightarrow \quad & \lambda=7 \& \mu=10 \\
\therefore \quad & \lambda^3+\mu^3+5=1348
\end{aligned}
\) -
Question 128 of 202
128. Question
The angle between the lines whose direction cosines satisfy the equations \(l+m+n=0\) and \(l^2+m^2+n^2\) is [JEE 2014]
CorrectIncorrectHint
Given, \(l+m+n=0\) and \(l^2=m^2+n^2\)
Now, \((-m-n)^2=m^2+n^2\)
\(\Rightarrow m n=0 \Rightarrow m=0\) or \(n=0\)
If \(m=0\) then \(l=-n\)
We know \(l^2+m^2+n^2=1 \Rightarrow n= \pm \frac{1}{\sqrt{2}}\)
i.e. \(\left(l_1, m_1, n_1\right)=\left(-\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}\right)\)
If \(n=0\) then \(l=-m\)
\(l^2+m^2+n^2=1 \quad \Rightarrow 2 m^2=1\)
\(\Rightarrow m= \pm \frac{1}{\sqrt{2}}\)
Let \(m=\frac{1}{\sqrt{2}} \Rightarrow l=-\frac{1}{\sqrt{2}}\) and \(n=0\)
\(
\begin{aligned}
& \quad\left(l_2, m_2, n_2\right)=\left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0\right) \\
& \therefore \quad \cos \theta=\frac{1}{2} \Rightarrow \theta=\frac{\pi}{3}
\end{aligned}
\) -
Question 129 of 202
129. Question
Let \(A (2,3,5), B (-1,3,2)\) and \(C (\lambda, 5, \mu)\) be the vertices of a \(\triangle ABC\). If the median through \(A\) is equally inclined to the coordinate axes, then: [Online April 11, 2014]
CorrectIncorrectHint
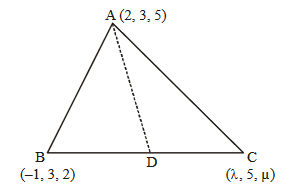
If \(D\) be the mid-point of \(BC\), then
\(
D=\left(\frac{\lambda-1}{2}, 4, \frac{\mu+2}{2}\right)
\)
Direction ratios of \(AD\) are \(\frac{\lambda-5}{2}, 1, \frac{\mu-8}{2}\)
Since median \(AD\) is equally inclined with coordinate axes, therefore direction ratios of \(AD\) will be equal, i.e,
\(
\begin{aligned}
& \frac{\left(\frac{\lambda-5}{2}\right)^2}{\left(\frac{\lambda-5}{2}\right)^2+1+\left(\frac{\mu-8}{2}\right)^2}=\frac{1}{\left(\frac{\lambda-5}{2}\right)^2+1+\left(\frac{\mu-8}{2}\right)^2} \\
& =\frac{\left(\frac{\mu-8}{2}\right)^2}{\left(\frac{\lambda-5}{2}\right)^2+1+\left(\frac{\mu-8}{2}\right)^2} \\
& \Rightarrow\left(\frac{\lambda-5}{2}\right)^2=1=\left(\frac{\mu-8}{2}\right)^2 \\
& \Rightarrow \lambda=7,3 \text { and } \mu=10,6 \\
& \text { If } \lambda=7 \text { and } \mu=10 \\
& \text { Then } \frac{\lambda}{\mu}=\frac{7}{10} \Rightarrow 10 \lambda-7 \mu=0
\end{aligned}
\) -
Question 130 of 202
130. Question
A line in the 3-dimensional space makes an angle \(\theta\) \(\left(0<\theta \leq \frac{\pi}{2}\right)\) with both the \(x\) and \(y\) axes. Then the set of all values of \(\theta\) is the interval: [Online April 9, 2014]
CorrectIncorrectHint
It makes \(\theta\) with \(x\) and \(y\)-axes.
\(
\begin{aligned}
& l=\cos \theta, m=\cos \theta, n=\cos (\pi-2 \theta) \\
& \text { we have } l^2+m^2+n^2=1 \\
& \Rightarrow \cos ^2 \theta+\cos ^2 \theta+\cos ^2(\pi-2 \theta)=1 \\
& \Rightarrow 2 \cos ^2 \theta+(-\cos 2 \theta)^2=1 \\
& \Rightarrow 2 \cos ^2 \theta-1+\cos ^2 2 \theta=0 \\
& \Rightarrow \cos 2 \theta [1+\cos 2 \theta]=0 \\
& \Rightarrow \cos 2 \theta=0 \text { or } \cos 2 \theta=-1 \\
& \Rightarrow 2 \theta=\pi / 2 \text { or } 2 \theta=\pi \\
& \Rightarrow \theta=\pi / 4 \text { or } \theta=\frac{\pi}{2} \\
& \Rightarrow \theta=\left[\frac{\pi}{4}, \frac{\pi}{2}\right]
\end{aligned}
\) -
Question 131 of 202
131. Question
Let \(ABC\) be a triangle with vertices at points \(A (2,3,5)\), \(B(-1,3,2)\) and \(C(\lambda, 5, \mu)\) in three dimensional space. If the median through \(A\) is equally inclined with the axes, then \((\lambda, \mu)\) is equal to : [Online April 25, 2013]
CorrectIncorrectHint
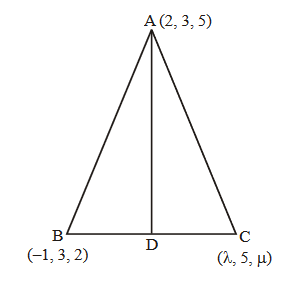
Since \(AD\) is the median
\(
\therefore D=\left(\frac{\lambda-1}{2}, 4, \frac{\mu+2}{2}\right)
\)
Now, dR’s of \(A D\) is
\(
\begin{aligned}
& a=\left(\frac{\lambda-1}{2}-2\right)=\frac{\lambda-5}{2} \\
& b=4-3=1, c=\frac{\mu+2}{2}-5=\frac{\mu-8}{2}
\end{aligned}
\)
Also, \(a, b, c\) are dR’s
\(\therefore a=k l, b=k m, c=k n\) where \(l=m=n\)
and \(l^2+m^2+n^2=1\)
\(\Rightarrow l=m=n=\frac{1}{\sqrt{3}}\)
Now, \(a=1, b=1\) and \(c=1\)
\(\Rightarrow \lambda=7\) and \(\mu=10\) -
Question 132 of 202
132. Question
If the projections of a line segment on the \(x, y\) and \(z\)-axes in 3-dimensional space are 2,3 and 6 respectively, then the length of the line segment is : [Online April 23, 2013]
CorrectIncorrectHint
Length of the line segment
\(
=\sqrt{(2)^2+(3)^2+(6)^2}=7
\) -
Question 133 of 202
133. Question
The acute angle between two lines such that the direction cosines \(l, m, n\), of each of them satisfy the equations \(l+m+n=0\) and \(l^2+m^2-n^2=0\) is :[Online April 22, 2013]
CorrectIncorrectHint
Let \(l_1, m_1, n_1\) and \(l_2, m_2, n_2\) be the d.c of line 1 and 2 respectively, then as given
\(
l_1+m_1+n_1=0
\)
and \(l_2+m_2+n_2=0\)
and \(l_1^2+m_1^2-n_1^2=0\) and
\(
\begin{aligned}
& l_2^2+m_2^2-n_2^2=0 \\
& \left(\because l+m+n=0 \text { and } l^2+m^2-n^2=0\right)
\end{aligned}
\)
Angle between lines, \(\theta\) is
\(
\cos \theta=l_1 l_2+m_1 m_2+n_1 n_2 \dots(1)
\)
As given \(l^2+m^2=n^2\) and \(l+m=-n\)
\(
\Rightarrow(-n)^2-2 l m=n^2 \Rightarrow 2 l m=0 \text { or } l m=0
\)
So \(l_1 m_1=0, l_2 m_2=0\)
If \(l_1=0, m_1 \neq 0\) then \(l_1 m_2=0\)
If \(m_1=0, l_1 \neq 0\) then \(l_2 m_1=0\)
If \(l_2=0, m_2 \neq 0\) then \(l_2 m_1=0\)
If \(m_2=0, l_2 \neq 0\) then \(l_1 m_2=0\)
Also \(l_1 l_2=0\) and \(m_1 m_2=0\)
\(
l^2+m^2-n^2=l^2+m^2+n^2-2 n^2=0
\)
\(
\begin{aligned}
& \Rightarrow 1-2 n^2=0 \Rightarrow n= \pm \frac{1}{\sqrt{2}} \\
& \therefore n_1= \pm \frac{1}{\sqrt{2}}, n_2= \pm \frac{1}{\sqrt{2}} \\
& \therefore \cos \theta=\frac{1}{2} \theta=60^{\circ} \text { (acute angle) }
\end{aligned}
\) -
Question 134 of 202
134. Question
A line \(AB\) in three-dimensional space makes angles \(45^{\circ}\) and \(120^{\circ}\) with the positive \(x\)-axis and the positive \(y\)-axis respectively. If \(A B\) makes an acute angle \(\theta\) with the positive z-axis, then \(\theta\) equals [JEE 2010]
CorrectIncorrectHint
Direction cosines of the line:
\(
\ell=\cos 45^{\circ}=\frac{1}{\sqrt{2}}, m=\cos 120^{\circ}=\frac{-1}{2}, n=\cos \theta
\)
where \(\theta\) is the angle, which line makes with positive \(z\) axis.
\(
\begin{aligned}
& \text { Now } \ell^2+m^2+n^2=1 \\
& \Rightarrow \frac{1}{2}+\frac{1}{4}+\cos ^2 \theta=1 \\
& \cos ^2 \theta=\frac{1}{4} \\
& \Rightarrow \cos \theta=\frac{1}{2} \text { ( } \theta \text { being acute) }\\
& \Rightarrow \theta=\frac{\pi}{3}
\end{aligned}
\) -
Question 135 of 202
135. Question
The projections of a vector on the three coordinate axis are 6 , \(-3,2\) respectively. The direction cosines of the vector are : [JEE 2009]
CorrectIncorrectHint
Let \(P\left(x_1, y_1, z_1\right)\) and \(Q\left(x_2, y_2, z_2\right)\) be the initial and final points of the vector whose projections on the three coordinate axes are \(6,-3,2\) then
\(
x_2-x_1=6 ; y_2-y_1=-3 ; z_2-z_1=2
\)
So that direction ratios of \(\overrightarrow{P Q}\) are \(6,-3,2\)
\(\therefore\) Direction cosines of \(\overrightarrow{P Q}\) are
\(
\begin{aligned}
& \frac{6}{\sqrt{6^2+(-3)^2+2^2}}, \frac{-3}{\sqrt{6^2+(-3)^2+2^2}} \\
& \frac{2}{\sqrt{6^2+(-3)^2+2^2}}=\frac{6}{7}, \frac{-3}{7}, \frac{2}{7}
\end{aligned}
\) -
Question 136 of 202
136. Question
If a line makes an angle of \(\pi / 4\) with the positive directions of each of \(x\) – axis and \(y\)-axis, then the angle that the line makes with the positive direction of the \(z\)-axis is [JEE 2007]
CorrectIncorrectHint
Let the angle of line makes with the positive direction of \(z\)-axis is \(\alpha\) direction cosines of line with the + ve directions of \(x\)-axis, \(y\)-axis, and \(z\)-axis is \(l, m, n\) respectively.
\(
\therefore l=\cos \frac{\pi}{4}, m=\cos \frac{\pi}{4}, n=\cos \alpha
\)
as we know that, \(l^2+m^2+n^2=1\)
\(
\begin{aligned}
& \therefore \cos ^2 \frac{\pi}{4}+\cos ^2 \frac{\pi}{4}+\cos ^2 \alpha=1 \\
& \Rightarrow \frac{1}{2}+\frac{1}{2}+\cos ^2 \alpha=1 \\
& \Rightarrow \cos ^2 \alpha=0 \Rightarrow \alpha=\frac{\pi}{2}
\end{aligned}
\)
Hence, angle with positive direction of the \(z\)-axis is \(\frac{\pi}{2}\). -
Question 137 of 202
137. Question
A line makes the same angle \(\theta\), with each of the \(x\) and \(z\) axis. If the angle \(\beta\), which it makes with \(y\)-axis, is such that \(\sin ^2 \beta=3 \sin ^2 \theta\), then \(\cos ^2 \theta\) equals [JEE 2004]
CorrectIncorrectHint
The direction cosines of the line are \(\cos \theta, \cos \beta, \cos \theta\)
\(
\begin{aligned}
& \therefore \cos ^2 \theta+\cos ^2 \beta+\cos ^2 \theta=1 \\
& \Rightarrow 2 \cos ^2 \theta=\sin ^2 \beta=3 \sin ^2 \theta \text { (given) } \\
& \Rightarrow 2 \cos ^2 \theta=3-3 \cos ^2 \theta \\
& \therefore \cos ^2 \theta=\frac{3}{5}
\end{aligned}
\) -
Question 138 of 202
138. Question
The number of distinct real values of \(\lambda\) for which the lines \(\frac{x-1}{1}=\frac{y-2}{2}=\frac{z+3}{\lambda^2}\) and \(\quad \frac{x-3}{1}=\frac{y-2}{\lambda^2}=\frac{z-1}{2} \quad\) are coplanar is : [Online April 10, 2016]
CorrectIncorrectHint
Lines are coplanar.
\(
\begin{aligned}
&\left|\begin{array}{ccc}
3-1 & 2-2 & 1-(-3) \\
1 & 2 & \lambda^2 \\
1 & \lambda^2 & 2
\end{array}\right|=0 \\
& \Rightarrow\left|\begin{array}{ccc}
2 & 0 & 4 \\
1 & 2 & \lambda^2 \\
1 & \lambda^2 & 2
\end{array}\right|=0 \\
& \Rightarrow 2\left(4-\lambda^4\right)+4\left(\lambda^2-2\right)=0 \\
& \Rightarrow 4-\lambda^4+2 \lambda^2-4=0 \\
& \Rightarrow \lambda^2\left(\lambda^2-2\right)=0 \\
& \Rightarrow \lambda=0, \sqrt{2,}-\sqrt{2}
\end{aligned}
\) -
Question 139 of 202
139. Question
The shortest distance between the lines \(\frac{x}{2}=\frac{y}{2}=\frac{z}{1}\) and \(\frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4}\) lies in the interval : [Online April 9, 2016]
CorrectIncorrectHint
Shortest distance between two lines
\(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}\) and
\(\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}\) is given by,
\(\left|\frac{\left|\begin{array}{ccc}x_2-x_1 & y_2-y_1 & z_2-z_1 \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2\end{array}\right|}{\sqrt{\left(b_1 c_2-b_2 c_1\right)^2+\left(c_1 a_2-c_2 a_1\right)^2+\left(a_1 b_2-a_2 b_1\right)^2}}\right|\)
The shortest distance between given lines are \(\left|\frac{\left|\begin{array}{ccc}-2 & 4 & 5 \\ 2 & 2 & 1 \\ -1 & 8 & 4\end{array}\right|}{\sqrt{(8-8)^2+(-1-8)^2+(16+2)^2}}\right|\)
\(=\left|\frac{0-36+90}{\sqrt{405}}\right|=\frac{54}{20.1}=2.68\) -
Question 140 of 202
140. Question
Equation of the line of the shortest distance between the lines \(\frac{x}{1}=\frac{y}{-1}=\frac{z}{1}\) and \(\frac{x-1}{0}=\frac{y+1}{-2}=\frac{z}{1}\) is: [Online April 19, 2014]
CorrectIncorrectHint
Let equation of the required line be
\(
\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c} \dots(i)
\)
Given two lines
\(
\frac{x}{1}=\frac{y}{-1}=\frac{z}{1} \dots(ii)
\)
and \(\frac{x-1}{0}=\frac{y+1}{0}=\frac{z}{1} \dots(iii)\)
Since the line (i) is perpendicular to both the lines (ii) and (iii), therefore
\(
\begin{aligned}
& a-b+c=0 \dots(iv)\\
& -2 b +c=0 \dots(v)
\end{aligned}
\)
From (iv) and (v) \(c =2 b\) and \(a+b=0\), which are not satisfy by options (c) and (d). Hence options (c) and (d) are rejected.
Thus point \(\left(x_1, y_1, z_1\right)\) on the required line will be either \((0,0,0)\) or \((1,-1,0)\).
Now foot of the perpendicular from point \((0,0,0)\) to the line (iii)
\(
=(1,-2 r-1, r)
\)
The direction ratios of the line joining the points \((0,0,0)\) and \((1,-2 r-1, r)\) are \(1,-2 r-1, r\) Since sum of the \(x\) and \(y\)-coordinate of direction ratio of the required line is 0 .
\(
\therefore 1-2 r-1=0, \Rightarrow r=0
\)
Hence direction ratio are \(1,-1,0\) But the \(z\)-direction ratio of the required line is twice the \(y\)-direction ratio of the required line i.e. \(0=2(-1)\), which is not true.
Hence the shortest line does not pass through the point \((0,0,0)\). Therefore option (a) is also rejected. -
Question 141 of 202
141. Question
If the lines \(\frac{x-2}{1}=\frac{y-3}{1}=\frac{z-4}{-k}\) and \(\frac{x-1}{k}=\frac{y-4}{2}=\frac{z-5}{1}\) are coplanar, then \(k\) can have [JEE 2013]
CorrectIncorrectHint
Given lines will be coplanar
\(
\begin{aligned}
& \text { If }\left|\begin{array}{ccc}
-1 & 1 & 1 \\
1 & 1 & -k \\
k & 2 &
\end{array}\right|=0 \\
& \Rightarrow-1(1+2 k)-\left(1+k^2\right)+1(2-k)=0 \\
& \Rightarrow k=0,-3
\end{aligned}
\) -
Question 142 of 202
142. Question
If two lines \(L_1\) and \(L_2\) in space, are defined by
\(
\begin{aligned}
& L_1=\{x=\sqrt{\lambda} y+(\sqrt{\lambda}-1), z=(\sqrt{\lambda}-1) y+\sqrt{\lambda}\} \text { and } \\
& L_2=\{x=\sqrt{\mu} y+(1-\sqrt{\mu}), z=(1-\sqrt{\mu}) y+\sqrt{\mu}\}
\end{aligned}
\)
then \(L_1\) is perpendicular to \(L_2\), for all non-negative reals \(\lambda\) and \(\mu\), such that : [Online April 23, 2013]CorrectIncorrectHint
For \(L _1\),
\(
\begin{aligned}
& x=\sqrt{\lambda} y+(\sqrt{\lambda}-1) \Rightarrow y=\frac{x-(\sqrt{\lambda}-1)}{\sqrt{\lambda}} \dots(i)\\
& z=(\sqrt{\lambda}-1) y+\sqrt{\lambda} \Rightarrow y=\frac{z-\sqrt{\lambda}}{\sqrt{\lambda}-1} \dots(ii)
\end{aligned}
\)
From (i) and (ii)
\(
\frac{x-(\sqrt{\lambda}-1)}{\sqrt{\lambda}}=\frac{y-0}{1}=\frac{z-\sqrt{\lambda}}{\sqrt{\lambda}-1} \dots(A)
\)
The equation (A) is the equation of line \(L_1\). Similarly equation of line \(L _2\) is
\(
\frac{x-(1-\sqrt{\mu})}{\sqrt{\mu}}=\frac{y-0}{1}=\frac{z-\sqrt{\mu}}{1-\sqrt{\mu}} \dots(B)
\)
Since \(L _1 \perp L _2\), therefore
\(
\begin{aligned}
& \sqrt{\lambda} \sqrt{\mu}+1 \times 1+(\sqrt{\lambda}-1)(1-\sqrt{\mu})=0 \\
& \Rightarrow \sqrt{\lambda}+\sqrt{\mu}=0 \Rightarrow \sqrt{\lambda}=-\sqrt{\mu} \\
& \Rightarrow \lambda=\mu
\end{aligned}
\) -
Question 143 of 202
143. Question
If the lines \(\frac{x+1}{2}=\frac{y-1}{1}=\frac{z+1}{3}\) and \(\frac{x+2}{2}=\frac{y-k}{3}=\frac{z}{4}\) are coplanar, then the value of \(k\) is: [Online April 9, 2013]
CorrectIncorrectHint
Two given planes are coplanar, if
\(
\begin{aligned}
& \left|\begin{array}{ccc}
-2-(-1) & k-1 & 0-(-1) \\
2 & 1 & 3 \\
2 & 3 & 4
\end{array}\right|=0 \\
& \Rightarrow\left|\begin{array}{ccc}
-1 & k-1 & 1 \\
2 & 1 & 3 \\
2 & 3 & 4
\end{array}\right|=0 \\
& \Rightarrow(-1)(4-9)-(k-1)(8-6)+6-2=0 \\
& \Rightarrow k=\frac{11}{2}
\end{aligned}
\) -
Question 144 of 202
144. Question
If the line \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4}\) and \(\frac{x-3}{1}=\frac{y-k}{2}=\frac{z}{1}\) intersect, then \(k\) is equal to: [JEE 2012]
CorrectIncorrectHint
Given lines are \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4}\) and \(\frac{x-3}{1}=\frac{y-k}{2}=\frac{z}{1}\)
Thus, \(\vec{a}, \vec{b}, \vec{c}\) and \(\vec{d}\) are given as \(\vec{a}(1,-1,1), \vec{b}(2,3,4), \vec{c}(3, k, 0)\); and \(\vec{d}(1,2,1)\)
These lines will intersect if lines are coplanar i.e., \(\vec{a}-\vec{c}, \vec{b} \& \vec{d}\) are coplanar
\(
\therefore[\vec{a}-\vec{c}, \vec{b}, \vec{d}]=0
\)
Now, \(\vec{a}-\vec{c}=(3-1, k+1,0-1)\)
\(
\begin{gathered}
=(2, k+1,-1) \\
\Rightarrow\left|\begin{array}{ccc}
2 & k+1 & -1 \\
2 & 3 & 4 \\
1 & 2 & 1
\end{array}\right|=0
\end{gathered}
\)
\(
\begin{aligned}
& \Rightarrow \quad 2(3-8)-k+1(2-4)-1(4-3)=0 \\
& \Rightarrow \quad 2(-5)-(k+1)(-2)-1(1)=0 \\
& \Rightarrow \quad-10+2 k+2-1=0 \Rightarrow k=\frac{9}{2}
\end{aligned}
\) -
Question 145 of 202
145. Question
The distance of the point \(-\hat{i}+2 \hat{j}+6 \hat{k}\) from the straight line that passes through the point \(2 \hat{i}+3 \hat{j}-4 \hat{k}\) and is parallel to the vector \(6 \hat{i}+3 \hat{j}-4 \hat{k}\) is [Online May 26, 2012]
CorrectIncorrectHint
Point is \((-1,2,6)\)
Line passes through the point \((2,3,-4)\) parallel to vector whose direction ratios is \(6,3,-4\).
Equation is \(\frac{x-2}{6}=\frac{y-3}{3}=\frac{z+4}{-4}=\lambda\)
Any point on this line is given by \(x=6 \lambda+2\), \(y=3 \lambda+3, z=-4 \lambda-4\)
Now, \(d\).Rs of line passing through \((-1,2,6)\) and \(\perp\) to this line is
\(
\{(x+1),(y-2),(z-6)\}
\)
So, \(6(x+1)+3(y-2)-4(z-6)=0\)
\(
\Rightarrow 6 x+3 y-4 z+24=0
\)
Now, \(6(6 \lambda+2)+3(3 \lambda+3)+4(4 \lambda+4)+24=0\)
\(
\Rightarrow 61 \lambda+61=0 \Rightarrow \lambda=-1
\)
So, \(x=-4, y=0, z=0\)
Now, distance between \((-1,2,6)\) and \((-4,0,0)\) is
\(
\sqrt{9+4+36}=\sqrt{49}=7
\) -
Question 146 of 202
146. Question
Statement 1: The shortest distance between the lines \(\frac{x}{2}=\frac{y}{-1}=\frac{z}{2}\) and \(\frac{x-1}{4}=\frac{y-1}{-2}=\frac{z-1}{4}\) is \(\sqrt{2}\).
Statement 2: The shortest distance between two parallel lines is the perpendicular distance from any point on one of the lines to the other line. [Online May 19, 2012]CorrectIncorrectHint
\(
\text { On solving we will get shortest distance } \neq \sqrt{2}
\) -
Question 147 of 202
147. Question
The coordinates of the foot of perpendicular from the point \((1,0,0)\) to the line
\(
\frac{x-1}{2}=\frac{y+1}{-3}=\frac{z+10}{8} \text { are }
\) [Online May 12, 2012]CorrectIncorrectHint
Let the equation of \(A B\) is
\(
\frac{x-1}{2}=\frac{y-(-1)}{-3}=\frac{z-(-10)}{8}=k
\)
Let \(L\) be the foot of the perpendicular drawn from \(P(1,0,0)\).
\(
\therefore \quad L=(2 k+1,-3 k -1,8 k-10) \text {. }
\)
Now, direction ratio of \(P L=(2 k,-3 k-1,8 k-10)\) and direction ratio of \(A B=(2,-3,8)\)
Since, \(P L\) is perpendicular to \(A B\)
\(
\therefore 2(2 k)-3(-3 k-1)+8(8 k-10)=0
\)
Now, \(k=\frac{2(1-1)+(-3)(0+1)+8(0+10)}{(2)^2+(-3)^2+(8)^2}\)
\(
=\frac{0-3+80}{4+9+64}=\frac{77}{77}=1
\)
\(\therefore\) Required co-ordinate
\(
=L=(2+1,-3-1,8-10)=(3,-4,-2) \text {. }
\) -
Question 148 of 202
148. Question
The length of the perpendicular drawn from the point \((3,-1,11)\) to the line \(\frac{x}{2}=\frac{y-2}{3}=\frac{z-3}{4}\) is : [JEE 2011RS]
CorrectIncorrectHint
Let feet of perpendicular is
\(
(2 \alpha, 3 \alpha+2,4 \alpha+3)
\)
\(\Rightarrow\) Direction ratio of the \(\perp\) line is \(2 \alpha-3,3 \alpha+3,4 \alpha-8\). and Direction ratio of the line \(2,3,4\) are
\(
\begin{aligned}
& 2(2 \alpha-3)+3(3 \alpha+3)+4(4 \alpha-8)=0 \\
& 29 \alpha-29=0 \\
& \alpha=1
\end{aligned}
\)
Feet of \(\perp\) is \((2,5,7)\)
Length \(\perp\) is \(\sqrt{1^2+6^2+4^2}=\sqrt{53}\) -
Question 149 of 202
149. Question
Statement-1: The point \(A(1,0,7))\) is the mirror image of the point \(B(1,6,3)\) in the line : \(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\)
Statement-2: The line \(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\) bisects the line segment joining \(A(1,0,7)\) and \(B(1,6,3)\). [JEE 2011]CorrectIncorrectHint
The direction ratio of the line segment joining points \(A (1,0,7)\) and \(B (1,6,3)\) is \(0,6,-4\).
The direction ratio of the given line is \(1,2,3\).
Clearly \(1 \times 0+2 \times 6+3 \times(-4)=0\)
So, the given line is perpendicular to line \(AB\).
Also, the mid point of \(A\) and \(B\) is \((1,3,5)\) which lies on the given line.
So, the image of \(B\) in the given line is \(A\), because the given line is the perpendicular bisector of line segment joining points \(A\) and \(B\). -
Question 150 of 202
150. Question
The line \(L\) given by \(\frac{x}{5}+\frac{y}{b}=1\) passes through the point ( 13 ,32). The line \(K\) is parallel to \(L\) and has the equation \(\frac{x}{c}+\frac{y}{3}=1\). Then the distance between \(L\) and \(K\) is [JEE 2010]
CorrectIncorrectHint
Slope of line \(L =-\frac{b}{5}\)
Slope of line \(K =-\frac{3}{c}\)
Line \(L\) is parallel to line \(k\).
\(
\Rightarrow \frac{b}{5}=\frac{3}{c} \Rightarrow b c=15
\)
\((13,32)\) is a point on \(L\).
\(
\begin{aligned}
& \therefore \frac{13}{5}+\frac{32}{b}=1 \Rightarrow \frac{32}{b}=-\frac{8}{5} \\
& \Rightarrow b=-20 \Rightarrow c=-\frac{3}{4}
\end{aligned}
\)
Equation of \(K\) :
\(
y-4 x=3 \Rightarrow 4 x-y+3=0
\)
Distance between \(L\) and \(K\)
\(
=\frac{|52-32+3|}{\sqrt{17}}=\frac{23}{\sqrt{17}}
\) -
Question 151 of 202
151. Question
If the straight lines \(\frac{x-1}{k}=\frac{y-2}{2}=\frac{z-3}{3}\) and \(\frac{x-2}{3}=\frac{y-3}{k}=\frac{z-1}{2}\) intersect at a point, then the integer \(k\) is equal to [JEE 2008]
CorrectIncorrectHint
The two lines intersect if shortest distance between them is zeroi.e.
\(
\frac{\left(\vec{a}_2-\vec{a}_1\right) \cdot \vec{b}_1 \times \vec{b}_2}{\left|\vec{b}_1 \times \vec{b}_2\right|}=0 \Rightarrow\left(\vec{a}_2-\vec{a}_1\right) \cdot \vec{b}_1 \times \vec{b}_2=0
\)
where \(\vec{a}_1=\hat{i}+2 \hat{j}+3 \hat{k}, \vec{b}_1=k \hat{i}+2 \hat{j}+3 \hat{k}\)
\(
\begin{aligned}
& \vec{a}_2=2 \hat{i}+3 \hat{j}+\hat{k}, \hat{b}_2=3 \hat{i}+k \hat{j}+2 \hat{k} \\
& \Rightarrow\left|\begin{array}{ccc}
1 & 1 & -2 \\
k & 2 & 3 \\
3 & k & 2
\end{array}\right|=0
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow 1(4-3 k)-1(2 k-9)-2\left(k^2-6\right)=0 \\
& \Rightarrow-2 k^2-5 k+25=0 \Rightarrow k=-5 \text { or } \frac{5}{2} \\
& \because k \text { is an integer, therefore } k=-5
\end{aligned}
\) -
Question 152 of 202
152. Question
If non zero numbers \(a, b, c\) are in H.P., then the straight line \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}=0\) always passes through a fixed point. That point is [JEE 2005]
CorrectIncorrectHint
\(a, b, c\) are in H.P. \(\Rightarrow \frac{1}{a}, \frac{1}{b}, \frac{1}{c}\) are in A.P.
\(
\begin{aligned}
& \Rightarrow \frac{2}{b}=\frac{1}{a}+\frac{1}{c} \Rightarrow \frac{1}{a}-\frac{2}{b}+\frac{1}{c}=0 \\
& \therefore \frac{x}{a}+\frac{y}{a}+\frac{1}{c}=0 \text { passes through }(1,-2)
\end{aligned}
\) -
Question 153 of 202
153. Question
The angle between the lines \(2 x=3 y=-z\) and \(6 x=-y=-4 z\) is [JEE 2005]
CorrectIncorrectHint
The given lines are \(2 x=3 y=-z\)
or \(\frac{x}{3}=\frac{y}{2}=\frac{z}{-6}\) [Dividing by 6]
and \(\quad 6 x=-y=-4 z\)
or \(\frac{x}{2}=\frac{y}{-12}=\frac{z}{-3}\) [Dividing by 12]
\(\therefore\) Angle between two lines is
\(
\begin{aligned}
& \cos \theta=\frac{3 \cdot 2+2 \cdot(-12)+(-6) \cdot(-3)}{\sqrt{3^2+2^2+(-6)^2} \sqrt{2^2+(-12)^2+(-3)^2}} \\
& =\frac{6-24+18}{\sqrt{49} \sqrt{157}}=0 \Rightarrow \theta=90^{\circ}
\end{aligned}
\) -
Question 154 of 202
154. Question
If the straight lines
\(
x=1+s, y=-3-\lambda s, z=1+\lambda s
\)
and \(x=\frac{t}{2}, y=1+t, z=2-t\), with parameters \(s\) and \(t\) respectively, are co-planar, then \(\lambda\) equals. [JEE 2004]CorrectIncorrectHint
The given lines are
\(
x-1=\frac{y+3}{-\lambda}=\frac{z-1}{\lambda}=s \dots(1)
\)
and \(2 x=y-1=\frac{z-2}{-1}=t \dots(2)\)
The lines are coplanar, if
\(
\begin{aligned}
& \left|\begin{array}{ccc}
0-(-1) & -1-3 & -2-(-1) \\
1 & -\lambda & \lambda \\
\frac{1}{2} & 1 & -1
\end{array}\right|=0 \\
& c_2 \rightarrow c_2+c_3 ;\left|\begin{array}{ccc}
1 & -5 & -1 \\
1 & 0 & \lambda \\
\frac{1}{2} & 0 & -1
\end{array}\right|=0 \\
& \Rightarrow 5\left(-1-\frac{\lambda}{2}\right)=0 \Rightarrow \lambda=-2
\end{aligned}
\) -
Question 155 of 202
155. Question
A line with direction cosines proportional to \(2,1,2\) meets each of the lines \(x=y+a=z\) and \(x+a=2 y=2 z\). The co-ordinates of each of the points of intersection are given by [JEE 2004]
CorrectIncorrectHint
Let a point on the line \(x=y+a=z\) is \((\lambda, \lambda-a, \lambda)\) and a point on the line \(x+a=2 y=2 z\) is \(\left(\mu-a, \frac{\mu}{2}, \frac{\mu}{2}\right)\), then direction ratio of the line joining these points are \(\lambda-\mu+a, \lambda-a-\frac{\mu}{2}, \lambda-\frac{\mu}{2}\) If it respresents the required line, then
\(
\frac{\lambda-\mu+a}{2}=\frac{\lambda-a-\frac{\mu}{2}}{1}=\frac{\lambda-\frac{\mu}{2}}{2}
\)
on solving we get \(\lambda=3 a, \mu=2 a\)
\(\therefore\) The required points of intersection are \((3 a, 3 a-a, 3 a)\) and \(\left(2 a-a, \frac{2 a}{2}, \frac{2 a}{2}\right)\)
or \((3 a, 2 a, 3 a)\) and \((a, a, a)\) -
Question 156 of 202
156. Question
The lines \(\frac{x-2}{1}=\frac{y-3}{1}=\frac{z-4}{-k}\)
and \(\frac{x-1}{k}=\frac{y-4}{1}=\frac{z-5}{1}\) are coplanar if [JEE 2003]CorrectIncorrectHint
\(
\begin{aligned}
& \left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
l_1 & m_1 & n_1 \\
l_2 & m_2 & n_2
\end{array}\right|=0 \\
& \left|\begin{array}{ccc}
1 & -1 & -1 \\
1 & 1 & -k \\
k & 2 & 1
\end{array}\right|=0 \Rightarrow\left|\begin{array}{ccc}
0 & 0 & -1 \\
2 & 1+k & -k \\
k+2 & 1 & 1
\end{array}\right|=0 \\
& k^2+3 k=0 \Rightarrow k(k+3)=0 \text { or } k=0 \text { or }-3
\end{aligned}
\) -
Question 157 of 202
157. Question
The two lines \(x=a y+b, z=c y+d\) and \(x=a^{\prime} y+b^{\prime}, z=c^{\prime} y+d^{\prime}\) will be perpendicular, if and only if [JEE 2003]
CorrectIncorrectHint
\(
\frac{x-b}{a}=\frac{y}{1}=\frac{z-d}{c} ; \frac{x-b^{\prime}}{a^{\prime}}=\frac{y}{1}=\frac{z-d^{\prime}}{c^{\prime}} .
\)
For perpendicularity of lines
\(
a a^{\prime}+1+c c^{\prime}=0
\) -
Question 158 of 202
158. Question
The distance of the point \((1,3,-7)\) from the plane passing through the point \((1,-1,-1)\), having normal perpendicular to both the lines
\(\frac{x-1}{1}=\frac{y+2}{-2}=\frac{z-4}{3}\) and \(\frac{x-2}{2}=\frac{y+1}{-1}=\frac{z+7}{-1}\), is: [JEE 2017]CorrectIncorrectHint
Let the plane be
\(
a ( x -1)+ b ( y +1)+ c ( z +1)=0
\)
Normal vector
\(
\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & -2 & 3 \\
2 & -1 & -1
\end{array}\right|=5 \hat{i}+7 \hat{j}+3 \hat{k}
\)
So plane is \(5(x-1)+7(y+1)+3(z+1)=0\)
\(
\Rightarrow 5 x+7 y+3 z+5=0
\)
Distance of point \((1,3,-7)\) from the plane is
\(
\frac{5+21-21+5}{\sqrt{25+49+9}}=\frac{10}{\sqrt{83}}
\) -
Question 159 of 202
159. Question
If the image of the point \(P(1,-2,3)\) in the plane, \(2 x+3 y-4 z+22=0\) measured parallel to line, \(\frac{x}{1}=\frac{y}{4}=\frac{z}{5}\) is \(Q\), then \(P Q\) is equal to: [JEE 2017]
CorrectIncorrectHint
Equation of line \(P Q\) is \(\frac{x-1}{1}=\frac{y+2}{4}=\frac{z-3}{5}\)
Let \(F\) be \((\lambda+1,4 \lambda-2,5 \lambda+3)\)
Since \(F\) lies on the plane
\(
\begin{aligned}
& \therefore 2(\lambda+1)+3(4 \lambda-2)-4(5 \lambda+3)+22=0 \\
& 2 \lambda+2+12 \lambda-6-20 \lambda-12+22=0
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow-6 \lambda+6=0 \Rightarrow \lambda=1 \\
& \therefore F \text { is }(2,2,8) \\
& PQ =2 PF =2 \sqrt{1^2+4^2+5^2}=2 \sqrt{42}
\end{aligned}
\) -
Question 160 of 202
160. Question
If \(x=a, y= b , z=c\) is a solution of the system of linear equations
\(
\begin{aligned}
& x+8 y+7 z=0 \\
& 9 x+2 y+3 z=0 \\
& x+y+z=0
\end{aligned}
\)
such that the point \((a, b, c)\) lies on the plane \(x+2 y+z=6\), then \(2 a+b+c\) equals: [Online April 9, 2017]CorrectIncorrectHint
\(
\begin{aligned}
& x+8 y+7 z=0 \ldots (1)\\
& 9 x+2 y+3 z=0 \dots(2)\\
& x+y+z=0 \ldots(3)
\end{aligned}
\)
Multiply eqn. (3) by 3 & subtract from eqn. (2)
we get \(6 x-y=0\)
\(y=6 x \dots(4)\)
Substitute in Eqn (1). we get
\(
\begin{aligned}
& x+8(6 x)+7 z=0 \\
& 49 x+7 z=0 \\
& 7 x+z=0 \\
& z=-7 x \ldots \ldots .(5)
\end{aligned}
\)
\(
\Rightarrow x = a , y = b \cdot z = c
\)
is the solutions of the system of linear equation
\(
\therefore b=6 a \text { and } c=-7 a \dots(6)
\)
Also, \((a, b, c)\) lies on the plane \(x+2 y+z=6\)
\(
\therefore a +2 b + c =6 \dots(7)
\)
Substitute eq. (6) in eq(7)
\(
\begin{aligned}
& \therefore a+2(6 a)-7 a=6 \\
& \therefore a+12 a-7 a=6 \\
& \therefore 6 a=6 \\
& \therefore a=1
\end{aligned}
\)
So, \(b=6\) and \(c=-7\)
\(
\therefore 2 a+b+c=2(1)+6-7=1 \text {. }
\) -
Question 161 of 202
161. Question
If a variable plane, at a distance of 3 units from the origin, intersects the coordinate axes at \(A , B\) and \(C\), then the locus of the centroid of \(\triangle A B C\) is : [Online April 9, 2017]
CorrectIncorrectHint
Let the plane equation be \(a x+b y+c z+d=0\). The distance of the plane from the origin is 3 .
Therefore,
\(
\frac{d}{\sqrt{a^2+b^2+c^2}}=3
\)
That is,
\(
d^2=9\left(a^2+b^2+c^2\right) \dots(1)
\)
Now, the plane intersects \(x\)-axis at point \(A(-d / a, 0,0) ; y\)-axis at point \((0,-d / b, 0)\) and \(z\)-axis at point \(C (0,0,- d / c )\).
Let \(h =- d / 3 a , k =- d / 3 b , l =- d / 3 c\).
Therefore, from Eq. (1), we get
\(
\begin{aligned}
& \frac{1}{9 h^2}+\frac{1}{9 k^2}+\frac{1}{9 l^2}=\frac{1}{9}=\frac{1}{h^2}+\frac{1}{k^2}+\frac{1}{l^2}=1 \\
& \Rightarrow \frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}=1
\end{aligned}
\) -
Question 162 of 202
162. Question
If the line, \(\frac{x-3}{1}=\frac{y+2}{-1}=\frac{z+\lambda}{-2}\) lies in the plane, \(2 x-\) \(4 y+3 z=2\), then the shortest distance between this line and the line, \(\frac{x-1}{12}=\frac{y}{9}=\frac{z}{4}\) is: [Online April 9, 2017]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Point }(3,-2,-\lambda) \text { on } p \text { line } 2 x-4 y+3 z-2=0 \\
&=6+8-3 \lambda-2=0 \\
&=3 \lambda=12 \\
& \lambda=4
\end{aligned}
\)
Now,
\(
\begin{aligned}
& \frac{x-3}{1}=\frac{y+2}{-1}=\frac{z+4}{-2}=k_1 \dots(i) \\
& \frac{x-1}{12}=\frac{y}{9}=\frac{z}{4}=k_2 \dots(ii)
\end{aligned}
\)
\(
\begin{aligned}
& \text { Point on equation (i) } P \left( k _1+3,- k _1-2,-2 k _1-4\right) \\
& \text { Point on equation (ii) } Q \left(12 k _2+1,9 k _2, 4 k _2\right) \\
& k _1+3=12 k _2+1\left|- k _1-2=9 k _2\right|-2 k _1-4=4 k _2 \\
& \quad k _2=0 \\
& k _1=-2 \\
& p (1,0,0) \text { lie on equation of a line } 1 \\
& \text { gives shortest distance }=0
\end{aligned}
\) -
Question 163 of 202
163. Question
The coordinates of the foot of the perpendicular from the point \((1,-2,1)\) on the plane containing the lines, \(\frac{x+1}{6}=\frac{y-1}{7}=\frac{z-3}{8}\) and \(\frac{x-1}{3}=\frac{y-2}{5}=\frac{z-3}{7}\), is : [Online April 8, 2017]
CorrectIncorrectHint
\(
\begin{aligned}
\vec{n} & =\overrightarrow{n_1} \times \overrightarrow{n_2}=\left|\begin{array}{lll}
\hat{i} & \hat{j} & \hat{k} \\
6 & 7 & 8 \\
3 & 5 & 7
\end{array}\right| \\
& =(9,-18,9) \\
& =(1,-2,1)
\end{aligned}
\)
Equation of plane is
\(
\begin{aligned}
& 1(x+1)-2(y-1)+(z-3)=0 \\
& x-2 y+z=0
\end{aligned}
\)
foot to \(z\)
\(
\begin{gathered}
\frac{x-1}{1}=\frac{y+2}{-2}=\frac{z-1}{1}=-\frac{[1+4+1]}{6} \\
x=0, y=0, z=0
\end{gathered}
\) -
Question 164 of 202
164. Question
The line of intersection of the planes \(\vec{r} \cdot(3 \hat{i}-\hat{j}+\hat{k})=1\) and \(\overrightarrow{ r } \cdot(\hat{ i }+4 \hat{ j }-2 \hat{ k })=2\), is: [Online April 8, 2017]
CorrectIncorrectHint
\(
\begin{aligned}
\vec{n}=\overrightarrow{n_1} \times \overrightarrow{n_2} \\
& \Rightarrow\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
3 & -1 & 1 \\
1 & 4 & -2
\end{array}\right|=\hat{i}(-2)-\hat{j}(-7)+\hat{k}(13) \\
& \Rightarrow \vec{n}=-2 \hat{i}+7 \hat{j}+13 \hat{k}
\end{aligned}
\)
Now,
\(
\begin{aligned}
& 3 x-y+z=1 \\
& x+4 y-2 z=2
\end{aligned}
\)
but \(z=0 \&\) solving the given
\(
x=6 / 13 \text { and } y=5 / 13
\)
\(\therefore\) required equation of a line is
\(
\frac{x-6 / 13}{2}=\frac{y-5 / 13}{-7}=\frac{z}{-13}
\) -
Question 165 of 202
165. Question
If the line, \(\frac{x-3}{2}=\frac{y+2}{-1}=\frac{z+4}{3}\) lies in the plane, \(lx+m y-z=9\), then \(l^2+ m ^2\) is equal to : [JEE 2016]
CorrectIncorrectHint
Line lies in the plane \(\Rightarrow(3,-2,-4)\) lie in the plane
\(
\Rightarrow 3 \ell-2 m +4=9 \text { or } 3 \ell-2 m =5 \text {…. }(1)
\)
Also, \(\ell, m ,-1\) are dr’s of line perpendicular to plane and \(2,-1,3\) are dr’s of line lying in the plane
\(
\Rightarrow 2 \ell- m -3=0 \text { or } 2 \ell- m =3 \dots(2)
\)
Solving (1) and (2) we get \(\ell=1\) and \(m =-1\) \(\Rightarrow \ell^2+ m ^2=2\). -
Question 166 of 202
166. Question
The distance of the point \((1,-5,9)\) from the plane \(x-y+z=5\) measured along the line \(x=y=z\) is : [JEE 2016]
CorrectIncorrectHint
Equation of line passing through the point \((1,-5,9)\) and parallel to \(x=y=z\) is
\(
\frac{x-1}{1}=\frac{y+5}{1}=\frac{z-9}{1}=\lambda
\)
Thus, any point on this line is of the form
\(
\lambda+1, \lambda-5, \lambda+9 \text {. }
\)
Now, if \(P(\lambda+1, \lambda-5, \lambda+9)\) is the point of intersection of line and plane, then
\(
\begin{aligned}
& (\lambda+1)-(\lambda-5)+\lambda+9=5 \\
& \Rightarrow \lambda+15=5 \Rightarrow \lambda=-10
\end{aligned}
\)
\(\therefore\) Coordintes of point \(P\) are ( \(-9,-15,-1\) ).
Hence, required distance
\(
\begin{aligned}
& =\sqrt{(1+9)^2+(-5+15)^2+(9+1)^2} \\
& =\sqrt{10^2+10^2+10^2}=10 \sqrt{3}
\end{aligned}
\) -
Question 167 of 202
167. Question
The distance of the point \((1,-2,4)\) from the plane passing through the point \((1,2,2)\) and perpendicular to the planes \(x-y+2 z=3\) and \(2 x-2 y+z+12=0\), is : [Online April 9, 2016]
CorrectIncorrectHint
Let equation of plane be
\(
a(x-1)+b(y-2)+c(z-2)=0 \dots(1)
\)
(1) is perpendicular to given planes then
\(
\begin{aligned}
& a-b+2 c=0 \\
& 2 a-2 b+c=0
\end{aligned}
\)
Solving above equation \(c=0\) and \(a=b\) equation of plane (1) can be
\(
x+y-3=0
\)
distance from \((1,-2,4)\) will be
\(
D=\frac{|1-2-3|}{\sqrt{1+1}}=\frac{4}{\sqrt{2}}=2 \sqrt{2}
\) -
Question 168 of 202
168. Question
The equation of the plane containing the line \(2 x-5 y+z=3\); \(x+y+4 z=5\), and parallel to the plane, \(x+3 y+6 z=1\), is : [JEE 2015]
CorrectIncorrectHint
Equation of the plane containing the lines
\(2 x-5 y+z=3\) and \(x+y+4 z=5\) is
\(
\begin{aligned}
& 2 x-5 y+z-3+\lambda(x+y+4 z-5)=0 \\
& \Rightarrow(2+\lambda) x+(-5+\lambda) y+(1+4 \lambda) z+(-3-5 \lambda)=0 \dots(i)
\end{aligned}
\)
Since the plane (i) parallel to the given plane \(x+3 y+6 z\) \(=1\)
\(
\begin{aligned}
& \therefore \frac{2+\lambda}{1}=\frac{-5+\lambda}{3}=\frac{1+4 \lambda}{6} \\
& \Rightarrow \lambda=-\frac{11}{2}
\end{aligned}
\)
Hence equation of the required plane is
\(
\begin{aligned}
& \left(2-\frac{11}{2}\right) x+\left(-5-\frac{11}{2}\right) y+\left(1-\frac{44}{2}\right) z+\left(-3+\frac{55}{2}\right)=0 \\
& \Rightarrow(4-11) x+(-10-11) y+(2-44) z+(-6+55)=0 \\
& \Rightarrow-7 x-21 y-42 z+49=0 \\
& \Rightarrow x+3 y+6 z-7=0 \\
& \Rightarrow x+3 y+6 z=7
\end{aligned}
\) -
Question 169 of 202
169. Question
The distance of the point \((1,0,2)\) from the point of intersection of the line \(\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{12}\) and the plane \(x-y+z=16\), is [JEE 2015]
CorrectIncorrectHint
General point on given line \(\equiv P(3 r+2,4 r-1,12 r+2)\)
Point \(P\) must satisfy equation of plane
\(
\begin{aligned}
& (3 r+2)-(4 r-1)+(12 r+2)=16 \\
& 11 r+5=16 \\
& r =1 \\
& P (3 \times 1+2,4 \times 1-1,12 \times 1+2)= P (5,3,14)
\end{aligned}
\)
distance between \(P\) and \((1,0,2)\)
\(
D =\sqrt{(5-1)^2+3^2+(14-2)^2}=13
\) -
Question 170 of 202
170. Question
The shortest distance between the \(z\)-axis and the line \(x\) \(+y+2 z-3=0=2 x+3 y+4 z-4\), is [Online April 11, 2015]
CorrectIncorrectHint
The equation of any plane passing through given line is
\(
\begin{aligned}
& (x+y+2 z-3)+\lambda(2 x+3 y+4 z-4)=0 \\
& \Rightarrow(1+2 \lambda) x+(1+3 \lambda) y+(2+4 \lambda) z-(3+4 \lambda)=0
\end{aligned}
\)
If this plane is parallel to \(z\)-axis then normal to the plane will be perpendicular to \(z\)-axis.
\(
\begin{aligned}
& \therefore(1+2 \lambda)(0)+(1+3 \lambda)(0)+(2+4 \lambda)(1)=0 \\
& \lambda=-\frac{1}{2}
\end{aligned}
\)
Thus, Required plane is
\(
\begin{aligned}
& (x+y+2 z-3)-\frac{1}{2}(2 x+3 y+4 z-4)=0 \Rightarrow y+2=0 \\
& \therefore S . D=\frac{2}{\sqrt{(1)^2}}=2
\end{aligned}
\) -
Question 171 of 202
171. Question
A plane containing the point \((3,2,0)\) and the line \(\frac{x-1}{1}=\frac{y-2}{5}=\frac{z-3}{4}\) also contains the point : [Online April 11, 2015]
CorrectIncorrectHint
Equation of the plane containing the given line \(\frac{x-1}{1}\) \(=\frac{y-2}{5}=\frac{z-3}{4}\) is
\(
A ( x -1)+ B ( y -2)+ C ( z -3)=0 \dots(i)
\)
where \(A +5 B +4 C =0 \dots(ii)\)
Since the point \((3,2,0)\) contains in the plane (i), therefore
\(
2 A +0 . B -3 C =0 \dots(iii)
\)
From equations (ii) and (iii),
\(
\frac{ A }{-15-0}=\frac{ B }{6+3}=\frac{ C }{0-10}= k \text { (let) }
\)
\(
\Rightarrow A =-15 k , B =9 k \text { and } C =-10 k
\)
Putting the value of \(A , B\) and \(C\) in equation (i), we get
\(
-15(x-1)+9(y-2)-10(z-3)=0 \dots(iv)
\)
Now the coordinates of the point \((0,-3,1)\) satisfy the equation of the plane (iv) as
\(
\begin{aligned}
& -15(0-1)+9(-3-2)-10(1-3) \\
& =15-45+20=0
\end{aligned}
\)
Hence the point \((0,-3,1)\) contains in the plane. -
Question 172 of 202
172. Question
If the points \((1,1, \lambda)\) and \((-3,0,1)\) are equidistant from the plane, \(3 x+4 y-12 z+13=0\), then \(\lambda\) satisfies the equation : [Online April 10, 2015]
CorrectIncorrectHint
\(
\begin{aligned}
& |3+4-12 \lambda+13|=|-9+0-12+13| \\
& \Rightarrow|-12 \lambda+20|=|8| \\
& \Rightarrow|3 \lambda-5|=2 \\
& \Rightarrow 9 \lambda^2+25-30 \lambda=4 \\
& \Rightarrow 9 \lambda^2-30 \lambda+21=0 \\
& \Rightarrow 3 \lambda^2-10 \lambda+7=0
\end{aligned}
\) -
Question 173 of 202
173. Question
If the shortest distance between the lines \(\frac{x-1}{\alpha}=\frac{y+1}{-1}=\frac{z}{1},(\alpha \neq-1)\) and \(x+y+z+1=0\) \(=2 x-y+z+3\) is \(\frac{1}{\sqrt{3}}\), then a value \(\alpha\) is : [Online April 10, 2015]
CorrectIncorrectHint
Plane passing through \(x+y+z+1=0\) and \(2 x-y+z+3=0\)
\(
\begin{aligned}
& \text { is } x+y+z+1+\lambda(2 x-y+z+3)=0 \\
& \Rightarrow(2 \lambda+1) x+(1-\lambda) y+(1+\lambda) z+3 \lambda+1=0
\end{aligned}
\)
Parallel to the given line if
\(
\begin{aligned}
& \alpha(2 \lambda+1)-1(1-\lambda)+1(1+\lambda)=0 \\
& \Rightarrow \alpha=\frac{-2 \lambda}{2 \lambda+1} \dots(i)
\end{aligned}
\)
\(
\begin{gathered}
\text { Also, }\left|\frac{2 \lambda+1-(1-\lambda)+0+3 \lambda+1}{\sqrt{(2 \lambda+1)^2+(1-\lambda)^2+(1+\lambda)^2}}\right|=\frac{1}{\sqrt{3}} \\
\Rightarrow \lambda=0, \frac{-32}{102} ; \alpha=0 \text { or } \alpha=\frac{32}{19}
\end{gathered}
\) -
Question 174 of 202
174. Question
The image of the line \(\frac{x-1}{3}=\frac{y-3}{1}=\frac{z-4}{-5}\) in the plane \(2 x-y+z+3=0\) is the line: [JEE 2014]
CorrectIncorrectHint
\(
\begin{aligned}
\frac{a-1}{2} & =\frac{b-3}{-1}=\frac{c-4}{1}=\lambda \text { (let) } \\
\Rightarrow \quad a & =2 \lambda+1 \\
b & =3-\lambda \\
c & =4+\lambda
\end{aligned}
\)
\(
\begin{aligned}
& P=\left(\frac{a+1}{2}, \frac{b+3}{2}, \frac{c+4}{2}\right)=\left(\lambda+1, \frac{6-\lambda}{2}, \frac{\lambda+8}{2}\right) \\
& \therefore \quad 2(\lambda+1)-\frac{6-\lambda}{2}+\frac{\lambda+8}{2}+3=0 \\
& 3 \lambda+6=0 \Rightarrow \lambda=-2 \\
& a=-3, b=5, c=2
\end{aligned}
\)
Required line is \(\frac{x+3}{3}=\frac{y-5}{1}=\frac{z-2}{-5}\) -
Question 175 of 202
175. Question
If the angle between the line \(2(x+1)=y=z+4\) and the plane \(2 x-y+\sqrt{\lambda} z+4=0\) is \(\frac{\pi}{6}\), then the value of \(\lambda\) is: [Online April 19, 2014]
CorrectIncorrectHint
Given equation of line can be written as
\(
\frac{x+1}{1}=\frac{y}{2}=\frac{z+4}{2}
\)
Eqn of plane is \(2 x-y+\sqrt{\lambda} z+4=0\)
Since, angle between the line and the plane is \(\frac{\pi}{6}\) therefore
\(
\begin{aligned}
& \sin \frac{\pi}{6}=\frac{2(1)+2(-1)+2(\sqrt{\lambda})}{\sqrt{1+4+4} \sqrt{4+1+\lambda}} \\
& \frac{1}{2}=\frac{2-2+2 \sqrt{\lambda}}{\sqrt{9} \sqrt{5+\lambda}} \\
& \Rightarrow \frac{\sqrt{\lambda}}{\sqrt{5+\lambda}}=\frac{3}{4} \Rightarrow \frac{\lambda}{5+\lambda}=\frac{9}{16} \\
& \Rightarrow 7 \lambda=45 \Rightarrow \lambda=\frac{45}{7}
\end{aligned}
\) -
Question 176 of 202
176. Question
If the distance between planes, \(4 x-2 y-4 z+1=0\) and \(4 x-2 y-4 z+d=0\) is 7, then \(d\) is: [Online April 12, 2014]
CorrectIncorrectHint
Given planes are
\(
4 x-2 y-4 z+1=0
\)
and \(4 x-2 y-4 z+d=0\)
They are parallel.
Distance between them is \(\pm 7=\frac{d-1}{\sqrt{16+4+16}}\)
\(
\begin{aligned}
& \Rightarrow \frac{d-1}{6}= \pm 7 \Rightarrow d=42+1 \\
& \text { or }-42+1 \text { i.e. } d=-41 \text { or } 43 \text {. }
\end{aligned}
\) -
Question 177 of 202
177. Question
A symmetrical form of the line of intersection of the planes \(x=a y+b\) and \(z=c y+d\) is [Online April 12, 2014]
CorrectIncorrectHint
Given two planes :
\(
x-a y-b=0 \text { and } c y-z+d=0
\)
Let, \(l, m, n\) be the direction ratio of the required line. Since the required line is perpendicular to normal of both the plane, therefore \(l-a m=0\) and \(c m-n=0\)
\(
\begin{aligned}
& \Rightarrow l-a m+0 . n=0 \text { and } 0 . l+c m-n=0 \\
& \therefore \frac{l}{a-0}=\frac{m}{0+1}=\frac{n}{c-0}
\end{aligned}
\)
Hence, \(d . R\) of the required line are \(a, 1, c\). Hence, options (c) and (d) are rejected.
Now, the point \((a+b, 1, c+d)\) satisfy the equation of the two given planes.
\(\therefore\) Option (b) is correct. -
Question 178 of 202
178. Question
The plane containing the line \(\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{3}\) and parallel to the line \(\frac{x}{1}=\frac{y}{1}=\frac{z}{4}\) passes through the point: [Online April 11, 2014]
CorrectIncorrectHint
Equation of the plane containing the line \(\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{3}\) is
\(
a(x-1)+b(y-2)+c(z-3)=0 \dots(i)
\)
where \(a .1+b .2+c .3=0\)
\(
\text { i.e., } \quad a+2 b+3 c=0 \dots(ii)
\)
Since the plane (i) parallel to the line
\(
\frac{x}{1}=\frac{y}{1}=\frac{z}{4}
\)
\(
\begin{aligned}
& \therefore \quad a .1+b .1+c .4=0 \\
& \text { i.e., } \quad a + b +4 c =0 \dots(iii) \\
& \text { From (ii) and (iii), } \\
& \frac{a}{8-3}=\frac{b}{3-4}=\frac{c}{1-2}=k \text { (let) } \\
& \therefore \quad a=5 k, b=-k, c=-k
\end{aligned}
\)
On putting the value of \(a, b\) and \(c\) in equation (i),
\(
\begin{aligned}
& 5(x-1)-(y-2)-(z-3)=0 \\
& \Rightarrow \quad 5 x-y-z=0 \dots(iv)
\end{aligned}
\)
when \(x=1, y=0\) and \(z=5\); then
L.H.S. of equation (iv) \(=5 x-y-2\)
\(
=5 \times 1-0-5
\)
\(
\begin{aligned}
& =0 \\
& =\text { R.H.S. of equation (iv) }
\end{aligned}
\)
Hence coordinates of the point \((1,0,5)\) satisfy the equation plane represented by equations (iv), Therefore the plane passes through the point \((1,0,5)\) -
Question 179 of 202
179. Question
Equation of the plane which passes through the point of intersection of lines \(\frac{x-1}{3}=\frac{y-2}{1}=\frac{z-3}{2}\) and
\(
\frac{x-3}{1}=\frac{y-1}{2}=\frac{z-2}{3}
\)
and has the largest distance from the origin is: [Online April 9, 2014]CorrectIncorrectHint
Given equation of lines are
\(
\begin{aligned}
& \frac{x-1}{3}=\frac{y-2}{1}=\frac{z-3}{2} \dots(1) \\
& \text { and } \frac{x-3}{1}=\frac{y-1}{2}=\frac{z-2}{3} \dots(2)
\end{aligned}
\)
Any point on line (1) is \(P (3 \lambda+1, \lambda+2,2 \lambda+3)\) and on line (2) is \(Q (\mu+3,2 \mu+1,3 \mu+2)\).
On solving \(3 \lambda+1=\mu+3\) and \(\lambda+2=2 \mu+1\) we get \(\lambda=1, \mu=1\)
\(\therefore\) Point of intersection of two lines is \(R (4,3,5)\)
So, equation of plane \(\perp\) to \(OR\) where \(O\) is \((0,0,0)\) and passing through \(R\) is
\(
4 x+3 y+5 z=50
\) -
Question 180 of 202
180. Question
Distance between two parallel planes \(2 x+y+2 z=8\) and \(4 x+2 y+4 z+5=0\) is [JEE 2013]
CorrectIncorrectHint
\(2 x+y+2 z-8=0\) …(Plane 1)
\(2 x+y+2 z+\frac{5}{2}=0\) …(Plane 2)
Distance between Plane 1 and 2
\(
=\left|\frac{-8-\frac{5}{2}}{\sqrt{2^2+1^2+2^2}}\right|=\left|\frac{-21}{6}\right|=\frac{7}{2}
\) -
Question 181 of 202
181. Question
The equation of a plane through the line of intersection of the planes \(x+2 y=3, y-2 z+1=0\), and perpendicular to the first plane is: [Online April 25, 2013]
CorrectIncorrectHint
Equation of a plane through the line of intersection of the planes
\(
\begin{aligned}
& x+2 y=3, y-2 z+1=0 \text { is } \\
& (x+2 y-3)+\lambda(y-2 z+1)=0 \\
& \Rightarrow x+(2+\lambda) y-2 \lambda(z)-3+\lambda=0 \dots(i)
\end{aligned}
\)
Now, plane (i) is \(\perp\) to \(x+2 y=3\)
\(\therefore\) Their dot product is zero
i.e. \(1+2(2+\lambda)=0 \Rightarrow \lambda=-\frac{5}{2}\)
Thus, required plane is
\(
\begin{aligned}
& x+\left(2-\frac{5}{2}\right) y-2 \times \frac{-5}{2}(z)-3-\frac{5}{2}=0 \\
& \Rightarrow x-\frac{y}{2}+5 z-\frac{11}{2}=0 \\
& \Rightarrow 2 x-y+10 z-11=0
\end{aligned}
\) -
Question 182 of 202
182. Question
Let \(Q\) be the foot of perpendicular from the origin to the plane \(4 x-3 y+z+13=0\) and \(R\) be a point \((-1,-6)\) on the plane. Then length \(QR\) is : [Online April 22, 2013]
CorrectIncorrectHint
Let \(P\) be the image of \(O\) in the given plane.
Equation of the plane, \(4 x-3 y+z+13=0\)
\(OP\) is normal to the plane, therefore direction ratio of \(OP\) are proportional to \(4,-3,1\)
Since \(OP\) passes through \((0,0,0)\) and has direction ratio proportional to \(4,-3,1\). Therefore equation of \(O P\) is
\(
\frac{x-0}{4}=\frac{y-0}{-3}=\frac{z-0}{1}=r \text { (let) }
\)
\(
\therefore x=4 r, y=-3 r, z=r
\)
Let the coordinate of \(P\) be \((4 r,-3 r, r)\)
Since \(Q\) be the mid point of \(O P\)
\(
\therefore Q =\left(2 r,-\frac{3}{2} r, \frac{r}{2}\right)
\)
Since \(Q\) lies in the given plane
\(
\begin{aligned}
& 4 x-3 y+z+13=0 \\
& \therefore 8 r+\frac{9}{2} r+\frac{r}{2}+13=0 \\
& \Rightarrow r=\frac{-13}{8+\frac{9}{2}+\frac{1}{2}}=\frac{-26}{26}=-1 \\
& \therefore Q =\left(-2, \frac{3}{2},-\frac{1}{2}\right)
\end{aligned}
\)
\(
\begin{aligned}
QR & =\sqrt{(-1+2)^2+\left(1-\frac{3}{2}\right)^2+\left(-6+\frac{1}{2}\right)^2} \\
& =\sqrt{1+\frac{1}{4}+\frac{121}{4}}=3 \sqrt{\frac{7}{2}}
\end{aligned}
\) -
Question 183 of 202
183. Question
A vector \(\vec{n}\) is inclined to \(x\)-axis at \(45^{\circ}\), to \(y\)-axis at \(60^{\circ}\) and at an acute angle to \(z\)-axis. If \(\vec{n}\) is a normal to a plane passing through the point \((\sqrt{2},-1,1)\) then the equation of the plane is: [Online April 9, 2013]
CorrectIncorrectHint
Direction cosines of \(\vec{n}\) are \(\frac{1}{2}, \frac{1}{4}, \frac{1}{2}\). Equation of the plane,
\(
\frac{1}{2}(x-\sqrt{2})+\frac{1}{4}(y+1)+\frac{1}{2}(z-1)=0
\)
\(
\begin{aligned}
& \Rightarrow 2(x-\sqrt{2})+(y+1)+2(z-1)=0 \\
& \Rightarrow 2 x+y+2 z=2 \sqrt{2}-1+2 \\
& \Rightarrow 2 x+y+2 z=2 \sqrt{2}+1
\end{aligned}
\) -
Question 184 of 202
184. Question
A equation of a plane parallel to the plane \(x-2 y+2 z-5=0\) and at a unit distance from the origin is : [JEE 2012]
CorrectIncorrectHint
Given equation of a plane is \(x-2 y+2 z-5=0\)
So, Equation of parallel plane is given by
\(
x-2 y+2 z+d=0
\)
Now, it is given that distance from origin to the parallel plane is 1 .
\(
\therefore\left|\frac{d}{\sqrt{1^2+2^2+2^2}}\right|=1 \Rightarrow d= \pm 3
\)
So equation of required plane
\(
x-2 y+2 z \pm 3=0
\) -
Question 185 of 202
185. Question
The equation of a plane containing the line \(\frac{x+1}{-3}=\frac{y-3}{2} \quad \frac{z+2}{1}\) and the point \((0,7,-7)\) is [Online May 26, 2012]
CorrectIncorrectHint
The equation of the plane containing the line \(\frac{x+1}{-3}=\frac{y-3}{2}=\frac{z+2}{1}\) is a \((x+1)+b(y-3)+c(z\) \(+2)=0\) where
\(
-3 a+2 b+c=0 \dots(A)
\)
This passes through \((0,7,-7)\)
\(
\begin{aligned}
& \therefore a(0+1)+b(7-3)+c(-7+2)=0 \\
& \Rightarrow a+4 b-5 c=0 \dots(B)
\end{aligned}
\)
On solving equation (A) and (B) we get
\(
a=1, b=1, c=1
\)
\(\therefore\) Required plane is
\(
\begin{aligned}
& x+1+y-3+z+2=0 \\
& \Rightarrow x+y+z=0
\end{aligned}
\) -
Question 186 of 202
186. Question
Consider the following planes
\(
\begin{aligned}
& P: x+y-2 z+7=0 \\
& Q: x+y+2 z+2=0 \\
& R: 3 x+3 y-6 z-11=0
\end{aligned}
\) [Online May 26, 2012]CorrectIncorrectHint
Given planes are
\(
\begin{aligned}
& P: x+y-2 z+7=0 \\
& Q: x+y+2 z+2=0 \\
& \text { and } R: 3 x+3 y-6 z-11=0
\end{aligned}
\)
Consider Plane \(P\) and \(R\).
Here \(a_1=1, b_1=1, c_1=-2\)
and \(a_2=3, b_2=3, c_2=-6\)
Since, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}=\frac{1}{3}\)
therefore \(P\) and \(R\) are parallel. -
Question 187 of 202
187. Question
If the three planes \(x=5,2 x-5 a y+3 z-2=0\) and \(3 b x+y-3 z=0\) contain a common line, then \((a, b)\) is equal to [Online May 19, 2012]
CorrectIncorrectHint
Let the direction ratios of the common line be \(l, m\) and n.
\(
\begin{aligned}
& \therefore l \times 1+ m \times 0+ n \times 0=0 \Rightarrow l=0 \dots(1) \\
& 2 l-5 m a+3 n=0 \Rightarrow 5 m a-3 n=0 \dots(2) \\
& 3 l b+m-3 n=0 \Rightarrow m-3 n=0 \dots(3)
\end{aligned}
\)
Subtracting (3) from (1), we get
\(
m(5 a-1)=0
\)
Now, value of \(m\) can not be zero because if \(m=0\) then \(n=0\)
\(\Rightarrow l=m=n=0\) which is not possible.
Hence, \(5 a-1=0 \Rightarrow a=\frac{1}{5}\)
Thus, option (b) is correct. -
Question 188 of 202
188. Question
A line with positive direction cosines passes through the point \(P(2,-1,2)\) and makes equal angles with the coordinate axes. If the line meets the plane \(2 x+y+z=9\) at point \(Q\), then the length \(P Q\) equals [Online May 7, 2012]
CorrectIncorrectHint
Point \(P\) is \((2,-1,2)\)
Let this line meet at \(Q(h, k, w)\)
Direction ratio of this line is
\(
(h-2, k+1, w-2)
\)
Since, \(d c_s\) are equal \(\& d r_s\) are also equal,
So, \(h-2=k+1+w-2\)
\(\Rightarrow k=h-3\) and \(w=h\)
This line meets the plane
\(
\begin{aligned}
& 2 x+y+z=9 \text { at } Q, \text { so, } \\
& 2 h+k+w=9 \text { or } 2 h+h-3+h=9 \\
& \Rightarrow \quad 4 h-3=9 \Rightarrow h=3
\end{aligned}
\)
and \(k=0\) and \(w=3\)
Distance
\(
\begin{aligned}
P Q & =\sqrt{(3-2)^2+(0-(-1))^2+(3-2)^2} \\
& =\sqrt{1^2+1^2+1^2}=\sqrt{3}
\end{aligned}
\) -
Question 189 of 202
189. Question
The values of a for which the two points \((1, a, 1)\) and \((-3,0, a)\) lie on the opposite sides of the plane \(3 x+4 y-12 z\) \(+13=0\), satisfy [Online May 7, 2012]
CorrectIncorrectHint
Given equation of plane is
\(
3 x+4 y-12 z+13=0
\)
\((1, a, 1)\) and \((-3,0, a)\) satisfy the equation of plane.
\(\therefore\) We have
\(
3+4(a)-12+13=0 \text { and } 3(-3)-12(a)+13=0
\)
\(\Rightarrow 4+4 a=0\) and \(4-12 a=0\)
\(
\Rightarrow a=-1 \text { and } a=\frac{1}{3}
\)
Since, \((1, a, 1)\) and \((-3,0, a)\) lie on the opposite sides of the plane \(\therefore a=0\) -
Question 190 of 202
190. Question
The distance of the point \((1,-5,9)\) from the plane \(x-y+z\) \(=5\) measured along a straight \(x=y=z\) is [JEE 2011RS]
CorrectIncorrectHint
Equation of line through \(P(1,-5,9)\) and parallel to the plane \(x=y=z\) is
\(
\frac{x-1}{1}=\frac{y+5}{1}=\frac{z-9}{1}=\lambda(\text { say })
\)
\(
Q =(x=1+\lambda, y=-5+\lambda, z=9+\lambda)
\)
Given plane \(x-y+z=5\)
\(
\begin{aligned}
& \therefore \quad 1+\lambda+5-\lambda+9+\lambda=5 \\
& \Rightarrow \quad \lambda=-10 \\
& \therefore \quad Q=(-9,-15,-1)
\end{aligned}
\)
\(
\begin{aligned}
\therefore \quad PQ & =\sqrt{(1+9)^2+(15-5)^2+(9+1)^2} \\
& =\sqrt{300}=10 \sqrt{3}
\end{aligned}
\) -
Question 191 of 202
191. Question
If the angle between the line \(x=\frac{y-1}{2}=\frac{z-3}{\lambda}\) and the plane \(x+2 y+3 z=4\) is \(\cos ^{-1}\left(\sqrt{\frac{5}{14}}\right)\), then \(\lambda\) equals [2011]
CorrectIncorrectHint
If \(\theta\) be the angle between the given line and plane, then
\(
\begin{aligned}
& \sin \theta=\frac{1 \times 1+2 \times 2+\lambda \times 3}{\sqrt{1^2+2^2+\lambda^2} \cdot \sqrt{1^2+2^2+3^2}} \\
&=\frac{5+3 \lambda}{\sqrt{14} \cdot \sqrt{5+\lambda^2}} \\
& \Rightarrow \cos \theta=\sqrt{1-\frac{(5+3 \lambda)^2}{14\left(5+\lambda^2\right)}} \\
& \therefore \theta=\cos ^{-1} \sqrt{1-\frac{(5+3 \lambda)^2}{14\left(5+\lambda^2\right)}}
\end{aligned}
\)
But it is given that \(\theta=\cos ^{-1} \sqrt{\frac{5}{14}}\)
\(
\begin{aligned}
& \therefore \sqrt{1-\frac{(5+3 \lambda)^2}{14\left(5+\lambda^2\right.}}=\sqrt{\frac{5}{14}} \\
& \Rightarrow \lambda=\frac{2}{3}
\end{aligned}
\) -
Question 192 of 202
192. Question
Statement -1 : The point \(A(3,1,6)\) is the mirror image of the point \(B (1,3,4)\) in the plane \(x-y+z=5\).
Statement -2 : The plane \(x-y+z=5\) bisects the line segment joining \(A (3,1,6)\) and \(B (1,3,4)\). [JEE 2010]CorrectIncorrectHint
\(A (3,1,6) ; B =(1,3,4)\)
Mid-point of \(AB =(2,2,5)\) lies on the plane.
and d.r’s of \(A B=(2,-2,2)\)
d.r’s of normal to plane \(=(1,-1,1)\).
Direction ratio of \(AB\) and normal to the plane are
proportional therefore,
\(AB\) is perpendicular to the plane
\(\therefore\) A is image of \(B\)
Statement-2 is correct but it is not correct explanation. -
Question 193 of 202
193. Question
Let the line \(\frac{x-2}{3}=\frac{y-1}{-5}=\frac{z+2}{2}\) lie in the plane \(x+3 y-\alpha z+\beta=0\). Then \((\alpha, \beta)\) equals [JEE 2009]
CorrectIncorrectHint
\(\because\) The line \(\frac{x-2}{3}=\frac{y-1}{-5}=\frac{z+2}{2}\) lie in the plane \(x+3 y-\alpha z+\beta=0\)
\(\therefore P t(2,1,-2)\) lies on the plane
i.e. \(2+3+2 \alpha+\beta=0\)
or \(2 \alpha+\beta+5=0 \dots(i)\)
Also normal to plane will be perpendicular to line,
\(
\begin{aligned}
& \therefore 3 \times 1-5 \times 3+2 \times(-\alpha)=0 \\
& \Rightarrow \alpha=-6
\end{aligned}
\)
From equation (i) then, \(\beta=7\)
\(
\therefore(\alpha, \beta)=(-6,7)
\) -
Question 194 of 202
194. Question
The line passing through the points \((5,1, a)\) and \((3, b, 1)\) crosses the yz-plane at the point \(\left(0, \frac{17}{2}, \frac{-13}{2}\right)\). Then [JEE 2008]
CorrectIncorrectHint
Equation of line through \((5,1, a)\) and \((3, b, 1)\) is \(\frac{x-5}{-2}=\frac{y-1}{b-1}=\frac{z-a}{1-a}=\lambda\)
\(\therefore\) Any point on this line is a
\(
[-2 \lambda+5,(b-1) \lambda+1,(1-a) \lambda+a]
\)
It crosses yz plane where \(-2 \lambda+5=0\)
\(
\begin{aligned}
& \lambda=\frac{5}{2} \\
& \therefore \quad\left(0,(b-1) \frac{5}{2}+1,(1-a) \frac{5}{2}+a\right)=\left(0, \frac{17}{2}, \frac{-13}{2}\right) \\
& \Rightarrow(b-1) \frac{5}{2}+1=\frac{17}{2} \text { and }(1-a) \frac{5}{2}+a=-\frac{13}{2} \\
& \Rightarrow b=4 \text { and } a=6
\end{aligned}
\) -
Question 195 of 202
195. Question
Let \(L\) be the line of intersection of the planes \(2 x+3 y+z=1\) and \(x+3 y+2 z=2\). If \(L\) makes an angle \(\alpha\) with the positive \(x\)-axis, then \(\cos \alpha\) equals [JEE 2007]
CorrectIncorrectHint
Let the direction cosines of line \(L\) be \(l, m, n\), then
\(
2 l+3 m+n=0 \dots(i)
\)
and \(l+3 m+2 n=0 \dots(ii)\)
on solving equation (i) and (ii), we get
\(
\frac{l}{6-3}=\frac{m}{1-4}=\frac{n}{6-3} \quad \Rightarrow \quad \frac{l}{3}=\frac{m}{-3}=\frac{n}{3}
\)
Now \(\frac{l}{3}=\frac{m}{-3}=\frac{n}{3}=\frac{\sqrt{l^2+m^2+n^2}}{\sqrt{3^2+(-3)^2+3^2}}\)
\(
\because l^2+m^2+n^2=1
\)
\(
\begin{aligned}
& \therefore \frac{l}{3}=\frac{m}{-3}=\frac{n}{3}=\frac{1}{\sqrt{27}} \\
& \Rightarrow l=\frac{3}{\sqrt{27}}=\frac{1}{\sqrt{3}}, m=-\frac{1}{\sqrt{3}}, n=\frac{1}{\sqrt{3}}
\end{aligned}
\)
Line \(L\), makes an angle \(\alpha\) with +ve \(x\)-axis
\(
\therefore l=\cos \alpha \Rightarrow \cos \alpha=\frac{1}{\sqrt{3}}
\) -
Question 196 of 202
196. Question
The image of the point \((-1,3,4)\) in the plane \(x-2 y=0\) is [JEE 2006]
CorrectIncorrectHint
If \((\alpha, \beta, \gamma)\) be the image, then mid point of \((\alpha, \beta, \gamma)\) and \((-1,3,4)\) must lie on \(x-2 y=0\)
\(
\begin{aligned}
& \therefore \frac{\alpha-1}{2}-2\left(\frac{\beta+3}{2}\right)=0 \\
& \therefore \alpha-1-2 \beta-6=0 \Rightarrow \alpha-2 \beta=7 \dots(1)
\end{aligned}
\)
Also line joining \((\alpha, \beta, \gamma)\) and \((-1,3,4)\) should be parallel to the normal of the plane \(x-2 y=0\)
\(
\begin{aligned}
& \therefore \frac{\alpha+1}{1}=\frac{\beta-3}{-2}=\frac{\gamma-4}{0}=\lambda \\
& \Rightarrow \alpha=\lambda-1, \beta=-2 \lambda+3, \gamma=4 \ldots(2)
\end{aligned}
\)
From (1) and (2)
\(
\alpha=\frac{9}{5}, \beta=-\frac{13}{5}, \gamma=4
\)
None of the option matches. -
Question 197 of 202
197. Question
The distance between the line \(\vec{r}=2 \hat{i}-2 \hat{j}+3 \hat{k}+\lambda(i-j+4 k)\) and the plane \(\vec{r} \cdot(\hat{i}+5 \hat{j}+\hat{k})=5\) is [JEE 2005]
CorrectIncorrectHint
The given line is \(\vec{r}=2 \vec{i}-2 \vec{j}+3 \vec{k}+\lambda(\vec{i}-\vec{j}+4 \vec{k})\) and the plane is \(\vec{r} \cdot(\vec{i}+5 \vec{j}+\vec{k})=5\) or \(x+5 y+z=5\)
\(
\text { Required distance }=\left|\frac{2-10-2+3-5}{\sqrt{1+25+1}}\right|=\frac{10}{3 \sqrt{3}}
\) -
Question 198 of 202
198. Question
If the angle \(\theta\) between the line \(\frac{x+1}{1}=\frac{y-1}{2}\) \(=\frac{z-2}{2}\) and the plane \(2 x-y+\sqrt{\lambda} z+4=0\) is such that \(\sin \theta=\frac{1}{3}\) then the value of \(\lambda\) is [JEE 2005]
CorrectIncorrectHint
If \(\theta\) is the angle between line and plane then \(\left(\frac{\pi}{2}-\theta\right)\) is the angle between line and normal to plane given by
\(
\begin{aligned}
& \cos \left(\frac{\pi}{2}-\theta\right)=\frac{(\hat{i}+2 \hat{j}+2 \hat{k}) \cdot(2 \hat{i}-\hat{j}+\sqrt{\lambda} \hat{k})}{3 \sqrt{4+1+\lambda}} \\
& \cos \left(\frac{\pi}{2}-\theta\right)=\frac{2-2+2 \sqrt{\lambda}}{3 \times \sqrt{5}+\lambda} \\
& \Rightarrow \sin \theta=\frac{2 \sqrt{\lambda}}{3 \sqrt{5}+\lambda}=\frac{1}{3} \Rightarrow 4 \lambda=5+\lambda \\
& \Rightarrow \lambda=\frac{5}{3} .
\end{aligned}
\) -
Question 199 of 202
199. Question
Distance between two parallel planes \(2 x+y+2 z=8\) and \(4 x+2 y+4 z+5=0\) is [JEE 2004]
CorrectIncorrectHint
The planes are \(2 x+y+2 z-8=0 \dots(1)\).
and \(4 x+2 y+4 z+5=0\) or \(2 x+y+2 z+\frac{5}{2}=0 \dots(2)\)
\(\therefore\) Distance between (1) and (2)
\(
=\left|\frac{\frac{5}{2}+8}{\sqrt{2^2+1^2+2^2}}\right|=\left|\frac{21}{2 \sqrt{9}}\right|=\frac{7}{2}
\) -
Question 200 of 202
200. Question
Two system of rectangular axes have the same origin. If a plane cuts them at distances \(a, b, c\) and \(a^{\prime}, b^{\prime}, c^{\prime}\) from the origin then [JEE 2003]
CorrectIncorrectHint
Eq. of planes be \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 \& \frac{x}{a^{\prime}}+\frac{y}{b^{\prime}}+\frac{z}{c^{\prime}}=1\)
( \(\perp r\) distance on plane from origin is same.)
\(
\begin{aligned}
& \left|\frac{-1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}}\right|=\left|\frac{-1}{\sqrt{\frac{1}{a^{\prime 2}}+\frac{1}{b^{\prime 2}}+\frac{1}{c^{\prime 2}}}}\right| \\
& \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}-\frac{1}{a^{\prime 2}}-\frac{1}{b^{\prime 2}}-\frac{1}{c^{\prime 2}}=0
\end{aligned}
\) -
Question 201 of 202
201. Question
The d.r. of normal to the plane through \((1,0,0),(0,1,0)\) which makes an angle \(\pi / 4\) with plane \(x+y=3\) are [JEE 2002]
CorrectIncorrectHint
Equation of plane through \((1,0,0)\) is
\(
a(x-1)+b y+c z=0 \dots(i)
\)
(i) passes through \((0,1,0)\).
\(
\begin{aligned}
& -a+b=0 \Rightarrow b=a ; \text { Also, } \\
& \cos 45^{\circ}=\frac{a+a}{\sqrt{2\left(2 a^2+c^2\right)}} \Rightarrow 2 a=\sqrt{2 a^2+c^2} \\
& \Rightarrow 2 a^2=c^2 \quad \Rightarrow c=\sqrt{2} a .
\end{aligned}
\)
So d.r of normal are a, a \(\sqrt{2} a\) i.e. \(1,1, \sqrt{2}\). -
Question 202 of 202
202. Question
A plane which passes through the point \((3,2,0)\) and the line \(\frac{x-4}{1}=\frac{y-7}{5}=\frac{z-4}{4}\) is [JEE 2002]
CorrectIncorrectHint
As the point \((3,2,0)\) lies on the given line
\(
\frac{x-4}{1}=\frac{y-7}{5}=\frac{z-4}{4}
\)
There can be infinite many planes passing through this line. But here out of the four options only first option is satisfied by the coordinates of both the points \((3,2,0)\) and \((4,7,4)\)
\(\therefore \quad x-y+z=1\) is the required plane.