NCERT Exercise Probelms and Solution

Examples

Example 1: Locate the points (i) \((2,3,4)\)
(ii) \((-2,-2,3)\) in space.

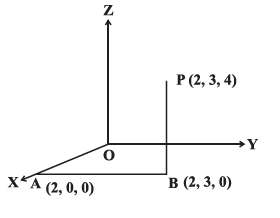
Solution: (i) To locate the point \((2,3,4)\) in space, we move 2 units from \(O\) along the positive direction of \(x\)-axis. Let this point be \(A\) \((2,0,0)\). From the point A moves 3 units parallel to +ve direction of \(y\)-axis. Let this point be \(B(2,3,0)\). From the point \(B\) moves 4 units along positive direction of \(z\)-axis. Let this point be \(P (2,3,4)\) Figure below.

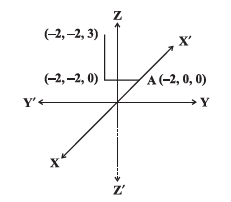
(ii) From the origin, move 2 units along the negative direction of \(x\)-axis. Let this point be \(A (-2,0,0)\). From the point A move 2 units parallel to negative direction of \(y\)-axis.
Let this point be \(B(-2,-2,0)\). From \(B\) move 3 units parallel to positive direction of \(z\) – axis. This is our required point \(Q (-2,-2,3)\) (Figure below.)

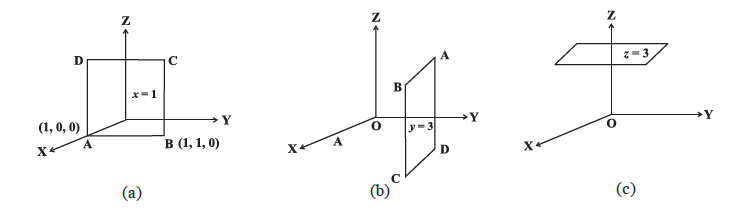
Example 2: Sketch the plane (i) \(x=1\) (ii) \(y=3\) (iii) \(z=4\)

Solution: (i) The equation of the plan \(x=0\) represents the \(y z\)-plane and equation of the plane \(x=1\) represents the plane parallel to \(y z\)-plane at a distance 1 unit above \(y z\) plane. Now, we draw a plane parallel to \(y z\)-plane at a distance 1 unit above \(y z\) plane Figure(a).
(ii) The equation of the plane \(y=0\) represents the \(x z\) plane and the equation of the plane \(y=3\) represents the plane parallel to \(x z\) plane at a distance 3 unit above \(x z\) plane (Figure (b)).
(iii) The equation of the plane \(z=0\) represents the \(x y\)-plane and \(z=3\) represents the plane parallel to \(x y\)-plane at a distance 3 unit above \(x y\)-plane (Figure(c)).

Example 3: Let \(L, M, N\) be the feet of the perpendiculars drawn from a point \(P(3,4,5)\) on the \(x, y\) and \(z\)-axes respectively. Find the coordinates of \(L, M\) and \(N\).

Solution: Since \(L\) is the foot of perpendicular from \(P\) on the \(x\)-axis, its \(y\) and \(z\) coordinates are zero. The coordinates of \(L\) is \((3,0,0)\). Similarly, the coordinates of \(M\) and \(N\) are \((0,4,0)\) and \((0,0,5)\), respectively.

Example 4: Let \(L , M , N\) be the feet of the perpendicular segments drawn from a point \(P (3,4,5)\) on the \(x y, y z\) and \(z x\)-planes, respectively. What are the coordinates of \(L , M\) and \(N\) ?

Solution: Since \(L\) is the foot of perpendicular segment from \(P\) on the \(x y\)-plane, \(z\)-coordinate is zero in the \(x y\)-plane. Hence, coordinates of \(L\) is \((3,4,0)\). Similarly, we can find the coordinates of of \(M(0,4,5)\) and \(N(3,0,5)\)

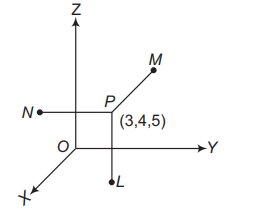
Example 5: Let \(L , M , N\) are the feet of the perpendiculars drawn from the point \(P(3,4,5)\) on the \(x y, y z\) and \(z x\)-planes, respectively. Find the distance of these points \(L , M , N\) from the point P, Figure below.

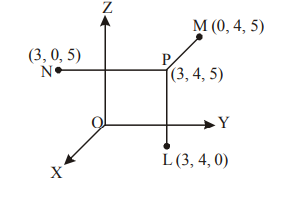
Solution: \(L\) is the foot of perpendicular drawn from the point \(P (3,4,5)\) to the \(x y\)-plane. Therefore, the coordinate of the point \(L\) is \((3,4,0)\). The distance between the point \((3,4\), 5 ) and \((3,4,0)\) is 5 . Similarly, we can find the lengths of the foot of perpendiculars on \(y z\) and \(z x\)-plane which are 3 and 4 units, respectively.

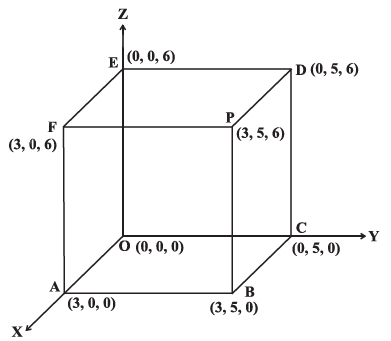
Example 6: Describe the vertices and edges of the rectangular parallelopiped with vertex \((3,5,6)\) placed in the first octant with one vertex at origin and edges of parallelopiped lie along \(x, y\) and \(z\)-axes.

Solution: The six planes of the parallelopiped are as follows:
Plane OABC lies in the \(x y\)-plane. The \(z\)-coordinate of every point in this plane is zero. \(z=0\) is the equation of this \(x y\)-plane. Plane PDEF is parallel to \(x y\)-plane and 6 unit distance above it. The equation of the plane is \(z=6\). Plane ABPF represents plane \(x=3\). Plane OCDE lies in the \(y z\)-plane and \(x=0\) is the equation of this plane. Plane AOEF lies in the \(x z\)-plane. The \(y\) coordinate of everypoint in this plane is zero. Therefore, \(y=0\) is the equation of plane.
Plane BCDP is parallel to the plane AOEF at a distance \(y=5\).
Edge OA lies on the \(x\)-axis. The \(x\)-axis has equation \(y=0\) and \(z=0\).
Edges OC and OE lie on \(y\)-axis and \(z\)-axis, respectively. The \(y\)-axis has its equation \(z=0, x=0\). The \(z\)-axis has its equation \(x=0, y=0\). The perpendicular distance of the point \(P(3,5,6)\) from the \(x\) -axis is \(\sqrt{5^2+6^2}=\sqrt{61}\).
The perpendicular distance of the point \(P (3,5,6)\) from \(y\)-axis and \(z\)-axis are \(\sqrt{3^2+6^2}=\sqrt{45}\) and \(\sqrt{3^2+5^2}=\), respectively.
The coordinates of the feet of perpendiculars from the point \(P(3,5,6)\) to the coordinate axes are A, C, E. The coordinates of feet of perpendiculars from the point \(P\) on the coordinate planes \(x y, y z\) and \(z x\) are \((3,5,0),(0,5,6)\) and \((3,0,6)\). Also, perpendicular distance of the point \(P\) from the \(x y, y z\) and \(z x\)-planes are 6,5 and 3 , respectively(Figure below shows it).

Exercise Problems