JEE Type Practice Problems
Circle
- A circle is the set of all points in a plane that are equidistant from a fixed point in the plane.
The equation of a circle with centre \((h, k)\) and the radius \(r\) is
\(
(x-h)^2+(y-k)^2=r^2 .
\) - The general equation of the circle is given by \(x^2+y^2+2 g x+2 f y+c=0\), where \(g, f\) and \(c\) are constants.
(a) The centre of this circle is \((-g,-f)\)
(b) The radius of the circle is \(\sqrt{g^2+f^2-c}\) - The general equation of the circle passing through the origin is given by \(x^2+y^2+2 g x+2 f y=0\).
- General equation of second degree i.e., \(a x^2+2 h x y+b y^2+2 g x+2 f y+c=0\) represent a circle if (i) the coefficient of \(x^2\) equals the coefficient of \(y^2\), i.e., \(a=b \neq 0\) and (ii) the coefficient of \(x y\) is zero, i.e., \(h=0\).
- The parametric equations of the circle \(x^2+y^2=r^2\) are given by \(x=r \cos \theta, y=r \sin \theta\) where \(\theta\) is the parameter and the parametric equations of the circle \((x-h)^2+(y-k)^2=r^2\) are given by
\(
\begin{aligned}
x-h & =r \cos \theta, y-k=r \sin \theta \\
x & =h+r \cos \theta, y=k+r \sin \theta .
\end{aligned}
\)
Parabola
- A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point in the plane.
- The equation of the parabola with focus at \((a, 0) a>0\) and directrix \(x=-a\) is
\(
y^2=4 a x
\) - Latus rectum of a parabola is a line segment perpendicular to the axis of the parabola, through the focus and whose end points lie on the parabola.
- Length of the latus rectum of the parabola \(y^2=4 a x\) is \(4 a\).
- Focal distance of a point: Let the equation of the parabola be \(y^2=4 a x\) and \(P (x, y)\) be a point on it. Then the distance of \(P\) from the focus \((a, 0)\) is called the focal distance of the point, i.e.,
\(
\begin{aligned}
FP & =\sqrt{(x-a)^2+y^2} \\
& =\sqrt{(x-a)^2+4 a x} \\
& =\sqrt{(x+a)^2} \\
& =|x+a|
\end{aligned}
\)
Ellipse
- An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant.
- The equation of an ellipse with foci on the \(x\)-axis is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\).
- Latus rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose end points lie on the ellipse.
- Length of the latus rectum of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is \(\frac{2 b^2}{a}\).
- The eccentricity of an ellipse is the ratio between the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse.
- We have two standard forms of the ellipse, i.e.,
(i) \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \quad\) and
(ii) \(\frac{x^2}{b^2}+\frac{y^2}{a^2}=1\),
In both cases \(a>b\) and \(b^2=a^2\left(1-e^2\right), e<1\). - Focal Distance: The focal distance of a point \((x, y)\) on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is
\(a-e|x|\) from the nearer focus
\(a+e|x|\) from the farther focus - Sum of the focal distances of any point on an ellipse is constant and equal to the length of the major axis.
Hyperbola
- The equation of a hyperbola with foci on the \(x\)-axis is : \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
- Latus rectum of hyperbola is a line segment perpendicular to the transverse axis through any of the foci and whose end points lie on the hyperbola.
- Length of the latus rectum of the hyperbola : \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is: \(\frac{2 b^2}{a}\).
- The eccentricity of a hyperbola is the ratio of the distances from the centre of the hyperbola to one of the foci and to one of the vertices of the hyperbola.
- We have two standard forms of the hyperbola, i.e.,
(i) \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) and
(ii) \(\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\)
Here \(b^2=a^2\left(e^2-1\right), e>1\). - Focal distance: The focal distance of any point \((x, y)\) on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is \(e|x|-a\) from the nearer focus
\(e|x|+a\) from the farther focus
Differences of the focal distances of any point on a hyperbola is constant and equal to the length of the transverse axis.
Quiz Summary
0 of 250 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 250 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 250
1. Question
A circle is given by \(x^2+(y-1)^2=1\), another circle \(C\) touches it externally and also the \(X\)-axis, then the locus of its centre is
CorrectIncorrectHint
Let the centre of circle \(C\) be \((h, k)\). Then as this circle touches axis of \(x\), its radius \(=|k|\)
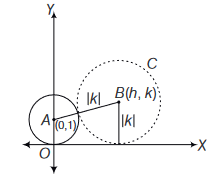
Also, it touches the given circle \(x^2+(y-1)^2=1\), centre \((0,1)\) radius 1 , externally
Therefore, the distance between centres = sum of radii
\(
\begin{array}{lc}
\Rightarrow & \sqrt{(h-0)^2+(k-1)^2}=1+|k| \\
\Rightarrow & h^2+k^2-2 k+1=(1+|k|)^2 \\
\Rightarrow & h^2+k^2-2 k+1=1+2|k|+k^2 \\
\Rightarrow & h^2=2 k+2|k|
\end{array}
\)
\(\therefore\) Locus of \((h, k)\) is, \(x^2=2 y+2|y|\)
Now if \(y>0\), it becomes \(x^2=4 y\)
and if \(y \leq 0\), it becomes \(x=0\)
\(\therefore\) Combining the two, the required locus is
\(
\left\{(x, y): x^2=4 y\right\} \cup\{(0, y): y \leq 0\}
\) -
Question 2 of 250
2. Question
If the circles \(x^2+y^2+2 a x+c y+a=0\) and \(x^2+y^2-3 a x+d y-1=0\) intersect in two distinct points \(P\) and \(Q\), then the line \(5 x+b y-a=0\) passes through \(P\) and \(Q\) for
CorrectIncorrectHint
\(
\begin{aligned}
& s_1=x^2+y^2+2 a x+c y+a=0 \\
& \quad s_2=x^2+y^2-3 a x+d y-1=0
\end{aligned}
\)
Equation of common chord of circles \(s_1\) and \(s_2\) is given by
\(
\begin{array}{ll}
s_1-s_2=0 & \\
\Rightarrow & 5 a x+(c-d) y+a+1=0
\end{array}
\)
Given, that \(5 x+b y-a=0\) passes through \(P\) and \(Q\)
\(\therefore\) The two equations should represent the same line
\(
\begin{array}{ll}
\Rightarrow & \frac{a}{1}=\frac{c-d}{b}=\frac{a+1}{-a} \\
\Rightarrow \quad & a+1=-a^2 \\
& a^2+a+1=0
\end{array}
\)
No real value of \(a\). -
Question 3 of 250
3. Question
A circle touches the \(X\)-axis and also touches the circle with centre at \((0,3)\) and radius 2 . The locus of the centre of the circle is
CorrectIncorrectHint
Equation of circle with centre \((0,3)\) and radius 2 is
\(
x^2+(y-3)^2=4
\)
Let centre of the variable circle is \((\alpha, \beta)\)
\(\because\) It touches \(X\)-axis.
\(\therefore\) It’s equation is \((x-\alpha)^2+(y+\beta)^2=\beta^2\)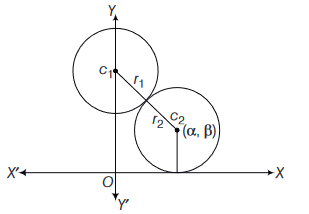
Circle touch externally
\(
\begin{array}{ll}
\Rightarrow & c_1 c_2=r_1+r_2 \\
\therefore & \sqrt{\alpha^2+(\beta-3)^2}=2+\beta \\
& \alpha^2+(\beta-3)^2=\beta^2+4+4 \beta \\
\Rightarrow & \alpha^2=10(\beta-1 / 2)
\end{array}
\)
\(\therefore\) Locus is \(x^2=10\left(y-\frac{1}{2}\right)\) which is a parabola. -
Question 4 of 250
4. Question
If a circle passes through the point \((a, b)\) and cuts the circle \(x^2+y^2=p^2\) orthogonally, then the equation of the locus of its centre is
CorrectIncorrectHint
Let the centre be \((\alpha, \beta)\)
\(\because\) It cuts the circle \(x^2+y^2=p^2\) orthogonally
\(\therefore\) Using \(2 g_1 g_2+2 f_1 f_2=c_1+c_2\), we get
\(
\begin{aligned}
& 2(-\alpha) \times 0+2(-\beta) \times 0=c_1-p^2 \\
& \Rightarrow \quad c_1=p^2 \\
&
\end{aligned}
\)
Let equation of circle is
\(
x^2+y^2-2 \alpha x-2 \beta y+p^2=0
\)
It passes through
\(
(a, b) \Rightarrow a^2+b^2-2 \alpha a-2 \beta b+p^2=0
\)
\(\therefore\) Locus of \((\alpha, \beta)\) is
\(
\therefore \quad 2 a x+2 b y-\left(a^2+b^2+p^2\right)=0
\) -
Question 5 of 250
5. Question
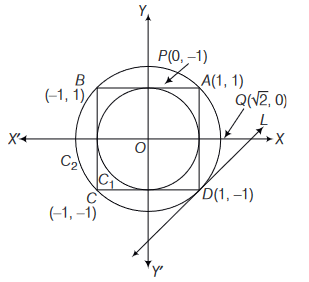
\(A B C D\) is a square of side length 2 units. \(C_1\) is the circle touching all the sides of the square \(A B C D\) and \(C_2\) is the circumcircle of square \(A B C D\). Lis a fixed line in the same plane and \(R\) is a fixed point.
If \(P\) is any point of \(C_1\) and \(Q\) is another point on \(C_2\), then \(\frac{P A^2+P B^2+P C^2+P D^2}{Q A^2+Q B^2+Q C^2+Q D^2}\) is equal toCorrectIncorrectHint
Without loss of generally it we can assume the square \(A B C D\) with its vertices \(A(1,1), B(-1,1), C(-1,-1), D(1,-1)\) \(P\) to be the point \((0,1)\) and \(Q\) as \((\sqrt{2}, 0)\).
\(
\begin{aligned}
& \text { Then, } \frac{P A^2+P B^2+P C^2+P D^2}{Q A^2+Q B^2+Q C^2+Q D^2} \\
& =\frac{1+1+5+5}{2\left[(\sqrt{2}-1)^2+1\right]+2\left((\sqrt{2}+1)^2+1\right)} \\
& =\frac{12}{16}=0.75 \\
&
\end{aligned}
\) -
Question 6 of 250
6. Question
\(A B C D\) is a square of side length 2 units. \(C_1\) is the circle touching all the sides of the square \(A B C D\) and \(C_2\) is the circumcircle of square \(A B C D\). Lis a fixed line in the same plane and \(R\) is a fixed point. If a circle is such that it touches the line \(L\) and the circle \(C_1\) externally, such that both the circles are on the same side of the line, then the locus of centre of the circle is
CorrectIncorrectHint
Let \(C^{\prime}\) be the circle touching circle \(C_1\) and \(L\), so that \(C_1\) and \(C^{\prime}\) are on the same side of \(L\). Let us draw a line \(T\) parallel to \(L\) at a distance equal to the radius of circle \(C_1\), on opposite side of \(L\). Then, the centre of \(C^{\prime}\) is equidistant from the centre of \(C_1\) and from line \(T\).
\(\Rightarrow\) locus of centre of \(C^{\prime}\) is a parabola.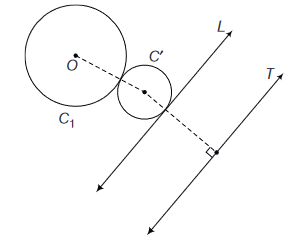
-
Question 7 of 250
7. Question
\(A B C D\) is a square of side length 2 units. \(C_1\) is the circle touching all the sides of the square \(A B C D\) and \(C_2\) is the circumcircle of square \(A B C D\). Lis a fixed line in the same plane and \(R\) is a fixed point. A line \(L^{\prime}\) through \(A\) is drawn parallel to \(B D\). Point \(S\) moves such that its distances from the line \(B D\) and the vertex \(A\) are equal. If locus of \(S\) cuts \(L^{\prime}\) at \(T_2\) and \(T_3\) and \(A C\) at \(T_1\), then area of \(\Delta T_1 T_2 T_3\) is
CorrectIncorrectHint
Since, \(S\) is equidistant from \(A\) and line \(B D\), it traces a parabola. Clearly, \(A C\) is the axis, \(A(1,1)\) is the focus and \(T_1\left(\frac{1}{2}, \frac{1}{2}\right)\) is the vertex of parabola.
\(
A T_1=\frac{1}{\sqrt{2}} .
\)
\(T_2 T_3\) = latusrectum of parabola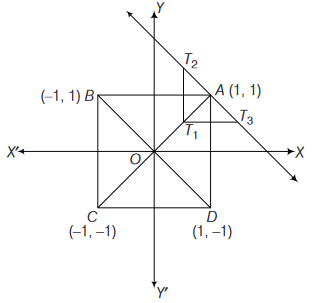
\(
\begin{gathered}
=4 \times \frac{1}{\sqrt{2}}=2 \sqrt{2} \\
\therefore \quad \text { Area }\left(\Delta T_1 T_2 T_3\right)=\frac{1}{2} \times \frac{1}{\sqrt{2}} \times 2 \sqrt{2}=1 \text { sq units. }
\end{gathered}
\) -
Question 8 of 250
8. Question
If the lines \(3 x-4 y-7=0\) and \(2 x-3 y-5=0\) are two diameters of a circle of area \(49 \pi\) square units, the equation of the circle is
CorrectIncorrectHint
Point of intersection of \(3 x-47-7=0\) and \(2 x-3 y-5=0\) is \((1,-1)\) which is the centre of the circle and radius \(=7\)
\(\therefore\) Equation is \((x-1)^2+(y+1)^2=49\)
\(
\Rightarrow \quad x^2+y^2-2 x+2 y-47=0
\) -
Question 9 of 250
9. Question
Let \(C\) be the circle with centre \((0,0)\) and radius 3 units. The equation of the locus of the mid-points of the chords of the circle \(C\) that subtend an angle of \(\frac{2 \pi}{3}\) at its centre is
CorrectIncorrectHint
Let \(M(h, k)\) be the mid-point of chord \(A B\) where
\(
\angle A O B=\frac{2 \pi}{3}
\)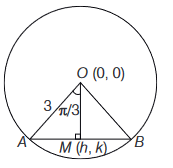
\(\therefore \quad \angle A O M=\frac{\pi}{3}\).
Also, \(\quad O M=3 \cos \frac{\pi}{3}=\frac{3}{2}\)
\(\Rightarrow \quad \sqrt{h^2+k^2}=\frac{3}{2}\)
\(\Rightarrow \quad h^2+k^2=\frac{9}{4}\)
\(\therefore\) Locus of \((h, k)\) is \(x^2+y^2=\frac{9}{4}\) -
Question 10 of 250
10. Question
Tangents are drawn from the point \((17,7)\) to the circle \(x^2+y^2=169\).
Statement I: The tangents are mutually perpendicular.
Statement II: The locus of the points from which mutually perpendicular tangents can be drawn to the given circle is \(x^2+y^2=338\)CorrectIncorrectHint
Equation of director circle of the given circle \(x^2+y^2=169\) is \(x^2+y^2=2 \times 169=338\).
We know from every point on director circle, the tangents drawn to given circle are perpendicular to each other. Here, \((17,7)\) lies on director circle.
\(\therefore\) The tangent from \((17,7)\) to given circle are mutually perpendicular. -
Question 11 of 250
11. Question
Consider a family of circles which are passing through the point \((-1,1)\) and are tangent to \(X\)-axis. If \((h, k)\) are the coordinate of the centre of the circles, then the set of values of \(k\) is given by the interval
CorrectIncorrectHint
Equation of circle whose centre is \((h, k)\)
\(
(x-h)^2+(y-k)^2=k^2
\)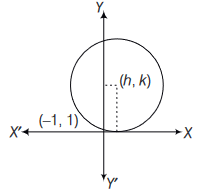
(radius of circle \(=k\) because circle is tangent to \(x\)-axis)
Equation of circle passing through \((-1,+1)\)
\(
\begin{array}{ll}
\therefore & (-1-h)^2+(1-k)^2=k^2 \\
\Rightarrow & 1+h^2+2 h+1+k^2-2 k=k^2 \\
\Rightarrow & h^2+2 h-2 k+2=0 D \geq 0 \\
\therefore & (2)^2-4 \times 1 .(-2 K+2) \geq 0 \\
\Rightarrow & 4-4(-2 k+2) \geq 0 \\
\Rightarrow & 1+2 k-2 \geq 0 \Rightarrow k \geq \frac{1}{2}
\end{array}
\) -
Question 12 of 250
12. Question
A circle \(C\) of radius 1 is inscribed in an equilateral triangle \(P Q R\). The points of contact of \(C\) with the sides \(P Q, Q R, R P\) are \(D, E, F\), respectively. The line \(P Q\) is given by the equation \(\sqrt{3} x+y-6=0\) and the point D is \(\left(\frac{3 \sqrt{3}}{2}, \frac{3}{2}\right)\) Further, it is given that the origin and the centre of \(C\) are on the same side of the line \(P Q\). The equation of circle \(C\) is
CorrectIncorrectHint
Slope of \(C D=\frac{1}{\sqrt{3}}\)
\(\therefore\) Parametric equation of \(C D\) is
\(
\frac{x-\frac{3 \sqrt{3}}{2}}{\frac{\sqrt{3}}{2}}=\frac{y-\frac{3}{2}}{\frac{1}{2}}= \pm 1
\)
\(\therefore\) Two possible coordinates of \(C\) are
\(
\left(\frac{\sqrt{3}}{2}+\frac{3 \sqrt{3}}{2}, \frac{1}{2}+\frac{3}{2}\right) \text { or }\left(\frac{-\sqrt{3}}{2}+\frac{3 \sqrt{3}}{2},-\frac{1}{2}+\frac{3}{2}\right)
\)
i.e. \((2 \sqrt{3}, 2)\) or \((\sqrt{3}, 1)\)
As \((0,0)\) and \(C\) lie on the same side of \(P Q\) \(\therefore(\sqrt{3}, 1)\) should be the coordinates of \(C\).
Remark : Remember \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) lie on the same or opposite side of a line \(a x+b y+c=0\) according as \(\frac{a x_1+b y_1+c}{a x_2+b y_2+c}>0\) or \(<0 . \therefore\) Equation of the circle is \((x-\sqrt{3})^2+(y-1)^2=1\) -
Question 13 of 250
13. Question
A circle \(C\) of radius 1 is inscribed in an equilateral triangle \(P Q R\). The points of contact of \(C\) with the sides \(P Q, Q R, R P\) are \(D, E, F\), respectively. The line \(P Q\) is given by the equation \(\sqrt{3} x+y-6=0\) and the point D is \(\left(\frac{3 \sqrt{3}}{2}, \frac{3}{2}\right)\) Further, it is given that the origin and the centre of \(C\) are on the same side of the line \(P Q\). Points \(E\) and \(F\) are given by
CorrectIncorrectHint
\(\triangle P Q R\) is an equilateral triangle, the incentre \(C\) must coincide with centroid of \(\triangle P Q R\) and \(D, E, F\) must coincide with the mid points of sides \(P Q, Q R\) and \(R P\) respectively.
Also, \(\quad \angle C P D=30^{\circ} \Rightarrow P D=\sqrt{3}\)
Writing the equation of side \(P Q\) in symmetric form we get,
\(
\begin{gathered}
\frac{x-\frac{3 \sqrt{3}}{2}}{-\frac{1}{2}}=\frac{y-\frac{3}{2}}{\frac{\sqrt{3}}{2}}=\mp \sqrt{3} \\
\therefore \text { Coordinates of } P=\left(\frac{\sqrt{3}}{2}+\frac{3 \sqrt{3}}{2}, \frac{-3}{2}+\frac{3}{2}\right)=(2 \sqrt{3}, 0) \\
\text { and coordinates of } Q=\left(\frac{-\sqrt{3}}{2}+\frac{3 \sqrt{3}}{2}, \frac{3}{2}+\frac{3}{2}\right)=(\sqrt{3}, 3)
\end{gathered}
\)
Let coordinates of \(R\) be \((\alpha, \beta)\), then using the formula for centriod of \(\Delta\) we get
\(
\frac{\sqrt{3}+2 \sqrt{3}+\alpha}{3}=\sqrt{3} \text { and } \frac{3+0+\beta}{3}=1
\)
\(\Rightarrow \quad \alpha=0\) and \(\beta=0\)
\(\therefore\) Coordinates of \(R=(0,0)\)
Now, coordinates of \(E=\) mid point of \(Q R=\left(\frac{\sqrt{3}}{2}, \frac{3}{2}\right)\) and coordinates of \(F=\) mid-point of \(P R=(\sqrt{3}, 0)\) -
Question 14 of 250
14. Question
A circle \(C\) of radius 1 is inscribed in an equilateral triangle \(P Q R\). The points of contact of \(C\) with the sides \(P Q, Q R, R P\) are \(D, E, F\), respectively. The line \(P Q\) is given by the equation \(\sqrt{3} x+y-6=0\) and the point D is \(\left(\frac{3 \sqrt{3}}{2}, \frac{3}{2}\right)\) Further, it is given that the origin and the centre of \(C\) are on the same side of the line \(P Q\). Equations of the sides \(Q R, R P\) are
CorrectIncorrectHint
Equation of side \(Q R\) is \(y=\sqrt{3} x\) and equation of side \(R P\) is
\(
y=0
\) -
Question 15 of 250
15. Question
Consider \(L_1: 2 x+3 y+p-3=0 ; L_2: 2 x+3 y+p+3=0\) where, \(p\) is a real number, and \(C: x^2+y^2+6 x-10 y+30=0\)
Statement I If line \(L_1\) is a chord of circle \(C\), then line \(L_2\) is not always a diameter of circle \(C\) and
Statement II If line \(L_1\) is a diameter of circle \(C\), then line \(L_2\) is not a chord of circle \(C\)CorrectIncorrectHint
The given circle is \(x^2+y^2+6 x-10 y+30=0\) Centre \((-3,5)\), radius \(=2\)
\(
\begin{array}{r}
L_1: 2 x+3 y+(p-3)=0 ; \\
L_2: 2 x+3 y+p+3=0
\end{array}
\)
Clearly, \(L_1 \| L_2\)
Distance between \(L_1\) and \(L_2\)
\(
=\left|\frac{p+3-p+3}{\sqrt{2^2+3^2}}\right|=\frac{6}{\sqrt{13}}<2
\)
\(\Rightarrow\) If one line is a chord of the given circle, other line may or may not the diameter of the circle.
Statement \(I\) is true and statement \(II\) is false. -
Question 16 of 250
16. Question
The point diametrically opposite to the point \(P(1,0)\) on the circle \(x^2+y^2+2 x+4 y-3=0\) is
CorrectIncorrectHint
The given circle is \(x^2+y^2+2 x+4 y-3=0\)
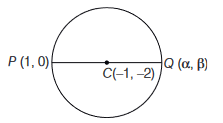
Centre \((-1,-2)\)
Let \(Q(\alpha, \beta)\) be the point diametrically opposite to the point \(P(1,0)\),
then, \(\frac{1+\alpha}{2}=-1\) and \(\frac{0+\beta}{2}=-2\)
\(
\Rightarrow \quad \alpha=-3, \beta=-4 \text {, So, } Q \text { is }(-3,-4)
\) -
Question 17 of 250
17. Question
Tangents drawn from the point \(P(1,8)\) to the circle \(x^2+y^2-6 x-4 y-11=0\) touch the circle at the points \(A\) and \(B\). The equation of the circumcircle of the triangle \(P A B\) is
CorrectIncorrectHint
Tangents \(P A\) and \(P B\) are drawn from the point \(P(1,3)\) to circle \(x^2+y^2-6 x-4 y-11=0\) with centre \(C(3,2)\)
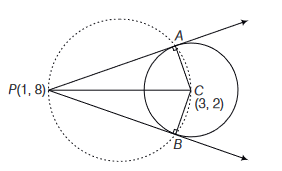
Clearly the circumcircle of \(\triangle P A B\) will pass through \(C\) and as \(\angle A=90^{\circ}, P C\) must be a diameter of the circle.
\(\therefore\) Equation of required circle is
\(
\Rightarrow \quad \begin{aligned}
(x-1)(x-3)+(y-2) & =0 \\
\Rightarrow \quad x^2+y^2-4 x-10 y+19 & =0
\end{aligned}
\) -
Question 18 of 250
18. Question
The centres of two circles \(C_1\) and \(C_2\) each of unit radius are at a distance of 6 units from each other. Let \(P\) be the mid point of the line segment joining the centres of \(C_1\) and \(C_2\) and \(C\) be a circle touching circles \(C_1\) and \(C_2\) externally. If a common tangent to \(C_1\) and \(C\) passing through \(P\) is also a common tangent to \(C_2\) and \(C\), then the radius of the circle \(C\) is
CorrectIncorrectHint
Let \(r\) be the radius of required circle.
Clearly, in \(\Delta C_1 C C_2, C_1 C=C_2 C=r+1\) and \(P\) is mid-point of \(C_1 C_2\)
\(
\begin{array}{ll}
\therefore & C P \perp C_1 C_2 \\
\text { Also, } & P M \perp C C_1
\end{array}
\)
Now, \(\triangle P M C_1 \sim \triangle C P C_1\) (by \(A A\) similarity)
\(
\therefore \quad \frac{M C_1}{P C_1}=\frac{P C_1}{C C_1}
\)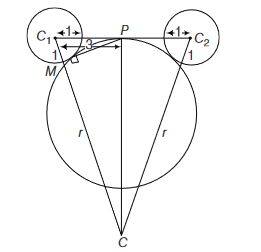
\(
\Rightarrow \quad \frac{1}{3}=\frac{3}{r+1} \Rightarrow r+1=9 \Rightarrow r=8 \text {. }
\) -
Question 19 of 250
19. Question
If \(P\) and \(Q\) are the points of intersection of the circles \(x^2+y^2+3 x+7 y+2 p-5=0\) and \(x^2+y^2+2 x+2 y-p^2=0\) then there is a circle passing through \(P, Q\) and \((1,1)\) for :
CorrectIncorrectHint
The given circles are
\(
\begin{aligned}
& S_1 \equiv x^2+y^2+3 x+7 y+2 p-5=0 \dots(i) \\
& S_2 \equiv x^2+y^2+2 x+2 y-p^2=0 \dots(ii)
\end{aligned}
\)
\(\therefore\) Equation of common chord \(P Q\) is \(S_1-S_2=0\)
\(
\Rightarrow \quad L \equiv x+5 y+p^2+2 p-5=0
\)
\(\Rightarrow\) Equation of circle passing through \(P\) and \(Q\) is \(S_1+\lambda L=0\)
\(
\Rightarrow\left(x^2+y^2+3 x+7 y+2 p-5\right)+\lambda\left(x+5 y+p^2+2 p-5\right)=0
\)
As it passes through \((1,1)\), therefore
\(
\begin{array}{ll}
\Rightarrow & (7+2 p)+\lambda\left(2 p+p^2+1\right)=0 \\
\Rightarrow \quad & \lambda=-\frac{2 p+7}{(p+1)^2}
\end{array}
\)
which does not exist for \(p=-1\) -
Question 20 of 250
20. Question
The circle \(x^2+y^{2}=4 x+8 y+5\) intersects the line \(3 x-4 y=m\) at two distinct points if
CorrectIncorrectHint
Circle \(x^2+y^2-4 x-8 y-5=0\)
\(
\begin{aligned}
& \text { Centre }=(2,4) \\
& \text { Radius }=\sqrt{4+16+5}=5
\end{aligned}
\)
If circle is intersecting line \(3 x-4 y=m\), at two distinct points. \(\Rightarrow\) length of perpendicular from centre to the line \(<\) radius
\(
\begin{array}{lc}
\Rightarrow & \frac{|6-16-m|}{5}<5 \\
\Rightarrow & |10+m|<25 \\
\Rightarrow & -25<m+10<25 \\
\Rightarrow & -35<m<15
\end{array}
\) -
Question 21 of 250
21. Question
The circle passing through the point \((-1,0)\) and touching the \(Y\)-axis at \((0,2)\) also passes through the point.
CorrectIncorrectHint
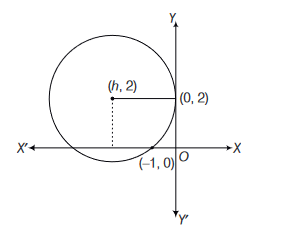
\(\Rightarrow \quad(-1-h)^2+4=h^2 \Rightarrow h=\frac{-5}{2}\)
\(\therefore \quad\) Centre \(\left(\frac{-5}{2}, 2\right)\) and \(r=\frac{5}{2}\)
Distance of centre from \((-4,0)\) is \(\frac{5}{2}\)
\(\therefore\) It lies on the circle. -
Question 22 of 250
22. Question
The straight line \(2 x-3 y=1\) divides the circular region \(x^2+y^2 \leq 6\) into two parts.
If \(S=\left\{\left(2 \frac{3}{4}\right)\left(\frac{5}{2}, \frac{3}{4}\right)\left(\frac{1}{4},-\frac{1}{4}\right)\left(\frac{1}{8}, \frac{1}{4}\right)\right\}\) then the number of point(s) in \(S\) lying inside the smaller part isCorrectIncorrectHint
The smaller region of circle is the region given by
\(
\begin{array}{ll}
& x^2+y^2 \leq 6 \dots(i) \\
\text { and } \quad & 2 x-3 y \geq 1 \dots(ii)
\end{array}
\)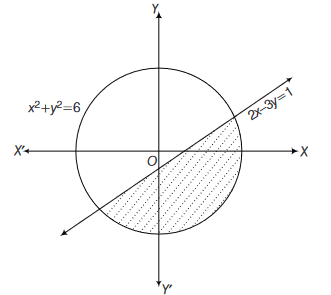
We observe that only two points \(\left(2, \frac{3}{4}\right)\) and \(\left(\frac{1}{4},-\frac{1}{4}\right)\) satisfy both the inequations Eqs. (i) and (ii), we get \(\therefore 2\) points in \(S\) lie inside the smaller part.
-
Question 23 of 250
23. Question
The two circles \(x^2+y^2=a x\) and \(x^2+y^2=c^2(c>0)\) touch each other if
CorrectIncorrectHint
As centre of one circle is \((0,0)\) and other circle passes through \((0,0)\), therefore
\(
\begin{array}{ll}
\text { Aslo, } \quad & C_1\left(\frac{a}{2}, 0\right) C_2(0,0) \\
& r_1=\frac{|a|}{2}, r_2=c \\
& C_1 C_2=r_1-r_2=\frac{|a|}{2} \\
\Rightarrow \quad & c-\frac{|a|}{2}=\frac{|a|}{2} \Rightarrow c=|a|
\end{array}
\)
If the two circles touch each other, then they must touch each other internally. -
Question 24 of 250
24. Question
The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line \(4 x-5 y=20\) to the circle \(x^2+y^2=9\) is
CorrectIncorrectHint
Any point \(P\) on line \(4 x-5 y=20\) is \(\left(\alpha, \frac{4 \alpha-20}{5}\right)\)
Equation of chord of contact \(A B\) to the circle \(x^2+y^2=9\)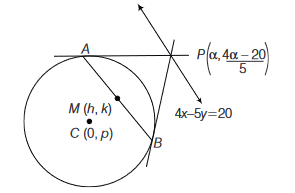
drawn from point \(P\left(\alpha, \frac{4 \alpha-20}{5}\right)\) is
\(
x \cdot \alpha+y \cdot\left(\frac{4 \alpha-20}{5}\right)=9 \dots(i)
\)
Also, the equation of chord \(A B\) whose mid-point is \((h, k)\) is
\(
h x+k y=h^2+k^2 \dots(ii)
\)
\(\because\) Eqs. (i) and (ii) represent the same line, therefore
\(
\frac{h}{\alpha}=\frac{k}{\frac{4 \alpha-20}{5}}=\frac{h^2+k^2}{9}
\)
\(
\begin{array}{lrl}
\Rightarrow & 5 k \alpha & =4 h \alpha-20 h \\
\text { and } & 9 h & =\alpha\left(h^2+k^2\right) \\
\Rightarrow & \alpha & =\frac{20 h}{4 h-5 k} \text { and } \alpha=\frac{9 h}{h^2+k^2}
\end{array}
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{20 h}{4 h-5 k}=\frac{9 h}{h^2+k^2} \\
& \Rightarrow \quad 20\left(h^2+k^2\right)=9(4 h-5 k) \\
& \therefore \text { Locus of }(h, k) \text { is } 20\left(x^2+y^2\right)-36 x+45 y=0
\end{aligned}
\) -
Question 25 of 250
25. Question
A tangent PT is drawn to the circle \(x^2+y^2=4\) at the point \(P(\sqrt{3}, 1)\). A straight line \(L\) perpendicular to PT is a tangent to the circle \((x-3)^2+y^2=1\). A possible equation of \(L\) is
CorrectIncorrectHint
Equation of tangent \(P T\) to the circle \(x^2+y^2=4\) at the point \(P(\sqrt{3}, 1)\) is \(x \sqrt{3}+y=4\)
Let the line \(L\), perpendicular to tangent \(P T\) be
\(
x-y \sqrt{3}+\lambda=0 \dots(i)
\)
As it is tangent to the circle \((x-3)^2+y^2=1\)
\(\therefore\) length of perpendicular from centre of circle to the tangent
\(=\) radius of circle.
\(\Rightarrow \quad\left|\frac{3+\lambda}{2}\right|=1 \Rightarrow \lambda=-1\) or -5
From Eq. (i)
Equation of \(L\) can be
\(
\begin{aligned}
& x-\sqrt{3} y=1 \\
& x-\sqrt{3} y=5
\end{aligned}
\) -
Question 26 of 250
26. Question
A tangent PT is drawn to the circle \(x^2+y^2=4\) at the point \(P(\sqrt{3}, 1)\). A straight line \(L\) perpendicular to PT is a tangent to the circle \((x-3)^2+y^2=1\). A common tangent of the two circles is
CorrectIncorrectHint
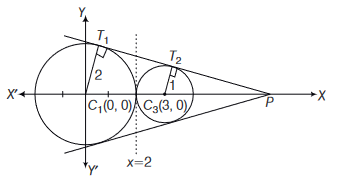
Equation of tangent \(P T\) to the circle \(x^2+y^2=4\) at the point \(P(\sqrt{3}, 1)\) is \(x \sqrt{3}+y=4\)
Let the line \(L\), perpendicular to tangent \(P T\) be
\(
x-y \sqrt{3}+\lambda=0 \dots(i)
\)
As it is tangent to the circle \((x-3)^2+y^2=1\)
\(\therefore\) length of perpendicular from centre of circle to the tangent
\(=\) radius of circle.
\(\Rightarrow \quad\left|\frac{3+\lambda}{2}\right|=1 \Rightarrow \lambda=-1\) or -5
From the figure it is clear that the intersection point of two direct common tangents lies on \(X\)-axis.
Aslo
\(\Delta P T_1 C_1 \sim \Delta P T_2 C_2\)
\(\Rightarrow \quad P C_1: P C_2=2: 1\)
or \(P\) divides \(C_1 C_2\) in the ratio \(2: 1\) externally
\(\therefore\) Coordinates of \(P\) are \((6,0)\)
Let the equation of tangent through \(P\) be
\(
y=m(x-6)
\)
As it touches \(x^2+y^2=4\)
\(
\begin{aligned}
& \therefore \quad\left|\frac{6 m}{\sqrt{m^2+1}}\right|=2 \\
& \Rightarrow \quad 36 m^2=4\left(m^2+1\right) \\
& \Rightarrow \quad m= \pm \frac{1}{2 \sqrt{2}} \\
&
\end{aligned}
\)
\(\therefore\) Equations of common tangents are \(y= \pm \frac{1}{2 \sqrt{2}}(x-6)\)
Also \(x=2\) is the common tangent to the two circles. -
Question 27 of 250
27. Question
The length of the diameter of the circle which touches the \(X\)-axis at the point \((1,0)\) and passes through the point \((2,3)\) is
CorrectIncorrectHint
Let centre of the circle be \((1,4)\)
\([\because\) circle touches \(x\)-axis at \((1,0)]\)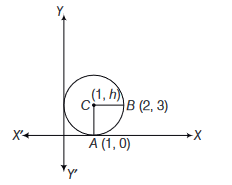
Let the circle passes through the point \(B(2,3)\)
\(\therefore \quad C A=C B \text { (radius) }\)
\(
\begin{array}{lc}
\Rightarrow & C A^2=C B^2 \\
\Rightarrow & (1-1)^2+(h-0)^2=(1-2)^2+(h-3)^2 \\
\Rightarrow & h^2=1+h^2+9-6 h \\
\Rightarrow & h=\frac{10}{6}=\frac{5}{3}
\end{array}
\)
Thus, diameter is \(2 h=\frac{10}{3}\). -
Question 28 of 250
28. Question
The circle passing through \((1,-2)\) and touching the axis of \(x\) at \((3,0)\) also passes through the point
CorrectIncorrectHint
Since, circle touches \(X\)-axis at \((3,0)\)
\(\therefore\) The equation of circle be
\(
(x-3)^2+(y-0)^2+\lambda y=0
\)
As it passes through \((1,-2)\)
\(\therefore\) Put \(x=1, y=-2\)
\(
\Rightarrow \quad(1-3)^2+(-2)^2+\lambda(-2)=0 \Rightarrow \lambda=4
\)
\(\therefore\) Equation of circle is \((x-3)^2+y^2-8=0\)
Now, from the options \((5,-2)\) satisfies equation of circle. -
Question 29 of 250
29. Question
Circle(s) touching \(X\)-axis at a distance 3 from the origin and having an intercept of length \(2 \sqrt{7}\) on \(Y\)-axis is (are)
CorrectIncorrectHint
There can be two possibilities for the given circle as shown in the figure
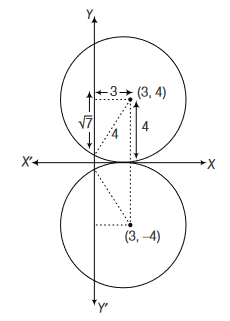
\(\therefore\) The equations of circle can be
\(
\begin{array}{ll}
& (x-3)^2+(y-4)^2=4^2 \\
\text { or } & (x-3)^2+(y+4)^2=4^2 \\
\text { i.e. } & x^2+y^2-6 x+8 y+9=0 \\
\end{array}
\) -
Question 30 of 250
30. Question
Let \(C\) be the circle with centre at \((1,1)\) and radius \(=1\). If \(T\) is the circle centred at \((0, y)\), passing through origin and touching the circle \(C\) externally, then the radius of \(T\) is equal to
CorrectIncorrectHint
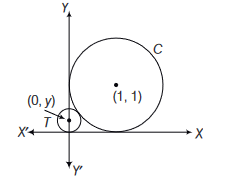
Equation of circle \(C=(x-1)^2+(y-1)^2=1\)
Radius of \(T=|y|\)
\(T\) touches \(C\) externally therefore,
Distance between the centres \(=\) sum of their radii
\(
\begin{array}{cc}
\Rightarrow & \sqrt{(0-1)^2+(y-1)^2}=1+|y| \\
\Rightarrow & (0-1)^2+(y-1)^2=(1+|y|)^2 \\
\Rightarrow & 1+y^2+1-2 y=1+y^2+2|y| \\
& 2|y|=1-2 y
\end{array}
\)
If \(y>0\) then, \(2 y=1-2 y \Rightarrow y=\frac{1}{4}\)
If \(y<0\) then, \(-2 y=1-2 y \Rightarrow 0=1\) (not possible)
\(
\therefore \quad y=\frac{1}{4}
\) -
Question 31 of 250
31. Question
A circle \(S\) passes through the point \((0,1)\) and is orthogonal to the circles \((x-1)^2+y^2=16\) and \(x^2+y^2=1\). Then
CorrectIncorrectHint
Let the equation of circle be
\(
x^2+y^2+2 g x+2 f y+c=0
\)
It passes through \((0,1)\)
\(
\therefore \quad 1+2 f+c=0 \dots(i)
\)
This circle is orthogonal to \((x-1)^2+y^2=16\) i.e.
\(
\begin{array}{r}
x^2+y^2-2 x-15=0 \\
x^2+y^2-1=0
\end{array}
\)
\(\therefore\) We should have
\(
2 g(-1)+2 f(0)=c-15
\)
\(
2 g+c-15=0 \dots(ii)
\)
Solving Eqs. (i), (ii) and (iii), we get
\(
c=1, g=7, f=-1
\)
\(\therefore\) Required circle is
\(
x^2+y^2+14 x-2 y+1=0
\)
With centre \((-7,1)\) and radius \(=7\) -
Question 32 of 250
32. Question
Locus of the image of the point \((2,3)\) in the line \((2 x-3 y+4)+k(x-2 y+3)=0, k \in R\), is a
CorrectIncorrectHint
Intersection point of \(2 x-3 y+4=0\) and \(x-2 y+3=0\) is \((1,2)\)
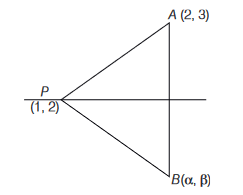
Since, \(P\) is the fixed point for given family of lines
So,
\(
\begin{aligned}
& P B=P A \\
& (\alpha-1)^2+(\beta-2)^2=(2-1)^2+(3-2)^2 \\
& (\alpha-1)^2+(\beta-2)^2=1+1=2 \\
& (x-1)^2+(y-2)^2=(\sqrt{2})^2
\end{aligned}
\)
\(
(x-a)^2+(y-b)^2=r^2
\)
Therefore, given locus is a circle with centre \((1,2)\) and radius \(\sqrt{2}\). -
Question 33 of 250
33. Question
The number of common tangents to the circles \(x^2+y^2-4 x-6 x-12=0\) and \(x^2+y^2+6 x+18 y+26=0\), is
CorrectIncorrectHint
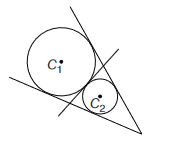
\(
x^2+y^2-4 x-6 y-12=0 \dots(i)
\)
Centre \(C_1=(2,3)\) and Radius, \(r_1=5\) units
\(
x^2+y^2+6 x+18 y+26=0 \dots(ii)
\)
\(
\begin{aligned}
& \text { Centre, } C_2=(-3,-9) \\
& \text { and radius, } r_2=8 \text { units } \\
& \left|C_1 C_2\right|=\sqrt{(2+3)^2+(3+9)^2}=13 \text { units } \\
& r_1+r_2=5+8=13 \\
& \therefore\left|C_1 C_2\right|=r_1+r_2 \\
&
\end{aligned}
\)
Therefore, there are three common tangents. -
Question 34 of 250
34. Question
The centres of those circles which touch the circle, \(x^2+y^2-8 x-8 y-4=0\), externally and also touch the \(X\)-axis, lie on
CorrectIncorrectHint
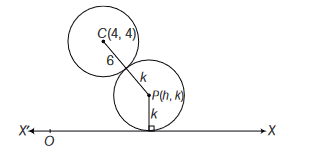
For the given circle, centre \(:(4,4)\), radius \(=6\)
\(
\begin{aligned}
6+k & =\sqrt{(h-4)^2+(k-4)^2} \\
(h-4)^2 & =20 k+20
\end{aligned}
\)
\(\therefore\) locus of \((h, k)\) is \((x-4)^2=20(y+1)\), which is parabola. -
Question 35 of 250
35. Question
If one of the diameters of the circle, given by the equation, \(x^2+y^2-4 x+6 y-12=0\), is a chord of a circle \(S\), whose centre is at \((-3,2)\), then the radius of \(S\) is
CorrectIncorrectHint
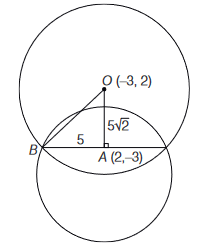
Centre of \(S: O(-3,2)\) and centre of given circle is \(A(2,-3)\)
\(
\Rightarrow \quad O A=5 \sqrt{2}
\)
Also, \(\quad A B=5 \quad(\because A B=\) radius of the given circle)
Now, in \(\triangle O A B\),
\(
\begin{aligned}
& (O B)^2=(A B)^2+(O A)^2=25+50=75 \\
& \therefore \quad O B=5 \sqrt{3} \\
&
\end{aligned}
\) -
Question 36 of 250
36. Question
Let \(R S\) be the diameter of the circle \(x^2+y^2=1\), where \(S\) is the point \((1,0)\). Let \(P\) be a variable point (other than \(R\) and \(S\) ) on the circle and tangents to the circle at \(S\) and \(P\) meet at the point \(Q\). The normal to the circle at \(P\) intersects a line drawn through \(Q\) parallel to \(R S\) at point \(E\). Then the locus of \(E\) passes through the point(s)
CorrectIncorrectHint
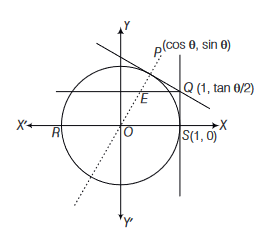
Circle : \(x^2+y^2=1\)
Equation of tangent at \(P(\cos \theta, \sin \theta)\)
\(
x \cos \theta+y \sin \theta=1 \dots(i)
\)
Equation of normal at \(P\)
\(
y=x \tan \theta \dots(ii)
\)
Equation of tangent at \(S\) is \(x=1\)
\(
\therefore \quad Q\left(1, \frac{1-\cos \theta}{\sin \theta}\right)=Q\left(1, \tan \frac{\theta}{2}\right)
\)
\(\therefore\) Equation of line through \(Q\) and parallel to \(R S\) is \(y=\tan \frac{\theta}{2}\)
\(\therefore\) Intersection point \(E\) of normal and \(y=\tan \frac{\theta}{2}\)
\(
\tan \frac{\theta}{2}=x \tan \theta
\)
\(
\begin{array}{cc}
\Rightarrow & x=\frac{1-\tan ^2 \frac{\theta}{2}}{2} \\
\therefore & \text { Locus of } E: x=\frac{1-y^2}{2} \text { or } y^2=1-2 x
\end{array}
\)
It is satisfied by the points \(\left(\frac{1}{3}, \frac{1}{\sqrt{3}}\right)\) and \(\left(\frac{1}{3}, \frac{-1}{\sqrt{3}}\right)\). -
Question 37 of 250
37. Question
For how many values of \(p\), the circle \(x^2+y^2+2 x+4 y-p=0\) and the co-ordinate axes have exactly three common points?
CorrectIncorrectHint
(2) Equation of circle can be written as
\(
(x+1)^2+(y+2)^2=p+5 \dots(i)
\)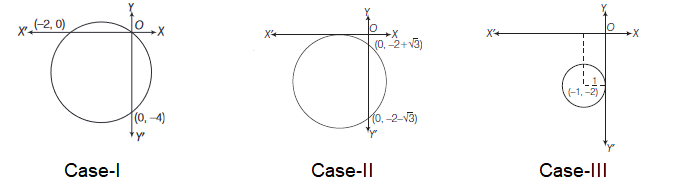
Case I. For \(p=0\), circle passes through origin and cuts \(x\)-axis and \(y\)-axis at \((-2,0)\) and \((0,-4)\) respectively.
Case II. If circle touch X-axis, then
\(
(1)^2=-p \Rightarrow p=-1
\)
From Eq. (i), we get
\(
(x+1)^2+(y+2)^2=2^2
\)
Cut off \(Y\)-axis at (put \(x=0\) )
\(
\begin{aligned}
&(y+2)^2=3 \\
& \Rightarrow y=-2 \pm \sqrt{3} \\
& \text { or }(0,-2 \pm \sqrt{3})
\end{aligned}
\)
Case III. If circle touch \(Y\)-axis, then
\((2)^2=-p\)
\(
\Rightarrow \quad p=-4
\)
From Eq. (i), we get
\(
(x+1)^2+(y+2)^2=1
\)
Cut off \(X\)-axis at (put \(y=0\) )
\(
(x+1)^2=-3 \text { (impossible) }
\) -
Question 38 of 250
38. Question
Tangent to the curve \(y=x^2+6\) at a point \((1,7)\) touches the circle \(x^2+y^2+16 x+12 y+c=0\) at a point \(Q\). Then the coordinates of \(Q\) are
CorrectIncorrectHint
Equation of tangent at \((1,7)\) to \(y=x^2+6\)
\(\Rightarrow \quad \frac{1}{2}(y+7)=x \cdot 1+6\)
\(\Rightarrow \quad y=2 x+5 \dots(i)\)
This tangent also touches the circle.
\(
x^2+y^2+16 x+12 y+c=0 \dots(ii)
\)
Now, solving Eqs. (i) and (ii), we get
\(
\Rightarrow \quad \begin{aligned}
x^2+(2 x+5)^2+16 x+12(2 x+5)+c & =0 \\
\Rightarrow \quad 5 x^2+60 x+85+c & =0
\end{aligned}
\)
Since, roots are equal, so
\(
\begin{aligned}
& B^2-4 A C=0 \\
& \Rightarrow \quad(60)^2-4 \times 5 \times(85+c)=0 \\
& \Rightarrow \quad 85+c=180 \\
& \Rightarrow \quad 5 x^2+60 x+180=0 \\
& \Rightarrow \quad x=-\frac{60}{10}=-6 \quad \Rightarrow \quad y=-7 \\
&
\end{aligned}
\)
Hence, point of contact is \((-6,-7)\). -
Question 39 of 250
39. Question
Let \(P\) be a point \((1,0)\) and \(Q\) a point on the locus \(y^2=8 x\). The locus of mid-point of \(P Q\) is
CorrectIncorrectHint
\(P \equiv(1,0)\), let \(Q \equiv(h, k)\)
such that \(\quad k^2=8 h \dots(i)\)
Let \((\alpha, \beta)\) be the mid-point of \(P Q\).
\(
\begin{array}{ll}
\therefore & \alpha=\frac{h+1}{2}, \beta=\frac{k+0}{2} \\
\Rightarrow & h=2 \alpha-1, k=2 \beta
\end{array}
\)
From Eq. (i), we get
\(
\begin{aligned}
(2 \beta)^2 & =8(2 \alpha-1) \\
\Rightarrow \quad \beta^2 & =4 \alpha-2 \\
\Rightarrow \quad \beta^2-4 \alpha+2 & =0
\end{aligned}
\)
\(\therefore\) Required locus is \(y^2-4 x+2=0\). -
Question 40 of 250
40. Question
The axis of a parabola is along the line \(y=x\) and the distance of its vertex from origin is \(\sqrt{2}\) and that from its focus is \(2 \sqrt{2}\). If vertex and focus both lie in the first quadrant, the equation of the parabola is
CorrectIncorrectHint
Coordinates of \(S\) are \(\left(2 \sqrt{2} \cos 45^{\circ}, 2 \sqrt{2} \sin 45^{\circ}\right)\) i.e. \((2,2)\).
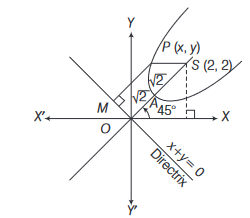
\(
\begin{aligned}
& \therefore \quad S P=P M \\
& \Rightarrow \quad(S P)^2=(P M)^2 \\
& \Rightarrow \quad(x-2)^2+(y-2)^2=\left[\frac{(x+y)}{\sqrt{2}}\right]^2 \\
& \Rightarrow \quad 2\left(x^2+y^2-4 x-4 y+8\right)=x^2+y^2+2 x y \\
& \Rightarrow x^2+y^2-2 x y-8 x-8 y+16=0 \\
& \therefore \quad(x-y)^2=8(x+y-2) \\
&
\end{aligned}
\) -
Question 41 of 250
41. Question
The equations of the common tangents to the parabolas \(y=x^2\) and \(y=-(x-2)^2\) is/are
CorrectIncorrectHint
Equation of tangent to \(y=x^2\) is
\(
y=m x-\frac{1}{4} m^2 \dots(i)
\)
Equation of tangent to \((x-2)^2=-y\) is
\(
y=m(x-2)+\frac{1}{4} m^2 \dots(ii)
\)
\(\because\) Eqs. (i) and (ii) are identical.
\(
\Rightarrow \quad m=0 \text { or } 4
\)
\(\therefore\) Common tangents are \(y=0\) and \(y=4 x-4=4(x-1)\). -
Question 42 of 250
42. Question
The locus of the vertices of the family of parabolas \(y=\frac{a^3 x^2}{3105}+\frac{a^2 x}{2}-2 a\) is
CorrectIncorrectHint
Given parabola is
\(
y=\frac{a^3 x^2}{3}+\frac{a^2 x}{2}-2 a \dots(i)
\)
For vertex \(\frac{d y}{d x}=0 \Rightarrow x=-\frac{3}{4 a}\)
Substitute \(x=-\frac{3}{4 a}\) in Eq. (i), we get
\(
y=-\frac{35 a}{16}
\)
\(\therefore\) Coordinates of vertex are \(\left(-\frac{3}{4 a},-\frac{35 a}{16}\right)\).
For locus let \(x=-\frac{3}{4 a}\) and \(y=-\frac{35 a}{16}\).
\(\therefore \quad x y=\frac{105}{64}\), which is the required locus. -
Question 43 of 250
43. Question
Angle between the tangents to the curve \(y=x^2-5 x+6\) at the points \((2,0)\) and \((3,0)\) is
CorrectIncorrectHint
\(
y=x^2-5 x+6
\)
\(\therefore\) Equation of tangent at \((2,0)\) is
\(
\begin{aligned}
\frac{y+0}{2} & =x \cdot 2-\frac{5}{2}(x+2)+6 \\
\Rightarrow \quad y & =-x+2 \dots(i)
\end{aligned}
\)
and equation of tangent at \((3,0)\) is
\(
\Rightarrow \quad y=x-3
\)
\(\because\) Eqs. (i) and (ii) are perpendicular.
\(\therefore\) Angle between tangents is \(\pi / 2\). -
Question 44 of 250
44. Question
Consider the circle \(x^2+y^2=9\) and the parabola \(y^2=8 x\). They intersect at \(P\) and \(Q\) in the first and fourth quadrants, respectively. Tangents to the circle at \(P\) and \(Q\) intersect the \(X\)-axis at \(R\) and tangents to the parabola at \(P\) and \(Q\) intersect the \(X\)-axis at \(S\).
(i) The ratio of the areas of the \(\triangle P Q S\) and \(\triangle P Q R\) is
(a) \(1: \sqrt{2}\)
(b) \(1: 2\)
(c) \(1: 4\)
(d) \(1: 8\)
(ii) The radius of the circumcircle of the \(\triangle P R S\) is
(a) 5
(b) \(3 \sqrt{3}\)
(c) \(3 \sqrt{2}\)
(d) \(2 \sqrt{3}\)
(iii) The radius of the incircle of the \(\triangle P Q R\) is
(a) 4
(b) 3
(c) \(8 / 3\)
(d) 2CorrectIncorrectHint
(i) Coordinates of \(P\) and \(Q\) are \((1,2 \sqrt{2})\) and \((1,-2 \sqrt{2})\).
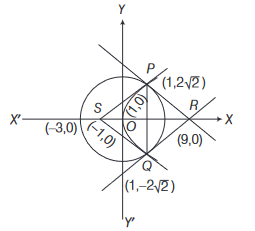
Area of \(\triangle P Q R=\frac{1}{2} \cdot 4 \sqrt{2} \cdot 8=16 \sqrt{2}\)
Area of \(\triangle P Q S=\frac{1}{2} \cdot 4 \sqrt{2} \cdot 2=4 \sqrt{2}\)
\(\therefore\) Ratio of area of \(\triangle P Q S\) and \(\triangle P Q R\) is \(1: 4\).
(ii) Equation of circumcircle of \(\triangle P R S\) is
\(
(x+1)(x-9)+y^2+\lambda y=0
\)
It will pass through \((1,2 \sqrt{2})\), then
\(
-16+8+\lambda 2 \sqrt{2}=0 \Rightarrow \lambda=\frac{8}{2 \sqrt{2}}=2 \sqrt{2}
\)
Equation of circumcircle is
\(
x^2+y^2-8 x+2 \sqrt{2} y-9=0
\)
Hence, radius is \(3 \sqrt{3}\).
Alternate :
\(
\begin{aligned}
& \text { Let } \angle P S R=\theta \Rightarrow \sin \theta=\frac{2 \sqrt{2}}{2 \sqrt{3}} \\
& \Rightarrow \quad P R=6 \sqrt{2}=2 R \cdot \sin \theta \Rightarrow R=3 \sqrt{3} .
\end{aligned}
\)
(iii) Radius of incircle is \(r=\frac{\Delta}{ s }\).
\(
\begin{aligned}
\text { As } & \Delta=16 \sqrt{2} \\
& \therefore \quad s=\frac{6 \sqrt{2}+6 \sqrt{2}+4 \sqrt{2}}{2}=8 \sqrt{2} \\
& \therefore \quad r=\frac{16 \sqrt{2}}{8 \sqrt{2}}=2 \\
&
\end{aligned}
\) -
Question 45 of 250
45. Question
Statement I: The curve \(y=-\frac{x^2}{2}+x+1\) is symmetric with respect to the line \(x=1\) because
Statement II: A parabola is symmetric about its axis.CorrectIncorrectHint
\(
y=-\frac{x^2}{2}+x+1 \Rightarrow y-\frac{3}{2}=-\frac{1}{2}(x-1)^2
\)
\(\Rightarrow\) It is symmetric about \(x=1\).
Hence, both statement are true and Statement II is correct explanation of Statement I. -
Question 46 of 250
46. Question
The equation of a tangent to the parabola \(y^2=8 x\) is \(y=x+2\). The point on this line from which the other tangent to the parabola is perpendicular to the given tangent is
CorrectIncorrectHint
Point of intersection of two perpendicular tangents to the parabola lies on directrix of the parabola.
\(\therefore\) Equation of directrix is \(x+2=0\).
So, point is \((-2,0)\). -
Question 47 of 250
47. Question
Consider the two curves \(C_1: y^2=4 x, C_2: x^2+y^2-6 x+1=0\), then
CorrectIncorrectHint
The circle and the parabola touch each other at \(x=1\), i.e. at the points \((1,2)\) and \((1,-2)\) as shown in figure.
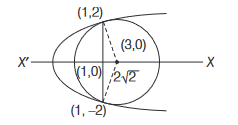
-
Question 48 of 250
48. Question
A parabola has the origin as its focus and the line \(x=2\) as the directrix. The vertex of the parabola is at
CorrectIncorrectHint
Focus of the parabola is \((0,0)\) and \(x=2\) is the directrix
And we know that axis of the parabola is perpendicular to the directrix and pass through the focus of the parabola
Thus foot of directrix is \((2,0)\)
Also we know that, vertex of the parabola is the mid point of its focus and the foot of directrix
So vertex of parabola is \(\left(\frac{0+2}{2}, \frac{0+0}{2}\right)=(1,0)\)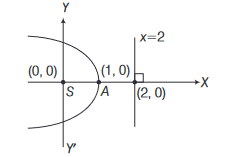
-
Question 49 of 250
49. Question
The tangent \(P T\) and the normal \(P N\) to the parabola \(y^2=4 a x\) at a point \(P\) on it meet its axis at points \(T\) and \(N\), respectively. The locus of the centroid of the \(\triangle P T N\) is a parabola whose
CorrectIncorrectHint
\(
\begin{aligned}
G & \equiv(h, k) \\
\Rightarrow \quad h & =\frac{2 a+a t^2}{3}, k=\frac{2 a t}{3}
\end{aligned}
\)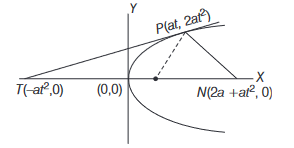
\(
\Rightarrow \quad\left(\frac{3 h-2 a}{a}\right)=\frac{9 k^2}{4 a^2}
\)
\(\therefore\) Required parabola is
\(
\begin{aligned}
& \quad \frac{9 y^2}{4 a^2}=\frac{(3 x-2 a)}{a}=\frac{3}{a}\left(x-\frac{2 a}{3}\right) \\
& \Rightarrow \quad y^2=\frac{4 a}{3}\left(x-\frac{2 a}{3}\right) \\
& \therefore \text { Vertex } \equiv\left(\frac{2 a}{3}, 0\right) \text {; Focus } \equiv(a, 0) .
\end{aligned}
\) -
Question 50 of 250
50. Question
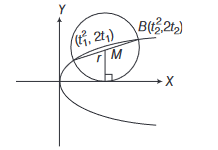
Let \(A\) and \(B\) be two distinct points on the parabola \(y^2=4 x\). If the axis of the parabola touches a circle of radius \(r\) having \(A B\) as its diameter, The slope of the line joining \(A\) and \(B\) can be
CorrectIncorrectHint
\(
\text { Slope of } A B=\frac{2 t_2-2 t_1}{\left(t_2^2-t_1^2\right)}=\frac{2}{\left(t_2+t_1\right)} \dots(i)
\)
\(
\begin{aligned}
& M=\text { Mid-point of } A B=\left(\frac{t_1^2+t_2^2}{2}, t_1+t_2\right) \\
\therefore & r=\left|t_1+t_2\right| \Rightarrow t_1+t_2= \pm r
\end{aligned}
\)
Now, from Eq. (i),
\(
\text { slope of } A B= \pm \frac{2}{r} \text {. }
\) -
Question 51 of 250
51. Question
If two tangents drawn from a point \(P\) to the parabola \(y^2=4 x\) are at right angles, the locus of \(P\) is
CorrectIncorrectHint
Given equation of parabola is \(y^2=4 x\)
We know that the locus of point \(P\) from which two perpendicular tangents are drawn to the parabola is the directrix of the parabola.
The standard equation of parabola \((y-k)^2=4 p(x-h)\) has focus \((h+p, k)\) and the directrix is \(x = h – p\)
From (i), we get
\(
h = 0 , k = 0 , p =1
\)
\(\Rightarrow\) Directrix of (i) is \(x=0-1=-1\)
Hence, required locus is \(x =- 1\). -
Question 52 of 250
52. Question
Consider the parabola \(y^2=8 x\). Let \(\Delta_1\) be the area of the triangle formed by the end points of its latusrectum and the point \(P\left(\frac{1}{2}, 2\right)\) on the parabola and \(\Delta_2\) be the area of the triangle formed by drawing tangent at \(P\) and at the end points of the latusrectum. Then, \(\frac{\Delta_1}{\Delta_2}\) is
CorrectIncorrectHint
\(
\begin{aligned}
\Delta_1 & =\text { Area of } \triangle P L L^{\prime} \\
& =\frac{1}{2} \times 8 \times\left(2-\frac{1}{2}\right)=6 \text { sq units }
\end{aligned}
\)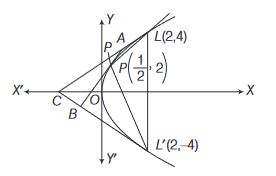
Now, equation of \(A B\) is \(y=2 x+1\), equation of \(A C\) is \(y=x+2\) and equation of \(B C\) is \(y=-x-2\)
On solving above equations, we get
\(
A(1,3), B(-1,-1) \text { and } C(-2,0)
\)
\(
\begin{array}{ll}
\therefore & \Delta_2=\frac{1}{2}\left\|\begin{array}{cc}
1+2 & 3-0 \\
-1+2 & -1-0
\end{array}\right\|=3 \text { sq units } \\
\therefore & \frac{\Delta_1}{\Delta_2}=2
\end{array}
\) -
Question 53 of 250
53. Question
Let \((x, y)\) be any point on the parabola \(y^2=4 x\). Let \(P\) be the point that divides the line segment from \((0,0)\) to \((x, y)\) in the ratio \(1: 3\). Then, the locus of \(P\) is
CorrectIncorrectHint
Let \(A(x, y)=A\left(t^2, 2 t\right)\) be any point on the parabola \(y^2=4 x\), then
\(
x=\frac{t^2}{4} \dots(i)
\)
and \(y=\frac{2 t}{4} \dots(ii)\)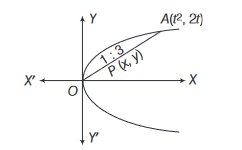
From Eqs. (i) and (ii), we get
\(
x=y^2
\) -
Question 54 of 250
54. Question
Let \(L\) be a normal to the parabola \(y^2=4 x\). If \(L\) passes through the point \((9,6)\), then \(L\) is given by
CorrectIncorrectHint
The equation of normal to
\(
y^2=4 x \text { is } y=m x-2 m-m^3 \dots(i)
\)
As it passes through \((9,6)\), then
\(
6=9 m-2 m-m^3
\)
\(
\begin{aligned}
& \Rightarrow \quad m^3-7 m+6=0 \\
& \Rightarrow(m-1)(m-2)(m+3)=0 \\
& \Rightarrow \quad m=1,2,-3 \\
&
\end{aligned}
\)
From Eq. (i), equations of normals are
\(
\begin{aligned}
& y=x-3, y=2 x-12, y=-3 x+33 \\
\Rightarrow & y-x+3=0, y-2 x+12=0, y+3 x-33=0
\end{aligned}
\) -
Question 55 of 250
55. Question
The shortest distance between line \(y-x=1\) and curve \(x=y^2\) is
CorrectIncorrectHint
The shortest distance between \(y=x-1\) and \(y^2=x\) is along the normal of \(y^2=x\).
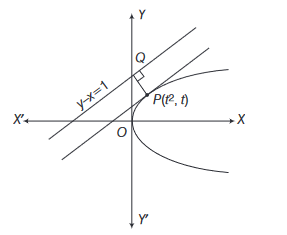
Let \(P\left(t^2, t\right)\) be any point on \(y^2=x\).
\(\therefore \quad\) Tangent at \(P\) is \(y=\frac{x}{2 t}+\frac{t}{2}\).
\(\therefore \quad\) Slope of tangent \(=\frac{1}{2 t}\)
and tangent at \(P\) is parallel to \(y-x=1\)
\(\therefore \quad \frac{1}{2 t}=1 \Rightarrow t=\frac{1}{2} \Rightarrow P\left(\frac{1}{4}, \frac{1}{2}\right)\)
Hence, shortest distance \(=P Q=\frac{\left|\frac{1}{2}-\frac{1}{4}-1\right|}{\sqrt{(1+1)}}=\frac{3}{4 \sqrt{2}}=\frac{3 \sqrt{2}}{8}\) -
Question 56 of 250
56. Question
Let \(S\) be the focus of the parabola \(y^2=8 x\) and let \(P Q\) be the common chord of the circle \(x^2+y^2-2 x-4 y=0\) and the given parabola. The area of the \(\triangle P Q S\) is
CorrectIncorrectHint
We observe that both parabola \(y^2=8 x\) and circle \(x^2+y^2-2 x-4 y=0\) pass through origin say \(P(0,0)\).

Let \(Q\) be the point \(\left(2 t^2, 4 t\right)\), then it will satisfy the equation of circle.
\(
\begin{array}{lc}
\therefore & \left(2 t^2\right)^2+(4 t)^2-2\left(2 t^2\right)-4(4 t)=0 \\
\Rightarrow & 4 t^4+12 t^2-16 t=0 \\
\Rightarrow & t(t-1)\left(t^2+t-4\right)=0 \Rightarrow t=0 \text { or } 1
\end{array}
\)
For \(t=0\), we get point \(P\), therefore \(t=1\) gives point \(Q\) as \((2,4)\). Here, \(P(0,0)\) and \(Q(2,4)\) are end points of diameter of the given circle and focus of the parabola is the point \(S(2,0)\).
\(\therefore \quad \angle P S Q=90^{\circ}\)
Hence, area of \(\triangle P Q S=\frac{1}{2} \times 2 \times 4=4\) sq units. -
Question 57 of 250
57. Question
Let \(P Q\) be a focal chord of the parabola \(y^2=4 a x\). The tangent to the parabola at \(P\) and \(Q\) meet at a point lying on the line \(y=2 x+a, a>0\). If chord \(P Q\) subtends an angle \(\theta\) at the vertex of \(y^2=4 a x\), then \(\tan \theta\) is equal to
CorrectIncorrectHint
\(\because P Q\) is the focal chord of \(y^2=4 a x\).
\(\therefore\) Coordinates of \(P\) and \(Q\) are \(\left(a t^2, 2 a t\right)\) and \(\left(\frac{a}{t^2},-\frac{2 a}{t}\right)\).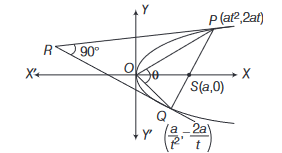
Tangents at \(P\) and \(Q\) are
\(
t y=x+a t^2 \text { and } t y=x t^2+a
\)
which intersect each other at \(R\left(-a, a\left(t-\frac{1}{t}\right)\right)\).
As \(R\) lies on the line \(y=2 x+a, a>0\)
\(
\begin{aligned}
& \therefore \quad a\left(t-\frac{1}{t}\right)=-2 a+a & \Rightarrow \quad t-\frac{1}{t}=-1
\end{aligned}
\)
\(\because\) Slope of \(O P=\frac{2}{t}\) and slope of \(O Q=-2 t\)
\(
\begin{aligned}
& \therefore \quad \tan \theta=\left|\frac{\frac{2}{t}+2 t}{1-4}\right|=\frac{2}{3}\left|t+\frac{1}{t}\right| \\
& =\frac{2}{3} \sqrt{\left(t-\frac{1}{t}\right)^2+4}=\frac{2}{3} \sqrt{5} \quad\left[\because t-\frac{1}{t}=-1\right] \\
& \because \quad \theta>90^{\circ} & \therefore \quad \tan \theta=-\frac{2}{3} \sqrt{5}
&
\end{aligned}
\)
\(\because\) Slope of \(O P=\frac{2}{t}\) and slope of \(O Q=-2 t\)
\(
\begin{aligned}
& \therefore \quad \tan \theta=\left|\frac{\frac{2}{t}+2 t}{1-4}\right|=\frac{2}{3}\left|t+\frac{1}{t}\right| \\
& =\frac{2}{3} \sqrt{\left(t-\frac{1}{t}\right)^2+4}=\frac{2}{3} \sqrt{5} \quad\left[\because t-\frac{1}{t}=-1\right] \\
& \because \quad \theta>90^{\circ} & \therefore \quad \tan \theta=-\frac{2}{3} \sqrt{5} \\
&
\end{aligned}
\) -
Question 58 of 250
58. Question
Let \(P Q\) be a focal chord of the parabola \(y^2=4 a x\). The tangent to the parabola at \(P\) and \(Q\) meet at a point lying on the line \(y=2 x+a, a>0\). Length of chord \(P Q\) is
CorrectIncorrectHint
\(\because P Q\) is the focal chord of \(y^2=4 a x\).
\(\therefore\) Coordinates of \(P\) and \(Q\) are \(\left(a t^2, 2 a t\right)\) and \(\left(\frac{a}{t^2},-\frac{2 a}{t}\right)\).
Tangents at \(P\) and \(Q\) are
\(
t y=x+a t^2 \text { and } t y=x t^2+a
\)
which intersect each other at \(R\left(-a, a\left(t-\frac{1}{t}\right)\right)\).
As \(R\) lies on the line \(y=2 x+a, a>0\)
\(
\begin{aligned}
& \therefore \quad a\left(t-\frac{1}{t}\right)=-2 a+a \\
& \Rightarrow \quad t-\frac{1}{t}=-1 \\
&
\end{aligned}
\)
\(
\begin{aligned}
&\begin{aligned}
P Q & =a\left(t+\frac{1}{t}\right)^2=a\left\{\left(t-\frac{1}{t}\right)^2+4\right\} \\
& =a(1+4)=5 a
\end{aligned}\\
&\left[\because t-\frac{1}{t}=-1\right]
\end{aligned}
\) -
Question 59 of 250
59. Question
The slope of the line touching the parabolas \(y^2=4 x\) and \(x^2=-32 y\) is
CorrectIncorrectHint
Equation of tangent of \(y^2=4 x\) in terms of slope is
\(
y=m x+\frac{1}{m} \dots(i)
\)
\(\because\) Line Eq. (i) touches \(x^2=-32 y\)
\(
\begin{aligned}
\Rightarrow & x^2 =-32\left(m x+\frac{1}{m}\right) \\
\Rightarrow & x^2+32 m x+\frac{32}{m} =0 \dots(ii)
\end{aligned}
\)
For touching roots of Eq. (ii) are equal.
\(
\begin{aligned}
& \therefore \quad D=0 \\
& \Rightarrow \quad(32 m)^2=4 \cdot 1 \cdot\left(\frac{32}{m}\right) \\
& \Rightarrow \quad m^3=\frac{1}{8} \\
& \therefore \quad m=1 / 2 \\
&
\end{aligned}
\) -
Question 60 of 250
60. Question
The common tangent to the circle \(x^2+y^2=2\) and the parabola \(y^2=8 x\) touch the circle at the points \(P, Q\) and the parabola at the points \(R, S\). Then, the area of the quadrilateral \(P Q R S\) is
CorrectIncorrectHint
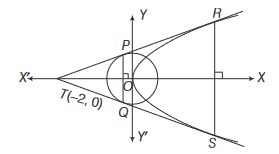
Let the tangent to, \(y^2=8 x\) be \(y=m x+\frac{2}{m}\).
If it is common tangent to parabola and circle, then \(y=m x+\frac{2}{m}\) is a tangent to \(x^2+y^2=2\).
\(
\begin{aligned}
& & \frac{\frac{2}{m}}{\sqrt{\left(1+m^2\right)}} & =\sqrt{2} \\
\Rightarrow & & \frac{4}{m^2\left(1+m^2\right)} & =2 \\
\Rightarrow & & m^4+m^2-2 & =0 \\
\Rightarrow & & \left(m^2+2\right)\left(m^2-1\right) & =0 \\
& \therefore & & m= \pm 1
\end{aligned}
\)
\(\therefore\) Required tangents are \(y=x+2\) and \(y=-x-2\).
Their common point is \(T(-2,0)\).
Chord of contact \(P Q\) to circle is
\(
\begin{aligned}
& & x \cdot(-2)+y \cdot 0 & =2 \\
\Rightarrow & & x & =-1
\end{aligned}
\)
Hence, coordinates of \(P\) and \(Q\) are \((-1,1)\) and \((-1,-1)\) and chord of contact \(R S\) to parabola is
\(
\begin{aligned}
& y \cdot 0=4(x-2) \\
& \Rightarrow \quad x=2 \\
&
\end{aligned}
\)
Hence, coordinates of \(R\) and \(S\) are \((2,4)\) and \((2,-4)\).
\(\therefore\) Area of trapezium \(P Q R S=\frac{1}{2}(2+8) \times 3=15\) sq units -
Question 61 of 250
61. Question
Let \(a, r, s\) and \(t\) be non-zero real numbers. Let \(P\left(a t^2, 2 a t\right)\), \(Q\left(\frac{a}{t^2}, \frac{-2 a}{t}\right), R\left(a r^2, 2 a r\right)\) and \(S\left(a s^2, 2 a s\right)\) be distinct points on the parabola \(y^2=4 a x\). Suppose that \(P Q\) is the focal chord and lines \(Q R\) and \(P K\) are parallel, where \(K\) is the point \((2 a, 0)\). The value of \(r\) is
CorrectIncorrectHint
\(\because P Q\) is a focal chord, then \(Q\left(\frac{a}{t^2}, \frac{-2 a}{t}\right)\).
Also,
\(
Q R \| P K \Rightarrow m_{Q R}=m_{P K}
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{2 a r+\frac{2 a}{t}}{a r^2-\frac{a}{t^2}}=\frac{0-2 a t}{2 a-a t^2} \\
& \Rightarrow \quad \frac{2}{r-\frac{1}{t}}=\frac{-2 t}{2-t^2} \\
& {\left[\because r+\frac{1}{t} \neq 0 \text {, otherwise } Q \text { will coincide with } R\right]} \\
& \Rightarrow \quad 2-t^2=-r t+1 \\
& \therefore \quad r=\frac{t^2-1}{t} \\
&
\end{aligned}
\) -
Question 62 of 250
62. Question
Let \(a, r, s\) and \(t\) be non-zero real numbers. Let \(P\left(a t^2, 2 a t\right)\), \(Q\left(\frac{a}{t^2}, \frac{-2 a}{t}\right), R\left(a r^2, 2 a r\right)\) and \(S\left(a s^2, 2 a s\right)\) be distinct points on the parabola \(y^2=4 a x\). Suppose that \(P Q\) is the focal chord and lines \(Q R\) and \(P K\) are parallel, where \(K\) is the point \((2 a, 0)\). If \(s t=1\), then the tangent at \(P\) and the normal at \(S\) to the parabola meet at a point whose ordinate is
CorrectIncorrectHint
Tangent at \(P\) is \(\quad t y=x+a t^2 \dots(i)\)
Normal at \(S\) is \(\quad y+s x=2 a s+a s^3 \dots(ii)\)
Putting the value of \(x\) from Eq. (i) in Eq. (ii), then
\(
\begin{aligned}
& y+s\left(t y-a t^2\right)=2 a s+a s^3 \\
& \Rightarrow \quad y+(s t) y-a(s t) t=2 a s+a s^3 \\
& \Rightarrow \quad y+y-a t=\frac{2 a}{t}+\frac{a}{t^3} \quad[\because s t=1] \\
& \Rightarrow \quad 2 y=a\left(t+\frac{2}{t}+\frac{1}{t^3}\right) \\
& \therefore \quad y=\frac{a\left(t^2+1\right)^2}{2 t^3} \\
&
\end{aligned}
\) -
Question 63 of 250
63. Question
Let \(O\) be the vertex and \(Q\) be any point on the parabola \(x^2=8 y\). If the point \(P\) divides the line segment \(O Q\) internally in the ratio \(1: 3\), then the locus of \(P\) is
CorrectIncorrectHint
Let any point \(Q\) on \(x^2=8 y\) is \(\left(4 t, 2 t^2\right)\) and given \(P(h, k)\) divides \(O Q\) in the ratio \(1: 3\) (internally).
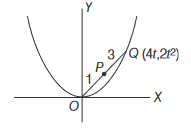
Then, \(\quad h=\frac{4 t}{4}=t\) and \(k=\frac{2 t^2}{4} \Rightarrow 2 k=h^2\)
\(\therefore\) Required locus of \(P\) is \(x^2=2 y\). -
Question 64 of 250
64. Question
If the normals of the parabola \(y^2=4 x\) drawn at the end points of its latusrectum are tangents to the circle \((x-3)^2+(y+2)^2=r^2\), then the value of \(r^2\) is
CorrectIncorrectHint
End points of latusrectum of
\(
y^2=4 x \text { are }(1, \pm 2) .
\)
Equation of normal to \(y^2=4 x\) at \((1,2)\) is
\(
\begin{aligned}
y-2 & =-\frac{2}{2}(x-1) \\
\Rightarrow \quad x+y-3 & =0
\end{aligned}
\)
As it is tangent to circle \((x-3)^2+(y+2)^2=r^2\)
\(
\therefore \quad \frac{|3-2-3|}{\sqrt{(1+1)}}=r \Rightarrow r^2=2
\) -
Question 65 of 250
65. Question
Let the curve \(C\) be the mirror image of the parabola \(y^2=4 x\) with respect to the line \(x+y+4=0\). If \(A\) and \(B\) are the points of intersection of \(C\) with the line \(y=-5\), the distance between \(A\) and \(B\) is
CorrectIncorrectHint
Let \(\left(t^2, 2 t\right)\) be any point on \(y^2=4 x\). Let \((h, k)\) be image of \(\left(t^2, 2 t\right)\) with respect to the line \(x+y+4=0\), then
\(
\frac{h-t^2}{1}=\frac{k-2 t}{1}=\frac{-2\left(t^2+2 t+4\right)}{1+1}
\)
\(
\begin{aligned}
& \Rightarrow \quad h=-(2 t+4) \text { and } k=-\left(t^2+4\right) \\
& \Rightarrow \quad(k+4)=-\left(\frac{h+4}{-2}\right)^2 \\
& \Rightarrow \quad(h+4)^2=-4(k+4) \\
&
\end{aligned}
\)
Locus of \((h, k)\) is \((x+4)^2=-4(y+4)\).
\(
\therefore \quad \text { Curve } C \text { is }(x+4)^2=-4(y+4)
\)
Now, intersection of \(C\) with \(y=-5\), then
\(
\begin{array}{lc}
& (x+4)^2=-4(-5+4)=4 \\
\therefore & x+4= \pm 2 \Rightarrow x=-6,-2 \\
\therefore & A(-6,-5) \text { and } B(-2,-5) \\
\therefore & A B=4
\end{array}
\) -
Question 66 of 250
66. Question
Let \(P\) and \(Q\) be distinct points on the parabola \(y^2=2 x\) such that a circle with \(P Q\) as diameter passes through the vertex \(O\) of the parabola. If \(P\) lies in the first quadrant and the area of the \(\triangle O P Q\) is \(3 \sqrt{2}\), then which of the following is (are) the coordinates of \(P\)?
CorrectIncorrectHint
Let \(P\left(\frac{t_1^2}{2}, t_1\right)\) and \(Q\left(\frac{t_2^2}{2}, t_2\right)\) such that \(t_1>0\)
\([\because P\) lies in first quadrant \(]\)
\(\because\) Circle with \(P Q\) as diameter passes through the vertex \(O(0,0)\) of the parabola.
\(
\begin{aligned}
& \therefore \quad \angle P O Q=90^{\circ} \\
& \Rightarrow \text { Slope of } O P \times \text { Slope of } O Q=-1 \\
& \Rightarrow \quad \frac{2}{t_1} \times \frac{2}{t_2}=-1 \\
& \Rightarrow \quad t_1 t_2=-4 \quad\left[\because t_2<0\right] \\
&
\end{aligned}
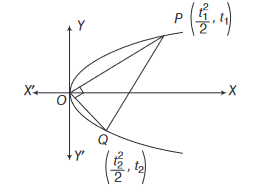
\)
\(
\begin{aligned}
& \text { Now, area of } \triangle O P Q=3 \sqrt{2} \\
& \Rightarrow \quad \frac{1}{2}\left|\begin{array}{cc}
\frac{t_1^2}{2} & t_1 \\
\frac{t_2^2}{2} & t_2
\end{array}\right|=3 \sqrt{2} \\
& \Rightarrow \quad \frac{1}{4} t_1 t_2\left(t_1-t_2\right)= \pm 3 \sqrt{2} \\
& \Rightarrow \quad t_1-t_2= \pm 3 \sqrt{2} \left[\because t_1 t_2=-4\right]
\end{aligned}
\)
\(
\begin{array}{ll}
\Rightarrow & t_1+\frac{4}{t_1}= \pm 3 \sqrt{2} \\
\text { or } & t_1+\frac{4}{t_1}=3 \sqrt{2} \left[\because t_1>0\right]
\end{array}
\)
\(
\begin{array}{lc}
\Rightarrow & t_1^2-3 \sqrt{2} t_1+4=0 \\
\therefore & t_1=\frac{3 \sqrt{2} \pm \sqrt{2}}{2}=2 \sqrt{2}, \sqrt{2} . \\
\therefore & \text { Point } P \text { can be }(4,2 \sqrt{2}) \text { or }(1, \sqrt{2}) .
\end{array}
\) -
Question 67 of 250
67. Question
Let \(P\) be the point on the parabola \(y^2=8 x\), which is at a minimum distance from the centre \(C\) of the circle \(x^2+(y+6)^2=1\), the equation of the circle passing through \(C\) and having its centre at \(P\), is
CorrectIncorrectHint
Let \(P\left(2 t^2, 4 t\right)\) and \(C(0,-6)\).
\(
\therefore \quad(C P)^2=4 t^4+(4 t+6)^2=z \text { say }
\)
\(
\begin{aligned}
& \therefore \quad \frac{d z}{d t}=0 \\
& \Rightarrow \quad 16 t^3+2(4 t+6) \cdot 4=0 \\
& \Rightarrow \quad t^3+2 t+3=0 \\
& \Rightarrow \quad(t+1)\left(t^2-t+3\right)=0 \\
&
\end{aligned}
\)
\(
\begin{array}{lc}
\therefore & t=-1 \\
\Rightarrow & P(2,-4)
\end{array}
\)
Equation of circle is
\(
\begin{aligned}
(x-2)^2+(y+4)^2 & =(2-0)^2+(-4+6)^2 \\
\Rightarrow x^2+y^2-4 x+8 y+12 & =0
\end{aligned}
\) -
Question 68 of 250
68. Question
The circle \(C_1: x^2+y^2=3\) with centre at \(O\), intersects the parabola \(x^2=2 y\) at the point \(P\) in the first quadrant. Let the tangent to the circle \(C_1\) at \(P\) touches other two circles \(C_2\) and \(C_3\) at \(R_2\) and \(R_3\), respectively. Suppose \(C_2\) and \(C_3\) have equal radii \(2 \sqrt{3}\) and centres \(Q_2\) and \(Q_3\), respectively. If \(Q_2\) and \(Q_3\) lie on the \(Y\)-axis, then
CorrectIncorrectHint
\(\because C_1: x^2+y^2=3\) and parabola \(x^2=2 y\), then
\(
y^2+2 y-3=0 \Rightarrow y=1,-3
\)
\(\therefore \quad P(\sqrt{2}, 1)\) \([\because P\) lies in first quadrant \(]\)
Now, tangent at \(P(\sqrt{2}, 1)\) on the circle \(C_1\) is
\(
x \sqrt{2}+y=3
\)
Let \(Q_2\) or \(Q_3(0, \lambda)\)
\(
\begin{aligned}
& \therefore \quad \frac{|0+\lambda-3|}{\sqrt{(2+1)}}=2 \sqrt{3} \\
& \Rightarrow \quad|\lambda-3|=6 \\
& \therefore \quad \lambda=9 \text { or }-3 \\
& \Rightarrow Q_2(0,-3) \text { and } Q_3(0,9) \text {. } \\
&
\end{aligned}
\)
Alternate (a) \(Q_2 Q_3=12\)
Alternate (b) \(R_2 R_3=\) Length of external common tangent
\(
\begin{aligned}
& =\sqrt{\left(Q_2 Q_3\right)^2-(2 \sqrt{3}+2 \sqrt{3})^2} \\
& =\sqrt{(144-48}=4 \sqrt{6}
\end{aligned}
\)
Alternate (c) Area of \(\triangle O R_2 R_3=\frac{1}{2} \times R_2 R_3 \times \frac{|0+0-3|}{\sqrt{(2+1)}}\)
\(
=\frac{1}{2} \times 4 \sqrt{6} \times \frac{3}{\sqrt{3}}=6 \sqrt{2}
\)
Alternate (d) Area of \(\triangle P Q_2 Q_3=\frac{1}{2} \times Q_2 Q_3 \times \sqrt{2}\)
\(
=\frac{1}{2} \times 12 \times \sqrt{2}=6 \sqrt{2}
\) -
Question 69 of 250
69. Question
Let \(P\) be the point on the parabola \(y^2=4 x\) which is at the shortest distance from the centre \(S\) of the circle \(x^2+y^2-4 x-16 y+64=0\). Let \(Q\) be the point on the circle dividing the line segment \(S P\) internally. Then,
CorrectIncorrectHint
Let \(P\left(t^2, 2 t\right), S(2,8)\) and \(r=\sqrt{(4+64-64)}=2\)
We know that, shortest distance between two curves lies along their common normal. The common normal will pass through centre of circle.
\(\therefore\) Slope of \(P S=\) Slope of normal to the parabola \(y^2=4 x\) at \(P\left(t^2, 2 t\right)\)
\(
\Rightarrow \quad \frac{2 t-8}{t^2-2}=-t \text { or } t^3=8 \Rightarrow t=2
\)
\(
\therefore P(4,4)
\)
Alternate (a) \(\quad S P=\sqrt{(2-4)^2+(8-4)^2}=2 \sqrt{5}\)
Alternate (b) \(\quad S Q=r=2\)
\(
\begin{aligned}
\therefore \quad \frac{S Q}{Q P} & =\frac{S Q}{S P-S Q}=\frac{2}{2 \sqrt{5}-2} \\
& =\frac{1}{(\sqrt{5}-1)} \times \frac{(\sqrt{5}+1)}{(\sqrt{5}+1)}=\frac{\sqrt{5}+1}{4} \\
\Rightarrow \quad S Q: Q P & =(\sqrt{5}+1): 4
\end{aligned}
\)
Alternate (c) Equation of normal at \(P(4,4)\) is
\(
\begin{array}{rlrl}
& & y-4 & =-\frac{4}{2}(x-4) \\
\Rightarrow & & y-4 & =-2 x+8 \\
\Rightarrow & 2 x+y & =12
\end{array}
\)
\(\therefore\) Intercept on \(X\)-axis is 6 .
Alternate (d) Slope of tangent at \(Q=\) Slope of tangent at
\(
P=\frac{1}{2}
\) -
Question 70 of 250
70. Question
The radius of a circle, having minimum area, which touches the curve \(y=4-x^2\) and the lines, \(y=|x|\) is
CorrectIncorrectHint
Centre of circle
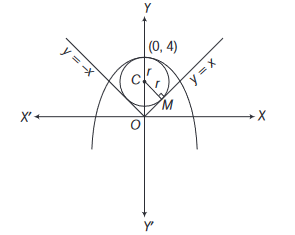
\(
\begin{aligned}
& C \equiv(0,4-r) \\
& \because \quad C M=r \\
& \therefore \quad \frac{|10-(4-r)|}{\sqrt{2}}=r \\
& \Rightarrow \quad 4-r=r \sqrt{2} \\
& \text { or } \\
& r=\frac{4}{\sqrt{2}+1} \\
& =4(\sqrt{2}-1) \\
&
\end{aligned}
\) -
Question 71 of 250
71. Question
If a chord, which is not a tangent of the parabola \(y^2=16 x\) has the equation \(2 x+y=p\), and mid-point \((h, k)\), then which of the following is (are) possible value(s) of \(p, h\) and \(k\) ?
CorrectIncorrectHint
(a) Equation of chord of parabola \(y^2=16 x\) whose mid-point \((h, k)\) is
\(
\begin{aligned}
T & =S_1 \\
k y-8(x+h) & =k^2-16 h \\
8 x-k y & =8 h-k^2 \dots(i)
\end{aligned}
\)
Now comparing Eq. (i) and \(2 x+y=p\), then
\(
\begin{array}{ll}
& \frac{8}{2}=\frac{-k}{1}=\frac{8 h-k^2}{p} \\
\Rightarrow & k=-4 \text { and } 4 p=8 h-k^2 \\
\text { or } & k=-4 \text { and } p=2 h-4 \\
\text { Hence, } & p=2, h=3, k=-4
\end{array}
\) -
Question 72 of 250
72. Question
The minimum area of triangle formed by the tangent to the \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) and coordinate axes is
CorrectIncorrectHint
Any tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) at \(P(a \cos \theta, b \sin \theta)\) is \(\frac{x \cos \theta}{a}+\frac{y \sin \theta}{b}=1\)
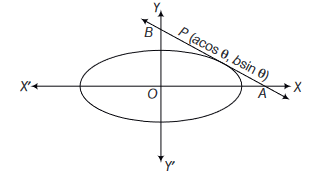
It meets coordinate axes at \(A(a \sec \theta, 0)\) and \(B(0, b \operatorname{cosec} \theta)\).
\(
\begin{aligned}
& \therefore \quad \text { Area of } \triangle O A B & =\frac{1}{2} \times a \sec \theta \times b \operatorname{cosec} \theta \\
\Rightarrow & \Delta =\frac{a b}{\sin 2 \theta}
\end{aligned}
\)
For \(\Delta\) to be min, \(\sin 2 \theta\) should be max and we know max value of \(\sin 2 \theta=1\).
\(
\therefore \quad \Delta_{\max }=a b \text { sq units. }
\) -
Question 73 of 250
73. Question
Find the equation of the common tangent in 1st quadrant to the circle \(x^2+y^2=16\) and the ellipse \(\frac{x^2}{25}+\frac{y^2}{4}=1\). Also find the length of the intercept of the tangent between the coordinate axes.
CorrectIncorrectHint
Let the common tangent to circle \(x^2+y^2=16\) and ellipse
\(
\begin{aligned}
x^2 / 25+y^2 / 4 & =1 \text { be } \\
y & =m x+\sqrt{25 m^2+4} \dots(i)
\end{aligned}
\)
As it is tangent to circle \(x^2+y^2=16\), we should have
\(
\begin{array}{rlrl}
& & \frac{\sqrt{25 m^2+4}}{\sqrt{m^2+1}} & =4 \quad \begin{array}{r}
\text { [Using: length of perpendicular } \\
\text { from }(0,0) \text { to }(1)=4]
\end{array} \\
\Rightarrow & & 25 m^2+4 & =16 m^2+16 \\
\Rightarrow & 9 m^2 & =12 \\
\Rightarrow & m & =\frac{-2}{\sqrt{3}}
\end{array}
\)
[Leaving + ve sign to consider tangent in I quadrant]
\(\therefore\) Equation of common tangent is
\(
\begin{aligned}
y & =-\frac{2}{\sqrt{3}} x+\sqrt{25 \cdot \frac{4}{3}+4} \\
\Rightarrow \quad y & =-\frac{2}{\sqrt{3}} x+4 \sqrt{\frac{7}{3}}
\end{aligned}
\)
This tangent meets the axes at \(A(2 \sqrt{7}, 0)\) and \(B\left(0,4 \sqrt{\frac{7}{3}}\right)\).
\(\therefore\) Length of intercepted portion of tangent between axes
\(
\begin{aligned}
A B & =\sqrt{(2 \sqrt{7})+\left(4 \sqrt{\frac{7}{3}}\right)^3} \\
& =14 / \sqrt{3}
\end{aligned}
\) -
Question 74 of 250
74. Question
An ellipse has \(O B\) as semi minor axis, \(F\) and \(F^{\prime}\) its focii and the angle \(F B F^{\prime}\) is a right angle. Then, the eccentricity of the ellipse is
CorrectIncorrectHint
\(
\begin{aligned}
& \because \angle F B F^{\prime}=90^{\circ} \Rightarrow F B^2+F^{\prime} B^2=F F^{\prime 2} \\
& \therefore\left(\sqrt{a^2 e^2+b^2}\right)^2+\left(\sqrt{a^2 e^2+b^2}\right)^2=(2 a e)^2
\end{aligned}
\)
\(
\begin{array}{rlrl}
\Rightarrow & & 2\left(a^2 e^2+b^2\right) & =4 a^2 e^2 \\
\Rightarrow & e^2 =\frac{b^2}{a^2}
\end{array}
\)
\(
\begin{array}{ll}
\text { Also, } & e^2=1-b^2 / a^2=1-e^2 \\
\Rightarrow & 2 e^2=1, e=\frac{1}{\sqrt{2}}
\end{array}
\) -
Question 75 of 250
75. Question
In an ellipse, the distance between its foci is 6 and minor axis is 8 . Then, its eccentricity is
CorrectIncorrectHint
\(
\begin{aligned}
& 2 a e=6 \Rightarrow a e=3 ; 2 b=8 \\
& \Rightarrow \quad b=4 \\
& b^2=a^2\left(1-e^2\right) ; 16=a^2-a^2 e^2 \\
& \Rightarrow \quad a^2=16+9=25 \Rightarrow a=5 \\
& \therefore \quad e=\frac{3}{a}=\frac{3}{5} \\
&
\end{aligned}
\) -
Question 76 of 250
76. Question
Let \(P\left(x_1, y_1\right)\) and \(Q\left(x_2, y_2\right), y_1<0, y_2<0\) be the end points of the latusrectum of the, ellipse \(x^2+4 y^2=4\). The equations of parabolas with latusrectum \(P Q\) are
CorrectIncorrectHint
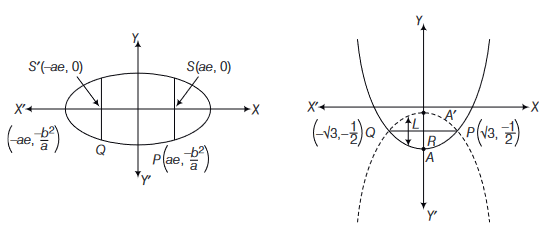
Given, ellipse is \(x^2+4 y^2=4\)
\(
\begin{array}{ll}
\text { or } & \frac{x^2}{2^2}+\frac{y^2}{1}=1 \Rightarrow a=2, b=1 \\
\therefore & e=\sqrt{1-\frac{1}{4}}=\frac{\sqrt{3}}{2} \\
\therefore & a e=\sqrt{3}
\end{array}
\)
As per question \(P \equiv\left(a e,-b^2 / a\right)=\left(\sqrt{3},-\frac{1}{2}\right)\)
\(
\begin{aligned}
& Q \equiv\left(-a e,-b^2 / a\right)=\left(-\sqrt{3},-\frac{1}{2}\right) \\
& \therefore \quad P Q=2 \sqrt{3} \\
&
\end{aligned}
\)
Now, if \(P Q\) is the length of latusrectum to be found, then
\(
P Q=4 a=2 \sqrt{3} \Rightarrow a=\frac{\sqrt{3}}{2}
\)
Also, as \(P Q\) is horizontal, parabola with \(P Q\) as latusrectum can be upward parabola (with vertex at \(A\) ) or down ward parabola (with vertex at \(A^{\prime}\) ).
For upward parabola, \(A r=a=\frac{\sqrt{3}}{2}\)
\(\therefore\) Coordinates of \(A=\left(0,-\left(\frac{\sqrt{3}+1}{2}\right)\right)\)
So, Equation of upward parabola is given by
\(
x^2=2 \sqrt{3}\left(y+\frac{\sqrt{3}+1}{2}\right) \text { or } x^2-2 \sqrt{3} y=3+\sqrt{3} \dots(i)
\)
For downward parabola \(A^{\prime} R=a=\frac{\sqrt{3}}{2}\)
\(\therefore\) Coordinates of \(A^{\prime}=\left(0,-\left(\frac{1-\sqrt{3}}{2}\right)\right)\)
So, equation of downward parabola is given by
\(
\begin{aligned}
& x^2=-2 \sqrt{3}\left(y+\frac{1-\sqrt{3}}{2}\right) \\
& x^2+2 \sqrt{3} y=3-\sqrt{3} \dots(ii)
\end{aligned}
\)
\(\therefore\) Equation of required parabola is given by Eqs. (i) and (ii). -
Question 77 of 250
77. Question
A focus of an ellipse is at the origin. The directrix is the line \(x=4\) and the eccentricity is \(\frac{1}{2}\). Then, the length of the semi-major axis is
CorrectIncorrectHint
Perpendicular distance of directrix from focus
\(
\begin{aligned}
& =\frac{a}{e}-a e=4 \\
\Rightarrow a\left(2-\frac{1}{2}\right) & =4 \Rightarrow a=\frac{8}{3}
\end{aligned}
\)
\(
\therefore \text { Semi major axis }=8 / 3
\) -
Question 78 of 250
78. Question
The line passing through the extermity \(A\) of the major axis and extremity \(B\) of the minor axis of the ellipse \(x^2+9 y^2=9\) meets its auxiliary circle at the point \(M\). Then, the area of the triangle with vertices at \(A, M\) and the origin \(O\) is
CorrectIncorrectHint
The given ellipse is \(x^2+9 y^2=9\) or \(\quad \frac{x^2}{3^2}+\frac{y^2}{1^2}=1\)
So, the \(A(3,0)\) and \(B(0,1)\)
\(\therefore\) Equation of \(A B\) is \(\frac{x}{3}+\frac{y}{1}=1\) or \(x+3 y-3=0 \dots(i)\)
Also, auxillary circle of given ellipse is
\(
x^2+y^2=9 \dots(ii)
\)
Solving Eqs. (i) and (ii), we get the point \(M\) where line \(A B\) meets the auxillary circle.
Putting \(x=3-3 y\) from Eqs. (i) and (ii)
\(
\begin{array}{rlrl}
\text { we get } & (3-3 y)^2+y^2 =9 \\
\Rightarrow & 9-18 y+9 y^2+y^2 =9 \\
\Rightarrow & 10 y^2-18 y =0 \\
\Rightarrow & y=0, \frac{9}{5} \Rightarrow x =3, \frac{-12}{5}
\end{array}
\)
Clearly, \(M\left(\frac{-12}{5}, \frac{9}{5}\right)\)
\(
\therefore \text { Area of } \triangle O A M=\frac{1}{2} \times\left|\begin{array}{ccc}
0 & 0 & 1 \\
3 & 0 & 1 \\
\frac{-12}{5} & \frac{9}{5} & 1
\end{array}\right|=\frac{27}{10} \text { (Take only the magnitude) }
\) -
Question 79 of 250
79. Question
The normal at a point \(P\) on the ellipse \(x^2+4 y^2=16\) meets the \(X\)-axis at \(Q\). If \(M\) is the mid-point of the line segment \(P Q\), then the locus of \(M\) intersects the latusrectum of the given ellipse at the points
CorrectIncorrectHint
The given ellipse is \(\frac{x^2}{4^2}+\frac{y^2}{2^2}=1\)
such that \(a^2=16\) and \(b^2=4\)
\(
\begin{array}{ll}
\therefore & e^2=1-\frac{4}{16}=\frac{3}{4} \\
\Rightarrow & e=\frac{\sqrt{3}}{2}
\end{array}
\)
Let \(P(4 \cos \theta, 2 \sin \theta)\) be any point on the ellipse, then equation of normal at \(P\) is
\(
\begin{aligned}
\quad 4 x \sin \theta-2 y \cos \theta & =12 \sin \theta \cos \theta \\
\Rightarrow \quad \frac{x}{3 \cos \theta}-\frac{y}{6 \sin \theta} & =1
\end{aligned}
\)
\(\therefore Q\), the point where normal at \(P\) meets \(X\)-axis, has coordinates \((3 \cos \theta, 0)\)
\(\therefore\) Mid-point of \(P Q\) is \(M\left(\frac{7 \cos \theta}{2}, \sin \theta\right)\)
For locus of point \(M\) we consider
\(
x=\frac{7 \cos \theta}{2} \text { and } y=\sin \theta
\)
\(
\Rightarrow \cos \theta=\frac{2 x}{7} \text { and } \sin \theta=y \Rightarrow \frac{4 x^2}{49}+y^2=1 \dots(i)
\)
Also, the latusrectum of given ellipse is
\(
\begin{aligned}
x & = \pm a e= \pm 4 \times \frac{\sqrt{3}}{2}= \pm 2 \sqrt{3} \\
\text { or } \quad x & = \pm 2 \sqrt{3} \dots(ii)
\end{aligned}
\)
Solving Eqs. (i) and (ii), we get
\(
\begin{gathered}
\frac{4 \times 12}{49}+y^2=1 \\
\Rightarrow \quad y^2=\frac{1}{49} \text { or } y= \pm \frac{1}{7} \\
\therefore \text { The required points are }\left( \pm 2 \sqrt{3}, \pm \frac{1}{7}\right) \text {. }
\end{gathered}
\) -
Question 80 of 250
80. Question
In a triangle \(A B C\) with fixed base \(B C\), the vertex \(A\) moves such that
\(
\cos B+\cos C=4 \sin ^2 \frac{A}{2}
\)
If \(a, b\) and \(c\) denote the lengths of the sides of the triangle opposite to the angles \(A, B\) and \(C\), respectively, thenCorrectIncorrectHint
In \(\triangle A B C\), given that \(\cos B+\cos C=4 \sin ^2 \frac{A}{2}\)
\(
\begin{aligned}
& \Rightarrow \quad 2 \cos \frac{B+C}{2} \cos \frac{B-C}{2}-4 \sin ^2 \frac{A}{2}=0 \\
& \Rightarrow \quad 2 \sin \frac{A}{2}\left[\cos \frac{B-C}{2}-2 \sin \frac{A}{2}\right]=0 \\
& \Rightarrow \quad \sin \frac{A}{2}=0 \text { or }\left(\cos \frac{B-C}{2}-2 \cos \frac{B+C}{2}\right)=0 \qquad\left(\because \frac{A}{2}=90^{\circ}-\left(\frac{B+C}{2}\right)\right)
\end{aligned}
\)
But in a triangle \(\sin \frac{A}{2} \neq 0\)
\(
\begin{aligned}
& \cos \frac{B-C}{2}-2 \cos \frac{B+C}{2}=0 \\
\Rightarrow \quad & \frac{\cos \left(\frac{B+C}{2}\right)}{\cos \left(\frac{B-C}{2}\right)}=\frac{1}{2}
\end{aligned}
\)
Applying componendo and dividendo, we get
\(
\begin{aligned}
& \frac{\cos \left(\frac{B+C}{2}\right)+\cos \left(\frac{B-C}{2}\right)}{\cos \left(\frac{B+C}{2}\right)-\cos \left(\frac{B-C}{2}\right)}=\frac{1+2}{1-2}=-3 \\
\Rightarrow & -\frac{2 \cos \frac{B}{2} \cos \frac{C}{2}}{2 \sin \frac{B}{2} \sin \frac{C}{2}}=-3 \\
\Rightarrow & \quad \tan \frac{B}{2} \tan \frac{C}{2}=\frac{1}{3} \\
\Rightarrow & \sqrt{\frac{(s-a)(s-c)}{s(s-b)}} \sqrt{\frac{(s-a)(s-b)}{s(s-c)}}=\frac{1}{3}
\end{aligned}
\)
\(
\begin{array}{rlrl}
\Rightarrow & \frac{s-a}{s} =\frac{1}{3} \\
& \text { or } & 2 s =3 a \\
\Rightarrow & a+b+c =3 a \\
\text { or } & b+c =2 a \\
\text { i.e. } & A C+A B & =\text { constant } \text { [ } \because \text { base } B C=a \text { is given to be constant] }
\end{array}
\)
\(\Rightarrow A\) moves on an ellipse. -
Question 81 of 250
81. Question
The conic having parametric representation \(x=\sqrt{3}\left(\frac{1-t^2}{1+t^2}\right), y=\frac{2 t}{1+t^2}\) is
CorrectIncorrectHint
\(
\begin{aligned}
\left(\frac{x}{\sqrt{3}}\right)^2+(y)^2 & =\left(\frac{1-t^2}{1+t^2}\right)^2+\left(\frac{2 t}{1+t^2}\right)^2 \\
& =\frac{\left(1+t^2\right)^2}{\left(1+t^2\right)^2}=1 \\
\Rightarrow \quad \frac{x^2}{3}+y^2 & =1
\end{aligned}
\)
Which is an ellipse. -
Question 82 of 250
82. Question
The ellipse \(x^2+4 y^2=4\) is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point \((4,0)\). Then, the equation of the ellipse is
CorrectIncorrectHint
The given ellipse is \(\frac{x^2}{4}+\frac{y^2}{1}=1\)
So, \(A=(2,0)\) and \(B=(0,1)\)
If \(P Q R S\) is the rectangle in which it is inscribed, then
\(
P=(2,1) \text {. }
\)
Let \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) be the ellipse circumscribing the rectangle \(P Q R S\). Then it passes through \(P(2,1)\)
\(
\therefore \quad \frac{4}{a^2}+\frac{1}{b^2}=1 \dots(i)
\)
Also, given that, it passes through \((4,0)\)
\(
\begin{aligned}
& \therefore \quad \frac{16}{a^2}+0=1 \\
& \Rightarrow \quad a^2=16 \\
& \Rightarrow \quad b^2=4 / 3 \quad \text { [substituting } a^2=16 \text { in Eq. (i)] } \\
& \therefore \text { The required ellipse is } \frac{x^2}{16}+\frac{y^2}{4 / 3}=1 \\
& \text { or } x^2+12 y^2=16 \\
&
\end{aligned}
\) -
Question 83 of 250
83. Question
Tangents are drawn from the point \(P(3,4)\) to the ellipse \(\frac{x^2}{9}+\frac{y^2}{4}=1\) touching the ellipse at points \(A\) and \(B\).
The coordinates of \(A\) and \(B\) areCorrectIncorrectHint
Tangent to \(\frac{x^2}{3^2}+\frac{y^2}{2^2}=1\) at the point \((3 \cos \theta, 2 \sin \theta)\) is
\(
\frac{x \cos \theta}{3}+\frac{y \sin \theta}{2}=1
\)
As it passes through \((3,4)\), we get
\(
\begin{array}{ll}
& \cos \theta+2 \sin \theta=1 \\
\Rightarrow \quad & 4 \sin ^2 \theta=1+\cos ^2 \theta-2 \cos \theta \\
\Rightarrow \quad & 5 \cos ^2 \theta-2 \cos \theta-3=0 \\
\Rightarrow \quad & \cos \theta=1,-\frac{3}{5} \\
\Rightarrow \quad & \sin \theta=0, \frac{4}{5}
\end{array}
\)
\(\therefore\) Required points are \(A(3,0)\) and \(B\left(\frac{9}{5}, \frac{8}{5}\right)\). -
Question 84 of 250
84. Question
Tangents are drawn from the point \(P(3,4)\) to the ellipse \(\frac{x^2}{9}+\frac{y^2}{4}=1\) touching the ellipse at points \(A\) and \(B\).
The orthocenter of the triangle \(P A B\) isCorrectIncorrectHint
Let \(H\) be orthocentre of \(\triangle P A B\), then as \(B H \perp A P, B H\) is a horizontal line through \(B\).
\(\therefore y\)-coordinate of \(B=8 / 5\)
Let \(H\) has coordinate \((\alpha, 8 / 5)\)
Then, slope of \(P H=\frac{\frac{8}{5}-4}{\alpha-3}=\frac{-12}{5(\alpha-3)}\)
and slope of \(A B=\frac{\frac{8-0}{5}}{-\frac{9}{5-3}}=\frac{8}{-24}=\frac{-1}{3}\)
But \(P H \perp A B\)
\(
\begin{array}{ll}
\Rightarrow & \frac{-12}{5(\alpha-3)} \times\left(\frac{-1}{3}\right)=-1 \\
\Rightarrow & 4=-5 \alpha+15 \text { or } \alpha=11 / 5
\end{array}
\)
Hence \(H\left(\frac{11}{5}, \frac{8}{5}\right)\). -
Question 85 of 250
85. Question
The equation of the locus of the point whose distances from the point \(P\) and the line \(A B\) are equal, is
CorrectIncorrectHint
Clearly, the moving point traces a parabola with focus at \(P(3,4)\) and directrix as
\(
\begin{aligned}
& A B: \frac{y-0}{x-3}=\frac{-1}{3} \\
& x+3 y-3=0
\end{aligned}
\)
\(\therefore\) Equation of parabola is
\(
(x-3)^2+(y-4)^2=\frac{(x+3 y-3)^2}{10}
\)
\(
9 x^2+y^2-6 x y-54 x-62 y+241=0
\) -
Question 86 of 250
86. Question
Equation of the ellipse whose axes are the axes of coordinates which passes through the point \((-3,1)\) and has eccentricity \(\sqrt{\frac{2}{5}}\) is
CorrectIncorrectHint
Let the ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
It passes through \((-3,1)\), so
\(
\frac{9}{a^2}+\frac{1}{b^2}=1 \dots(i)
\)
Also,
\(
b^2=a^2(1-2 / 5)
\)
\(\Rightarrow\) \(5 b^2=3 a^2 \dots(ii)\)
Solving Eqs. (i) and (ii), we get
\(
a^2=\frac{32}{3}, b^2=\frac{32}{5}
\)
So, the equation of the ellipse is \(3 x^2+5 y^2=32\) -
Question 87 of 250
87. Question
The ellipse \(E_1: \frac{x^2}{9}+\frac{y^2}{4}=1\) is inscribed in a rectangle \(R\) whose sides are parallel to the coordinate axes. Another ellipse \(E_2\) passing through the point \((0,4)\) circumscribes the rectangle \(R\). the eccentricity of the ellipse \(E_2\) is
CorrectIncorrectHint
As rectangle \(A B C D\) circumscribed the ellipse
\(
\frac{x^2}{9}+\frac{y^2}{4}=1
\)
\(
\therefore \quad A=(3,2)
\)
Let the ellipse circumscribing the rectangle \(A B C D\) is
\(
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\)
Given that, it passes through \((0,4)\)
\(\therefore \quad b^2=16\)
Also, it passes through \(A(3,2)\)
\(
\begin{array}{ll}
\therefore & \frac{9}{a^2}+\frac{4}{16}=1 \Rightarrow a^2=12 \\
\therefore & e=\sqrt{1-\frac{12}{16}}=\sqrt{\frac{1}{4}}=\frac{1}{2}
\end{array}
\) -
Question 88 of 250
88. Question
Statement I : An equation of a common tangent to the parabola \(y^2=16 \sqrt{3} x\) and the ellipse \(2 x^2+y^2=4\) is \(y=2 x+2 \sqrt{3}\)
Statement II : If the line \(y=m x+\frac{4 \sqrt{3}}{m},(m \neq 0)\) is a common tangent to the parabola \(y^2=16 \sqrt{3} x\) and the ellipse \(2 x^2+y^2=4\), then \(m\) satisfies \(m^2+2 m^2=24\)CorrectIncorrectHint
Given, equation of ellipse is \(2 x^2+y^2=4\)
\(
\Rightarrow \quad \frac{2 x^2}{4}+\frac{y^2}{4}=1 \Rightarrow \frac{x^2}{2}+\frac{y^2}{4}=1
\)
Equation of tangent to the ellipse \(\frac{x^2}{2}+\frac{y^2}{4}=1\) is
\(
y=m x \pm \sqrt{2 m^2+4} \dots(i)
\)
\(\because\) equation of tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is \(y=m x+c\), where \(c= \pm \sqrt{a^2 m^2+b^2}\)
Now, equation of tangent to the parabola
\(
\because y^2=16 \sqrt{3} x \text { is } y=m x+\frac{4 \sqrt{3}}{m} \dots(ii)
\)
( \(\because\) Equation of tangent to the parabola \(y^2=4 a x\) is \(\left.y=m x+\frac{a}{m}\right)\)
On comparing Eqs. (i) and (ii), we get
\(
\frac{4 \sqrt{3}}{m}= \pm \sqrt{2 m^2+4}
\)
Squaring on both the sides, we get
\(
\begin{aligned}
& 16(3)=\left(2 m^2+4\right) m^2 \\
& \Rightarrow \quad 48=m^2\left(2 m^2+4\right) \\
& \Rightarrow \quad 2 m^2+4 m^2-48=0 \\
& \Rightarrow \quad m^4+2 m^2-24=0 \\
& \Rightarrow \quad\left(m^2+6\right)\left(m^2-4\right)=0 \\
& \Rightarrow \quad m^2=4 \quad\left(\because m^2 \neq-6\right) \\
& \Rightarrow \quad m= \pm 2 \\
& \Rightarrow \text { Equation of common tangents are } y= \pm 2 x \pm 2 \sqrt{3} \\
&
\end{aligned}
\)
Thus, statement I is true. statement II is obviously true. -
Question 89 of 250
89. Question
An ellipse is drawn by taking a diameter of the circle \((x-1)^2+y^2=1\) as its semi-minor axis and diameter of the circle \(x^2+(y-2)^2=4\) is semi-major axis. If the centre of the ellipse is at the origin and its axes are the coordinate axes, then the equation of the ellipse is
CorrectIncorrectHint
Equation of circle is \((x-1)^2+y^2=1\)
\(\Rightarrow\) Radius \(=1\) and Diameter \(=2\)
\(\therefore\) Length of semi-minor axis is 2 .
Equation of circle is \(x^2+(y-2)^2=4=(2)^2\)
\(\Rightarrow\) Radius \(=2\) and Diameter \(=4\)
\(\Rightarrow\) Length of semi-major axis is 4
We know, equation of ellipse is given by
\(
\frac{x^2}{\text { (Major-axis) }^2}+\frac{y^2}{(\text { Major-axis) })^2}=1
\)
\(
\begin{aligned}
\Rightarrow \quad \frac{x^2}{(4)^2}+\frac{y^2}{(2)^2}=1 \Rightarrow \frac{x^2}{16}+\frac{y^2}{4} & =1 \\
\Rightarrow \quad x^2+4 y^2 & =16
\end{aligned}
\) -
Question 90 of 250
90. Question
The equation of the circle passing through the foci of the ellipse \(\frac{x^2}{16}+\frac{y^2}{9}=1\), and having centre at \((0,3)\) is
CorrectIncorrectHint
From the given equation of ellipse, we have
\(
\begin{aligned}
& \quad a=4, b=3 e=\sqrt{1-\frac{9}{16}} \\
& \Rightarrow \quad e=\frac{\sqrt{7}}{4}
\end{aligned}
\)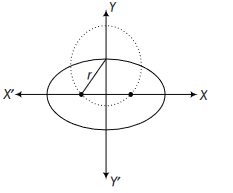
Now, radius of this circle \(=a^2=16\)
\(
\Rightarrow \quad \text { Foci }=( \pm \sqrt{7}, 0)
\)
Now, equation of circle is \((x-0)^2+(y-3)^2=16\)
\(
x^2+y^2-6 y-7=0
\) -
Question 91 of 250
91. Question
A vertical line passing through the point \((h, 0)\) intersects the ellipse \(\frac{x^2}{4}+\frac{y^2}{9}=1\) at the points \(P\) and \(Q\). Let the tangents to the ellipse at \(P\) and \(Q\) meet at the point \(R\). If \(\Delta(h)=\) area of the triangle \(P Q R, \Delta_1=\) \(\frac{1}{2} \leq h \leq \max \Delta(h)\) and \(\Delta_2=\frac{1}{2} \leq h \leq \min \Delta(h)\), then \(\frac{8}{\sqrt{5}} \Delta_1-8 \Delta_2=\)
CorrectIncorrectHint
Vertical line \(x=h\), meets the ellipse \(\frac{x^2}{4}+\frac{y^2}{3}=1\) at
\(
P\left(h, \frac{\sqrt{3}}{2} \sqrt{\left(4-h^2\right)}\right) \text { and } Q\left(h, \frac{-\sqrt{3}}{2} \sqrt{\left(4-h^2\right)}\right)
\)
By symmetry, tangents at \(P\) and \(Q\) will meet each other at \(X\)-axis
Tangent at \(P\) is \(\frac{x h}{4}+\frac{y \sqrt{3}}{6} \sqrt{\left(4-h^2\right)}=1\)
Which meets \(X\)-axis at \(R\left(\frac{4}{h}, 0\right)\)
\(
\text { Area of } \begin{aligned}
\triangle P Q R & =\frac{1}{2} \times \sqrt{3} \sqrt{\left(4-h^2\right)} \times\left(\frac{4}{h}-h\right) \\
\text { i.e. } \quad \Delta(h) & =\frac{\sqrt{3}}{2} \frac{\left(4-h^2\right)^{3 / 2}}{h} \\
\frac{d \Delta}{d h} & =-\sqrt{3}\left[\frac{\sqrt{\left(4-h^2\right)}\left(h^2+2\right)}{h^2}\right]<0
\end{aligned}
\)
\(\therefore \Delta(h)\) is a decreasing function.
\(
\begin{array}{ll}
\therefore & \frac{1}{2} \leq h \leq 1 \\
\Rightarrow & \Delta_{\max }=\Delta\left(\frac{1}{2}\right) \text { and } \Delta_{\max }=\Delta(1)
\end{array}
\)
\(
\begin{aligned}
& \therefore \quad \Delta_1=\frac{\sqrt{3}}{2}\left(\frac{\left(4-\frac{1}{4}\right)^{3 / 2}}{\frac{1}{2}}\right)=\frac{45}{8} \sqrt{5} \\
& \Delta_2=\frac{\sqrt{3}}{2} \cdot \frac{3 \sqrt{3}}{1}=\frac{9}{2} \\
& \therefore \quad \frac{8}{\sqrt{5}} \Delta_1-8 \Delta_2=45-36=9 \\
&
\end{aligned}
\) -
Question 92 of 250
92. Question
The locus of the foot of perpendicular drawn from the centre of the ellipse \(x^2+3 y^2=6\) on any tangent to it is
CorrectIncorrectHint
Given, equation of ellipse can be written as
\(
\Rightarrow \quad \begin{aligned}
& \frac{x^2}{6}+\frac{y^2}{2}=1 \\
& \Rightarrow \quad a^2=6, b^2=2
\end{aligned}
\)
Now, equation of any variable tangent is
\(
y=m x \pm \sqrt{a^2 m^2+b^2} \dots(i)
\)
where \(m\) is slope of the tangent
So, equation of perpendicular line drawn from centre to tangent is
\(
y=\frac{-x}{m} \dots(ii)
\)
Eliminating \(m\),we get
\(
\begin{aligned}
& & \left(x^4+y^4+2 x^2 y^2\right) & =a^2 x^2+b^2 y^2 \\
\Rightarrow & & \left(x^2+y^2\right)^2 & =a^2 x^2+b^2 y^2 \\
\Rightarrow & & \left(x^2+y^2\right)^2 & =6 x^2+2 y^2
\end{aligned}
\) -
Question 93 of 250
93. Question
The area (in sq units) of the quadrilateral formed by the tangents at the end points of the latus rectum to the ellipse \(\frac{x^2}{9}+\frac{y^2}{5}=1\) is
CorrectIncorrectHint
The end point of latusrectum of ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) in first quadrant is \(\left(a e, \frac{b^2}{a}\right)\) and the tangent at this point intersects \(X\)-axis at \(\left(\frac{a}{e}, 0\right)\) and \(Y\) – axis at \((0, a)\).
The given ellipse is \(\frac{x^2}{9}+\frac{y^2}{5}=1\)
Then, \(a^2=9, b^2=5\)
\(
\Rightarrow \quad e=\sqrt{\left(1-\frac{5}{9}\right)}=\frac{2}{3}
\)
\(\therefore\) End point of latusrectum in first quadrant is \(L(2,5 / 3)\)
Equation of tangent at \(L\) is \(\frac{2 x}{9}+\frac{y}{3}=1\)
It meets \(X\)-axis at \(A(9 / 2,0)\) and \(Y\)-axis at \(B(0,3)\)
\(
\therefore \text { Area of } \triangle O A B=\frac{1}{2} \times \frac{9}{2} \times 3=\frac{27}{4}
\)
By symmetry area of quadrilateral
\(
=4 \times(\text { Area } \triangle O A B)=4 \times \frac{27}{4}=27 \text { sq units }
\) -
Question 94 of 250
94. Question
Let \(E_1\) and \(E_2\) be two ellipses whose centers are at the origin. The major axes of \(E_1\) and \(E_2\) lie along the \(X\)-axis and the \(Y\)-axis, respectively. Let \(S\) be the circle \(x^2+(y-1)^2=2\). The straight line \(x+y=3\) touches the curves, \(S, E_1\) and \(E_2\) at \(P, Q\) and \(R\) respectively. Suppose that \(P Q=P R=\frac{2 \sqrt{2}}{3}\). If \(e_1\) and \(e_2\) are the eccentricities of \(E_1\) and \(E_2\), respectively, then the correct expression(s) is (are)
CorrectIncorrectHint
Let \(E_1: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), where \(a>b\) and \(E_2: \frac{x^2}{c^2}+\frac{y^2}{d^2}=1\), where \(c<d\)
Also, \(S: x^2+(y-1)^2=2\)
Tangent at \(P\left(x_1, y_1\right)\) to \(S\) is \(x+y=3\)
To find point of contact put \(x=3-y\) in \(S\), we get \(P(1,2)\) writing equation of tangent in parametric form
\(
\begin{aligned}
& \frac{x-1}{\frac{-1}{\sqrt{2}}}=\frac{y-2}{\frac{1}{\sqrt{2}}}= \pm \frac{2 \sqrt{2}}{3} \\
& x=\frac{-2}{3}+1 \text { or } \frac{2}{3}+1 \text { and } y=\frac{2}{3}+2 \text { or } \frac{-2}{3}+2 \\
\Rightarrow \quad & x=\frac{1}{3} \text { or } \frac{5}{3} \text { and } y=\frac{8}{3} \text { or } \frac{4}{3} \\
\therefore \quad & Q\left(\frac{5}{3}, \frac{4}{3}\right) \text { and } R\left(\frac{1}{3}, \frac{8}{3}\right)
\end{aligned}
\)
Equation of tangent to \(E_1\) at \(Q\) is \(\frac{5 x}{3 a^2}+\frac{4 y}{3 b^2}=1\) which is identical to \(\frac{x}{3}+\frac{y}{3}=1\) \(\Rightarrow a^2=5\) and \(b^2=4 \Rightarrow e_1^2=1-\frac{4}{5}=\frac{1}{5}\)
Equation of tangent to \(E_2\) at \(R\) is
\(
\begin{aligned}
& \frac{x}{3 c^2}+\frac{8 y}{3 d^2}=1 \text { identical to } \frac{x}{3}+\frac{y}{3}=1 \\
& \Rightarrow \quad c^2=1, d^2=8 \Rightarrow e_2^2=1-\frac{1}{8}=\frac{7}{8} \\
& \therefore \quad e_1^2+e_2^2=\frac{43}{40}, e_1 e_2=\frac{\sqrt{7}}{2 \sqrt{10}},\left|e_1^2-e_2^2\right|=\frac{27}{40}
\end{aligned}
\) -
Question 95 of 250
95. Question
Suppose that the foci of the ellipse \(\frac{x^2}{9}+\frac{y^2}{5}=1\) are \(\left(f_1, 0\right)\) and \(\left(f_2, 0\right)\) where \(f_1>0\) and \(f_2>0\). Let \(P_1\) and \(P_2\) be two parabolas with a common vertex at \((0,0)\) and with foci at \(\left(f_1, 0\right)\) and \(\left(2 f_2, 0\right)\), respectively. Let \(T_1\) be a tangent to \(P_1\) which passes through \(\left(2 f_2, 0\right)\) and \(T_2\) be a tangent to \(P_2\) which passes through \(\left(f_1, 0\right)\). If \(m_1\) is the slope of \(T_1\) and \(m_2\) is the slope of \(T_2\), then the value of \(\left(\frac{1}{m_1^2}+m_2^2\right)\) is
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Ellipse } \frac{x^2}{9}+\frac{y^2}{5}=1 \Rightarrow a=3, b=\sqrt{5} \text { and } e=\frac{2}{3} \\
& \therefore \quad f_1=2 \text { and } f_2=-2 \\
& P_1: y^2=8 x \text { and } P_2: y^2=-16 x \\
& T_1: y=m_1 x+\frac{2}{m_1} \\
& 0=-4 m_1+\frac{2}{m_1} \Rightarrow m_1^2=\frac{1}{2} \\
&
\end{aligned}
\)
It passes through \((-4,0)\),
\(
T_2: y=m_2 x-\frac{4}{m_2}
\)
It passes through \((2,0)\)
\(
\begin{array}{rcrl}
& 0=2 m_2-\frac{4}{m_2} \Rightarrow m_2^2=2 \\
\therefore & \frac{1}{m_1^2}+m_2^2=4
\end{array}
\) -
Question 96 of 250
96. Question
Let \(F_1\left(x_1, 0\right)\) and \(F_2\left(x_2, 0\right)\) for \(x_1<0\) and \(x_2>0\), be the foci of the ellipse \(\frac{x^2}{9}+\frac{y^2}{8}=1\). Suppose a parabola having vertex at the origin and focus at \(F_2\) intersects the ellipse at point \(M\) in the first quadrant and at point \(N\) in the fourth quadrant. The orthocentre of the triangle \(F_1 M N\) is
CorrectIncorrectHint
For ellipse \(\frac{x^2}{9}+\frac{y^2}{8}=1, e=\sqrt{\left(1-\frac{8}{9}\right)}=\frac{1}{3}\)
\(
\therefore \quad F_1(-1,0) \text { and } F_2(1,0)
\)
Parabola with vertex at \((0,0)\) and focus at \(F_2(1,0)\) is \(y^2=4 x\). Intersection points of ellipse and parabola are \(M\left(\frac{3}{2}, \sqrt{6}\right)\) and \(N\left(\frac{3}{2},-\sqrt{6}\right)\)
For orthocentre of \(\Delta F_1 M N\), clearly one altitude is \(X\)-axis i.e. \(y=0\) and altitude from \(M\) to \(F_1 N\) is
\(
y-\sqrt{6}=\frac{5}{2 \sqrt{6}}\left(x-\frac{3}{2}\right)
\)
Putting \(y=0\) in above equation, we get \(x=-\frac{9}{10}\)
Orthocentre \(\left(-\frac{9}{10}, 0\right)\) -
Question 97 of 250
97. Question
Let \(F_1\left(x_1, 0\right)\) and \(F_2\left(x_2, 0\right)\) for \(x_1<0\) and \(x_2>0\), be the foci of the ellipse \(\frac{x^2}{9}+\frac{y^2}{8}=1\). Suppose a parabola having vertex at the origin and focus at \(F_2\) intersects the ellipse at point \(M\) in the first quadrant and at point \(N\) in the fourth quadrant. If the tangents to the ellipse at \(M\) and \(N\) meet at \(R\) and the normal to the parabola at \(M\) meets the \(X\)-axis at \(Q\), then the ratio of area of the triangle \(M Q R\) to area of the quadrilateral \(M F_1 N F_2\) is
CorrectIncorrectHint
Tangents to ellipse at \(M\) and \(N\) are
\(
\frac{x}{6}+\frac{y \sqrt{6}}{8}=1 \text { and } \frac{x}{6}-\frac{y \sqrt{6}}{8}=1
\)
their intersection point is \(R(6,0)\)
Also, normal to parabola at \(M\left(\frac{3}{2}, \sqrt{6}\right)\) is
\(
y-\sqrt{6}=-\frac{\sqrt{6}}{2}\left(x-\frac{3}{2}\right)
\)
Its intersection with \(x\)-axis is \(Q\left(\frac{7}{2}, 0\right)\)
Now, \(\quad \operatorname{ar}(\triangle M Q R)=\frac{1}{2} \times \frac{5}{2} \times \sqrt{6}=\frac{5 \sqrt{6}}{4}\)
Also, \(\operatorname{area}\left(M F_1 N F_2\right)=2 \times\) Area of \(\left(F_1 M F_2\right)\)
\(
\begin{aligned}
= & 2 \times \frac{1}{2} \times 2 \times \sqrt{6}=2 \sqrt{6} \\
\frac{\operatorname{arca}(\triangle M Q R)}{\operatorname{area}\left(M F_1 N F_2\right)} & =\frac{5 \sqrt{6}}{4 \times 2 \sqrt{6}}=5: 8
\end{aligned}
\) -
Question 98 of 250
98. Question
Let \(F_1\left(x_1, 0\right)\) and \(F_2\left(x_2, 0\right)\) for \(x_1<0\) and \(x_2>0\), be the foci of the ellipse \(\frac{x^2}{9}+\frac{y^2}{8}=1\). Suppose a parabola having vertex at the origin and focus at \(F_2\) intersects the ellipse at point \(M\) in the first quadrant and at point \(N\) in the fourth quadrant. The eccentricity of an ellipse whose centre is at the origin is \(1 / 2\). If one of its directices is \(x=-4\), then the equation of the normal to it at \((1,3 / 2)\) is
CorrectIncorrectHint
Here, \(e=\frac{1}{2}\) and \(x=-\frac{a}{e}=-4\)
\(\therefore \quad a=2\)
and \(b^2=a^2\left(1-e^2\right)=4(1-1 / 4)=3\)
\(\therefore\) Equation of ellipse is \(\frac{x^2}{4}+\frac{y^2}{3}=1\)
\(\Rightarrow\) Equation of normal at \((1,3 / 2)\) is
\(
\frac{4 x}{1}-\frac{3 y}{3 / 2}=4-3
\)
or \(4 x-2 y=1\) -
Question 99 of 250
99. Question
The locus of a point \(P(\alpha, \beta)\) moving under the condition that the line \(y=\alpha x+\beta\) is a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is
CorrectIncorrectHint
Tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is
\(
y=m x \pm \sqrt{a^2 m^2-b^2}
\)
Given that \(y=\alpha x+\beta\) is the tangent of hyperbola
\(
\begin{aligned}
& \Rightarrow & m=\alpha \text { and } a^2 m^2-b^2 & =\beta^2 \\
& & a^2 \alpha^2-b^2 & =\beta^2
\end{aligned}
\)
Locus is \(a^2 x^2-y^2=b^2\) which is hyperbola. -
Question 100 of 250
100. Question
Let a hyperbola passes through the focus of the ellipse \(\frac{x^2}{25}+\frac{y^2}{16}=1\). The transverse and conjugate axes of this hyperbola coincide with the major and minor axes of the given ellipse, also the product of eccentricities of given ellipse and hyperbola is 1 , then
CorrectIncorrectHint
For the given ellipse \(\frac{x^2}{25}+\frac{y^2}{16}=1\)
\(
\Rightarrow \quad e=\sqrt{\left(1-\frac{16}{25}\right)}=\frac{3}{5}
\)
\(\Rightarrow\) Eccentricity of hyperbola \(=\frac{5}{3}\)
Let the hyperbola be \(\frac{x^2}{A^2}-\frac{y^2}{B^2}=1\) then
\(
B^2=A^2\left(\frac{25}{9}-1\right)=\frac{16}{9} A^2
\)
\(\therefore \frac{x^2}{A^2}-\frac{9 y^2}{16 A^2}=1\), As it passes through focus of ellipse i.e. \((3,0)\)
\(\therefore\) We get \(A^2=9 \Rightarrow B^2=16\)
\(\therefore\) Equation of hyperbola is \(\frac{x^2}{9}-\frac{y^2}{16}=1\), focus of hyperbola is \((5,0)\), vertex of hyperbola is \((3,0)\). -
Question 101 of 250
101. Question
A hyperbola, having the transverse axis of length \(2 \sin \theta\), is confocal with the ellipse \(3 x^2+4 y^2=12\). Then, its equation is
CorrectIncorrectHint
The length of transverse axis \(=2 \sin \theta=2 a\)
\(
\Rightarrow \quad a=\sin \theta
\)
Also for ellipse \(3 x^2+4 y^2=12\)
\(
\begin{gathered}
\text { or } \frac{x^2}{4}+\frac{y^2}{3}=1, a^2=4, b^2=3 \\
e=\sqrt{1-\frac{b^2}{a^2}}=\sqrt{1-\frac{3}{4}}=\frac{1}{2}
\end{gathered}
\)
\(\therefore\) Focus of ellipse \(=\left(2 \times \frac{1}{2}, 0\right) \Rightarrow(1,0)\)
As hyperbola is confocal with ellipse, focus of hyperbola \(=(1,0)\)
\(
\begin{array}{rlrl}
\Rightarrow & & a e & =1 \Rightarrow \sin \theta \times e=1 \\
\Rightarrow & & e & =\operatorname{cosec} \theta \\
& & b^2 & =a^2\left(e^2-1\right) \\
& & =\sin ^2 \theta\left(\operatorname{cosec}^2 \theta-1\right)=\cos ^2 \theta
\end{array}
\)
\(\therefore\) Equation of hyperbola is
\(
\frac{x^2}{\sin ^2 \theta}-\frac{y^2}{\cos ^2 \theta}=1
\)
or, \(x^2 \operatorname{cosec}^2 \theta-y^2 \sec ^2 \theta=1\) -
Question 102 of 250
102. Question
Two branches of a hyperbola
CorrectIncorrectHint
Two branches of hyperbola have no common tangent but have a common normal joining \(S S^{\prime}\).
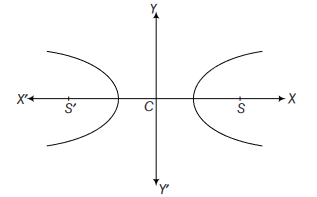
-
Question 103 of 250
103. Question
For the hyperbola \(\frac{x^2}{\cos ^2 \alpha}-\frac{y^2}{\sin ^2 \alpha}=1\), which of the following remains constant when \(\alpha\) varies
CorrectIncorrectHint
Given, equation of hyperbola is
\(
\frac{x^2}{\cos ^2 \alpha}-\frac{y^2}{\sin ^2 \alpha}=1
\)
Here, \(a^2=\cos ^2 \alpha\) and \(b^2=\sin ^2 \alpha\)
\(
\begin{array}{rlrl}
\because & b^2 & =a^2\left(e^2-1\right) \\
& \therefore & \sin ^2 \alpha & =\cos ^2 \alpha\left(e^2-1\right) \\
& \text { or } & \sin ^2 \alpha+\cos ^2 \alpha & =\cos ^2 \alpha \cdot e^2
\end{array}
\)
\(
\begin{aligned}
& \text { or } e^2=1+\tan ^2 \alpha=\sec ^2 \alpha \Rightarrow e=\sec \alpha \\
& \therefore \quad a e=\cos \alpha \cdot \frac{1}{\cos \alpha}=1
\end{aligned}
\)
Coordinates of foci are \(( \pm a e, 0)\) i.e. \(( \pm 1,0)\)
Hence, abscissae of foci remain constant, when \(\alpha\) varies. -
Question 104 of 250
104. Question
Consider a branch of the hyperbola
\(
x^2-2 y^2-2 \sqrt{2} x-4 \sqrt{2} y-6=0
\)
with vertex at the point \(A\). Let \(B\) be one of the end points of its latusrectum. If \(C\) is the focus of the hyperbola nearest to the point \(A\), then the area of the triangle \(A B C\) isCorrectIncorrectHint
The given hyperbola is
\(
\begin{aligned}
x^2-2 y^2-2 \sqrt{2} x-4 \sqrt{2} y-6 & =0 \\
\Rightarrow\left(x^2-2 \sqrt{2} x+2\right)-2\left(y^2+2 \sqrt{2} y+2\right) & =6+2-4
\end{aligned}
\)
\(
\begin{array}{ll}
\Rightarrow & (x-\sqrt{2})^2-2(y+\sqrt{2})^2=4 \\
\Rightarrow & \frac{(x-\sqrt{2})^2}{2^2}-\frac{(y+\sqrt{2})^2}{(\sqrt{2})^2}=1
\end{array}
\)
\(
\therefore \quad a=2, b=\sqrt{2} \Rightarrow e=\sqrt{\left(1+\frac{2}{4}\right)}=\sqrt{\frac{3}{2}}
\)
Clearly, \(\triangle A B C\) is a right triangle.
\(
B\left(a e, \frac{b^2}{a}\right)
\)
\(
\begin{aligned}
\therefore \quad \text { Area of }(\triangle A B C) & =\frac{1}{2} \times A C \times B C \\
& =\frac{1}{2} \times(a e-a) \times \frac{b^2}{a}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{2}(e-1) b^2=\frac{1}{2}\left(\sqrt{\frac{3}{2}}-1\right) \cdot 2 \\
& =\left(\sqrt{\frac{3}{2}}-1\right)
\end{aligned}
\) -
Question 105 of 250
105. Question
An ellipse intersects the hyperbola \(2 x^2-2 y^2=1\) orthogonally. The eccentricity of the ellipse is reciprocal of that of the hyperbola. If the axes of the ellipse are along the coordinate axes, then
CorrectIncorrectHint
The given hyperbola is
\(
x^2-y^2=\frac{1}{2} \dots(i)
\)
which is rectangular hyperbola
\(\therefore \quad e=\sqrt{2}\)
Let the ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Its eccentricity \(=\frac{1}{\sqrt{2}}\)
\(
\therefore \quad b^2=a^2\left(1-e^2\right)=a^2\left(1-\frac{1}{2}\right)=\frac{a^2}{2}
\)
So, the equation of ellipse becomes
\(
x^2+2 y^2=a^2 \dots(ii)
\)
Let the hyperbola (i) and ellipse (ii) intersect each other at \(P\left(x_1, y_1\right)\).
\(\therefore\) (Slope of hyperbola (i) at \(\left.\left(x_1, y_1\right)\right) \times\) (Slope of ellipse (ii) at \(\left(x_1, y_1\right)=-1\)
\(
\Rightarrow \quad \frac{x_1}{y_1} \times \frac{-x_1}{2 y_1}=-1
\)
or \(x_1^2=2 y_1^2 \dots(iii)\)
Also \(\left(x_1, y_1\right)\) lies on \(x^2-y^2=\frac{1}{2}\)
\(
\therefore \quad x_1^2-y_1^2=\frac{1}{2} \dots(iv)
\)
From Eqs. (iii) and (iv), we get \(y_1^2=\frac{1}{2}\) and \(x_1^2=1\) and \(\left(x_1, y_1\right)\) lies on ellipse \(x^2+2 y^2=a^2\)
\(
\therefore \quad x_1^2+2 y_1^2=a^2
\)
\(
\Rightarrow \quad 1+1=a^2 \text { or } a^2=2
\)
\(\therefore\) Equation of ellipse is \(x^2+2 y^2=2\) whose foci \(( \pm 1,0)\). -
Question 106 of 250
106. Question
The circle \(x^2+y^2-8 x=0\) and hyperbola \(\frac{x^2}{9}-\frac{y^2}{4}=1\) intersect at the points \(A\) and \(B\). Equation of a common tangent with positive slope to the circle as well as to the hyperbola is
CorrectIncorrectHint
The intersection points of given circle
\(
x^2+y^2-8 x=0 \dots(i)
\)
and hyperbola
\(
4 x^2-9 y^2=36 \dots(ii)
\)
can be obtained by solving these equations substituting value of \(y^2\) from Eq. (i) in Eq. (ii), we get
\(
\begin{aligned}
4 x^2-9\left(8 x-x^2\right) & =36 \\
13 x^2-72 x-36 & =0 \\
x & =6,-\frac{6}{13} \\
y^2 & =12,-\frac{660}{169} \text { (not possible) }
\end{aligned}
\)
\(
\therefore A(6,2 \sqrt{3}) \text { and } B(6,-2 \sqrt{3}) \text { are points of intersection. }
\)
Equation of tangent to hyperbola having slope \(m\) is
\(
y=m x+\sqrt{\left(9 m^2-4\right)} \dots(iii)
\)
Equation of tangent to circle is
\(
y=m(x-4)+\sqrt{\left(16 m^2+16\right)} \dots(iv)
\)
Eqs. (iii) and (iv) will be identical, then
\(
m=\frac{2}{\sqrt{5}}
\)
So, equation of common tangents
\(
\begin{aligned}
y & =\frac{2 x}{\sqrt{5}}+\sqrt{\left(\frac{36}{5}-4\right)} \\
\Rightarrow \quad y & =\frac{2 x}{\sqrt{5}}+\frac{4}{\sqrt{5}}
\end{aligned}
\)
or \(2 x-\sqrt{5} y+4=0\) -
Question 107 of 250
107. Question
The circle \(x^2+y^2-8 x=0\) and hyperbola \(\frac{x^2}{9}-\frac{y^2}{4}=1\) intersect at the points \(A\) and \(B\). Equation of the circle with \(A B\) as its diameter is
CorrectIncorrectHint
The intersection points of given circle
\(
x^2+y^2-8 x=0 \dots(i)
\)
and hyperbola
\(
4 x^2-9 y^2=36 \dots(ii)
\)
can be obtained by solving these equations substituting value of \(y^2\) from Eq. (i) in Eq. (ii), we get
\(
\begin{aligned}
4 x^2-9\left(8 x-x^2\right) & =36 \\
13 x^2-72 x-36 & =0 \\
x & =6,-\frac{6}{13} \\
y^2 & =12,-\frac{660}{169} \text { (not possible) }
\end{aligned}
\)
\(
\therefore A(6,2 \sqrt{3}) \text { and } B(6,-2 \sqrt{3}) \text { are points of intersection. }
\)
Equation of circle with \(A B\) as its diameter is
\(
\begin{aligned}
& (x-6)(x-6)+(y-2 \sqrt{3})(y+2 \sqrt{3})=0 \\
& \Rightarrow \quad x^2+y^2-12 x+24=0 \\
&
\end{aligned}
\) -
Question 108 of 250
108. Question
The line \(2 x+y=1\) is tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\). If this line passes through the point of intersection of the nearest directrix and the \(X\)-axis, then the eccentricity of the hyperbola is
CorrectIncorrectHint
\(\because\) line \(2 x+y=1\) is tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
\(
\begin{aligned}
\therefore & (1)^2 =a^2(-2)^2-b^2 \\
\Rightarrow & 4 a^2-b^2 =1
\end{aligned}
\)
Intersection point of nearest directrix \(x=\frac{a}{e}\) and \(X\)-axis is \(\left(\frac{a}{e}, 0\right)\) As, \(2 x+y=1\) passes through \(\left(\frac{a}{e}, 0\right)\)
\(\therefore \quad \frac{2 a}{e}+0=1 \Rightarrow a=\frac{e}{2} \dots(ii)\)
and \(b^2=a^2\left(e^2-1\right)=\frac{e^2}{4}\left(e^2-1\right) \dots(iii)\)
Substituting the values of \(a\) and \(b\) from Eqs. (ii) and (iii) in Eq. (i), then
\(
\begin{aligned}
& e^2-\frac{e^2}{4}\left(e^2-1\right)=1 \\
& \Rightarrow \quad\left(e^2-4\right)\left(e^2-1\right)=0 \\
& \therefore \quad e^2=4, e^2 \neq 1 \quad(\because e>1) \\
& \text { Hence } e=2 \\
&
\end{aligned}
\) -
Question 109 of 250
109. Question
Let \(P(6,3)\) be a point on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\). If the normal at the point \(P\) intersects the \(X\)-axis at \((9,0)\), then the eccentricity of the hyperbola is
CorrectIncorrectHint
Equation of normal at \(P(6,3)\) is
\(
\frac{a^2 x}{6}+\frac{b^2 y}{3}=a^2+b^2
\)
\(\because\) Normal intersects the \(X\)-axis at \((9,0)\), then
\(
\frac{9 a^2}{6}+0=a^2+b^2 \Rightarrow 3 a^2=2 a^2+2 b^2
\)
or \(a^2=2 b^2\)
or \(a^2=2 a^2\left(e^2-1\right)\)
\(\therefore \quad e^2=\frac{3}{2}\)
Hence, \(e=\sqrt{\frac{3}{2}}\) -
Question 110 of 250
110. Question
Let the eccentricity of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) be reciprocal to that of the ellipse \(x^2+4 y^2=4\). If the hyperbola passes through a focus of the ellipse, then
CorrectIncorrectHint
Given, ellipse is \(x^2+4 y^2=4\)
or \(\quad \frac{x^2}{4}+\frac{y^2}{1}=1\)
\(\therefore \quad e=\sqrt{\left(1-\frac{1}{4}\right)}=\frac{\sqrt{3}}{2}\)
and foci are \(( \pm \sqrt{3}, 0)\)
\(\therefore\) Eccentricity of hyperbola \(=\frac{2}{\sqrt{3}}=e_1\)
and \(b^2=a^2\left(e_1^2-1\right)=a^2\left(\frac{4}{3}-1\right)=\frac{a^2}{3}\)
then equation of hyperbola becomes
\(
x^2-3 y^2=a^2
\)
which pass through \(( \pm \sqrt{3}, 0)\)
\(
\begin{aligned}
3-0 & =a^2 \\
\Rightarrow a^2 & =3
\end{aligned}
\)
\(\therefore\) Equation of hyperbola is
\(
x^2-3 y^2=3
\)
and foci of hyperbola are \(\left( \pm \sqrt{3} \times \frac{2}{\sqrt{3}}, 0\right)\) i.e., \(( \pm 2,0)\) -
Question 111 of 250
111. Question
Tangents are drawn to the hyperbola \(\frac{x^2}{9}-\frac{y^2}{4}=1\), parallel to the straight line \(2 x-y=1\). The points of contact of the tangents on the hyperbola are
CorrectIncorrectHint
Equation of tangent at \(\left(x_1, y_1\right)\) is
\(
\frac{x x_1}{9}-\frac{y y_1}{4}=1 \dots(i)
\)
Equation of line parallel to
\(
2 x-y=\lambda \dots(ii)
\)
\(\because\) Line (ii) is tangent of \(\frac{x^2}{9}-\frac{y^2}{4}=1\), then
\(
\begin{array}{rlrl}
& & \lambda^2 & =9 \times 2^2-4 \\
\therefore \quad & \lambda & = \pm 4 \sqrt{2}
\end{array}
\)
From Eq. (ii), Equation of tangent is
\(
2 x-y= \pm 4 \sqrt{2} \dots(iii)
\)
Comparing Eqs. (i) and (iii), we get \(\frac{x_1}{18}=\frac{y_1}{4}= \pm \frac{1}{4 \sqrt{2}}\)
or \(\quad x_1= \pm \frac{9}{2 \sqrt{2}}\) and \(y_1= \pm \frac{1}{\sqrt{2}}\)
Hence, points of contact of the tangents on the hyperbola are
\(
\left(\frac{9}{2 \sqrt{2}}, \frac{1}{\sqrt{2}}\right) \text { and }\left(-\frac{9}{2 \sqrt{2}},-\frac{1}{\sqrt{2}}\right)
\) -
Question 112 of 250
112. Question
Consider the hyperbola \(H: x^2-y^2=1\) and a circle \(S\) with centre \(N\left(x_2, 0\right)\). Suppose that \(H\) and \(S\) touch each other at a point \(P\left(x_1, y_1\right)\) with \(x_1>1\) and \(y_1>0\). The common tangent to \(H\) and \(S\) at \(P\) intersects the \(X\)-axis at point \(M\). If \((l, m)\) is the centroid of the triangle \(P M N\), then the correct expression(s) is(are)
CorrectIncorrectHint
\(
H: x^2-y^2=1
\)
\(S:\) Circle with centre \(N\left(x_2, 0\right)\)
Common tangent to \(H\) and \(S\) at \(P\left(x_1, y_1\right)\) is
\(
x x_1-y y_1=1 \Rightarrow m_1=\frac{x_1}{y_1}
\)
Also radius of circle \(S\) with centre \(N\left(x_2, 0\right)\) through point of contact \(\left(x_1, y_1\right)\) is perpendicular to tangent.
\(
\begin{array}{lll}
\therefore & m_1 m_2=-1 \Rightarrow \frac{x_1}{y_1} \times \frac{0-y_1}{x_2-x_1}=-1 \\
\Rightarrow & x_1=x_2-x_1 \text { or } x_2=2 x_1
\end{array}
\)
\(M\) is the point of intersection of tangent at \(P\) and \(X\)-axis
\(
\therefore \quad M\left(\frac{1}{x_1}, 0\right)
\)
\(\because\) Centroid of \(\triangle P M N\) is \((\ell, m)\)
\(
\therefore \quad x_1+\frac{1}{x_1}+x_2=3 \ell \text { and } y_1=3 m
\)
Using \(x_2=2 x_1\),
\(
\begin{array}{ll}
\Rightarrow & \frac{1}{3}\left(3 x_1+\frac{1}{x_1}\right)=l \text { and } \frac{y_1}{3}=m \\
\therefore & \frac{d l}{d x_1}=1-\frac{1}{3 x_1^2}, \frac{d m}{d y_1}=\frac{1}{3}
\end{array}
\)
Also, \(\left(x_1, y_1\right)\) lies on \(H\),
\(
\begin{aligned}
& \therefore \quad x_1^2-y_1^2=1 \text { or } y_1=\sqrt{\left(x_1^2-1\right)} \\
& \therefore \quad m=\frac{1}{3} \sqrt{\left(x_1^2-1\right)} \\
& \therefore \quad \frac{d m}{d x_1}=\frac{x_1}{3 \sqrt{\left(x_1^2-1\right)}} \\
&
\end{aligned}
\) -
Question 113 of 250
113. Question
The eccentricity of the hyperbola whose length of the latusrectum is equal to 8 and the length of its conjugate axis is equal to half of the distance between its foci, is
CorrectIncorrectHint
\(\because \frac{2 b^2}{a}=8\) and \(2 b=\frac{1}{2}(2 a e)\)
\(\Rightarrow \quad b^2=4 a\) and \(b=\frac{1}{2} a e\) or \(b^2=\frac{1}{4} a^2 e^2\)
\(\Rightarrow \quad a^2\left(e^2-1\right)=\frac{1}{4} a^2 e^2 \Rightarrow 4 e^2-4=e^2 \quad\) or \(e^2=\frac{4}{3}\)
\(\therefore \quad e=\frac{2}{\sqrt{3}}\)
\(\Rightarrow b^2=4 a\) and \(b=\frac{1}{2} a e\) or \(b^2=\frac{1}{4} a^2 e^2\) -
Question 114 of 250
114. Question
A hyperbola passes through the point \(P(\sqrt{2}, \sqrt{3})\) and has foci at \(( \pm 2,0)\). Then the taught to this hyperbola at \(P\) also passes through the point
CorrectIncorrectHint
Let Equation of hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) When it passes through \(P(\sqrt{2}, \sqrt{3})\), then \(\frac{2}{a^2}-\frac{3}{b^2}=1\)
\(
\begin{aligned}
& \Rightarrow \quad 2 b^2-3 a^2=a^2 b^2 \dots(i) \\
& \text { and } a e=2 \Rightarrow a^2+b^2=4 \dots(ii)
\end{aligned}
\)
From Eqs. (i) and (ii), we get \(2\left(4-a^2\right)-3 a^2=a^2\left(4-a^2\right)\)
\(
\begin{aligned}
& \Rightarrow a^2-9 a^2+8=0 \Rightarrow\left(a^2-1\right)\left(a^2-8\right)=0 \\
& \therefore a^2=1 \quad\left(\because a^2 \neq 8\right) \\
&
\end{aligned}
\)
From Eq. (ii), \(b^2=3\)
\(\therefore\) Equation of Hyperbola is \(\frac{x^2}{1}-\frac{y^2}{3}=1\)
Equation of tangent at \(P(\sqrt{2}, \sqrt{3})\) is \(\frac{x \sqrt{2}}{1}-\frac{y \sqrt{3}}{3}=1\)
Which is passes through \((2 \sqrt{2}, 3 \sqrt{2})\) -
Question 115 of 250
115. Question
If \(2 x-y+1=0\) is a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{16}=1\), then which of the following cannot be sides of a right angled triangle?
CorrectIncorrectHint
\(( a , b , c ) \because 2 x-y+1=0\) is a tangent of \(\frac{x^2}{a^2}-\frac{y^2}{16}=1\), then
\(
(1)^2=a^2(2)^2-16 \text { or }(2 a)^2=(1)^2+(4)^2
\)
\(\therefore 2 a, 4,1\) are the sides of a right angled triangle. -
Question 116 of 250
116. Question
Matching the information given in the three columns of the following table. Columns 1, 2 and 3 contain conics, equations of tangents to the conics and points of contact, respectively.
\(
\begin{array}{|c|c|c|c|c|c|}
\hline & \text { Column } 1 & & \text { Column } 2 & & \text { Column } 3 \\
\hline \text { (I) } & \begin{array}{l}
x^2+y^2 \\
=a^2
\end{array} & \text { (i) } & m y=m^2 x+a & \text { (P) } & \left(\frac{a}{m^2}, \frac{2 a}{m}\right) \\
\hline \text { (II) } & \begin{array}{l}
x^2+a^2 y^2 \\
=a^2
\end{array} & \text { (ii) } & \begin{array}{l}
y=m x \\
+a \sqrt{m^2+1}
\end{array} & \text { (Q) } & \left(\frac{-m a}{\sqrt{m^2+1}}, \frac{a}{\sqrt{m^2+1}}\right) \\
\hline \text { (III) } & y^2=4 a x & \text { (iii) } & \begin{array}{l}
y=m x \\
+\sqrt{a^2 m^2-1}
\end{array} & \text { (R) } & \left(\frac{-a^2 m}{\sqrt{a^2 m^2+1}}, \frac{1}{\sqrt{a^2 m^2+1}}\right. \\
\hline \text { (IV) } & \begin{array}{l}
x^2-a^2 y^2 \\
=a^2
\end{array} & \text { (iv) } & \begin{array}{l}
y=m x \\
+\sqrt{a^2 m^2+1}
\end{array} & \text { (S) } & \left(\frac{-a^2 m}{\sqrt{a^2 m^2-1}}, \frac{-1}{\sqrt{a^2 m^2-1}}\right) \\
\hline
\end{array}
\)
The tangent to a suitable conic (Column 1 ) at \(\left(\sqrt{3}, \frac{1}{2}\right)\) is found to be \(\sqrt{3} x+2 y=4\), then which of the following options is the only correct combination?CorrectIncorrectHint
I. \(x^2+y^2=a^2\)
Equations of tangents in terms of slopes are
\(
y=m x+a \sqrt{\left(m^2+1\right)}
\)
and points of contact in terms of slopes are
\(
\left(\frac{-m a}{\sqrt{\left(m^2+1\right)}}, \frac{a}{\sqrt{\left(m^2+1\right)}}\right)(Q)
\)
\(\therefore I\) (ii) (Q) (Ans. Q.No. 112) (Here, \(a=\sqrt{2}, m= \pm 1\) )
II. \(x^2+a^2 y^2=a^2\) or \(\frac{x^2}{a^2}+\frac{y^2}{1^2}=1\)
Equations of tangents in terms of slopes are
\(
y=m x+\sqrt{\left(a^2 m^2+1\right)}
\)
and points of contact in terms of slopes are
\(
\left(\frac{-a^2 m}{\sqrt{\left(a^2 m^2+1\right)}}, \frac{1}{\sqrt{\left(a^2 m^2+1\right)}}\right)
\)
\(\therefore\) II (iv) (R) (Ans. Q.No. 111) (Here, \(a=2, m=\frac{-\sqrt{3}}{2}\) )
III. \(y^2=4 a x\)
Equation of tangent in terms of slopes are
\(
y=m x+\frac{a}{m} \text { or } m y=m^2 x+a
\)
and points of contact in terms of slopes are
\(
\left(\frac{a}{m^2}, \frac{2 a}{m}\right)
\)
\(\therefore\) III (i) (P) (Ans. Q.No. 113) (Here, \(a=8, m=1\) ) -
Question 117 of 250
117. Question
Matching the information given in the three columns of the following table. Columns 1, 2 and 3 contain conics, equations of tangents to the conics and points of contact, respectively.
\(
\begin{array}{|c|c|c|c|c|c|}
\hline & \text { Column } 1 & & \text { Column } 2 & & \text { Column } 3 \\
\hline \text { (I) } & \begin{array}{l}
x^2+y^2 \\
=a^2
\end{array} & \text { (i) } & m y=m^2 x+a & \text { (P) } & \left(\frac{a}{m^2}, \frac{2 a}{m}\right) \\
\hline \text { (II) } & \begin{array}{l}
x^2+a^2 y^2 \\
=a^2
\end{array} & \text { (ii) } & \begin{array}{l}
y=m x \\
+a \sqrt{m^2+1}
\end{array} & \text { (Q) } & \left(\frac{-m a}{\sqrt{m^2+1}}, \frac{a}{\sqrt{m^2+1}}\right) \\
\hline \text { (III) } & y^2=4 a x & \text { (iii) } & \begin{array}{l}
y=m x \\
+\sqrt{a^2 m^2-1}
\end{array} & \text { (R) } & \left(\frac{-a^2 m}{\sqrt{a^2 m^2+1}}, \frac{1}{\sqrt{a^2 m^2+1}}\right. \\
\hline \text { (IV) } & \begin{array}{l}
x^2-a^2 y^2 \\
=a^2
\end{array} & \text { (iv) } & \begin{array}{l}
y=m x \\
+\sqrt{a^2 m^2+1}
\end{array} & \text { (S) } & \left(\frac{-a^2 m}{\sqrt{a^2 m^2-1}}, \frac{-1}{\sqrt{a^2 m^2-1}}\right) \\
\hline
\end{array}
\)
For \(a=\sqrt{2}\), if a tangent is drawn to a suitable conic (Column 1 ) at the point of contact \((-1,1)\), then which of the following options is the only correct combination for obtaining its equation?CorrectIncorrectHint
I. \(x^2+y^2=a^2\)
Equations of tangents in terms of slopes are
\(
y=m x+a \sqrt{\left(m^2+1\right)}
\)
and points of contact in terms of slopes are
\(
\left(\frac{-m a}{\sqrt{\left(m^2+1\right)}}, \frac{a}{\sqrt{\left(m^2+1\right)}}\right)(Q)
\)
\(\therefore I\) (ii) (Q) (Ans. Q.No. 112) (Here, \(a=\sqrt{2}, m= \pm 1\) )
II. \(x^2+a^2 y^2=a^2\) or \(\frac{x^2}{a^2}+\frac{y^2}{1^2}=1\)
Equations of tangents in terms of slopes are
\(
y=m x+\sqrt{\left(a^2 m^2+1\right)}
\)
and points of contact in terms of slopes are
\(
\left(\frac{-a^2 m}{\sqrt{\left(a^2 m^2+1\right)}}, \frac{1}{\sqrt{\left(a^2 m^2+1\right)}}\right)
\)
\(\therefore\) II (iv) (R) (Ans. Q.No. 111) (Here, \(a=2, m=\frac{-\sqrt{3}}{2}\) )
III. \(y^2=4 a x\)
Equation of tangent in terms of slopes are
\(
y=m x+\frac{a}{m} \text { or } m y=m^2 x+a
\)
and points of contact in terms of slopes are
\(
\left(\frac{a}{m^2}, \frac{2 a}{m}\right)
\)
\(\therefore\) III (i) (P) (Ans. Q.No. 113) (Here, \(a=8, m=1\) ) -
Question 118 of 250
118. Question
Matching the information given in the three columns of the following table. Columns 1, 2 and 3 contain conics, equations of tangents to the conics and points of contact, respectively.
\(
\begin{array}{|c|c|c|c|c|c|}
\hline & \text { Column } 1 & & \text { Column } 2 & & \text { Column } 3 \\
\hline \text { (I) } & \begin{array}{l}
x^2+y^2 \\
=a^2
\end{array} & \text { (i) } & m y=m^2 x+a & \text { (P) } & \left(\frac{a}{m^2}, \frac{2 a}{m}\right) \\
\hline \text { (II) } & \begin{array}{l}
x^2+a^2 y^2 \\
=a^2
\end{array} & \text { (ii) } & \begin{array}{l}
y=m x \\
+a \sqrt{m^2+1}
\end{array} & \text { (Q) } & \left(\frac{-m a}{\sqrt{m^2+1}}, \frac{a}{\sqrt{m^2+1}}\right) \\
\hline \text { (III) } & y^2=4 a x & \text { (iii) } & \begin{array}{l}
y=m x \\
+\sqrt{a^2 m^2-1}
\end{array} & \text { (R) } & \left(\frac{-a^2 m}{\sqrt{a^2 m^2+1}}, \frac{1}{\sqrt{a^2 m^2+1}}\right. \\
\hline \text { (IV) } & \begin{array}{l}
x^2-a^2 y^2 \\
=a^2
\end{array} & \text { (iv) } & \begin{array}{l}
y=m x \\
+\sqrt{a^2 m^2+1}
\end{array} & \text { (S) } & \left(\frac{-a^2 m}{\sqrt{a^2 m^2-1}}, \frac{-1}{\sqrt{a^2 m^2-1}}\right) \\
\hline
\end{array}
\)
If a tangent of a suitable conic (Column 1 ) is found to be \(y=x+8\) and its point of contact is \((8,16)\), then which of the following options is the only correct combination?CorrectIncorrectHint
I. \(x^2+y^2=a^2\)
Equations of tangents in terms of slopes are
\(
y=m x+a \sqrt{\left(m^2+1\right)}
\)
and points of contact in terms of slopes are
\(
\left(\frac{-m a}{\sqrt{\left(m^2+1\right)}}, \frac{a}{\sqrt{\left(m^2+1\right)}}\right)(Q)
\)
\(\therefore I\) (ii) (Q) (Ans. Q.No. 112) (Here, \(a=\sqrt{2}, m= \pm 1\) )
II. \(x^2+a^2 y^2=a^2\) or \(\frac{x^2}{a^2}+\frac{y^2}{1^2}=1\)
Equations of tangents in terms of slopes are
\(
y=m x+\sqrt{\left(a^2 m^2+1\right)}
\)
and points of contact in terms of slopes are
\(
\left(\frac{-a^2 m}{\sqrt{\left(a^2 m^2+1\right)}}, \frac{1}{\sqrt{\left(a^2 m^2+1\right)}}\right)
\)
\(\therefore\) II (iv) (R) (Ans. Q.No. 111) (Here, \(a=2, m=\frac{-\sqrt{3}}{2}\) )
III. \(y^2=4 a x\)
Equation of tangent in terms of slopes are
\(
y=m x+\frac{a}{m} \text { or } m y=m^2 x+a
\)
and points of contact in terms of slopes are
\(
\left(\frac{a}{m^2}, \frac{2 a}{m}\right)
\)
\(\therefore\) III (i) (P) (Ans. Q.No. 113) (Here, \(a=8, m=1\) ) -
Question 119 of 250
119. Question
Find the equation of the parabola whose focus is \((-3,2)\) and the directrix is \(x+y=4\).
CorrectIncorrectHint
Let \(P(x, y)\) be any point on the parabola whose focus is \(S(-3,2)\) and the directrix \(x+y-4=0\). Draw \(P M\) perpendicular to \(x+y-4=0\). Then,
\(
\begin{array}{ll}
& S P=P M \\
\Rightarrow \quad & S P^2=P M^2 \\
\Rightarrow \quad & (x+3)^2+(y-2)^2=\left|\frac{x+y-4}{\sqrt{1+1}}\right|^2 \\
\Rightarrow \quad & 2\left(x^2+y^2+6 x-4 y+13\right)=\left(x^2+y^2+16+2 x y-8 x-8 y\right) \\
\Rightarrow \quad & x^2+y^2-2 x y+20 x+10=0
\end{array}
\) -
Question 120 of 250
120. Question
Find the equation of the parabola whose focus is \((-3,0)\) and the directrix is \(x+5=0\).
CorrectIncorrectHint
Let \(P(x, y)\) be any point on the parabola having its focus at \(S(-3,0)\) and directrix as the line \(x+5=0\). Then,
\(S P=P M\), where \(P M\) is the length of the perpendicular from \(P\) on the directrix
\(
\Rightarrow \quad S P^2=P M^2
\)
\(
\Rightarrow \quad(x+3)^2+(y-0)^2=\left|\frac{x+0 y+5}{\sqrt{1}+0}\right|^2
\)
\(\Rightarrow \quad y^2=4 x+16\), which is the required equation of the parabola. -
Question 121 of 250
121. Question
Find the vertex, focus and directrix of the parabola \(4 y^2+12 x-12 y+39=0\).
CorrectIncorrectHint
The given equation is
\(
\begin{array}{ll}
& 4 y^2+12 x-12 y+39=0 \\
\Rightarrow \quad & 4 y^2-12 y=-12 x-39 \\
\Rightarrow \quad & 4\left(y^2-3 y\right)=-12 x-39 \\
\Rightarrow \quad & 4\left(y^2-3 y+\frac{9}{4}\right)=-12 x-39+9
\end{array}
\)
\(
\begin{aligned}
& \Rightarrow \quad 4\left(y-\frac{3}{2}\right)^2=-12\left(x+\frac{5}{2}\right) \\
& \Rightarrow \quad\left(y-\frac{3}{2}\right)^2=-3\left(x+\frac{5}{2}\right) \dots(i)
\end{aligned}
\)
Shifting the origin to the point \((-5 / 2,3 / 2)\) without rotating the axes and denoting the new coordinates with respect to these axes by \(X\) and \(Y\), we obtain
\(
x=X+\left(-\frac{5}{2}\right), y=Y+\frac{3}{2} \dots(ii)
\)
Using these relations equation (i), reduces to
\(
Y^2=-3 X \dots(iii)
\)
This is of the form \(Y^2=-4 a X\). On comparing, we get: \(a=\frac{3}{4}\).
Vertex: The coordinates of the vertex with respect to new axes are \((X=0, Y=0)\). So, coordinates of the vertex with respect to old axes are \((-5 / 2,3 / 2) \text { [Putting } X=0, Y=0 \text { in (ii)] }\).
Focus: The coordinates of the focus of the parabola with respect to new axes are
\(
\left(X=-\frac{3}{4}, Y=0\right) \text {. }
\)
So, coordinates of the focus with respect to old axes are
\(
\left(-\frac{13}{4}, \frac{3}{2}\right) \quad\left[\text { Putting } X=-\frac{3}{4}, Y=0 \text { in (ii) }\right]
\)
Directrix: The equation of the directrix of the parabola with respect to new axes is \(X=\frac{3}{4}\). So, equation of the directrix of the parabola with respect to old axes is
\(
x=-\frac{7}{4} \text { [Putting } X=3 / 4 \text { in (ii)] }
\) -
Question 122 of 250
122. Question
If the tangent at \((1,7)\) to the curve \(x^2=y-6\) touches the circle \(x^2+y^2+16 x+12 y+c=0\) then the value of \(c\) is : [JEE Main 2018]
CorrectIncorrectHint
(c) Equation of tangent at \((1,7)\) to \(x^2=y-6\) is
\(
2 x-y+5=0
\)
Now, perpendicular from centre \(O(-8,-6)\) to \(2 x-y+5=0\) should be equal to radius of the circle
\(
\begin{aligned}
& \therefore\left|\frac{-16+6+5}{\sqrt{5}}\right|=\sqrt{64+36- C } \\
& \quad \Rightarrow \sqrt{5}=\sqrt{100- c } \\
& \quad \Rightarrow c=95
\end{aligned}
\) -
Question 123 of 250
123. Question
If a circle \(C\), whose radius is 3 , touches externally the circle, \(x^2+y^2+2 x-4 y-4=0\) at the point \((2,2)\), then the length of the intercept cut by this circle \(c\), on the \(x\)-axis is equal to [Online April 16, 2018]
CorrectIncorrectHint
Given circle is:
\(
x^2+y^2+2 x-4 y-4=0
\)
its centre is \((-1,2)\) and radius is 3 units.
Let \(A=(x, y)\) be the centre of the circle \(C\)
\(
\therefore \frac{x-1}{2}=2 \Rightarrow x=5 \text { and } \frac{y+2}{2}=2 \Rightarrow y=2
\)
So the centre of \(C\) is \((5,2)\) and its radius is 3
\(\therefore\) equation of centre \(C\) is:
\(
x^2+y^2-10 x-4 y+20=0
\)
\(\therefore\) The length of the intercept it cuts on the \(x\)-axis
\(
=2 \sqrt{g^2-c}=2 \sqrt{25-20}=2 \sqrt{5}
\) -
Question 124 of 250
124. Question
A circle passes through the points \((2,3)\) and \((4,5)\). If its centre lies on the line, \(y-4 x+3=0\), then its radius is equal to [Online April 15, 2018]
CorrectIncorrectHint
(c) Equation of the line passing through the points \((2,3)\) and \((4,5)\) is
\(
y-3=\left(\frac{5-3}{4-2}\right) (x-2) \Rightarrow x-y+1=0 \dots(1)
\)
Equation of the perpendicular line passing through the midpoint \((3,4)\) is \(x+y-7=0 \ldots .\). (2)
Lines (1) and (2) intersect at the center of the circle. So, the center of the circle is \((3,4)\)
Therefore, the radius is
\(
\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}=\sqrt{(2-3)^2+(3-4)^2}=\sqrt{2} \text { units. }
\) -
Question 125 of 250
125. Question
Two parabolas with a common vertex and with axes along \(x\) axis and \(y\)-axis, respectively, intersect each other in the first quadrant. if the length of the latus rectum of each parabola is 3 , then the equation of the common tangent to the two parabolas is? [Online April 15, 2018]
CorrectIncorrectHint
(c) As origin is the only common point to \(x\)-axis and \(y\)-axis, so, origin is the common vertex
Let the equation of two of parabolas be \(y^2=4 a x\) and \(x^2=4 b y\)
Now latus rectum of both parabolas \(=3\)
\(\therefore 4 a=4 b=3\)
\(\Rightarrow a=b=\frac{3}{4}\)
\(\therefore\) Two parabolas are \(y^2=3 x\) and \(x^2=3 y\)
Suppose \(y=m x+c\) is the common tangent.
\(\therefore y^2=3 x \Rightarrow(m x+c)^2=3 x \Rightarrow m^2 x^2+(2 m c-3) x+c^2=0\)
As, the tangent touches at one point only
So, \(b^2-4 a c=0\)
\(\Rightarrow(2 m c-3)^2-4 m^2 c^2=0\)
\(\Rightarrow 4 m^2 c^2+9-12 m c-4 m^2 c^2=0\)
\(\Rightarrow c=\frac{9}{12 m}=\frac{3}{4 m} \dots(i)\)
\(\therefore x^2=3 y \Rightarrow x^2=3(m x+c) \Rightarrow x^2-3 m x-3 c=0\)
Again, \(b^2-4 a c=0\)
\(\Rightarrow 9 m^2-4(1)(-3 c)=0\)
\(\Rightarrow 9 m^2=-12 c \dots(ii)\)
Form \((i)\) and (ii)
\(m^2=\frac{-4 c}{3}=\frac{-4}{3}\left(\frac{3}{4 m}\right)\)
\(\Rightarrow m^3=-1 \Rightarrow m=-1 \Rightarrow c=\frac{-3}{4}\)
Hence, \(y=m x+c=-x-\frac{3}{4}\)
\(\Rightarrow 4(x+y)+3=0\) -
Question 126 of 250
126. Question
The tangent to the circle \(C_1: x^2+y^2-2 x-1=0\) at the point \((2,1)\) cuts off a chord of length 4 from a circle \(C_2\) whose centre is \((3,-2)\). The radius of \(C_2\) is [Online April 15, 2018]
CorrectIncorrectHint
(a) Here, equation of tangent on \(C_1\) at \((2,1)\) is:
\(
\begin{aligned}
& 2 x+y-(x+2)-1=0 \\
& \text { Or } x+y=3
\end{aligned}
\)
If it cuts off the chord of the circle \(C_2\) then the equation of the chord is:
\(
x+y=3
\)
\(\therefore\) distance of the chord from \((3,-2)\) is :
\(
d=\left|\frac{3-2-3}{\sqrt{2}}\right|=\sqrt{2}
\)
Also, length of the chord is \(l=4\)
\(
\begin{aligned}
\therefore \text { radius of } C_2=r & =\sqrt{\left(\frac{l}{2}\right)^2+d^2} \\
& =\sqrt{(2)^2+(\sqrt{2})^2}=\sqrt{6}
\end{aligned}
\) -
Question 127 of 250
127. Question
Tangent and normal are drawn at \(P(16,16)\) on the parabola \(y^2=16 x\), which intersect the axis of the parabola at \(A\) and \(B\), respectively. If \(C\) is the centre of the circle through the points \(P, A\) and \(B\) and \(\angle C P B=\theta\), then the value of \(\tan \theta\) is : [JEE Main 2018]
CorrectIncorrectHint
(a) Equation of tangent at \(P (16,16)\) is given as:
\(
x-2 y+16=0
\)
Slope of \(PC \left( m _1\right)=\frac{4}{3}\)
Slope of PB \(\left(m_2\right)=-2\)
Hence, \(\tan \theta=\left|\frac{ m _1- m _2}{1+ m _1 \cdot m _2}\right|=\left|\frac{\frac{4}{3}+2}{1-\frac{4}{3} \cdot 2}\right|\)
\(\Rightarrow \tan \theta=2\) -
Question 128 of 250
128. Question
Tangents drawn from the point \((-8,0)\) to the parabola \(y^2=8 x\) touch the parabola at \(P\) and \(Q\). If \(F\) is the focus of the parabola, then the area of the triangle \(P F Q\) (in sq. units) is equal to Online April 15, 2018]
CorrectIncorrectHint
(a) Equation of the chord of contact \(P Q\) is given by:
\(T=0\)
or \(T \equiv y y_1-4\left(x+x_1\right)\), where \(\left(x_1, y_1\right) \equiv(-8,0)\)
\(\therefore\) Equation becomes: \(x=8\)
& Chord of contact is \(x=8\)
\(\therefore\) Coordinates of point \(P\) and \(Q\) are \((8,8)\) and \((8,-8)\)
and focus of the parabola is \(F(2,0)\)
\(\therefore\) Area of triangle \(P Q F=\frac{1}{2} \times(8-2) \times(8+8)=48\) sq. units -
Question 129 of 250
129. Question
Two sets \(A\) and \(B\) are as under :
\(
\begin{aligned}
& A=\{(a, b) \in R \times R:|a-5|<1 \text { and }|b-5|<1\} ; \\
& B=\left\{(a, b) \in R \times R: 4(a-6)^2+9(b-5)^2 \leq 36\right\} . \text { Then : }
\end{aligned}
\) [2018]CorrectIncorrectHint
(a) \(A =\{( a , b ) \in R \times R : |a -5|<1,| b -5|<1\}\)
Let \(a-5=x, b-5=y\)
Set A contains all points inside \(|x|<1,|y|<1\)
\(
B =\left\{( a , b ) \in R \times R : 4( a -6)^2+9( B -5)^2 \leq 36\right\}
\)
Set \(B\) contains all points inside or on
\(
\frac{(x-1)^2}{9}+\frac{y^2}{4}=1
\)
\(\therefore \quad( \pm 1, \pm 1)\) lies inside the ellipse.
Hence, \(A \subset B\). -
Question 130 of 250
130. Question
If the length of the latus rectum of an ellipse is 4 units and the distance between a focus and its nearest vertex on the major axis is \(\frac{3}{2}\) units, then its eccentricity is? [Online April 16, 2018]
CorrectIncorrectHint
(d) Let for ellipse coordinates of focus and vertex are \((a e, 0)\) and \((a, 0)\) respectively.
\(\therefore\) Distance between focus and vertex \(=a(1-e)=\frac{3}{2}\) (given)
\(\Rightarrow a-\frac{3}{2}=a e\)
\(\Rightarrow a^2+\frac{9}{4}-3 a=a^2 e^2 \dots(i)\)
Length of latus rectum \(=\frac{2 b^2}{a}=4\)
\(\Rightarrow b^2=2 a \dots(ii)\)
\(
e^2=1-\frac{b^2}{a^2}
\)
\(\Rightarrow e^2=1-\frac{2 a}{a^2} \text { (from(ii)) }\)
(from(ii))
\(\Rightarrow e^2=1-\frac{2}{a} \dots(iii)\)
Substituting the value of \(e^2\) in eq. (i) we get;
\(\Rightarrow a^2+\frac{9}{4}-3 a=a^2\left(1-\frac{2}{a}\right)\)
\(\Rightarrow a=\frac{9}{4}\)
\(\therefore\) from eq. (iii) we get;
\(e^2=1-\frac{2}{a}=1-\frac{8}{9}=\frac{1}{9}\)
\(\Rightarrow e=\frac{1}{3}\) -
Question 131 of 250
131. Question
Tangents are drawn to the hyperbola \(4 x^2-y^2=36\) at the points \(P\) and \(Q\). If these tangents intersect at the point \(T(0,3)\) then the area (in sq. units) of \(\triangle PTQ\) is : [JEE Main 2018]
CorrectIncorrectHint
(d) Here equation of hyperbola is \(\frac{x^2}{9}-\frac{y^2}{36}=1\) Now, \(PQ\) is the chord of contact
\(\therefore \quad\) Equation of \(P Q\) is : \(\frac{x(0)}{9}-\frac{y(3)}{36}=1\)
\(\Rightarrow y=-12\)
\(\therefore \quad\) Area of \(\triangle PQT =\frac{1}{2} \times TR \times PQ\)
\(\because \quad P \equiv(3 \sqrt{5},-12) \quad \therefore TR =3+12=15\),
\(\therefore \quad\) Area of \(\triangle PQT =\frac{1}{2} \times 15 \times 6 \sqrt{5}=45 \sqrt{5}\) sq. units -
Question 132 of 250
132. Question
The locus of the point of intersection of the lines, \(\sqrt{2} x-y+4 \sqrt{2} k=0\) and \(\sqrt{2} k x+k y-4 \sqrt{2}=0(k\) is any non-zero real parameter) is. [Online April 16, 2018]
CorrectIncorrectHint
(a) Here, lines are:
\(
\begin{aligned}
& \sqrt{2} x-y+4 \sqrt{2} k=0 \\
& \Rightarrow \sqrt{2} x+4 \sqrt{2} k=y \dots(i)
\end{aligned}
\)
\(
\text { and } \sqrt{2} k x+k y-4 \sqrt{2}=0 \dots(ii)
\)
Put the value of \(y\) from (i) in (ii) we get;
\(
\begin{aligned}
& \Rightarrow 2 \sqrt{2} k x+4 \sqrt{2}\left(k^2-1\right)=0 \\
& \Rightarrow x=\frac{2\left(1-k^2\right)}{k}, y=\frac{2 \sqrt{2}\left(1+k^2\right)}{k} \\
& \therefore\left(\frac{y}{4 \sqrt{2}}\right)^2-\left(\frac{x}{4}\right)^2=1
\end{aligned}
\)
\(\therefore\) length of transverse axis
\(
2 a=2 \times 4 \sqrt{2}=8 \sqrt{2}
\)
Hence, the locus is a hyperbola with length of its transverse axis equal to \(8 \sqrt{2}\) -
Question 133 of 250
133. Question
The radius of a circle, having minimum area, which touches the curve \(y=4-x^2\) and the lines, \(y=|x|\) is: [JEE Main 2017]
CorrectIncorrectHint
It is given that the radius of circle is minimum and it touches the curve \(y=4-x^2\) and the lines,
\(
y=|x|
\)
Let us draw \(y=4-x^2\) and \(y=|x|\)
Let us assume that the radius of the circle is \(r\). Then from figure it is clear that the center of the circle will be \((0,4-r)\)
Since \(y=x\) is tangent to the circle, the line obtained by joining the center with the contact point will be perpendicular to the line \(y=x\). The length of this perpendicular is equal to the radius of the circle.
We know that the length of perpendicular (d) drawn from point \((\alpha, \beta)\) on the line
\(A x+B y+C=0\) is given by
\(
d=\frac{|A \alpha+B \beta+C|}{\sqrt{A^2+B^2}}
\)
Hence, we have
\(
\begin{gathered}
\alpha=0 \\
\beta=4-r \\
d=r \\
\therefore r=\frac{|0-(4-r)+0|}{\sqrt{1^2+(-1)^2}} \\
\Rightarrow r=\frac{|-(4-r)|}{\sqrt{2}} \\
\Rightarrow r=\frac{|(4-r)|}{\sqrt{2}}
\end{gathered}
\)
From the figure, it is clear that radius \(r\) is less than 4. Therefore,
\(
\begin{aligned}
& |4-r|=4-r \\
& \therefore r=\frac{4-r}{\sqrt{2}} \\
& \Rightarrow \sqrt{2} r+r=4 \\
& \Rightarrow r=\frac{4}{\sqrt{2}+1} \\
&
\end{aligned}
\)
Let is rationalize the number
\(
r=\frac{4(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}=\frac{4(\sqrt{2}-1)}{2-1}=4(\sqrt{2}-1)
\) -
Question 134 of 250
134. Question
The equation \(\operatorname{Im}\left(\frac{i z-2}{z-i}\right)+1=0, z \in C , z \neq i\) represents a part of a circle having radius equal to: [Online April 9, 2017]
CorrectIncorrectHint
(c) Let \(z=x+iy\)
\(
\operatorname{Im}\left[\left(\frac{i x-y-2}{x+(y-1) i}\right)\left(\frac{x-(y-1) i}{x-(y-1) i}\right)\right]+1=0
\)
On solving, we get:
\(
\begin{gathered}
2 x^2+2 y^2-y-1=0 \\
\Rightarrow x^2+y^2-1 / 2 y-1 / 2=0 \\
\Rightarrow x^2+\left(y-\frac{1}{4}\right)^2=\frac{9}{16} \\
\Rightarrow \quad r=\frac{3}{4}
\end{gathered}
\) -
Question 135 of 250
135. Question
A line drawn through the point \(P (4,7)\) cuts the circle \(x^2+y^2=9\) at the points \(A\) and \(B\). Then \(P A \cdot P B\) is equal to : [Online April 9, 2017]
CorrectIncorrectHint
\(
\begin{aligned}
\text { (b) } \quad & P(4,7) \cdot \text { Here, } x=4, y=7 \\
x-y & =-3 \\
\therefore \quad & P A \times P B=P T^2
\end{aligned}
\)
\(
\begin{aligned}
& \text { Also; } PT =\sqrt{ x ^2+ y ^2-( x – y )^2} \\
\Rightarrow \quad & PT =\sqrt{16+49-9}=\sqrt{56} \\
\Rightarrow \quad & PT ^2=56 \therefore PA \times PB =56
\end{aligned}
\) -
Question 136 of 250
136. Question
The two adjacent sides of a cyclic quadrilateral are 2 and 5 and the angle between them is \(60^{\circ}\). If the area of the quadrilateral is \(4 \sqrt{3}\), then the perimeter of the quadrilateral is : [Online April 9, 2017]
CorrectIncorrectHint
Here; \(\cos \theta=\frac{a^2+b^2-c^2}{2 a b}\) and \(\theta=60^{\circ}\)
\(
\begin{aligned}
& \Rightarrow \cos 60^{\circ}=\frac{4+25-c^2}{2.2 .5} \\
& \Rightarrow 10=29-c^2 \\
& \Rightarrow c^2=19 \\
& \Rightarrow c=\sqrt{19}
\end{aligned}
\)
also; \(\cos \theta=\frac{a^2+b^2-c^2}{2 a b}\) and \(\theta=120^{\circ}\)
\(
\begin{aligned}
& \Rightarrow-\frac{1}{2}=\frac{ a ^2+ b ^2-19}{2 ab } \\
& \Rightarrow a^2+b^2-19=-a b \\
& \Rightarrow a^2+b^2+a b=19 \\
& \therefore \text { Area }=\frac{1}{2} \times 2 \times 5 \sin 60+\frac{1}{2} ab \sin 120^{\circ}=4 \sqrt{3} \\
& \Rightarrow \frac{5 \sqrt{3}}{2}+\frac{ ab \sqrt{3}}{4}=4 \sqrt{3} \\
& \Rightarrow \frac{ ab }{4}=4-\frac{5}{2}=\frac{3}{2} \\
& \Rightarrow ab =6 \\
& \therefore a ^2+ b ^2=13 \\
& \Rightarrow a =2, b =3 \\
& \text { Perimeter }=\text { Sum of all sides } \\
& =2+5+2+3=12 \\
&
\end{aligned}
\) -
Question 137 of 250
137. Question
Let \(z \in C\), the set of complex numbers. Then the equation, \(2|z+3 i|-|z-i|=0\) represents : [Online April 8, 2017]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (a) Let } z = x +1 y \\
& \Rightarrow 2|x+i(y+3)=| x+i(y-1) \mid \\
& \Rightarrow \quad 2 \sqrt{x^2+(y+3)^2}=\sqrt{x^2+(y-1)^2}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad 4 x^2+4(y+3)^2=x^2+(y-1)^2 \\
& \Rightarrow \quad 3 x^2=y^2-2 y+1-4 y^2-24 y-36 \\
& \Rightarrow \quad 3 x^2+3 y^2+26 y+35=0 \quad \text { (which is a circle) } \\
& \Rightarrow \quad x^2+y^2+\frac{26}{3} y+\frac{35}{3}=0
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow r=\sqrt{0+\frac{169}{9}-\frac{35}{3}} \\
& \Rightarrow r=\sqrt{\frac{64}{9}}=\frac{8}{3}
\end{aligned}
\) -
Question 138 of 250
138. Question
If a point \(P\) has co-ordinates \((0,-2)\) and \(Q\) is any point on the circle, \(x^2+y^2-5 x-y+5=0\), then the maximum value of \(( PQ )^2\) is : [Online April 8, 2017]
CorrectIncorrectHint
(b) Given that \(x^2+y^2-5 x-y+5=0\)
\(
\begin{aligned}
\Rightarrow & ( x -5 / 2)^2-\frac{25}{4}+( y -1 / 2)^2-1 / 4=0 \\
\Rightarrow & ( x -5 / 2)^2+( y -1 / 2)^2=3 / 2 \\
& \text { on circle }\left[Q \equiv\left(5 / 2+\sqrt{3 / 2} \cos Q, \frac{1}{2}+\sqrt{3 / 2} \sin Q\right)\right]
\end{aligned}
\)
\(
\begin{aligned}
\Rightarrow PQ ^2 & =\left(\frac{5}{2}+\sqrt{3 / 2} \cos Q\right)^2+\left(\frac{5}{2}+\sqrt{3 / 2} \sin Q\right)^2 \\
\Rightarrow \quad PQ ^2 & =\frac{25}{2}+\frac{3}{2}+5 \sqrt{3 / 2}(\cos Q+\sin Q) \\
& =14+5 \sqrt{3 / 2}(\cos Q+\sin Q)
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \text { Maximum value of } PQ ^2 \\
& \qquad=14+5 \sqrt{3 / 2} \times \sqrt{2}=14+5 \sqrt{3}
\end{aligned}
\) -
Question 139 of 250
139. Question
If two parallel chords of a circle, having diameter 4 units, lie on the opposite sides of the centre and subtend angles \(\cos ^{-1}\left(\frac{1}{7}\right)\) and \(\sec ^{-1}(7)\) at the centre respectively, then the distance between these chords, is : [Online April 8, 2017]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Since } \cos 2 \theta=1 / 7 \Rightarrow 2 \cos ^2 Q-1=1 / 7 \\
\Rightarrow & 2 \cos ^2 \theta=8 / 7 \\
\Rightarrow & \cos ^2 \theta=4 / 7 \\
\Rightarrow & \cos ^2 \theta=\frac{4}{7} \\
\Rightarrow & \cos ^2 \phi=\frac{2}{\sqrt{7}}
\end{aligned}
\)
\(
\text { Also, } \begin{aligned}
\sec ^2 \phi & =7=\frac{1}{2 \cos ^2 \phi-1}=7 \\
& =\cos ^2 \phi-1=\frac{1}{7} \\
& =2 \cos ^2 \phi=\frac{8}{7} \\
& =\cos \phi=\frac{2}{\sqrt{7}} \\
P _1 P _2 & = r \cos \theta+ r \cos \phi \\
& =\frac{4}{\sqrt{7}}+\frac{4}{\sqrt{7}}=\frac{8}{\sqrt{7}}
\end{aligned}
\) -
Question 140 of 250
140. Question
If one of the diameters of the circle, given by the equation, \(x^2\) \(+y^2-4 x+6 y-12=0\), is a chord of a circle \(S\), whose centre is at \((-3,2)\), then the radius of \(S\) is: [JEE Main 2016]
CorrectIncorrectHint
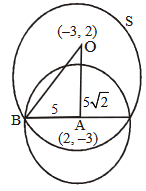
Centre of S : \(O (-3,2)\) centre of given circle \(A (2,-3)\)
\(
\Rightarrow OA =5 \sqrt{2}
\)
Also \(AB =5(\because AB = r\) of the given circle \()\)
\(\Rightarrow\) Using pythagoras theorem in \(\triangle OAB\)
\(
r =5 \sqrt{3}
\) -
Question 141 of 250
141. Question
Equation of the tangent to the circle, at the point \((1,-1)\) whose centre is the point of intersection of the straight lines \(x-y=1\) and \(2 x+y=3\) is : [Online April 10, 2016]
CorrectIncorrectHint
(a) Point of intersection of lines
\(
\begin{aligned}
& x-y=1 \text { and } 2 x+y=3 \text { is }\left(\frac{4}{3}, \frac{1}{3}\right) \\
& \text { Slope of } O P=\frac{\frac{1}{3}+1}{\frac{4}{3}-1}=\frac{\frac{4}{3}}{\frac{1}{3}}=4 \\
& \text { Slope of tangent }=-\frac{1}{4}
\end{aligned}
\)
Equation of tangent \(y+1=-\frac{1}{4}(x-1)\)
\(
\begin{aligned}
& 4 y+4=-x+1 \\
& x+4 y+3=0
\end{aligned}
\) -
Question 142 of 250
142. Question
A circle passes through \((-2,4)\) and touches the \(y\)-axis at \((0,2)\). Which one of the following equations can represent a diameter of this circle? [Online April 9, 2016]
CorrectIncorrectHint
\(EF =\) perpendicular bisector of chord \(AB\)
\(BG =\) perpendicular to \(y\)-axis
Here \(C =\) centre of the circle
mid-point of chord \(A B, D=(-1,3)\)
slope of \(A B=\frac{4-2}{-2-0}=-1\)
\(\because \quad EF \perp AB\)
\(\therefore \quad\) Slope of EF \(=1\)
Equation of \(EF , y-3=1(x+1)\)
\(\Rightarrow y=x+4 \dots(i)\)
Equation of BG
\(
y=2 \dots(ii)
\)
From equations (i) and (ii)
\(
x=-2, y=2
\)
since \(C\) be the point of intersection of \(E F\) and \(B G\), therefore centre, \(C =(-2,2)\)
Now coordinates of centre \(C\) satisfy the equation
\(
2 x-3 y+10=0
\)
Hence \(2 x-3 y+10=0\) is the equation of the diameter -
Question 143 of 250
143. Question
Locus of the image of the point \((2,3)\) in the line \((2 x-3 y+4)\) \(+ k ( x -2 y +3)=0, k \in R\), is a : [JEE Main 2015]
CorrectIncorrectHint
(a) Intersection point of \(2 x-3 y+4=0\) and \(x-2 y+3=0\) is \((1,2)\)
Since, \(P\) is the fixed point for given family of lines
So,
\(
\begin{aligned}
& \text { PB }=\text { PA } \\
& (\alpha-1)^2+(\beta-2)^2=(2-1)^2+(3-2)^2 \\
& (\alpha-1)^2+(\beta-2)^2=1+1=2 \\
& (x-1)^2+(y-2)^2=(\sqrt{2})^2 \\
& (x-a)^2+(y-b)^2=r^2
\end{aligned}
\)
Therefore, given locus is a circle with centre \((1,2)\) and radius \(\sqrt{2}\). -
Question 144 of 250
144. Question
The number of common tangents to the circles \(x^2+y^2-4 x\) \(-6 x-12=0\) and \(x^2+y^2+6 x+18 y+26=0\), is : [JEE Main 2015]
CorrectIncorrectHint
(a) \(x^2+y^2-4 x-6 y-12=0 \dots(i)\)
Centre, \(C _1=(2,3)\)
Radius, \(r_1=5\) units
\(
x^2+y^2+6 x+18 y+26=0 \dots(ii)
\)
Centre, \(C_2=(-3,-9)\)
Radius, \(r_2=8\) units
\(C _1 C _2=\sqrt{(2+3)^2+(3+9)^2}=13\) units
\(
\begin{aligned}
& r_1+r_2=5+8=13 \\
& \therefore C_1 C_2=r_1+r_2
\end{aligned}
\)
Therefore there are three common tangents.
-
Question 145 of 250
145. Question
If the incentre of an equilateral triangle is \((1,1)\) and the equation of its one side is \(3 x+4 y+3=0\), then the equation of the circumcircle of this triangle is : [Online April 11, 2015]
CorrectIncorrectHint
(a) Let radius of circumcircle be According to the question,
\(
\frac{ r }{2}=\frac{10}{5} \Rightarrow r =4
\)
So equation of required circle is
\(
\begin{aligned}
& (x-1)^2+(y-1)^2=16 \\
& \Rightarrow x^2+y^2-2 x-2 y-14=0
\end{aligned}
\) -
Question 146 of 250
146. Question
If a circle passing through the point \((-1,0)\) touches \(y\)-axis at \((0,2)\), then the length of the chord of the circle along the \(x\)-axis is : [Online April 11, 2015]
CorrectIncorrectHint
(b) Let ‘ \(h\) ‘ be the radius of the circle and since circle touches \(y\)-axis at \((0,2)\) therefore centre \(=(h, 2)\)
Now, eqn of circle is
\(
\begin{aligned}
& (h+1)^2+2^2=h^2 \\
& \Rightarrow 2 h+5=0
\end{aligned}
\)
\(
h =-\frac{5}{2}
\)
From the figure, it is clear that \(AB\) is the chord along \(x\)-axis
\(
\therefore AB =2( AM )=2 \sqrt{\frac{25}{4}-4}=2\left(\frac{3}{2}\right)=3
\) -
Question 147 of 250
147. Question
Let the tangents drawn to the circle, \(x^2+y^2=16\) from the point \(P(0, h)\) meet the \(x\)-axis at point \(A\) and \(B\). If the area of \(\triangle A P B\) is minimum, then \(h\) is equal to: [Online April 10, 2015]
CorrectIncorrectHint
(a) \(OP =\frac{4}{\sin \theta}\)
\(
OB =\frac{4}{\cos \theta}
\)
\(
\begin{aligned}
& \text { Area }=O P \times O B=\frac{16}{\sin \theta \cos \theta}=\frac{32}{\sin 2 \theta} \\
& \text { least value } \sin 2 \theta=1 ; \theta=45^{\circ}
\end{aligned}
\)
So, \(h =\frac{4}{\sin 45^{\circ}}=4 \sqrt{2}\) -
Question 148 of 250
148. Question
If \(y+3 x=0\) is the equation of a chord of the circle, \(x^2+y^2-30 x=0\), then the equation of the circle with this chord as diameter is: [Online April 10, 2015]
CorrectIncorrectHint
(d) Given that \(y+3 x=0\) is the equation of a chord of the circle then
\(
\begin{aligned}
& y=-3 x \dots(i)\\
& \left(x^2\right)+(-3 x)^2-30 x=0 \\
& 10 x^2-30 x=0 \\
& 10 x(x-3)=0 \\
& x=0, y=0
\end{aligned}
\)
so the equation of the circle is
\(
\begin{aligned}
& (x-3)(x-0)+(y+9)(y-0)=0 \\
& x^2-3 x+y^2+9 y=0 \\
& x^2+y^2-3 x+9 y=0
\end{aligned}
\) -
Question 149 of 250
149. Question
The largest value of \(r\) for which the region represented by the set \(\{\omega \in C|\omega-4-i| \leq r\}\) is contained in the region represented by the set \((z \in c: |z-1| \leq|z+i|)\), is equal to: [Online April 10, 2015]
CorrectIncorrectHint
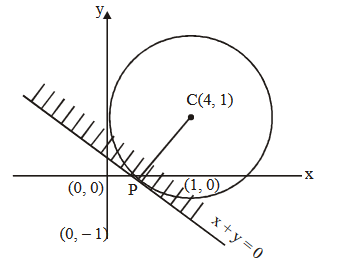
(a) Radius
\(
CP =\frac{4+1}{\sqrt{2}}
\)
\(
=\frac{5}{\sqrt{2}}=\frac{5}{2} \sqrt{2}
\) -
Question 150 of 250
150. Question
Let \(C\) be the circle with centre at \((1,1)\) and radius \(=1\). If \(T\) is the circle centred at \((0, y)\), passing through origin and touching the circle \(C\) externally, then the radius of \(T\) is equal to [JEE Main 2014]
CorrectIncorrectHint
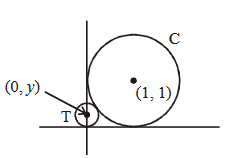
Equation of circle
\(
\begin{aligned}
& C \equiv(x-1)^2+(y-1)^2=1 \\
& \text { Radius of } T =|y| \\
&
\end{aligned}
\)
\(T\) touches \(C\) externally therefore, Distance between the centres \(=\) sum of their radii
\(
\begin{aligned}
\Rightarrow & \sqrt{(0-1)^2+(y-1)^2}=1+|y| \\
\Rightarrow & (0-1)^2+(y-1)^2=(1+|y|)^2 \\
\Rightarrow & 1+y^2+1-2 y=1+y^2+2|y| \\
& 2|y|=1-2 y
\end{aligned}
\)
If \(y>0\) then \(2 y=1-2 y \Rightarrow y=\frac{1}{4}\)
If \(y<0\) then \(-2 y=1-2 y \Rightarrow 0=1\) (not possible)
\(
\therefore \quad y=\frac{1}{4}
\) -
Question 151 of 250
151. Question
The equation of circle described on the chord \(3 x+y+5=0\) of the circle \(x^2+y^2=16\) as diameter is: [Online April 19, 2014]
CorrectIncorrectHint
(a) Given circle is \(x^2+y^2-16=0\)
Eqn of chord say \(A B\) of given circle is
\(
3 x+y+5=0 \text {. }
\)
Equation of required circle is
\(
\begin{aligned}
& x^2+y^2-16+\lambda(3 x+y+5)=0 \\
& \Rightarrow x^2+y^2+(3 \lambda) x+(\lambda) y+5 \lambda-16=0 \dots(1) \\
& \text { Centre } C =\left(\frac{-3 \lambda}{2}, \frac{-\lambda}{2}\right) .
\end{aligned}
\)
If line \(A B\) is the diameter of circle (1), then
\(C\left(\frac{-3 \lambda}{2}, \frac{-\lambda}{2}\right)\) will lie on line \(AB\)
i.e. \(3\left(\frac{-3 \lambda}{2}\right)+\left(\frac{-\lambda}{2}\right)+5=0\)
\(
\Rightarrow-\frac{9 \lambda-\lambda}{2}+5=0 \Rightarrow \lambda=1
\)
Hence, required eqn of circle is
\(
\begin{aligned}
& x^2+y^2+3 x+y+5-16=0 \\
& \Rightarrow x^2+y^2+3 x+y-11=0
\end{aligned}
\) -
Question 152 of 250
152. Question
For the two circles \(x^2+y^2=16\) and \(x^2+y^2-2 y=0\), there is/are [Online April 12, 2014]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (d) Let, } S_1 \text { : } x^2+y^2=16 \text { or } x^2+y^2=4^2 \\
& \text { Center of } S_1 \text { is } C_1 \text { : } \text { radius of circle } r_1=4 \text {, centre } C _1(0,0) \\
& \text { we have, } \text { and } S_2 \text { : } x^2+y^2-2 y=0 \\
& \Rightarrow x^2+\left(y^2-2 y+1\right)-1=0 \text { or } x^2+(y-1)^2=1^2 \\
& \text { Center of } S _2 \text { is } C _2 \text { : } \text { Radius } 1 \text {, centre } C_2(0,1) \\
& \left|C_1 C_2\right|=1 \\
& \left|r_2-r_1\right|=|4-1|=3 \\
& \left|C_1 C_2\right|<\left|r_2-r_1\right|
\end{aligned}
\)
\(\therefore S _2\) is completely within \(S _1\) and hence there are no common tangents to the two circles. -
Question 153 of 250
153. Question
The set of all real values of \(\lambda\) for which exactly two common tangents can be drawn to the circles \(x^2+y^2-4 x-4 y+6=0\) and \(x^2+y^2-10 x-10 y+\lambda=0\) is the interval: [Online April 11, 2014]
CorrectIncorrectHint
(b) The equations of the circles are
\(
x^2+y^2-10 x-10 y+\lambda=0 \dots(1)
\)
and \(x^2+y^2-4 x-4 y+6=0 \dots(2)\)
\(C _1=\) centre of \((1)=(5,5)\)
\(C _2=\) centre of \((2)=(2,2)\)
\(d=\) distance between centres
\(
\begin{aligned}
& = C _1 C _2=\sqrt{9+9}=\sqrt{18} \\
& r_1=\sqrt{50-\lambda}, r_2=\sqrt{2}
\end{aligned}
\)
For exactly two common tangents we have
\(
\begin{aligned}
& r_1-r_2<C_1 C_2<r_1+r_2 \\
& \Rightarrow \sqrt{50-\lambda}-\sqrt{2}<3 \sqrt{2}<\sqrt{50-\lambda}+\sqrt{2} \\
& \Rightarrow \sqrt{50-\lambda}-\sqrt{2}<3 \sqrt{2} \text { or } 3 \sqrt{2}<\sqrt{50-\lambda}+\sqrt{2} \\
& \Rightarrow \sqrt{50-\lambda}<4 \sqrt{2} \text { or } 2 \sqrt{2}<\sqrt{50-\lambda} \\
& \Rightarrow 50-\lambda<32 \text { or } 8<50-\lambda \\
& \Rightarrow \lambda>18 \text { or } \lambda<42
\end{aligned}
\)
Required interval is \((18,42)\) -
Question 154 of 250
154. Question
If the point \((1,4)\) lies inside the circle \(x^2+y^2-6 x-10 y+P=0\) and the circle does not touch or intersect the coordinate axes, then the set of all possible values of \(P\) is the interval: [Online April 9, 2014]
CorrectIncorrectHint
The equation of circle is
\(
\begin{aligned}
& x^2+y^2-6 x-10 y+P=0 \dots(i)\\
& (x-3)^2+(y-5)^2=(\sqrt{34- P })^2
\end{aligned}
\)
Centre \((3,5)\) and radius ‘ \(r\) ‘ \(=\sqrt{34-P}\)
If circle does not touch or intersect the \(x\)-axis then radius \(x<y\) – coordinate of centre \(C\)
\(
\begin{aligned}
& \text { or } \sqrt{34- P }<5 \\
& \Rightarrow 34- P <25 \\
& \Rightarrow P >9 \dots(ii)
\end{aligned}
\)
Also if the circle does not touch or intersect \(x\)-axis the radius \(r<x\)-coordinate of centre \(C\).
or \(\sqrt{34- P }<3 \Rightarrow 34- P <9 \Rightarrow P >25\)
If the point \((1,4)\) is inside the circle, then its distance from centre \(C < r\).
or \(\sqrt{34- P }<3 \Rightarrow 34- P <9 \Rightarrow P >25 \dots(iii)\)
If the point \((1,4)\) is inside the circle, then its distance from centre \(C < r\).
or \(\sqrt{\left[(3-1)^2+(5-4)^2\right]}<\sqrt{34-P}\)
\(\Rightarrow 5<34- K\)
\(\Rightarrow P <29 \dots(iv)\)
Now all the conditions (ii), (iii) and (iv) are satisfied if \(25< P <29\) which is required value of \(P\). -
Question 155 of 250
155. Question
Let \(a\) and \(b\) be any two numbers satisfying \(\frac{1}{ a ^2}+\frac{1}{ b ^2}=\frac{1}{4}\). Then, the foot of perpendicular from the origin on the variable line, \(\frac{ x }{ a }+\frac{ y }{ b }=1\), lies on: [Online April 9, 2014]
CorrectIncorrectHint
(c) Let the foot of the perpendicular from \((0,0)\) on the variable line \(\frac{x}{a}+\frac{y}{b}=1\) is \(\left(x_1>y_1\right)\) Hence, perpendicular distance of the variable line \(\frac{x}{a}+\frac{y}{b}=1\) from the point \(O (0,0)= OA\)
\(
\Rightarrow \frac{|-1|}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}}=\sqrt{x_1^2+y_1^2}
\)
\(
\Rightarrow \frac{1}{\frac{1}{a^2}+\frac{1}{b^2}}=x_1^2+y_1^2
\)
\(
\Rightarrow 4=x_1^2+y_1^2\left[\because \frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{4}\right] \text {, }
\)
which is equation of a circle with radius 2 .
Hence \(\left(x_1, y_1\right)\) i.e., the foot of the perpendicular from
the point \((0,0)\) to the variable line \(\frac{x}{a}+\frac{x}{b}=1\) is lies on a circle with radius \(=2\) -
Question 156 of 250
156. Question
The circle passing through \((1,-2)\) and touching the axis of \(x\) at \((3,0)\) also passes through the point [JEE Main 2013]
CorrectIncorrectHint
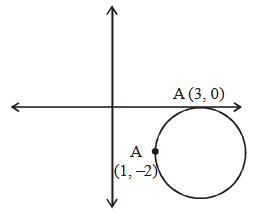
(c) Since circle touches \(x\)-axis at \((3,0)\) \(\therefore\) the equation of circle be
\(
(x-3)^2+(y-0)^2+\lambda y=0
\)
As it passes through \((1,-2)\)
\(
\begin{aligned}
& \therefore \text { Put } x=1, y=-2 \\
& \Rightarrow(1-3)^2+(-2)^2+\lambda(-2)=0 \\
& \Rightarrow \lambda=4
\end{aligned}
\)
\(\therefore\) equation of circle is
\(
(x-3)^2+y^2-8=0
\)
Now, from the options \((5,-2)\) satisfies equation of circle. -
Question 157 of 250
157. Question
If a circle of unit radius is divided into two parts by an arc of another circle subtending an angle \(60^{\circ}\) on the circumference of the first circle, then the radius of the arc is: [Online April 25, 2013]
CorrectIncorrectHint
Let us denote the centre of the unit circle as \(O\) and the points of intersection of circle of unit radius with the other circle as \(A, B\). Let us consider the intercepted \(\operatorname{arc} A B\) as less than semicircle. Let \(C\) be any point on the circumference. Since intercepted arc less than semicircle will only subtend an obtuse angle \(C\) will not lie on intercepted arc AB. We drop perpendicular \(OD\) on \(AB\). So we have the diagram as
We know that the central angle subtended by an arc at the centre is twice the inscribed angle. Here \(\angle A C B\) is an inscribed angle of arc \(AB\) with measure given to us as \(\angle A C B=60^{\circ}\). So the central angle \(\angle A O B\) will have the measure
\(
\angle A O B=2 \times \angle A C B=2 \times 60^{\circ}=120^{\circ}
\)
Now we observe the triangle AOB where the lengths of radii are given to us as
\(O A=O B=1\). Here \(AOB\) is an isosceles triangle whose perpendicular from apex \(O\) that is \(A D\) will bisect the angle at \(O\) and the opposite \(A B\). So we have
\(
\begin{aligned}
& \angle A O D=\angle B O D=\frac{120^{\circ}}{2}=60^{\circ} \\
& A D=B D=\frac{A B}{2}
\end{aligned}
\)
So in triangle AOD we have
\(
\begin{aligned}
& \sin (\angle A O D)=\frac{A D}{O A} \\
& \Rightarrow \sin \left(60^{\circ}\right)=\frac{A D}{1} \\
& \Rightarrow A D=1 \cdot \sin 60^{\circ}=1 \times \frac{\sqrt{3}}{2} \\
& \Rightarrow A D=\frac{\sqrt{3}}{2}
\end{aligned}
\)
So we have the required length of the chord as;
\(
A B=A D+B D=2 A D=2 \times \frac{\sqrt{3}}{2}=\sqrt{3}
\) -
Question 158 of 250
158. Question
Statement 1: The only circle having radius \(\sqrt{10}\) and a diameter along line \(2 x+y=5\) is \(x^2+y^2-6 x+2 y=0\).
Statement 2: \(2 x+y=5\) is a normal to the circle \(x^2+y^2-6 x+2 y=0\) [Online April 25, 2013]CorrectIncorrectHint
(a) Circle: \(x^2+y^2-6 x+2 y=0 \dots(i)\)
Line: \(2 x+y=5 \dots(ii)\)
Centre \(=(3,-1)\)
Now, \(2 \times 3-1=5\), hence centre lies on the given line. Therefore line passes through the centre. The given line is normal to the circle.
Thus statement- 2 is true, but statement- 1 is not true as there are infinite circle according to the given conditions.
-
Question 159 of 250
159. Question
If the circle \(x^2+y^2-6 x-8 y+\left(25-a^2\right)=0\) touches the axis of \(x\), then a equals. [Online April 23, 2013]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2+y^2-6 x-8 y+\left(25-a^2\right)=0 \\
& \text { Radius }=4=\sqrt{9+16+\left(25-a^2\right)} \\
& \Rightarrow a = \pm 4
\end{aligned}
\) -
Question 160 of 250
160. Question
If a circle \(C\) passing through \((4,0)\) touches the circle \(x^2+y^2\) \(+4 x-6 y-12=0\) externally at a point \((1,-1)\), then the radius of the circle \(C\) is: [Online April 22, 2013]
CorrectIncorrectHint
(a) Let \(A\) be the centre of given circle and \(B\) be the centre of circle C.
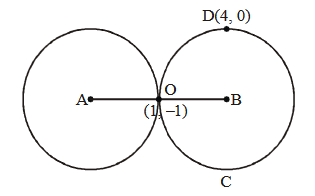
\(
\begin{aligned}
& x ^2+ y ^2+4 x -6 y -12=0 \\
& \therefore A =(-2,3) \text { and } B =(g, f)
\end{aligned}
\)
Now, from the figure, we have
\(
\begin{aligned}
& \frac{-2+g}{2}=1 \text { and } \frac{3+f}{2}=-1 \text { (By mid point formula) } \\
& \Rightarrow g=4 \text { and } f=-5
\end{aligned}
\) -
Question 161 of 250
161. Question
If two vertices of an equilateral triangle are \(A (-a, 0)\) and \(B(a, 0), a>0\), and the third vertex \(C\) lies above \(x\)-axis then the equation of the circumcircle of \(\triangle A B C\) is : [Online April 22, 2013]
CorrectIncorrectHint
(a) Let \(C =(x, y)\)
Now, \(CA ^2= CB ^2= AB ^2\)
\(\Rightarrow(x+a)^2+y^2=(x-a)^2+y^2=(2 a)^2\)
\(\Rightarrow x^2+2 a x+a^2+y^2=4 a^2 \dots(i)\)
and \(x^2-2 a x+a^2+y^2=4 a^2 \dots(ii)\)
From (i) and (ii), \(x=0\) and \(y= \pm \sqrt{3} a\)
Since point \(C (x, y)\) lies above the \(x\)-axis and \(a>0\), hence \(y=\sqrt{3} a\)
\(
\therefore \quad C =(0, \sqrt{3} a)
\)
Let the equation of circumcircle be
\(
x^2+y^2+2 g x+2 f y+C=0
\)
Since points \(A (-a, 0), B (a, 0)\) and \(C (0, \sqrt{3} a)\) lie on the circle, therefore
\(
\begin{aligned}
& a^2-2 g a+ C =0 \dots(iii) \\
& a^2+2 g a+ C =0 \dots(iv) \\
& \text { and } 3 a^2+2 \sqrt{3} a f+ C =0 \dots(v)
\end{aligned}
\)
From (iii), (iv), and (v)
\(
g=0, c=-a^2, f=-\frac{a}{\sqrt{3}}
\)
Hence equation of the circumcircle is
\(
x^2+y^2-\frac{2 a}{\sqrt{3}} y-a^2=0
\)
\(
\begin{aligned}
& \Rightarrow x^2+y^2-\frac{2 \sqrt{3} a y}{3}-a^2=0 \\
& \Rightarrow 3 x^2+3 y^2-2 \sqrt{3} a y=3 a^2
\end{aligned}
\) -
Question 162 of 250
162. Question
If each of the lines \(5 x+8 y=13\) and \(4 x-y=3\) contains a diameter of the circle \(x^2+y^2-2\left(a^2-7 a+11\right) x-2\left(a^2-6 a+6\right) y+b^3+1=0\), then [Online April 9, 2013]
CorrectIncorrectHint
(d) Point of intersection of two given lines is \((1,1)\). Since each of the two given lines contains a diameter of the given circle, therefore the point of intersection of the two given lines is the centre of the given circle.
Hence centre \(=(1,1)\)
\(
\begin{aligned}
& \therefore a^2-7 a+11=1 \Rightarrow a=2,5 \dots(i) \\
& \text { and } a^2-6 a+6=1 \Rightarrow a=1,5 \dots(ii)
\end{aligned}
\)
From both (i) and (ii), \(a=5\)
Now on replacing each of \(\left(a^2-7 a+11\right)\) and \(\left(a^2-6 a+6\right)\) by 1 , the equation of the given circle is
\(
\begin{aligned}
& x^2+y^2-2 x-2 y+b^3+1=0 \\
& \Rightarrow(x-1)^2+(y-1)^2+b^3=1 \\
& \Rightarrow b^3=1-\left[(x-1)^2+(y-1)^2\right] \\
& \therefore b \in(-\infty, 1)
\end{aligned}
\) -
Question 163 of 250
163. Question
The length of the diameter of the circle which touches the \(x\)-axis at the point \((1,0)\) and passes through the point \((2,3)\) is: [JEE Main 2012]
CorrectIncorrectHint
(a) Let centre of the circle be \((1, h )\) \([\because\) circle touches \(x\)-axis at \((1,0)]\)
Let the circle passes through the point \(B(2,3)\)
\(
\begin{array}{ll}
\therefore & C A=C B \text { (radius) } \\
\Rightarrow & C A^2=C B^2 \\
\Rightarrow & (1-1)^2+(h-0)^2=(1-2)^2+(h-3)^2 \\
\Rightarrow & h^2=1+h^2+9-6 h \\
\Rightarrow & h=\frac{10}{6}=\frac{5}{3}
\end{array}
\) -
Question 164 of 250
164. Question
The number of common tangents of the circles given by \(x^2+y^2-8 x-2 y+1=0\) and \(x^2+y^2+6 x+8 y=0\) is [Online May 26, 2012]
CorrectIncorrectHint
Given circles are
\(
\begin{aligned}
& x^2+y^2-8 x-2 y+1=0 \\
& \text { and } x^2+y^2+6 x+8 y=0
\end{aligned}
\)
Their centres and radius are
\(
\begin{aligned}
& C_1(4,1), r_1=\sqrt{16}=4 \\
& C_2(-3,-4), r_2=\sqrt{25}=5
\end{aligned}
\)
Now, \(C_1 C_2=\sqrt{49+25}=\sqrt{74}\)
\(
r_1-r_2=-1, r_1+r_2=9
\)
Since, \(r_1-r_2<C_1 C_2<r_1+r_2\) \(\therefore\) Number of common tangents \(=2\) -
Question 165 of 250
165. Question
If the line \(y=m x+1\) meets the circle \(x^2+y^2+3 x=0\) in two points equidistant from and on opposite sides of \(x\)-axis, then [Online May 19, 2012]
CorrectIncorrectHint
(b) Circle: \(x^2+y^2+3 x=0\)
Centre, \(B=\left(-\frac{3}{2}, 0\right)\)
Radius \(=\frac{3}{2}\) units.
\(
\begin{aligned}
& \text { Line: } y=m x+1 \\
& y \text {-intercept of the line }=1 \\
& \therefore A =(0,1)
\end{aligned}
\)
Slope of line, \(m=\tan \theta=\frac{O A}{O B}\)
\(
\begin{aligned}
& \Rightarrow m=\frac{1}{\frac{3}{2}}=\frac{2}{3} \\
& \Rightarrow 3 m-2=0
\end{aligned}
\) -
Question 166 of 250
166. Question
If three distinct points \(A, B, C\) are given in the 2-dimensional coordinate plane such that the ratio of the distance of each one of them from the point \((1,0)\) to the distance from \((-1,0)\) is equal to \(\frac{1}{2}\), then the circumcentre of the triangle \(A B C\) is at the point [Online May 19, 2012]
CorrectIncorrectHint
(a) Let \(P(1,0)\) and \(Q(-1,0), A(x, y)\)
\(
\begin{aligned}
& \text { Given: } \frac{A P}{A Q}=\frac{B P}{B Q}=\frac{C P}{C Q}=\frac{1}{2} \\
& \Rightarrow 2 A P=A Q \\
& \Rightarrow 4(A P)^2=A Q^2 \\
& \Rightarrow 4\left[(x-1)^2+y^2\right]=(x+1)^2+y^2 \\
& \Rightarrow 4\left(x^2+1-2 x\right)+4 y^2=x^2+1+2 x+y^2 \\
& \Rightarrow 3 x^2+3 y^2-8 x-2 x+4-1=0 \\
& \Rightarrow 3 x^2+3 y^2-10 x+3=0 \\
& \Rightarrow x^2+y^2-\frac{10}{3} x+1=0 \dots(1)
\end{aligned}
\)
\(\therefore \quad\) A lies on the circle given by (1). As \(B\) and \(C\) also follow the same condition.
\(\therefore\) Centre of circumcircle of \(\triangle A B C=\) centre of circle given by (1)
\(
=\left(\frac{5}{3}, 0\right) .
\) -
Question 167 of 250
167. Question
The equation of the circle passing through the point \((1,2)\) and through the points of intersection of \(x^2+y^2-4 x-6 y-21=0\) and \(3 x+4 y+5=0\) is given by [Online May 7, 2012]
CorrectIncorrectHint
(d) Point \((1,2)\) lies on the circle \(x^2+y^2+2 x+2 y-11=0\), because coordinates of point \((1,2)\) satisfy the equation \(x^2+y^2+2 x+2 y-11=0\)
Now, \(x^2+y^2-4 x-6 y-21=0 \dots(i)\)
\(
\begin{aligned}
& x^2+y^2+2 x+2 y-11=0 \dots(ii)\\
& 3 x+4 y+5=0 \dots(iii)
\end{aligned}
\)
From (i) and (iii),
\(
\begin{aligned}
& x^2+\left(-\frac{3 x+5}{4}\right)^2-4 x-6\left(-\frac{3 x+5}{4}\right)-21=0 \\
& \Rightarrow 16 x^2+9 x^2+30 x+25-64 x+72 x+120-336=0 \\
& \Rightarrow 25 x^2+38 x-191=0 \quad \text { (iv) }
\end{aligned}
\)
From (ii) and(iii),
\(
\begin{aligned}
& x^2+\left(-\frac{3 x+5}{4}\right)^2+2 x+2\left(-\frac{3 x+5}{4}\right)-11=0 \\
& \Rightarrow 16 x^2+9 x^2+30 x+25+32 x-24 x-40-176=0 \\
& \Rightarrow 25 x^2+38 x-191=0 \quad \ldots \text { (v) }
\end{aligned}
\)
Thus we get the same equation from (ii) and (iii) as we get from equation (i) and (iii). Hence the point of intersections of (ii) and (iii) will be same as the point of intersections of (i) and (iii). Therefore the circle (ii) passing through the point of intersection of circle(i) and point \((1,2)\) also as shown in the figure.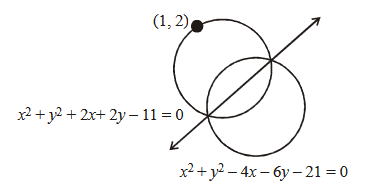
Hence equation(ii) i.e. \(x^2+y^2+2 x+2 y-11=0\) is the equation of required circle.
-
Question 168 of 250
168. Question
The equation of the circle passing through the point \((1,0)\) and \((0,1)\) and having the smallest radius is – [JEE Main 2011 RS]
CorrectIncorrectHint
(b) Circle whose diametric end points are \((1,0)\) and \((0,1)\) will be of smallest radius. Equation of this smallest circle is
\(
\begin{aligned}
& (x-1)(x-0)+(y-0)(y-1)=0 \\
& \Rightarrow x^2+y^2-x-y=0
\end{aligned}
\) -
Question 169 of 250
169. Question
The two circles \(x^2+y^2=a x\) and \(x^2+y^2=c^2(c>0)\) touch each other if [JEE Main 2011]
CorrectIncorrectHint
(a) If the two circles touch each other, then they must touch each other internally.
So, \(\frac{|a|}{2}=c-\frac{|a|}{2} \Rightarrow|a|=c\) -
Question 170 of 250
170. Question
The circle \(x^2+y^2=4 x+8 y+5\) intersects the line \(3 x-4 y=m\) at two distinct points if [JEE Main 2010]
CorrectIncorrectHint
(a) Circle \(x^2+y^2-4 x-8 y-5=0\)
Centre \(=(2,4)\), Radius \(=\sqrt{4+16+5}=5\)
If circle is intersecting line \(3 x-4 y=m\), at two distinct points.
\(\Rightarrow\) length of perpendicular from centre to the line <radius
\(\Rightarrow \frac{|6-16-m|}{5}<5 \Rightarrow|10+m|<25\)
\(\Rightarrow-25<m+10<25 \Rightarrow-35<m<15\) -
Question 171 of 250
171. Question
If \(P\) and \(Q\) are the points of intersection of the circles \(x^2+y^2+3 x+7 y+2 p-5=0\) and \(x^2+y^2+2 x+2 y-p^2=0\) then there is a circle passing through \(P, Q\) and \((1,1)\) for: [JEE Main 2009]
CorrectIncorrectHint
(a) The given circles are
\(
\begin{aligned}
& S_1 \equiv x^2+y^2+3 x+7 y+2 p-5=0 \dots(1) \\
& S_2 \equiv x^2+y^2+2 x+2 y-p^2=0 \dots(2)
\end{aligned}
\)
\(\therefore \quad\) Equation of common chord \(P Q\) is
\(
\begin{aligned}
& S_1-S_2=0 \\
& \Rightarrow \quad L \equiv x+5 y+p^2+2 p-5=0 \\
&
\end{aligned}
\)
\(\Rightarrow\) Equation of circle passing through \(P\) and \(Q\) is
\(
S_1+\lambda L =0
\)
\(
\begin{aligned}
\Rightarrow\left(x^2+y^2+3 x+7 y+2 p-5\right) & \\
& +\lambda\left(x+5 y+p^2+2 p-5\right)=0
\end{aligned}
\)
As it passes through \((1,1)\), therefore
\(
\begin{aligned}
& (7+2 p )+\lambda\left(2 p + p ^2+1\right)=0 \\
\Rightarrow & \lambda=-\frac{2 p+7}{(p+1)^2}
\end{aligned}
\)
which does not exist for \(p=-1\) -
Question 172 of 250
172. Question
Three distinct points \(A, B\) and \(C\) are given in the 2-dimensional coordinates plane such that the ratio of the distance of any one of them from the point \((1,0)\) to the distance from the point \((-1,0)\) is equal to \(\frac{1}{3}\). Then the circumcentre of the triangle \(ABC\) is at the point: [JEE Main 2009]
CorrectIncorrectHint
(a) Given that \(P(1,0), Q(-1,0)\)
and \(\frac{A P}{A Q}=\frac{B P}{B Q}=\frac{C P}{C Q}=\frac{1}{3}\)
\(
\Rightarrow 3 A P=A Q
\)
Let \(A=(x, y)\) then
\(
\begin{aligned}
& 3 A P=A Q \Rightarrow 9 A P^2=A Q^2 \\
& \Rightarrow 9(x-1)^2+9 y^2=(x+1)^2+y^2 \\
& \Rightarrow 9 x^2-18 x+9+9 y^2=x^2+2 x+1+y^2 \\
& \Rightarrow 8 x^2-20 x+8 y^2+8=0 \\
& \Rightarrow x^2+y^2-\frac{5}{3} x+1=0 \dots(1)
\end{aligned}
\)
\(\therefore \quad\) A lies on the circle given by eq (1). As \(B\) and \(C\) also follow the same condition, they must lie on the same circle.
\(\therefore\) Centre of circumcircle of \(\triangle A B C\)
\(=\) Centre of circle given by \((1)=\left(\frac{5}{4}, 0\right)\) -
Question 173 of 250
173. Question
The point diametrically opposite to the point \(P(1,0)\) on the circle \(x^2+y^2+2 x+4 y-3=0\) is [JEE Main 2008]
CorrectIncorrectHint
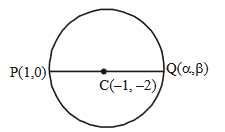
(c) The given circle is \(x^2+y^2+2 x+4 y-3=0\)
Centre \((-1,-2)\)
Let \(Q(\alpha, \beta)\) be the point diametrically opposite to the point \(P(1,0)\), then \(\frac{1+\alpha}{2}=-1\) and \(\frac{0+\beta}{2}=-2\)
\(
\Rightarrow \alpha=-3, \beta=-4
\)
So, \(Q\) is \((-3,-4)\) -
Question 174 of 250
174. Question
Consider a family of circles which are passing through the point \((-1,1)\) and are tangent to \(x\)-axis. If \((h, k)\) are the coordinate of the centre of the circles, then the set of values of \(k\) is given by the interval [JEE Main 2007]
CorrectIncorrectHint
Equation of circle whose centre is \((h, k)\)
i.e \((x-h)^2+(y-k)^2=k^2\)
\(
\begin{aligned}
& \text { (radius of circle }=k \text { because circle is tangent to } x \text {-axis) } \\
& \text { Equation of circle passing through }(-1,+1) \\
& \therefore(-1-h)^2+(1-k)^2=k^2 \\
& \Rightarrow 1+h^2+2 h+1+k^2-2 k=k^2 \\
& \Rightarrow h^2+2 h-2 k+2=0 \\
& D \geq 0 \\
& \therefore(2)^2-4 \times 1 .(-2 k+2) \geq 0 \\
& \Rightarrow 4-4(-2 k+2) \geq 0 \Rightarrow 1+2 k-2 \geq 0 \Rightarrow k \geq \frac{1}{2} \\
&
\end{aligned}
\) -
Question 175 of 250
175. Question
Let \(C\) be the circle with centre \((0,0)\) and radius 3 units. The equation of the locus of the mid points of the chords of the circle \(C\) that subtend an angle of \(\frac{2 \pi}{3}\) at its center is [JEE Main 2006]
CorrectIncorrectHint
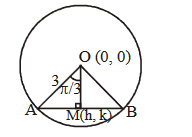
(d) Let \(M(h, k)\) be the mid point of chord \(A B\) where
\(
\angle A O B=\frac{2 \pi}{3}
\)
\(
\begin{aligned}
& \therefore \angle A O M=\frac{\pi}{3} \text {. Also } O M=3 \cos \frac{\pi}{3}=\frac{3}{2} \\
& \Rightarrow \sqrt{h^2+k^2}=\frac{3}{2} \Rightarrow h^2+k^2=\frac{9}{4}
\end{aligned}
\)
\(\therefore\) Locus of \((h, k)\) is \(x^2+y^2=\frac{9}{4}\) -
Question 176 of 250
176. Question
If the lines \(3 x-4 y-7=0\) and \(2 x-3 y-5=0\) are two diameters of a circle of area \(49 \pi\) square units, the equation of the circle is [JEE Main 2006]
CorrectIncorrectHint
(d) Point of intersection of \(3 x-4 y-7=0\) and \(2 x-3 y-5=0\) is \((1,-1)\) which is the centre of the circle and radius \(=7\)
\(\therefore\) Equation is \((x-1)^2+(y+1)^2=49\)
\(\Rightarrow x^2+y^2-2 x+2 y-47=0\) -
Question 177 of 250
177. Question
If a circle passes through the point \((a, b)\) and cuts the circle \(x^2+y^2=p^2\) orthogonally, then the equation of the locus of its centre is [JEE 2005]
CorrectIncorrectHint
(d) Let the centre be \((\alpha, \beta)\)
\(\because\) It cuts the circle \(x^2+y^2=p^2\) orthogonally
\(\therefore\) Using \(2 g_1 g_2+2 f_1 f_2=c_1+c_2\), we get
\(
2(-\alpha) \times 0+2(-\beta) \times 0=c_1-p^2
\)
\(
c_1=p^2
\)
Let equation of circle is
\(
x^2+y^2-2 \alpha x-2 \beta y+p^2=0
\)
It passes through
\(
(a, b) \Rightarrow a^2+b^2-2 \alpha a-2 \beta b+p^2=0
\)
\(\therefore\) Locus of \((\alpha, \beta)\) is
\(
\therefore 2 a x+2 b y-\left(a^2+b^2+p^2\right)=0 .
\) -
Question 178 of 250
178. Question
If the pair of lines \(a x^2+2(a+b) x y+b y^2=0\) lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [JEE 2005]
CorrectIncorrectHint
As per question area of one sector \(=3\) area of another sector
\(\Rightarrow\) angle at centre by one sector \(=3 \times\) angle at centre by another sector
Let one angle be \(\theta\) then other \(=3 \theta\)
Clearly \(\theta+3 \theta=180 \Rightarrow \theta=45^{\circ}\)
\(\therefore\) Angle between the diameters represented by combined equation
\(
a x^2+2(a+b) x y+b y^2=0 \text { is } 45^{\circ}
\)
\(\therefore\) Using \(\tan \theta=\frac{2 \sqrt{h^2-a b}}{a+b}\)
we get \(\tan 45^{\circ}=\frac{2 \sqrt{(a+b)^2-a b}}{a+b}\)
\(\Rightarrow 1=\frac{2 \sqrt{a^2+b^2+a b}}{a+b}\)
\(\Rightarrow(a+b)^2=4\left(a^2+b^2+a b\right)\)
\(\Rightarrow a^2+b^2+2 a b=4 a^2+4 b^2+4 a b\)
\(\Rightarrow 3 a^2+3 b^2+2 a b=0\) -
Question 179 of 250
179. Question
If the circles \(x^2+y^2+2 a x+c y+a=0\) and \(x^2+y^2-3 a x+d y-1=0\) intersect in two distinct points \(P\) and \(Q\) then the line \(5 x+b y-a=0\) passes through \(P\) and \(Q\) for [JEE 2005]
CorrectIncorrectHint
(b)
\(
\begin{aligned}
& s_1=x^2+y^2+2 a x+c y+a=0 \\
& s_2=x^2+y^2-3 a x+d y-1=0
\end{aligned}
\)
Equation of common chord of circles \(s_1\) and \(s_2\) is given by \(s_1-s_2=0\)
\(
\Rightarrow 5 a x+(c-d) y+a+1=0
\)
Given that \(5 x+b y-a=0\) passes through \(P\) and \(Q\)
\(\therefore\) The two equations should represent the same line
\(
\begin{aligned}
& \Rightarrow \frac{a}{1}=\frac{c-d}{b}=\frac{a+1}{-a} \Rightarrow a+1=-a^2 \\
& a^2+a+1=0
\end{aligned}
\)
No real value of \(a\). -
Question 180 of 250
180. Question
If a circle passes through the point \((a, b)\) and cuts the circle \(x^2+y^2=4\) orthogonally, then the locus of its centre is [JEE Main 2004]
CorrectIncorrectHint
(b) Let the variable circle is
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(1)
\)
It passes through \((a, b)\)
\(
\therefore a^2+b^2+2 g a+2 f b+c=0 \dots(2)
\)
(1) cuts \(x^2+y^2=4\) orthogonally
\(
\therefore 2(g \times 0+f \times 0)=c-4 \Rightarrow c=4
\)
\(\therefore\) from (2) \(a^2+b^2+2 g a+2 f b+4=0\)
\(\therefore\) Locus of centre \((-g,-f)\) is
\(
a^2+b^2-2 a x-2 b y+4=0
\)
or \(2 a x+2 b y=a^2+b^2+4\) -
Question 181 of 250
181. Question
A variable circle passes through the fixed point \(A(p, q)\) and touches \(x\)-axis. The locus of the other end of the diameter through \(A\) is [JEE 2004]
CorrectIncorrectHint
(d) Let the variable circle be
\(
\begin{aligned}
& x^2+y^2+2 g x+2 f y+c=0 \dots(1) \\
& \therefore p^2+q^2+2 g p+2 f q+c=0 \dots(2)
\end{aligned}
\)
Circle (1) touches \(x\)-axis,
\(
\begin{aligned}
& \therefore g^2-c=0 \Rightarrow c=g^2 . \text { From }(2) \\
& p^2+q^2+2 g p+2 f q+g^2=0 \dots(3)
\end{aligned}
\)
Let the other end of diameter through \((p, q)\) be \((h, k)\), then
\(
\frac{h+p}{2}=-g \text { and } \frac{k+q}{2}=-f
\)
Put in (3)
\(
\begin{aligned}
& p^2+q^2+2 p\left(-\frac{h+p}{2}\right)+2 q\left(-\frac{k+q}{2}\right)+\left(\frac{h+p}{2}\right)^2=0 \\
& \Rightarrow h^2+p^2-2 h p-4 k q=0
\end{aligned}
\)
\(\therefore\) locus of \((h, k)\) is \(x^2+p^2-2 x p-4 y q=0\)
\(
\Rightarrow(x-p)^2=4 q y
\) -
Question 182 of 250
182. Question
If the lines \(2 x+3 y+1=0\) and \(3 x-y-4=0\) lie along diameter of a circle of circumference \(10 \pi\), then the equation of the circle is [JEE 2004]
CorrectIncorrectHint
(d) Two diameters are along
\(
\begin{aligned}
& 2 x+3 y+1=0 \text { and } 3 x-y-4=0 \\
& \text { solving we get centre }(1,-1) \\
& \text { circumference }=2 \pi r=10 \pi \\
& \therefore r=5 .
\end{aligned}
\)
Required circle is, \((x-1)^2+(y+1)^2=5^2\)
\(
\Rightarrow x^2+y^2-2 x+2 y-23=0
\) -
Question 183 of 250
183. Question
Intercept on the line \(y=x\) by the circle \(x^2+y^2-2 x=0\) is \(A B\). Equation of the circle on \(A B\) as a diameter is [JEE 2004]
CorrectIncorrectHint
(d) Solving \(y=x\) and the circle
\(x^2+y^2-2 x=0\), we get
\(x=0, y=0\) and \(x=1, y=1\)
\(\therefore\) Extremities of diameter of the required circle are \((0,0)\) and \((1,1)\). Hence, the equation of circle is
\(
\begin{aligned}
& (x-0)(x-1)+(y-0)(y-1)=0 \\
& \Rightarrow x^2+y^2-x-y=0
\end{aligned}
\) -
Question 184 of 250
184. Question
If the two circles \((x-1)^2+(y-3)^2=r^2\) and \(x^2+y^2-8 x+2 y+8=0\) intersect in two distinct point, then [JEE 2003]
CorrectIncorrectHint
(b) \(\left|r_1-r_2\right|<C_1 C_2\) for intersection
\(
\begin{aligned}
& \Rightarrow r-3<5 \Rightarrow r<8 \quad \ldots \text { (1) } \\
& \text { and } r_1+r_2>C_1 C_2, r+3>5 \Rightarrow r>2 \dots(ii) \\
& \text { From(1) and (2), } 2< r <8 \text {. }
\end{aligned}
\)
From(1) and (2), \(2< r <8\). -
Question 185 of 250
185. Question
The lines \(2 x-3 y=5\) and \(3 x-4 y=7\) are diameters of a circle having area as 154 sq.units. Then the equation of the circle is [JEE 2003]
CorrectIncorrectHint
(d) \(\pi r^2=154 \Rightarrow r=7\)
For centre on solving equation
\(2 x-3 y=5 \& 3 x-4 y=7\) we get \(x=1, y=-1\)
\(\therefore\) centre \(=(1,-1)\)
Equation of circle, \((x-1)^2+(y+1)^2=7^2\)
\(
x^2+y^2-2 x+2 y=47
\) -
Question 186 of 250
186. Question
If the chord \(y=m x+1\) of the circle \(x^2+y^2=1\) subtends an angle of measure \(45^{\circ}\) at the major segment of the circle then value of \(m\) is [JEE 2002]
CorrectIncorrectHint
(c) Equation of circle \(x^2+y^2=1=(1)^2\)
\(\Rightarrow x^2+y^2=(y-m x)^2\)
\(\Rightarrow x^2=m^2 x^2-2 m x y ;\)
\(\Rightarrow x^2\left(1-m^2\right)+2 m x y=0\). Which represents the pair of lines between which the angle is \(45^{\circ}\).
\(
\begin{aligned}
& \tan 45= \pm \frac{2 \sqrt{m^2-0}}{1-m^2}=\frac{ \pm 2 m}{1-m^2} ; \\
& \Rightarrow 1-m^2= \pm 2 m \Rightarrow m^2 \pm 2 m-1=0 \\
& \Rightarrow m=\frac{-2 \pm \sqrt{4+4}}{2} \\
& =\frac{-2 \pm 2 \sqrt{2}}{2}=-1 \pm \sqrt{2} .
\end{aligned}
\) -
Question 187 of 250
187. Question
The centres of a set of circles, each of radius 3, lie on the circle \(x^2+y^2=25\). The locus of any point in the set is [JEE 2002]
CorrectIncorrectHint
(a) For any point \(P ( x , y )\) in the given circle,
we should have
\(
O A \leq O P \leq O B
\)
\(
\begin{aligned}
& \Rightarrow(5-3) \leq \sqrt{x^2+y^2} \leq 5+3 \\
& \Rightarrow 4 \leq x^2+y^2 \leq 64
\end{aligned}
\) -
Question 188 of 250
188. Question
The centre of the circle passing through \((0,0)\) and \((1,0)\) and touching the circle \(x^2+y^2=9\) is [JEE 2002]
CorrectIncorrectHint
(b) Let the required circle be
\(
x^2+y^2+2 g x+2 f y+c=0
\)
Since it passes through \((0,0)\) and \((1,0)\)
\(
\Rightarrow c=0 \text { and } g=-\frac{1}{2}
\)
Points \((0,0)\) and \((1,0)\) lie inside the circle \(x^2+y^2=9\), so two circles touch internally
\(
\begin{aligned}
& \Rightarrow c_1 c_2=r_1-r_2 \\
& \therefore \sqrt{g^2+f^2}=3-\sqrt{g^2+f^2} \Rightarrow \sqrt{g^2+f^2}=\frac{3}{2} \\
& \Rightarrow f^2=\frac{9}{4}-\frac{1}{4}=2 \quad \therefore f= \pm \sqrt{2} .
\end{aligned}
\)
Hence, the centres of required circle are
\(
\left(\frac{1}{2}, \sqrt{2}\right) \text { or }\left(\frac{1}{2},-\sqrt{2}\right)
\) -
Question 189 of 250
189. Question
The equation of a circle with origin as a centre and passing through equilateral triangle whose median is of length \(3 a\) is [JEE 2002]
CorrectIncorrectHint
(c) Let \(A B C\) be an equilateral triangle, whose median is \(A D\).
\(
\begin{aligned}
& \text { Given } A D=3 a \text {. } \\
& \text { In } \triangle A B D, A B^2=A D^2+B D^2 \text {; } \\
& \Rightarrow x^2=9 a^2+\left(x^2 / 4\right) \text { where } A B=B C=A C=x \text {. } \\
& \frac{3}{4} x^2=9 a^2 \Rightarrow x^2=12 a^2 . \\
& \text { In } \triangle O B D, O B^2=O D^2+B D^2
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow r^2=(3 a-r)^2+\frac{x^2}{4} \\
& \Rightarrow r^2=9 a^2-6 a r+r^2+3 a^2 ; \Rightarrow 6 a r=12 a^2 \\
& \Rightarrow r=2 a
\end{aligned}
\)
So equation of circle is \(x^2+y^2=4 a^2\) -
Question 190 of 250
190. Question
If \(y=m x+c\) is the normal at a point on the parabola \(y^2=8 x\) whose focal distance is 8 units, then \(|c|\) is equal to: [Online April 9, 2017]
CorrectIncorrectHint
\(
\begin{aligned}
\text { (c) } & c =-29 m -9 m ^3 \\
& a =2 \\
& \text { Given }\left( at ^2- a \right)^2+4 a ^2 t ^2=64 \\
\Rightarrow & \left( a \left( t ^2+1\right)\right)=8 \\
\Rightarrow & t ^2+1=4 \Rightarrow t ^2=3 \\
\Rightarrow & t =\sqrt{3} \\
\therefore \quad & c =2 at \left(2+ t ^2\right)
\end{aligned}
\)
\(
\begin{aligned}
= & 2 \sqrt{3}(5) \\
|c| & =10 \sqrt{3}
\end{aligned}
\) -
Question 191 of 250
191. Question
If the common tangents to the parabola, \(x^2=4 y\) and the circle, \(x^2+y^2=4\) intersect at the point \(P\), then the distance of \(P\) from the origin, is : [Online April 8, 2017]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Tangent to } x^2+y^2=4 \text { is } \\
& y= mx \pm 2 \sqrt{1+m^2} \\
& \text { Also, } x^2=4 y \\
& x^2=4 mx +8 \sqrt{1+m^2} \text { or } x^2=4 mx -8 \sqrt{1+m^2} \\
& \text { For } D =0 \\
& \text { we have; } 16 m ^2+4.8 \sqrt{1+m^2}=0 \\
& \Rightarrow m ^2+2 \sqrt{1+m^2}=0 \\
& \Rightarrow m ^2=-2 \sqrt{1+m^2} \\
& \Rightarrow m ^4=4+4 m ^2 \\
& \Rightarrow m ^4-4 m ^2-4=0 \\
& \Rightarrow m ^2=\frac{4 \pm \sqrt{16+16}}{2} \\
& \Rightarrow m ^2=\frac{4 \pm 4 \sqrt{2}}{2} \\
& \Rightarrow \quad m ^2=2+2 \sqrt{2} \\
&
\end{aligned}
\) -
Question 192 of 250
192. Question
Let \(P\) be the point on the parabola, \(y^2=8 x\) which is at a minimum distance from the centre \(C\) of the circle, \(x^2+(y+6)^2=1\). Then the equation of the circle, passing through \(C\) and having its centre at \(P\) is: [JEE 2016]
CorrectIncorrectHint
(c) Minimum distance \(\Rightarrow\) perpendicular distance
Eqn of normal at \(p\left(2 t^2, 4 t\right)\)
\(
y=-t x+4 t+2 t^3
\)
It passes through \(C (0,-6)\)
\(
\Rightarrow t^3+2 t+3=0 \Rightarrow t=-1
\)
\(
\begin{aligned}
& \text { Centre of new circle }= P \left(2 t ^2, 4 t \right) \\
& = P (2,-4) \\
& \text { Radius }=\text { PC } \\
& =\sqrt{(2-0)^2+(-4+6)^2} \\
&
\end{aligned}
\)
\(
=2 \sqrt{2}
\)
\(\therefore\) Equation of circle is :
\(
\begin{aligned}
& (x-2)^2+(y+4)=(2 \sqrt{2})^2 \\
\Rightarrow & x^2+y^2-4 x+8 y+12=0
\end{aligned}
\) -
Question 193 of 250
193. Question
\(P\) and \(Q\) are two distinct points on the parabola, \(y^2=4 x\), with parameters \(t\) and \(t_1\) respectively. If the normal at \(P\) passes through \(Q\), then the minimum value of \(t_1^2\) is: [Online April 10, 2016]
CorrectIncorrectHint
(a) \(t_1=-t-\frac{2}{t}\)
\(
\begin{aligned}
& t_1^2=t^2+\frac{4}{t^2}+4 \\
& t^2+\frac{4}{t^2} \geq 2 \sqrt{t^2 \cdot \frac{4}{t^2}}=4
\end{aligned}
\)
Minimum value of \(t_1^2=8\) -
Question 194 of 250
194. Question
Let \(O\) be the vertex and \(Q\) be any point on the parabola, \(x ^2=8 y\). If the point \(P\) divides the line segment \(OQ\) internally in the ratio \(1: 3\), then locus of \(P\) is : [JEE Main 2015]
CorrectIncorrectHint
(b) Let \(P ( h , k )\) divides
\(OQ\) in the ratio \(1: 3\)
Let any point \(Q\) on \(x ^2=8 y\) is \(\left(4 t , 2 t ^2\right)\).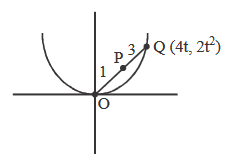
Then by section formula
\(
\begin{aligned}
& \Rightarrow \quad k =\frac{ t ^2}{2} \text { and } h = t \\
& \Rightarrow \quad 2 k = h ^2
\end{aligned}
\)
Required locus of \(P\) is \(x ^2=2 y\) -
Question 195 of 250
195. Question
Let PQ be a double ordinate of the parabola, \(y^2=-4 x\), where \(P\) lies in the second quadrant. If \(R\) divides \(P Q\) in the ratio \(2: 1\) then the locus of \(R\) is : [Online April 11, 2015]
CorrectIncorrectHint
\(
\text { (d) Let } P \left(- at _1^2, 2 at _1\right), Q \left(- at _1^2,-2 at _1\right) \text { and } R ( h , k )
\)
By using section formula, we have
\(
\begin{aligned}
& h =- at _1^2, k =\frac{-2 at _1}{3} \\
& k =-\frac{2 at _1}{3}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow 3 k =-2 at _1 \\
& \Rightarrow 9 k ^2=4 a ^2 t _1^2=4 a (- h ) \\
& \Rightarrow 9 k ^2=-4 a h \\
& \Rightarrow 9 k ^2=-4 h \Rightarrow 9 y ^2=-4 x
\end{aligned}
\) -
Question 196 of 250
196. Question
The slope of the line touching both the parabolas \(y^2=4 x\) and \(x^2=-32 y\) is [JEE Main 2014]
CorrectIncorrectHint
(c) Given parabolas are
\(
\begin{aligned}
& y^2=4 x \dots(i) \\
& x^2=-32 y \dots(ii)
\end{aligned}
\)
Let \(m\) be slope of common tangent
Equation of tangent of parabola (i)
\(
y=m x+\frac{1}{m} \dots(iii)
\)
Equation of tangent of parabola (ii)
\(
y=m x+8 m^2 \dots(iv)
\)
(iii) and (iv) are identical
\(
\Rightarrow \frac{1}{m}=8 m^2 \Rightarrow m^3=\frac{1}{8} \Rightarrow m=\frac{1}{2}
\)Alternate:
Let tangent to \(y^2=4 x\) be \(y=m x+\frac{1}{m}\)
Since this is also tangent to \(x^2=-32 y\)
\(
\begin{aligned}
& \therefore x^2=-32\left(m x+\frac{1}{m}\right) \\
& \Rightarrow x^2+32 m x+\frac{32}{m}=0
\end{aligned}
\)
Now, \(D =0\)
\(
\begin{aligned}
(32)^2-4\left(\frac{32}{m}\right) & =0 \\
\Rightarrow m^3=\frac{4}{32} \quad \Rightarrow m & =\frac{1}{2}
\end{aligned}
\) -
Question 197 of 250
197. Question
A chord is drawn through the focus of the parabola \(y^2=6 x\) such that its distance from the vertex of this parabola is \(\frac{\sqrt{5}}{2}\), then its slope can be: [Online April 19, 2014]
CorrectIncorrectHint
(a) Equation of parabola, \(y^2=6 x\)
\(
\begin{aligned}
& \Rightarrow y^2=4 \times \frac{3}{2} x \\
& \therefore \text { Focus }=\left(\frac{3}{2}, 0\right)
\end{aligned}
\)
Let equation of chord passing through focus be \(a x+b y+c=0 \dots(1)\)
Since chord is passing through \(\left(\frac{3}{2}, 0\right)\)
\(\therefore\) Put \(x=\frac{3}{2}, y=0\) in eqn (1), we get \(\frac{3}{2} a+c=0\)
\(\Rightarrow c=-\frac{3}{2} a \dots(2)\)
distance of chord from origin is \(\frac{\sqrt{5}}{2}\)
\(
\frac{\sqrt{5}}{2}=\left|\frac{a(0)+b(0)+c}{\sqrt{a^2+b^2}}\right|=\frac{c}{\sqrt{a^2+b^2}}
\)
Squaring both sides
\(
\begin{aligned}
& \frac{5}{4}=\frac{c^2}{a^2+b^2} \\
& \Rightarrow a^2+b^2=\frac{4}{5} c^2
\end{aligned}
\)
Putting value of \(c\) from (2), we get
\(
\begin{aligned}
& a^2+b^2=\frac{4}{5} \times \frac{9}{4} a^2 \\
& b^2=\frac{9}{5} a^2-a^2=\frac{4}{5} a^2 \\
& \frac{a^2}{b^2}=\frac{5}{4}, \frac{a}{b}= \pm \frac{\sqrt{5}}{2}
\end{aligned}
\)
Slope of chord, \(\frac{d y}{d x}=-\frac{a}{b}=-\left(\frac{ \pm \sqrt{5}}{2}\right)=\mp \frac{\sqrt{5}}{2}\) -
Question 198 of 250
198. Question
Two tangents are drawn from a point \((-2,-1)\) to the curve, \(y^2=4 x\). If \(\alpha\) is the angle between them, then \(|\tan \alpha|\) is equal to: [Online April 12, 2014]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (d) The locus of the point of intersection of tangents to } \\
& \text { the parabola } y^2=4 a x \text { inclined at an angle } \alpha \text { to each } \\
& \text { other is } \\
& \tan ^2 \alpha(x+a)^2=y^2-4 a x \\
& \text { Given equation of Parabola } y^2=4 x\{a=1\} \\
& \text { Point of intersection }(-2,-1) \\
& \tan ^2 \alpha(-2+1)^2=(-1)^2-4 \times 1 \times(-2) \\
& \Rightarrow \quad \tan ^2 \alpha=9 \\
& \Rightarrow \quad \tan \alpha= \pm 3 \\
& \Rightarrow \quad|\tan \alpha|=3
\end{aligned}
\) -
Question 199 of 250
199. Question
Let \(L_1\) be the length of the common chord of the curves \(x^2+y^2=9\) and \(y^2=8 x\), and \(L_2\) be the length of the latus rectum of \(y^2=8 x\), then: [Online April 11, 2014]
CorrectIncorrectHint
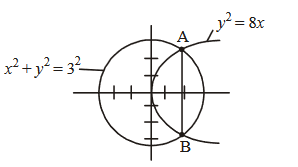
We have
\(
\begin{aligned}
& x^2+(8 x)=9 \\
& x^2+9 x-x-9=0 \\
& x(x+9)-1(x+9)=0 \\
& (x+9)(x-1)=0 \\
& x=-9,1 \\
& \text { for } x=1, y= \pm 2 \sqrt{2 x}= \pm 2 \sqrt{2} \\
& L _1=\text { Length of } AB \\
& \qquad=\sqrt{(2 \sqrt{2}+2 \sqrt{2})^2+(1-1)^2}=4 \sqrt{2} \\
& L _2=\text { Length of latus rectum }=4 a=4 \times 2=8 \\
& L _1< L _2
\end{aligned}
\) -
Question 200 of 250
200. Question
Given : A circle, \(2 x^2+2 y^2=5\) and a parabola, \(y^2=4 \sqrt{5} x\).
Statement-1 : An equation of a common tangent to these curves is \(y=x+\sqrt{5}\).
Statement-2 : If the line, \(y=m x+\frac{\sqrt{5}}{m}(m \neq 0)\) is their common tangent, then \(m\) satisfies \(m^4-3 m^2+2=0\). [JEE Main 2013]CorrectIncorrectHint
(b) Let common tangent be
\(
y=m x+\frac{\sqrt{5}}{m}
\)
Since, perpendicular distance from centre of the circle to the common tangent is equal to radius of the circle,
therefore \(\frac{\frac{\sqrt{5}}{m}}{\sqrt{1+m^2}}=\sqrt{\frac{5}{2}}\)
On squaring both the side, we get
\(
\begin{aligned}
& m^2\left(1+m^2\right)=2 \\
\Rightarrow & m^4+m^2-2=0 \\
\Rightarrow & \left(m^2+2\right)\left(m^2-1\right)=0 \\
\Rightarrow & m= \pm 1 \quad(\because m \neq \pm \sqrt{2})
\end{aligned}
\)
\(y= \pm(x+\sqrt{5})\), both statements are correct as \(m= \pm 1\) satisfies the given equation of statement-2. -
Question 201 of 250
201. Question
The point of intersection of the normals to the parabola \(y^2=4 x\) at the ends of its latus rectum is : [Online April 23, 2013]
CorrectIncorrectHint
(b) We know that point of intersection of the normal to the parabola \(y^2=4 a x\) at the ends of its latus rectum is \((3 a, 0)\)
Hence required point of intersection \(=(3,0)\) -
Question 202 of 250
202. Question
Statement-1: The line \(x-2 y=2\) meets the parabola, \(y^2+2 x=0\) only at the point \((-2,-2)\).
Statement-2: The line \(y=m x-\frac{1}{2 m}(m \neq 0)\) is tangent to the parabola, \(y^2=-2 x\) at the point \(\left(-\frac{1}{2 m^2},-\frac{1}{m}\right)\). [Online April 22, 2013]CorrectIncorrectHint
(b) Both statements are true and statement- 2 is the correct explanation of statement-1
\(\therefore \quad\) The straight line \(y=m x+\frac{a}{m}\) is always a tangent to the parabola \(y^2=4 a x\) for any value of \(m\).
The co-ordinates of point of contact \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\)
Now, required radius \(= OB =\sqrt{9+16}=\sqrt{25}=5\) -
Question 203 of 250
203. Question
The normal at \(\left(2, \frac{3}{2}\right)\) to the ellipse, \(\frac{x^2}{16}+\frac{y^2}{3}=1\) touches a parabola, whose equation is [Online May 26, 2012]
CorrectIncorrectHint
(a) Ellipse is \(\frac{x^2}{16}+\frac{y^2}{3}=1\)
Now, equation of normal at \((2,3 / 2)\) is
\(
\begin{aligned}
& \frac{16 x}{2}-\frac{3 y}{3 / 2}=16-3 \\
& \Rightarrow \quad 8 x-2 y=13 \\
& \Rightarrow \quad y=4 x-\frac{13}{2}
\end{aligned}
\)
Let \(y=4 x-\frac{13}{2}\) touches a parabola
\(
y^2=4 a x \text {. }
\)
We know, a straight line \(y=m x+c\) touches a parabola \(y^2=4 a x\) if \(a-m c=0\)
\(
\therefore \quad a-(4)\left(-\frac{13}{2}\right)=0 \Rightarrow a=-26
\)
Hence, required equation of parabola is
\(
y^2=4(-26) x=-104 x
\) -
Question 204 of 250
204. Question
The chord \(P Q\) of the parabola \(y^2=x\), where one end \(P\) of the chord is at point \((4,-2)\), is perpendicular to the axis of the parabola. Then the slope of the normal at \(Q\) is [Online May 26, 2012]
CorrectIncorrectHint
(a) Point \(P\) is \((4,-2)\) and \(P Q \perp x\)-axis So, \(Q=(4,2)\)
Equation of tangent at \((4,2)\) is
\(
\begin{aligned}
& y y_1=\frac{1}{2}\left(x+x_1\right) \\
& \Rightarrow 2 y=\frac{1}{2}(x+2) \Rightarrow 4 y=x+2 \\
& \Rightarrow y=\frac{x}{4}+\frac{1}{2}
\end{aligned}
\)
So, slope of tangent \(=\frac{1}{4}\)
\(\therefore\) Slope of normal \(=-4\) -
Question 205 of 250
205. Question
Statement \(1: y=m x-\frac{1}{m}\) is always a tangent to the parabola, \(y^2=-4 x\) for all non-zero values of \(m\).
Statement 2: Every tangent to the parabola, \(y^2=-4 x\) will meet its axis at a point whose abscissa is non-negative. [Online May 7, 2012]CorrectIncorrectHint
\(
y^2=-4 x
\)
Eqn of tangent
\(
\begin{gathered}
y=m x-\frac{a}{m} . \\
y=m x-\frac{1}{m}
\end{gathered}
\)
\(
-4 a=-4; a=1
\)Both the given statements are true.
Statement – 2 is not the correct explanation for statement – 1. -
Question 206 of 250
206. Question
The shortest distance between line \(y-x=1\) and curve \(x=y^2\) is [JEE Main 2011]
CorrectIncorrectHint
(a) Shortest distance between two curve occurred along the common normal, so \(-2 t=-1\) \(\Rightarrow t=1 / 2\)
\(
\text { So shortest distance between them is } \frac{3 \sqrt{2}}{8}
\) -
Question 207 of 250
207. Question
If two tangents drawn from a point \(P\) to the parabola \(y^2=4 x\) are at right angles, then the locus of \(P\) is [JEE Main 2010]
CorrectIncorrectHint
(b) The locus of perpendicular tangents is directrix i.e., \(x=-a ; x=-1\)
-
Question 208 of 250
208. Question
A parabola has the origin as its focus and the line \(x=2\) as the directrix. Then the vertex of the parabola is at [JEE 2008]
CorrectIncorrectHint
(b) Vertex of a parabola is the mid point of focus and the point where directrix meets the axis of the parabola.
Here focus is \(O(0,0)\) and directrix meets the axis at \(B(2,0)\)
\(\therefore\) Vertex of the parabola is \((1,0)\)
-
Question 209 of 250
209. Question
The equation of a tangent to the parabola \(y^2=8 x\) is \(y=x+2\). The point on this line from which the other tangent to the parabola is perpendicular to the given tangent is [JEE Main 2007]
CorrectIncorrectHint
\(
\text { (b) Parabola } y^2=8 x
\)
We know that the locus of point of intersection of two perpendicular tangents to a parabola is its directrix.
Point must be on the directrix of parabola
\(\because\) equation of directrix \(x+2=0\)
\(
\Rightarrow x=-2
\)
Hence the point is \((-2,0)\) -
Question 210 of 250
210. Question
The locus of the vertices of the family of parabolas \(y=\frac{a^3 x^2}{3}+\frac{a^2 x}{2}-2 a\) is [JEE 2006]
CorrectIncorrectHint
(a) Given parabola is \(y=\frac{a^3 x^2}{3}+\frac{a^2 x}{2}-2 a\)
\(
\begin{aligned}
& \Rightarrow y=\frac{a^3}{3}\left(x^3+\frac{3}{2 a} x+\frac{9}{16 a^2}\right)-\frac{3 a}{16}-2 a \\
& \Rightarrow y+\frac{35 a}{16}=\frac{a^3}{3}\left(x+\frac{3}{4 a}\right)^2
\end{aligned}
\)
\(\therefore\) Vertex of parabola is \(\left(\frac{-3}{4 a}, \frac{-35 a}{16}\right)\)
To find locus of this vertex, \(x=\frac{-3}{4 a}\) and \(y=\frac{-35 a}{16}\)
\(\Rightarrow a=\frac{-3}{4 x}\) and \(a=-\frac{16 y}{35}\)
\(\Rightarrow \frac{-3}{4 x}=\frac{-16 y}{35} \Rightarrow 64 x y=105\)
\(\Rightarrow x y=\frac{105}{64}\) which is the required locus. -
Question 211 of 250
211. Question
Let \(P\) be the point \((1,0)\) and \(Q\) a point on the locus \(y^2=8 x\). The locus of mid point of \(P Q\) is [JEE 2005]
CorrectIncorrectHint
(a) \(P=(1,0) Q=(h, k)\) Such that \(K^2=8 h\) Let \((\alpha, \beta)\) be the midpoint of \(P Q\)
\(
\begin{array}{ll}
\alpha=\frac{h+1}{2}, & \beta=\frac{k+0}{2} \\
2 \alpha-1=h & 2 \beta=k .
\end{array}
\)
\(
\begin{aligned}
& (2 \beta)^2=8(2 \alpha-1) \Rightarrow \beta^2=4 \alpha-2 \\
& \Rightarrow y^2-4 x+2=0 .
\end{aligned}
\) -
Question 212 of 250
212. Question
A circle touches the \(x\) – axis and also touches the circle with centre at \((0,3)\) and radius 2 . The locus of the centre of the circle is [JEE 2005]
CorrectIncorrectHint
(d) Equation of circle with centre \((0,3)\) and radius 2 is \(x^2+(y-3)^2=4\)
Let locus of the variable circle is \((\alpha, \beta)\)
\(\because \quad\) It touches \(x\)-axis.
\(\therefore \quad\) It’s equation is \((x-\alpha)^2+(y+\beta)^2=\beta^2\)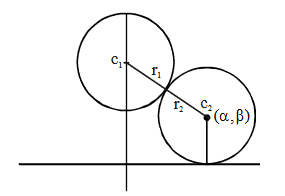
Circle touch externally \(\Rightarrow c_1 c_2=r_1+r_2\)
\(
\begin{aligned}
& \therefore \sqrt{\alpha^2+(\beta-3)^2}=2+\beta \\
& \alpha^2+(\beta-3)^2=\beta^2+4+4 \beta \\
& \Rightarrow \alpha^2=10(\beta-1 / 2)
\end{aligned}
\)
\(\therefore\) Locus is \(x^2=10\left(y-\frac{1}{2}\right)\)
Which is parabola. -
Question 213 of 250
213. Question
If \(a \neq 0\) and the line \(2 b x+3 c y+4 d=0\) passes through the points of intersection of the parabolas \(y^2=4 a x\) and \(x^2 = 4 a y\), then [JEE 2004]
CorrectIncorrectHint
(d) Solving equations of parabolas
\(
y^2=4 a x \text { and } x^2=4 a y
\)
we get \((0,0)\) and \((4 a, 4 a)\)
Substituting in the given equation of line
\(
2 b x+3 c y+4 d=0 \text {, }
\)
we get \(d=0\) and \(2 b+3 c=0\)
\(
\Rightarrow d^2+(2 b+3 c)^2=0
\) -
Question 214 of 250
214. Question
The normal at the point \(\left(b t_1{ }^2, 2 b t_1\right)\) on a parabola meets the parabola again in the point \(\left(b t_2{ }^2, 2 b t_2\right)\), then [JEE 2003]
CorrectIncorrectHint
(b) Equation of the normal to a parabola \(y^2=4 b x\) at point \(\left(b t_1^2, 2 b t_1\right)\) is \(y=-t_1 x+2 b t_1+b t_1^3\) As given, it also passes through \(\left(b t_2^2, 2 b t_2\right)\) then
\(
\begin{aligned}
& 2 b t_2=-t_1 b t_2^2+2 b t_1+b t_1^3 \\
& 2 t_2-2 t_1=-t_1\left(t_2^2-t_1^2\right) \\
& =-t_1\left(t_2+t_1\right)\left(t_2-t_1\right) \\
& \Rightarrow 2=-t_1\left(t_2+t_1\right) \Rightarrow t_2+t_1=-\frac{2}{t_1} \\
& \Rightarrow t_2=-t_1-\frac{2}{t_1}
\end{aligned}
\) -
Question 215 of 250
215. Question
Two common tangents to the circle \(x^2+y^2=2 a^2\) and parabola \(y^2=8 a x\) are [JEE 2002]
CorrectIncorrectHint
(b) Any tangent to the parabola \(y^2=8 a x\) is
\(
y=m x+\frac{2 a}{m} \dots(i)
\)
If (i) is a tangent to the circle, \(x^2+y^2=2 a^2\) then,
\(
\begin{aligned}
& \sqrt{2} a= \pm \frac{2 a}{m \sqrt{m^2+1}} \\
& \Rightarrow m^2\left(1+m^2\right)=2 \Rightarrow\left(m^2+2\right)\left(m^2-1\right)=0 \Rightarrow m= \pm 1 .
\end{aligned}
\)
So from (i), \(y= \pm(x+2 a)\). -
Question 216 of 250
216. Question
The eccentricity of an ellipse having centre at the origin, axes along the co-ordinate axes and passing through the points \((4,-1)\) and \((-2,2)\) is : [Online April 9, 2017]
CorrectIncorrectHint
(c) Centre at \((0,0)\)
\(
\begin{aligned}
& \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\
& \text { at point }(4,-1) \\
& \frac{16}{a^2}+\frac{1}{b^2}=1 \\
\Rightarrow \quad & 16 b^2+a^2=a^2 b^2 \dots(i)\\
& \text { at point }(-2,2) \\
& \frac{4}{a^2}+\frac{4}{b^2}=1 \\
\Rightarrow & 4 b^2+4 a^2=a^2 b^2 \dots(ii) \\
\Rightarrow & 16 b^2+a^2=4 a^2+4 b^2
\end{aligned}
\)
From equations (i) and (ii)
\(
\begin{aligned}
& \Rightarrow \quad 3 a^2=12 b^2 \\
& \Rightarrow \quad a^2=4 b^2 \\
& b ^2= a ^2\left(1-e^2\right) \\
& \Rightarrow \quad e ^2=\frac{3}{4} \\
& \Rightarrow \quad e =\frac{\sqrt{3}}{2}
\end{aligned}
\) -
Question 217 of 250
217. Question
Consider an ellipse, whose centre is at the origin and its major axis is along the \(x\)-axis. If its eccentricity is \(\frac{3}{5}\) and the distance between its foci is 6 , then the area (in sq. units) of the quadrilateral inscribed in the ellipse, with the vertices as the vertices of the ellipse, is : [Online April 8, 2017]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (d) } e =3 / 5 \& 2 ae =6 \Rightarrow a =5 \\
& \because b ^2= a ^2\left(1- e ^2\right) \\
& \Rightarrow b ^2=25(1-9 / 25)
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad b =4 \\
& \therefore \quad \text { area of required quadrilateral }=4(1 / 2 ab ) \\
&=2 ab =40
\end{aligned}
\) -
Question 218 of 250
218. Question
If the tangent at a point on the ellipse \(\frac{x^2}{27}+\frac{y^2}{3}=1\) meets the coordinate axes at \(A\) and \(B\), and \(O\) is the origin, then the minimum area (in sq. units) of the triangle \(O A B\) is : [Online April 9, 2016]
CorrectIncorrectHint
(c) Equation of tangent to ellipse
\(
\frac{x}{\sqrt{27}} \cos \theta+\frac{y}{\sqrt{3}} \sin \theta=1
\)
Area bounded by line and co-ordinate axis
\(
\begin{aligned}
& \Delta=\frac{1}{2} \cdot \frac{\sqrt{27}}{\cos \theta} \cdot \frac{\sqrt{3}}{\sin \theta}=\frac{9}{\sin 2 \theta} \\
& \Delta=\text { will be minimum when } \sin 2 \theta=1 \\
& \Delta_{\min }=9
\end{aligned}
\) -
Question 219 of 250
219. Question
The area (in sq. units) of the quadrilateral formed by the tangents at the end points of the latus rectum to the ellipse \(\frac{x^2}{9}+\frac{y^2}{5}=1\), is : (JEE Main 2015)
CorrectIncorrectHint
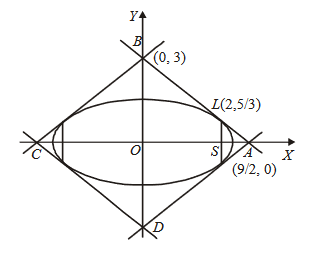
(b) The end point of latus rectum of ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) in first quadrant is \(\left(a e, \frac{b^2}{a}\right)\) and the tangent at this point intersects \(x\)-axis at \(\left(\frac{a}{e}, 0\right)\) and \(y\)-axis at \((0, a)\).
The given ellipse is \(\frac{x^2}{9}+\frac{y^2}{5}=1\)
Then \(a^2=9, b^2=5\)
\(\Rightarrow e=\sqrt{1-\frac{5}{9}}=\frac{2}{3}\)
\(\therefore\) end point of latus rectum in first quadrant is \(L(2,5 / 3)\)
Equation of tangent at \(L\) is \(\frac{2 x}{9}+\frac{y}{3}=1\)
It meets \(x\)-axis at \(A(9 / 2,0)\) and \(y\)-axis at \(B(0,3)\)
\(\therefore \quad\) Area of \(\triangle OAB =\frac{1}{2} \times \frac{9}{2} \times 3=\frac{27}{4}\)
By symmetry area of quadrilateral \(=4 \times(\) Area \(\triangle O A B)=4 \times \frac{27}{4}=27\) sq. units. -
Question 220 of 250
220. Question
If the distance between the foci of an ellipse is half the length of its latus rectum, then the eccentricity of the ellipse is: [Online April 11, 2015]
CorrectIncorrectHint
\(
\begin{aligned}
& S_1 S_2=\text { distance between foci } \\
& =2 a e=\frac{1}{2}\left(\text { length of latus rectum }=\frac{2 b^2}{a}\right. \text { ) } \\
& \therefore 2 a e=\frac{1}{2}\left(\frac{2 b^2}{a}\right) \\
& \Rightarrow 2 a^2 e=b^2 \\
& \Rightarrow e=\frac{b^2}{2 a^2}=\frac{a^2\left(1-e^2\right)}{2 a^2}=\frac{1-e^2}{2} \\
& \Rightarrow e^2+2 e-1=0 \\
& \Rightarrow e=\frac{-2+\sqrt{4+4}}{2}=\frac{\sqrt{8-2}}{2}=\sqrt{2}-1
\end{aligned}
\) -
Question 221 of 250
221. Question
The locus of the foot of perpendicular drawn from the centre of the ellipse \(x^2+3 y^2=6\) on any tangent to it is [JEE Main 2014]
CorrectIncorrectHint
(a) Given equation of ellipse can be written as
\(
\begin{aligned}
& \frac{x^2}{6}+\frac{y^2}{2}=1 \\
& \Rightarrow a^2=6, b^2=2
\end{aligned}
\)
Now, equation of any variable tangent is
\(
y=m x \pm \sqrt{a^2 m^2+b^2} \dots(i)
\)
where \(m\) is slope of the tangent
So, equation of perpendicular line drawn from centre to tangent is
\(
y=\frac{-x}{m} \dots(ii)
\)
Eliminating \(m\), we get
\(
\begin{aligned}
& \left(x^4+y^4+2 x^2 y^2\right)=a^2 x^2+b^2 y^2 \\
\Rightarrow & \left(x^2+y^2\right)^2=a^2 x^2+b^2 y^2 \\
\Rightarrow & \left(x^2+y^2\right)^2=6 x^2+2 y^2
\end{aligned}
\) -
Question 222 of 250
222. Question
A stair-case of length \(l\) rests against a vertical wall and a floor of a room. Let \(P\) be a point on the stair-case, nearer to its end on the wall, that divides its length in the ratio \(1: 2\). If the stair-case begins to slide on the floor, then the locus of P is: [Online April 11, 2014]
CorrectIncorrectHint
(b) Let point \(A (a, 0)\) is on \(x\)-axis and \(B (0, b)\) is on \(y\)-axis.
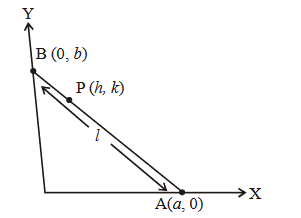
Let \(P (h, k)\) divides \(AB\) in the ratio \(1: 2\).
So, by section formula
\(
h=\frac{2(0)+1(a)}{1+2}=\frac{a}{3}
\)
\(
k=\frac{2(b)+1(0)}{3}=\frac{2 b}{3}
\)
\(\Rightarrow a=3 h\) and \(b=\frac{3 k}{2}\)
Now, \(a^2+b^2=l^2\)
\(\Rightarrow 9 h^2+\frac{9 k^2}{4}=l^2\)
\(
\Rightarrow \frac{h^2}{\left(\frac{l}{3}\right)^2}+\frac{k^2}{\left(\frac{2 l}{3}\right)^2}=1
\)
Now \(e=\sqrt{1-\left(\frac{l^2}{9} \times \frac{9}{4 l^2}\right)}=\sqrt{1-\frac{1}{4}}=\frac{\sqrt{3}}{2}\)
Thus, required locus of \(P\) is an ellipse with eccentricity \(\frac{\sqrt{3}}{2}\). -
Question 223 of 250
223. Question
If \(OB\) is the semi-minor axis of an ellipse, \(F _1\) and \(F _2\) are its foci and the angle between \(F_1 B\) and \(F_2 B\) is a right angle, then the square of the eccentricity of the ellipse is: [Online April 9, 2014]
CorrectIncorrectHint
(a) Let \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) be the equation of ellipse.
Given that \(F_1 B\) and \(F_2 B\) are perpendicular to each other.
Slope of \(F_1 B \times\) slope of \(F_2 B=-1\)
\(
\left(\frac{0-b}{-a e-0}\right) \times\left(\frac{0-b}{a e-0}\right)=-1
\)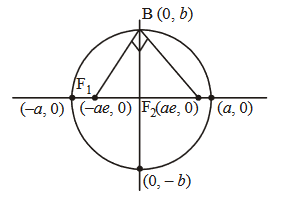
\(
\begin{aligned}
& \left(\frac{b}{a e}\right) \times\left(\frac{-b}{a e}\right)=-1 \\
& b^2=a^2 e^2 \\
& e^2=\frac{b^2}{a^2} \\
& \left\{\because e^2=1-\frac{b^2}{a^2}\right\} \\
&
\end{aligned}
\)
\(
\begin{aligned}
& 1-\frac{b^2}{a^2}=\frac{b^2}{a^2} \\
& 1=2 \frac{b^2}{a^2} \Rightarrow \frac{b^2}{a^2}=\frac{1}{2} \\
& e^2=1-\frac{b^2}{a^2}=1-\frac{1}{2}=\frac{1}{2} \\
& e^2=\frac{1}{2}
\end{aligned}
\)
No common tangents for these two circles. -
Question 224 of 250
224. Question
The equation of the circle passing through the foci of the ellipse \(\frac{x^2}{16}+\frac{y^2}{9}=1\), and having centre at \((0,3)\) is [JEE Main 2013]
CorrectIncorrectHint
(a) From the given equation of ellipse, we have
\(
a=4, b=3, e=\sqrt{1-\frac{9}{16}}
\)
\(
\Rightarrow e=\frac{\sqrt{7}}{4}
\)
Now, radius of this circle \(=a^2=16\)
\(
\Rightarrow \text { Focii }=( \pm \sqrt{7}, 0)
\)
Now equation of circle is \((x-0)^2+(y-3)^2=16\)
\(
x^2+y^2-6 y-7=0
\) -
Question 225 of 250
225. Question
A point on the ellipse, \(4 x^2+9 y^2=36\), where the normal is parallel to the line, \(4 x-2 y-5=0\), is: [Online April 25, 2013]
CorrectIncorrectHint
(c) Given ellipse is \(4 x^2+9 y^2=36\)
\(
\Rightarrow \frac{x^2}{9}+\frac{y^2}{4}=1
\)
Normal at the point is parallel to the line
\(
4 x-2 y-5=0
\)
Slope of normal \(=2\)
Slope of tangent \(=\frac{-1}{2}\)
Point of contact to ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
and line is \(\left(\frac{a^2 m}{\sqrt{a^2 m^2+b^2}}, \frac{b}{\sqrt{a^2 m^2+b^2}}\right)\)
Now, \(a^2=9, b^2=4\)
\(
\therefore \quad \text { Point }=\left(\frac{-9}{5}, \frac{8}{5}\right)
\) -
Question 226 of 250
226. Question
Let the equations of two ellipses be
\(
E_1: \frac{x^2}{3}+\frac{y^2}{2}=1 \text { and } E_2: \frac{x^2}{16}+\frac{y^2}{b^2}=1,
\)
If the product of their eccentricities is \(\frac{1}{2}\), then the length of the minor axis of ellipse \(E_2\) is : [Online April 22, 2013]CorrectIncorrectHint
(c) Given equations of ellipses
\(
\begin{aligned}
& E _1: \frac{x^2}{3}+\frac{y^2}{2}=1 \\
& \Rightarrow e_1=\sqrt{1-\frac{2}{3}}=\frac{1}{\sqrt{3}} \\
& \text { and } E _2: \frac{x^2}{16}+\frac{y^2}{b^2}=1 \\
& \Rightarrow e_2=\sqrt{\frac{1-b^2}{16}}=\sqrt{\frac{16-b^2}{4}}
\end{aligned}
\)
Also, given \(e_1 \times e_2=\frac{1}{2}\)
\(
\begin{aligned}
& \Rightarrow \frac{1}{\sqrt{3}} \times \sqrt{\frac{16-b^2}{4}}=\frac{1}{2} \Rightarrow 16-b^2=12 \\
& \Rightarrow b^2=4
\end{aligned}
\)
\(\therefore\) Length of minor axis of
\(
E _2=2 b=2 \times 2=4
\) -
Question 227 of 250
227. Question
Equation of the line passing through the points of intersection of the parabola \(x^2=8 y\) and the ellipse \(\frac{x^2}{3}+y^2=1\) is : [Online April 9, 2013]
CorrectIncorrectHint
(d)
\(
x^2=8 y \dots(i)
\)
\(
\frac{x^2}{3}+y^2=1 \dots(ii)
\)
From (i) and (ii),
\(
\frac{8 y}{3}+y^2=1 \Rightarrow y=-3, \frac{1}{3}
\)
When \(y=-3\), then \(x^2=-24\), which is not possible.
When \(y=\frac{1}{3}\), then \(x= \pm \frac{2 \sqrt{6}}{3}\)
Point of intersection are
\(
\left(\frac{2 \sqrt{6}}{3}, \frac{1}{3}\right) \text { and }\left(-\frac{2 \sqrt{6}}{3}, \frac{1}{3}\right)
\)
Required equation of the line,
\(
y-\frac{1}{3}=0 \Rightarrow 3 y-1=0
\) -
Question 228 of 250
228. Question
If \(P_1\) and \(P_2\) are two points on the ellipse \(\frac{x^2}{4}+y^2=1\) at which the tangents are parallel to the chord joining the points \((0,1)\) and \((2,0)\), then the distance between \(P_1\) and \(P_2\) is [Online May 12, 2012]
CorrectIncorrectHint
(d) Any tangent on an ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is given by \(y=m x \pm \sqrt{a^2 m^2+b^2}\)
Here \(a=2, b=1\)
\(
\begin{aligned}
& m=\frac{1-0}{0-2}=-\frac{1}{2} \\
& c=\sqrt{4\left(-\frac{1}{2}\right)^2+1^2}=\sqrt{2}
\end{aligned}
\)
So, \(y=-\frac{1}{2} x \pm \sqrt{2}\)
For ellipse : \(\frac{x^2}{4}+\frac{y^2}{1}=1\)
We put \(y=-\frac{1}{2} x+\sqrt{2}\)
\(
\begin{aligned}
& \therefore \frac{x^2}{4}+\left(-\frac{x}{2}+\sqrt{2}\right)^2=1 \\
& \frac{x^2}{4}+\left(\frac{x^2}{4}-2\left(\frac{x}{2}\right) \sqrt{2}+2\right)=1 \\
& \Rightarrow x^2+2 \sqrt{2} x+2=0 \\
& \text { or } x^2-2 \sqrt{2} x+2=0 \\
& \Rightarrow x=\sqrt{2} \text { or }-\sqrt{2}
\end{aligned}
\)
If \(x=\sqrt{2}, y=\frac{1}{\sqrt{2}}\) and \(x=-\sqrt{2}, y=-\frac{1}{\sqrt{2}}\)
\(\therefore\) Points are \(\left(\sqrt{2}, \frac{1}{\sqrt{2}}\right),\left(-\sqrt{2},-\frac{1}{\sqrt{2}}\right)\)
\(
\begin{aligned}
& \therefore P_1 P_2=\sqrt{\left\{\frac{1}{\sqrt{2}}-\left(-\frac{1}{\sqrt{2}}\right)\right\}^2+\{\sqrt{2}-(-\sqrt{2})\}^2} \\
= & \sqrt{\left(\frac{2}{\sqrt{2}}\right)^2+(2 \sqrt{2})^2}=\sqrt{2+8}=\sqrt{10}
\end{aligned}
\) -
Question 229 of 250
229. Question
Equation of the ellipse whose axes are the axes of coordinates and which passes through the point \((-3,1)\) and has eccentricity \(\sqrt{\frac{2}{5}}\) is [JEE Main 2011]
CorrectIncorrectHint
(d) Let the ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
It passes through \((-3,1)\) so \(\frac{9}{a^2}+\frac{1}{b^2}=1 \dots(i) \)
\(Also , b^2=a^2(1-2 / 5)\)
\(
\Rightarrow 5 b^2=3 a^2 \dots(ii)
\)
Solving (i) and (ii) we get \(a ^2=\frac{32}{3}, b^2=\frac{32}{5}\)
So, the equation of the ellipse is
\(
3 x^2+5 y^2=32
\) -
Question 230 of 250
230. Question
The ellipse \(x^2+4 y^2=4\) is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point \((4,0)\). Then the equation of the ellipse is : [JEE Main 2009]
CorrectIncorrectHint
(a) The given ellipse is \(\frac{x^2}{4}+\frac{y^2}{1}=1\)
So \(A=(2,0)\) and \(B=(0,1)\)
If \(P Q R S\) is the rectangle in which it is inscribed, then \(P=(2,1)\).
Let \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) be the ellipse
circumscribing the rectangle \(P Q R S\).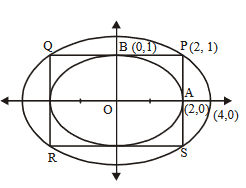
Then it passed through \(P(2,1)\)
\(
\therefore \frac{4}{a^2}+\frac{1}{b^2}=1
\)
Also, given that, it passes through \((4,0)\)
\(
\begin{aligned}
& \therefore \frac{16}{a^2}+0=1 \Rightarrow a^2=16 \\
& \Rightarrow b^2=4 / 3\left[\text { substituting a } a ^2=16 \text { in } eqn ( A )\right]
\end{aligned}
\)
\(\therefore \quad\) The required ellipse is \(\frac{x^2}{16}+\frac{y^2}{4 / 3}=1\)
\(
\text { or } x^2+12 y^2=16
\) -
Question 231 of 250
231. Question
A focus of an ellipse is at the origin. The directrix is the line \(x=4\) and the eccentricity is \(\frac{1}{2}\). Then the length of the semimajor axis is [JEE Main 2008]
CorrectIncorrectHint
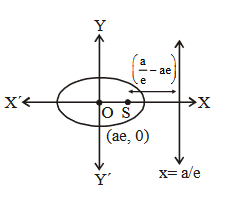
(a) Perpendicular distance of directrix from focus \(=\frac{a}{e}-a e=4\)
\(
\Rightarrow a\left(2-\frac{1}{2}\right)=4
\)
\(
\Rightarrow a=\frac{8}{3}
\)
\(\therefore\) Semi major axis \(=8 / 3\) -
Question 232 of 250
232. Question
In an ellipse, the distance between its foci is 6 and minor axis is 8 . Then its eccentricity is [JEE 2006]
CorrectIncorrectHint
\(
\text { (a) } \begin{aligned}
& 2 a e=6 \Rightarrow a e=3 ; 2 b=8 \Rightarrow b=4 \\
& b^2=a^2\left(1-e^2\right) ; 16=a^2-a^2 e^2 \\
& \Rightarrow a^2=16+9=25 \Rightarrow a=5 \\
& \therefore e=\frac{3}{a}=\frac{3}{5}
\end{aligned}
\) -
Question 233 of 250
233. Question
An ellipse has \(O B\) as semi minor axis, \(F\) and \(F^{\prime}\) its focii and the angle \(F B F^{\prime}\) is a right angle. Then the eccentricity of the ellipse is [JEE Main 2005]
CorrectIncorrectHint
\(
\begin{aligned}
\because & \angle F B F^{\prime}=90^{\circ} \Rightarrow F B^2+F^{\prime} B^2=F^{\prime} F^2 \\
& \therefore\left(\sqrt{a^2 e^2+b^2}\right)^2+\left(\sqrt{a^2 e^2+b^2}\right)^2=(2 a e)^2
\end{aligned}
\)
\(
\Rightarrow 2\left(a^2 e^2+b^2\right)=4 a^2 e^2 \Rightarrow e^2=\frac{b^2}{a^2}
\)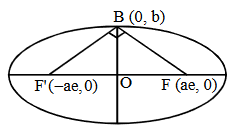
\(
\begin{aligned}
& \text { Also } e^2=1-b^2 / a^2=1-e^2 \\
& \Rightarrow 2 e^2=1, e=\frac{1}{\sqrt{2}}
\end{aligned}
\) -
Question 234 of 250
234. Question
The eccentricity of an ellipse, with its centre at the origin, is \(\frac{1}{2}\). If one of the directrices is \(x=4\), then the equation of the ellipse is: [JEE 2004]
CorrectIncorrectHint
(b) \(e=\frac{1}{2}\). Directrix, \(x=\frac{a}{e}=4\)
\(\therefore a=4 \times \frac{1}{2}=2\)
\(
\therefore b=2 \sqrt{1-\frac{1}{4}}=\sqrt{3}
\)
Equation of ellipse is
\(
\frac{x^2}{4}+\frac{y^2}{3}=1 \Rightarrow 3 x^2+4 y^2=12
\) -
Question 235 of 250
235. Question
A hyperbola passes through the point \(P (\sqrt{2}, \sqrt{3})\) and has foci at \(( \pm 2,0)\). Then the tangent to this hyperbola at \(P\) also passes through the point : [JEE Main 2017]
CorrectIncorrectHint
(c) Equation of hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
foci is \(( \pm 2,0) \Rightarrow a e=2 \Rightarrow a^2 e^2=4\)
\(
\begin{aligned}
\text { Since } b ^2 & = a ^2\left( e ^2-1\right) \\
b ^2 & = a ^2 e ^2- a ^2 \\
\therefore \quad a ^2 & + b ^2=4 \dots(i)
\end{aligned}
\)
Hyperbola passes through \((\sqrt{2}, \sqrt{3})\)
\(
\therefore \frac{2}{ a ^2}-\frac{3}{ b ^2}=1 \dots(ii)
\)
\(
\begin{aligned}
& \frac{2}{4-b^2} – \frac{3}{b^2}=1 \\
\Rightarrow & b^4+b^2-12=0 \\
\Rightarrow & \left(b^2-3\right)\left(b^2+4\right)=0 \\
\Rightarrow & b^2=3 \\
& b^2=-4 \text { (Not possible) }
\end{aligned}
\)
For \(b ^2=3\)
\(
\begin{aligned}
& \Rightarrow a ^2=1 \\
& \therefore \frac{x^2}{1}-\frac{y^2}{3}=1
\end{aligned}
\)
Equation of tangent is \(\frac{\sqrt{2} x}{1}-\frac{\sqrt{3} y}{3}=1\)
Clearly \((2 \sqrt{2}, 3 \sqrt{3})\) satisfies it. -
Question 236 of 250
236. Question
The locus of the point of intersection of the straight lines, \(tx -2 y -3 t =0\) \(x -2 ty +3=0( t \in R )\), is : [Online April 8, 2017]
CorrectIncorrectHint
(d) Here, \(t x-2 y-3 t=0 \& x-2 t y+3=0\) On solving, we get;
\(
\begin{aligned}
& y=\frac{6 t}{2 t^2-2}=\frac{3 t}{t^2-1} \& x =\frac{3 t ^2+3}{ t ^2-1} \\
& \text { Put } t =\tan \theta \\
\therefore \quad & x =-3 \sec 2 \theta \& 2 y=3(-\tan 2 \theta) \\
\because \quad & \sec ^2 2 \theta-\tan ^2 2 \theta=1
\end{aligned}
\)
\(
\Rightarrow \quad \frac{x^2}{9}-\frac{y^2}{9 / 4}=1
\)
which represents a hyperbola
\(
\therefore \quad a^2=9 \& b^2=9 / 4
\)
\(
\lambda(\text { T.A. })=6 ; e^2=1+\frac{9 / 4}{9}=1+\frac{1}{4} \Rightarrow e=\frac{\sqrt{5}}{2}
\)Also, semi conjugate axis \(=\sqrt{\frac{9}{4}}=\frac{3}{2}\)
Therefore, the length of conjugate axis would be 3 . -
Question 237 of 250
237. Question
The eccentricity of the hyperbola whose length of the latus rectum is equal to 8 and the length of its conjugate axis is equal to half of the distance between its foci, is : [JEE Main 2016]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (a) } \frac{2 b ^2}{ a }=8 \text { and } 2 b =\frac{1}{2}(2 ae ) \\
& \Rightarrow 4 b ^2= a ^2 e ^2 \Rightarrow 4 a ^2\left( e ^2-1\right)= a ^2 e ^2 \\
& \Rightarrow 3 e ^2=4 \Rightarrow e =\frac{2}{\sqrt{3}}
\end{aligned}
\) -
Question 238 of 250
238. Question
A hyperbola whose transverse axis is along the major axis of the conic, \(\frac{x^2}{3}+\frac{y^2}{4}=4\) and has vertices at the foci of this conic. If the eccentricity of the hyperbola is \(\frac{3}{2}\), then which of the following points does NOT lie on it ? [Online April 10, 2016]
CorrectIncorrectHint
(c) \(\frac{x^2}{12}+\frac{y^2}{16}=1\)
\(
e=\sqrt{1-\frac{12}{16}}=\frac{1}{2}
\)
Foci \((0,2) \&(0,-2)\)
So, transverse axis of hyperbola \(=2 b=4 \Rightarrow b=2\)
\(\& a^2=1^2\left(e^2-1\right)\)
\(\Rightarrow a^2=4\left(\frac{9}{4}-1\right)\)
\(\Rightarrow a^2=5\)
\(\therefore\) It’s equation is \(\frac{x^2}{5}-\frac{y^2}{4}=-1\)
The point \((5,2 \sqrt{3})\) does not satisfy the above equation. -
Question 239 of 250
239. Question
Let \(a\) and \(b\) respectively be the semitransverse and semiconjugate axes of a hyperbola whose eccentricity satisfies the equation \(9 e^2-18 e+5=0\). If \(S(5,0)\) is a focus and \(5 x=9\) is the corresponding directrix of this hyperbola, then \(a^2-b^2\) is equal to : [Online April 9, 2016]
CorrectIncorrectHint
\(S(5,0)\) is focus \(\Rightarrow a e=5 \text { (focus) } \dots(a)\)
\(
x=\frac{a}{5} \Rightarrow \frac{a}{e}=\frac{9}{5} \text { (directrix) } \dots(b)
\)
(a) & (b) \(\Rightarrow a^2=9\)
\(
\begin{aligned}
& \text { (a) } \Rightarrow(e)=\frac{5}{3} \\
& b^2=a^2\left(e^2-1\right) \Rightarrow b^2=16 \\
& a^2-b^2=9-16=-7
\end{aligned}
\) -
Question 240 of 250
240. Question
An ellipse passes through the foci of the hyperbola, \(9 x^2-4 y^2=36\) and its major and minor axes lie along the transverse and conjugate axes of the hyperbola respectively. If the product of eccentricities of the two conics is \(\frac{1}{2}\), then which of the following points does not lie on the ellipse? [Online April 10, 2015]
CorrectIncorrectHint
(c) Equation of hyperbola is
\(
\begin{aligned}
& \frac{x^2}{4}-\frac{y^2}{9}=1 \\
& \text { Its Foci }=( \pm \sqrt{13}, 0)
\end{aligned}
\)
\(
e =\frac{\sqrt{13}}{2}
\)
If e, be the eccentricity of the ellipse, then
\(
e_1 \times \frac{\sqrt{13}}{2}=\frac{1}{2} \quad \Rightarrow e_1=\frac{1}{\sqrt{13}}
\)
Equation of ellipse is
\(
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\)
Since ellipse passes through the foci \(( \pm \sqrt{13}, 0)\) of the hyperbola, therefore
\(
a^2=13
\)
Now \(\sqrt{ a ^2- b ^2}= ae _1\)
\(
\begin{aligned}
& \therefore 13-b^2=1 \\
& \Rightarrow b^2=12
\end{aligned}
\)
Hence, equation of ellipse is
\(
\frac{x^2}{13}+\frac{y^2}{12}=1
\)
Now putting the coordinate of the point \(\left(\frac{\sqrt{13}}{2}, \frac{\sqrt{3}}{2}\right)\) in the equation of the ellipse, we get
\(
\frac{13}{4 \times 13}+\frac{3}{4 \times 12}=1
\)
\(\Rightarrow \frac{1}{4}+\frac{1}{16}=1\), which is not true,
Hence the point \(\left(\frac{\sqrt{13}}{2}, \frac{\sqrt{3}}{2}\right)\) does not lie on the ellipse. -
Question 241 of 250
241. Question
The tangent at an extremity (in the first quadrant) of latus rectum of the hyperbola \(\frac{x^2}{4}-\frac{y^2}{5}=1\), meet \(x\)-axis and \(y\)-axis at \(A\) and \(B\) respectively. Then \((O A)^2-(O B)^2\), where \(O\) is the origin, equals: [Online April 19, 2014]
CorrectIncorrectHint
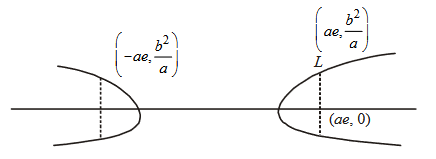
\(
\begin{aligned}
& \quad \text { Given } \frac{x^2}{4}-\frac{y^2}{5}=1 \\
& \Rightarrow \quad a^2=4, b^2=5 \\
& e=\sqrt{\frac{a^2+b^2}{a^2}}=\sqrt{\frac{4+5}{4}}=\frac{3}{2} \\
& L =\left(2 \times \frac{3}{2}, \frac{5}{2}\right)=\left(3, \frac{5}{2}\right)
\end{aligned}
\)
Equation of tangent at \(\left(x_1, y_1\right)\) is
\(
\frac{x x_1}{a^2}-\frac{y y_1}{b^2}=1
\)
Here \(x_1=3, y_1=\frac{5}{2}\)
\(
\Rightarrow \frac{3 x}{4}-\frac{y}{2}=1 \Rightarrow \frac{x}{\frac{4}{3}}+\frac{y}{-2}=1
\)
\(x\)-intercept of the tangent, \(OA =\frac{4}{3}\)
\(y\)-intercept of the tangent, \(OB =-2\)
\(
OA ^2- OB ^2=\frac{16}{9}-4=-\frac{20}{9}
\) -
Question 242 of 250
242. Question
Let \(P (3 \sec \theta, 2 \tan \theta)\) and \(Q (3 \sec \phi, 2 \tan \phi)\) where \(\theta+\phi=\frac{\pi}{2}\), be two distinct points on the hyperbola \(\frac{x^2}{9}-\frac{y^2}{4}=1\). Then the ordinate of the point of intersection of the normals at \(P\) and \(Q\) is: [Online April 11, 2014]
CorrectIncorrectHint
(d) Let the coordinate at point of intersection of normals at \(P\) and \(Q\) be \((h, k)\)
Since, equation of normals to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) At point \(\left(x_1, y_1\right)\) is \(\frac{a^2 x}{x_1}+\frac{b^2 y}{y_1}=a^2+b^2\) therefore equation of normal to the hyperbola \(\frac{x^2}{3^2}-\frac{y^2}{2^2}=1\) at point \(P (3 \sec \theta, 2 \tan \theta)\) is
\(
\begin{aligned}
& \frac{3^2 x}{3 \sec \theta}+\frac{2^2 y}{2 \tan \theta}=3^2+2^2 \\
& \Rightarrow 3 x \cos \theta+2 y \cot \theta=3^2+2^2 \dots(1)
\end{aligned}
\)
Similarly, Equation of normal to the hyperbola \(\frac{x^2}{3^2}-\frac{y^2}{2^2}\) at point \(Q (3 \sec \phi, 2 \tan \phi)\) is
\(
\begin{aligned}
& \frac{3^2 x}{3 \sec \phi}+\frac{2^2 y}{2 \tan \phi}=3^2+2^2 \\
& \Rightarrow 3 x \cos \phi+2 y \cot \phi=3^2+2^2 \dots(2)
\end{aligned}
\)
Given \(\theta+\phi=\frac{\pi}{2} \Rightarrow \phi=\frac{\pi}{2}-\theta\) and these passes through \((h, k)\)
\(\therefore\) From eq. (2)
\(
3 x \cos \left(\frac{\pi}{2}-\theta\right)+2 y \cot \left(\frac{\pi}{2}-\theta\right)=3^2+2^2
\)
\(
\Rightarrow 3 h \sin \theta+2 k \tan \theta=3^2+2^2 \dots(3)
\)
and \(3 h \cos \theta+2 k \cot \theta=3^2+2^2 \dots(4)\)
Comparing equation (3) & (4), we get
\(
\begin{aligned}
& 3 h \cos \theta+2 k \cot \theta=3 h \sin \theta+2 k \tan \theta \\
& 3 h \cos \theta-3 h \sin \theta=2 k \tan \theta-2 k \cot \theta \\
& 3 h(\cos \theta-\sin \theta)=2 k(\tan \theta-\cot \theta)
\end{aligned}
\)
\(
\begin{aligned}
& 3 h(\cos \theta-\sin \theta)=2 k \frac{(\sin \theta-\cos \theta)(\sin \theta+\cos \theta)}{\sin \theta \cos \theta} \\
& \text { or, } 3 h=\frac{-2 k(\sin \theta+\cos \theta)}{\sin \theta \cos \theta} \dots(5)
\end{aligned}
\)
Now, putting the value of equation (5) in eq. (3)
\(
\begin{aligned}
& \frac{-2 k(\sin \theta+\cos \theta) \sin \theta}{\sin \theta \cos \theta}+2 k \tan \theta=3^2+2^2 \\
& \Rightarrow 2 k \text { tan } \theta-2 k+2 k \text { tan } \theta=13 \\
& -2 k=13 \Rightarrow k=\frac{-13}{2}
\end{aligned}
\)
Hence, ordinate of point of intersection of normals at \(P\) and \(Q\) is \(\frac{-13}{2}\) -
Question 243 of 250
243. Question
A common tangent to the conics \(x^2=6 y\) and \(2 x^2-4 y^2=9\) is: [Online April 25, 2013]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2-6 y \dots(i) \\
& 2 x^2-4 y^2=9 \dots(ii)
\end{aligned}
\)
Consider the line,
\(
x-y=\frac{3}{2} \dots(iii)
\)
On solving (i) and (iii), we get only
\(
x=3, y=\frac{3}{2}
\)
Hence \(\left(3, \frac{3}{2}\right)\) is the point of contact of conic (i), and line(iii)
On solving (ii) and (iii), we get only \(x=3, y=\frac{3}{2}\)
Hence \(\left(3, \frac{3}{2}\right)\) is also the point of contact of conic (ii) and line (iii).
Hence line (iii) is the common tangent to both the given conics. -
Question 244 of 250
244. Question
A tangent to the hyperbola \(\frac{x^2}{4}-\frac{y^2}{2}=1\) meets \(x\)-axis at \(P\) and \(y\)-axis at \(Q\). Lines \(P R\) and \(Q R\) are drawn such that \(O P R Q\) is a rectangle (where \(O\) is the origin). Then \(R\) lies on : [Online April 23, 2013]
CorrectIncorrectHint
(d) Equation of the tangent at the point ‘ \(\theta\) ‘ is \(\frac{x \sec \theta}{a}-\frac{y \tan \theta}{b}=1\)
\(\Rightarrow P=(a \cos \theta, 0)\) and \(Q=(0,-b \cot \theta)\)
Let \(R\) be \(( h , k ) \Rightarrow h =a \cos \theta, k =-b \cot \theta\)
\(\Rightarrow \frac{k}{h}=\frac{-b}{a \sin \theta} \Rightarrow \sin \theta=\frac{-b h}{a k}\) and \(\cos \theta=\frac{h}{a}\)
By squaring and adding,
\(
\frac{b^2 h^2}{a^2 k^2}+\frac{h^2}{a^2}=1
\)
\(
\Rightarrow \frac{b^2}{k^2}+1=\frac{a^2}{h^2}
\)
\(
\Rightarrow \frac{a^2}{h^2}-\frac{b^2}{k^2}=1
\)
Now, given eq \({ }^{ n }\) of hyperbola is \(\frac{x^2}{4}-\frac{y^2}{2}=1\)
\(
\begin{aligned}
& \Rightarrow a^2=4, b^2=2 \\
& \therefore \text { R lies on } \frac{a^2}{x^2}-\frac{b^2}{y^2}=1 \text { i.e., } \frac{4}{x^2}-\frac{2}{y^2}=1
\end{aligned}
\) -
Question 245 of 250
245. Question
If the foci of the ellipse \(\frac{x^2}{16}+\frac{y^2}{b^2}=1\) coincide with the foci of the hyperbola \(\frac{x^2}{144}-\frac{y^2}{81}=\frac{1}{25}\), then \(b^2\) is equal to [Online May 19,2012 ]
CorrectIncorrectHint
(c) Given equation of ellipse is
\(
\begin{aligned}
& \frac{x^2}{16}+\frac{y^2}{b^2}=1 \\
& \text { eccentricity }=e=\sqrt{1-\frac{b^2}{16}} \\
& \text { foci: } \pm a e= \pm 4 \sqrt{1-\frac{b^2}{16}}
\end{aligned}
\)
Equation of hyperbola is \(\frac{x^2}{144}-\frac{y^2}{81}=\frac{1}{25}\)
\(
\begin{aligned}
& \Rightarrow \frac{x^2}{\frac{144}{25}}-\frac{y^2}{\frac{81}{25}}=1 \\
& \text { eccentricity }=e=\sqrt{1+\frac{81}{25} \times \frac{25}{144}}=\sqrt{1+\frac{81}{144}} \\
& =\sqrt{\frac{225}{144}}=\frac{15}{12} \\
& \text { foci: } \pm a e= \pm \frac{12}{5} \times \frac{15}{12}= \pm 3 \\
&
\end{aligned}
\)
Since, foci of ellipse and hyperbola coincide
\(
\therefore \pm 4 \sqrt{1-\frac{b^2}{16}}= \pm 3 \Rightarrow b^2=7
\) -
Question 246 of 250
246. Question
If the eccentricity of a hyperbola \(\frac{x^2}{9}-\frac{y^2}{b^2}=1\), which passes through \((k, 2)\), is \(\frac{\sqrt{13}}{3}\), then the value of \(k^2\) is [Online May 7, 2012]
CorrectIncorrectHint
(a) Given hyperbola is
\(
\frac{x^2}{9}-\frac{y^2}{b^2}=1
\)
Since this passes through \((K, 2)\), therefore
\(
\frac{K^2}{9}-\frac{4}{b^2}=1 \dots(1)
\)
Also, given \(e=\sqrt{1+\frac{b^2}{a^2}}=\frac{\sqrt{13}}{3}\)
\(
\begin{aligned}
& \Rightarrow \sqrt{1+\frac{b^2}{9}}=\frac{\sqrt{13}}{3} \Rightarrow 9+b^2=13 \\
& \Rightarrow b= \pm 2
\end{aligned}
\)
Now, from eq \({ }^{ n }(1)\), we have
\(
\begin{aligned}
& \frac{K^2}{9}-\frac{4}{4}=1 \quad(\because b= \pm 2) \\
\Rightarrow \quad & K^2=18
\end{aligned}
\) -
Question 247 of 250
247. Question
The equation of the hyperbola whose foci are \((-2,0)\) and \((2,0)\) and eccentricity is 2 is given by: [JEE 2011]
CorrectIncorrectHint
(b)
\(
\begin{aligned}
& a e=2 \\
& e=2 \\
& \therefore \quad a=1 \\
& b^2=a^2\left(e^2-1\right) \\
& b^2=1(4-1) \\
& b^2=3
\end{aligned}
\)
Equation of hyperbola, \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
\(
\begin{array}{r}
\Rightarrow \quad \frac{x^2}{1}-\frac{y^2}{3}=1 \\
3 x^2-y^2=3
\end{array}
\) -
Question 248 of 250
248. Question
For the Hyperbola \(\frac{x^2}{\cos ^2 \alpha}-\frac{y^2}{\sin ^2 \alpha}=1\), which of the following remains constant when \(\alpha\) varies =? [JEE 2007]
CorrectIncorrectHint
(b) Given, equation of hyperbola is
\(
\frac{x^2}{\cos ^2 \alpha}-\frac{y^2}{\sin ^2 \alpha}=1
\)
We know that the equation of hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) Here, \(a^2=\cos ^2 \alpha\) and
\(
b^2=\sin ^2 \alpha
\)
We know that, \(b^2=a^2\left(e^2-1\right)\)
\(
\begin{aligned}
& \Rightarrow \sin ^2 \alpha=\cos ^2 \alpha\left(e^2-1\right) \\
& \Rightarrow \sin ^2 \alpha+\cos ^2 \alpha=\cos ^2 \alpha \cdot e^2 \\
& \Rightarrow e^2=1+\tan ^2 \alpha=\sec ^2 \alpha \\
& \Rightarrow e=\sec \alpha
\end{aligned}
\)
\(
\therefore a e=\cos \alpha \cdot \frac{1}{\cos \alpha}=1
\)
Co-ordinates of foci are \(( \pm a e, 0)\)
i.e. \(( \pm 1,0)\)
Hence, abscissae of foci remain constant when \(\alpha\) varies. -
Question 249 of 250
249. Question
The locus of a point \(P(\alpha, \beta)\) moving under the condition that the line \(y=\alpha x+\beta\) is a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is [JEE 2005]
CorrectIncorrectHint
(d) Tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is
\(
y=m x \pm \sqrt{a^2 m^2-b^2}
\)
Given that \(y=\alpha x+\beta\) is the tangent of hyperbola
\(
\begin{aligned}
& \Rightarrow \quad m=\alpha \text { and } a^2 m^2-b^2=\beta^2 \\
& \therefore \quad a^2 \alpha^2-b^2=\beta^2
\end{aligned}
\)
Locus is \(a^2 x^2-y^2=b^2\) which is hyperbola. -
Question 250 of 250
250. Question
The foci of the ellipse \(\frac{x^2}{16}+\frac{y^2}{b^2}=1\) and the hyperbola \(\frac{x^2}{144}-\frac{y^2}{81}=\frac{1}{25}\) coincide. Then the value of \(b^2\) is [JEE 2003]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (d) } \frac{x^2}{144}-\frac{y^2}{81}=\frac{1}{25} \\
& a=\sqrt{\frac{144}{25}}, b=\sqrt{\frac{81}{25}}, \quad e=\sqrt{1+\frac{81}{144}}=\frac{15}{12}=\frac{5}{4}
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \quad \text { Foci }=( \pm 3,0) \\
& \therefore \quad \text { foci of ellipse }=\text { foci of hyperbola } \\
& \therefore \quad \text { for ellipse } a e=3 \text { but } a=4, \\
& \therefore \quad e=\frac{3}{4} \\
& \text { Then } b^2=a^2\left(1-e^2\right) \\
& \Rightarrow b^2=16\left(1-\frac{9}{16}\right)=7
\end{aligned}
\)