10.7 Ncert Exercise Problem and Solution

EXERCISE 10.1

Q1. Draw a quadrilateral in the Cartesian plane, whose vertices are \((-4,5),(0,7)\), \((5,-5)\) and \((-4,-2)\). Also, find its area.

Answer: Let \(A B C D\) be the given quadrilateral with vertices \(A(-4,5), B(0,7), C(5\), – 5) and \(D(-4,-2)\). Then, by plotting A, B, C and D on the Cartesian plane and joining \(A B, B C, C D\) and \(D A\), the given quadrilateral can be drawn as

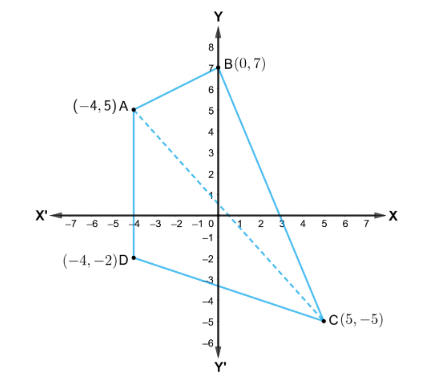
To find the area of quadrilateral \(ABCD\), we draw one diagonal, say \(AC\).
Accordingly, area \(( ABCD )=\operatorname{area}(\triangle ABC )+\operatorname{area}(\triangle ACD )\)
We know that the area of a triangles whose vertices are \(\left(x_1, y_1\right),\left(x_2, y_2\right)\) and \(\left(x_3, y_3\right)\) is
\(
1 / 2\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|
\)
Therefore,
\(
\begin{aligned}
& \operatorname{ar}(\triangle ABC )=1 / 2|-4(7+5)+0(-5+5)+5(5-7)| \\
& =1 / 2|-48+0-10| \\
& =1 / 2|-58| \\
& =1 / 2(58) \\
& =29
\end{aligned}
\)
\(
\begin{aligned}
& \operatorname{ar}(\triangle ACD )=1 / 2|(-4)(-5+2)+5(-2-5)+(-4)(5+5)| \\
& =1 / 2|12-35-40| \\
& =1 / 2|-63| \\
& =1 / 2(63) \\
& =63 / 2
\end{aligned}
\)
Thus, area \(( ABCD )=\operatorname{area}(\triangle ABC )+\operatorname{area}(\triangle ACD )\)
\(
\begin{aligned}
& =29+63 / 2 \text { sq. unit } \\
& =(58+63) / 2 \text { sq. unit } \\
& =121 / 2 \text { sq. unit }
\end{aligned}
\)

Q2. The base of an equilateral triangle with side \(2 a\) lies along the \(y\)-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.

Answer: Let \(ABC\) be the given equilateral triangle with side 2a.
Accordingly, \(AB = BC = CA =2 a\)
Assume that base \(BC\) (the base of the triangle) lies along the \(y\)-axis such that the mid-point of \(BC\) is at the origin. i.e., \(BO = OC = a\), where \(O\) is the origin.

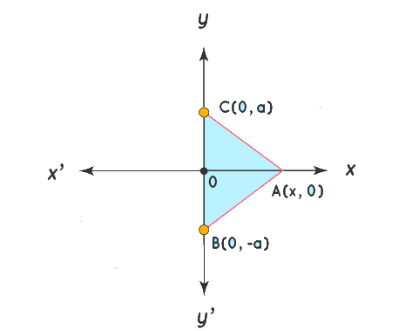
Now, it is clear that the coordinates of point \(C(0, a)\), while the coordinates of point \(B ( 0 ,- a )\).
It is known that the line joining a vertex of an equilateral triangle with the mid-point of its opposite side is perpendicular.
Hence, vertex A lies on the y-axis.
On applying Pythagoras theorem to DAOC, we obtain
\(
\begin{aligned}
& A C^2=O A^2+O C^2 \\
& O A^2=A C^2-O C^2 \\
& O A^2=(2 a)^2+(a)^2 \\
& O A^2=4 a^2-a^2 \\
& O A^2=3 a^2 \\
& O A= \pm \sqrt{3} a
\end{aligned}
\)
Therefore, coordinates of point \(A( \pm \sqrt{3} a, 0)\)
Thus, the vertices of the given equilateral triangle are \((0, a),(0,-a)\) and \((\sqrt{ } 3 a, 0)\) or \((0, a),(0,-a)\) and \((-\sqrt{ } 3 a, 0)\)

Q3. Find the distance between \(P \left(x_1, y_1\right)\) and \(Q \left(x_2, y_2\right)\) when : (i) \(PQ\) is parallel to the \(y\)-axis, (ii) \(PQ\) is parallel to the \(x\)-axis.

Answer: The given points are \(P \left(x_1, y_1\right)\) and \(Q \left(x_2, y_2\right)\).
(i) When \(PQ\) is parallel to the \(y\)-axis, \(x_1=x_2\).
In this case, distance between \(P\) and \(Q =\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
\(
\begin{aligned}
& =\sqrt{\left(y_2-y_1\right)^2} \\
& =\left|y_2-y_1\right|
\end{aligned}
\)
(ii) When \(PQ\) is parallel to the \(x\)-axis, \(y_1=y_2\).
In this case, distance between \(P\) and \(Q =\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
\(
\begin{aligned}
& =\sqrt{\left(x_2-x_1\right)^2} \\
& =\left|x_2-x_1\right|
\end{aligned}
\)

Q4. Find a point on the \(x\)-axis, which is equidistant from the points \((7,6)\) and \((3,4)\).

Answer: Let \((a, 0)\) be the point on the \(x\) axis that is equidistant from the points \((7,6)\) and \((3,4)\).
Accordingly, \(\sqrt{(7-a)^2+(6-0)^2}=\sqrt{(3-a)^2+(4-0)^2}\)
\(
\begin{aligned}
& \Rightarrow \sqrt{49+a^2-14 a+36}=\sqrt{9+a^2-6 a+16} \\
& \Rightarrow \sqrt{a^2-14 a+85}=\sqrt{a^2-6 a+25}
\end{aligned}
\)
On squaring both sides, we obtain
\(
\begin{aligned}
& a^2-14 a+85=a^2-6 a+25 \\
& \Rightarrow-14 a+6 a=25-85 \\
& \Rightarrow-8 a=-60 \\
& \Rightarrow a=\frac{60}{8}=\frac{15}{2}
\end{aligned}
\)
Thus, the required point on the \(x\)-axis is \(\left(\frac{15}{2}, 0\right)\).

Q5. Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points \(P (0,-4)\) and \(B (8,0)\).

Answer: The coordinates of the mid-point of the line segment joining the points
\(P(0,-4)\) and \(B(8,0)\) are \(\left(\frac{0+8}{2}, \frac{-4+0}{2}\right)=(4,-2)\)
It is known that the slope (m) of a non-vertical line passing through the points \(\left[x_1\right.\), \(\left.y_1\right)\) and \(\left(x_2, y_2\right)\) is given by \(m=\frac{y_2-y_1}{x_2-x_1}, x_2 \neq x_1\).
Therefore, the slope of the line passing through \((0,0)\) and \((4,-2)\) is
\(
\frac{-2-0}{4-0}=\frac{-2}{4}=-\frac{1}{2} \text {. }
\)
Hence, the required slope of the line is \(-\frac{1}{2}\).

Q6. Without using the Pythagoras theorem, show that the points \((4,4),(3,5)\) and \((-1,-1)\) are the vertices of a right angled triangle.

Answer: The vertices of the given triangle are \(A(4,4), B(3,5)\), and \(C(-1,-1)\).
It is known that the slope (m) of a non-vertical line passing through the points \(\left[x_1\right.\), \(\left.y_1\right)\) and \(\left(x_2, y_2\right)\) is given by \(m=\frac{y_2-y_1}{x_2-x_1}, x_2 \neq x_1\).
\(\therefore\) Slope of AB \(\left(m_1\right)=\frac{5-4}{3-4}=-1\)
Slope of BC \(\left(m_2\right)=\frac{-1-5}{-1-3}=\frac{-6}{-4}=\frac{3}{2}\)
Slope of \(CA \left( m _3\right)=\frac{4+1}{4+1}=\frac{5}{5}=1\)
It is observed that \(m_1 m_3=-1\)
This shows that line segments \(AB\) and \(CA\) are perpendicular to each other i.e., the given triangle is right-angled at \(A (4,4)\).
Thus, the points \((4,4),(3,5)\), and \((-1,-1)\) are the vertices of a right-angled triangle.

Q7. Find the slope of the line, which makes an angle of \(30^{\circ}\) with the positive direction of \(y\)-axis measured anticlockwise.

Answer: 

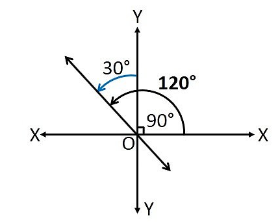
If a line makes an angle of \(30^{\circ}\) with the positive direction of the \(y\)-axis measured anticlockwise, then the angle made by the line with the positve direction of the \(x\)-axis measured anticlockwise is \(90^{\circ}+30^{\circ}=120^{\circ}\).
Thus, the slope of the given line is \(\tan 120^{\circ}=\tan \left(180^{\circ}-60^{\circ}\right)=-\tan 60^{\circ}=-\sqrt{3}\)

Q8. Find the value of \(x\) for which the points \((x,-1),(2,1)\) and \((4,5)\) are collinear.

Answer: If points \(A (x,-1), B (2,1)\), and \(C (4,5)\) are collinear, then
Slope of \(A B=\) Slope of \(B C\)
\(
\begin{aligned}
& \Rightarrow \frac{1-(-1)}{2-x}=\frac{5-1}{4-2} \\
& \Rightarrow \frac{1+1}{2-x}=\frac{4}{2} \\
& \Rightarrow \frac{2}{2-x}=2 \\
& \Rightarrow 2=4-2 x \\
& \Rightarrow 2 x=2 \\
& \Rightarrow x=1
\end{aligned}
\)
Thus, the required value of \(x\) is 1.

Q9. Without using distance formula, show that points \((-2,-1),(4,0),(3,3)\) and \((-3,2)\) are the vertices of a parallelogram.

Answer: 

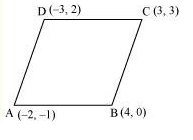
Let points \((-2,-1),(4,0),(3,3)\), and \((-3,2)\) be respectively denoted by \(A, B, C\), and D.
Slope of \(A B=\frac{0+1}{4+2}=\frac{1}{6}\)
Slope of CD \(=\frac{2-3}{-3-3}=\frac{-1}{-6}=\frac{1}{6}\)
\(\Rightarrow\) Slope of \(A B=\) Slope of \(C D\)
\(\Rightarrow A B\) and \(C D\) are parallel to each other.
Now, slope of \(B C=\frac{3-0}{3-4}=\frac{3}{-1}=-3\)
Slope of \(A D=\frac{2+1}{-3+2}=\frac{3}{-1}=-3\)
\(\Rightarrow\) Slope of \(B C=\) Slope of AD
\(\Rightarrow B C\) and \(A D\) are parallel to each other.
Therefore, both pairs of opposite sides of quadrilateral \(A B C D\) are parallel.
Hence, \(A B C D\) is a parallelogram.
Thus, points \((-2,-1),(4,0),(3,3)\), and \((-3,2)\) are the vertices of a parallelogram.

Q10. Find the angle between the \(x\)-axis and the line joining the points \((3,-1)\) and \((4,-2)\).

Answer: The slope of the line joining the points \((3,-1)\) and \((4,-2)\) is
\(
m=\frac{-2-(-1)}{4-3}=-2+1=-1
\)
Now, the inclination \((\theta)\) of the line joining the points \((3,-1)\) and \((4,-2)\) is given by
\(\tan \theta=-1\)
\(
\Rightarrow \theta=\left(90^{\circ}+45^{\circ}\right)=135^{\circ}
\)
Thus, the angle between the \(x\)-axis and the line joining the points \((3,-1)\) and \((4,-\) 2) is \(135^{\circ}\).

Q11. The slope of a line is double of the slope of another line. If tangent of the angle between them is \(\frac{1}{3}\), find the slopes of the lines.

Answer: We know that if \(\theta\) is the angle between the lines \(I_1\) and \(I_2\) with slopes \(m_1\) and \(m_2\) then
\(
\tan \theta=\left|\left(m_2-m_1\right) /\left(1+m_1 m_2\right)\right|
\)
It is given that the tangent of the angle between the two lines is \(1 / 3\) and slope of a line is double of the slope of another line.
Let \(m\) and \(2 m\) be the slopes of the given lines.
Therefore,
\(
\begin{aligned}
& 1 / 3=\mid(2 m-m) /(1+m(2 m) \mid \\
& 1 / 3=\left|(m) /\left(1+2 m^2\right)\right| \\
& 1 / 3=(m) /\left(1+2 m^2\right) \text { (or) } 1 / 3=(-m) /\left(1+2 m^2\right)
\end{aligned}
\)

Case l:
\(
\begin{aligned}
& 1 / 3=(-m) /\left(1+2 m^2\right) \\
& 1+2 m^2=-3 m \\
& 2 m^2+3 m+1=0 \\
& 2 m^2+2 m+m+1=0 \\
& 2 m(m+1)+1(m+1)=0 \\
& (m+1)(2 m+1)=0 \\
& \Rightarrow m=-1 \text { or } m=-1 / 2
\end{aligned}
\)
If \(m=-1\), then the slopes of the lines are -1 and -2.
If \(m=-1 / 2\), then the slopes of the lines are \(-1 / 2\) and -1.
Case II:
\(
\begin{aligned}
& 1 / 3=-(m) /\left(1+2 m^2\right) \\
& 2 m^2+1=3 m \\
& 2 m^2-3 m+1=0 \\
& 2 m^2-2 m-m+1=0 \\
& 2 m(m-1)-1(m-1)=0 \\
& (2 m-1)(m-1)=0 \\
& \Rightarrow m=1 \text { or } m=1 / 2
\end{aligned}
\)
If \(m =1\), then the slopes of the lines are 1 and 2 .
If \(m=1 / 2\), then the slopes of the lines are \(1 / 2\) and 1 .
Hence, the slopes of the lines are – 1 and – 2 or \(-1 / 2\) and -1 or 1 and 2 , or \(1 / 2\) and 1.

Q12. A line passes through \(\left(x_1, y_1\right)\) and \((h, k)\). If slope of the line is \(m\), show that
\(
k-y_1=m\left(h-x_1\right) \text {. }
\)

Answer: The slope of the line passing through \(\left(x_1, y_1\right)\) and \((h, k)\) is \(\frac{k-y_1}{h-x_1}\).
It is given that the slope of the line is \(m\).
\(
\begin{aligned}
& \therefore \frac{k-y_1}{h-x_1}=m \\
& \Rightarrow k-y_1=m\left(h-x_1\right)
\end{aligned}
\)
Hence. \(k-y_1=m\left(h-x_1\right)\)

Q13. If three points \((h, 0),(a, b)\) and \((0, k)\) lie on a line, show that \(\frac{a}{h}+\frac{b}{k}=1\).

Answer: If the points \(A (h, 0), B (a, b)\), and \(C (0, k)\) lie on a line, then
Slope of \(A B=\) Slope of BC
\(
\begin{aligned}
& \frac{b-0}{a-h}=\frac{k-b}{0-a} \\
& \Rightarrow \frac{b}{a-h}=\frac{k-b}{-a} \\
& \Rightarrow-a b=(k-b)(a-h) \\
& \Rightarrow-a b=k a-k h-a b+b h \\
& \Rightarrow k a+b h=k h
\end{aligned}
\)
On dividing both sides by \(k h\), we obtain
\(
\begin{aligned}
& \frac{k a}{k h}+\frac{b h}{k h}=\frac{k h}{k h} \\
& \Rightarrow \frac{a}{h}+\frac{b}{k}=1
\end{aligned}
\)
Hence, \(\frac{a}{h}+\frac{b}{k}=1\)

Q14. Consider the following population and year graph (Fig 10.10), find the slope of the line \(A B\) and using it, find what will be the population in the year 2010 ?

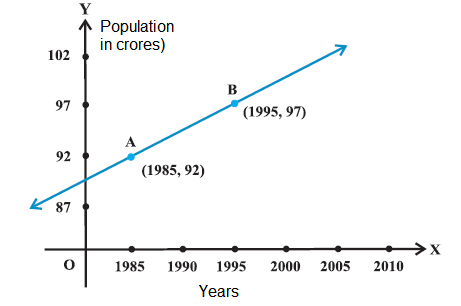
Answer: Since line AB passes through points \(A(1985,92)\) and \(B(1995,97)\), its slope is
\(
(97-92) /(1995-1985)=5 / 10=1 / 2
\)
Let \(y\) be the population in the year 2010 .
Then, according to the given graph, line AB must pass through point \(C\) (2010, y).
Therefore, Slope of AB = Slope of BC
\(
\begin{aligned}
& 1 / 2=(y-97) /(2010-1995) \\
& 1 / 2=(y-97) / 15 \\
& 15 / 2=(y-97) \\
& y=7.5+97 \\
& y=104.5
\end{aligned}
\)
Thus, the slope of line AB is \(1 / 2\), while in the year 2010 , the population will be 104.5 crores.

EXERCISE 10.2

Q1. Find the equation of the line which satisfy the given conditions:
a. Write the equations for the \(x\)-and \(y\)-axes.
b. Passing through the point \((-4,3)\) with slope \(\frac{1}{2}\).
c. Passing through \((0,0)\) with slope \(m\).
d. Passing through \((2,2 \sqrt{3})\) and inclined with the \(x\)-axis at an angle of \(75^{\circ}\).
e. Intersecting the \(x\)-axis at a distance of 3 units to the left of origin with slope -2 .
f. Intersecting the \(y\)-axis at a distance of 2 units above the origin and making an angle of \(30^{\circ}\) with positive direction of the \(x\)-axis.
g. Passing through the points \((-1,1)\) and \((2,-4)\).
h. Perpendicular distance from the origin is 5 units and the angle made by the perpendicular with the positive \(x\)-axis is \(30^{\circ}\). 

Answer:

(a) The \(y\)-coordinate of every point on the \(x\)-axis is 0 . Therefore, the equation of the \(x\)-axis is \(y=0\).
The \(x\)-coordinate of every point on the \(y\)-axis is 0 . Therefore, the equation of the \(y\)-axis is \(x=0\).

(b) We know that the equation of the line passing through point \(\left(x_0, y_0\right)\), whose slope is \(m\), is \(\left(y-y_0\right)=m\left(x-x_0\right)\)
Thus, the equation of the line passing through point \((-4,3)\), whose slope is \(\frac{1}{2}\),
\(
\begin{aligned}
(y-3) & =\frac{1}{2}(x+4) \\
2(y-3) & =x+4 \\
2 y-6 & =x+4 \\
x-2 y+10 & =0
\end{aligned}
\)
Hence the equation is \(x-2 y+10=0\).

(c) We know that the equation of the line passing through point \(\left(x_0, y_0\right)\), whose slope is \(m\), \(\left(y-y_0\right)=m\left(x-x_0\right)\)
Thus, the equation of the line passing through point \((0,0)\), whose slope is \(m\), is
\(
\begin{aligned}
(y-0) & =m(x-0) \\
y & =m x
\end{aligned}
\)
Hence the equation is \(y=m x\).

(d) The slope of the line that inclines with the \(x\)-axis at an angle of \(75^{\circ}\) is \(m=\tan 75^{\circ}\)
\(
\begin{aligned}
m & =\tan \left(45^{\circ}+30^{\circ}\right) \\
& =\frac{\tan 45^{\circ}+\tan 30^{\circ}}{\left.1-\tan 45^{\circ} \tan 30^{\circ}\right)} \\
& =\frac{1+\frac{1}{\sqrt{3}}}{1-1 \times \frac{1}{\sqrt{3}}} \\
& =\frac{\frac{\sqrt{3}+1}{\sqrt{3}}}{\frac{\sqrt{3}-1}{\sqrt{3}}} \\
& =\frac{\sqrt{3}+1}{\sqrt{3}-1}
\end{aligned}
\)
We know that the equation of the line passing through point \(\left(x_0, y_0\right)\), whose slope is \(m\),
\(
\left(y-y_0\right)=m\left(x-x_0\right)
\)
Thus, if a line passes through \((2,2 \sqrt{3})\) and inclines with the \(x\)-axis at angle of \(75^{\circ}\), then the equation of the line is given as
\(
\begin{aligned}
(y-2 \sqrt{3}) & =\frac{\sqrt{3}+1}{\sqrt{3}-1}(x-2) \\
(y-2 \sqrt{3})(\sqrt{3}-1) & =(\sqrt{3}+1)(x-2) \\
y(\sqrt{3}-1)-2 \sqrt{3}(\sqrt{3}-1) & =x(\sqrt{3}+1)-2(\sqrt{3}+1) \\
x(\sqrt{3}+1)-y(\sqrt{3}-1) & =2 \sqrt{3}+2-6+2 \sqrt{3} \\
x(\sqrt{3}+1)-y(\sqrt{3}-1) & =4 \sqrt{3}-4 \\
(\sqrt{3}+1) x-(\sqrt{3}-1) y & =4(\sqrt{3}-1)
\end{aligned}
\)
Hence the equation is \((\sqrt{3}+1) x-(\sqrt{3}-1) y=4(\sqrt{3}-1)\).

(e) It is known that if a line with slope \(m\) makes \(x\)-intercept \(d\), then the equation of the time is given as \(y=m(x-d)\)
For the line intersecting the \(x\)-axis at a distance of 3 units to the left of the origin, \(d=-3\).
The slope of the line is given as \(m=-2\)
Thus, the required equation of the given line is
\(
\begin{aligned}
y & =-2[x-(-3)] \\
y & =-2 x-6 \\
2 x+y+6 & =0
\end{aligned}
\)
Hence the equation is \(2 x+y+6=0\)

(f) It is known that if a line with slope \(m\) makes \(y\)-intercept \(c\), then the equation of the line is given as \(y=m x+c\)
Here, \(c=2\) and \(m=\tan 30^{\circ}=\frac{1}{\sqrt{3}}\)
Thus, the required equations of the given line is
\(
\begin{aligned}
y & =\frac{1}{\sqrt{3}} x+2 \\
y & =\frac{x+2 \sqrt{3}}{\sqrt{3}} \\
\sqrt{3} y & =x+2 \sqrt{3} \\
x-\sqrt{3} y+2 \sqrt{3} & =0
\end{aligned}
\)
Hence, the equation of the line is \(x-\sqrt{3} y+2 \sqrt{3}=0\)

(g) It is known that the equation of the line passes through points \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) is
\(
y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)
\)
Therefore, the equation of the line passing through the points \((-1,1)\) and \((2,-4)\) is
\(
\begin{aligned}
(y-1) & =\frac{-4-1}{2+1}(x+1) \\
(y-1) & =-\frac{5}{3}(x+1) \\
3(y-1) & =-5(x+1) \\
3 y-3 & =-5 x-5 \\
5 x+3 y+2 & =0
\end{aligned}
\)
Hence, the equation of the line is \(5 x+3 y+2=0\)

(h) If \(p\) is the length of the normal from the origin to a line and \(\omega\) is the angle made by the normal with the positive direction of the \(x\)-axis, then the equation of the line given by
\(
x \cos \omega+y \sin \omega=p
\)
Here, \(p=5\) units and \(\omega=30^{\circ}\)
Thus, the required equation of the given line is
\(
\begin{array}{r}
x \cos 30^{\circ}+y \sin 30^{\circ}=5 \\
x \cdot \frac{\sqrt{3}}{2}+y \cdot \frac{1}{2}=5 \\
\sqrt{3} x+y-10=0
\end{array}
\)
Hence, the equation of the line is \(\sqrt{3} x+y-10=0\)

Q2. The vertices of \(\triangle PQR\) are \(P (2,1), Q (-2,3)\) and \(R (4,5)\). Find equation of the median through the vertex \(R\).

Answer: 

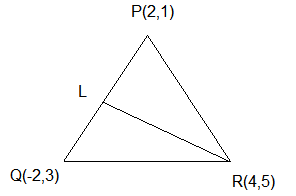
It is given that the vertices of \(\triangle P Q R\) are \(P(2,1), Q(-2,3)\) and \(R(4,5)\). Let \(R L\) be the median through vertex \(R\).
Accordingly, \(L\) be the mid-point of \(PQ\).
By mid-point formula, the coordinates of point \(L\) are given by \(\left(\frac{2-2}{2}, \frac{1+3}{2}\right)=(0,2)\)
Therefore, the equation of the line passing through points \((4,5)\) and \((0,2)\) is
\(
\begin{aligned}
y-5 & =\frac{2-5}{0-4}(x-4) \\
y-5 & =\frac{-3}{-4}(x-4) \\
4(y-5) & =3(x-4) \\
4 y-20 & =3 x-12 \\
3 x-4 y+8 & =0
\end{aligned}
\)
Thus, the equation of the median through vertex \(R\) is \(3 x-4 y+8=0\).

Q3. Find the equation of the line passing through \((-3,5)\) and perpendicular to the line through the points \((2,5)\) and \((-3,6)\).

Answer: The slope of the line joining the points \((2,5)\) and \((-3,6)\) is \(m=\frac{6-5}{-3-2}=-\frac{1}{5}\)
We know that two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other.
Therefore, slope of the line perpendicular to the line through the points \((2,5)\) and \((-3,6)\) is \(-\frac{1}{m}=-\frac{1}{\left(-\frac{1}{5}\right)}=5\)
Now, the equation of the line passing through point \((-3,5)\), whose slope is 5 , is
\(
\begin{aligned}
(y-5) & =5(x+3) \\
y-5 & =5 x+15 \\
5 x-y+20 & =0
\end{aligned}
\)
Hence, the equation of the line is \(5 x-y+20=0\).

Q4. A line perpendicular to the line segment joining the points \((1,0)\) and \((2,3)\) divides it in the ratio \(1: n\). Find the equation of the line.

Answer: According to the section formula, the coordinates of the point that divides the line segment joining the points \((1,0)\) and \((2,3)\) in the ratio \(1: n\) is given by
\(
\left(\frac{n(1)+1(2)}{1+n}, \frac{n(0)+1(3)}{1+n}\right)=\left(\frac{n+2}{n+1}, \frac{3}{n+1}\right)
\)
The slope of the line joining the points \((1,0)\) and \((2,3)\) is \(m=\frac{3-0}{2-1}=3\)
We know that two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other.
Therefore, slope of the line that is perpendicular to the line joining the points \((1,0)\) and \((2,3)\) is \(-\frac{1}{m}=-\frac{1}{3}\)
Now the equation of the line passing through \(\left(\frac{n+2}{n+1}, \frac{3}{n+1}\right)\) and whose slope is \(-\frac{1}{3}\), given by
\(
\begin{aligned}
\left(y-\frac{3}{n+1}\right) & =-\frac{1}{3}\left(x-\frac{(n+2)}{(n+1)}\right) \\
3[(n+1) y-3] & =-[x(n+1)-(n-2)] \\
3(n+1) y-9 & =-(n+1) x+n+2 \\
(1+n) x+3(1+n) y & =n+11
\end{aligned}
\)
Hence, the equation of the line is \((1+n) x+3(1+n) y=n+11\)

Q5. Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point \((2,3)\).

Answer: The equation of the line in the intercept form is
\(
\frac{x}{a}+\frac{y}{b}=1 \dots(1)
\)
Here, \(a\) and \(b\) are the intercepts on \(x\) and \(y\) axes respectively.
It is given that the line cuts off equal intercepts on both the axes. This means that \(a=b\). Accordingly, equation (1) reduces to
\(
x+y=a \dots(2)
\)
Since the given line passes through point \((2,3)\), equation (2) reduces to
\(
\begin{aligned}
2+3 & =a \\
a & =5
\end{aligned}
\)
On substituting the value of \(a\) in equation (2), we obtain \(x+y=5\), which is the required equation of the line.

Q6. Find equation of the line passing through the point \((2,2)\) and cutting off intercepts on the axes whose sum is 9.

Answer: The equation of a line in the intercept form is \(\frac{x}{a}+\frac{y}{b}=1 \dots(1)\)
Here, \(a\) and \(b\) are the intercepts on \(x\) and \(y\) axis respectively.
It is given that
\(
\begin{aligned}
a+b & =9 \\
b & =9-a \dots(2)
\end{aligned}
\)
From equation (1) and (2), we obtain
\(
\frac{x}{a}+\frac{y}{9-a}=1 \dots(3)
\)
It is given that the line passes through point \((2,2)\).
Therefore, equation (3) reduces to
\(
\begin{aligned}
& \Rightarrow \frac{2}{a}+\frac{2}{9-a}=1 \\
& \Rightarrow \frac{2(9-a)+2 a}{a(9-a)}=1 \\
& \Rightarrow \frac{18-2 a+2 a}{\left(9 a-a^2\right)}=1 \\
& \Rightarrow \frac{18}{9 a-a^2}=1 \\
& \Rightarrow 18=9 a-a^2 \\
& \Rightarrow a^2-9 a+18=0 \\
& \Rightarrow a^2-6 a-3 a+18=0 \\
& \Rightarrow a(a-6)-3(a-6)=0 \\
& \Rightarrow(a-6)(a-3)=0 \\
& \Rightarrow a=6 \text { or } a=3
\end{aligned}
\)
If \(a=6\) then \(b=9-6=3\),
Hence, the equation of the line is
\(
\begin{aligned}
& \Rightarrow \frac{x}{6}+\frac{y}{3}=1 \\
& \Rightarrow x+2 y-6=0
\end{aligned}
\)
If \(a=3\) then \(b=9-3=6\)
Hence, the equation of the line is
\(
\begin{aligned}
& \Rightarrow \frac{x}{3}+\frac{y}{6}=1 \\
& \Rightarrow 2 x+y-6=0
\end{aligned}
\)
Thus, the equation of the line is \(x+2 y-6=0\) or \(2 x+y-6=0\).

Q7. Find equation of the line through the point \((0,2)\) making an angle \(\frac{2 \pi}{3}\) with the positive \(x\)-axis. Also, find the equation of line parallel to it and crossing the \(y\)-axis at a distance of 2 units below the origin.

Answer: The slope of the line making an angle \(\frac{2 \pi}{3}\) with the positive \(x\)-axis is \(m=\tan \left(\frac{2 \pi}{3}\right)=-\sqrt{3}\) Now, the equation of the line passing through points \((0,2)\) and having a slope \(-\sqrt{3}\) is
\(
\begin{aligned}
& (y-2)=-\sqrt{3}(x-0) \\
& \sqrt{3} x+y-2=0
\end{aligned}
\)
The slope of line parallel to line \(\sqrt{3} x+y-2=0\) is \(-\sqrt{3}\)
It is given that the line parallel to line \(\sqrt{3} x+y-2=0\) crosses the \(y\)-axis 2 units below the origin, i.e., it passes through point \((0,2)\).
Hence, the equation of the line passing through points \((0,2)\) and having a slope \(-\sqrt{3}\) is
\(
\begin{aligned}
y-(-2) & =-\sqrt{3}(x-0) \\
y+2 & =-\sqrt{3} x \\
\sqrt{3} x+y+2 & =0
\end{aligned}
\)
Thus, the equation of the line is \(\sqrt{3} x+y+2=0\)

Q8. The perpendicular from the origin to a line meets it at the point \((-2,9)\), find the equation of the line.

Answer: The slope of the line joining the origin \((0,0)\) and point \((-2,9), m=\frac{9-0}{-2-0}=-\frac{9}{2}\) Accordingly, the slope of the line perpendicular to the line joining the origin and point \((-2,9)\) is
\(
m_2=\frac{1}{m_1}=-\frac{1}{\left(-\frac{9}{2}\right)}=\frac{2}{9}
\)
Now, the equation of the line passing through point \((-2,9)\) and having a slope \(m_2\) is
\(
\begin{aligned}
(y-9) & =\frac{2}{9}(x+2) \\
9 y-81 & =2 x+4 \\
2 x-9 y+85 & =0
\end{aligned}
\)
Thus, the equation of the line is \(2 x-9 y+85=0\)

Q9. The length \(L\) (in centimetre) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if \(L =124.942\) when \(C =20\) and \(L =125.134\) when \(C=110\), express \(L\) in terms of \(C\).

Answer: It is given that when \(C=20\), the value of \(L=124.942\), whereas when \(C=110\), the value of \(L=125.134\).
Accordingly, points \((20,124.942)\) and \((110,125.134)\) satisfy the linear relation between \(L\) and C.
Now, assuming \(C\) along the \(x\)-axis and \(L\) along the \(y\)-axis, we have two points i.e., \((20,124.942)\) and \((110,125.134)\) in the XY plane.
Therefore, the linear relation between \(L\) and \(C\) is the equation of the line passing through points \((20,124.942)\) and \((110,125.134)\).
\(
\begin{aligned}
& (L-124.942)=\frac{125.134-124.942}{110-20}(C-20) \\
& (L-124.942)=\frac{0.192}{90}(C-20) \\
& L=\frac{0.192}{90}(C-20)+124.942
\end{aligned}
\)
Thus, the required linear relation is \(L=\frac{0.192}{90}(C-20)+124.942\)

Q10. The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs 14/litre and 1220 litres of milk each week at Rs 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs \(17 /\) litre?

Answer: The relationship between selling price and demand is linear.
Assuming selling price per liter along the \(x\)-axis and demand along the \(y\)-axis, we have two points i.e., \((14,980)\) and \((16,1220)\) in the XY plane that satisfy the linear relationship between selling price and demand.
Therefore, the line passing through points \((14,980)\) and \((16,1220)\).
\(
\begin{aligned}
& y-980=\frac{1220-980}{16-14}(x-14) \\
& y-980=\frac{240}{2}(x-14) \\
& y-980=120(x-14) \\
& y=120(x-14)+980
\end{aligned}
\)
When \(x=17\),
\(
\begin{aligned}
y & =120(17-14)+980 \\
& =120 \times 3+980 \\
& =360+980 \\
& =1340
\end{aligned}
\)
Thus, the owner of the milk store could sell 1340 litres of milk weekly at ₹ 17/litre.

Q11. \(P (a, b)\) is the mid-point of a line segment between axes. Show that equation of the line is \(\frac{x}{a}+\frac{y}{b}=2\).

Answer: Let \(AB\) be the line segment between the axis and let \(P(a, b)\) be its mid-point.
Let the coordinates of \(A\) and \(B\) be \((0, y)\) and \((x, 0)\) respectively.
Since \(P(a, b)\) is the mid-point of \(AB\),
\(
\begin{aligned}
& \left(\frac{0+x}{2}, \frac{y+0}{2}\right)=(a, b) \\
& \Rightarrow\left(\frac{x}{2}, \frac{y}{2}\right)=(a, b) \\
& \Rightarrow \frac{x}{2}=a \text { and } \frac{y}{2}=b \\
& \Rightarrow x=2 a \text { and } y=2 b
\end{aligned}
\)
Thus, the respective coordinates of A and B are \((0,2 b)\) and \((2 a, 0)\). The equation of the line passing through points \((0,2 b)\) and \((2 a, 0)\) is
\(
\begin{aligned}
(y-2 b) & =\frac{(0-2 b)}{(2 a-0)}(x-0) \\
(y-2 b) & =-\frac{2 b}{2 a}(x) \\
a(y-2 b) & =-b x \\
a y-2 a b & =-b x \\
b x+a y & =2 a b
\end{aligned}
\)
On dividing both sides by \(a b\), we obtain
\(
\begin{aligned}
& \frac{b x}{a b}+\frac{a y}{a b}=\frac{2 a b}{a b} \\
& \Rightarrow \frac{x}{a}+\frac{y}{b}=2
\end{aligned}
\)
Hence, the equation of the line is \(\frac{x}{a}+\frac{y}{b}=2\) proved.

Q12. Point \(R (h, k)\) divides a line segment between the axes in the ratio \(1: 2\). Find equation of the line.

Answer: Let \(AB\) be the line segment between the axes such that point \(R(h, k)\) divides \(AB\) in the ratio \(1: 2\).
Let the respective coordinates of \(A\) and \(B\) be \((x, 0)\) and \((0, y)\).
Since point \(R(h, k)\) divides \(AB\) in the ratio \(1: 2\), according to the section formula,
\(
\begin{aligned}
& (h, k)=\left(\frac{1(0)+2(x)}{1+2}, \frac{1(y)+2(0)}{1+2}\right) \\
& \Rightarrow(h, k)=\left(\frac{2 x}{3}, \frac{y}{3}\right) \\
& \Rightarrow h=\frac{2 x}{3} \text { and } k=\frac{y}{3} \\
& \Rightarrow x=\frac{3 h}{2} \text { and } y=3 k
\end{aligned}
\)
Therefore, the respective coordinates of \(A\) and \(B\) are \(\left(\frac{3 h}{2}, 0\right)\) and \((0,3 k)\)
Now, the equation of the line \(AB\) passing through points \(\left(\frac{3 h}{2}, 0\right)\) and \((0,3 k)\) is
\(
\begin{aligned}
& (y-0)=\frac{3 k-0}{0-\frac{3 h}{2}}\left(x-\frac{3 h}{2}\right) \\
& y=-\frac{2 k}{h}\left(x-\frac{3 h}{2}\right) \\
& h y=-2 k\left(\frac{2 x-3 h}{2}\right) \\
& h y=-k(2 x-3 h) \\
& h y=-2 k x+3 k h \\
& 2 k x+h y=3 k h
\end{aligned}
\)
Thus, the required equation of a line is \(2 k x+h y=3 k h\)

Q13. By using the concept of equation of a line, prove that the three points \((3,0)\), \((-2,-2)\) and \((8,2)\) are collinear.

Answer: In order to show that the points \((3,0),(-2,-2)\) and \((8,2)\) are collinear, it suffices to show that the line passing through points \((3,0)\) and \((-2,-2)\) also passes through point \((8,2)\).
The equation of the line passing through points \((3,0)\) and \((-2,-2)\) is
\(
\begin{aligned}
& (y-0)=\frac{(-2-0)}{(-2-3)}(x-3) \\
& y=\frac{-2}{-5}(x-3) \\
& 5 y=2 x-6 \\
& 2 x-5 y-6=0
\end{aligned}
\)
It is observed that at \(x=8, y=2\)
\(
\begin{aligned}
L H S & =2 \times 8-5 \times 2-6 \\
& =16-10-6 \\
& =0 \\
& =R H S
\end{aligned}
\)
Therefore, the line passing through points \((3,0)\) and \((-2,-2)\) also passes through point \((8,2)\). Hence, points \((3,0),(-2,-2)\) and \((8,2)\) are collinear, proved.

EXERCISE 10.3

Q1. Reduce the following equations into slope – intercept form and find their slopes and the \(y\) – intercepts.
(i) \(x+7 y=0\),
(ii) \(6 x+3 y-5=0\),
(iii) \(y=0\).

Answer: (i) The given equation is \(x+7 y=0\)
It can be written as
\(
y=-\frac{1}{7} x+0
\)
This equation is of the form \(y=m x+c\), where \(m=-\frac{1}{7}\) and \(c=0\)
Therefore, equation \(x+7 y=0\) is the slope-intercept form, where the slope and the \(y\) intercept are \(-\frac{1}{7}\) and 0 respectively.
(ii) The given equation is \(6 x+3 y-5=0\)
It can be written as
\(
\begin{aligned}
& y=\frac{1}{3}(-6 x+5) \\
& y=-2 x+\frac{5}{3}
\end{aligned}
\)
This equation is of the form \(y=m x+c\), where \(m=-2\) and \(c=\frac{5}{3}\)
Therefore, equation \(6 x+3 y-5=0\) is the slope-intercept form, where the slope and the \(y\) intercept are -2 and \(\frac{5}{3}\) respectively.
(iii) The given equation is \(y=0\).
It can be written as \(y=0 . x+0\)
This equation is of the form \(y=m x+c\), where \(m=0\) and \(c=0\).
Therefore, equation \(y=0\) is in the slope-intercept form, where the slope and the \(y\) intercept are 0 and 0 respectively.

Q2. Reduce the following equations into intercept form and find their intercepts on the axes.
(i) \(3 x+2 y-12=0\),
(ii) \(4 x-3 y=6\),
(iii) \(3 y+2=0\).

Answer: (i) The given equation is \(3 x+2 y-12=0\)
It can be written as
\(
\begin{aligned}
& 3 x+2 y=12 \\
& \frac{3 x}{12}+\frac{2 y}{12}=1 \\
& \frac{x}{4}+\frac{y}{6}=1 \dots(1)
\end{aligned}
\)
This equation is of the form \(\frac{x}{a}+\frac{y}{b}=1\), where \(a=4\) and \(b=6\).
Therefore, equation (1) is in the intercept form, where the intercepts on the \(x\) and \(y\) axes are 4 and 6 respectively.
(ii) The given equation is \(4 x-3 y=6\).
It can be written as
\(
\begin{aligned}
& \frac{4 x}{6}-\frac{3 y}{6}=1 \\
& \frac{2 x}{3}-\frac{y}{2}=1 \\
& \frac{x}{3}+\frac{y}{(-2)}=1 \dots(2)
\end{aligned}
\)
This equation is of the form \(\frac{x}{a}+\frac{y}{b}=1\), where \(a=\frac{3}{2}\) and \(b=-2\).
Therefore, equation (2) is in the intercept form, where the intercepts on \(x\) and \(y\)-axes are \(\frac{3}{2}\) and -2 respectively.
(iii) The given equation is \(3 y+2=0\)
It can be written as
\(
\begin{aligned}
& 3 y=-2 \\
& \frac{y}{\left(-\frac{2}{3}\right)}=1 \dots(3)
\end{aligned}
\)
This equation is of the form \(\frac{x}{a}+\frac{y}{b}=1\), where \(a=0\) and \(b=-\frac{2}{3}\).
Therefore, equation (3) is in the intercept form, where the intercepts on the \(y\)-axis is \(-\frac{2}{3}\) and it has no intercept on the \(x\)-axis.

Q3. Reduce the following equations into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive \(x\)-axis.
(i) \(x-\sqrt{3} y+8=0\),
(ii) \(y-2=0\),
(iii) \(x-y=4\).

Answer: (i) The given equation is \(x-3 \sqrt{y}+8=0\)
It can be written as
\(
\begin{aligned}
x-3 \sqrt{y} & =-8 \\
-x+3 \sqrt{y} & =8
\end{aligned}
\)
On dividing both sides by \(\sqrt{(-1)^2+(\sqrt{3})^2}=\sqrt{4}=2\), we obtain
\(
\begin{aligned}
& -\frac{x}{2}+\frac{\sqrt{3}}{2} y=\frac{8}{2} \\
& \left(-\frac{1}{2}\right) x+\left(\frac{\sqrt{3}}{2}\right) y=4 \\
& x \cos 120^{\circ}+y \sin 120^{\circ}=4 \dots(1)
\end{aligned}
\)
Equation (1) is in the normal form.
On comparing equation (1) with the normal form of equation of the line \(x \cos \omega+y \sin \omega=p\), we obtain \(\omega=120^{\circ}\) and \(p=4\).
Thus, the perpendicular distance of the line from the origin is 4 , while the angle between the perpendicular and the positive \(x\)-axis is \(120^{\circ}\).
(ii) The given equation is \(y-2=0\)
It can be represented as \(0 . x+1 . y=2\)
On dividing both sides by \(\sqrt{0^2+1^2}=1\), we obtain
\(
\begin{aligned}
& 0 . x+1 . y=2 \\
& \Rightarrow x \cos 90^{\circ}+y \sin 90^{\circ}=2 \dots(2)
\end{aligned}
\)
Equation (2) is in the normal form.
On comparing equation (2) with the normal form of equation of line
\(
x \cos \omega+y \sin \omega=p \text {, we obtain } \omega=90^{\circ} \text { and } p=2 \text {. }
\)
Thus, the perpendicular distance of the line from the origin is 2 , while the angle between the perpendicular and the positive \(x\)-axis is \(90^{\circ}\).
(iii) The given equation is \(x-y=4\).
It can be reduced as \(1 . x+(-1) y=4\)
On dividing both sides by \(\sqrt{1^2+(-1)^2}=\sqrt{2}\), we obtain
\(
\begin{aligned}
& \frac{1}{\sqrt{2}} x+\left(-\frac{1}{\sqrt{2}}\right) y=\frac{4}{\sqrt{2}} \\
& \Rightarrow x \cos \left(2 \pi-\frac{\pi}{4}\right)+y \sin \left(2 \pi-\frac{\pi}{4}\right)=2 \sqrt{2} \\
& \Rightarrow x \cos 315^{\circ}+y \sin 315^{\circ}=2 \sqrt{2} \dots(3)
\end{aligned}
\)
Equation (3) is in the normal form.
On comparing equation (3) with the normal form of the equation of the line \(x \cos \omega+y \sin \omega=p\), we obtain \(\omega=315^{\circ}\) and \(p=2 \sqrt{2}\).
Thus, the perpendicular distance of the line from the origin is \(2 \sqrt{2}\), while the angle between the perpendicular and the positive \(x\)-axis is \(315^{\circ}\).

Q4. Find the distance of the point \((-1,1)\) from the line \(12(x+6)=5(y-2)\).

Answer: The given equation of the line is \(12(x+6)=5(y-2)\)
\(
\begin{aligned}
& \Rightarrow 12 x+72=5 y-10 \\
& \Rightarrow 12 x-5 y+82=0
\end{aligned}
\)
On comparing equation (1) with general equation of line \(A x+B y+C=0\) we obtain \(A=12, B=-5\) and \(C=82\).
It is known that the perpendicular distance (d) of a line \(A x+B y+C=0\) from a point
\(\left(x_1, y_1\right)\) is given by \(d=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}}\)
The given point is \(\left(x_1, y_1\right)=(-1,1)\).
Therefore, the distance of point \((-1,1)\) from the given line is
\(
\begin{aligned}
\frac{\mid 12(-1)+(-5)(1)+82}{\sqrt{12^2+(-5)^2}} & =\frac{|-12-5+82|}{\sqrt{169}} \\
& =\frac{|65|}{13} \\
& =5
\end{aligned}
\)
Hence, the distance of point \((-1,1)\) from the given line is 5 units.

Q5. Find the points on the \(x\)-axis, whose distances from the line \(\frac{x}{3}+\frac{y}{4}=1\) are 4 units.

Answer: The given equation of line is
\(
\begin{aligned}
& \frac{x}{3}+\frac{y}{4}=1 \\
& 4 x+3 y-12=0 \dots(1)
\end{aligned}
\)
On comparing equation (1) with general equation of line \(A x+B y+C=0\) we obtain \(A=4\), \(B=3\), and \(C=-12\).
Let \((a, 0)\) be the point on the \(x\)-axis whose distance from the given line is 4 units.
It is known that the perpendicular distance (d) of a line \(A x+B y+C=0\) from a point \(\left(x_1, y_1\right)\) is given by \(d=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}}\)
Therefore,
\(
\begin{aligned}
& \Rightarrow(4 a-12)=20 \text { or }-(4 a-12)=20 \\
& \Rightarrow 4 a=20+12 \text { or } 4 a=-20+12 \\
& \Rightarrow a=8 \text { or } a=-2
\end{aligned}
\)
Thus, the required points on \(x\)-axis are \((-2,0)\) and \((8,0)\).

Q6. Find the distance between parallel lines
(i) \(15 x+8 y-34=0\) and \(15 x+8 y+31=0\)
(ii) \(l(x+y)+p=0\) and \(l(x+y)-r=0\).

Answer: It is known that the distance (d) between parallel lines \(A x+B y+C_1=0\) and \(A x+B y+C_2=0\) is given by \(d=\frac{\left|C_1-C_2\right|}{\sqrt{A^2+B^2}}\)
(i) The given parallel lines are \(15 x+8 y-34=0\) and \(15 x+8 y+31=0\)
Here, \(A=15, B=8, C_1=-34\) and \(C_2=-31\)
Therefore, the distance between the parallel lines is
\(
\begin{aligned}
d & =\frac{\left|C_1-C_2\right|}{\sqrt{A^2+B^2}} \\
& =\frac{|34-31|}{\sqrt{(15)^2+(8)^2}} \text { units } \\
& =\frac{|-65|}{\sqrt{289}} \text { units } \\
& =\frac{65}{17} \text { units }
\end{aligned}
\)
(ii) The given parallel lines are \(l(x+y)+p=0\) and \(l(x+y)-r=0\) Here, \(A=B=l, C_1=p\) and \(C_2=-r\)
Therefore, the distance between the parallel lines is
\(
\begin{aligned}
d & =\frac{\left|C_1-C_2\right|}{\sqrt{A^2+B^2}} \\
& =\frac{|p+r|}{\sqrt{l^2+l^2}} \text { units } \\
& =\frac{|p+r|}{\sqrt{2 l^2}} \text { units } \\
& =\frac{|p+r|}{l \sqrt{2}} \text { units } \\
& =\frac{1}{\sqrt{2}} \frac{|p+r|}{l} \text { units }
\end{aligned}
\)

Q7. Find equation of the line parallel to the line \(3 x-4 y+2=0\) and passing through the point \((-2,3)\).

Answer: The equation of the given line is
\(
\begin{aligned}
& 3 x-4 y+2=0 \\
& y=\frac{3 x}{4}+\frac{2}{4}
\end{aligned}
\)
\(y=\frac{3}{4} x+\frac{2}{4}\), which is of the form \(y=m x+c\)
Therefore, slope of the given line is \(\frac{3}{4}\)
It is known that parallel lines have the same slope.
Slope of the other line is \(m=\frac{3}{4}\)
Now, the equation of the line that has a slope of \(\frac{3}{4}\) and passes through the points \((-2,3)\) is
\(
\begin{aligned}
& (y-3)=\frac{3}{4}\{x-(-2)\} \\
& 4 y-12=3 x+6 \\
& 3 x-4 y+18=0
\end{aligned}
\)

Q8. Find equation of the line perpendicular to the line \(x-7 y+5=0\) and having \(x\) intercept 3.

Answer: The given equation of the line is \(x-7 y+5=0\) Or \(y=\frac{1}{7} x+\frac{5}{7}\), which is of the form \(y=m x+c\) Therefore, slope of the given line is \(\frac{1}{7}\)
The slope of the line perpendicular to the line having a slope is \(m=-\frac{1}{\left(\frac{1}{7}\right)}=-7\)
The equation of the line with slope -7 and \(x\)-intercept 3 is given by
\(
\begin{aligned}
& y=m(x-d) \\
& y=-7(x-3) \\
& y=-7 x+21 \\
& 7 x+y-21=0
\end{aligned}
\)
Hence, the required equation of the line is \(7 x+y-21=0\)

Q9. Find angles between the lines \(\sqrt{3} x+y=1\) and \(x+\sqrt{3} y=1\).

Answer: The given lines are \(\sqrt{3} x+y=1\) and \(x+\sqrt{3} y=1\)
\(
y=-\sqrt{3} x+1 \dots(1)
\)
and
\(
y=-\frac{1}{\sqrt{3}} x+\frac{1}{\sqrt{3}} \dots(2)
\)
The slope of line (1) is \(m_1=-3\), while the slope of the line (2) is \(m_2=-\frac{1}{\sqrt{3}}\)
The actual angle i.e., \(\theta\) between the two lines is given by
\(
\begin{aligned}
\tan \theta & =\left|\frac{m_1-m_2}{1+m_1 m_2}\right| \\
& =\left|\frac{-\sqrt{3}+\frac{1}{\sqrt{3}}}{1+\left(-\sqrt{3}\left(-\frac{1}{\sqrt{3}}\right)\right)}\right| \\
& =\left|\frac{-3+1}{\sqrt{3}}\right|=\left|\frac{-2}{2 \times \sqrt{3}}\right|
\end{aligned}
\)
\(
\begin{aligned}
\tan \theta & =\frac{1}{\sqrt{3}} \\
\theta & =30^{\circ}
\end{aligned}
\)
Thus, the angle between the given lines is either \(30^{\circ}\) or \(180^{\circ}-30^{\circ}=150^{\circ}\).

Q10. The line through the points \((h, 3)\) and \((4,1)\) intersects the line \(7 x-9 y-19=0\). at right angle. Find the value of \(h\).

Answer: The slope of the line passing through points \((h, 3)\) and \((4,1)\) is
\(
m_1=\frac{1-3}{4-h}=\frac{-2}{4-h}
\)
The slope of the line \(7 x-9 y-19=0\) or \(y=\frac{7}{9} x-\frac{19}{9}\) is \(m_2=\frac{7}{9}\) It is given that the two lines are perpendicular Therefore,
\(
\begin{aligned}
& \Rightarrow m_1 \times m_2=-1 \\
& \Rightarrow \frac{-14}{36-9 h}=-1 \\
& \Rightarrow 14=36-9 h \\
& \Rightarrow 9 h=36-14 \\
& \Rightarrow h=\frac{22}{9}
\end{aligned}
\)
Thus, the value of \(h=\frac{22}{9}\).

Q11. Prove that the line through the point \(\left(x_1, y_1\right)\) and parallel to the line \(A x+ B y+ C =0\) is \(A \left(x-x_1\right)+ B \left(y-y_1\right)=0\).

Answer: The slope of line \(A x+B y+C=0\) or \(y=\left(-\frac{A}{B}\right) x+\left(-\frac{C}{B}\right)\) is \(m=-\frac{A}{B}\) It is known that parallel lines have the same slope.
Therefore, slope of the other line \(=m=-\frac{A}{B}\)
The equation of the line passing through point \(\left(x_1, y_1\right)\) and having slope \(m=-\frac{A}{B}\) is
\(
\begin{aligned}
& y-y_1=m\left(x-x_1\right) \\
& y-y_1=-\frac{A}{B}\left(x-x_1\right) \\
& B\left(y-y_1\right)=-A\left(x-x_1\right) \\
& A\left(x-x_1\right)+B\left(y-y_1\right)=0
\end{aligned}
\)
Hence, the line through point \(\left(x_1, y_1\right)\) and parallel to line \(A x+B y+C=0\) is \(A\left(x-x_1\right)+B\left(y-y_1\right)=0\)

Q12. Two lines passing through the point \((2,3)\) intersects each other at angle of \(60^{\circ}\). If slope of one line is 2 , find equation of the other line.

Answer: It is given that the slope of the first line, \(m_1=2\).
Let the slope of the other line be \(m_2\).
The angle between the two lines is \(60^{\circ}\).
\(
\begin{aligned}
& \tan { \theta }=\left|\frac{m_1-m_2}{1+m_1 m_2}\right| \\
& \tan 60^{\circ}=\left|\frac{2-m_2}{1+2 m_2}\right| \\
& \sqrt{3}= \pm\left(\frac{2-m_2}{1+2 m_2}\right)
\end{aligned}
\)
\(
\begin{array}{ll}
\sqrt{3}=\left(\frac{2-m_2}{1+2 m_2}\right) & \sqrt{3}=-\left(\frac{2-m_2}{1+2 m_2}\right) \\
\sqrt{3}\left(1+2 m_2\right)=2-m_2 & \sqrt{3}\left(1+2 m_2\right)=-\left(2-m_2\right) \\
\sqrt{3}+2 \sqrt{3} m_2+m_2=2 & \sqrt{3}+2 \sqrt{3} m_2-m_2=-2 \\
\sqrt{3}+(2 \sqrt{3}+1) m_2=2 & \sqrt{3}+(2 \sqrt{3}-1) m_2=-2 \\
m_2=\frac{2-\sqrt{3}}{(2 \sqrt{3}+1)} & m_2=\frac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}
\end{array}
\)
Case 1:
\(
m_2=\frac{2-\sqrt{3}}{(2 \sqrt{3}+1)}
\)
The equation of the line passing through the point \((2,3)\) and having a slope of \(\frac{2-\sqrt{3}}{(2 \sqrt{3}+1)}\) is
\(
\begin{aligned}
& (y-3)=\frac{2-\sqrt{3}}{(2 \sqrt{3}+1)}(x-2) \\
& (2 \sqrt{3}+1) y-3(2 \sqrt{3}+1)=(2-\sqrt{3}) x-2(2-\sqrt{3}) \\
& (\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}
\end{aligned}
\)
In this case, the equation of the other line is \((\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}\)
Case 2:
\(
m_2=\frac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}
\)
The equation of the line passing through the point \((2,3)\) and having a slope of \(\frac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}\) is
\(
\begin{aligned}
& (y-3)=\frac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}(x-2) \\
& (2 \sqrt{3}-1) y-3(2 \sqrt{3}-1)=-(2-\sqrt{3}) x+2(2-\sqrt{3}) \\
& (2-\sqrt{3}) x+(2 \sqrt{3}-1) y=4-2 \sqrt{3}+6 \sqrt{3}-3 \\
& (2-\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}
\end{aligned}
\)
If the case of the equation of the other line is \((2-\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}\)
Thus, the required equation of the other line is \((\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}\) or \((2-\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}\).

Q13. Find the equation of the right bisector of the line segment joining the points \((3,4)\) and \((-1,2)\).

Answer: The right bisector of a line segment bisects the line segment at \(90^{\circ}\).
The end points of the line segment are given as \(A(3,4)\) and \(B(-1,2)\).
Accordingly, mid-point of \(A B=\left(\frac{3-1}{2}, \frac{4+2}{0}\right)=(1,3)\)
Slope of \(A B=\frac{2-4}{-1-3}=\frac{-2}{-4}=\frac{1}{2}\)
Slope of the line perpendicular to
\(
A B=-\frac{1}{\left(\frac{1}{2}\right)}=-2
\)
The equation of the line passing through \((1,3)\) and having a slope of -2 is
\(
\begin{aligned}
& (y-3)=-2(x-1) \\
& y-3=-2 x+2 \\
& 2 x+y=5
\end{aligned}
\)
Thus, the required equation of the line is \(2 x+y=5\).

Q14. Find the coordinates of the foot of perpendicular from the point \((-1,3)\) to the line \(3 x-4 y-16=0\).

Answer: Let \((a, b)\) be the coordinates of the foot of the perpendicular from the points \((-1,3)\) to the line \(3 x-4 y-16=0\).

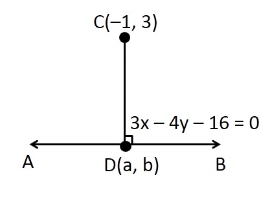
Slope of the line joining \((-1,3)\) and \((a, b), m_1=\frac{b-3}{a+1}\) Slope of the line \(3 x-4 y-16=0\) or \(y=\frac{3}{4} x-4, m_2=\frac{3}{4}\) Since these two lines are perpendicular, \(m_1 \times m_2=-1\) Therefore,
\(
\begin{aligned}
& \Rightarrow\left(\frac{b-3}{a+1}\right) \times\left(\frac{3}{4}\right)=-1 \\
& \Rightarrow \frac{3 b-9}{4 a+4}=-1 \\
& \Rightarrow 3 b-9=-4 a-4 \\
& \Rightarrow 4 a+3 b=5 \dots(1)
\end{aligned}
\)
Point \((a, b)\) lies on the line \(3 x-4 y-16=0\)
Therefore,
\(
\Rightarrow 3 a-4 b=16 \dots(2)
\)
On solving equations (1) and (2), we obtain
\(
a=\frac{68}{25} \text { and } b=-\frac{49}{25}
\)
Thus, the required coordinates of the foot of the perpendicular are \(\left(\frac{68}{25}, \frac{49}{25}\right)\)

Q15. The perpendicular from the origin to the line \(y=m x+c\) meets it at the point \((-1,2)\). Find the values of \(m\) and \(c\).

Answer: The given equation of line is \(y=m x+c\)
It is given that the perpendicular from the origin meets the given line at \((-1,2)\).
Therefore, the line joining the points \((0,0)\) and \((-1,2)\) is perpendicular to the given line
Slope of the line joining \((0,0)\) and \((-1,2)\) is \(\frac{2}{-1}=-2\)
The slope of the given line is \(m\)
Therefore,
\(m \times(-2)=-1 \quad\) [The two lines are perpendicular]
\(
\Rightarrow m=\frac{1}{2}
\)
Since points \((-1,2)\) lies on the given line, it satisfies the equation \(y=m x+c\) Therefore,
\(
\begin{aligned}
& \Rightarrow 2=m(-1)+c \\
& \Rightarrow 2=2+\frac{1}{2}(-1)+c \\
& \Rightarrow c=2+\frac{1}{2}=\frac{5}{2}
\end{aligned}
\)
Thus, the respective values of \(m\) and \(c\) are \(\frac{1}{2}\) and \(\frac{5}{2}\)

Q16. If \(p\) and \(q\) are the lengths of perpendiculars from the origin to the lines \(x \cos \theta-y \sin \theta=k \cos 2 \theta\) and \(x \sec \theta+y \operatorname{cosec} \theta=k\), respectively, prove that \(p^2+4 q^2=k^2\).

Answer: The equations of given lines are
\(
\begin{aligned}
& x \cos \theta-y \sin \theta=k \cos 2 \theta \dots(1) \\
& x \sec \theta+y \operatorname{cosec} \theta=k \dots(2)
\end{aligned}
\)
The perpendicular distance(d) of a line \(A x+B y+C=0\) from a point \(\left(x_1, x_2\right)\) is given by
\(
d=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}}
\)
On comparing equation(1) to the general equation of a line i.e., \(A x+B y+C=0\), we obtain \(A=\cos \theta, B=-\sin \theta\) and \(C=-k \cos 2 \theta\)
It is given that \(p\) is the length of the perpendicular from \((0,0)\) to line (1).
Therefore,
\(
p=\frac{|A(0)+B(0)+C|}{\sqrt{A^2+B^2}}=\frac{|C|}{\sqrt{A^2+B^2}}=\frac{|-k \cos 2 \theta|}{\sqrt{\cos ^2 \theta+\sin ^2 \theta}}=|-k \cos 2 \theta| \dots(3)
\)
On comparing equation (2) to the general equation of line i.e., \(A x+B y+C=0\), we obtain \(A=\sec \theta, B=\operatorname{cosec} \theta\) and \(C=-k\)
It is given that \(q\) is the length of the perpendicular from \((0,0)\) to line (2)
Therefore,
\(
p=\frac{|A(0)+B(0)+C|}{\sqrt{A^2+B^2}}=\frac{|C|}{\sqrt{A^2+B^2}}=\frac{|-k|}{\sqrt{\sec ^2 \theta+\operatorname{cosec}^2 \theta}} \dots(4)
\)
From (3) and (4), we have
\(
p^2+4 q^2=(|-k \cos 2 \theta|)^2+4\left(\frac{|-k|}{\sqrt{\sec ^2 \theta+\operatorname{cosec}^2 \theta}}\right)^2
\)
\(
\begin{aligned}
& =k^2 \cos ^2 2 \theta+\frac{4 k^2}{\left(\sec ^2 \theta+\operatorname{cosec}^2 \theta\right)} \\
& =k^2 \cos ^2 2 \theta+\frac{4 k^2}{\left(\frac{1}{\cos ^2 \theta}+\frac{1}{\sin ^2 \theta}\right)}
\end{aligned}
\)
\(
\begin{aligned}
& =k^2 \cos ^2 2 \theta+\left(\frac{4 k^2}{\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin ^2 \theta \cos ^2 \theta}}\right) \\
& =k^2 \cos ^2 2 \theta+\left(\frac{4 k^2}{\frac{1}{\sin ^2 \theta \cos ^2 \theta}}\right)
\end{aligned}
\)
\(
\begin{aligned}
& =k^2 \cos ^2 2 \theta+4 k^2 \sin ^2 \theta \cos ^2 \theta \\
& =k^2 \cos ^2 2 \theta+k^2(2 \sin \theta \cos \theta)^2 \\
& =k^2 \cos ^2 2 \theta+k^2 \sin ^2 2 \theta \\
& =k^2\left(\cos ^2 2 \theta+\sin ^2 2 \theta\right) \\
& =k^2
\end{aligned}
\)
Hence, we proved that \(p^2+4 q^2=k^2\)

Q17. n the triangle \(A B C\) with vertices \(A(2,3), B(4,-1)\) and \(C(1,2)\), find the equation and length of altitude from the vertex \(A\).

Answer: Let \(A D\) be the altitude of triangle \(A B C\) from vertex \(A\). Accordingly, \(A D \perp B C\)
The equation of the line passing through point \((2,3)\) and having a slope of 1 is
\(
\begin{aligned}
& \Rightarrow(y-3)=1(x-2) \\
& \Rightarrow x-y+1=0 \\
& \Rightarrow y-x=1
\end{aligned}
\)
Therefore, equation of the altitude from vertex \(A=y-x=1\)
Length of \(AD =\) Length of the perpendicular from \(A(2,3)\) to \(BC\) The equation of \(BC\) is
\(
\begin{aligned}
& \Rightarrow(y+1)=\frac{2+1}{1-4}(x-4) \\
& \Rightarrow(y+1)=-1(x-4) \\
& \Rightarrow y+1=-x+4 \\
& \Rightarrow x+y-3=0 \dots(1)
\end{aligned}
\)
The perpendicular distance (d) of a line \(A x+B y+C=0\) from a point \(\left(x_1, y_1\right)\) is given by
\(
d=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}}
\)
On comparing equation (1) to the general equation of line \(A x+B y+C=0\), we obtain \(A=1, B=1\) and \(C=3\).
Length of \(A D=\frac{|1 \times 2+1 \times 3-3|}{\sqrt{1^2+1^2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\) units
Thus, the equation and length of the altitude from vertex A are \(y-x=1\) and \(\sqrt{2}\) units.

Q18. If \(p\) is the length of perpendicular from the origin to the line whose intercepts on the axes are \(a\) and \(b\), then show that \(\frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}\).

Answer: It is known that the equation of a line whose intercepts on the axis \(a\) and \(b\) is
\(
\begin{aligned}
& \frac{x}{a}+\frac{y}{b}=1 \\
& b x+a y=a b \\
& b x+a y-a b=0 \dots(1)
\end{aligned}
\)
he perpendicular distance (d) of a line \(A x+B y+C=0\) from a point \(\left(x_1, y_1\right)\) is given by
\(
d=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}}
\)
On comparing equation (1) to the general equation of line \(A x+B y+C=0\), we obtain \(A=b, B=a\) and \(C=-a b\).
Therefore, if \(p\) is the length of the perpendicular from point \(\left(x_1, y_1\right)=(0,0)\) to line (1), We obtain
\(
\begin{aligned}
p & =\frac{|A(0)+B(0)-a b|}{\sqrt{a^2+b^2}} \\
& =\frac{|-a b|}{\sqrt{a^2+b^2}}
\end{aligned}
\)
On squaring both sides, we obtain
\(
\begin{aligned}
& \Rightarrow p^2=\frac{(-a b)^2}{a^2+b^2} \\
& \Rightarrow p^2\left(a^2+b^2\right)=a^2 b^2 \\
& \Rightarrow \frac{a^2+b^2}{a^2 b^2}=\frac{1}{p^2} \\
& \Rightarrow \frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}
\end{aligned}
\)
Hence, we showed \(\frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}\)

Miscellaneous Exercise

Q1. Find the values of \(k\) for which the line \((k-3) x-\left(4-k^2\right) y+k^2-7 k+6=0\) is
(a) Parallel to the \(x\)-axis,
(b) Parallel to the \(y\)-axis,
(c) Passing through the origin.

Answer: The given equation of the line is
\(
(k-3) x-\left(4-k^2\right) y+k^2-7 k+6=0 \dots(1)
\)
(a) If the given line is parallel to the \(x\)-axis then, Slope of the given line \(=\) Slope of the \(x\)-axis Then given line can be written as
\(
\begin{aligned}
& (k-3) x+k^2-7 k+6=\left(4-k^2\right) y \\
& y=\frac{(k-3)}{\left(4-k^2\right)} x+\frac{k^2-7 k+6}{\left(4-k^2\right)}
\end{aligned}
\)
Which is of the form \(y=m x+c\)
Slope of the given line \(=\frac{(k-3)}{\left(4-k^2\right)}\)
Slope of the \(x\)-axis \(=0\)
\(
\Rightarrow \frac{k-4}{\left(4-k^2\right)}=0
\)
\(
\begin{aligned}
& \Rightarrow k-3=0 \\
& \Rightarrow k=3
\end{aligned}
\)
Thus, the given line is parallel to \(x\)-axis, then the value of \(k=3\).
(b) If the given line is parallel to the \(y\)-axis, it is vertical.
Hence, its slope will be undefined.
\(
=\frac{(k-3)}{\left(4-k^2\right)}
\)
The slope of the given line is Now, \(\frac{(k-3)}{\left(4-k^2\right)}\) is defined at \(k^2=4\)
\(
\begin{aligned}
& \Rightarrow k^2=4 \\
& \Rightarrow k= \pm 2
\end{aligned}
\)
Thus, if the given line is parallel to the \(y\)-axis, then the value of \(k= \pm 2\).
(c) if the given line is passing through the origin, then point \((0,0)\) satisfies the given equation of the line.
\(
\begin{aligned}
& (k-3)(0)-\left(4-k^2\right)(0)+k^2-7 k+6=0 \\
& k^2-7 k+6=0 \\
& k^2-6 k-k+6=0 \\
& (k-6)(k-1)=0 \\
& \Rightarrow k=6 \text { or } k=1
\end{aligned}
\)
Thus, if the given line is passing through the origin, then the values of \(k\) is either 1 or 6.

Q2. Find the values of \(\theta\) and \(p\), if the equation \(x \cos \theta+y \sin \theta=p\) is the normal form of the line \(\sqrt{3} x+y+2=0\).

Answer: The equation of the given line is \(\sqrt{3} x+y+2=0\)
This equation can be reduced as
\(
\begin{aligned}
& \Rightarrow \sqrt{3} x+y+2=0 \\
& \Rightarrow-\sqrt{3} x-y=2
\end{aligned}
\)
On dividing both sides by \(\sqrt{(-\sqrt{3})^2+(-1)^2}=2\), we obtain
\(
\begin{aligned}
& \Rightarrow-\frac{\sqrt{3}}{2} x-\frac{1}{2} y=\frac{2}{2} \\
& \Rightarrow\left(-\frac{\sqrt{3}}{2}\right) x-\left(\frac{1}{2}\right) y=1 \dots(1)
\end{aligned}
\)
On comparing equation (1) to \(x \cos \theta+y \sin \theta=p\), we obtain \(\cos \theta=-\frac{\sqrt{3}}{2}, \sin \theta=-\frac{1}{2}\) and \(p=1\)
Since the value of \(\sin \theta\) and \(\cos \theta\) are negative \(\theta=\pi+\frac{\pi}{6}=\frac{7 \pi}{6}\)
Thus, the respective values of \(\theta\) and \(p\) are \(\frac{7 \pi}{6}\) and 1.

Q3. Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and -6 , respectively.

Answer: Let the intercepts cut by the given lines on the axis be \(a\) and \(b\).
It is given that
\(
\begin{aligned}
& a+b=1 \dots(1) \\
& a b=-6 \dots(2)
\end{aligned}
\)
On solving equation (1) and (2), we obtain \(a=3\) and \(b=-2\) or \(a=-3\) and \(b=3\)
It is known that the equation of the line whose intercepts on the axis are a and b is \(\frac{x}{a}+\frac{y}{b}=1\) or \(b x+a y-a b=0\)
Case I: \(a=3\) and \(b=-2\)
In this case, the equation of the line is \(-2 x+3 y+6=0 \Rightarrow 2 x-3 y=6\)
Case II: \(a=-3\) and \(b=3\)
In this case, the equation of the line is \(3 x-2 y+6=0 \Rightarrow-3 x+2 y=6\)
Thus, the required equations of the lines are \(2 x-3 y=6\) and \(-3 x+2 y=6\)

Q4. What are the points on the \(y\)-axis whose distance from the line \(\frac{x}{3}+\frac{y}{4}=1\) is 4 units.

Answer: Let \((0, b)\) be the point on \(y\)-axis whose distance from line \(\frac{x}{3}+\frac{y}{4}=1\) is 4 units.
The given line can be written as
\(
4 x+3 y-12=0 \dots(1)
\)
On comparing equation (1) to the general equation of line \(A x+B y+C=0\), we obtain \(A=4, B=-3\) and \(C=-12\).
It is known that the perpendicular distance (d) of a line \(A x+B y+C=0\) from a point \(\left(x_1, y_1\right)\) is given by \(d=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}}\)
Therefore, if \((0, b)\) is the point on the \(y\)-axis whose distance from line \(\frac{x}{3}+\frac{y}{4}=1\) is 4 units, Then,
\(
\begin{aligned}
& \Rightarrow 4=\frac{|4(0)+3(b)-12|}{\sqrt{4^2+3^2}} \\
& \Rightarrow 4=\frac{|3 b-12|}{5} \\
& \Rightarrow 20=|3 b-12| \\
& \Rightarrow 20= \pm(3 b-12) \\
& \Rightarrow(3 b-12)=20 \text { or }(3 b-12)=-20 \\
& \Rightarrow 3 b=20+12 \text { or } 3 b=-20+12 \\
& \Rightarrow b=\frac{32}{3} \text { or } b=\frac{-8}{3}
\end{aligned}
\)
Thus, the required points are \(\left(0, \frac{32}{3}\right)\) and \(\left(0,-\frac{8}{3}\right)\)

Q5. Find perpendicular distance from the origin to the line joining the points \((\cos \theta, \sin \theta)\) and \((\cos \phi, \sin \phi)\).

Answer: The equation of the line joining the points \((\cos \theta, \sin \theta)\) and \((\cos \phi, \sin \phi)\) is given by
\(
\begin{aligned}
& \frac{y-\sin \theta}{x-\cos \theta}=\frac{\sin \phi-\sin \theta}{\cos \phi-\cos \theta} \\
& y-\sin \theta=\frac{\sin \phi-\sin \theta}{\cos \phi-\cos \theta}(x-\cos \theta) \\
& y(\cos \phi-\cos \theta)-\sin \theta(\cos \phi-\cos \theta)=x(\sin \phi-\sin \theta)-\cos \theta(\sin \phi-\sin \theta) \\
& x(\sin \phi-\sin \theta)+y(\cos \phi-\cos \theta)+\cos \theta \sin \phi-\cos \theta \sin \theta-\sin \theta \cos \phi+\sin \theta \cos \theta=0 \\
& x(\sin \phi-\sin \theta)+y(\cos \phi-\cos \theta)+\sin (\phi-\theta)=0 \\
& A x+B y+C=0, \text { where } A=\sin \theta-\sin \phi, B=\cos \phi-\cos \theta \text { and } C=\sin (\phi-\theta)
\end{aligned}
\)
It is known that the perpendicular distance (d) of a line \(A x+B y+C=0\) from a point \(\left(x_1, y_1\right)\) is given by \(d=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}}\)
Therefore, the perpendicular distance (d) of the given line from point \(\left(x_1, y_1\right)=(0,0)\) is
\(
\begin{aligned}
& d=\frac{|(\sin \phi-\sin \theta)(0)+(\cos \phi-\cos \theta)(0)+\sin (\phi-\theta)|}{\sqrt{(\sin \phi-\sin \theta)^2+(\cos \phi-\cos \theta)^2}} \\
& =\frac{|\sin (\phi-\theta)|}{\sqrt{\sin ^2 \phi+\sin ^2 \theta-2 \sin \theta \sin \phi+\cos ^2 \phi+\cos ^2 \theta-2 \cos \phi \cos \theta}} \\
& =\frac{|\sin (\phi-\theta)|}{\sqrt{\left(\sin ^2 \phi+\cos ^2 \phi\right)+\left(\sin ^2 \theta+\cos ^2 \theta\right)-2(\sin \theta \sin \phi+\cos \phi \cos \theta)}} \\
& =\frac{|\sin (\phi-\theta)|}{\sqrt{1+1-2(\cos (\phi-\theta))}} \\
& =\frac{|\sin (\phi-\theta)|}{\sqrt{2(1-\cos (\phi-\theta))}} \\
& =\frac{|\sin (\phi-\theta)|}{\sqrt{2\left(2 \sin ^2\left(\frac{\phi-\theta}{2}\right)\right)}} \\
& =\frac{|\sin (\phi-\theta)|}{\left|2 \sin \left(\frac{\phi-\theta}{2}\right)\right|} \\
&
\end{aligned}
\)
Then,
\(
\frac{\left|2 \cos \left(\frac{\phi-\theta}{2}\right) \sin \left(\frac{\phi-\theta}{2}\right)\right|}{\left|2 \sin \left(\frac{\phi-\theta}{2}\right)\right|}=\left|\cos \left(\frac{\phi-\theta}{2}\right)\right|
\)

Q6. Find the equation of the line parallel to \(y\)-axis and drawn through the point of intersection of the lines \(x-7 y+5=0\) and \(3 x+y=0\).

Answer: The equation of any line parallel to the \(y\)-axis is of the form
\(
x=a \dots(1)
\)
The two given lines are
\(
\begin{aligned}
& x-7 y+5=0 \dots(2) \\
& 3 x+y=0 \dots(3)
\end{aligned}
\)
On solving equation (2) and (3), we obtain \(x=-\frac{5}{22}\) and \(x=-\frac{15}{22}\)
Therefore, \(\left(-\frac{5}{22},-\frac{15}{22}\right)\) is the point of intersection of lines (2) and (3).
Since, line \(x=a\) passes through point \(\left(-\frac{5}{22},-\frac{15}{22}\right), a=-\frac{5}{22}\)
Thus, the required equation of the line is \(x=-\frac{5}{22}\).

Q7. Find the equation of a line drawn perpendicular to the line \(\frac{x}{4}+\frac{y}{6}=1\) through the point, where it meets the \(y\)-axis.

Answer: The equation of the given line is \(\frac{x}{4}+\frac{y}{6}=1\)
This equation can also be written as \(3 x+2 y-12=0\) \(y=-\frac{3}{2} x+6\), which is of the form \(y=m x+c\) Hence, the slope of the given line is \(-\frac{3}{2}\)
Slope of the line perpendicular to the given line is \(-\frac{1}{\left(-\frac{3}{2}\right)}=\frac{2}{3}\)
Let the given line intersect the \(y\)-axis at \((0, y)\).
On substituting \(x=0\) in the equation of the given line, we obtain \(\frac{y}{6}=1 \Rightarrow y=6\) The given line intersects the \(y\)-axis at \((0,6)\).
The equation of the line that has a slope of \(\frac{2}{3}\) and passes through point \((0,6)\) is
\(
\begin{aligned}
& (y-6)=\frac{2}{3}(x-0) \\
& 3 y-18=2 x \\
& 2 x-3 y+18=0
\end{aligned}
\)
Thus, the required equation of the line is \(2 x-3 y+18=0\).

Q8. Find the area of the triangle formed by the lines \(y-x=0, x+y=0\) and \(x-k=0\).

Answer: The equations of the given lines are:
\(
\begin{aligned}
& y-x=0 \dots(1) \\
& x+y=0 \dots(2) \\
& x-k=0 \dots(3)
\end{aligned}
\)
The point of interaction of lines (1) and (2) is given by
\(
x=0 \text { and } y=0 .
\)
The point of interaction of lines (2) and (3) is given by
\(
x=k \text { and } y=-k \text {. }
\)
The point of interaction of lines (3) and (1) is given by
\(
x=k \text { and } y=k \text {. }
\)
Thus, the vertices of the triangle formed by the three given lines are \((0,0),(k,-k)\) and \((k,-k)\). We know that the area of a triangle whose vertices are \(\left(x_1, y_1\right),\left(x_2, y_2\right)\) and \(\left(x_3, y_3\right)\) is
\(
\frac{1}{2}\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|
\)
Therefore, area of the triangle formed by three given lines
\(
\begin{aligned}
& =\frac{1}{2}|0(-k-k)+k(k-0)+k(0+k)| \\
& =\frac{1}{2}\left|k^2+k^2\right| \\
& =\frac{1}{2} 2 k^2 \\
& =k^2
\end{aligned}
\)
Hence, the area of the triangle is \(k^2\) square units.

Q9. Find the value of \(p\) so that the three lines \(3 x+y-2=0, p x+2 y-3=0\) and \(2 x-y-3=0\) may intersect at one point.

Answer: The equation of the given lines are
\(
\begin{aligned}
& 3 x+y-2=0 \dots(1) \\
& p x+2 y-3=0 \dots(2) \\
& 2 x-y-3=0 \dots(3)
\end{aligned}
\)
On solving equations (1) and (3), we obtain
\(
x=1 \text { and } y=-1
\)
Since these three lines may intersect at one point, the point of intersection of lines (1) and (3) will also satisfy line (2)
\(
\begin{aligned}
& p(1)+2(-1)-3=0 \\
& p-2-3=0 \\
& p=5
\end{aligned}
\)
Thus, the required value of \(p=5\).

Q10. If three lines whose equations are \(y=m_1 x+c_1, y=m_2 x+c_2\) and \(y=m_3 x+c_3\) are concurrent, then show that \(m_1\left( c _2- c _3\right)+m_2\left( c _3- c _1\right)^2+m_3\left( c _1- c _2\right)=0\).

Answer: The equations of the given lines are:
\(
\begin{aligned}
& y=m_1 x+c_1 \dots(1) \\
& y=m_2 x+c_2 \dots(2) \\
& y=m_3 x+c_3 \dots(3)
\end{aligned}
\)
On subtracting equation (1) from (2) we obtain
\(
\begin{aligned}
\left(m_2-m_1\right) x+\left(c_2-c_1\right) & =0 \\
\left(m_1-m_2\right) x & =\left(c_2-c_1\right) \\
x & =\frac{\left(c_2-c_1\right)}{\left(m_1-m_2\right)}
\end{aligned}
\)
On substituting this value of \(x\) in (1), we obtain
\(
\begin{aligned}
y & =m_1\left(\frac{c_2-c_1}{m_1-m_2}\right)+c_1 \\
& =\frac{m_1 c_2-m_1 c_1}{m_1-m_2}+c_1 \\
& =\frac{m_1 c_2-m_1 c_1+c_1\left(m_1-m_2\right)}{m_1-m_2} \\
& =\frac{m_1 c_2-m_1 c_1+m_1 c_1-m_2 c_1}{m_1-m_2} \\
y & =\frac{m_1 c_2-m_2 c_1}{m_1-m_2}
\end{aligned}
\)
Therefore,
\(\left(\frac{c_2-c_1}{m_1-m_2}, \frac{m_1 c_2-m_2 c_1}{m_1-m_2}\right)\) is the point of intersection of line (1) and (2)
It is given that lines (1), (2) and (3) are concurrent.
Hence the point of intersection of lines (1) and (2) will also satisfy equation (3).
On substituting this value of \(x\) and \(y\) in (3), we obtain
\(
\begin{aligned}
& \frac{m_1 c_2-m_2 c_1}{m_1-m_2}=m_3\left(\frac{c_2-c_1}{m_1-m_2}\right)+c_3 \\
& \frac{m_1 c_2-m_2 c_1}{m_1-m_2}=\frac{m_3 c_2-m_3 c_1+c_3 m_1-c_3 m_2}{m_1-m_2} \\
& m_1 c_2-m_2 c_1-m_3 c_2+m_3 c_1-m_1 c_3+m_2 c_3=0 \\
& m_1 c_2-m_1 c_3-m_2 c_1+m_2 c_3-m_3 c_2+m_3 c_1=0 \\
& m_1\left(c_2-c_3\right)+m_2\left(c_3-c_1\right)+m_3\left(c_1-c_2\right)=0
\end{aligned}
\)
Hence, \(m_1\left(c_2-c_3\right)+m_2\left(c_3-c_1\right)+m_3\left(c_1-c_2\right)=0\) proved.

Q11. Find the equation of the line through the points \((3,2)\) which make an angle of \(45^{\circ}\) with the line \(x-2 y=3\).

Answer: Let the slope of the required line be \(m_1\)
The given line can be represented as \(y=\frac{1}{2} x-\frac{3}{2}\), which is of the form \(y=m x+c\)
Slope of the given line \(=m_2=\frac{1}{2}\)
It is given that the angle between the required line and line \(x-2 y=3\) is \(45^{\circ}\).
We know that if \(\theta\) is the acute angle between lines \(l_1\) and \(l_2\) with the slopes \(m_1\) and \(m_2\) respectively,
Then,
\(
\begin{aligned}
\tan \theta & =\left|\frac{m_2-m_1}{1+m_1 m_2}\right| \\
\tan 45^{\circ} & =\left|\frac{m_2-m_1}{1+m_1 m_2}\right| \\
1 & =\left|\frac{\frac{1}{2}-m_1}{1+\frac{m_1}{2}}\right| \\
1 & =\left|\frac{1-2 m_1}{\frac{2+m_1}{2}}\right| \\
1 & =\left|\frac{1-2 m_1}{2+m_1}\right| \\
1 & = \pm\left(\frac{1-2 m_1}{2+m_1}\right)
\end{aligned}
\)
\(
\begin{array}{ll}
\Rightarrow 1=\left(\frac{1-2 m_1}{2+m_1}\right) & \Rightarrow 1=-\left(\frac{1-2 m_1}{2+m_1}\right) \\
\Rightarrow 2+m_1=1-2 m_1 & \Rightarrow 2+m_1=-1+2 m_1 \\
\Rightarrow m_1=-\frac{1}{3} & \text { or } \Rightarrow m_1=3
\end{array}
\)
Case I: \(m_1=3\)
The equation of the line passing through \((3,2)\) and having a slope of 3 is:
\(
\begin{aligned}
& y-2=3(x-3) \\
& y-2=3 x-9 \\
& 3 x-y=7
\end{aligned}
\)
Case II: \({m_1}=-\frac{1}{3}\)
The equation of the line passing through \((3,2)\) and having a slope of \(-\frac{1}{3}\) is
\(
\begin{aligned}
& y-2=-\frac{1}{3}(x-2) \\
& 3 y-6=-x+3 \\
& x+3 y=9
\end{aligned}
\)
Thus, the equations of the line are \(3 x-y=7\) and \(x+3 y=9\).

Q12. Find the equation of the line passing through the point of intersection of the lines \(4 x+7 y-3=0\) and \(2 x-3 y+1=0\) that has equal intercepts on the axes.

Answer: Let the equation of the line having equal intercepts on the axes be
\(
\begin{aligned}
& \frac{x}{a}+\frac{y}{b}=1 \\
& \Rightarrow x+y=a b \dots(1)
\end{aligned}
\)
On solving equations \(4 x+7 y-3=0\) and \(2 x-3 y+1=0\), we obtain \(x=\frac{1}{13}\) and \(y=\frac{5}{13}\) Therefore,
\(\left(\frac{1}{13}, \frac{5}{13}\right)\) is the point of the intersection of the two given lines.
Since equation (1) passes through point \(\left(\frac{1}{13}, \frac{5}{13}\right)\)
\(
\begin{aligned}
& \frac{1}{13}+\frac{5}{13}=a \\
& \Rightarrow a=\frac{6}{13}
\end{aligned}
\)
Equation (1) becomes
\(
\begin{aligned}
& \Rightarrow x+y=\frac{6}{13} \\
& \Rightarrow 13 x+13 y=6
\end{aligned}
\)
Thus, the required equation of the line \(13 x+13 y=6\)

Q13. Show that the equation of the line passing through the origin and making an angle \(\theta\) with the line \(y=m x+c\) is \(\frac{y}{x}=\frac{m \pm \tan \theta}{1 \mp m \tan \theta}\).

Answer: Let the equation of the line passing through the origin be \(y=m_1 x\)
If this line makes an angle of \(\theta\) with line \(y=m x+c\), then angle \(\theta\) is given by
\(
\begin{aligned}
\tan \theta & =\left|\frac{m_1-m}{1+m_1 m}\right| \\
& =\left|\frac{\frac{y}{x}-m}{1+\frac{y}{x} m}\right| \\
\tan \theta & = \pm\left(\left.\frac{\frac{y}{x}-m}{1+\frac{y}{x} m} \right\rvert\,\right. \\
\Rightarrow \tan \theta & =\frac{\frac{y}{x}-m}{1+\frac{y}{x} m} \text { or } \tan \theta=-\left(\frac{\frac{y}{x}-m}{1+\frac{y}{x} m}\right)
\end{aligned}
\)
Case I:
\(
\begin{gathered}
\tan \theta=\frac{\frac{y}{x}-m}{1+\frac{y}{x} m} \\
\tan \theta+\frac{y}{x} m \tan \theta=\frac{y}{x}-m \\
m+\tan \theta=\frac{y}{x}(1-m \tan \theta) \\
\frac{y}{x}=\frac{m+\tan \theta}{1-m \tan \theta} \\
\tan \theta=-\left(\frac{\frac{y}{x}-m}{1+\frac{y}{x} m}\right)
\end{gathered}
\)
Case II:
\(
\begin{aligned}
& \tan \theta=-\left(\frac{\frac{y}{x}-m}{1+\frac{y}{x} m}\right) \\
& \tan \theta+\frac{y}{x} m \tan \theta=-\frac{y}{x}+m \\
& m-\tan \theta=\frac{y}{x}(1+m \tan \theta) \\
& \frac{y}{x}=\frac{m-\tan \theta}{1+m \tan \theta}
\end{aligned}
\)
Thus, the required line is given by \(\frac{y}{x}=\frac{m \pm \tan \theta}{1 \mp m \tan \theta}\)

Q14. In what ratio, the joining \((-1,1)\) and \((5,7)\) is divisible by the line \(x+y=4\) ?

Answer: The solution of the line joining the points \((-1,1)\) and \((5,7)\) is given by
\(
\begin{aligned}
& y-1=\frac{7-1}{5+1}(x+1) \\
& y-1=\frac{6}{6}(x+1) \\
& x-y+2=0 \dots(1)
\end{aligned}
\)
The equation of the line is
\(
x+y=4 \dots(2)
\)
The points of intersection of line (1) and (2) is given by
\(
x=1 \text { and } y=3
\)
Let point \((1,3)\) divides the line segment joining \((-1,1)\) and \((5,7)\) in the ratio \(1: k\). Accordingly, by section formula
\(
\begin{aligned}
& (1,3)=\left(\frac{k(-1)+1(5)}{1+k}, \frac{k(1)+1(7)}{1+k}\right) \\
& \Rightarrow(1,3)=\left(\frac{-k+5}{1+k}, \frac{k+7}{1+k}\right) \\
& \Rightarrow \frac{-k+5}{1+k}=1, \frac{k+7}{1+k}=3
\end{aligned}
\)
Therefore,
\(
\begin{aligned}
& \Rightarrow \frac{-k+5}{1+k}=1 \\
& \Rightarrow-k+5=1+k \\
& \Rightarrow 2 k=4 \\
& \Rightarrow k=2
\end{aligned}
\)
Thus, the line joining the points \((-1,1)\) and \((5,7)\) is divided by line \(x+y=4\) in the ratio \(1: 2\).

Q15. Find the distance of the line \(4 x+7 y+5=0\) from the point \((1,2)\) along the line \(2 x-y=0\).

Answer: The given lines are
\(
\begin{aligned}
& 2 x-y=0 \dots(1) \\
& 4 x+7 y+5=0 \dots(2)
\end{aligned}
\)
Let \(A(1,2)\) is a point on the line (1) and B be the point intersection of line (1) and (2).
On solving equations (1) and (2), we obtain \(x=-\frac{5}{18}\) and \(y=-\frac{5}{9}\)
Coordinates of point B are \(\left(-\frac{5}{18},-\frac{5}{9}\right)\)
By using distance formula, the distance between points \(A\) and \(B\) can be obtained as
\(
\begin{aligned}
A B & =\sqrt{\left(1+\frac{5}{18}\right)^2+\left(2+\frac{5}{9}\right)^2} \\
& =\sqrt{\left(\frac{23}{18}\right)^2+\left(\frac{23}{9}\right)^2} \\
& =\sqrt{\left(\frac{23}{9 \times 2}\right)^2+\left(\frac{23}{9}\right)^2} \\
& =\sqrt{\left(\frac{23}{9}\right)^2\left(\frac{1}{2}\right)^2+\left(\frac{23}{9}\right)^2} \\
& =\sqrt{\left(\frac{23}{9}\right)^2\left(\frac{1}{4}+1\right)} \\
& =\frac{23}{9} \sqrt{\left(\frac{5}{4}\right)} \\
& =\frac{23}{9} \times \frac{\sqrt{5}}{2} \\
& =\frac{23 \sqrt{5}}{18}
\end{aligned}
\)
Thus, the required distance is \(\frac{23 \sqrt{5}}{18}\) units.

Q16. Find the direction in which a straight line must be drawn through the point \((-1,2)\) so that its point of intersection with the line \(x+y=4\) may be at a distance of 3 units from this point.

Answer: Let \(y=m x+c\) be the line through point \((-1,2)\)
Accordingly,
\(
\begin{aligned}
& \Rightarrow 2=m(-1)+c \\
& \Rightarrow 2=-m+c \\
& \Rightarrow c=m+2 \\
& \Rightarrow y=m x+m+2 \dots(1)
\end{aligned}
\)
The given line is
\(
x-y=4 \dots(2)
\)
On solving equation (1) and (2), we obtain
\(
x=\frac{2-m}{m+1} \text { and } y=\frac{5 m+2}{m+1}
\)
Therefore,
\(\left(\frac{2-m}{m+1}, \frac{5 m+2}{m+1}\right)\) is the point of intersection of line (1) and (2)
Since this point is at a distance of 3 units from point \((-1,2)\), accordingly to distance formula,
\(
\begin{aligned}
& \Rightarrow \sqrt{\left(\frac{2-m}{m+1}+1\right)^2+\left(\frac{5 m+2}{m+1}-2\right)^2}=3 \\
& \Rightarrow\left(\frac{2-m+m+1}{m+1}\right)^2+\left(\frac{5 m+2-2 m-2}{m+1}\right)^2=3^2 \\
& \Rightarrow \frac{9}{(m+1)^2}+\frac{9 m^2}{(m+1)^2}=9 \\
& \Rightarrow \frac{1+m^2}{(m+1)^2}=1 \\
& \Rightarrow 1+m^2=m^2+1+2 m \\
& \Rightarrow 2 m=0 \\
& \Rightarrow m=0
\end{aligned}
\)
Thus, the slope of the required line must be zero i.e., the line must be parallel to the \(x\)-axis.

Q17. The hypotenuse of a right angled triangle has its ends at the points \((1,3)\) and \((-4,1)\). Find an equation of the legs (perpendicular sides) of the triangle.

Answer: Let \(ABC\) be the right-angled triangle, where \(\angle C=90^{\circ}\)
Let the slope of \(A C=m\)
Hence, the slope of \(B C=-\frac{1}{m}\)
Equation of \(AC\) :
\(
\begin{aligned}
& \Rightarrow y-3=m(x-1) \\
& \Rightarrow(x-1)=\frac{y-3}{m}
\end{aligned}
\)
Equation of \(BC\) :
\(
x+4=-m(y-1)
\)
For a given value of \(m\), we can get these equations
For, \(m=0, y-3=0 ; x+4=0\)
For \(m \rightarrow \infty, x-1=0 ; y-1=0\)

Q18. Find the image of the point \((3,8)\) with respect to the line \(x+3 y=7\) assuming the line to be a plane mirror.

Answer: The equation of the given line is
\(
x+3 y=7 \dots(1)
\)
Let point \(B(a, b)\) be the image of point \(A(3,8)\)
Accordingly, line (1) is the perpendicular bisector of \(A B\)
Slope of \(A B=\frac{b-8}{a-3}\), while the slope of the line (1) is \(-\frac{1}{3}\)
Since line (1) is perpendicular to \(A B\)
\(
\begin{aligned}
& \Rightarrow\left(\frac{b-8}{a-3}\right)\left(-\frac{1}{3}\right)=1 \\
& \Rightarrow \frac{b-8}{3 a-9}=1 \\
& \Rightarrow b-8=3 a-9 \\
& \Rightarrow 3 a-b=1 \dots(2)
\end{aligned}
\)
Mid-point of
\(
A B=\left(\frac{a+3}{2}, \frac{b+8}{2}\right)
\)
The mid-point of the line segments \(A B\) will also satisfy line (1).
Hence, from equation (1), we have
\(
\begin{aligned}
& \Rightarrow\left(\frac{a+3}{2}\right)+3\left(\frac{b+8}{2}\right)=7 \\
& \Rightarrow a+3+3 b+24=14 \\
& \Rightarrow a+3 b=-13 \ldots \ldots .(3)
\end{aligned}
\)
On solving equations (2) and (3), we obtain
\(
a=-1 \text { and } b=-4 \text {. }
\)
Thus, the image of the given point with respect to the given line is \((-1,-4)\).

Q19. If the lines \(y=3 x+1\) and \(2 y=x+3\) are equally inclined to the line \(y=m x+4\), find the value of \(m\).

Answer: The equations of the given lines are:
\(
\begin{aligned}
& y=3 x+1 \dots(1) \\
& 2 y=x+3 \dots(2) \\
& y=m x+4 \dots(3)
\end{aligned}
\)
Slope of line (1), \(m_1=3\)
Slope of line (2), \(m_2=\frac{1}{2}\)
Slope of line (3), \(m_3=m\)
It is given that lines (1) and (2) are equally inclined to line (3). This means that the given angle between lines (1) and (3) equals the angle between lines (2) and (3).
Therefore,
\(
\begin{aligned}
& \Rightarrow\left|\frac{m_1-m_3}{1+m_1 m_3}\right|=\left|\frac{m_2-m_3}{1+m_2 m_3}\right| \\
& \Rightarrow\left|\frac{3-m}{1+3 m}\right|=\left|\frac{\frac{1}{2}-m}{1+\frac{1}{2} m}\right| \\
& \Rightarrow\left|\frac{3-m}{1+3 m}\right|=\left|\frac{1-2 m}{m+2}\right| \\
& \Rightarrow\left|\frac{3-m}{1+3 m}\right|= \pm\left(\frac{1-2 m}{m+2}\right) \\
& \Rightarrow \frac{3-m}{1+3 m}=\frac{1-2 m}{m+2} \text { or } \frac{3-m}{1+3 m}=-\left(\frac{1-2 m}{m+2}\right)
\end{aligned}
\)
Case I: If \(\frac{3-m}{1+3 m}=\frac{1-2 m}{m+2}\)
Then,
\(
\begin{aligned}
& \Rightarrow(3-m)(m+2)=(1-2 m)(1+3 m) \\
& \Rightarrow-m^2+m-6=1+m-6 m^2 \\
& \Rightarrow 5 m^2+5=0 \\
& \Rightarrow m^2+1=0 \\
& \Rightarrow m^2=-1 \\
& \Rightarrow m=\sqrt{-1}
\end{aligned}
\)
Here, \(m=\sqrt{-1}\), which is not real Hence, this case is not possible
Case II: If \(\frac{3-m}{1+3 m}=-\left(\frac{1-2 m}{m+2}\right)\)
Then,
\(
\begin{aligned}
& \Rightarrow(3-m)(m+2)=-(1-2 m)(1+3 m) \\
& \Rightarrow-m^2+m-6=-\left(1+m-6 m^2\right) \\
& \Rightarrow 7 m^2-2 m-7=0 \\
& \Rightarrow m=\frac{-2 \pm \sqrt{4-4(7)(-7)}}{2(7)} \\
& \Rightarrow m=\frac{2 \pm 2 \sqrt{1+49}}{14} \\
& \Rightarrow m=\frac{1 \pm 5 \sqrt{2}}{7}
\end{aligned}
\)
Thus, the required value of \(m=\frac{1 \pm 5 \sqrt{2}}{7}\).

Q20. If sum of the perpendicular distances of a variable point \(P (x, y)\) from the lines \(x+y-5=0\) and \(3 x-2 y+7=0\) is always 10 . Show that \(P\) must move on a line.

Answer: The equations of the lines are
\(
\begin{aligned}
& x+y-5=0 \dots(1) \\
& 3 x-2 y+7=0 \dots(2)
\end{aligned}
\)
The perpendicular distance of \(P(x, y)\) from lines (1) and (2) are respectively given by
\(
\begin{aligned}
& d_1=\frac{|x+y-5|}{\sqrt{(1)^2+(1)^2}} \text { and } d_2=\frac{|3 x-2 y+7|}{\sqrt{(3)^2+(-2)^2}} \\
& \text { i.e., } d_1=\frac{|x+y-5|}{\sqrt{2}} \text { and } d_2=\frac{|3 x-2 y+7|}{\sqrt{13}}
\end{aligned}
\)
It is given that \(d_1+d_2=10\)
Therefore,
\(
\begin{aligned}
& \Rightarrow \frac{|x+y-5|}{\sqrt{2}}+\frac{|3 x-2 y+7|}{\sqrt{13}}=10 \\
& \Rightarrow \sqrt{13}|x+y-5|+\sqrt{2}|3 x-2 y+7|-10 \sqrt{26}=0 \\
& \Rightarrow \sqrt{13}(x+y-5)+\sqrt{2}(3 x-2 y+7)-10 \sqrt{26}=0
\end{aligned}
\)
Assuming \(x+y-5=0\) and \(3 x-2 y+7=0\) are positive.
\(
\begin{aligned}
& \Rightarrow \sqrt{13} x+\sqrt{13} y-5 \sqrt{13}+3 \sqrt{2} x-2 \sqrt{2} y+7 \sqrt{2}-10 \sqrt{26}=0 \\
& \Rightarrow(\sqrt{13}+3 \sqrt{2}) x+(\sqrt{13}-2 \sqrt{2}) y+(7 \sqrt{2}-5 \sqrt{13}-10 \sqrt{26})=0
\end{aligned}
\)
Since, \((\sqrt{13}+3 \sqrt{2}) x+(\sqrt{13}-2 \sqrt{2}) y+(7 \sqrt{2}-5 \sqrt{13}-10 \sqrt{26})=0\) is the equation of a line.
Similarly, we can obtain the equation of line for any signs of \(x+y-5=0\) and \(3 x-2 y+7=0\).
Thus, point \(P\) must move on a line.

Q21. Find equation of the line which is equidistant from parallel lines \(9 x+6 y-7=0\) and \(3 x+2 y+6=0\).

Answer: The equations of the given lines are
\(
\begin{aligned}
& 9 x+6 y-7=0 \dots(1) \\
& 3 x+2 y+6=0 \dots(2)
\end{aligned}
\)
Let \(P(h, k)\) be the arbitrary point, is equidistant from lines (1) and (2).
Then the perpendicular distance of \(P(h, k)\) from the line (1) is given by
\(
\begin{aligned}
d_1 & =\frac{|9 h+6 k-7|}{\sqrt{(9)^2+(6)^2}} \\
& =\frac{|9 h+6 k-7|}{\sqrt{117}} \\
& =\frac{|9 h+6 k-7|}{3 \sqrt{13}}
\end{aligned}
\)
And the perpendicular distance of \(P(h, k)\) from line (2) is given by
\(
\begin{aligned}
d_2 & =\frac{|3 h+2 k+6|}{\sqrt{(3)^2+(2)^2}} \\
& =\frac{|3 h+2 k+6|}{\sqrt{13}}
\end{aligned}
\)
Since \(P(h, k)\) is equidistant from lines (1) and (2), \(d_1=d_2\)
Therefore,
\(
\begin{aligned}
& \Rightarrow \frac{|9 h+6 k-7|}{3 \sqrt{13}}=\frac{|3 h+2 k+6|}{\sqrt{13}} \\
& \Rightarrow|9 h+6 k-7|=3|3 h+2 k+6| \\
& \Rightarrow 9 h+6 k-7= \pm 3(3 h+2 k+6)
\end{aligned}
\)
Case I:
\(
\begin{aligned}
& 9 h+6 k-7=3(3 h+2 k+6) \\
& \quad \Rightarrow 9 h+6 k-7=3(3 h+2 k+6) \\
& \quad \Rightarrow 9 h+6 k-7=9 h+6 k+18 \\
& \quad \Rightarrow 9 h+6 k-7-9 h-6 k-18=0 \\
& \quad \Rightarrow 25=0
\end{aligned}
\)
Which is an absurd, hence this case is not possible.

Case II:
\(
\begin{aligned}
& 9 h+6 k-7=-3(3 h+2 k+6) \\
& \quad \Rightarrow 9 h+6 k-7=-3(3 h+2 k+6) \\
& \quad \Rightarrow 9 h+6 k-7=-9 h-6 k-18 \\
& \quad \Rightarrow 18 h+12 k+11=0
\end{aligned}
\)
Thus, the required equation of the line is \(18 x+12 y+11=0\).

Q22. A ray of light passing through the point \((1,2)\) reflects on the \(x\)-axis at point \(A\) and the reflected ray passes through the point \((5,3)\). Find the coordinates of A.

Answer:

Let the coordinates of point A be \((a, 0)\).
Draw a line, AL perpendicular to the \(x\)-axis
We know that angle of incidence is equal to angle of reflection.
Hence, let \(\angle B A L=\angle C A L=\phi\) and \(\angle C A X=\theta\) Now,
\(
\begin{aligned}
\angle O A B & =180^{\circ}-(\theta+2 \phi) \\
& =180^{\circ}-\left[\theta+2\left(90^{\circ}-\theta\right)\right] \\
& =180^{\circ}-\left[\theta+180^{\circ}-2 \theta\right] \\
& =180^{\circ}-180^{\circ}+\theta \\
& =\theta
\end{aligned}
\)
Therefore,
\(
\angle B A X=180^{\circ}-\theta
\)
Now,Slope of line
\(
A C=\frac{3-0}{5-a}
\)
\(
\Rightarrow \tan \theta=\frac{3-0}{5-a} \dots(1)
\)
Slope of line \(A C=\frac{2-0}{1-a}\)
\(
\begin{aligned}
& \Rightarrow \tan \left(180^{\circ}-\theta\right)=\frac{2}{1-a} \\
& \Rightarrow-\tan \theta=\frac{2}{1-a} \\
& \Rightarrow \tan \theta=\frac{2}{a-1} \dots(2)
\end{aligned}
\)
From equations (1) and (2), we obtain
\(
\begin{aligned}
& \Rightarrow \frac{3}{5-a}=\frac{2}{a-1} \\
& \Rightarrow 3 a-3=10-2 a \\
& \Rightarrow a=\frac{13}{5}
\end{aligned}
\)
Thus, the coordinates of point A are \(\left(\frac{13}{5}, 0\right)\).

Q23. Prove that the product of the lengths of the perpendiculars drawn from the points \(\left(\sqrt{a^2-b^2}, 0\right)\) and \(\left(-\sqrt{a^2-b^2}, 0\right)\) to the line \(\frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta=1\) is \(b^2\).

Answer: The equation of the given line is
\(
\begin{aligned}
& \frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta=1 \\
& b x \cos \theta+a y \sin \theta-a b=0 \dots(1)
\end{aligned}
\)
Length of the perpendicular from point \(\left(\sqrt{a^2+b^2}, 0\right)\) to the line (1) is
\(
\begin{aligned}
p_1 & =\frac{\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)+a \sin \theta(0)-a b\right|}{\sqrt{b^2 \cos ^2 \theta+a^2 \sin ^2 \theta}} \\
& =\frac{\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)-a b\right|}{\sqrt{b^2 \cos ^2 \theta+a^2 \sin ^2 \theta}} \dots(2)
\end{aligned}
\)
Length of the perpendicular from point \(\left(-\sqrt{a^2+b^2}, 0\right)\) to the line (2) is
\(
\begin{aligned}
p_2 & =\frac{\left|b \cos \theta\left(-\sqrt{a^2-b^2}\right)+a \sin \theta(0)-a b\right|}{\sqrt{b^2 \cos ^2 \theta+a^2 \sin ^2 \theta}} \\
& =\frac{\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)-a b\right|}{\sqrt{b^2 \cos ^2 \theta+a^2 \sin ^2 \theta}} \dots(3)
\end{aligned}
\)
On multiplying equations (2) and (3), we obtain
\(
\begin{aligned}
p_1 p_2 & =\frac{\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)-a b\right|\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)-a b\right|}{\left(\sqrt{b^2 \cos ^2 \theta+a^2 \sin ^2 \theta}\right)^2} \\
& =\frac{\left|\left(b \cos \theta\left(\sqrt{a^2-b^2}\right)-a b\right)\left(b \cos \theta\left(\sqrt{a^2-b^2}\right)-a b\right)\right|}{\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{\left|\left(b \cos \theta \sqrt{a^2-b^2}\right)^2-(a b)^2\right|}{\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)} \\
& =\frac{\left|b^2 \cos ^2 \theta\left(a^2-b^2\right)-a^2 b^2\right|}{\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)} \\
& =\frac{\left|a^2 b^2 \cos ^2 \theta-b^4 \cos ^2 \theta-a^2 b^2\right|}{\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)} \\
& =\frac{b^2\left|a^2 \cos ^2 \theta-b^2 \cos ^2 \theta-a^2\right|}{\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)} \\
& =\frac{b^2\left|a^2 \cos ^2 \theta-b^2 \cos ^2 \theta-a^2 \sin ^2 \theta-a^2 \cos ^2 \theta\right|}{\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)} \quad\left[\because \sin ^2 \theta+\cos ^2 \theta=1\right] \\
& =\frac{b^2\left|-\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)\right|}{\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)} \\
& =\frac{b^2\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)}{\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)} \\
& =b^2 \\
&
\end{aligned}
\)
Hence, proved.

Q24. A person standing at the junction (crossing) of two straight paths represented by the equations \(2 x-3 y+4=0\) and \(3 x+4 y-5=0\) wants to reach the path whose equation is \(6 x-7 y+8=0\) in the least time. Find equation of the path that he should follow.

Answer: The equations of the given lines are
\(
\begin{aligned}
& 2 x-3 y+4=0 \dots(1) \\
& 3 x+4 y-5=0 \dots(2) \\
& 6 x-7 y+8=0 \dots(3)
\end{aligned}
\)
The person is standing at the junction of the paths represented by lines (1) and (2).
On solving equations (1) and (2), we obtain \(x=-\frac{1}{17}\) and \(y=\frac{22}{17}\)
Thus, the person is standing at point \(\left(-\frac{1}{17}, \frac{22}{17}\right)\)
The person can reach path (3) in the least time if he walks along the perpendicular line to (3) from point \(\left(-\frac{1}{17}, \frac{22}{17}\right)\)
Now,
Slope of the line (3) \(=\frac{6}{7}\)
Slope of the line perpendicular to line (3)
\(
=-\frac{1}{\left(\frac{6}{7}\right)}=-\frac{7}{6}
\)
The equation of the line passing through \(\left(-\frac{1}{17}, \frac{22}{17}\right)\) and having a slope of \(-\frac{7}{6}\) is given by
\(
\begin{aligned}
& \Rightarrow\left(y-\frac{22}{17}\right)=-\frac{7}{6}\left(x+\frac{1}{17}\right) \\
& \Rightarrow 6(17 y-22)=-7(17 x+1) \\
& \Rightarrow 102 y-132=-119 x-7 \\
& \Rightarrow 119 x+102 y=125
\end{aligned}
\)
Hence, the path that the person should follow is \(119 x+102 y=125\).