Common Forces in Mechanics
Some of the common forces that we come across in mechanics are described below
Weight (w)
The weight of an object is equal to the gravitational force with which the earth pulls it downwards.
Weight of an object, \(w=m g\)
where, \(m=\) mass of the object and \(g=\) acceleration due to gravity.
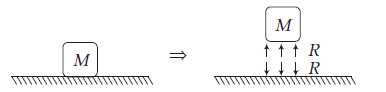
Normal reaction ( \(R\) or \(N\) )
It is a contact force between two surfaces in contact, which is always perpendicular to the surfaces in contact. The following diagrams show normal reaction between two surfaces.
Block pushes ground downward with force \(R\) and ground pushes the block back with force \(R\), where \(R=\) normal reaction force. Three cases are shown below.
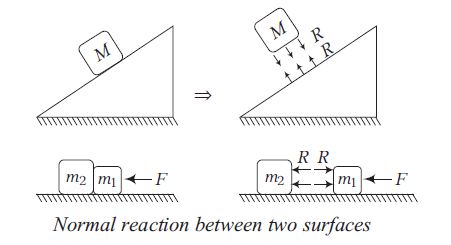
Here, \(m_1\) pushes \(m_2\) towards left by force \(R\) and \(m_2\) pushes \(m_1\) towards right by force \(R\).
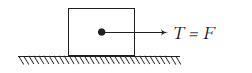
Tension (T)
All physical objects that are in contact can exert forces on each other. We give these contact forces different names based on the types of objects in contact. If one of the objects exerting the force happens to be a rope, string, chain, or cable we call the force tension.
Regarding tension and string, the following points are important to remember
- Force of tension acts on a body in the direction away from the point of contact or tied ends of the string.
- If a string is inextensible, the magnitude of acceleration of any number of masses connected through string is always same.
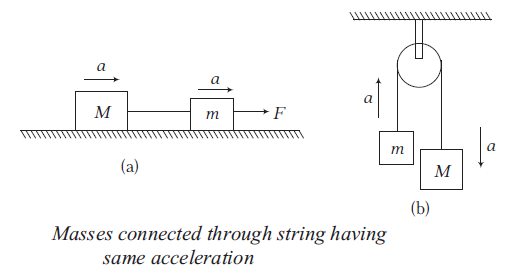
- If a string is massless, the tension in it is same everywhere. However, if a string has a mass, tension at different points will be different.
- If there is friction between string and pulley, tension is different on two sides of the pulley, but if there is no friction between pulley and string, tension will be same on both sides of the pulley.
These points can be understood in diagram as follows
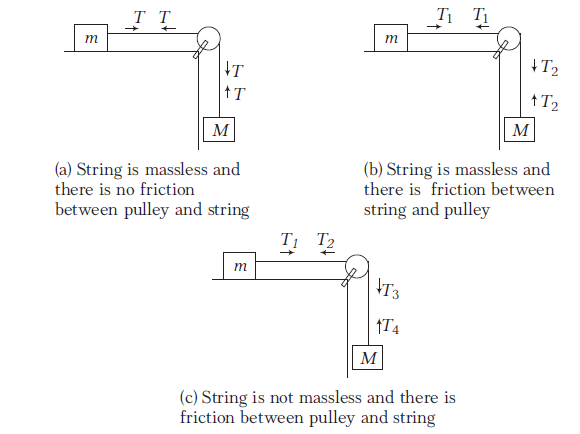
- If a force is directly applied on the string, the tension will be equal to the applied force irrespective of the motion of the pulling agent.
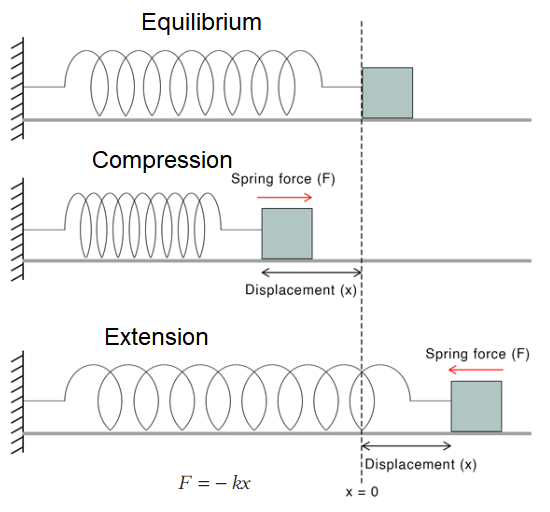
Spring force
The resistive force developed in a spring, when its length is changed is called spring force.
\(\therefore \quad\) Spring force, \(F=-k x\)
where, \(x=\) change in length of the spring
and \(\quad k=\) spring constant.
Free Body Diagram (FBD)
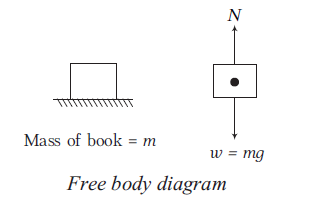
A free body diagram (FBD) consists of a diagrammatic representation of a single body or a sub-system of bodies isolated from its surroundings showing all the forces acting on it.
Consider, for example, a book lying on a horizontal surface as shown below. A free body diagram of the book alone would consist of its weight \((w=m g)\), acting through the centre of gravity and the reaction \((N)\) exerted on the book by the surface.
Example 1: A cylinder of weight \(w\) is resting on a \(V\)-groove as shown in figure. Draw its free body diagram.

Answer: The free body diagram of the cylinder is as shown in figure.
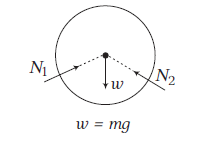
Here, \(w=\) weight of cylinder and \(N_1\) and \(N_2\) are the normal reactions between the cylinder and the two inclined walls.
Example 2: Three blocks A, B and C are placed one over the other as shown in figure. Draw free body diagrams of all the three blocks.
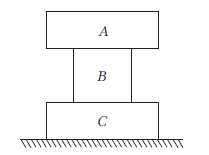
Answer: Free body diagrams of A, B and C are shown below.
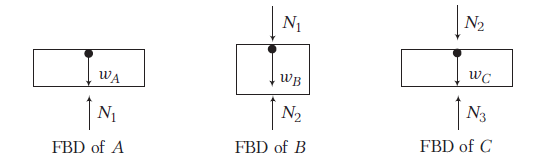
Here, \(N_1=\) normal reaction between \(A\) and \(B\),
\(N_2=\) normal reaction between \(B\) and \(C\)
and \(\quad N_3=\) normal reaction between \(C\) and ground.
Example 3: A block of mass \(m\) is attached with two strings as shown in figure. Draw the free body diagram of the block.
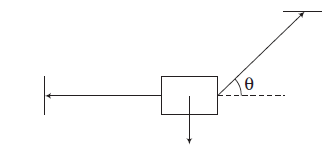
Answer: The free body diagram of the block is as shown in figure.
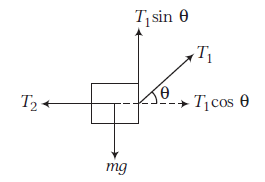
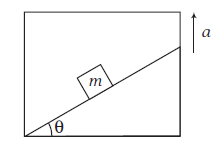
Example 4: All surfaces are smooth in following figure. Find F such that block remains stationary with respect to wedge.
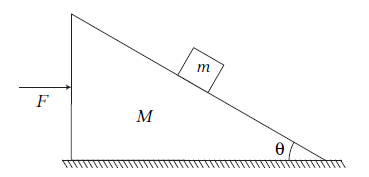
Answer: Acceleration of (block + wedge), \(a=\frac{F}{(M+m)}\)
From inertial frame of reference (ground) FBD of block (only real forces) with respect to ground, which is moving with an acceleration a is shown below.
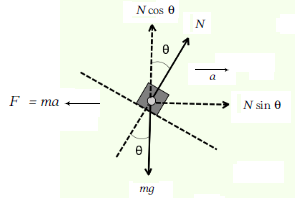
Since there is No vertical acceleration, \(a=0\)
\(
\Sigma F_y=0
\)
\(
N \cos \theta=m g \dots(i)
\)
\(
N \sin \theta=m a \dots(ii)
\)
From Eqs. (i) and (ii), we get
\(
\begin{array}{rlrl}
a & =g \tan \theta \\
\therefore \quad & F =(M+m) a=(M+m) g \tan \theta
\end{array}
\)
Example 5: A bob of mass \(m\) is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle \(\theta\) in equilibrium position.

Answer: FBD of the problem is shown below.
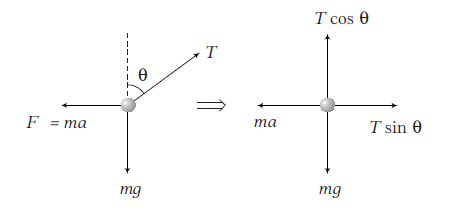
As, with respect to train, bob is in equilibrium.
\(
\begin{array}{rlrlrl}
& \therefore & \Sigma F_x =0 \dots(i) \\
\Rightarrow & T \sin \theta =m a \\
& \therefore & \Sigma F_y =0 \dots(ii) \\
\Rightarrow & T \cos \theta =m g
\end{array}
\)
From Eqns. (i) and (ii), we get the same result, i.e.
\(
\theta=\tan ^{-1}\left(\frac{a}{g}\right)
\)
Apparent weight of a man in a lift
Let us consider a man of mass \(m\) is standing on a weighing machine placed in an elevator/lift. The actual weight \(m g\) of the man acts on the weighing machine and offers a reaction \(R\) given by the reading of the weighing machine. This reaction \(R\) exerted by the surface of contact on the man is apparent weight of the person.
Now, we consider how \(R\) is related to \(m g\) in the different conditions.
Case-I: When the lift moves upwards with acceleration \(a\) as shown in figure, the net upward force on the man is
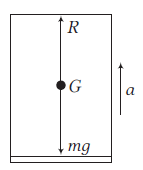
\(
R-m g=m a \Rightarrow R=m a+m g
\)
Apparent weight, \(R=m(g+a)\)
So, when a lift accelerates upwards, the apparent weight of the man inside it increases.
Case-II: When the lift moves downwards with acceleration \(a\) as shown in figure, the net downward force on the man is
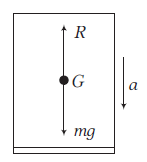
\(
\begin{aligned}
m g-R =m a \\
\text { Apparent weight, } R =m(g-a)
\end{aligned}
\)
So, when a lift accelerates downwards, the apparent weight of the man inside it decreases.
Case-III: When the lift is at rest or moving with uniform velocity \({v}\) downward or upward as shown in figure.
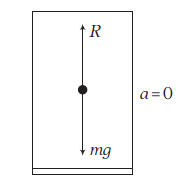
Then, acceleration \(a=0\). So, net force on the man is
\(
\begin{array}{rlrl}
R-m g & =m \times 0 \\
\Rightarrow R =m g \\
\text { or Apparent weight } & =\text { Actual weight }
\end{array}
\)
So, when the lift is at rest, the apparent weight of the man is his actual weight.
Case-IV: When the lift falls freely under gravity, if the supporting cable of the lift breaks. Then, \(a=g\).
The net downward force on the man is
\(
R=m(g-g) \Rightarrow R=0
\)
Thus, the apparent weight of the man becomes zero. This is because both the lift and man are moving downwards with the same acceleration \(g\) and so there is no force of action and reaction existing between the man and lift. Hence, a person develops a feeling of weightlessness when the lift falls freely under gravity.
Example 6: A spring balance is attached to the ceiling of an elevator. A boy hangs his bag on the spring and the spring reads \(49 \mathrm{~N}\), when the elevator is stationary. If the elevator moves downward with an acceleration of \(5 \mathrm{~ms}^{-2}\), what will be the reading of the spring balance?
Answer: When the elevator is stationary, then
\(
\begin{array}{rlrl}
& w =m g \\
\Rightarrow & 49 =m \times 9.8 \\
\Rightarrow & m =\frac{49}{9.8}=5 \mathrm{~kg}
\end{array}
\)
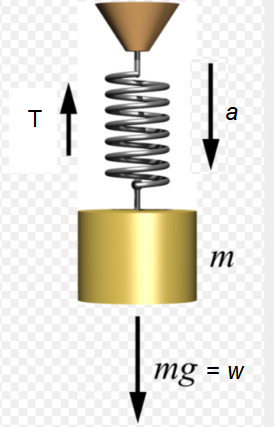
When the elevator is moving downward with an acceleration,
\(
m a=m g-T
\)
\(
\begin{aligned}
\Rightarrow T =m g-m a \\
=m(g-a)
\end{aligned}
\)
\(
T=m(9.8-a)=5(9.8-5)=24 \mathrm{~N}
\)
Example 7: If in a stationary elevator, a man is standing with a bucket full of water. The bucket has a hole at its bottom. The rate of flow of water through this hole is \(R_0\). If the elevator starts to move up and then down with same acceleration, then the rate of flow of water are \(R_u\) and \(R_d\). Find the relation between \(R_0, R_u\) and \(R_d\).
Answer: Rate of flow will be more when elevator will move in upward direction with some acceleration because the net downward pull will be more and vice-versa.
\(
\begin{array}{l}
F_{\text {upward }}=R_u=m(g+a) \\
F_{\text {downward }}=R_d=m(g-a) \\
\Rightarrow \quad F_{\text {at rest }}=R_0=m g \\
\end{array}
\)
Thus, relation between \(R_u, R_0\) and \(R_d\) is \(R_u>R_0>R_d\).
Example 8: In the adjoining figure, a wedge is fixed to an elevator moving upwards with an acceleration a. A block of mass \(m\) is placed over the wedge. Find the acceleration of the block with respect to wedge. Neglect friction.
Answer: Since, acceleration of block w.r.t. wedge (an accelerating or non-inertial frame of reference) is to be find out. FBD of block w.r.t. wedge is shown in figure.
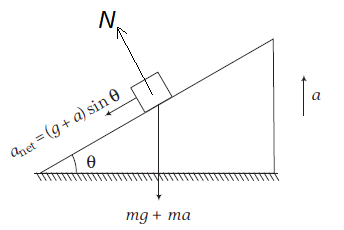
The acceleration would had been \(g \sin \theta\) (down the plane), if the lift were stationary or when only weight (i.e. \(\mathrm{mg}\) ) acts downwards.
Here, downward force is \(m(g+a)\)
\(\therefore\) Acceleration of the block (of course w.r.t. wedge) will be \((g+a) \sin \theta\) down the plane.
Applications Of Newton’s Laws Of Motion
Consider two bodies of masses \(m_1\) and \(m_2\) placed in direct contact with each other on a smooth platform.
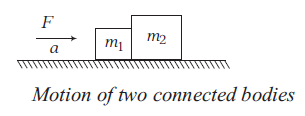
Suppose a horizontal force is applied and both the bodies moves with acceleration \(a\), then
\(
F=\left(m_1+m_2\right) a
\)
Now, we can calculate normal reaction bet|ween the bodies, using free body diagram (FBD).
FBD of 1st body
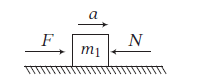
\(\therefore \quad F-N=m_1 a \quad\) (From Newton’s 2nd law)
FBD of 2nd body
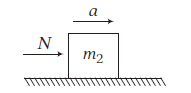
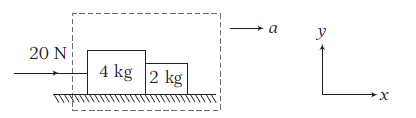
Example 9: Two blocks of masses \(4 \mathrm{~kg}\) and \(2 \mathrm{~kg}\) are placed side-by-side on a smooth horizontal surface as shown in the figure. A horizontal force of \(20 \mathrm{~N}\) is applied on \(4 \mathrm{~kg}\) block.
Find
(i) the acceleration of each block
(ii) and the normal reaction between two blocks.
Answer: (i) Since, both the blocks will move with same acceleration (say a) in horizontal direction. Let us take both the blocks as a system. Net external force on the system is \(20 \mathrm{~N}\) in horizontal direction.
Using
\(
\begin{array}{l}
\quad \begin{aligned}
\Sigma F_x & =m a_x \\
20 & =(4+2) a=6 a \text { or } a=\frac{10}{3} \mathrm{~ms}^{-2}
\end{aligned}
\end{array}
\)
(ii) The free body diagram of both the blocks are shown in the figure.
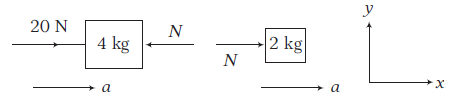
Using \(\quad \Sigma F_x=m a_x\)
For \(4 \mathrm{~kg}\) block, \(20-N=4 a=4 \times \frac{10}{3}\)
\(
\Rightarrow \quad N=20-\frac{40}{3}=\frac{20}{3} \mathrm{~N}
\)
For \(2 \mathrm{~kg}\) block, \(N=2 a=2 \times \frac{10}{3}=\frac{20}{3} \mathrm{~N}\)
Here, \(N\) is the normal reaction between the two blocks.
Note: In free body diagram of the blocks, we have not shown the forces acting on the blocks in vertical direction, because normal reaction between the blocks and acceleration of the system can be obtained without using \(\Sigma F_y=0\).
Example 10: Three blocks of masses \(3 \mathrm{~kg}, 2 \mathrm{~kg}\) and \(1 \mathrm{~kg}\) are placed side-by-side on a smooth surface as shown in figure. A horizontal force of \(12 \mathrm{~N}\) is applied on \(3 \mathrm{~kg}\) block. Find the net force on \(2 \mathrm{~kg}\) block.
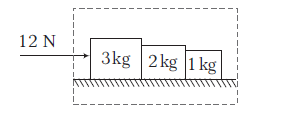
All the blocks will move with same acceleration (say a) in horizontal direction. Let us take all the blocks as a system, net external force on the system is \(12 \mathrm{~N}\) in horizontal direction.
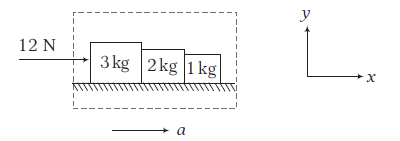
Using \(\Sigma F_x=m a_x\), we get
\(
12=(3+2+1) a=6 a \text { or } a=\frac{12}{6}=2 \mathrm{~ms}^{-2}
\)
Now, let \(F\) be the net force on \(2 \mathrm{~kg}\) block in \(x\)-direction, then using \(\Sigma F_x=m a_x\) for \(2 \mathrm{~kg}\) block, we get
\(
F=(2)(2)=4 \mathrm{~N}
\)
Note: Here, net force \(F\) on \(2 \mathrm{~kg}\) block is the resultant of \(N_1\) and \(N_2\left(N_1>N_2\right)\), where \(N_1=\) normal reaction between \(3 \mathrm{~kg}\) and \(2 \mathrm{~kg}\) block and \(N_2=\) normal reaction between \(2 \mathrm{~kg}\) and \(1 \mathrm{~kg}\) block. Thus, \(F=N_1-N_2\).
Motion of bodies connected through strings or springs
Horizontal motion
When two bodies are connected through an inextensible weightless string and a force is applied to impart an acceleration \(a\) in both the bodies, as given in the figure below, then equation of motion from the FBD can be given by
For \(A\),
\(T=m_1 a \dots(i)\)
For \(B\),
\(F-T=m_2 a \dots(ii)\)
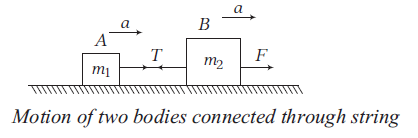
From Eqs. (i) and (ii), \(F=m_1 a+m_2 a \dots(iii)\)
From Eqns. (i) and (iii), \(T=\frac{m_1 F}{\left(m_1+m_2\right)}\)
Example 11: A block of mass \(M\) is pulled along a horizontal frictionless surface by a rope of mass \(m\) as shown in figure. A horizontal force \(F\) is applied to one end of the rope. Find (i) the acceleration of the rope and block, (ii) the force that the rope exerts on the block (iii) and tension in the rope at its mid-point.
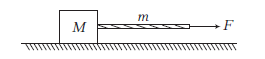
Answer: (i) Acceleration, \(a=\frac{F}{(m+M)}\)
(ii) Force exerted by rope on the block is
\(
T=M a=\frac{M \cdot F}{(m+M)}
\)
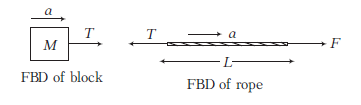
(iii) \(T_1=\left(\frac{m}{2}+M\right) a=\left(\frac{m+2 M}{2}\right)\left(\frac{F}{m+M}\right)\)
Tension in rope at mid-point, \(T_1=\frac{(m+2 M) F}{2(m+M)}\)
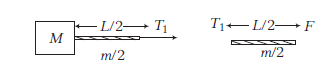
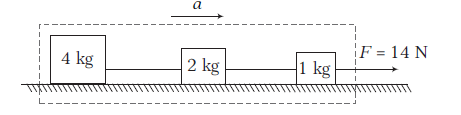
Example 12: In the arrangement shown in the figure, the strings are light and inextensible. The surface over which blocks are placed is smooth. Find
(i) the acceleration of each block
(ii) the tension in each string.

(i) Let \(a\) be the acceleration of each block and \(T_1\) and \(T_2\) be the tensions, in the two strings as shown in the figure.

Taking the three blocks and the two strings as the system.
\begin{array}{l}
\text { Using } \quad \Sigma F_x=m a_x \\
\text { or } \quad 14=(4+2+1) a \text { or } a=\frac{14}{7}=2 \mathrm{~ms}^{-2} \\
\end{array}
\)
(ii) Free body diagram (showing the forces in \(x\)-direction only) of \(4 \mathrm{~kg}\) block and \(1 \mathrm{~kg}\) block are shown in figure.
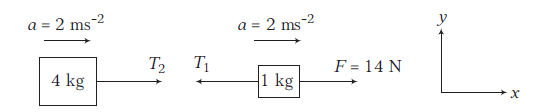
Using \(\Sigma F_x=m a_x\)
For \(1 \mathrm{~kg}\) block, \(\quad F-T_1=(1)(a)\) or \(14-T_1=(1)(2)=2\)
\(\therefore \quad T_1=14-2=12 \mathrm{~N}\)
For \(4 \mathrm{~kg}\) block, \(\quad T_2=(4)(a)\)
\(\therefore \quad T_2=(4)(2)=8 \mathrm{~N}\)
Vertical motion
In the same manner, as discussed above, we can calculate acceleration, tension in the string and common force in two or more blocks in vertical direction also.
Example 13: The blocks of masses \(2 \mathrm{~kg}, 3 \mathrm{~kg}\) and \(5 \mathrm{~kg}\) are connected by light, inextensible strings as shown in figure.
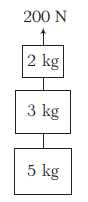
The system of blocks is raised vertically upwards by applying a force \(F_0=200 \mathrm{~N}\). Find the common acceleration and tension in the strings.
Answer:
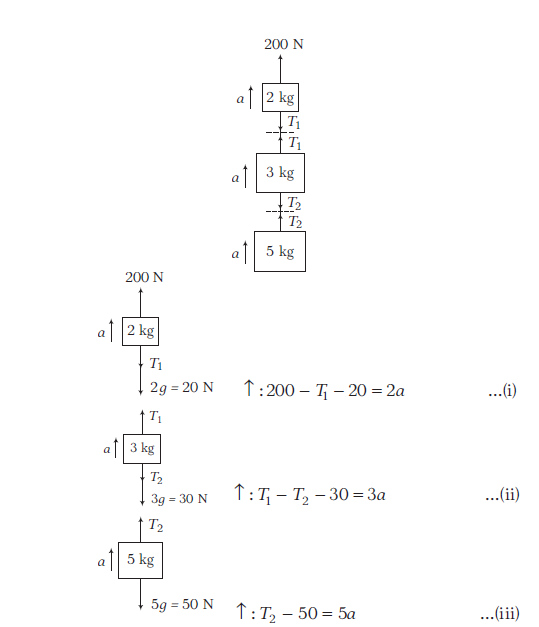
Adding Eqns. (i), (ii) and (iii), we get
\(
\begin{aligned}
100 & =10 a \quad \Rightarrow a=10 \mathrm{~ms}^{-2} \\
T_1 & =160 \mathrm{~N} \text { and } T_2=100 \mathrm{~N}
\end{aligned}
\)
Alternate Method: Taking three blocks together as a system
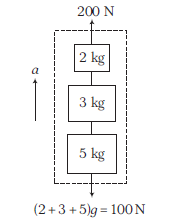
\begin{array}{c}
\uparrow: 200-100=(2+3+5) a \\
a=10 \mathrm{~ms}^{-2}
\end{array}
\)
Taking two blocks at a time
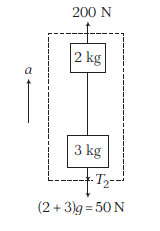
\begin{aligned}
200-50-T_2 & =(2+3) a \\
150-T_2 & =5 \times 10 \\
\Rightarrow \quad T_2 & =100 \mathrm{~N}
\end{aligned}
\)
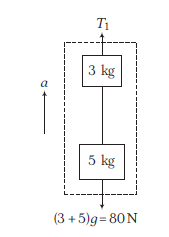
\begin{aligned}
T_1-80 & =(3+5) a \\
T_1-80 & =8 \times 10 \\
T_1 & =160 \mathrm{~N}
\end{aligned}
\)
For spring-block system
In the same manner, as discussed above, we can calculate the tension in a spring connected to a block of mass \(m\), which produces an extension \(x\) in it, i.e. \(T=k x\).
where, \(k=\) spring constant.
Example 14: Two masses are connected to two identical springs of spring constant \(100 \mathrm{~N} / \mathrm{m}\) as shown in figure. Find the extension in both the springs.
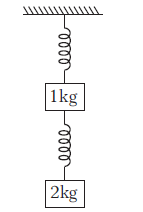
Answer: The FBD for mass \(2 \mathrm{~kg}\),
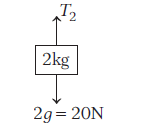
\(\Rightarrow \quad T_2-20=0\) or \(T_2=20 \mathrm{~N} \dots(i)\)
The FBD for mass \(1 \mathrm{~kg}\),
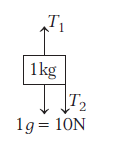
\(
\Rightarrow \quad T_1=T_2+10 \Rightarrow T_1=30 \mathrm{~N} \quad \text { [Using Eq. (i)] }
\)
As, these tensions in the springs are the spring forces,
\(
\begin{array}{ll}
\therefore & T_1=k x_1 \Rightarrow 30=100 \times x_1 \text { or } x_1=0.3 \mathrm{~m} \\
\text { and } & T_2=k x_2 \Rightarrow 20=100 \times x_2 \text { or } x_2=0.2 \mathrm{~m}
\end{array}
\)
Bodies attached through pulley (using strings or springs )
Case I: Consider two bodies of masses \(m_1\) and \(m_2\left(m_2>m_1\right)\) connected to a massless and inextensible string which passes through a smooth pulley. If they are allowed to move freely, they move with common acceleration \(a\). The tension in the string due to mass \(m_1\) and \(m_2\) is \(T\).
From FBD,
For \(A, \quad T-m_1 g=m_1 a \dots(i)\)
For \(B, \quad m_2 g-T=m_2 a \dots(ii)\)
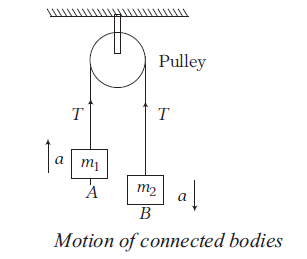
On solving Eqs. (i) and (ii), we get
\(
\begin{aligned}
\Rightarrow & a=\frac{\left(m_2-m_1\right)}{\left(m_2+m_1\right)} g \\
\Rightarrow & T=\left(\frac{2 m_1 m_2}{m_1+m_2}\right) g
\end{aligned}
\)
Reaction at suspension of pulley \(R=2 T\).
Example 15: Two blocks of masses \(2.6 \mathrm{~kg}\) and \(4.1 \mathrm{~kg}\) are tied together by a light string looped over a frictionless pulley.
(a) What will the acceleration of each mass be?
(b) Find the value of tension in the string.
Answer: Here, \(m_1=2.6 \mathrm{~kg}, m_2=4.1 \mathrm{~kg}\)
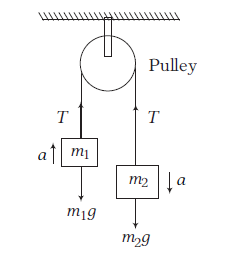
FBD for \(m_1\),
\(
\begin{aligned}
T-m_1 g & =m_1 a \text { (upward) }\\
T-2.6 g & =2.6 a \dots(i)
\end{aligned}
\)
FBD for \(m_2\),
\(
\begin{array}{l}
m_2 g-T=m_2 a \text { (downward) }\\
4.1 g-T=4.1 a \dots(ii)
\end{array}
\)
(a) Adding Eqs. (i) and (ii), we get
\(
\begin{aligned}
4.1 g-2.6 g & =(2.6+4.1) a \\
\Rightarrow \quad a & =\frac{1.5 g}{6.7}=\frac{1.5 \times 10}{6.7} \\
& =2.2 \mathrm{~ms}^{-2}
\end{aligned}
\)
(b) Putting the value of \(a\) in Eq. (i), we get
\(
T-2.6 g=2.6 \times 2.2
\)
\(
\begin{aligned}
T & =2.6 \times 2.2+2.6 \times 10 \\
& =31.72 \mathrm{~N}
\end{aligned}
\)
Example 16: The pulley is light and smooth; the strings are inextensible and light. The system is released from rest. Find the acceleration of each block, tensions in the strings and reaction on pulley.

Answer:
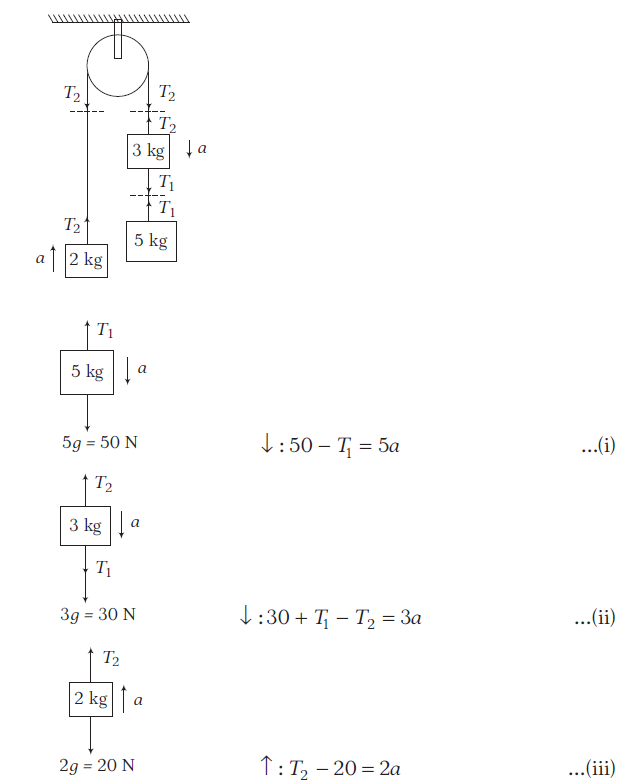
Solving Eqs. (i), (ii) and (iii), we get
\(
a=6 \mathrm{~ms}^{-2}, T_1=20 \mathrm{~N}, T_2=32 \mathrm{~N}
\)
Forces on pulley, \(R-2 T_2=0\)
(Pulley is massless)
\(
R=2 T_2=64 \mathrm{~N}
\)
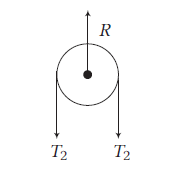
where, \(R\) is the reaction on the pulley.
Case II: When two bodies are attached through a pulley as given in the figure below.
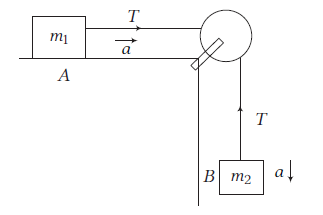
Here, \(m_2>m_1\), then from FBD,
For \(A, \quad T=m_1 a \dots(i)\)
For \(B, \quad m_2 a=m_2 g-T \dots(ii)\)
Solving Eqs. (i) and (ii), we get
\(
\begin{aligned}
a & =\frac{m_2}{\left(m_1+m_2\right)} g \\
\Rightarrow \quad T & =\frac{m_1 m_2}{\left(m_1+m_2\right)} g
\end{aligned}
\)
Example 17: A \(2 \mathrm{~kg}\) mass placed on a level table is attached to a \(5 \mathrm{~kg}\) mass by a string passing over the edge of a table as illustrated in the diagram.
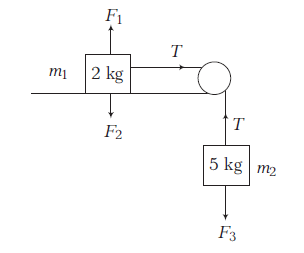
(a) Calculate the magnitude of acceleration of the system.
(b) Calculate the tension in the string.
Answer: From FBD in \(m_1\),
\(
\begin{aligned}
T-m_1 a & =0 \\
\Rightarrow \quad T-2 a & =0 \dots(i)
\end{aligned}
\)
FBD in \(m_2\),
\(
\begin{array}{c}
m_2 g-T=m_2 a \\
5 g-T=5 a
\end{array}
\)
Putting \(T=2 a\) from Eq. (i), we get
\(
\begin{array}{r}
5 g-2 a=5 a \\
7 a=5 g
\end{array}
\)
(a) \(a=\frac{5}{7} \times 10=\frac{50}{7} \mathrm{~ms}^{-2}\)
(b) Again, tension in the string,
\(
T=2 a=2 \times \frac{50}{7}=\frac{100}{7} \mathrm{~N}
\)
Example 18: The strings are inextensible and light; the pulleys are smooth and light. Find the acceleration of each block and tensions in the strings.
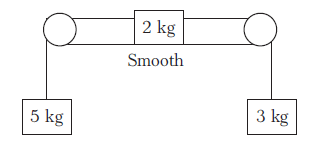
Answer:
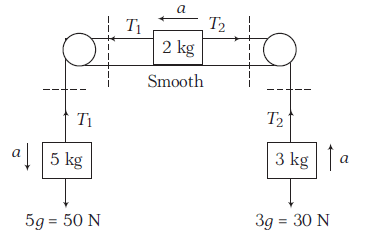
\(
5 \mathrm{~kg}: \quad \downarrow: 50-T_1=5 a \dots(i)
\)
\(
2 \mathrm{~kg}: \quad \leftarrow: T_1-T_2=2 a \dots(ii)
\)
\(
3 \mathrm{~kg}: \quad \uparrow: T_2-30=3 a \dots(iii)
\)
Adding Eqs. (i), (ii) and (iii), we get
\(
\begin{array}{l}
20=10 a \Rightarrow a=2 \mathrm{~ms}^{-2} \\
T_1=40 \mathrm{~N} \text { and } T_2=36 \mathrm{~N}
\end{array}
\)
Example 19: Consider the situation shown in figure. Initially the spring is unstretched when the block of mass is released from rest. Assume the pulley frictionless and light, the spring and string massless. Find the maximum extension of the spring.
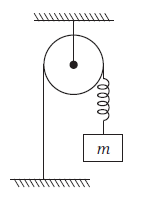
Answer:
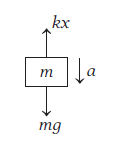
The FBD of given mass \(m\)
\(
\begin{aligned}
m g-k x & =m a \text { or } a=g-\frac{k}{m} x \\
v d v & =\left(g-\frac{k}{m} x\right) d x
\end{aligned}
\)
Integrating both sides, we get or
\(
\begin{aligned}
\int_0^v v d v & =\int_0^x\left(g-\frac{k}{m} x\right) d x \Rightarrow \frac{v^2}{2}=g x-\frac{k x^2}{2 m} \\
v & =\left(2 g x-\frac{k x^2}{m}\right)^{1 / 2}
\end{aligned}
\)
When the block will stop, \(v=0\) (at maximum extension),
\(
\left(2 g x-\frac{k x^2}{m}\right)^{1 / 2}=0 \Rightarrow 2 g x=\frac{k x^2}{m} \Rightarrow x=x_m=\frac{2 m g}{k}
\)
Case III: When pulley is attached to the edge of an inclined plane To understand this case, first of all we need to understand the motion of an object placed on a frictionless inclined plane.
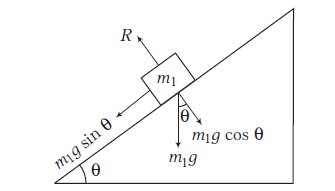
Consider an object of mass \(m_1\) is placed on a smooth inclined plane with angle of inclination \(\theta\). From the FBD of object, different forces acting on it, are
(i) Normal reaction \(R\), acting perpendicular to the plane.
(ii) Component of weight \(m_1 g \cos \theta\), acting perpendicular to plane.
(iii) Component of weight \(m_1 g \sin \theta\) downward along the inclined plane.
Here, \(R\) and \(m_1 g \cos \theta\) will cancel each other (as here is no motion in vertically upward and vertical downward direction), so these forces can be ignored.
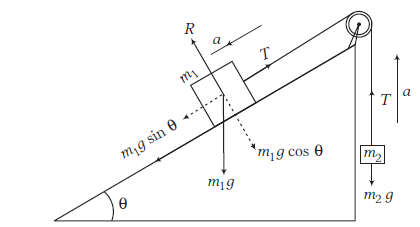
Now, a pulley is connected at the edge of inclined plane and a block of mass \(m_2\left(m_1>m_2\right)\) is connected through a string passing over the pulley to mass \(m_1\) as shown in Figure above.
Now, equation of motion for \(m_2\),
\(
T-m_2 g=m_2 a \dots(i)
\)
Equation of motion for \(m_1\),
\(
m_1 g \sin \theta-T=m_1 a \dots(ii)
\)
From Eqs. (i) and (ii), we get
\(
a=\frac{\left(m_1 g \sin \theta-m_2 g\right)}{\left(m_1+m_2\right)}
\)
\(
T=\frac{m_1 m_2}{m_1+m_2}(1+\sin \theta) g
\)
Example 20: Consider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.
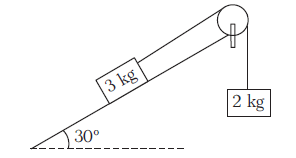
Answer:
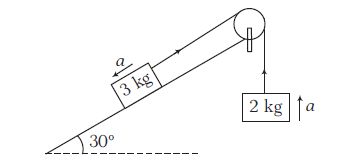
Let \(3 \mathrm{~kg}\) block be moving downward.
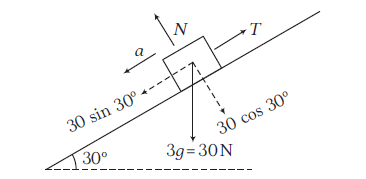
Along the plane: \(30 \sin 30^{\circ}-T=3 a \dots(i)\)
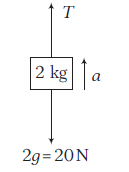
\(
T-20=2 a \dots(ii)
\)
Adding Eqs. (i) and (ii), we get
\(
a=-1 \mathrm{~ms}^{-2} \Rightarrow T=18 \mathrm{~N}
\)
Since, the acceleration is negative, i.e. the block of mass \(3 \mathrm{~kg}\) is moving upward.
Example 21: In the arrangement shown, inclined plane is smooth, strings and pulleys are massless. Find \(\frac{T_1}{T_2}\).
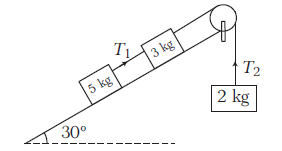
Answer:
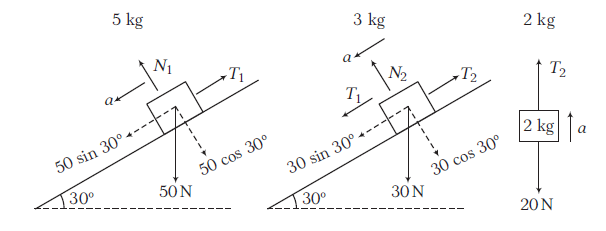
\(5 \mathrm{~kg}\) : along the plane : \(50 \sin 30^{\circ}-T_1=5 a \dots(i)\)
\(3 \mathrm{~kg}\) : along the plane : \(30 \sin 30^{\circ}+T_1-T_2=3 a \dots(ii)\)
\(2 \mathrm{~kg}: \uparrow: T_2-20=2 a \dots(iii)\)
Adding Eqs. (i), (ii) and (iii), we get
\(
\begin{array}{rlrl}
20 & =10 a \Rightarrow a=2 \mathrm{~ms}^{-2} \\
T_1 & =15 \mathrm{~N} \text { and } T_2=24 \mathrm{~N} \\
\therefore \quad & \frac{T_1}{T_2}=\frac{15}{24}=\frac{5}{8}
\end{array}
\)
Example 22: In the arrangement shown, all the surfaces are smooth, strings and pulleys are light. Find the tension in the string.
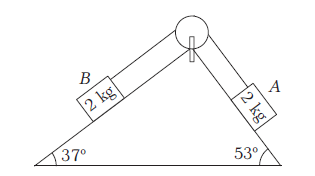
Answer:
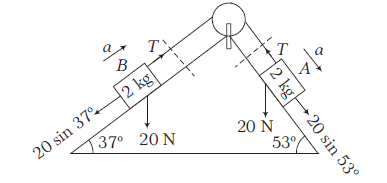
Block \(A\) : along the plane, \(20 \sin 53^{\circ}-T=2 a \dots(i)\)
Block \(B\) : along the plane, \(T-20 \sin 37^{\circ}=2 a \dots(ii)\)
Adding Eqs. (i) and (ii), we get
\(
\begin{array}{l}
20\left(\sin 53^{\circ}-\sin 37^{\circ}\right)=4 a \\
20\left(\frac{4}{5}-\frac{3}{5}\right)=4=4 a \Rightarrow a=1 \mathrm{~ms}^{-2} \\
T=20 \sin 37^{\circ}+2 a=20 \times \frac{3}{5}+2 \times 1=14 \mathrm{~N}
\end{array}
\)
Example 23: In the adjacent figure, masses of \(A, B\) and \(C\) are \(1 \mathrm{~kg}, 3 \mathrm{~kg}\) and \(2 \mathrm{~kg}\), respectively. Find
(i) the acceleration of the system
(ii) and tension in the string.
Neglect friction. \(\left(g=10 \mathrm{~ms}^{-2}\right)\)
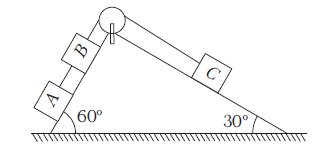
Answer: (i) In this case, net pulling force
\(
\begin{array}{l}
=m_A g \sin 60^{\circ}+m_B g \sin 60^{\circ}-m_C g \sin 30^{\circ} \\
=(1)(10)\left(\frac{\sqrt{3}}{2}\right)+(3)(10)\left(\frac{\sqrt{3}}{2}\right)-(2)(10)\left(\frac{1}{2}\right) \\
=24.64 \mathrm{~N}
\end{array}
\)
Total mass being pulled \(=1+3+2=6 \mathrm{~kg}\)
\(\therefore\) Acceleration of the system, \(a=\frac{24.64}{6}=4.10 \mathrm{~ms}^{-2}\)
(ii) For the tension in the string between \(A\) and \(B\)
FBD of A
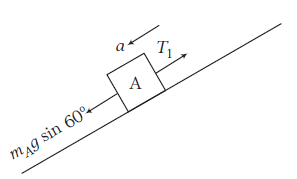
\(
\begin{array}{l}
m_A g \sin 60^{\circ}-T_1=\left(m_A\right)(a) \\
T_1=m_A g \sin 60^{\circ}-m_A a \\
\quad=m_A\left(g \sin 60^{\circ}-a\right) \\
T_1=(1)\left(10 \times \frac{\sqrt{3}}{2}-4.10\right)=4.56 \mathrm{~N}
\end{array}
\)
For the tension in the string between \(B\) and \(C\)
FBD of C
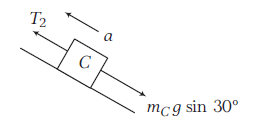
\begin{array}{l}
T_2-m_C g \sin 30^{\circ}=\left(m_C\right)(a) \\
T_2=m_C\left(a+g \sin 30^{\circ}\right) \\
T_2=2\left[4.10+10\left(\frac{1}{2}\right)\right]=18.2 \mathrm{~N}
\end{array}
\)
Example 24: Calculate the net acceleration produced in the arrangements shown below.
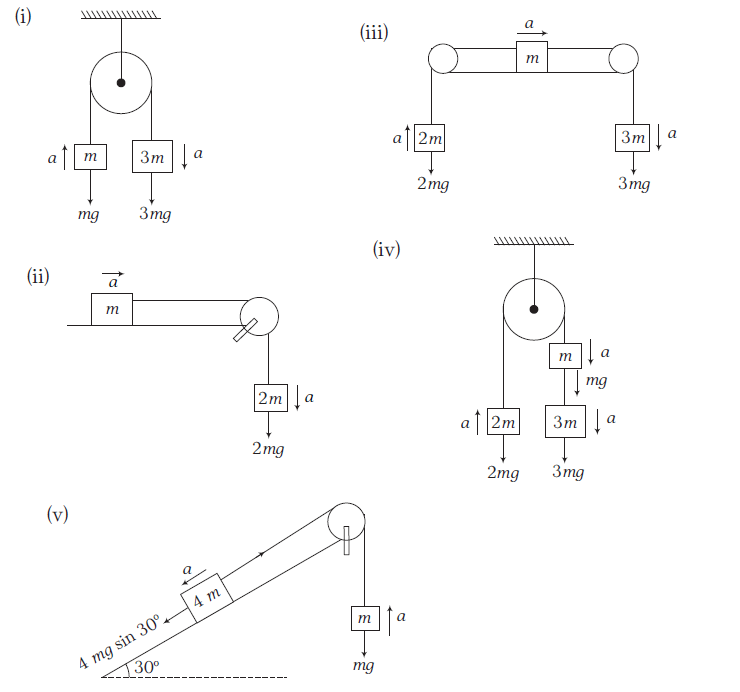
Answer:
\(
\begin{array}{l}
\text { (i) Net pulling force }=3 m g-m g=2 m g \\
\text { Total mass }=3 m+m=4 m \\
\qquad a=\frac{2 m g}{4 m}=\frac{g}{2}
\end{array}
\)
\(
\begin{array}{l}
\text { (ii) Pulling force }=2 \mathrm{mg} \\
\text { Total mass }=3 \mathrm{~m} \\
a=\frac{2 m g}{3 m}=\frac{2 g}{3} \\
\end{array}
\)
(iii) Net pulling force \(=3 m g-2 m g=m g\)
\(
\begin{aligned}
\text { Total mass } & =3 m+m+2 m=6 m \\
a & =\frac{m g}{6 m}=\frac{g}{6}
\end{aligned}
\)
\(
\begin{array}{l}
\text { (iv) Net pulling force }=3 m g+m g-2 m g \\
=2 \mathrm{mg} \\
\text { Total mass }=3 m+m+2 m=6 m \\
a=\frac{2 m g}{6 m}=\frac{g}{3} \\
\text { (v) Net pulling force }=4 m g \sin 30^{\circ}-m g \\
=m g \\
\text { Total mass }=4 m+m=5 m \\
\Rightarrow \quad a=\frac{m g}{5 m}=\frac{g}{5} \\
\end{array}
\)