JEE Physics Test Series Quiz-10
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
Match List I with List II
\(
\begin{array}{|l|l|l|l|}
\hline & \text { List I } & & \text { List II } \\
\hline \text { A } & \text { Plank’s constant }(h) & \text { I. } & {\left[M^1 L^2 T^{-2}\right]} \\
\hline \text { B } & \text { stopping potential }(Vs) & \text { II. } & {\left[M^1 L^1 T^{-1}\right]} \\
\hline \text { C } & \text { Work function }(\phi) & \text { III. } & {\left[M^1 L^2 T^{-1}\right]} \\
\hline \text { D } & \text { Momentum }(p) & \text { IV } & {\left[M^1 L^2 T^{-3} A^{-1}\right]} \\
\hline
\end{array}
\)CorrectIncorrectHint
(A) Planck’s constant
\(
\begin{aligned}
& \mathrm{h} \nu=\mathrm{E} \\
& \mathrm{h}=\frac{\mathrm{E}}{\mathrm{\nu}}=\frac{\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2}}{\mathrm{~T}^{-1}}=\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-1}
\end{aligned}
\)
(B)
\(
\begin{aligned}
& E=q V_s \\
& V_s=\frac{E}{q}=\frac{M^1 L^2 T^{-2}}{A^1 T^1}=M^1 L^2 T^{-3} A^{-1}
\end{aligned}
\)
(C)
\(
\begin{aligned}
& \phi(\text { work function })=\text { energy } \\
& =\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2}
\end{aligned}
\)
(D)
\(
\begin{aligned}
& \text { Momentum }(p)=\text { F x time } \\
& =M^1 L^1 T^{-2} T^1 \\
& =M^1 L^1 T^{-1}
\end{aligned}
\) -
Question 2 of 50
2. Question
The frequency \((\nu)\) of an oscillating liquid drop may depend upon radius (r) of the drop, density \((\rho)\) of liquid and the surface tension (s) of the liquid as : \(v=r^a \rho^b s^c\). The values of \(a, b\) and \(c\) respectively are
CorrectIncorrectHint
\(
\begin{aligned}
& {\left[\mathrm{T}^{-1}\right]=\left[\mathrm{L}^1\right]^{\mathrm{a}}\left[\mathrm{M}^1 \mathrm{~L}^{-3}\right]^{\mathrm{b}}\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}}\right]^{\mathrm{c}}} \\
& \Rightarrow \mathrm{T}^{-1}=\mathrm{M}^{\mathrm{b}+\mathrm{c}} \cdot \mathrm{L}^{\mathrm{a}-3 \mathrm{~b}} \cdot \mathrm{T}^{-2 \mathrm{c}} \\
& \mathrm{c}=\frac{1}{2}, \mathrm{~b}=-\frac{1}{2}, \quad \mathrm{a}-3 \mathrm{~b}=0 \\
& \mathrm{a}+\frac{3}{2}=0 \Rightarrow \mathrm{a}=-\frac{3}{2}
\end{aligned}
\) -
Question 3 of 50
3. Question
Match List I with List II
\(
\begin{array}{|l|l|l|l|}
\hline & \text { List I } & & \text { List II } \\
\hline \text { A } & \text { Surface Tension } & \text { I. } & {\mathrm{Kg} \mathrm{~m}^{-1} \mathrm{~s}^{-1}} \\
\hline \text { B } & \text { Pressure } & \text { II. } & {\mathrm{Kg} \mathrm{~ms}^{-1}} \\
\hline \text { C } & \text { Viscocity } & \text { III. } & {\mathrm{Kg} \mathrm{~m}^{-1} \mathrm{~s}^{-2}} \\
\hline \text { D } & \text { Impulse } & \text { IV } & {\mathrm{Kg} \mathrm{~s}^{-2}} \\
\hline
\end{array}
\)
Choose the correct answer from the options given below:CorrectIncorrectHint
(A) Surface Tension
\(
\begin{aligned}
=\frac{\mathrm{F}}{\ell} & =\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}}=\mathrm{ML}^{-1} \mathrm{~T}^{-2} \\
& =\mathrm{Kg} \mathrm{s}^{-2}(\mathrm{IV})
\end{aligned}
\)
\(
\begin{aligned}
\text { (B) Pressure }=\frac{\mathrm{F}}{\mathrm{A}} & =\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^2} \\
& =\mathrm{kg} \mathrm{m}^{-1} \mathrm{~s}^{-2} \text { (III) }
\end{aligned}
\)
\(
\begin{aligned}
& \text { (C) Viscosity }==\frac{F}{A\left(\frac{d V}{d z}\right)}=\frac{\text { MLT }^{-2}}{L^2\left(\frac{LT{-1}}{L}\right)} \\
& =\mathrm{ML}^{-1} \mathrm{~T}^{-1}=\mathrm{kg} \mathrm{m}^{-1} \mathrm{~s}^{-1}(\mathrm{I}) \\
& \text { (D) Impulse }=\int \mathrm{Fdt}=\mathrm{MLT}^{-2} \times \mathrm{T} \\
& =\mathrm{MLT}^{-1}=\mathrm{Kgms}^{-1} \text { (II) } \\
&
\end{aligned}
\) -
Question 4 of 50
4. Question
Match List I with List II
\(
\begin{array}{|l|l|l|l|}
\hline & \text { List I } & & \text { List II } \\
\hline \text { A } & \text { Young’s Modulus } (\mathrm{Y}) & \text { I. } & {\left[\mathrm{M} \mathrm{L}^{-1} \mathrm{~T}^{-1}\right]} \\
\hline \text { B } & \text { Co-efficient of Viscosity } (\eta) & \text { II. } & {\left[\mathrm{M} \mathrm{L}^2 \mathrm{~T}^{-1}\right]} \\
\hline \text { C } & \text { Planck’s Constant } (\mathrm{h}) & \text { III. } & {\left[\mathrm{M} \mathrm{L}^{-1} \mathrm{~T}^{-2}\right]} \\
\hline \text { D } & \text { Work Function } & (\phi) \text { IV } & {\left[\mathrm{M} \mathrm{L}^2 \mathrm{~T}^{-2}\right]} \\
\hline
\end{array}
\)
Choose the correct answer from the options given below:CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{Y}=\frac{\text { Stress }}{\text { Strain }}=\frac{\mathrm{F} / \mathrm{A}}{\Delta \ell / \ell}=\frac{\left[\mathrm{MLT}^{-2}\right]}{\left[\mathrm{L}^2\right]}=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right] \\
& \mathrm{F}=6 \pi \eta \mathrm{rv} \Rightarrow \eta=\frac{\mathrm{F}}{6 \pi \mathrm{rv}} \\
& {[\eta]=\frac{\left[\mathrm{MLT}^{-2}\right]}{[\mathrm{L}]\left[\mathrm{LT}^{-1}\right]}=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-1}\right]} \\
& \mathrm{E}=\mathrm{h} \nu \Rightarrow \mathrm{h}=\frac{\mathrm{E}}{v}=\frac{\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]}{\left[\mathrm{T}^{-1}\right]}=\left[\mathrm{ML}^2 \mathrm{~T}^{-1}\right]
\end{aligned}
\)
Work function has same dimension as that of energy, so \([\phi]=\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]\) -
Question 5 of 50
5. Question
Match List I with List II :
\(
\begin{array}{|l|l|}
\hline \begin{array}{l}
\text { List-I } \\
\text { (Physical Quantity) }
\end{array} & \begin{array}{l}
\text { List-II } \\
\text { (Dimensional Formula) }
\end{array} \\
\hline \text { A. Pressure gradient } & \mathrm{I. }\left[\mathrm{M}^0 \mathrm{~L}^2 \mathrm{~T}^{-2}\right] \\
\hline \text { B. Energy density } & \text { II. }\left[\mathrm{M}^1 \mathrm{~L}^{-1} \mathrm{~T}^{-2}\right] \\
\hline \text { C. Electric Field } & \text { III. }\left[\mathrm{M}^1 \mathrm{~L}^{-2} \mathrm{~T}^{-2}\right] \\
\hline \text { D. Latent heat } & \mathrm{IV. }\left[\mathrm{M}^1 \mathrm{~L}^1 \mathrm{~T}^{-3} \mathrm{~A}^{-1}\right] \\
\hline
\end{array}
\)
Choose the correct answer from the options given below:CorrectIncorrectHint
\(
\begin{aligned}
& \text { Pressure gradient }=\frac{\mathrm{dp}}{\mathrm{dx}}=\frac{\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]}{[\mathrm{L}]} \\
& =\left[\mathrm{M}^1 \mathrm{~L}^{-2} \mathrm{~T}^{-2}\right] \\
& \text { Energy density }=\frac{\text { energy }}{\text { volume }}=\frac{\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]}{\left[\mathrm{L}^3\right]} \\
& =\left[\mathrm{M}^1 \mathrm{~L}^{-1} \mathrm{~T}^{-2}\right] \\
& \text { Electric field }=\frac{\text { Force }}{\text { charge }}=\frac{\left[\mathrm{MLT}^{-2}\right]}{[\mathrm{A} . \mathrm{T}]} \\
& =\left[\mathrm{M}^1 \mathrm{~L}^1 \mathrm{~T}^{-3} \mathrm{~A}^{-1}\right] \\
& \text { Latent heat }=\frac{\text { heat }}{\text { mass }}=\frac{\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]}{[\mathrm{M}]} \\
& =\left[\mathrm{M}^0 \mathrm{~L}^2 \mathrm{~T}^{-2}\right] \\
&
\end{aligned}
\) -
Question 6 of 50
6. Question
The equation of a circle is given by \(x^2+y^2=a^2\), where \(a\) is the radius. If the equation is modified to change the origin other than \((0,0)\), then find out the correct dimensions of \(\mathrm{A}\) and \(\mathrm{B}\) in a new equation: \((x-A t)^2+\left(y-\frac{t}{B}\right)^2=a^2\).
The dimensions of \(\mathrm{t}\) is given as \(\left[\mathrm{T}^{-1}\right]\).CorrectIncorrectHint
\(
\begin{aligned}
& (\mathrm{x}-\mathrm{At})^2+\left(\mathrm{y}-\frac{\mathrm{t}}{\mathrm{B}}\right)^2=\mathrm{a}^2 \\
& {[\mathrm{At}]=\mathrm{A} \times \frac{1}{\mathrm{~T}}=\mathrm{L}} \\
& \therefore \quad[\mathrm{A}]=\mathrm{T}^1 \mathrm{~L}^1 \\
& \frac{\mathrm{t}}{\mathrm{B}} \text { is in meters } \\
& \therefore \quad \frac{1}{\mathrm{~T}[\mathrm{~B}]}=\mathrm{L} \\
& \therefore \quad[\mathrm{B}]=\mathrm{T}^{-1} \mathrm{~L}^{-1}
\end{aligned}
\) -
Question 7 of 50
7. Question
\(\left(P+\frac{a}{V^2}\right)(V-b)=R T\) represents the equation of state of some gases. Where \(P\) is the pressure, \(V\) is the volume, \(T\) is the temperature and \(a, b, R\) are the constants. The physical quantity, which has dimensional formula as that of \(\frac{b^2}{a}\), will be :
CorrectIncorrectHint
\(
\begin{aligned}
& {[b]=[V]} \\
& \quad\left[\frac{a}{b^2}\right]=[P] \quad \therefore\left[\frac{b^2}{a}\right]=\frac{1}{[P]}=\frac{1}{[B]}=[K]
\end{aligned}
\) -
Question 8 of 50
8. Question
Electric field in a certain region is given by \(\dot{E}=\left(\frac{A}{x^2} \hat{i}+\frac{B}{y^3} \hat{j}\right)\). The SI unit of \(A\) and \(B\) are:
CorrectIncorrectHint
\(
\begin{aligned}
& \vec{E}=\frac{A}{x^2} \hat{i}+\frac{B}{y^3} \hat{j} \\
& {\left[\frac{A}{x^2}\right]=N C^{-1} \Rightarrow[A]=N^2 C^{-1}}
\end{aligned}
\) -
Question 9 of 50
9. Question
Match List I with List II
\(
\begin{array}{|l|l|l|l|}
\hline & \text { List I } & & \text { List II } \\
\hline \text { A } & \text { Torque } & \text { I. } & {\mathrm{kg} \mathrm{~m}^{-1} \mathrm{~s}^{-2}} \\
\hline \text { B } & \text { Energy Density } & \text { II. } & {\mathrm{kg} \mathrm{~ms}^{-1}} \\
\hline \text { C } & \text { Pressure Gradient } & \text { III. } & {\mathrm{kg} \mathrm{~m}^{-2} \mathrm{~s}^{-2}} \\
\hline \text { D } & \text { Impulse } & \text { IV } & {\mathrm{kg} \mathrm{~m}^2 \mathrm{~s}^{-2}} \\
\hline
\end{array}
\)
Choose the correct answer from the options given below:CorrectIncorrectHint
\(
\text { A-IV, B-I, C-III, D-II }
\) -
Question 10 of 50
10. Question
If \(\mathrm{R}, \mathrm{X}_{\mathrm{L}}\) and \(\mathrm{X}_{\mathrm{C}}\) represent resistance, inductive reactance and capacitive reactance. Then which of the following is dimensionless:
CorrectIncorrectHint
All three have same dimension therefore \(\frac{\mathrm{R}}{\sqrt{\mathrm{X}_{\mathrm{L}} \mathrm{X}_{\mathrm{C}}}}\) is dimensionless.
-
Question 11 of 50
11. Question
Match List I with List II
\(
\begin{array}{|l|l|l|l|}
\hline & \text { List-I } & & \text { List-II } \\
\hline \text { A. } & \begin{array}{l}
\text { Angular } \\
\text { momentum }
\end{array} & \text { I } & {\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]} \\
\hline \text { B } & \text { Torque } & \text { II } & {\left[\mathrm{ML}^{-2} \mathrm{~T}^{-2}\right]} \\
\hline \text { C } & \text { Stress } & \text { III } & {\left[\mathrm{ML}^2 \mathrm{~T}^{-1}\right]} \\
\hline \text { D } & \text { Pressure gradient } & \text { IV } & {\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]} \\
\hline
\end{array}
\)
Choose the correct answer from the options given below:CorrectIncorrectHint
A-III, B-I, C-IV, D-II
-
Question 12 of 50
12. Question
If the velocity of light \(\mathbf{c}\), universal gravitational constant \(\mathrm{G}\) and planck’s constant \(\mathrm{h}\) are chosen as fundamental quantities. The dimensions of mass in the new system is:
CorrectIncorrectHint
Say dimensional formale of mass is \(\mathrm{H}^{\mathrm{x}} \mathrm{C}^{\mathrm{y}} \mathrm{G}^{\mathrm{z}}\)
\(
\begin{aligned}
& M^1=\left(M L^2 T^{-1}\right)^x\left(L^{-1}\right)\left(M^{-1} L^3 T^{-2}\right)^z \\
& M^1 L^0 T^0=M^{x-z} L^{2 x+y+3 z} T^{-x-y-2 z}
\end{aligned}
\)
on comparing both side
\(
\begin{aligned}
& x-z=1 \\
& 2 x+y+3 z=0 \\
& -x-y-2 z=0
\end{aligned}
\)
On solving above equations we get
\(
x=\frac{1}{2} \quad y=\frac{1}{2} \quad z=\frac{-1}{2}
\) -
Question 13 of 50
13. Question
The velocity time graph of a body moving in a straight line is shown in figure.
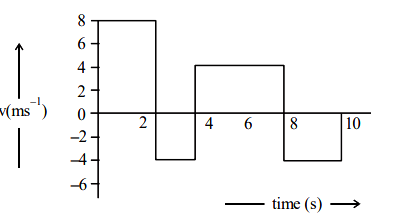
The ratio of displacement to distance travelled by the body in time 0 to \(10 \mathrm{~s}\) is
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Displacement }=\Sigma \text { area }=16-8+16-8=16 \mathrm{~m} \\
& \text { Distance }=\Sigma \mid \text { area } \mid=48 \mathrm{~m} \\
& \frac{\text { displacement }}{\text { Distance }}=\frac{1}{3}
\end{aligned}
\) -
Question 14 of 50
14. Question
A car travels a distance of ‘ \(x\) ‘ with speed \(V_1\) and then same distance ‘ \(x\) ‘ with speed \(V_2\) in the same direction. The average speed of the car is:
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Average velocity }=\frac{\text { Total displacement }}{\text { Total time }} \\
& =\frac{\mathrm{x}+\mathrm{x}}{\frac{\mathrm{x}}{\mathrm{v}_1}+\frac{\mathrm{x}}{\mathrm{v}_2}}=\frac{2 \mathrm{v}_1 \mathrm{v}_2}{\mathrm{v}_1+\mathrm{v}_2}
\end{aligned}
\) -
Question 15 of 50
15. Question
The distance travelled by a particle is related to time \(t\) as \(x=4 t^2\). The velocity of the particle at \(t=\) \(5 \mathrm{~s}\) is .
CorrectIncorrectHint
\(
\begin{aligned}
& x=4 t^2 \\
& v=\frac{d x}{d t}=8 t
\end{aligned}
\)At \(\mathrm{t}=5 \mathrm{sec}\)
\(
\mathrm{v}=8 \times 5=40 \mathrm{~m} / \mathrm{s}
\) -
Question 16 of 50
16. Question
A tennis ball is dropped on to the floor from a height of \(9.8 \mathrm{~m}\). It rebounds to a height \(5.0 \mathrm{~m}\). Ball comes in contact with the floor for \(0.2 \mathrm{~s}\). The average acceleration during contact is _______ \(\mathrm{ms}^{-2}\). [Given \(\mathrm{g}=10 \mathrm{~ms}^{-2}\) ]
CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{v}_{\mathrm{i}}=\sqrt{2 \mathrm{gh}_{\mathrm{i}}} \\
& =\sqrt{2 \times 10 \times 9.8} \downarrow \\
& =14 \mathrm{~m} / \mathrm{s} \downarrow
\end{aligned}
\)
\(
\begin{aligned}
& \mathrm{v}_{\mathrm{f}}=\sqrt{2 \mathrm{gh}_{\mathrm{f}}} \\
& =\sqrt{2 \times 10 \times 5} \uparrow \\
& =\mathbf{1 0} \mathbf{~ m} / \mathbf{s} \uparrow
\end{aligned}
\)
\(
\left|\overrightarrow{\mathrm{a}}_{\mathrm{avg}}\right|=\left|\frac{\Delta \overrightarrow{\mathrm{v}}}{\Delta \mathrm{t}}\right|=\frac{24}{0.2}=120 \mathrm{~m} / \mathrm{s}^2
\) -
Question 17 of 50
17. Question
Match Column-I with Column-II :
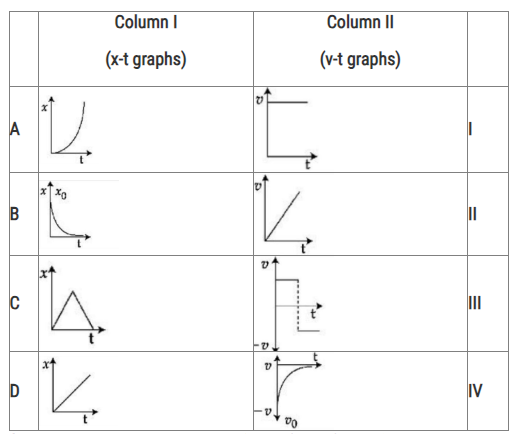
Choose the correct answer from the options given below:
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{\mathrm{dx}}{\mathrm{dt}}=\text { slope } \geq 0 \text { always increasing } \\
& (\mathrm{A}-\mathrm{II}) \\
& \frac{\mathrm{dx}}{\mathrm{dt}}<0 ; \text { and at } \mathrm{t} \rightarrow \infty \frac{\mathrm{dx}}{\mathrm{dt}} \rightarrow 0 \\
& (\mathrm{~B}-\mathrm{IV}) \\
& \frac{\mathrm{dx}}{\mathrm{dt}}>0 \text { for first half } \frac{\mathrm{dx}}{\mathrm{dt}}<0 \text { for second half } \\
& (\mathrm{C}-\mathrm{III}) \\
& \frac{\mathrm{dx}}{\mathrm{dt}}=\text { constant }
\end{aligned}
\) -
Question 18 of 50
18. Question
A horse rider covers half the distance with \(5 \mathrm{~m} / \mathrm{s}\) speed. The remaining part of the distance was travelled with speed \(10 \mathrm{~m} / \mathrm{s}\) for half the time and with speed \(15 \mathrm{~m} / \mathrm{s}\) for other half of the time. The mean speed of the rider averaged over the whole time of motion is \(x / 7 \mathrm{~m} / \mathrm{s}\). The value of \(x\) is
CorrectIncorrectHint
\(
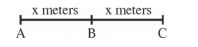
t_{A B}=\frac{x}{5 m / s}
\)
In motion \(B C\)
\(
x=d_1+d_2
\)
where \(d_1 \& d_2\) we the distance travelled with \(10 \mathrm{~m} / \mathrm{s}\) and \(15 \mathrm{~m} / \mathrm{s}\) respectively in equal time intervals \(\frac{t}{2}\) each
\(
\begin{aligned}
& d_1=\frac{10 t}{2}, d_2=\frac{15 t}{2} \\
& d_1+d_2=x=\frac{t}{2}(10+15)=\frac{25 t}{2}
\end{aligned}
\)
\(
\langle v\rangle=\frac{2 x}{\frac{x}{5}+\frac{2 x}{25}}=\frac{2 \times 25}{5+2}=\frac{50}{7} \mathrm{~m} / \mathrm{s}
\) -
Question 19 of 50
19. Question
An object is allowed to fall from a height \(\mathrm{R}\) above the earth, where \(\mathrm{R}\) is the radius of earth. Its velocity when it strikes the earth’s surface, ignoring air resistance, will be :
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Loss in } \mathrm{PE}=\text { Gain in KE } \\
& \left(-\frac{\mathrm{GMm}}{2 \mathrm{R}}\right)-\left(-\frac{\mathrm{GMm}}{\mathrm{R}}\right)=\frac{1}{2} \mathrm{mv}^2 \\
& \Rightarrow \mathrm{v}^2=\frac{\mathrm{GM}}{\mathrm{R}}=\mathrm{gR} \\
& \Rightarrow \mathrm{v}=\sqrt{\mathrm{gR}}
\end{aligned}
\) -
Question 20 of 50
20. Question
A vehicle travels \(4 \mathrm{~km}\) with speed of \(3 \mathrm{~km} / \mathrm{h}\) and another \(4 \mathrm{~km}\) with speed of \(5 \mathrm{~km} / \mathrm{h}\), then its average speed is :
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{2}{\mathrm{~V}_{\mathrm{av}}}=\frac{1}{3}+\frac{1}{5}=\frac{8}{15} \\
& \Rightarrow \mathrm{V}_{\mathrm{av}}=\frac{15}{4}=3.75 \mathrm{~km} / \mathrm{h}
\end{aligned}
\) -
Question 21 of 50
21. Question
A body is moving with constant speed, in a circle of radius \(10 \mathrm{~m}\). The body completes one revolution in \(4 \mathrm{~s}\). At the end of 3rd second, the displacement of body (in \(\mathrm{m}\) ) from its starting point is:
CorrectIncorrectHint
\(
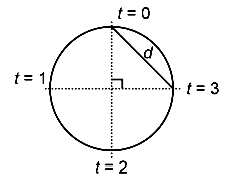
\begin{aligned}
& \omega=\frac{2 \pi}{\mathrm{T}}=\frac{2 \pi}{4}=\frac{\pi}{2} \mathrm{rad} / \mathrm{s} \\
& \theta=\omega \mathrm{t} \\
& \theta=\frac{\pi}{2} \times 3 \\
& \theta=\frac{3 \pi}{2} \mathrm{rad}
\end{aligned}
\)
\(
\begin{aligned}
&r=10 \mathrm{~m}\\
&T=4 \mathrm{sec}\\
&d=\sqrt{2}(10) \mathrm{m}
\end{aligned}
\) -
Question 22 of 50
22. Question
An object moves with speed \(v_1, v_2\), and \(v_3\) along a line segment \(A B, B C\) and \(C D\) respectively as shown in figure. Where \(\mathrm{AB}=\mathrm{BC}\) and \(\mathrm{AD}=3 \mathrm{AB}\), then average speed of the object will be :
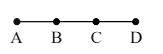CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{AB}=x \\
& \mathrm{BC}=x \\
& 2 x+\mathrm{CD}=3 x \\
& \mathrm{CD}=x \\
& \langle\mathrm{v}\rangle=\frac{3 x}{\frac{x}{v_1}+\frac{x}{v_2}+\frac{x}{v_3}}=\frac{3 v_1 v_2 v_3}{v_2 v_3+v_1 v_3+v_1 v_2}
\end{aligned}
\) -
Question 23 of 50
23. Question
For a train engine moving with speed of \(20 \mathrm{~ms}^{-1}\). the driver must apply brakes at a distance of \(500 \mathrm{~m}\) before the station for the train to come to rest at the station. If the brakes were applied at half of this distance, the train engine would cross the station with speed \(\sqrt{\mathrm{x}} \mathrm{ms}^{-1}\). The value of \(\mathrm{x}\) is _____. (Assuming same retardation is produced by brakes)
CorrectIncorrectHint
\(
\mathrm{u}=20 \mathrm{~m} / \mathrm{s}, \mathrm{S}_1=500 \mathrm{~m}, \mathrm{v}=0
\)
By third equation of mation
\(
\begin{aligned}
& 0=(20)^2-2 \mathrm{a} \cdot 500 \Rightarrow \mathrm{a}=\frac{4}{10} \mathrm{~m} / \mathrm{s}^2 \\
& \mathrm{u}=20 \mathrm{~m} / \mathrm{s}, \mathrm{S}_2=250 \mathrm{~m}, \mathrm{v}=? \\
& \mathrm{v}^2=(20)^2-2 \mathrm{a} \cdot 250 \\
& =\mathrm{v}=\sqrt{200} \mathrm{~m} / \mathrm{s} \\
& \mathrm{x}=200
\end{aligned}
\) -
Question 24 of 50
24. Question
The maximum vertical height to which a man can throw a ball is \(136 \mathrm{~m}\). The maximum horizontal distance upto which he can throw the same ball is
CorrectIncorrectHint
\(
\mathrm{H}_{\max }=\frac{\mathrm{v}^2}{2 \mathrm{~g}}=136 \mathrm{~m}
\)\(
\begin{aligned}
& \mathrm{R}_{\max }=\frac{\mathrm{v}^2}{\mathrm{~g}}=2 \mathrm{H}_{\max } \\
& =2(136) \\
& =272 \mathrm{~m}
\end{aligned}
\) -
Question 25 of 50
25. Question
Two objects are projected with same velocity ‘ \(u\) ‘ however at different angles \(\alpha\) and \(\beta\) with the horizontal. If \(\alpha+\beta=90^{\circ}\), the ratio of horizontal range of the first object to the \(2^{\text {nd }}\) object will be :
CorrectIncorrectHint
\(
\text { Range }=\frac{\mathrm{u}^2 \sin 2 \theta}{\mathrm{g}}
\)Range for projection angle ” \(\alpha\) “
\(
\mathrm{R}_1=\frac{\mathrm{u}^2 \sin 2 \alpha}{\mathrm{g}}
\)Range for projection angle ” \(\beta\) “
\(
\mathrm{R}_2=\frac{\mathrm{u}^2 \sin 2 \beta}{\mathrm{g}}
\)
\(
\begin{aligned}
& \alpha+\beta=90^{\circ}(\text { Given }) \\
& \Rightarrow \beta=90^{\circ}-\alpha \\
& \mathrm{R}_2=\frac{\mathrm{u}^2 \sin 2\left(90^{\circ}-\alpha\right)}{\mathrm{g}} \\
& \mathrm{R}_2=\frac{\mathrm{u}^2 \sin \left(180^{\circ}-2 \alpha\right)}{\mathrm{g}} \\
& \mathrm{R}_2=\frac{\mathrm{u}^2 \sin 2 \alpha}{\mathrm{g}} \\
& \Rightarrow \frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{\left(\frac{\mathrm{u}^2 \sin 2 \alpha}{\mathrm{g}}\right)}{\left(\frac{\mathrm{u}^2 \sin 2 \alpha}{\mathrm{g}}\right)}=\frac{1}{1}
\end{aligned}
\) -
Question 26 of 50
26. Question
A stone is projected at angle \(30^{\circ}\) to the horizontal. The ratio of kinetic energy of the stone at point of projection to its kinetic energy at the highest point of flight will be :
CorrectIncorrectHint
\(
\frac{\mathrm{KE}_{\text {pop }}}{\mathrm{KE}_{\text {top }}}=\frac{\frac{1}{2} \mathrm{M}(\mathrm{u})^2}{\frac{1}{2} \mathrm{M}\left(\mathrm{u} \cos 30^{\circ}\right)^2}=\frac{4}{3}
\) -
Question 27 of 50
27. Question
A particle of mass \(100 \mathrm{~g}\) is projected at time \(\mathrm{t}=0\) with a speed \(20 \mathrm{~ms}^{-1}\) at an angle \(45^{\circ}\) to the horizontal as given in the figure. The magnitude of the angular momentum of the particle about the starting point at time \(t=2 \mathrm{~s}\) is found to be \(\sqrt{\mathrm{K}} \mathrm{kg} \mathrm{m}^2 / \mathrm{s}\). The value of \(\mathrm{K}\) is ____. \(\left(\text { Take } g=10 \mathrm{~ms}^{-2}\right)\)
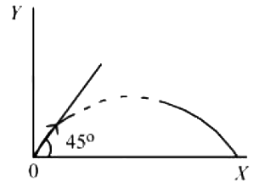CorrectIncorrectHint
\(
\text { Use } \Delta \mathrm{L}=\int_0^{\mathrm{t}} \tau \mathrm{dt}
\)
\(
L_0=\int_0^2 m g\left(v_x t\right) d t
\)
\(
=\operatorname{mg} {{v_x}} \frac{\mathrm{t}^2}{2}=(0.1)(10)(10 \sqrt{2}) \frac{2^2}{2}
\)
\(
\begin{aligned}
& =20 \sqrt{2} \\
& =\sqrt{800} \mathrm{~kg} \mathrm{~m}^2 / \mathrm{s}
\end{aligned}
\) -
Question 28 of 50
28. Question
The initial speed of a projectile fired from ground is \(u\). At the highest point during its motion, the speed of projectile is \(\frac{\sqrt{3}}{2} \mathrm{u}\). The time of flight of the projectile is:
CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{u} \cos \theta=\frac{\sqrt{3} \mathrm{u}}{2} \Rightarrow \cos \theta=\frac{\sqrt{3}}{2} \\
& \Rightarrow \theta=30^{\circ} \\
& \mathrm{T}=\frac{2 \mathrm{u} \sin 30^{\circ}}{\mathrm{g}}=\frac{\mathrm{u}}{\mathrm{g}}
\end{aligned}
\) -
Question 29 of 50
29. Question
The speed of a swimmer is \(4 \mathrm{~km} \mathrm{~h}^{-1}\) in still water. If the swimmer makes his strokes normal to the flow of river of width \(1 \mathrm{~km}\), he reaches a point \(750 \mathrm{~m}\) down the stream on the opposite bank. The speed of the river water is ___ \(\mathrm{km} \mathrm{h}^{-1}\).
CorrectIncorrectHint
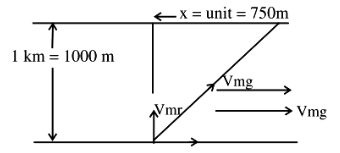
Time to cross the River width \(\omega=1000 \mathrm{~m} \text { is }=\frac{1 \mathrm{~km}}{4 \mathrm{~km} / \mathrm{h}}\)
Drift \(\mathrm{x}=\mathrm{Vm} / \mathrm{g} \times \mathrm{t}\)
Where \(\mathrm{Vm} / \mathrm{g}\) is velocity of River w.r. to ground.
\(
\begin{aligned}
& \mathrm{x}=\mathrm{Vm} / \mathrm{g} \times \frac{1}{4}=750 \mathrm{~m}=\frac{3}{4} \mathrm{~km} \\
& \mathrm{Vm} / \mathrm{g}=3 \mathrm{~km} / \mathrm{hr}
\end{aligned}
\) -
Question 30 of 50
30. Question
Two bodies are projected from ground with same speeds \(40 \mathrm{~ms}^{-1}\) at two different angles with respect to horizontal. The bodies were found to have same range. If one of the body was projected at an angle of \(60^{\circ}\), with horizontal then sum of the maximum heights, attained by the two projectiles, is ____ m. (Given \(\mathrm{g}=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
\(
\begin{aligned}
& \theta_1+\theta_2=90^{\circ} \\
& \Rightarrow \theta_2=30^{\circ} \\
& \Rightarrow\left(H_{\max }\right)_1+\left(H_{\max }\right)_2 \\
& =\frac{U^2 \sin ^2 \theta_1}{2 g}+\frac{U^2 \sin ^2 \theta_2}{2 g} \\
& =\frac{40^2}{20}\left(\frac{1}{4}+\frac{3}{4}\right)=80 \mathrm{~m}
\end{aligned}
\) -
Question 31 of 50
31. Question
A child stands on the edge of the cliff \(10 \mathrm{~m}\) above the ground and throws a stone horizontally with an initial speed of \(5 \mathrm{~ms}^{-1}\). Neglecting the air resistance, the speed with which the stone hits the ground will be _____ \(\mathrm{ms}^{-1}\) (given, \(\mathrm{g}=10 \mathrm{~ms}^{-2}\) ).
CorrectIncorrectHint
\(
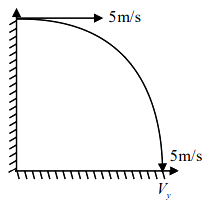
\begin{aligned}
& \mathrm{v}_{\mathrm{y}}=\sqrt{2 g h}=\sqrt{200} \\
& v_{n e t}=\sqrt{25+200}=15 \mathrm{~m} / \mathrm{s}
\end{aligned}
\) -
Question 32 of 50
32. Question
As per given figure, a weightless pulley \(P\) is attached on a double inclined frictionless surface. The tension in the string (massless) will be (if \(g=\) \(10 \mathrm{~m} / \mathrm{s}^2\) )
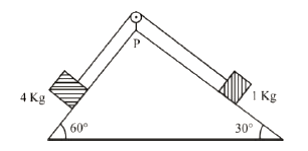CorrectIncorrectHint
\(
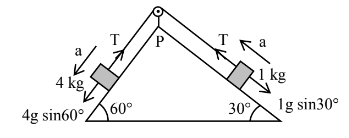
4 g \sin 60^{\circ}-T=4 a \dots(1)
\)\(
\mathrm{T}-\mathrm{g} \sin 30^{\circ}=\mathrm{a} \dots(2)
\)\(
\begin{aligned}
& 4 \mathrm{~g} \frac{\sqrt{3}}{2}-\mathrm{T}=4 \mathrm{a} \\
& \mathrm{T}-\frac{\mathrm{g}}{2}=1 \mathrm{a} \\
& 2 \sqrt{3} \mathrm{~g}-\mathrm{T}=4\left(\mathrm{~T}-\frac{\mathrm{g}}{2}\right) \Rightarrow 5 \mathrm{~T}=(2 \sqrt{3}+2) \mathrm{g} \\
& \mathrm{T}=\frac{10}{5}(2 \sqrt{3}+2) \Rightarrow \mathrm{T}=4(\sqrt{3}+1) \mathrm{N}
\end{aligned}
\) -
Question 33 of 50
33. Question
Given below are two statements :
Statement-I : An elevator can go up or down with uniform speed when its weight is balanced with the tension of its cable.
Statement-II : Force exerted by the floor of an elevator on the foot of a person standing on it is more than his/her weight when the elevator goes down with increasing speed.
In the light of the above statements, choose the correct answer from the options given below :CorrectIncorrectHint
Statement-1: When elevator is moving with uniform speed \(\mathrm{T}=\mathrm{F}_{\mathrm{g}}\)
Statement-2
When elevator is going down with increasing speed, its acceleration is downward.
Hence
\(
\mathrm{W}-\mathrm{N}=\frac{\mathrm{W}}{\mathrm{g}} \times \mathrm{a}
\)
\(\mathrm{N}=\mathrm{W}\left(1-\frac{\mathrm{a}}{\mathrm{g}}\right)\) i.e. less than weight. -
Question 34 of 50
34. Question
Consider a block kept on an inclined plane (inclined at \(45^{\circ}\) ) as shown in the figure. If the force required to just push it up the incline is 2 times the force required to just prevent it from sliding down, the coefficient of friction between the block and inclined plane \((\mu)\) is equal to :
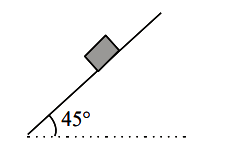CorrectIncorrectHint
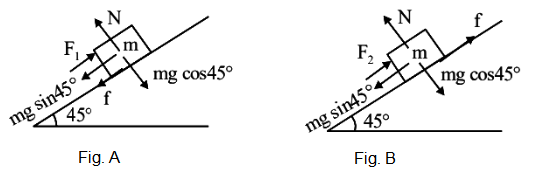
From Fig.A:
\(
\begin{aligned}
& \mathrm{F}_1=\mathrm{mg} \sin 45^{\circ}+\mathrm{f}=\mathrm{mg} \sin 45^{\circ}+\mu \mathrm{N} \\
& \mathrm{F}_1=\frac{\mathrm{mg}}{\sqrt{2}}+\mu \mathrm{mg} \cos 45^{\circ} \\
& \mathrm{F}_1=\frac{\mathrm{mg}}{\sqrt{2}}(1+\mu)
\end{aligned}
\)From Fig.B:
\(
\begin{aligned}
& \mathrm{F}_2=\mathrm{mg} \sin 45^{\circ}-\mathrm{f}=\mathrm{mg} \sin 45^{\circ}-\mu \mathrm{N} \\
& =\frac{\mathrm{mg}}{\sqrt{2}}(1-\mu) \\
& \mathrm{F}_1=2 \mathrm{~F}_2 \\
& \frac{\mathrm{mg}}{\sqrt{2}}(1+\mu)=2 \frac{\mathrm{mg}}{\sqrt{2}}(1-\mu) \\
& 1+\mu=2-2 \mu \\
& \mu=1 / 3=0.33
\end{aligned}
\) -
Question 35 of 50
35. Question
A block of mass \(m\) slides down the plane inclined at angle \(30^{\circ}\) with an acceleration \(\frac{g}{4}\). The value of coefficient of kinetic friction will be :
CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{Mg} \sin 30^{\circ}-\mu \mathrm{mg} \cos 30^{\circ}=\mathrm{ma} \\
& \frac{\mathrm{g}}{2}-\frac{\sqrt{3}}{2} \cdot \mu \mathrm{g}=\frac{\mathrm{g}}{4}
\end{aligned}
\)
\(
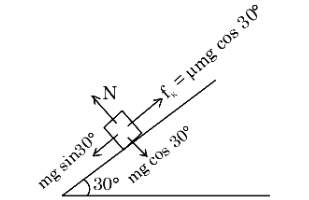
\begin{aligned}
& \frac{\sqrt{3}}{2} \mu=\frac{1}{4} \\
& \mu=\frac{1}{2 \sqrt{3}}
\end{aligned}
\) -
Question 36 of 50
36. Question
Force acts for \(20 \mathrm{~s}\) on a body of mass \(20 \mathrm{~kg}\), starting from rest, after which the force ceases and then body describes \(50 \mathrm{~m}\) in the next \(10 \mathrm{~s}\). The value of force will be :
CorrectIncorrectHint
\(
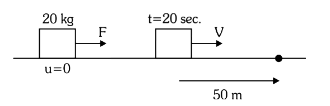
\begin{aligned}
& 50=\mathrm{V} \times 10 \\
& \mathrm{~V}=5 \mathrm{~m} / \mathrm{s} \\
& \mathrm{V}=0+\mathrm{a} \times 20 \\
& 5=\mathrm{a} \times 20 \\
& \mathrm{a}=\frac{1}{4} \mathrm{~m} / \mathrm{s}^2 \\
& \mathrm{~F}=\mathrm{ma}=20 \times \frac{1}{4}=5 \mathrm{~N}
\end{aligned}
\) -
Question 37 of 50
37. Question
The time taken by an object to slide down \(45^{\circ}\) rough inclined plane is \(\mathrm{n}\) times as it takes to slide down a perfectly smooth \(45^{\circ}\) incline plane. The coefficient of kinetic friction between the object and the incline plane is
CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{a}_1=\mathrm{g} \sin \theta=\mathrm{g} / \sqrt{2} \\
& \mathrm{a}_2=\mathrm{g} \sin \theta-\mathrm{{\mu_k}g} \cos \theta=\frac{\mathrm{g}}{\sqrt{2}}-\frac{\mathrm{{\mu_k}g}}{\sqrt{2}} \\
& \mathrm{t}_2=\mathrm{nt}_1 \quad \& \quad \mathrm{a}_1 \mathrm{t}_1^2=\mathrm{a}_2 \mathrm{t}_2^2 \\
& \frac{\mathrm{g}}{\sqrt{2}} \mathrm{t}_1^2=\left(\frac{\mathrm{g}}{\sqrt{2}}-\frac{\mathrm{{\mu_k}g}}{\sqrt{2}}\right) \mathrm{n}^2 \mathrm{t}_1^2 \\
& \mathrm{~\mu_k}=1-\frac{1}{\mathrm{n}^2}Â
\end{aligned}
\)Note:
since both starts From \(\mathrm{O}\) i.e. from rest and the distance (S) is same then
\(
\begin{aligned}
& \mathrm{S}_1=\mathrm{S}_2 \\
& \frac{1}{2} \mathrm{{a_1}{t_1}}^2=\frac{1}{2} \mathrm{a_2}(\mathrm{nt_2})^2
\end{aligned}
\)
-
Question 38 of 50
38. Question
The figure represents the momentum time \((p-t)\) curve for a particle moving along an axis under the influence of the force. Identify the regions on the graph where the magnitude of the force is maximum and minimum respectively?
\(
\text { If }\left(t_3-t_2\right)<t_1 \text {. }
\)
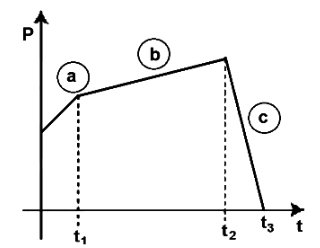CorrectIncorrectHint
\(\left|\frac{\mathrm{d} \overrightarrow{\mathrm{p}}}{\mathrm{dt}}\right|=|\overrightarrow{\mathrm{F}}| \Rightarrow \frac{\mathrm{d} \overrightarrow{\mathrm{p}}}{\mathrm{dt}}=\) Slope of curve
max slope (c)
min slope (b) -
Question 39 of 50
39. Question
A block of \(\sqrt{3} \mathrm{~kg}\) is attached to a string whose other end is attached to the wall. An unknown force \(\mathrm{F}\) is applied so that the string makes an angle of \(30^{\circ}\) with the wall. The tension \(\mathrm{T}\) is :
(Given \(\mathrm{g}=10 \mathrm{~ms}^{-2}\) )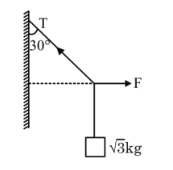
CorrectIncorrectHint
\(
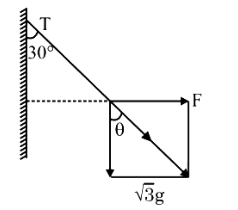
\begin{aligned}
& \theta=30^{\circ} \\
& \cos \theta=\frac{\sqrt{3} \mathrm{~g}}{\mathrm{~T}} \\
& \Rightarrow \frac{\sqrt{3}}{2}=\frac{\sqrt{3} \mathrm{~g}}{\mathrm{~T}} \\
& \Rightarrow \mathrm{T}=20 \mathrm{~N}
\end{aligned}
\) -
Question 40 of 50
40. Question
A stone tied to \(180 \mathrm{~cm}\) long string at its end is making 28 revolutions in horizontal circle in every minute. The magnitude of acceleration of stone is \(\frac{1936}{\mathrm{x}} \mathrm{ms}^{-2}\). The value of \(\mathrm{x}\) ____.
\(
\left(\text { Take } \pi=\frac{22}{7}\right)
\)CorrectIncorrectHint
Acceleration of stone \(a=\frac{v^2}{r}=\omega^2 R\)
\(
\begin{aligned}
a & =\left(\frac{28 \times 2}{60} \times \frac{22}{7}\right)^2 \times 1.8 \\
& =\frac{1936}{125}
\end{aligned}
\)So, \(x=125\)
-
Question 41 of 50
41. Question
As shown in figure, a \(70 \mathrm{~kg}\) garden roller is pushed with a force of \(\overrightarrow{\mathrm{F}}=200 \mathrm{~N}\) at an angle of \(30^{\circ}\) with horizontal. The normal reaction on the roller is (Given \(\mathrm{g}=10 \mathrm{~m} \mathrm{~s}^{-2}\) )
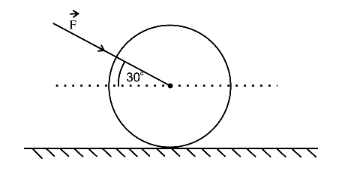CorrectIncorrectHint
\(
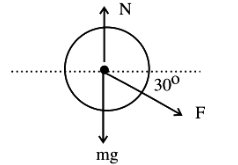
\begin{aligned}
\mathrm{N} & =\mathrm{mg}+\mathrm{F} \sin 30^{\circ} \\
& =700+200 \times \frac{1}{2}=800 \text { newton } .
\end{aligned}
\) -
Question 42 of 50
42. Question
A lift of mass \(M=500 \mathrm{~kg}\) is descending with speed of \(2 \mathrm{~ms}^{-1}\). Its supporting cable begins to slip thus allowing it to fall with a constant acceleration of \(2 \mathrm{~ms}^{-2}\). The kinetic energy of the lift at the end of fall through to a distance of \(6 \mathrm{~m}\) will be ______ \(\mathrm{kJ}\).
CorrectIncorrectHint
\(
\begin{aligned}
&\begin{aligned}
v^2 & =u^2+2 a s \\
& =2^2+2(2)(6) \\
& =4+24=28
\end{aligned}\\
&\begin{aligned}
\mathrm{KE} & =\frac{1}{2} \mathrm{mv}^2 \\
& =\frac{1}{2}(500) 28 \\
& =7000 \mathrm{~J} \\
& =7 \mathrm{~kJ}
\end{aligned}
\end{aligned}
\) -
Question 43 of 50
43. Question
A stone of mass \(1 \mathrm{~kg}\) is tied to end of a massless string of length \(1 \mathrm{~m}\). If the breaking tension of the string is \(400 \mathrm{~N}\), then maximum linear velocity, the stone can have without breaking the string, while rotating in horizontal plane, is:
CorrectIncorrectHint
\(
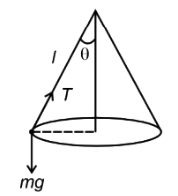
\begin{aligned}
& T \sin \theta=\frac{m v^2}{l \sin \theta} \\
& \cos \theta=\frac{m g}{T} \ldots \ldots(1) \\
& \sin ^2 \theta=\frac{m v^2}{T l} \ldots(2)
\end{aligned}
\)From (1) and (2),
\(
\begin{aligned}
& 1=\left(\frac{m g}{T}\right)^2+\frac{m v^2}{T l} \\
& \Rightarrow 1=\left(\frac{10}{400}\right)^2+\frac{v^2}{400} \\
& \Rightarrow v^2=399.78 \\
& \Rightarrow v=20 \mathrm{~m} / \mathrm{s}
\end{aligned}
\) -
Question 44 of 50
44. Question
A body of mass \(10 \mathrm{~kg}\) is moving with an initial speed of \(20 \mathrm{~m} / \mathrm{s}\). The body stops after \(5 \mathrm{~s}\) due to friction between body and the floor. The value of the coefficient of friction is: (Take acceleration due to gravity \(\mathrm{g}=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
\(
\begin{aligned}
& a=-\mu g \\
& \because v=u+a t \\
& 0=20+(-\mu \times 10) \times 5 \\
& 50 \mu=20 \\
& \mu=\frac{2}{5}=0.4
\end{aligned}
\) -
Question 45 of 50
45. Question
A block of mass \(5 \mathrm{~kg}\) is placed at rest on a table of rough surface. Now, if a force of \(30 \mathrm{~N}\) is applied in the direction parallel to surface of the table, the block slides through a distance of \(50 \mathrm{~m}\) in an interval of time \(10 \mathrm{~s}\). Coefficient of kinetic friction is (given, \(\mathrm{g}=10 \mathrm{~ms}^{-2}\) ):
CorrectIncorrectHint
\(
\begin{aligned}
& S=u t+\frac{1}{2} a t^2 \\
& 50=0+\frac{1}{2} \times a \times 100 \\
& a=1 \mathrm{~m} / \mathrm{s}^2 \\
& F-\mu m g=m a \\
& 30-\mu \times 50=5 \times 1 \\
& 50 \mu=25 \\
& \mu=\frac{1}{2}
\end{aligned}
\) -
Question 46 of 50
46. Question
As shown in the figure a block of mass \(10 \mathrm{~kg}\) lying on a horizontal surface is pulled by a force \(\mathrm{F}\) acting at an angle \(30^{\circ}\), with horizontal. For \(\mu_{\mathrm{s}}=0.25\), the block will just start to move for the value of \(\mathrm{F}\) : [Given \(\mathrm{g}=10 \mathrm{~ms}^{-2}\) ]
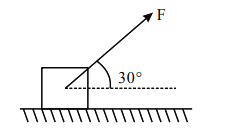CorrectIncorrectHint
\(
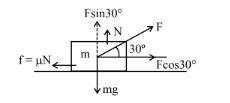
\begin{aligned}
& F \cos 30^{\circ}=\mu_s N \ldots \ldots(1) \\
& F \sin 30^{\circ}+\mathrm{N}=\mathrm{mg} \\
& \Rightarrow \mathrm{N}=\mathrm{mg}-\mathrm{F} \sin 30^{\circ} \ldots(2)
\end{aligned}
\)From equation 1,
\(
\begin{aligned}
& \mathrm{F} \cos 30^{\circ}=\mu_{\mathrm{s}}\left(\mathrm{mg}-\mathrm{F} \sin 30^{\circ}\right) \\
& \mathrm{F} \cos 30^{\circ}=\mu_{\mathrm{s}} \mathrm{mg}-\mu_{\mathrm{s}} \mathrm{F} \sin 30^{\circ} \\
& \mathrm{F}\left(\cos 30^{\circ}+\mu_{\mathrm{s}} \sin 30^{\circ}\right)=\mu_{\mathrm{s}} \mathrm{mg} \\
& \mathrm{F}=\frac{\mu_{\mathrm{s}} \mathrm{mg}}{\cos 30^{\circ}+\mu_{\mathrm{s}} \sin 30^{\circ}}=\frac{0.25 \times 10 \times 10}{\sqrt{3} / 2 \times 0.25 \times 1 / 2} \\
& \Rightarrow \mathrm{F}=\frac{25}{\sqrt{3} / 2+\frac{0.25}{2}}=\frac{50}{1.73+0.25}=\frac{50}{1.98}=25.2 \mathrm{~N}
\end{aligned}
\) -
Question 47 of 50
47. Question
Identify the pair of physical quantities which have different dimensions :
CorrectIncorrectHint
\(
\begin{aligned}
&\mathrm{S}=\frac{\mathrm{Q}}{\mathrm{m} \Delta \mathrm{T}}=\frac{\mathrm{J}}{\mathrm{Kg}^{\circ} \mathrm{C}}\\
&\mathrm{L}=\frac{\mathrm{Q}}{\mathrm{m}}=\frac{\mathrm{J}}{\mathrm{Kg}}
\end{aligned}
\)Therefore, they have different dimensions.
-
Question 48 of 50
48. Question
Identify the pair of physical quantities that have same dimensions :
CorrectIncorrectHint
Velocity gradient \(=\frac{d v}{d x}=\frac{1}{S}\)
\(\Rightarrow\) Dimensions are \(\frac{\left[L T^{-1}\right]}{[L]}=\left[T^{-1}\right]\)
Decay constant \(\lambda\) has dimensions of \(\left[T^{-1}\right]\) because of the relation \(
\lambda=\frac{1}{\mathrm{~S}}
\)
\(\Rightarrow\) Velocity gradient and decay constant have same dimensions. -
Question 49 of 50
49. Question
An expression for a dimensionless quantity \(\mathrm{P}\) is given by \(\mathrm{P}=\frac{\alpha}{\beta} \log _{\mathrm{e}}\left(\frac{\mathrm{kt}}{\beta \mathrm{x}}\right)\); where \(\alpha\) and \(\beta\) are constants, \(\mathrm{x}\) is distance ; \(\mathrm{k}\) is Boltzmann constant and \(t\) is the temperature. Then the dimensions of \(\alpha\) will be :
CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{P}=\frac{\alpha}{\beta} \log _{\mathrm{e}}\left(\frac{\mathrm{kt}}{\beta \mathrm{x}}\right) \\
& \frac{\mathrm{kt}}{\beta \mathrm{x}}=1 \Rightarrow \beta=\frac{\mathrm{kt}}{\mathrm{x}}=\frac{\mathrm{ML}^2 \mathrm{~T}^{-2}}{\mathrm{~L}} \\
& \left(\because \mathrm{E}=\frac{1}{2} \mathrm{kt}\right)
\end{aligned}
\)As \(\mathrm{P}\) is dimensionless
\(
\Rightarrow[\alpha]=[\beta]=\left[\mathrm{MLT}^{-2}\right]
\) -
Question 50 of 50
50. Question
The dimension of mutual inductance is :
CorrectIncorrectHint
\(\mathrm{e}_2\) : induced emf in secondary coil
\({i}_1\) : Current in primary coil
\(M\) : Mutual inductance
\(
\begin{aligned}
& e_2=-M \frac{d i_1}{d t} \\
& \mathrm{M}=-\frac{\mathrm{e}_2}{\frac{\mathrm{di_1}}{\mathrm{dt}}} \\
&
\end{aligned}
\)
\(
\begin{aligned}
& {[\mathrm{M}]=\frac{\left[\mathrm{e}_2\right]}{\left[\frac{\mathrm{di}_1}{\mathrm{dt}}\right]}=\frac{\left[\frac{\mathrm{W}}{\mathrm{q}}\right]}{\left[\frac{\mathrm{di}_1}{\mathrm{dt}}\right]}=\frac{\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]}{[\mathrm{AT}]}} \\
& =\left[\mathrm{ML}^2 \mathrm{~T}^{-2} \mathrm{~A}^{-2}\right]
\end{aligned}
\)