Thermodynamics Quiz-1
Multiple Choice Questions with one Correct Answer
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
1 point(s)The true statement amongst the following is :
CorrectIncorrect -
Question 2 of 50
2. Question
1 point(s)Five moles of an ideal gas at 1 bar and \(298 \mathrm{~K}\) is expanded into vacuum to double the volume. The work done is :
CorrectIncorrect -
Question 3 of 50
3. Question
1 point(s)Among the following, the set of parameters that represents path functions, is:
(A) \(q+w\)
(B) \(q\)
(C) \(w\)
(D) \(H-T S\)CorrectIncorrect -
Question 4 of 50
4. Question
1 point(s)Which one of the following equations does not correctly represent the first law of thermodynamics for the given processes involving an ideal gas? (Assume non-expansion work is zero)
CorrectIncorrect -
Question 5 of 50
5. Question
1 point(s)5 moles of an ideal gas at \(100 \mathrm{~K}\) are allowed to undergo reversible compression till its temperature becomes \(200 \mathrm{~K}\). If \(\mathrm{C}_V=28 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\), calculate \(\Delta \mathrm{U}\) and \(\Delta \mathrm{pV}\) for this process. \(\left(\mathrm{R}=8.0 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right)\)
CorrectIncorrect -
Question 6 of 50
6. Question
1 point(s)For a diatomic ideal gas in a closed system, which of the following plots does not correctly describe the relation between various thermodynamic quantities?
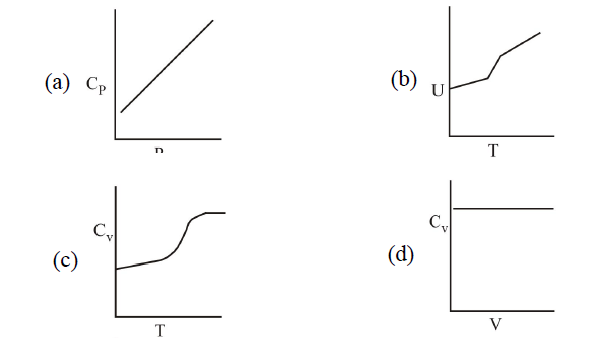 CorrectIncorrect
CorrectIncorrect -
Question 7 of 50
7. Question
1 point(s)The process with negative entropy change is:
CorrectIncorrect -
Question 8 of 50
8. Question
1 point(s)Which of the following lines correctly show the temperature dependence of equilibrium constant, \(\mathrm{K}\), for an exothermic reaction?
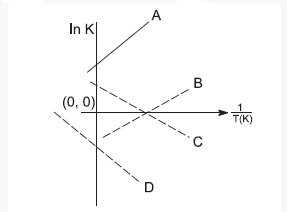 CorrectIncorrect
CorrectIncorrect -
Question 9 of 50
9. Question
1 point(s)For which of the following processes, \(\Delta \mathrm{S}\) is negative?
CorrectIncorrect -
Question 10 of 50
10. Question
1 point(s)\(\Delta \mathrm{U}\) is equal to
CorrectIncorrect -
Question 11 of 50
11. Question
1 point(s)A gas undergoes change from state A to state B. In this process, the heat absorbed and work done by the gas is \(5 \mathrm{~J}\) and \(8 \mathrm{~J}\), respectively. Now gas is brought back to A by another process during which \(3 \mathrm{~J}\) of heat is evolved. In this reverse process of B to A :
CorrectIncorrect -
Question 12 of 50
12. Question
1 point(s)If 100 mole of \(\mathrm{H}_2 \mathrm{O}_2\) decomposes at 1 bar and \(300 \mathrm{~K}\), the work done \((\mathrm{kJ})\) by one mole of \(\mathrm{O}_2(\mathrm{~g})\) as it expands against 1 bar pressure is : \(\left(\mathrm{R}=83 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\right)\)
\(
2 \mathrm{H}_2 \mathrm{O}_2(l) \rightleftharpoons \mathrm{H}_2 \mathrm{O}(l)+\mathrm{O}_2(g)
\)CorrectIncorrect -
Question 13 of 50
13. Question
1 point(s)A reaction at 1 bar is non-spontaneous at low temperature but becomes spontaneous at high temperature. Identify the correct statement about the reaction among the following :
CorrectIncorrect -
Question 14 of 50
14. Question
1 point(s)One mole of an ideal gas at \(300 \mathrm{~K}\) in thermal contact with surroundings expands isothermally from \(1.0 \mathrm{~L}\) to \(2.0 \mathrm{~L}\) against a constant pressure of \(3.0 \mathrm{~atm}\). In this process, the change in entropy of surroundings \(\left(\Delta S_{\text {surr }}\right)\) in \(\mathrm{JK}^{-1}\) is \((1 \mathrm{~L} \mathrm{~atm}=101.3 \mathrm{~J})\)
CorrectIncorrect -
Question 15 of 50
15. Question
1 point(s)A piston filled with \(0.04 \mathrm{~mol}\) of an ideal gas expands reversibly from \(50.0 \mathrm{~mL}\) to \(375 \mathrm{~mL}\) at a constant temperature of \(37.0^{\circ} \mathrm{C}\). As it does so, it absorbs \(208 \mathrm{~J}\) of heat. The values of \(\mathrm{q}\) and \(\mathrm{w}\) for the process will be: \((\mathrm{R}=8.314 \mathrm{~J} / \mathrm{mol} \mathrm{K})(\ln 7.5=2.01)\)
CorrectIncorrect -
Question 16 of 50
16. Question
1 point(s)Which of the following statements/relationships is not correct in thermodynamic changes?
CorrectIncorrect -
Question 17 of 50
17. Question
1 point(s)When one mole of monoatomic ideal gas at \(T \mathrm{~K}\) undergoes adiabatic change under a constant external pressure of \(1 \mathrm{~atm}\), volume changes from 1 litre to 2 litre. The final temperature in Kelvin would be
CorrectIncorrect -
Question 18 of 50
18. Question
1 point(s)A mono-atomic ideal gas undergoes a process in which the ratio of \(P\) to \(V\) at any instant is constant and equals to 1 . What is the molar heat
CorrectIncorrect -
Question 19 of 50
19. Question
1 point(s)Two moles of an ideal gas is expanded isothermally and reversibly from 1 litre to 10 litres at \(300 \mathrm{~K}\). The enthalpy change (in \(\mathrm{kJ}\) ) for the process is
CorrectIncorrect -
Question 20 of 50
20. Question
1 point(s)One mole of a non-ideal gas undergoes a change of state \((2.0 \mathrm{~atm}\), \(3.0 \mathrm{~L}, 95 \mathrm{~K}) \rightarrow(4.0 \mathrm{~atm}, 5.0 \mathrm{~L}, 245 \mathrm{~K})\) with a change in internal energy, \(\Delta U=30.0 \mathrm{~L} \mathrm{~atm}\). The change in enthalpy \((\Delta H)\) of the process in \(\mathrm{L}\) atm is
CorrectIncorrect -
Question 21 of 50
21. Question
1 point(s)In thermodynamics, a process is called reversible when
CorrectIncorrect -
Question 22 of 50
22. Question
1 point(s)Which one of the following statements is false?
CorrectIncorrect -
Question 23 of 50
23. Question
1 point(s)One mole of an ideal gas is taken from \(a\) to \(b\) along two paths denoted by the solid and the dashed lines as shown in the graphs below. If the work done along the solid line path \(w_s\) and that along the dotted line path is \(w_d\), then the integer closest to the ratio \(w_d / w_s\) is:
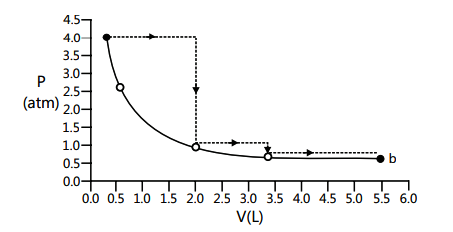 CorrectIncorrect
CorrectIncorrect -
Question 24 of 50
24. Question
1 point(s)In a constant volume calorimeter, \(3.5 \mathrm{~g}\) of a gas with molecular weight 28 was burnt in excess oxygen at \(298.0 \mathrm{~K}\). The temperature of the calorimeter was found to increase from \(298.0 \mathrm{~K}\) to \(298.45 \mathrm{~K}\) due to the combustion process. Given that the heat capacity of the calorimeter is \(2.5 \mathrm{~kJ} \mathrm{~K}^{-1}\), the numerical value for the enthalpy of combustion of the gas in \(\mathrm{kJ} \mathrm{mol}^{-1}\) is
CorrectIncorrect -
Question 25 of 50
25. Question
1 point(s)For a dimerization reaction, \(\quad 2 \mathrm{~A}(\mathrm{~g}) \rightarrow \mathrm{A}_2(\mathrm{~g})\), at \(298 \mathrm{~K}, \Delta \mathrm{U}^{\Theta}=-20 \mathrm{~kJ} \mathrm{~mol}^{-1}, \Delta \mathrm{S}^{\Theta}=-30 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\), then the \(\Delta \mathrm{G}^{\Theta}\) will be _____ J.
CorrectIncorrect -
Question 26 of 50
26. Question
1 point(s)One mole of an ideal monoatomic gas is subjected to changes as shown in the graph. The magnitude of the work done (by the system or on the system) is ____ \(\mathrm{J}\) (nearest integer).
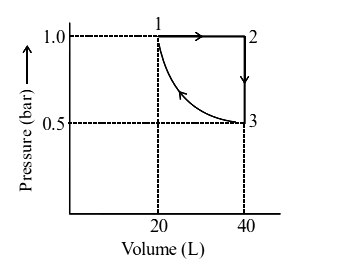
\(
\text { Given }: \log 2=0.3, \ln 10=2.3
\)CorrectIncorrect -
Question 27 of 50
27. Question
1 point(s)An athlete is given \(100 \mathrm{~g}\) of glucose \(\left(\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6\right)\) for energy. This is equivalent to \(1800 \mathrm{~kJ}\) of energy. The \(50 \%\) of this energy gained is utilized by the athlete for sports activities at the event. In order to avoid storage of energy, the weight of extra water he would need to perspire is ____ g (Nearest integer)
Assume that there is no other way of consuming stored energy.
Given : The enthalpy of evaporation of water is 45 \(\mathrm{kJ} \mathrm{mol}^{-1}\)
Molar mass of \(\mathrm{C}, \mathrm{H} \& \mathrm{O}\) are 12.1 and \(16 \mathrm{~g} \mathrm{~mol}^{-1}\).CorrectIncorrect -
Question 28 of 50
28. Question
1 point(s)The magnitude of work done by a gas that undergoes a reversible expansion along the path \(A B C\) shown in the figure is _____.
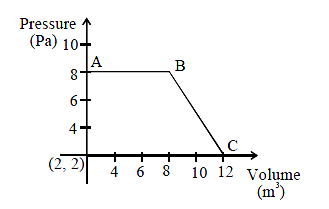 CorrectIncorrect
CorrectIncorrect -
Question 29 of 50
29. Question
1 point(s)At constant volume, \(4 \mathrm{~mol}\) of an ideal gas when heated from \(300 \mathrm{~K}\) to \(500 \mathrm{~K}\) changes its internal energy by \(5000 \mathrm{~J}\). The molar heat capacity at constant volume is ________.
CorrectIncorrect -
Question 30 of 50
30. Question
1 point(s)For the reaction, \(2 \mathrm{CO}+\mathrm{O}_2 \longrightarrow 2 \mathrm{CO}_2 ; \Delta H=-560 \mathrm{~kJ}\). Two moles of \(\mathrm{CO}\) and one mole of \(\mathrm{O}_2\) are taken in a container of volume \(1 \mathrm{~L}\). They completely form two moles of \(\mathrm{CO}_2\), the gases deviate appreciably from ideal behaviour. If the pressure in the vessel changes from 70 to \(40 \mathrm{~atm}\), find the magnitude (absolute value) of \(\Delta U\) at \(500 \mathrm{~K} .(1 \mathrm{~L} \mathrm{~atm}\) \(=0.1 \mathrm{~kJ})\)
CorrectIncorrect -
Question 31 of 50
31. Question
1 point(s)A sample of argon gas at \(1 \mathrm{~atm}\) pressure and \(27^{\circ} \mathrm{C}\) expands reversibly and adiabatically from \(1.25 \mathrm{dm}^3\) to \(2.50 \mathrm{dm}^3\). Calculate the enthalpy change in this process. \(C_{V, m}\) for argon is \(12.48 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\).
CorrectIncorrect -
Question 32 of 50
32. Question
1 point(s)An athlete is given \(100 \mathrm{~g}\) of glcuose \(\left(\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6\right)\) of energy equivalent to \(1560 \mathrm{~kJ}\). He utilizes 50 percent of this gained energy in the event. In order to avoids storage of energy in the body, calculate the weight of water he would need to perspire. The enthalpy of evaporation of water is \(44 \mathrm{~kJ} / \mathrm{mole}\).
CorrectIncorrect -
Question 33 of 50
33. Question
1 point(s)Lattice enthalpy and enthalpy of solution of \(\mathrm{NaCl}\) are \(788 \mathrm{~kJ} \mathrm{~mol}^{-1}\) and \(4 \mathrm{~kJ} \mathrm{~mol}^{-1}\), respectively. The hydration enthalpy of \(\mathrm{NaCl}\) is :
CorrectIncorrect -
Question 34 of 50
34. Question
1 point(s)For one mole of an ideal gas, which of these statements must be true?
(1) \(\mathrm{U}\) and \(\mathrm{H}\) each depends only on temperature
(2) Compressibility factor \(z\) is not equal to 1
(3) \(\mathrm{C}_{\mathrm{P}, \mathrm{m}}-\mathrm{C}_{\mathrm{V}, \mathrm{m}}=\mathrm{R}\)
(4) \(\mathrm{dU}=\mathrm{C}_{\mathrm{V}} \mathrm{dT}\) for any processCorrectIncorrect -
Question 35 of 50
35. Question
1 point(s)The intermolecular potential energy for the molecules \(A, B, C\) and \(D\) given below suggests that :
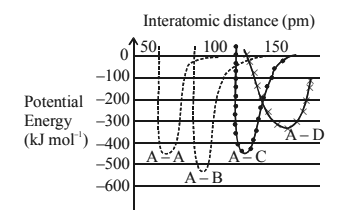 CorrectIncorrect
CorrectIncorrect -
Question 36 of 50
36. Question
1 point(s)If enthalpy of atomisation for \(\mathrm{Br}_2(l)\) is \(x \mathrm{~kJ} / \mathrm{mol}\) and bond enthalpy for \(\mathrm{Br}_2\) is \(y \mathrm{~kJ} / \mathrm{mol}\), the relation between them:
CorrectIncorrect -
Question 37 of 50
37. Question
1 point(s)The difference between \(\Delta \mathrm{H}\) and \(\Delta \mathrm{U}(\Delta \mathrm{H}-\Delta \mathrm{U})\), when the combustion of one mole of heptane (I) is carried out at a temperature T, is equal to
CorrectIncorrect -
Question 38 of 50
38. Question
1 point(s)The combustion of benzene (l) gives \(\mathrm{CO}_2(\mathrm{~g})\) and \(\mathrm{H}_2 \mathrm{O}(l)\). Given that heat of combustion of benzene at constant volume is \(-3263.9 \mathrm{~kJ} \mathrm{~mol}^{-1}\) at \(25^{\circ} \mathrm{C}\); heat of combustion (in \(\mathrm{kJ} \mathrm{mol}^{-1}\) ) of benzene at constant pressure will be : \(\left(\mathrm{R}=8.314 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\right)\)
CorrectIncorrect -
Question 39 of 50
39. Question
1 point(s)For which of the following reactions, \(\Delta \mathrm{H}\) is equal to \(\Delta \mathrm{U}\) ?
CorrectIncorrect -
Question 40 of 50
40. Question
1 point(s)Given
\(
\begin{aligned}
& \mathrm{C}_{\text {(graphite) }}+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) ; \Delta_r \mathrm{H}^{\ominus}=-393.5 \mathrm{~kJ} \mathrm{~mol}^{-1} \\
& \mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l}) ; \Delta_r \mathrm{H}^{\ominus}=-285.8 \mathrm{~kJ} \mathrm{~mol}^{-1}
\end{aligned}
\)
\(
\mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{CH}_4(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}); \Delta_r \mathrm{H}^{\ominus}=+890.3 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
Based on the above thermochemical equations, the value of \(\Delta_r \mathrm{H}^{\ominus}\) at \(298 \mathrm{~K}\) for the reaction
\(\mathrm{C}_{\text {(graphite) }}+2 \mathrm{H}_2(\mathrm{~g}) \rightarrow \mathrm{CH}_4(\mathrm{~g})\) will be :CorrectIncorrect -
Question 41 of 50
41. Question
1 point(s)For a reaction, \(\mathrm{A}(\mathrm{g}) \rightarrow \mathrm{A}(\mathrm{l}) ; \Delta \mathrm{H}=-3 \mathrm{RT}\). The correct statement for the reaction is :
CorrectIncorrect -
Question 42 of 50
42. Question
1 point(s)The heats of combustion of carbon and carbon monoxide are -393.5 and \(-283.5 \mathrm{~kJ} \mathrm{~mol}^{-1}\), respectively. The heat of formation (in \(\mathrm{kJ}\) ) of carbon monoxide per mole is :
CorrectIncorrect -
Question 43 of 50
43. Question
1 point(s)The heat of atomization of methane and ethane are \(360 \mathrm{~kJ} / \mathrm{mol}\) and 620 \(\mathrm{kJ} / \mathrm{mol}\), respectively. The longest wavelength of light capable of breaking the \(\mathrm{C}-\mathrm{C}\) bond is (Avogadro number \(=6.02 \times 10^{23}, \mathrm{~h}=6.62\) \(\left.\times 10^{-34} \mathrm{~J} \mathrm{~s}\right):\)
CorrectIncorrect -
Question 44 of 50
44. Question
1 point(s)For complete combustion of ethanol,
\(
\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}(l)+3 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{CO}_2(\mathrm{~g})+3 \mathrm{H}_2 \mathrm{O}(l)
\)
the amount of heat produced as measured in bomb calorimeter, is 1364.47 \(\mathrm{~kJ} \mathrm{~mol}{ }^{-1}\) at \(25^{\circ} \mathrm{C}\). Assuming ideality the enthalpy of combustion, \(\Delta_{\mathrm{c}} \mathrm{H}\), for the reaction will be:
\(
\left(\mathrm{R}=8.314 \mathrm{~kJ} \mathrm{~mol}^{-1}\right)
\)CorrectIncorrect -
Question 45 of 50
45. Question
1 point(s)The standard enthalpy of formation of \(\mathrm{NH}_3\) is \(-46.0 \mathrm{~kJ} / \mathrm{mol}\). If the enthalpy of formation of \(\mathrm{H}_2\) from its atoms is \(-436 \mathrm{~kJ} / \mathrm{mol}\) and that of \(\mathrm{N}_2\) is \(-712 \mathrm{~kJ} / \mathrm{mol}\), the average bond enthalpy of \(\mathrm{N}-\mathrm{H}\) bond in \(\mathrm{NH}_3\) is:
CorrectIncorrect -
Question 46 of 50
46. Question
1 point(s)For the process
\(\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)
at \(T=100^{\circ} \mathrm{C}\) and 1 atmosphere pressure, the correct choice isCorrectIncorrect -
Question 47 of 50
47. Question
1 point(s)Given
(I) \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{H}_2 \mathrm{O}(l)\);
\(
\Delta \mathrm{H}^{\ominus}{ }_{298 \mathrm{~K}}=-285.9 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
(II) \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g})\);
\(
\Delta \mathrm{H}^{\ominus}{ }_{298 \mathrm{~K}}=-241.8 \mathrm{~kJ} \mathrm{~mol}^{-1}
\)
The molar enthalpy of vapourisation of water will be :CorrectIncorrect -
Question 48 of 50
48. Question
1 point(s)The species which by definition has ZERO standard molar enthalpy of formation at \(298 \mathrm{~K}\) is
CorrectIncorrect -
Question 49 of 50
49. Question
1 point(s)For the process \(\mathrm{H}_2 \mathrm{O}(1)(1 \mathrm{bar}, 373 \mathrm{~K}) \rightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g})(1 \mathrm{bar}, 373 \mathrm{~K})\), the correct set of thermodynamic parameters is
CorrectIncorrect -
Question 50 of 50
50. Question
1 point(s)The value of \(\log _{10} K\) for a reaction \(A \rightleftharpoons B\) is (Given :
\(\Delta_r H_{298 \mathrm{~K}}^{\ominus}=-54.07 \mathrm{~kJ} \mathrm{~mol}^{-1}, \Delta_r S_{298 \mathrm{~K}}^{\ominus}\)
\(=10 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\) and \(R=8.314 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\); \(2.303 \times 8.314 \times 298=5705)\)CorrectIncorrect