Structure of Atom Quiz-1
Multiple Choice Questions with one Correct Answer
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
1 point(s)The difference between the radii of \(3^{\text {rd }}\) and \(4^{\text {th }}\) orbits of \(\mathrm{Li}^{2+}\) is \(\Delta R_1\). The difference between the radii of \(3^{\text {rd }}\) and \(4^{\text {th }}\) orbits of \(\mathrm{He}^{+}\)is \(\Delta \mathrm{R}_2\). Ratio \(\Delta \mathrm{R}_1: \Delta \mathrm{R}_2\) is:
CorrectIncorrect -
Question 2 of 50
2. Question
1 point(s)The region in the electromagnetic spectrum where the Balmer series lines appear is :
CorrectIncorrect -
Question 3 of 50
3. Question
1 point(s)The shortest wavelength of \(\mathrm{H}\) atom in the Lyman series is \(\lambda_1\). The longest wavelength in the Balmer series is \(\mathrm{He}^{+}\)is :
CorrectIncorrect -
Question 4 of 50
4. Question
1 point(s)For the Balmer series in the spectrum of \(\mathrm{H}\) atom, \(\bar{\nu}=R_H\left\{\frac{1}{n_1^2}-\frac{1}{n_2^2}\right\}\), the correct statements among (I) to (IV) are:
(I) As the wavelength decreases, the lines in the series converge
(II) The integer \(n_1\) is equal to 2
(III) The lines of the longest wavelength correspond to \(n_2=3\)
(IV) The ionization energy of hydrogen can be calculated from the wave number of these linesCorrectIncorrect -
Question 5 of 50
5. Question
1 point(s)The radius of the second Bohr orbit, in terms of the Bohr radius, \(a_0\), in \(\mathrm{Li}^{2+}\) is:
CorrectIncorrect -
Question 6 of 50
6. Question
1 point(s)Among the following, the energy of \(2 s\) orbital is lowest in:
CorrectIncorrect -
Question 7 of 50
7. Question
1 point(s)The ratio of the shortest wavelength of two spectral series of hydrogen spectrum is found to be about 9. The spectral series are :
CorrectIncorrect -
Question 8 of 50
8. Question
1 point(s)For any given series of spectral lines of atomic hydrogen, let \(\Delta \bar{\nu}=\bar{\nu}_{\max }-\bar{\nu}_{\min }\) be the difference in maximum and minimum frequencies in \(\mathrm{cm}^{-1}\). The ratio \(\Delta \bar{\nu}\) Lyman \(/ \Delta \bar{\nu}_{\text {Balmer }}\) is :
CorrectIncorrect -
Question 9 of 50
9. Question
1 point(s)What is the work function of the metal if the light of wavelength \(4000\)Å generates photoelectrons of velocity \(6 \times 10^5 \mathrm{~ms}^{-1}\) from it ?
(Mass of electron \(=9 \times 10^{-31} \mathrm{~kg}\)
Velocity of light \(=3 \times 10^8 \mathrm{~ms}^{-1}\)
Planck’s constant \(=6.626 \times 10^{-34} \mathrm{Js}\)
Charge of electron \(=1.6 \times 10^{-19} \mathrm{JeV}^{-1}\) )CorrectIncorrect -
Question 10 of 50
10. Question
1 point(s)Heat treatment of muscular pain involves radiation of wavelength of about 900 nm. Which spectral line of \(\mathrm{H}\)-atom is suitable for this purpose?
\(
\left[R_H=1 \times 10^5 \mathrm{~cm}^{-1} \cdot \mathrm{h}=6.6 \times 10^{-34} \mathrm{Js}, \mathrm{c}=3 \times 10^8 \mathrm{~ms}^{-1}\right]
\)CorrectIncorrect -
Question 11 of 50
11. Question
1 point(s)The ground state energy of hydrogen atom is \(-13.6 \mathrm{eV}\). The energy of second excited state of \(\mathrm{He}^{+}\)ion in \(\mathrm{eV}\) is:
CorrectIncorrect -
Question 12 of 50
12. Question
1 point(s)Which of the following statements is false?
CorrectIncorrect -
Question 13 of 50
13. Question
1 point(s)Ejection of the photoelectron from metal in the photoelectric effect experiment can be stopped by applying \(0.5 \mathrm{~V}\) when the radiation of \(250 \mathrm{~nm}\) is used. The work function of the metal is :
CorrectIncorrect -
Question 14 of 50
14. Question
1 point(s)The radius of the second Bohr orbit for hydrogen atom is : (Plank’s const. \(h=6.6262 \times 10^{-34} \mathrm{Js}\); mass of electron \(=9.1091 \times 10^{-31} \mathrm{~kg}\); charge of electron \(\mathrm{e}=1.60210 \times 10^{-19} \mathrm{C}\); permittivity of vaccum \(\left.\in_0=8.854185 \times 10^{-12} \mathrm{~kg}^{-1} \mathrm{~m}^{-3} \mathrm{~A}^2\right)\)
CorrectIncorrect -
Question 15 of 50
15. Question
1 point(s)If the shortest wavelength in Lyman series of hydrogen atom is A, then the longest wavelength in Paschen series of \(\mathrm{He}^{+}\)is :
CorrectIncorrect -
Question 16 of 50
16. Question
1 point(s)A stream of electrons from a heated filaments was passed two charged plates kept at a potential difference \(\mathrm{V}\) esu. If ‘ \(\mathrm{e}\) ‘ and \(m\) are charge and mass of an electron, respectively, then the value of \(h / \lambda\) (where \(\lambda\) is wavelength associated with electron wave) is given by:
CorrectIncorrect -
Question 17 of 50
17. Question
1 point(s)Which of the following is the energy of a possible excited state of hydrogen?
CorrectIncorrect -
Question 18 of 50
18. Question
1 point(s)If \(m\) and \(e\) are the mass and charge of the revolving electron in the orbit of radius \(r\) for hydrogen atom, the total energy of the revolving electron will be:
CorrectIncorrect -
Question 19 of 50
19. Question
1 point(s)If \(\lambda_0\) and \(\lambda\) be threshold wavelength and wavelength of incident light, the velocity of photoelectron ejected from the metal surface is:
CorrectIncorrect -
Question 20 of 50
20. Question
1 point(s)Energy of an electron is given by \(\mathrm{E}=-2.178 \times 10^{-18} \mathrm{~J}\left(\frac{Z^2}{n^2}\right)\).
Wavelength of light required to excite an electron in an hydrogen atom from level \(n=1\) to \(n=2\) will be:
\(
\left(h=6.62 \times 10^{-34} \mathrm{Js} \text { and } \mathrm{c}=3.0 \times 10^8 \mathrm{~ms}^{-1}\right)
\)CorrectIncorrect -
Question 21 of 50
21. Question
1 point(s)The wave number of the first emission line in the Balmer series of \(\mathrm{H}\)-Spectrum is :
( \(\mathrm{R}=\) Rydberg constant \()\) :CorrectIncorrect -
Question 22 of 50
22. Question
1 point(s)The kinetic energy of an electron in the second Bohr orbit of a hydrogen atom is \(\left[a_0\right.\) is Bohr radius \(]\) :
CorrectIncorrect -
Question 23 of 50
23. Question
1 point(s)Given that the abundances of isotopes \({ }^{54} \mathrm{Fe},{ }^{56} \mathrm{Fe}\) and \({ }^{57} \mathrm{Fe}\) are \(5 \%, 90 \%\) and \(5 \%\), respectively, the atomic mass of \(\mathrm{Fe}\) is
CorrectIncorrect -
Question 24 of 50
24. Question
1 point(s)The radius of which of the following orbit is same as that of the first Bohr’s orbit of hydrogen atom?
CorrectIncorrect -
Question 25 of 50
25. Question
1 point(s)Rurtherford’s experiment, which established the nuclear model of the atom, used a beam of
CorrectIncorrect -
Question 26 of 50
26. Question
1 point(s)Which of the following does not characterise X-rays?
CorrectIncorrect -
Question 27 of 50
27. Question
1 point(s)The wavelength of a spectral line for an electronic transition is inversely related to :
CorrectIncorrect -
Question 28 of 50
28. Question
1 point(s)The triad of nuclei that is isotonic is
CorrectIncorrect -
Question 29 of 50
29. Question
1 point(s)The ratio of the energy of a photon of \(2000\)Å wavelength radiation to that of \(4000\)Å radiation is :
CorrectIncorrect -
Question 30 of 50
30. Question
1 point(s)Rutherford’s alpha particle scattering experiment eventually led to the conclusion that :
CorrectIncorrect -
Question 31 of 50
31. Question
1 point(s)Electromagnetic radiation with maximum wavelength is :
CorrectIncorrect -
Question 32 of 50
32. Question
1 point(s)The radius of an atomic nucleus is of the order of :
CorrectIncorrect -
Question 33 of 50
33. Question
1 point(s)Bohr model can explain :
CorrectIncorrect -
Question 34 of 50
34. Question
1 point(s)Which electronic level would allow the hydrogen atom to absorb a photon but not to emit a photon?
CorrectIncorrect -
Question 35 of 50
35. Question
1 point(s)The increasing order (lowest first) for the values of \(\mathrm{e} / \mathrm{m}\) (charge/mass) for electron \((e)\), proton \((p)\), neutron \((n)\) and alpha particle \((\alpha)\) is :
CorrectIncorrect -
Question 36 of 50
36. Question
1 point(s)Rutherford’s scattering experiment is related to the size of the
CorrectIncorrect -
Question 37 of 50
37. Question
1 point(s)Rutherford’s experiment on scattering of \(\alpha\)-particles showed for the first time that the atom has
CorrectIncorrect -
Question 38 of 50
38. Question
1 point(s)The number of neutrons in dipositive zinc ion with mass number 70 is
CorrectIncorrect -
Question 39 of 50
39. Question
1 point(s)The work function \((\varphi)\) of some metals is listed below. The number of metals which will show photoelectric effect when light of \(300 \mathrm{~nm}\) wavelength falls on the metal is
CorrectIncorrect -
Question 40 of 50
40. Question
1 point(s)The figure that is not a direct manifestation of the quantum nature of atoms is :
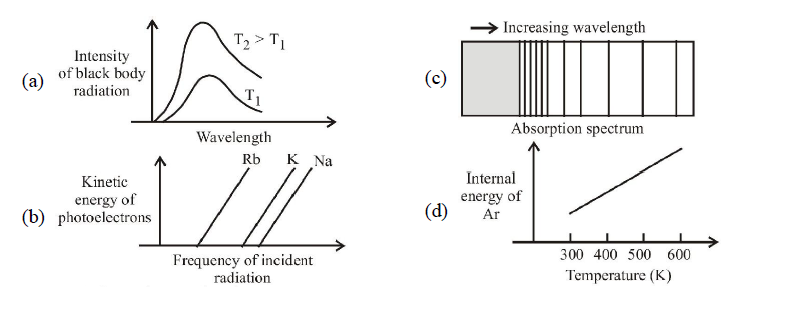 CorrectIncorrect
CorrectIncorrect -
Question 41 of 50
41. Question
1 point(s)The de Broglie wavelength of an electron in the \(4^{\text {th }}\) Bohr orbit is:
CorrectIncorrect -
Question 42 of 50
42. Question
1 point(s)If \(p\) is the momentum of the fastest electron ejected from a metal surface after the irradiation of light having wavelength \(\lambda\), then for \(1.5 p\) momentum of the photoelectron, the wavelength of the light should be:
(Assume the kinetic energy of ejected photoelectron to be very high in comparison to work function):CorrectIncorrect -
Question 43 of 50
43. Question
1 point(s)If the de Broglie wavelength of the electron in \(n^{\text {th }}\) Bohr orbit in a hydrogenic atom is equal to \(1.5 \pi \mathrm{a}_0\left(\mathrm{a}_0\right.\) is Bohr radius), then the value of \(\mathrm{n} / \mathrm{z}\) is :
CorrectIncorrect -
Question 44 of 50
44. Question
1 point(s)The de-Broglie’s wavelength of electron present in first Bohr orbit of ‘H’ atom is:
CorrectIncorrect -
Question 45 of 50
45. Question
1 point(s)At temperature \(\mathrm{T}\), the average kinetic energy of any particle is \(\frac{3}{2} \mathrm{kT}\). The de Broglie wavelength follows the order :
CorrectIncorrect -
Question 46 of 50
46. Question
1 point(s)The de-Broglie wavelength of a particle of mass \(6.63 \mathrm{~g}\) moving with a velocity of \(100 \mathrm{~ms}^{-1}\) is:
CorrectIncorrect -
Question 47 of 50
47. Question
1 point(s)The de Broglie wavelength of a car of mass \(1000 \mathrm{~kg}\) and velocity \(36 \mathrm{~km} / \mathrm{hr}\) is :
CorrectIncorrect -
Question 48 of 50
48. Question
1 point(s)The wavelength associated with a golf ball weighing \(200 \mathrm{~g}\) and moving at a speed of \(5 \mathrm{~m} / \mathrm{h}\) is of the order
CorrectIncorrectHint
According to de-Broglie’s equation
\(
\begin{aligned}
& \lambda=\frac{h}{p}=\frac{h}{m v}=\frac{6.63 \times 10^{-34}}{0.2 \times 5} \times 3600 \approx 2.4 \\
& \times 10^{-30}
\end{aligned}
\) -
Question 49 of 50
49. Question
1 point(s)Which of the following relates to photons both as wave motion and as a stream of particles?
CorrectIncorrect -
Question 50 of 50
50. Question
1 point(s)The work function of sodium metal is \(4.41 \times 10^{-19} \mathrm{~J}\). If photons of wavelength \(300 \mathrm{~nm}\) are incident on the metal, the kinetic energy of the ejected electrons will be ____ \(\times 10^{-21} \mathrm{~J}\).
\(
\left(h=6.63 \times 10^{-34} \mathrm{~J} \mathrm{~s} ; c=3 \times 10^8 \mathrm{~m} / \mathrm{s}\right)
\)CorrectIncorrect