4.11 Exercise Problems and Solutions

Q1. Explain the formation of a chemical bond.

Answer: A chemical bond formation is attributed to the tendency of a system to attain stability. It was observed that the inertness of noble gases was because of their fully filled outermost orbitals. According to Kossel and Lewis, atoms combine together in order to complete their respective octets so as to acquire the stable inert gas configuration. This can occur in two ways; by the transfer of one or more electrons from one atom to other or by sharing of electrons between two or more atoms. The chemical bond formed as a result of sharing of electrons between atoms is called a covalent bond. An ionic bond is formed as a result of the transference of electrons from one atom to another.

Q2. Write Lewis dot symbols for atoms of the following elements : \(\mathrm{Mg}, \mathrm{Na}, \mathrm{B}, \mathrm{O}, \mathrm{N}, \mathrm{Br}\).

Answer: 

Q3. Write Lewis symbols for the following atoms and lons:
\(
\mathrm{S} \text { and } \mathrm{S}^{2-} ; \mathrm{Al} \text { and } \mathrm{Al}^{3+}; \mathrm{H} \text { and } \mathrm{H}^{-}
\)

Answer: 

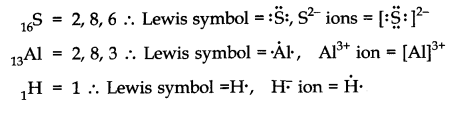
Q4. Draw the Lewis structures for the following molecules and ions :
\(
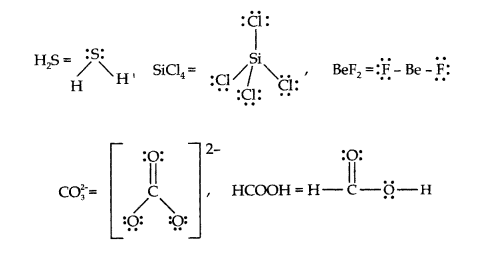
\mathrm{H}_2 \mathrm{~S}, \mathrm{SiCl}_4, \mathrm{BeF}_2, \mathrm{CO}_3^{2-}, \mathrm{HCOOH}
\)

Answer: 

Q5. Define octet rule. Write its significance and limitations.

Answer:

Octet rule: Atoms of elements combine with each other in order to complete their respective octets so as to acquire the stable gas configuration.

Significance: It helps to explain why different atoms combine with each other to form ionic compounds or covalent compounds.

Limitations of Octet rule:

• According to Octet rule, atoms take part in chemical combinations to achieve the configuration of the nearest noble gas elements. However, some of noble gas elements like Xenon have formed compounds with fluorine and oxygen. For example: \(\mathrm{XeF}_2, \mathrm{XeF}_4\) etc.
  Therefore, the validity of the octet rule has been challenged.
• This theory does not account for shape of molecules.

Q6. Write the favourable factors for the formation of ionic bond.

Answer: 

• Low ionization enthalpy of metal atoms
• High electron gain enthalpy of non-metal atoms
• High lattice enthalpy of the compound formed.

Q7. Discuss the shape of the following molecules using the VSEPR model:
\(
\mathrm{BeCl}_2, \mathrm{BCl}_3, \mathrm{SiCl}_4, \mathrm{AsF}_5, \mathrm{H}_2 \mathrm{~S}, \mathrm{PH}_3
\)

Answer:

(i) \(\mathrm{BeCl}_2=\mathrm{Cl}: \mathrm{Be}: \mathrm{Cl}\).
The central atom has only two bond pairs and there is no lone pair, i.e., it is of the type \(\mathrm{AB}_2\). Hence, the shape is linear.
(ii) \(\mathrm{BCl}_3=\mathrm{Cl}: \ddot{\mathrm{B}}: \mathrm{Cl}\).
The central atom has only 3 bond pairs and no lone pair, i.e., it is of the type \(\mathrm{AB}_3\). Hence, the shape is triangular planar.
(iii)

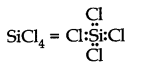
Bond pairs \(=4\), lone pairs \(=0\), i.e., it is of the type \(\mathrm{AB}_4\). Hence, the shape is Tetrahedral.
(iv)

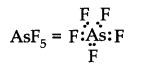
Bond pairs \(=5\), lone pairs \(=0\), i.e., it is of the type \(\mathrm{AB}_5\). Hence, the shape is Trigonal bipyramidal.
(v)

Bond pairs \(=2\), lone pairs \(=2\), i.e., it is of the type \(\mathrm{AB}_2 \mathrm{~L}_2\). Hence, the shape is Bent/V-shaped.
(vi)

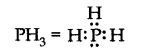
Bond pairs \(=3\), lone pair \(=1\), i.e., it is of the type \(\mathrm{AB}_3 \mathrm{~L}\). Hence, the shape is Trigonal.

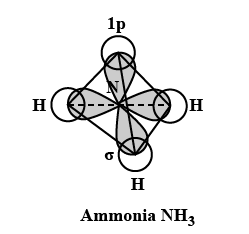
Q8. Although geometries of \(\mathrm{NH}_3\) and \(\mathrm{H}_2 \mathrm{O}\) molecules are distorted tetrahedral, bond angle in water is less than that of ammonia. Discuss.

Answer:

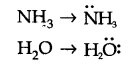
Because of two lone pairs of electrons on \(\mathrm{O}\)-atom, repulsion on bond pairs is greater in \(\mathrm{H}_2 \mathrm{O}\) in comparison to \(\mathrm{NH}_3\). Thus, the bond angle is less in \(\mathrm{H}_2 \mathrm{O}\) molecules.

Alternate: The molecular geometry of \(\mathrm{NH}_3\) and \(\mathrm{H}_2 \mathrm{O}\) can be shown as:

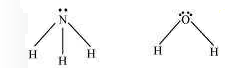
The central atom \((\mathrm{N})\) in \(\mathrm{NH}_3\) has one lone pair and there are three bond pairs. In \(\mathrm{H}_2 \mathrm{O}\), there are two lone pairs and two bond pairs.
The two lone pairs present in the oxygen atom of \(\mathrm{H}_2 \mathrm{O}\) molecule repels the two bond pairs. This repulsion is stronger than the repulsion between the lone pair and the three bond pairs on the nitrogen atom. the bond angle in water is less than that of ammonia.

Q9. How do you express the bond strength in terms of bond order?

Answer: Bond strength represents the extent of bonding between two atoms forming a molecule. The larger the bond energy, the stronger is the bond and the greater is the bond order. Bond strength is directly proportional to the bond order.

Q10. Define the bond length.

Answer: Bond length is defined as the equilibrium distance between the nuclei of two bonded atoms in a molecule. Bond lengths are measured by spectroscopic methods.
Bond lengths are expressed in terms of Angstrom \(\left(10^{-10} \mathrm{~m}\right)\) or picometer \(\left(10^{-12} \mathrm{~m}\right)\) and are measured by spectroscopic X-ray diffractions and electron-diffraction techniques.
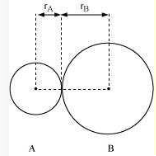
In an ionic compound, the bond length is the sum of the ionic radii of the constituting atoms \(\left(\mathrm{d}=\mathrm{r}_{+}+\mathrm{r}_{-}\right)\). In a covalent compound, it is the sum of their covalent radii \(\left(\mathrm{d}=\mathrm{r}_{\mathrm{A}}+\mathrm{r}_{\mathrm{B}}\right)\)

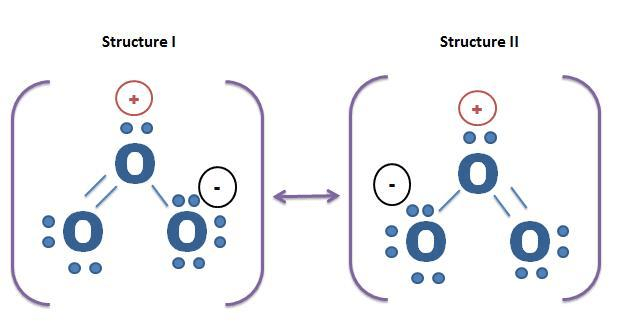
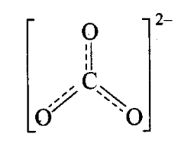
Q11. Explain the important aspects of resonance with reference to the \(\mathrm{CO}_3^{2-}\) ion.

Answer: According to experimental findings, all carbon to oxygen bonds in \(\mathrm{CO}_3^{2-}\) are equivalent.
Hence, it is inadequate to represent \(\mathrm{CO}_3^{2-}\) by a single Lewis structure having two single bonds and one double bond. Therefore, carbonate ion is described as a resonance hybrid of the following structures:

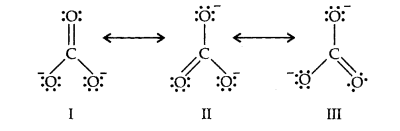
Resonance in \(\mathrm{CO}_3{ }^{2-}, \mathrm{I}, \mathrm{II}\) and \(\mathrm{III}\) represent the three canonical forms.

• In these structures, the positions of nuclei are the same.
• All three forms have almost equal energy.
• Same number of paired and impaired electrons, they differ only in their position.

Q12. \(\mathrm{H}_3 \mathrm{PO}_3\) can be represented by structures 1 and 2 shown below. Can these two structures be taken as the canonical forms of the resonance hybrid representing \(\mathrm{H}_3 \mathrm{PO}_3\)? If not, give reasons for the same.

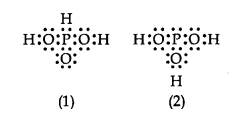
Answer: No, these cannot be taken as canonical forms because the positions of atoms have been changed.

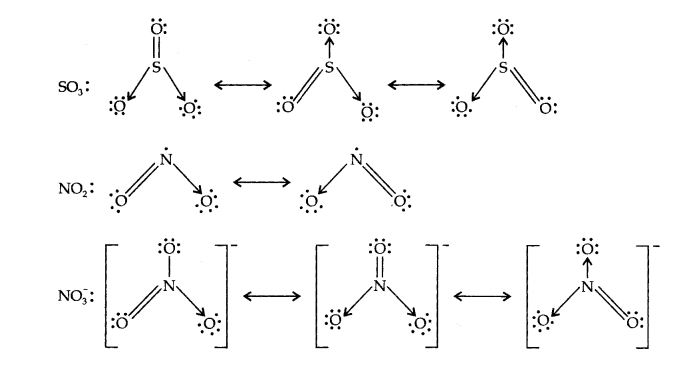
Q13. Write the resonance structures for \(\mathrm{SO}_3, \mathrm{NO}_2\) and \(\mathrm{NO}_3^{-}\).

Answer: The resonance structures are:

Q14. Use Lewis symbols to show electron transfer between the following atoms to form cations and anions : (a) \(\mathrm{K}\) and \(\mathrm{S}\) (b) \(\mathrm{Ca}\) and \(\mathrm{O}\) (c) \(\mathrm{Al}\) and \(\mathrm{N}\).

Answer: 

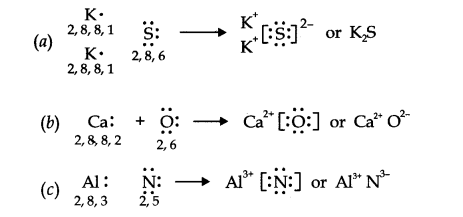
Q15. Although both \(\mathrm{CO}_2\) and \(\mathrm{H}_2 \mathrm{O}\) are trlatomic molecules, the shape of \(\mathrm{H}_2 \mathrm{O}\) molecule is bent while that of \(\mathrm{CO}_2\) is linear. Explain this on the basis of dipole moment.

Answer: In \(\mathrm{CO}_2\), there are two \(\mathrm{C}=\mathrm{O}\) bonds. Each \(\mathrm{C}=\mathrm{O}\) bond is a polar bond.
The net dipole moment of \(\mathrm{CO}_2\) molecule is zero. This is possible only if \(\mathrm{CO}_2\) is a linear molecule. \((\mathrm{O}=\mathrm{C}=\mathrm{O})\).
The bond dipoles of two \(\mathrm{C}=\mathrm{O}\) bonds cancel the moment of each other.
Whereas, \(\mathrm{H}_2 \mathrm{O}\) molecule has a net dipole moment (1.84 D). \(\mathrm{H}_2 \mathrm{O}\) molecule has a bent structure because here the \(\mathrm{O}-\mathrm{H}\) bonds are oriented at an angle of \(104.5^{\circ}\) and do not cancel the bond moments of each other.

Q16. Write the significance/applications of dipole moment.

Answer: 

• In predicting the nature of the molecules: Molecules with specific dipole moments are polar in nature and those of zero dipole moments are non-polar in nature.
• In the determination of the shapes of molecules.
• In calculating the percentage of ionic characters.

In heteronuclear molecules, polarization arises due to a difference in the electronegativities of the constituents of atoms. As a result, one end of the molecule acquires a positive charge while the other end becomes negative. Hence, a molecule is said to possess a dipole.
The product of the magnitude of the charge and the distance between the centres of positive-negative charges is called the dipole moment ( \(\mu\) ) of the molecule. It is a vector quantity and is represented by an arrow with its tail at the positive centre and head pointing towards a negative centre.
Dipole moment \((\mu)=\) charge \((Q) \times\) distance of separation \((r)\) The
Sl unit of a dipole moment is ‘esu’.
\(
1 \text { esu }=3.335 \times 10^{-30} \mathrm{~cm}
\)
Dipole moment is the measure of the polarity of a bond. lt is used to differentiate between polar and non-polar bonds since all non-polar molecules (e.g. \(\mathrm{H}_2, \mathrm{O}_2\) ) have zero dipole moments. It is also helpful in calculating the percentage ionic character of a molecule.

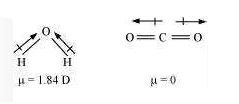
Q17. Define electronegativity. How does it differ from electron gain enthalpy?

Answer: Electronegativity: Electronegativity is the tendency of an atom to attract a shared pair of electrons. It is the property of bonded atom. The electronegativity of any given element is not constant. It varies according to the element to which it is bound. It is not a measurable quantity. It is only a relative number.
Whereas, electron gain enthalpy is the tendency of an atom to attract outside electrons. It is the property of an isolated atom. On the other hand, electron gain enthalpy is the enthalpy change that takes place when an electron is added to a neutral gaseous atom to form an anion. It can be negative or positive depending upon whether the electron is added or removed. An element has a constant value of the electron gain enthalpy that can be measured experimentally.

Q18. Explain with the help of a suitable example polar covalent bond.

Answer: when two atoms with different electronegativity are linked to each other by covalent bond, the shared electron pair will not in the centre because of the difference in electronegativity. For example, in hydrogen flouride molecule, flouride has greater electronegativity than hydrogen. Thus, the shared electron pair is displaced more towards fluorine atom, the later will acquire a partial negative charge \(\left(\partial^{-}\right)\). At the same time, hydrogen atom will have a partial positive charge \(\left(\partial^{+}\right)\). Such a covalent bond is known as polar covalent bond or simply polar bond. It is represented as

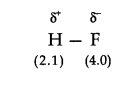
Alternate: When two dissimilar atoms having different electronegativities combine to form a covalent bond, the bond pair of electrons is not shared equally. The bond pair shifts towards the nucleus of the atom having greater electronegativity. As a result, electron distribution gets distorted and the electron cloud is displaced towards the electronegative atom.
As a result, the electronegative atom becomes slightly negatively charged while the other atom becomes slightly positively charged. Thus, opposite poles are developed in the molecule and this type of a bond is called a polar covalent bond.
\(\mathrm{HCl}\), for example, contains a polar covalent bond. The chlorine atom is more electronegative than hydrogen atom. Hence, the bond pair lies towards chlorine and therefore, it acquires a partial negative charge.

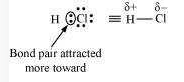
Q19. Arrange the bonds in order of increasing ionic character in the molecules: \(\mathrm{LiF}\), \(\mathrm{K}_2 \mathrm{O}, \mathrm{N}_2, \mathrm{SO}_2\) and \(\mathrm{ClF}_3\).

Answer: The ionic character in a molecule is dependent upon the electronegativity difference between the constituting atoms. The greater the difference, the greater will be the ionic character of the molecule.
On this basis, the order of increasing ionic character in the given molecules is
\(
\mathrm{N}_2<\mathrm{SO}_2<\mathrm{CIF}_3<\mathrm{K}_2 \mathrm{O}<\text { LiF. }
\)

Q20. The skeletal structure of \(\mathrm{CH}_3 \mathrm{COOH}\) as shown below is correct, but some of the bonds are shown incorrectly. Write the correct Lewis structure for acetic acid.

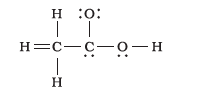
Answer: The correct Lewis structure for acetic acid is as follows:

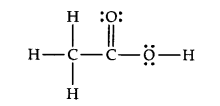
Q21. Apart from tetrahedral geometry, another possible geometry for \(\mathrm{CH}_4\) is square planar with the four \(\mathrm{H}\) atoms at the corners of the square and the \(\mathrm{C}\) atom at its centre. Explain why \(\mathrm{CH}_4\) is not square planar.

Answer: According to VSEPR theory, if \(\mathrm{CH}_4\) were square planar, the bond angle would be \(90^{\circ}\). For tetrahedral structure, the bond angle is \(109^{\circ} 28^{\prime}\). Therefore, in square planar structure, repulsion between bond pairs would be more and thus the stability will be less.

Q22. Explain why \(\mathrm{BeH}_2\) molecule has a zero dipole moment although the \(\mathrm{Be}-\mathrm{H}\) bonds are polar.

Answer: 

\(\mathrm{BeH}_2\) is a linear molecular \((\mathrm{H}-\mathrm{Be}-\mathrm{H})\), the bond angle \(=180^{\circ}\).
\(\mathrm{Be}-\mathrm{H}\) bonds are polar due to difference in their electronegativity but the bond polarities cancel each other. Thus, the molecule has a resultant dipole moment of zero.

Q23. Which out of \(\mathrm{NH}_3\) and \(\mathrm{NF}_3\) has higher dipole moment and why?

Answer: \(\ln \mathrm{NH}_3\) and \(\mathrm{NF}_3\), the difference in electronegativity is nearly same but the dipole moment of \(\mathrm{NH}_3=\) (1.46D) For Example, \(\mathrm{NH}_3=(0.24 \mathrm{D})\)
In \(\mathrm{NH} 3\), the dipole moments of the three \(\mathrm{N}-\mathrm{H}\) bonds are in the same direction as the lone pair of electron. But in \(\mathrm{NF}_3\), the dipole moments of the three \(\mathrm{N}-\mathrm{F}\) bonds are in the direction opposite to that of the lone pair. Therefore, the resultant dipole moment in \(\mathrm{NH}_3\) is more than in \(\mathrm{NF}_3\).

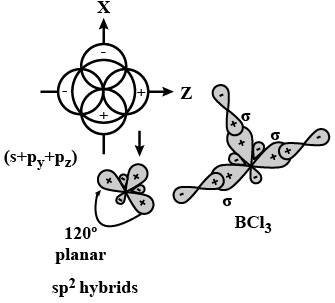
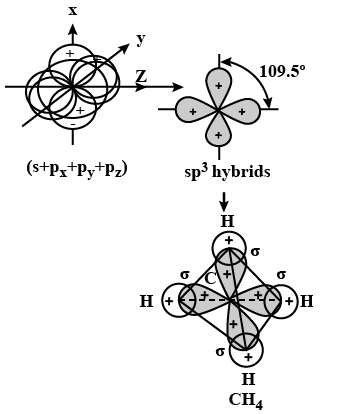
Q24. What is meant by hybridisation of atomic orbitals? Describe the shapes of \(s p\), \(s p^2, s p^3\) hybrid orbitals.

Answer: Hybridisation: It is defined as the process of intermixing of atomic orbitals of slightly different energies to give rise to new hybridized orbitals having equivalent energy and identical shapes.
Shapes of Orbitals:
sp hybridisation: When one s-and one p-orbital, intermix then it is called sp-hybridisation. For example, in BeF2, Be atom undergoes sp-hybridisation. It has linear shape. Bond angle is \(180^{\circ}\).
\(\mathrm{sp}^2\) hybridisation: One s-and two p-orbitals get hybridised to form three equivalent hybrid orbitals. The three hybrid orbitals directed towards three corners of an equilateral triangle. It is, therefore, known as trigonal hybridisation.
\(\mathrm{sp}^3\) hybridisation: One s-and three p-orbitals get hybridised to form four equivalent hybrid orbitals. These orbitals are directed towards the four corners of a regular tetrahedron.

Q25. Describe the change in hybridisation (if any) of the \(\mathrm{Al}\) atom in the following reaction.
\(
\mathrm{AlCl}_3+\mathrm{Cl}^{-} \rightarrow \mathrm{AlCl}_4^{-}
\)

Answer:

\(
\text { Electronic configuration of }{ }_{13} \mathrm{Al}=1 \mathrm{~s}^2 2 \mathrm{~s}^2 2 \mathrm{p}^6 3 \mathrm{~s}^1 3 \mathrm{p}_{\mathrm{x}}{ }^1 3 \mathrm{p}_{\mathrm{y}}{ }^1
\)
(excited state)
Hence, hybridisation will be \(\mathrm{SP}^2\)
In \(\mathrm{AlCl}_4^{-}\), the empty \(3 \mathrm{p}_z\) orbital is also involved. So, the hybridisation is \(\mathrm{sp}^3\) and the shape is tetrahedral.

Q26. Is there any change in the hybridisation of \(\mathrm{B}\) and \(\mathrm{N}\) atoms as a result of the following reaction?
\(
\mathrm{BF}_3+\mathrm{NH}_3 \rightarrow \mathrm{F}_3 \mathrm{~B} \cdot \mathrm{NH}_3
\)

Answer: In \(\mathrm{BF}_3, \mathrm{~B}\) atom is \(\mathrm{sp}^2\) hybridised. In \(\mathrm{NH}_3, \mathrm{~N}\) is \(\mathrm{sp}^3\) hybridised. After the reaction, hybridisation of \(\mathrm{B}\) changes from \(\mathrm{sp}^2\) to \(\mathrm{sp}^3\).

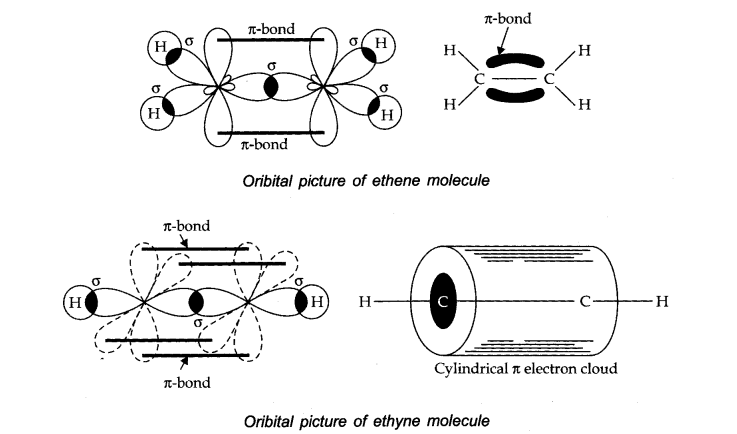
Q27. Draw diagrams showing the formation of a double bond and a triple bond between carbon atoms in \(\mathrm{C}_2 \mathrm{H}_4\) and \(\mathrm{C}_2 \mathrm{H}_2\) molecules.

Answer: 

\(\mathrm{C}_2 \mathrm{H}_4\) :
The electronic configuration of \(\mathrm{C}\)-atom in the excited state is:
\(
{ }_6 \mathrm{C}=1 \mathrm{~s}^2 2 \mathrm{~s}^1 2 \mathrm{p}_{\mathrm{x}}^1 2 \mathrm{p}_{\mathrm{y}}^1 2 \mathrm{p}_{\mathrm{z}}^1
\)
In the formation of an ethane molecule \(\left(\mathrm{C}_2 \mathrm{H}_4\right)\), one \(\mathrm{sp}^2\) hybrid orbital of carbon overlaps a \(\mathrm{sp}^2\) hybridized orbital of another carbon atom, thereby forming a \(\mathrm{C}\) C sigma bond.

The remaining two \(\mathrm{sp}^2\) orbitals of each carbon atom form a \(\mathrm{sp}^2-\mathrm{s}\) sigma bond with two hydrogen atoms. The unhybridized orbital of one carbon atom undergoes sidewise overlap with the orbital of a similar kind present on another carbon atom to form a weak \(\pi \text {-bond.}\)

\(\mathrm{C}_2 \mathrm{H}_2\) : In the formation of \(\mathrm{C}_2 \mathrm{H}_2\) molecule, each \(\mathrm{C}\)-atom is \(\mathrm{sp}\) hybridized with two \(2 \mathrm{p}\)-orbitals in an unhybridized state.
One \(s p\) orbital of each carbon atom overlaps with the other along the internuclear axis forming a C-C sigma bond. The second sp orbital of each Catom overlaps a half-filled 1s- orbital to form a \(\sigma\) bond.

The two unhybridized \(2 p\)-orbitals of the first carbon undergo sidewise overlap with the \(2 p\) orbital of another carbon atom, thereby forming two pi ( \(\pi\) ) bonds between carbon atoms. Hence, the triple bond between two carbon atoms is made up of one sigma and two \(\pi\)-bonds.

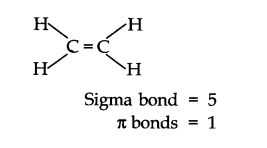
Q28. What is the total number of sigma and pi bonds in the following molecules?
(a) \(\mathrm{C}_2 \mathrm{H}_2\)
(b) \(\mathrm{C}_2 \mathrm{H}_4\)

Answer: (a) \(\mathrm{H}-\mathrm{C}\equiv\mathrm{C}-\mathrm{H}\)
Sigma bond \(=3; (\pi)\) bonds \(=2\)

(b) 

Q29. Considering \(\mathrm{x}\)-axis as the internuclear axis which out of the following will not form a sigma bond and why?
(a) \(1 s\) and is (b) \(1 s\) and \(2 p_x\);
(c) \(2 p_y\) and \(2 p_y\)
(d) \(1 s\) and \(2 s\).

Answer: \(2 \mathrm{p}_y\) and \(2 \mathrm{p}_y\) orbitals will not a form a sigma bond. Taking \(\mathrm{x}\)-axis as the internuclear axis, \(2 \mathrm{p}_y\) and \(2 \mathrm{p}_y\) orbitals will undergo lateral overlapping, thereby forming a pi \((\pi)\) bond.

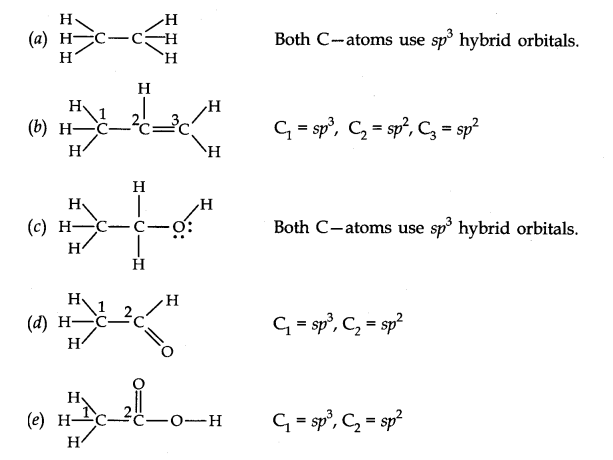
Q30. Which hybrid orbitals are used by carbon atoms in the following molecules?
(a) \(\mathrm{CH}_3-\mathrm{CH}_3\)
(b) \(\mathrm{CH}_3-\mathrm{CH}=\mathrm{CH}_2\);
(c) \(\mathrm{CH}_3-\mathrm{CH}_2-\mathrm{OH}\);
(d) \(\mathrm{CH}_3-\mathrm{CHO}\)
(e) \(\mathrm{CH}_3 \mathrm{COOH}\)

Answer: 

Q31. What do you understand by bond pairs and lone pairs of electrons? Illustrate by giving one example of each type.

Answer: The electron pair involved in sharing between two atoms during covalent bonding is called shared pair or bond pair. At the same time, the electron pair which is not involved in sharing is called lone pair of electrons.

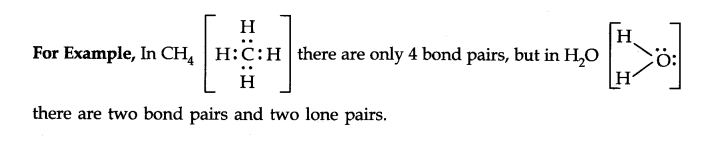
Q32. Distinguish between a sigma and a pi bond.

Answer: 

\(
\begin{array}{|l|l|}
\hline {\text { Sigma Bond }} & {\text { Pi Bond }} \\
\hline \begin{array}{l}
\text { 1. The bond is formed by the axial overlap of atomic } \\
\text { orbitals. }
\end{array} & \begin{array}{l}
\text { 1. The bond formed by the sidewise overlap of } \\
\text { atomic orbitals. }
\end{array} \\
\hline \begin{array}{l}
\text { 2. This bond can be formed by s-s, s-p or p-p } \\
\text { orbitals. }
\end{array} & \text { 2. It involves of overlap of p-orbitals only. } \\
\hline \begin{array}{l}
\text { 3. The bond is stronger because overlapping can take } \\
\text { place to a larger extent. }
\end{array} & \begin{array}{l}
\text { 3. The bond is weaker because the overlapping } \\
\text { occurs to a smaller extent. }
\end{array} \\
\hline \begin{array}{l}
\text { 4. The molecular orbital is symmetrical about the } \\
\text { internuclear axis and consists of single charged } \\
\text { cloud. }
\end{array} & \begin{array}{l}
\text { 4. The molecular orbital is discontinuous } \\
\text { and consists of two charged clouds above and below } \\
\text { the plane of atoms. }
\end{array} \\
\hline \begin{array}{l}
\text { 5. There can be a free rotation of atoms around the a } \\
\text { bond. }
\end{array} & \begin{array}{l}
\text { 5. Free rotation of atoms around } \pi \text { bond is not } \\
\text { possible because it involves breaking of } \pi \text { bond. }
\end{array} \\
\hline \begin{array}{l}
\text { 6. The shape of the molecule is determined by the sigma } \\
\text { framework around the central atom }
\end{array} & \begin{array}{l}
\text { 6. The } \pi \text { bonds do not contribute to the shape } \\
\text { however they modify the dimensions of the } \\
\text { molecule. }
\end{array} \\
\hline
\end{array}
\)

Q33. Explain the formation of \(\mathrm{H}_2\) molecule on the basis of valence bond theory.

Answer:Let us assume that two hydrogen atoms ( \(\mathrm{A}\) and \(\mathrm{B})\) with nuclei \(\left(\mathrm{N}_A\right.\) and \(\mathrm{N}_B\) ) and electrons \(\left(\mathrm{e}_A\right.\) and \(\left.\mathrm{e}_B\right)\) are taken to undergo a reaction to form a hydrogen molecule.
When A and B are at a large distance, there is no interaction between them. As they begin to approach each other, the attractive and repulsive forces start operating.
Attractive force arises between:
(a) Nucleus of one atom and its own electron i.e., \(\mathrm{N}_A-\mathrm{e}_A\) and \(\mathrm{N}_B-\mathrm{e}_B\).
(b) Nucleus of one atom and electron of another atom i.e., \(\mathrm{N}_A-\mathrm{e}_B\) and \(\mathrm{N}_B-\mathrm{e}_A\).
Repulsive force arises between:
(a) Electrons of two atoms i.e., \(\mathrm{e}_A-\mathrm{e}_B\).
(b) Nuclei of two atoms i.e., \(\mathrm{N}_A-\mathrm{N}_B\).
The force of attraction brings the two atoms together, whereas the force of repulsion tends to push them apart.
The magnitude of the attractive forces is more than that of the repulsive forces. Hence, the two atoms approach each other. As a result, the potential energy decreases. Finally, a state is reached when the attractive forces balance the repulsive forces and the system acquires minimum energy. This leads to the formation of a dihydrogen molecule.

As they tend to come closer, two different forces operate between the nucleus and the electron of the other and vice versa. The nuclei of the atoms as well as their electrons repel each other. Energy is needed to overcome the force of repulsion. Although the number of new attractive and repulsive forces is the same, but the magnitude of the attractive forces is more. Thus, when two hydrogen atoms approach each other, the overall potential energy of the system decreases. Thus, a stable molecule of hydrogen is formed.

Q34. Write the important conditions required for the linear combination of atomic orbitals to form molecular orbitals.

Answer:

• The combining atomic orbitals should have comparable energies.
  For example, Is orbital of one atom can combine with Is atomic orbital of another atom, \(2 \mathrm{~s}\) can combine with \(2 \mathrm{~s}\).
• The combining atomic orbitals must have proper orientations. So that they are able to overlap to a considerable extent.
• The extent of overlapping should be large.

Q35. Use molecular orbital theory to explain why the \(\mathrm{Be}_2\) molecule does not exist.

Answer:

\(
\text { E.C. of } \mathrm{Be}=1 \mathrm{~s}^2 2 \mathrm{~s}^2
\)
\(
\text { M.O.E.C. of } \mathrm{~Be}_2=\sigma 1s^2 \sigma^{*} 1s^2 \sigma 2s^2 \sigma^{*} 2s^2
\)
\(
\begin{aligned}
\text { Bond order } & =\frac{1}{2}(4-4) = 0\\
\end{aligned}
\)
Hence, \(\mathrm{Be}_2\) does not exist.

Q36. Compare the relative stability of the following species and indicate their magnetic properties;
\(\mathrm{O}_2, \mathrm{O}_2^{+}, \mathrm{O}_2^{-}\)(superoxide), \(\mathrm{O}_2^{2-}\) (peroxide)

Answer:

\(\mathrm{O}_2-\) Bond order \(=2\), paramagnetic
\(\mathrm{O}_2{ }^{+}\)– Bond order \(=2.5\), paramagnetic
\(\mathrm{O}_2{ }^{-}-\)Bond order \(=1.5\), paramagnetic
\(\mathrm{O}_2{ }^{2-}\) – Bond order \(=1\), diamagnetic
The order of relative stability is
\(
\begin{aligned}
& \mathrm{O}_2^{+}>\mathrm{O}_2>\mathrm{O}_2^{-}>\mathrm{O}_2^{2-} \\
& (2.5)(2.0)(1.5)(1.0)
\end{aligned}
\)

Q37. Write the significance of a plus and a minus sign shown in representing the orbitals.

Answer: The plus and minus sign is used to identify the nature of electron wave. Plus (+ve) sign denotes crest, while (-ve) sign denotes trough.

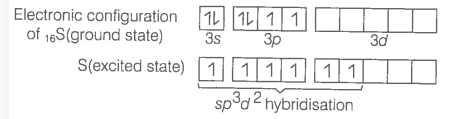
Q38. Describe the hybridisation in the case of \(\mathrm{PCl}_5\). Why are the axial bonds longer as compared to equatorial bonds?

Answer: The ground state E.C. and the excited state E.C. of phosphorus are represented as:

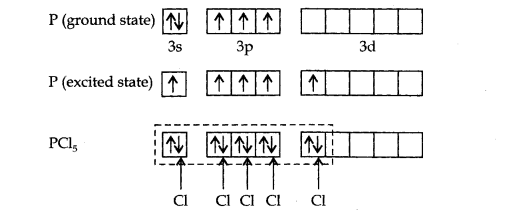
\(s p^3\) hybrid orbitals filled by electron pairs donated by five \(\mathrm{Cl}\) atoms

The one s, three-p and one d-orbitals hybridise to yield five sets of \(\mathrm{SP}^3 \mathrm{~d}\) hybrid orbitals which are directed towards the five corners of a trigonal bipyramidal as in Fig.

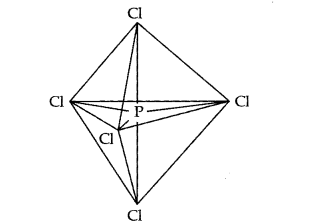
Trigonal bipyramidal geometry of \(\mathrm{PCl}_5\) molecule

Because axial bond pairs suffer more repulsive interaction from the equatorial bond pairs, therefore axial bonds have been found to be slightly longer and hence slightly weaker than equatorial bonds.

Q39. Define hydrogen bond. Is it weaker or stronger than the van der Waals forces?

Answer: When hydrogen is attached with highly electronegative element in a covalent bonding the electrons of the covalent bond are shifted towards the more electronegative atom. Thus, a partially positively charged hydrogen atom forms a bond with the other more electronegative atom. This bond is known as a hydrogen bond. Hydrogen bond is stronger than the van der Waals forces.

Q40. What is meant by the term bond order? Calculate the bond order of : \(\mathrm{N}_2, \mathrm{O}_2, \mathrm{O}_2^{+}\) and \(\mathrm{O}_2^{-}\).

Answer: Bond order is defined as the half of the difference between the number of electrons present in bonding and antibonding molecular orbitals.

Exemplar  Problems

Q1. Explain the non linear shape of \(\mathrm{H}_2 \mathrm{~S}\) and non planar shape of \(\mathrm{PCl}_3\) using valence shell electron pair repulsion theory.

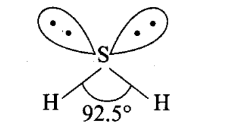
Answer: Central atom of \(\mathrm{H}_2\) is \(\mathrm{S}\). There are 6 electrons in its valence shell \(\left({ }_{16} \mathrm{~S}=2,8,6\right)\). Two electrons are shared with two \(\mathrm{H}\)-atoms and the remaining four electrons are present as two lone pairs. Hence, the total pairs of electrons are four ( 2 bond pairs and 2 lone pairs). Due to the presence of 2 lone pairs the shape becomes distorted tetrahedral or angular or bent (non-linear).

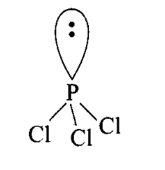
\(\mathrm{PCl}_3\)-Central atom is phosphorus. There are 5 electrons in its valence shell \(\left({ }_{15} \mathrm{P}=2,8,5\right)\). Three electrons are shared with three \(\mathrm{Cl}\)-atoms and the remaining two electrons are present as one lone pair.Hence, the total pairs of electrons are four ( 1 lone pair and 3 bond pairs). Due to the presence of one lone pair, the shape becomes pyramidal (non-planar).

Q2. Using molecular orbital theory, compare the bond energy and magnetic character of \(\mathrm{O}_2^{+}\)and \(\mathrm{O}_2^{-}\)species.

Answer:

\(
\begin{aligned}
& \mathrm{O}_2^{+}(15): \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2=\pi 2 p_y^2 \pi^* 2 p_x^1 \\
& \text { B.O. }=\frac{1}{2}(10-5)=2.5 \\
& \mathrm{O}_2^{-}(17): \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2=\pi 2 p_y^2 \pi^* 2 p_x^2=\pi^* 2 p_y^1 \\
& \text { B.O. }=\frac{1}{2}(10-7)=1.5
\end{aligned}
\)
Bond energy of \(\mathrm{O}_2^{+}>\mathrm{O}_2^{-}\)
Both are paramagnetic due to the presence of unpaired electrons. Higher bond order of \(\mathrm{O}_2^{+}\)shows that it is more stable than \(\mathrm{O}_2^{-}\). Both the species have unpaired electrons. So, both are paramagnetic in nature.

Q3. Explain the shape of \(\mathrm{BrF}_5\).

Answer: The central atom \(\mathrm{Br}\) has seven electrons in the valence shell. Five of these will form bonds with five fluorine atoms and the remaining two electrons are present as one lone pair. \(\mathrm{Br}\)-atom has configuration:
\(
1 s^2, 2 s^2 2 p^6, 3 s^2 3 p^6 3 d^{10}, 4 s^2 4 p^5
\)
To get pentavalency, two of the p-orbitals are unpaired and electrons are shifted to \(4 \mathrm{~d}\)-orbitals. Hence, the total pairs of electrons are six ( 5 bond pairs and 1 lone pair). To minimize repulsion.

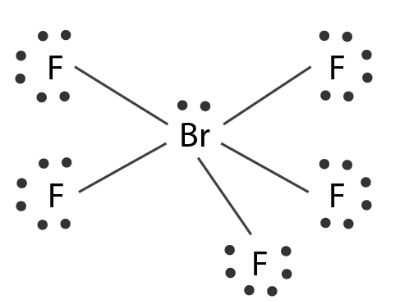
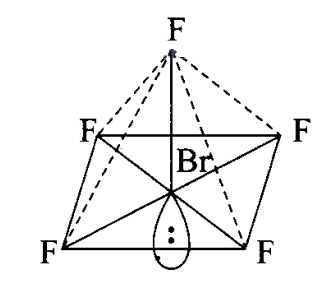
In this excited state, \(s p^3 d^2\)-hybridisation occurs giving octahedral structure. Five positions are occupied by \(F\) atoms forming sigma bonds with hybrid bonds and one position occupied by lone pair, i.e., the molecule as a square pyramidal shape.

Q4. Structures of molecules of two compounds are given below :

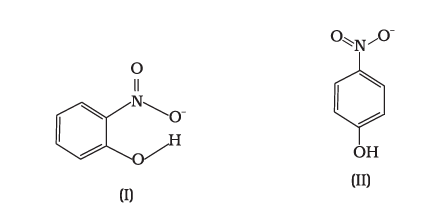
(a) Which of the two compounds will have intermolecular hydrogen bonding and which compound is expected to show intramolecular hydrogen bonding?
(b) The melting point of a compound depends on, among other things, the extent of hydrogen bonding. On this basis explain which of the above two compounds will show the higher melting point.
(c) Solubility of compounds in water depends on power to form hydrogen bonds with water. Which of the above compounds will form hydrogen bond with water easily and be more soluble in it?

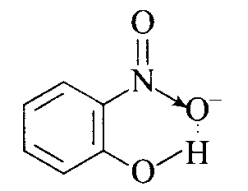
Answer: (a) Compound I will form intramolecular hydrogen bond because \(\mathrm{NO} 2\) and \(\mathrm{OH}\) groups are close together whereas it is not so in compound II. Compound (I) will form intramolecular \(\mathrm{H}\)-bonding. Intramolecular \(\mathrm{H}\)-bonding is formed when \(\mathrm{H}\)-atom, in between the two highly electronegative atoms, is present within the same molecule. In ortho-nitrophenol (compound I), \(\mathrm{H}\)-atom is in between the two oxygen atoms.

Compound II will have intermolecular hydrogen bonding. Bonding in both the cases is shown below: Compound (II) forms intermolecular \(\mathrm{H}\)-bonding. In para-nitrophenol (II) there is a gap between \(\mathrm{NO}_2\) and \(\mathrm{OH}\) group. So, \(\mathrm{H}\)-bond exists between \(\mathrm{H}\)-atom of one molecule and \(\mathrm{O}\)-atom of another molecule as depicted below.

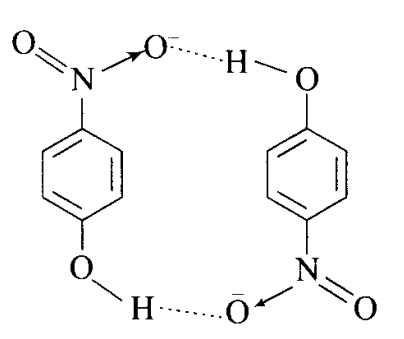
(b) As a large number of molecules can be linked together through intermolecular hydrogen bonding, compound II will show higher melting point.
(c) Due to intramolecular hydrogen bonding, compound I will not be able to form hydrogen bonds with \(\mathrm{H}_2 \mathrm{O}\) molecules. Hence, it will be less soluble in water. However, compound II can form hydrogen bonds with \(\mathrm{H}_2 \mathrm{O}\) molecules easily and hence it will be more soluble in water.

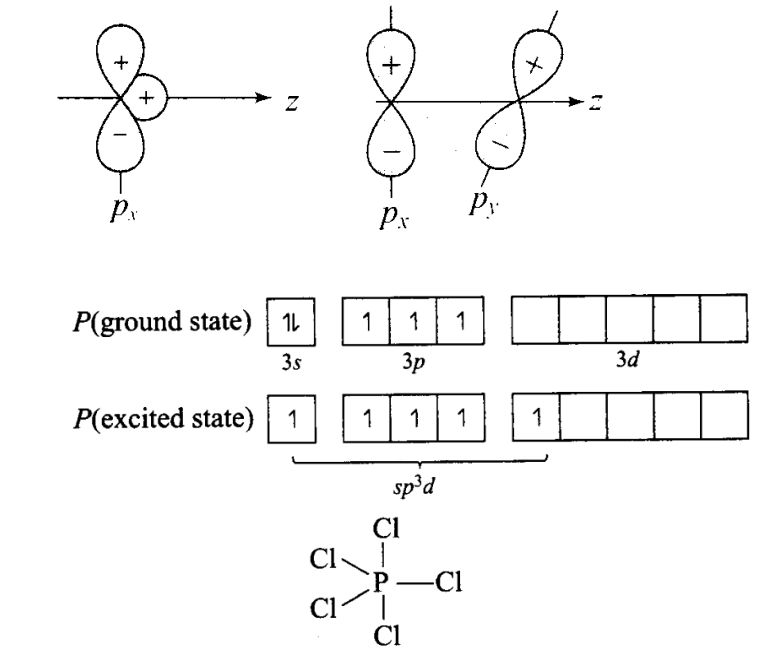
Q5. Why does type of overlap given in the following figure not result in bond formation?

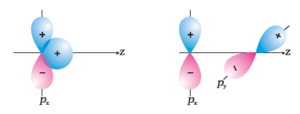
Answer:  In first figure, the ++ overlap is equal to +- overlap and therefore, these cancel out and the net overlap is zero.
In the second figure, no overlap is possible because the two orbitals are perpendicular to each other.

Q6. Explain why \(\mathrm{PCl}_5\) is trigonal bipyramidal whereas \(\mathrm{IF}_5\) is square pyramidal.

Answer: \(P C l_5\) – The ground state and the excited state outer electronic configurations of phosphorus \((Z=15)\) are represented below.

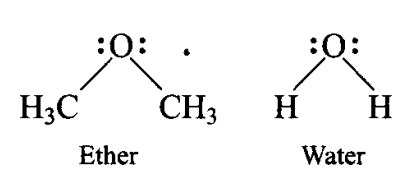
Q7. In both water and dimethyl ether oxygen atom is central atom, and has the same hybridisation, yet they have different bond angles. Which one has greater bond angle? Give reason.

Answer: Dimethyl ether has larger bond angle than water. This is because there is more repulsion between bond pairs of \(\mathrm{CH}_3\) groups attached in ether than between bond pairs of hydrogen atoms attached to oxygen in water. The carbon of \(\mathrm{CH}_3\) group in ether is attached to three hydrogen atoms through c bonds and electron pairs of these bonds add to the electron charge density on carbon atom. Hence, repulsion between two \(\mathrm{CH}_3\) groups will be more than that between two \(\mathrm{H}\) atoms.

Q8. Write Lewis structure of the following compounds and show the formal charge on each atom.
\(
\mathrm{HNO}_3, \mathrm{NO}_2, \mathrm{H}_2 \mathrm{SO}_4
\)

Answer: Formal charge on an atom in a Lewis structure = [total number of valence electrons in free atom] – [total number of non-bonding (lone pairs) electrons] \(-1 / 2\) [total number of bonding or shared electrons]

\(
\mathrm{F}=\mathrm{V}-\mathrm{L}-\frac{B}{2}
\)
Where,
\(\mathrm{F}=\) Formal Charge
\(V=\) Valence Electron of the neutral atom in isolation
\(\mathrm{L}=\) Number of non-bonding valence electrons on this atom in the molecule
\(\mathrm{B}=\) Total number of electrons shared in bonds with other atoms in the molecule

(i) \(\mathrm{HNO}_3\)
Formal charge \(=1 / 2\) [total no: of bonding or shared electrons]
Oxygen with single bond will have formal charge of \(=6-6-2 / 2=-1\)
Oxygen with double bond will have formal charge of \(=6-4-4 / 2=0\)
Therefore, nitrogen will have a formal charge of \(=5-2-6 / 2=0\)
Oxygen 1 and 4 will have a formal charge \(=6-4-4 / 2=0\)
Oxygen 2 and 3 will have a formal charge \(=6-4-4 / 2=0\)
Hydrogen 1 and 2 will have a formal charge \(=1-0-2 / 2=0\)
Sulfur will have a formal charge \(=6-0-12 / 2=0\)

\(
\text { (ii) } \mathrm{NO}_2
\)

F.C. on \(\mathrm{O}(1) \rightarrow 6-6-\frac{1}{2}(2)=-1\)
F.C. on \(\mathrm{O}(2) \rightarrow 6-4-\frac{1}{2}(4)=0\)
F.C. on \(\mathrm{N} \rightarrow 5-2-\frac{1}{2}(6)=0\)

\(
\text { (iii) } \mathrm{H}_2 \mathrm{SO}_4
\)

\(
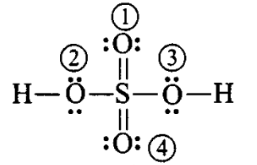
\begin{aligned}
& \text { F.C. on } \mathrm{O}(1) \text { and }(4) \rightarrow 6-4-\frac{1}{2}(4)=0 \\
& \text { F.C. on } \mathrm{O}(2) \text { and }(3) \rightarrow 6-4-\frac{1}{2}(4)=0 \\
& \text { F.C. on } \mathrm{H} \longrightarrow 1-0-\frac{1}{2}(2)=0 \\
& \text { F.C. on } \mathrm{S} \longrightarrow 6-0-\frac{1}{2}(12)=0
\end{aligned}
\)

Q9. The energy of \(\sigma 2 p_z\) molecular orbital is greater than \(\pi 2 p_x\) and \(\pi 2 p_y\) molecular orbitals in nitrogen molecule. Write the complete sequence of energy levels in the increasing order of energy in the molecule. Compare the relative stability and the magnetic behaviour of the following species :
\(
\mathrm{N}_2, \mathrm{~N}_2^{+}, \mathrm{N}_2^{-}, \mathrm{N}_2^{2+}
\)

Answer: Sequence of energy levels
\(
\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\pi 2 p_x=\pi 2 p_y<\sigma 2 p_z
\)
For \(\mathrm{N}_2\) molecule the M.O. configuration is:
\(
\sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_x^2=\pi 2 p_y^2 \sigma 2 p_z^2
\)
B.O. \(=\frac{1}{2}(10-4)=3\), diamagnetic
\(
\mathrm{N}_2^{+}: \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_x^2=\pi 2 p_y^2 \sigma 2 p_z^1
\)
\(
\begin{aligned}
& \text { B.O. }=\frac{1}{2}(9-4)=2.5, \text { paramagnetic } \\
& \mathrm{N}_2^{-}: \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_x^2=\pi 2 p_y^2 \sigma 2 p_z^2 \pi^* 2 p_x^1
\end{aligned}
\)
B.O. \(=\frac{1}{2}(10-5)=2.5\), paramagnetic
\(\mathrm{N}_2^{2+}: \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_x^2=\pi 2 p_y^2\)
B.O. \(=\frac{1}{3}(8-4)=2\), diamagnetic
\(
\text { B.O. }=\frac{1}{2}(8-4)=2 \text {, diamagnetic }
\)
Stability order: \(\mathrm{N}_2>\mathrm{N}_2^{-}>\mathrm{N}_2^{+}>\mathrm{N}_2^{2+}\) ( \(\mathrm{N}_2^{-}\)has more bonding electrons as compared to \(\mathrm{N}_2^{+}\)).

Q10. What is the effect of the following processes on the bond order in \(\mathrm{N}_2\) and \(\mathrm{O}_2\)?
(i) \(\mathrm{N}_2 \rightarrow \mathrm{N}_2^{+}+\mathrm{e}^{-}\)
(ii) \(\quad \mathrm{O}_2 \rightarrow \mathrm{O}_2^{+}+\mathrm{e}^{-}\)

Answer:

(i)
\(
\begin{array}{|c|c|l|c|}
\hline \text { Species } & \begin{array}{c}
\text { Total } \\
\text { electrons }
\end{array} & \begin{array}{c}
\text { Configuration } \\
\end{array} & \begin{array}{c}
\text { Bond } \\
\text { order }
\end{array} \\
\hline \mathrm{N}_2 & 14 & \mathrm{KK} \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_{\mathrm{x}}{ }^2=\pi 2 p_{\mathrm{y}}{ }^2 \sigma 2 p_{\mathrm{z}}{ }^2 & \frac{8-2}{2}=3 \\
\hline \mathrm{N}_2^{+} & 13 & \mathrm{KK} \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_{\mathrm{x}}{ }^2=\pi 2 p_{\mathrm{y}}{ }^2 \sigma 2 p_{\mathrm{z}}{ }^1 & \frac{7-2}{2}=2.5 \\
\hline
\end{array}
\)
Bond order decreases from 3 to 2.5.

(ii) 
\(
\begin{array}{|c|c|l|l|}
\hline \text { Species } & \begin{array}{c}
\text { Total } \\
\text { electrons }
\end{array} & \begin{array}{c}
\text { Configuration } \\
\end{array} & \begin{array}{c}
\text { Bond } \\
\text { order }
\end{array} \\
\hline \mathrm{O}_2 & 16 & \begin{array}{l}
\mathrm{KK} \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_{\mathrm{z}}{ }^2 \pi 2 p_{\mathrm{x}}{ }^2=\pi 2 p_{\mathrm{y}}{ }^2 \pi^* 2 p_{\mathrm{x}}{ }^1 \\
=\pi^* 2 p_{\mathrm{y}}{ }^1
\end{array} & \frac{8-4}{2}=2.0 \\
\hline \mathrm{O}_2^{+} & 15 & \mathrm{KK} \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_{\mathrm{z}}{ }^2 \pi 2 p_{\mathrm{x}}{ }^2=\pi 2 p_{\mathrm{y}}{ }^2 \pi^* 2 p_{\mathrm{x}}{ }^1 & \frac{8-3}{2}=2.5 \\
\hline
\end{array}
\)
Bond order increases from 2 to 2.5.

Q11. Give reasons for the following :
(i) Covalent bonds are directional bonds while ionic bonds are nondirectional.
(ii) Water molecule has bent structure whereas carbon dioxide molecule is linear.
(iii) Ethyne molecule is linear.

Answer: (i) Since the covalent bond depends on the overlapping of orbitals between different orbitals, the geometry of the molecule is different. The orientation of overlap is different. The orientation of overlap is the factor responsible for their directional nature.
(ii) Due to the presence of two lone pairs of electrons on the oxygen atom in \(\mathrm{HiO}\) the repulsion between lp-lp is more. \(\mathrm{CO}_2\) undergoes sp hybridization resulting in linear shape \((\mathrm{O}=\mathrm{C}=0)\) while \(\mathrm{H}_2 \mathrm{O}\) undergoes \({sp}^3\) hybridisation resulting in distorted tetrahedral or bent structure.

(iii) In ethyne molecule carbon undergoes sp hybridization with two unhybridised orbitals. One sp hybrid orbital of one carbon atom overlaps axially with \(\mathrm{sp}\) hybrid orbital of the other carbon atom to form \(\mathrm{C}-\mathrm{C}\) sigma bond while the other hybridized orbital of each carbon atom overlaps axially with \(S\) orbitals of hydrogen atoms forming \(\sigma\) bonds. Unhybridised orbitals form \(\pi\) bonds

Q12. What is an ionic bond? With two suitable examples explain the difference between an ionic and a covalent bond.

Answer: An ionic bond is formed as a result of the electrostatic attraction between the positive and negative ions formed by the transfer of electrons from one atom to another.
Ionic bond: The bond which is formed by the transferring electrons from one atom to other atom completely, and as a result positive and negative ions are formed in this bond. Here, the ions are held together through the electrostatic force of attraction. e.g.,
The formation of calcium fluoride,
\(
\mathrm{Ca} \rightarrow \mathrm{Ca}^{2+}+2 e^{-}
\)
\(
[A r] 4 s^2[A r]
\)
\(
\begin{aligned}
& \mathrm{F}+e^{-} \rightarrow F^{-} \\
& {[\mathrm{He}] 2 s^2 2 p^5[\mathrm{He}] 2 s^2 2 p^6 \text { or }[\mathrm{Ne}]} \\
& \mathrm{Ca}^{2+}+2 F^{-} \rightarrow \mathrm{CaF}_2 \text { or } \mathrm{Ca}^{2+}\left(\mathrm{F}^{-}\right)_2
\end{aligned}
\)
The information of \(\mathrm{NaCl}\)
\(
\begin{aligned}
& \mathrm{Na} \rightarrow \mathrm{Na}^{+}+e^{-} \\
& {[\mathrm{Ne}] 3 s^2 3 p^5[\mathrm{Ne}] 3 s^2 3 p^6 \text { or }[\mathrm{Ar}]} \\
& \mathrm{Na}^{+}+\mathrm{Cl}^{-} \rightarrow \mathrm{NaCl} \text { or } \mathrm{Na}^{+} \mathrm{Cl}^{-}
\end{aligned}
\)
Covalent bond: The bond which is formed between the two atoms of non-metals by the mutual sharing of electrons between them is called a covalent bond, e.g., the formation of a chlorine molecule can be explained as

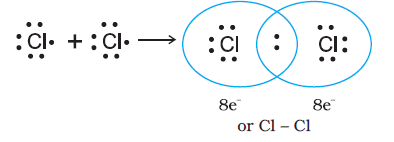
Also formation of \(\mathrm{HCl}\):

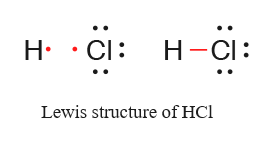
Q13. Arrange the following bonds in order of increasing ionic character giving reason.
\(
\mathrm{N}-\mathrm{H}, \mathrm{F}-\mathrm{H}, \mathrm{C}-\mathrm{H} \text { and } \mathrm{O}-\mathrm{H}
\)

Answer:The ionic character of the bond depends on the electronegativity. Ionic character \(\alpha\) to the difference of electronegativity.
In the following bonds, hydrogen is in all but have different electronegativity.
\(N-H, F-H, C-H\) and \(O-H\)
Increasing order of electronegativity is:
\(
C<N<O<F
\)
Therefore, the ionic character of the bond in increasing order will be
\(
C-H<N-H<O-H<F-H
\)
Increasing order of electronegativity difference: \(\mathrm{C}-\mathrm{H}<\mathrm{N}-\mathrm{H}<\mathrm{O}-\mathrm{H}<\mathrm{F}-\mathrm{H}\)
The greater is the difference in electronegativity between two bonded atoms, the greater is the ionic character.

Q14. Explain why \(\mathrm{CO}_3^{2-}\) ion cannot be represented by a single Lewis structure. How can it be best represented?

Answer: A single Lewis structure of \(\mathrm{CO}_3^{2-}\) ion cannot explain all the properties of this ion. It can be represented as a resonance hybrid of the following structures:

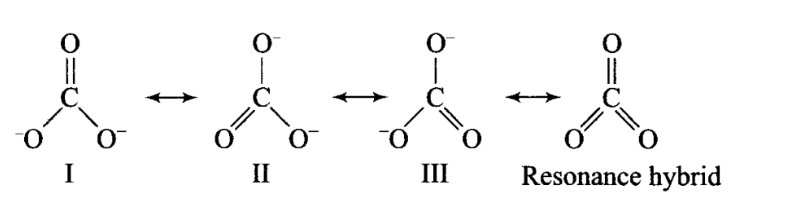
If it were represented only by one structure, there should be two types of bonds, i.e., \(\mathrm{C}=\mathrm{O}\) double bond and \(\mathrm{C}-\mathrm{O}\) single bonds but actually all bonds are found to be identical with same bond length and same bond strength.

Q15. Predict the hybridisation of each carbon in the molecule of the organic compound given below. Also, indicate the total number of sigma and pi bonds in this molecule.

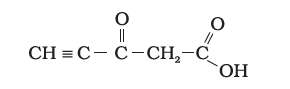
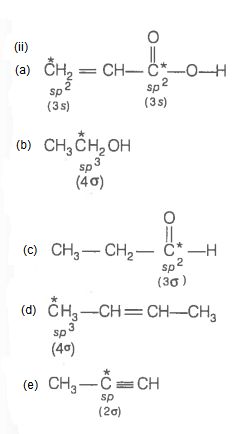
Answer: 

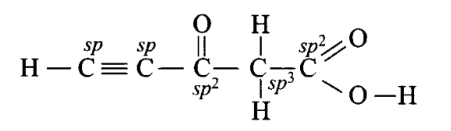
Number of \(\sigma\) bonds \(=11\)
Number of \(\pi\) bonds \(=4\)

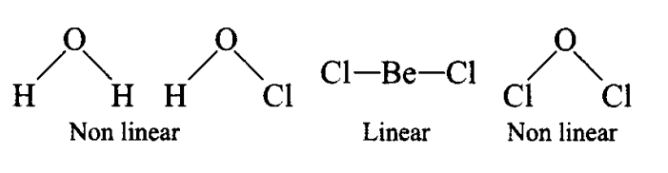
Q16. Group the following as linear and non-linear molecules:
\(
\mathrm{H}_2 \mathrm{O}, \mathrm{HOCl}, \mathrm{BeCl}_2, \mathrm{Cl}_2 \mathrm{O}
\)

Answer: 

Q17. Elements \(\mathrm{X}, \mathrm{Y}\) and \(\mathrm{Z}\) have 4,5 and 7 valence electrons respectively. (i) Write the molecular formula of the compounds formed by these elements individually with hydrogen. (ii) Which of these compounds will have the highest dipole moment?

Answer: 

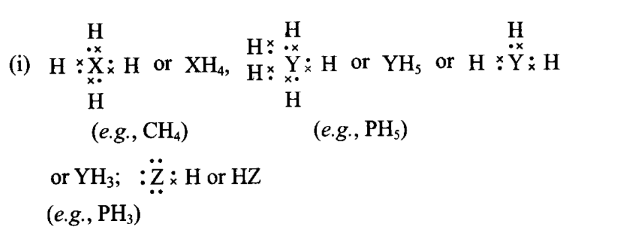
(ii) \(Z\) will be most electronegative element and hence \(\mathrm{HZ}\) will have highest dipole moment.

Q18. Draw the resonating structure of
(i) Ozone molecule
(ii) Nitrate ion

Answer: (i) Resonating structure of Ozone \((O)_3\) :

(ii) Resonating structure of \(\mathrm{NO}_3^{-}\):

Q19. Predict the shapes of the following molecules on the basis of hybridisation.
\(
\mathrm{BCl}_3, \mathrm{CH}_4, \mathrm{CO}_2, \mathrm{NH}_3
\)

Answer: \(\mathrm{BCl}_3-\mathrm{sp}^2\) hybridisation – Trigonal planar 

\(\mathrm{CH}_4-\mathrm{sp}{ }^3\) hybridisation – Tetrahedral.

\(\mathrm{NH}_3-\mathrm{sp}^3\) hybridisation – Distorted tetrahedral or Pyramidal

\(\mathrm{CO}_2\) show linear shape because of \(\mathrm{sp}\) hybridisation.

• The central element is carbon. It is a neutral molecule.
• The electronic contribution from carbon is \(\mathbf{4}\) and from two oxygen is \(\mathbf{4}\). The total electronic pair is thus \(\mathbf{4}\) out of which two are sigma bonds are two are pi bonds.
• As pi bonds do not contribute toward hybridization, the total electronic pairs are two.
• Two-electron pairs mean sp hybridization and the shape is linear.

Q20. All the \(\mathrm{C}-\mathrm{O}\) bonds in carbonate ion \(\left(\mathrm{CO}_3^{2-}\right)\) are equal in length. Explain.

Answer: Carbonate ion is represented by resonating structures as given below:

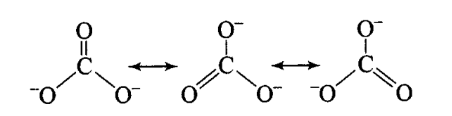
The actual structure will be the mixture of all resonating structures, also called resonance hybrid structures.

Q21. What is meant by the term average bond enthalpy? Why is there difference in bond enthalpy of \(\mathrm{O}-\mathrm{H}\) bond in ethanol \(\left(\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}\right)\) and water?

Answer: All the similar bonds in a molecule do not have the same bond enthalpies, e.g., in \(\mathrm{CH}_4\)

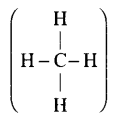
the four \(\mathrm{C}-\mathrm{H}\) bonds do not have the same bond enthalpies because after breaking of the bonds one by one, the electronic environment around carbon changes. Hence, the actual bond enthalpy of \(\mathrm{C}-\mathrm{H}\) bond is taken as the average value. \(\mathrm{O}-\mathrm{H}\) bond in ethanol 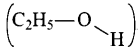and that in water 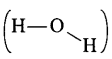do not have similar electronic Environment around oxygen atom. Hence, their \(\mathrm{O}-\mathrm{H}\) bond enthalpies are different.

Q22. (i) Discuss the significance/ applications of dipole moment.
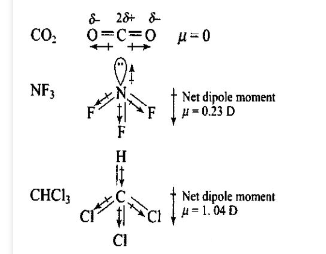
(ii) Represent diagrammatically the bond moments and the resultant dipole moment in \(\mathrm{CO}_2, \mathrm{NF}_3\) and \(\mathrm{CHCl}_3\).

Answer: (i) Dipole moment plays a very important role in understanding the nature of the chemical bond. A few applications are given below:
(a) Distinction between, polar and non-polar molecules: The measurement of dipole moment can help us to distinguish between polar and non-polar molecules. Non-polar molecules have zero dipole moment while polar molecules have some value of dipole moment.
(b) Degree of polarity in a molecule: Dipole moment measurement also gives an idea about the degree of polarity especially in a diatomic molecule. The greater the dipole moment, the greater is the polarity in such a molecule.
(c) Shape of molecules: In the case of molecules containing more than two atoms, the dipole moment not only depends upon the individual dipole moments of the bonds but also on the arrangement of bonds. Thus, dipole moment is used to find the shapes of molecules.
(d) Ionic character in a molecule: Knowing the electronegativities of atoms involved in a molecule, it is possible to predict the nature of the chemical bond formed. If the difference in electronegativities of two atoms is large, the bond will be highly polar. As an extreme case, when the electron is completely transferred from one atom to another, an ionic bond is formed. Therefore, the ionic bond is regarded as an extreme case of covalent bond. The greater the difference in electronegativities of the bonded atoms, the higher is the ionic character.
(e) Distinguish between cis- and trans-isomers: Dipole moment measurements help to distinguish between cis- and trans- isomers because the cis-isomer has usually higher dipole moment than trans isomer.
(f) Distinguish between ortho, meta and para isomers: Dipole moment measurements help to distinguish between \(\mathrm{o-}, \mathrm{m}\) – and \(\mathrm{p}\)-isomers because the dipole moment of \(\mathrm{p}\)-isomer is zero and that of \(\mathrm{o}\)-isomers is more than that of m-isomer.

(ii)

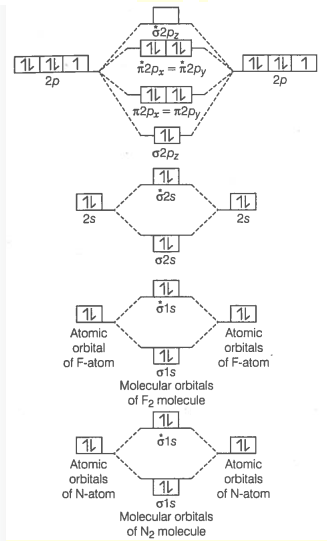
Q23. Use the molecular orbital energy level diagram to show that \(N_2\) would be expected to have a triple bond, \(\mathrm{F}_2\), a single bond and \(\mathrm{Ne}_2\), no bond.

Answer: The general sequence of the energy level of molecular orbitals for nitrogen is:
\(
\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\pi 2 p_x=\pi 2 p_y<\sigma 2 p_z
\)
The molecular orbitals in the sequence of their energy levels for the given \(\mathrm{N}_2\) molecule molecules have hereby been described below:
\(
\sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_x{ }^2=\pi 2 p_y{ }^2 \sigma 2 p_z{ }^2
\)
Bond order \(=\frac{1}{2}\left[\mathrm{~N}_{\mathrm{b}}-\mathrm{N}_{\mathrm{a}}\right]=\frac{1}{2}(10-4)=3\).
Bond order value of 3 means that \(\mathrm{N}_2\) contains a triple bond.

Fluorine molecule \(\left(\mathrm{F}_2\right)\) : Electronic configuration of \(\mathrm{F}\)-atom \((Z=9)\) is \(1 s^2 2 s^2 2 p_x^2 2 p_y^2 2 p_z^1\). Total number of electron in \(\mathrm{F}_2\) molecule is 18,9 from each \(\mathrm{F}\)-atom. Thus, it has two electrons more than \(\mathrm{O}_2\) molecule. These two additional electrons will enter into \(\pi^*\left(2 p_x\right)\) and \(\pi^*\left(2 p_y\right)\) orbitals, one in each of them so that pairing of electrons takes place in these orbitals. Thus, the electronic configuration of \(\mathrm{F}_2\) will be
\(
\begin{aligned}
& {[\sigma(1 s)]^2\left[\sigma^*(1 s)\right]^2[\sigma(2 s)]^2\left[\sigma^*(2 s)\right]^2\left[\sigma\left(2 p_z\right)\right]^2\left[\pi\left(2 p_x\right)\right]^2\left[\pi\left(2 p_y\right)\right]^2\left[\pi^*\left(2 p_x\right)\right]^2} {\left[\pi^*\left(2 p_y\right)\right]^2}
\end{aligned}
\)

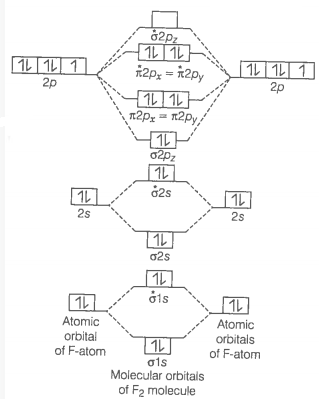
The molecular orbital of Fluorine has been described below:
\(
F_2=\sigma 1 s^2, \sigma^* 1 s^2, \sigma 2 s^2, \sigma^* 2 s^2, \sigma 2 p x^2, \pi 2 p x^2=\pi 2 p y^2
\)

Bond order \(=\frac{1}{2}\left[N_b-N_a\right]=\frac{1}{2}(10-8)=1\)
Bond order value 1 means that \(F_2\) contains single bond. Thus, we can imply that when the bond order is 1, the number of bonds must also be 1.

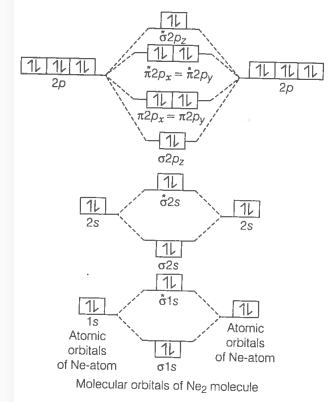
Formation of \(\mathrm{Ne}_2\) molecule \({ }_{10} \mathrm{Ne}=1 \mathrm{~s}^2, 2 \mathrm{~s}^2, 2 \mathrm{p}_{\mathrm{x}}{ }^2, 2 \mathrm{p}_{\mathrm{y}}{ }^2, 2 \mathrm{p}_{\mathrm{z}}{ }^2\)
\(
N e_2=\sigma 1 s^2, \sigma^* 1 s^2, \sigma 2 s^2, \sigma^* 2 s^2, \sigma 2 p x^2, \pi 2 p x^2=\pi 2 p y^2, \pi^* 2 p_x{ }^2=\pi^* 2 p_y{ }^2
\)
Now, we can calculate the bond order of \(N e_2\)
\(
\text { Bond order }=\frac{1}{2}\left[\mathrm{~N}_{\mathrm{b}}-\mathrm{N}_{\mathrm{a}}\right]=\frac{1}{2}(10-10)=0
\)
Bond order value zero means that there is no formation of bond between two \(\mathrm{Ne}\)-atoms. Hence, \(\mathrm{Ne}_2\) molecule does not exist.

Q24. Briefly describe the valence bond theory of covalent bond formation by taking an example of hydrogen. How can you interpret energy changes taking place in the formation of dihydrogen?

Answer:The valence bond theory was put forward by Heitler and London in 1927. It was later improved and developed by L. Pauling and J.C. Slater in 1931. The valence bond theory is based on the knowledge of atomic orbitals and electronic configurations of elements, overlap criteria of atomic orbitals, and stability of molecules.
The main points of valence bond theory are
(i) Atoms do not lose their identity even after the formation of the molecule.
(ii) The bond is formed due to the interaction of only the valence electrons as the two atoms come close to each other. The inner electrons do not participate in the bond formation.
(iii) During the formation of bond, only the valence electrons from each bonded atom lose their identity. The other electrons remain unaffected.
(iv) The stability of bond is accounted by the fact that the formation of the bond is accompanied by the release of energy. The molecule has minimum energy at a certain distance between the atoms known as internuclear distance. The larger the decrease in energy, the stronger will be the bond formed.
Valence bond Treatment of Hydrogen Molecule:
Consider two hydrogen atoms \(A\) and \(B\) approaching each other having nuclei \(H_a\) and \(H_B\) and the corresponding electrons \(\mathrm{e}_{\mathrm{A}}\) and \(\mathrm{e}_{\mathrm{B}}\) respectively.
When atoms come closer to form molecules new forces begin to operate.
(a) The force of attraction between the nucleus of atom and the electron of another atom.
(b) The force of repulsion between two nuclei of the atom and the electron of two atoms.

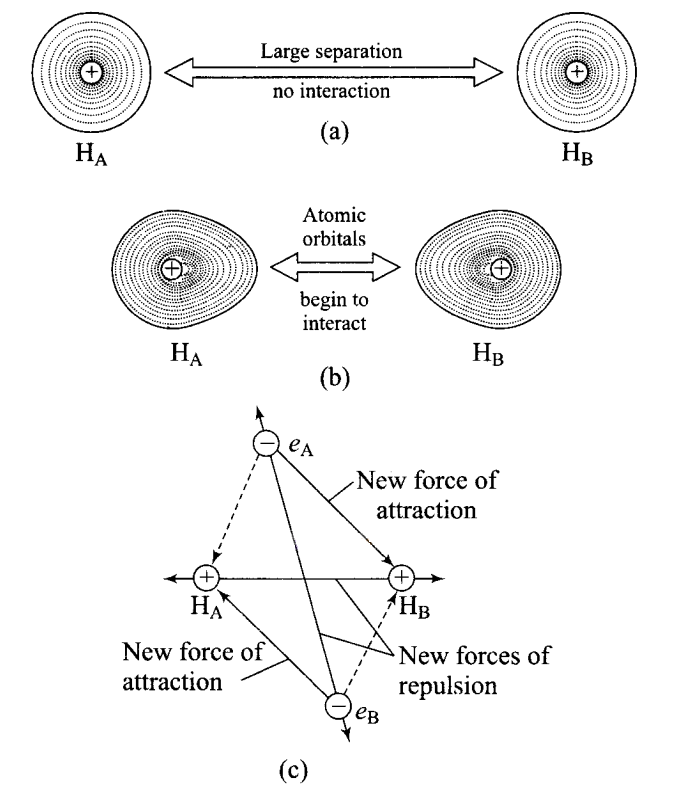
Fig. (a) Two hydrogen atoms at a large distance and hence, no interaction, (b) Two hydrogen atom closer to each other atomic orbitals begin to interact, (c) Attractive and repulsive forces in hydrogen atoms when interaction begins. In the case of hydrogen: Figure ‘a’ shows that two hydrogen atoms are at the farthest distances and their electron distribution is absolutely symmetrical.
(a) When two hydrogen atom start coming closer to each other, the electron cloud becomes distorted, and new attractive and repulsive forces begin to operate as shown in figure ‘ \(c\) ‘
(b) In Figure ‘c’ dotted lines show attractive forces present in the atom already and bold lines show the new attractive and repulsive forces.
(c) It has been found experimentally that the magnitude of net attractive forces is more than net repulsive forces. Thus stable hydrogen molecule is formed.

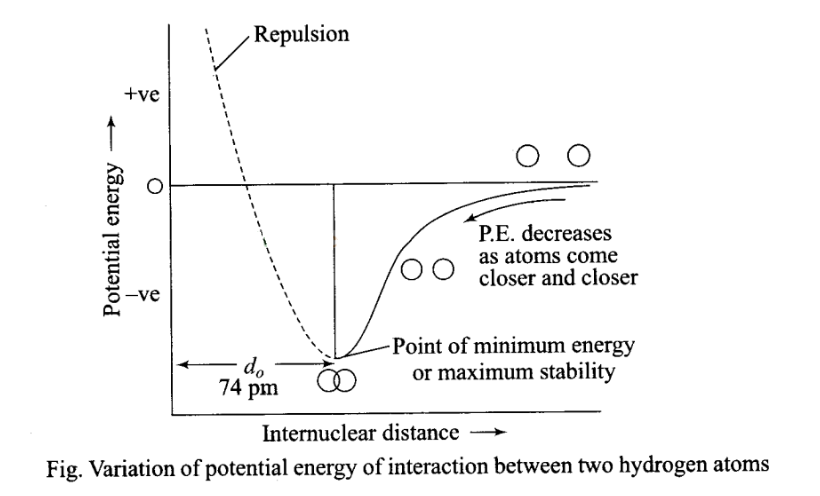
Potential energy diagram for formation of hydrogen molecules:
When two hydrogen atoms are at farther distance, there is no force operating between them, when they start coming closer to each other, the force of attraction comes into play and their potential energy starts decreasing. As they come closer to each other potential goes on decreasing, but a point is reached when potential energy acquires minimum value.
Note:
(a) This distance corresponding to this minimum energy value is called the distance of maximum possible approach, i.e. the point which corresponds to minimum energy and maximum stability.
(b) If atoms come further closer than this distance of maximum possible approach, then potential energy starts increasing and force of repulsion comes into play and molecules start becoming unstable.

Q25. Describe hybridisation in the case of \(\mathrm{PCl}_5\) and \(\mathrm{SF}_6\). The axial bonds are longer as compared to equatorial bonds in \(\mathrm{PCl}_5\) whereas in \(\mathrm{SF}_6\) both axial bonds and equatorial bonds have the same bond length. Explain.

Answer: Formation of \(\mathrm{PCl}_5\):

In \(\mathrm{PCl}_5\), phosphorus is \(\mathrm{sp}^3 \mathrm{~d}\) hybridised to produce a set of five \(\mathrm{sp}^3 \mathrm{~d}\) hybrid orbitals which are directed towards the five corners of a trigonal bipyramidal. These five \(\mathrm{sp}^3 \mathrm{~d}\) hydrid orbitals overlap with singly occupied \(\mathrm{p}\)-orbitals to \(\mathrm{Cl}\)-atoms to form five \(\mathrm{P}-\mathrm{Cl}\) sigma bonds.

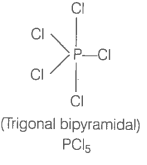
Three \(\mathrm{P}-\mathrm{Cl}\) bonds lie in one plane make an angle of \(120^{\circ}\) with each other. These bonds are called equatorial bonds. The remaining two \(\mathrm{P}-\mathrm{Cl}\) bonds one lying above and other lying below the plane make and angle of \(90^{\circ}\) with the equatorial plane.
These bonds are called axial bonds. Axial bonds are slightly longer than equatorial bonds because axial bond pairs suffer more repulsive interaction from the equatorial bond pairs.

Formation of \(\mathbf{S F}_6\):

In \(\mathrm{SF}_6\), sulphur is \(\mathrm{sp}^3 \mathrm{~d}^2\) hybridised to produce a set of six \(\mathrm{sp}^3 \mathrm{~d}^2\) hybrid orbitals which are directed towards the six corners of a regular octahedron. These six \(\mathrm{sp}^3 \mathrm{~d}^2\) hybrid orbitals overlap with singly occupied orbitals of fluorine atoms to form six S-F sigma bonds. Thus, \(\mathrm{SF}_6\) molecule has a regular octahedral geometry and all S-F bonds have same bond length.

Q26. (i) Discuss the concept of hybridisation. What are its different types in a carbon atom.
(ii) What is the type of hybridisation of carbon atoms marked with star?

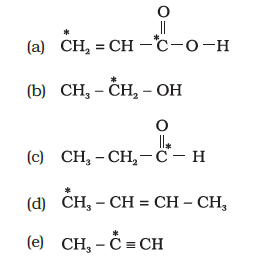
Answer: (i) Hybridisation It can be defined as the process of intermixing of the orbitals of slightly different energy or of the same energy to produce entirely new orbitals of equivalent energy, identical shapes and symmetrically disposed of in plane. New orbitals formed are called hybrid orbitals.
Only the orbitals of an isolated single atom can undergo hybridisation. The hybrid orbitals generated are equal in number to that of the pure atomic orbitals which mix up.
Hybrid orbitals do not make \(\pi\), pi-bonds. If there are \(\pi\)-bonds, an equal number of atomic orbitals must be left unhybridised for \(\pi\)-bonding.
Like atomic orbitals, hybrid orbitals cannot have more than two electrons of opposite spins.
Types of hybridisation in carbon atoms
(a) Diagonal or sp-hybridisation All compounds of carbon-containing \(\mathrm{C} \equiv \mathrm{C}\) triple bond like ethyne \(\left(\mathrm{C}_2 \mathrm{H}_2\right)\).
(b) Trigonal or \(\mathrm{sp}^2\)-hybridisation All compounds of carbon containing \(\mathrm{C}=\mathrm{C}\) (double bond) like ethene \(\left(\mathrm{C}_2 \mathrm{H}_4\right)\).
(c) Tetrahedral or \(\mathrm{sp}^3\)-hybridisation All compounds of carbon containing \(\mathrm{C}-\mathrm{C}\) single bonds only like ethane \(\left(\mathrm{C}_2 \mathrm{H}_6\right)\).